0 引言
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）具有结构简单、效率高、控制性能好等优点，被广泛应用于机械制造、轨道交通等工业领域[1-2]。
为提高控制系统的动态性能，模型预测控制被引入控制领域中，并根据所控制对象的不同，可以将其分为模型预测电流控制（Model Predictive Current Control, MPCC）[3-5]和模型预测转矩控制（Model Predictive Torque Control, MPTC）[6-8]。模型预测电流控制主要以电流为控制目标，其价值函数中只包含电流项；而模型预测转矩控制主要以磁链和转矩为控制目标，由于这两者的量纲不同，导致价值函数中需要权重系数来对其占比进行调整。但与MPCC 相比，MPTC 能直接控制转矩，使系统更加直观简洁[9]。
传统MPTC 方法的思想与传统直接转矩控制（Direct Torque Control, DTC）方法相似[10]，但后者通过滞环控制器进行电压矢量选择，而前者则是将转矩和磁链的控制作为一个优化问题进行讨论[11]。传统MPTC 通过提前一个采样周期对下个时刻的电机数学模型控制量进行预测，选取使价值函数值最小的基本电压矢量为最优电压矢量，并作用于两电平逆电器进行输出，该方法具有控制结构简单的优点，但由于两电平逆变器只能输出8 个电压矢量（6个有效电压矢量和2 个零电压矢量），导致可选电压矢量受限，使得输出转矩脉动和磁链波动过大。针对此问题，文献[12-13]将扇区细分为多个扇区，通过增加扇区划分来增加电压矢量的选择精度，最终达到减小转矩误差的效果，但扇区划分有限，且容易导致计算量过大。文献[14-16]采用双矢量方法，在传统MPTC 的基础上增加一个电压矢量，通过查表进行有效电压矢量寻找，并将电压矢量和其动作时间同时纳入预测模型中，最后合成所需要的电压矢量，该方法将电压矢量选择范围扩大，并有效减小转矩脉动。文献[17]采用离散占空比控制方法对转矩脉动和磁链波动进行抑制，提出一种精确选择合适有效电压矢量的方法，并在该有效电压矢量中插入零电压矢量进行输出电压矢量幅值调节。虽然该方法有效地减小了转矩脉动和磁链波动，但由于需要对每个电压矢量占比进行分配，导致算法中所占用的储存空间增加。文献[18]提出了一种三矢量MPTC 策略，通过多次模型预测选出最优电压矢量，最后将该电压矢量与相邻电压矢量、零电压矢量进行虚拟电压矢量合成达到减小转矩脉动的效果进而改善系统性能。文献[19-20]在三矢量MPTC 基础上进行优化，将电压矢量范围扩大到任意电压矢量，对最优电压矢量与另外4 个有效电压矢量以及零电压矢量组成的四种组合依次进行模型预测，从而得出最优组合。该方法能达到有效减小转矩脉动和磁链波动的效果，但是在进行预测时需要对最优电压矢量进行多次模型预测，计算量大，且算法较为复杂。
为了减少双矢量MPTC 的计算量并抑制转矩脉动和磁链波动，本文提出一种基于快速选择表的改进型模型预测转矩控制策略。在该策略中通过快速选择表直接进行所需的2 个有效电压矢量选择以此提高控制性能和减少模型预测次数。首先，对电压矢量与转矩和定子磁链之间的关系进行综合分析，得到快速选择表，并进行扇区判断；其次，依据转矩差值和扇区值在快速选择表中进行有效电压矢量选择，降低对有效电压矢量的选择时间和预测次数；最后，根据无差拍控制原理计算出各个电压矢量作用时间。仿真和实验结果表明，该方法与双矢量MPTC 具有相似的动态性能，但该方法能够有效改善动态性能，减小转矩脉动和磁链波动。
1 PMSM 预测模型
本文以表贴式PMSM 为研究对象，为了避免控制复杂性和坐标变换，选择静止坐标系下的电机数学模型，具体表达式为
在静止坐标系中的电磁转矩方程表达式为
式中，
；us、is、 s、 f、Ls 和R 分别为电机的定子电压矢量、定子电流矢量、定子磁链矢量、永磁体磁链矢量、定子电感和定子电阻； e、 e 和p 分别为转子电角速度、电角度和电机极对数。
采用一阶欧拉法对式（1）～式（4）进行离散化，可得到k+1 时刻定子磁链、定子电流和电磁转矩的预测值分别为
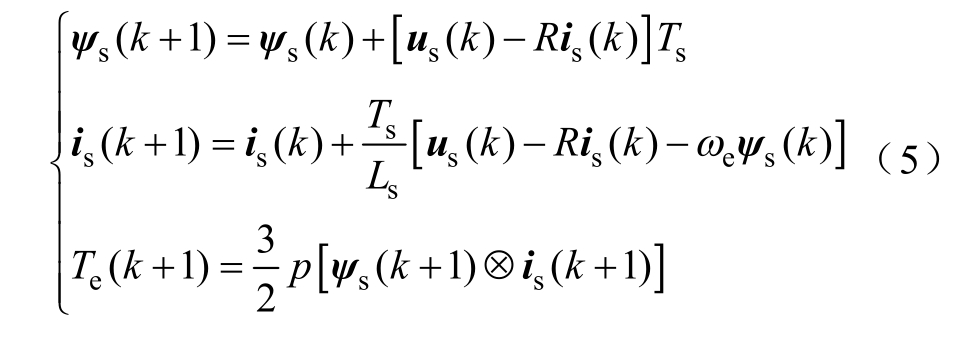
式中，Ts 为采样时间。
2 双矢量模型预测转矩控制
单矢量MPTC 通过将8 个基本电压矢量的预测值逐个代入到价值函数式（6）中，选取使价值函数最小的基本电压矢量作为最优电压矢量。在一个周期内仅输出一个电压矢量，而文献[14]在其基础上再引入一个电压矢量，提出一种新的双矢量MPTC（Novel Two Vector MPTC, NTV-MPTC），在一个控制周期结束时，输出一个零电压矢量和一个有效电压矢量。
式中，F 为价值函数；Q 为定子磁链参数权重系数；
为给定定子磁链幅值参考值；
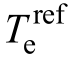为给定转矩参考值。
首先，根据上个周期所得定子磁链参数，进行扇区数判断；其次，对转矩预测值与实际转矩参考值进行求差，并依据所得差值进行有效电压矢量选择，该策略将可选电压矢量由最初的6 个有效电压矢量缩减至2 个电压矢量，再分别将这2 个有效电压矢量代入式（5）进行转矩和磁链预测值计算；最后，通过传统的价值函数进行最优电压矢量选择，从而降低了模型预测次数。定子磁链矢量与电压矢量如图1 所示，若定子磁链矢量位于扇区S1 中，且所求转矩差值大于0，那么此时选择U2 和U3 作为备选电压矢量，采用权重系数式（6）进行最优电压矢量判断。
图1 定子磁链矢量与电压矢量
Fig.1 Stator flux vector and voltage vector
但需要进行考虑的是，尽管该方法相比于单矢量MPTC，在其基础上引入了零电压矢量，逆变器所发出的电压矢量幅值变得可调，但在其方向上仍有一定局限，依旧固定在有效电压矢量所在方向上，因此电压矢量选择上依旧存在一定局限，导致转矩脉动过大。
3 三矢量模型预测转矩控制
3.1 总体控制框图
针对双矢量 MPTC（Two Vector MPTC, TVMPTC）中合成电压矢量范围有限的问题，本文在TV-MPTC 的基础上进行改进，通过再引入一个有效电压矢量，与TV-MPTC 策略中原有的有效电压矢量和零电压矢量进行合成，得到一个方向和幅值皆可调节的合成虚拟电压矢量，最终达到扩大合成电压矢量选择范围的目的，即改进三矢量模型预测转矩控制（Improve Three Vector MPTC, ITV-MPTC）策略，其控制框图如图2 所示。
图2 永磁同步电机ITV-MPTC 控制框图
Fig.2 Block diagram of the ITV-MPTC for PMSM
根据最大转矩电流比原理将转矩与定子磁链幅值之间的关系简化，可以在线得到定子磁链幅值参考值，其计算式为
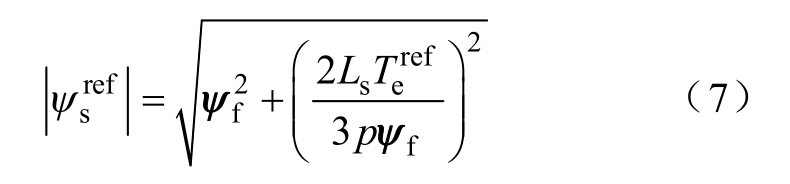
3.2 转矩和磁链斜率分析
在下一时刻要选取合适的最优电压矢量来对磁链误差和转矩误差进行补偿，因此，需要准确分析直接转矩控制系统性能中影响电磁转矩和定子磁链斜率的参数。首先，考虑基本电压矢量对转矩斜率的影响，对转矩式（4）进行求导，得到瞬时转矩变化量为
式（8）表明，转矩的变化值与定子磁链矢量和定子电流之间为函数关系，将式（1）～式（4）代入其斜率式（8）中，可推导出简化后转矩变化斜率表达式为
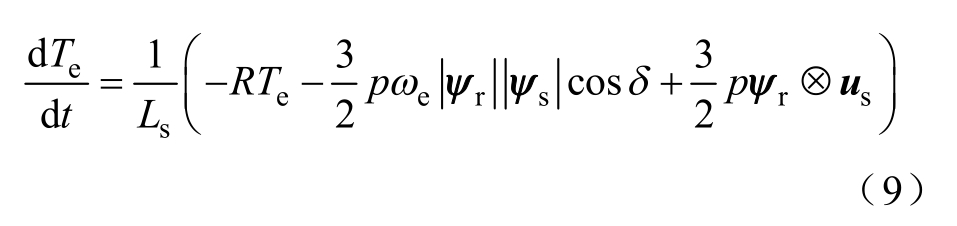
式中， 为负载角，即定子磁链和转子磁链之间的夹角。
由转矩斜率式（9）可以看出，转矩斜率公式主要可以分成三部分，前两部分总是负值，分别与瞬时电磁转矩和机械角速度成正比，而第三部分则为正值，主要反映电磁转矩受电压矢量的影响。当电压矢量为零电压矢量时，其电磁转矩斜率表达式为
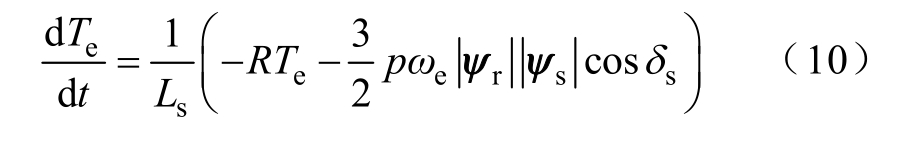
由此可见，零电压矢量所引起的转矩斜率始终为负值，并且该参数会随着电机的转矩和所带负载值增加而增加，特别是在电机高速和带大转矩负载运行时，电机转矩脉动会受较大影响。
根据电压矢量与定子磁链的关系式（1），若忽略定子电阻压降的影响，式（10）可以转换为
对式（3）进行离散化，得到一个采样周期内定子磁链的变化值为
由此可见，定子磁链变化值主要受有效电压矢量参数的影响，如果能合理控制下一个采样周期内作用于电机的电压矢量，则可以减小定子磁链的变化量，并且当电压矢量为零电压矢量时，定子磁链的变化值几乎为零。
3.3 基本电压矢量选择
由三相PMSM 传统的直接转矩开关表可知，图1 为扇区分布。例如，当定子磁链位于S1 扇区时，有效电压矢量U2、U3 都是用于增大转矩，而对于定子磁链，两个电压矢量所产生作用则是相反的；同理，有效电压矢量U5、U6 则是减小转矩，在定子磁链上所产生的作用也是相反。因此，本文所使用的电压矢量快速选择表根据传统的直接转矩开关表的特性，进行有效电压矢量选择时只涉及转矩误差，而定子磁链误差只需通过合理分配2 个有效电压矢量的作用时间则可维持定子磁链不变或减小、增大定子磁链，从而达到减小定子磁链波动的效果。
第一步，准确判断定子磁链所在扇区位置。为准确判断其位置，引入辅助参数 ，其表达式为
通过判断 、 和 的符号确定具体扇区数，扇区判断见表1，其中 在扇区S1 和扇区S4 中正负号皆可。
表1 扇区判断表
Tab.1 The table of sector judgment
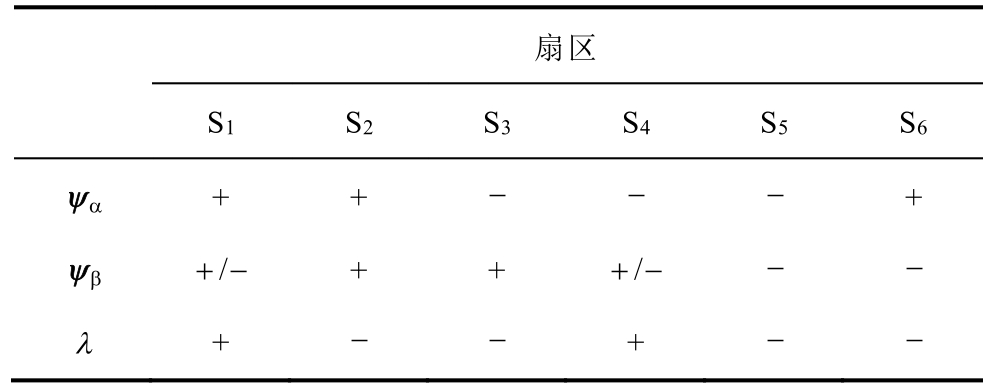
扇区S1 S2 S3 S4 S5 S6 + + + / + + / + +
第二步，根据转矩差值和定子磁链所在扇区位置进行合适的有效电压矢量选择。电压矢量快速选择表见表2，其中，该表没有提供具体的零电压矢量选择值，而需要根据当前逆变器所处状态进行零电压矢量选择，其选取原则是最大程度地减小开关损耗，以确保逆变器开关切换次数最少。如当电压矢量为U3(100)时，零电压矢量选择U0(000)。
表2 电压矢量快速选择表
Tab.2 The fast selection table for voltage vectors
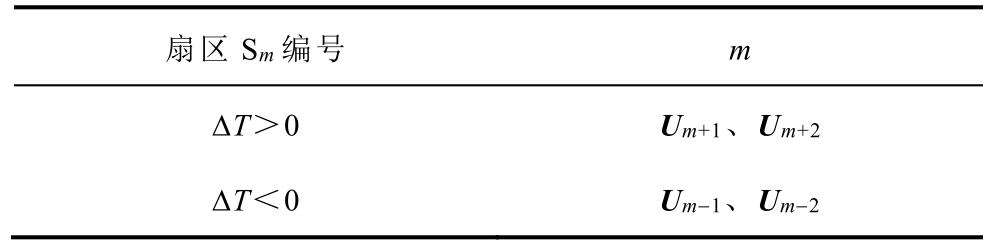
扇区Sm 编号 m T＞0 Um+1、Um+2 T＜0 Um 1、Um 2
表2 中，扇区编号m∈{1, 2,…, 6}，电压矢量Um+n 中参数m+n 表示电压矢量选择索引，当参数m+n＞6 时，参数m+n 为实际参数m+n 对6 进行求余所得。
3.4 作用时间分配
在获得所需的2 个有效电压矢量和1 个零电压矢量后，需要分别对这3 个电压矢量的作用时间进行计算。假设有效电压矢量的作用时间分别为t1 和t2，零电压矢量的作用时间为t0=Ts t1 t2。本文采用基于转矩差值和磁链差值的无差拍原则计算方法，其计算公式如式（14）所示。由零电压矢量对磁链影响分析可知，零电压矢量所引起的磁链斜率几乎为零，因此只需假设零电压矢量作用时转矩斜率为
，有效电压矢量时转矩和磁链的斜率分别为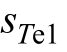
、 sTe2 和s1 、s2 ，如式（15）所示。
式中，Tei 和 i（i=0, 1, 2）分别为所选定3 个电压矢量u0、uopt1、uopt2 作用下转矩和磁链的预测值，联立式（14）和式（15）求解，可得有效矢量作用时间t1 和t2 分别为
因此，得到合成虚拟电压矢量us，表示为
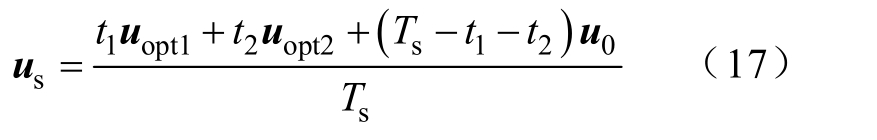
该虚拟电压矢量主要由2 个有效电压矢量和1个零电压矢量合成所得，有效电压矢量选择则直接通过选择表进行选择，并将模型预测次数由文献[13]中的6 次预测降为2 次预测，达到适当减小算法计算量的效果；时间分配上，利用无差拍原理和零电压矢量作用的影响，求得各个电压矢量的作用时间，最终合成并输出虚拟电压矢量，在下个采样周期结束时，预测值能与参考值更为接近。
4 结果及分析
为了验证本文所提出的ITV-MPTC 方法的正确性和有效性，对该方法和NTV-MPTC 方法在Matlab/Simulink 环境下进行了综合仿真。两种控制策略的采样频率、PI 环参数设置均相同，并都采用离散时间仿真，电机参数见表3。同时，本文对NTV-MPTC和ITV-MPTC 两种控制方法进行实验对比分析，搭建了以TI 公司TMS320F28335 芯片为控制器的永磁同步电机实验平台，实验平台如图3 所示，并采用2 500 线编码器对转子位置进行实时获取，控制系统采样频率为10 kHz。实验数据主要通过上位机和示波器进行采集，其中转矩、转速和磁链等主要参数数据通过上位机采集，保存至 Excel 中，并采用Matlab 软件进行图形绘制；而电流波形则直接通过电流钳和示波器进行测量。对两种策略在稳态和暂态运行条件下分别进行了实验对比，实验过程中仿真和实验结果如图4～图9 所示。
表3 永磁同步电机参数
Tab.3 The parameters of PMSM
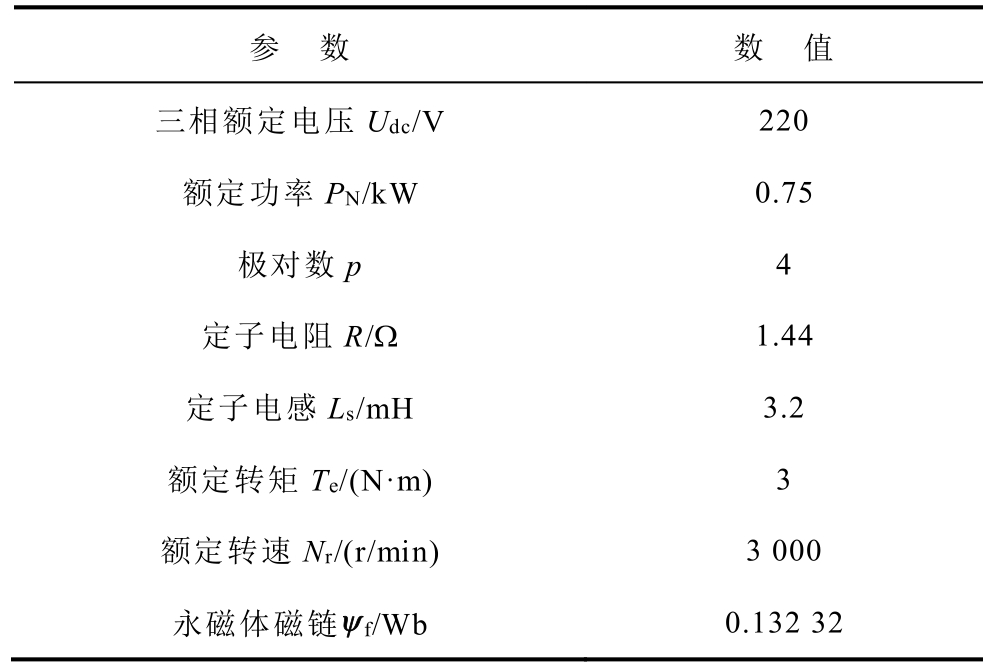
参 数 数 值三相额定电压Udc/V 220额定功率PN/kW 0.75极对数p 4定子电阻R/ 1.44定子电感Ls/mH 3.2额定转矩Te/(N·m) 3额定转速Nr/(r/min) 3 000永磁体磁链 f/Wb 0.132 32
图3 PMSM 实验平台
Fig.3 Experimental system for PMSM
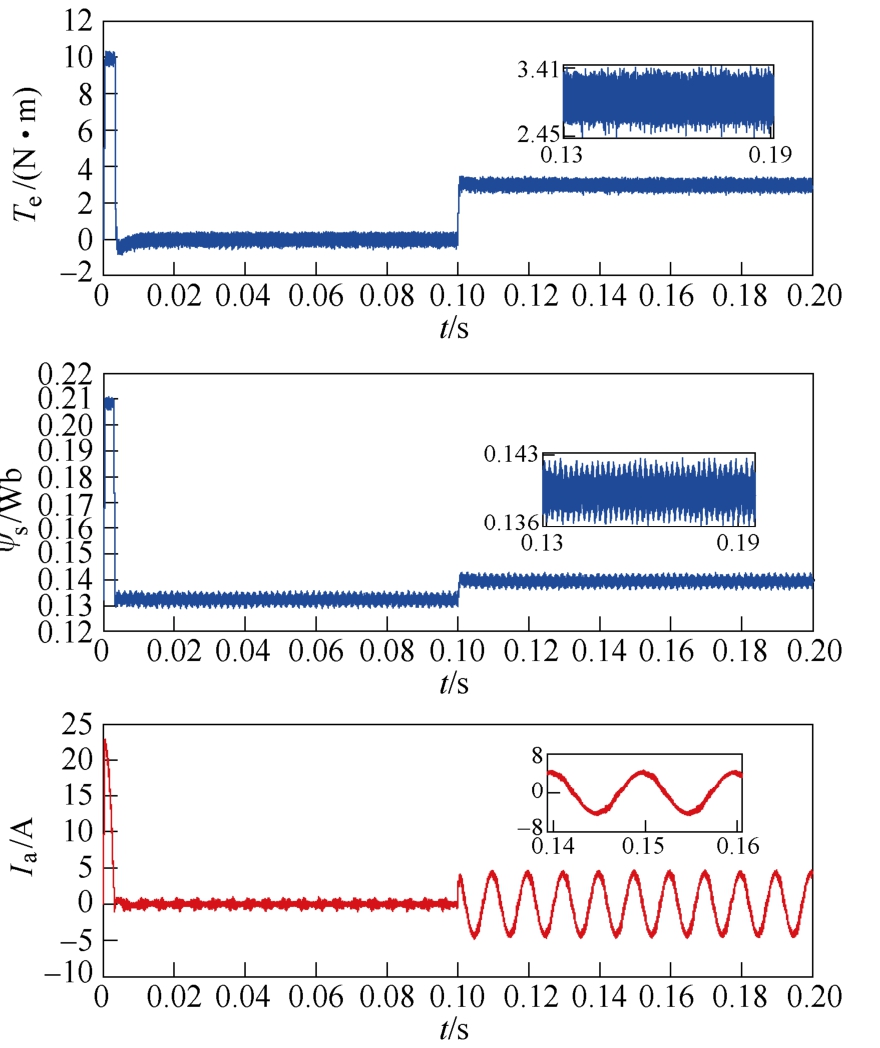
图4 NTV-MPTC 仿真波形
Fig.4 Simulation waveforms of NTV-MPTC
4.1 仿真结果
图4 和图5 分别为NTV-MPTC、ITV-MPTC 两种策略在电机转速设定为1 500 r/min，并以空载状态进行起动情况下，待电机稳定运行至1 500 r/min后，在0.1 s 时突加负载转矩3 N·m 的仿真波形，从上到下分别是转矩脉动波形、磁链波动波形及在3 N·m 稳定运行时的A 相电流波形。通过对比可以看出，ITV-MPTC 的转矩脉动和磁链波动明显小于NTV-MPTC 策略的转矩脉动和磁链波动，并且NTV-MPTC 方法下的电流纹波略大于ITV-MPTC 方法下的电流纹波，因此该方法能有效减少磁链波动和转矩脉动。为了更清晰地分析电流性能，采用快速傅里叶变换（Fast Fourier Transformation, FFT）进行分析，基频为100 Hz，NTV-MPTC、ITV-MPTC的A 相电流总谐波畸变率（Total Harmonic Distortion,THD）分别为13.27%、6.77%，因此，该方法可以有效地抑制电流谐波。
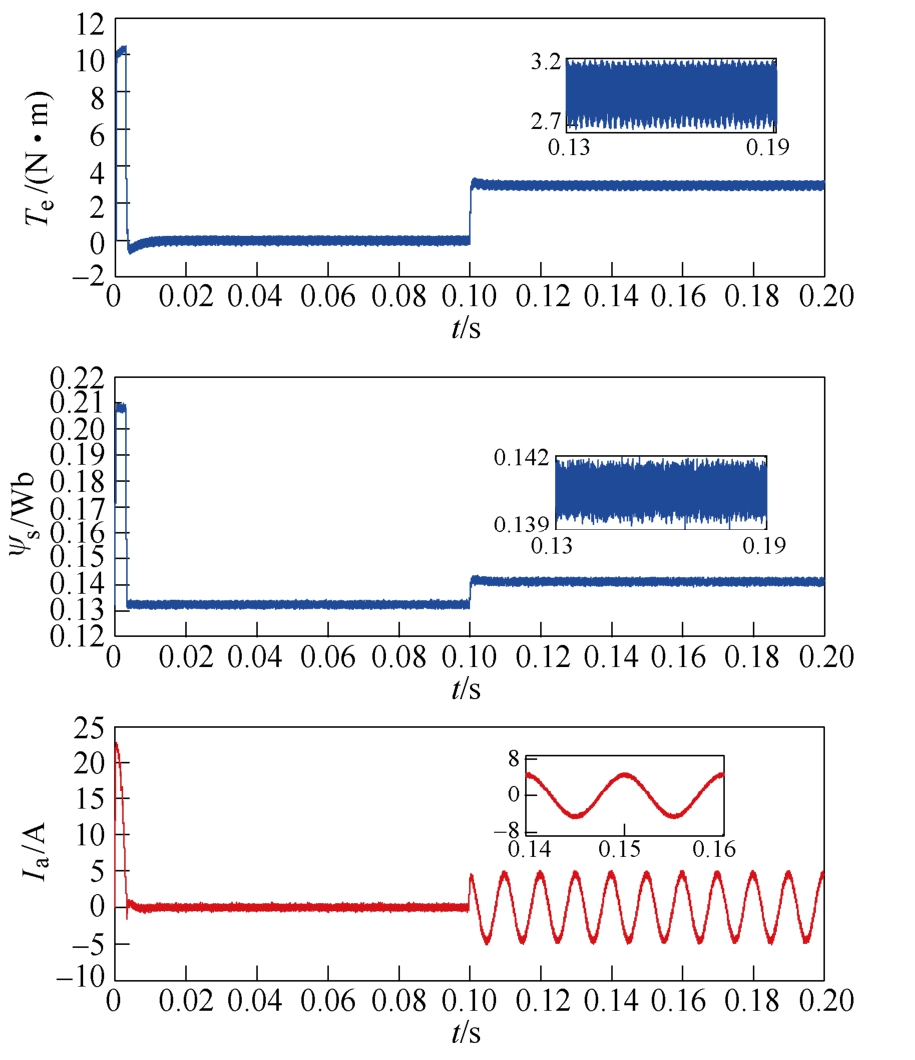
图5 ITV-MPTC 仿真波形
Fig.5 Simulation waveforms of ITV-MPTC
4.2 实验结果
图6 为NTV-MPTC 策略和本文所提ITV-MPTC策略在电机空载运行条件下的磁链和转矩稳态实验波形，其给定速度为800 r/min。通过上位机将实验中所测10 000 组数据Excel 导出，并进行图形绘制。实验结果对比分析，相较于NTV-MPTC 策略，本文所提ITV-MPTC 策略能有效抑制转矩脉动和磁链波动。
图6 转速800 r/min 空载时稳态实验结果
Fig.6 Experimental results at steady speed of 800 r/min without load
图7 为两种控制策略在转速为2 000 r/min 并带2 N·m 负载条件下的磁链、转矩以及电流波形，同时通过泰克示波器保存 10 000 组数据，并导入Matlab 软件中进行快速傅里叶分析，分析结果如图8 所示，NTV-MPTC 总谐波分量为32.37%，ITVMPTC 总谐波分量为25.68%，可以得出，其电流得到有效改进，降低了谐波含量。
图7 转速2 000 r/min 带载运行稳态实验结果
Fig.7 Experimental results at steady speed of 2 000 r/min with load
图8 转速2 000 r/min 带载稳态运行时电流波形和FFT 分析
Fig.8 Current waveform and FFT analysis at steady speed of 2 000 r/min with load
图9 为NTV-MPTC 策略和本文所提ITV-MPTC策略在电机速度为2 000 r/min 条件下稳定运行，并且其所带负载突然由1 N·m 变为2 N·m 的转矩和转速实验波形，在突变时，虽然两者转速都有一定影响，但本文所提ITV-MPTC 策略转速所受影响较小、动态性能更好。
图9 NTV-MPTC 和ITV-MPTC 突加负载实验结果
Fig.9 Experimental results of NTV-MPTC and ITV-MPTC at changed torque
综上所述，本文所提ITV-MPTC 策略与NTVMPTC 策略具有类似的暂态和稳态控制性能，而在减小转矩脉动和磁链波动的效果上，本文所提ITVMPTC 策略的改进效果更为明显，同时能降低电流谐波，稳态性能明显更好，并且在转矩突变时，虽然两者转速都会受到一定影响，但是ITV-MPTC 策略的结果所受影响较小，并能保持较快动态响应。分析可知，本文在NTV-MPTC 策略的基础上额外添加一个有效电压矢量，使得逆变器输出的电压矢量的幅值和方向更为灵活，因此相对来说具有较好的控制性能。
5 结论
本文针对NTV-MPTC 策略中电压矢量范围受限、转矩脉动和磁链波动过大等问题，提出了一种改进的三矢量模型预测转矩控制策略，在其基础上额外添加一个有效电压矢量来扩大有效电压矢量选择范围，得到一个电压幅值和方向均可调节的合成电压矢量，最后通过引入快速选择表在减小转矩脉动和磁链波动的同时减小相应的计算量。综合实验结果，相较于NTV-MPTC 策略，本文所提ITV-MPTC策略能有效抑制转矩脉动和磁链波动，并保持良好的动稳态性能和较少的预测次数。
[1] 宋文祥, 任航, 杨煜, 等.双三相永磁同步电机的双矢量模型预测转矩控制[J].电机与控制学报,2022, 26(9): 97-107.Song Wenxiang, Ren Hang, Yang Yu, et al.Dual three phase permanent synchronous magnet machines model predictive torque control harmonic current suppression two voltage vectors operating time of vector[J].Electric Machines and Control, 2022, 22(9):97-107.
[2] 姚绪梁, 黄乘齐, 王景芳, 等.两相静止坐标系下的永磁同步电动机模型预测功率控制[J].电工技术学报, 2021, 36(1): 60-67.Yao Xuliang, Huang Shengqi, Wang Jingfang, et al.Model predictive power control of permanent magnet synchronous motor in two-phase static coordinate system[J].Transactions of China Electrotechnical Society, 2021, 36(1): 60-67.
[3] 章回炫, 范涛, 边元均, 等.永磁同步电机高性能电流预测控制[J].电工技术学报, 2022, 37(17):4335-4345.Zhang Huixuan, Fan Tao, Bian Yuanjun, et al.Predictive current control strategy of permanent magnet synchronous motors with high performance[J].Transactions of China Electrotechnical Society, 2022,37(17): 4335-4345.
[4] 史婷娜, 张维, 肖萌, 等.基于矢量作用时间的永磁同步电机预测电流控制[J].电工技术学报, 2017,32(19): 1-10.Shi Tingna, Zhang Wei, Xiao Meng, et al.Predictive current control for permanent magnet synchronous motor based on operating time of vector[J].Transactions of China Electrotechnical Society, 2017,32(19): 1-10.
[5] 周湛清, 夏长亮, 陈炜, 等.具有参数鲁棒性的永磁同步电机改进型预测转矩控制[J].电工技术学报,2018, 33(5): 965-972.Zhou Zhanqing, Xia Changliang, Chen Wei, et al.Modified predictive torque control for PMSM drives with parameter robustness[J].Transactions of China Electrotechnical Society, 2018, 33(5): 965-972.
[6] Zhang Yongchang, Zhu Jianguo.A novel duty cycle control strategy to reduce both torque and flux ripples for DTC of permanent magnet synchronous motor drives with switching frequency reduction[J].IEEE Transactions on Power Electronics, 2011, 26(10):3055-3067.
[7] 刘珅, 高琳.永磁同步电机的改进模型预测直接转矩控制[J].电机与控制学报, 2020, 24(1): 10-17.Liu Shen, Gao Lin.Improved model of predictive direct torque control for permanent magnet synchronous motor[J].Electric Machines and Control,2020, 24(1): 10-17.
[8] Niu Feng, Li Kui, Wang Bingsen, et al.Comparative evaluation of direct torque control strategies for permanent magnet synchronous machines[C]//2014 IEEE Applied Power Electronics Conference and Exposition-APEC, Fort Worth, TX, USA, 2014: 2438-2445.
[9] 牛峰, 李奎, 王尧.基于占空比调制的永磁同步电机直接转矩控制[J].电工技术学报, 2014, 29(11):20-29.Niu Feng, Li Kui, Wang Yao.Model predictive direct torque control for permanent magnet synchronous machines based on duty ratio modulation[J].Transactions of China Electrotechnical Society, 2014, 29(11):20-29.
[10] Wang Fengxiang, Li Shihua, Mei Xuezhu, et al.Model-based predictive direct control strategies for electrical drives: an experimental evaluation of PTC and PCC methods[J].IEEE Transactions on Industrial Informatics, 2015, 11(3): 671-681.
[11] Zhang Yongchang, Yang Haitao.Model predictive torque control of induction motor drives with optimal duty cycle control[J].IEEE Transactions on Power Electronics, 2014, 29(12): 6593-6603.
[12] 廖晓钟, 邵立伟.直接转矩控制的十二区段控制方法[J].中国电机工程学报, 2006, 26(6): 167-173.Liao Xiaozhong, Shao Liwei.The twelve-section control methods of direct torque control[J].Proceedings of the CSEE, 2006, 26(6): 167-173.
[13] 吕帅帅, 林辉, 李兵强, 等.一种改进的PMSM 模型预测直接转矩控制方法[J].电机与控制学报,2020, 24(7): 102-111.Lü Shuaishuai, Lin Hui, Li Bingqiang, et al.Improved model predictive direct torque control for permanent magnet synchronous motor[J].Electric Machines and Control, 2020, 24(7): 102-111.
[14] Wu Minkai, Sun Xiaodong, Zhu Jianguo, et al.Improved model predictive torque control for PMSM drives based on duty cycle optimization[J].IEEE Transactions on Magnetics, 2021, 57(2): 1-5.
[15] 徐艳平, 李园园, 周钦, 等.矢量双选取的永磁同步电动机直接转矩控制策略[J].中国电机工程学报,2018, 38(17): 5211-5218, 5318.Xu Yanping, Li Yuanyuan, Zhou Qin, et al.A double vectors selection direct torque control strategy of permanent magnet synchronous motor[J].Proceedings of the CSEE, 2018, 38(17): 5211-5218, 5318.
[16] 夏长亮, 仇旭东, 王志强, 等.基于矢量作用时间的新型预测转矩控制[J].中国电机工程学报, 2016,36(11): 3045-3053.Xia Changliang, Qiu Xudong, Wang Zhiqiang, et al.Predictive torque control based on optimal operating time of vector[J].Proceedings of the CSEE, 2016,36(11): 3045-3053.
[17] Nikzad M R, Asaei B, Ahmadi S O.Discrete dutycycle-control method for direct torque control of induction motor drives with model predictive solution[J].IEEE Transactions on Power Electronics,2018, 33(3): 2317-2329.
[18] Zhang Yongchang, Zhu Jianguo.Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency[J].IEEE Transactions on Power Electronics, 2011, 26(1):235-248.
[19] 徐艳平, 李园园, 张保程, 等.一种消除权重系数三矢量模型预测转矩控制[J].电工技术学报, 2018,33(16): 3925-3934.Xu Yanping, Li Yuanyuan, Zhang Baocheng, et al.Three-vector based model predictive torque control of eliminating weighting factor[J].Transactions of China Electrotechnical Society, 2018, 33(16): 3925-3934.
[20] 陈炜, 曾思坷, 张国政, 等.永磁同步电机改进型三矢量模型预测转矩控制[J].电工技术学报, 2018,33(增刊2): 420-426.Chen Wei, Zeng Sike, Zhang Guozheng, et al.Improved three-vector model predictive torque control of permanent magnet synchronous motor[J].Transactions of China Electrotechnical Society, 2018,33(S2): 420-426.