0 引言
近年来,我国加大力度进行电网改造,电缆线路增长十分迅速,交联聚乙烯(Cross-Linked Polyethylene, XLPE)电缆因具有良好的电气性能及较好的环境适应性而被广泛应用于各电压等级的输配电线路中。电缆的运行环境复杂多变,其绝缘性能在实际运行过程中会受到极大的考验[1-3],极易发生局部缺陷。然而,输配电线路中的电缆多采用埋地敷设,本体位于地下难以直接观测,电缆沟内部空间狭小,进行离线检测操作困难,且代价高昂。因此,实现对XLPE 电缆绝缘状态的带电在线监测,可在局部缺陷造成重大损失之前进行告警,降低运维成本,提高电网的可靠性。此外,实现在线监测还可以优化电缆的使用,减少能量损失,对保证电力系统安全、高效、可靠运行有着重要意义[4-5]。
目前应用于XLPE 电缆绝缘状态评估的方法主要有介电谱检测法、局部放电检测法、电流检测法。其中,电流检测法包括直流分量法、直流叠加法、交流叠加法和损耗电流谐波特征法[6-9]。然而,介电谱检测法无法实现在线监测,且商用设备功率有限,无法应用于较长的电缆线路[8];局部放电检测法的检测准确性与灵敏度受干扰信号的影响严重,且对一些老化类型不敏感[9]。电流检测法从地线获取信号,设备简单、操作简易、经济适用,具有发展为在线监测方法的潜力。其中,直流分量法很容易受到环境腐蚀电流的影响,对测试环境的要求较高[9];直流叠加法在测试时施加的直流电压容易引起地电位互感器磁饱和;交流叠加法需要加装额外的电桥等设备,测试前的调试操作过程复杂[9]。损耗电流谐波特征法可以实现在线监测,且不需要加装额外的供电设备,特别地,损耗电流中含有丰富的绝缘信息,可以较好地反映电缆的绝缘状况,已有相应的在线监测设备尝试应用于现场[10-12]。
在电缆损耗电流的实际检测方面,已有学者开展了基于损耗电流谐波特征的XLPE 电缆水树老化诊断的研究,以损耗电流中的三次谐波分量为特征参数,实现了对水树老化程度的诊断[13-15],但相关研究缺乏对损耗电流中谐波分量成因的物理解释。还有学者对XLPE 电缆存在大规模、大尺寸、均匀绝缘缺陷时的损耗电流谐波特征进行了分析[16-17],但相关成果缺乏针对小尺寸、不均匀局部缺陷的研究。在机理研究方面,针对损耗电流谐波分量的分析大多基于由麦克斯韦方程组和洛伦兹力构建的应力模型,这种物理模型无法对局部不均匀缺陷下损耗电流中存在的高次谐波分量作出合理的解释。针对电缆局部缺陷的损耗电流变化的原因,已有研究发现聚合物在高电场强度下会呈现出非线性的伏安特性,并用跳跃电导模型描述了XLPE 在高电场下的电导特性[18-21];相关研究也在直流电压下发现了带有局部缺陷的电缆损耗电流随电压的增大而出现非线性增长的现象[22-23]。然而,目前还没有针对于在交流电压下,电缆绝缘层中存在局部缺陷时损耗电流谐波成分的研究。
尖刺缺陷是电缆的一种典型局部缺陷,本文主要基于这种局部缺陷开展相关研究。首先,基于聚合物在高电场下的非线性电导特性,对XLPE 绝缘内部存在导体尖刺时的损耗电流密度进行仿真,从载流子的发射输运过程角度来解释损耗电流中谐波分量的形成机理;然后,制作了XLPE 典型导体尖刺缺陷试样,在试样上进行实验;最后,结合仿真与实验的结果,提取总谐波畸变率(Total Harmonic Distortion, THD)和各次谐波贡献率为特征参量,分析当XLPE 绝缘中出现导体尖刺时损耗电流的谐波特征,以及上述参量随缺陷严重程度的变化规律,为实现基于损耗电流高次谐波特性的电缆局部不均匀缺陷诊断提供理论和实验参考。
1 基于非线性电导理论的尖刺缺陷损耗电流仿真模型
当XLPE 材料内部存在尖刺缺陷时,局部电场会发生明显的畸变,电场强度剧增。为了能从机理上分析当绝缘内部存在尖刺缺陷时损耗电流的频域特性,本节主要对XLPE 在高电场下的非线性电导现象进行分析,并在此基础上建立基于载流子输运过程的尖刺缺陷损耗电流密度仿真模型。
1.1 高电场下非线性电导理论及双极性载流子模型
聚合物固体介质在高电场下的电导特性与传统意义上的电导有很大差别,后者是用欧姆定律来描述的线性规律,而前者是非线性的。
较低电场下,聚合物介质中的载流子主要由两部分组成,一部分是电子(或空穴)热激发带间跃迁所产生的本征载流子;另一部分是杂质能级中电子(或空穴)热激发所产生的非本征载流子。由于聚合物的禁带宽度(>5 eV)远大于半导体和导体,这种由热激发产生的本征和非本征载流子浓度非常低,且与外施电场的大小无关。
当强电场施加于介质时,将引起电极处的电荷注入或者介质内的电子发射等一系列载流子增殖过程,使得介质内部的载流子浓度由与外电场无关变为随着外施电场强度变化而剧烈变化,稳态电流密度与电场强度之间的欧姆定律不再成立,介质的电导率成为电场强度的函数。
国内外众多学者对聚合物在高电场下的非线性电导机理进行了研究,XLPE 在高电场下的电导特性可以用跳跃电导模型来描述,基于跳跃电导模型的电导率的解析表达式[18]为
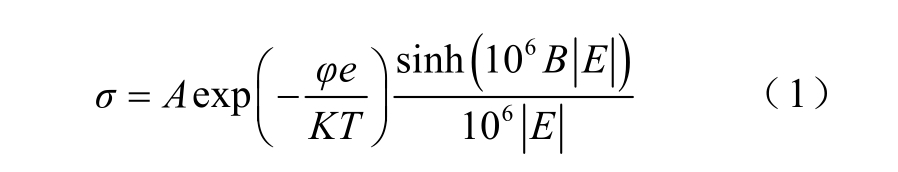
式中,A 和B 为常数;φ 为活化能;e 为单位电荷即元电荷;T 为热力学温度;E 为电场强度;K 为Boltzmann 常数[24]。
按照电介质物理学中的论述,材料电导率的物理定义可表示为
式中,ei、ni、μi 分别为第i 种载流子的电荷量、数密度与迁移率。可见,电导率与材料中的空间电荷行为紧密相关[25]。
双极性载流子模型被广泛应用于聚合物空间电荷行为的仿真计算,模型通过注入\抽出、电荷迁移、入陷\脱陷、复合、输运五个方面来描述介质内部电荷的行为,从而实现聚合物内部空间电荷的数值模拟[26-30]。
电极处的注入采用Schottky 公式来描述。阳极处注入时有
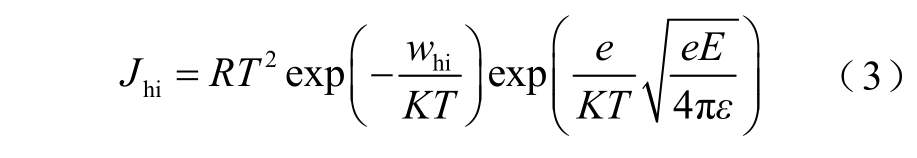
阴极处注入时有
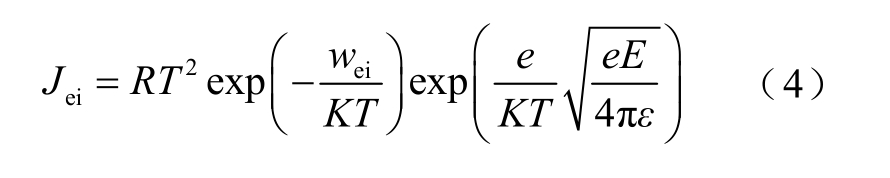
式中,R 为Richardson 常数;wei 和whi 分别为阴极和阳极与复合材料之间的注入势垒;J 为电流密度;ε 为复合材料的介电常数。
对应于载流子的界面注入,相应地也会有载流子的界面抽出,二者在机理上是相似的,因而在数学上也具有相似的形式。阳极处抽出时有
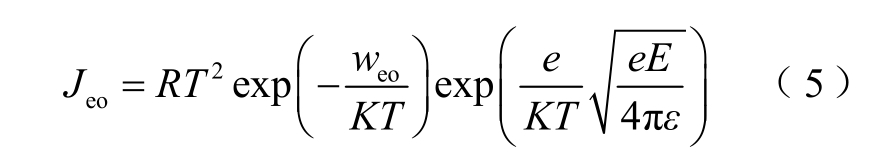
阴极抽出时有
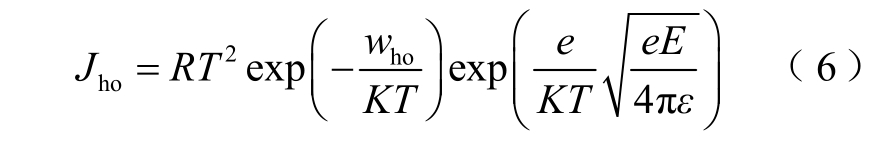
式中,weo、who 为对应过程的界面抽出势垒。
电介质内部的双极性载流子输运模型为
1)传导方程
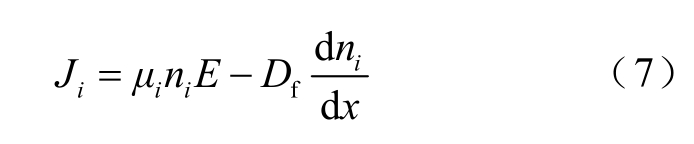
2)泊松方程

3)连续方程
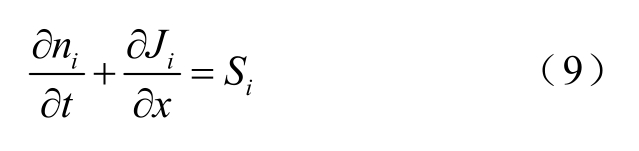
式中,下角标“i”为介质中存在的电荷种类,代表移动电子、受陷电子、移动空穴和受陷空穴;Df 为扩散系数;ρ 为单位体积的净电荷密度;连续方程右侧Si 为源项,其是由局域范围内非电荷传导输运引起的各类载流子电荷密度变化量的总和,主要包含内部电荷的产生、复合、入陷与脱陷。
1.2 模型有效性验证
为了验证仿真方法的有效性,利用双极性载流子模型,对30℃时不同电场强度下的XLPE 的电导率进行仿真分析,结果如图1 所示。可以看出XLPE的电导率随外施电场强度大小的不同,会呈现不同的特性:较低电场范围内,电导率随电场强度的变化较小;电场强度升高到一定程度之后,电导率随着电场强度的升高急剧增大,即聚合物的伏安特性随电场强度的变化均包含低电场下的线性区和高电场下的非线性区。
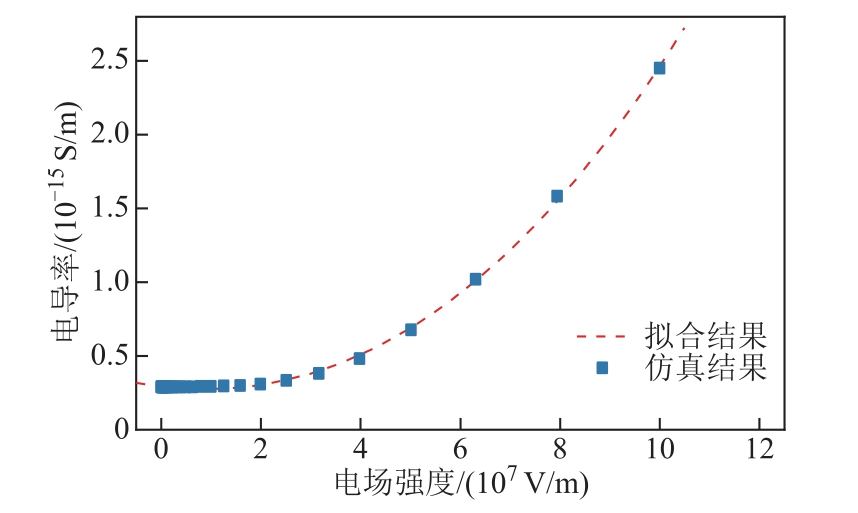
图1 不同电场下XLPE 的电导率仿真与拟合曲线
Fig.1 Conductivity simulation and fitting curve of XLPE under different temperatures and electric fields
利用仿真得到的数据,对式(1)进行拟合,得到的电导率计算式见式(10),所得参数的值与现有研究结论相符合[31],证明非线性电导理论在这里适用,双极性载流子模型在此处有效。
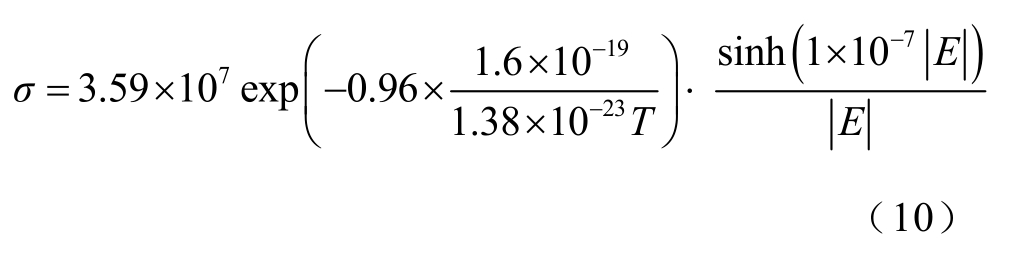
1.3 损耗电流模型的设置与诊断参数的提出
1.3.1 尖刺缺陷模型的设置
与直流电压下的情况不同,当交变的电压施加于内部存在金属尖刺缺陷的绝缘介质时,介质局部会处于交变的高电场下,材料的电导率不可再看作一个常数,而成为了一个随电压的交变而产生周期性变化的时变量,即介质的电导特性会在一个电压周期内发生线性区和非线性区间之间的波动,导致损耗电流产生畸变。
为模拟在电缆绝缘中出现金属尖刺情况时损耗电流的谐波特征,基于双极性载流子模型,建立简化二维轴对称XLPE 电缆尖刺缺陷模型。仿真模型的几何结构如图2 所示。为了对不同尖刺曲率半径以及不同电极间距的情况进行仿真,将尖刺的几何形状定义为
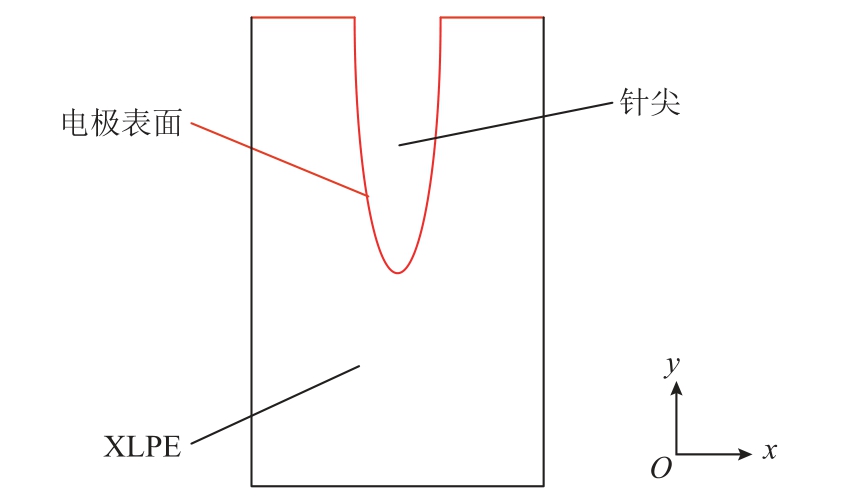
图2 尖刺缺陷试样几何结构
Fig.2 Geometric structure of tip defect specimen

式中,x、y、r、h 分别为平面坐标系中的横坐标、纵坐标、尖刺曲率半径和尖刺到平板电极之间的距离。通过改变r 和h 的值来实现对不同严重程度缺陷的仿真。
为更好地从机理上对损耗电流的畸变进行分析,选取与电导率线性相关的损耗电流密度作为计算量,其中损耗电流密度为电极表面(见图2)的面平均值,电导率为对二维轴对称模型的回转体内部的体平均值。损耗电流密度为
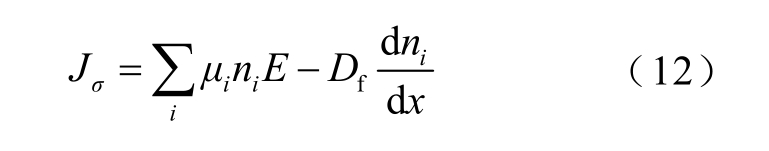
考虑到实际运行情况和后续实测实验的可行性,同时为了避免电树枝对于实验结果的影响,仿真与实验检测的电压均采用6 kV[32-34]。
1.3.2 诊断参数的提出
为了更直观地对不同情况下损耗电流的谐波特征进行量化分析,引入总谐波畸变率与各次谐波贡献率来描述损耗电流的频域特性,表达式分别为
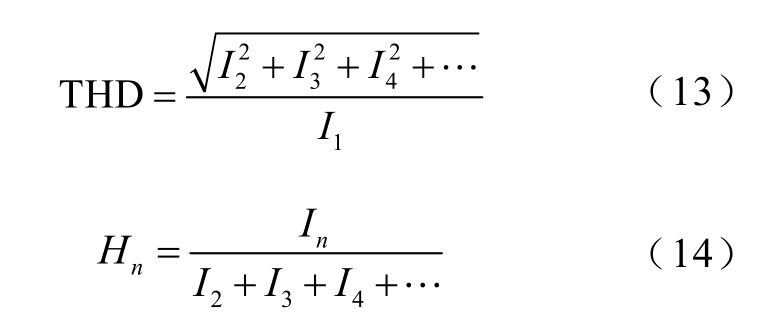
式中,Hn 为第n 次谐波贡献率,n≠1;In 为第n 次谐波的有效值;I1 为基波有效值。
为了更直观地对电导率的波动程度作量化分析,定义电导率畸变率(Conductivity Distortion Rate,CDR)为
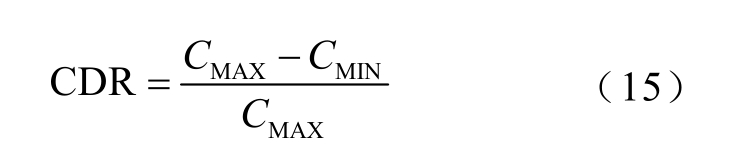
式中,CMAX 和CMIN 分别为电导率最大值与最小值。
2 XLPE 尖刺缺陷损耗电流谐波特性分析
在第1 节的基础上,对不同尖刺曲率半径及不同电极间距下的尖刺缺陷的损耗电流进行仿真分析,并探究缺陷严重程度对损耗电流的谐波特性的影响。
2.1 不同尖刺曲率半径的影响
本节主要探究不同尖刺曲率半径对损耗电流密度和电导率及第1 节所提出参数的影响。在前期预研究中发现,较大曲率半径下,损耗电流的畸变程度并不显著,且较小曲率半径的尖刺缺陷在实际电缆中并不常见,在25、30、35、40 μm 四种曲率半径下,已可以呈现出完整的各次谐波含量的变化过程。因此,为了更好地分析针尖曲率半径对损耗电流频域特性的影响,本节将尖刺与平板电极之间的距离设置为3 mm,对25、30、35、40 μm 四种不同尖刺曲率半径下模型的损耗电流密度以及平均电导率进行分析。
2.1.1 对损耗电流密度的影响
不同尖刺曲率半径下损耗电流密度的时域波形如图3 所示。从图3 中可以看出,由于尖刺缺陷的存在,损耗电流的波形与工频正弦相比发生了明显的畸变。直观来看,波形中出现了较为明显的“尖峰”,电流中叠加有较大的3 次谐波分量,且随着尖刺曲率半径的减小,损耗电流密度逐渐增大。曲率半径减小15 μm,损耗电流密度幅值增大12.3 倍(1 个数量级);损耗电流的波形畸变程度也在增大。

图3 不同尖刺曲率半径下损耗电流密度时域波形
Fig.3 Time domain waveforms of loss current density under different curvature radii of tip
为了更直观地对损耗电流的畸变程度进行量化分析,对1.3 节所述的THD 进行计算,不同尖刺曲率半径下损耗电流THD 的计算结果见表1。
表1 不同尖刺曲率半径下损耗电流THD
Tab.1 THD of loss current under different curvature radii of tip

尖刺曲率半径/μm 25 30 35 40 THD(%) 71.03 48.68 30.74 20.28
从表1 中可以看出,随着尖刺曲率半径的减小,THD 的值逐步上升。尖刺曲率半径由40 μm 减小至35 μm 时,THD 上升10.46%;尖刺曲率半径由35 μm 减小至30 μm 时,THD 上升17.94%;尖刺曲率半径由30 μm 减小至25 μm 时,THD 上升22.35%。综上分析可知,THD 与尖刺曲率半径之间呈非线性的单调递减关系。
对损耗电流密度进行快速傅里叶分析(Fast Fourier Transform, FFT),得到不同尖刺曲率半径下损耗电流密度的频域分析结果如图4 所示。由分析结果可知,损耗电流中的谐波以3 次和5 次谐波为主。

图4 不同尖刺曲率半径下损耗电流密度频域分布
Fig.4 Frequency domain distribution of loss current density under different electrode spacings
根据频域计算结果,对1.3 节中所述的Hn 进行计算,图5 展示了不同尖刺曲率半径下,2~7 次谐波的贡献率。可见,随着尖刺曲率半径的增大,3 次谐波贡献率逐步上升,5 次、7 次谐波贡献率逐渐降低。尖刺曲率半径由25 μm 增大至30 μm,3 次谐波贡献率上升8.63%,5 次谐波贡献率下降5.09%,7 次谐波贡献率下降3.69%;尖刺曲率半径由30 μm增大至35 μm,3 次谐波贡献率上升6.51%,5 次谐波贡献率下降5.63%,7 次谐波贡献率下降1.96%;尖刺曲率半径由35 μm 增大至40 μm,3 次谐波贡献率上升3.49%,5 次谐波贡献率下降4.90%,7 次谐波贡献率下降0.77%。

图5 不同尖刺曲率半径下损耗电流各次谐波贡献率
Fig.5 Contribution rate of each harmonic of loss current under different curvature radii of tip
2.1.2 对电导率的影响
不同尖刺曲率半径下的电导率时域波形如图6所示。从图6 中可以看出,电导率随着工频电压的周期性变化也发生了周期性的波动,其波动的周期为工频的两倍。且随着尖刺曲率半径的减小,电导率的峰谷差增大,即波动程度也在加大。

图6 不同尖刺曲率半径下电导率时域波形
Fig.6 Time domain waveforms of conductivity under different curvature radii of tip
为了对电导率的波动程度进行量化分析,对1.3节中所述的CDR 参数进行计算,得到不同尖刺曲率半径下损耗电流CDR 的计算结果见表2。
表2 不同尖刺曲率半径下损耗电流CDR
Tab.2 CDR of loss current under different curvature radii of tip

尖刺曲率半径/μm 25 30 35 40 CDR(%) 83.48 42.96 21.73 14.85
从表2 中可以看出,随着尖刺曲率半径的减小,CDR 的值逐步上升。尖刺曲率半径由40 μm减小至35 μm,CDR 上升6.88%;尖刺曲率半径由35 μm 减小至30 μm,CDR 上升21.23%;尖刺曲率半径由30 μm 减小至25 μm,CDR 上升40.52%。CDR与尖刺曲率半径之间呈非线性的单调递减关系。
2.2 不同电极间距的影响
本节主要探究不同电极间距对损耗电流密度和电导率及第1 节所提出参数的影响。实验与仿真所采用的电压为6 kV,与10 kV 电缆在运行过程中的相电压相当。10 kV 电缆绝缘厚度约为5 mm,1、2、3、4 mm 四种不同电极间距与实际工况中缺陷的不同严重程度相对应,在前期预研究中也发现,这四种电极间距下可以呈现出完整的各次谐波含量的变化过程。因此,本节保持尖刺曲率半径为30 μm,对1、2、3、4 mm 四种不同电极间距下模型的损耗电流密度及平均电导率进行分析。
2.2.1 对损耗电流密度的影响
不同电极间距下损耗电流密度的时域波形如图7 所示。从图7 中可以看出,随着电极间距的减小,损耗电流密度逐渐增大,针板间距减小3 mm,损耗电流密度幅值增大约10 000 倍(4 个数量级);损耗电流密度的波形畸变程度也有着明显的扩大。

图7 不同电极间距下损耗电流密度时域波形
Fig.7 Time domain waveforms of loss current density under different electrode spacings
为了更直观地对损耗电流的畸变程度进行量化分析,对1.3 节中所述的THD 进行计算。表3 中展示了不同尖刺曲率半径下损耗电流THD 的计算结果。可见,随着电极间距的减小,损耗电流的THD逐步扩大。
表3 不同电极间距下损耗电流THD
Tab.3 THD of loss current under different electrode spacings

电极间距/mm 1 2 3 4 THD(%) 84.85 75.98 48.68 27.46
由表3 可知,电极间距由4 mm 减小至3 mm,THD 上升21.22%;电极间距由3 mm 减小至2 mm,THD 上升27.30%;电极间距由2 mm 减小至1 mm,THD 上升8.87%。THD 与电极间距之间呈单调递减关系。
对损耗电流密度进行FFT 分析,不同电极间距下损耗电流的频域分析结果如图8 所示。由图8 可知,损耗电流中的谐波以3 次和5 次谐波为主。

图8 不同电极间距下损耗电流密度频域分布
Fig.8 Frequency domain distribution of loss current density under different electrode spacing
根据频域计算结果,对1.3 节中所述的Hn 进行计算,不同尖刺曲率半径下,2~7 次谐波的贡献率如图9 所示。随着电极间距的增大,3 次谐波贡献率逐步上升,5 次、7 次谐波贡献率逐渐降低。电极间距由1 mm 扩大至2 mm,3 次谐波贡献率上升3.07%,5 次谐波贡献率下降1.93%,7 次谐波贡献率下降2.47%;电极间距由2 mm 扩大至3 mm,3 次谐波贡献率上升10.68%,5 次谐波贡献率下降6.07%,7 次谐波贡献率下降4.82%;电极间距由3 mm 扩大至4 mm,3 次谐波贡献率上升6.94%,5 次谐波贡献率下降6.41%,7 次谐波贡献率下降2.09%。
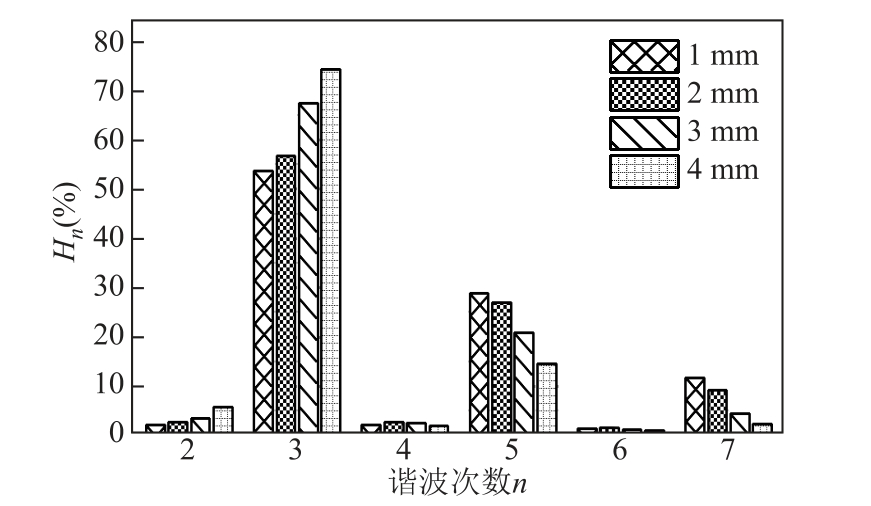
图9 不同电极间距下各次谐波贡献率
Fig.9 Contribution rate of each harmonic under different electrode spacings
2.2.2 对电导率的影响
不同电极间距下电导率的时域波形如图10 所示,随着电极间距的减小,电导率的波动程度增大。

图10 不同电极间距下电导率时域波形
Fig.10 Time domain waveforms of conductivity under different electrode spacings
为了对电导率的波动程度进行量化分析,对1.3节中所述的CDR 参数进行计算。表4 中展示了不同电极间距下的CDR,可见,随着电极间距的减小,CDR 的值逐步上升。
表4 不同电极间距下CDR
Tab.4 CDR of loss current under different electrode spacings

电极间距/mm 1 2 3 4 CDR(%) 99.88 96.41 42.96 16.42
由表4 可知,电极间距由4 mm 减小至3 mm,CDR 上升26.54%;电极间距由3 mm 减小至2 mm,CDR 上升53.45%;电极间距由2 mm 减小至1 mm,CDR 上升3.47%。CDR 与电极间距之间呈单调递减关系。
2.3 损耗电流谐波特性分析
如前所述,随着缺陷严重程度的增加(尖刺曲率半径的减小以及电极间距的缩短),THD 和CDR均会有明显的上升。为了进一步量化上述两个参数与缺陷严重程度的关系,本节分析了THD 与CDR随局部最大电场强度的变化,以及THD 与CDR 之间的关系。此外,为了进一步分析谐波成分随缺陷严重程度的变化规律,给出了5 次和7 次谐波贡献率之和H5+7 随CDR 变化的量化关系。
对不同缺陷严重程度下的电场强度进行计算,结果见表5 和表6。
表5 不同尖刺曲率半径下电场强度最大值
Tab.5 Maximum electric field strength under different curvature radii of tip

尖刺曲率半径/μm 25 30 35 40最大电场强度/(V/m) 1.10×108 8.01×107 6.17×107 4.94×107
表6 不同电极间距下电场强度最大值
Tab.6 Maximum electric field strength under different electrode spacings

电极间距/mm 1 2 3 4最大电场强度/(V/m) 1.59×108 1.18×108 8.01×107 6.04×107
从表5 和表6 中可以看出,缺陷严重程度的增加会造成局部最大电场强度的明显上升,在电极间距为3 mm 时,尖刺曲率半径减小15 μm,局部最大电场强度上升了1.23 倍;当尖刺曲率半径为30 μm 时,电极间距缩短3 mm,局部最大电场强度上升了1.63 倍。
图11 中展示了THD 与CDR 随局部最大电场强度的变化曲线。可以发现,随着局部最大电场强度的增大,THD 与CDR 单调上升,电场强度增加了2.22 倍,THD 上升3.18 倍,CDR 上升5.73 倍。
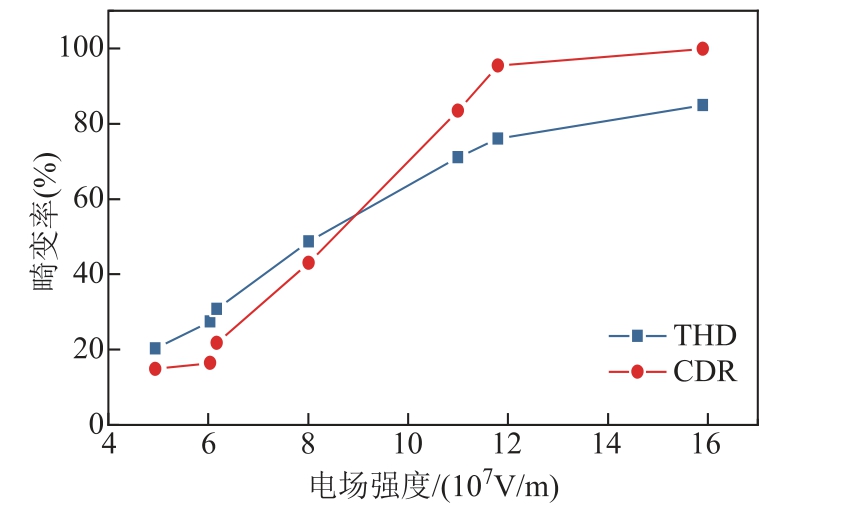
图11 THD 与CDR 随局部最大电场强度的变化曲线
Fig.11 The variation curve of THD and CDR with local maximum electric field intensity
THD 随CDR 的变化趋势如图12 所示,可以看出,THD 随CDR 线性增长。对二者的关系进行最小二乘拟合,可得到

图12 THD 随CDR 的变化趋势
Fig.12 The variation trend of THD with local CDR
基于以上分析可以发现,局部缺陷的存在会使得局部电场强度发生畸变,且缺陷越严重,电场强度的畸变程度也越大;畸变的局部高电场使得绝缘材料的电导率随着交流电压波形的变化而发生波动,且电场强度的畸变越严重,波动程度也越大,这一现象体现在CDR 随电场强度变化的规律上。电导率随时间发生的波动,会导致损耗电流中叠加高次谐波分量,电导率随时间的波动程度越大,谐波的含量越高,这一现象可以从THD 随CDR 变化的趋势中看出。
从2.1 节和2.2 节的分析中还可以发现,5 次、7 次谐波贡献率之和与缺陷严重程度呈正相关。为了分析这种现象产生的原因,以2.1 和2.2 节所述的八种情况下的CDR 为自变量,5 次和7 次谐波贡献率之和H5+7 为因变量,变化曲线如图13所示。
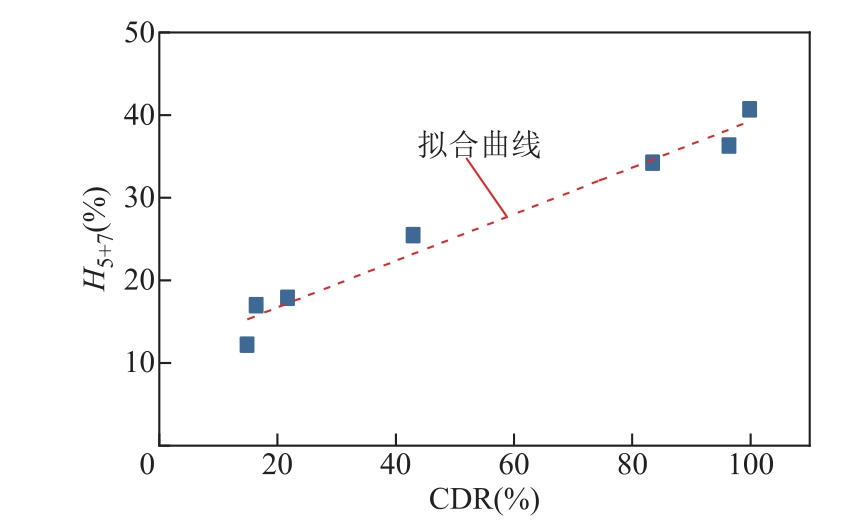
图13 H5+7 随CDR 的变化曲线
Fig.13 The variation trend of H5+7 with local CDR
对二者的关系进行最小二乘拟合,结果为
由式(17)可知,电导率的波动程度越大,损耗电流中5 次、7 次谐波成分的占比越高,即5 次、7 次谐波贡献率之和随缺陷严重程度的增大主要是由CDR 增大引起的。
3 尖刺缺陷试样实测分析
为了对实际XLPE 绝缘尖刺缺陷下损耗电流的谐波特征进行实测,搭建了尖刺缺陷试样损耗电流检测平台,对三种不同规格尖刺缺陷试样的损耗电流进行检测,并对比分析了仿真与实测的结果。
3.1 实验平台与检测方法
尖刺试样模型如图14 所示。为避免XLPE 材料与电极之间存在的微小气隙对实验结果产生影响,试样采用预埋式电极,XLPE 注入电极凹槽中浇注/挤压一体成型。试样主体宽25 mm、长50 mm、厚4 mm。共制作了三种规格的尖刺模型:尖刺曲率半径30 μm/电极间距3 mm、尖刺曲率半径25 μm/电极间距3 mm 和尖刺曲率半径30 μm/电极间距2 mm,分别记为30(3)、25(3)和30(2)。其中,钢针直径为0.5 mm,尖刺角度为30°,针尖为专业加工机构定制,并在显微镜下对针尖表面光滑程度及曲率半径进行测量。其余尺寸如图14 中标注所示。
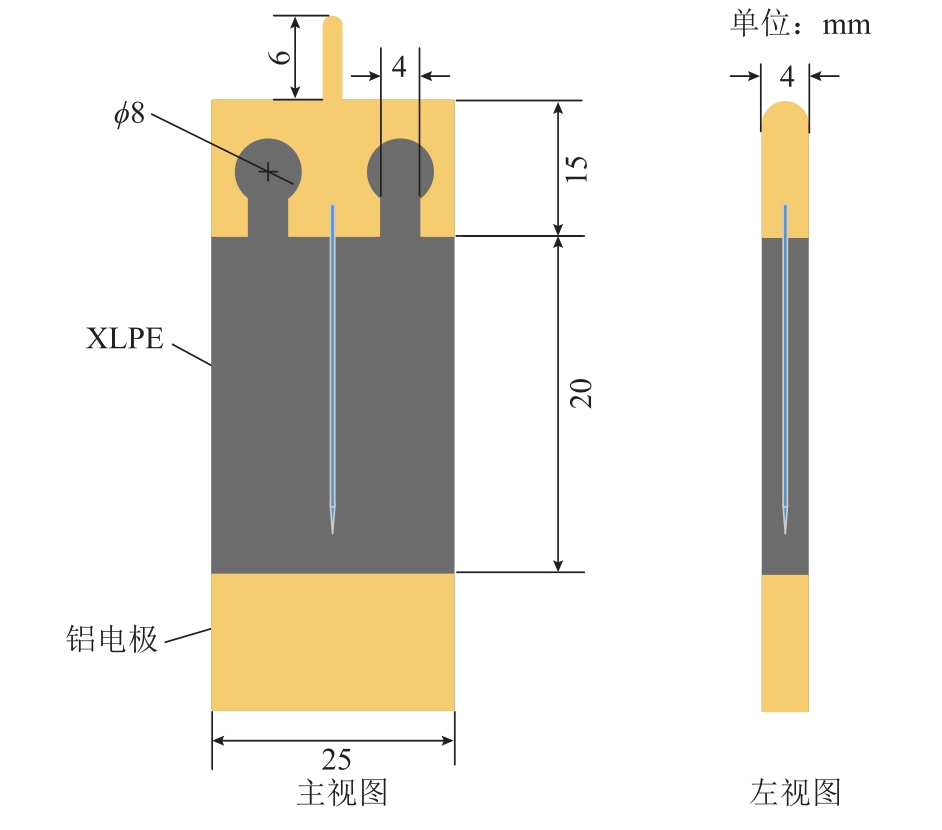
图14 尖刺试样模型
Fig.14 The sample of tip
现场实际测试中,无法对损耗电流密度进行直接测量,因此在实验室测试中,也只能对损耗电流进行测量。在三种规格的尖刺试样中,30(3)试样的绝缘电阻最大,损耗电流信号最小,经测量该试样绝缘电阻的数量级约为1011 Ω,在有效值为6 kV 的实验电压下,损耗电流的数量级在10-7 A 左右。为保证测量精度,选取10 kΩ 无感电阻对泄漏电流信号进行测量,并将信号接入pico5442D 高分辨率示波器(垂直分辨率为16 bit,在100 mV 量程下,测量精度为1.53×10-6 V)进行采集。
实验接线示意图如图15 所示。实验中将10 kΩ无感电阻串联在试样接地线中,将电阻两端的电压信号接入高分辨率示波器,对泄漏电流信号进行采集;同时通过电容分压器对施加在试样上的电压信号进行同步采集。为避免表面泄漏电流对实验结果的影响,在实验过程中将试样浸没在变压器油中。

图15 实验接线示意图
Fig.15 Experimental wiring diagram
3.2 实测结果
以30(3)试样为例,导体尖刺缺陷试样承受电压与泄漏电流的时域波形如图16 所示。

图16 导体尖刺缺陷试样承受电压与泄漏电流
Fig.16 Withstand voltage and leakage current of conductor tip defect sample
由图16 可知,泄漏电流与试样承受电压之间存在约90°的相位差,即泄漏电流的主要成分为容性电流,电流波形并没有发生明显畸变。本文分析的是泄漏电流中的阻性分量,即损耗电流。图17 中展示了泄漏电流I 中容性分量IC、阻性分量(损耗电流)IR 与试样承受电压U 之间的相位关系,其中β为I 与U 之间的夹角,利用两者的相对相位可以将泄漏电流中的损耗电流分离出来。从图中可以看出,IC 与IR 为一组正交矢量,经运算得到的损耗电流中不会含有容性电流的成分。因此,容性电流不会对损耗电流中的谐波成分产生影响[25]。
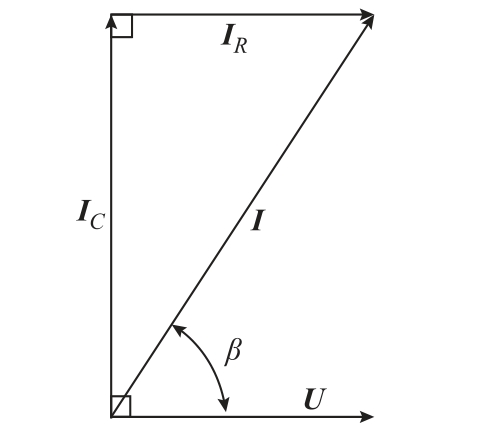
图17 导体尖刺缺陷试样承受电压与泄漏电流
Fig.17 Withstand voltage and leakage current of conductor tip defect sample
三种规格试样下损耗电流的频域计算结果如图18 所示。由图18 可知,在三种规格试样下,损耗电流中均存在明显的3 次与5 次谐波分量,进一步对实测结果进行量化分析,计算三种规格下的损耗电流有效值与THD 见表7。从实测结果来看,在尖刺曲率半径为30 μm 时,电极间距由3 mm 缩小至2 mm,损耗电流有效值上升9 190.32 nA,THD 上升14.12%;在电极间距为3 mm 时,尖刺曲率半径减小5 μm,损耗电流有效值上升1 356.72 nA,THD上升10.1%。
表7 损耗电流有效值与THD
Tab.7 Effective value of loss current and THD
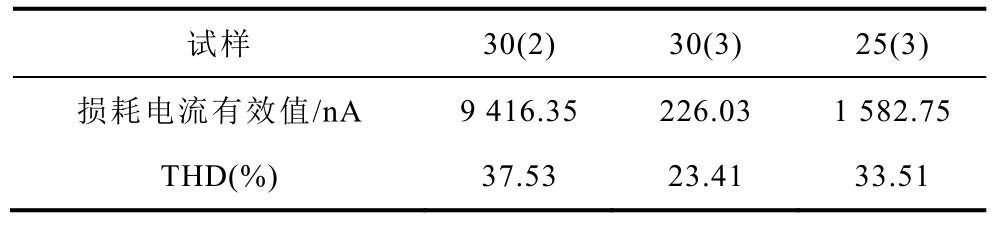
试样 30(2) 30(3) 25(3)损耗电流有效值/nA 9 416.35 226.03 1 582.75 THD(%) 37.53 23.41 33.51

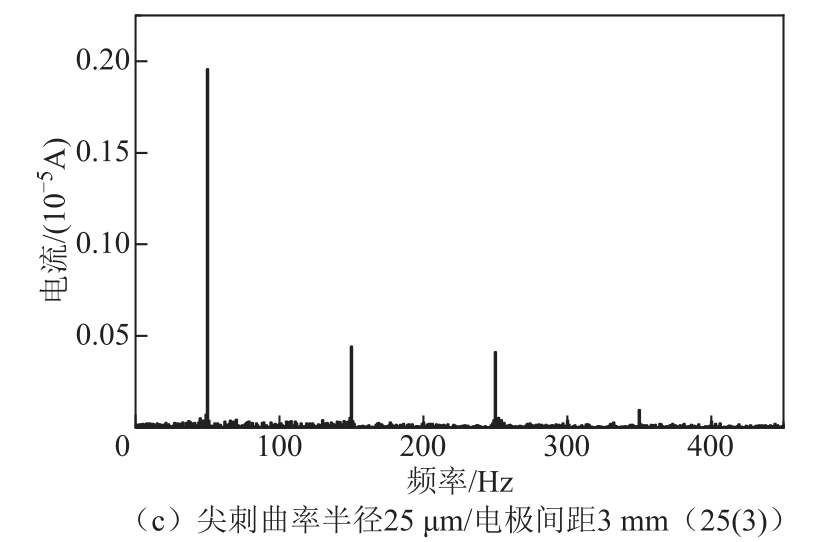
图18 损耗电流频谱
Fig.18 Loss current spectrum
3.3 实测与仿真结果对比分析
出于机理分析的明确性,在仿真分析中,选取与电导率线性相关的损耗电流密度作为计算量;但现场实际测试中,无法对损耗电流密度进行直接测量,因此在实验室测试中,也只能对损耗电流进行测量。因此3.2 节实验与2.2.1 节仿真中所获的结果存在差异。然而,根据式(14),Hn 为各次谐波分量的占比,能较大程度地去除仿真中损耗电流密度和实测中损耗电流的差异,较好地联系了理论分析和实际测量的结果。因此,在后续的对比分析中,选取Hn 为特征量,对仿真及实测结果中的谐波成分进行对比。损耗电流各次谐波贡献率的仿真与实测对比如图19 所示。


图19 仿真与实验各次谐波贡献率对比
Fig.19 Comparison of harmonic contribution rates between simulation and experiment
以实测结果的中位数为基准,由图19a 可知,实测结果表明,电极间距由2 mm 增大至3 mm,3 次谐波贡献率上升9.42%,5 次谐波贡献率下降7.02%,7 次谐波贡献率下降4.53%;由2.2 节可知,在仿真结果中,电极间距由2 mm 扩大至3 mm,3 次谐波贡献率上升10.68%,5 次谐波贡献率下降6.07%,7 次谐波贡献率下降4.82%。由图19b 可知,实测结果表明,尖刺曲率半径由25 μm 增大至30 μm,3 次谐波贡献率上升8.73%,5 次谐波贡献率下降4.99%,7 次谐波贡献率下降3.49%;由2.2 节得到,在仿真结果中,尖刺曲率半径由 25 μm 增大至30 μm,3 次谐波贡献率上升8.63%,5 次谐波贡献率下降5.09%,7 次谐波贡献率下降3.69%。
由对比结果可发现,仿真与实测结果在不同缺陷严重程度下的损耗电流谐波成分上保持了较好的一致性。损耗电流谐波特征分析的方法针对电缆局部尖刺缺陷诊断是有效的。特别地,谐波组成成分与尖刺缺陷的形貌密切相关。本文主要针对的缺陷是尖刺缺陷,因此在本文中,尖刺的形貌代表了尖刺缺陷的严重程度。同时,在对电缆进行实际诊断时,缺陷形貌也表明不同缺陷类型。由此可见,Hn不仅可以评估严重程度,还具有辨识缺陷类型的潜力,是一个具有工程实际应用价值的诊断特征量。特征参量与不同缺陷类型、严重程度的一一对应关系以及特征参量变化背后的物理规律值得继续探索,也是本文下一步努力的方向。
4 结论
本文开展了基于损耗电流谐波特征分析的电缆局部缺陷诊断研究,进行了仿真机理研究和针对典型局部尖刺缺陷的实测研究,得出主要结论如下:
1)电缆发生尖刺缺陷时,损耗电流中存在高次谐波,主要成分为3 次与5 次谐波分量。仿真分析可知,当XLPE 绝缘中存在导体尖刺缺陷时,由于局部电场强度急剧增大,使得绝缘材料的电导特性在一个工频周期内发生于欧姆区和非欧姆区间之间的反复波动,造成损耗电流中叠加了3 次与5 次谐波分量。
2)提取THD 作为诊断特征量,发现这一参数与缺陷严重程度之间存在明确的相关关系,可以将其作为电缆缺陷严重程度诊断的特征量。分析了产生这一现象的原因,发现导体尖刺缺陷的严重程度增加,使得局部电场畸变程度加大,进而导致了CDR 的升高,损耗电流的THD 也随之上升。
3)对比分析结果表明,导体尖刺缺陷的严重程度和缺陷形貌的改变,都会使得损耗电流中的谐波成分发生改变。缺陷严重程度越高、尖刺形状越尖锐,3 次谐波占比越低,5 次、7 次谐波占比越高;且5 次、7 次谐波贡献率之和与CDR 之间呈线性正相关关系。损耗电流的各次谐波贡献率Hn 是一个具有工程实际应用价值的诊断特征量。
[1] 陈向荣, 洪泽林, 朱光宇, 等.高温下电压稳定剂对交联聚乙烯电树枝化及局部放电特性的影响[J].电工技术学报, 2023, 38(3): 577-586.Chen Xiangrong, Hong Zelin, Zhu Guangyu, et al.Effect of voltage stabilizer on electrical treeing and partial discharge characteristics of crosslinked polyethylene at high temperature[J].Transactions of China Electrotechnical Society, 2023, 38(3): 577-586.
[2] 王昊月, 李成榕, 王伟, 等.高压频域介电谱诊断XLPE 电缆局部绝缘老化缺陷的研究[J].电工技术学报, 2022, 37(6): 1542-1553.Wang Haoyue, Li Chengrong, Wang Wei, et al.Local aging diagnosis of XLPE cables using high voltage frequency domain dielectric spectroscopy[J].Transactions of China Electrotechnical Society, 2022, 37(6):1542-1553.
[3] Al-Arainy A, Malik N H, Qureshi M I, et al.The performance of strippable and bonded screened medium-voltage XLPE-insulated cables under longterm accelerated aging[J].IEEE Transactions on Power Delivery, 2007, 22(2): 744-751.
[4] 李蓉, 周凯, 万航, 等.基于输入阻抗谱的电力电缆本体局部缺陷类型识别及定位[J].电工技术学报, 2021, 36(8): 1743-1751.Li Rong, Zhou Kai, Wan Hang, et al.Identification and location of local defects in power cable body based on input impedance spectroscopy[J].Transactions of China Electrotechnical Society, 2021, 36(8): 1743-1751.
[5] 王昊月, 孙茂伦, 赵凯杰, 等.电缆绝缘老化的高压频域介电谱诊断评估方法[J].中国电机工程学报, 2023, 43(9): 3630-3642.Wang Haoyue, Sun Maolun, Zhao Kaijie, et al.High voltage FDS diagnosis and evaluation method for cable insulation aging[J].Proceedings of the CSEE,2023, 43(9): 3630-3642.
[6] 张牧烨.电力电缆故障定位和故障诊断方法研究[D].济南: 山东大学, 2022.
[7] 吴沛航, 吴旭升, 高嵬.舰船电缆绝缘在线监测技术综述[J].电工技术学报, 2021, 36(增刊 2): 713-722.Wu Peihang, Wu Xusheng, Gao Wei.A review of online conditon monitoring of marine cable insulation[J].Transactions of China Electrotechnical Society, 2021, 36(S2): 713-722.
[8] 王昊月, 王晓威, 孙茂伦, 等.XLPE 电缆绝缘热老化的高压频域介电谱诊断方法[J].电工技术学报,2022, 37(17): 4497-4507.Wang Haoyue, Wang Xiaowei, Sun Maolun, et al.High voltage frequency domain dielectric spectroscopy diagnosis method for thermal aging of XPLE cables[J].Transactions of China Electrotechnical Society, 2022,37(17): 4497-4507.
[9] CIGRE WG JWG D1/B1.20.Non-destructive watertree detection in XLPE cable insulation[R].CIGRE,2012.
[10] Yagi Y, Tanaka H, Kimura H.Study on diagnostic method for water treed XLPE cable by loss current measurement[C]//1998 Annual Report Conference on Electrical Insulation and Dielectric Phenomena (Cat.No.98CH36257), Atlanta, GA, USA, 2002: 653-656.
[11] Hvidsten S, Ildstad E, Sletbak J, et al.Understanding water treeing mechanisms in the development of diagnostic test methods[J].IEEE Transactions on Dielectrics and Electrical Insulation, 1998, 5(5): 754-760.
[12] 赵世纯, 凌标灿, 朱希安, 等.HDS 电气设备带电状态诊断技术及应用[M].北京: 电子工业出版社,2017.
[13] 魏强.基于谐波分量法XLPE 电缆水树老化测试系统的研究[D].哈尔滨: 哈尔滨理工大学, 2004.
[14] 高震.变频谐振电源条件下电缆绝缘损耗电流谐波分量的测量[D].哈尔滨: 哈尔滨理工大学, 2012.
[15] 李闯.损耗电流谐波分量测试系统的研制[D].哈尔滨: 哈尔滨理工大学, 2010.
[16] 靳雪君.基于谐波特征的电缆绝缘带电诊断技术[D].北京: 北方工业大学, 2022.
[17] 符劲松, 陈俊武, 舒舟, 等.含水树枝的 XLPE 电力电缆损耗电流建模仿真计算[J].高压电器, 2013,49(5): 86-89.Fu Jinsong, Chen Junwu, Shu Zhou, et al.Modeling water tree for XLPE cable loss current numerical calculation[J].High Voltage Apparatus, 2013, 49(5):86-89.
[18] 兰莉.温度对聚合物绝缘中空间电荷行为的影响[D].上海: 上海交通大学, 2015.
[19] 刘德远.交直流电场下电缆绝缘中空间电荷测量与数值模拟技术研究[D].上海: 上海交通大学, 2019.
[20] 钟琼霞, 兰莉, 吴建东, 等.交联副产物对交联聚乙烯中空间电荷行为的影响[J].中国电机工程学报, 2015, 35(11): 2903-2910.Zhong Qiongxia, Lan Li, Wu Jiandong, et al.The influence of cross-linked by-products on space charge behaviour in XLPE[J].Proceedings of the CSEE, 2015,35(11): 2903-2910.
[21] 陈驰, 李佳兴, 王霞, 等.交联聚乙烯试样中空间电荷输运特性的数值模拟[J].高电压技术, 2023,49(1): 311-320.Chen Chi, Li Jiaxing, Wang Xia, et al.Numerical simulation of space charge transport characteristics in crosslinked polyethylene samples[J].High Voltage Engineering, 2023, 49(1): 311-320.
[22] 黄光磊, 李喆, 杨丰源, 等.直流交联聚乙烯电缆泄漏电流试验特性研究[J].电工技术学报, 2019,34(1): 192-201.Huang Guanglei, Li Zhe, Yang Fengyuan, et al.Experimental research on leakage current of DC cross linked polyethylene cable[J].Transactions of China Electrotechnical Society, 2019, 34(1): 192-201.
[23] 黄光磊.直流电缆局部放电与泄漏电流特性及类型识别研究[D].上海: 上海交通大学, 2019.
[24] 严有祥, 朱婷, 王蕾.基于有限元法对±320 kV 直流XLPE 电缆中间接头电场与空间电荷的仿真计算[J].高电压技术, 2017, 43(11): 3591-3598.Yan Youxiang, Zhu Ting, Wang Lei.Simulation calculation of electric field and space charge in the joint of DC ±320 kV XLPE cable based on finite element method[J].High Voltage Engineering, 2017,43(11): 3591-3598.
[25] 曹政钦, 石岩, 魏钢.高电压技术[M].重庆: 重庆大学出版社, 2020.
[26] 李进, 梁虎成, 杜伯学, 等.基于双极性载流子输运模型的高压直流电缆附件绝缘EPDM/LDPE 界面电荷的数值模拟[J].高电压技术, 2018, 44(5): 1443-1449.Li Jin, Liang Hucheng, Du Boxue, et al.Numerical simulation of interface charge behaviors between LDPE/EPDM for HVDC cable accessory insulation based on the bipolar charge transport model[J].High Voltage Engineering, 2018, 44(5): 1443-1449.
[27] 张灵, 陈健宁, 周远翔, 等.聚合物绝缘空间电荷动力学的理论模型与数值仿真研究进展[J].中国电机工程学报, 2022, 42(8): 3037-3055.Zhang Ling, Chen Jianning, Zhou Yuanxiang, et al.Progress on theoretical models and numerical simulation of space charge kinetics in polymeric insulation[J].Proceedings of the CSEE, 2022, 42(8):3037-3055.
[28] Liu Hongbo, Liao Ruijin, Zhu Qingdai, et al.Calculation of space charge density in negative corona based on finite-element iteration and sound pulse method[J].IEEE Transactions on Magnetics, 2018,54(3): 1-4.
[29] 于弘洋, 周飞, 荆平, 等.城市电网紧凑化输电增容技术探讨[J].智能电网, 2014, 2(8): 26-30.Yu Hongyang, Zhou Fei, Jing Ping, et al.Discussion of compact design and capacity increase technology of power transmission in urban power grid[J].Smart Grid,2014, 2(8): 26-30.
[30] Lan Li, Wu Jiandong, Yin Yi, et al.Effect of temperature on space charge trapping and conduction in cross-linked polyethylene[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(4):1784-1791.
[31] 刘士利, 李丛健, 沈方, 等.交流XLPE 电缆改为直流运行时空间电荷积累特性仿真[J].高电压技术, 2017, 43(11): 3576-3582.Liu Shili, Li Congjian, Shen Fang, et al.Simulation on the characteristics of space charge accumulation when converting the AC XLPE cable to DC operation[J].High Voltage Engineering, 2017, 43(11): 3576-3582.
[32] 陶文彪, 朱光亚, 宋述勇, 等.交联聚乙烯中丛状电树枝的生长机制[J].中国电机工程学报, 2018,38(13): 4004-4012, 4042.Tao Wenbiao, Zhu Guangya, Song Shuyong, et al.The growth mechanism of brush-type electrical tree in XLPE[J].Proceedings of the CSEE, 2018, 38(13):4004-4012, 4042.
[33] Wang Haoyue, Wang Wei, Wu Feng, et al.Characteristics analysis of water needle induced electrical trees in XLPE[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2021, 28(6):1988-1995.
[34] 马鑫, 张怀垠, 吴继岩, 等.温度对交联聚乙烯电缆尖刺缺陷局部放电特性的影响[J].高压电器,2021, 57(5): 151-156.Ma Xin, Zhang Huaiyin, Wu Jiyan, et al.Effect of temperature on partial discharge characteristics of needle defects in cross-linked polyethylene cable[J].High Voltage Apparatus, 2021, 57(5): 151-156.