0 引言
电气系统通常由多个以串联方式连接的元件或装置组成,其中任何一个元件发生故障都可能导致整个系统故障。例如,在高压直流输电系统中,电缆附件绝缘故障占线路故障的70%[1];在水轮发电机等电机系统中,绝缘损坏导致的故障率高达50%[2]。而绝缘聚合物的老化速率取决于所施加应力的性质,其承受的主要应力形式包括电应力、热应力和机械应力[3-5]。尤其在直流系统中,绝缘被施加高应力时,电荷很容易注入到聚合物内部并产生积聚,进而使得绝缘内部电场分布不均匀。由于空间电荷累积、局部放电和电树枝的共同作用,造成聚合物绝缘性能下降,甚至导致不可逆转的击穿行为[6-8]。
高压直流电力电缆绝缘主要采用低密度聚乙烯(Low Density Polyethylene, LDPE)和交联聚乙烯(Cross-Linked Polyethylene, XLPE)。在施加电场、温度、材料结构、添加剂、杂质等因素的影响下,空间电荷或者极化的非均匀分布会显著增加绝缘内部电场的畸变,进而造成绝缘故障[9-11]。电缆接头和电缆终端是电力系统运行中较为薄弱的环节,其故障也是高压直流电缆运行中的主要问题[12]。电缆端部电场分布如图1 所示,可知当电缆屏蔽层未采取任何措施时,于金属/电介质/空气三相交接处可见明显的电应力集中,而较为集中的电场则会直接导致局部的放电、闪络和击穿[13]。

图1 电缆端部电场分布[13]
Fig.1 Electric field distribution at cable end[13]
此外,在高压旋转电机中,定子系统绝缘会受到集中电场的作用,在热应力、机械应力、电应力和环境应力共同作用下产生缺陷,导致环氧树脂(Epoxy Resin, EP)等绝缘逐渐劣化,特别是电应力会导致系统空隙中产生局部放电,从而使得绝缘产生电树枝。在叠层铁心端部的绝缘也会受到切向的电应力,使得靠近端匝绝缘层的空气发生放电或导致表面产生电晕放电[14-15]。表面电晕放电和内部的放电均会加速绝缘聚合物的劣化,最终导致绝缘的失效[16]。大功率绝缘栅双极晶体管(Insulated Gate Bipolar Transistor, IGBT)模块是工业、牵引和高压直流输电应用中的关键部件。尽管功率模块的故障率已大幅降低,但就系统可靠性而言,IGBT 模块仍然是最脆弱的组件之一[17]。随着对更大功率密度需求的日益增长,需要提高电压、温度和频率,嵌入硅凝胶中的金属化氮化铝陶瓷基板将会受到很大的影响,由于金属化基板边缘电场强度有可能超过硅胶的耐电强度,进而发生局部击穿,甚至绝缘击穿[18]。
高压系统用绝缘器件的电场控制已被广泛关注,工程上致力于实现在固定系统电压下获得尽可能低的电场强度,并且尽可能实现电场均匀分布。应力控制主要有两种方法:一种是电容应力控制,例如,通过控制导电部件的形状进行几何电极分级,通过高介电常数材料进行电位分布调控,以及通过将具有特定电阻率的结构层施加到屏蔽层和绝缘层来控制阻抗应力[19];还有一种是施加直流电应力时,使用特定电流-电场特性的材料进行电阻应力控制[20]。本文将从调控电场分布的措施进行介绍,总结相关无机导电颗粒与聚合物基复合材料的导电机理,并对非线性电导材料研究的进展与应用进行综述。
1 高压应用中均化电场的措施
几何应力控制主要通过优化电极的几何形状来优化电场分布,实现电势线沿电极分布,例如将电缆屏蔽层设计为应力锥接头结构,如图2 所示[19]。几何应力还可以通过导电层的设计实现电场均匀分布,将典型的导电材料包括石墨、导电聚合物、炭黑胶带及金属箔片等应用于最高应力区域,使用具有高介电常数的复合材料实现电应力控制,例如在具有高电应力的区域周围缠绕胶带或在绝缘中引入高介电材料来实现,如图3 所示。但是随着复合材料介电常数的增加,介质损耗也会增加,在高频下会产生局部过热[21-22]。阻抗应力控制则是将具有特定电阻率的结构层应用于屏蔽和电缆绝缘,这些结构层通常使用收缩管或贴片[23]。
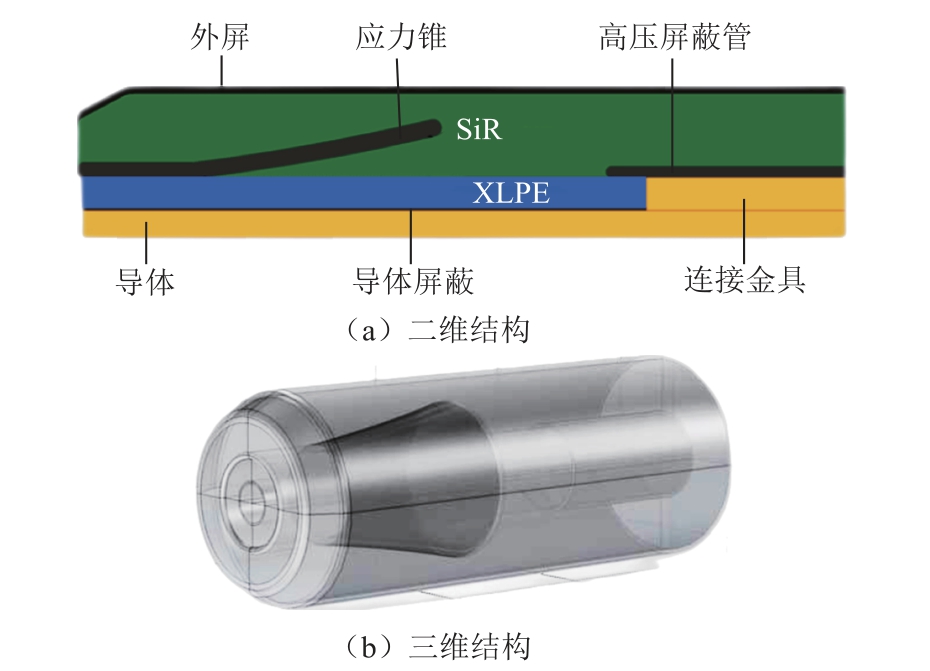
图2 电缆应力锥接头结构[19]
Fig.2 Cable stress cone joint structure[19]

图3 带有高介电材料的电缆端部电场分布[21]
Fig.3 Electric field distribution at the end of cable with high dielectric material[21]
几何控制往往比较复杂,在高介电材料介质损耗、聚合物材料传热、电应力曲线峰值位置不可控等方面存在较大的限制,结构的设计涉及材料结构、电气、机械、热力学等诸多因素,成本相对较高且较为复杂[21-23]。为了解决这个问题,研究人员创造了一种非线性应力控制的方法,主要采用电导率随所施加电压增加而非线性变化的非线性电导材料作为绝缘材料,通常将具有非线性功能的无机填料掺入绝缘材料中实现,这种复合材料也常被称作“智能”绝缘材料[24]。非线性电导材料已经被广泛应用于电缆附件、电机等领域。用于电机定子线棒、电缆附件应力锥根部和绝缘子电晕保护的常见无机填料有碳化硅(SiC)、氧化锌(ZnO)、炭黑(CB)、钛酸钡(BaTiO3)、二氧化钛(TiO2)、二氧化硅(SiO2)、SiOx 或不同氧化物的混合物[25-34]。
高压电缆附件绝缘使用非线性电导材料不仅可以将电应力控制在较低水平,也可更好地控制绝缘的尺寸,使得电缆附件体积更小、更易安装并降低制备成本[25]。在高压电机线圈中使用非线性电导材料也是较为普遍的选择,主绝缘通常采用半导体涂料或绝缘胶带进行外部电晕保护,碳基半导体胶带和碳化硅基非线性分级胶带则被广泛应用于大型旋转机械定子杆出口槽处,且模拟分析也表明,高导电的非线性电导带可以降低该区域的最大电场,使定子杆表面电场分布更加均匀[35]。非线性电阻层也被应用于大功率IGBT 模块金属边缘,可以显著地降低金属铜、陶瓷基板和有机硅凝胶或聚酰亚胺封装三相交界处的电场强度[36]。
2 非线性电导复合材料的导电机理
非线性电导分级材料具有复杂的物理化学结构,当施加电场时,载流子在材料内部的输运方式会变得非常复杂。为了探索非线性电导材料的电荷输运机理,一般假设存在两种导电路径:欧姆导电路径和非线性导电路径。欧姆导电路径中电流的流动方向与电场矢量保持一致,电流的流动路径始终遵循最小电阻的原则。非线性导电路径中电流流动路径与电场矢量不一致,载流子的传导路径较为错乱,电导机制遵循传导粒子的界面原理[37]。然而,简单的物理模型并不能解释复杂的输运方式,目前有关导电聚合物的导电理论有较多的研究,经典的理论包括跳跃电导理论、肖特基效应、普尔-弗兰凯尔效应、隧穿效应、空间电荷限制电流理论等;推广的导电理论包括渗流理论、有效介质理论、场致发射理论等。本节将从无机导电颗粒和聚合物基复合材料的非线性导电原理入手,介绍现有较为成熟的导电理论,并分析各理论的局限性。
ZnO 是一种优良的陶瓷材料,在避雷器、非线性开关、断路器等电源设备上有着广泛的应用[38-39]。G.D.Mahan 等提出了ZnO 非线性电导行为的两步输运模型,研究者假设两个ZnO 颗粒之间的边界层厚度不完全相同,如果两相颗粒之间边界层的厚度很薄(<3 nm),由于内部存在缺陷,大量的电子可以积累在界面层,将建立一个负电荷区域。因此,为了保持静电平衡,颗粒的另一边就会表现出带正电荷的特性,如图4 所示。其中XL0、XR0 分别为耗尽层左右两侧宽度;E0 为真空能级,Ec 为导带底能级,Ev 为价带顶能级,EF 为费米能级;ΦL 与ΦR 分别为左右两侧势垒;IL 和IR 分别为注入电流与流出电流。如图4a 所示,当未施加电场时,左右耗尽层具有相同的宽度,即XL0=XR0,且左右肖特基势垒的高度是相等的[40]。当电场作用时,电子会注入两个相邻ZnO 之间的界面层,然后进入另一个ZnO 颗粒,在低电场条件下,热激发是电荷传递的主要因素,此时界面层势垒两侧发生变化,界面一侧电荷增加,隧穿效应导致势垒减小,如图4b 所示,这可以解释在低电场条件下出现的一些非线性电导现象。当电场进一步升高时,势垒会进一步降低,且界面处积聚的正电荷也会增多,并使得隧穿效应更加明显,更多的载流子可以跨越势垒进行传输,传输电流急剧增加[40]。

图4 ZnO 肖特基势垒模型[40]
Fig.4 Schottky barrier model of the ZnO[40]
SiC 最初被用于定子绝缘涂层,以解决定子绕组末端的电晕现象[41-42]。由于SiC 具有非线性电导特性,进而也被广泛用于电场分级调控[43]。然而到目前为止,SiC 的非线性电导机制并没有统一的理论解释。有一种是基于SiC 颗粒表面的氧化行为进行解释,SiC 本身的电阻率非常小,但SiC 表面通常存在一层较薄的二氧化硅(SiO2),SiO2 电阻率较高,当施加高电场时,这一薄层会产生较大的电压降,载流子可以很容易地通过这一薄层,形成一个隧穿电流。当外加电场进一步增加时,载流子数量增多,将触发颗粒的非线性电导行为[44]。还有一种是基于场致发射理论来解释,SiC 颗粒具有高度不规则的形状,当颗粒聚集时会产生一些明显的尖角接触区域,在两个相邻的颗粒之间可能存在一个带有一定距离的气隙,当气隙中施加的电场超过其临界电场时,将自动在SiC 颗粒的边缘或尖角处产生电子发射。当外施电场较低时,载流子在两个颗粒之间相互接触的区域内流动,仍然服从欧姆定律;当外加电场不断增长,越来越多的气隙产生电子发射,使得非线性电导现象发生[45-46]。也有基于局部加热理论进行解释,当外加电场增加时,SiC 本身的电阻率会由于热阻效应而降低,从而发生非线性电导行为[47]。当然,由于SiC 本身具有复杂的结构,单一的理论并不能很好地解释其非线性电导现象,因此需要将多种理论相结合来合理地解释其非线性电导特性。
除了上述介绍的两种无机半导体颗粒(SiC和ZnO)外,还有其他的无机导电颗粒,如氧化铝(Al2O3)[48]、钛酸铜钙(Copper Calcium Titanate,CCTO)[49]、二硫化钨(WS2)[50]、碳纳米管(Carbon Nanotube, CNT)[51]等,它们都具有一定的非线性电导特性,其传导机制也都有所不同。例如具有明显长径比的碳基材料(如CNT),主要通过在渗流阈值之上构建较为稳定且相互连接的导电路径,从而实现电学性能的快速变化;而具有任意纵横比的颗粒(如CB)则不会构建这种互连的路径,仅通过颗粒的直接接触改变其属性[52]。目前对于聚合物非线性电导理论的传输机制还不统一,研究人员对于相同颗粒的导电机理往往也给出较为不同的解释。因此,需要将半导体颗粒的导电机理与聚合物基体的导电机理相结合,进而更好地解释其传输机理。
针对复合材料非线性电导机制有一定的共识,主要是复合材料内部的载流子在高电场作用下可以传输形成电流,也就是说必须通过电场因素建立导电路径[53-55]。典型的渗流理论被广泛使用于解释非线性电导特性,该理论认为复合材料是一个完整的系统,当掺杂颗粒含量超过一定的占比即其渗透阈值时,导电颗粒将形成一条相互接触的导电路径,形成传输电流[56]。但这种渗流理论只从统计学的角度解释了某些导电复合材料的传导机理,忽略了聚合物基体与导电颗粒之间的界面相互作用。
也有研究认为聚合物基体与导电颗粒之间的界面是影响导电通道建立的重要因素,如果复合材料中的界面急剧增加,颗粒间导电通道的建立就会较为容易。但是由于微观颗粒性能测试较为困难,并不能直接探索其真正的作用机理,该理论具有较大的局限性。也有研究采用隧穿效应解释相关行为,认为载流子的传导过程不依赖两个颗粒之间的接触界面,而是依赖于它们之间的电子跃迁过程。当两个颗粒之间的间隙宽度很大时,电子跃迁较为困难,流过复合材料的电流密度就会很小,隧穿效应较难发生;当颗粒增多时,颗粒之间的距离减小,电子跃迁更容易,隧穿效应也更易发生,电流密度增加[57]。场致发射理论也被广泛应用,该理论假设当相邻颗粒之间的间隙宽度较小时,电子会在高电场的作用下脱离束缚进行跃迁,从而使得电流密度随着电场的增加呈现指数级增加,且不需要考虑温度的影响[58]。
实际上,上述的传导理论,包括跳跃电导、渗流和隧穿传导理论,都存在于传导过程中,哪种导电机制占主导地位取决于导电颗粒的形状、含量及聚合物基体的特性。上述电导理论可以解释部分改性复合材料在不同电场条件下的非线性电导行为,但研究者仍不能应用一种固定的理论来解释所有改性复合材料的非线性电导行为,许多理论忽略了颗粒本征的非线性电导特性,不能很好地将导电颗粒特性与聚合物结合起来,非线性电导理论仍然需要进一步探索。
3 非线性电导复合材料研究
复合材料的理想电气性能取决于多种因素:填料的含量和结构、填料与基体材料之间的分子间相互作用等。复合材料的非线性电导参数(阈值电场强度和非线性系数)取决于填料的特性,例如填料掺杂含量、尺寸、形态和组成成分,所有这些因素都显著地影响了填料渗流网络的形成,本节将从这几部分对现有研究进行介绍。
3.1 基于填料掺杂含量的非线性电导研究
填料掺杂含量是影响复合材料性能的重要因素,针对填料掺杂含量的影响,已有较多的研究者基于ZnO 无机填料进行研究。曼彻斯特大学K.Tavernier等将质量分数为10%、20%、30%、40%和50%的ZnO 颗粒掺入聚酯树脂中制备了复合绝缘材料。研究表明,复合绝缘材料的阈值电场强度和填料含量依赖性较强,且当ZnO 质量分数为30%时,复合树脂聚酯材料中的电导率与电场强度开始呈现明显的非线性关系[25]。曼彻斯特大学D.W.Auckland 等于聚酯树脂中引入适量的ZnO 颗粒,确定了产生非线性电导特性的临界ZnO 填充体积分数为14%,且表明掺杂含量越高,非线性电导特性出现时的电场强度就越低[59]。曼彻斯特大学B.R.Varlow 等将不同含量的ZnO 掺入环氧树脂中,研究显示掺杂ZnO 体积分数为15%时的阈值电场强度为2 kV/mm,掺杂ZnO 体积分数为 20%时的阈值电场强度为1 kV/mm[60]。D.W.Auckland 等研究了ZnO/LDPE复合材料的J-E(电流密度-电场强度)曲线,表明ZnO 掺杂质量分数高于10%时,能够观察到非线性的J-E 曲线,并且随着ZnO 含量的增加,阈值电场强度减小[61]。清华大学杨霄等的研究也表明,当硅橡胶(Silicone Rubber, SiR)中ZnO 填料体积分数高于渗流阈值(39%)时,ZnO/SiR 才具有非线性电导特性,且可以通过改变填料含量来控制阈值电场强度,填料含量越高,阈值电场强度数值越小[62]。清华大学高磊等将自制的ZnO 微球掺入硅橡胶中,ZnO 形貌及复合材料电学性能如图5a 所示,可知当掺杂体积分数为39%、46.5%、52%和60%时,复合材料的非线性系数为12.5、15.8、17.1 和19.0,表明复合材料的非线性电导特性随着掺杂含量的提升而增强[63]。

图5 无机填料含量对复合材料电学性能的影响
Fig.5 Influence of inorganic filler content on electrical properties of composites
这些研究表明,复合材料的非线性电导在很大程度上取决于无机填料的含量。当填料含量增加时,阈值电场强度减小,这主要取决于ZnO 的特性。ZnO在晶界的两侧能够产生肖特基势垒,在足够高的填料含量下,产生非线性电导特性[64]。也有研究者绘制出ZnO 于基体复合材料中的分布示意图,用来解释其非线性电导机理,填料含量对渗流路径的影响如图6 所示。由图6 可知,在低掺杂含量时并无传导路径产生,此时电导率较低;当填料含量超过渗流阈值时,电流传导路径形成,电导率剧烈增加;当掺杂填料含量更高时,传导路径更多。因此,非线性电导对应的阈值电场强度更小,非线性电导特性更优异[62]。

图6 填料含量对渗流路径的影响[62]
Fig.6 Effect of filler content on seepage path[62]
基于SiC 无机填料的非线性复合材料也有较多的研究。天津大学杜伯学等将质量分数为10%、30%、50%和100%的球形α-SiC 六方晶体掺入硅橡胶中。α-SiC 形貌及复合材料电学性能如图5b 所示,可知,当填料质量分数超过10%时,SiR/SiC 复合材料的电导率是电场强度的非线性函数。随着填料含量的增加,非线性电导的阈值电场强度减小,非线性系数减小。根据渗流理论,对于填料含量低的复合材料,颗粒间的平均距离很大,在整个复合材料中不能形成导电路径。填料含量进一步增加并超过渗流阈值时,会导致颗粒间的平均距离减小,从而在基体内形成传导路径,当电场强度超过阈值电场强度时,直流电导率呈指数增长。在低电场条件下,SiR/SiC 复合材料处于欧姆电导区域。在该区域中,载流子难以克服SiC 颗粒界面上的势垒。当电场强度增大并超过一定的阈值电场强度时,相邻颗粒之间会发生隧穿现象。在此情况下,大量的载流子通过颗粒的界面,SiR/SiC 复合材料的电导率急剧上升[65]。天津大学李进等研究了SiC 作为填料,三元乙丙橡胶(Ethylene Propylene Diene Monomer,EPDM)作为基体的复合材料的非线性电导特性。研究表明,一定含量的SiC 可以引发复合材料非线性电导特性,且阈值电场强度随着SiC 掺杂含量的增加而减小。这主要是因为在低电场强度条件下,很少有载流子能通过热激发越过界面势垒,当电场强度超过一定的阈值时,就会产生隧穿效应。作者认为SiC 填料将大量的载流子引入复合材料中,从而促进了载流子在局部应力下的迁移。当填料含量增加时,载流子迁移率增加,又由于SiC 之间平均距离减小,从而形成较多的导电通路[66]。
除了较为常见的ZnO 和SiC 无机填料,其余无机填料掺杂含量对材料电学性能的影响也有较多报道。哈尔滨理工大学迟庆国等在EPDM 中引入了金属元素Ag,研究表明Ag/EPDM 复合材料中极少量的Ag 即可诱导出明显的非线性电导特性,最大非线性系数能够达到2.45。作者认为随着Ag含量的增加,载流子浓度增加,陷阱势垒能级降低,隧穿效应更容易发生,非线性电导特性更为明显[67]。哈尔滨理工大学尚南强等制备了不同掺杂含量的TiO2/液体硅橡胶复合材料,研究结果显示,在70℃下,掺杂TiO2 质量分数为4%的复合材料的非线性电导特性最强,8%次之,2%最差。作者认为这是由于TiO2 掺杂会形成无机填料/基体界面,而界面处是高导电区,外电场的施加会使得载流子获得足够的能量越过势垒进行传输。而更高含量的掺杂却又会导致填料的团聚,阻碍载流子的传输[29]。哈尔滨理工大学刘静怡等制备了BaTiO3/环氧树脂复合材料,实验结果表明,在纯环氧树脂中加入质量分数3%以下的BaTiO3 时,复合材料的电导率随着电场强度增加平稳上升,而当BaTiO3 掺杂质量分数达到5%时,复合材料出现明显的非线性电导特性。这主要是因为非线性电导特性由BaTiO3 的性质和BaTiO3/环氧树脂基体界面所决定,当填料含量较低时,颗粒之间的距离较远,跳跃和隧穿的势垒非常高,所以电导率很低;随着填充量的增加,填料间聚合物层厚度逐渐减小,电子跳跃和隧穿势垒逐渐减小,电导率增加[30]。吉林大学汤浩和香港城市大学贺鳞翔等采用高密度聚乙烯(High Density Polyethylene, HDPE)作为基体,不同掺杂含量的炭黑(CB)和碳纳米纤维(Carbon Nanofibers, CNFs)作为填料,研究了复合材料的非线性电导行为。研究结果表明,碳基导电聚合物复合材料的电导率源于两种机理:欧姆传导和非欧姆传导。欧姆传导主要是由于导电填料在渗流阈值以上的直接接触,而非欧姆传导则是由于导电填料之间的势垒隧穿,通常当碳基填料之间的距离小于10 nm 时,就会发生隧穿传导[27,51]。
总之,在基体/填料复合材料中,当填料掺杂含量超过渗流阈值时,会出现由填料接触而形成的渗流路径,而渗流路径作为传导路径,对复合材料电学性能的影响很大。特别是含有微压敏电阻填料的复合材料,其非线性电导行为在很大程度上取决于填料形成的传导路径。当然不仅仅只存在这一种导电机理,很多导电颗粒的掺杂引入了大量的载流子,也有很多氧化物与基体形成界面,填料的数量能够决定载流子的引入数量及界面的形成数量,从而影响复合材料非线性电导特性形成的难易程度。但是高填充量会导致成本增加、质量增加和力学性能降低,这些都会降低相关设备的使用性能。本节涉及的部分文献中掺杂不同含量无机填料的复合材料电学性能见表1。
表1 掺杂不同含量无机填料的复合材料电学性能
Tab.1 Electrical properties of composites doped with different contents of inorganic fillers

基体材料 填料 尺寸 渗流阈值 掺杂含量 阈值电场强度/(kV/mm) 非线性系数 文献聚酯树脂 ZnO — 体积分数14%硅橡胶 ZnO 约1 μm 体积分数15%体积分数14% 10体积分数30% 3体积分数15% 2体积分数20% 1— [59]— [60]
(续)

基体材料 填料 尺寸 渗流阈值 掺杂含量 阈值电场强度/(kV/mm) 非线性系数 文献质量分数15% 55低密度聚乙烯 ZnO 约1 μm 质量分数10%~15%质量分数20% 13质量分数25% 10质量分数30% 5— [61]硅橡胶 ZnO 100~125 μm 体积分数39%体积分数39% 0.57 10体积分数46.5% 0.4 12.7[62]体积分数39%12.5硅橡胶 ZnO 120 μm 体积分数39%体积分数46.5% 15.8体积分数52% 17.1体积分数60% 19—[63]质量分数30% 3.5 0.97硅橡胶 SiC 约0.45 μm 质量分数30%质量分数50% 1.4 1.04质量分数100% 0.9 1.07[65]质量分数10% 12三元乙丙橡胶 SiC 约0.5 μm 质量分数10%质量分数30% 9质量分数50% 7— [66]质量分数0.2% 18.49 1.26三元乙丙橡胶 Ag 100~200 nm 质量分数0.2%质量分数0.3% 14.40 1.97质量分数0.5% 10.47 2.45[67]质量分数2% 12低密度硅橡胶 TiO2 300 nm 质量分数2%质量分数4% 5质量分数8% 3环氧树脂 BaTiO3 50 nm 质量分数3%~5% 质量分数5% 20 — [30]— [29]
3.2 基于填料形貌和尺寸的非线性电导研究
填料的形貌、尺寸也是影响复合材料非线性电导特性的重要因素。西安交通大学田晶晶等将体积分数为20%的ZnO 掺入环氧树脂中,控制填料的尺寸范围为50~100 μm、100~150 μm、150~200 μm和200~300 μm。结果表明,阈值电场强度随着填料尺寸的增加而显著减小,非线性系数也略增加[68]。
杨霄等首先将直径范围为 50~75 μm、75~100 μm、100~125 μm 和125~150 μm 的ZnO 微球掺入硅橡胶中,掺杂体积分数控制为31%、35%、39%、46.5%。研究结果表明,ZnO/硅橡胶复合材料的J-E 曲线非线性特性受到填料含量和尺寸的显著影响。当填料含量增加到35%左右的渗流阈值时,复合材料开始呈现非线性特性,随着掺杂含量的增多阈值电场强度减小,非线性系数增大;当填料掺杂含量略高于渗流阈值时,随着填料直径增大,复合材料的阈值电场强度会减小,而非线性系数保持不变[62]。
然后,杨霄等在掺杂体积分数46.5%的基础上,又将掺杂填料分为球形颗粒和不规则颗粒,球形颗粒按照50~75 μm、75~100 μm、100~125 μm 和125~150 μm 直径范围分为四组,不规则形状的颗粒也按照20~35 μm、35~50 μm、50~75 μm 和75~125 μm 的尺寸范围筛成四组。研究表明随着填料尺寸的增加,同一形态掺杂填料下的非线性系数没有明显变化,但不规则形状填料的阈值电场强度和非线性系数均高于球形填料[69]。不同形状填料的影响可由图7 解释,由于不规则形状填料的表面不平坦,其面接触可以视为两个曲率半径较大的圆形填料之间的接触,而由于不规则形状填料之间边缘接触的接触界面非常复杂,考虑点接触为最简单的情况,不管是面接触还是点接触,不规则形状填料之间的边缘接触电阻均会涉及绝缘基体的电阻,因此边缘接触电阻将远高于球形填料颗粒之间的边缘接触电阻,阈值电场强度也将更大。
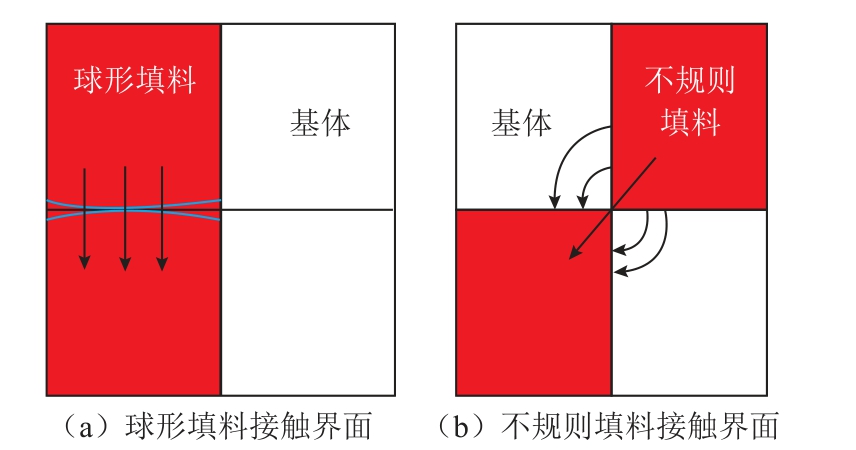
图7 填料接触界面示意图[69]
Fig.7 Schematic diagram of filler contact interface[69]
最后,杨霄等研究了晶粒尺寸对微压敏电阻及其复合材料性能的影响,晶粒尺寸分别为10~15 μm、5~8 μm、1~4 μm。研究表明,通过控制ZnO 微压敏电阻的晶粒尺寸,可以在较大范围内调节ZnO 复合材料的阈值电场强度,同时拥有较稳定的非线性系数[70]。C.Önneby 等研究了SiC 基复合材料中填料尺寸的影响,在EPDM 基体中控制SiC 颗粒的掺杂体积分数为40%,填料尺寸分别为22.8 μm、9.3 μm、3.0 μm 和0.7 μm。研究表明,所有复合材料均表现出非线性电导特性,且当晶粒尺寸增大时,阈值电场强度减小,复合材料的电阻率也会降低[71]。
为了探明WS2 的尺寸和形态对EPDM 基复合材料导电性的影响,北京科技大学韩澎等对WS2 进行剥离,并测量原始WS2 和剥离WS2 填充EPDM 基复合材料的直流电导特性。研究表明剥离后WS2 的叠层较少,且剥离后颗粒的大小和形貌更加均匀,尺寸约为200 nm。复合材料直流电导性能测试表明,随着WS2 含量的增加,复合材料的阈值电场强度急剧下降,电导率迅速增加。且原始WS2/EPDM 复合材料的导电性随填料含量的增加呈现无序且不稳定的趋势;对于剥离WS2/EPDM 复合材料,导电性的变化更为规律和明显。作者认为这可以用WS2 的厚度或层数的变化来解释,WS2 采用共价键合的S—W—S单层结构,通过范德华力相互作用,WS2 的带隙可以从1.3 eV 的多层结构的间接带隙改变为2.1 eV 的直接带隙。剥离操作减少了WS2 的层数和厚度,从而增加了WS2 的带隙,直接影响了其非线性电导[50]。
含有微压敏电阻填料的复合材料非线性电导传导在很大程度上取决于填料形成的传导路径,当填料含量低于渗流阈值时,复合材料表现为绝缘体;当填料含量达到一定的渗流阈值时,复合材料电导随着电场强度增加表现出非线性特性[72]。以上研究也表明,在给定的填料含量下,填料尺寸越大,复合材料中的填料颗粒将越少。对于随机分布的填料,较少和较大的填料形成传导路径的概率高于许多较小填料的概率。当更多的传导路径形成时,更短路径出现的概率也将增大,从而能够大大降低复合材料非线性电导的阈值电场强度。此外,复合材料体积电阻率与填料接触界面的数量和电阻也有关[68]。
复合材料的传导路径示意图如图8 所示,圆圈表示接触ZnO 微压敏电阻填料在复合材料中形成传导路径,圆圈内的多边形表示 ZnO 晶粒。由图8a、图8c 可知,对于相同体积分数的填料,较大颗粒之间的接触概率和接触电阻小于较小颗粒之间的接触概率和接触电阻[71]。对于填料尺寸较大的复合材料,每个界面处的接触电阻较小。当施加较低的电场时,更多的电荷载流子可以通过聚合物传输,导电路径更容易、更快速地形成,因此具有较大填料的复合材料拥有更佳的非线性电学性能[68]。填料晶粒尺寸对复合材料阈值电场强度的影响如图8a、图8b 所示,当晶粒尺寸较小时,电流在单个导通路径中流过更多的晶界。由于每个晶界具有相似的阈值电压(约为3 V),因此传导路径中的晶界数量越多,复合材料的阈值电场强度就越高[71]。

图8 复合材料的传导路径示意图[68]
Fig.8 Schematic diagram of conduction path of composites[68]
基于SiC 填料晶粒尺寸也有相关的研究,英国皇家理工学院E.Mårtensson 等分别使用360 目、600 目和1 200 目的SiC 填料研究了SiC 填料中的晶粒尺寸效应,分别对应于22.8 μm、9.3 μm 和3.0 μm 的晶粒粒径。测试显示晶粒尺寸显著影响填料的性能,当晶粒尺寸减小时,电流密度也随之减小,并且所有晶粒尺寸均可以观察到非线性电导特性,作者同样认为晶粒尺寸可以通过填料接触界面的数量来影响阈值电压[73]。然而,过大粒径与形状不规则填料不仅容易造成填料团聚,且不利于导电通路的形成。在工程制造方面,填料的形貌把控比较困难,在复合材料制备时容易造成缺陷。本节涉及部分文献中掺杂不同形貌、尺寸无机填料的复合材料电学性能见表2。
表2 掺杂不同形貌、尺寸无机填料的复合材料电学性能
Tab.2 Electrical properties of composites doped with different appearances and sizes of inorganic fillers

基体材料 填料 掺杂含量 尺寸 填料形貌 阈值电场强度/(kV/mm) 非线性系数 文献50~100 μm 0.5 14.98环氧树脂 ZnO 体积分数20%100~150 μm 0.12 15.56 150~200 μm 0.07 15.58 200~300 μm 0.05 16.08颗粒[68]20~35 μm 1.73 15硅橡胶 ZnO 体积分数46.5%35~50 μm 1.54 15 50~75 μm 1.29 14 75~125 μm 1.33 15 50~75 μm不规则0.52 10.2[62, 69]75~100 μm 0.42 12.6 100~125 μm 0.41 12.7 125~150 μm 0.33 17.5微球硅橡胶ZnO(75~125 μm)体积分数39%晶粒尺寸10~15 μm 0.36 12.3 5~8 μm 0.52 14.9 1~4 μm 1.56 14.5微球[70]三元乙丙橡胶 SiC 体积分数40%22.8 μm<0.3 9.3 μm 3.0 μm 0.3 0.7 μm 0.6颗粒— [71]质量分数16.23%三元乙丙橡胶 WS2质量分数22.52%质量分数27.93%质量分数32.63%质量分数36.76% 约1.5质量分数27.93%薄层均匀结构约13多层簇结构约4~5 200 nm 18 4.27质量分数32.63% 13 4.42质量分数36.76% 7 5.44[50]
3.3 基于多类型填料掺杂的非线性电导研究
如3.1 节和3.2 节所述,复合材料的性能取决于填料的性能,多种填料的共掺杂可获得与单一填料不同的特性。使用两种或多种填料的想法是通过结合其优点来提高复合材料的性能[74]。英国皇家理工学院E.Mårtensson 等于基体EPDM 中掺杂一定比例的SiC 和CB 颗粒制备得到复合材料。研究表明,复合材料的电学特征表现出非线性行为,当CB掺杂含量增加时,复合材料的阈值电场强度和非线性系数减小。作者认为SiC 颗粒在基体内大多是孤立的,彼此之间没有接触,CB 颗粒可以作为半导体SiC 颗粒之间的连接,使导电路径变得更为丰富[75]。
哈尔滨理工大学胡海涛等以纳米SiC、纳米ZnO和微米ZnO 颗粒为填料,制备了五种基于环氧树脂(EP)的非线性导电复合材料(纳米SiC/EP、纳米ZnO/EP、微米ZnO/EP、纳米SiC/ZnO/EP 和微米SiC/ZnO/EP)。复合材料的直流电压特性表明,采用单一填料的复合材料的电导率和非线性系数随着无机填料含量的增加而增加。相同条件下,微米ZnO/EP的电导率大于纳米ZnO/EP 的电导率,这主要是因为微米ZnO 比纳米ZnO 更容易在介质中形成导电网络,从而促进载流子的迁移。在相同条件下,SiC/EP的电导率和非线性系数均大于纳米ZnO/EP 和微米ZnO/EP。共掺杂填料复合材料电学性能测试表明,SiC 填料的引入,能够大大提高复合材料的非线性系数,作者认为这主要是因为在含有纳米SiC 的EP 复合材料中,容易形成界面结构,在高电场强度下,界面结构中的导电通道能够使得载流子迁移率增加。因此SiC 和ZnO 的结合在EP 体内形成了良好的导电通路,促进了不同导电基团之间的载流子迁移。而较小尺寸的纳米ZnO 和SiC 颗粒之间更有可能发生团聚,这使得纳米ZnO/SiC/EP 复合材料的电导率低于微米ZnO/SiC/ EP 复合材料的电导率。这些结果表明,使用不同填料组合有助于调整复合材料的电气性能,并根据应用规格获得不同的非线性传导性能[76]。
迟庆国等为了实现ZnO/SiR 复合介质在较少无机填料掺杂下拥有较为优异的非线性电导特性,将少量多壁碳纳米管(Multi Walled Carbon Nanotubes,MWCNTs)与ZnO 纳米片混合掺入SiR 中制备了MWCNTs/ZnO/SiR 复合材料。研究表明,填充适当含量的MWCNTs/ZnO 填料可以诱导非线性电导特性,与非线性电导对应的阈值电场强度随着MWCNTs 填充质量分数的增加而逐渐降低,如图9a所示。这主要是由于MWCNTs 填料可以为复合材料提供更多的载流子,从而导致阈值电场强度降低。且未掺杂MWCNTs 填料时,相邻的ZnO 填料之间的距离较长,载流子无法有效地在基体中传输,引入具有一维形貌特征的分子填料,促进了氧化锌纳米片之间连接路径的形成。随着MWCNTs 填充含量的进一步增加,连接路径逐渐增加,使载流子更容易传输,阈值电场强度更低,非线性电导变得更加明显[77]。韩澎等也使用相同的方法将MWCNTs 与WS2 按照一定比例掺入EPDM 中获得了优异的非线性电导性能。作者认为MWCNTs 的引入,使得载流子在WS2 中隧穿概率增加,载流子在外电场作用下定向运动的概率也增加[78]。

图9 多类型填料掺杂对复合材料电学性能的影响
Fig.9 Effects of multi-type filler doping on electrical properties of composites
清华大学王军等将自制的核-壳结构 CCTO@ZnO 填料掺杂到硅橡胶中,并与相同填料含量的CCTO 和ZnO 的混合物进行了比较。电学性能测试结果表示,掺杂核-壳结构的CCTO@ZnO 的复合介质具有更高的非线性系数,作者认为这主要是因为ZnO 和CCTO 颗粒的混合物分散在基体中时,除非填料的含量足够高,否则很难形成电流路径,而核-壳结构的CCTO@ZnO 粒径大于ZnO 或CCTO,填料也更容易接触,吸附在CCTO 表面的ZnO 纳米颗粒可以形成电流传输路径的三维结构,ZnO 与CCTO 的接触也可以形成一条路径,如图10 所示。而电流传输可以选择更多、更短的路径,导致渗流阈值降低,且非线性电导系数增大[49]。

图10 电流路径示意图[49]
Fig.10 Schematic diagram of current path[49]
在迟庆国教授课题组的另一项研究中,制备了掺杂铁离子的纳米ZnO 无机填料,然后加入EPDM橡胶中制备了复合材料,电学实验结果显示,随着Fe3+的增加,复合材料的非线性电导系数显著增加。作者认为这是因为由于铁离子比锌离子多一个价电子,引入铁离子后使得载流子的含量增大,在外电场作用下可以降低势垒,导致电导增大[79]。当然,引入无机填料或金属元素会牺牲复合材料的击穿性能,为了实现协同提升复合介质的非线性电导特性与击穿性能,研究者往往也会同时掺杂部分绝缘性能良好的填料,例如BN 等填料。掺杂银元素纳米颗粒(AgNPs)/BN 的EPDM 复合材料的电学性能如图9b 所示[80-81]。
具有大长径比的导电纤维、纳米管和纳米片等填料具有形成导电网络结构的优势,且其余多种填料的掺杂在很大程度上也是为了增加填料的传导路径。对于随机分布的填料,较少但较大的填料形成传导路径的概率高于较多但较小填料的相应概率。多种填料的配合可以在较低掺杂含量下实现更多的传导路径,且主传导路径也就越短,复合材料的阈值电场强度就越低。当然引入金属元素等物质,可直接使得载流子输入数量增多,在施加电场后,电导增大,性能提升。但在多填料共掺研究中,均会涉及多填料共掺导致的结构缺陷,且存在制备工艺不成熟、填料分散不均、配比调控量不可控等因素。本节涉及部分文献中掺杂多类型无机填料的复合材料电学性能见表3。
表3 掺杂多类型无机填料的复合材料电学性能
Tab.3 Electrical properties of composites doped with various types of inorganic fillers

基体材料填料1 填料2 阈值电场强度/(kV/mm)名称 形貌、尺寸 掺杂含量 名称 形貌、尺寸 掺杂含量非线性系数 文献三元乙丙橡胶SiC 10 μm 体积分数17.5% CB 1 μm体积分数11.7% 随着CB 含量的增加,阈值电场强度减小,非线性系数减小体积分数13.1%[75]环氧树脂微米ZnO针状、直径约1.5~2 μm、长度约20~27 μm质量分数1%质量分数4% — 2.57质量分数2% 质量分数3% 1.51 3.50质量分数3% 质量分数2% 1.52 2.31质量分数4% 质量分数1% 1.56 —SiC均匀颗粒、约30~40 μm质量分数1% 质量分数4% 2.45 2.32[76]纳米ZnO不规则、约30~40 μm质量分数2% 质量分数3% 4.69 2.96质量分数3% 质量分数2% 6.28 2.05质量分数4% 质量分数1% 6.26 1.44硅橡胶 ZnO不规则片状、约200~300 nm质量分数5% MWCNTs光滑的管状表面且直径约为50~70 nm 0 14.51 2.71质量分数0.03% 11.11 2.74质量分数0.05% 10.52 2.68质量分数0.07% 8.15 2.99质量分数0.1% 3.77 2.89[78]三元乙丙橡胶WS2薄层均匀结构、200 nm质量分数22.52% MWCNTs光滑的管状表面且直径约为10~20 nm,长度约为10~ 30 μm质量分数0.37%低电场时,复合材料电导率相对未掺杂提高一个数量级左右质量分数0.56% 17 —质量分数0.74% 13 4.42质量分数0.93% 5 —[77]
(续)

基体材料填料1 填料2 阈值电场强度/(kV/mm)名称 形貌、尺寸 掺杂含量 名称 形貌、尺寸 掺杂含量非线性系数 文献ZnO 197.5 nm 20.61 0.63三元乙丙橡胶Fe0.01ZnO0.99 197.16 nm 18.44 0.40 Fe0.02ZnO0.98 183.39 nm 18.97 1.11 Fe0.03ZnO0.97 175.31 nm 19.78 1.22质量分数10% — — —[79]质量分数6.7%质量分数13.3%2.72硅橡胶ZnO纤锌矿结构,约50 nm质量分数10.0% 质量分数20.0% 3.25质量分数13.3% 质量分数27.7% 3.62质量分数16.7% 质量分数33.3% 4.03质量分数20.0% 质量分数40.0% 4.31 CCTO正方钙钛矿,约500 nm—质量分数20%3.46[49]CaCu3Ti4O12@ZnO —质量分数30% 3.95质量分数40% 4.00质量分数50% 6.91质量分数60% 10.87— — — —
3.4 基于无机填料表面处理的非线性电导研究
为了确保复合材料具有良好的非线性电导特性,需要在聚合物基体中掺杂大量无机填料,这会严重降低复合材料的力学性能,并且使其不适用于实际应用。同时,较小尺寸的无机填料具有较低的比表面积,将导致基体与填料融合不良,在基体与填料之间的界面处会产生大量缺陷,并导致复合材料发生严重局部放电,使绝缘材料老化,从而影响设备寿命和运行可靠性。纳米复合材料中纳米填料的渗流网络形成受到多种因素的影响,纳米填料的分散性是决定渗流阈值的关键因素之一,为了更好地实现分散纳米填料并降低渗流阈值,通常采用引入表面活性剂或修改填料表面等实验方法。纳米颗粒经过表面功能化可以抑制团聚,表面处理可以使纳米颗粒均匀分布,增强复合材料中填料和基体之间的界面结合。
表面改性分为表面物理改性和表面化学改性。表面物理改性是指无机填充相与有机物之间的结合为物理吸附。伦斯勒理工学院王星等对63 nm 的ZnO纳米颗粒进行表面物理改性处理,将ZnO 纳米颗粒混合到SnF2 水溶液中,在27℃下处理4 min,将处理后的ZnO 掺入EPDM 中得到ZnO/EPDM 复合材料。ZnO 电学性能测试表明,表面处理过的填料显示出增强的非线性传导特性,掺杂表面处理ZnO 的复合材料的非线性系数和电导率均比未处理的复合材料要高,作者认为这是因为ZnO 表面形成的SnO具有较高的电导率,能够大大降低聚合物基体隧穿的势垒,并且复合材料中较高的非线性可能是处理后的ZnO 在某一电场区域(电场强度为105 V/m)有极大的电导率,可以在较低的电场中隧穿[34]。
而表面化学改性则是采用硅烷偶联剂进行改性,使得有机物与无机填充相之间形成牢固的化学键,主要是应用偶联剂分子一端与无机填料结合,另一端与有机物结合的两性结构。清华大学赵小蕾等采用硅烷偶联剂对ZnO 表面进行处理,将未处理的ZnO 与处理之后的ZnO 按照不同的掺杂组分掺入SiR 中,制备得到ZnO/SiR 复合材料。复合材料电学性能测试表明,ZnO 表面处理仅略微改善了填料分散的均匀性,对阈值电场强度Eb 仅有轻微影响,掺杂经表面处理填料的复合材料的非线性系数值略高于未处理复合材料的非线性系数值,这意味着与掺杂未经表面处理的微球填料的复合材料相比,掺杂经表面处理的微球填料的复合材料具有更大的分级电场效应。作者还测量了单轴拉伸应变的J-E 曲线,与掺杂未处理填料的复合材料相比,掺杂表面处理微球填料的复合材料在变形下的非线性电性能更稳定,这主要归因于应力条件下,处理后的ZnO微球能够维持与基体紧密结合的关系[82]。
哈尔滨理工大学迟庆国等使用硅烷偶联剂(KH550)对碳化硅晶须(SiCw)进行改性,改性过程如图11 所示。研究表明,采用适量的硅烷偶联剂对碳化硅进行修饰,可以使得碳化硅晶须在树脂基体中分散更为均匀,继而形成导电通道,非线性电导特性也能够更加优异。但是过量的硅烷偶联剂修饰反而会导致填料表层产生一层较厚的包覆,使得载流子传输势垒提高,载流子传输受制[32]。张宇轩等将多壁碳纳米管(MWCNT)进行混酸化处理,然后按照不同比例掺入环氧树脂(EP)中制备得到MWCNT/EP 复合材料。复合材料电导特性研究表明,混酸处理的MWCNT/EP 复合材料电导率丧失了非线性电导特性。这主要是由于混酸法处理之后的MWCNT 长径比减小,填料之间不容易接触,导电路径不易形成。同时混酸处理之后的MWCNT 由于其表面形成羟基和羧基,更容易和材料结合,导致其场致发射能力较弱[33]。

图11 偶联剂作用机理示意图[32]
Fig.11 Schematic diagram of coupling reagent[32]
由以上分析可知,对填料表面进行改性,主要是可以提高分散性,进一步增强聚合物与填料之间的相互作用,能够保证在力学状态下非线性电导特性的维持。但是填料分散性对于填料/基体复合材料电导的影响,不同的研究者有各自不同的见解,有的认为分散性的提高可以使得导电通道更为容易形成,有的学者则认为分散性提高后填料不容易直接接触,对其电导特性产生负面影响。填料分散性对于复合材料的非线性电学特性还需进一步探究。本节涉及部分文献中掺杂表面处理无机填料的复合材料电学性能见表4。
表4 掺杂表面处理无机填料的复合材料电学性能
Tab.4 Electrical properties of composites doped with surface treated inorganic fillers

基体材料 填料 掺杂含量 改性方式 尺寸 填料形貌 阈值电场强度/(kV/mm)非线性系数 文献乙丙橡胶 ZnO 体积分数20% SnF2溶液三元0 3.8 0.23 mol/L 约13 0.5 mol/L 约13 63 nm 核-壳结构颗粒 —[34]质量分数35%2.02 13.0硅橡胶 ZnO质量分数40% 1.80 11.7质量分数45% 1.57 10.0质量分数50% 1.31 9.4质量分数35%正庚烷溶液与KH550 偶联剂—10~30 μm 微球2.14 13.9质量分数40% 1.89 12.4质量分数45% 1.67 12.2质量分数50% 1.37 9.2[82]质量分数1%—环氧树脂 SiC质量分数2% 1.25质量分数3% 6.43质量分数4% 6.57质量分数1%——直径100~500 nm 晶须— —[32]质量分数2% 7.3 3.03质量分数3% 7 4.62质量分数4% 6 6.29 KH550 偶联剂环氧树脂 MWCNT 质量分数0.05%未处理外径10~20 nm、长度10~30 μm缠结长纤维状J-E 曲线呈现明显非线性混酸法处理 未缠结短纤维状 J-E 曲线线性增长[33]
4 非线性电导复合材料调控电场研究
非线性电导材料的主要特征是,在施加高于阈值电场强度的电场时,电导率呈现较快的增长速度并达到较高的数值,因此可用于降低绝缘系统内关键位置的最大电场应力。研究者往往通过测试介质表面电位、界面电场强度及建立仿真模型模拟电场分布来验证非线性电导材料调控电场的能力。
天津大学杜伯学等采用脉冲电声法(Pulsed Electro-Acoustic, PEA)研究了不同SiC 掺杂含量对SiR 基复合材料电场分布的影响。研究表明,随着SiC 掺杂含量的提升,材料内部电场畸变显著减弱。非线性电导复合材料调控电场研究部分成果如图12 所示。由图12a 可知,当SiC 的质量分数达到100%时,电场非常接近理想电场,证明具有非线性电导特性的SiR/SiC 复合材料可提高载流子迁移率,有效地降低电场畸变的程度[65]。天津大学李忠磊等通过二维表面电位衰减(Surface Potential Decay, SPD)测试研究了ZnO/SiR 复合材料的表面电荷积累和耗散特性,如图12b 所示。在样品的去极化过程中,样品中间的最大表面电荷密度随时间减小,表明ZnO 填料引入的非线性电导可以通过垂直电荷传输到地面和表面水平移动加速电荷耗散,如图12b 中箭头所指电荷包所示,最终抑制表面电荷积累[40]。天津大学梁虎成等的研究也表明具有非线性电导特性的环氧树脂/SiC 可以有效地抵抗表面电位的上升,增强表面电荷耗散过程[83]。

图12 非线性电导复合材料调控电场研究
Fig.12 Study on electric field regulation of nonlinear conductive composites
在仿真模拟应用中,有大量的研究建立了IGBT、气体绝缘开关设备(Gas Insulated Switchgear, GIS)及电缆附件模型,并对非线性电导材料调控相关器件电场进行了验证模拟。清华大学李锴宣等通过仿真模拟了非线性电导材料作为IGBT 涂层后关键部位的电场分布,如图12c 所示,结合处的最大电场强度和高场区的电场畸变率显著降低[36]。Li Rui 等的仿真研究也表明,具有非线性电导的复合材料可以降低电场应力,且SiC 改性环氧树脂得到的新兴绝缘材料,可以有效地促进电场分布均匀,保证功率模块的安全运行[47]。天津大学杜伯学等将不同重量份数(phr)SiC 掺杂的环氧树脂/SiC 复合材料作为GIS 隔板的涂层材料,模拟了间隔物周围的电场分布,如图12d 所示,在正极性脉冲电压与直流电压叠加条件下,SiC 掺杂可以有效地降低结合处的最大电场强度[84]。清华大学赵小蕾等研究发现,由非线性导电材料制成的电缆终端附件比传统的电缆终端附件具有更强的电场分级作用[85]。哈尔滨理工大学李中原等的研究也表明 CCTO 掺杂体积分数为8%的CCTO/EPDM 表现出明显的非线性电导特性,且由图12e 可知,掺杂体积分数为8%的CCTO/EPDM 可以更有效地降低电缆终端应力锥根部的电场强度[86]。
以上研究表明,具有非线性电导特性的材料能够调控电场的不均匀性,降低绝缘材料中的电应力,并且通过减少电气系统中的应力集中,可以在很大程度上降低整体绝缘退化,在高电压应用中发挥重要作用。但是现有研究模型较为简单,并且多为分立模型,不能够准确地搭建复合材料的应用场景。
5 有待解决的关键问题
国内外学者对非线性电场分级材料已经做了大量的研究,但是研究的结果仅仅能够反映填料界面特性,相关理论研究较少,因此需要从复合材料的电导机制、基础理论等方面开展深入研究,对无机填料本身的特性、复合材料的特性、无机填料对复合材料的作用机理等均需要进行深入的探索,为电场调控绝缘材料研究提供支撑。
各种形式无机填料掺杂的复合材料已经被考虑用作高压设备绝缘,以期达到均匀电场的效果,但是在实际应用中局限性却很大。例如高压电缆运行过程中,电流流过线芯产生大量的热,而绝缘外围所处的环境温度较低,导致绝缘内外存在温差。由于聚合物绝缘材料的电阻率依赖温度,这种温度梯度可能导致电场于介质中分布不均匀,所以必须考虑复合材料电阻率与温度及电场的耦合影响。高压器件绝缘在安装和运行时也必须考虑机械应力的影响,例如弯曲应力、热膨胀系数差所导致的应力等。因此提升非线性电导特性材料综合性能也是亟待解决的关键问题之一,可为解决国内电场调控材料国产化的空白提供依据。
6 结论
1)复合材料中填料含量对非线性传导渗流路径的形成、载流子的注入及填料与基体的界面效应均会产生一定的影响,从而影响复合材料非线性电导特性形成的难易程度。
2)填料形貌的影响主要依赖填料间接触电阻的大小,填料尺寸主要影响载流子传导路径形成的概率,且也与界面电阻相关,而晶粒尺寸的影响则可以通过填料接触界面的数量来影响接触电压。
3)填料共掺主要调控导电网络结构形成的难易程度,且引入金属元素可以使载流子数目剧增。
4)填料表面可提高填料于基体中的分散性,进而增强聚合物与填料之间的相互作用,但填料分散性对于复合材料非线性电学特性的影响仍没有较为统一的认知。
5)非线性电导材料能够有效地调控IGBT、GIS及电缆附件等部件的电场分布,为电气用绝缘部件的安全运行提供保障。
尽管非线性电场调控已开始应用于中高压电缆附件和旋转电机等部件,但其实际应用仍然存在有限性,例如复合材料无法兼具良好的非线性电导特性与高击穿特性,在瞬时电压响应和脉冲应力下实现有效的电场调控具有较大的困难。包括非线性电导理论、实际应用中的热应力与机械应力的影响机制及工艺的可实施性均需在未来研究中逐步探索。
因此,需要进行大量研究,以拓宽可用于合成非线性电导复合材料制备方法的范围,同时提高材料的拉伸强度和韧性。填料的表面改性是另一个较为新兴的研究领域,可实现聚合物基体中高含量纳米填料的均匀分散,是一个可深入研究的方向。聚合物接枝也是未来研究的一个领域。总之,新兴方法的优异特性和高效性将推进国内相关技术的提升和产业的发展。
[1] 陈杰, 吴世林, 胡丽斌, 等.退役高压电缆附件绝缘状态及理化性能分析[J].电工技术学报, 2021,36(12): 2650-2658.Chen Jie, Wu Shilin, Hu Libin, et al.Analysis of insulation state and physicochemical property of retired high-voltage cable accessories[J].Transactions of China Electrotechnical Society, 2021, 36(12):2650-2658.
[2] Sumereder C.Statistical lifetime of hydro generators and failure analysis[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2008, 15(3):678-685.
[3] Zhou Haolong, Hanafusa W, Udo K, et al.Aging behavior of flame-retardant cross-linked polyolefin under thermal and radiation stresses[J].IEEE Transactions on Dielectrics and Electrical Insulation,2021, 28(1): 303-309.
[4] 王孟夏, 周生远, 杨明, 等.计及海底电缆热特性的可接纳海上风电装机容量评估方法[J].电力系统自动化, 2021, 45(6): 195-202.Wang Mengxia, Zhou Shengyuan, Yang Ming, et al.Assessment method for acceptable installed capacity of offshore wind farms considering thermal characteristics of submarine cables[J].Automation of Electric Power Systems, 2021, 45(6): 195-202.
[5] Liu A Y H, Rottler J.Physical aging and structural relaxation in polymer nanocomposites[J].Journal of Polymer Science Part B: Polymer Physics, 2009,47(18): 1789-1798.
[6] Tan D.Structured microgrids (SμGs) and flexible electronic large power transformers (FeLPTs)[J].CES Transactions on Electrical Machines and Systems,2020, 4(4): 255-263.
[7] Pleşa I, Noţingher P V, Stancu C, et al.Polyethylene nanocomposites for power cable insulations[J].Polymers, 2018, 11(1): 24.
[8] Wu Kai, Su Rui, Wang Xia.Space charge behavior in polymeric materials under temperature gradient[J].IEEE Electrical Insulation Magazine, 2020, 36(2): 37-49.
[9] Andersson M G, Hynynen J, Andersson M R, et al.Highly insulating polyethylene blends for highvoltage direct-current power cables[J].ACS Macro Letters, 2017, 6(2): 78-82.
[10] Li Yuan, Zhu Guangya, Zhou Kai, et al.Evaluation of graphene/crosslinked polyethylene for potential high voltage direct current cable insulation applications[J].Scientific Reports, 2021, 11: 18139.
[11] Paramane A, Chen Xiangrong, Dai Chao, et al.Electrical insulation performance of cross-linked polyethylene/MgO nanocomposite material for ±320 kV high-voltage direct-current cables[J].Polymer Composites, 2020, 41(5): 1936-1949.
[12] Ye Hanyu, Fechner T, Lei Xianzhang, et al.Review on HVDC cable terminations[J].High Voltage, 2018,3(2): 79-89.
[13] 刘彬, 马骏逸.中压电缆附件电场应力控制的发展[J].工业设计, 2011(6): 204, 206.
[14] Andraschek N, Wanner A J, Ebner C, et al.Mica/epoxy-composites in the electrical industry:applications, composites for insulation, and investigations on failure mechanisms for prospective optimizations[J].Polymers, 2016, 8(5): 201.
[15] Wang Peng, Hui Suxin, Akram S, et al.Influence of repetitive square voltage duty cycle on the electrical tree characteristics of epoxy resin[J].Polymers, 2020,12(10): 2215.
[16] Dabbak S Z, Illias H A, Ang B C.Effect of surface discharges on different polymer dielectric materials under high field stress[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(6):3758-3765.
[17] 丁雪妮, 陈民铀, 赖伟, 等.多芯片并联IGBT 模块老化特征参量甄选研究[J].电工技术学报, 2022,37(13): 3304-3316, 3340.Ding Xueni, Chen Minyou, Lai Wei, et al.Selection of aging characteristic parameter for multi-chips parallel IGBT module[J].Transactions of China Electrotechnical Society, 2022, 37(13): 3304-3316,3340.
[18] Hirao K, Zhou You, Hyuga H, et al.Evaluation of thermal resistance for metalized ceramic substrates using a microheater chip[J].International Journal of Applied Ceramic Technology, 2022, 19(1): 232-240.
[19] Yu Jingzhe, Chen Xiangrong, Zhou Hao.Electric field calculation and optimization for stress cone of DC cable joint based on the coaxial double-layer insulation model[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(1): 33-41.
[20] Abd-Rahman R, Haddad A, Harid N, et al.Stress control on polymeric outdoor insulators using Zinc oxide microvaristor composites[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(2):705-713.
[21] Eigner A, Semino S.50 years of electrical-stress control in cable accessories[J].IEEE Electrical Insulation Magazine, 2013, 29(5): 47-55.
[22] 孙中玉, 徐丙垠, 王玮, 等.电缆故障脉冲电流测距系统建模与仿真[J].电力系统自动化, 2021,45(4): 142-147.Sun Zhongyu, Xu Bingyin, Wang Wei, et al.Modeling and simulation of cable fault location system based on pulse current[J].Automation of Electric Power Systems, 2021, 45(4): 142-147.
[23] Lupo G, Miano G, Tucci V, et al.Field distribution in cable terminations from a quasi-static approximation of the Maxwell equations[J].IEEE Transactions on Dielectrics and Electrical Insulation, 1996, 3(3): 399-409.
[24] Yang Xiao, Hu Jun, Chen Shuiming, et al.Understanding the percolation characteristics of nonlinear composite dielectrics[J].Scientific Reports,2016, 6: 30597.
[25] Tavernier K, Varlow B R, Auckland D W, et al.Improvement in electrical insulators by nonlinear fillers[J].IEE Proceedings - Science, Measurement and Technology, 1999, 146(2): 88.
[26] Yin Yi, Chen Jiong, Li Zhe, et al.High field conduction of the composites of low-density polyethylene/nano SiOx and low-density polyethylene/micrometer SiO2[C]//Proceedings of 2005 International Symposium on Electrical Insulating Materials,Kitakyushu, Japan, 2005: 405-408.
[27] Tang Hao, Chen Xinfang, Tang Aoqing, et al.Studies on the electrical conductivity of carbon black filled polymers[J].Journal of Applied Polymer Science,1996, 59(3): 383-387.
[28] Han Peng, Zha Junwei, Wang Sijiao, et al.Theoretical analysis and application of polymer-matrix field grading materials in HVDC cable terminals[J].High Voltage, 2017, 2(1): 39-46.
[29] 尚南强, 陈庆国, 秦君.纳米TiO2/液体硅橡胶直流电缆附件绝缘复合材料的介电性能[J].复合材料学报, 2019, 36(1): 104-113.Shang Nanqiang, Chen Qingguo, Qin Jun.Dielectric properties of nano TiO2/liquid silicone rubber composites for direct current cable accessories insulation[J].Acta Materiae Compositae Sinica, 2019,36(1): 104-113.
[30] Liu Jingyi, Li Zhonghua, Han Yongsen, et al.Study on polarization and depolarization characteristics of epoxy/BaTiO3 nano-composites[C]//2019 2nd International Conference on Electrical Materials and Power Equipment (ICEMPE), Guangzhou, China,2019: 305-308.
[31] Vu T T N, Teyssedre G, Vissouvanadin B, et al.Correlating conductivity and space charge measurements in multi-dielectrics under various electrical and thermal stresses[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(1):117-127.
[32] 迟庆国, 崔爽, 张天栋, 等.碳化硅晶须/环氧树脂复合介质非线性电导特性研究[J].电工技术学报,2020, 35(20): 4405-4414.Chi Qingguo, Cui Shuang, Zhang Tiandong, et al.Study on nonlinear characteristics on conductivity of silicon carbide whisker/epoxy resin composites[J].Transactions of China Electrotechnical Society, 2020,35(20): 4405-4414.
[33] 张宇轩, 李禾, 王闯, 等.混酸功能化方法对碳纳米管/环氧树脂复合材料电导性能的影响[J].绝缘材料, 2017, 50(1): 23-27.Zhang Yuxuan, Li He, Wang Chuang, et al.Effects of mixed acid functionalization on electric conductance properties of carbon nanotube/epoxy resin composite[J].Insulating Materials, 2017, 50(1): 23-27.
[34] Wang X, Herth S, Hugener T, et al.Nonlinear electrical behavior of treated ZnO-EPDM nanocomposites[C]//2006 IEEE Conference on Electrical Insulation and Dielectric Phenomena,Kansas City, MO, USA, 2006: 421-424.
[35] Koktsinskaya E M, Vakser B D, Polonskii Y A.Filler selection for nonlinear anti-corona bands used in high voltage electric machines[J].Russian Electrical Engineering, 2007, 78(3): 118-122.
[36] Li Kaixuan, Zhang Boya, Li Xingwen, et al.Electric field mitigation in high-voltage high-power IGBT modules using nonlinear conductivity composites[J].IEEE Transactions on Components, Packaging and Manufacturing Technology, 2021, 11(11): 1844-1855.
[37] Liu Chenyang, Zheng Xiaoquan, Peng Ping.The nonlinear conductivity experiment and mechanism analysis of modified polyimide (PI) composite materials with inorganic filler[J].IEEE Transactions on Plasma Science, 2015, 43(10): 3727-3733.
[38] Roberts A.Stress grading for high voltage motor and generator coils[J].IEEE Electrical Insulation Magazine, 1995, 11(4): 26-31.
[39] 胡琦, 李庆民, 刘智鹏, 等.基于表层梯度电导调控的直流三支柱绝缘子界面电场优化方法[J].电工技术学报, 2022, 37(7): 1856-1865.Hu Qi, Li Qingmin, Liu Zhipeng, et al.Interfacial electric field optimization of DC tri-post insulator based on gradient surface conductance regulation[J].Transactions of China Electrotechnical Society, 2022,37(7): 1856-1865.
[40] Li Zhonglei, Yang Zhuoran, Du Boxue.Surface charge transport characteristics of ZnO/silicone rubber composites under impulse superimposed on DC voltage[J].IEEE Access, 2018, 7: 3008-3017.
[41] Vaferi K, Vajdi M, Nekahi S, et al.Thermomechanical simulation of ultrahigh temperature ceramic composites as alternative materials for gas turbine stator blades[J].Ceramics International, 2021,47(1): 567-580.
[42] Taylor N, Edin H.Stator end-winding currents in frequency-domain dielectric response measurements[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(5): 1489-1498.
[43] Gartner J, Gockenbach E, Borsi H.Field-grading with semi-conducting materials based on silicon carbide(SiC)[C]//Conference Record of the 1998 IEEE International Symposium on Electrical Insulation,Arlington, VA, USA, 2002: 202-205.
[44] 贺西民.碳化硅非线性电阻导电机理[J].电瓷避雷器, 1992(6): 47-49.
[45] 郭磊, 宁叔帆, 于开坤, 等.碳化硅非线性导电特性的研究进展[J].绝缘材料, 2005, 38(3): 60-64.Guo Lei, Ning Shufan, Yu Kaikun, et al.Study progress of silicon carbide non-linear property[J].Insulating Materials, 2005, 38(3): 60-64.
[46] Han Yongsen, Li Shengtao, Min Daomin.Nonlinear conduction and surface potential decay of epoxy/SiC nanocomposites[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(5): 3154-3164.
[47] Li Rui, Wang Yufan, Zhang Cheng, et al.Non-linear conductivity epoxy/SiC composites for emerging power module packaging: fabrication, characterization and application[J].Materials, 2020, 13(15): 3278.
[48] Zebouchi N, Li Haoluan, Haddad M A.Development of future compact and eco-friendly HVDC gasinsulated systems: shape optimization of a DC spacer model and novel materials investigation[J].Energies,2020, 13(12): 3288.
[49] Wang Jun, Wang Xilin, Yao Youwei, et al.Nonlinear electrical characteristics of core-satellite CaCu3Ti4O12@ZnO doped silicone rubber composites[J].RSC Advances, 2017, 7(50): 31654-31662.
[50] Han Peng, Zha Junwei, Zheng Mingsheng, et al.Nonlinear electric conductivity and thermal conductivity of WS2/EPDM field grading materials[J].Journal of Applied Physics, 2017, 122(19): 195106.
[51] He L X, Tjong S C.Direct current conductivity of carbon nanofiber-based conductive polymer composites: effects of temperature and electric field[J].Journal of Nanoscience and Nanotechnology, 2011,11(5): 3916-3921.
[52] Köckritz T, Jansen I, Beyer E.Integration of carbon allotropes into polydimethylsiloxane to control the electrical conductivity for novel fields of application[J].International Journal of Adhesion and Adhesives, 2018, 82: 240-253.
[53] Mitic G, Lefranc G.Localization of electricalinsulation and partial-discharge failures of IGBT modules[J].IEEE Transactions on Industry Applications, 2002, 38(1): 175-180.
[54] Christen T, Donzel L, Greuter F.Nonlinear resistive electric field grading part 1: theory and simulation[J].IEEE Electrical Insulation Magazine, 2010, 26(6): 47-59.
[55] Donzel L, Schuderer J.Nonlinear resistive electric field control for power electronic modules[J].IEEE Transactions on Dielectrics and Electrical Insulation,2012, 19(3): 955-959.
[56] Ouyang Benhong, Liu Zongxi, Wang Xubin, et al.Investigation of electrical properties of ZnO@Ag/EPDM composites[J].AIP Advances, 2020, 10(9):095108.
[57] 李忠磊, 赵宇彤, 韩涛, 等.高压电缆半导电屏蔽材料研究进展与展望[J].电工技术学报, 2022,37(9): 2341-2354.Li Zhonglei, Zhao Yutong, Han Tao, et al.Research progress and prospect of semi-conductive shielding composites for high-voltage cables[J].Transactions of China Electrotechnical Society, 2022, 37(9): 2341-2354.
[58] Rokhlenko A, Jensen K L, Lebowitz J L.Space charge effects in field emission: one dimensional theory[J].Journal of Applied Physics, 2010, 107(1): 014904.
[59] Auckland D W, Su W, Varlow B R.Nonlinear fillers in electrical insulation[J].IEE Proceedings - Science,Measurement and Technology, 1997, 144(3): 127-133.
[60] Varlow B R, Robertson J, Donnelly K P.Nonlinear fillers in electrical insulating materials[J].IET Science, Measurement & Technology, 2007, 1(2): 96-102.
[61] Auckland D W, Brown N E, Varlow B R.Non-linear conductivity in electrical insulation[C]//IEEE 1997 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Minneapolis, MN, USA,1997: 186-189.
[62] Yang Xiao, He Jinliang, Hu Jun.Tailoring the nonlinear conducting behavior of silicone composites by ZnO microvaristor fillers[J].Journal of Applied Polymer Science, 2015, 132(40): 42645.
[63] Gao Lei, Yang Xiao, Hu Jun, et al.ZnO microvaristors doped polymer composites with electrical field dependent nonlinear conductive and dielectric characteristics[J].Materials Letters, 2016, 171: 1-4.
[64] Xie Pengkang, Wang Ziyue, Wu Kangning.Evolution of intrinsic and extrinsic electron traps at grain boundary during sintering ZnO based varistor ceramics[J].Materials, 2022, 15(3): 1098.
[65] Du Boxue, Li Zhonglei, Yang Zhuoran.Fielddependent conductivity and space charge behavior of silicone rubber/SiC composites[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(5):3108-3116.
[66] Li Jin, Du Boxue, Kong Xiaoxiao, et al.Nonlinear conductivity and interface charge behaviors between LDPE and EPDM/SiC composite for HVDC cable accessory[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(3): 1566-1573.
[67] Chi Qingguo, Yang Meng, Zhang Tiandong, et al.Investigation of electrical and mechanical properties of silver-hexagonal boron nitride/EPDM composites[J].Journal of Materials Science: Materials in Electronics,2019, 30(14): 13321-13329.
[68] Tian Jingjing, Xu Ran, He Hongliang, et al.Influence of ZnO filler size on the nonlinear electrical properties of ZnO ceramic-epoxy composite material[J].Journal of Materials Science: Materials in Electronics, 2017,28(7): 5102-5105.
[69] Yang Xiao, Zhao Xiaolei, Hu Jun, et al.Grading electric field in high voltage insulation using composite materials[J].IEEE Electrical Insulation Magazine, 2018, 34(1): 15-25.
[70] Yang Xiao, Meng Pengfei, Zhao Xiaolei, et al.How nonlinear V-I characteristics of single ZnO microvaristor influences the performance of its silicone rubber composite[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(2):623-630.
[71] Önneby C, Mårtensson E, Gäfvert U, et al.Electrical properties of field grading materials influenced by the silicon carbide grain size[C]//Proceedings of the 2001 IEEE 7th International Conference on Solid Dielectrics,Eindhoven, Netherlands, 2001: 43-45.
[72] Zha Junwei, Dang Zhimin, Zhao Kai, et al.Prominent nonlinear electrical conduction characteristic in TZnOw/PTFE composites with low threshold field[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(2): 567-573.
[73] Mårtensson E, Gäfvert U, Lindefelt U.Direct current conduction in SiC powders[J].Journal of Applied Physics, 2001, 90(6): 2862-2869.
[74] Yu Aiping, Ramesh P, Sun Xiaobo, et al.Enhanced thermal conductivity in a hybrid graphite nanoplateletcarbon nanotube filler for epoxy composites[J].Advanced Materials, 2008, 20(24): 4740-4744.
[75] Mårtensson E, Nettelbled B, Gäfvert U, et al.Electrical properties of field grading materials with silicon carbide and carbon black[C]//Proceedings of the 1998 IEEE 6th International Conference on Conduction and Breakdown in Solid Dielectrics,Vasteras, Sweden, 1998: 548-552.
[76] Hu Haitao, Zhang Xiaohong, Zhang Dingping, et al.Study on the nonlinear conductivity of SiC/ZnO/epoxy resin micro-and nanocomposite materials[J].Materials, 2019, 12(5): 761.
[77] Chi Qingguo, Meng Zhaotong, Zhang Tiandong, et al.Effect of MWCNTs/ZnO inorganic fillers on the electrical, mechanical and thermal properties of SiRbased composites[J].Journal of Materials Science:Materials in Electronics, 2021, 32(23): 27676-27687.
[78] 韩澎, 郑明胜, 查俊伟, 等.MWCNTs 改善WS2/三元乙丙橡胶复合材料的非线性电导特性与热导性能[J].复合材料学报, 2019, 36(3): 748-755.Han Peng, Zheng Mingsheng, Zha Junwei, et al.Improved nonlinear conductivity and thermal conductivity of WS2/ethylene propylene diene monomer composites with MWCNTs[J].Acta Materiae Compositae Sinica, 2019, 36(3): 748-755.
[79] Chi Qingguo, Jiang Longkun, Zhang Tiandong, et al.Study on electrical properties of donor ZnO nanoparticles/EPDM composites[J].Journal of Materials Science: Materials in Electronics, 2021,32(22): 26894-26904.
[80] Chi Q G, Yang M, Zhang C H, et al.Nonlinear electrical conductivity and thermal properties of AgNPs/BN/EPDM composites for cable accessory[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(4): 1081-1088.
[81] Chi Qingguo, Hao Yuyi, Zhang Tiandong, et al.Study on nonlinear conductivity and breakdown characteristics of zinc oxide-hexagonal boron nitride/EPDM composites[J].Journal of Materials Science: Materials in Electronics, 2018, 29(23): 19678-19688.
[82] Zhao Xiaolei, Yang Xiao, Hu Jun, et al.Globally reinforced mechanical, electrical, and thermal properties of nonlinear conductivity composites by surface treatment of varistor microspheres[J].Composites Science and Technology, 2019, 175: 151-157.
[83] Liang Hucheng, Du Boxue, Li Jin, et al.Effects of non-linear conductivity on charge trapping and detrapping behaviours in epoxy/SiC composites under DC stress[J].IET Science, Measurement &Technology, 2018, 12(1): 83-89.
[84] Du Boxue, Dong Jianan, Liang Hucheng.Electric field control by permittivity functionally graded and superficially non-linear conductivity materials for DC-GIS spacer[J].High Voltage, 2022, 7(5): 992-1000.
[85] Zhao Xiaolei, Meng Pengfei, Hu Jun, et al.Simulation and design of 500 kV DC cable terminal accessory based on ZnO varistor microsphere composites[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(1): 10-16.
[86] Li Zhongyuan, Zhao Hong, Zhang Changhai.Study on nonlinear conductivity of CCTO/EPDM rubber composites[J].Materials, 2018, 11(9): 1590.