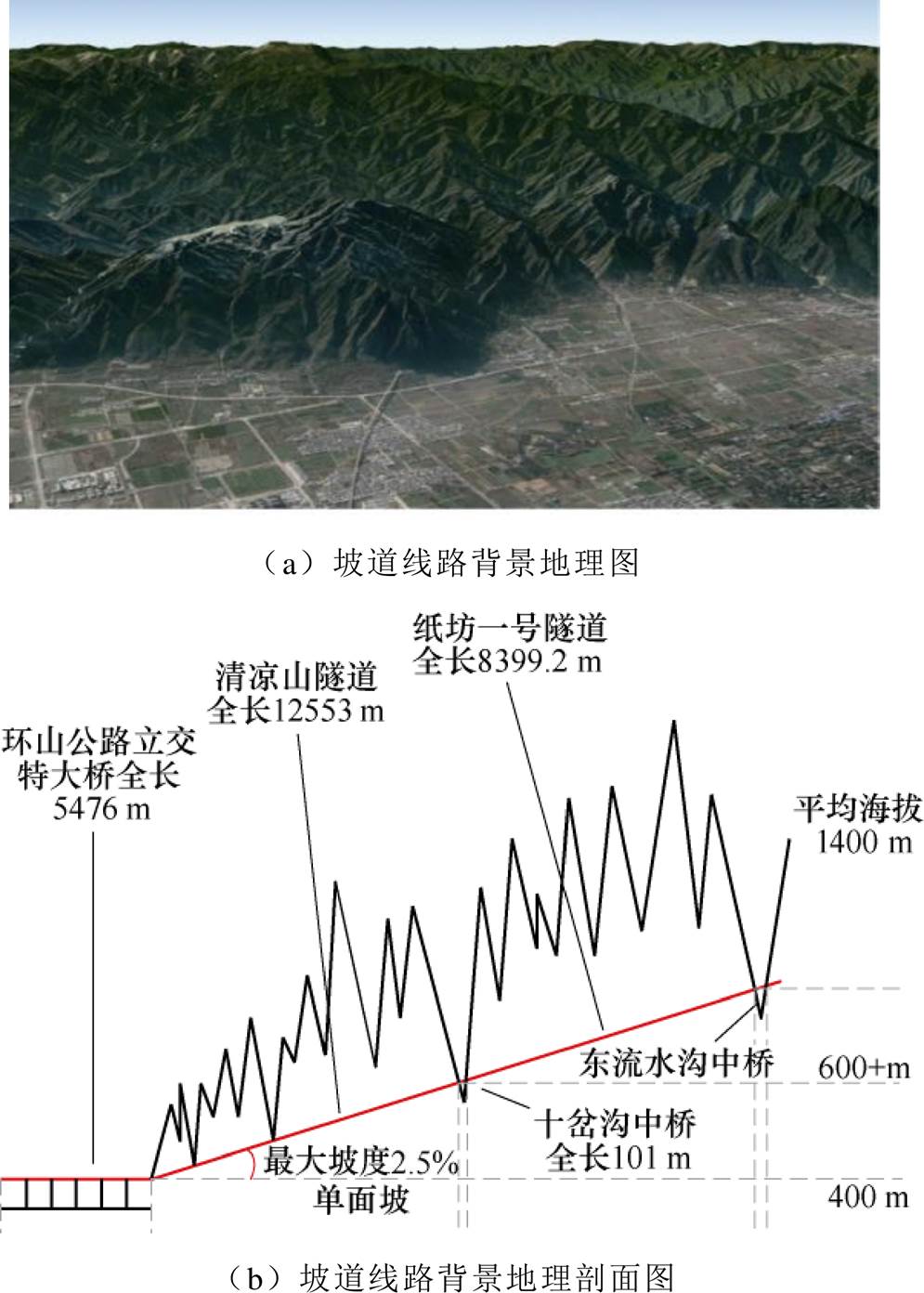
图1 坡道线路背景
Fig.1 Geographic background of slope
摘要 高速铁路列车在以下坡方向经过长大坡道路段时会产生大量的再生制动能量,若将此能量合理回收利用将有利于低碳交通与节能减排,实现“3060”双碳目标,更有利于列车行车安全。针对地面式再生制动能量混合储能系统容量高效合理配置问题,该文在分析高铁长大坡道的再生制动能量实测数据基础上,根据其功率分层的特性给出了混合储能系统的分段配置方案;考虑全域经济性能水平建立混合储能系统容量优化模型,针对传统优化算法迭代次数高、求解效率低等问题,利用Levy飞行产生初始解并在求解过程中不断记忆更新,给出了一种基于Levy飞行的改进模拟退火算法(LESA);最后,选取西成高铁秦岭北麓长大坡道路段,鄠邑(户县东)站牵引变电所实测数据进行算例仿真。结果表明,该方法可使混合储能系统在寿命期内回收大量再生制动能量,占牵引耗电量16.3 %。
关键词:高铁长大坡道 再生制动能量 混合储能系统 容量优化配置 改进模拟退火算法
我国作为铁路运输大国,截至2021年12月30日,高铁运营里程突破4万km,稳居世界第一,在里程上涨的同时,其能耗问题也值得关注。电能为铁路消耗最主要的能源类型,虽然近年来我国的新能源发展速度很快,并且风电、太阳能发电数量都是全球最高的,但火力发电依然占据主导地位。交流电气化铁路作为电网单体最大负荷,其耗电仍然会带来大量的碳排放[1]。
根据2019年全国铁路运营耗能显示,全年共耗电755.84亿kW·h时,较2018年711亿kW·h时上涨6.2 %[2](2020年后受疫情影响不予统计),因耗电量巨大,而存在可观的节能降耗潜力。降低电能消耗对我国铁路节能减排具有重要意义,有利于实现“3060”双碳目标。对再生制动能量的回收、利用是减少耗能的重要方式之一[3-7]。
我国西部地区地形复杂,共存高、亚高中山、盆地地貌,一些线路累计拔起高程超过10 km[8],铁路网整体呈现出设计坡度大、坡道线路长的特 点[9]。其中,典型长大坡道线路如川藏铁路雅安至林芝段,全线采用最大3%设计坡度,紧坡地段达到了300多km[10];西成客专秦岭隧道群段,最大设计坡度2.5%,大坡道持续长度达46 km[11-12]。列车以下坡方向运行至此时,为保证行车安全,多采取再生制动方式降速,此时列车电机将工作在发电状态产生电能并返送至牵引网[13]。根据西成客专线路内某变电所测量数据所示,瞬时牵引有功功率趋近于120 MW,再生制动有功功率接近60 MW,再生制动功率瞬时反馈比达50 %[11],再生制动能量不容小觑。
供电方面,再生制动能量会引起牵引网电压抬升,严重的情况下甚至会造成列车电气制动失效,危害行车安全[4,14-15];经济方面,由于列车的返送能量对外电网存在负序、谐波等电能质量的影 响[16-17],属于“劣质”电能,电力企业对其采取“返送不计费”的管理方式[5],对于电能质量影响较大的情况甚至要求支付罚款,浪费掉的电能给铁路企业造成了一定的经济损失。
在列车再生制动能量回收技术的研究中,主要有三种技术类型:基于优化列车时刻表、考虑引出至外部耗能场景[18]、基于储能系统的能量储存利用技术[6,19]。其中,基于优化列车时刻表的方式可实现能量就近高效利用,损耗最小[20-21]。但其优化方式单一,受列车运行规划局限性过强,优化灵活性欠佳。考虑长大坡道路段多为单线运行,且所处环境外电网鲜有可大量消纳再生制动能量的用电需求。以储能系统回收高铁列车长大坡道再生制动能量的方式受外部因素影响较小,线路改造少,建设成本适中,可灵活调度或接入多种用能、产能场景,环境适用性较强,优势更为突出[22]。
目前,该技术在电压低、能量少、对储能系统容量要求不高的城市轨道交通中研究较为深入。国内已有多条地铁线路安装储能型再生制动能量回收装置[23-25]。根据《“十四五”铁路科技创新规划》,我国正大力推进储能应用于电气化铁路的技术发展。回收储存可为供电臂内过剩能量构建通道,保证有效的电气制动、保证行车安全。同时可降低对外电网电能质量的影响[26]。储存的能量补充上坡列车耗电需求,进而对牵引网进行削峰,可进一步降低对牵引变压器最大功率需求、降低牵引变电所建设成本。研究长大坡道再生制动能量回收、储存、利用具有环境、经济、行车安全等多方面意义[27]。
在此方面,文献[3]根据电气化铁路再生制动能量特点,结合牵引负荷的运行状态提出了一种再生制动能量综合管理及控制系统,实现再生制动能量回收利用及平衡牵引负荷。文献[28]提出了一种储能型列车再生制动能量利用方案,其仿真结果表明该方案对提升再生制动能量利用率、稳定牵引网网压两方面均有利。文献[29]提出了一种基于铁路功率调节器的高速铁路牵引供电系统储能方案及控制策略。特别地,文献[5]指出混合储能系统回收高铁再生制动能量比单一储能装置更具有优势,且部分回收时的放电功率利用率也远高于完全回收。其中,值得注意的是,文献[23]指出混合储能装置又可分为车载式和地面式,地面式因不增加车体自重而被广泛关注,但需要考虑其容量配置问题。结合以上研究,不难看出混合储能系统用于回收高铁列车的再生制动能量具有优势及可行性。
目前少有结合制动情况,对高铁长大坡道制动特性的分析,且少有对如何配置混合储能系统进行明确说明。若储能系统配置过低,则回收能量有限,无法做到再生制动能量的高效利用;若配置过高,在运行周期内鲜有能量达到峰值,储能介质容量利用率低、成本回收困难[30]。故研究混合储能系统的优化配置意义重大。考虑多应用混合储能系统的新能源发电领域的配置方法,文献[31]采用小波分解光伏出力功率曲线得到高、低频波动信号,分别通过功率型、储能型器件进行回收,结合全生命周期成本最小与目标出力满足度最大为目标的混合储能容量优化配置模型。文献[32]采用集合经验模态分解系统总功率,分别得到锂电池和超级电容器的充放电功率指令,其中文献[33]将其方法应用于铁路领域,通过变分模态分解的方法将再生制动功率分解为高频、低频段后分别配置超级电容器、蓄电池的参数指标。以上文献通过频率分解的容量配置方法,在计算过程中始终无法避免出现模态混杂、影响计算结果、增加储能介质压力[30]等问题。且上述领域与本文背景的功率变化情况存在较大差异,将该技术直接应用显然会带来较大误差。但其对能量进行“分界”配置的方案为本文提供了一定的参考。
优化算法方面,工程背景下的实际问题,常因数据不可导、不可微的离散特性导致连续变量优化中的许多有效的解析数学算法和优化条件对此无 效[34],从而限制了很多优化方法的运用。对于离散采样数据,若拟合为函数后进行优化求解,将产生大量误差,影响计算精度[35]。模拟退火(Simulated Annealing, SA)算法是一种全局优化算法,其特点在于对目标函数的性质限制程度小,可以是不连续的,即可用于求解离散问题。其思想来自热力学与统计物理学中的固体退火过程,结合Metropolis接受准则在解空间中搜索最优解,可概率性地跳出局部解并最终趋于全局最优解[36]。但是为保证求解结果足够好,需保证退火过程降温速度足够慢,需要足够多的迭代次数,优化效率较低,这一问题阻碍了其实用性的发展[37]。文献[37-40]提出了多种改进思路及解决方案。其中指出增加补充搜索、尽可能多地获得算法已知信息、避免迂回判断和增加记忆功能是有效的改进措施。
综上所述,本文以地面式混合储能系统为研究对象,对高铁列车于长大坡道的再生制动能量特性进行了分析。考虑列车实际运行情况,从能量回收可行性的角度,将全日制动整合为多组制动段。随后结合制动能量特性及储能系统能量回收方式给出了混合储能系统分段配置方案。通过以寿命为条件的配置取值域筛选,考虑全域经济性能水平建立了混合储能系统容量优化模型。针对传统SA算法求解效率低的缺点,利用Levy飞行产生初始解并在求解过程中不断记忆更新,给出了基于Levy飞行的改进模拟退火算法(Levy flight Enhancement Simulated Annealing algorithm, LESA)。采用该算法对模型进行优化求解,得到最佳的配置方案。通过实例分析,证明了该方法的有效性,储能系统在寿命内可大量回收再生制动能量。
为合理配置混合储能系统,需充分了解高铁列车于长大坡道段再生制动能量特性。首先分析了单次制动功率变化并总结特点,在此基础上进一步分析了全日内再生制动功率曲线,得到其整体特性。
本文选用我国西成高铁秦岭北麓长大坡道路段,鄠邑(户县东)站牵引变电所主变压器日功率数据。数据范围辐射鄠邑至东流水沟供电臂,该臂内路段包括:环山公路立交特大桥、清凉山隧道、十岔沟中桥、纸坊一号隧道、东流水沟中桥。该坡道线路背景如图1所示。
西安方向上行列车运行至此路段时需以再生制动方式进行下坡降速制动。此时,列车将产生大量再生制动能量返送至供电臂,考虑行车运行规划,一部分能量可由同时段臂内其他车辆消耗,仍有能量未经利用通过线路经牵引供电系统与大电网的连接点送出,造成了能量浪费与损耗[12]。本文即针对此部分能量进行回收计算,实测数据如图2所示。
将全日再生制动能量进行提取分析。认为返送功率持续时长小于10 s的再生制动过程产生的能量较少,不足以影响储能系统容量设置,故舍弃持续时长小于10 s的再生制动,共提取出59次再生制动过程。通过逐一对比分析,可将单次再生制动分为四种基础类型,典型制动状态功率如图3所示。图3a显示再生制动能量以稳定3.6 MW功率持续全制动时长,全段无功率波动,记为恒功率返送状态;图3b显示再生制动功率于制动时段在3 MW附近按照±1 MW左右幅度小范围波动,记为波动功率返送状态;图3c显示再生制动功率先以小幅波动功率返送状态维持一定时间后,在某一时刻出现功率突增,并以较大功率水平保持一段时间后,逐渐减弱,记为混合功率返送状态;图3d显示再生制动功率先以近似恒功率返送状态维持一段时间后出现短时功率突增,形成功率尖点,记为尖峰功率返送状态。

图1 坡道线路背景
Fig.1 Geographic background of slope
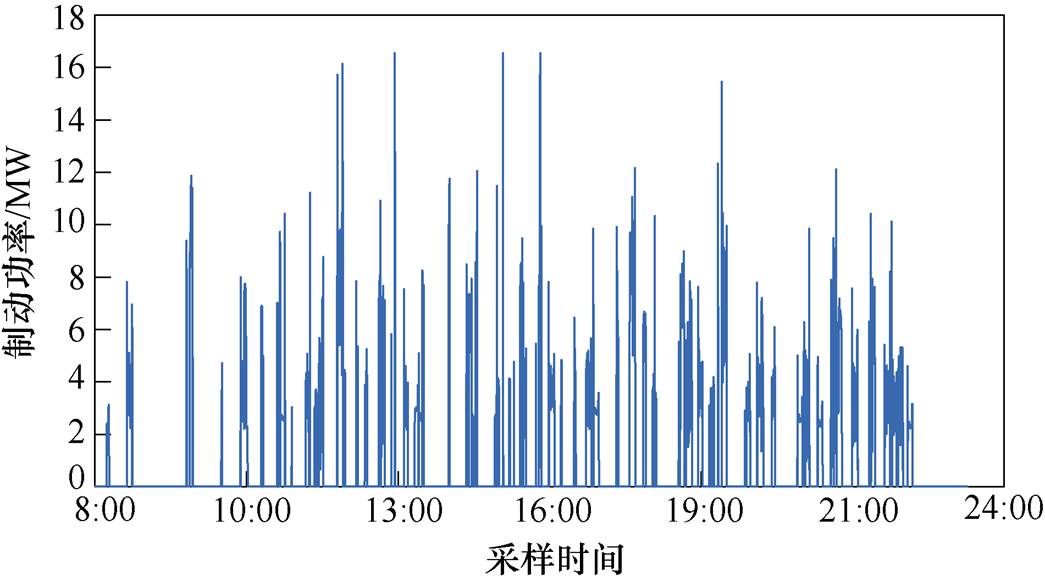
图2 再生制动功率实测值
Fig.2 Measured regenerative braking power
全日任意时段再生制动功率变化情况均可由上述四种基础类型单独或组合构成。各类型出现次数及数量见表1。查列车运行图,第7次制动过程为D6858次列车产生,在该制动时段有且仅有此车次通过,再生制动功率无同臂或对向车次影响,制动功率变化情况正如图3c所示。
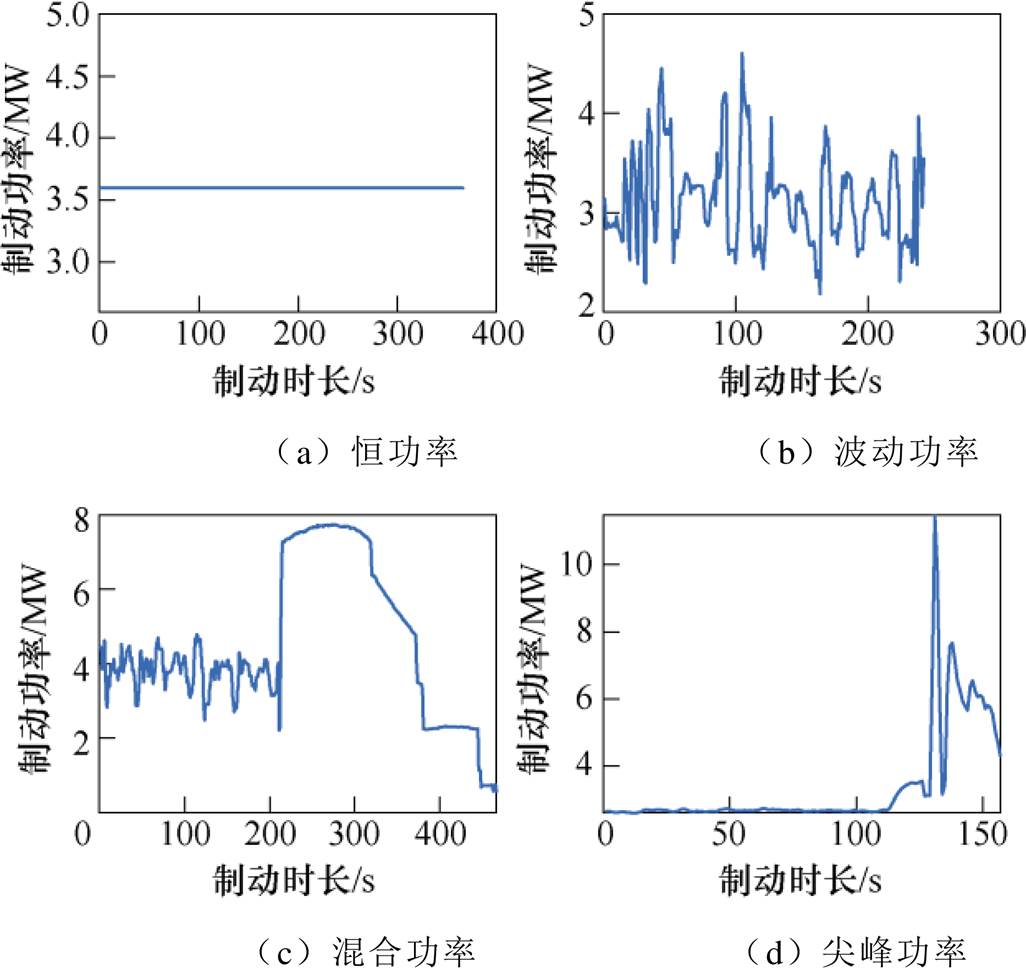
图3 典型制动状态功率
Fig.3 Typical braking power
表1 各类型功率对应制动次数及数量
Tab.1 Number and number of brakes corresponding to various types of power

制动类型制动次数数量 恒功率返送状态5、8、10、31、335 波动功率返送状态2、3、12、16、17、18、21、26、27、29、34、40、42、44、45、46、48、50、55、5720 混合功率返送状态1、7、13、19、22、23、32、35、38、47、49、53、5613 尖峰功率返送状态6、11、25、37、39、54、597 基础类型组合4、9、14、15、20、24、28、30、36、41、43、51、52、5814
经过分析比对,以上四种制动类型中,均有较大比例的、功率波动范围在2.5~4.5 MW之间的恒功率或小范围功率波动的制动,该类型的总时长占全日总再生制动时长的58.9 %。为充分了解该部分能量的总体情况,故从全日制动的角度进行分析。
将全日59次再生制动能量功率变化曲线按同一坐标尺度进行重合处理,如图4所示。图4所示功率曲线有明显堆叠带,产生分层效果。在低功率部分,曲线产生的堆叠较多,集中在2~5 MW功率范围,时长多在300 s内;在高功率段,较少功率突破12 MW,且其中多数维持时间较短。由此,进一步验证了小范围波动或恒功率返送状态的再生制动能量充分、功率维持时间长,具有极强的回收价值。同时,以上数据为混合储能系统的配置情况提供了部分功率约束参考。
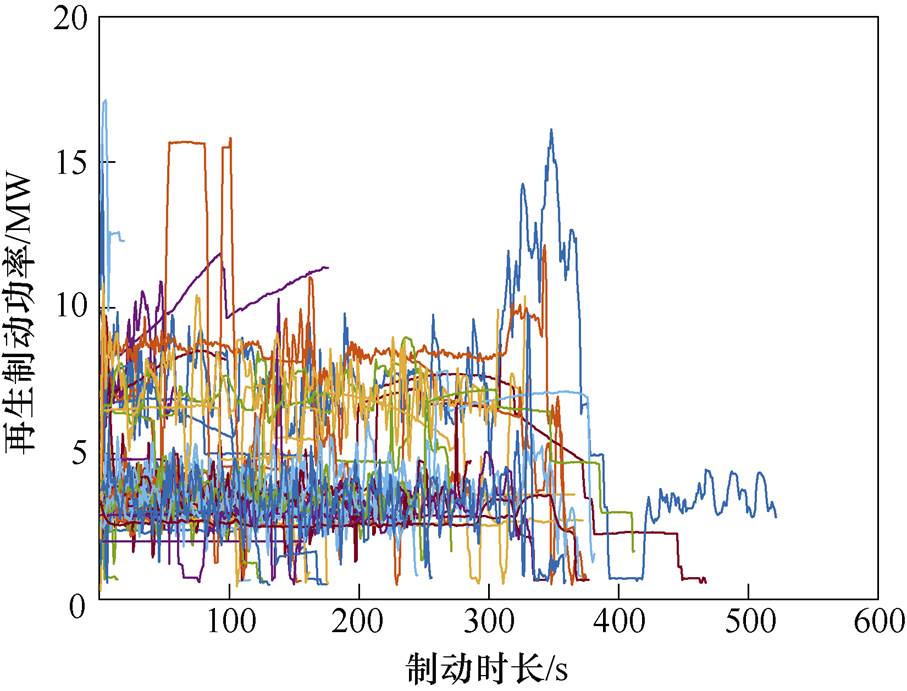
图4 可回收再生制动功率曲线重叠
Fig.4 Recoverable regenerative braking power curves overlap diagram
本文所选数据中,在全日内有多次列车再生制动能量返送。为保证储能系统“有充有放”,需将全日内再生制动能量进行整理分析,以此可合理确定储能系统容量上下限。
(1)考虑再生制动能量维持时间,如1.2节中所述,共提取出59次具有回收价值的制动能量返送时段。
(2)结合运行规划,分析每时段制动能量对储能系统的容量需求的影响。将一时段内单次或连续的同牵引或同制动过程为记为一个动作段。
经分析,其中第4、13、22、25、30、34、36、38、40、43、46、51次制动后无牵引消耗,存在连续制动情况。这表明,在相应时段中,储能系统需进行多次充电动作后才出现放电需求。进一步地,系统容量上限应考虑上述情况的能量累加值。故将上述次数进行整合处理,累计每次制动后直至出现牵引消耗为一次制动段,共得到了36次制动段,以负向表示。同理,将多次牵引间无能量返送的过程记为一个牵引段,以正向表示,得到36次牵引段。共计72次动作段,如图5所示。
(3)考虑放电需求,分析这36次制动段回收的能量是否可被消耗利用。
其中前35次制动段的累计制动能量均小于其后的列车牵引耗能,储能系统可完全释放能量。但第36次制动段,即单次制动第51~59次之和,电量数值远超前35次,且在当日内其后无牵引耗电。为避免扩大计算范围,影响配置结果,故不将第36段列入可回收能量的计算范围内。但在运行过程中,由于前次牵引段已将储能系统内能量耗尽,系统仍可回收该段部分能量,用于次日的首次牵引耗电。
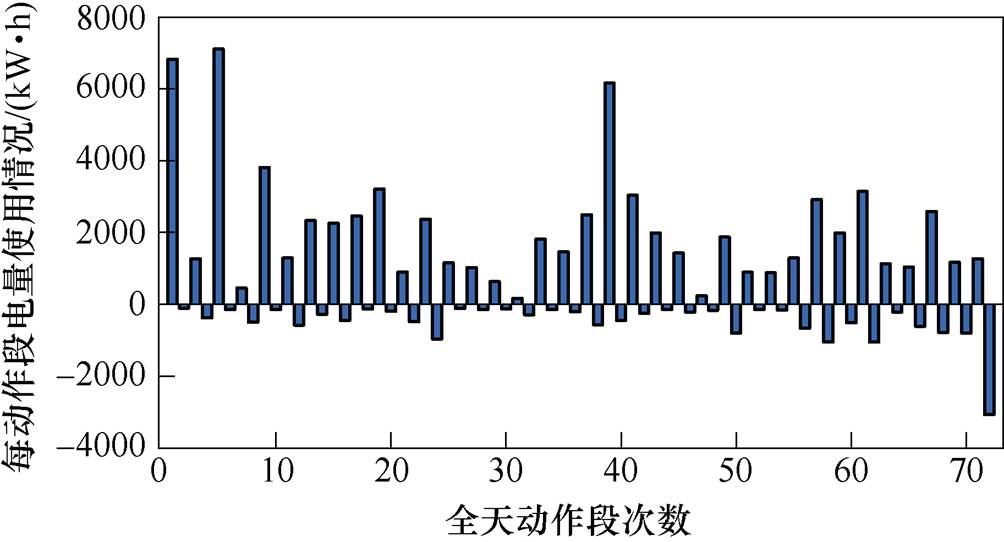
图5 全天每动作段电量使用情况
Fig.5 The electricity consumption of each action in the whole day
通过以上分析共得到35次制动段及其累计能量,列入可回收范围。
如1.3节所述,高铁列车长大坡道的再生制动能量功率有明显高、低功率段之分且高功率段能量密集度明显小于低功率段。考虑超级电容特性:功率密度较大,充放电速度快,状态响应快,可承受大电流场景,但在能量密度上不及蓄电池;蓄电池特性:能量密度大、适合大规模储存电能,但功率密度小、承受大电流能力有限[30,41]。更为重要的是,超级电容与蓄电池在循环寿命方面有数量级上的差异,蓄电池100 %充放电深度(Depth of Discharge, DOD)循环寿命仅为3 000次[4,42],且功率密度问题导致其功率单价较高,配置时应考虑投入成本以及其是否能在寿命周期内满足盈利条件;超级电容器循环寿命可达100万次,但其能量密度以及较高的造价制约了其部分应用需求。若仅用一种储能介质回收再生制动能量,对超级电容而言,容量压力势必会导致成本大幅增加;对蓄电池而言,功率需求、充放电循环次数都将成为配置的制约条件[32]。
将二者结合成为混合储能系统,为充分利用二者特性,需考虑其功率配置范围、容量、盈利条件、储能系统循环寿命等相关需求,设定储能系统的配置方案。结合第2节内容,考虑由超级电容—蓄电池二者以相互补充的回收方式,分别负责回收各功率段的一部分能量。因此需要设置功率阈值,将功率低于阈值的能量由超级电容或蓄电池其中一者回收,将功率高于阈值的能量由另一者储能介质回收。记功率阈值为Pth,该值即为回收低功率段能量的储能介质L的最大充电功率PL。另记回收高功率部分能量的储能介质为介质H。混合储能系统充电工作流程如图6所示。
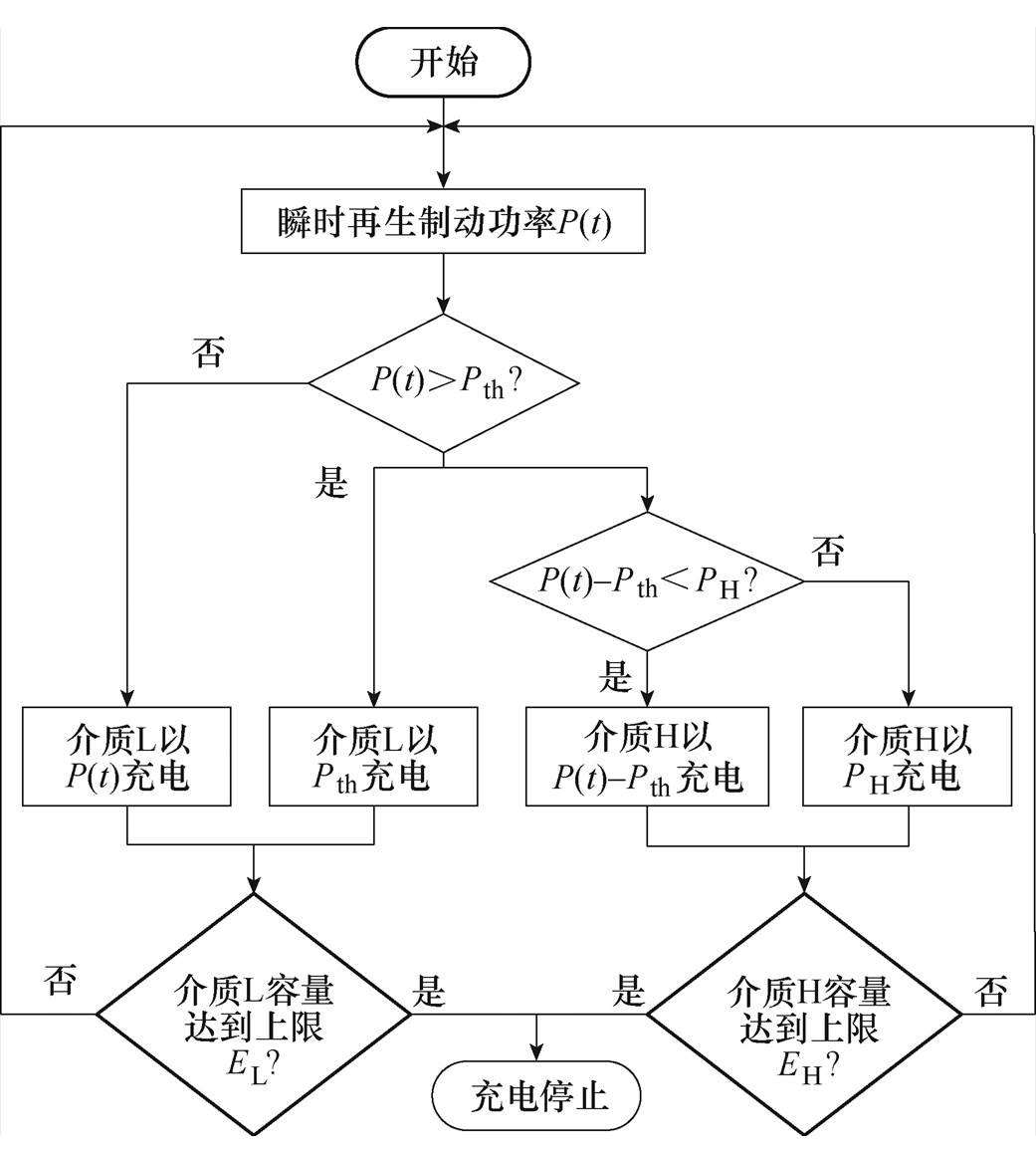
图6 混合储能系统充电工作流程
Fig.6 Charging workflow of hybrid energy storage system
图6中,认为再生制动功率是关于时间的映射函数,记为P(t),PL、PH分别为储能介质L、H最大充电功率,EL、EH分别为介质L、H最大充电容量。
针对第3节所述的高铁列车在长大坡道的再生制动能量功率曲线有明显分层的情况,分别对混合储能系统中回收低功率段能量的储能介质L、高功率段的储能介质H进行配置。
1)介质L最大充电功率
如图4所示,选择低功率段曲线密集区域上边界与下边界为回收该段再生制动能量储能介质L的最大充电功率计算上限与下限,记为PL_max与PL_min。
2)介质L最大储能容量
已知储能介质L最大充电功率计算范围,考虑在不同功率下每次制动可回收能量值为
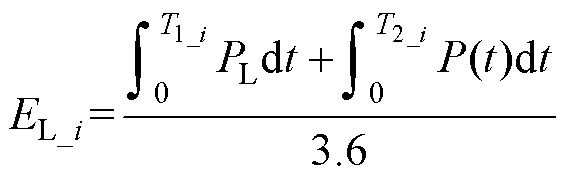 (1)
(1)
其中
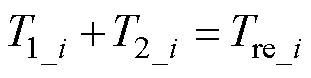 (2)
(2)
式中,T1_i为第i次制动中,再生制动功功率大于或等于PL的时长;T2_i为再生制动功功率小于PL的时长;T1_i与T2_i之和构成第i次制动总时长Tre_i;EL_i为在介质L取最大充电功率为PL时,第i次制动可回收的能量。
在已知逐次制动可回收能量的基础上,按第2节所述整合,即将共计59次EL_i整合为36次的EL_re_n,表示在该功率PL下第n次制动段实际可用于回收的能量。选取前35次中的最值EL_re_min、EL_re_max作为储能介质L 的容量回收计算范围。
考虑第3节所述,储能介质H应负责回收再生制动功率大于PL的部分能量,同样需对介质H进行最大充电功率PH、最大容量EH_set配置计算。
1)介质H最大充电功率
PL与PH共同构成混合储能系统的最大充电功率Pmax,即
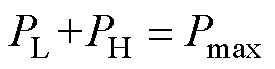 (3)
(3)
对PH进行计算时应考虑混合储能系统的最大充电功率利用率R为
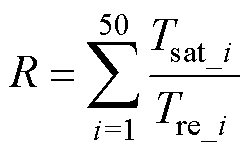 (4)
(4)
式中,Tsat_i为第i次制动功率小于Pmax的时长。式(4)表征混合储能系统功率满足全日再生制动功率需求的占比。在R的值域内,设定系统最大充电功率利用率不低于Rset,则可得Rset计算位置处Tsat_i所对应的Pmax,在已知PL的情况下可通过式(3)得到PH的最大值,记为PH_max作为介质H的最大充电功率配置上限,下限为0。
2)介质H最大储能容量
为除去低功率段介质L所回收的部分功率,需对原再生制动功率曲线进行重造,得到应由介质H负责回收的功率曲线PH(t)为
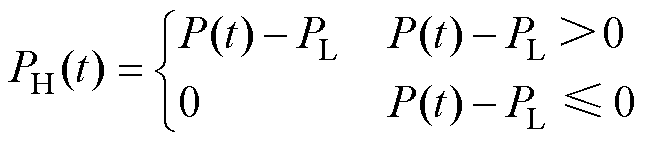 (5)
(5)
得到P(t)H后,对介质H进行容量配置计算,计算方式同式(1)、式(2),分别将式(1)、式(2)中PL、P(t)替换为PH与PH(t)得到计算结果EH_i,选其最值EH_re_min、EH_re_max作为储能介质H的容量回收计算范围。
为保证储能系统安全高效地运行,切实通过储能进行节能降耗,应考虑其电能回收价值、建设成本投入、成本回收年限等经济性指标。
以储能介质L为例:首先,考虑其储能介质在各功率-容量下运行一日可回收的电能EL_re_day与所回收电量的电度电价CL_re分别为
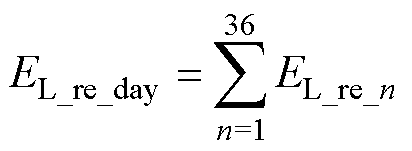 (6)
(6)
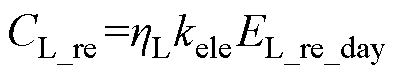 (7)
(7)
式中,hL为储能介质L充放电效率;kele为电度电价(元/(kW·h))。储能介质L建设成本表示为
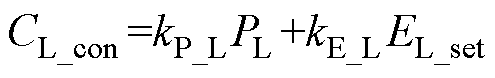 (8)
(8)
式中,kP_L为储能介质L功率单价(元/kW);kE_L为储能介质L容量单价(元/(kW·h));EL_set为储能介质L配置容量,表示为
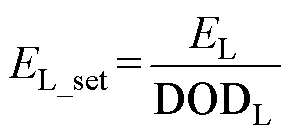 (9)
(9)
式中,DODL为储能介质L所设定的最大充放电深度。由式(7)、式(8)可得介质L的成本回收年限yearL为
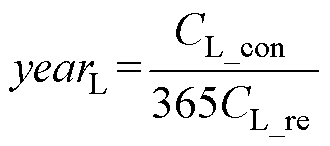 (10)
(10)
介质H成本回收年限计算原理同式(6)~式(10),计算各功率-容量下介质H可回收电能EH_re_day及所回收电量电度电价CH_re,通过其最大充放电深度DODH可得配置容量EH_set进而可得建设成本CH_con,通过式(10)计算介质H的成本回收年限yearH。由于计算逻辑关系相同,仅需替换对应条件参数,故不再赘述。
为保证储能系统优化配置过程合理、结果准确,本节首先针对配置取值范围进行了考虑寿命条件的筛选,得到配置取值域。进而考虑全域经济性能水平建立混合储能系统容量优化模型。在此基础上,通过基于Levy飞行的改进模拟退火算法,对模型求解。
考虑储能介质本身特性,其寿命与充放电深度、循环次数息息相关[43]。为保证优化计算速度,在计算起始,应首先排除储能介质在回本年限内以设定深度充放电工作,理论循环次数大于循环寿命的取值点。即有约束条件,以储能介质L为例
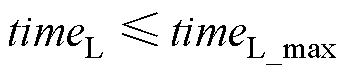 (11)
(11)
式中,timeL表示储能介质L以PL、EL_set配置时运行yearL年共产生的全设计充放电深度循环次数;timeL_max为储能介质L在全设计充放电深度下的循环寿命。其中timeL计算方式为
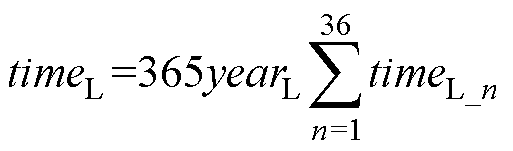 (12)
(12)
式中,timeL_n为储能介质L以PL、EL_set配置时,第n制动段是否达到设计充放电深度循环的判断函数,可表示为
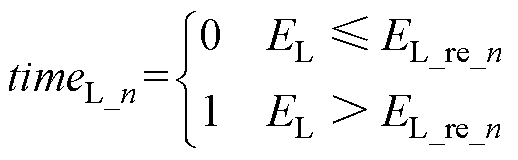 (13)
(13)
通过上述计算范围筛选,可排除掉一部分不满足条件的功率—容量配置组合,得到新的可配置组合取值范围,记为取值域UL。
储能介质H的配置取值域UH计算方法同理。
5.2.1 考虑全域经济性能水平的优化配置
混合储能系统的经济性能主要表现在成本回收年限,决定其大小的建设成本和所回收电量随配置参数的增加也会增长。若只考虑以成本回收年限作为优化求解目标则可能受单次制动能量最小值的影响,出现因配置过小而产生的每次制动均为“满充”的情况,这会导致大量电能无法回收利用,产生浪费。因此,考虑全域配置条件下的经济性能,以最低配置、最高配置情况下最佳的成本回收年限构建经济性能水平参考函数,该函数反映全域内随配置的增加,经济性能变化的情况。构建目标函数,求解优于性能水平的最佳配置取值。
以储能介质L为例,经济性能水平参考函数yearL_ref表示为
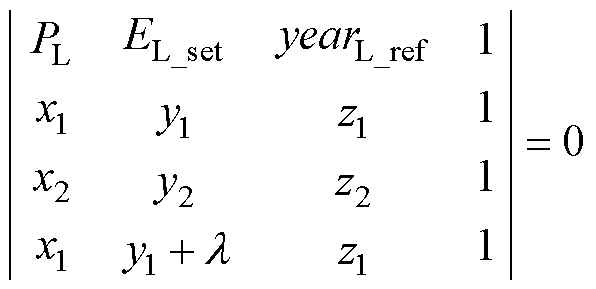 (14)
(14)
式中,x1、y1、z1分别为在最低配置情况下的最大充电功率、介质配置容量、最佳成本回收年限;x2、y2、z2为最高配置情况下的相应取值;l 为非零任意实数。
构建优化配置目标函数为
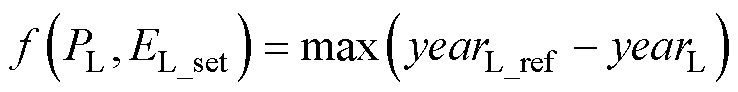 (15)
(15)
约束条件为
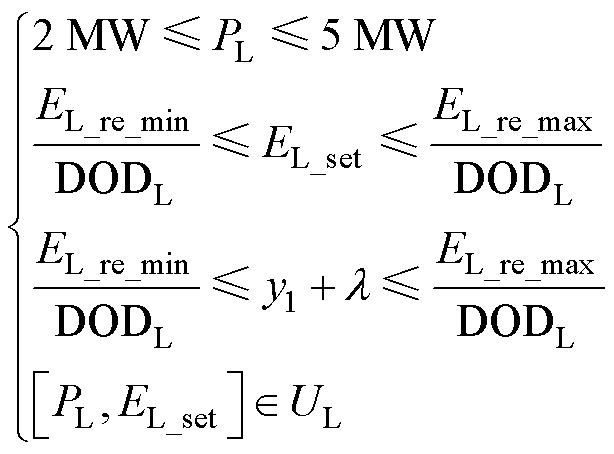 (16)
(16)
对于储能介质H,经济性能水平参考函数yearH_ref以及目标函数表示方式与式(14)、式(15)相同,其约束条件为
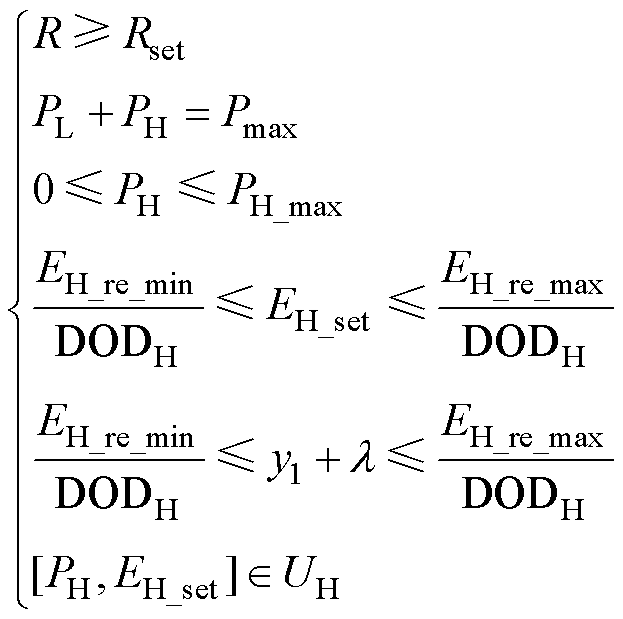 (17)
(17)
5.2.2 基于Levy飞行的改进模拟退火算法
Levy飞行模型是根据鸟类和昆虫类的觅食轨迹而研究的一种随机行走策略,其特点是移动步长符合一个重尾的稳定分布,表现为短距离移动和长距离移动交错产生[44-45]。Levy飞行过程可以产生变化多样的随机步长,可产生多个小范围内的密集搜索,具有随机性和一定的遍历性。其更新公式为
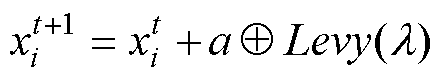 (18)
(18)
式中,a为步长控制参数; 表示点乘运算;Levy(l)为一个随机搜索路径;其随机步长表现为一个Levy分布,即
表示点乘运算;Levy(l)为一个随机搜索路径;其随机步长表现为一个Levy分布,即
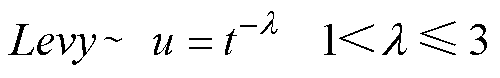 (19)
(19)
利用Mantegna算法计算随机步长为
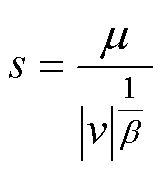 (20)
(20)
式中,m、v服从正态分布,可表示为
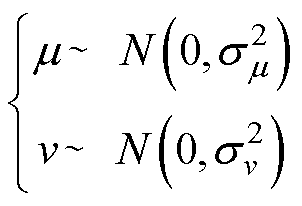 (21)
(21)
其中
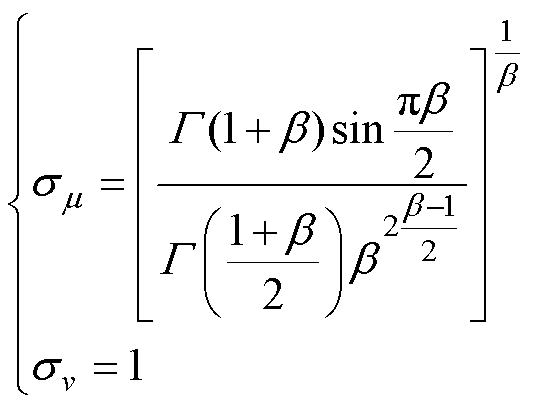 (22)
(22)
式中,b 通常取值1.5。
本文结合以上方法,给出基于Levy飞行的改进模拟退火算法(LESA)。其目的是在进入模拟退火算法前,先通过Levy飞行模型在可行域内对目标函数进行不完全遍历的随机求解,飞行路径中有概率经过较优值点,记录所求得解的最优值及解的位置,令其成为模拟退火算法中的初始最优值及起始位置。在求解过程中出现当前最优解后,通过记忆不断更新初始最优值,且将其作为进入Metropolis接受准则的判断条件,具体计算流程如图7所示。

图7 LESA算法计算流程
Fig.7 LESA calculation process
因此,改进的模拟退火算法将起始在一个较好的位置。由计算时长更短的Levy飞行取代了传统SA以多次迭代向上述的初始最优值逼近的过程。通过最优解的记忆功能,可直接舍弃当前解的过劣值,避免过多进入Metropolis接受准则。可在有限的迭代次数下更趋近于最优解,提升算法效率。
本文选用西成高铁长大坡道路段,鄠邑站牵引变电所主变压器日实际运行功率数据,数据涉及路线长度超21 km,为西安方向0.025°单面下坡。拟在沿线配置地面式混合储能系统,其由超级电容及蓄电池构成,结合第3节中分析及系统工作流程,存在两种配置方案:
方案1:由蓄电池承担低功率部分能量回收,即储能介质L;由超级电容承担剩余及高功率部分能量回收,即储能介质H。
方案2:由超级电容承担低功率部分能量回收,即储能介质L;由蓄电池承担剩余及高功率部分能量回收,即储能介质H。
通过改进的LESA对比传统SA分别对两种条件下的混合储能系统进行优化配置计算,设计迭代次数均为100次。参考文献[2, 4, 42],设置混合储能系统基本参数,见表2。电费方面,高速铁路采取电度电费和基本电费构成的两部制电费计价方 式[5],由于本文未涉及关于变压器容量的相关研究,故未计算基本电费。
表2 混合储能系统基本参数
Tab.2 Basic parameters of hybrid energy storage system

基本参数数 值 蓄电池超级电容 功率成本单价/(元/kW)2 000500 容量成本单价/[元/(kW·h)]64013 500 循环寿命4 2861 000 000 充放电深度(%)7080 充放电效率(%)8095 电度电费/[元/(kW·h)]0.60.6
两种方案优化配置过程如下:
1)方案1
由1.3节分析可知,低功率段能量回收最大功率需求取值范围为2~5 MW,计算PL在不同功率取值下每制动段可回收的电量,计算结果如图8a所示,其电量回收上限为1 092.83 kW·h。考虑介质储能效率及充放电深度,容量配置上限为1 561 kW·h,故低功率段储能介质容量计算范围为0~1 561 kW·h。通过计算,得到蓄电池的日累计回收电量如图8b所示,建设成本投入如图8c所示,成本回收年限如图8d所示。
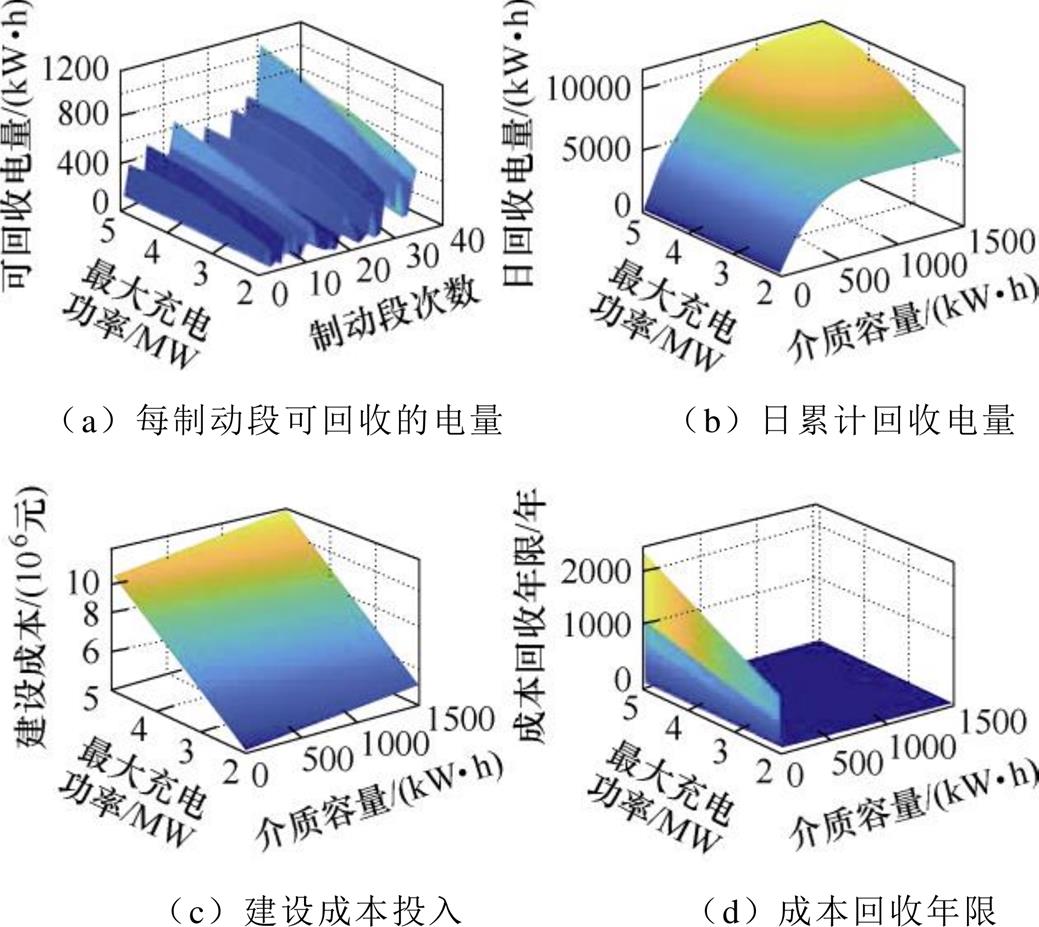
图8 方案1蓄电池计算结果
Fig.8 Scheme 1 battery calculation result
通过取值域筛选,去除不满足寿命的取值点,得到可行的功率—容量组合范围以及其对应的成本回收年限,构成取值域UL。根据式(14)构建经济性能水平参考函数yearL_ref,如图9所示。
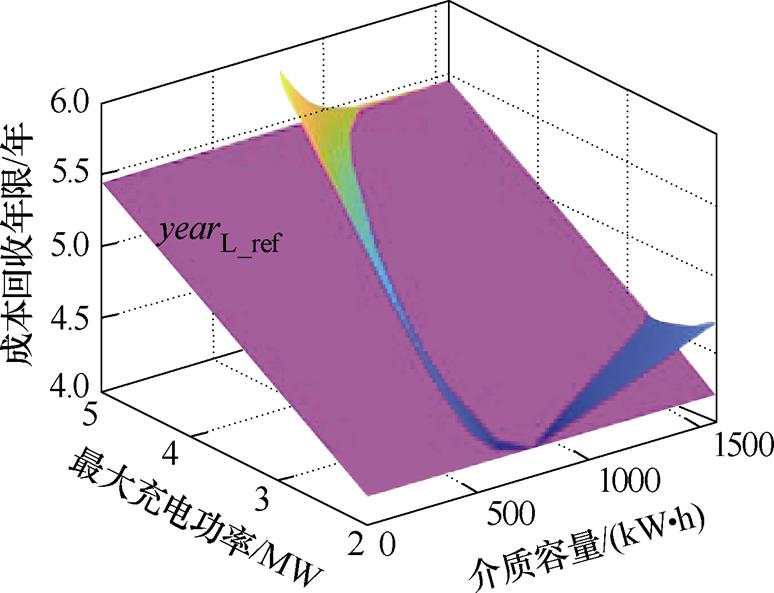
图9 方案1蓄电池取值域筛选结果及参考函数
Fig.9 Selection results of configuration range and reference function of battery in scheme 1
在取值域UL中进行优化配置计算:首先,随机产生Levy飞行路径,将PL、EL_set所构成路径点代入f (PL、EL_set) 目标函数,选取最佳位置作为初始点,通过两种算法求解最佳配置参数。图10a所示为飞行过程,图10b为目标函数在两种算法下的计算结果。
对方案1中超级电容进行优化配置,首先计算系统最大充电功率利用率,结果如图11所示。图像以5 MW为界,分别形成了低、高功率的“Z”形下降曲线,同时验证了1.3节中对日再生制动能量特性的分析。取Rset=5 %,即系统最大充电功率Pmax=9 MW,从而得到方案1中PH的取值范围为0~5.80 MW。
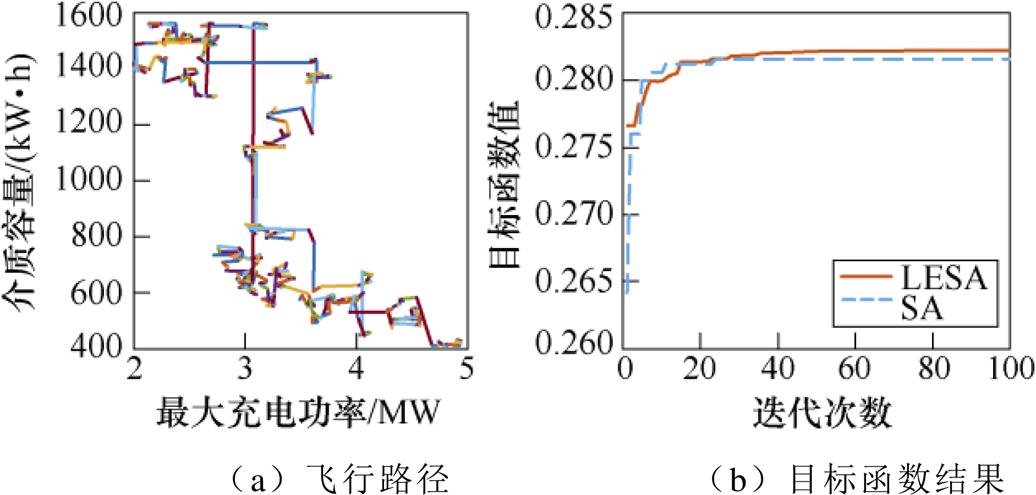
图10 方案1蓄电池求解Levy飞行路径及目标函数结果
Fig.10 Scheme 1 Levy flight path and results of objective function for battery
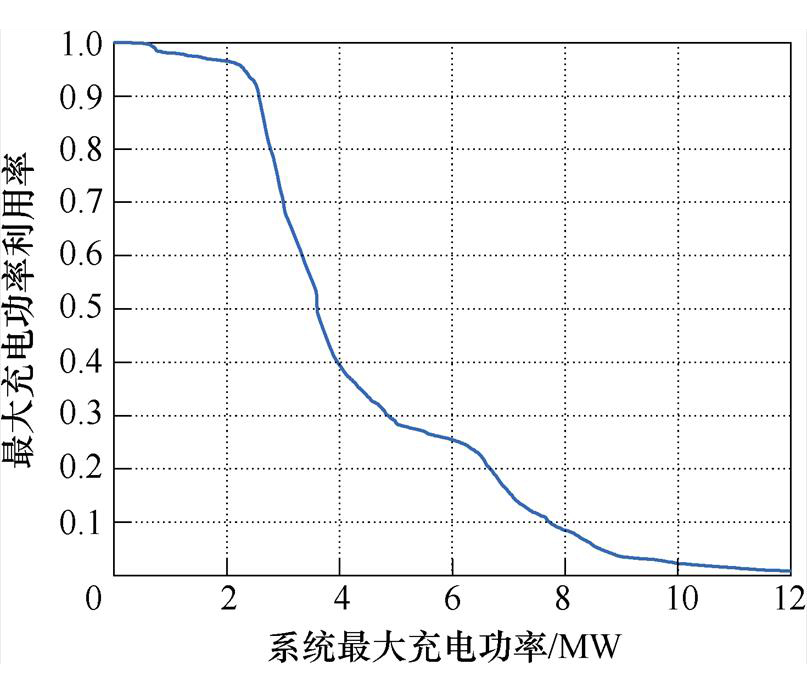
图11 系统最大充电功率利用率
Fig.11 System maximum charging power utilization
得到其可回收电量以及各功率—容量取值下的日累计回收电量、建设成本投入、成本回收年限如图12所示。
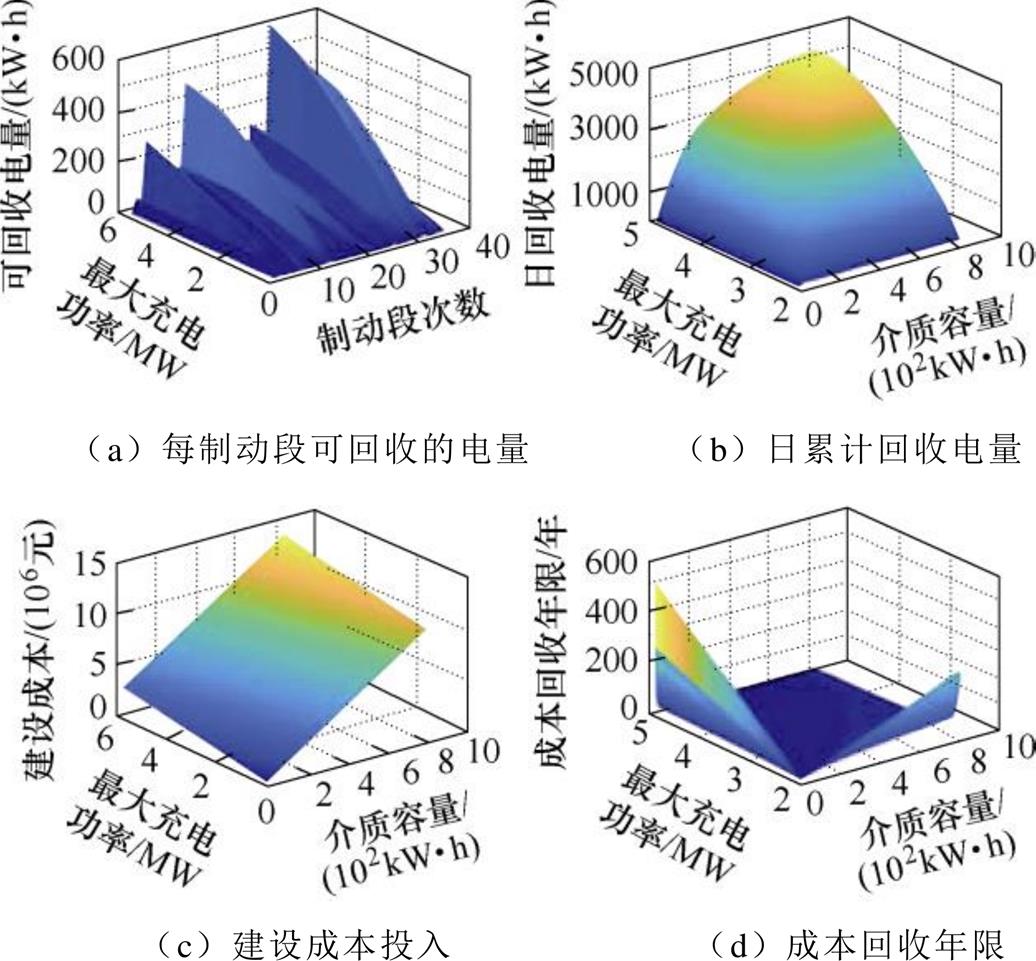
图12 方案1超级电容计算结果
Fig.12 Scheme 1 supercapacitor calculation result
经取值域筛选后可行的功率—容量组合范围以及其对应的成本回收年限、经济性能水平参考函数yearH_ref如图13所示。
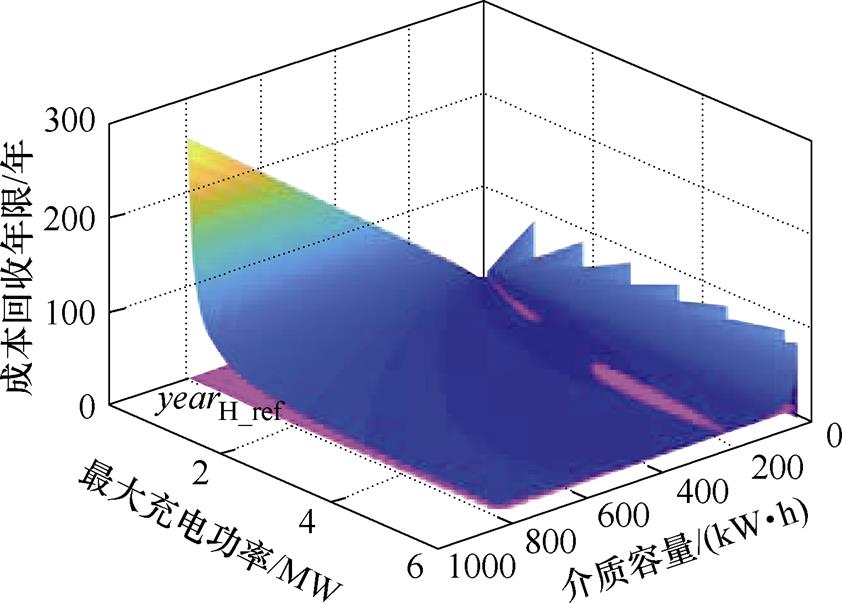
图13 方案1超级电容取值域筛选结果及参考函数
Fig.13 Selection results of configuration range and reference function of supercapacitor in scheme 1
在取值域UH中进行优化配置计算,Levy飞行路径及目标函数收敛情况如图14所示。
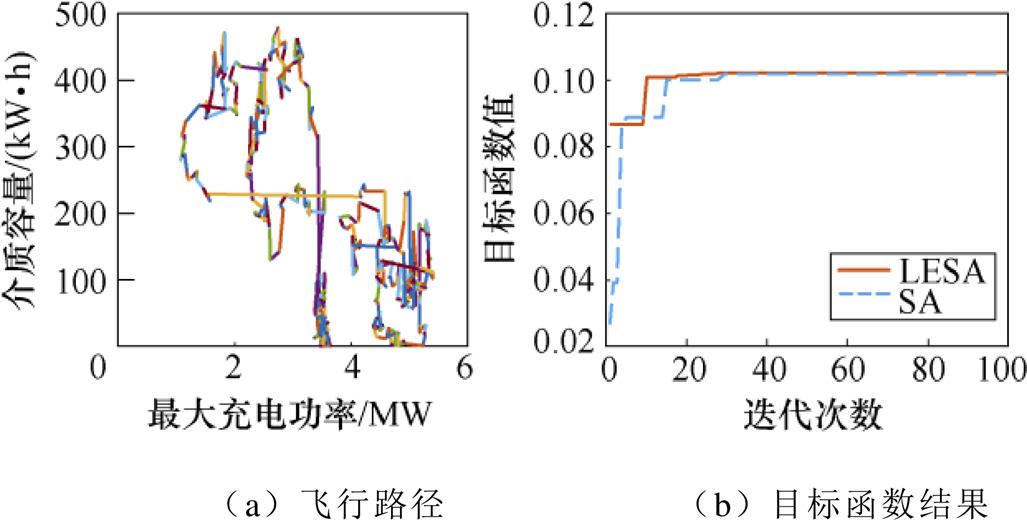
图14 方案1超级电容求解Levy飞行路径及目标函数结果
Fig.14 Scheme 1 Levy flight path and results of objective function for supercapacitor
2)方案2
首先对超级电容进行配置,得到各制动段可回收电量以及各功率—容量取值下的日累计回收电量、建设成本投入、成本回收年限,如图15所示。
筛选超级电容取值域并建立参考平面,如图16所示。
通过LESA、SA算法求解目标函数,如图17所示。

图15 方案2超级电容计算结果
Fig.15 Scheme 2 supercapacitor calculation result
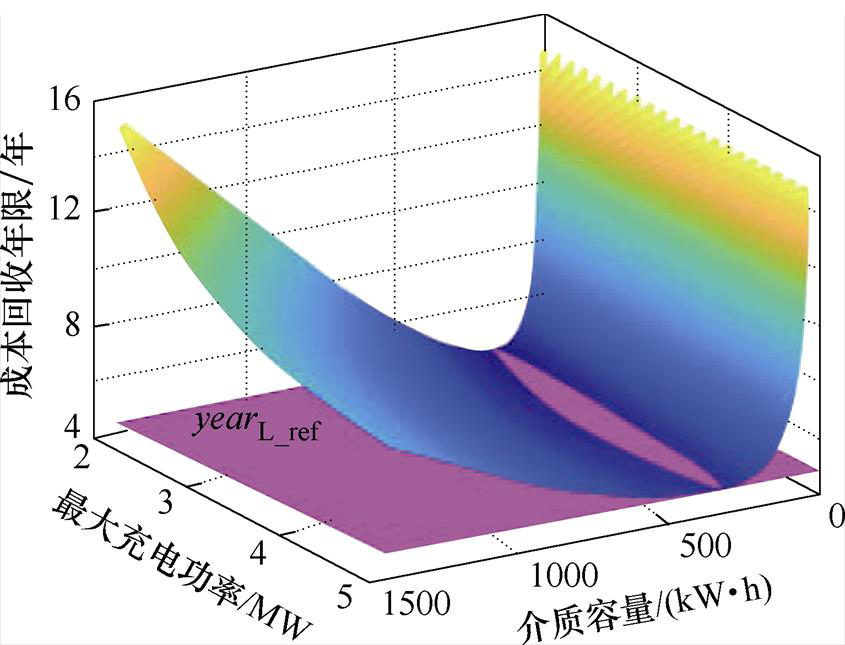
图16 方案2超级电容取值域筛选结果及参考函数
Fig.16 Selection results of configuration range and reference function of supercapacitor in scheme 2
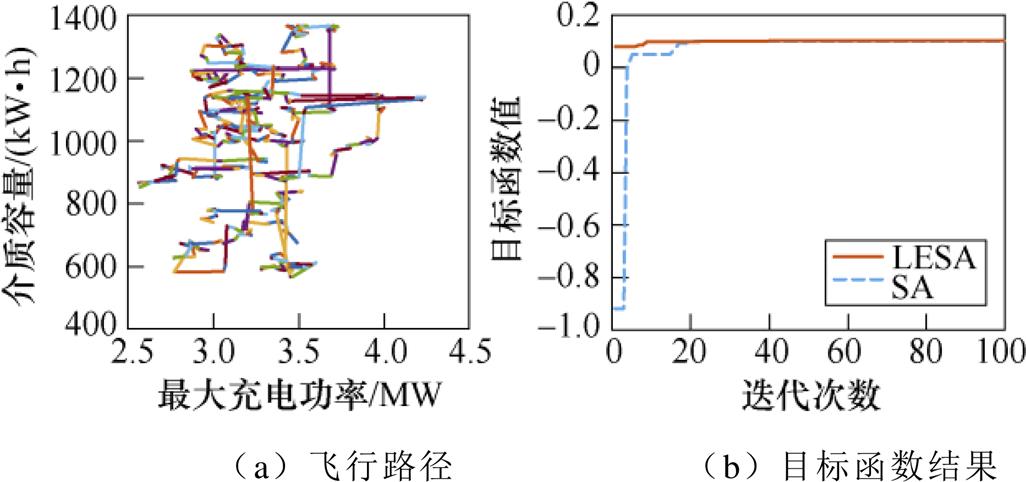
图17 方案2超级电容求解Levy飞行路径及目标函数结果
Fig.17 Scheme 2 Levy flight path and results of objective function for supercapacitor
同方案1中计算,取Rset=5 %,PH的取值范围为0~5.72 MW。进而对蓄电池进行优化配置,得到已知超级电容配置条件下各制动段可回收电量以及各功率—容量取值下的日累计回收电量、建设成本投入、成本回收年限,如图18所示。
筛选蓄电池取值域并建立参考平面,如图19所示。
通过LESA、SA算法求解目标函数,结果如图20所示。
混合储能系统两种配置方案下的优化配置结果见表3、表4。
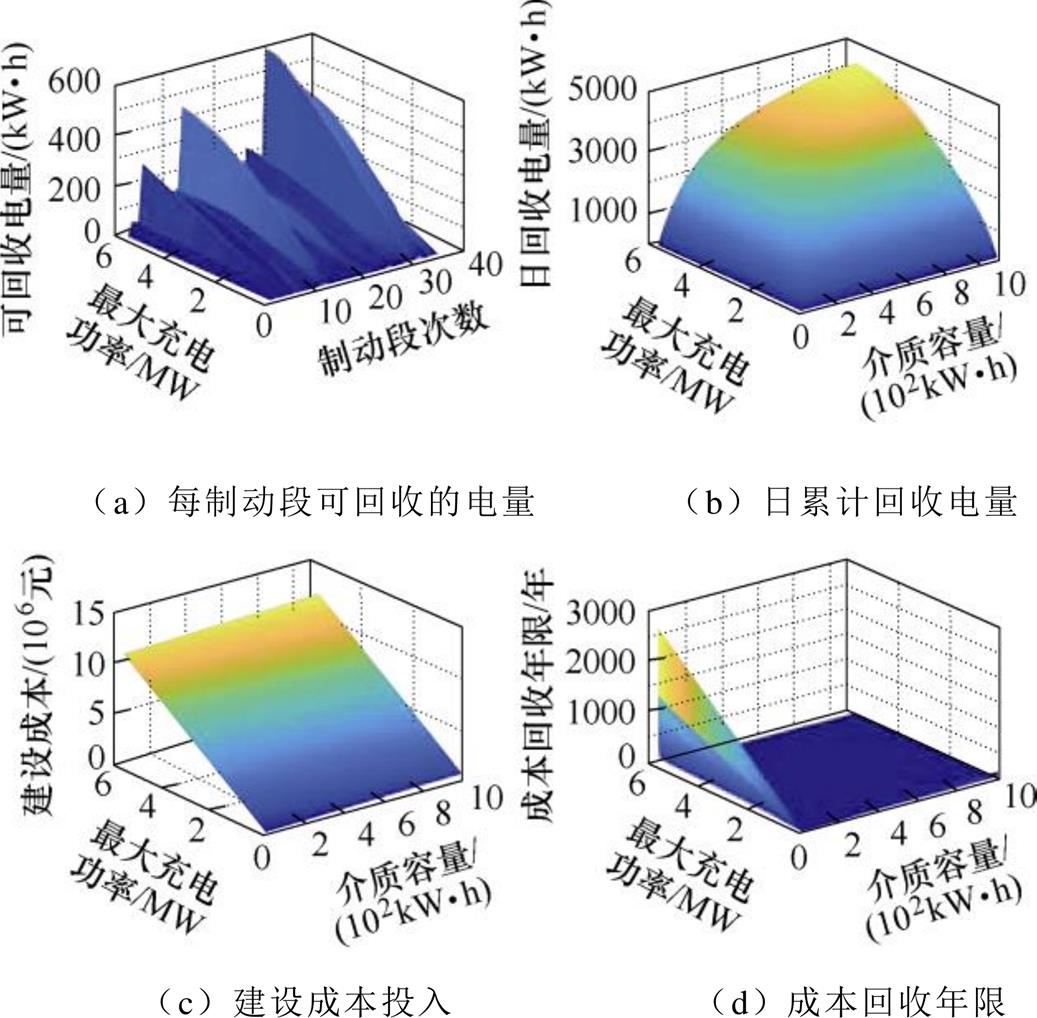
图18 方案2蓄电池计算结果
Fig.18 Scheme 2 battery calculation result
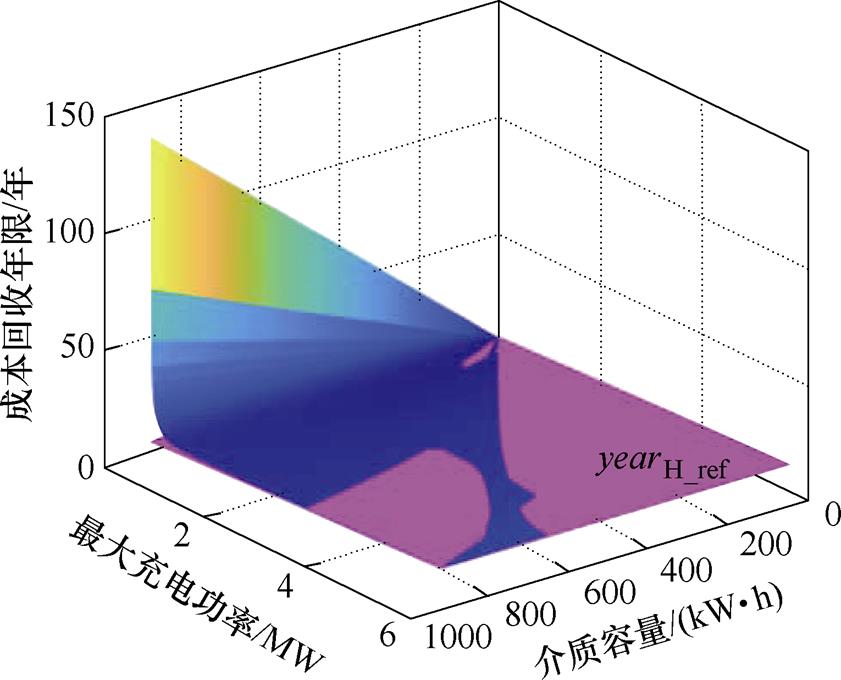
图19 方案2蓄电池取值域筛选结果及参考函数
Fig.19 Selection results of configuration range and reference function of battery in condition 2
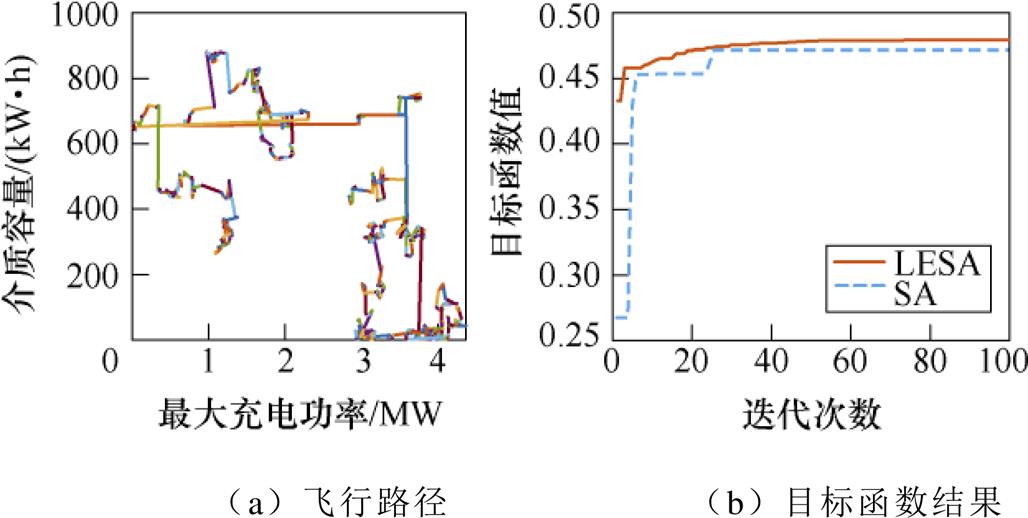
图20 方案2蓄电池求解Levy飞行路径及目标函数结果
Fig.20 Scheme 2 Levy flight path and results of objective function for battery
对比表3、表4,在有限的迭代次数下,LESA求解得到的配置方案较SA计算结果更具优势。主要表现为:在同等或更少的成本回收年限下回收更多的电量,具有更佳的经济性。
表3 混合储能系统LESA优化配置结果
Tab.3 Hybrid energy storage system optimization configuration results by LESA

项 目方案1方案2 蓄电池最大充电功率/MW3.203.89 配置容量/(kW·h)1 051681 成本回收年限/年4.419.75 日回收电量/(kW·h)9 137.093 846.89 超级电容最大充电功率/MW3.833.28 配置容量/(kW·h)172256 成本回收年限/年8.024.35 日回收电量/(kW·h)2 536.395 344.26 系统日累计回收电量/(kW·h)11 673.489 191.15
表4 混合储能系统SA优化配置结果
Tab.4 Hybrid energy storage system optimization configuration results by SA

项 目方案1方案2 蓄电池最大充电功率/MW3.183.88 配置容量/(kW·h)1 048673 成本回收年限/年4.419.76 日回收电量/(kW·h)9 099.823 829.58 超级电容最大充电功率/MW3.823.24 配置容量/(kW·h)167253 成本回收年限/年8.034.35 日回收电量/(kW·h)2 490.535 301.66 系统日累计回收电量/(kW·h)11 290.359 131.24
从表中数据可见,方案1与方案2均体现出了混合储能系统在功率、容量上的双重优势。对于列车长大坡道背景下的再生制动能量,日均回收电量达万kW·h左右,回收价值巨大。
方案1中的配置方法,虽然在成本回收年限、回收电量上较方案2有优势,但蓄电池承担了大量的充放电任务,考虑其存在衰减情况,不利于其长期使用。超级电容因均价高于蓄电池且电能回收量较少,成本回收周期长,但较现有文献中多取的15年设计寿命计算,仍可创造可观盈利。
对于方案2,主要充放电任务由超级电容承担,可减小蓄电池的储能压力及充放电循环次数,作为主要的储能角色,其成本回收年限较方案1大幅缩短。对蓄电池来讲,其作为补充储能,有利于长期使用的寿命优势。但因高功率段能量较少,故为保证充分回收能量而提高了功率配置,导致成本回收周期较方案1延长。
为避免算法存在随机性结果,以相同条件进行了20次计算,结果如图21所示。由图21可见,LESA较SA计算效果更佳、运行结果更稳定、计算效率显著提升。
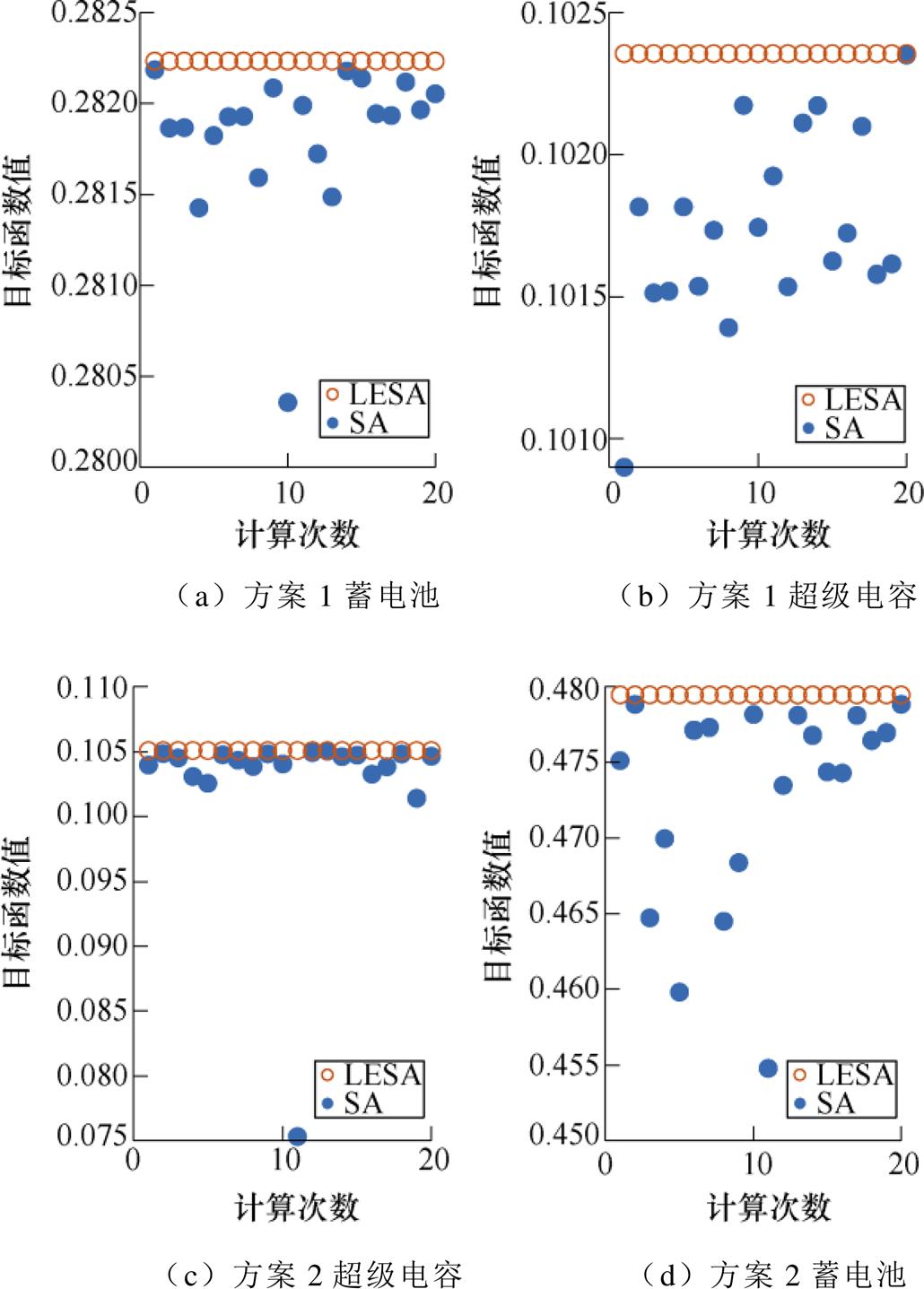
图21 LESA、SA 20次运行结果
Fig.21 Results of 20 runs of LESA and SA
本文根据高速列车及长大坡道段牵引变电所日实际运行数据,分析得到高速列车于长大坡道的再生制动能量特点为功率产生明显分层、低功率段能量十分富集。考虑选用地面式混合储能装置回收再生制动能量,在此基础上设计了分段回收配置方案,并以寿命条件对取值域进行了筛选。考虑实测数据离散的特点,选用并改进SA,以基于Levy飞行的改进模拟退火算法求解最优值,得到优化配置结果。
通过优化配置长大坡道混合储能系统,可充分利用超级电容、蓄电池的各自特点,在满足寿命的条件下,系统日可回收万kW·h制动能量,回收的电量占全日牵引耗电的16.3 %。回收利用价值极高。
基于Levy飞行的改进模拟退火算法在有限迭代次数条件下,求解结果较传统SA更优且结果稳定,一定程度上解决了原始算法的求解效率问题。在进行算法寻优前,通过图像法经大量的比较与计算得到初步配置结果,本文结果较前期在成本回收年限相近的情况下电能回收量提升10 %。
在本文优化配置过程中,蓄电池受功率成本因素、超级电容受容量成本因素的影响仍是主导经济计算的重要方面。随着储能新技术、新材料的不断发展进步,介质性能不断更新、单位成本不断降低,可回收电量将持续提升,成本回收年限将持续下降,因此也将会出现综合性能更好的储能配置方案。为利用好列车再生制动能量,在后续的研究中应考虑在交通能源互联网背景下结合其他产、用电环节甚至连接外电网对再生制动能量进行优化调度。在碳交易时代背景下,应考虑如何高效利用再生制动能量,减小发电或购电端碳权需量,甚至可以考虑通过利用列车再生制动能量为铁路或上游发电企业在碳交易中创造经济效益。
参考文献
[1] 耿安琪, 胡海涛, 张育维, 等. 基于阶梯能量管理的电气化铁路混合储能系统控制策略[J]. 电工技术学报, 2021, 36(23): 4916-4925.
Geng Anqi, Hu Haitao, Zhang Yuwei, et al. Control strategy of hybrid energy storage system for elec- trified railway based on increment energy manage- ment[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4916-4925.
[2] 胡海涛, 陈俊宇, 葛银波, 等. 高速铁路再生制动能量储存与利用技术研究[J]. 中国电机工程学报, 2020, 40(1): 246-256, 391.
Hu Haitao, Chen Junyu, Ge Yinbo, et al. Research on regenerative braking energy storage and utilization technology for high-speed railways[J]. Proceedings of the CSEE, 2020, 40(1): 246-256, 391.
[3] 李明林. 电气化铁路再生制动能量利用系统研究[D]. 成都: 西南交通大学, 2020.
[4] 刘华伟, 耿安琪, 何正友, 等. 重载铁路再生制动能量利用方案研究[J]. 电气工程学报, 2021, 16(1): 157-165.
Liu Huawei, Geng Anqi, He Zhengyou, et al. Research on energy utilization scheme of regenerative braking for heavy haul railway[J]. Journal of Elec- trical Engineering, 2021, 16(1): 157-165.
[5] 袁佳歆, 曲锴, 郑先锋, 等. 高速铁路混合储能系统容量优化研究[J]. 电工技术学报, 2021, 36(19): 4161-4169, 4182.
Yuan Jiaxin, Qu Kai, Zheng Xianfeng, et al. Opti- mizing research on hybrid energy storage system of high speed railway[J]. Transactions of China Elec- trotechnical Society, 2021, 36(19): 4161-4169, 4182.
[6] 邓文丽, 戴朝华, 韩春白雪, 等. 计及再生制动能量回收和电能质量改善的铁路背靠背混合储能系统及其控制方法[J]. 中国电机工程学报, 2019, 39(10): 2914-2924.
Deng Wenli, Dai Chaohua, Han Chunbaixue, et al. Back-to-back hybrid energy storage system of electric railway and its control method considering regen- erative braking energy recovery and power quality improvement[J]. Proceedings of the CSEE, 2019, 39(10): 2914-2924.
[7] 何棒棒, 高志宣, 马超. 一种基于储能系统的混合铁路功率调节器及其控制策略[J]. 电工技术学报, 2021, 36(23): 4905-4915.
He Bangbang, Gao Zhixuan, Ma Chao. A hybrid railway power conditioner based on energy storage system and its control strategy[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4905- 4915.
[8] 李炳元, 潘保田, 程维明, 等. 中国地貌区划新论[J]. 地理学报, 2013, 68(3): 291-306.
Li Bingyuan, Pan Baotian, Cheng Weiming, et al. Research on geomorphological regionalization of China[J]. Acta Geographica Sinica, 2013, 68(3): 291-306.
[9] 莫志松. 西部高原山区高速铁路列控系统方案探讨[J]. 中国铁路, 2021(5): 77-83.
Mo Zhisong. Discussion on train control system scheme of high speed railway in mountainous area of western plateau[J]. China Railway, 2021(5): 77-83.
[10] 邓云川, 林宗良. 川藏铁路电气化工程面临的挑战和对策思考[J]. 电气化铁道, 2019, 30(增刊1): 5-11, 15.
Deng Yunchuan, Lin Zongliang. Thoughts on challenges faced by Sichuan-Tibet railway electrification project and its solutions[J]. Electric Railway, 2019, 30(S1): 5-11, 15.
[11] 章鹏. 超长大坡道条件下西成高铁节能优化研究[D]. 成都: 西南交通大学, 2020.
[12] 乔忠伟. 西成高铁列车再生对供电系统影响及解决方案研究[D]. 西安: 西安理工大学, 2020.
[13] 吕顺凯. 电气化铁路再生制动能量利用装置节能检验与计量方案研究[J]. 铁道技术监督, 2021, 49(3): 21-25.
Lü Shunkai. Research on energy-saving inspection and metrology scheme of regenerative braking energy utilization device for electrified railway[J]. Railway Quality Control, 2021, 49(3): 21-25.
[14] 黄文勋. 复杂艰险山区列车再生制动对牵引网电压影响及相关抑制措施研究[J]. 铁道标准设计, 2020, 64(10): 143-147.
Huang Wenxun. Study on voltage rise of traction network and related restraining measures under the condition of train regenerative braking in complex and difficult mountainous area[J]. Railway Standard Design, 2020, 64(10): 143-147.
[15] 杨创, 冯鉴, 李天成, 等. 基于Simulink的高速铁路长大坡道储能系统设计[J]. 机电工程技术, 2020, 49(9): 151-153.
Yang Chuang, Feng Jian, Li Tiancheng, et al. Design of energy storage system for long steep grade of high speed railway based on Simulink[J]. Mechanical & Electrical Engineering Technology, 2020, 49(9): 151- 153.
[16] 张民, 何正友, 胡海涛, 等. 高速动车组再生制动下网侧电流谐波特性分析[J]. 电网技术, 2012, 36(9): 257-261.
Zhang Min, He Zhengyou, Hu Haitao, et al. Analysis on harmonic characteristics of grid-side current during regenerative braking of high speed train[J]. Power System Technology, 2012, 36(9): 257-261.
[17] 周琪琛, 雷杰, 杨磊. 高速列车再生制动对电能质量的影响[J]. 甘肃科技, 2019, 35(9): 53-55, 35.
Zhou Qichen, Lei Jie, Yang Lei. Influence of regenerative braking on power quality of high-speed train[J]. Gansu Science and Technology, 2019, 35(9): 53-55, 35.
[18] 黄文龙, 胡海涛, 陈俊宇, 等. 枢纽型牵引变电所再生制动能量利用系统能量管理及控制策略[J]. 电工技术学报, 2021, 36(3): 588-598.
Huang Wenlong, Hu Haitao, Chen Junyu, et al. Energy management and control strategy of regen- erative braking energy utilization system in hub traction substation[J]. Transactions of China Elec- trotechnical Society, 2021, 36(3): 588-598.
[19] Ceraolo M, Lutzemberger G, Meli E, et al. Energy storage systems to exploit regenerative braking in DC railway systems: different approaches to improve efficiency of modern high-speed trains[J]. Journal of Energy Storage, 2018, 16: 269-279.
[20] 赵乐. 基于再生制动的地铁列车时刻表优化模型与算法研究[D]. 北京: 北京交通大学, 2014.
[21] Yuksel T. A survey on energy-efficient timetable optimization model based on the utilization of regenerative braking[C]//International Symposium on Multidisciplinary Studies and Innovative Techno- logies, Kizilcahamam, 2018: 1-6.
[22] 陈启鑫, 房曦晨, 郭鸿业, 等. 储能参与电力市场机制: 现状与展望[J]. 电力系统自动化, 2021, 45(16): 14-28.
Chen Qixin, Fang Xichen, Guo Hongye, et al. participation mechanism of energy storage in elec- tricity market: status quo and prospect[J]. Automation of Electric Power Systems, 2021, 45(16): 14-28.
[23] 安秋颖. 城市轨道交通供电系统再生制动能量回收装置节能影响因素分析[J]. 铁道车辆, 2021, 59(1): 31-34, 116.
An Qiuying. Analysis of affecting factors of energy saving of regenerative braking energy recovery device in power supply system for urban rail transit[J]. Rolling Stock, 2021, 59(1): 31-34, 116.
[24] 毕文骏. 基于飞轮储能的地铁再生制动能量利用研究[D]. 成都: 西南交通大学, 2016.
[25] 申宁, 石广保, 陈亮. 储能型再生制动能量吸收装置在青岛地铁的应用[J]. 自动化应用, 2020(9): 25-27.
Shen Ning, Shi Guangbao, Chen Liang. Application of energy storage type regenerative braking energy absorber in Qingdao metro[J]. Automation Appli- cation, 2020(9): 25-27.
[26] Kaleybar H J, Brenna M, Foiadelli F, et al. Regen- erative braking energy and power quality analysis in 2×25 kV high-speed railway lines operating with 4QC locomotives[C]//Power Electronics, Drive Systems, and Technologies Conference, Tehran, 2020: 1-6.
[27] 贺启甫. 电气化铁路再生储能系统经济最优化运行方案研究[D]. 成都: 西南交通大学, 2020.
[28] 刘方中. 长大坡道储能型列车再生制动能量利用方案研究[J]. 电气化铁道, 2020, 31(5): 27-31.
Liu Fangzhong. Research on energy utilization scheme of regenerative braking for energy storage trains on tracks with long steep gradient[J]. Electric Railway, 2020, 31(5): 27-31.
[29] 魏文婧. 高速铁路再生制动能量存储与利用控制策略研究[D]. 成都: 西南交通大学, 2019.
[30] 王慧娟. 超级电容器—蓄电池混合储能系统容量优化配置方法研究[D]. 北京: 华北电力大学, 2017.
[31] 马超, 董森, 华正操. 多种光伏组件组合光伏电站的混合储能容量优化配置研究[J]. 天津大学学报(自然科学与工程技术版), 2020, 53(11): 1128-1135.
Ma Chao, Dong Sen, Hua Zhengcao. Capacity configuration of hybrid energy storage system for PV power stations using multiple solar trackers[J]. Journal of Tianjin University(Science and Tech- nology), 2020, 53(11): 1128-1135.
[32] 郭玲娟, 魏斌, 韩肖清, 等. 基于集合经验模态分解的交直流混合微电网混合储能容量优化配置[J]. 高电压技术, 2020, 46(2): 527-537.
Guo Lingjuan, Wei Bin, Han Xiaoqing, et al. Capacity optimal configuration of hybrid energy storage in hybrid AC/DC micro-grid based on ensemble empi- rical mode decomposition[J]. High Voltage Engin- eering, 2020, 46(2): 527-537.
[33] 杨宏伟. 基于混合储能的电气化铁路再生制动能量存储策略研究[D]. 兰州: 兰州交通大学, 2020.
[34] 李彦苍, 赵丽娜. 离散变量结构优化方法研究现状及趋势[J]. 河北工程大学学报(自然科学版), 2011, 28(4): 22-26.
Li Yancang, Zhao Lina. Current research and trends of structural optimization with discrete variables[J]. Journal of Hebei University of Engineering (Natural Science Edition), 2011, 28(4): 22-26.
[35] 张园. 基于进化多目标优化的智能拟合方法[D]. 西安: 西安电子科技大学, 2018.
[36] 陈华根, 吴健生, 王家林, 等. 模拟退火算法机理研究[J]. 同济大学学报(自然科学版), 2004(6): 802-805.
Chen Huagen, Wu Jiansheng, Wang Jialin, et al. Mechanism study of simulated annealing algorithm[J]. Journal of Tongji University (Natural Science), 2004(6): 802-805.
[37] 肖晓伟, 肖迪, 林锦国, 等. 多目标优化问题的研究概述[J]. 计算机应用研究, 2011, 28(3): 805-808, 827.
Xiao Xiaowei, Xiao Di, Lin Jinguo, et al. Overview on multi-objective optimization problem research[J]. Application Research of Computers, 2011, 28(3): 805-808, 827.
[38] 朱颢东, 钟勇. 一种改进的模拟退火算法[J]. 计算机技术与发展, 2009, 19(6): 32-35.
Zhu Haodong, Zhong Yong. A kind of renewed simulated annealing algorithm[J]. Computer Tech- nology and Development, 2009, 19(6): 32-35.
[39] 杨若黎, 顾基发. 一种高效的模拟退火全局优化算法[J]. 系统工程理论与实践, 1997, 17(5): 29-35.
Yang Ruoli, Gu Jifa. An efficient simulated annealing algorithm for global optimization[J]. Systems Engin- eering-Theory & Practice, 1997, 17(5): 29-35.
[40] 张九龙, 王晓峰, 芦磊, 等. 改进的模拟退火算法求解规则可满足性问题[J]. 现代电子技术, 2022, 45(5): 122-128.
Zhang Jiulong, Wang Xiaofeng, Lu Lei, et al. Improved simulated annealing algorithm for regular satisfiability problem[J]. Modern Electronics Tech- nique, 2022, 45(5): 122-128.
[41] Tang Lianfu, Wu Lixin. Research on the integrated braking energy recovery strategy based on super- capacitor energy storage[C]//International Conference on Smart Grid and Electrical Automation, Changsha, 2017: 175-178.
[42] 娄素华, 罗鹏, 吴耀武, 等. 计及负荷可控性的微网储能容量优化配置[J]. 电工技术学报, 2016, 31(21): 39-45.
Lou Suhua, Luo Peng, Wu Yaowu, et al. Sizing of energy storage in microgrid with controllable load[J]. Transactions of China Electrotechnical Society, 2016, 31(21): 39-45.
[43] 郭明萱, 穆云飞, 肖迁, 等. 考虑电池寿命损耗的园区综合能源电/热混合储能优化配置[J]. 电力系统自动化, 2021, 45(13): 66-75.
Guo Mingxuan, Mu Yunfei, Xiao Qian, et al. Optimal configuration of electric/thermal hybrid energy storage for park-level integrated energy system con- sidering battery life loss[J]. Automation of Electric Power Systems, 2021, 45(13): 66-75.
[44] 张前图, 房立清, 赵玉龙. 具有Levy飞行特征的双子群果蝇优化算法[J]. 计算机应用, 2015, 35(5): 1348-1352.
Zhang Qiantu, Fang Liqing, Zhao Yulong. Double subgroups fruit fly optimization algorithm with characteristics of Levy flight[J]. Journal of Computer Applications, 2015, 35(5): 1348-1352.
[45] 王庆喜, 郭晓波. 基于莱维飞行的粒子群优化算法[J]. 计算机应用研究, 2016, 33(9): 2588-2591.
Wang Qingxi, Guo Xiaobo. Particle swarm opti- mization algorithm based on Levy flight[J]. Appli- cation Research of Computers, 2016, 33(9): 2588- 2591.
Abstract High-speed railway trains will generate a large amount of regenerative braking energy and send it back to the traction network when they pass through the long ramp section, which will cause the voltage uplift of the traction network, harm traffic safety, and even cause economic losses to the railway enterprises. If this energy is reasonably recycled, it will be beneficial to reduce the energy consumption of high-speed rail, low-carbon transportation, energy conservation, and emission reduction, and achieve the ‘3060’ dual carbon target, which is more conducive to train safety. Studies have shown that it is a good method to recover regenerative braking energy by ground hybrid energy storage system, but it needs to be reasonably configured. Therefore, this paper presents a segmented configuration scheme and capacity optimization model for a hybrid energy storage system. The improved simulated annealing algorithm based on Levy flight (LESA) is used to optimize the capacity of the hybrid energy storage system on a long ramp of a high-speed railway.
Firstly, the characteristics of regenerative braking power are analyzed from each and all day respectively. On this basis, considering the capacity requirements of the energy storage system, the energy is combined with the same type in chronological order to form the action segment, analyze the feasibility of the utilization of regenerative braking energy, and determine the recovery range. Accordingly, considering the respective characteristics of different media of the hybrid energy storage system, the energy recovery method with the threshold Pth as the boundary condition is formulated, the segmented configuration scheme of the hybrid energy storage system is established, and the economic indicators are calculated. Secondly, in the aspect of optimization algorithm, because the traditional simulated annealing algorithm (SA) has low efficiency, Levy flight is used to generate the initial solution, and it is constantly memorized and updated in the process of algorithm solution. An improved simulated annealing algorithm based on Levy flight (LESA) is proposed. This method can reduce the number of times to enter the Metropolis criterion, and is closer to the optimal solution under a limited number of iterations, improving the efficiency of the algorithm. Finally, according to the actual operation data of a long steep slope of Xi'an-Chengdu high-speed railway, two kinds of configuration schemes are analyzed.
The analysis results of regenerative braking power show that the single braking power is low and has small fluctuation. Moreover, in the analysis of the whole day conditions, the power curve has obvious stratification, and the energy of the low-power section is more enriched than the high-power section. In the feasibility analysis of regenerative braking energy utilization, a total of 36 braking sections and 36 traction sections were obtained. The first 35 times were included in the configuration calculation range considering the discharge demand. According to the actual operation data, through the given configuration scheme, optimization model, and LESA algorithm, the results of optimal configuration are obtained: Scheme 1 of recovering low-power energy with battery, the daily cumulative recovery power reaches 1 1673.48 kW·h; scheme 2 of recovering low-power energy with supercapacitors has a daily cumulative recovery of 9 191.15 kW·h. The configuration results obtained by the LESA algorithm are better than the 11 290.35 kW·h and 9 131.24 kW·h calculated by the SA algorithm.
The improved simulated annealing algorithm based on the Levy flight presented in this paper has better and more stable results than the traditional SA under the finite number of iterations, which solves the solving efficiency problem of the original algorithm to a certain extent. After optimized configuration, the hybrid energy storage system can recover a large amount of regenerative braking energy during its life, and the recovered electricity accounts for 16.3 % of the traction power consumption, which has a high recycling significance.
keywords:High-speed rail long steep slope, regenerative braking energy, hybrid energy storage system, capacity optimized configuration, improved simulated annealing algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.221199
中图分类号:TM922.3
国家自然科学基金(51767015)、甘肃省科技计划即甘肃省自然科学基金(22JR5RA317)、兰州交通大学“天佑创新团队”支持计划(TY202009)和甘肃省教育厅:优秀研究生“创新之星”(2022CXZX-609)资助项目。
收稿日期 2022-06-22
改稿日期 2022-07-30
李 欣 男,1978年生,博士,教授,研究方向为电气化交通与能源融合、非接触供电。E-mail: lxfp167@163.com(通信作者)
卢景涛 男,1998年生,硕士研究生,研究方向为电气化交通与能源融合。E-mail: lujingtao0722@163.com
(编辑 陈 诚)