（1）
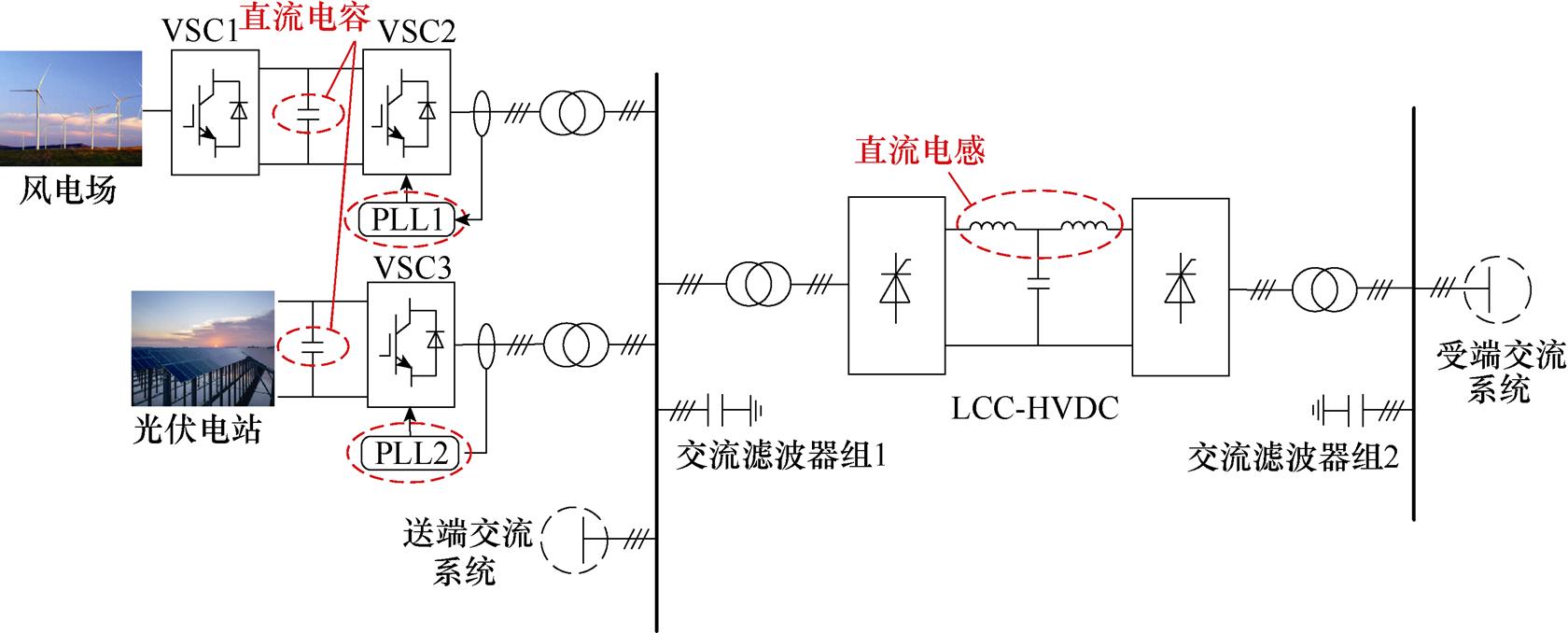
图1 新能源经LCC-HVDC送出系统结构
Fig.1 Structure diagram of renewable energy power generation integrated with LCC-HVDC system
摘要 大规模新能源通过电网换相型高压直流输电（LCC-HVDC）送出时，新能源发电设备的电压源换流器（VSC）与LCC-HVDC之间的交互作用存在诱发次同步振荡（SSO）的风险，因此迫切需要开展相关研究。该文提出一种阻尼路径分析法，研究新能源经LCC-HVDC送出系统的次同步交互作用。阻尼路径能够清楚地显示次同步频率扰动的传递过程，揭示系统内的次同步交互作用。根据扰动通过设备的不同，阻尼路径可分为三类，分别反映设备内部的阻尼作用以及不同设备之间的次同步交互作用。通过阻尼重构，可得到每条路径的阻尼，并使用类Heffron- Phillips模型中的阻尼系数对路径阻尼进行定量评估，从而达到分析次同步交互作用对SSO模式阻尼影响的目的。最后以直驱风电场经LCC-HVDC送出系统为算例，验证了阻尼路径分析法的有效性。
关键词：新能源发电 LCC-HVDC 次同步交互作用 阻尼路径 阻尼重构
在我国，风电、光伏发电等大型新能源多分布在西北部地区，离负荷中心较远，多和当地的常规电源一起经电网换相型高压直流输电（Line- Commutated Converter-Based High Voltage Direct Current, LCC-HVDC）送出[1-2]。为早日实现“双碳”目标规划，近年来，我国新能源发电的装机容量增长迅速[3]，并且其占比的增加削弱了送端常规电源的支撑能力，导致新能源发电设备的电压源换流器（Voltage Source Converter, VSC）与LCC-HVDC之间的交互作用增强，并且这种交互作用存在诱发次同步振荡（Sub-Synchronous Oscillation, SSO）的风险[4]。因此，新能源发电经LCC-HVDC送出系统的次同步交互作用问题亟待研究。
现有研究主要采用阻抗分析法[5-8]或特征值分析法[8-11]研究新能源经LCC-HVDC送出系统的SSO特性。文献[11-12]分别建立了直驱风电场和双馈风电场经LCC-HVDC送出系统的小信号模型，并进行了特征值和参与因子分析。文献[13]通过谐波线性化方法分别建立了直驱风电机组、LCC-HVDC和静止同步补偿器（Static Synchronous Compensator, STATCOM）的正序和负序阻抗模型，并使用阻抗稳定性准则分析了系统的稳定性。文献[14]解析推导了LCC-HVDC和直驱风电机组的谐波阻抗模型，并使用奈奎斯特曲线判断系统的稳定性。可以看出，现有研究大多是判断系统的SSO稳定性，或是分析系统参数和运行状态对SSO稳定性的影响，而很少对系统内部的次同步交互作用展开分析。
然而，特征值分析法和阻抗分析法难以分析系统内的次同步交互作用。特征值分析法可以给出SSO模式的主要参与变量，但作为一种数学分析方法，很难从物理层面上揭示系统的次同步交互作 用[15]。阻抗分析法物理意义清晰，能够在物理层面上对SSO产生机理进行解释，并且可以对“黑（灰）箱”系统进行建模；然而，仅通过分析设备的外部阻抗特性，很难清楚地揭示系统内的次同步交互作用[16]。因此，有必要在物理层面上，从新的角度对次同步交互作用进行分析。
当系统发生SSO时，分析次同步频率扰动的传递过程可以清楚地揭示系统内的次同步交互作 用[17-18]。次同步频率扰动的传递过程具有明确的物理意义，可以揭示扰动在各种设备和环节中的传播路径，从而清晰直观地显示SSO特性的主要影响环节，揭示系统的次同步交互作用。考虑到特征值分析法和阻抗分析法的局限性，本文选择使用传递函数框图分析系统的扰动传递过程。传递函数框图可以清楚地显示设备内的各个环节，便于对扰动传递过程的分析。此外，基于闭环传递函数框图，可以将扰动的传递过程以“路径”的形式展现，从而直观地显示各个环节之间以及各设备之间的交互作用。由于传递函数可以表示扰动传递过程的阻尼[19]，因此本文将该“路径”称为“阻尼路径”。
为了分别分析每条阻尼路径对系统总阻尼的影响，本文选择利用阻尼转矩法[20-21]来定量评估路径阻尼。阻尼转矩法将所研究元件的动态过程推导为同步机转子Heffron-Phillips模型的形式[20]，从而利用阻尼系数等参数定量评估SSO模式的阻尼。文献[20-21]类比Heffron-Phillips模型建立了并网VSC的小信号模型，并进行稳定性分析。文献[22-23]利用阻尼转矩法分别建立了LCC-HVDC和双馈风电机组的小信号模型。文献[24]则利用阻尼转矩法分析了并网VSC电流内环对直流电压环节稳定性的影响。阻尼转矩法具有明确的物理意义，得到的模型形式上和同步机转子Heffron-Phillips模型非常相似，因此能够运用类似的方法分析系统的稳定性[20]。
在本文的研究中，需要分析每条阻尼路径的阻尼特性，因此，有必要重构闭环传递函数框图，以便将系统的总阻尼分离到每条阻尼路径中，本文称之为“阻尼重构”。然后，利用阻尼系数对每条路径的阻尼进行评估。将阻尼转矩法和阻尼路径、阻尼重构相结合是本文相较于文献[19-22]最大的创新之处：阻尼路径以一种新的方式分析系统的次同步交互作用，阻尼重构能够分离出每条阻尼路径的阻尼，最后应用阻尼转矩法定量评估每条路径的阻尼。阻尼转矩法、阻尼路径和阻尼重构三者相辅相成，相互补充，共同实现对次同步交互作用的分析。
对于新能源经LCC-HVDC送出系统，存在多种SSO模式，包括VSC的直流电容SSO模式和锁相环（Phase Locked Loop, PLL）SSO模式，以及LCC-HVDC的直流电感SSO模式[21-25]。通常，系统中最容易失稳的模式称为主导模式。在不同的系统参数和运行条件下，主导模式也会发生变化。因此，本文根据不同参数或运行条件下的主导模式，推导不同振荡主导元件的类Heffron-Phillips模型，从而可以利用系统闭环传递函数和阻尼重构法分析不同SSO模式的阻尼路径和阻尼特性。
本文提出了一种阻尼路径分析法，用于研究新能源经LCC-HVDC送出系统的次同步交互作用。首先，利用阻尼转矩法，建立了反映VSC的直流电容、PLL，以及LCC-HVDC的直流电感动态特性的类Heffron-Phillips模型；其次，基于上述模型，推导了系统的闭环传递函数框图，以揭示子系统之间的耦合关系，并获得了SSO模式的三种阻尼路径；然后，对闭环传递函数框图进行阻尼重构，分离出每条路径的阻尼，从而进行路径阻尼特性分析；最后，以直驱风电场经LCC-HVDC送出系统为例，分析了直流电感SSO模式下的阻尼路径和路径阻尼特性，验证了该方法的有效性。
新能源经LCC-HVDC送出系统的结构如图1所示。新能源发电场，如风电场和光伏电站，和当地常规电源（等效为送端交流系统）一同经LCC- HVDC送到负荷中心（等效为受端交流系统）。
如图1所示，系统主要包括以下两种电力电子设备：VSC（直驱风机、双馈风机、光伏）和晶闸管换流器（LCC-HVDC）。在VSC中，直流电容器和PLL是次同步频带中的主要元件；在晶闸管换流器中，直流电感是次同步频带的主要元件。这三种元件分别主导一种SSO模式。上述元件在图1中用（红色）椭圆虚线标出。为了分析由上述三种元件主导的SSO模式的特性，推导了它们的动态方程，得到对应的二阶运动方程，并与Heffron-Phillips模型进行类比，得到它们的类Heffron-Phillips模型。
直流电容的动态过程如图2所示。Pin和Pe分别是机侧换流器（Machine Side Converter, MSC）的输出功率和网侧换流器（Grid Side Converter, GSC）的输入功率，C为直流电容，Udc为直流电容电压。
直流电容的动态方程为
（1）
图1 新能源经LCC-HVDC送出系统结构
Fig.1 Structure diagram of renewable energy power generation integrated with LCC-HVDC system
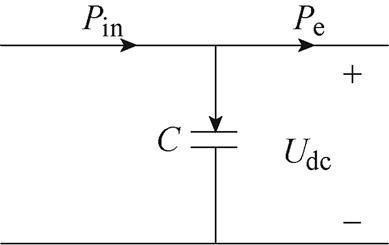
图2 直流电容动态过程
Fig.2 Dynamic of DC-link capacitor
式中，D 表示对应变量的小扰动信号；Udc0为稳定工作点处的直流电容电压；Dxdc=DUdc/s；Gdc(s)为从Dxdc到DPe的开环传递函数。
在频率w 上，算子s=jw，可将Gdc(s)表示为
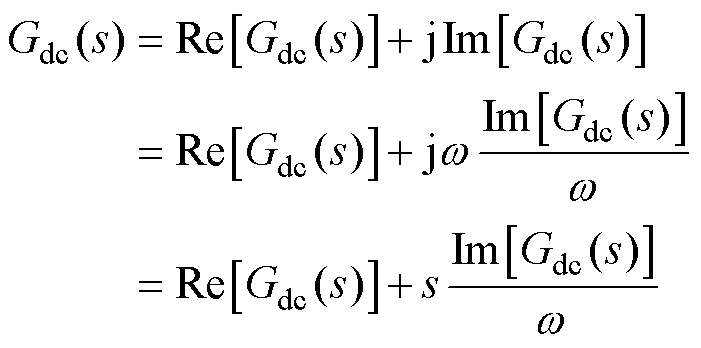（2）
当MSC的输出功率维持恒定时，DPin=0。将式（2）代入式（1），可以得到直流电容的二阶运动方程为
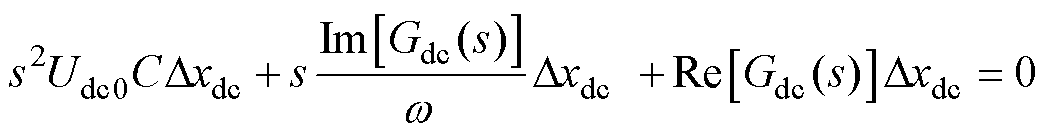（3）
直流电感的动态过程如图3所示。Pr和Pdc分别是交流系统的输出功率和直流线路上的功率，Lr为直流电感，Idcr是流经直流线路的电流。直流电感的动态方程为
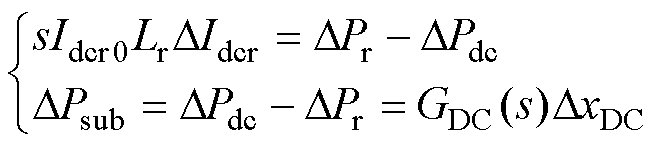（4）
式中，Idcr0为稳定工作点处的直流线路电流，DxDC= DIdcr/s；GDC(s)为从DxDC到DPsub的开环传递函数。
通过类比直流电容的推导过程，可以得到直流电感的二阶运动方程为
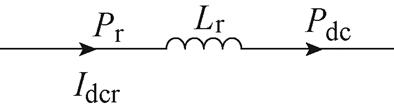
图3 直流电感动态过程
Fig.3 Dynamic of DC-link inductor
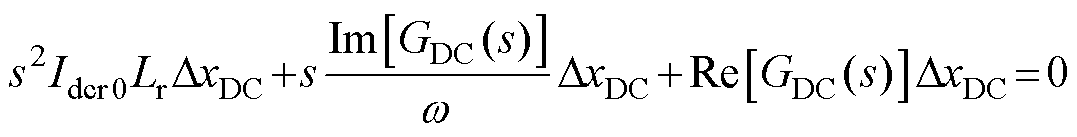（5）
锁相环的动态过程如图4所示。图中，U为锁相电压，Ud和Uq是U的dq轴分量；KP和KI分别为PLL的PI控制器比例系数和积分系数；wpll、qpll分别为PLL输出的角频率和锁相角。
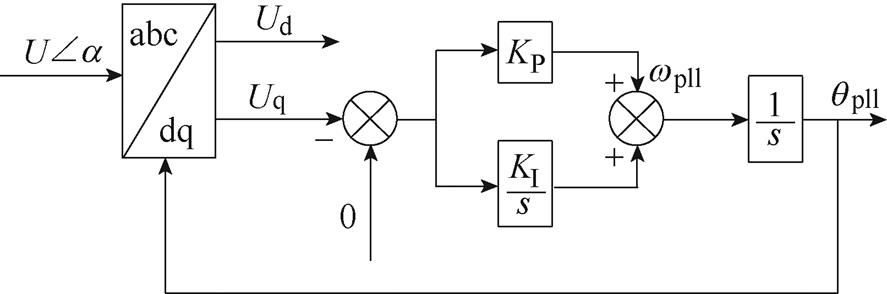
图4 PLL动态过程
Fig.4 Dynamic of PLL
PLL的动态方程线性化为
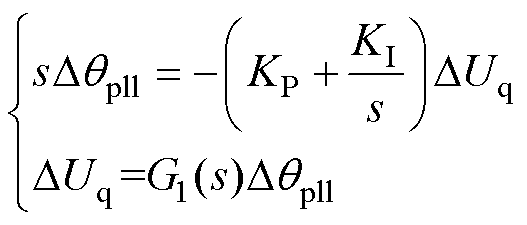（6）
式中，G1(s)为锁相角qpll到DUq的开环传递函数。
对式（6）进行推导，可得
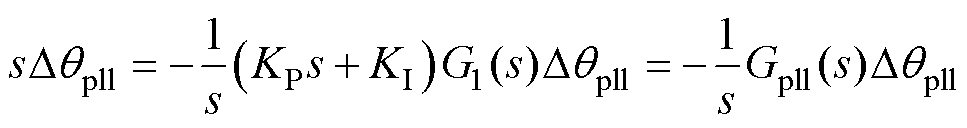（7）
式（7）可以推导为s2Dqpll+Gpll(s)Dqpll=0的形式。通过类比直流电容的推导过程，可以得到PLL的二阶运动方程为
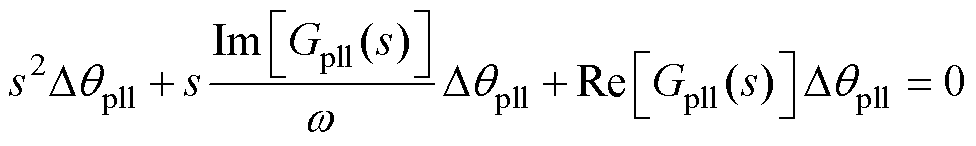（8）
根据式（3）、式（5）、式（8），直流电容、直流电感和PLL的动态方程与式（9）所示的二阶运动方程具有相同的形式。
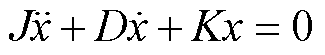（9）
式中，
、
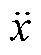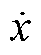和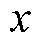
分别为惯性元件状态变量的加速度、速度和位移。J、D和K分别为元件的等效惯性、等效阻尼系数和等效同步系数。当判别式D= D2-4JK＜0时，认为相应元件主导了一种SSO模式。式（9）的特征值为
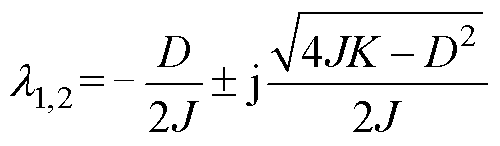（10）
根据特征值的实部，当等效阻尼系数D＞0时，SSO模式是稳定的；当D＜0时，SSO模式不稳定，系统在该SSO模式下表现为负阻尼，且D越小，负阻尼作用越强。
通过类比Heffron-Phillips模型，可得式（9）对应的频域小信号模型，如图5所示，并将其称为类Heffron-Phillips模型。
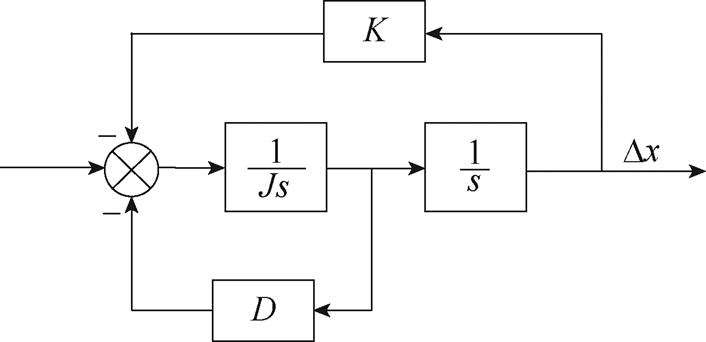
图5 类Heffron-Phillips模型
Fig.5 Heffron-Phillips-like model
直流电容、直流电感和PLL对应的状态变量、等效惯量、等效阻尼系数和等效同步系数见表1。从表1可以看出，直流电容和直流电感的等效惯量与稳态工作点、元件参数有关。每个元件的等效阻尼系数和等效同步系数主要受外部传递函数的频域特性影响。由此，可利用元件的类Heffron-Phillips模型对其主导振荡模式的稳定性进行分析。
表1 振荡主导元件等效系数
Tab.1 Equivalent coefficient of SSO dominant elements
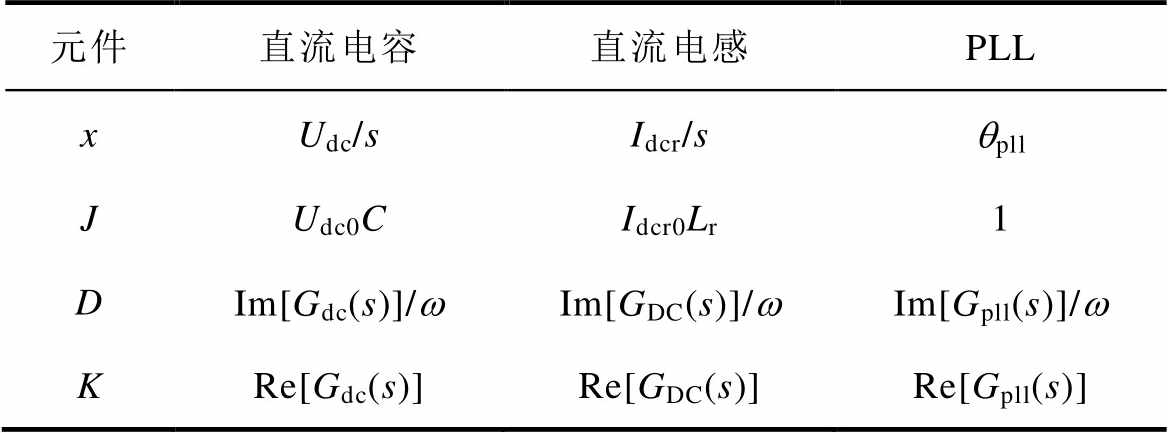
元件直流电容直流电感PLL xUdc/sIdcr/sqpll JUdc0CIdcr0Lr1 DIm[Gdc(s)]/wIm[GDC(s)]/wIm[Gpll(s)]/w KRe[Gdc(s)]Re[GDC(s)]Re[Gpll(s)]
值得说明的是，本文推导的类Heffron-Phillips模型与同样运用阻尼转矩法的文献存在不同。文献[20-24]在推导设备的运动方程时，针对具体的系统结构以及控制策略进行小信号模型的推导。而本文考虑到实际的新能源经LCC-HVDC送出系统的控制策略和系统结构不同，在推导三种振荡主导元件的二阶运动方程时，并未针对具体的系统结构以及控制策略，而是将外部系统用一个传递函数表示，从而得到三种元件结构相同的类Heffron-Phillips模型，并将具体的传递函数推导放在后文的阻尼路径推导过程中。按照本文的处理方法，针对不同系统，振荡主导元件的类Heffron-Phillips模型是相同的，不同之处仅体现在阻尼路径推导部分，便于本文的方法在其他系统的应用。
本节基于第1节中得到的类Heffron-Phillips模型建立研究系统的闭环传递函数框图，以分析系统的阻尼路径。
参考新能源经LCC-HVDC送出系统的工程实际场景，假设系统中存在一个新能源发电厂，该发电厂具有相同参数和运行状态的相同类型新能源发电设备，并与当地常规电源（等效为交流系统）一起经LCC-HVDC送出。需要说明的是，由于新能源发电设备主要是通过并网VSC与外部系统进行交互作用[20]，因此，本文在介绍阻尼路径分析法时，以并网VSC模型表示新能源发电设备。
本节中，在建立系统闭环传递函数框图时，LCC-HVDC围绕直流电感的动态过程进行建模，VSC围绕直流电容的动态过程进行建模。围绕PLL进行建模的VSC传递函数框图与围绕直流电容进行建模时具有相同的结构，本节将不再展开介绍。
根据式（1），直流电容的动态方程可以表示为
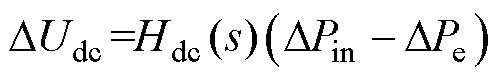（11）
其中，Hdc(s)的表达式为
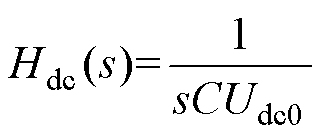（12）
围绕直流电容的动态过程，在交流系统xy坐标系中对VSC进行建模。VSC设备的电磁功率可以表示为
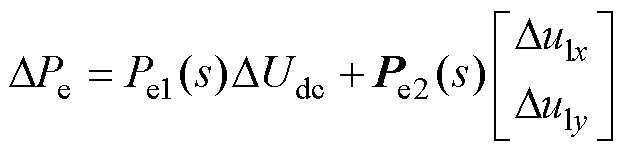（13）
式中，Pe1(s)为直流电容电压DUdc到DPe的开环传递函数；Pe2(s)为输入电压Dul到DPe的开环传递函数矩 阵，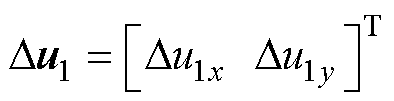
。
VSC的输出电流Dil可以表示为
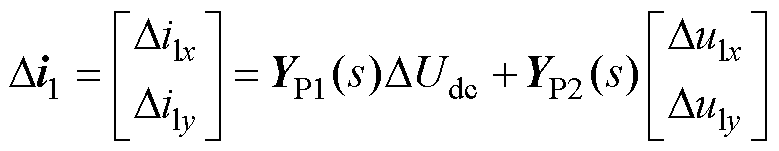（14）
式中，YP1(s)和YP2(s)分别为直流电容电压DUdc和输入电压Dul到输出电流Dil的开环传递函数矩阵。
系统闭环的传递函数框图如图6所示。根据式（11）、式（13）和式（14），VSC的传递函数框图如图6中的左侧点画线框内部分所示。VSC的输入为端口电压的x、y轴分量，输出为线路电流的x、y轴分量。
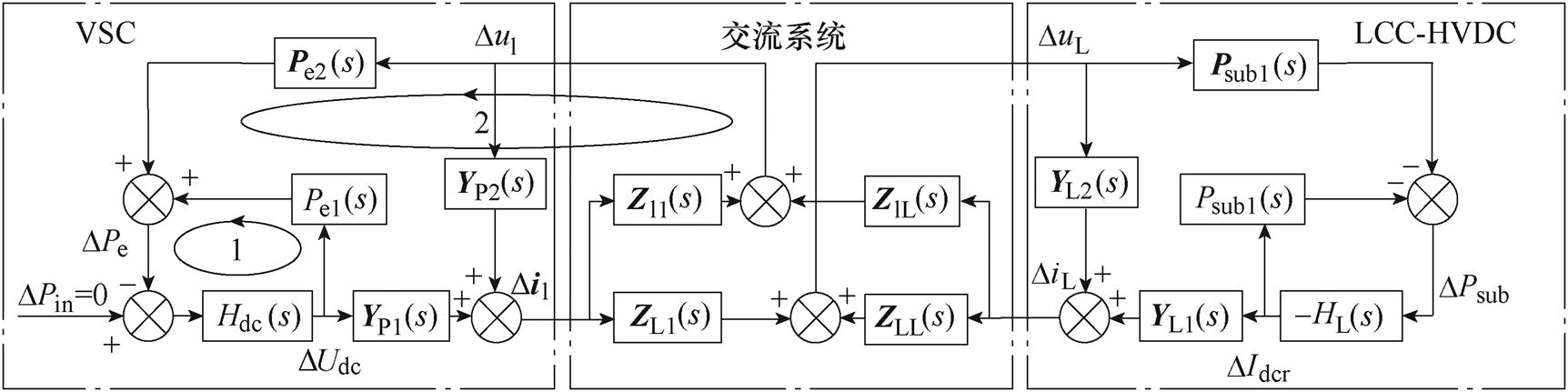
图6 系统闭环传递函数框图
Fig.6 System closed-loop transfer function block diagram
根据式（4），直流电感的动态方程可以表示为
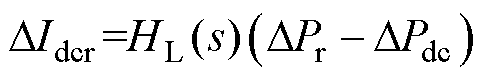（15）
式中，HL(s)的表达式为
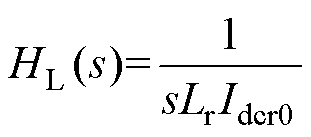（16）
围绕直流电感的动态过程，在交流系统的xy坐标系中对LCC-HVDC进行建模。直流功率DPdc减去交流系统功率DPr之差DPsub可表示为
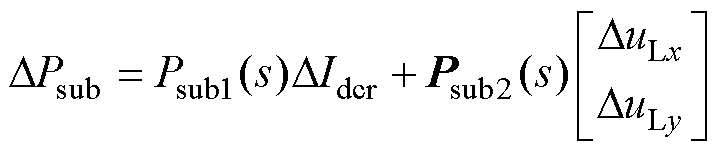（17）
式中，Psub1(s)和Psub2(s)分别为直流电流DIdcr和输入电压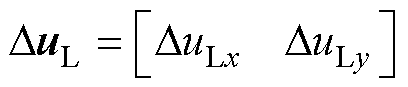
到DPsub的开环传递函数和传递函数矩阵。
LCC-HVDC系统的输出电流DiL可表示为
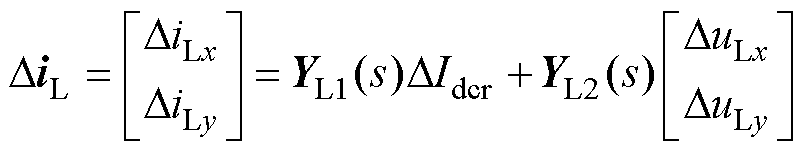（18）
式中，YL1(s)和YL2(s)分别为直流电流DIdcr和输入电压DuL到输出电流DiL的开环传递函数矩阵。
根据式（15）、式（17）和式（18），可得LCC-HVDC的传递函数框图，如图6中右侧点画线框内的部分所示。LCC-HVDC的输入是整流侧交流母线电压的x、y轴分量，输出是整流侧交流电流的x、y轴分量。
在对交流系统建模时，考虑到其与VSC和LCC-HVDC的外部接口特性，可得动态方程为
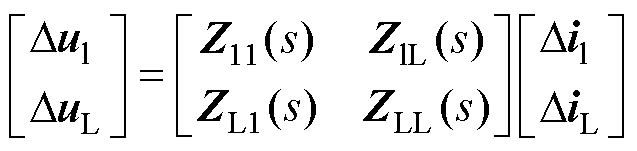（19）
式中，Dul、DuL、Dil和DiL为二维向量；Zll、ZlL、ZLl和ZLL为二阶矩阵，为从相应电流到电压的开环传递函数矩阵。
根据式（19），可以得到交流系统的传递函数框图，如图6中中间框内的部分所示。
将VSC、LCC-HVDC和交流系统的传递函数框图按照接口连接，可得系统的闭环传递函数框图，如图6所示。图6清楚地显示了次同步频率扰动的传递过程。基于闭环传递函数框图，将经过SSO主导元件形成的回路定义为次同步扰动传递的阻尼路径。以VSC直流电容主导的SSO模式为例，从图6中可以看出，在该SSO模式中，系统存在两条阻尼路径（阻尼路径1和2），并在图中用椭圆形实线标示。阻尼路径1形成在VSC内部，仅与其自身参数相关；阻尼路径2形成于VSC、交流系统以及LCC-HVDC之间，表征了设备之间的次同步交互作用。
从图6可以看出，阻尼路径1揭示了VSC的一次系统和控制器对SSO模式阻尼的影响。根据扰动是否通过LCC-HVDC，阻尼路径2可分为两类：①VSC的输出Di1通过交流系统直接影响其自身的输入Du1，反映了VSC和交流系统之间的交互作用对SSO模式阻尼的影响；②VSC的输出Di1通过交流系统影响LCC-HVDC的输入DuL，从而导致LCC- HVDC的输出DiL产生扰动，并通过交流系统对VSC输入Du1产生扰动；在扰动传递过程中，扰动通过VSC、交流系统、LCC-HVDC、交流系统，最后返回VSC，形成闭合路径，因此，该阻尼路径反映了VSC和LCC-HVDC之间的交互作用对SSO模式阻尼的影响。
综上所述，VSC的SSO模式阻尼由上述三种阻尼路径提供。将上述结论推广到电力电子设备中，可以得到三类阻尼路径的一般结论，并总结于表2中。除了VSC直流电容SSO模式外，VSC的PLL主导的SSO模式和LCC-HVDC的直流电感主导的SSO模式也可以利用本节中的方法分析阻尼路径，只需替换电力电子设备的模型。
表2 三类阻尼路径
Tab.2 Three kinds of damping paths
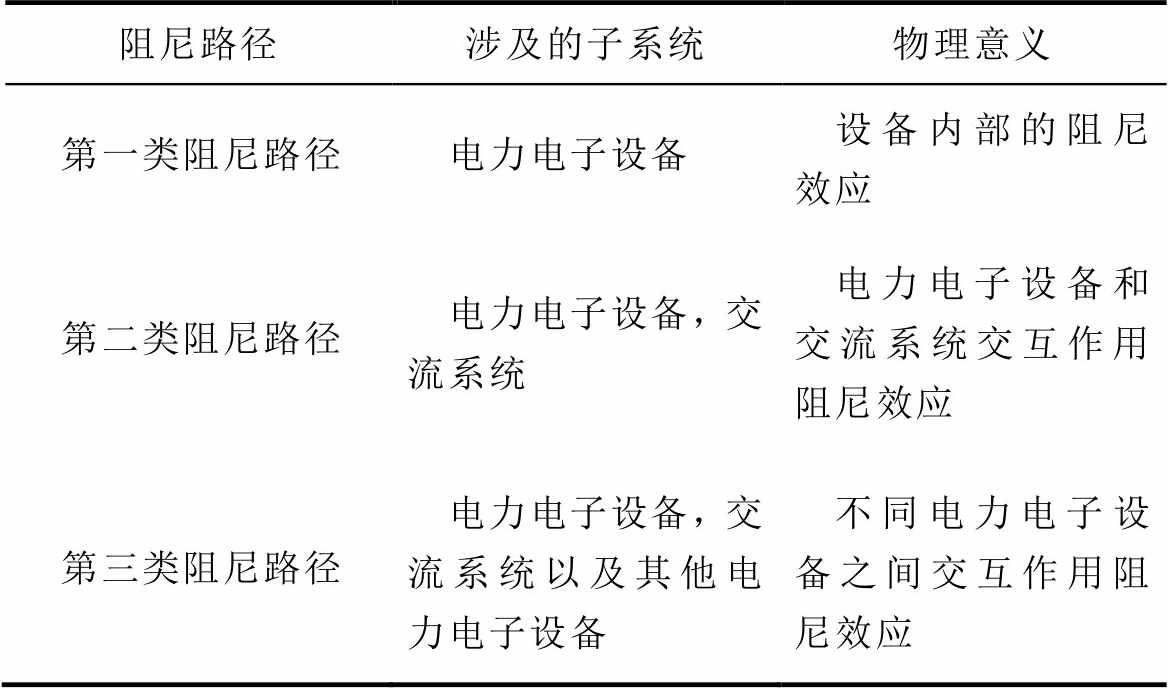
阻尼路径涉及的子系统物理意义 第一类阻尼路径电力电子设备设备内部的阻尼效应 第二类阻尼路径电力电子设备，交流系统电力电子设备和交流系统交互作用阻尼效应 第三类阻尼路径电力电子设备，交流系统以及其他电力电子设备不同电力电子设备之间交互作用阻尼效应
在第2节中，初步推导了系统的三条阻尼路径，为了进一步对路径的阻尼进行定量分析，需要进行“阻尼重构”过程，即对闭环传递函数框图进行推导、变形，得到每条阻尼路径的传递函数表达式。为了能够利用阻尼系数评估SSO模式的阻尼，需要将系统的两输入两输出传递函数矩阵转换为单输入单输出传递函数，其中输入变量为DUdc，输出变量为DPe。
对于图6所示的闭环传递函数框图，第一类阻尼路径提供的阻尼可从传递函数Pe1(s)获得。阻尼路径2可细分为第二类和第三类阻尼路径：①当LCC-HVDC输出DiL设置为0时，VSC的输入不受LCC-HVDC输出扰动的影响，在这种情况下，阻尼路径2仅包括第二类阻尼路径；②当LCC-HVDC输出DiL≠0时，阻尼路径2包含第二类阻尼路径和第三类阻尼路径。通过从②的传递函数中减去①的传递函数，即可分离出第三类阻尼路径对SSO模式阻尼的影响。具体步骤如下：
1）根据LCC-HVDC的开环传递函数框图，可以获得其输入和输出之间的关系为
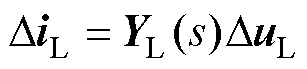（20）
式中，YL(s)为LCC-HVDC输入DuL到输出DiL的传递函数矩阵。
根据式（20），可以得到从DiL到DuL的动态方程，即
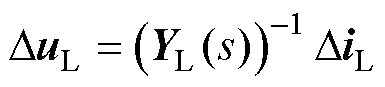（21）
根据式（19），DuL可以表示为
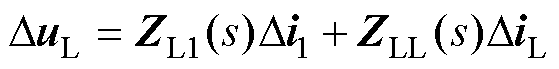（22）
联立式（21）和式（22），消去中间变量DuL，可得
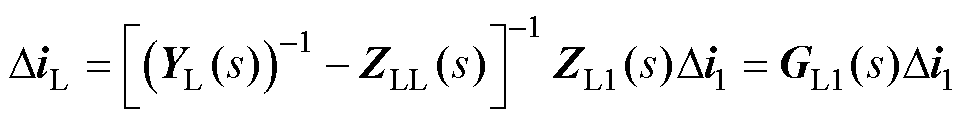（23）
根据式（19）和式（23），可以得到VSC输入和输出关系式为
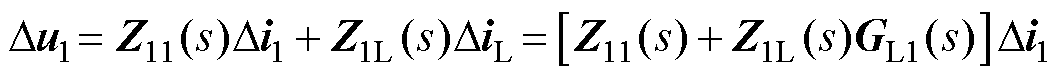（24）
从式（24）可以看出，VSC的输入完全由其自身的输出表示。因此，可以得到如图7a所示的系统闭环传递函数框图。图7a中右侧点画线框内的部分定义为Z1(s)，反映了交流系统和LCC-HVDC的动态特性，其表达式为
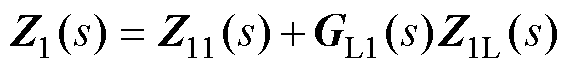（25）
式（24）给出了传递函数矩阵形式的阻尼路径的解析形式。通过分析式（24）的构成，可以对次同步交互作用进行分析。由式（19）可知，Z11(s)反映了VSC的输出扰动Dil通过交流系统影响VSC的输入扰动Dul的过程；Z1L(s)反映了LCC-HVDC的输出扰动DiL通过交流系统影响VSC的输入扰动Dul的过程。由式（23）可知，GL1(s)反映了VSC的输出扰动Dil通过交流系统影响LCC-HVDC的输入扰动DuL，然后影响LCC-HVDC的输出扰动DiL的过程。因此，Z11(s)反映了VSC与交流系统之间的相互作用，即Z11(s)反映了第二类阻尼路径的频域特性；Z1L(s)GL1(s)反映了VSC和LCC-HVDC之间的交互作用，即Z1L(s)GL1(s)反映了第三类阻尼路径的频域特性。在图7a中，用椭圆形曲线标示三类阻尼路径，其中闭环Ⅰ、Ⅱ、Ⅲ分别表示第一类、第二类和第三类阻尼路径。
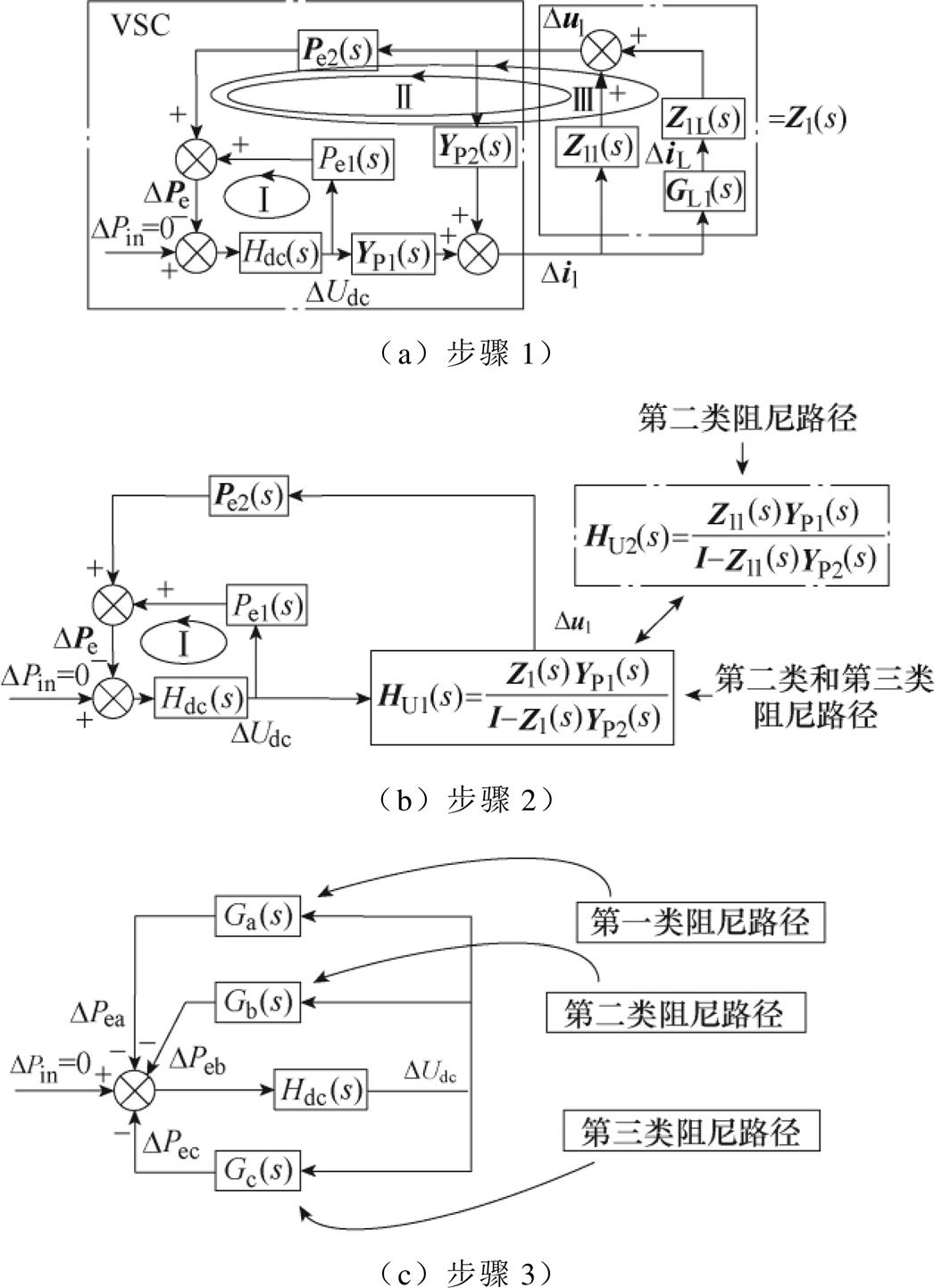
图7 阻尼重构过程
Fig.7 System closed-loop transfer function block diagram
2）进一步简化步骤1）中的闭环传递函数框图，得到从DUdc到Du1的传递函数矩阵HU1(s)。HU1(s)包含第二类和第三类阻尼路径。当不考虑VSC和LCC-HVDC通过交流系统的交互作用时，DiL为0，图7a中的外部传递函数矩阵变为Z11(s)。此时，DUdc到Du1的传递函数矩阵变为反映第二类阻尼路径的HU2(s)，如图7b中点画线框内部分所示。
3）从传递函数矩阵HU1(s)中减去传递函数矩阵HU2(s)，得到反映第三类阻尼路径的传递函数矩阵HU3(s)，即HU3(s)=HU1(s)-HU2(s)。通过将HU1(s)分解为HU2(s)和HU3(s)，外部系统的阻尼路径得以分离。将电磁功率DPe分解到三条阻尼路径上，得到DPea、DPeb和DPec三个分量。然后保留DUdc和DPe的分量，并消去其他中间变量，得到从DUdc到DPe的三个传递函数Ga(s)、Gb(s)和Gc(s)，并分别形成三条阻尼路径，如图7c所示。Ga(s)、Gb(s)和Gc(s)表达式为
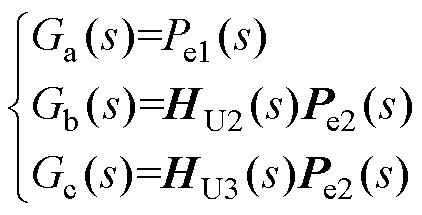（26）
Ga(s)仅与VSC的内部结构和参数相关，构成了VSC的内部阻尼；Gb(s)构成VSC和交流系统之间的次同步交互作用阻尼；Gc(s)构成了VSC和LCC- HVDC之间的次同步交互作用阻尼。
由第2节可知，直流电容SSO模式的阻尼系数Kd=Im[Gdc(jw)]/w。对于图7c中的三条阻尼路径，Gdc(s)=sGa(s), sGb(s), sGc(s)，因此可以分别计算出每条阻尼路径的阻尼系数。Ga(s)反映了VSC内部的阻尼效应，将其对应的阻尼系数表示为Kd1；Gb(s)反映了VSC和交流系统之间的交互作用阻尼，将其对应的阻尼系数表示为Kd2；Gc(s)反映了VSC和LCC-HVDC之间的交互作用阻尼，将其对应的阻尼系数表示为Kd3。系统的总阻尼系数Kd=Kd1+Kd2+ Kd3，反映了三条阻尼路径提供的阻尼之和，即该SSO模式下系统提供的总阻尼。由此，可以利用阻尼系数进行路径阻尼特性分析。
本节以直驱风电场经LCC-HVDC送出系统为例，说明阻尼路径分析方法分析次同步交互作用时的有效性。
直驱风电场经LCC-HVDC送出系统的拓扑结构和控制策略如图8所示。为了便于分析，将研究系统分为三个子系统：直驱风电场系统、交流系统和LCC-HVDC系统。系统划分如图8所示。系统的主要参数详见附表1。
直驱风电场系统包括直驱风电场和输电线路。其中，直驱风电场采用单机等值的建模方式[26]，由50台直驱风电机组聚合而成，1台直驱风机的容量为5 MW。工程实际中，对于本文算例研究的中小型风电场，内部风速的空间分布基本相同，各风电机组的参数和运行状态也是基本相同的，因此，分析系统的次同步交互作用时，风电场可视为一个整体[27]，即风电场单机等值的建模方式是合理的。风电场出口电压为3 kV，经过两次升压变压器后分别升压至35 kV和345 kV，然后接入交流母线。直驱风电机组的GSC控制母线电压和输出到电网的无功功率[28-29]，具体控制策略如图8所示，控制系统的参数详见附表2。直驱风电场系统相关变量定义如下：Pin和Pe分别为MSC输出功率和GSC输入功率，Udc为直流电容电压，ut和ig分别为GSC的端口电压和出口电流，ug为一级升压变压器高压侧电压，i1为输电线路电流，qpll为GSC锁相环的锁相角。
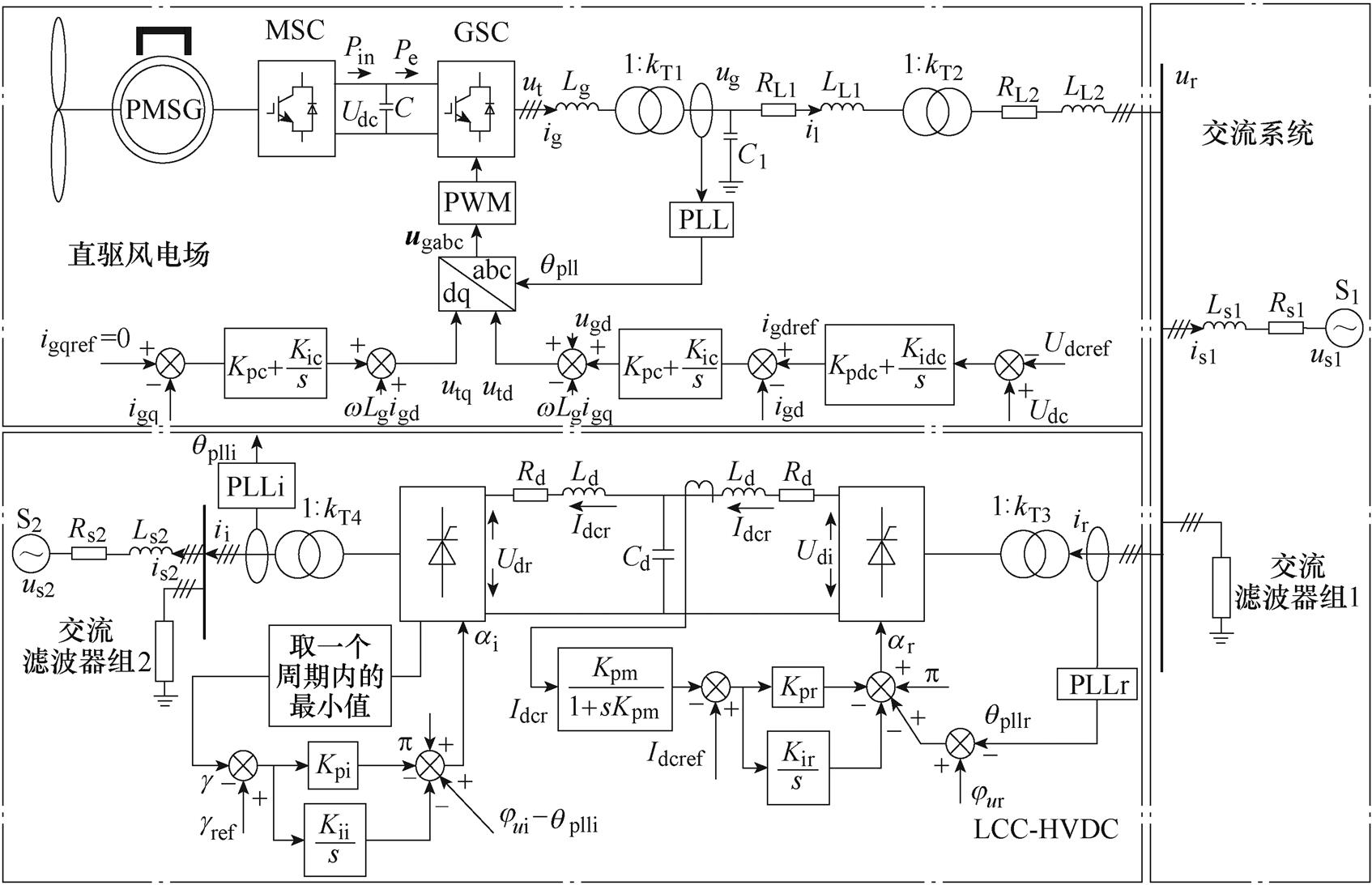
图8 直驱风电场经LCC-HVDC送出系统结构
Fig.8 Schematic diagram of the D-PMSG-based wind farm integrated with LCC-HVDC system
LCC-HVDC系统包括LCC-HVDC、交流系统S2和交流滤波器组2。LCC-HVDC采用CIGRE HVDC基准模型，整流侧和逆变侧分别采用定电流和定关断角控制策略[29]。控制系统参数详见附表3。相关参数定义如下：ur、ir分别为整流侧的母线电压和线电流，ui、ii分别为逆变侧的母线电压和线电流，Udr、Idcr分别为整流侧直流电压和直流电流，Udi、Idci分别为逆变侧直流电压和直流电流，us2和is2分别是交流系统S2的电压和电流，qpllr、qplli分别为整流器、逆变器锁相环的锁相角，jur、jui分别为ur、ui的相位，g 为逆变器关断角，ar、ai分别为整流器和逆变器的触发延迟角。
交流系统包括交流系统S1和交流滤波器组1。相关参数定义如下：us1和is1分别为送端交流系统的电压和电流。
考虑到第2、3节在介绍阻尼路径分析法时，是以VSC直流电容主导的SSO模式为例进行说明的，为了体现阻尼路径分析法的适用性，本节选取LCC-HVDC直流电感主导的SSO模式为例进行阻尼路径分析和仿真验证。
首先建立系统闭环传递函数框图如图9所示。直驱风电场、LCC-HVDC、交流系统模型的建立和第2节相同，此处不再赘述，并直接给出标示阻尼路径的系统闭环传递函数框图。需要说明的是，由于直驱风电场并网系统的SSO特性仅与GSC和直流电容有关，而与MSC以及风力机无关[30]，因此直驱风电场建模时仅考虑GSC和直流电容的动态特性。并且在风电场建模时，考虑35 kV和345 kV传输线路的动态过程。
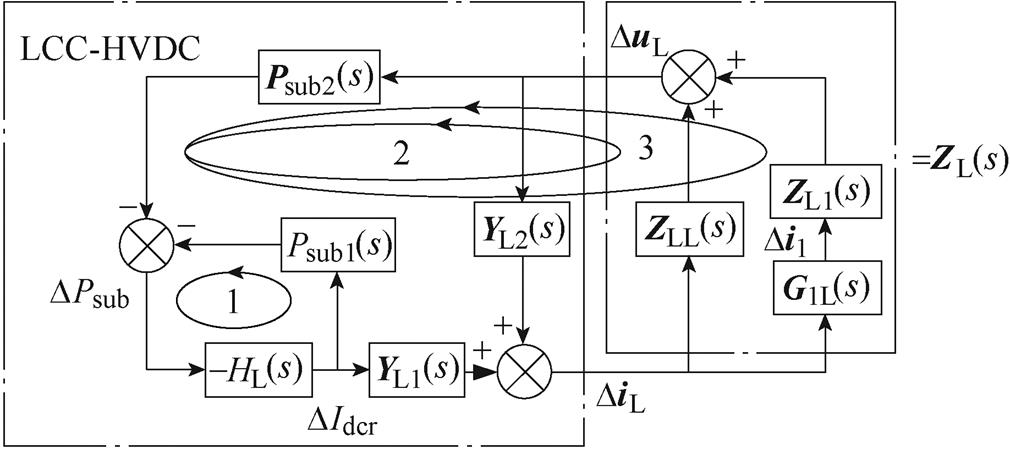
图9 系统闭环传递函数框图
Fig.9 System closed-loop transfer function block diagram
图9中的传递函数以及传递函数矩阵和图6具有相同的定义，其中G1L(s)和GL1(s)具有相似的含义，即反映电力电子设备的输出扰动影响其他电力电子设备输出扰动的过程，并且通过推导可知，G1L(s)=1/GL1(s)。ZL(s)=ZLL(s)+G1L(s)ZL1(s)，反映了交流系统和直驱风电场的动态特性。可以看出，阻尼路径分析法便于在其他振荡模式以及系统中应用。
图9中，直流电感主导的SSO模式下阻尼路径已用不同的椭圆形框线标记。可以看出，该SSO模式下同样包含三条阻尼路径，分别对应第2节介绍的三类阻尼路径，即反映LCC-HVDC内部阻尼的阻尼路径1，反映LCC-HVDC和交流系统之间交互作用的阻尼路径2，以及反映LCC-HVDC和直驱风电场之间交互作用的阻尼路径3。通过进一步地对图9所示的闭环传递函数框图进行阻尼重构，即可分离出每条路径的阻尼，进而进行路径阻尼特性分析。
根据第3节的内容，可以利用阻尼重构得到LCC-HVDC的直流电感SSO模式的三类阻尼路径的阻尼系数Kd1、Kd2、Kd3。通过分析每条路径的阻尼特性，达到分析次同步交互作用对SSO模式阻尼影响的目的，并结合时域仿真验证阻尼路径分析法的有效性。
将LCC-HVDC的定电流控制器积分系数Kir设置为20Kir0，其他参数保持不变。在这种情况下，系统的总阻尼系数Kd以及各路径阻尼系数Kd1、Kd2、Kd3的频率特性曲线如图10所示。
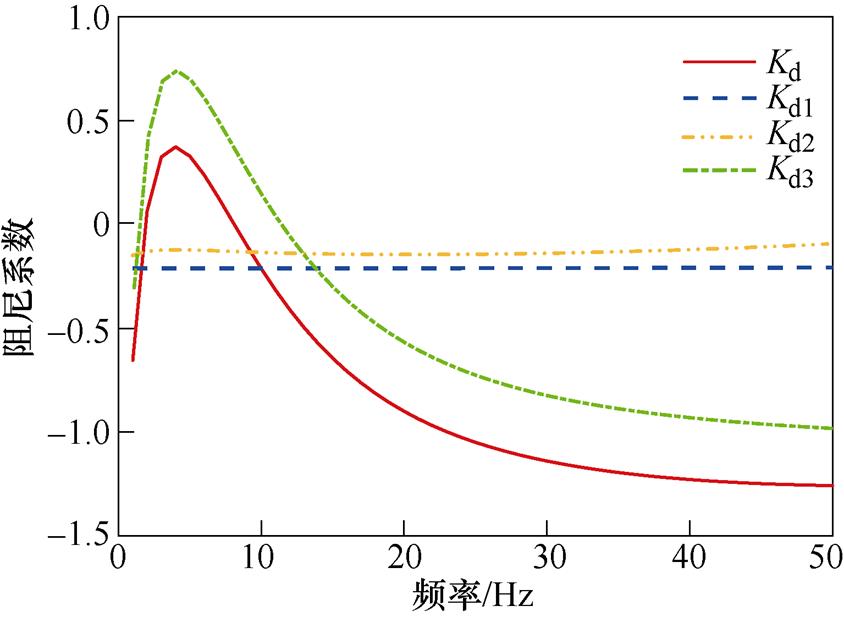
图10 阻尼系数频率特性曲线
Fig.10 Frequency characteristic curves of damping coefficient
从图10中可以看出，LCC-HVDC内部阻尼系数Kd1的频率特性曲线是一条几乎与横轴平行的直线，在该工况下，Kd1始终小于0，即LCC-HVDC自身表现为负阻尼，不利于系统的稳定。LCC- HVDC和交流系统交互作用阻尼系数Kd2特性曲线表现为略微向下凸的形状，且在0～50 Hz频率范围内都小于0，表明LCC-HVDC和交流系统交互作用提供负阻尼，不利于系统的稳定。LCC-HVDC和直驱风电场的次同步交互作用阻尼系数Kd3的频率特性曲线呈现出先上升、后下降的趋势，在频率大于12 Hz时，Kd3＜0，表明此时直驱风电场和LCC- HVDC之间的次同步交互作用提供负阻尼，不利于系统的稳定。Kd1、Kd2、Kd3叠加即为系统总阻尼系数Kd。Kd的频率特性曲线同样表现为先上升后下降的趋势，在频率大于8 Hz时，Kd＜0，表明此时SSO模式的总阻尼为负，系统可能会失稳并发生SSO。此外，从图10可以看出，Kd的负阻尼主要由Kd3提供，即LCC-HVDC和直驱风电场的次同步交互作用是系统在该SSO模式下表现为负阻尼的主要原因，这种次同步交互作用会使得SSO更加剧烈。
为了验证上述理论分析结果的正确性和阻尼路径分析法的有效性，在PSCAD/EMTDC中建立了图8所示系统的电磁暂态模型，并设置了以下两个工况。工况1：忽略直驱风电场的动态特性，使用电流源代替直驱风电场等值模型。工况2：考虑直驱风电场的动态特性，使用详细的直驱风电场模型。工况1和工况2保证系统潮流相同。由于工况1忽略了直驱风电场的动态特性，即不考虑LCC-HVDC和直驱风电场之间的次同步交互作用，因此该工况体现了LCC-HVDC内部的阻尼特性Kd1以及LCC- HVDC和交流系统之间的交互作用阻尼特性Kd2。工况2采用了详细的直驱风电场模型，即体现了系统的总阻尼特性Kd。
在3 s时，将LCC-HVDC定电流控制器积分系数修改为20Kir0以激发SSO，分别在两种工况下启动仿真。两种工况下，直流电流Idcr的仿真波形如图11所示。
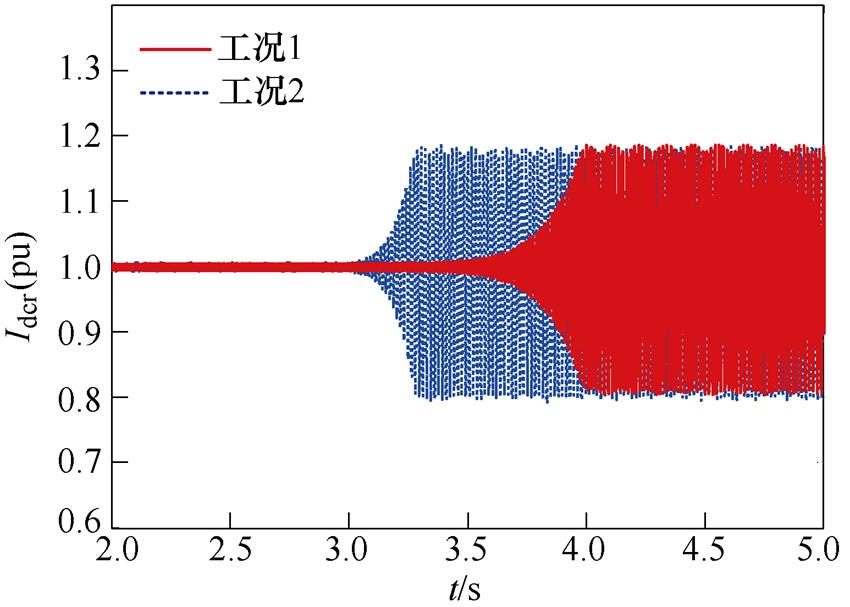
图11 直流电流Idcr波形
Fig.11 Waveforms of DC current Idcr
由图11可知，3 s时，在两种工况下都发生了SSO，这与理论分析中次同步频段内Kd和Kd1+Kd2都小于0相符。此外，从图11可以看出，工况1下Idcr缓慢失稳并逐渐发展为等幅振荡，工况2下Idcr迅速失稳并发展为等幅振荡，即工况2下系统发生的SSO比工况1中的更为剧烈，表明LCC-HVDC和直驱风电场之间的次同步交互作用提供负阻尼，加剧了系统的SSO，与理论分析中次同步频段内 Kd3＜0相符。时域仿真验证了LCC-HVDC和直驱风电场之间的次同步交互作用提供负阻尼的理论分析结果，并验证了阻尼路径分析法的有效性。
本节进行路径阻尼特性的影响因素分析，并选取了LCC-HVDC定电流控制器参数以及直驱风电机组网侧电压外环控制器参数，研究参数变化对路径阻尼特性的影响。此外，本文同样以直驱风电场直流电容振荡模式为算例进行了路径阻尼特性分析，详见附录。
4.4.1 LCC-HVDC定电流控制器参数
本节分析LCC-HVDC定电流控制器比例系数和积分系数对路径阻尼特性的影响。分别改变LCC-HVDC定电流控制器的积分系数Kir和比例系数Kpr，得到系统在不同运行状况下的路径阻尼特性曲线，如图12所示。图12a中，定电流控制器积分系数分别为10Kir0、12Kir0以及15Kir0；图12b中，定电流控制器的比例系数分别为Kpr0、1.5Kpr0以及2Kpr0，并将积分系数设为12Kir0以激发振荡。图中箭头的方向为相应控制器参数增大的方向。
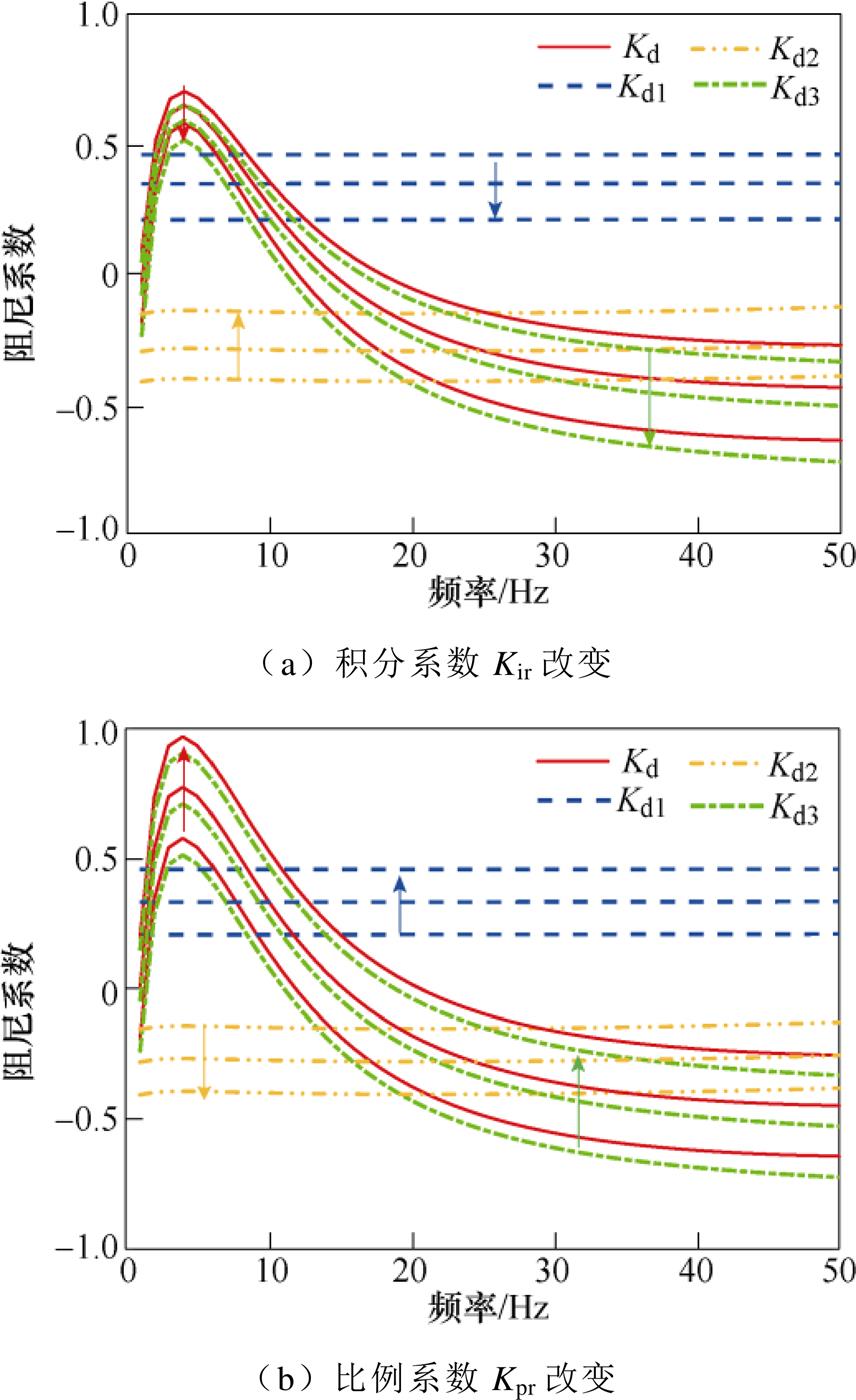
图12 定电流控制器参数对阻尼特性的影响
Fig.12 Influence of constant current controller parameters on damping characteristics
从图12a中可以看出，随着Kir的增大，Kd1曲线逐渐下移，表明LCC-HVDC内部提供的阻尼作用逐渐减小，不利于系统的稳定；Kd2曲线逐渐上移，表明LCC-HVDC和交流系统交互作用提供的阻尼作用逐渐增大，有利于系统的稳定；Kd3曲线逐渐下移，且在20～50 Hz频率范围内下降幅度明显大于其他频率范围，表明LCC-HVDC与直驱风电场在次同步频段内提供的阻尼明显减小，不利于系统的稳定。在三条路径的共同作用下，随着积分系数的增大，系统总阻尼系数Kd频率特性曲线下移，且在12～50 Hz频率范围内下移最大，因此系统在次同步频率范围内负阻尼作用明显增强，系统的稳定性降低，振荡将变得更加剧烈。
从图12b中可以看出，随着Kpr的增大，Kd1曲线逐渐上移，表明LCC-HVDC内部提供的阻尼逐渐增大，系统稳定性增强；Kd2曲线逐渐下移，表明LCC-HVDC与交流系统交互作用阻尼逐渐减小，不利于系统的稳定；Kd3曲线逐渐上移，表明LCC- HVDC与直驱风电场之间的交互作用阻尼逐渐增强，系统稳定性增强。在三条路径的共同作用下，随着Kpr的增大，Kd频率特性曲线上移，阻尼作用增强，振荡在一定程度上将得到抑制。
对阻尼特性分析结果进行时域仿真验证。在3 s时改变控制器参数，并使用直流电流Idcr反映SSO模式的阻尼。仿真结果如图13所示。
从图13a中可以看出，随着积分系数Kir的增加，Idcr的振荡变得越来越剧烈，对应阻尼特性分析过程中，Kd频率特性曲线下移，SSO模式负阻尼增强，验证了阻尼特性分析结果的正确性。
从图13b中可以看出，随着比例系数Kpr的增加，Idcr振荡的强度逐渐减小，对应阻尼特性分析过程中，Kd频率特性曲线上移，SSO模式阻尼增强，验证了阻尼特性分析结果的正确性。
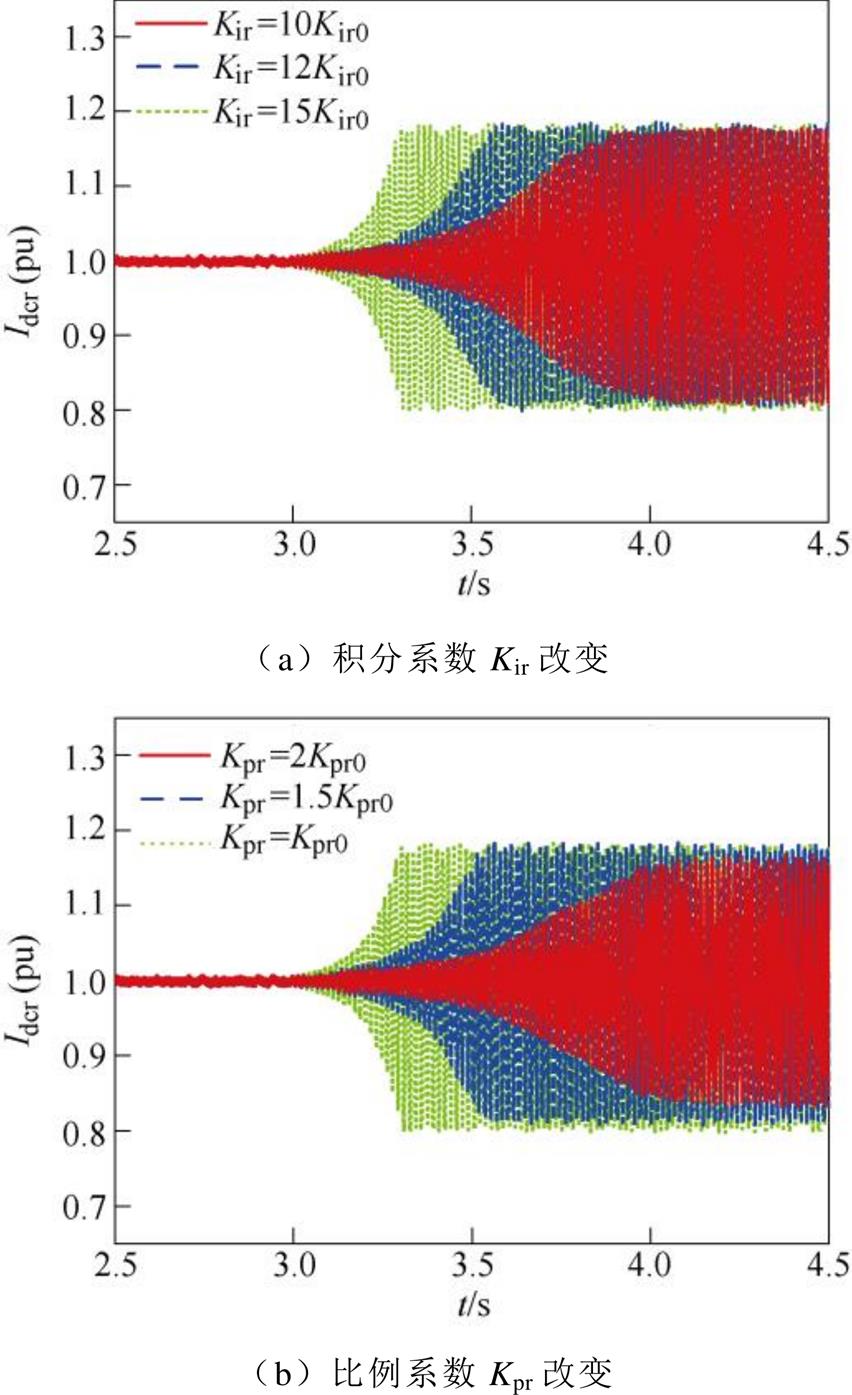
图13 直流电流仿真结果（定电流控制器参数变化）
Fig.13 DC current simulation results (constant current controller parameter changes)
4.4.2 直驱风电机组网侧电压外环控制器参数
本节分析直驱风电机组网侧电压外环控制器比例和积分系数对路径阻尼特性的影响。将LCC- HVDC定电流控制器积分系数修改为12Kir0，并分别改变直驱风电机组电压外环积分系数Kidc和比例系数Kpdc，得到系统在不同运行状况下的路径阻尼特性曲线，如图14所示。图14a中，电压外环积分系数分别为0.5Kidc0、0.75Kidc0以及Kidc0；图14b中，电压外环比例系数分别为Kpdc0、2Kpdc0以及4Kpdc0。图中箭头的方向为相应控制器参数增大的方向。
从图14a中可以看出，Kd1和Kd2并不随电压外环积分系数Kidc的变化而改变，由图9也可看出，Kd1和Kd2与LCC-HVDC和交流系统的参数有关，而和直驱风电机组的参数无关。而随着Kidc的增大，Kd3在大于20 Hz的频率范围内的值会逐渐减小，而对其他频率的值基本无影响；即在大于20 Hz的频率范围内，阻尼频率特性曲线有“上翘”的趋势，次同步交互作用提供的负阻尼作用略有减小。因此，Kidc的改变主要通过影响LCC-HVDC与直驱风电场次同步交互作用阻尼从而影响系统总阻尼。随着Kidc的减小，Kd频率特性在大于20 Hz的频率范围内的值会逐渐增大，且有“上翘”趋势，阻尼作用略有增强，振荡将一定程度上得到抑制。
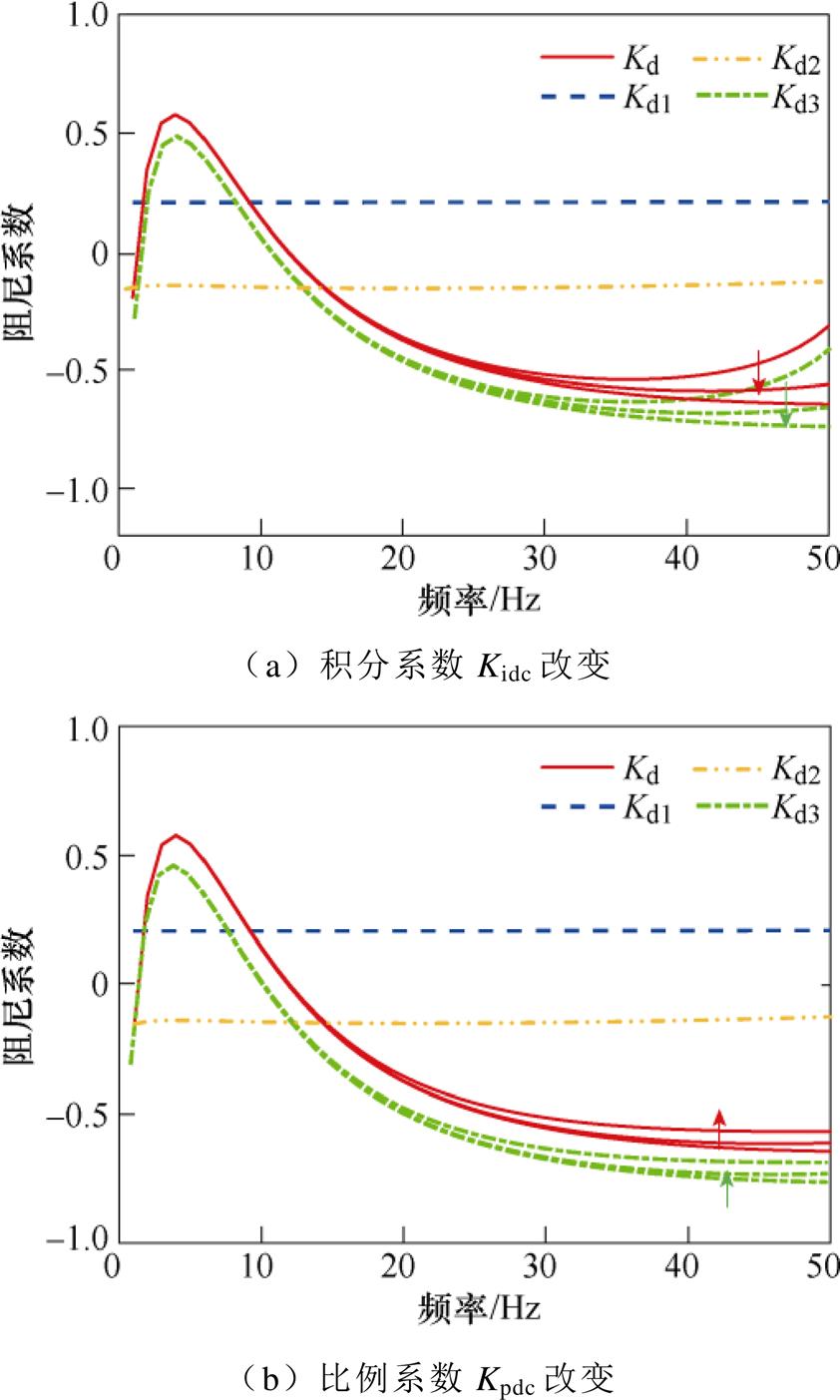
图14 电压外环制器参数对阻尼特性的影响
Fig.14 Influence of voltage outer loop controller parameters on damping characteristics
从图14b可以看出，Kd1和Kd2也不随电压外环比例系数Kpdc的变化而改变。而随着Kpdc的增大，次同步交互作用阻尼特性在大于20 Hz频率范围内的值略有增大，而对其他频率范围内的值基本无影响；即在次同步频段内，次同步交互作用提供的负阻尼作用略有减小。因此，Kpdc的改变也主要通过影响LCC-HVDC与直驱风电场的次同步交互作用阻尼从而影响系统总阻尼。随着Kpdc的增大，系统总阻尼特性在大于20 Hz的频率范围内的值会逐渐增大，阻尼作用略有增强，振荡将一定程度上得到抑制。
对阻尼特性分析结果进行时域仿真验证。在3 s时改变控制器参数，并使用直流电流Idcr反映SSO模式的阻尼。仿真结果如图15所示。
从图15a中可以看出，随着积分系数Kidc的减小，Idcr振荡的强度略有减小，对应阻尼特性分析过程中，Kd在次同步频率范围内略有增大，SSO模式阻尼增强，验证了阻尼特性分析结果的正确性。
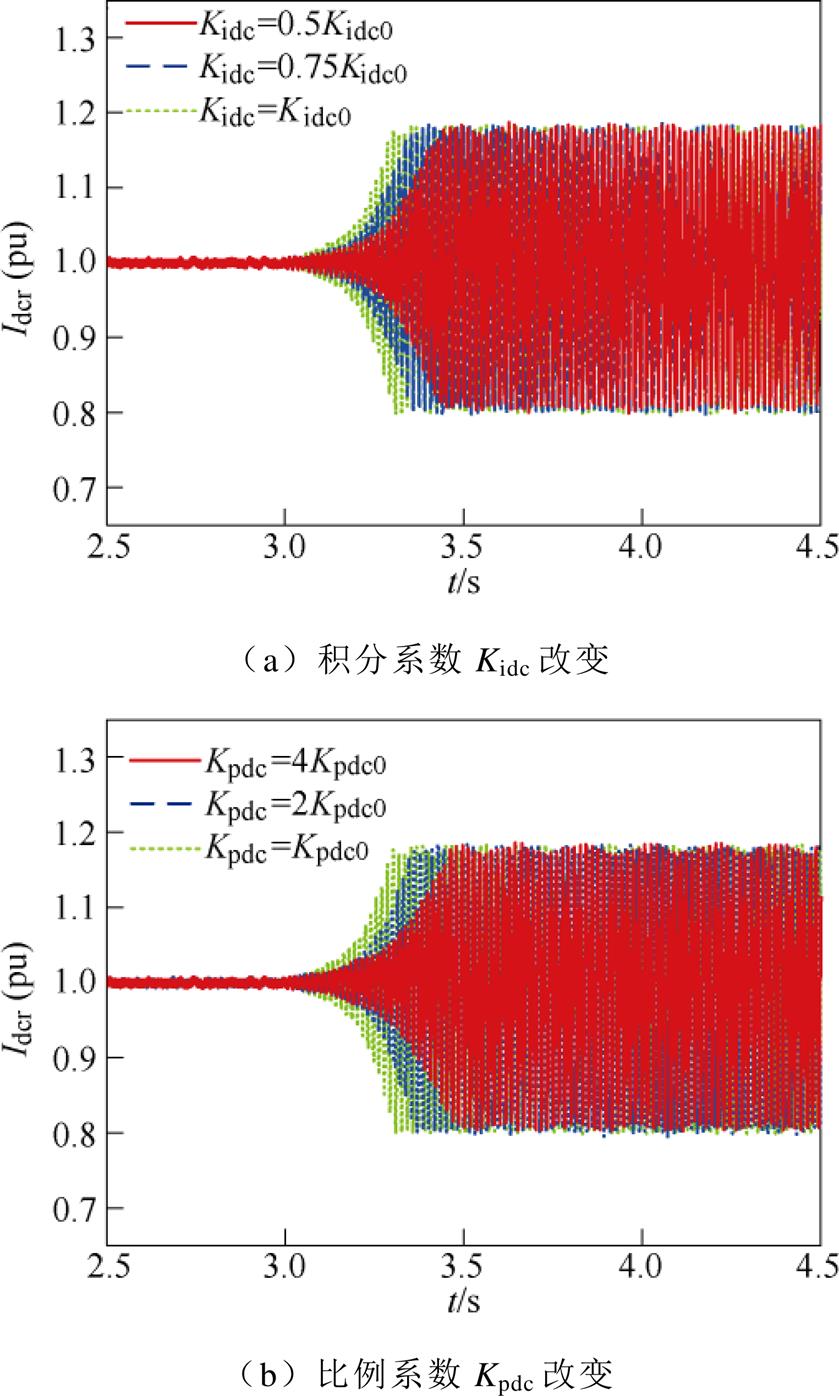
图15 直流电流仿真结果（电压外环控制器参数变化）
Fig.15 DC current simulation results (voltage outer loop controller parameter changes)
从图15b中可以看出，随着比例系数Kpdc的增加，Idcr振荡的强度略有减小，对应阻尼特性分析过程中，Kd在次同步频率范围内略有增大，SSO模式阻尼增强，验证了阻尼特性分析结果的正确性。
本文提出了一种阻尼路径分析方法，研究新能源经LCC-HVDC送出系统的次同步交互作用。主要结论如下：
1）当直流电容、PLL和直流电感的动态过程可以用二阶运动方程的形式表示时，可以基于SSO主导元件建立相应的类Heffron-Phillips模型，以分析相应SSO模式的阻尼特性。
2）根据闭环传递函数框图，在特定SSO模式下，可以分离出三种扰动传递的阻尼路径。这三种阻尼路径分别反映了电力电子设备内部的SSO特性、电力电子设备与交流系统之间的次同步交互作用以及不同电力电子设备之间的次同步交互作用。
3）使用阻尼重构法，能够分离出每条阻尼路径提供的阻尼，并利用阻尼系数对路径阻尼进行定量评估，从而可对每条阻尼路径进行阻尼特性分析。
4）利用本文的方法，以直驱风电场经LCC- HVDC送出系统为算例，分析了LCC-HVDC直流电感SSO模式下的阻尼路径，验证了阻尼路径分析法的有效性。利用路径阻尼分析和时域仿真，分析了控制器参数对路径阻尼特性的影响。所得结论可为工程中控制器参数的设计提供指导。
附 录
1. 仿真系统参数
附表1 系统主要参数
App.Tab.1 Main parameters of the system
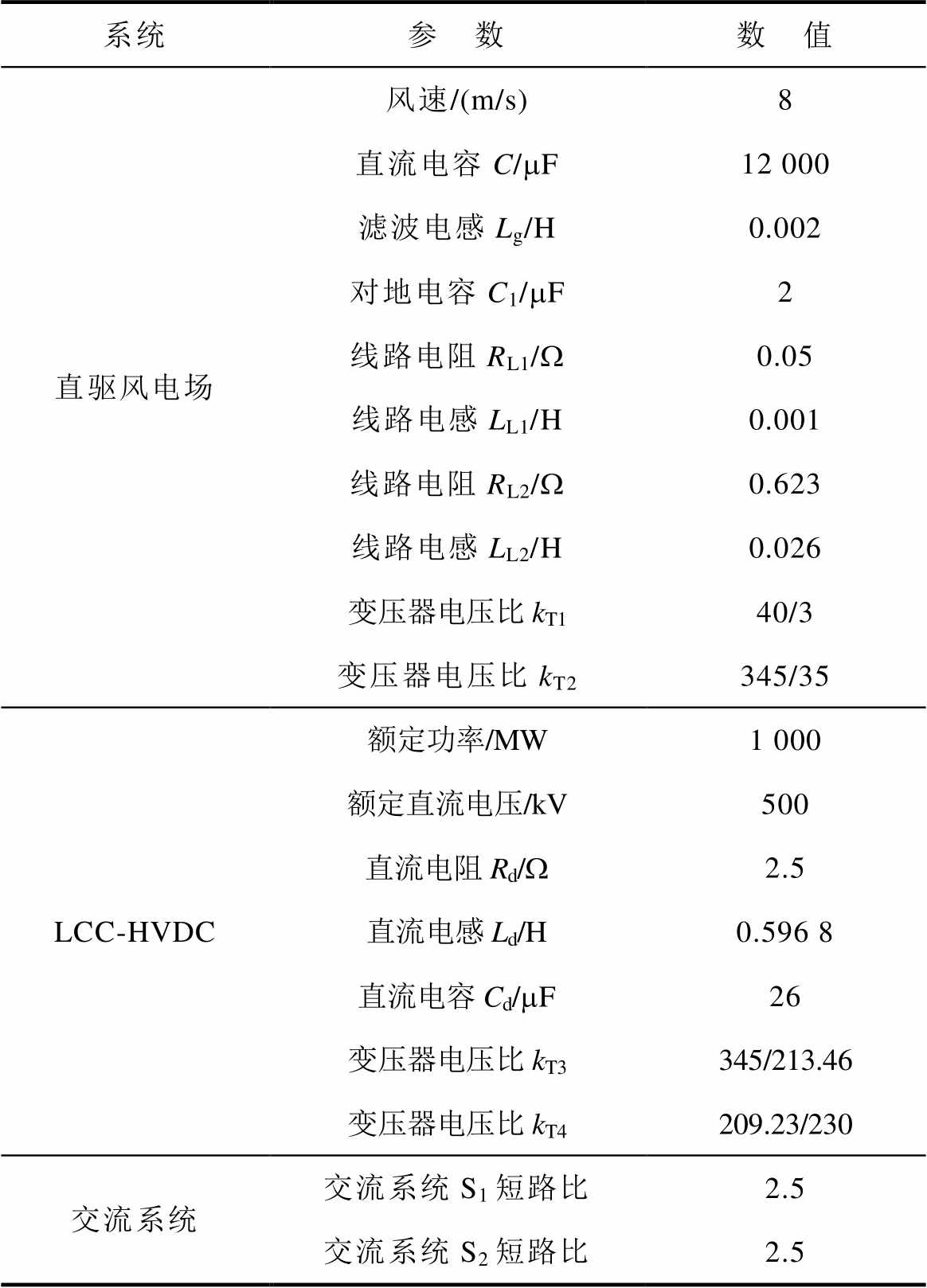
系统参 数数 值 直驱风电场风速/(m/s)8 直流电容C/mF12 000 滤波电感Lg/H0.002 对地电容C1/mF2 线路电阻RL1/W0.05 线路电感LL1/H0.001 线路电阻RL2/W0.623 线路电感LL2/H0.026 变压器电压比kT140/3 变压器电压比kT2345/35 LCC-HVDC额定功率/MW1 000 额定直流电压/kV500 直流电阻Rd/W2.5 直流电感Ld/H0.596 8 直流电容Cd/mF26 变压器电压比kT3345/213.46 变压器电压比kT4209.23/230 交流系统交流系统S1短路比2.5 交流系统S2短路比2.5
附表2 直驱风电机组控制器参数
App.Tab.2 D-PMSG controller parameters
控制器参 数数 值 GSC外环比例系数Kpdc0.2 外环积分系数Kidc20 内环比例系数Kpc0.6 内环积分系数Kic2.5 PLL比例系数Kpp100 积分系数Kip900
附表3 LCC-HVDC控制器参数
App.Tab.3 LCC-HVDC controller parameters
控制器参 数数 值 整流器比例系数Kpr1.098 9 积分系数Kir1/0.010 92 逆变器比例系数Kpi0.750 6 积分系数Kii1/0.054 4 PLL比例系数KpP10 积分系数KiP50 测量环节比例系数Kpm0.5 积分系数Kim0.001 2
2. 直流电容模式仿真算例分析
1）直驱风电机组网侧电压外环控制器参数的影响
本节分析直驱风电机组的直流电压外环控制器参数对路径阻尼特性的影响。分别改变直流电压外环控制积分系数Kidc和比例系数Kpdc，得到系统的在不同运行状况下的路径阻尼特性曲线，如附图1所示。在附图1a中，外环积分系数分别为150、200和250；在附图1b中，外环比例系数分别为Kpdc0、1.5Kpdc0和2Kpdc0，积分系数为250。图中箭头的方向为相应控制器参数增大的方向。
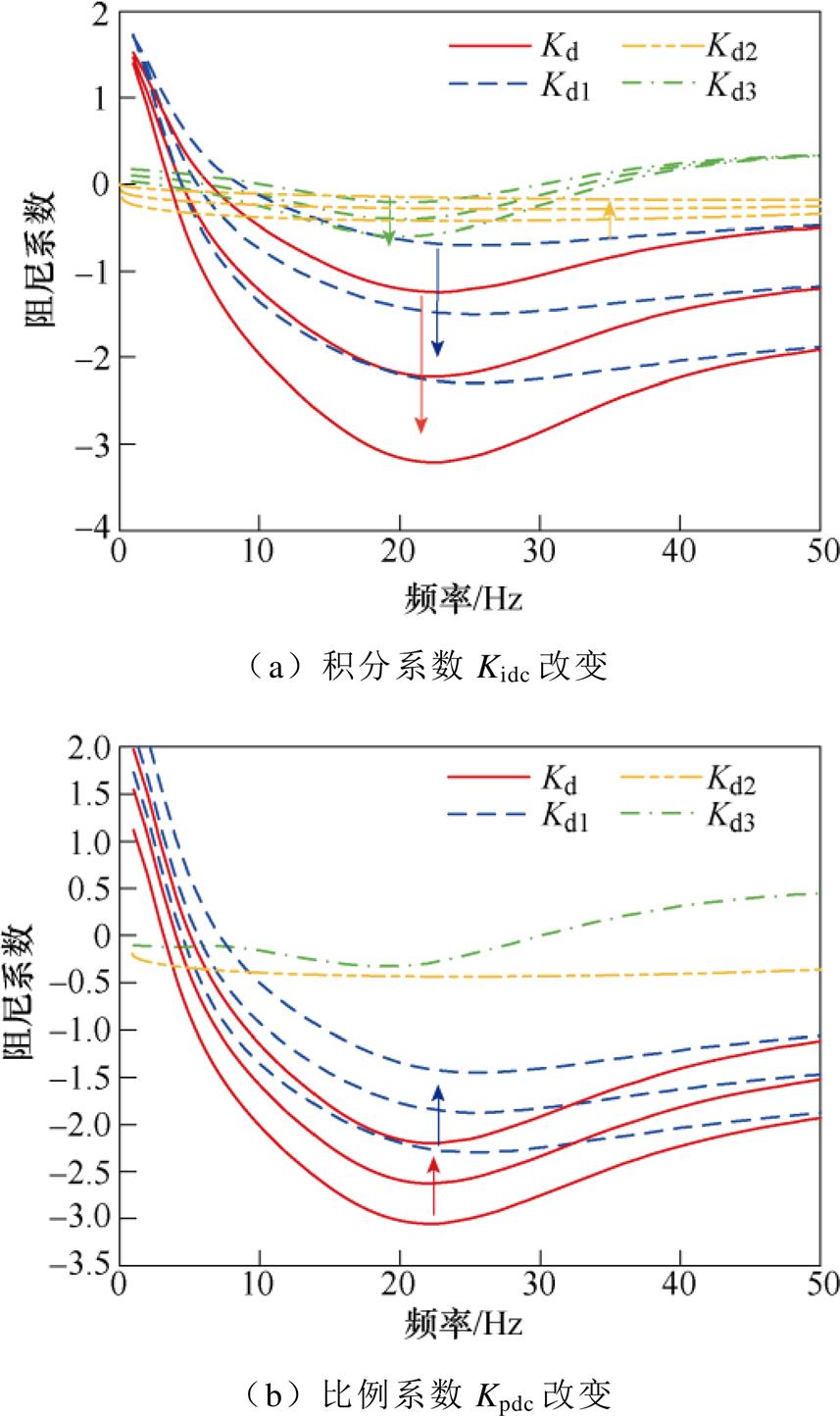
附图1 电压外环控制器参数对阻尼特性的影响
App.Fig.1 Influence of voltage outer loop controller parameters on damping characteristics
如附图1a所示，随着Kidc的增加，Kd1对应的曲线向下移动，表明直驱风电场内部提供的阻尼作用逐渐减小，不利于系统的稳定；Kd2对应的曲线上移，表明直驱风电场和交流系统的交互作用阻尼增大，有利于系统的稳定；Kd3对应的曲线下移，表明直驱风电场和LCC- HVDC的交互作用阻尼减小，不利于系统的稳定。在三条阻尼路径的作用下，随着Kidc的增大，系统总阻尼系数Kd减小，并且在10～50 Hz的频率范围内减小最为明显。系统在次同步频率范围内的负阻尼作用明显增强，系统的稳定性降低，振荡将变得更加剧烈。
如附图1b所示，随着Kpdc的增加，Kd1对应的曲线向上移动，表明直驱风电场内部提供的阻尼作用增强，有利于系统的稳定；Kd2和Kd3基本上不受Kpdc变化的影响。根据上述分析，可以看出Kpdc的变化主要通过改变直驱风电场内部阻尼Kd1来影响系统的总阻尼。因此，随着Kpdc的增大，系统总阻尼Kd频率特性曲线上移，阻尼作用增强，振荡一定程度上得到抑制。
对上述阻尼特性分析结果进行时域仿真验证。在3 s时，改变控制器参数，并使用直流电容电压Udc反映SSO模式阻尼。仿真结果如附图2所示。
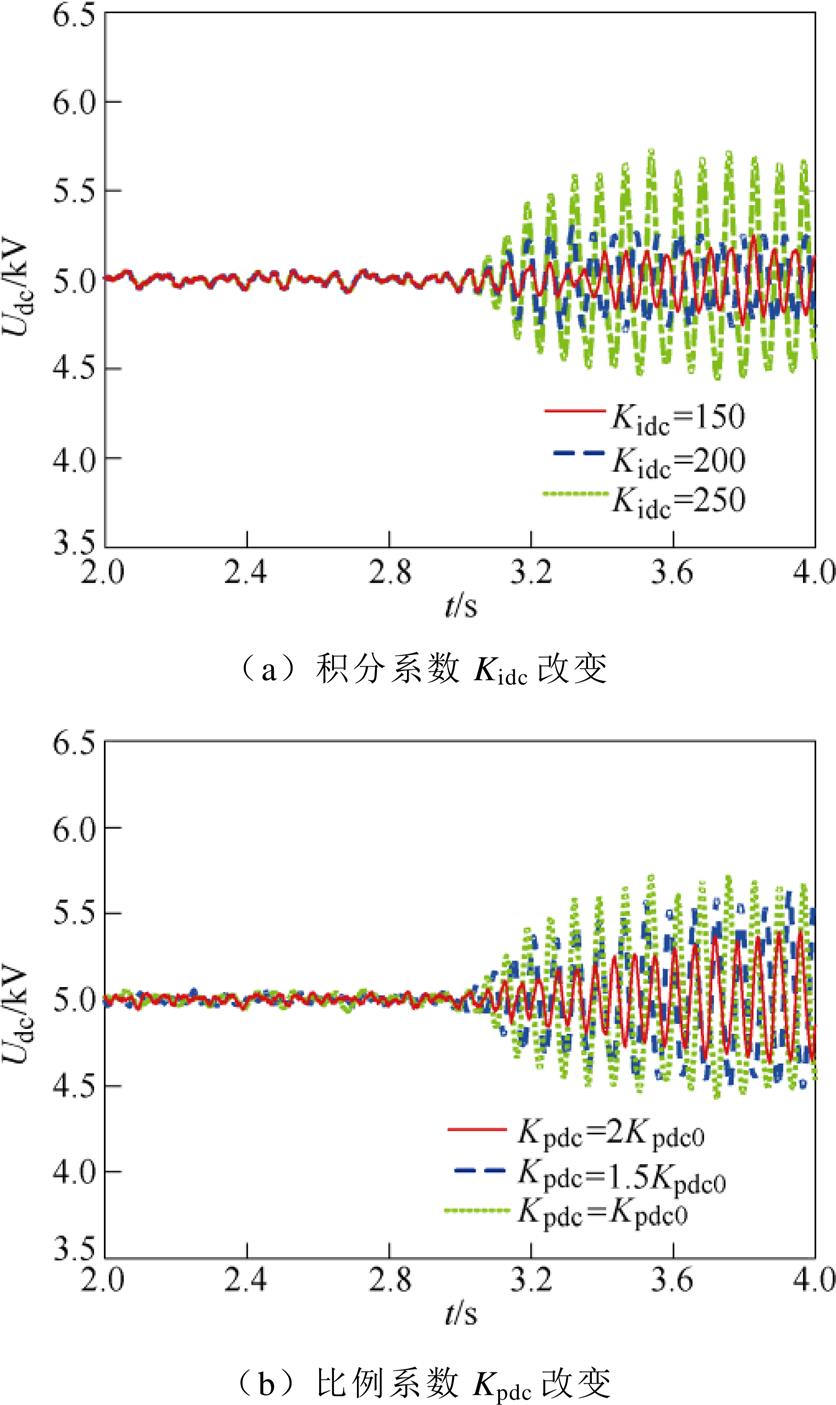
附图2 直流电压仿真结果（电压外环控制器参数变化）
App.Fig.2 DC voltage simulation results (parameter changes of voltage outer loop controller)
从附图2a中可以看出，随着Kidc的增加，Udc的振荡幅度逐渐增加。对应阻尼特性分析中Kd逐渐减小，SSO模式负阻尼增强，验证了阻尼特性分析结果的正确性。
从附图2b中可以看出，随着Kpdc的增加，Udc的振荡幅度逐渐减小。对应阻尼特性分析中Kd逐渐增大，SSO模式阻尼增强，验证了阻尼特性分析结果的正确性。
2）LCC-HVDC定电流控制器参数的影响
本节分析LCC-HVDC的定电流控制器参数对路径阻尼特性的影响。分别改变定电流控制积分系数Kir和比例系数Kpr，并将直驱风电机组GSC外环积分系数设置为250以激发振荡，保持其他参数不变，得到系统的在不同运行状况下的路径阻尼特性曲线，如附图3所示。在附图3a中，LCC-HVDC定电流控制器的积分系数分别为Kir0、2Kir0和3Kir0；在附图3b中，定电流控制器的比例系数分别为Kpr0、2Kpr0和3Kpr0。图中箭头的方向为相应控制器参数增大的方向。
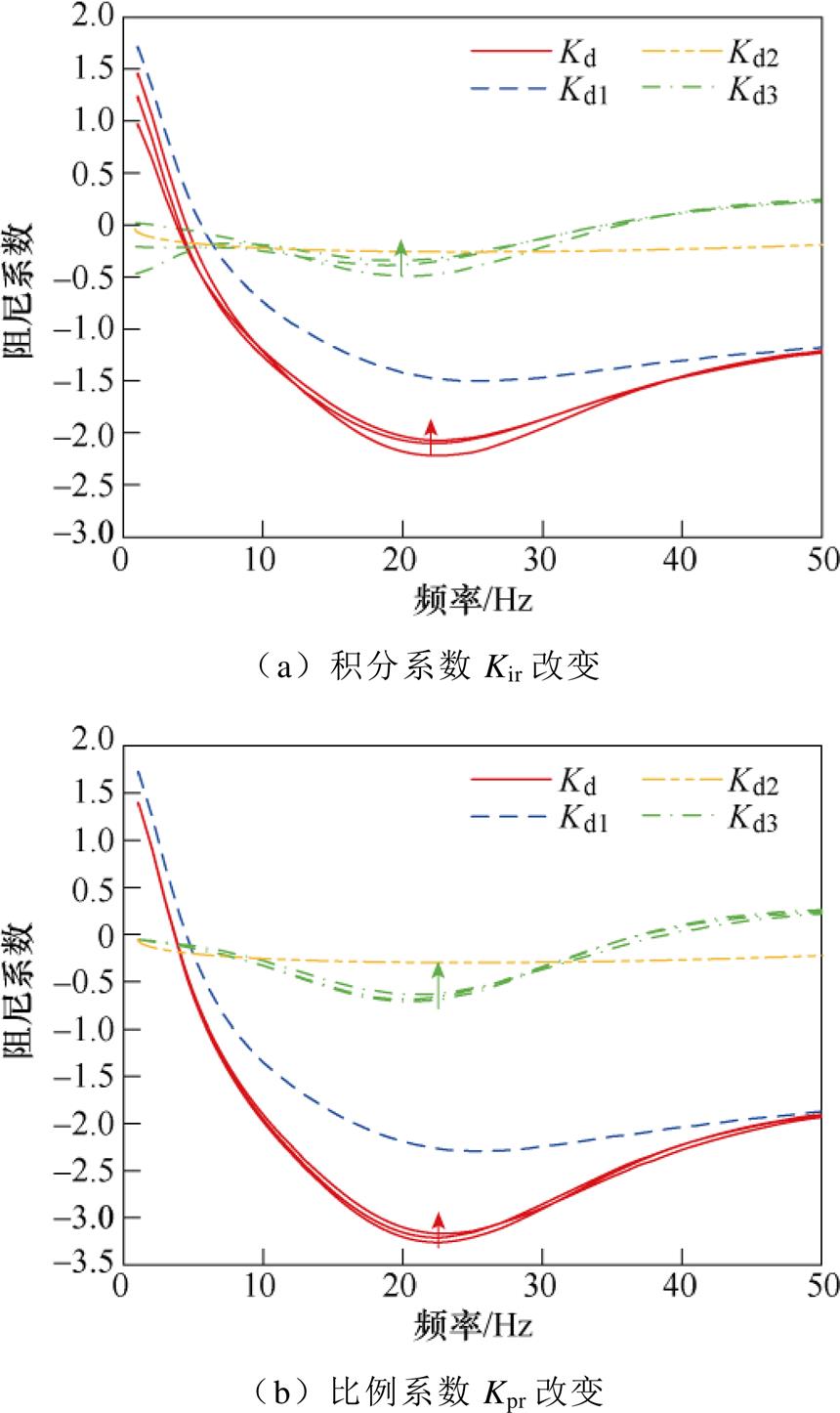
附图3 定电流控制器参数对阻尼特性的影响
App.Fig.3 Influence of constant current controller parameters on damping characteristics
从附图3a中可以看出，Kd1和Kd2不随Kir的变化而变化。随着Kir的增加，Kd3在10～50 Hz范围内略有增加，在0～10 Hz频率范围内略有减少。因此，Kir的变化主要通过改变直驱风电场和LCC-HVDC交互作用阻尼来影响系统的总阻尼。随着Kir的增加，总阻尼系数Kd在10～50 Hz范围内略有增加，系统的阻尼作用增强，振荡一定程度上得到抑制。
从附图3b中可以看出，Kd1和Kd2同样不随Kpr的变化而变化。随着Kpr的增加，Kd3略有增加，表明直驱风电场和LCC-HVDC之间的负阻尼作用增强。因此，Kpr的变化主要通过改变直驱风电场和LCC-HVDC交互作用阻尼来影响系统的总阻尼。随着Kpr的增加，系统的总阻尼系数Kd略有增加，系统的阻尼作用增强，振荡一定程度上得到抑制。
对上述阻尼特性分析结果进行时域仿真验证。在3 s时，将直驱风电机组的GSC外环积分系数更改为250以激发SSO，并使用直流电容电压Udc反映SSO模式阻尼。仿真结果如附图4所示。
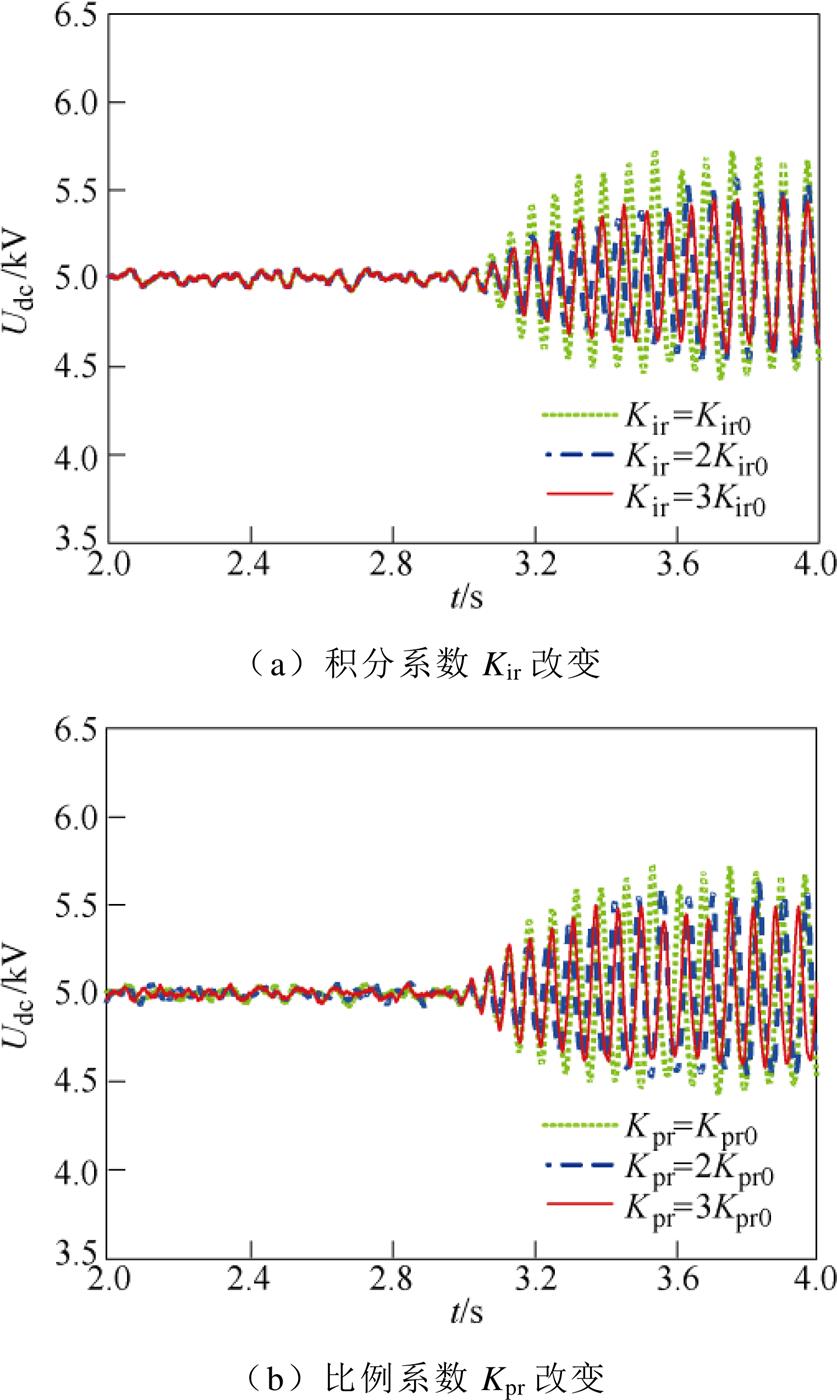
附图4 直流电压仿真结果（定电流控制器参数变化）
App.Fig.4 DC voltage simulation results (parameter changes of LCC-HVDC constant current controller)
从附图4a中可以看出，随着Kir的增加，Udc的振荡幅度逐渐减小，对应阻尼特性分析中Kd逐渐增大，SSO模式阻尼增强，验证了阻尼特性分析结果的正确性。
从附图4b中可以看出，随着Kpr的增加，Udc的振荡幅度逐渐减小，对应理论分析中Kd逐渐增大，SSO模式阻尼增强，验证了阻尼特性分析结果的正确性。
参考文献
[1] 文福拴, 鲁刚, 黄杰. 面向碳达峰、碳中和的综合能源系统[J]. 全球能源互联网, 2022, 5(2): 116-117.
Wen Fushuan, Lu Gang, Huang Jie. Integrated energy system towards carbon peak and neutrality targets[J]. Global Energy Interconnection, 2022, 5(2): 116-117.
[2] 高本锋, 陈淑平, 刘毅. 光伏与LCC-HVDC系统的次同步振荡耦合路径及阻尼特性分析[J]. 电力系统自动化, 2022, 46(24): 66-75.
Gao Benfeng, Chen Shuping, Liu Yi. Analysis on coupling path and damping characteristics of sub- synchronous oscillation between photovoltaic and LCC-HVDC system[J]. Automation of Electric Power Systems, 2022, 46(24): 66-75.
[3] 魏泓屹, 卓振宇, 张宁,等. 中国电力系统碳达峰·碳中和转型路径优化与影响因素分析[J]. 电力系统自动化, 2022, 46(19): 1-12.
Wei Hongyi, Zhuo Zhenyu, Zhang Ning, et al. Transition path optimization and influencing factor analysis of carbon emission peak and carbon neutrality for power system of China[J]. Automation of Electric Power Systems, 2022, 46 (19): 1-12.
[4] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97.
Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[5] 王利超, 于永军, 张明远, 等. 直驱风电机组阻抗建模及次同步振荡影响因素分析[J]. 电力工程技术, 2020, 39(1): 170-177.
Wang Lichao, Yu Yongjun, Zhang Mingyuan, et al. Impedance model and analysis of subsynchronous oscillation influence factors for grid-connected full-converter wind turbines[J]. Jiangsu Electrical Engineering, 2020, 39(1): 170-177.
[6] 刘其辉, 洪晨威, 逄思敏, 等. 基于弹性系数的双馈风电机组控制参数对次同步振荡作用分析及调整方法[J]. 电工技术学报, 2022, 37(14): 3528- 3541.
Liu Qihui, Hong Chenwei, Pang Simin, et al. Analysis and adjustment method of doubly-fed fan control parameters on subsynchronous oscillation based on impedance elastic sensitivity[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3528- 3541.
[7] 汪春江, 孙建军, 宫金武, 等. 并网逆变器与电网阻抗交互失稳机理及阻尼策略[J]. 电工技术学报, 2020, 35(增刊2): 503-511.
Wang Chunjiang, Sun Jianjun, Gong Jinwu, et al. Mechanism and damping strategy of interactive instability between grid-connected inverter and grid impedance[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 503-511.
[8] 刘一锋, 周小平, 洪乐荣, 等. 虚拟惯性控制的负荷变换器接入弱电网的序阻抗建模与稳定性分析[J]. 电工技术学报, 2021, 36(4): 843-856.
Liu Yifeng, Zhou Xiaoping, Hong Lerong, et al. Sequence impedance modeling and stability analysis of load converter with virtual inertia control con- nected to weak grid[J]. Transactions of China Electro- technical Society, 2021, 36(4): 843-856.
[9] 赖林琛, 周强, 杜文娟, 等. 同型光热发电机并联聚合对光热发电场振荡稳定性影响[J]. 电工技术学报, 2022, 37(1): 179-191, 231
Lai Linchen, Zhou Qiang, Du Wenjuan, et al. Impact of dynamic aggregation of same concentrating solar power generators in parallel connection on the oscillation stability of a CSP plant[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 179-191, 231
[10] Liu Huakun, Xie Xiaorong, He Jingbo, et al. Sub- synchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708- 4720.
[11] 高本锋, 崔意婵, 李蕴红, 等. D-PMSG经LCC- HVDC送出系统的次同步振荡特性分析[J]. 中国电机工程学报, 2022, 42(6): 2084-2095, 4.
Gao Benfeng, Cui Yichan, Li Yunhong, et al. Analysis of subsynchronous oscillation characteristics of D-PMSG integrated with LCC-HVDC system[J]. Proceedings of the CSEE, 2022, 42(6): 2084-2095, 4.
[12] 高本锋, 刘毅, 宋瑞华, 等. 双馈风电场经LCC- HVDC送出的次同步振荡特性研究[J]. 中国电机工程学报, 2020, 40(11): 3477-3488, 9.
Gao Benfeng, Liu Yi, Song Ruihua, et al. Study on subsynchronous oscillation characteristics of DFIG- based wind farm integrated with LCC-HVDC system[J]. Proceedings of the CSEE, 2020, 40(11): 3477-3488, 9.
[13] Liu Hanchao, Sun Jian. Small-signal stability analysis of offshore wind farms with LCC HVDC[C]//2013 IEEE Grenoble Conference, Grenoble, France, 2013: 1-8.
[14] Añó-Villalba S, Bernal-Perez S, Martinez-Turegano J, et al. Impedance-based stability analysis for HVDC diode-rectifier connected off-shore wind farms[C]// IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 2019: 2389-2394.
[15] 薛安成, 付潇宇, 乔登科, 等. 风电参与的电力系统次同步振荡机理研究综述和展望[J]. 电力自动化设备, 2020, 40(9): 118-128.
Xue Ancheng, Fu Xiaoyu, Qiao Dengke, et al. Review and prospect of research on sub-synchronous oscillation mechanism for power system with wind power participation[J]. Electric Power Automation Equipment, 2020, 40(9): 118-128.
[16] Du Wenjuan, Ren Bixing, Wang Haifeng, et al. Comparison of methods to examine sub-synchronous oscillations caused by grid-connected wind turbine generators[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4931-4943.
[17] 高本锋, 刘毅, 李蕴红, 等. 直驱风电场与LCC- HVDC次同步交互作用的扰动传递路径及阻尼特性分析[J]. 中国电机工程学报, 2021, 41(5): 1713- 1728, 18.
Gao Benfeng, Liu Yi, Li Yunhong, et al. Analysis on disturbance transfer path and damping characteristics of sub-synchronous interaction between D-PMSG- based wind farm and LCC-HVDC[J]. Proceedings of the CSEE, 2021, 41(5): 1713-1728, 18.
[18] 高本锋, 王义, 曾四鸣, 等. 直驱风电场并入弱交流电网的次同步分量通路及阻尼特性分析[J]. 中国电机工程学报, 2022, 42(14): 5089-5102, 8.
Gao Benfeng, Wang Yi, Zeng Siming, et al. Analysis of sub-synchronous component path and damping characteristics of D-PMSG-based wind farm incor- porated into weak AC grid[J]. Proceedings of the CSEE, 2022, 42(14): 5089-5102, 8.
[19] 王一珺, 杜文娟, 陈晨, 等. 基于改进复转矩系数法的风电场并网引发电力系统次同步振荡研究[J]. 电工技术学报, 2020, 35(15): 3258-3269.
Wang Yijun, Du Wenjuan, Chen Chen, et al. Study on sub-synchronous oscillations of power systems caused by grid-connected wind farms based on the improved complex torque coefficients method[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3258-3269.
[20] Yuan Hao, Yuan Xiaoming, Hu Jiabing. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control times- cale[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3981-3991.
[21] 张思东, 黄云辉, 周党生, 等. 弱电网下VSC控制环路对直流电压稳定性的影响分析[J]. 高电压技术, 2021, 47(8): 2730-2741.
Zhang Sidong, Huang Yunhui, Zhou Dangsheng, et al. Impacts analysis of VSC control loop on DC voltage control stability in weak-grid[J]. High Voltage Engineering, 2021, 47(8): 2730-2741.
[22] Lu Jun, Yuan Xiaoming, Hu Jiabing, et al. Motion equation modeling of LCC-HVDC stations for analyzing DC and AC network interactions[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1563- 1574.
[23] Hu Jiabing, Yuan Hao, Yuan Xiaoming. Modeling of DFIG-based WTs for small-signal stability analysis in DVC timescale in power electronized power systems[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1151-1165.
[24] Huang Yunhui, Zhai Xuebing, Hu Jiabing, et al. Modeling and stability analysis of VSC internal voltage in DC-link voltage control timescale[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(1): 16-28.
[25] 董文凯, 杜文娟, 王海风. 弱连接条件下锁环动态主导的并网直驱风电场小干扰稳定性研究[J]. 电工技术学报, 2021, 36(3): 609-622.
Dong Wenkai, Du Wenjuan, Wang Haifeng. Small- signal stability of a grid-connected PMSG wind farm dominated by dynamics of PLLs under weak grid connection[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 609-622.
[26] Xu Yanhui, Gao Tianchu. Sub-synchronous frequency domain-equivalent modeling for wind farms based on rotor equivalent resistance characteristics[J]. Global Energy Interconnection, 2022, 5(3): 293-300.
[27] Wu Meng, Xie Le, Cheng Lin, et al. A study on the impact of wind farm spatial distribution on power system sub-synchronous oscillations[J]. IEEE Transa- ctions on Power Systems, 2016, 31(3): 2154-2162.
[28] Wang Cong, Li Yan, Fan Yiwen, et al. Development of wind-energy modeling technology and standards[J]. Global Energy Interconnection, 2022, 5(2): 206- 216.
[29] 叶运铭, 汪娟娟, 陈威, 等. LCC-HVDC系统直流控制回路小干扰稳定性分析[J]. 电力系统自动化, 2021, 45(16): 178-188.
Ye Yunming, Wang Juanjuan, Chen Wei, et al. Analysis of small interference stability in the DC control circuit of LCC-HVDC system[J]. Automation of Electric Power Systems, 2021, 45(16): 178-188.
[30] 徐衍会, 曹宇平. 直驱风机网侧换流器引发次/超同步振荡机理研究[J]. 电网技术, 2018, 42(5): 1556- 1564.
Xu Yanhui, Cao Yuping. Research on mechanism of sub/sup-synchronous oscillation caused by GSC controller of direct-drive permanent magnetic syn- chronous generator[J]. Power System Technology, 2018, 42(5): 1556-1564.
Abstract In China, wind power, photovoltaic, and other renewable energy are mainly distributed in the western and northern regions, far from the load center in the eastern and central regions. Consequently, line-commutated converter-based high voltage direct current (LCC-HVDC) has become the main form of renewable energy transmission. However, according to the rapid technological development of renewable energy, more and more renewable energy bases will be connected to the near area of the LCC-HVDC transmission end. The proportion of renewable energy will increase, weakening the support capacity of conventional power supply. The interaction between the grid-connected voltage source converter (VSC) of renewable energy power generation equipment and LCC-HVDC is increasingly obvious, and this interaction has the risk of inducing sub-synchronous oscillation (SSO). The current research methods for the SSO characteristics of renewable energy generations integrated with the LCC-HVDC system mainly focus on the impedance analysis method and eigenvalue analysis method, and the research content also focuses on the judgment of SSO stability. It is necessary to study the sub-synchronous interaction at the physical level from a new perspective.
This paper uses the damping path to analyze the transmission process of the sub-synchronous frequency disturbance to analyze the sub-synchronous interaction of the system. Firstly, the second-order motion equations of three kinds of oscillation dominant elements are derived. By analogy with the Heffron-Phillips model of synchronous machine rotor, the “Heffron-Phillips-like model” is obtained to analyze the stability of oscillation dominant elements. Afterward, based on the dynamic process of the dominant oscillation element, the closed-loop transfer function block diagram of the system is established, and three kinds of damping paths are obtained through analysis. The first kind of damping path reflects the internal damping of power electronic equipment, the second kind of damping path reflects the interaction between the power electronic equipment and the AC system, and the third kind of damping path reflects the interaction between different power electronic equipment. Subsequently, the closed-loop transfer function block diagram of the system is reconstructed to separate the damping of each path, and the damping of SSO mode is quantitatively evaluated using the concept of damping coefficient in the Heffron-Phillips-like model, thereby achieving the purpose of analyzing the influence of sub-synchronous interaction on SSO stability. For example, in the case of the direct drive wind farm integrated with the LCC-HVDC system, the path-damping characteristics of LCC-HVDC DC-link inductor dominated SSO mode are searched, and the influence of controller parameters on path damping is analyzed. The results show that the sub-synchronous interaction between LCC-HVDC and direct-driven wind farm mainly provides negative damping in the DC-link inductor SSO mode, which is not conducive to the stability of the system. The controller parameters obviously affect the path-damping characteristics. By analyzing the influence of the system parameters on the path damping, the main influence links of the sub-synchronous interaction can be obtained, and relevant measures can be taken to suppress SSO better. The conclusions can guide the design of controller parameters in engineering practice.
keywords：Renewable energy generation, LCC-HVDC, sub-synchronous interaction, damping path, damping reconstruction
DOI: 10.19595/j.cnki.1000-6753.tces.221579
中图分类号：TM712
收稿日期 2022-08-15
改稿日期 2022-11-18
高本锋 男，1981年，博士，副教授，研究方向为高压直流输电和电力系统次同步振荡。E-mail: gaobenfeng@126.com
王 义 男，1998年生，硕士研究生，研究方向为电力系统分析与控制。E-mail: wy15653653183@163.com（通信作者）
（编辑 郭丽军）