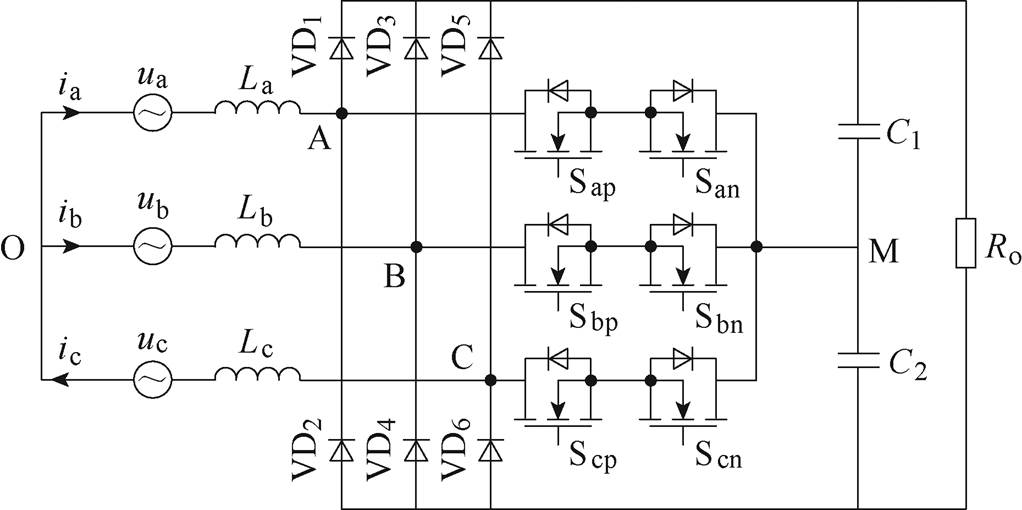
图1 三相三线制Vienna整流器拓扑原理
Fig.1 Topology of three-phase three-wire Vienna rectifier
摘要 Vienna整流器因其高功率密度、高可靠性等优点，适用于多电飞机的交流供电系统。航空电网对可靠性有很高的要求，需要考虑电网不平衡甚至缺相故障的情况。当电网出现三相不平衡情况时，需要采取合适的控制方法消除电网负序分量对整流器输入输出性能的影响。而当电网出现缺相故障时，常规的三相控制方法失效，整流器通常需要停机保护，但降低了供电系统的可靠性。为了使整流器在电网缺相故障下维持输出功能，该文通过分析缺相状态下Vienna整流器的工作模态，提出一种单相空间矢量脉宽调制方法，并设计相应的控制环路，使得Vienna整流器在缺相状态下能够维持稳定的直流输出，并同时给出一种缺相判断方法。通过仿真和实验验证了所提Vienna整流器缺相控制方法的有效性。
关键词：Vienna整流器 电网不平衡 单相空间矢量脉宽调制 缺相控制
新型飞机交流变频供电系统，通过发动机直接带动交流发电机产生360～800 Hz三相交流电，具有结构简单、效率高等优点，已在Boeing787等多电飞机上得到了应用[1-2]。随着多电飞机技术的发展，机载电子设备容量越来越大，航空电网的谐波污染以及电压不平衡等问题日益严重，这会影响飞机供电质量，甚至带来安全隐患[3-6]。
三相整流器起到将交流输入转化为直流高压输出，为负载设备供电的作用，在航空电网中应用广泛[6]。传统的无源整流器，虽然可靠性较高，但存在体积质量大、功率因数低、谐波含量高等缺点，不适用于未来多电飞机。相比于无源多脉冲整流系统，Vienna整流器在系统效率与功率密度方面更具优势，并且具有功率因数校正（Power Factor Correction, PFC）功能，能够实现电压电流闭环控制，适用于对整流器性能要求较高的航空电网[7-9]。但是由于在可靠性方面仍有欠缺，Vienna整流器无法应用于关键负载供电。因此，研究Vienna整流器的故障诊断与容错控制方法，提高整流器的可靠性具有重要意义。
在理想电网下，Vienna整流器可以实现低输入电流谐波和稳定的直流输出电压。然而，在实际的航空电网中，各相的幅值、相位均会产生偏差，出现三相不平衡的情况。根据瞬时功率理论，不平衡电网存在的负序分量会导致输入功率和直流电压存在二倍频波动，进而影响输入电流质量与输出电压稳定性[10-11]。通常可以采用正负序锁相环，如解耦双同步坐标系锁相环（Decoupled dual Synchronous Rotating Frame filtering-based Phase-Locked Loop, DSRF-PLL）和双二阶广义积分器锁相环（Dual Second Order Generalized Integrator PLL, DSOGI- PLL），提取电网负序分量并产生电流参考信号，可以维持恒定的输入功率，消除负序分量带来的二倍频波动，实现整流器的控制[12-15]。
航空供电系统对可靠性有很高的要求，需要考虑在缺相等故障情况下的应用[16]。对于三相PWM整流器，当电网出现缺相故障时，常规的三相控制方法失效，通常需要及时地判断出缺相故障并停机保护[17]。这会导致整流器无法为后级负载设备持续供电，降低了供电系统的可靠性。因此，为了满足航空电网高可靠性的需求，需要研究Vienna整流器在电网缺相情况下的控制方法。
目前，针对三相PWM整流器的缺相控制方法研究较少，且大多集中于缺相故障判断方法。文献[18]介绍了一种基于三相锁相环的缺相故障软件检测方法。文献[19]提出了一种缺相故障硬件检测电路。文献[20]研究了采用单周期控制的三相四线制Vienna整流器在电网不平衡以及缺相情况下的应用。由于三相四线制Vienna整流器可以物理解耦成三路单相Boost型整流器，因此当电网一相缺相时，其余两路仍可正常工作。而对于三相三线制整流器，由于三相之间相互耦合，当电网一相缺相时，其余两相无法独立解耦，可以将其视为单相PWM整流器，输入电压为线电压。因此，对于三相三线制Vienna整流器，可以考虑借鉴单相三电平PWM整流器的控制方法，实现电网缺相情况下的控制。
单相三电平变流器拓扑主要有二极管钳位型、T型等[21-22]。其调制方式主要包括正弦脉宽调制（Sinusoidal Pulse Width Modulation, SPWM）与单相空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）。其中，单相SVPWM方法借鉴于三相拓扑结构广泛应用的SVPWM方法，具有物理含义清晰、易于数字实现等优点[22]。利用单相SVPWM原理分析电网缺相下Vienna整流器模型，有助于理解单相Vienna整流器的工作原理，设计相应的控制环路，实现整流器缺相状态下的控制。
本文以Vienna整流器在航空电网中的应用为研究目标，首先，分析了航空电网不平衡下Vienna整流器的控制方法，采用了一种双坐标变换矢量控制方法以消除电网负序分量带来的输入电流谐波与直流电压波动；其次，分析了电网缺相下Vienna整流器的数学模型，提出了一种单相空间矢量调制方法，能够实现Vienna整流器在缺相情况下的控制；然后，根据正负序锁相环设计了一种电网缺相故障判断方法，并给出了考虑电网缺相故障情况的Vienna整流器控制方法；最后，通过仿真与实验验证了所提控制方法在航空宽变频电网中应用的有效性。
本文所研究的三相三线制Vienna整流器基本拓扑原理如图1所示，主要由交流侧输入电感La、Lb、Lc，直流侧输出电容C1、C2，三相整流桥VD1～VD6和三对反向串联MOSFET（Sap～Scn）组成的双向开关构成。三相之间相互耦合，工作模态由输入电流极性和开关状态共同决定。
在理想电网情况下，Vienna整流器通常采用基于dq坐标系的电压电流双环PI控制，利用矢量调制的方法完成控制[23-24]。但实际航空电网易受后级负载设备的影响，各相幅值和相位均会存在偏差，出现三相不平衡的情况。不平衡电网中负序分量的存在会导致整流器直流侧出现二倍频电压波动，输入电流谐波含量增加[14-15]。因此，为了使Vienna整流器在航空电网中实现良好的输入输出性能，需要考虑在不平衡电网中的控制方法。
图1 三相三线制Vienna整流器拓扑原理
Fig.1 Topology of three-phase three-wire Vienna rectifier
对于三相三线制系统，零序分量没有通路，电网电压u可以分解为正序分量up和负序分量un。根据文献[10]中给出的瞬时有功和无功功率的定义，可以得到三相系统在dq坐标系下的功率表达式为
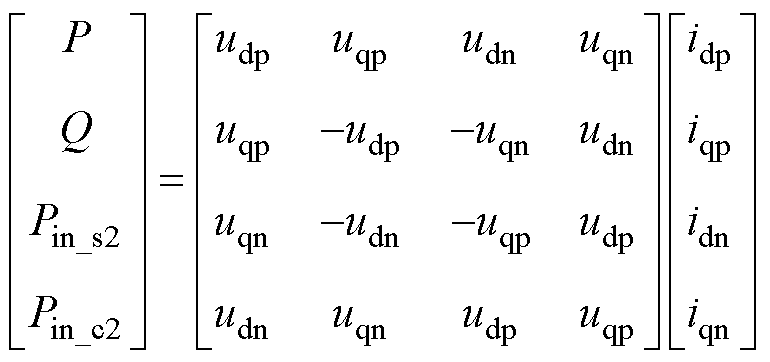（1）
式中，udp、uqp、udn、uqn为电网电压在dq坐标系下正负序分量；idp、iqp、idn、iqn为输入电流的正负序分量；P为有功功率；Q为无功功率；Pin_c2、Pin_s2为负序分量所带来的二倍频功率波动。对于三相整流器，有功功率P决定了直流电压，有功功率波动分量Pin_c2、Pin_s2会在直流侧引入二次纹波，而瞬时无功功率Q决定了电路的功率因数[12]。为抑制直流电压波动和实现单位功率因数，可以令[P Q Pin_c2 Pin_s2]T=[Po 0 0 0]T，Po为输出功率，从而计算得到满足控制目标的电流表达式为
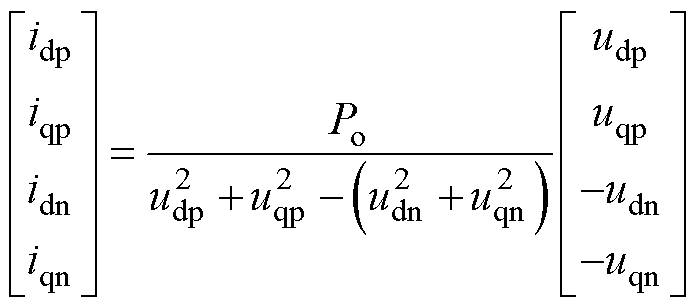（2）
因此，只需要设计控制环路使得输入电流满足式（2），即可消除电网不平衡带来的直流电压波动与输入电流谐波，维持整流器的稳定工作。
由式（2）可知，满足控制目标的电流参考值包含电网的正序和负序分量，因此电网电压各序分量的计算是三相不平衡电网中Vienna整流器控制首先需要解决的问题。
三相输入电压可以通过Clarke变换转化到ab 坐标系下，同时正负序电压分量可以由对称分量法获得，因此可以计算得到ab 坐标系下电网正序电压分量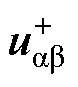
和负序电压分量
表达式[11]分别为
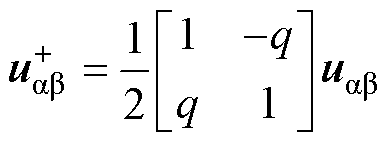（3）
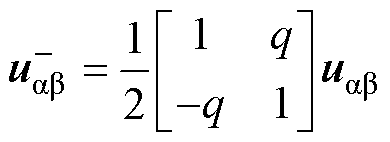（4）
式中，q为滞后电压信号90 °的正交分量，q=e-j(p/2)。
文献[11]提出的基于二阶广义积分（Second Order Generalized Integrator, SOGI）的正交信号发生器，起到产生90 °相位偏移信号和带通滤波的作用。可以借助SOGI计算得到电网的正序和负序分量，进而对电网电压进行锁相，得到电网相位与dq坐标系下的电网电压分量，该方法即为基于双二阶广义积分器的锁相环（DSOGI-PLL），其结构框图如图2所示。
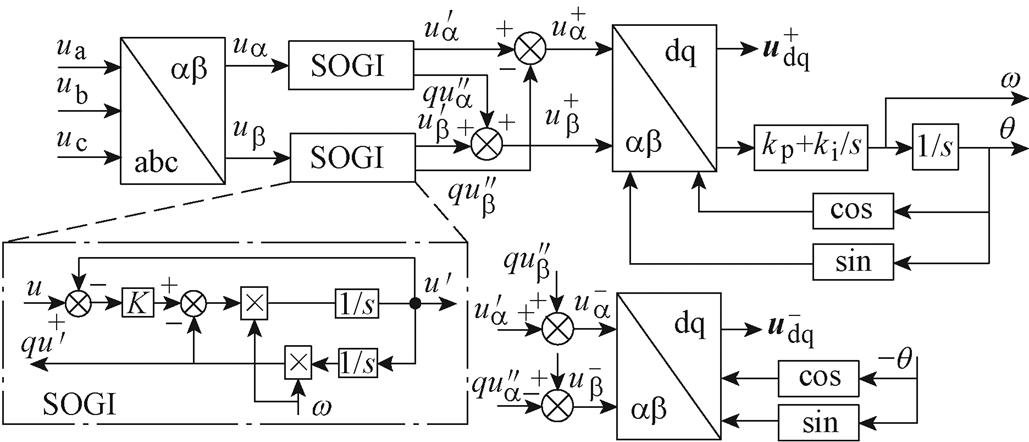
图2 DSOGI-PLL结构框图
Fig.2 Block diagram of DSOGI-PLL
该方法通过SOGI计算得到ab 坐标系下电网电压正交信号，并根据式（3）、式（4）得到电网的正序和负序电压分量。利用锁相环对正序电压分量进行锁相，即可得到电网频率w 与相位q。根据电网相位进行坐标变换即可得到电网电压在dq坐标系下的正序与负序分量。
基于式（2）与DSOGI-PLL，可以将电网电压与电流通过双坐标变换转换到正负序dq坐标系下，对正负序的dq轴电流分量分别进行控制，再通过矢量调制方法产生占空比信号（da, db, dc）。控制框图如图3所示。
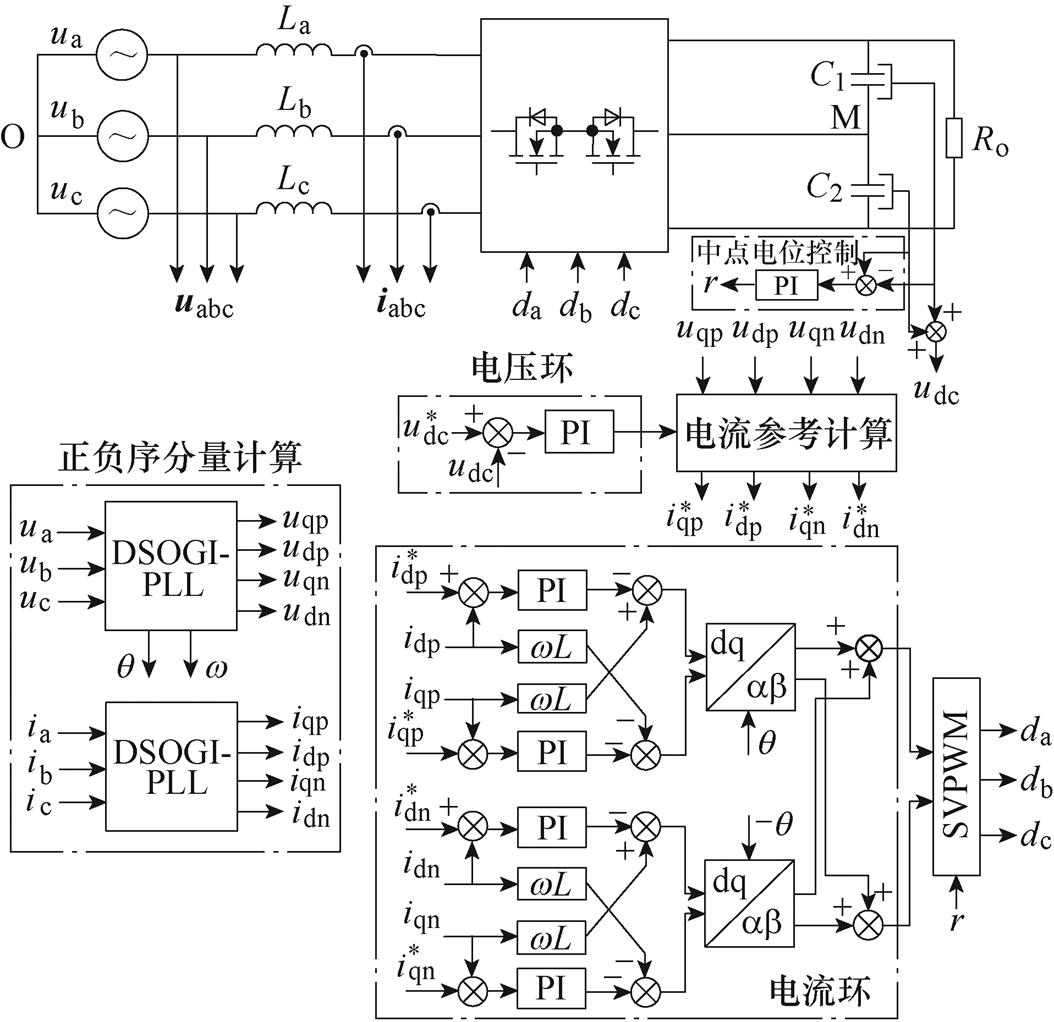
图3 电网不平衡下Vienna整流器控制框图
Fig.3 Block diagram of control strategy for Vienna rectifier under unbalanced grids
通过上述双坐标变换矢量控制方法，可以使Vienna整流器在电网不平衡情况下维持良好的输入输出特性。但是，相比于工频电网，航空电网相对独立且脆弱，除了三相不平衡等情况，还存在电网缺相的问题。通常，为了整流器自身的安全，当电网出现缺相故障时，需要识别并进行停机保护，但这会影响对负载供电的连续性。为了提高整流系统供电的可靠性，需要研究Vienna整流器在电网缺相下的运行控制方法。
对于三相三线制系统，当有两相缺相时，电路无法构成回路，因此只需考虑电网单相缺相故障的情况。为便于叙述分析且不失一般性，本文中电网缺相故障均假设为A相缺相。
当电网A相缺相时，Vienna整流器A相通路对电路不起任何作用，因此整流器可以视作单相系统运行，此时整流器的输入电压为BC两相线电压ubc，A相缺相时Vienna整流器拓扑如图4所示。
对于缺相下的Vienna整流器，将其视作一单相PWM整流器。设直流侧电压为Udc，直流侧电容C1=C2，直流侧电容电压相同（即Udc1=Udc2=Udc/2）；以M为参考点，则每相桥臂uxM可以输出三种电平：+Udc/2, 0, -Udc/2。整流器交流侧输入ubc有五种电平状态：±Udc, ±Udc/2, 0。假设开关管为理想开关管，可以用开关函数Sx（x=b, c）表示每相开关管的导通和关断，表达式为
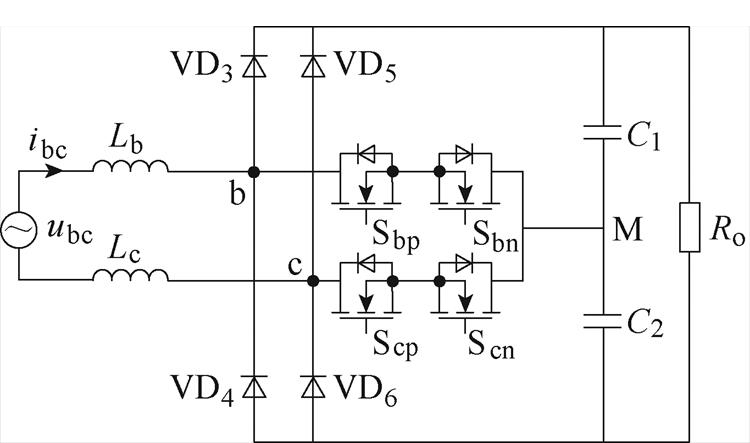
图4 A相缺相时Vienna整流器拓扑
Fig.4 Topology of Vienna rectifier when phase A losses
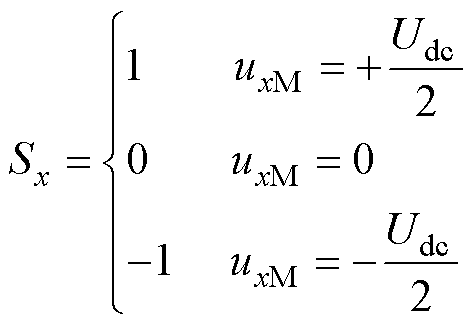（5）
由于Vienna整流器输入端电压受限于交流侧电流的极性，两相输入电流不可能同时为正或负，因此缺相状态下Vienna整流器共存在七种不同的工作状态，见表1。这七种工作状态形成七种不同的电压矢量，记为Vi，i=1,…, 7。七种基本电压矢量对应整流器的工作状态如图5所示。
表1 缺相下空间电压矢量表
Tab.1 Voltage space vectors when phase A losses
电压矢量SbScubMucMubc V11-1+-Udc V210+0+ V30-10-+ V400000 V5-11-+-Udc V6-10-0- V7010+-
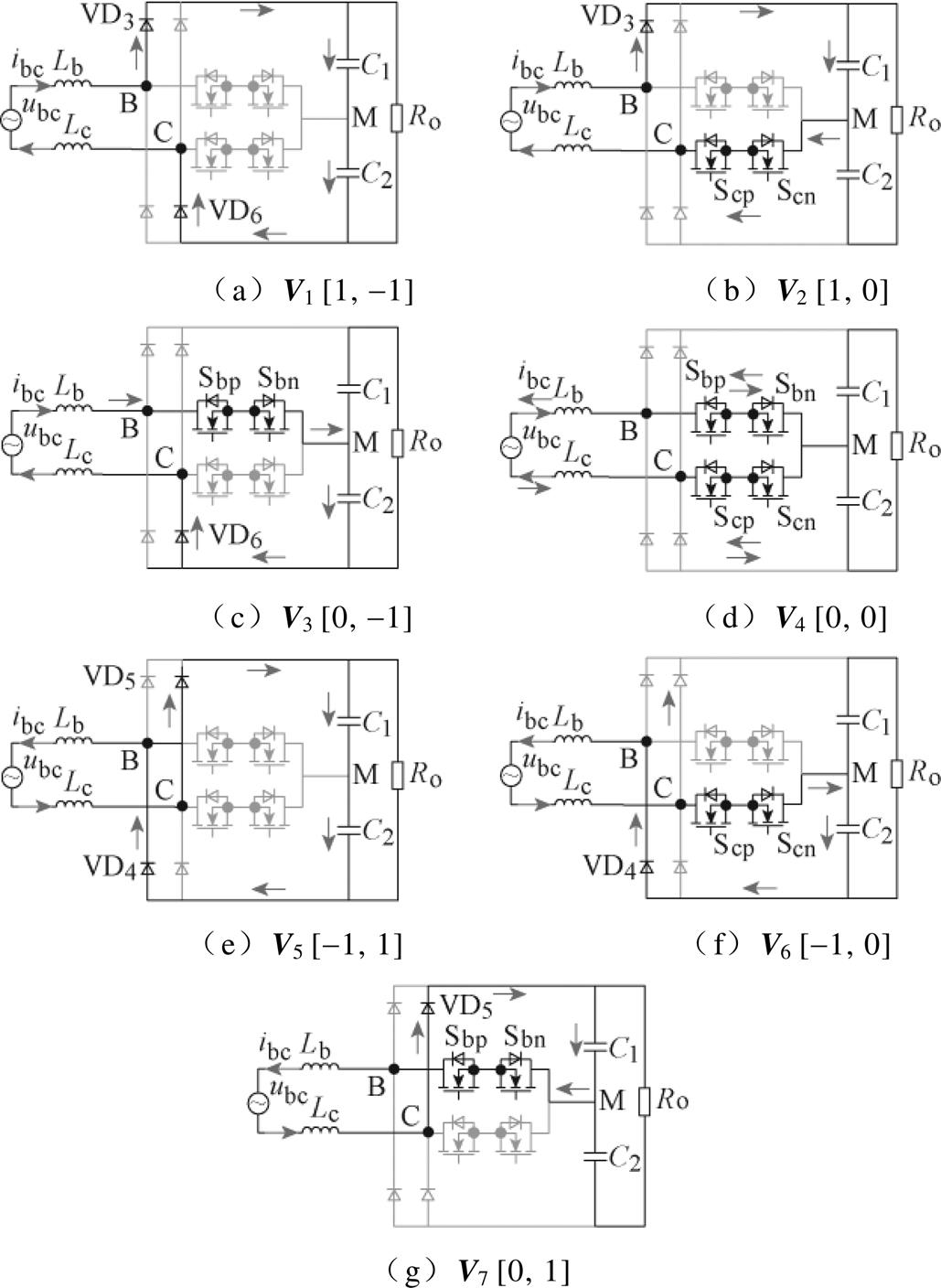
图5 A相缺相下Vienna整流器工作状态
Fig.5 Operational modes of Vienna rectifier when phase A losses
SVPWM方法在三相拓扑结构中得到广泛应用，基本思想是采用邻近的基本电压矢量来合成参考电压矢量[23-24]。参考Vienna整流器在正常工作状态下的SVPWM方法，本文推导出一种单相空间矢量调制方法，以实现Vienna整流器在电网缺相故障下的调制。
根据表1，Vienna整流器在缺相情况下共有七种不同的工作状态，根据每个工作状态交流侧输入电压ubc模值的大小，可以将七种基本电压矢量分为大矢量（V1, V5）、小矢量（V2, V3, V6, V7）和零矢量（V4），对应的模值分别为Udc、Udc/2和0。其中V2与V3, V6与V7对矢量合成作用相同，互为冗余小矢量。绘制这些矢量可以得到单相空间矢量平面，如图6所示。
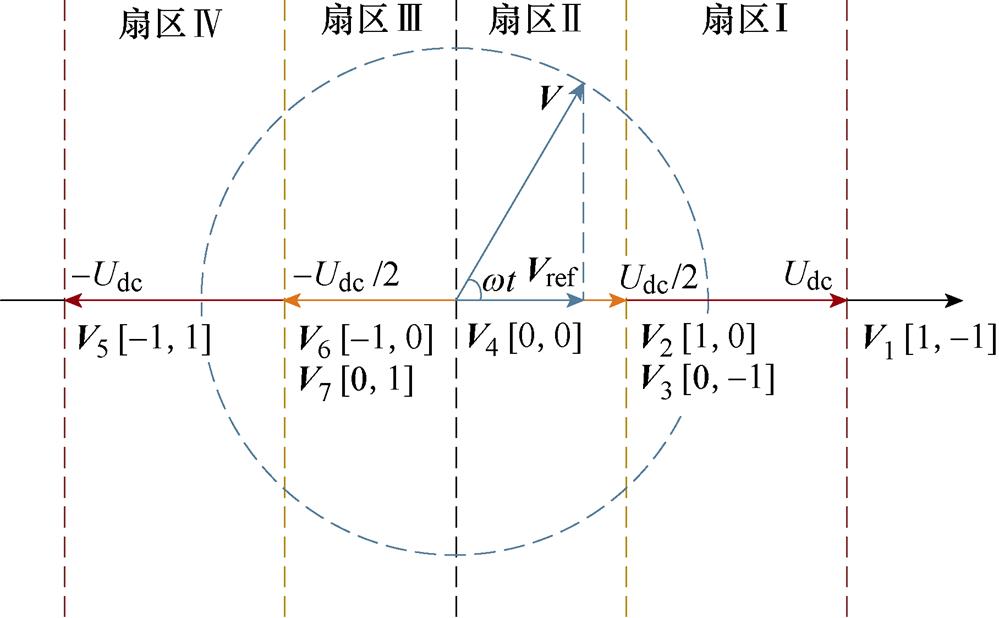
图6 单相空间矢量平面
Fig.6 Space vector diagram for single-phase SVPWM
单相空间矢量平面是一维平面，根据矢量模值的不同，可以将该平面划分为扇区Ⅰ～Ⅳ。根据参考电压矢量所在的扇区，选择该扇区内的基本电压矢量进行合成，即可实现单相空间矢量调制。参考电压矢量为输入电压ubc，设ubc=mUdccos(wt)，其中m为调制比，范围在0～1之间。如图6所示，参考电压矢量Vref可以视作长度为mUdc的矢量V在该平面的投影，矢量V以角频率w逆时针旋转。
根据参考电压矢量的幅值即可判断其所在的扇区，确定参与合成的基本电压矢量，扇区判断规则见表2。
表2 扇区判断规则
Tab.2 Sector j udgement rules
扇区判断规则合成矢量 Ⅰ＜Vref＜UdcV1、V2、V3 Ⅱ0＜Vref＜V2、V3、V4 Ⅲ-＜Vref＜0V4、V6、V7 Ⅳ-Udc＜Vref＜-V1、V2、V3
确定参与合成的基本电压矢量后，根据伏秒平衡原理，即式（6），可以求得每个基本矢量的作用时间（一对冗余矢量算作一个小矢量）。
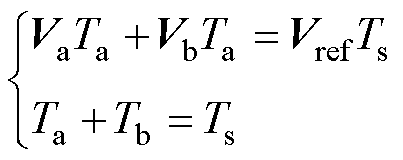（6）
式中，Ta、Tb分别为Va、Vb矢量对应的作用时间。可以解得
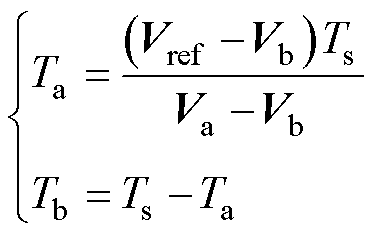（7）
在计算矢量作用时间后，需要确定一个开关周期内开关管的动作顺序。为了减少器件的开关损耗，本文采取一种五段式矢量合成方法，从小矢量开始，每次只改变一个开关动作。参考电压矢量在各个扇区内的输出矢量的作用顺序见表3，其中首发小矢量可以为一对冗余小矢量中的任意一个。图7为参考电压矢量位于扇区Ⅰ时开关动作时序，图中PWMx（x=B, C）表示该相开关管导通或关断信号。当参考电压矢量位于其他扇区时，情况类似。
作为三电平变换器，Vienna整流器在运行中需要保持直流侧中点电位平衡，否则会造成部分器件偏压等问题，不利于整流器的安全运行。在正常运行情况下，Vienna整流器利用一对冗余小矢量对中点电位有相反的电压调节作用，通过分配冗余小矢量的作用时间实现中点电位平衡[15]。
表3 五段式合成矢量作用顺序
Tab.3 Output vectors sequence of five-segement Synthetis
扇区矢量作用顺序 ⅠV2-V1-V3-V1-V2 ⅡV3-V4-V2-V4-V3 ⅢV6-V4-V7-V4-V6 ⅣV5-V7-V6-V7-V5
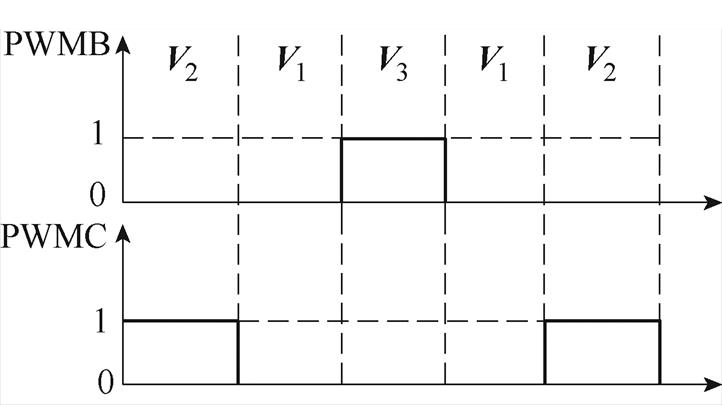
图7 扇区Ⅰ开关状态时序
Fig.7 Timing diagram of space vector in Sector Ⅰ
在电网缺相的情况下，由图5可知，大矢量V1、V5和零矢量V4对中点电位没有影响，而一对冗余小矢量（V2与V3，V6与V7），以V2与V3为例，其中V2状态下电路对上母线电容C1充电，V3状态下电路对下母线电容C2充电，二者对中点电位的作用相反。因此，与正常运行情况下方法相同，在电网缺相情况下，Vienna整流器仍然可以通过调整正负小矢量的作用时间来实现中点电位平衡控制。
引入分配系数r（0＜r＜1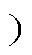
对小矢量作用时间进行调节，以扇区Ⅰ为例，其中V2与V3互为冗余矢量，若其总的作用时间为Ta，令V2的作用时间T2=rTa，则V3的作用时间T3=(1-r)Ta。这样在得到直流侧电容电压差的情况下，通过调整一对冗余小矢量的作用时间即可实现中点电位平衡控制。
在分析Vienna整流器在缺相故障下的工作状态与空间矢量调制方法后，需要设计缺相检测方法以及控制环路以实现Vienna整流器在缺相状态下的控制。
对于三相三线制变换器，由于没有中线接入，输入电压采样通常需要构建额外的中性点
实现，如图8所示。
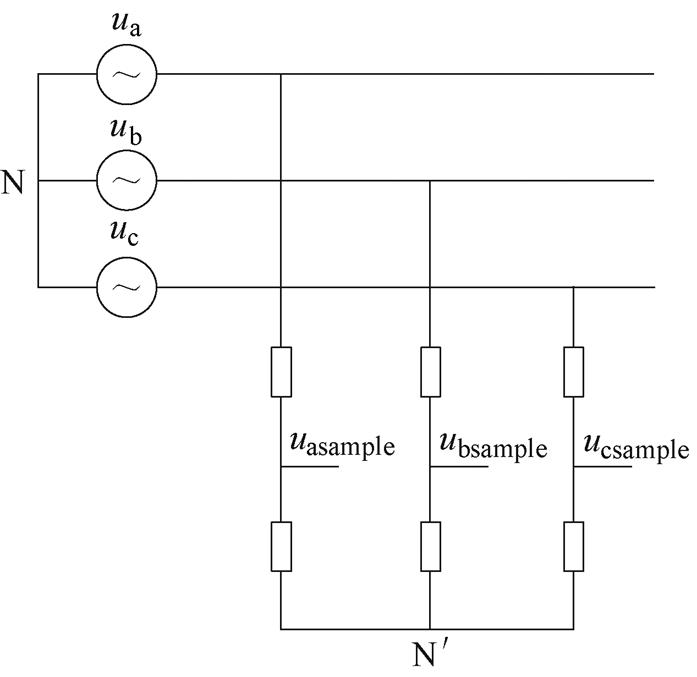
图8 三线制输入电压采样
Fig.8 Voltage sample of three-wire system
当A相缺相时，三相通路并不存在，此时B相和C相采样得到的电压为输入线电压ubc的一半，即
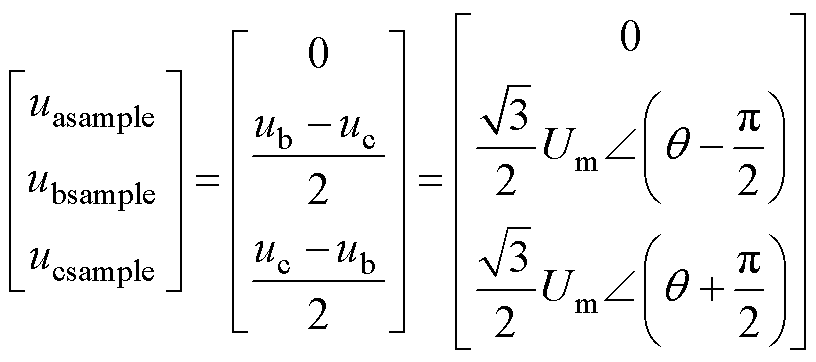（8）
式中，Um为输入相电压有效值。根据对称分量法，可以计算得到采样电压的正负序分量为
（9）
此时d轴的正负序电压分量udp=Um/2，udn= Um/2。由于本文考虑电网不平衡下Vienna整流器的控制，采用DSOGI-PLL计算电网的正负序分量。因此，可以利用DSOGI-PLL检测电网的缺相故障。
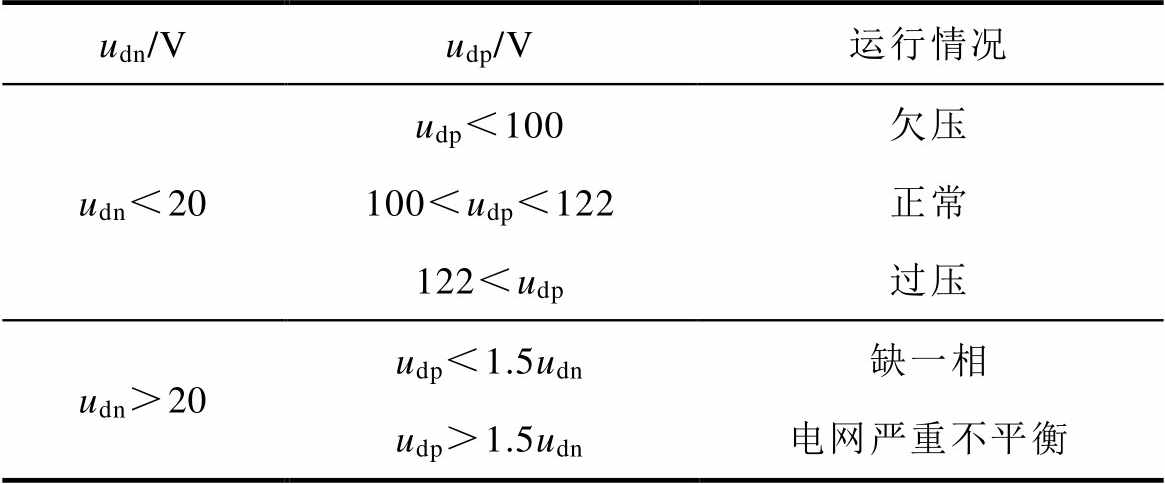
航空宽变频电网的输入电压正常在100 Vrms～122 Vrms范围变化，当电网出现过电压、欠电压以及缺相故障时，可以根据采用得到的电网正序和负序电压分量udp与udn判断电网状况。本文根据电网的运行情况，采用的判断标准见表4。
根据表4，当DSOGI-PLL计算得到电网的正序分量udp与负序分udn满足udn＞20 V且udp＜1.5udn时，即可判断电网出现缺相故障。在电网缺相情况下，Vienna整流器的该相通路没有电流流过，因此当检测某相电流为零时，即可判断该相出现了缺相故障。
表4 电网运行情况判断
Tab.4 Grid conditions detection criterion
udn/Vudp/V运行情况 udn＜20udp＜100欠压 100＜udp＜122正常 122＜udp过压 udn＞20udp＜1.5udn缺一相 udp＞1.5udn电网严重不平衡
在PLECS软件中搭建仿真模型验证缺相检测方法的有效性。设置电网三相输入为115 Vrms/400 Hz，在0.3 s时刻A相缺相，此时B相和C相采样得到的电压ubsample、ucsample为输入线电压ubc的一半，DSOGI-PLL计算得到电网电压正序和负序分量udp与udn由162.6 V和0 V经过约5 ms的调节时间变为81 V。根据表4中判断标准，在A相缺相后经过约0.6 ms检测到缺相故障。缺相故障检测仿真如图9所示，仿真结果验证了通过DSOGI-PLL计算电网正负序分量的方法可以较快的检测出电网的缺相故障。
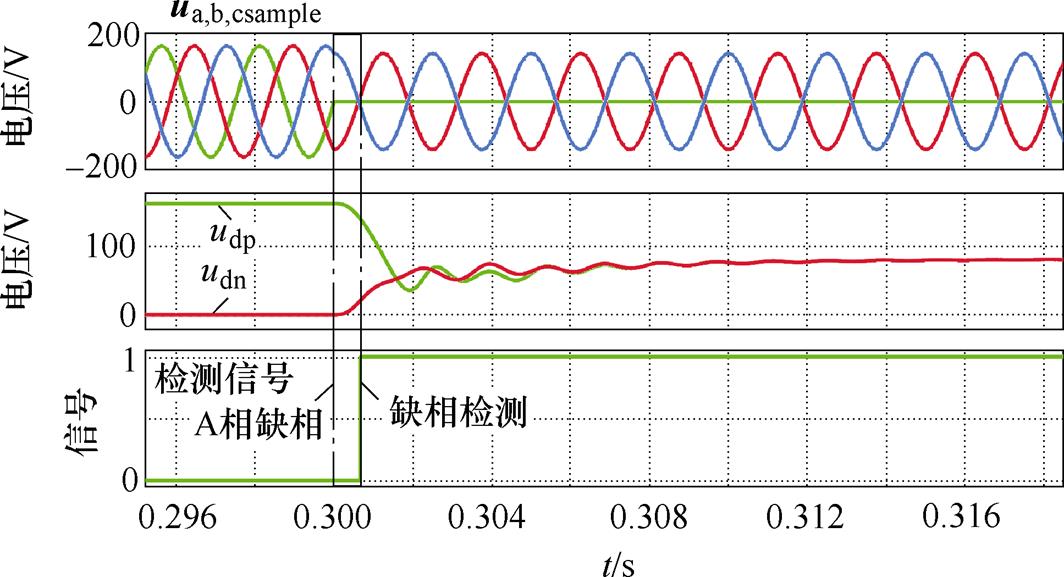
图9 缺相故障检测仿真
Fig.9 Simulation of lack phase detection
根据第2节的分析，当电网出现某一相缺相故障，此时Vienna整流器可以视为单相PWM整流器。因此，与单相Boost型PFC控制方法类似，可以设计Vienna整流器在电网缺相故障下的控制方法，如图10所示。图10中各控制环路功能如下：
（1）电压环：采样直流电压与参考值对比，误差经PI控制器计算得到电流参考值的功率系数km。电压环传递函数表达式为
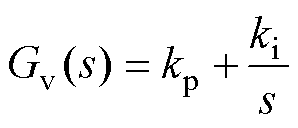（10）
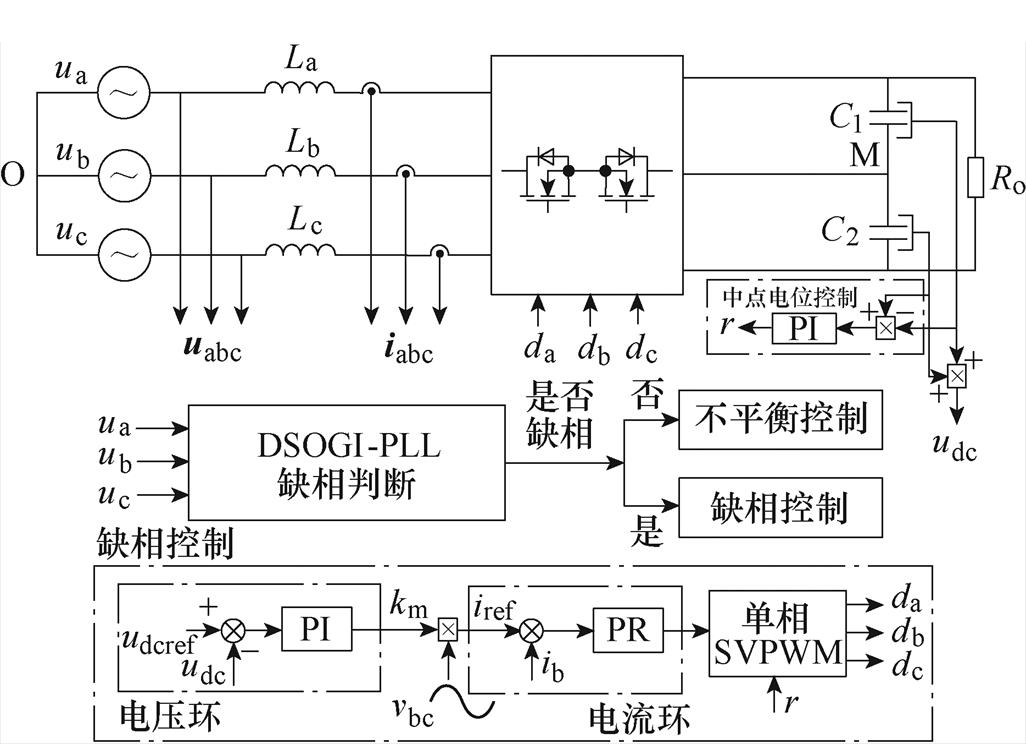
图10 Vienna整流器缺相控制方法
Fig.10 Lack phase control strategy of Vienna rectifier
式中，kp为比例系数；ki为积分系数。
（2）电流环：电网缺相下的Vienna整流器视作单相Boost型PWM整流器，假设A相缺相，那么输入电压为线电压vbc。可以将电压环的输出km与线电压vbc相乘作为电流环的参考值iref。由于参考电流为正弦信号，为了实现无静态误差跟踪，采用准比例谐振（Quasi Proportional Resonant, QPR）控制器实现，传递函数如式（11）所示。由于应用在宽变频电网，控制器的谐振频率由DSOGI-PLL计算得到。
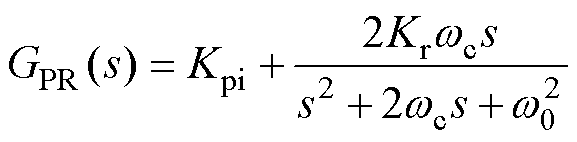（11）
式中，Kpi为比例系数；Kr为谐振增益系数；w0为谐振频率；wc为控制器带宽。
（3）中点电位控制环路：根据2.3节分析，在电网缺相情况下，Vienna整流器的一对冗余小矢量对中点电位作用效果相反，但对矢量合成作用效果相同，可以通过调整正负小矢量的作用时间来实现中点电位平衡控制。采样上下母线电容电压计算差值，并通过PI控制器计算出冗余小矢量作用时间的分配系数r，将r送入调制环节实现中点电位平衡控制。
（4）单相空间矢量调制：根据第2节分析，Vienna整流器在电网缺相情况下可以采用一种单相空间矢量调制方法产生占空比信号。将电流环输出送入单相矢量调制环节，经过扇区判断、矢量合成以及占空比信号产生，即可完成控制。
在实际运行中，首先根据DSOGI-PLL计算得到的电网正负序分量进行判断：若电网三相输入正常，则采用图3所示不平衡控制；若检测到电网存在某一相输入缺相，则切换为图10所示缺相控制。
为验证本文所提电网缺相故障下Vienna整流器控制方法的有效性，通过4.5 kW Vienna整流器样机进行了实验验证，样机如图11所示，样机参数见表5。
图11 Vienna整流器样机
Fig.11 Vienna rectifier prototype
表5 航空Vienna整流器样机参数
Tab.5 Parameters of aviation Vienna rectifier
参 数数 值 额定功率Po/kW4.5 输入电压有效值ua/V100 ub/V122 uc/V122 额定输出电压Vdc/V360 输入电压频率f/Hz360～800 开关频率fs/kHz200 控制频率fc/kHz100 输入电感La, Lb, Lc/mH150 输入电容C1, C2/mF1 410
航空交流供电系统可以分为恒频（400 Hz）、窄变频（360～650 Hz）与宽变频（360～800 Hz）供电系统，本文选择宽变频交流供电系统作为测试标准（对窄变频和恒频供电系统具有同等效果）。RCTA/DO-160G定义了航空电网三相输入电压与频率变化的相关测试标准，见表6[18]。在正常运行情况下，航空宽变频电网电压范围在100～122 V之间，且输入电压不平衡程度不超过10 V；电网频率在360～800 Hz缓慢变化，频率跳变不超过5 Hz。
表6 航空宽变频电网测试标准
Tab.6 Test requirements for a wide variable frequency category equipment
参 数标 准 额定三相输入电压115Vrms 输入电压范围/V100～122 输入电压不平衡≤10Vrms 输入频率范围/Hz360～800 频率跳变/Hz≤5
实验中，设置三相输入电压为100Vrms、122Vrms和122Vrms；输入电压频率范围360～800 Hz，频率跳变10 Hz，满足电网运行测试标准。
图12为三相输入100Vrms、122Vrms和122Vrms，频率为400 Hz稳态运行下，三相输入电流与输出电压波形。三相输入电流总谐波畸变率（Total Harmonic Distortion, THD）见表7。
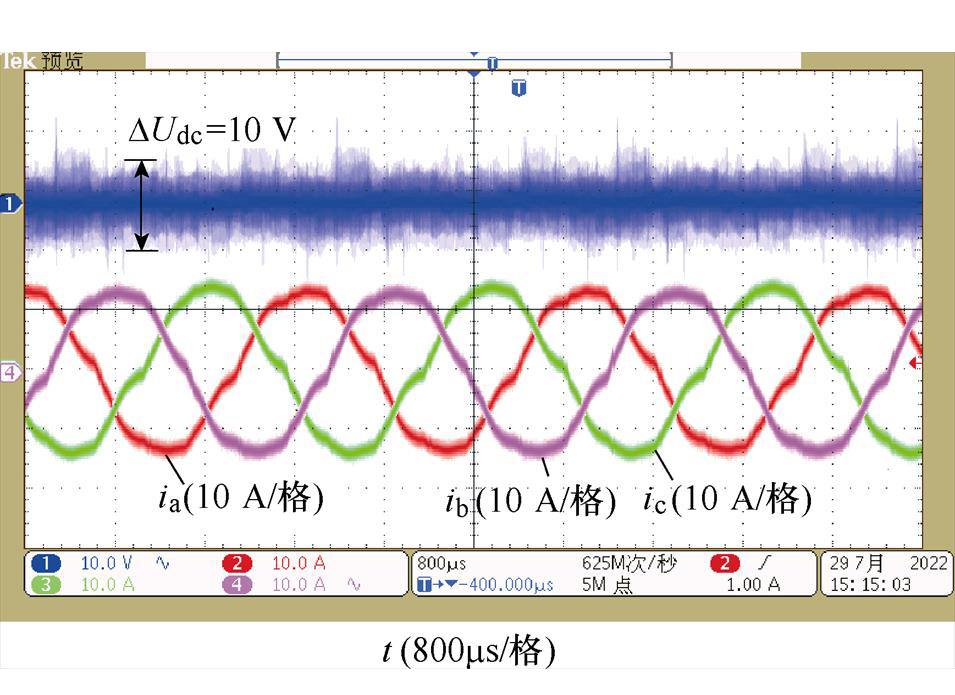
图12 电网不平衡运行实验结果
Fig.12 Experimental results under unbalanced grid
表7 400 Hz电网不平衡下输入电流THD
Tab.7 THD performance under unbalanced grid
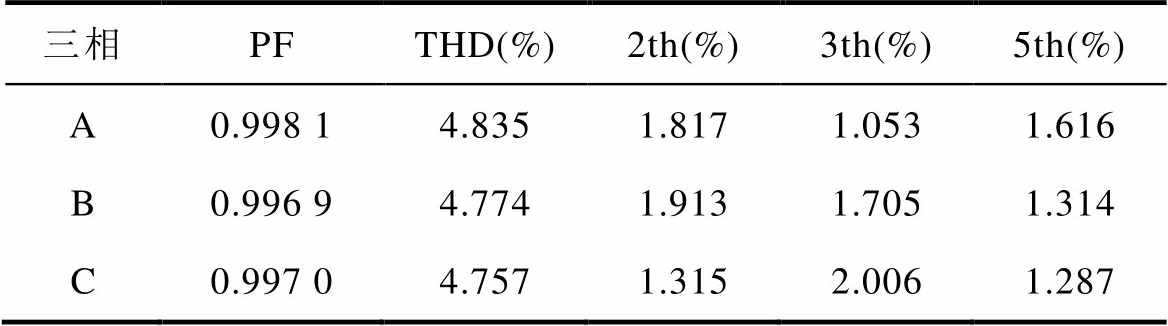
三相PFTHD(%)2th(%)3th(%)5th(%) A0.998 14.8351.8171.0531.616 B0.996 94.7741.9131.7051.314 C0.997 04.7571.3152.0061.287
可以看到，在电网三相电压不平衡输入情况下，采用电网不平衡控制，输入电流正弦度高，THD均在5 %以下，输出电压纹波小于10 V，满足航空电网运行标准。
设置电网频率从360 Hz跳变至370 Hz，从800 Hz跳变至790 Hz，在三相输入100Vrms、122Vrms和122Vrms条件下，输出电压与输入电流波形如图13所示。可以看到，当电网频率出现10 Hz跳变时，输出电压出现不到10 V波动，输入电流也存在一定的波动，约10 ms左右恢复稳定；当电网频率发生突变时，采用不平衡控制方法整流器依然可以维持稳定运行。
进一步地，在A相输入线路串入一双向开关（由一对MOSFET反向串联构成），模拟缺相故障。为避免开关器件过电流，将输出功率降为2 kW。图14为A相缺相故障下，采用缺相控制Vienna整流器输入电流与输出电压波形。设置此时输入电压ub= uc=115Vrms，频率为400 Hz。由实验波形可知，此时输入电流与线电压ubc同相位，输出电压稳定在360 V，输出电压纹波约为10 V。可以看到，在电网缺相故障下，采用本文所提缺相控制方法可以维持整流器输出电压稳定，保障后级负载设备的供电。
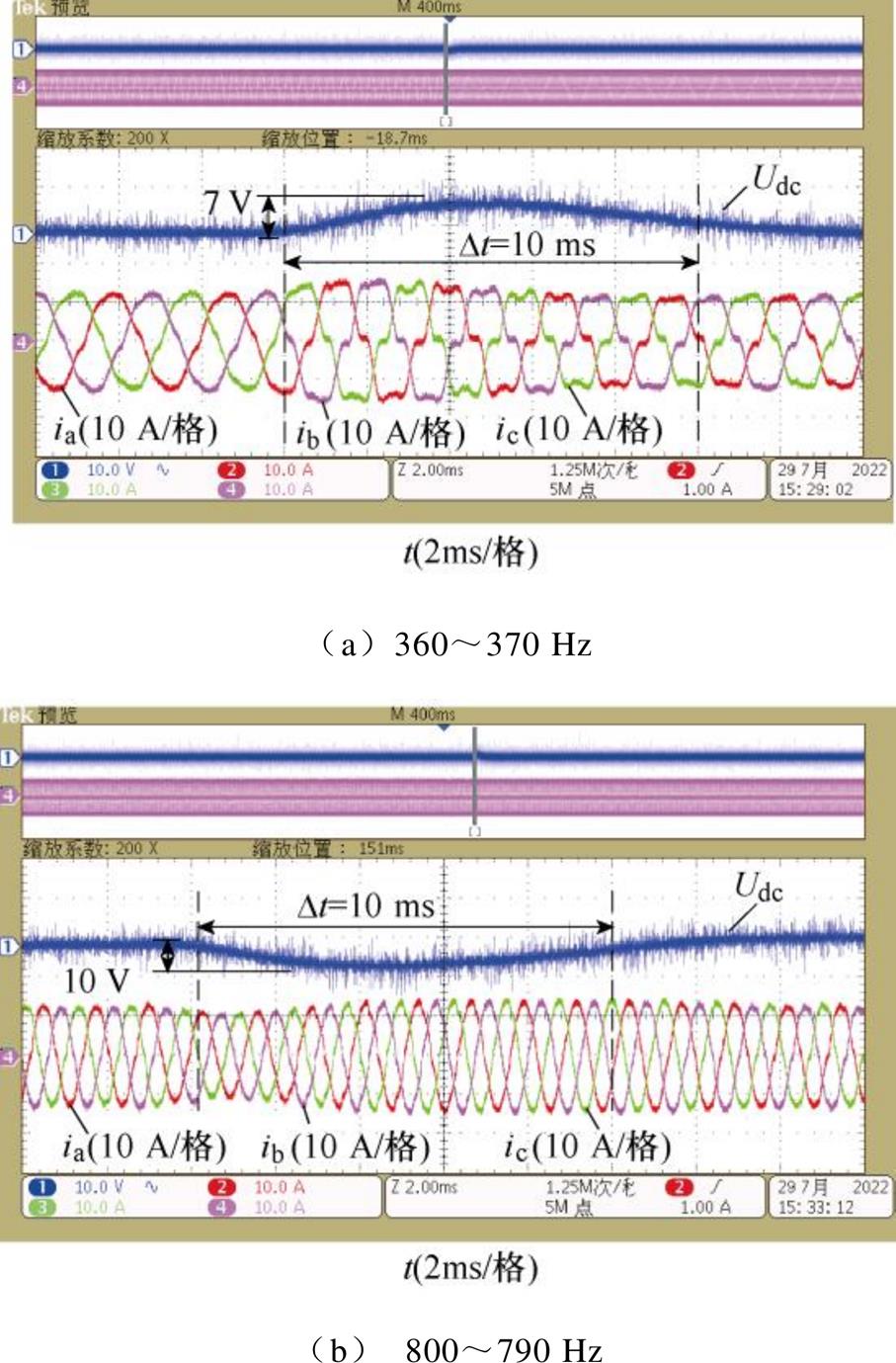
图13 电网变频运行实验结果
Fig.13 Experimental results under variable frequency grid
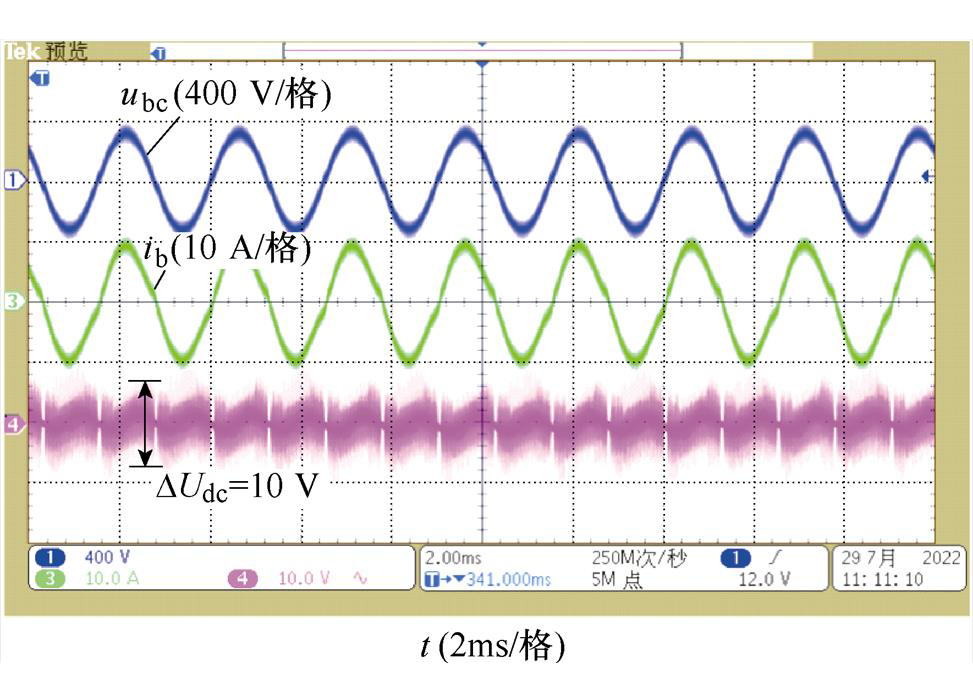
图14 电网缺相运行实验结果
Fig.14 Experimental results when phase A losses
设置电网频率从360 Hz跳变至370 Hz，从800 Hz跳变至790 Hz，在A相缺相，ub=uc=115Vrms条件下，输出电压输入电流波形如图15所示。可以看到，在缺相控制情况下，当电网频率出现10 Hz跳变时，输出电压存在不到6 V波动，输入电流也存在一定的波动，不到10 ms恢复稳定。在电网缺相情况下，采用所提缺相控制方法依然可以在电网频率跳变情况下维持稳定运行。
图15 电网缺相运行变频实验结果
Fig.15 Experimental results when phase A losses and frequency changes
图16为采用缺相控制时，Vienna整流器上下母线电容电压波形。可以看到，在稳态运行情况下，采用本文所提的单相空间矢量调制方法，整流器上下母线电容电压维持在180 V，实现了很好的均压。
图17为缺相故障检测波形。设置某一时刻A相突然缺相，由图中可以看到，当电网A相出现缺相故障时，缺相检测方法经过约1 ms检测到缺相故障，缺相检测信号跳变为1，整流器切换为缺相控制。
图18为缺相故障切换波形。设置某一时刻A相突然缺相，从图中可以看到，当检测到缺相故障后，整流器立刻切换缺相控制算法，平稳的过渡到缺相控制状态，在几个工频周期后即恢复稳定，输出电压跌落不超过5 V。
根据上述实验结果，采用本文所提的控制方法，整流器可以在航空电网不平衡以及某一相缺相的情况下维持稳定的运行，提高了整流系统的可靠性，为后级负载设备供电提供了可靠的保证。
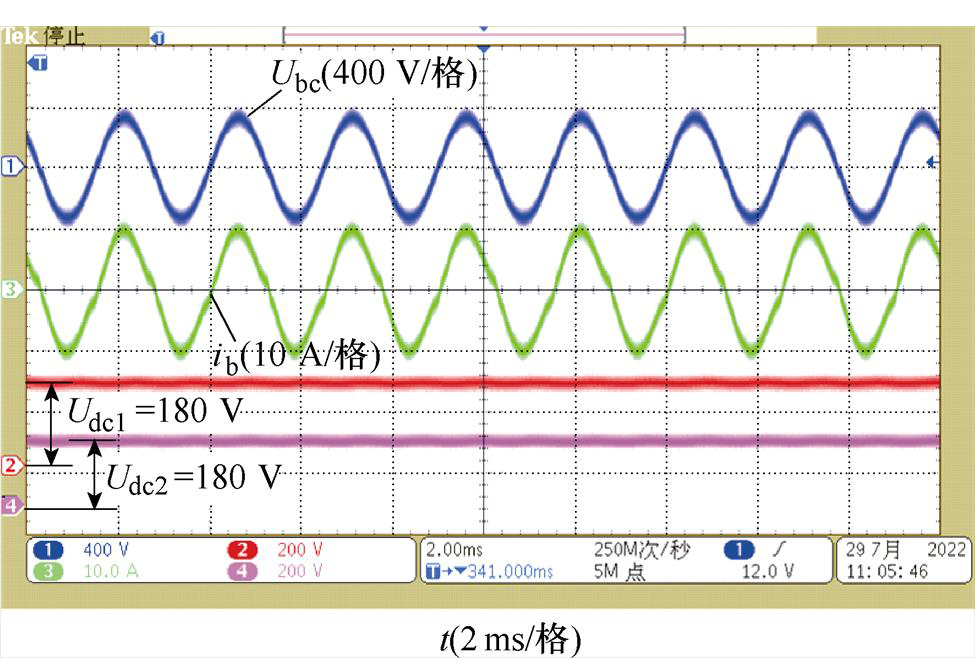
图16 电网缺相运行中点电位波形
Fig.16 Neutral point voltage waveforms when phase A losses
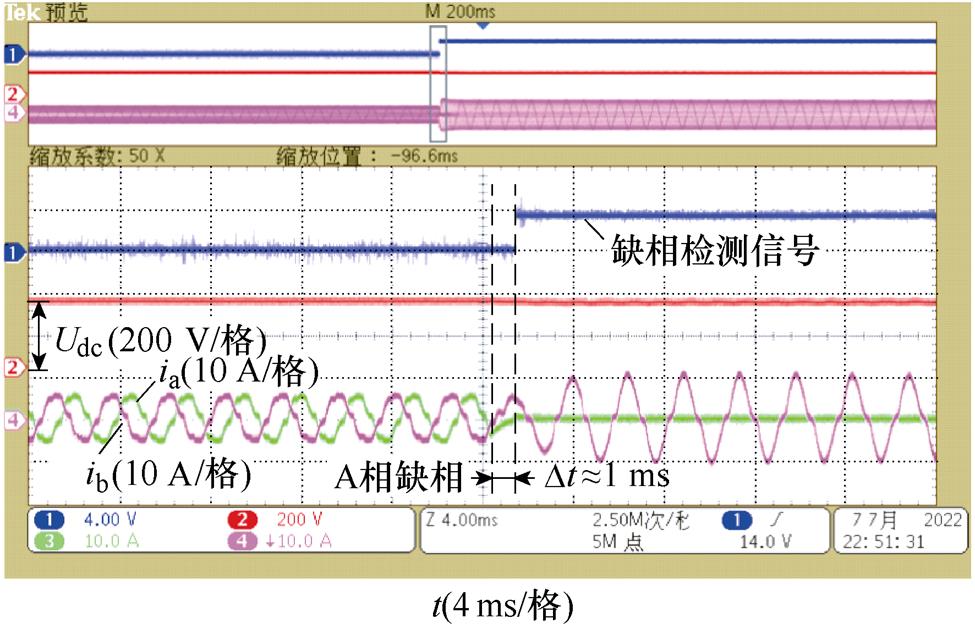
图17 缺相故障检测波形
Fig.17 Waveforms of lack phase detection when phase A losses
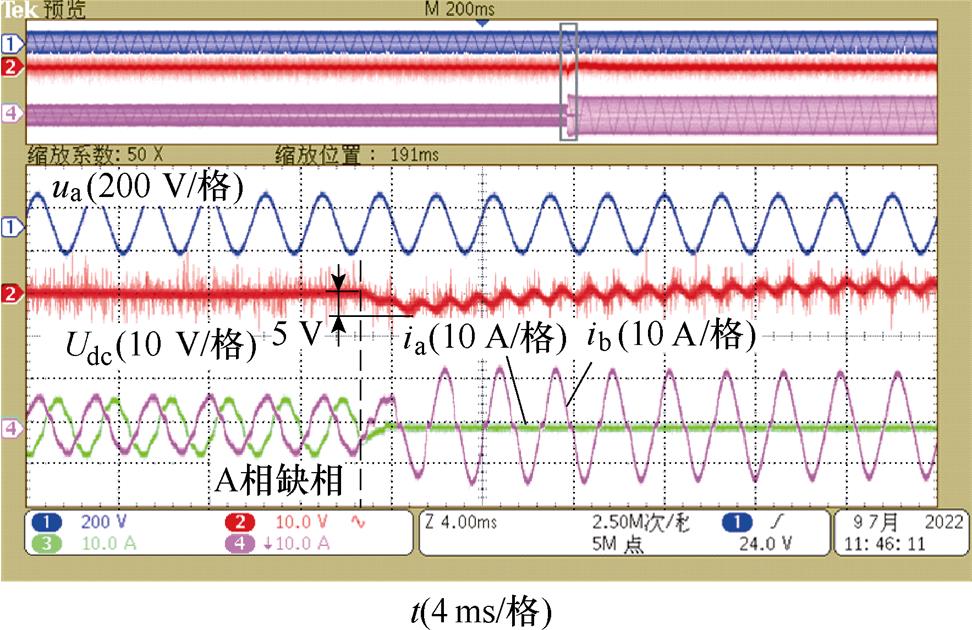
图18 缺相故障切换波形
Fig.18 Waveforms of switching when phase A losses
针对Vienna整流器在航空电网中的应用，首先，本文给出了一种考虑电网缺相故障的Vienna整流器控制方法。首先，当电网三相正常输入时，采用一种双坐标变换矢量控制方法，通过DSOGI-PLL提取不平衡电网的负序分量并产生参考电流，以消除不平衡电网带来的输入电流谐波与输出电压波动。其次，通过分析Vienna整流器在电网缺相下的工作模态，提出了一种单相空间矢量调制方法，能够实现Vienna整流器缺相下的控制。然后，根据DSOGI-PLL计算得到的电网正负序分量给出了电网缺相故障判断方法，并设计了考虑电网缺相故障的Vienna整流器控制方法。最后，通过仿真和实验验证了所提控制方法在航空宽变频电网中应用的有效性。
参考文献
[1] Wheeler P. Technology for the more and all electric aircraft of the future[C]//2016 IEEE International Conference on Automatica (ICA-ACCA), Curico, Chile, 2016: 1-5.
[2] Chen Jiawei, Wang Chengjun, Chen Jie. Investigation on the selection of electric power system architecture for future more electric aircraft[J]. IEEE Transactions on Transportation Electrification, 2018, 4(2): 563- 576.
[3] Ren Xiaoyong, Zhou Yuting, Guo Zhehui, et al. Analysis and improvement of capacitance effects in 360-800 Hz variable on-time controlled CRM Boost PFC converters[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(7): 7480-7491.
[4] 周运红, 张爱民, 黄晶晶, 等. 基于动态事件触发的Vienna整流器模型预测控制[J]. 电工技术学报, 2022, 37(8): 2040-2050.
Zhou Yunhong, Zhang Aimin, Huang Jingjing, et al. Dynamic event-triggered model predictive control for Vienna rectifier[J]. Transactions of China Electro- technical Society, 2022, 37(8): 2040-2050.
[5] 陈杰, 沈禹廷, 沈佳茜, 等. 三相VIENNA整流器的混合空间矢量脉宽调制策略[J]. 电工技术学报, 2021, 36(增刊2): 665-675.
Chen Jie, Shen Yuting, Shen Jiaqian, et al. Hybrid space vector pulse width modulation strategy for three-phase VIENNA rectifier[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 665- 675.
[6] 肖蕙蕙, 苏新柱, 郭强, 等. 三相Vienna整流器无网压传感器预测电流控制策略[J]. 电工技术学报, 2021, 36(6): 1304-1312.
Xiao Huihui, Su Xinzhu, Guo Qiang, et al. Predictive current control of three-phase Vienna rectifier without grid voltage sensors[J]. Transactions of China Electro- technical Society, 2021, 36(6): 1304-1312.
[7] Kolar J W, Zach F C. A novel three-phase utility interface minimizing line current harmonics of high- power telecommunications rectifier modules[J]. IEEE Transactions on Industrial Electronics, 1997, 44(4): 456-467.
[8] Gong G, Heldwein M L, Drofenik U, et al. Comparative evaluation of three-phase high-power- factor AC/DC converter concepts for application in future more electronic aircraft[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3): 727-737.
[9] Chen Xudong, Ren Xiaoyong, Zhang Zhiliang, et al. Dynamic response optimization for three-phase Vienna rectifier with load feedforward control[C]// 2016 IEEE Energy Conversion Congress and Exposi- tion, Milwaukee, 2017: 1-7.
[10] Enjeti P N, Choudhury S A. A new control strategy to improve the performance of a PWM AC to DC con- verter under unbalanced operating conditions[J]. IEEE Transactions on Power Electronics, 1993, 8(4): 493-500.
[11] Rodriguez P, Pou J, Bergas J, et al. Decoupled double synchronous reference frame PLL for power con- verters control[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 584-592.
[12] Teshnizi H M, Moallem A, Zolghadri M, et al. A dual-frame hybrid vector control of vector modulated VIENNA I rectifier for unity power factor operation under unbalanced mains condition[C]//IEEE Applied Power Electronics Conference, Austin, TX, USA, 2008: 1402-1408.
[13] Rodríguez P, Luna A, Muñoz-Aguilar R S, et al. A stationary reference frame grid synchronization system for three-phase grid-connected power con- verters under adverse grid conditions[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(1): 99-112.
[14] Burgos R, Lai Rixin, Pei Yunqing, et al. Space vector modulator for Vienna-type rectifiers based on the equivalence between two- and three-level converters: a carrier-nased implementation[J]. IEEE Transactions on Power Electronics, 2008, 23(4): 1888-1898.
[15] Hang Lijun, Li Bin, Zhang Ming, et al. Equivalence of SVM and carrier-based PWM in three-phase/wire/ level Vienna rectifier and capability of unbalanced- load control[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 20-28.
[16] RTCA. DO-160G-2010. Environmental conditions and test procedures for aircraft equipment[M]. Washington USA: TRCA, 2010.
[17] Kolar J W, Friedli T. The essence of three-phase PFC rectifier systems-part I[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 176-198.
[18] 王达开, 常越, 王娇娇, 等. 变频器缺相故障检测及相序自适应方法[J]. 电机与控制应用, 2018, 45(8): 110-115, 123.
Wang Dakai, Chang Yue, Wang Jiaojiao, et al. Phase- loss detection and phase-sequence adaption method of frequency converter[J]. Electric Machines and Control Application, 2018, 45(8): 110-115,123.
[19] 王栋, 刘利. 一种基于单片机的相序检测及电机缺相保护方法[J]. 电机与控制应用, 2006, 33(9): 50-52.
Wang Dong, Liu Li. A novel method for phase dequence test and phase-break protection based on MCU[J]. Electric Machines & Control Application. 2006, 33(9): 50-52.
[20] Zhang Xianjin, Fan Caihong. Research on 3-phase 4-wire VIENNA rectifier based on one cycle control[C]//2012 Fifth International Conference on Intelligent Computation Technology and Automation, Zhangjiajie, China, 2012: 280-282.
[21] 张志, 谢运祥, 乐江源, 等. 二极管钳位型单相三电平逆变器空间矢量脉宽调制方法[J]. 中国电机工程学报, 2010, 30(27): 62-68.
Zhang Zhi, Xie Yunxiang, Le Jiangyuan, et al. Study of SVPWM method for single-phase three-level diode-clamped inverter[J]. Proceedings of the CSEE, 2010, 30(27): 62-68.
[22] 王建华, 骆芳芳, 季振东, 等. T型三电平变换器的通用PWM平均模型[J]. 中国电机工程学报, 2018, 38(2): 573-581, 688.
Wang Jianhua, Luo Fangfang, Ji Zhendong, et al. A unified PWM averaged model for T-type three-level converter[J]. Proceedings of the CSEE, 2018, 38(2): 573-581, 688.
[23] Hang Lijun, Zhang Hao, Liu Sensen, et al. A novel control strategy based on natural frame for Vienna- type rectifier under light unbalanced-grid condi- tions[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1353-1362.
[24] Zhang Ming, Hang Lijun, Yao Wenxi, et al. A novel strategy for three-phase/switch/level (Vienna) recti- fier under severe unbalanced grids[J]. IEEE Transa- ctions on Industrial Electronics, 2013, 60(10): 4243- 4252.
Abstract Vienna rectifier is one of the most potential topologies for aircraft electrical systems due to its high power density, high efficiency, and high reliability. With the onboard electrical equipment increasing, the electrical power consumption increases significantly in more-electrical aircraft, resulting in harmonics and grid unbalanced issues in aircraft electrical systems. Three-phase rectifiers must maintain stable operation under unbalanced grid and lack phase condition, which presents a challenge to the control strategy of the Vienna rectifier.
According to the instantaneous symmetrical component, the unbalanced grid voltage comprises fundamental positive-, negative- and zero-sequence components. The negative-sequence component leads to second-harmonic ripples in dc-link voltage and low-order harmonics in input currents. The mathematical model of the Vienna rectifier under unbalanced conditions is derived. DSOGI-PLL is utilized to calculate positive- and negative- sequence components of the grid and generate current references. In this way, input current harmonics and dc-link voltage ripples are suppressed well under the unbalanced grid.
For higher reliability requirements, the application under the grid lack phase should be considered. Under a lack-phase grid, the conventional three-phase control strategy is invalid. Rectifiers usually detect the lack-phase fault condition and shutdown for protection, which decreases the reliability of the electrical system.
In order to make Vienna rectifiers maintain stable output under a lack-phase grid, this paper first analyzes the mathematical model. The rectifier under the lack-phase grid is regarded as a single-phase PWM rectifier. By analyzing operational modes, a single-phase space vector pulse width modulation method is proposed, and the implementation process is introduced in detail. Different operational modes can be seen as seven basic voltage vectors, divided into zero, short, and long vectors according to the vector length. Like conventional three-phase space vector modulation, seven basic voltage vectors are used to synthesize the reference voltage vector. Not all switch combinations for each vector can be achieved at each moment, and four sectors are divided for exact synthetization. The dwell time for each basic vector satisfies the voltage-second balance principle. The vectors sequence is selected to be a five-segment form for minimizing the switching loss. The voltage of output capacitors can be balanced by adjusting the dwell times of a pair of redundant short vectors.
Furthermore, according to the three-phase voltage sampling conditions under a lack-phase grid, a lack-phase fault detection method based on the phase locked loop is proposed. Different grid fault conditions can be determined by calculating the positive- and negative-sequence components of sampling grid voltages. The corresponding control loop is also designed for stable dc output under lack-phase conditions. If the grid voltages are three-phase input, a control strategy for the unbalanced grid is applied. If a lack-phase fault occurs, the corresponding control strategy is switched for lack phase control.
A 4.5 kW aircraft Vienna rectifier prototype is built to verify the proposed control strategy. Experiment results prove that the Vienna rectifier can maintain stable operation under the unbalanced grid and lack-phase grid with the proposed control strategy.
keywords：Vienna rectifier, unbalanced grids, single-phase space vector pulse width modulation (SVPWM), lack phase control
DOI: 10.19595/j.cnki.1000-6753.tces.221501
中图分类号：TM46
国家自然科学基金资助项目（52177181）。
收稿日期 2022-08-03
改稿日期 2022-11-14
徐子梁 男，1998年生，硕士研究生，研究方向为Vienna整流器技术。E-mail: xuziliang@nuaa.edu.cn
任小永 男，1979年生，教授，博士生导师，研究方向为高功率密度集成技术、高电压调节模块、分布式电源系统和GaN晶体管应用技术。E-mail: renxy@nuaa.edu.cn（通信作者）
（编辑 陈 诚）