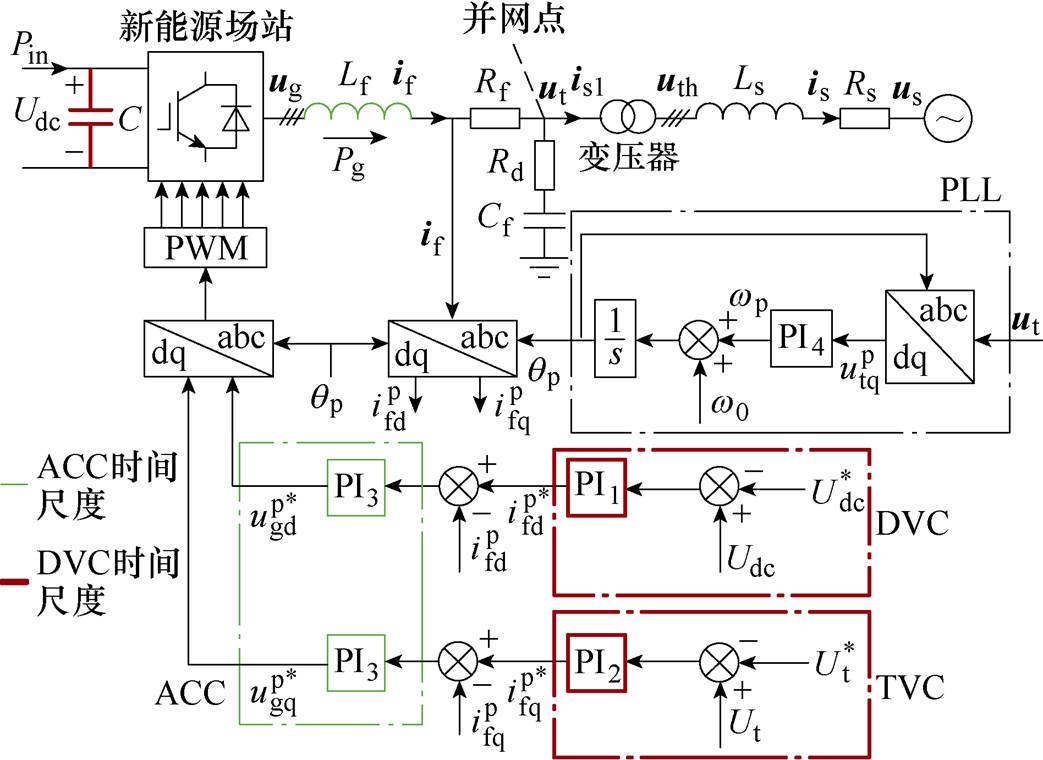
图1 VSC并网系统拓扑及控制结构
Fig.1 The topology and the control scheme of the grid-tied VSC
摘要 电压源型变流器（VSC）的控制环节及其与网络间的相互作用是造成VSC并网系统失稳的重要因素。而VSC的控制具有多时间尺度特征，具体可划分为直流电压控制（DVC）时间尺度和交流电流控制（ACC）时间尺度。现有文献大多仅针对单一时间尺度的稳定性问题开展研究，对于多时间尺度环节间的相互作用则鲜有涉及。对此，该文基于模式分析方法，提出衡量多时间尺度间相互作用的量化指标，揭示多时间尺度间相互作用随锁相环带宽和系统短路比的变化规律。进而通过对比不同时间尺度模型的阻尼比和振荡频率，明确多时间尺度间相互作用对系统稳定性分析结果的影响。最后探讨DVC、ACC时间尺度模型的适用范围，并从物理角度对分析结果进行初步阐释。
关键词：电压源型变流器 多时间尺度 直流电压控制（DVC）时间尺度 交流电流控制（ACC）时间尺度 相互作用 模式分析
由于风电、光伏等新能源发电发展迅速，电压源型变流器（Voltage Source Converter, VSC）作为典型的电力电子变换装置广泛应用于现代电力系统中，其动态特征对于系统稳定性具有重要影响。近年来，VSC并网系统振荡问题频发，严重威胁系统安全稳定运行。例如，双馈风电机群和线路串补装置引发的次同步振荡[1-2]、直驱风电场和弱交流电网之间的次同步振荡[3]、光伏电站引发的高频振荡[4]等。与传统同步机主导的稳定性问题不同，VSC控制环节及其与网络间的相互作用是引起VSC并网系统失稳的重要因素[5-7]。而VSC的控制具有多时间尺度特征，具体可划分为响应时间约100 ms的直流电压控制（DC-link Voltage Control, DVC）时间尺度和响应时间约10 ms的交流电流控制（Alternating Current Control, ACC）时间尺度[8]。然而，现有文献大多针对单一时间尺度下的稳定性问题开展研究。
文献[9-12]研究了VSC并网系统的DVC时间尺度稳定性。文献[9]基于幅相运动方程建立了VSC的DVC时间尺度小信号模型，并针对单台VSC并网系统，分析了直流电压控制、锁相环（Phase Locked Loop, PLL）等控制环节对于系统稳定性的影响规律；文献[10]指出弱电网下锁相环、无功控制等环节给直流电压环带来相位滞后，这是影响VSC并网系统稳定性的关键因素，进而设计了VSC直流电压时间尺度稳定器，以增强系统阻尼；文献[11]基于自稳/致稳作用系数，提出了解析量化研究DVC尺度下多台VSC间相互作用的分析方法，并指出控制环节通过影响VSC间相互作用路径从而影响系统的稳定性；文献[12]推导了DVC尺度下直驱风电场的传递函数模型，并基于劳斯-赫尔维茨判据研究控制参数和运行参数稳定域，分析了风电场内风机参数的差异性对于稳定域分析结果的影响。
文献[13-16]针对VSC并网系统的ACC时间尺度稳定性开展研究。文献[13]基于电流平衡-内电动势运动的建模方法，提出VSC的ACC时间尺度小信号模型，并指出锁相环带宽增加会引入负阻尼，进而导致VSC并网系统失稳；文献[14]将VSC并网系统等效为RLC电路，发现在系统谐振点处电流控制会提供正阻尼，而锁相环在特定参数范围内提供负阻尼，二者相互作用会导致系统发生振荡失稳；文献[15]重点关注VSC交流电流控制和电压前馈环节的影响，说明弱电网下电压前馈环节会恶化VSC的端电压稳定性；文献[16]建立了考虑机侧、网侧电流控制和锁相环的双馈风机并网系统阻抗模型，详细研究了各控制器参数对于系统次同步振荡特性的影响，并给出了相应的参数调整策略，以达到抑制次同步振荡的效果。
以上两类文献分别研究VSC并网系统的DVC时间尺度和ACC时间尺度稳定性，其重要假设前提是不同尺度环节间相互解耦。而对于DVC时间尺度和ACC时间尺度环节间的相互作用，目前的研究鲜有涉及。文献[17]针对直驱风电场并网系统，利用模式分析法，研究了功率控制外环对系统ACC时间尺度稳定性的影响，并指出外环功率控制和内环电流控制的耦合会恶化系统稳定性，进而分析了功率控制外环对电流控制内环与锁相环间动态交互的影响。然而，文献[17]重点关注DVC时间尺度环节对于ACC时间尺度稳定性的影响，而ACC时间尺度环节对于DVC时间尺度稳定性分析结果的影响则并未涉及。另外，有关DVC、ACC时间尺度环节间的相互作用，还存在两方面问题有待进一步研究：一方面，多时间尺度环节间相互作用随VSC控制参数和网络参数的变化规律尚不明确；另一方面，对于DVC时间尺度模型和ACC时间尺度模型各自的适用范围，目前的研究尚属空白。
针对现有研究存在的缺陷，本文首先介绍VSC并网系统拓扑及控制结构，并说明其多时间尺度动态特征，然后建立VSC并网系统的多时间尺度、DVC时间尺度、ACC时间尺度小信号模型，并基于模式分析方法提出多时间尺度间相互作用的量化衡量指标，进而揭示了尺度间相互作用随锁相环带宽、系统短路比的变化规律，明确了多时间尺度间相互作用对于系统稳定性分析结果的影响，进而探讨了DVC、ACC时间尺度模型的适用范围并进行验证，最后从物理层面初步解释多时间尺度间相互作用的影响。
VSC并网系统拓扑及控制结构如图1所示。新能源场站包含100台参数相同的2 MW变流器，经升压变压器、输电线路接入无穷大电网。为简化分析，将新能源场站等值聚合为一台VSC。图1中，上标p为锁相坐标系下变量，上标*为参考值；下标d和q为变量的d轴和q轴分量；C为直流母线电容；Lf和Rf分别为交流滤波电感和电阻；Cf和Rd分别为交流滤波电容及其串联电阻；Ls和Rs分别为并网线路电感和电阻；Pin为新能源场站输入有功功率，Pg为新能源场站输出有功功率；if为滤波电感电流，isl和is分别为变压器低压侧电流和输电线路电流；ug为新能源场站输出电压，ut为端电压，uth为变压器高压侧电压，us为无穷大电网电压；Ut为端电压幅值，Udc为直流母线电压；wp和qp分别为锁相环输出频率和相位；w0为基频。由图1可以看到，VSC中包含了不同类型、不同容量的储能元件。其中，交流滤波电感响应速度较快，约为10 ms，而直流母线电容稳定直流电压，响应速度较慢，约为100 ms[8]。对应于不同类型的储能元件，VSC中分别设计了响应速度与之匹配的控制器。VSC的内环交流电流控制带宽一般设计为开关频率的1/10左右，响应时间约为10 ms。而对于外环控制，如直流电压控制和端电压控制（Terminal Voltage Control, TVC），其带宽一般设计为内环电流控制的1/10左右，响应时间约为100 ms。另外，PLL检测端电压相位，为坐标变换提供相位信息。根据响应时间的不同，可以将上述控制器的动态划分到不同时间尺度[18]，具体情况如图2所示。需要说明的是，锁相环根据其控制带宽可以划分到DVC时间尺度或ACC时间尺度。而本文中锁相环带宽不超过50 Hz，因此将其划分在DVC时间尺度下。
图1 VSC并网系统拓扑及控制结构
Fig.1 The topology and the control scheme of the grid-tied VSC
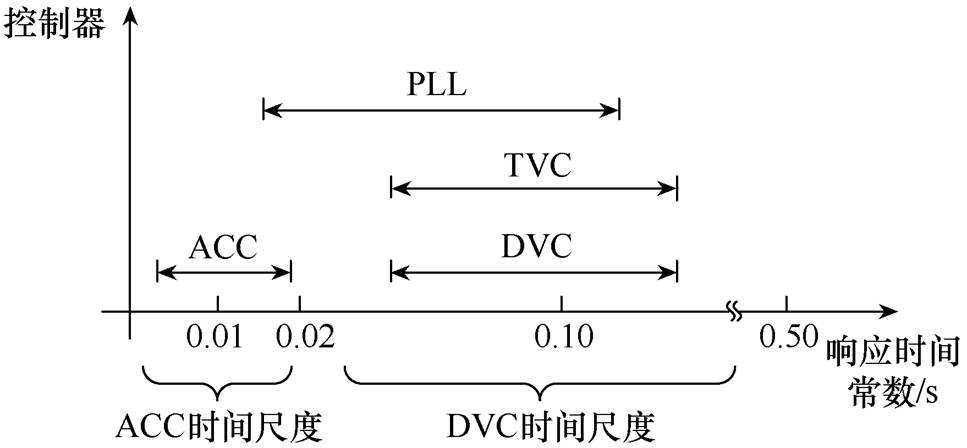
图2 VSC时间尺度划分
Fig.2 Timescale classification in VSC
本节分别建立VSC并网系统的多时间尺度、DVC时间尺度和ACC时间尺度小信号模型，并进行验证，为后续的分析奠定基础。需要说明的是，本文在建模过程中假设三相对称。
如图1所示，VSC并网系统可进一步分为直流母线部分、控制器部分及交流网络部分。下面针对上述三部分分别进行建模。
对于直流母线部分，输入输出VSC直流母线的有功功率决定了直流母线电压的动态，因此，VSC直流母线部分的关系式可以表示为
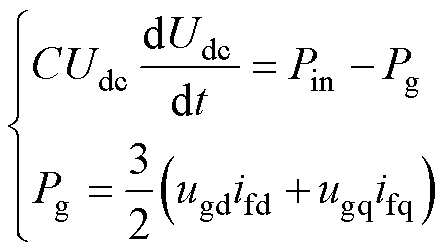（1）
VSC锁相环的控制结构如图1所示，采用d轴端电压定向控制策略。其数学关系式如下
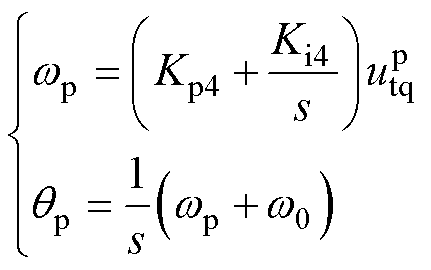（2）
式中，Kp4和Ki4分别为PLL的比例、积分系数。另外，VSC控制系统中包含DVC、TVC和ACC，均采用PI控制，因此有
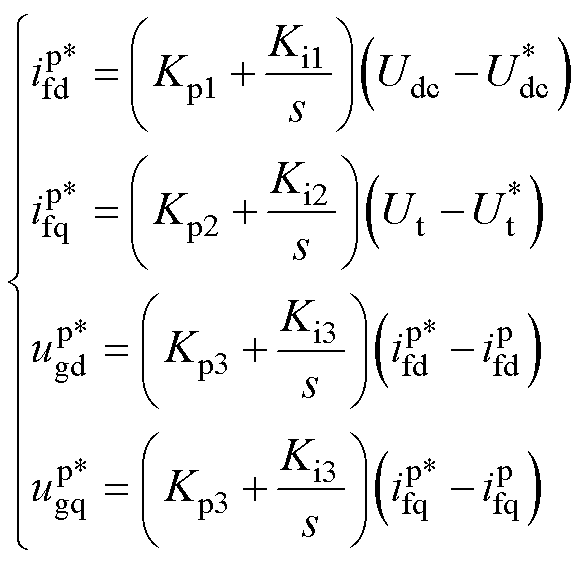（3）
式中，Kpn和Kin（n=1, 2, 3）分别为DVC、TVC和ACC的比例、积分系数。VSC的采样及PWM过程会引入控制延时，本文采用二阶Pade近似模拟该控制延时的影响。二阶Pade近似表达式为
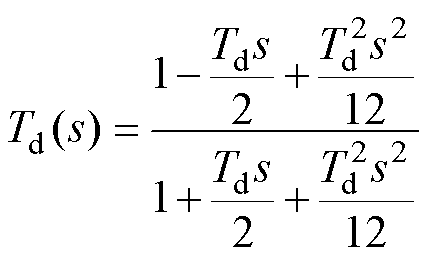（4）
式中，Td为控制延时。交流网络部分主要包含VSC的LC滤波电路及并网线路，在同步速dq坐标系下对其进行建模，关系式为
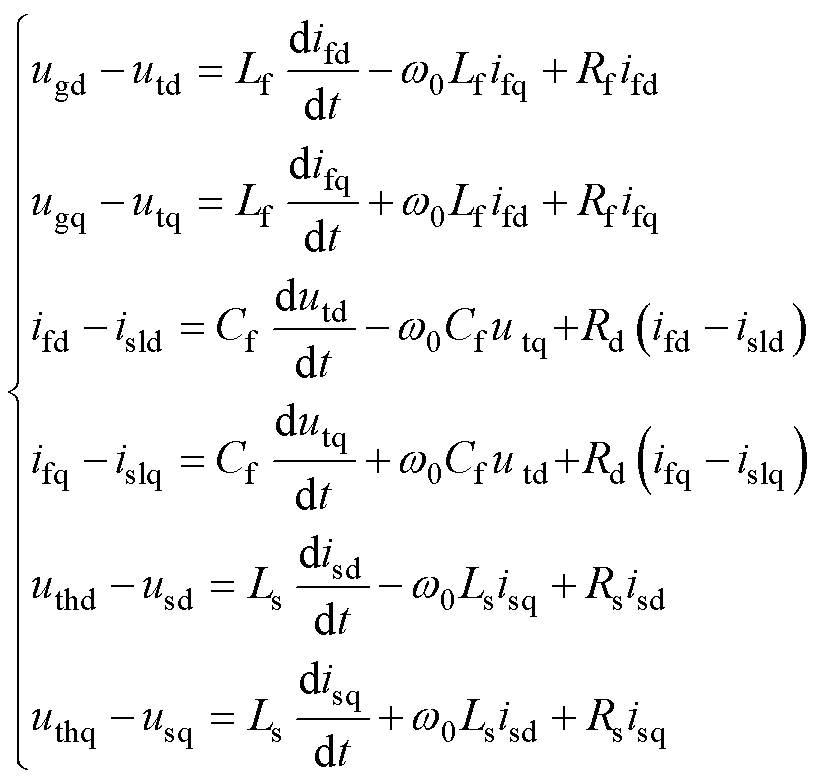（5）
另外，VSC控制系统和交流网络分别在锁相dq坐标系和同步速dq坐标系下建模，必须通过坐标变换才能实现互联。上述两类dq坐标系及电气量的关系如图3所示。其中，F为电压或电流矢量，而qpll表示两坐标系间的相位差，有
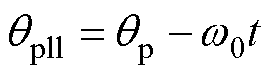（6）
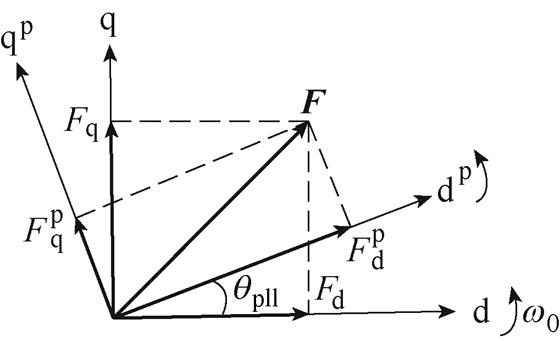
图3 不同dq坐标系位置关系
Fig.3 Position relationships between different dq coordinates
根据图3可以推导得坐标转换关系为
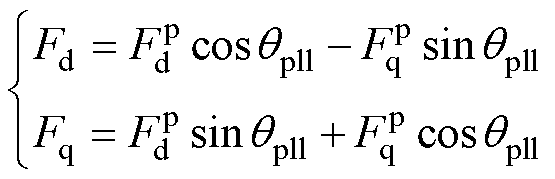（7）
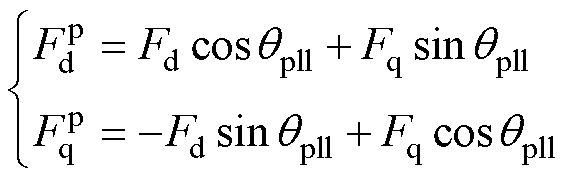（8）
针对式（1）～式（8），在其稳态工作点附近线性化，构建VSC并网系统的小信号模型。模型状态变量选取如下
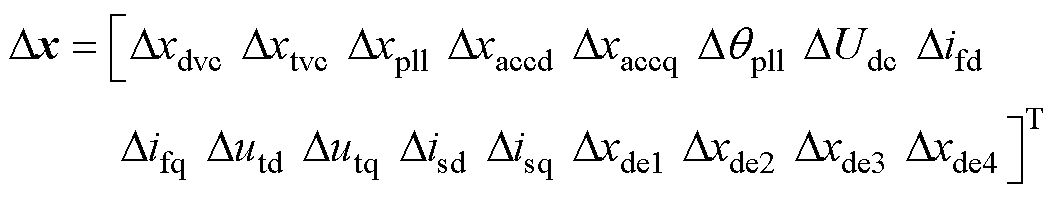（9）
式中，前5个状态变量与VSC的控制器相关，具体含义为
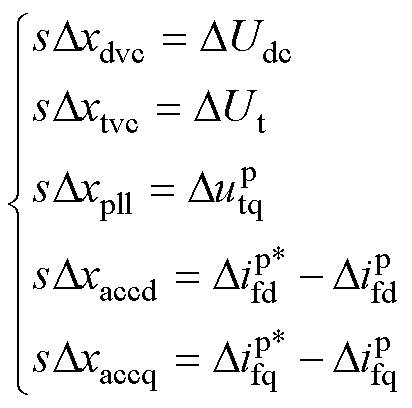（10）
另外，Dxde1、Dxde2、Dxde3、Dxde4为与延时环节相关的状态变量。
联立式（1）～式（10）获得VSC并网系统多时间尺度小信号模型为
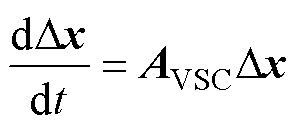（11）
式中，AVSC为小信号模型的系统矩阵。
本节在VSC并网系统多时间尺度模型的基础上，经过假设简化，建立DVC时间尺度、ACC时间尺度小信号模型。
VSC并网系统的DVC时间尺度动态主要包含直流母线电压动态、外环电压控制动态及PLL动态，因此，假设[9-12]：
（1）滤波电感电流的实际值瞬时跟踪外环给定的指令值，即忽略内环电流控制器动态。
（2）忽略交流网络的电压、电流动态，即交流网络部分采用导纳矩阵等代数环节进行建模。
基于上述两方面假设，建立VSC并网系统的DVC时间尺度小信号模型。
而VSC并网系统的ACC时间尺度动态主要包含网络电流、电压动态，以及内环电流控制器动态和PLL动态，因此假设[13-16]：
（1）电压外环给定的电流指令值恒定，即忽略外环电压控制器的动态。
（2）忽略直流母线电压动态，即认为直流母线电压恒定。
基于上述两方面假设，建立VSC并网系统的ACC时间尺度小信号模型。
本节通过电磁暂态仿真和特征值分析法验证2.1节和2.2节构建的VSC并网系统不同时间尺度小信号模型的准确性。系统参数见附表1。
对于系统多时间尺度小信号模型和电磁暂态仿真模型，在2 s时对VSC输入功率Pin施加2 %扰动，其时域响应波形如图4所示。可以看到，在不同输入功率下，两种模型的扰动响应均相互吻合，从而验证了系统多时间尺度小信号模型的准确性。
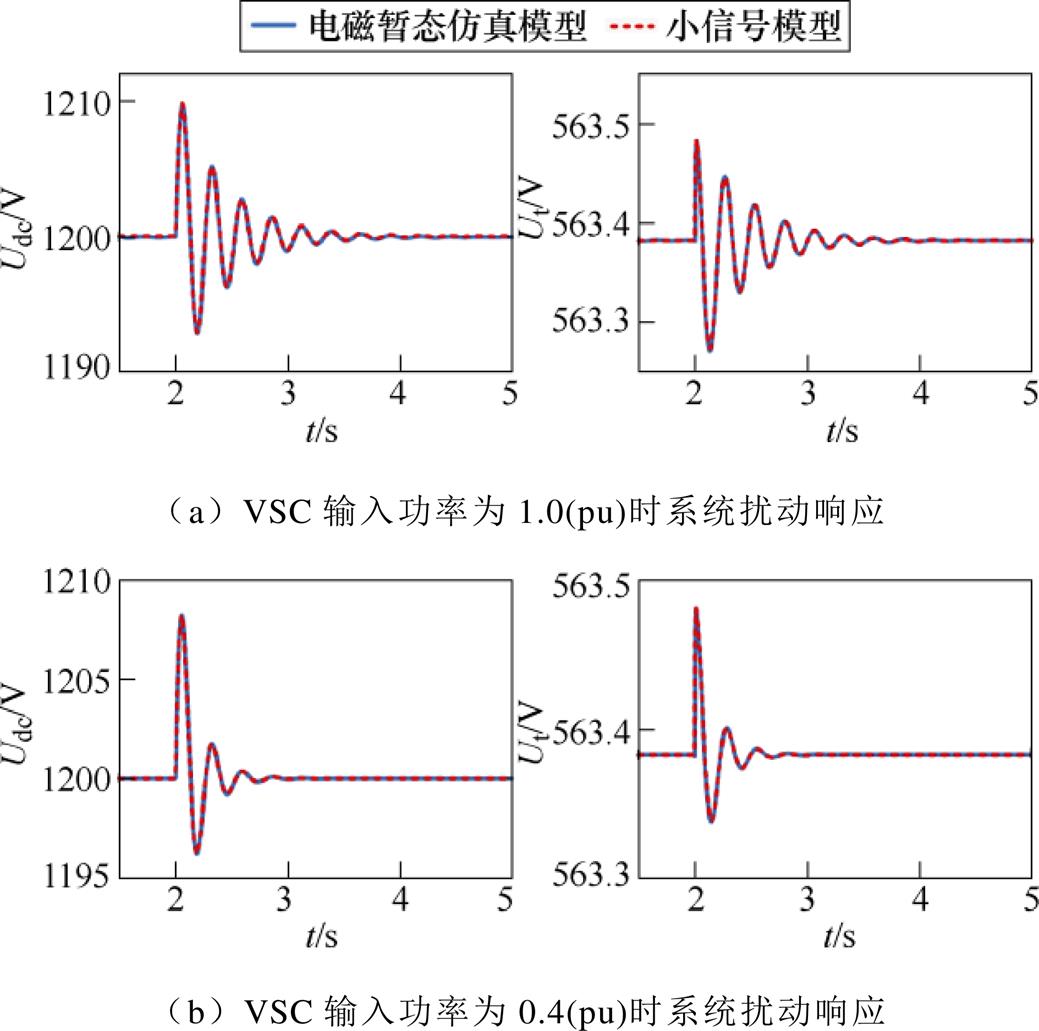
图4 多时间尺度小信号模型和电磁暂态仿真模型时域仿真结果对比
Fig.4 The comparison of the time-domain simulation between the small-signal model in multiple timescales and the electromagnetic transient model
对于DVC和ACC时间尺度小信号模型，一般通过特征值分析验证其准确性[9,18]。基于式（11）中系统矩阵AVSC计算得VSC并网系统多时间尺度模型的特征值。基于2.2节内容，更改系统矩阵，计算得DVC、ACC时间尺度模型的特征值。不同时间尺度模型的特征值见表1。可以看到，当VSC输入功率不同时，DVC、ACC时间尺度模型均能准确反映对应尺度下的特征值。这验证了上述两类单一时间尺度模型的准确性。
本节利用模式分析方法提出VSC并网系统多时间尺度间相互作用的量化衡量指标，并基于该指标研究尺度间相互作用随PLL带宽、短路比等参数的变化规律。
表1 VSC并网系统不同时间尺度模型的特征值对比
Tab.1 Eigenvalue comparison of the grid-tied VSC in different timescales
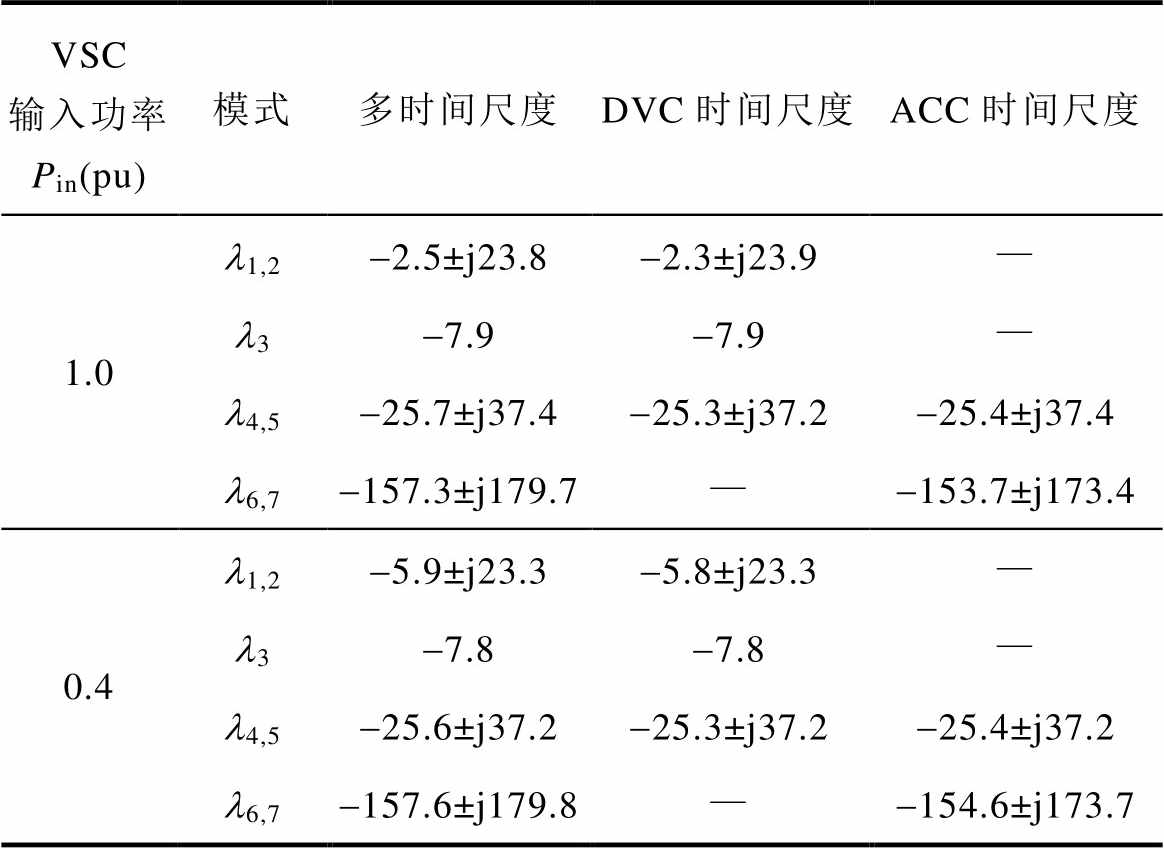
VSC输入功率Pin(pu)模式多时间尺度DVC时间尺度ACC时间尺度 1.0l1,2-2.5±j23.8-2.3±j23.9— l3-7.9-7.9— l4,5-25.7±j37.4-25.3±j37.2-25.4±j37.4 l6,7-157.3±j179.7—-153.7±j173.4 0.4l1,2-5.9±j23.3-5.8±j23.3— l3-7.8-7.8— l4,5-25.6±j37.2-25.3±j37.2-25.4±j37.2 l6,7-157.6±j179.8—-154.6±j173.7
模式分析基于振荡模式、参与因子等概念，刻画系统稳定性以及状态变量与振荡模式间的关联特性[19-20]。其中，参与因子定义为
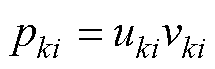（12）
式中，uki和vki分别为第i个特征值对应的左特征向量ui和右特征向量vi的第k个元素[19]。从模式分析的角度看，当多个状态变量共同参与同一振荡模式时，说明这些状态变量间存在耦合作用[20]。而系统的多时间尺度间相互作用，本质上是不同尺度状态变量之间的耦合。因此，可以利用参与因子反映对于同一振荡模式不同尺度状态的参与程度，进而衡量多时间尺度间相互作用的相对强弱。下面结合具体案例进行说明。
短路比（Short Circuit Ratio, SCR）是衡量交流系统强弱的重要指标[21-22]。等比例改变并网线路电感和电阻参数，当SCR=3时，VSC并网系统多时间尺度模型参与因子的分析结果如图5所示。l1,2、l3和l4,5振荡频率较低，且均由DVC时间尺度状态DUdc、Dxdvc、Dxtvc和Dqpll主导，因此将上述振荡模式定义为DVC时间尺度模式。而l6,7振荡频率较高，主要由ACC时间尺度状态Dxaccd和Dxaccq主导，因此将其定义为ACC时间尺度模式。另外，由图5可以看到，对于DVC时间尺度模式l4,5，除DVC时间尺度状态Dqpll起主导作用外，ACC时间尺度状态也会参与该模式。而对于ACC时间尺度模式l6,7，DVC时间尺度状态DUdc、Dxtvc和Dqpll参与程度较高。因此，l4,5和l6,7说明多时间尺度状态间存在相互作用，并且这类相互作用可以通过不同时间尺度状态——模式间的参与因子（定义为异尺度参与因子）衡量。当异尺度参与因子较高时，说明不同时间尺度状态间的耦合作用较强。在后续研究中，将异尺度参与因子作为系统多时间尺度间相互作用的量化衡量指标，分析尺度间相互作用随控制参数和网络参数的变化规律。
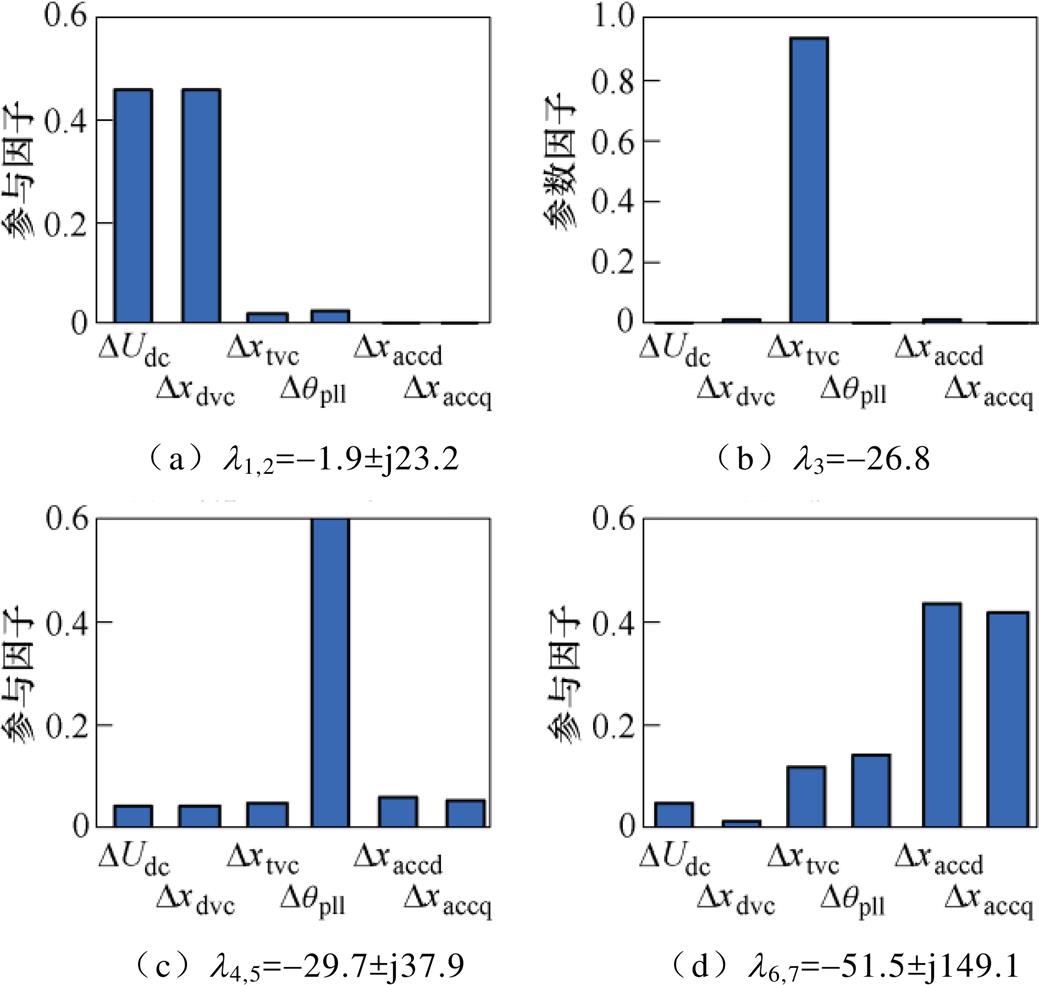
图5 VSC并网系统参与因子结果
Fig.5 Participation factors of the grid-tied VSC
本文以PLL带宽对多时间尺度间相互作用的影响为例进行分析。根据式（2）、式（7）以及PLL结构，可得PLL的闭环传递函数为
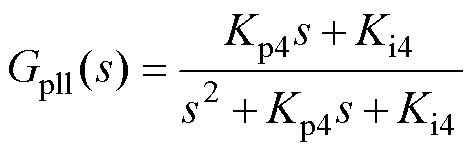（13）
在保持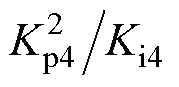
不变（即保持PLL阻尼比不变[23]）的基础上改变Kp4和Ki4大小（即改变PLL带宽），其余系统参数均按照附录取值，振荡模式l4,5（振荡频率最高的DVC时间尺度模式）和l6,7（振荡频率最低的ACC时间尺度模式）的参与因子变化情况如图6所示。可以看到，当PLL带宽较低时，l4,5和l6,7分别由DVC时间尺度状态和ACC时间尺度状态主导。随着PLL带宽提高，ACC时间尺度状态Dxaccd和Dxaccq对于l4,5以及DVC时间尺度状态Dqpll对于l6,7参与因子显著提高，说明多时间尺度状态间的相互作用逐渐增强。
针对上述现象解释如下。随着带宽提高，PLL可以响应系统中较快尺度的扰动，因此，与ACC时间尺度状态间的相互作用增强。从模式分析的角度，具体体现为PLL状态Dqpll对于ACC时间尺度模式以及ACC时间尺度状态对于PLL主导模式的参与程度提高。
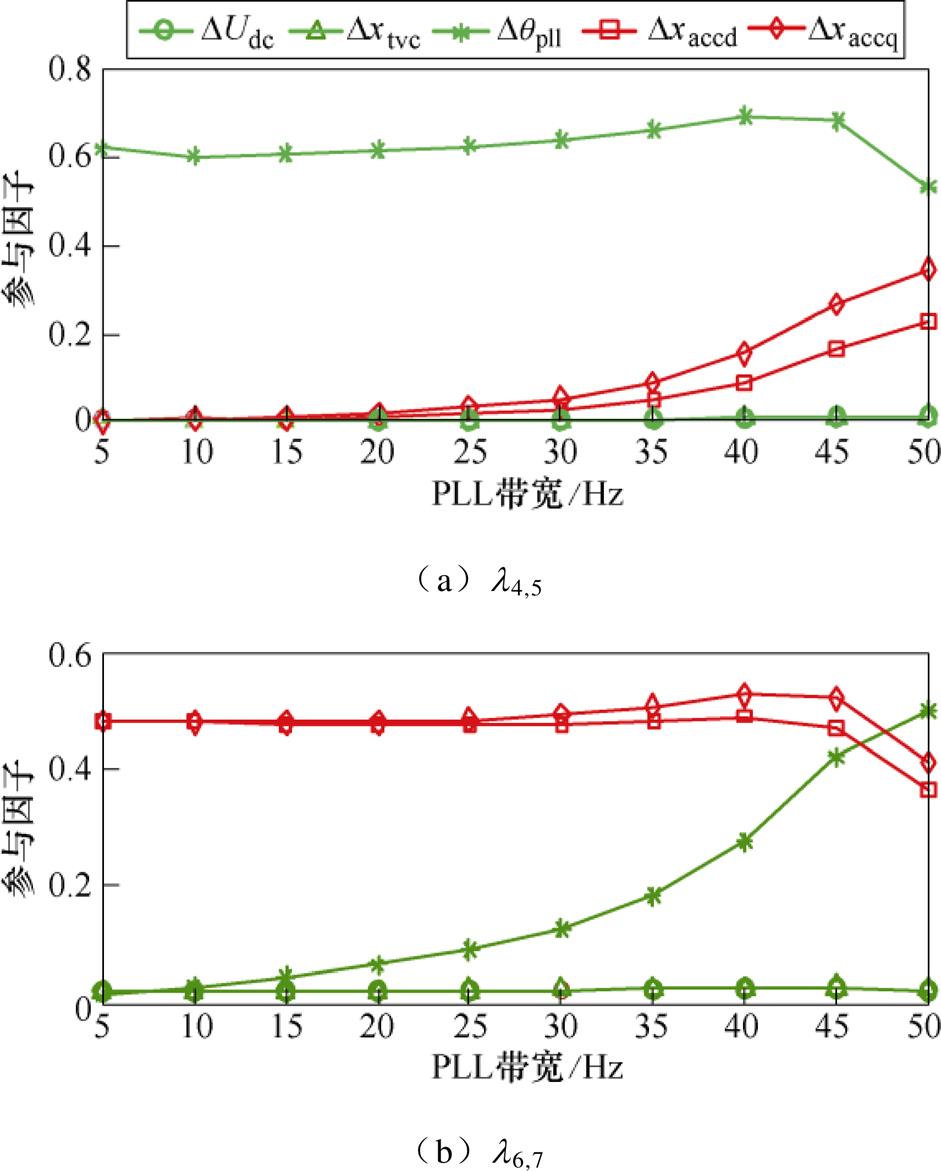
图6 l4,5和l6,7参与因子随PLL带宽的变化情况
Fig.6 Participation factors of l4,5 and l6,7 when the bandwidth of PLL varies
本文通过改变SCR研究网络参数对于多时间尺度间相互作用的影响，等比例改变并网线路电阻、电感参数（即改变SCR），其余参数均按照附录取值，振荡模式l4,5（振荡频率最高的DVC时间尺度模式）和l6,7（振荡频率最低的ACC时间尺度模式）的参与因子变化情况如图7所示。可以看到，当SCR较高时，异尺度参与因子较低，多时间尺度间相互作用较弱。而随着SCR降低，异尺度参与因子逐渐提高，多时间尺度间相互作用增强。
对于上述现象初步解释如下：PLL通过检测并网点电压相位，为交流电流的坐标变换提供相位信息，进而影响内环电流控制。同时，DVC、TVC和内环电流控制等通过调节VSC输出的有功、无功电流，控制VSC输出功率。当系统中发生功率扰动后，并网点电压波动，PLL受扰动作，影响内环电流控制；而内环电流控制会影响VSC输出功率，导致并网点电压受扰波动，进一步影响PLL和TVC动作。SCR越低，并网点电压受功率扰动的影响越大，进而使PLL、TVC和内环电流控制的耦合性增强，即多时间尺度间相互作用增强。
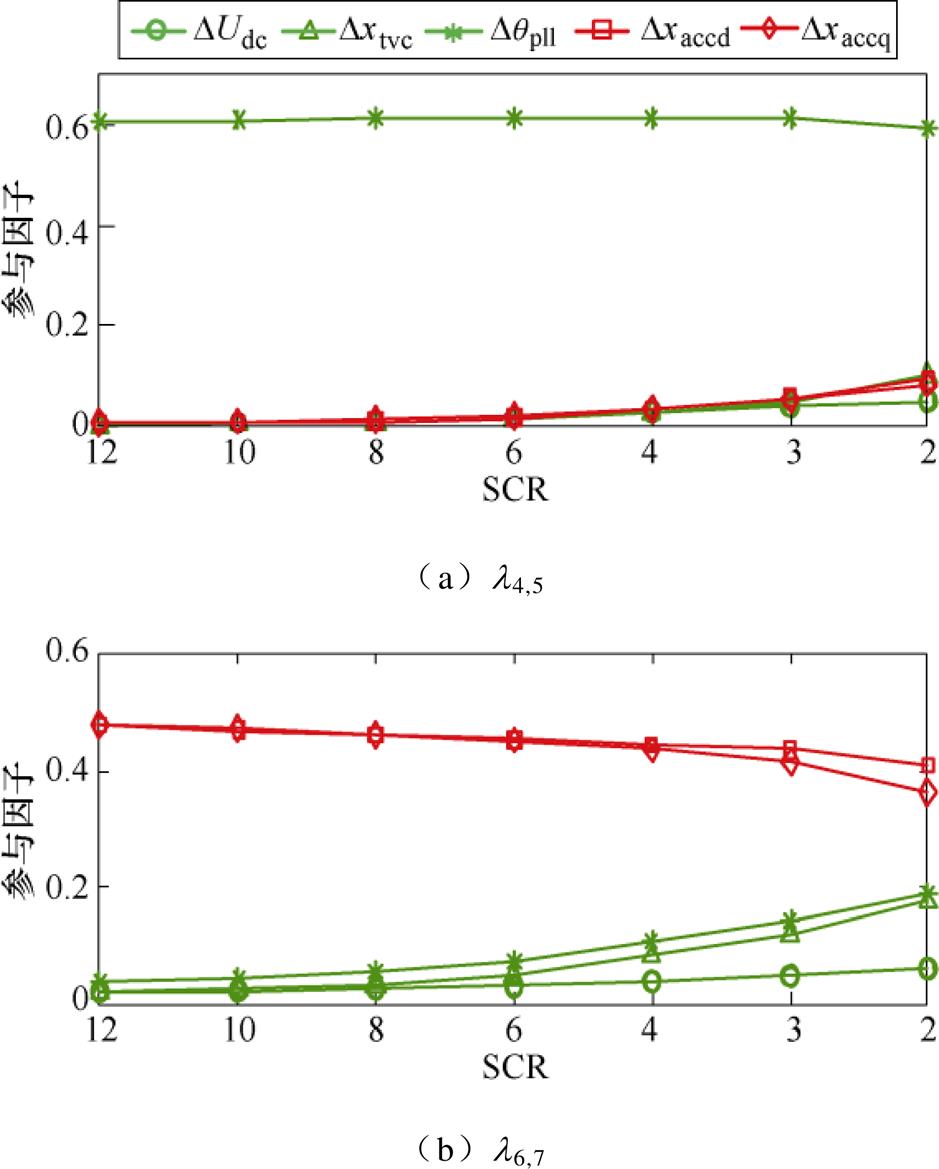
图7 l4,5和l6,7参与因子随SCR的变化情况
Fig.7 Participation factors of l4,5 and l6,7 when SCR varies
基于第3节研究结论，本节研究多时间尺度间相互作用对于系统稳定性分析结果的影响，说明DVC时间尺度和ACC时间尺度模型的适用范围，并进行案例分析与验证，最后对多时间尺度间相互作用的影响初步做物理性解释。
本节通过对比多时间尺度、DVC时间尺度和ACC时间尺度模型的特征值，说明多时间尺度间相互作用对于系统稳定性分析结果的影响。
如图8所示为SCR=12时不同时间尺度模型特征值的对比情况。其中，图8a和图8b分别对比了多时间尺度模型和DVC时间尺度模型的主导特征值阻尼比和振荡频率。随着PLL带宽提高，尺度间相互作用增强，多时间尺度和DVC时间尺度模型主导特征值l4,5阻尼比和振荡频率的偏差均逐渐增大。而对于ACC时间尺度模型，PLL带宽提高，其主导特征值分析结果与多时间尺度模型相比差距不大。
如图9所示为SCR=3时不同时间尺度模型特征值的对比情况。其中，图9a和图9b分别对比多时间尺度模型和DVC时间尺度模型的主导特征值阻尼比和振荡频率。可以看到，多时间尺度模型和DVC时间尺度模型的特征值l4,5阻尼比和振荡频率偏差随PLL带宽提高而增大。另外，相比于多时间尺度模型，DVC时间尺度模型特征值l4,5阻尼比偏低，振荡频率偏高。图9c和图9d分别对比了多时间尺度模型和ACC时间尺度模型的主导特征值阻尼比和振荡频率。根据图9c，当PLL带宽较小时，多时间尺度模型和ACC时间尺度模型阻尼比存在一定偏差，随着PLL带宽提高，阻尼比偏差逐渐降低。根据图9d，ACC时间尺度模型的特征值l6,7相比多时间尺度模型振荡频率偏低，且偏差较大。
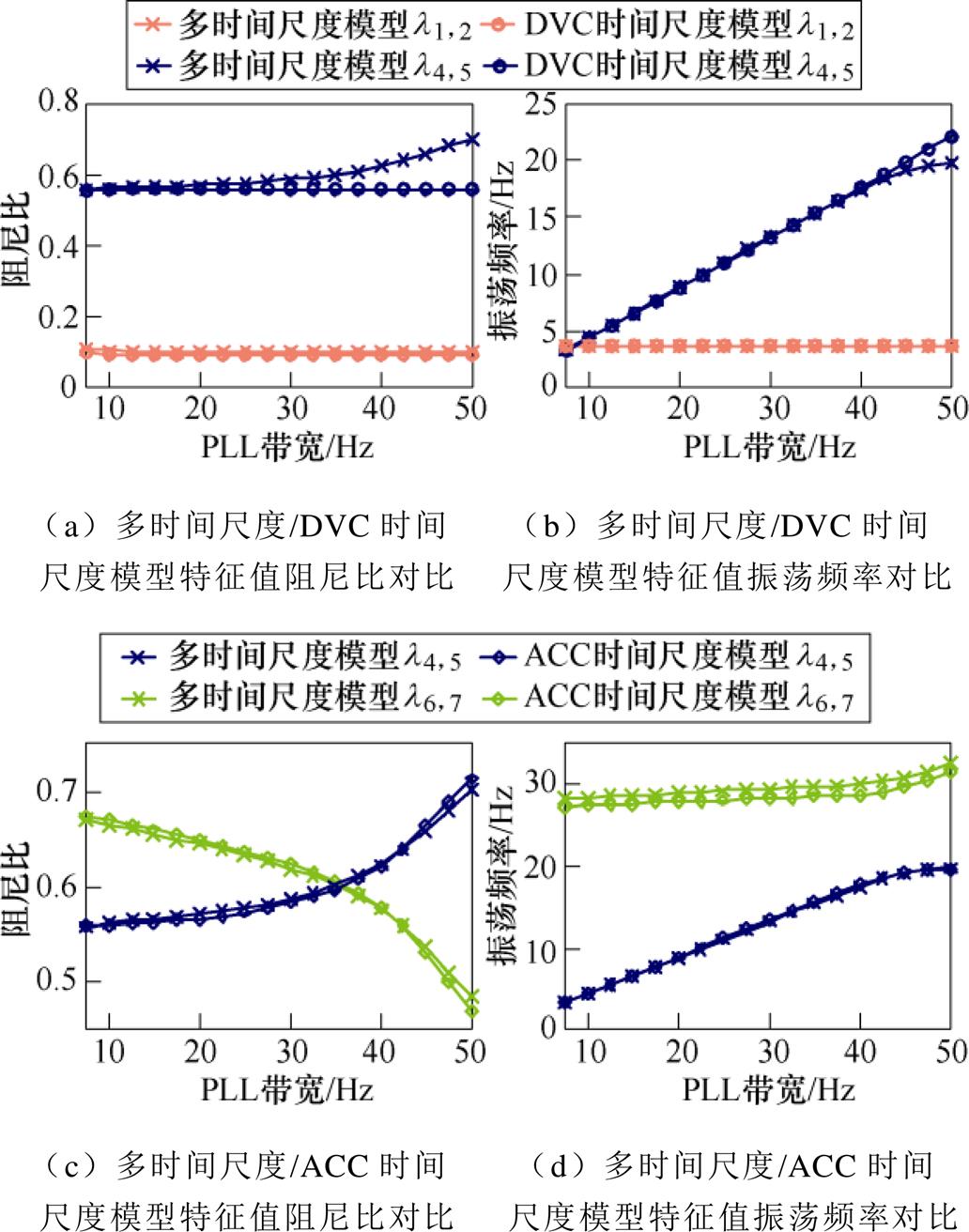
图8 SCR=12时不同时间尺度模型特征值对比
Fig.8 Eigenvalue comparison of the models in the different timescales when SCR is 12
进一步对比图8和图9不同时间尺度模型特征值分析结果的偏差，可以发现：当SCR降低即电网减弱时，多时间尺度、DVC时间尺度和ACC时间尺度模型的特征值偏差增大。综合图8和图9对比结果，并结合第3节多时间尺度间相互作用的变化规律，可以发现：SCR降低或PLL带宽提高，多时间尺度间相互作用增强，单一时间尺度模型的特征值分析结果偏差增大。
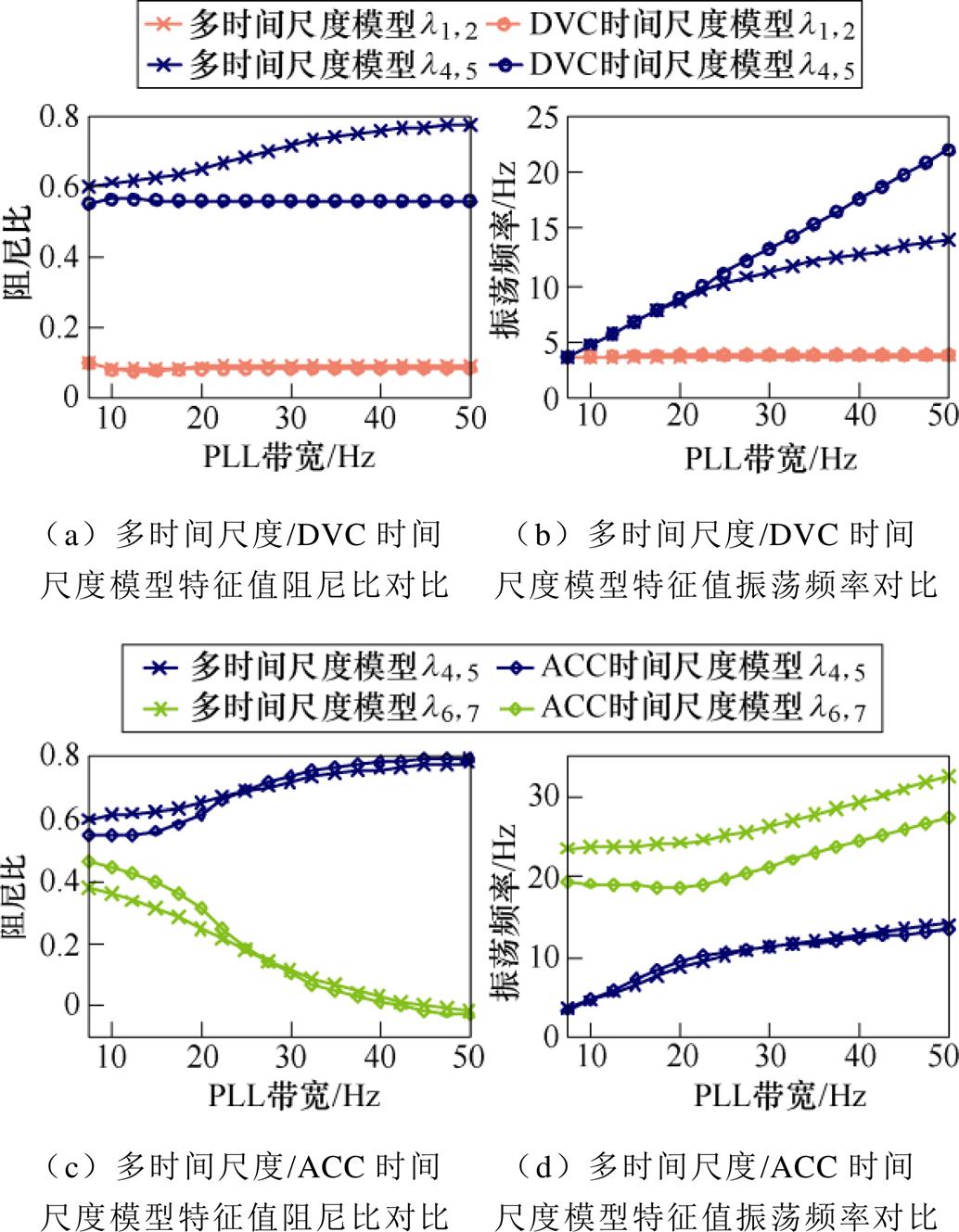
图9 SCR=3时不同时间尺度模型特征值对比
Fig.9 Eigenvalue comparison of the models in the different timescales when SCR is 3
本节说明DVC和ACC时间尺度模型特征值分析结果在不同PLL带宽和SCR下的偏差情况，并确定上述模型的适用范围。
定义DVC时间尺度模型特征值阻尼比偏差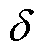
为
=
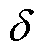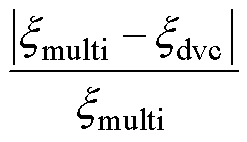（14）
式中，ξmulti和ξdvc分别为多时间尺度、DVC时间尺度模型的特征值阻尼比。其余特征值偏差均类此定义。在特定PLL带宽和SCR下，计算DVC时间尺度模型和ACC时间尺度模型的阻尼比偏差和振荡频率偏差，分别取最大值，可绘制PLL带宽和SCR变化时不同时间尺度模型的特征值偏差，如图10所示。根据图10a和图10b，随着PLL带宽提高或SCR降低，DVC时间尺度模型阻尼比和振荡频率偏差均增大。而由图10c和图10d可以看到，ACC时间尺度模型阻尼比和振荡频率偏差主要与SCR相关。随着SCR降低，ACC时间尺度模型特征值偏差提高。
根据图10的分析结果可以进一步确定DVC、ACC时间尺度模型的适用范围。从系统分析需求的角度看，DVC时间尺度模型和ACC时间尺度模型需要准确反映实际系统在对应时间尺度的动态特性，即特征值的阻尼比和振荡频率。因此，本文将DVC、ACC时间尺度模型的适用范围定义为：单一时间尺度模型的稳定性分析结果与多时间尺度模型相同，且其最大阻尼比偏差和振荡频率偏差均不超过10 %。根据该定义，可以获得DVC、ACC时间尺度模型的适用范围，如图11所示。
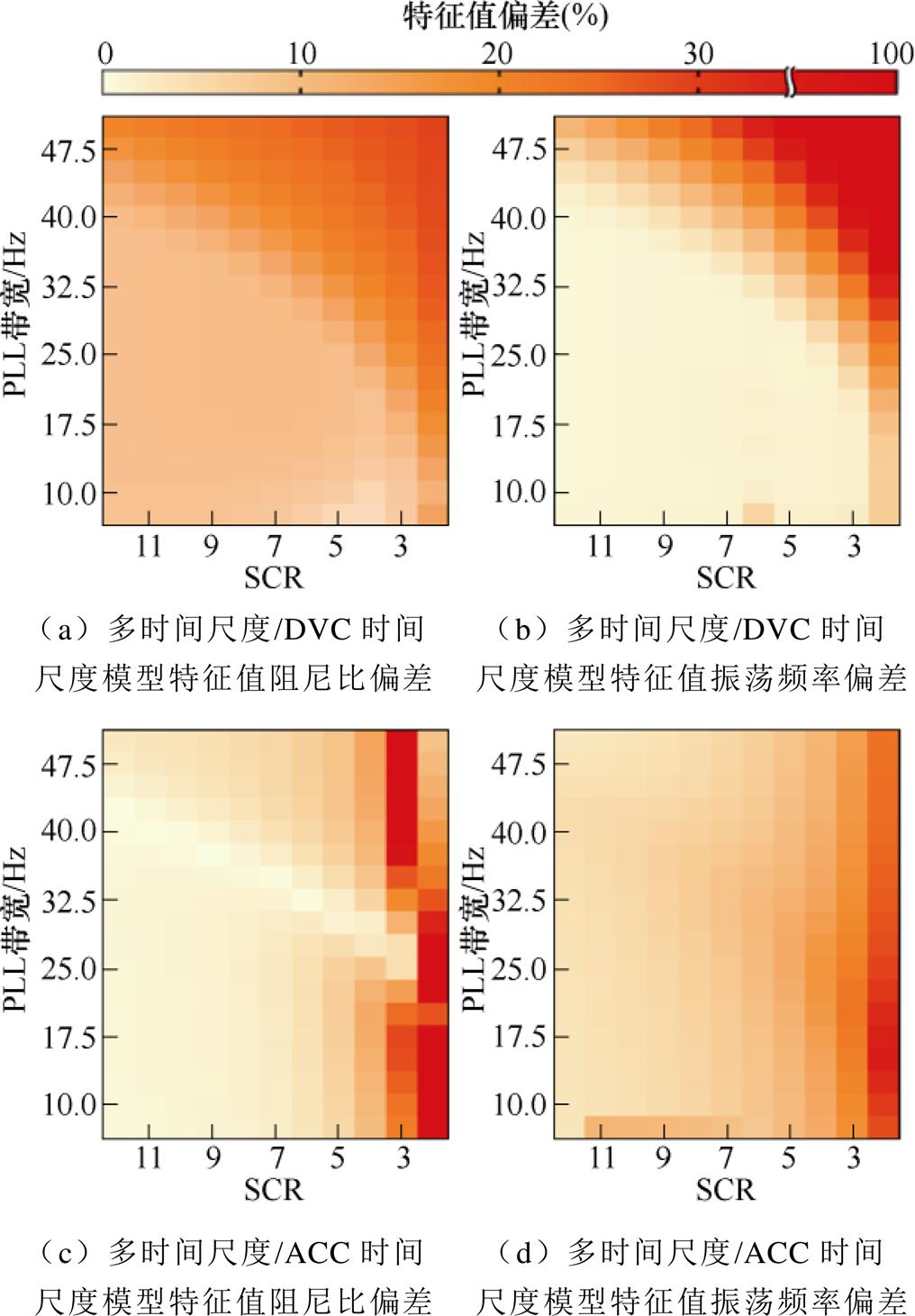
图10 PLL带宽和SCR变化时不同时间尺度模型的特征值偏差
Fig.10 Eigenvalue deviation of models in the different timescales when the PLL bandwidth and SCR vary
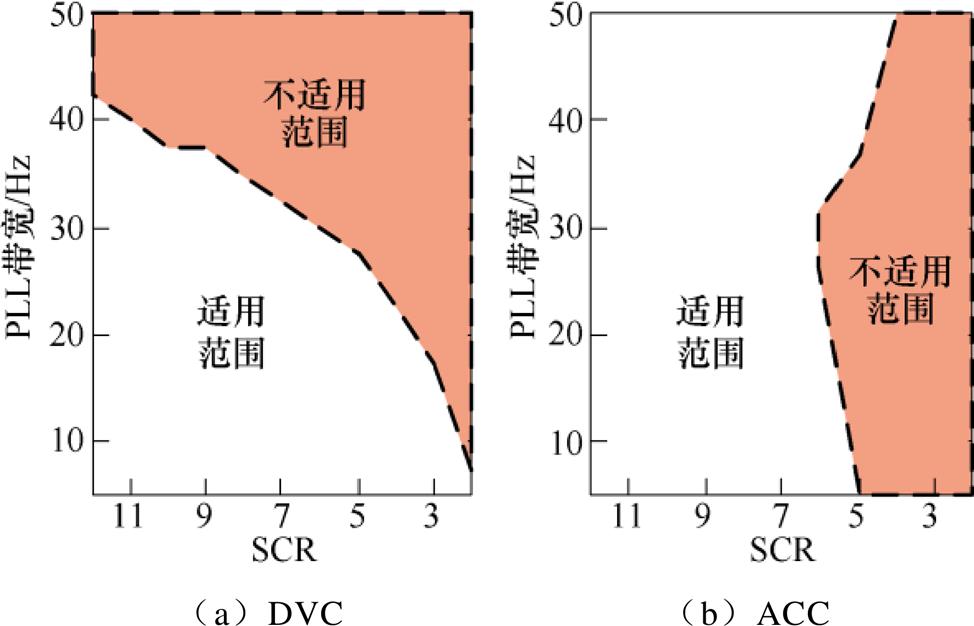
图11 DVC时间尺度及ACC时间尺度模型的适用范围
Fig.11 Applicable scope of the model in DVC/ACC timescale
本节针对图1所示的VSC并网系统，通过对比不同PLL带宽和SCR下电磁暂态仿真分析结果和DVC、ACC时间尺度模型分析结果，验证4.1节和4.2节的分析结论。本节案例的参数设置如下：
（1）案例1：PLL带宽取40 Hz，SCR=7。
（2）案例2：PLL带宽取10 Hz，SCR=3。
（3）案例3：PLL带宽取40 Hz，SCR=3。
其余参数见附录。在案例1参数下，2.5 s时对于电磁暂态仿真模型施加扰动，VSC并网系统的端电压幅值时域响应波形如图12所示。针对该仿真波形进行Prony分析，结果见表2。DVC、ACC时间尺度模型在案例1参数下的阻尼比、振荡频率及其偏差的分析结果见表3。对比表2和表3的分析结果可以看到，在案例1高SCR且高PLL带宽的情况下，DVC时间尺度模型特征值l4,5阻尼比与Prony分析结果相比偏低，偏差超过10 %；而ACC时间尺度模型特征值与Prony分析结果较为接近，这与4.1节图8高PLL带宽情况下的分析结论相符。根据本文对模型适用范围的定义，对于案例1，DVC时间尺度模型不适用，而ACC时间尺度模型在适用范围内，准确度较高。这与4.2节图11模型适用范围的分析结果相符。
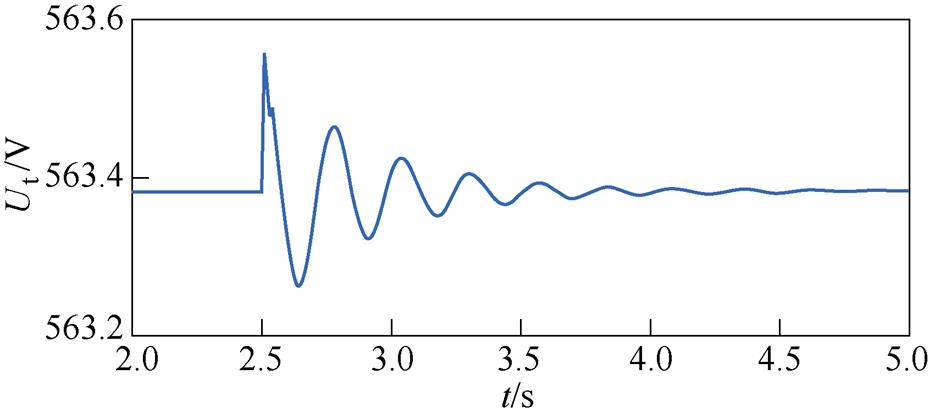
图12 案例1仿真结果
Fig.12 Simulation results of Case 1
表2 案例1的Prony分析结果
Tab.2 Prony analysis results of Case 1
模式阻尼比振荡频率/Hz l1,20.103.8 l4,50.6916 l6,70.3831
表3 案例1不同时间尺度模型的特征值分析结果
Tab.3 Eigenvalue analysis results of models in the different timescales for Case 1
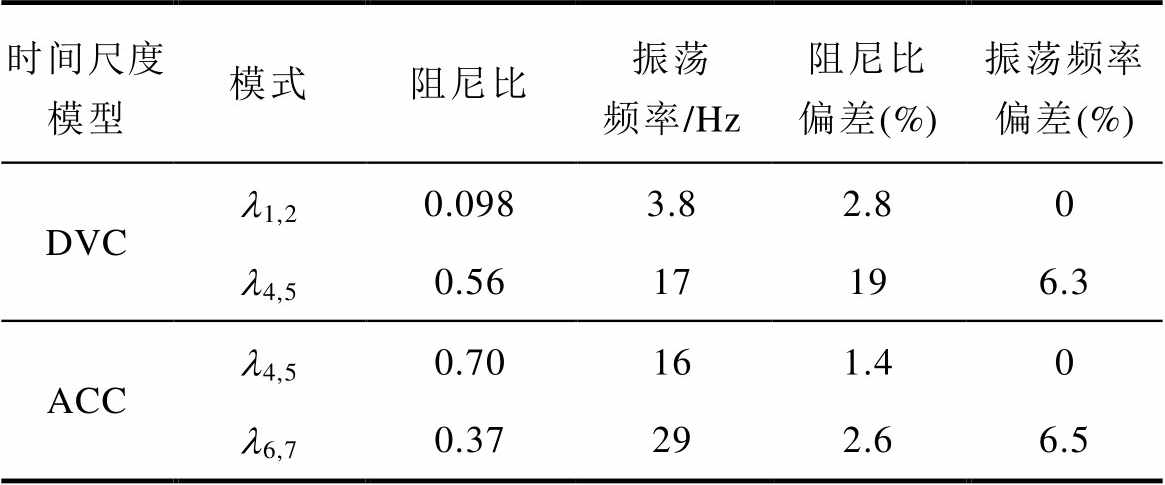
时间尺度模型模式阻尼比振荡频率/Hz阻尼比偏差(%)振荡频率偏差(%) DVCl1,20.0983.82.80 l4,50.5617196.3 ACCl4,50.70161.40 l6,70.37292.66.5
在案例2参数下，VSC并网系统的端电压幅值扰动响应时域波形及其Prony分析结果分别如图13所示和见表4。DVC、ACC时间尺度模型的特征值分析结果见表5。通过对比表4和表5，可见在案例2低SCR且低PLL带宽下，DVC时间尺度模型的特征值与Prony分析结果接近；而ACC时间尺度模型的特征值阻尼比存在较大偏差，同时特征值l6,7振荡频率偏低，偏差超过10 %。以上结果验证了4.1节图9低PLL带宽情况下的分析结论。另外，对比表4与表5说明，对于案例2，DVC时间尺度模型适用，而ACC时间尺度模型不在适用范围内。这与4.2节图11有关模型适用范围的结论相符。
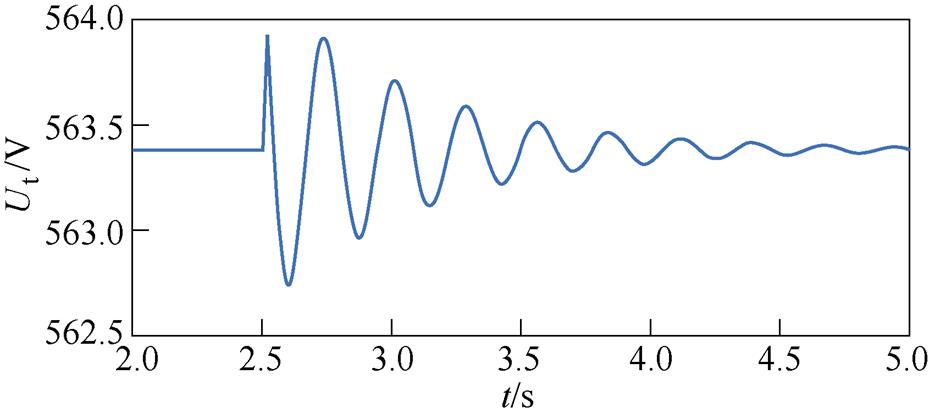
图13 案例2仿真结果
Fig.13 Simulation results of Case 2
表4 案例2的Prony分析结果
Tab.4 Prony analysis results of Case 2
模式阻尼比振荡频率/Hz l1,20.0753.6 l4,50.614.6 l6,70.3524
表5 案例2不同时间尺度模型的特征值分析结果
Tab.5 Eigenvalue analysis results of models in the different timescales for Case 2
时间尺度模型模式阻尼比振荡频率/Hz阻尼比偏差(%)振荡频率偏差(%) DVCl1,20.0783.74.02.8 l4,50.564.78.22.2 ACCl4,50.544.711.52.2 l6,70.44192621
在案例3参数下，VSC并网系统的端电压幅值扰动响应时域波形及其Prony分析结果分别如图14所示和见表6。表7为对应参数下单一时间尺度模型的特征值分析结果。对比表6和表7可以看到，在案例3低SCR且高PLL带宽下，DVC、ACC时间尺度模型的特征值分析结果均存在较大偏差。其中，DVC时间尺度模型特征值l4,5阻尼比偏低，振荡频率偏高。ACC时间尺度模型的特征值l6,7振荡频率偏低。上述结果与4.1节图9高PLL带宽情况下的理论分析结论相符。另外，对比表6与表7说明，对于案例3，DVC、ACC时间尺度模型均不适用，验证了4.2节图11模型适用范围的准确性。
图14 案例3仿真结果
Fig.14 Simulation results of Case 3
表6 案例3的Prony分析结果
Tab.6 Prony analysis results of Case 3
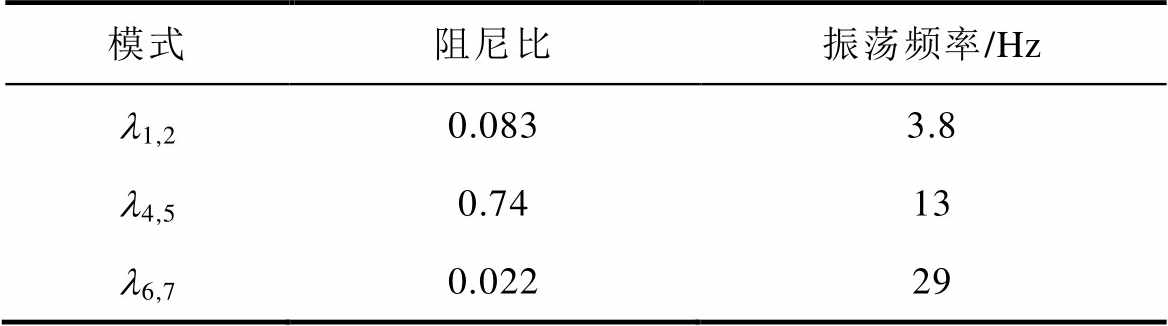
模式阻尼比振荡频率/Hz l1,20.0833.8 l4,50.7413 l6,70.02229
表7 案例3不同时间尺度模型的特征值分析结果
Tab.7 Eigenvalue analysis results of models in the different timescales for Case 3
时间尺度模型模式阻尼比振荡频率/Hz阻尼比偏差(%)振荡频率偏差(%) DVCl1,20.0843.81.20 l4,50.56182438 ACCl4,50.78125.47.7 l6,70.011245017
此外，通过对比案例1和案例3可以发现，当SCR降低时，单一时间尺度模型的特征值偏差增大。而案例2和案例3的对比说明，PLL带宽提高时也存在类似结论。这验证了4.1节对比图8和图9获得的规律性结论。
解释多时间尺度间相互作用对于DVC时间尺度模型分析结果的影响。DVC时间尺度模型假设网络电流能够瞬时跟踪电压外环给定的电流指令值。但是，在实际动态过程中，由于电流内环存在积分环节并且交流网络中存在电感、电容等储能元件，网络电流无法突变，需要一定响应时间才能跟踪外环给定的指令值。因此，从DVC时间尺度环节的视角看，电流内环和交流网络等相当于阻尼环节，阻滞了电流指令值动态产生的影响。而从特征值分析的角度看，由于忽略电流控制等环节的阻尼作用，DVC时间尺度模型分析得到的特征值阻尼比更低而振荡频率更高，这与图8和图9所观察到的现象相符。
解释多时间尺度间相互作用对于ACC时间尺度模型分析结果的影响。从ACC时间尺度环节的视角看，电压外环给定电流指令，相当于激励环节。以d轴电流控制为例，假设VSC输出的d轴电流受扰增大，VSC有功功率输出随之增大。如果忽略直流电压外环，则d轴电流指令值恒定，内环控制器动作使实际d轴电流下降。而如果考虑直流电压外环，d轴电流指令值则会减小，导致d轴电流指令值与实际值间的误差增大，电流内环更快动作。因此，从特征值分析的角度，ACC时间尺度模型的特征值振荡频率相比多时间尺度模型更低，这与图8d和图9d所观察到的现象相符。
针对VSC并网系统多时间尺度间相互作用，本文基于模式分析方法，研究了系统多时间尺度间相互作用的量化衡量指标、变化规律及其对系统稳定性分析结果的影响，并对分析结果做了初步的物理解释。本文的主要工作和结论如下：
1）提出将不同时间尺度状态-模式间参与因子定义为异尺度参与因子，并将异尺度参与因子作为衡量系统多时间尺度间相互作用的量化指标。
2）揭示了多时间尺度间相互作用随PLL带宽和SCR的变化规律，明确当PLL带宽提高或SCR降低时，系统异尺度参与因子提高，多时间尺度间相互作用增强。
3）研究了多时间尺度间相互作用对于系统稳定性分析结果的影响，提出了DVC、ACC时间尺度模型的适用范围。PLL带宽提高或SCR降低，将导致系统多时间尺度间相互作用增强，进而使单一时间尺度模型的特征值分析结果偏差增大。
4）初步解释了多时间尺度间相互作用的影响。从DVC时间尺度环节的视角看，内环相当于阻尼环节，因此DVC时间尺度模型的特征值分析结果阻尼比偏低而振荡频率偏高。而从ACC时间尺度环节的视角看，外环相当于激励，因此ACC时间尺度模型分析得到的特征值振荡频率偏低。
然而，本文仅研究了三相对称情况下VSC并网系统的多时间尺度间相互作用。在三相不对称情况下，VSC控制策略及网络拓扑等与三相对称情况相比呈现出较大差异，VSC并网系统的建模及多时间尺度间相互作用也会更为复杂。后续将对此进行深入研究。
附 录
VSC并网系统参数见附表1。
附表1 VSC并网系统参数
App.Tab.1 VSC grid-connected system parameters
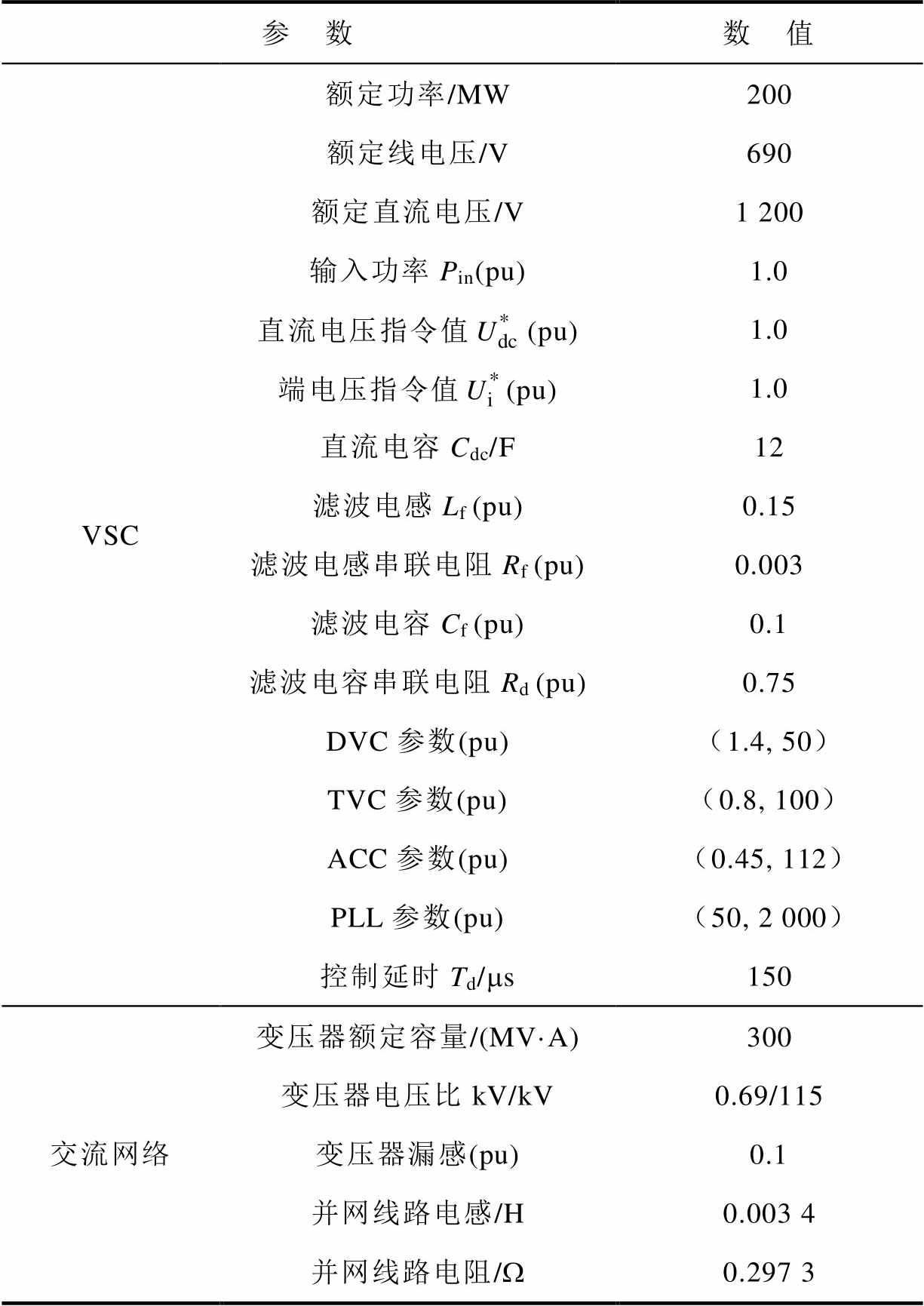
参 数数 值 VSC额定功率/MW200 额定线电压/V690 额定直流电压/V1 200 输入功率Pin(pu)1.0 直流电压指令值(pu)1.0 端电压指令值(pu)1.0 直流电容Cdc/F12 滤波电感Lf(pu)0.15 滤波电感串联电阻Rf (pu)0.003 滤波电容Cf(pu)0.1 滤波电容串联电阻Rd(pu)0.75 DVC参数(pu)（1.4, 50） TVC参数(pu)（0.8, 100） ACC参数(pu)（0.45, 112） PLL参数(pu)（50, 2 000） 控制延时Td/ms150 交流网络变压器额定容量/(MV·A)300 变压器电压比kV/kV0.69/115 变压器漏感(pu)0.1 并网线路电感/H0.003 4 并网线路电阻/W0.297 3
参考文献
[1] Xie Xiaorong, Zhang Xu, Liu Huakun, et al. Charac- teristic analysis of subsynchronous resonance in practical wind farms connected to series-compensated transmissions[J]. IEEE Transactions on Energy Con- version, 2017, 32(3): 1117-1126.
[2] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97.
Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[3] Liu Huakun, Xie Xiaorong, He Jingbo, et al. Sub- synchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708- 4720.
[4] 张东辉, 陈新, 杨舒婷, 等. 含静止无功补偿装置的光伏电站高频谐振分析及抑制策略研究[J/OL]. 中国电机工程学报. https://kns.cnki.net/kcms/detail/ 11.2107.TM.20220707.1548.014.html.
Zhang Donghui, Chen Xin, Yang Shuting, et al. Analysis of high-frequency resonance and suppression strategy of photovoltaic power plant with static reactive power compensation device[J/OL]. Pro- ceedings of the CSEE. https://kns.cnki.net/kcms/detail/ 11.2107.TM.20220707.1548.014.html.
[5] 颜湘武, 常文斐, 崔森, 等. 基于线性自抗扰控制的静止无功补偿器抑制弱交流风电系统次同步振荡策略[J]. 电工技术学报, 2022, 37(11): 2825-2836.
Yan Xiangwu, Chang Wenfei, Cui Sen, et al. Sub- synchronous oscillation suppression strategy of weak AC wind power system with static var compensator based on linear active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2825-2836.
[6] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324.
Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low- frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electro- technical Society, 2023, 38(5): 1312-1324.
[7] 徐海亮, 吴瀚, 李志, 等. 低短路比电网下含负序控制双馈风机稳定性研究的几个关键问题[J]. 电工技术学报, 2021, 36(22): 4688-4702.
Xu Hailiang, Wu Han, Li Zhi, et al. Several key issues on stability study of DFIG-based wind turbines with negative sequence control during low short-circuit ratio power grids[J]. Transactions of China Electro- technical Society, 2021, 36(22): 4688-4702.
[8] 袁小明, 程时杰, 胡家兵. 电力电子化电力系统多尺度电压功角动态稳定问题[J]. 中国电机工程学报, 2016, 36(19): 5145-5154, 5395.
Yuan Xiaoming, Cheng Shijie, Hu Jiabing. Multi- timescale voltage and power angle dynamics in power electronics dominated large power systems[J]. Pro- ceedings of the CSEE, 2016, 36(19): 5145-5154, 5395.
[9] Yuan Hao, Yuan Xiaoming, Hu Jiabing. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control times- cale[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3981-3991.
[10] 黄云辉, 宋泽凡, 唐金锐, 等. 连接弱电网的并网变换器直流电压时间尺度稳定器的设计与分析[J].电工技术学报, 2018, 33(增刊1): 185-192.
Huang Yunhui, Song Zefan, Tang Jinrui, et al. Design and analysis of DC-link voltage stabilizer for voltage source converter as connected to weak grid[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 185-192.
[11] Zheng Wanning, Hu Jiabing, Yuan Xiaoming. Analytic quantification of interactions in MTDC systems based on self-/en-stabilizing coefficients in DC voltage control timescale[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 2980-2991.
[12] 王一珺, 王海风. 直流电压动态时间尺度下大规模直驱风电场振荡稳定性及参数稳定域分析[J]. 中国电机工程学报, 2021, 41(增刊1): 92-107.
Wang Yijun, Wang Haifeng. Analysis of oscillation stability and stability region of parameters in large- scale direct-drive wind farms under DC voltage dynamic time scale[J]. Proceedings of the CSEE, 2021, 41(S1): 92-107.
[13] 严亚兵, 苗淼, 李胜, 等. 静止坐标系下变换器电流平衡-内电势运动模型: 一种装备电流控制尺度物理化建模方法[J]. 中国电机工程学报, 2017, 37(14): 3963-3972, 4274.
Yan Yabing, Miao Miao, Li Sheng, et al. Current- balancing driven internal voltage motion model of voltage source converter in stationary frame: a physical modeling method in current-control times- cale[J]. Proceedings of the CSEE, 2017, 37(14): 3963-3972, 4274.
[14] 张琛, 蔡旭, 李征. 电压源型并网变流器的机-网电气振荡机理及稳定判据研究[J].中国电机工程学报, 2017, 37(11): 3174-3183, 3372.
Zhang Chen, Cai Xu, Li Zheng. Stability criterion and mechanisms analysis of electrical oscillations in the grid-tied VSC system[J]. Proceedings of the CSEE, 2017, 37(11): 3174-3183, 3372.
[15] Zhao Mingquan, Yuan Xiaoming, Hu Jiabing, et al. Voltage dynamics of current control time-scale in a VSC-connected weak grid[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2925-2937.
[16] 刘其辉, 洪晨威, 逄思敏, 等. 基于弹性系数的双馈风电机组控制参数对次同步振荡作用分析及调整方法[J]. 电工技术学报, 2022, 37(14): 3528-3541.
Liu Qihui, Hong Chenwei, Pang Simin, et al. Analysis and adjustment method of doubly-fed fan control parameters on subsynchronous oscillation based on impedance elastic sensitivity[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3528- 3541.
[17] 王一珺, 王海风. 并网直驱风电场在交流电流时间尺度下的小干扰稳定性—功率控制外环影响[J]. 高电压技术, 2022, 48(4): 1411-1421.
Wang Yijun, Wang Haifeng. Small-disturbance stabi- lity of grid-connected PMSG wind farms under AC current time scales-the influence of power control outer loop[J]. High Voltage Engineering, 2022, 48(4): 1411-1421.
[18] Li Sheng, Yan Yabing, Yuan Xiaoming. SISO equi- valent of MIMO VSC-dominated power systems for voltage amplitude and phase dynamic analyses in current control timescale[J]. IEEE Transactions on Energy Conversion, 2019, 34(3): 1454-1465.
[19] 刘取. 电力系统稳定性及发电机励磁控制[M]. 北京: 中国电力出版社, 2007.
[20] 王锡凡. 现代电力系统分析[M]. 北京: 科学出版社, 2003.
[21] Zhang Yang, Huang S H F, Schmall J, et al. Evaluating system strength for large-scale wind plant integr- ation[C]//2014 IEEE PES General Meeting Con- ference & Exposition, National Harbor, MD, USA, 2014: 1-5.
[22] 朱凌志, 曲立楠, 刘纯, 等. 新能源发电集群的改进等效短路比计算方法[J]. 电力系统自动化, 2021, 45(22): 74-82.
Zhu Lingzhi, Qu Linan, Liu Chun, et al. Improved calculation method of equivalent short-circuit ratio for power generation cluster of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(22): 74-82.
[23] Zhu Jianhang, Guo Zeren, Hu Jiabing, et al. Trun- cation number selection of harmonic state-space model based on the Floquet characteristic expo- nent[J/OL]. IEEE Transactions on Industrial Elec- tronics. https://ieeexplore.ieee.org/document/9772947.
Abstract The voltage source converter's (VSC) control system and its interactions with the network are important factors that cause the instability of the grid-tied VSC. The control of VSC has a multiple timescale feature, which can be divided into DC-link voltage control (DVC) timescale and alternating current control (ACC) timescale. Existing research focuses on stability in a single timescale and rarely deals with the interaction between multiple timescales. Therefore, this paper uses the modal analysis to investigate the quantitative indicators and influencing factors of the interaction between different timescales of the grid-tied VSC. At the same time, the applicable scope of the models in DVC and ACC timescales is clarified, and the analysis results are preliminarily explained from a physical point of view.
First, this paper briefly introduces the topology and control scheme of the grid-tied VSC and illustrates its multiple timescale dynamic characteristics. Next, the small-signal models of the grid-tied VSC in multiple timescales, DVC timescales, and ACC timescales are constructed. The accuracy of the above models is verified by the electromagnetic transient simulation and eigenvalue analysis. The participation factors for state variables and modes in different timescales are used based on the modal analysis method to measure the relative strength of the interaction between different timescales. The interaction variation between different timescales with the bandwidth of the phase-locked loop (PLL) and the short circuit ratio (SCR) is analyzed. By comparing the eigenvalue damping ratios and oscillation frequencies of the grid-tied VSC models in multiple timescales, DVC timescale, and ACC timescale, this paper shows that the interaction between multiple timescales has an impact on the system stability analysis results. Then, the deviations of eigenvalue damping ratios and oscillation frequencies of the DVC or ACC timescale models are analyzed when the PLL bandwidth and SCR vary. The applicable scope of the above models in a single timescale is clarified. Moreover, the theoretical analysis results are verified by electromagnetic transient simulation. Finally, the effects of the interaction between multiple timescales are initially explained from the physical level.
The main conclusions of this paper are as follows. (1) The participation factors for state variables and modes in different timescales are defined as the different-scale participation factors, and different-scale participation factors can be used as a quantitative index to measure the interaction between multiple timescales. (2) When the PLL bandwidth increases or SCR decreases, the different-scale participation factors increase, which enhances the interaction between multiple timescales. (3) The influence of the interaction between multiple timescales on the analysis results of system stability is studied, and the applicable scope of the models in DVC and ACC timescales is proposed. The increase of PLL bandwidth or the decrease of SCR will enhance the interaction between multiple timescales, thus increasing the deviation of the eigenvalue analysis results of the models in a single timescale. (4) From the perspective of the parts in the DVC timescale, the inner control loops are equivalent to the damping links. Therefore, the eigenvalue analysis results of the model in the DVC timescale are lower in damping ratio and higher in oscillation frequency than those in the multiple timescale model. From the perspective of the parts in the ACC timescale, the outer control loops are equivalent to the excitation, so the eigenvalue oscillation frequency obtained by the model in the ACC timescale is much lower.
keywords：Voltage source converter, multiple timescales, DC-link voltage control (DVC) timescale, alternating current control (ACC) timescale, interaction, modal analysis
DOI: 10.19595/j.cnki.1000-6753.tces.221496
中图分类号：TM712
国家电网有限公司科技资助项目（5214DK210010）。
收稿日期 2022-08-02
改稿日期 2022-09-16
杜步阳 男，1998年生，博士研究生，研究方向为新能源发电、高压直流输电系统建模及其稳定性分析。E-mail: buyang_du@hust.edu.cn
朱建行 男，1992年生，博士，博士后，研究方向为大规模新能源发电系统、高压直流输电系统电磁动态稳定分析与控制。E-mail: jh_zhu@hust.edu.cn（通信作者）
（编辑 陈 诚）