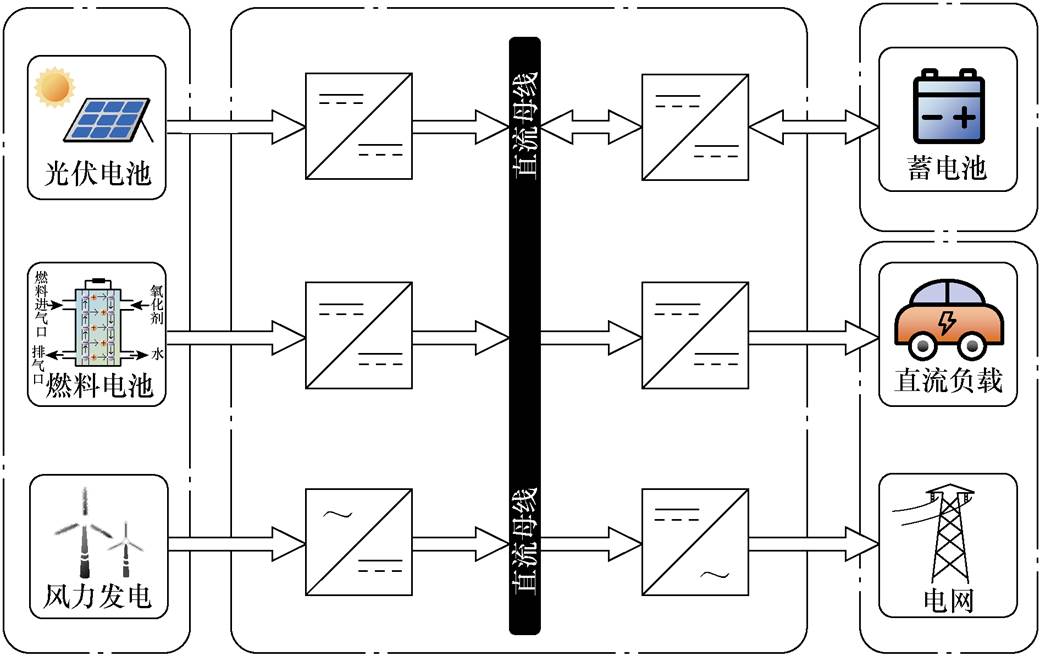
图1 直流微电网结构示意图
Fig.1 Schematic diagram of the DC microgrid architecture
摘要 针对清洁能源输出电压等级较低难以实现直流微电网并网的问题，提出一种基于开关耦合电感的无源钳位结构的高升压DC-DC变换器。所提变换器采用开关耦合电感结构连接变换器的输入端与输出端。通过调整耦合电感的匝比提高电压增益。此外，采用无源钳位结构回收漏感能量，抑制功率开关管上的电压尖峰，降低功率开关管的电压应力，提高变换器的电能转换效率。该文介绍变换器的工作原理，推导了变换器的稳态特性和各元件的设计参数，详细分析变换器的损耗以及选择有利的参数提高效率，如合理设计耦合电感匝比。搭建一台输入电压为40 V、输出电压为400 V、满载功率为250 W的实验样机，验证了变换器的可行性和理论分析的正确性。实测的最高效率和满载效率分别为97.59 %和97.10 %。
关键词：开关耦合电感 高升压 DC-DC变换器 效率优化 直流微电网
传统化石能源的储量难以满足日益增长的消费需求，并且过度使用会造成碳排放量上升，导致全球气候变暖等全球性环境污染问题[1-3]。为了加快能源转型，减小化石能源在能源结构中所占比例，实现“碳达峰”和“碳中和”的战略目标，开发清洁能源已成为世界各国研究的热点[4-6]。光伏电池、燃料电池、风力发电等由清洁能源发电构成的分布式电源结合储能装置以及负载组成的直流微电网，可以降低分布式电源并网对电网运行的影响。此外，分布式电源及储能装置多为直流电，直流微电网可减少变换环节，转化效率高；与交流微电网相比，无需考虑电压相位、频率、无功功率等问题。因此直流微电网具有灵活可靠、损耗小、控制难度相对较低、便于拓展等优点[7-9]。然而，这些清洁能源发电装置输出电压低，难以达到直流微电网并网所需的电压。因此，高升压DC-DC变换器已被广泛应用于低电压转换场合[10-11]。图1为直流微电网结构示意图。
图1 直流微电网结构示意图
Fig.1 Schematic diagram of the DC microgrid architecture
由于传统Boost变换器结构简单和成本较低，能够通过调节占空比实现升压，在工业生产中被广泛应用[12-14]。理想情况下，当占空比趋向于1时，电压增益接近于无穷大。但是，功率开关管的电压应力等于输出电压，过高的占空比会导致功率开关管的电压应力较大，且二极管反向恢复问题严重。此外，电容和电感的等效串联电阻会限制电压增益和降低变换器的转换效率[15-18]。因此，在高升压比的电路应用中，传统的Boost电路难以满足。
为了在适当的占空比下实现高升压和高效率转换，国内外对Boost变换器的拓扑结构进行了广泛研究。文献[19-22]采用耦合电感结构，改变耦合电感的匝比实现高升压。此外，耦合电感还可与电感、电容组成无源零输入电流纹波电路[23]。文献[24]结合双开关管实现谐振软开关耦合电感变换器。不可忽略的是，在功率开关管关断时，由于功率开关管的输出电容与耦合电感的漏感产生谐振，功率开关管两端会产生较高的电压尖峰。采用RCD缓冲电路尽管可以有效降低功率开关管的电压应力，但RCD中的电阻会消耗一部分能量导致功率损耗增加，降低了转换效率[25]。文献[26-27]通过增加功率开关管及相应的驱动电路构成有源钳位电路，实现漏感能量回收和抑制功率开关管的电压尖峰，但电路结构复杂，降低了变换器的可靠性。文献[28-30]采用二极管和电容构成的无源钳位电路，电路结构和控制简单。
此外，开关电感结构近年来也被运用于升压变换器以提高输出电压[31-32]，但磁性元件数量的增加，降低了转换效率和功率密度。因此，结合开关电感与耦合电感的优点，将两个开关电感结构集成到一个耦合电感上。文献[33]采用开关耦合电感结构提高了电压转换比。然而，漏感能量无法被回收利用，降低了变换器效率且功率开关管产生很大的电压尖峰。
本文提出一种基于开关耦合电感结构的无源钳位高升压DC-DC变换器。该变换器的拓扑结构如图2所示，耦合电感由励磁电感Lm、理想变压器和漏感Lk组成，其中一次绕组和二次绕组的匝比np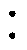
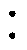ns=1n。二极管VD1和电容C1组成无源钳位电路用于抑制功率开关管S产生的电压尖峰和回收漏感能量。电容C2从直流输入电压源Vin、电容C1和二次绕组ns获得能量，通过二极管VD3为输出电容Co和负载Ro提供能量。所提变换器具有的特点如下：①所需元器件数量较少，结构简单，提高了可靠性；②输入端和输出端共地；③调节耦合电感的匝比和占空比提高电压增益；④无源钳位电路抑制功率开关管的电压尖峰，降低功率开关管的电压应力，同时回收漏感能量，提高转换效率。
本文首先对变换器的工作原理进行分析，推导了稳态特性与设计参数。然后详细分析变换器的损耗，通过合理设计耦合电感，选择电压应力低且导通电阻小的开关管实现效率的优化。最后制作一台250 W的实验样机，验证了理论分析的正确性。
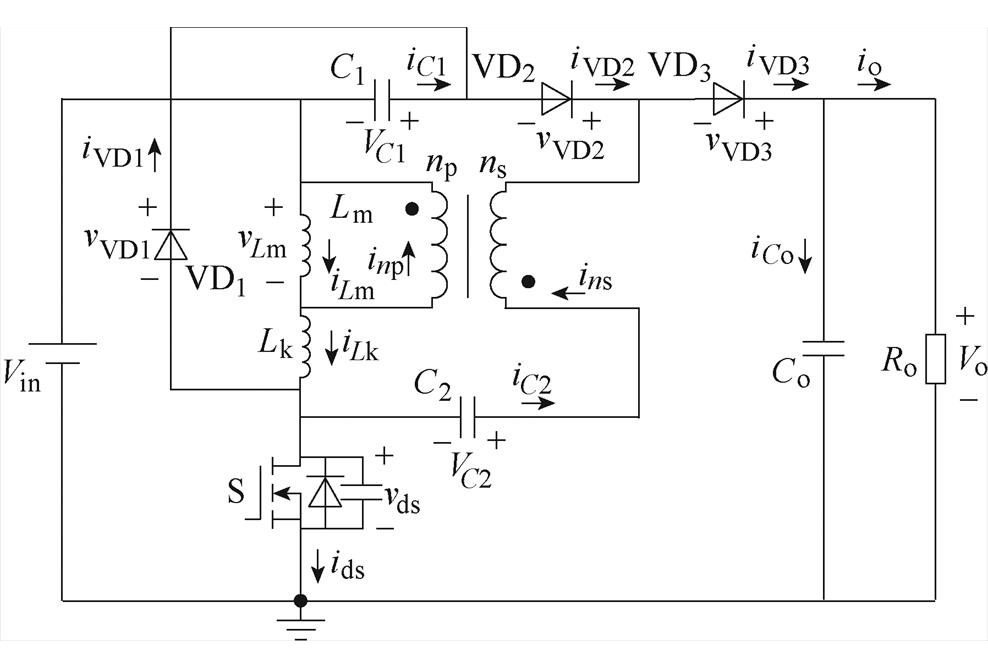
图2 所提变换器的等效电路
Fig.2 Equivalent circuit of the proposed converter
变换器的工作原理分析主要包括两种运行模式：连续导电模式（Continuous Conduction Mode, CCM）和不连续导电模式（Discontinuous Conduction Mode, DCM）。为了便于理论分析，假定条件如下：
（1）除了功率开关管的输出电容和反并联二极管外，变换器中所有二极管、电感、电容均为理想元器件，忽略等效阻抗产生的影响。
（2）电解电容C1、C2、Co足够大，其电容两端电压纹波可以忽略，电容电压保持恒定。
（3）考虑漏感对变换器运行模式的影响。
（4）vVDx（x=1, 2, 3）为二极管电压瞬时值；vds为开关管电压瞬时值；vLm为励磁电感电压瞬时值。
图3为所提变换器在CCM下的主要波形，D为占空比，Ts为开关周期；图4为在一个开关周期Ts内，变换器的4个工作模态。详细分析如下。
（1）模态1 [t0, t1]：能量流动如图4a所示，功率开关管S导通，二极管VD3正向导通，VD1、VD2反向截止。直流输入电压源Vin向漏感Lk提供能量，漏感电流iLk增加。储存在励磁电感Lm和电容C2的能量，通过二次绕组ns和二极管VD3传输到输出电容Co和负载Ro中，励磁电感电流iLm减小。当t=t1，流过二极管VD3的电流变为零时，此模态结束。
（2）模态2 
t1, t2]：能量流动如图4b所示，功率开关管S继续导通，二极管VD2正向导通，VD1、VD3反向截止。直流输入电压源Vin向励磁电感Lm和漏感Lk提供能量，励磁电感电流iLm和漏感电流iLk均增加。同时，输入电压源Vin和电容C1通过二极管VD2和耦合电感二次绕组ns向电容C2传输能量。电容Co向负载Ro提供能量。当t=t2，功率开关管S关断时，此模态结束。
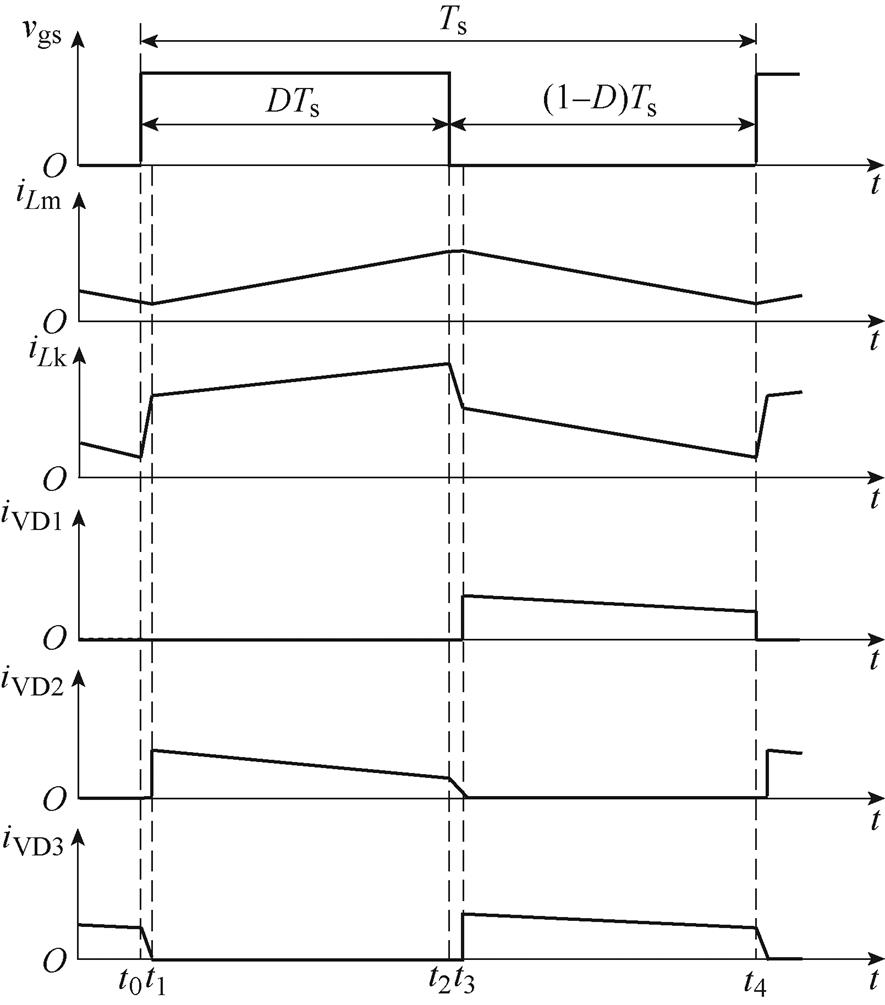
图3 CCM下变换器的主要波形
Fig.3 Key waveforms of the proposed converter in CCM
（3）模态3 t2, t3]：能量流动如图4c所示，功率开关管S关断，二极管VD2继续正向导通，VD1和VD3反向截止。输入电压源Vin继续提供能量给励磁电感Lm。功率开关管的输出电容被充电，vds增加。由于漏感非常小，故漏感电流iLk以较大斜率值减小。电压源Vin和电容C1继续通过二极管VD2和耦合电感二次绕组ns向电容C2传输能量。当t =t3，VD1导通时，此模态结束。
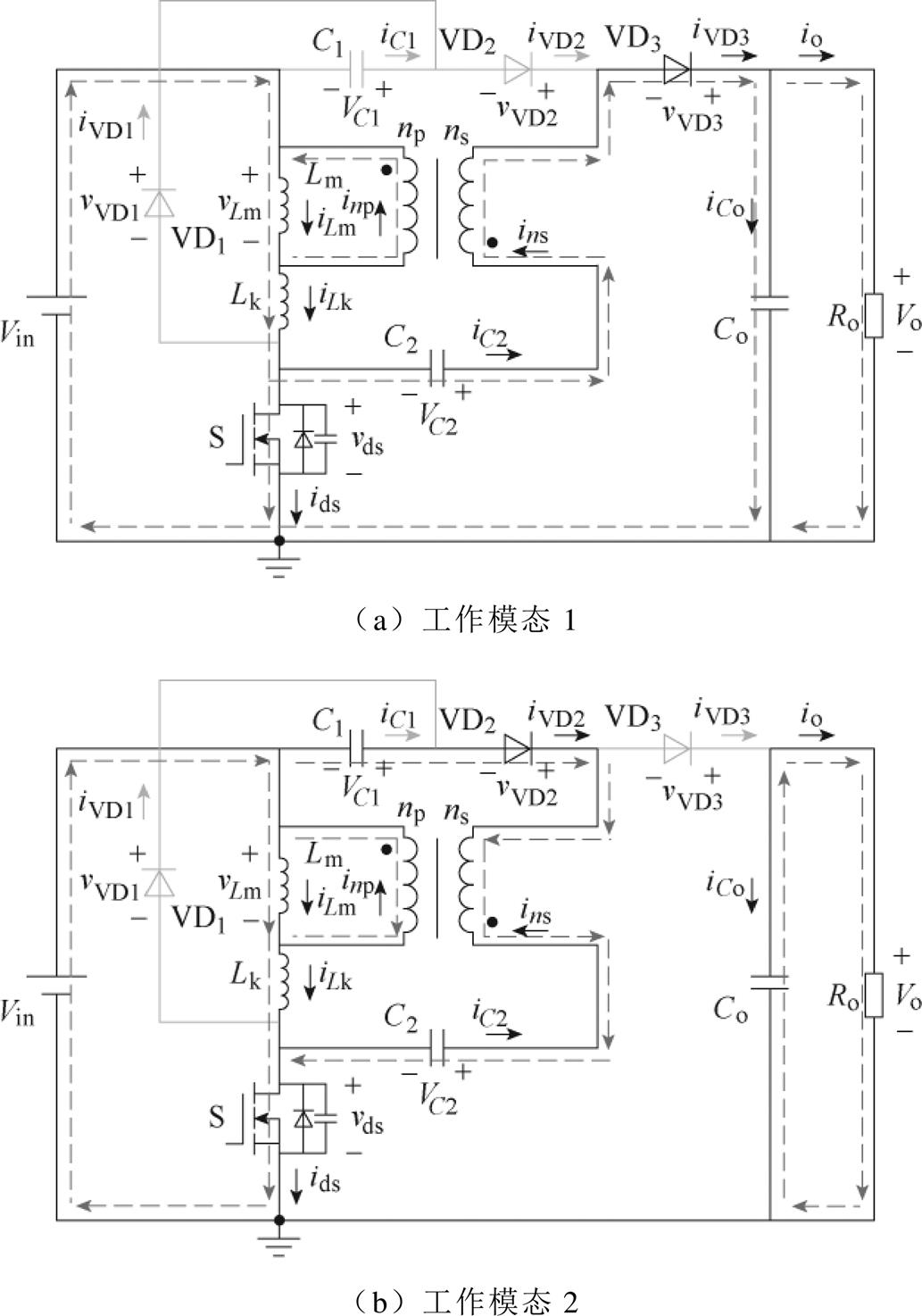
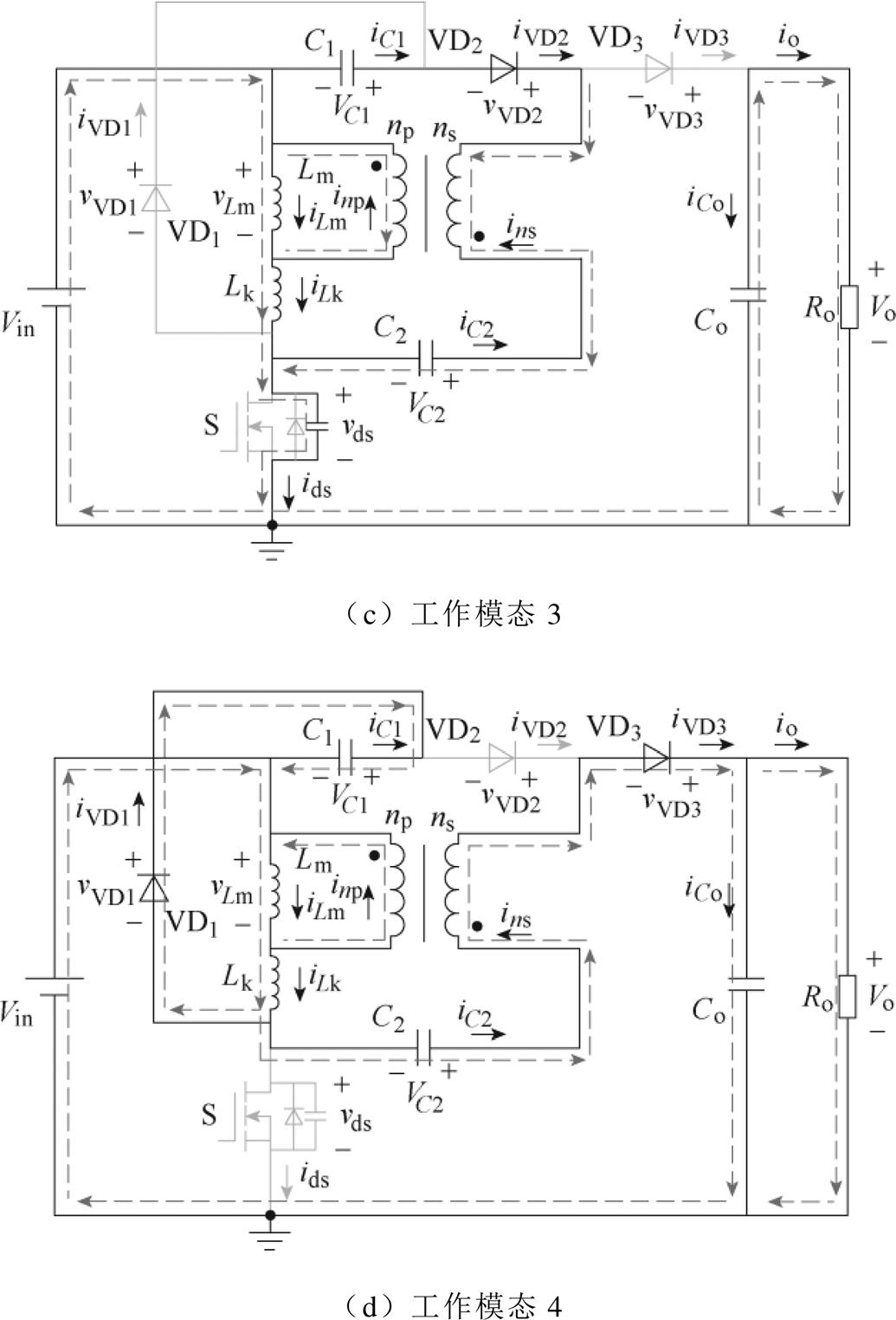
图4 CCM下所提变换器各个工作模态的等效电路
Fig.4 The equivalent circuits of the proposed converter under different operating modes in CCM
（4）模态4 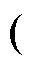t3, t4]：能量流动如图4d所示，功率开关管S关断，二极管VD1和VD3正向导通，VD2反向截止。输入电压源Vin与励磁电感Lm和电容C2串联，通过耦合电感二次绕组ns和二极管VD3，向输出电容Co和负载Ro提供能量。漏感Lk继续通过二极管VD1为电容C1提供能量。励磁电感电流iLm和漏感电流iLk均减小。当t=t4，二极管VD1关断，功率开关管S在下一个开关周期导通时，此模态结束。
DCM下，变换器的工作模态可以分为5个，主要的工作波形如图5所示，DL为漏感电流下降至0时的占空比。其中DCM下模态1、模态2、模态3、模态4与CCM下近似一致，在此仅分析DCM下的工作模态5。
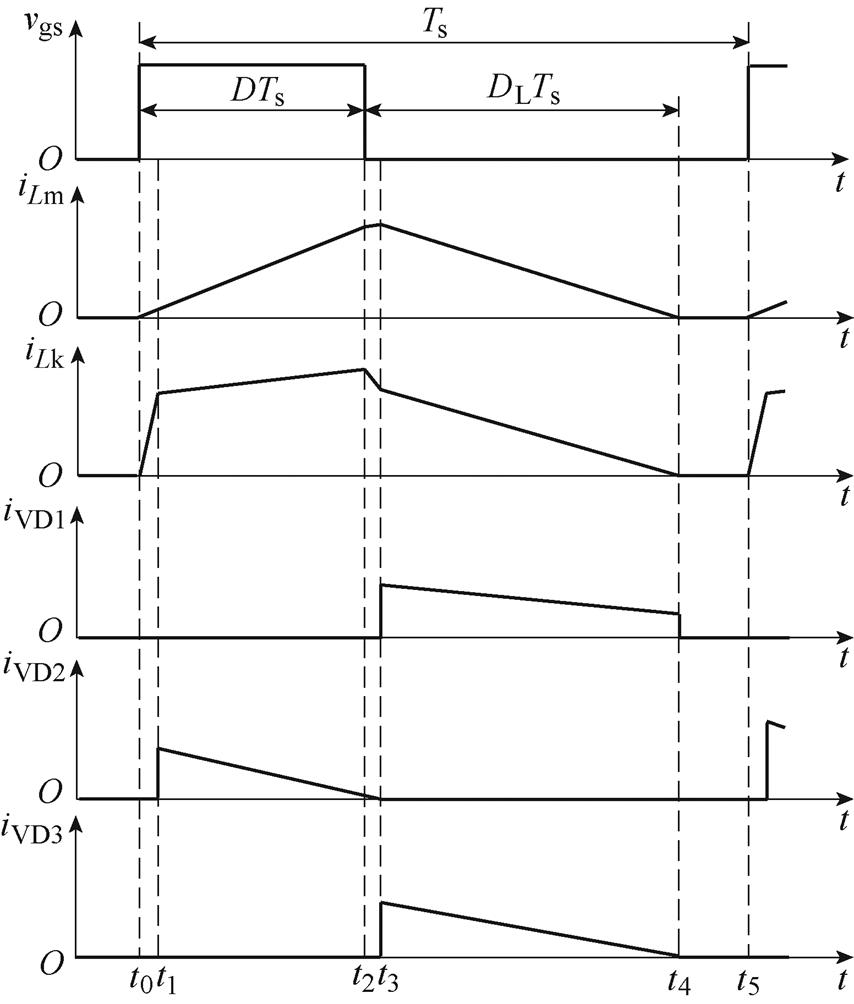
图5 DCM下变换器的主要波形
Fig.5 Key waveforms of the proposed converter in DCM
模态5 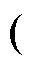t4, t5]：DCM下变换器在工作模态5的等效电路如图6所示，功率开关管S处于关断状态，二极管VD1、VD2、VD3反向截止。储存在耦合电感中的能量为零，只有输出电容Co向负载Ro提供能量。当功率开关管S在t=t5导通时，此模态结束。
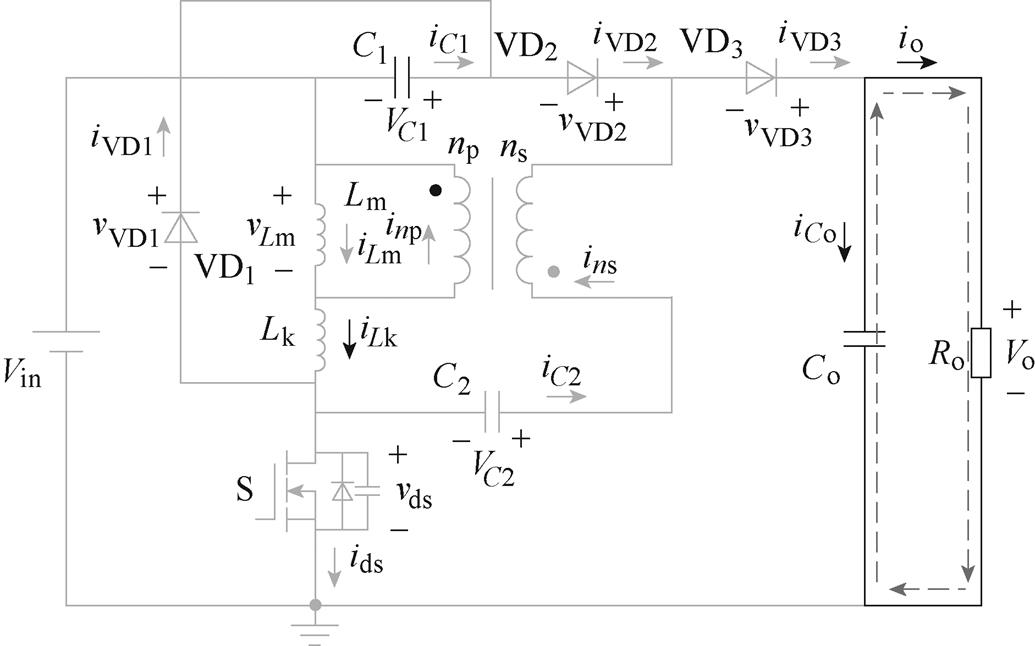
图6 DCM下变换器在工作模态5的等效电路
Fig.6 The equivalent circuit of the converter under the operating mode five in DCM
CCM和DCM下的模态1和模态3因漏感产生，因两个模态时间短暂，为方便分析将其忽略。
2.1.1 变换器电压增益分析
设电感的耦合系数为k，则
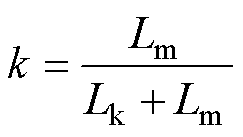（1）
在0～DTs时间段内，根据图4b，励磁电感电压VLm与电容C2的电压VC2可表示为
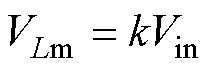（2）
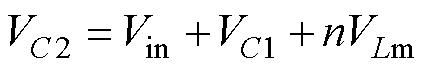（3）
式中，VC1为电容C1电压。
在DTs～Ts时间段内，根据图4d，励磁电感电压VLm与输出电压Vo可表示为
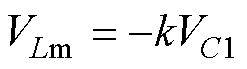（4）
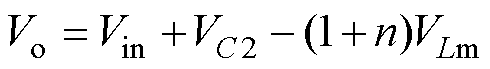（5）
根据电感的伏秒平衡原理，励磁电感Lm电压在一个开关周期内满足
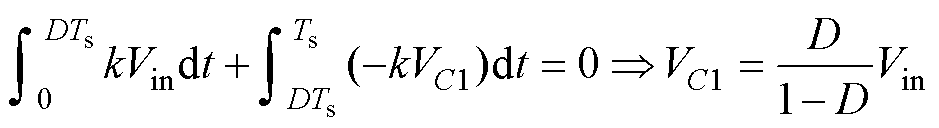（6）
结合式（2）、式（3）和式（6），电容C2的电压表示为
（7）
将式（4）、式（6）、式（7）代入式（5），在CCM下，电压增益为
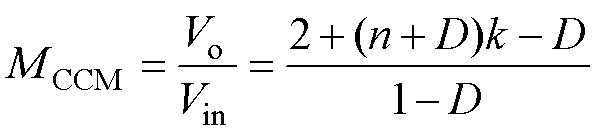（8）
根据式（8），图7给出了变换器的电压增益MCCM在不同占空比D、匝比n和耦合系数k下的特性。可以看出，匝比n对电压增益产生明显影响，但耦合系数k对电压的增益影响较小，因此取耦合系数的理想值k=1。
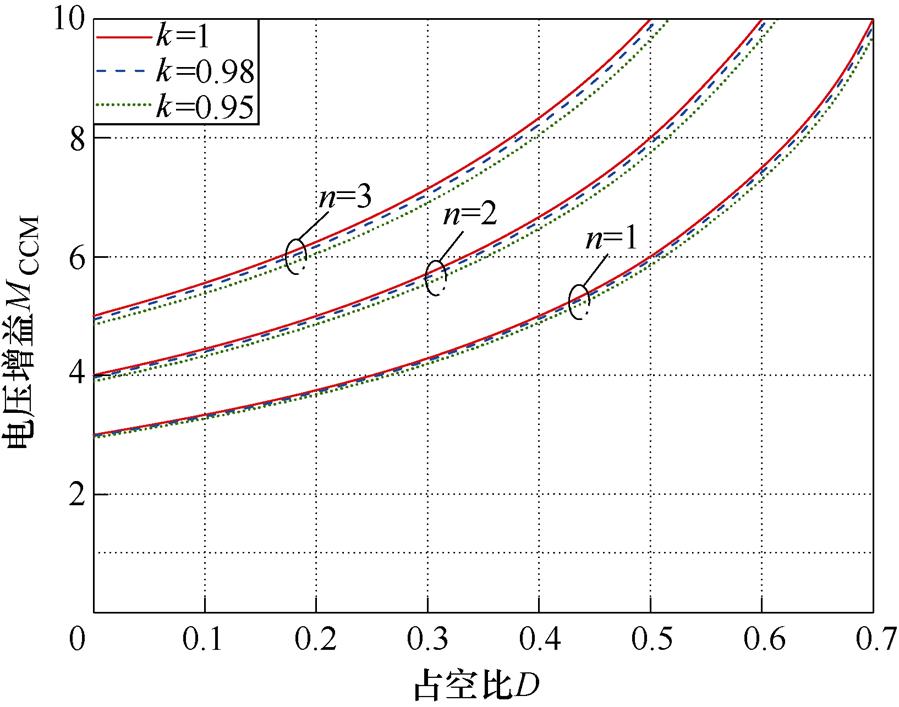
图7 变换器电压增益MCCM与占空比D、匝比n、耦合系数k的关系曲线
Fig.7 The voltage gain versus the duty cycle D, turns ratio n and the coupling coefficient k
当k=1时，变换器的电压增益为
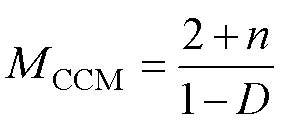（9）
2.1.2 变换器电压应力分析
在DTs～Ts时间段内，如图4d所示，功率开关管S的电压应力为
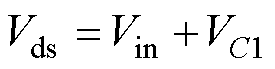（10）
结合式（6）可得
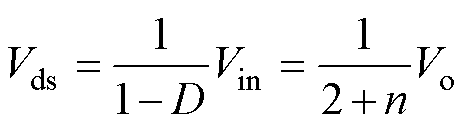（11）
由图4b和图4d所示，二极管VD1、VD2、VD3的电压应力分别为
（12）
2.1.3 变换器电流应力分析
根据电容的安秒平衡原理，在一个开关周期Ts内，流经电容C1、C2、Co的平均电流为零。由图2可以得出，通过二极管VD1、VD2、VD3的平均电流等于输出电流Io，即
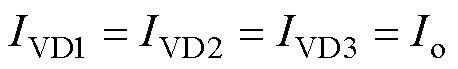（13）
二极管VD1、VD2、VD3的电流应力可表示为
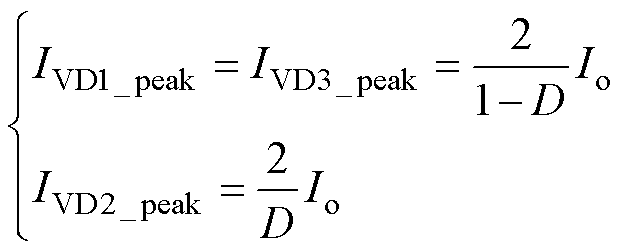（14）
在功率开关管关断阶段DTs～Ts，如图4d所示，流经励磁电感的电流iLm的表达式为
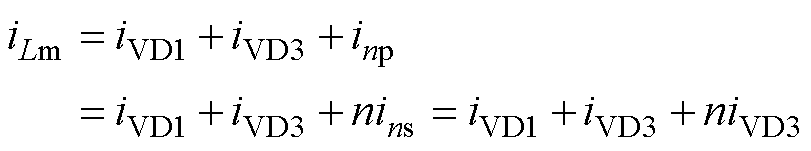（15）
式中，iVD1、iVD3分别为流经二极管VD1、VD3的电流；inp、ins分别为流经一次绕组np和二次绕组ns的电流。
式（15）两边同时积分可得
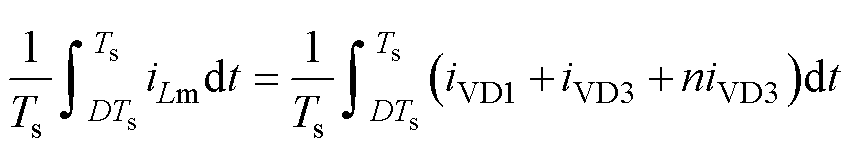（16）
化简式（16）并结合式（13），流经励磁电感的平均电流ILm可以表示为
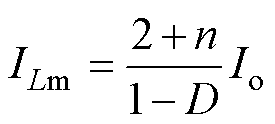（17）
在功率开关管导通阶段0～DTs，如图4b所示，流经功率开关管S的电流ids的表达式为
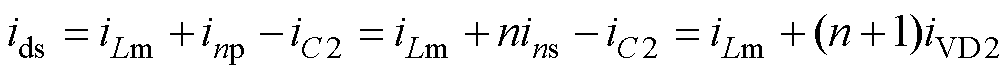（18）
式中，iC2为流经电容C2的电流；iVD2为流经二极管VD2的电流。
式（18）两边同时积分可得
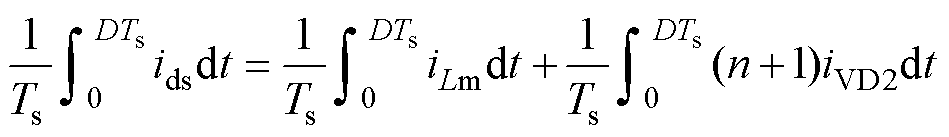（19）
化简式（19）并结合式（13）和式（17），功率开关管S的平均电流Ids和电流有效值Ids_RMS分别为
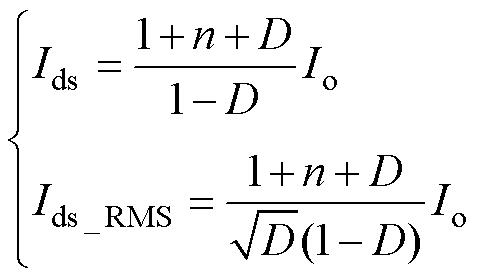（20）
功率开关管导通情况下0～DTs，根据图4b，电容C2的电压VC2与CCM情况下0～DTs时间段内式（3）相同，励磁电感电压VLm可表示为
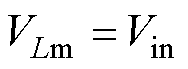（21）
在DTs～(D+DL)Ts时间段，根据图4d，输出电压Vo与CCM情况下DTs～Ts时间段内式（5）相同，励磁电感电压VLm可表示为
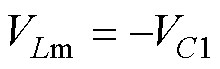（22）
根据电感Lm的伏秒平衡原理可得
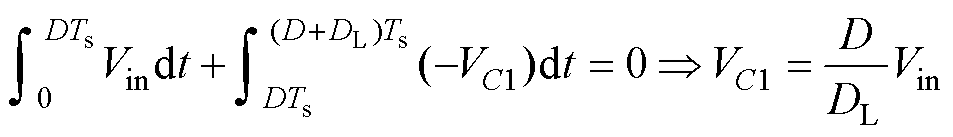（23）
式中，DL为漏感电流下降至0时的占空比。
结合式（21）和式（23）代入式（3），电容C2的电压为
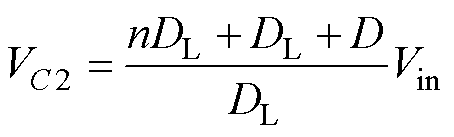（24）
将式（22）～式（24）代入式（5），在DCM下，电压增益的表达式为
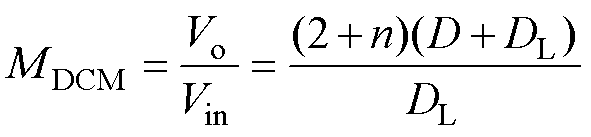（25）
由式（25）可得，DL的表达式为
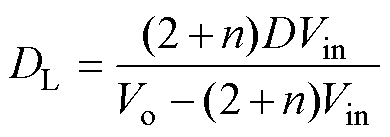（26）
在功率开关管关断阶段DTs～(D+DL)Ts，励磁电感的电流iLm与CCM情况下DTs～Ts时间段内式（15）相同，对式（15）在DTs～(D+DL)Ts时间段内积分可得
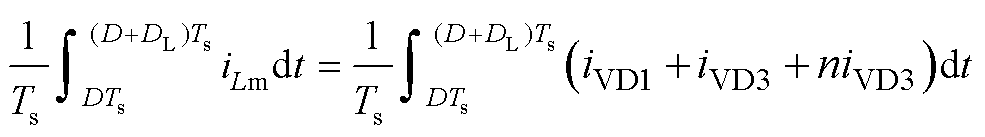（27）
假设IoDCM为DCM下的输出电流。由式（27），可得励磁电感电流在时间段DTs～(D+DL)Ts内的平均值为
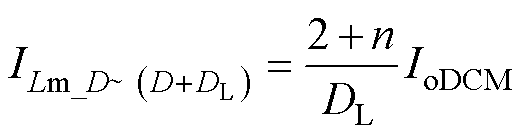（28）
由图5可得，DCM下励磁电感的电流在时间段DTs～(D+DL)Ts平均值表达式为
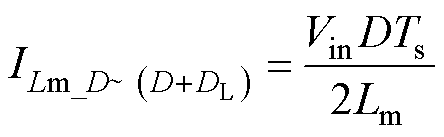（29）
设励磁电感的时间常数tLm为
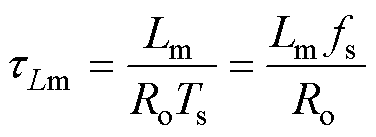（30）
式中，fs为功率开关管的工作频率。
联立式（26）、式（28）～式（30）可得，DCM下变换器的电压增益表达式为
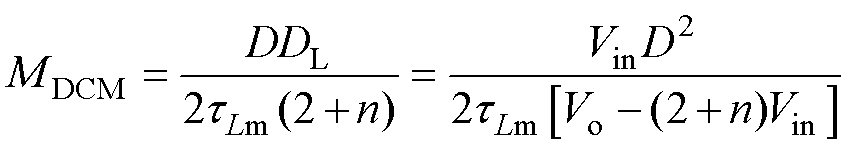（31）
当变换器工作在临界导通模式（Boundary Con- duction Mode，BCM）下，D+DL=1；且CCM下的电压增益与DCM下的电压增益相等。联立式（9）和式（31）可得BCM下励磁电感的时间常数为
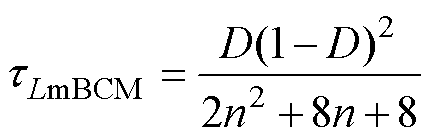（32）
变换器在BCM下励磁电感的电流波形如图8所示，图中，ILmpeak为BCM情况下的最大值。励磁电感Lm的平均电流ILm_BCM等于电感电流纹波DILm_BCM的一半，即
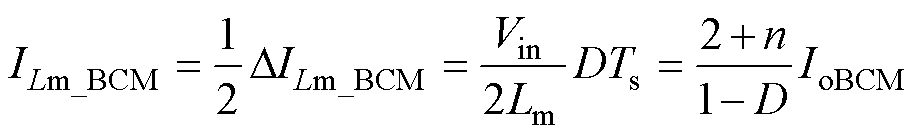（33）
式中，IoBCM为BCM下的输出电流。
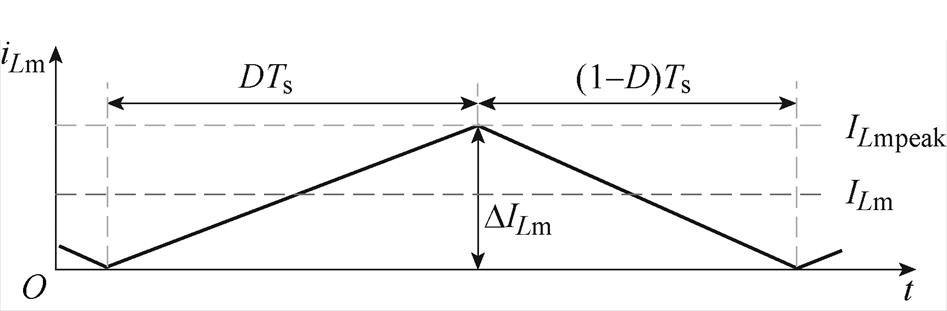
图8 变换器在BCM下励磁电感的电流波形
Fig.8 The magnetic inductor current waveform of the converter in BCM
根据式（33），可以推导出励磁电感Lm取值为
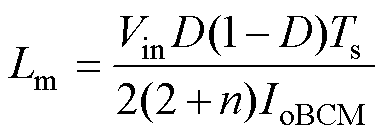（34）
励磁电感Lm电流的最大值和最小值可分别表示为
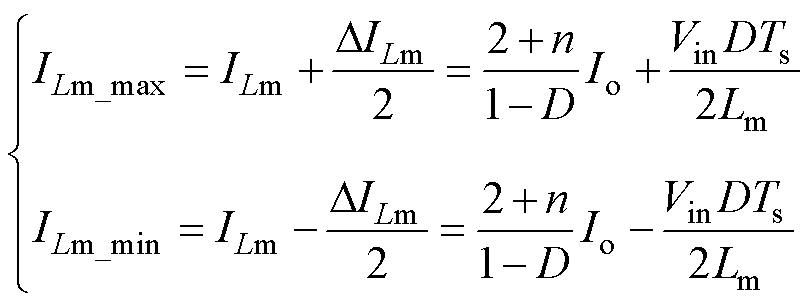（35）
式中，DILm为电感电流纹波。
结合式（6）和式（7），电容C1、C2和Co的电压纹波分别为
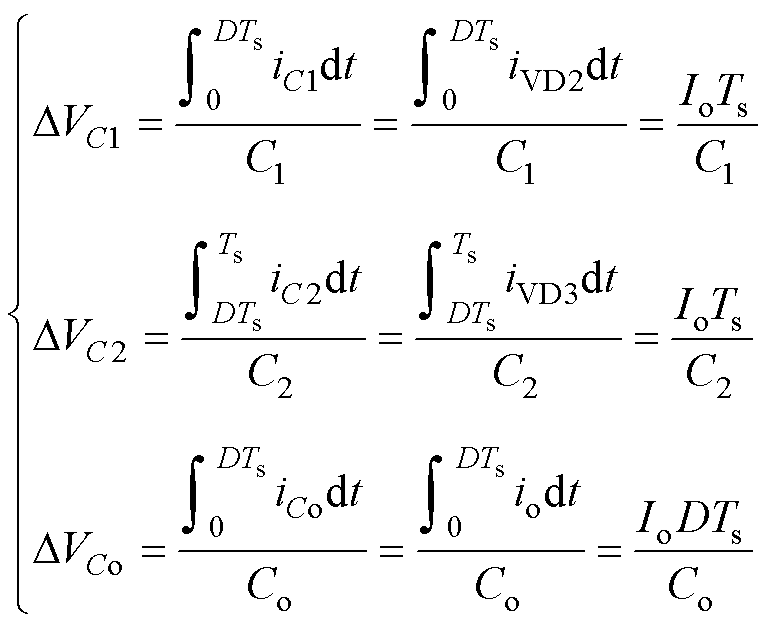（36）
式中，iC1、iCo为流经电容C1和Co的电流；io为流经负载Ro的电流。
变换器的损耗主要分为功率开关管损耗、二极管损耗、电容损耗和耦合电感损耗四部分。ton为功率开关管开通持续时间，包括开通延迟时间和上升时间，toff为功率开关管关断持续时间，包括关断延迟时间和下降时间；rds_on为功率开关管的开通电阻；VF1、VF2、VF3分别为二极管VD1、VD2、VD3的正向导通压降；rVD1、rVD2、rVD3为二极管VD1、VD2、VD3的正向导通电阻；rC1、rC2、rCo分别为电容C1、C2、Co的串联等效电阻；rLp、rLs分别耦合电感一次绕组和二次绕组的等效电阻；Pcv为单位体积磁心损耗；Ve为选用的磁心体积。所提变换器结合寄生参数的等效电路如图9所示。
图9 结合寄生参数的所提变换器的等效电路
Fig.9 Equivalent circuit of the proposed converter with parasitic parameters
开关管的功率损耗主要包括：开关损耗PS_Switching和稳态损耗PS_Conduction，为简化计算，用导通过程的平均电流作为开关损耗的计算电流[34]，可得
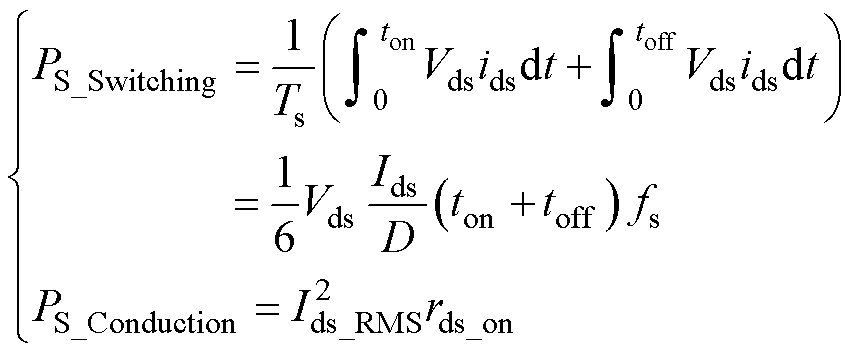（37）
结合式（11）和式（20），开关管的总功率损耗PS_Loss为
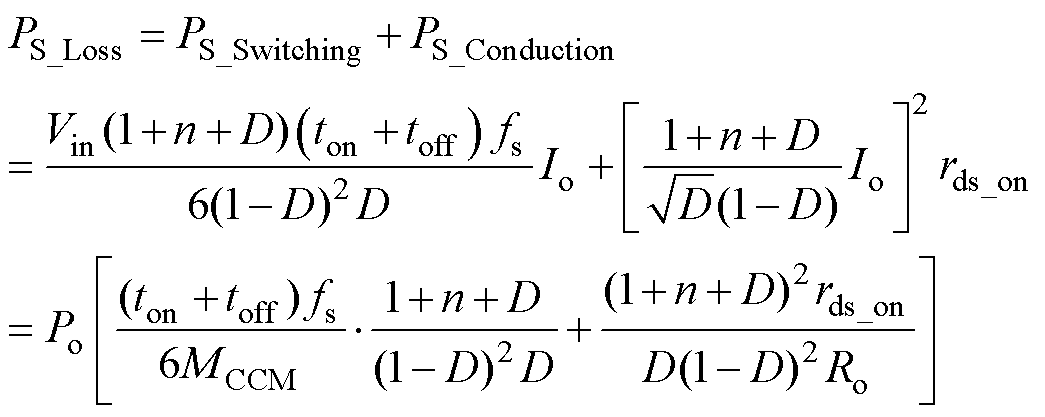（38）
由式（13）可得二极管VD1、VD2和VD3的平均电流等于输出电流，则二极管VD1、VD2和VD3电流有效值分别为
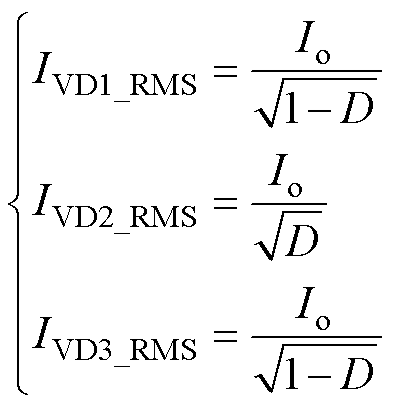（39）
二极管的总损耗PD_Loss为
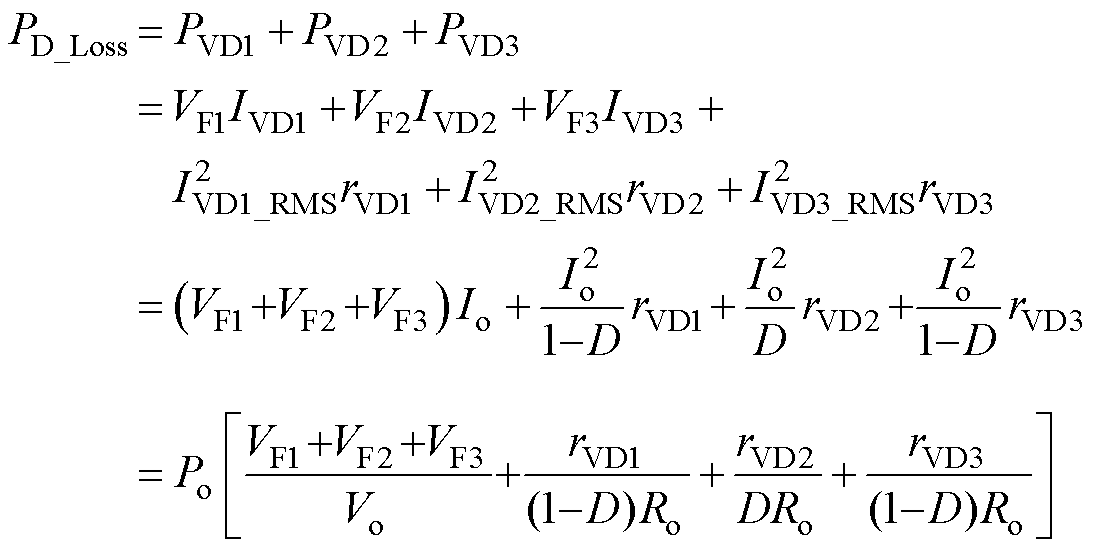（40）
式中，PVD1、PVD2和PVD3为二极管VD1、VD2和VD3的损耗。
在功率开关管S导通或关断情况下，电容C1、C2和Co的电流分别为
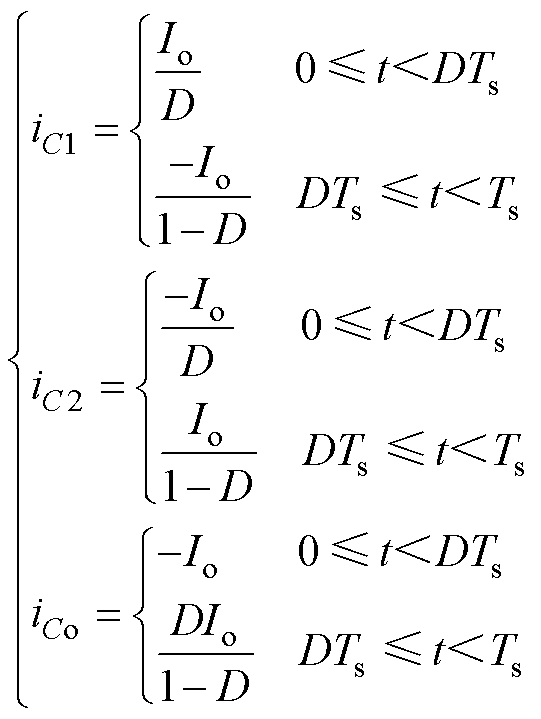（41）
由式（41）可得，电容C1、C2和Co的电流有效值为
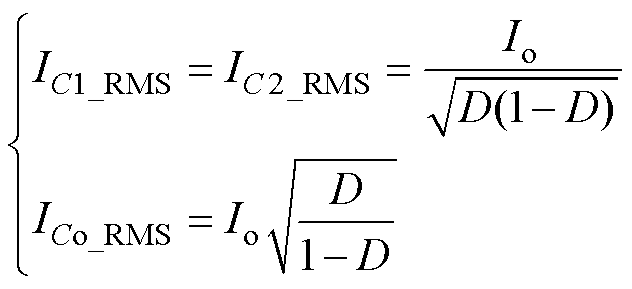（42）
则电容C1、C2和Co的功率损耗分别为
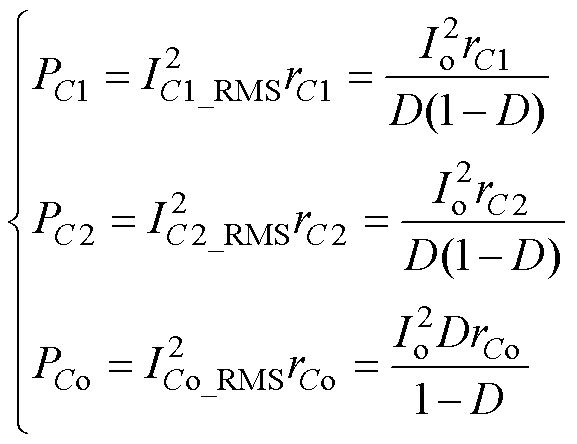（43）
电容的总功率损耗PC_Loss为
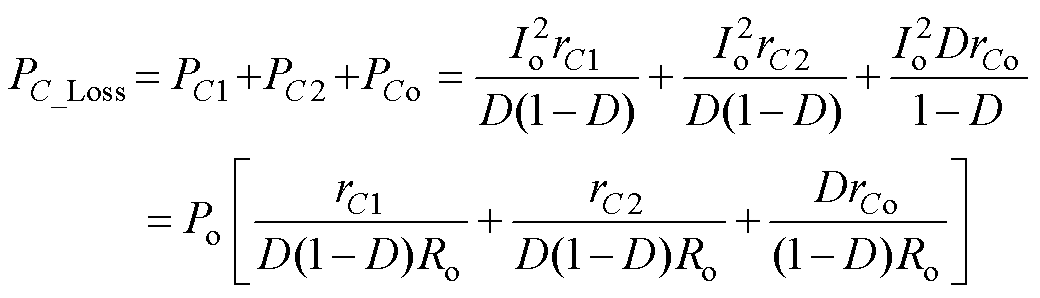（44）
在功率开关管S导通或关断时，通过耦合电感漏感电流iLk和二次绕组电流ins的表达式分别为
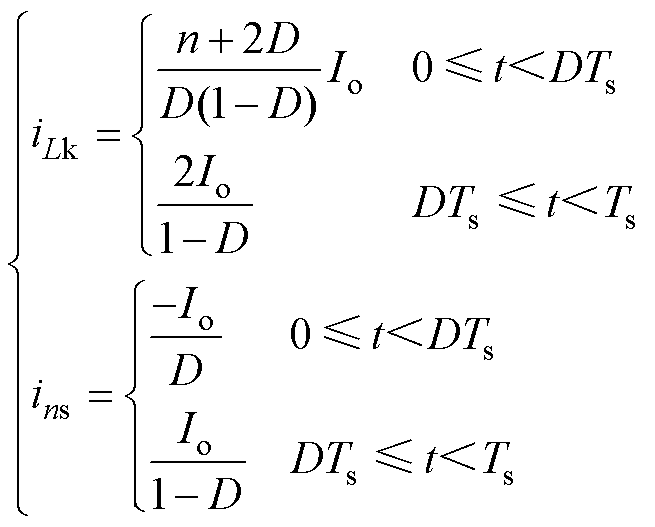（45）
由式（45）可得，通过耦合电感的一次和二次绕组的电流有效值ILk_RMS、Ins_RMS分别为
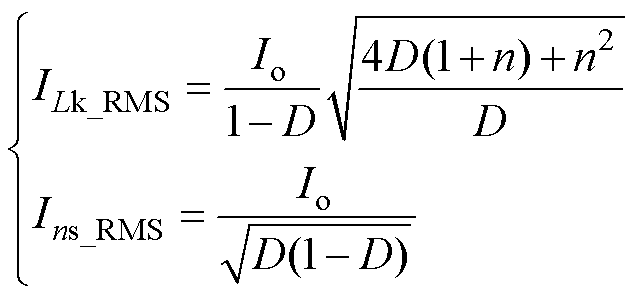（46）
耦合电感的绕组损耗PL_Winding为
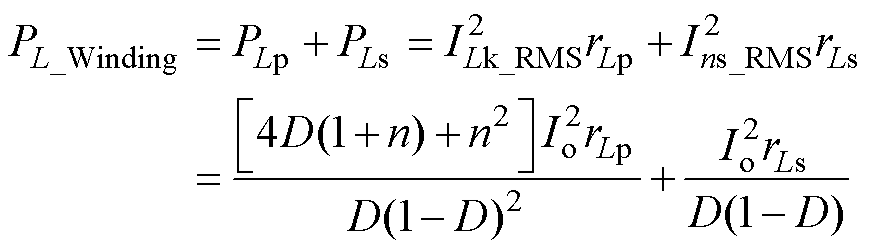（47）
式中，PLp、PLs为一次绕组和二次绕组的绕组损耗。
耦合电感的磁心损耗PL_Core为
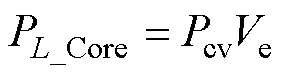（48）
耦合电感的总损耗PL_Loss为
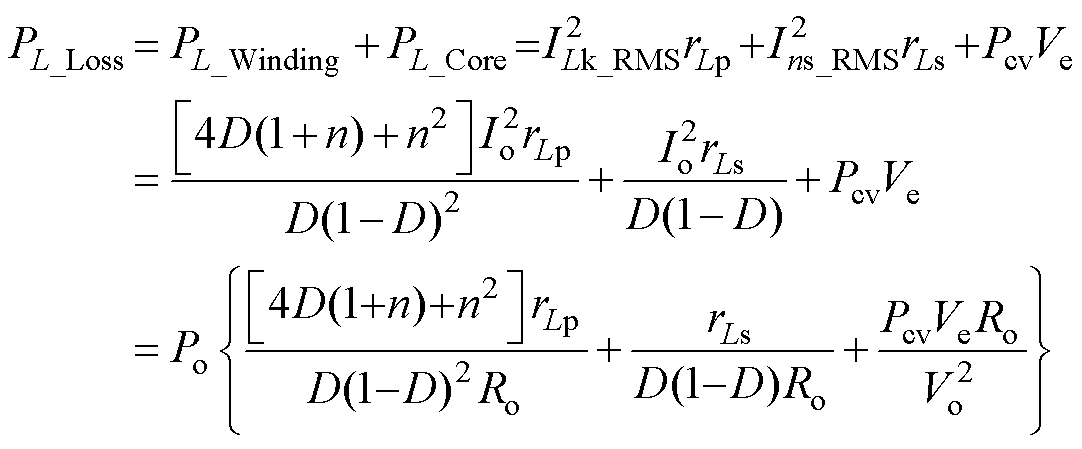（49）
基于式（38）、式（40）、式（44）及式（49），所提变换器的效率可表示为
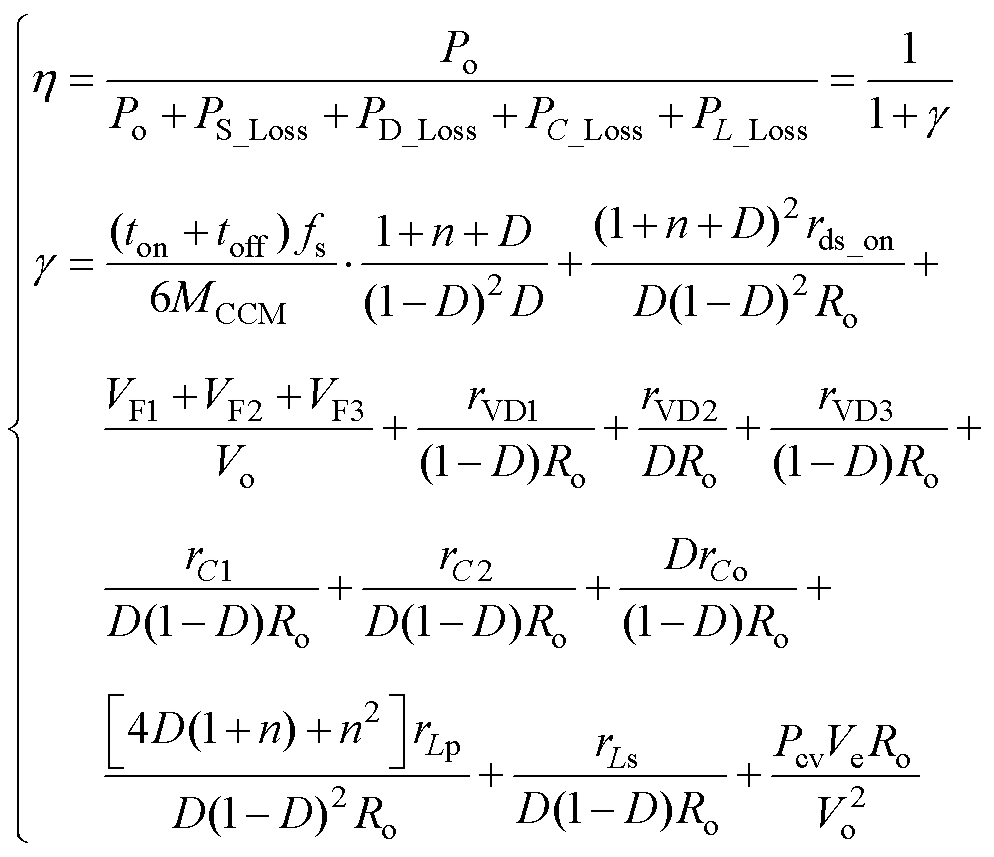（50）
式中，Po为所提变换器的输出功率，Po=VoIo；g 为变量。
在实际中，元件存在寄生参数会对电压产生影响，为了计算转换器在非理想情况下的电压增益，根据表1、式（8）和式（50），所提变换器非理想状态电压增益MCCM_nonideal可表示为
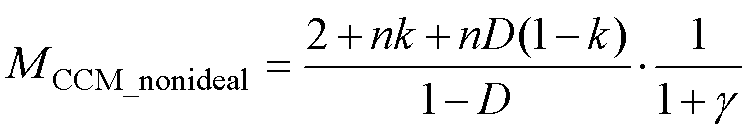（51）
当变换器工作在工况1时所选择的元器件的寄生参数见表1。
图10为k=1时所提变换器在表1所述工况下理想与非理想情况的电压增益。由图10可知，占空比D为0.1～0.8时，电压增益在理想与非理想情况下相近，寄生参数对电压增益的影响较小，所提变换器具有高升压、高效率的特性。
表1 元件的寄生参数
Tab.1 Parasitic parameters of the components
参 数数 值 rds_on/mW10 ton/ns44 toff/ns52 rC1/mW240 rC2/mW360 rCo/mW180 VF1/V0.65 VF2, VF3/V0.60 rVD1/mW100 rVD2, rVD3/mW160 rLp/mW10 rLs/mW100
根据上述CCM下的稳态分析，将所提变换器与文献[13, 19-20, 23, 29, 33]的拓扑结构进行了比较。各个变换器的元件数量、电压增益、功率开关管的电压应力与电压尖峰情况、输入输出电压、满载功率和满载效率见表2。由表2可得，所提变换器与采用耦合电感的变换器[19-20,23,29,33]相比，具有更高的转换效率。所提变换器与文献[19-20, 29]均采用无源钳位技术，能够有效抑制开关管电压尖峰。文献[33]具有较少的元器件个数，但开关管的电压尖峰很大。
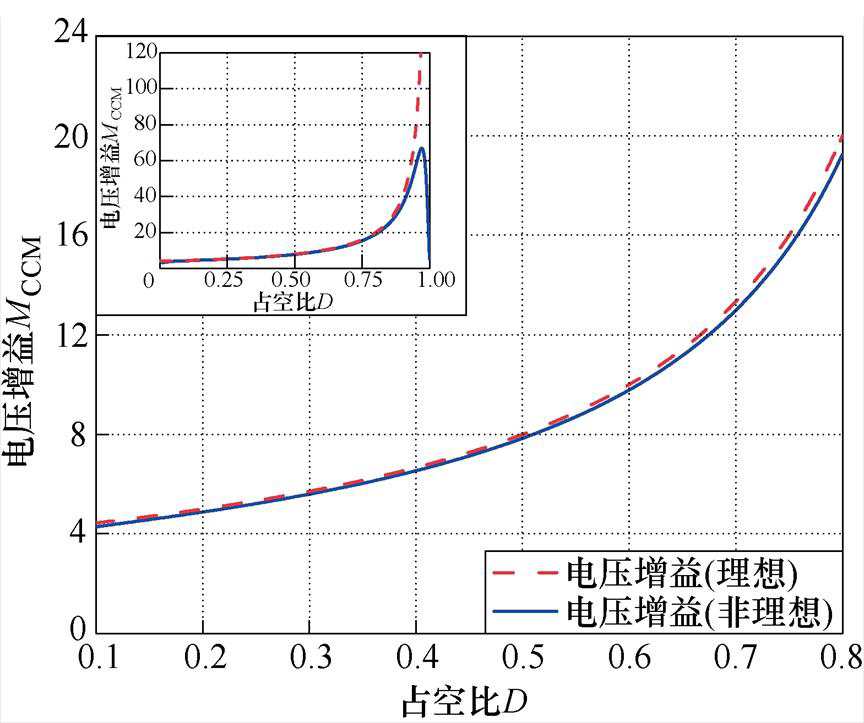
图10 k=1时所提变换器在理想与非理想情况的电压增益
Fig.10 Voltage gain under ideal and non-ideal conditions of the proposed converter when k=1
表2 所提变换器与相关变换器的对比
Tab.2 Comparisons of the proposed converter with relevant converters
变换器元器件数量总数电压增益MCCM功率开关管电压应力Vds/Vin功率开关管电压尖峰输入电压/V输出电压/V满载功率/W满载效率h(%) SVDLC 所提变换器13138低4040025097.1 文献[13]12238低4830025097.3 文献[19]12238低2020020093.8 文献[20]13138低1515010090.3 文献[23]224614低4838025093.5 文献[29]12238低4020010093.0 文献[33]12126高2022025093.6
当耦合系数k =1，匝比n=2时，各个变换器的电压增益与占空比关系如图11所示，功率开关管的电压应力与电压增益关系如图12所示。所提变换器与其他6个变换器都能通过调节占空比实现高电压增益。在相同占空比条件下，所提变换器的电压增益高于其他6个变换器。在相同电压增益条件下，所提变换器比其他变换器具有更低的功率开关管电压应力。因此，采用电压低且导通电阻小的开关管可实现更高的效率。
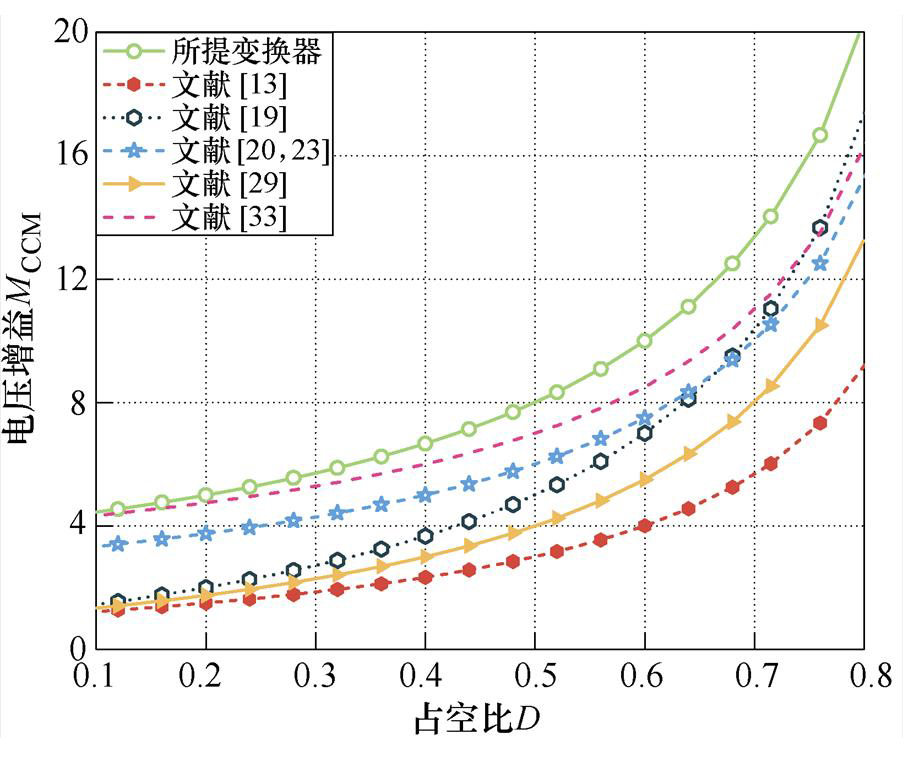
图11 匝比为2时所提变换器与相关变换器的电压增益与占空比关系
Fig.11 The voltage gain versus duty cycle of proposed converter and relevant converters under n=2
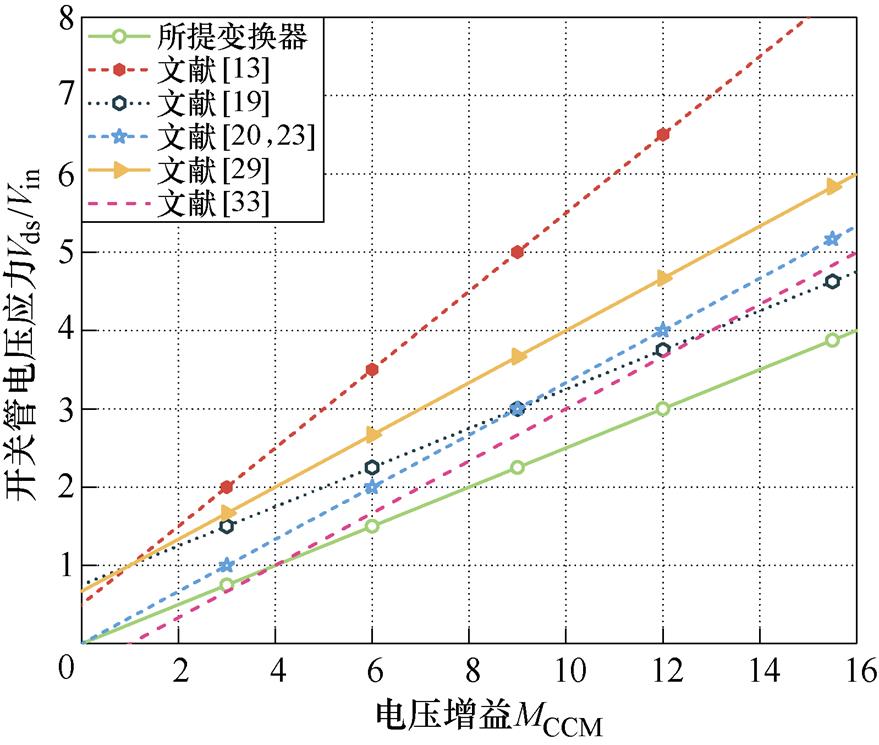
图12 匝比为2时所提变换器与相关变换器的开关管电压应力与电压增益关系
Fig.12 The voltage stress of the switch versus the voltage gain of proposed converter and relevant converters under n=2
图13给出在所提变换器的基础上实现软开关等效电路，即将图2的二极管VD1替换为开关管S2，利用开关管的寄生电容与漏感进行谐振可以实现开关管的零电压导通从而降低开通损耗。但需设置死区时间且需控制漏感在死区时间内将储存于寄生电容的能量完全消耗，增加了控制及电感设计的复杂性。
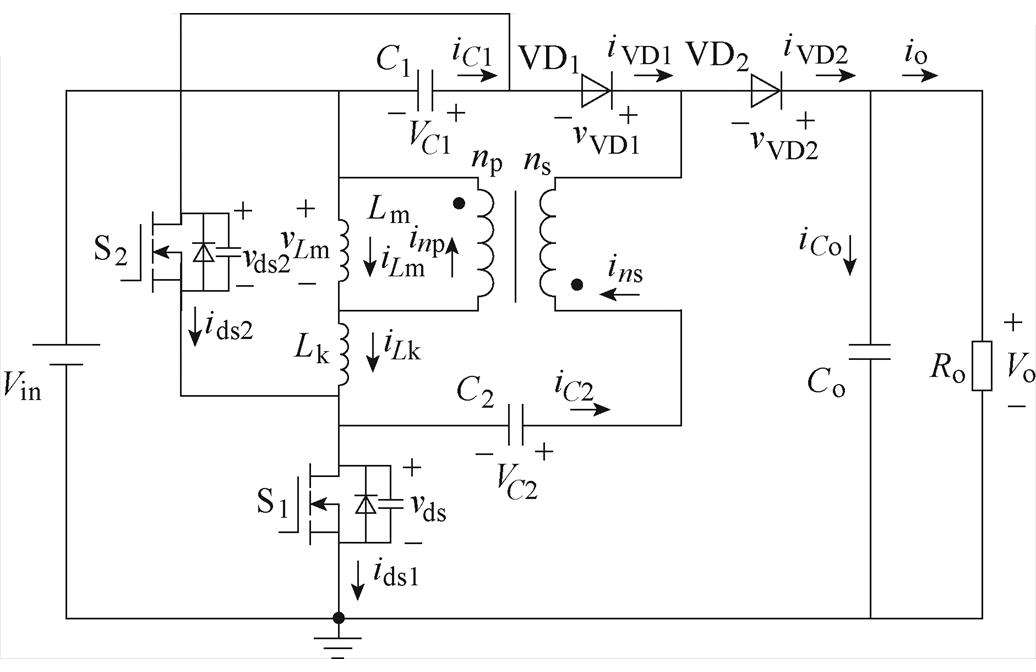
图13 软开关变换器等效电路
Fig.13 Equivalent circuit of the soft-switching converter
为验证理论分析的正确性和可行性，搭建一个输入电压40 V，输出电压400 V，满载功率250 W的实验样机进行测试，主要参数见表3。图14为所提变换器的实物。
表3 所提变换器的主要参数
Tab.3 The key parameters of the proposed converter
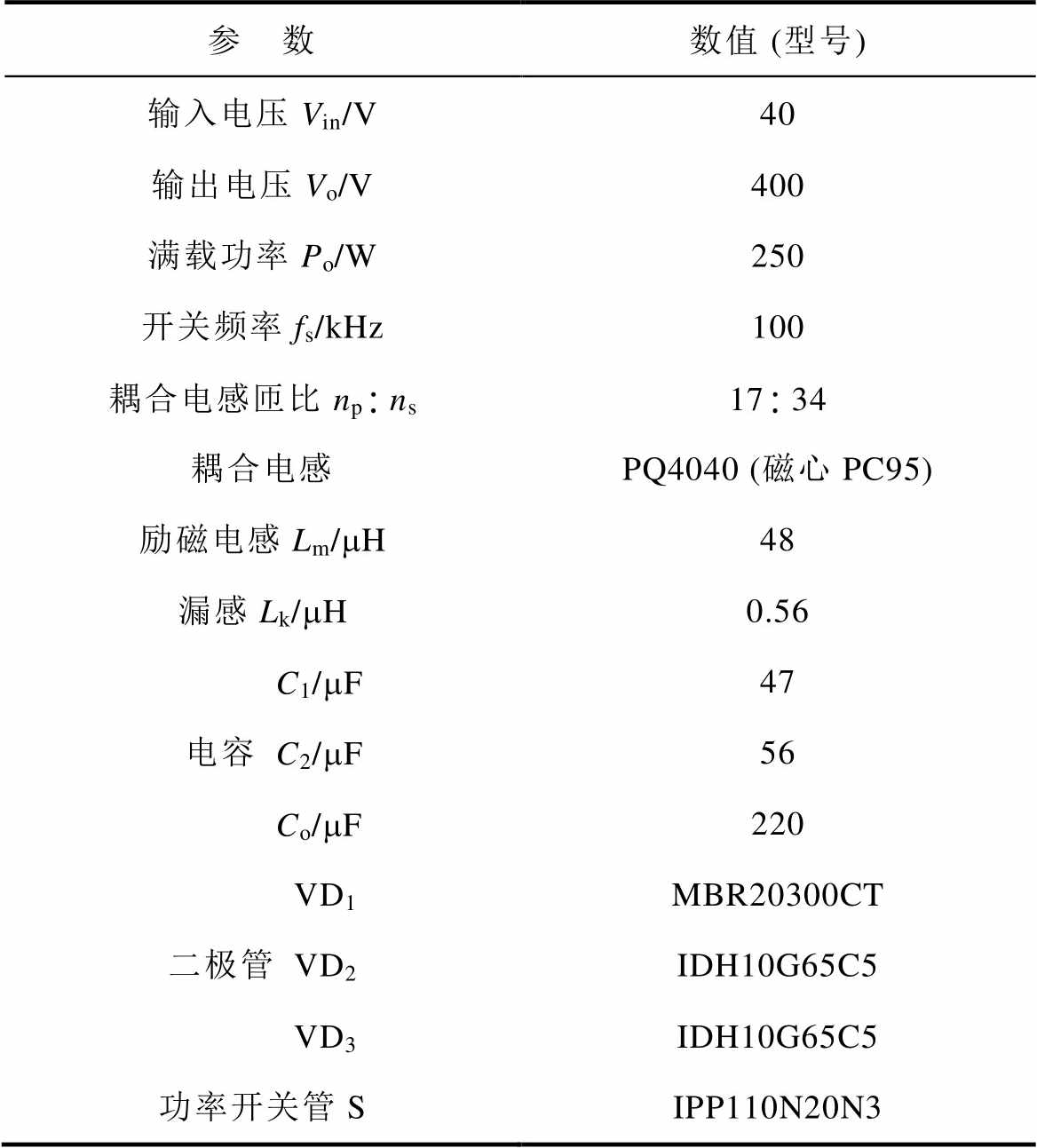
参 数数值 (型号) 输入电压Vin/V40 输出电压Vo/V400 满载功率Po/W250 开关频率fs/kHz100 耦合电感匝比npns1734 耦合电感PQ4040 (磁心PC95) 励磁电感Lm/mH48 漏感Lk/mH0.56 电容C1/mF47 C2/mF56 Co/mF220 二极管VD1MBR20300CT VD2IDH10G65C5 VD3IDH10G65C5 功率开关管SIPP110N20N3
图14 所提变换器实物
Fig.14 Experimental prototype of the proposed converter
由式（9）可得，在CCM下，在匝比n=1、n=2、n=3的不同情况下，所提变换器的电压增益MCCM与占空比D的关系如图15所示。为了避免所提变换器在极高占空比条件下工作，减少磁心损耗，提高转换效率，选择n=2。
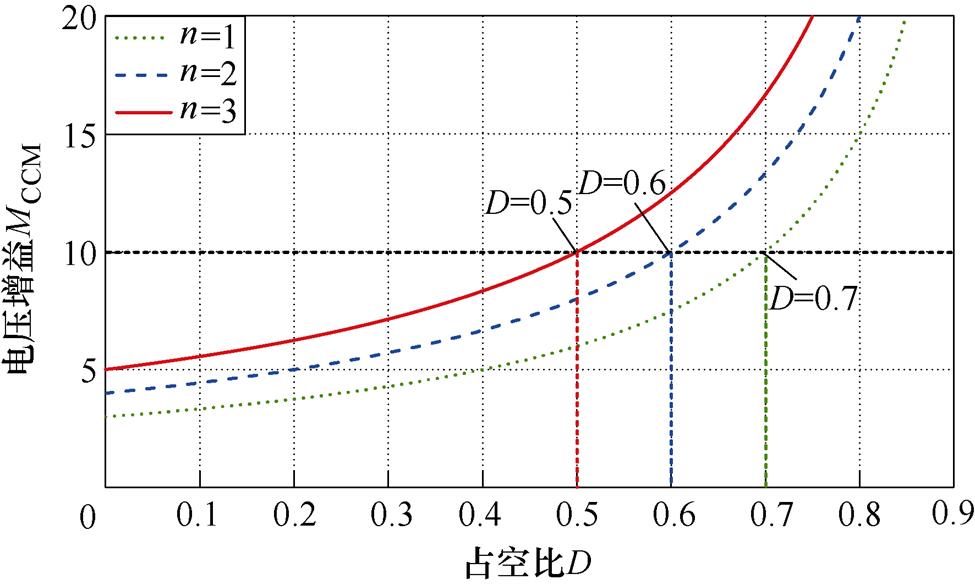
图15 电压增益与不同匝比之间的关系
Fig.15 The voltage gain versus the duty cycle under different turns ratio
设置IoBCM=0.25 A，通过表3中的输入输出电压以及耦合电感匝比，由式（34），励磁电感Lm的电感值为
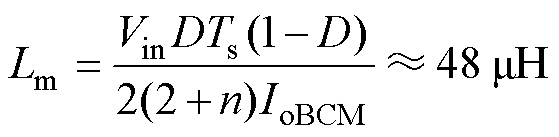（52）
所提变换器可以通过无源钳位电路回收漏感能量，而漏感产生的原因为部分磁通通过磁心外的空气闭合到绕组中，为了减小漏感带来的损耗，漏感设计值应小于3 %，即
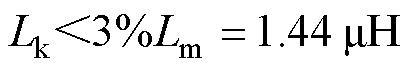（53）
根据式（32），在匝比n=2情况下，励磁电感时间常数与占空比之间的关系如图16所示。当励磁电感时间常数tLm高于临界模式下的励磁电感时间常数tLmBCM时，所提变换器工作在CCM；反之，工作在DCM。
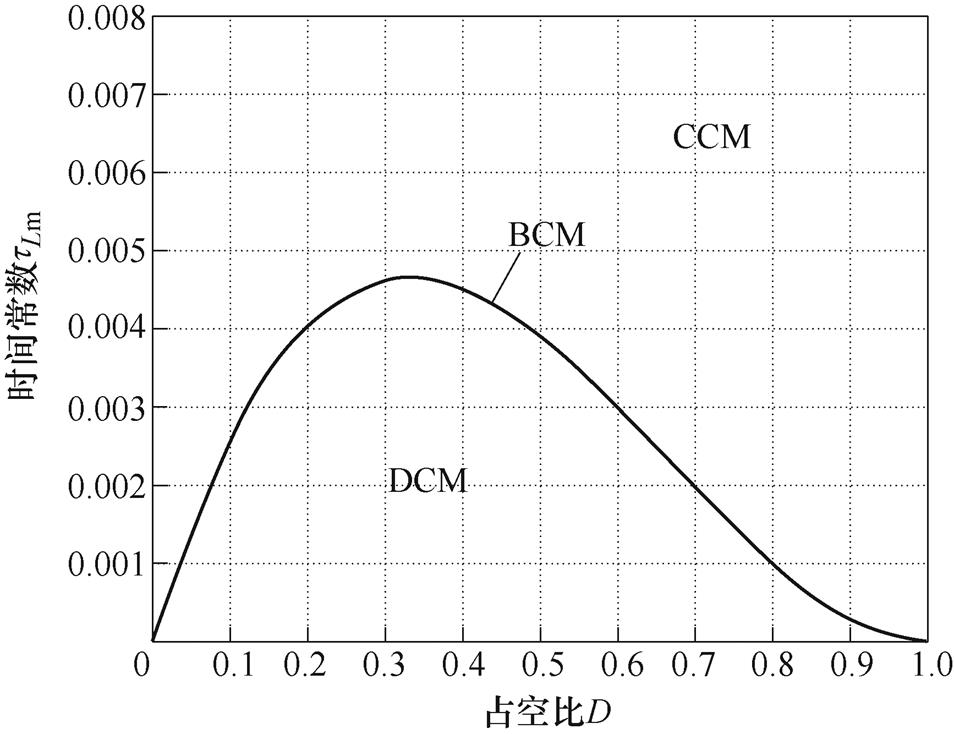
图16 时间常数tLm与占空比D的关系曲线
Fig.16 Time constant versus the duty cycle D
根据不同磁心材质数据手册，图17给出不同磁心材质在100 ℃及100 kHz下单位磁心损耗与磁通密度的关系曲线。选择单位体积磁心损耗较小的PC95材质作为磁心的材料。
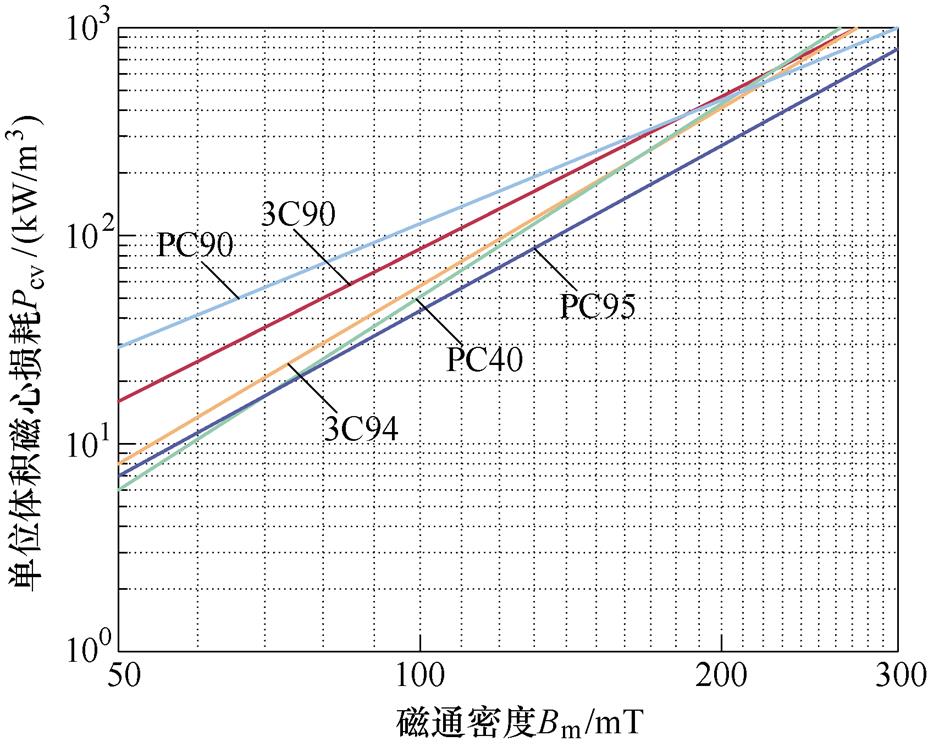
图17 不同材料在100 ℃和100 kHz下的单位功率损耗与磁通密度的关系
Fig.17 Specific power loss versus flux density for the various materials under 100 ℃ and 100 kHz
根据式（47）～式（49），可得图18耦合电感的磁心损耗、绕组损耗与总损耗随匝比变化的关系。总损耗最小值出现在匝比为17
34的情况下。
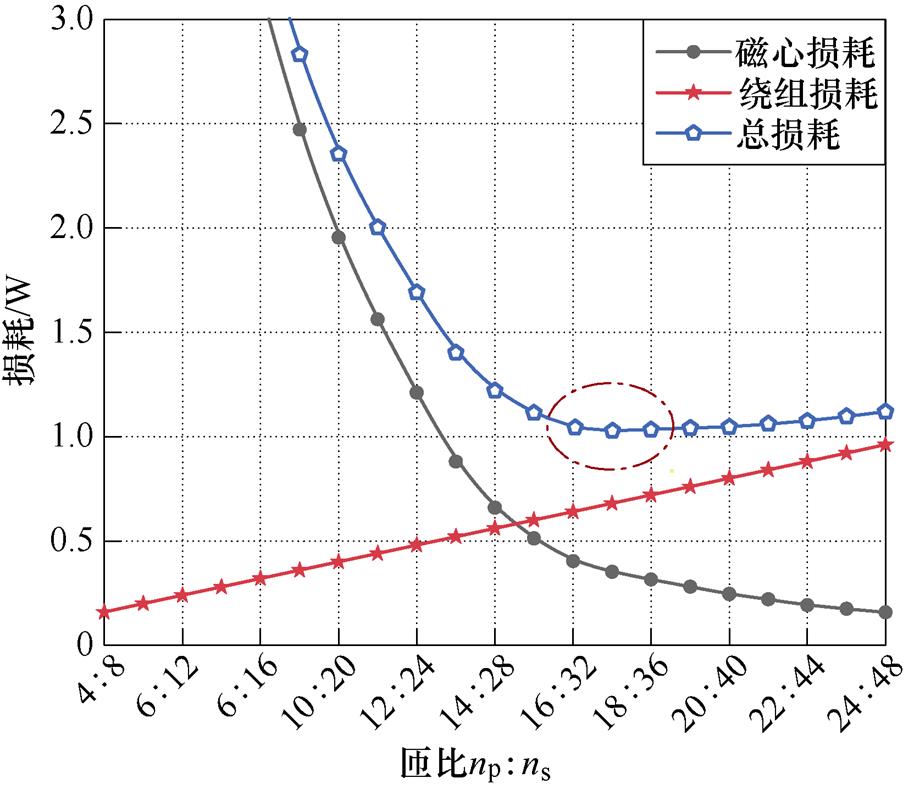
图18 耦合电感损耗与匝比的关系
Fig.18 Coupled inductor power loss versus turns ratio
通过表3的输入输出电压以及耦合电感匝比，取耦合系数k=1，由式（6）和式（7），电容C1、C2以及Co两端电压为
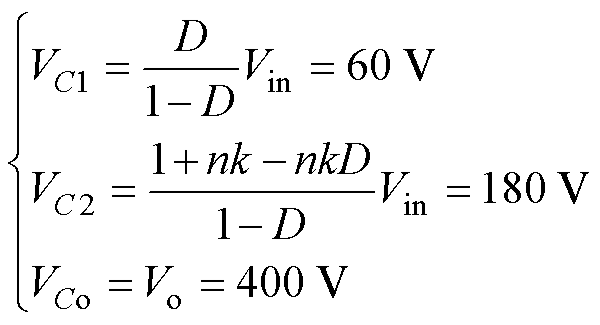（54）
通过表2的输入输出电压及开关频率，由上述电容两端电压和式（36），取电容纹波小于1 %，可求得电容C1、C2以及Co的取值分别为
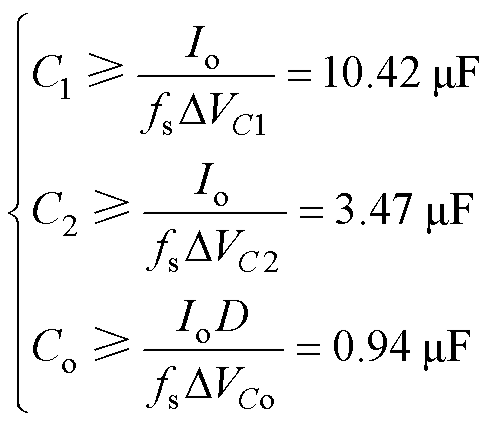（55）
图19显示了在输出功率250 W条件下，变换器工作在CCM主要元件的实验波形。图19a为功率开关管S的驱动信号vgs、两端电压vds、漏感电流iLk的波形。由实验波形可得：二极管VD1和电容C1组成的钳位电路能有效抑制功率开关管S的电压尖峰，其电压应力Vds=100 V，与理论分析值相符。流经耦合电感漏感的电流iLk是连续的。图19b、图19c、图19d为二极管VD1、VD2、VD3的电压vVD1、vVD2、vVD3和电流iVD1、iVD2、iVD3波形。二极管电压应力VVD2与VVD3几乎相等，符合理论计算值。当VD1关断时，其反向电流是由于二极管本身的反向恢复特性造成的。图19e可得测量的电容电压VC1=59 V，VC2=179 V，符合理论分析值。
在输出功率50 W条件下，变换器工作在DCM。图20显示了主要元件的实验波形。在功率开关管关断时，由于开关管和二极管的寄生电容的影响，功率开关管电压vds和二极管电压vVD1、vVD2、vVD3与等效的漏感或线路中寄生电感发生了谐振；漏感电流iLk和二极管电流iVD1、iVD2、iVD3在下一刻驱动信号来临前实现了自然关断。
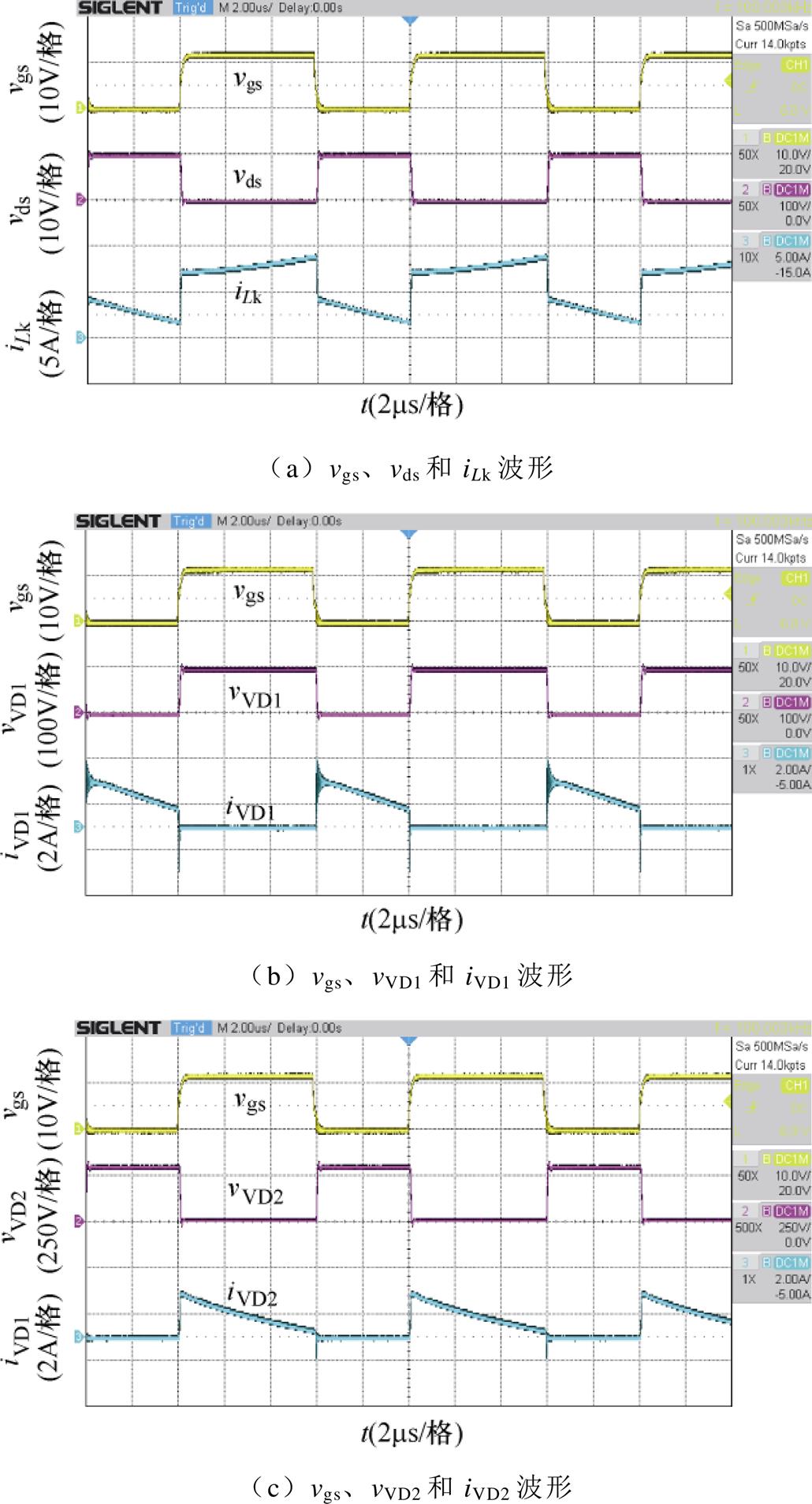
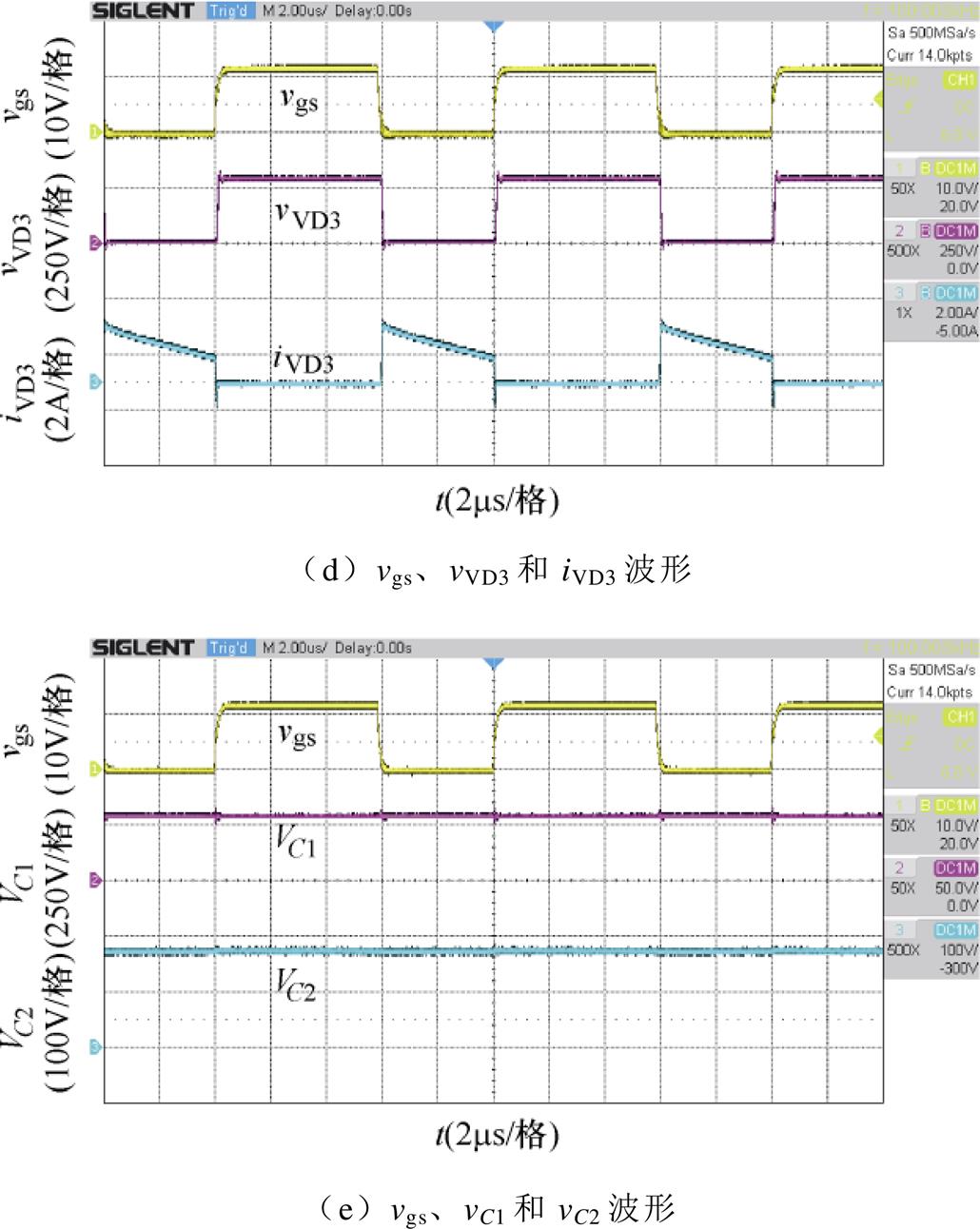
图19 在Po=250 W时，变换器的实验波形
Fig.19 Experimental waveforms of the converter at Po=250 W
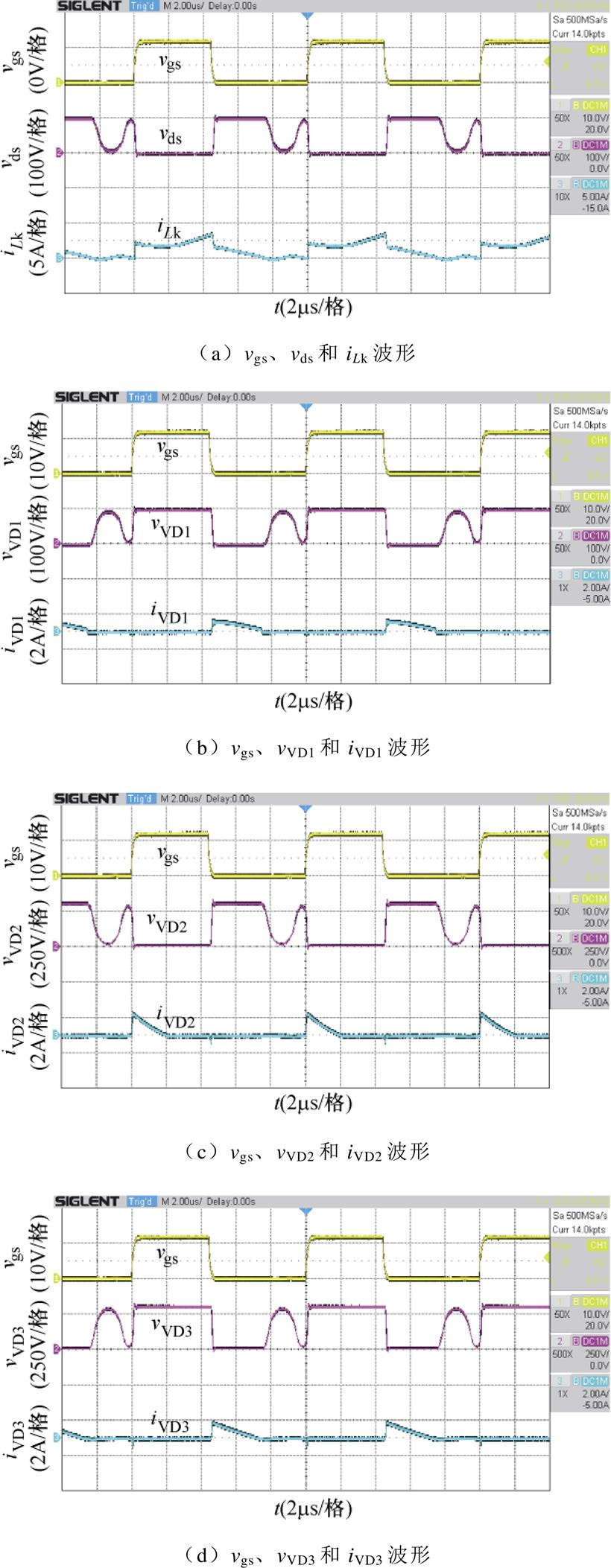
图20 在Po=50 W时，变换器的实验波形
Fig.20 Experimental waveforms of the converter at Po=50 W
图21为所提变换器输入电压40 V，输出电压400 V情况下的计算效率与实验效率曲线。因DCM下占空比会随功率而变化，因此效率计算使用的是CCM下的增益，计算效率只取100～250 W的效率。根据表1和式（50）可得图21中计算出的最大效率和满载效率分别为98.19 %以及97.81 %。实验测量的最大效率和满载效率分别为97.59 %以及97.10 %。因此，所提变换器具有高增益、高效率的特性。
图22为所提变换器输入电压40 V、输出电压400 V、输出功率250 W情况下的功率分布损耗。由图22可知，所提变换器在输入电压40 V，输出电压400 V以及输出功率250 W情况下，总损耗为5.49 W。开关损耗管损耗占比最大，损耗为2.04 W。
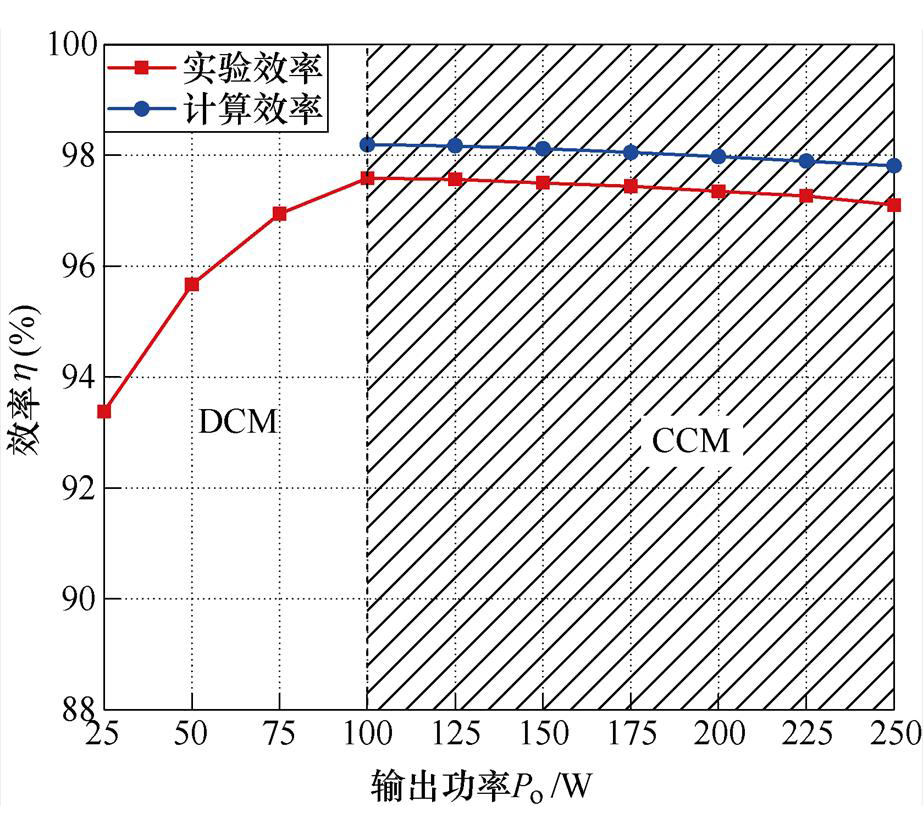
图21 所提变换器效率曲线
Fig.21 The efficiency curves of the proposed converter
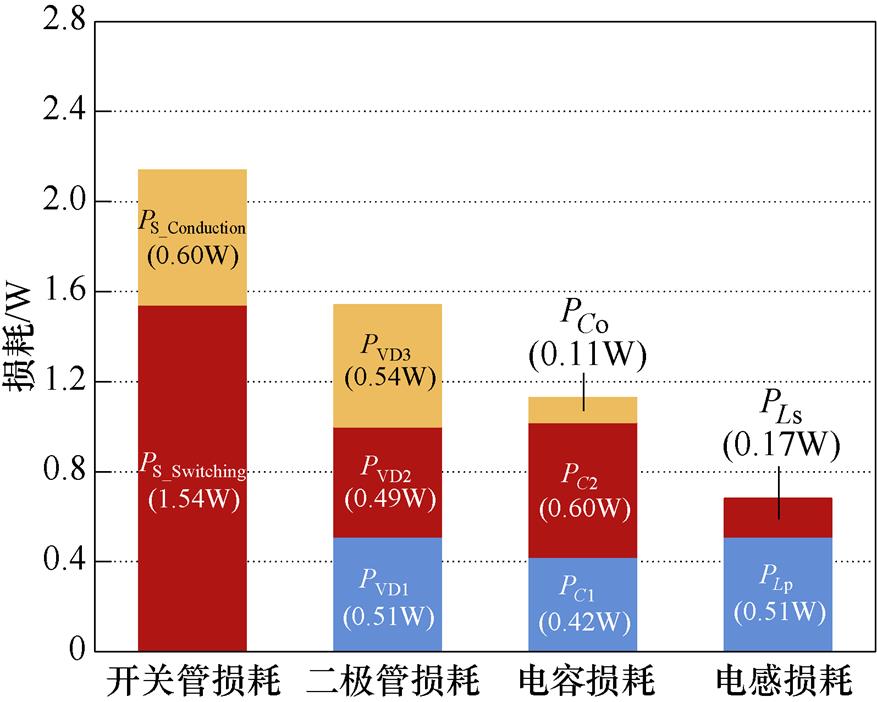
图22 变换器在Po=250 W时功率损耗分布
Fig.22 The power loss distribution of the proposed converter at Po=250 W
本文提出一种用于直流微电网的基于开关耦合电感高升压直流变换器。通过开关耦合电感结构提高电压增益，同时利用无源钳位电路回收漏感能量，抑制功率开关管两端的电压尖峰，降低功率开关管两端的电压应力，提高变换器的转换效率。在CCM和DCM下，对所提变换器的工作原理和稳定状态下的特性进行计算，并对损耗进行详细分析，给出耦合电感和开关管的效率优化方法。最后，搭建一个满载功率为250 W，输入电压为40 V，输出电压为400 V的实验样机验证了变换器理论分析的正确性和可行性，测量的满载效率为97.10 %。
参考文献
[1] 姚子睿, 曾君, 刘俊峰. 基于耦合电感的高增益低电压应力Boost变换器[J]. 中国电机工程学报, 2019, 39(12): 3659-3667.
Yao Zirui, Zeng Jun, Liu Junfeng. High step-up low- voltage stress Boost converter based on coupled inductor[J]. Proceedings of the CSEE, 2019, 39(12): 3659-3667.
[2] Liang T J, Luo Peng, Chen Kaihui. A high step-up DC-DC converter with three-winding coupled indu- ctor for sustainable energy systems[J]. IEEE Transa- ctions on Industrial Electronics, 2022, 69(10): 10249- 10258.
[3] 孙孝峰, 张绘欣, 张涵, 等. 一种用于电-氢多能互补型微电网的双有源桥集成Boost拓扑及其控制[J]. 电工技术学报, 2021, 36(10): 2092-2104.
Sun Xiaofeng, Zhang Huixin, Zhang Han, et al. Topo- logy and control strategy of dual active bridge integrated Boost circuit for electro-hydrogen multi- energy complementary microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2092- 2104.
[4] 张沈习, 王丹阳, 程浩忠, 等. 双碳目标下低碳综合能源系统规划关键技术及挑战[J]. 电力系统自动化, 2022, 46(8): 189-207.
Zhang Shenxi, Wang Danyang, Cheng Haozhong, et al. Key technologies and challenges of low-carbon integrated energy system planning for carbon emission peak and carbon neutrality[J]. Automation of Electric Power Systems, 2022, 46(8): 189-207.
[5] 侯金鸣, 孙蔚, 肖晋宇, 等. 电力系统关键技术进步与低碳转型的协同优化[J]. 电力系统自动化, 2022, 46(13): 1-9.
Hou Jinming, Sun Wei, Xiao Jinyu, et al. Collabo- rative optimization of key technology progress and low-carbon transition of power systems[J]. Auto- mation of Electric Power Systems, 2022, 46(13): 1-9.
[6] Majeed Y E, Ahmad I, Habibi D. A multiple-input cascaded DC-DC converter for very small wind tur- bines[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4414-4423.
[7] 佟子昂, 武建文, 马速良, 等. 一种基于主动电压扰动的直流微网负载均流控制策略[J]. 电工技术学报, 2019, 34(24): 5199-5208.
Tong Ziang, Wu Jianwen, Ma Suliang, et al. A load current-sharing control strategy for DC microgrid converters based on active voltage disturbance[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5199-5208.
[8] 吴卫民, 何远彬, 耿攀, 等. 直流微网研究中的关键技术[J]. 电工技术学报, 2012, 27(1): 98-106, 113.
Wu Weimin, He Yuanbin, Geng Pan, et al. Key tech- nologies for DC micro-grids[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 98-106, 113.
[9] 郭慧, 汪飞, 顾永文, 等. 基于电压分层控制的直流微电网及其储能扩容单元功率协调控制策略[J]. 电工技术学报, 2022, 37(12): 3117-3131.
Guo Hui, Wang Fei, Gu Yongwen, et al. Coordinated Power control strategy for DC microgrid and storage expansion unit based on voltage hierarchical con- trol[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3117-3131.
[10] 王攀攀, 段森, 于东升, 等. 一种新型高增益零输入纹波DC-DC变换器[J]. 太阳能学报, 2020, 41(12): 18-25.
Wang Panpan, Duan Sen, Yu Dongsheng, et al. A novel high voltage gain zero input-current ripple DC-DC converter[J]. Acta Energiae Solaris Sinica, 2020, 41(12): 18-25.
[11] 郭英军, 孔德楷, 汤雨, 等. 考虑寄生参数的双管升压变换器高频工作特性分析[J]. 电工技术学报, 2022, 37(6): 1431-1441.
Guo Yingjun, Kong Dekai, Tang Yu, et al. Analysis of operating characteristics of dual-switch Boost converter considering parasitic parameters under high frequency conditions[J]. Transactions of China Elec- trotechnical Society, 2022, 37(6): 1431-1441.
[12] Ai Jian, Lin Mingyao, Yin Ming. A family of high step-up cascade DC-DC converters with clamped circuits[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 4819-4834.
[13] 周磊, 张宇妍, 秦岭, 等. 低电应力无变压器单管高增益Boost变换器族[J]. 中国电机工程学报, 2020, 40(21): 7036-7047.
Zhou Lei, Zhang Yuyan, Qin Ling, et al. A family of transformer-less single-switch high gain Boost con- verters with low electric stress[J]. Proceedings of the CSEE, 2020, 40(21): 7036-7047.
[14] 唐钧涛, 戚志东, 裴进, 等. 基于电荷泵的燃料电池有源网络升压变换器[J]. 电工技术学报, 2022, 37(4): 905-917.
Tang Juntao, Qi Zhidong, Pei Jin, et al. An active network DC-DC Boost converter with a charge pump employed in fuel cells[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 905-917.
[15] Liang T J，Chen S M，Yang L S, et al. Ultra-large gain step-up switched-capacitor DC-DC converter with coupled inductor for alternative sources of energy[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2012, 59(4): 864-874.
[16] 罗全明, 高伟, 吕星宇, 等. 耦合电感型高增益Boost变换器拓扑分析[J]. 中国电机工程学报, 2017, 37(24): 7266-7275, 7441.
Luo Quanming, Gao Wei, Lü Xingyu, et al. Topology analysis of high step-up Boost converters with coupled inductors[J]. Proceedings of the CSEE, 2017, 37(24): 7266-7275, 7441.
[17] Hu Renjun, Zeng Jun, Liu Junfeng, et al. An ultrahigh step-up quadratic Boost converter based on coupled- inductor[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13200-13209.
[18] 丁杰, 高双, 赵世伟, 等. 基于耦合电感的对称式交错并联低输入电流纹波高增益DC-DC变换器[J]. 电工技术学报, 2021, 36(7): 1507-1515.
Ding Jie, Gao Shuang, Zhao Shiwei, et al. Symmetri- cal interleaved low input current ripple high step-up DC-DC converter based on coupled inductor[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1507-1515.
[19] Zheng Yifei, Smedley K M. Analysis and design of a single-switch high step-up coupled-inductor Boost converter[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 535-545.
[20] 皇金锋, 谢锋, 罗全明. 一种改进型低电压应力耦合电感高增益Boost变换器[J]. 电机与控制学报, 2020, 24(10): 69-76.
Huang Jinfeng, Xie Feng, Luo Quanming. High step-up improved low voltage-stress Boost converter with coupled inductors[J]. Electric Machines and Control, 2020, 24(10): 69-76.
[21] Hsieh Y P, Chen J F, Liang T J P, et al. Novel high step-up DC-DC converter with coupled-inductor and switched-capacitor techniques for a sustainable energy system[J]. IEEE Transactions on Power Elec- tronics, 2011, 26(12): 3481-3490.
[22] 李洪珠, 刘飞扬, 刘艳, 等. 一种新型磁集成高增益耦合电感倍压Boost变换器[J]. 电工技术学报, 2020, 35(增刊2): 450-460.
Li Hongzhu, Liu Feiyang, Liu Yan, et al. A new magnetically integrated high gain coupled inductance voltage-doubled Boost converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 450- 460.
[23] 高伟, 罗全明, 张阳, 等. 一种零输入电流纹波高增益DC-DC变换器[J]. 电工技术学报, 2018, 33(2): 284-292.
Gao Wei, Luo Quanming, Zhang Yang, et al. A high step-up DC-DC converter with zero input current ripple[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 284-292.
[24] 林雪凤, 许建平, 周翔. 谐振软开关耦合电感高增益DC-DC变换器[J]. 电工技术学报, 2019, 34(4): 747-755.
Lin Xuefeng, Xu Jianping, Zhou Xiang. Soft-switched high step-up DC-DC converter with coupled inductor of resonance[J]. Transactions of China Electro- technical Society, 2019, 34(4): 747-755.
[25] Lee S W, Do H L. High step-up coupled-inductor cascade Boost DC-DC converter with lossless passive snubber[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(10): 7753-7761.
[26] Mirzaee A, Moghani J S. Coupled inductor-based high voltage gain DC-DC converter for renewable energy applications[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 7045-7057.
[27] 罗全明, 张阳, 闫欢, 等. 一种带耦合电感的有源钳位高增益Boost变换器[J]. 中国电机工程学报, 2014, 34(27): 4576-4583.
Luo Quanming, Zhang Yang, Yan Huan, et al. An active-clamp high step-up Boost converter with coupled-inductor[J]. Proceedings of the CSEE, 2014, 34(27): 4576-4583.
[28] Wang Yijie, Qiu Yuping, Bian Qing, et al. A single switch quadratic Boost high step up DC-DC con- verter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4387-4397.
[29] 陈章勇, 许建平, 吴建雪, 等. 耦合电感零输入纹波高增益非隔离DC-DC变换器[J]. 中国电机工程学报, 2014, 34(33): 5836-5845.
Chen Zhangyong, Xu Jianping, Wu Jianxue, et al. High voltage gain zero-ripple non-isolated converters with a coupled-inductor[J]. Proceedings of the CSEE, 2014, 34(33): 5836-5845.
[30] Hassan W, Lu D D C, Xiao Weidong. Single-switch high step-up DC-DC converter with low and steady switch voltage stress[J]. IEEE Transactions on Industrial Electronics, 2019, 66(12): 9326-9338.
[31] Kumar G G, Sundaramoorthy K, Karthikeyan V, et al. Switched capacitor-inductor network based ultra-gain DC-DC converter using single switch[J]. IEEE Transa- ctions on Industrial Electronics, 2020, 67(12): 10274- 10283.
[32] Bao Danyang, Kumar A, Pan Xuewei, et al. Switched inductor double switch high gain DC-DC converter for renewable applications[J]. IEEE Access, 2021, 9: 14259-14270.
[33] Chen S M, Lao Manlong, Hsieh Y H, et al. A novel switched-coupled-inductor DC-DC step-up converter and its derivatives[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 309-314.
[34] Ding Xinping, Zhou Mingzhu, Cao Yichang, et al. A high step-up coupled-inductor-integrated DC-DC multilevel Boost converter with continuous input current[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 7346-7360.
Abstract Since the excessive use of fossil energy has caused global warming and an energy crisis, clean energy development has gained much more attention. In order to reduce the impact of clean energy based distributed generation grid-connect, improving the conversion efficiency and reliable performance, DC microgrid plays an important role. However, the low output voltage of clean energy should be boosted to a suitable voltage level of the DC microgrid grid-connected. Therefore, a high step-up DC-DC converter using switched coupled inductor and passive clamp circuit is proposed. The switched coupled inductor technique is connected to the input and the output parts, and the voltage gain can be further improved by adjusting the turns ratio of the coupled inductor. In addition, by applying a passive clamp circuit, the energy stored in the leakage inductor is recycled, and the voltage spike on the power switch can be suppressed. Hence, the voltage stress on the switch is reduced, and the efficiency can be improved.
The operating principles and steady-state performance in continuous conduction mode (CCM) and discontinuous conduction mode (DCM) are analyzed in detail. The operating mode is analyzed through the key waveforms and equivalent circuits. Considering the coupling coefficient has no significant effect on the voltage gain, the ideal voltage gain is (2+n)/(1-D) where n=ns/np. Under n=2 and D=0.6, the voltage gain can reach 10. Hence, the proposed converter can achieve high voltage gain. Meanwhile, the voltage stress and current stress of components are studied, including semiconductor devices and passive devices. Moreover, the parameters of the magnetizing inductor and capacitors are designed.
The power loss is divided into four parts: power switch, diode, capacitor, and inductor losses. The theoretical efficiency and non-ideal voltage gain are obtained. Compared with the ideal and non-ideal voltage gains at the appropriate duty cycle, the effect of parasitic parameters of components is negligible. The proposed converter has higher voltage gain and efficiency, lower voltage stress of the power switch, and fewer components than the high step-up converter.
A 40 V-input, 400 V-output, 250 W experimental prototype is built by choosing the proper value and type of components. Considering the inductor loss, the material of core and turns ratio are selected to achieve the highest efficiency. The measured voltage and current of components are consistent with the theoretical analysis. Also, the measured maximum and full-load efficiencies are 97.59 % and 97.10 %, respectively. Total power loss is 5.49 W at 250 W. The proposed converter has the following advantages.
(1) The high voltage gain is obtained by switched coupled inductor, suitable for the DC microgrid grid-connected.
(2) Through the experiment results, the low voltage stress of the power switch validates that the passive clamp circuit inhibits the voltage spike effectively.
(3) The beneficial parameters are chosen to improve the efficiency, verifying the power loss analyses through the experiment.
(4) Fewer components are required, which improves reliability.
keywords：Switched coupled inductor, high step-up, DC-DC converter, efficiency optimization, DC microgrid
DOI: 10.19595/j.cnki.1000-6753.tces.222228
中图分类号：TM46
国家自然科学基金（62171143, 61871465）和广东省自然科学基金（2021A1515011948）资助项目。
收稿日期 2022-11-29
改稿日期 2023-02-06
罗 朋 男，1988年生，讲师，博士研究生，研究方向为电力电子变换技术。E-mail: dqluopeng@163.com
刘洺辛 男，1976年生，博士，教授，博士生导师，研究方向为无线传感网络和新能源电力变换技术。E-mail: liumx@gdou.edu.cn（通信作者）
（编辑 陈 诚）