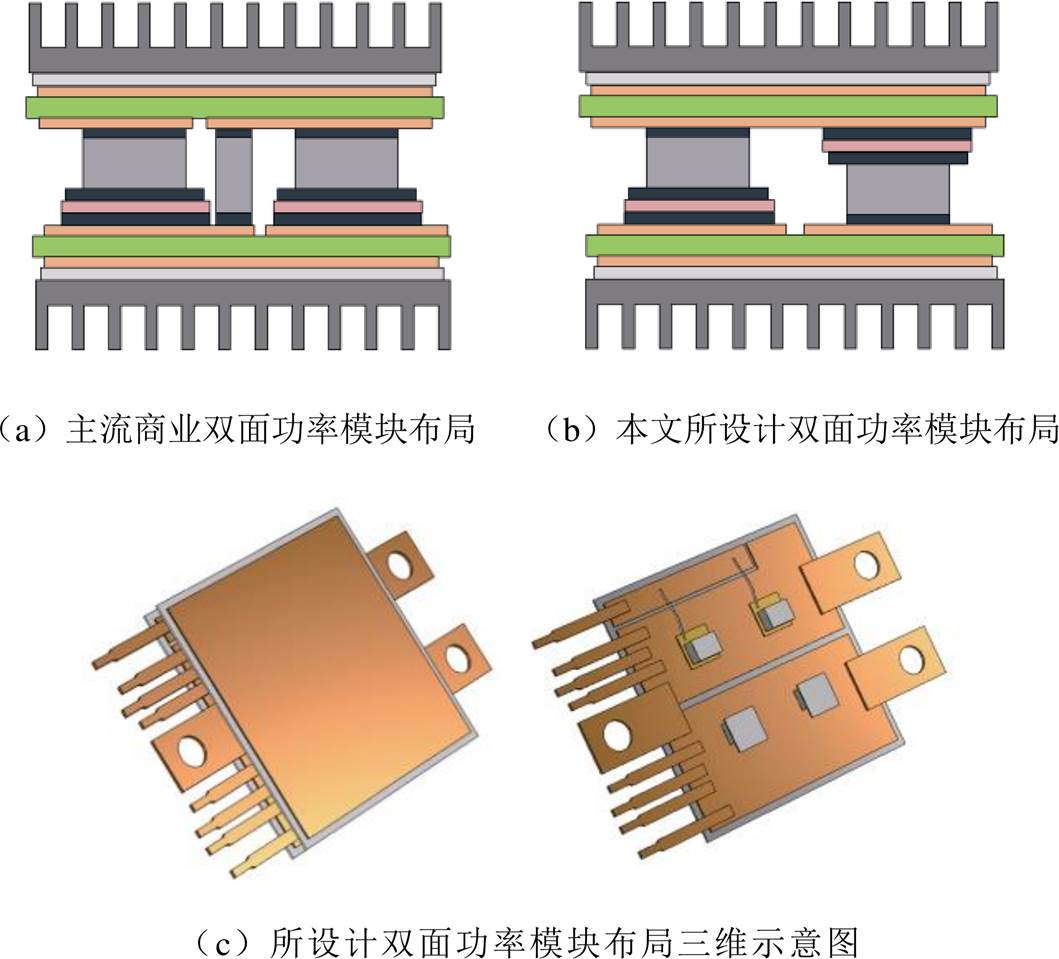
图1 功率模块布局示意图
Fig.1 Power module layout diagram
摘要 双面散热功率模块凭借优异的电热特性,能够满足SiC器件封装的性能要求。但双面散热模块的电学、热学及力学特性互相制约,难以实现各性能的全部最优,为此,该文提出一种基于智能算法的多目标优化设计方法。首先,通过参数化仿真对功率模块的电热力性能进行了建模,并分析了待优化的尺寸参数对各性能指标的影响规律。然后,基于参数化仿真与流程控制方法得到学习样本,通过神经网络训练得到了待优化尺寸变量与各性能指标之间的函数关系,解决了尺寸变量与性能指标之间的函数难以获取的问题。得到目标函数后,基于遗传算法进行多目标优化求解,实现了定制化的多目标优化设计。最后,基于优化结果分别制备了优化前后的功率模块,并对其性能指标进行了测试和对比,结果证明了所提出的多目标优化设计方法的正确性。
关键词:SiC功率模块 双面散热 多目标优化 人工神经网络 遗传算法
随着以SiC、GaN为代表的第三代半导体的迅速发展,对功率模块封装的性能提出了更高的要求,传统的功率模块封装结构已经无法满足新型功率器件的封装要求[1]。功率模块的设计需要综合考虑多方面的性能,主要包括电学性能、热学性能及力学性能。其中封装引入的电学性能指标主要为寄生参数,热学性能指标主要为热阻,力学性能指标主要为热应力。
为了提高功率模块各方面的性能,许多新型封装结构不断被提出。减小寄生参数的方法包括端子直焊技术[2]、柔性印制电路板(Printed Circuit Board, PCB)封装[3]、双面散热结构[4]、3D封装[5]等。为了降低热阻,可以采用高热导率DBC(direct bonded copper)材料、双面散热结构、微通道散热[6]、相变散热技术[7]等方法。在热应力的作用下,键合线和焊层的退化是造成功率模块老化失效的主要原因[8],使用铜线、铝包铜线、铝带、铜带以及引线框等代替铝键合线实现芯片顶部的互连,能够降低顶部铝键合线互连带来的可靠性问题[9],通过采用新型的高可靠性互连技术,如瞬态液相键合[10]及纳米银烧结[11]等工艺取代传统钎焊,能够提高功率模块互连层的可靠性。
在上述众多封装结构创新中,双面散热功率模块通过取消键合线实现双通道散热,凭借其优良的电气特性、热特性以及极高的功率密度,已经取得了商业化落地,多家企业的双面散热功率模块已经上市,在电动汽车中取得了广泛的应用。但相较于传统的单面散热功率模块,双面散热功率模块中芯片两侧的刚性连接带来了另外的高应力可靠性问题。在双面散热功率模块的设计过程当中,电-热-力三场紧密耦合,电学、热学及力学特性互相制约,无法达到多个目标全部最优,因此,需要进行多目标优化设计。
对于功率模块的封装结构多目标优化问题,文献[12]针对传统功率模块的封装结构,提出了一种基于遗传算法的多目标优化方法,其目标函数通过采用物理解析表达式进行推导获取,在推导过程中进行了简化因而准确性不高。文献[13]提出了一种针对双面散热功率模块的热力协同优化设计方法,研究方法与文献[12]类似,但未考虑对寄生参数的优化。文献[14]以功率模块的功率循环以及温度循环寿命为优化目标对功率模块的各层厚度进行优化,同样采用了解析方式获取目标函数的方法。文献[15]采用有限元软件中的优化模块对功率模块的结构参数进行优化,但由于有限元软件的限制,优化目标仅仅选取热学以及力学性能指标,且采用的优化算法为传统的对多目标设定各目标权值进而转化为单目标优化的方法,无法得到帕累托前沿进行定制化的多目标优化。从现有的功率模块多目标优化方法可以看出,大多存在优化目标与优化变量选取不合理、目标函数获取方法不准确等问题。因此有必要提出一种能够兼顾准确性以及灵活性的功率模块多目标优化设计方法,对功率模块的电学、热学及力学性能指标进行多目标优化设计。
针对现有的功率模块设计方法存在的问题,本文以双面散热SiC功率模块为研究对象,提出了一种基于智能算法的多目标优化设计方法,能够实现对功率模块高效灵活的定制化设计。首先对电学、热学及力学特性进行了建模仿真分析,并研究了各尺寸参数变化对功率模块各性能指标的影响规律,揭示了各性能指标与参数变化之间的制约关系。接着基于Q3D寄生参数仿真及有限元电热力多物理场耦合仿真,通过神经网络获取了目标函数。然后采用遗传算法进行求解,实现了对功率模块定制化的设计。
功率模块的设计需要综合考虑电学、热学及力学性能,本节首先对双面散热SiC功率模块的结构布局进行设计并确定模块内部各关键组件的材料,进而对所设计双面散热SiC功率模块的电学、热学及力学性能进行仿真建模,并分析各尺寸变量对各性能指标的影响规律,探究各性能指标之间的制约关系。
目前商用的双面散热功率模块,如英飞凌的FF450R08A03P2、安森美的NVG800A75L4DSC,普遍采用图1a所示的双层DBC、芯片、垫片与焊层构成的三明治结构,需要额外增加垫片实现半桥上下管的电气连接。针对这种双面散热封装结构所存在的问题,本文采用图1b所示的令上、下管分别位于上、下两个DBC的布局,不需增加垫片实现电气连接,能够使得散热效率更高、热耦合与寄生参数达到最小化。

图1 功率模块布局示意图
Fig.1 Power module layout diagram
本文所设计的双面散热SiC功率模块的各尺寸参数与选用材料如图2所示,其中DBC选用Al2O3陶瓷基板,垫片选用热膨胀系数较小的钼铜合金以缓冲应力。由于双面散热功率模块功率回路不含键合线,因此芯片互连层是双面散热封装结构的主要薄弱点,加上刚性连接带来的高应力问题,双面散热功率模块对互连层的可靠性要求十分高,为了提高互连层的可靠性,采用纳米银烧结工艺实现互连。
功率模块所采用材料的电学、热学及力学基本属性见表1。
根据设计经验,选取功率模块各尺寸参数的初始值与取值范围见表2,其中芯片的长度d0、宽度d1与厚度h0已经确定,纳米银烧结层的厚度h3依据工艺参数选取0.06 mm,待优化的尺寸变量为芯片在DBC上的布局间距d2~d5,DBC铜层厚度h1、陶瓷厚度h2与垫片厚度h4共7个参数变量。另外,两块主回路DBC铜排之间的距离为1 mm,驱动回路DBC和功率回路DBC之间的距离为0.5 mm。
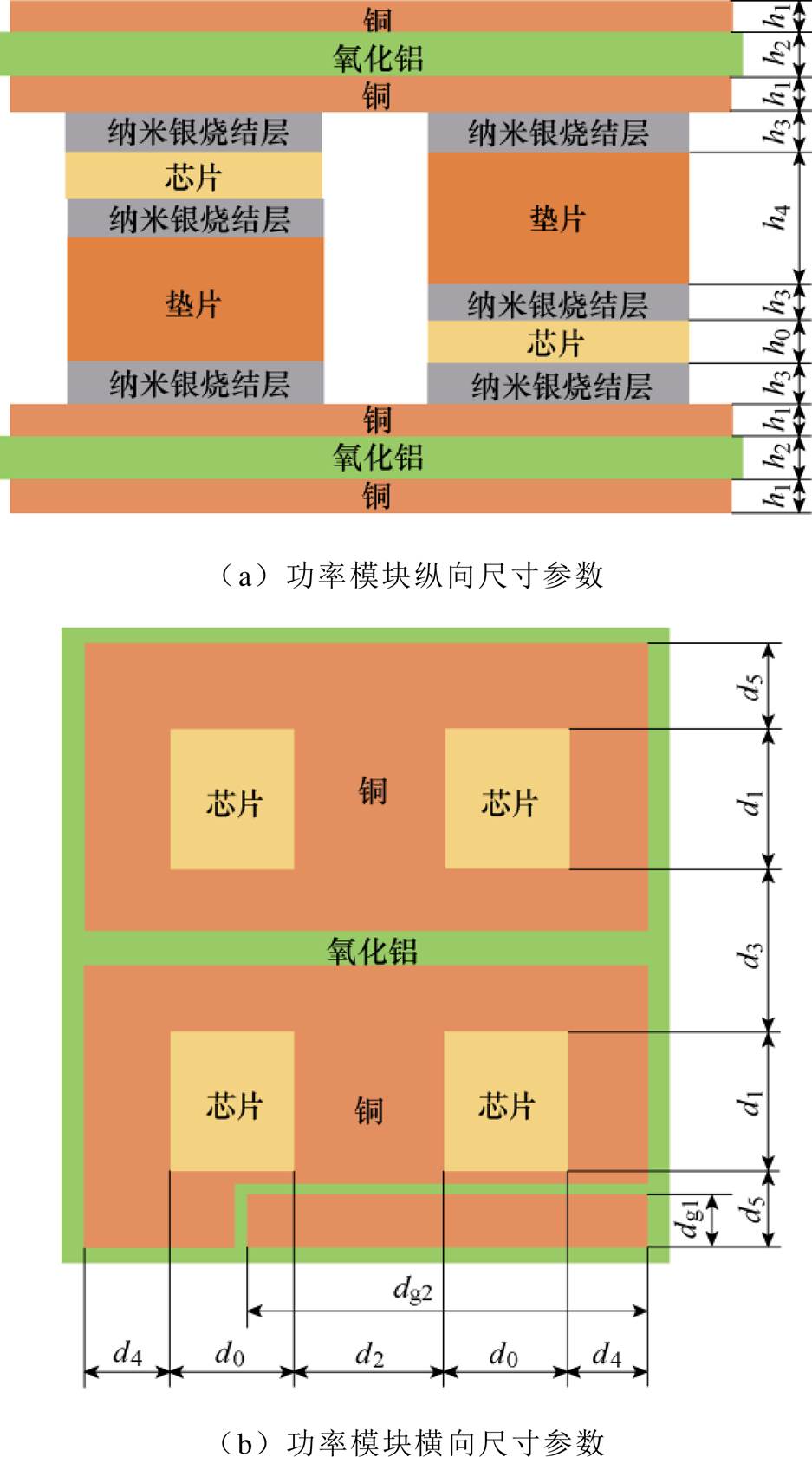
图2 功率模块尺寸参数
Fig.2 Dimensions of the power module
表1 功率模块各材料属性
Tab.1 The material property

材料属性SiCAgAl2O3CuMoCu30 电导率/(106S/m)—63—5722.7 相对介电常数9.66—9.8—— 热导率/[W/(m·K)]37042924394208 热膨胀系数/(10-6/K)4.318.96.817.59.1 杨氏模量/GPa16174310135280 泊松比0.260.380.220.350.3
表2 功率模块尺寸参数的初始值与取值范围
Tab.2 The power module dimensions Initial value and value range (单位: mm)

尺寸类型参数初始值下限上限 纵向尺寸h00.15—— h10.30.11 h20.380.11 h30.06—— h42110 横向尺寸d05—— d15—— d28220 d38220 d48420 d58220 dg1min(d5,4)-0.5—— dg2d0+d2+d4+3.5——
功率模块的寄生电感是表征功率模块电气性能的重要指标。采用Q3D软件建模提取所设计功率模块的寄生电感,本文采用的SiC芯片关断阶段电流下降时间tf=17 ns,其等效频率[16]为
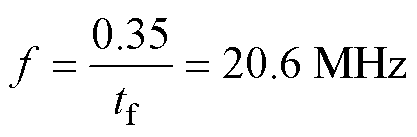 (1)
(1)
提取20.6 MHz下的寄生电感,电流从DC+端子流入,DC-端子流出,求解得到回路的寄生电感大小为7.335 nH。
为了研究各尺寸变量的变化对功率模块寄生电感的影响,进行参数化建模,对各变量在其取值范围内进行参数扫描的结果如图3所示。参数扫描过程中对一个变量进行分析时,其他变量取初始值。从寄生电感随尺寸参数的变化关系可以看出:①间距d5与d2对L的影响较小;②L与h2、h4、d3、d4呈正相关,与h1、d5呈负相关,对通流回路分析可知,h4、d3、d4的提高会增大通流路径长度,h2的增大则降低了外侧DBC铜层的涡流效应[17],h1、d5的增大会增大通流回路的横截面,从而减小寄生电感;③h4、d3、d4增加回路面积引起的L的变化显著大于其他尺寸参数。
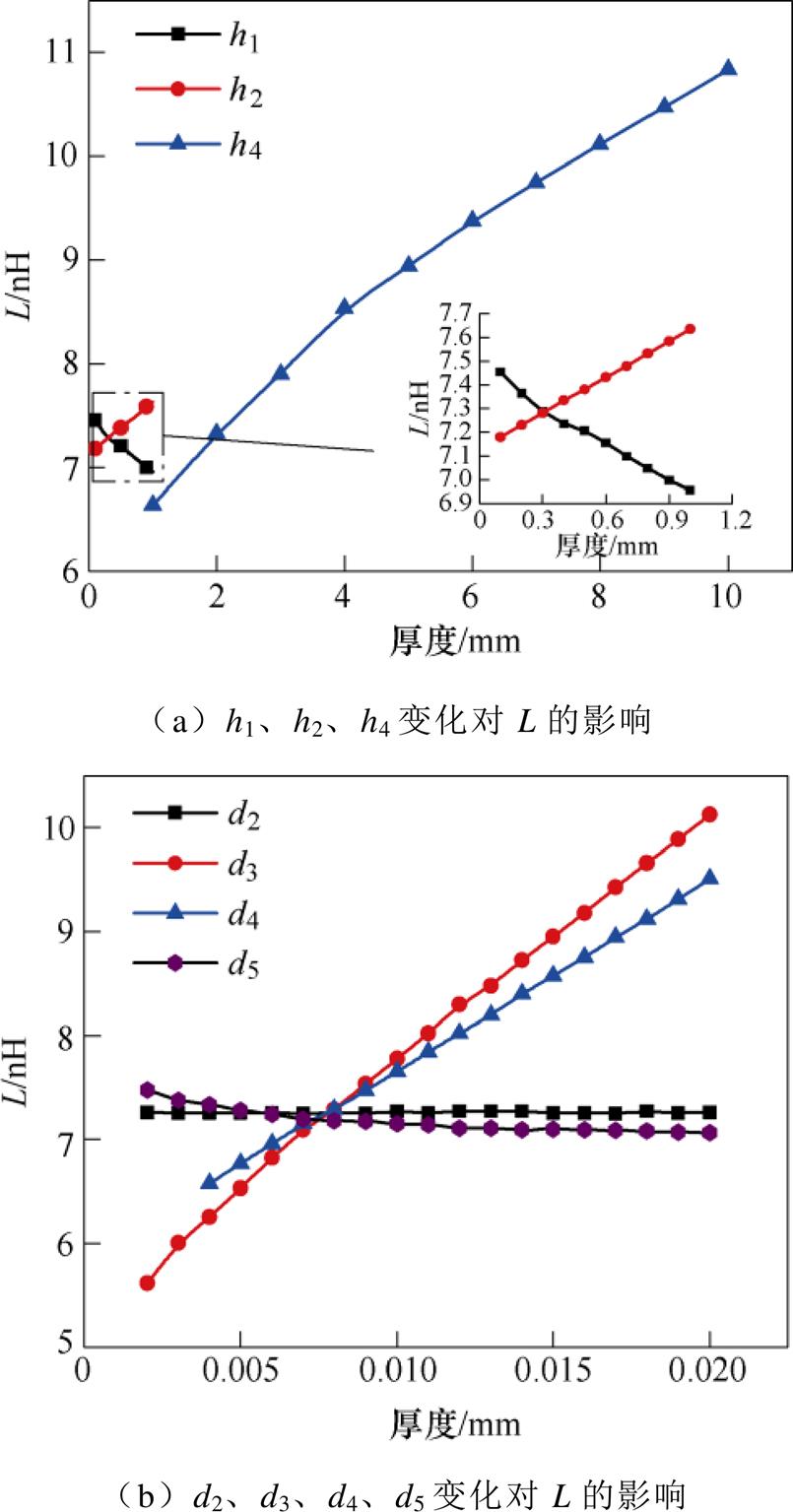
图3 寄生电感随尺寸参数的变化关系
Fig.3 The relationship between parasitic inductance and dimension parameters
热阻是表征功率模块散热特性的重要指标[18],对于多芯片双面散热功率模块而言,由于两侧壳温的不一致,难以对结壳热阻进行表征。与结壳热阻相比,在散热条件一定的情况下,结环热阻计算简便且能够反映功率模块的散热性能。因此本文采用结环热阻表征功率模块的热学性能指标,即
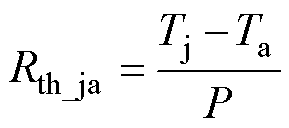 (2)
(2)
式中,Tj为四个芯片的芯片结温;Ta为散热器流体温度;P为损耗。
对所设计功率模块的传热过程进行有限元电热耦合仿真建模,芯片的导通电阻Ron与结温Tj之间具有耦合关系[19],其相关性如图4所示,热源可表示为
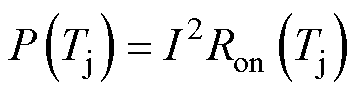 (3)
(3)
Ron-Tj的关系如图4所示,设置上下管电流为140 A,代入式(3)设置热载荷从而实现电热耦合,取表面传热系数为8 000 W/(m2·K),该系数按照热阻测试平台的水冷散热器设置,水冷温度为50 ℃,有限元仿真中使用芯片平均温度近似芯片结温。
初始功率模块的温度分布如图5所示,其中图5a为整体温度分布云图,最高温度为159 ℃,最低温度为55.1 ℃;图5b为芯片的温度分布,整个芯片的温度梯度达到35 ℃;图5c为温度分布的剖面图,垂直与水平方向均有很大的温度梯度,单个芯片两侧散发的热功率分别为110.94 W和38.74 W。有限元后处理可得芯片平均温度为150.15 ℃,模块的结环热阻为0.334 ℃/W。
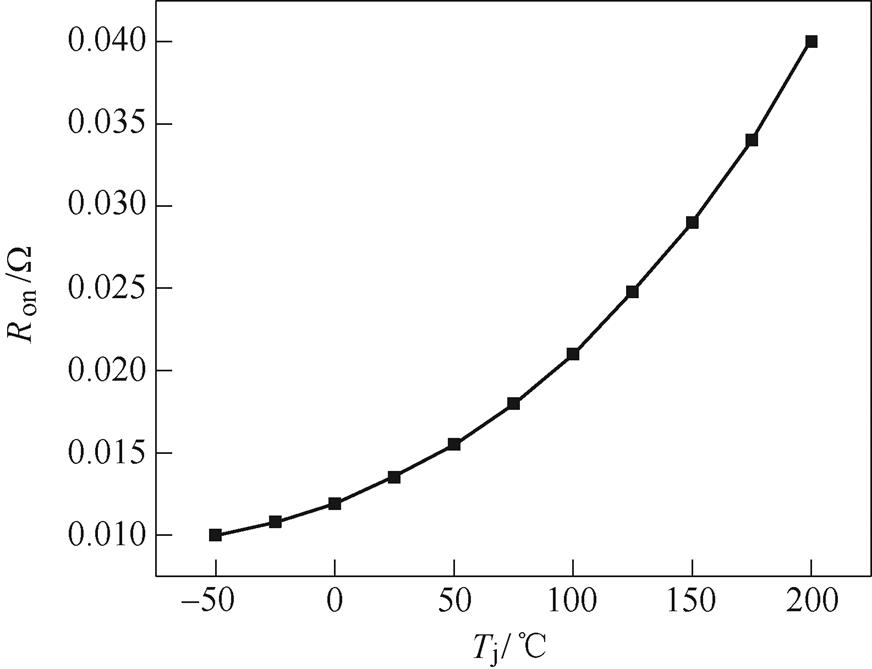
图4 导通电阻与结温的关系
Fig.4 Relationship between conduction resistance and junction temperature
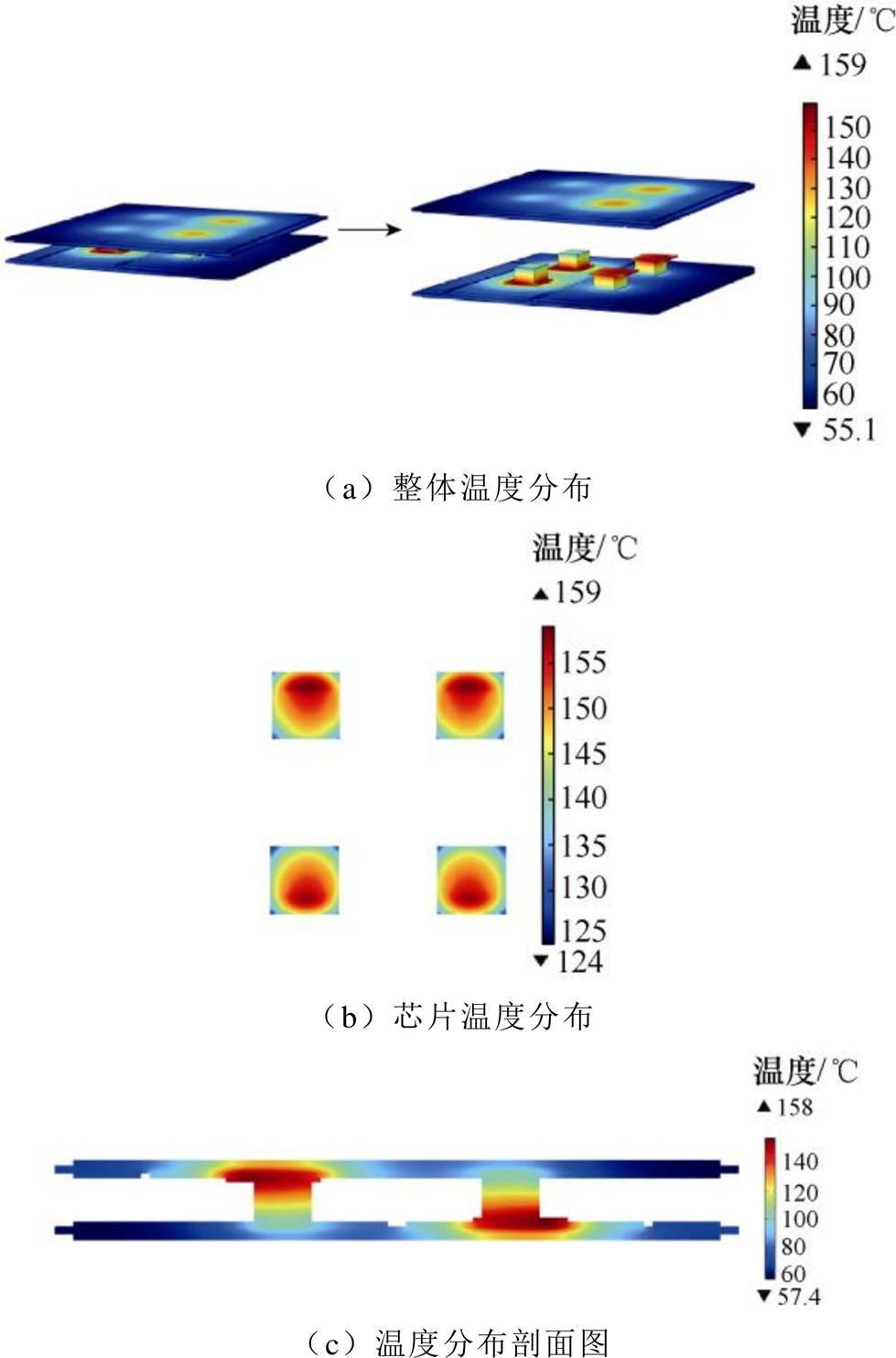
图5 功率模块温度分布
Fig.5 Power module temperature distribution
为了研究各尺寸变量与功率模块结环热阻之间的关系,在有限元软件中进行参数化建模,分别对各变量在取值范围内进行参数扫描,过程中对一个变量进行分析时,其他变量取初始值。得到如图6所示的结果。从结环热阻随尺寸参数的变化关系,可以看出:
(1)各尺寸参数与结环热阻之间具有非线性相关性。
(2)结环热阻与h2、h4呈正相关,与h1、d2、d3、d4、d5呈负相关。h2、h4的增大会增加散热路径的长度,因此引起热阻的增大。DBC铜层厚度h1的增大会增加散热路径的长度,同时也会增强热流的横向扩散,热阻随h1增大而减小说明在目前的范围内,h1的增大引起的热扩散的效果更为显著。d2、d3、d4、d5的增加则减小了芯片间的热耦合,从而减小了热阻。
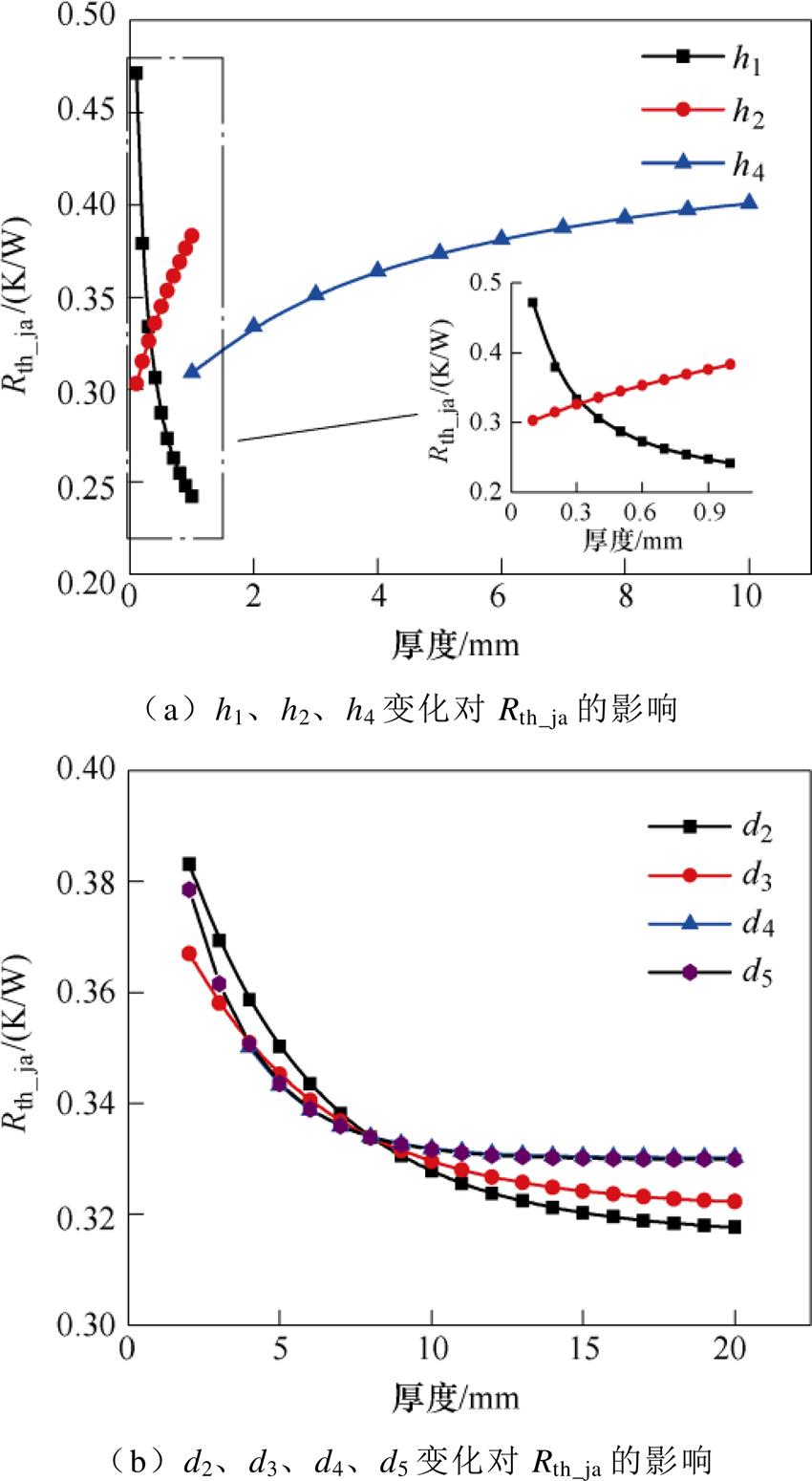
图6 结环热阻随尺寸参数的变化关系
Fig.6 The relationship between thermal resistance and dimension parameters
(3)在尺寸参数的约束范围内,铜层厚度h1变化引起的热阻变化要显著大于其他参数。
热应力是功率模块的重要力学性能指标,双面散热功率模块由于刚性连接,热应力问题相对传统功率模块更为严峻[20]。在热应力的作用下,芯片以及互连层有较高的失效风险,芯片在高应力下容易发生脆性断裂,互连层在热应力的长期作用下会产生蠕变退化。纳米银烧结层为金属材料,其可靠性评估适用于第四强度理论,需要读取纳米银烧结层的Von Mises应力,SiC芯片为脆性材料,其可靠性评估适用于第二强度理论,需要读取第一主应力。
进行有限元热力耦合分析,热学仿真采用电热耦合仿真的结果,在电热耦合的基础上加入力学仿真,采用刚体运动抑制作为力学仿真的边界条件,得到功率模块在自由膨胀下的热应力。
有限元仿真求解得到的模块整体应力场如图7b所示,由于各层材料属性不一,各层材料间的应力存在突变,在不同材料界面的边缘存在应力集中,与温度分布对比可知,在温度梯度较高的区域热应力也较大。
芯片的第一主应力分布如图7c所示,最大应力集中在垫片对应区域的边缘,芯片平均应力为123.8 MPa。
纳米银烧结层应力分布如图7d~图7f所示,各纳米银烧结层对应位置示意图如7a所示,烧结层1和烧结层3的应力中间区域大而边缘区域小,芯片和垫片之间的烧结层2的应力则边缘区域更大,因此在长期运行过程中可能出现不同的老化失效模式,纳米银烧结层的平均应力为175.9 MPa,以下应力未说明均为平均应力,平均应力能够反映模块的可靠性,同时避免被仿真中出现的应力奇异现象影响。
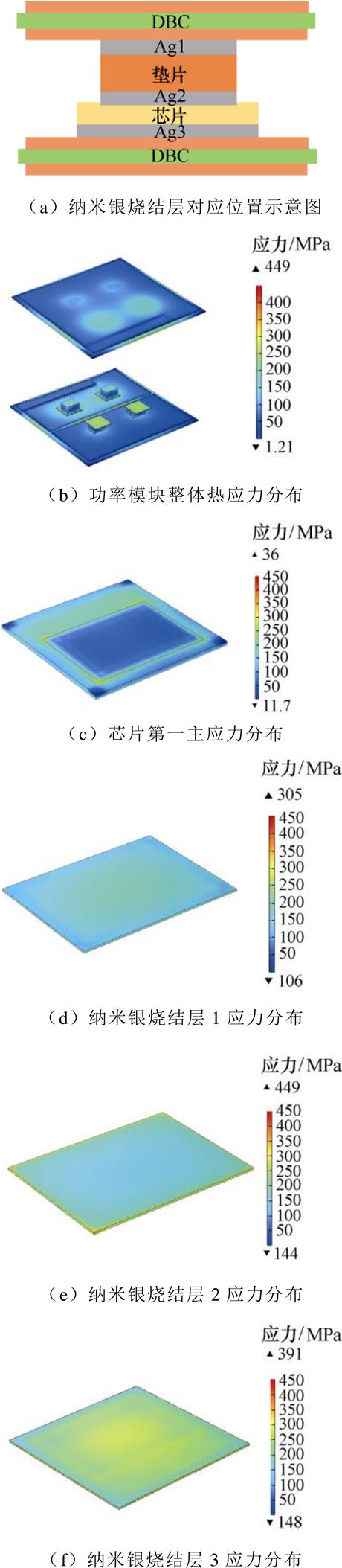
图7 功率模块热应力分布
Fig.7 Thermal stress distribution of the power module
为了研究各尺寸参数与功率模块热应力之间的关系,在有限元软件中进行参数化建模,分别对各变量在取值范围内进行参数扫描,过程中对一个变量进行分析时,其他变量取初始值。得到的纳米银烧结层应力随尺寸参数的变化关系如图8所示、芯片应力随尺寸参数的变化关系如图9所示。
从纳米银烧结层应力与芯片应力随尺寸参数的变化关系,可以看出:
(1)各尺寸参数与纳米银烧结层应力以及芯片应力非线性相关。
(2)纳米银烧结层应力随尺寸参数的变化规律与结环热阻一致,这是因为热应力是由于模块内部的温度梯度加上功率模块内部各材料的热膨胀系数不一致导致,而热阻的增加会导致内部功率模块温度的上升,也会进一步导致温度梯度的增大,从而使得热应力增加,因此热应力随尺寸参数的变化相关性与结环热阻一致。
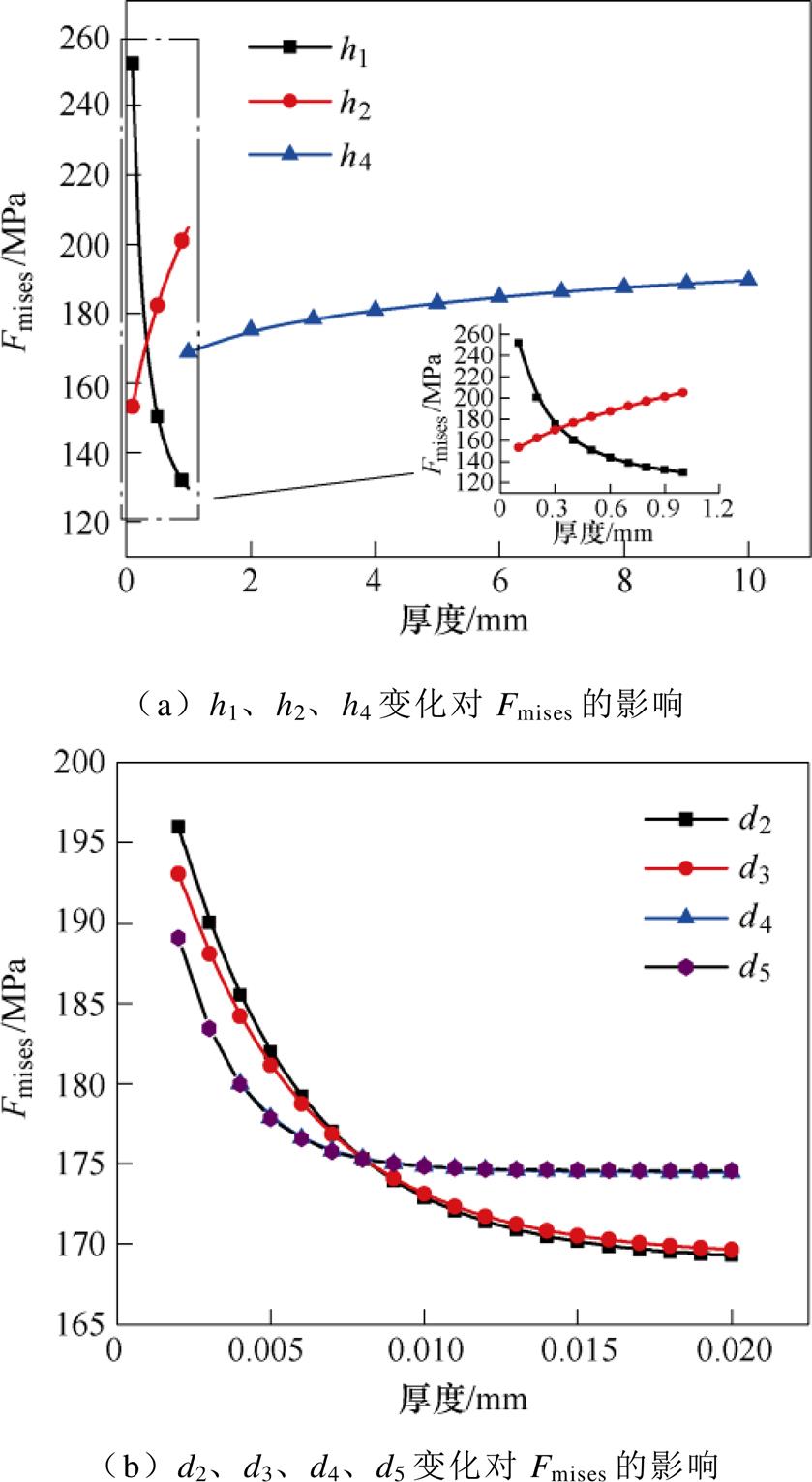
图8 纳米银烧结层应力随尺寸参数的变化关系
Fig.8 The relationship between stress of sintered layer and dimension parameters
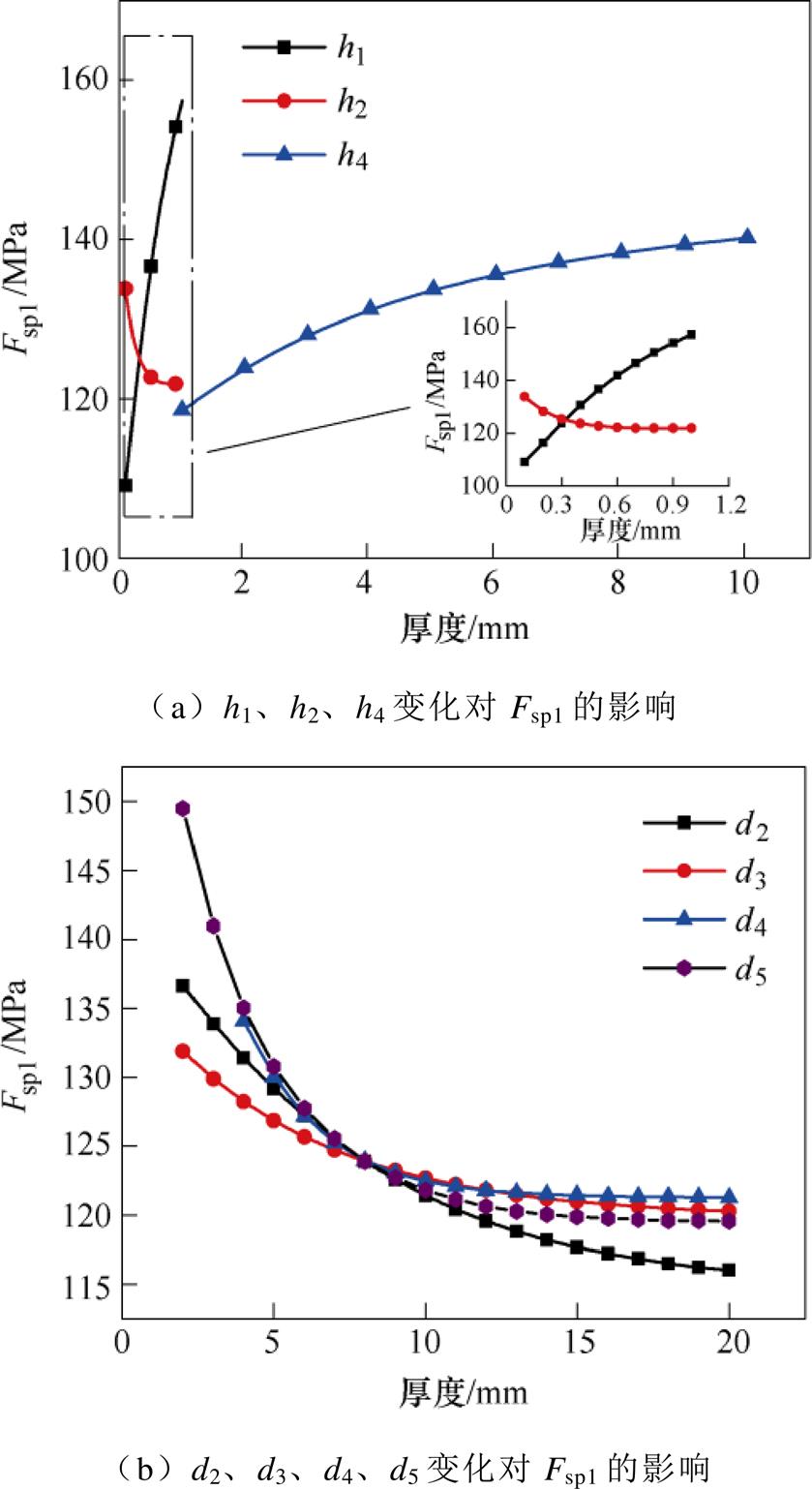
图9 芯片应力随尺寸参数的变化关系
Fig.9 The relationship between chip stress and size parameters
(3)芯片第一主应力与h1呈正相关,与h2呈负相关,这与纳米银烧结层应力随h1和h2的变化规律相反,其原因是纵向尺寸的变化除了会影响温度梯度的分布,还会影响热膨胀前的初始体积,因此对于芯片而言,热膨胀初始体积的影响效果相较温度梯度更为显著。
对电学、热学及力学性能的仿真建模分析,揭示了双面散热功率模块各性能指标之间的制约关系,因此需要进行多目标优化。本节首先提出一种基于神经网络的目标函数提取方法,以解决目标函数难以准确获取的问题。得到目标函数后采用遗传算法进行多目标优化求解,通过对不同的优化目标以及不同约束的多目标优化,实现定制化的优化 设计。
本文目标函数包含7输入4输出,可表示为
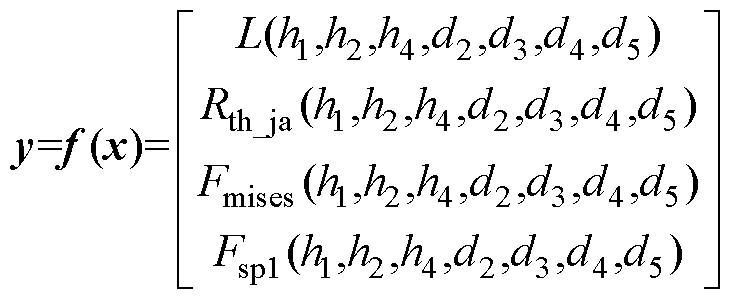 (4)
(4)
式中,h1、h2、h4、d2、d3、d4、d5为待优化的尺寸变量;L为寄生电感;Rth_ja为结环热阻;Fmises为纳米银烧结层Von Mises应力;Fsp1为芯片第一主应力。
人工神经网络具有强大的函数拟合能力,对所求函数的要求很低,理论上能够对所有的函数进行拟合,尤其适用于本文所求的目标函数这一类多输入多输出、无解析形式的非线性函数,因此本文采用神经网络进行目标函数的拟合[21]。
神经网络的训练就是通过对样本的学习不断调整神经网络各节点之间的权重的过程。当经过迭代计算后,预测误差小于设定的精度,对神经网络的训练即可完成。本文通过采用Matlab中的神经网络工具进行函数拟合,通过输入足够的学习样本,并设置适合的神经网络参数,即可得到所需的目标函数。
采用神经网络拟合目标函数,学习样本的获取是关键,足够的样本数量以及准确的样本信息对于神经网络的训练至关重要[22]。本文采用如图10所示的学习样本自动化获取方法,能够实现学习样本的高效获取,并保证所获取的样本能够反映函数整个可行域内的信息。首先,在约束范围内随机生成N×7的参数变量矩阵P,每一行向量为一个样本的输入量。样本的输出量分别通过Q3D参数化仿真以及COMSOL有限元参数化仿真获得,其中在Q3D中通过参数化仿真模型进行电磁场寄生电感提取,得到在给定尺寸参数下的寄生电感L,在COMSOL中进行电热力多物理场耦合参数化仿真,通过后处理得到在给定尺寸参数下的结环热阻Rth_ja、纳米银烧结层Von Mises应力Fmises以及芯片第一主应力Fsp1,通过运用COMSOL with Matlab接口实现COMSOL软件与Matlab软件之间的信息传递进行流程控制,实现学习样本的自动化获取,大大节省了有限元仿真的所需计算空间以及获取样本所需的计算时间。

图10 学习样本自动化获取方法
Fig.10 Automatic acquisition of learning samples
得到训练样本后,采用如图11所示的流程进行神经网络训练获取目标函数。对于仿真所获取得到的学习样本,各性能指标的数量级以及量纲存在很大的差别,需要采用归一化对样本进行预处理,将样本各特征的取值范围归一化到0~1之间。神经网络的训练需要将训练样本分为训练集、验证集和测试集,选取样本的80 %作为训练集,用于训练神经网络的权值,10 %作为验证集,用于验证神经网络的性能,当神经网络的性能满足要求时停止继续训练,10 %作为测试集,测试集独立用于测试判断神经网络的性能而不会影响神经网络的训练。由于目标函数的不确定性,所需样本的数量也是不确定的,首先选取N为100,训练过程中对神经网络的神经元个数以及训练算法等参数进行调整,训练得到一定学习样本下最小的误差结果e,如果e<1 %,则直接输出目标函数,若误差e≥1 %,则增加学习样本的个数,直至误差小于1 %。
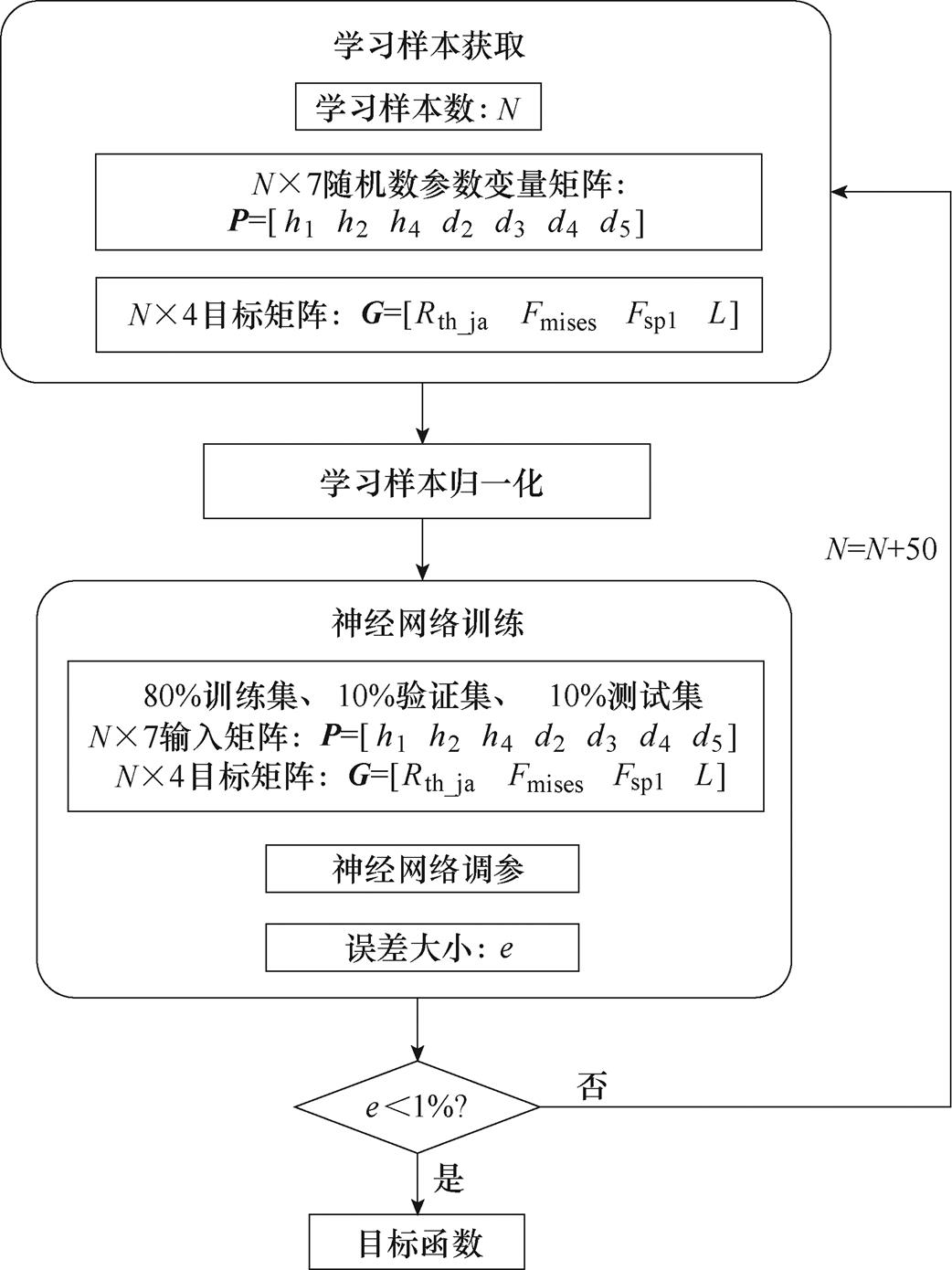
图11 神经网络拟合目标函数
Fig.11 The method of fitting objective function with neural network
对100组样本进行训练,所得神经网络各样本的误差在5 %左右,进一步增加样本量直至200个,所训练得到的神经网络各样本的误差减小到1 %以内,误差满足需求。通过仿真手动验证所训练得到的目标函数的准确性,拟合得到的目标函数计算结果与仿真结果的误差最大不超过2 %,平均误差在1 %以内,拟合效果满足需要。
在众多的多目标优化算法中,遗传算法的适用范围广,对目标函数的要求低,对于不连续不可微的目标函数依然可以求解,并且能够实现全局的优化,可以充分满足本文进行多目标优化的需求,因此本文采用遗传算法进行多目标优化求解[23-24]。
采用如图12所示的流程进行遗传算法多目标优化求解,首先设置待求解目标函数以及各变量的约束,其中目标函数由神经网络拟合得来,约束根据设计需要进行设定。然后进行遗传算法的参数设置,将种群规模大小设置为200,最大迭代次数设为800,函数值容差设置为0.000 1。接着对7个尺寸变量进行编码生成初始种群,将连续的变量转化为类似染色体的离散变量。再根据目标函数计算出种群个体的适应度,适应度的大小为即为每个个体的结环热阻Rth_ja、纳米银烧结层Von Mises应力Fmises、芯片第一主应力Fsp1以及寄生电感L的值。由于适应度为向量,不可能全部取得最优值,但可以求解其帕累托前沿。得到种群的适应度后,可以判断是否满足收敛条件,若不满足收敛条件,则进行一次种群的选择、交叉和变异操作,从而实现种群的进化,直至达到收敛条件。达到收敛条件后对种群进行解码,最后进行反归一化得到帕累托前沿,完成多目标优化求解。帕累托前沿的解中,不能在不降低其他目标的情况下,改进某一个目标[13]。
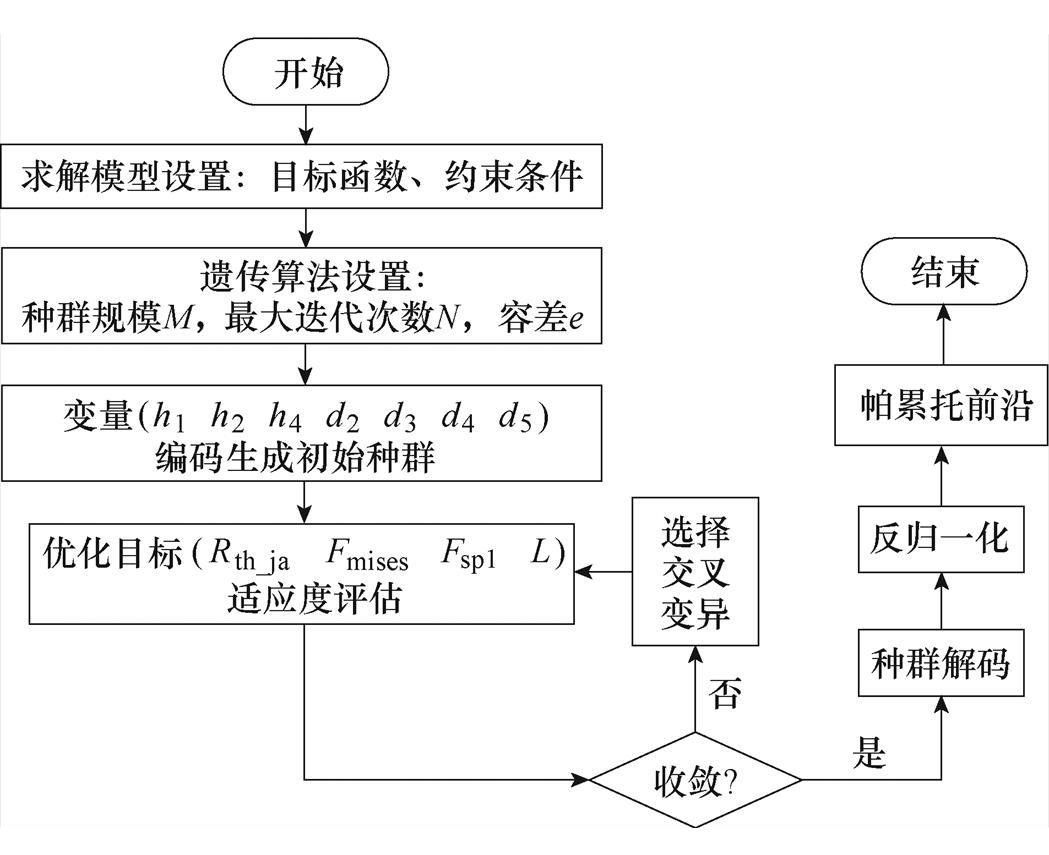
图12 遗传算法多目标优化求解流程
Fig.12 Multi-objective optimization solution flow of genetic algorithm
采用图12的遗传算法多目标优化求解流程,能够灵活地选取优化目标,同时可以自定义约束条件,再从得到的众多帕累托解中灵活选取优化结果从而实现定制化的优化设计。首先选取三目标进行优化,分别以寄生电感L、结环热阻Rth_ja、纳米银烧结层Von Mises应力Fmises,以及寄生电感、结环热阻、芯片第一主应力作为优化目标,通过对三个性能指标进行多目标优化并绘制帕累托前沿,验证所采用遗传算法的合理性与正确性,再根据需要进行四目标的优化设计。
2.3.1 三目标优化
对寄生电感、结环热阻、纳米银烧结层Von Mises应力进行多目标优化,尺寸的约束除了上、下限,选取的其他约束包括:DBC的陶瓷厚度大于铜层厚度,垫片厚度大于2 mm,模块的长度与宽度尽可能相等,相差在5 mm以内,约束为
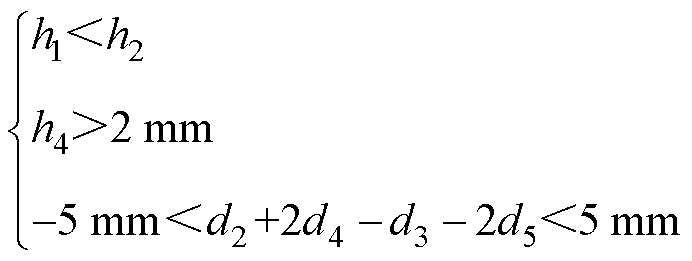 (5)
(5)
添加式(5)的约束条件后,对寄生电感、热阻、纳米银烧结层应力多目标优化的帕累托前沿如图13所示,由于热阻和纳米银烧结层应力随尺寸参数的变化趋势一致,因此二者的优化方向相同,对寄生电感、热阻、烧结层应力三目标优化的帕累托前沿为一条曲线。
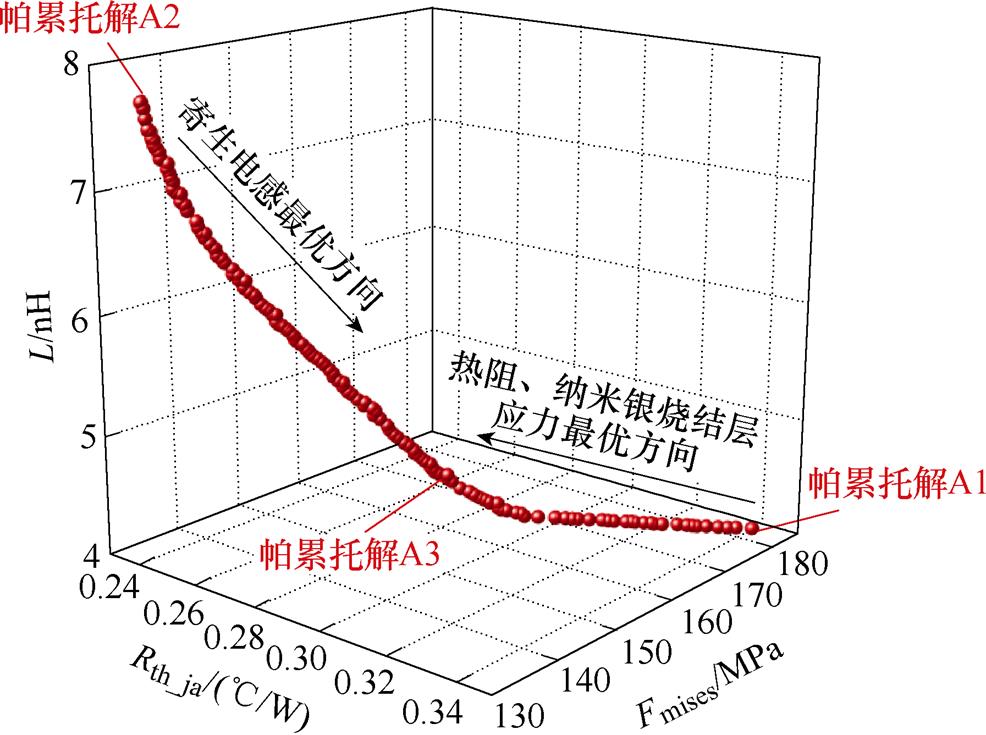
图13 对L、Rth_ja、Fmises多目标优化的帕累托前沿
Fig.13 Pareto fronts for optimization of L、Rth_ja、Fmises
选取其中三组帕累托解变量值和目标值见表3和表4,其中帕累托解A1使得寄生电感最优,帕累托解A2使得热阻、纳米银烧结层应力最优,帕累托解A3使得三目标均得到不同程度的优化,性能较为均衡,优化结果相对初始解有较大的性能提升。
表3 对L、Rth_ja、Fmises多目标优化的帕累托解变量值
Tab.3 Pareto solution variable value for multi-objective optimization of L、Rth_ja、Fmises (单位: mm)

组别h1h2h4d2d3d4d5 初始解0.30.382.008.008.008.008.00 解A11.001.002.017.792.014.019.20 解A20.980.982.0316.3910.447.459.89 解A31.001.002.0115.792.475.669.91
表4 对L、Rth_ja、Fmises多目标优化的帕累托解目标值
Tab.4 Pareto solution target value for multi-objective optimization of L、Rth_ja、Fmises
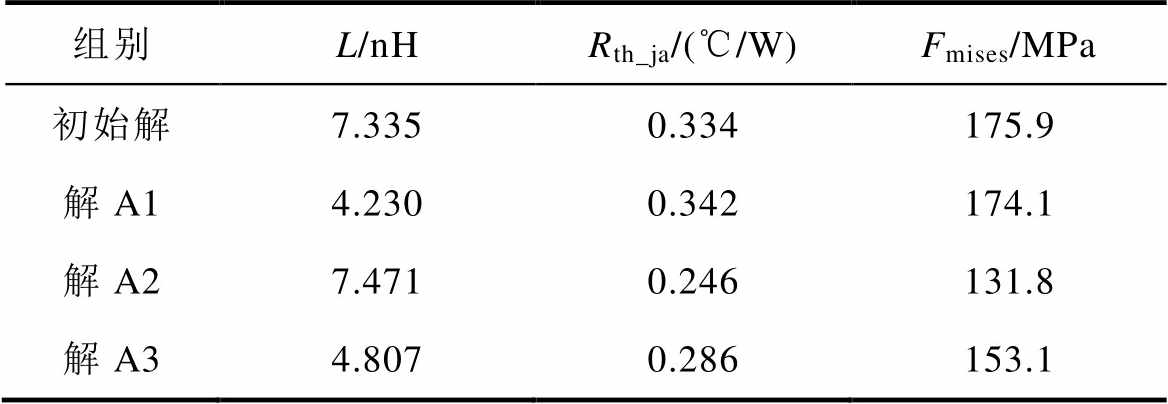
组别L/nHRth_ja/(℃/W)Fmises/MPa 初始解7.3350.334175.9 解A14.2300.342174.1 解A27.4710.246131.8 解A34.8070.286153.1
采用帕累托解A3的参数进行电热力性能建模仿真,并与初始解的结果进行对比。其中Q3D得到寄生电感为4.725 nH,相较初始解的7.335 nH显著下降。有限元电热耦合仿真温度分布结果如图14所示,对比图5的初始解的温度分布,芯片最高温度由159 ℃下降到139 ℃,结温显著下降。有限元热力耦合仿真得到的纳米银烧结层平均应力由175.9 MPa下降至152.3 MPa,仿真结果与神经网络预测结果相近,验证了使用神经网络方法预测目标函数的准确性。
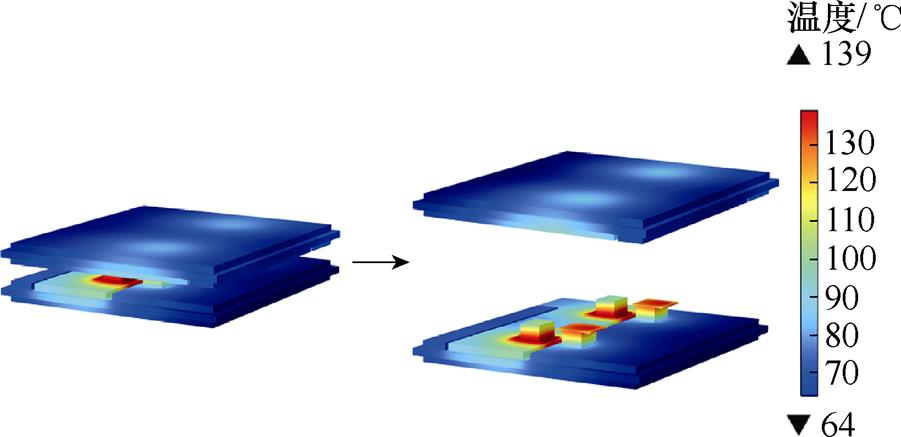
图14 帕累托解A3的温度分布
Fig.14 Temperature distribution of Pareto solution A3
对寄生电感、热阻、芯片应力多目标优化的帕累托前沿如图15所示,由于寄生电感、热阻、芯片应力互相制约,因此帕累托前沿解分布在一个曲面上。
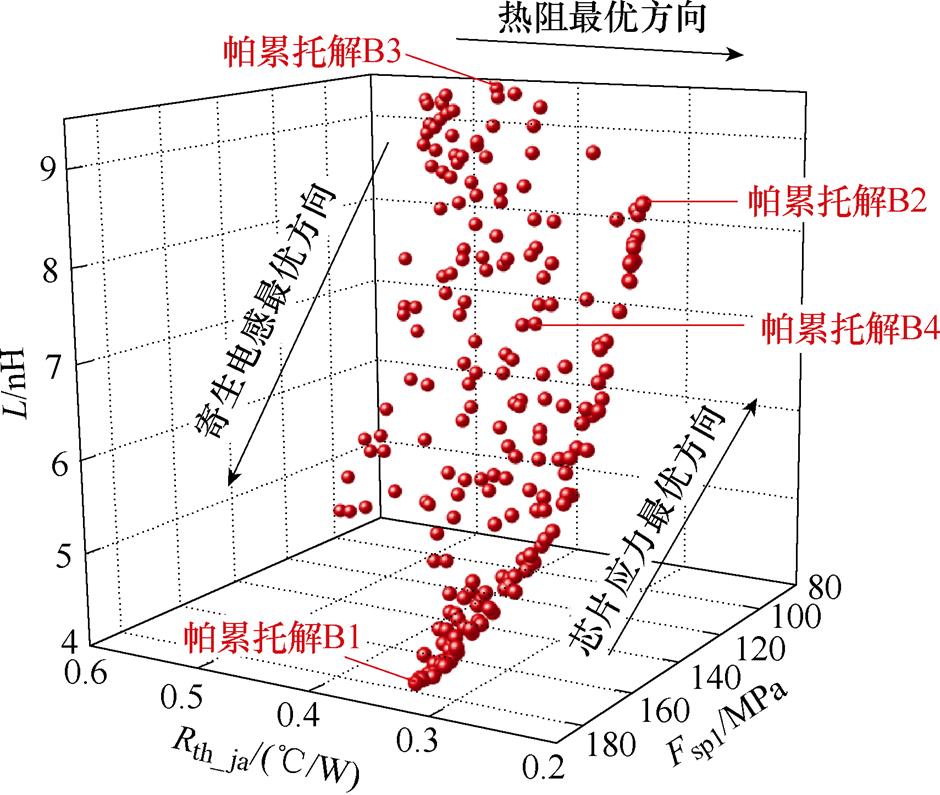
图15 对L、Rth_ja、Fsp1多目标优化的帕累托前沿
Fig.15 Pareto fronts for optimization of L、Rth_ja、Fsp1
选取其中四组帕累托解变量值与目标值见表5和表6,其中帕累托解B1、帕累托解B2、帕累托解B3分别使得寄生电感、热阻、芯片应力最优,帕累托解B4使得三目标性能较为均衡。
表5 对L、Rth_ja、Fsp1多目标优化的帕累托解变量值
Tab.5 Pareto solution variable value for multi-objective optimization of L、Rth_ja、Fsp1 (单位: mm)

组别h1h2h4d2d3d4d5 初始解0.300.382.008.008.008.008.00 解B10.980.992.019.292.044.099.05 解B20.970.982.2311.7610.8914.3615.14 解B30.110.952.2412.6410.9714.7216.11 解B40.590.952.1010.932.3713.716.78
表6 对L、Rth_ja、Fsp1多目标优化的帕累托解目标值
Tab.6 Pareto solution target value for multi-objective optimization of L、Rth_ja、Fsp1

组别L/nHRth_ja/(℃/W)Fsp1/MPa 初始解7.3350.334123.8 解B14.1850.324183.8 解B28.6090.238135.7 解B39.2940.51792.4 解B46.3900.301128.3
采用帕累托解B4的参数进行电热力性能建模仿真,并与初始解的结果进行对比。其中Q3D得到寄生电感为6.405 nH,相较初始解的7.335 nH明显下降。有限元电热耦合仿真温度分布结果如图16所示,芯片最高温度由159 ℃下降到149 ℃。有限元热力耦合仿真得到的芯片平均第一主应力由123.8 MPa略微上升至127.5 MPa。
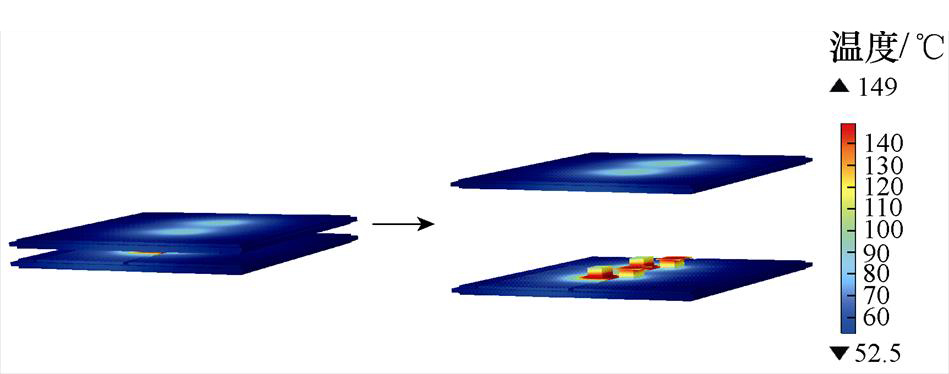
图16 帕累托解B4的温度分布
Fig.16 Temperature distribution of pare to solution B4
2.3.2 四目标优化
对寄生电感、热阻、纳米银烧结层应力以及芯片应力多目标优化,由于四目标的优化问题无法绘制帕累托前沿,因此需要在求解得到的帕累托解集中根据设计的需求选取合适的解。在实际优化求解过程中还可根据需要添加更多约束,以实现定制化的优化,本文选取与初始模块在同一DBC下进行优化,根据DBC尺寸的限制,约束条件进一步调整为
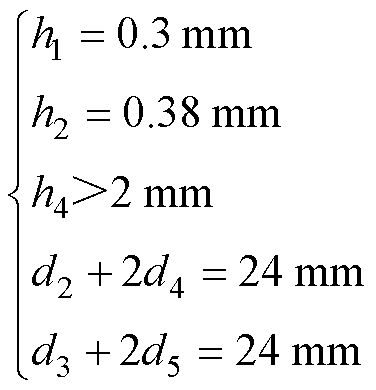 (6)
(6)
帕累托集设置为80个,选取其中四组帕累托解变量值和目标值见表7和表8。其中帕累托解C1使得寄生电感最优;帕累托解C2使得热阻与纳米银烧结层应力最优;帕累托解C3使得芯片应力最优;帕累托解C4使得四目标性能较为均衡。
表7 对L、Rth_ja、Fmises、Fsp1优化的帕累托解变量值
Tab.7 Pareto solution variable value for optimization of L、Rth_ja、Fmises、Fsp1 (单位: mm)

组别h1h2h4d2d3d4d5 初始解0.30.382.008.008.008.008.00 解C10.300.382.002.002.0011.0111.00 解C20.300.382.0010.6611.006.676.50 解C30.300.382.009.826.757.098.62 解C40.300.382.0010.147.176.938.42
表8 对L、Rth_ja、Fmises、Fsp1优化的帕累托解目标值
Tab.8 Pareto solution target value for optimization of L、Rth_ja、Fmises、Fsp1

组别L/nHRth_ja/(℃/W)Fmises/MPaFsp1/MPa 初始解7.3350.334175.9123.8 解C15.9400.401208.0135.7 解C27.7990.321168.4123.5 解C36.7680.328172.5122.2 解C46.8570.327171.8122.3
采用帕累托解C4的参数进行电热力性能建模仿真,并与初始解的结果进行对比。其中Q3D得到寄生电感为6.783 nH,相较初始解的7.335 nH有所下降。有限元电热耦合仿真温度分布结果如图17所示,芯片最高温度由160 ℃下降到156 ℃。有限元热力耦合仿真的纳米银烧结层应力与芯片应力分布结果如图18所示,经计算纳米银烧结层平均应力由175.9 MPa下降至170.6 MPa,芯片平均应力由123.8 MPa下降至122.6 MPa。虽然受DBC约束的限制,优化自由度较小,但仍能取得一定的性能提升。
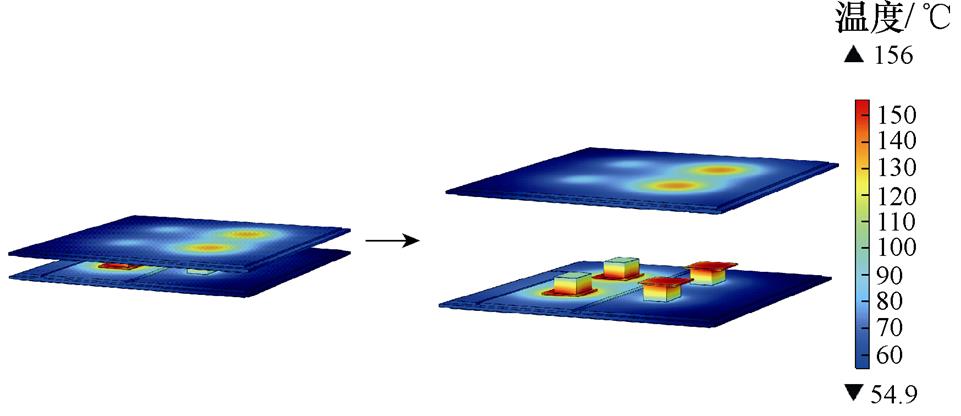
图17 帕累托解C4的温度分布
Fig.17 Temperature distribution of Pareto solution C4
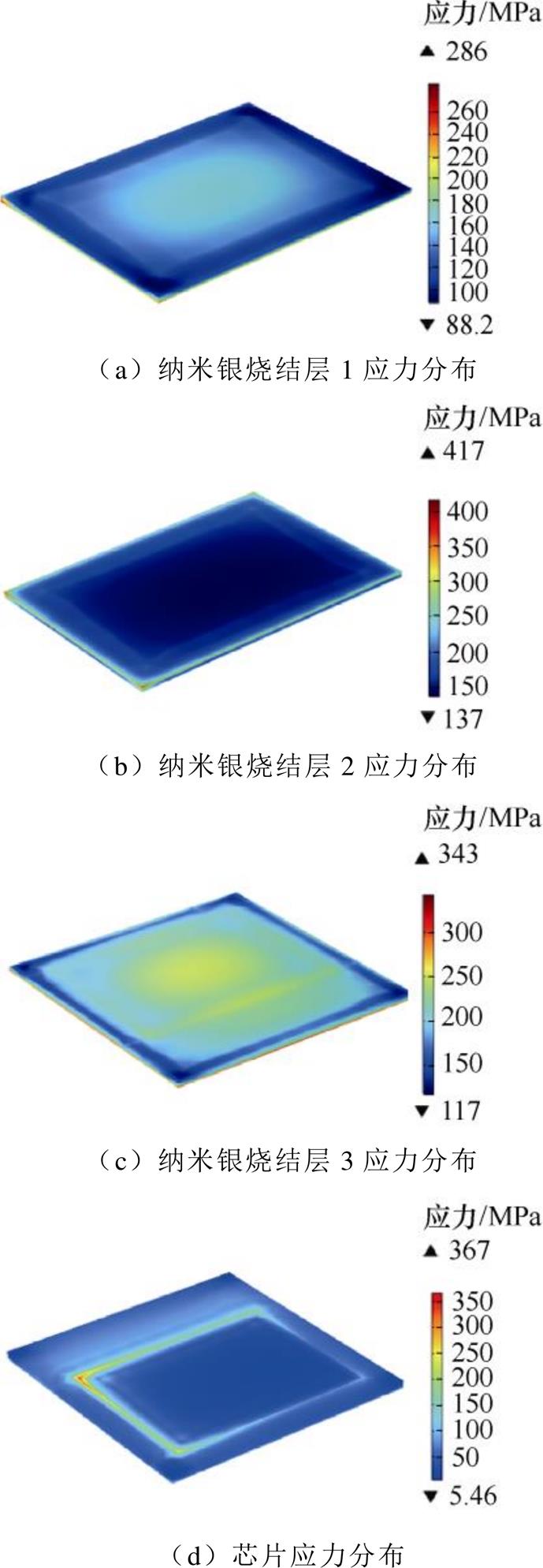
图18 帕累托解C4的各位置应力分布
Fig.18 Stress distribution in the sintered layer of pareto solution C4
为了验证所提出的多目标优化方法的正确性,选取表8和表9中的帕累托解C4作为优化解,分别制备优化前的初始功率模块以及经过优化后的功率模块,并对其性能指标进行测试。
根据本文所设计的双面散热SiC功率模块的特点,其制备流程如图19所示。
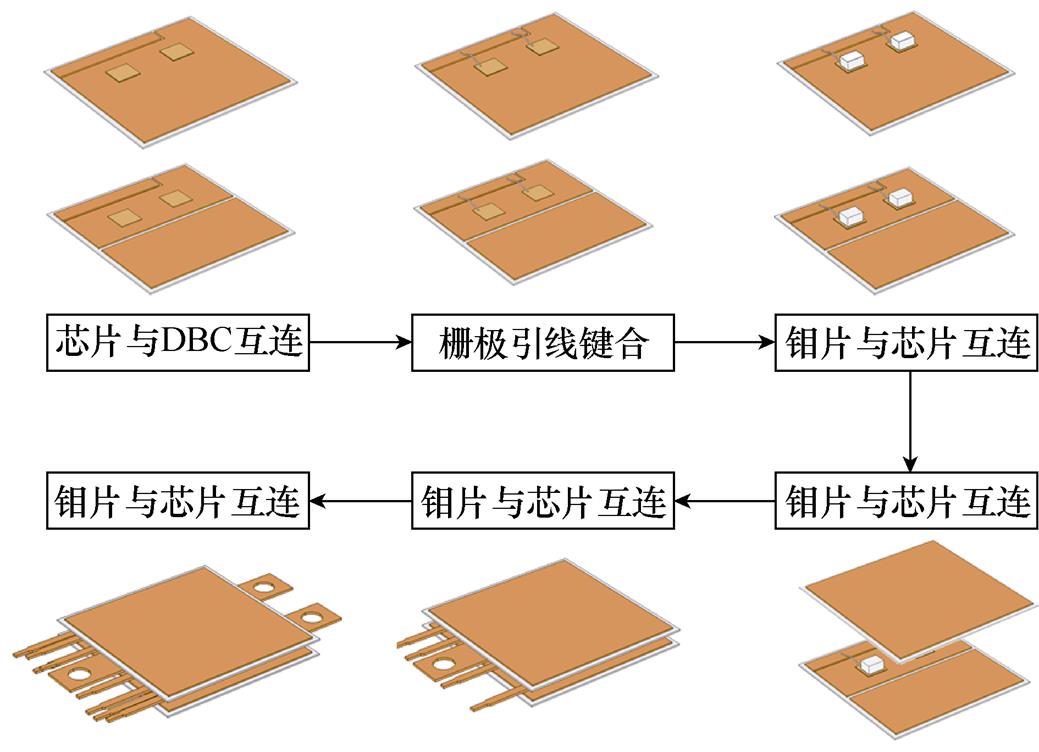
图19 功率模块制备流程
Fig.19 Preparing process of the power module
分别以功率模块初始尺寸以及优化后的尺寸制备得到的功率模块样品如图20所示。两个功率模块端子布局一致,内部芯片布局间距根据优化前后的尺寸参数存在差异。

图20 功率模块样品及其芯片布局
Fig.20 Power module sample and chip layout
功率模块寄生电感的测量可采用精密电桥进行测量,由于精密电桥无法直接测试含有芯片的功率模块,因此需要制备不含芯片的功率模块样品以测试其通流回路的寄生参数。制备得到样品后进行寄生电感测量,图21为精密电桥测量装置,初始功率模块寄生电感大小为7.475 nH,与计算得到的寄生电感值7.335 nH相差约2 %,优化后的功率模块寄生电感大小为6.489 nH,与计算得到的寄生电感值6.783 nH相差约4.3 %,对于寄生电感的测量结果验证了所提出的设计方法的准确性。实际上,不管是测量时的频率1 MHz还是仿真计算得到的20.6 MHz频率下的寄生参数,均具有较强的趋肤效应,在这种情况下,频率对寄生电感大小的影响较小,经多次仿真,1 MHz和20.6 MHz频率下的寄生电感相差小于1 %。

图21 寄生电感测量装置
Fig.21 Parasitic inductance measurement results
进行结环热阻测量,向SiC MOSFET体二极管通加热电流,分别获取热平衡后的芯片损耗、结温以及散热器的水温Ta进而计算得到结环热阻。其中结温通过温敏电参数法测得[25],对SiC MOSFET的体二极管压降与结温之间的关系式进行标定,得到在100 mA检测电流不同结温下的体二极管压降如图22所示。
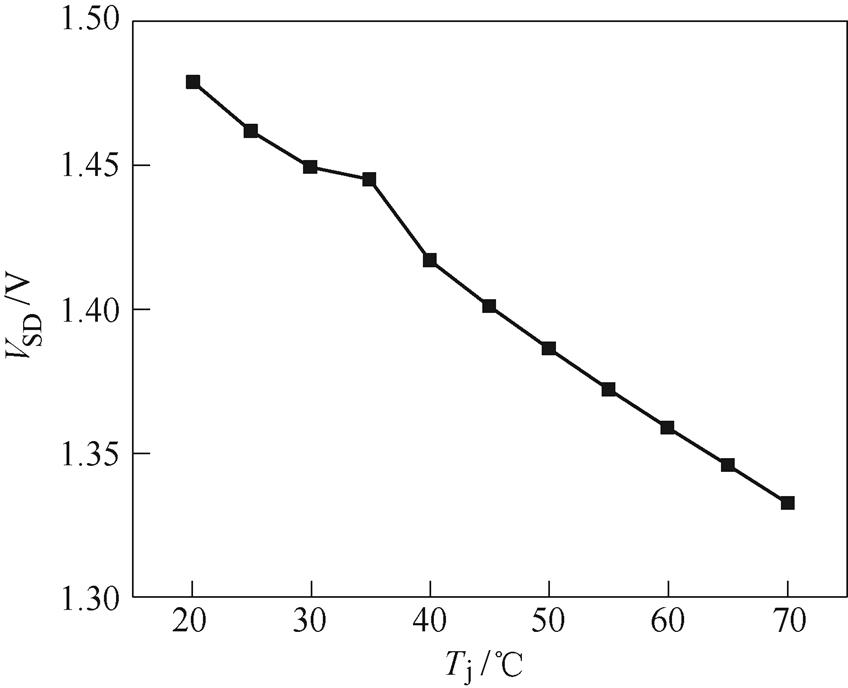
图22 不同结温下的体二极管压降
Fig.22 Body diode voltage at different junction temperatures
拟合得到在100 mA的检测电流下SiC MOSFET体二极管的压降与结温之间关系为
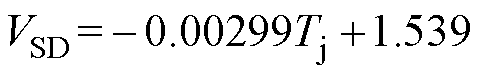 (7)
(7)
对温敏电参数与结温之间的关系标定完成后,对功率模块的结环热阻进行测量,热阻测试平台如图23所示,分别测量底面散热通道的热阻以及顶面散热通道的热阻,进而得到整个功率模块的结环热阻,如式(8)所示。测量得到初始功率模块总的结环热阻为0.373 ℃/W,优化后的功率模块总的结环热阻为0.355 ℃/W,均与计算得到的结环热阻值相差不大,对于结环热阻的测量结果验证了设计的准确性。

图23 热阻测试平台
Fig.23 Thermal resistance test platform
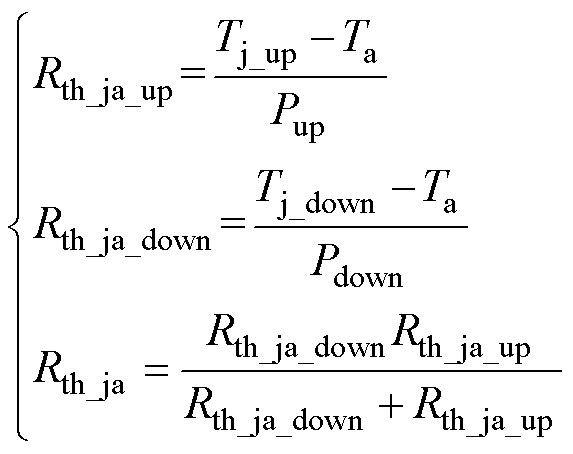 (8)
(8)
双面散热SiC功率模块凭借优异的电热性能成为功率的发展方向之一,但由于其电-热-力三场的紧密耦合,电学、热学及力学特性互相制约,需要进行多目标优化设计,针对现有功率模块封装多目标优化方法的不足,本文提出了一种基于智能算法的多目标优化设计方法,能够实现对功率模块高效灵活的定制化设计。通过研究各尺寸参数变化对功率模块各性能指标的影响规律,揭示了各性能指标随参数变化之间的制约关系,证明了进行多目标优化的必要性。所提出的基于参数化仿真与神经网络的目标函数拟合方法,能够高效准确地拟合各尺寸参数与各性能指标之间的函数关系,解决目标函数难以获得的问题。基于遗传算法的多目标优化方法,能够灵活地设定目标以及约束条件,实现功率模块定制化的设计。通过制备初始解以及优化解的功率模块,并对二者的性能指标进行测试和对比,证明了本文所提出的多目标优化方法的正确性。
参考文献
[1] 王来利, 赵成, 张彤宇, 等. 碳化硅功率模块封装技术综述[J/OL]. 电工技术学报: 1-16[2022-09-23]. DOI: 10.19595/j.cnki.1000-6753.tces.221214.
Wang Laili, Zhao Cheng, Zhang Tongyu, et al. Review of packaging and integration technology insilicon carbide power modules[J/OL]. Transactions of China Electrotechnical Society, 1-16[2022-09-23], DOI: 10.19595/j.cnki.1000-6753.tces.221214.
[2] Temple V, Waldron J, Azotea J, et al. High frequency SiC majority carrier modules[C]//Proceedings of PCIM Europe 2015; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Ger- many, 2015: 1-7.
[3] Kasko I, Berberich S E, Gross M, et al. High efficient approach to utilize SiC MOSFET potential in power modules[C]//2017 29th International Symposium on Power Semiconductor Devices and IC's (ISPSD), Sapporo, Japan, 2017: 259-262.
[4] Yang Fengtao, Jia Lixin, Wang Laili, et al. Inter- leaved planar packaging method of multichip SiC power module for thermal and electrical performance improvement[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(2): 1615-1629.
[5] Vagnon E, Jeannin P O, Crebier J C, et al. A bus- bar-like power module based on three-dimensional power-chip-on-chip hybrid integration[J]. IEEE Transactions on Industry Applications, 2010, 46(5): 2046-2055.
[6] Liang Zhenxian, Ning Puqi, Wang F. Development of advanced all-SiC power modules[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(5): 2289-2295.
[7] Mu Wei, Wang Laili, Wang Binyu, et al. Direct integration of optimized phase-change heat spreaders into SiC power module for thermal performance improvements under high heat flux[J]. IEEE Transa- ctions on Power Electronics, 2022, 37(5): 5398-5410.
[8] Ni Ze, Lü Xiaofeng, Yadav O P, et al. Overview of real-time lifetime prediction and extension for SiC power converters[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 7765-7794.
[9] Dornic N, Khatir Z, Tran S H, et al. Stress-based model for lifetime estimation of bond wire contacts using power cycling tests and finite-element modeling[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(3): 1659-1667.
[10] Lee H, Smet V, Tummala R. A review of SiC power module packaging technologies: challenges, advances, and emerging issues[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 239-255.
[11] Ding Chao, Liu H, Ngo K D T, et al. A double-side cooled SiC MOSFET power module with sintered- silver interposers: I-design, simulation, fabrication, and performance characterization[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(10): 11672- 11680.
[12] 曾正, 李晓玲, 林超彪, 等. 功率模块封装的电-热-力多目标优化设计[J]. 中国电机工程学报, 2019, 39(17): 5161-5171, 5297.
Zeng Zheng, Li Xiaoling, Lin Chaobiao, et al. Electric-thermal-stress oriented multi-objective opti- mal design of power module package[J]. Proceedings of the CSEE, 2019, 39(17): 5161-5171, 5297.
[13] 曾正, 欧开鸿, 吴义伯, 等. 车用双面散热功率模块的热-力协同设计[J]. 电工技术学报, 2020, 35(14): 3050-3064.
Zeng Zheng, Ou Kaihong, Wu Yibo, et al. Thermo- mechanical Co-design of double sided cooling power module for electric vehicle application[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(14): 3050-3064.
[14] Ji Bing, Song Xueguan, Sciberras E, et al. Multiob- jective design optimization of IGBT power modules considering power cycling and thermal cycling[J]. IEEE Transactions on Power Electronics, 2014, 30(5): 2493-2504.
[15] 能立强. 多芯片并联SiC MOSFET模块的电-热-力多物理场仿真设计研究[D]. 天津: 天津大学, 2020.
[16] Hall S H, Hall G W, McCall J A. High-speed digital system design: a handbook of interconnect theory and design practices[M]. New York: Wiley, 2000.
[17] Le Quang, Al Razi I, Evans T M, et al. Fast and accurate parasitic extraction in multichip power module design automation considering eddy-current losses[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, PP(99): 1.
[18] Wang Jianpeng, Chen Wenjie, Wang Laili, et al. A transient 3-D thermal modeling method for IGBT modules considering uneven power losses and cooling conditions[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 3959- 3970.
[19] 陈宇, 周宇, 罗皓泽, 等. 计及芯片导通压降温变效应的功率模块三维温度场解析建模方法[J]. 电工技术学报, 2021, 36(12): 2459-2470.
Chen Yu, Zhou Yu, Luo Haoze, et al. Analytical 3D temperature field model for power module con- sidering temperature effect of semiconductor voltage drop[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2459-2470.
[20] Le Henaff F, Azzopardi S, Woirgard E, et al. Lifetime evaluation of nanoscale silver sintered power modules for automotive application based on experiments and finite-element modeling[J]. IEEE Transactions on Device and Materials Reliability, 2015, 15(3): 326- 334.
[21] Dragičević T, Wheeler P, Blaabjerg F. Artificial intelligence aided automated design for reliability of power electronic systems[J]. IEEE Transactions on Power Electronics, 2018, 34(8): 7161-7171.
[22] Wang Jianpeng, Chen Wenjie, Wu Yuwei, et al. Chip- level electrothermal stress calculation method of high-power IGBT modules in system-level simu- lation[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 10546-10561.
[23] (美)埃德温, (美)扎克著. 最优化导论[M]. 孙志强等译. 北京: 电子工业出版社, 2015.
[24] 袁立强, 陆子贤, 孙建宁, 等. 电能路由器设计自动化综述—设计流程架构和遗传算法[J]. 电工技术学报, 2020, 35(18): 3878-3893.
Yuan Liqiang, Lu Zixian, Sun Jianning, et al. Design automation for electrical energy router-design work- flow framework and genetic algorithm: a review[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3878-3893.
[25] 陈杰, 邓二平, 赵子轩, 等. 不同老化试验方法下SiC MOSFET失效机理分析[J]. 电工技术学报, 2020, 35(24): 5105-5114.
Chen Jie, Deng Erping, Zhao Zixuan, et al. Failure mechanism analysis of SiC MOSFET under different aging test methods[J]. Transactions of China Elec- trotechnical Society, 2020, 35(24): 5105-5114.
Abstract Double-sided cooling power module has low parasitic parameters and excellent heat dissipation performance, which is one of the development directions of power modules. However, its electrical, thermal, and mechanical properties are contradictory, so achieving the complete optimization of all performance is difficult. As a new packaging structure type, the double-sided cooling power module lacks a systematic multi-objective optimization design method. Therefore, this paper proposes a multi-objective optimization design method based on an intelligent algorithm.
Firstly, the structure of the double-sided cooling SiC power module was designed, and the material of each key component within the module was determined. The electrical, thermal, and mechanical properties of the designed power module were analyzed by parasitic parameter simulation and finite element electro-thermal coupling simulation. The parasitic inductance was calculated using ANSYS Q3D, and the junction-to-ambient thermal resistance was calculated using COMSOL. The mechanical properties, including die attach stress and chip stress, were calculated using COMSOL considering the temperature gradient in the heat conduction process. After that, the influence of the size parameters on the performance indexes of the power module was studied. There are three key points: (1) h2 has a large effect on the parasitic inductance through eddy current effect; (2) a negative relationship between h1 and the thermal resistance exists because a thicker copper layer can spread more heat horizontally; (3) the chip stress optimization and the die attach stress is contradicted.
Secondly, a multi-objective optimization method based on an intelligent algorithm was proposed using the method of parametric modeling and simulation. Based on the randomly generated size parameters, hundreds of module samples were simulated, and the results were used as training samples for the artificial neural network. The functional relationship between size parameters and performance indexes can be obtained, which can speed up the calculation of the performance index and ensure calculation accuracy. After obtaining the objective function, a genetic algorithm is used to solve the multi-objective optimization. A three-objective optimization of die attach stress, parasitic inductance, and thermal resistance was conducted. The Pareto front is a curve because thermal resistance and die-attach stress have the same optimization direction. Then a three-objective optimization of chip stress, parasitic inductance, and thermal resistance was conducted. The Pareto front is a curved surface because these performance indexes have different optimization directions. To achieve customized optimization, a stricter size constraint was set, and a four-objective optimization was conducted including die-attach stress, chip stress, parasitic inductance, and junction-to-ambient thermal resistance. A solution that can improve all performance exists.
Finally, based on four-objective optimization, the power modules before and after optimization were manufactured, and their performance indexes were tested and compared. The parasitic inductance was measured using an LCR meter, and junction-to-ambient thermal resistance was measured using a thermal characteristic test platform. The results show that the multi-objective optimization method can significantly improve the overall performance of the double-sided cooling SiC power module, the loop parasitic inductance is reduced from 7.475 nH to 6.489 nH, and the thermal resistance is reduced from 0.373 K/W to 0.355 K/W.
keywords:SiC power module, double-sided cooling, multi-objective optimization, artificial neural network, genetic algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.221526
中图分类号:TM23
收稿日期 2022-08-04
改稿日期 2022-08-24
张 缙 男,1998年生,博士研究生,研究方向为功率半导体器件的封装与可靠性。E-mail: z062626@stu.xjtu.edu.cn
王来利 男,1982年生,教授,博士生导师,研究方向为电力电子封装集成。E-mail: llwang@mail.xjtu.edu.cn(通信作者)
(编辑 郭丽军)