1，其漏感可作为Lr2的一部分参与谐振，由于励磁电感未参与谐振，其值可设为理想的无穷大；二次侧采用VD1～VD4组成的全桥整流结构；Cf为输出的滤波电容。iC为谐振电流，VAB为谐振腔输入电压。变换器采用变频控制方式，通过改变开关频率来调节输出电压。摘要 CLL谐振变换器在工作中谐振电流会回流到输入源产生回流功率，回流功率的增加会导致变换器产生更多的传导损耗，这限制了转化效率的提高。对此，基于回流功率的定义对全桥CLL变换器的工作模态进行详细分析，指出在正负模态中都会有回流功率的产生。同时，分析CLL变换器的交流等效模型，并结合产生回流功率的模态，得出回流功率可用谐振腔输入电压和电流的相移角间接表征。在此基础上，提出一种CLL变换器回流功率的简单表征方法，通过对谐振参数的优化设计来减小回流功率，从而提高转化效率。最后，通过两组谐振参数的仿真和实验对该设计方法进行验证，结果表明在谐振频率点和满载条件下，转化效率提高约1.8%，验证了理论分析的正确性和可行性。
关键词：全桥CLL谐振变换器 回流功率 参数优化 设计转化效率 软开关
谐振变换器由于其高效率、高功率密度和电磁干扰小等优点[1]，近年来在工程应用中已成为研究的热点，广泛应用在分布式电源系统、便携式计算机、通信设备以及新能源电动汽车等领域[2-4]。在众多谐振拓扑中，国内外专家、学者对LLC谐振变换器研究得最多，其在应用中也最为广泛。而本文将研究另一种新型谐振拓扑结构的变换器，其谐振腔为一个T型的CLL结构，工作特性与传统LLC十分相似，同样可实现一次侧MOS管的零电压开通（Zero Voltage Switching, ZVS）以及二次侧二极管的零电流关断（Zero Current Switching, ZCS）[5]。由于励磁电感未参与到谐振中，且不存在变压器气隙涡流损耗问题，因此在磁元件设计方面具有一定的优势[6-8]。谐振变换器最大的优点就是它的高转化效率，而变换器在工作中无法避免回流功率的产生，回流功率的增加会导致换流开关的传导损耗和电流应力急剧增加，从而降低转化效率[9]。因此研究回流功率的优化方法在工程应用上具有一定的指导作用。
现有文献对回流功率的优化研究主要是针对移相全桥、双有源桥（Dual-Active-Bridge, DAB）结构，通过各种混合控制策略能在一定程度上减小回流功率，提高效率[10-12]。文献[13]针对DAB的固态变压器（Solid State Transformer, SST）转换器两侧进行全面分析，在此基础上，建立了完整的传输功率、回流功率和峰值电流的数学模型，提出一种基于扩展移相的最小回流功率控制策略，可提高输出功率的调节灵活性，最大限度地减少回流功率提高效率。文献[14]针对混合三电平双向DC-DC变换器提出一种变占空比与移相结合的控制方法，将系统工作分为四种模式，根据每种模式的等效电路推导变换器传输功率及软开关条件，实现最小回流功率控制。
总体而言，通过移相控制的方法对回流功率进行优化已经研究得比较成熟，但是对于非移相全桥来讲则研究较少，因此需要找到其他的方法来解决问题。针对谐振变换器的性能优化问题，有不少文献通过谐振参数的优化设计来解决。文献[15]提出一种半桥LLC谐振变换器回流功率表征方法，在一定程度上能减小变换器在负半谐振周期所产生的回流功率，但在分析回流功率特性时未考虑死区时间的影响，可能使ZVS无法实现。文献[16]针对双向T-LCL变换器提出通过谐振参数的设计，变换器在固定输入输出电压条件下成功地降低了回流功率，但未能实现整个开关频率范围的软开关，带来了更多的损耗。文献[17]针对半桥CLL变换器提出一种基于等效谐振腔的参数设计方法优化回流功率，该方法无需直接分析变换器的各种工作特性，通过与LLC的等效关系便可间接获得其回流功率特性。文献[18]利用时域分析法分析了LLC变换器ZVS上下边界处的工作状态，计算出变换器软开关运行所允许的输出电压范围，揭示了变换器的软开关特性与工作频率、谐振参数之间的关系，为变换器的参数设计和变频控制提供了理论指导。
综上所述，针对全桥CLL谐振变换器产生回流功率的问题，提出一种简单的回流功率表征方法，该方法相对于传统定义式表征更加简单且便于计算，能清晰地描述谐振参数与回流功率之间的动态关系，通过对谐振参数的优化设计来减小回流功率，提高转化效率。本文首先根据回流功率定义对变换器产生回流功率的模态进行详细分析，并且结合CLL交流等效模型得出了回流功率的简单表征方法，分析了CLL谐振参数与回流功率之间的内在关系；其次，基于全桥CLL的回流功率特性，并结合电压增益及零电压导通（ZVS）的约束设计最优谐振参数优化回流功率；最后通过仿真分析和搭建一个100 W的实验平台验证了所提方法的正确性和有效性。
图1为全桥CLL谐振变换器拓扑结构，主要由方波发生器、CLL谐振腔、中间变压器、全桥整流、滤波输出五部分组成。方波发生器包括开关管S1～S4，Coss1～Coss4为4个MOS管的寄生电容，Coss1= Coss2=Coss3=Coss4=Coss，同一桥臂的2个开关管互补导通，中间留出一定死区；CLL谐振网络由1个谐振电容Cr和2个谐振电感Lr1和Lr2组成，呈现出一个T形结构；中间变压器部分，匝数比为n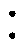1，其漏感可作为Lr2的一部分参与谐振，由于励磁电感未参与谐振，其值可设为理想的无穷大；二次侧采用VD1～VD4组成的全桥整流结构；Cf为输出的滤波电容。iC为谐振电流，VAB为谐振腔输入电压。变换器采用变频控制方式，通过改变开关频率来调节输出电压。
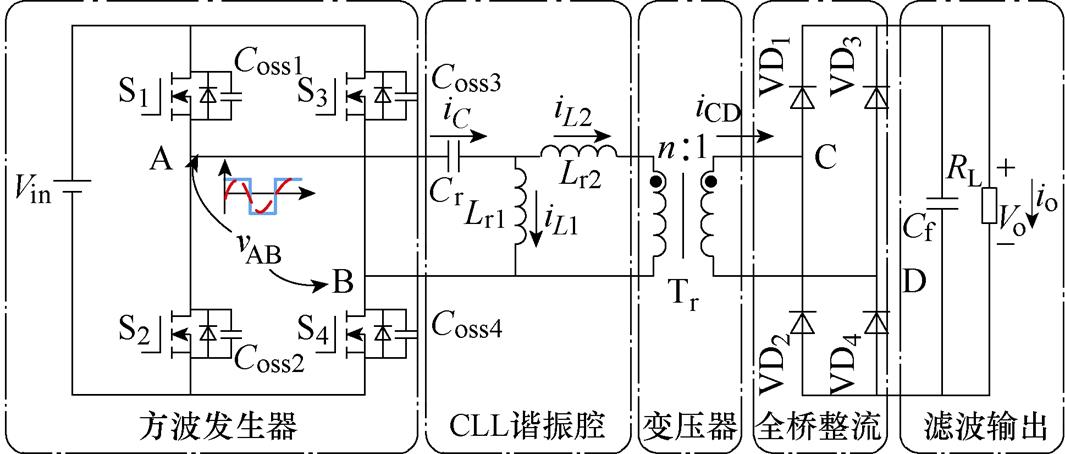
图1 全桥CLL谐振变换器拓扑
Fig.1 Topology of full-bridge CLL resonant converter
CLL谐振变换器有两个谐振频率，即
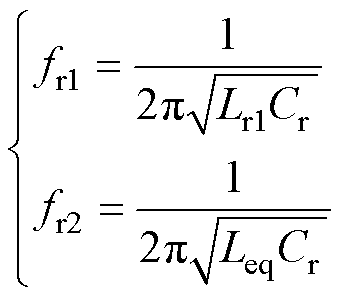（1）
式中，Leq=Lr1Lr2/(Lr1+Lr2)为等效电感；fr2为特征频率。
图2为全桥CLL谐振变换器的工作模态及典型波形。由于CLL变换器在欠谐振（fs＜fr2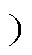
状态下的工作模态包括了准谐振和过谐振时的工作模态，因此以欠谐振时的模态进行分析。以谐振电流波形为基准，在一个谐振周期Ts中，将变换器的工作分为八种模态，其中正向和负向各四种，且它们是对称的。在全桥CLL变换器中正向和负向模态都有产生回流功率的现象，这里以它的4个负向工作模态为例进行分析。
图2 全桥CLL工作模态和典型波形
Fig.2 Full-bridge CLL working mode and typical waveforms
1）模态1[t0, t1
：从t0时刻谐振电流过零点开始，电流方向由正变到负，且谐振电容Cr、谐振电感Lr1和Lr2都参与谐振，其谐振频率为fr2，此时变换器一次侧向二次侧传递能量，变压器一次电压被钳位到-nVo，二次侧二极管VD2、VD3导通，直到t1时刻iC与iL1重合，模态1结束。其模态等效电路如图3a所示。
2）模态2[t1, t2：此时iL2为0，谐振电感Lr2未参与谐振，谐振频率为fr1，一次侧不再向二次侧传递能量，二次侧二极管VD2、VD3电流为0，为之后ZCS的实现提供条件，负载由滤波电容供电。其模态等效电路如图3b所示。
3）模态3[t2, t4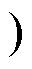：在t2时刻，S2、S3关断，进入死区时间，由于电路谐振的作用，二次侧二极管VD2、VD3此时实现ZCS，同时VD1、VD4开始换流导通。谐振电流流过4个MOS管的寄生电容并进行充放电，其中对Coss1、Coss4的放电为之后S1、S4的ZVS实现提供条件。t3时刻寄生电容完成充放电后，谐振电流通过S1、S4体二极管回流到输入源，此时谐振腔输入电压VAB已充电至Vin，由于iC＜0，因此会产生一个电流回流的负功率。直到t4时刻S1、S4驱动信号到达，死区时间结束，且两端电压为0，实现ZVS。其模态等效电路如图3c和图3d所示。
4）模态4[t4, t5]：S1、S4开始导通，谐振电流继续回流到输入电源Vin缓冲回流功率，直到t5时刻电流过零点处回流功率为0，之后电流由负变为正，电源输入电流与谐振电流同向，进入到正向模态。其模态等效电路如图3e所示。
根据对图2的负向模态分析可知，在模态3和模态4中，谐振电流回流到输入电源中产生回流功率，因此在一个谐振周期中，将有4个模态有回流功率的产生，图2中阴影部分可表示回流功率。
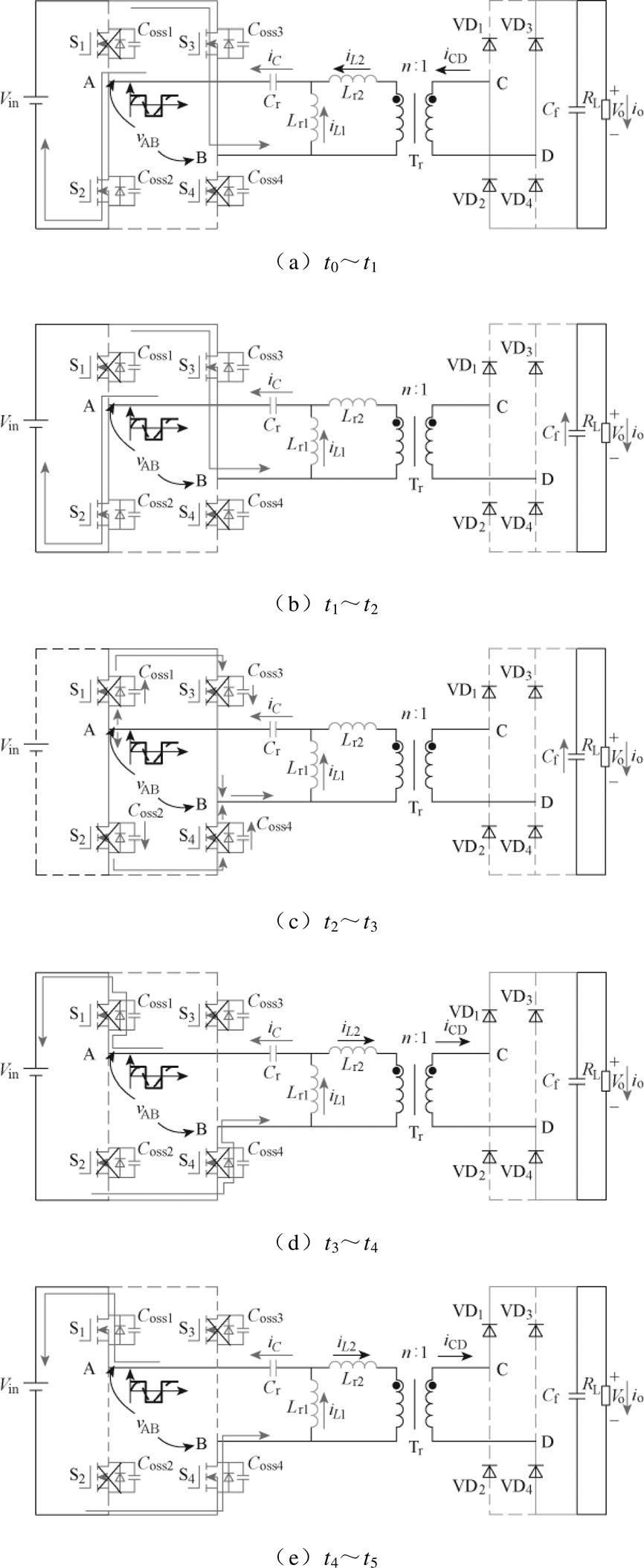
图3 模态等效电路
Fig.3 Modal equivalent circuit
当fs=fr2时，变换器工作在准谐振模式，谐振电流等效为一个正弦波，其时域解析表达式[8]为
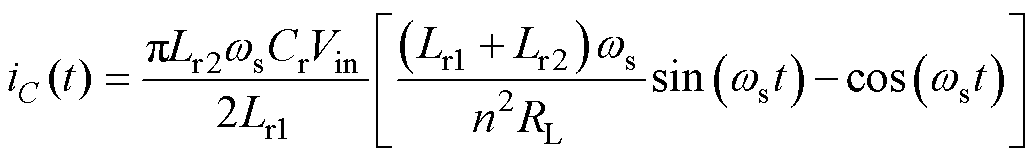（2）
根据以上对负向模态的分析，回流功率在t2～t5这段时间内产生。根据回流功率的定义为谐振腔输入电压VAB与谐振电流iC的乘积。在模态3中由于对寄生电容的充放电时间很短，可忽略不计，因此在t2～t5这段时间内，VAB=Vin，在负半周期中的回流功率表达式为
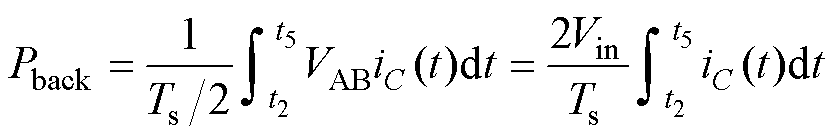（3）
将式（2）代入式（3）中，整理得出回流功率的时域表达式为
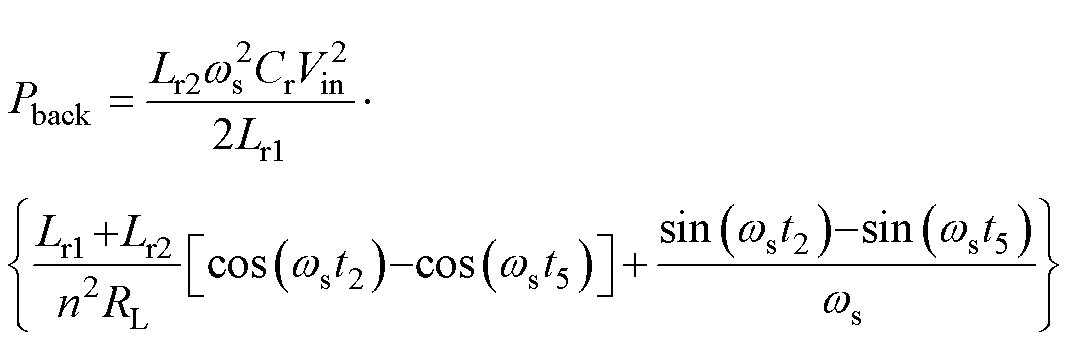（4）
由于CLL谐振变换器是变频控制，当开关频率偏离谐振频率时，谐振电流不能等效于一个正弦波，因此式（4）中对回流功率的求解具有一定的局限性。在其他开关频率条件下，谐振电流不能用式（2）直接计算，只能在等效电路中通过列写KVL求解状态方程得出，并且由于状态变量的解析解本身具有高度复杂性，需通过数学计算软件中的迭代循环来获得精确的解析解，这带来了计算的复杂性。因此通过直接分析定义式的方法来优化回流功率具有一定困难，传统的表征方法难以优化回流功率。
从回流功率的模态分析中可以看出，回流功率本质上是在电路中循环的无功功率，而不是直接等同于功率损耗。电路中大量回流功率导致的功率损失仅消耗在无功路径中的有源和无源元件的等效电阻中。因此无需直接计算，用一个能指示回流功率的变量来表征即可，这样能避免复杂的数学求解。
在全桥结构中，一个谐振周期有2个回流功率模态，且它们是对称的关系。以负向模态为例，对产生回流功率的部分进行分析。如图4a所示，以S2、S3关断进入死区时刻为0时刻，谐振电流开始回流到输入源产生回流功率（忽略寄生电容充放电时间），直到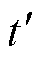
时谐振电流换向，回流功率为零。因此可以用一个产生回流功率的时间变量来描述回流功率的大小，即可用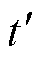来统一表征正、负模态中的回流功率。从图4中可以看出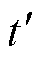，实质上是谐振电流滞后于谐振腔输入电压的时间，
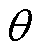为谐振电流的相位，由于VAB的相角为0，因此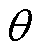在数值上为谐振电流滞后于谐振腔输入电压的相位，且满足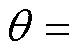
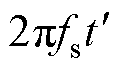，即回流功率还可用图4b中谐振等效电路的输入阻抗角来表征，其中CLL谐振等效电路的输入阻抗为
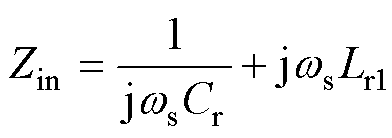
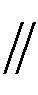
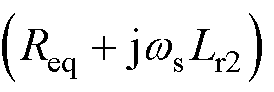（5）
将式（5）归一化处理为
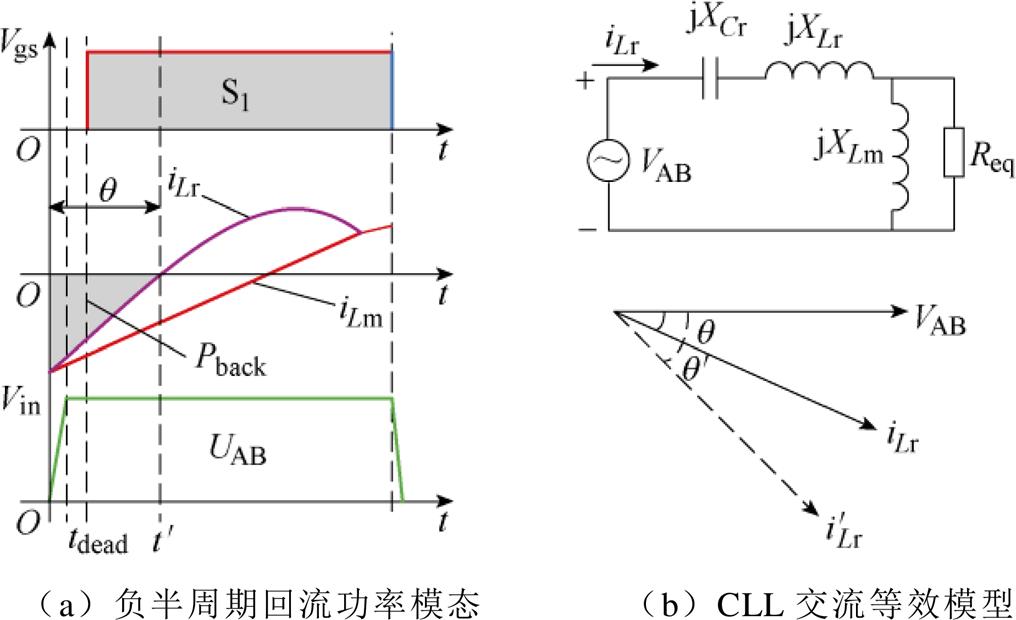
图4 回流功率表征示意图
Fig.4 Schematic diagram of backflow power
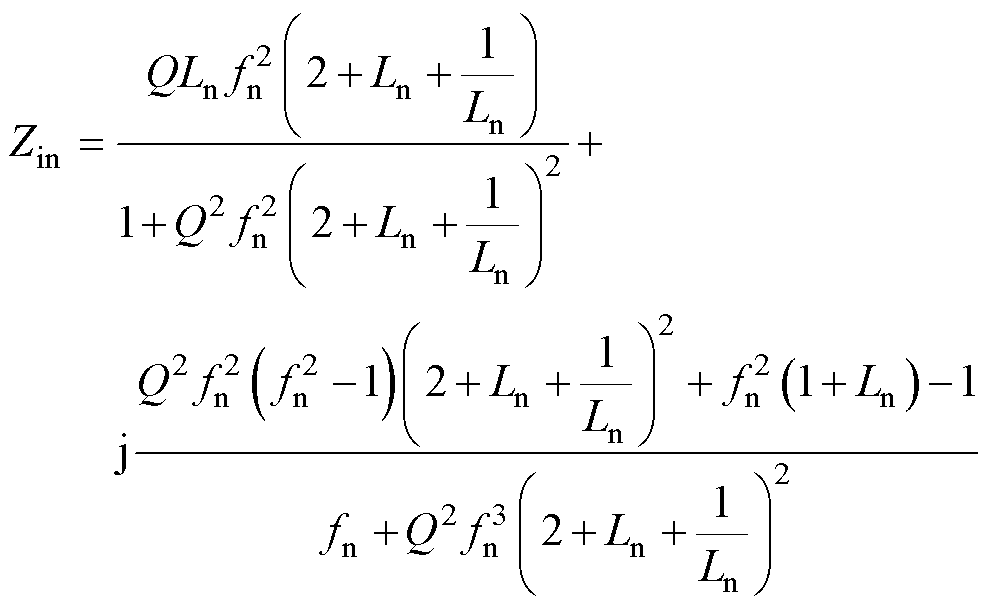（6）
式中，Req为二次侧等效到一次侧的等效电阻，Req= 8n2RL/p2；Ln为电感比，Ln=Lr1/Lr2；fn为归一化开关频率，fn=fs/fr2；Q为品质因数，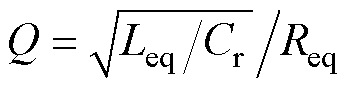
。
因此输入阻抗角可表示为
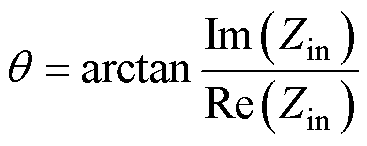（7）
其中
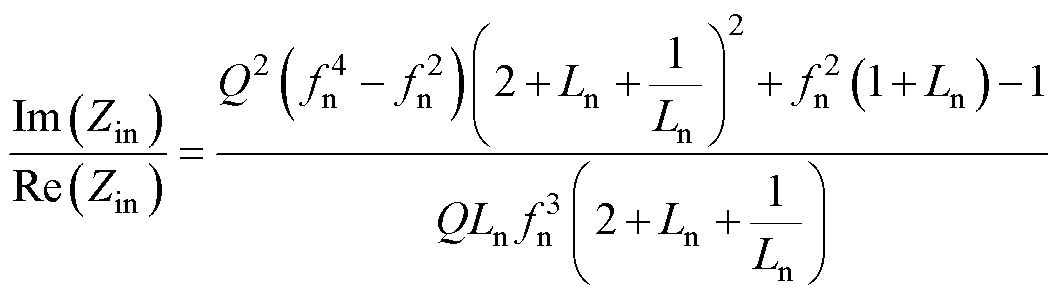（8）
为能更好地预测谐振参数与回流功率之间的动态关系，用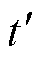表征的回流功率表达式为
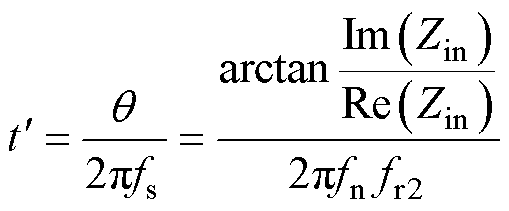（9）
通过第2节的分析，回流功率可用其产生时间来描述，从式（9）中可以看出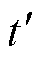，是关于谐振腔参数的一个函数，即可用设计谐振参数的方式来优化回流功率。
在设计谐振参数优化回流功率的同时，还需考虑变换器的ZVS以及电压增益的约束。为保证一次侧MOS管的ZVS，需要足够的死区时间来让MOS管的寄生电容完成充放电，使在下一个开关导通信号到来前，MOS管的寄生电容能放电至0，体二极管导通，实现ZVS。此外，当谐振电流的过零点时间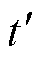＜tdead时（在死区时间内谐振电流换向），会对寄生电容进行反向充放电，导致在下一个开关导通信号到来时，MOS管两端的电压从0又回升到一定电压值，使ZVS失败。因此为了保证ZVS的实现，需满足
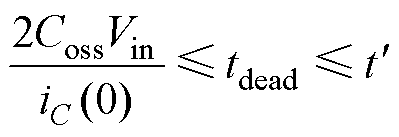（10）
从式（10）中可以看出，较大的死区时间需要较小的关断电流iC(0)来实现ZVS，意味着对死区时间的适当设计，可实现较小的循环电流，从而减小回流功率。
此外，还需对变换器的电压增益进行讨论。为了方便设计并且使变换器在宽输出电压范围内达到要求，设计输入电压为额定值时，交流电压增益约束条件为
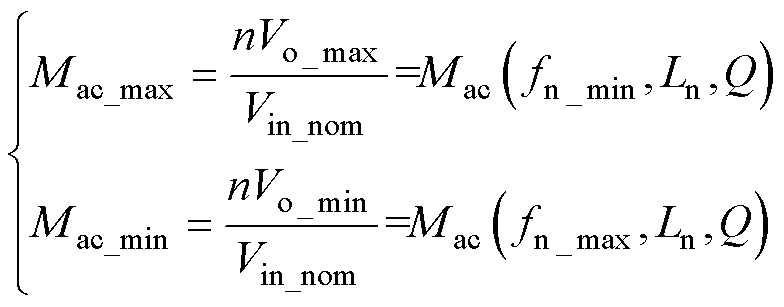（11）
式中，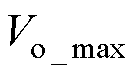
为输出电压最大值；
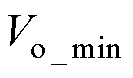为输出电压最小值；
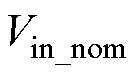为Vin的额定值。
式（11）中，CLL交流电压增益函数为
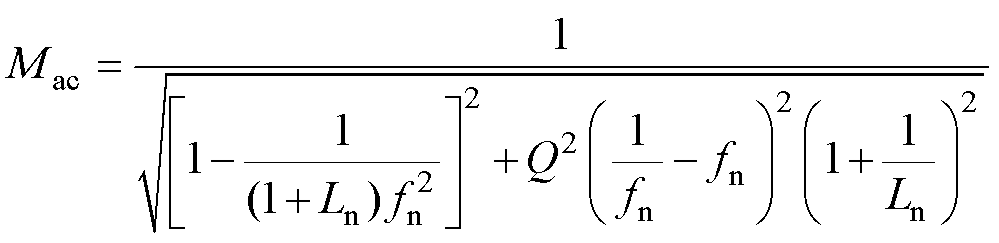（12）
为对其性能进行评估，全桥CLL变换器具体设计规格见表1。
在确定谐振频率的情况下，CLL谐振参数可以有多种配置方式，根据需求选择Q与Ln的组合，最终确定谐振参数。本文以优化回流功率为目的，通过谐振参数对回流功率的影响，找到一条最优回流功率曲线，确定最优谐振参数。
表1 变换器设计要求
Tab.1 Converter design requirements
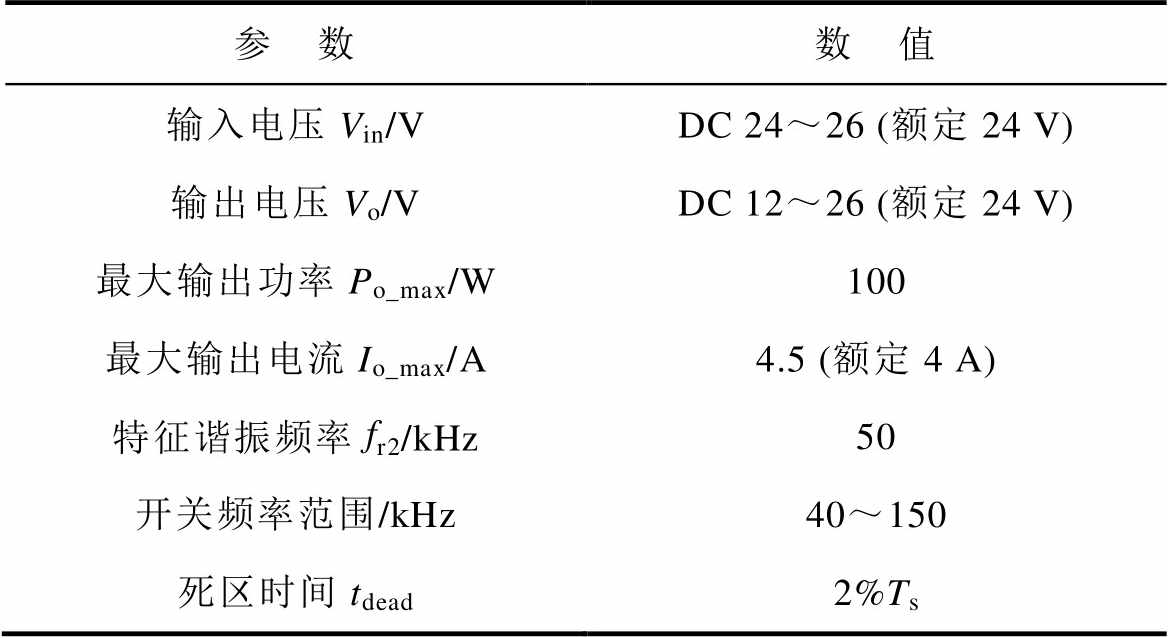
参 数数 值 输入电压Vin/VDC 24～26 (额定24 V) 输出电压Vo/VDC 12～26 (额定24 V) 最大输出功率Po_max/W100 最大输出电流Io_max/A4.5 (额定4 A) 特征谐振频率fr2/kHz50 开关频率范围/kHz40～150 死区时间tdead2%Ts
在LLC谐振变换器中，电感比被定义为励磁电感与谐振电感的比值Lm/Lr，励磁电感越大，回流功率越小，但为满足ZVS条件，励磁电感的上限约束式为
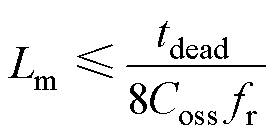（13）
式中，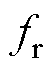
为LLC的谐振频率，
。
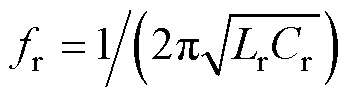若Lm取最大值，可能导致较高的电感比，增益减小，励磁电流峰值降低，效率提高，但是对于低电压输入满足最大增益来讲，可能无法满足变换器的增益条件，因此根据设计经验，在LLC中电感比一般会选择2～6之间。而对于CLL变换器，励磁电感将不作为谐振元件参与谐振，为减小损耗可设为无穷大。在文献[5]中，对于谐振元件部分，定义了一个等效特征电感Lp来表示关断电流，即
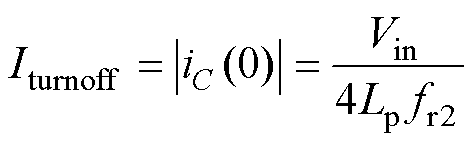（14）
其中
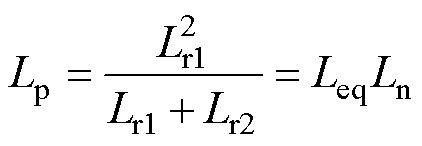（15）
结合式（14）和式（10）可得
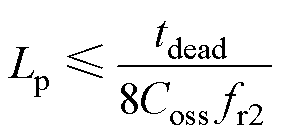（16）
对比式（13）和式（16）不难发现，Lp与Lm等价，Leq与Lr等价，因此针对Ln的选取，CLL变换器可参考与LLC类似的设计方法。
需要注意的是，在设计全桥CLL的变压器匝比时，在谐振频率点处电压增益始终大于1，且与电感比Ln有关，变压器匝比设计为
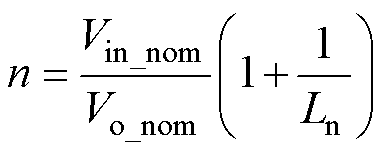（17）
式中，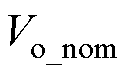
为Vo的额定值。
因此相较于LLC，在CLL中Ln的变化会影响匝比n的设计，间接影响了等效电阻Req，从而对CLL的回流功率分析又多了一个影响因素。图5为不同Ln条件下的回流功率特性，从图5中可以看出，Ln增大，Q=0.15的曲线在谐振频率点的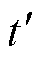值从2.593 ms减小到2.284 ms，说明较大的Ln值有助于回流功率的减小，同时最小回流功率曲线对应的Q值也会相应减小，这对系统的稳定响应来说是有利的。
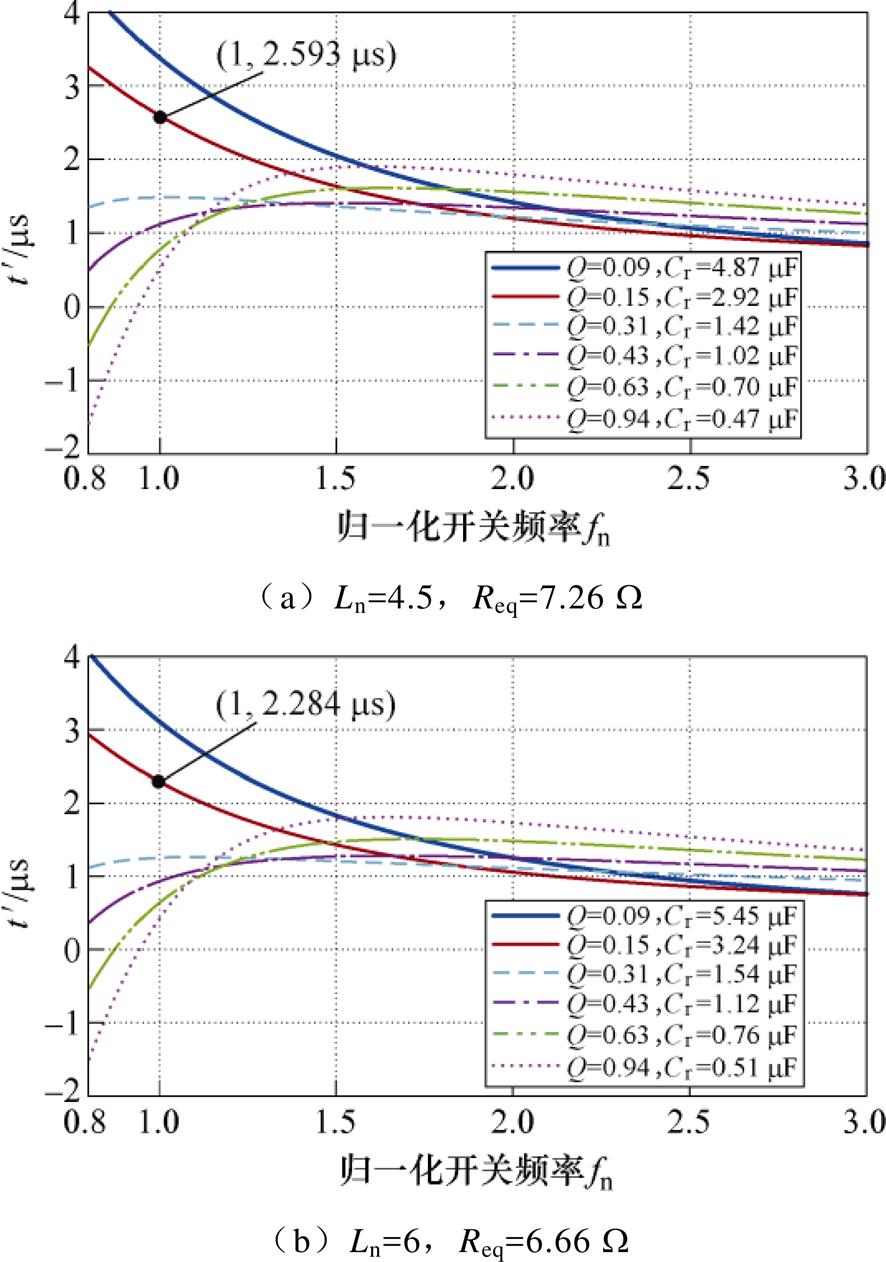
图5 不同Ln值的回流功率特性比较
Fig.5 Comparison of backflow power characteristics with different Ln values
图6为在Ln=6，负载电阻RL=6 W（满载）条件下，不同CLL谐振参数对回流功率表征值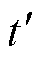的影响。可从图中看出，在整个归一化开关频率范围（0.8～3）内，若谐振电容Cr＜1.25 mF，则在低频时可能无法实现ZVS，甚至进入容性区域。而与较小的谐振电容相比，较大的谐振电容可实现全开关频率范围的ZVS，但是若谐振电容值过大会导致较大的回流功率，增大损耗。当变换器工作在谐振点时具有最高的转化效率，同时也是最理想的工况，图6中显示在谐振频率点附近谐振参数对回流功率的影响较大，因此对谐振参数的合理选取成为减小回流功率、提高转化效率的关键。为满足优化要求，谐振电容需要折中选取，当Cr取1.25～2.20 mF之间时，既保证了全开关频率范围内的ZVS，又产生了较小的回流功率。
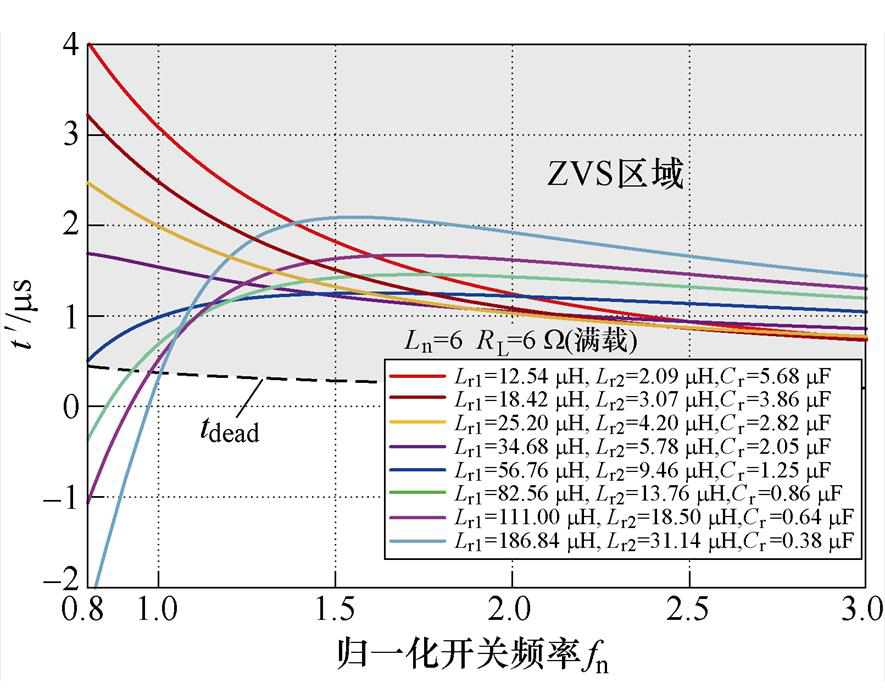
图6 谐振参数对回流功率的影响
Fig.6 Influence of resonance parameters on backflow power
图7为CLL谐振参数设计的三维绘图，区域一在低频时不易实现ZVS，区域二和三均可实现全开关频率的ZVS，但区域三在谐振频率点附近有较大的回流功率，因此区域二为设计谐振参数的建议区域。图8为对全桥CLL谐振变换器进行效率优化的参数设计流程。
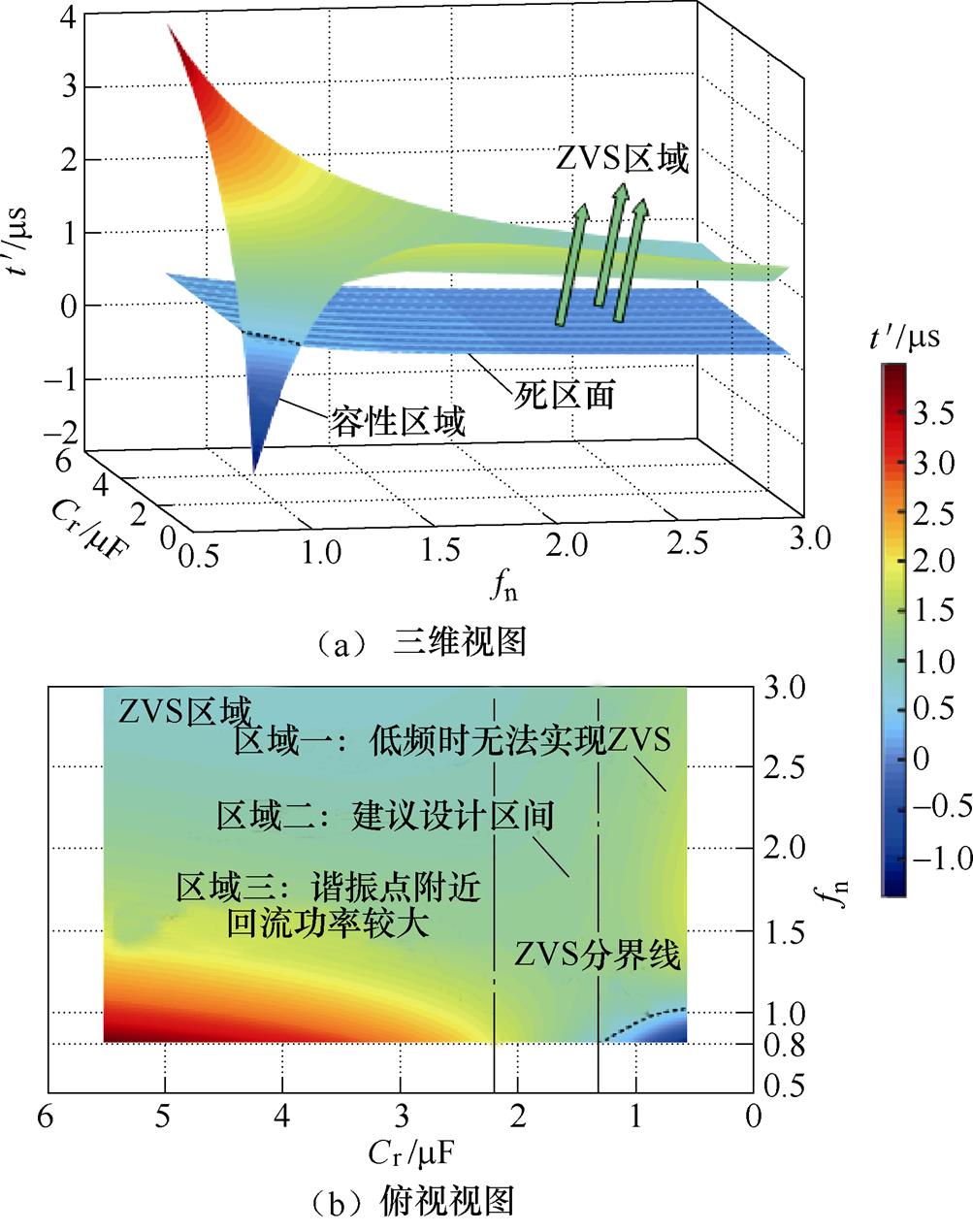
图7 设计方法的三维绘图
Fig.7 Three-dimensional plots of the design method
为验证本文所提方法的正确性，在Matlab/ Simulink平台上搭建了全桥CLL谐振变换器进行仿真分析，并设计了一台100 W的实验样机进行了进一步的验证。输入直流电压源为额定24 V，负载为满载6 W 电阻，用两组不同谐振参数来评估优化谐振参数对变换器转化效率的影响。两组谐振参数见表2。两组谐振腔参数各自的回流功率特性如图9所示。
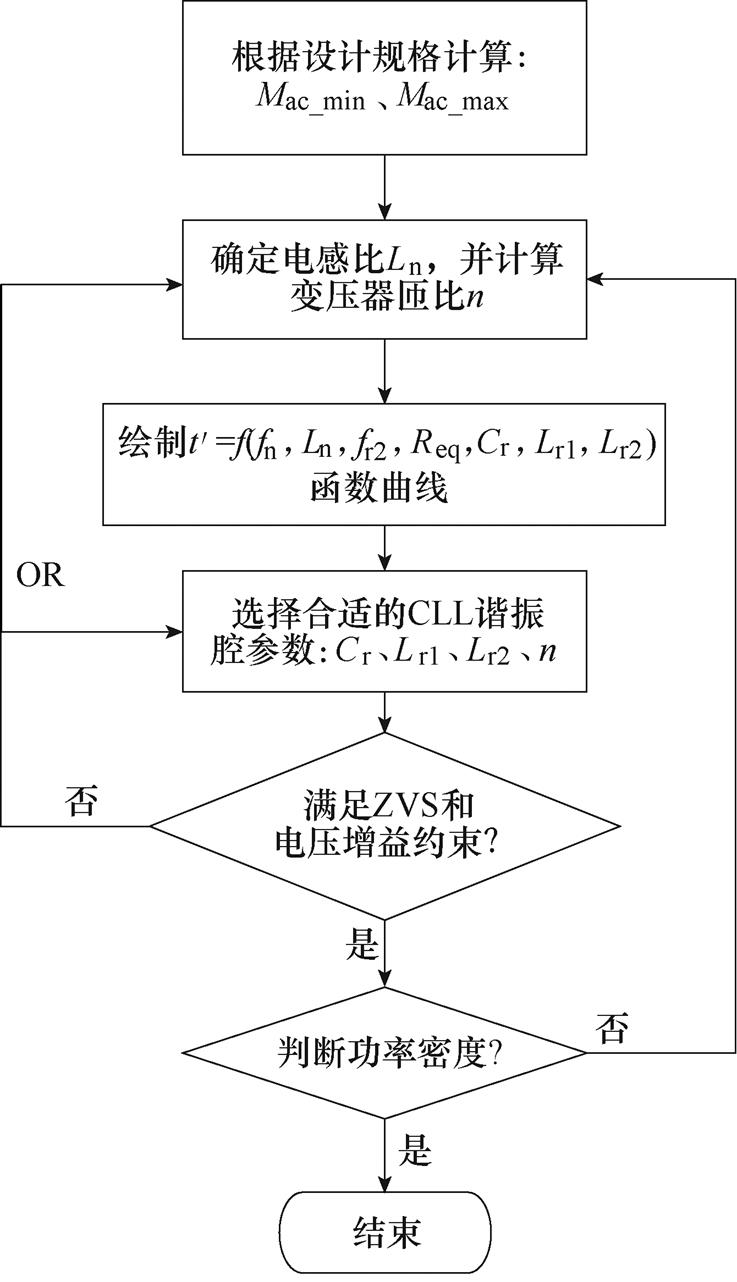
图8 设计流程
Fig.8 Design process
表2 谐振腔参数
Tab.2 Resonance tank parameters
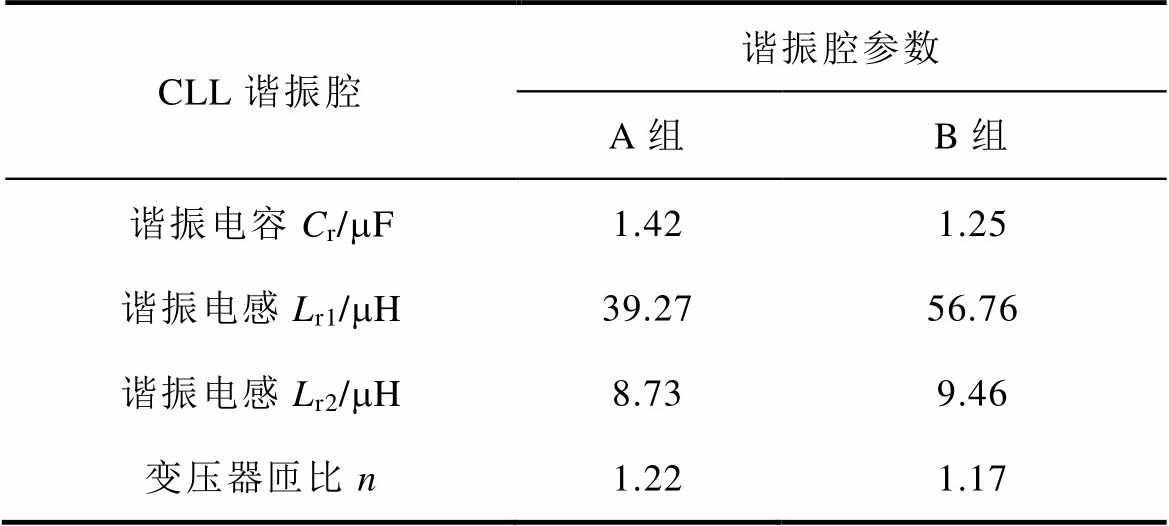
CLL谐振腔谐振腔参数 A组B组 谐振电容Cr/mF1.421.25 谐振电感Lr1/mH39.2756.76 谐振电感Lr2/mH8.739.46 变压器匝比n1.221.17
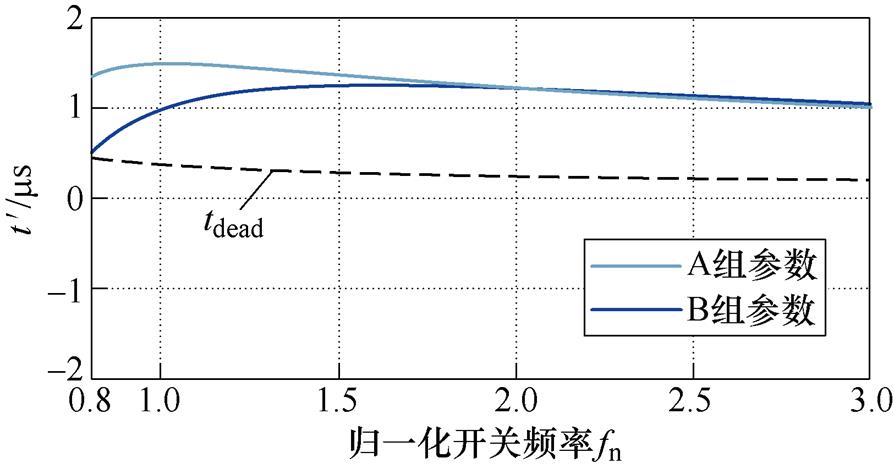
图9 两组谐振参数的回流功率特性
Fig.9 Backflow power characteristics of two groups of resonance parameters
对表2中的两组谐振参数进行仿真，分别在归一化开关频率fn=0.8（fs=40 kHz）、fn=1（fs=50 kHz）、fn=2（fs=100 kHz）条件下进行对比。图10为全桥CLL谐振变换器关键波形仿真，图10a～图10c为A组谐振参数波形，图10d～图10f为B组谐振参数波形。表3为两组谐振参数回流功率表征值的仿真结果。
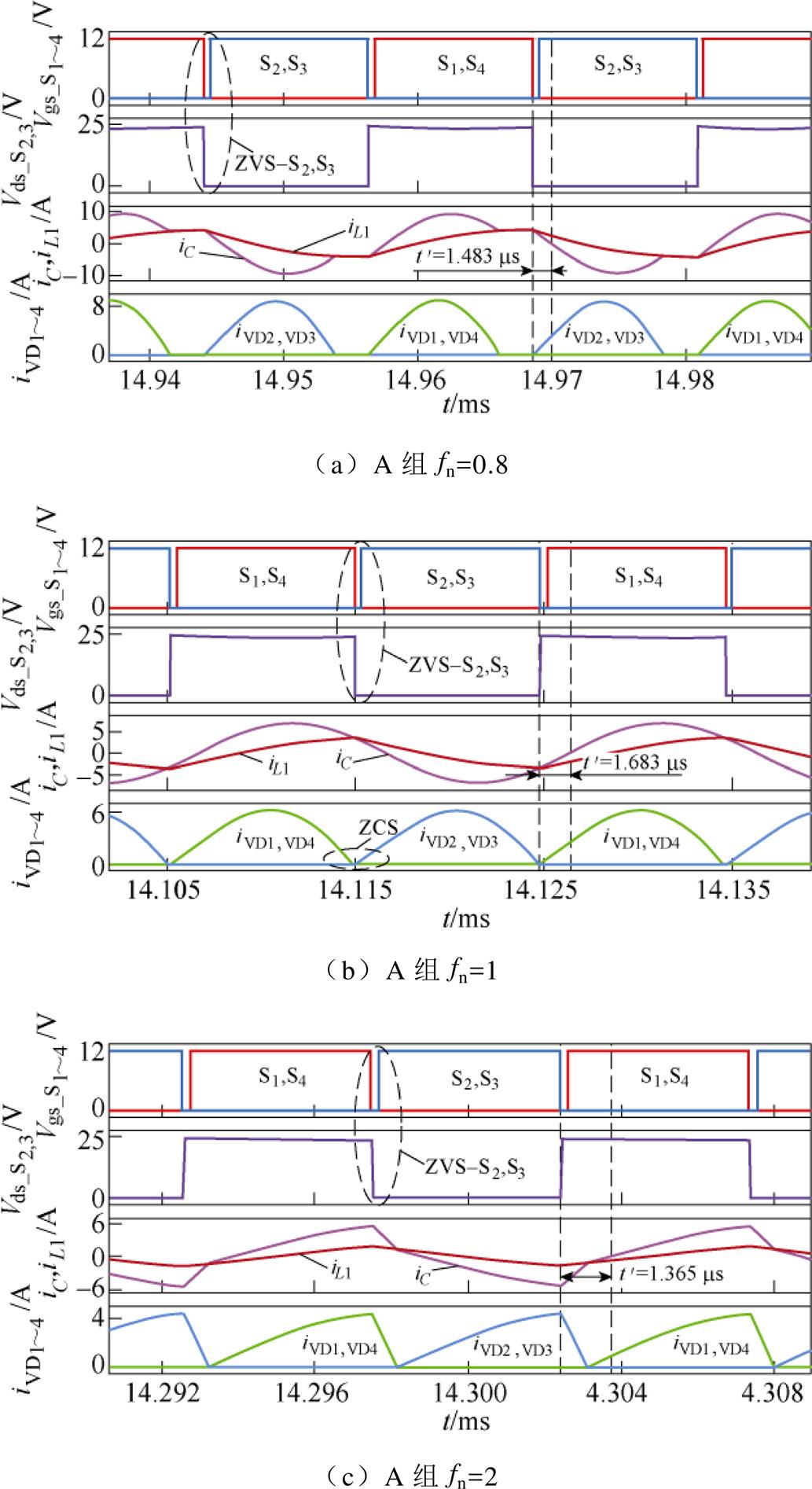
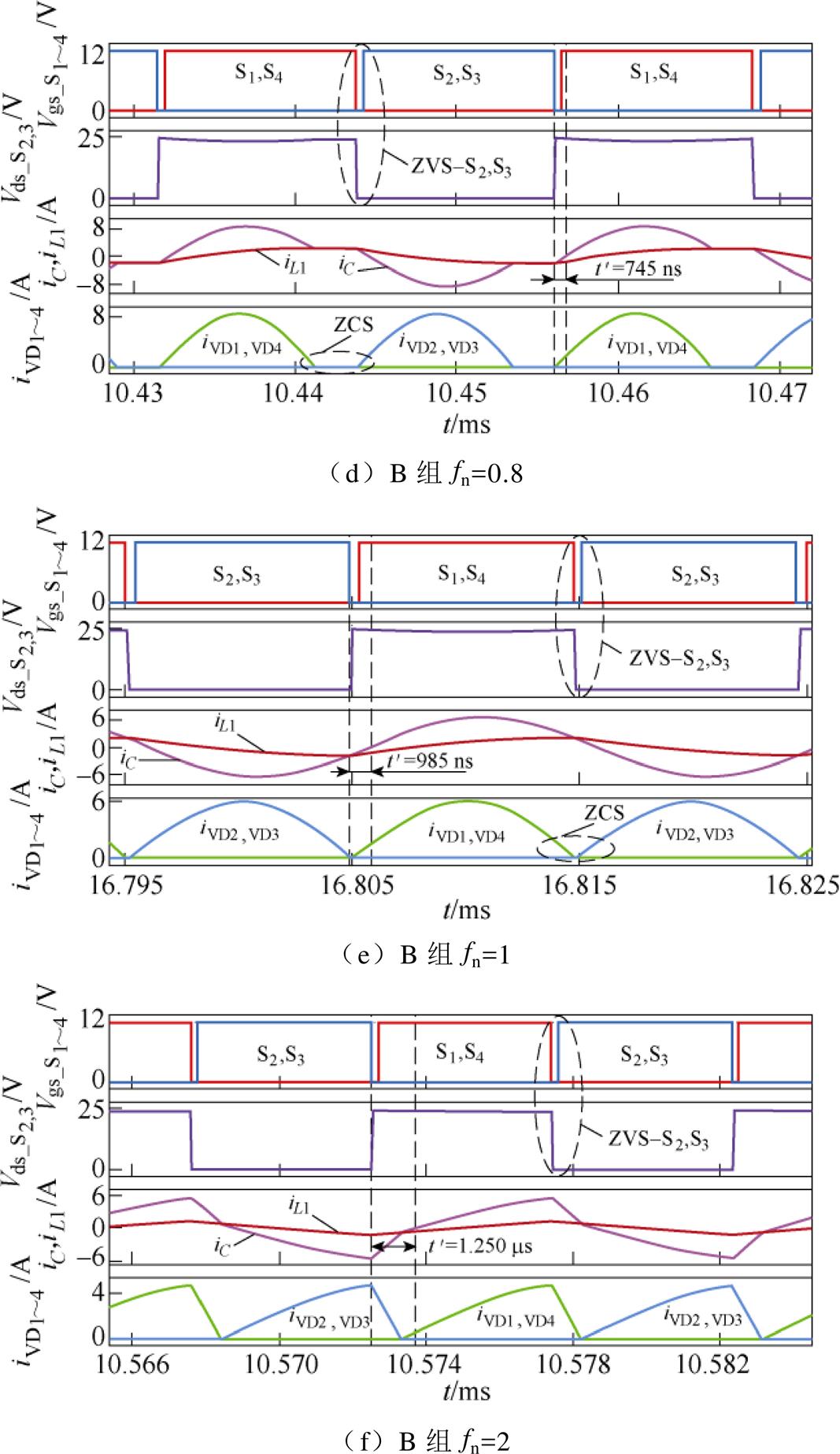
图10 两组谐振参数下关键波形比较
Fig.10 Comparison of key waveforms under two sets of resonance parameters
表3 谐振电流过零时间
Tab.3 Zero-crossing time of resonant current
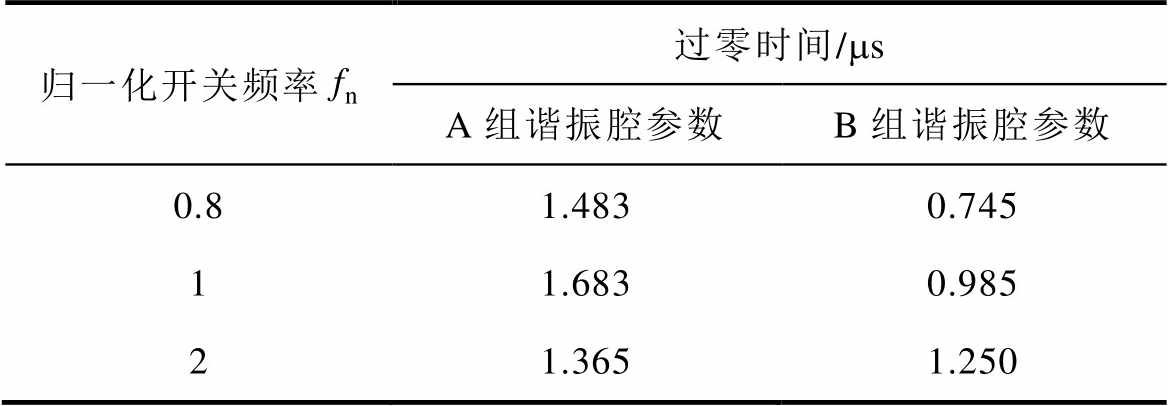
归一化开关频率fn过零时间/ms A组谐振腔参数B组谐振腔参数 0.81.4830.745 11.6830.985 21.3651.250
为进一步验证理论分析的正确性，搭建了一个100 W的实验样机平台如图11所示，采用TI公司的TMS320F28034型DSP实现数字控制，并使用表2中A、B两组不同的CLL谐振参数进行实验验证。
图11 实验平台
Fig.11 Experimental platform
图12为两组谐振参数下的波形对比，其中图12a～图12c为A组实验波形，12d～图12f为B组实验波形。在A组参数条件下，当fn=0.8时，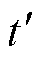
= 1.64 ms，理论值为1.436 ms，误差为204 ns；fn=1时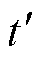，=1.76 ms，理论值为1.526 ms，误差为234 ns；fn=2时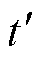，=1.28 ms，理论值为1.21 ms，误差为70 ns。由于电流纹波、电路的一些实际寄生元件参数和测量误差的关系，导致实验值和理论值的最大误差约200 ns，总体来说，两者是基本吻合的。
在B组参数条件下，变换器有最小回流功率。当fn=0.8和fn=1时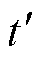，分别为680 ns和1.04 ms，与A组参数相比，谐振参数优化后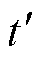时间明显减小，分别优化了960 ns和720 ns；当fn=2时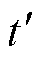，=1.2 ms，从图9中可以看到，随着fs的增大，它们的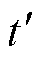值逐渐相等，这说明了结果与分析是一致的。
为保证在优化回流功率的同时，不会影响变换器的软开关，图13为fn=0.8时的软开关实现。
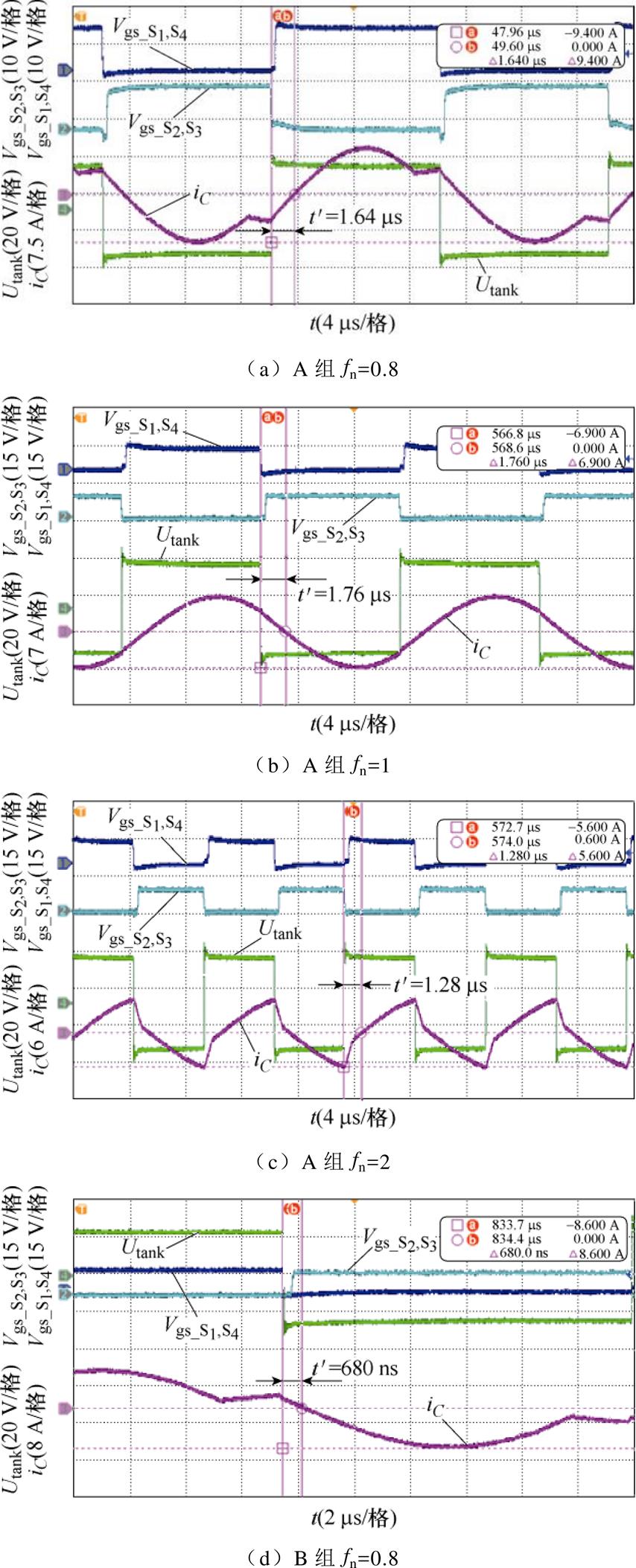
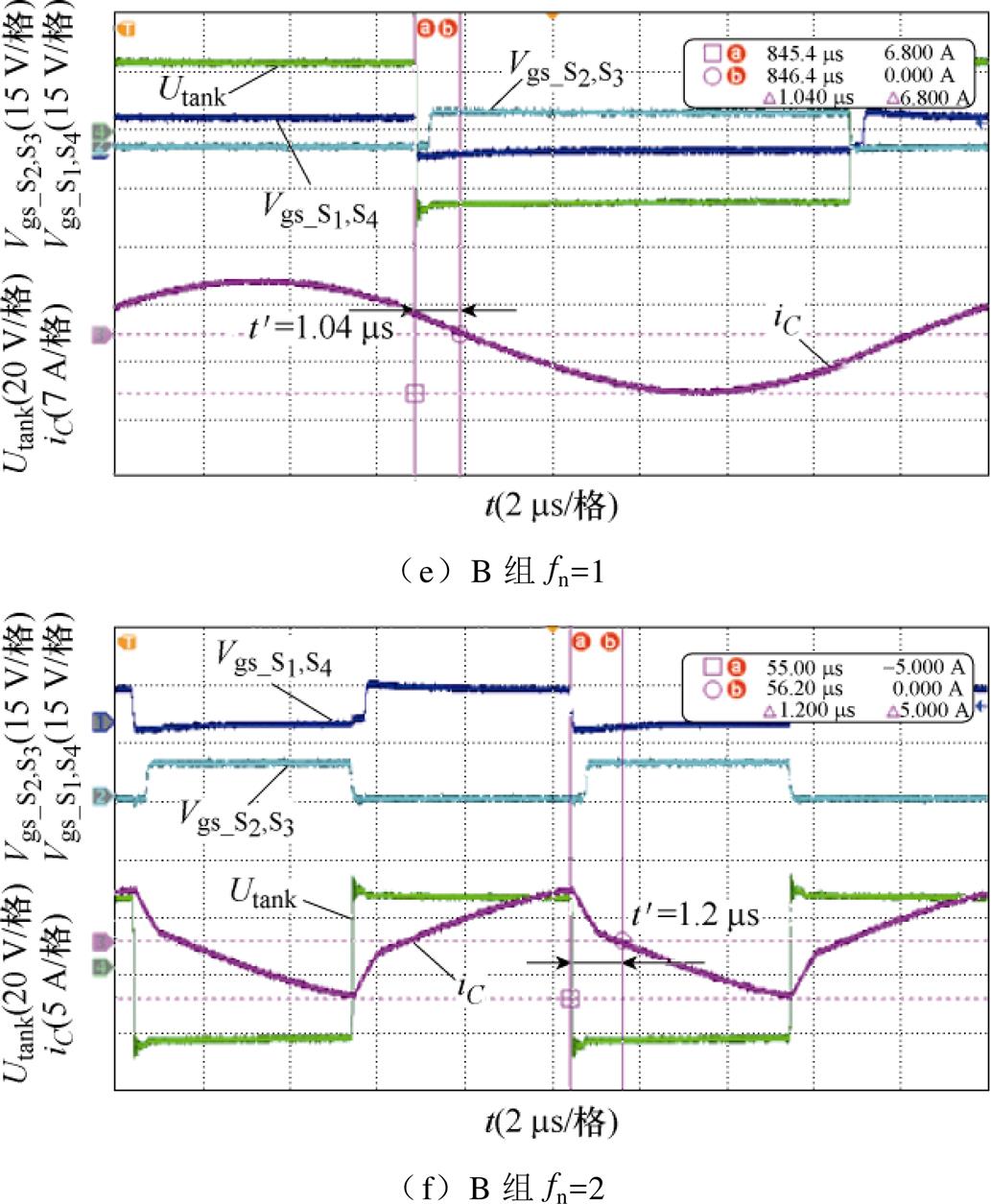
图12 实验波形
Fig.12 Experimental waveforms
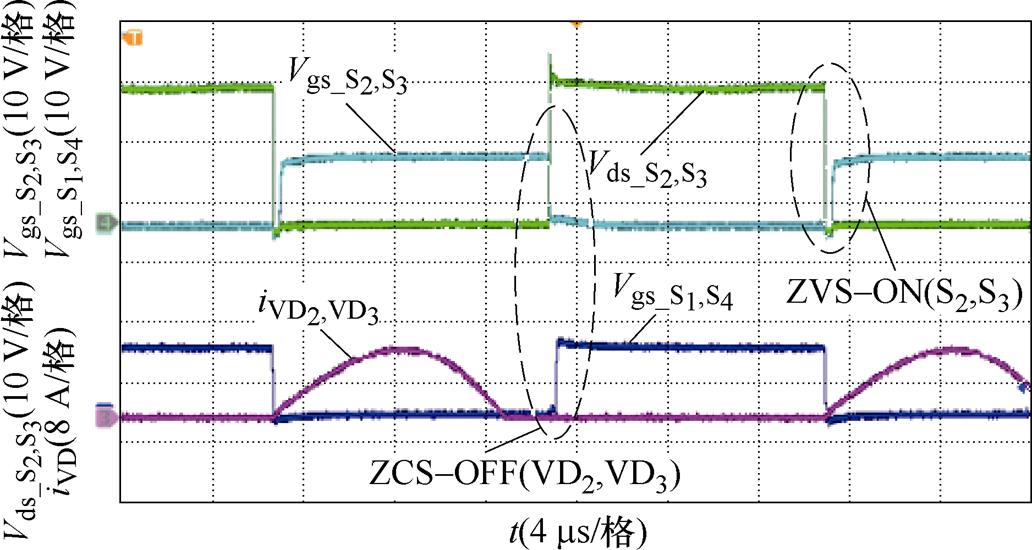
图13 软开关实现
Fig.13 Soft-switching realization
图14显示了B组谐振参数的理论值、仿真结果和实验结果的比较，可以看出三种结果相对接近，拟合程度良好，说明了理论分析的正确性和参数设计的有效性。图15显示了两组谐振参数的转化效率情况，在谐振频率点处，变换器有最高的转化效率，当负载为满载时，可以看到B组参数的转化效率明显高于A组参数，效率提高约1.8%，并且随着负载的增大，效率提升也越明显，这是由于当负载越重时，回流功率在电路中循环，电路元件的等效电阻损失越大，因此谐振参数改善后，效率提高越明显。当变换器工作在过谐振状态时，由于副边整流二极管无法实现ZCS，因此效率较低，这里可引入同步整流技术来提高效率，并且相较于LLC，CLL会更有优势。
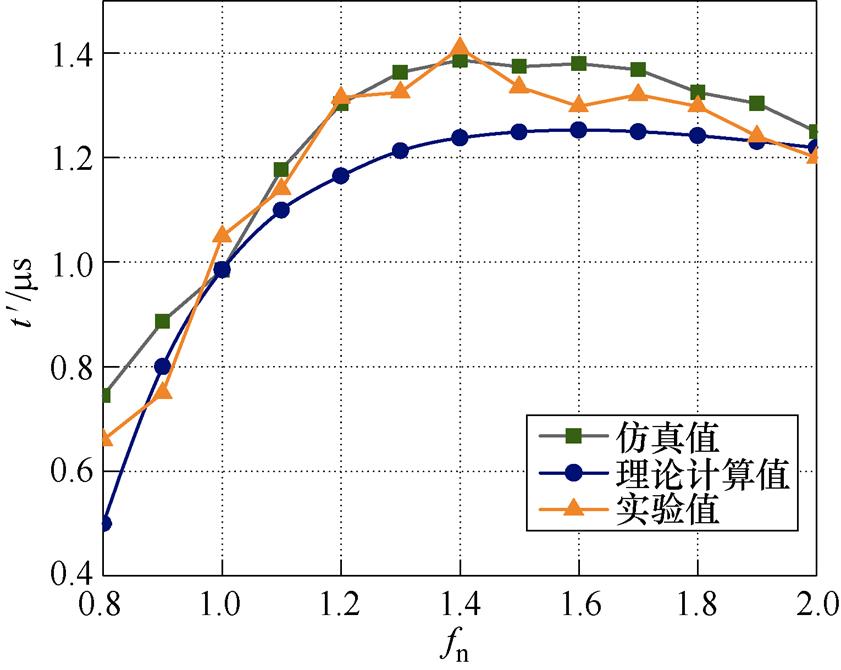
图14 理论值、仿真值、实验值比较
Fig.14 Comparison of the theoretical calculation, simulation and experimental results
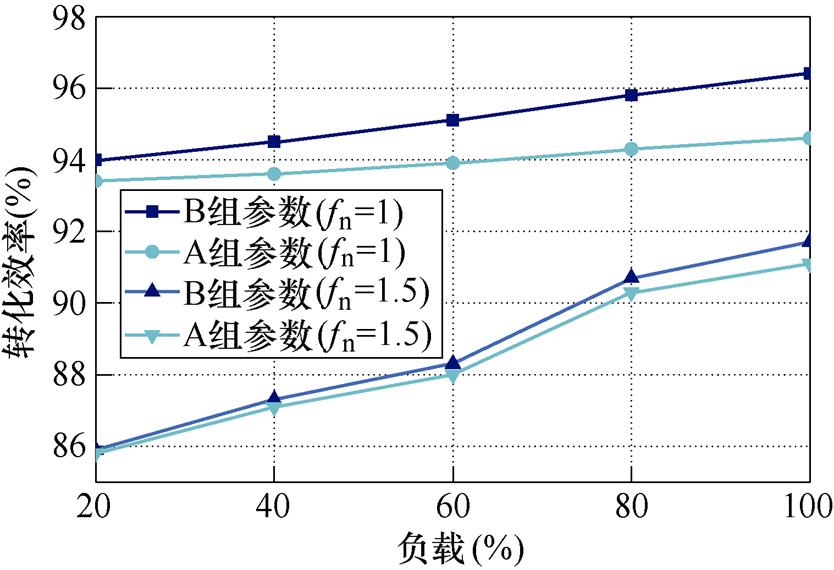
图15 转化效率
Fig.15 Transformation efficiency
本文针对全桥CLL谐振变换器，提出一种优化谐振参数的设计方法减小回流功率，提高了变换器的转化效率。理论分析和实验结果表明：
1）根据变换器在工作中产生回流功率的原理，提出了全桥CLL变换器回流功率的简单表征方法，相较于传统定义式表征，减小了计算的复杂性。
2）全桥谐振变换器在一个谐振周期中会有两次回流功率的产生，相较于半桥结构而言，优化更加有意义。
3）本文所提方法避免了复杂的控制算法，减小了电路的复杂性，无需额外的控制电路就能达到优化回流功率的目的，节约了器件成本并保证了电路的稳定性。仿真和实验验证了表征函数的正确性以及所提方法减小回流功率的有效性。
参考文献
[1] 赵烈, 裴云庆, 刘鑫浩, 等. 基于基波分析法的车载充电机CLLC谐振变换器参数设计方法[J]. 中国电机工程学报, 2020, 40(15): 4965-4976, 23.
Zhao Lie, Pei Yunqing, Liu Xinhao, et al. Design methodology of CLLC resonant converters for electric vehicle battery chargers[J]. Proceedings of the CSEE, 2020, 40(15): 4965-4976, 23.
[2] 丁超, 李勇, 姜利, 等. 电动汽车直流充电系统LLC谐振变换器软开关电压边界分析[J]. 电工技术学报, 2022, 37(1): 3-11.
Ding Chao, Li Yong, Jiang Li, et al. Analysis of soft switching voltage boundary of LLC resonant converter for EV DC charging system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(1): 3-11.
[3] 王皓, 朱金大, 侯凯, 等. 基于混合控制式交错并联LLC谐振变换器的充电模块研制[J]. 电力系统自动化, 2017, 41(7): 108-113.
Wang Hao, Zhu Jinda, Hou Kai, et al. Development of charging module based on interleaving paralleled LLC resonant converter with hybrid control[J]. Automation of Electric Power Systems, 2017, 41(7): 108-113.
[4] Zhao Bin, Zhang Xin. An efficiency-oriented two- stage optimal design methodology of high-frequency LCLC resonant converters for space travelling-wave tube amplifier applications[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1068-1080.
[5] Huang Daocheng, Fu Dianbo, Lee F C, et al. High-frequency high-efficiency-resonant converters with synchronous rectifiers[J]. IEEE Transactions on Industrial Electronics, 2010, 58(8): 3461-3470.
[6] Asa E, Colak K, Czarkowski D. Analysis of a CLL resonant converter with semi-bridgeless active rectifier and hybrid control[J]. IEEE Transactions on Industrial Electronics, 2015, 62(11): 6877-6886.
[7] Liu Yue, Wu Hongfei, Zou Jun, et al. CLL resonant converter with secondary side resonant inductor and integrated magnetics[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11316-11325.
[8] 吴建雪, 许建平, 陈章勇. CLL谐振变换器谐振电路参数优化设计[J]. 电力自动化设备, 2015, 35(1): 79-84, 152.
Wu Jianxue, Xu Jianping, Chen Zhangyong. Optimal design of resonant circuit parameters for CLL resonant converter[J]. Electric Power Automation Equipment, 2015, 35(1): 79-84, 152.
[9] Zhao Biao, Yu Qingguang, Sun Weixin. Extended- phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.
[10] 范恩泽, 李耀华, 葛琼璇, 等. 基于优化移相的双有源串联谐振变换器前馈控制策略[J]. 电工技术学报, 2022, 37(20): 5324-5333.
Fan Enze, Li Yaohua, Ge Qiongxuan, et al. Feed- forward control strategy of dual active bridge series resonant converter based on optimized phase shift[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5324-5333.
[11] 周路遥, 姜久春. LCL谐振型双有源全桥双向DC-DC变换器分析与控制[J]. 电力系统自动化, 2016, 40(19): 82-86, 93.
Zhou Luyao, Jiang Jiuchun. Analysis and control of dual active bridge DC-DC converter based on LCL resonant network[J]. Automation of Electric Power Systems, 2016, 40(19): 82-86, 93.
[12] 王武, 雷文浩, 蔡逢煌, 等. 结合电流应力优化的双有源全桥DC-DC变换器自抗扰控制[J]. 电工技术学报, 2022, 37(12): 3073-3086.
Wang wu, Lei Wenhao, Cai Fenghuang, et al. Active disturbance rejection control of dual-active-bridge DC-DC converter with current stress optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3073-3086.
[13] Shi Haochen, Wen Huiqing, Chen Jie, et al. Minimum-backflow-power scheme of DAB-based solid-state transformer with extended-phase-shift control[J]. IEEE Transactions on Industry Appli- cations, 2018, 54(4): 3483-3496.
[14] 杨超, 许海平, 张祖之, 等. PWM与移相结合控制下的混合三电平隔离型双向DC-DC最小回流功率控制研究[J]. 电工技术学报, 2019, 34(15): 3186- 3197.
Yang Chao, Xu Haiping, Zhang Zuzhi, et al. Minimum backflow power control of the hybrid three level isolated bi-directional DC-DC converters based on PWM-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3186- 3197.
[15] Shi Zhe, Tang Yu, Guo Yingjun, et al. Optimal design method of LLC half-bridge resonant converter considering backflow power analysis[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3599-3608.
[16] Kan Jiarong, Xie Shaojun, Tang Yu, et al. Voltage-fed dual active bridge bidirectional DC/DC converter with an immittance network[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3582-3590.
[17] 黄何伟, 曹太强, 李蔚, 等. 基于等效谐振腔的半桥CLL谐振变换器回流功率优化方法[J/OL]. 电源学报, 2023: 1-15. [2023-04-28] http://kns.cnki.net/kcms/ detail/12.1420.tm.20230427.1103.004.html.
Huang Hewei, Cao Taiqiang, Li Wei, et al. Optimi- zation method of backflow power of half-bridge CLL resonant converter based on equivalent resonant tanks[J/OL]. Journal of Power Supply, 2023: 1-15. [2023-04-28] http://kns.cnki.net/kcms/detail/12.1420.tm.20230427. 1103.004.html.
[18] 丁超, 李勇, 姜利, 等. 电动汽车直流充电系统LLC谐振变换器软开关电压边界分析[J]. 电工技术学报, 2022, 37(1): 3-11.
Ding Chao, Li Yong, Jiang Li, et al. Analysis of soft switching voltage boundary of LLC resonant converter for EV DC charging system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(1): 3-11.
Abstract Resonant converters are widely used in distributed power systems, notebook computers, communication equipment, and new energy electric vehicles due to their excellent performance. However, the parameters of resonant elements are the main factors affecting the gain, loss, volume of the converter, and overall performance. Therefore, optimizing these parameters can lead to improvements in converter performance.
Among many resonant topologies, the LLC resonant converter hasreceived significant attention and is widely used in practical applications. This paper studies a new resonant topology converter with a T-type CLL structure resonant tank. Its operating characteristics are very similar to the traditional LLC, which can be realized in the ZVS of the primary-side MOSFETs and the ZCS of the secondary-side diodes. The advantage of the resonant converter is its high conversion efficiency. Nonetheless, the converter cannot avoid generating backflow power during the operation, and the increase in backflow power can lead to a sharp increase in the conduction loss and current stress of the converter switch, ultimately reducing conversion efficiency. Therefore, this paper analyzes and optimizes the backflow power generated by the CLL resonant converter.
Firstly, the operating modes of the full-bridge CLL converter are analyzed based on the backflow power definition. It is pointed out that backflow power is generated in both positive and negative operating modes. In addition, a time-domain expression for backflow power is derived, though its complexity makes direct calculation and characterization challenging. Secondly, two insights emerge from the modal analysis of backflow power: (1) Backflow power is essentially reactive power circulating in the circuit and is not directly equivalent to power loss. (2) Power loss due to the substantial backflow power in the circuit is dissipated mainly within the equivalent resistance of the active and passive components in the reactive path. As a result, direct calculation is unnecessary, and it suffices to characterize backflow power using a relevant variable. Thirdly, by analyzing the AC equivalent model of the CLL converter and combining it with the modes that generate backflow power, it is derived that backflow power can be indirectly characterized by the phase shift angle of the resonant tank’s input voltage and current. Accordingly, a simple characterization method for the backflow power of CLL resonant converters is proposed. Backflow power is reduced by optimizing resonance parameters within the constraints of voltage gain and ZVS, thereby enhancing conversion efficiency. Finally, the design method is verified by simulation and experiment using two sets of resonant parameters. The results show that conversion efficiency is improved by about 1.8% at the resonant frequency point under full-load conditions.
keywords：Full-bridge CLL resonant converter, backflow power, parameter optimization design, trans- formation efficiency, soft-switching
DOI: 10.19595/j.cnki.1000-6753.tces.230368
中图分类号：TM46
四川省科技计划项目（2023YFG0338, 2023YFG0191, 2022ZHCG0015）和四川省科技成果转移转化示范项目（2023ZHCG0039, 2023ZHCG0021）资助。
收稿日期 2023-03-25
改稿日期 2023-06-29
黄何伟 男，1997年生，硕士研究生，主要研究方向为谐振DC-DC变换器拓扑分析及其性能优化。E-mail: 634326231@qq.com
曹太强 男，1969年生，博士，教授，硕士生导师，主要研究方向为电力电子与电力传动、光伏发电技术等。E-mail: ctq815@126.com（通信作者）
（编辑 郭丽军）