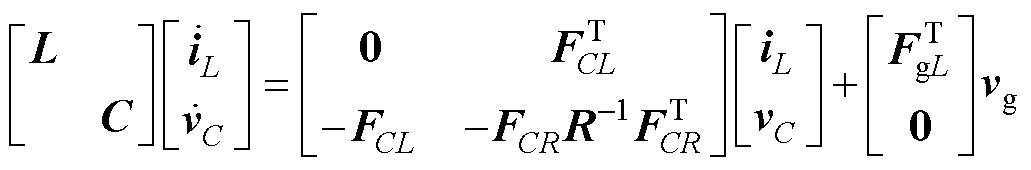（1）
摘要 DC-DC变换器广泛应用于开关电源、电机传动等传统领域，以及新能源发电、电动汽车等新兴领域。不同应用场景通常对DC-DC变换器有不同的要求，当现有变换器的性能不能满足需求时，需要构造新的变换器。然而，凭经验或灵感构造出的DC-DC变换器往往缺乏普遍适用性。为了能够根据具体应用需求构造DC-DC变换器，该文在总结现有大部分DC-DC变换器构造方法的基础上，按“元器件-电路单元-变换器”三个层级，将DC-DC变换器的构造方法分为一次构造和二次构造。重点介绍一些典型构造方法的构造原理和构造步骤，并将构造方法进行分析和比较，为今后利用计算机技术智能构造和科学评价DC-DC变换器提供了参考。
关键词：DC-DC变换器 构造方法 拓扑 图论
DC-DC变换器将一种电压的直流电变换为另一种电压的直流电，以向不同电压等级的直流负载供电。传统上，DC-DC变换器可应用于开关电源、直流电动机传动等领域。近年来，随着新能源产业的兴起，DC-DC变换器在风力和光伏发电、微电网、电动汽车等领域得到了更广泛的应用。各种应用场景对DC-DC变换器有不同的需求，如应用于直流微电网的DC-DC变换器需要满足故障隔离、功率双向流动、维持母线电压稳定的要求[1]；应用于海上风电并网的DC-DC变换器需要具有高增益、大容量以及一定的故障隔离能力[2]；而应用于储能系统和电动汽车充电的DC-DC变换器需要适应宽范围的输入输出电压[3-4]。因此，当现有的DC-DC变换器不能满足需求时，需要构造新的变换器。
在实际应用中，由于变换器工作环境不同，对其性能指标的要求往往是多样化的。除电压增益之外，通常还要考虑器件电压电流应力、电压电流纹波、稳定性等指标[5]，且不同的性能指标要求可能相互制约。为了满足DC-DC变换器的性能要求，设计者们通常根据自己的经验去设计变换器拓扑，且设计过程严重依赖灵感。运用此方法通常只能构造出满足当前场景需求的少量变换器，且往往缺乏普适性[6-7]。目前，一些系统性的拓扑构造理论和方法先后被提出，但大部分的构造步骤仍需人工参与。对于一些包含遍历、搜索等步骤的构造方法，可以采用计算机编程实现，因此有必要探索计算机辅助技术与DC-DC变换器构造相结合的方法。
本文在总结现有大部分DC-DC变换器拓扑构造方法的基础上，按“元器件-电路单元-变换器”三个层级，将DC-DC变换器的构造方法分成一次构造和二次构造。其中，一次构造是指将独立的元器件组合成变换器，二次构造则是以现有变换器为基本单元，构造出新的变换器。文中具体介绍了一些典型构造方法的实现方式，并讨论了这些构造方法的优缺点、关键技术、应用场景、适用范围以及发展趋势等。通过上述工作，为今后结合具体需求使用计算机辅助技术构造DC-DC变换器提供参考。
在“元器件-电路单元-变换器”三个层级中，“元器件”是指独立的元器件，如电力电子开关、电感、电容等；“电路单元”本身也是功能完整的DC-DC变换器，通常是一些比较基本的变换器，可作为构造其他变换器的基本单元。本文将从元器件出发直接构造变换器电路的方法称为一次构造，一次构造方法主要包括状态方程法[8-9]、磁通平衡设计法[7,10-12]和图论搜索法[6, 13-16]。
每个电力电子变换器都可用状态方程进行描述，若对状态方程的参数进行设置，则可构造出一个新的变换器[8]。
对于一般的DC-DC变换器，设电容、电感、独立电压源、负载的数量分别为m、n、p、q，某一工作模态下的状态方程为
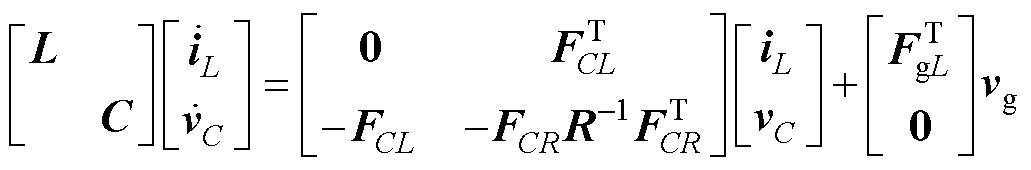（1）
式中，iL为电感电流列向量（n×1阶）；vC为电容电压列向量（m×1阶）；vg为电压源电压列向量（p×1阶）；L为n阶对称矩阵，如果网络中不含耦合电感，则L成为对角矩阵，对角线元素为相应电感值；C和R为对角矩阵，对角线元素为相应电容、电阻值；FCL为描述电容与电感回路关系的矩阵（m×n阶）；FCR为描述电容与负载电阻回路关系的矩阵（m×q阶）；FgL为描述独立电压源与电感回路关系的矩阵（p×n阶）。如果网络中不含变压器，FCL、FCR、FgL中的元素只取±1或0。
定义电压源、电感、电容、电阻的参考方向均为高电位指向低电位，回路的参考方向为顺时针。以FCL为例，若Cs与Lt在同一回路且在该回路中同向，则第s行第t列元素FCL(s,t)=-1；若Cs与Lt在同一回路且在该回路中反向，则FCL(s,t)=1；若Cs与Lt不在同一回路，则FCL(s,t)=0。对于不同的工作模态，其对应的关系矩阵会不同，通常FCL会改变，而FCR和FgL可能不变。
下面以如图1a所示的Cuk变换器及其等效电路为例说明关系矩阵的提取。当开关管导通时，其等效电路如图1b所示。根据元器件的参考方向，可得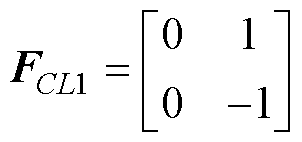
，
，
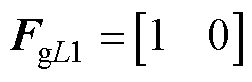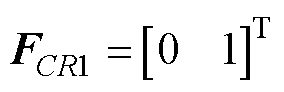。当开关管关断时，其等效电路如图1c所示，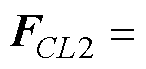
，
，
。
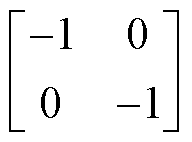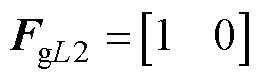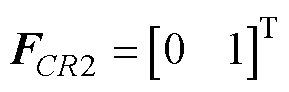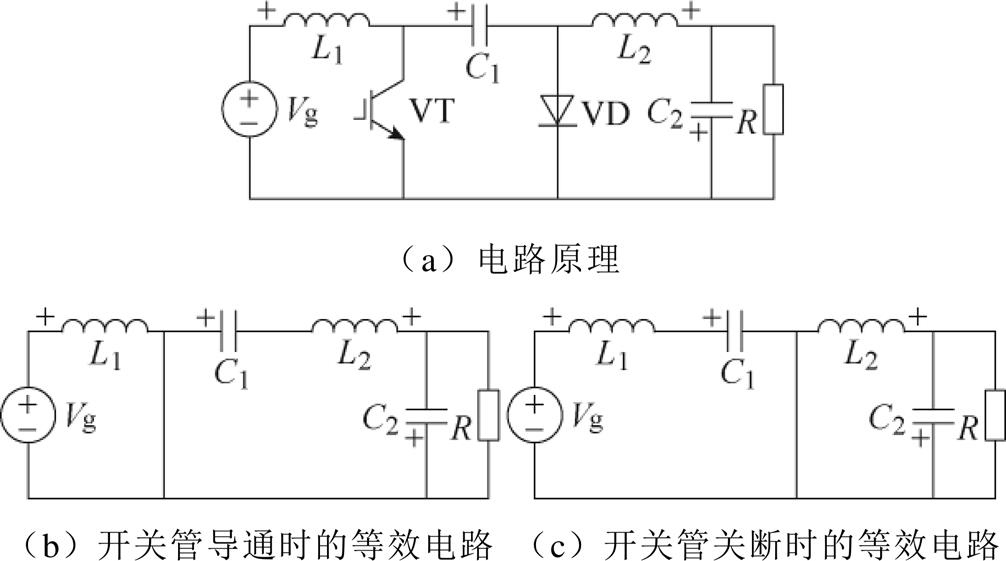
图1 Cuk变换器及其等效电路
Fig.1 Cuk converter and its equivalent circuits
利用状态方程法构造DC-DC变换器的思路简述如下：
（1）确定DC-DC变换器的类型，如是否含有变压器或耦合电感等。
（2）确定电压源、负载、电感、电容的数量。
（3）综合考虑开关管数量、控制策略以及变换器工作在连续导通模式（Continous Conduction Mode, CCM）还是断续导通模式（Discontinous Conduction Mode, DCM），确定开关状态数量。
（4）根据需求设置矩阵FCLi、FCRi、FgLi中的元素值，进而采用遍历算法，排除冗余和无法构成电路的组合，得到若干组有效的关系矩阵。
（5）关系矩阵确定后，状态方程也随之确定，可根据具体的状态方程构造出DC-DC变换器。
设所构造的DC-DC变换器不含变压器或耦合电感，为单输入单输出，含2个电容和2个电感，具有2个工作模态，要求输入电流连续，输出电阻与电容并联。根据上述信息，可知：
（1）FCL为2×2阶矩阵，FCR为2×1阶矩阵，FgL为1×2阶矩阵，矩阵元素可以取±1或0。
（2）关系矩阵FCLi、FCRi、FgLi各有两组，对应两个工作模态。
（3）因为输入电流连续，所以电压源始终串联一个电感（设为L1），即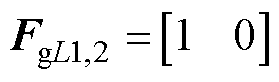
。因为输出电阻与电容（设为C2）并联，所以
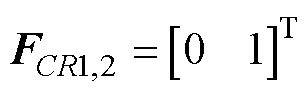。由于FCL1和FCL2共有8个元素，每个元素有三种取值，故共有38=6 561种情况，其中一组合理取值为
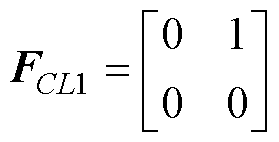和
。
（4）由FCL1可知，当变换器工作在工作模态1时，C1与L2在同一回路，C2与L1、L2均不在同一回路；由FCL2可知，当变换器工作在工作模态2时，C1与L1、L2在同一回路，C2与L2在同一回路。又由FgL1,2及FCR1,2可知，Vg与L1始终在同一回路，C2与R始终在同一回路。
根据上述讨论，分别作出两个工作模态下的等效电路，如图2a、图2b所示。整合两个电路并加入开关管和二极管，可构造出完整的变换器电路，如图2c所示。其中，开关管导通、二极管关断时为模态1，开关管关断、二极管导通时为模态2。
图2 运用状态方程法构造的一种DC-DC变换器
Fig.2 A DC-DC converter synthesized by state equation method
从上述分析可见，只要给定元器件类型及其数量，根据附加需求设定部分关系矩阵的元素值，就可以利用计算机程序遍历生成并筛选关系矩阵，从而构造出与之对应的变换器。该方法理论上能构造出多种类型的DC-DC变换器，包括多输入、多输出、多工作模态、含变压器、耦合电感的DC-DC变换器。然而，该方法的主要难点是需要排除无效和冗余的关系矩阵，以及根据关系矩阵构造电路，尤其是构造含多个工作模态、多个元器件的变换器（如准谐振变换器）时，该方法会变得十分复杂。
磁通平衡原理也称伏秒平衡原理，常用于DC- DC变换器的稳态分析。假设电感电流和电容电压的纹波很小，则在开关导通或关断的时间段内，电感电压可看作是恒定的，即为电源电压与各个电容电压的线性组合。根据伏秒平衡原理，当电路处于稳态时，在一个开关周期内，电感电压对时间的积分为零[10]，由此可推导出电源电压与电容电压的关系，最终得到电压增益表达式。
对于含1个电感、1个电容的变换器，电感L1的伏秒平衡表达式为
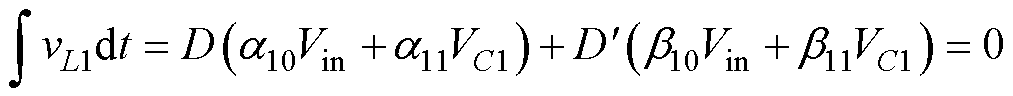（2）
式中，D为占空比，D'=1-D；Vin、VC1和vL1分别为电压源、电容C1和电感L1的电压；系数aij、bij只能取0或±1，表示开关导通（或关断）时，电感电压由哪些电压组成。
若取电容C1的电压为输出电压，由式（2）得到的电压增益表达式为
（3）
对于含2个电感、2个电容的变换器，电感L1和L2的伏秒平衡表达式为
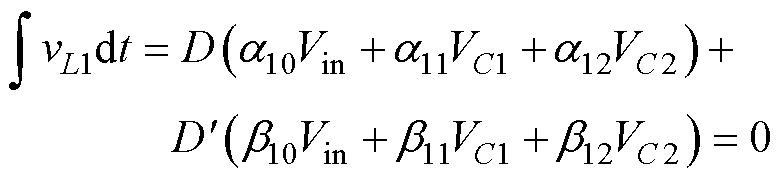（4）
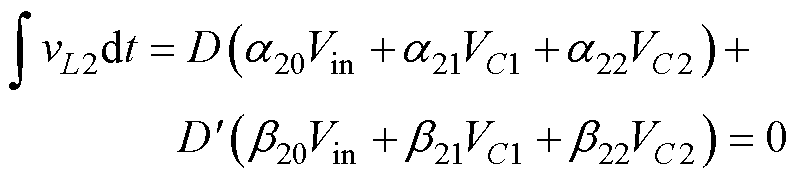（5）
若取电容C2的电压为输出电压，由式（4）和（5）得到的电压增益表达式为
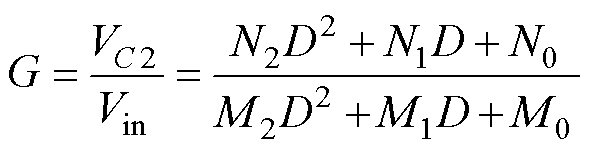（6）
其中
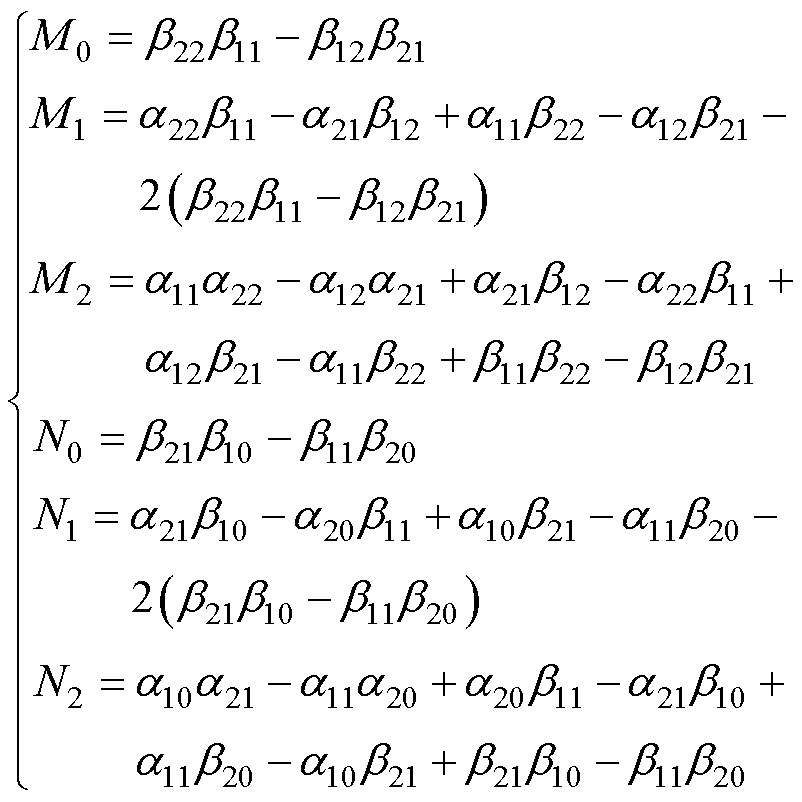（7）
磁通平衡设计法的思路是对于一个给定的电压增益表达式，求解出表达式中的未知系数，即不同模态下电感与电压源、电容的连接关系，从而得到DC-DC变换器拓扑。运用磁通平衡设计法构造的一种DC-DC变换器如图3所示。
以电压增益G=1/(1-D)2为例，磁通平衡设计法的步骤如下[10]：
（1）比较电压增益表达式与式（6）中的系数，得[N2 N1 N0 M2 M1 M0]=[0 0 1 1 -2 1]或[0 0 -1-1 2 -1]。
（2）将[N2 N1 N0 M2 M1 M0]的取值代入方程组式（7），得到包含12个未知数的6个方程。由于aij、bij只能取0或±1，所以解的个数是有限的，总共312种情况，可以用枚举法求出初解[11]。
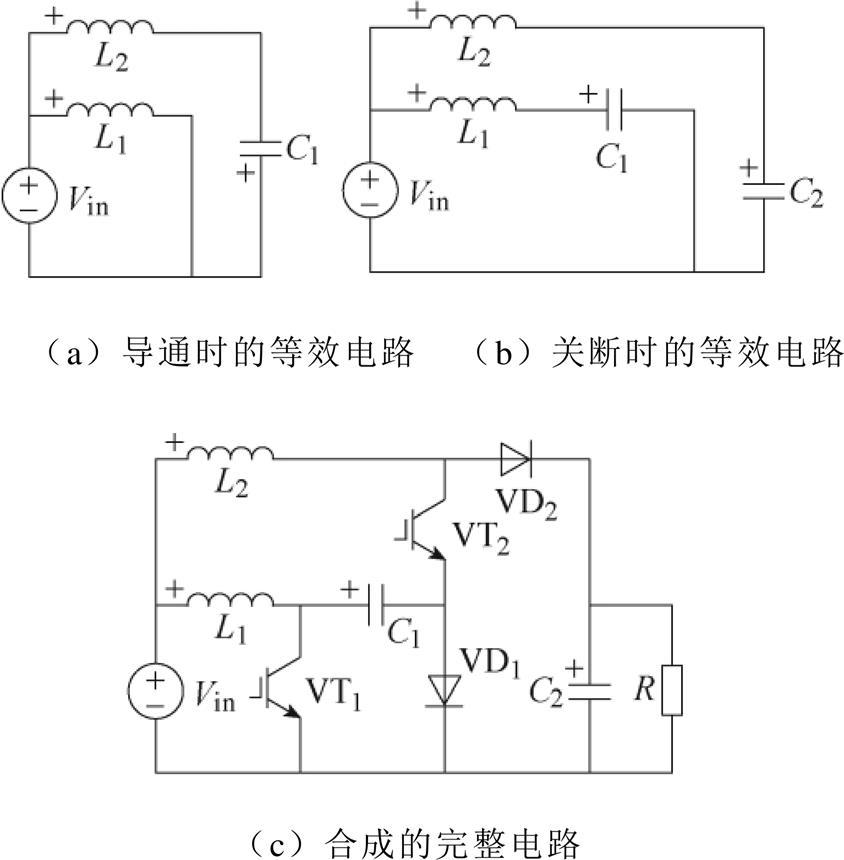
图3 运用磁通平衡设计法构造的一种DC-DC变换器
Fig.3 A DC-DC converter synthesized by flux balance method
（3）排除冗余解和无效解。冗余解是指不同的解对应同一电路，如将电感、电容的极性取反。此外，某些解可能无法形成电路，为无效解。
排除冗余解和无效解之后，得到若干可行解，其中一组解为
将其代入式（4）和式（5）可得
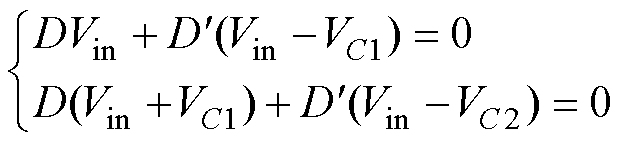（8）
（4）根据式（8），作出开关导通和关断两个模态下的等效电路，如图3a、图3b所示。
（5）加入开关器件，按一定方法合成完整的DC-DC变换器[12]，如图3c所示。其中开关管VT1和VT2在一个开关周期内的D时段导通，二极管VD1和VD2在余下的D'时段导通。
（6）进一步地，可按照输入输出是否共地、开关管数量、电感电流应力等指标，在可行解中选出最优解[11]。
综上所述，磁通平衡设计法适用于构造电压型输出的DC-DC变换器，即输出电压为电容两端电压。该方法的初解求取、冗余解和无效解剔除可利用编程实现，主要涉及循环、枚举等算法，故具有快速性和较好的完备性等优点。但由伏秒平衡方程构造分模态等效电路，再加入开关合成完整电路仍需要手工尝试。此外，某些电压增益表达式可能无法实现。
图论是电路分析的一种常用工具。将电路表示为几何图的形式，从而可用图论的理论和方法对电路进行分析。图论已在电网络方程的推导[17]、对偶理论的应用[18]等方面发挥了重要作用。
文献[13]从一个包含输入电源与输出负载的子图出发，通过添加新的节点和支路，推导出一系列DC-DC变换器。文献[14]首次将同构图应用到构造电力电子变换器，并提出同构图对应的变换器可以采用相同的控制策略。文献[15]通过对变换器的邻接矩阵进行降阶变换后实现变换器化简的目标。然而，上述方法都是采用手工推导变换器，当变换器包含元器件较多、节点和支路较多时，手工推导将会变得繁杂。
给定元器件类型及其数量后，由于形成的拓扑个数是有限的，因此可以编写程序，通过遍历或搜索得到所有拓扑，然后根据元器件组合规则选出有效拓扑。文献[6]提出了图论搜索法，即一种指定元器件类型及其数量的可编程拓扑搜索算法。该文以包含1个开关管、1个二极管、2个电感、1个电容的DC-DC变换器为例，首先通过算法搜索出所有可能的拓扑，并生成非同构图；然后根据元器件组合的规则和环路有效的条件，剔除无法正常工作的拓扑，识别电气特性冗余的拓扑；最后得到非冗余拓扑32种。下面介绍该方法的工作流程。
1）建立数据结构
（1）将负载等效为输出电压源，将DC-DC变换器电路抽象为无向图和有向图。定义电路元器件为图的边（或称支路），元器件之间的节点为图的顶点。有向图支路的方向与元器件电流流向一致。如果支路电流双向流动，则支路也为双向。将电路表示为图的形式后，可用矩阵存储图的信息。
（2）建立简化关联矩阵C。该矩阵存储搜索到的所有图的支路-节点关联信息，每一行对应一个图，行中的元素为边两端的顶点编号，每两个元素为一个分隔。
（3）建立元器件类型矩阵T。该矩阵存储每个图中边代表的元器件类型。指定元器件类型和数量的情况下，令每个图中边的排序不变，则统一的元器件类型矩阵为
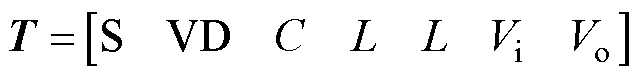（9）
（4）建立环路矩阵L。环路矩阵存储单个图中环路的信息。每一行存储一个环路，行中的元素为组成环路的边。
2）生成非同构图
由程序生成一系列图之后，必定会有一些是同构的。如同一个电路改变节点编号，简化关联矩阵就会不同，但它们是同构的。筛除边有序同构图和边类型同构图之后，剩下均为非同构图[6]。
3）初步筛除无效图
（1）筛除存在顶点度为1的图。度为1的顶点只连接一条边，该边不参与组成闭合回路。
（2）筛除存在顶点度为2，且该顶点关联的一条边不是Vi或Vo类型的图。度为2的顶点关联的两条边是串联的。输入端、输出端可以与其他元器件串联，而S、VD、L、C类型元器件相互串联都是不能工作或存在冗余的，两个元器件串联的无效情况见表1。
表1 两个元器件串联的无效情况
Tab.1 Invalid situations of two components connected in series
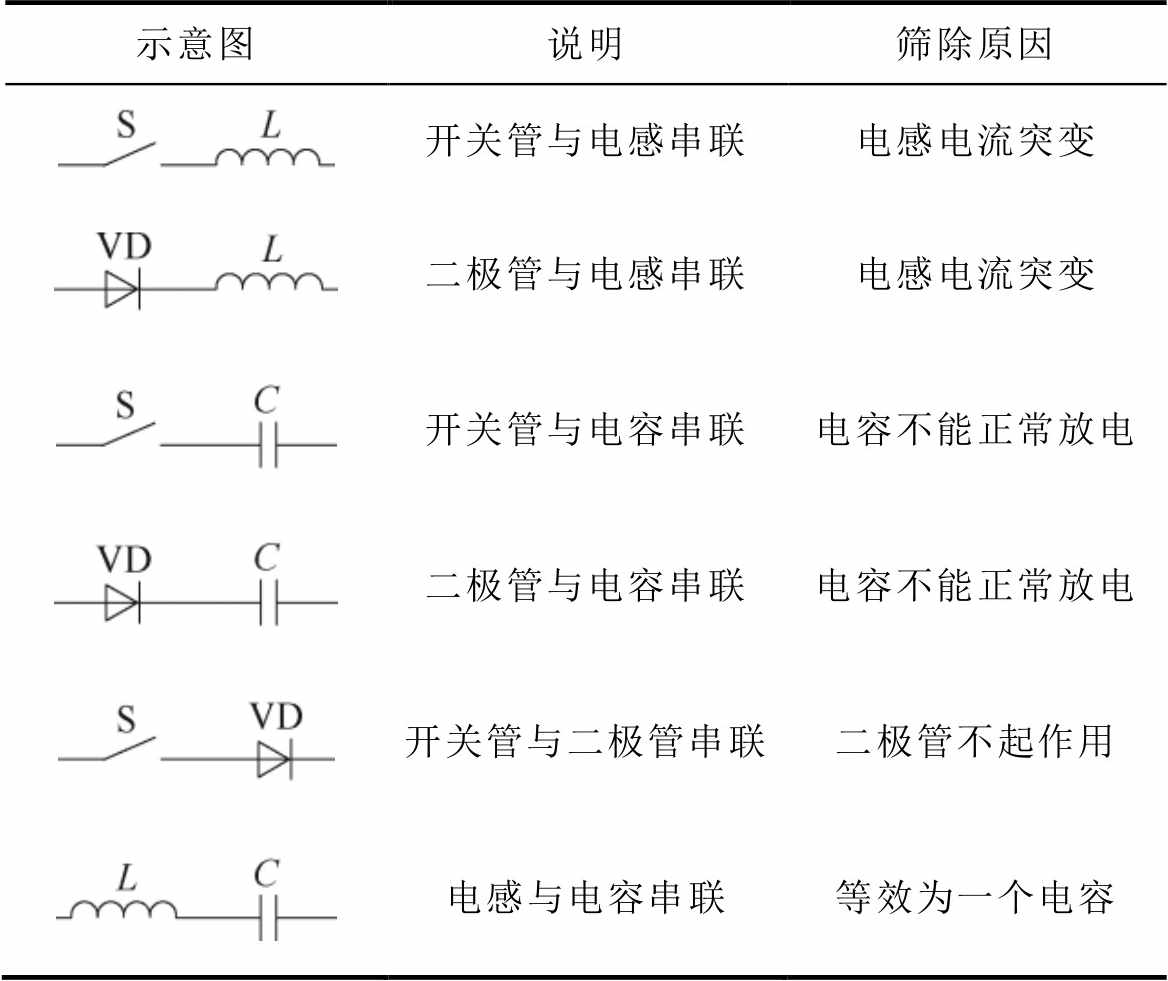
示意图说明筛除原因 开关管与电感串联电感电流突变 二极管与电感串联电感电流突变 开关管与电容串联电容不能正常放电 二极管与电容串联电容不能正常放电 开关管与二极管串联二极管不起作用 电感与电容串联等效为一个电容
4）搜索环路
将非同构的无向图转化为有向图，使用深度优先算法搜索出每个图的环路信息，存储在环路矩阵中。
5）选择有效拓扑
该步骤分为合法筛选和冗余筛选。其中合法筛选主要考虑电路的电气特性，例如：
（1）至少存在2个环路，否则电路不能正常工作。
（2）所有元器件都要在环路矩阵中出现。
（3）开关管和二极管不能同时在一个回路中。
（4）每一个电感和电容至少要出现在2个环路中，并且电容电流方向不能相同，否则无法正常充放电。
（5）环路不能出现短路、直通的情况。
从上述分析可见，图论搜索法将变换器表示为图的形式，进而表示为矩阵的形式，成为一种易于计算机存储的数据结构，通过搜索和筛选算法就能构造出变换器。然而，该方法需给定元器件类型及其数量，未能实现根据实用需求构造对应的变换器，且目前尚不支持含有多端元器件（如变压器、耦合电感）的变换器构造。
从上述分析可见，状态方程法、磁通平衡设计法和图论搜索法都是从元器件直接构造出变换器，运用了遍历、搜索等算法，适合编程实现。表2对比了上述三种方法的构造条件、适用范围、优缺点、难点和关键技术、未来的发展趋势，从计算机辅助构造变换器的角度出发，得出的结论如下：
（1）磁通平衡设计法能实现根据较为具体的需求（电压增益）构造DC-DC变换器，而状态方程法和图论搜索法实现的需求比较宽泛，且遍历或搜索得到的变换器数量较多，需进一步筛选。
表2 一次构造方法的比较
Tab.2 Comparison of primary synthesis methods
方法构造条件适用范围优点缺点难点和关键技术发展趋势 状态方程法元器件类型及其数量确定元器件数量较少的变换器通用性强，理论上能构造出多种类型的DC-DC变换器不适合构造复杂变换器排除无效和冗余的关系矩阵；由关系矩阵构造对应电路自动实现由关系矩阵构造对应电路 磁通平衡设计法电压增益表达式确定电压型输出的变换器具有快速性和较好的完备性，结果满足增益需求某些增益表达式不能实现；由伏秒平衡方程构造电路尚无明确步骤根据求解系数的结果构造电路编写构造算法，实现自动构造 图论搜索法元器件类型及其数量确定不含变压器或耦合电感的变换器具有较好的完备性和确定性构造过程产生大量中间体，占用计算机资源较多；未能按照具体需求构造变换器用算法搜索出符合要求的图；筛除无效和冗余的图支持多端元器件，增加其他需求（如电压增益）作为约束
（2）状态方程法和磁通平衡设计法对变量取值进行遍历，程序实现较简单。图论搜索法需要对图进行搜索，程序较为复杂。
（3）目前三种构造方法只在部分环节借助了计算机，计算机的参与度仍有提升空间，今后可通过编写软件实现从输入需求到输出电路的全流程。
当一次构造方法得到的变换器不满足需求时，可对现有的变换器进行改进，即二次构造。因此，二次构造是指从现有的变换器单元出发，通过改变单元的连接方式、组合单元、增删元器件或单元等，构造出另一个变换器，即实现“电路单元-变换器”的构造。属于二次构造的方法主要有：开关网络单元法[19-21]、对偶法[18, 22-23]、级联法[24-26]、Layer和Graft法[27-29]、交错并联法[30-32]、R2P2法[33-36]、阻抗网络置换-嵌入法[37-44]和多输出串并级联法[45]。
开关网络单元如图4所示，是一个含有开关管、二极管、电感和电容的三端网络[19]，其基本结构如图4a所示，每个端子可以轮流作为输入端、输出端和公共端。因此，开关网络单元法是指将开关网络单元的三个端子与输入电源、输出负载进行不同的连接组合，从而构造出一系列拓扑。
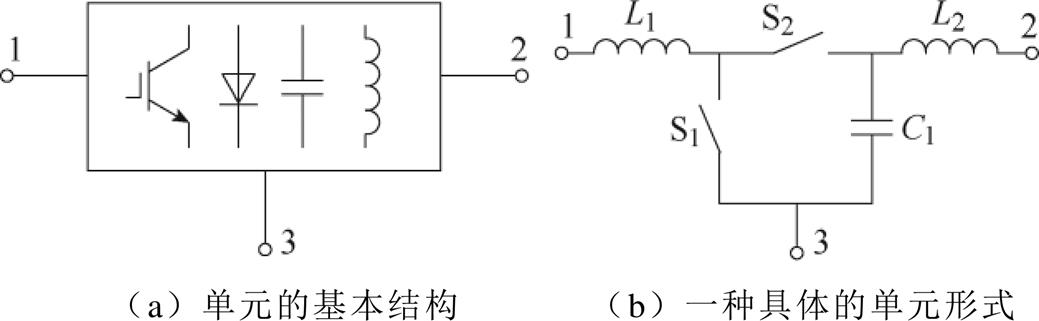
图4 开关网络单元
Fig.4 Switching converter cell
由于开关网络单元具有三个端子，故与电源、负载的连接方式有六种见表3。若开关网络单元是轴对称的，其实际连接方式只有三种。假设方式①的电压增益为f(D)，其他连接方式的电压增益也列于表3。
表3 开关网络单元的六种连接方式
Tab.3 Six connectionmodes of switching converter cells
方式①②③④⑤⑥ 输入端121323 输出端213132 公共端332211 增益f(D)1-f(D)
以图4b所示的一种开关网络单元[19]为例，根据表3，将该单元的3个端口分别与输入电压源、输出负载进行组合，可以得到六种DC-DC变换器拓扑，如图5所示。
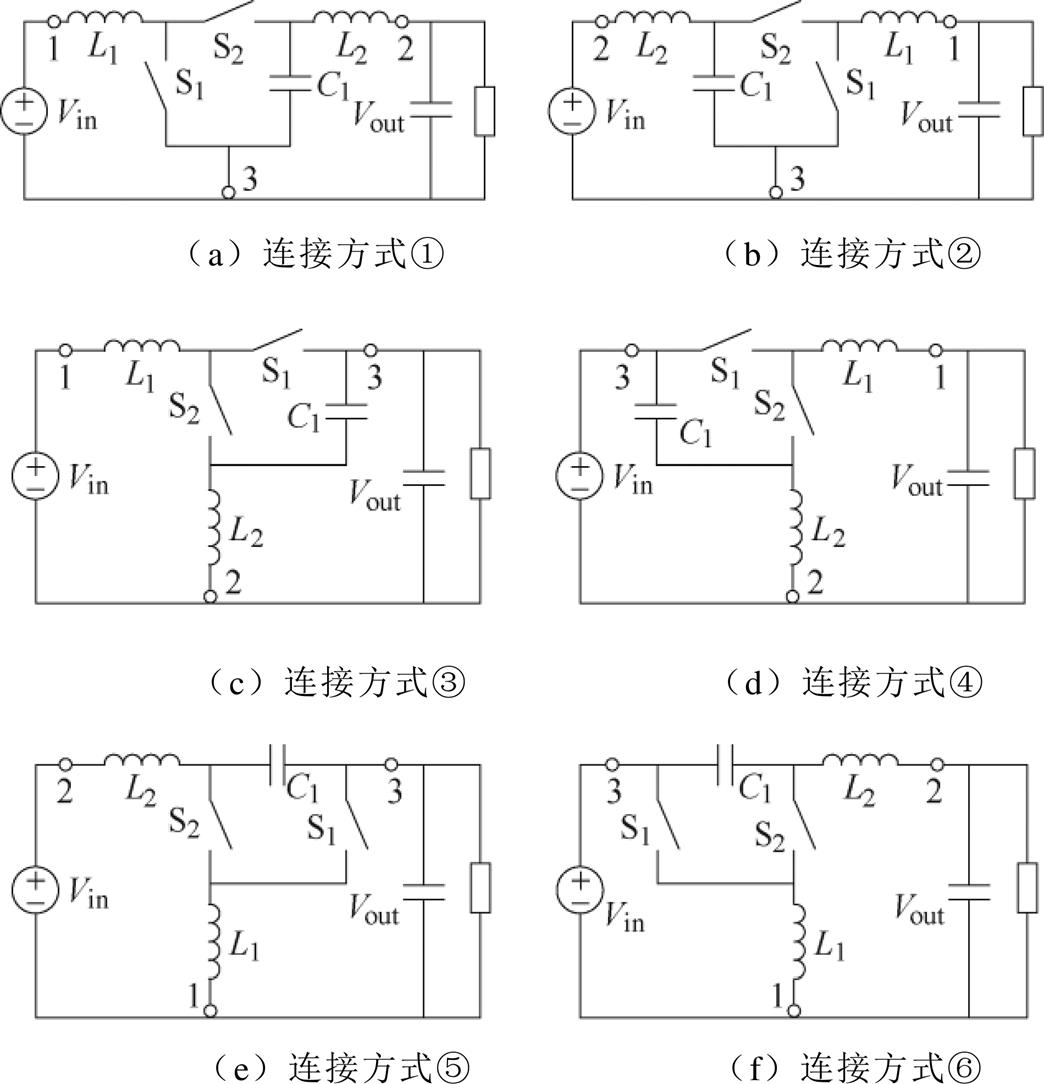
图5 采用开关网络单元法构造的六种DC-DC变换器
Fig.5 Six DC-DC converters synthesized by switching converter cell method
按上述方法，对于一个开关网络单元，就能推导出最多六种拓扑。已知其中一种拓扑的电压增益，就可推导出其他拓扑的电压增益。因此，该方法适用于有具体电压增益需求的应用场合。例如，构造升压变换器时，可将现有降压变换器的输出端和输入端调换（即从①到②的变换），此时电压增益变为原来的倒数。除了表3的构造方式之外，开关网络单元法还可以采用输出变换、输入变换等构造方 式[20]。由于开关网络单元只有三个端子，故该方法适用于构造输出电源和输入负载共地的变换器。
电路的对偶特性是指电路中的许多变量、元器件、结构等都是成对出现的，存在一一对应的关系，如表4中的电压和电流、网孔和节点等。而对偶变换是指根据上述对偶特性和对偶规则，将一个初始电路或网络变换成具有对偶关系的另一电路或网络。变换前后的电路在许多方面具有可以类比的特性[18]。
常用的对偶规则如下[18]：
（1）元器件参数。在原电路和对偶电路中，具有对偶关系的两个元器件参数在数值上是相等的。如10 W 电阻的对偶元器件是10 S电导，即0.1 W 电阻。
表4 对偶元器件的类型
Tab.4 Types of dual elements
原元器件对偶元器件 电压电流 网孔节点 电压源电流源 电感电容 电阻电导 阻抗导纳 二极管（通）二极管（断） 开关管（通）开关管（断）
（2）元器件的参考方向。规定电压源和电流源的参考方向是电位从低到高的方向，其他所有元器件的参考方向是电位从高到低的方向。
（3）对偶元器件支路的旋转。对偶元器件支路的位置由原元器件支路顺时针或逆时针旋转90 °得到。其中电压源、电流源、二极管的对偶元器件按顺时针旋转90 °；开关管、电阻、电容、电感的对偶元器件按逆时针旋转90 °。
运用对偶法构造的Boost变换器如图6所示。下面结合从Buck变换器构造Boost变换器的过程，说明对偶法构造DC-DC变换器的步骤[18]。
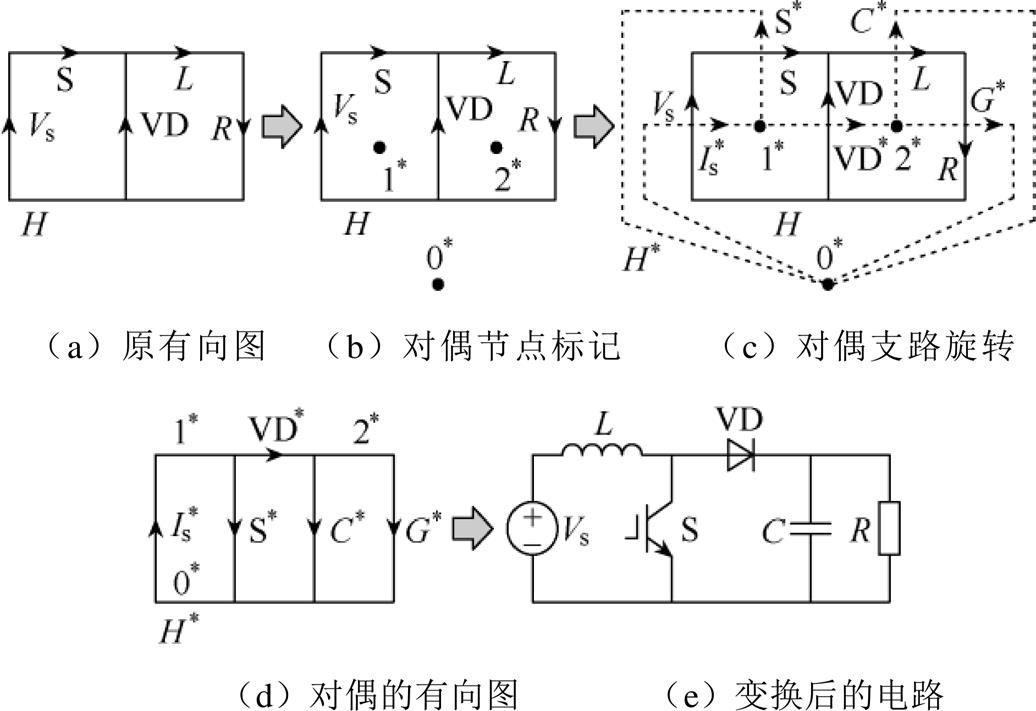
图6 运用对偶法构造的Boost变换器
Fig.6 Boost converter synthesized by duality method
（1）将Buck变换器的每个元器件用有向支路表示，支路方向为元器件参考方向，得到有向图H，如图6a所示。
（2）在图G中，将每个网孔标记一个节点n*，n=1, 2,…；外网孔则标记为节点0*，如图6b所示。
（3）根据对偶支路的旋转规则，将图H中的每条支路进行旋转，得到对偶支路b*。b*的元器件类型由表4决定。旋转后，支路b*两端连接的节点应对应原电路的网孔，如图6c所示。
（4）提取出n*和b*，形成有向图H*，如图6d所示。将图H*还原成电路，如有需要，可进行适当变换，如将电流源变换成电压源串联一个电感。得到的对偶电路如图6e所示。
在实际应用中，利用对偶性质可构造出满足特定需求的变换器。例如，因电压和电流是对偶量，可得
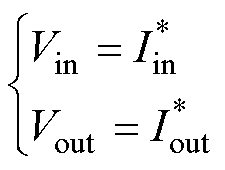（10）
式中，Vin和Vout分别为原电路的输入端和输出端电压；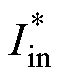
和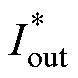
分别为对偶电路的输入端和输出端电流；“=”指在数值上相等。
因此
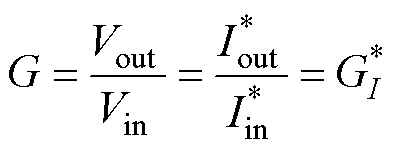（11）
即原电路的电压增益G等于对偶电路的电流增益
。如要求电流增益较大，可选择现有的电压增益较高的变换器为初始电路，求解对偶电路。
从上述分析可见，对偶法有明确的步骤，便于计算机编程实现。只要输入原电路的支路类型向量、支路与节点的连接矩阵、节点坐标矩阵等信息，就能获得对偶电路。但该方法目前只适用于平面电路，即所有支路都布置在一个平面内，除节点处以外不发生交叉的电路。该方法的优点是确定性强，只要原电路是能工作的，那么对偶电路一般也能正常工作。而缺点是对于一个原电路，只能构造出一个对偶电路。
级联就是将一个变换单元的输入端口接到另一个变换单元的输出端口，得到新的两级变换器。根据具体需求，可将升压或降压单元进行级联，实现更大范围的电压变换[24-25]，如图7所示的级联Boost变换器。
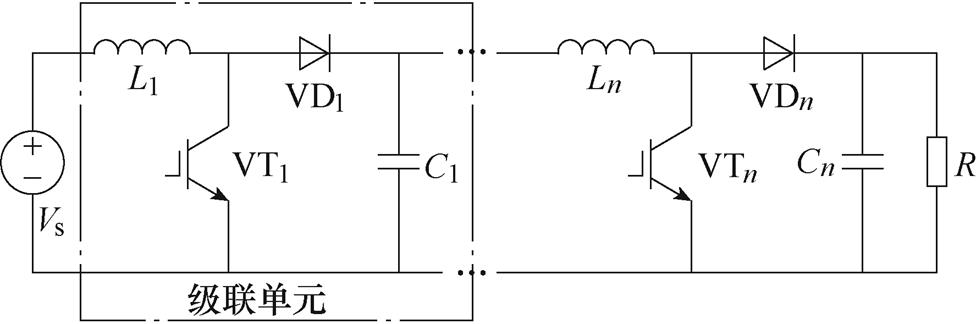
图7 级联Boost变换器
Fig.7 Cascaded Boost converter
然而，级联变换器用到了更多的开关管。当级数较多时，控制和驱动电路复杂。此外，级联变换器效率等于各级单元的效率之积，所以整体效率较低。因此，级联级数不宜过多。
Layer意为“压条”，是指取DC-DC变换器的输出反馈到输入端，就像取植物的枝条插到土壤中让其繁殖一样[27]。Graft意为“嫁接”，是指将不同的DC-DC变换单元进行级联，然后使用一些方法进行化简[28]。有公共端的两个开关管、多个二极管的化简[28-29]如图8所示。
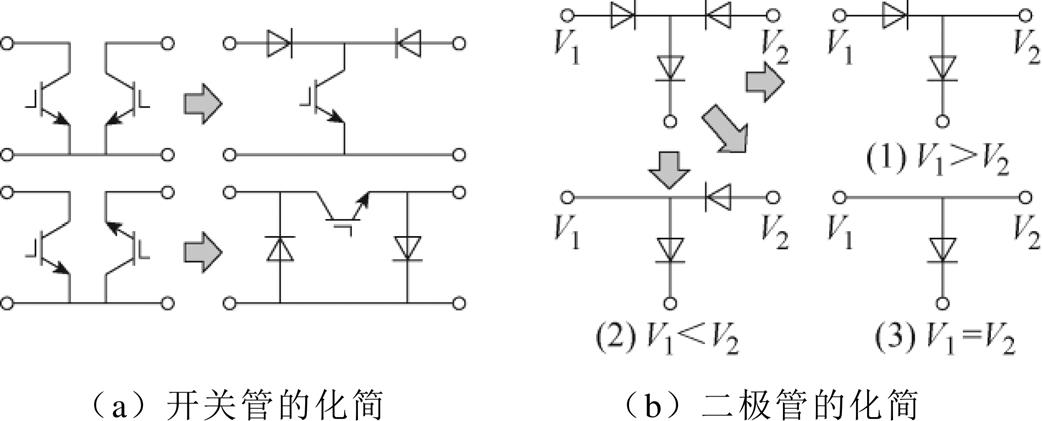
图8 开关管和二极管的Graft变换
Fig.8 Graft conversions of switches and diodes
文献[29]对Layer和Graft两种方法进行了综合改进，可根据给定电压增益表达式构造出对应的变换器。该方法的基本思想是：将电压增益表达式分解为基本DC-DC变换器的电压增益表达式，如D、1/(1-D)、D/(1-D)等，然后借助方框图，在基本DC- DC变换器上引入反馈等变换，得到符合给定电压增益的变换器。
设给定电压增益G=(1-D)/(1-2D)，可将其分解为
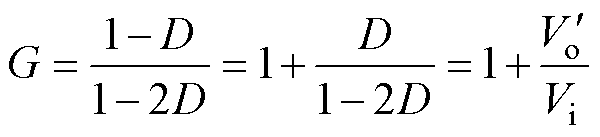（12）
式中，
为去除增益为1的并联环节后的输出电压。
进一步地
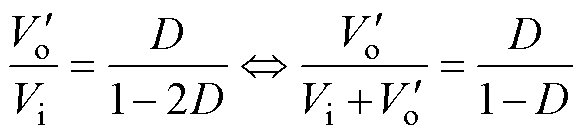（13）
可知，电压增益G=(1-D)/(1-2D)对应的系统由并联环节、反馈环节和一个传递函数为D/(1-D)的环节组成，系统框图如图9所示。
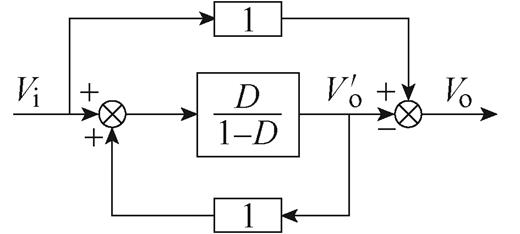
图9 电压增益G=(1-D)/(1-2D)对应的系统框图
Fig.9 Block diagram of a converter with voltage gain G=(1-D)/(1-2D)
根据图9，若传递函数为D/(1-D)的环节选择Sepic变换器，则实现输出电压为的电路如图10a所示。然后，在Vi的正极和的负极之间并联电容Co，如图10b所示。最后，将负载R与电容Co并联，得到的负载电压为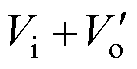
。重新布置元器件，得到电压增益为(1-D)/(1-2D)的变换器如图10c所示。
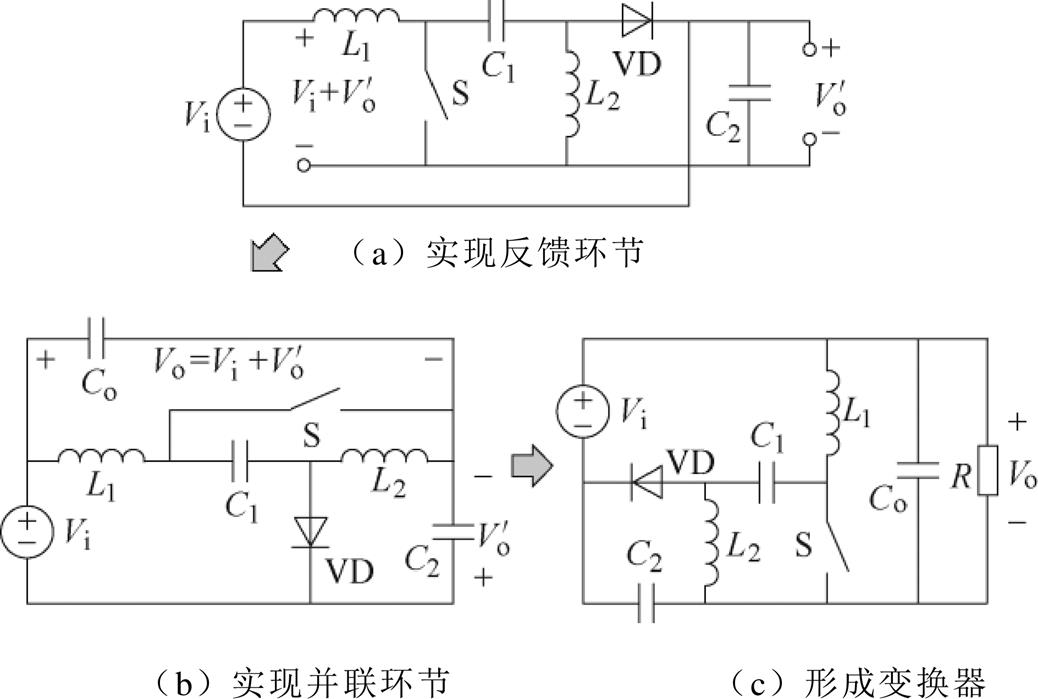
图10 采用Layer和Graft方法构造的一种DC-DC变换器
Fig.10 A DC-DC converter synthesized by Layer and Graft method
由上述分析可见，改进Layer和Graft方法可根据给定电压增益表达式，构造出对应的DC-DC变换器。然而，将电压增益表达式进行数学处理的过程需手工进行，且某些电压增益表达式可能无法实现分解。
交错并联法的思想是将若干个相同开关单元的输入端并联、输出端并联，从而构造出新的变换器。该方法增加了通过电流和功率的支路，可容纳更大的电流，传输更大的功率。
以两个Boost变换单元为例，交错并联的连接方式如图11所示，其中开关管S1和S2的导通时刻需要错开。
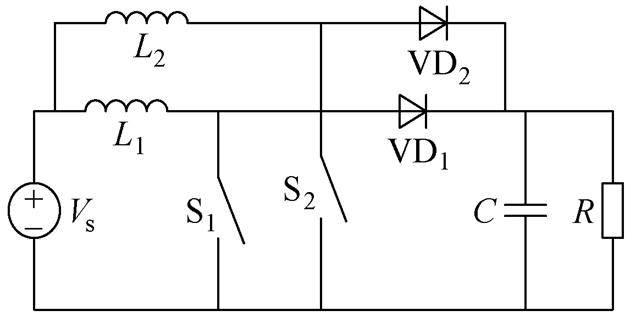
图11 交错并联的Boost变换器
Fig.11 Interleaving Boost converter
采用交错并联法构造的变换器有以下优点：
（1）各支路开关管的导通时刻错开，使各支路电流的脉动互相抵消，从而减小输出电流纹波、功率器件的开关损耗和电流应力[30]。
（2）在大功率应用场合，各支路共同分担系统总功率，便于功率器件选型[30]。
（3）各支路可互为备用，当某一支路发生故障时，其余支路可以继续工作，提高了总体可靠性[31]。
类似地，将其他变换器单元进行交错并联，可获得更多新的变换器，但需要考虑各支路元器件的应力大小及不同支路间的功率分配。
减少不必要的功率处理（Reduced Redundant Power Processing, R2P2）方法早期用于构造非级联的功率因数校正电路[33]，后来推广到DC-DC变换器的构造中[34-36]。
R2P2方法与级联法类似，也是对多个变换单元进行组合，以获得较高的电压增益。R2P2方法中主要的几种连接方式如图12所示[34]。图中，A和B代表基本变换单元。设单元A和B的电压增益分别为MA和MB，则变换器整体的电压增益见表5。
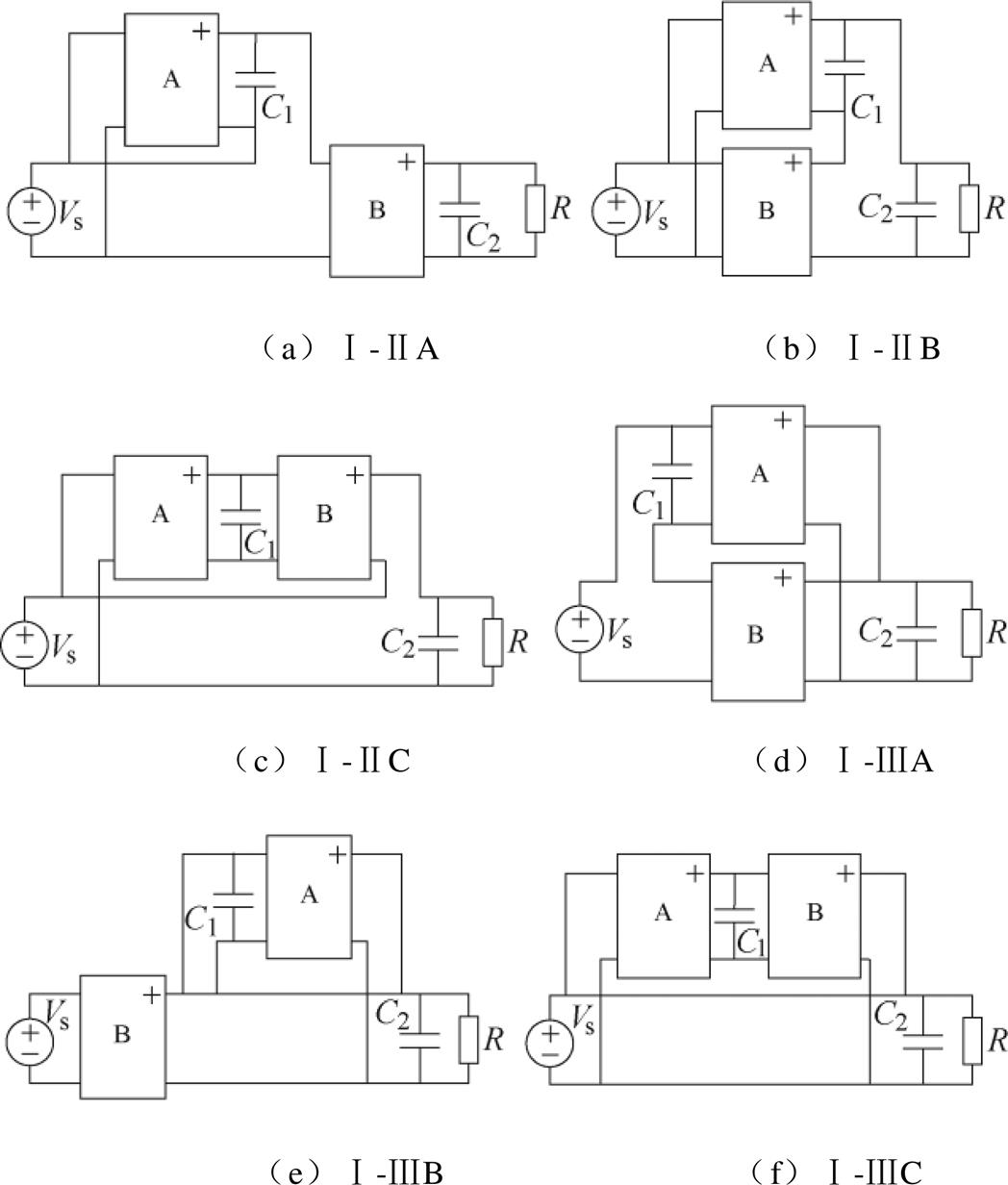
图12 R2P2方法的连接方式
Fig.12 Connection modes of R2P2 method
以Ⅰ-ⅡA结构为例，若A单元选择Buck-Boost单元，B单元选择Boost单元，得到的变换器如图13所示[34]，其电压增益为1/(1-D)2。
从上述分析可见，R2P2方法适用于构造有明确电压增益需求的变换器。由于变换单元之间的连接关系不是级联，故R2P2方法有效地克服了级联法的不足，在提高电压增益的同时，保证了较高的效率。此外，该方法有多种连接方式可选，灵活性较高。
表5 R2P2方法不同连接方式的电压增益
Tab.5 Voltage gains of different modes of R2P2 method
连接方式电压增益 Ⅰ-ⅡAMB(MA+1) Ⅰ-ⅡBMA+MB Ⅰ-ⅡC Ⅰ-ⅢA Ⅰ-ⅢB Ⅰ-ⅢC
图13 运用R2P2方法构造的一种DC-DC变换器
Fig.13 A DC-DC converter synthesized by R2P2 method
阻抗网络（单元）泛指含有电感、电容、开关管和二极管的网络。通过开关器件对电流通路的控制，使网络中的电感、电容有序充电和放电，实现升压等功能。置换法的思路是用一个阻抗单元代替一个元器件，且可迭代多次；嵌入法的思路则是在电路中插入一个阻抗单元。阻抗网络置换-嵌入法常用于构造高电压增益的DC-DC变换器。下面按不同类型的阻抗网络进行介绍。
2.7.1 Z源网络
传统Z源网络是由两个相同电感和两个相同电容构成的四端阻抗网络，并连接成X型[37]，如图14a所示。传统Z源网络衍生出的多种变体统称为Z源网络，常用于DC-DC变换器的Z源网络有准Z源、共阳二次型、共阴二次型、开关电感型等[38]，分别如图14b～图14e所示。
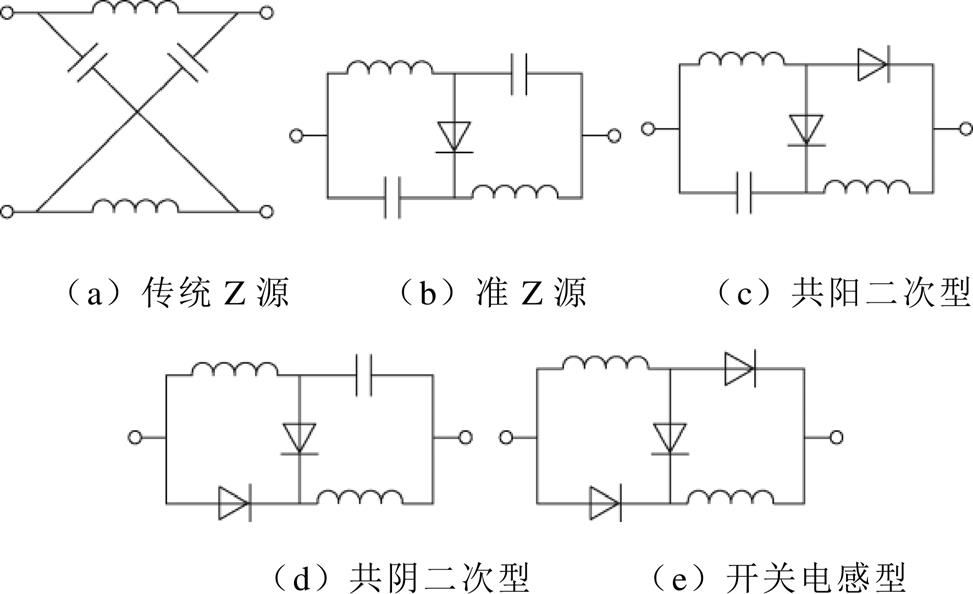
图14 常用的Z源网络
Fig.14 Frequently-used Z-source networks
将上述Z源网络适当地嵌入DC-DC变换器，或置换DC-DC变换器中的元器件，可以得到新的变换器。例如，用共阳二次型网络置换Boost变换器中的电感，得到电压增益为1/(1-D)2的共阳二次型Boost变换器[39]如图15所示。由于Z源网络有多种类型，置换和嵌入方式又比较灵活，因此可构造出数量巨大的新型变换器。
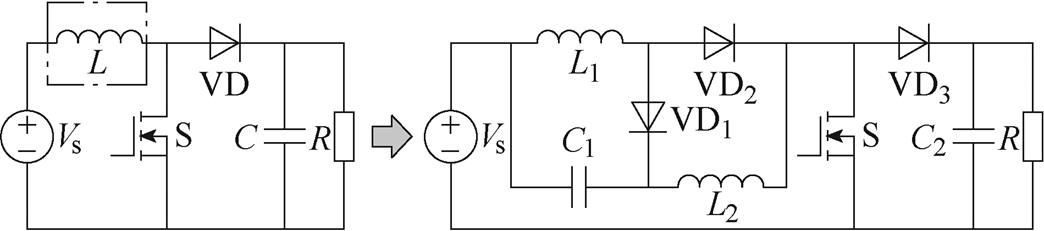
图15 共阳二次型Boost变换器
Fig.15 Common-anode quadratic Boost converter
2.7.2 开关电容网络
开关电容网络只含电容、开关管和二极管。最简单的开关电容网络[41]如图16所示，其中，开关管S和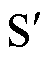
交替导通，使电容C交替充电和放电。
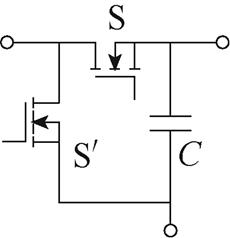
图16 开关电容网络
Fig.16 Switched capacitor network
将开关电容网络置换Boost变换器中的电感，可构造出倍压开关电容变换器和多级开关电容变换器[41]。开关电容变换器如图17所示，其基本原理是开关电容C1～Cn并联充电，串联向输出电容Co及负载放电，实现升压功能。当开关电容网络的个数为n时，输出电压为输入电压的n+1倍。由于开关电容网络不含磁性元器件，故功率密度相对较高，但输出电压与输入电压成倍数关系，无法调节[41]。此外，如要求很高的增益，需要的开关电容和开关管数目较多，不仅结构复杂，而且累计导通压降较大。
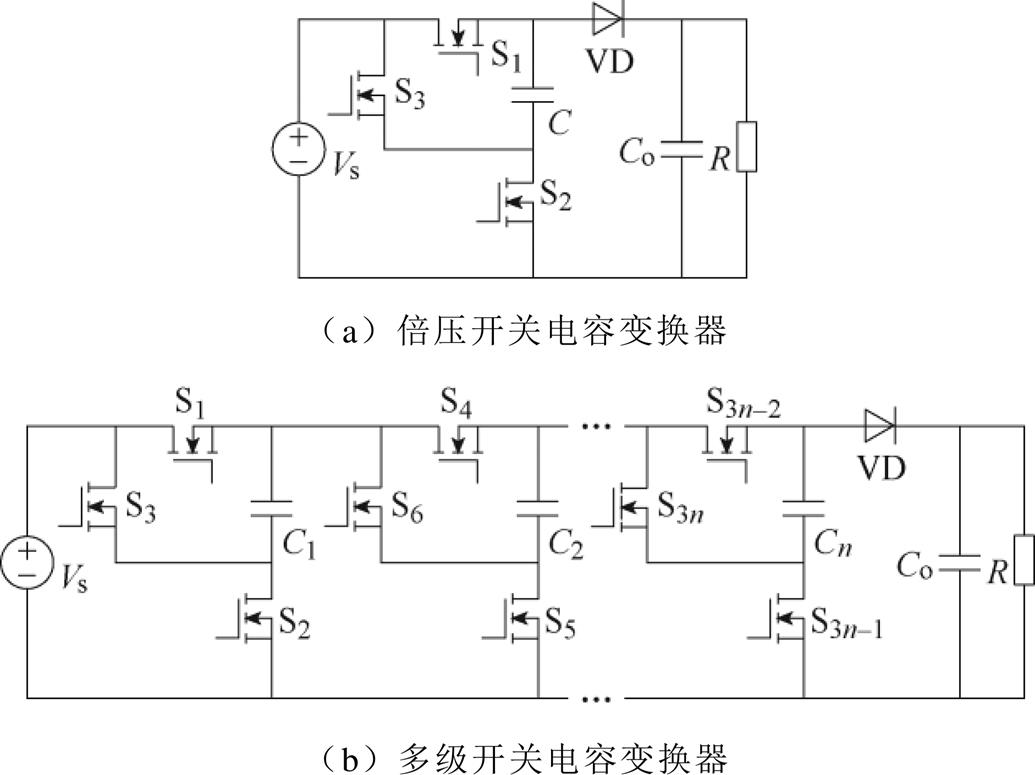
图17 开关电容变换器
Fig.17 Switched capacitor converters
2.7.3 其他阻抗网络
文献[42-43]提出一种“单开关级联”的连接方式，该连接方式与传统的级联不同，但本质属于阻抗网络的嵌入和置换。常见的单开关级联DC-DC变换器如图18所示，该类变换器具有以下优势：①与传统级联DC-DC变换器类似，可实现更大范围的电压变换；②仅釆用一个开关管，简化了驱动电路和控制回路的设计。
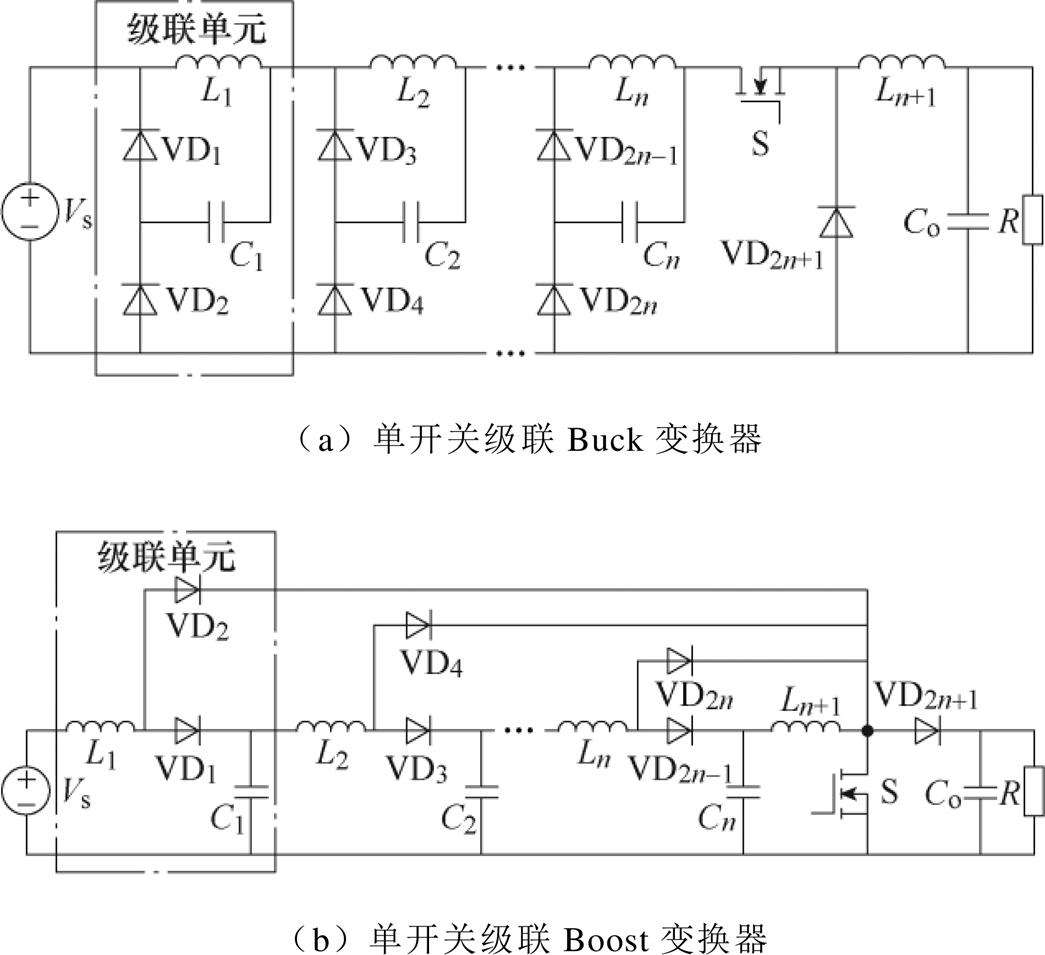
图18 单开关级联变换器
Fig.18 Single-switch cascaded converters
文献[44]提出“外衣电路”的概念，将阻抗网络一层一层地嵌入基本DC-DC变换器中，实现电压增益的提高。该文提出了一种适用于Boost、Buck- Boost等基本DC-DC变换器的外衣电路拓扑，一种嵌入外衣电路的Boost变换器如图19所示。嵌入外衣电路的优点是提高了电压增益，降低了开关管电压应力，而且外衣电路内部电容电压应力相对均匀，方便了器件选型。同时，外衣电路没有增加开关管数量，因此不影响原控制环节。
综上所述，阻抗网络置换-嵌入法通过在基本DC-DC变换器中置换或嵌入阻抗网络单元，从而满足电压增益需求，灵活性较高。单一的置换或嵌入操作可以由计算机完成并可视化，但是选择何种基本变换器和阻抗网络、置换哪个元器件、在何处嵌入等关键问题仍需人工参与。
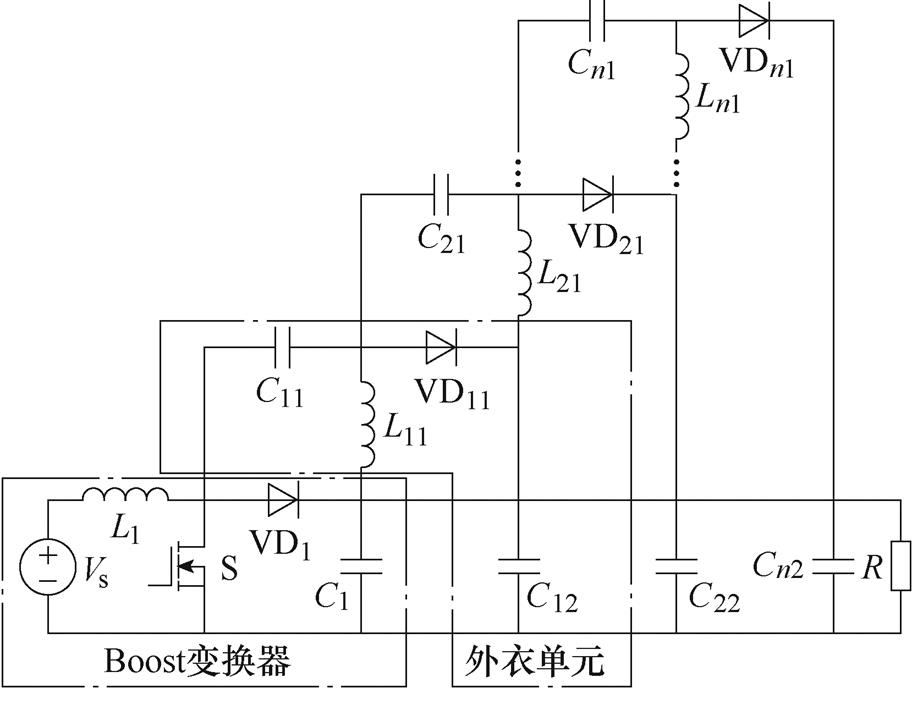
图19 嵌入外衣电路的Boost变换器
Fig.19 Boost converter inserting coat circuit
对于多负载的应用场合，要求DC-DC变换器具有多路输出。文献[45]介绍了两级单输入多输出DC-DC变换器的串并级联法，其中第一级只有一个变换单元，第二级有多个变换单元，第一级与第二级之间有串联和并联两种连接方式，分别如图20a和图20b所示。按照前后级输入输出是V型（电压型）还是I型（电流型）、前后级的连接方式是串联（S型）还是并联（P型），可得到24=16种连接方式。
该方法满足了DC-DC变换器多路输出的需求，可选连接方式较多，可根据其他需求（如电压增益）进行选择，如第二级之间串联的结构适用于高降压比的场景。然而，该方法构造得到的变换器各路输出不完全独立，某些连接方式的前后级也会相互影响[45]。
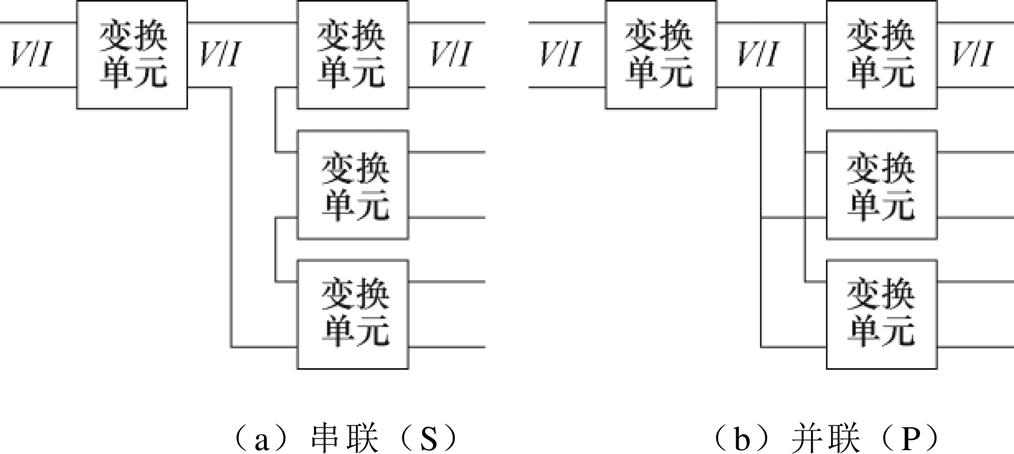
图20 两级单输入多输出DC-DC变换器
Fig.20 Two-stage single-input multi-output DC-DC converters
以输入级为V型、中间级为I型、中间级串联、输出级为I型（V-I-S-I）的连接方式为例，若前后级均选择Buck单元，输出为两路，构造出的变换器如图21所示[45]。
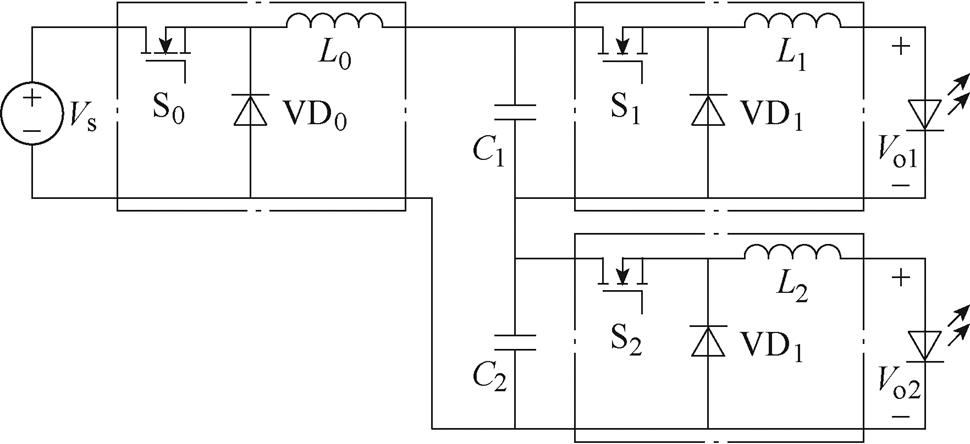
图21 一种V-I-S-I型单输入双输出DC-DC变换器
Fig.21 A V-I-S-I configured single-input double-output DC-DC converter
表6对比了上述几种典型二次构造方法的构造条件、适用范围、优缺点、难点和关键技术、发展趋势，从计算机辅助设计的角度出发，上述方法可分为三类：
表6 二次构造方法的比较
Tab.6 Comparison of secondary synthesis methods
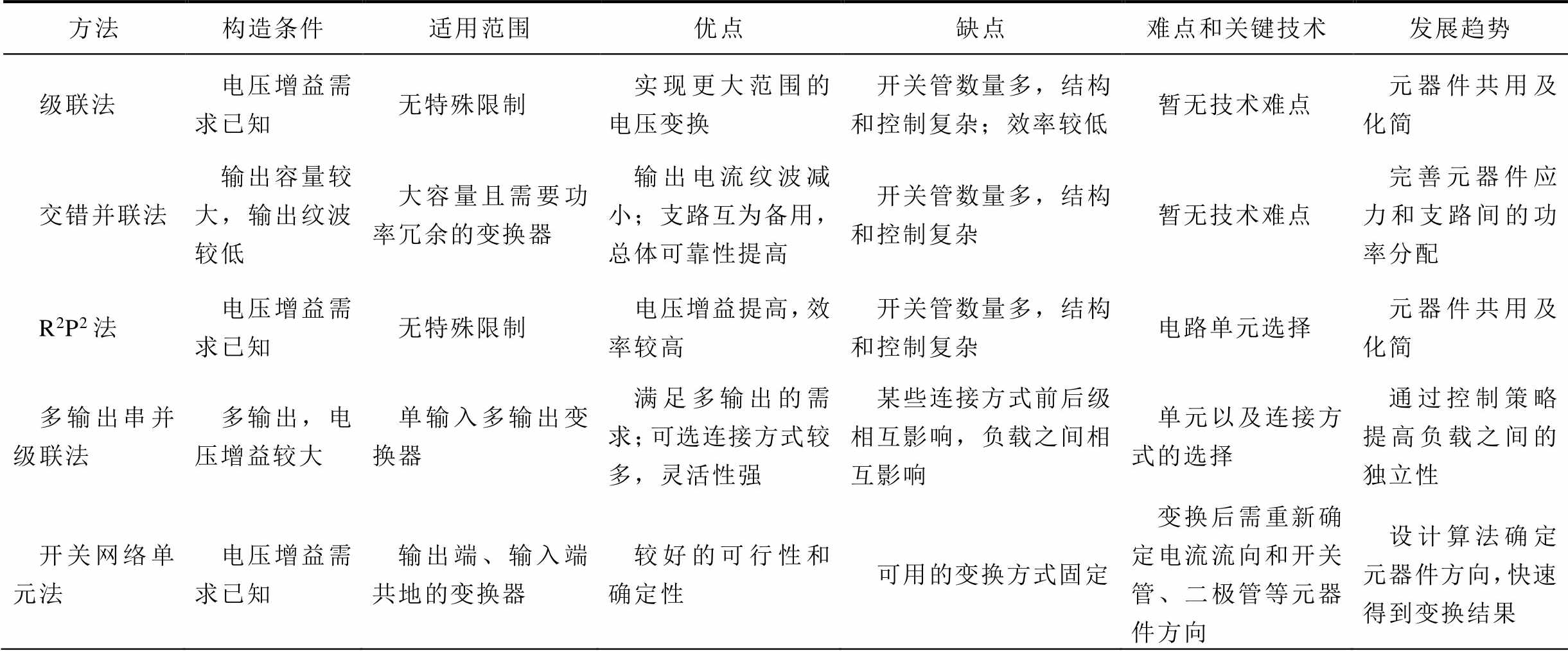
方法构造条件适用范围优点缺点难点和关键技术发展趋势 级联法电压增益需求已知无特殊限制实现更大范围的电压变换开关管数量多，结构和控制复杂；效率较低暂无技术难点元器件共用及化简 交错并联法输出容量较大，输出纹波较低大容量且需要功率冗余的变换器输出电流纹波减小；支路互为备用，总体可靠性提高开关管数量多，结构和控制复杂暂无技术难点完善元器件应力和支路间的功率分配 R2P2法电压增益需求已知无特殊限制电压增益提高，效率较高开关管数量多，结构和控制复杂电路单元选择元器件共用及化简 多输出串并级联法多输出，电压增益较大单输入多输出变换器满足多输出的需求；可选连接方式较多，灵活性强某些连接方式前后级相互影响，负载之间相互影响单元以及连接方式的选择通过控制策略提高负载之间的独立性 开关网络单元法电压增益需求已知输出端、输入端共地的变换器较好的可行性和确定性可用的变换方式固定变换后需重新确定电流流向和开关管、二极管等元器件方向设计算法确定元器件方向，快速得到变换结果
（续）
方法构造条件适用范围优点缺点难点和关键技术发展趋势 对偶法电压增益需求已知平面电路确定性强，对偶电路特性已知目前只适用于平面电路，且只能构造出一个对偶变换器采用算法搜索网孔推广到非平面电路 Layer和Graft方法电压增益表达式确定无特殊限制开关管数量较少手工推导，具有不确定性，某些电压增益无法实现对给定的电压增益表达式进行数学处理自动判断一个电压增益表达式能否转换成有效的框图 阻抗网络置换-嵌入法电压增益需求已知无特殊限制灵活性强，可满足增益、应力等需求具有不确定性，构造过程难量化，需要设计者经验用于置换的单元以及单元嵌入的位置选择编写构造算法，实现自动构造
（1）级联法、交错并联法、R2P2方法、多输出串并级联法仅需将变换单元填入特定结构中，因此可不借助计算机辅助技术。
（2）开关网络单元法、对偶法、Layer和Graft方法有比较明确的步骤，因此适合编程实现辅助设计。
（3）阻抗网络置换-嵌入法的电路形式丰富，但一些关键问题仍需人工决策，是今后计算机辅助设计需要解决的问题。
本文总结了现有大部分DC-DC变换器的构造方法，并按照“元器件-电路单元-变换器”三个层级，将构造方法分为一次构造和二次构造。其中一次构造从元器件出发直接构造出变换器，故适用于构造元器件较少、功能简单的变换器，同时为二次构造提供各种不同功能的原型变换器。而二次构造则对已有电路单元或变换器进行改造，适用于根据实际需要构造变换器。
本文重点介绍了DC-DC变换器一些典型构造方法的原理和步骤，分析了各种方法的优缺点和适用场合，进而探讨了在构造方法中运用计算机辅助技术的可行性。虽然每种构造方法解决的应用需求有所不同，但未来可将大部分构造方法编成程序，一方面进一步减少构造过程对人工的依赖；另一方面可根据特定需求由程序选择并执行合适的构造方法，从而构造出符合需求的DC-DC变换器。
参考文献
[1] 张辉, 梁誉馨, 孙凯, 等. 直流微电网中多端口隔离型DC-DC变换器的改进虚拟电容控制策略[J]. 电工技术学报, 2021, 36(2): 292-304.
Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port isolated DC-DC converter in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 292-304.
[2] 蔡旭, 杨仁炘, 周剑桥, 等. 海上风电直流送出与并网技术综述[J]. 电力系统自动化, 2021, 45(21): 2-22.
Cai Xu, Yang Renxin, Zhou Jianqiao, et al. Review on offshore wind power integration via DC trans- mission[J]. Automation of Electric Power Systems, 2021, 45(21): 2-22.
[3] 管乐诗, 温兆亮, 许晓志, 等. 适用于宽增益范围的可重构单级DC-DC变换器及其磁元件设计[J]. 电工技术学报, 2023, 38(6): 1571-1583.
Guan Leshi, Wen Zhaoliang, Xu Xiaozhi, et al. A modular reconfigurable single-stage DC-DC converter suitable for wide gain range and its magnetic design[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1571-1583..
[4] 佟明昊, 程明, 许芷源, 等. 电动汽车用车载集成式充电系统若干关键技术问题及解决方案[J]. 电工技术学报, 2021, 36(24): 5125-5142.
Tong Minghao, Cheng Ming, Xu Zhiyuan, et al. Key issues and solutions of integrated on-board chargers for electric vehicles[J]. Transactions of China Elec- trotechnical Society, 2021, 36(24): 5125-5142.
[5] Chen Manxin, Loh P C, Yang Yongheng, et al. A six-switch seven-level triple-Boost inverter[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1225-1230.
[6] 李虹, 王文财, 李亚敏, 等. 基于图论的S1D1L2C1型DC-DC变换器可编程拓扑搜索算法[J]. 中国电机工程学报, 2021, 41(16): 5670-5683.
Li Hong, Wang Wencai, Li Yamin, et al. Program- mable topology searching algorithm for S1D1L2C1 type DC-DC converters based on graph theory[J]. Proceedings of the CSEE, 2021, 41(16): 5670-5683.
[7] Nag S S, Panigrahi R, Mishra S K, et al. A theory to synthesize nonisolated DC-DC converters using flux balance principle[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10910-10924.
[8] Erickson R W. Synthesis of switched-mode conver- ters[C]//1983 IEEE Power Electronics Specialists Conference, Albuquerque, USA, 2015: 9-22.
[9] Maksimovic D, Cuk S. General properties and synthesis of PWM DC-to-DC converters[C]//20th Annual IEEE Power Electronics Specialists Con- ference, Milwaukee, USA, 2002: 515-525.
[10] Panigrahi R, Mishra S K, Joshi A. Synthesizing a family of converters for a specified conversion ratio using flux balance principle[J]. IEEE Transactions on Industrial Electronics, 2021, 68(5): 3854-3864.
[11] Panigrahi R, Mishra S K, Joshi A. Synthesis of an optimum converter topology for a specified voltage conversion ratio[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 3923-3934.
[12] Panigrahi R, Mishra S K, Joshi A, et al. DC-DC converter synthesis: an inverse problem[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 12633-12638.
[13] Pietkiewicz A, Tollik D. Systematic derivation of two-state switching DC-DC converter structures[C]// International Telecommunications Energy Conference, New Orleans, USA, 2009: 473-477.
[14] Li Yuzhuo, Ding Li, Li Yunwei. Isomorphic relation- ships between voltage-source and current-source converters[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(8): 7131-7135.
[15] Zhang Guidong, Liao Yukai, Yu S S, et al. A graph-modeling approach to topology simplification in power converters[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 8248-8261.
[16] Mo Liping, Chen Guipeng, Huang Jiangming, et al. Graph theory based programmable topology deriva- tion of multi-port DC-DC converters with reduced switches[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 69(6): 5745-5755.
[17] 吴宁. 电网络分析与综合(修订版)[M]. 北京: 科学出版社, 2020.
[18] 张兴. 高等电力电子技术[M]. 北京: 机械工业出版社, 2011.
[19] Tymerski R, Vorperian V. Generation and classi- fication of PWM DC-to-DC converters[J]. IEEE Transactions on Aerospace and Electronic Systems, 1988, 24(6): 743-754.
[20] Williams B W. Generation and analysis of canonical switching cell DC-to-DC converters[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 329-346.
[21] Marquez R, Contreras-Ordaz M A. The three-terminal converter cell, graphs, and generation of DC-to-DC converter families[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 7725-7728.
[22] Freeland S D. Techniques for the practical application of duality to power circuits[J]. IEEE Transactions on Power Electronics, 1992, 7(2): 374-384.
[23] Bai Zhihong, Zhang Zhongchao. Conformation of multilevel current source converter topologies using the duality principle[J]. IEEE Transactions on Power Electronics, 2008, 23(5): 2260-2267.
[24] Matsuo H, Harada K. The cascade connection of switching regulators[J]. IEEE Transactions on Industry Applications, 1976, IA-12(2): 192-198.
[25] Cuk S, Middlebrook R D. A new optimum topology switching DC-to-DC converter[C]//IEEE Power Elec- tronics Specialists Conference, Palo Alto, USA, 2015: 160-179.
[26] 李福, 邓红雷, 张国驹, 等. 一种中间电容谐振型级联双向DC-DC变换器[J]. 电工技术学报, 2022, 37(20): 5253-5266.
Li Fu, Deng Honglei, Zhang Guoju, et al. A cascaded bidirectional DC-DC converter with intermediate capacitor resonance[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5253-5266.
[27] Wu T P, Chen Y K. A systematic and unified approach to modeling PWM DC/DC converters using the layer scheme[C]//27th Annual IEEE Power Electronics Specialists Conference, Baveno, Italy, 2002: 575-580.
[28] Wu T F, Chen Yukai. A systematic and unified approach to modeling PWM DC/DC converters based on the graft scheme[J]. IEEE Transactions on Industrial Electronics, 1998, 45(1): 88-98.
[29] Wu T F. Decoding and synthesizing transformerless PWM converters[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6293-6304.
[30] Zhang M T, Jovanovic M M, Lee F C Y. Analysis and evaluation of interleaving techniques in forward converters[J]. IEEE Transactions on Power Elec- tronics, 1998, 13(4): 690-698.
[31] 汪元鑫, 苏瑾, 胡金高. 电动汽车车载充电系统的设计与研究[J]. 电气技术, 2019, 20(7): 5-8, 17.
Wang Yuanxin, Su Jin, Hu Jingao. Research on on-board charging system for electric vehicle[J]. Electrical Engineering, 2019, 20(7): 5-8, 17.
[32] 丁杰, 高双, 赵世伟, 等. 基于耦合电感的对称式交错并联低输入电流纹波高增益DC-DC变换器[J]. 电工技术学报, 2021, 36(7): 1507-1515.
Ding Jie, Gao Shuang, Zhao Shiwei, et al. Sym- metrical interleaved low input current ripple high step-up DC-DC converter based on coupled indu- ctor[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1507-1515.
[33] Tse C K, Chow M H L, Cheung M K H. A family of PFC voltage regulator configurations with reduced redundant power processing[J]. IEEE Transactions on Power Electronics, 2001, 16(6): 794-802.
[34] Loera-Palomo R, Morales-Saldaña J A. Family of quadratic step-up DC-DC converters based on non- cascading structures[J]. IET Power Electronics, 2015, 8(5): 793-801.
[35] Zogogianni C G, Tatakis E C, Vekic M S. Non- isolated reduced redundant power processing DC/DC converters: a systematic study of topologies with wide voltage ratio for high-power applications[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 8491-8502.
[36] Salvador M A, de Andrade J M, Lazzarin T B, et al. Methodology for synthesis of high-gain step-up DC-DC converters based on differential con- nections[J]. International Journal of Circuit Theory and Applications, 2021, 49(2): 306-326.
[37] Peng Fangzheng. Z-source inverter[J]. IEEE Transa- ctions on Industry Applications, 2003, 39(2): 504- 510.
[38] Siwakoti Y P, Peng Fangzheng, Blaabjerg F, et al. Impedance-source networks for electric power conver- sion part I: a topological review[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(2): 699-716.
[39] Ye Yuanmao, Eric Cheng K W. Quadratic Boost converter with low buffer capacitor stress[J]. IET Power Electronics, 2014, 7(5): 1162-1170.
[40] Li Kerui, Hu Yafei, Ioinovici A. Generation of the large DC gain step-up nonisolated converters in conjunction with renewable energy sources starting from a proposed geometric structure[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(7): 5323- 5340.
[41] Wu Gang, Ruan Xinbo, Ye Zhihong. Nonisolated high step-up DC-DC converters adopting switched- capacitor cell[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 383-393.
[42] Carbajal-Gutierrez E E, Morales-Saldana J A, Leyva- Ramos J. Modeling of a single-switch quadratic Buck converter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1450-1456.
[43] 杨平, 许建平, 董政, 等. 二次型Boost变换器工作模式及输出电压纹波分析[J]. 电工技术学报, 2014, 29(8): 110-118.
Yang Ping, Xu Jianping, Dong Zheng, et al. Output voltage ripple of quadratic Boost converter[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 110-118.
[44] Zhu Binxin, Ding Feng, Vilathgamuwa D M. Coat circuits for DC-DC converters to improve voltage conversion ratio[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3679-3687.
[45] Li Xiaolu, Dong Zheng, Tse C K. Complete family of two-stage single-input multioutput configurations of interconnected power converters[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(4): 3713-3728.
Abstract In order to synthesize DC-DC converters for specific application requirements, most of the existing synthesis methods of DC-DC converters are summarized. As listed in Tab, these methods can be divided into primary and secondary synthesis according to the three levels of “component-circuit cell-converter”. The principles and steps of typical synthesis methods are highlighted, and the requirements, scope, key technologies, development trends, advantages, and disadvantages of these methods are analyzed and compared. Moreover, the feasibility of using computer-aided technology in the above synthesis methods is discussed.
Tab Classification of Synthesis Methods of DC-DC Converters
ClassificationHierarchyTypical Methods Primary synthesisComponent-circuit cellState equation method, flux balance method, graph search method Secondary synthesisCircuit cell-converterSwitching cell method, duality, cascading, layer and graft method, interleaving, R2P2 method, replacing and inserting of impedance networks, serial-parallel-cascading connection of multioutput converters
The primary synthesis method refers to the synthesis of circuit cells directly from separate components. A circuit cell is a full-featured but relatively basic DC-DC converter that can be used as a basic unit to synthesize other converters. Regarding primary synthesis methods, some conclusions are listed as follows.
(1) The flux balance method synthesis DC-DC converters according to specific requirements (e.g., voltage gain), while the state equation method and graph search method do not. In addition, the latter two methods derive a large number of converters with various features that require further screening.
(2) The state equation method and the flux balance method traverse numerical values, so the implementation programs are simple. However, the graph search method traverses the graphs, which is more difficult to be programmed.
(3) Computer programs can be utilized in some steps of primary synthesis methods, but the utilization of the program still needs to be improved. In the future, full-featured software is expected to realize the whole process, from inputting the requirements to outputting the converter circuits.
Secondary synthesis methods involve synthesizing new topologies from existing topologies by changing connections of circuit cells, combining circuit cells, and adding or removing components or cells. Regarding secondary synthesis methods, some conclusions are listed as follows.
(1) Cascading, interleaving, R2P2 method and serial-parallel-cascading connection of multioutput converters only need to fill the converter cells into specific structures, which require little computer-aided technology.
(2) Switching cell method, duality, layer and graft method have relatively clear steps, which are suitable for programming.
(3) The replacing and inserting method of impedance networks is flexible, and some significant problems still need to be solved manually. Therefore, programming is not appropriate for this method currently.
In conclusion, the primary synthesis method is usually suitable for synthesizing DC-DC converters with fewer components and simpler functions, providing prototypes with different functions for the secondary synthesis. On the other hand, the secondary synthesis method is suitable for synthesizing complex converters. In the future, most of the synthesis methods are expected to be programmed, which can select and execute appropriate synthesis methods intelligently to synthesize a DC-DC converter that meets the given requirements.
keywords：DC-DC converter, synthesis method, topology, graph theory
DOI: 10.19595/j.cnki.1000-6753.tces.221521
中图分类号：TM46
国家自然科学基金资助项目（52277177, 52077085）。
收稿日期 2022-08-05
改稿日期 2022-10-26
张 洋 男，1998年生，硕士研究生，研究方向为电力电子变换器拓扑构造与设计。E-mail: 202120115175@mail.scut.edu.cn
丘东元 女，1972年生，教授，博士生导师，研究方向为电力电子变换器拓扑构造与设计、无线电能传输机理及应用等。E-mail: epdyqiu@scut.edu.cn（通信作者）
（编辑 陈 诚）