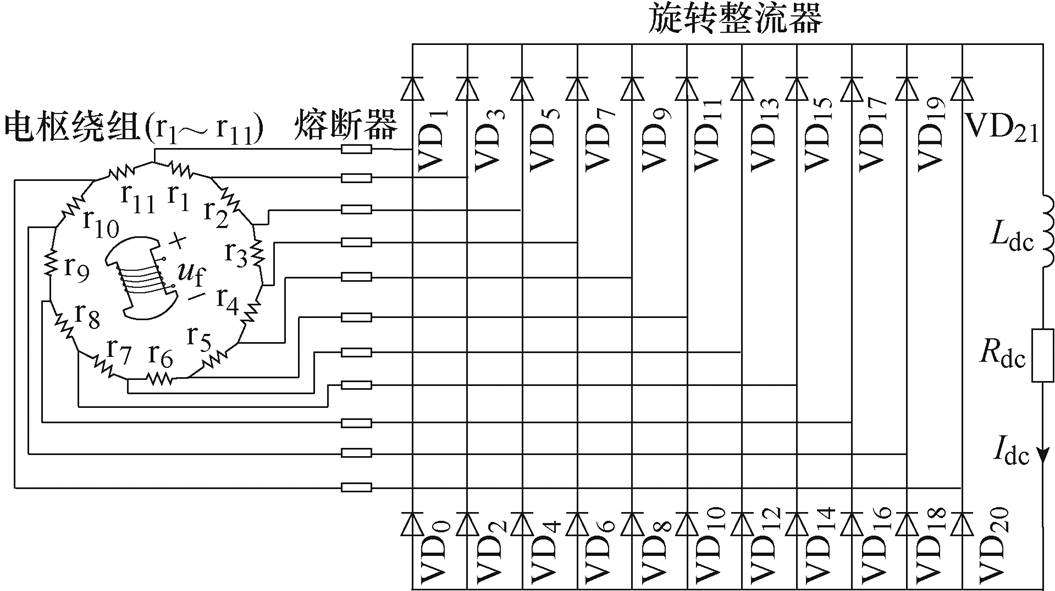
图1 11相环形无刷励磁机及旋转整流系统示意图
Fig.1 Schematic diagram of 11-phase angular brushless exciter and rotating rectifier system
摘要 多相无刷励磁系统广泛应用于大容量核电机组，对其旋转整流器故障的准确判断是保障机组安全稳定运行的重要前提，但是现有方法难以准确区分所有类型故障。为此，该文提出基于卷积神经网络的多相无刷励磁系统旋转整流器故障诊断方案。在给出故障诊断信号选取的理论基础上，将励磁电流作为输入特征，采用一维空洞卷积神经网络实现励磁电流的特征提取和故障模式分类，并结合置信度指标对诊断结果的可靠程度进行评价。进一步使用Score-CAM类激活映射算法分析模型的诊断机制，兼顾了准确性和可解释性。通过11相无刷励磁系统的动模实验进行验证，结果表明，所提方法能够准确区分旋转整流器的不同二极管开路故障模式，在含噪声情况下仍然有较高的准确率，具有良好的应用前景。
关键词：无刷励磁系统 旋转整流器 深度学习 卷积神经网络 故障诊断
核能发电清洁高效，可长期稳定运行，对于节能减排发挥了重要作用，在“双碳”目标背景下具有很大的发展潜力[1]。近年来，我国核电发电量逐年增加，核电机组的安全性和可靠性也逐渐成为关注的重点。无刷励磁系统不使用电刷和集电环[2]，显著提高了励磁系统的可靠性[3]，是大容量核电机组首选的励磁方式。新型的多相无刷励磁系统进一步改善了励磁机性能，广泛应用于我国红沿河、宁德、台山等电厂的大容量核电机组。
旋转整流器是多相无刷励磁系统的关键组成部分之一。然而，由于旋转整流器随励磁机转子侧电枢绕组一直高速旋转，极易受到离心力、电磁作用等的影响，且二极管数量比普通三相整流器多[4]，导致旋转整流器更易发生故障。现场运行中经常发生由于二极管损坏引起的故障事件，如某电厂3号核电机组主变C相故障引起励磁机旋转二极管断相故障和定子绕组接地故障，导致旋转二极管被误判为两相断相故障，机组抢修近20天。因此，及时准确地识别旋转整流器的故障模式，采取灵敏可靠的保护措施避免事故恶化，对核电站运行的安全性和经济性至关重要。
目前，针对多相无刷励磁系统旋转整流器的故障诊断研究相对较少。文献[5-6]提出将探测线圈安装在定子上，利用探测线圈感应电动势的特定频率谐波幅值变化来诊断旋转二极管开路故障。但是这种方法需要改造现有的励磁机，增加了运营成本；还额外要求运行机组具备一定的安装条件，存在较大局限性。文献[4-7]以直流侧电压谐波含量作为判别依据对十二相整流发电机缺桥运行、单个二极管开路故障进行诊断。文献[8]提出定子励磁电流谐波判据对某39相角形无刷励磁系统正常运行和旋转二极管一管开路的故障特征进行研究。文献[9]研究了某11相角形无刷励磁系统正常运行、旋转二极管一管开路和一相开路时定子励磁电流的谐波特征。但是，现有基于谐波分析的方法丢失了能够表征位置的相位信息，导致不同故障模式的输入信号谐波特征存在混叠，仅能区分部分故障模式，未涉及多相旋转二极管更多故障模式的精细区分，难以满足工程实际需求。
近年来，以深度学习为代表的人工智能方法快速发展，为上述问题提供了新的解决思路。人工智能方法不严格依赖复杂的机理分析，可以从数据出发[10]，利用故障数据自适应地构建输入特征与故障模式之间的非线性关系[11]，准确快速地实现故障诊断。已有部分文献将深度学习等方法应用于旋转整流器的故障诊断[12-15]，但仅局限于三相旋转整流系统。与之相比，本文关注的多相无刷励磁系统拓扑结构更复杂，故障类型更多，不同故障类型之间的区分难度随之增大，亟须寻求准确有效的故障诊断方法。
目前，尚未有研究将深度学习方法应用于核电多相无刷励磁系统旋转整流器故障诊断。深度学习模型结构复杂，类似黑盒的工作方式使其准确性高但可解释性差，形成一种相互矛盾的关系[16]。而故障诊断方法要真正地实现落地应用，需要同时兼顾准确性和可解释性，才能为后续制定故障监测与保护方案提供可信的依据。
卷积神经网络作为一种被广泛使用的深度学习算法，具备强大的特征提取能力、优秀的泛化能力和较好的抗噪性能，在时间序列分类问题中展示出显著的优势[17]。卷积层是卷积神经网络区别于其他深度学习方法的重要组成，包括普通卷积、空洞卷积等多种卷积方式。同时，卷积神经网络不仅能给出输入样本的诊断结果，还能提供输出结果的置信度指标，以便对诊断结果的可信度进行评价，有助于减少错判情况的发生。此外，对于卷积神经网络的可解释性研究也受到广泛关注，主要分为两种思路：一种是构造自身具有可解释能力的模型，例如构造可解释的滤波器[18]等，但这类方法在实现可解释性的同时可能会牺牲模型本身的准确性；另一种是对已经训练好的模型进行解释，例如类激活映射方法[19-21]、基于反向传播的方法[22]、基于扰动的方法[23]等，这类方法能够在保证准确率的基础上为模型内部工作机制提供解释。相较而言，类激活映射方法无需额外修改模型输入，仅基于卷积层良好的类别定位能力就能实现对决策机制的解释，为探索卷积神经网络应用于多相无刷励磁系统旋转整流器故障诊断的可解释性创造了有利的条件。
为解决现有方法难以准确识别所有故障模式的问题，本文引入深度卷积神经网络进行多相无刷励磁系统旋转整流器的故障诊断。考虑到输入信号为一维时间序列，且空洞卷积能够在不增加模型计算负担的基础上提高准确率，故采用一维空洞卷积神经网络（One-Dimensional Dilated Convolutional Neural Network, 1D-DCNN）实现故障模式的准确识别，从而降低模型复杂度，并使得模型具备一定的抗噪能力。为减少模型错判情况的发生，通过定义置信度指标来评估分类结果的可靠程度。此外，为了兼顾深度卷积神经网络应用的准确性和可解释性，进一步结合Score-CAM方法分析模型的诊断机制。
利用深度学习方法进行旋转整流器故障识别的首要前提是选取能够充分表征故障信息的诊断信号，即深度模型的输入特征。多相无刷励磁系统的旋转整流器和电枢绕组一直处于高速旋转状态，这种转枢式结构导致获取励磁机转子侧电气量较为困难，定子侧励磁电流是唯一可以被直接监测的电气量。此外，不同二极管故障模式下的励磁电流具有不同的特征。因此，励磁电流是诊断旋转二极管故障最直接有效的信号。以下从转子侧电枢绕组入手分析旋转整流器发生故障后的励磁电流特征产生机理，说明励磁电流用于故障诊断的理论可行性。
以实际中常用的11相环形无刷励磁机及其旋转整流系统为例进行分析，结构示意图如图1所示。励磁机的励磁绕组位于定子侧，电枢绕组与由二极管组成的旋转整流器一起高速旋转，整流电压用于给负载即主发电机励磁绕组供电。交流侧的每相电枢绕组等效为理想电压源与电感串联，各相电枢绕组依次首尾相连形成环形回路，每相电枢绕组两端各接一对反向并联二极管构成多相全波整流电路。
图1 11相环形无刷励磁机及旋转整流系统示意图
Fig.1 Schematic diagram of 11-phase angular brushless exciter and rotating rectifier system
在理论分析时忽略二极管的实际换相过程且假设电枢回路电感足够大。正常运行时，整流电路中上、下桥臂的二极管在线电压达到最大值时导通。各相电枢绕组依次相差4p/11电角度，则第m相电枢电流可表示为
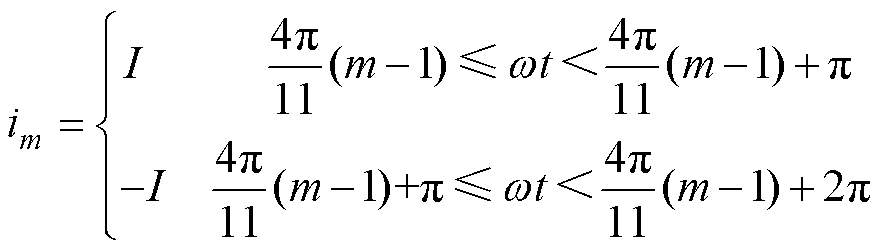（1）
式中，I为电枢电流幅值；wt为电角度；m为相数。
对电枢电流进行傅里叶分析，第m相电枢绕组的m 次谐波电流im,m 及其产生的n 次空间谐波磁动势fa,m,n 分别为
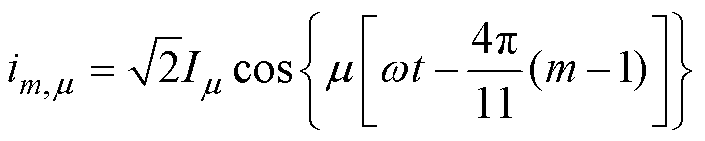（2）
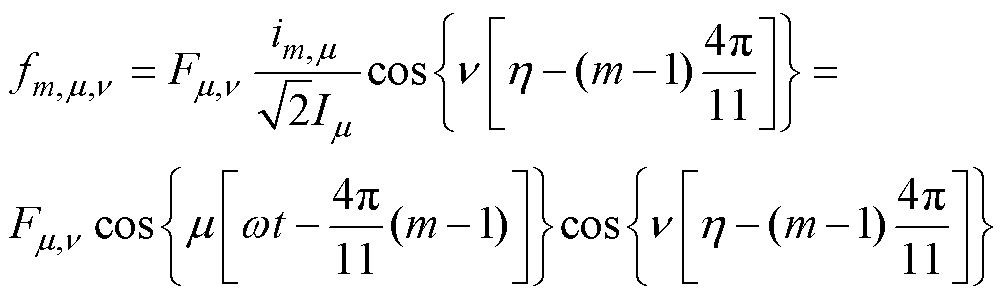（3）
式中，Im 为m 次谐波电流有效值；Fm,n 为谐波磁动势幅值；n 为空间磁动势谐波次数，n =1, 2, 3,…；h 为沿励磁机转子圆周方向的电角度。
凸极同步电机的气隙磁导系数和定、转子空间坐标之间的关系分别为
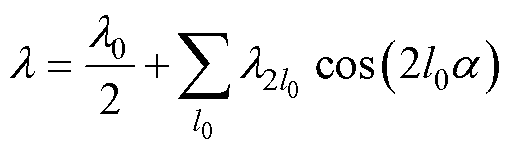（4）
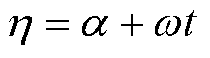（5）
式中，l为气隙磁导系数；l0/2为磁导系数的常数项；2l0为磁导系数的谐波次数，l0=1, 2, 3,…；l2l0为2l0次谐波磁导的幅值；a 为沿励磁机定子圆周方向的电角度。
各相转子电枢绕组空间谐波磁动势合成的电枢反应磁场的磁感应强度可表示为
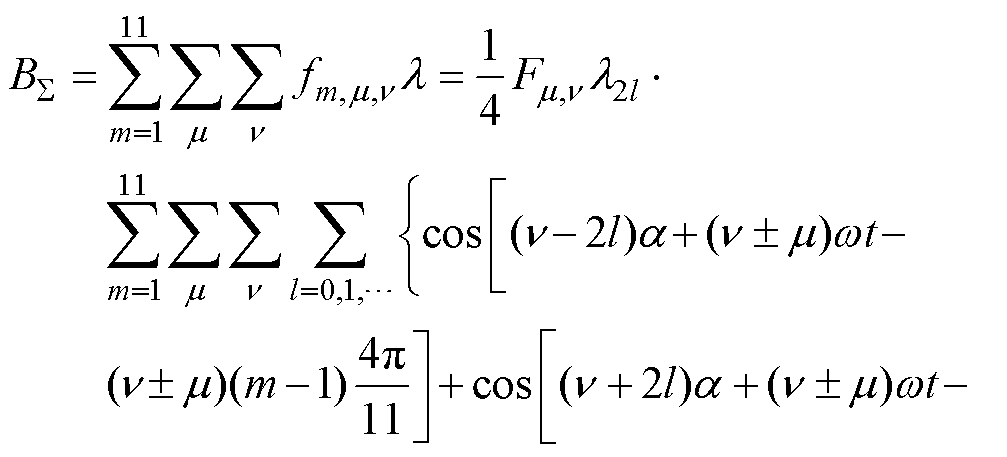
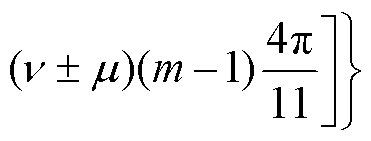（6）
式中，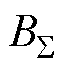
为合成电枢反应磁场磁感应强度；m 为谐波电流次数；2l为磁导系数的谐波次数，l=0,1, 2, 3,…；l2l为2l次谐波磁导的幅值。
正常运行时电枢反应磁场将在定子励磁绕组上感应出谐波电动势和谐波电流。而当旋转二极管发生不同相数或故障相的相对位置不同的故障时，将引起励磁机转子电枢绕组电流出现不同于正常运行时的变化。相数的不同引起电流幅值的变化，而故障相的相对位置的差异会引起电流相位的变化，导致电枢电流具有不同的畸变程度。各相电枢电流产生的合成电枢反应磁场在定子励磁绕组中感应出不同次数和相位的谐波电动势，进而产生不同次数和相位的谐波电流分量，使得旋转二极管不同运行状态下励磁电流呈现出不同的故障特性。不同类型故障在频谱分布上存在相似特征[24]，但故障谐波相位并不相同，实际励磁电流时域波形也有着不同的 表现。
因此，励磁电流包含了所有故障谐波幅值及相位信息，能够反映旋转整流器不同故障模式下的独有特征，可作为故障诊断信号用以区分旋转整流器的运行状态。
卷积神经网络因其稀疏连接和权值共享的特点具备优秀的非线性拟合能力[25]，它能够通过卷积核的局部感受野捕捉到不同故障模式下励磁电流信号微弱的特征差异，自动进行特征提取和模式分类，有望解决现有方法进行旋转整流器故障诊断面临的难题。基于励磁电流信号构建的输入特征本质上是一维时序数据，适合于采用一维卷积神经网络进行处理，这种方式不需要将输入数据转换为其他形式，在一定程度上降低了模型的复杂度，有助于实时检测速度的提升。此外，空洞卷积能够在不增加模型计算负担的基础上进一步优化模型的诊断性能。因此，本文采用1D-DCNN方法实现多相无刷励磁系统旋转整流器故障的智能诊断。
卷积神经网络是一种特殊的前馈神经网络，通常包括卷积层、池化层和全连接层[26]。一维卷积神经网络（One-Dimensional Convolutional Neural Net- work, 1D-CNN）常用于序列模型、自然语言处理等，卷积核只沿着一个方向移动。其核心部分为一维卷积层，通过卷积操作将低级别特征映射为高级别特征[27]，具体运算式为
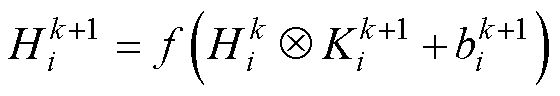（7）
式中，k为卷积层的层数；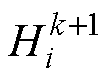
为第i个卷积核在第k+1个卷积层上生成的特征映射；
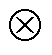为卷积运算符；
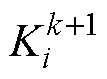和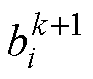
分别为卷积核对应的权重项和偏置项；f为激活函数。
一维卷积神经网络可以用于处理时序数据，如图2所示。同一卷积核作用于原始数据时间序列的不同滑动窗口，得到不同的卷积核输出，实现了对原始数据时间序列的特征提取。
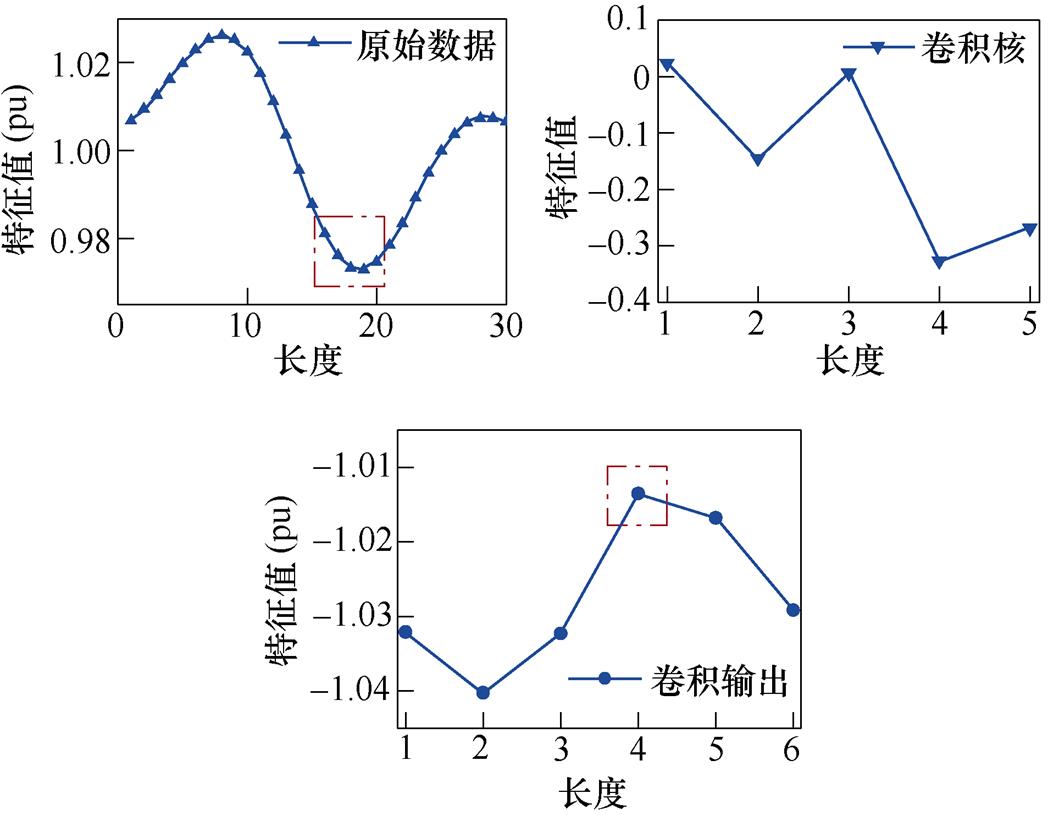
图2 一维卷积过程
Fig.2 One-dimensional convolution process
空洞卷积是一种特殊的卷积模块，能够在不增加参数量的情况下扩大感受野[28]。设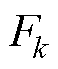
为第k层卷积层的输入，
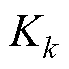为同一卷积层的离散卷积，传统离散卷积运算为
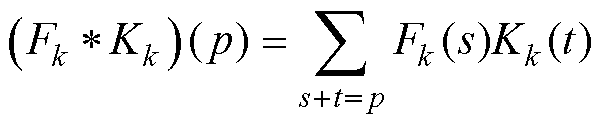（8）
式中，p为卷积后特征图内的点；s为原始特征图内的点；t为卷积层内的特征点。
在传统卷积运算中引入膨胀系数n，表示向原始卷积核的两个相邻元素内添加n-1的空洞数目，构成新的卷积核即空洞卷积，运算公式为
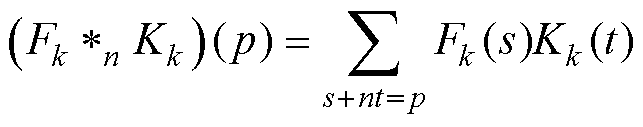（9）
当n=1时空洞卷积退化为传统卷积。膨胀系数越大，表示空洞卷积等间隔采样的范围越大。
感受野被定义为某个卷积层输出结果中一个元素所对应的输入层的区域大小。空洞卷积运算通过膨胀系数控制感受野的大小，传统卷积和空洞卷积各自的感受野为
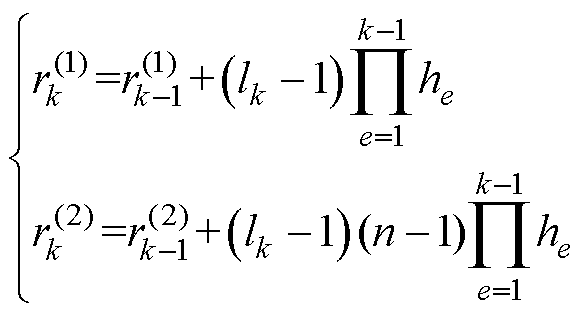（10）
式中，
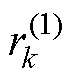和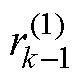
分别表示传统卷积第k层和第k-1层的感受野；
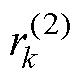和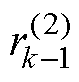
分别表示空洞卷积第k层和第k-1层的感受野；lk为第k层原始卷积核的大小；he为k层前第e层卷积的步长。
本文构建的用于旋转整流器故障诊断的1D- DCNN模型如图3所示。1D-DCNN模型建立起从输入励磁电流信号到输出故障模式的映射关系，从而实现了旋转整流器的故障诊断。
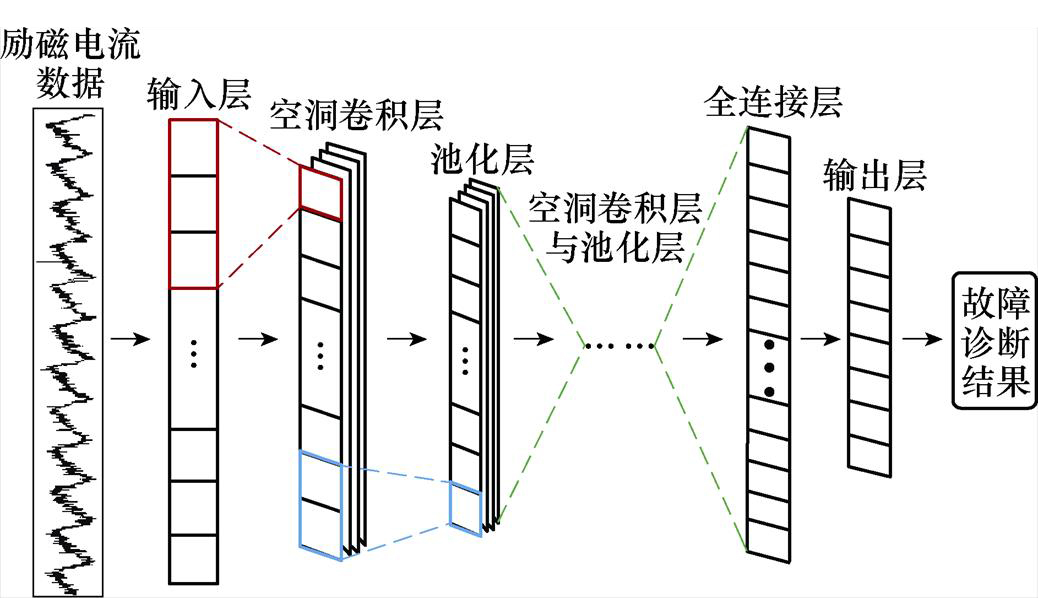
图3 用于旋转整流器故障诊断的1D-DCNN模型
Fig.3 1D-DCNN model for rotating rectifier fault diagnosis
1D-DCNN模型的输入为励磁电流信号组成的一维向量，可以表示为
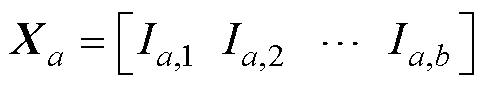（11）
式中，Xa为第a个输入样本；Ia,b为第a个样本中第b个采样时刻的电流值。
输入样本Xa通过空洞卷积层和池化层实现特征提取，其中，空洞卷积层能够充分挖掘局部窗口长度内的故障信息，发现不同故障模式中励磁电流信号的区分性特征；池化层能够提取上一空洞卷积层中最有用的特征，采用最大池化方式降低噪声干扰，增强模型应用于故障诊断的抗噪能力。
由空洞卷积层和池化层提取到的特征展平后输入至全连接层。考虑到旋转二极管的故障模式识别属于多分类问题，故采用softmax函数[29]作为激活函数对整体故障特征进行分类输出，有
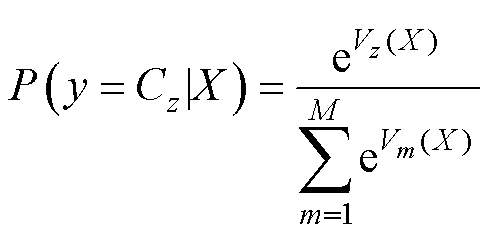（12）
式中，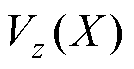
为样本X在输出层第z个神经元的输入值；M为输出层的神经元个数；
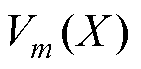为样本X在输出层第m个神经元的输入值，m=1, 2, 3,…, M；
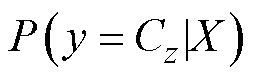为样本X属于第z个类别的条件概率；概率输出最大值对应的故障模式即为诊断网络的输出结果。
在模型给出样本属于不同故障模式条件概率的基础上，可进一步定义输出结果的置信度，以表征诊断结果的可靠程度，本文将置信度定义为模型输出最大概率值和第二大概率值之差，有
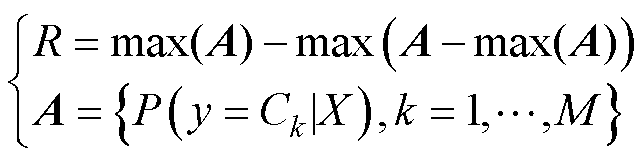（13）
式中，R为模型对样本X诊断结果的置信度；A为由所有条件概率值组成的集合。置信度R越大，表明模型对故障诊断结果的正确程度更加确定。
为实现多相无刷励磁系统旋转整流器故障的准确识别，本文提出了基于1D-DCNN模型的故障诊断的整体流程，如图4所示，包括三个阶段：励磁电流数据获取与预处理、模型训练与在线诊断、模型进行故障诊断的机制分析。
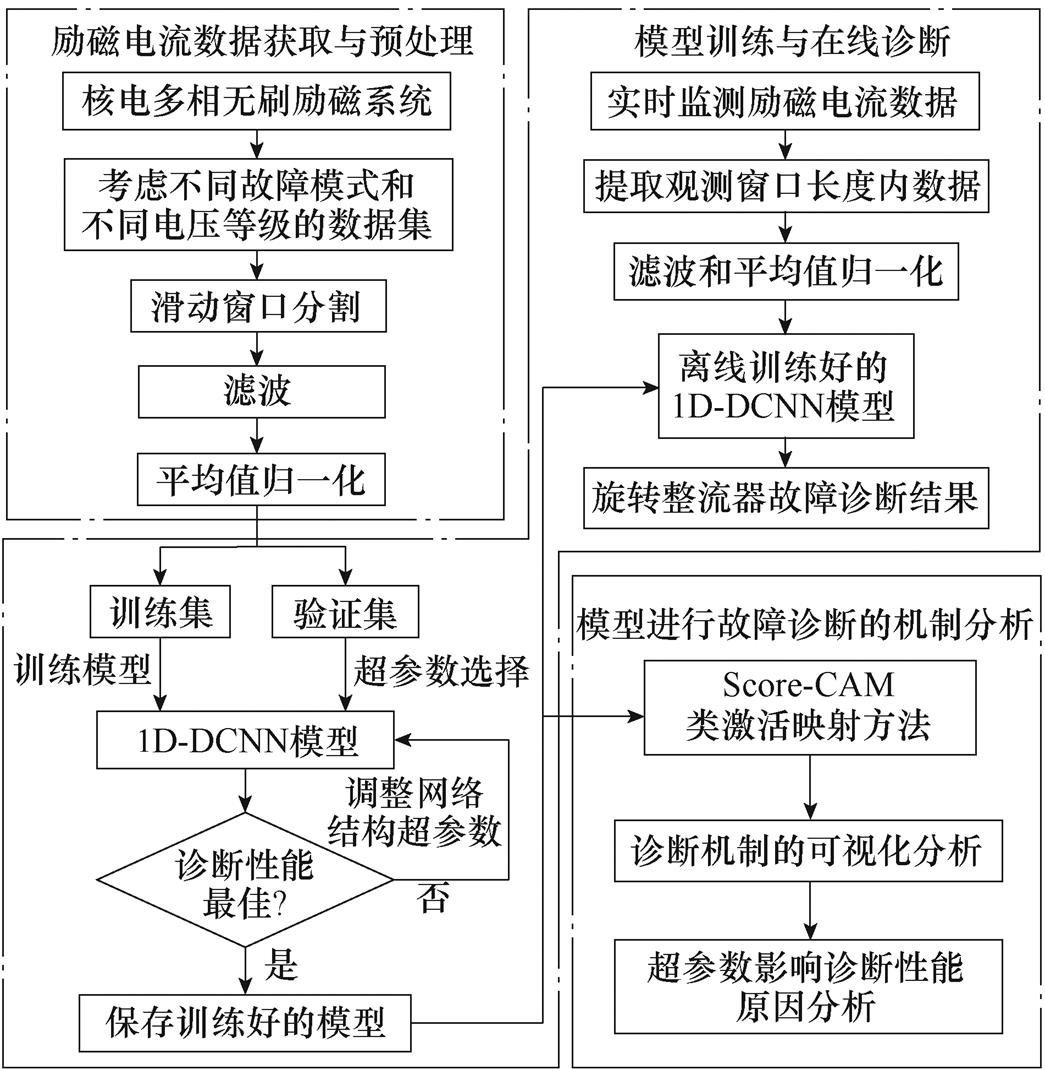
图4 旋转整流器故障诊断的整体流程
Fig.4 The flow chart of rotating rectifier fault diagnosis
励磁电流是对多相无刷励磁系统旋转整流器进行故障诊断的输入信号，实验过程中的电压等级将影响励磁电流的数据特征。为了保证故障诊断网络对不同电压等级具有适用性及泛化能力，在数据获取时应考虑多种电压等级情况。
输入励磁电流信号的可区分性、数据质量均会影响模型的故障诊断表现，因此很有必要对原始信号进行预处理。在此考虑的预处理方法包括滑动窗口分割、滤波和平均值归一化。
首先，考虑到实际系统发生故障的时刻具有不确定性，不同时刻采集信号的起始点不同，本文采用滑动窗口分割励磁电流信号，得到分割后的数据。
实际采集到的数据可能包含较多噪声，为避免噪声影响故障识别准确率，进一步对分割后的数据进行滤波。滤除高次谐波后能够更加突出地展示励磁电流信号的波形特征。值得注意的是，滤波频率过高不会对波形特征起到明显的改善效果。
此外，不同电压等级下采集的励磁电流幅值具有明显差异。为了避免输入信号幅值的差异影响模型性能，需要对滤波后的数据采用归一化处理。由多相无刷励磁系统的旋转整流器故障实验结果得知，随着电压等级的升高，励磁电流波形幅值大小也会随之增加。根据励磁电流信号这一变化特点，提出平均值归一化方法，每个采样点除以所在样本中所有采样点的平均值，有
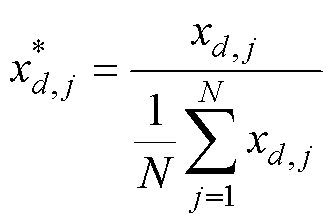（14）
式中，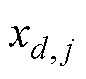
为第d个样本的第j个采样点；N为第d个样本的采样点数；
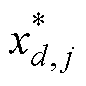为归一化后的数据。
对输入数据进行预处理后，需要利用预处理后的数据离线训练一个性能较优的深度学习模型，并用于在线诊断。
在离线训练阶段，将预处理后的数据样本集按一定比例划分为训练集和验证集，划分时确保故障类型分布均衡。训练集样本用于训练1D-DCNN模型的网络参数，同时根据验证集样本上的诊断效果调整网络结构超参数选出最优模型。训练模型的过程中，以交叉熵损失函数[30]为目标函数来量化模型输出结果和真实标签之间的差异，通过Adam算法最小化目标函数，优化各神经层的权重和偏置量，得到性能最佳的模型。目标函数的表达式为
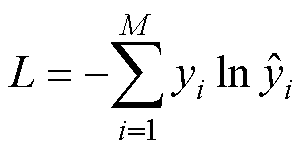（15）
式中，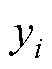
为第i个类别以独热编码表示的真实标签；
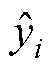为网络Softmax层的目标输出概率。
在线诊断阶段，调用离线训练好的模型用于旋转整流器运行状态诊断。在实时监测多相环形无刷励磁系统的前提下，采集预设采样点数的实测励磁电流数据，进行滤波和平均值归一化操作，再输入至1D-DCNN模型，即可得到最终的故障诊断结果，为后续制定旋转整流器的保护策略提供参考依据。
深度学习模型存在可解释性差的问题，黑箱式的模型使得决策者不能理解模型内部的工作机制，难以信任决策结果。为此，本文采用Score-CAM方法对1D-DCNN模型的诊断机制进行可解释性分析。Score-CAM是一种特定于卷积神经网络模型的事后可解释性方法[21]，可将输出诊断结果映射回输入变量，进而确定模型决策的核心依据。与Grad- CAM、Grad-CAM++等方法相比，Score-CAM方法能够避免梯度不稳定产生的影响，生成的类激活图中噪声更少、可视化效果较为稳定。
设模型的输入向量和输出分别为x和y=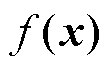
，若被判为目标类别c，相应的预测得分表示为
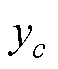。令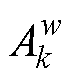
为模型中第k个卷积层第w个通道的输出特征图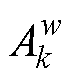，对于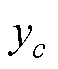的贡献可表示[21]为
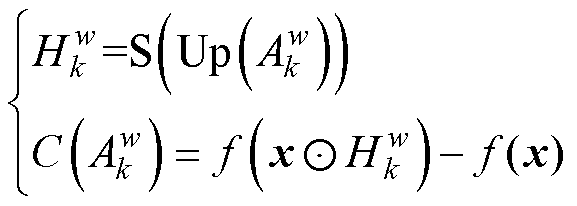（16）
式中，Up(·)为上采样到输入大小的操作；S为将元素映射到0和1之间的操作；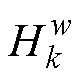
为经采样和映射之后的特征图；表示哈达玛乘积；
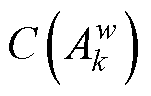为特征图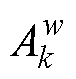
的贡献大小。
该方法首先为每一个特征图分配一个全局权重，再对特征映射和权重进行线性加权求和，最后采用ReLU操作去除负响应，具体计算表达式[21]为
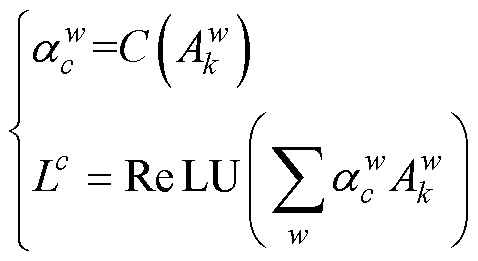（17）
式中，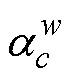
为各通道的权重，决定了类激活图中包含的特定类别信息，每个特征图对应的全局权重即为对应的预测分数贡献值
。
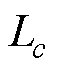利用Score-CAM方法对1D-DCNN模型进行故障诊断的机制展开分析，根据式（16）和式（17）可以计算出励磁电流样本输入特征的归因值，该值代表着输入特征对于诊断结果的影响程度，从而可以发现输入特征和模型输出类别之间的关联性。一方面，通过观察模型在决策过程中更关注励磁电流信号中的哪些特征区域，能够分析模型对于不同故障模式样本的决策依据；另一方面，结合网络结构超参数变化过程中错判样本的决策依据分析，能够更直观地解释网络结构超参数对故障诊断的影响。
本节将通过动模样机的实验数据验证所提故障诊断方案的有效性。动模样机根据实际无刷励磁机设计而成，容量较小便于开展实验，并且能够模拟旋转整流器的各种运行工况。
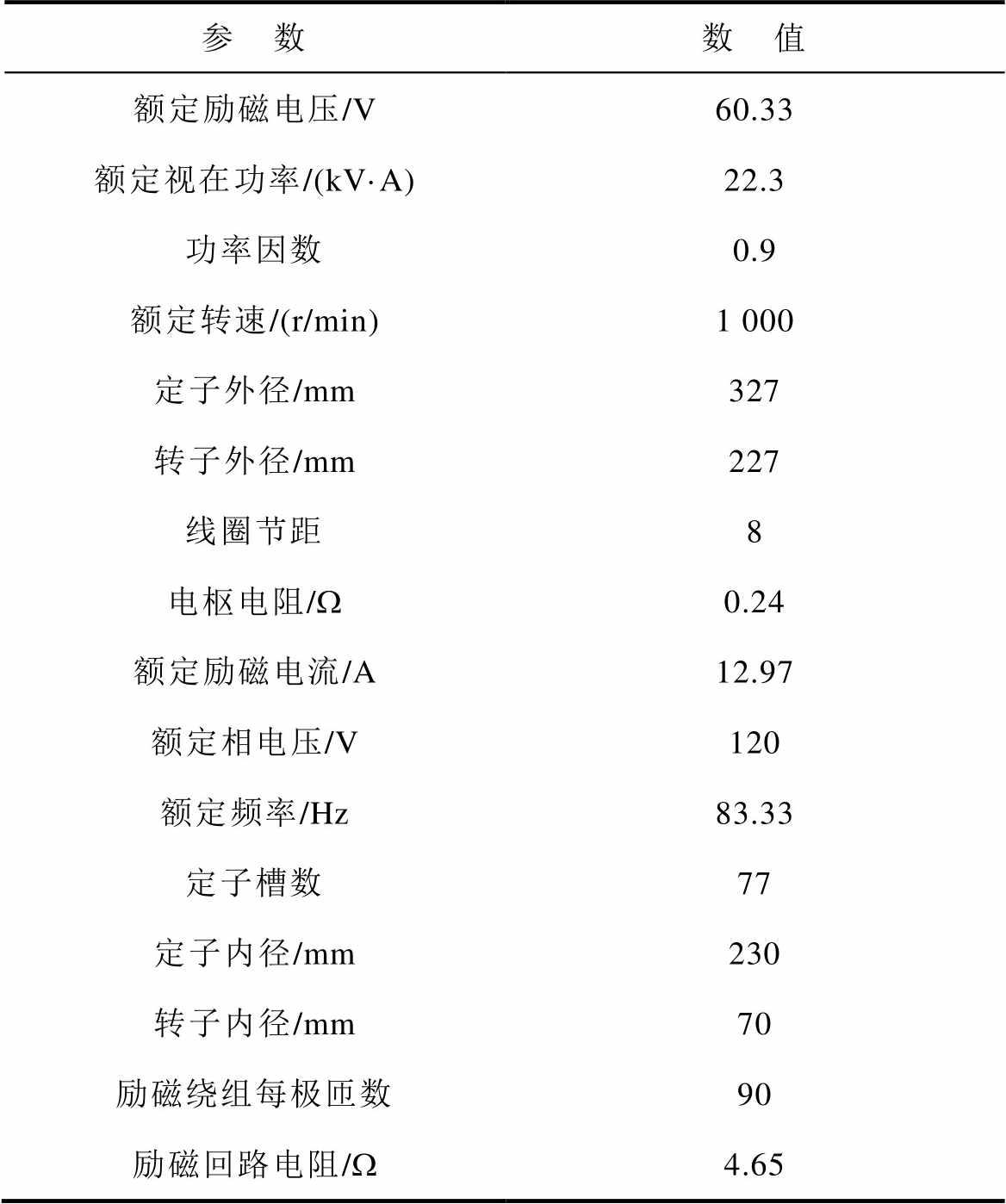
算例使用的数据集来源于以实际电厂同型无刷励磁机为原型制造的一台5对极11相环形凸极同步发电机，其主要技术参数见表1。
表1 无刷励磁样机的基本参数
Tab.1 Basic parameters of brushless excitation prototype
参 数数 值 额定励磁电压/V60.33 额定视在功率/(kV·A)22.3 功率因数0.9 额定转速/(r/min)1 000 定子外径/mm327 转子外径/mm227 线圈节距8 电枢电阻/W0.24 额定励磁电流/A12.97 额定相电压/V120 额定频率/Hz83.33 定子槽数77 定子内径/mm230 转子内径/mm70 励磁绕组每极匝数90 励磁回路电阻/W4.65
动模样机的实验平台装置如图5所示。直流电源和SIEMENS 6RA80调速设备通入380 V三相交流电，直流电机经调速器调节至恒定转速。励磁机用直流电机驱动，动模样机的励磁绕组由稳压开关直流电源提供励磁电流，数字存储示波器负责记录旋转整流器故障实验的数据。
图5 实验平台装置
Fig.5 Diagram of experimental platform installation
在装设有熔断器的无刷励磁系统中，即使旋转整流器中的二极管发生短路故障，在熔断器的保护作用下也会很快转变为开路故障，因此本文主要研究二极管开路故障。除正常运行状态以外，常见的开路故障类型主要包括单个二极管开路、同一相两个二极管开路和不同相对位置的两相二极管开路。针对11相无刷励磁机，共包含八种故障，其中，两相二极管开路故障分为五种：AB两相开路、AC两相开路、AD两相开路、AE两相开路和AF开路。
在5对极11相无刷励磁机的动模实验过程中，控制电机转速维持在960 r/min，负载条件为阻感性负载，其中电阻为1.567 W，电感为0.357 H。实验中需重点考虑励磁电压等级的变化，但是，励磁电压越低，对波形的干扰性越强；励磁电压越高，越不利于动模实验的安全性。基于上述因素的考量，分别针对20、22、24和26 V电压等级进行实验。使用数字示波器记录旋转二极管开路故障数据时，采样频率设为20 kHz。为使单个样本保留足够丰富的特征且兼顾训练效率，在滑动窗口分割原始数据时选取滑动窗口长度为两个电周期0.025 s，每个励磁电流样本的采样点为125。
每种励磁电压水平下的每种故障各生成240个样本，四种电压等级八种故障共计获取7 680个故障样本。为全面评估模型对已学习的和未学习的电压等级样本集的性能，将20 V电压等级下的数据按照4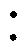
1的比例划分到训练集和验证集，22 V电压等级下的数据全部划分给验证集。由于现场应用中会面临新的电压等级，将24 V和26 V电压等级下的故障数据构造为测试集，具体划分见表2。
表2 数据样本集划分
Tab.2 Data sample set division
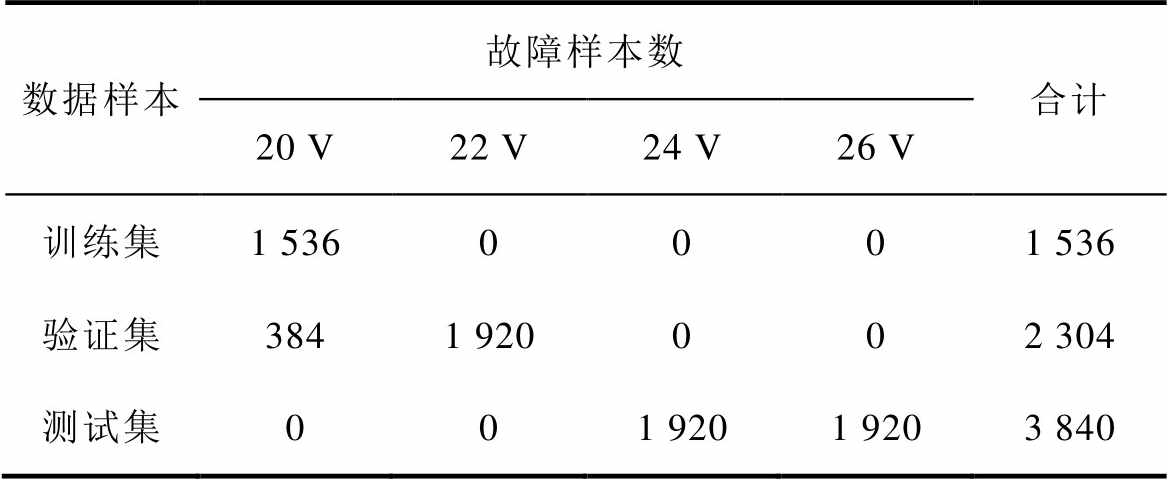
数据样本故障样本数合计 20 V22 V24 V26 V 训练集1 5360001 536 验证集3841 920002 304 测试集001 9201 9203 840
得到初始数据样本集后，进一步对数据进行预处理。考虑到电枢感应电动势基波频率为80 Hz，将傅里叶低通滤波的截止频率设为320 Hz，滤除4次以上的谐波成分，滤波后再进行平均值归一化处理。图6展示了八种旋转整流器二极管开路故障模式的样本在预处理前后的波形，将以下故障模式依次编号为0～7。从图6可以看出，预处理后的波形更加清晰地表现出不同类别故障的差异，说明选择励磁电流作为故障诊断依据是合理且可行的。
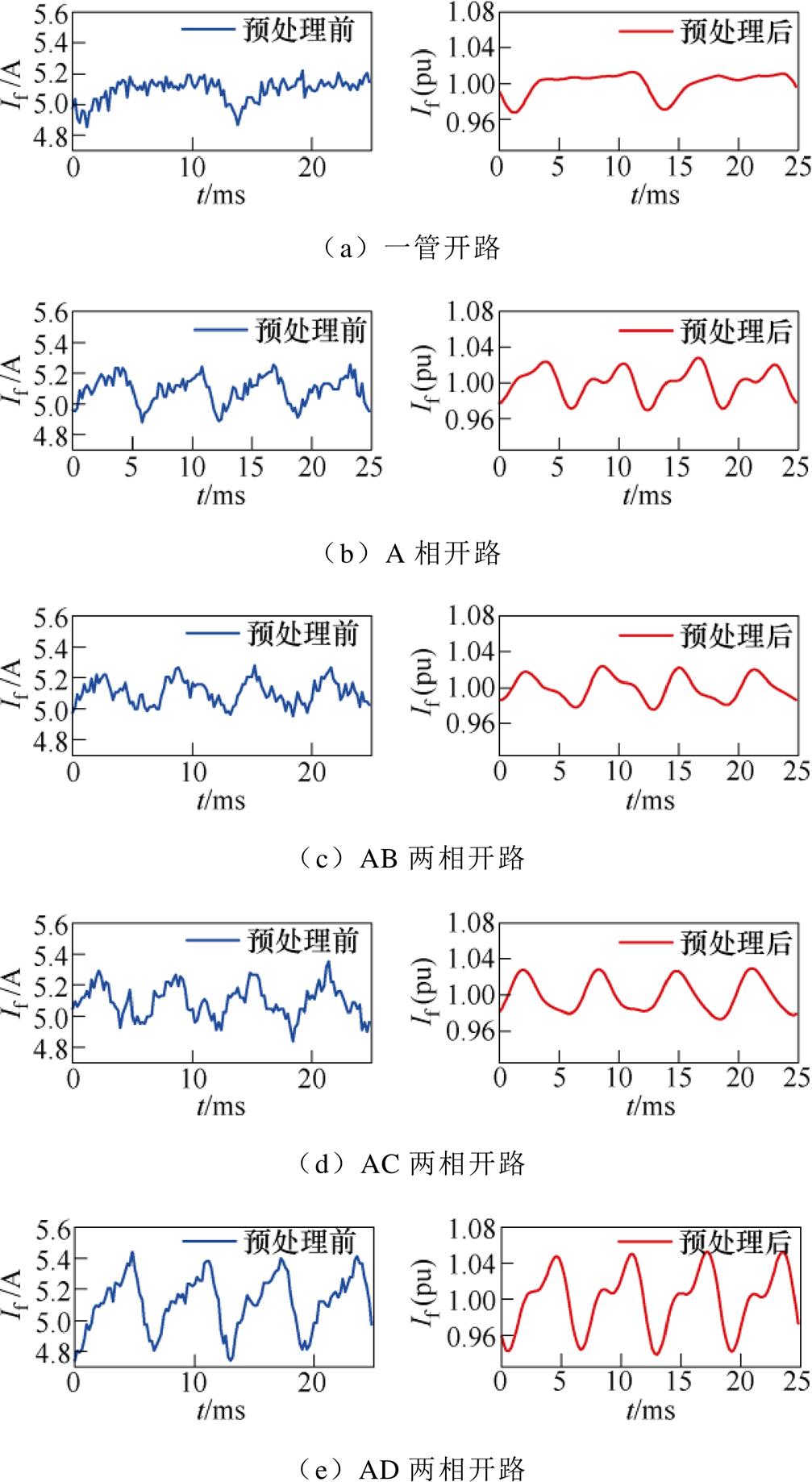
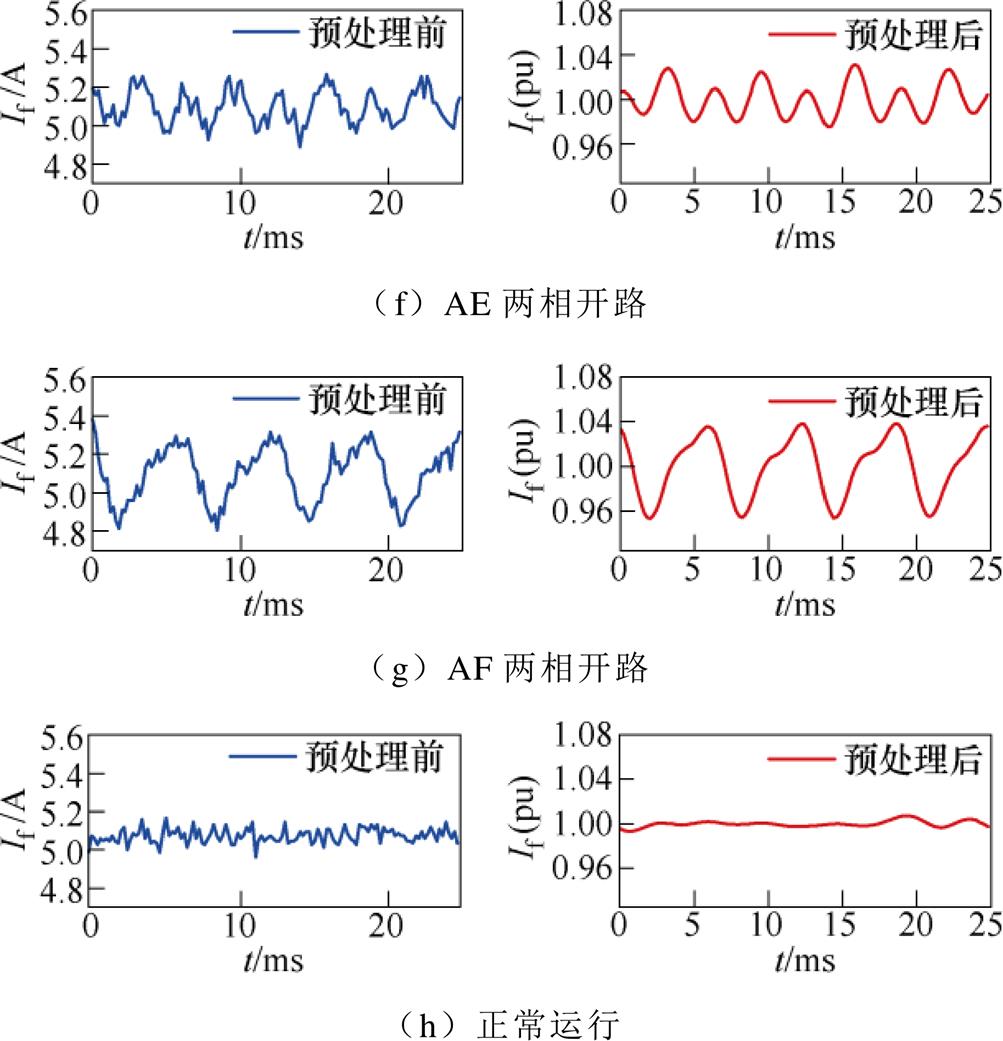
图6 预处理前后的励磁电流波形
Fig.6 Excitation current waveforms diagram before and after preprocessing
不同参数的人工智能模型的性能不同，在实际应用中往往需要设置相对合适的参数保证模型具有较优的故障诊断性能。在本文的1D-DCNN方法中，网络结构超参数主要包括卷积核数量、卷积核大小、卷积核步长、膨胀系数。这些超参数对于1D-DCNN模型的诊断表现具有较为明确的作用，能够用于指导参数设置，例如：卷积核数量代表着模型提取励磁电流波形局部故障特征的种类；卷积核尺寸影响着模型对输入励磁电流信号的感受野范围；卷积核步长决定了相邻感受野之间的重叠范围，关系到提取故障特征的有效性；膨胀系数具备在不增加模型参数量的前提下扩大感受野范围的优势。
在确定网络结构超参数的过程中，采用控制变量法依次对每一层的超参数进行逐层寻优，以网络在验证集上的准确率作为评价指标，直到准确率不再提高。设置批量训练样本数为128，学习率为0.000 1，迭代周期数为150。不同超参数设置的网络在验证集上的准确率如图7所示。
由图7可知，卷积核数量、卷积核尺寸设置得过小时识别准确率较低，但是增加到一定大小后准确率也不会显著提升，反而增加了模型参数量。这是因为卷积核过多会导致学习到的局部特征存在冗余，卷积核过大会导致学习到无用信息，不利于模型训练和性能提升。卷积核步长设置过大会降低模型的识别准确率。此外，通过设置一定的膨胀系数可以在原有卷积核大小的基础上进一步提高模型的识别准确率，由此表明，加入空洞卷积能够有效提升模型的诊断表现。
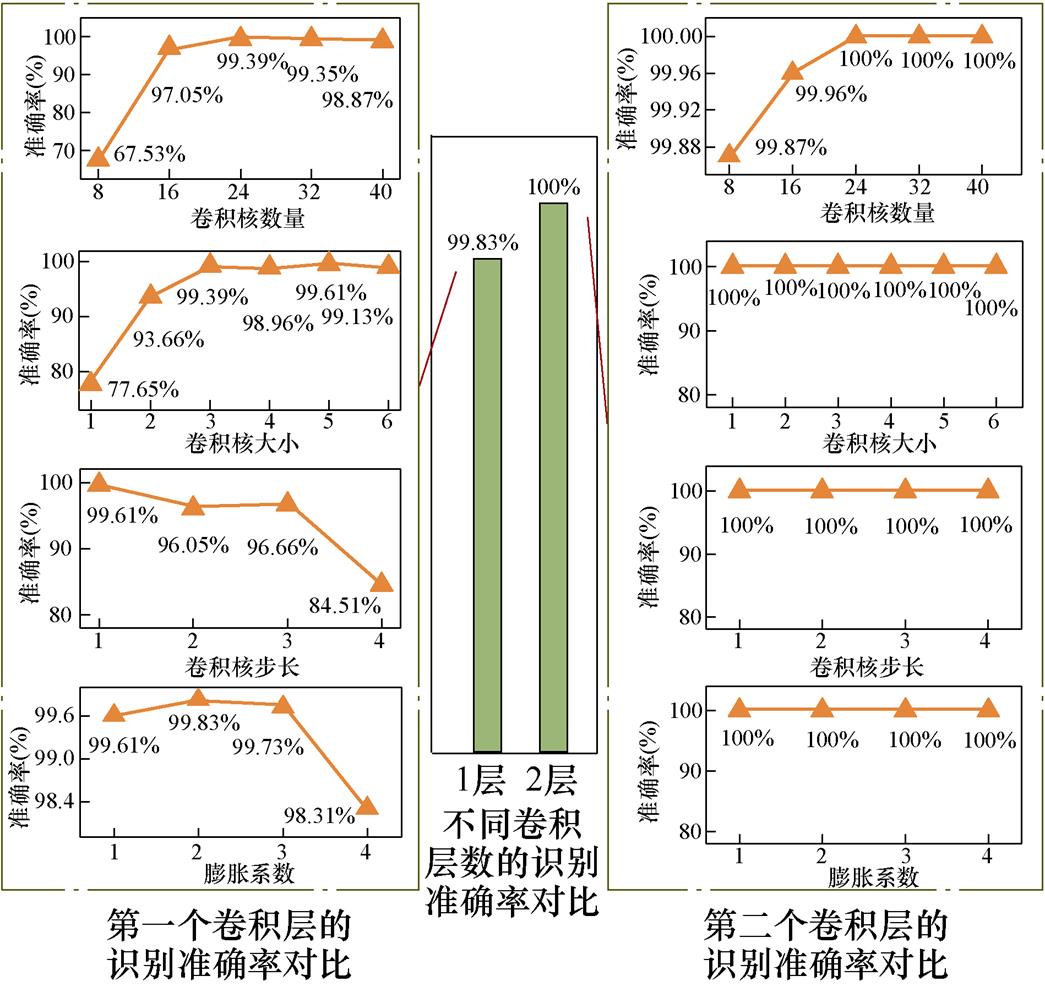
图7 网络结构超参数的寻优过程
Fig.7 Optimization process of network structure hyperparameters
基于超参数寻优最终确定的1D-DCNN网络结构见表3。故障诊断网络输出层的维度为8，代表八种故障模式。为避免训练过程收敛过慢，在卷积层后加入批量归一化层提升网络的优化效率。
表3 1D-DCNN网络结构
Tab.3 1D-DCNN network structure
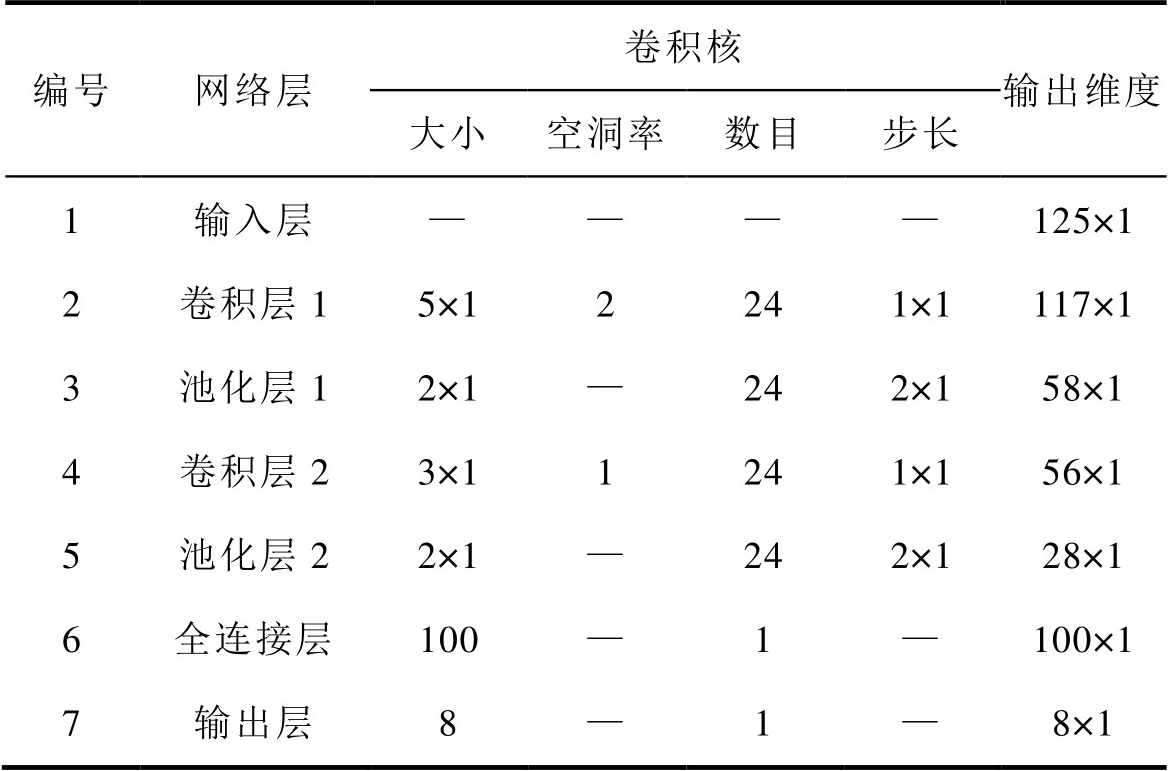
编号网络层卷积核输出维度 大小空洞率数目步长 1输入层————125×1 2卷积层15×12241×1117×1 3池化层12×1—242×158×1 4卷积层23×11241×156×1 5池化层22×1—242×128×1 6全连接层100—1—100×1 7输出层8—1—8×1
为进一步验证数据预处理以及所搭建的1D- DCNN网络的有效性，采用t-SNE算法[31]对两种电压等级的不同数据进行可视化，如图8所示。
从图8可以看出，预处理前的原始数据分布呈现出按电压等级聚集的现象。数据预处理后，不同电压等级的同类故障样本不再各自聚集，但仍有部分故障模式样本存在混叠，如AB两相开路（类别2）和AC两相开路（类别3）故障样本、AD两相开路（类别4）和AF两相开路（类别6）故障样本均互相重叠，原因在于这两组样本自身的波形特征较为相似，难以区分。经过两个卷积池化层的处理后，从图8d可以观察到，不同故障模式的样本间形成了明显的分类边界，说明通过两个卷积池化层能够充分提取到励磁电流数据的特征，进而实现旋转整流器故障模式的有效识别。
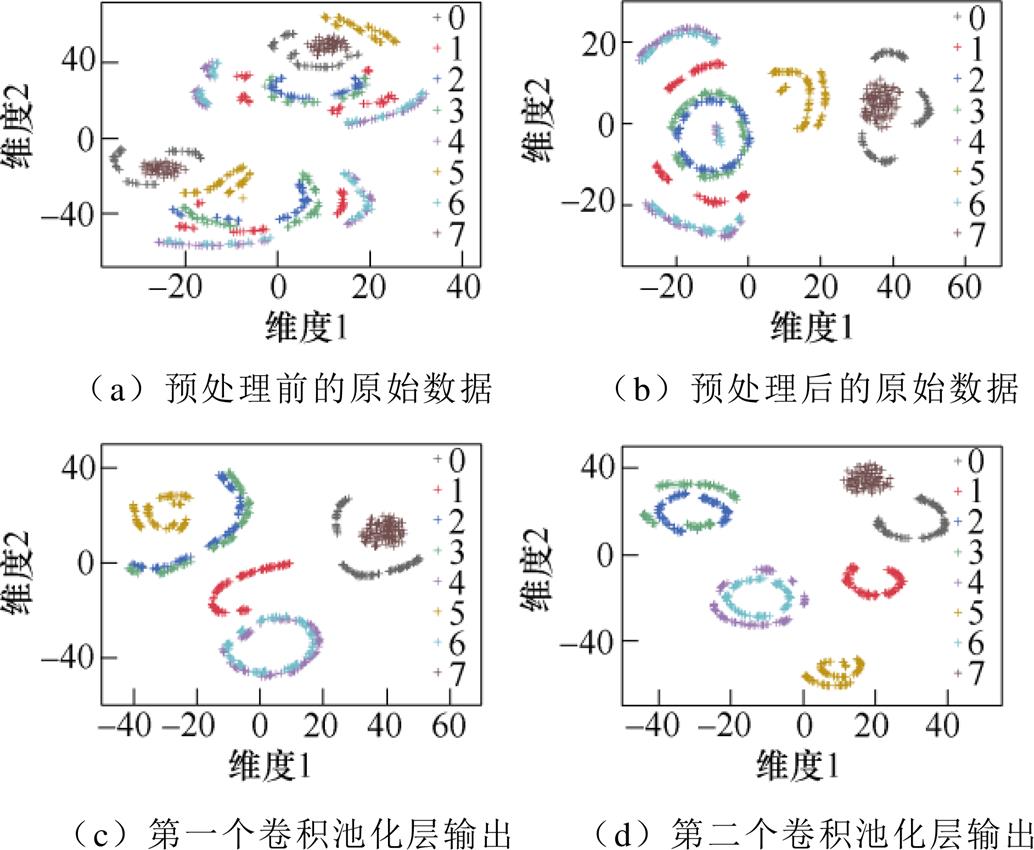
图8 数据可视化结果
Fig.8 Data visualization result
4.4.1 诊断机制的可视化分析
为了分析1D-DCNN模型进行旋转整流器故障诊断的工作机制，采用Score-CAM方法得到励磁电流信号的归因热度图，定位对诊断结果贡献最大的关键特征段，从而理解模型的决策依据。
随机选取诊断结果为发生旋转整流器一管开路故障的两个样本，通过Score-CAM分析训练好的模型对输入样本的决策依据，如图9所示。在样本的归因热度图中，归因值的范围处于0～1之间，其大小用不同颜色展示，颜色越黄表示对故障诊断结果的影响程度越高；颜色越蓝则表示影响程度越低。从图9可以观察到，样本1和样本2的差别体现在滑动窗口分割样本导致的起点不对齐以及实验设备等客观条件引起的波形形态差异，而两个样本中影响模型诊断结果最重要的特征区域都位于励磁电流波形中较大的波谷附近，其次是一些小波峰周围，说明训练好的模型在判别同一故障模式下不同样本时关注到了类似的波形特征。
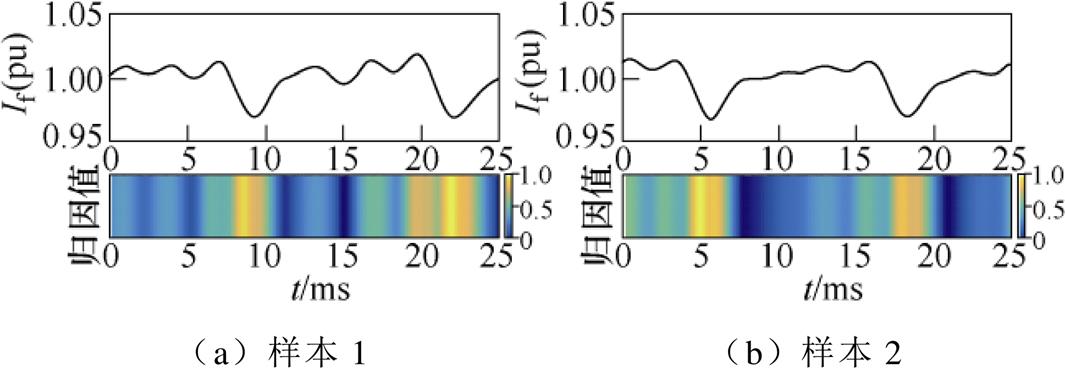
图9 一管开路故障样本的决策依据
Fig.9 Decision basis of one-tube open circuit sample
图10展示了采用Score-CAM方法对八种故障模式下样本的诊断机制分析结果。从图10a～图10f可以看出，影响1D-DCNN模型故障分类结果的关键在于励磁电流波形的波峰或波谷区域，而这些故障模式下励磁电流信号的波峰波谷区域实际上具有不同的畸变程度和幅值差异；图10h中，当旋转整流器正常运行时，无刷励磁电机输出的励磁电流基本上维持在恒定水平，此时模型主要关注的区域是几个小范围内波动不大的特征段。由此可知，1D- DCNN模型学习到了不同故障模式下励磁电流波形的关键特征段，并且这些特征段能够呈现出不同故障类别间的差异，一定程度上说明了该方法的有效性。
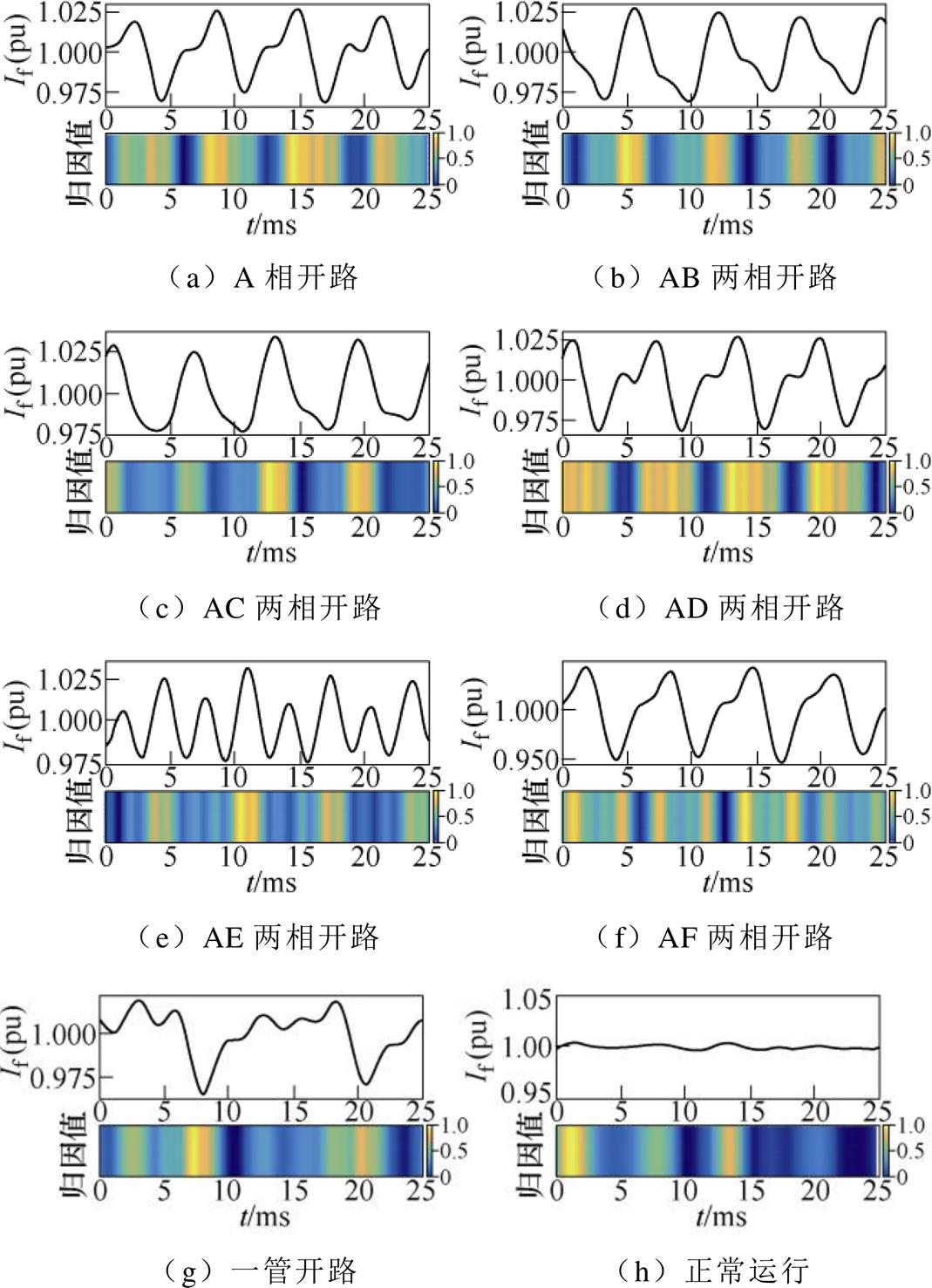
图10 不同故障模式样本的决策依据
Fig.10 Decision basis of different fault mode samples
4.4.2 不同超参数对模型性能的影响分析
模型超参数的选取通常需要进行反复试探，有时带有一定盲目性，比较费时但不一定能达到理想的效果。本文采用的可解释性分析方法能够解释超参数对模型性能的影响，分析样本被错判的原因，为模型的设计和优化提供针对性指导和有力支撑。
在第4.3节的超参数寻优过程中，第一个卷积层采用不同卷积核步长得到的模型具有不同的准确率，其中较多错判是将旋转二极管AF两相开路故障误判为AD两相开路故障。对于同一个AF两相开路故障样本，卷积核步长为2或3的模型将该样本错判，而卷积核步长为1的模型将该样本分类正确，图11展示了具体的决策依据可视化结果。
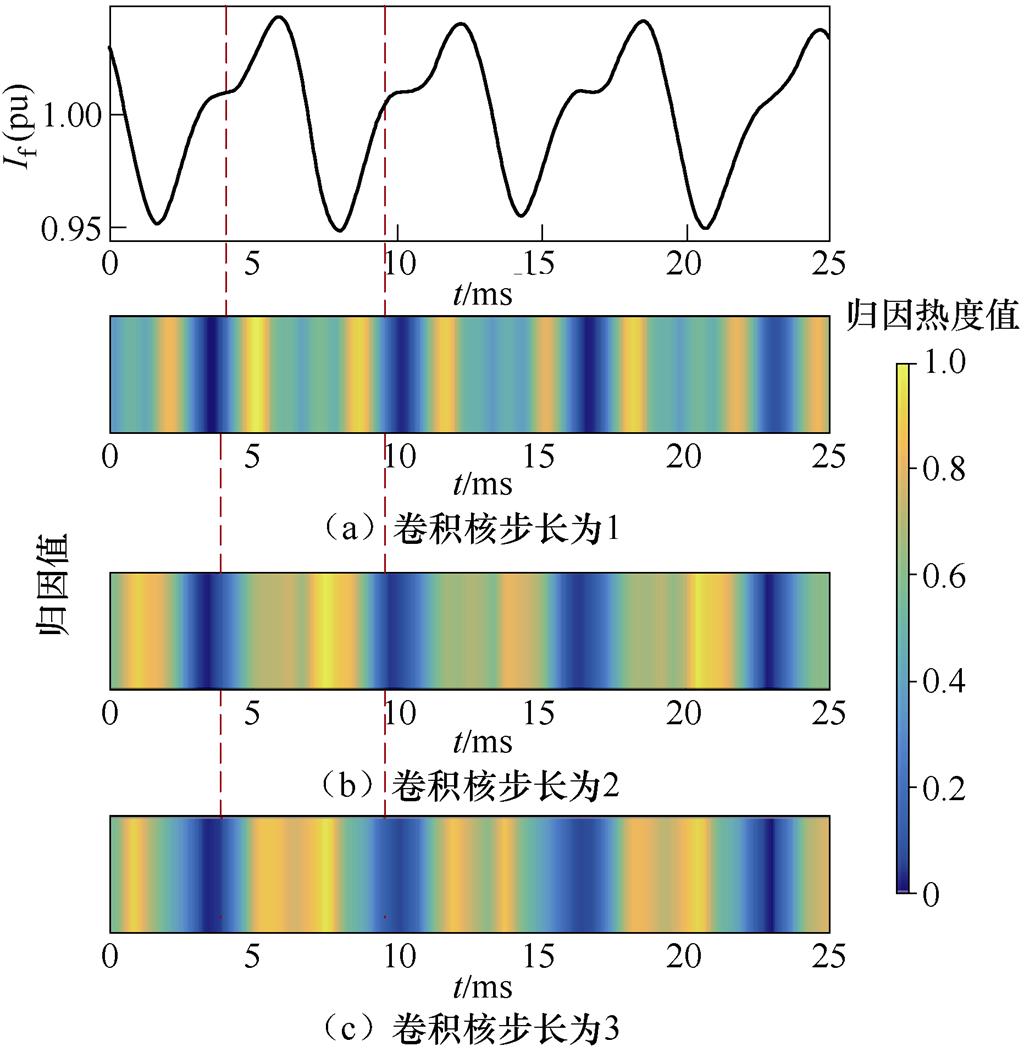
图11 不同卷积核步长对决策的影响
Fig.11 The influence of convolution kernel step size on decision-making
从图11可以观察到，不同卷积核步长的三种模型都关注到了励磁电流波形较为完整的波峰和波谷特征，但是学习到的重点特征区域随着卷积核步长的减小逐渐向波峰和波谷两侧进行偏移。由此可知，卷积核步长的改变使得模型的重点关注特征区域发生偏移，从而影响了分类正确性。
此外，不同卷积核大小训练得到的模型存在较多将AB两相开路故障误判为AC两相开路的情况。对于同一个旋转二极管AB两相开路样本，卷积核大小分别为1和3的模型将其误判，而卷积核大小为5的模型给出了正确的分类结果，图12展示了这三种不同卷积核大小下训练好的模型对该样本诊断结果的决策依据可视化结果。
由图12可知，随着卷积核大小逐渐增加，模型提取到越来越大范围内的波谷和波峰特征，说明卷积核大小的增加能够扩充模型的诊断依据范围，使得样本由分类错误到分类正确。
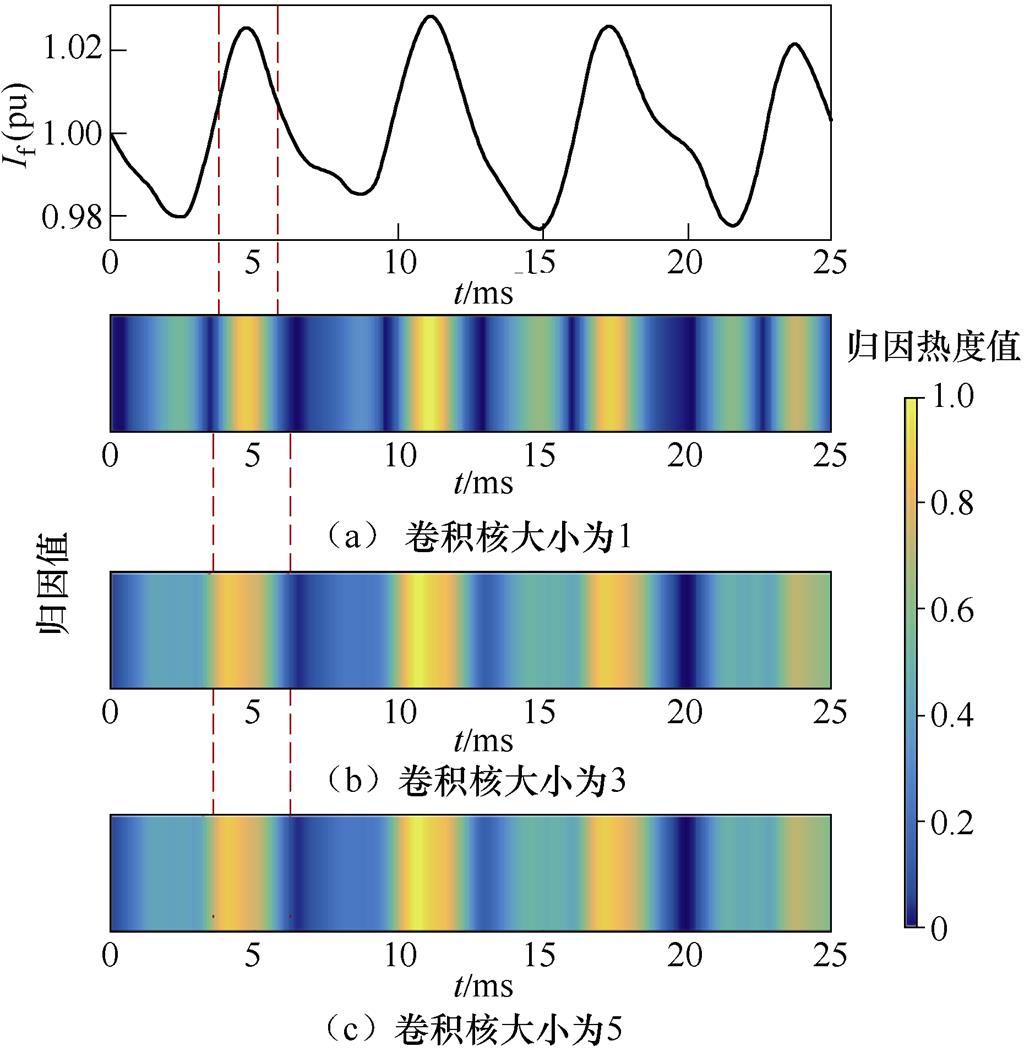
图12 不同卷积核大小对决策的影响
Fig.12 The influence of different convolution kernel size on decision-making
为了验证本文所提1D-DCNN算法在旋转二极管故障模式识别的性能优势，选择随机森林（Random Forest, RF）、分类回归树（Classification and Regression Tree, CART）和多层感知机（Multi- Layer Perceptron, MLP）算法进行对比。采用相同的验证集对上述算法进行参数寻优，最终确定诊断效果最好且参数量最少的模型。其中：RF选择的树棵数为30，该参数在验证集上可获得最高准确率；MLP的结构为五层全连接层，各网络层神经元数分别为125、80、50、30、8，激活函数选择ReLU，选取Adam作为优化算法。为使得到的故障诊断结果更加严谨，采用交叉验证的方式进行多次实验，保证每次实验中训练集具有不同的组成，然后逐一记录每次实验的测试准确率指标。不同模型对于原始测试集的分类准确率见表4。
从表4的交叉验证结果可知，CART决策树的分类准确率最低，RF、MLP和1D-DCNN这三种算法的总体分类准确率都达到了99%以上，这是因为原始数据经过预处理后已经具备了较好的特征区分度，使得判别旋转整流器故障模式的难度大大降低，导致这几种模型均表现出良好的诊断性能。
考虑到实际应用中的实测数据往往包含较多噪声，可能会影响模型的识别准确率。为模拟实测数据含噪声的情况，向原始测试集中添加高斯白噪声得到新的测试集，含噪声的励磁电流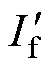
可表示为
表4 不同模型在原始测试集中的交叉验证结果
Tab.4 Cross validation results of different models in the original test set
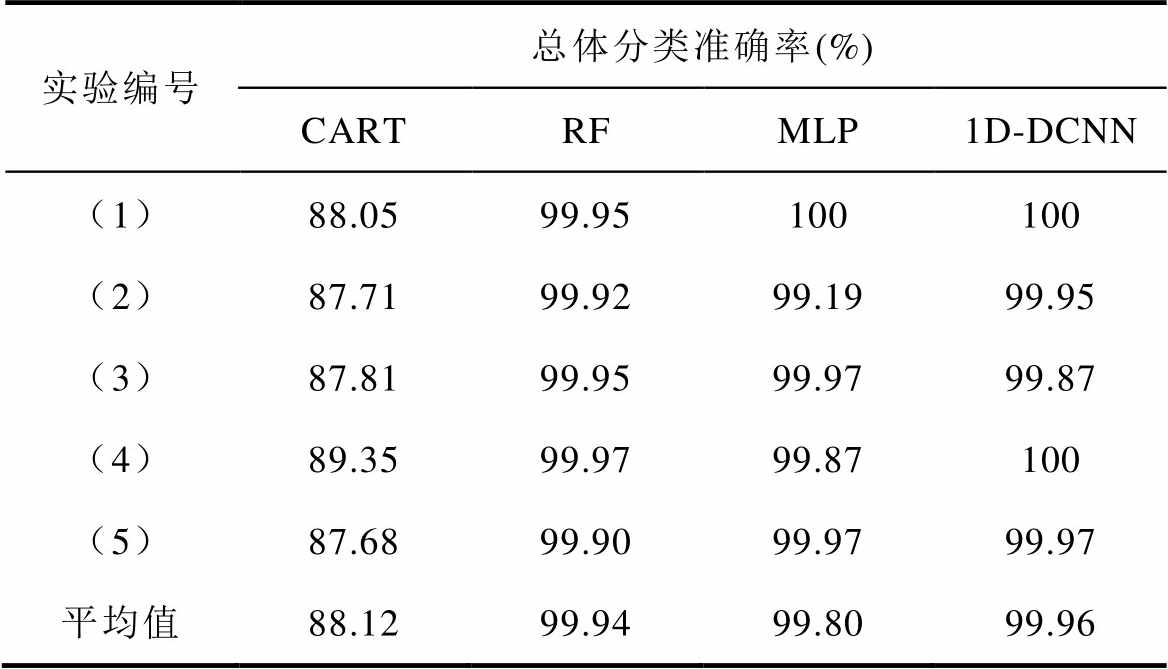
实验编号总体分类准确率(%) CARTRFMLP1D-DCNN （1）88.0599.95100100 （2）87.7199.9299.1999.95 （3）87.8199.9599.9799.87 （4）89.3599.9799.87100 （5）87.6899.9099.9799.97 平均值88.1299.9499.8099.96
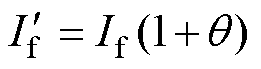（18）
式中，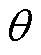
为噪声幅值服从均值为0、方差为
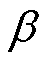的正态分布；If为原始的励磁电流。
为检验不同模型在实际应用时的诊断效果，分别向原始测试集中添加方差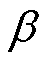为0.01～0.08的高斯白噪声构造新的测试集。需要说明的是，此处的添加噪声是在数据预处理步骤之前进行。选取第一次交叉验证实验的结果，对比本文所提方法和其他算法在含噪声测试集下的故障分类结果见表5。
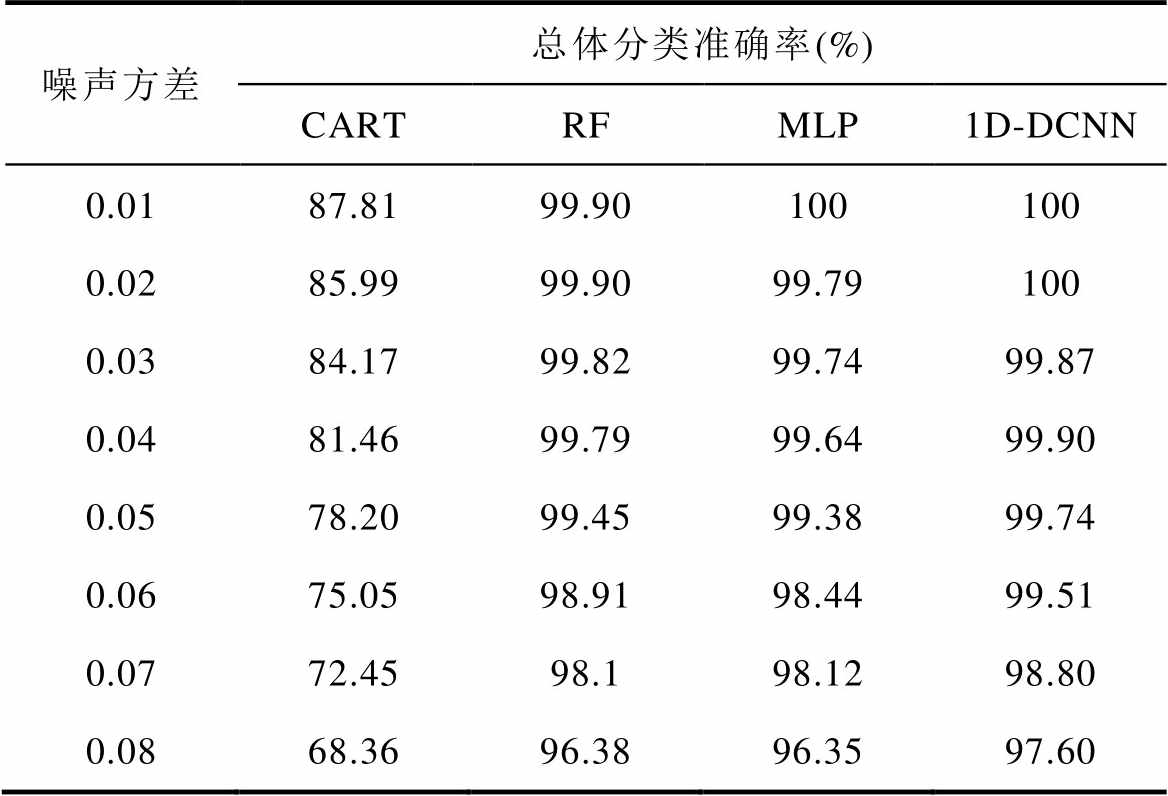
表5 不同模型在含噪声测试集中的性能对比
Tab.5 Performance comparison of different models in noisy test sets
噪声方差总体分类准确率(%) CARTRFMLP1D-DCNN 0.0187.8199.90100100 0.0285.9999.9099.79100 0.0384.1799.8299.7499.87 0.0481.4699.7999.6499.90 0.0578.2099.4599.3899.74 0.0675.0598.9198.4499.51 0.0772.4598.198.1298.80 0.0868.3696.3896.3597.60
从表5得知，不同算法在含噪声测试集下的故障识别准确率都有所降低。随着高斯白噪声方差的增大，模型的诊断性能基本上呈现下降趋势，但是1D-DCNN方法相比于其他算法有着更高的识别准确率，说明1D-DCNN模型的抗噪声干扰能力较强，这是因为搭建模型的过程中池化层采用最大池化方式，即使在一定范围内出现噪声干扰，对选取最大值影响较小。由此表明，本文提出的1D-DCNN模型在实际应用时具有更大的优势。
由4.5节的结果可知，即使模型在原始测试集上能达到很高的诊断准确率，但是在受到较多噪声干扰的情况下还是会导致准确率下降。而本文提出的1D-DCNN模型的诊断结果置信度指标，为诊断结果提供了更多信息，可以用于进一步降低错判。
图13展示了第一次交叉验证实验中原始测试集和方差为0.08的含噪声测试集上样本的置信度分布情况。由此得知，样本集中分布在置信度比较高的区间，置信度比较低的区间样本很少。对于原始测试集而言，从图13a可以看出，全部样本的置信度在0.4以上，其中3 815个样本的置信度达到0.9以上，只有25个样本的置信度低于0.9，说明模型对于原始测试集的故障诊断结果基本上是可靠的。而对于含噪声测试集而言，从图13b可以观察到，其中有3 241个样本的置信度达到0.9以上，分别有227和108个样本的置信度分布在区间[0.8, 0.9]和[0.7, 0.8]，剩余样本的置信度分别位于0.7以下的每个区间。与原始测试集相比，模型对含噪声测试集的置信度整体上有所下降，说明外界噪声的干扰会减小模型对输出结果的确定程度。
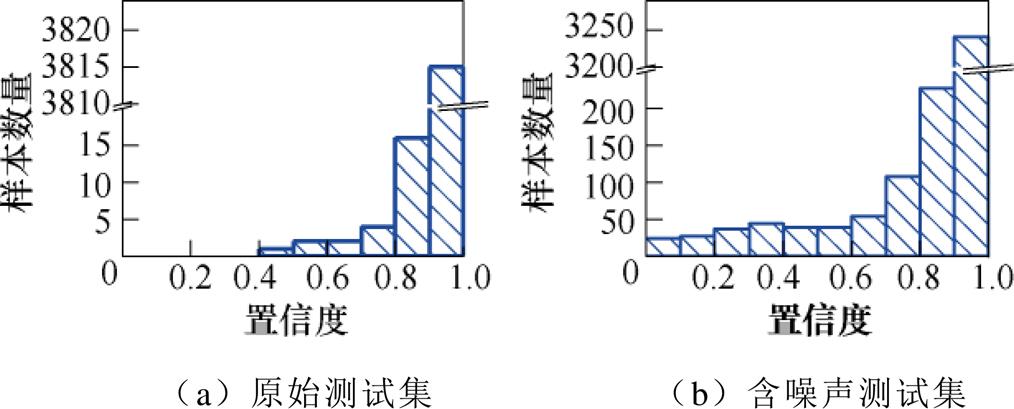
图13 不同置信度区间的样本数量分布
Fig.13 Sample distribution diagram with different confidence intervals
进一步分析模型在不同置信度区间上的准确率。原始测试集的识别准确率已经达到100%，不存在错判的样本。而含噪声测试集的总体识别准确率为97.6%，在不同置信度区间的准确率分布情况如图14所示。可以观察到，置信度越高的区间，模型的分类准确率越高；置信度越低的区间，模型的分类准确率相对来说会越低。
基于上述结果可以看出，为了进一步降低1D- DCNN模型对故障模式的错判，可以设置置信度阈值以提高模型的分类准确率。图15比较了不同置信度阈值下模型对含噪声数据集的识别准确率。
从图15可以看出，随着置信度阈值的增加，识别准确率呈上升趋势。这是因为置信度阈值越高，筛选样本中的错判样本都会减少，准确率随之提高。在实际应用中可以通过增加测试数据并结合运行人员需求来选择合适的置信度阈值。
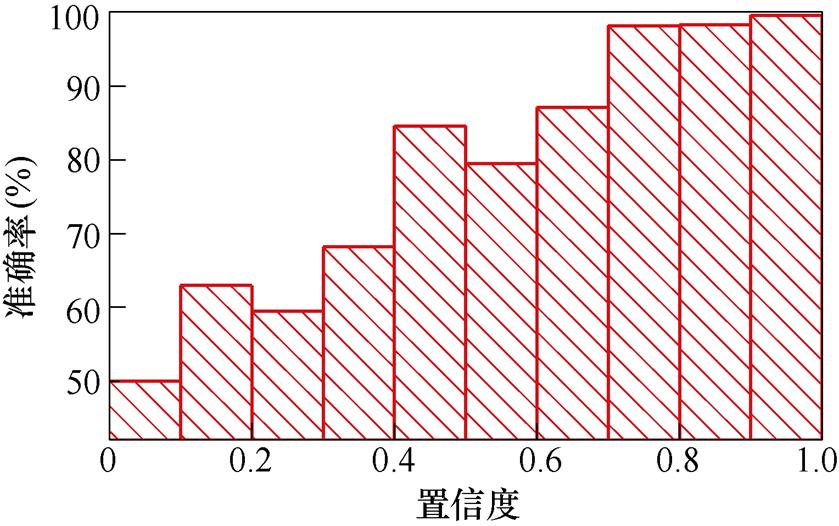
图14 不同置信度区间的准确率分布
Fig.14 Accuracy distribution diagram of different confidence intervals
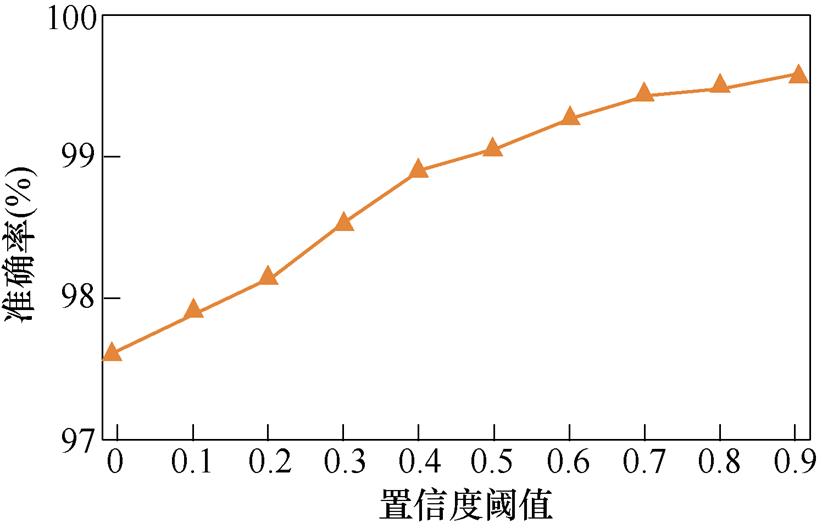
图15 不同置信度阈值对模型识别准确率的影响
Fig.15 Influence of different confidence threshold on model recognition accuracy
针对现有方法无法准确识别出多相无刷励磁系统旋转整流器所有故障模式的难题，本文提出了一种基于卷积神经网络的故障诊断方案，并通过11相环形无刷励磁系统的动模样机实验数据验证了所提方案的有效性，得到如下结论：
1）选取的故障诊断信号励磁电流能够充分反映旋转二极管的不同运行状态，原始励磁电流信号经滤波和平均值归一化等预处理步骤后具有更明显的区分度，为所提方法学习故障特征打下良好的基础。
2）所提出的1D-DCNN模型能够充分挖掘励磁电流波形的深层特征，有效识别出旋转整流器的不同二极管开路故障模式。采用1D-DCNN可以极大程度地降低故障诊断模型的复杂度，并且在考虑噪声干扰的情况下具有良好的应用潜力。
3）使用Score-CAM类激活映射方法能够直观地展示1D-DCNN模型对不同故障模式样本的决策依据，分析网络结构超参数影响故障诊断性能的原因，从而为模型内部工作机制提供解释，也为模型的设计优化提供了重要依据。
4）定义置信度指标能够评估分类结果的可靠程度，通过设定置信度阈值减少了模型错判情况的发生。并且置信度指标为诊断结果提供了更多信息，可以供现场人员借鉴和参考。
本文初步探索了通过基于卷积神经网络的故障诊断方法解决精细区分旋转整流器故障模式识别问题的可行性，为旋转整流器的故障诊断提供了数据驱动的新思路。然而实际应用中面临着故障实测数据缺乏等问题，如何将所提故障诊断方法推广到现场运行机组是下一步工作的研究重点，后续可以考虑将该方法与数据增强或者迁移学习等方法相结合以达到实际应用的要求。
参考文献
[1] 张蕴. 双碳目标下我国核电发展趋势分析[J]. 核科学与工程, 2021, 41(6): 1347-1351.
Zhang Yun. Analysis on the development trend of nuclear energy in China under the dual carbon target[J]. Nuclear Science and Engineering, 2021, 41(6): 1347-1351.
[2] 郝亮亮, 常江, 李洪学, 等. 核电多相角形无刷励磁机定子匝间短路故障特征分析[J]. 中国电机工程学报, 2019, 39(22): 6726-6736.
Hao Liangliang, Chang Jiang, Li Hongxue, et al. Characteristics analysis of stator inter-turn short circuits in nuclear power multi-phase angular brush- less exciter[J]. Proceedings of the CSEE, 2019, 39(22): 6726-6736.
[3] 郝亮亮, 李佳慧, 段贤稳, 等. 核电多相环形无刷励磁机转子绕组短路故障特征分析[J]. 电工技术学报, 2020, 35(6): 1251-1261.
Hao Liangliang, Li Jiahui, Duan Xianwen, et al. Characteristic analysis of short-circuit fault in rotor winding of nuclear power multi-phase annular brushless exciter[J]. Transactions of China Electro- technical Society, 2020, 35(6): 1251-1261.
[4] 吴新振, 张伟玲, 董海涛, 等. 十二相整流发电机二极管开路的故障运行分析[J]. 电工技术学报, 2017, 32(3): 157-163.
Wu Xinzhen, Zhang Weiling, Dong Haitao, et al. Analysis of diode-open fault operation for 12-phase rectifier generators[J]. Transactions of China Elec- trotechnical Society, 2017, 32(3): 157-163.
[5] Bui H K, Bracikowski N, Hecquet M, et al. Simulation of a large power brushless synchronous generator (BLSG) with a rotating rectifier by a reluctance network for fault analysis and diagnosis[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 4327-4337.
[6] Wu Yucai, Cai Bochong, Ma Qianqian. An online diagnostic method for rotary diode open-circuit faults in brushless exciters[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1677-1685.
[7] 张伟玲, 吴新振, 魏锟, 等. 十二相整流发电机缺桥故障运行分析[J]. 中国电机工程学报, 2016, 36(6): 1724-1730.
Zhang Weiling, Wu Xinzhen, Wei Kun, et al. Analysis of bridge-loss fault operation of 12-phase generators with rectifier-load[J]. Proceedings of the CSEE, 2016, 36(6): 1724-1730.
[8] 蔡波冲, 武玉才, 赵艳军. 基于定子电流谐波法的无刷励磁机旋转二极管开路故障检测[J]. 大电机技术, 2018(4): 61-65.
Cai Bochong, Wu Yucai, Zhao Yanjun. The detection of open-circuit fault of rotary diode in brushless exciter using stator current harmonic method[J]. Large Electric Machine and Hydraulic Turbine, 2018(4): 61-65.
[9] 郝亮亮, 李佳慧, 李洪学, 等. 核电多相角形无刷励磁系统旋转二极管开路故障特征分析[J]. 电力系统自动化, 2019, 43(11): 112-120.
Hao Liangliang, Li Jiahui, Li Hongxue, et al. Characteristic analysis of open-circuit fault of rotating diode in nuclear multi-phase angular brush- less excitation system[J]. Automation of Electric Power Systems, 2019, 43(11): 112-120.
[10] 朱继忠, 骆腾燕, 吴皖莉, 等. 综合能源系统运行可靠性评估评述Ⅱ: 数据驱动法与模型-数据混合驱动法[J]. 电工技术学报, 2022, 37(13): 3227-3240.
Zhu Jizhong, Luo Tengyan, Wu Wanli, et al. A review of operational reliability assessment of integrated energy systems Ⅱ: data-driven method and model- data hybrid driven method[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3227-3240.
[11] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636.
Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[12] 崔江, 冯赛, 张卓然, 等. 基于BLS的无刷发电机旋转整流器特征提取技术研究[J]. 中国电机工程学报, 2020, 40(12): 4004-4013.
Cui Jiang, Feng Sai, Zhang Zhuoran, et al. Research on feature extraction technology of brushless gener- ator rotating rectifier based on BLS[J]. Proceedings of the CSEE, 2020, 40(12): 4004-4013.
[13] 崔江, 郭瑞东, 张卓然, 等. 基于改进DBN的发电机旋转整流器故障特征提取技术[J]. 中国电机工程学报, 2020, 40(7): 2369-2376, 2415.
Cui Jiang, Guo Ruidong, Zhang Zhuoran, et al. Generator rotating rectifier fault feature extraction technique based on improved DBN[J]. Proceedings of the CSEE, 2020, 40(7): 2369-2376, 2415.
[14] Rahnama M, Vahedi A, Alikhani A M, et al. Diode open-circuit fault detection in rectifier bridge of the brushless synchronous generator[C]//2018 XIII Inter- national Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 2018: 1821-1826.
[15] Mohammad-Alikhani A, Rahnama M, Vahedi A. Neighbors class solidarity feature selection for fault diagnosis of brushless generator using thermal imaging[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(9): 6221-6227.
[16] 纪守领, 李进锋, 杜天宇, 等. 机器学习模型可解释性方法、应用与安全研究综述[J]. 计算机研究与发展, 2019, 56(10): 2071-2096.
Ji Shouling, Li Jinfeng, Du Tianyu, et al. Survey on techniques, applications and security of machine learning interpretability[J]. Journal of Computer Research and Development, 2019, 56(10): 2071-2096.
[17] 任守纲, 张景旭, 顾兴健, 等. 时间序列特征提取方法研究综述[J]. 小型微型计算机系统, 2021, 42(2): 271-278.
Ren Shougang, Zhang Jingxu, Gu Xingjian, et al. Overview of feature extraction algorithms for time series[J]. Journal of Chinese Computer Systems, 2021, 42(2): 271-278.
[18] Zhang Quanshi, Wu Ying Nian, Zhu Songchun. Interpretable convolutional neural networks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 2018: 8827-8836.
[19] Selvaraju R R, Cogswell M, Das A, et al. Grad-CAM: visual explanations from deep networks via gradient- based localization[C]//2017 IEEE International Con- ference on Computer Vision (ICCV), Venice, Italy, 2017: 618-626.
[20] Chattopadhay A, Sarkar A, Howlader P, et al. Grad- CAM: generalized gradient-based visual explanations for deep convolutional networks[C]//2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 2018: 839-847.
[21] Wang Haofan, Wang Zifan, Du Mengnan, et al. Score-CAM: score-weighted visual explanations for convolutional neural networks[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recog- nition Workshops (CVPRW), Seattle, WA, USA, 2020: 111-119.
[22] Zeiler M D, Fergus R. Visualizing and understanding convolutional networks[C]//Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 2014: 818-833.
[23] Fong R C, Vedaldi A. Interpretable explanations of black boxes by meaningful perturbation[C]//2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 2017: 3449-3457.
[24] Chen Jianlin, Hao Liangliang, Li Huazhong, et al. Time-frequency characteristics analysis and diagnosis of rotating rectifier faults in multiphase annular brushless system[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3233-3244.
[25] 张大海, 张晓炜, 孙浩, 等. 基于卷积神经网络的交直流输电系统故障诊断[J]. 电力系统自动化, 2022, 46(5): 132-145.
Zhang Dahai, Zhang Xiaowei, Sun Hao, et al. Fault diagnosis for AC/DC transmission system based on convolutional neural network[J]. Automation of Electric Power Systems, 2022, 46(5): 132-145.
[26] 王艳新, 闫静, 王建华, 等. 基于域对抗迁移卷积神经网络的小样本GIS绝缘缺陷智能诊断方法[J]. 电工技术学报, 2022, 37(9): 2150-2160.
Wang Yanxin, Yan Jing, Wang Jianhua, et al. Intelligent diagnosis for GIS with small samples using a novel adversarial transfer learning in convolutional neural network[J]. Transactions of China Electro- technical Society, 2022, 37(9): 2150-2160.
[27] 蔡智超, 孙翼虎, 赵振勇, 等. 基于时频分析和深度学习的表面粗糙度超声模式识别方法[J]. 电工技术学报, 2022, 37(15): 3743-3752.
Cai Zhichao, Sun Yihu, Zhao Zhenyong, et al. A deep learning-based electromagnetic ultrasonic recognition method for surface roughness of workpeice[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3743-3752.
[28] Yu F, Koltun V. Multi-scale context aggregation by dilated convolutions[EB/OL]. 2015, arXiv: 1511.07122. https://arxiv.org/abs/1511.07122.
[29] Bridle J S. Probabilistic interpretation of feedforward classification network outputs, with relationships to statistical pattern recognition[J]. Neurocomputing: Algorithms, Architectures and Applications, 1989, 68: 227-236.
[30] Rubinstein R. The cross-entropy method for combi- natorial and continuous optimization[J]. Methodology and Computing in Applied Probability, 1999, 1(2): 127-190.
[31] Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(86): 2579-2605.
Abstract The multi-phase brushless excitation system is widely used in large-capacity nuclear power plants. The safe and stable operation of nuclear power plants depends on accurately diagnosing rotating rectifier faults. However, the existing methods cannot accurately distinguish all types of faults, which makes it challenging to meet the demands in practice. Recently, as a representative artificial intelligence method, deep learning has provided new ideas for solving this problem. Therefore, this paper develops a fault diagnosis scheme for the rotating rectifier based on a convolutional neural network.
First, taking an 11-phase brushless excitation system as an example, the excitation current characteristics after the rotating rectifier fault are analyzed. The results show that the excitation current waveforms contain amplitude and phase information of all fault harmonics, which can be varied under different fault modes and used for fault diagnosis of the rotating rectifier.
Then, a one-dimensional dilated convolutional neural network (1D-DCNN) model is introduced to realize fault diagnosis. The 1D-DCNN establishes a mapping relationship from the input (excitation current waveforms) to the output (fault mode). Meanwhile, the difference between the largest and second-largest probability of the output is defined as the confidence based on the conditional probability of samples belonging to different fault modes given by the model, which is used to measure the reliability of the diagnosis results. The process of fault diagnosis based on the 1D-DCNN model includes three stages. At stage 1, raw data at several voltage levels are acquired to ensure the model has applicability and generalizability under different voltage levels. Then, the data are preprocessed regarding sliding window segmentation, filtering, and mean normalization. At stage 2, the 1D-DCNN model is trained to diagnose rotating rectifier faults online. At stage 3, the Score-CAM method is introduced to clarify the interpretability of the 1D-DCNN model.
Finally, the prototype experiment verifies the effectiveness of the proposed 1D-DCNN model. Diode open-circuit faults in an 11-phase brushless excitation system are mainly studied, which includes eight fault types. The processed samples are divided into training, verification, and test sets. The verification set is utilized to determine the hyperparameters of the model. The variable control method is used to optimize the hyperparameters of each layer sequentially. Next, the Score-CAM method provides interpretability for the 1D-DCNN model and explains the hyperparameter influence on fault diagnosis performance. The diagnostic accuracy and confidence of different models are compared by the original test set and the test sets with noise. The 1D-DCNN model shows better anti-noise ability, which indicates that selecting the appropriate confidence threshold improves the classification accuracy of the model.
In conclusion, the feasibility of fault diagnosis of rotating rectifiers based on a convolutional neural network is verified, providing a new data-driven idea for the fault diagnosis of rotating rectifiers.
keywords：Brushless excitation system, rotating rectifier, deep learning, convolutional neural network, fault diagnosis
DOI: 10.19595/j.cnki.1000-6753.tces.221531
中图分类号：TM341
中央高校基本科研业务费专项资金项目（2020JBM070）和中广核集团公司科技项目（3100077013）资助。
收稿日期 2022-08-08
改稿日期 2022-12-20
梁郑秋 女，1999年生，硕士研究生，研究方向为多相无刷励磁系统故障监测。E-mail: 21121435@bjtu.edu.cn
周艳真 女，1990年生，博士，研究方向为电力系统分析与控制、人工智能在复杂电网调控及故障诊断中的应用。E-mail: zhouyzh@126.com（通信作者）
（编辑 崔文静）