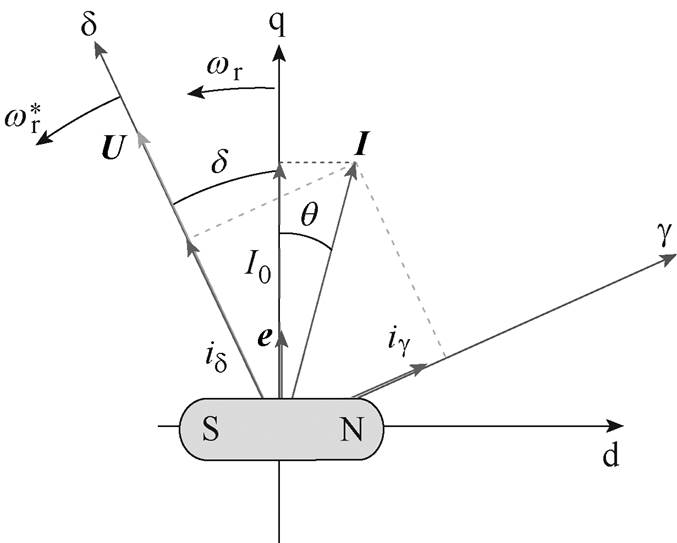
图1 单相电机空间旋转坐标系矢量图
Fig.1 Vector diagram of space rotation coordinate system of single-phase motor
摘要 以单相无刷直流电机（SPBLDC）控制系统为研究对象，针对小型风机位置传感器安装受限等问题，提出基于单相无刷直流电机的高效全速域无位置控制策略，该策略通过单相I/f电流幅值与功率因数补偿相结合的控制方法实现。通过构建SPBLDC的小信号模型，根据小信号根轨迹分析法，分别对单相I/f电流幅值控制以及单相I/f电流幅值与功率因数补偿相结合控制方法下系统全速域稳态及动态调速过程进行稳定性分析，选取了合适的升速斜率，理论分析了该控制策略能够提高电机运行效率，同时保证系统全速域均具备良好的稳定性能。在Matlab/Simulink环境中仿真验证该控制策略下系统全速域均高效运行于最大转矩/电流比状态，电机转速、电流收敛性能及稳定性均有提升。最后，实验验证了该控制策略的有效性及工程应用的可行性。
关键词：单相无刷直流电机 无位置传感器控制 单相I/f电流幅值控制 功率因数补偿 小信号分析
无刷直流电机凭借其运行效率高、调速性能好等优点，广泛应用于电动汽车、民用家电、军事等领域。一方面，单相无刷直流电机（Single-Phase Brushless DC motor, SPBLDC）由于定子绕组数的减小，控制电路的功率器件数量也大大减小，且本体结构简化，使得控制系统的成本大大降低，在风机、泵类应用场合占据着绝对优势[1-2]。另一方面，无位置传感器控制技术可以克服位置传感器在体积结构、成本、温度、可靠性等方面带来的限制，满足小型单相无刷直流风机的技术特点，并实现系统效率优化[3-6]。因此近年来，无位置传感器控制技术已经成为了单相无刷直流电机控制系统的研究热点。
反电动势法检测是目前无刷直流电机无位置传感器控制运用最为成熟的方法[7-8]，其中文献[8]根据转速变化时换向误差角度与反电动势过零时间间隔关系调整了过零点的延时，实时补偿了换向误差。但由于单相无刷直流电机在运行时无不通电绕组，无法直接测得反电动势。文献[9-10]采用基于相电流分时复用的方法来实现对转子位置的检测，需提前关断功率开关管，使相电流归零并持续一段时间，容易使得电机电磁转矩产生波动，降低电机性能。有学者采用磁链观测法[11-12]，通过电压电流积分补偿得到磁链估计转子位置，要求主控芯片不断计算当前磁链并进行查表，占用芯片大量的计算内存，且该方法本身易受电机参数变化的影响。文献[13]结合了改进I/f与磁链观测法，实现了全速域稳定控制，为本文的研究提供了思路。有学者提出将相电流延时90°构建虚拟dq坐标轴的双环控制方法[14-15]，该方法难点在于延时模块的宽频带滤波器难以设计。文献[16-18]采用高频注入结合自适应位置观测器的方法对转子位置进行观测，文献[19]在高频电压注入基础上采用位置反馈的电流解调方法，提高了电流环的带宽与控制性能，文献[20]采用滑模观测器重构单电阻电流方法实现无位置控制。但上述控制算法的复杂度均会提高控制器的成本，实际工程应用价值不高。
电流幅值/频率（I/f）控制与传统恒压频比（V/f）控制[21]相比，采用电流环调节，改善了电流响应，可防止起动阶段电流失控[22-23]。然而，开环I/f控制无法保持调速及稳态情况下反电动势与电流相位同步一致，存在中高速阶段易振荡、稳定性较差、效率低的缺点。因此，通过功率因数补偿控制实现反电动势与电流相位一致，使电机运行于最大转矩/电流比状态，提高电机效率。功率因数补偿可通过调节给定频率或者电流幅值来实现，文献[24]采用通过瞬时有功功率和无功功率反馈来补偿电流幅值和给定频率，从而增加电磁转矩中阻尼分量的方法。由于单相电机不易进行坐标变换和对有功、无功功率分量进行提取，文献[1]提出了一种基于I/f电流瞬时值功率因数补偿的控制方法，并在稳态条件下进行了仿真与实验验证。但电流瞬时值控制法的电流反馈量为正弦量，会导致电流脉动与振荡，对电流环调节器的带宽性能要求较高。
考虑到本文研究对象为风机类负载，对系统伺服控制精度要求并不高。因此，本文提出了一种基于单相无刷直流电机的高效全速域无位置控制策略，通过单相I/f电流幅值控制与功率因数补偿相结合的控制方法实现。其中单相I/f电流幅值控制将相电流幅值作为电流环反馈，降低电流脉动，能够实现全速域无位置控制；同时结合功率因数补偿控制，将逆变器瞬时输出电压与电流反电动势同相位时的理想电压幅值作误差，闭环调节给定电流幅值，使电机运行于最大转矩/电流比状态，保证电机全速域高效运行。通过小信号建模对系统进行稳定性分析，理论分析该方法能够提高电机在全速域各稳态转速及动态调速范围的稳定裕度及稳定性。最后，通过仿真和实验验证本文控制策略的正确性及有效性。
在电机低速起动阶段，采用电流幅值/频率开环给定、并用电流幅值作为反馈的矢量控制方法具有算法简单、不依赖电机参数、电流响应良好等优势，可以抑制起动电流过电流和转矩脉动，实现电机平滑起动与升速。
根据文献[1]，建立单相无刷直流电机的空间矢量旋转参考坐标系模型。如图1所示，两个旋转坐标系分别为转子dq轴坐标系和电压空间矢量gd 轴坐标系，其中定义d轴为转子永磁体磁通参考方向，定义q轴为电机反电动势空间矢量e参考方向；定义gd 轴为逆变器输出电压矢量U参考坐标系，d 轴为单相逆变器电压矢量参考方向，g 轴在相位上滞后d 轴90°。图2所示为单相电机H桥逆变器拓扑。定义单相绕组的瞬时电压和电流分别为u和i；直流母线电压和电流分别为Udc和idc；Q1, Q4开通、Q2, Q3关断时绕组施加正向参考电压，并以该参考方向建立静止坐标系，此时u和i的参考方向为正方向，与Udc的参考方向相同，x轴为该静止坐标系的参考轴。
图1 单相电机空间旋转坐标系矢量图
Fig.1 Vector diagram of space rotation coordinate system of single-phase motor
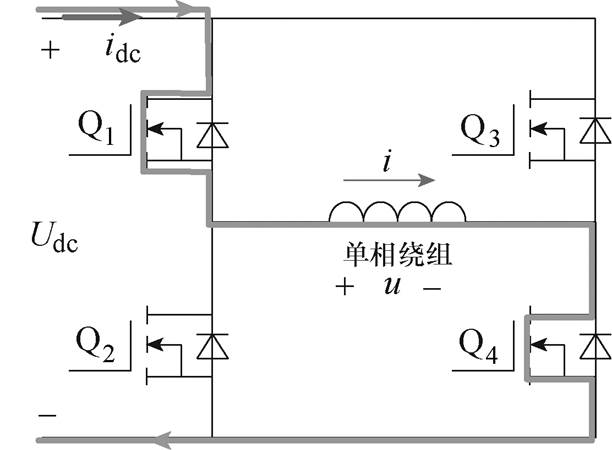
图2 单相电机H桥逆变器拓扑
Fig.2 Single-phase motor H-bridge inverter topology
矢量控制下，绕组瞬时电压可近似视为时变正弦量，可表示为u=Umcosqu，其中Um为相电压幅值，qu为瞬时电压的相位值。同理，绕组瞬时电流也可表示为i=Imcosqi，其中Im为相电流幅值，qi为瞬时电流的相位值。瞬时电压和电流所对应的相量形式分别为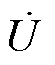
和
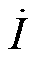，其中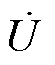=Um∠qu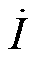，=Im∠qi。当qu=0时，绕组两端瞬时电压u达到相电压幅值Um；同理，当qi=0时，绕组两端瞬时电流i达到相电流幅值Im。
由于单相电机运行时的转子磁场为旋转空间矢量，为了更直观地反映单相绕组电压、电流和反电动势三者在旋转坐标系中的相位和幅值关系，从而实现高精度高性能的矢量控制，本文通过等效方法构造了电压空间矢量U和电流空间矢量I，如图3所示。以静止坐标系作为参考系，定义电压空间矢量的幅值为Um，且相位为qu；定义电流空间矢量的幅值为Im，且相位为qi。此时，绕组瞬时电压u和瞬时电流i即可等效为电压空间矢量U和电流空间矢量I在静止坐标轴上投影的模（符号取x轴参考方向为正）。当qu和qi分别为0时，U与I分别与x轴同向。以空间旋转坐标系作为参考系，稳态下U和I随着转子dq轴旋转坐标系同步旋转，二者与反电动势空间矢量e之间存在近似固定的矢量关系。
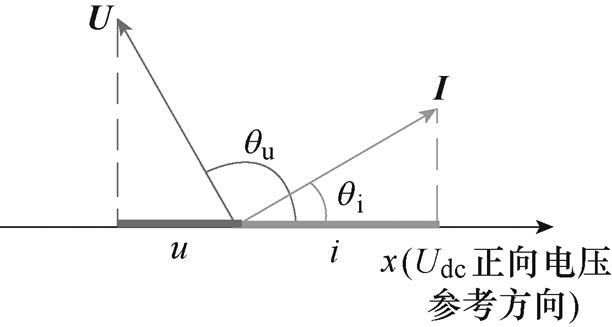
图3 静止坐标系电压电流瞬时值与空间矢量示意图
Fig.3 Schematic diagram of voltage and current instantaneous value and space vector in static coordinate system
图1中，d 为电压空间矢量gd 轴与电机转子矢量dq轴的夹角，q 为电机转子矢量dq轴与电流空间矢量I的夹角，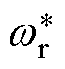
为gd 轴坐标系角频率，wr为dq轴坐标系角频率。以电压空间矢量坐标系为参考系，将U分解得到g、d 轴下的标量vg、vd，其中vg=0，vd=Um，vd 即为逆变器输出相电压幅值；同理，将电流空间矢量I分解得到g、d 轴下的标量ig、id，需要注意，此处定义电流分量目的是为了建立电压空间矢量参考轴下的电流电压微分方程，通过小信号建模即可判定电流电压在gd 轴分量的稳定性，若电流分量ig、id 均能够稳态收敛于定值，那么认为电流空间矢量I的幅值和相位均趋于稳定。
根据永磁无刷直流电机的开环数学模型[25]，建立电机gd 轴下的电压微分方程为
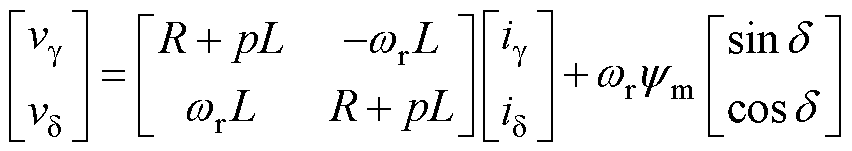（1）
式中，vg、vd 分别为g、d 轴下的电压分量；ig、id 分别为g、d 轴下的电流分量；p为微分算子；R为相电阻；L为相电感；ym为永磁体磁链。
单相电机电磁转矩方程为
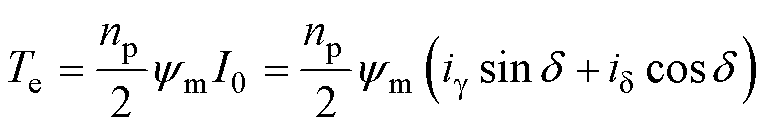（2）
式中，Te为电磁转矩；np为电机极对数；I0为有功电流幅值，可由ig、id 在q轴上的分量叠加得到。
由于电机负载为风机类负载，负载转矩TL可表示为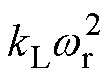
，进而得到电机运动方程为
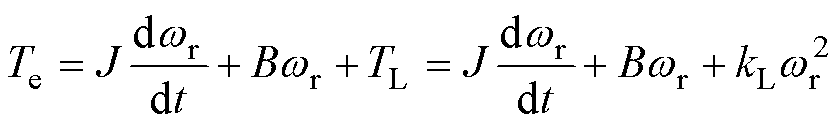（3）
式中，J为转动惯量；B为阻尼系数；kL为负载转矩系数。
图4所示为单相I/f电流幅值控制框图。
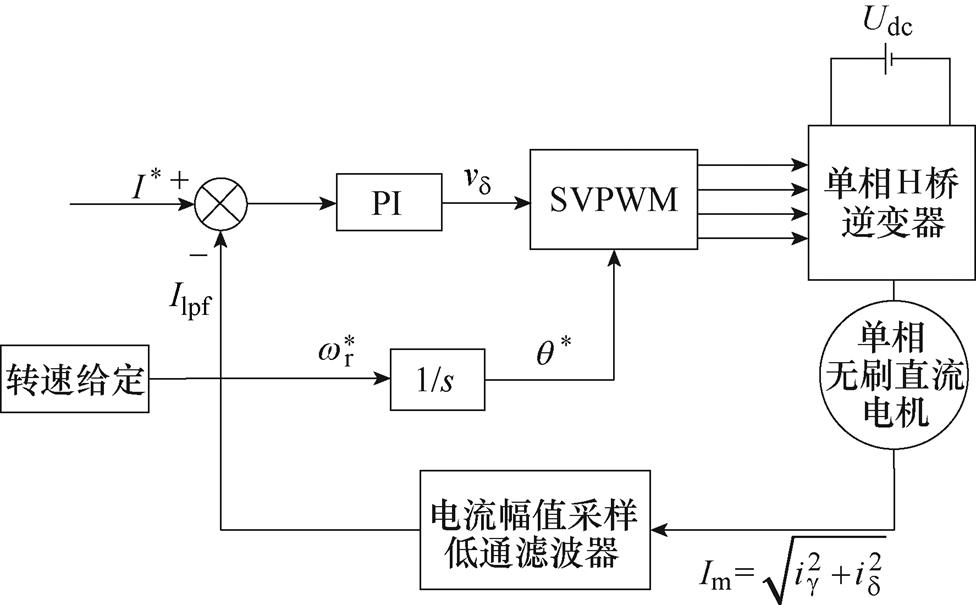
图4 单相I/f电流幅值控制框图
Fig.4 Single-phase I/f current amplitude control block diagram
该控制方法为电流闭环、转速开环控制，通过离线给定电流幅值和斜坡转速，产生旋转电磁场和电磁转矩，拖动转子运动。
电流环方程为
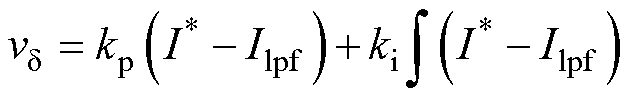（4）
式中，kp和ki分别为电流环PI控制器的比例和积分系数；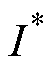
为给定电流幅值；Ilpf为经过低通滤波后的采样电流幅值，稳态下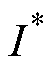与Ilpf相等。
该方法将相电流幅值作为电流环反馈，相对于相电流瞬时值反馈，可有效抑制反馈量脉动带来的振荡，对PI调节器带宽要求不高。
单相电机的起动分为预定位和起动两个阶段。初始静止状态下，由于单相电机定子不对称气隙的作用，定子绕组轴与转子磁通方向d轴之间存在一定夹角；预定位时，逆变器施加微小的正向电压vd，绕组中产生正向电流，此时转子受到电磁力矩，产生偏移使得转子d轴与定子绕组轴向重合；给定起动指令时，逆变器正向电压置为零，在顿转转矩的作用下，转子会产生向着初始静止位置偏移的初速度，此时给定电流幅值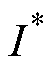为一正值，而电流幅值反馈为零，依据电流环方程，输出电压vd 为一正值且不断增大，同时给定位置角度，使电机绕组产生等效旋转的电压矢量，电磁转矩逐渐增大，电机完成起动并升速。由于风机类负载的起动转矩较小[26]，因此采用电流幅值控制可以大大改善起动时的电流响应。
根据式（1），将g、d 轴电流ig、id 为作为状态变量，并以微分算子形式表示为
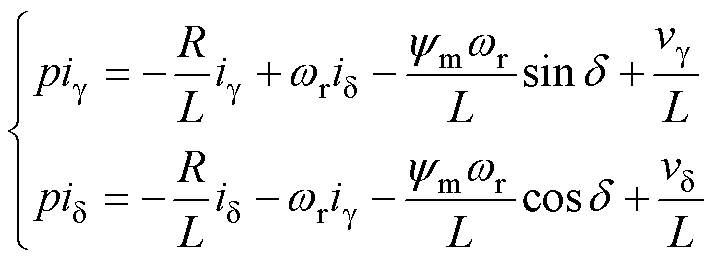（5）
根据运动方程，得到角频率的微分算子表达式为
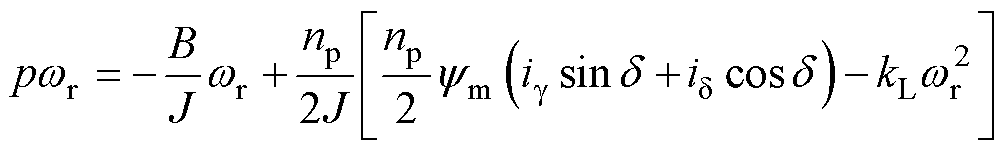（6）
电压空间矢量轴与电机转子位置夹角的微分算子表达式为
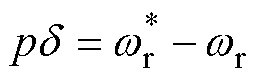（7）
对电流幅值采样环节进行低通滤波处理，有
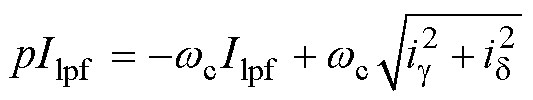（8）
式中，wc为低通滤波器的截止频率。
根据电流环方程式（4），将电流误差量作为新状态变量w，得到电流环误差的微分算子表达式为
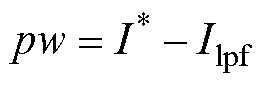（9）
通过在稳态条件下对系统施加小扰动，系统中各变量将在稳态值附近产生一定增量，将状态量近似表示为线性增量，即可得到线性化状态方程表达形式为
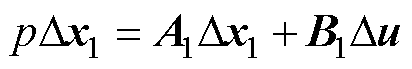（10）
式中，x1为单相I/f电流幅值控制系统的状态变量；u为输入变量；A1和B1分别为系统的状态矩阵和输入矩阵，其中，A1见附录。
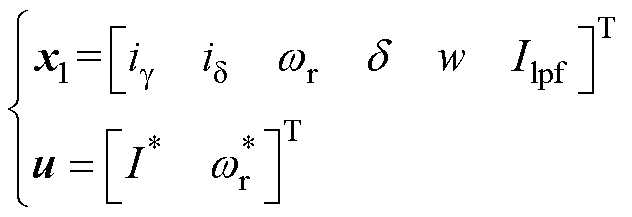（11）
对于连续时域的线性定常系统而言，系统内部渐进稳定的充分必要条件是状态矩阵特征根均位于复平面左半平面，系统的特征根可由式（12）求得。
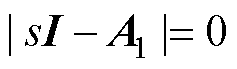（12）
为分析电机在不同稳态转速下的系统稳定性，首先需要计算出稳态工作点下各状态变量的稳态值。
在稳态转速下，电机运动方程可简化为
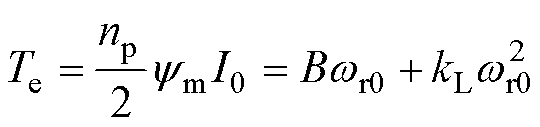（13）
式中，wr0为wr的稳态值；I0为有功电流幅值，即给定电流幅值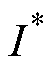在反电动势矢量q轴上有功分量的稳态值，根据稳态下有功电流与相电流矢量关系（见图1），得到对应I0与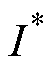关系为
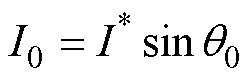（14）
式中，q0为q 的稳态值。
根据空间矢量图，电压与反电动势矢量夹角的稳态值d0为
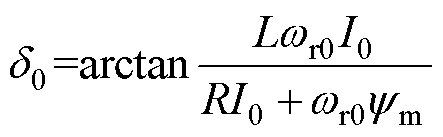（15）
综上所述，各状态变量的稳态值为
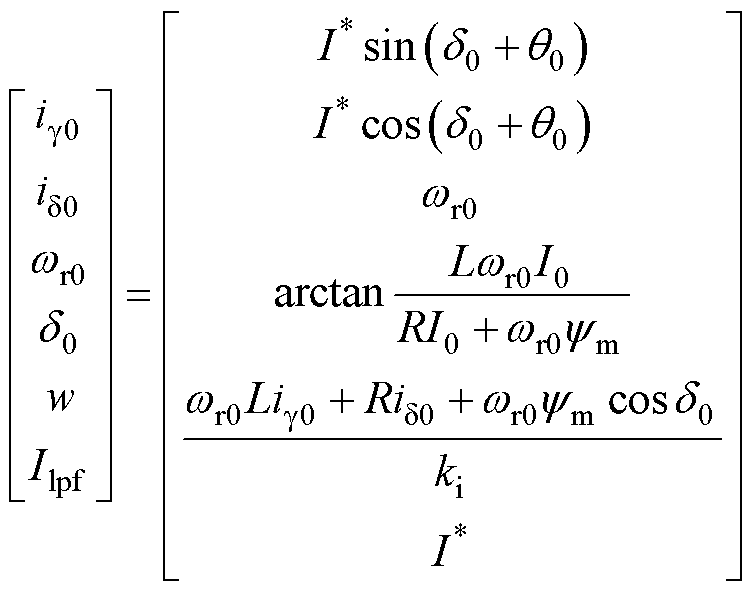（16）
式中，ig0、id0 分别为g、d 轴电流ig、id 的稳态值。
结合表3所示单相无刷直流电机参数，建立单相I/f电流幅值控制的小信号模型，对各稳态转速的系统进行稳定性分析。由于单相无刷直流电机的额定转速nN为4 200 r/min，因此绘制转速N为0～4 200 r/min系统闭环极点根轨迹如图5所示。
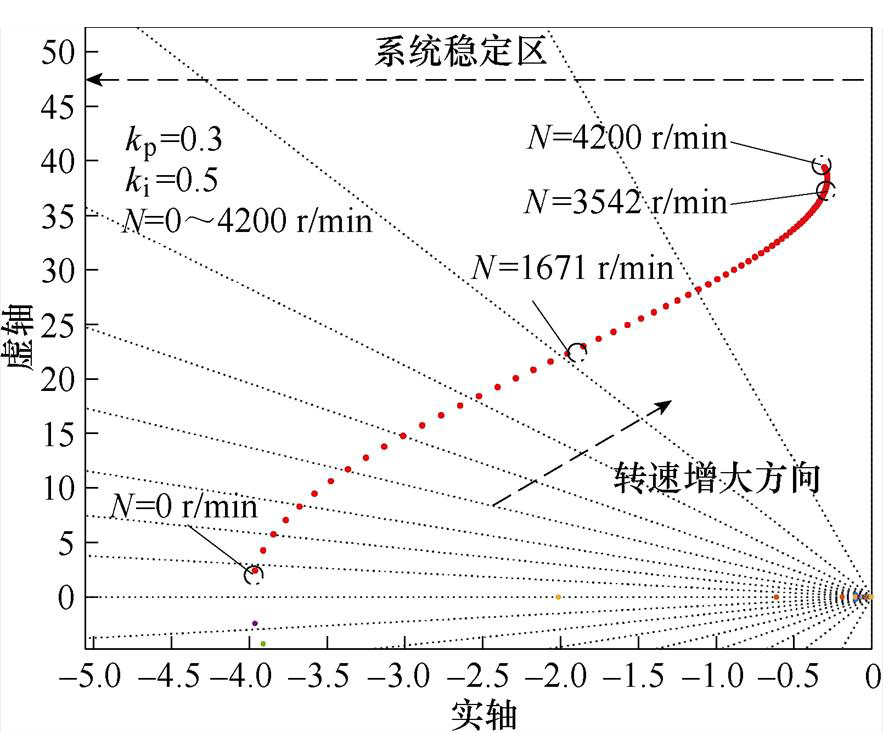
图5 单相I/f电流幅值控制闭环极点根轨迹
Fig.5 Single phase I/f current amplitude control closed-loop pole root locus diagram
由图5可得，随着转速升高，闭环极点总体呈靠近虚轴趋势，稳定性下降。当转速在3 542 r/min至额定转速4 200 r/min时，根轨迹距虚轴较近，趋近等幅振荡区，系统稳定性较差。
因此，单相I/f电流幅值控制方法在低速起动阶段具备较好的稳定性能，但随着转速增加，系统稳定裕度降低，尤其在实际升速斜率较高的工况下易导致电机失步。在性能效率方面，为使电机在受扰动时拥有足够的稳定裕量，该方法需要将电流幅值给定为较大值，使得功角增加，远离临界稳定区域，但同时增加了电机的无功损耗。
针对上述问题，本文提出了一种基于单相I/f电流幅值与功率因数补偿相结合的无位置控制策略。
该控制方法能够降低电机运行时的无功损耗，提高运行效率；同时保证系统在全速域均具备良好的稳定性能。一方面，通过闭环调节电流指令控制反电动势和电流空间矢量相位一致，降低电流无功分量，提高电机的运行效率，使电机运行于最大转矩/电流比；另一方面，提高系统全速段稳态转速及调速范围内的稳定性，使之具备一定的稳定裕度。
图6为单相I/f电流幅值与功率因数补偿系统控制框图，在开环I/f电流幅值控制的基础上加入了电压幅值补偿环路，根据电压幅值比较判断来调节瞬时电流指令，从而保证反电动势与电流相位一致，使电机运行于最佳功率因数状态。
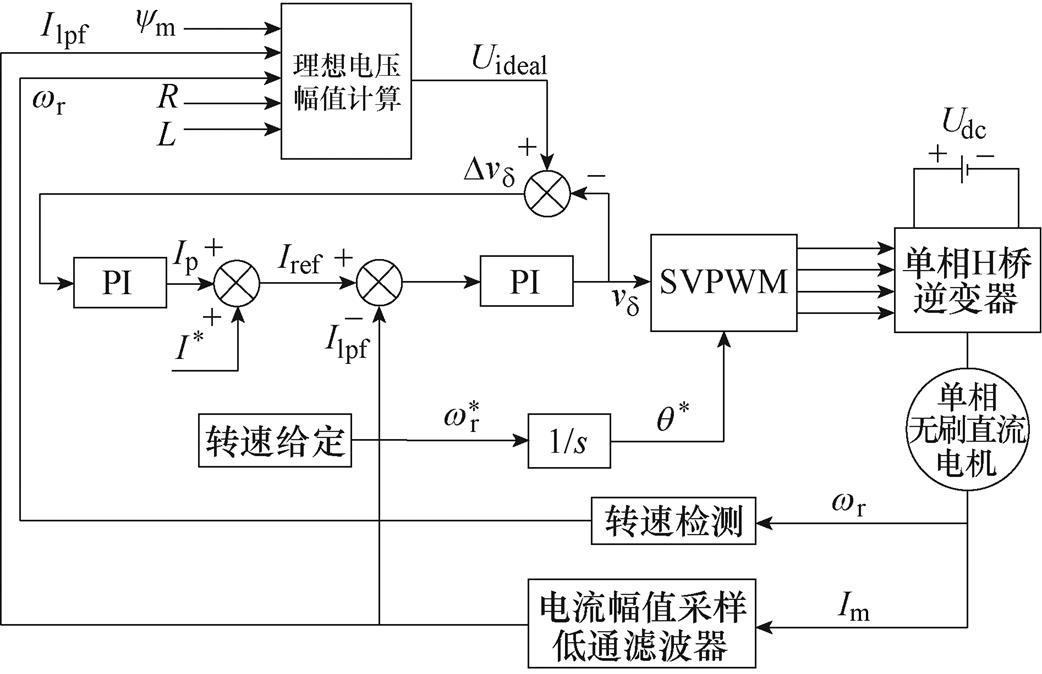
图6 单相I/f电流幅值与功率因数补偿控制结构框图
Fig.6 Single-phase I/f current amplitude power factor compensation control structure block diagram
图7为单相电机反电动势空间矢量e和电流空间矢量I依次重合、超前、滞后电流矢量的电机矢量相位关系。
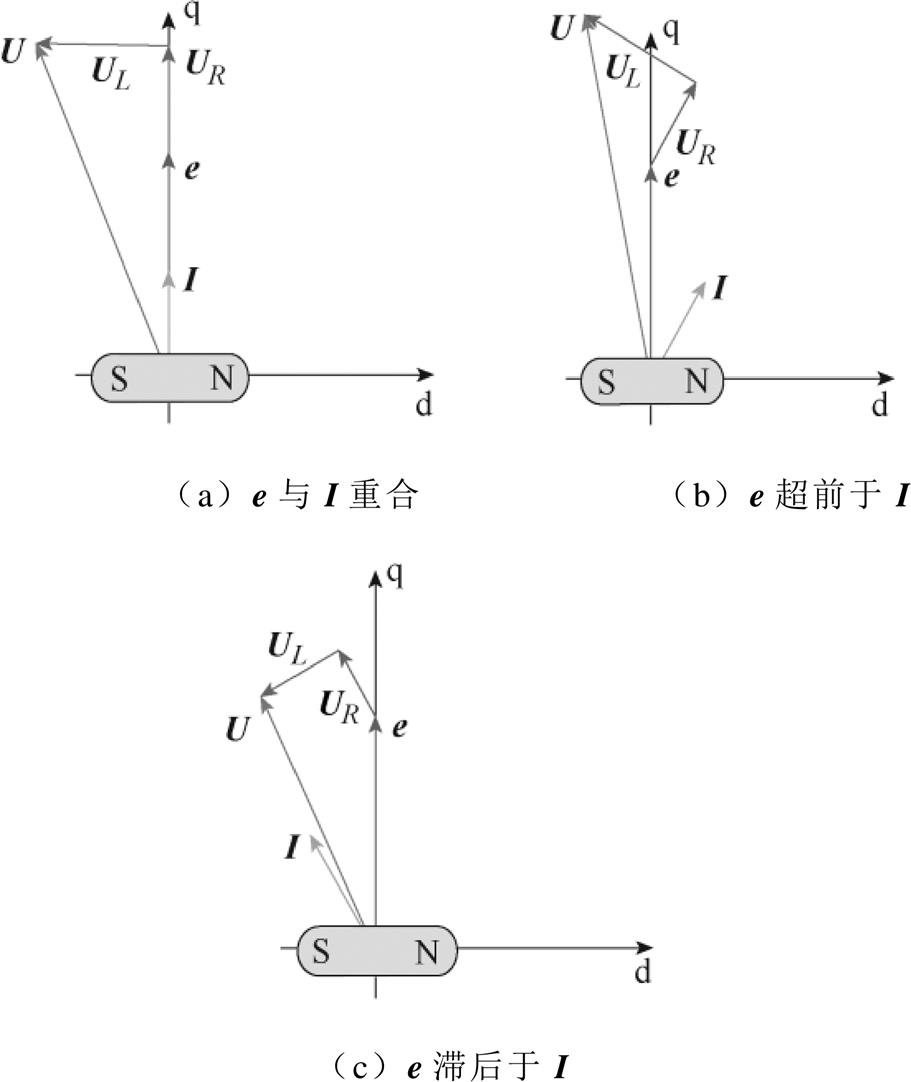
图7 单相电机空间矢量图
Fig.7 Single-phase motor space vector diagram
电机的电压矢量方程为
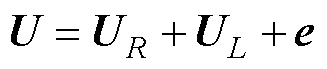（17）
其中
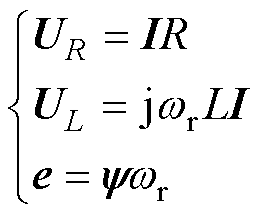（18）
式中，U为逆变器输出电压空间矢量；UR、UL分别为电机绕组电阻和电感上的电压矢量；e为反电动势矢量；y 为永磁体磁链空间矢量。
当电流矢量I与反电动势矢量同相位时，逆变器输出电压幅值为理想电压幅值，不同稳态转速下的理想电压幅值通过滤波后采样电流幅值Ilpf、实际检测角频率wr与实际电机参数等在线计算得到。
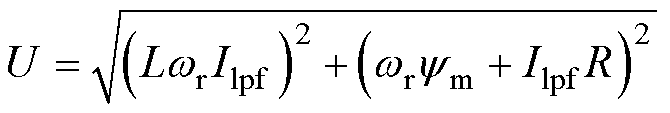（19）
当I超前于e时，瞬时电压幅值大于理想电压幅值，此时PI调节器需要增大给定电流指令，增大瞬时有功电流从而提高电磁转矩，使电机加速，e收敛至与I同向；反之，当I滞后于e时，减小给定电流指令，使电机减速。
电压幅值补偿环方程为
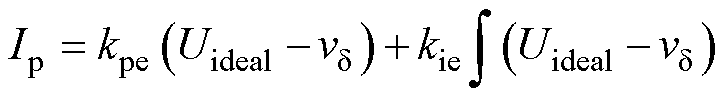（20）
式中，Uideal为理想电压幅值；kpe和kie分别为补偿环PI控制器的比例和积分系数；Ip为补偿环电流给定幅值。
当瞬时电压幅值与理想电压幅值存在误差时，通过PI控制器调节Ip，控制电流环的输出电压幅值vd 收敛于Uideal，保持相电流与反电动势相位一致，电机运行于最佳功率因数状态。
同1.2节，对功率因数补偿控制稳态条件下的系统进行稳定性分析。将电压误差量作为新状态变量v，得到状态量微分算子方程为
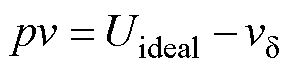（21）
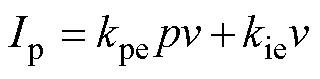（22）
功率因数补偿控制下稳态电流近似为有功电流，因此将各转速下的有功电流幅值I0作为Ilpf的稳态值。将式（22）用线性增量表示，近似得到电压线性增量为
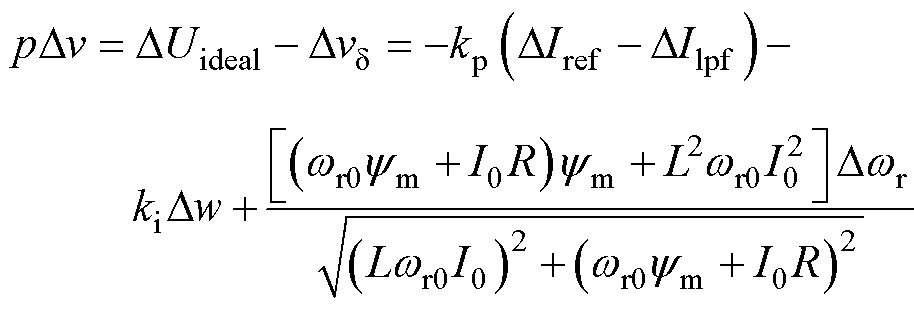（23）
式中，Iref为加入补偿环后的给定电流幅值；DIref、DIlpf、DUideal、Dvd、Dv、Dw、Dwr分别为状态量Iref、Ilpf、Uideal、vd、v、w、wr在小扰动下的线性增量。
由于开环给定电流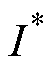为离线给定值，因此电流环输入的微小扰动量等效为电压补偿环输出的电流扰动量，有
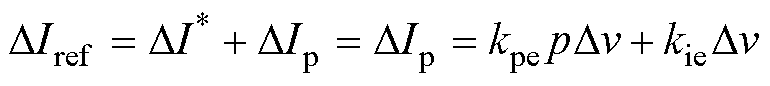（24）
此时电流环方程改写为
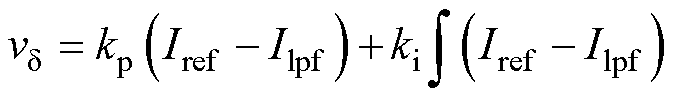（25）
整理式（21）～式（25），建立单相I/f电流幅值结合功率因数补偿的系统线性化状态方程为
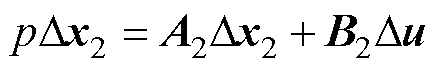（26）
式中，x2为功率因数补偿下系统的状态变量；A2和B2分别为功率因数补偿控制下系统的状态矩阵和输入矩阵，其中，A2见附录。
功率因数补偿控制下系统的状态变量表示为
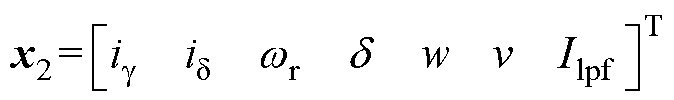（27）
功率因数补偿下有功电流幅值I0可表示为
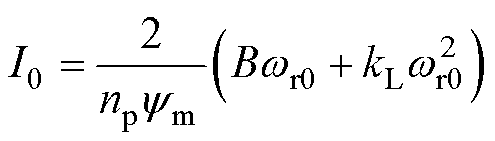（28）
稳态下电流与反电动势夹角q0近似为零，绘制转速为0～4 200 r/min系统闭环极点根轨迹如图8所示。
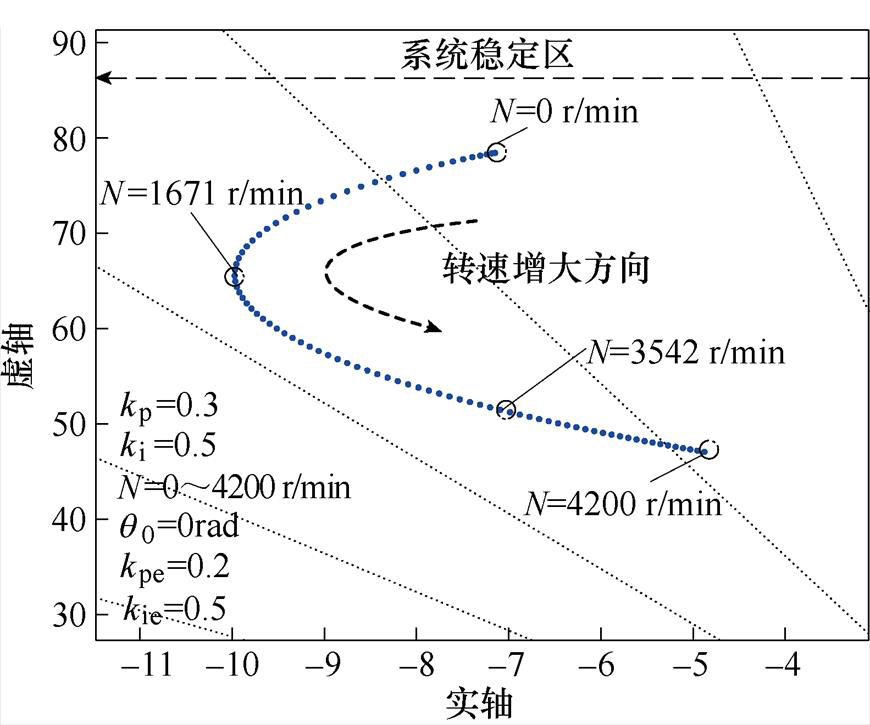
图8 功率因数补偿控制系统闭环极点根轨迹
Fig.8 I/f power factor compensation control dominant pole diagram
功率因数补偿后系统在0～1 671 r/min转速范围内，随着转速增加，闭环极点距虚轴距离增加，系统稳定性增加；转速在1 671～4 200 r/min范围内，随着转速增加，闭环极点距虚轴距离减小，同时距实轴距离也减小，系统响应速度有提升，但稳定性逐渐下降。
对比功率因数补偿前后系统闭环极点，如图9所示。功率因数补偿前后根轨迹对比见表1。
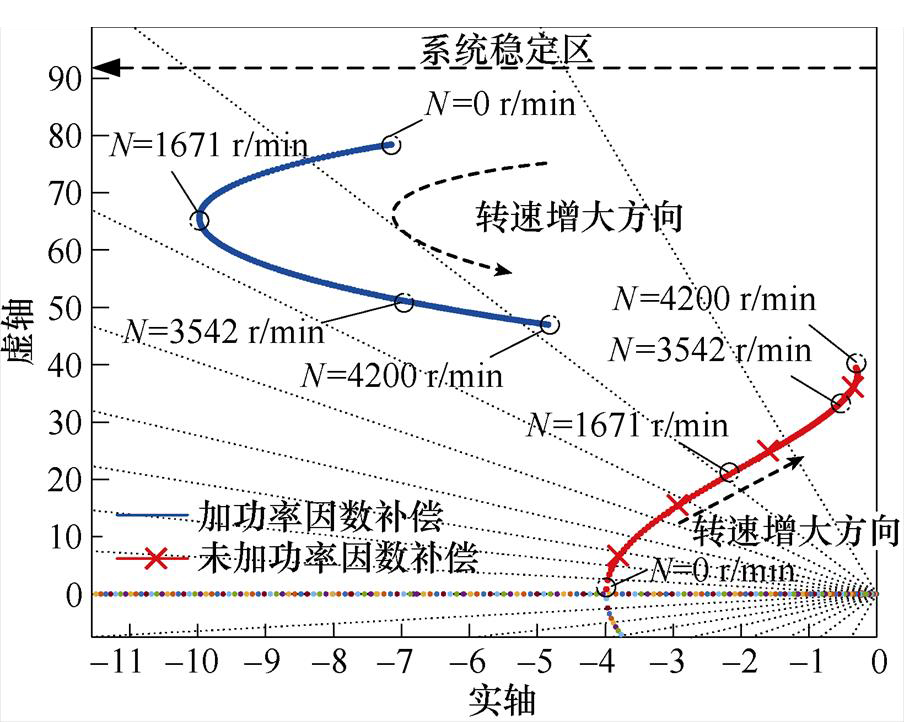
图9 功率因数补偿前后系统闭环极点
Fig.9 Comparison of root locus before and after power factor compensation
表1 功率因数补偿前后根轨迹对比
Tab.1 Improvement table of wind direction characteristic for forecast performance
转速/(r/min)未加功率因数补偿加功率因数补偿 0-3.9+1.5j-7.1+79.1j 1 671-2.1+20j-79.4+66.5j 3 542-0.5+31.8j-7+48.5j 4 200-0.3+45.3j-4.8+47j
由图9可得，功率因数补偿前，全速段系统闭环极点实部的模均小于4，随着转速增大，根轨迹不断靠近虚轴，系统振荡加剧，稳定性降低；功率因数补偿后，全速段系统闭环极点实部的模均大于4，系统振荡降低，稳定性提升。
在电机低速起动阶段，功率因数补偿后系统的振荡量增大，响应快速性有所提高；中低速阶段（1 671～3 542 r/min），功率因数补偿后系统闭环极点明显向远离虚轴方向移动，阻尼比增加，系统稳定性显著提高，是功率因数补偿主要的改进阶段；接近额定转速4 200 r/min阶段，功率因数补偿后闭环极点靠近虚轴方向移动，稳定性略有下降，但相对于未加补偿仍有提升。
综上所述，基于单相I/f电流幅值与功率因数补偿相结合的控制方法可以提高系统在全速段的阻尼比，降低振荡，系统的稳定性显著提升。
2.2节针对功率因数补偿控制系统进行了稳态稳定性分析。而在实际工程应用中，需考虑电机动态调速过程系统的稳定性。本节依据不同升速斜率下系统各速段的稳定性，得到合适的升速斜率区间。
电机以某一固定升速斜率升速至额定转速过程中，角频率wr为一斜坡函数，根据稳态下电磁转矩方程式（29），升速斜率可由Jdwr0/dt项表示（注意此处的dwr0/dt在固定升速斜率下为一恒定值，与状态变量无关），因此可将其等效为各稳态转速下的恒定负载，得到不同转速下的有功电流幅值I0。同2.2节，由于功率因数补偿后功角d 近似为90°，稳态下电流幅值Ilpf近似为I0，如式（30）所示。
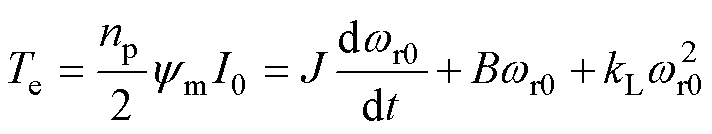（29）
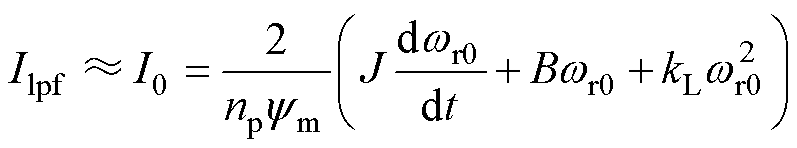（30）
将升速斜率单位转换为r/min/s，分别令其为100、200、400、600和1 000 r/min/s进行不同升速斜率下0～4 200 r/min全速段的稳定性分析，闭环极点分布如图10所示，转速接近额定转速4 200 r/min时的闭环极点如图11所示。
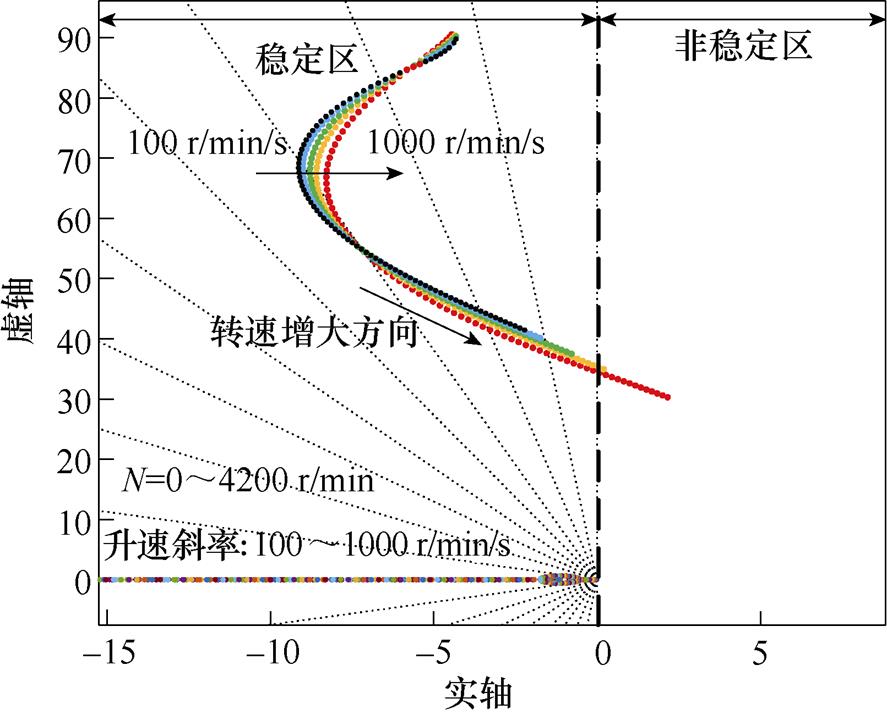
图10 不同升速斜率下系统闭环极点分布
Fig.10 Root locus diagram of different acceleration slopes
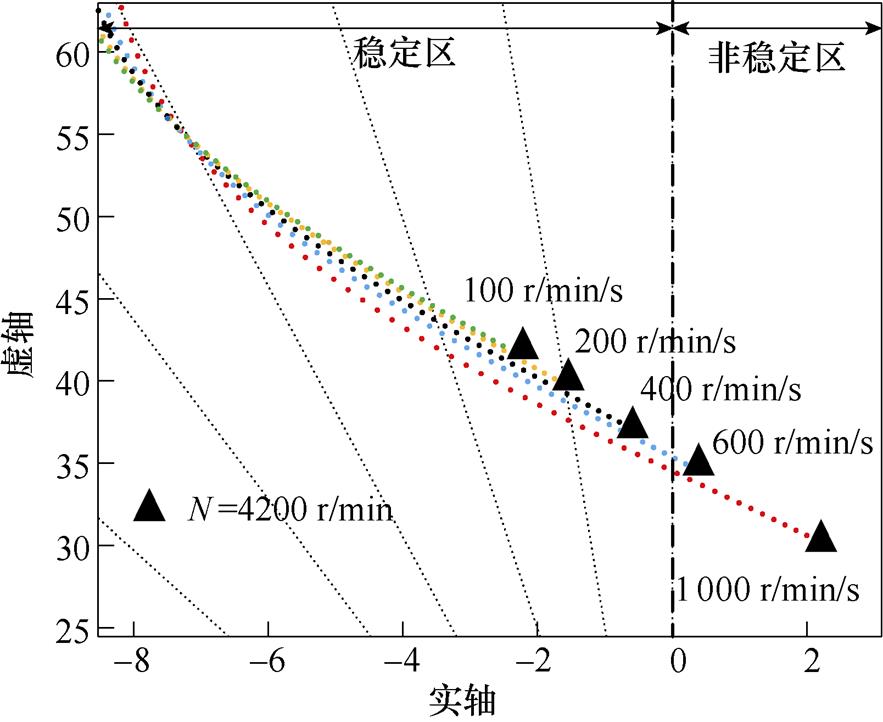
图11 4 200 r/min附近不同升速斜率闭环极点
Fig.11 Closed-loop pole diagram of different ramp-up slopes around 4 200 r/min
加入功率因数补偿后，随着升速斜率的增加，接近4 200 r/min区间的闭环根轨迹总体向虚轴偏移，系统稳定性降低，若升速斜率大于600 r/min/s，接近额定转速时系统趋于不稳定区。
实际动态调速的升速斜率的选取需根据实验调整，升速斜率选取为500 r/min/s，功率因数补偿前后的根轨迹对比如图12所示。升速阶段功率因数补偿前后根轨迹见表2。
由图12可得，给定升速斜率下，在转速为3 542～4 200 r/min的中高速区间内，加入功率因数补偿后闭环极点的实部扩大约9倍，而虚部几乎不变，极点接近向左平移，表明系统阻尼增大、收敛性能提高，升速至该转速范围内系统的稳定性显著提升。
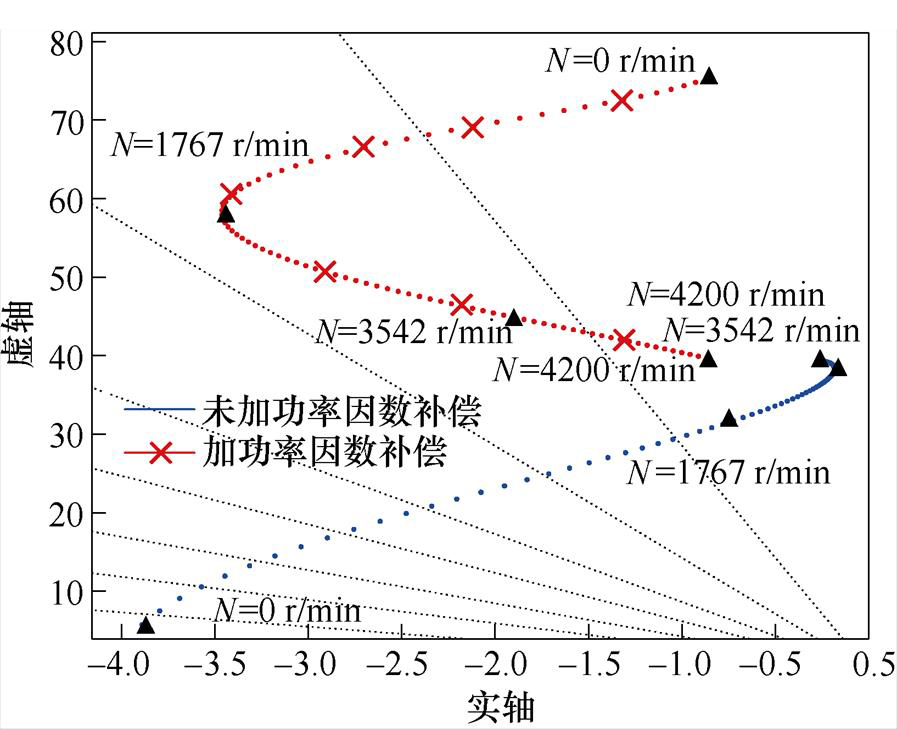
图12 动态调速阶段功率因数补偿前（蓝）后（红）根轨迹
Fig.12 Root locus before (blue) and after (red) power factor compensation during acceleration
表2 升速阶段功率因数补偿前后根轨迹
Tab.2 Root locus before and after power factor compensation during acceleration
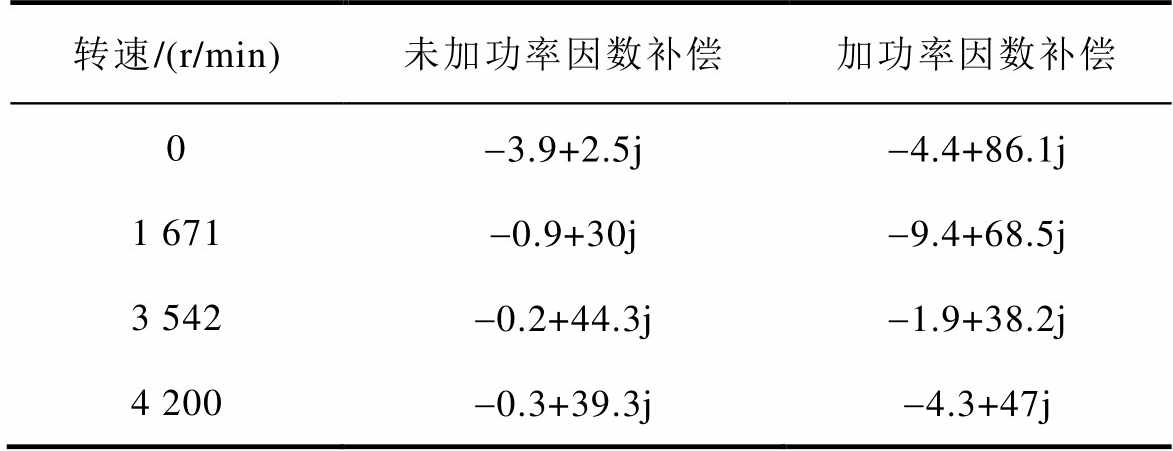
转速/(r/min)未加功率因数补偿加功率因数补偿 0-3.9+2.5j-4.4+86.1j 1 671-0.9+30j-9.4+68.5j 3 542-0.2+44.3j-1.9+38.2j 4 200-0.3+39.3j-4.3+47j
为验证本文提出的单相电机I/f电流幅值控制功率因数补偿控制方法的可行性，本节在Matlab/ Simulink环境下搭建了系统模型，对功率因数补偿前后系统在稳态转速/调速过程的转速、电流响应情况进行了仿真分析。
单相双极性无刷直流电机的负载类型为风机类型负载，仿真模型参数设置见表3。
为了验证调速范围及稳态转速下功率因数补偿控制的有效性，电机分别采用I/f电流幅值控制和I/f电流幅值加功率因数补偿控制，从0 r/min起动至额定转速4 200 r/min，升速斜率设为500 r/min/s，仿真得到给定转速、实际转速波形如图13a和图13b所示。由于电流环采用PI调节，转速存在振荡，功率因数补偿后稳态转速脉动由正负50 r/min降低至正负20 r/min，由于功率因数补偿增加了系统阻尼，使转速脉动减小、振荡量降低、收敛性能提升。
功率因数补偿前后全速段相电流、反电动势、相电压仿真波形如图14所示，图中，e为反电动势在相绕组上的交流分量。展开图分别对应升速阶段3 542 r/min和稳态阶段4 200 r/min。起动、稳态阶段对比分别见表4、表5。
表3 仿真模型参数
Tab.3 Simulation parameters
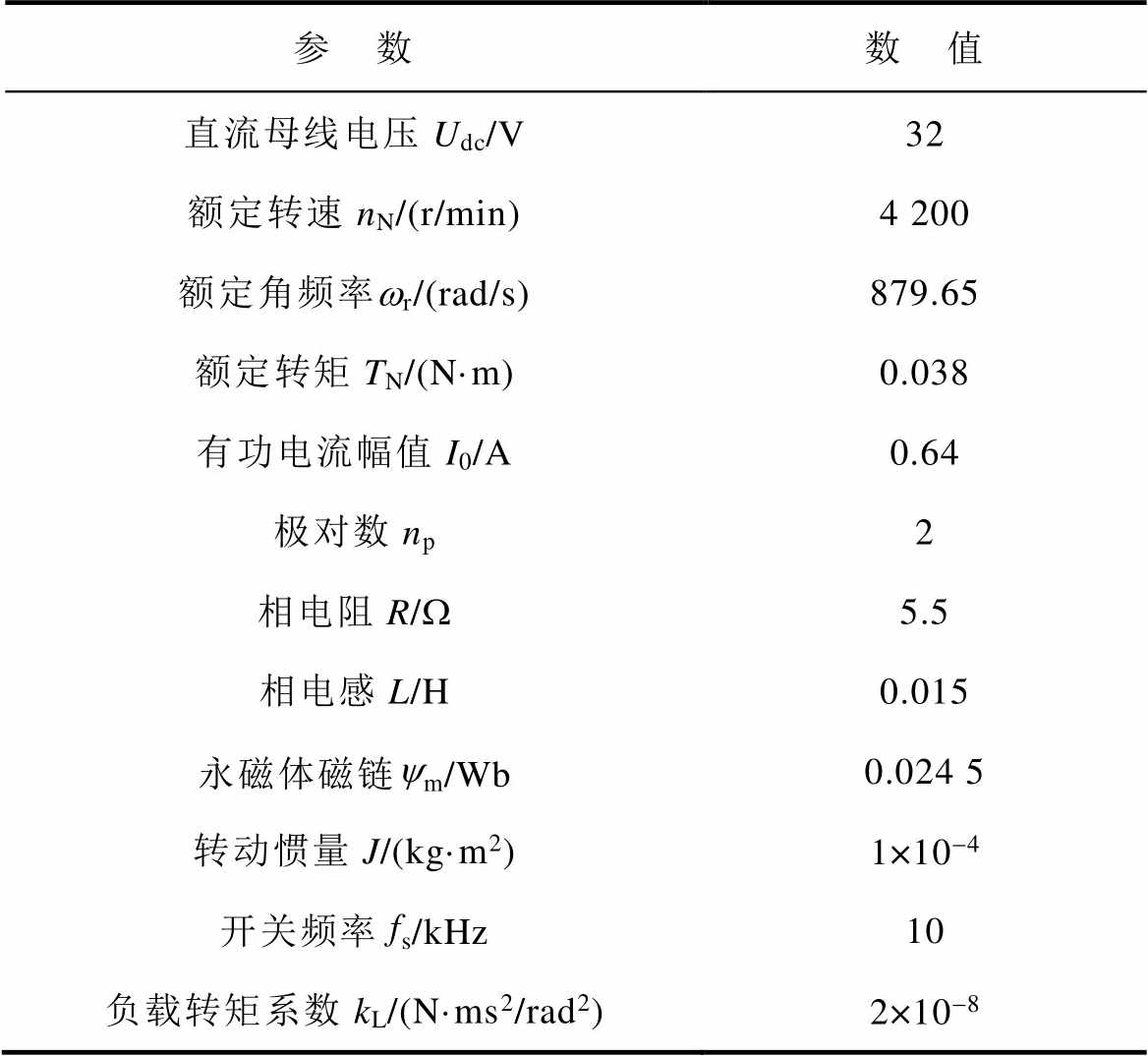
参 数数 值 直流母线电压Udc/V32 额定转速nN/(r/min)4 200 额定角频率wr/(rad/s)879.65 额定转矩TN/(N·m)0.038 有功电流幅值I0/A0.64 极对数np2 相电阻R/W5.5 相电感L/H0.015 永磁体磁链ym/Wb0.024 5 转动惯量J/(kg·m2)1×10-4 开关频率fs/kHz10 负载转矩系数kL/(N·ms2/rad2)2×10-8
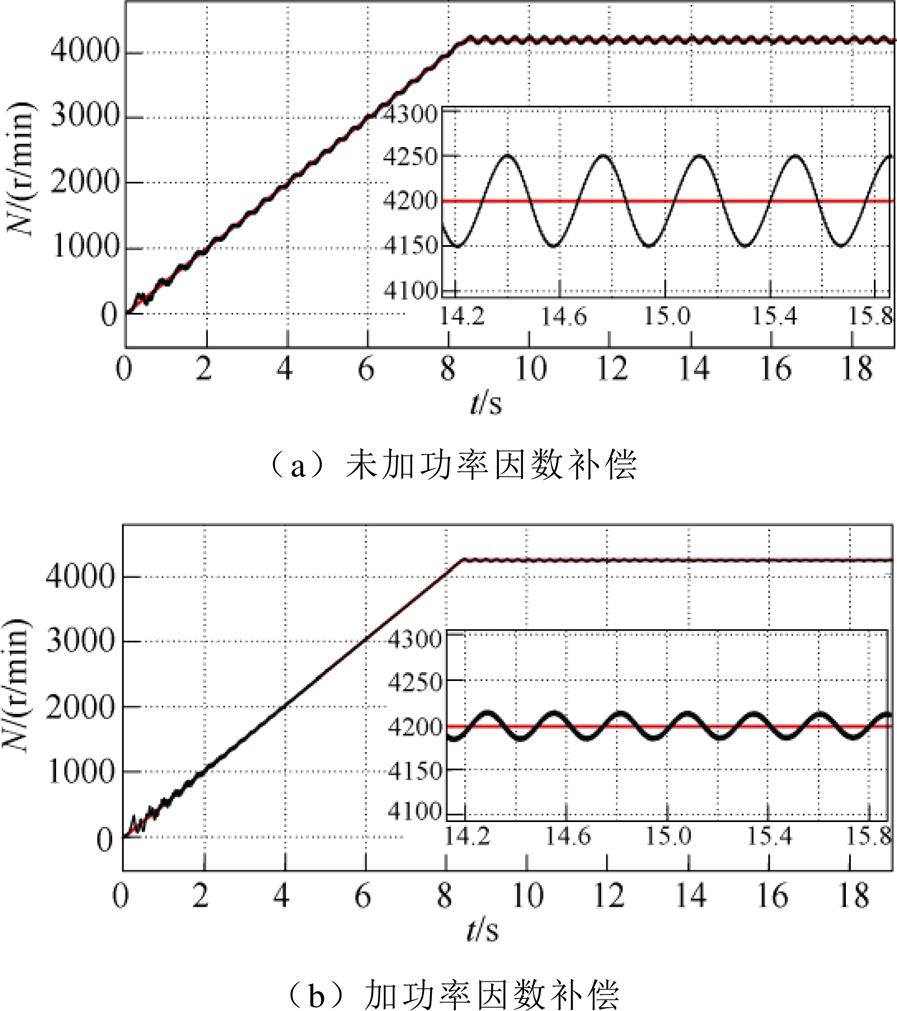
图13 功率因数补偿前后转速波形
Fig.13 Speed waveforms before and after power factor compensation
由图14可得，功率因数补偿控制后升速过程全速段的电流幅值、反电动势与电流相位差均显著降低，且在3 542 r/min附近转速区间的电流振荡明显降低，验证了2.3节的理论推导：在中高速转速区间内，功率因数补偿控制可以显著提升系统的电流收敛性能和稳定性。
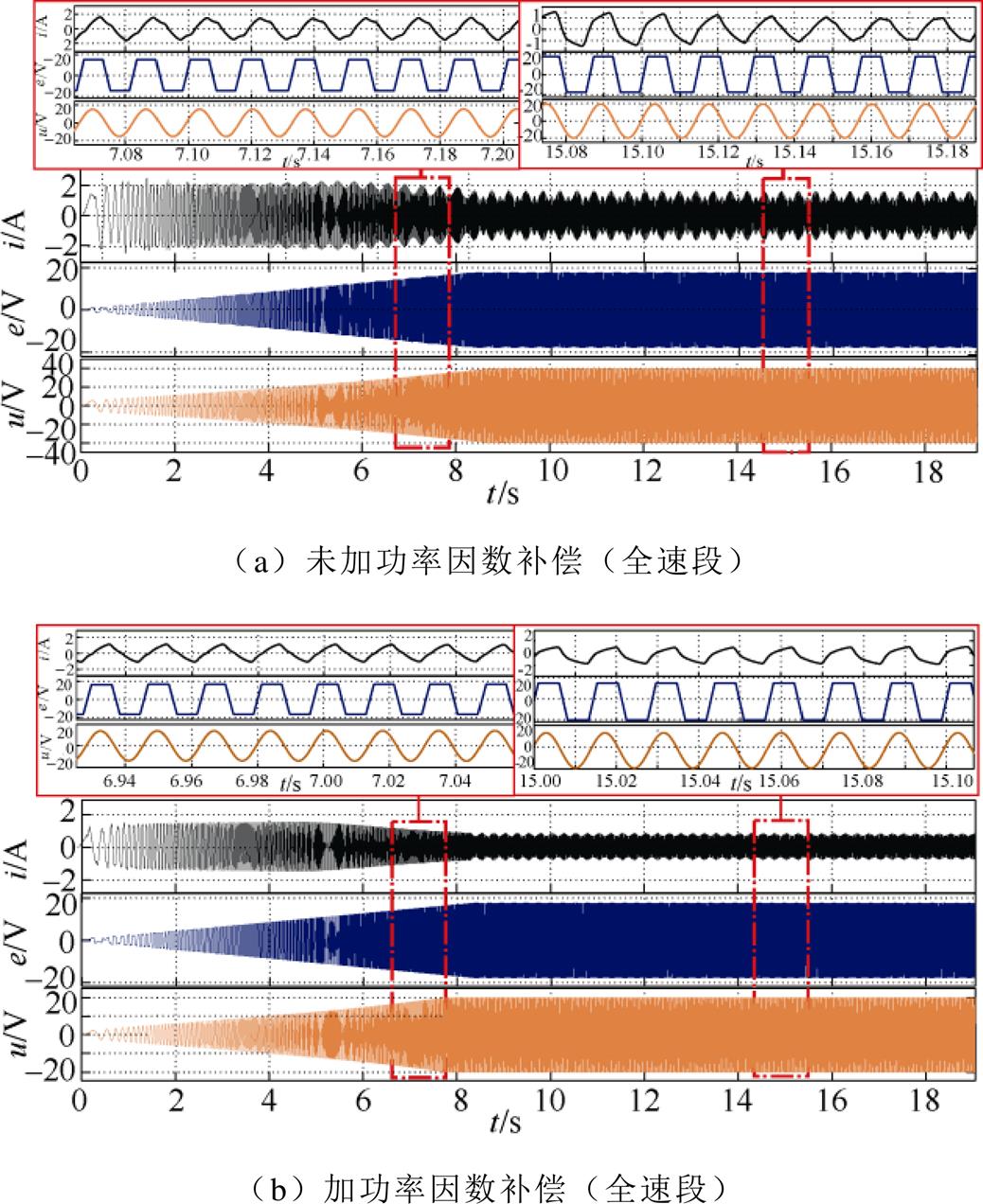
图14 全速域相电流i、反电动势e、相电压u波形
Fig.14 Waveforms of current i, back electromotive force e and voltage u at full speed
表4 起动阶段对比
Tab.4 Start-up comparison
参 数未加功率因数补偿加功率因数补偿 相电流幅值Im/A1.81.1 反电动势e与相电流i相位差/(°)6030
表5 稳态阶段对比
Tab.5 Steady state phase comparison
参 数未加功率因数补偿加功率因数补偿 相电流幅值Im/A1.40.7 反电动势e与相电流i相位差/(°)358
系统硬件平台架构包括控制板、上位机调试界面和单相无刷直流风机。其中控制板的控制部分由国产DSP28027芯片及其外围电路构成；驱动部分采用单相H桥结构；电流采样部分采用桥臂下管电阻采样。实验所用电机参数与仿真参数基本相同。实验平台及其工作运行状态如图15所示。
图16验证了单相电机无位置控制算法在额定转速下的可行性，进行了额定转速4 200 r/min实验，电流基频为140 Hz。
图15 单相无刷直流电机实验平台及其工作运行状态
Fig.15 Single-phase brushless DC motor experimental platform and its working and operating status
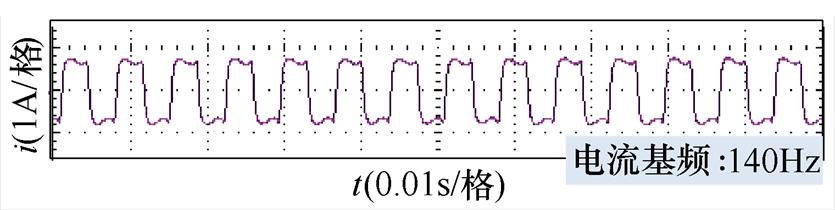
图16 额定转速电流波形
Fig.16 Current waveform at rated speed
为验证稳态转速下功率因数补偿控制的可行性，在转速为3 000 r/min的电压线性调制区内，由I/f电流幅值控制切换至功率因数补偿控制，调节时间约为0.15 s，补偿过程电压电流波形如图17所示，补偿前后相电压u、相电流i波形如图18所示。
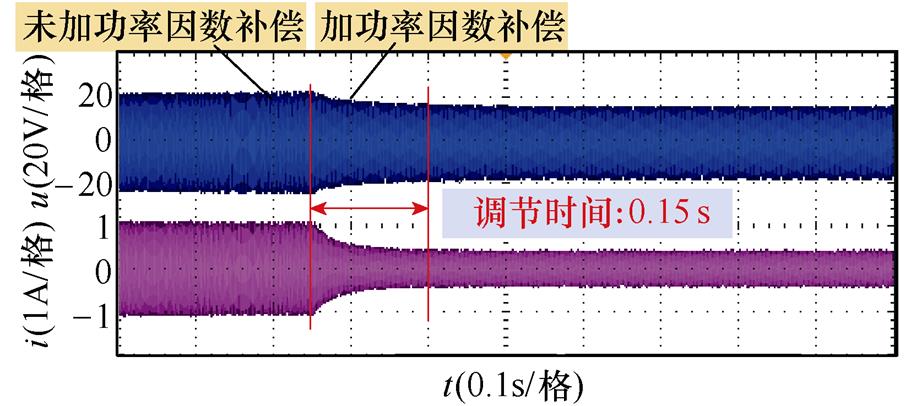
图17 3 000 r/min功率因数补偿切换过程波形
Fig.17 3 000 r/min power factor compensation switchingprocess waveforms
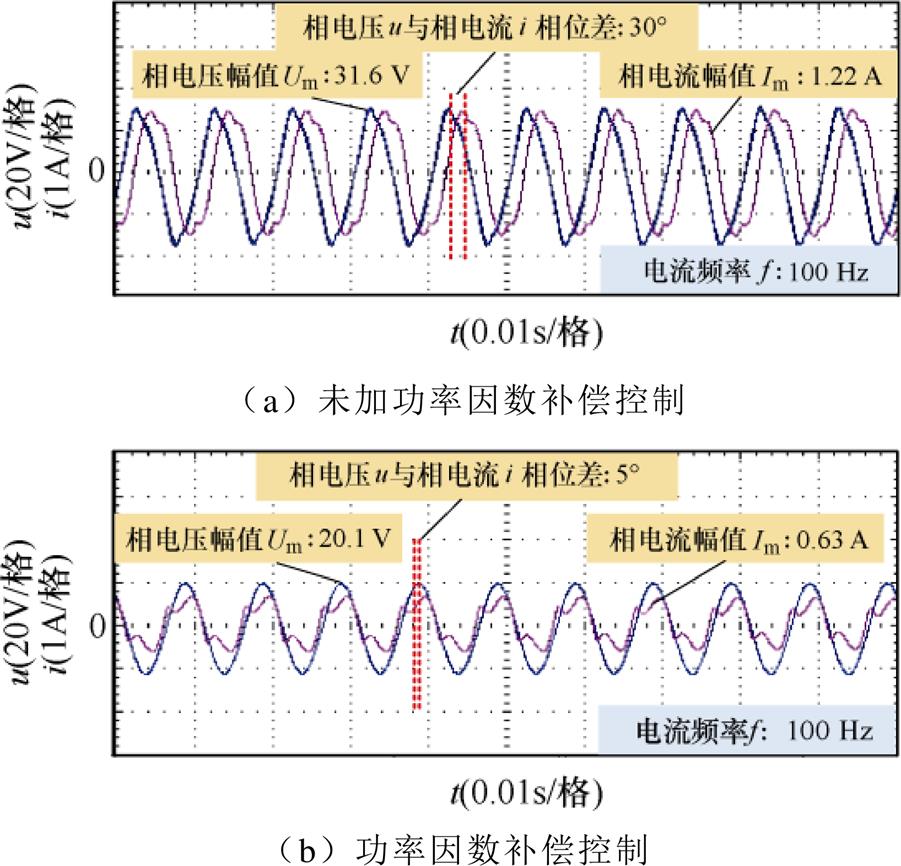
图18 功率因数补偿前后电压电流波形
Fig.18 Voltage and current waveforms before and afterpower factor compensation
稳态转速下加入功率因数补偿后，相电压幅值Um由31.6 V降低至20.1 V，相电流幅值Im由1.22 A降低至0.63 A，且u超前i的相位差由30°减小至5°。结合电机空间矢量图可得，加入功率因数补偿后，电机的反电动势矢量e与电流矢量I夹角降低至几乎为零，电流无功分量与相电流幅值降低，功率因数补偿控制可以有效降低电流的有效值和峰值，使电机运行于最大转矩/电流比状态，提高电机效率。
为验证调速范围下功率因数补偿对系统的影响，在升速斜率为500 r/min/s的升速过程中，对比了3 542 r/min转速区间功率因数补偿控制前后的直流母线电流idc及相电流i的波形，分别如图19和图20所示。
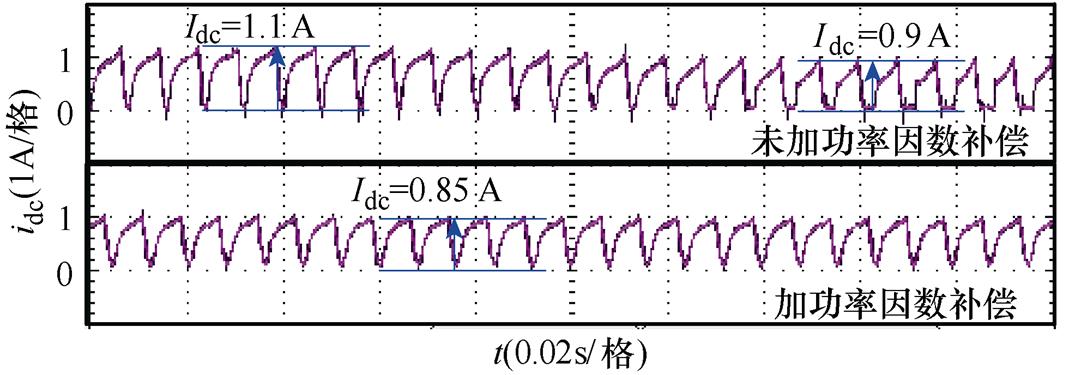
图19 调速范围功率因数补偿前后直流母线电流波形对比
Fig.19 Comparison of DC bus current waveforms before and after power factor compensation in speed regulation range
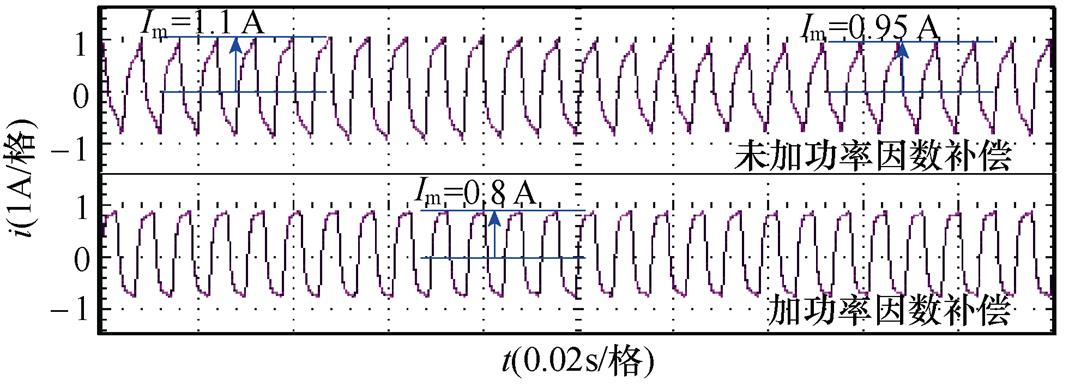
图20 调速范围功率因数补偿前后相电流波形对比
Fig.20 Comparison of phase current waveforms before and after power factor compensation in speed regulation range
图19中，Idc为母线电流幅值。在3 542 r/min转速区间内，未加功率因数补偿时，Idc在0.9～1.1 A范围内波动，相电流幅值Im在0.95～1.1 A范围内波动；加入功率因数补偿后，Idc稳定在0.85 A，Im稳定在0.8 A左右，电流幅值脉动均显著降低，表明加入功率因数补偿控制后，在转速为3 342～4 200 r/min的中高速区间内，系统阻尼增大、稳定性提升，电机具备更好的调速性能，验证了2.3节稳定性分析结果的正确性。
本文主要针对基于SPBLDC的高效全速域无位置控制策略进行研究与设计，提出单相I/f电流幅值与功率因数补偿控制相结合的控制方法，得到结论如下：
1）建立开环I/f电流幅值及I/f电流幅值加功率因数补偿控制的小信号模型，对稳态转速及动态调速范围系统进行全速域稳定性分析：①稳态转速下，功率因数补偿控制后闭环极点向复平面左侧偏移，提高系统在全速域的阻尼比，降低振荡，系统稳定裕度增大，稳定性显著提升。②动态调速范围下，在3 542 r/min的中高速转速区间内，功率因数补偿控制可以降低振荡，显著提升系统的稳定性；若升速斜率大于600 r/min/s，则接近额定转速时系统趋于不稳定，由此得到了合适的升速斜率区间。
2）仿真验证功率因数补偿控制在全速域稳态转速、动态调速范围内电流幅值、反电动势与电流相位差均显著降低：在升速阶段3 542 r/min相电流幅值由1.8 A降低至1.1 A，反电动势与电流相位差由60°降低至30°，在稳态阶段4 200 r/min相电流幅值由1.4 A降低至0.7 A，反电动势与电流相位差由35°降低至8°，电机运行效率提高，均接近工作于最大转矩/电流比状态。
3）实验验证在3000 r/min恒转速下加入功率因数补偿控制，相电流幅值由1.22 A降低至0.63 A，降低了49%，电机运行效率显著提升；升速斜率为500 r/min/s升速至3 542 r/min转速区间，功率因数补偿控制下母线电流及相电流幅值及振荡显著降低，稳定性提升。验证了控制策略的有效性及工程应用的可行性。
附 录
线性化系统矩阵的形式为
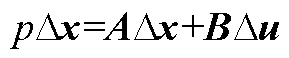
其中，I/f电流幅值控制的线性化系统矩阵的形式为
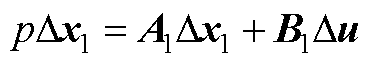
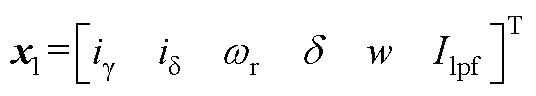
其中，状态矩阵A1为
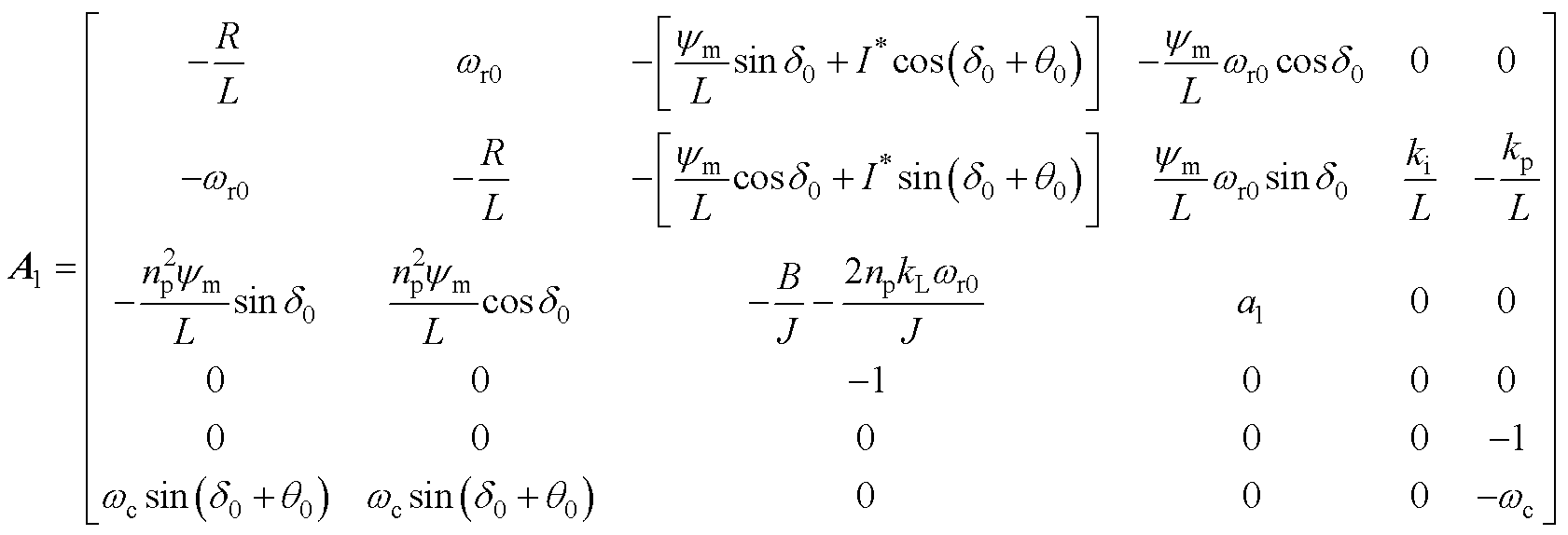
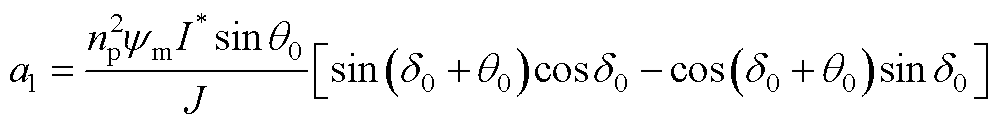
功率因数补偿控制的线性化系统矩阵的形式为
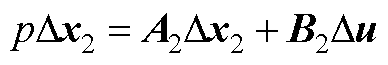
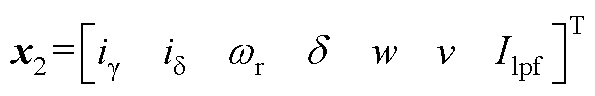
其中，状态矩阵A2为
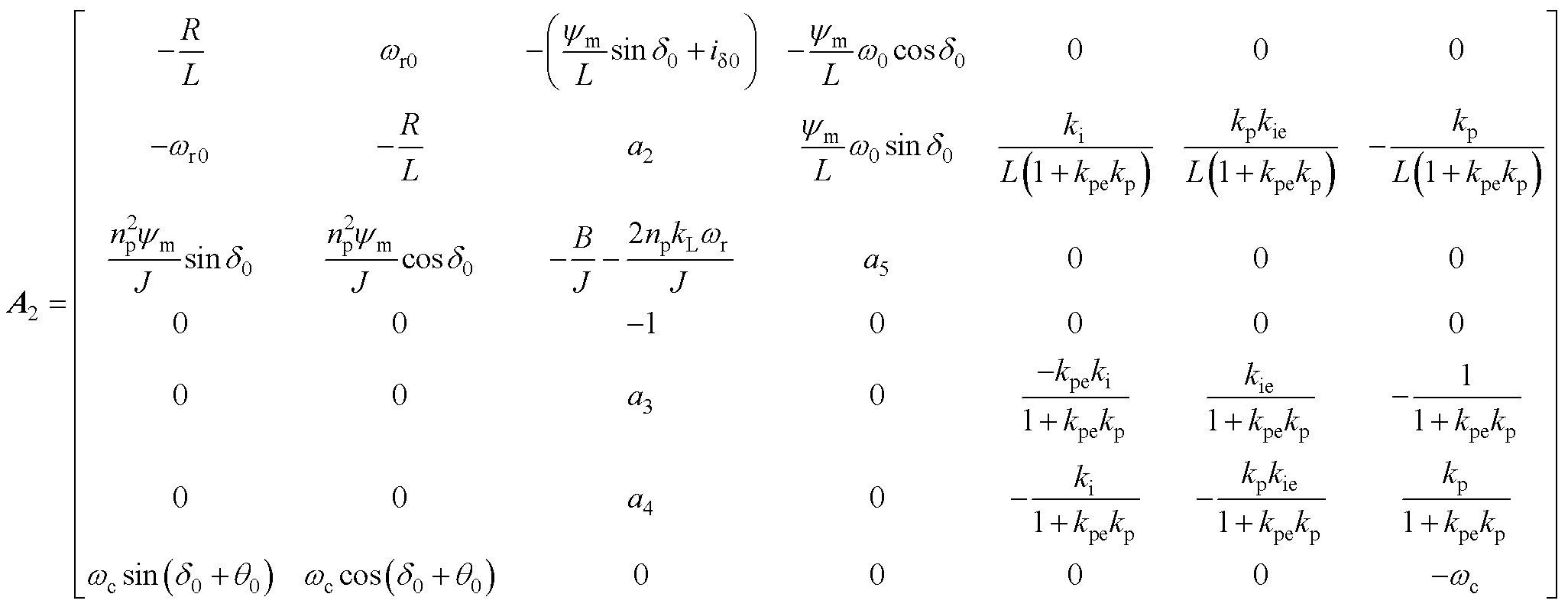
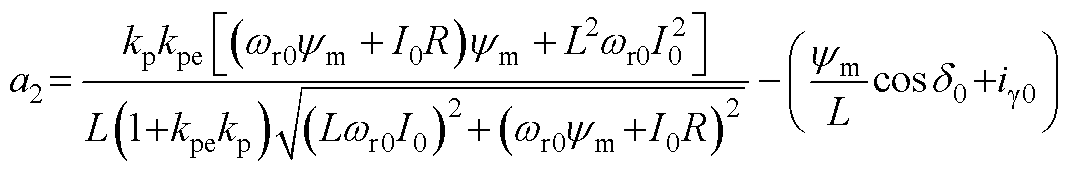
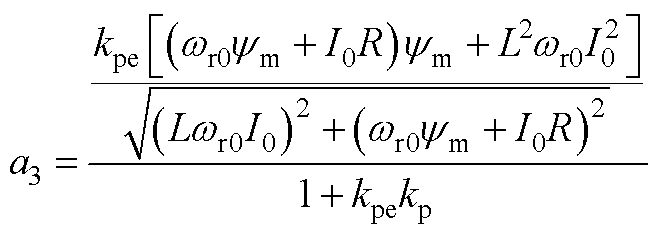
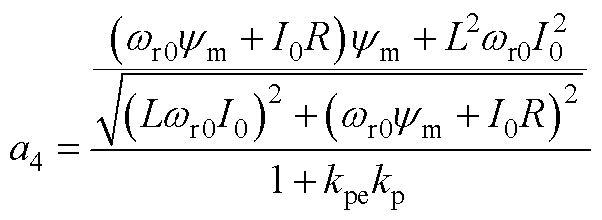
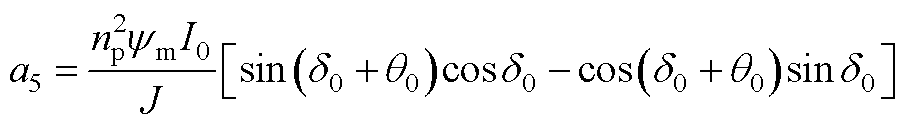
参考文献
[1] Kan Kaisheng, Tzou Y Y. A sensorless I/f control method for single-phase BLDC fan motors with efficiency optimization by power factor control[C]// Proceedings of The 7th International Power Elec- tronics and Motion Control Conference, Harbin, China, 2012: 2537-2541.
[2] Dunkl S, Muetze A, Schoener G. Design constraints of small single-phase permanent magnet brushless DC drives for fan applications[J]. IEEE Transactions on Industry Applications, 2015, 51(4): 3178-3186.
[3] Gruebler H, Leitner S, Muetze A, et al. Improved switching strategy for a single-phase brushless direct current fan drive and its impact on efficiency[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6050-6059.
[4] Sun Jiang, Chen Xiangdong, Wang Zhigang, et al. Current spike and efficiency optimization by using dynamic model of open-loop voltage mode single- phase BLDC cooling fan motor[C]//2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 2018: 1209-1214.
[5] Chen Weichao, Tzou Y Y. Efficiency optimization control for single-phase brushless DC fan motors[C]// 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 2009: 1913-1918.
[6] Lee W, Kim J H, Choi W, et al. Torque ripple minimization control technique of high-speed single- phase brushless DC motor for electric turbocharger[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10357-10365.
[7] Wu Lijian, Wu Zhigan, Jin Wanbing, et al. A novel magnetization failure detection method for 1-phase BLDC motor based on back-EMF test[C]//2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 2007: 2200-2204.
[8] 边春元, 邢海洋, 李晓霞, 等. 基于速度变化率的无位置传感器无刷直流电机风力发电系统换相误差补偿策略[J]. 电工技术学报, 2021, 36(11): 2374- 2382.
Bian Chunyuan, Xing Haiyang, Li Xiaoxia, et al. Compensation strategy for commutation error of sensorless brushless DC motor wind power generation system based on speed change rate[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2374- 2382.
[9] 梁伟. 单相无刷直流电机及其无位置传感器控制系统研究[D]. 杭州: 浙江大学, 2014.
[10] 陈兵兵. 单相无刷直流电机无位置传感器控制系统[D]. 杭州: 浙江理工大学, 2012.
[11] 周子馨. 单相无刷直流电机无传感器控制系统[D]. 杭州: 浙江大学, 2021.
[12] Xu Wei, Wang Lei, Liu Yi, et al. Improved rotor flux observer for sensorless control of PMSM with adaptive harmonic elimination and phase compen- sation[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 151-159.
[13] 付康壮, 刘计龙, 麦志勤, 等. 改进型IF控制结合有效磁链法的永磁同步电机全速域无位置传感器控制策略[J]. 电工技术学报, 2022, 37(22): 5704- 5716.
Fu Kangzhuang, Liu Jilong, Mai Zhiqin, et al. Sensorless control strategy of permanent magnet synchronous motor in full speed domain based on improved IF control and effective flux linkage method[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5704-5716.
[14] 候海波. 单相永磁无刷直流电机控制系统的研究[D]. 杭州: 浙江大学, 2017.
[15] Kang H D, Hwang S H. Starting method of high speed operation sinlge-phase BLDC motor based on virtual DQ current control[C]//2018 21st International Con- ference on Electrical Machines and Systems (ICEMS), Jeju, Korea (South), 2018: 1518-1521.
[16] Iepure L I, Boldea I, Blaabjerg F. Hybrid I-f starting and observer-based sensorless control of single-phase BLDC-PM motor drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(9): 3436-3444.
[17] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet syn- chronous motor based on adaptive notch filter online decoupling[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 344-354.
[18] 王菁, 颜建虎, 季国东, 等. 一种基于双位置观测器的永磁同步电机低速无位置传感器控制方法[J]. 电工技术学报, 2023, 38(2): 375-386.
Wang Jing, Yan Jianhu, Ji Guodong, et al. A low- speed sensorless control method of permanent magnet synchronous motor based on dual-position observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 375-386.
[19] 麦志勤, 刘计龙, 肖飞, 等. 基于估计位置反馈电流解调算法的改进型高频旋转电压注入无位置传感器控制策略[J]. 电工技术学报, 2022, 37(4): 870- 881, 891.
Mai Zhiqin, Liu Jilong, Xiao Fei, et al. Sensorless control strategy of improved HF rotating voltage injection based on estimated position feedback current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 870-881, 891.
[20] Sun Qingguo, Zhu Xiaolei, Niu Feng. Sensorless control of permanent magnet synchronous motor based on new sliding mode observer with single resistor current reconstruction[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(4): 378-383.
[21] Perera P D C, Blaabjerg F, Pedersen J K, et al. A sensorless, stable V/f control method for permanent- magnet synchronous motor drives[J]. IEEE Transa- ctions on Industry Applications, 2003, 39(3): 783- 791.
[22] Chen Weichao, Tzou Y Y. Current-mode sensorless control of single-phase brushless DC fan motors[C]// 2011 IEEE Ninth International Conference on Power Electronics and Drive Systems, Singapore, 2012: 659- 663.
[23] Wang Zihui, Lu Kaiyuan, Blaabjerg F. A simple startup strategy based on current regulation for back-EMF-based sensorless control of PMSM[J]. IEEE Transactions on Power Electronics, 2012, 27(8): 3817-3825.
[24] 王萌, 杨家强, 张翔, 等. 一种表贴式永磁同步电机电流矢量闭环I/f控制方法[J]. 中国电机工程学报, 2015, 35(10): 2513-2521.
Wang Meng, Yang Jiaqiang, Zhang Xiang, et al. An I/f control method with closed-loop regulation of current vector for surface permanent magnet syn- chronous motor drives[J]. Proceedings of the CSEE, 2015, 35(10): 2513-2521.
[25] 李槐树, 周羽, 曹晴, 等. 永磁同步电机开环控制系统稳定性的数学推导与分析[J]. 电工技术学报, 2014, 29(增刊1): 36-43.
Li Huaishu, Zhou Yu, Cao Qing, et al. Mathematical deduction and stability analysis of PMSM open-loop control system[J]. Transactions of China Electro- technical Society, 2014, 29(S1): 36-43.
[26] 雷金莉, 窦满峰, 李延升. 带风机类负载的无刷直流电机控制系统建模与仿真[J]. 微电机, 2009, 42(8): 57-60.
Lei Jinli, Dou Manfeng, Li Yansheng. Modeling and simulation of BLDCM control system with fans load[J]. Micromotors, 2009, 42(8): 57-60.
Abstract This study focuses on the single-phase brushless DC motor (SPBLDC). The small DC fan has some problems, such as the complex installation of position sensors, low reliability under high & low temperatures, and low operating efficiency. Therefore, this paper proposes a control strategy based on power factor compensation based on the traditional I/f current amplitude control. By controlling the back electromotive force (EMF) and the current vector of SPBLDC in the same direction, the SPBLDC can operate at the optimal power factor state, thereby improving the operating efficiency and stability of the system.
The methods of this paper are as follows. In the single-phase motor H-bridge inverter topology, the voltage and current of the single-phase winding under vector control are approximately sinusoidal functions. The back EMF of the single-phase motor is a rotating space vector. In order to reflect and analyze the phase and amplitude relationship of single-phase winding voltage, current and back EMF in the rotating coordinate system more intuitively and realize the high-precision and high-performance vector control. The space rotation coordinate system of the single-phase motor is then constructed. The single-phase winding voltage and current are equivalent to the space vector.
According to the three different phase relations between the current and the back EMF, a power factor compensation control strategy is proposed based on the traditional I/f current amplitude control. Assume that the voltage amplitude of the inverter when the motor operates at the optimal power factor is the ideal voltage amplitude. To make the back electromotive force and current converge in the same direction, the ideal voltage amplitude is subtracted from the instantaneous output voltage of the inverter. Afterward, the given current amplitude is adjusted through a PI controller to reduce the current amplitude and allow the motor to operate at the maximum torque/current ratio.
Based on the spatial rotation coordinate system, the small signal model of SPBLDC is constructed. According to the small-signal root locus analysis method, the full-speed stability analysis of single-phase I/f current amplitude control and power factor compensation control methods is carried out. The closed-loop pole positions of the system before and after the power factor compensation control are compared. After adding the power factor compensation control, the closed-loop poles in the middle and high-speed sections shift significantly to the left. The real part expands about 9 times, while the imaginary part is almost unchanged. The system has a greater damping ratio and stability margin. The stability of the system under different ramp rates is analyzed, and the appropriate ramp rates in practical engineering applications are selected.
The experimental results show that the phase voltage amplitude decreases by 36%, the phase current amplitude decreases by 49%, and the phase difference between voltage and current decreases from 30° to 5° at the steady speed of 3 000 r/min with power factor compensation.
According to the motor space vector diagram, the back EMF vector and the current vector are almost in phase, with an angle close to zero degree. The current reactive component and the phase current amplitude are reduced, indicating that the power factor compensation control can make the motor close to the maximum torque/current ratio state. Accordingly, the motor operation efficiency is improved. The pulsation and oscillation of DC bus current and phase current amplitude are significantly reduced under the power factor compensation control when the speed is increased to 3 542r/min at the theoretically designed ramp. This reduction in pulsation and oscillation indicates that the damping of the system is increased, and the stability is improved.
Theoretical analysis and experimental results show that the system can achieve low current oscillation and low-speed pulsation under steady state and dynamic speed regulation process using the sensorless control strategy of single-phase I/f control combined with power factor compensation. The motor operates efficiently at the optimal power factor state in the full speed range and has good dynamic and steady performance, making it highly valuable for engineering applications.
keywords：Single-phase brushless DC motor, sensorless control, single-phase I/f current amplitude control, power factor compensation, small signal analysis
DOI: 10.19595/j.cnki.1000-6753.tces.221655
中图分类号：TM351
国家自然科学基金（52077100）和航空科学资金（201958052001）资助项目。
收稿日期 2022-08-30
改稿日期 2022-10-13
郝振洋 男，1981年生，教授，0究生，研究方向为永磁无刷直流电机驱动控制。E-mail: 1843548705@qq.com（通信作者）
（编辑 崔文静）