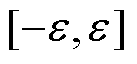 区域内的光滑函数。当变量向区域边界
区域内的光滑函数。当变量向区域边界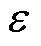 接近时,其输出值随之增大;当变量向零接近时,其输出值向零趋近。此功能可以实现“切换控制”的约束。
接近时,其输出值随之增大;当变量向零接近时,其输出值向零趋近。此功能可以实现“切换控制”的约束。摘要 针对永磁直线同步电机的位置跟踪性能易受负载扰动、动子质量变化等不确定性的影响,提出一种基于半正定屏障函数的自适应分数阶终端滑模控制策略。首先,采用分数阶终端滑模控制方法来抑制不确定性对系统的影响,保证了跟踪误差在有限时间收敛,且能够有效地减小系统稳态误差。然后,为了进一步改善系统鲁棒跟踪性能,设计基于半正定屏障函数的自适应控制对不确定扰动的上界进行估计,避免了控制增益的过高估计且削弱了系统抖振。此外,该自适应策略在不需要外界扰动先验信息的情况下,可以使得系统误差收敛到一个预定的零邻域内。最后,实验结果表明,该策略提高了系统的跟踪精度,对负载扰动和附加有效载荷具有较强鲁棒性。
关键词:永磁直线同步电机 自适应分数阶终端滑模控制 半正定屏障函数 鲁棒性
随着电力电子技术的进步和稀土永磁材料的发展,永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)受到极大重视。因其具有高响应、高刚度、高精度等优点,在机器人、光刻机和高精密数控机床等各类场合具有重要应用价值[1-3]。由于省去了机械传动环节,负载扰动、动子质量变化等不确定因素会严重影响PMLSM的位置跟踪性能[4-5]。为此,如何克服不确定因素影响,获得高品质的跟踪性能是亟待解决的关键问题。
近年来,滑模控制(Sliding Mode Control, SMC)因响应速度快、对外部扰动具有很强的鲁棒性,在PMLSM伺服系统中得到了广泛的应用[6]。但是SMC仅用于不确定性有界的情况。如果切换项增益值选取过大,系统可能会发生严重的抖振现象。若不确定扰动突然增加,滑模控制也可能因选取的切换增益值过小而失去抑制扰动的功能,此时将无法保证系统的跟踪性能。因此,为了削弱抖振,文献[7-8]采用了边界层技术,减小了系统抖振,但跟踪误差只能收敛到边界层内,降低了系统的鲁棒性。文献[9]中,针对快速刀具直线伺服系统的跟踪问题,设计了一种模糊自适应滑模控制策略,将模糊自适应控制方法引入滑模控制算法设计中,去除了对扰动不确定性上界信息的先验要求,且通过仿真证明了理论分析的可靠性,但文中缺少实验证明。在文献[10]中,设计了一种基于径向基函数神经网络自适应的永磁直线电机的超扭曲滑模控制算法,采用径向基函数神经网络对系统扰动进行观测估计,实验验证了系统的鲁棒性能和稳态性能。但神经网络结构复杂,且在线训练会对系统动态性能造成影响。文献[11]提出了一种快速非奇异终端滑模控制策略,该策略由于取消开关项而产生的连续输入保证了直线电机运动控制系统“弱抖振”。但是,由于不确定性因素的存在,跟踪精度下降,且滑模收敛区域的大小仍然取决于系统不确定扰动的上界。为了进一步减小稳态误差,一些学者提出在滑模动态面中引入整数阶积分项,并成功应用于直线电机控制领域。而近些年由于计算机技术高速发展,分数阶微积分算子的近似方法不断改进,分数阶滑模控制技术成为当前研究热点。尽管分数阶滑模控制技术在PMLSM控制领域应用罕见,但在旋转电机[12]、四旋翼飞行器[13]等其他领域得到广泛应用。其中,文献[14]提出了分数阶积分型终端滑模控制策略,将传统整数阶终端滑模面扩展为分数维空间的分数阶积分型终端滑模面,即滑模面增加了一个额外的控制参数。实验结果证明了分数阶系统的优越性,但是同快速非奇异终端滑模控制一样,控制器的设计仍然依赖系统扰动的上界信息。文献[15]介绍了半正定屏障函数,是一个定义在零附近的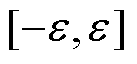 区域内的光滑函数。当变量向区域边界
区域内的光滑函数。当变量向区域边界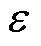 接近时,其输出值随之增大;当变量向零接近时,其输出值向零趋近。此功能可以实现“切换控制”的约束。
接近时,其输出值随之增大;当变量向零接近时,其输出值向零趋近。此功能可以实现“切换控制”的约束。
通过以上分析,整数阶滑模在PMLSM控制领域得到广泛应用,且分数阶滑模控制技术的优越性也在控制领域得到验证。但对于强耦合、多变量直线电机系统,滑模控制器的设计最主要问题就是过度依赖扰动上界。因此,本文为了改善易受动子质量变化、负载扰动等不确定性影响的PMLSM系统的鲁棒跟踪性能,提出一种基于半正定屏障函数的自适应分数阶终端滑模控制(Adaptive Fractional- order Terminal Sliding Mode Control based on Positive Semi-definite Barrier-function, PSB-AFTSMC)策略。该控制策略在抑制不确定因素影响的同时保证了跟踪误差在有限时间内收敛,提高了系统的跟踪性能。在系统不确定上界未知的情况下,自适应滑模控制律对不确定扰动的上界进行实时估计,提高了系统的鲁棒性,保证系统误差在有限时间内收敛到一个预定的零邻域。最后,实验验证了本文所提控制策略的可行性。
永磁体基波励磁磁场轴线为d轴,其逆时针旋转90°为q轴,忽略电机初级绕组和永磁体阻尼作用,不考虑磁路饱和、铁心损耗等因素的影响,则PMLSM电气和机械运动方程表示[16]为
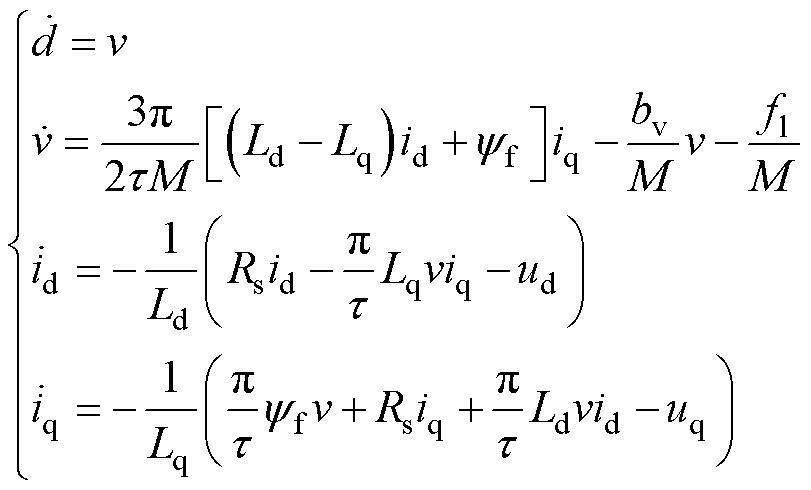 (1)
(1)
式中,d为动子所在位置;ud, uq、id, iq分别为d、q轴动子电压、电流;v为运动速度;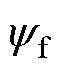 为定子永磁体磁链;
为定子永磁体磁链;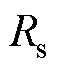 为定子电阻;Ld、Lq为定子d、q轴电感;
为定子电阻;Ld、Lq为定子d、q轴电感;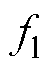 为系统外部扰动、非线性摩擦力等;M为PMLSM的动子及所带负载的总质量;
为系统外部扰动、非线性摩擦力等;M为PMLSM的动子及所带负载的总质量;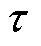 为极距;bv为粘滞摩擦系数。为保证稳态时d轴动子电流不影响q轴动子电流,根据磁场定向原理,式(1)改写为
为极距;bv为粘滞摩擦系数。为保证稳态时d轴动子电流不影响q轴动子电流,根据磁场定向原理,式(1)改写为
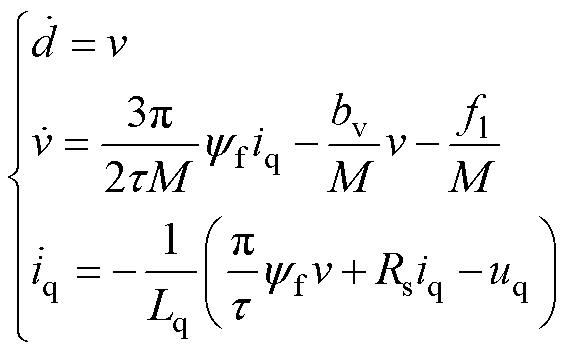 (2)
(2)
在实际的运动系统中,标称参数与实际值将会存在偏差。因此,考虑系统参数变化,式(2)中动态方程改写为
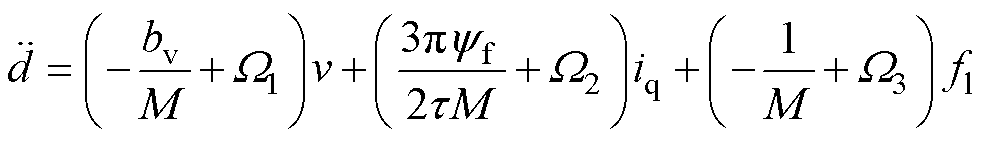
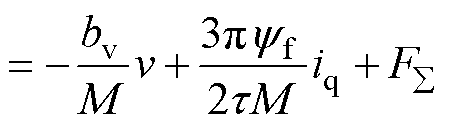 (3)
(3)
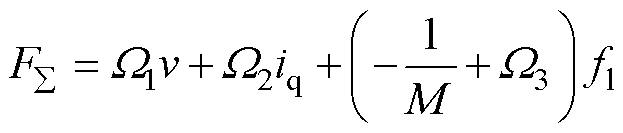 (4)
(4)
式中, 、
、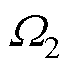 和
和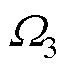 为系统参数的不确定性;
为系统参数的不确定性;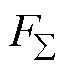 表示系统总不确定性,且假设
表示系统总不确定性,且假设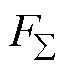 有界,即
有界,即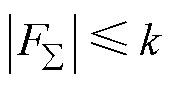 ,
,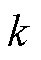 为一正常数,是系统总不确定性的上界,同时作为分数阶终端滑模控制器的控制增益。
为一正常数,是系统总不确定性的上界,同时作为分数阶终端滑模控制器的控制增益。
由于PMLSM伺服系统易受负载扰动、动子质量变化等不确定性的影响,则需要控制器必须具有强鲁棒性。因此,提出了一种PSB-AFTSMC方法来提高系统的鲁棒跟踪性能。该方法可以更好地克服系统不确定性,提高位置跟踪性能与鲁棒性能,使得系统误差在有限时间内收敛到一个预定的零邻域。最后,采用Lyapunov理论证明了系统的稳定性。基于PSB-AFTSMC的系统框图如图1所示。
位置跟踪误差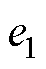 为
为
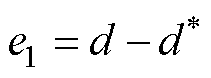 (5)
(5)
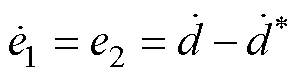 (6)
(6)
式中,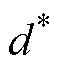 为参考轨迹;e2为跟踪误差的一阶导数。下面对滑模面和控制律进行设计,则分数阶终端滑模面S定义为
为参考轨迹;e2为跟踪误差的一阶导数。下面对滑模面和控制律进行设计,则分数阶终端滑模面S定义为
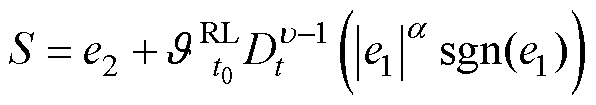 (7)
(7)
式中,u 为分数阶参数,0<u<1;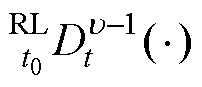 为分数阶积分算子,具体定义详见附录第1节;
为分数阶积分算子,具体定义详见附录第1节;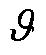 为分数阶项增益,
为分数阶项增益,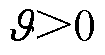 ;a 为幂次,0<a<1;
;a 为幂次,0<a<1;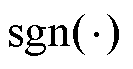 为符号函数。则对S求导,并将式(3)代入得
为符号函数。则对S求导,并将式(3)代入得
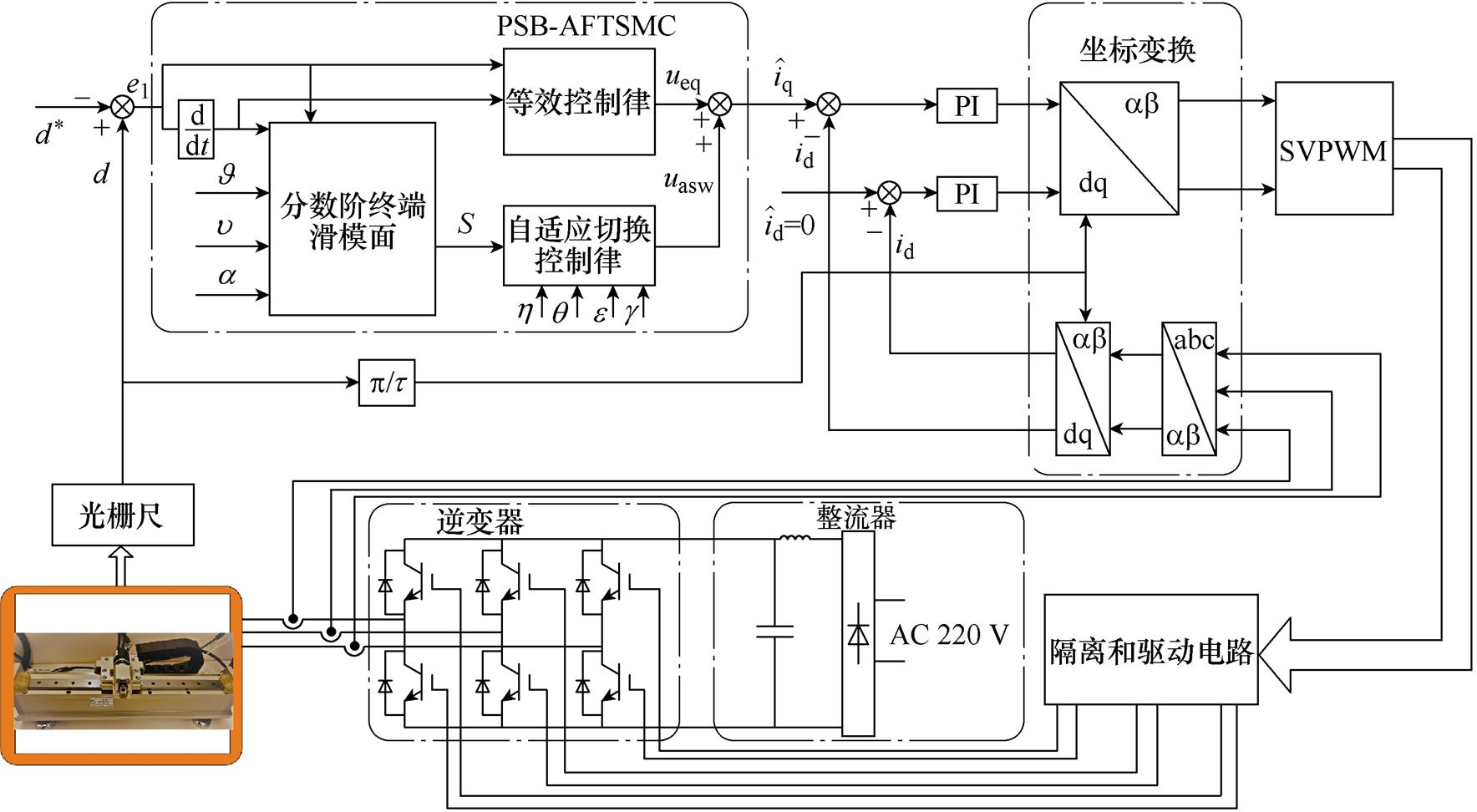
图1 基于PSB-AFTSMC的系统框图
Fig.1 Block diagram of the system based on PSB-AFTSMC
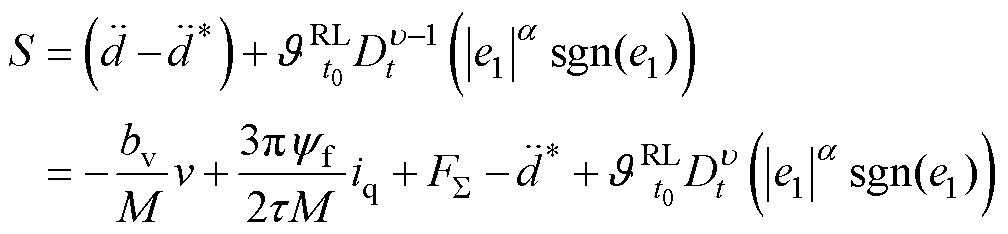 (8)
(8)
在忽略集总不确定性的情况下,令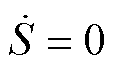 得等效控制律为
得等效控制律为
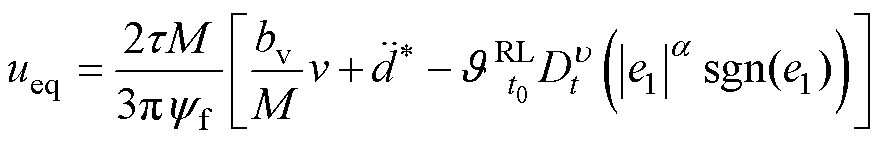 (9)
(9)
切换控制律为
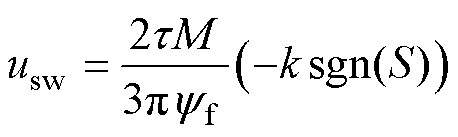 (10)
(10)
式中,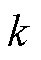 为切换控制增益。
为切换控制增益。
定义1:假设存在零附近的很小正常数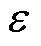 ,半正定屏障函数定义为一个连续的偶函数KPSB(x):
,半正定屏障函数定义为一个连续的偶函数KPSB(x):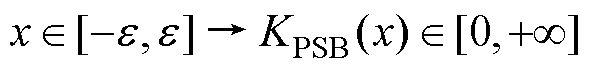 ,在区间
,在区间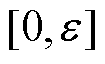 内严格单调递增[15]。
内严格单调递增[15]。
(1)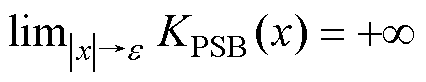 。
。
(2)在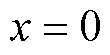 时,KPSB(x)为最小值。
时,KPSB(x)为最小值。
(3)半正定屏障函数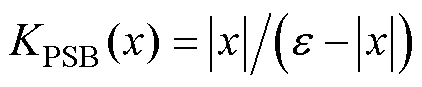 ,KPSB(0)=0。
,KPSB(0)=0。
在实际应用中,系统不确定性的未知上界是很难获得的。则在系统不确定上界未知的情况下,自适应切换控制律设计为
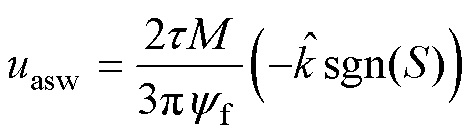 (11)
(11)
其中,自适应切换控制增益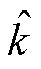 为
为
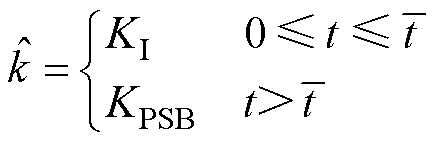 (12)
(12)
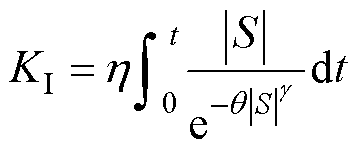 (13)
(13)
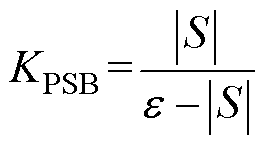 (14)
(14)
式中,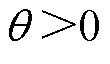 ,
,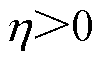 ,
,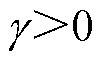 且初始值
且初始值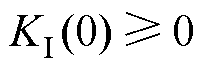 ;
;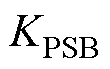 为半正定屏障函数。当
为半正定屏障函数。当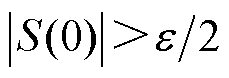 时,选择切换控制增益
时,选择切换控制增益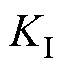 ,使得
,使得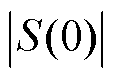 第一次到达
第一次到达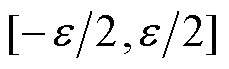 区域内,记录时间为
区域内,记录时间为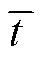 。否则,
。否则,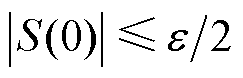 ,
,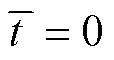 。当
。当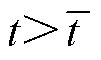 时,选择自适应切换增益KPSB。则PSB-AFTSMC控制律设计为
时,选择自适应切换增益KPSB。则PSB-AFTSMC控制律设计为
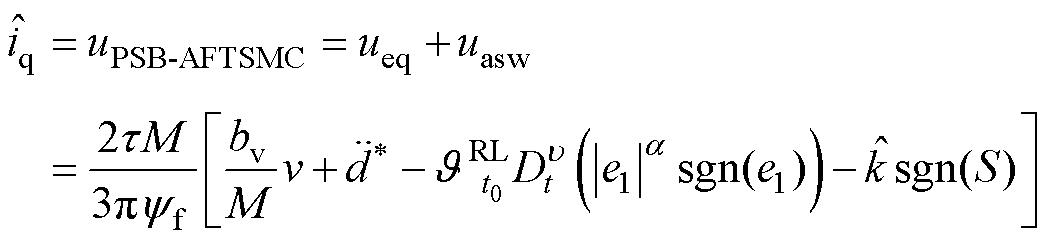 (15)
(15)
推论1:式(13)中的指数项可以获得快速收敛速率,使得滑动模态S在较短时间内快速收敛到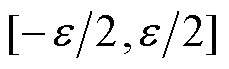 区域,且当S距离原点较远时,收敛效果更佳[17]。
区域,且当S距离原点较远时,收敛效果更佳[17]。
推论2:图2为基于半正定屏障函数自适应律(即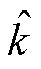 相对于
相对于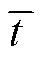 时刻后的S的变化曲线)。可以看出,当系统不确定扰动存在,致使滑模面S在[-e, e]区域内的值增加时,自适应切换增益
时刻后的S的变化曲线)。可以看出,当系统不确定扰动存在,致使滑模面S在[-e, e]区域内的值增加时,自适应切换增益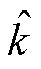 将显著增加,直到
将显著增加,直到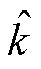 增加到可以抵消系统不确定性,将S迅速拉回原点。另一方面,S逐渐减小到0的过程中,
增加到可以抵消系统不确定性,将S迅速拉回原点。另一方面,S逐渐减小到0的过程中,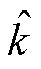 值也会相应减少,直到达到可以抵消系统不确定,此过程避免了控制输入的过饱和,并可以使系统滑动变量最终收敛到指定区域
值也会相应减少,直到达到可以抵消系统不确定,此过程避免了控制输入的过饱和,并可以使系统滑动变量最终收敛到指定区域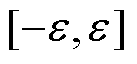 内。
内。
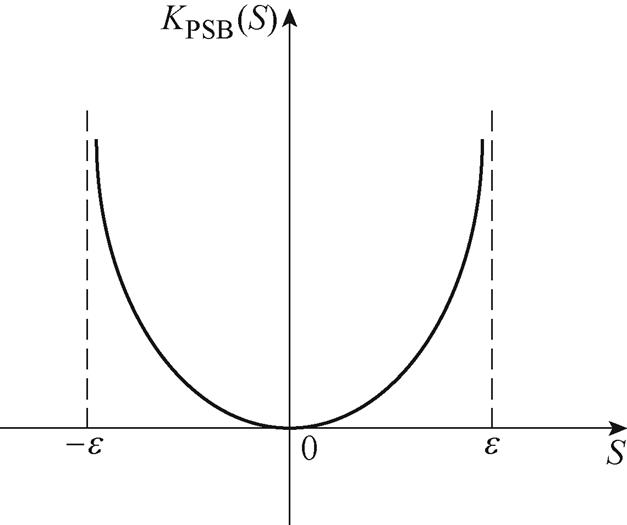
图2 基于半正定屏障函数的自适应律
Fig.2 Adaptive law based on positive semi-definite barrier function
引理1:针对PMLSM非线性系统式(3),滑模面式(7),在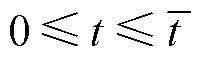 的时间段,PSB-AFTSMC的切换增益采用式(13),则PSB-AFTSMC的自适应切换增益
的时间段,PSB-AFTSMC的切换增益采用式(13),则PSB-AFTSMC的自适应切换增益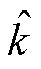 存在一个正常数上界
存在一个正常数上界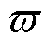 ,满足
,满足
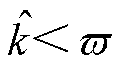 (16)
(16)
引理1的证明过程详见附录第2节。
(1)在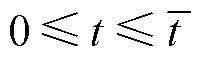 时间段时,自适应切换增益为
时间段时,自适应切换增益为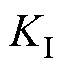 。选择一个Lyapunov函数
。选择一个Lyapunov函数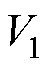 为
为
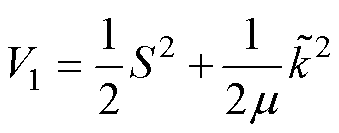 (17)
(17)
式中,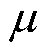 为一正常数,在稳定性证明中起到辅助作用;
为一正常数,在稳定性证明中起到辅助作用;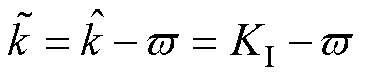 。则对
。则对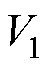 求导,可得
求导,可得
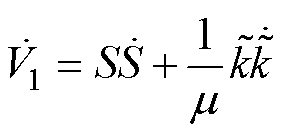 (18)
(18)
结合式(8)和式(15),可得
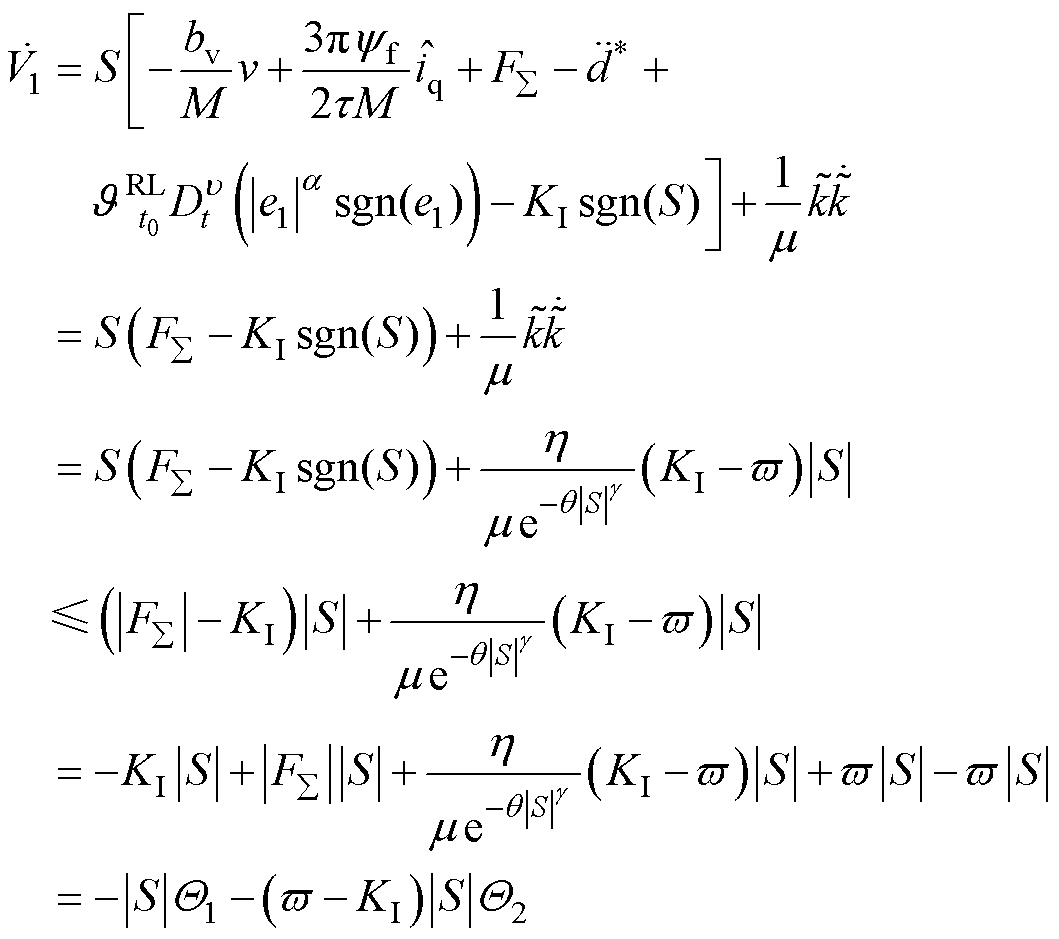 (19)
(19)
其中
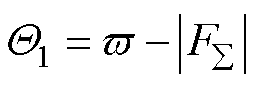
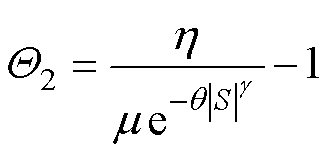
根据引理1可得,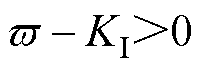 ,
,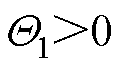 ;由于总是存在一个正常数
;由于总是存在一个正常数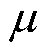 使得
使得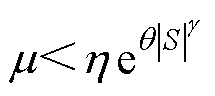 ,即
,即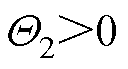 。因此,
。因此,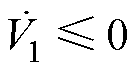 。由Lyapunov稳定性定理可知,在不确定性存在的情况下,系统状态能够收敛到滑模面附近,最终到达
。由Lyapunov稳定性定理可知,在不确定性存在的情况下,系统状态能够收敛到滑模面附近,最终到达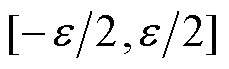 区域。
区域。
(2)在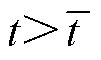 时间段时,自适应切换增益为KPSB。
时间段时,自适应切换增益为KPSB。
首先,引入一个辅助变量: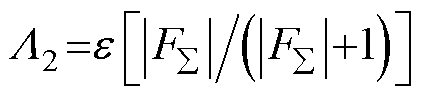 。从
。从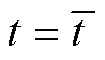 开始,自适应控制律可以保证在有限时间
开始,自适应控制律可以保证在有限时间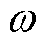 内使得
内使得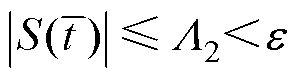 。如果
。如果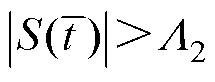 ,则
,则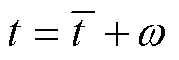 ;否则,对于
;否则,对于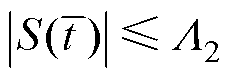 ,
,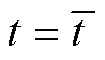 。假设
。假设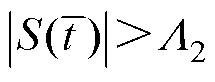 ,选择Lyapunov函数
,选择Lyapunov函数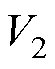 为
为
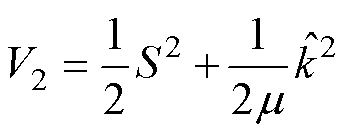 (20)
(20)
结合式(8)和式(15),并对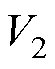 进行求导可得
进行求导可得
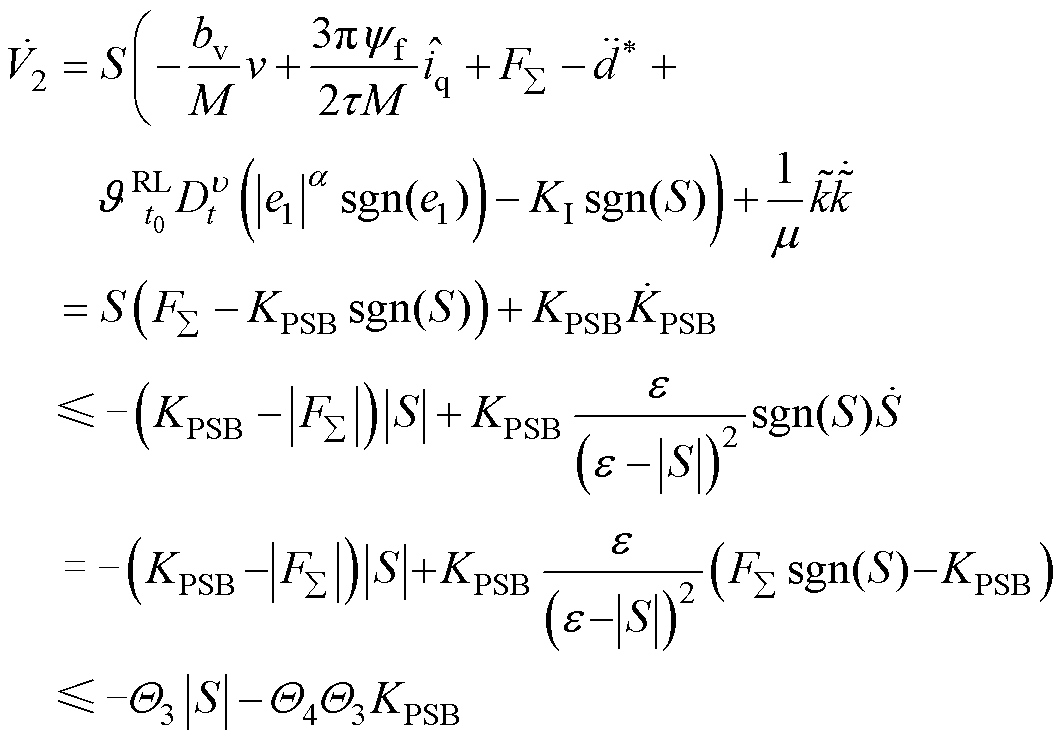 (21)
(21)
其中
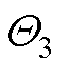 =
=
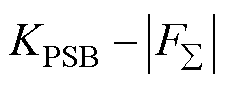
 =
=
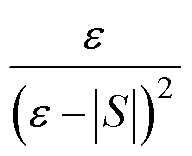
式中,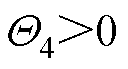 ;根据半正定屏障函数的性质可得
;根据半正定屏障函数的性质可得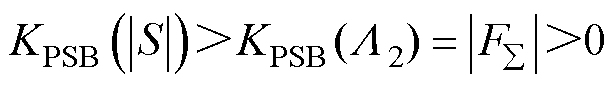 ,所以
,所以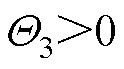 。因此,当自适应切换控制增益
。因此,当自适应切换控制增益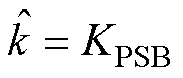 时,本文中提出的控制策略可以确保系统有限时间稳定,并且对于所有的
时,本文中提出的控制策略可以确保系统有限时间稳定,并且对于所有的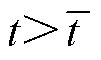 ,滑动变量收敛到指定的零邻域
,滑动变量收敛到指定的零邻域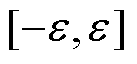 内。
内。
图3为基于cSPACE的PMLSM实验测试平台。实验装置包括PMLSM(额定推力30 N)、cSPACE控制平台、带有Matlab/Simulink的计算机、直线电机驱动器、位移光栅传感器(精度1 mm)等。在Simulink中搭建设计的控制算法,将输入输出接口替换为cSPACE模块,编译整个模块自动生成DSP代码,在控制卡上运行后生成相应的控制信号。运行过程中通过cSPACE提供的Matlab接口模块,可实时修改控制参数。其中,PMLSM的主要参数: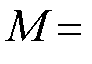
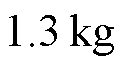 ,
,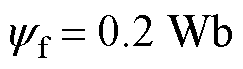 ,
,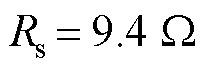 ,
,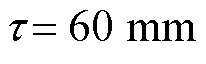 ,
,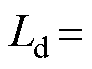
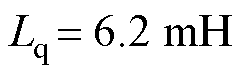 。最后,下载保存变量数据到硬盘,并利用Origin软件处理数据,完成图像化显示。
。最后,下载保存变量数据到硬盘,并利用Origin软件处理数据,完成图像化显示。

图3 PMLSM实验平台
Fig.3 Experimental platform of PMLSM
首先,利用Matlab仿真软件分析不同阶次下分数阶滑模面的动态。通过选取不同的阶次(0.2, 0.5, 0.8)来分析分数阶滑模面解的轨迹为
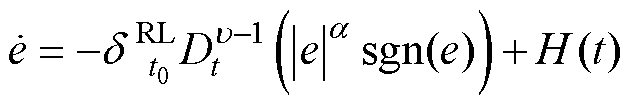 (22)
(22)
式中,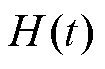 为扰动,且存在上界。
为扰动,且存在上界。
从图4的分数阶终端滑模面动态性能对比可以发现,不同阶次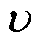 值都能够保证系统的稳定,当
值都能够保证系统的稳定,当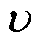 =0.2时,由于系统的解受扰动的影响,振动幅值较大,且相较于其他阶次超调值最大;当
=0.2时,由于系统的解受扰动的影响,振动幅值较大,且相较于其他阶次超调值最大;当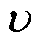 =0.8时,振幅较大,但系统稳定到期望值附近的过程中超调很小;而
=0.8时,振幅较大,但系统稳定到期望值附近的过程中超调很小;而 =0.5时,振动幅值最小。可以得出结论,由于扰动的存在而导致系统出现稳态误差时,阶次越小,其超调越大,但0.5阶次抑制稳态误差的性能最强。因此,综合考虑系统动态和稳态性能,实验部分选择
=0.5时,振动幅值最小。可以得出结论,由于扰动的存在而导致系统出现稳态误差时,阶次越小,其超调越大,但0.5阶次抑制稳态误差的性能最强。因此,综合考虑系统动态和稳态性能,实验部分选择 =0.5来验证系统的跟踪性能。
=0.5来验证系统的跟踪性能。
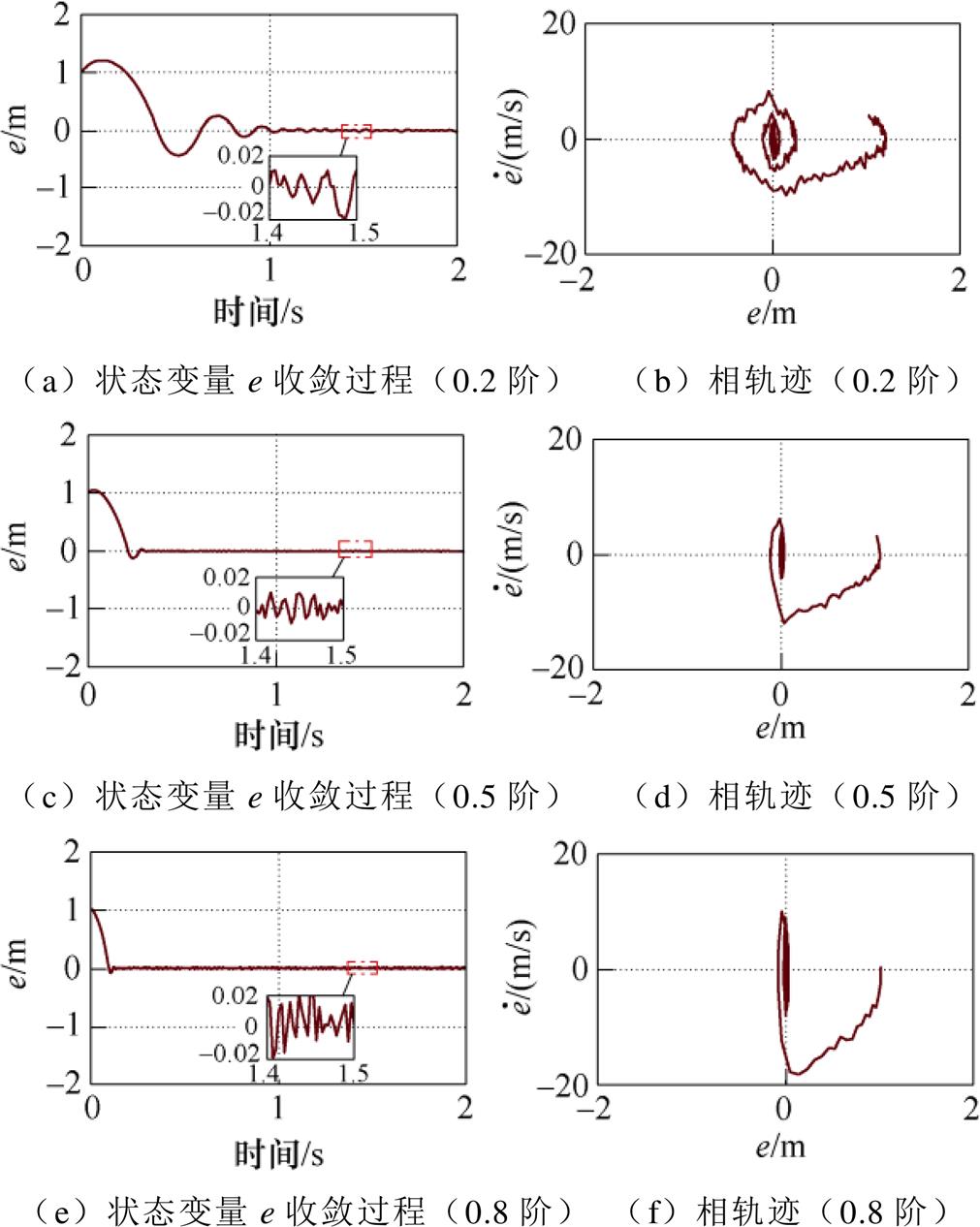
图4 分数阶终端滑模面动态性能对比
Fig.4 Dynamic performance comparison of fractional order terminal sliding mode surface
为了验证所提出控制方法的优越性以及有效性,将分数阶终端滑模控制(FTSMC)方法[14]与本文提出的基于半正定屏障函数的自适应分数阶终端滑模控制(PSB-AFTSMC)方法在直线电机运动平台上依次进行两组位置跟踪对比实验(Case 1,Case 2)。此外,额外进行一组(Case 3)实验来确定不同分数阶参数 对控制系统的影响,此组实验仅改变分数阶阶次,其他条件不变。经过多次重复实验调试参数,系统处于最佳的运行状态。PSB- AFTSMC策略的参数:
对控制系统的影响,此组实验仅改变分数阶阶次,其他条件不变。经过多次重复实验调试参数,系统处于最佳的运行状态。PSB- AFTSMC策略的参数: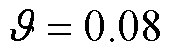 ,
,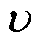 =0.5,a=0.5,
=0.5,a=0.5,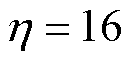 ,
,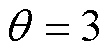 ,
,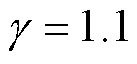 ;
;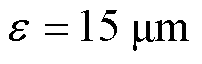 。
。
Case 1为在标称状态条件和附加有效载荷条件下跟踪给定参考信号。Case 2为在变化负载扰动条件下跟踪给定参考信号。Case 3为在不同阶次条件下跟踪给定参考信号。
Case 1:在标称状态条件下,FTSMC和PSB- AFTSMC两种方法下的位置跟踪曲线如图5所示。从图5可以看出,这两种控制方法均可以使电机动子跟踪给定参考信号,但PSB-AFTSMC跟踪曲线的偏差较小,而FTSMC跟踪曲线与给定位置信号的偏差较大。该结果表明PSB-AFTSMC方法具有更好的跟踪性能。
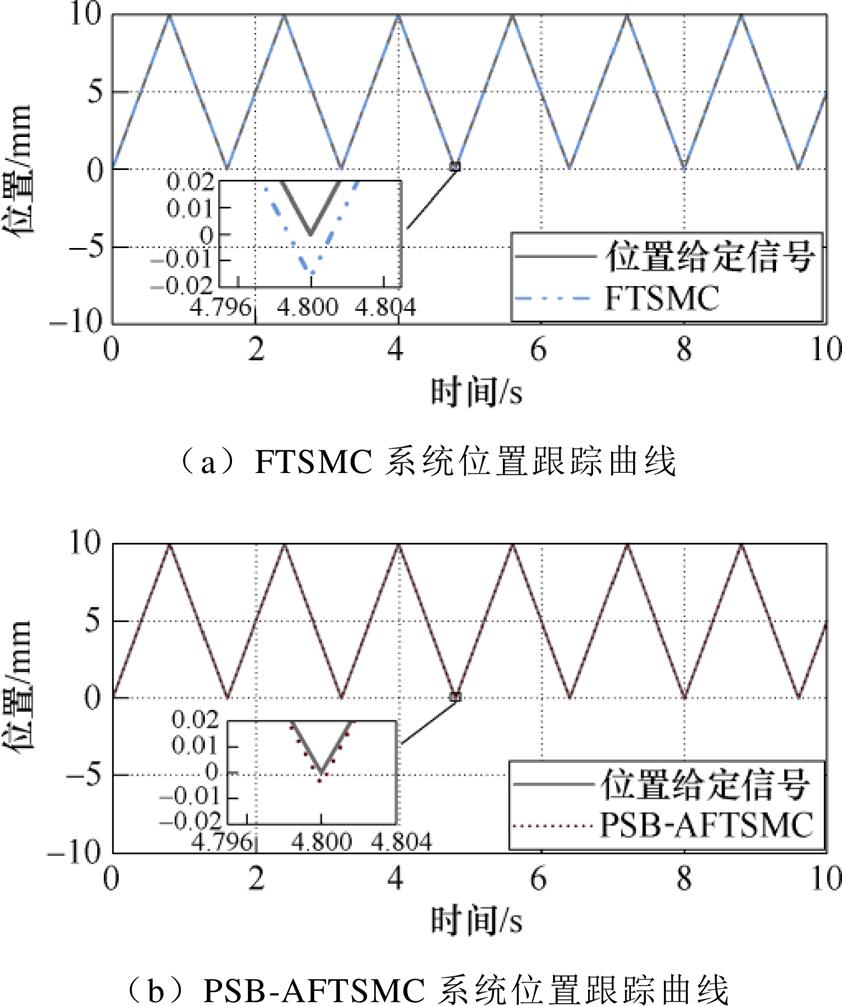
图5 位置跟踪曲线(标称条件)
Fig.5 Position tracking curve (nominal condition)
为了研究动子质量变化对PMLSM系统的影响,在直线电机平台上安装2 kg有效载荷,且测试的过程中不改变其他控制参数以及实验条件。图6、图7分别为附加有效载荷条件下的FTSMC和PSB- AFTSMC跟踪误差曲线。其中,图6a和图7a分别为附加0 kg条件下的FTSMC和PSB-AFTSMC跟踪误差曲线,也就是标称状态下的跟踪误差曲线。而对比图6a和图6b看出,附加2 kg有效载荷的FTSMC方法的稳态误差曲线波动频率和幅值均明显大于附加0 kg条件下的稳态误差曲线。对比图7a和图7b可以看出,尽管附加2 kg有效载荷的PSB-AFTSMC方法的稳态误差曲线波动频率大于附加0 kg条件下的稳态误差曲线波动频率,但误差曲线的波动幅值变化不大。且相较于FTSMC方法,PSB-AFTSMC方法具有更小的跟踪误差,跟踪误差大小减小了60%左右。这表明PSB-AFTSMC方法对于附加有效载荷的影响具有更好的抑制效果。
此外,为了定量比较FTSMC方法与PSB- AFTSMC方法的跟踪性能,定义了三项位置误差性能指标[18-19],分别为最大误差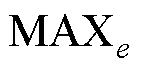 、绝对平均误差
、绝对平均误差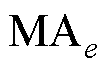 、方均根误差
、方均根误差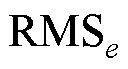 ,有
,有
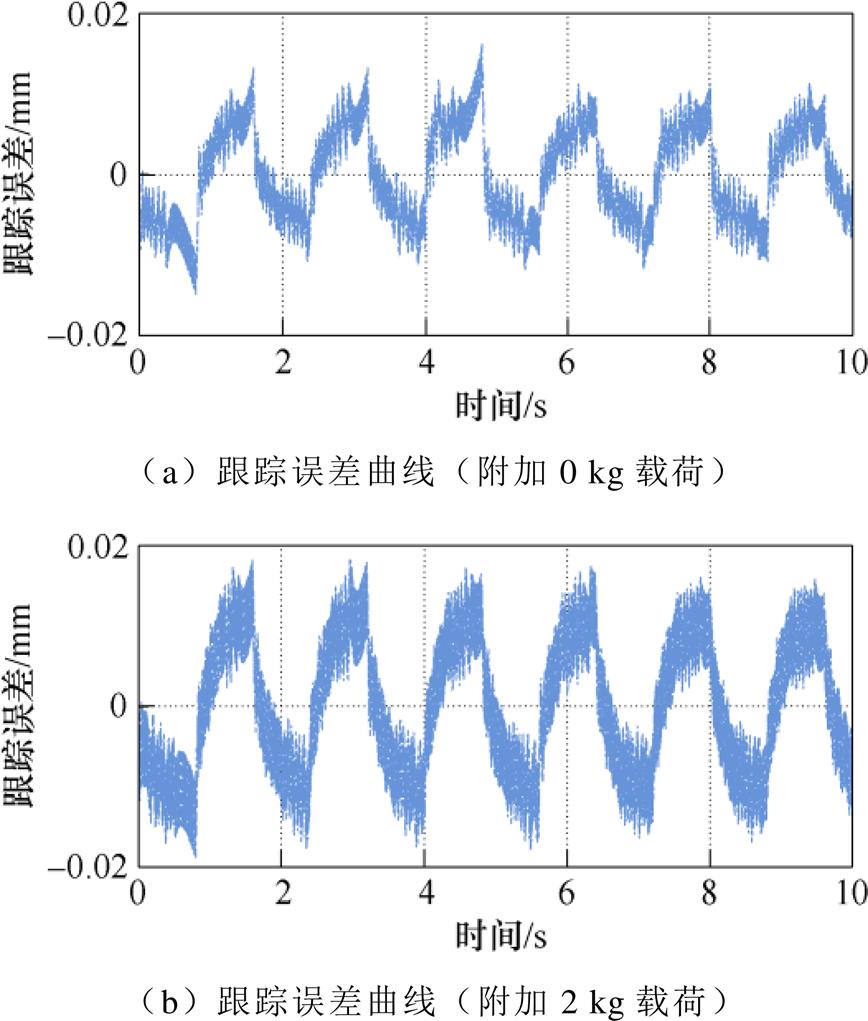
图6 FTSMC系统跟踪误差(附加载荷)
Fig.6 FTSMC system tracking error (additional load)
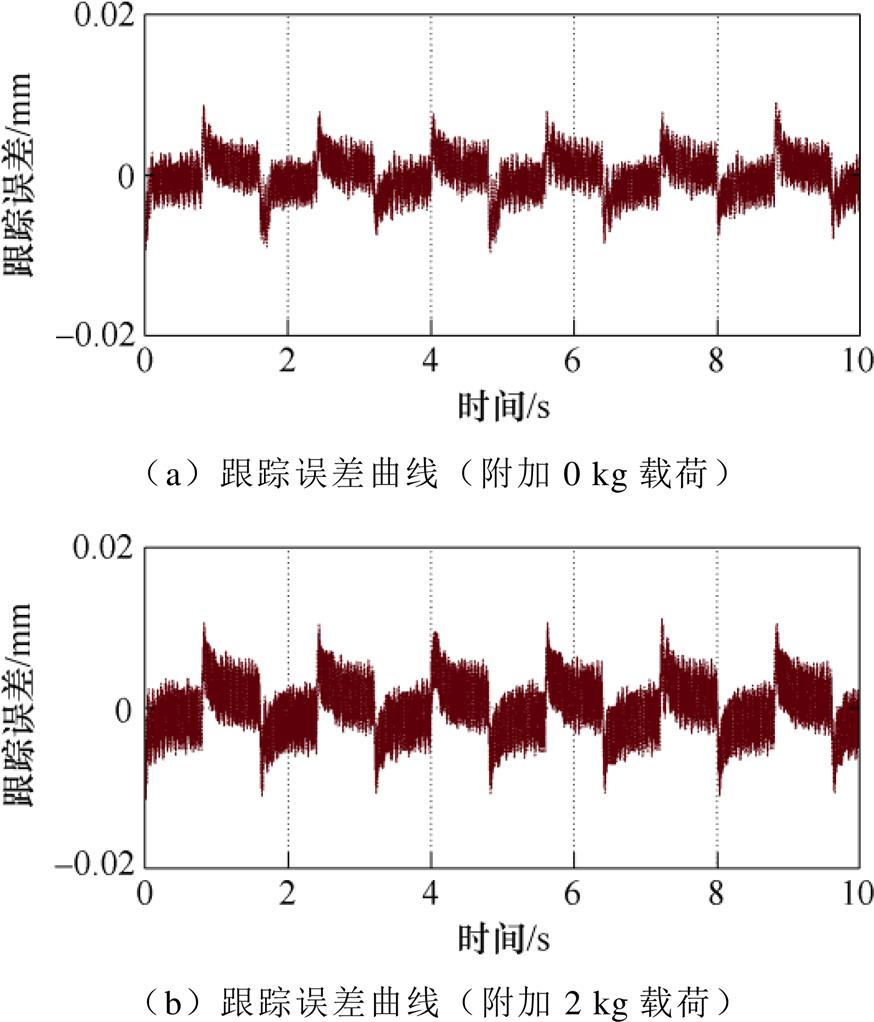
图7 PSB-AFTSMC系统跟踪误差(附加载荷)
Fig.7 PSB-AFTSMC system tracking error (additional load)
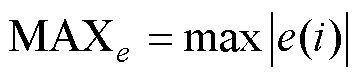 (23)
(23)
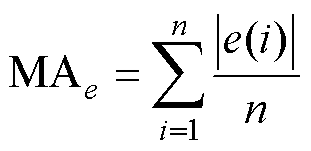 (24)
(24)
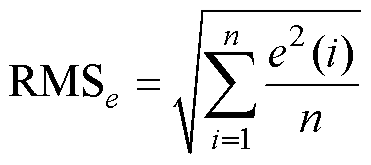 (25)
(25)
式中,n为位置误差信号序列长度。位置误差的详细数据见表1。从表1可以看出,PSB-AFTSMC方法的性能指标均优于FTSMC方法。
表1 稳态性能的比较
Tab.1 The comparison of steady-state performance (单位: mm)

控制策略MAXeMAeRMSe FTSMC(0 kg/2 kg)16.16/18.805.23/7.876.12/9.30 PSB-AFTSMC(0 kg/2 kg)9.75/11.062.66/3.723.16/4.37
Case 2:在1 s时向PMLSM系统突加变负载扰动,其在1~3 s、3~6 s和6~10 s的值大小约为额定推力的15%、30%和15%,具体如图8所示。两种控制方法下的系统跟踪误差曲线如图9所示。在变负载扰动条件下,两种控制方法均出现了明显波动,但PSB-AFTSMC方法到达稳态时间较短,约0.1 s,跟踪误差曲线的波动幅值也较小,仍保持在15 mm以内。而FTSMC方法的跟踪误差曲线波动幅值较大,尤其3~6 s时间段,大幅度波动两次,最大幅值达到40 mm左右,且到达稳态时间较长,约0.4 s。详细的性能指标见表2。本组实验证明了PSB-AFTSMC系统可以很好地克服负载扰动变化的影响,使系统具有较强鲁棒性,保证了位置跟踪性能。这是由于PSB-AFTSMC方法在不需要扰动上界信息的情况下,可以有效地使切换控制自适应幅值变化的扰动,而FTSMC方法依赖扰动幅值的上界,如果扰动大小超过设定的上界,系统的鲁棒性降低,甚至系统的控制性能将会恶化。
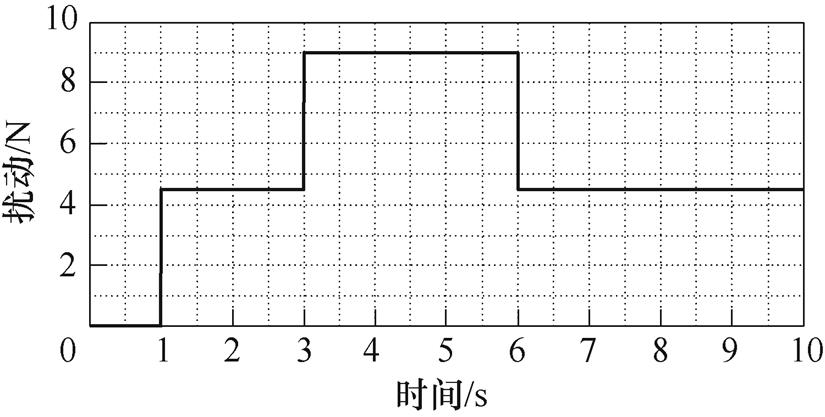
图8 变负载扰动
Fig.8 Variable load disturbance
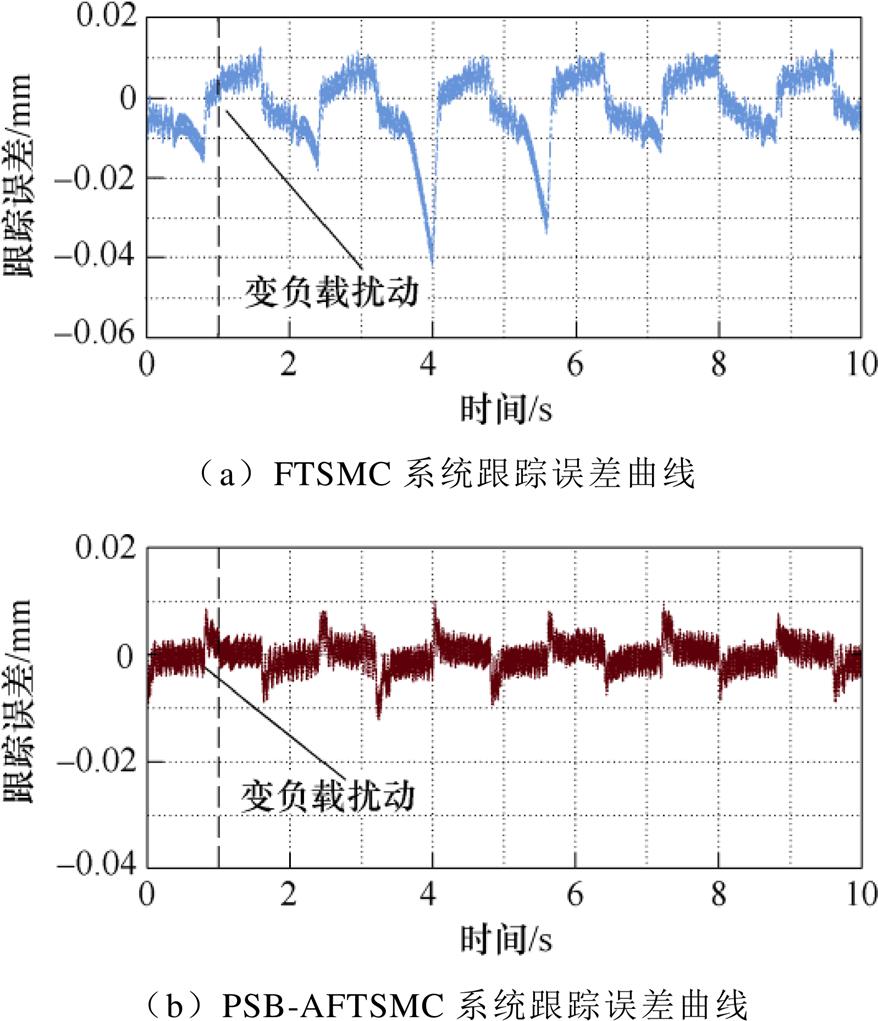
图9 系统跟踪误差(存在扰动)
Fig.9 System tracking error (presence of disturbance)
表2 突加负载扰动下稳态性能的比较
Tab.2 Comparison of steady-state performance under sudden load disturbance (单位: mm)
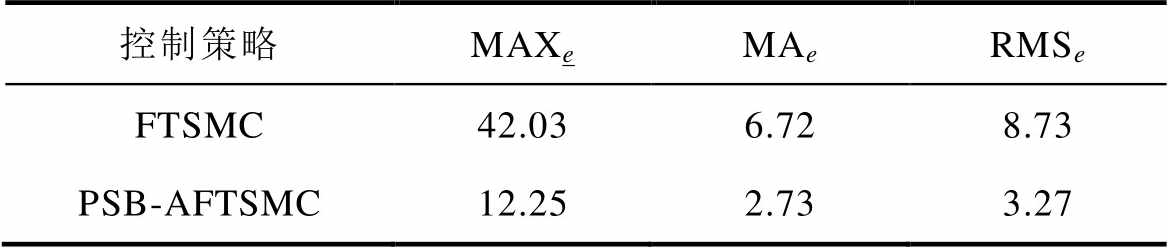
控制策略MAXeMAeRMSe FTSMC42.036.728.73 PSB-AFTSMC12.252.733.27
Case 3:此组实验只改变分数阶阶次,不改变其他控制参数以及实验条件。则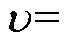 0.2, 0.5, 0.8时的系统位置跟踪误差如图10所示。当
0.2, 0.5, 0.8时的系统位置跟踪误差如图10所示。当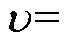 0.2时,跟踪误差曲线在系统响应初期的时刻,其响应时间太慢,跟踪误差波动幅值也较大,最大幅值达到30 mm左右。当
0.2时,跟踪误差曲线在系统响应初期的时刻,其响应时间太慢,跟踪误差波动幅值也较大,最大幅值达到30 mm左右。当 0.8时,跟踪误差的波动幅值大幅度增加,尤其在速度方向变化的时刻,跟踪误差明显增大。这是由于一些不确定性集中体现在速度方向变化的过程中,而0.8阶次的分数阶系统对不确定扰动的抑制能力较差,使得该时刻的跟踪性能下降,甚至实验结果已经无法保证高精度跟踪要求。当
0.8时,跟踪误差的波动幅值大幅度增加,尤其在速度方向变化的时刻,跟踪误差明显增大。这是由于一些不确定性集中体现在速度方向变化的过程中,而0.8阶次的分数阶系统对不确定扰动的抑制能力较差,使得该时刻的跟踪性能下降,甚至实验结果已经无法保证高精度跟踪要求。当 0.5时,跟踪误差的波动幅值最小,且在速度变化时刻跟踪误差仍保持在10 mm以内。该实验现象与仿真中的分析结果基本一致。因此,为了保证整个直线电机伺服系统的跟踪精度,并且响应速度快,本实验分数阶参数适宜在0.5附近进行选择。
0.5时,跟踪误差的波动幅值最小,且在速度变化时刻跟踪误差仍保持在10 mm以内。该实验现象与仿真中的分析结果基本一致。因此,为了保证整个直线电机伺服系统的跟踪精度,并且响应速度快,本实验分数阶参数适宜在0.5附近进行选择。
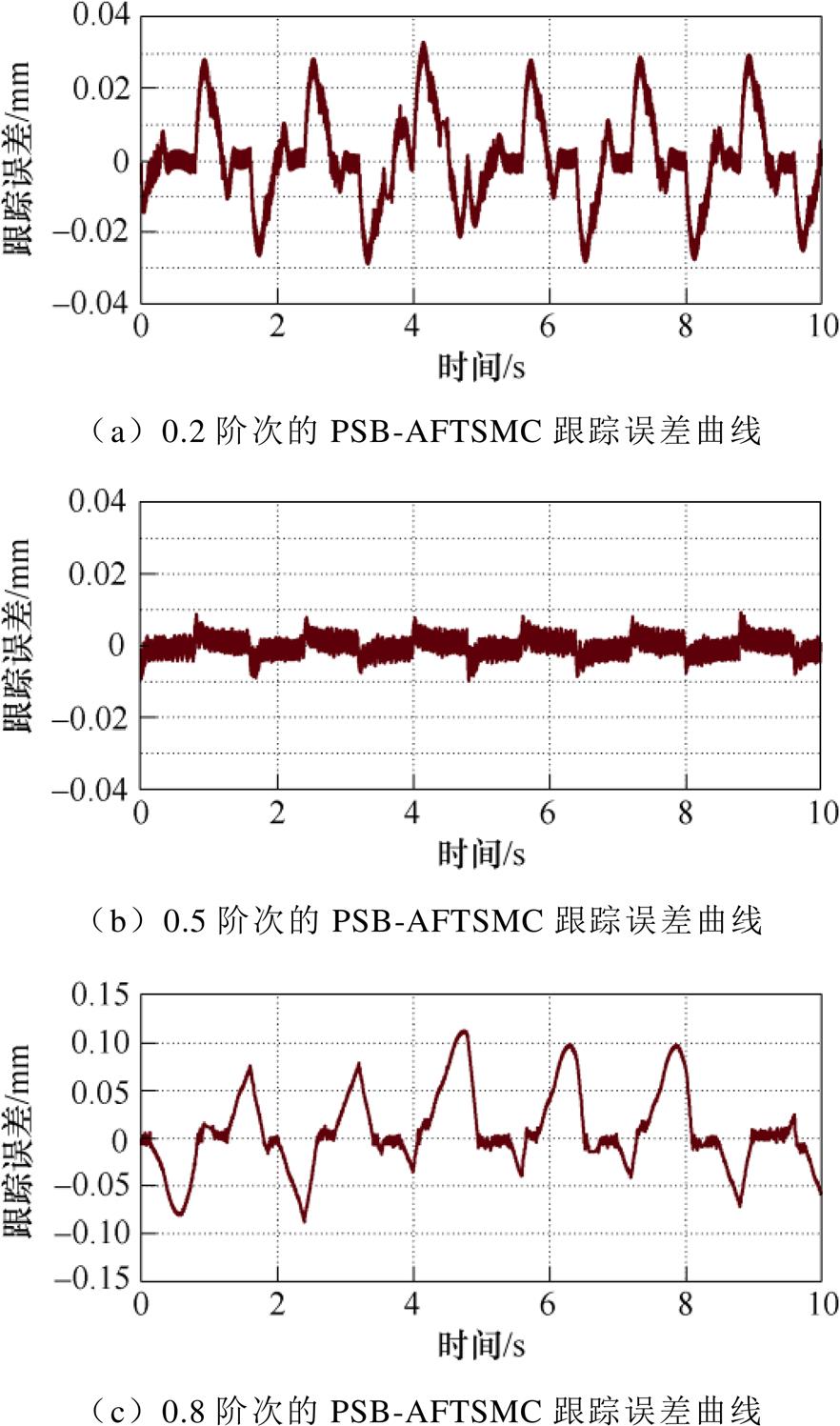
图10 系统跟踪误差(不同阶次)
Fig.10 System tracking error (different order)
1)针对不确定因素影响下的永磁直线同步电机运动平台,基于PSB-AFTSMC系统具有较强的鲁棒性,跟踪性能较好,精度保持在15 mm以内,且不同阶次下的控制系统的跟踪性能存在较大差异,0.5阶次附近的分数阶滑模控制系统具有更好的稳态性能。此外,与传统的控制方法相比,PSB- AFTSMC方法具有更高跟踪精度,更强的鲁棒性。
2)用半正定屏障函数对控制输入幅值进行自适应调整,解决了滑模控制依赖系统扰动上界信息的问题,更适合于实际应用。
附 录
1. 在实际控制工程中,已有三种类型的分数阶微积分算子被应用,分别为Riemann-Liouville(RL)型、Caputo型和Grunwald-Letnikov型。其中,RL型的应用较为广泛,定义[20]为
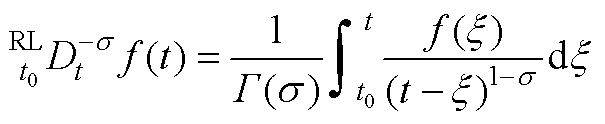 (A1)
(A1)
式中,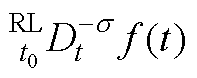 为分数阶积分算子,其中
为分数阶积分算子,其中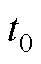 、
、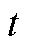 为算子上、下限;
为算子上、下限;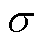 为其阶次,
为其阶次,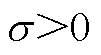 ;
;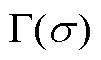 为Gamma函数,其表达式为
为Gamma函数,其表达式为
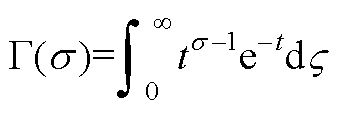 (A2)
(A2)
分数阶的积分运算相比于整数阶的积分运算,增加了额外的自由度。因此,对函数f(t)=t进行分数阶积分运算,附图1结果说明了不同阶次分数阶积分运算的结果存在一定差异。
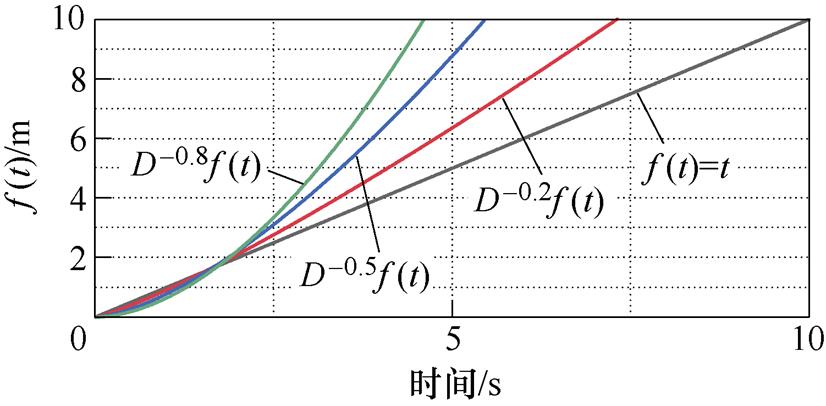
附图1 函数f(t)的分数阶积分运算结果
App.Fig.1 The results of fractional order integrals of the function f(t)
2. 假设滑模面初始值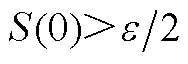 。首先,根据式(13),由于存在
。首先,根据式(13),由于存在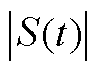 的积分项,
的积分项,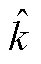 将持续增加,直到满足
将持续增加,直到满足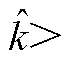
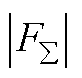 ,此时的时间记为
,此时的时间记为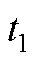 。则从
。则从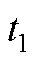 开始,
开始,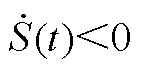 且
且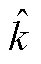 继续增加,直到满足
继续增加,直到满足 。当
。当 时,此时的
时,此时的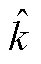 由
由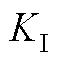 状态切换为
状态切换为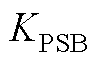 状态,并取得趋近过程中的最大值
状态,并取得趋近过程中的最大值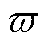 ,且时间记为
,且时间记为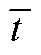 。因此,在
。因此,在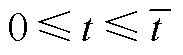 时间内,
时间内,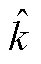 总是存在一个正常数上界
总是存在一个正常数上界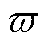 ,满足
,满足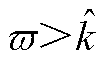 ,
,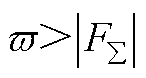 。类比推理,对于
。类比推理,对于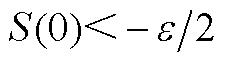 情况,有类似动态过程。
情况,有类似动态过程。
引理1得证。
参考文献
[1] 沈燚明, 卢琴芬. 初级励磁型永磁直线电机研究现状与展望[J]. 电工技术学报, 2021, 36(11): 2325- 2343.
Shen Yiming, Lu Qinfen. Overview of permanent magnet linear machines with primary excitation[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2325-2343.
[2] 李雄松, 崔鹤松, 胡纯福, 等. 平板型永磁直线同步电机推力特性的优化设计[J]. 电工技术学报, 2021, 36(5): 916-923.
Li Xiongsong, Cui Hesong, Hu Chunfu, et al. Optimal design of thrust characteristics of flat-type permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 916-923.
[3] 李争, 安金峰, 肖宇, 等. 基于自适应观测器的永磁同步直线电机模型预测控制系统设计[J]. 电工技术学报, 2021, 36(6): 1190-1200.
Li Zheng, An Jinfeng, Xiao Yu, et al. Design of model predictive control system for permanent magnet synchronous linear motor based on adaptive observer[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1190-1200.
[4] 方馨, 王丽梅, 张康. H型平台直驱伺服系统离散积分滑模平滑控制[J]. 电机与控制学报, 2022, 26(6): 101-111.
Fang Xin, Wang Limei, Zhang Kang. Discrete integral sliding mode smoothing control of H-type platform direct drive servo system[J]. Electric Machines and Control, 2022, 26(6): 101-111.
[5] 苏光靖, 李红梅, 李争, 等. 永磁同步直线电机无模型电流控制[J]. 电工技术学报, 2021, 36(15): 3182-3190.
Su Guangjing, Li Hongmei, Li Zheng, et al. Research on model-free current control of permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3182-3190.
[6] 张月玲, 党选举. 基于死区迟滞函数的永磁同步直线电机滑模控制[J]. 中国电机工程学报, 2011, 31(3): 67-74.
Zhang Yueling, Dang Xuanju. Sliding mode control based on dead-zone hysteresis function for PMLSM[J]. Proceedings of the CSEE, 2011, 31(3): 67-74.
[7] Gandikota G, Das D K. Disturbance observer-based adaptive boundary layer sliding mode controller for a type of nonlinear multiple-input multiple-output system[J]. International Journal of Robust and Nonlinear Control, 2019, 29(17): 5886-5912.
[8] 赵希梅, 赵久威. 精密直驱龙门系统的交叉耦合互补滑模控制[J]. 电工技术学报, 2015, 30(11): 7-12.
Zhao Ximei, Zhao Jiuwei. Cross-coupled comple- mentary sliding mode control for precision direct- drive gantry system[J]. Transactions of China Elec- trotechnical Society, 2015, 30(11): 7-12.
[9] 刘春芳, 杜昭童. 快速刀具伺服系统的模糊自适应滑模控制[J]. 沈阳工业大学学报, 2015, 37(2): 126- 131.
Liu Chunfang, Du Zhaotong. Fuzzy adaptive sliding mode control of fast tool servo system[J]. Journal of Shenyang University of Technology, 2015, 37(2): 126-131.
[10] 许德智, 黄泊珉, 杨玮林. 神经网络自适应的永磁直线同步电机超扭曲终端滑模控制[J]. 电力系统保护与控制, 2021, 49(13): 64-71.
Xu Dezhi, Huang Bomin, Yang Weilin. Neural net- work adaptive super twist terminal sliding mode control for a permanent magnet linear synchronous motor[J]. Power System Protection and Control, 2021, 49(13): 64-71.
[11] Zheng Jinchuan, Wang Hai, Man Zhihong, et al. Robust motion control of a linear motor positioner using fast nonsingular terminal sliding mode[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(4): 1743-1752.
[12] 熊林云, 王杰. 永磁同步电机电能质量分数阶滑模控制[J]. 中国电机工程学报, 2019, 39(10): 3065- 3075.
Xiong Linyun, Wang Jie. Fractional order sliding mode control of PMSG wind turbine for power quality enhancement[J]. Proceedings of the CSEE, 2019, 39(10): 3065-3075.
[13] Labbadi M, Nassiri S, Bousselamti L, et al. Fractional- order fast terminal sliding mode control of uncertain quadrotor UAV with time-varying disturbances[C]// 2019 8th International Conference on Systems and Control (ICSC), Marrakesh, Morocco, 2020: 417-422.
[14] Wang Yaoyao, Gu Linyi, Xu Yihong, et al. Practical tracking control of robot manipulators with con- tinuous fractional-order nonsingular terminal sliding mode[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6194-6204.
[15] Obeid H, Fridman L M, Laghrouche S, et al. Barrier function-based adaptive sliding mode control[J]. Automatica, 2018, 93: 540-544.
[16] 武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512.
Wu Zhitao, Li Shuai, Cheng Wansheng. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512.
[17] Maaruf M, El Ferik S, Mahmoud M S. Integral sliding mode control with power exponential reaching law for DFIG[C]//2020 17th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 2021: 1122-1127.
[18] Shao Ke, Zheng Jinchuan, Huang Kang, et al. Finite- time control of a linear motor positioner using adaptive recursive terminal sliding mode[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6659-6668.
[19] Du Haibo, Chen Xiuping, Wen Guanghui, et al. Discrete-time fast terminal sliding mode control for permanent magnet linear motor[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9916-9927.
[20] 薛定宇. 分数阶微积分学与分数阶控制[M]. 北京: 科学出版社, 2018.
Abstract Permanent magnet linear synchronous motor (PMLSM) has been increasingly used in many high-precision machining applications due to its high response, stiffness, and precision. However, the position tracking performance of PMLSM is susceptible to various uncertainties, such as load disturbance and mass change of actuator, because of the omission of the mechanical transmission. Recently, researchers have proposed terminal sliding mode control methods to improve the tracking performance of PMLSM. However, the design of the controller depends on the upper bound of system disturbances. Therefore, an adaptive fractional-order terminal sliding mode control strategy based on a positive semi-definite barrier function (PSB-AFTSMC) is proposed.
Firstly, the dynamic model of PMLSM with uncertainties is established. Secondly, the fractional-order terminal sliding mode control method is used to suppress the influence of uncertain factors on the system, which ensures that the tracking error converges in finite time and reduces the steady-state error. To further improve the robust performance of the system, the upper bound of the uncertain disturbance is estimated in real time using the adaptive sliding mode control law. This method avoids the overestimation of the control gain, enhances the robustness of the system, and makes the system error converge to a predefined zero neighborhood. Finally, experimental results show that the strategy improves the tracking accuracy of the system and has strong robustness to load disturbance and payload variations.
In order to highlight the superiority of the proposed method, the fractional-order terminal sliding mode control (FTSMC) method and the PSB-AFTSMC method are sequentially performed on a linear motor motion stage for position tracking experiments. When a 2 kg payload is added, the fluctuation frequency of the steady-state error curve of the PSB-AFTSMC is greater than that under nominal conditions, but the fluctuation amplitude remains relatively constant. Compared with the FTSMC, the PSB-AFTSMC has a smaller tracking error, and the tracking error is reduced by 60% around. Furthermore, in the nominal state, the sudden application of variable load disturbance to the linear motor system shows significant fluctuations in the error curve based on both control methods, but the fluctuation amplitude of the PSB-AFTSMC is small, which remains below 15 mm. However, the tracking error curve of the FTSMC method fluctuates with large amplitude, especially in 3~6 seconds, and fluctuates greatly twice with a maximum amplitude of approximately 40 mm. The superiority of the PSB-AFTSMC is reflected in the ability to adapt switching control to amplitude-varying disturbances without the constraint information of disturbances. In contrast, the FTSMC control method depends on the upper bound of uncertain disturbance. Finally, to verify that different orders have a specific impact on the control performance, additional experiments that only change order-value are done. The experimental results demonstrate that the fractional-order terminal sliding mode controller based on 0.5 order has superior control performance.
The following conclusions can be drawn from the experimental analysis: (1) Regarding the permanent magnet linear synchronous motor motion platform under uncertain factors, the PSB-AFTSMC-based system demonstrates strong robustness, better tracking performance, and maintains accuracy within 15 mm. Furthermore, the tracking performance varies at different orders, and the fractional-order sliding mode control system near the 0.5 order has good steady-state performance. (2) The adaptive amplitude adjustment of the control input by the positive semi-definite barrier function solves the problem of sliding mode control relying on the bound information of the system disturbance, which is more suitable for practical applications.
keywords:Permanent magnet linear synchronous motor, adaptive fractional-order terminal sliding mode control, positive semi-definite barrier function, robustness
DOI: 10.19595/j.cnki.1000-6753.tces.221489
中图分类号:TM36
国家自然科学基金资助项目(51875366)。
收稿日期 2022-08-01
改稿日期 2022-09-05
赵鑫宇 男,1996年生,博士研究生,研究方向为永磁直驱伺服系统及其控制。E-mail: zhaoxy_sut@163.com
王丽梅 女,1969年生,教授,博士生导师,研究方向为交流伺服驱动技术。E-mail: wanglm@sut.edu.cn(通信作者)
(编辑 崔文静)