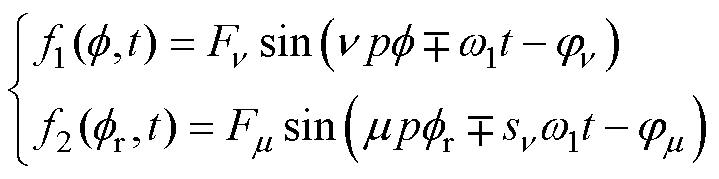（1）
摘要 特定槽配合感应电机输出转矩与电机起动位置有关。为抑制转矩随起动位置周期变化引起的转矩波动，提出一种削弱同步附加转矩的轴向分段错开转子结构。建立电磁转矩计算模型，推导关于转子初始位置的转矩幅值表达式，确定产生恒定转矩的磁场阶次和电机转速条件。基于磁动势线性分布假设，探讨转子分段错开结构减小谐波电动势的机理，量化同步附加转矩削弱程度与转子错开段数的关系。以四种特殊槽配合为例，仿真分析单斜槽转子、分段错开转子及两者组合结构转子，对电机基波转矩和同步附加转矩的影响。最后，选择等槽配合方案试制双斜槽转子样机，开展电机堵转转矩和空载特性试验。结果表明，转子分段错开结构有效削弱了同步附加转矩，解决了等槽配合感应电机起动困难的问题，为抑制电机转矩波动和槽配合选取方法的研究提供了理论参考。
关键词：轴向分段错开转子 同步附加转矩 转矩波动 槽配合 感应电机
近些年，在电动汽车等新兴应用领域中，电机输出转矩的平滑性与稳定性要求逐渐提高[1-3]。相较于永磁同步电机，感应电机（Induction Machine, IM）凭借着价格低廉、可靠性高和过载能力强等优点，仍具有一定的竞争优势和应用需求[4]。因此，众多科技工作者开展了抑制感应电机转矩波动的理论研究与实践验证。感应电机转矩波动主要源于气隙谐波磁场产生的谐波电磁转矩[5]，而谐波磁场可分为由变频供电方式导致的时间谐波分量，以及由分布绕组与铁心开槽结构引起的空间谐波分量[6-7]。相应的转矩脉动抑制措施可以从谐波磁场来源展开，一方面可以优化电机控制算法，减小谐波电流分量来降低电机转矩脉动[8-9]；另一方面也可以调整电机结构参数来降低由空间谐波磁场导致的转矩脉动[10-12]。基于削弱空间谐波磁场的转矩研究，主要从电机定子侧与转子侧结构优化两个方向展开。Li Yanxin等探究定子集中绕组与铁心结构对转矩特性的影响，对比分析不同拓扑电机的转矩分量，研究表明齿间不对称饱和是导致转矩脉动差异的主要原因[10]。T. Gundogdu等优化电机转子槽形参数，在转子闭口槽槽口处设置U型槽桥结构，改善转子侧磁场分布来降低磁饱和程度，从而减小电机转矩脉动[11]。G. Joksimović等对比研究定、转子槽配合参数对电机负载时转矩脉动的影响，根据转子直槽或斜槽类型，分别总结八极电机槽配合参数的选取范围，并按照转矩脉动大小依次排序[12]。笼型转子轴向斜槽是一种传统且有效的抑制转矩波动的措施。基于单斜槽转子结构，一种带中间环的斜槽转子逐步发展并应用在双速电机中，有助于减小电机高速运行时的转矩脉动，并提高电机低速运行时的输出转矩[13]。通过对中环斜槽转子结构参数的组合设计，优化后的转子相较于单斜槽转子进一步削弱了空间谐波磁场，从而降低电机转矩脉动[14]。但是，考虑感应电机附加转矩与杂散损耗的槽配合选取矛盾仍然存在[15-16]，已有的转矩脉动抑制研究往往基于电机常规的槽配合选取范围。
感应电机结构优化措施可以为其他类型电机抑制转矩脉动研究提供思路。永磁同步电机采用类似于单斜槽转子的轴向分段倾斜磁极，有助于削弱齿槽转矩、减小转矩脉动等[17-18]。为避免单向倾斜磁极引起的不平衡磁拉力问题，永磁电机采用轴向分段错开的非斜极转子，并结合其他措施抑制电机齿槽转矩[19-20]。这种转子分段错开的斜槽代替结构也可以抑制感应电机转矩脉动[21]。但是，转子轴向分段错开结构减小谐波转矩的工作原理还未明确。相较于随转子位置周期变化的齿槽转矩[22]，很少有文献研究感应电机电磁转矩的空间周期性，尤其是针对起动过程中的附加转矩分量，基于削弱附加转矩以拓宽电机槽配合选取范围的研究还不够充分。
本文针对感应电机输出转矩随起动位置周期变化的现象，提出一种转子轴向分段错开结构削弱同步附加转矩，降低电机转矩波动。通过建立电磁转矩计算模型，推导恒定转矩幅值与转子初始位置的关系，确定典型槽配合电机恒定转矩的空间周期性。仿真分析单斜槽转子、分段错开转子及其组合结构转子削弱同步附加转矩的效果，并采用等槽配合样机试验来验证理论分析的合理性。为抑制电机转矩波动提供设计思路，并为探索感应电机新的槽配合选取规则提供理论参考。
感应电机电磁转矩可利用虚位移法求解，根据转矩表达式的数学意义，确定不随时间或空间位置角变化的恒定电磁转矩的产生条件。对于三相笼型感应电机，分别在定子侧和转子侧建立绕组磁动势坐标系，电机合成气隙磁动势包括定子合成磁动势和转子合成磁动势，可表示[14]为
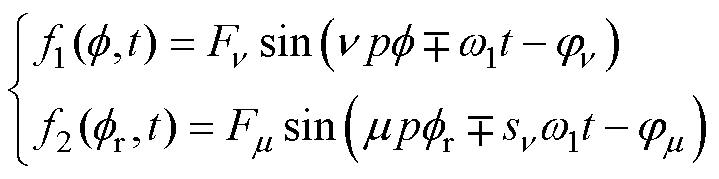（1）
其中，定、转子谐波磁动势的阶次可分别表示为
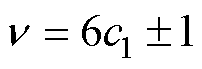（2）
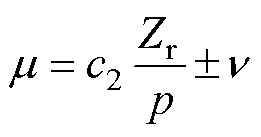（3）
式中，Fν和Fm 分别为定、转子谐波磁动势幅值；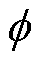
和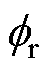
分别为定、转子空间机械角；jν和jm分别为定、转子谐波磁动势的初相位；p为电机极对数；w1为电源角频率；
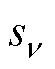为谐波转差率；“∓”分别为气隙磁动势正向旋转和反向旋转两种情况；c1和c2为非负整数，若当c1,2=0，则对应的谐波磁动势相当于基波磁动势；Zr为电机转子槽数。定子齿谐波磁场阶次νt=c1Zs/p±1，Zs为电机定子槽数。
为便于后续电磁转矩的计算，将转子磁动势表达式转换至定子静止坐标系中。利用空间机械位置角的变换关系，转子合成磁动势又可表示为
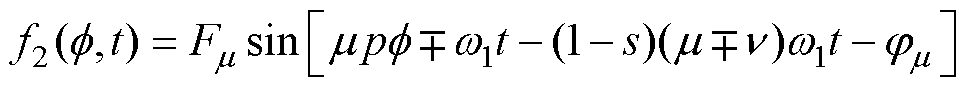（4）
式中，s为转差率。
根据虚位移法的定义，电机电磁转矩等于气隙磁场能量对转角的偏导数。若该角度表示为转子虚位移D，忽略磁能中的恒定部分，电机电磁转矩通用表达式可化简为
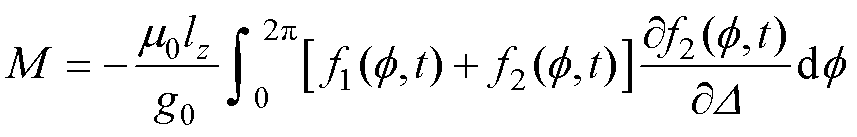（5）
式中，m0为真空磁导率；lz为电机轴向长度；g0为气隙的径向长度。在此不考虑电机定、转子开槽等因素引起的气隙谐波磁导分量。
电磁转矩表达式可以化简为关于磁动势的两项三角函数乘积项。对于第一项由不同阶次定、转子磁场产生的转矩分量，以及第二项由转子磁场自身产生的转矩分量，转矩幅值在空间周期内的平均值恒为零，表现为空间转矩脉动分量。仅当产生转矩的定、转子磁场阶次绝对值相同，即|ν|=|m|时，电磁转矩幅值与转子空间位置角无关，可表示为
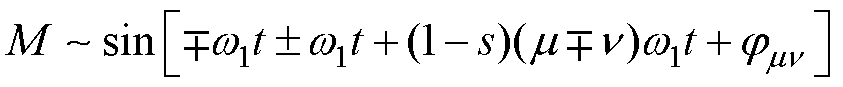（6）
式中，jmν为定、转子谐波磁动势初相位之差。
由式（6）可进一步分析转矩幅值与时间无关的条件，在此分为两种情况。第一种情况为ma次转子谐波磁场与感生它的νa次定子谐波磁场相互作用，即式（3）中c2=0，该转矩分量可称为异步转矩[15]。在第二种情况中，转矩由ma次转子谐波磁场与非感生它的νb次定子谐波磁场相互作用，该转矩分量可称为同步转矩[15]。若产生同步转矩的两种磁动势的转向相同，恒定转矩还应满足电机转速nr=0的条件；若这两种磁动势的转向相反，则转速条件应满足
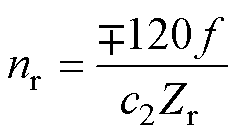（7）
式中，f为电源频率。对于式（6）中的其他转矩分量，其幅值在时间周期内的平均值恒为零，表现为时间转矩脉动分量。
恒定电磁转矩可分为异步转矩和同步转矩两类，由基波磁动势产生的异步转矩称为基波转矩，其他恒定转矩分量相应地称为附加转矩[15]。本节对恒定转矩随起动位置变化的空间周期性展开分析，在1.1节建立气隙磁动势的坐标系中，假设转子的初始位置角滞后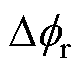
，由式（1）可知，此时转子谐波磁动势可以表示为
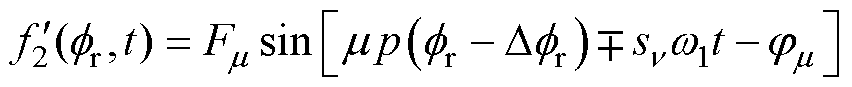（8）
由转子初始位置改变导致的转子磁动势初相位变化，相当于建立转子磁动势的坐标系移动。根据笼型感应电机的工作原理，定、转子磁动势在任意转速时保持相对静止，因此，若保持建立定子磁动势坐标系不变的假设，则定子谐波磁动势相当于滞后时间相位差Dt=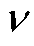
pD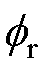
/w1，即可表示为
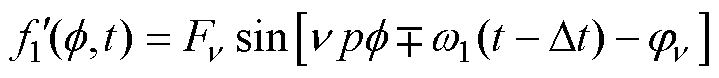（9）
考虑转子初始位置变化后的气隙磁动势表达式（8）与式（9）之间存在一一对应关系，即转子m 次磁动势是由定子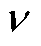
次磁动势感生，而非式（1）中的气隙磁动势通用表达式。若保持定子磁动势表达式不变，则将式（9）中的时间相位差转换至式（8）中的空间相位差中，由此转子谐波磁动势的等效初相位可以表示为
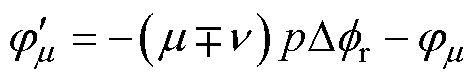（10）
由式（6）可知，恒定转矩幅值与产生转矩的定、转子磁动势的相位差的正弦值成正比。若谐波转矩最大值表示为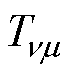
，将式（3）代入式（10）中，此时恒定转矩幅值与转子初始位置角的关系可以表示为
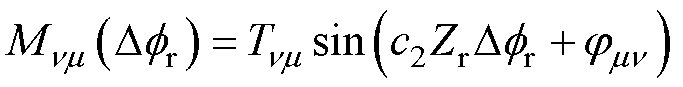（11）
由此可知，转矩幅值随起动位置角变化的空间周期与转子谐波磁动势阶次c2成反比，其最小公倍数为一个转子齿距。由于产生异步转矩的磁场阶次条件为c2=0，故转子初始位置变化不影响异步转矩，仅需考虑同步转矩的空间周期性。在此以四极感应电机为例，同步附加转矩的产生条件见表1，分别列出电机四种槽配合时，产生主要同步转矩分量的磁场阶次和电机转速条件。气隙谐波磁场正向与反向旋转的差异性直接反映在阶次正负号上。当Zr=24时，同阶定、转子谐波磁场转向相同，同步转矩的转速条件均为零。当Zr=26, 28, 16时，产生同步转矩的定、转子磁场旋转方向相反，由式（7）可知，相应的电机正向转速条件。根据产生同步转矩的转子磁场阶次，可推断四种槽配合电机最大同步附加转矩的空间周期分别为1.0、0.5、1.0和1.0个转子齿距。
表1 四极感应电机同步附加转矩的产生条件
Tab.1 Generation conditions for synchronous parasitic torque of four-pole induction machine
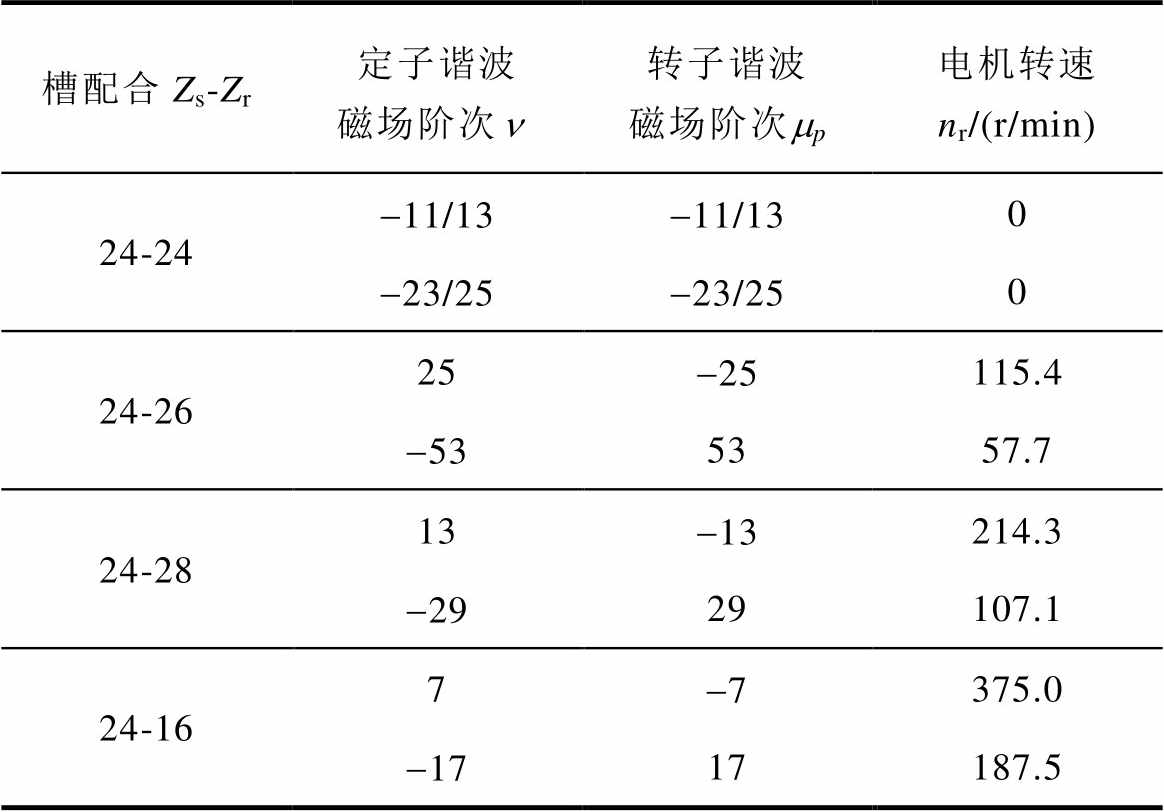
槽配合Zs-Zr定子谐波磁场阶次转子谐波磁场阶次mp电机转速nr/(r/min) 24-24-11/13-11/130 -23/25-23/250 24-2625-25115.4 -535357.7 24-2813-13214.3 -2929107.1 24-167-7375.0 -1717187.5
为抑制恒定转矩分量随起动位置周期变化而引起的转矩波动，本节提出一种轴向分段错开转子结构，如图1所示，转子沿轴向分为n段，每段转子轴向长度为lz/n，相邻转子间的圆周错开距离为t2/n，其中，t2为转子齿距。轴向分段错开转子削弱谐波电动势的工作原理如图2所示，以错开段数n=4为例，转子任意一根导条沿轴向分为四段导体并相互错开，依次标记为1～4。根据电磁感应原理，定子一阶和二阶齿谐波磁场在各导条中分别感生谐波电动势eν1和eν2，同阶感生电动势的幅值相等。由于各段导条沿圆周均匀分布，导条12与导条34感生的一阶谐波电动势的方向相反，四段错开转子合成电动势中的一阶齿谐波分量被抵消，二阶齿谐波电动势同理也被抵消。但是对于两段错开转子，即单根转子导条分别错开为导条13或导条24，相邻导条中二阶齿谐波电动势方向相同，故仅能抵消转子一阶齿谐波电动势。通过各段错开转子电动势之间的合成作用，可以抵消部分阶次的谐波电动势，进而削弱由齿谐波磁动势产生的同步附加转矩。假设合成转子磁动势为各段错开转子磁动势的矢量和，由式（11）可知，此时感应电机的谐波电磁转矩可以表示为
（12）
式中，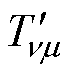
为考虑转子分段错开效应后的谐波电磁转矩最大值；a2为转子齿距角。
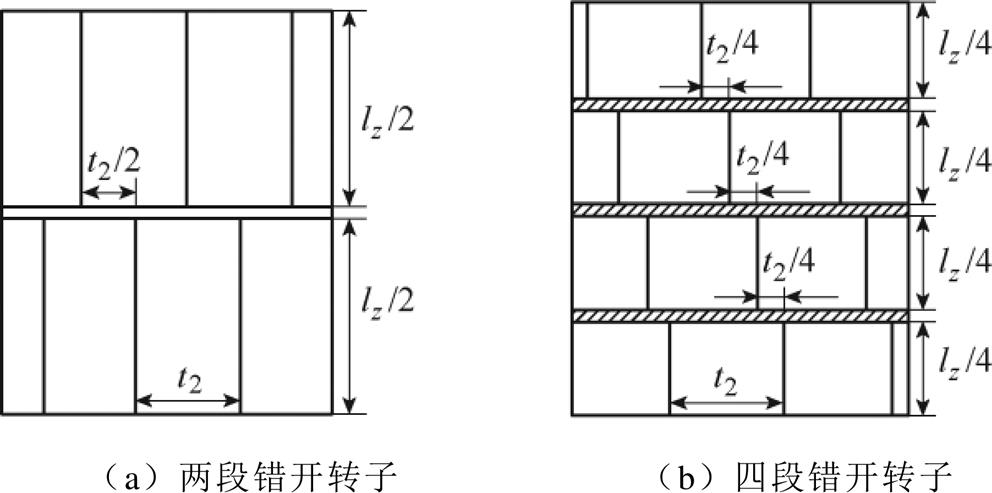
图1 轴向分段错开转子示意图
Fig.1 Illustration of axial piecewise staggered rotor
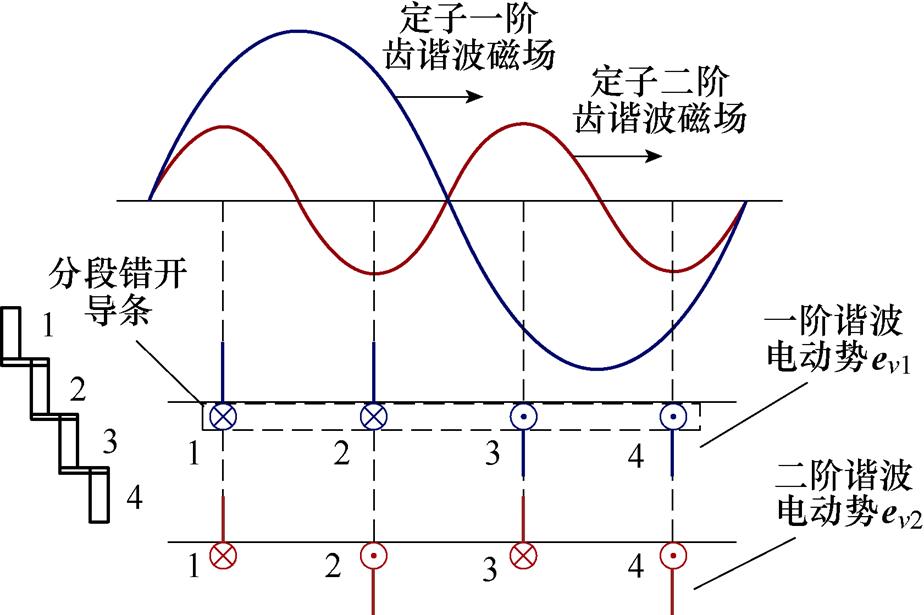
图2 轴向分段错开转子削弱谐波电动势原理
Fig.2 Schematic diagram of axial piecewise staggered rotor weakening harmonic electromotive force
为描述分段错开转子对电机电磁转矩的削弱程度，引入转子错开系数kstm，定义该系数为分段错开转子与完整转子时电机谐波转矩的幅值比。考虑到当前电机制造工艺水平，以错开段数n≤4为例，由式（12）化简可知转子错开系数为
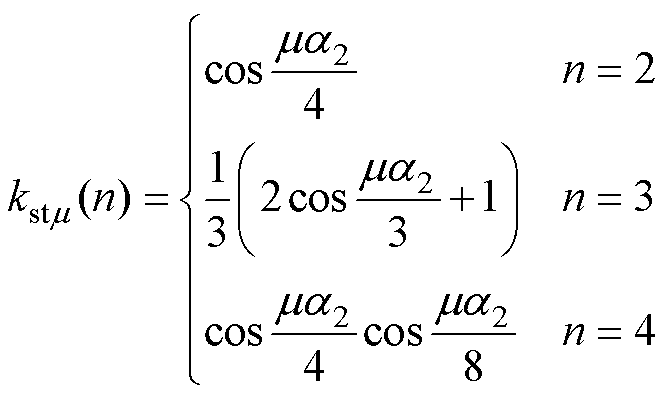（13）
将式（3）代入式（13）中，可计算轴向分段错开转子对两类恒定转矩的削弱程度。对于c2=0时的异步转矩，谐波阶次越低则错开系数越接近于1，转矩幅值近似不变。对于c2≠0时的同步转矩，特定谐波阶次时的错开系数接近于零，转矩分量近似被抵消。若以k为正序数，轴向分段错开转子抵消同步转矩的转子齿谐波磁场阶次为
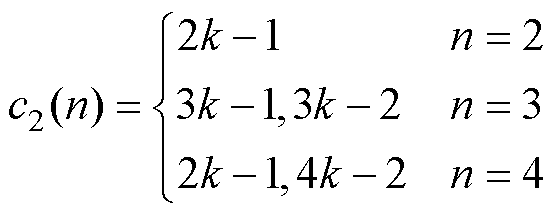（14）
在气隙磁动势线性分布的前提下，轴向分段错开转子可以抵消转子谐波电动势及其产生的同步附加转矩，作用谐波的类型与错开段数有关。若考虑错开转子轴向连接区域导致的漏磁，则谐波的削弱程度存在一定的折扣，并且会引起电机主磁通部分降低、附加损耗增加等不利因素。
传统感应电机设计理论通常采用转子斜槽措施，并限制槽配合参数的选取范围，从而避免电机在起动过程中产生较大的同步附加转矩[15]。为对比不同转子类型削弱同步附加转矩的效果，本文选取表1中的四种非常规槽配合，建立相应的电机模型，每种槽配合电机分别采用转子直槽与单斜槽两种结构，其他参数完全相同，三相感应电机的主要参数见表2。在产生最大同步转矩的转速条件下，分别计算电机齿距范围内不同起动位置时的转矩。直槽和单斜槽转子感应电机输出转矩波形如图3所示，四种槽配合电机的输出转矩波形正弦周期变化，周期分别为1.0、0.5、1.0和1.0个转子齿距，验证了转矩空间周期性的理论结果。若忽略异步附加转矩分量，输出转矩的平均值约等于基波转矩，转矩波形的峰-峰值近似等于两倍最大同步转矩值。相较于直槽转子，单斜槽转子有效削弱了电机同步附加转矩，四种槽配合电机的最大同步转矩幅值分别减小了58.2%、55.0%、42.9%和61.8%。但是，单斜槽转子仍无法改变特殊槽配合电机输出转矩的空间周 期性。
表2 三相感应电机的主要参数
Tab.2 Main parameters of three-phase induction machine
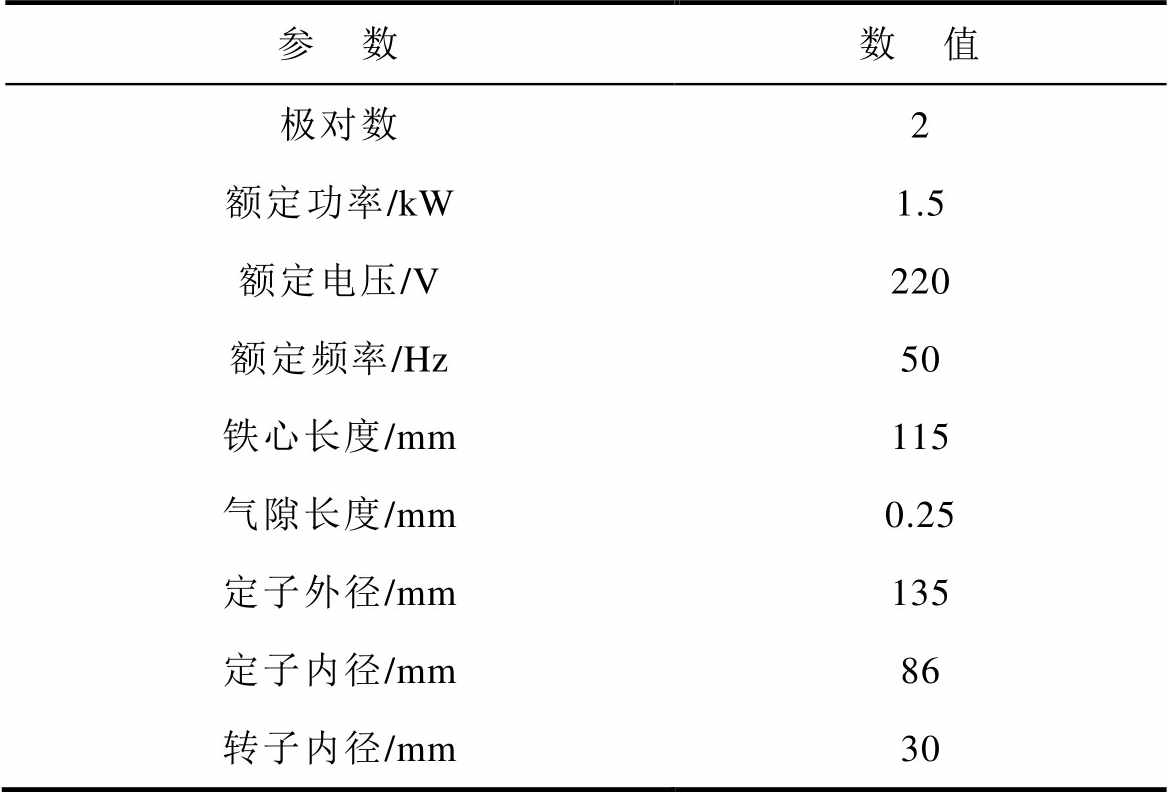
参 数数 值 极对数2 额定功率/kW1.5 额定电压/V220 额定频率/Hz50 铁心长度/mm115 气隙长度/mm0.25 定子外径/mm135 定子内径/mm86 转子内径/mm30
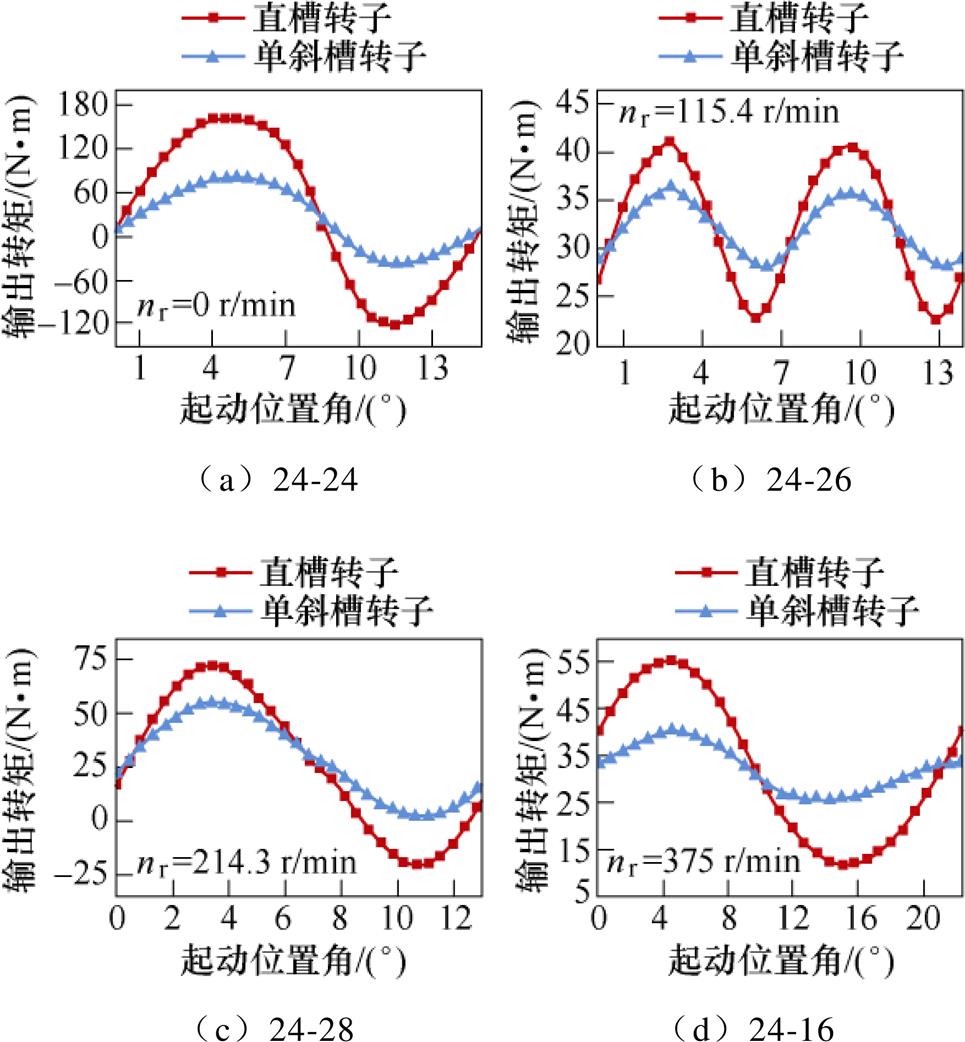
图3 直槽和单斜槽转子感应电机输出转矩波形
Fig.3 Output torque waveforms of straight-slot and single-skewed rotor induction motors
以两段和三段错开转子为例，根据表2中的电机参数，分别建立轴向分段错开转子电机模型，在此忽略错开转子间的轴向连通区域。电机输出转矩随起动位置角的波形如图4所示。在两段错开转子情况下，四种槽配合电机输出转矩的波形为正弦波，空间周期均为1/2个转子齿距。在三段错开转子情况下，Zr=24, 16时转矩波形的空间周期为1/3个转子齿距，Zr=26, 28时电机转矩近似为恒定值，转矩脉动分别为0.55%和1.0%。转矩空间周期性的变化反映了最大同步转矩类型的改变，特定转子谐波磁场产生的同步转矩近似被消除，验证了两段错开转子能抵消转子一阶齿谐波磁场产生的同步转矩，三段错开转子能分别抵消转子一阶和二阶齿谐波磁场各自产生的同步转矩分量的分析结果。
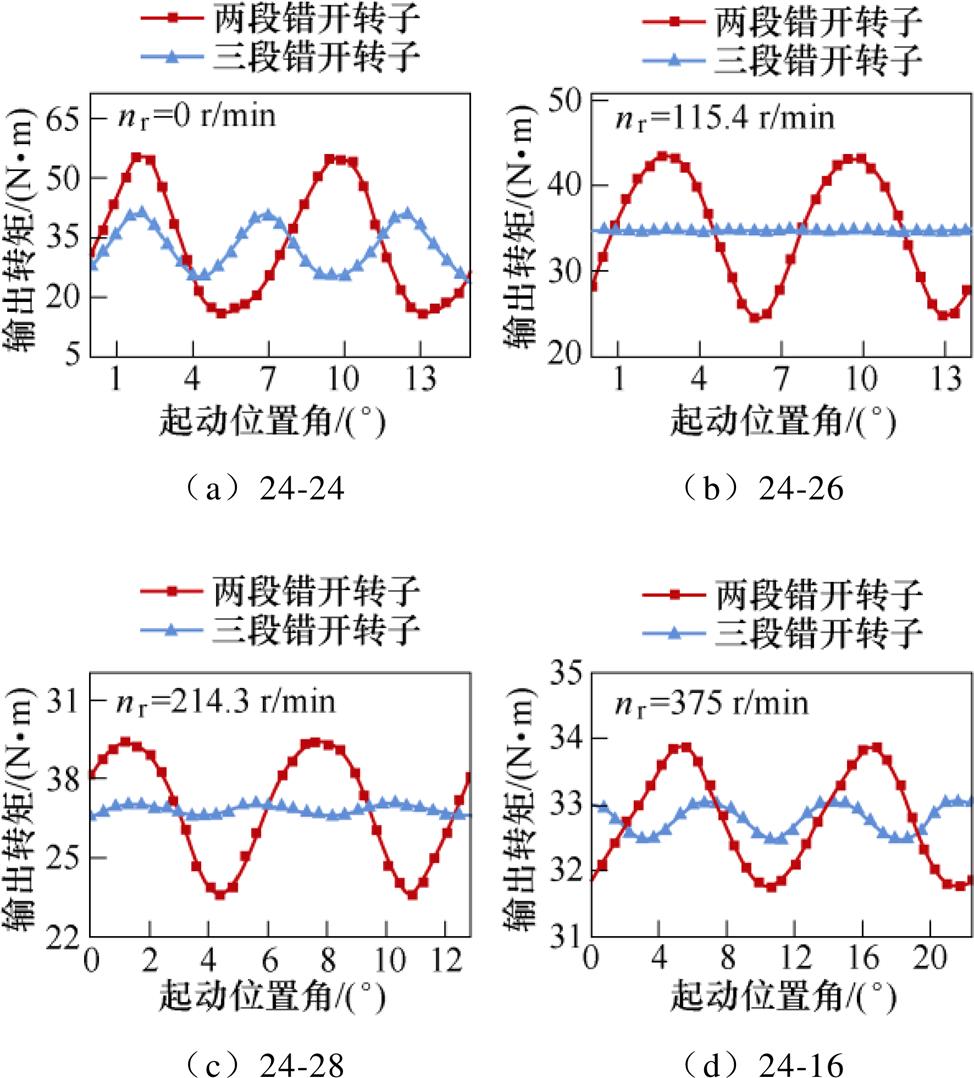
图4 轴向分段错开转子感应电机输出转矩波形
Fig.4 Output torque waveforms of piecewise-stagger rotor induction motors
不同转子类型时感应电机的转矩值对比见表3，分别列出转子类型为直槽、单斜槽、两段错开和三段错开时，四种槽配合电机的基波转矩和最大同步转矩值。通过对比可知，相较于直槽转子，单斜槽转子有助于削弱不同槽配合电机的同步转矩，并且略微降低基波转矩；而分段错开转子仅削弱特定槽配合时的同步附加转矩，基波转矩的幅值近似不变。分段错开转子适用的槽配合范围取决于同步附加转矩的谐波磁场来源。
表3 不同转子类型时感应电机的转矩值对比
Tab.3 Comparison of torque values of induction machines with different rotor types （单位: N·m）
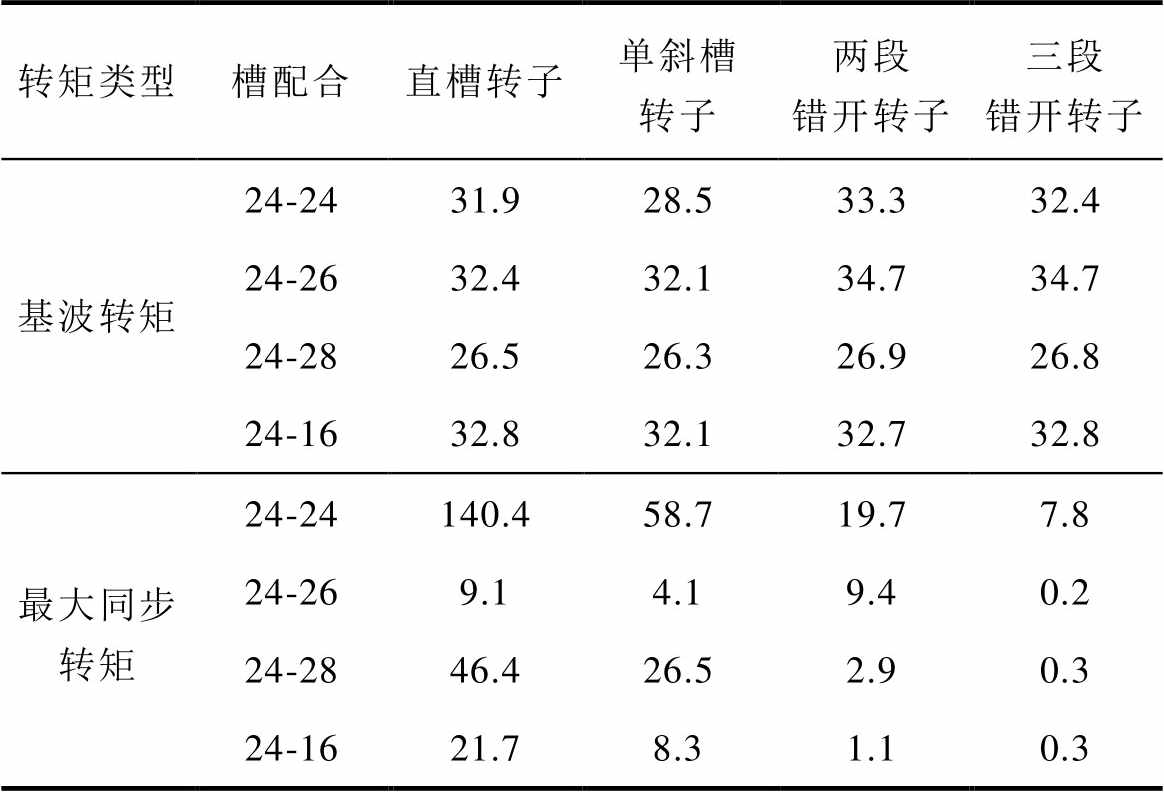
转矩类型槽配合直槽转子单斜槽转子两段错开转子三段错开转子 基波转矩24-2431.928.533.332.4 24-2632.432.134.734.7 24-2826.526.326.926.8 24-1632.832.132.732.8 最大同步转矩24-24140.458.719.77.8 24-269.14.19.40.2 24-2846.426.52.90.3 24-1621.78.31.10.3
通过第3节对四种槽配合电机的仿真计算，验证了单斜槽转子与分段错开转子对同步附加转矩的削弱效果。为保证附加转矩的削弱程度，本节将这两种转子结构结合，形成两段错开斜槽结构的双斜槽转子，转子模型如图5所示。考虑到电机等槽配合时，最大同步附加转矩的产生条件为电机转速nr=0 r/min，为简化后续样机的试验过程，在此以24-24等槽配合为例。建立转子单斜槽、两段错开和双斜槽时的电机对比模型，转子斜槽距离均为一个齿距，电机除转子类型外其他参数完全相同（见表2）。三台电机堵转转矩仿真波形对比如图6所示，转矩幅值随起动位置角近似正弦变化，其空间周期性与二维有限元仿真中的结果相同。相较于前两种转子，电机采用双斜槽转子组合结构时，最大同步附加转矩幅值分别减小80.3%和50.2%，转矩空间周期性为半个齿距。转矩对比结果验证了双斜槽转子削弱一阶齿谐波磁场产生同步转矩的优越性，其削弱程度优于任意一种单独转子结构时的效果。
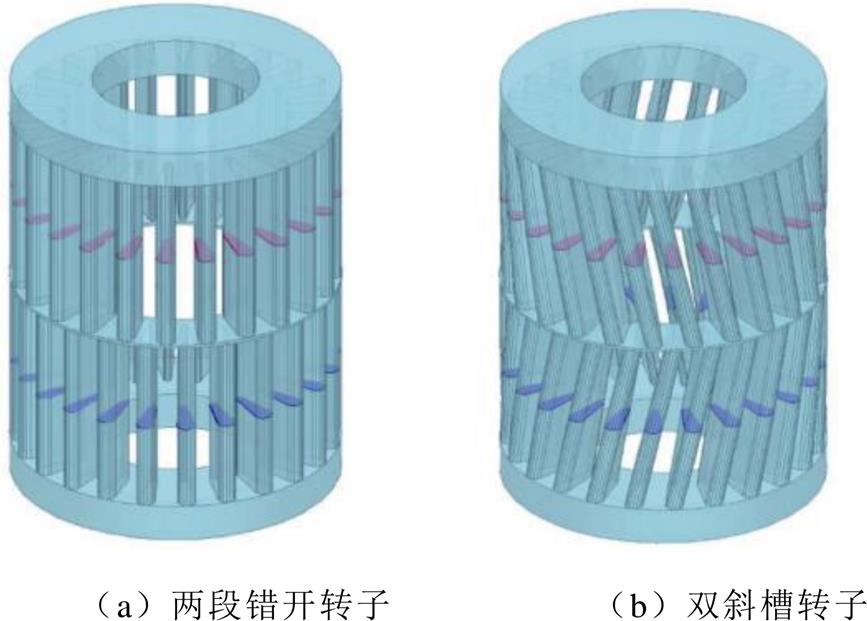
图5 笼型转子的三维有限元模型
Fig.5 3D finite element models of cage rotors
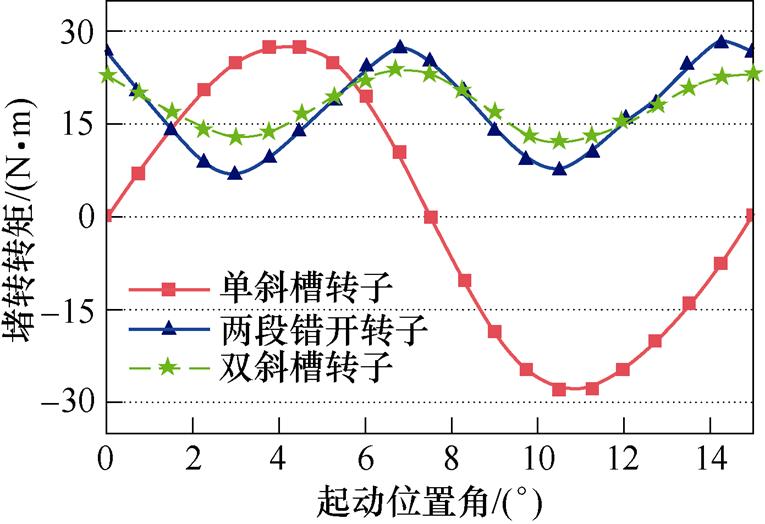
图6 等槽配合电机堵转转矩的仿真波形
Fig.6 Simulation waveforms of locked-rotor torque of IMs with equivalent slot combination
在各导条中设置随转子旋转的电流横截面，计算导条电流在圆周内的空间分布。双斜槽转子导条电流的谐波分析如图7所示，相较于单侧转子电流，合成转子电流的基波分量略微减小，11次与13次的一阶齿谐波电流幅值大幅降低，分别减小84.2%和87.8%，而23次与25次的二阶齿谐波电流的减小程度分别为1.15%和0.43%，可近似忽略不计。谐波电流的对比结果验证了转子分段错开结构的作用效果，双斜槽转子具有削弱转子一阶齿谐波电动势的优越效果，但不影响转子二阶齿谐波电动势。
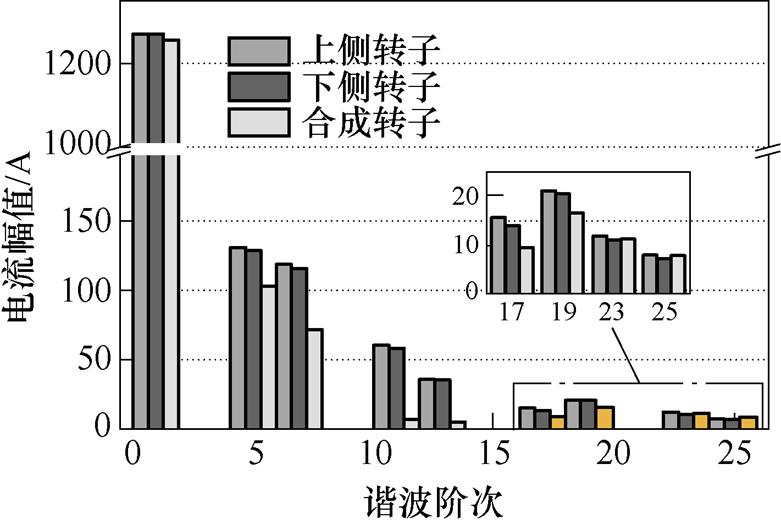
图7 双斜槽转子感应电机导条电流谐波分析
Fig.7 Harmonic analysis of bar currents in an IM with the dual skewed rotor
笼型感应电机斜槽转子的最佳斜槽距离通常为一个齿距，有助于削弱奇次齿谐波磁场。为探讨双斜槽转子组合结构中，转子斜槽度参数对同步附加转矩抑制效果的影响，试制两台不同斜槽度的双斜槽转子样机，斜槽距离分别为0.9以及1个齿距。样机转子实物如图8所示。搭建如图9所示的堵转转矩试验平台，以目测读取的转矩最大值作为该转子位置时的电机堵转转矩值。
图8 闭口槽形的双斜槽转子
Fig.8 Dual skewed rotor with closed-slot shape
图9 电机堵转转矩试验平台
Fig.9 Test platform of motor locked-rotor torque
样机堵转转矩波形如图10所示，转矩幅值随转子机械位置角近似正弦变化，其空间周期约为半个转子齿距（t2/2）。由此推断，同步附加转矩以二阶齿谐波磁场产生的转矩分量为主。相较于4.1节的仿真结果，样机基波转矩的试验值较为接近，但是最大同步转矩的估算值偏大，导致堵转转矩的最值存在误差。考虑转子斜槽设计对样机转矩的影响，相较于斜槽距离bsk=0.9t2时的情况，样机转子bsk=1.0t2时的堵转转矩最小值增加4.7 N·m，最大值减小8.1 N·m。转矩对比结果表明，在组合转子结构中，转子导条斜槽效应与错开效应对转子谐波磁动势存在耦合的削弱作用。错开导条结构对奇次谐波产生同步转矩的抵消效果存在误差，仍需补充采取最佳斜槽角的转子斜槽设计，从而最大程度削弱同步附加转矩。
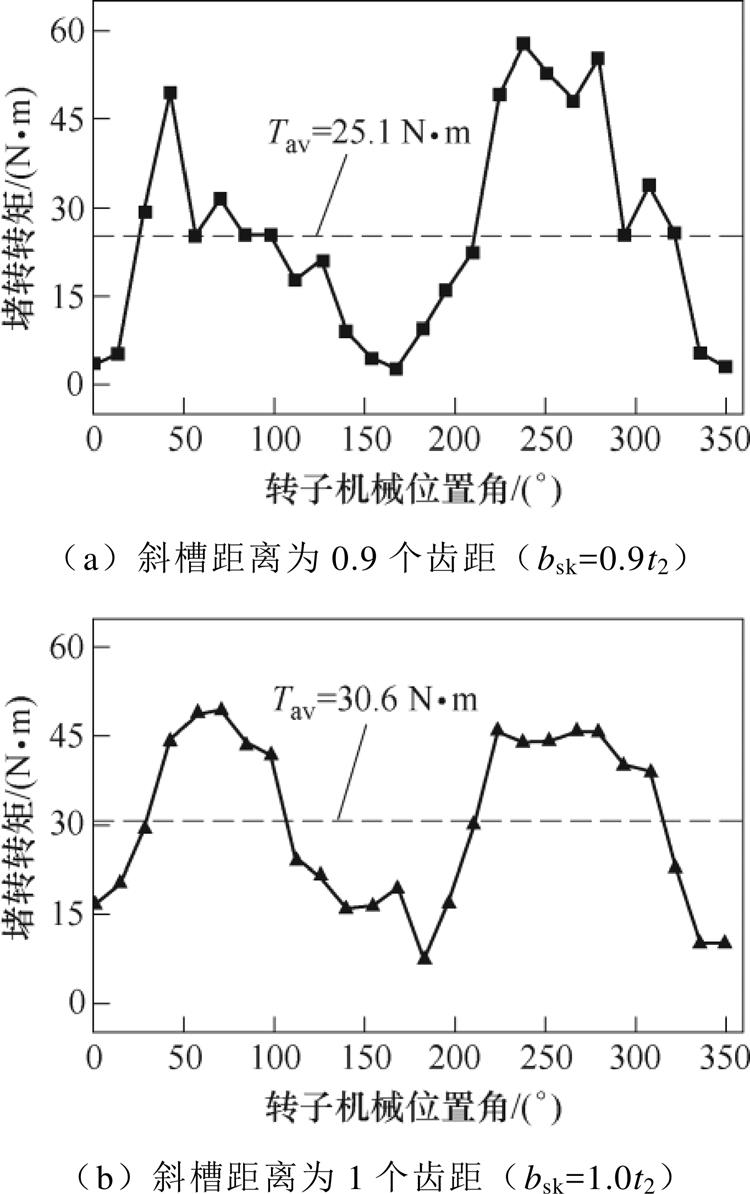
图10 双斜槽转子样机堵转转矩的试验波形
Fig.10 Test waveforms of locked-rotor torque of dual skewed rotor prototype machines
为探究双斜槽转子组合结构对定子侧磁场的影响，在此开展样机空载特性试验。利用测定的线电压、相电流和输入功率参数，样机空载特性曲线如图11所示，绘制其中一台双斜槽转子样机的空载特性曲线。由铁耗与机械损耗组成的恒定损耗Pcon近似与电压比的二次方线性相关，其拟合曲线的纵轴截距约等于机械损耗。图中，U0和UN分别为空载电压和额定电压。两台样机空载试验结果见表4，相较于斜槽距离bsk=0.9t2时的情况，样机转子bsk=1.0t2时的空载电流增加约2.8%，由此导致定子空载铜耗增加5.5 W，而恒定损耗值共增加7.26 W。样机对比试验表明，双斜槽转子有助于削弱同步附加转矩，解决等槽配合电机起动困难的问题。但是，错开转子连接区域会引起边缘漏磁，降低了电机的有效磁通，进而导致功率因数降低和空载损耗增加等。
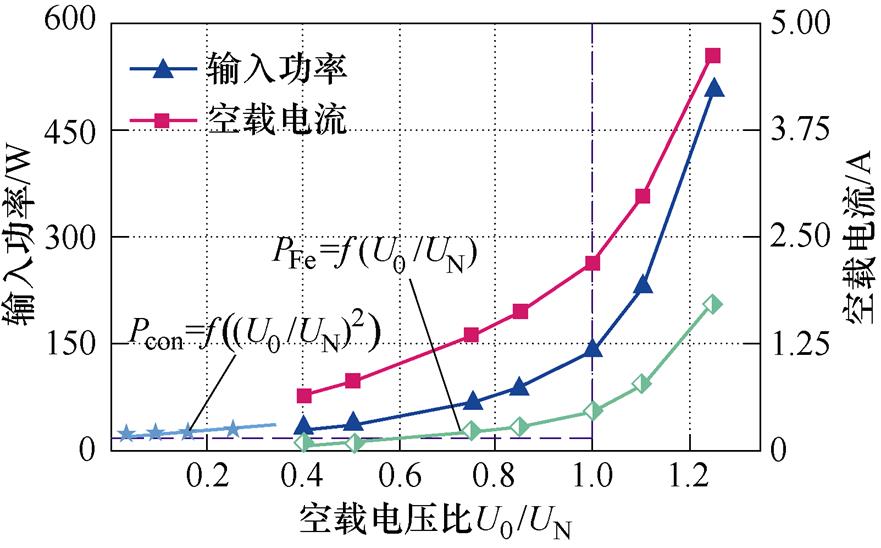
图11 样机空载特性曲线
Fig.11 No-load characteristic curves of prototype machine
表4 双斜槽转子样机空载试验结果对比
Tab.4 Comparison of no-load test results of dual skewed rotor prototype machines
转子斜槽距离输入功率P0/W空载电流I0/A定子铜耗P0Cu1/W铁耗PFe/W机械损耗Pfw/W 0.9t2125.882.1759.0954.7012.08 1.0t2138.642.2364.5956.4617.59
本文提出一种转子轴向分段错开结构削弱电机同步附加转矩，抑制转矩幅值随起动位置周期变化引起的转矩波动。通过仿真分析转子单斜槽、分段错开及其组合结构时的电机转矩特性，对比试验两台等槽配合样机，可以得到以下主要结论：
1）感应电机恒定转矩包括异步转矩与同步转矩两类，仅同步转矩幅值随电机起动位置周期性变化，其空间周期大小与产生转矩的转子谐波磁场阶次成反比，周期最小公倍数为一个转子齿距。
2）转子轴向分段错开结构可以减小转子谐波电动势，改变特殊槽配合电机输出转矩的空间周期性，提高输出转矩最小值。当错开段数n=2时，可近似抵消转子奇次齿谐波磁场产生的同步转矩分量。
3）相较于轴向斜槽和分段错开转子，两者组合结构削弱同步附加转矩效果更佳。双斜槽转子斜槽距离为一个齿距时，样机起动转矩比的最小值约为1.5倍，有助于实现等槽配合电机正常起动，但转子局部漏磁会引起空载损耗增加等缺点。
参考文献
[1] Zhu Z Q, Chu W Q, Guan Y. Quantitative comparison of electromagnetic performance of electrical machines for HEVs/EVs[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(1): 37-47.
[2] Wang Zhikun, Ching T W, Huang Shaojia, et al. Challenges faced by electric vehicle motors and their solutions[J]. IEEE Access, 2020, 9: 5228-5249.
[3] 王道涵, 彭晨, 王柄东, 等. 电动汽车新型转子内置式永磁同步电动机转矩脉动与电磁振动抑制研究[J]. 中国电机工程学报, 2022, 42(14): 5289- 5300.
Wang Daohan, Peng Chen, Wang Bingdong, et al. Research on a novel interior permanent magnet machine with segmented rotor to mitigate torque ripple and electromagnetic vibration[J]. Proceedings of the CSEE, 2022, 42(14): 5289-5300.
[4] Thomas R, Husson H, Garbuio L, et al. Comparative study of the tesla model S and audi e-tron induction motors[C]//2021 17th Conference on Electrical Machines, Drives and Power Systems, Sofia, Bulgaria, 2021: 1-6.
[5] Mishra A K, Rajpurohit B S, Kumar R. Induction machine drive design for enhanced torque profile[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1283-1291.
[6] 肖阳, 宋金元, 屈仁浩, 等. 变频谐波对电机振动噪声特性的影响规律[J]. 电工技术学报, 2021, 36(12): 2607-2615.
Xiao Yang, Song Jinyuan, Qu Renhao, et al. The effect of harmonics on electromagnetic vibration and noise characteristic in inverter-duty motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(12): 2607-2615.
[7] Keerthipati S, Nallamekala K K. UPSC SVPWM controlled multi-level inverter topology for multiple pole-pair induction motor drive for minimising torque ripple[J]. IET Power Electronics, 2016, 9(6): 1306- 1314.
[8] 黄林森, 赵文祥, 吉敬华, 等. 稳态性能改善的双三相永磁电机直接转矩控制[J]. 电工技术学报, 2022, 37(2): 355-367.
Huang Linsen, Zhao Wenxiang, Ji Jinghua, et al. Direct torque control for dual three-phase permanent- magnet machine with improved steady-state perfor- mance[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 355-367.
[9] 贾慧利, 杨家强, 杨光辉. 基于转子磁链优化的五相感应电机电子变极策略[J]. 电工技术学报, 2022, 37(14): 3587-3597, 3631.
Jia Huili, Yang Jiaqiang, Yang Guanghui. Electronic pole-changing strategy for five-phase induction motor based on rotor flux optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3587- 3597, 3631.
[10] Li Yanxin, Zhu Ziqiang, Li Guang jin. Influence of stator topologies on average torque and torque ripple of fractional-slot SPM machines with fully closed slots[J]. IEEE Transactions on Industry Applications, 2018, 54(3): 2151-2164.
[11] Gundogdu T, Zhu Z Q, Mipo J C. Optimization and improvement of advanced nonoverlapping induction machines for EVs/HEVs[J]. IEEE Access, 2022, 10: 13329-13353.
[12] Joksimović G, Melecio J I, Tuohy P M, et al. Towards the optimal ‘slot combination’ for steady-state torque ripple minimization: an eight-pole cage rotor indu- ction motor case study[J]. Electrical Engineering, 2020, 102(1): 293-308.
[13] Cheraghi M, Bayati B M, Mahmoudian E M, et al. Determination of torque-speed characteristic for a two-speed elevator induction machine[J]. IET Electric Power Applications, 2018, 12(2): 239-246.
[14] Xu Wei, Bao Xiaohua, Di Chong, et al. Optimal angle combination for improving electromagnetic torque in induction motor with double-skewed rotor[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-5.
[15] Boldea I, Nasar S A. The induction machines design handbook[M]. 2nd ed. Boca Raton, FL: CRC Press/ Taylor & Francis, 2010.
[16] 安俊义, 赵海森, 刘晓芳, 等. 槽配合对单绕组双速直槽异步电动机空载磁场及损耗的影响[J]. 微特电机, 2015, 43(5): 17-21.
An Junyi, Zhao Haisen, Liu Xiaofang, et al. Influence of slot combination change on no-load magnetic field and loss of single-winding two-speed motor with straight slot system[J]. Small & Special Electrical Machines, 2015, 43(5): 17-21.
[17] Barman D, Pillay P. Effect of skewing in a variable flux interior permanent magnet synchronous machine[J]. IEEE Transactions on Industry Applications, 2020, 56(6): 6399-6410.
[18] Ullah W, Khan F, Umair M. Design and optimization of segmented PM consequent pole hybrid excited flux switching machine for EV/HEV application[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 206-214.
[19] Hong Jianfeng, Wang Shanming, Sun Yuguang, et al. Piecewise stagger poles with continuous skew edge for vibration reduction in surface-mounted PM synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8498-8506.
[20] Peng Chen, Wang Daohan, Feng Zhenkang, et al. A new segmented rotor to mitigate torque ripple and electromagnetic vibration of interior permanent magnet machine[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1367-1377.
[21] Darjazini A, Vahedi A, Nobahari A, et al. Analysis of electromagnetic torque for induction motors with a novel non-skewed rotor structure[J]. COMPEL-the International Journal for Computation and Mathe- matics in Electrical and Electronic Engineering, 2021, 41(1): 238-257.
[22] 刘家琦, 白金刚, 郑萍, 等. 基于磁场调制原理的齿槽转矩研究[J]. 电工技术学报, 2020, 35(5): 931- 941.
Liu Jiaqi, Bai Jingang, Zheng Ping, et al. Investi- gation of cogging torque based on magnetic field modulation principle[J]. Transactions of China Elec- trotechnical Society, 2020, 35(5): 931-941.
Abstract The smoothness and stability requirements of motor output torque have gradually increased in recent years, especially in emerging applications such as electric vehicles. The induction machine (IM), due to its low price, high reliability, and strong overload capacity, still has certain competitive advantages and application needs. In classical motor design theory, the range of slot combinations is limited to ignore the large synchronous parasitic torque, such as the equivalent slot combination. However, the stray loss of IM is small when the number of stator slots and rotor slots is similar. For some of these special slot combinations, the output torque of the induction machine is related to the starting position of the motor. In order to suppress the torque ripple caused by the periodic torque variation with the starting position, a rotor axial piecewise staggered structure is proposed to weaken the synchronous parasitic torque. The selection range of slot combinations can be expanded by solving the starting difficulty of the IM with an equivalent slot combination.
The electromagnetic torque calculation model is established, the torque amplitude expression about the initial rotor position is deduced, and the magnetic field order and the motor speed conditions for generating constant torque are determined. Based on the assumption of the linearly distributed magnetic potential, the mechanism of weakening the harmonic electromotive force is discussed using a piecewise staggered rotor structure. The relationship between the weakening degree of synchronous parasitic torque and the number of staggered rotor segments is quantified. Taking four kinds of special slot combinations as examples, the effects of the single skewed rotor, the piecewise staggered rotor, and the rotor with the combined structure on the fundamental torque and synchronous parasitic torque are simulated and analyzed. Finally, the dual skewed rotor prototype machines are trial-produced with the equivalent slot combination scheme, and the motor locked-rotor torque tests are carried out.
Simulation results on the torque components show that the single skewed rotor weakens the synchronous torque of the motor with different slot combinations while slightly reducing the fundamental torque. However, the single skewed rotor still cannot change the spatial periodicity of the output torque. For the piecewise staggered rotor, the synchronous torque is weakened only for certain slot combinations, and the amplitude of the fundamental torque remains approximately unchanged. Regarding the combined rotor structure, taking the two-stage staggered skewed rotor as an example, the attenuation degree of the harmonic magnetic field is greater than that of any single rotor structure. Experimental results on the locked-rotor torque show that the offset effect of the staggered bar structure on the synchronous torque generated by the odd harmonics deviates from the simulation results by a degree. An optimal skewed rotor design is necessary to minimize the synchronous parasitic torque.
The following conclusions can be drawn from the simulation analysis and prototype test. (1) The amplitude of synchronous torque changes periodically with the starting position of the motor, and the spatial period is inversely proportional to the order of the rotor harmonic magnetic field that generates torque. The rotor pitch is the least common multiple of the period. (2) The rotor axial staggered structure can reduce the rotor harmonic electromotive force, change the spatial periodicity of the output torque of the motor with certain slot combinations, and improve the minimum output torque. (3) Compared with the skewed rotor and the piecewise staggered rotor, the combined structure of the two has a better effect of weakening the synchronous parasitic torque. When the skewed distance of the dual skewed rotor is one tooth pitch, the minimum value of the starting torque ratio of the prototype is about 1.5 times, thus helping the normal starting of the motor with equal stator and rotor slot number. However, the partial magnetic flux leakage of the rotor may result in certain disadvantages. For example, it may increase no-load loss.
keywords：Axial piecewise staggered rotor, synchronous parasitic torque, torque fluctuation, slot combination, induction machine
DOI: 10.19595/j.cnki.1000-6753.tces.221534
中图分类号：TM343
国家自然科学基金（51977055）和安徽省科技重大专项（201903a05020042）资助项目。
收稿日期 2022-08-08
改稿日期 2022-09-01
徐 威 男，1994年生，博士，讲师，研究方向为电机电磁场分析与计算、电机优化设计、电机谐波磁场理论等。E-mail: xuwei@sdju.edu.cn（通信作者）
任晓明 男，1977年生，博士，副教授，研究方向为高电压技术、储能技术、工业控制及图像处理等。E-mail: renxm@sdju.edu.cn
（编辑 崔文静）