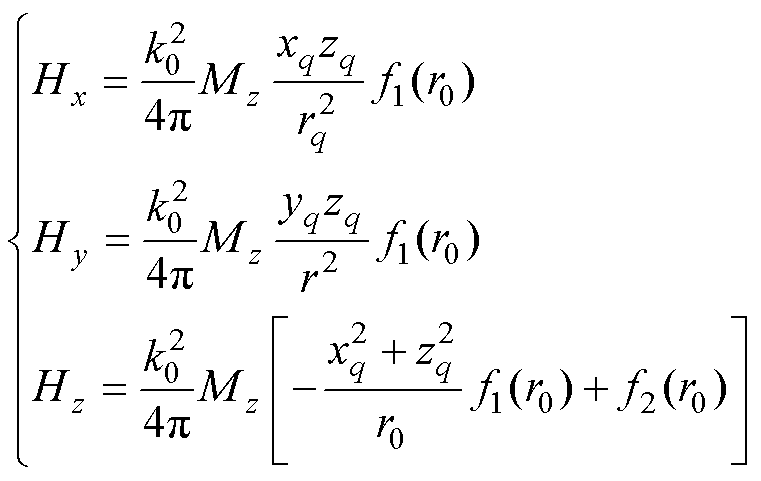 (1)
(1)
摘要 随着高开关频率的新型电力电子器件广泛应用到舰船等平台上的强电磁设备中,强电磁设备产生的低频辐射会对平台上的敏感设备产生严重的影响,因此必须对强电磁设备的低频辐射特性进行准确建模表征,支撑开展强电磁设备低频场分布特征的量化预测,以便提升整个平台的电磁兼容性能。传统等效偶极子法在对大尺寸辐射源进行等效建模时,存在偶极子阵列所需的等效偶极子源数量多,高度、位置选择困难等问题。为解决上述问题,该文提出一种基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模的方法。该方法从强电磁设备附近的近场辐射特性测试数据出发,将强电磁设备低频辐射等效为分布在多个区域的偶极子阵列组合的分布式辐射源,并通过自适应差分进化算法优化各区域偶极子阵列的数量、位置以及高度等等效源参数,并通过试验和算例验证该方法可在满足一定精度条件下,能大幅度减小偶极子数量,得到强电磁设备最优的低频分布式等效源模型。
关键词:低频辐射干扰 等效源法 三维磁偶极子阵列 自适应差分进化算法 近场数据
随着高频、高开关频率等新型电力电子器件在飞机、舰船等平台上新型强电磁设备上应用越来越广泛。由于半导体开关在进行开关状态变换时不可避免地引入与开关频率倍频、电力电子器件拓扑结构等因素相关的谐波电流,并叠加在一定频率的工作电流上,然后会在设备内部形成电流环路,进而产生低频电磁辐射,因此新型电力电子器件的广泛应用导致新型强电磁设备产生更加严重的低频电磁辐射,且产生的低频电磁辐射对平台监控、通信等敏感设备的影响越来越大,带来很多潜在的电磁兼容风险[1]。强电磁设备是指基于电磁原理工作的大功率、大电流和大体积的电气设备,如:永磁推进电机、发电机和变流装置等。为此,需要研究强电磁设备低频辐射特性的建模方法[2],进而开展飞机、舰船等平台的低频电磁环境准确量化分析,进一步对低频电磁干扰环境的控制进行支撑。
强电磁设备的辐射特性建模方法主要分为两类。一类是全波分析方法,该方法根据辐射源的电路拓扑得到电流路径计算电流,特别是共模电流,后在全波仿真软件根据实际辐射源的电磁参数建立仿真模型,以计算的电流作为激励源,仿真得到辐射源的辐射特性。A. Rosales等针对开关频率对电力驱动系统辐射场影响的研究需求,在三维全波仿真软件中建立了IGBT驱动器、电缆和永磁电机组成的驱动系统[3]。文献[4]为研究永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)驱动系统产生的电磁辐射干扰,建立了整个系统的有限元模型,将变流器输出的共模电流作为系统有限元模型的激励进行仿真计算。S. Shinde等利用DC-DC功率变换器的等效电路模型得到共模电流,再联合全波仿真软件,预测了DC-DC转换器和直流无刷电机做负载组成的系统的辐射场[5]。文献[6]为研究DC-DC变换器系统的电磁辐射,用高频电流回路双环模型替代该系统,并将其嵌入到印制电路板(Printed Circuit Board, PCB)上,在HFSS软件里进行了辐射特性仿真研究。上述均要求得到辐射源准确的电路拓扑、具体结构以及详细的电磁参数,而实际上复杂强电磁设备难以知道完整的辐射源建模信息,因此该类方法不适用于处理复杂强电磁设备辐射特性建模。
另一类是等效源方法,该方法是根据电磁场理论和近场数据建立辐射特性的等效模型,主要包括模式展开法[7]、积分方程法[8]、等效电/磁流法[9]以及等效偶极子法[10-19]。模式展开法和积分方程法原理类似,就是将辐射源等效为不同模式的波或一系列积分方程的叠加,模式展开法和积分方程法的局限性在于需要知道封闭面上的电磁场数据且封闭面必须包含辐射源[7-8];等效电/磁流法与等效偶极子法原理相近,但是等效偶极子法在得到辐射源等效阵列模型后,十分方便地和现有三维仿真软件进行联合仿真分析强电磁设备附近辐射特性。在根据等效偶极子法对PCB辐射源等效建模方面,Yu Zhenwei等学者为提高近场噪声耦合分析时的精确度,采用截断奇异值分解方法与正则化方法减小近场扫描误差带来的影响[10]。文献[11]针对估计噪声源与受扰天线之间的耦合问题,应用等效偶极子阵列建模,并利用互易理论进行耦合分析。Shu Yufei等采用人工神经网络解决了高速密集电路中干扰源和附近元件存在的多重反射导致集成电路干扰源建模时的偶极子模型不准确的问题[12]。为进一步提高等效偶极子阵列表征辐射源特性的准确性,文献[13]采用重复粒子群优化(Reduced Particle Swarm Optimization, RPSO)算法和迭代源重构算法相结合来解决。孔文杰为进一步提高PCB辐射源偶极子阵列建模的精确度,选取切向磁偶极子分量和法向电偶极子分量构成混合偶极子阵列,提升了建模的精确度[14]。此外,Zhao Yuan等针对PCB上宽频带辐射源建模,提出了一种由时域近场扫描数据得到时变等效偶极子阵列的方法[15]。
此外,等效偶极子法也能用于船舰等平台上的磁场建模。文献[16]研究了磁偶极子分布形式等参数的选取对舰船磁场重构的影响,提出了三种典型的磁偶极子阵列用于舰船磁场的反演建模。文献[17]针对舰船磁场建模的精度问题,以系数矩阵条件数为目标函数,采用模拟退火算法提高了偶极子阵列等效建模精度。戴中华等以建模精度和稳定性为目标,利用多目标粒子群优化算法得到合理的磁偶极子阵列模型[18]。针对卫星磁特性研究,文献[19]利用遗传算法建立了多磁偶极子模型。但是,当将等效偶极子模型应用到舰船等平台上的强电磁设备等效建模时,满足一定精度时存在等效源偶极子数量膨胀,等效偶极阵列分布方式、距离强电磁设备的高度等参数严重影响等效源建模精度等问题。
为此,本文针对上述问题,提出一种基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模方法,根据近场数据将强电磁设备低频辐射等效为分布在多个区域的偶极子阵列组合的分布式辐射源。该方法可在不知道强电磁设备具体结构和电路拓扑结果时得到辐射特性的高精度等效模型,同时可将等效偶极子阵列优化模型导入仿真软件中,得到强电磁设备附近辐射特性。该方法首先通过测量得到近场幅值和相位信息,再通过幅值信息将整个磁偶极子阵列组合按照一定的磁场强度划分为几个区域,再通过自适应差分进化算法确定各区域磁偶极子的数量、位置以及磁偶极子阵列的高度。最后,通过试验和算例验证本方法的准确性和可靠性。
强电磁设备低频辐射特性等效建模是利用磁偶极子构成分布式等效辐射源对强电磁设备的低频辐射特性进行等效表征。z方向磁偶极子(xq, yq, zq)与其辐射场任意一点(xp, yp, zp)的磁场之间的关系为
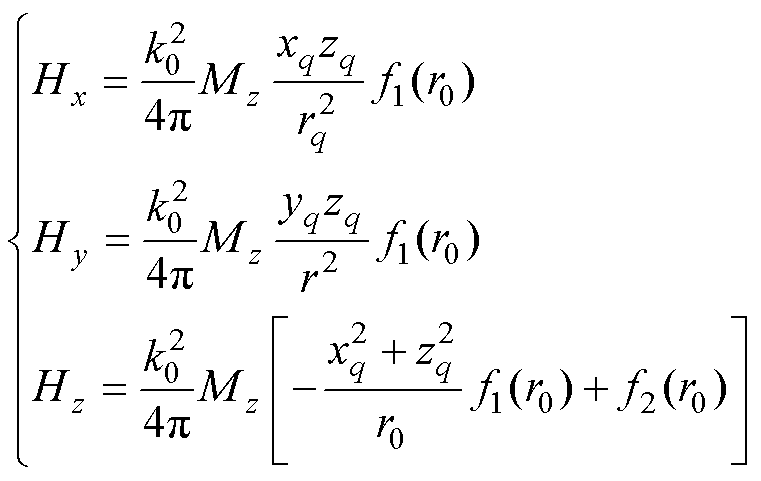 (1)
(1)
式中,Mz为z方向磁偶极子的磁偶极矩;Hx、Hy和Hz分别为x、y和z方向的磁场强度分量;k0为自由空间常数;r0为磁偶极子和其辐射场任意一点的距离。f1(r0)、f2(r0)、r0分别为
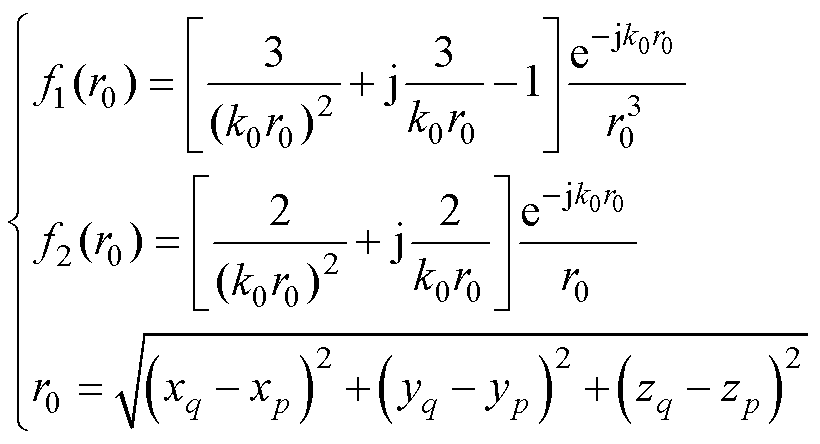 (2)
(2)
式中,j为虚部单位。磁偶极矩Mx、My与磁场之间的关系可以由式(1)利用直角坐标系各分量的对称性推导出来[13]。鉴于篇幅长度,在此不赘述。
对强电磁设备进行低频辐射特性等效建模时,考虑到建模方法和应用对象的普适性,本文以三维结构的偶极子阵列模型为例进行讨论。
三维结构的偶极子阵列模型是利用不同平面上的近场测量数据建立等效辐射源三维模型。本节以利用两个测量平面上的近场数据建立辐射源等效模型为例,其中,近场测量平面和偶极子阵列均包含两个面,位置如图1所示。
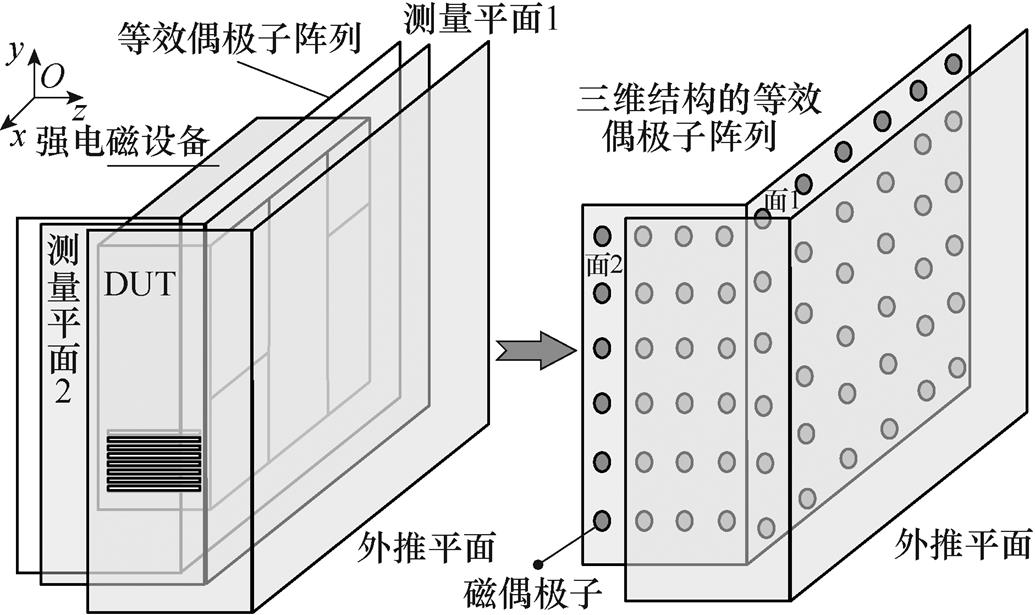
图1 辐射特性的等效偶极子法建模示意图
Fig.1 Schematic diagram of equivalent dipole method modeling of radiation characteristics
假设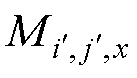 、
、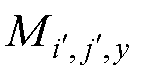 和
和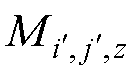 分别是偶极子阵列第
分别是偶极子阵列第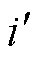 个面中第
个面中第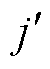 个磁偶极子的磁偶极矩x、y和z分量,
个磁偶极子的磁偶极矩x、y和z分量,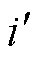 =1, 2,×××,
=1, 2,×××,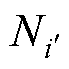 ,其中
,其中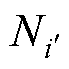 是偶极子平面的数量,故此时
是偶极子平面的数量,故此时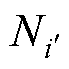 =2;
=2;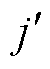 =1, 2,×××,
=1, 2,×××, 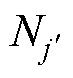 ,其中
,其中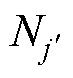 是各偶极子平面中磁偶极子的数量;Hi,j,x、Hi,j,y和Hi,j,z是近场平面第i个面中第j个测量点的磁场强度x、y和z分量,i=1, 2,j=1, 2,×××, Nj,则有
是各偶极子平面中磁偶极子的数量;Hi,j,x、Hi,j,y和Hi,j,z是近场平面第i个面中第j个测量点的磁场强度x、y和z分量,i=1, 2,j=1, 2,×××, Nj,则有
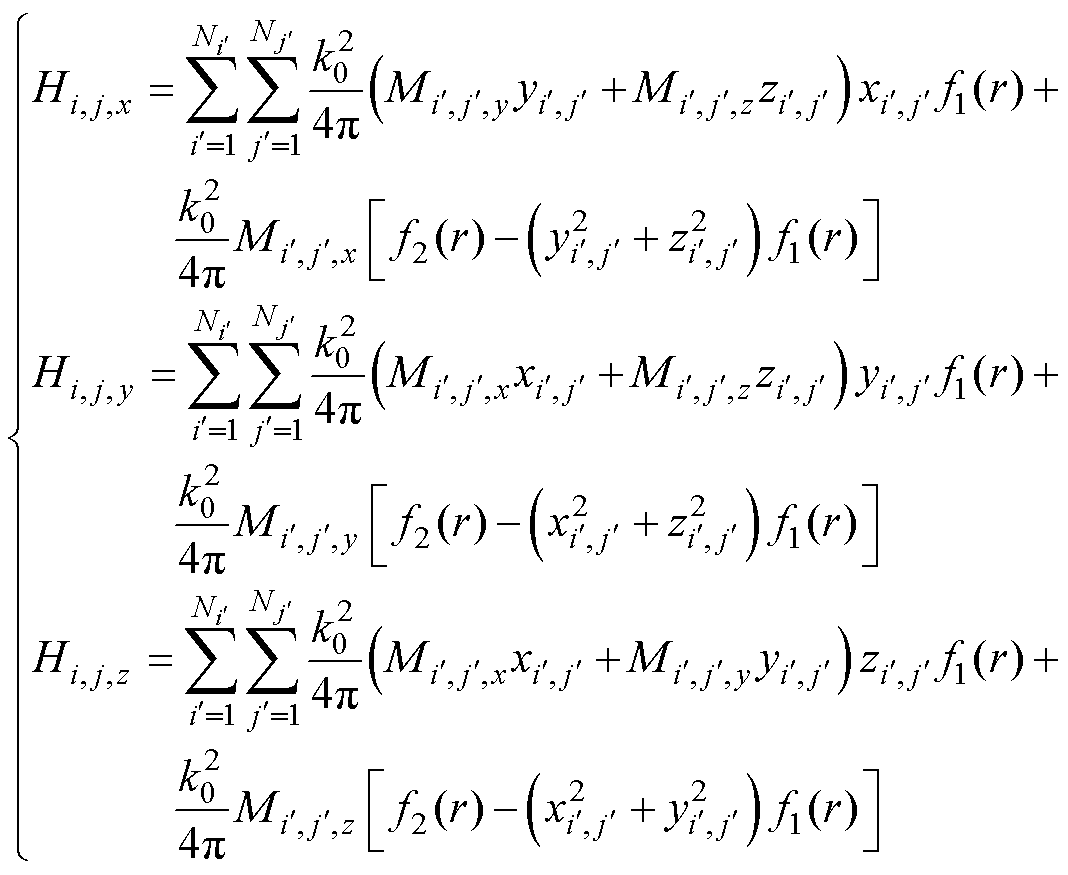 (3)
(3)
其中,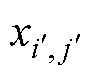 、
、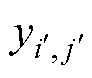 和
和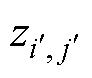 的表达式分别为
的表达式分别为
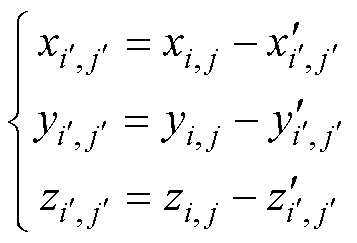 (4)
(4)
r为位置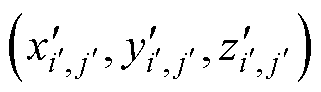 处的磁偶极子和测量点
处的磁偶极子和测量点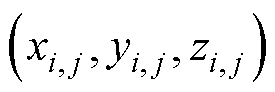 的距离,此处每个磁偶极子的位置是在各自区域里随机选取的。
的距离,此处每个磁偶极子的位置是在各自区域里随机选取的。
由于每个磁偶极子的磁偶极矩为未知量,因此将式(3)转化为一个矩阵方程便于求解,即
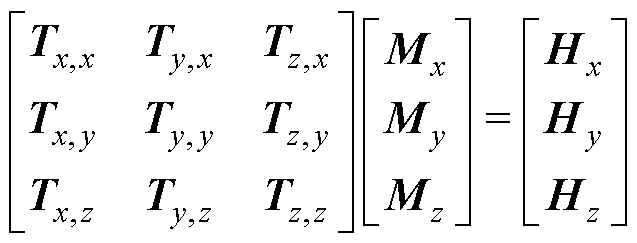 (5)
(5)
式中,Tx,x、Ty,x、Tz,x分别为磁偶极子x、y、z分量的磁偶极矩和测量数据Hx之间的转换系数矩阵;Mx、My和Mz为待求的磁偶极子阵列中磁偶极子各分量的磁偶极矩;等式右侧Hx、Hy和Hz是近场测量点磁场在x、y、z方向的磁场值。
在式(5)中,磁偶极矩M是未知量,磁场测量值H是已知量,转换系数矩阵T可以由式(3)得到,其中,Tx,x、Ty,x、Tz,x、Tx,y、Ty,y、Tz,y、Tx,z、Ty,z、Tz,z的计算公式为
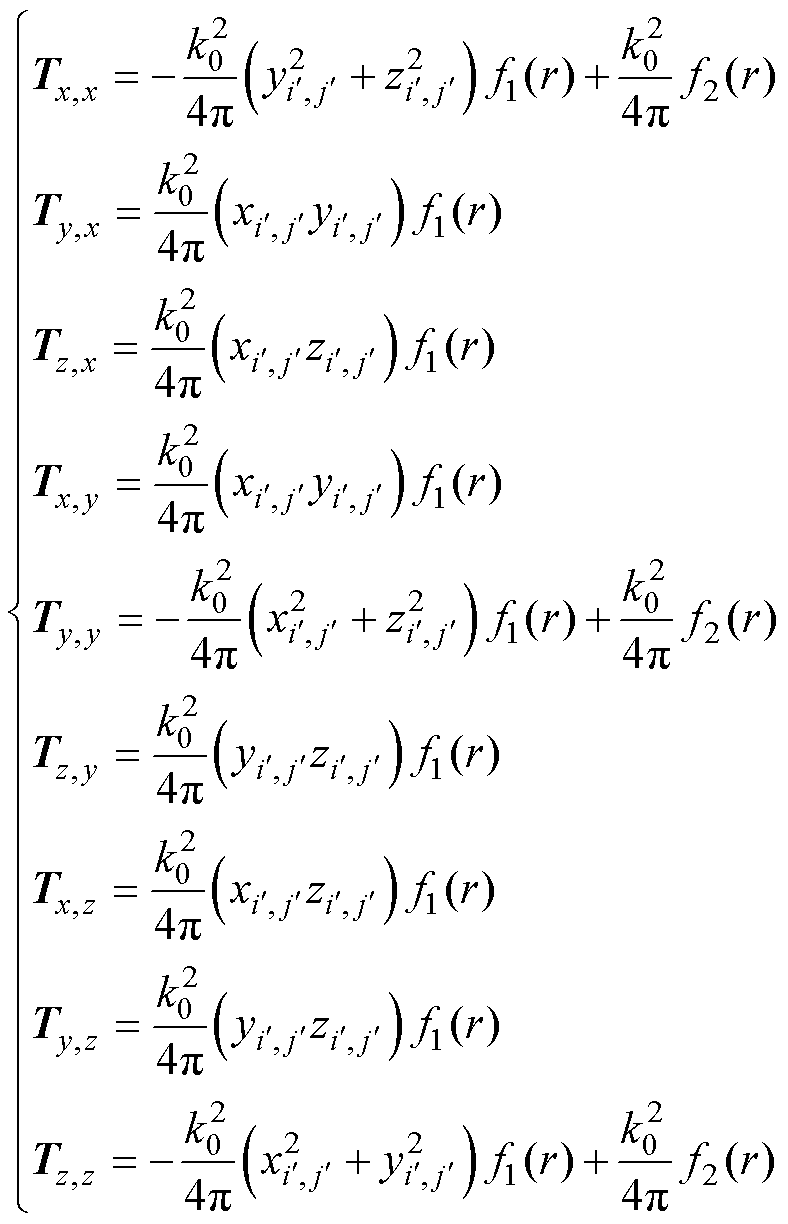 (6)
(6)
由式(3)、式(5)和式(6)可知,磁偶极子阵列中每个磁偶极子的x、y、z坐标(即磁偶极子的分布以及阵列的位置)以及磁偶极子的数量都会影响辐射特性的建模结果。
2.2.1 自适应差分进化算法基本原理
自适应差分进化(Adaptive Differential Evolution with Optional External Archive, JADE)算法的基本原理和差分进化算法一致,通过变异、交叉和选择操作,一次次迭代寻找到最优解。
JADE在每一次变异和交叉操作中,每个个体都产生服从正态分布的交叉概率因子CR和服从柯西分布的缩放因子F,分别储存于集合SCR和集合SF,最后取均值按照指定公式产生更新CR和F。另外通过引入可选的外部存档种群A和一种新的变异策略,A在迭代过程中记录成功参与选择操作的个体。以上操作提高了算法的收敛速度、全局寻优能力以及高维问题求解能力。
本文将自适应差分进化算法引入强电磁设备低频辐射特性等效建模优化中,涉及的待优化量包括各区域磁偶极子的位置、数量,以及阵列的高度等。
2.2.2 磁偶极子阵列建模优化
为了减少磁偶极子阵列偶极子单元的数量,根据近场数据将强电磁设备低频辐射等效为分布在多个区域的偶极子阵列组合的分布式辐射源,首先利用近场幅值数据将偶极子阵列按照一定的磁场强度划分为几个区域。不失一般性,本文按照式(7)以划分A、B和C三个区域为例进行讨论。
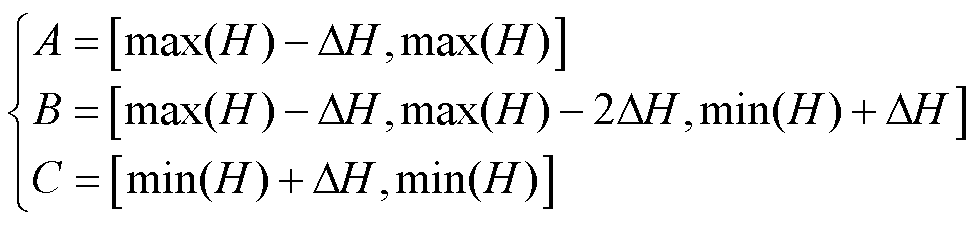 (7)
(7)
式中,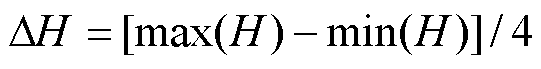 ;H为磁场强度的测量值。
;H为磁场强度的测量值。
本文结合JADE算法[20],给出了一种基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模方法,如图2所示,其计算步骤如下:
(1)初始化种群,并计算初始种群的适应度值。设置种群数量为NP,且每个种群的规模为N= N1+N2,即磁偶极子的总数,其中N1和N2分别是磁偶极子阵列中面1和面2偶极子的总数,种群中个体为一个维数D=18的行向量。
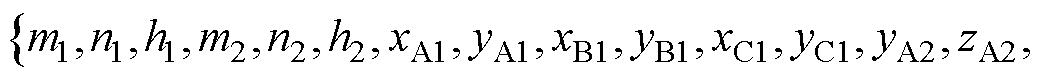
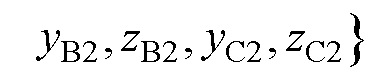 (8)
(8)
式中,m1和m2分别为磁偶极子阵列面1和面2中A区域的偶极子数量;n1和n2分别为磁偶极子阵列面1和面2中B区域的偶极子数量;h1和h2为磁偶极子阵列平面的高度;xA1、yA1、xB1、yB1、xC1和yC1为面1区域A、B和C中磁偶极子的x和y坐标;yA2、zA2、yB2、zB2、yC2和zC2为面2区域A、B和C中磁偶极子的y和z坐标。
以式(9)适应度函数表达式作为相对误差,即
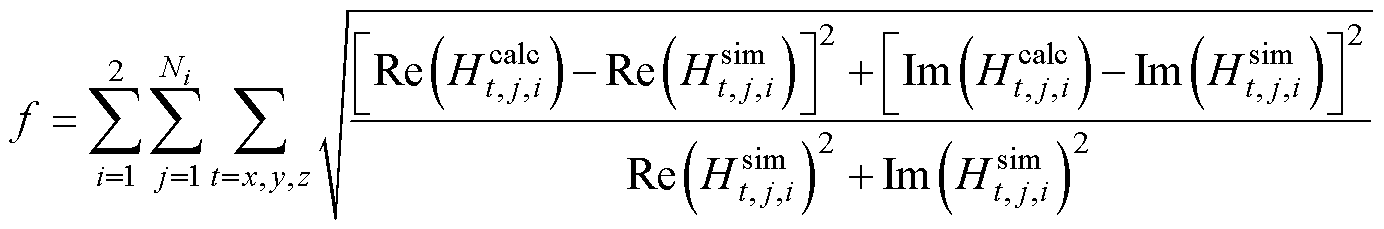 (9)
(9)
式中,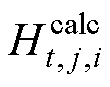 为偶极子阵列等效模型计算得到的磁场强度;
为偶极子阵列等效模型计算得到的磁场强度;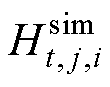 为已知的磁场强度;Re(×)为取磁场数据的实部;Im(×)是取磁场数据的虚部。
为已知的磁场强度;Re(×)为取磁场数据的实部;Im(×)是取磁场数据的虚部。
(2)计算第G代种群中第i个种群的CRi和Fi。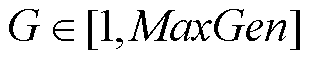 ,其中MaxGen是最大迭代次数,CRi服从正态分布,Fi服从柯西分布[19],计算公式分别为
,其中MaxGen是最大迭代次数,CRi服从正态分布,Fi服从柯西分布[19],计算公式分别为
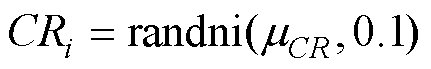 (10)
(10)
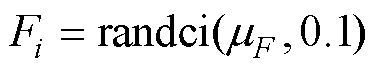 (11)
(11)
(3)进行变异、交叉和选择操作。计算公式依次为式(12)~式(14)。
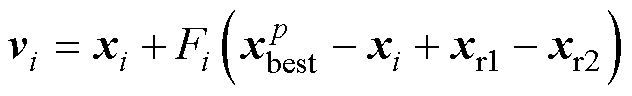 (12)
(12)
式中,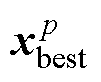 为从当前NP个种群适应度值的前100p%个种群中随机选择一个种群;xr1是从当前NP个种群中随机选择;xr2是从当前NP个种群和存档种群A的并集中随机选择,满足
为从当前NP个种群适应度值的前100p%个种群中随机选择一个种群;xr1是从当前NP个种群中随机选择;xr2是从当前NP个种群和存档种群A的并集中随机选择,满足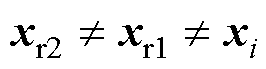 。
。
本节中选择操作是认为适应度值小时为更优解。
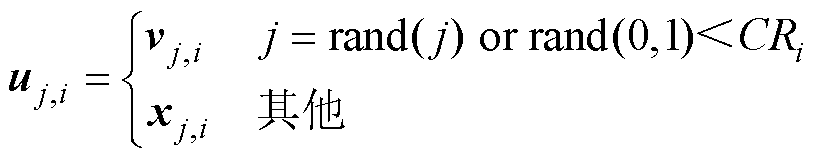
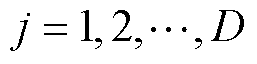 (13)
(13)
即式(14)是对第G代时种群中第i个个体的第j维操作的。
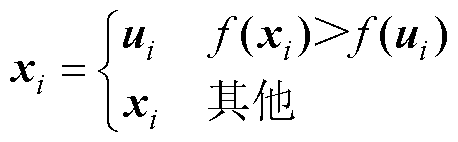 (14)
(14)
其中,满足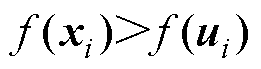 时,将
时,将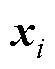 存储在外部存档种群A,与
存储在外部存档种群A,与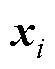 对应的CRi和Fi分别存储在SCR和SF中。
对应的CRi和Fi分别存储在SCR和SF中。
(4)更新外部存档种群A、mCR和mF。判断外部存档种群A的个体数量是否大于N,大于N则随机移除个体使其规模不大于N。最后更新mCR和mF,公式为
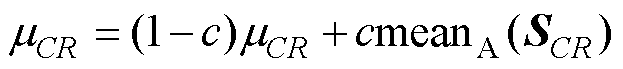 (15)
(15)
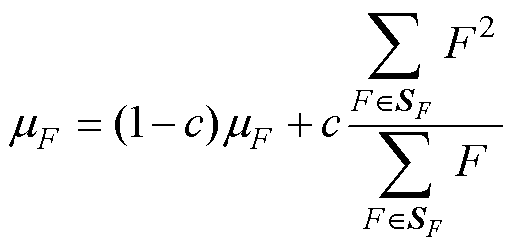 (16)
(16)
式中,c为控制因子,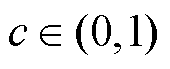 ;
;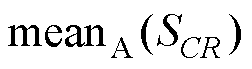 为集合SCR元素的均值。
为集合SCR元素的均值。
(5)判断群体最优适应度值是否满足预设的迭代停止条件。
基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模方法的流程如图2所示。
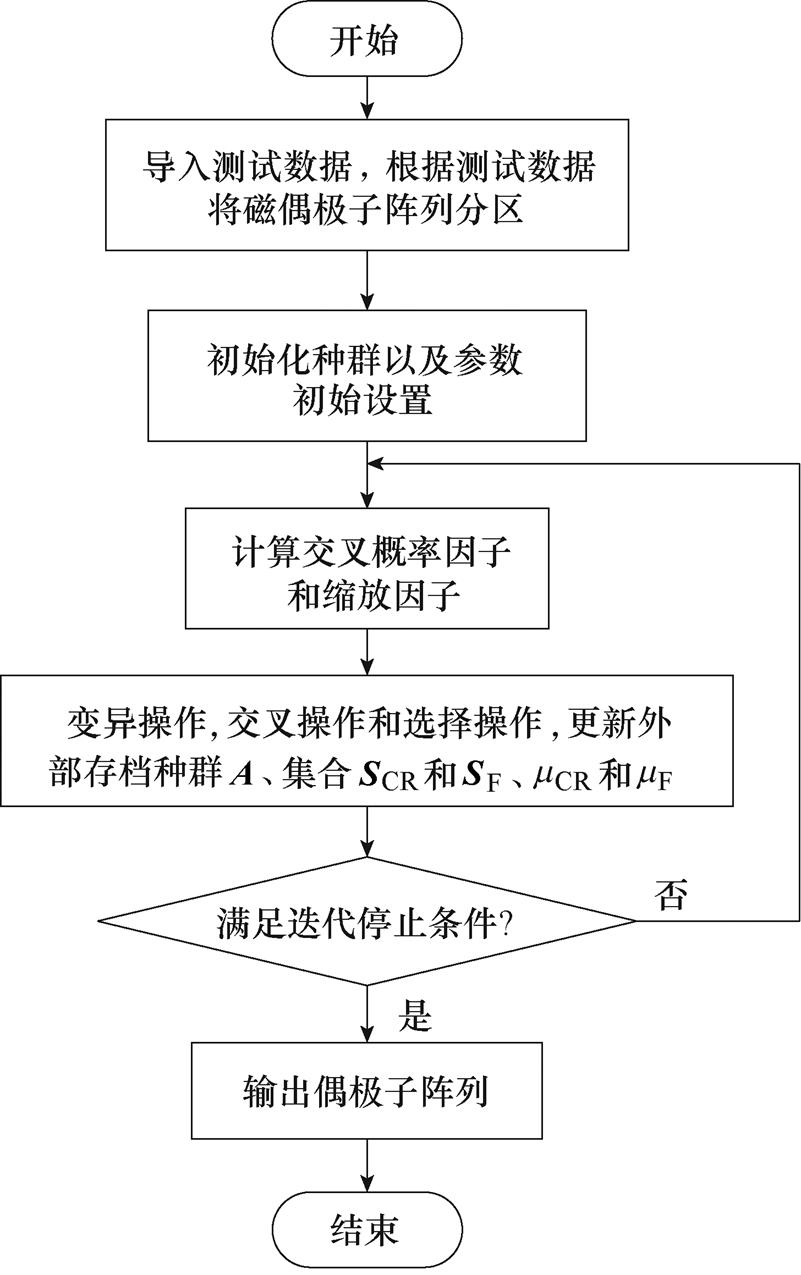
图2 基于自适应差分进化算法的等效偶极子法流程
Fig.2 Flow chart of the equivalent dipoles method based on JADE
在图2所示的建模流程中,每迭代一次就会求解一次式(5)。而在求解式(5)的过程中,转换系数矩阵T由于其条件数很大,是一个高度病态的矩阵。
本文通过最小二乘法和吉洪诺夫正则化来进行病态矩阵的计算。吉洪诺夫正则化是通过增加一个正则化参数,来修正待求解量的误差,使病态矩阵的求解结果为一个稳定的近似解。
式(5)可以简写为
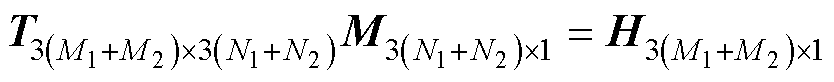 (17)
(17)
式中,M1和M2分别为已知磁场平面中各面的数据点总数;N1和N2分别为偶极子阵列中各面的偶极子总数。
结合吉洪诺夫正则化的最小二乘法的形式为
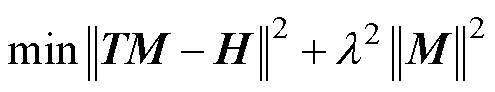 (18)
(18)
式中,l 为正则化系数,是一个未知量。一个合适的正则化系数l 可以保证待求解量M尽量接近真实值。通过吉洪诺夫正则化求解病态矩阵的解为
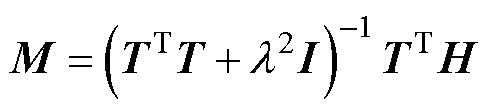 (19)
(19)
式中,I为3(N1+N2)×3(N1+N2)的单位矩阵。
常用的两种正则化参数求解方法是广义交叉验证法(Generalized Cross Validation, GCV)[13]和L-Curve法[13]。由于GCV不需要知道关于误差的先验信息,并且具有很强的适应性,本文采用GCV来求解正则化参数l。GCV的原理就是将已知量H分为两部分:一部分求近似解;另一部分验证该近似解,从而得到一个合适的正则化参数。得到正则化参数后就可以根据式(19)得到式(5)方程的解。
针对第2节提出的基于自适应差分进化算法的强电磁设备低频辐射特性的偶极子阵列建模优化方法,本节用试验和算例来验证,验证内容包含磁场幅值和相位分布以及长距离测量线上测量点的磁场。
3.1.1 试验验证
为了模拟设备的低频磁场辐射,本文选择信号频率为60 Hz、峰-峰值为2 V的低频正弦波信号,信号经频率特性模块通入低频环形天线后,在天线中会产生一定强度的电流,从而对外产生低频辐射,低频环形天线置于铝制外壳中作为低频辐射源,外壳开有孔缝。试验现场如图3所示。
利用磁通门以及电网磁效应测量系统测量辐射源周围的低频近场数据,在被测设备的7.5 cm处和12.5 cm处测得两个长85 cm和宽100 cm大小的面的磁场,设定长度的范围为-35~50 cm,宽度的范围为-50~50 cm。测量示意图如图4所示。

图3 试验现场
Fig.3 Test site
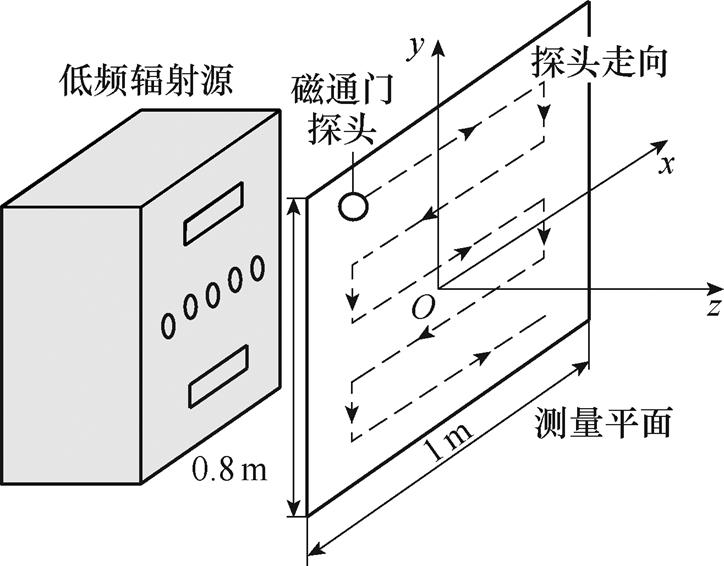
图4 测量示意图
Fig.4 Demonstration of the measurement
以7.5 cm处的平面为测量平面,以12.5 cm处的平面为外推平面,每个平面间隔5 cm取一个测量点,故有378个测量点。12.5 cm的磁场分布如图5所示。
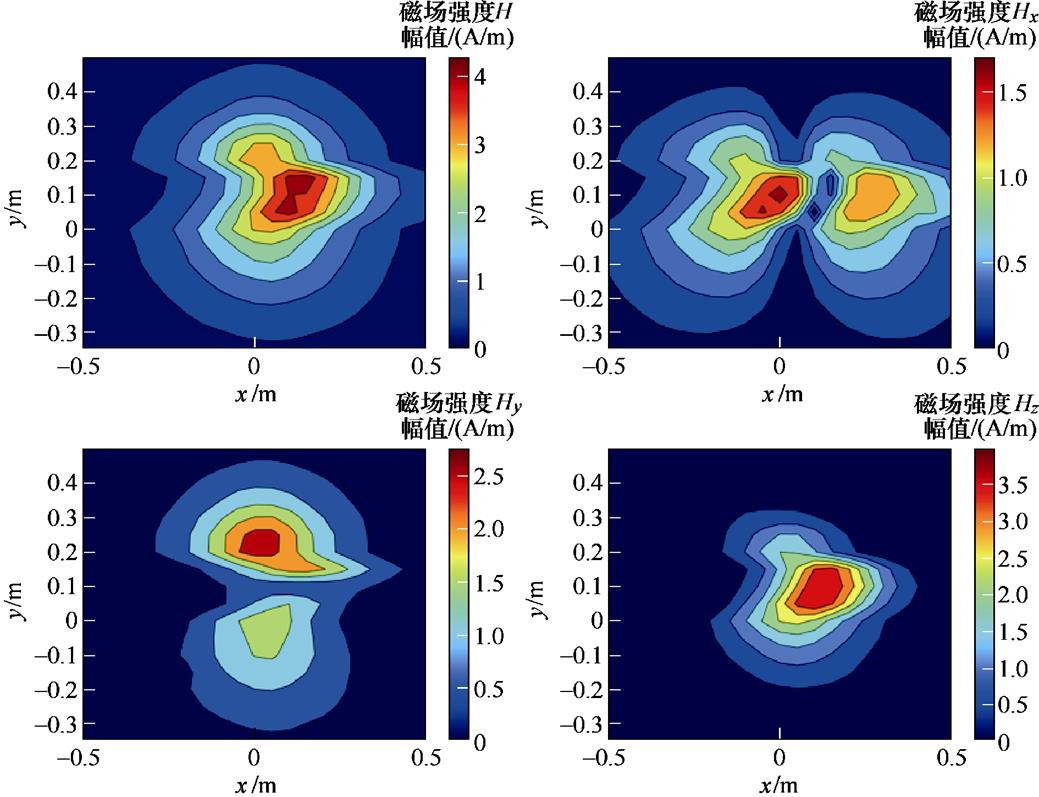
图5 12.5 cm处测量磁场的幅值分布
Fig.5 Amplitude distribution of the measured magnetic field at 12.5 cm
在基于自适应差分进化算法的强电磁设备低频辐射特性的偶极子阵列建模方法中,设置磁偶极子数量为18,p=0.2,初始交叉概率因子mCR=0.5,初始缩放因子mF=0.5,控制因子c=0.1,当种群最优适应度值小于0.2时,迭代停止。
利用JADE算法优化后的偶极子阵列平面距被测设备4.3 cm,磁偶极子阵列得到的外推平面的磁场幅值分布如图6所示。
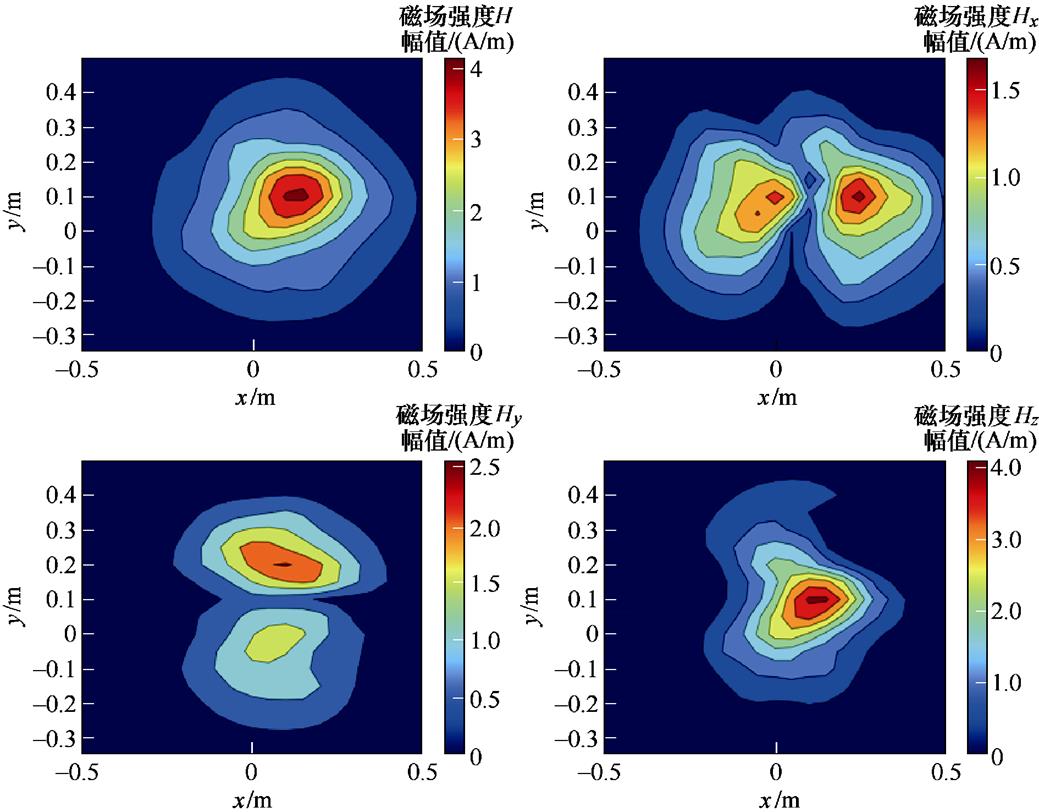
图6 等效偶极子阵列计算出的12.5 cm处磁场幅值分布
Fig.6 The distribution of the magnetic amplitude at 12.5 cm calculated by the equivalent dipole array
根据式(9)得到的磁场幅值的相对误差见表1。
表1 等效偶极子阵列得到的磁场幅值相对误差
Tab.1 Relativeerrors of magnetic field amplitudes obtained by equivalent dipole arrays

磁场强度分量幅值误差(%) Hx23.16 Hy22.74 Hz17.06 H19.11
选择40个点进行相位结果对比,相位对比结果和相对误差分别如图7和图8所示。
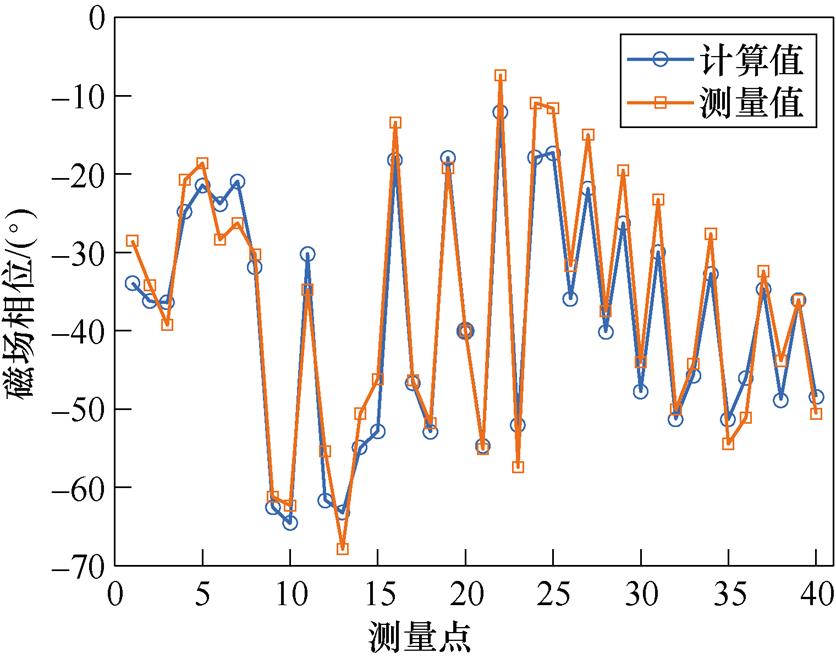
图7 测量点的测量值和计算值的相位对比
Fig.7 Phase comparison of measured and calculated values at the measuring points
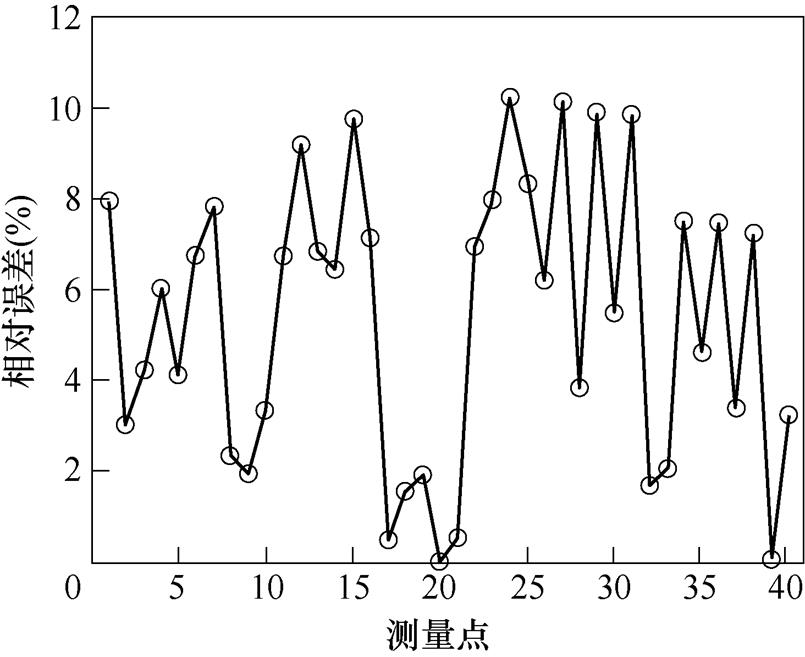
图8 测量点测量值和计算值的相对误差
Fig.8 Relative error of the measured and calculated values at the measuring point
图7中每个点相位的测量值和计算值的相对误差基本都在10%以下,同时结合幅值分布来看,试验测量结果和等效模型计算结果吻合度很好,说明本文的方法可以准确地对强电磁设备低频辐射特性进行等效。
3.1.2 强电磁设备机柜辐射特性建模验证
进一步对基于自适应差分进化算法的强电磁设备低频辐射特性的偶极子阵列建模方法进行验证。首先在仿真软件Maxwell 3D里建立某强电磁设备及其机柜模型。如图9所示,无侧边开缝机柜模型的长×宽×高为1.70 m×1.10 m×2.24 m,由三个小机柜构成,其中布置有一个线圈,用作低频辐射源,线圈流过的电流为1 kA,匝数为15,设置仿真频率为60 Hz。
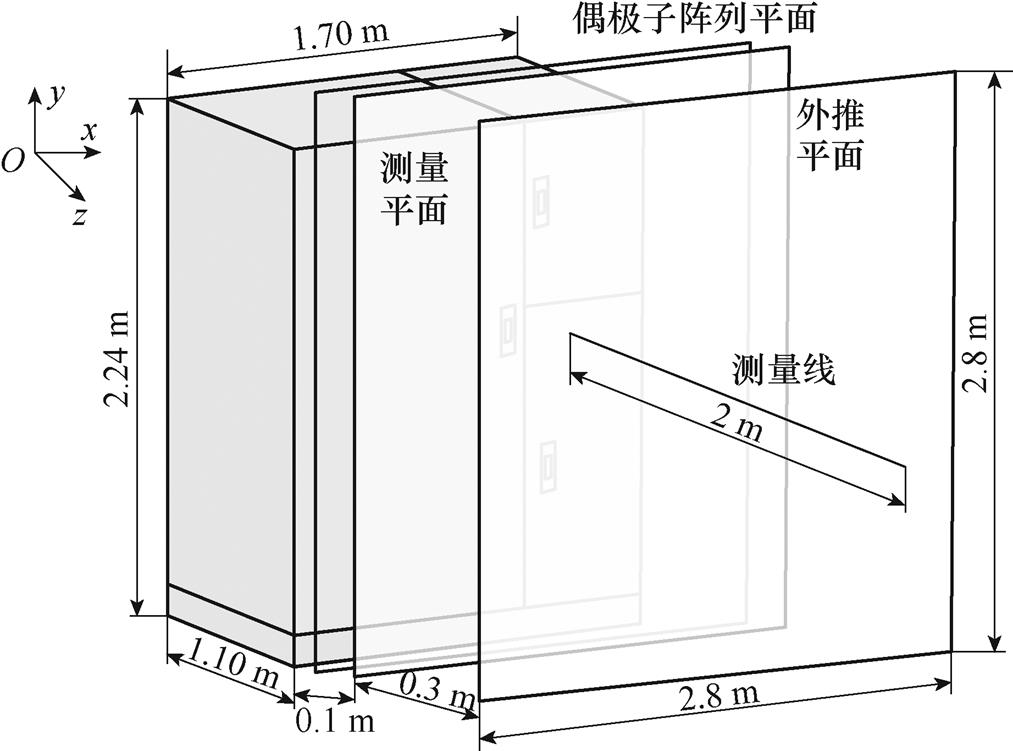
图9 无侧边开缝的机柜模型
Fig.9 Electronic cabinet model without side slits
选择磁偶极子阵列平面、测量平面和外推平面地大小均为2.8 m×2.8 m;测量平面和外推平面分别距离机柜0.1 m和0.4 m,两个平面均间隔4 cm取一个测量点,故各平面有5 041个点。通过Maxwell 3D仿真得到的外推平面磁场分布如图10所示。
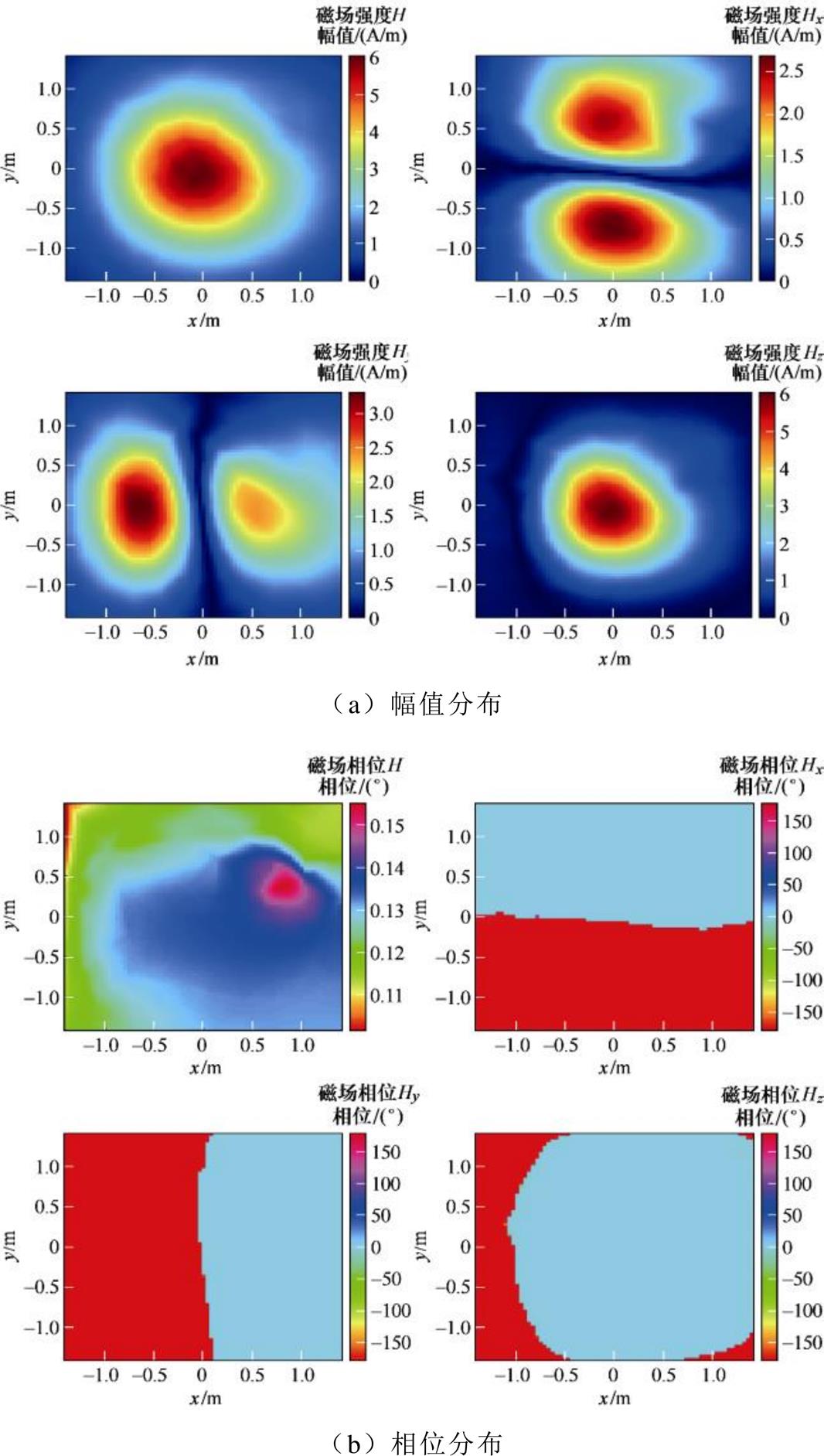
图10 等效模型计算得到的磁场分布
Fig.10 The distribution of the magnetic fieldcalculated by the equivalent model
为验证基于自适应差分进化算法的等效偶极子法在减少磁偶极子数量、选择最优阵列参数以及提高等效精度等方面的效果,现用18个磁偶极子组成阵列进行等效建模。JADE算法参数设置:p=0.2,μCR=0.5,μF=0.5,c=0.1,当最优适应度值小于0.03时,迭代停止。
利用2.2.2节的优化方法可得最优磁偶极子分布如图11所示,其中3.683 5和9.580 9是各自等位线上的磁场大小,A、B、C区域分别分布了10、5、3个磁偶极子,优化得到磁偶极子阵列最佳的位置是距被测设备表面0.04 m处。

图11 磁偶极子的分布
Fig.11 The distribution of magnetic dipoles
由磁偶极子阵列计算得到的外推平面磁场分布如图12所示。从图中可知,基于优化后的偶极子阵列模型得到的磁场幅值分布和相位分布与Maxwell 3D有限元仿真结果基本一致。
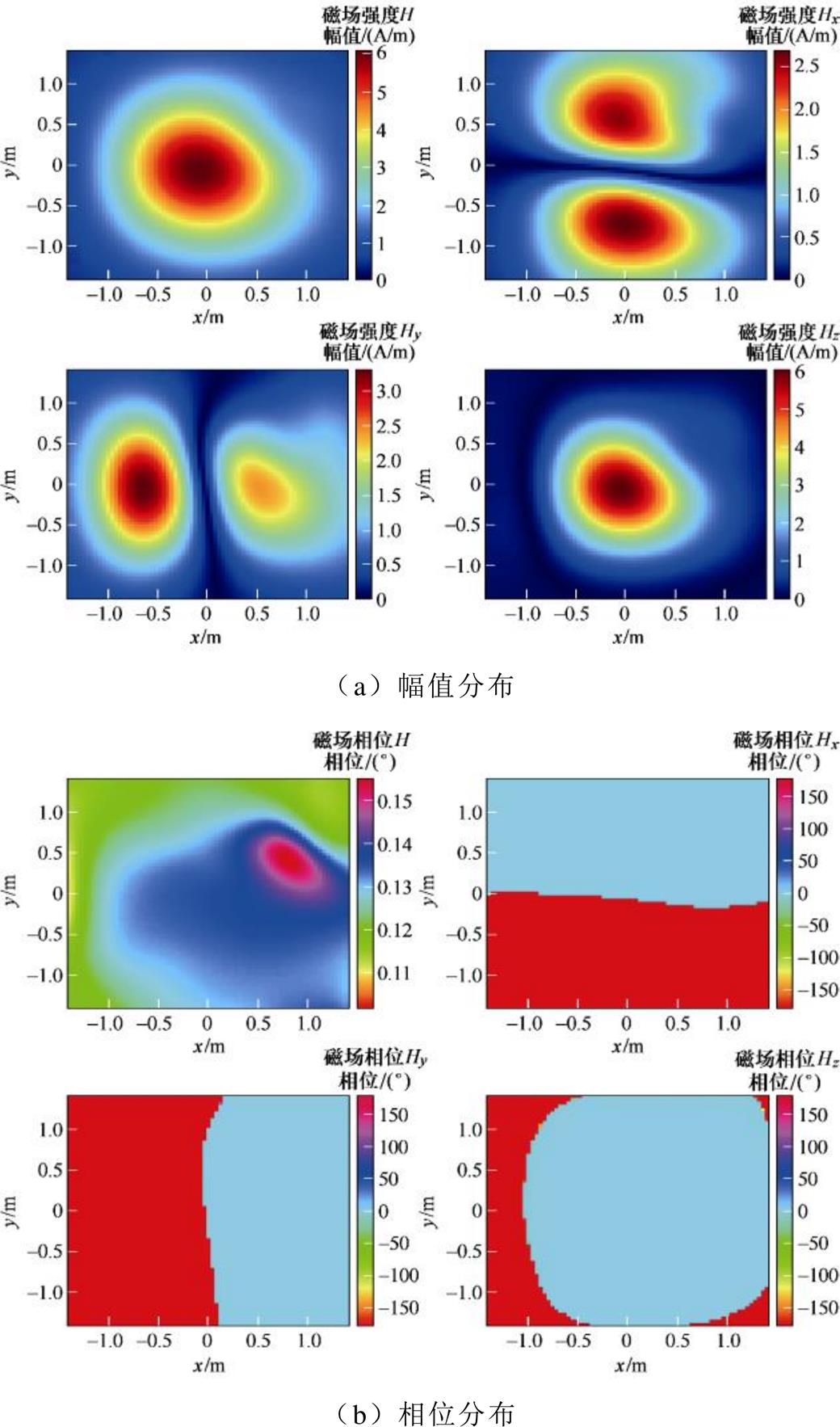
图12 等效偶极子阵列计算出的磁场分布
Fig.12 The distribution of magnetic field calculated by the equivalent dipole array
进一步对均匀分布磁偶极子阵列和优化的磁偶极子阵列的偶极子数量、建模精度和建模效率等进行了比较,见表2。表2中,sH、sHx、sHy和sHz依次是磁场各分量的幅值的相对误差。
表2 算例1中两种磁偶极子阵列等效对比结果
Tab.2 Comparison of results of two magnetic dipole arrays in example 1
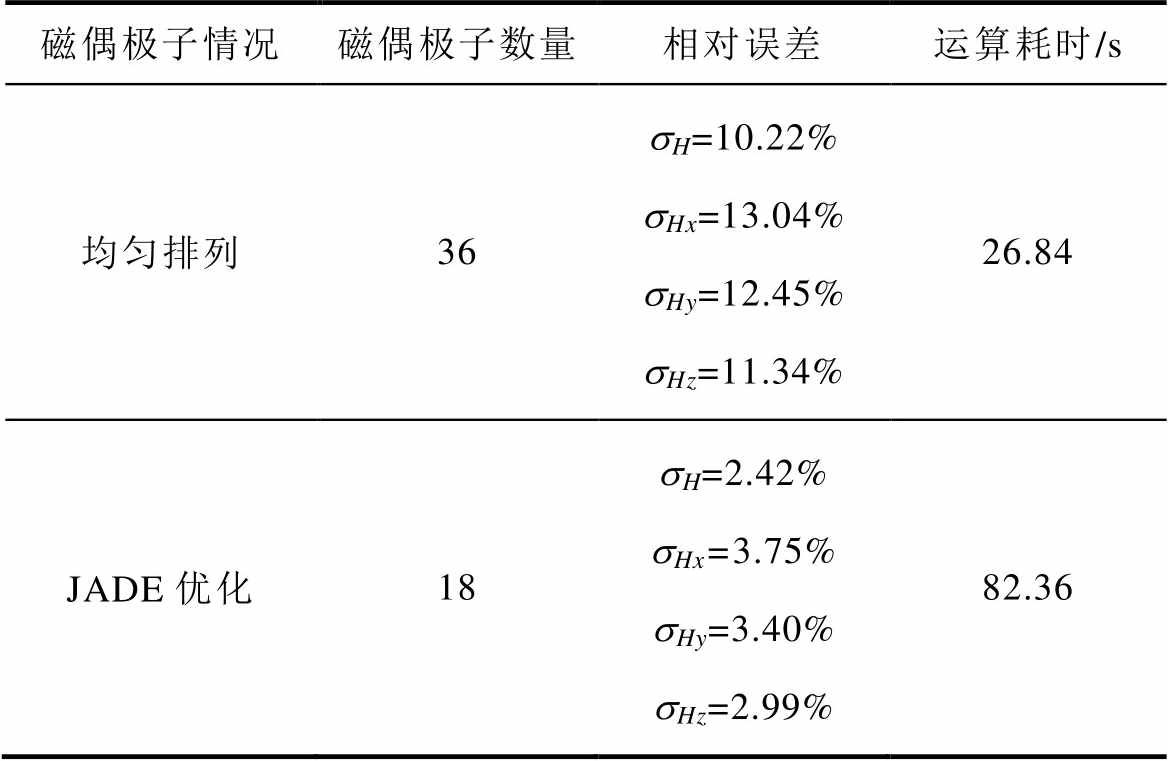
磁偶极子情况磁偶极子数量相对误差运算耗时/s 均匀排列36sH=10.22%sHx=13.04%sHy=12.45%sHz=11.34%26.84 JADE优化18sH=2.42%sHx=3.75%sHy=3.40%sHz=2.99%82.36
另外,由表2得到在减小一半偶极子数量的前提下,等效精度大大提高。同时,基于JADE方法的偶极子阵列法需要耗时82.36 s,比均匀排列时的计算耗时略长,这是因为在优化过程中需要多次计算得到磁偶极子阵列,而均匀排列的磁偶极子阵列的结果是在相同阵列高度时计算一次得到。
最后在垂直于电子机柜表面正中心的位置,沿z轴方向选择一条2 m长的测量线,起点位置在距表面正中心3 m处,间隔0.05 m测量一个点,测量线位置图9所示。将仿真值与磁偶极子阵列得到的计算值进行对比如图13所示。
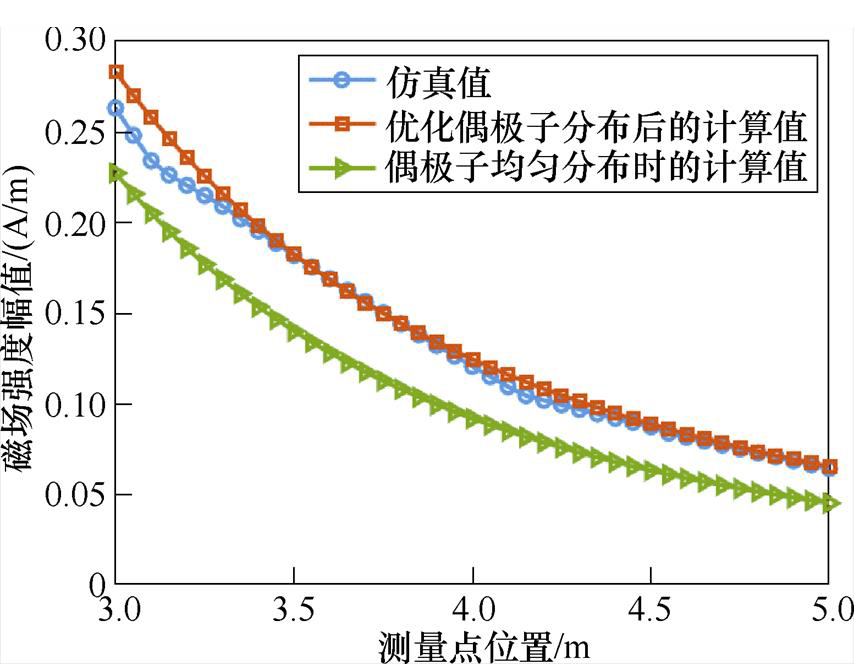
图13 算例1中测量线上仿真值与计算值的对比
Fig.13 Comparison of simulated and computed values on the measurement line in example 1
测量线上各点的仿真值和优化偶极子分布后得到的计算值的相对误差均在10%以下,因此基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模方法在开展远距离低频磁场预测时,也能很好地保证精度。
3.1.3 多相永磁推进电机低频辐射特性等效建模验证
通过对多相永磁同步电机的低频辐射特性建模来验证本文提出的基于自适应差分进化算法的强电磁设备低频辐射特性的偶极子阵列建模方法。首先在Maxwell 3D中建立十二相永磁同步电机的仿真模型,如图14所示。电机定子布置4套三相绕组,它们相位依次相差15°电角度,电流幅值为10 A。
图14 十二相永磁同步电机模型
Fig.14 Model of the twelve-phase permanent magnet synchronous motor
选择磁偶极子阵列平面、测量平面和外推平面的大小均为2 m×2 m;测量平面和外推平面分别距离电机0.2 m和0.8 m,两个平面均间隔3 cm取一个测量点,故各平面有4 489个点。通过Maxwell 3D仿真得到的外推平面磁场分布如图15所示。
在基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模方法中,本案例中JADE参数的设置与3.1.2节保持一致,当适应度值(总体相对误差)满足小于0.08时,循环停止。
为验证基于自适应差分进化算法的等效偶极子法在减少磁偶极子数量、选择最优阵列参数以及提高等效精度等方面的效果,将磁偶极子数量减少一半,即18个磁偶极子,由算法得到的磁偶极子最优分布如图16所示。A、B、C区域分别分布了9、5、4个磁偶极子,优化得到磁偶极子阵列最佳的位置是距被测设备表面0.137 m处。
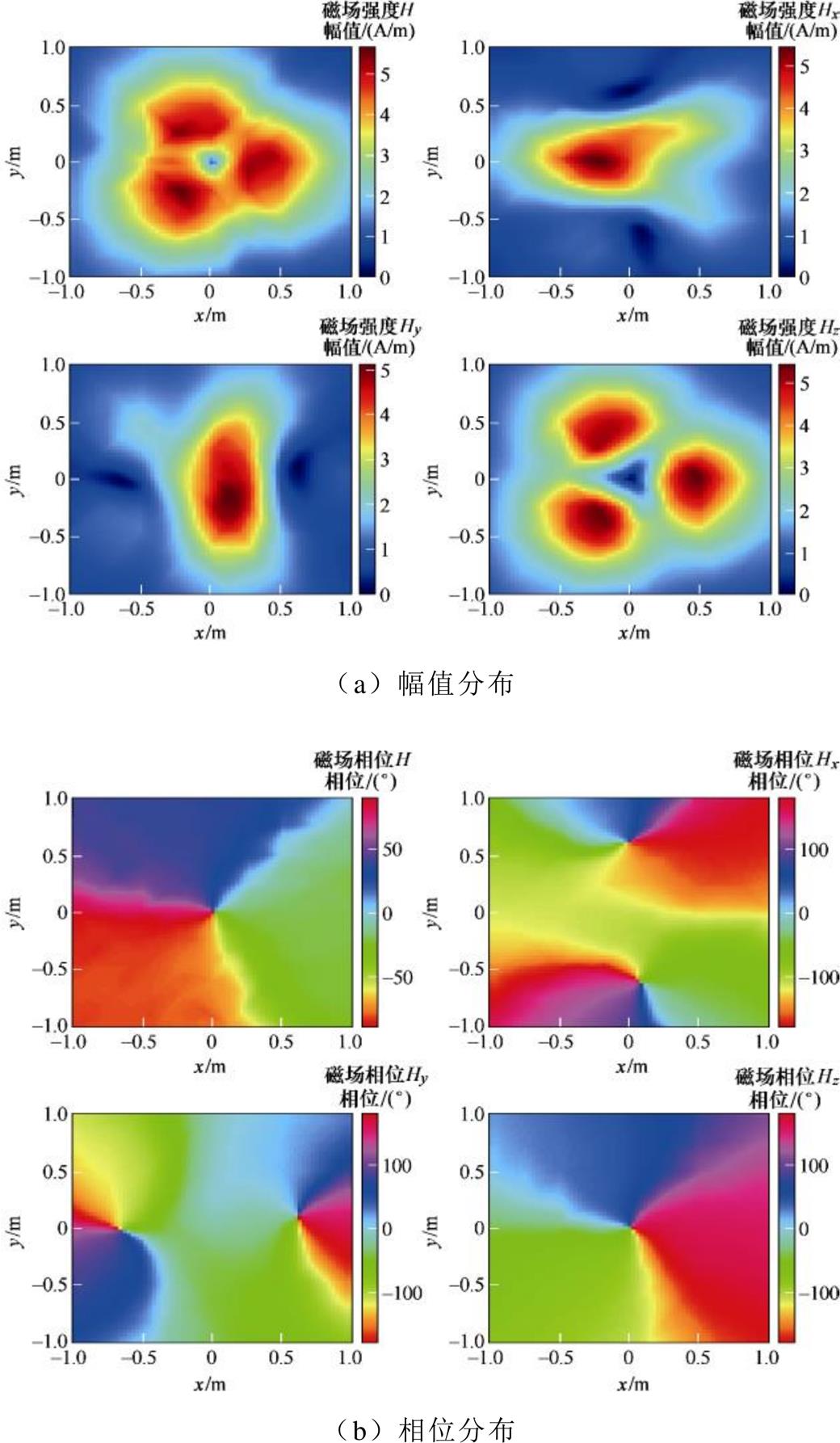
图15 算例2中等效模型计算得到的磁场分布
Fig.15 The distribution of the magnetic field calculated by the equivalent model in example 2
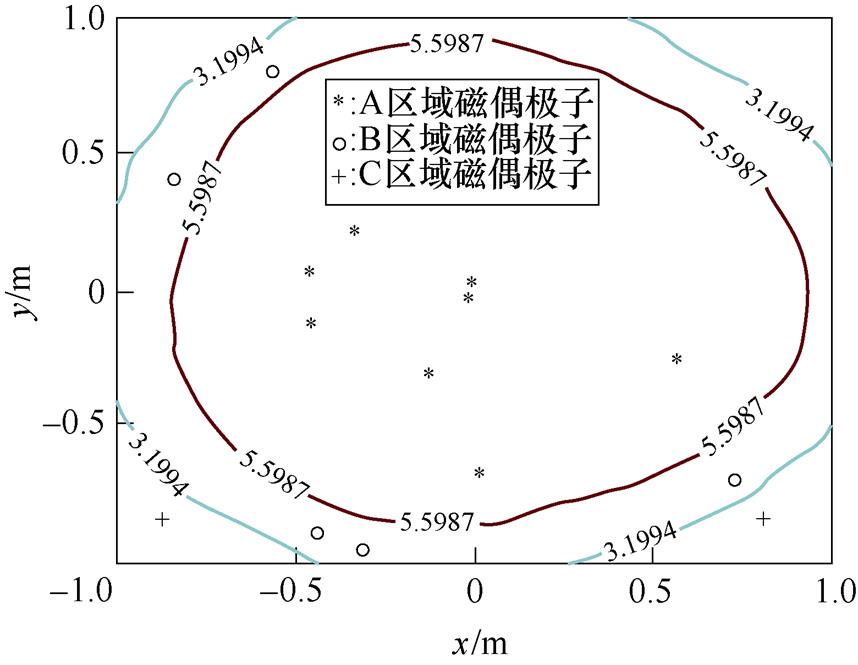
图16 算例2中磁偶极子的分布
Fig.16 The distribution of magnetic dipoles in example 2
由磁偶极子阵列计算得到的外推平面磁场分布如图17所示。从图17中可知,基于优化后的偶极子阵列模型得到的磁场幅值分布和相位分布与Maxwell 3D有限元仿真结果基本一致。
进一步对均匀分布磁偶极子阵列和优化的磁偶极子阵列的偶极子数量、建模精度和建模效率等进行了比较,见表3。
由表3得到在减小一半偶极子数量的前提下,等效精度大大提高。同时,基于JADE方法的偶极子阵列法耗时42.12 s,比均匀排列时的计算耗时略长,这是因为本文方法需多次计算得到磁偶极子阵列,而均匀排列的磁偶极子阵列的结果只需计算一次得到。
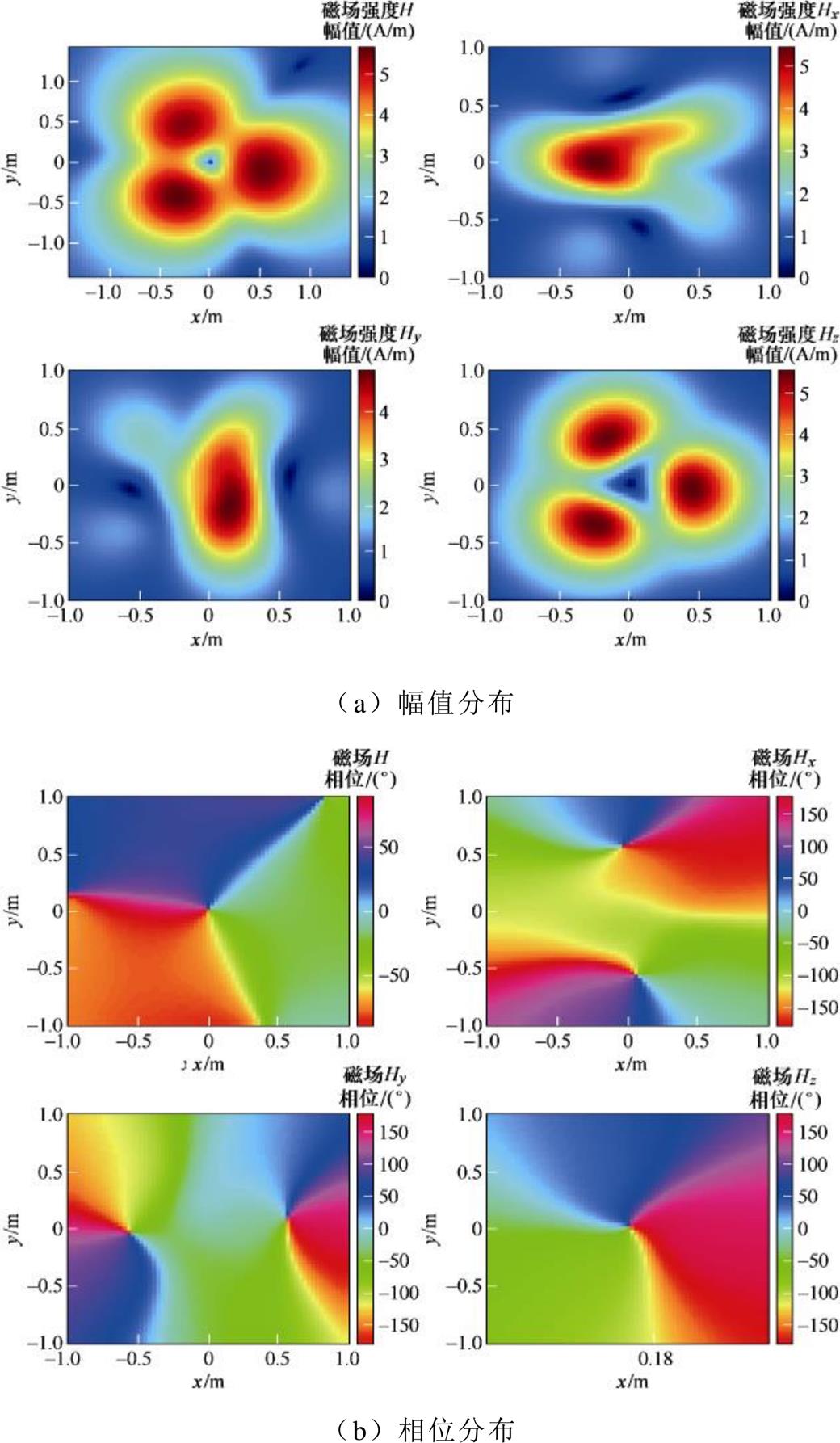
图17 算例2中等效偶极子阵列计算出的磁场分布
Fig.17 The distribution of magnetic field calculated by the equivalent dipole array in example 2
表3 算例2中两种磁偶极子阵列等效对比结果
Tab.3 Comparison of results of two magnetic dipole arrays in example 2
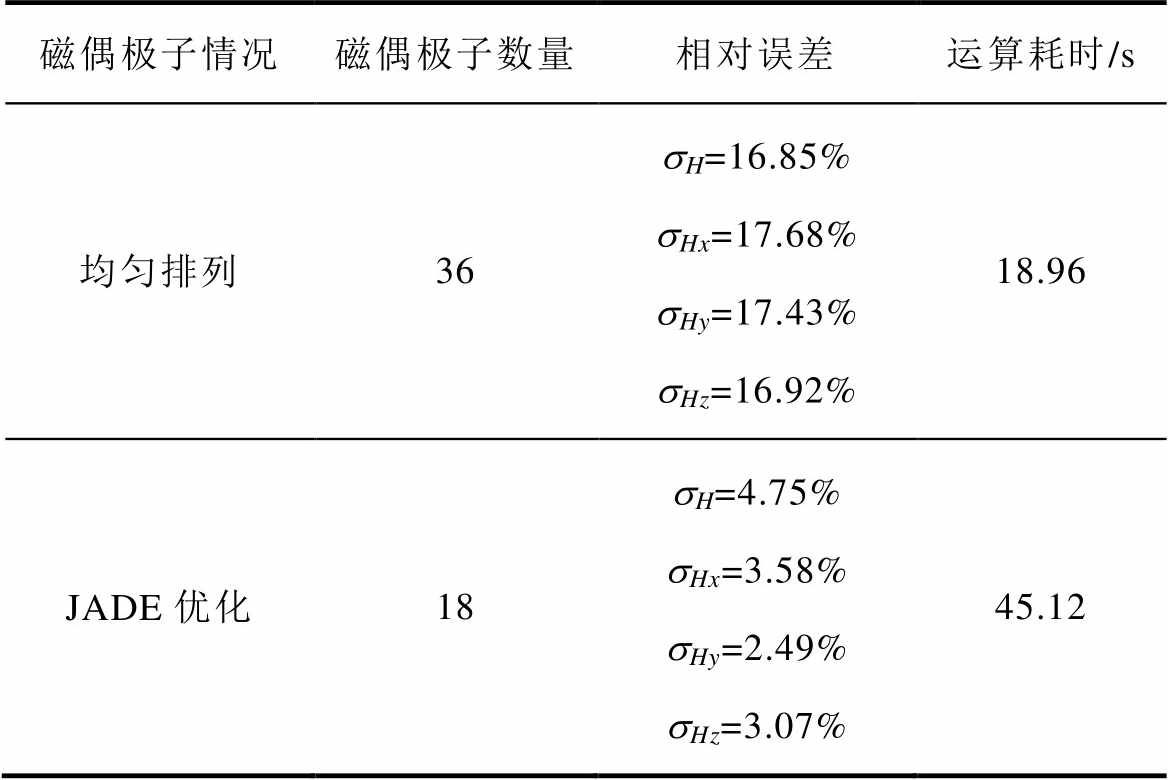
磁偶极子情况磁偶极子数量相对误差运算耗时/s 均匀排列36sH=16.85%sHx=17.68%sHy=17.43%sHz=16.92%18.96 JADE优化18sH=4.75%sHx=3.58%sHy=2.49%sHz=3.07%45.12
最后在垂直于电子机柜表面正中心的位置,沿z方向选择一条2 m长的测量线,起点位置在距表面正中心1 m处,间隔0.05 m测量一个点,测量线位置如图14所示。将仿真值与磁偶极子阵列得到的计算值进行对比如图18所示。
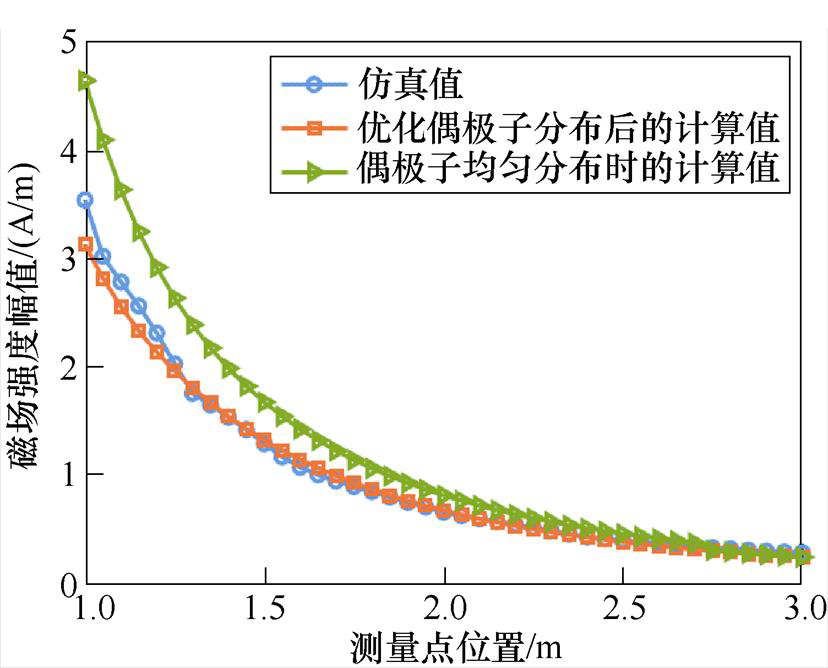
图18 算例2中测量线上仿真值与计算值的对比
Fig.18 Comparison of simulated and computed values on the measurement line in example 2
测量线上各点的仿真值和优化偶极子分布后得到的计算值的相对误差均在10%以下,因此基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模方法在开展远距离低频磁场预测时,也能很好地保证精度。
通过3.1节的仿真和试验验证,最后用本文提出的方法对侧边开缝的复杂强电磁设备机柜进行低频辐射特性等效建模应用。
在Maxwell 3D里建立低频设备机柜几何模型如图19所示,长×宽×高为2.26 m×1.10 m×2.24 m,厚度为2 cm,由4个小机柜构成,其中左侧两个机柜开有通风散热孔缝,右侧上方开有小窗。同样在机柜中布置一个和3.1.2节一样的线圈,用于模拟强电磁设备透过机柜外壳的低频辐射,故线圈置于小窗后。选取的强电磁设备的磁偶极子阵列平面、测量平面和外推平面相对位置见图19。
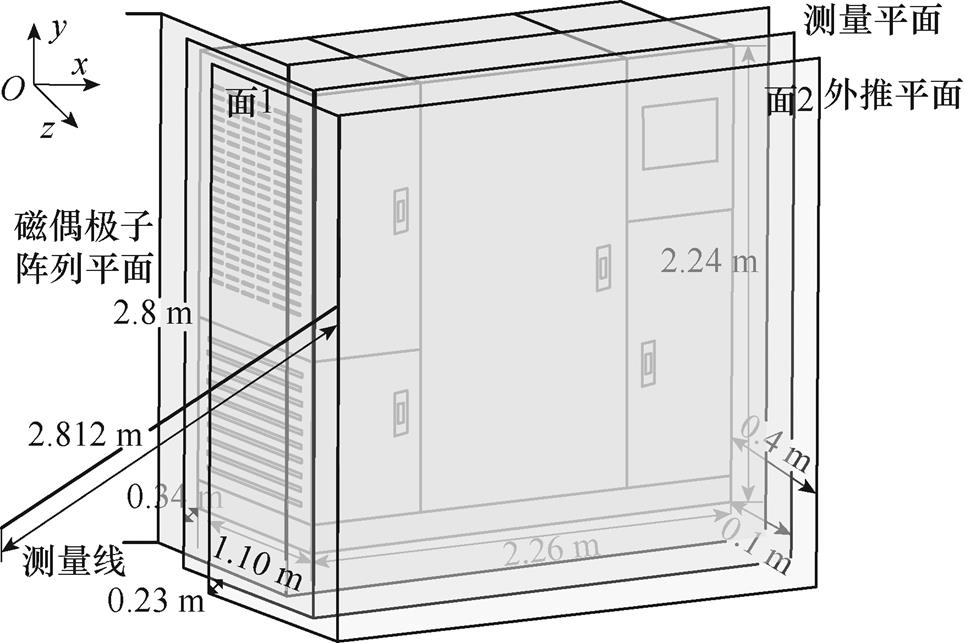
图19 侧边开缝的电子机柜模型
Fig.19 Electronic cabinet model with side slits
两个测量平面长宽分别为2.8 m×2.8 m和2.8 m× 1.3 m,共有9 727个已知的仿真数据点,分别距被测设备0.1 m和0.34 m;外推平面大小分别为:3.4 m×3.4 m和3.4 m×1.9 m,共有15 652个待计算的点,分别距被测设备0.4 m和0.57 m。仿真得到的外推平面磁场分布如图20和图21所示。

图20 仿真得到的面1磁场分布
Fig.20 The distribution of the magnetic field of first face by simulating
在基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模方法中,本案例中JADE参数的设置与3.1.2节保持一致,当适应度值(总体相对误差)满足小于0.11时,循环停止。
为验证基于自适应差分进化算法的等效偶极子法在减少磁偶极子数量、选择最优阵列参数以及提高等效精度等方面的效果,将磁偶极子数量减少一半,即36个磁偶极子,由算法得到的磁偶极子最优分布如图22所示。
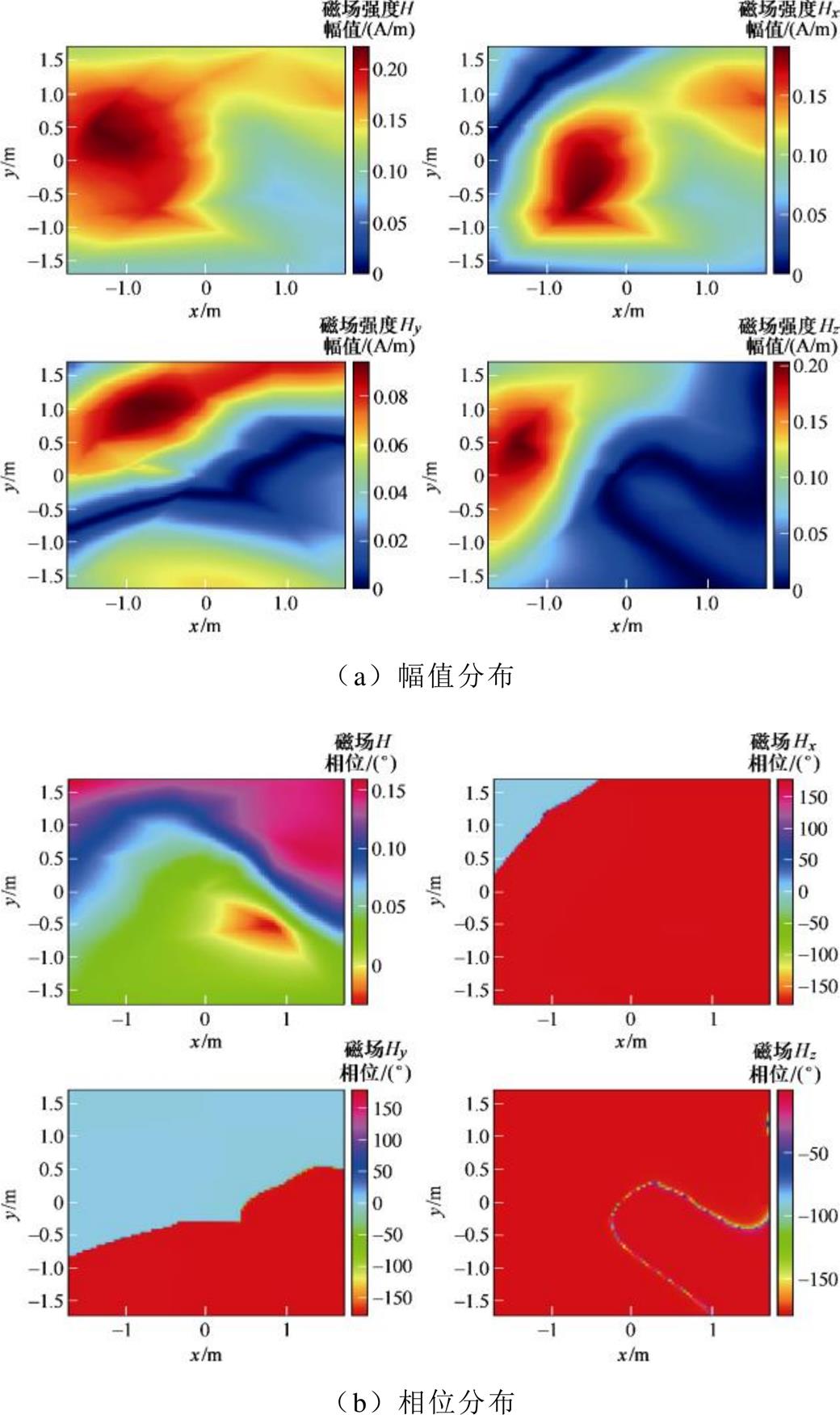
图21 仿真得到的面2磁场分布
Fig.21 The distribution of the magnetic field of second face by simulating
由图18可知,面1和面2在各自的A、B、C区域分别分布了8、5、5和6、7、5个磁偶极子,且优化得到磁偶极子阵列面1和面2的最佳位置分别在被测设备侧正面0.085 m处和表面0.235 m处。阵列得到的外推平面磁场分布如图23和图24所示。从图23和图24中可知,基于优化后的偶极子阵列模型得到的磁场幅值分布和相位分布与Maxwell 3D有限元仿真结果基本一致。
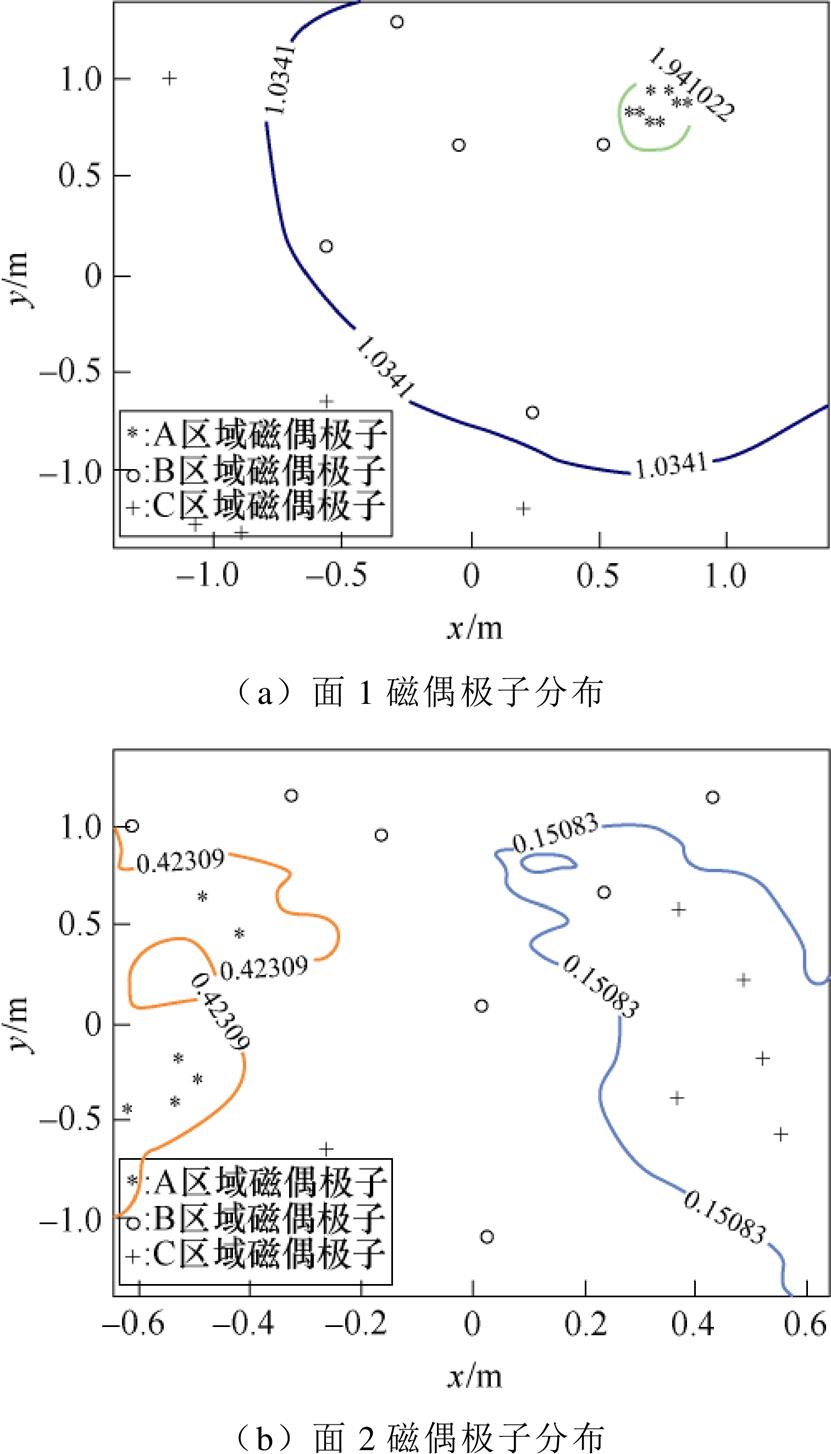
图22 磁偶极子的分布
Fig.22 The distribution of magnetic dipoles of first face
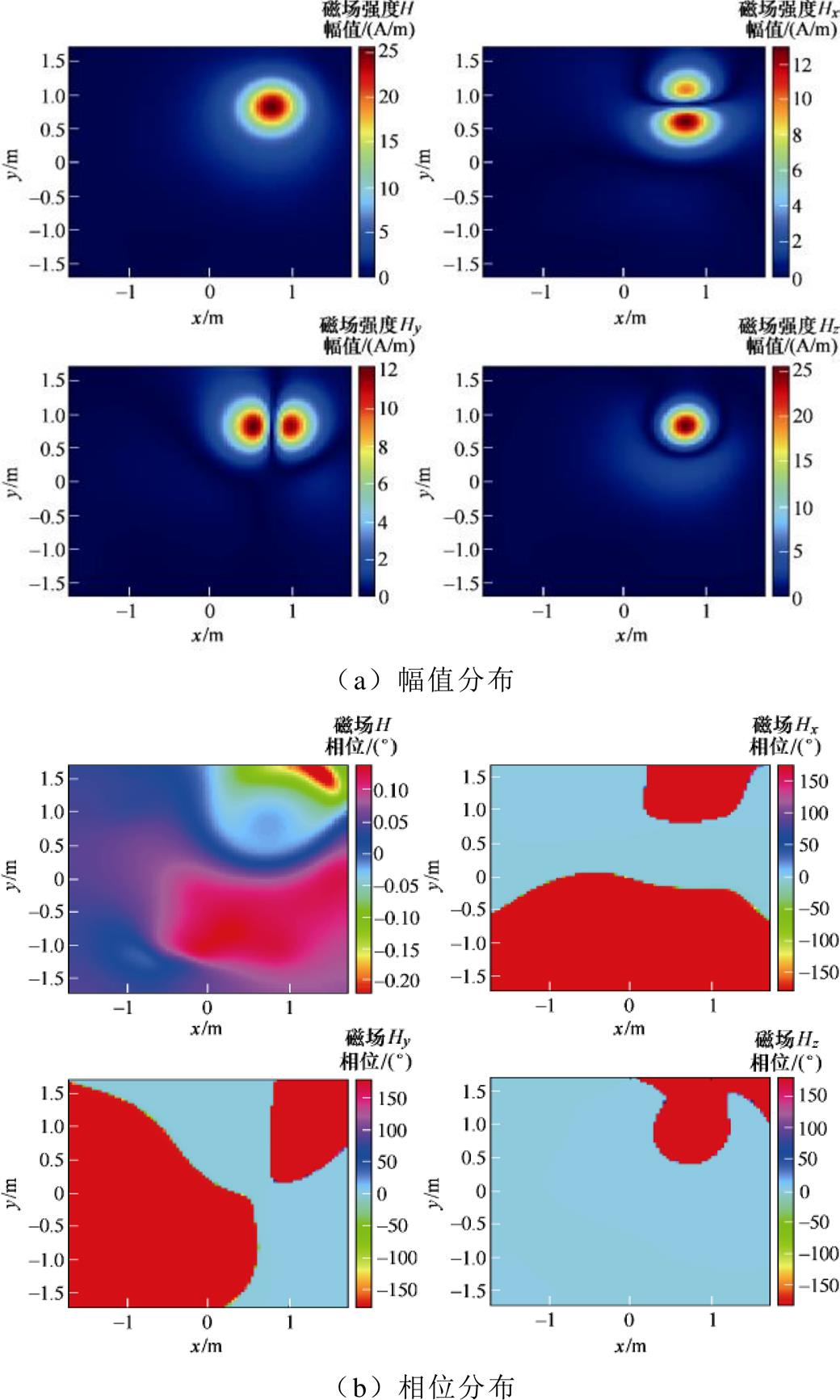
图23 等效偶极子阵列计算出的面1磁场分布
Fig.23 The distribution of magnetic field of first face calculated by the equivalent dipole array

图24 等效偶极子阵列计算出的面2磁场分布
Fig.24 The distribution of magnetic field of second face calculated by the equivalent dipole array
进一步对均匀分布磁偶极子阵列和优化的磁偶极子阵列的偶极子数量、建模精度和建模效率等进行了比较,见表4。表4中,s1,H、s1,Hx、s1,Hy和s1,Hz依次是面1磁场各分量的幅值的相对误差;s2,H、s2,Hx、s2,Hy和s2,Hz依次是面2磁场各分量的幅值的相对误差。
表4 两种磁偶极子阵列等效对比结果
Tab.4 Comparison of results of two magnetic dipole arrays
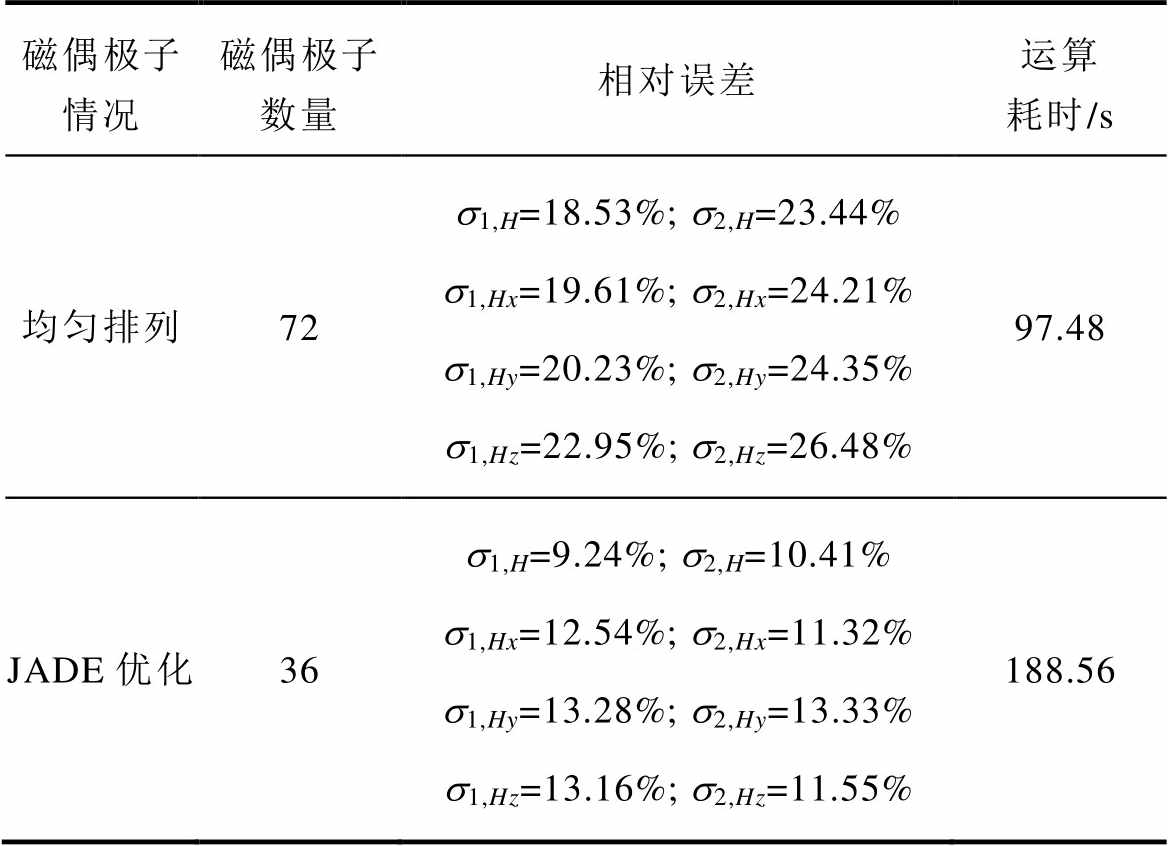
磁偶极子情况磁偶极子数量相对误差运算耗时/s 均匀排列72s1,H=18.53%; s2,H=23.44%s1,Hx=19.61%; s2,Hx=24.21%s1,Hy=20.23%; s2,Hy=24.35%s1,Hz=22.95%; s2,Hz=26.48%97.48 JADE优化36s1,H=9.24%; s2,H=10.41%s1,Hx=12.54%; s2,Hx=11.32%s1,Hy=13.28%; s2,Hy=13.33%s1,Hz=13.16%; s2,Hz=11.55%188.56
由表4得到在减小一半偶极子数量的前提下,等效精度大大提高,本文方法需要耗时188.56 s,比均匀排列时的计算耗时略长,这是因为本文方法需多次计算得到磁偶极子阵列,而均匀排列的磁偶极子阵列的结果只需计算一次得到。
最后选择一条总长2.812 m,垂直于设备侧边棱线且与z轴正半轴成45°的测量线,间隔0.07 m测量一个点。将仿真值与阵列得到的计算值进行对比如图25所示。
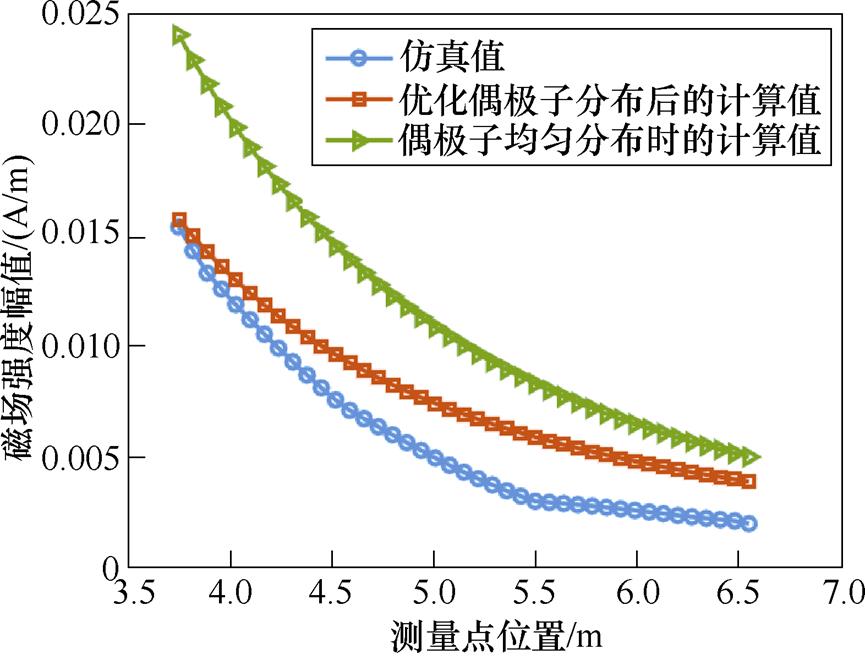
图25 侧边开缝机柜中测量线上仿真值与计算值的对比
Fig.25 Comparison of the simulation value and the calculated value of the measurement line in the side slit cabinet
测量线上各点的仿真值和优化偶极子分布后阵列得到的计算值的相对误差均在20%以下。因此基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模方法在开展远距离测试时,也能保证很好的预测精度。
本文针对强电磁设备低频辐射特性高精度建模时面临的等效偶极子数量多、位置、高度选择困难等问题,提出了一种基于自适应差分进化算法的强电磁设备低频辐射特性等效偶极子建模方法,该方法可以在不知道辐射源的具体结构以及电路拓扑的情况下将强电磁设备低频辐射等效为分布在多个区域的偶极子阵列最优组合的分布式辐射源。该方法首先利用近场测试得到幅值和相位信息,再通过幅值信息将磁偶极子阵列组合中的磁偶极子按照一定的磁场强度梯度分布在一定的区域中,再利用JADE优化算法,优化各区域磁偶极子的数量、位置以及阵列的高度。最后通过试验和仿真算例验证了该方法的有效性,并对舰船平台上典型的强电磁设备的低频辐射特性进行了等效建模。
参考文献
[1] 汪泉弟, 刘青松, 安宗裕, 等. 混合动力客车低频电磁辐射机理及抑制方法[J]. 电工技术学报, 2014, 29(1): 202-207, 228.
Wang Quandi, Liu Qingsong, An Zongyu, et al. Electromagnetic radiation mechanism and noise suppression method for hybrid electric bus[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 202-207, 228.
[2] 华阳, 华成超. 舰船设备低频磁场传播特性仿真研究及试验验证[J]. 舰船电子工程, 2020, 40(12): 87-90.
Hua Yang, Hua Chengchao. Simulation and test verification of low frequency magnetic field dis- tribution characteristics of ship equipment[J]. Ship Electronic Engineering, 2020, 40(12): 87-90.
[3] Rosales A, Sarikhani A, Mohammed O A. Evaluation of radiated electromagnetic field interference due to frequency swithcing in PWM motor drives by 3D finite elements[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1474-1477.
[4] Huangfu Youpeng, Wang Shuhong, Di Rienzo L, et al. Radiated EMI modeling and performance analysis of a PWM PMSM drive system based on field-circuit coupled FEM[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-4.
[5] Shinde S, Masuda K, Shen Guangyao, et al. Radiated EMI estimation from DC-DC converters with attached cables based on terminal equivalent circuit mode- ling[J]. IEEE Transactions on Electromagnetic Com- patibility, 2018, 60(6): 1769-1776.
[6] 苏利捷, 黄保栋, 次仁罗布. 混联式PHEV中DC/DC变换器辐射电磁干扰分析与抑制[J]. 电测与仪表, 2019, 56(7): 35-42.
Su Lijie, Huang Baodong, Ci Renluobu. Analysis and suppression on radiated EMI of DC/DC converter in parallel-series PHEV[J]. Electrical Measurement & Instrumentation, 2019, 56(7): 35-42.
[7] 刘子剑. 非均匀介质中低频电磁波的散射与传输[D]. 成都: 电子科技大学, 2019.
[8] Solís D M, Martín V F, Araújo M G, et al. Accurate EMC engineering on realistic platforms using an integral equation domain decomposition approach[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(4): 3002-3015.
[9] Kornprobst J, Knapp J, Mauermayer R A M, et al. Accuracy and conditioning of surface-source based near-field to far-field transformations[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(8): 4894-4908.
[10] Yu Zhenwei, Mix J A, Sajuyigbe S, et al. An improved dipole-moment model based on near-field scanning for characterizing near-field coupling and far-field radiation from an IC[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55(1): 97- 108.
[11] Pan Jingnan, Wang Hanfeng, Gao Xu, et al. Radio- frequency interference estimation using equivalent dipole-moment models and decomposition method based on reciprocity[J]. IEEE Transactions on Elec- tromagnetic Compatibility, 2016, 58(1): 75-84.
[12] Shu Yufei, Wei Xingchang, Fan Jun, et al. An equivalent dipole model hybrid with artificial neural network for electromagnetic interference prediction[J]. IEEE Transactions on Microwave Theory and Tech- niques, 2019, 67(5): 1790-1797.
[13] 项方品. 基于近场扫描的高速电路电磁辐射建模研究[D]. 杭州: 浙江大学, 2015.
[14] 孔文杰. 板级电磁辐射偶极子阵列等效建模研[D]. 杭州: 浙江大学, 2016.
[15] Zhao Yuan, Baharuddin M H, Smartt C, et al. Measurement of near-field electromagnetic emissions and characterization based on equivalent dipole model in time-domain[J]. IEEE Transactions on Electro- magnetic Compatibility, 2020, 62(4): 1237-1246.
[16] 郭成豹, 殷琦琦. 舰船磁场磁单极子阵列法建模技术[J]. 物理学报, 2019, 68(11): 114101.
Guo Chengbao, Yin Qiqi. Magnetic monopole array model for modeling ship magnetic signatures[J]. Acta Physica Sinica, 2019, 68(11): 114101.
[17] 戴忠华, 周穗华, 单珊. 基于模拟退火算法的舰船磁场高精度建模方法[J]. 电子学报, 2018, 46(6): 1524-1529.
Dai Zhonghua, Zhou Suihua, Shan Shan. High accuracy method for ship magnetic field based on simulated annealing algorithm[J]. Acta Electronica Sinica, 2018, 46(6): 1524-1529.
[18] 戴忠华, 周穗华, 张晓兵. 多目标优化的舰船磁场建模方法[J]. 物理学报, 2021, 70(16): 164101.
Dai Zhonghua, Zhou Suihua, Zhang Xiaobing. Multi-objective optimization of ship magnetic field modeling method[J]. Acta Physica Sinica, 2021, 70(16): 164101.
[19] 徐超群, 易忠, 孟立飞, 等. 基于遗传算法的卫星磁模型研究[J]. 电子学报, 2020, 48(6): 1108-1112.
Xu Chaoqun, Yi Zhong, Meng Lifei, et al. Research on satellite magnetic model based on genetic algorithm[J]. Acta Electronica Sinica, 2020, 48(6): 1108-1112.
[20] Zhang Jingqiao, Sanderson A C. JADE: adaptive differential evolution with optional external archive[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958.
Abstract As new power electronics with high switching frequencies are widely used in high-power, high-current, and large-volume electrical equipment on aircraft, ships, and other platforms, the low-frequency radiation generated by high-power electromagnetic equipment seriously impactssensitive equipment. Therefore, it is important to accurately model and characterize the low-frequency radiation characteristics of the equipment and support the predictions of its low-frequency field distribution characteristics to improve the entire platform's electromagnetic compatibility. When the traditional equivalent dipole method is used for equivalent modeling of the radiation characteristics of the large radiation sources, the required dipole array contains many equivalent dipole sources, and choosing the array height and dipole positionis challenging. Therefore, this paper proposes an equivalent dipole method based on the adaptive differential evolution algorithm for the low-frequency radiation characteristics of high-power electromagnetic equipment.
Firstly, to reduce the number of dipoles in the array, the low-frequency radiation of the high-power electromagnetic equipment is equivalent to the distributed radiation source equivalent model of dipole arrays distributed in multiple regions according to the near-field test data. Secondly, the adaptive differential evolution with an optional external archive (JADE) is introduced to optimize the equivalent modeling of the low-frequency radiation characteristics to obtain the number, position, and height of dipole arrays that meet the requirements of high-precision equivalent modeling. Finally, to solve the ill-conditioned matrix in each iteration of the equivalent dipole method based on JADE, the least squares method, and Tikhonov regularization are used to solve the ill-conditioned matrix. The generalized cross-validation method (GCV) solves the corresponding Tikhonov regularization parameters of the matrix equation to obtain the stable solution of the equation. The distributed radiation source equivalent model of the optimal dipole array can be obtained using the equivalent dipole method based on JADE and the near-field data.
Experiments verify the correctness and reliability of the method. Firstly, the low-frequency magnetic field radiation generated by high-power electromagnetic equipment is physically modeled, and the accuracy and reliability of the method in this paper are verified by equivalently modeling the radiation characteristics of the low-frequency radiation source in the test. Secondly, the method is further validated by equivalent modeling of the low-frequency radiation characteristics of an electronic cabinet and a twelve-phase permanent magnet motor. Then, the equivalent modeling method is applied to the low-frequency equivalent modeling of a complex high-power electromagnetic equipment cabinet The proposed method can significantly reduce the number of dipole arrays under certain accuracy conditions, so the optimal low-frequency, distributed equivalent source model for high-power electromagnetic equipment is obtained.
keywords:Low-frequency interference, equivalent source method, three-dimensional magnetic dipole array, adaptive differential evolution algorithm, near-field data
DOI: 10.19595/j.cnki.1000-6753.tces.221607
中图分类号:TM155
射频系统强电磁脉冲环境效应预测与防护技术研究(cstc2021ycjh- bgzxm0330)和随机电磁环境中汽车线缆网络电磁干扰特性的高效预测方法研究(cstc2020jcyj-msxmX0825, 2020CDJ-LHZZ-078)资助项目。
收稿日期 2022-08-21
改稿日期 2023-01-04
陈 豪 男,1997年生,硕士研究生,研究方向电磁辐射干扰等效建模。E-mail: 202011021042@cqu.edu.cn
刘其凤 男,1981年生,博士,研究方向电磁兼容、电磁计算及微波无线能量传输。E-mail: liuqifeng@cqu.edu.cn(通信作者)
(编辑 郭丽军)