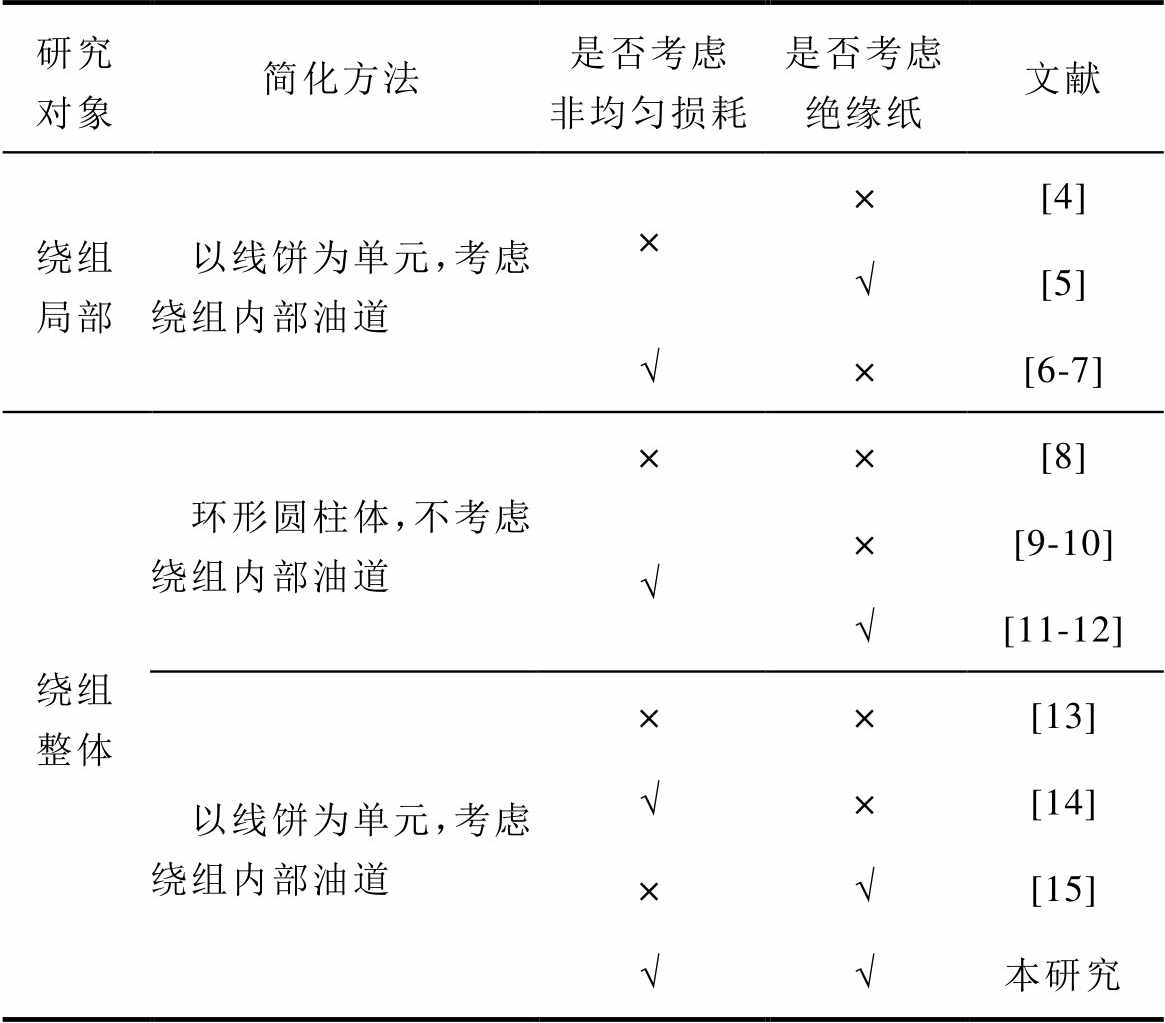
表1 现有绕组温度数值计算模型
Tab.1 Existing numerical calculation models for winding temperature
研究对象简化方法是否考虑非均匀损耗是否考虑绝缘纸文献 绕组局部以线饼为单元，考虑绕组内部油道××[4] √[5] √×[6-7] 绕组整体环形圆柱体，不考虑绕组内部油道××[8] √×[9-10] √[11-12] 以线饼为单元，考虑绕组内部油道××[13] √×[14] ×√[15] √√本研究
摘要 针对谐波电流引起的换流变压器绕组局部过热、绝缘老化加速的问题，该文对现有绕组温度计算模型进行了改进，并采用电磁-热-流多物理场耦合的方法定量分析了谐波电流对绕组损耗和温度分布特性的影响规律。结果表明，采用该文提出的计算模型，绕组热点和平均温度与实测结果的误差分别为0.4%和2.9%，辐向油道内油流质量流量和线饼温度的分布规律与参考文献十分吻合。基波工况下，受涡流效应的影响，绕组端部附近2～3个线饼以及辐向内侧线饼单元的损耗明显较大。相比于基波工况，谐波电流不仅使各线饼的损耗增大，同时加剧了端部和辐向内侧线饼单元的涡流效应，使端部和辐向内侧线饼单元损耗显著增大，导致绕组温度沿辐向分布不均匀，热点集中在绕组辐向内侧，热点和平均温度分别升高了8.6℃和3.5℃。
关键词：换流变压器 绕组 谐波电流 损耗 温度 多物理场耦合
换流变压器处在交流与直流输电系统连接的核心位置[1]，在其实际运行过程中，负载电流含有大量的高次谐波分量，导致其内部损耗分布不均匀，引起其内部某一区域的局部过热。过高的温度会加速绝缘材料的老化，从而降低换流变压器的性能及缩短其寿命[2]。在换流变压器的组成中，绕组的损耗和局部过热现象受谐波电流的影响最为显著[3]。因此，在绕组热设计时必须考虑谐波损耗，以确保在换流变压器运行时绕组热点温升低于规定的温升，提高变压器运行的稳定性和延长其使用寿命。
除了考虑上述的非均匀损耗，绕组具有结构复杂、组件尺寸差异大等特点，因此，准确的热建模对于研究谐波电流对绕组温度分布特性的影响至关重要。在绕组温度数值计算中必须解决以下关键问题，具体为：①需对整个绕组建模且进行高质量网格剖分；②需考虑绕组内部油道对绕组换热的影响；③需考虑绝缘纸对绕组散热的影响。本文对现有绕组温度数值计算模型进行了调研，并将其进行了分类，现有绕组温度数值计算模型见表1。其中，苏小平等[6]、马永强等[7]和井永腾等[14]尽管考虑了绕组内部油道和非均匀损耗，但并未考虑绝缘纸对绕组散热的影响。李永建等[11]和J. Smolka等[12]尽管通过建立电磁-热-流耦合模型考虑了绕组的非均匀损耗，同时采用电热类比的方法考虑了绝缘纸对绕组散热的影响，但并未考虑绕组内部油道对绕组散热的影响。Tan Youbo等[15]采用均匀损耗对影响绕组内部流动与传热的因素进行了参数化研究。可见，现有的绕组温度数值计算模型都有不同程度的简化，综合考虑上述关键问题，建立完整的电磁-热-流耦合模型计算绕组温度的研究比较匮乏。
国内外学者针对谐波电流对绕组损耗和热点温度的影响进行了广泛的研究。蔡国伟等[16]分析了谐波电流的频变效应问题，并通过修正频变指数修正了谐波损耗计算模型。张占龙等[17]分析了变压器负载不平衡引起的谐波损耗问题，提出了一种谐波损耗在线监测方法。李琼林等[18]提出了一种时频域结合的三相变压器谐波模型，并用实验和仿真证明了该模型。刘书铭等[19]在考虑趋肤效应与邻近效应的前提下建立了变压器谐波损耗模型。马铁军等[20]和周卫华等[21]采用公式法预测了谐波工况下绕组的热点温度。T. Dao等[22]比较了无谐波电流、基波电流与3%的3次谐波电流叠加以及基波电流与3%的5次谐波电流叠加三种工况下的绕组热点温度。Zhang Jie等[23]总结了各次谐波电流对绕组热点温度的影响规律，但缺乏各次谐波电流叠加的结果。Wu Jie等[24]通过仿真得到了交流变压器低压绕组在不同频率、相同幅值电流作用下的绕组热点温度，并建立了电流频率与绕组热点温度之间的定量关系。目前的研究大多聚焦于谐波电流对损耗值和热点温度大小的影响，而缺乏谐波电流对损耗和温度分布特性影响的定量分析。然而，研究绕组损耗和温度分布特性是必要的，一方面，在绕组热设计时能够指导局部强化散热，有利于降低热点温度和提高均温性；另一方面，能够为后期故障排查提供参考，从而缩短检修时间，对于提高经济效应和保障社会用电稳定具有重要意义[25]。因此，本研究采用电磁-热-流多物理场耦合的有限元方法，综合考虑前述绕组温度数值计算中的关键问题，对一工程实际应用的换流变压器阀侧绕组全尺寸建模，分别计算基波和额定工况下绕组的损耗和温度，定量分析谐波电流对绕组损耗和温度分布特性的影响规律。
表1 现有绕组温度数值计算模型
Tab.1 Existing numerical calculation models for winding temperature
研究对象简化方法是否考虑非均匀损耗是否考虑绝缘纸文献 绕组局部以线饼为单元，考虑绕组内部油道××[4] √[5] √×[6-7] 绕组整体环形圆柱体，不考虑绕组内部油道××[8] √×[9-10] √[11-12] 以线饼为单元，考虑绕组内部油道××[13] √×[14] ×√[15] √√本研究
注：“√”代表“是”，“×”代表“否”。
本研究基于一工程实际应用的工频50Hz、容量376.6MV·A的强油风冷油浸式换流变压器的阀侧绕组。由于绕组的轴对称结构，目前通常采用二维轴对称模型计算绕组的损耗和温度[3, 5]，本研究沿用了这一方法。计算域如图1所示。如图1a所示，损耗计算域包含铁心、网侧绕组和阀侧绕组；图1b展示了包含线饼、绕组壁面和纵横交错油道网络的温度计算域。油流入口位于绕组底部的中间位置，油流出口位于绕组顶部，与油流入口同轴。变压器油在压差和密度差的双重作用下流入绕组，经过油道网络流出绕组，带走线饼产生的热量。按变压器油的流动方向，油道网络分为轴向油道和辐向油道，如图1c所示。沿轴向，72个线饼均匀排列。为增强线饼散热，在每个线饼中间增加了4个轴向油道，油道将每个线饼沿辐向分成了5个线饼单元，如图1c所示。绕组的主要结构尺寸标注于图1c。
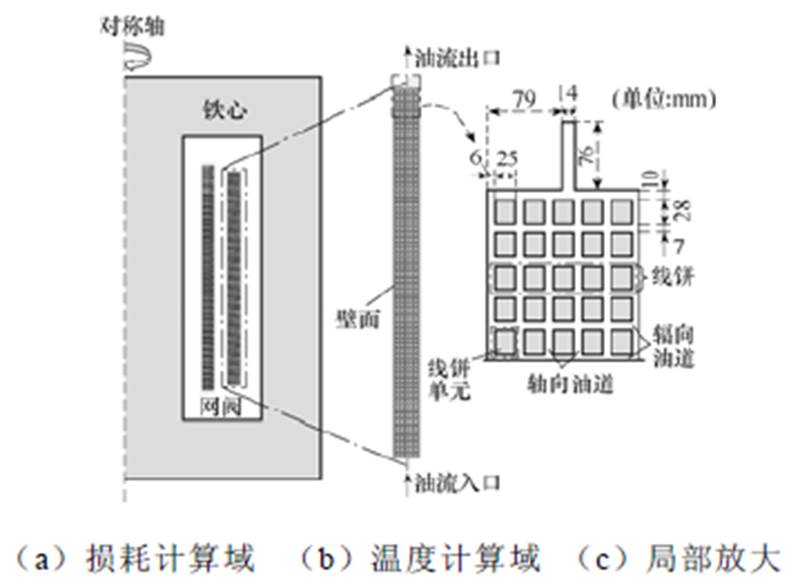
图1 计算域
Fig.1 Calculation domain
为提高计算精度，本研究采用全结构化网格将计算域离散，网格剖分示意图与部分细节如图2所示。为捕捉线饼表面附近的速度和温度变化，线饼附近流体域的网格被加密，并将固体域和流体域界面的网格节点对齐，以保证共轭传热的准确性。
绕组和铁心的电物性参数见表2。其中，绕组的电导率受温度的影响较大，采用关于温度的函数s(T)表示，定义见式（1）；铁心的相对磁导率用B-H曲线表示，如图3所示。
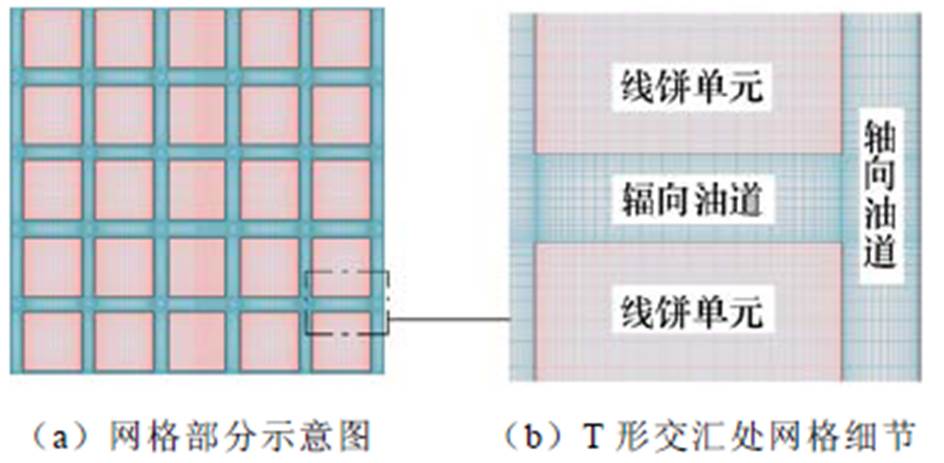
图2 网格剖分示意图与部分细节
Fig.2 Schematic of meshing and partial details
表2 电物性参数
Tab.2 Electrophysical property parameters
组件电导率s/(S/m)相对磁导率mr 绕组s(T)1 铁心2.2×106B-H曲线
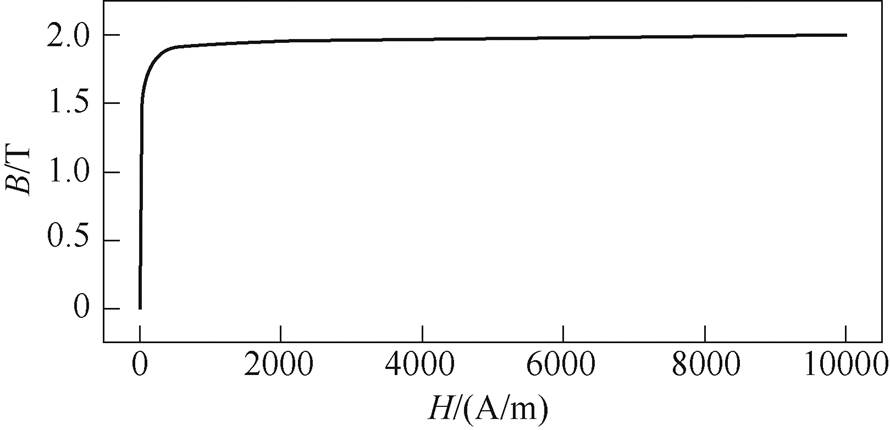
图3 铁心B-H曲线
Fig.3 B-H curve of core
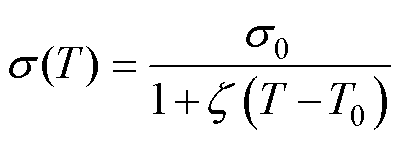（1）
式中，T0和s0分别为参考温度及其对应的电导率，取值为20℃和5.8×107S/m；T和s(T)分别为绕组的实际温度及其对应的电导率；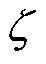
为温度补偿系数，取值为0.003 93/℃[11]。
变压器油的热物性参数受温度影响较大，见 表3。表中，Tf为变压器油油温。
表3 变压器油热物性参数
Tab.3 Thermophysical property parameters of transformer oil
物性参数表达式 密度rf/(kg/m3) 比热容cp,f/[J/(kg·K)] 热导率lf/[W/(m·K)] 动力黏度hf/(Pa·s)
线饼单元结构及有限元物理模型如图4所示。线饼主要由铜线和绝缘纸组成，铜线被绝缘纸包裹，如图4a所示。由于绝缘纸的热导率相比于铜线而言极小（见表4），因此绝缘纸对线饼散热的影响无法忽略。由于绝缘纸厚度相比于整个绕组而言极小（10-1：103mm，相差4个数量级），如果对整个绕组的绝缘纸建模，计算难度较大，且会造成计算资源的巨大浪费。目前，通常采用电热类比的方法简化线饼，即将热阻类比于电阻，建立热阻网络，计算线饼的等效热导率。但该方法存在不足：①对于结构复杂的线饼，需要建立复杂的热阻网络，计算难度较大，且对于异形的线饼结构不再适用；②计算某一方向的等效热导率时仅考虑该方向的导热，但实际上导热是同时沿各个方向进行的，因此计算存在一定误差。针对上述不足，本研究对现有计算模型进行了改进，提出了一种新的线饼简化方法，具体步骤如下：
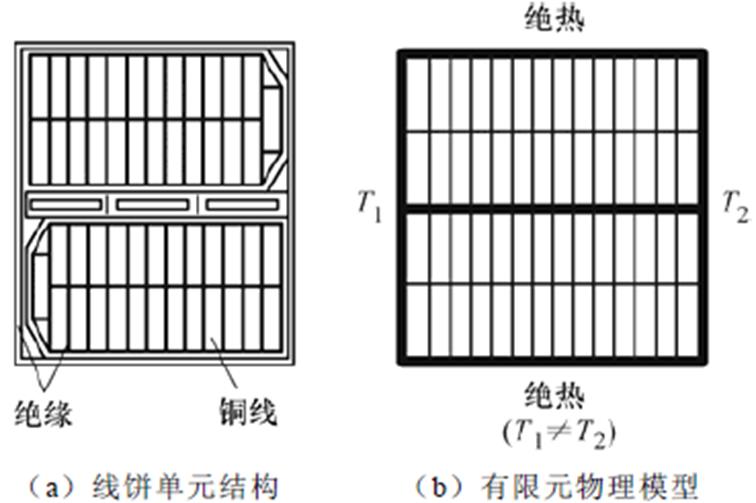
图4 线饼单元结构及有限元物理模型
Fig.4 Disc unit structure and finite element physical model
表4 绕组材料属性
Tab.4 Winding material properties
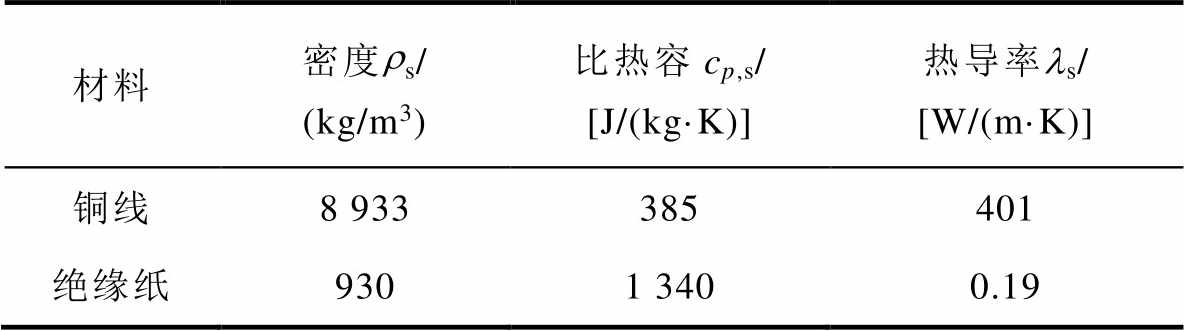
材料密度rs/ (kg/m3)比热容cp,s/ [J/(kg·K)]热导率ls/ [W/(m·K)] 铜线8 933385401 绝缘纸9301 3400.19
（1）对单个线饼单元以铜线和绝缘纸为单元建立有限元稳态导热模型。
（2）对铜线和绝缘纸施加各自的材料属性（见表4）。
（3）计算线饼辐向等效热导率时，在线饼的两个轴向壁面分别设置不同温度的温度边界条件（温度值非特定，只要保证温度不同，即有温差即可），同时将线饼辐向壁面设置为绝热壁面，如图4b所示。
（4）计算得到线饼单元的辐向等效热导率为
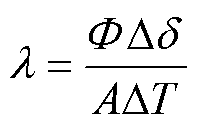（2）
式中，F 为换热量（W）；A为热流穿过截面的截面积（m2）；DT为施加温度边界条件的两壁面的温差（℃），它是一个正数；Dd 为施加温度边界条件的两壁面之间的距离（m）。
（5）同理，计算轴向等效热导率。
（6）然后，在绕组热建模时，将每个线饼单元简化为具有等效热导率的块，如图1c所示。
本文研究的绕组的线饼单元有两种线规：一种是内部含屏线，位于绕组顶部和底部，各10个线饼，共20个线饼；另一种是内部不含屏线，位于绕组中部，共52个线饼。本研究分别对两种线规的线饼单元的等效热导率进行了计算，计算结果见表5。
表5 线饼单元等效热导率计算结果
Tab.5 Calculation results of disc unit equivalent thermal conductivity
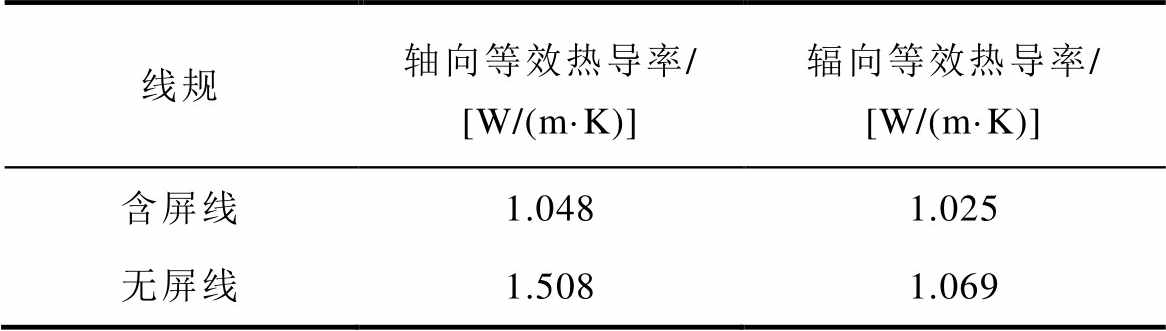
线规轴向等效热导率/ [W/(m·K)]辐向等效热导率/ [W/(m·K)] 含屏线1.0481.025 无屏线1.5081.069
为验证上述简化方法的准确性，将具有等效热导率的线饼单元简化模型的换热量与以铜线和绝缘纸为单元建立的有限元稳态导热模型（称为无简化模型）进行对比，对比结果见表6。结果显示，简化模型的轴向换热量与无简化模型几乎相同；辐向换热量的偏差在2%以内。可见，本研究提出的简化方法是十分准确的。
表6 简化模型与无简化模型换热量的对比结果
Tab.6 Comparison results of heat transfer rate between simplified and non-simplified model
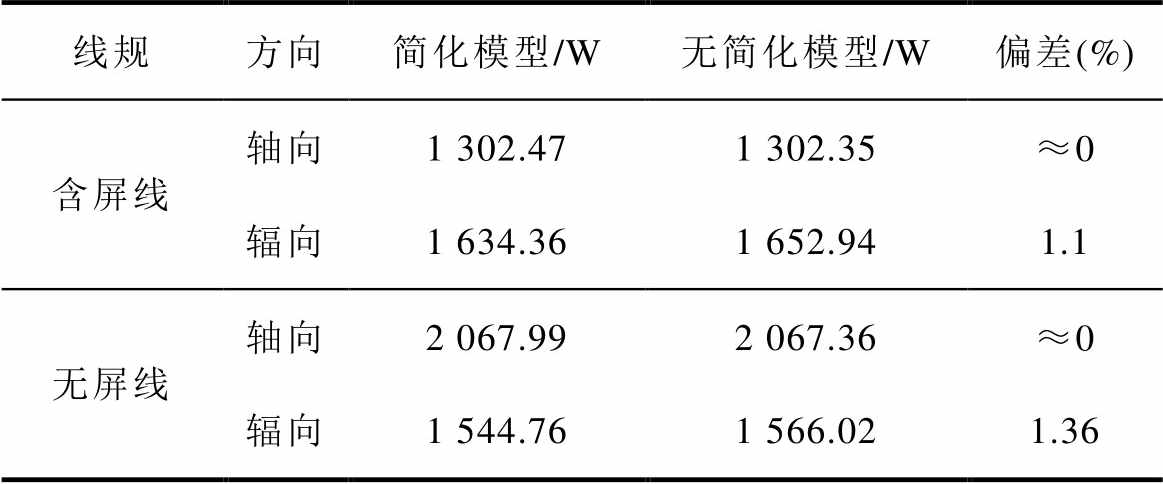
线规方向简化模型/W无简化模型/W偏差(%) 含屏线轴向1 302.471 302.35≈0 辐向1 634.361 652.941.1 无屏线轴向2 067.992 067.36≈0 辐向1 544.761 566.021.36
相比于传统的电热类比的线饼简化方法，采用本研究提出的简化方法，不仅避免了建立热阻网络时的庞大工作量，降低了计算难度，对于异形线饼结构也同样适用。
负载电流中谐波分量的主要成分为6n±1次谐波电流。各次谐波电流占基波电流的百分比随次数的增加逐渐减少。当次数大于13时，该次谐波分量对于损耗的影响可以忽略不计[26]。因此，本研究在损耗计算时只考虑5、7、11、13次谐波电流。负载电流的波形及频谱分量如图5所示。
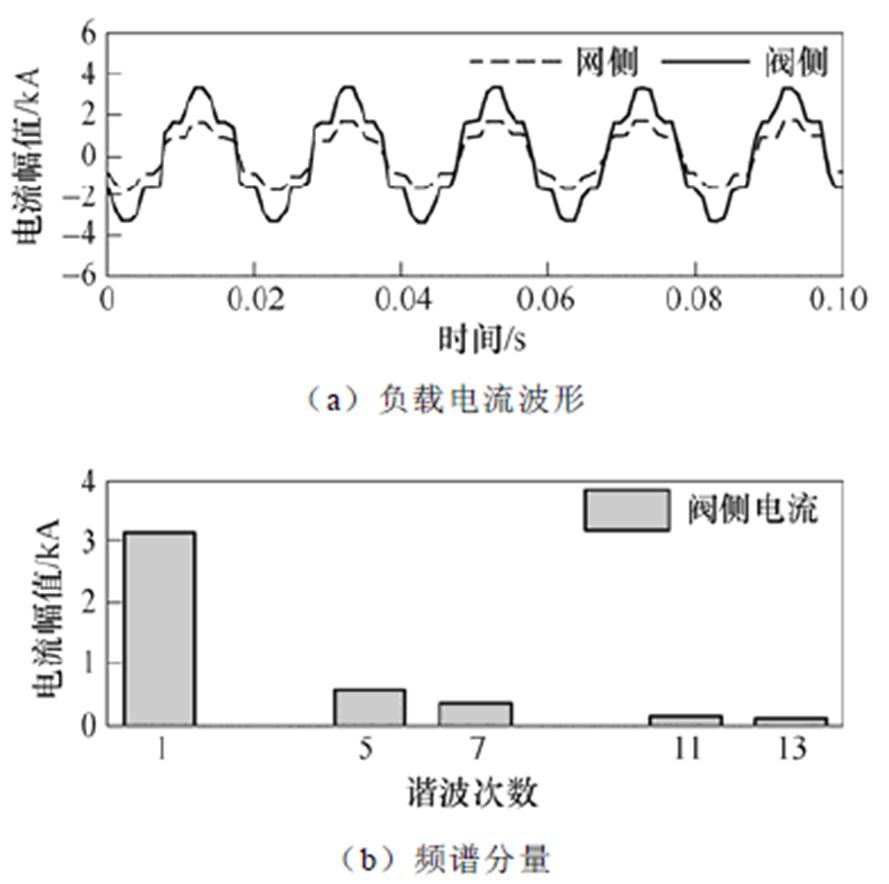
图5 负载电流波形及频谱分量
Fig.5 Waveforms and spectrum component of load current
绕组损耗Q由欧姆损耗Qo和涡流损耗Qe两部分组成。欧姆损耗Qo可由电流有效值I和绕组电阻R计算得到，即
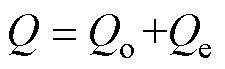（3）
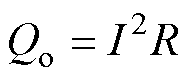（4）
对于二维轴对称模型，单一频率电流激励下绕组的涡流损耗Qe[27]为
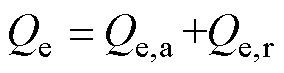（5）
其中
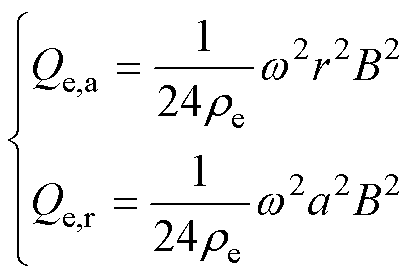（6）
式中，Qe,a和Qe,r分别为轴向和辐向涡流损耗密度；re为电阻率；w 为角频率；B为磁感应强度；r和a分别为辐向和轴向线规尺寸。
又根据Parseval理论[3]，额定工况下绕组损耗可以简化为基波电流以及各次谐波电流单独激励下绕组的损耗之和，即
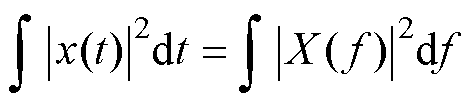（7）
雷诺数（Re）是用来表征流体流动情况的无量纲数，其定义为
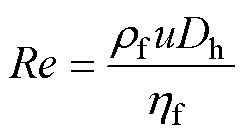（8）
式中，rf、hf分别为变压器油的密度和动力黏度；u为油流速度；Dh为水力直径。
水力直径定义为
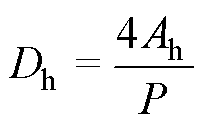（9）
式中，Ah和P分别为变压器油流经截面的截面积和润湿周长。
对于本研究的计算模型，入口雷诺数为696.7，远小于临界雷诺数2 300。因此本研究采用层流模型，其控制方程如式（10）～式（13）所示。
连续性方程为
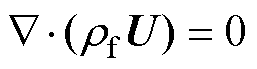（10）
动量方程为
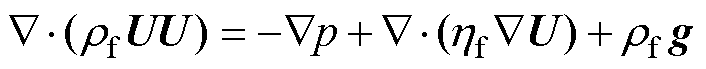（11）
对于固体域，能量方程为
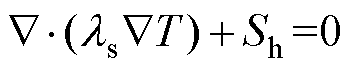（12）
对于流体域，能量方程为
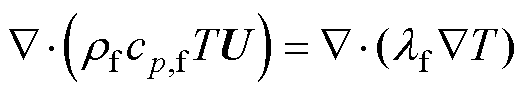（13）
式中，p为压力；U为速度矢量；g为重力加速度；Sh为热源项。
采用速度入口、压力出口边界条件。将固体域和流体域的接触面设置为耦合面，以实现固体域与流体域传热的相互耦合，即共轭传热。将绕组壁面设置为绝热表面，因为围屏的热导率很低且本研究不考虑围屏的换热。
多物理场耦合计算流程如图6所示。由于在计算前无法得知绕组的实际温度，故先假定一个初始温度，该温度可取一个接近工程测量值的值，施加该温度下的电物性，通过求解损耗方程（见式（3）～式（7））得到绕组的损耗分布，再将损耗作为热源施加给固体域，即固体域能量方程（见式（12））中的Sh=Q，然后联立求解式（10）～式（13）得到绕组的流场和温度场分布，此过程称为单向耦合计算。在得到流场和温度场分布后，再根据温度计算结果更新绕组的电物性，重复上述的单向耦合计算过程。然后反复迭代，直到相邻两次单向耦合计算得到的温度值的最大偏差（迭代误差）小于或等于0.01℃[11]，即可认为迭代收敛，结束迭代，此过程称为双向耦合计算。值得说明的是，假定的初始温度值的大小只会影响收敛的快慢，而不会影响计算的最终结果。初始温度值越接近实际温度值，达到收敛所需的时间越短。
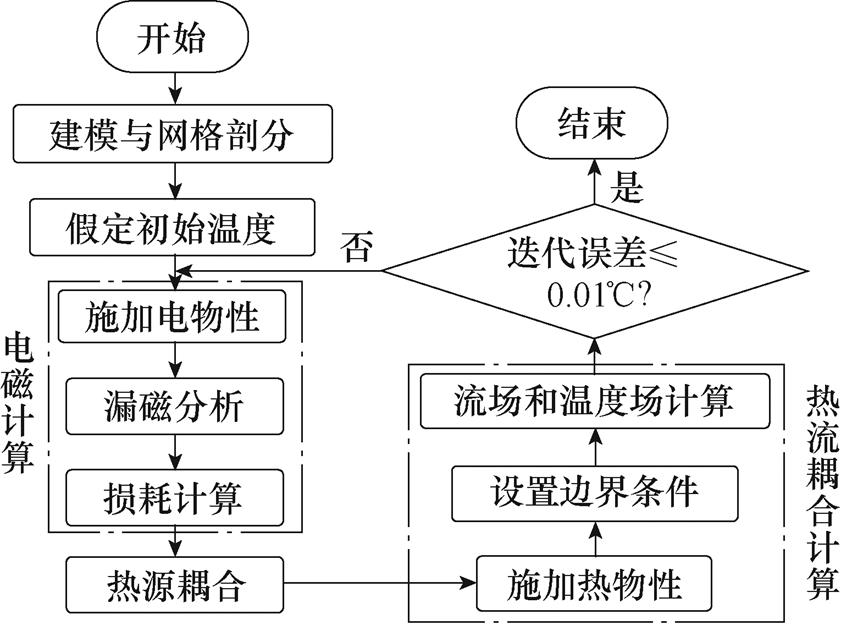
图6 多物理场耦合计算流程
Fig.6 Multi-physics coupling calculation process
在换流变压器实际运行过程中，绕组温度是基波电流和各次谐波电流叠加作用下的结果。因此，本研究仅对基波电流单独作用下（即基波工况）以及基波电流叠加各次谐波电流作用下（即额定工况）两种工况下绕组的损耗和温度进行计算。
为研究线饼温度和辐向油道内油流速度分布规律，将线饼和辐向油道分别沿轴向从绕组底部至顶部依次编号为D1～D72和d1～d73。为研究谐波电流对线饼轴向损耗分布的影响，将绕组顶部和底部的4个线饼分别从绕组顶部和底部向绕组中部依次编号为AT1～AT4和AB1～AB4。为研究谐波电流对线饼辐向损耗分布的影响，将线饼单元沿辐向从绕组内侧到外侧依次编号为R1～R5。各编号如图7所示。
将辐向油道内油流质量流量、线饼平均温度和油流速度进行无量纲化[28]。
油流无量纲质量流量（MFR）定义为
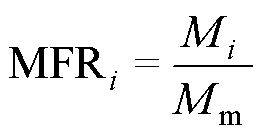（14）
式中，MFRi和Mi分别为编号为di的辐向油道内的油流无量纲质量流量和实际质量流量；Mm为所有辐向油道内油流质量流量的平均值。
线饼无量纲平均温度（MT）定义为
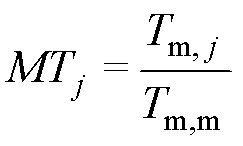（15）
式中，MTj和Tm, j分别为编号为Dj的线饼的无量纲平均温度和实际平均温度；Tm,m为所有线饼平均温度的平均值。
油流无量纲速度（U）定义为
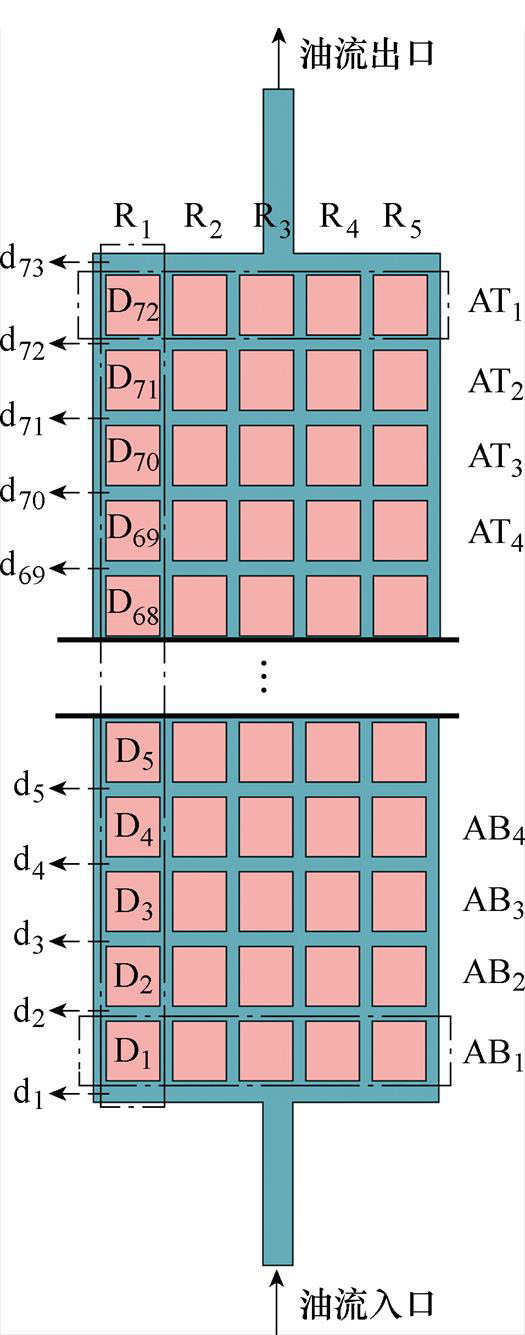
图7 编号示意图
Fig.7 Numbering diagram
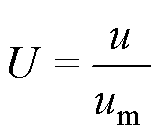（16）
式中，U和u分别为油流的无量纲速度和实际速度；um为绕组内油流的平均速度。
温升（DT）定义为
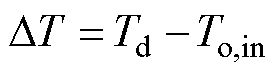（17）
式中，Td和To,in分别为线饼温度和入口油温。
为研究谐波电流对线饼损耗的影响，定义损耗增长率G为
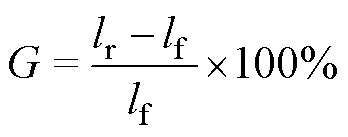（18）
式中，lr为额定工况下的线饼损耗；lf为基波工况下的线饼损耗。
数值计算结果应与网格数量无关。由于网格单元的纵横比过大会影响计算精度，本研究将油流通道横截面和每个线饼单元表面的网格单元数分别设为Ng和2Ng，并通过增加Ng来增加网格的总单元数。Ng从5逐渐增加到30，增加幅度为5。网格无关性验证如图8所示。当Ng达到20后，继续增加Ng，绕组的热点温度和总压降几乎不变，说明当Ng＞20时计算结果与网格数量无关。因此，本研究采用Ng=20对计算模型进行网格剖分。
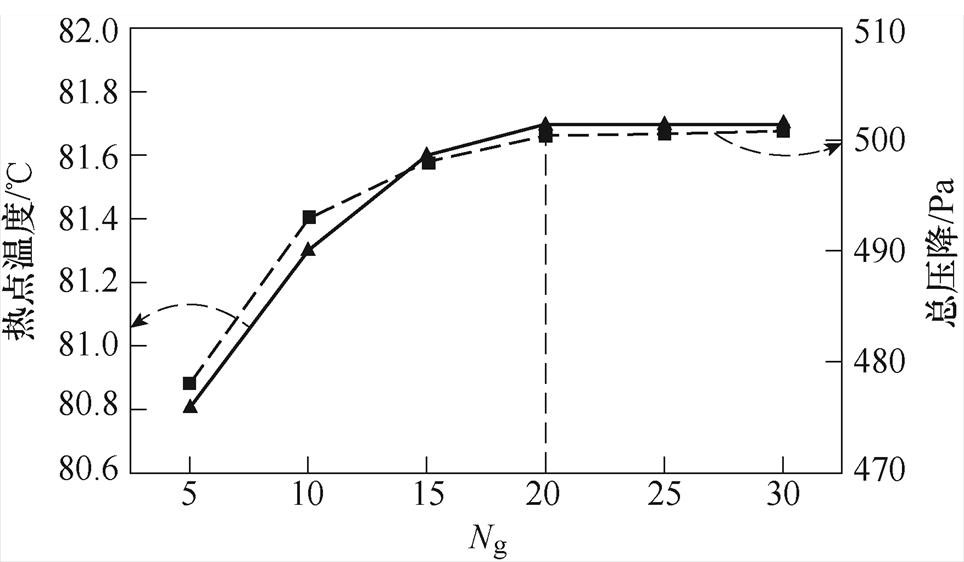
图8 网格无关性验证
Fig.8 Grid independence verification
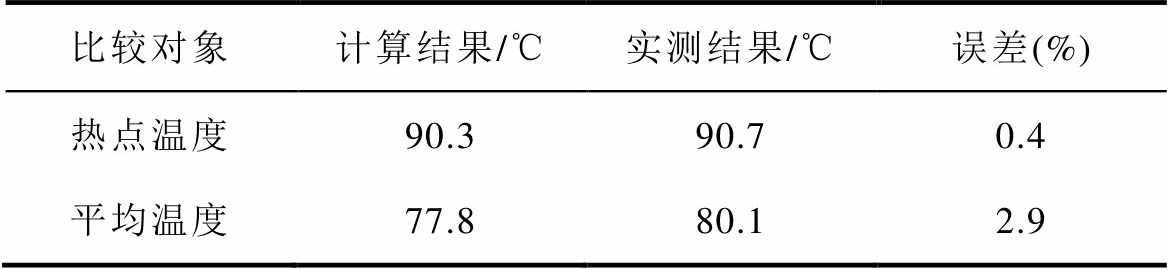
通常采用热电偶法或光纤法对绕组温度进行实际测量，但由于绝缘等限制，布置的测点有限，因此实际测量能够提供的温度细节有限，且无法提供绕组内部的油流分布情况，而数值模拟可以弥补这一不足，能够提供绕组内部温度和油流分布细节。因此，本研究采用实际测量和数值模拟相结合的方式来验证本研究计算模型的准确性，计算结果与实测结果的比较见表7，计算结果与文献结果的比较如图9所示。结果表明，采用本研究的计算模型，绕组热点和平均温度与实测结果的误差分别为0.4%和2.9%，辐向油道内油流质量流量和线饼温度的分布规律与文献[28]十分吻合。这表明本研究采用的计算模型是准确而可靠的。
表7 计算结果与实测结果的比较
Tab.7 Comparison between calculated and measured results
比较对象计算结果/℃实测结果/℃误差(%) 热点温度90.390.70.4 平均温度77.880.12.9
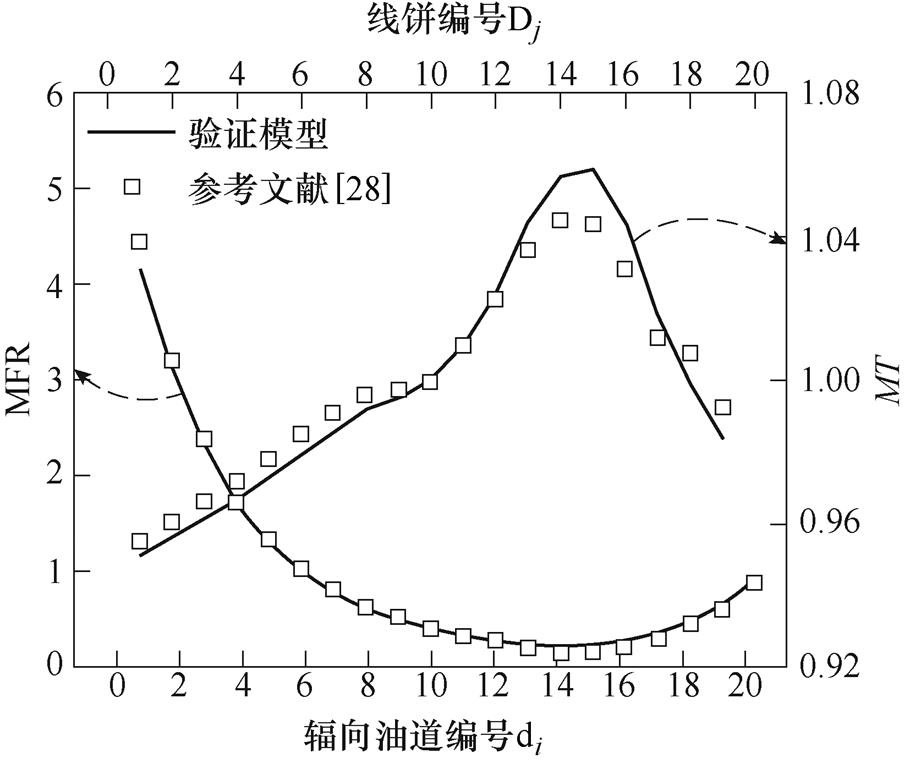
图9 计算结果与文献结果的比较
Fig.9 Comparison between calculated and literature results
基波和额定工况下线饼损耗分布的比较如图10所示。基波工况下，如图10a所示，沿轴向，受涡流效应的影响，绕组端部附近2～3个线饼的损耗明显较大，其余线饼的损耗无明显差异。绕组顶部和底部各4个线饼的损耗见表8。表中，Y为沿轴向从绕组顶部或底部向绕组中部数的第Y个线饼。由表8可知，顶部和底部第1个线饼的损耗分别比第4个线饼大27.27%和26.07%。沿辐向，涡流效应使内侧列线饼单元的总损耗较大，其余列线饼单元的总损耗无明显差异。辐向各列线饼单元的总损耗见表9。表中，X为沿辐向从绕组内侧向外侧数的第X列线饼单元。由表9可知，辐向最内侧列线饼单元的总损耗比最外侧列大10.71%。
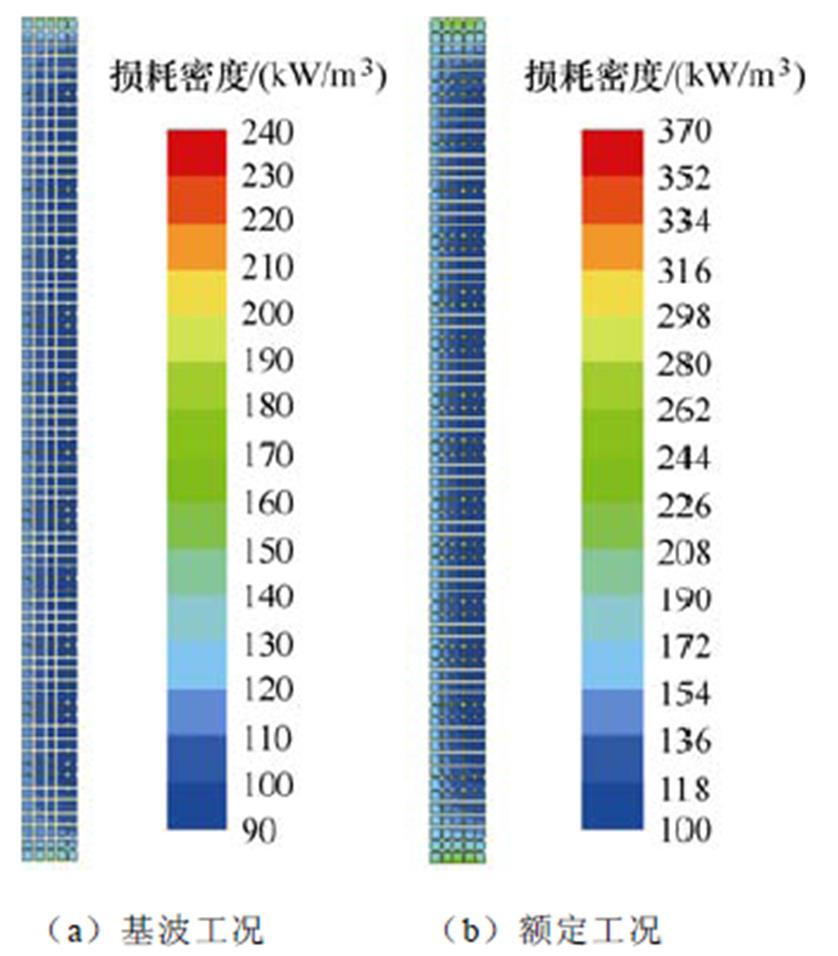
图10 基波和额定工况下线饼损耗分布的比较
Fig.10 Comparison of disc loss distributions under fundamental wave and rated conditions
表8 绕组顶部和底部各4个线饼的损耗
Tab.8 Losses of four discs at winding top and bottom
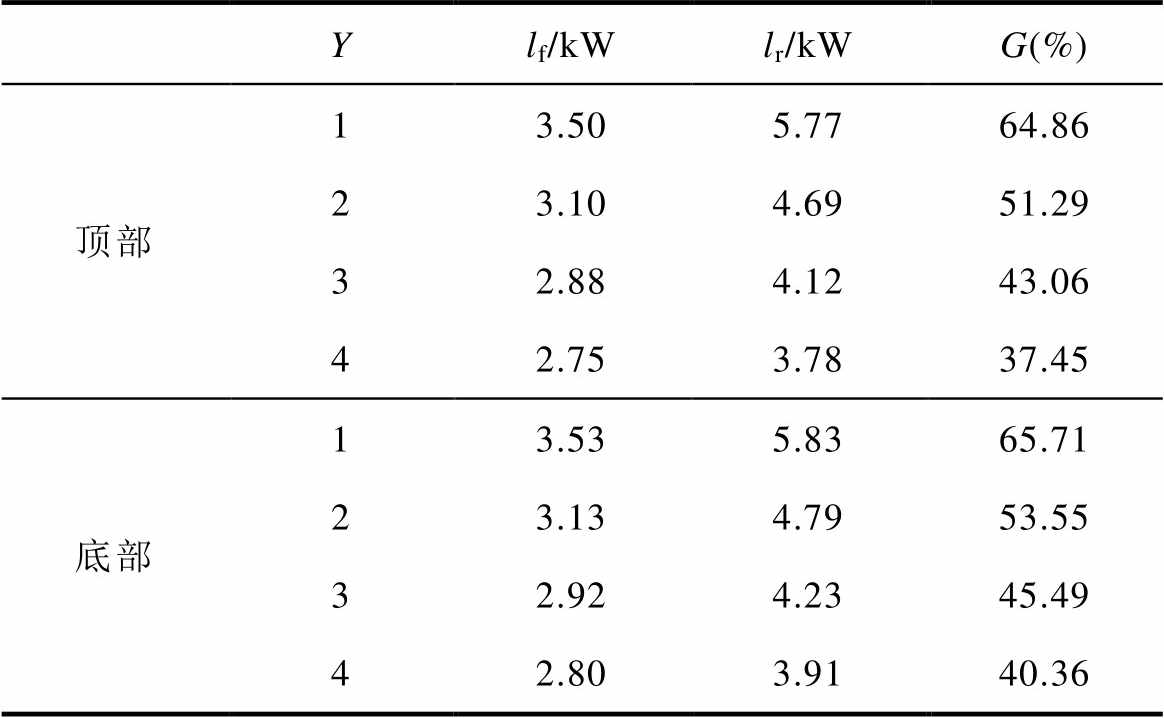
Ylf/kWlr/kWG(%) 顶部13.505.7764.86 23.104.6951.29 32.884.1243.06 42.753.7837.45 底部13.535.8365.71 23.134.7953.55 32.924.2345.49 42.803.9140.36
表9 辐向各列线饼单元的总损耗
Tab.9 Total losses of disc units at each column
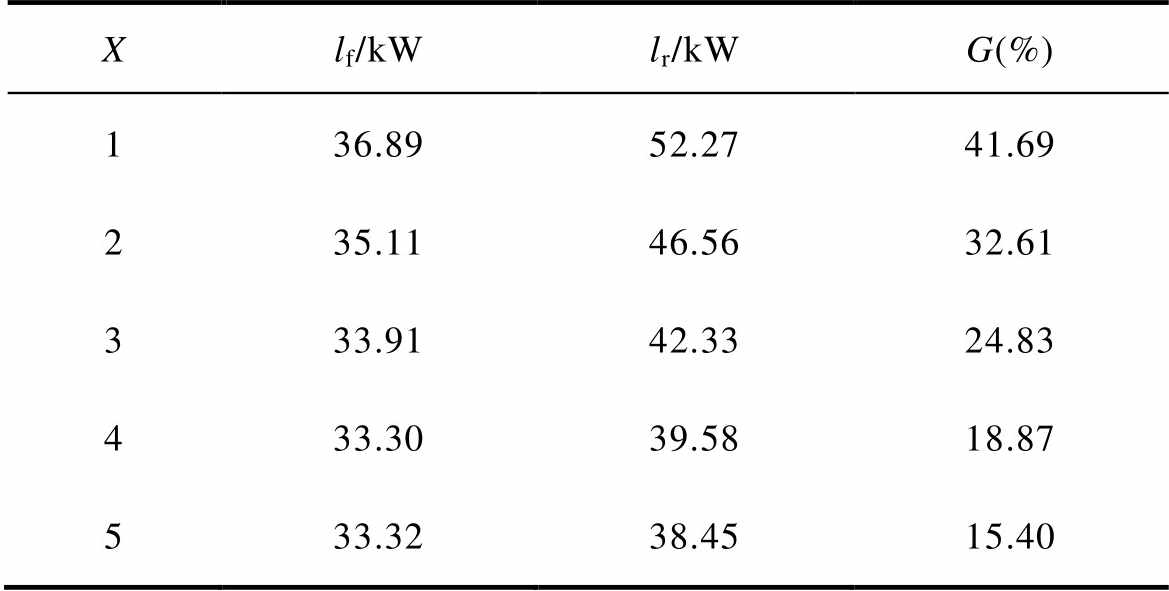
Xlf/kWlr/kWG(%) 136.8952.2741.69 235.1146.5632.61 333.9142.3324.83 433.3039.5818.87 533.3238.4515.40
额定工况下，如图10b所示，沿轴向，与基波工况相比，各线饼的总损耗有不同程度的增加。由表8可知，顶部第1～第4个线饼的损耗增长率分别为64.86%、51.29%、43.06%和37.45%，底部第1～第4个线饼的损耗增长率分别为65.71%、53.55%、45.49%和40.36%。可见，越靠近绕组端部，线饼损耗的增加幅度越大，说明谐波电流加剧了端部线饼的涡流效应。沿辐向，与基波工况相比，各列线饼单元的总损耗有不同程度的增加。由表9可知，辐向最内侧列到最外侧列线饼单元的损耗增长率分别为41.69%、32.61%、24.83%、18.87%和15.40%，可见，从最外侧列到最内侧列，线饼单元总损耗的增加幅度依次增大，说明谐波电流加剧了辐向内侧列线饼单元的涡流效应。
辐向油道油流质量流量和线饼平均温度分布特性如图11所示。油流无量纲速度云图如图12所示。靠近油流入口和油流出口的辐向油道内的油流流量较大，而绕组中部辐向油道内的油流流量较小，且变化幅度很小。分析其原因，如图12d所示，变压器油从油流入口流入绕组后，会首先充满底部第一个辐向油道，然后分流，一部分流入轴向油道，一部分流入下一个辐向油道。因此，辐向油道内油流流量随着高度的升高会先减小。油流的主流方向为轴向，辐向油道与主流方向垂直，所以变压器油流入辐向油道的阻力较大。随着高度升高，油压会逐渐减小。当油压不足以克服阻力时，会在辐向油道的入口和出口附近形成回流，从而阻塞辐向油道，如图12c所示。因此，绕组中部辐向油道内的油流流量较小且变化幅度很小。当油流靠近油流出口时，由于油流出口位于绕组的中间位置，两侧轴向油道内的变压器油必须经过辐向油道才能流出绕组。因此，靠近油流出口附近的辐向油道内的油流流量明显增大，如图12b所示。
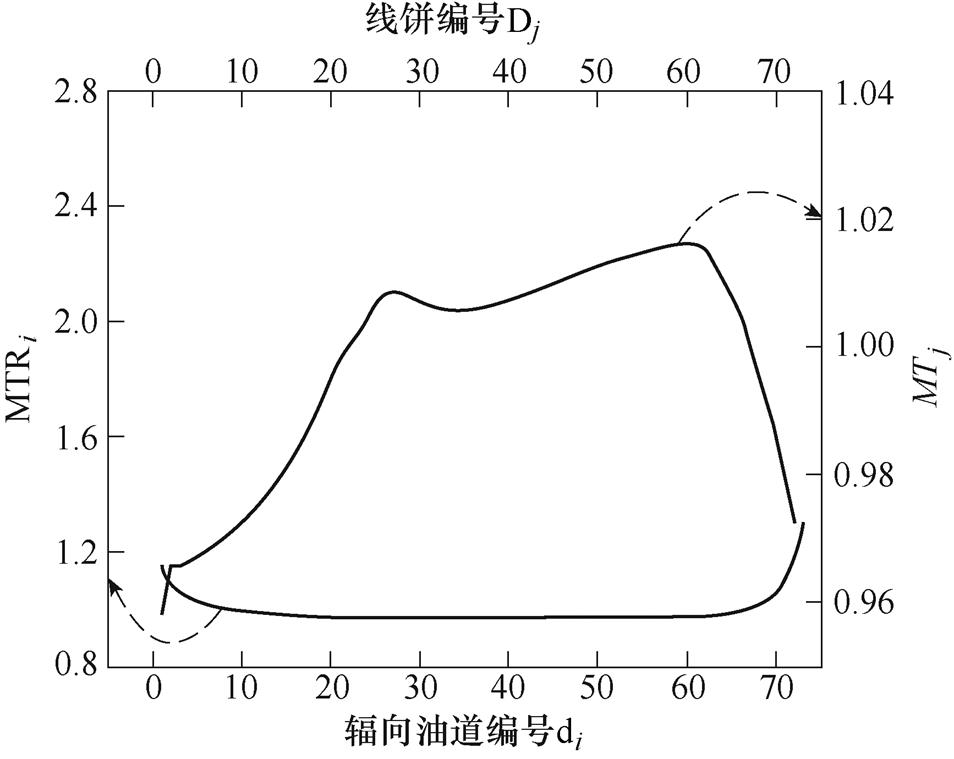
图11 辐向油道油流质量流量和线饼平均温度分布特性
Fig.11 Distribution characteristics of mass flow rate in radial oil duct and disc mean temperature
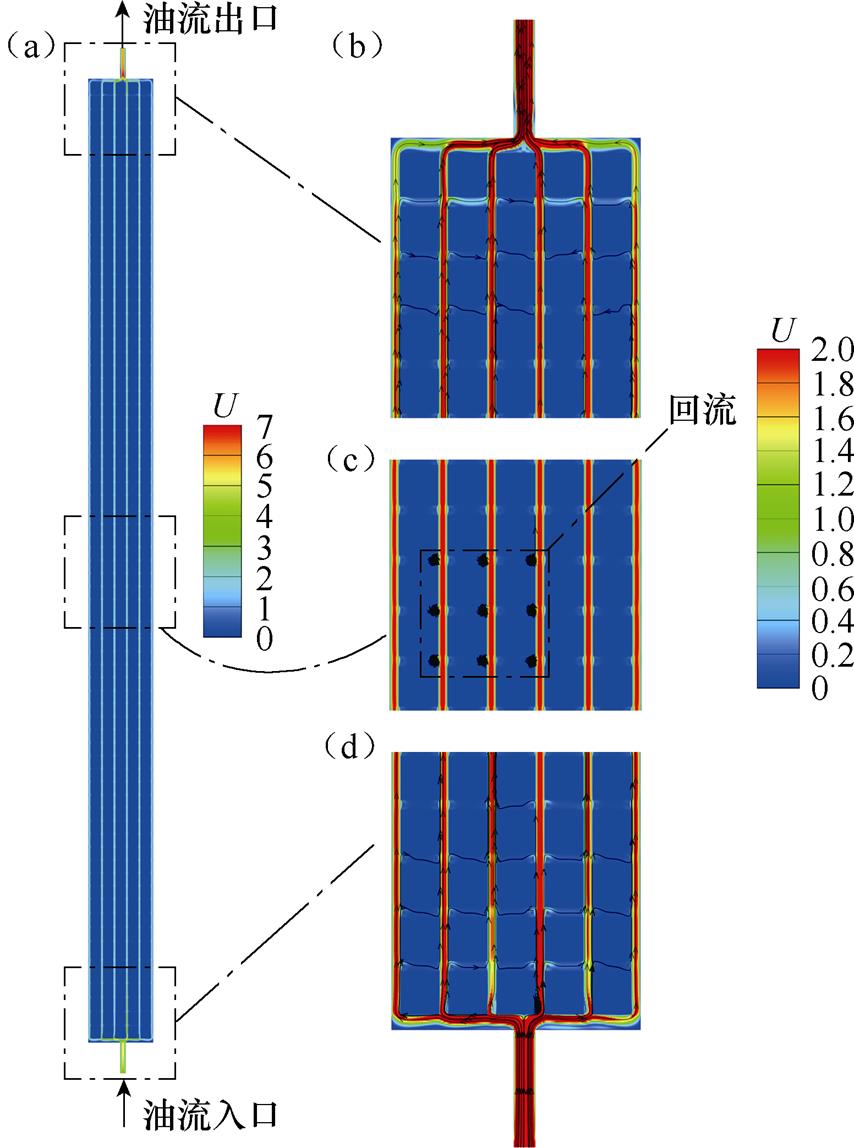
图12 油流无量纲速度云图
Fig.12 Contour of oil dimensionless velocity
基波工况下绕组的温度分布如图13a所示。绕组热点温度为81.7℃，平均温度为74.3℃，热点位于绕组的中上部。如图11所示，沿轴向，从绕组底部至顶部，线饼平均温度先逐渐升高，后逐渐下降。分析其原因，由损耗计算结果可知，仅绕组端部附近2～3个线饼的损耗明显较大，其他线饼的损耗无明显差异。线饼平均温度先升高的原因是随着高度增加，油温逐渐升高，线饼和变压器油之间的温差减小，而且绕组中部辐向油道内油流流量很小且几乎不变，可认为线饼与变压器油之间的热阻几乎不变，因此线饼与变压器油之间的换热量减少，导致线饼平均温度升高。由于靠近油流出口附近的辐向油道内油流流量明显增大，油速加快导致线饼与变压器油之间的热阻减小，因此线饼与变压器油之间的换热量增大，导致线饼的平均温度下降。沿辐向，由于油流入口和出口均位于绕组的中间位置，因此绕组内部流场沿辐向接近于对称分布，如图12所示。而且，线饼损耗沿辐向变化不大。因此线饼温度沿辐向变化不大。
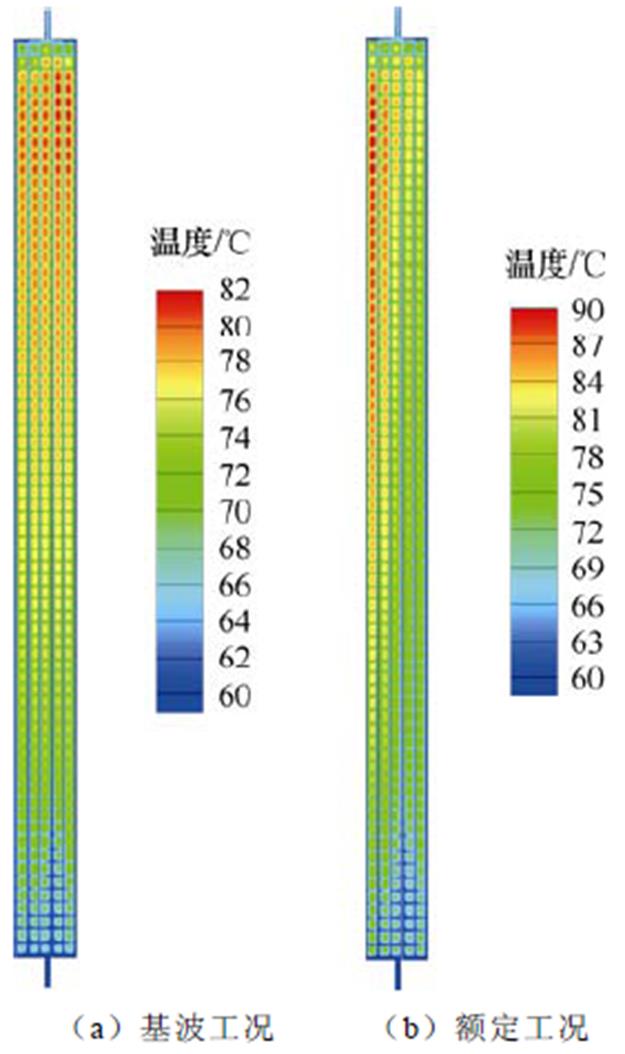
图13 基波和额定工况下绕组温度分布的比较
Fig.13 Comparison of winding temperature distributions under fundamental wave and rated conditions
额定工况下绕组的温度分布如图13b所示。绕组热点温度为90.3℃，平均温度为77.8℃。相比于基波工况，热点温度升高了8.6℃，平均温度升高了3.5℃。热点位于绕组的中上部，且位于绕组辐向内侧。沿轴向，和基波工况下一致，线饼温度随着高度的增加先升高后降低。沿辐向，由于辐向内侧列线饼单元的总损耗明显大于外侧列。因此，相比于基波工况，额定工况下线饼温度沿辐向分布不均匀，热点集中在绕组辐向内侧。
本研究针对传统电热类比线饼简化方法的不足提出了一种新的线饼简化方法，并综合考虑绕组温度数值计算中的关键问题，建立了完整的电磁-热-流多物理场耦合模型，基于计算结果定量分析了谐波电流对绕组损耗和温度分布特性的影响规律，主要结论总结如下：
1）采用本研究提出的线饼简化方法建立的简化模型，与无简化模型相比，轴向换热量几乎相同，辐向换热量的偏差在2%以内。相比于传统的电热类比的简化方法，不仅避免了建立热阻网络时的庞大工作量，降低了计算难度，对于异形线饼结构也同样适用。
2）综合考虑绕组温度数值计算中关键问题的多物理场耦合模型减少了现有计算模型部分简化导致的不确定性，并经过了实测结果和文献结果的双重验证。
3）基波工况下，受涡流效应的影响，绕组端部附近2～3个线饼以及辐向内侧列线饼单元的损耗明显较大。相比于基波工况，谐波电流不仅使各线饼的损耗增大，同时加剧了端部线饼和辐向内侧列线饼单元的涡流效应，使端部线饼和辐向内侧列线饼单元的损耗显著增大。
4）基波工况下线饼温度沿辐向变化不明显。相比于基波工况，谐波电流使线饼温度沿辐向方向分布不均匀，热点集中在绕组辐向内侧，使热点和平均温度分别升高了8.6℃和3.5℃。
参考文献
[1] 李冰, 王泽忠, 刘恪, 等. 特高压变压器直流偏磁对绕组电流的影响[J]. 电工技术学报, 2020, 35(7): 1422-1431.
Li Bing, Wang Zezhong, Liu Ke, et al. Research on winding current of UHV transformer under DC- bias[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1422-1431.
[2] 刘骥, 张明泽, 赵春明, 等. 基于频域介电响应分频段优化计算的变压器油纸绝缘老化参数定量计算方法[J]. 电工技术学报, 2020, 35(9): 2020-2031.
Liu Ji, Zhang Mingze, Zhao Chunming, et al. Quanti- tative calculation method of transformer oil-paper insulation aging parameters based on frequency dielectric spectrum frequency range optimized calculation[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2020-2031.
[3] 张良县, 陈模生, 彭宗仁, 等. 非正弦负载电流下特高压换流变压器绕组的谐波损耗分析[J]. 中国电机工程学报, 2014, 34(15): 2452-2459.
Zhang Liangxian, Chen Mosheng, Peng Zongren, et al. Study on the harmonic losses of UHV converter transformer windings subject to non-sinusoidal load current[J]. Proceedings of the CSEE, 2014, 34(15): 2452-2459.
[4] 谢裕清, 李琳, 宋雅吾, 等. 油浸式电力变压器绕组温升的多物理场耦合计算方法[J]. 中国电机工程学报, 2016, 36(21): 5957-5965, 6040.
Xie Yuqing, Li Lin, Song Yawu, et al. Multi-physical field coupled method for temperature rise of winding in oil-immersed power transformer[J]. Proceedings of the CSEE, 2016, 36(21): 5957-5965, 6040.
[5] Zhang Xiang, Wang Zhongdong, Liu Qiang, et al. Numerical investigation of oil flow and temperature distributions for ON transformer windings[J]. Applied Thermal Engineering, 2018, 130: 1-9.
[6] 苏小平, 陈伟根, 胡启元, 等. 基于解析-数值技术的变压器绕组温度分布计算[J]. 高电压技术, 2014, 40(10): 3164-3170.
Su Xiaoping, Chen Weigen, Hu Qiyuan, et al. Calculation for transformer winding temperature distribution by numerical analytical technology[J]. High Voltage Engineering, 2014, 40(10): 3164-3170.
[7] 马永强, 刘刚, 李德波, 等. 绕组损耗分布对油浸式变压器温升的影响分析[J]. 华北电力大学学报(自然科学版), 2018, 45(3): 34-43.
Ma Yongqiang, Liu Gang, Li Debo, et al. Analyses of effect of winding loss distribution on temperature rise of oil-immersed transformer[J]. Journal of North China Electric Power University (Natural Science Edition), 2018, 45(3): 34-43.
[8] 王永强, 马伦, 律方成, 等. 基于有限差分和有限体积法相结合的油浸式变压器三维温度场计算[J]. 高电压技术, 2014, 40(10): 3179-3185.
Wang Yongqiang, Ma Lun, Lü Fangcheng, et al. Calculation of 3D temperature field of oil immersed transformer by the combination of the finite element and finite volume method[J]. High Voltage Engin- eering, 2014, 40(10): 3179-3185.
[9] 曾非同, 关向雨, 黄以政, 等. 基于多尺度多物理场的油浸式变压器流动-传热数值研究[J]. 电工技术学报, 2020, 35(16): 3436-3444.
Zeng Feitong, Guan Xiangyu, Huang Yizheng, et al. Numerical study on flow-heat transfer of oil- immersed transformer based on multiple-scale and multiple-physical fields[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3436-3444.
[10] 王泽忠, 李明洋, 宣梦真, 等. 单相四柱式变压器直流偏磁下的温升试验及仿真分析[J]. 电工技术学报, 2021, 36(5): 1006-1013.
Wang Zezhong, Li Mingyang, Xuan Mengzhen, et al. Temperature rise test and simulation of single-phase four-column transformer under DC-bias[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(5): 1006-1013.
[11] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491.
Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal- fluid model[J]. Transactions of China Electro- technical Society, 2020, 35(21): 4483-4491.
[12] Smolka J, Nowak A J. Experimental validation of the coupled fluid flow, heat transfer and electromagnetic numerical model of the medium-power dry-type electrical transformer[J]. International Journal of Thermal Sciences, 2008, 47(10): 1393-1410.
[13] Tenbohlen S, Schmidt N, Breuer C, et al. Investi- gation of thermal behavior of an oil-directed cooled transformer winding[J]. IEEE Transactions on Power Delivery, 2018, 33(3): 1091-1098.
[14] 井永腾, 王宁, 李岩, 等. 电磁-热-流弱耦合的变压器绕组温升研究[J]. 电机与控制学报, 2019, 23(10): 41-48.
Jing Yongteng, Wang Ning, Li Yan, et al. Research on temperature rise of transformer windings with electromagnetic-thermal-flow weak coupling[J]. Electric Machines and Control, 2019, 23(10): 41-48.
[15] Tan Youbo, Yu Xiaoling, Ji Shengchang, et al. Para- metric study and optimization of a full-scale converter transformer winding[J]. International Journal of Heat and Mass Transfer, 2021, 181: 121861.
[16] 蔡国伟, 孔令国, 潘超, 等. 基于频变特性的变压器谐波损耗分析[J]. 电网技术, 2011, 35(11): 120- 124.
Cai Guowei, Kong Lingguo, Pan Chao, et al. Harmonic loss analysis of transformer based on frequency dependent characteristics[J]. Power System Technology, 2011, 35(11): 120-124.
[17] 张占龙, 王科, 李德文, 等. 变压器谐波损耗计算及影响因素分析[J]. 电力系统保护与控制, 2011, 39(4): 68-72, 78.
Zhang Zhanlong, Wang Ke, Li Dewen, et al. Transformer harmonic loss calculation and influence factor analysis[J]. Power System Protection and Control, 2011, 39(4): 68-72, 78.
[18] 李琼林, 邹磊, 刘会金, 等. 电力变压器谐波损耗仿真计算与实验研究[J]. 电网技术, 2013, 37(12): 3521-3527.
Li Qionglin, Zou Lei, Liu Huijin, et al. Simulation calculation and experimental research on harmonic losses in power transformers[J]. Power System Technology, 2013, 37(12): 3521-3527.
[19] 刘书铭, 施红, 冯蕾. 考虑集肤效应与邻近效应的变压器谐波损耗模型[J]. 电力自动化设备, 2015, 35(3): 133-139.
Liu Shuming, Shi Hong, Feng Lei. Transformer harmonic loss model considering skin effect and proximity effect[J]. Electric Power Automation Equipment, 2015, 35(3): 133-139.
[20] 马铁军, 刘念, 张云红, 等. 谐波对油浸式变压器顶层油温和绕组热点温度影响的研究[J]. 变压器, 2012, 49(6): 26-29.
Ma Tiejun, Liu Nian, Zhang Yunhong, et al. Research on influence of harmonic wave to top oil temperature and winding hot spot temperature in oil-immersed transformer[J]. Transformer, 2012, 49(6): 26-29.
[21] 周卫华, 万代, 江红成, 等. 谐波电流下油浸式配电变压器负载损耗及绕组热点温度分析[J]. 高压电器, 2018, 54(9): 135-141.
Zhou Weihua, Wan Dai, Jiang Hongcheng, et al. Analysis of load loss and winding hot spot tempera- ture of oil immersed distribution transformer under harmonic current[J]. High Voltage Apparatus, 2018, 54(9): 135-141.
[22] Dao T, Phung B T. Study of voltage harmonic effect on temperature rise in distribution transformer[C]// 2016 IEEE International Conference on Power System Technology (POWERCON), Wollongong, NSW, Australia, 2016: 1-5.
[23] Zhang Jie, Cheng Lin, Wen Hao, et al. Simulation analysis of the influence of harmonics current on the winding temperature distribution of converter trans- former[C]//2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 2021: 1566-1571.
[24] Wu Jie, Liu Cong, Zhang Xianliang, et al. Influence of harmonic current on the winding loss and temperature distribution of AC transformer[C]//2021 6th Asia Conference on Power and Electrical Engin- eering (ACPEE), Chongqing, China, 2021: 1492- 1498.
[25] 叶建新, 黄健豪, 张禄亮, 等. 东莞配电网谐波对配电变压器危害分析[J]. 电力自动化设备, 2011, 31(7): 146-149.
Ye Jianxin, Huang Jianhao, Zhang Luliang, et al. Analysis of harmonic harm to distribution trans- formers[J]. Electric Power Automation Equipment, 2011, 31(7): 146-149.
[26] 于岭. 直流偏磁及谐波条件下换流变压器温升的计算[D]. 沈阳: 沈阳工业大学, 2017.
[27] 王婷婷. 电力变压器绕组的涡流损耗和温升研究[D]. 天津: 河北工业大学, 2014.
[28] Zhang Yunpeng, Ho S L, Fu Weinong, et al. Numerical study on natural convective heat transfer of nanofluids in disc-type transformer windings[J]. IEEE Access, 2019, 7: 51267-51275.
The Influence of Harmonic Current on The Loss and Temperature Distribution Characteristics of a Converter Transformer Winding
Abstract Since the harmonic current aggravated the local overheating and insulation aging of converter transformer windings, studying the influence of harmonic current on the loss and temperature distribution characteristics of windings attributed to improve the stability of transformer operation and prolong its service life. Accurate thermal modeling was critical for this study. However, there were different degrees of simplifications in the existing numerical calculation models of winding temperature. Moreover, most of current research focused on the influence of harmonic current on the loss and hot-spot temperature values, whereas there was a lack of quantitative analysis on the influence of harmonic current on the loss and temperature distribution characteristics of windings. To address these issues, this study improved winding temperature numerical calculation model, and based on this improved model, the influence of harmonic current on the loss and temperature distribution characteristics of windings was investigated.
Firstly, a novel simplification method of disc was developed and an electromagnetic-thermo-flow coupling numerical model of a full-scale valve-side winding of a converter transformer practically applied in engineering was established, in which the key factors affecting the calculation accuracy of the winding temperature were comprehensively considered. The model was validated by both measured and literature results. Secondly, the losses and temperature of the winding under the fundamental wave and rated conditions were calculated, respectively. Finally, the influence of harmonic current on the loss and temperature distribution characteristics of the winding was quantitatively analyzed.
The results showed that compared with the non-simplified model, the axial heat transfer rate of the simplified model established by the simplification method of disc proposed in this study was almost the same, and the deviation of the radial heat transfer rate was within 2%. Moreover, compared with the fundamental wave condition, under the rated condition, along the axial direction, the losses of the first to fourth disc in winding top increased by 64.86%, 51.29%, 43.06% and 37.45%, respectively, and the losses of the first to fourth disc in winding bottom increased by 65.71%, 53.55%, 45.49% and 40.36%, respectively. And along the radial direction, the total losses of each disc unit column increased by 41.69%, 32.61%, 24.83%, 18.87% and 15.40% from the innermost to the outermost column. Besides, under the fundamental wave condition, the winding hot-spot and mean temperatures were 81.7℃ and 74.3℃, respectively. The difference of winding temperature distribution along the radial direction was not obvious. By contrast, under the rated condition, the winding hot-spot and mean temperatures were 90.3℃ and 77.8℃, respectively. The winding temperature was unevenly distributed along the radial direction, and the hot spot was concentrated on the winding inside.
The following conclusions were drawn: ①The simplification method of disc proposed in this study was accurate for calculating the heat transfer of the disc. Compared with the traditional simplification method, i.e. electrothermal analogy, adopting the simplification method proposed in this study, not only the huge workload of establishing thermal resistance network was avoided and the computational hardness was lowered, but also this method was applicable to the special-shaped disc structure. ② The uncertainty caused by partial simplification of existing numerical calculation models was reduced after adopting the multi-physics coupling model established in this work. ③ Compared with the fundamental wave condition, the harmonic current intensified the eddy current effect of the end and radial inside disc unit, which increased the losses of the end and radial inside disc unit. ④Compared with the fundamental wave condition, the harmonic current made winding temperature unevenly distributed along the radial direction, and the hot spot was concentrated on the winding inside. The hot spot and mean temperatures were increased by 8.6℃ and 3.5℃, respectively.
Keywords：Converter transformer, winding, harmonic current, loss, temperature, multi-physics coupling
中图分类号：TM411
DOI: 10.19595/j.cnki.1000-6753.tces.211812
西安交通大学电力设备电气绝缘国家重点实验室（EIPE20206）和国家电网公司总部科技项目（5200-201955096A-0-0-00）资助。
收稿日期 2021-11-10
改稿日期 2021-12-02
E-mail: bo969349690@stu.xjtu.edu.cn
余小玲 女，1978年生，教授，博士生导师，研究方向为电力电子设备热管理。
E-mail: xlingyu@mail.xjtu.edu.cn（通信作者）
（编辑 崔文静）