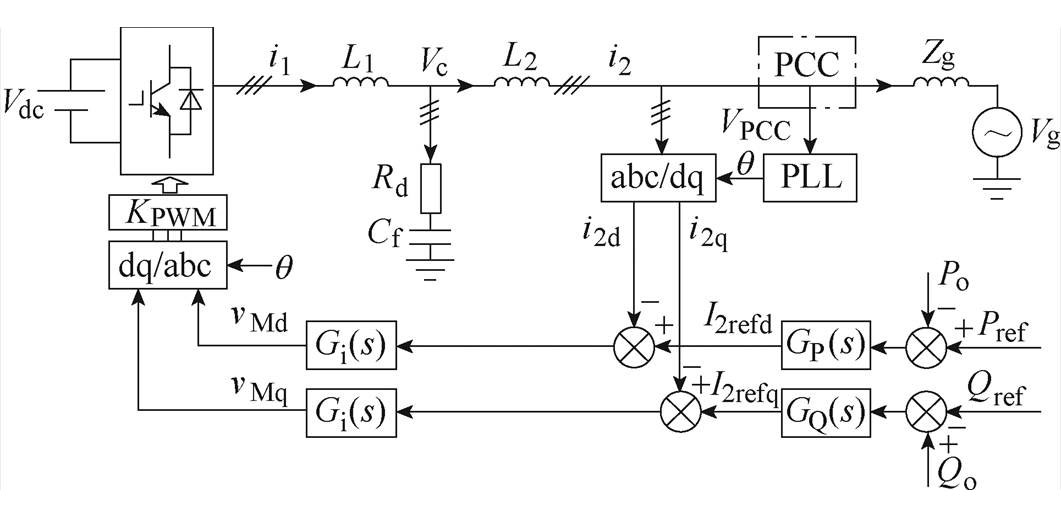
图1 PQ功率控制下LCL型GCI的系统结构
Fig.1 System structure diagram of LCL type GCI under PQ power control
摘要 针对弱电网下PQ功率控制并网逆变器的稳定性问题，该文通过构建有功/无功环的小信号控制框图，首次揭示弱电网下PQ功率控制是一种不对称控制的本质，即无功环控制器会在有功和无功控制环中形成不对称的正负反馈环路。同时，基于PQ功率环小信号控制框图的不对称现象，揭示有功/无功环控制器参数变化对并网逆变器稳定性影响存在差异性的机理，指出无功环控制器参数变化对并网系统稳定性的影响程度要明显强于有功环控制器参数变化。在此基础上，借助有功与无功环小信号控制框图中的正负反馈效应，分析并网逆变器稳定性随无功环控制器参数增加而出现先增强后减弱的“拐点”现象。最后，通过仿真与实验验证了该文理论分析的正确性。
关键词：弱电网 并网逆变器 PQ功率控制 小信号模型 不对称正负反馈效应 稳定性
随着传统化石能源的大量消耗及其对环境带来的不利影响，分布式发电技术受到广泛的关注和应用[1]。而并网逆变器（Grid-Connected Inverter, GCI）作为分布式发电与电网之间的接口设备，将在可再生能源输送到电网中发挥着重要作用[2-3]。但可再生能源分布不均导致其发电单元通常部署在偏远地区，长距离输电线路的阻抗较大，使电网表现出弱电网特性[4-5]。因此，逆变器接入电网后极易与电网阻抗发生交互作用而导致并网系统出现宽频振荡等稳定性问题，严重威胁新型电力系统的安全、可靠运行[6-8]。
目前，大量研究成果表明弱电网下并网逆变器的外环控制对并网系统稳定性的影响不容忽视[9-11]。文献[9]指出在弱电网条件下，逆变器功率外环、电压外环与锁相环之间的交互作用会更加明显，不利于GCI的稳定性。文献[10]研究了有功功率和无功功率参考值对GCI阻抗特性的影响，表明在PQ功率控制模式下，给定有功功率超过阈值时，可能诱发并网系统出现低频振荡现象。文献[11]利用传递函数模型分析了PQ功率控制下GCI的稳定性，指出增加有功功率输出对GCI稳定性的负面影响要强于增加无功功率输出。此外，文献[12]比较了不同外环控制方式下GCI的稳定裕度，发现在定无功功率控制时GCI的稳定性最差。文献[13]重构了有功和无功控制环路，并用d轴电流来表征功率耦合，同时提出一种基于自适应无功补偿的解耦策略以提升系统稳定性。但以上研究并未分析有功/无功环控制器参数变化对GCI稳定性的影响。为此，文献[14-16]通过构建考虑无功功率外环影响的GCI阻抗模型，分析了无功环控制器参数对并网系统稳定性的影响规律，指出并网系统的稳定性会随着无功环参数增加而逐渐减弱。然而，上述研究在分析PQ功率控制对GCI运行特性的影响时，并未同时考虑有功/无功环控制器参数变化对GCI稳定性的影响，难以揭示PQ功率外环控制器参数对并网系统稳定性影响的真实特性。
为了充分研究PQ功率外环控制器参数对GCI稳定性的影响，文献[17]通过构建PQ功率控制下GCI的直流侧阻抗模型，分析了电流内环与PQ外环控制器参数对直流侧阻抗特性的影响，并指出电流内环控制带宽减小会减弱PQ外环控制器参数对直流侧阻抗的影响。文献[18]分析表明，采用PQ功率控制的GCI在单位功率因数运行下，功率外环控制器参数变化对并网系统稳定性影响较小，系统是否稳定主要取决于有功功率对d轴电流的灵敏度。文献[19]构建了模块化多电平变换器（Modular Multilevel Converters, MMC）的阻抗模型，并基于该模型指出MMC的阻抗特性会随着功率外环控制器比例系数增加而向较低频段移动，从而恶化MMC的稳定性。文献[20]基于风电变流器分析了功率外环控制器参数变化对额定风速下并网系统稳定性的影响，并提出一种提高风电变流器稳定性的控制器参数设计方法。文献[21-22]构建了考虑PQ功率外环的风电变流器机组简化阻抗模型，详细分析了功率外环控制器参数变化对变流器阻抗特性的影响规律，并指出所建简化阻抗模型和详细阻抗模型的偏差会随着功率外环控制带宽与阻尼比的增加而增大。
通过以上分析不难发现，现有针对PQ功率控制下GCI稳定性的研究依旧没有深入分析有功/无功环控制器参数变化对GCI稳定性影响存在的差异性，更没有从不对称正负反馈效应的角度揭示导致这种差异性的内在机理。
因此，针对以上研究存在的不足，本文首先推导了PQ功率控制下并网逆变器的小信号数学模型，并构建了计及电网阻抗影响的并网逆变器的小信号控制框图；基于控制框图首次揭示了弱电网下PQ功率控制是一种不对称控制的本质，即无功环控制器不仅会出现在自身控制环中，而且还会以正负反馈环路的形式出现在有功控制环中。其次，通过阻抗模型分析了有功/无功环参数变化对并网逆变器稳定性的影响特性，指出无功环控制器参数变化对并网系统稳定性的影响程度要明显强于有功环控制器参数变化，进一步验证了弱电网下有功/无功环小信号控制框图的不对称性。在此基础上，借助小信号控制框图中形成的正负反馈环效应，分析了并网逆变器稳定性随无功环控制器参数增加而出现先增强后减弱的“拐点”现象。最后，通过仿真与实验验证了本文理论分析的正确性。
为了分析PQ功率控制的不对称机理及其对GCI稳定性的影响特性，本文以三相LCL型并网逆变器为例，构建了GCI系统的小信号数学模型。图1给出了PQ功率控制下GCI的系统结构，图中，功率外环的输出作为电流内环的参考值。
图1 PQ功率控制下LCL型GCI的系统结构
Fig.1 System structure diagram of LCL type GCI under PQ power control
图1中，Vdc为直流侧电压；逆变器侧滤波电感L1、滤波电容Cf和网侧滤波电感L2构成LCL滤波器；Rd为抑制LCL滤波器谐振尖峰的阻尼电阻；i1为桥臂输出电流，VC为电容支路电压，i2为并网电流，VPCC为并网点电压，Vg为电网电压，Zg为电网阻抗；P/Q、Pref/Qref分别为GCI有功/无功功率输出值和参考值；I2refd、I2refq分别为GCI输出电流在d轴和q轴的参考值；vMd、vMq分别为调制信号的d、q轴分量；q 为锁相环输出相位；KPWM为并网逆变器等效调制增益。
在系统dq坐标系下，LCL型GCI主电路的小信号数学模型[23]为
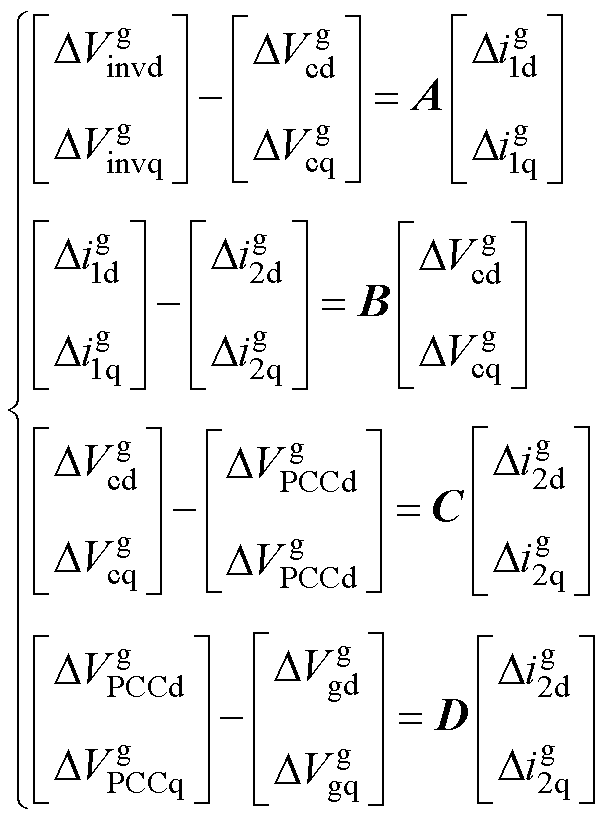（1）
式中，上标“g”表示系统dq坐标系；“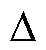
”表示扰动信号；
、
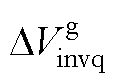分别为并网逆变器桥臂输出电压的d、q分量；
、
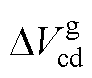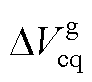分别为电容支路电压的d、q轴分量；
、
分别为并网点电压的d、q轴分量；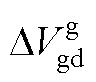
、
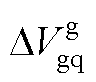分别为电网电压的d、q轴分量；
、
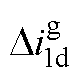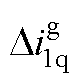分别为并网逆变器桥臂输出电流的d、q轴分量；
、
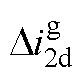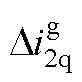分别为并网电流的d、q轴分量；矩阵A～D在频域下的具体表达式为
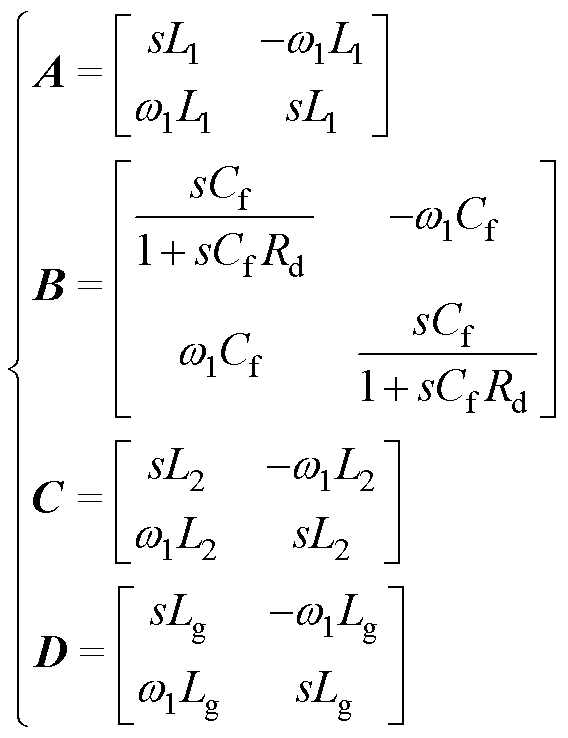（2）
GCI系统输出的有功/无功功率与电压电流之间的关系为
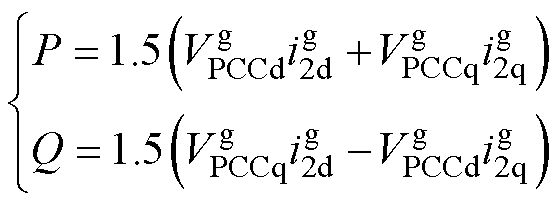（3）
对式（3）进行小信号线性化处理后可得
（4）
其中
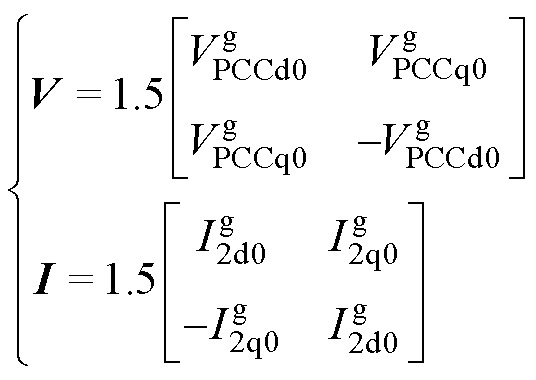（5）
式中，w1为无穷大电网的角频率。
1）锁相环
为了实现GCI与电网同步，本文采用同步参考坐标系锁相环（Synchronous Reference Frame Phase Locked Loop, SRF-PLL）结构来实现相位跟踪。通过对锁相环进行小信号建模[24]，可以得到表征其输出特性的小信号数学模型为
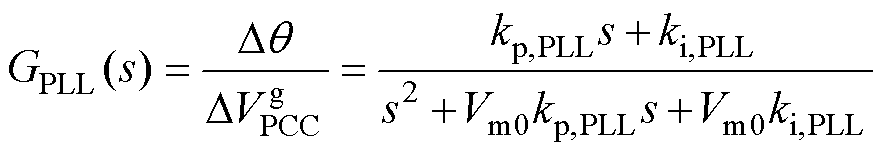（6）
式中，kp,PLL、ki,PLL分别为锁相环内部PI控制器的比例和积分系数；Vm0为PCC电压幅值。
2）PQ功率外环
根据图1可以得到外环PQ功率控制的输出与内环电流参考值之间的小信号模型为
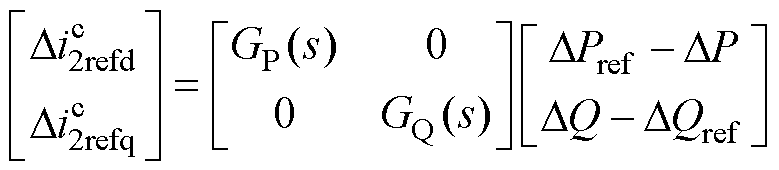（7）
式中，上标“c”表示控制器dq坐标系；GP(s)=kpp+kip/s为有功环PI控制器；GQ(s)=kqp+kqi/s为无功环PI控制器。
3）电流内环
由于PLL小信号扰动影响，导致并网逆变器的状态变量在系统dq坐标系与控制器dq坐标系之间存在关系[24]为
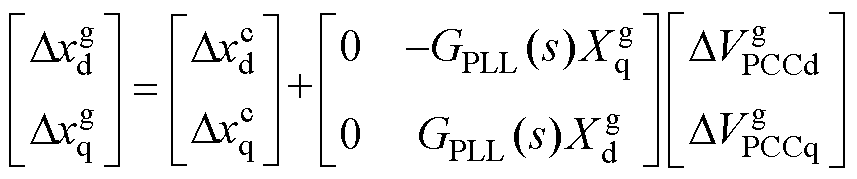（8）
式中，上标“c”表示控制器dq坐标系的变量；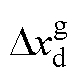
、
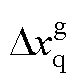和
、
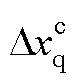分别可以代表电压、电流以及占空
比等状态变量在系统dq坐标系和控制器dq坐标系的d、q轴分量。
基于以上关系，可以得到系统dq坐标系下调制信号VMdq的小信号数学模型为
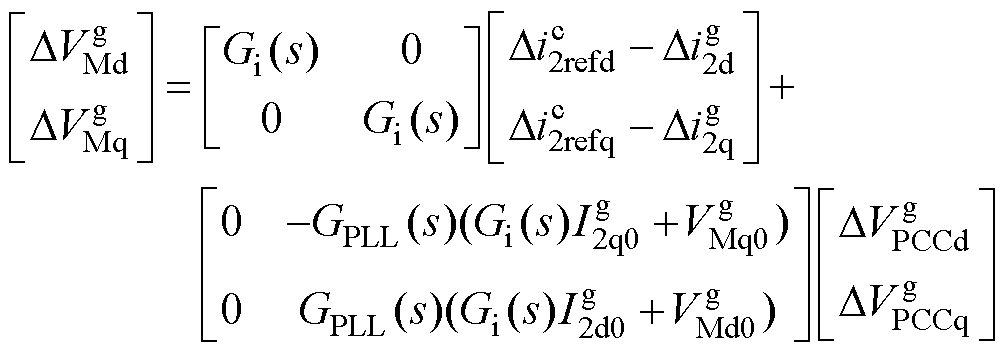（9）
式中，Gi(s)=kp,i+ki,i/s为电流内环PI控制器。
4）延时环节
考虑PWM与计算延时，通常将其线性化[5]为
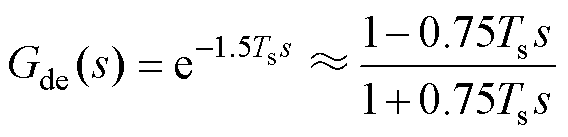（10）
利用控制电路输出调制信号与逆变器桥臂输出信号之间的关系，可以得到主电路与控制电路之间的数学表达式为
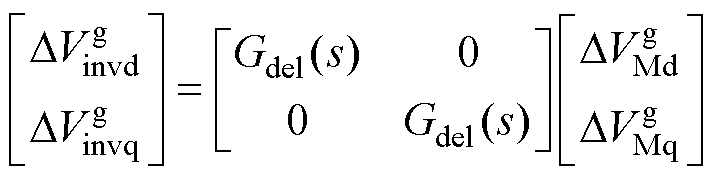（11）
式中，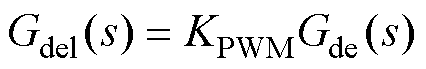
，KPWM为调制增益。
结合式（4）～式（7）、式（9）～式（11），忽略有功/无功环功率参考值的扰动，可以得到逆变器桥臂输出电压与并网电流和PCC电压之间的关系为
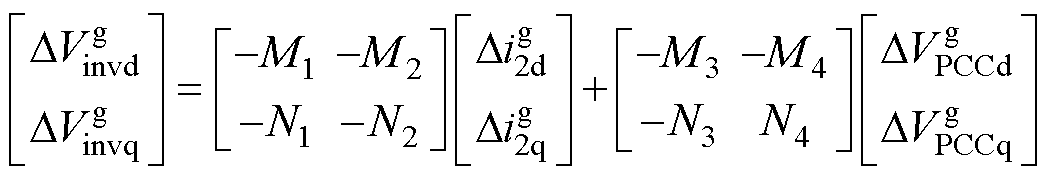（12）
其中
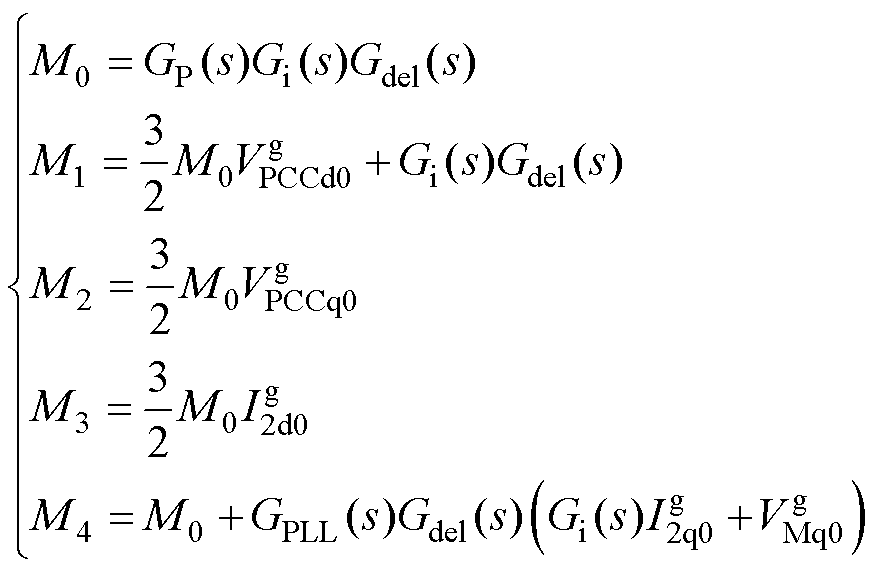
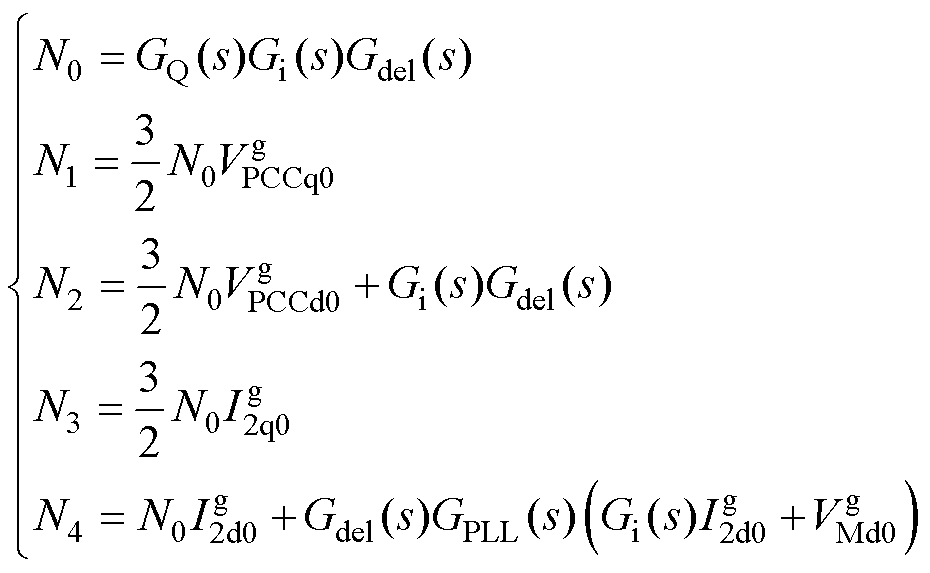
考虑到在稳态值附近，LCL滤波电感和电容引入的耦合量远小于系统电压和电流的稳态值，为了简化计算分析过程，暂且忽略这些耦合量的影响。结合式（1）与式（12）可以得到q轴并网电流与PCC电压d轴、q轴分量之间的表达式为
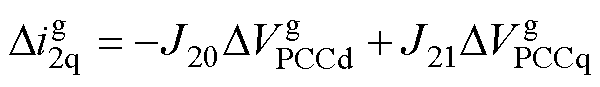（13）
其中
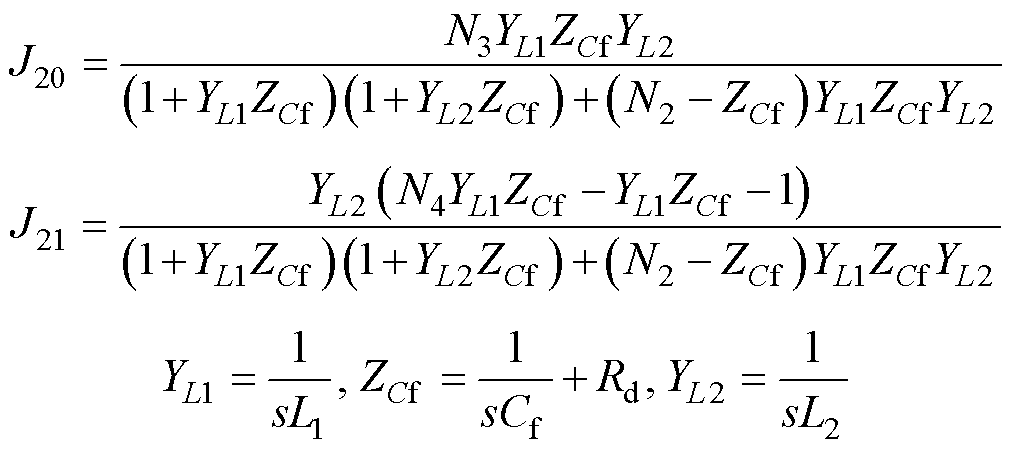
此外，本文忽略等效电网电压Vg的小信号扰动。在弱电网下，由于电网阻抗会通过PLL结构在控制环中形成并网电流正反馈环，严重影响系统的稳定性[24]。因此，在构建PQ功率控制的小信号模型时，需要将电网阻抗引入到控制环的等效变换过程中，并以此来反映弱电网对GCI稳定性的影响。基于此，联立式（12）、式（13）可得d轴电压与dq轴电流以及q轴电压与dq轴电流之间的表达式分别为
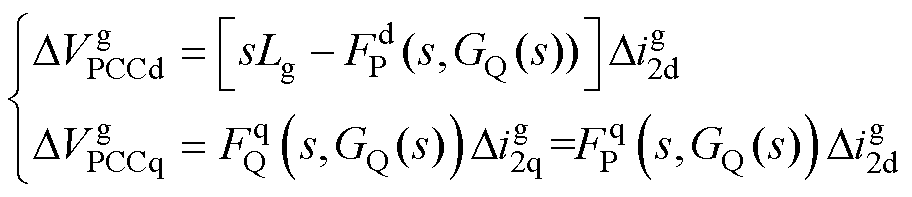（14）
式中，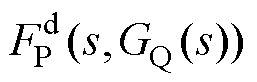
、
、
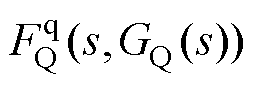分别为无功环PI控制器GQ(s)的隐函数，其具体表示为
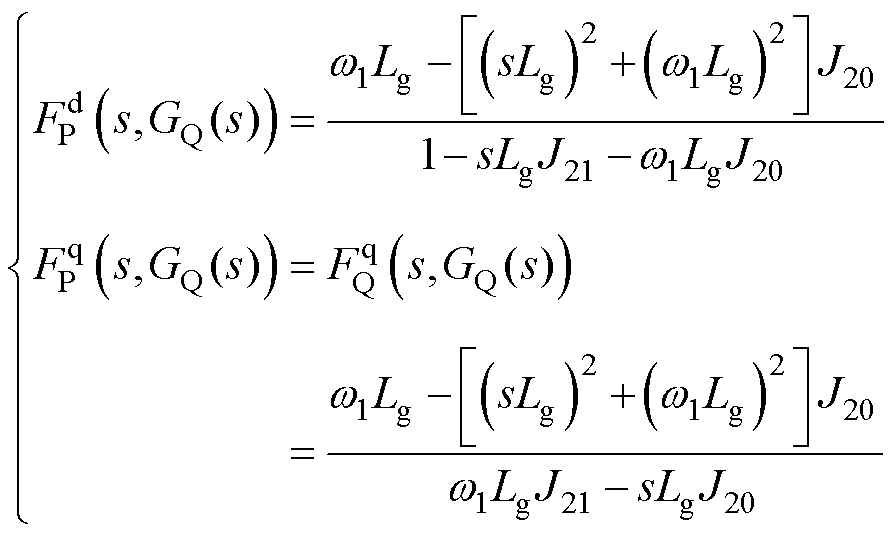（15）
根据式（15），并结合式（4）、式（5），得到有功功率与d轴电流、无功功率与q轴电流之间的关系为
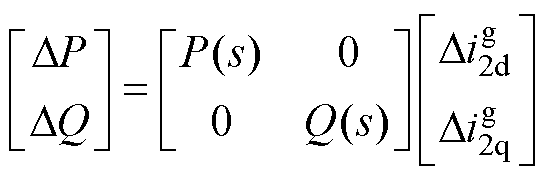（16）
其中
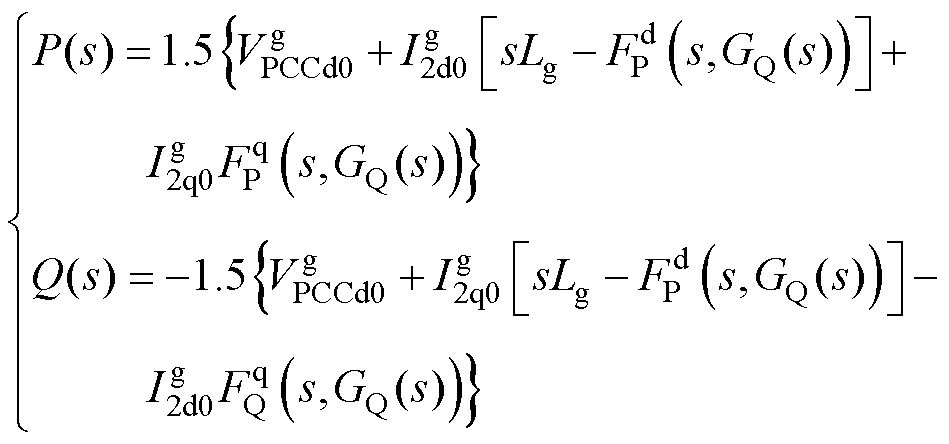
基于以上分析，可得PQ功率控制下GCI有功环与无功环的小信号控制框图，如图2所示。由于电网阻抗的存在，PLL会在电流参考值和调制信号处诱发产生相应的正负反馈环路[24]，等效到图2中即形成负反馈环路1中的Gasy,q(s)与正反馈环路4中的Gasy,d(s)。此外，当并网逆变器以单位功率因数运行时，并网电流的q轴分量为0，式（15）可进一步简化为
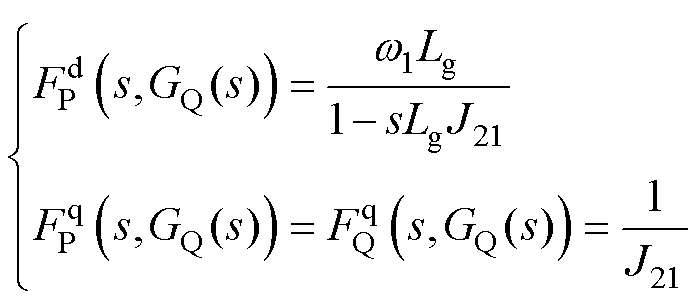（17）
由式（17）可知，此时环路3中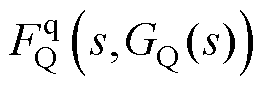
的表达式不再含有电网阻抗信息。然而，现有研究表明，并网逆变器的稳定性会随着电网阻抗的增加而逐渐减弱[3-4,7-11,15-20,24]，因此包含电网阻抗信息的环路2势必会在小信号控制框图中形成正反馈环效应，以达到削弱系统稳定性的目的。
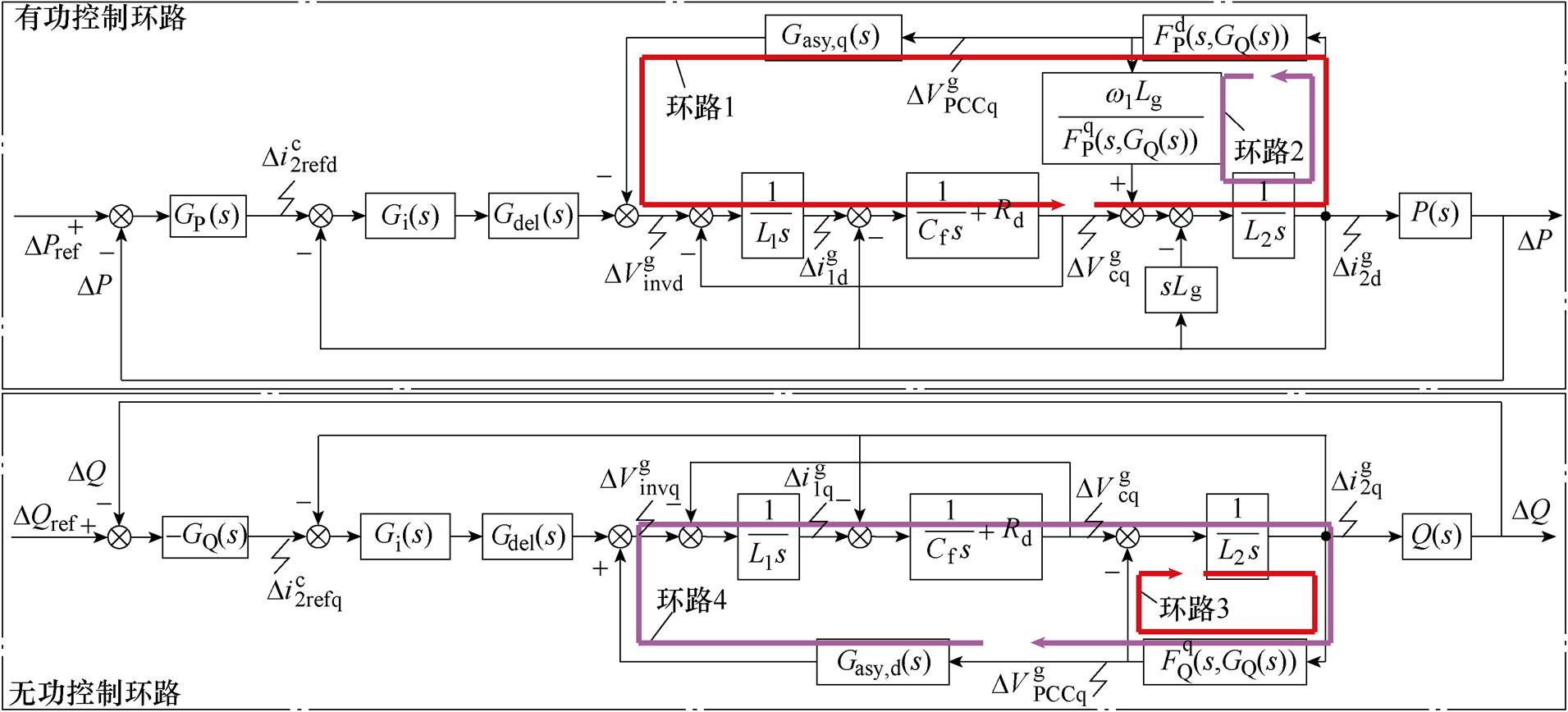
图2 PQ功率控制中有功环路和无功环路的等效小信号控制框图
Fig.2 Equivalent small signal control block diagram of active loop and reactive loop in PQ power control
与此同时，根据图2可以看出，无功环控制器参数GQ(s)不仅存在于自身控制环路中，而且还会以正负反馈环的形式存在于有功环路中，这意味着无功环控制器参数将同时影响有功环和无功环的稳定性。然而，有功环控制器参数却只出现在有功环中，仅对自身环路稳定性产生影响。因此，在考虑电网阻抗影响时，PQ功率控制并网逆变器的小信号控制框图表现出一种不对称控制现象，揭示了PQ功率控制是一种不对称控制的数学本质。
值得说明的是，上述推导的PQ功率控制下并网逆变器的小信号控制框图是在考虑电网阻抗影响与PLL小信号扰动的情形下构建的，图2中所形成的正负反馈环路都与电网阻抗或PLL传递函数直接相关。若不考虑电网阻抗影响，则图2中的正负反馈环路就不会被形成。因此，本文所推导的分析模型仅适用于新能源装机容量不断增加下考虑电网阻抗影响的并网逆变器稳定性分析场景。
通过第1节的分析不难发现，PQ功率控制GCI小信号控制框图中的正负反馈环路都只与无功环控制器有关。这意味着相较于有功环控制器参数而言，GCI的稳定性对无功环参数变化会表现的更加敏感。为了验证上述猜想，本文通过构建PQ功率控制下GCI的阻抗模型，并利用基于阻抗的稳定性判据分析有功/无功环参数变化对GCI稳定性影响程度的差异性。图3给出了矩阵形式下PQ功率控制GCI的小信号控制框图模型。
基于图3可以求得GCI的等效输出阻抗模型为
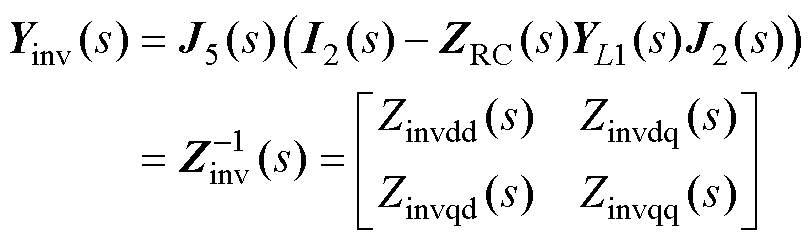（18）
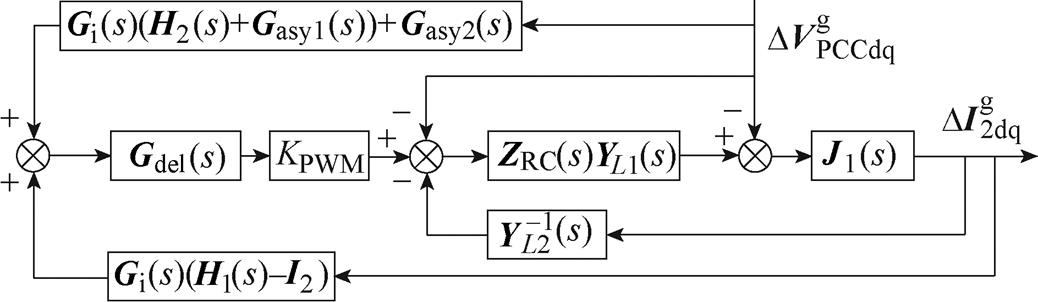
图3 矩阵形式下PQ功率控制GCI的小信号控制框图
Fig.3 Small signal control block diagram of PQ power control in the form of GCI matrix
其中
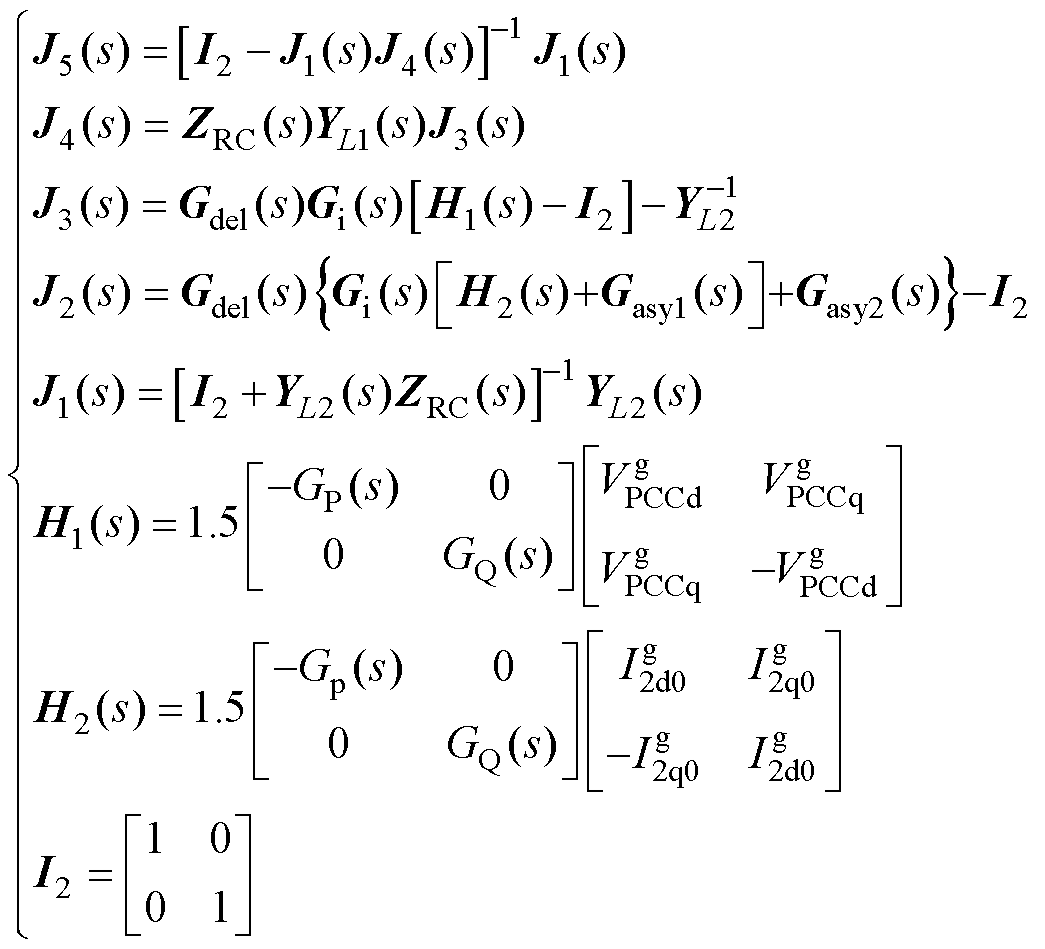
需要说明的是，式（18）中LCL滤波环节、延时环节、内环控制器及Gasy1(s)、Gasy2(s)的具体表达式详见文献[24]。同时，电网阻抗的矩阵表示为
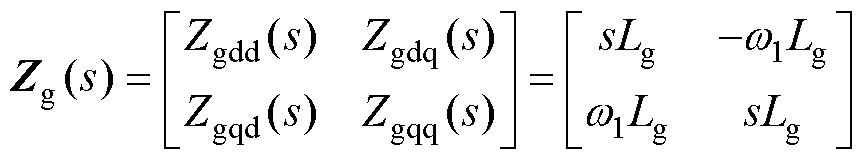（19）
根据基于阻抗的稳定性判据可知，弱电网下GCI的稳定性可以通过回率矩阵L(s)的特征值是否包围点（-1, j0）来进行判定[24-25]。其中，GCI系统回率矩阵L(s)的表达式为
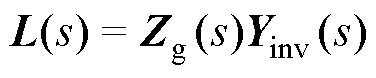（20）
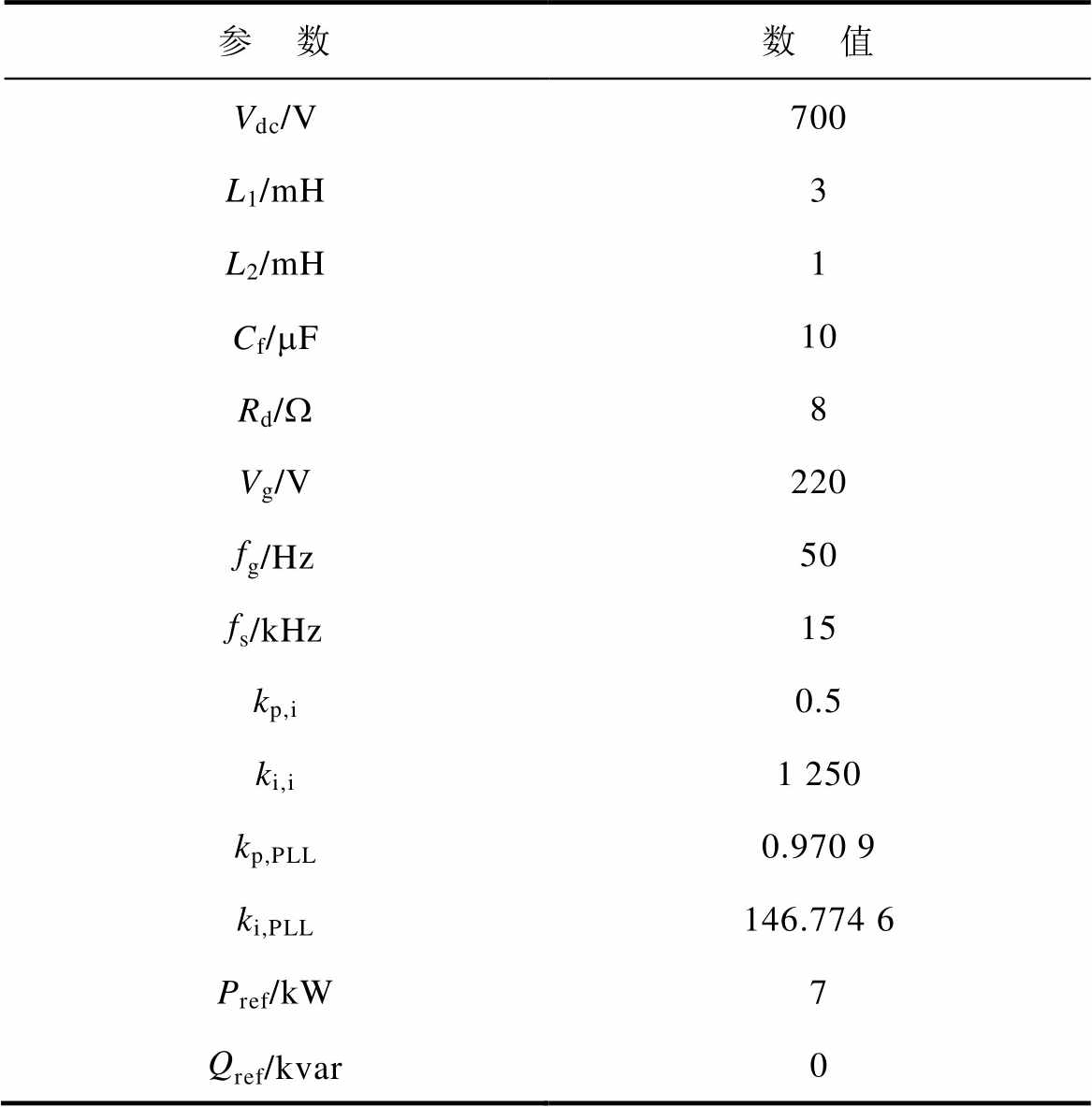
本文所采用LCL型GCI系统的主要参数见表1，并分四种情形来分析有功/无功环参数变化对并网系统稳定性的影响。其中，PQ功率环控制器参数见表2。
表1 系统主要参数
Tab.1 Main system parameters
参 数数 值 Vdc/V700 L1/mH3 L2/mH1 Cf/mF10 Rd/W8 Vg/V220 fg/Hz50 fs/kHz15 kp,i0.5 ki,i1 250 kp,PLL0.970 9 ki,PLL146.774 6 Pref/kW7 Qref/kvar0
表2 有功与无功环PI控制器参数
Tab.2 PI parameter of active and reactive power loops
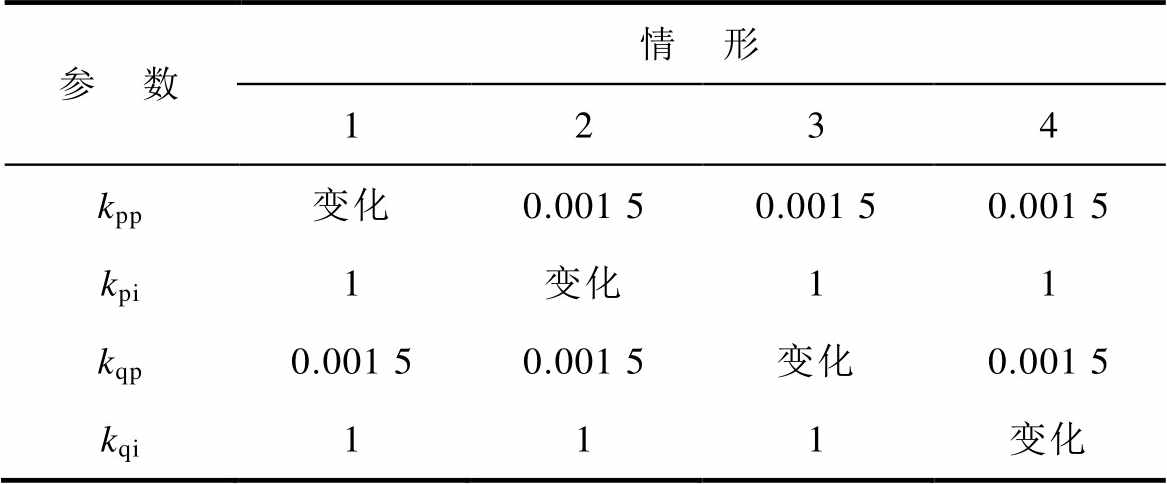
参 数情 形 1234 kpp变化0.001 50.001 50.001 5 kpi1变化11 kqp0.001 50.001 5变化0.001 5 kqi111变化
在表1与表2参数下，图4a给出了有功控制环比例系数kpp变化时，即情形1的稳定性分析结果。观察图4a可以看出：当kpp从0.000 6增大到0.005 2时，回率矩阵L(s)的特征值l1(s)的Nyquist曲线均不包围点（-1, j0），此时GCI系统处于稳定运行状态。图4b给出了有功控制环积分系数kpi变化时，即情形2的稳定性分析结果。观察图4b可以看出：当kpi从0.5增大到5时，回率矩阵L(s)的特征值l1(s)的Nyquist曲线都不包围点（-1, j0），此时并网逆变器系统同样处于稳定运行状态。值得说明的是：当kpi从0.5增大到1，再增大到1.6时，特征值l1(s)与实轴的交点先远离再靠近点（-1, j0）；当kpi从1.6增大到5时，特征值l1(s)与实轴的交点明显靠近点（-1, j0）。这意味着，随着kpi的增大，GCI系统的稳定裕度先小幅度提升，而后再降低。
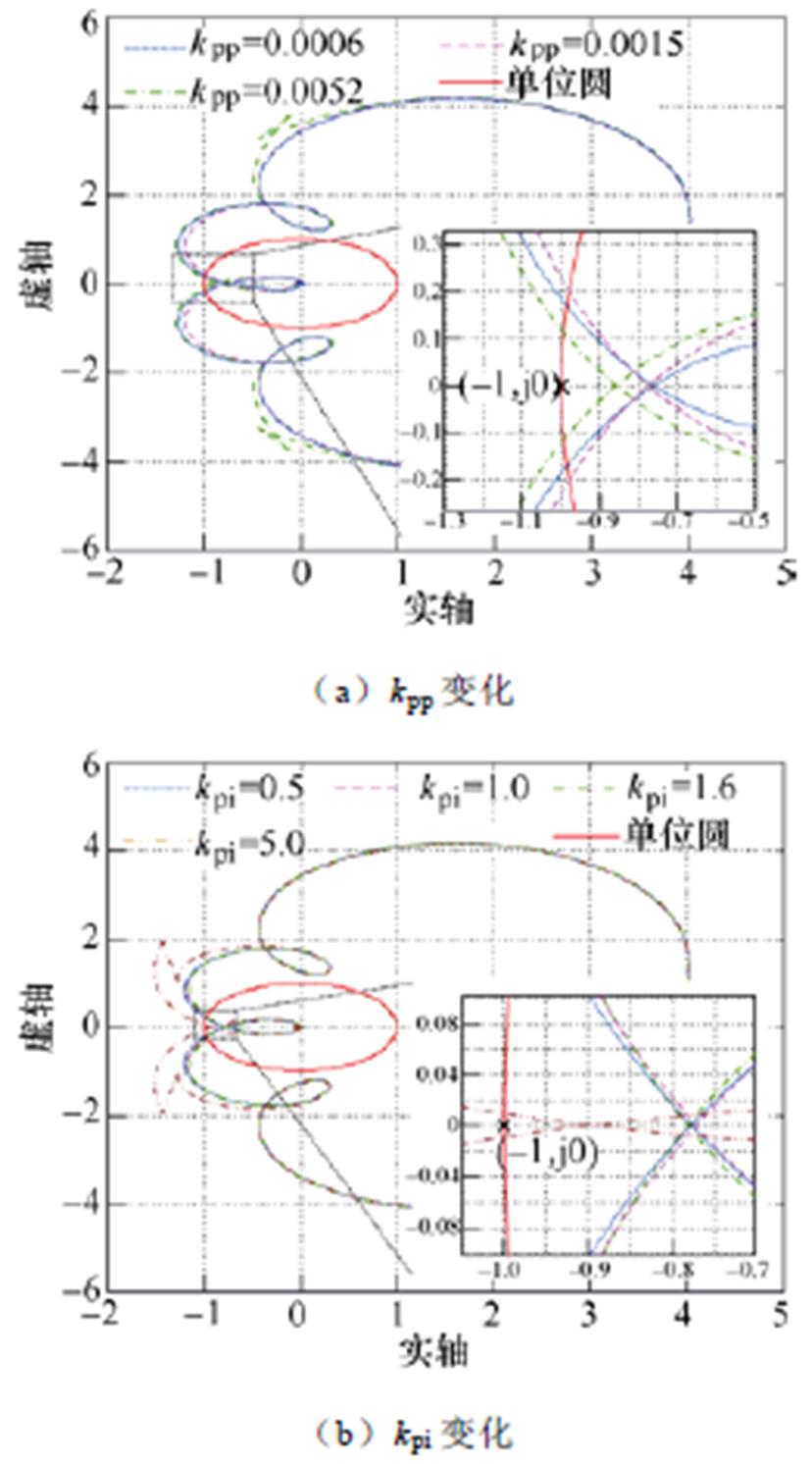
图4 情形1与情形2下GCI的稳定性分析结果
Fig.4 Stability analysis results of GCI under Case 1 and 2
为了验证有功环参数变化对GCI系统稳定性影响分析的正确性，图5a与图5b分别给出了kpp与kpi变化时GCI的输出电流仿真结果。
观察图5a可以看出：当有功环比例系数kpp从0.000 6增大到0.005 2时，GCI输出电流波形都能够保持稳定运行。而且，通过对三组参数下的并网电流进行快速傅里叶变换（Fast Fourier Transform, FFT）分析，得到相应的总谐波畸变率（Total Harmonic Distortion, THD）分别为2.21%、2.37%和3.80%。FFT分析结果表明，随着kpp的增大，并网电流的谐波含量也随之增加，即GCI系统的稳定裕度逐渐降低。以上分析验证了图4a理论分析的正确性。
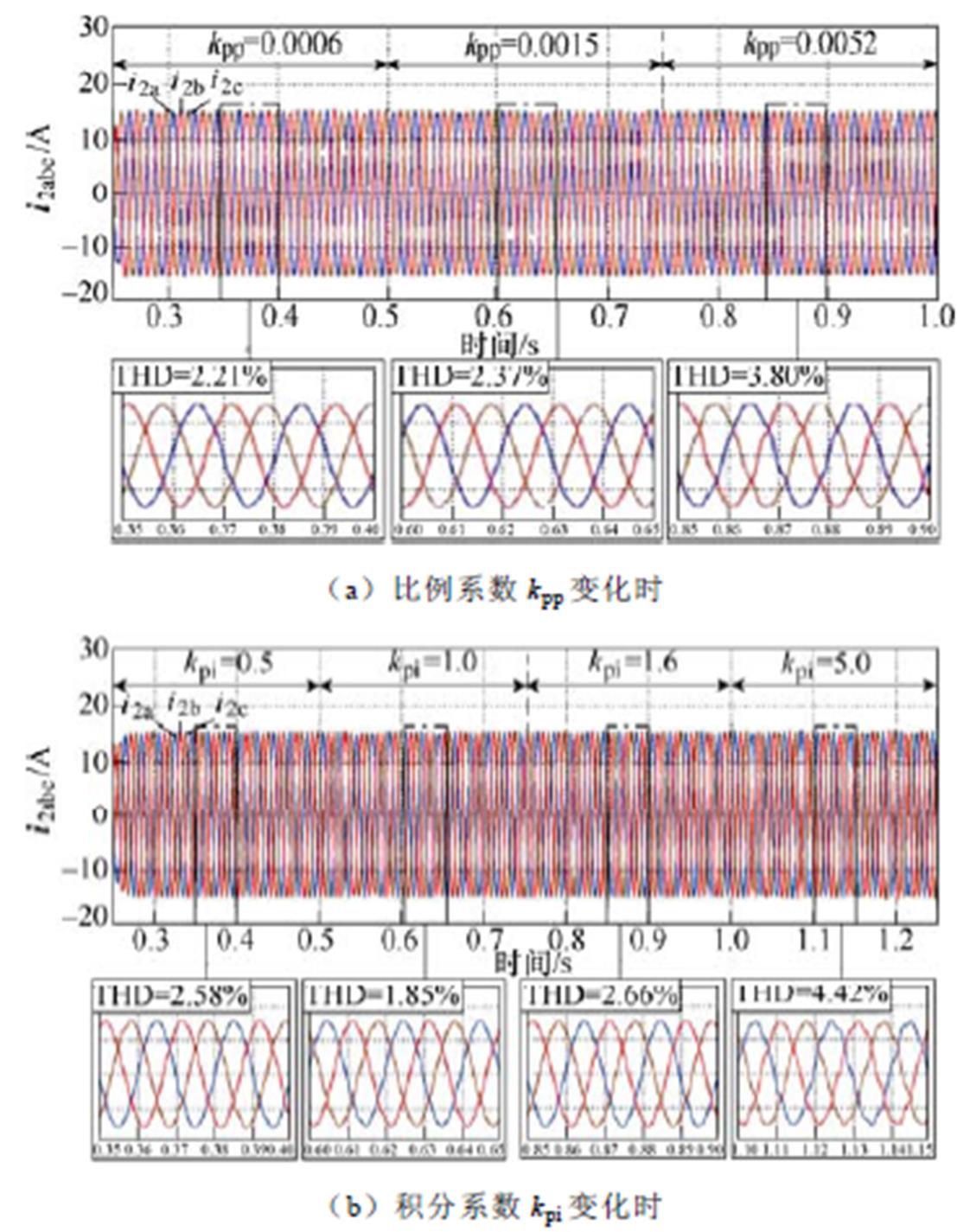
图5 有功环控制器参数变化时的并网电流仿真结果
Fig.5 Simulation results of grid-connected current when active loop controller parameters change
观察图5b可以看出：当有功环积分系数kpi从0.5增大到5时，GCI输出电流同样能够保持稳定运行。同时，通过对kpi=0.5、1.0、1.6、5.0时的并网电流进行FFT分析，可得相应的THD分别为2.58%、1.85%、2.66%和4.42%。FFT分析结果表明：随着kpi增大，并网电流的谐波含量表现出先减小后增大的特性，这意味着GCI系统的稳定裕度先增加后减小，与图4b的理论分析结果一致。
同理，图6给出了无功环参数变化时GCI的稳定性分析结果。
观察图6a可以看出：当比例系数kqp=0.001 5时，回率矩阵L(s)的特征值曲线都不包围点（-1, j0），此时并网系统处于稳定运行状态；而当kqp继续增加到0.005 2时，特征值l1(s)的Nyquist曲线包围了点（-1, j0），此时系统失稳。
观察图6b可以看出，当积分系数kqi从0.5增大到1时，回率矩阵L(s)的特征值曲线l1(s)都不包围点（-1, j0），此时系统能够保持稳定运行；而当kqi增大到1.6时，特征值l1(s)的Nyquist曲线包围点（-1, j0），此时GCI处于失稳状态。
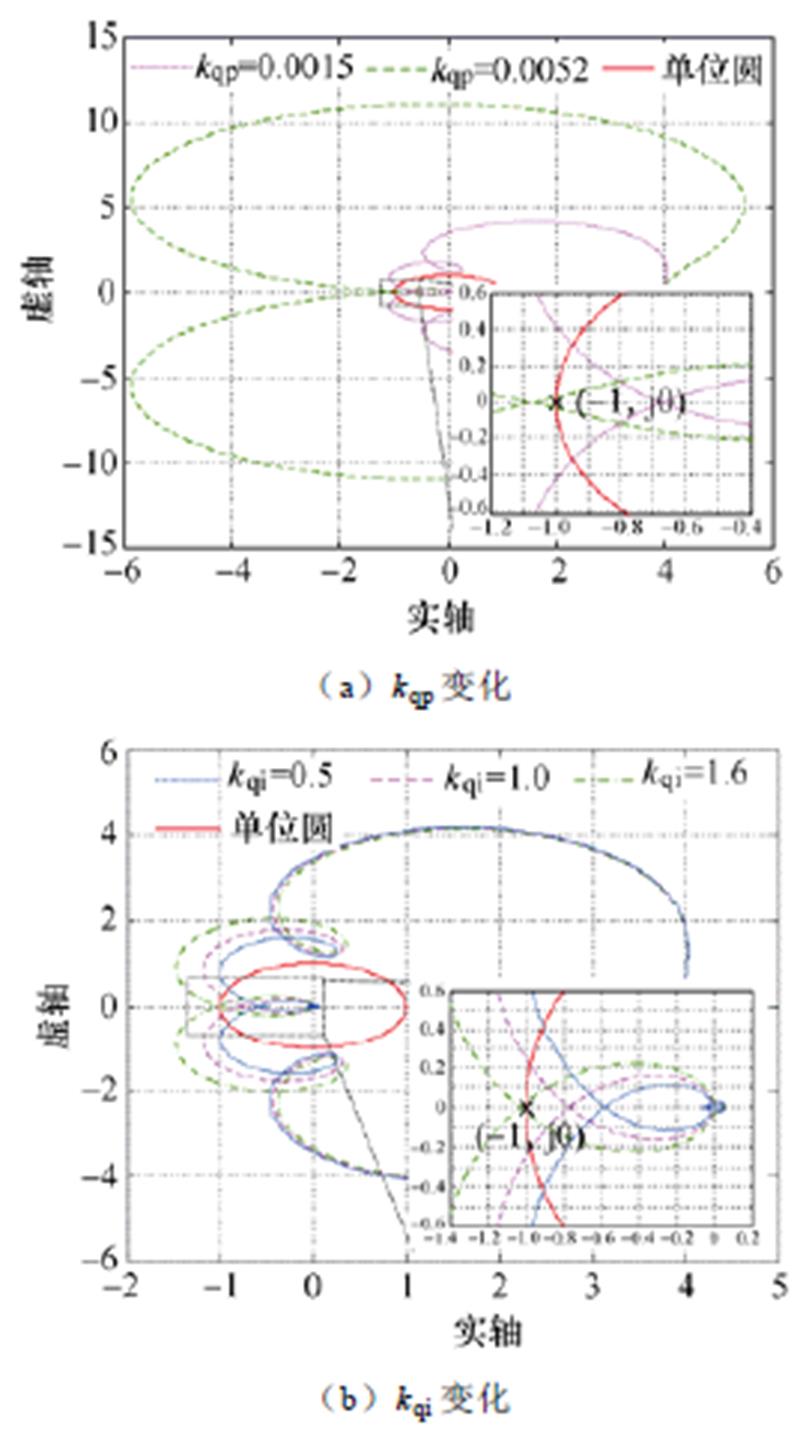
图6 情形3与情形4下GCI的稳定性分析结果
Fig.6 Stability analysis results of GCI under Case 3 and 4
为了验证图6理论分析的正确性，图7给出了相应情形下的并网电流仿真结果。
图7 无功环控制器参数变化时的并网电流仿真结果
Fig.7 Simulation results of grid-connected current when reactive loop controller parameters change
观察图7a可以看出：当比例系数kqp=0.001 5时，GCI输出电流波形稳定；而当kqp增加到0.005 2时，输出电流波形发生明显畸变，表现出谐波失稳现象。同时，观察图7b可以看出：当kqi增大到1.6时，GCI输出电流已经明显失稳。上述仿真结果验证了图6理论分析的正确性。
对比有功环和无功环参数变化对GCI系统稳定性的影响分析可以发现：当有功环比例系数kpp从0.000 6增大到0.005 2时，GCI依旧能够保持稳定运行；然而无功环比例系数kqp增加到0.005 2，系统已经失稳。除此之外，当有功环积分系数kpi从0.5增大到5时，GCI同样能够保持稳定运行；然而无功环积分系数kqi增大到1.6时，系统就已经表现出失稳。以上对比分析表明，GCI系统的稳定性对无功环参数变化更加敏感，换句话说就是无功环参数变化对系统稳定性的影响程度要明显强于有功环参数，这也证明了弱电网下PQ功率控制在本质上是一种不对称控制。
在第1节中通过构建的有功/无功环小信号控制框图已经表明，无功环参数不仅会出现在自身的小信号控制环路中，而且还会以正负反馈环的形式出现在有功环的小信号控制环路中，如图2中的负反馈“环路1”和正反馈“环路2”。其中，“环路1”的反馈增益由传递函数Gasy,q(s)、LCL滤波电容和滤波电感的传递函数及GQ(s)的隐函数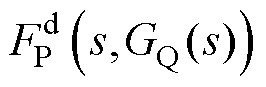
决定；“环路2”的反馈增益由滤波电感L2的传递函数
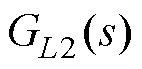、GQ(s)的隐函数
以及电网阻抗Lg决定。同时无功环参数也会在自身控制环中形成正反馈“环路3”和负反馈“环路4”。
由以上分析可以看出，无功环控制器GQ(s)对GCI的稳定性将产生“双重影响”。当调整无功环控制器参数使“环路1”与“环路4”的负反馈效应强于“环路2”与“环路3”的正反馈效应时，GCI的稳定性会增强；当调整无功环控制器参数使“环路2”与“环路3”的正反馈效应强于“环路1”与“环路4”的负反馈效应时，GCI的稳定性会减弱。
为验证由无功环控制器参数引入的不对称正负反馈环路对GCI稳定性影响特性分析的正确性，图8给出了无功环控制器参数kqp变化时的稳定性分析结果。
观察图8a可以看出：当无功环参数kqp从0.000 6增大到0.002 25时，回率矩阵L(s)的特征值l1(s)与实轴的交点向坐标原点移动，即逐渐由包围点（-1, j0）向不包围点（-1, j0）移动，并网系统的稳定裕度增加。这表明随着kqp的增加，由无功环控制器参数所形成的负反馈环效应要强于正反馈环效应，GCI系统的稳定性增强。当无功环参数kqp从0.002 25继续增加到0.005 2时，回率矩阵L(s)的特征值l1(s)与实轴的交点向远离坐标原点的方向移动，即逐渐由不包围点（-1, j0）向包围点（-1, j0）移动，如图8b所示。这意味着此时由无功环控制器参数形成的正反馈环效应要强于负反馈环效应，GCI系统的稳定性减弱。
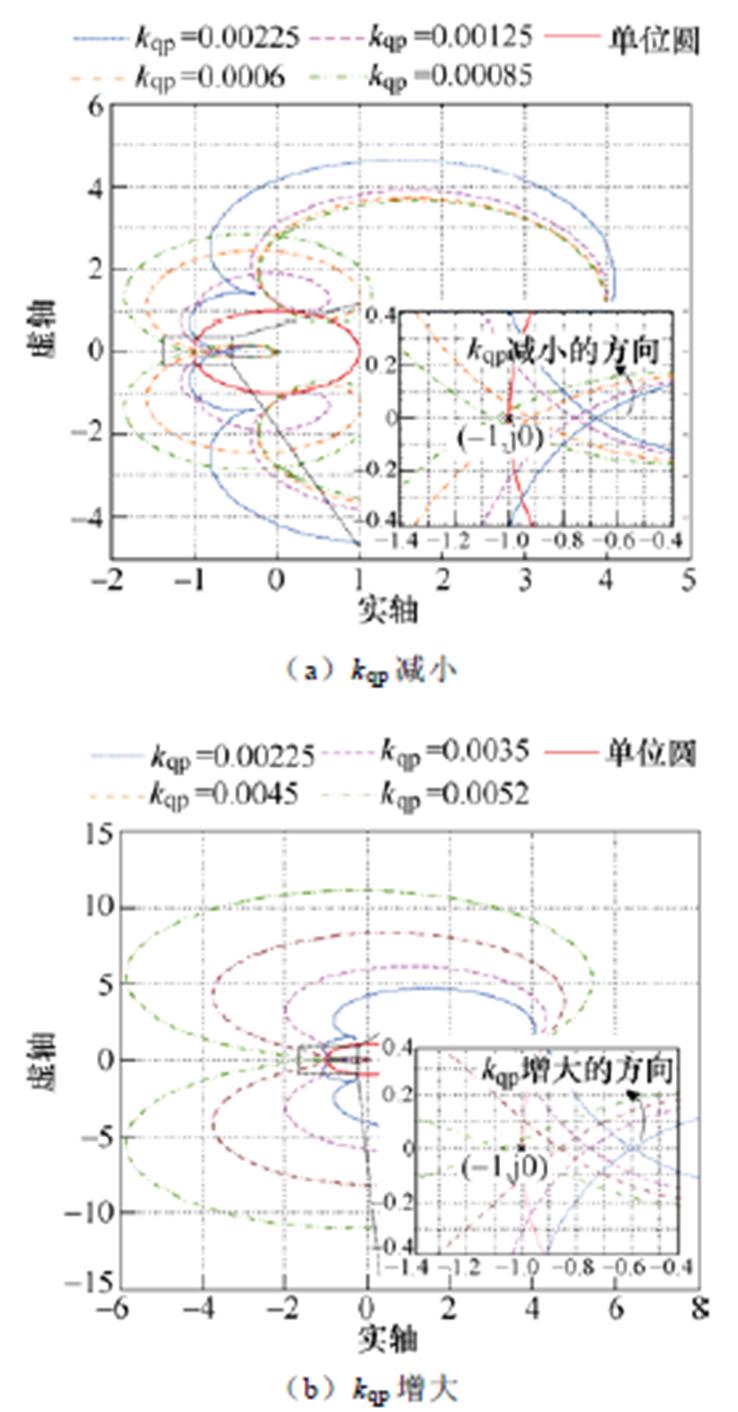
图8 无功环控制器参数变化时的稳定性分析结果
Fig.8 Stability analysis results when reactive power loop controller parameters change
为了更加直观地展示无功环控制器参数对并网逆变器稳定性的影响规律，图9给出了用GCI输出阻抗Zinvqq(s)与电网阻抗Zgqq(s)表征的GCI稳定裕度随参数kqp变化的Bode图。
观察图9可以看出，随着无功环控制器参数kqp的增大，GCI表现出由不稳定向稳定，再向不稳定变化的规律，即GCI的稳定性表现出一种“拐点”行为，而非现有研究中表明的系统稳定性随无功环参数增加而逐渐减弱[14-16]。
图9 无功环控制器参数变化时的Bode图
Fig.9 The Bode diagram when the parameters of the reactive power loop controller change
为了验证上述理论分析的正确性，图10给出了无功环控制器参数kqp变化时的并网电流仿真结果。
观察图10可以看出：当kqp=0.000 6时，GCI输出电流发生明显畸变，对输出电流进行FFT分析可得，此时并网电流的THD=67.84%，系统失稳。而当kqp增加到0.002 25时，GCI输出电流波形稳定。当kqp进一步增加到0.005 2时，与kqp=0.000 6类似，GCI系统同样出现明显的谐波失稳现象。以上仿真结果验证了本文理论分析的正确性。
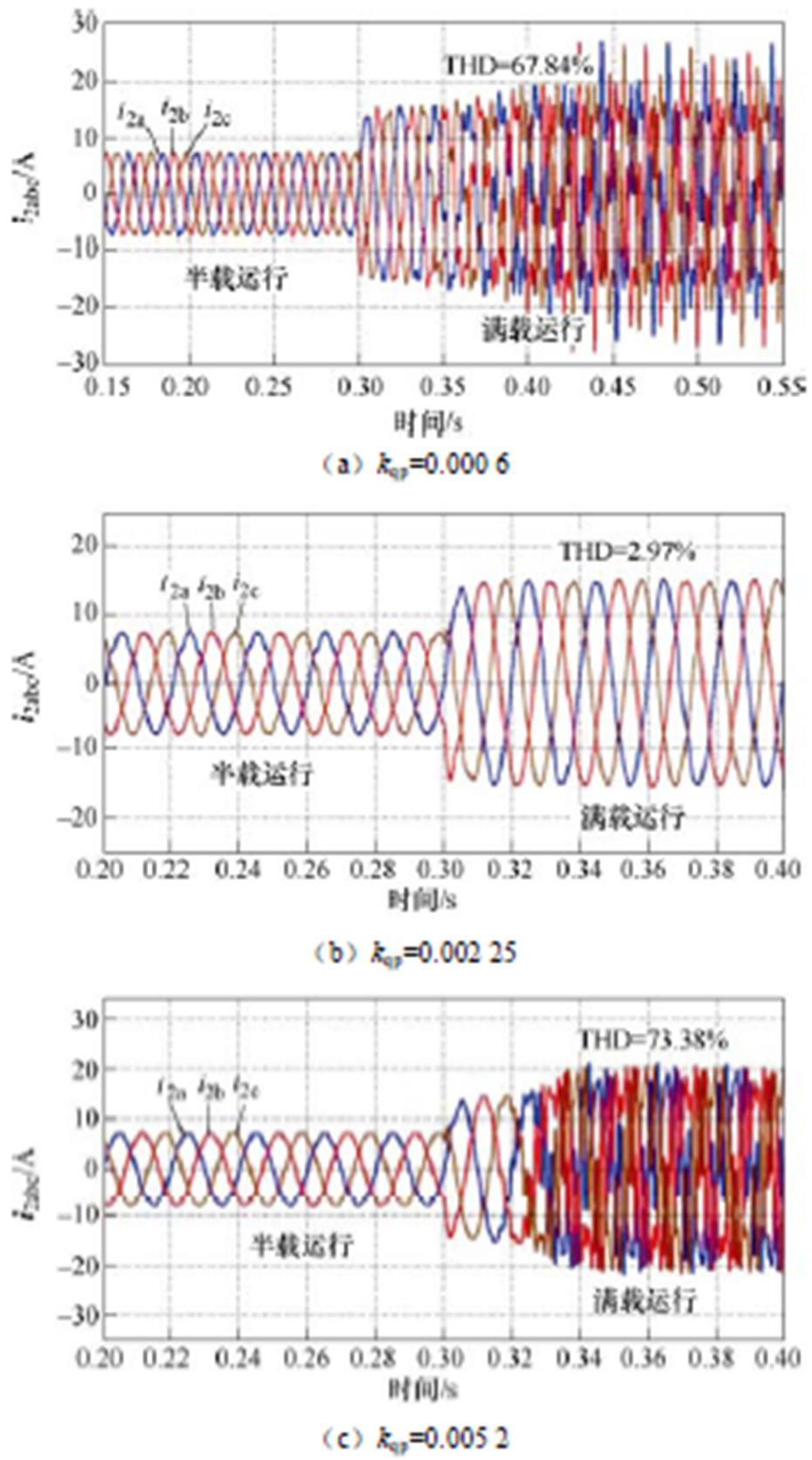
图10 无功环控制器参数变化时的并网电流仿真结果
Fig.10 Simulation results of grid-connected current when reactive loop controller parameters change
为验证上述理论分析的正确性，在实验室搭建了一套三相LCL型并网逆变器实验平台，其中平台实验参数与表1一致。图11和图12分别给出了有功/无功环参数变化时的并网实验波形。
观察图11a可以看出，在初始参数条件下，并网逆变器能够输出稳定的并网电流波形，即系统稳定。在图11a初始参数基础上，当调整有功环比例系数kpp从0.001 5变化到0.005 2时，并网电流依旧稳定，如图11b所示；而当无功环比例系数kqp从0.001 5变化到0.005 2时，并网电流发生明显畸变，如图11c所示。同样观察图12可以看出，在初始参数条件下，当调整有功环积分系数kpi从1变化到1.6时，并网电流依旧稳定，如图12a所示；而当无功环积分系数kqi从1变化到1.6时，并网电流发生明显畸变，如图12b所示。通过以上实验结果对比分析表明，无功环参数变化对系统稳定性的影响程度要明显强于有功环参数，这与图4、图6理论分析结果相一致。
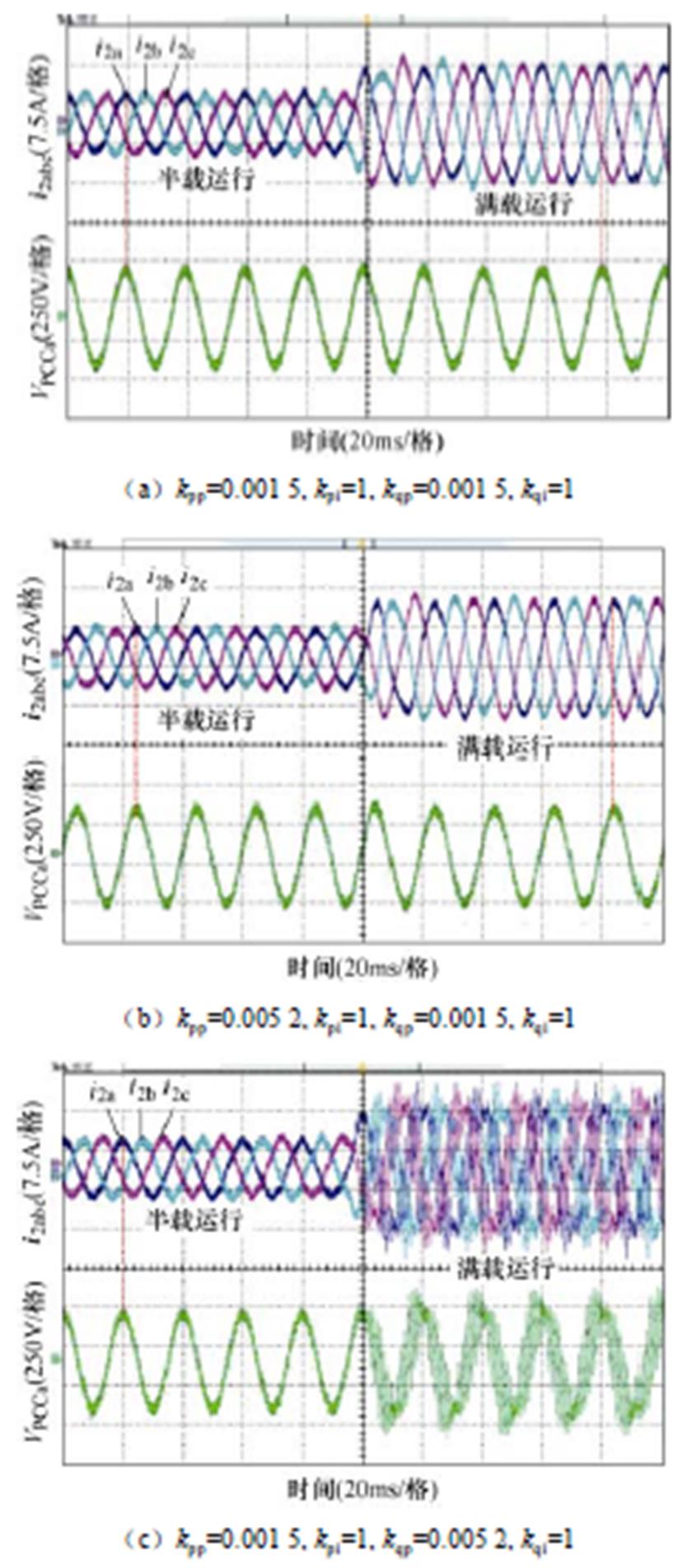
图11 有功/无功环比例系数变化时的实验波形
Fig.11 Experimental waveforms when active/reactive loop proportional parameters change
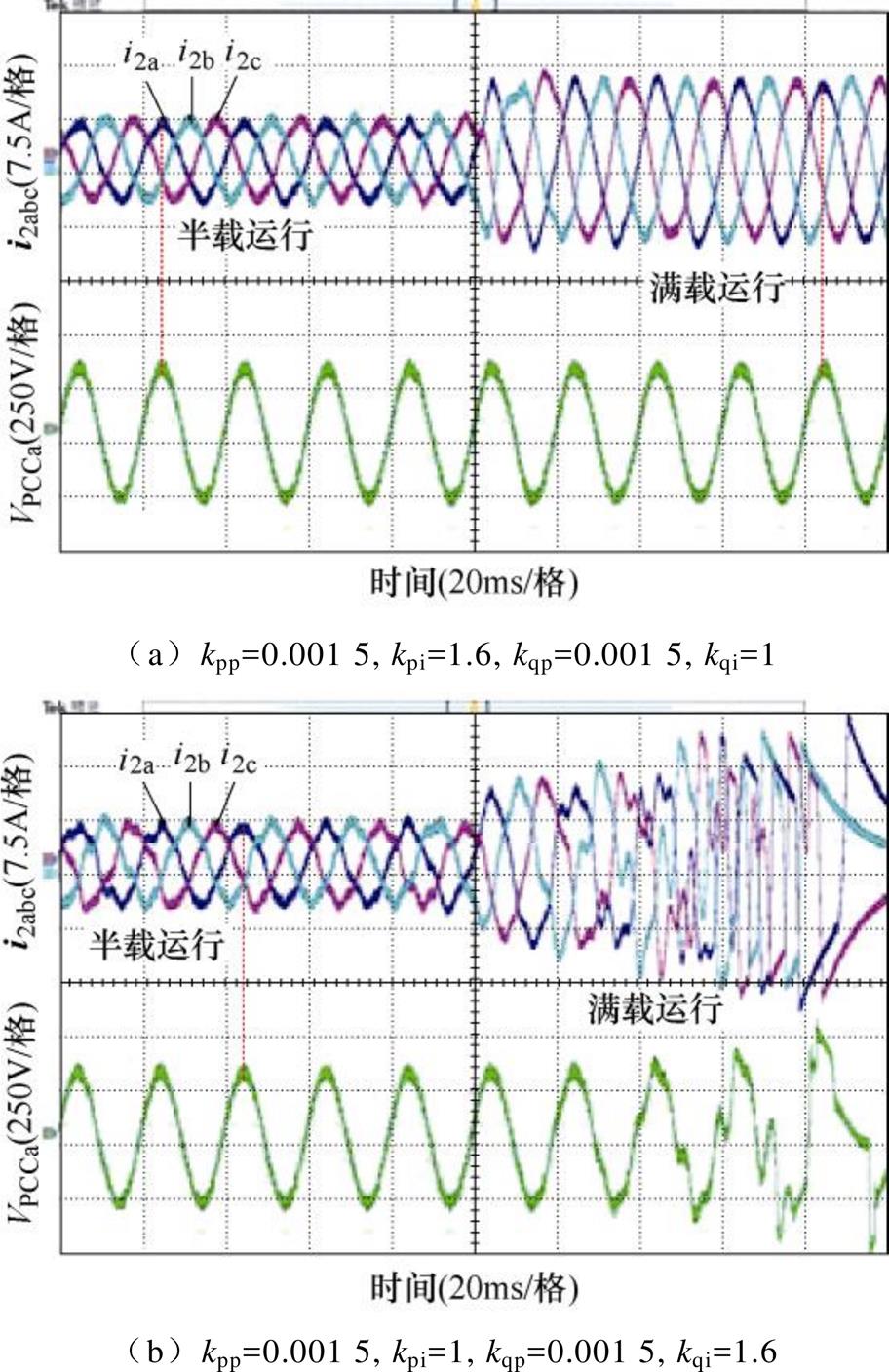
图12 有功/无功环积分系数变化时的实验波形
Fig.12 Experimental waveforms when active/reactive loop integral parameters change
为验证无功环参数形成的正负反馈环效应对GCI稳定性影响特性分析的正确性，图13给出了无功环参数分别为0.000 6与0.002 25时的实验结果。
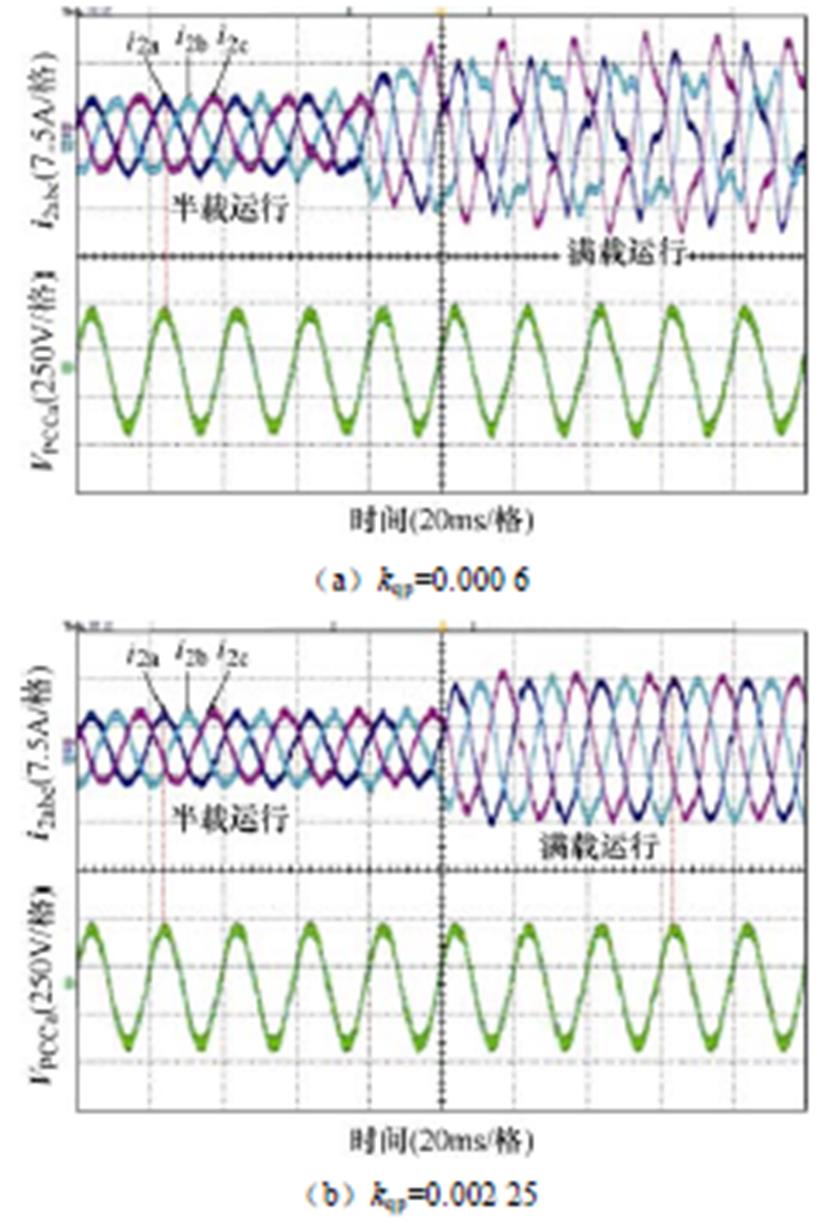
图13 无功环比例系数变化时的实验波形
Fig.13 Experimental waveforms when reactive power loop proportional parameters change
结合图11c和图13不难发现：当无功环参数kqp从0.000 6增加到0.005 2时，GCI会出现由最初的不稳定运行过渡到稳定运行，而后随着参数增加又再次失稳的一个变化过程，即GCI的稳定性随无功环参数增加会出现“拐点”现象。以上实验结果进一步验证了图8与图9理论分析的正确性。
本文通过构建PQ功率控制GCI的小信号数学模型，揭示了弱电网下PQ功率控制是一种不对称
控制的数学本质；同时利用有功与无功环路中的正负反馈环效应，揭示了有功/无功环控制器参数变化对GCI稳定性影响存在差异性的机理，并得出以下重要结论：
1）揭示了弱电网下PQ功率控制是一种不对称控制的本质，即无功环控制器会在有功和无功控制环路中形成不对称的正负反馈环路。
2）无功环控制器参数变化对GCI稳定性的影响程度要强于有功环控制器参数变化，即GCI的稳定性对无功环参数变化更加敏感。
3）调整无功环控制器参数时，不对称正负反馈环效应会出现彼此抵消的现象，导致系统稳定性出现不稳定到稳定再到不稳定的一个变化过程，即“拐点”现象，并非是并网系统稳定性随无功环控制器参数增加而逐渐减弱。
值得说明的是，如何通过构建解析表达式或者量化指标的方式寻求正、负反馈环效应相互抵消的临界点，将是未来需要进一步探索的工作。
参考文献
[1] 张学广, 夏丹妮, 陈文佳, 等. 三相并网变流器弱电网下频率耦合抑制控制方法[J]. 电工技术学报, 2019, 34(21): 4559-4571.
Zhang Xueguang, Xia Danni, Chen Wenjia, et al. Frequency coupling suppression control method for three-phase grid-connected converter under weak grid[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4559-4571.
[2] 陈燕东, 王伊, 周乐明, 等. 弱电网下LCL逆变器阻尼谐振抑制与功率快速调节方法[J]. 电工技术学报, 2018, 33(11): 2564-2574.
Chen Yandong, Wang Yi, Zhou Leming, et al. Damping resonance suppression and fast power regulation method for LCL-type inverter under weak grid[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2564-2574.
[3] Zhu Donghai, Zhou Shiying, Zou Xudong, et al. Improved design of PLL controller for LCL-type grid-connected converter in weak grid[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 4715-4727.
[4] 张旸, 陈新, 王昀, 等. 弱电网下并网逆变器的阻抗相角动态控制方法[J]. 电工技术学报, 2017, 32(1): 97-106.
Zhang Yang, Chen Xin, Wang Yun, et al. Impedance phased dynamic control method of grid-connected inverters under weak grid condition[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 97- 106.
[5] Zhang Xueguang, Xia Danni, Fu Zhichao, et al. An improved feedforward control method considering PLL dynamics to improve weak grid stability of grid-connected inverters[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5143-5151.
[6] 涂春鸣, 高家元, 赵晋斌, 等. 弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计[J]. 电工技术学报, 2020, 35(6): 1327-1335.
Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.
[7] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J/OL]. 电工技术学报, 2022, DOI: 10.19595/j.cnki.1000-6753.tces.211555.
Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs[J/OL]. Transa- ctions of China Electrotechnical Society: 2022, DOI: 10.19595/j.cnki.1000-6753.tces.211555.
[8] 张占俊, 李建文, 董耀, 等. 弱电网下多逆变器并网谐振失稳分析方法[J]. 电气技术, 2020, 21(10): 21-28.
Zhang Zhanjun, Li Jianwen, Dong Yao, et al. Method of resonance instability analysis of multiple grid- connected inverters in weak grid[J]. Electrical Engineering, 2020, 21(10): 21-28.
[9] Arani M F M, Mohamed Y A I. Analysis and per- formance enhancement of vector-controlled VSC in HVDC links connected to very weak grids[J]. IEEE Transactions on Power Systems, 2017, 32(1): 684- 693.
[10] Zhou Weihua, Wang Yanbo, Torres-Olguin R E, et al. Effect of reactive power characteristic of offshore wind power plant on low-frequency stability[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 837-853.
[11] Wu Guanglu, Sun Huadong, Zhang Xi, et al. Parameter design oriented analysis of the current control stability of the weak-grid-tied VSC[J]. IEEE Transactions on Power Delivery, 2021, 36(3): 1458- 1470.
[12] Huang Linbin, Xin Huanhai, Li Zhiyi, et al. Grid- synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control[J]. IEEE Transactions on Smart Grid, 2020, 11(1): 501-516.
[13] 姜静雅, 王玮, 吴学智, 等. 基于自适应无功功率补偿的虚拟同步机功率解耦策略[J]. 电工技术学报, 2020, 35(13): 2747-2756.
Jiang Jingya, Wang Wei, Wu Xuezhi, et al. Power decoupling strategy in virtual synchronous generator based on adaptive reactive power compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2747-2756.
[14] 徐路遥, 兰洲, 陈飞, 等. 弱电网下无功控制对并网变流器稳定性影响分析[J]. 电力系统自动化, 2019, 43(15): 56-63.
Xu Luyao, Lan Zhou, Chen Fei, et al. Analysis on impact of reactive power control on stability of grid-connected converter in weak grid[J]. Automation of Electric Power Systems, 2019, 43(15): 56-63.
[15] Xu Luyao, Yuan Hui, Lan Zhou, et al. Impedance- based analysis of constant reactive power control for voltage source converter in weak AC grids[C]//2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 2019: 1-5.
[16] 任必兴, 孙蓉, 李强, 等. 弱连接下并网VSC外环控制稳定性分析[J]. 高电压技术, 2022, 48(2): 762- 771.
Ren Bixing, Sun Rong, Li Qiang, et al. Stability analysis of power control outer loop of grid- connected VSC under weak connection conditions[J]. High Voltage Engineering, 2022, 48(2): 762-771.
[17] Xue Danhong, Liu Jinjun, Liu Zeng, et al. Modeling and analysis of DC terminal impedance of voltage- source converters with different control modes[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 5883-5896.
[18] 邵冰冰, 赵书强, 高本锋, 等. 连接弱交流电网的VSC-HVDC失稳机理及判据研究[J]. 电工技术学报, 2019, 34(18): 3884-3889.
Shao Bingbing, Zhao Shuqiang, Gao Benfeng, et al. Instability mechanism and criterion analysis of VSC- HVDC connected to the weak AC power grid[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3884-3889.
[19] Yin Taiyuan, Wang Yue, Wang Xiaolei, et al. Mode- ling and analysis of high-frequency MMC impedance considering different control modes and voltage feed- forward[J]. IEEE Access, 2020, 8: 218575- 218584.
[20] Jia Yanbing, Huang Tao, Li Yubo, et al. Parameter setting strategy for the controller of the DFIG wind turbine considering the small-signal stability of power grids[J]. IEEE Access, 2020, 8: 31287-31294.
[21] 李光辉, 王伟胜, 张兴, 等. 双馈风电场并网次/超同步振荡建模与机理分析(一): 考虑功率外环的阻抗建模[J]. 中国电机工程学报, 2022, 42(7): 2438- 2448.
Li Guanghui, Wang Weisheng, Zhang Xing, et al. Modeling and suppression method of sub/super- synchronous oscillation of grid-connected DFIG wind farms (part Ⅰ): sequence impedance modeling and analysis of DFIG wind turbines considering power loop[J]. Proceedings of the CSEE, 2022, 42(7): 2438-2448.
[22] 李光辉, 王伟胜, 张兴, 等. 双馈风电场并网次/超同步振荡建模与机理分析(二): 阻抗特性与振荡机理分析[J]. 中国电机工程学报, 2022, 42(10): 3614- 3627.
Li Guanghui, Wang Weisheng, Zhang Xing, et al. Modeling and mechanism analysis of sub/super- synchronous oscillation of grid-connected DFIG wind farms (part Ⅱ): analysis of impedance characteristic and oscillation mechanism[J]. Proceedings of the CSEE, 2022, 42(10): 3614-3627.
[23] 张琦, 李锐, 张永平, 等. 具有主动阻尼特征的LCL并网逆变器状态反馈控制方法[J]. 电工技术学报, 2019, 34(8): 1698-1707.
Zhang Qi, Li Rui, Zhang Yongping, et al. Active damping method based on state-feedback for grid- connected inverter with LCL filter[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1698- 1707.
[24] 高家元, 涂春鸣, 肖凡, 等. 弱电网下PLL结构引入的不对称正反馈环路对并网逆变器稳定性的影响分析[J]. 中国电机工程学报, 2022, 42(3): 1113- 1124.
Gao Jiayuan, Tu Chunming, Xiao Fan, et al. Analysis of the influence of the asymmetric positive-feedback loop introduced by the PLL structure on the stability of grid-connected inverter in weak grids[J]. Pro- ceedings of the CSEE, 2022, 42(3): 1113-1124.
[25] 刘一锋, 周小平, 洪乐荣, 等. 虚拟惯性控制的负荷变换器接入弱电网的序阻抗建模与稳定性分析[J]. 电工技术学报, 2021, 36(4): 843-856.
Liu Yifeng, Zhou Xiaoping, Hong Lerong, et al. Sequence impedance modeling and stability analysis of load converter with virtual inertia control con- nected to weak grid[J]. Transactions of China Elec- trotechnical Society, 2021, 36(4): 843-856.
Stability Analysis of Grid-Connected Inverter under PQ Power Control Based on Asymmetric Positive-Negative-Feedback Effects
Abstract With the large consumption of traditional fossil energy and its adverse impact on the environment, distributed power generation technology has been widely concerned and applied. The stability problem brought by PQ power control to grid-connected inverter (GCI) system under a weak grid has been widely studied.
Firstly, the small signal mathematical model of grid connected inverter under PQ power control is derived, and the small signal control block diagram of grid connected inverter considering the influence of grid impedance is constructed. In the small signal control block diagram, there are two positive feedback loops and two negative feedback loops at the same time. At the same time, from the composition of positive feedback and negative feedback loops, it can be seen that the parameters of the reactive power loop controller not only exist in the self control loop, but also exist in the active power loop in the form of positive and negative feedback loops, which means that the parameters of the reactive power loop controller will affect the stability of the active power loop and the reactive power loop at the same time. However, the parameters of the active power loop controller only appear in the active power loop, which only affects the stability of its own loop. Therefore, when considering the influence of grid impedance, the small signal control block diagram of PQ power control grid connected inverter shows an asymmetric control phenomenon, revealing the mathematical essence of PQ power control as an asymmetric control. Secondly, in order to verify the influence of active/reactive loop parameters on the stability of grid connected inverter, the impedance model of PQ power controlled grid connected inverter under weak current grid is built. It can be seen from the simulation and experimental results that, within the same parameter variation range, the influence of the parameter variation of the reactive power loop controller on the stability of the grid connected system is obviously stronger than the parameter variation of the active power loop controller, which further verifies the asymmetry of the small signal control block diagram of the active/reactive power loop under the weak current network. On this basis, with the help of the positive and negative feedback loop effect formed in the small signal control block diagram, the law of the stability of grid connected inverter changing with the parameters of the reactive power loop controller is analyzed. When the parameters of the reactive power loop controller are adjusted, the asymmetric positive and negative feedback loop effects will cancel each other, leading to a change process of system stability from instability to stability and then to instability. This is not a gradual weakening of the stability of the grid connected system as the parameters of the reactive power loop controller increase.
The following conclusions can be drawn from the simulation analysis: ① It is revealed that PQ power control in weak current network is the essence of asymmetric control, that is, the reactive power loop controller will form an asymmetric positive and negative feedback loop in the active and reactive power control loops. ② The change of reactive power loop controller parameters has a stronger influence on the stability of GCI than the change of active power loop controller parameters, that is, the stability of GCI is more sensitive to the change of reactive power loop parameters. ③ When the parameters of the reactive power loop controller are adjusted, the asymmetric positive and negative feedback loop effects will cancel each other, leading to a change process of system stability from instability to stability and then to instability, that is, the “inflection point” phenomenon. It is not that the stability of the grid connected system gradually weakens with the increase of the parameters of the reactive power loop controller. It is worth noting that how to find the critical point of mutual cancellation of positive and negative feedback loop effects by constructing analytical expressions or quantitative indicators will be the work that needs further exploration in the future.
Keywords：Weak grid, grid-connected inverter, PQ power control, small-signal model, asymmetric positive- negative-feedback effects, stability
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.220653
国家自然科学基金项目（52077072, 51907057）、湖南省科技创新领军人才项目（2019RS3014）资助。
收稿日期 2022-04-24
改稿日期 2022-05-30
E-mail: chunming_tu@263.net
高家元 男，1991年生，博士研究生，研究方向为电力电子技术，分布式发电和逆变器控制技术。
E-mail: Jiayuan_gao@163.com（通信作者）
（编辑 陈 诚）