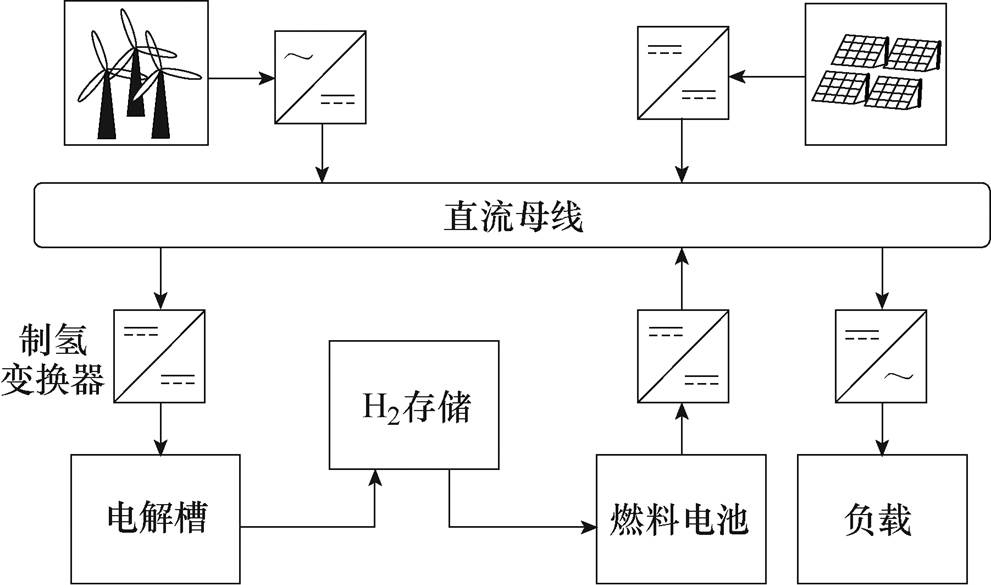
图1 可再生能源制氢系统
Fig.1 Renewable energy hydrogen production systems
摘要 制氢变换器的效率和输出纹波等指标在氢能应用中至关重要。多相交错并联Buck变换器（MPIBC）输出纹波的减小需要以增加并联支路、开关频率和滤波电感为代价，这将导致成本和损耗的提高。为此该文提出多相堆叠交错并联Buck变换器（MPSIBC），MPSIBC在MPIBC基础上增加纹波补偿并联支路。补偿支路采用具有补偿特性的PWM控制，输出交流电流与MPIBC输出电流纹波波形互补。MPSIBC利用输出补偿思想使得变换器输出纹波的消除不依赖开关频率等因素。该文从理论上对MPSIBC拓扑和纹波补偿原理进行了分析，并通过PSIM仿真和实验进行了验证，结果表明MPSIBC具有显著纹波抑制效果的同时可有效降低开关频率和滤波电感。
关键词：制氢变换器 堆叠交错并联Buck 输出纹波 效率
近年来随着我国能源转型的推进，全国风电机和光伏等可再生能源装机容量持续增长，高比例可再生能源的消纳问题日渐突出[1]。储能技术不仅能有效缓解可再生能源的消纳问题，还可保证可再生能源的供电可靠性[2-3]。氢作为高效能源载体，被认为是未来可持续发展的重要储能方式之一[4]，氢与可再生能源的结合受到越来越多的关注[5-6]。
可再生能源制氢系统如图1所示，电解槽为产氢设备，需要小电压大电流的直流供电[7]。制氢变换器为电解槽供电，其需要满足高效率、高容错性、高降压转换比、低纹波和低成本等要求[8-10]。
图1 可再生能源制氢系统
Fig.1 Renewable energy hydrogen production systems
传统Buck变换器在大电流应用中存在降压比不高、效率低等诸多问题。为提高传统Buck变换器降压比，文献[11]采用二次Buck变换器，使用全控开关器件级联两个Buck变换器。文献[12]提出抽头电感Buck变换器，通过调节抽头电感的一次侧与二次侧的匝数比，获得更高的降压比。不局限于Buck拓扑，近年来隔离型DC-DC降压变换器得到广泛关注[13]，其利用高频变压器可实现高降压比。
然而高频变换器的效率问题较为关键，文献[14]使用LLC谐振方式，在变压器一次侧加入电感和电容组合谐振电路，借助软开关技术提高效率。但值得注意的是，软开关电路通常采用MOSFET，电路功率等级受限。制氢大电流应用中，开关器件将使用大功率IGBT，而普通的IGBT受物理极限和导通死区的制约，其开关频率一般不超过20kHz，因此通常不采用软开关技术。
制氢变换器除降压比、效率等指标外，输出纹波指标也极为重要。文献[15-16]分别对碱性和质子交换膜（Polymer Electrolyte Membrane, PEM）电解槽进行了纹波实验，结论为制氢变换器输出的电流纹波会降低电解槽的制氢效率。此外，纹波带来电流冲击将损坏电解槽内部，缩短电解槽的使用寿命，因此需尽可能降低制氢变换器的电流纹波[17]。
目前，多相交错并联Buck变换器（Multi-Phase Interleaved Buck Converter, MPIBC）较适合用于大电流场合[18-21]，其通过移相交错导通的方式，可减小输出电流纹波，但较好的电流纹波抑制效果需依赖并联支路数、开关频率和滤波电感，这将导致损耗和成本的增加。文献[22-24]采用交错并联磁集成Buck变换器，通过电感耦合的方式来提高实际电感的等效感值，可有效降低变换器中的电感，但等效感值提升有限，且开关频率较高。
本文提出多相堆叠交错并联Buck变换器（Multi-Phase Stacked Interleaved Buck Converter, MPSIBC），旨在消除输出电流纹波的同时可有效降低开关频率和滤波电感。MPSIBC在MPIBC基础上增加纹波补偿并联支路，利用输出补偿思想使得变换器输出纹波的消除不依赖开关频率等因素。本文首先介绍MPSIBC拓扑和控制方式，并给出拓扑参数计算公式；其次以四相堆叠交错并联Buck变换器（4-Phase Stacked Interleaved Buck Converter, 4PSIBC）为例对变换器输出纹波公式进行数学推导，对变换器的效率进行理论分析；然后通过PSIM仿真验证变换器的输出纹波、效率和容错性；最后通过400W样机实验完成对理论和仿真的验证。
MPIBC拓扑如图2a所示，该拓扑为N个Buck电路并联，各并联Buck电路采用相同的开关频率，但导通时刻依次相差1/N个开关周期。本文提出的MPSIBC拓扑如图2b所示，该拓扑在MPIBC基础上增加了一个电容CS，不失一般性，以第一相支路串联电容CS为例，该支路通过一定的控制策略可对输出纹波进行补偿。SD1、SP1、SP2、…、SPn为IGBT模块，VDP2、VDP3、…、VDPn为续流二极管，LP1、LP2、…、LPn为滤波电感，CS、CP为变换器电容。
电路中SP1、SD1、LP1所在的第一相支路由于增加了电容CS，该支路的功能从原来的功率传输变为纹波补偿，因此本文将该支路称为纹波补偿支路，其中CS起分压和隔直流的作用。其余IGBT模块、二极管及电感构成功率支路，用于功率传输，其中SP2、VDP2、LP2构成第二相支路，依此类推，SPn、VDPn、LPn构成第N相支路。
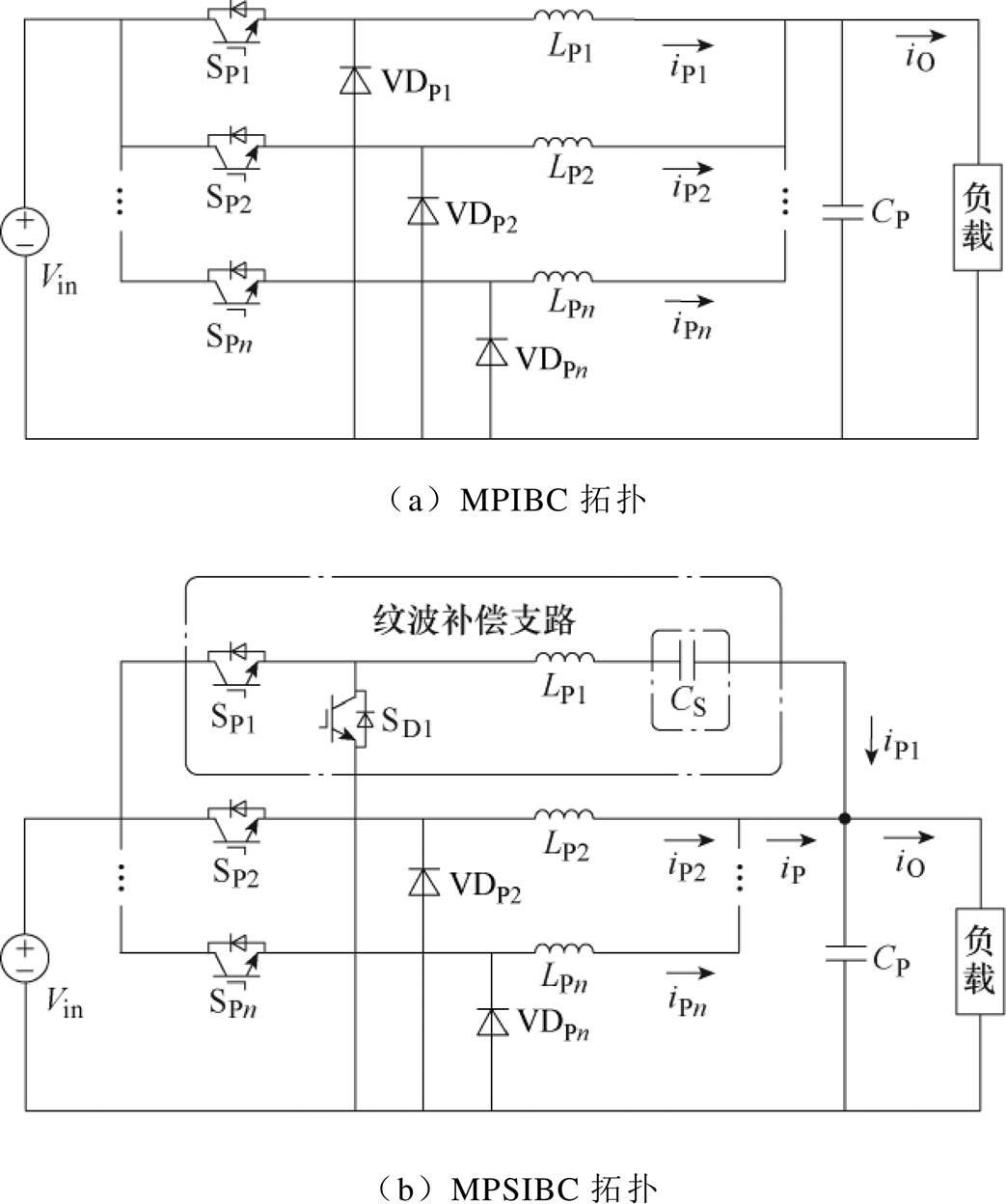
图2 MPIBC和MPSIBC拓扑对比
Fig.2 Topology comparison between MPIBC and MPSIBC
图3为MPSIBC控制框图，其中以第二相支路PWM控制信号的相位为参考相位，且第二相支路至第N相支路的PWM依次相差360°/(N-1)的相位。这些支路的PWM采用相同的占空比DP和开关频率fP。第一相支路为纹波补偿支路，该支路的PWM控制信号超前第二相支路TA时间，开关频率fS是第二相支路开关频率fP的N-1倍，占空比为DS，DS和TA可表示为
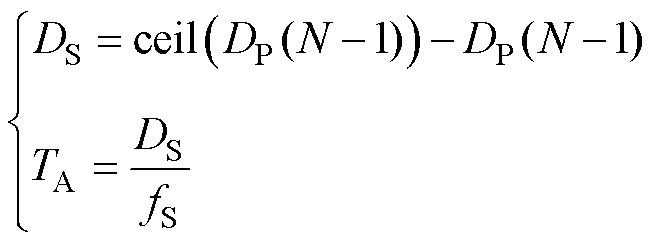（1）
式中，ceil()运算符的含义为向上取整。
纹波补偿支路和功率支路的占空比、开断频率不同，会导致输出电压存在差异，因此补偿支路上CS的一个重要作用是实现分压，电容CS两端的直流偏置电压VCS表示为
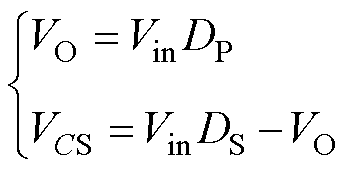（2）
式中，Vin为输入电压；VO为输出电压。
纹波补偿支路采用同步Buck电路，因此IGBT模块SP1、SD1的PWM控制信号互补。
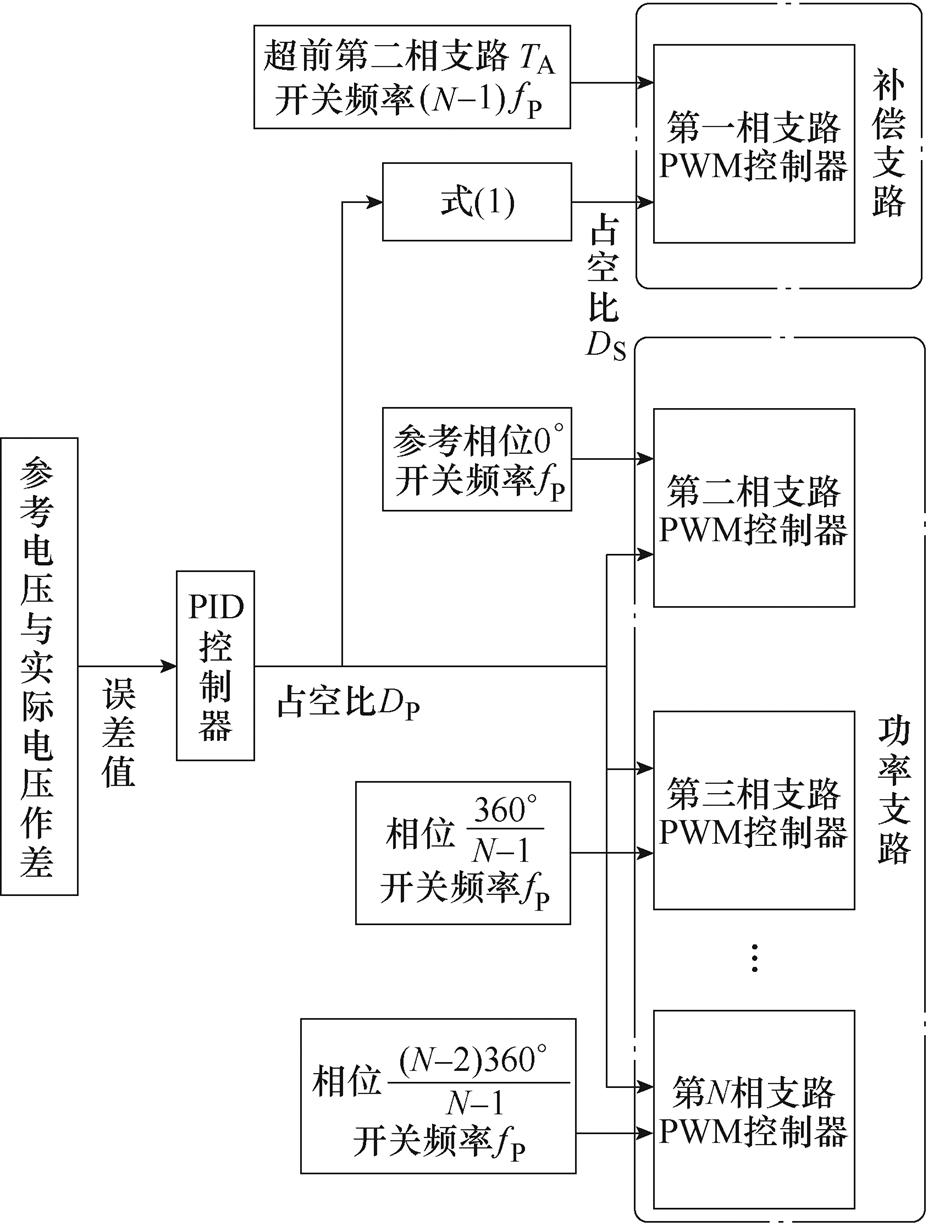
图3 MPSIBC控制框图
Fig.3 Control diagram of the MPSIBC
MPSIBC各功率支路应工作在连续导通模式，以此配合纹波补偿支路达到补偿效果。MPSIBC在选择开关频率和滤波电感时需保证变换器连续导通，因此功率支路上电感值计算表达式为
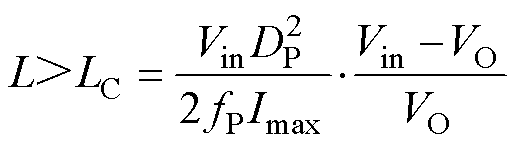（3）
式中，LC为临界电感；Imax为功率支路的最大电流。
值得注意的是，纹波补偿支路和各功率支路上的电感参数需要保持一致，这将有利于变换器的输出纹波抑制，后续将通过2.1节理论推导证明。
变换器中的电容CP直接影响输出电压的稳定性及系统的瞬态响应性能。CP电容值太大会导致系统的瞬态响应较慢，电容值太小会影响系统稳定性。CP表达式为
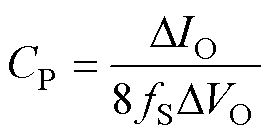（4）
式中，DIO为输出纹波电流；DVO为输出纹波电压。
变换器中的电容CS的作用是分压和隔直流，并直接影响变换器输出纹波抑制效果。CS电容值需要足够大以至于其两端电压波动量DvCS在充放电过程中变化极小。DvCS是纹波补偿支路电流峰-峰值ISp-p、电容值CS及其充放电周期Dt的函数，即
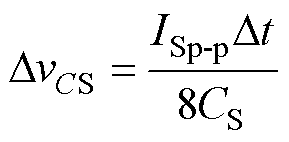（5）
式中，ISp-p为功率支路数N-1和占空比DP相关的函数[21]，即
（6）
式中，m=floor[DP(N-1)]，floor()运算符表示向下 取整。
根据式（5）和式（6）可计算得到合理的CS电容值。
本节以4PSIBC为例进行输出电流纹波分析。为了简化电流纹波公式的数学推导过程，此处假设IGBT为理想开关，电感电容没有寄生参数。下面以功率支路占空比DP=0.3为例来推导输出电流纹波公式，其余占空比的情况分析同理。变换器各IGBT单个周期的PWM控制信号时序如图4所示，纵坐标Vgs表示各个IGBT的门控信号，TP为功率支路开关周期，每个周期对应六个运行阶段，如图5所示。
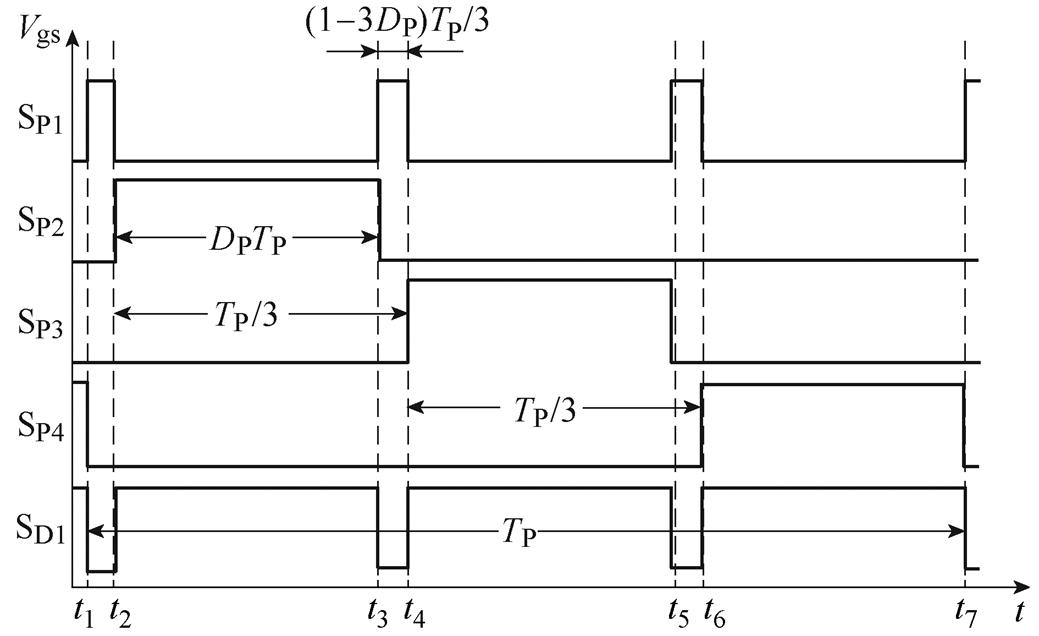
图4 DP=0.3时PWM控制信号时序图
Fig.4 Timing diagram of the PWM control signal at DP=0.3
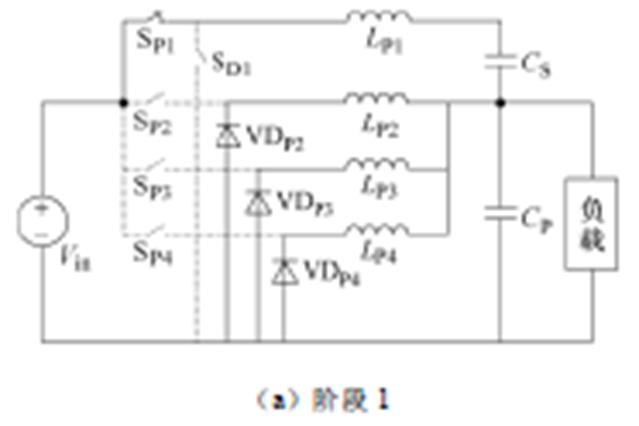
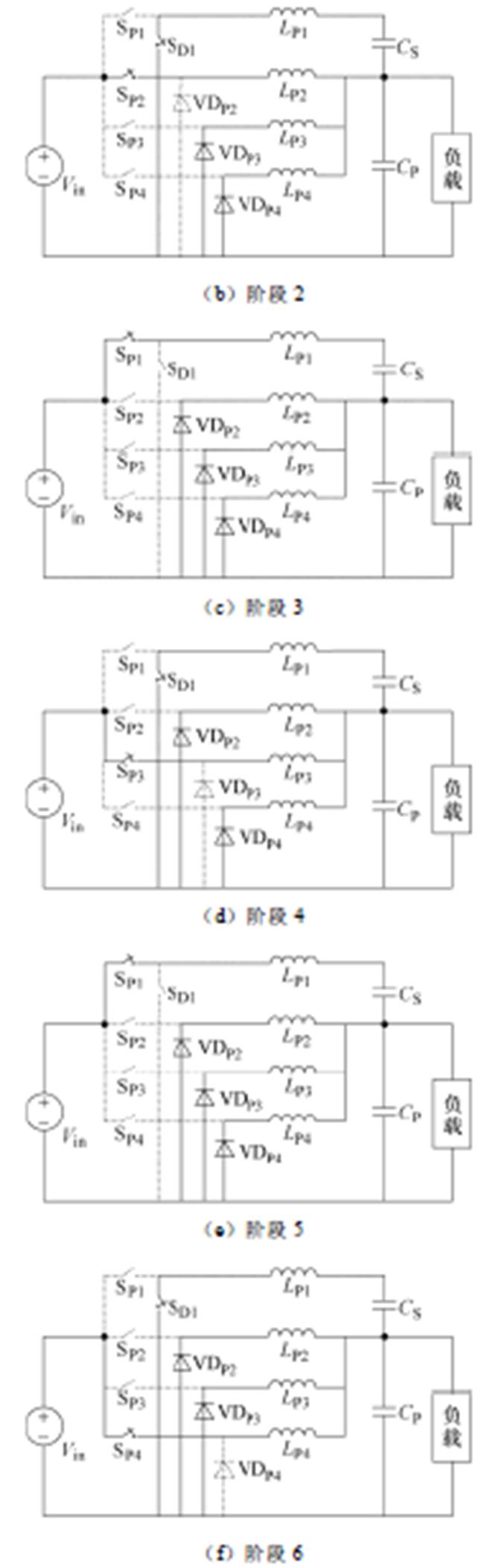
图5 DP=0.3时各运行阶段变换器电路图
Fig.5 Circuit diagram of each operating stage at DP=0.3
阶段1[t1, t2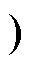
：SP1导通，SD1、SP2、SP3、SP4关断，此时电感LP1被充电，电感LP2、LP3、LP4放电。根据基尔霍夫电压定律有
（7）
式中，DvCS为电容CS两端电压波动量；Dt可表示为
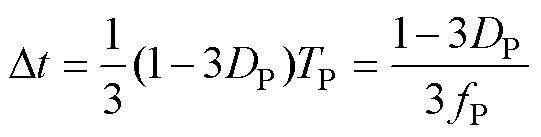（8）
联立式（1）、式（2）、式（7）、式（8），得到各支路电感电流纹波表达式为
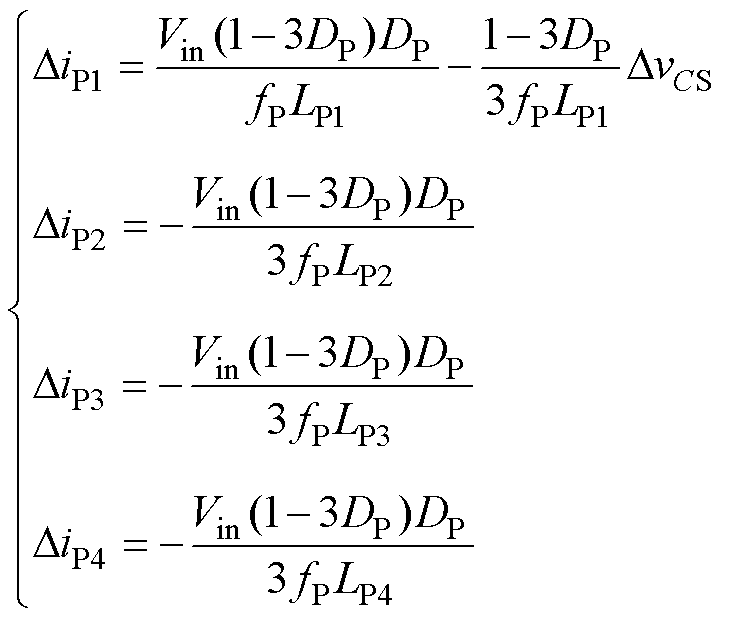（9）
当LP1=LP2=LP3=LP4=LP时，由式（9）得到总的输出电流纹波为
（10）
阶段2[t2, t3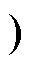：SD1、SP2导通，SP1、SP3、SP4关断，此时电感LP2充电，电感LP1、LP3、LP4放电。由基尔霍夫电压定律可得
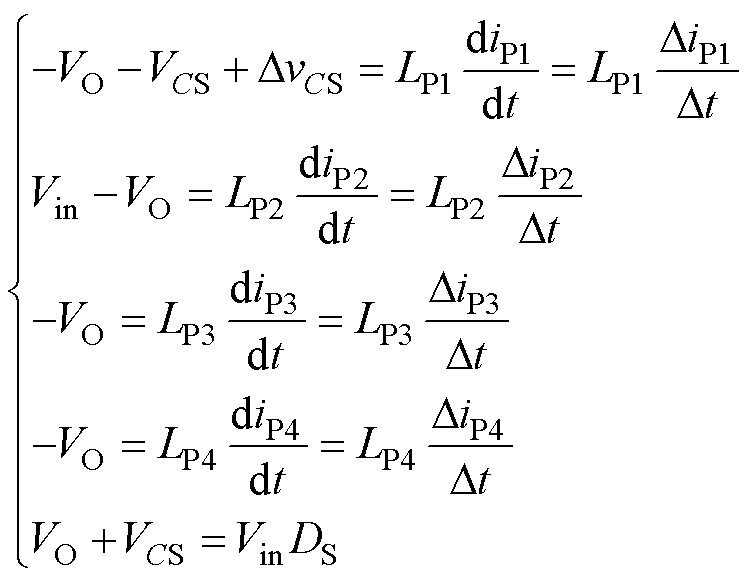（11）
式中，Dt=DPTP。由式（1）、式（2）、式（11）得到各支路电感电流纹波表达式为
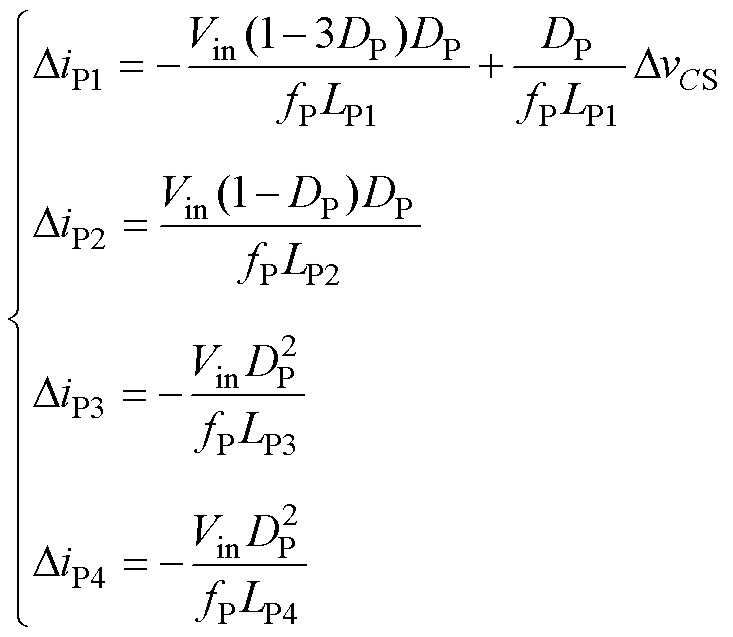（12）
因此当LP1=LP2=LP3=LP4=LP时，由式（12）计算得到总的输出电流纹波为
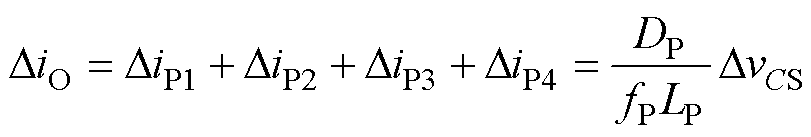（13）
阶段3[t3, t4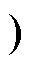、阶段5[t5, t6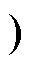和阶段1一样，电感LP1充电，其余支路电感放电，因此这三个阶段电流纹波公式是相同的。阶段4[t4, t5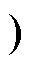、阶段6[t6, t7]和阶段2相似，某一功率支路电感充电，其余支路电感放电，因此这三个阶段电流纹波公式相似。
通过上述对4PSIBC各个运行阶段电流纹波的分析可得，该变换器各功率支路产生的总电流纹波可被补偿支路消除，总输出纹波DiO最终由补偿支路的DvCS决定，当CS容值适当，即DvCS足够小，则该变换器可实现近乎零电流纹波的输出。
本文采用一种快速IGBT损耗计算方法对MPSIBC损耗进行评估，IGBT在1s内的导通损耗PSS可表示为
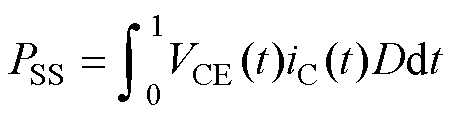（14）
式中，VCE为IGBT端电压；iC为IGBT电流；D为IGBT导通时间，即占空比。
VCE和iC的关系曲线是非线性的，为了简化计算，对其进行线性化处理，VCE可写为
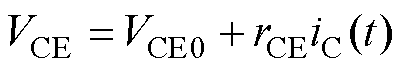（15）
式中，VCE0为IGBT导通电压；rCE为IGBT导通电阻。
将式（15）代入式（14）中，可得
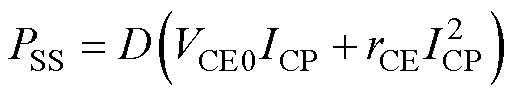（16）
式中，ICP为iC中的直流分量。
IGBT在1s内的开关损耗PSW可表示为
（17）
式中，fSW为变换器开关频率；ESW(on)为IGBT开通一次的损耗；ESW(off)为IGBT关断一次的损耗。
对ESW(on)和ESW(off)进行线性化处理，PSW进一步可写成
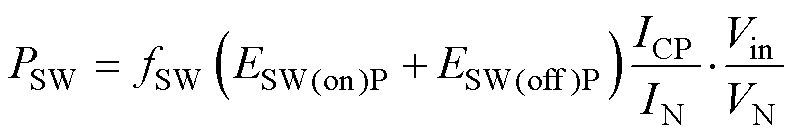（18）
式中，ESW(on)P和ESW(off)P为IGBT在额定功率下的开通关断一次的损耗；IN为额定电流；VN为额定 电压。
二极管损耗包括导通损耗和开关损耗。导通损耗计算式为
（19）
式中，TDon为1s时间内的二极管导通时间；UF(t)为正向压降；iF(t)为正向电流。
开关损耗又分为开通损耗和关断损耗。由于二极管开通时间非常短，因此与关断损耗相比，导通损耗非常小，可以忽略不计。关断损耗的计算公式为
（20）
式中，Urf为最大瞬态电压；Irf为最大瞬态电流；tf为反向恢复时间；fD为二极管的开关频率。
变换器中电感损耗主要分为磁滞损耗、涡流损耗和电阻损耗，电阻损耗又分为直流电阻损耗和交流电阻损耗。本文提出的变换器开关频率较小，因此电感的磁滞损耗涡流损耗和交流电阻损耗可忽略。
直流电阻损耗PR计算公式为
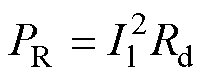（21）
式中，Il为电感流过的电流；Rd为电感直流电阻。
由MPSIBC纹波分析结论可知，当CS容值适当，即DvCS足够小时，输出纹波对开关频率和滤波电感的需求小。根据上述效率分析，较小的开关频率和滤波电感将意味着变换器开关损耗和电感损耗成倍地降低。
本文在PSIM仿真软件中搭建了4PSIBC仿真模型。
仿真模型中仿真参数见表1。全控开关器件选用PSIM仿真软件中Thermal Module的IGBT，型号为CM600HA-24A，续流二极管型号为150EBU04，在仿真中设置器件外壳温度为40℃，热阻为0.034W，电容CS容值根据式（5）、式（6）确定。
表1 仿真模型参数
Tab.1 Parameters of the simulation model
参 数数 值 电感LP1、LP2、LP3、LP4/mH50 电感寄生电阻RP1、RP2、RP3、RP4/mW80 补偿电容CS/mF200 输出电容CP/mF100 负载电阻RO/mW12.5 负载反电动势Vint/V15 输入电压Vin/V50 输出参考电压Vref/V20 IGBT模块SP1、SP2、SP3、SP4、SD1CM600HA-24A 续流二极管VDP2、VDP3、VDP4150EBU04 功率支路开关频率fP/Hz2 000 纹波补偿支路开关频率fS/Hz6 000
图6给出了理论和仿真计算的纹波值，理论值是将仿真参数代入电流纹波公式得到的结果。变换器处于稳定运行状态时，各支路电流波形呈现周期性。图中4PSIBC电流波形的理论值和仿真值几乎重合，补偿支路电流iP1和功率支路总电流iP波形互补，叠加之后总输出电流iO的纹波得以消除。iO仿真结果表明其纹波系数为0.125%，与理论上的纹波系数基本相符，通过仿真结果验证了理论的正确性。此外，对比相同仿真参数下4PSIBC和4PIBC的输出纹波，由仿真结果可见，4PIBC由于开关频率低、电感小的缘故，其输出纹波较大，而4PSIBC具有纹波补偿特性，即使开关频率低、电感小也能保证低纹波输出。
为验证仿真，实验室中搭建了400W的4PSIBC实验样机，实验样机如图7所示。变换器的PWM控制信号由DSP（TMS320F28335）提供，IGBT选用英飞凌公司的FF50R12RT4，输出电流设置为20A，样机电感参数选用400mH，实验样机中其他元件参数与仿真相同。
图8给出了各支路电流纹波波形。从图8中可看出，iP2、iP3、iP4依次相差120°相位，频率为2kHz，纹波峰-峰值为6A左右，iP由iP2、iP3、iP4叠加得到，iP纹波峰-峰值为1.2A，频率为6kHz，此时iP1纹波波形相位与iP纹波几乎互补，iP和iP1叠加得到最终的输出电流iO，输出电流iO纹波约为0.2A。
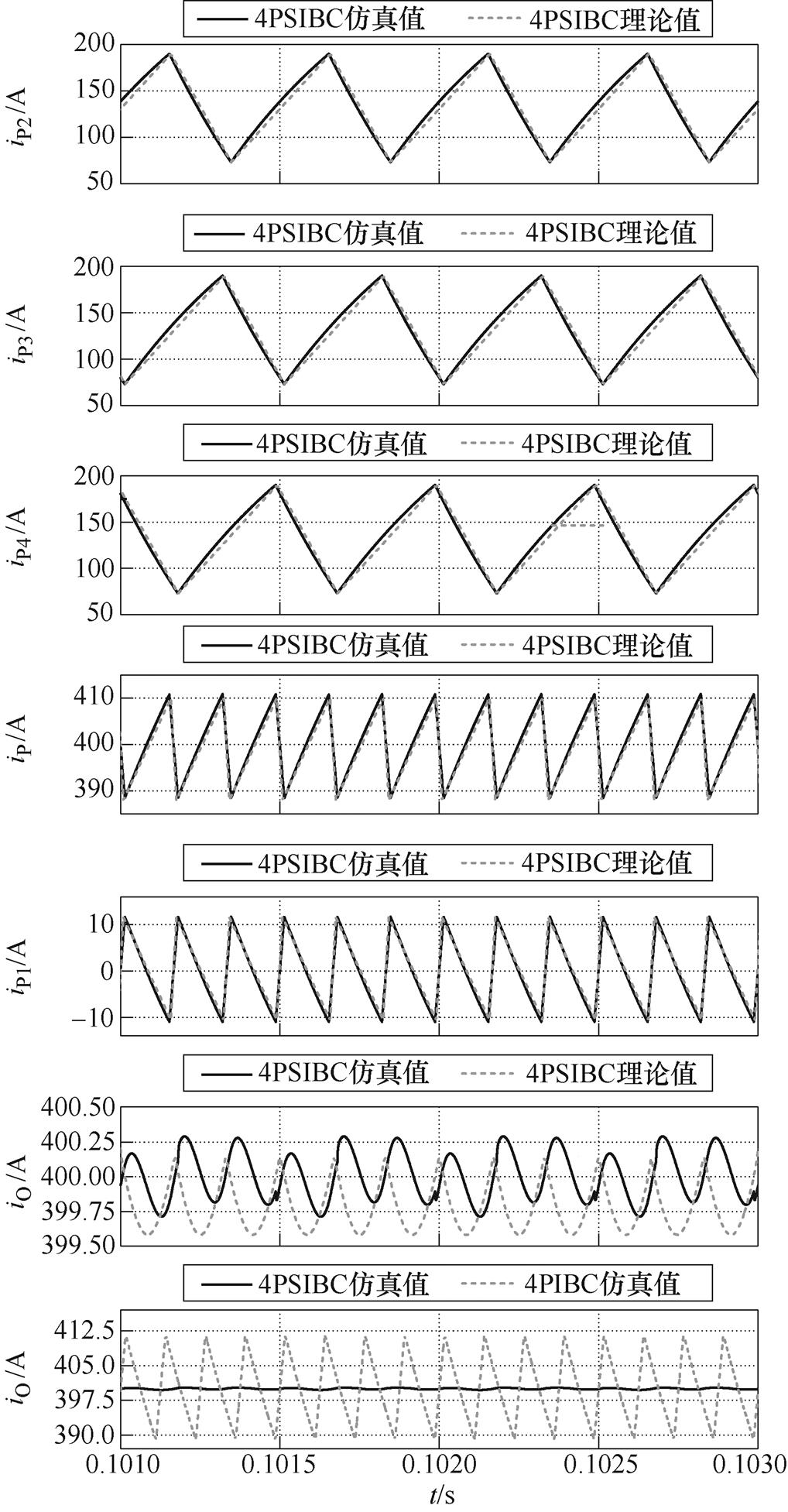
图6 4PSIBC各支路电流波形
Fig.6 Current waveforms of each branch in the 4PSIBC
图7 实验样机
Fig.7 Experimental prototype
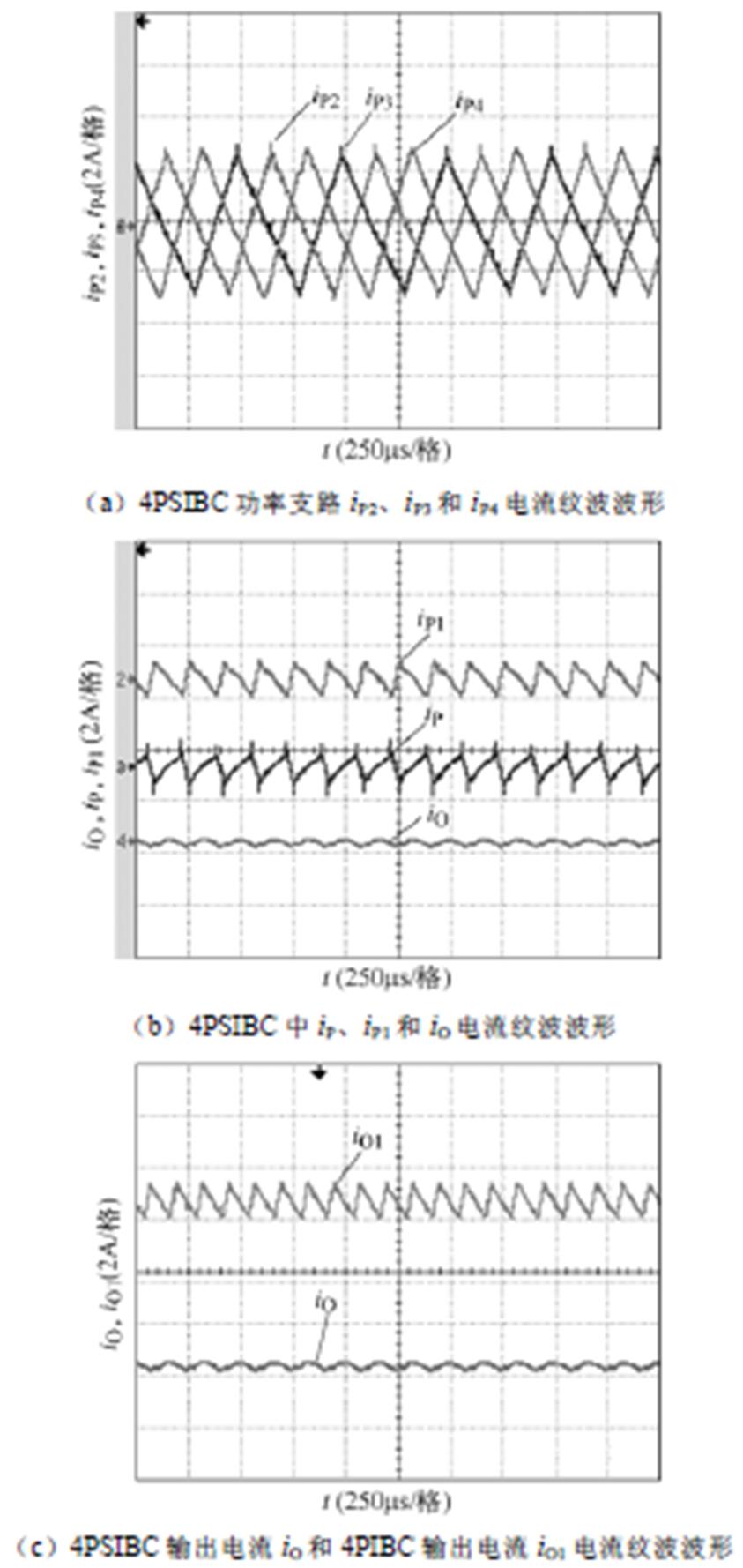
图8 实验样机各支路电流纹波
Fig.8 Current ripple of each branch in the experimental prototype
样机实验得到的结果与理论、仿真相近，该实验结果有效验证了4PSIBC的纹波消除效果。
容错性是指变换器在发生故障后，持续有效运行的能力，因此变换器是否具有良好的容错性同样值得关注。
图9给出了变换器某一功率支路故障时的输出电流变化。故障前，4PSIBC输出电流为400A；0.3s时变换器某一功率支路发生故障，故障的功率支路被切除；支路切除后，4PSIBC的补偿支路PWM控制信号频率和占空比按式（1）进行调整，变换器从四相运行转变到三相运行，输出电流iO出现暂降的原因为故障后变换器短暂功率缺额，但20ms后重新恢复至400A，恢复后iO纹波峰-峰值为0.1A、纹波系数为0.025%。由此可见MPSIBC在功率支路发生故障后仍可有效运行。
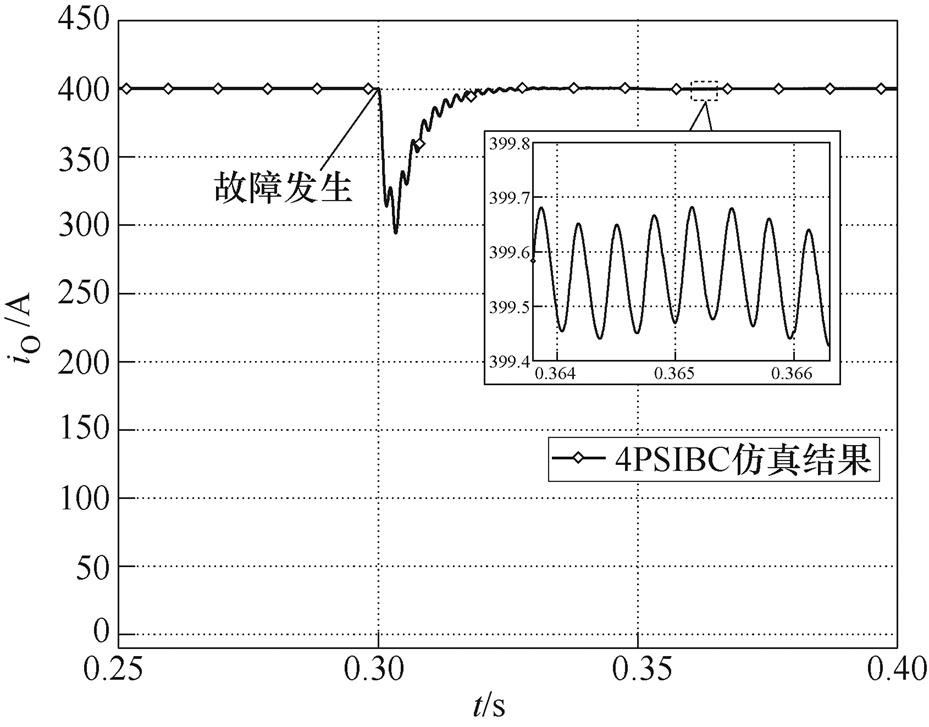
图9 4PSIBC容错性分析
Fig.9 Fault tolerance analysis of the 4PSIBC
图10给出了变换器容错性的实验结果。实验样机正常运行时设置输出电流iO=20A，则每一条功率支路电流平均值约为6.6A，波形如图10a所示。某一功率支路发生故障时，故障功率支路被切除；支路切除后，故障功率支路iP4变为0，另外两条功率支路iP2、iP3分别承担平均值为9A的电流。故障后iP、iP1和iO的纹波波形如图10b所示，故障后iP和iP1的纹波峰-峰值变大，频率变小，但iP和iP1的纹波波形仍然满足相位互补，即补偿支路可有效补偿纹波，最终输出纹波约为0.2A左右。该实验结果有效验证了变换器的容错性。
图10 实验样机容错性分析
Fig.10 Fault tolerance analysis of the experimental prototype
利用PSIM仿真软件中的Thermal Module可对4PSIBC进行快速功率损耗评估。图11对比了4PSIBC和4PIBC的滤波电感和开关器件损耗。图中横坐标为输出电流，其大小通过改变负载电阻RO的大小来调整，纵坐标分别是变换器电感值、开关频率和IGBT损耗。参考中电联《锂电池储能系统接入直流配电网技术要求》中的电能质量标准，本文设定4PSIBC和4PIBC输出电流纹波系数为0.5%，在此要求下进行后续验证。
图11 PSIM仿真效率分析
Fig.11 Efficiency analysis in PSIM simulation
首先固定4PSIBC和4PIBC的功率支路开关频率为2kHz，图11中柱状图对比了不同输出电流下两种变换器对滤波电感值的需求，结果表明4PSIBC的电感远远小于4PIBC，且最多可减小96%的电感值。然后固定4PSIBC和4PIBC的滤波电感值为50mH，图11中点线对比了不同输出电流下两种变换器对功率支路开关频率的需求，结果表明4PSIBC的开关频率远远小于4PIBC，且最多可减小94%的开关频率。从图中可看出，由于4PSIBC的开关频率的降低，其IGBT损耗相较于4PIBC也有明显的下降。
图12对4PSIBC和4PIBC的效率进行了实验对比，结果表明由于滤波电感和开关频率的降低，4PSIBC比4PIBC的效率平均高5%左右。
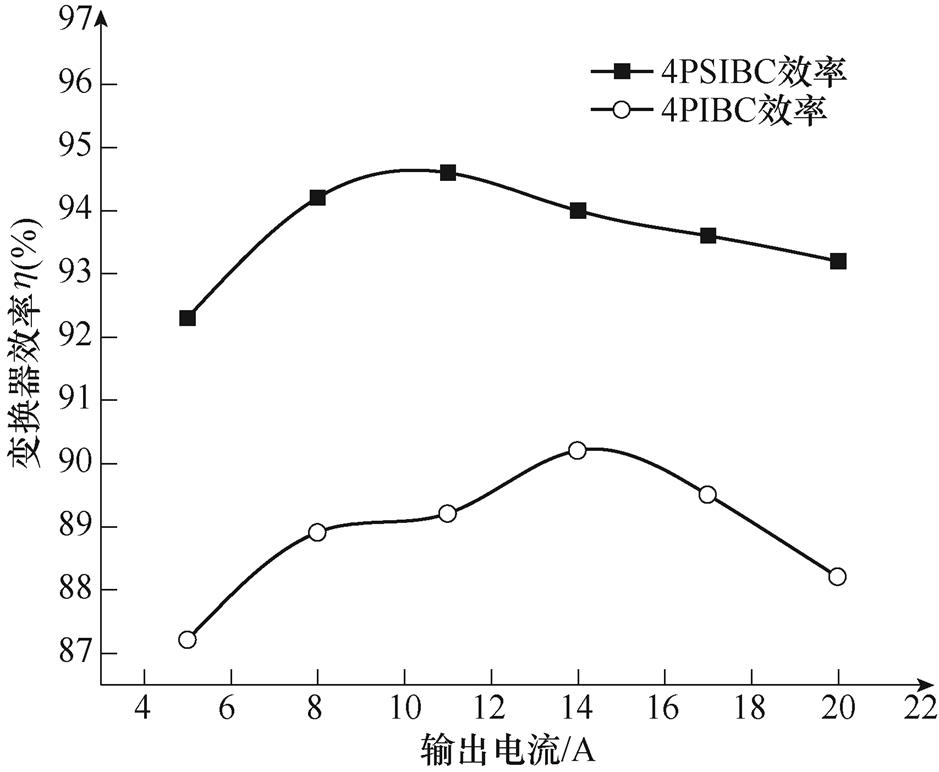
图12 4PIBC和4PSIBC实验样机效率对比
Fig.12 Efficiency comparison between 4PIBC and 4PSIBC experimental prototype
本文提出的MPSIBC在MPIBC拓扑上增加一个电容构成纹波补偿支路，从而解决了MPIBC输出纹波和效率之间的矛盾。MPSIBC拓扑结构简单，兼具输出纹波小和效率高的优点。本文对MPSIBC的输出纹波和效率进行了详细的理论、仿真和实验分析，结果表明MPSIBC具有一定的容错性和显著的纹波抑制效果，输出纹波系数几乎为0，且在输出纹波小的同时，MPSIBC的开关频率和滤波电感低，效率得到提高。仿真和实验表明，在同等运行条件下，MPSIBC的平均效率比MPIBC提高了5%左右。
参考文献
[1] 孙惠, 翟海保, 吴鑫. 源网荷储多元协调控制系统的研究及应用[J]. 电工技术学报, 2021, 36(15): 3264-3271.
Sun Hui, Zhai Haibao, Wu Xin. Research and appli- cation of multi-energy coordinated control of gener- ation, network, load and storage[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3264- 3271.
[2] 李建林, 牛萌, 周喜超, 等. 能源互联网中微能源系统储能容量规划及投资效益分析[J]. 电工技术学报, 2020, 35(4): 874-884.
Li Jianlin, Niu Meng, Zhou Xichao, et al. Energy storage capacity planning and investment benefit analysis of micro-energy system in energy inter- connection[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 874-884.
[3] 潘光胜, 顾伟, 张会岩, 等. 面向高比例可再生能源消纳的电氢能源系统[J]. 电力系统自动化, 2020, 44(23): 1-10.
Pan Guangsheng, Gu Wei, Zhang Huiyan, et al. Electri- city and hydrogen energy system towards accomodation of high proportion of renewable energy[J]. Auto- mation of Electric Power Systems, 2020, 44(23): 1-10.
[4] 李争, 张蕊, 孙鹤旭, 等. 可再生能源多能互补制-储-运氢关键技术综述[J]. 电工技术学报, 2021, 36(3): 446-462.
Li Zheng, Zhang Rui, Sun Hexu, et al. Review on key technologies of hydrogen generation, storage and transportation based on multi-energy complementary renewable energy[J]. Transactions of China Electro- technical Society, 2021, 36(3): 446-462.
[5] 李健强, 余光正, 汤波, 等. 考虑风光利用率和含氢能流的多能流综合能源系统规划[J]. 电力系统保护与控制, 2021, 49(14): 11-20.
Li Jianqiang, Yu Guangzheng, Tang Bo, et al. Multi- energy flow integrated energy system planning considering wind and solar utilization and containing hydrogen energy flow[J]. Power System Protection and Control, 2021, 49(14): 11-20.
[6] 李奇, 赵淑丹, 蒲雨辰, 等. 考虑电氢耦合的混合储能微电网容量配置优化[J]. 电工技术学报, 2021, 36(3): 486-495.
Li Qi, Zhao Shudan, Pu Yuchen, et al. Capacity optimization of hybrid energy storage microgrid con- sidering electricity-hydrogen coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 486- 495.
[7] Buttler A, Spliethoff H. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: a review[J]. Renewable and Sustainable Energy Reviews, 2018, 82(3): 2440-2454.
[8] Guilbert D, Collura S M, Scipioni A. DC-DC converter topologies for electrolyzers: state-of-the-art and remaining key issues[J]. International Journal of Hydrogen Energy, 2017, 42(38): 23966-23985.
[9] Guilbert D, Sorbera D, Vitale G. A stacked inter- leaved DC-DC Buck converter for proton exchange membrane electrolyzer applications: design and experimental validation[J]. International Journal of Hydrogen Energy, 2020, 45(1): 64-79.
[10] 郭小强, 魏玉鹏, 万燕鸣, 等. 新能源制氢电力电子变换器综述[J]. 电力系统自动化, 2021, 45(20): 185-199.
Guo Xiaoqiang, Wei Yupeng, Wan Yanming, et al. Review on power electronic converters for producing hydrogen from renewable energy sources[J]. Auto- mation of Electric Power Systems, 2021, 45(20): 185-199.
[11] Vázquez N, Reyes-malanche J A, Vázquez E, et al. Delayed quadratic Buck converter[J]. 2016, 9: 2534- 2542.
[12] Dc H S, Application D C, Zhang L, et al. An interleaved series-capacitor tapped Buck[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6565-6574.
[13] Kolli A, Gaillard A, De Bernardinis A, et al. A review on DC-DC converter architectures for power fuel cell applications[J]. Energy Conversion and Management, 2015, 105: 716-730.
[14] 童军, 吴伟东, 李发成, 等. 基于GaN器件的高频高效LLC谐振变换器[J]. 电工技术学报, 2021, 36(增刊2): 635-643.
Tong Jun, Wu Weidong, Li Facheng, et al. High- frequency and high-efficiency LLC resonant con- verter based on GaN devices[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 635- 643.
[15] Dobó Z, Palotás Á B. Impact of the current fluctuation on the efficiency of alkaline water electrolysis[J]. International Journal of Hydrogen Energy, 2017, 42(9): 5649-5656.
[16] Buitendach H P C, Gouws R, Martinson C A, et al. Effect of a ripple current on the efficiency of a PEM electrolyser[J]. Results in Engineering, 2021, 10.
[17] Palma L. Current source converter topology selection for low frequency ripple current reduction in PEM fuel cell applications[C]//IECON Proceedings (IndustrialElectronics Conference), Vienna, Austria, 2013: 1577- 1582.
[18] 赵清林, 刘会峰, 袁精, 等. 基于移相补偿的全桥LLC谐振变换器交错并联技术[J]. 电工技术学报, 2018, 33(12): 2777-2787.
Zhao Qinglin, Liu Huifeng, Yuan Jing, et al. An interleaved full-bridge LLC resonant converter with phase shift compensation[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2777-2787.
[19] 汪元鑫, 苏瑾, 胡金高. 电动汽车车载充电系统的设计与研究[J]. 电气技术, 2019, 20(7): 5-8, 17.
Wang Yuanxin, Su Jin, Hu Jingao. Research on onboard charging system for electric vehicle[J]. Electrical Engineering, 2019, 20(7): 5-8,17.
[20] 王朝强, 曹太强, 郭筱瑛, 等. 三相交错并联双向DC-DC变换器动态休眠控制策略[J]. 电工技术学报, 2020, 35(15): 3214-3223.
Wang Chaoqiang, Cao Taiqiang, Guo Xiaoying, et al. Dynamic dormancy control strategy of three-phase staggered parallel bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3214-3223.
[21] 高青. 低纹波输出的多相交错并联Buck变换器研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
[22] 杨玉岗, 祁鳞, 李龙华. 交错并联磁集成Buck变换器本质安全性输出纹波电压的分析[J]. 电工技术学报, 2014, 29(6): 181-188.
Yang Yugang, Qi Lin, Li Longhua. Analysis of output ripple voltage of essential safety for interleaving magnetics Buck converter[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 181-188.
[23] 陈东, 王磊, 赵君君. 基于改进平均电流控制的交错型磁耦合DC-DC变换器研究[J]. 电力系统保护与控制, 2016, 44(24): 58-65.
Chen Dong, Wang Lei, Zhao Junjun. Research of staggered parallel magnetic DC-DC converters based on improved average current control[J]. Power System Protection and Control, 2016, 44(24): 58-65.
[24] 郭瑞, 王磊. 混合储能系统六通道双向DC-DC变换器耦合电感研究[J]. 电工技术学报, 2017, 32(1): 117-128.
Guo Rui, Wang Lei. Research on coupled inductors of 6-channel bi-directional DC-DC converters for hybrid energy storage system[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 117-128.
Control Strategy and Characteristic Analysis of Multi-Phase Stacked Interleaved Buck Converter for Hydrogen Production
Abstract Efficiency and output ripple of hydrogen generation converters are critical metrics in hydrogen energy applications. Multi-phase interleaved Buck converter (MPIBC) suppresses the output ripple by increasing parallel branches, adopting the higher switching frequency, and adding filter inductance. However, that will lead to an increment in both costs and losses. To solve this deficiency, adding a ripple compensating shunt branch to MPIBC, a new topology, multi-phase stacked interleaved Buck converter (MPSIBC), is proposed in this paper. PWM control with the compensation characteristic is adopted in the compensation branch, in which the output AC current is complementary to the ripple of the MPIBC output current. The idea of output compensation is used to eliminate the output ripple of the converter without dependence on other factors, such as switching frequency. Based on the theoretical analysis of MPSIBC topology and the principle of ripple compensation, simulation on PSIM and physical experiments are established accordingly. Both the simulation and experimental results prove the ripple suppression capability of the proposed MPSIBC, with the reduction of the switching frequency and the inductance of the filters.
By adding a capacitor to one of the branches in MPIBC, the function of that branch changes from the original power flow to ripple compensation. This paper refers to the branch as a ripple compensation branch, where the capacitor acts as a voltage divider and a DC blocker. The MPSIBC proposed in this paper is MPIBC with the ripple compensation branch, and its topology and control strategy is first described in detail. Different pulse width modulation signals control the ripple compensation branch and other branches in MPSIBC. The control result is that the compensation branch provides a path for the converter output ripple, thus preventing the ripple from output to the load. The parameter calculations for the converter are then illustrated. The switching frequency and inductance are chosen for continuous conduction mode, and the capacitance is determined for ripple compensation. Next, the converter operation is divided into six stages in combination with the timing diagram of the control signal. The output current ripple of each stage is analyzed theoretically using the formula derivation. Theoretical results show that MPSIBC can achieve almost zero current ripple output under ideal conditions. Finally, the losses of the converter are calculated. The lower switching frequency and the filter inductor in MPSIBC significantly reduce the switching and inductor losses, respectively.
This paper builds an MPSIBC simulation model in the PSIM professional tool. In order to estimate the converter losses, the IGBT is simulated using a thermal physical model. The simulation model diagram and parameter table are provided in the paper. A 400W 4PSIBC experimental prototype is also built in the laboratory to verify the simulation. The experiments are implemented in three aspects: output current ripple, fault tolerance, and efficiency. The experimental results indicate that the current ripple output by MPSIBC is approximately 0.2A, a reduction of 83.3% compared to the MPIBC. In the fault tolerance test, one of the power branches in the MPSIBC is set to a fault, and the results show that the compensation branch can still effectively cancel the current ripple after the fault. An experimental comparison of MPSIBC and MPIBC shows that MPSIBC is about 5% more efficient than MPIBC due to the reduction in filter inductance and switching frequency. The experimental results of the prototype verify the correctness of the theoretical analysis and simulation.
The MPSIBC proposed in this paper adds a capacitor to the MPIBC topology to form a ripple compensation branch, thus resolving the conflict between MPIBC output ripple and efficiency.
Keywords：Hydrogen generation converters, multi-phase stacked interleaved Buck, output ripple, efficiency
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.211878
国家科技部重点研发资助项目（2018YFB0904700）。
收稿日期 2021-11-17
改稿日期 2022-03-06
E-mail: zl1846720683@163.com
韩民晓 男，1961年生，教授，博士生导师，研究方向为电力电子在电力系统中的应用。
E-mail: hanminxiao@263.net（通信作者）
（编辑 郭丽军）