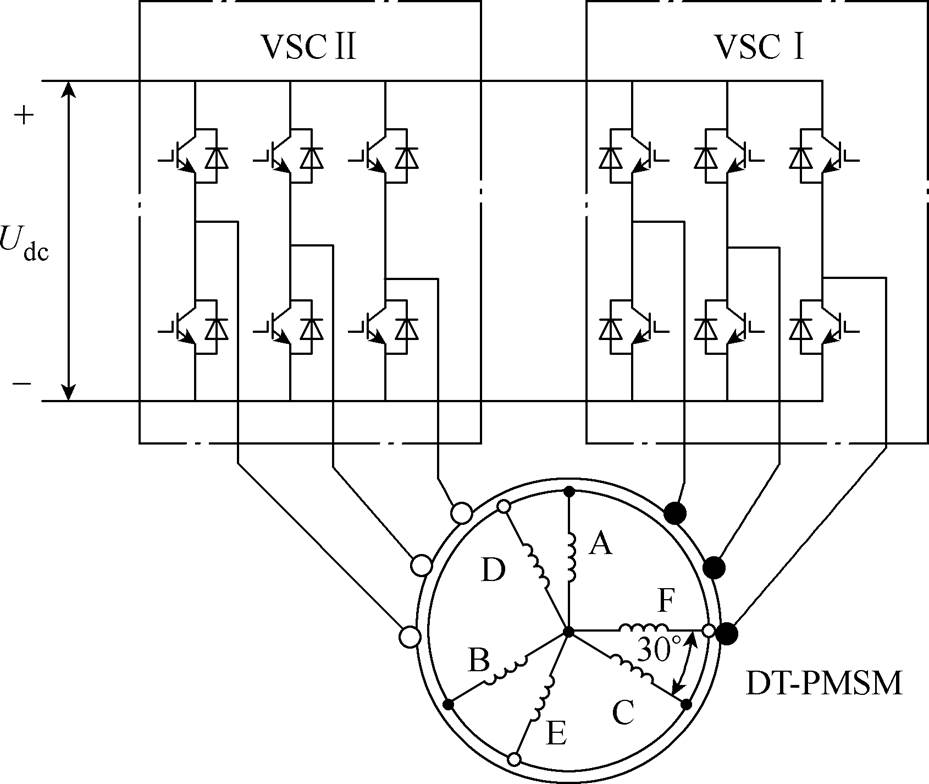
图1 定子绕组和变流器的拓扑结构
Fig.1 Topology of stator windings and converters
摘要 双三相永磁同步电机发生断相故障时，转速及电流中将会出现明显的周期性扰动。为了解决这一问题，该文提出了一种容错控制器，该控制器包含基于主控制器的参考值跟踪环路和基于重复控制器的周期性扰动抑制环路。所提出的容错控制器不仅可以实现对周期性扰动的闭环抑制，有效降低断相故障后系统中的转速脉动和谐波电流，还能够实现系统参考值追踪与周期性扰动抑制之间的解耦，避免重复控制器对暂态性能的影响。将所提出的控制器分别应用于驱动系统的转速环和电流环中，实验结果表明，与传统策略相比，该容错控制策略不仅能够有效抑制周期性扰动，还拥有更快更平稳的暂态跟踪响应。
关键词：双三相永磁同步电机 容错控制 周期扰动抑制 解耦控制 重复控制器
双三相永磁同步电机（Dual-Three-phase Per- manent Magnet Synchronous Machine, DT-PMSM）具有高功率密度、低转矩波动和强容错性能等优点，在航空航天、船舶推进和风力发电等场合中得到了应用[1-3]。容错控制是DT-PMSM驱动系统的重要研究方向之一，国内外学者针对断相、短路、退磁等多种故障下的容错控制策略开展了深入研究[4-5]。目前，主流方案是通过故障隔离方法将多数故障转化为断相故障进而进行容错控制，以此降低控制策略的复杂程度[6-7]。其中，单相断相故障是最常见的故障类型，因此，本文所提出的容错控制策略基于DT-PMSM驱动系统的单相断相故障。
断相故障会在转速和电流中引入周期性扰动，这会导致电机振动，同时降低系统的运行效率。为了实现对故障后双三相电机驱动系统的平稳控制，部分文献将断相后的电机视为不对称的多相电机，并提出了基于降维模型的容错控制策略[8-11]。但采用此种容错控制策略，故障前后需要切换控制器，这会提升控制系统的复杂度，并且切换过程可能在系统中引发振荡。
为了解决以上问题，国内外学者更加关注故障前后控制器无需重构的容错控制策略。其中，在故障后对扰动进行前馈补偿是一种被广泛应用的策略。文献[12-13]在故障后重新整定相电流的参考值，以补偿因断相而缺失的磁动势。文献[14-15]则在断相后对相电流进行了补偿。文献[16]建立了更加详尽的扰动模型，并采用遗传算法求解模型参数，但是该策略复杂度较高。文献[17]则在计算扰动模型参数时引入了查找表，简化了计算流程。尽管上述策略可以在一定程度上抑制周期性扰动，但是其扰动抑制效果会受到参数变化、变频器死区、齿槽转矩和永磁体磁链高次谐波等因素干扰[17-18]。
为了避免容错控制策略受到外部因素干扰，部分文献采用了基于谐振控制器的闭环控制策略，谐振控制器结构简单且能够有效抑制周期性扰动，闭环控制则不易受外部干扰的影响。文献[19]在原有的比例积分（Proportional Integral, PI）控制器的基础上并联了比例谐振（Proportional Resonant, PR）控制器，以抑制故障后出现的周期性扰动。文献[20]采用了类似的结构，对断相故障发生后零序电流引起的二倍和四倍频的电磁转矩脉动进行了抑制。然而，这种控制器结构尽管可以在系统稳态运行时有效抑制周期性扰动，但也会导致系统的参考值跟踪和扰动抑制之间产生耦合，在系统暂态过程中引入不必要的振荡。
为了避免传统前馈补偿策略对外部干扰抵抗力弱，以及传统的并联结构控制器暂态响应较差的问题，在文献[21]的基础上，本文提出了一种新型容错控制器，该控制器包含两个环路分别实现参考值跟踪和周期性扰动抑制。与传统的前馈控制策略相比，本文提出的控制器采用了闭环控制抑制扰动，不易受外部干扰的影响；与并联控制器相比，本文提出的控制器实现了系统参考追踪与扰动抑制之间的解耦，提升了暂态性能。此外，与传统隔离中性点结构相比，单中性点结构有更高的故障后控制自由度，可以实现更高的转矩输出[12]。因此，本文主要关注单中性点结构DT-PMSM的容错控制策略，但该策略同样可以应用于隔离中性点结构DT- PMSM。通过实验，验证了本文所提出方案的可行性和有效性。
本文研究的DT-PMSM采用表贴式转子结构、两套绕组相移30°电角度、单中性点连接方式，电机定子绕组由两电平电压源型变流器（Voltage Source Converter, VSC）供电，如图1所示。图中，Udc为母线电压。
图1 定子绕组和变流器的拓扑结构
Fig.1 Topology of stator windings and converters
采用矢量空间解耦矩阵，可以将六相自然坐标系下的物理量映射到dq、z1z2和o1o2三个正交的子平面上，即
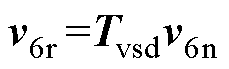（1）
式中，ν6r=[νd νq νz1 νz2 νo1 νo2]T为三个正交子平面上的物理量；ν6n=[νA νB νC νD νE νF]T为六相自然坐标系下的物理量；变换矩阵Tvsd的具体表达式可见文献[22]。经上述变换后，表贴式DT- PMSM各平面电压方程可以表示为
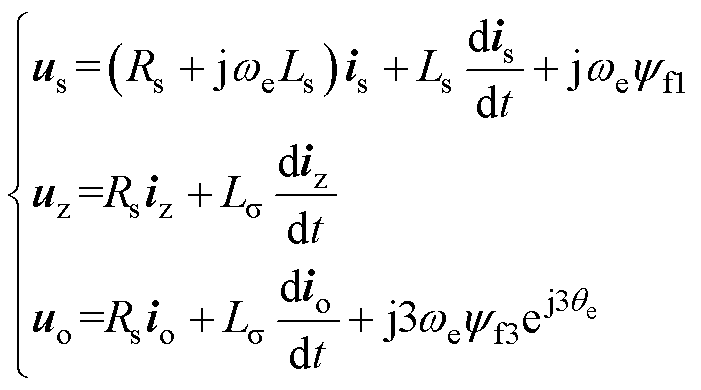（2）
式中，us=ud+juq、uz=uz1+juz2、uo=uo1+juo2为电压矢量；is=id+jiq、iz=iz1+jiz2、io=io1+jio2为电流矢量；Rs为相电阻；Ls和Ls 分别为dq平面的电感和漏电感；we为转子的电角速度；yf1和yf3分别为转子磁链的基波和3次谐波分量的幅值；qe为转子位置的电 角度。
采用单中性点结构，DT-PMSM中存在零序电流通路，因此电磁转矩方程的推导应综合考虑磁通基波和3次分量的影响，可以表示[23]为
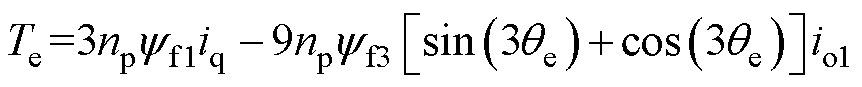（3）
式中，Te为电磁转矩；np为电机极对数。
DT-PMSM的运动方程可以表示为
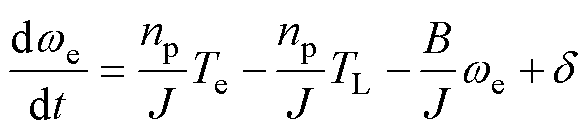（4）
式中，J为转动惯量；TL为负载转矩；B为摩擦因数；d 为转速环中存在的扰动，包含周期性扰动dp和非周期性扰动dn。
当单相断相故障发生时，定子绕组的某一相电流将无法控制且始终为零。若其余各相和DT-PMSM的参数（如电阻、电感和转子磁链）不受故障影响，则故障后的电压方程、电磁转矩方程和运动方程也与故障前保持一致。
为了维持恒定的电磁转矩，在故障前后的运行中，磁动势应保持不变。基于这一原理，文献[12]给出了两种常规的故障后电流优化算法，即最大转矩控制和最小铜耗控制。为了节省篇幅，本文在之后的内容中仅讨论最大转矩控制，但本文所提出的策略同样可以采用其他优化算法。
以F相断相为例，因为断相前后电磁转矩需维持一致，所以dq平面的电流不应变化，但断相故障会降低控制自由度，电流将满足约束条件
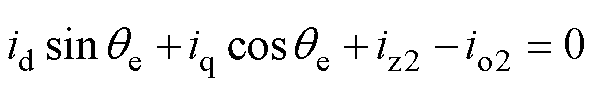（5）
为了避免各电流平面控制器互相影响，故障后电流参考值整定需要考虑约束条件式（5）。若断相后仍采用id=0控制策略，各平面的故障后电流可以用iq表示为
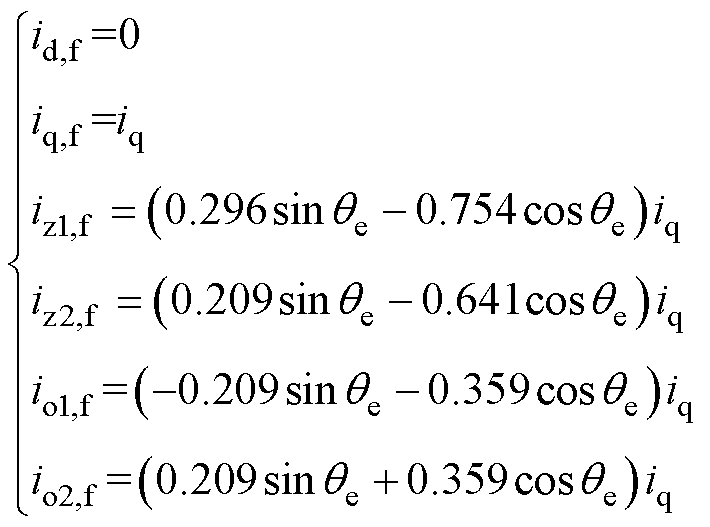（6）
式中，id,f、iq,f、iz1,f、iz2,f、io1,f和io2,f分别为故障后的d轴、q轴、z1轴、z2轴、o1轴和o2轴电流。
本文所提容错控制策略的结构如图2所示，图中，Ts为转速环和电流环的采样时间，上标“*”为参考值。本节将介绍转速环容错控制器，并对其性能进行分析。
在离散域中，式（4）可表示为
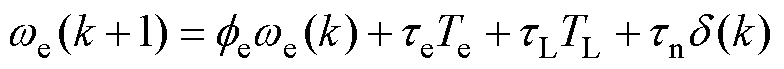（7）
其中
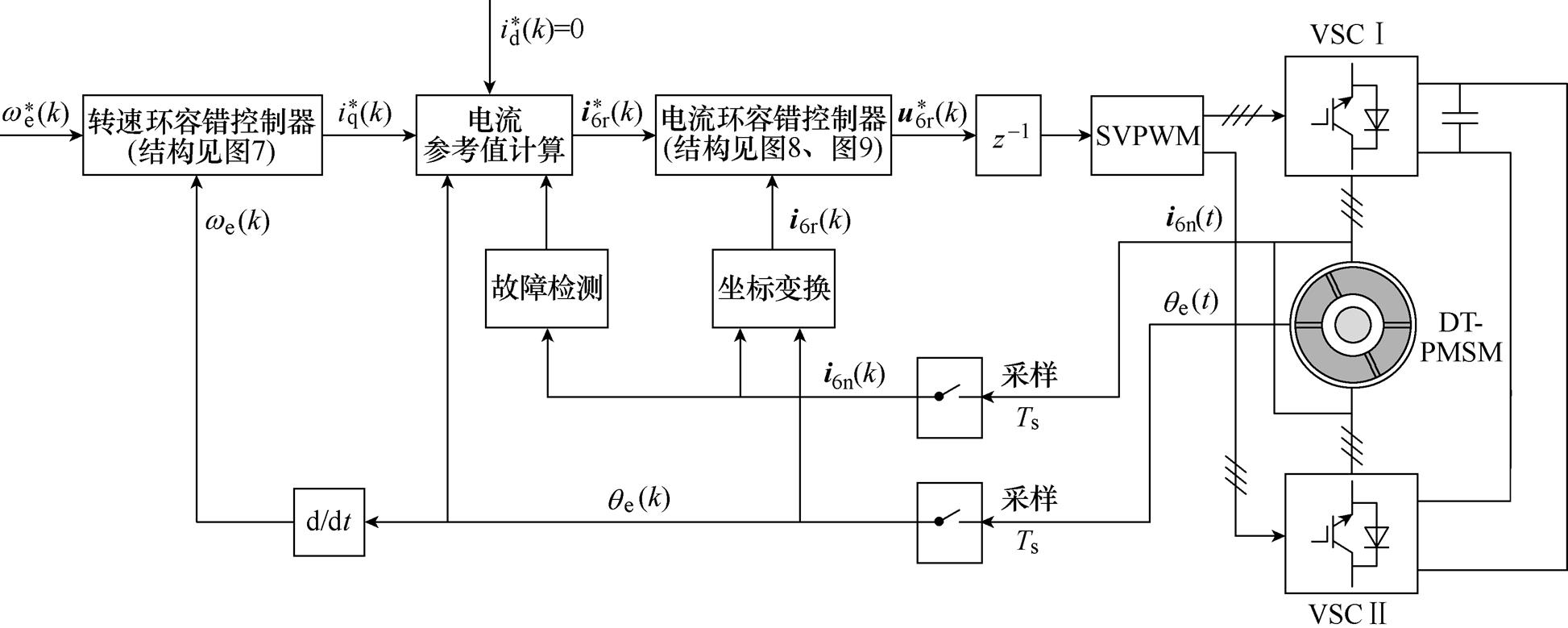
图2 本文提出的DT-PMSM驱动系统容错控制结构
Fig.2 The proposed fault-tolerant control scheme of DT-PMSM drive system
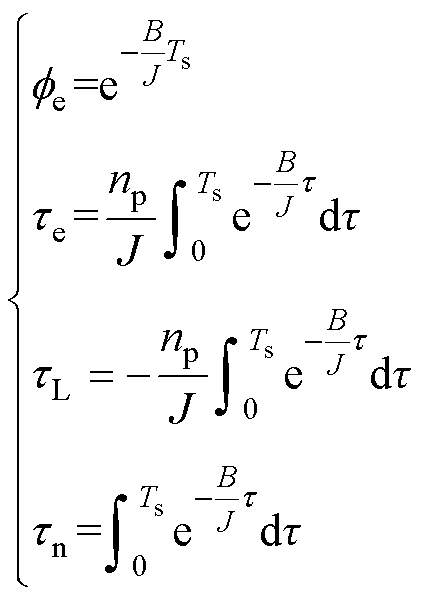（8）
当F相断开后，将式（3）和式（6）代入式（7），则可以得到断相故障发生后系统的运动方程为
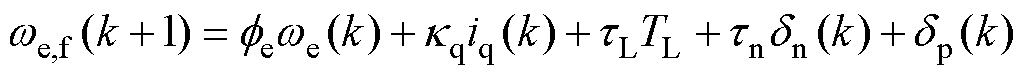（9）
其中
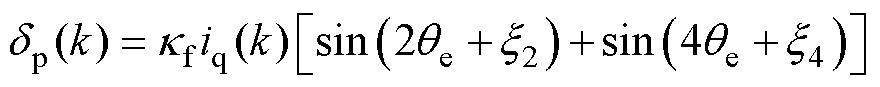
式中，we,f为故障后电角速度。其他参数为
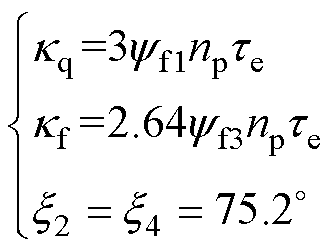（10）
可以注意到，故障后转速中将存在明显的周期性扰动，其频率主要为二倍和四倍基频。同时，由于永磁体磁链的高次谐波和齿槽转矩等因素的影响，电磁转矩中还会存在其他偶次谐波[17]。转速扰动会造成电机振动，这会影响产品使用的舒适性，严重时会损坏电机主轴和联轴器，降低系统寿命。因此，需要设计具有良好周期扰动抑制性能的转速环容错控制器。
图3给出了三种可以抑制周期性扰动的控制结构，图中，CM为主控制器，CR为谐振控制器，M为系统的实际模型，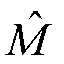
为转速观测器。前馈控制器如图3a所示，该结构直接将扰动补偿加入主控制器的输出中。图3b引入了CR，并将之与CM并联，这种控制器下文简称并联控制器。图3c为本文所提出的控制器，首先由PI控制器输出iq,pi，并根据iq,pi估计k时刻转速的预测值，然后将预测值与实际值的误差信号输入重复控制器（Repetitive Controller, RC），最后将PI控制器与RC输出信号相加得到最终的q轴电流参考值。其中，PI控制器作为主控制器以实现参考信号跟踪，RC则用来抑制周期性扰动。在离散域中，RC的传递函数可以表示为
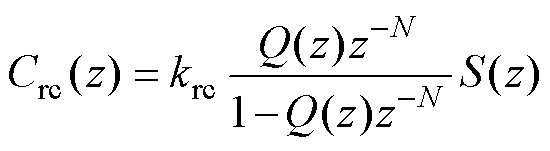（11）
式中，krc为控制器增益；为了保证控制器所有的极点都位于单位圆内，根据文献[24]，Q(z)可以配置为低通滤波器；定义N=R( fs/fc)，R为取整函数，fs为采样频率，fc为被控信号的频率；S(z)可以补偿相位延迟，通常设置为S(z)=zl，l为一个小于N的整数。
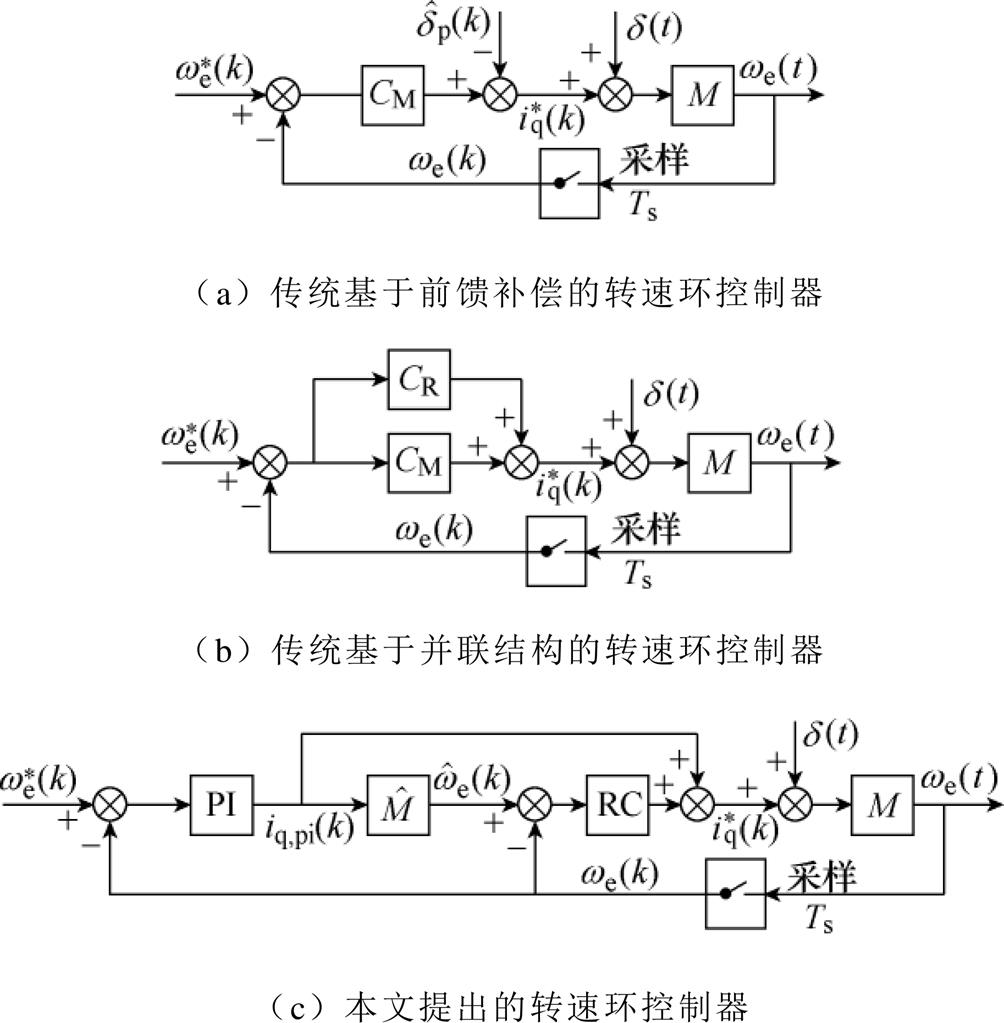
图3 传统与本文提出的转速环容错控制器框图
Fig.3 Block diagram of conventional and proposed fault-tolerant speed-loop controllers
RC的频率响应如图4所示，图中fs和fc分别选择为10kHz和50Hz。由图4可以看出，RC在kfc（k =1, 2, 3,…）频率附近具有显著的增益，因此可以控制一系列具有相同基频的谐波。提高krc会带来更高的幅值增益，但可能会降低系统的稳定性，增大l可以降低相位延迟。因为转速环中出现的周期性扰动为偶次谐波，所以可以设置fc=2fe，其中fe=we/(2p)。
为了统一对比三种控制结构，在下文中将图3a和图3b中的CM和CR分别选为PI和RC。当采用前馈补偿时，转速环从参考值到输出的闭环传递函数可以描述为
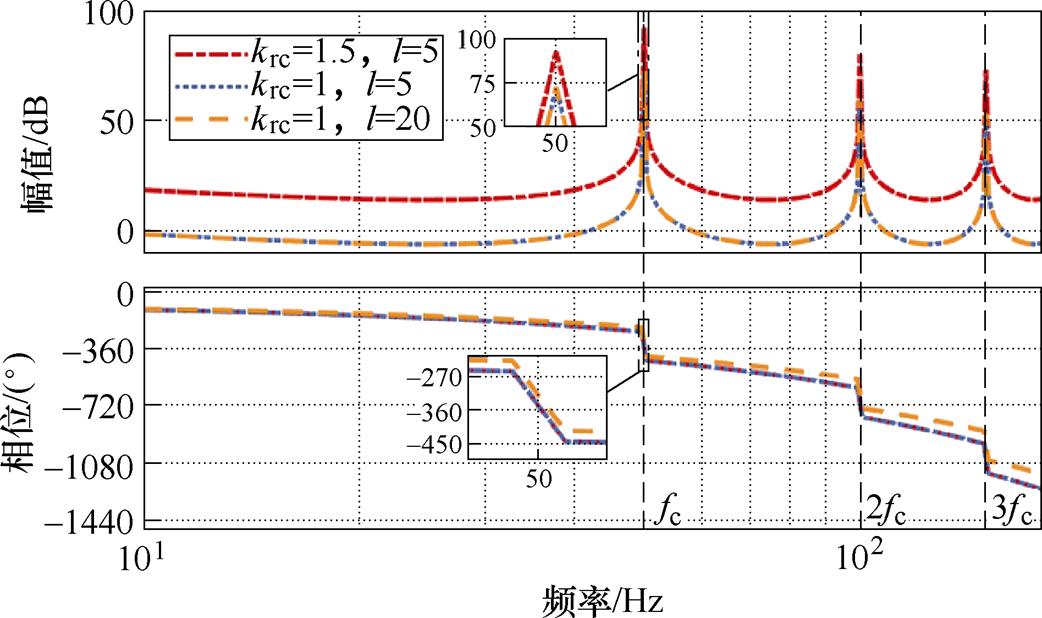
图4 RC的频率响应
Fig.4 The frequency response of RC
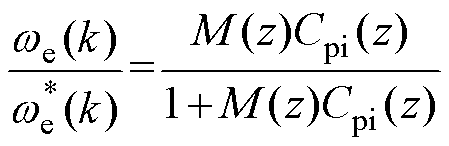（12）
式中，Cpi为PI控制器的传递函数。
从扰动到输出的闭环传递函数可以表示为
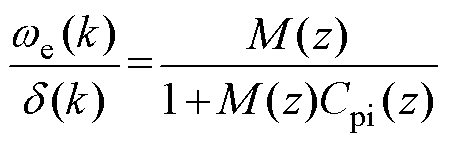（13）
采用并联控制器时，以上两个传递函数可以表示为
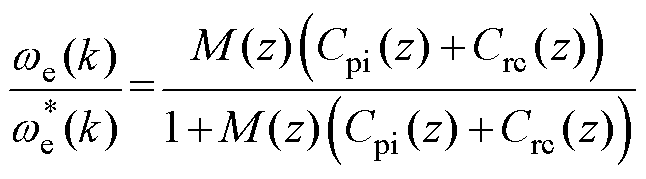（14）
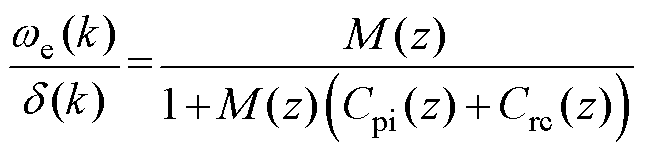（15）
从式（14）和式（15）可以看出，采用并联结构时，RC不仅在扰动抑制过程中发挥作用，还会对参考信号跟踪性能产生影响。
而采用本文提出的控制器时，转速环的传递函数可以表示为
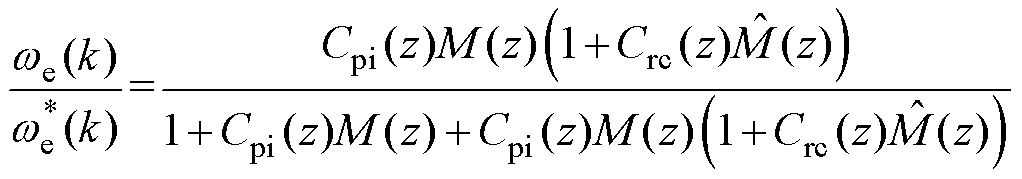（16）
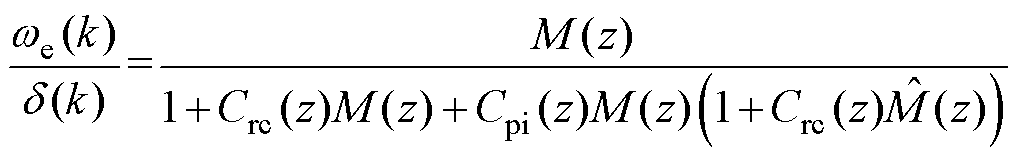（17）
若转速估计较为精确，可以认为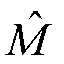≈M，则式（16）和式（17）可以化简为
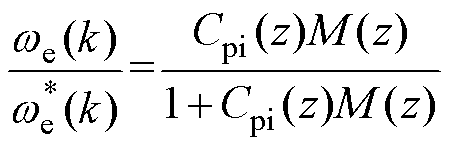（18）
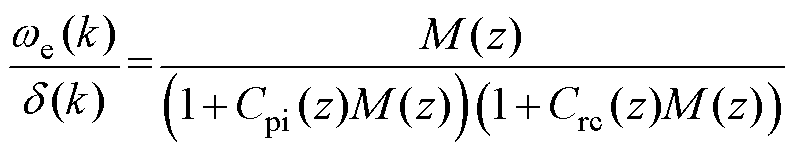（19）
可以看到，采用本文提出的控制器时，RC仅作用于转速环的扰动抑制过程，而其主传递函数与采用前馈补偿时相同，并没有受到RC的影响，这说明本文所提出控制器的参考值跟踪性能和周期性扰动抑制性能实现了解耦。
图5展示了分别采用传统控制结构和本文提出的控制结构时转速环的参考值跟踪特性。图中，fs=10kHz, fe=25Hz。由图5可以看出，采用并联控制器时，RC会在谐振频率处引入额外的增益，这会放大暂态过程中的振荡，在后续的实验环节中可以明显观察到这一现象，而采用前馈补偿或本文提出的控制器则避免了RC的影响，转速环呈现低通滤波特性。
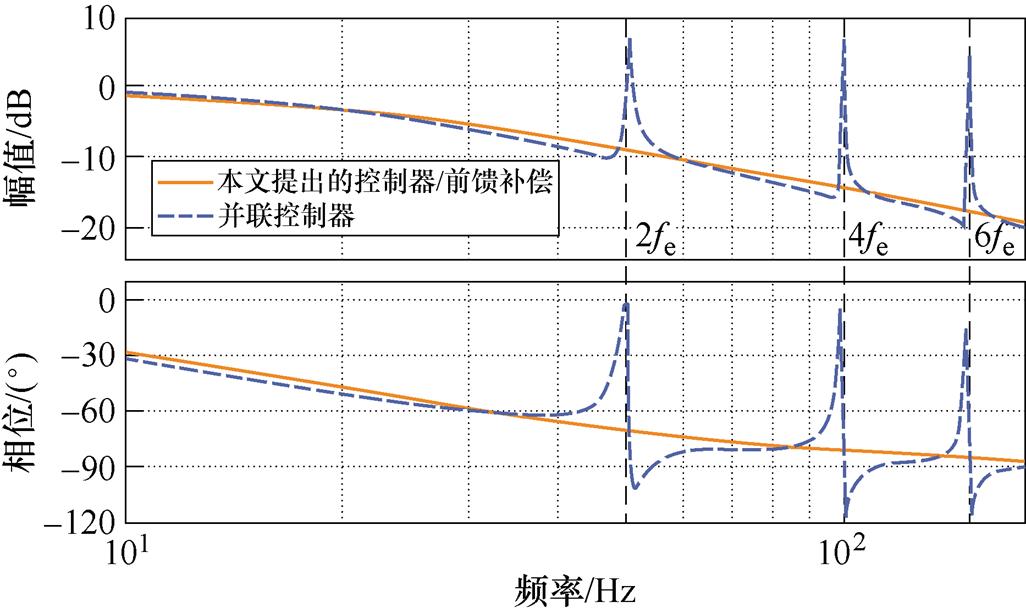
图5 分别采用传统控制器以及本文提出的控制器时从参考值到输出的闭环传递函数频率响应
Fig.5 The frequency response of the close-loop transfer function from reference to output with conventional and proposed controller adopted respectively
图6则展示了三种控制器的扰动抑制能力，可以看到，并联控制器与本文提出的控制器在扰动频率处有较大的负增益，因此这两种控制器可以有效抑制周期性扰动；而采用前馈补偿策略时，控制器本身缺乏对周期性扰动的抑制能力，扰动抑制效果取决于补偿项的准确度。同时从图6中可以看到，本文提出的控制器在绝大多数频域内有最低的幅值增益，可以更加有效地抑制扰动。
根据2.2节分析，本文提出的控制器实现周期性扰动抑制与参考值跟踪解耦的前提是有较为精准的转速估计，本文使用了扩展状态观测器（Extended State Observer, ESO）来实现这一目标。本文中周期性扰动可以被结构简单的RC有效抑制，因此ESO
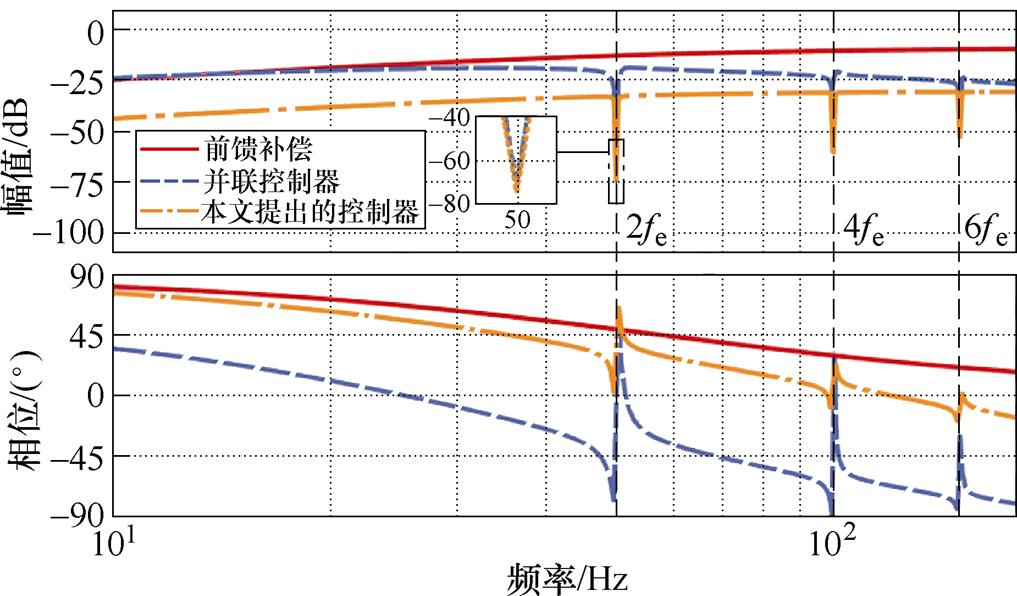
图6 分别采用传统控制器以及本文提出的控制器时从扰动到输出的传递函数频率响应
Fig.6 The frequency response of the close-loop transfer function from disturbance to output with conventional and proposed controller adopted respectively
仅需观测非周期性扰动dn。根据式（7）可以建立增广转速环状态方程为
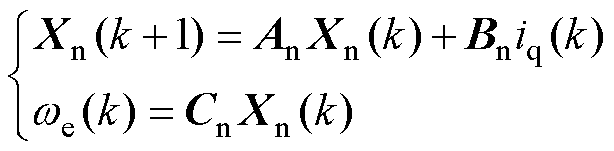（20）
其中
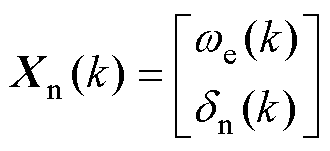
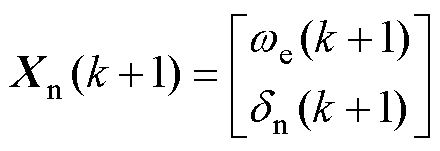
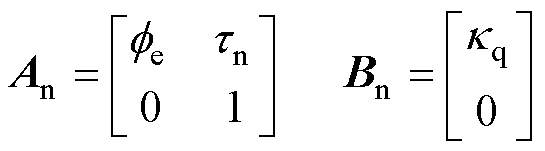
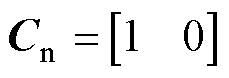
式中，Χn为包含扰动的转速环状态矢量；An、Bn和Cn为相应的系数矩阵。
根据式（20），本文建立的ESO为
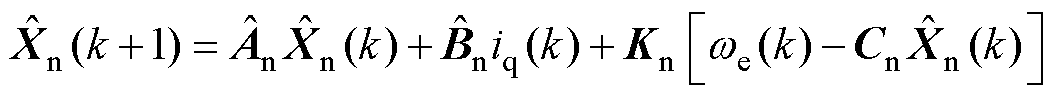（21）
式中，上标“
”为观测值；Kn=[kno1 kno2]T为观测器系数矩阵。
文献[25]详细分析了ESO的收敛条件，该文献指出，若系统中扰动是有界的，那么选择合适的观测器参数，ESO的观测误差满足
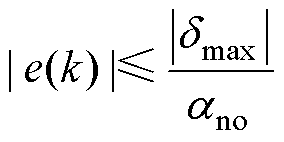（22）
式中，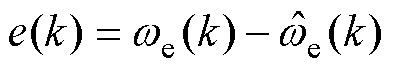
为转速环ESO观测误差；dmax为扰动最大边界值；ano为观测器环宽。
根据式（22）可知，ano越大，测误差越小，ESO的模型估计越精确，但观测噪声使得ano不能无限大。ano等观测器参数的整定方法可参见文献[26]。
采用ESO建立系统模型，图3c中的结构可以详细表示为图7，可以看到，ESO不仅可以获得较为精准的转速估计值，还可以对非周期扰动进行补偿。
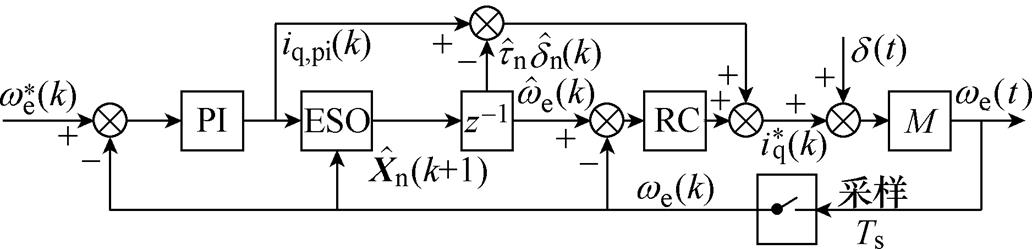
图7 本文提出的基于ESO的转速控制器框图
Fig.7 Diagram of proposed speed controller based on ESO
本文在矢量空间解耦坐标系下设计了电流环的容错控制策略，电流控制器将在dq、z1z2和o1o2平面中分别讨论。
首先讨论dq平面的控制策略。根据式（2）可得到正常工况下dq平面的离散化模型为
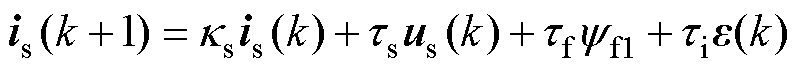（23）
式中，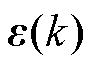
为电流环扰动。其余各系数可以表示为
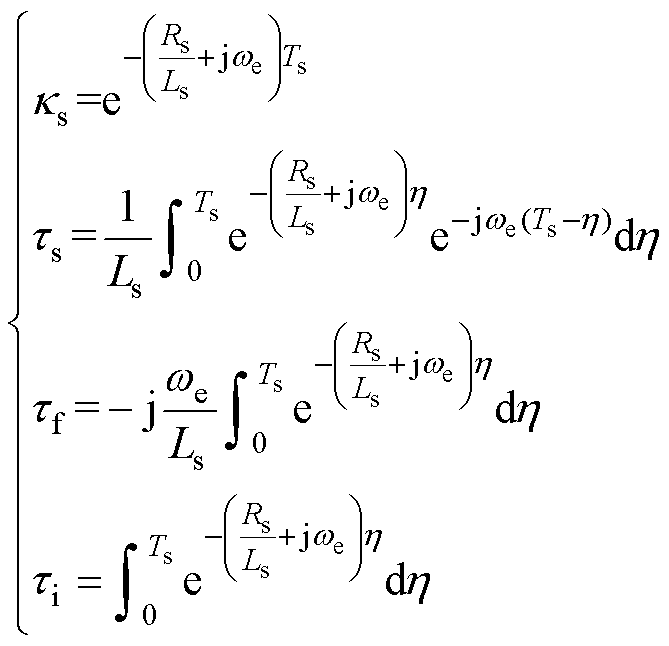（24）
F相断相后，SVPWM模块仍然会输出六相占空比信号，然后由变流器调制出六相电压uA～uF。但uF无法对电流产生影响，因此故障后dq平面的电流可以表示为
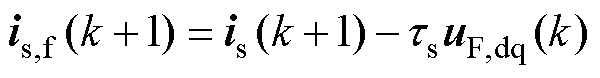（25）
式中，is,f为断相后的dq平面电流矢量；uF,dq为uF在dq平面上的投影，有
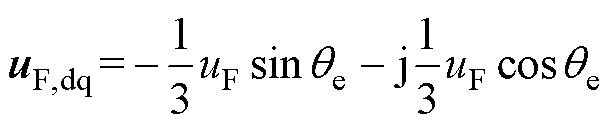（26）
uF主要包含基频分量和奇次谐波，其表达式为
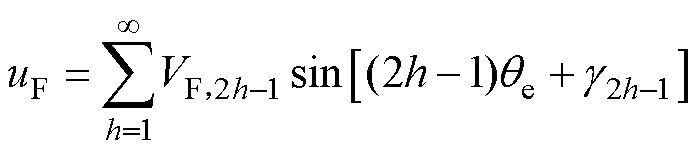（27）
式中，VF,2h-1为2h-1（h=1, 2, 3,…）次电压的幅值；g2h-1为2h-1次电压的相位。
将式（26）和式（27）代入式（25），可得
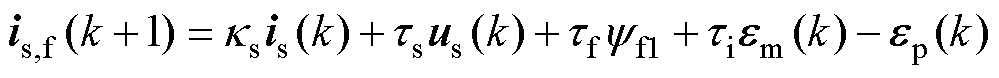（28）
其中
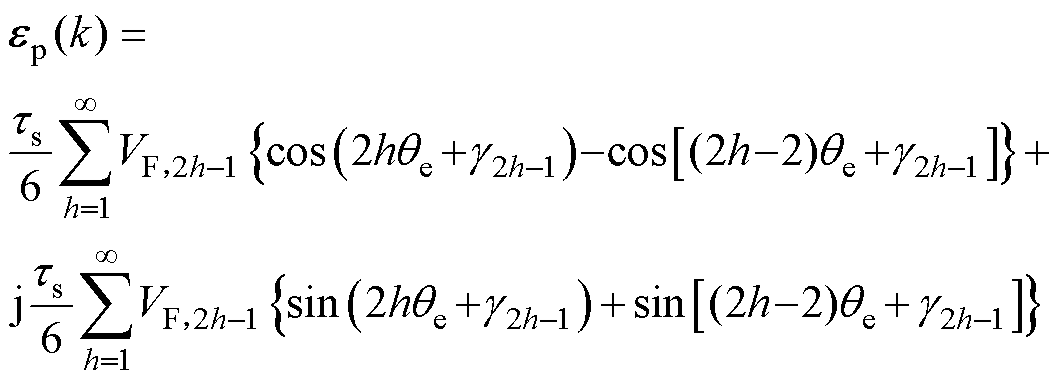
式中，em和ep分别为电流环非周期性和周期性扰动。
由式（28）可以看出，断相故障会在dq平面电流中引入偶次扰动。dq平面电流扰动不仅会引发转矩波动，还会产生谐波电流。谐波电流会导致系统运行效率降低，控制性能下降。此外，谐波电流过大还会损坏绕组绝缘和设备中的电容，降低系统使用寿命。为了抑制电流扰动，图3中的三种控制器也可以应用于电流环。本文在dq平面的控制器同样采用了转速环中的结构，其结构框图如图8所示，以PI控制器作为主控制器以跟踪参考信号，同时采用RC来抑制周期性扰动。另外两种控制器结构以及不同控制器的性能分析与转速环类似，此处不再详述。
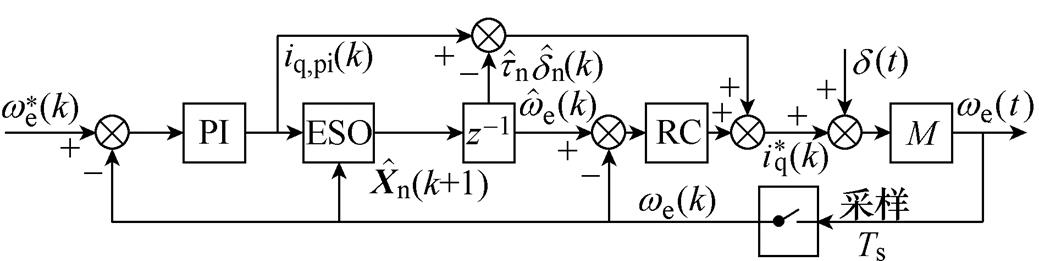
图8 本文提出的dq平面电流环控制器框图
Fig.8 Block diagram of proposed current-loop controller in dq frame
dq平面电流也可以由ESO估计，电流ESO的数学模型为
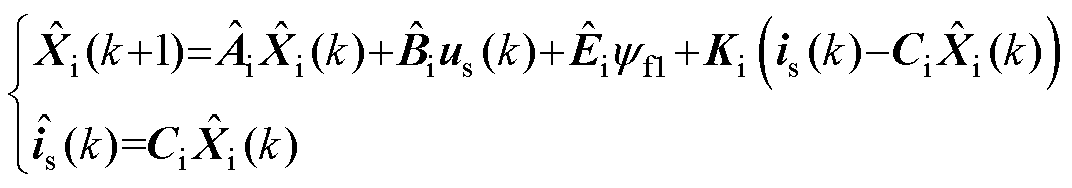（29）
式中，Ki=[kio1 kio2]T为观测器系数矩阵，其整定方法与转速环相同。其他系数矩阵表达式为
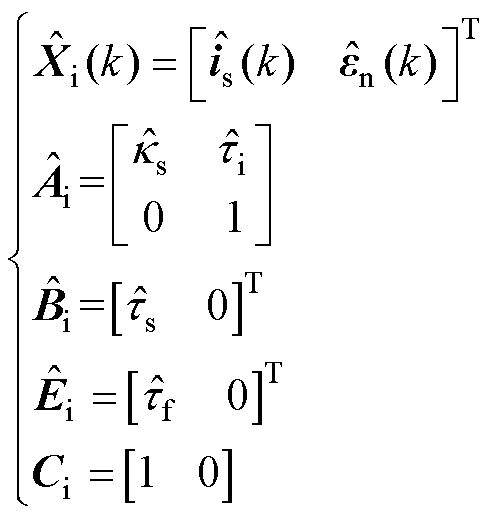（30）
在矢量空间解耦坐标系中，z1z2平面的电流主要成分为6k±1（k =1, 3, 5,…）次谐波，该电流不参与直流转矩的形成，但会产生额外的损耗，正常工况下应该被抑制为0。由于z1z2平面电流中同时存在正序和负序分量，为方便控制，本文对其进行如下坐标变换，有
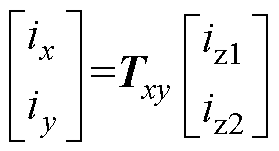（31）
其中
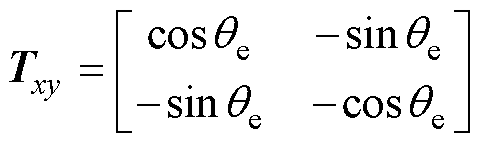
式中，Txy为变换矩阵。经过坐标变换后，ix与iy中的谐波成分变为6k（k =1, 3, 5,…）次。
经过坐标变后，正常工况下xy平面的控制器可以采用RC，其fc设置为6fe。在断相故障发生后，根据式（6），需要在z1z2平面注入基频电流，但是上述RC不能实现对基频的控制，因此，本文在RC上并联了准PR控制器，其离散域传递函数可以表示为
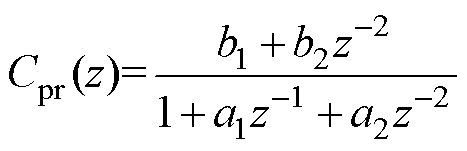（32）
其中
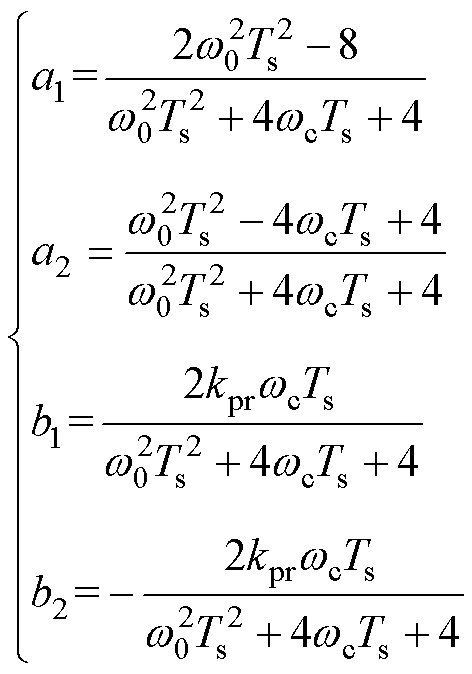（33）
式中，kpr为谐振增益；wc为截止频率；w0为谐振频率，为了使得准PR控制器在基频处有较大增益，此处取w0=we。
z1z2平面电流控制器框图如图9所示，与dq平面相比，z1z2平面不需要跟踪直流参考信号，因此无需采用图8中的结构以实现参考值跟踪与扰动抑制的解耦。同时，z1z2平面电流主要成分为周期性谐波，非周期扰动相对较小，即使存在一定的非周期扰动，其对电磁转矩和转速的影响也极小，因此该平面可以不考虑非周期性扰动的抑制。
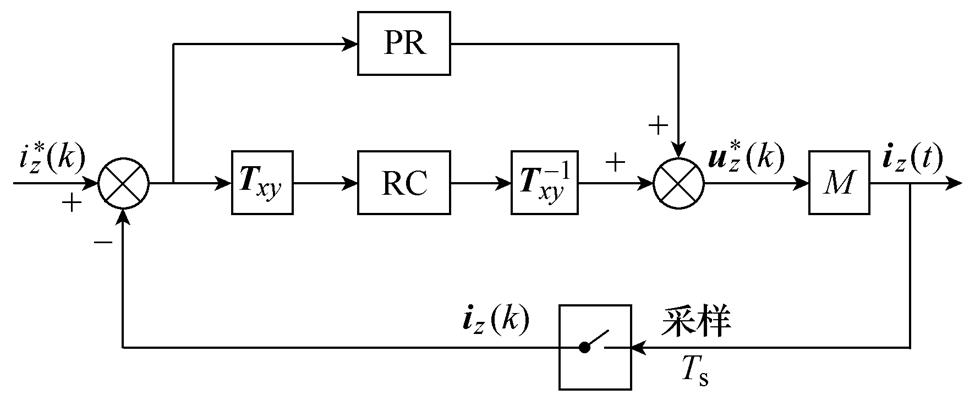
图9 z1z2平面电流控制器框图
Fig.9 Block diagram of current-loop controller in z1z2 frame
o1o2平面的情况与z1z2平面类似。其电流组成以3k（k =1, 3, 5,…）次谐波为主，在正常工况下需要对其进行抑制，断相故障发生后也需要向平面中注入基频电流。因此，图9所示控制器结构同样也可以应用于o1o2平面，只需要删除坐标变换环节Txy和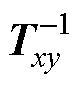
并将RC的fc设置为3fe即可。
本节通过实验验证了所提出的容错策略的性能。实验装置如图10所示，两套定子绕组由两台共直流母线的Danfoss变流器供电，选用TMS320F28379D数字信号处理器实现控制算法。西门子变频器控制的感应负载电机与DT-PMSM同轴连接。实验装置的详细参数见表1。
图10 实验平台实物
Fig.10 Pictures of the experimental platform
表1 实验平台参数
Tab.1 Parameters of the experimental platform
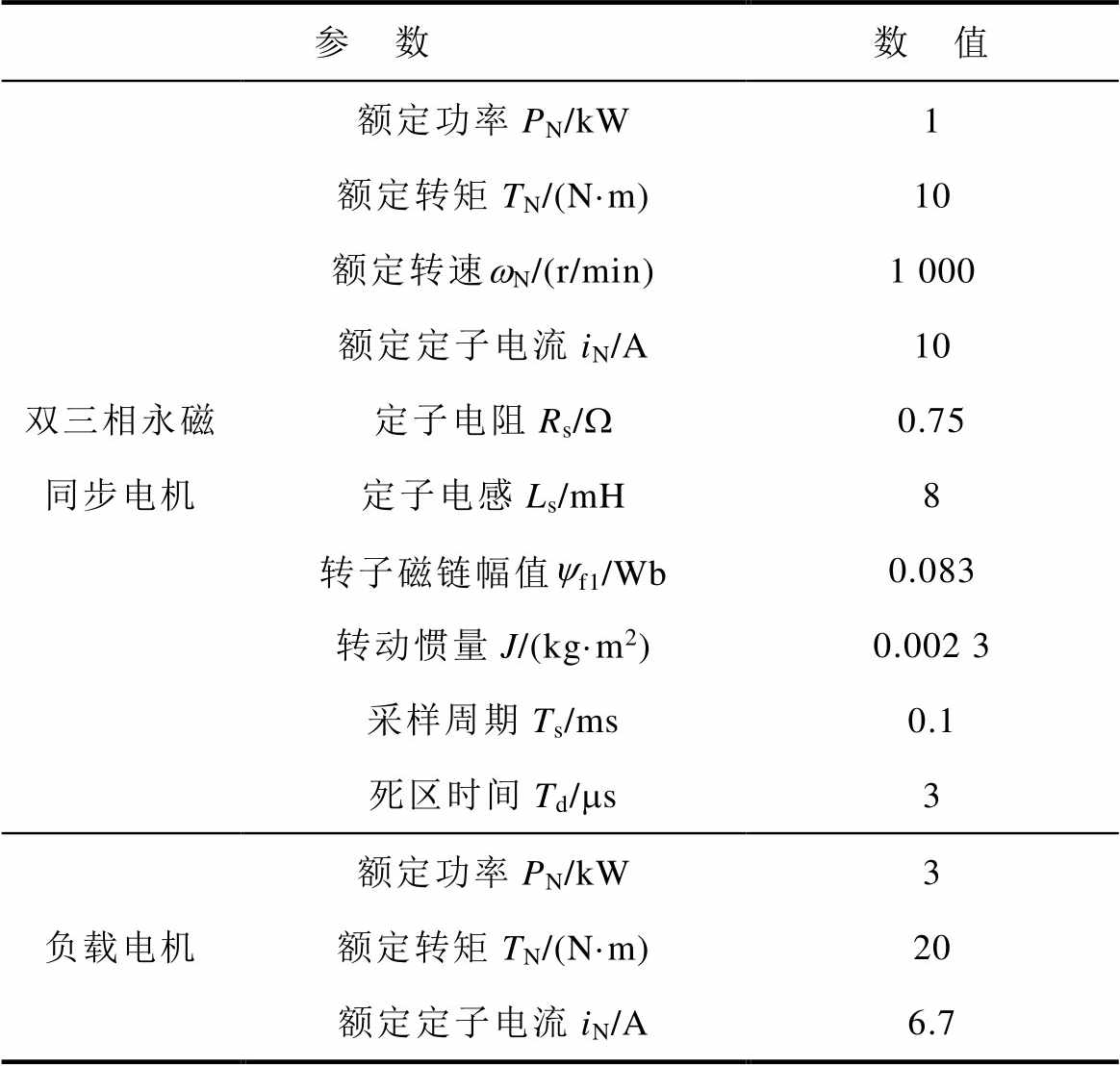
参 数数 值 双三相永磁同步电机额定功率PN/kW1 额定转矩TN/(N·m)10 额定转速wN/(r/min)1 000 额定定子电流iN/A10 定子电阻Rs/W0.75 定子电感Ls/mH8 转子磁链幅值yf1/Wb0.083 转动惯量J/(kg·m2)0.002 3 采样周期Ts/ms0.1 死区时间Td/ms3 负载电机额定功率PN/kW3 额定转矩TN/(N·m)20 额定定子电流iN/A6.7
为了验证本文提出的容错控制策略在系统稳态运行时有较好的控制性能，采用了基于前馈补偿的控制策略、基于并联控制器的控制策略和基于本文所提出控制器的控制策略分别进行实验，三种控制策略除控制器结构外，其他条件均相同。表2给出了控制器的详细参数。
表2 转速及电流控制器参数
Tab.2 Parameters of the speed and current controllers
参 数数 值 转速控制器转速环PI环宽as/(rad/s)40 RC谐振增益krc0.1 RC补偿步长l3 ESO增益矩阵Kn[0.013 0.805] dq电流控制器电流环PI环宽ac/(rad/s)600 RC谐振增益krc1 RC补偿步长l3 ESO增益矩阵Ki[0.259-j0.004 43.242-j0.085] z1z2及o1o2电流控制器RC谐振增益krc1 RC补偿步长l3 PR谐振增益kpr150 PR截止频率wc2
图11～图13分别展示了三种策略故障前后的稳态性能，图11a～图13a为A相和D相电流波形；图11b～图13b为电机转速nr和电磁转矩Te波形，nr参考值为额定转速1 000r/min，而故障后电机的输出转矩需要降额，因此Te参考值选为5N·m，D 表示物理量波动的峰峰值；图11c～图13c则给出了相电流的快速傅里叶变换（Fast Fourier Transform, FFT）分析。为了方便比较不同控制器的稳态性能，表3将稳态实验的数据进行了汇总，其中转速和电磁转矩波动为波动量峰峰值相对参考值的百分比。
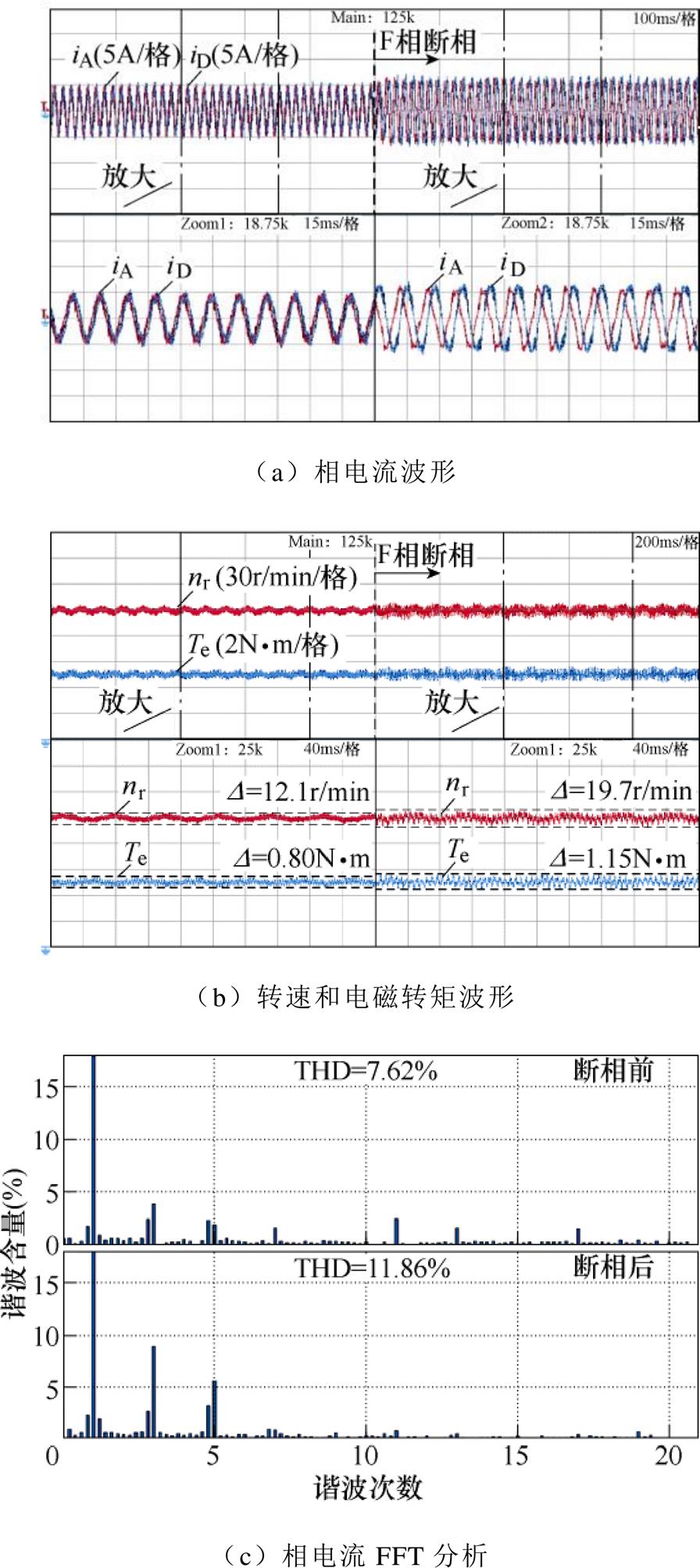
图11 采用传统基于前馈补偿的控制器时断相故障发生前后的实验波形
Fig.11 Experimental waveforms on pre- and post-fault condition with the conventional feedforward compensation controller
由图11可以看出，正常工况下，前馈补偿方案因为没有采用重复控制器，系统抑制周期性扰动的效果差，相电流的总谐波畸变率（Total Harmonic Distortion, THD）较高，达到了7.62%，其转速和转矩的波动高于其他两种方案，分别为12.1r/min和0.80N·m。而根据图12和图13，采用并联控制器和本文所提出控制器时，转速和转矩的波动更小，THD也更低。同时，本文所提出控制器对非周期性扰动进行了补偿，因此稳态性能略优于并联控制器。
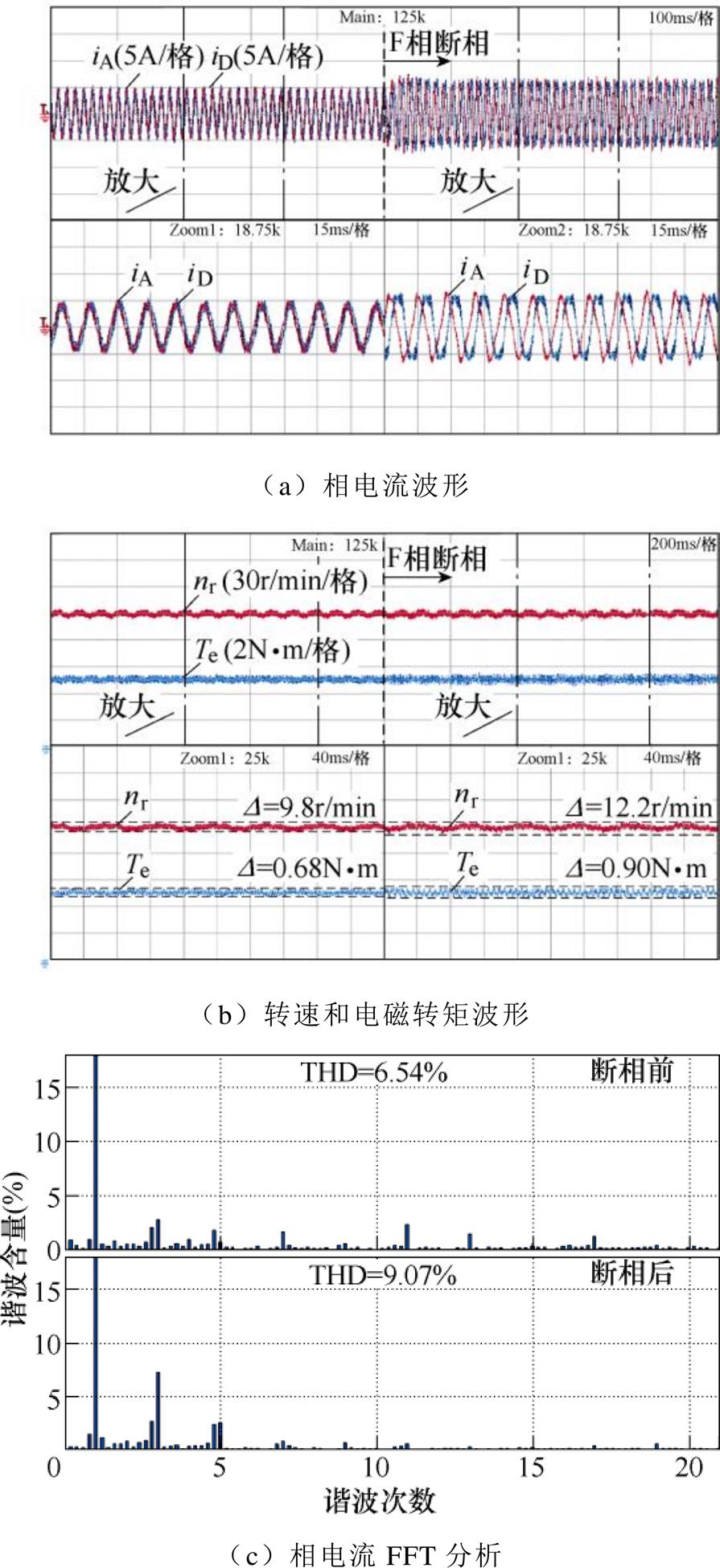
图12 采用传统并联控制器时断相故障发生前后的实验波形
Fig.12 Experimental waveforms on pre- and post-fault condition with the conventional parallel controller
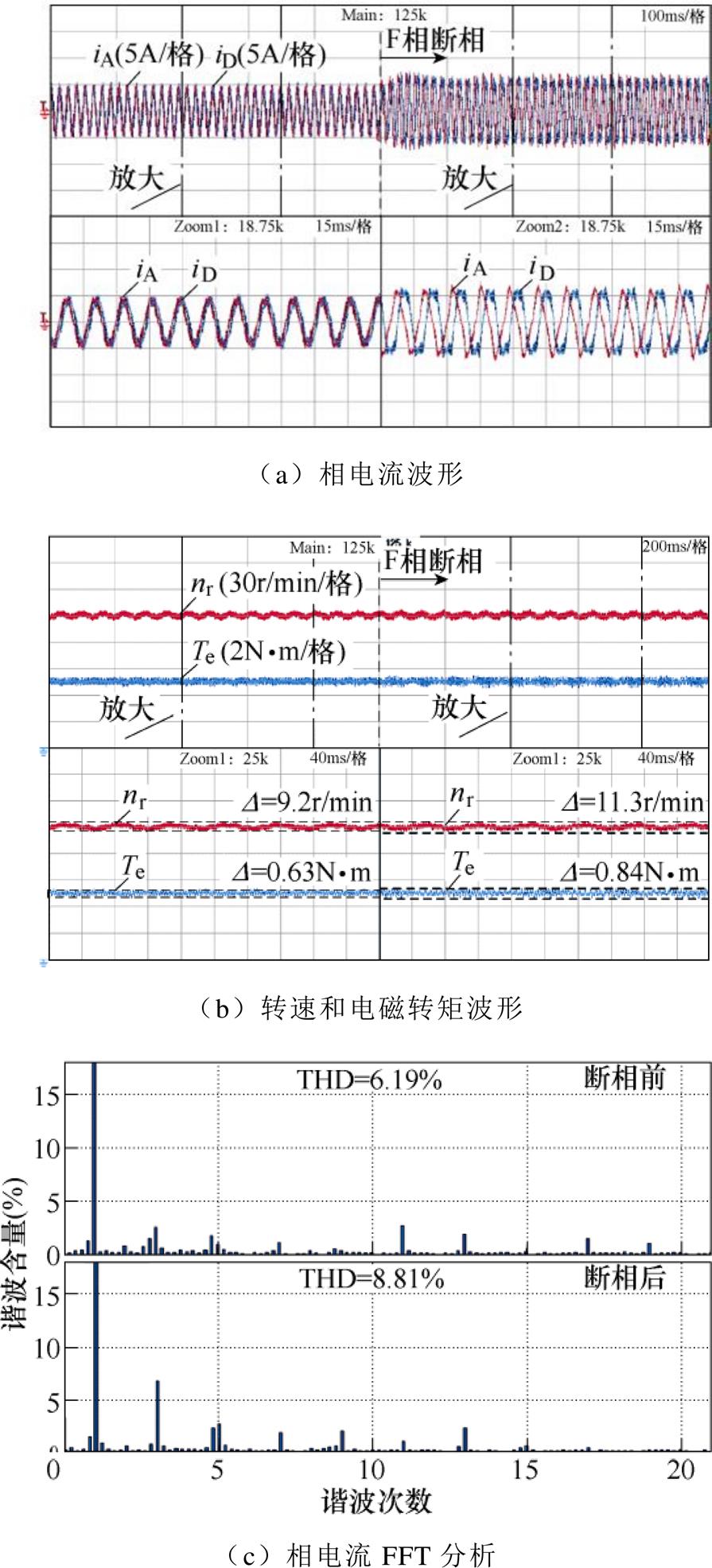
图13 采用本文提出的控制器时断相故障发生前后的实验波形
Fig.13 Experimental waveforms on pre- and post-fault condition with the proposed controller
表3 不同控制器稳态实验效果对比
Tab.3 Comparison of steady experimental results among different controllers
控制器结构转速波动 (%)电磁转矩波动(%)相电流 THD(%)计算时间/ms 故障前故障后故障前故障后故障前故障后故障前故障后 前馈补偿1.211.971623.07.6211.8616.217.3 并联控制器0.981.2213.618.06.549.0719.220.5 本文提出的控制器0.921.1312.616.86.198.8124.826.1
断相故障发生后，转速和转矩中出现了较大的波动，同时相电流中3次和5次谐波含量明显升高，这与断相会在dq平面引发偶次周期性扰动的分析吻合。对比三种控制器，由图11中可以看出，采用前馈补偿方案时，断相后相电流THD达到了11.86%，转速和转矩扰动也提升至19.7r/min和1.15N·m。而根据图12和图13，采用并联控制器和本文所提出控制器时，相电流THD分别为9.07%和8.81%，转速和转矩的扰动分别为12.2r/min和0.90N·m以及11.3r/min和0.84N·m。可以看到，前馈补偿结构与后两种控制结构相比，系统中的扰动更大，这是因为受参数漂移和外部干扰等因素的影响，前馈补偿所建立的扰动项模型与实际扰动相比往往存在一定的误差，扰动并不能被完全补偿。而采用并联控制器和本文提出的控制器依靠闭环控制实现扰动抑制，受外部因素的干扰更小，因此这两种控制结构有更好的故障后稳态性能。而且与正常工况时类似，本文提出的控制器在断相后转速和转矩波动也略小于并联控制器。
当系统的控制周期为100ms时，故障前后三种控制器的计算时间Tc如图14所示，图中波形处于高位时表明数字信号处理器（Digital Signal Processor, DSP）正在执行算法，波形处于低位时表明DSP处于空闲状态。与前馈补偿控制器相比，并联控制器超出的计算时间主要用来执行转速环和dq平面电流环RC的运算程序，约为3ms。而本文提出的控制器则在并联控制器的基础上增加了转速环和电流环ESO，需要额外占用约5.5ms的计算时间。
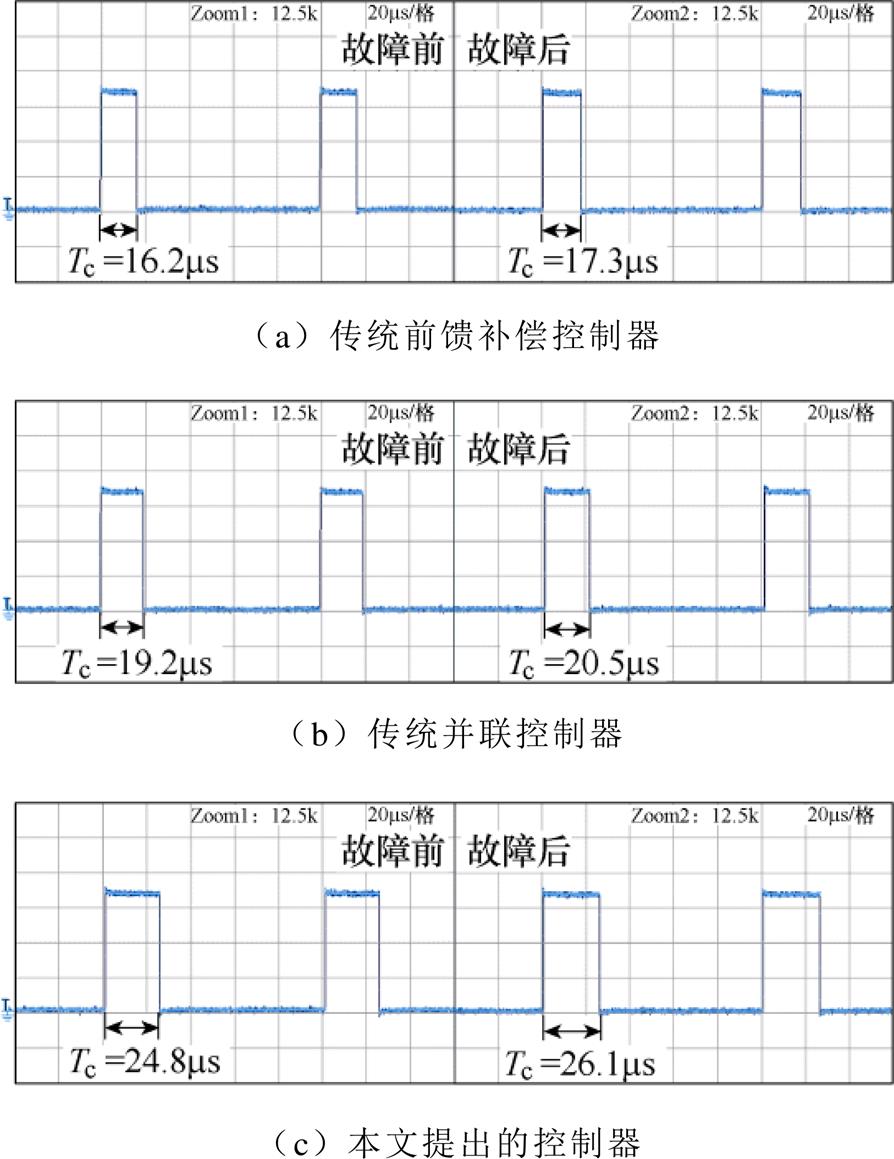
图14 不同控制器故障前后在DSP中的计算时间
Fig.14 Calculation time of different controllers in DSP on pre- and post-fault condition
综合上述实验，可以看到并联控制器和本文所提出控制器的稳态性能要明显优于前馈补偿，而且由于加入了对非周期性扰动的补偿，本文所提出控制器的稳态性能略好于并联控制器。然而控制器性能提升意味着消耗更多的计算资源，对数字信号处理器的性能提出了更高的要求。
并联控制器和本文提出的控制器在故障前和故障后的稳态性能并没有特别显著的差别，这是因为两种控制器都拥有对周期性扰动的闭环抑制能力，并且系统稳态运行时参考值跟踪和周期性扰动抑制之间的耦合效应不明显。为了验证所提出控制器的优越性，本文还进行了暂态性能的对比实验。图15～图17分别展示了断相故障发生后，不同暂态实验中三种控制器的暂态响应。表4将三组实验的数据进行了汇总，表中，Dr和Df分别为上升沿和下降沿物理量波动，以波动量与稳态值的百分比表示，trec,r和trec,f分别为上升沿和下降沿的恢复时间。
图15中转速参考值由100r/min阶跃至200r/min然后再变回100r/min，电磁转矩参考值维持在5N·m。由图15b可以看出，采用并联控制器时，由于RC的影响，电磁转矩中出现了较明显的暂态振荡，因此导致上升沿和下降沿转速的波动达到了74.6r/min和27.8r/min，系统恢复时间为0.13s和0.11s。与之相对，在图15c中，采用本文所提出控制器时电磁转矩振荡大幅减小，过渡过程更加平稳，上升沿和下降沿转速的波动也仅为9.5r/min和6.1r/min，系统的恢复时间也缩短为0.05s左右。尽管根据之前的分析，采用前馈补偿控制器时，系统的参考跟踪能力理论上与采用本文提出的控制器时相同，但是受参数不匹配等因素影响，前馈补偿往往会在系统中引入额外的振荡，因此由图15a可以看到，其暂态性能与本文提出的控制器相比较差，无论是转速的波动量还是恢复时间都更大。
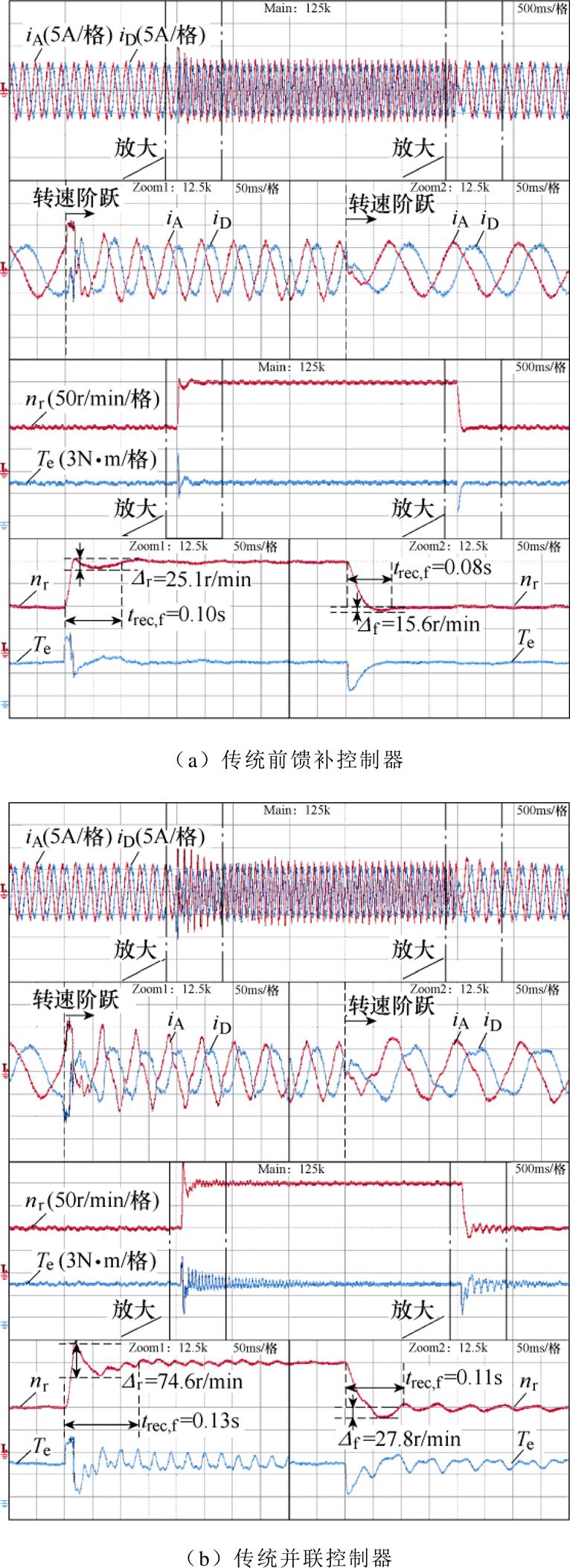
图15 断相故障下转速参考值阶跃变化时系统的暂态响应
Fig.15 System dynamic responses under open-phase fault when the speed reference is step changed
图16则展示了当负载转矩TL由2N·m突变至4N·m再变回2N·m，转速参考值为200r/min时，不同控制器的暂态响应。采用并联控制器时，电磁转矩在过渡过程中同样存在明显的振荡，转速波动分别为35.6r/min和34.8r/min，恢复时间分别为0.37s和0.26s。采用前馈补偿时，暂态性能明显优于并联控制器，转速波动降至24.2r/min和25.7r/min，恢复时间只有0.19s和0.20s。采用本文提出的控制器时，系统的过渡过程最平稳，转速超调量和恢复时间仅为并联控制器的一半左右。
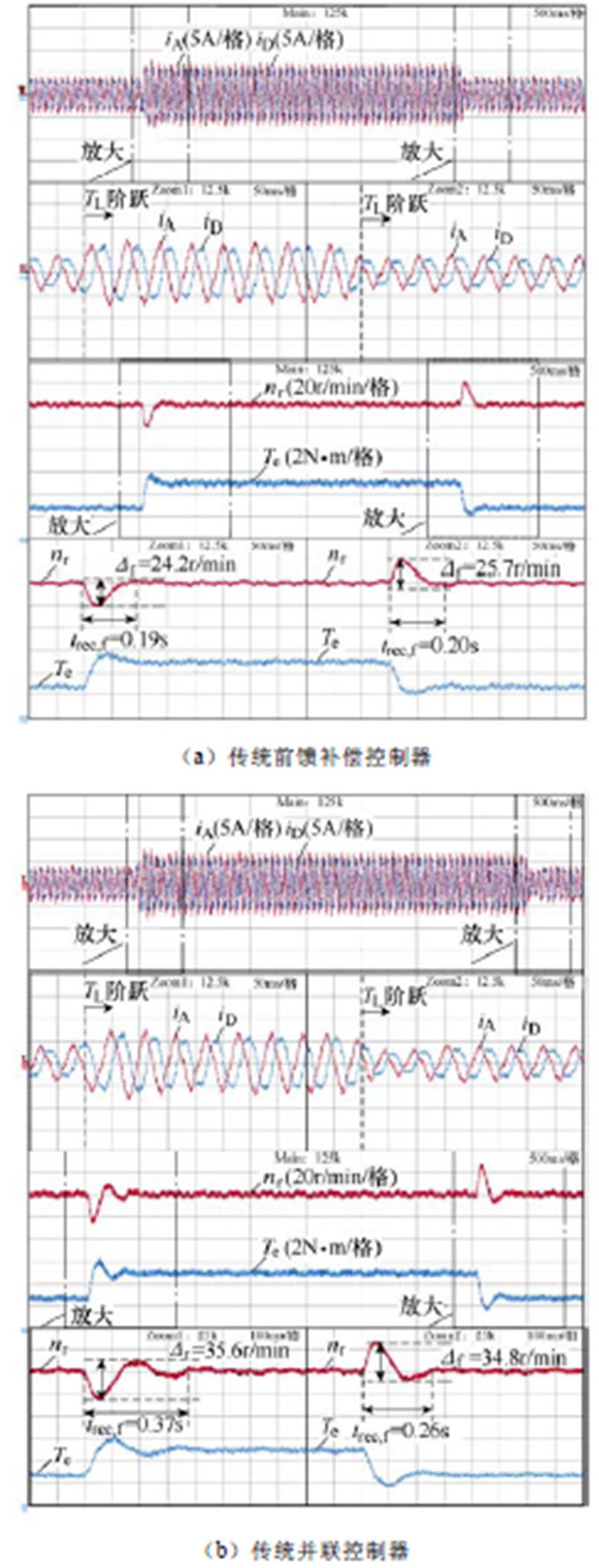
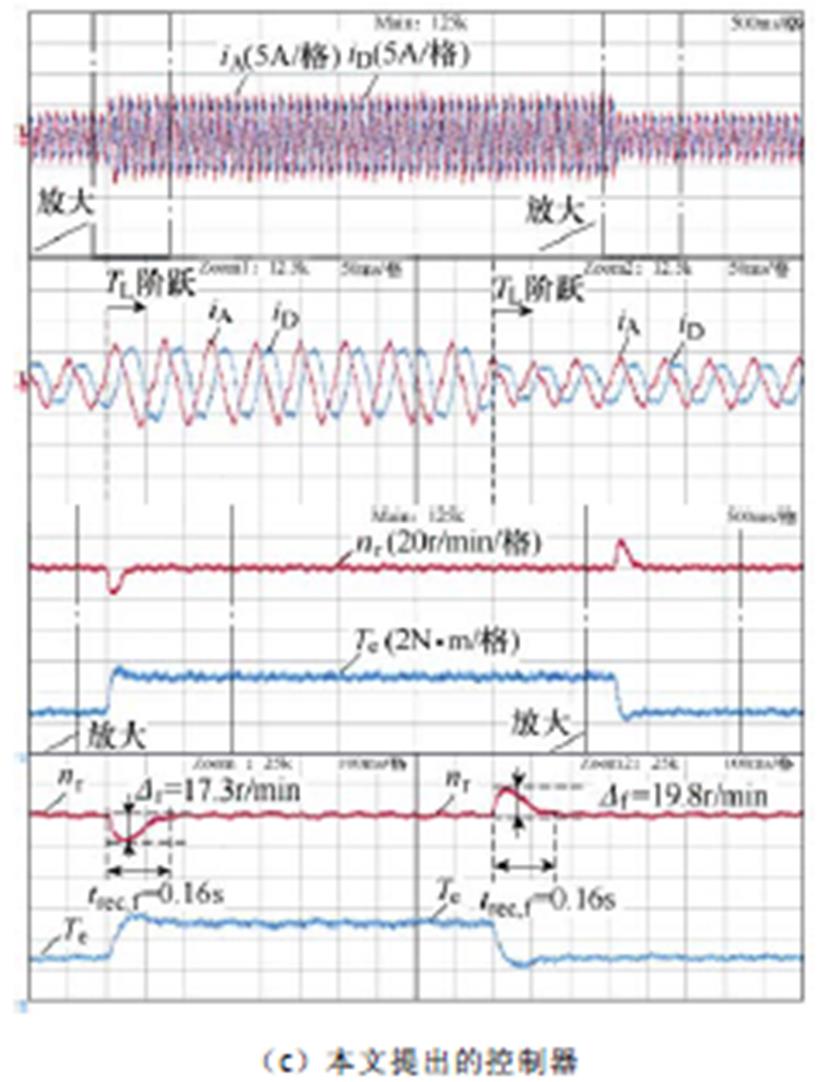
图16 断相故障下负载转矩阶跃变化时系统的暂态响应
Fig.16 System dynamic responses under open-phase fault when the load torque is step changed
图17对比了三种控制器在电流环中的暂态响应，该实验中DT-PMSM由负载感应电机拖动，转速维持在150r/min，id参考值为0，iq参考值由2A突变为5A再变回2A。采用并联控制器时，暂态过程中可以观察到明显的振荡，iq波动量为1.12A和1.39A，恢复时间为36ms和22ms。采用前馈补偿控制器时系统的暂态性能比并联控制器有所提高，但是iq也有明显超调，其波动量为0.95A和0.73A，但系统恢复时间缩短至10ms和14ms。而采用本文提出的控制器，暂态响应中几乎没有超调，iq波动量仅为0.44A和0.42A，系统恢复到稳态所用时间也最短，仅有6ms。
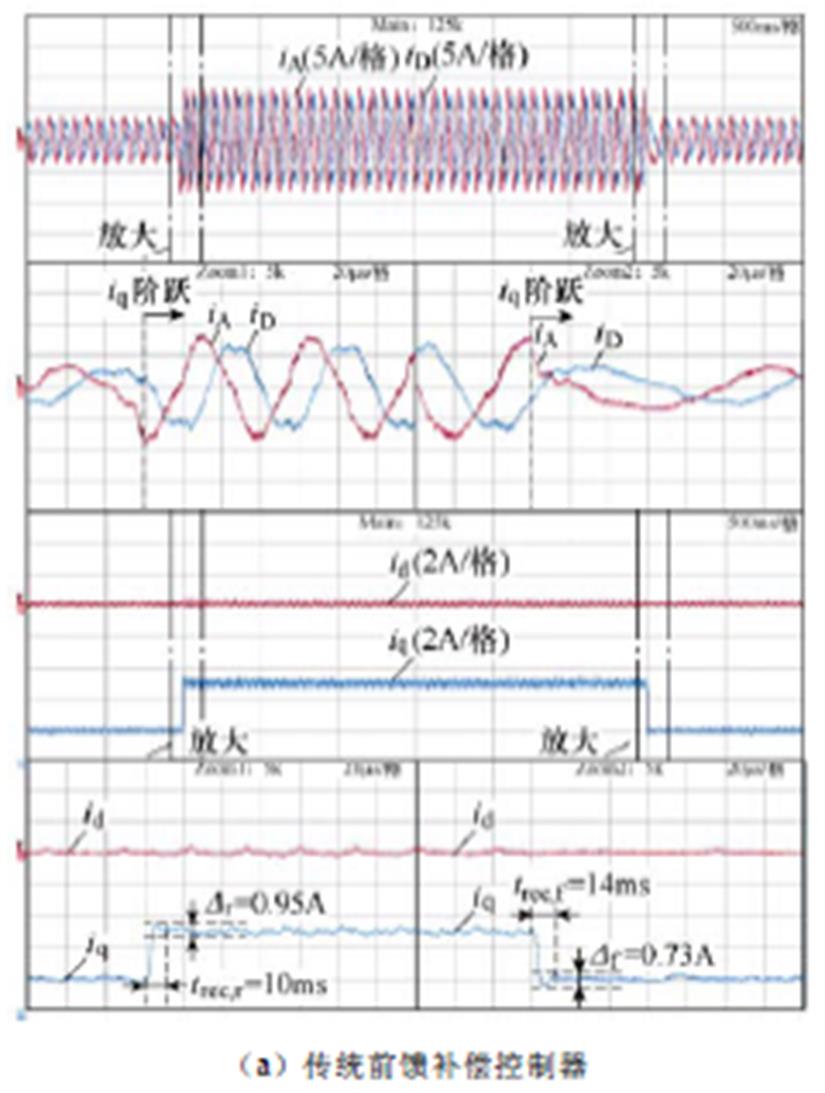
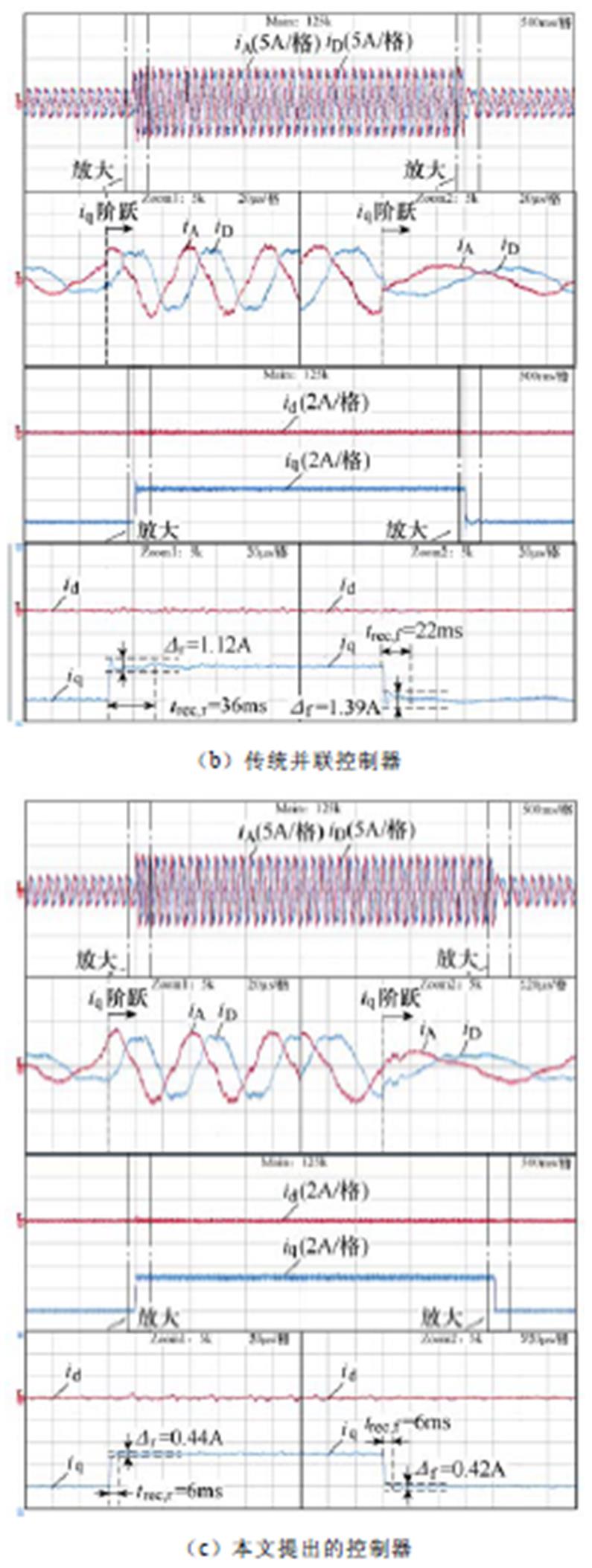
图17 断相故障下q轴电流参考值阶跃变化时系统的暂态响应
Fig.17 System dynamic responses under open-phase fault when the q-axis current reference is step changed
表4 不同控制器暂态实验效果对比
Tab.4 Comparison of dynamic experimental results among different controllers
控制器结构转速阶跃负载转矩阶跃电流阶跃 Dr, Df (%)trec,r, trec.f /sDr, Df (%)trec,r, trec.f /sDr, Df (%)trec,r, trec.f /ms 前馈控制12.6, 15.60.10, 0.0812.1, 12.80.19, 0.2019.0, 14.610, 14 并联控制器37.3, 27.80.13, 0.1117.8, 17.40.37, 0.2622.4, 27.836, 22 本文提出的控制器3.7, 6.10.05, 0.068.7, 9.90.16, 0.168.8, 8.46, 6
综合上述实验，可以验证与传统的前馈补偿和并联结构控制器相比，本文提出的控制器拥有最好的暂态跟踪性能，也证明了本文提出的控制器可以将系统的参考跟踪能力和周期性扰动抑制能力有效地解耦。
为了保障所提出控制器的控制性能，转速环和电流环的ESO对状态量的观测不能有较大的误差。根据文献[25]的分析，系统稳态运行时ESO的观测值可以收敛到实际状态量。然而暂态过程中转速和电流快速变化，系统扰动较大，可能会导致ESO观测值出现偏差。为了验证本文中转速环和电流环的ESO在暂态过程中也能够精准且快速地收敛，本文对不同暂态实验中ESO观测值与实际状态量进行了对比，波形如图18所示，实验条件与图15～图17对应的暂态实验完全相同，图中，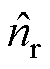
和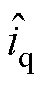
分别为转速和q轴电流的观测值，转速环和电流环ESO观测误差分别为ezs和edl。由图18可以看到，在不同暂态过程中，转速环和电流环ESO观测误差最大值分别为2.4%和2.3%，而且ESO的收敛速度也较快，因此，可以认为暂态过程中ESO同样满足控制需求。
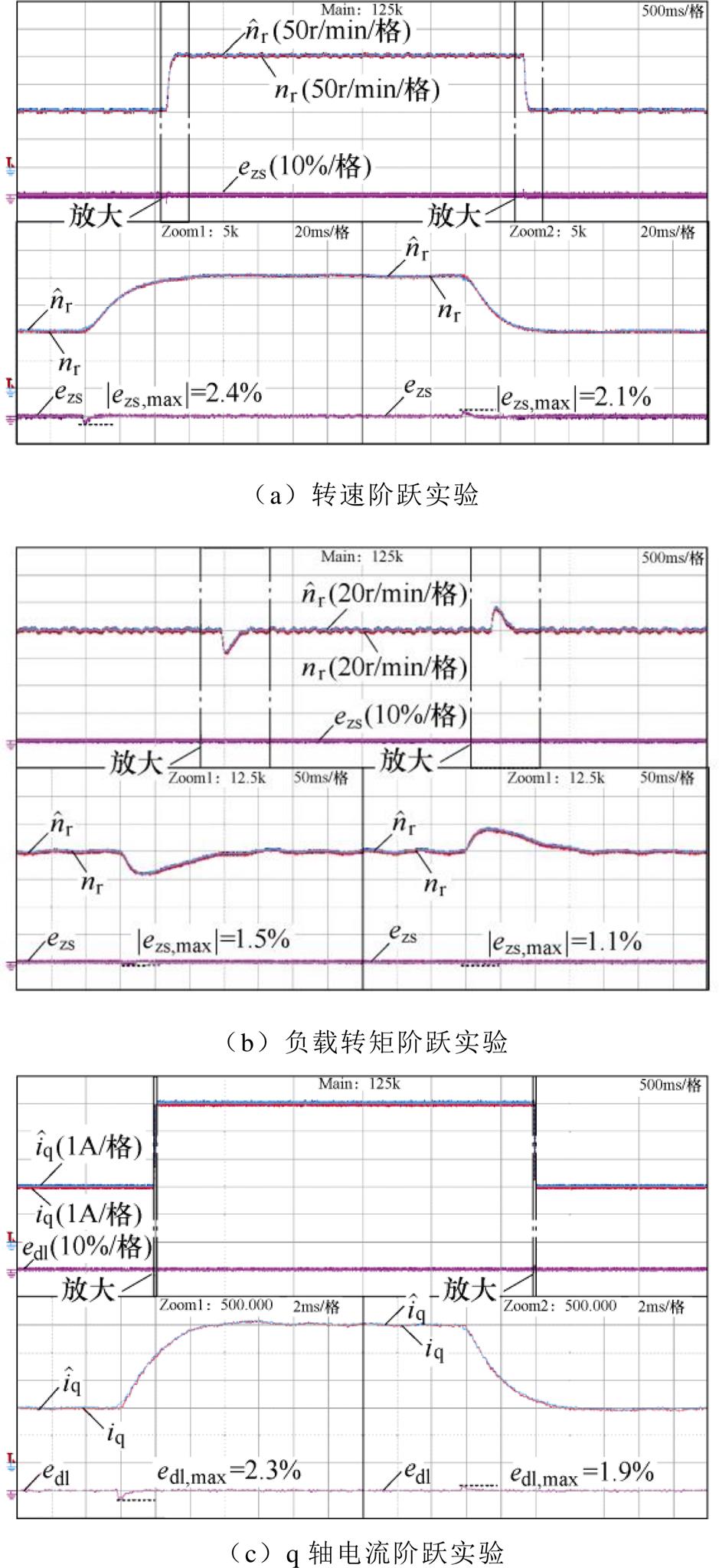
图18 不同暂态实验中ESO观测值与实际值对比
Fig.18 Comparison between estimated values of ESO and actual values in different dynamic tests
为了在DT-PMSM发生断相故障后既可以有效抑制系统中的扰动，又能够拥有较好的暂态性能，本文提出了一种新型容错控制器。该控制器采用闭环控制来抑制系统中的扰动，同时还实现了参考跟踪和周期性扰动抑制之间的解耦。与传统基于前馈补偿策略和传统基于并联控制器策略进行对比实验，验证了本文提出的控制策略有更好的抑制扰动能力和暂态跟踪性能。但本文提出的控制策略较为复杂，占用的计算资源也更大。
参考文献
[1] 赵勇, 黄文新, 林晓刚, 等. 基于权重系数消除和有限控制集优化的双三相永磁容错电机快速预测直接转矩控制[J]. 电工技术学报, 2021, 36(1): 3-14.
Zhao Yong, Huang Wenxin, Lin Xiaogang, et al. Fast predictive direct torque control of dual three-phase permanent magnet fault tolerant machine based on weighting factor elimination and finite control set optimization[J]. Transactions of China Electrotech- nical Society, 2021, 36(1): 3-14.
[2] 黄林森, 赵文祥, 吉敬华, 等. 稳态性能改善的双三相永磁电机直接转矩控制[J]. 电工技术学报, 2022, 37(2): 355-367.
Huang Linsen, Zhao Wenxiang, Ji Jinghua, et al. Direct torque control for dual three-phase permanent- magnet machine with improved steady-state perfor- mance[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 355-367.
[3] 佟明昊, 程明, 许芷源, 等. 电动汽车用车载集成式充电系统若干关键技术问题及解决方案[J]. 电工技术学报, 2021, 36(24): 5125-5142.
Tong Minghao, Cheng Ming, Xu Zhiyuan, et al. Key issues and solutions of integrated on-board chargers for electric vehicles[J]. Transactions of China Elec- trotechnical Society, 2021, 36(24): 5125-5142.
[4] Faiz J, Nejadi-Koti H. Demagnetization fault indexes in permanent magnet synchronous motors-an over- view[J]. IEEE Transactions on Magnetics, 2016, 52(4): 1-11.
[5] Wang Xueqing, Wang Zheng, Xu Zhixian, et al. Comprehensive diagnosis and tolerance strategies for electrical faults and sensor faults in dual three-phase PMSM drives[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(7): 6669-6684.
[6] 刘胜, 郭晓杰, 张兰勇. 六相永磁同步电机鲁棒自适应反步滑模容错控制[J]. 电机与控制学报, 2020, 24(5): 68-78, 88.
Liu Sheng, Guo Xiaojie, Zhang Lanyong. Robust adaptive backstepping sliding mode control for six- phase PMSM system with open phases[J]. Electric Machines and Control, 2020, 24(5): 68-78, 88.
[7] Kommuri S K, Defoort M, Karimi H R, et al. A robust observer-based sensor fault-tolerant control for PMSM in electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7671-7681.
[8] Ryu H M, Kim J W, Sul S K. Synchronous-frame current control of multiphase synchronous motor under asymmetric fault condition due to open phases[J]. IEEE Transactions on Industry Appli- cations, 2006, 42(4): 1062-1070.
[9] Lu Hanxiao, Li Jian, Qu Ronghai, et al. Fault-tolerant predictive control of six-phase PMSM drives based on pulsewidth modulation[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 4992-5003.
[10] 杨金波, 李铁才, 杨贵杰. 一相开路双三相永磁同步电机建模与控制[J]. 电工技术学报, 2011, 26(10): 167-173, 187.
Yang Jinbo, Li Tiecai, Yang Guijie. Modeling and control of dual three-phase PMSM with one open phase[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 167-173, 187.
[11] Hu Yashan, Feng Yaojing, Li Xuefei. Fault-tolerant hybrid current control of dual three-phase PMSM with one phase open[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 3418-3426.
[12] 周长攀, 杨贵杰, 苏健勇, 等. 基于正常解耦变换的双三相永磁同步电机缺相容错控制策略[J]. 电工技术学报, 2017, 32(3): 86-96.
Zhou Changpan, Yang Guijie, Su Jianyong, et al. The control strategy for dual three-phase PMSM based on normal decoupling transformation under fault con- dition due to open phases[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 86-96.
[13] 高闯, 赵文祥, 吉敬华, 等. 低谐波双三相永磁同步电机及其容错控制[J]. 电工技术学报, 2017, 32(增刊1): 124-130.
Gao Chuang, Zhao Wenxiang, Ji Jinghua, et al. Low harmonic dual three-phase permanent magnet syn- chronous motor and fault-tolerant control[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(S1): 124-130.
[14] González-Prieto I, Duran M J, Barrero F J. Fault- tolerant control of six-phase induction motor drives with variable current injection[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7894-7903.
[15] Luo Yixiao, Liu Chunhua. Pre- and post-fault tolerant operation of a six-phase PMSM motor using FCS-
MPC without controller reconfiguration[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 254-263.
[16] Feng Guodong, Lai Chunyan, Li Wenlong, et al. Open-phase fault modeling and optimized fault- tolerant control of dual three-phase permanent magnet synchronous machines[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11116-11127.
[17] Feng Guodong, Lai Chunyan, Li Wenlong, et al. Computation-efficient solution to open-phase fault tolerant control of dual three-phase interior PMSMs with maximized torque and minimized ripple[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4488-4499.
[18] 蒋钱, 卢琴芬, 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J]. 电工技术学报, 2021, 36(5): 883-892.
Jiang Qian, Lu Qinfen, Li Yanxin. Thrust ripple and depression method of dual three-phase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 883-892.
[19] Li Zhuohang, Wu Lijian, Chen Zekai, et al. Single- and two-phase open-circuit fault tolerant control for dual three-phase PM motor without phase shifting[J]. IEEE Access, 2020, 8: 171945-171955.
[20] Liang Zhe, Liang Deliang, Kou Peng, et al. Postfault control and harmonic current suppression for a symmetrical dual three-phase SPMSM drive under single-phase open-circuit fault[J]. IEEE Access, 2020, 8: 67674-67686.
[21] Song Zhanfeng, Wang Yaqi, Shi Tingna. A dual-loop predictive control structure for permanent magnet synchronous machines with enhanced attenuation of periodic disturbances[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 760-774.
[22] Suhel S M, Maurya R. A new switching sequences of SVPWM for six-phase induction motor with features of reduced switching losses[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 100- 107.
[23] Akay A, Lefley P. Research on torque ripple under healthy and open-circuit fault-tolerant conditions in a PM multiphase machine[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 349- 359.
[24] 兰梓冉, 郝瑞祥, 角宏林, 等. 基于重复控制和状态反馈的三相逆变器最优预见控制[J]. 电工技术学报, 2022, 37(6): 1473-1481.
Lan Ziran, Hao Ruixiang, Jiao Honglin, et al. Optimal preview control of three-phase inverter based on repetitive control and state-feedback[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1473- 1481.
[25] 高钦和, 董家臣. 扩张状态观测器的观测误差前馈补偿设计[J]. 国防科技大学学报, 2019, 41(5): 93- 102.
Gao Qinhe, Dong Jiachen. Feedforward compensation design for observation error of extended state obser- ver[J]. Journal of National University of Defense Technology, 2019, 41(5): 93-102.
[26] Song Zhanfeng, Zhou Fengjiao, Yu Yun, et al. Open- phase fault-tolerant predictive control strategy for open-end-winding permanent magnet synchronous machines without postfault controller reconfigu- ration[J]. IEEE Transactions on Industrial Electronics, 2021, 68(5): 3770-3781.
Abstract Under open-phase fault conditions, the dual three-phase permanent magnet synchronous machine (DT-PMSM) suffers from periodic disturbances, which may cause significant performance degradation. Therefore, it is regarded as a major concerno of fault-tolerant control. The feed-forward compensation method is widely used under postfault situation to suppress periodic disturbances. However, the effect of disturbance suppression can be easily affected by non-ideal factors, such as parameter variation, inverter dead-time, cogging torque, and flux harmonic of permanent magnet. In order to solve this problem, the proportional resonance (PR) controller is paralleled to the original proportional integral (PI) controller in some references. The closed-loop control structure can effectively suppress the periodic disturbances without being affected by non-ideal factors. However, the coupling effects between reference tracking and periodic disturbance attenuation will lead to significant transient oscillations under the situation of a reference step change. In order to realize decoupling between reference tracking and disturbance attenuation, this paper proposes a novel fault-tolerant controller which contains two independent control loops. The reference tracking is only determined by the primary controller, and the disturbance rejection loop is embedded to achieve periodic disturbance attenuation. Firstly, the PI controller outputs the initial reference value, while the extended state observer (ESO) predicts the system output value based on the initial reference value. Then, the error signal between the predicted value and actual value is input to resonant controller. Finally, the initial reference value and output signal of resonant controller are added to obtain the final reference value. The main transfer function of the proposed controller is consistent with that of the feed-forward compensation controller, and the resonant controller only responds to periodic disturbances. With the proposed controller adopted, periodic disturbances are strongly attenuated while smooth and fast transient performances are simultaneously guaranteed. The performances of different controllers are compared experimentally in this paper. Firstly, when the speed is 1 000r/min and load torque is 5N·m, the steady-state performances are compared under open-phase fault condition. With the feed-forward compensation controller, parallel controller, and the proposed controller adopted, the total harmonic distortion (THD) of phase current is 11.86%, 9.07%, and 8.81%, respectively. The speed fluctuation is 19.7r/min, 12.2r/min, and 11.3r/min, respectively. And the torque fluctuation is 1.15N·m, 0.9N·m, and 0.84N·m, respectively. From the above experimental results, it can be seen that the steady-state performance of the proposed controller is obviously better than that of the feed-forward compensation method. The transient experiments are also carried out in this paper. When the speed reference is step changed from 100r/min to 200r/min, the transient responses are compared. With the feed-forward compensation controller, parallel controller, and the proposed controller adopted, the speed fluctuation is 25.1r/min, 74.6r/min, and 9.5r/min, respectively. The adjustment time is 0.1s, 0.13s, and 0.06s, respectively. When the reference value of iq is step changed from 2A to 5A, the transient responses are compared. The iq fluctuation is 0.95A, 1.12A, and 0.44A, respectively. The adjustment time is 10ms, 36ms, and 6ms, respectively. The experimental results prove the efficiency of the proposed method. The reference tracking loop and periodic disturbance suppression loop are decoupled. The proposed fault-tolerant controller improves the transient performance and steady-state performance simultaneously.
Keywords：Dual-three-phase permanent magnet synchronous machine, fault-tolerant control, periodic disturbance attenuation, decoupled control, repetitive controller
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.211972
国家自然科学基金资助项目（51877150）。
收稿日期 2021-12-06
改稿日期 2022-03-21
E-mail: zfsong@tju.edu.cn（通信作者）
毛丰羽 男，1996年生，硕士研究生，研究方向为电机及其控 制等。
E-mail: maofy@tju.edu.cn
（编辑 崔文静）