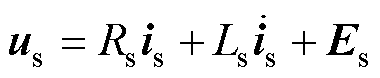（1）
摘要 五相容错永磁同步电机（PMSM）开路故障模型的不对称性，影响了其无位置运行性能。该文提出一种基于转子磁链观测器的无位置控制策略。首先，该策略在容错模型基础上，构建基于指数趋近律的滑模观测器（SMO）以获取反电动势信号；其次，为抑制所观测反电动势中直流偏置、低频和高频谐波对转子位置观测精度的影响，设计一种改进型二阶广义积分器（ISOGI），并将其和SMO级联构成转子磁链观测器；然后，采用锁相环技术从转子磁链中提取转子位置信息；最后，将该转子磁链观测器和容错控制策略相结合。实验结果表明，该策略提高了转子位置观测精度，实现了PMSM开路故障下的无位置高性能运行。
关键词：永磁同步电机 开路故障 滑模观测器 改进二阶广义积分器 转子磁链观测器
五相永磁同步电机（Permanent Magnet Syn- chronous Motor, PMSM）具有功率密度高、转矩脉动低、容错能力强等优点[1-3]，在不增加额外硬件的基础上加入容错策略，就能实现故障后的平稳运行。因此，五相PMSM在新能源车、航空航天等高可靠性领域得到了广泛关注[4-6]。
PMSM发生开路故障后，可采用合适的基于机械位置传感器的容错控制策略改善其在开路故障情况下的稳态和动态性能[7-8]。然而，机械位置传感器较脆弱，易发生故障[9]。当PMSM发生开路故障后，如果机械位置传感器也发生了故障，即使采用这些开路容错策略，也无法实现该故障电机的平稳运行。另外，PMSM发生开路故障后，非故障相绕组运行在不对称状态，其电压或电流发生畸变，电机模型不再对称，导致现有的基于对称电机模型的无位置控制策略无法直接用于故障状态[10-11]。因此，为进一步提高PMSM运行的可靠性和安全性，需对适用于电机故障状态下的无位置控制技术进行研究[12-14]。
无位置控制技术一般可分为信号注入法[15-17]和模型法[18-20]两种基本类型。模型法由于不依赖转子凸极特性和额外信号注入，仅利用电机模型便可实现转子位置辨识，在无位置控制系统中被广泛应用。其大致需通过反电动势（Electromotive Force, EMF）观测、反电动势滤波以及转子位置信息提取三个环节方能实现。转子位置信息提取通常采用锁相环（Phase-Locked Loop, PLL）技术实现，该环节对位置估计性能影响较小[21]。当电机发生故障之后，在反电动势观测环节，除了建模不确定性、逆变器非线性和采样误差等因素外，还有电机模型的不对称性问题以及非故障相电压或电流的畸变等原因，致使所观测到的反电动势中含有大量的高频、低频和直流偏置噪声[22]，给无位置控制性能带来极大影响。反电动势滤波作为一种能够消除噪声的方法，通过滤除干扰信号提取基波分量，从而精确观测转子位置。因此，反电动势滤波器性能的优劣将直接决定电机故障情况下的转子位置观测精度。文献[22]提出了适用于PMSM单相开路故障的无位置控制策略。由于在反电动势滤波环节采用低通滤波器，且没有幅相误差补偿，导致位置误差较大。文献[23]针对五相PMSM提出了一种基于强鲁棒滑模观测器（Sliding Mode Observer, SMO）的无位置容错控制策略，尽管实现了电机开路故障下的无位置运行，但该策略采用的反电动势滤波器仅针对高频噪声具有抑制作用，无法有效消除频率较低的干扰信号和直流偏置。文献[10]针对六相电机提出了一种基于鲁棒观测器的容错无位置控制策略。然而，该策略采用固定截止频率的低通滤波器平滑反电动势，导致观测反电动势幅值衰减和相位滞后，进而影响位置观测精度。文献[11]采用两个可变截止频率的低通滤波器级联的方法，并结合自适应补偿消除了幅相误差。但是，该滤波器的性能仍呈低通特性，且未考虑反电动势中直流偏置及低频扰动对位置观测的影响。文献[24]设计了一种基于二阶广义积分器（Second-Order Generalized Integrator, SOGI）的转子磁链观测器。虽然SOGI对低频域内的信号起到了衰减作用，但是信号衰减速率太小，且通过调节SOGI的阻尼因子无法显著提升SOGI在低频域区的滤波性能。
本文针对五相PMSM开路故障的特点，提出了一种基于SMO和改进型二阶广义积分器（Improved Second-Order Generalized Integrator, ISOGI）的转子磁链观测器，将其与容错矢量控制策略相结合，不但提高了PMSM开路故障情况下的转子位置估计精度，而且有效抑制了故障导致的转矩脉动，提升了PMSM在开路故障下的无位置传感器运行时的稳态和动态性能。首先，根据五相PMSM非故障相容错电流推导降阶变换矩阵，建立故障解耦模型；其次，设计基于指数趋近律的SMO，用于观测反电动势并抑制滑模抖振；然后，为抑制所观测反电动势中的干扰噪声，尤其是直流偏置和低频扰动，设计ISOGI以获取基波转子磁链，并采用PLL技术提取转子位置及转速信息；最后，以五相开路故障PMSM为控制对象，对基于SMO+ISOGI转子磁链观测器的无位置控制策略进行实验研究。
本文研究对象为20槽22极的五相外转子PMSM。该电机采用内嵌式V型永磁体，分数槽单层集中绕组配合容错齿实现了相与相之间的磁和热的机械隔离。电机互感相对自感很小，可忽略不计。自感在一个周期中的变化幅值相对均值非常小，可视为常数[7]。相反电动势谐波含量很少，可假设只含有基波成分。在三维空间中采用电流控制器能有效地将3次谐波电流抑制为零[25]。由此，五相PMSM在两相静止坐标系ab 上的数学模型为
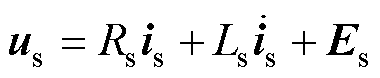（1）
其中
（2）
式中，us、is分别为定子电压、电流；Rs、Ls分别为定子电阻、电感；Es为反电动势；
为转子磁链；wr为转子电角速度；yf为永磁磁链幅值；qr为转子位置。
不失一般性，假设PMSM的A相发生开路故障，此时该相电流为零。为确保故障电机能继续平稳运行，需重新调整非故障相电流以实现磁动势不变。由此可得
（3）
其中
（4）
式中，I为电机正常运行时的相电流幅值；s =0.4p；
、
、
、
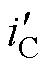为非故障相容错电流；xb、yb、xc、yc、xd、yd、xe和ye为电流系数。将式（4）代入式（3）可得
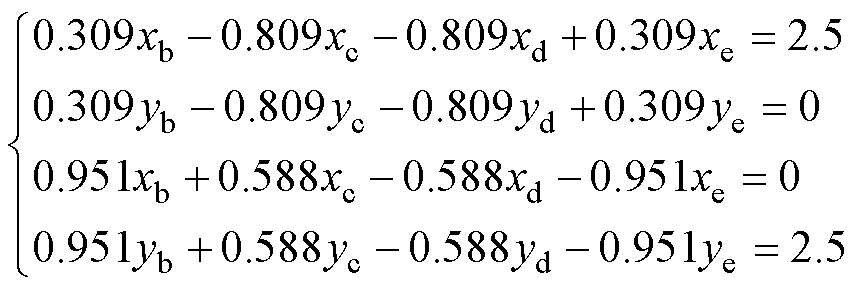（5）
根据非故障相电流和为零以及铜耗最小原则，由式（5）可推导出非故障相电流为
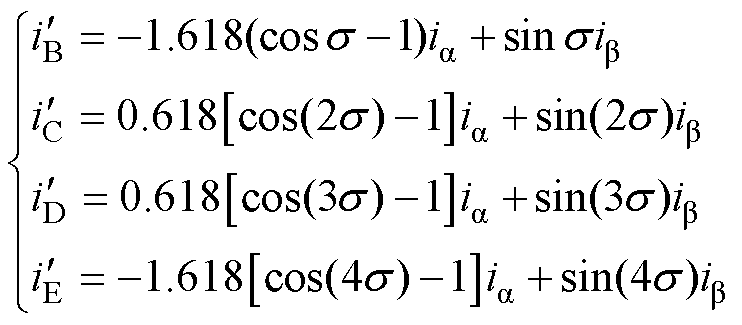（6）
由于电机绕组星形联结，由传统Clarke变换矩阵可得x轴电流ix=-ia。可见，在开路故障情况下，ia 和ix存在耦合，无法独立控制。因此，故障电机的控制自由度由4个变为3个。这3个自由度可被分配到两个正交的平面上。其中，两个自由度分配到ab 平面上，用于能量转换；另一个自由度在xy平面上，将其控制为零以抑制损耗。因此，根据空间矢量分解思想和式（6），推导出将自然坐标系上的变量变换到两相静止坐标系上的容错变换矩阵为
（7）
采用式（7）将故障PMSM在自然坐标系上的电压模型变换到ab 轴上，得到的电压模型如式（1）所示。因此，PMSM在开路故障前后在ab 轴上具有相同的电压模型。在此基础上，采用Park变换将该故障模型变换到同步旋转坐标系上。因此，在传统矢量控制策略基础上，采用式（7）容错变换矩阵及其逆矩阵代替传统Clarke变换矩阵及其逆变换矩阵，同时去掉x轴电流的闭环控制，进而得到PMSM在A相开路故障情况下的容错矢量控制策略，如图1所示[26]。由于载波脉宽调制（Carrier-based Pulse Width Modulation, CPWM）技术无需进行电压矢量夹角的三角函数和无理数运算，避免了复杂运算，降低了CPU计算载荷[27]，因此本文采用CPWM技术。
图1 容错矢量控制框图
Fig.1 Diagram of fault-tolerant vector control
将式（1）进一步改写成
（8）
其中
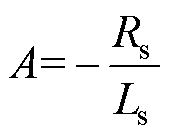
根据式（8）设计PMSM反电动势观测方程为
（9）
其中
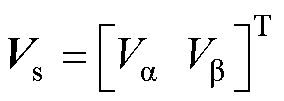
式中，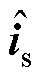
为电流估计值；
为滑模控制率。选择滑模切换面为
（10）
其中
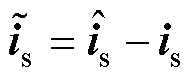
式中，c为滑模参数，c＞0；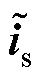
为电流估计误差。
采用指数趋近律
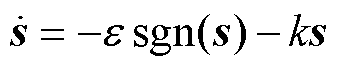（11）
式中，e、k为趋近系数，且e＞0、k＞0，其大小影响了系统运动点趋近滑模面的速率。为了保证运动点快速趋近滑模面的同时削弱抖振影响，需在增大k的同时相应减小e 以达到最优状态。
为确保观测器稳定，结合式（9）～式（11）设计滑模控制律为
（12）
利用Lyapunov稳定性理论证明滑模观测器的收敛性，选取Lyapunov函数
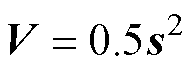（13）
对式（13）求导，并将式（11）代入，可得
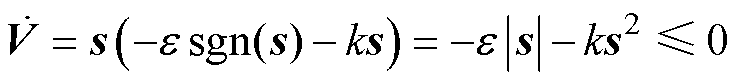（14）
因此，在式（12）滑模控制律作用下，滑模切换面s将在有限时间内收敛，即满足
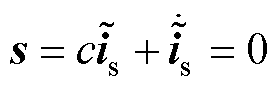（15）
从而解得
（16）
式中，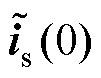
为电流估计误差的初始状态。可见，当状态点到达滑模切换面后，电流估计误差及其变化率按照指数形式趋近于零。将式（9）减去式（8），得电流误差方程为
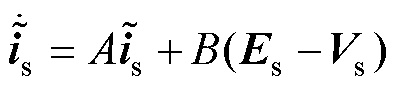（17）
由以上分析可知，在滑模切换面上有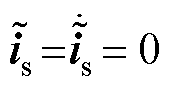
，于是Es=Vs。由此，根据等效滑模控制律可得反电动势观测值[28]。
由式（12）可知，SMO观测到的反电动势Vs中含有定子电压和电流。当PMSM发生开路故障后，其模型不再对称，致使非故障相电压畸变。此时，定子电压不但与电压源逆变器的开关状态有关，还与故障相的反电动势相关，它们的关系可表示为
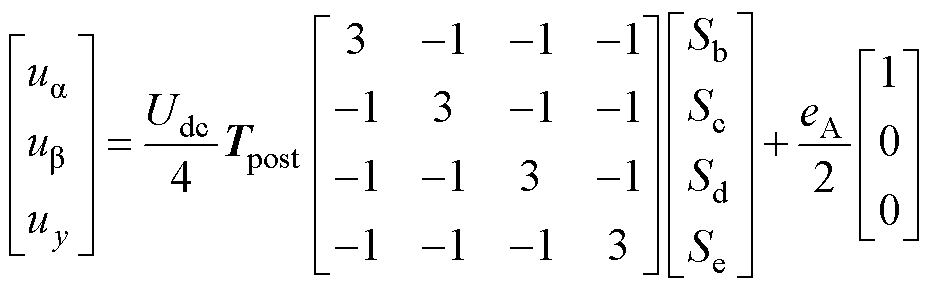（18）
式中，ua、ub 分别为定子电压在a、b 轴上的分量；uy为定子电压在y轴上的分量；Sb～Se为开关状态；Udc为直流母线电压；eA为A相的反电动势。可见，定子电压中存在开关器件的高频成分，同时A相反电动势需要通过估算获得，必然存在一定误差。另外，电机模型的不对称致使出现直流偏置和低频扰动。定子电流需通过电流传感器、运放和A-D转换电路后方能采集到。因此，采样值不可避免地存在直流偏置、噪声等现象。此外，由于逆变器非线性和死区效应，导致被测电流中含有大量谐波。因此，Vs中将包含定子电压和电流的高频、低频和直流偏置，以及滑模抖振等干扰噪声。为了更加精确地描述所观测到的反电动势，式（12）可进一步表示为
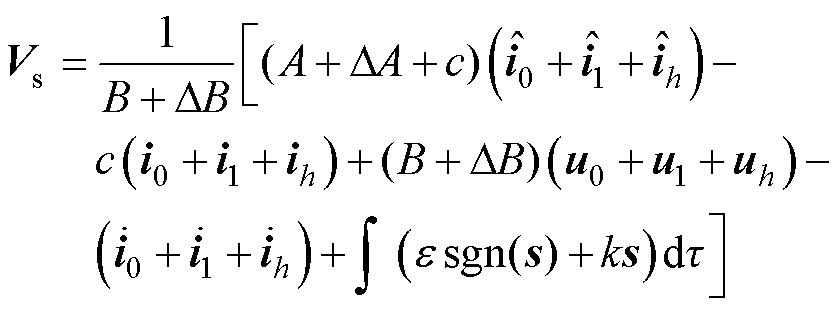（19）
式中，DA和DB分别为参数A和B的摄动；下标“0”、“1”和“h”分别为定子电压和电流的直流、基波和谐波分量。将式（19）展开[29-30]得
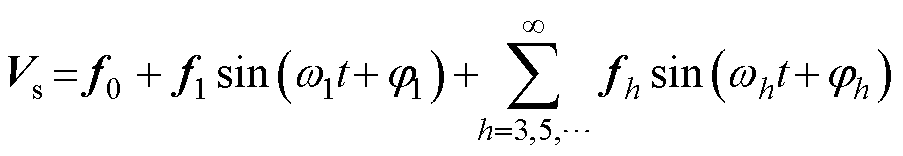（20）
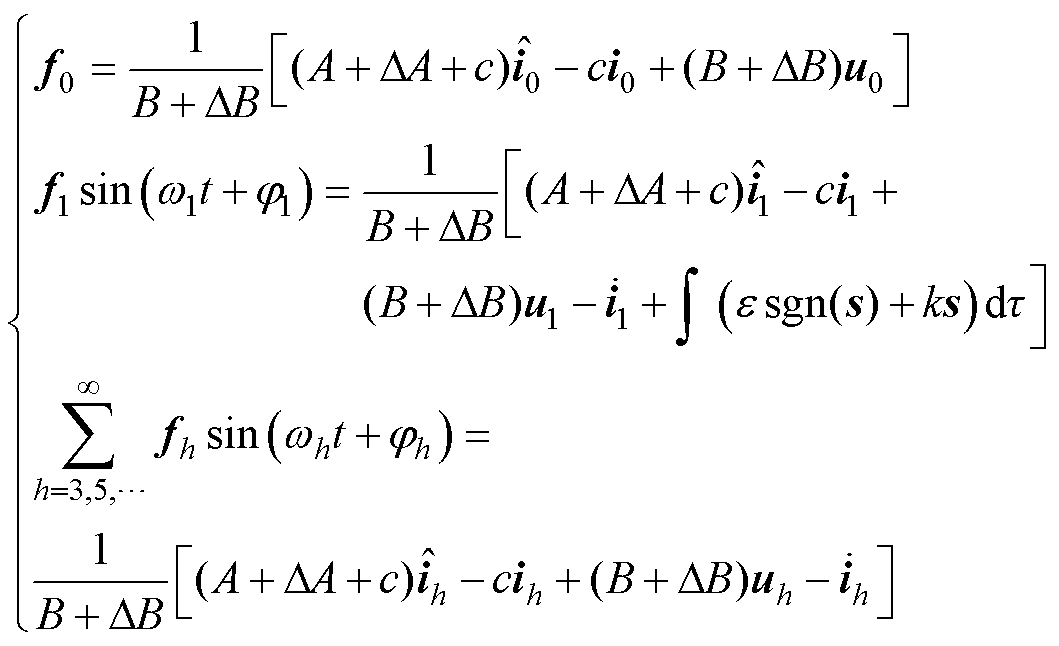（21）
式中，f0为观测到的反电动势的直流分量；f1sin(w1t+j1)为观测到的反电动势的基波分量；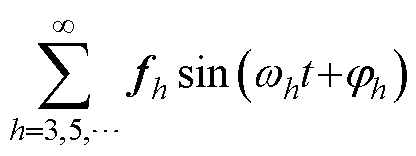
为观测到的反电动势的谐波分量；w1为基波电角频率；wh为谐波电角频率，wh=hw1，h为谐波阶次；j1和jh分别为基波和谐波初始相位。
式（20）中存在直流、低频和高频扰动噪声，无法直接用于提取转子位置信号。因此，在SMO观测到反电动势信号基础上，先将该反电动势信号积分得到转子磁链，以提高电机开路故障情况下的位置估计精度。
根据式（2），并结合反电动势Es的观测值Vs，转子磁链可表示为
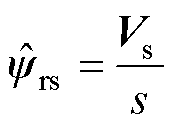（22）
其中
式中，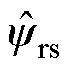
为转子磁链估计值。
分析式（22）可知，采用纯积分器将会在观测的转子磁链中引入直流偏置误差，引起积分漂移，导致转子磁链观测产生较大误差，进而影响位置估计精度。
若采用SOGI，其传递函数表示[24]为
（23）
式中，k0为阻尼因子；
为中心频率，故障PMSM稳态运行时存在
。图2所示为SOGI幅频和相频特性曲线，中心频率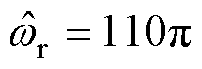
rad/s，阻尼因子k0分别取1、0.25、0.1。可见，SOGI对高频信号起到较好的衰减作用，衰减速率为-40dB/dec。然而，在低频域内，信号幅值衰减速率恒为0dB/dec，且减小k0时，信号衰减幅度变化较小。因此，仅调节k0大小，无法满足抑制低频（包括直流）信号的要求。另外，在中心频率附近，相频曲线斜率随着k0减小而减小（绝对值增大），导致积分性能较好的频带在中心频率附近变窄。然而，当负载变化或外部扰动时，电机转速存在一定的波动，积分器需具有较宽的频带才能确保转子磁链观测器观测到较好的转子磁链。因此，为保证SOGI在中心频率附近具有较好的积分特性，k0取1。
在此基础上，提出了一种ISOGI，其传递函数表示为
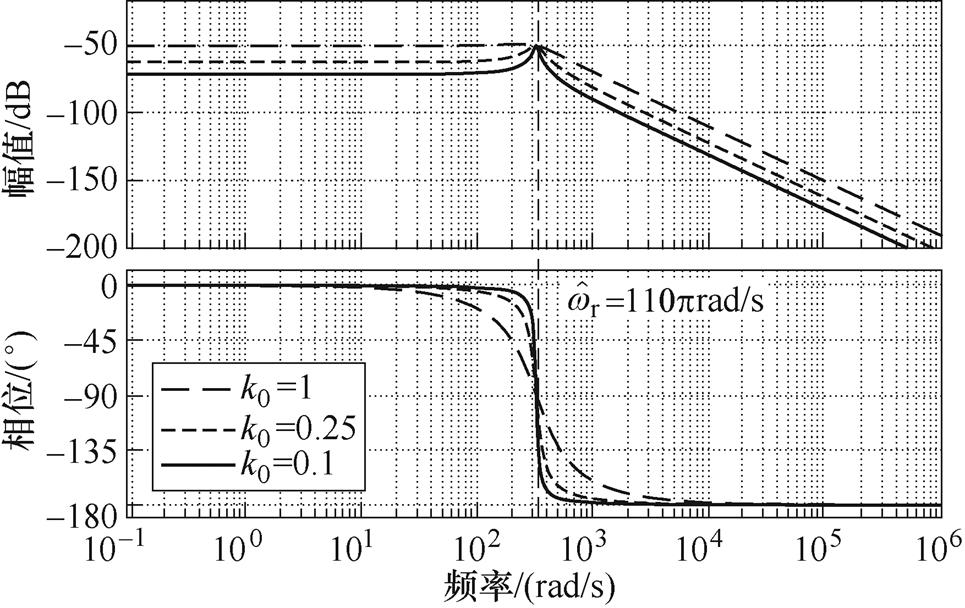
图2 SOGI伯德图
Fig.2 Bode diagram of SOGI
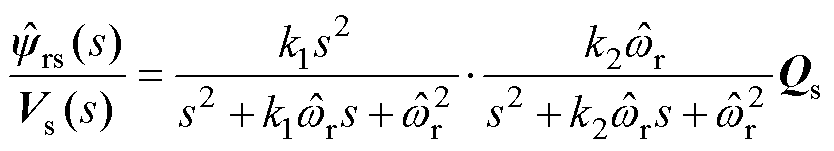（24）
式中，k1、k2为阻尼因子；Qs为补偿环节。
故障电机稳态运行时，通过补偿环节将中心频率处的幅频和相频特性与纯积分等效，从而对基波分量实现积分作用。结合s=jw1以及式（22）和式（24），可得其补偿值为
（25）
根据式（22）～式（24），绘制三种积分器的幅频和相频特性曲线，中心频率取110prad/s，如图3所示。为确保后续实验对比的公平性，k1、k2取值和k0相同，全部为1。可见，随着频率减小，纯积分器的输出信号幅值逐渐增大。因此，纯积分器无法抑制直流偏置和低频扰动。尽管SOGI对高频噪声具有较好的抑制作用，但是对直流偏置和低频扰动的衰减能力较弱。然而，无论是低频区扰动（包括直流）还是高频区噪声，ISOGI均能以-40dB/dec速率衰减。因此，相比纯积分器和SOGI，ISOGI不但对低频（包括直流）扰动的衰减能力更强，而且对高频噪声都具有较好的抑制能力，同时对中心频率及其附近的信号具有积分作用。因此，ISOGI具有更高的转子磁链观测精度。
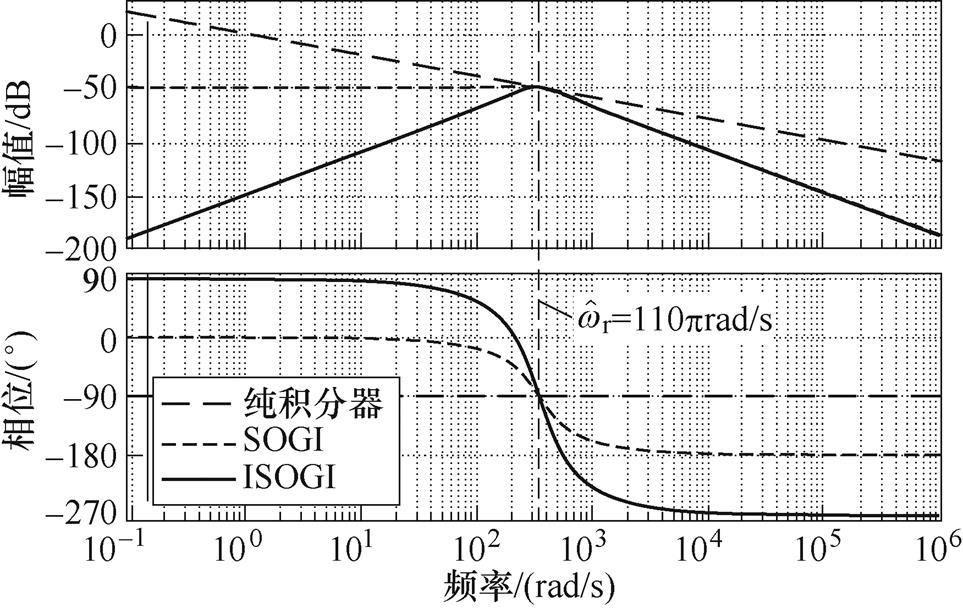
图3 三种积分器的伯德图对比
Fig.3 Comparison of Bode diagrams of the three integrators
为了进一步验证ISOGI的性能，分别对Vs中的直流、基波和谐波分量进行分析。
2.3.1 直流分量
将式（20）中f0作为ISOGI的输入，并结合式（24），可得
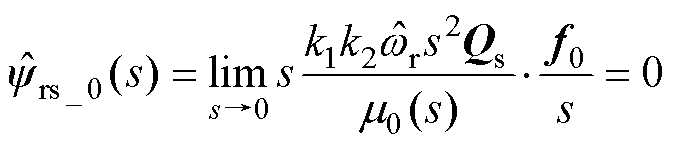（26）
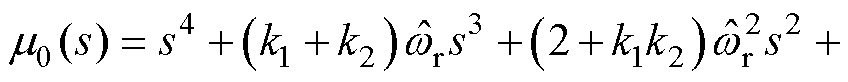
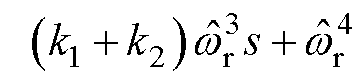（27）
由此可知，ISOGI能够完全抑制直流偏置。
2.3.2 基波分量
将式（20）中f1sin(w1t+j1)作为ISOGI的输入，并结合s=jw1和式（24），可得
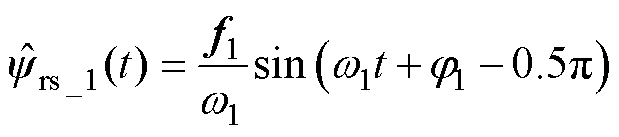（28）
可知，ISOGI对反电动势基波分量实现了纯积分作用，准确地观测到了转子磁链。
2.3.3 谐波分量
结合s=jhw1，将式（24）表示为
（29）
其中
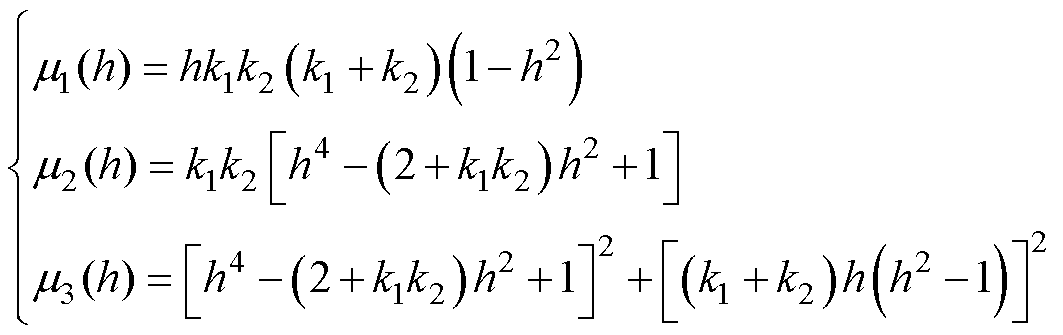（30）
式（29）在极坐标系上可表示为
（31）
其中
将式（20）中
作为ISOGI的输入，并结合式（31），可得
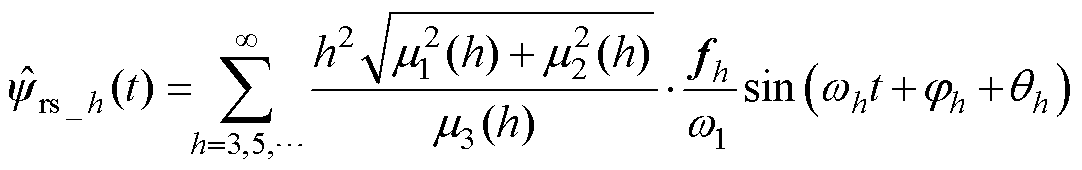（32）
可知，谐波阶次h越高，
值越小，进而谐波幅值越小。因此，ISOGI具有较好的抑制高次谐波的能力。
综上所述，本文提出的ISOGI对基波分量实现了积分作用，对直流偏置、低频和高频干扰实现了较好的抑制作用。因此，将ISOGI与SMO级联构成的基于SMO+ISOGI的转子磁链观测器能精确地观测到转子磁链。
采用PLL[21]从基于SMO+ISOGI观测器观测到的转子磁链中提取转子位置和转速信息。PLL原理框图如图4所示。电机稳态运行时，PLL闭环传递函数为
（33）
其中
K=yf
式中，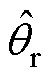
为转子位置估计值；Kp、Ki为PI参数。由于输入qr为斜坡信号，可求得PLL稳态误差为
（34）
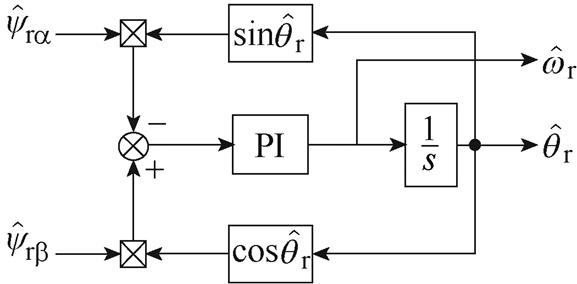
图4 锁相环原理框图
Fig.4 Block diagram of PLL
可见，当电机稳态运行时，位置稳态误差为零。因此，采用PLL能精确地获取转子位置和转速信息。
为验证所提出的无位置控制策略的参数鲁棒性，针对五相PMSM进行仿真分析。开路故障下基于转子磁链观测器的无位置控制框图如图5所示。五相PMSM具体参数见表1。图6～图8分别为五相PMSM电阻、电感和永磁磁链参数改变时的稳态性能。可知，当t=1.2s和t=1.4s时电机参数分别变为真实参数的0.5和2倍时，位置观测误差和速度观测误差几乎不变。可见，无论电阻、电感还是永磁磁链变大还是变小，位置观测误差和速度观测误差都和电机参数没有发生变化时几乎相同。因此，本文所提出用于开路故障电机的基于转子磁链观测器的无位置控制策略对参数摄动具有很好的鲁棒性。
图5 开路故障下基于转子磁链观测器的无位置控制框图
Fig.5 Control diagram of rotor-flux observer based sensorless control under open-circuit fault condition
表1 五相PMSM参数
Tab.1 Parameters of five-phase PMSM
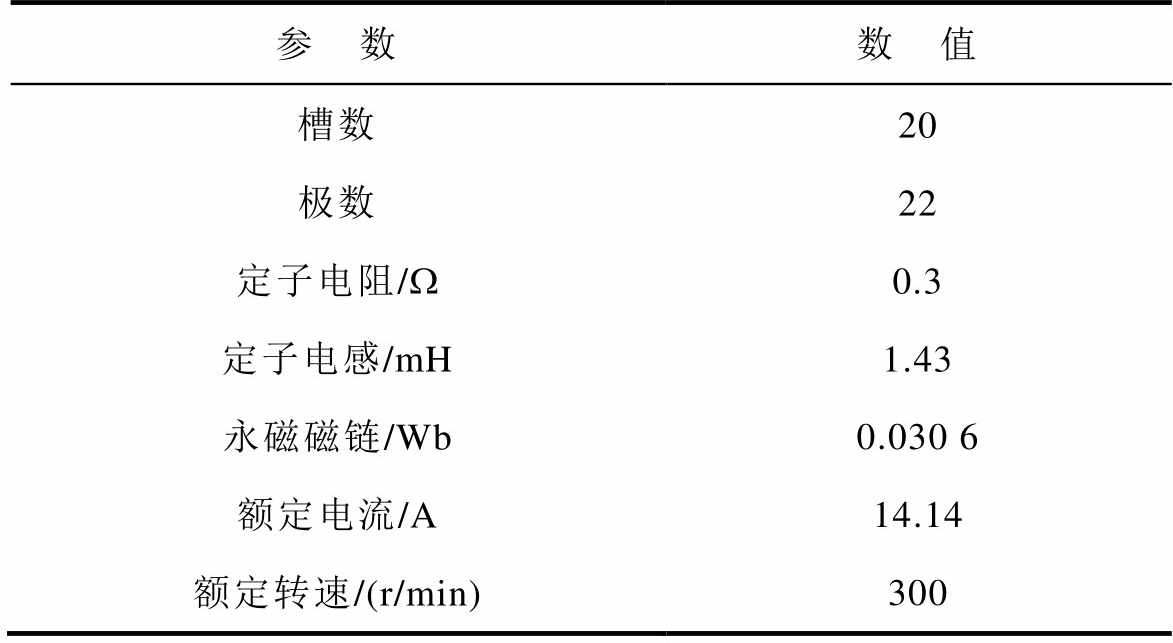
参 数数 值 槽数20 极数22 定子电阻/W0.3 定子电感/mH1.43 永磁磁链/Wb0.030 6 额定电流/A14.14 额定转速/(r/min)300
图6 电阻参数改变时的稳态性能
Fig.6 Steady-state performance when resistance parameters change
为验证所提出的PMSM开路故障下的基于转子磁链观测器的无位置控制策略的可行性，针对五相PMSM进行实验验证，并与基于SMO+SOGI转子磁链观测器的无位置控制策略进行对比研究。搭建如图9所示的驱动控制系统实验平台。
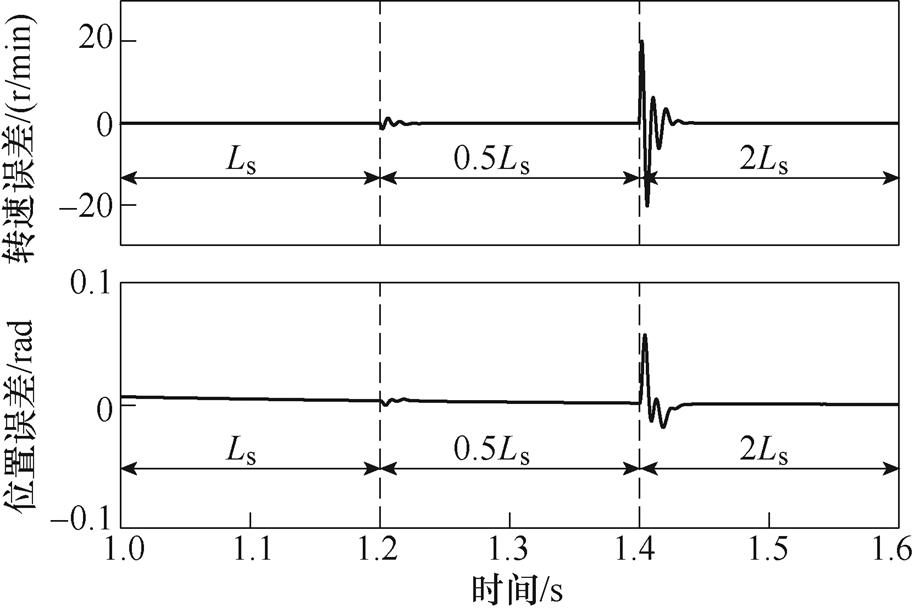
图7 电感参数改变时的稳态性能
Fig.7 Steady-state performance when inductance parameters change
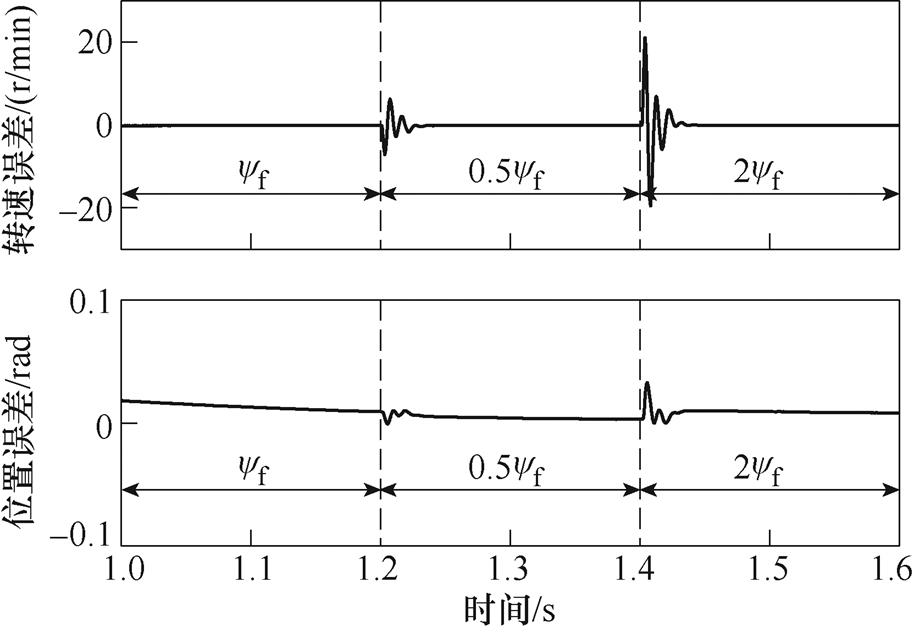
图8 永磁磁链参数改变时的稳态性能
Fig.8 Steady-state performance when permanent magnet flux parameter changes
图9 实验平台
Fig.9 Experimental platform
实验样机通过联轴器与永磁直流电机连接，直流电机串联电阻作为负载；通过光电编码器获取PMSM转子实际位置和转速信息，用于和估计值进行对比。
3.2.1 稳态性能分析
实验中电机转速为300r/min，负载转矩为4N·m。图10为采用两种观测器下的PMSM由正常无位置状态到A相开路故障再到容错无位置状态时的转矩、相电流波形。可见，当A相发生开路故障时，电机转矩脉动明显增大，且相电流畸变严重。当采用基于SMO+SOGI观测器的无位置容错控制策略后，转矩脉动由20.31%降至13.28%；而采用基于SMO+ISOGI观测器的无位置容错控制策略后，转矩脉动降至10.35%，且相电流畸变得到有效抑制。可见，采用基于SMO+ISOGI观测器的无位置容错控制策略有效地提高了PMSM开路故障情况下的稳态性能。
图10 正常到故障到容错运行时转矩、相电流波形
Fig.10 Waveforms of torque, phase current under healthy, fault and fault-tolerant conditions
图11～图14为五相PMSM由正常状态切换至容错状态时的无位置运行的稳态性能。图11为采用基于SMO+SOGI转子磁链观测器的反电动势与转子磁链观测波形。可知，正常工况下，由SMO观测到的反电动势中存在高频噪声，通过SOGI能有效抑制这部分干扰，获得平滑的转子磁链观测值。然而，当电机发生开路故障且容错运行后，观测到的反电动势中同时产生了高频扰动和2.2V幅值偏差，经SOGI处理后，转子磁链在ab 上的幅值仍存在0.005Wb的偏差。可见，基于SMO+SOGI转子磁链观测器对高频扰动具有较好的抑制作用，但无法消除直流偏置和低频扰动，进而极大地影响了位置和转速估计精度。
图11 基于SMO+SOGI无位置控制的反电动势与转子磁链
Fig.11 Estimated back EMFs and rotor-fluxes with flux observer based on SMO+SOGI
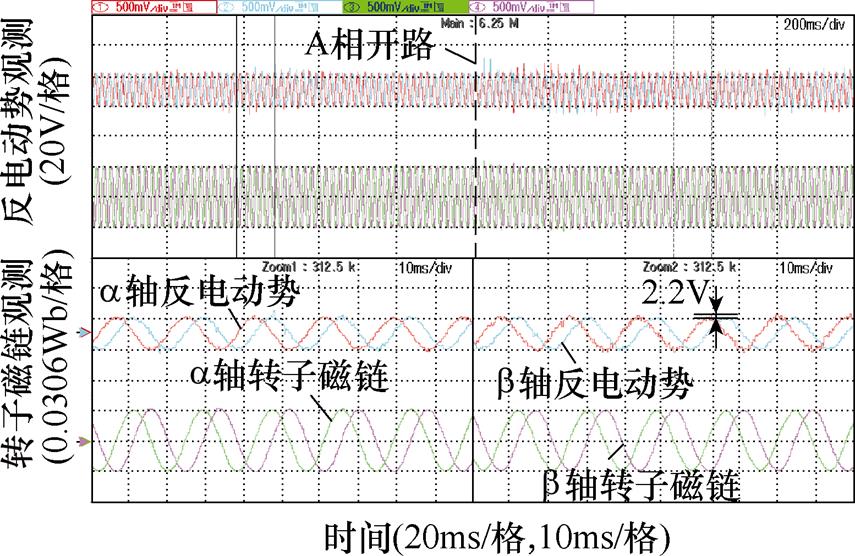
图12 基于SMO+ISOGI无位置控制的反电动势与转子磁链
Fig.12 Estimated back EMFs and rotor-fluxes with flux observer based on SMO+ISOGI
图13 转子位置、位置估算误差与B相电流波形
Fig.13 Waveforms of rotor position, position estimation error and B-phase current
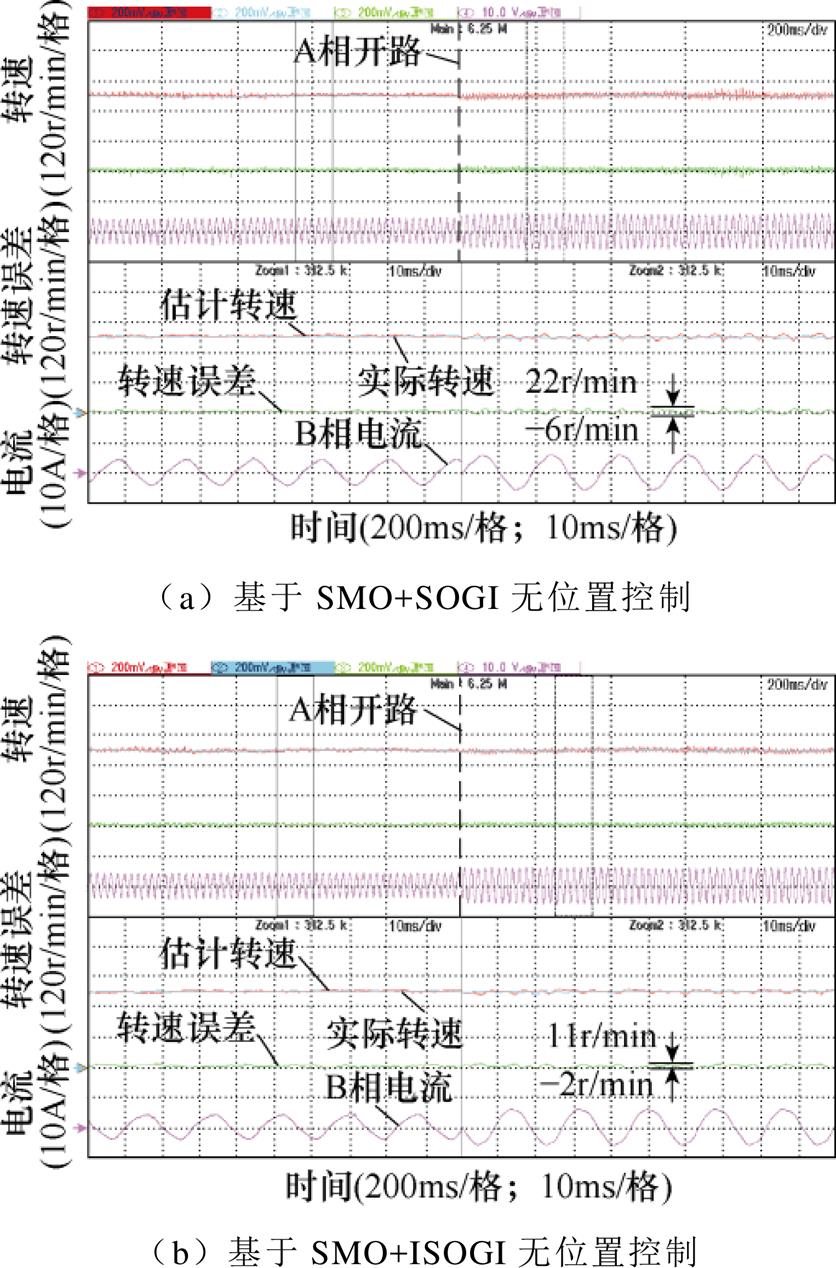
图14 转速、转速误差与B相电流波形
Fig.14 Waveforms of speed, speed estimation error and B-phase current
图12为采用基于SMO+ISOGI转子磁链观测器的反电动势与转子磁链观测波形。由转子磁链观测波形可知，正常运行时ISOGI能有效地滤除反电动势观测值中的高频成分，转子磁链不存在直流偏置且正弦度较好；切换至容错运行状态后，尽管SMO观测到的反电动势幅值仍然存在2.2V的差值，但是转子磁链在ab 上的幅值是相等的且具有较好的正弦度。可见，采用基于SMO+ISOGI转子磁链观测器时，故障状态下观测到的转子磁链性能与正常状态保持一致。
图13为采用两种观测器下的实际与估计位置、位置误差和B相电流波形。正常无位置运行时，采用基于SMO+SOGI观测器的位置估计误差为0.23rad；而采用基于SMO+ISOGI观测器时，位置估计误差为0.12rad。容错无位置运行状态下，基于SMO+ SOGI观测器的位置估计误差在0.16～0.55rad之间波动；而基于SMO+ISOGI观测器的误差在0.07～0.22rad之间波动，误差较小、波动更小。因此，在正常和故障状态下，相比基于SMO+SOGI无位置控制策略，基于SMO+ISOGI无位置控制策略具有更高的位置估计精度和更好的无位置运行的稳态性能。
图14为采用两种观测器下的实际与估计转速、转速误差和B相电流波形。正常无位置运行时，采用基于SMO+SOGI观测器的转速估计误差为15r/min；而基于SMO+ISOGI观测器的误差仅为8r/min。当电机进入容错无位置运行时，采用基于SMO+SOGI观测器的转速估计误差在-6～22r/min之间波动；而基于SMO+ISOGI观测器的误差在-2～11r/min之间波动。可见，误差较小且波动更小。因此，在正常和故障状态下，采用基于SMO+ISOGI无位置控制后速度跟踪效果更优。
3.2.2 转速突变工况下性能分析
图15为2N·m负载条件下容错无位置运行时，电机转速在200～300r/min之间阶跃时的动态性能对比实验。由图15a可知，采用基于SMO+SOGI观测器，在转速突变瞬间，估计转速无法较快地跟踪实际转速，进而转速和位置误差产生了较大脉动。在转速突增和突减瞬间，转速调节时间分别为0.55s和0.5s，转速误差的波动值分别为45r/min和51r/min，位置误差的波动值分别为0.23rad和0.31rad。由图15b可知，采用基于SMO+ISOGI观测器，在转速突增和突减瞬间，转速调节时间分别缩短至0.5s和0.45s，转速误差的波动值分别减小至30r/min和33r/min，位置误差的波动值分别减小至0.2rad和0.23rad。因此，在转速突变工况下，采用基于SMO+ ISOGI无位置控制时，速度跟踪性能更优，位置估计精度更高，动态性能得到显著改善。
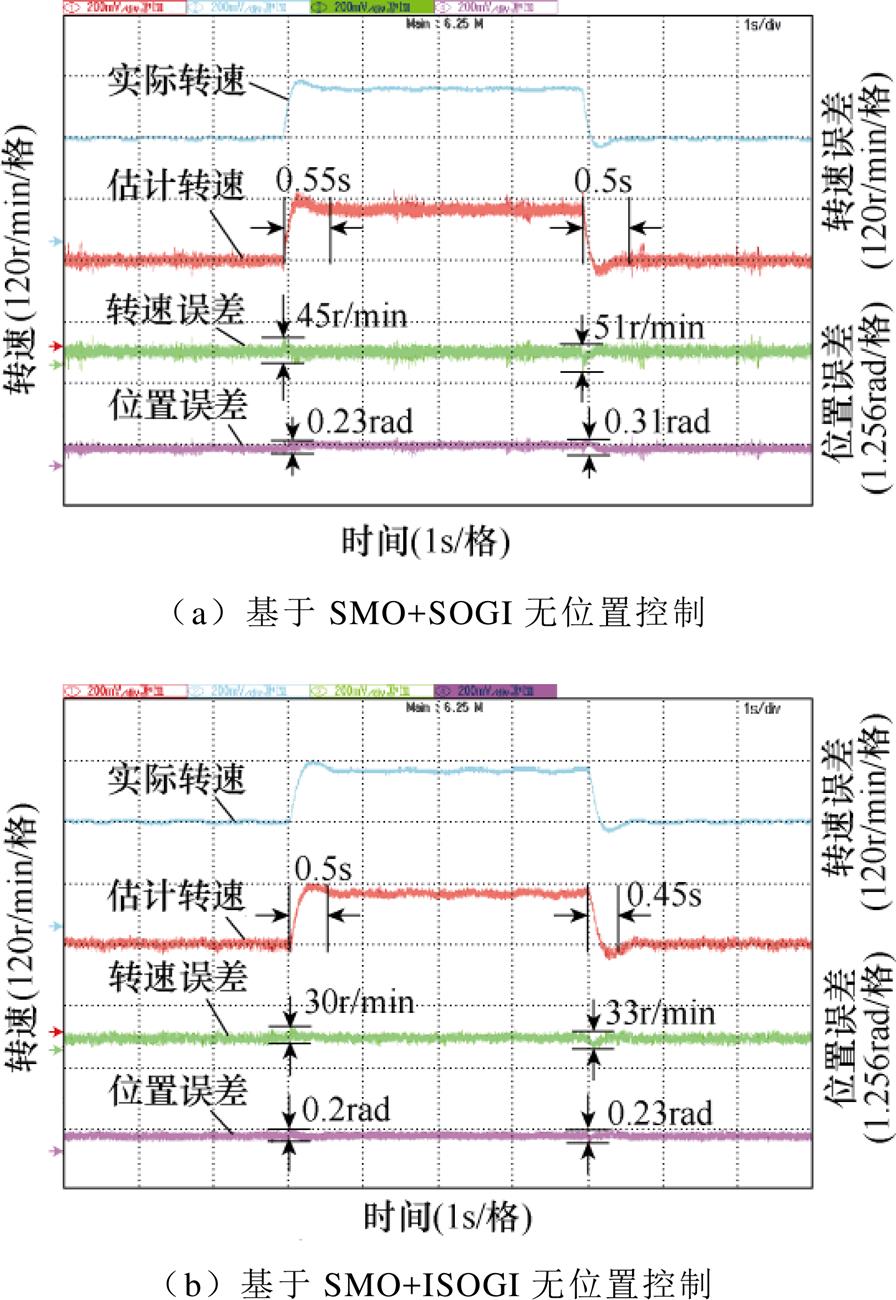
图15 容错运行时转速、转速和位置估算误差对速度阶跃的响应
Fig.15 Speed, speed and position estimation errors response to step speeds under fault-tolerant condition
3.2.3 负载转矩突变工况下性能分析
图16为300r/min容错无位置运行时，负载转矩在2N·m和6N·m之间阶跃时的动态性能对比实验。由图16a可知，采用基于SMO+SOGI无位置控制，在负载转矩突增和突减瞬间，估计转速出现了明显偏差，调节时间分别为0.55s和0.75s，且转速和位置误差的波动值分别达到43r/min和0.25rad；由图16b可知，采用基于SMO+ISOGI无位置控制，在负载转矩突变瞬间，估计转速的调节时间缩短至0.5s，且转速和位置误差的波动值分别减小至33r/min和0.19rad。由此可见，基于SMO+ISOGI无位置控制策略有效地提高了负载转矩突变下的转速跟随性能和位置估计精度，改善了电机开路故障下无位置运行的动态性能。
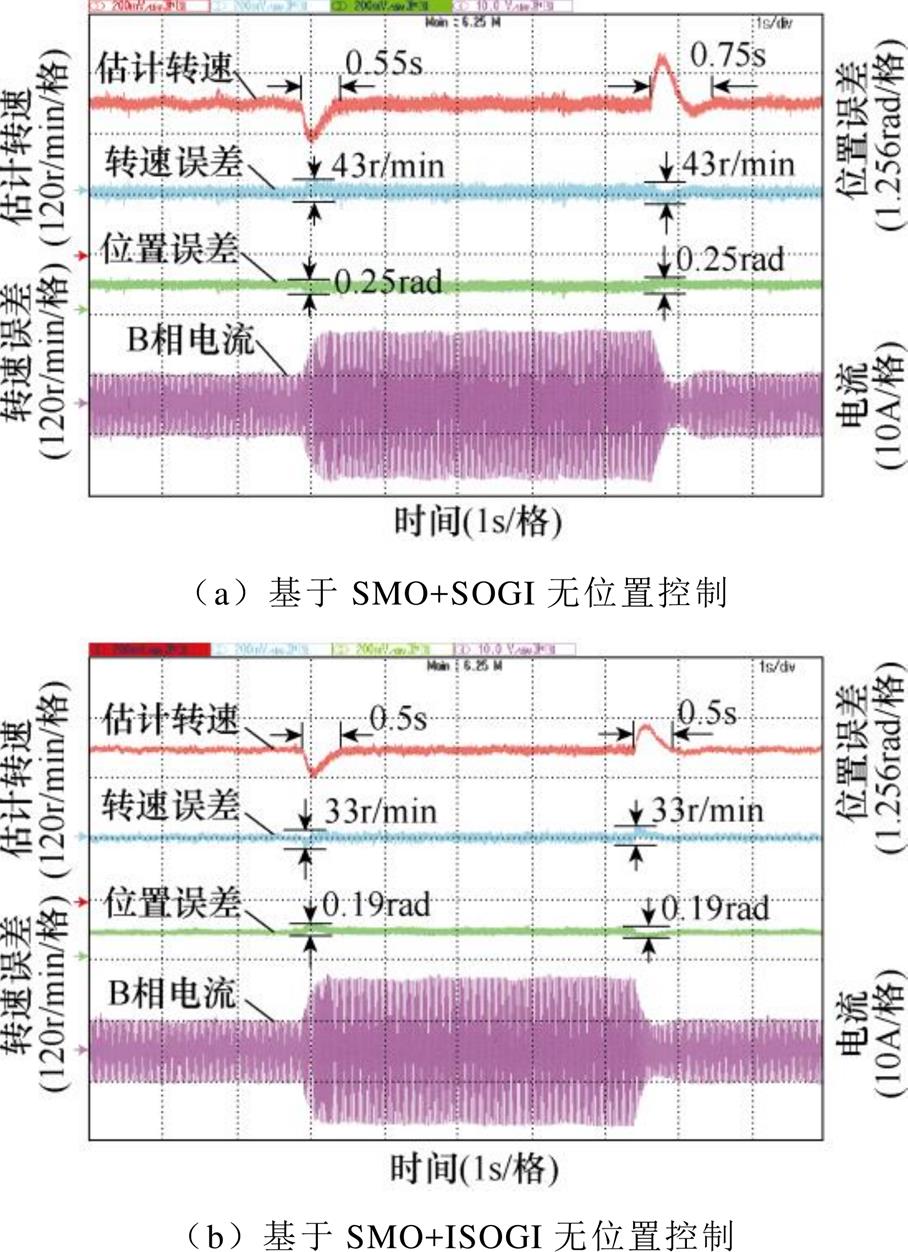
图16 容错运行时转速、转速和位置估算误差对负载转矩突变的响应
Fig.16 Speed, speed and position estimation errors response to step loads under fault-tolerant condition
本文针对五相PMSM开路故障的特点，提出了一种基于SMO+ISOGI转子磁链观测器的无位置控制策略，实现了PMSM单相开路故障情况下的高性能无位置运行。该策略具有如下优点：
1）相对基于SMO+SOGI转子磁链观测器的无位置控制策略，该策略不但具有较好的高频噪声抑制能力，而且能有效抑制低频（包括直流）扰动，降低了开路故障对位置观测精度的影响，提高了转子位置观测精度，同时具有较好的稳态和动态性能。
2）该策略融合基于指数趋近律的SMO，不但抑制了滑模抖振，而且具有较好的参数鲁棒性。
3）该策略不但能准确地观测到PMSM开路故障情况下的转子位置，而且能有效观测到无故障情况下的转子位置。
4）若电机发生两相开路故障，在容错控制基础上，采用基于SMO+ISOGI转子磁链观测器观测到磁链，并采用修正系数将其修正成等幅值的磁链，然后采用PLL提取出转子位置和速度信息，进而实现无位置传感器运行。
参考文献
[1] 陈前, 夏雨航, 赵文祥, 等. 采用无差拍电流跟踪的五相梯形反电动势永磁电机开路容错控制[J]. 电工技术学报, 2022, 37(2): 368-379.
Chen Qian, Xia Yuhang, Zhao Wenxiang, et al. Open- circuit fault-tolerant control for five-phase permanent magnet motors with trapezoidal back-EMF by deadbeat current tracking[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 368-379.
[2] Huang Wentao, Hua Wei, Fan Qigao. Performance analysis and comparison of two fault-tolerant model predictive control methods for five-phase PMSM drives[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(4): 311-320.
[3] Wei Yongqing, Qiao Mingzhong, Zhu Peng. Fault- tolerant operation of five-phase permanent magnet synchronous motor with independent phase driving control[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 105-110.
[4] Trabelsi M, Nguyen N K, Semail E. Real-time switches fault diagnosis based on typical operating characteristics of five-phase permanent-magnetic synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 4683-4694.
[5] Zhou Xinxiu, Sun Jun, Li Haitao, et al. PMSM open- phase fault-tolerant control strategy based on four-leg inverter[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 2799-2808.
[6] 周华伟, 周城, 刘国海, 等. 五相圆筒永磁电机统一容错矢量控制[J]. 中国电机工程学报, 2019, 39(5): 1479-1488.
Zhou Huawei, Zhou Cheng, Liu Guohai, et al. A unified fault-tolerant vector control for tubular per- manent magnet motors[J]. Proceedings of the CSEE, 2019, 39(5): 1479-1488.
[7] Zhou Huawei, Zhao Wenxiang, Liu Guohai, et al. Remedial field-oriented control of five-phase fault- tolerant permanent-magnet motor by using reduced- order transformation matrices[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 169-178.
[8] 陈文汉, 孙丹, 王铭泽. 断相故障下开绕组永磁同步电机模型预测控制容错控制策略研究[J]. 电工技术学报, 2021, 36(1): 77-86.
Chen Wenhan, Sun Dan, Wang Mingze. Research on fault-tolerance strategy based on model predictive control for open-winding PMSM system under open- phase fault[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 77-86.
[9] Lascu C, Andreescu G D. PLL position and speed observer with integrated current observer for sensor- less PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5990-5999.
[10] Xu Jinquan, Du Yutao, Fang Hao, et al. A robust observer and nonorthogonal PLL-based sensorless control for fault-tolerant permanent magnet motor with guaranteed postfault performance[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5959-5970.
[11] Xu Jinquan, Du Yutao, Zhang Boyi, et al. Sensorless fault-tolerant control with phase delay compensation for aerospace FTPMSM drives with phase open- circuit and short-circuit faults[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 4576-4585.
[12] Zhang Li, Zhu Xiaoyong, Gao Jian, et al. Design and analysis of new five-phase flux-intensifying fault- tolerant interior-permanent-magnet motor for sensor- less operation[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 6055-6065.
[13] Yepes A G, Doval-Gandoy J, Baneira F, et al. Speed estimation based on rotor slot harmonics in multi- phase induction machines under open-phase fault[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7980-7993.
[14] Cai Jun, Liu Zeyuan, Zeng Yu. Aligned position estimation based fault-tolerant sensorless control strategy for SRM drives[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7754-7762.
[15] 麦志勤, 刘计龙, 肖飞, 等. 基于估计位置反馈电流解调算法的改进型高频旋转电压注入无位置传感器控制策略[J]. 电工技术学报, 2022, 37(4): 870- 881, 891.
Mai Zhiqin, Liu Jilong, Xiao Fei, et al. Sensorless control strategy of improved HF rotating voltage injection based on estimated position feedback current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 870-881, 891.
[16] 杜博超, 崔淑梅, 宋立伟, 等. 一种基于变频电流信号的IPMSM无位置传感器高频注入电流噪声抑制方法[J]. 电工技术学报, 2020, 35(18): 3830-3837.
Du Bochao, Cui Shumei, Song Liwei, et al. A variable frequency current injection sensorless control strategy of IPMSM for audible noise reduction[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(18): 3830-3837.
[17] 赵文祥, 刘桓, 陶涛, 等. 基于虚拟信号和高频脉振信号注入的无位置传感器内置式永磁同步电机MTPA控制[J]. 电工技术学报, 2021, 36(24): 5092- 5100.
Zhao Wengxiang, Liu Huan, Tao Tao, et al. MTPA control of sensorless IPMSM based on virtual signal and high-frequency pulsating signal injection[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5092-5100.
[18] 章春娟, 王慧贞, 刘伟峰, 等. 基于宽频带同步基频提取滤波器的永磁同步电机转子位置与转速估计[J]. 电工技术学报, 2022, 37(4): 882-891.
Zhang Chunjuan, Wang Huizhen, Liu Weifeng, et al. Rotor position and speed estimation of permanent magnet synchronous motor based on wideband syn- chronous fundamental frequency extraction filter[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 882-891.
[19] Liang Donglai, Li Jian, Qu Ronghai. Sensorless control of permanent magnet synchronous machine based on second-order sliding-mode observer with online resistance estimation[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3672-3682.
[20] Liang Donglai, Li Jian, Qu Ronghai, et al. Adaptive second-order sliding-mode observer for PMSM sen- sorless control considering VSI nonlinearity[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8994-9004.
[21] Ji Jinghua, Jiang Yang, Zhao Wenxiang, et al. Sensor- less control of linear vernier permanent-magnet motor based on improved mover flux observer[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3869-3877.
[22] Gaeta A, Scelba G, Consoli A. Sensorless vector control of PM synchronous motors during single- phase open-circuit faulted conditions[J]. IEEE Transactions on Industry Applications, 2012, 48(6): 1968-1979.
[23] Zhang Li, Fan Ying, Li Chenxue, et al. Fault-tolerant sensorless control of a five-phase FTFSCW-IPM motor based on a wide-speed strong-robustness sliding mode observer[J]. IEEE Transactions on Energy Conversion, 2018, 33(1): 87-95.
[24] Zhao Rende, Xin Zhen, Loh P C, et al. A novel flux estimator based on multiple second-order generalized integrators and frequency-locked loop for induction motor drives[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(8): 6286-6296.
[25] Guzman H, Duran M J, Barrero F, et al. Comparative study of predictive and resonant controllers in fault- tolerant five-phase induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 606-617.
[26] Chen Qian, Zhao Wenxiang, Liu Guohai, et al. Extension of virtual-signal-injection-based MTPA control for five-phase IPMSM into fault-tolerant operation[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(2): 944-955.
[27] 刘国海, 赵万祥, 周华伟, 等. 基于零序电压谐波注入式脉宽调制的五相永磁电机直接转矩控制[J]. 中国电机工程学报, 2017, 37(5): 1517-1527.
Liu Guohai, Zhao Wanxiang, Zhou Huawei, et al. Direct torque control of five-phase permanent magnet motor based on zero-sequence voltage harmonic injection pulse width modulation[J]. Proceedings of the CSEE, 2017, 37(5): 1517-1527.
[28] 杨淑英, 刘世园, 李浩源, 等. 永磁同步电机无位置传感器控制谐波抑制策略研究[J]. 中国电机工程学报, 2019, 39(20): 6075-6084, 6188.
Yang Shuying, Liu Shiyuan, Li Haoyuan, et al. Research on harmonic suppression strategy of posi- tion sensorless control for permanent magnet syn- chronous motor[J]. Proceedings of the CSEE, 2019, 39(20): 6075-6084, 6188.
[29] Li Junfang, Wang Kai, Li Fan. Reduction of torque ripple in consequent-pole permanent magnet machines using staggered rotor[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 643-651.
[30] Jiang Yajie, Xu Wei, Mu Chaoxu, et al. An improved third-order generalized integral flux observer for sensorless drive of PMSMs[J]. IEEE Transactions on Industrial Electronics, 2019, 66(12): 9149-9160.
Abstract Due to the asymmetric state of the five-phase fault-tolerant permanent magnet synchronous motor (PMSM) under open-circuit faultconditions, the operating performancewith sensorless control is not satisfied. The estimated accuracy of rotor positiondeterioratessince the back electromotive forces (EMFs)estimated by traditional observerscontain DC bias and high-order harmonicsunder open-circuit fault conditions. Therefore, a novel sensorless control strategy based on a rotor-flux observerwas proposed.
Firstly, based on the fault-tolerant model, a sliding mode observer (SMO) according to the exponential approach law was established to estimate back electromotive forces (EMFs).However, they contain dc bias, and low and high-order harmonics, which seriously affect the estimated accuracy of rotor position. Secondly, an improved second-order generalized integrator (ISOGI) was designed. The ISOGI transfer function can be expressed as
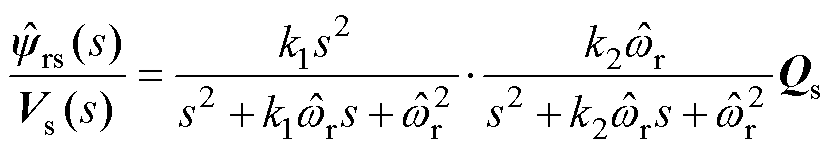(1)
Combined with the SMO, the ISOGIwas adopted to design a new rotor-flux observer.Then, a phase-locked loop (PLL) extracted the rotor position information from the rotor flux. Finally, the faulty PMSM can operate smoothly with a fault-tolerant method.
Simulated results on the parameter robustness show that when the resistance, inductance, or permanent magnet flux becomes 0.5 and 2 times the actual parameters, the estimated errors of position and speed are almost unchanged. Thus, whether the parameters become larger or smaller, the estimated errors are almost the same as thoseunder healthy conditions. An experimental platform was estimated to verify the feasibility and effectiveness of theproposed strategy. Steady-state experiments show that the maximum rotor position errors estimated by the SMO+SOGI andSMO+ISOGI are 0.55rad and 0.22rad, respectively. When reference speed changes, the maximum speed regulation time with the SMO+ISOGI strategy is 0.5s, while the SMO+SOGI strategy is 0.55s.When loads change, the maximum speed regulation time with the SMO+ISOGI strategy is 0.5s, while the SMO+SOGI strategy is 0.75s. The comparison between the SMO+SOGI and SMO+ISOGI strategies shows that the proposed strategy can reduce the estimated error of rotor positionand improve the steady-state and dynamic performanceunder open-circuit fault conditions.
The following conclusions can be drawn. ① Compared with the SMO+SOGI strategy, the proposed strategy has a strong filtering ability for DC bias, low and high order harmonics, effectively reduces the influence of open-circuit fault on estimated accuracy of rotor position, and improves the estimated accuracy of rotor position. Meanwhile, it has good steady-state and dynamic performance. ②Combined with the SMO based on the exponential reaching law, the proposed strategy can reduce sliding mode chattering and show good parameter robustness. ③The proposed rotor flux observer based on the SMO+ISOGI can be applied for the sensorless control of PMSM under healthy and open-circuit fault conditions. ④ If two-phase open-circuit faults occur, the proposed rotor flux observer can achieve sensorless control based on a fault-tolerant controlstrategy.
Keywords：Permanent magnet synchronous motor, open-circuit fault, sliding mode observer, improved second-order generalized integrator, rotor-flux observer
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.212119
国家自然科学基金项目（51877100）和江苏高校“青蓝工程”项目资助。
收稿日期 2021-12-27
改稿日期 2022-04-15
E-mail: zhouhuawei@ujs.edu.cn（通信作者）
叶 晨 男，1995年生，硕士研究生，研究方向为永磁电机控制。
E-mail: 1422687473@qq.com
（编辑 崔文静）