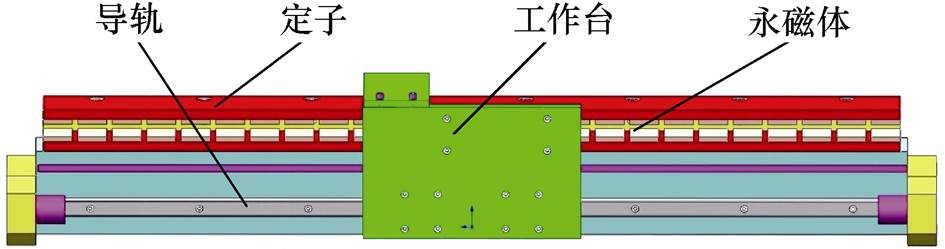
图1 PMLSM结构示意图
Fig.1 Structure diagram of PMLSM
摘要 针对永磁直线同步电机运行时存在模型不确定性、负载扰动、参数摄动等匹配/不匹配扰动等问题,该文提出一种基于扰动观测器的高阶非奇异快速终端滑模控制策略。利用非线性扰动观测器观测匹配/不匹配扰动,降低系统对多重扰动的保守性。此外,设计高阶非奇异快速终端滑模控制器,增强系统的鲁棒性,并将反馈电流引入滑模面,实现电机位置、速度和电流的整体控制,以提高位置跟踪系统的动态性能和稳态性能。基于李雅普诺夫稳定性理论,分析证明了闭环系统的稳定性和收敛性。最后,通过实验验证了所提控制方法的可行性,能够有效提高系统的跟踪精度和鲁棒性。
关键词:永磁直线同步电机 非线性扰动观测器 高阶非奇异快速终端滑模控制 匹配/不匹配扰动
永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)与旋转同步电机相比,具有更高的推力密度、更低的热损耗,而且不存在机械耦合和滚珠丝杠的问题,因此,广泛应用于高速度、高精度的数控加工领域[1-2]。由于电机运行在模型不确定性、负载扰动、参数摄动等复杂多变的工作环境,PMLSM系统通常会存在多种匹配/不匹配扰动,位置跟踪的快速性和精度恶化问题凸 显[3-4],因此采取有效的控制策略,提高PMLSM的位置跟踪性能,对于提高加工精度具有重要意义[5]。
为了提高PMLSM的位置跟踪性能,目前采用的控制策略主要有数控反推控制[6]、迭代学习控 制[7]、线性自抗扰控制[8]和滑模控制[9]等。反推控制可以对高阶系统的每一阶子系统设计虚拟控制律,实现全局调节和跟踪,但存在“微分爆炸”问题[10]。迭代学习控制对重复或周期性扰动有较强的处理能力,可实现有限区间内完全跟踪,但对非周期性扰动非常敏感,甚至导致系统发散[11]。线性自抗扰控制不依赖于扰动的具体数学模型,减少了整定参数,但损失了跟踪精度和抗扰性能。滑模控制(Sliding Mode Control, SMC)作为一种非线性控制方法,具有响应速度快、鲁棒性强、实现简单等优点[12],非常适用于PMLSM运动系统的位置控制[13]和推力控制[14]。理论上,当系统的参数摄动和外界扰动等不确定因素满足匹配性条件时,即扰动与控制输入在系统的同一通道中,SMC具有绝对鲁棒性[15]。但当扰动不满足匹配条件时,即扰动与控制输入在系统的不同通道中,控制系统的鲁棒性就不再存在,此时系统输出将无法精确跟踪给定输入[16]。同时,传统的SMC只能保证系统状态在无限时间内收敛到平衡点[17]。为了解决以上问题,文献[18]为提高系统的鲁棒性,采用二阶扰动观测器观测扰动并将观测值和反馈电流引入滑模控制器中,实现系统双重闭环控制。文献[19]设计了终端滑模面,保证系统状态在有限时间内收敛到平衡点,但控制律中存在的分数型次幂导致控制器出现奇异性问题。为此,文献[20]设计了非奇异终端滑模控制器(Nonsin- gular Terminal Sliding Mode Control, NTSMC)解决奇异性问题,进而保证了系统状态在有限时间内快速收敛。
为了实现PMLSM的高精度控制,本文提出了一种基于扰动观测器的高阶非奇异快速终端滑模控制策略。首先,建立包含匹配扰动和不匹配扰动的以位置误差、速度误差及反馈电流为状态量的PMLSM系统动力学模型。然后,设计非线性扰动观测器,同时观测匹配/不匹配扰动,从而降低系统对多重扰动的保守性。接着,基于PMLSM系统模型和观测扰动,设计高阶非奇异快速终端滑模控制器(High order Nonsingular Fast Terminal Sliding Mode Controller, HNFTSMC),其特点是在传统非奇异快速终端滑模面中加入加速度误差项,建立起滑模面与控制电压之间的连接纽带,实现电机位置、速度和电流的整体控制,进而提高位置跟踪系统的动态和稳态性能。该方法结合扰动观测器与滑模控制的优点,一方面,利用非线性扰动观测器削弱滑模控制的抖振现象,增强系统对不匹配扰动的抑制能力;另一方面,滑模控制能有效提高系统对扰动观测误差的鲁棒性,而将电流和观测扰动引入滑模面能够提高系统动态性能,且单个控制器即可实现传统的三环控制。最后,通过实验验证了所提控制策略的正确性和有效性。
图1为PMLSM结构示意图。PMLSM的动子上装有通电绕组,工作台固定于动子上,动子和工作台共同安装在线性导轨的滑块上,而定子上装有永磁体为动子提供励磁,以实现动子沿着直线方向运动。

图1 PMLSM结构示意图
Fig.1 Structure diagram of PMLSM
考虑系统的模型不确定性、负载扰动、参数摄动等影响因素,经过Park变换,PMLSM在两相旋转dq坐标系下的数学模型[18-21]为
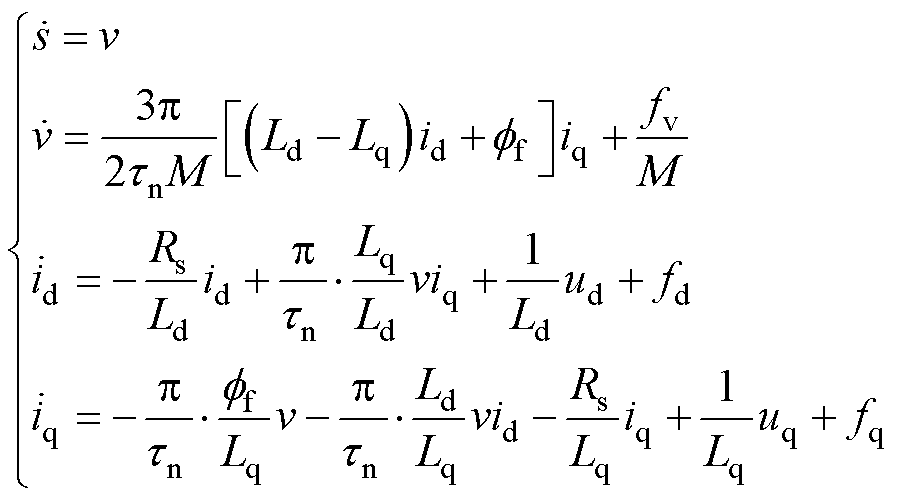 (1)
(1)
式中,Rs为相电阻;ud、uq分别为d、q轴电压;id、iq分别为d、q轴电流;Ld、Lq分别为d、q轴电感;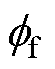 为永磁体磁链;s为动子所在位置;v为动子线速度;M为动子及所带负载的总质量;tn为极距;fd、fq和fv分别为参数摄动、外部扰动以及其他未建模动态引起的扰动。
为永磁体磁链;s为动子所在位置;v为动子线速度;M为动子及所带负载的总质量;tn为极距;fd、fq和fv分别为参数摄动、外部扰动以及其他未建模动态引起的扰动。
选取状态变量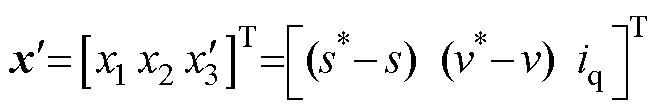 ,其中s*、v*分别为给定位置和线速度,基于
,其中s*、v*分别为给定位置和线速度,基于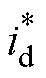 =0控制,由式(1)可得
=0控制,由式(1)可得
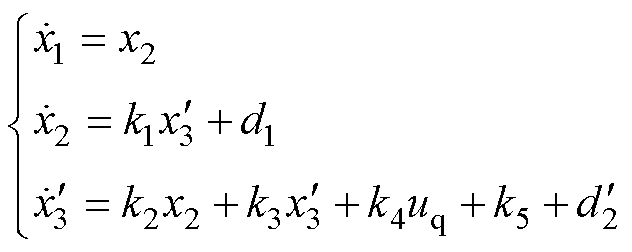 (2)
(2)
其中
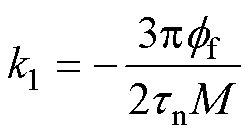
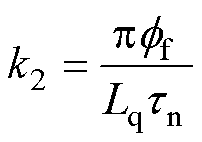
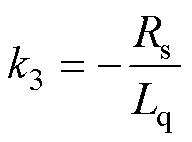
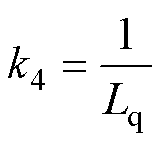

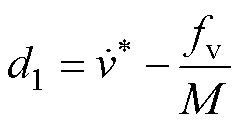
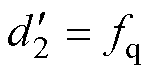
定义新状态变量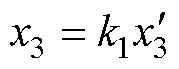 ;且令
;且令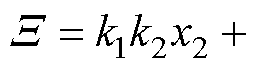
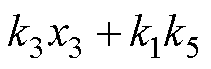 ;
;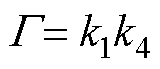 ,
,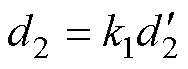 ,系统进一步表示为
,系统进一步表示为
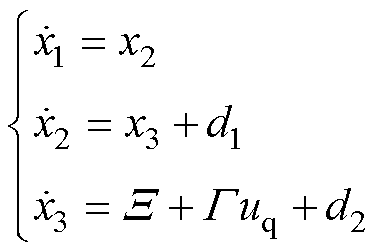 (3)
(3)
根据不匹配/匹配扰动的定义,由式(3)可知,d1为作用在不同通道的不匹配扰动,如摩擦力、纹波推力、负载力等,d2为与控制输入存在于同一通道的匹配扰动,如参数变化。同时,为保证严密性,假设系统扰动满足下面的条件:
假设1:扰动信号di是有界的,存在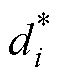 ∈R+,满足
∈R+,满足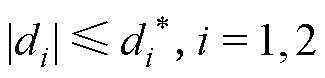 。
。
假设2:扰动信号di是缓慢变化的,故认为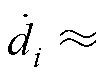
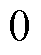 ,
,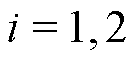 。
。
由于滑模控制对于不匹配扰动不具备鲁棒性,且为减小切换增益,削弱抖振现象,本文设计了非线性扰动观测器(Nonlinear Disturbance Observer, NDO)同时观测PMLSM系统中的匹配/不匹配扰动量[22],并用于滑模控制器设计。
取系统的状态变量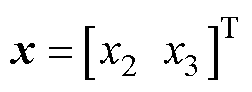 ,根据式(3),可重新表述为非线性系统的形式,有
,根据式(3),可重新表述为非线性系统的形式,有
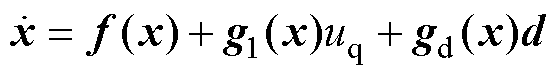 (4)
(4)
其中
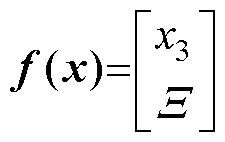
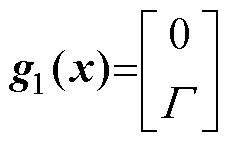
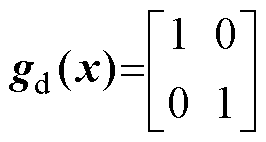
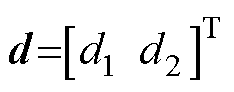
针对系统式(4),设计非线性扰动观测器为
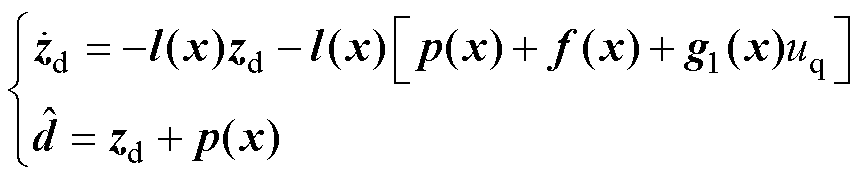 (5)
(5)
式中,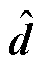 为扰动d的估计量,
为扰动d的估计量,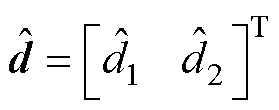 ;zd为定义的观测器内部状态变量;p(x)为观测器非线性向量函数,设计为
;zd为定义的观测器内部状态变量;p(x)为观测器非线性向量函数,设计为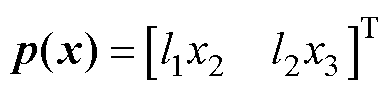 ;l(x)为观测器增益,且有
;l(x)为观测器增益,且有
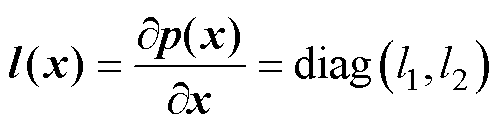 (6)
(6)
定义扰动观测误差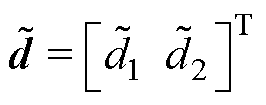 ,有
,有
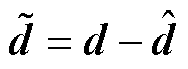 (7)
(7)
对式(7)求导并将式(5)代入,则观测误差动态方程可以表示为
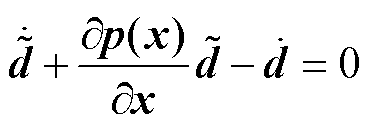 (8)
(8)
显然,根据假设1和假设2,存在观测器增益l(x)>0,使得观测误差是渐近收敛的。
为提高PMLSM系统的鲁棒性,设计高阶非奇异快速终端滑模控制器,同时为改善跟踪性能,将不匹配扰动观测值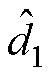 和反馈的q轴电流引入滑模面中。因此,高阶非奇异快速终端滑模面设计为
和反馈的q轴电流引入滑模面中。因此,高阶非奇异快速终端滑模面设计为
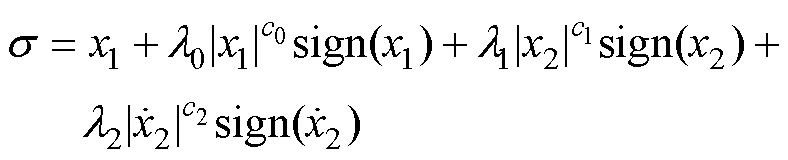 (9)
(9)
式中, ;为保证快速收敛和非奇异性能,c0、c1、c2的选取应满足c0>c1、1<c1<2且c2<1;
;为保证快速收敛和非奇异性能,c0、c1、c2的选取应满足c0>c1、1<c1<2且c2<1;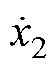 为加速度误差值,由式(3)可知,其可由扰动观测值
为加速度误差值,由式(3)可知,其可由扰动观测值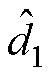 和反馈的q轴电流获得,这将大大缓解测量噪声在系统中的影响,利于跟踪性能的提高。
和反馈的q轴电流获得,这将大大缓解测量噪声在系统中的影响,利于跟踪性能的提高。
与文献[23]中传统的非奇异快速终端滑模面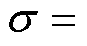
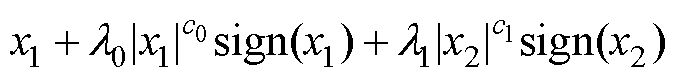 相比,高阶非奇异快速终端滑模面中增加了
相比,高阶非奇异快速终端滑模面中增加了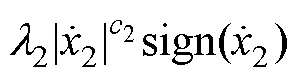 项,建立起滑模面与控制电压之间的连接纽带,提高了位置跟踪系统的动态性能和稳态性能。
项,建立起滑模面与控制电压之间的连接纽带,提高了位置跟踪系统的动态性能和稳态性能。
对式(9)求一阶导数,得
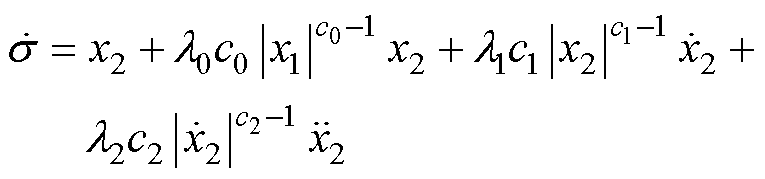 (10)
(10)
为削弱抖振现象并确保系统快速收敛,采用式(11)所示终端趋近律设计控制律,即
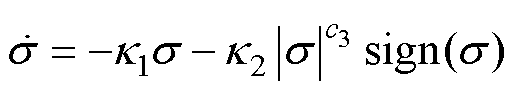 (11)
(11)
式中, ,
,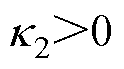 且
且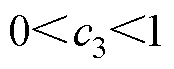 。
。
考虑系统式(11),通过仿真计算,对比终端趋近律、指数趋近律(c3=0)和等速趋近律(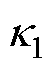 =0, c3=0)的收敛时间。仿真中,趋近律参数取值为
=0, c3=0)的收敛时间。仿真中,趋近律参数取值为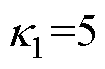 、
、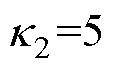 、
、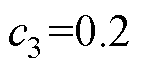 ;初始状态
;初始状态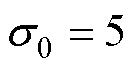 。初始状态
。初始状态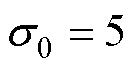 时
时 的收敛曲线如图2所示。可以看出,相比于指数趋近律和等速趋近律,终端趋近律在削弱抖振现象的同时兼顾了收敛时间。
的收敛曲线如图2所示。可以看出,相比于指数趋近律和等速趋近律,终端趋近律在削弱抖振现象的同时兼顾了收敛时间。
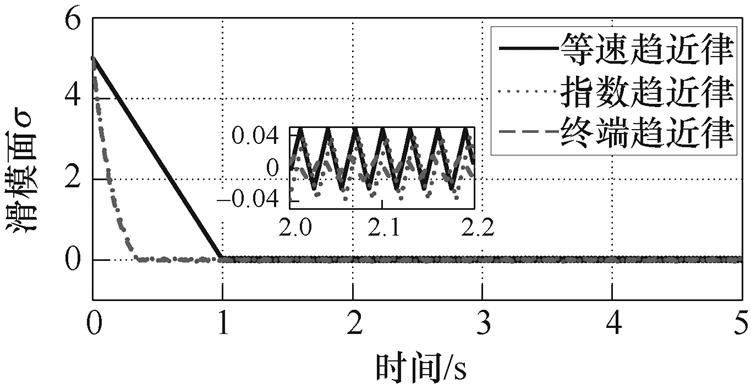
图2 初始状态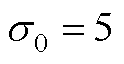 时
时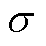 的收敛曲线
的收敛曲线
Fig.2 Convergence curves of 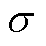 in the initial state
in the initial state 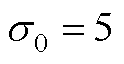
需要指出的是,本文采用终端趋近律改善趋近运动的动态品质。然而,切换增益为固定值,且当增益较大时会导致系统出现抖振现象。在这种情况下,自适应终端趋近律是一个可行的选择[12]。
联立式(10)和式(11),并结合式(3),可求解得到HNFTSMC-NDO控制律为
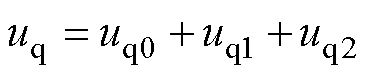 (12)
(12)
其中

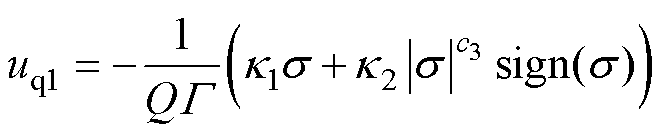
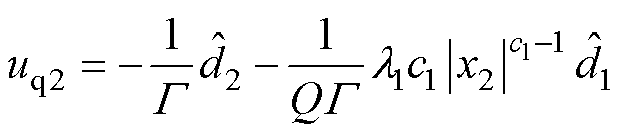
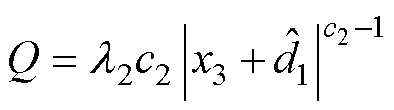
在实际应用中,由于跟踪性能往往会受到有限的控制输入、未建模动力学和测量噪声的影响,因此控制器参数选择准则为:
(1)在实际的HNFTSMC系统中,为克服较大集总不确定性的影响,增益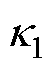 和
和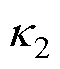 一般取较大正值,但增益过大易导致控制饱和;反之,则不能确保状态在有限时间内快速收敛至滑模面。在本文中,利用NDO对匹配和不匹配扰动进行补偿时,这两个增益依赖于扰动观测误差,因此它们可以取较小的值。
一般取较大正值,但增益过大易导致控制饱和;反之,则不能确保状态在有限时间内快速收敛至滑模面。在本文中,利用NDO对匹配和不匹配扰动进行补偿时,这两个增益依赖于扰动观测误差,因此它们可以取较小的值。
(2)因为c0、c1和c2的值越大,收敛速度越快,抖振越严重,所以在选择c0、c1和c2的值时,应兼顾收敛速度和控制抖振。
(3)由于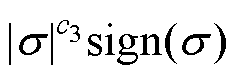 是切换控制(c3→0)和连续控制(c3→1)之间的桥梁,在选取c3的值时,需权衡系统的强鲁棒性和削弱抖振性能。
是切换控制(c3→0)和连续控制(c3→1)之间的桥梁,在选取c3的值时,需权衡系统的强鲁棒性和削弱抖振性能。
下面对整个控制系统在HNFTSMC-NDO作用下的稳定性进行分析。选取李雅普诺夫函数为
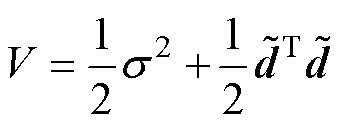 (13)
(13)
对式(13)求导,并代入式(10),可得
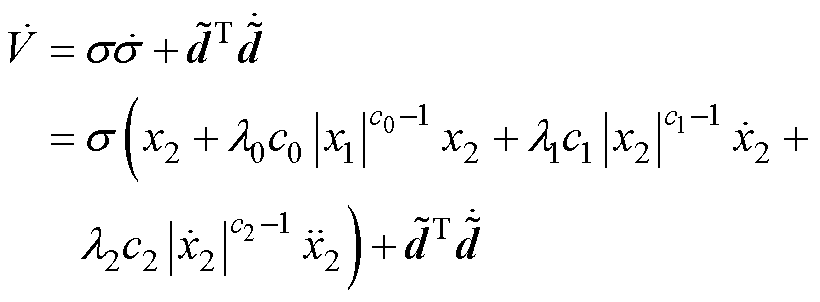 (14)
(14)
将被控对象(见式(3))和观测误差动态方程(见式(8))代入式(14),可得
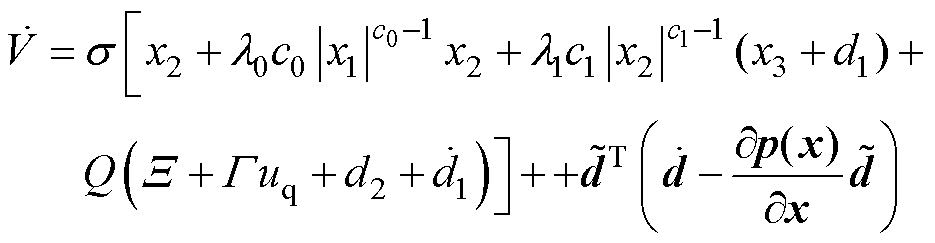 (15)
(15)
根据假设1和假设2,即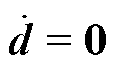 ,并将HNFTSMC- NDO控制律式(12)代入式(15),可得
,并将HNFTSMC- NDO控制律式(12)代入式(15),可得
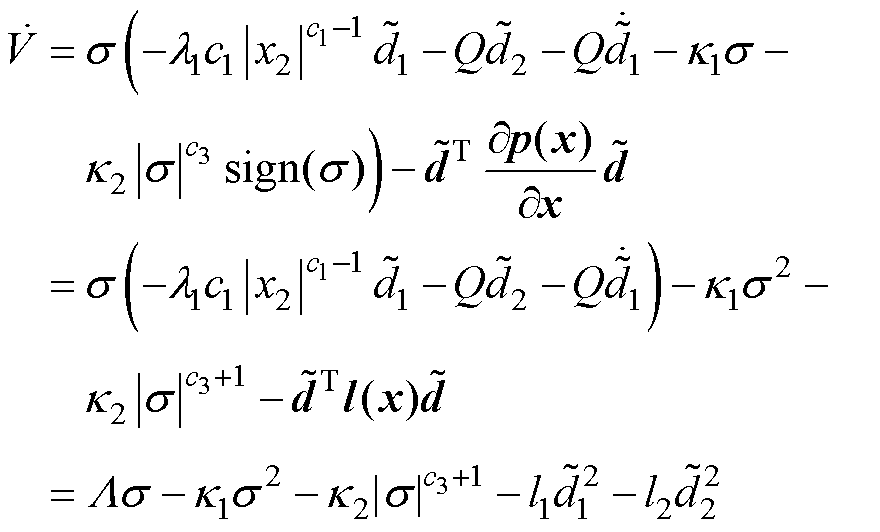 (16)
(16)
其中
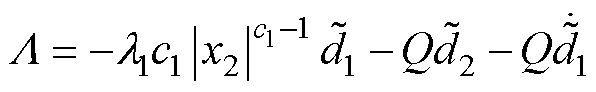
式(16)可以重新表述为
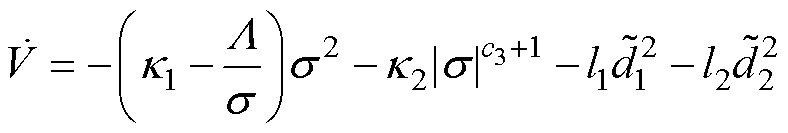 (17)
(17)
则可以得到
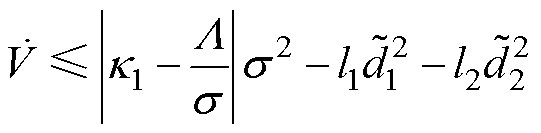 (18)
(18)
由假设1和假设2可知,存在正常数L1、L2,使得
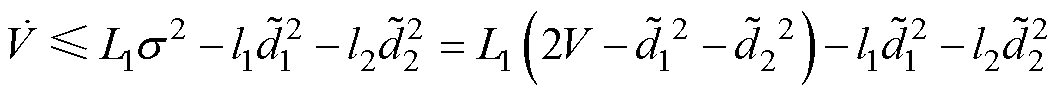
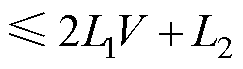 (19)
(19)
其中
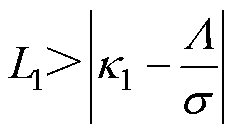
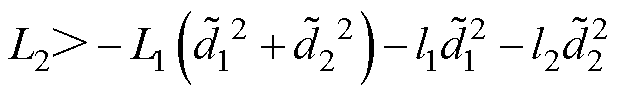
根据文献[24]可知,李雅普诺夫函数V、滑模面 和观测误差
和观测误差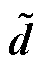 是渐进收敛的,因此,具有HNFTSMC- NDO控制律式(12)的系统式(3)在有限时间内稳定。收敛性分析见附录。
是渐进收敛的,因此,具有HNFTSMC- NDO控制律式(12)的系统式(3)在有限时间内稳定。收敛性分析见附录。
系统控制原理框图如图3所示。
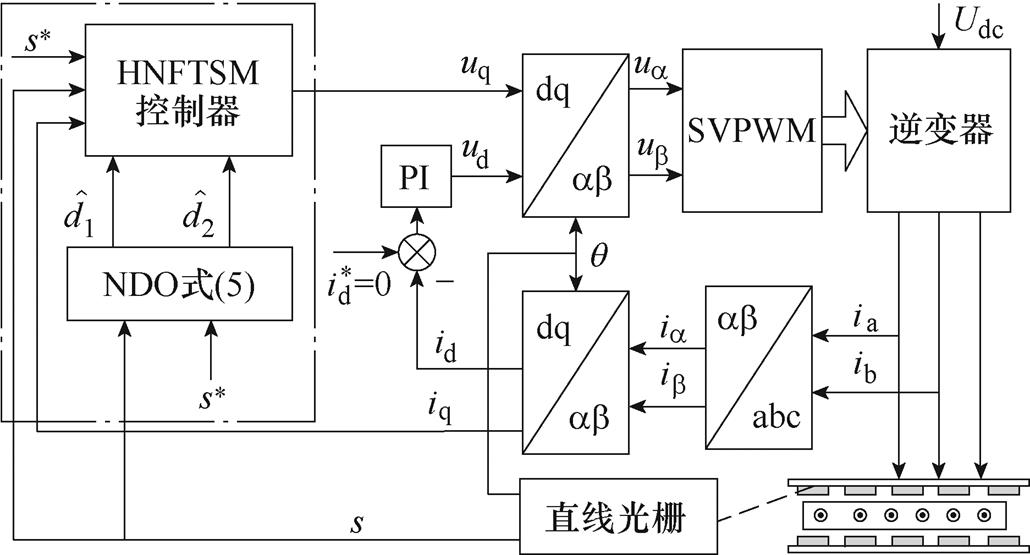
图3 系统控制原理框图
Fig.3 Block diagram of the control scheme
为验证所提控制方法的可行性,利用实验平台予以验证,图4为系统实验平台,图5为实验系统控制框图,系统主要由cSPACE控制平台、计算机、DSP控制卡、PMLSM、光栅编码器、直线电机驱动器组成。使用Matlab/Simulink软件搭建控制算法。将输入、输出接口替换为cSPACE模块,编译整个模块自动生成DSP代码,在控制卡上运行后生成相应的控制信号。在实验过程中通过限制电压的幅值,对电流进行限幅控制。运行过程中通过cSPACE提供的Matlab接口模块,可实时修改控制参数,能够简单高效地实现控制算法对直线电机的实时控制。DSP采集的数据可以保存到硬盘,利用Origin软件完成图形化显示,PMLSM参数见表1。

图4 PMLSM系统实验平台
Fig.4 Experimental platform of PMLSM
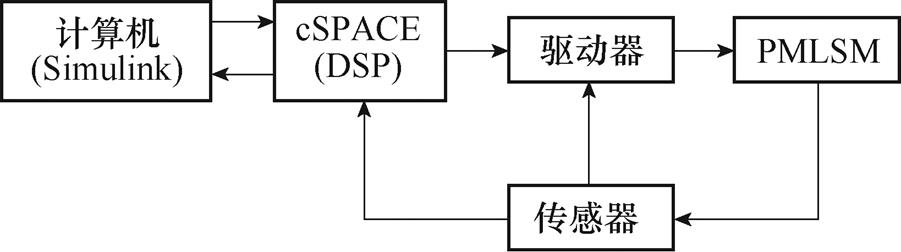
图5 实验系统控制框图
Fig.5 Control block diagram of experimental system
表1 PMLSM参数
Tab.1 Parameters of the PMLSM
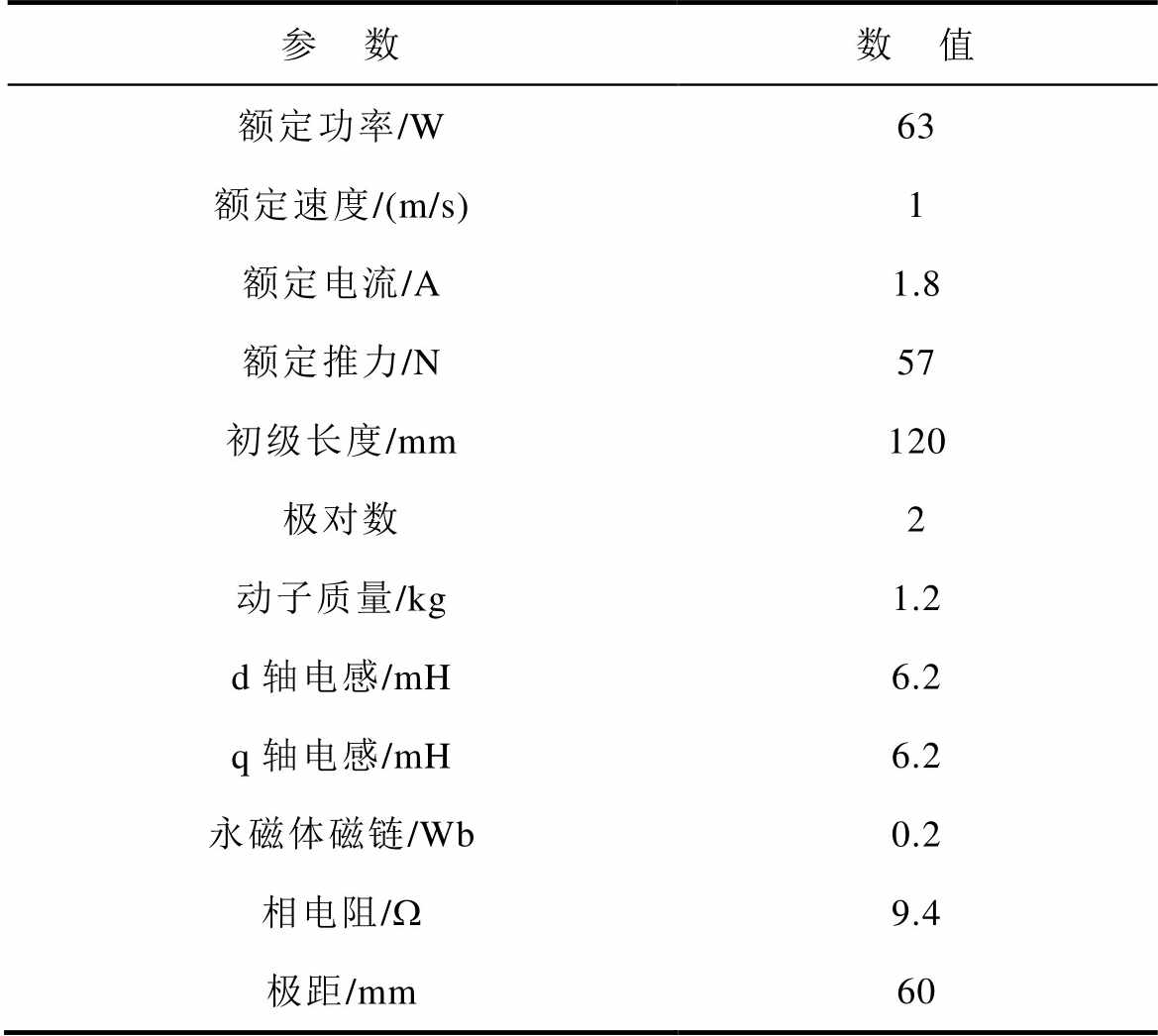
参 数数 值 额定功率/W63 额定速度/(m/s)1 额定电流/A1.8 额定推力/N57 初级长度/mm120 极对数2 动子质量/kg1.2 d轴电感/mH6.2 q轴电感/mH6.2 永磁体磁链/Wb0.2 相电阻/W9.4 极距/mm60
HNFTSMC-NDO控制器参数取:c0=1.52,c1=1.29,c2=0.78,c3=0.78,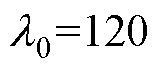 ,
,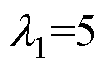 ,
,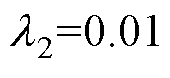 ,
,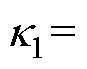
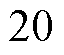 ,
,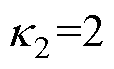 ,l=diag(5, 5)。NFTSMC控制器参数取:c0= 1.5,c1=1.29,c3=0.78,
,l=diag(5, 5)。NFTSMC控制器参数取:c0= 1.5,c1=1.29,c3=0.78,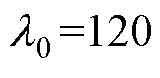 ,
,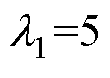 ,
,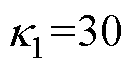 ,
,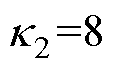 。
。
为研究PMLSM伺服系统的位置跟踪性能,设计余弦和三角波两种波形的位置参考指令,并分别在空载和载荷3kg(质量的变化会引起摩擦阻力的变化,表征系统不匹配扰动)时对伺服系统进行实验测试,且控制器中调整电阻为1.5Rs,电感为1.5Ld/Lq用于模拟系统参数变化(表征系统匹配扰动)。采用阶跃位置信号验证所采用的控制方法的动态性能。首先,对所提出的HNFTSMC-NDO系统进行了验证;随后,在无NDO的情况下,对HNFTSMC系统进行实验;然后,为验证本文方法在提高位置跟踪精度方面的优越性,与NFTSMC方法进行对比实验。
使用所提出的HNFTSMC-NDO、HNFTSMC和NFTSMC在如图6所示余弦给定指令下进行的实验结果如图7~图12所示。图7中,HNFTSMC-NDO方法的跟踪误差范围为-5.09~5.54mm、HNFTSMC的跟踪误差为-10.29~11.38mm、NFTSMC误差为-16.08~18.65mm,当运动方向改变时,跟踪性能明显变差,这是因为速度方向变化时瞬时速度接近零,放大了摩擦力模型中未建模部分对控制系统的影响,可知本文采用的HNFTSMC-NDO控制策略在速度方向改变时表现出更好的鲁棒性。图8为三种控制方法的速度误差曲线,为保证系统的稳定性,趋近律中切换控制增益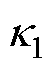 和
和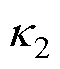 取值较大,造成HNFTSMC和NFTSMC方法中的速度误差存在明显的波动。在HNFTSMC-NDO中,利用非线性扰动观测器对系统匹配和不匹配扰动进行估计,并对系统进行动态补偿,因此增益
取值较大,造成HNFTSMC和NFTSMC方法中的速度误差存在明显的波动。在HNFTSMC-NDO中,利用非线性扰动观测器对系统匹配和不匹配扰动进行估计,并对系统进行动态补偿,因此增益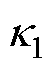 和
和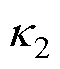 取值较小,波动现象得到抑制。图9为空载时三种控制方法的电流曲线,可以明显看出,HNFTSMC-NDO控制方法的电流曲线最平滑,考虑到相应的跟踪误差,即当参考信号变化时,可及时调整控制律,以保证高精度的跟踪。可见,HNFTSMC-NDO控制方法无论在跟踪精度还是在响应速度方面均优于HNFTSMC和NFTSMC。图10为负载时三种控制方法的误差跟踪曲线,其中HNFTSMC-NDO方法的跟踪误差范围为-6.28~6.85mm、HNFTSMC跟踪误差为-13.38~14.08mm、NFTSMC误差为-21.89~22.88mm。对比图7中的位置跟踪误差,显然无论是空载还是负载条件下,HNFTSMC-NDO方法的位置跟踪误差均为最小,负载时HNFTSMC和NFTSMC的误差增量更大。由于非线性扰动观测器的存在,所提出的HNFTSMC-NDO受负载的影响较小,能够始终保持较好的控制性能,且对施加负载具有较强的鲁棒性。图11为三种控制方法的速度误差曲线,可见负载时HNFTSMC-NDO速度误差波动程度最小。图12为负载时电流曲线,HNFTSMC- NDO方法通过平稳的输入就能保证系统跟踪精度,能最大程度减小外加负载影响。
取值较小,波动现象得到抑制。图9为空载时三种控制方法的电流曲线,可以明显看出,HNFTSMC-NDO控制方法的电流曲线最平滑,考虑到相应的跟踪误差,即当参考信号变化时,可及时调整控制律,以保证高精度的跟踪。可见,HNFTSMC-NDO控制方法无论在跟踪精度还是在响应速度方面均优于HNFTSMC和NFTSMC。图10为负载时三种控制方法的误差跟踪曲线,其中HNFTSMC-NDO方法的跟踪误差范围为-6.28~6.85mm、HNFTSMC跟踪误差为-13.38~14.08mm、NFTSMC误差为-21.89~22.88mm。对比图7中的位置跟踪误差,显然无论是空载还是负载条件下,HNFTSMC-NDO方法的位置跟踪误差均为最小,负载时HNFTSMC和NFTSMC的误差增量更大。由于非线性扰动观测器的存在,所提出的HNFTSMC-NDO受负载的影响较小,能够始终保持较好的控制性能,且对施加负载具有较强的鲁棒性。图11为三种控制方法的速度误差曲线,可见负载时HNFTSMC-NDO速度误差波动程度最小。图12为负载时电流曲线,HNFTSMC- NDO方法通过平稳的输入就能保证系统跟踪精度,能最大程度减小外加负载影响。
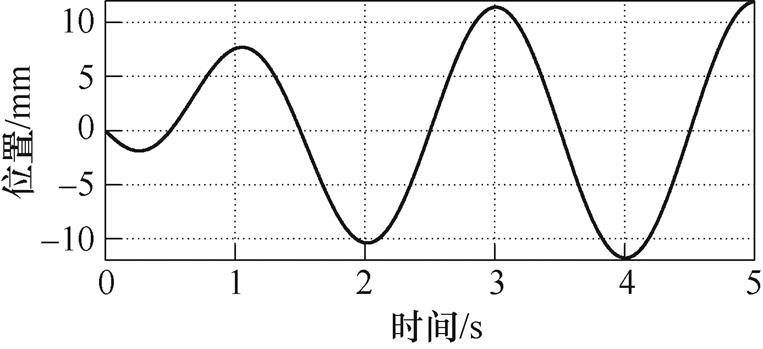
图6 给定位置曲线(余弦)
Fig.6 Tracking reference curve (cosine)
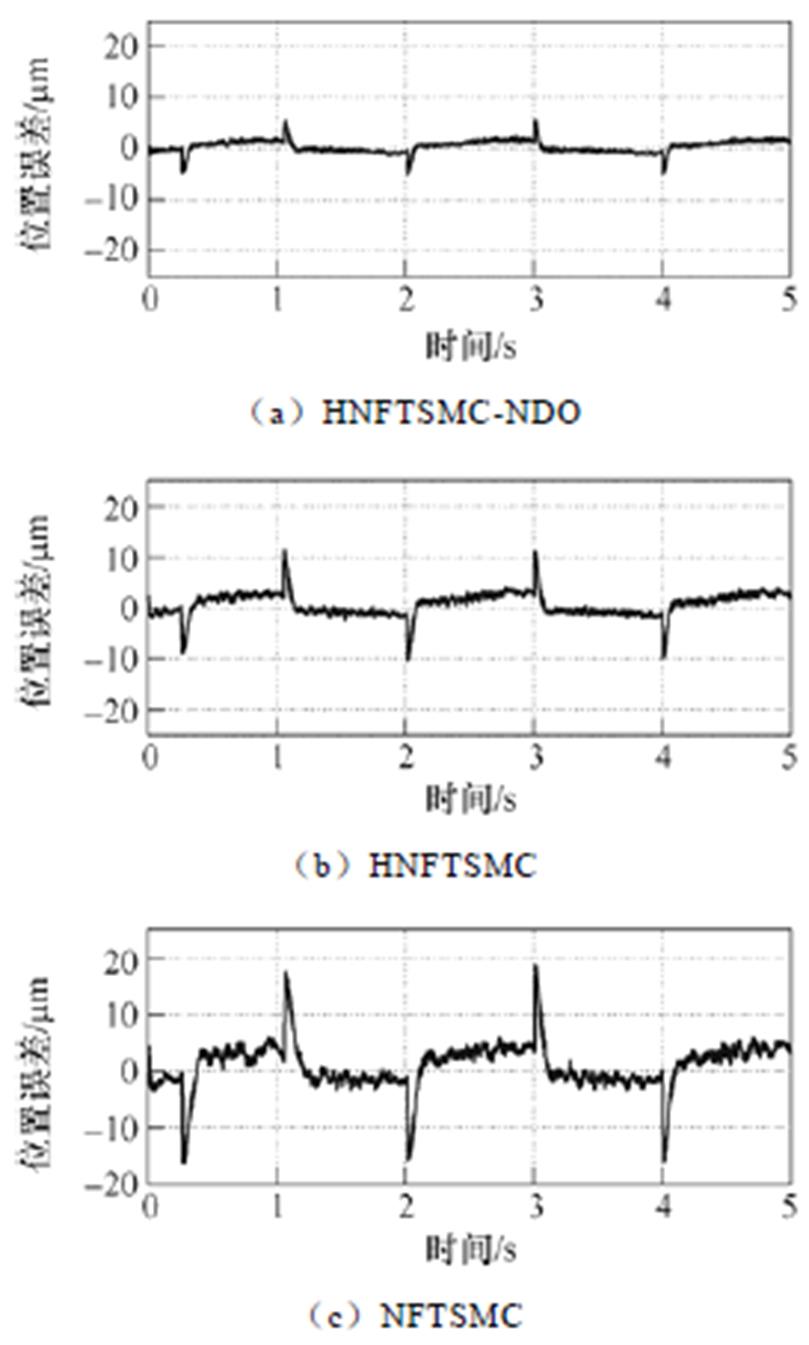
图7 空载下系统位置误差曲线(余弦)
Fig.7 Position error curves under no load (cosine)
使用HNFTSMC-NDO、HNFTSMC和NFTSMC在如图13所示三角波参考指令下进行的实验结果如图14~图19所示。由图14可知,三种方法的跟踪误差分别在-4.43~4.53mm、-6.97~10.25mm、-14.35~14.16mm之内。图15分别为三种控制方法的速度跟踪误差,由于扰动观测器的存在,HNFTSMC方法的速度误差波动幅度较其他两种方法小。图16为电流曲线,HNFTSMC和NFTSMC方法的电流曲线产生严重波动。负载时位置跟踪曲线如图17所示,三种方法跟踪误差曲线范围分别在-5.62~5.03mm、-10.44~14.35mm、-16.45~16.80mm之内。图18和图19分别为速度误差曲线和负载电流曲线,由图可知,其特点与余弦指令跟踪响应类似,无论在负载还是空载条件下,HNFTSMC- NDO的性能均优于HNFTSMC和NFTSMC。这也表明,HNFTSMC-NDO能够对不同类型的指令保持较好跟踪性能和鲁棒性。进一步验证了所提出控制方法的优越性,与HNFTSMC和NFTSMC相比,所提出的HNFTSMC-NDO不仅在整个跟踪过程中获得了最佳的控制精度和鲁棒性,而且削弱了抖振现象。
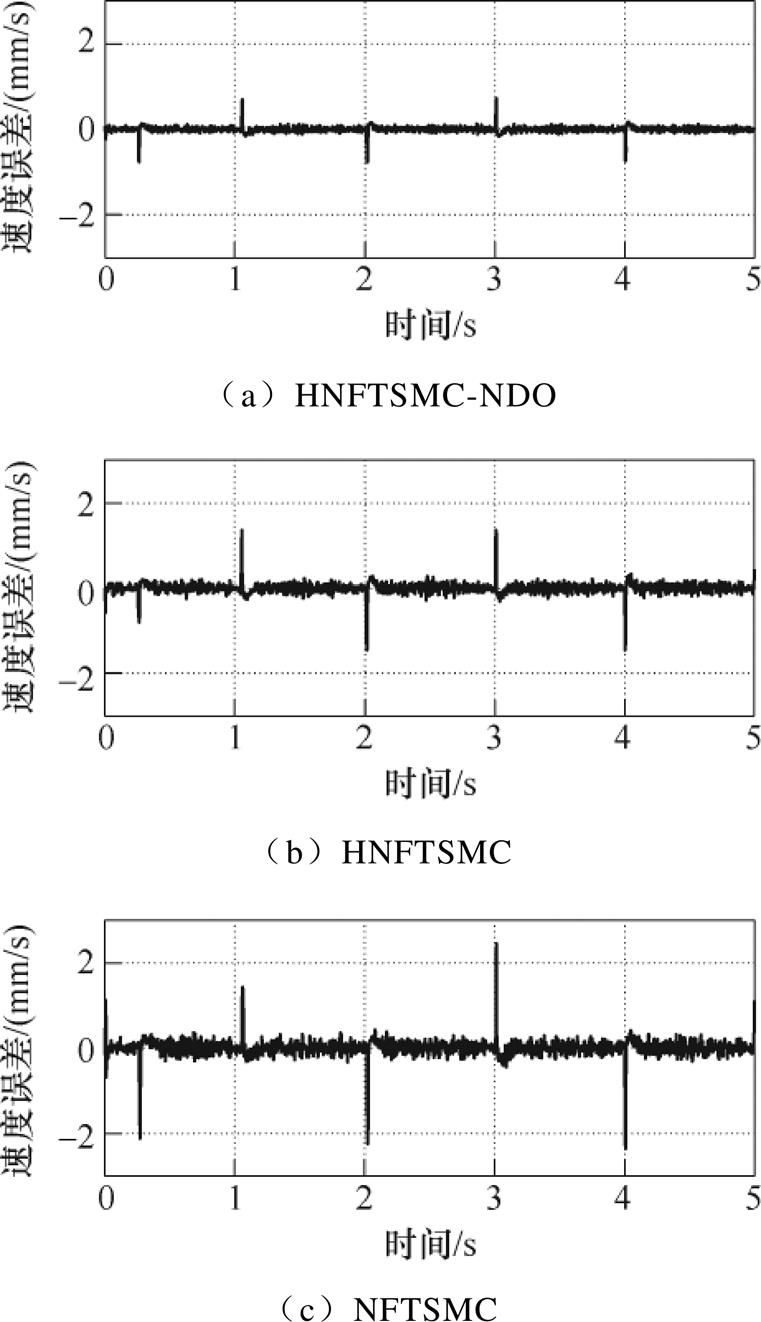
图8 空载下系统速度误差曲线(余弦)
Fig.8 Speed error curves under no load (cosine)
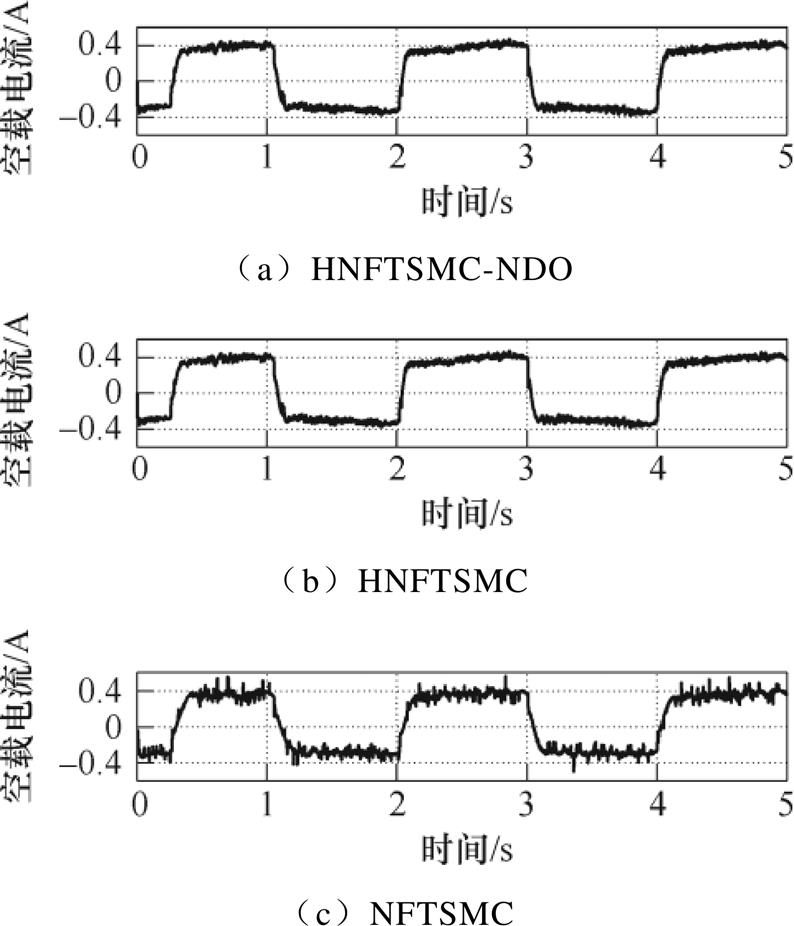
图9 空载电流曲线(余弦)
Fig.9 Current curves of no-load (cosine)
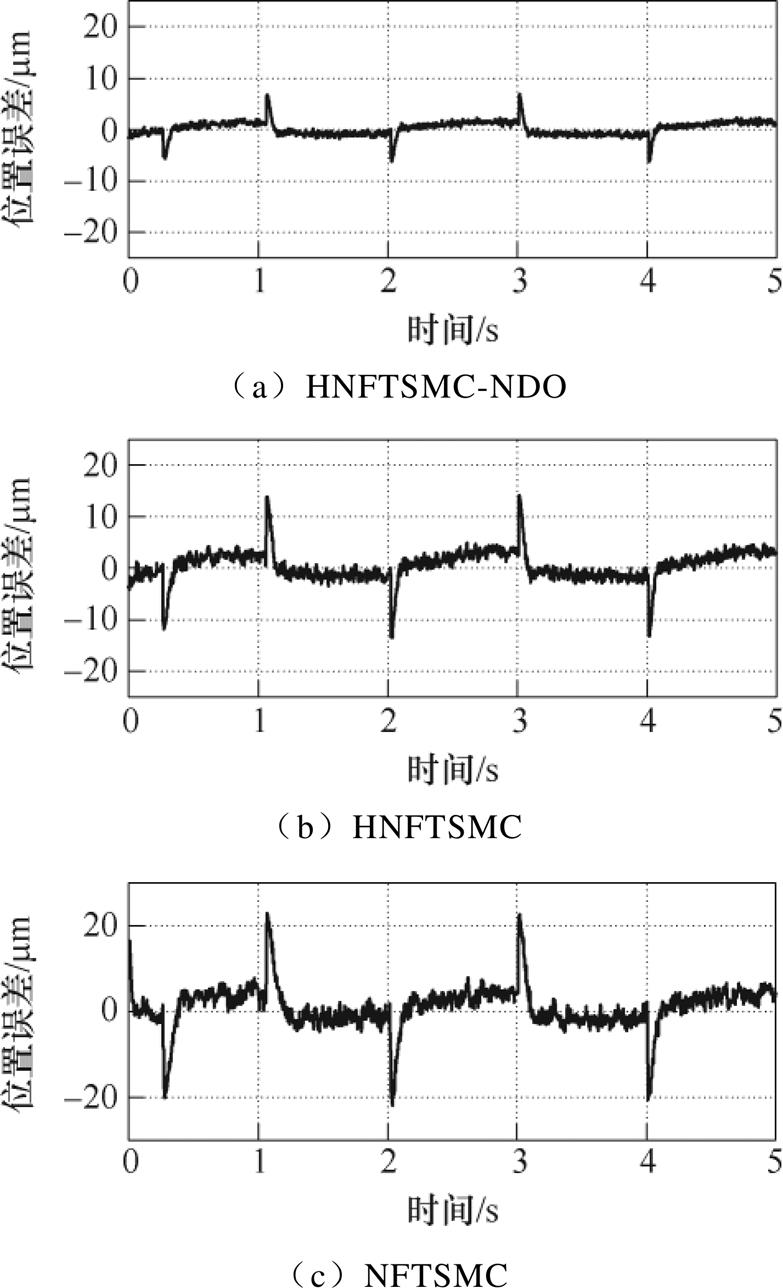
图10 负载下系统位置误差曲线(余弦)
Fig.10 Position error curves under load (cosine)
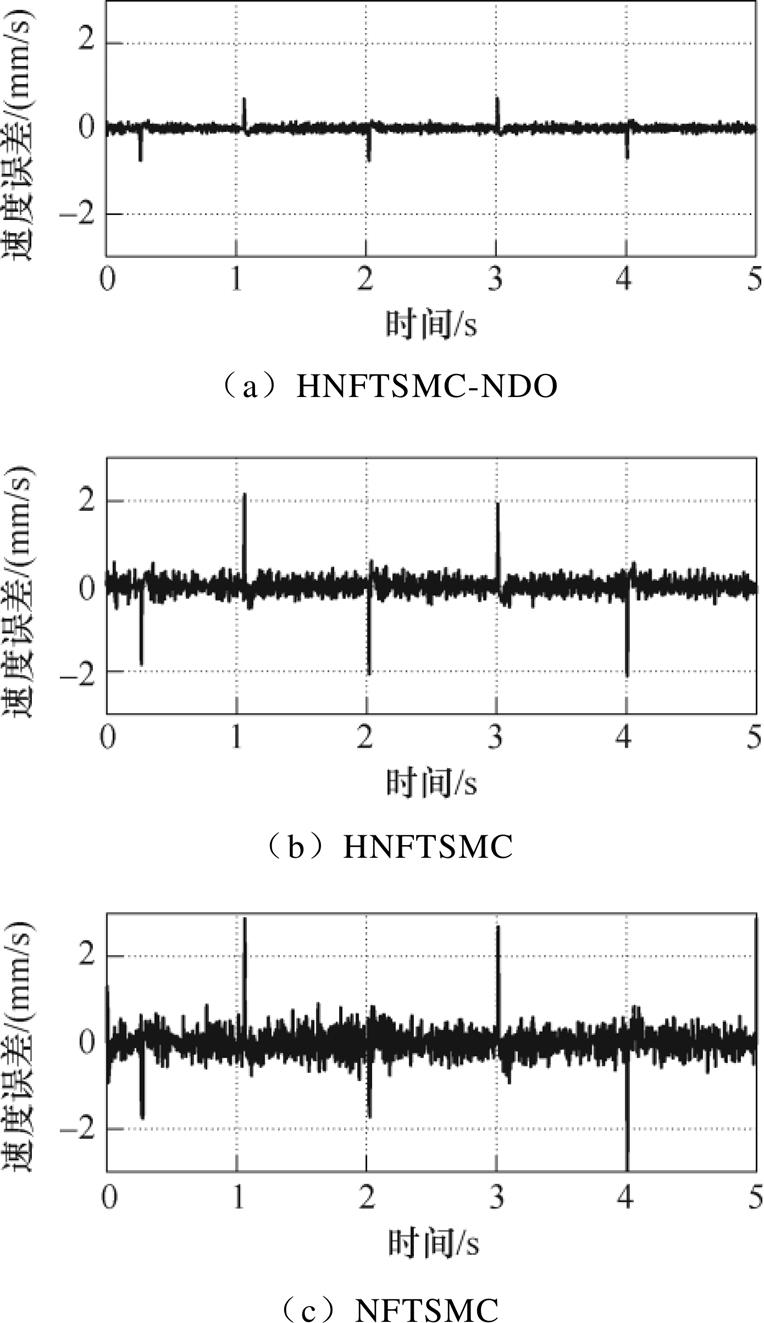
图11 负载下系统速度误差曲线(余弦)
Fig.11 Speed error curves under load (cosine)

图12 负载电流曲线(余弦)
Fig.12 Current curves under load (cosine)
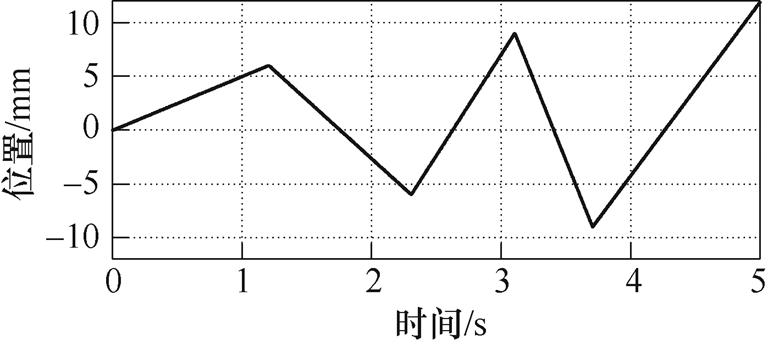
图13 给定位置曲线(三角)
Fig.13 Tracking reference curve (triangle)
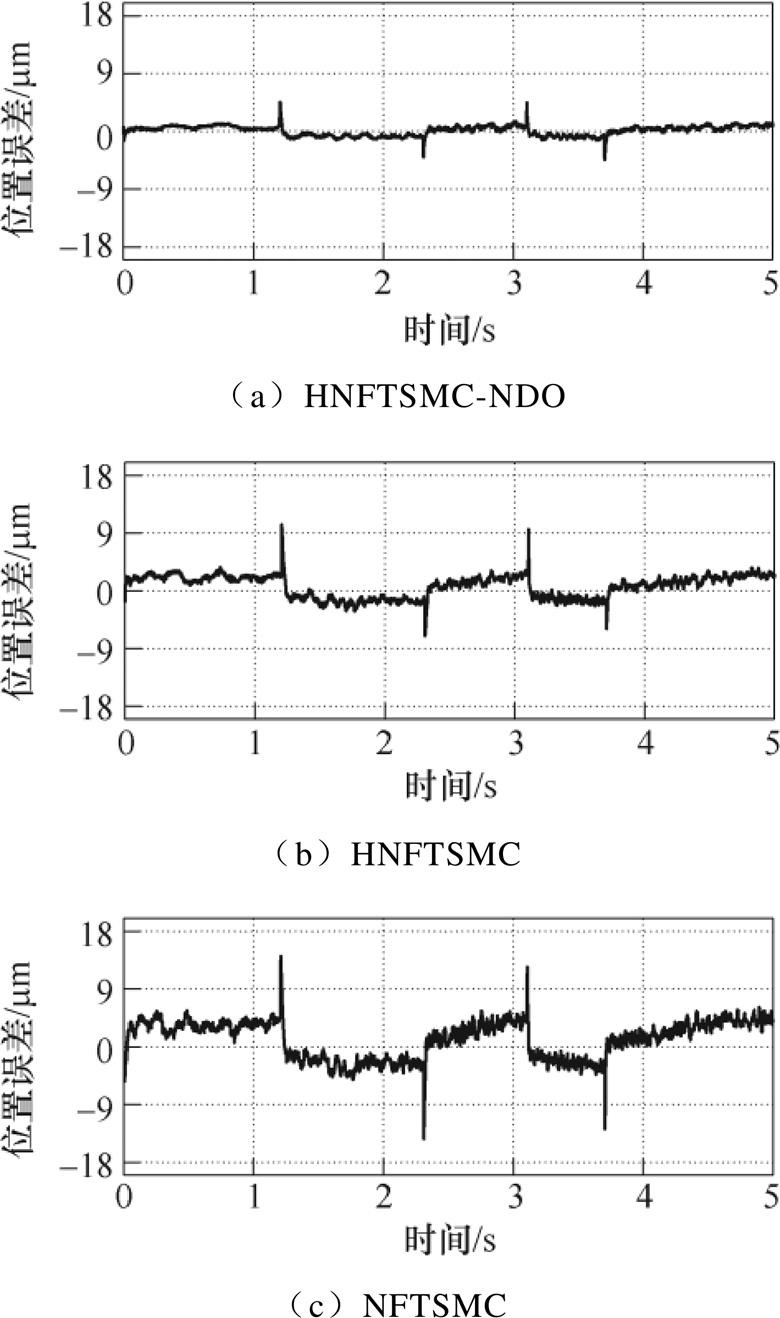
图14 空载下系统位置误差曲线(三角)
Fig.14 Position error curves of no load (triangle)
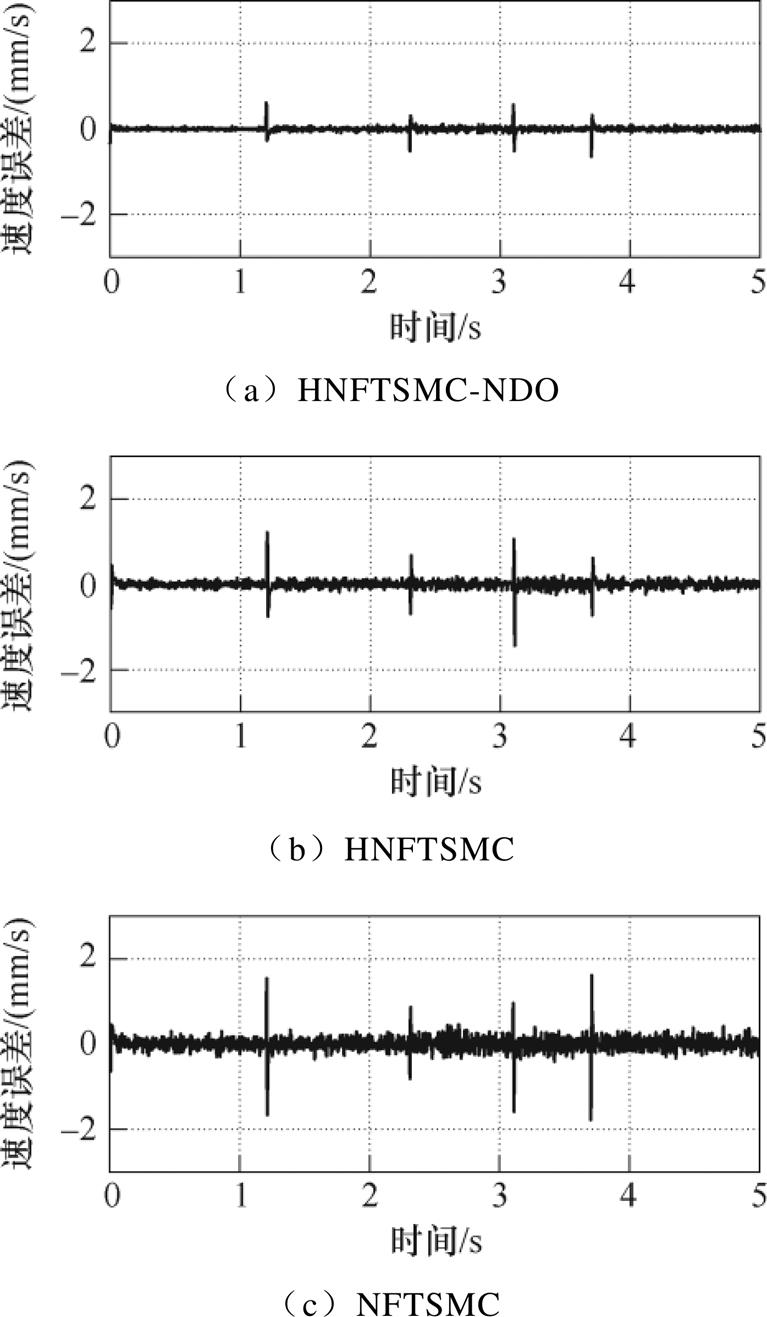
图15 空载下系统速度误差曲线(三角)
Fig.15 Speed error curves of no load (triangle)
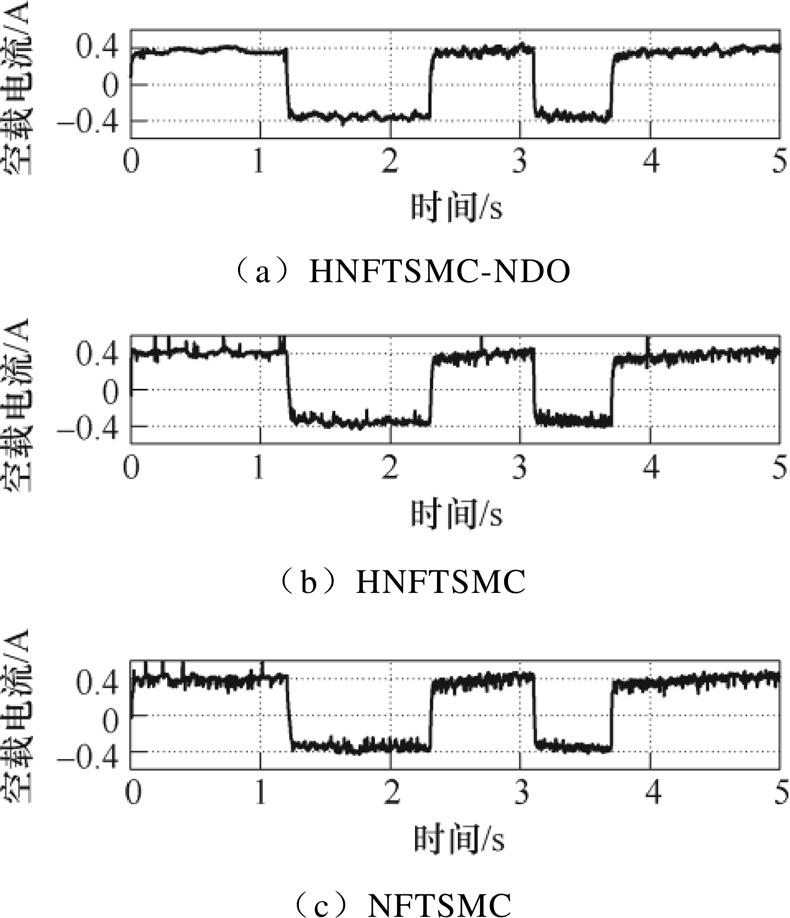
图16 空载电流曲线(三角)
Fig.16 Current curves of no-load (triangle)
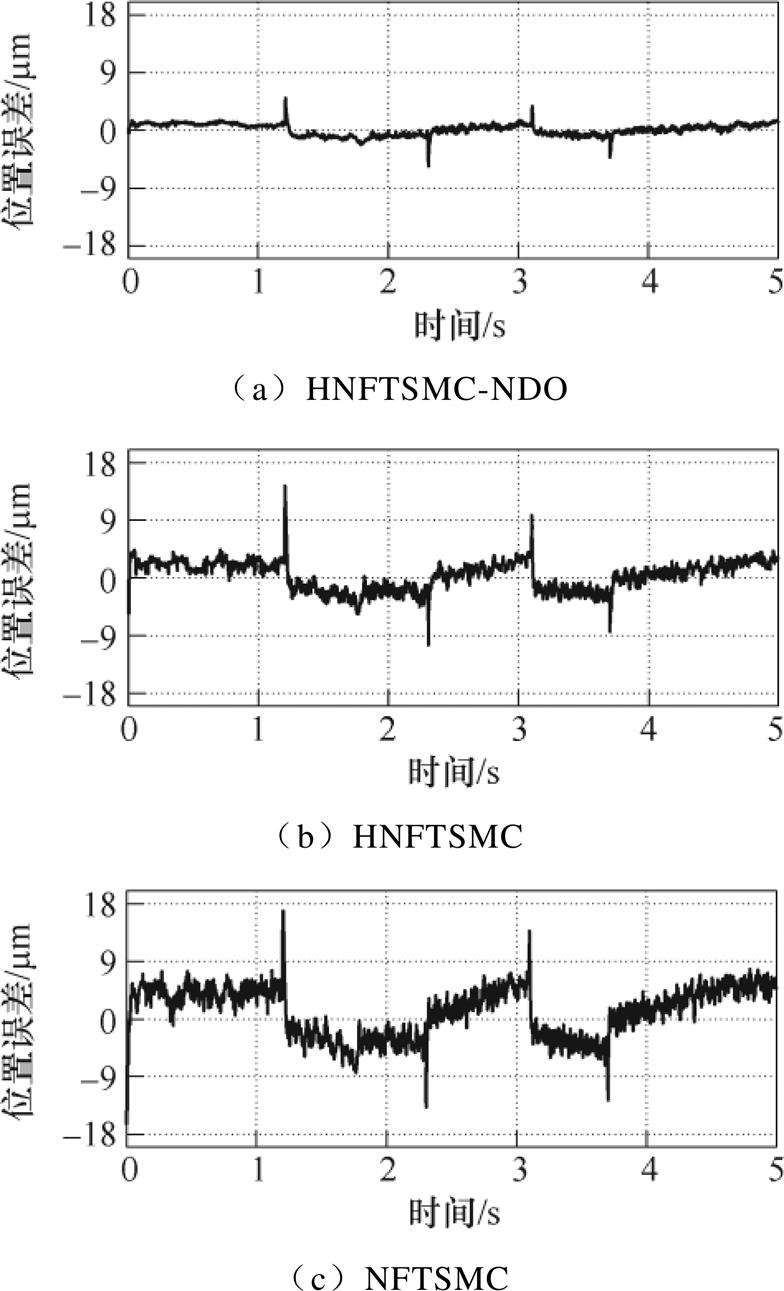
图17 负载下系统位置误差曲线(三角)
Fig.17 Position error curves under load (triangle)
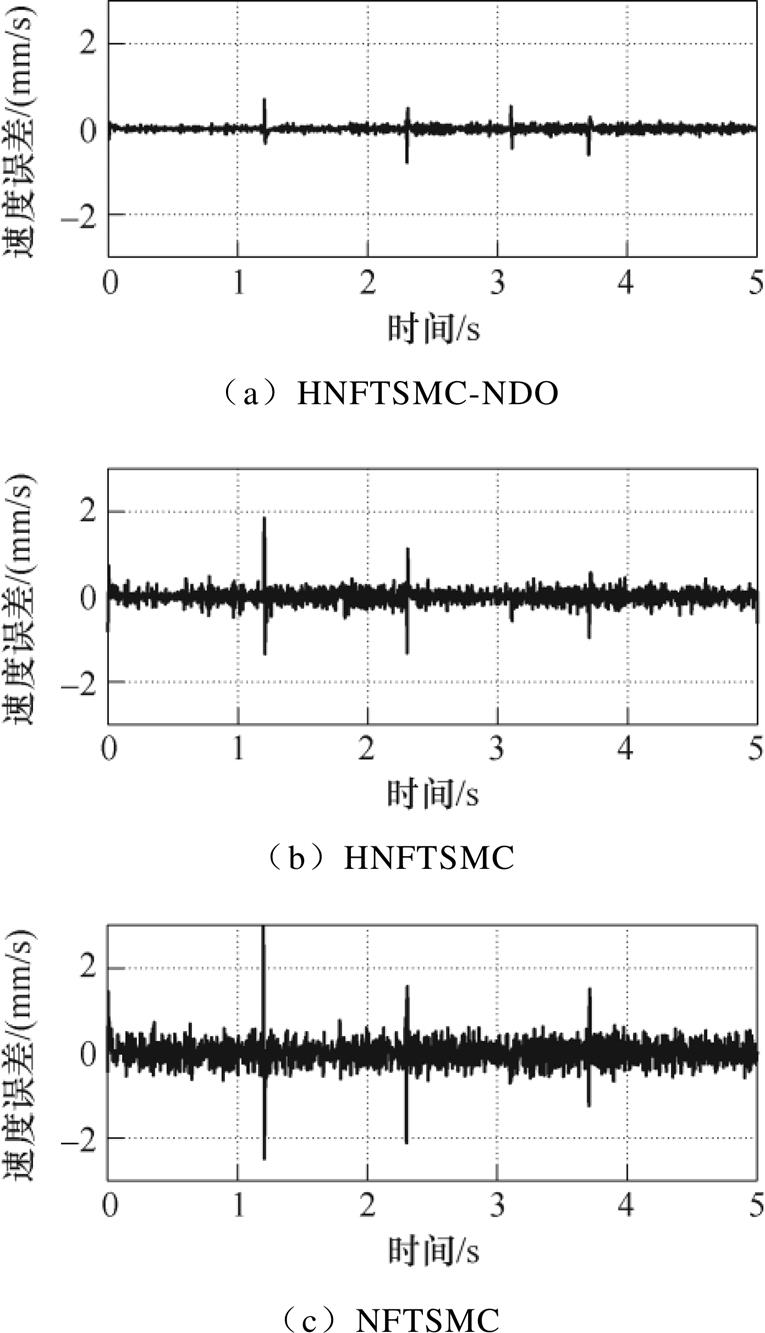
图18 负载下系统速度误差曲线(三角)
Fig.18 Speed error curves under load (triangle)
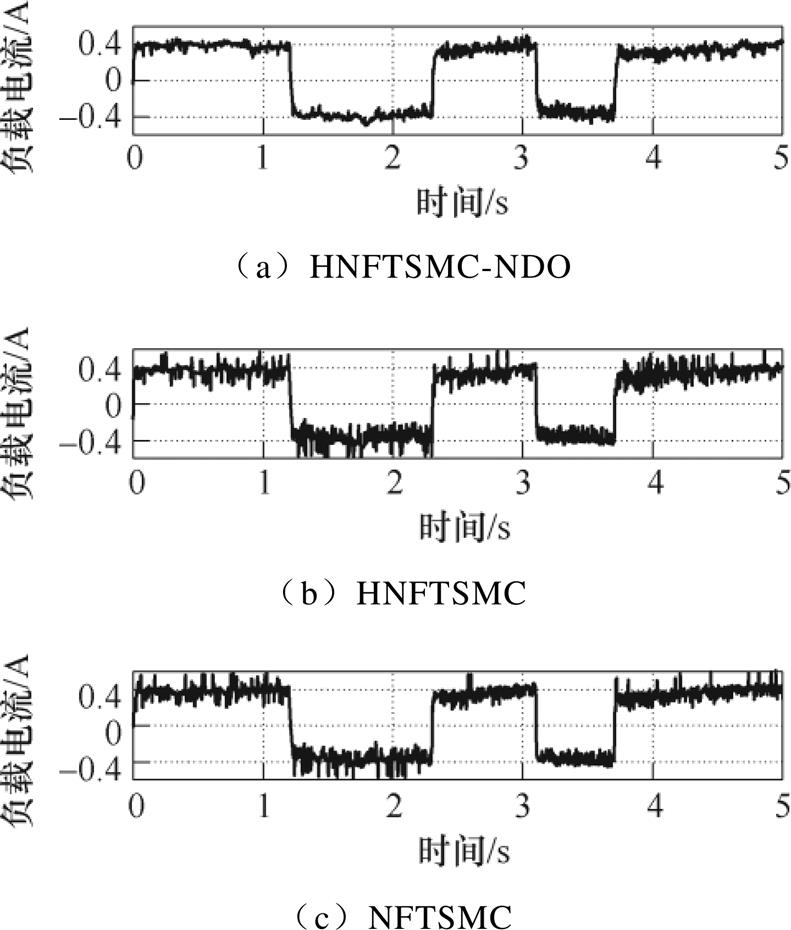
图19 负载电流曲线(三角)
Fig.19 Current curves under load (triangle)
当期望位置为阶跃信号(幅值5mm),并在0.25s突加10N负载时的位置响应曲线如图20所示。由图20a可以看出,在初始阶段NFTSMC响应速度较慢,且抖振严重,HNFTSMC能够提高响应速度,但是抖振现象依然存在,由于HNFTSMC-NDO的强鲁棒性和扰动观测器的动态补偿,使得系统的响应速度和抖振程度均得到改善。在0.25s时负载突变使得三种控制系统的位置均出现骤降,但在波动幅值和恢复时间上,HNFTSMC-NDO系统(0.11mm、0.013s)与HNFTSMC系统(0.2mm、0.014s)和NFTSMC系统(0.31mm、0.021s)相比均有减小,验证了所提出的控制策略对不匹配扰动具有较强鲁棒性。图20b、图20c所示分别为在突加负载前后的非匹配和匹配扰动(对应电压)观测波形。由图可知,NDO能够快速地估计负载变化和参数摄动引起的扰动,证明了观测器的有效性。但是,在本文中由于导轨长度的限制,直线电机不能设定到额定速度,否则会因运动太快无法达到单程的稳定状态,且频繁改变动子运动方向引起的振动也为系统带来了新的控制问题。因此所提出的控制策略在额定工况下的对比实验值得进一步研究。
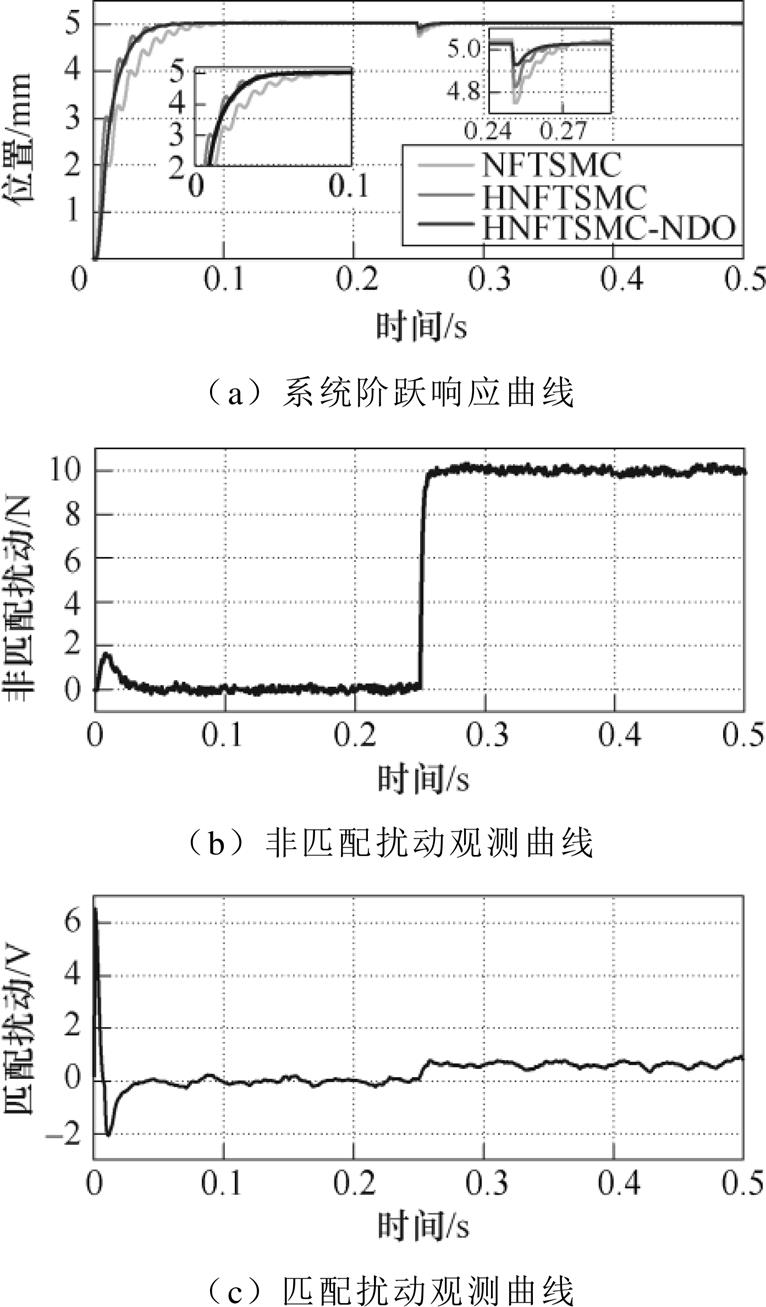
图20 阶跃指令下系统实验曲线
Fig.20 Experimental curves of the system with step reference
本文以PMLSM为研究对象,提出非线性扰动观测器与HNFTSMC相结合的控制策略,用于直线电机伺服系统控制。通过实验验证了该方案的正确性,并得到以下结论:
1)本文以位置误差、速度误差和反馈电流为状态量,同时考虑不匹配/匹配扰动的影响构建了PMLSM数学模型。
2)在此模型基础上,采用非线性扰动观测器,对不匹配/匹配扰动进行估计,降低系统对多重扰动的保守性,并削弱滑模控制中的抖振问题。
3)通过在滑模面中引入系统扰动值和反馈q轴电流,设计HNFTSMC-NDO,实现位置、速度、加速度(电流)整体控制,能有效改善直线电机伺服系统的动态和稳态性能以及抑制扰动的性能。
附 录
当观测误差收敛到有界常数时,式(15)可以表示为
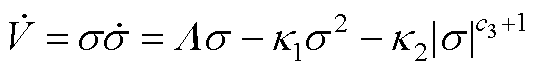 (A1)
(A1)
且式(A1)可以分为两种不同的情况。
情况1:将式(A1)改写为
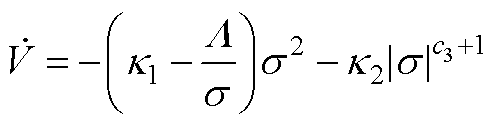 (A2)
(A2)
当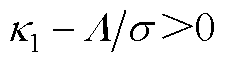 时,总存在两个正常数
时,总存在两个正常数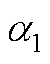 、
、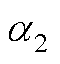 ,使得
,使得
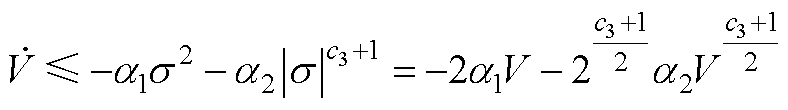 (A3)
(A3)
求解上述不等式,可得系统状态收敛时间tr为
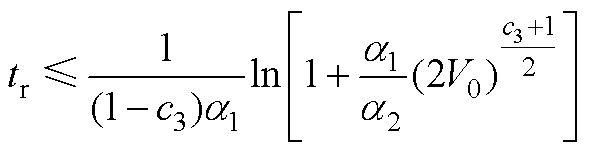 (A4)
(A4)
为了保证系统在有限时间tr内的稳定性,需要获得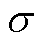 的收敛域,即
的收敛域,即
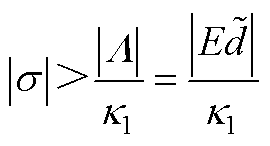 (A5)
(A5)
由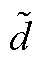 的边界
的边界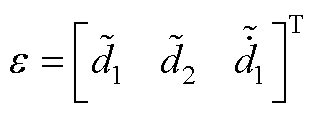 ,可得
,可得
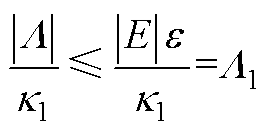 (A6)
(A6)
因此,当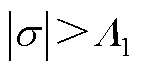 时,将确保
时,将确保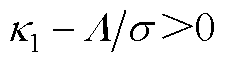 。则滑模面
。则滑模面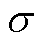 可以在有限的时间tr内到达以下区域
可以在有限的时间tr内到达以下区域
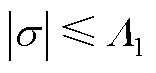 (A7)
(A7)
情况2:也可以将式(A1)改写为
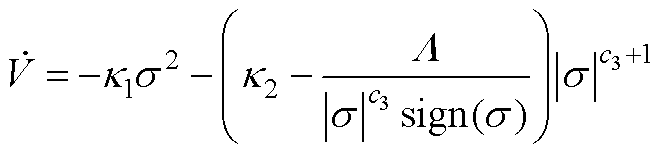 (A8)
(A8)
采用相同分析方法可得到收敛域的另一种表达方式为
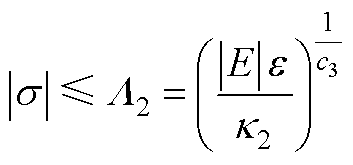 (A9)
(A9)
综上,系统状态轨迹将在有限时间内到达滑模面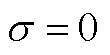 的一个邻域
的一个邻域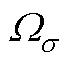 ,有
,有
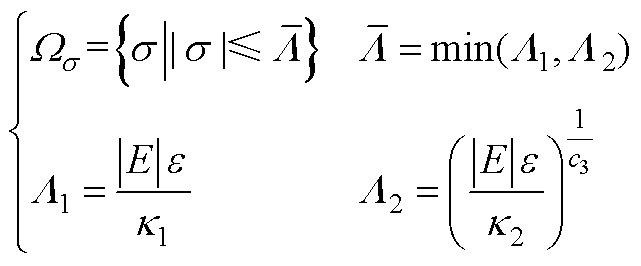 (A10)
(A10)
为了证明系统状态的收敛性,式(10)可重新表示为
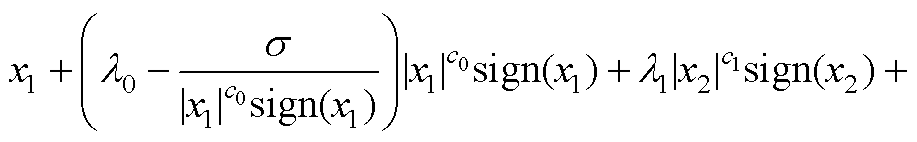
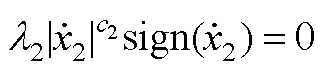 (A11)
(A11)
因此,当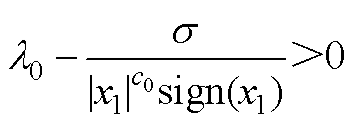 时,系统状态x1(位置误差)的收敛域为
时,系统状态x1(位置误差)的收敛域为
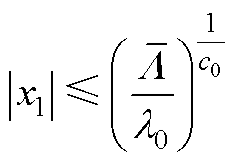 (A12)
(A12)
同理,式(10)也可重新表示为
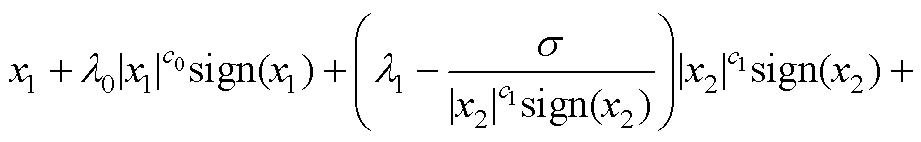
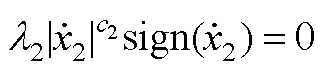 (A13)
(A13)
因此,在有限时间内,状态x2(速度误差)的收敛域为
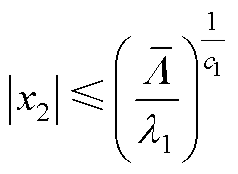 (A14)
(A14)
与上述两种情况类似,当式(10)表示为
 (A15)
(A15)
可知,系统状态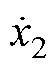 (加速度误差)的收敛域为
(加速度误差)的收敛域为
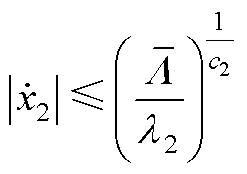 (A16)
(A16)
因此,系统状态将在有限时间内快速收敛到以下区域
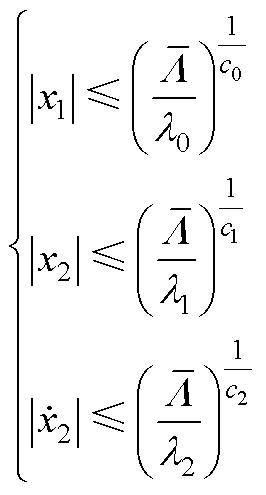 (A17)
(A17)
参考文献
[1] 凌志健, 赵文祥, 吉敬华. 高推力永磁直线作动器及其关键技术综述[J]. 电工技术学报, 2020, 35(5): 1022-1035.
Ling Zhijian, Zhao Wenxiang, Ji Jinghua. Overview of high force density permanent magnet linear actuator and its key technology[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1022- 1035.
[2] Zhang Kang, Wang Limei, Fang Xin. High-order fast nonsingular terminal sliding mode control of per- manent magnet linear motor based on double dis- turbance observer[J]. IEEE Transactions on Industry Applications, 2022, 58(3): 3696-3705.
[3] 李争, 安金峰, 肖宇, 等. 基于自适应观测器的永磁同步直线电机模型预测控制系统设计[J]. 电工技术学报, 2021, 36(6): 1190-1200.
Li Zheng, An Jinfeng, Xiao Yu, et al. Design of model predictive control system for permanent magnet synchronous linear motor based on adaptive observer[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1190-1200.
[4] 王立俊, 赵吉文, 董菲, 等. 基于自适应内模观测器的永磁同步直线电机高带宽强鲁棒预测电流控制策略研究[J]. 中国电机工程学报, 2019, 39(10): 3098-3107.
Wang Lijun, Zhao Jiwen, Dong Fei, et al. High- bandwidth and strong robust predictive current control strategy research for permanent-magnet synchronous linear motor based on adaptive internal model observer[J]. Proceedings of the CSEE, 2019, 39(10): 3098-3107.
[5] Sun Guanghui, Ma Zhiqiang, Yu Jinyong. Discrete- time fractional order terminal sliding mode tracking control for linear motor[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3386-3394.
[6] 付东学, 赵希梅. 永磁直线同步电机自适应反推全局快速终端滑模控制[J]. 电工技术学报, 2020, 35(8): 1634-1641.
Fu Dongxue, Zhao Ximei. Adaptive backstepping global fast terminal sliding mode control for per- manent magnet linear synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(8): 1634-1641.
[7] 曹荣敏, 郑鑫鑫, 侯忠生. 基于改进多入多出无模型自适应控制的二维直线电机迭代学习控制[J]. 电工技术学报, 2021, 36(19): 4025-4034.
Cao Rongmin, Zheng Xinxin, Hou Zhongsheng. An iterative learning control based on improved multiple input and multiple output model free adaptive control for two-dimensional linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4025- 4034.
[8] 刘川, 朱非甲, 马伟, 等. 直线电机的线性自抗扰控制[J]. 电机与控制学报, 2013, 17(1): 71-76.
Liu Chuan, Zhu Feijia, Ma Wei, et al. Research on linear active disturbance rejection control over linear motor[J]. Electric Machines and Control, 2013, 17(1): 71-76.
[9] Shao Ke, Zheng Jinchuan, Huang Kang, et al. Finite- time control of a linear motor positioner using adaptive recursive terminal sliding mode[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6659-6668.
[10] 余洋, 田夏, 从乐瑶, 等. 基于反推控制和模态估计的永磁同步电机驱动柔性涡簧储能控制方法[J]. 电工技术学报, 2019, 34(24): 5084-5094.
Yu Yang, Tian Xia, Cong Leyao, et al. Energy storage control method of flexible spiral springs driven by permanent magnet synchronous motor based on back- stepping control and modal estimation[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(24): 5084-5094.
[11] Butcher M, Karimi A. Linear parameter-varying iterative learning control with application to a linear motor system[J]. IEEE/ASME Transactions on Mechatronics, 2010, 15(3): 412-420.
[12] Junejo A K, Xu Wei, Mu Chaoxu, et al. Adaptive speed control of PMSM drive system based a new sliding-mode reaching law[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12110-12121.
[13] Chen S Y, Chiang H H, Liu T S, et al. Precision motion control of permanent magnet linear syn- chronous motors using adaptive fuzzy fractional-order sliding-mode control[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 741-752.
[14] 成瑀, 赵文祥, 吉敬华, 等. 直线永磁游标电机的开绕组单位功率因数直接推力控制[J]. 中国电机工程学报, 2019, 39(7): 1870-1878.
Cheng Yu, Zhao Wenxiang, Ji Jinghua, et al. Unity power factor direct thrust force control of linear permanent-magnet vernier motor fed by dual inverter[J]. Proceedings of the CSEE, 2019, 39(7): 1870-1878.
[15] Chaudhari S, Shendge P D, Phadke S B. Disturbance observer based controller under noisy measurement for tracking of nDOF uncertain mismatched nonlinear interconnected systems[J]. IEEE/ASME Transactions on Mechatronics, 2020, 25(3): 1600-1611.
[16] Aghababa M P. Sliding-mode control composite with disturbance observer for tracking control of misma- tched uncertain nDoF nonlinear systems[J]. IEEE/ ASME Transactions on Mechatronics, 2018, 23(1): 482-490.
[17] 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024.
Zhang Kang, Wang Limei. Adaptive dynamic sliding mode control of permanent magnet linear syn- chronous motor based on feedback linearization[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4016-4024.
[18] 周华伟, 于晓东, 高猛虎, 等. 基于不匹配干扰观测器的圆筒型永磁直线电机新型滑模速度控制[J]. 中国电机工程学报, 2018, 38(7): 2163-2170, 2231.
Zhou Huawei, Yu Xiaodong, Gao Menghu, et al. Novel sliding mode speed control for tubular permanent magnet linear motors based on mismatched disturbance observers[J]. Proceedings of the CSEE, 2018, 38(7): 2163-2170, 2231.
[19] Sun Guanghui, Ma Zhiqiang. Practical tracking control of linear motor with adaptive fractional order terminal sliding mode control[J]. IEEE/ASME Transa- ctions on Mechatronics, 2017, 22(6): 2643-2653.
[20] Qiao Jianzhong, Li Zhenxing, Xu Jianwei, et al. Composite nonsingular terminal sliding mode attitude controller for spacecraft with actuator dynamics under matched and mismatched disturbances[J]. IEEE Transactions on Industrial Informatics, 2020, 16(2): 1153-1162.
[21] Boldea I. Linear electric machines, drives, and MAGLEVs handbook[M]. Boca Raton: CRC, 2013.
[22] 刘旭东, 李珂, 张奇, 等. 基于非线性扰动观测器的永磁同步电机单环预测控制[J]. 中国电机工程学报, 2018, 38(7): 2153-2162, 2230.
Liu Xudong, Li Ke, Zhang Qi, et al. Single-loop predictive control of PMSM based on nonlinear disturbance observers[J]. Proceedings of the CSEE, 2018, 38(7): 2153-2162, 2230.
[23] Zheng Jinchuan, Wang Hai, Man Zhihong, et al. Robust motion control of a linear motor positioner using fast nonsingular terminal sliding mode[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(4): 1743-1752.
[24] Li Shihua, Tian Yuping. Finite-time stability of cascaded time-varying systems[J]. International Journal of Control, 2007, 80(4): 646-657.
High Order Nonsingular Fast Terminal Sliding Mode Control of Permanent Magnet Linear Motor Based on Disturbance Observer
Abstract Permanent magnet linear synchronous motor (PMLSM) has higher thrust density and lower heat loss. There are no mechanical coupling and ball screw problems, so it is widely used in the field of high-speed, high-precision CNC machining. Because the motor works in complex and changeable working environment such as model uncertainty, load disturbance, parameter perturbation. PMLSM system usually has a variety of matched/mismatched disturbances, and the problems of the rapidity and accuracy deterioration of position tracking are shown. To address these issues, a high order nonsingular fast terminal sliding mode control strategy based on disturbance observer is proposed in this paper.
Firstly, a PMLSM dynamic model including matched/unmatched disturbances is established. The dynamic model takes position error, velocity error and feedback current as state variables. Then, a nonlinear disturbance observer (NDO) is designed to observe matched/unmatched disturbances, thus reducing the conservatism of the system to multiple disturbances. Then, based on the PMLSM system model and observation disturbance, a high-order nonsingular fast terminal sliding mode controller (HNFTSMC) is designed. Its characteristic is that the acceleration error term is added to the sliding mode surface of the traditional nonsingular fast terminal to establish the connection between the sliding mode surface and the control voltage. Realize the overall control of motor position, speed and current, and improve the dynamic and stable performance of the position tracking system. On the one hand, nonlinear disturbance observer is used to weaken chattering of sliding mode control and enhance the ability to suppress mismatched disturbances. On the other hand, sliding mode control can effectively improve the robustness of the system to the disturbance observation error. The introduction of current and observation disturbances into the sliding mode surface can improve the dynamic performance of the system. Finally, the correctness and effectiveness of the proposed control strategy are verified by experiments.
Under no load condition, the tracking error of HNFTSMC-NDO method under cosine command is -5.09~5.54mm, the tracking error of HNFTSMC is -10.29~11.38mm, and the tracking error of NFTSMC is -16.08~18.65mm. Under load conditions, the tracking error of HNFTSMC-NDO method is -6.28~6.85mm, the error of HNFTSMC is -13.38~14.08mm, and the error of NFTSMC is -21.89~22.88mm. The tracking errors of the three methods under the triangle wave command at no load are respectively within 4.43~4.53mm, 6.97~10.25mm, and 14.35~14.16mm. The tracking error range of the three methods under load is 5.62~5.03mm, 10.44~14.35mm and 16.45~16.80mm respectively. When the command is a step signal, the sudden change of load makes the positions of the three control systems change suddenly, but in terms of fluctuation amplitude and recovery time, HNFTSMC-NDO (0.11mm, 0.013s), HNFTSMC (0.2mm, 0.014s) and NFTSMC (0.31mm, 0.021s). The above results show that HNFTSMC-NDO achieves better control accuracy and robustness in the tracking process.
The following conclusions can be drawn from the above analysis: ① In this paper, the position error, velocity error and feedback current are taken as state variables, and the influence of matched/mismatched disturbance is considered to construct the PMLSM mathematical model. ② A nonlinear disturbance observer is used to estimate the matched/mismatched disturbances, which provides an idea to reduce the conservatism of the system to multiple disturbances and weaken the chattering problem in sliding mode control. ③ By adding system disturbance value and feedback q axis current to the sliding mode surface, HNFTSMC-NDO is designed to achieve the overall control of position, speed and acceleration, which can effectively improve the dynamic and stable performance of the linear motor servo system and the performance of restraining disturbance.
Keywords:Permanent magnet linear synchronous motor, nonlinear disturbance observer, high order nonsingular fast terminal sliding mode control, matched/mismatched disturbances
中图分类号:TP273
DOI: 10.19595/j.cnki.1000-6753.tces.211779
国家自然科学基金资助项目(51875366)。
收稿日期 2021-11-03
改稿日期 2021-11-18
E-mail: fx23296016@163.com
王丽梅 女,1969年生,博士,教授,研究方向为交流伺服系统及其控制。
E-mail: wanglm@sut.edu.cn(通信作者)
(编辑 崔文静)