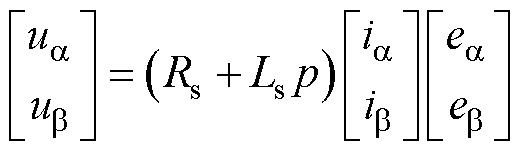 (1)
(1)
摘要 转子位置精度对于永磁同步电机无位置传感器控制至关重要。基于滑模观测器的转子位置估计方法因对参数敏感性低、鲁棒性强的优势得到了广泛的研究和应用。针对滑模观测器估计相位延迟导致的位置信号不准确问题,提出一种基于误差补偿的永磁同步电机无位置传感器控制策略。首先,详细分析了滑模观测器的位置误差产生机理,利用一阶滤波器设计了相位延迟补偿方法,以提高位置估计精度;然后,通过临界饱和切换函数改进滑模观测器收敛性能;最后,通过实验验证了所提方法的可行性。实验结果表明,所提方法的位置估计误差较传统方法减少了89.64%。
关键词:永磁同步电机 无位置传感器控制 滑模观测器 位置估计误差补偿
随着永磁材料的发展与应用,永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)以其功率密度高、转动惯量小、动态响应快、日趋高速化等特点,在大型舰船电力推进系统、先进电力传动系统、高速机床加工等领域具有巨大发展潜力,已成为国内外研究的热点[1-3]。
交流调速系统中,用作闭环反馈的转速和转子位置信息通常由编码器、旋转变压器等位置传感器测得,位置信息的测量精度决定着电机的驱动性能。然而在受运行环境、安装空间和成本等条件的限制时,位置传感器可能会出现测不准、易损坏的情况,因此无位置传感器控制方案是更为合适的选择[4-6]。经过去诸多学者的探究,PMSM无位置传感器驱动技术目前主要包括:基于电机基波模型的反电动势观测法[7-8]、磁链估计法[9]、模型参考自适应法[10],以及基于凸极跟踪的高频信号注入法[11-12]。其中,基于反电动势模型的滑模观测器(Sliding-Mode Observer, SMO)因参数敏感性低和鲁棒性强的优 势[13],得到了广泛研究和应用。
SMO本质上是根据两相静止坐标系下的电机定子电流状态方程,对系统状态进行重构,使其在滑模面上来回滑动,以快速地修正估计电流,从而让反电动势观测值接近真实值,从而得到估计的转子位置信息。然而,由于滤波器和符号函数等模块的引入,SMO存在着估计位置信息相位延迟、系统高频抖振等问题[14-15]。
针对位置估计相位延迟问题,常采用自适应算法补偿误差,其中一类是在SMO内部原有结构的基础上设计观测器或滤波器参数的自适应律,以提高估计反电动势信号精度[16-17],但这类自适应算法往往依赖电机参数,导致牺牲了系统的鲁棒性;另一类是根据位置估计误差会造成电流状态方程不平衡的特性,在SMO外部通过闭环调节,实现对估计误差自适应补偿[18-19],但这类方法往往直接将估计位置角与补偿角相加,并没有考虑估计转速相应的延迟,因而无法保证延迟较大时电机转速环输出依旧平稳。针对SMO固有的抖振问题,常采用S型函数或饱和函数等替代符号函数,减小高频开关信号影响[20-21],但采用常规切换函数替换,将改变系统向滑模面收敛的速度,导致位置估计精度降低。
为解决上述问题,提出了一种基于SMO误差补偿的实时位置估计方法。首先对不同因素所造成的位置信息估计误差进行分析;其次针对误差产生原因,提出一种基于滑模观测器估计误差反馈的位置补偿角计算方法,并利用一阶低通滤波器(Low- Pass Filter, LPF)和高通滤波器(High-Pass Filter, HPF)设计了一种前馈相位补偿器,能够直接对SMO观测到的反电动势进行相移,使估计转速和角度同时得到补偿;再次讨论了SMO响应速度对观测性能的影响,并提出了一种优化的切换函数以保持SMO收敛速度基本不变,同时削弱抖振;然后设计了一种参考转速发生器,用以配合算法中的其他模块工作,以及在低速下开环运行;最后在两台0.75kW永磁同步电机组成的同轴对拖平台上进行了实验,验证了所提出算法的有效性。
滑模观测器以永磁同步电机在两相静止坐标系下的电压方程为模型,对于本文所研究的表贴式永磁同步电机,其电压方程可表述[22]为
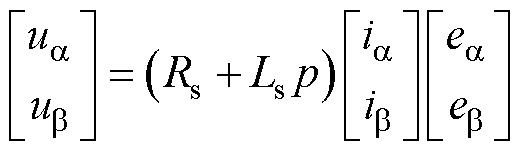 (1)
(1)
其中
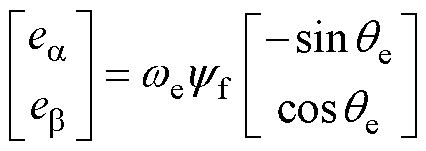 (2)
(2)
式中,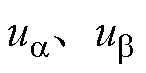 ,
,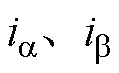 ,
,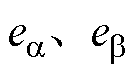 分别为PMSM两相静止坐标系下的定子电压、定子电流和反电动势在
分别为PMSM两相静止坐标系下的定子电压、定子电流和反电动势在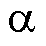 、
、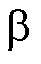 轴上的分量;Rs为电机定子等效电阻;Ls为电机定子等效电感;p为微分算子;
轴上的分量;Rs为电机定子等效电阻;Ls为电机定子等效电感;p为微分算子;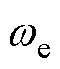 为电机转子的角转速;
为电机转子的角转速;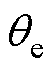 为位置角;
为位置角;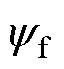 为永磁体磁链。只要能准确估计反电动势
为永磁体磁链。只要能准确估计反电动势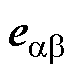 ,便能获得电机的当前位置。为了得到
,便能获得电机的当前位置。为了得到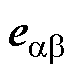 ,将式(1)改写成电流状态方程形式,并结合滑模变结构控制理论,以定子电流估计误差
,将式(1)改写成电流状态方程形式,并结合滑模变结构控制理论,以定子电流估计误差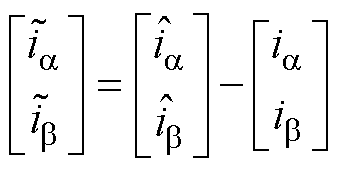 作为滑模面S,进而构建滑模观测器为
作为滑模面S,进而构建滑模观测器为
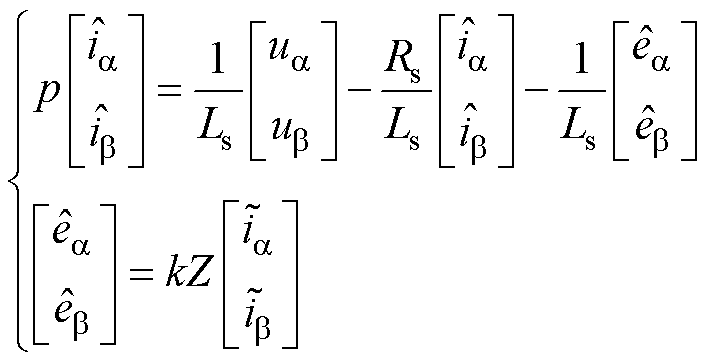 (3)
(3)
式中,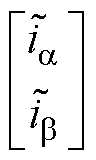 为电流估计误差;
为电流估计误差;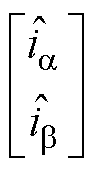 为
为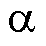 、
、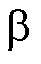 轴电流的估计值;
轴电流的估计值;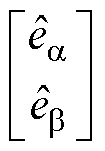 为
为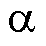 、
、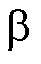 轴反电动势的估计值;k为滑模增益系数;Z(*)为切换函数,传统SMO中常采用符号函数。
轴反电动势的估计值;k为滑模增益系数;Z(*)为切换函数,传统SMO中常采用符号函数。
SMO将滑模面S作为系统的干扰量,通过切换函数不断产生调节量kZ(*),使S快速向零收敛,并将调节量作为估计反电动势,用于求解位置信息。为节省控制器内存、减少谐波影响,在得到反电动势信息后,常采用正交锁相环(Phase Locked Loop, PLL)求解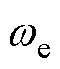 和
和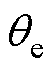 ,相比直接采用式(2)计算更为合适[23]。PLL基本模型[24]为
,相比直接采用式(2)计算更为合适[23]。PLL基本模型[24]为
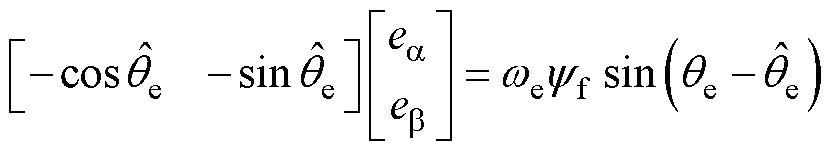 (4)
(4)
式中,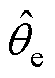 为转子位置角
为转子位置角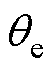 的估计值。当估计误差很小时,
的估计值。当估计误差很小时,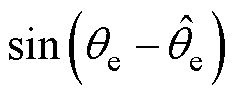 可近似等于
可近似等于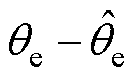 ,进而能够通
,进而能够通
过PI环对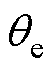 进行跟踪。SMO配合PLL估计转子位置原理如图1所示,其中实际电压信号由PWM调制的开关信号经Clarke变换得到,是非线性变量;实际电流信号由逆变电路中的电流传感器直接测得后经Clarke变换得到;输出为估计的电角速度和转子位置角。
进行跟踪。SMO配合PLL估计转子位置原理如图1所示,其中实际电压信号由PWM调制的开关信号经Clarke变换得到,是非线性变量;实际电流信号由逆变电路中的电流传感器直接测得后经Clarke变换得到;输出为估计的电角速度和转子位置角。
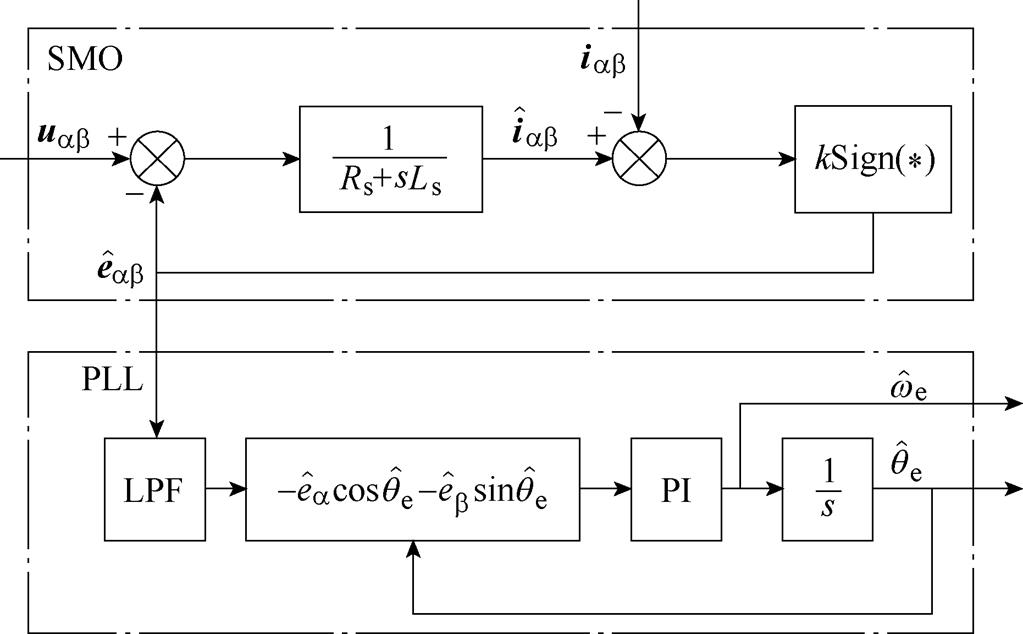
图1 采用PLL的SMO结构
Fig.1 SMO structure with PLL
基于图1原理所设计的位置观测器在估计转子位置时存在着固有误差,一般表现为估计角度滞后于实际角度[19],造成这些误差的因素是多方面的,下面具体分析产生误差的原因。
1.2.1 滤波环节的误差
为减小估计反电动势中非线性开关信号的影响,通常采用一阶LPF对反电动势信号平滑处理[25]。由于LPF的滞后效应,估计反电动势在平滑处理后将发生相移,进而使转速和转子位置角估计结果在相位上产生一定延迟。设LPF的截止频率为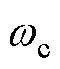 ,则其传递函数为
,则其传递函数为
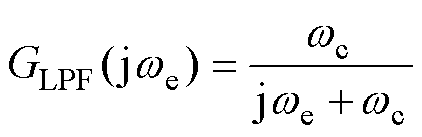 (5)
(5)
由式(5)可知,一阶LPF的相频特性为
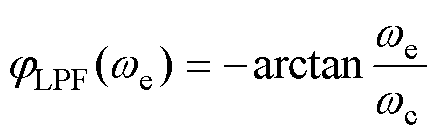 (6)
(6)
信号在经低通滤波处理后,相位产生了滞后,且延迟的角度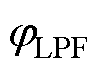 随着
随着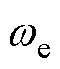 的增大而增大。故实际应用时应对该误差采取一定补偿措施。
的增大而增大。故实际应用时应对该误差采取一定补偿措施。
1.2.2 滑模观测环节的误差
对于SMO,根据文献[20, 25]的分析,要使所选取的滑模面具有存在性和可达性,滑模增益系数k应满足
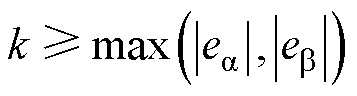 (7)
(7)
SMO中所设定的滑模增益系数大小会影响滑模面向零收敛的速度,这也将会使估计角度滞后,收敛越慢,滞后越多[26]。随着转速的提高,反电动势相应增大,使收敛速度相对变慢而引起一定延迟,故所取最佳滑模增益系数k也应随之变化[27],有
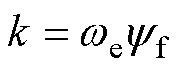 (8)
(8)
选取此值既能保证滑模面收敛,又不会因滑动幅度过大引起系统抖振。
对于PLL,根据式(4)将PLL中PI环的输入近似处理为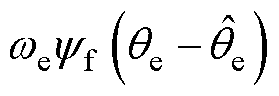 ,则其传递函数为
,则其传递函数为
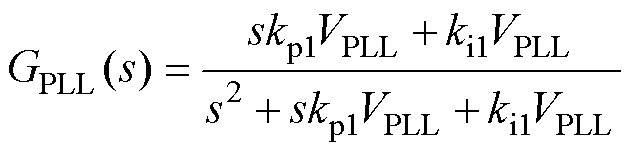 (9)
(9)
式中,kp1和ki1分别为PLL中PI环的比例、积分参数;VPLL为PI环的前馈增益,即VPLL=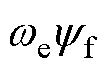 。若采用维纳方法进行参数整定,则有
。若采用维纳方法进行参数整定,则有
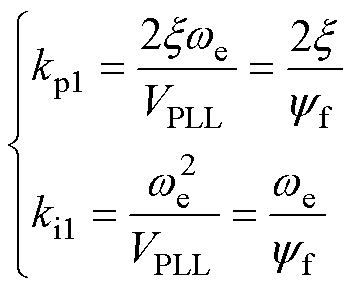 (10)
(10)
式中,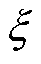 为阻尼比。可以看出,ki1的取值应与转速成正比,随着电机转速的升高,若ki1实际设定值远小于其整定值,会导致PLL传递函数近似于一阶LPF传递函数,从而引起类似的相位估计误差。因此,在实际应用中,将ki1按照
为阻尼比。可以看出,ki1的取值应与转速成正比,随着电机转速的升高,若ki1实际设定值远小于其整定值,会导致PLL传递函数近似于一阶LPF传递函数,从而引起类似的相位估计误差。因此,在实际应用中,将ki1按照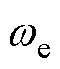 所能达到的最大值进行整定,能够有效减小此类误差。
所能达到的最大值进行整定,能够有效减小此类误差。
1.2.3 单位延迟环节和采样环节的误差
在离散数控系统中,由于时序性的约束,控制算法中存在的闭环反馈环节将会引入代数环,这会导致系统无法正常运行。要解决代数环问题就必须在反馈回路中加入单位延迟环节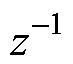 ,即人为地将反馈信号在时间上往后推迟一个采样步长Ts,这会产生一个固定时间的误差,随着转子频率的提高,其所引起的相位滞后增加。此外,采样环节中的某些因素也会导致固定时间延迟,例如逆变电路的开关延迟、模拟信号采样中零阶保持器的环路延迟以及控制器采样频率不高等。
,即人为地将反馈信号在时间上往后推迟一个采样步长Ts,这会产生一个固定时间的误差,随着转子频率的提高,其所引起的相位滞后增加。此外,采样环节中的某些因素也会导致固定时间延迟,例如逆变电路的开关延迟、模拟信号采样中零阶保持器的环路延迟以及控制器采样频率不高等。
上述的四类环节均会引起位置估计精度下降,导致调制的电压矢量不准,从而造成电机运行效率低、无法额定工况运行等不利结果。如果估计转速延迟较大,还会造成自动速度调节器(Automatic Speed Regulator, ASR)输出振荡,严重影响电机寿命。因此,探究转速和转子位置角误差补偿方法,是实现PMSM高效稳定运行的关键。
一方面针对上述所有造成误差的因素,提出一种相位延迟补偿方法,以提高位置信息估计的精度;另一方面针对SMO收敛速度和抖振问题,提出一种临界饱和的切换函数,以改善SMO的性能。
2.1.1 相位延迟计算
滤波环节和滑模观测环节中,由于SMO性能和LPF特性这类因素引起估计延迟,可以通过计算理论反电动势与估计反电动势之间的关系得到。将式(1)所示的电压方程写成复频域形式为
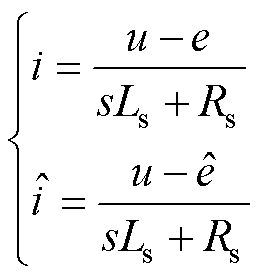 (11)
(11)
为避免u的非线性带来不利影响,将式(11)上下相减,得到定子电流估计误差与反电动势估计误差的数量关系为
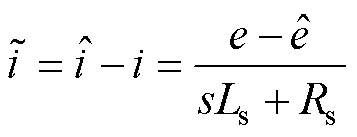 (12)
(12)
易知,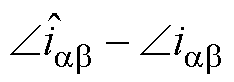 等于
等于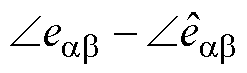 。以a 轴为基准,由式(2)中ea 与qe关系,将式(12)整理为
。以a 轴为基准,由式(2)中ea 与qe关系,将式(12)整理为
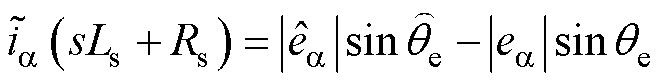 (13)
(13)
其中
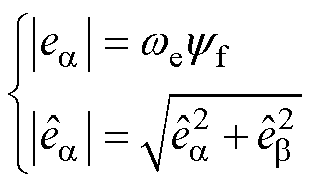 (14)
(14)
由于式(12)两边均为正弦曲线且其幅值相等,故将其左右同时取模并将其离散化可得
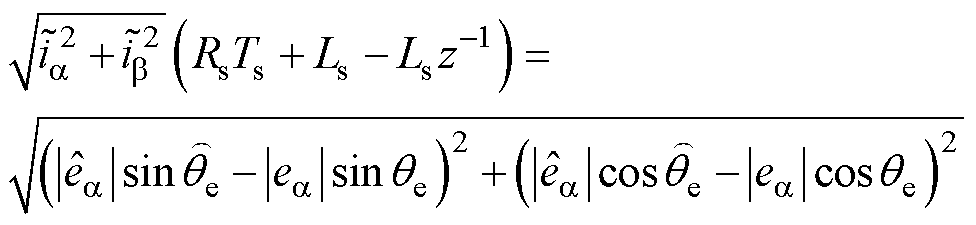 (15)
(15)
设该部分的误差为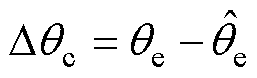 ,将式(15)两边之差作为观测误差,便能够利用PI构成闭环,实时地计算出补偿角
,将式(15)两边之差作为观测误差,便能够利用PI构成闭环,实时地计算出补偿角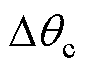 。
。
通过1.1节分析可知,SMO估计位置信息是否准确的判断标准之一是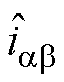 和
和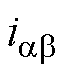 间相位差是否趋于0。采样环节中,延迟在传感器检测到定子电流信号iabc之前就已经存在,因此当使用一个本身有偏差的信号量作为输入,其估计结果也一定是不准的。对此,本文将其与单位延迟环节带来的误差一同归入固定时间延迟,由于位置角是电角速度对时间的一次积分,故对于这类延迟补偿量的计算为
间相位差是否趋于0。采样环节中,延迟在传感器检测到定子电流信号iabc之前就已经存在,因此当使用一个本身有偏差的信号量作为输入,其估计结果也一定是不准的。对此,本文将其与单位延迟环节带来的误差一同归入固定时间延迟,由于位置角是电角速度对时间的一次积分,故对于这类延迟补偿量的计算为
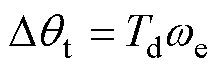 (16)
(16)
式中,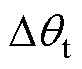 为固定时间延迟补偿角;Td为总延迟时间。因SMO模块、补偿角度计算模块和PLL模块中均存在一个积分环节,输出信号较输入信号共推后了3个采样步长,故不考虑硬件延迟时Td=3Ts。最终总角度延迟补偿为
为固定时间延迟补偿角;Td为总延迟时间。因SMO模块、补偿角度计算模块和PLL模块中均存在一个积分环节,输出信号较输入信号共推后了3个采样步长,故不考虑硬件延迟时Td=3Ts。最终总角度延迟补偿为
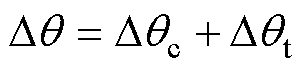 (17)
(17)
2.1.2 相位补偿器设计
PLL是根据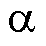 、
、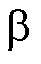 轴的估计反电动势的正弦基波频率来计算电机转速和转子位置角的,根据1.2节误差分析可知,估计反电动势的基波在输入到锁相环前就因滤波环节、观测环节、单位延迟环节和采样环节的延迟累计了误差。如果常规地在PLL模块后给估计位置角
轴的估计反电动势的正弦基波频率来计算电机转速和转子位置角的,根据1.2节误差分析可知,估计反电动势的基波在输入到锁相环前就因滤波环节、观测环节、单位延迟环节和采样环节的延迟累计了误差。如果常规地在PLL模块后给估计位置角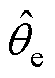 予相位补偿,而完全不考虑估计转速
予相位补偿,而完全不考虑估计转速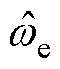 的延迟,那么在ASR调节灵敏度很高的情况下,反馈转速上的延迟会使ASR输出产生振荡,适当降低ASR参数可以缓解振荡,但这会降低控制器的响应速度、增大超调量。为在不牺牲控制器性能的前提下也能有效减小因转速延迟带来的振荡现象,本文基于一阶LPF和HPF设计了一种相位补偿器,能够使SMO观测到的反电动势基波在输入到PLL模块之前保持幅值不变进行相移,即同时对转速和位置角进行延迟补偿。
的延迟,那么在ASR调节灵敏度很高的情况下,反馈转速上的延迟会使ASR输出产生振荡,适当降低ASR参数可以缓解振荡,但这会降低控制器的响应速度、增大超调量。为在不牺牲控制器性能的前提下也能有效减小因转速延迟带来的振荡现象,本文基于一阶LPF和HPF设计了一种相位补偿器,能够使SMO观测到的反电动势基波在输入到PLL模块之前保持幅值不变进行相移,即同时对转速和位置角进行延迟补偿。
根据一阶LPF和HPF的幅频、相频特性可知,正弦信号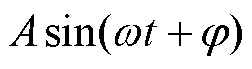 ,在经截止频率为
,在经截止频率为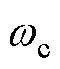 的一阶滤波器处理后,新信号的幅值
的一阶滤波器处理后,新信号的幅值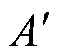 和相位
和相位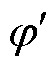 可表述为
可表述为
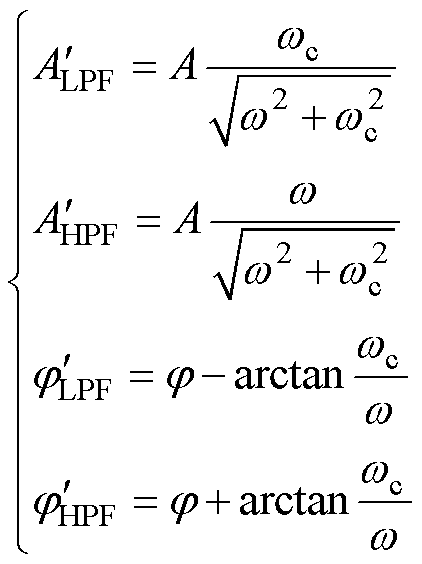 (18)
(18)
在离散系统中,若需要在不损失幅值的前提下使信号的基波相移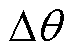 ,则可通过改变截止频率
,则可通过改变截止频率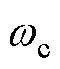 以及设定增益K的方式实现,设计的相位补偿器为
以及设定增益K的方式实现,设计的相位补偿器为
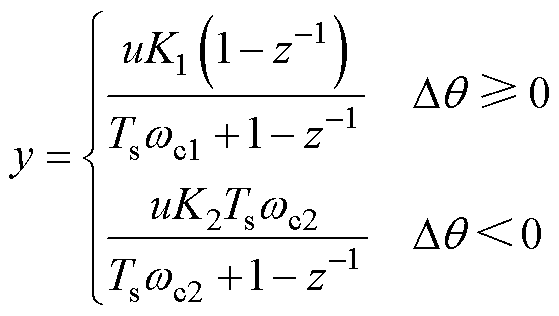 (19)
(19)
式中,y为相移后信号;u为频率为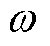 的原信号;
的原信号;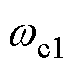 和
和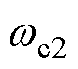 、K1和K2分别为使相位前移和使相位后移时的截止频率和增益,可表述为
、K1和K2分别为使相位前移和使相位后移时的截止频率和增益,可表述为
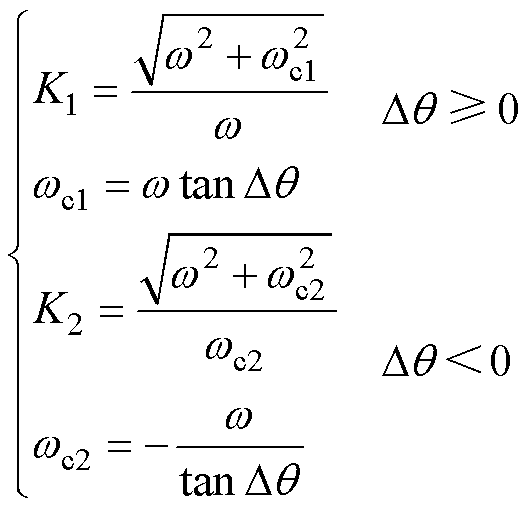 (20)
(20)
综上所述,相位延迟计算和补偿如图2所示,其中相位补偿器设置在估计误差补偿角计算和PLL之间,使得估计反电动势信号在输入到PLL之前就对其进行补偿,实现估计转速延迟的消除。
由于SMO以正弦信号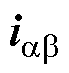 作为参考值,故当系统运动在滑模面上运动时S也呈正弦波,因此SMO收敛速度会影响位置估计精度。对于边界层为1且恒饱和的符号函数而言,滑模增益系数k决定了系统向滑模面收敛的速度,k值过小会导致收敛时间很长甚至发散,致使观测误差增大或观测器失效,而k值过大则会引起系统发生剧烈抖振[27-28]。这给切换函数的性能提出了要求:在S很小时,Z(*)输出应小于1,以减小SMO在单位采样周期里的调节量;在S很大时,Z(*)输出应能刚好达到饱和边界层且不会呈非线性突变,以保证收敛速度。综上所述,Z(*)输出应随着S的大小改变,来保证SMO响应时间不变,减少观测延迟,同时抑制抖振,提高观测质量和控制性能。为此设计了一种切换函数,即
作为参考值,故当系统运动在滑模面上运动时S也呈正弦波,因此SMO收敛速度会影响位置估计精度。对于边界层为1且恒饱和的符号函数而言,滑模增益系数k决定了系统向滑模面收敛的速度,k值过小会导致收敛时间很长甚至发散,致使观测误差增大或观测器失效,而k值过大则会引起系统发生剧烈抖振[27-28]。这给切换函数的性能提出了要求:在S很小时,Z(*)输出应小于1,以减小SMO在单位采样周期里的调节量;在S很大时,Z(*)输出应能刚好达到饱和边界层且不会呈非线性突变,以保证收敛速度。综上所述,Z(*)输出应随着S的大小改变,来保证SMO响应时间不变,减少观测延迟,同时抑制抖振,提高观测质量和控制性能。为此设计了一种切换函数,即
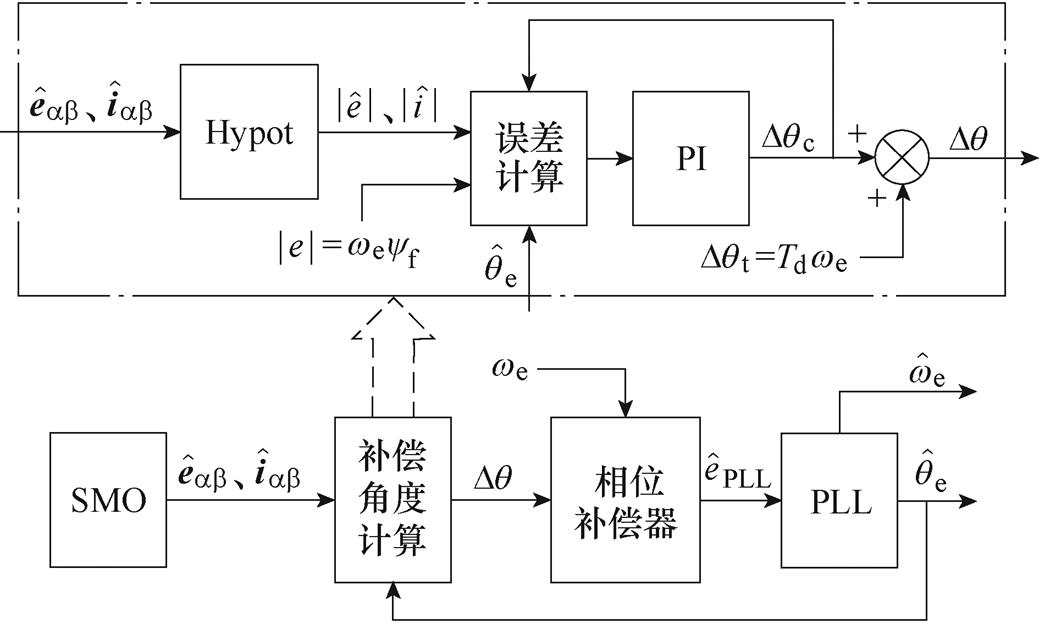
图2 相位延迟计算和补偿
Fig.2 Delay phase calculation and compensation
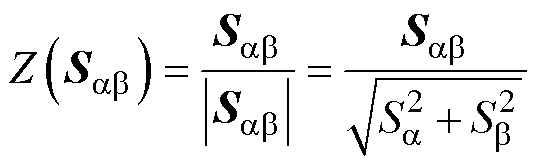 (21)
(21)
式中,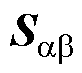 为
为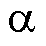 和
和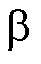 轴的滑模面,即定子电流误差。改进的切换函数效果示意图如图3所示,将
轴的滑模面,即定子电流误差。改进的切换函数效果示意图如图3所示,将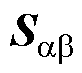 经切换函数的归一化处理后,无论
经切换函数的归一化处理后,无论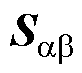 原频率和幅值大小如何变化,Z(*)的输出都是一组边界层厚度为1的保持原频率的正弦波,这使得SMO具有快速收敛性和平稳一致性。
原频率和幅值大小如何变化,Z(*)的输出都是一组边界层厚度为1的保持原频率的正弦波,这使得SMO具有快速收敛性和平稳一致性。
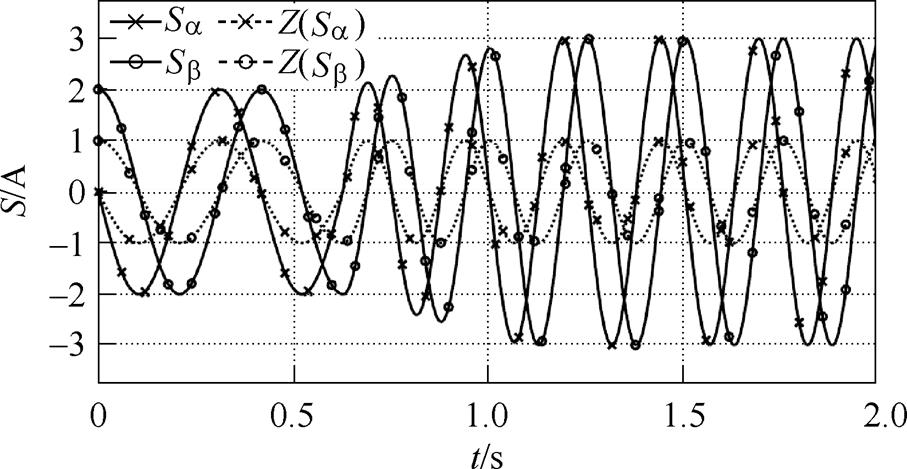
图3 改进的切换函数效果示意图
Fig.3 Schematic of the improved switching function
本文将参考转速由阶跃信号替换成了梯度可变的斜坡信号。设输入的给定转速为nset,经参考转速发生器处理后输出参考转速为nref。给定nref一个初始梯度,当反馈转速n接近nref时增大梯度,反之,当n跟不上nref变化速率时减小梯度,直至nref = nset,其效果如图4所示。这种做法的好处一是能够减小在转速设定值发生改变时的定子冲击电流,并且不影响转速环输出上限;二是将式(8)、式(14)、式(16)中的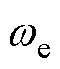 替换为
替换为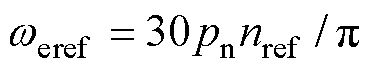 (pn为电机极对数),以提高动态性能;三是能够直接使用参考转速开环运行。
(pn为电机极对数),以提高动态性能;三是能够直接使用参考转速开环运行。
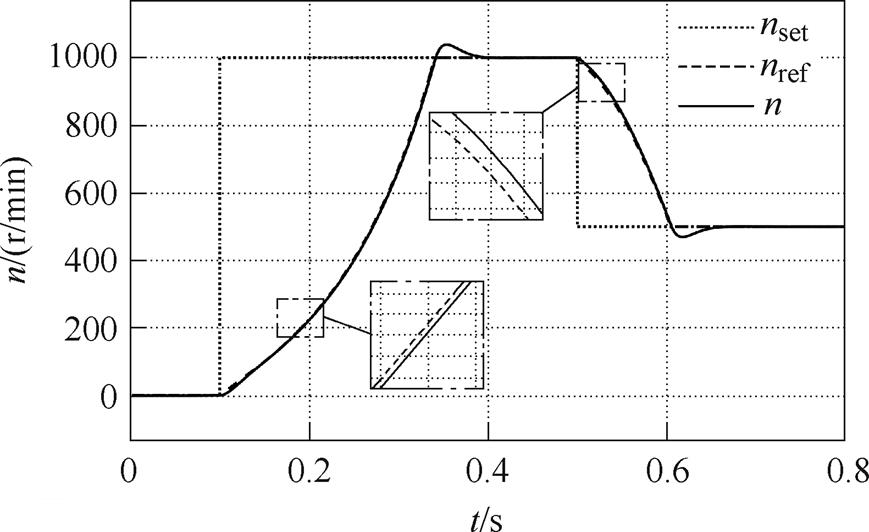
图4 参考转速发生器效果示意图
Fig.4 Schematic of the reference speed generator
最后,本文整体控制框图如图5所示,主要包括电压矢量调制模块、SMO模块、相位延迟计算与补偿模块、PLL模块以及参考转速发生模块。
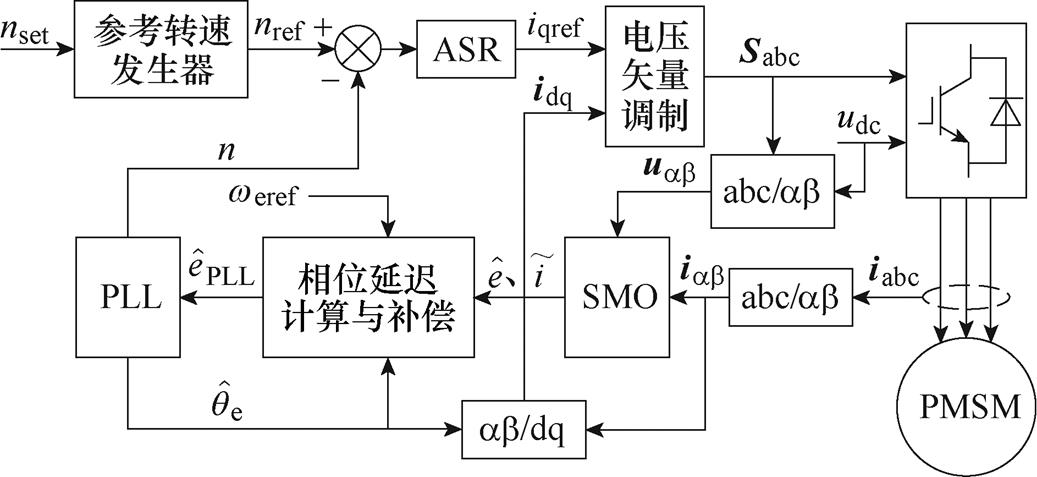
图5 基于观测误差补偿PMSM无位置传感器控制框图
Fig.5 Diagram of the sensorless control strategy of PMSM with observed error compensation
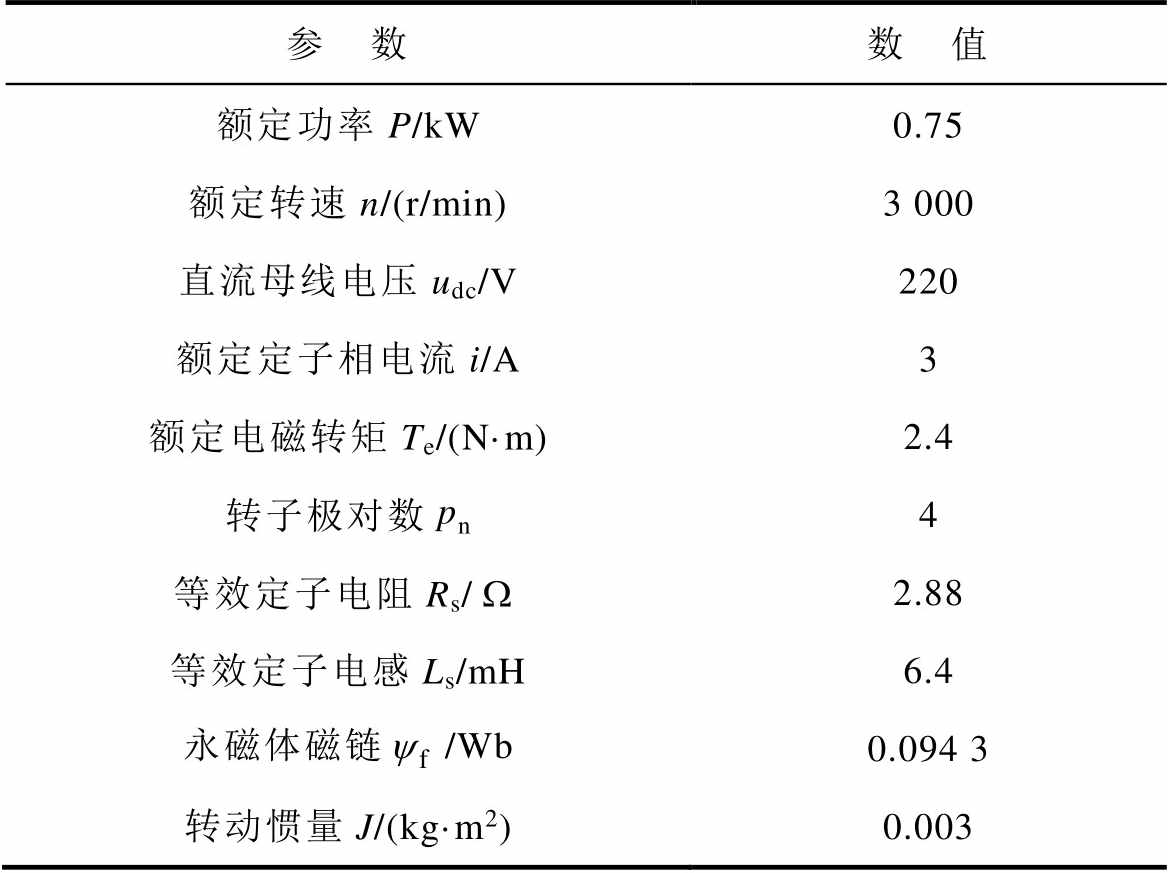
为验证本文所提出相位延迟补偿算法的控制效果,搭建了由两台参数相同的PMSM组成的同轴对拖平台,PMSM参数见表1,控制算法采用参数见表2,实验平台如图6所示。由于电压矢量调制方式采用模型预测控制,因此表2中没有给出电流环PI参数。被控电机控制器的主处理器采用了32位浮点型数字信号处理器TMS320C28346;直流电源经逆变电路为被控电机供电;负载电机工作在恒转矩模式。实验中,被控电机配备了2 500线增量式编码器,以检测转子实际转速和位置,用于与估计位置信息对比。系统采样频率设置为10kHz。
表1 实验电机参数
Tab.1 Parameters of experimental motor
参 数数 值 额定功率P/kW0.75 额定转速n/(r/min)3 000 直流母线电压udc/V220 额定定子相电流i/A3 额定电磁转矩Te/(N·m)2.4 转子极对数pn4 等效定子电阻Rs/2.88 等效定子电感Ls/mH6.4 永磁体磁链/Wb0.094 3 转动惯量J/(kg·m2)0.003
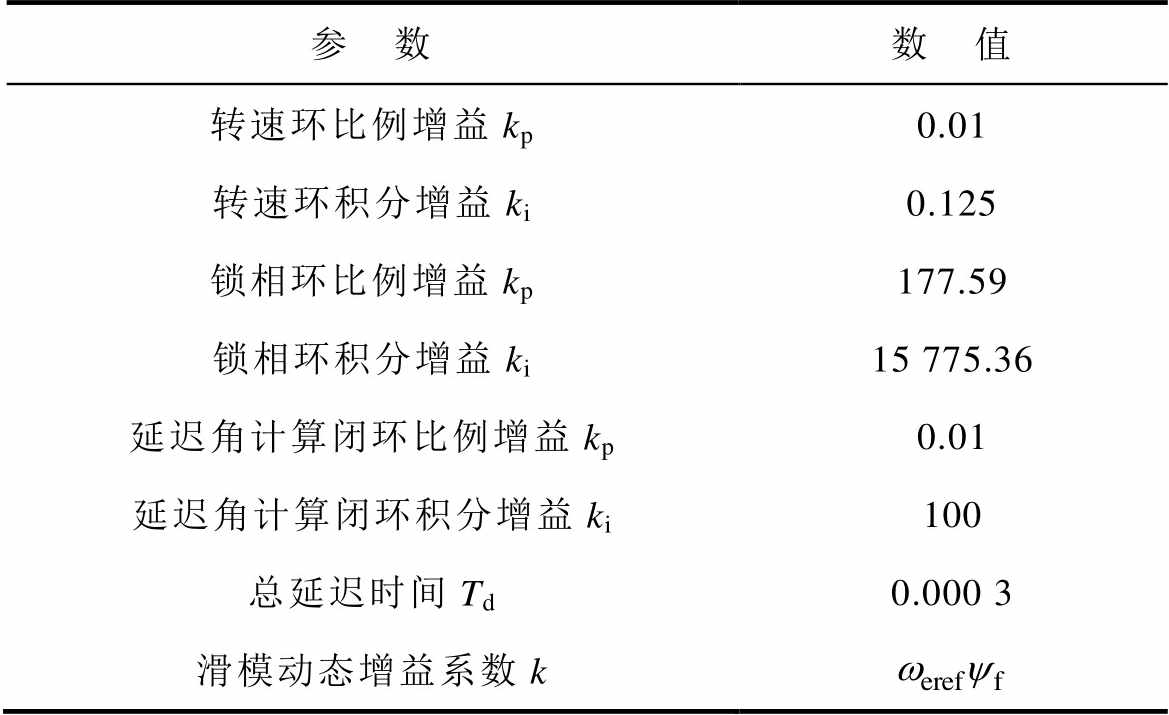
表2 控制算法参数
Tab.2 Parameters of control algorithm
参 数数 值 转速环比例增益kp0.01 转速环积分增益ki0.125 锁相环比例增益kp177.59 锁相环积分增益ki15 775.36 延迟角计算闭环比例增益kp0.01 延迟角计算闭环积分增益ki100 总延迟时间Td0.000 3 滑模动态增益系数k

图6 实验平台
Fig.6 Experimental platform
相位延迟补偿控制实验结果如图7所示。图7a为未采用本文所提出相位延迟补偿方法,被控电机转速设定为2 000r/min时的空载实验结果。可以看出,未进行相位延迟补偿时,转子估计位置角误差较大。其中,平均估计转速波动为6.80r/min,最大估计转速波动为71.95r/min,平均转子位置角估计误差为0.73rad。图7b为同工况下,采用本文所提出的补偿方法后的运行结果。可以看出,转子位置角估计偏差得到了有效的改善。其中,平均估计转速波动为5.99r/min,最大估计转速波动为53.59r/min,平均转子位置角估计误差为0.07rad。对比实验结果表明,所提出改进算法的位置估计误差较传统无补偿算法更准确,平均绝对误差减小了89.64%,验证了相位延迟补偿的必要性和有效性。
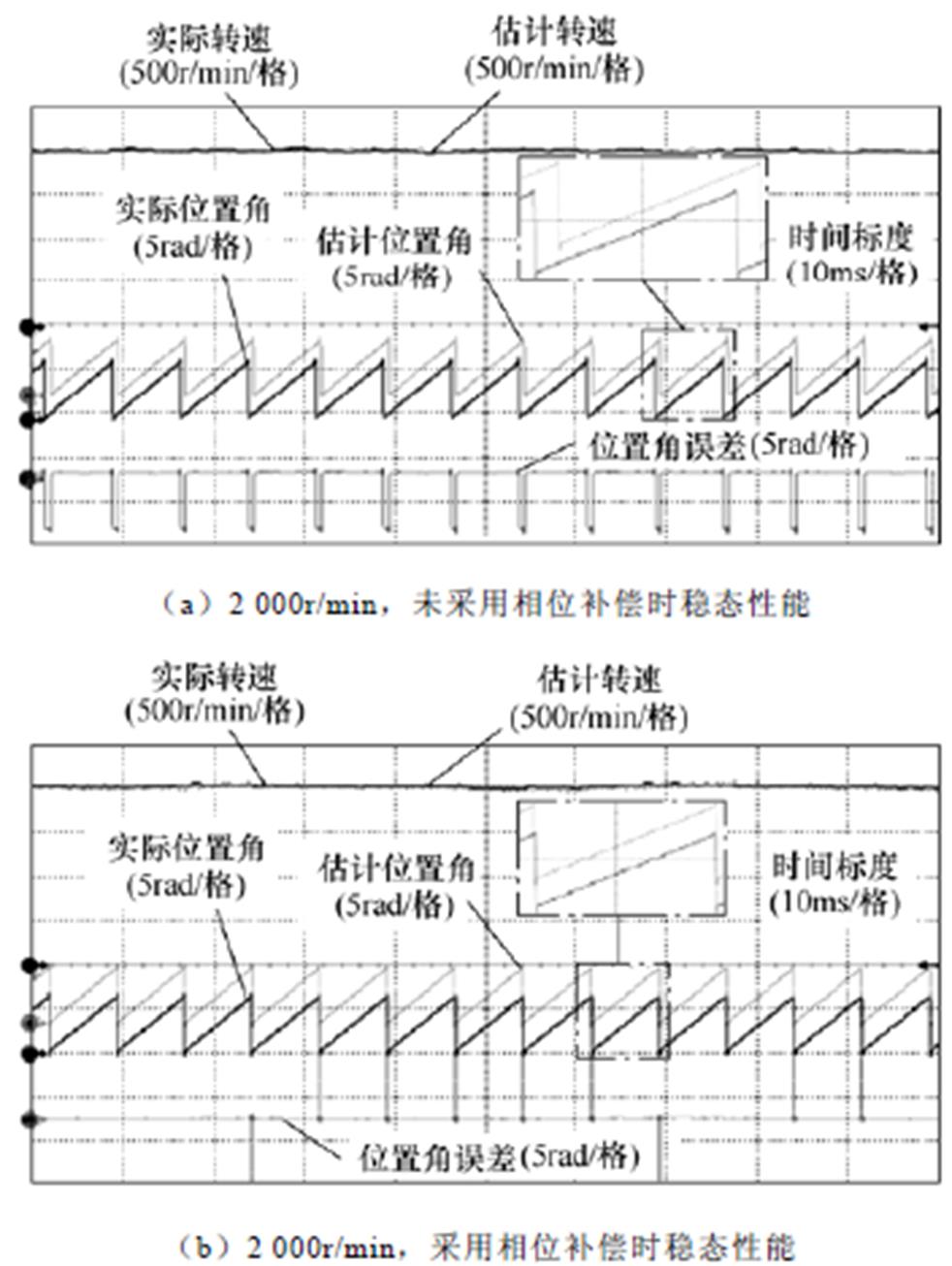
图7 相位延迟补偿控制实验结果
Fig.7 Experimental results of phase delay compensation
图8为空载运行在3 000r/min下,采用相位补偿算法,且SMO模块中设置不同切换函数时的对比实验结果。从图中可以明显看出,使用临界饱和切换函数相较常规切换函数,转速波动更小。其中,0~3.8s使用Sign函数,估计转速波动区间为[3 203.83, 2 795.39]r/min,转速波动标准差为54.79;3.8~6.5s使用Sigmoid函数,估计转速波动区间为[3 091.02, 2 933.59]r/min,转速波动标准差为21.87;6.5s后使用所提出的临界饱和切换函数,估计转速波动区间为[3 061.25, 2 968.44]r/min,转速波动标准差为13.22。
图9a和图9b为额定负载下,采用改进位置估计算法时,分别运行在300r/min和3 000r/min条件的稳态运行结果。可以看出,电机在低速和高速状态下均能够平稳运行。其中,平均估计转速波动分别为4.27r/min和26.06r/min,平均转子位置角估计误差均为0.08rad。上述稳态性能实验结果说明了所提出方法在低速和高速运行状态均有良好的控制性能。
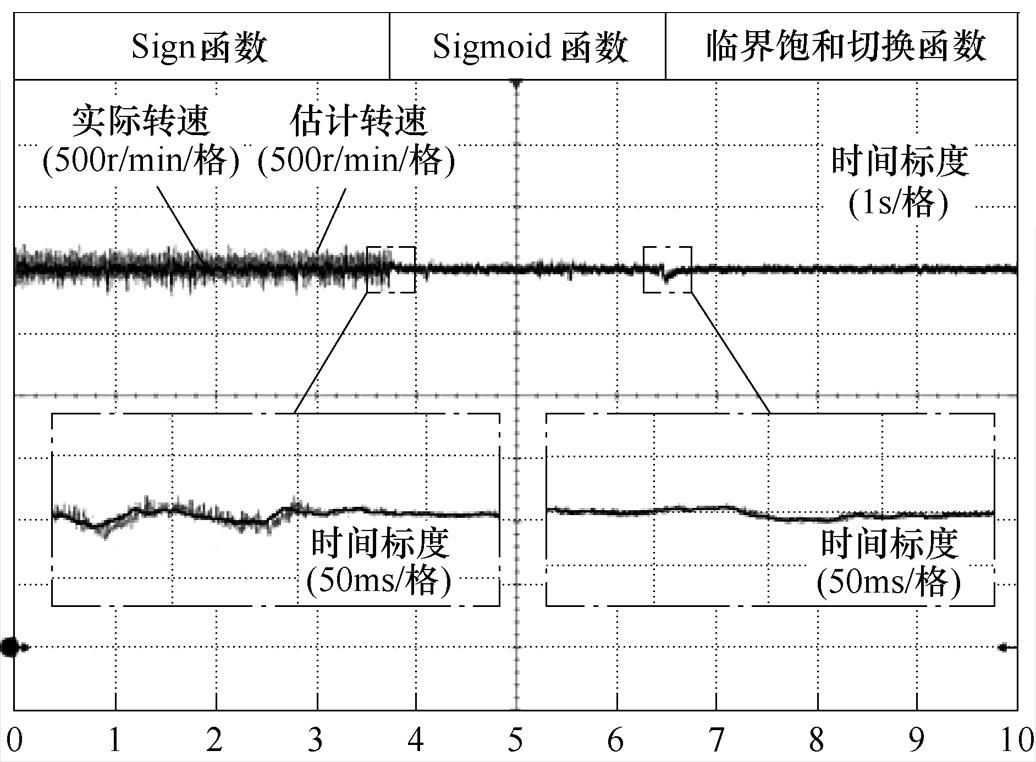
图8 3 000r/min时不同切换函数对比实验结果
Fig.8 Comparison of experimental results with various switching functions at 3 000r/min
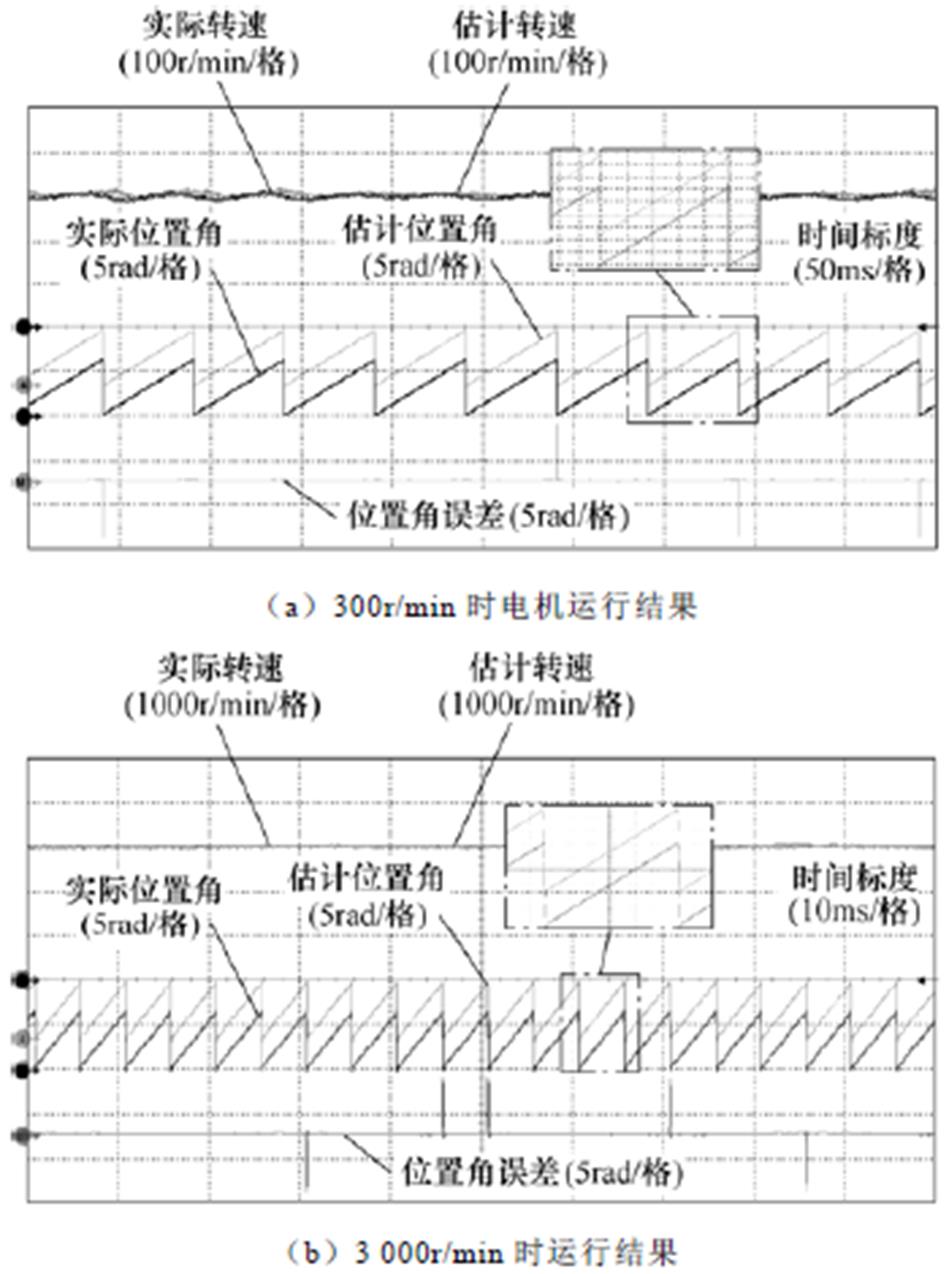
图9 不同设定转速下PMSM稳态实验结果
Fig.9 Steady-state experimental results of PMSM with different reference speeds
图10为动态调速实验结果。参考转速发生器最大梯度设定为5 000r/min/s,最小梯度设定为2 000r/min/s,由于SMO在转速极低时无法工作,因此转速在[-200, 200]r/min范围内时系统采用开环运行。在初始时电机轻载运行在-3 000r/min;3.4s时给定转速-500r/min,电机开始降速;5.1s时给定转速-100r/min,并在SMO反馈转速为-200r/min时将转速闭环切换为转速开环,并持续开环运行;5.5s时给定转速1 000r/min,并在SMO反馈转速为200r/min时将转速闭环重新切入,之后继续升速至1 000r/min和3 000r/min。
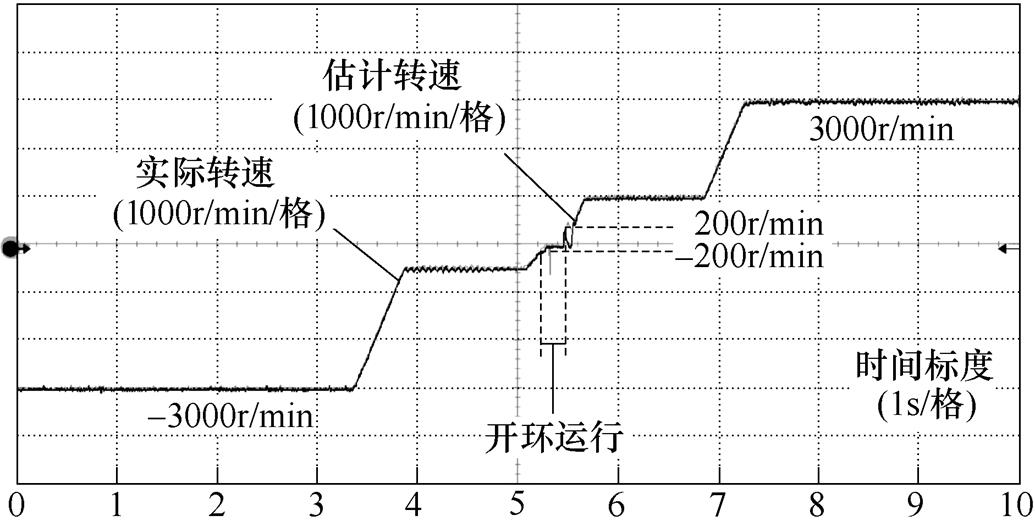
图10 变速实验结果
Fig.10 Experimental results under variable speed conditions
在实际转速过零时,估计转速存在波动,最大误差值为891r/min,原因是转速极低的状态下,定子电流和估计反电动势也趋近于零,从而导致估计位置信息不准确,在电机进入正转后该误差明显减小。在200r/min附近电机从转速开环状态切换进闭环时,实际转速存在下滑,原因是开环时用作反馈的转子位置角与实际位置角在数值上有偏差,直接切换存在突变。
为进一步验证系统的鲁棒性,使用负载电机控制器将负载电机控制在恒转矩模式,通过调节控制器参数,使之输出与被控电机旋转方向相反、大小可调的转矩。若被控电机具有良好的动态性能,则最终会稳定输出与所设定负载大小相同的转矩,以达到动态平衡。
图11为电机运行在1 500r/min下突变负载的实验结果,其中,图11a为0.18s时负载转矩从2N·m突变为0,图11b为0.18s时负载转矩从0突变为2N·m。可以看出,无论减载和加载,系统都在100ms内重新回归稳态。而整个暂态过程中,突卸负载估计转子位置角的最大误差为0.34rad,突增负载估计转子位置角的最大误差为0.41rad,均在可接受范围内。上述动态性能实验结果表明,在工况突变时,所提出方法具有良好的抗扰能力。
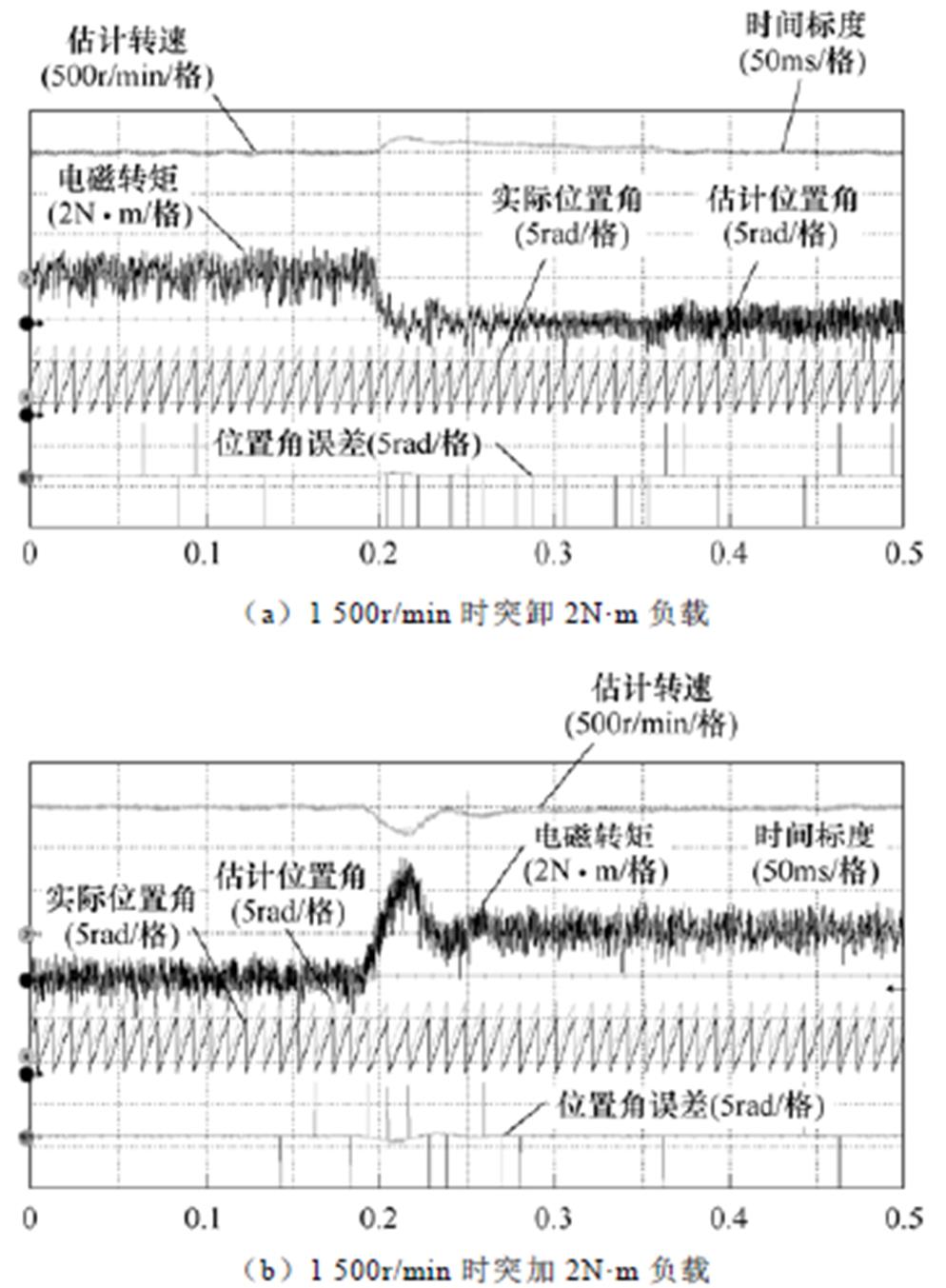
图11 负载突变实验结果
Fig.11 Experimental results under variable loads conditions
本文提出了一种基于滑模观测器估计误差反馈补偿的永磁同步电机无位置传感器控制策略。首先分析了采用正交锁相环的滑模观测器在估计转子位置时,引起估计误差和系统控制性能不佳的因素;其次针对误差产生的原因,提出了一种位置补偿角的计算与误差补偿方法;然后利用一种临界饱和的切换函数,提高了滑模观测器的收敛性能;最后在两台参数相同的永磁同步电机对拖平台上进行了实验。实验结果表明,所提方法可有效补偿转子位置误差,电机的运行具有良好的稳态和动态性能。
参考文献
[1] 刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017, 32(16): 76-88.
Liu Jilong, Xiao Fei, Shen Yang, et al. Position- sensorless control technology of permanent-magnet synchronous motor-a review[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 76-88.
[2] Xu Dianguo, Wang Bo, Zhang Guoqiang, et al. A review of sensorless control methods for AC motor drives[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 104-115.
[3] Bianchi N, Bolognani S, Luise F. Potentials and limits of high-speed PM motors[J]. IEEE Transactions on Industry Applications, 2004, 40(6): 1570-1578.
[4] 麦志勤, 肖飞, 刘计龙, 等. 基于改进型自调整轴系幅值收敛电流解调算法的旋转高频电压注入法[J]. 电工技术学报, 2021, 36(10): 2049-2060.
Mai Zhiqin, Xiao Fei, Liu Jilong, et al. Rotating high-frequency voltage injection method based on improved self-adjusting frame amplitude convergence current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2049- 2060.
[5] 张丽, 朱孝勇, 左月飞. 电动汽车用转子永磁型无刷电机与控制系统容错技术综述[J]. 中国电机工程学报, 2019, 39(6): 1792-1802, 1875.
Zhang Li, Zhu Xiaoyong, Zuo Yuefei. Overview of fault-tolerant technologies of rotor permanent magnet brushless machine and its control system for electric vehicles[J]. Proceedings of the CSEE, 2019, 39(6): 1792-1802, 1875.
[6] Yin Zhonggang, Gao Fengtao, Zhang Yanqing, et al. A review of nonlinear Kalman filter appling to sensorless control for AC motor drives[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 351-362.
[7] 李垣江, 董鑫, 魏海峰, 等. 表贴式永磁同步电机转速环复合PI无位置传感器控制[J]. 电工技术学报, 2020, 35(10): 2119-2129.
Li Yuanjiang, Dong Xin, Wei Haifeng, et al. Sensor- less compound PI control for surface permanent magnet synchronous motor speed regulation system[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2119-2129.
[8] Fan Ying, Zhang Li, Cheng Ming, et al. Sensorless SVPWM-FADTC of a new flux-modulated permanent- magnet wheel motor based on a wide-speed sliding mode observer[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 3143-3151.
[9] Sun Hongbo, Jiang Dong, Yang Jichang. Synchronous vibration suppression of magnetic bearing systems without angular sensors[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 70-77.
[10] 张洪帅, 王平, 韩邦成. 基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测[J]. 中国电机工程学报, 2014, 34(12): 1889-1896.
Zhang Hongshuai, Wang Ping, Han Bangcheng. Rotor position measurement for high-speed permanent magnet synchronous motors based on fuzzy PI MRAS[J]. Proceedings of the CSEE, 2014, 34(12): 1889-1896.
[11] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet syn- chronous motor based on adaptive Notch filter online decoupling[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 344-354.
[12] 刘旭, 牛大强, 曹阳, 等. 基于励磁绕组高频信号注入的混合励磁开关磁链永磁电机位置估计[J]. 电工技术学报, 2021, 36(20): 4297-4307.
Liu Xu, Niu Daqiang, Cao Yang, et al. Position estimation for hybrid excited switched flux PM machine by injecting high-frequency pulse into the field winding[J]. Transactions of China Electro- technical Society, 2021, 36(20): 4297-4307.
[13] Zhang Li, Fan Ying, Li Chenxue, et al. Fault-tolerant sensorless control of a five-phase FTFSCW-IPM motor based on a wide-speed strong-robustness sliding mode observer[J]. IEEE Transactions on Energy Conversion, 2018, 33(1): 87-95.
[14] 姜燕, 李博文, 吴轩, 等. 基于比例谐振滤波的改进永磁同步电机转子位置观测器[J]. 电工技术学报, 2020, 35(17): 3619-3630.
Jiang Yan, Li Bowen, Wu Xuan, et al. An improved rotor position observer for permanent magnet syn- chronous motors based on proportional resonant filtering[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3619-3630.
[15] Jung S Y, Nam K. PMSM control based on edge-field hall sensor signals through ANF-PLL processing[J]. IEEE Transactions on Industrial Electronics, 2011, 58(11): 5121-5129.
[16] Liang Donglai, Li Jian, Qu Ronghai, et al. Adaptive second-order sliding-mode observer for PMSM sensorless control considering VSI nonlinearity[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8994-9004.
[17] Song Xinda, Fang Jiancheng, Han Bangcheng, et al. Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1438-1449.
[18] 黄科元, 高丽真, 黄守道, 等. 基于电流环误差修正的高速永磁同步电机转子位置校正方法[J]. 中国电机工程学报, 2017, 37(8): 2391-2399.
Huang Keyuan, Gao Lizhen, Huang Shoudao, et al. A correction method of rotor positions for high speed permanent magnet synchronous motor based on the error correction of the current loop[J]. Proceedings of the CSEE, 2017, 37(8): 2391-2399.
[19] 顾聪, 王晓琳, 邓智泉. 一种基于双重锁相环的高速永磁同步电机转子位置估计误差全补偿方法[J]. 中国电机工程学报, 2020, 40(3): 962-970.
Gu Cong, Wang Xiaolin, Deng Zhiquan. A rotor position estimated error correction method for high- speed permanent magnet synchronous motor based on dual-phase-locked-loop[J]. Proceedings of the CSEE, 2020, 40(3): 962-970.
[20] 王要强, 冯玉涛, 秦明, 等. 表贴式永磁同步电机全阶滑模观测与控制策略[J]. 电工技术学报, 2018, 33(24): 5688-5699.
Wang Yaoqiang, Feng Yutao, Qin Ming, et al. Full- order sliding mode observation and control strategy for surface permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5688-5699.
[21] 武亚恒, 樊启高, 惠晶, 等. 基于改进型滑模观测器的无位置BLDCM控制[J]. 江南大学学报(自然科学版), 2015, 14(3): 278-282.
Wu Yaheng, Fan Qigao, Hui Jing, et al. Sensorless control research of BLDCM based on improved sliding mode observer[J]. Journal of Jiangnan University (Natural Science Edition), 2015, 14(3): 278-282.
[22] Elbuluk M, Li Changsheng. Sliding mode observer for wide-speed sensorless control of PMSM drives[C]// 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 2004: 480-485.
[23] Sun Xiaodong, Hu Changchang, Lei Gang, et al. Speed sensorless control of SPMSM drives for EVs with a binary search algorithm-based phase-locked loop[J]. IEEE Transactions on Vehicular Technology, 2020, 69(5): 4968-4978.
[24] 刘家曦, 李铁才, 杨贵杰. 永磁同步电机转子位置与速度预估[J]. 电机与控制学报, 2009, 13(5): 690- 694.
Liu Jiaxi, Li Tiecai, Yang Guijie. Rotor position and speed estimation for PMSM[J]. Electric Machines and Control, 2009, 13(5): 690-694.
[25] 尚喆, 赵荣祥, 窦汝振. 基于自适应滑模观测器的永磁同步电机无位置传感器控制研究[J]. 中国电机工程学报, 2007, 27(3): 23-27.
Shang Zhe, Zhao Rongxiang, Dou Ruzhen. Research on sensorless control method of PMSM based on an adaptive sliding mode observer[J]. Proceedings of the CSEE, 2007, 27(3): 23-27.
[26] 郑雪梅, 李秋明, 史宏宇, 等. 用于永磁同步电机的一种非奇异高阶终端滑模观测器[J]. 控制理论与应用, 2011, 28(10): 1467-1472.
Zheng Xuemei, Li Qiuming, Shi Hongyu, et al. Higher- order nonsingular terminal-sliding-mode observer for permanent-magnet synchronous motor[J]. Control Theory & Applications, 2011, 28(10): 1467-1472.
[27] Kim H, Son J, Lee J. A high-speed sliding-mode observer for the sensorless speed control of a PMSM[J]. IEEE Transactions on Industrial Elec- tronics, 2011, 58(9): 4069-4077.
[28] Sun Le, Li Xiaoxiang, Chen Longmiao. Motor speed control with convex optimization-based position estimation in the current loop[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10906-10919.
Sensorless Control Strategy of Permanent Magnet Synchronous Motor Based on Error Compensation Estimated by Sliding Mode Observer
Abstract With the rising demand for motor output power and speed control performance in various industries, and the rapid development of permanent magnet materials, Permanent Magnet Synchronous Motor (PMSM) has been widely used in electrical vehicle drive systems, marine electric propulsion systems and aerospace power systems.
All existing synchronous motor drive technologies must obtain real-time motor speed and rotor position angle information, usually using position sensors to obtain motor position information. In AC speed control systems, the speed and rotor position information used as closed-loop feedback are usually measured by position sensors such as encoders and rotary transformers, and the accuracy of the position information measurement determines the drive performance of the motor. However, due to the constraints of operating environment, installation space and cost, the position sensor may be inaccurate and easily damaged, so a sensorless control scheme is a more suitable choice.
The estimation accuracy of rotor position is crucial in the sensorless control technology of PMSM. The rotor position estimation method based on the Sliding-Mode Observer (SMO) has been widely studied and applied because of its low sensitivity to parameters and high robustness. However, due to the introduction of modules such as filters and symbolic functions, the estimated phase retardation and high frequency jitter in SMO can cause inaccurate position observation. Therefore, to address the inaccuracy of the position signal caused by the estimated phase delay of SMO, this paper proposes a sensorless control strategy of the PMSM based on error compensation, aiming to realize the sensorless control technology in the full-speed range for PMSMs.
Firstly, the mechanism of position observation error generation of SMO using phase locked loop was analyzed, and the position information estimation errors caused by different factors were discussed. A method of position compensation angle calculation and phase delay compensation based on SMO estimation error feedback was proposed to solve the cause of error, and a feedforward phase compensator was designed using a first order filter, which could directly phase shift the counter-electromotive force observed by SMO, so that the estimated speed and angle could be compensated at the same time.
Secondly, based on the analysis of the effect of SMO response speed on the observation performance, an optimized critical saturation switching function was designed, outputting a sine wave with boundary layer fixed at 1, which kept the convergence speed of SMO basically constant and weakened the jitter, thus the performance of SMO was improved.
Thirdly, a reference speed generator was designed to replace the reference speed from a step signal to a gradient-variable ramp signal for motor start-up and low-speed operation, which facilitated the control of the motor over the full speed range.
Finally, the feasibility of the proposed method was verified experimentally by using the constructed PMSM pair-tow platform with model predictive current control as the modulation of the voltage vector. In the steady-state comparison experiments, the average rotor position angle estimation error of the proposed method was 0.07rad, which was 89.64% less than that of the conventional method of 0.73rad under the same operating conditions. In the variable speed experiment, the motor was adjusted from negative to positive rated speed under no load. In the variable load experiment, the maximum error of rotor position angle estimated by sudden unloading was 0.34rad, and the maximum error of rotor position angle estimated by sudden increasing load was 0.41rad. The experimental results showed that the proposed method could effectively compensate the rotor position error, and the operation of the motor has good steady-state and dynamic performance.
Keywords:Permanent magnet synchronous motor, sensorless control, sliding mode observer, compensation of position estimated error
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.211876
江苏省“六大人才高峰”高层次人才项目(GDZB-138)和江苏省自然科学基金项目(BK20210475)资助。
收稿日期 2021-11-17
改稿日期 2021-12-27
E-mail: a16578123@gmail.com
樊启高 男,1986年生,博士,副教授,研究方向为高速电机控制技术、智能传感及机电一体化技术。
E-mail: qgfan@jiangnan.edu.cn(通信作者)
(编辑 崔文静)