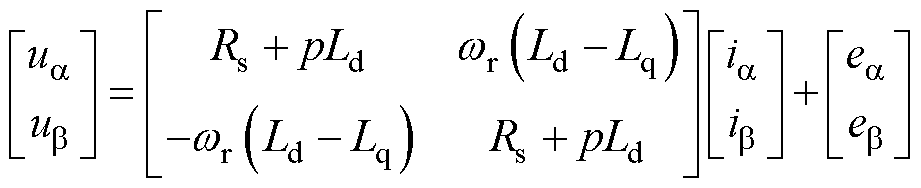（1）
摘要 滑模观测器由于对系统不确定性具有良好的鲁棒性，逐渐应用于永磁同步电机无位置传感器控制中，但是在实际应用中滑模观测器的抖振现象会严重影响系统控制性能。该文提出一种用于内置式永磁同步电机无位置传感器控制的改进的二阶滑模观测器，采用基于Super-twisting算法的二阶滑模观测器，不同于常规的通过滑模观测器估算得到反电动势分量的方法，该方法基于内模控制原理引入二阶广义积分器，通过滑模观测器估算得到反电动势误差分量，再经过二阶广义积分器得到估算的反电动势分量，能够在保证估算准确性的同时很好地抑制系统抖振。同时，为了消除数字实现过程中的离散化误差和估算反电动势分量的耦合项，提高估算的准确性，重新构建了基于扩展反电动势的离散域数学模型，并基于该模型设计了改进的离散域Super-twisting滑模观测器。最终将估算得到的扩展反电动势分量用于估算转子位置和转速。通过实验对该文提出方法的有效性进行了验证。
关键词：内置式永磁同步电机 无位置传感器控制 离散域模型 Super-twisting滑模观测器 二阶广义积分器
内置式永磁同步电机（Interior Permanent Magnet Synchronous Motor, IPMSM）由于具有功率密度高、效率高、调速范围宽等特点，在工业领域有着广阔的应用前景，近些年在轨道交通、家用电器、电动汽车等领域都有了一定的应用[1]。要实现IPMSM高性能的控制，准确的转子位置和转速信息必不可少。通常转子位置和转速信息可以通过位置传感器获得，如旋转变压器、绝对位置编码器等。然而位置传感器也给整个牵引传动系统带来了一些问题，如系统成本的增加、位置传感器故障造成的系统可靠性的降低、增大了牵引电机的安装体积等。为了解决位置传感器带来的问题，近些年无位置传感器控制受到了国内外越来越多的关注，经过这些年的研究有了一定的研究成果，在工业领域也有了一定的应用[2]。
根据目前的研究现状，IPMSM无位置传感器控制主要分为应用于零低速范围内的基于凸极特性的方法和应用于中高速范围内的基于基波模型的方 法[3-4]。通常在额定转速10%以上的范围内基于基波模型的方法能够获得令人满意的控制性能，但是随着转速的降低，受信噪比减小的影响，基于基波模型的方法性能变差，因此通常采用基于凸极特性的高频电压注入法[5-6]。基于基波模型的方法主要是通过估算反电动势分量，进而估算出转子位置和转速信息。对于IPMSM，由于其d、q轴电感不对称，无法直接采用基本的数学模型估算转子位置和转速，因此有学者提出扩展反电动势的概念，通过估算扩展反电动势来估算转子位置和转速[7]。扩展反电动势通常采用构建观测器的方法进行估算，如扰动观测器、全阶观测器、滑模观测器等[8-11]。
其中，滑模观测器作为一种非线性鲁棒控制策略，对系统模型的不确定性和扰动具有较好的鲁棒性，有着广阔的应用前景，也逐渐应用到了无位置传感器控制中。传统的滑模观测器为一阶滑模观测器，实现简单，但是其最大的问题在于开关函数的高频切换引起严重的系统抖振，这在实际工程应用中是不期望出现的[12]。为了解决抖振问题，有学者提出了边界层的方法，采用饱和函数或sigmoid函数抑制抖振，但边界层的引入使得系统成为准滑模动态，在抑制抖振的同时牺牲了滑模控制自身的一部分特性。还有学者提出了对滑模观测器输出的反电动势进行低通滤波，将引起抖振的高频信号滤除，但是低通滤波器的引入会造成估算反电动势相位的偏差，因此需要对滤波之后的信号进行相位的补偿[10]。随着滑模控制理论的发展，有学者提出了高阶滑模观测器的理论，其中Super-twisting滑模观测器由于只需要滑模变量的信息，而不需要滑模变量微分的信息，能够直接应用于相对阶为1的系统，并且可以抑制系统抖振，因此有较为广泛的应用[13]。有学者也将Super-twisting滑模观测器应用于无位置传感器控制中[14-16]。Super-twisting滑模观测器抑制抖振的作用在控制频率足够高的理想情况下能够达到很好的效果。在实际工程应用中，控制频率通常会受到限制，当控制频率较低时Super-twisting滑模观测器无法实现理想的控制性能，虽然相较于传统的一阶滑模观测器性能较好，但是依然会存在一定的抖振现象，影响整个系统的控制性能。
本文提出了一种用于IPMSM无位置传感器控制的改进的Super-twisting滑模观测器，基于内模控制原理引入二阶广义积分器（Second Order Generalized Integrator, SOGI），在保证估算扩展反电动势的准确性的同时能够有效抑制抖振，同时为了解决数字化实现中存在的离散化误差和反电动势交叉耦合问题，构建了离散域扩展反电动势模型，并基于该模型进一步设计了离散的改进型Super-twisting滑模观测器。最后在3kW的IPMSM牵引传动平台上对提出的控制策略进行了实验，验证了其有效性。
由于IPMSM的基础数学模型存在d、q轴电感不同带来的不对称性，无法直接用于无位置传感器控制。为了消除这种不对称性，扩展反电动势模型被用于IPMSM无位置传感器控制中[7]，连续域中扩展反电动势模型为
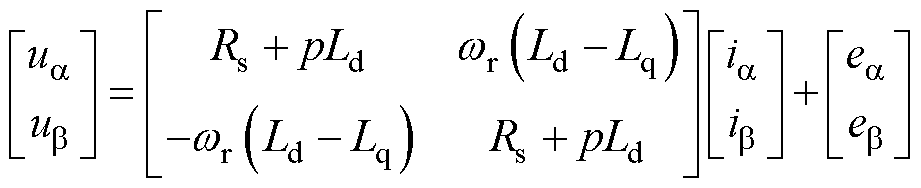（1）
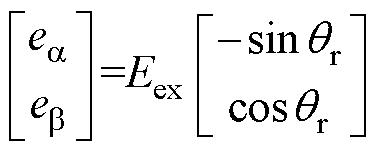（2）
式中，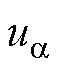
、
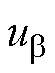分别为定子a、b 轴电压；
、
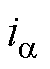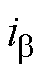分别为定子a、b 轴电流；Rs为定子电阻；Ld、Lq分别为d、q轴电感；
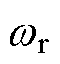为转速；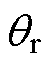
为转子位置；
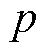为微分算子；
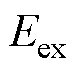为扩展反电动势的幅值，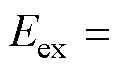
，
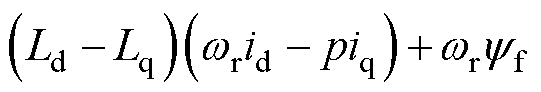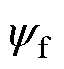为永磁体磁链；
、
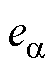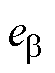为扩展反电动势。
从式（2）可以看出，扩展反电动势分量中包含转子位置信息，通过设计观测器可以估算出扩展反电动势，进一步估算出转子位置和转速。
在实际应用中控制算法通常需要在数字控制器中实现，基于连续域模型设计的观测器则需要选择合适的离散化方法对其进行离散化。连续域模型离散化的过程中，一方面会存在离散化误差，另一方面没有考虑反电动势分量的交叉耦合效应，最终会影响估算反电动势的准确性[17-18]。为了解决上述问题，本文重新构建离散域扩展反电动势模型。
如式（1）所示的连续域扩展反电动势模型可以重新写作复矢量形式为
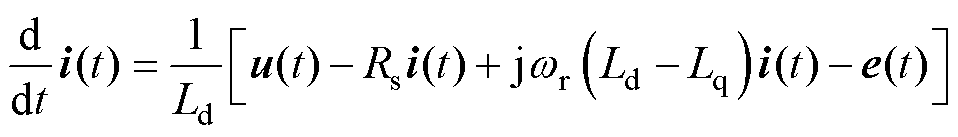（3）
对式（3）进行带初始条件的Laplace变换，得到
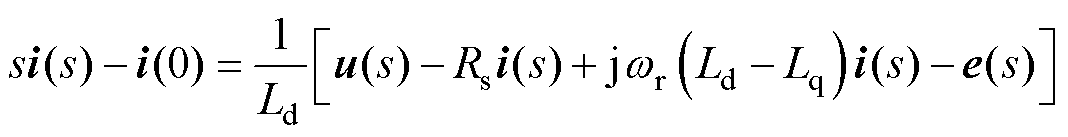（4）
由于实际应用中定子电压是通过电压源型逆变器经过脉宽调制产生，因此在静止坐标系中定子电压具有零阶保持作用，也称为在一个采样周期内处于锁存状态。在采样时刻（假定在一个采样周期内0时刻为采样时刻），定子电压认为是一个阶跃输入，其锁存模型的传递函数可以写作
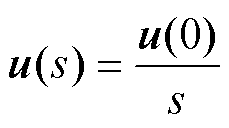（5）
另外，忽略扩展反电动势中电流变化量，认为转速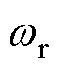
在一个采样周期内保持不变，则认为扩展反电动势在同步旋转坐标系中具有零阶保持作用，其在同步旋转坐标系下的锁存模型的传递函数为
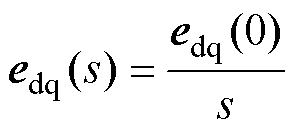（6）
经过坐标变换可以得到静止坐标系下扩展反电动势的锁存模型为
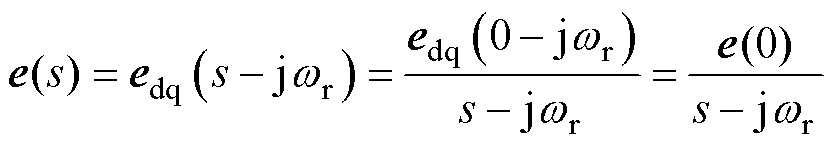（7）
将式（5）和式（7）代入式（4）得到
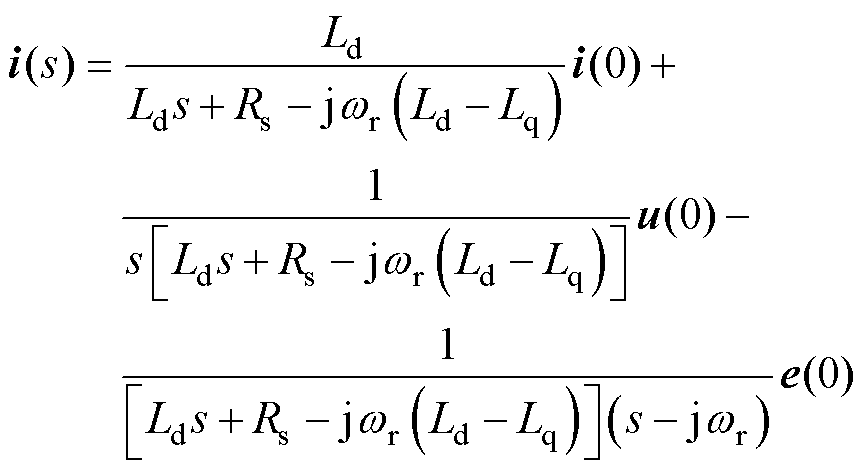（8）
对式（8）进行反Laplace变换得到
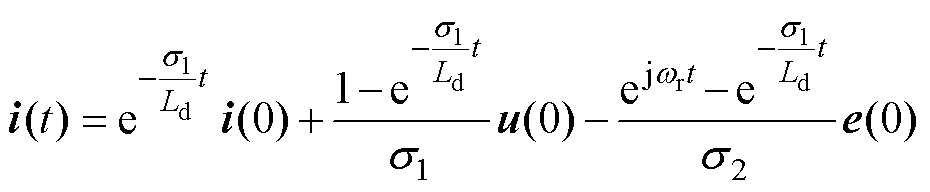（9）
式中，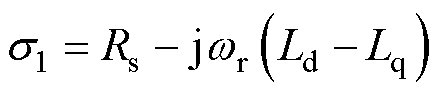
；
。
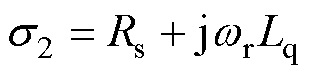在一个采样周期Ts内，认为式（9）中0为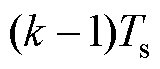
时刻，
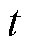为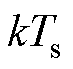
时刻，则离散域扩展反电动势模型为
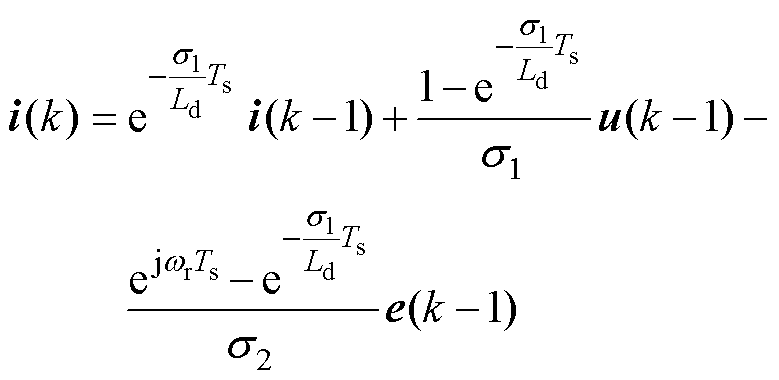（10）
基于IPMSM扩展反电动势数学模型式（1）可以构建Super-twisting滑模观测器估算扩展反电动 势[15]，观测器方程为
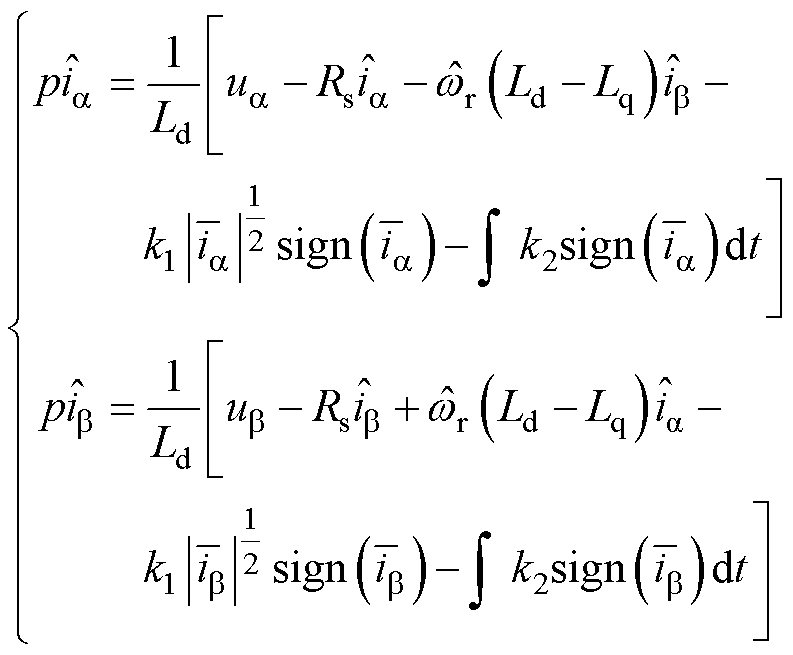（11）
式中，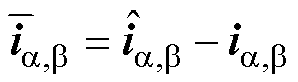
；sign(*)为开关函数；
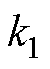和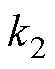
为滑模系数；“
”表示估计量。
估算的扩展反电动势可以通过Super-twisting算法得到，即
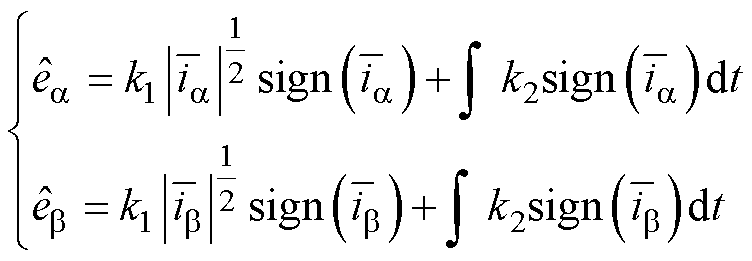（12）
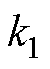滑模系数和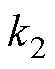可以选择[19]为
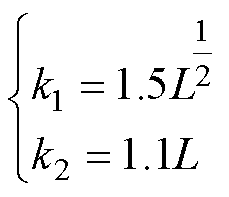（13）
式中，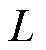
为扰动边界，取正实数。
Super-twisting滑模观测器结构如图1所示，其本质为二阶滑模观测器，理论上相比于传统的一阶滑模观测器具有很好的抑制抖振的效果，但这种理想状态只在控制频率足够大的时候能够实现。在实际应用中，控制频率通常会受到一些限制，因此抖振现象依然会存在，并且影响控制性能。
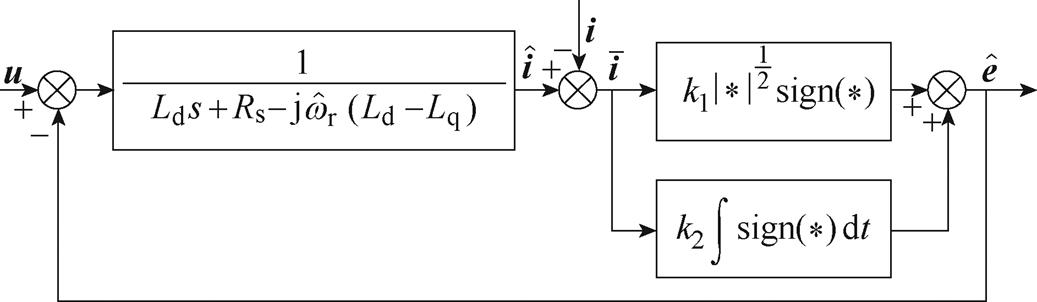
图1 Super-twisting滑模观测器结构
Fig.1 Structure of Super-twisting sliding mode observer
为了解决系统的抖振问题，本文基于内模控制原理[20]，在Super-twisting滑模观测器中引入一个正弦信号的二阶广义积分器（SOGI）作为估算的扩展反电动势的内模，带SOGI的Super-twisting滑模观测器结构如图2所示。不同于图1所示的常规结构，这里不是直接通过Super-twisting算法得到估算的扩展反电动势，而是获得实际扩展反电动势和估算扩展反电动势之间的误差信号，再将扩展反电动势误差信号作为SOGI的输入，最终输出估算的扩展反电动势。
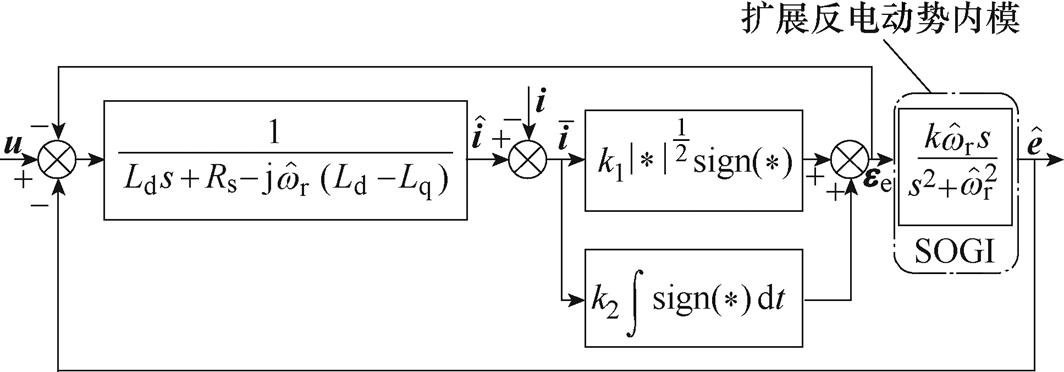
图2 带SOGI的Super-twisting滑模观测器结构
Fig.2 Structure of super-twisting sliding mode observer with SOGI
带SOGI的Super-twisting滑模观测器的方程为
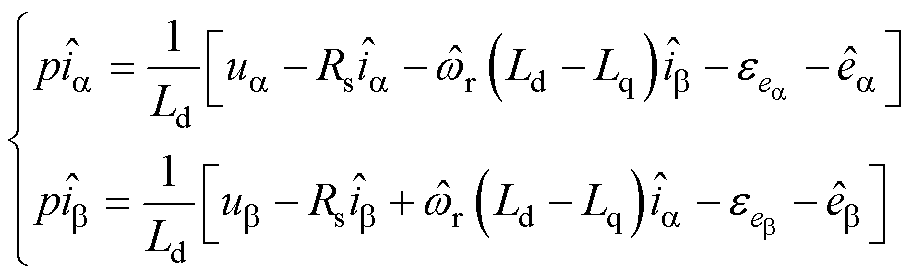（14）
式中，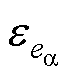
、
分别为实际扩展反电动势和扩展反电动势的误差，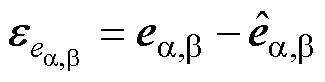
。
扩展反电动势误差通过Super-twisting算法计算获得
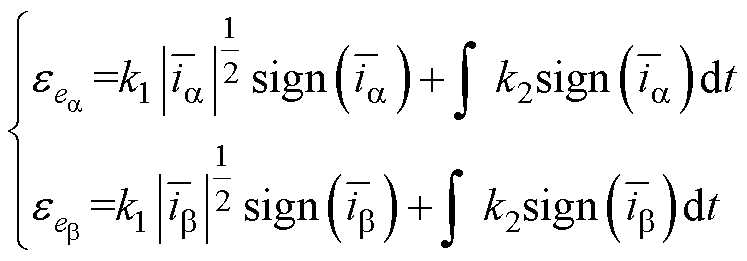（15）
式中，滑模系数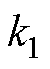和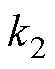依然可以按式（13）给定。
将获得的扩展反电动势误差信号输入如图3所示的SOGI，输出为估算的扩展反电动势，误差信号到估算的扩展反电动势之间的传递函数为
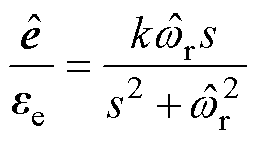（16）
式中，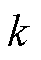
为增益系数，取值和SOGI动态性能有关[21]。
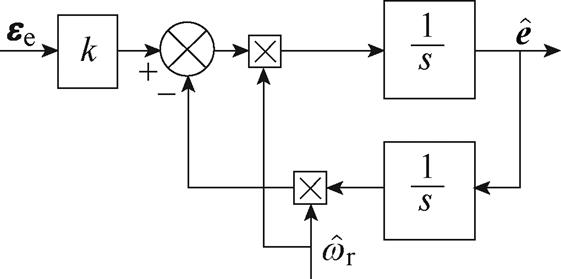
图3 SOGI结构
Fig.3 Structure of SOGI
为了分析所提出的改进的Super-twisting滑模观测器，首先推导得到实际扩展反电动势和估算扩展反电动势之间的传递函数关系。将式（14）写作复矢量的形式，有
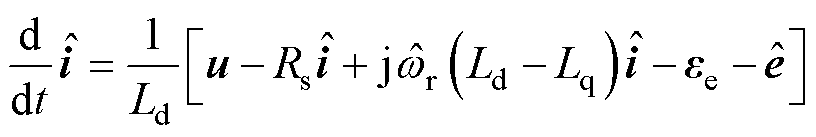（17）
式（17）与式（3）相减，考虑转速为机械量，相比于电气量变化较慢，这里认为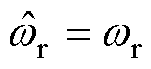
，得到
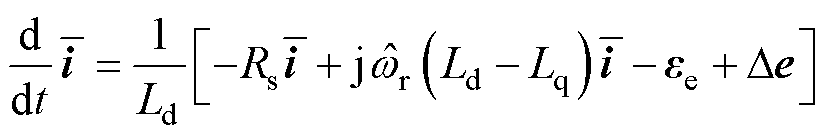（18）
这里，通过式（15）计算得到的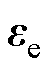
为估算的扩展反电动势误差，而
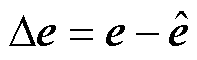为实际的扩展反电动势误差。由于式（15）中Super-twisting算法包含不连续项，无法直接采用传统的线性控制理论进行分析，因此为了便于分析，这里将式（15）简化为线性增益的形式，即
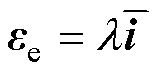（19）
式中，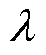
为正实数。
将式（19）代入式（18）中整理得到
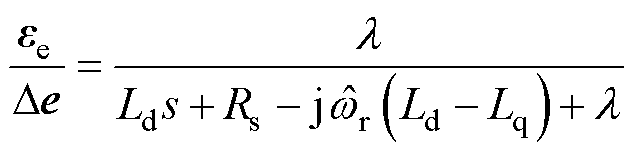（20）
然后将式（16）代入式（20）化简整理得到估算扩展反电动势和实际扩展反电动势之间的传递函数为
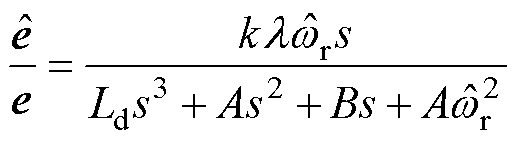（21）
其中
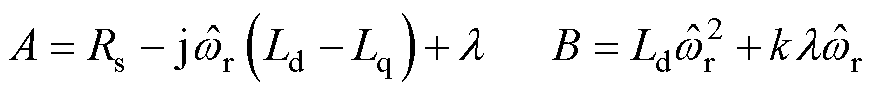
式（21）所示观测器传递函数的幅频特性如图4所示，从图中可以看出，在基频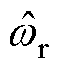
处幅值为0dB，相位为0°，能够实现扩展反电动势的准确估算。另外由于SOGI对高频信号具有滤波特性，因此在保证估算准确性的同时能够有效抑制滑模系统的高频抖振。
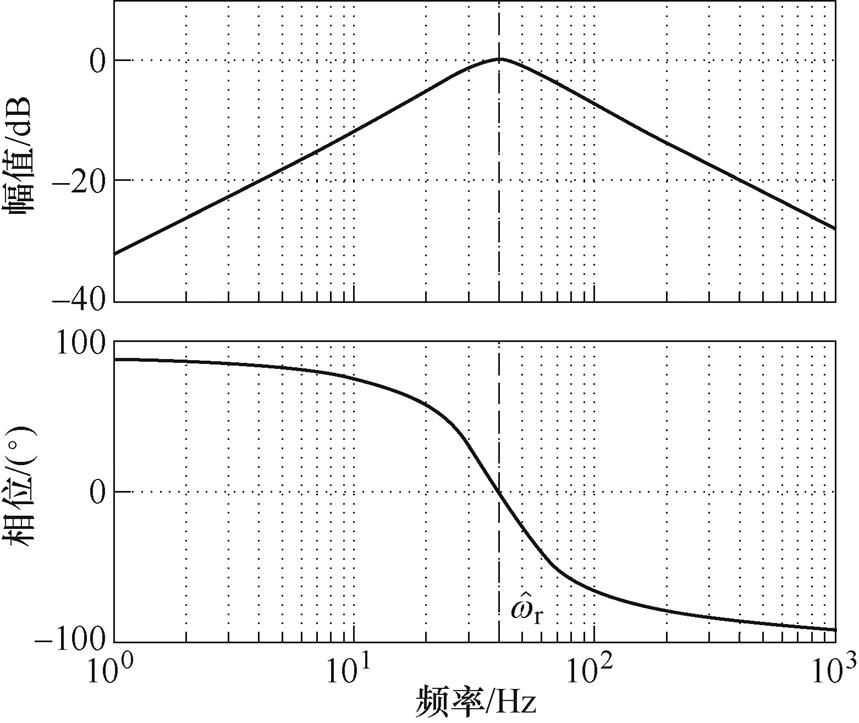
图4 扩展反电动势观测器传递函数伯德图
Fig.4 Bode plot of extended electromotive force observer
前面对滑模观测器做了一定简化，从线性控制理论的角度进行了分析，当设计的滑模观测器不做式（19）所示的简化时，可以采用构建李雅普诺夫函数的方法进行系统稳定性分析[16, 22]。将式（18）写作
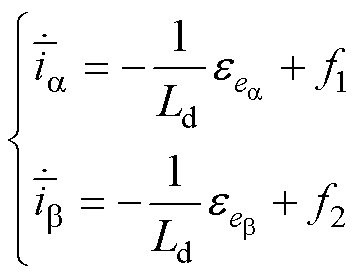（22）
其中
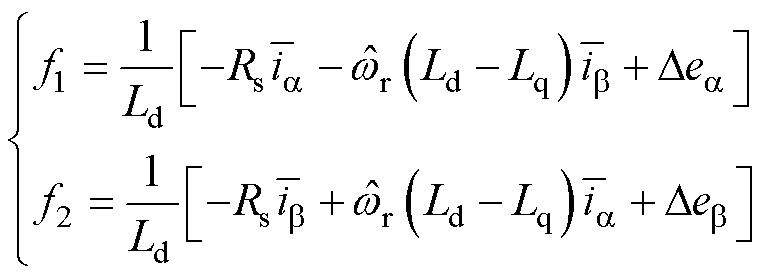
对于常数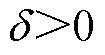
能够取足够大的值使得
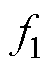和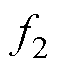
满足下面全局有界性的条件
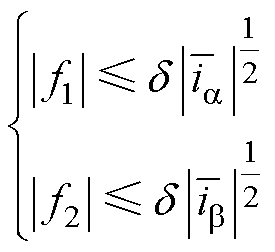（23）
定义李雅普诺夫函数为
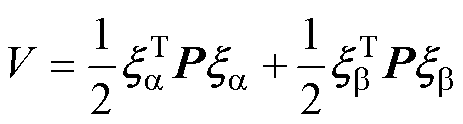（24）
其中
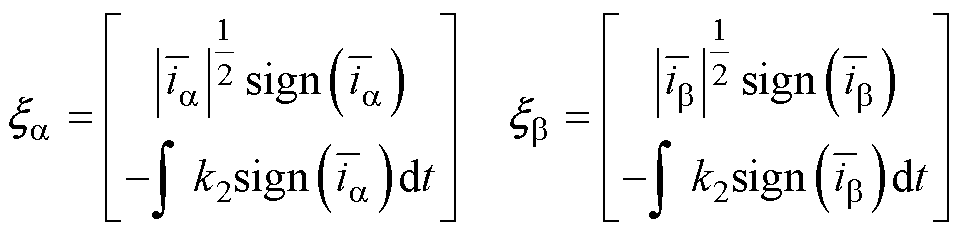
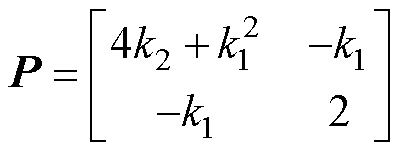
考虑式（23）的边界条件，并对李雅普诺夫函数求导，得到
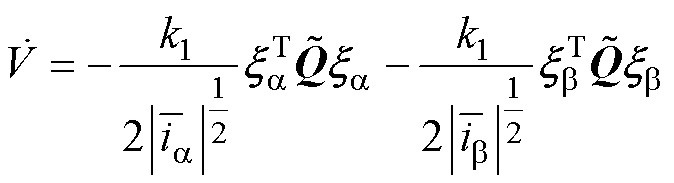（25）
其中
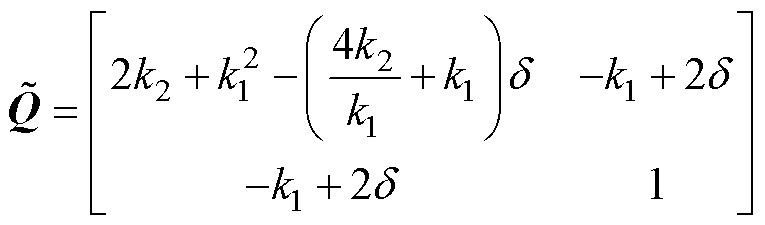
当滑模系数满足
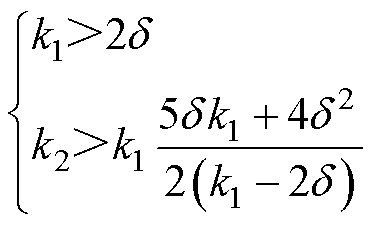（26）
则有
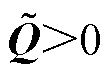，那么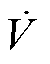
为负定，则系统满足李雅普诺夫稳定条件。其中式（13）为满足稳定条件的一种形式。
上述给出了连续域下改进Super-twisting滑模观测器的设计，为了方便工程应用中的数字化实现，以及解决连续域观测器离散化过程中存在的离散化误差和扩展反电动势的耦合问题，根据1.2节中构建的IPMSM离散域扩展反电动势模型直接设计离散域Super-twisting滑模观测器。
结合式（10）和式（14）、式（15），可以得到改进的离散域Super-twisting滑模观测器为
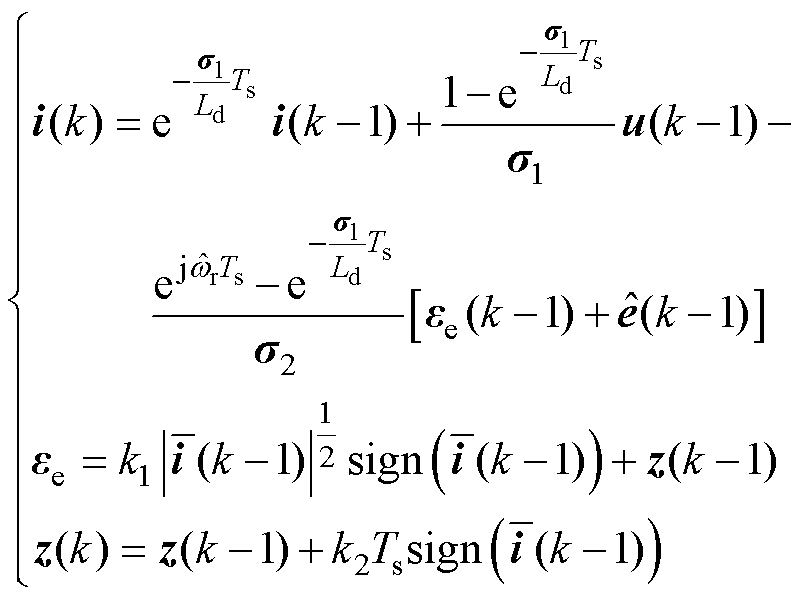（27）
对于图3所示的SOGI采用离散化积分器的方法进行离散化，由于扩展反电动势为交流信号，因此离散化方法选择防止频率畸变的双线性变换法，离散化之后的结构如图5所示。
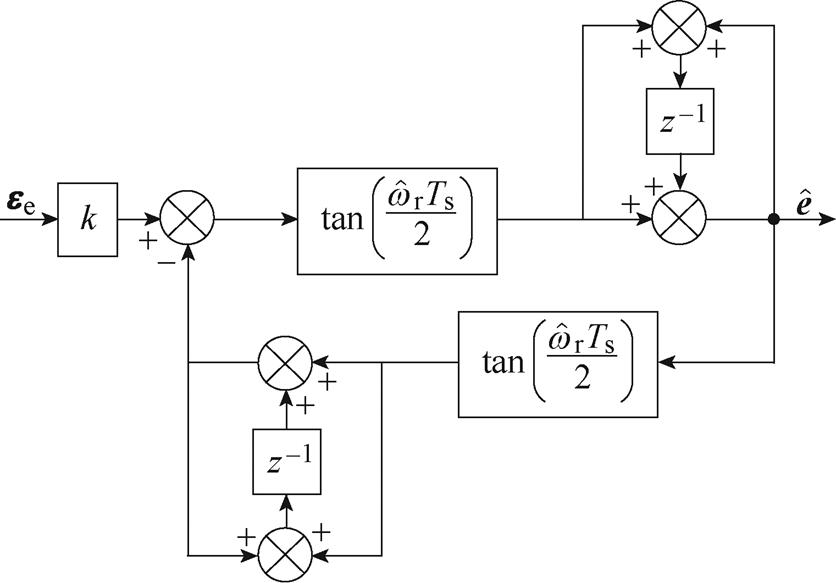
图5 SOGI离散化结构
Fig.5 Discrete structure of SOGI
在3kW的IMSM牵引传动平台上进行实验，验证本文提出的控制策略的有效性。整个IPMSM无位置传感器控制系统结构框图如图6所示，采用传统的矢量控制结构，坐标变换中用到的转子位置角度通过无位置控制算法获得。根据第2节中的Super-twisting滑模观测器估算得到扩展反电动势，利用估算得到的扩展反电动势可以进一步通过式（28）计算得到转子位置和转速，为了获得平滑的转速信息，这里采用低通滤波器（Low Pass Filter, LPF）对估算得到的转速进行滤波。
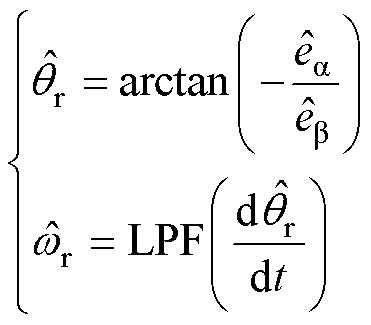（28）
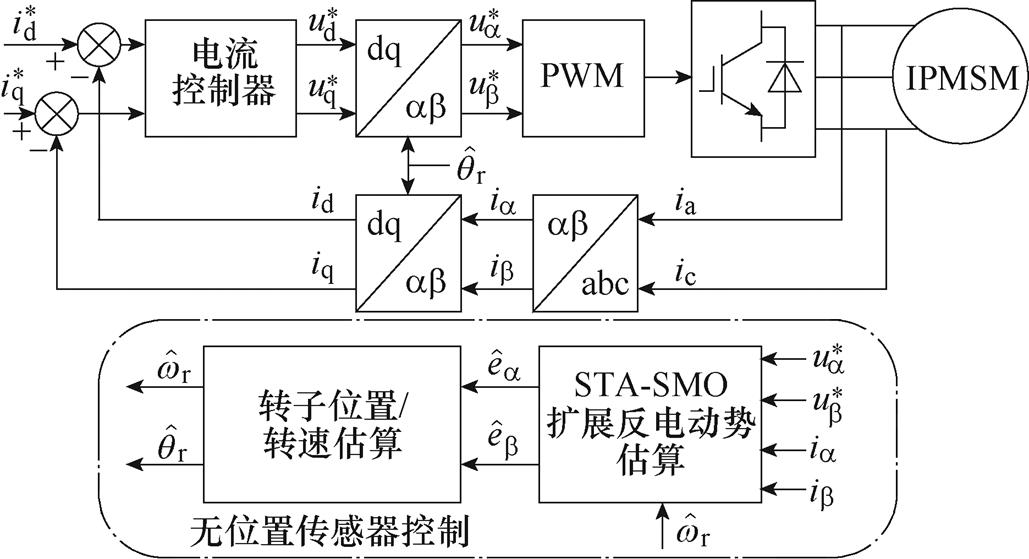
图6 无位置传感器控制系统结构框图
Fig.6 Structure diagram of sensorless control system
IPMSM实验平台如图7所示，包括二极管不控整流器和电压源型逆变器组成的主功率回路，基于TMS320F28335芯片的数字控制器，IPMSM作为被试电机，感应电机（Induction Motor, IM）作为陪试电机，陪试电机由负载控制柜进行控制。被试电机安装有旋转变压器，其输出信号经过解码芯片之后可以获得电机实际的转子位置和转速，在实验中实际的转子位置和转速不用于控制，只用于对比和评估无位置传感器控制中估算的转子位置和转速的性能。实验中采用在一个载波周期内双采样双更新的控制策略，能够减小数字控制的延时，提高系统动态响应，这里选取开关频率为2.5kHz，控制频率为5kHz。实验中IPMSM的各项参数见表1。
图7 IPMSM实验平台
Fig.7 Experimental platform of IPMSM
表1 IPMSM参数
Tab.1 The parameters of IPMSM
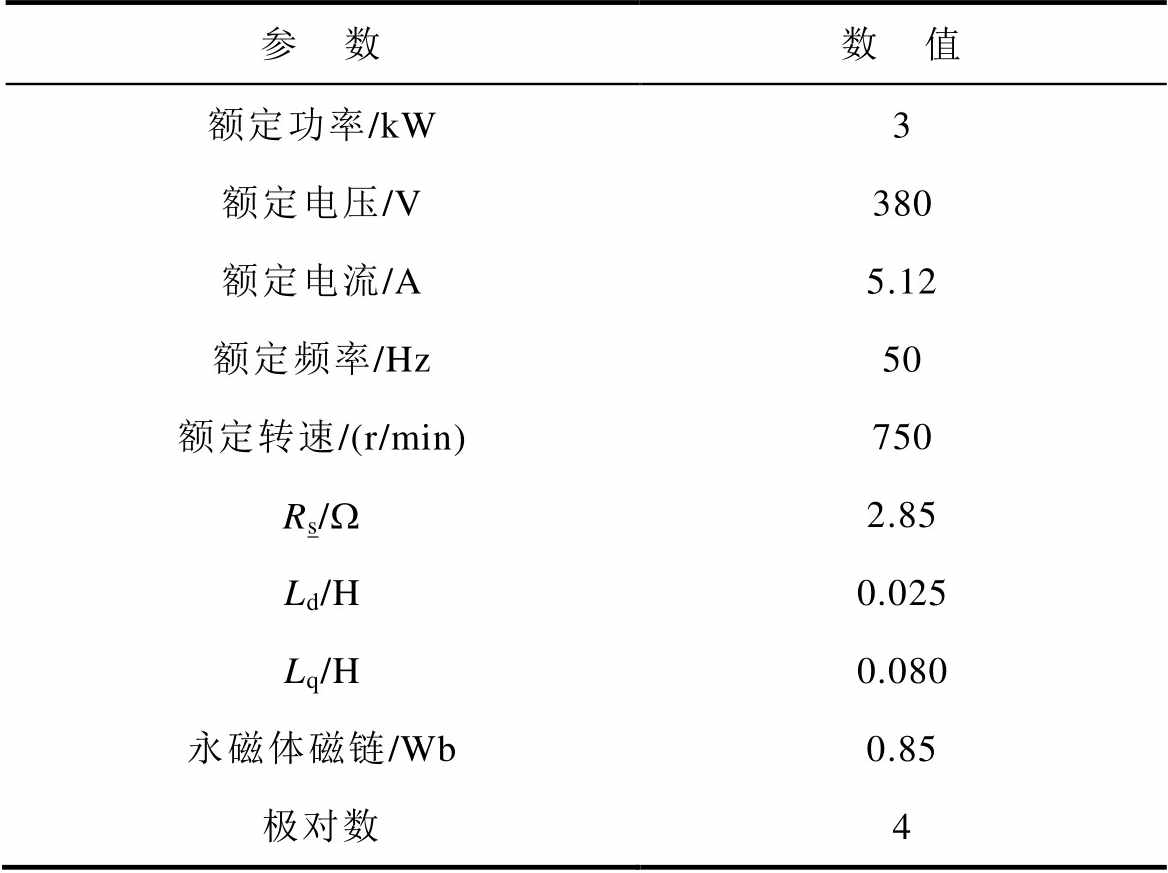
参 数数 值 额定功率/kW3 额定电压/V380 额定电流/A5.12 额定频率/Hz50 额定转速/(r/min)750 Rs/W2.85 Ld/H0.025 Lq/H0.080 永磁体磁链/Wb0.85 极对数4
图8为采用2.1节中常规Super-twisting滑模观测器估算定子电流和扩展反电动势的实验结果，电机运行在10Hz，转矩10N·m。根据式（13），并在实验中进行调试，分别选取不同范围内的两组滑模系数，当选取较小的滑模系数L=400时，抖振较小，但是会存在较大的估算误差；当选取较大的滑模系数L=2 000时，估算定子电流与实际定子电流之间的误差减小，但是出现了较大的抖振现象。图9为采用常规Super-twisting滑模观测器、系数选取为L=400时估算的反电动势计算得到的转子位置和转速结果，电机运行在10Hz，转矩为零，因为加载之后电机参数会发生变化进而影响估算转子位置的精度（会在后面加载实验中具体说明），为了排除电机参数因素变化带来的影响，因此这里设定转矩为零。从图9可以看出，虽然估算转速能够很好地跟踪实际转速，但是由于估算的扩展反电动势存在较大误差，因此估算的转子位置和实际转子位置之间的误差也较大，转子位置误差超过10°。因此，可以看出常规Super-twisting滑模观测器在实际应用中控制频率有限的情况下，无法获得令人满意的控制性能。
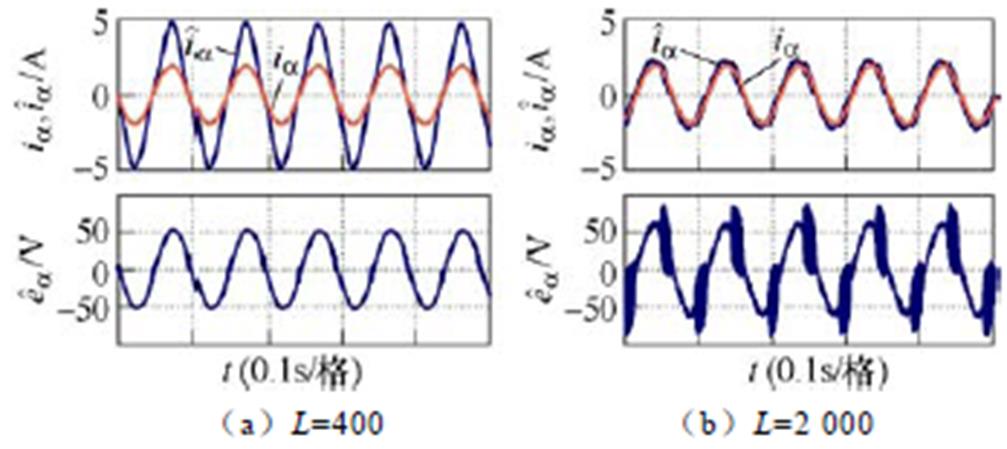
图8 常规Super-twisting滑模观测器估算定子电流和扩展反电动势的实验结果
Fig.8 Experimental results of stator current and EEMF estimation using the conventional super-twisting SMO
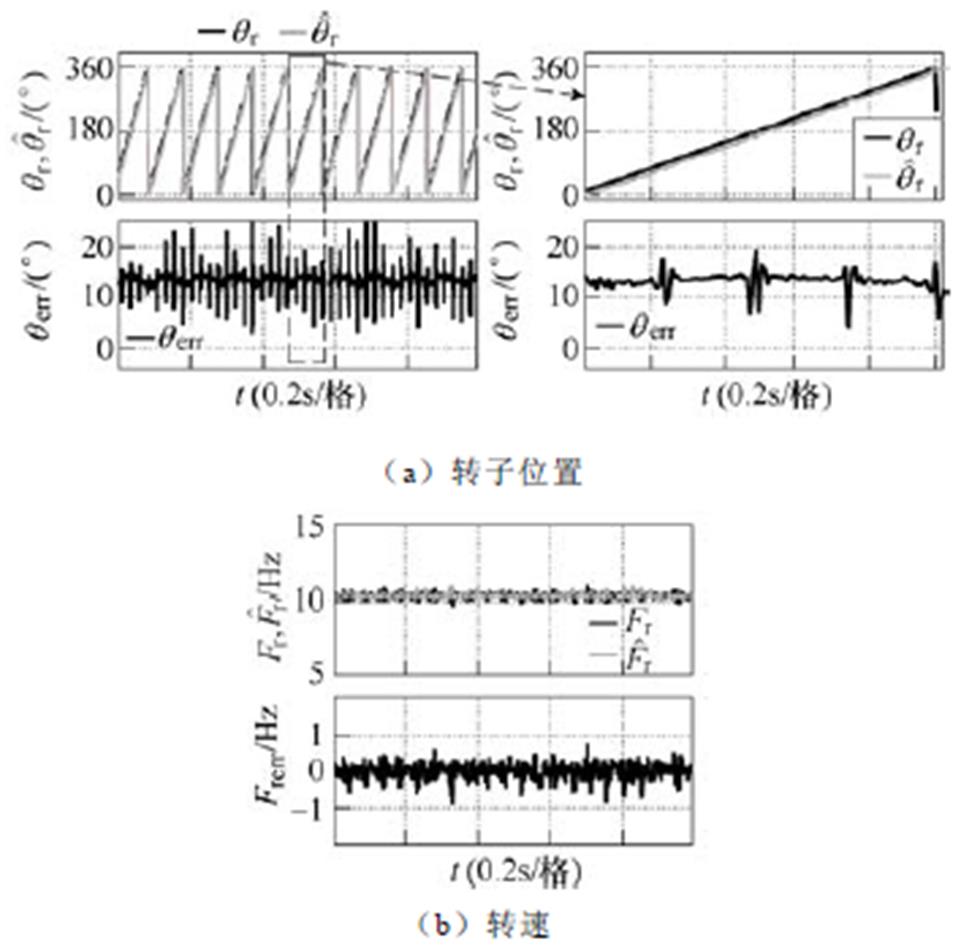
图9 采用常规Super-twisting滑模观测器时估算转子位置和转速的实验结果
Fig.9 Experimental results of the estimated rotor position and speed using the conventional super-twisting SMO
图10为采用带SOGI的Super-twisting滑模观测器估算定子电流和扩展反电动势的实验结果，电机运行在10Hz，转矩为10N·m，滑模系数选取为L= 400，SOGI增益系数k=2。从图中可以看出，估算定子电流能够很好地跟踪实际定子电流，同时也能够很好地抑制抖振。图11为采用带SOGI的Super- twisting滑模观测器在10Hz零转矩时估算转子位置和转速的实验结果，从图中可以看出，估算的转子位置和转速都能够很好地跟踪实际的转子位置和转速，转子位置误差在0°附近。图12为电机运行30Hz零转矩时估算转子位置和转速的实验结果，从图中可以看出，当转速升高之后，估算的转子位置和转速依然能够很好地跟踪实际值。图13给出了从5Hz加速到45Hz（转矩为零）的实验结果，从上往下依次是实际转速和估算转速、转速误差、转子位置误差，由于采用的如式（28）所示的直接计算法估算转子位置和转速，在动态过程中性能较差，不能做到无静差的跟踪，但整个动态加速过程中转速误差都保持在1Hz以内，估算转子位置误差最大不超过5°，恢复到稳态时转速误差和转子位置误差都能保持在零附近。减速工况和加速工况的实验结果一致，这里不再给出。
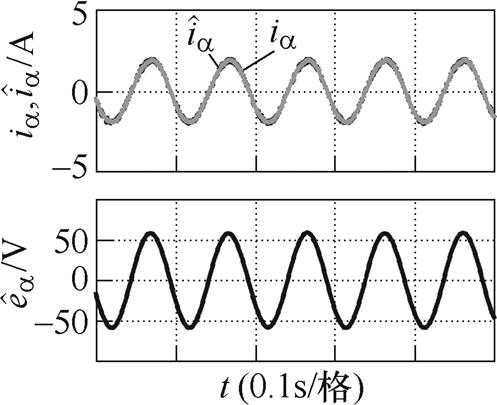
图10 带SOGI的Super-twisting滑模观测器估算定子电流和扩展反电动势的实验结果
Fig.10 Experimental results of stator current and EEMF estimation using the super-twisting SMO with SOGI
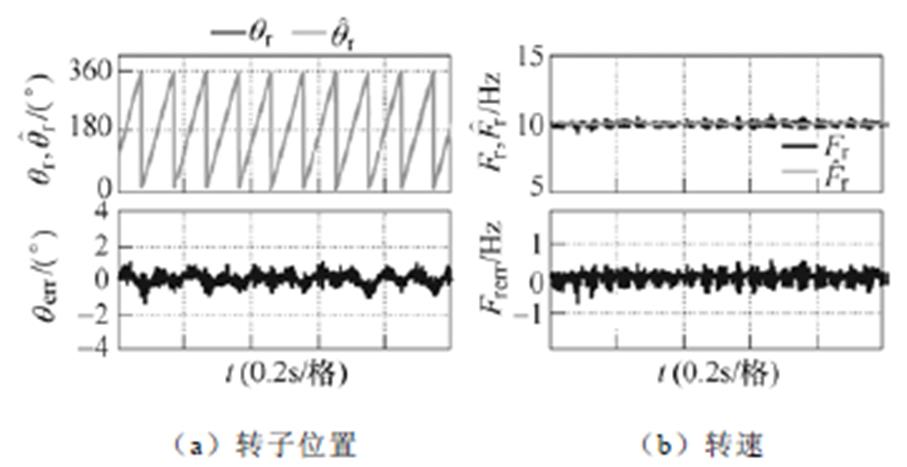
图11 带SOGI的Super-twisting滑模观测器时估算转子位置和转速的实验结果：10Hz
Fig.11 Experimental results of the estimated rotor position and speed using the super-twisting SMO with SOGI: 10Hz
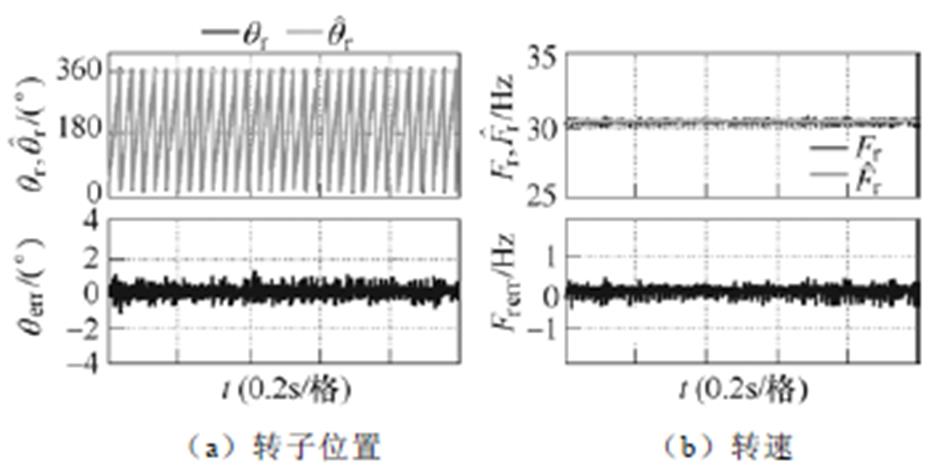
图12 带SOGI的Super-twisting滑模观测器时估算转子位置和转速的实验结果：30Hz
Fig.12 Experimental results of the estimated rotor position and speed using the super-twisting SMO with SOGI: 30Hz
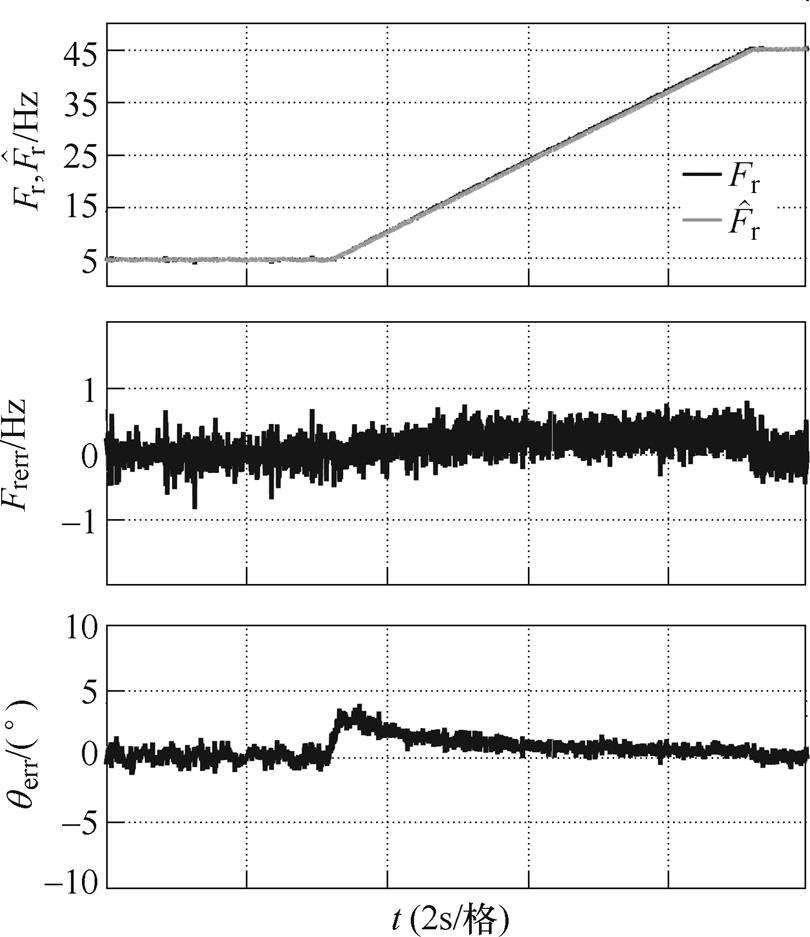
图13 带SOGI的Super-twisting滑模观测器时估算转子位置和转速的实验结果：加速工况
Fig.13 Experimental results of the estimated rotor position and speed using the super-twisting SMO with SOGI: acceleration operation
图14和图15分别为10Hz和40Hz时采用带SOGI的Super-twisting滑模观测器的方法负载变化的实验结果，分别给出了转速、转子位置误差、q轴电流（包括指令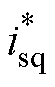值
和实际值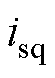
）、a相电流的实验结果。由于受数据采集手段的限制，没有同时采集d轴电流、b相和c相电流，但q轴电流和a相电流足以反映转矩变化过程中电流的性能。实验中转矩从零阶跃变化到10N·m，由于受实验条件所限，试验电机动态性能较差，当转矩发生阶跃变化时，电机短时间内加速，后续恢复到指令速度，为观察负载变化时刻的实验结果，图中所取时间较短，未显示速度恢复到稳态时的结果。从实验结果可以看出，转矩发生阶跃变化后估算转速和转子位置都能在很短的时间内跟踪实际值，电流控制也具有良好的性能。由于高速时电机扩展反电动势大，信噪比高，因此速度较高时能获得比速度较低时更好的动态性能。另外，转矩增大之后转子位置误差有所增大，主要是加载之后q轴电流增大引起磁饱和，进而使得电机参数Lq减小造成的，已有研究对此影响进行了验证和分析[23]。
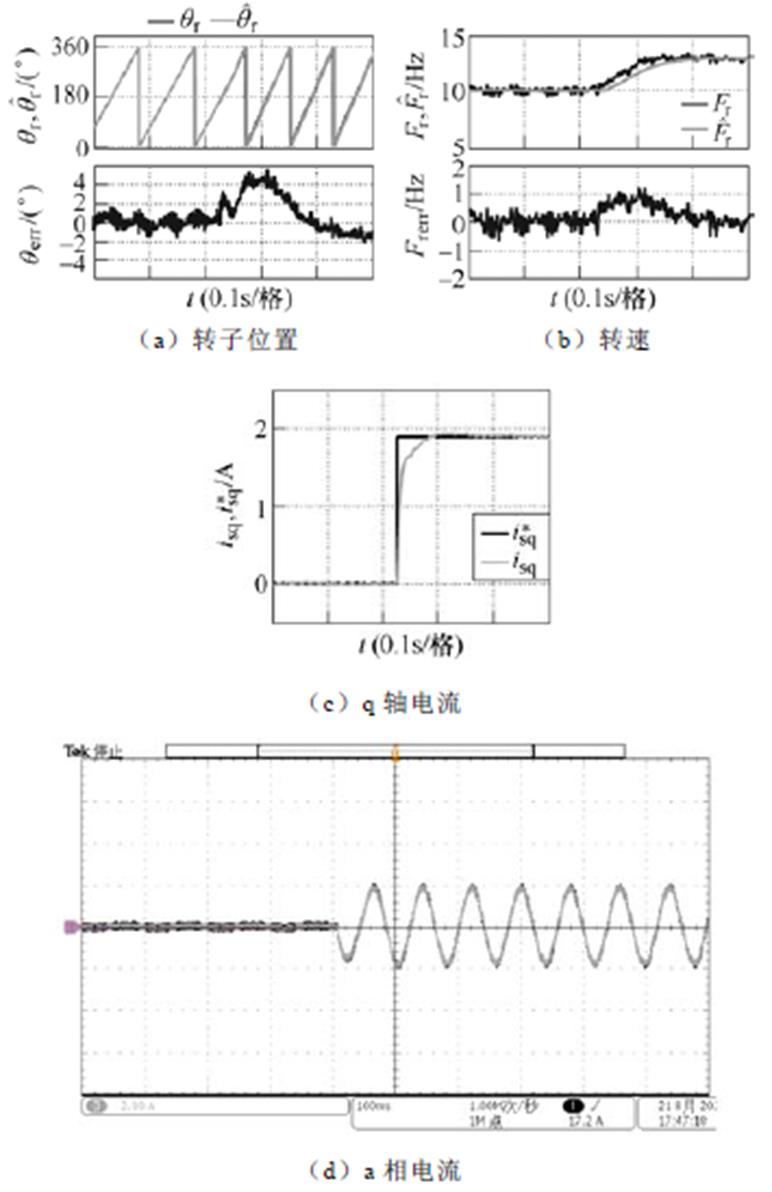
图14 带SOGI的Super-twisting滑模观测器方法负载变化实验结果:10Hz转矩阶跃变化
Fig.14 Experimental results of load change using the method of super-twisting SMO with SOGI: torque step change at 10Hz
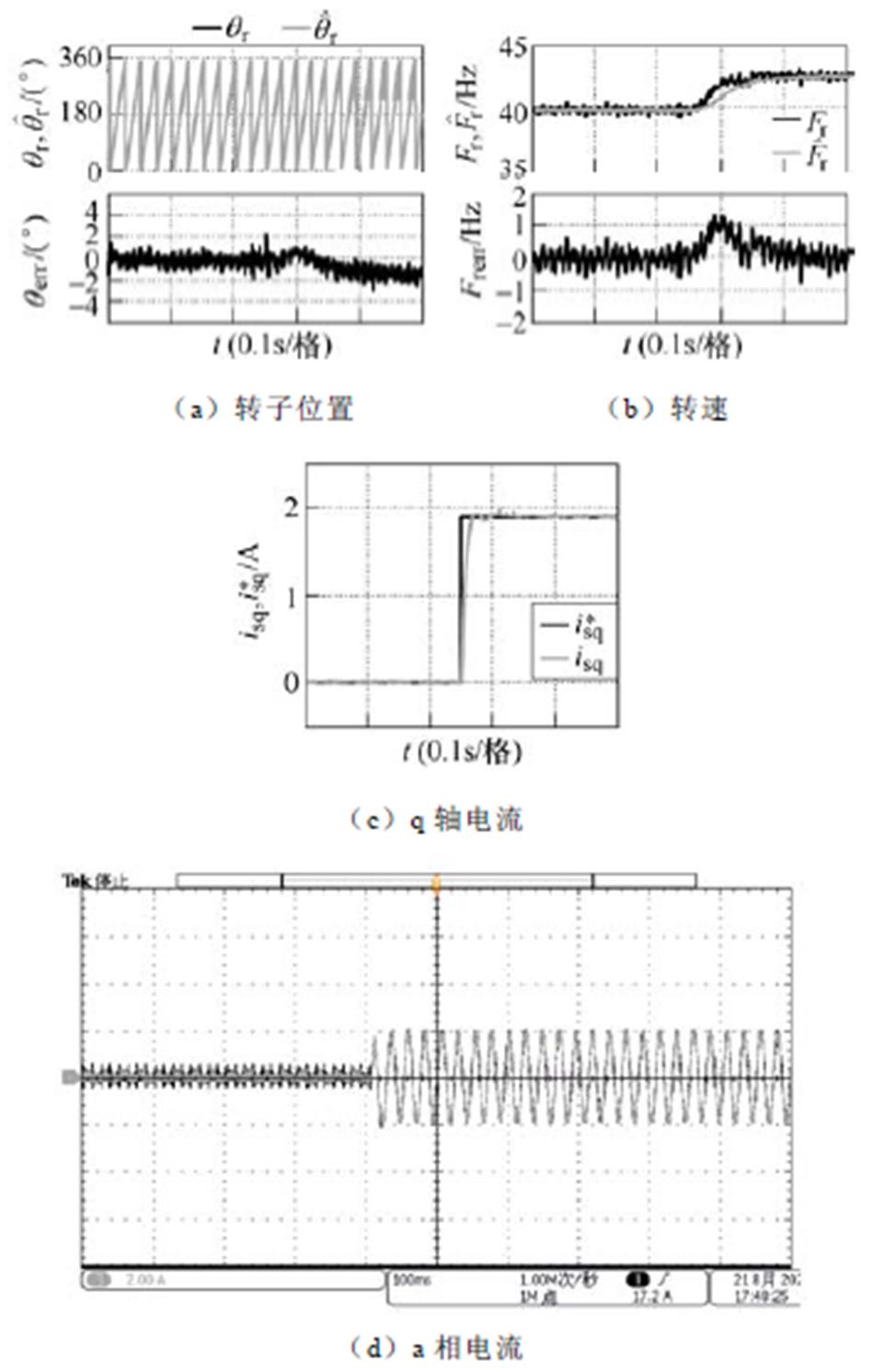
图15 带SOGI的Super-twisting滑模观测器方法负载变化实验结果：40Hz转矩阶跃变化
Fig.15 Experimental results of load change using the method of super-twisting SMO with SOGI: torque step change at 40Hz
针对基于Super-twisting滑模观测器的IPMSM无位置传感器控制在实际工程应用中存在的抖振现象和估算精度较差的问题，本文提出了一种改进的Super-twisting滑模观测器用于估算扩展反电动势，基于内模控制原理引入二阶广义积分器，使得在保证观测器估算准确性的同时能够有效抑制系统抖振，并对提出的改进Super-twisting滑模观测器的稳定性进行了分析。同时构建了精确的离散域扩展反电动势模型，并基于该模型设计了离散域Super- twisting滑模观测器，进一步提高了数字实现过程中的估算精度。通过实验验证了所提出的观测器的稳态和动态性能，实验结果证明，本文提出改进的Super-twisting滑模观测器在保证估算转子位置和转速准确性的同时能够有效抑制抖振，具有一定的实际工程应用价值。后续将在提高动态性能和减小电机参数变化对估算转子位置精度的影响方面开展进一步的研究工作。
参考文献
[1] 冯江华. 轨道交通永磁电机牵引系统关键技术及发展趋势[J]. 机车电传动, 2018(6): 9-17.
Feng Jianghua. Key technology and development trend of permanent magnet motor traction system for rail transit[J]. Electric Drive for Locomotives, 2018(6): 9-17.
[2] Pacas M. Sensorless drives in industrial appli- cations[J]. IEEE Industrial Electronics Magazine, 2011, 5(2): 16-23.
[3] 刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017, 32(16): 76-88.
Liu Jilong, Xiao Fei, Shen Yang, et al. Position- sensorless control technology of permanent-magnet synchronous motor-a review[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 76-88.
[4] Wang Gaolin, Valla M, Solsona J. Position sensorless permanent magnet synchronous machine drives-a review[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(7): 5830-5842.
[5] Lee Y, Kwon Y C, Sul S K. Comparison of rotor position estimation performance in fundamental- model-based sensorless control of PMSM[C]//2015 IEEE Energy Conversion Congress and Exposition, ontreal, QC, Canada, 2015: 5624-5633.
[6] 李浩源, 张兴, 杨淑英, 等. 基于高频信号注入的永磁同步电机无传感器控制技术综述[J]. 电工技术学报, 2018, 33(12): 2653-2664.
Li Haoyuan, Zhang Xing, Yang Shuying, et al. Review on sensorless control of permanent magnet synchronous motor based on high-frequency signal injection[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2653-2664.
[7] Chen Zhiqian, Tomita M, Doki S, et al. An extended electromotive force model for sensorless control of interior permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2003, 50(2): 288-295.
[8] 陆婋泉, 林鹤云, 韩俊林. 永磁同步电机的扰动观测器无位置传感器控制[J]. 中国电机工程学报, 2016, 36(5): 1387-1394.
Lu Xiaoquan, Lin Heyun, Han Junlin. Position sensorless control of permanent magnet synchronous machine using a disturbance observer[J]. Proceedings of the CSEE, 2016, 36(5): 1387-1394.
[9] Zhang Guoqiang, Wang Gaolin, Xu Dianguo, et al. Discrete-time low-frequency-ratio synchronous-frame full-order observer for position sensorless IPMSM drives[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(2): 870-879.
[10] 王高林, 张国强, 贵献国, 等. 永磁同步电机无位置传感器混合控制策略[J]. 中国电机工程学报, 2012, 32(24): 103-109, 17.
Wang Gaolin, Zhang Guoqiang, Gui Xianguo, et al. Hybrid sensorless control strategy for permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2012, 32(24): 103-109, 17.
[11] 刘计龙, 肖飞, 麦志勤, 等. IF控制结合滑模观测器的永磁同步电机无位置传感器复合控制策略[J]. 电工技术学报, 2018, 33(4): 919-929.
Liu Jilong, Xiao Fei, Mai Zhiqin, et al. Hybrid position-sensorless control scheme for PMSM based on combination of IF control and sliding mode observer[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 919-929.
[12] 苏健勇, 李铁才, 杨贵杰. PMSM无位置传感器控制中数字滑模观测器抖振现象分析与抑制[J]. 电工技术学报, 2009, 24(8): 58-64.
Su Jianyong, Li Tiecai, Yang Guijie. Chattering phenomenon analysis and suppression of sliding mode observer in PMSM sensorless control[J]. Transactions of China Electrotechnical Society, 2009, 24(8): 58-64.
[13] Fridman L, Levant A. Higher order sliding modes as a natural phenomenon in control theory[M]//Robust Control via Variable Structure and Lyapunov Tech- niques. London: Springer-Verlag, 2005.
[14] 张懿, 吴嘉欣, 韦汉培, 等. 离散型变增益永磁同步电机超螺旋滑模观测器[J]. 电工技术学报, 2018, 33(21): 4962-4970.
Zhang Yi, Wu Jiaxin, Wei Hanpei, et al. Discrete variable gain super-twisting sliding mode observer for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(21): 4962-4970.
[15] Liang Donglai, Li Jian, Qu Ronghai. Sensorless control of permanent magnet synchronous machine based on second-order sliding-mode observer with online resistance estimation[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3672-3682.
[16] Di Gennaro S, Rivera J, Castillo-Toledo B. Super- twisting sensorless control of permanent magnet synchronous motors[C]//49th IEEE Conference on Decision and Control, Atlanta, GA, USA, 2010: 4018- 4023.
[17] 许中阳, 郭希铮, 邹方朔, 等. 永磁同步电机无速度传感器控制离散化方法研究[J]. 电工技术学报, 2019, 34(增刊1): 52-61.
Xu Zhongyang, Guo Xizheng, Zou Fangshuo, et al. Research on digital discretization method of speed sensorless control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 52-61.
[18] Yang S C, Chen Guanren. High-speed position- sensorless drive of permanent-magnet machine using discrete-time EMF estimation[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 4444-4453.
[19] Fridman L, Levant A, Davila J. Observation of linear systems with unknown inputs via high-order sliding- modes[J]. International Journal of Systems Science, 2007, 38(10): 773-791.
[20] Francis B A, Wonham W M. The internal model principle of control theory[J]. Automatica, 1976, 12(5): 457-465.
[21] Xin Zhen, Wang Xiongfei, Qin Zian, et al. An improved second-order generalized integrator based quadrature signal generator[J]. IEEE Transactions on Power Electronics, 2016, 31(12): 8068-8073.
[22] Moreno J A, Osorio M. A Lyapunov approach to second-order sliding mode controllers and obser- vers[C]//2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 2008: 2856-2861.
[23] Bolognani S, Ortombina L, Tinazzi F, et al. Model sensitivity of fundamental-frequency-based position estimators for sensorless pm and reluctance syn- chronous motor drives[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 77-85.
Sensorless Control of IPMSM Based on Improved Discrete Second-Order Sliding Mode Observer
Abstract The model-based methods for the sensorless control of interior permanent magnet synchronous motor (IPMSM) are used for medium- and high-speed regions and can achieve satisfactory performance above 10% of the rated speed. Among the model-based methods, the sliding mode observer (SMO) has received increasing attention due to its great robustness to system uncertainty. However, the chattering phenomenon of the conventional first-order SMO seriously affect the performance of system control. A super-twisting algorithm based second-order sliding-mode observer (STA-SMO) has been proposed to alleviate chattering. However, the ideal control performance of STA-SMO cannot be achieved since the control frequency is limited in practice, and the STA-SMO exists the compromise between alleviating chattering and the estimation accuracy under the limited control frequency. To address the issue, an improved STA-SMO with a second order general integrator (SOGI) for sensorless control of an IPMSM is proposed in this paper. Furthermore, a discrete-time model of IPMSM based on the extended electromotive force (EEMF) is proposed to remove the cross-coupling effect for the EEMF estimation and improve the estimation accuracy.
In practice, the sensorless control is implemented by a digital controller, so the designed STA-SMO in the continue-time domain must be discretized. In the process of continue-time model discretization, there will be discretization errors and the cross-coupling effect on the estimated EEMF, which will affect the estimation accuracy of the EEMF finally. In this paper, based on the latched model of the stator voltage in the stationary frame and the latched model of the EEMF in the rotating frame, a discrete-time EEMF model is constructed by using a method for developing cross-coupled discrete-time model. Since the estimation accuracy of the rotor position and speed depends on the estimation accuracy of the EEMF, an improved STA-SMO is proposed to estimate the EEMF accurately. Based on the internal model principle, a SOGI is introduced as the internal model of the EEMF to alleviate chattering and improve the estimation accuracy. Different from the conventional STA-SMO which estimates the EEMF directly, the error between the actual and estimated EEMF can be regarded as a state variable in the proposed STA-SMO and estimated firstly, and then the EEMF error signal is used as the input of the SOGI, thus the EEMF can be estimated through the SOGI finally. In order to analyze the stability of the proposed STA-SMO with SOGI using the linear control theory, the transfer function between the actual and the estimated EEMF can be obtained by simplifying the super-twisting algorithm as a linear gain. The frequency response of the transfer function indicates that the magnitude is zero dB and the phase is zero degree at the estimated fundamental frequency. Therefore, not only the EEMF can be estimated accurately, but also the chattering can be alleviated due to the filter characteristic for the high-frequency harmonic. Moreover, the stability of the proposed STA-SMO is proved by Lyapunov approaches. Finally, based on the constructed discrete-time EEMF model, a discrete improved STA-SMO is proposed. In order to verify the effectiveness of the proposed sensorless control, the experiments are carried out on a 3kW IPMSM traction drive system. The EEMF estimation results of the conventional and proposed STA-SMO are compared. The error between the actual and estimated rotor position exceeds 10 degrees using the conventional STA-SMO. Using the proposed STA-SMO, the estimated rotor position and speed can track the actual values well and the chattering can also be well alleviated. The proposed sensorless control is also verified in the speed and load variation condition.
Keywords：Interior permanent magnet synchronous motor (PMSM) sensorless control, discrete-time model, Super-twisting sliding mode observer (SMO), second order generalized integrator (SOGI)
中图分类号：TM315
DOI: 10.19595/j.cnki.1000-6753.tces.211462
国家自然科学基金资助项目（51977006）。
收稿日期 2021-09-14
改稿日期 2022-03-21
E-mail: chchwang@bjtu.edu.cn
苟立峰 男，1988年生，博士，研究方向为电力电子与电力传动。
E-mail: 16117400@bjtu.edu.cn（通信作者）
（编辑 郭丽军）