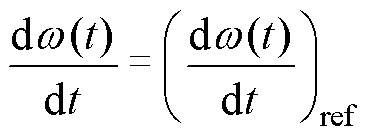（1）
摘要 电流传感器的使用会增加系统的成本和噪声干扰，降低系统的可靠性。而对于开关磁阻电机系统，缺少电流信号难以保证良好的控制性能。针对该问题，提出一种无电流传感器控制方法。该方法采用速度、加速度双闭环控制，因此反馈量均由位置传感器得到。首先，从两个方面分析了所提出控制方法的可行性：①证明了该方法的收敛性；②证明了在稳态下加速度和电磁转矩的近似线性关系，并依此分析了加速度控制和转矩控制的等效性。根据电机的磁链特性，对加速度环，提出具有三个滞环边界的滞环控制方法。兼顾电机效率和转矩脉动，合理地选择了开通角、关断角。实验电机为12/8开关磁阻电机。分别采用电压斩波控制方法、直接转矩控制方法和所提出的控制方法运行电机，对其电流、电磁转矩和转速波形进行了比较。结果表明，在控制效果上，所提出的控制方法与直接转矩控制方法相当，优于电压斩波控制方法。除此之外，电流与电磁转矩呈复杂的非线性关系，直接转矩控制方法需要进行电流和电磁转矩的换算。而由于加速度与电磁转矩的近似线性关系，所提控制方法无需计算电磁转矩，因此计算量更小。
关键词：开关磁阻电机 无电流传感器控制方法 加速度 电磁转矩
对于闭环控制系统，控制变量必须是已知的，控制变量主要通过传感器测量获得。传感器的使用存在以下弊端：①增加了系统的成本和体积；②安装需要增加接线，带来了电路干扰，降低了系统可靠性；③受环境约束，在恶劣条件下可能会失准或失效[1-2]。因此，为了减少传感器的使用数量，无传感器控制技术正在被研究并已取得大量的成果[3-8]。
开关磁阻电机结构简单坚固，其转子通常采用硅钢片叠压制成，无绕组或永磁体，因此不存在开、短路和退磁等问题，可靠性高，适用于恶劣环境[9-13]。在恶劣环境中，无传感器控制技术更为重要。开关磁阻电机常用的控制方法包括角度位置控制（Angular Position Control, APC）[14-15]、电压斩波控制（Voltage Pulse Width Modulation, VPWM）[16]、电流斩波控制（Chopping Current Control, CCC）[17-18]、直接转矩控制（Direct Torque Control, DTC）[19-22]等。与异步电机、同步电机等电机相比，开关磁阻电机主要缺点之一是具有较大的转矩脉动[23-24]。以上控制方法中，除APC和VPWM以外，其他方法都需要使用电流传感器。APC和VPWM虽然不需要使用电流传感器，但由于它们是单闭环控制，仅能跟踪速度，对转矩不具有控制能力。CCC能较好地控制电流，但由于电流和转矩是非线性关系，对转矩的控制效果不佳。DTC是直接跟踪转矩的控制方法，对转矩控制效果好[19-22]。通常，DTC需要将电流值换算成电磁转矩值跟踪参考转矩或者将参考转矩换算成参考电流值进行电流跟踪。因此，DTC除了需要每相电流值，还需要精确的电机模型参数。
开关磁阻电机的电流传感器通常安装在每相绕组的端部。为了减少电流传感器的使用数量，目前常见的方法是进行传感器的重构[25-27]。不对称半桥功率变换器（Asymmetric Half Bridge Converter, AHBC）是开关磁阻电机最常用的功率变换器。它的工作方式是依次逐相导通。在换相区间，通常有两相绕组同时导通。因此，任一时刻最多有两相绕组上有电流。通过重构，电流传感器与多相绕组耦合，任意时刻，先判断工作相，再根据耦合系数矩阵，将传感器上的电流值转换成当前工作相电流值。因此，电流传感器重构方法可以将电流传感器的数量降至两个[25-26]。文献[27]对功率变换器和电流传感器均进行了重构，将电流传感器的使用数量降至一个。对换相区的两个工作相，该方法通过切换测量的方式获取电流值。由于该方法不能测量退磁过程中的电流，因此通常用于CCC。
对于开关磁阻电机，在无电流传感器的情况下，要保证良好的转矩控制效果，需要找到一个新的不依赖电流的跟踪变量，并且该变量与转矩之间存在简单的函数关系。基于加速度变量，本文提出一种无电流传感器的开关磁阻电机控制方法。首先证明了基于加速度闭环控制方法的收敛性并分析了加速度控制和转矩控制的等效性。然后介绍了该控制方法的实现方式。最后通过实验比较了VPWM、DTC和该控制方法的控制效果。
对任何一种开关磁阻电机的控制方法，转子位置和转速都必须是已知的。它们通常由位置传感器测得，能够通过位置传感器直接或间接测得的量为转子位置及其n阶导数。转子位置的一阶导数为转速，二阶导数为加速度，三阶及以上导数无物理意义。当系统仅使用位置传感器一个传感器时，除了转速反馈，只有加速度适合作反馈量。以下将从收敛性和转矩控制效果两个方面分析基于加速度闭环控制方法的可行性。
基于加速度闭环控制方法的框图如图1所示。加速度为跟踪变量，因此近似认为
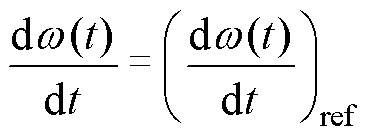（1）
式中，t为时间；
为转速；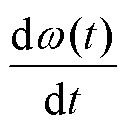
为加速度；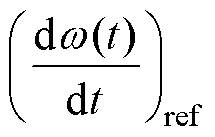
为参考加速度。参考加速度为PI调节器的输出。因此
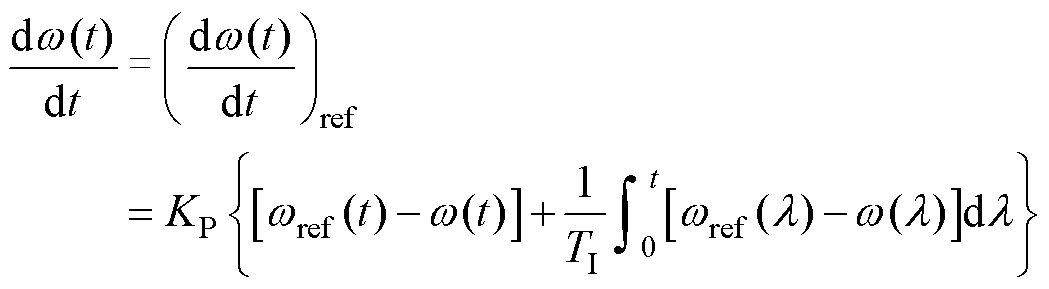（2）
式中，KP为PI调节器的比例常数；TI为积分常数；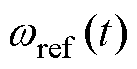
为给定速度。系统传递函数经过拉普拉斯变换得到
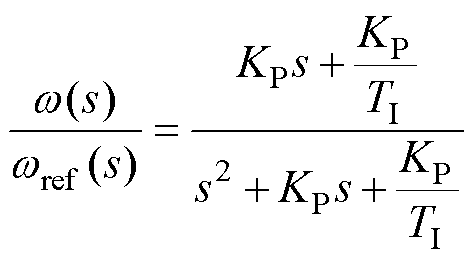（3）
式中，s为复频率。因此，当满足所有极点在左半平面时，该闭环系统稳定，即满足
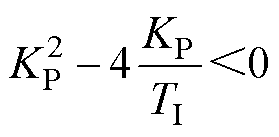（4）
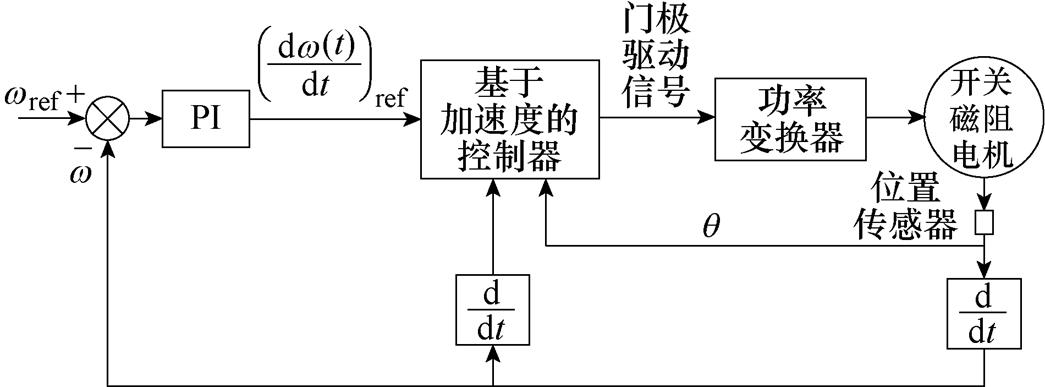
图1 基于加速度闭环控制方法的框图
Fig.1 Diagram of control method based on acceleration
电机的机械运动方程为
（5）
式中，Te(t)为电磁转矩；TL为负载转矩；J为转动惯量；D为摩擦系数。
当转速趋于稳定时，即
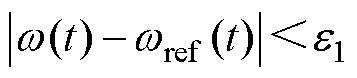（6）
其中
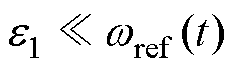（7）
根据机械运动方程式（5）得到
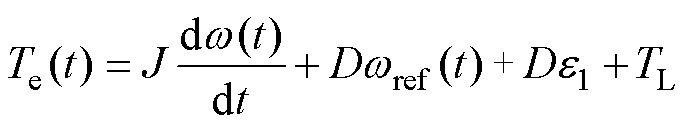（8）
根据式（7）可得
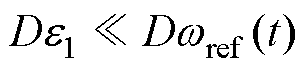（9）
因此，忽略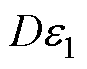
。在给定转速不变的情况下，有
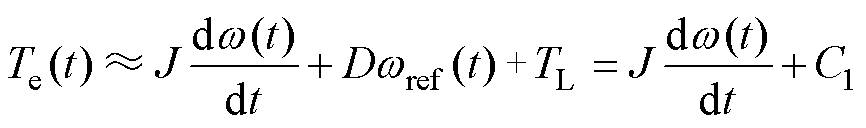（10）
式中，C1为常数，该常数与给定转速和负载转矩相关。电磁转矩和加速度近似呈线性关系。
假定在t1时转速趋于稳定，根据式（2），有
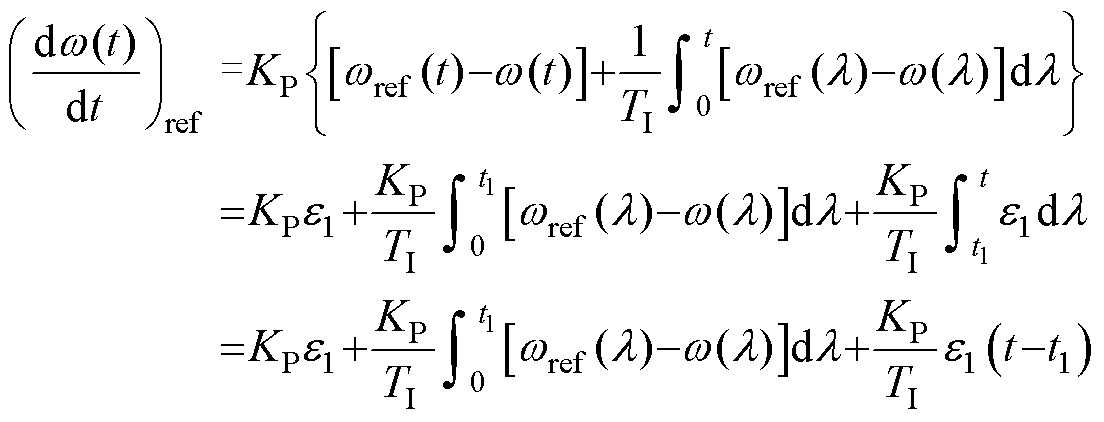（11）
在有限长的时间内，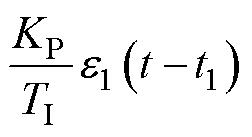
近似为零。因此有
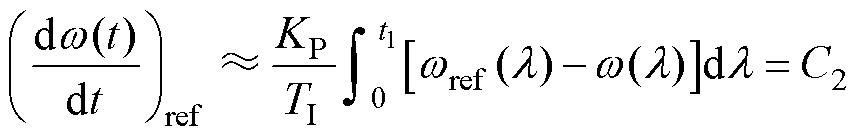（12）
式中，C2为常数，由转速稳定可知，C2必然约等于零。因此根据式（12），有
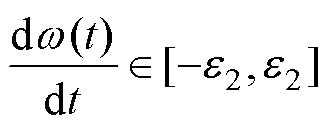（13）
式中，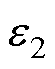
为一极小值。由于电磁转矩和加速度近似为线性关系，根据式（10），有
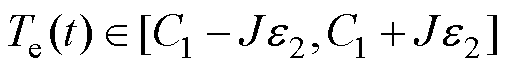（14）
因此，当加速度脉动小时，转矩脉动必然是小的。
不对称半桥功率变换器是开关磁阻电机最常用的功率变换器，其结构如图2所示。每相有四种开关状态，以A相为例，如图3所示，分别是（S1=1, S2=1），（S1=0, S2=1），（S1=1, S2=0），（S1=0, S2=0），其中，1代表开通，0代表关断。这四种开关状态对应三种绕组电压。不计晶体管导通压降和导线压降，（S1=1, S2=1）对应Udc，（S1=0, S2=1）和（S1=1, S2=0）对应0，（S1=0, S2=0）对应-Udc。Udc为母线电压。在电感值上升区，根据开关磁阻电机电路方程有
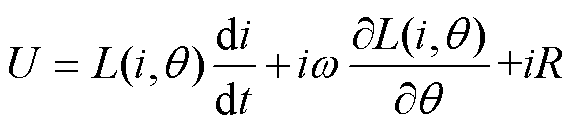（15）
式中，U为绕组端电压；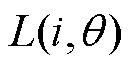
为绕组电感；i为相电流；
为位置角；R为绕组电阻。当（S1=1, S2=1）时，电流上升；当（S1=0, S2=1），（S1=1, S2=0），（S1=0, S2=0）时，电流下降；（S1=0, S2=0）的电流下降速率大于（S1=0, S2=1）和（S1=1, S2=0）的电流下降速率。一相的电磁转矩计算公式为
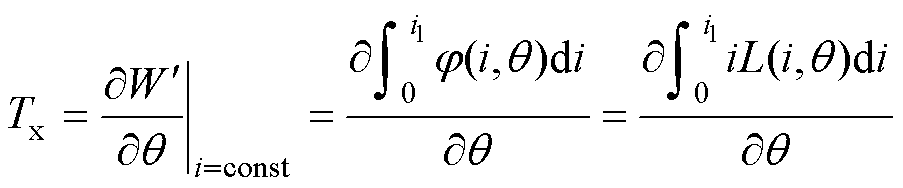
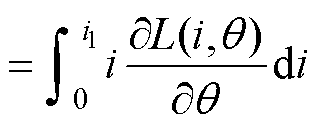（16）
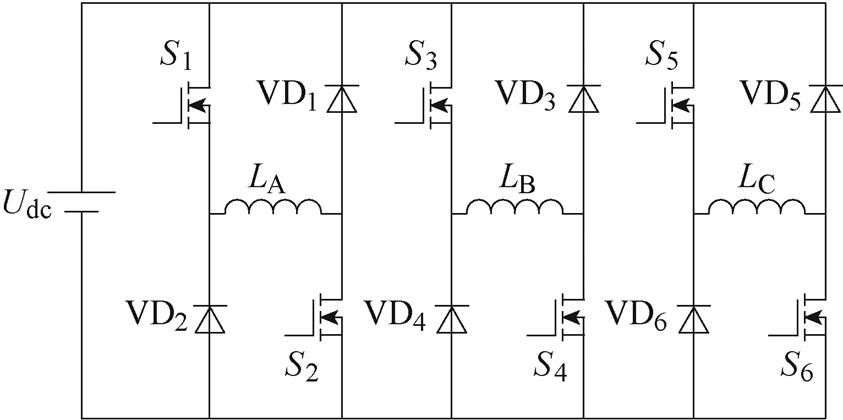
图2 不对称半桥功率变换器
Fig.2 Asymmetric half bridge converter
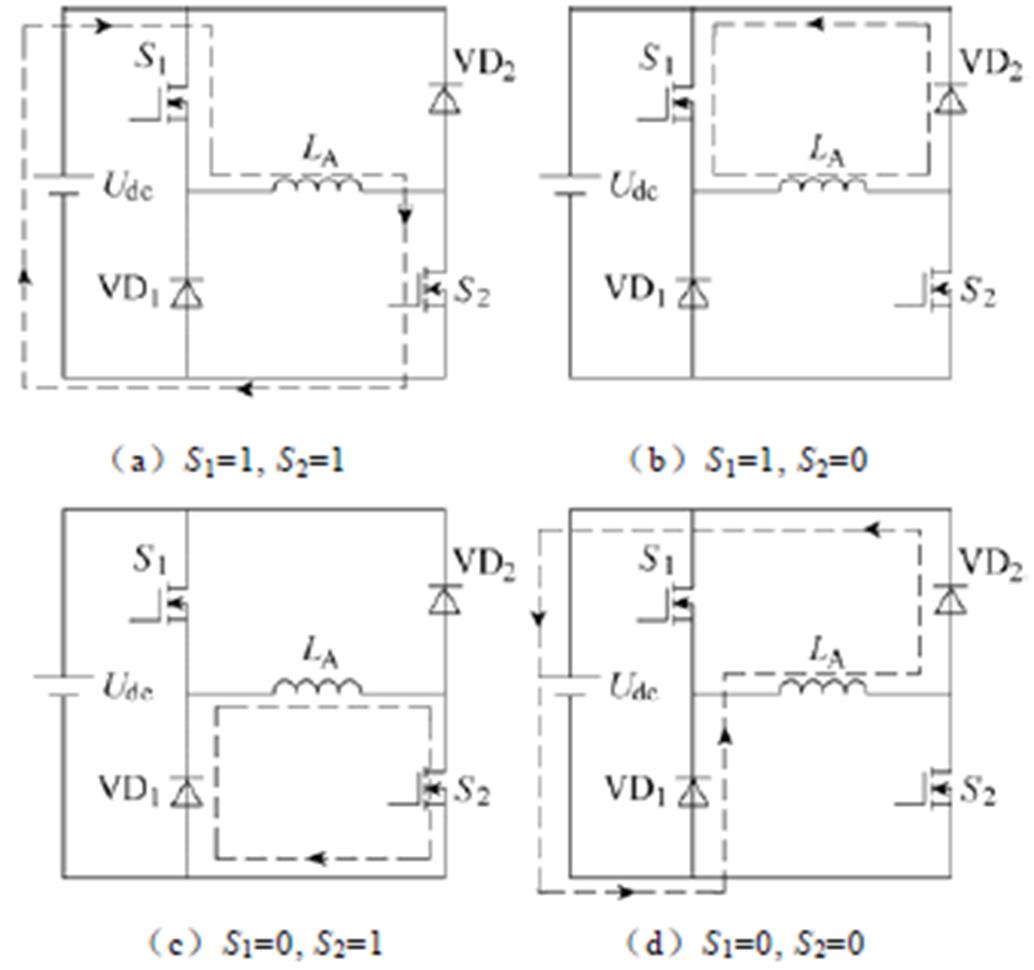
图3 不对称半桥功率变换器的四种开关状态
Fig.3 Four switch states of asymmetric half bridge converter
式中，
为磁共能；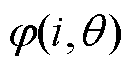
为磁链。根据式（16）可进一步推导当电流变化时的电磁转矩变化为
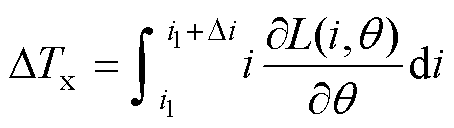（17）
因此，在电感上升区域，电磁转矩随着电流上升而上升，随着电流下降而下降。由式（10）可知，加速度随电磁转矩上升而上升，随电磁转矩下降而下降。综上所述，当（S1=1, S2=1）时，加速度上升，当（S1=0, S2=1），（S1=1, S2=0），（S1=0, S2=0）时，加速度下降，（S1=0, S2=0）的加速度下降速率大于（S1=0, S2=1）和（S1=1, S2=0）的加速度下降速率。
目前，开关磁阻电机系统的转矩环主要采用的控制方法为滞环控制方法或模型预测控制方法[19-22]。而开关磁阻电机的控制模型一般都涉及电流量，因此不适用于无电流传感器控制。基于转矩控制和加速度控制的等效性分析，本文采用滞环方法跟踪参考加速度。当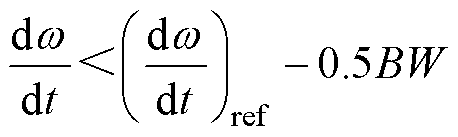
时，BW为环宽，开关状态选择为（S1=1, S2=1），使加速度上升。当
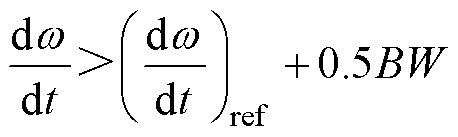时，选择加速度下降速率小的开关状态，即（S1=0, S2=1）或（S1=1, S2=0）。理由是：对于滞环控制，所控制变量的变化速率大会导致开关频率的上升。通过Simulink仿真观察该方法的控制效果。电机模型为三相12/8开关磁阻电机。设定子凸极中心和转子凹槽中心重合位置为0°，开通角和关断角分别设为0°和20°，负载转矩设为0.2N·m，给定转速为600r/min，滞环宽度设为10rad/s2，电机的转动惯量为0.002kg·m2，因此对应的转矩脉动应当约为0.02N·m。传统滞环控制的仿真结果如图4所示。
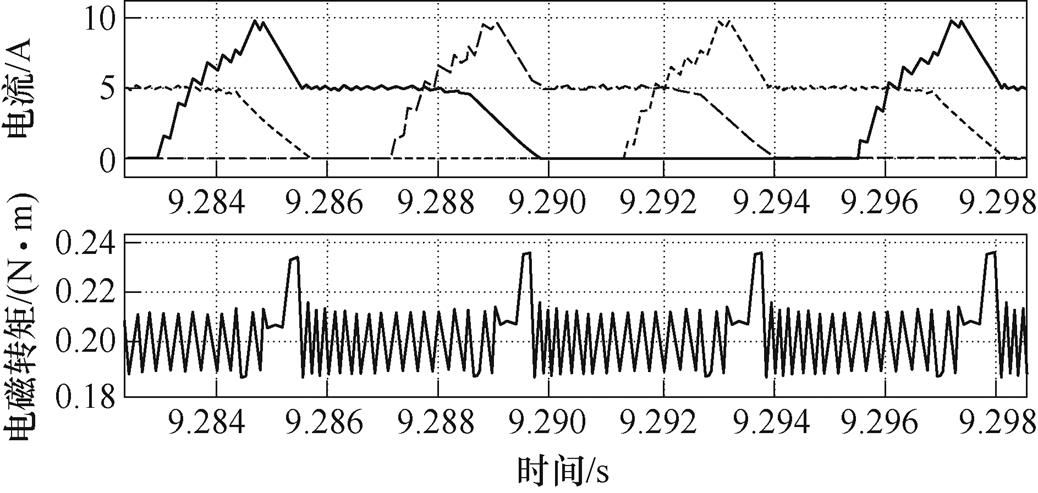
图4 传统滞环控制的仿真结果
Fig.4 Simulation results of traditional hysteresis control
电机的磁链曲线如图5所示。磁链曲线在7°位置附近有一个拐点，在该处电感值突升。在换相区，为了跟踪参考加速度，后一相电流会上升至一个较大值。当转子到达拐点处，如果电流不能迅速下降，由式（17）可知，电磁转矩会突升，因此在图4中，有一段时间电磁转矩显著超出预期值。为了解决该问题，本文的滞环控制方法增加一个滞环上界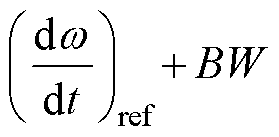
。当
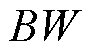时，选择加速度下降速率小的开关状态；当
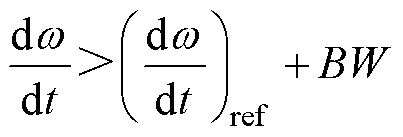时，选择加速度下降速率大的开关状态，即（S1=0, S2=0）。在磁链曲线拐点处，电流迅速下降，阻止电磁转矩突升。增加一个滞环上限的滞环控制的仿真结果如图6所示。
图5 电机磁链曲线
Fig.5 Flux curves of the motor
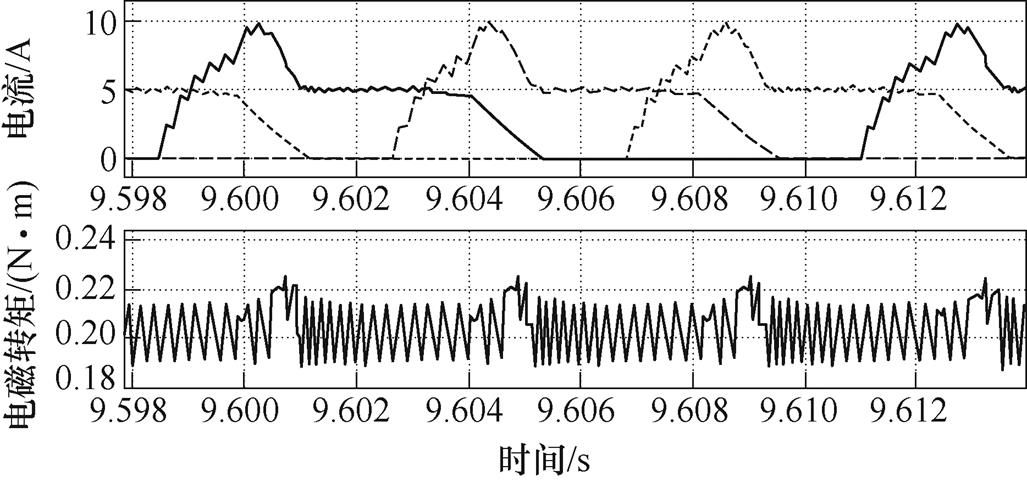
图6 增加一个滞环上限的滞环控制的仿真结果
Fig.6 Simulation results of hysteresis control with an extra upper bound
对于12/8开关磁阻电机，一个电角度周期对应45°机械角，每相相位差对应15°机械角。在0°～22.5°区间，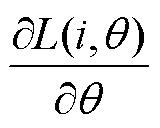
＞0，因此在该区间相电流产生正转矩。0°为相电流产生正转矩的起始位置角，因此选择为开通角。在换相时，当后一相处于0°～7°（磁链曲线拐点）时，前一相处于15°～22°。由图5可知，15°～22°区间的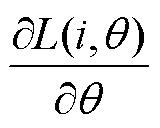远大于0°～7°区间的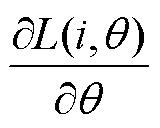，因此，在换相区，前一相应当提供更多的电磁转矩。关断角过小，则前一相的相电流过早地降为零，无法在换相区提供足够电磁转矩，使加速度难以跟踪参考值，造成转矩波动增大。将关断角设置为19°，仿真结果如图7所示。由于关断角过小，电磁转矩在换相区显著下降。相电流在22.5°之前未降为零，则会产生负转矩，降低电机效率。因此，关断角不宜过大，在保证能提供足够电磁转矩的前提下，应当尽可能小。由图6和图7可知，在换相区，当关断角为19°时，出现电磁转矩不足现象；当关断角为20°时，则无该现象，说明此时电机能提供足够的电磁转矩完成加速度滞环控制。因此，对于本文中的电机，关断角选择为20°。
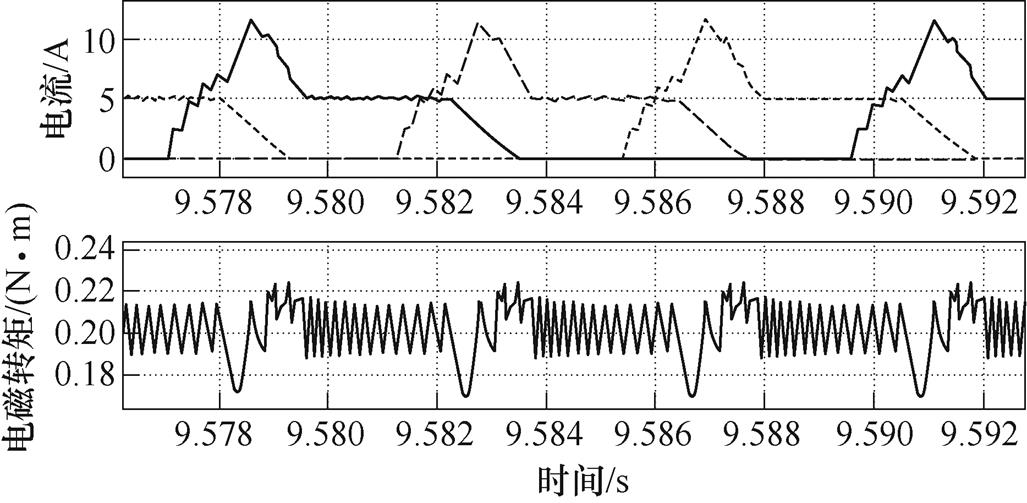
图7 关断角为19°时的仿真结果
Fig.7 Simulation results when turn-off angle is 19°
本文的实验平台如图8所示。实验电机采用12/8开关磁阻电机，其主要参数列在表1中。位置信号通过光电编码器E6B2-CWZ6C测得。对比实验中的电流信号通过电流传感器LT108-S7测得。位置信号和电流信号输入控制芯片DSP TMS320F28335，在DSP内计算速度、加速度以及执行控制方法，得到门极驱动信号。功率晶体管采用MOSFET，型号为IPP052N08N5。数模转换过程和模数转换过程分别由芯片AD5344和AD7606完成。电机的负载转矩由磁粉制动器提供。电磁转矩通过查T-i-q 表得到。
图8 实验平台
Fig.8 Experimental platform
表1 开关磁阻电机样机参数
Tab.1 The parameters of prototype switched reluctance motor
参 数数 值 相数3 定子极数12 转子极数8 额定电压/V12 额定功率/W100 额定电流/A8 额定转速/(r/min)1 500
由于本文方法的反馈量均直接或间接来自位置量，因此对位置量测量及速度计算方法进行简要的误差分析。对于光电编码器E6B2-CWZ6C，两个位置信号脉冲边沿间隔0.09°，因此位置量测量的最大误差为0.09°。测速采用的是测周法，其原理是以位置信号脉冲边沿间隔除以通过这段间隔所花时间。对于DSP，时间计量方式为时钟脉冲数乘以时钟周期。这种测速法的误差与光电编码器精度无关，取决于控制芯片的时钟频率，计时器最大误差为一个时钟周期。DSP28335的时钟频率为150MHz，如果QEP模块的时基不分频，那么时间计量的最大误差为6.67ns。以给定转速600r/min为例，转过0.09°需要25ms，一个位置间隔的时间计量的最大误差约为0.027%，因此速度计算误差极小。
APC和VPWM是两种常用的不需要电流传感器的开关磁阻电机控制方法，VPWM的转矩控制效果优于APC。因此，将VPWM作为本文控制方法的一个参照，在同样硬件条件下，验证本文控制方法在控制效果上的改进。DTC是目前转矩控制效果较好的控制方式。以DTC为参照，观察本文控制方法及其在控制效果上的差异。该DTC采用与本文相同的滞环方式实现。根据第2.3节的分析，开通角和关断角分别设为0°和20°。在低速轻载、高速重载、变转速和变负载条件下，分别采用VPWM、DTC和本文控制方法控制电机，观察并对比控制效果。转矩脉动Tripple定义为：Tripple=Tmax-Tmin, Tmax和Tmin分别为最大电磁转矩和最小电磁转矩。
母线电压设为12V。DTC的滞环下限为-0.01N·m，两个滞环上限分别为0.01N·m和0.02N·m。本文控制方法的滞环下限为-5rad/s2，两个滞环上限分别为5rad/s2和10rad/s2。当转速稳定时，取两个周期的波形，实验结果如图9所示。在该运行条件下，VPWM的Tmax约为0.4N·m，Tmin约为0.08N·m，Tripple约为0.32N·m；DTC和本文控制方法的Tmax约为0.32N·m，Tmin约为0.12N·m，Tripple约为0.2N·m。
图9 低速轻载时的实验结果
Fig.9 Experimental results under low speed and light load
母线电压设为36V。DTC的滞环下限为-0.03N·m，两个滞环上限分别为0.03N·m和0.06N·m。本文控制方法的滞环下限为-15rad/s2，两个滞环上限分别为15rad/s2、30rad/s2。当转速稳定时，取两个周期的波形，实验结果如图10所示。在该工作条件下，VPWM的Tmax约为1.8N·m，Tmin约为0.2N·m，Tripple约为1.6N·m；DTC和本文控制方法的Tmax约为1N·m，Tmin约为0.5N·m，Tripple约为0.5N·m。
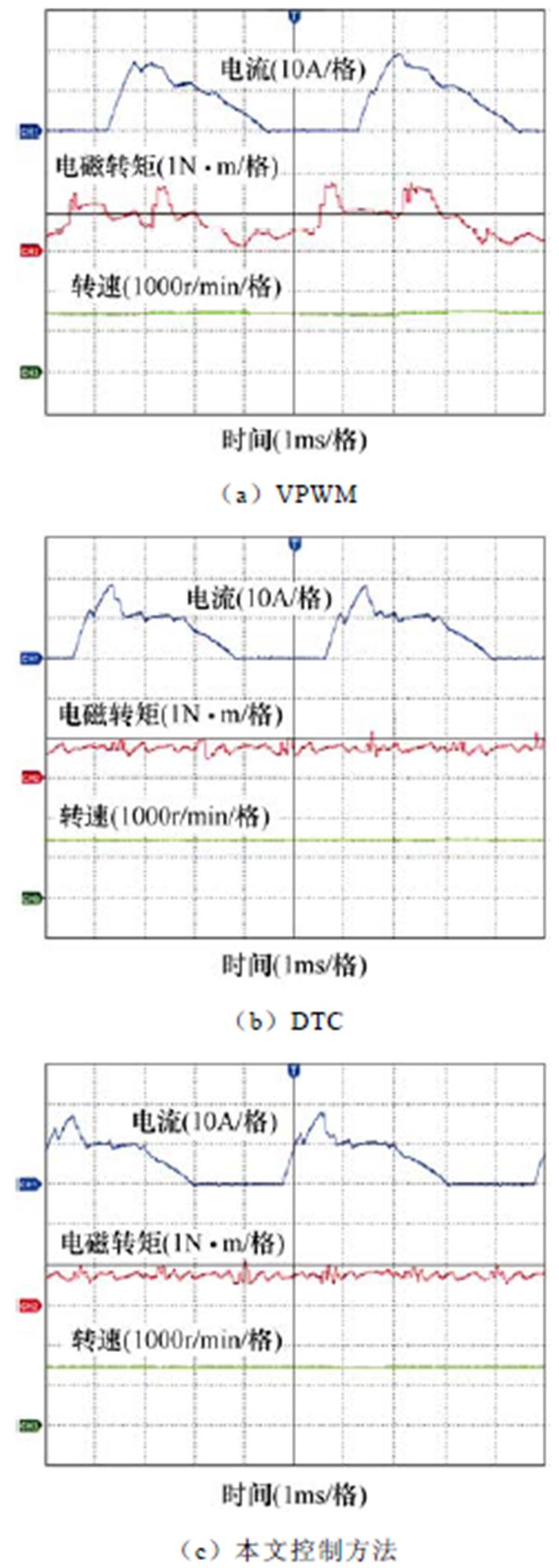
图10 高速重载时的实验结果
Fig.10 Experimental results under high speed and heavy load
母线电压设为24V。起始状态设为（600r/min, 0.2N·m）。变转速时的实验结果如图11所示。在变转速过程中，VPWM的Tmax接近4N·m；DTC和本文控制方法的Tmax约为3N·m。
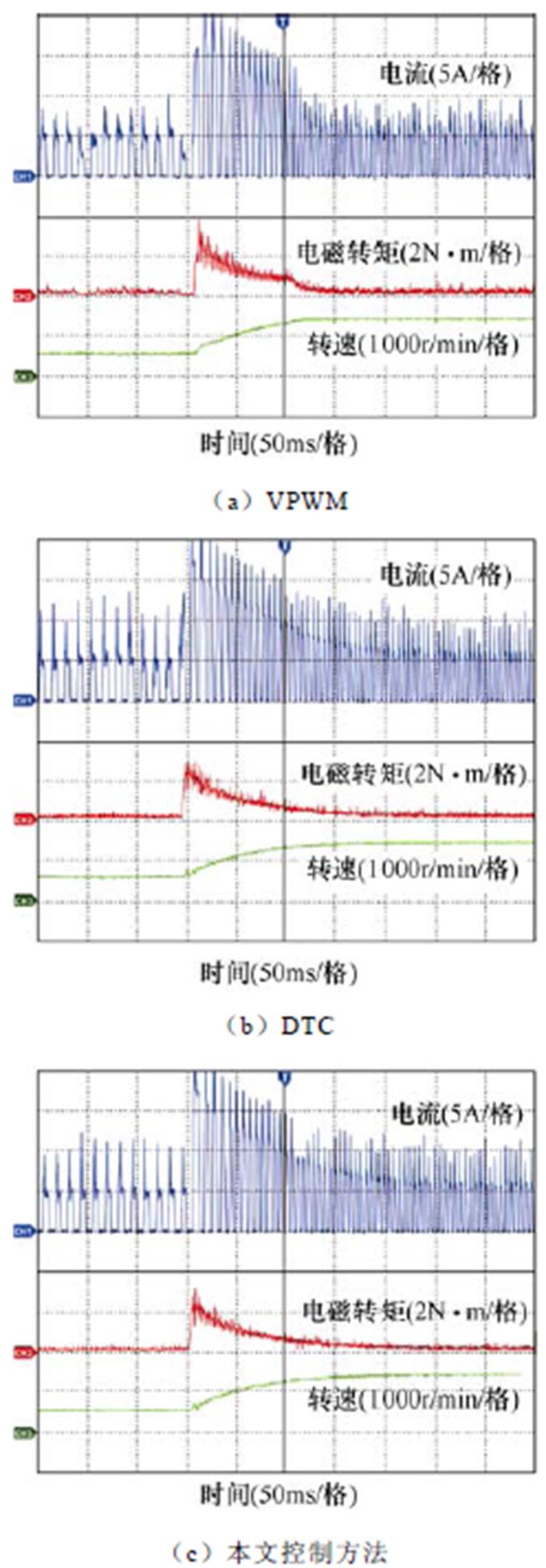
图11 变转速时的实验结果
Fig.11 Experimental results when speed changes
母线电压设为24V。起始状态为（600r/min, 0.2N·m）。变负载时的实验结果如图12所示。在变负载过程中，VPWM的一个周期的Tripple最大约为2N·m；DTC和本文控制方法的一个周期的Tripple最大约为0.5N·m。
由以上电机的动态过程和稳态过程的实验结果可知：和VPWM相比，在转矩控制效果上，本文控制方法具有显著优势；和DTC相比，对于电流波形、电磁转矩波形和转速波形，本文方法均与其相似。该结果证明了加速度控制和转矩控制的等效性，与第2节的理论分析相一致。
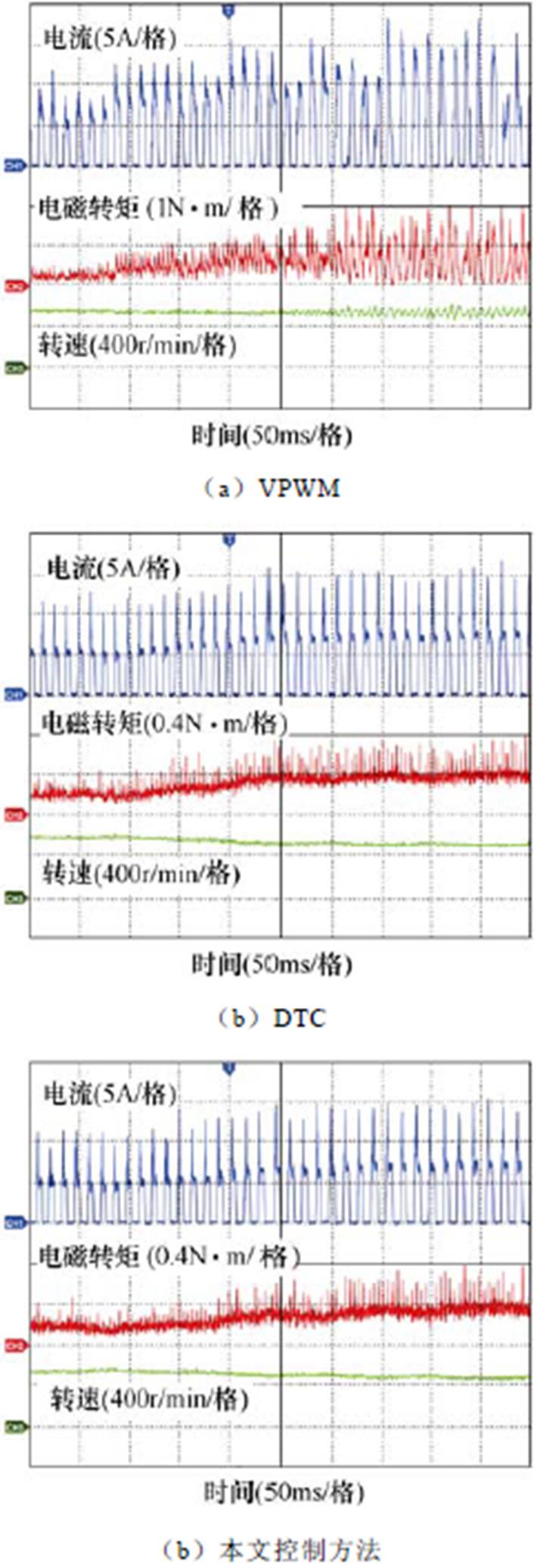
图12 变负载时的实验结果
Fig.12 Experimental results when load changes
本文提出了一种开关磁阻电机无电流传感器控制方法。电流传感器的省去提高了系统可靠性并降低了系统的成本。在缺少电流信息的情况下，该方法对位置信息进行了充分利用，将传统控制方法中不常使用的位置量二阶导数——加速度作为反馈量，取得了良好的控制效果。从理论上证明了该方法对转矩的间接控制能力。采用滞环方法跟踪参考加速度，根据开关磁阻电机的磁链特征，增加了一个滞环上界，减小了转矩脉动。根据实验结果，本文方法的控制性能优于现有的不依赖电流传感器的控制方法，与DTC相当。除此之外，与DTC相比，本文控制方法的优势还在于不需要进行电流-电磁转矩换算，减少了在线计算时间，并且不受电机参数限制，鲁棒性更好。旋转电机的机械运动方程相同，因此本文的控制方法能为其他类型旋转电机的控制提供参考。
参考文献
[1] Gou Lifeng, Wang Chenchen, Zhou Minglei, et al. Integral sliding mode control for starting speed sensorless controlled induction motor in the rotating condition[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4105-4116.
[2] Verrelli C M, Bifaretti S, Carfagna E, et al. Speed sensor fault tolerant PMSM machines: from position- sensorless to sensorless control[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3946-3954.
[3] Corne A, Yang Nanfang, Martin J P, et al. Nonlinear estimation of stator currents in a wound rotor syn- chronous machine[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3858-3867.
[4] Eull M, Mohamadian M, Luedtke D, et al. A current observer to reduce the sensor count in three-phase pm synchronous machine drives[J]. IEEE Transactions on Industry Applications, 2019, 55(5): 4780-4789.
[5] Martín C, Arahal M R, Barrero F, et al. Five-phase induction motor rotor current observer for finite con- trol set model predictive control of stator current[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4527-4538.
[6] Xiong Fei, Wu Junyong, Liu Zicheng, et al. Current sensorless control for dual active bridge DC-DC converter with estimated load-current feedforward[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 3552-3566.
[7] Das D, Madichetty S, Singh B, et al. Luenberger observer based current estimated Boost converter for PV maximum power extraction-a current sensorless approach[J]. IEEE Journal of Photovoltaics, 2019, 9(1): 278-286.
[8] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet syn- chronous motor based on adaptive Notch filter online decoupling[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 344-354.
[9] Ahn J W, Lukman G F. Switched reluctance motor: research trends and overview[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(4): 339-347.
[10] Zhang Man, Bahri I, Mininger X, et al. Vibration reduction controller for a switched reluctance machine based on HW/SW partitioning[J]. IEEE Transactions on Industrial Informatics, 2021, 17(6): 3879-3889.
[11] 闫文举, 陈昊, 刘永强, 等. 一种用于电动汽车磁场解耦型双定子开关磁阻电机的新型功率变换器[J]. 电工技术学报, 2021, 36(24): 5081-5091.
Yan Wenju, Chen Hao, Liu Yongqiang, et al. A novel power converter on magnetic field decoupling double stator switched reluctance machine for electric vehicles[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5081-5091.
[12] 丁文, 李可, 付海刚. 一种12/10极模块化定子混合励磁开关磁阻电机分析[J]. 电工技术学报, 2022, 37(8): 1948-1958.
Ding Wen, Li Ke, Fu Haigang. Analysis of a 12/10- pole modular-stator hybrid-excited switched reluctance machine[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 1948-1958.
[13] 孙德博, 胡艳芳, 牛峰, 等. 开关磁阻电机调速系统故障诊断和容错控制方法研究现状及展望[J]. 电工技术学报, 2022, 37(9): 2211-2229.
Sun Debo, Hu Yanfang, Niu Feng, et al. Status and prospect of fault diagnosis and tolerant control methods for switched reluctance motor drive system[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2211-2229.
[14] Davarpanah G, Faiz J. A novel structure of switched reluctance machine with higher mean torque and lower torque ripple[J]. IEEE Transactions on Energy Conversion, 2020, 35(4): 1859-1867.
[15] Aiso K, Akatsu K. High speed SRM using vector control for electric vehicle[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(1): 61-68.
[16] Cai Jun, Liu Zeyuan, Zeng Yu. Aligned position estimation based fault-tolerant sensorless control strategy for SRM drives[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7754-7762.
[17] Ho C Y, Wang J C, Hu Kaiwei, et al. Development and operation control of a switched-reluctance motor driven flywheel[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 526-537.
[18] Husain T, Uddin W, Sozer Y. Performance com- parison of short-pitched and fully pitched switched reluctance machines over wide speed operations[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4278-4287.
[19] 费晨, 颜建虎, 汪盼, 等. 基于改进的转矩分配函数法的开关磁阻电机转矩脉动抑制[J]. 电工技术学报, 2018, 33(增刊2): 394-400.
Fei Chen, Yan Jianhu, Wang Pan, et al. Torque ripple suppression of switched reluctance motor based on modified torque sharing function[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 394- 400.
[20] 卿龙, 王惠民, 葛兴来. 一种高效率开关磁阻电机转矩脉动抑制方法[J]. 电工技术学报, 2020, 35(9): 1912-1920.
Qing Long, Wang Huimin, Ge Xinglai. A high efficiency torque ripple suppression method for switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1912-1920.
[21] Valencia D F, Tarvirdilu-Asl R, Garcia C, et al. Vision, challenges, and future trends of model predictive control in switched reluctance motor drives[J]. IEEE Access, 2021, 9: 69926-69937.
[22] Valencia D F, Tarvirdilu-Asl R, Garcia C, et al. A review of predictive control techniques for switched reluctance machine drives. part Ⅱ: torque control, assessment and challenges[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 1323-1335.
[23] Dhale S, Nahid-Mobarakeh B, Emadi A. A review of fixed switching frequency current control techniques for switched reluctance machines[J]. IEEE Access, 2021, 9: 39375-39391.
[24] 闫文举, 陈昊, 马小平, 等. 不同转子极数下磁场解耦型双定子开关磁阻电机的研究[J]. 电工技术学报, 2021, 36(14): 2945-2956.
Yan Wenju, Chen Hao, Ma Xiaoping, et al. Deve- lopment and investigation on magnetic field decoupling double stator switched reluctance machine with different rotor pole numbers[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2945-2956.
[25] Han Guoqiang, Chen Hao, Shi Xianqiang, et al. Phase current reconstruction strategy for switched relu- ctance machines with fault-tolerant capability[J]. IET Electric Power Applications, 2017, 11(3): 399-411.
[26] Sun Qingguo, Wu Jianhua, Gan Chun, et al. A multiplexed current sensors-based phase current detection scheme for multiphase SRMs[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 6824-6835.
[27] Sun Qingguo, Wu Jianhua, Gan Chun, et al. A new phase current reconstruction scheme for four-phase SRM drives using improved converter topology without voltage penalty[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 133-144.
Current Sensorless Control Method of Switched Reluctance Motors
Abstract Control variables are usually measured by sensors. However, sensors can increase system costs, cause interference, and reduce reliability. Thus, the sensorless technique is widely studied. For switch reluctance motor (SRM) systems, according to present control methods, current information is necessary to torque control. A new control variable is toned to replace the current and have a simple relation with electromagnetic torque to achieve good control performance without current sensors. Rotor position and speed are necessary for any SRM control methods, usually measured by a position sensor. The first derivative of position is speed, the second derivative of position is acceleration, and the third and more derivatives of position have no physical meaning. When only a position sensor is used in the SRM system, besides the speed, the acceleration is the unique possible feedback variable. Therefore, a current sensorless control method of SRMs using double closed loops of speed and acceleration is proposed.
Firstly, the feasibility of the proposed method is analyzed in two points. ① Its convergence is proven; ② The approximate linear relation between electromagnetic torque and acceleration in a steady state is proven, and the equivalence of torque control and acceleration control is analyzed further. Subsequently, a hysteresis control method with three bounds is proposed to track reference acceleration. According to flux features of the SRM, there is a position where inductance increase sharply, and if the phase current cannot be reduced timely, the electromagnetic torque will also increase sharply, leading to a large torque ripple. Thus, an extra upper bound is set, and a negative voltage is used to quickly reduce the phase current when the acceleration is beyond the upper bound. Finally, Given both motor efficiency and torque ripple, turn-on and turn-off angle are appropriately selected.
Angle position control (APC) and voltage pulse width modulation (VPWM) are two existing current sensorless control methods of SRMs. VPWM has better control performance than APC. Therefore, taking VPWM as a comparison object, the improvement of the proposed method is verified by experiments. The direct torque control (DTC) method is another comparison object to demonstrate the equivalence of torque control and acceleration control. The experiments are carried out under four conditions: low speed and light load, high speed and heavy load, speed change, and load change. Under (600r/min, 0.2N·m), the torque ripple of VPMM is about 0.32N·m, and those of DTC and the proposed method are about 0.2N·m. Under (1 500r/min, 0.7N·m), the torque ripple of VPMM is about 1.6N·m, and those of DTC and the proposed method are about 0.5N·m. If the initial condition is set to (600r/min, 0.2N·m), during speed change, the max torque of VPMM is about 4N·m, and those of DTC and the proposed method are about 0.2N·m. If the initial condition is set to (600r/min, 0.2N·m), during load change, the torque ripple of VPMM is about 2N·m, and those of DTC and the proposed method are about 0.5N·m.
The experimental results show that the proposed method is comparable to the DTC and better than the VPWM in control performance. In addition, the relationship between the current and the electromagnetic torque is complex and nonlinear, but the conversion between them is needed in DTC. Due to the approximately linear relationship between electromagnetic torque and acceleration, the proposed method is independent of the electromagnetic torque, thus having a lower computational cost.
keywords：Switched reluctance motor, current sensorless control method, acceleration, electromagnetic torque
中图分类号：TM301
DOI: 10.19595/j.cnki.1000-6753.tces.212148
国家自然科学基金国际（地区）合作与交流项目、2019年度国家自然科学基金委员会与埃及科学研究技术院合作研究项目（51961145401）和徐州市推动科技创新专项资金项目-创新能力建设计划（KC21315）资助。
收稿日期 2021-12-30
改稿日期 2022-02-21
E-mail: shenweiqianchong@126.com
陈 昊 男，1969年生，教授，博士生导师，研究方向为开关磁阻电机系统及其控制。
E-mail: hchen@cumt.edu.cn（通信作者）
（编辑 崔文静）