图1 12/14 BSRM基本拓扑
Fig.1 Basic topology of 12/14 BSRM
摘要 12/14磁悬浮开关磁阻电机悬浮系统磁通与多个转子齿铰链，导致悬浮系统的等效磁路在整个转子位置周期内具有变结构特征，需要提出新的建模方法，揭示全位置周期内的悬浮力动态变化特性。针对上述问题，该文基于有限元模型开展了12/14磁悬浮开关磁阻电机悬浮力电磁特性分析，明晰了转子位置动态变化下的悬浮系统磁通铰链规律。利用麦克斯韦应力法“区域性”建模优势，提出“主-边磁路并行解析”策略，构建了考虑磁通多齿铰链的全周期悬浮力数学模型。通过有限元分析的方法验证了模型优良特性。开展实验研究，结果表明，建立的悬浮力模型可以有效揭示12/14磁悬浮开关磁阻电机独特本体结构下的悬浮力特性，实现稳定悬浮，进一步验证了所提建模方法的可行性。该方法可以推广至一类具有悬浮系统磁通多齿铰链特征的磁悬浮开关磁阻电机建模研究中。
关键词：悬浮系统磁通 悬浮力建模 磁悬浮开关磁阻电机 麦克斯韦应力法 有限元分析
我国大力发展纯电动城市公交，然而，蓄电池或氢燃料电池为代表的动力系统难以兼顾高比能量与高比功率，使得纯电动城市公交车的节能性、机动性和可靠性在频繁起停的城市工况下受到严重制约。大量研究表明，构建高比功率磁悬浮飞轮电池与高比能量动力电池的电-电混合动力系统是解决上述问题的有效途径[1-2]。
磁悬浮支承系统作为飞轮电池的核心部件直接决定了飞轮电池的运行品质[3-6]。磁悬浮开关磁阻电机（Bearingless Switched Reluctance Motor, BSRM）是由开关磁阻电机和磁悬浮轴承高度集成而得的磁悬浮支承系统，既保留了传统开关磁阻电机调速范围宽、电磁损耗几乎不随转速升高而增大、机械强度大等优点，也具备了磁悬浮轴承可以提供两自由度悬浮的特点，在飞轮电池中具有广阔的应用前景。
20世纪末，日本学者先提出了双绕组BSRM[7]，然而，双绕组BSRM存在悬浮-旋转强耦合的固有弊端。针对该问题，相继涌现出多类悬浮-旋转弱耦合的BSRM拓扑，代表性拓扑包括8/10宽窄极式、12/10宽窄极式、永磁偏置宽窄极式等[8-12]多类拓扑。8/10宽窄极式和12/10宽窄极式BSRM的悬浮力偏置磁场均采用了电励磁方式，悬浮功耗有待进一步降低。北京航空航天大学的王惠军等受偏置型磁悬浮轴承的启发，将永磁体引入BSRM定子轭，形成永磁偏置式BSRM[13-16]，有效降低了悬浮系统功耗，而12/14 BSRM是永磁偏置式BSRM的代表性拓 扑[17-18]，江苏大学、北京航空航天大学等高校开展了相关研究，研究重点主要集中于优化设计、温度场分析以及高性能控制器设计等方面[19-21]。
在上述研究过程中，12/14 BSRM的悬浮系统普遍采用了简化模型，即将悬浮系统等效为磁悬浮轴承系统，悬浮系统磁通面积等效为窄极转子的横截面积，其数值为恒定值。然而，由于边缘磁通的存在，12/14 BSRM的悬浮系统磁通与多个转子凸极产生铰链，受到转子位置的动态约束，使得构建的悬浮力模型无法真实有效地反映出悬浮力随着转子位置动态变化的特征。
目前，考虑边缘磁通的BSRM悬浮力建模方法已有研究，研究对象普遍集中于双绕组式BSRM和单绕组式BSRM，但该类对象不存在悬浮系统磁通多齿铰链特征（悬浮系统磁通多齿铰链具有宽窄极结构的BSRM独特的特征），建模过程也仅考虑定子与单一转子齿之间磁通铰链。因此，针对具有磁通多齿铰链特征的12/14 BSRM，悬浮力建模方法需要进一步探索。
本文基于有限元分析模型，探明了12/14 BSRM悬浮系统磁通在全转子位置周期内与多个转子齿的铰链规律；依据麦克斯韦应力法[22]具备的区域性建模优势，提出“主-边磁路并行建模”策略，实现等效磁路“变结构”特征下数学模型构建，并通过有限元分析（Finite Element Analysis, FEA）和实验验证了建模方法的可行性和悬浮力模型的有效性。
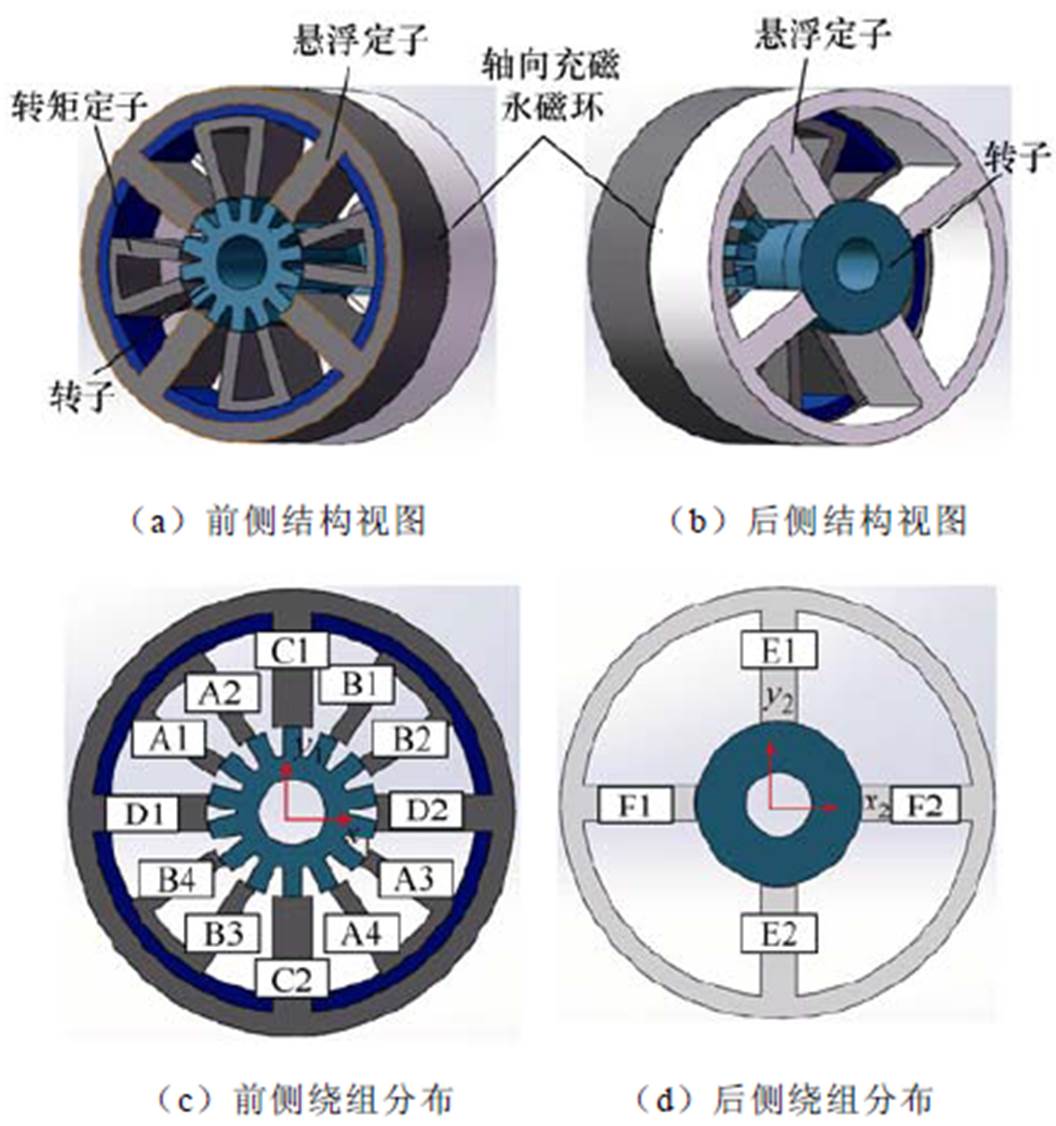
12/14 BSRM基本拓扑如图1所示，包括共用凸极转子的转矩系统和悬浮系统。转矩系统定子为U形结构，利用磁阻原理产生转矩。悬浮系统采用直流磁轴承式结构，提供悬浮力。
如图1a和图1b所示，12/14 BSRM在结构上包括前侧结构、后侧结构和永磁体（Permanent Magnet, PM）。其中，前侧结构主要由8个等距分布的转矩定子极（约12.85°）、4个等距分布的悬浮定子极（约25.7°）和14个等距分布的凸极转子（约12.85°）构成。后侧结构主要由4个等距分布的悬浮定子极（约25.7°）和圆柱形转子组成。前侧凸极转子与后侧圆柱形转子轴向一体化设计。
图1 12/14 BSRM基本拓扑
Fig.1 Basic topology of 12/14 BSRM
如图1b和图1c所示，转矩系统的定子采用了模块化U型结构，共包括了A、B两相。其中，A相由A1、A2、A3和A4极构成；B相由B1、B2、B3和B4极构成。基于“磁阻最小原理”，转矩系统的定子与凸极转子配合可以产生转矩。
悬浮系统共包括了C相、D相、E相和F相，如图1c和1d所示。其中，C相由C1极和C2极构成，产生的径向悬浮力方向定义为y1方向。D相由D1极和D2极构成，产生的径向悬浮力方向定义为x1方向。E相由E1极和E2极构成，产生的径向悬浮力方向定义为y2方向；F相由F1极和F2极构成，产生的径向悬浮力方向定义为x2方向。
因此，当C相与E相串联，D相与F相串联时，可实现两自由度径向悬浮；当C相、D相、E相，F相单独控制时，可实现四自由度径向悬浮。具体连接方式可由实际技术需求灵活配置。
针对12/14 BSRM悬浮系统，其前侧转子设计为多凸极结构，同时参与悬浮力和转矩的能量转换，在Ansys软件中构建有限元分析模型，模型参数见表1。
将转子极距作为一个分析研究周期。定义h为轴向长度，wr为凸极转子极宽，数值为a；ws为悬浮系统定子极宽，根据12/14 BSRM结构参数之间的物理关系，有ws=2wr=2a。以y1自由度为例，获得悬浮力特性如图2所示。
由图2可以看出，有限元分析获得悬浮力随着转子位移动态变化，悬浮力总体模型随着转子的位置变化而呈现类正弦分布，具有一定的周期性规律，且平均值几乎恒定。
然而，目前关于宽窄极结构特征的BSRM建模方法均忽略了悬浮系统磁通多齿极铰链特征，在建模过程中仅考虑了主磁通对悬浮力的影响。依据文献[23]建模方法所构建的浮力模型，在1个转子周期内的特性如图3所示。
表1 有限元模型参数
Tab.1 Parameters of Finite element model
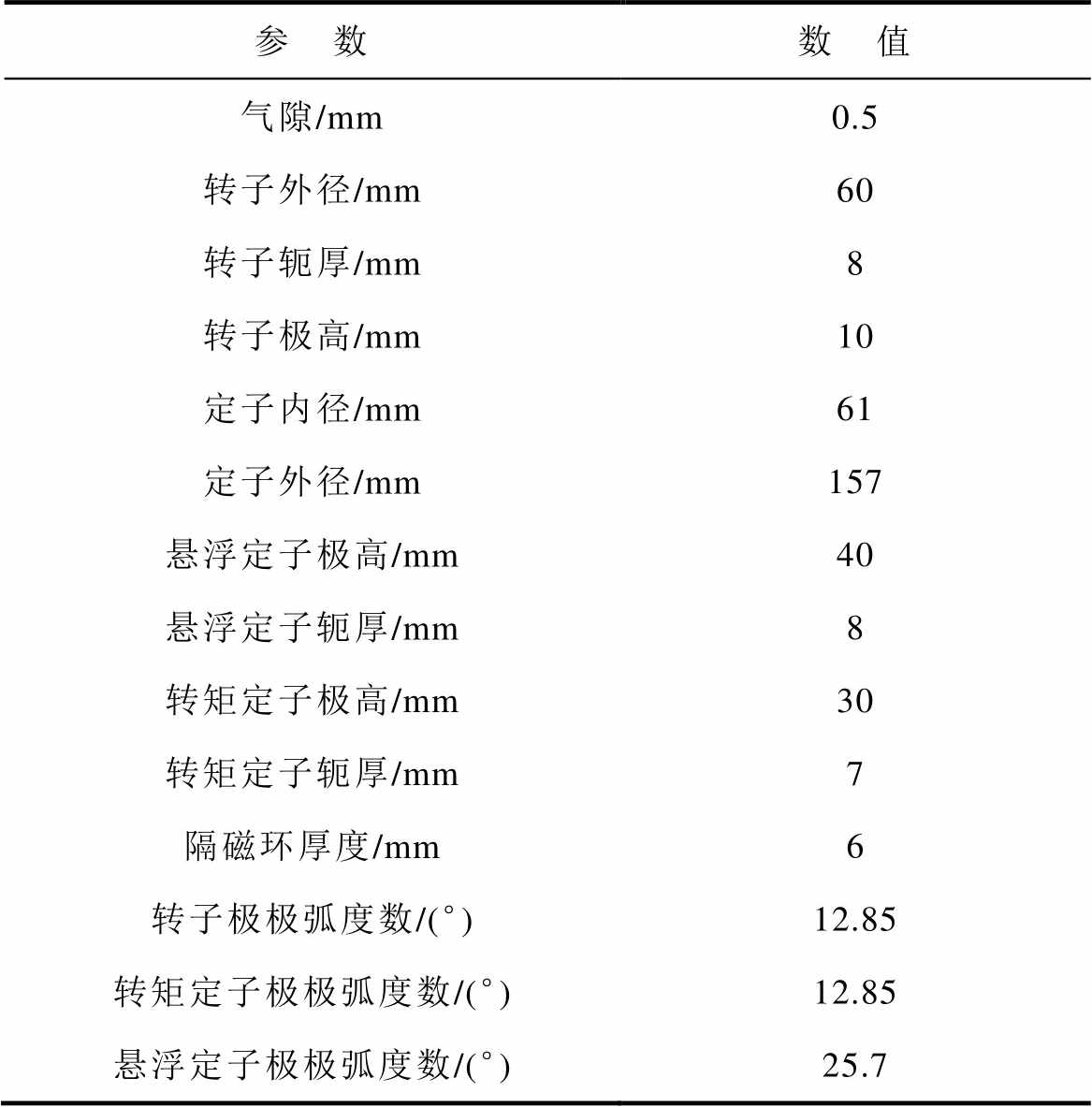
参 数数 值 气隙/mm0.5 转子外径/mm60 转子轭厚/mm8 转子极高/mm10 定子内径/mm61 定子外径/mm157 悬浮定子极高/mm40 悬浮定子轭厚/mm8 转矩定子极高/mm30 转矩定子轭厚/mm7 隔磁环厚度/mm6 转子极极弧度数/(°)12.85 转矩定子极极弧度数/(°)12.85 悬浮定子极极弧度数/(°)25.7
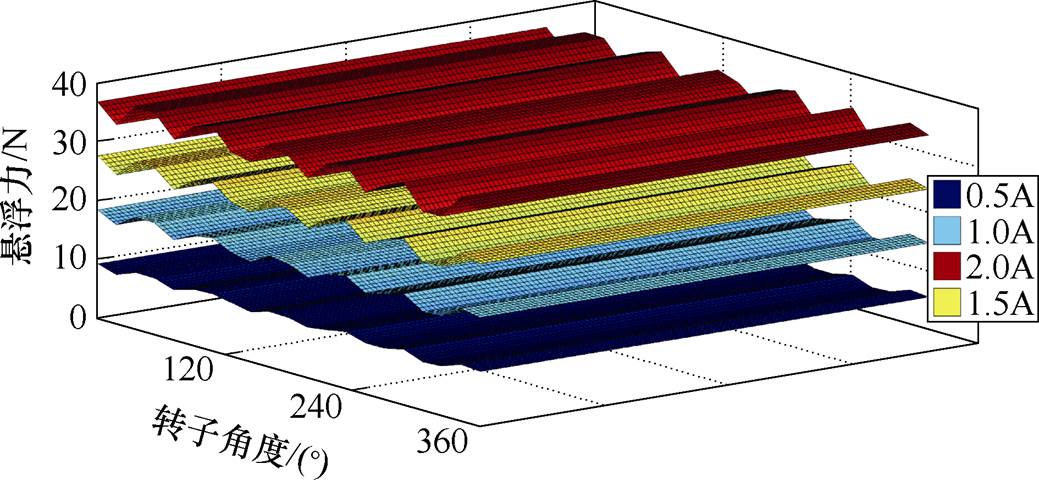
图2 基于有限元分析的悬浮力特性
Fig.2 Suspension force characteristics based on FEA
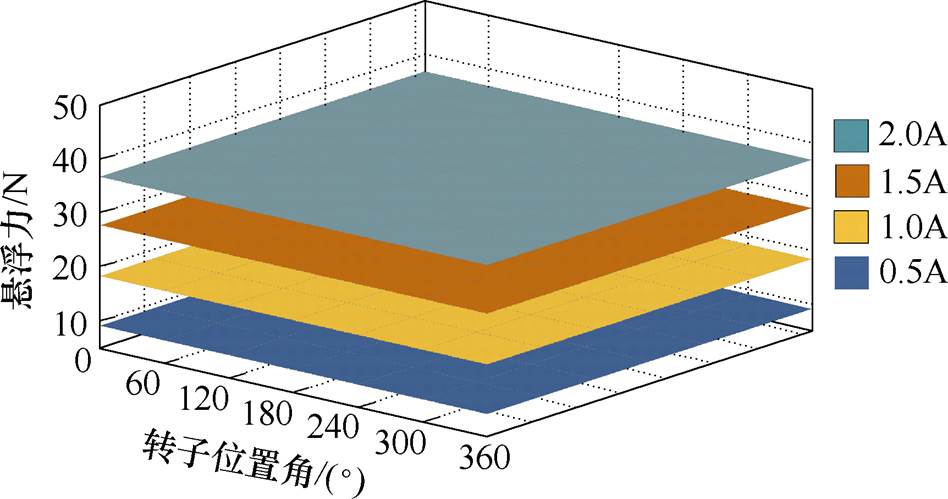
图3 忽略磁通多齿铰链的悬浮力模型
Fig.3 Suspension force model without considering flux multi teeth hinge
对比图2和图3可以看出，传统悬浮力模型忽略了边缘磁通变化对悬浮力的影响，仅能表征出主磁通与悬浮力的关系，无法揭示12/14 BSRM悬浮力值与转子位置的动态变化特征。
为进一步明晰悬浮力特性，将C1极作为参考对象，在飞轮电池立式放置条件下（忽略重力对径向悬浮力的影响），获取典型转子位置状态下悬浮系统磁通分布规律，如图4所示。
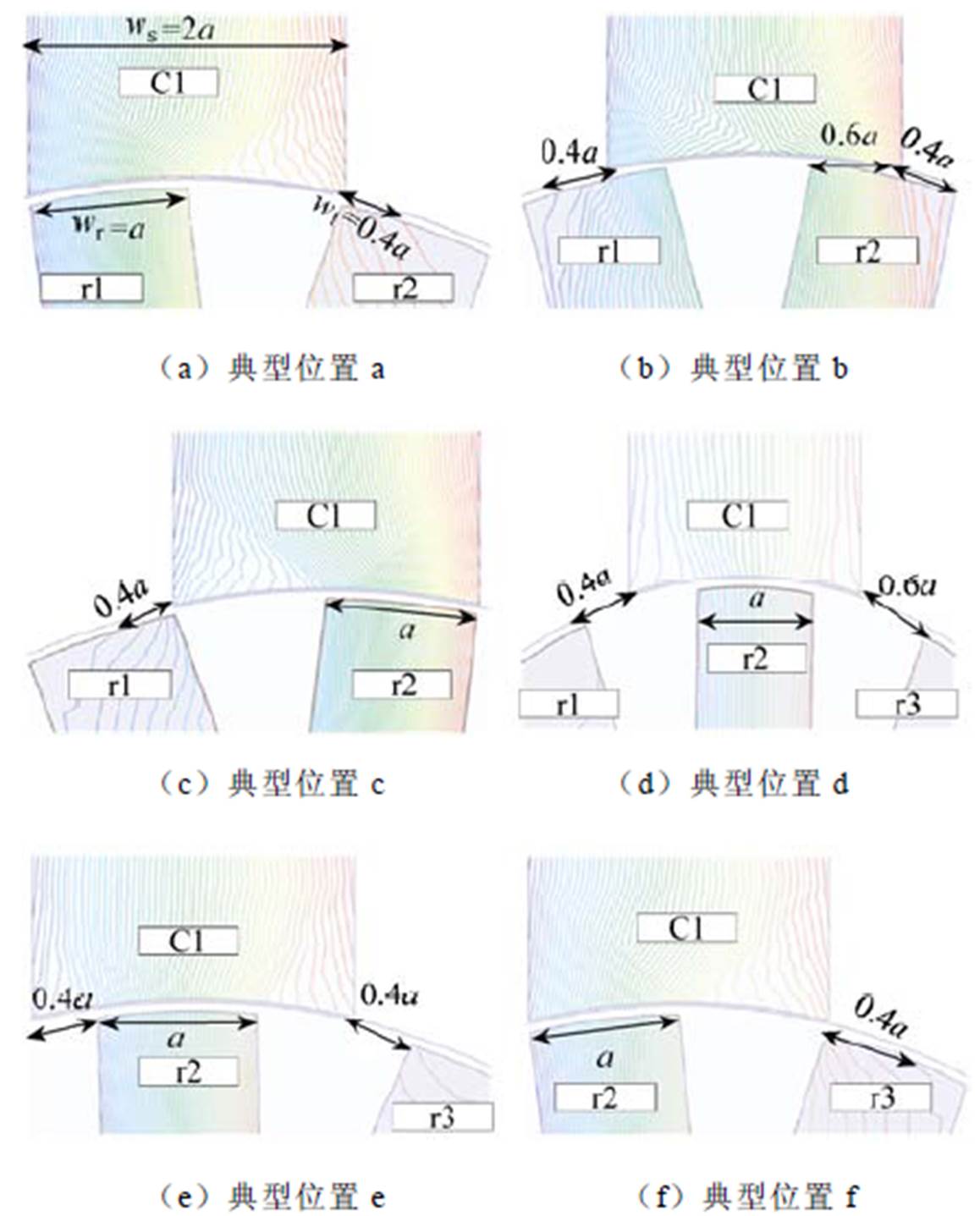
图4 悬浮磁场典型分布
Fig.4 Typical distribution of suspension magnetic field
由图4可知，悬浮系统磁通具有多齿铰链特征，共有6个典型铰链约束位置：
（1）典型位置a。其转子r1极与定子C1极完全重合，转子r2极与定子C1极临界重合。
（2）典型位置b。其相对转子a逆时针旋转0.6a距离，即转子r1极与定子C1极重合0.4a，转子r2极与定子C1极重合0.6a。
（3）典型位置c。其相对转子b逆时针旋转0.4a距离；即转子r1极与定子C1极临界重合，转子r2极与定子C1极完全重合。
（4）典型位置d。其相对转子c逆时针旋转0.4a距离；即转子r1极与定子C1极相距0.4a，转子r2极与定子C1极完全重合；此时，即转子r3极与定子C1极相距0.6a。
（5）典型位置e。其相对转子d逆时针旋转0.2a距离；转子r2极与定子C1极完全重合；转子r3极与定子C1极相距0.4a。
（6）典型位置f。其相对转子d逆时针旋转0.4a距离；转子r2极与定子C1极完全重合；转子r3极与定子C1极临界重合。
依据上述铰链规律，构建如图5所示的悬浮系统等效磁路。图中，Nph为悬浮绕组匝数，Pmr1和Pmr2分别为定子与转子r1和转子r2铰链的主磁路磁导，Pfr1、Pfr2、Pfr3分别为定子与转子r1、转子r2、转子r3铰链的边缘磁路磁导。
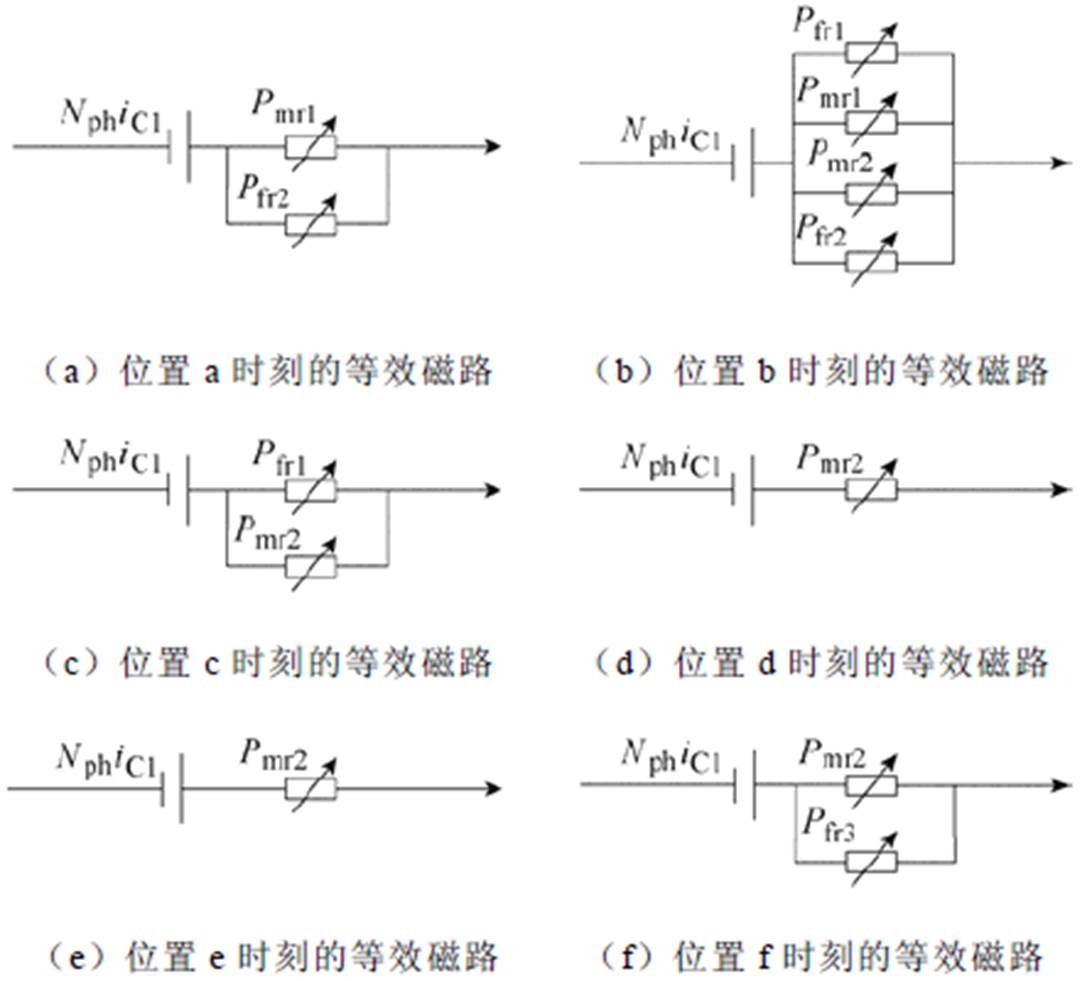
图5 典型位置下悬浮系统等效磁路
Fig.5 Equivalent magnetic circuit of for typical position
由图5可知，悬浮系统的等效磁路具有动态“变结构”特征，除了典型位置d和e的等效磁路相同外，每个典型位置下的悬浮系统等效磁路互不相同。现有悬浮力建模方法虽然考虑了边缘磁通影响，但建模过程仅针对定子与单一转子齿的铰链，构建出的悬浮力模型具有阶段性，难以有效揭示悬浮力的全周期变化特性（电机旋转过程中悬浮力随着转子位置的变化而产生变化，转子转过一个完整的电角度周期过程中悬浮力的变化特征称为悬浮力的全周期变化特征）。因此，需要探索12/14 BSRM悬浮力建模新方法。
本文利用麦克斯韦应力法能够实现悬浮力区域性建模的优势，对悬浮系统的主磁通和边缘磁通并行解析，该策略下的悬浮力模型结构为
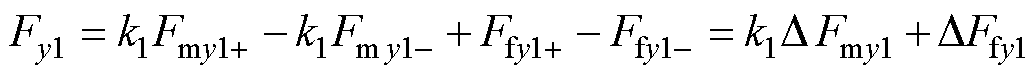（1）
式中，k1为悬浮系统磁通的漏磁系数[22]；Fmy1+为C1极主磁通产生的主悬浮力；Fmy1-为C2极主磁通产生的主悬浮力；Ffy1+为C1极边缘磁通产生的边缘悬浮力；Ffy1-为C2极边缘磁通产生的边缘悬浮力；DFmy1为Fmy1+与Fmy1-的合力；DFfy1为Ffy1+与Ffy1-的合力。DFmy1和DFfy1与气隙磁通密度、悬浮系统磁通面积等关系可一般性表示为
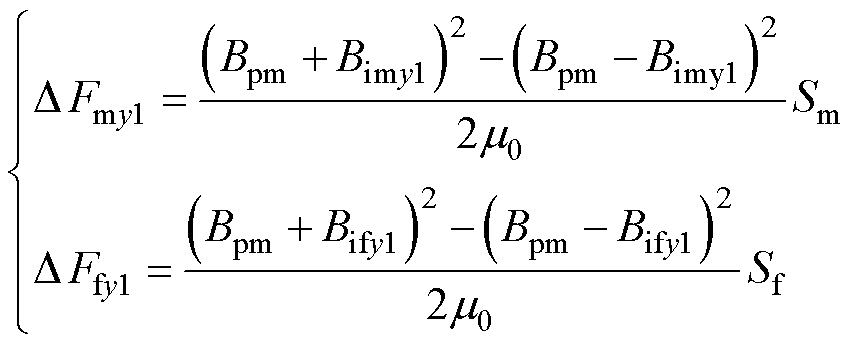（2）
式中，Bpm作为悬浮力偏置磁通密度；Bimy1为y1方向悬浮绕组产生的控制主磁通密度；Bify1为y1方向悬浮绕组产生的控制边缘磁通密度；Sm为主磁通面积；Sf为边缘磁通面积；m0为真空磁导率。
偏置磁通密度Bpm由轴向充磁永磁环提供，经过前侧悬浮系统定子、转子及后侧悬浮系统定子形成闭合回路且近似为常数[23]。
控制磁通密度包括了控制主磁通密度和控制边缘磁通密度。对于控制主磁通密度可以表示为
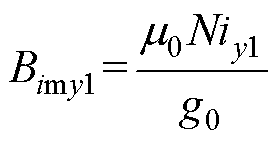（3）
式中，g0为主磁通路径长度，其数值等于定、转子之间的气隙长度；N为悬浮绕组匝数；iy1为悬浮电流。控制边缘磁通密度与电流、绕组匝数和气隙长度之间的数值关系可以表示为
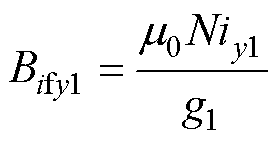（4）
式中，g1为边缘磁通路径长度。根据文献[22]提出的边缘磁通路径估算方法，g1可以近似表示为
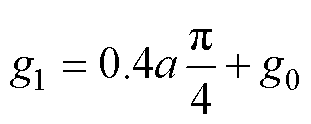（5）
悬浮系统磁通面积包括主磁通面积和边缘磁通面积。其中，主磁通面积Sm恒定，其值为ah。边缘磁通面积Sf数值与边缘磁通宽度af正相关。
定义旋转一个转子极距的时间为T，其与转速n、转子极数m的数学关系为
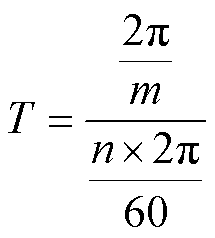（6）
定义6个典型位置对应的时刻分别为ta、tb、tc、td、te和tf。依据图4明晰的典型转子约束位置，悬浮系统磁通铰链规律可以明晰为：
（1）针对典型位置a。悬浮系统磁通面积包括r1极与C1极铰链的主磁通面积ah及r2极与C1极铰链的边缘磁通面积0.4ah。
（2）针对典型位置b。悬浮系统磁通面积包括r1极与C1极铰链的主磁通面积0.4ah，r2极与C1极铰链的主磁通面积0.6ah，r1极与C1极铰链的边缘磁通面积0.4ah，r2极与C1极铰链的边缘磁通面积0.4ah。
（3）针对典型位置c。悬浮系统磁通面积包括r2极与C1极铰链的主磁通面积ah及r1极与C1极铰链的边缘磁通面积0.4ah。
（4）针对典型位置d。悬浮系统磁通面积仅包括r2极与C1极铰链的主磁通面积ah。
（5）针对典型位置e。悬浮系统磁通面积仅包括r2极与C1极铰链的主磁通面积ah。
（6）针对典型位置f。悬浮系统磁通面积包括r2极与C1极铰链的主磁通面积ah，及r3极与C1极铰链的边缘磁通面积0.4ah。
综上所述，得到定子边缘磁通与转子铰链的宽度，见表2。
表2 边缘磁通铰链宽度
Tab.2 Hinge width of edge-flux value
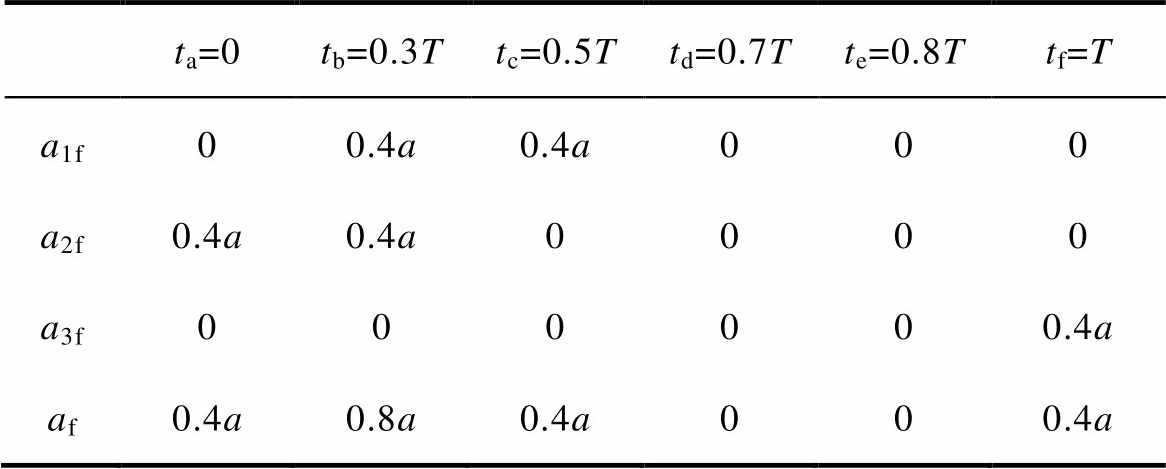
ta=0tb=0.3Ttc=0.5Ttd=0.7Tte=0.8Ttf=T a1f00.4a0.4a000 a2f0.4a0.4a0000 a3f000000.4a af0.4a0.8a0.4a000.4a
表2中，a1f、a2f、a3f分别为转子r1极、r2极、r3极与定子C1极铰链的边缘磁通宽度。且有
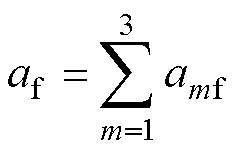（7）
依据表2，绘制边缘磁通宽度af在T内的变化趋势。鉴于悬浮力波形含有类正弦分量，对于af变化趋势傅里叶分析并取其基波，如图6所示。
因此，悬浮力全周期模型可以表示为
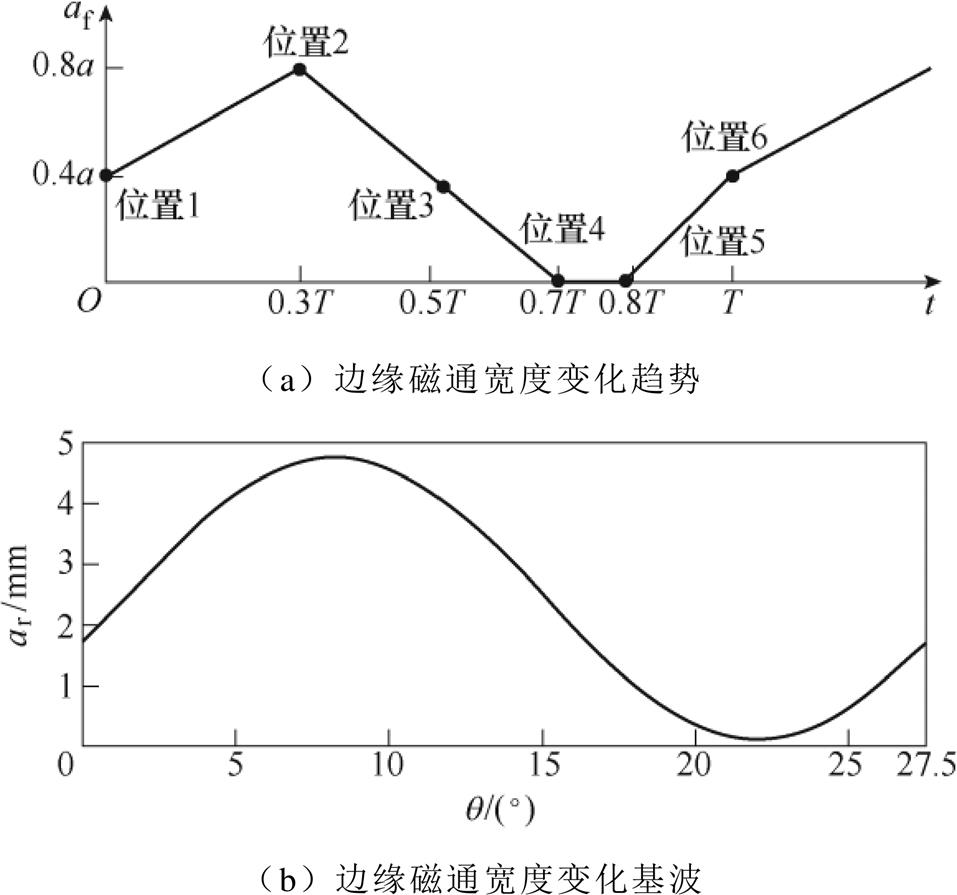
图6 边缘磁通宽度波形
Fig.6 Waveform of edge-flux width
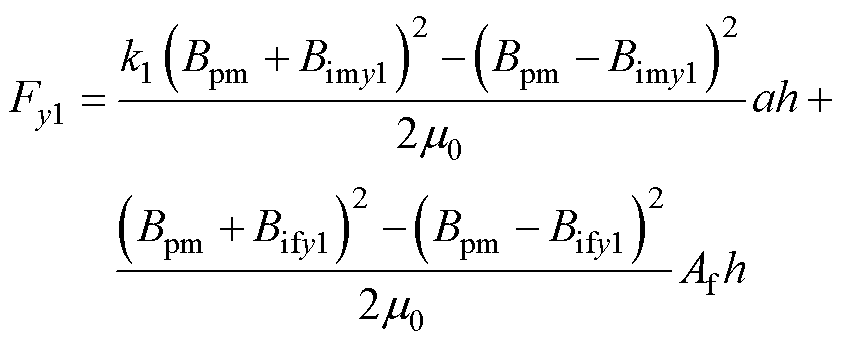（8）
式中，Af为af的基波分量，其解析模型为
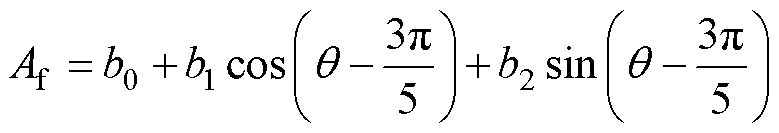（9）
且有
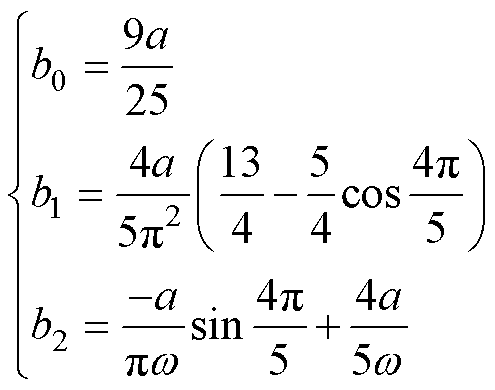（10）
式中，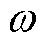
为Af的脉动频率，其与电机转速n之间的数学关系为
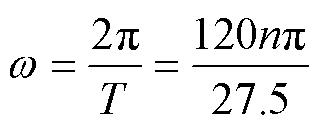（11）
分别通过有限元分析和实验验证模型的有效性和建模方法的可行性。
图7为悬浮电流iC=0A、1A和2A时，有限元分析值与模型计算值的对比。可以看出，构建的考虑磁通多齿铰链的全周期悬浮力模型能够描述悬浮力的动态变化特性，验证了模型的有效性。
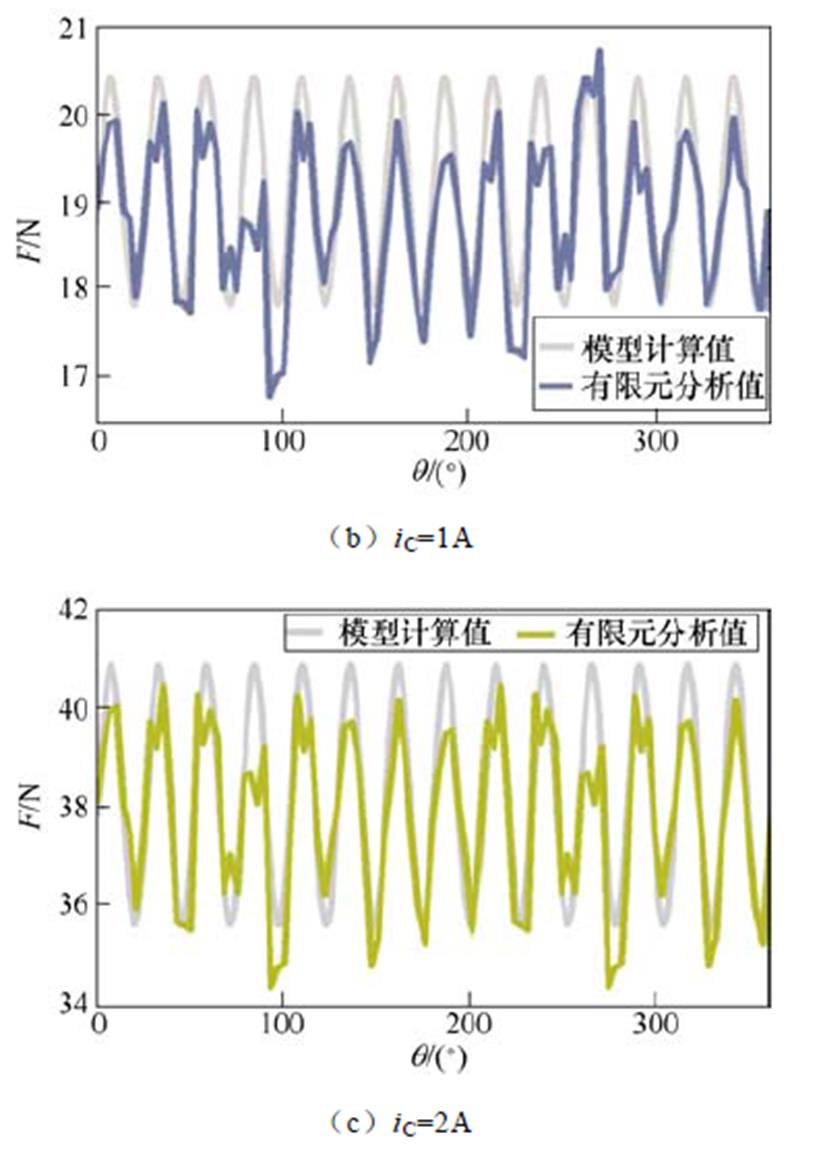
图7 基于有限元分析的悬浮力模型验证
Fig.7 Validation of levitation force model based on FEA
首先，基于构建的全周期悬浮力模型，提出相应的悬浮系统控制策略，通过转子悬浮验证悬浮模型的有效性。然后，再将基于本文悬浮模型的悬浮效果与基于考虑磁通多齿铰链模型的悬浮效果对比，验证建模方法的有效性。
12/14 BSRM中转矩系统和悬浮系统良好解耦效果[24]，采用直接转矩-悬浮力控制策略[19]，将控制系统分为独立控制的转矩系统和悬浮力系统。其中，转矩系统采用直接瞬时转矩控制方法，悬浮系统采用直接悬浮力控制方法。但由于本文建立的悬浮力模型中，自变量包括了动态时变的转子位置，因此需要在文献[19]的基础上，在悬浮控制系统中引入转子位置信号，形成悬浮系统全周期控制策略，如图8所示。图中，转子的位置信号q 由光电编码器测量获得，与转子的位移信号x、y和悬浮绕组电流共同反馈给悬浮力转换模块，该模块由式（8）所示的全周期悬浮力模型构建。
基于上述悬浮系统的控制策略，开展12/14 BSRM的实验研究。图9为基于DSPACE的实验测试平台。
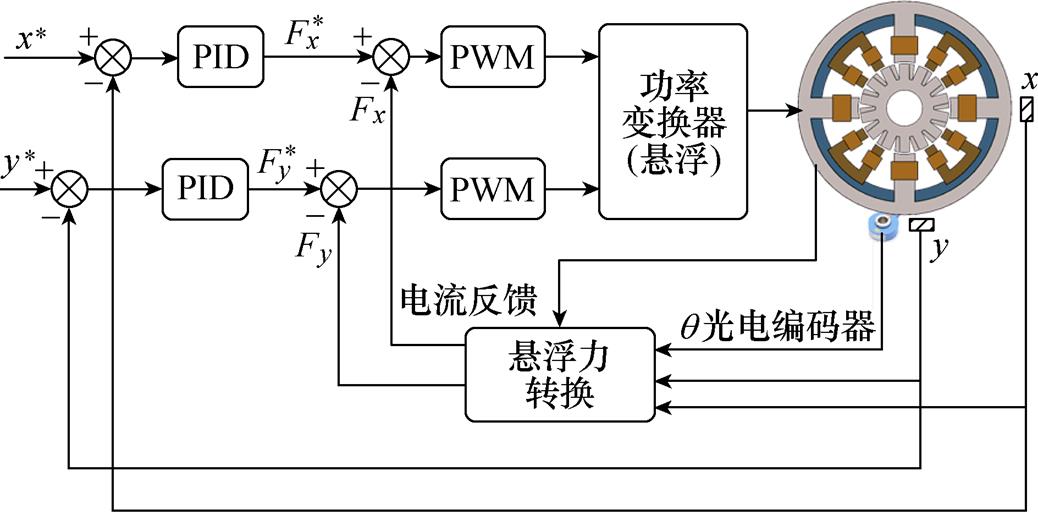
图8 悬浮系统全周期控制策略
Fig.8 Full-period control strategy of suspension system
图9 实验测试平台
图9 Experimental platform
图10为转子起浮时位移和电流波形，位移波形为200mm/格，电流波形为1A/格。
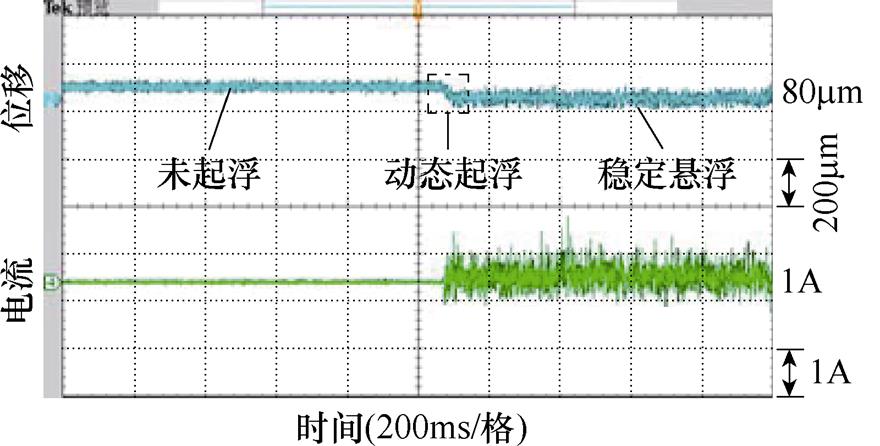
图10 起浮实验
Fig.10 Floating experiment
从图10中可以看出，转子从起浮到稳定悬浮用时约40ms，起伏后位移波动幅值约为80mm，占气隙总长度的8%，与之匹配的悬浮电流为1A，具有较好的悬浮控制精度和响应速度。
稳定悬浮实验对比如图11所示。稳定悬浮后，测得两自由度偏心位移，如图11a所示。进一步地，在DSPACE控制系统中，将式（8）右侧第二项设置为0，此时悬浮力模型仅保留了考虑主磁通的悬浮力模型且位置信号也相应置零，测得该情况下的两自由度偏心位移，作为基于传统悬浮力模型的两自由度悬浮位移结果，如图11b所示。
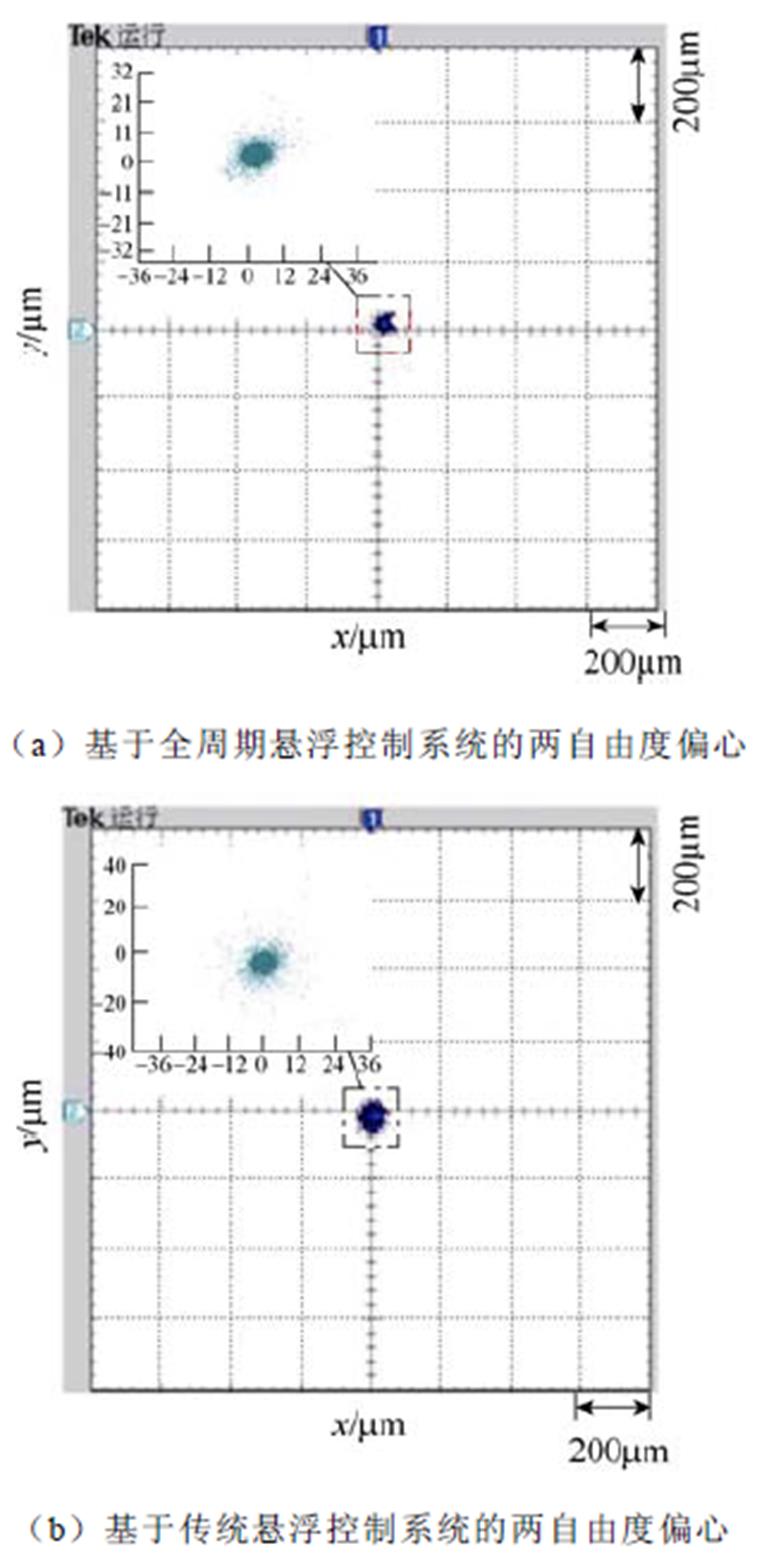
图11 稳定悬浮实验对比
Fig.11 Comparison of stable suspension experiments
相对于传统悬浮控制系统，全周期悬浮控制系统特征在于考虑了转子位置对悬浮系统的影响，控制系统的构造更加精确。从图11a与图11b对比可知，转子稳态悬浮时，基于全周期悬浮控制系统的两自由度偏心波动幅值为60mm，即单侧位移波动为30mm，占电机气隙总长度的6%，稳态悬浮精度良好。而传统悬浮控制系统，转子两自由度位移偏心幅值为80mm，即单侧位移波动为40mm，占电机气隙总长度的8%，稳态悬浮精度相对较差。
本文针对12/14 BSRM的结构特征构建了一种全周期建模方法。首先通过有限元分析探明了磁场的全周期铰链规律，然后利用麦克斯韦应力法能够实现区域性建模的优势，提出了主-边磁路并行建模策略，揭示了边缘磁通的动态时变特性，构建了考虑转子位置约束的全周期悬浮力模型。最后通过有限元分析和实验对模型进行了验证，分析结果与原理样机实验结果表明：
1）悬浮力全周期模型精准地表示了12/14 BSRM的悬浮力特征，为悬浮力的精确控制奠定了基础。
2）利用该模型很好地实现了12/14 BSRM稳定悬浮，且相较于传统的悬浮力模型及控制系统，稳定悬浮精度更高。
3）本文提出的建模方法可以进一步推广至其他具有悬浮系统磁通多齿铰链特征的BSRM悬浮力建模研究中，为该类电机高性能控制奠定基础。
参考文献
[1] Zhu Z Q, Cai Shun. Hybrid excited permanent magnet machines for electric and hybrid electric vehicles[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(3): 233-247.
[2] Correa G, Muñoz P M, Rodriguez C R. A comparative energy and environmental analysis of a diesel, hybrid, hydrogen and electric urban bus[J]. Energy, 2019, 187: 115906.
[3] 胡载东, 蒋栋, 孙宏博. 一种应用于磁悬浮轴承的四相四桥臂电力电子变换器[J]. 电工技术学报, 2020, 35(20): 4325-4335.
Hu Zaidong, Jiang Dong, Sun Hongbo. A four-phase four-leg power electronics converter for active magnetic bearing drive[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4325-4335.
[4] 周天豪, 杨智, 祝长生, 等. 电磁轴承高速电机转子系统的内模-PID控制[J]. 电工技术学报, 2020, 35(16): 3414-3425.
Zhou Tianhao, Yang Zhi, Zhu Changsheng, et al. Internal model control-PID control of an active magnetic bearing high-speed motor rotor system[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3414-3425.
[5] 黄威, 邓智泉, 李克翔, 等. 一种磁悬浮轴承支承刚性转子现场动平衡方法[J]. 电工技术学报, 2020, 35(22): 4636-4646.
Huang Wei, Deng Zhiquan, Li Kexiang, et al. A filed dynamic balancing method for rigid rotor supported by magnetic bearings[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4636-4646.
[6] 禹春敏, 邓智泉, 梅磊, 等. 基于精确磁路的新型混合型轴向-径向磁悬浮轴承研究[J]. 电工技术学报, 2021, 36(6): 1219-1228.
Yu Chunmin, Deng Zhiquan, Mei Lei, et al. Research of new hybrid axial-radial magnetic bearing based on accurate magnetic circuit[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1219-1228.
[7] Takemoto M, Suzuki H, Chiba A, et al. Improved analysis of a bearingless switched reluctance motor[J]. IEEE Transactions on Industry Applications, 2001, 37(1): 26-34.
[8] Lee D H, Ahn J W. Design and analysis of hybrid stator bearingless SRM[J]. Journal of Electrical Engineering and Technology, 2011, 6(1): 94-103.
[9] 孙玉坤, 于丰源, 袁野, 等. 一种混合双定子磁悬浮开关磁阻电机[J]. 电工技术学报, 2019, 34(1): 1-10.
Sun Yukun, Yu Fengyuan, Yuan Ye, et al. A hybrid double stator bearingless switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 1-10.
[10] Wang Huijun, Lee D H, Park T H, et al. Hybrid stator-pole switched reluctance motor to improve radial force for bearingless application[J]. Energy Conversion and Management, 2011, 52(2): 1371- 1376.
[11] Pang Mingqi, Wang Huijun, Zhou Guangxu, et al. Design and analysis of a two-phase permanent- magnet-assisted switched reluctance motor[C]//2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea (South), 2018: 1956-1961.
[12] Zhou Guangxu, Yang Ting, Li Fangxu, et al. Design and analysis of modular permanent bearingless switched reluctance motor[C]//2020 23rd Inter- national Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 2020: 1752- 1757.
[13] Liu Jianfeng, Wang Huijun, Bao Junfang, et al. A novel permanent magnet biased bearingless switched reluctance motor[C]//2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 2013: 4342-4347.
[14] Li Fangxu, Wang Huijun, Zhang Fengge, et al. Comprehensive analysis of suspending force for improved bearingless switched reluctance motor with permanent magnets in stator yoke[J]. CES Transa- ctions on Electrical Machines and Systems, 2018, 2(4): 348-354.
[15] Wang Huijun, Xue Bingkun, Tang Shaofei. New type 12/14 bearingless switched reluctance motor with double windings[J]. IET Electric Power Applications, 2015, 9(7): 478-485.
[16] Wang Huijun, Liu Jianfeng, Bao Junfang, et al. A novel bearingless switched reluctance motor with a biased permanent magnet[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6947-6955.
[17] Wang Huijun, Bao Junfang, Xue Bingkun, et al. Control of suspending force in novel permanent- magnet-biased bearingless switched reluctance motor[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4298-4306.
[18] Yuan Ye, Sun Yukun, Xiang Qianwen, et al. The study of switched reluctance motor for 4-DOF bearingless motor[J]. Journal of Electrical Engin- eering & Technology, 2019, 14(1): 179-189.
[19] 黄永红, 石姗姗, 袁野, 等. 磁悬浮开关磁阻电机的自适应终端滑模控制[J]. 控制与决策, 2021, 36(6): 1449-1456.
Huang Yonghong, Shi Shanshan, Yuan Ye, et al. Adaptive terminal sliding mode control of bearingless switched reluctance motor[J]. Control and Decision, 2021, 36(6): 1449-1456.
[20] Wang Huijun, Bao Junfang, Xue Bingkun, et al. Control of suspending force in novel permanent- magnet-biased bearingless switched reluctance motor[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4298-4306.
[21] Wang Huijun, Li Fangxu. Design consideration and characteristic investigation of modular permanent magnet bearingless switched reluctance motor[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 4326-4337.
[22] 曹鑫, 邓智泉, 杨钢, 等. 无轴承开关磁阻电机麦克斯韦应力法数学模型[J]. 中国电机工程学报, 2009, 29(3): 78-83.
Cao Xin, Deng Zhiquan, Yang Gang, et al. Mathe- matical model of bearingless switched reluctance motors based on Maxwell stress tensor method[J]. Proceedings of the CSEE, 2009, 29(3): 78-83.
[23] Yuan Ye, Huang Yonghong, Xiang Qianwen, et al. Mathematical modeling and control for a single winding bearingless flywheel motor in electric/ suspension mode[J]. Journal of Electrical Engineering and Technology, 2018, 13(5): 1935-1944.
[24] Yuan Ye, Sun Yukun, Xiang Qianwen, et al. The study of switched reluctance motor for 4-DOF bearingless motor[J]. Journal of Electrical Engin- eering & Technology, 2019, 14(1): 179-189.
Suspension Force Modeling for 12/14 Bearingless Switched Reluctance Motor Considering Flux Multi Teeth Hinge
Abstract Bearingless switched reluctance motor (BSRM) has the characteristics of traditional switched reluctance motor and magnetic suspension bearing. Therefore, it has broad application prospects in flywheel batteries. The inherent coupling between suspension and torque exists in the traditional dual winding BSRM. Profuse kinds of topologies, such as 8/10 BSRM, 12/10 BSRM, and permanent magnet biased BSRM, have been proposed successively. The 12/14 BSRM is a representative topology of permanent magnet bias BSRM. However, the 12/14 BSRM suspension system generally adopts a simplified model. The magnetic flux of the 12/14 BSRM suspension system intersects with multiple rotor salient poles, which is subject to the dynamic constraints of the rotor position. Therefore, it is necessary to further explore the modeling method of 12/14 BSRM suspension force.
The operating principle and topology of 12/14 BSRM are analyzed. The stator of torque system is U-shaped structure, and torque is generated by the principle of minimum reluctance. The suspension system has four phases, which are the same as the working principle of magnetic bearings. The finite element analysis model is built in the ANSYS software, and the rotor pole distance is taken as an analysis cycle. The result of finite element analysis shows that the suspension force changes dynamically with the rotor position, and the suspension force presents a quasi sinusoidal distribution with the rotor position. However, the traditional suspension force model cannot reveal the dynamic characteristics of 12/14 BSRM suspension force and rotor position. Therefore, by analyzing the finite element results, the cross link law between the stator pole and the rotor pole in typical positions is obtained and the equivalent magnetic circuit of the suspension system is constructed.
The magnetic flux density of the suspension system is analyzed. The bias flux density is provided by the axial magnetized permanent magnetic ring, which is approximately constant. The control main flux density and control edge flux density in the control flux density are calculated respectively. The magnetic flux area of the suspension system, including the main magnetic flux area and the edge magnetic flux area, is calculated. The main flux area is constant, and the edge flux area is positively related to the edge flux width. The corresponding change curve is obtained according to the clear width change rule of the stator edge flux and rotor cross link. Fourier analysis is carried out and the fundamental wave is taken to obtain the analytical model of the area change of the edge magnetic flux. Comparing the finite element analysis value with the model calculation value, the full cycle suspension force model considering the flux multi tooth hinge constructed can describe the dynamic variation characteristics of the suspension force, which verifies the validity of the model.
Based on the full cycle suspension force model and the experimental test platform of DSPACE, the experimental research of 12/14 BSRM was carried out. The rotor floating time is about 40ms. The displacement amplitude after fluctuation is about 80mm. The suspension control precision and response speed are good. The displacement amplitude of the two degrees of freedom based on the full cycle suspension control system is 60mm, When the rotor is stably suspended. In the traditional suspension control system, the displacement amplitude of the rotor with two degrees of freedom is 80mm. The model is verified by finite element analysis and experiment, and the results show that the full cycle suspension force model accurately represents the suspension force characteristics of 12/14 BSRM, establishing the foundation for accurate control of suspension force. The control strategy of 12/14 BSRM for more accurate suspension utilization of the model is realized. Implemented 12/14 BSRM for more precise suspension control utilizing the model.
Keywords：Suspension flux, suspension force modeling, bearingless switched reluctance motor, Maxwell stress method, finite element analysis
中图分类号：TM352
DOI: 10.19595/j.cnki.1000-6753.tces.211928
国家自然科学基金重点项目（51877101）、江苏省重点研发计划（BE2021094）、中国博士后科学基金项目（2021M702413）、江苏省优势学科（PAPD-2018-87）和江苏省研究生科研与实践创新计划项目（KYCX19_1607）资助。
收稿日期 2021-11-25
改稿日期 2022-02-22
E-mail: 1170557230@qq.com
袁 野 男，1991年生，副教授，硕士生导师，研究方向为磁悬浮电机设计与非线性控制。
E-mail: 1000050003@ujs.edu.cn（通信作者）
（编辑 崔文静）