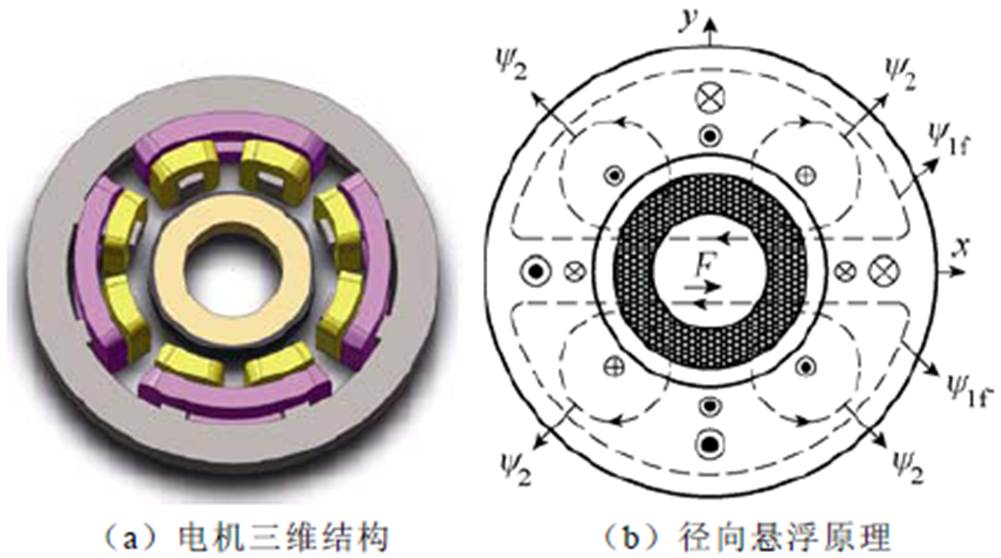
图1 双绕组无轴承永磁薄片电机示意图
Fig.1 Schematic diagram of double winding bearingless permanent magnet motor
摘要 在无轴承永磁薄片电机系统中,永磁转子因失去轴承支承容易发生偏心位移,为控制转子在几何中心稳定悬浮,径向悬浮力精确建模是无轴承系统高性能可靠运行的关键基础。针对大气隙无轴承永磁薄片电机因转子偏心程度大而引起的径向悬浮力模型非线性误差问题,该文提出一种基于频域拟合的径向悬浮力精确建模方法,将非线性分量转化为相应函数补偿至径向悬浮力模型中,从而提高了模型精确度。首先,对推导一般径向悬浮力模型过程中出现的多个误差因素及其影响进行系统分析;在此基础上,提出频域拟合方法重构径向悬浮力模型,并分析其非线性特性;最后,将解析模型与有限元仿真所得到的可控径向悬浮力、偏心磁拉力进行深入对比分析,验证了该解析模型的正确性与精确性。
关键词:无轴承永磁薄片电机 径向悬浮力 麦克斯韦应力张量法 频域拟合 有限元仿真
无轴承永磁薄片电机是将磁悬浮技术与永磁电机相结合的一种特种电机,其兼有前者无机械磨损、不需润滑的优势和后者结构简单、功率密度高的特点[1-3]。此外,电机中永磁转子具有轴向长度小于径向半径而呈薄片状的特征[4],提高经济效益的同时降低了电机结构复杂度。因此,采用无轴承永磁同步电机驱动的泵系统在半导体制造、医疗器械、航空航天等具有高洁净度指标要求的前沿领域具有重要的科研价值和广泛的应用前景[5-8]。
无轴承永磁薄片电机系统中,薄片转子的稳定悬浮是实现系统高性能可靠运行的必要条件[9]。为实现对薄片转子精确稳定、实时可靠的径向悬浮控制,需要建立精确的径向悬浮力数学模型[10-11]。文献[12-13]建立了无轴承永磁同步电机电感矩阵表达式,利用虚位移法对电感矩阵求偏导推导出径向悬浮力模型。该方法求解过程直接且考虑了两套绕组的耦合关系,但一系列电感参数难以准确获取,而且计算量较大。文献[14]利用机电能量变换的方法建立了无轴承永磁同步电机双绕组的磁链与电压方程,通过分析电机内各部分洛伦兹力得到电磁转矩和径向悬浮力的表达式。该方法具有直观清晰的建模概念,但需要繁琐的坐标变换且忽略了模型中存在的耦合因素。文献[15]对双绕组结构的无轴承永磁薄片电机进行磁路分析,在推导出气隙磁通密度表达式的基础上利用麦克斯韦应力张量法建立了径向悬浮力数学模型,该模型将悬浮力分成可控径向悬浮力和偏心磁拉力两部分,具有一定的普遍性。该方法虽然建模过程复杂、计算量较大,但模型的计算精度和准确性较高。
在影响无轴承永磁薄片电机径向悬浮力模型准确度的众多因素中,薄片转子的偏心位移不容忽视,尤其在电机起动或者突加扰动的情况下,较大的转子偏心会使径向悬浮力呈现出不同的模型特性。文献[16]所推导的无轴承永磁电机径向悬浮力模型由于缺失对转子偏心情况下悬浮力的研究分析而只能停留于非偏心条件下的理想方程;文献[17]将麦克斯韦张量法和磁路分析法相结合,推导出考虑转子偏心情况下的径向力数学模型,但对磁导函数的近似处理缺少相应分析与补偿,所得模型为近似形式,存在一定误差;文献[18]通过建立新的转子偏心坐标系并基于麦克斯韦张量法推导了径向悬浮力模型,但对悬浮力表达式所进行的一系列简化忽略了非线性悬浮力分量的存在。
本文针对无轴承永磁薄片电机因转子偏心位移大而引起的径向悬浮力非线性误差问题,在采用麦克斯韦张量法推导出一般径向悬浮力模型基础上,以提高模型精确度为目标,对磁导函数近似、径向悬浮力忽略项、等效气隙区别于绝对气隙等误差因素进行分析,提出一种基于频域拟合的径向悬浮力精确建模方法,将可控径向悬浮力、偏心磁拉力中的非线性分量转化为偏心系数的函数分别进行补偿,修正等效气隙长度的同时解决了磁导函数近似误差问题,从而提高了模型准确度。最后运用有限元法对无轴承永磁薄片电机样机的径向悬浮力进行分析,将仿真结果与解析模型计算值进行了对比分析和验证。
本文研究对象为永磁体极对数pf=1、转矩绕组极对数p1=1和悬浮绕组极对数p2=2的两相双绕组无轴承永磁薄片电机。文中与永磁体、转矩绕组及悬浮绕组三者相关的物理量分别用下标f、1和2指代以示区分。电机定子采用六极八齿集中式绕组结构,永磁转子采用平行充磁方式,电机三维结构如图1a所示。

图1 双绕组无轴承永磁薄片电机示意图
Fig.1 Schematic diagram of double winding bearingless permanent magnet motor
图1b为无轴承永磁薄片电机径向悬浮原理。电机定子内部嵌有转矩和悬浮两套绕组,当转子位于中心且未通入悬浮电流时,转矩绕组和永磁转子共同形成两极对称磁链y1f。当悬浮绕组中通入电流,所产生的四极磁链y2会与y1f叠加作用打破原本对称平衡的气隙磁场,使具有相同磁链方向的位置气隙磁通密度增大而相反方向的位置气隙磁通密度减小[19-20],从而产生径向悬浮力F。因此,当转子发生偏心时,可通过悬浮电流的一定组合形成与偏心方向相反的作用力,进而实现转子径向稳定悬浮。
基于对径向悬浮原理的分析,本节采用麦克斯韦应力张量法对图1无轴承永磁薄片电机进行径向悬浮力模型推导,其建模步骤如图2所示,可总结为:结合电机气隙磁导函数及磁动势表达式推导出气隙磁通密度分布,在此基础上由麦克斯韦应力公式求解出径向悬浮力模型。

图2 麦克斯韦应力张量法建模步骤
Fig.2 Modeling steps of Maxwell stress tensor method
图3所示为转子偏心示意图。图中,lp、lpx、lpy分别为转子偏心距离及其在x、y轴方向上的分量;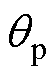 为转子偏心角度;
为转子偏心角度;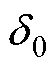 为绝对气隙长度;
为绝对气隙长度;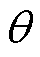 为气隙中任意处与x轴的夹角。其中,绝对气隙长度
为气隙中任意处与x轴的夹角。其中,绝对气隙长度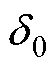 在此小节特指不考虑永磁体部分,只表示实际磁路中空气部分的长度[13-15],如图3a所示。
在此小节特指不考虑永磁体部分,只表示实际磁路中空气部分的长度[13-15],如图3a所示。
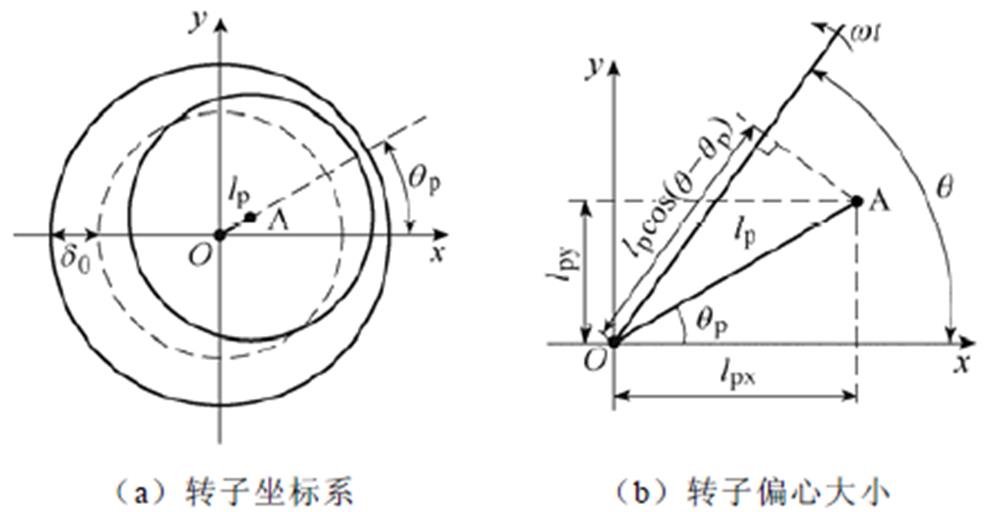
图3 转子偏心示意图
Fig.3 Diagram of rotor eccentricity
由图3可知,气隙长度分布函数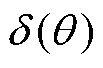 可表示为
可表示为
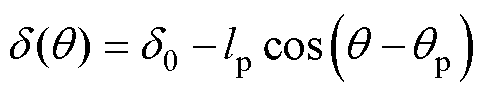 (1)
(1)
为衡量转子偏心程度,定义偏心系数k为
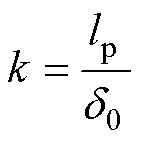 (2)
(2)
在此基础上,单位面积气隙磁导函数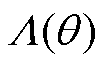 为
为
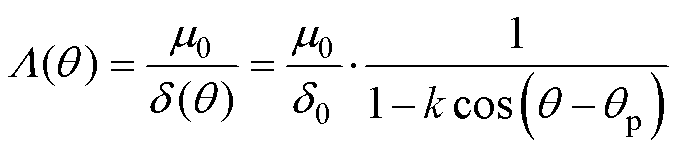 (3)
(3)
当偏心系数k很小时,式(3)可近似简化为
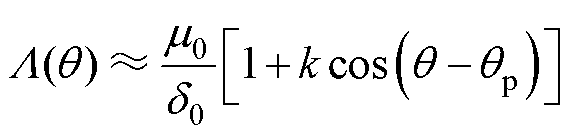 (4)
(4)
无轴承永磁电机的气隙磁场由转矩、悬浮绕组和永磁体共同建立,它们产生的磁动势基波分量为
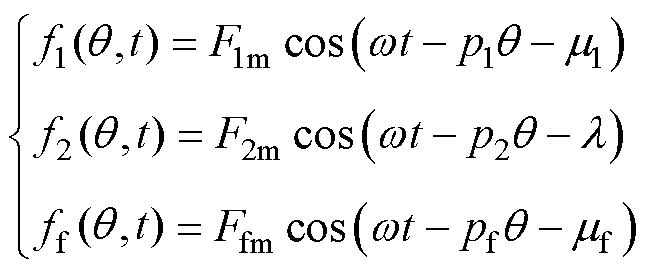 (5)
(5)
式中,F1m、F2m、Ffm分别为转矩绕组、悬浮绕组和永磁体产生的磁动势基波幅值;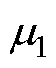 、
、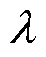 、
、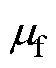 为各磁动势基波的初始相位;p1、p2、pf为各部分的极对数;
为各磁动势基波的初始相位;p1、p2、pf为各部分的极对数;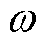 为三者共同的电流角频率。
为三者共同的电流角频率。
因转矩绕组和永磁体所产生磁场极对数相同,两者可共同建立合成磁动势,对应基波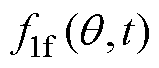 为
为
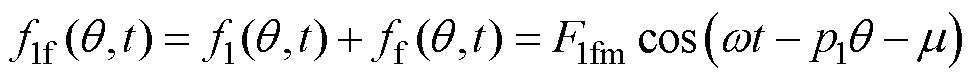 (6)
(6)
式中,F1fm、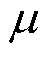 分别为
分别为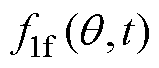 的基波幅值和初始相位。
的基波幅值和初始相位。
气隙中三者磁动势共同产生气隙磁通密度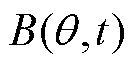 为
为
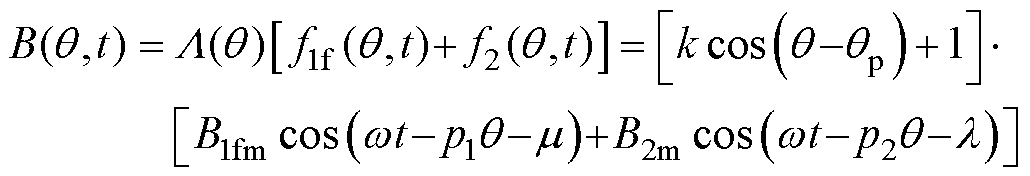 (7)
(7)
其中
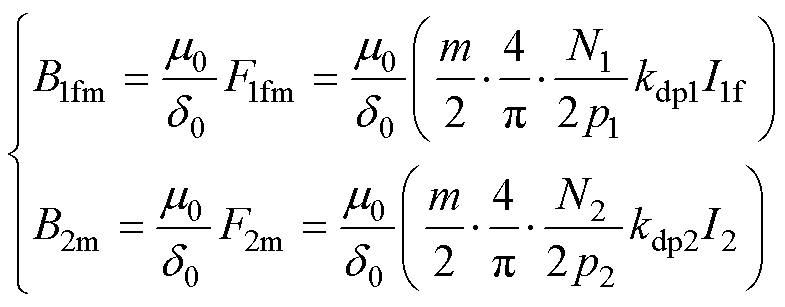 (8)
(8)
式中,B1fm、B2m分别为转子不偏心时气隙磁通密度基波幅值;I1f、I2为对应电流幅值;m为电机相数;N1、N2为转矩绕组和悬浮绕组每相串联总匝数;kdp1、kdp2为二者的绕组因数。
根据麦克斯韦张量法,转子沿x、y正交轴方向所受的总径向悬浮力可表示为
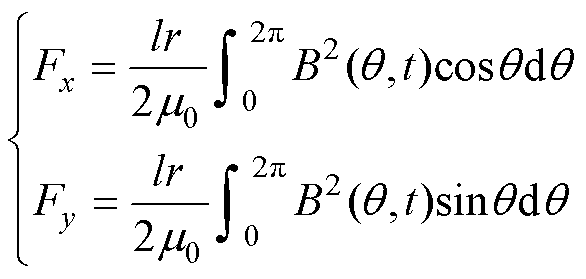 (9)
(9)
式中,l为转子轴向长度;r为转子半径。
对于p1=1、p2=2的无轴承永磁薄片电机,以x方向径向悬浮力Fx为例,计算得
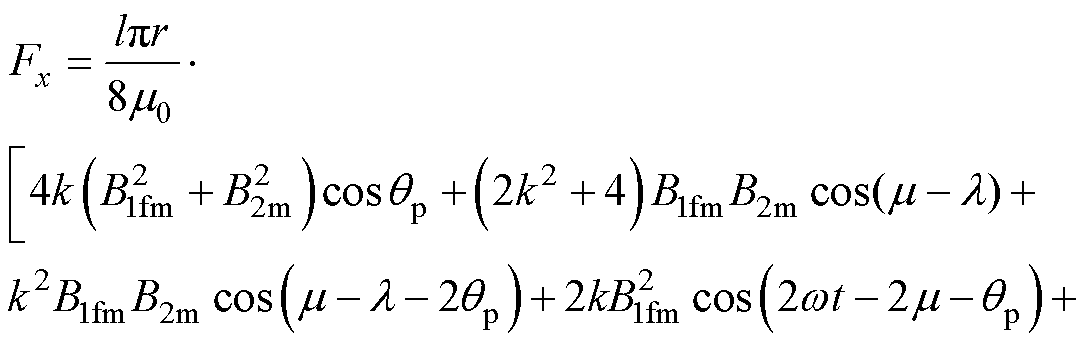
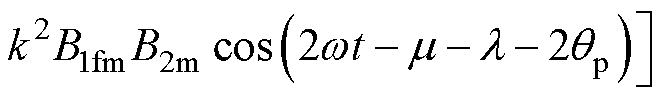 (10)
(10)
在本小节里,将式(10)所示Fx中k、B2m的二次方项与它们的乘积项忽略,同时不考虑含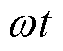 的交流脉动分量,Fy亦采用相同处理方法,可得
的交流脉动分量,Fy亦采用相同处理方法,可得
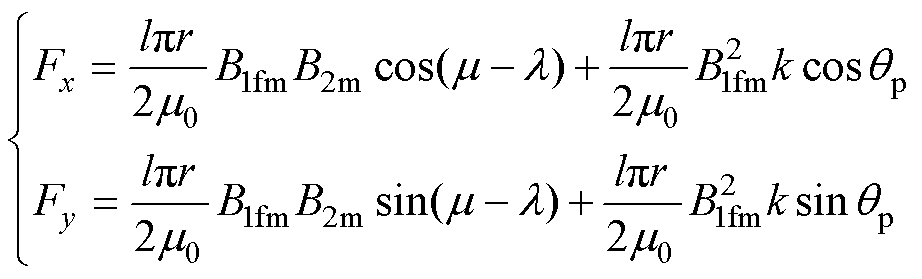 (11)
(11)
综上所述,式(11)构成一般径向悬浮力解析模型。其中,第一部分为可控径向悬浮力分量,大小可通过悬浮绕组电流进行调节;第二部分为偏心磁拉力分量,与偏心位移呈线性关系。
由第1节推导过程中可知,采用麦克斯韦应力张量法推导一般径向悬浮力解析模型时,常会引入一些等效近似或者忽略一些非理想因素,然而这些假设必然会引起误差。对无轴承永磁薄片电机而言,较大的转子偏心位移会使这些误差放大,带来控制模型不够精确的问题。本文对推导过程中引起模型误差的主要因素总结有:磁导函数近似、径向悬浮力忽略项和等效气隙区别于绝对气隙。下面将对这些因素逐一分析。
计算气隙磁导函数时,若采用式(3)形式则后续积分无法求解化简,因此将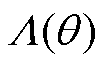 的表达式由式(3)近似成式(4)。然而,当偏心系数k不满足数值很小的条件时,近似处理的合理性就有待商榷。
的表达式由式(3)近似成式(4)。然而,当偏心系数k不满足数值很小的条件时,近似处理的合理性就有待商榷。
为便于分析,定义近似前后的磁导函数分别为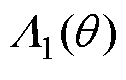 、
、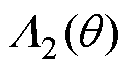 ,则二者的绝对误差
,则二者的绝对误差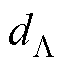 和相对误差
和相对误差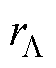 经计 算为
经计 算为
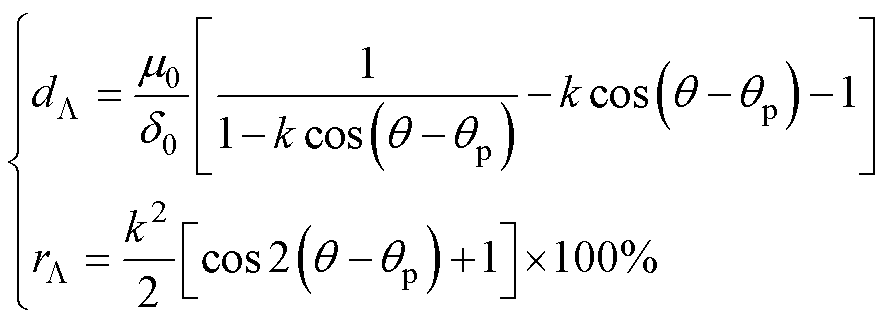 (12)
(12)
为衡量该因素所引起悬浮力误差大小,分别取磁导函数为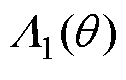 、
、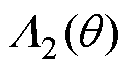 ,将本文第4节中表2样机参数代入式(9)并采用自适应辛普森积分法进行近似数值积分计算。以Fx为例,取绕组电流I1= I2=5A、
,将本文第4节中表2样机参数代入式(9)并采用自适应辛普森积分法进行近似数值积分计算。以Fx为例,取绕组电流I1= I2=5A、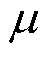 =
=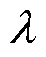 =0,记磁导函数近似前后所得Fx分别为
=0,记磁导函数近似前后所得Fx分别为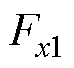 、
、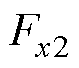 ,二者的绝对误差dF和相对误差rF为
,二者的绝对误差dF和相对误差rF为
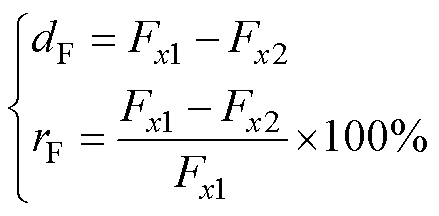 (13)
(13)
以偏心系数k和角度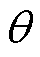 为自变量,绘制出
为自变量,绘制出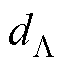 、
、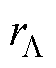 的三维图像如图4所示;以偏心系数k和时间t为自变量,绘制出dF、rF的三维图像如图5所示,其中偏心角度
的三维图像如图4所示;以偏心系数k和时间t为自变量,绘制出dF、rF的三维图像如图5所示,其中偏心角度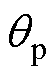 取为0。
取为0。
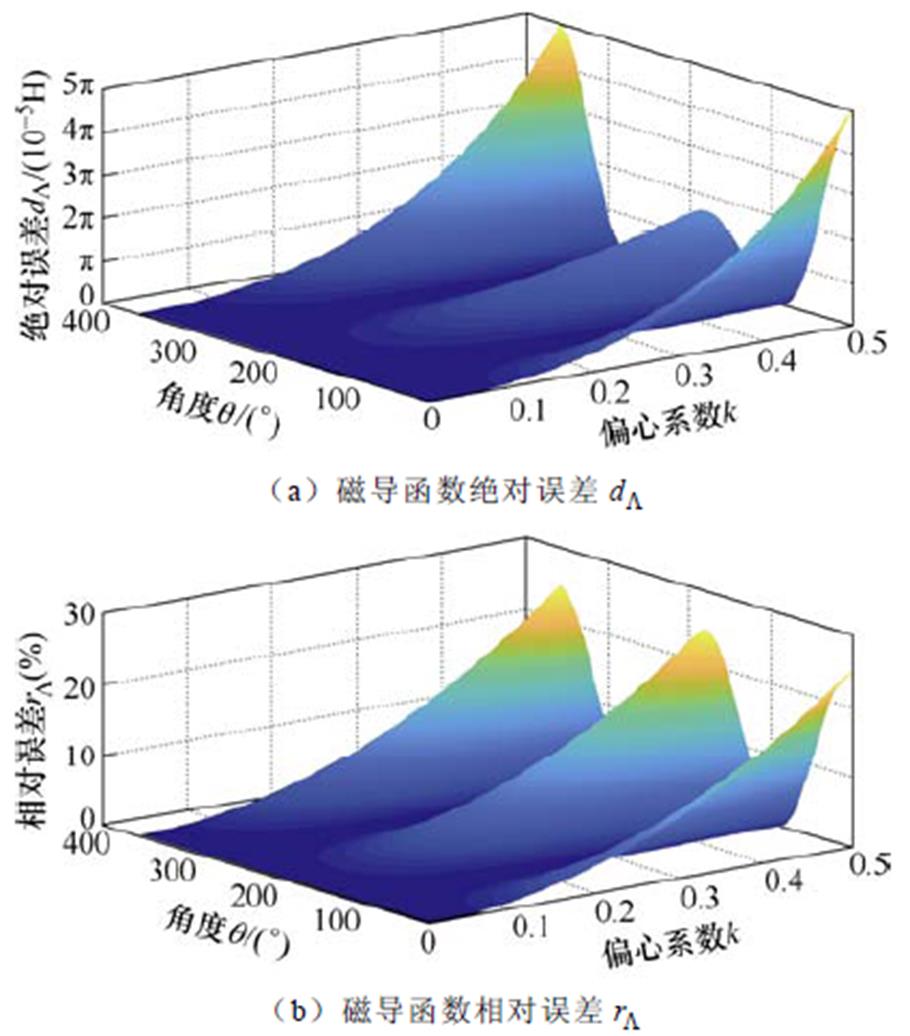
图4 磁导函数误差三维图像
Fig.4 Three-dimensional diagram of Magnetic conductivity function error
由图4、图5可知,磁导函数近似误差与其所引起的悬浮力误差具有相同变化趋势,都与偏心系数k呈正相关。若取k =0.3,此时气隙磁导的最大相对误差为9%,而引起的径向悬浮力最大相对误差可达15%。因此,磁导函数的近似误差会在后续模型推导过程中进一步放大。
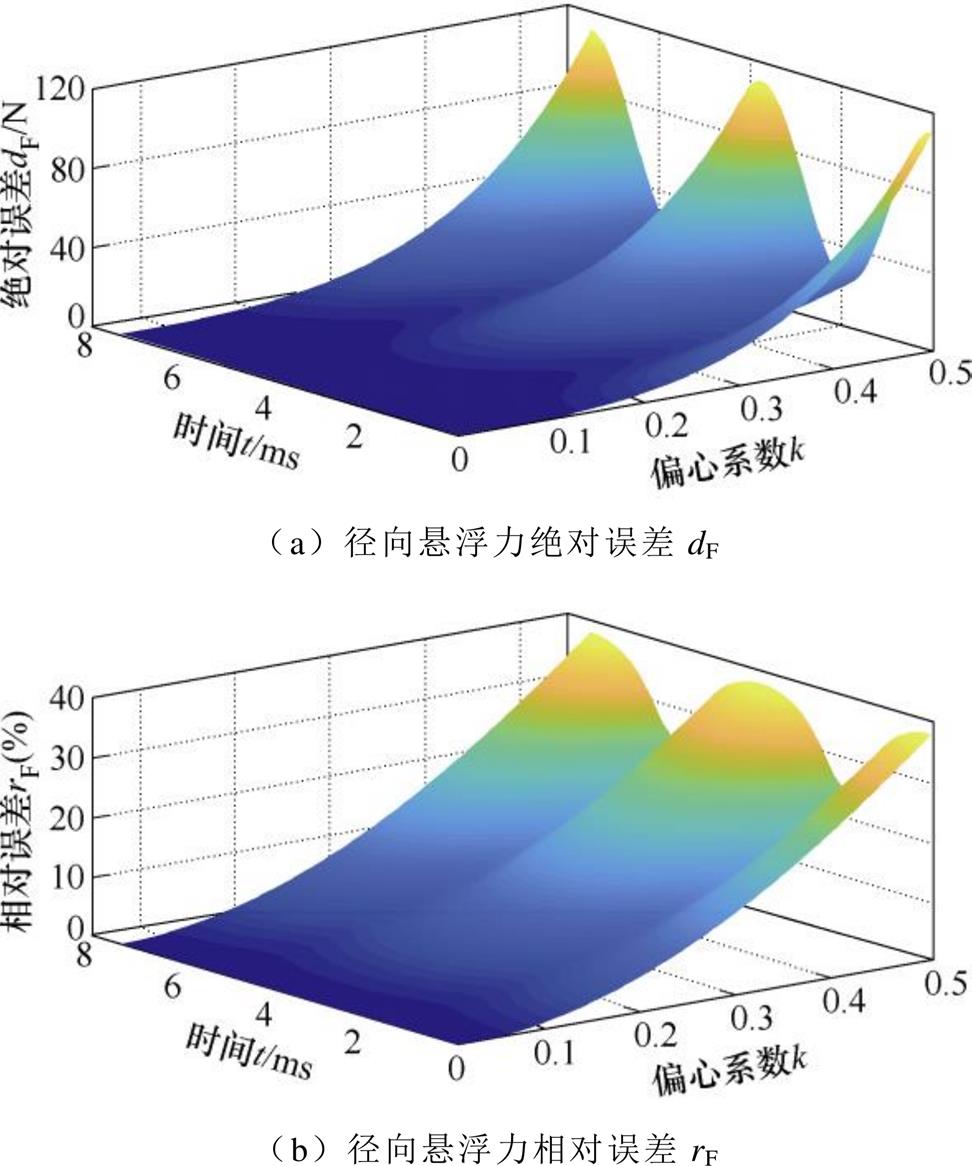
图5 径向悬浮力误差三维图像
Fig.5 Three-dimensional diagram of radial suspension force error
在径向悬浮力表达式由式(10)化简至式(11)过程中,k、B2m的二次方项、乘积项和含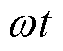 的交流项都予以忽略,而这也会带来模型误差。其中,含
的交流项都予以忽略,而这也会带来模型误差。其中,含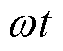 的交流项是磁动势函数的周期性所引起的径向悬浮力脉动分量,在一个周期内的平均值为0。在无轴承电机悬浮力模型研究中,径向悬浮力脉动分量一般被直接省略,本文也不多作分析。对于剩余忽略项部分,本节仍以Fx为例进行探究,记忽略前后径
的交流项是磁动势函数的周期性所引起的径向悬浮力脉动分量,在一个周期内的平均值为0。在无轴承电机悬浮力模型研究中,径向悬浮力脉动分量一般被直接省略,本文也不多作分析。对于剩余忽略项部分,本节仍以Fx为例进行探究,记忽略前后径
向悬浮力分别为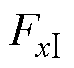 和
和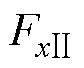 ,具体形式为
,具体形式为
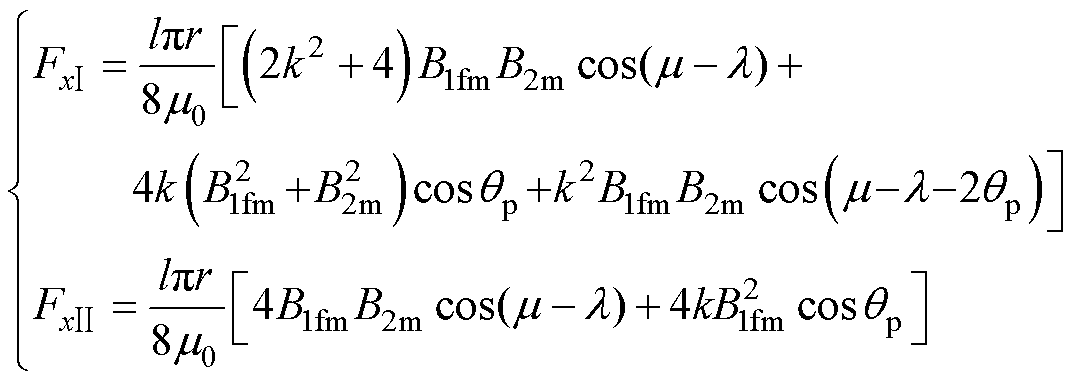 (14)
(14)
为分析忽略项所引起相对误差大小,定义
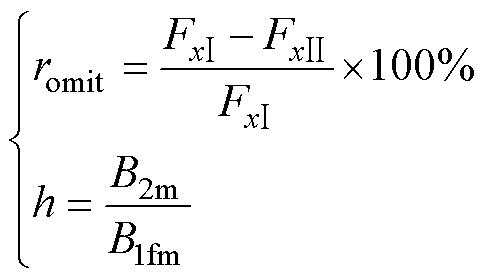 (15)
(15)
式中,romit为忽略前后Fx相对误差;h为悬浮绕组磁通密度与永磁体、转矩绕组合成磁通密度的基波幅值比值。
结合式(14)、式(15),各磁动势初始相位及偏心角度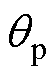 皆取为0,相对误差romit可展开成磁通密度比h和偏心系数k的函数为
皆取为0,相对误差romit可展开成磁通密度比h和偏心系数k的函数为
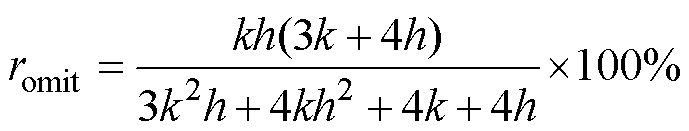 (16)
(16)
由于h、k都为正值,可做如下比较
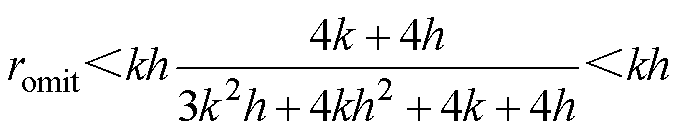 (17)
(17)
因此,径向悬浮力直流分量忽略项所引起的相对误差小于kh,而kh的数量级一般在1%左右,影响较小。
在径向悬浮力数学建模过程中,一般把转子不偏心时永磁转子外圆表面至定子内圆表面的距离定义为绝对气隙长度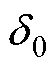 ,然而式(3)直接将
,然而式(3)直接将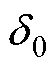 作为磁路总长度计算磁导的处理方式至少存在两方面 问题:
作为磁路总长度计算磁导的处理方式至少存在两方面 问题:
(1)永磁体作为非导磁材料未考虑至总等效气隙中。
(2)极对数不同的转矩绕组和悬浮绕组磁场被假设为磁路完全相同。
上述两个问题都会带来径向悬浮力模型误差。对仅有永磁体磁场作用下的无轴承永磁同步电机进行等效磁路分析,磁路分析对象可细分至每一角度微元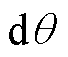 ,如图6所示,它们具有如下磁路特征:转子不偏心情况下磁导构成完全相同,磁动势在空间上呈正弦分布且随时间呈正弦变化如式(5)所示。图6中,Fc为永磁体磁动势源,幅值为Ffm;
,如图6所示,它们具有如下磁路特征:转子不偏心情况下磁导构成完全相同,磁动势在空间上呈正弦分布且随时间呈正弦变化如式(5)所示。图6中,Fc为永磁体磁动势源,幅值为Ffm;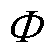 为磁路中走过的总磁通;
为磁路中走过的总磁通;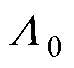 为永磁体内磁导;
为永磁体内磁导;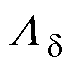 为外磁路主磁导;
为外磁路主磁导;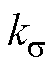 为漏磁系数,其值大于1。
为漏磁系数,其值大于1。
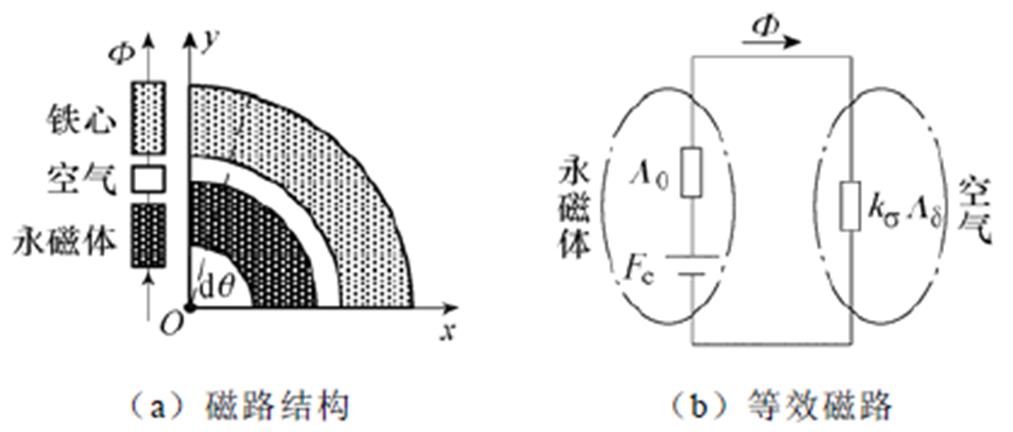
图6 等效磁路分析示意图
Fig.6 Diagram of equivalent magnetic circuit analysis
一般铁心的磁导率相较永磁体和空气而言很大,磁阻很小可以忽略不计。然而,永磁体的磁导率与空气相近,等效磁路中的内磁导部分必须予以考虑,因此磁路总磁阻Rm可以写成
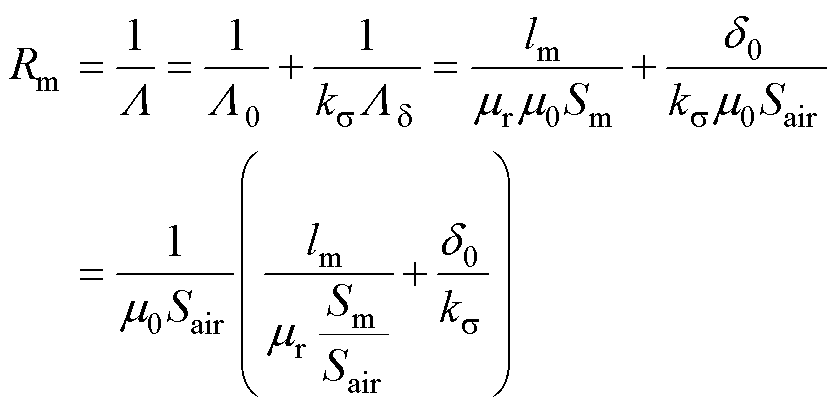 (18)
(18)
式中,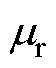 为永磁体相对磁导率;Sm、Sair分别为磁路中永磁体部分和空气部分的截面积;lm为磁路中永磁体部分的长度。
为永磁体相对磁导率;Sm、Sair分别为磁路中永磁体部分和空气部分的截面积;lm为磁路中永磁体部分的长度。
每一角度微元等效磁路中永磁体部分的磁动势源和内磁导都为圆环状永磁转子的一半,故lm一般取永磁转子平均磁化方向长度hMp的1/2,计算得
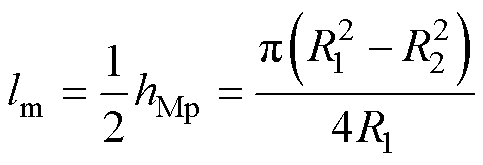 (19)
(19)
式中,R2和R1分别为圆环状永磁转子的内、外半径。
因此,模型推导过程中的绝对气隙长度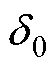 应修正为等效气隙长度
应修正为等效气隙长度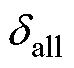 (总磁路长度),其表达式为
(总磁路长度),其表达式为
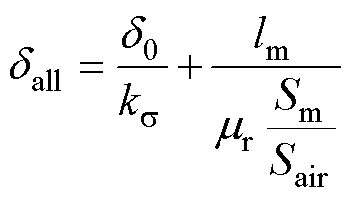 (20)
(20)
以上分析为仅有永磁体磁场作用的情况,当转矩或悬浮绕组通入电流建立起磁场时,采用相同的分析思路进行探究可得:转矩绕组磁场因与永磁体磁场极对数一致都为1,对应总磁路长度也为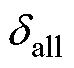 ;而悬浮绕组磁场的极对数为2,每一角度微元下等效磁路在永磁体中的路径长度大致为永磁体磁场情况下的一半,相应总磁路长度记为
;而悬浮绕组磁场的极对数为2,每一角度微元下等效磁路在永磁体中的路径长度大致为永磁体磁场情况下的一半,相应总磁路长度记为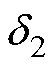 ,其表达式为
,其表达式为
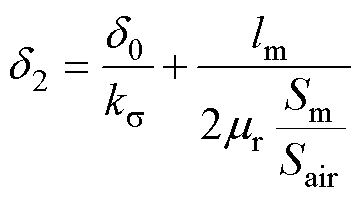 (21)
(21)
由式(20)、式(21)可知,绝对气隙长度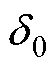 仅为等效气隙长度中的一部分,所表征的是转子最大可偏心距离;极对数不同的磁场所对应的等效气隙长度不一致。基于以上两点,1.1节一般径向悬浮力模型中气隙长度部分是不准确的,实际等效气隙长度可达绝对气隙长度
仅为等效气隙长度中的一部分,所表征的是转子最大可偏心距离;极对数不同的磁场所对应的等效气隙长度不一致。基于以上两点,1.1节一般径向悬浮力模型中气隙长度部分是不准确的,实际等效气隙长度可达绝对气隙长度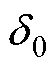 的几倍,所引起径向悬浮力相对误差很大,必须予以修正。
的几倍,所引起径向悬浮力相对误差很大,必须予以修正。
综上,由于磁导函数近似、径向悬浮力忽略项以及等效气隙区别于绝对气隙,一般径向悬浮力模型存在误差。经过分析可得出以下结论:
(1)磁导函数近似所引起的径向悬浮力误差与偏心系数呈正相关。
(2)径向悬浮力忽略项对模型准确度影响较小。
(3)等效气隙长度修正是建立准确径向悬浮力模型的必要条件。
针对第2节所分析的一般径向悬浮力模型误差,本节提出一种基于频域拟合的模型重构方法,主要包含以下环节:偏心系数及相关物理量修正、构造函数进行频域拟合、重构模型计算化简。最后,在对所建立模型进行特性分析的基础上,构建出无轴承永磁薄片电机径向悬浮力控制模型。
根据2.3节分析,极对数不相同磁场的等效气隙长度不一致:永磁体磁场及转矩绕组磁场的等效气隙长度由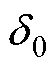 修正为
修正为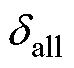 ;悬浮绕组磁场的等效气隙长度由
;悬浮绕组磁场的等效气隙长度由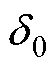 修正为
修正为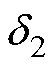 。在等效气隙修正后,式(2)所定义偏心系数不再适用。由于永磁体、转矩绕组及悬浮绕组三者所产生磁场分布随转子偏心位移的变化规律在本文中认为一致,故将偏心系数统一修正为
。在等效气隙修正后,式(2)所定义偏心系数不再适用。由于永磁体、转矩绕组及悬浮绕组三者所产生磁场分布随转子偏心位移的变化规律在本文中认为一致,故将偏心系数统一修正为
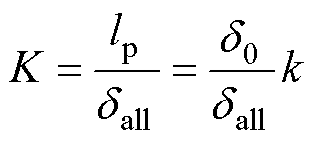 (22)
(22)
此外,转子不偏心时气隙磁通密度基波幅值B1fm、B2m随着等效气隙长度的变化也会发生相应改变,修正后表达式为
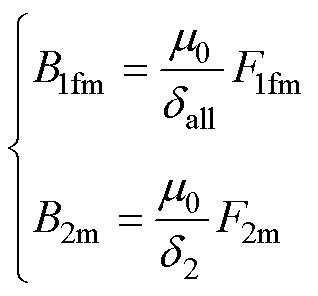 (23)
(23)
后文将统一采用如上修正后结果。
接下来对磁导函数近似所引起的模型误差进行补偿。以Fx为例,其计算式(9)可以写为
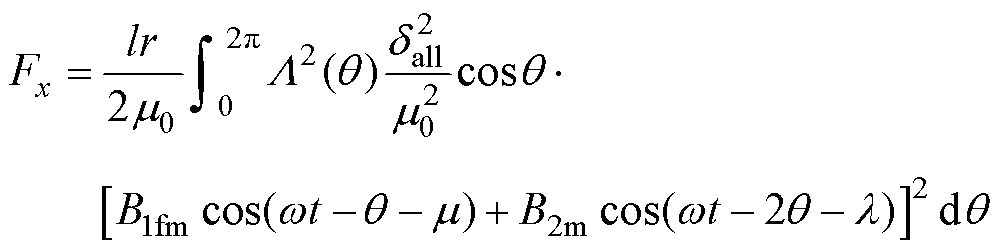 (24)
(24)
由式(24)计算过程可知,在一般径向悬浮力模型基础上将磁导函数由式(4)向式(3)进行补偿(由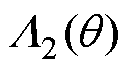 至
至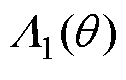 )有两个选择:磁导函数本身或它的二次方项。前者因补偿项会参与后续二次方计算增加表达式阶次,最终结果会更复杂;而后者是在磁导函数以二次方计算后引入补偿项,最终结果会更简单。为简化计算的复杂度,同时便于后续相关结论的证明,本文选择对磁导函数二次方项进行补偿,将常数项提出并构造差值函数
)有两个选择:磁导函数本身或它的二次方项。前者因补偿项会参与后续二次方计算增加表达式阶次,最终结果会更复杂;而后者是在磁导函数以二次方计算后引入补偿项,最终结果会更简单。为简化计算的复杂度,同时便于后续相关结论的证明,本文选择对磁导函数二次方项进行补偿,将常数项提出并构造差值函数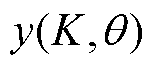 为
为
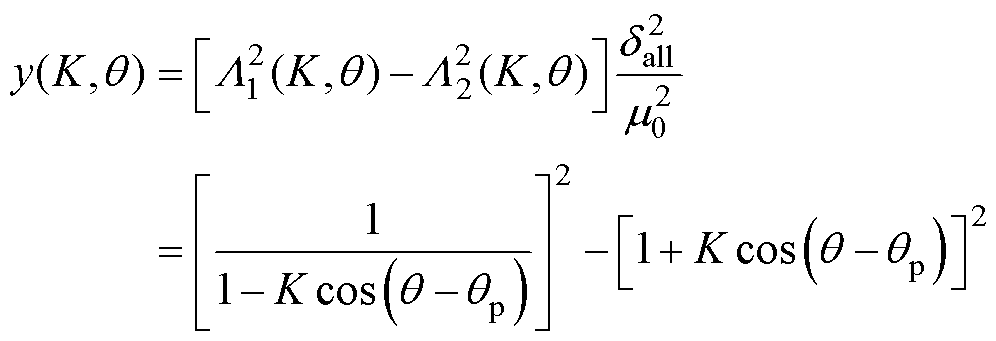 (25)
(25)
本文拟通过傅里叶变换将所构造差值函数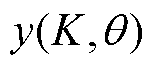 进行频域展开,并选取频域展开式中的前几项构成函数yfft去近似拟合复杂函数
进行频域展开,并选取频域展开式中的前几项构成函数yfft去近似拟合复杂函数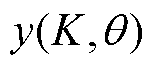 。下面进行具体说明,
。下面进行具体说明,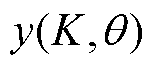 频域展开可得
频域展开可得
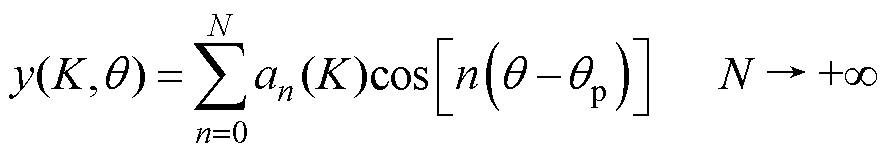 (26)
(26)
式中,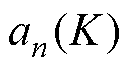 为差值函数
为差值函数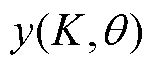 傅里叶分解展开式中各次谐波项的系数,大小只与偏心系数K唯一相关。
傅里叶分解展开式中各次谐波项的系数,大小只与偏心系数K唯一相关。
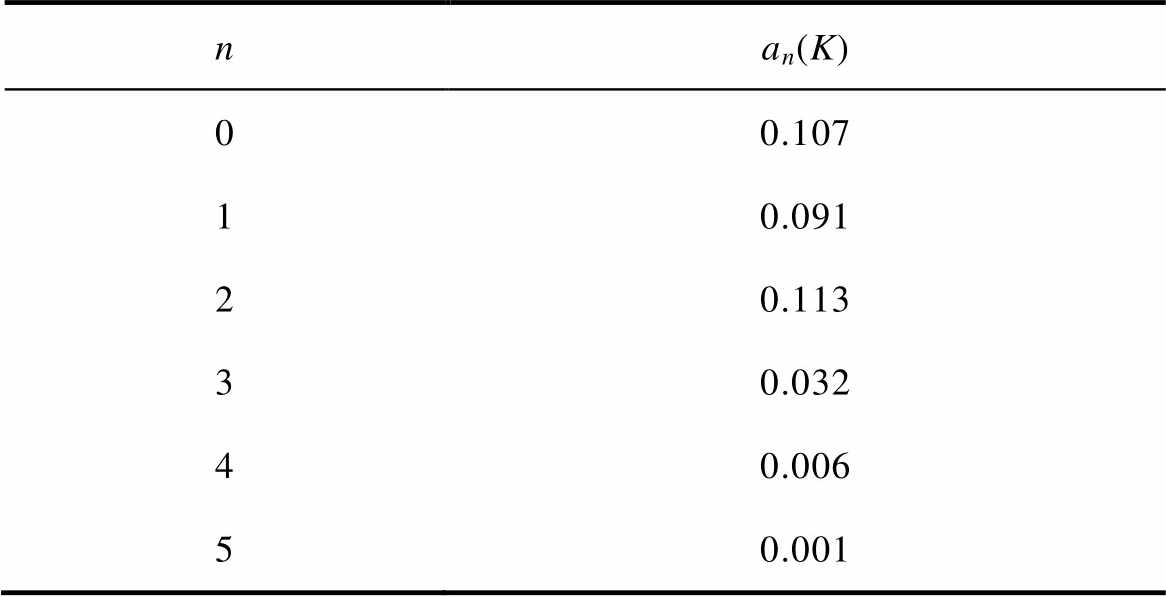
理论上,式(26)可以展开成无穷多项,将K=0.3时谐波项的系数整理见表1,可以发现,当谐波次数增大到一定程度时,其系数会急剧减小。
表1 K=0.3时谐波项系数
Tab.1 Harmonic coefficient when K=0.3
nan(K) 00.107 10.091 20.113 30.032 40.006 50.001
因此,本文选取频域展开式(26)中常数项至5次谐波项的和作为拟合函数yfft,有
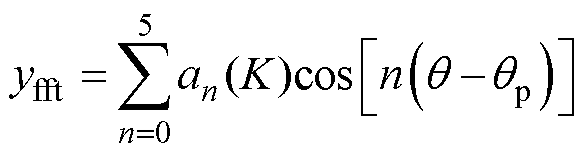 (27)
(27)
图7为K=0.3,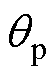 =0时yfft拟合
=0时yfft拟合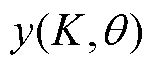 的示意图,上半部分是yfft和
的示意图,上半部分是yfft和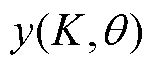 的函数值,下半部分是它们二者的差值,由图可知,yfft能够较好地还原
的函数值,下半部分是它们二者的差值,由图可知,yfft能够较好地还原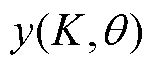 。
。
综上所述,本小节构造了差值函数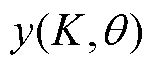 (见式(25)),并用频域展开函数yfft(见式(27))进行拟合。
(见式(25)),并用频域展开函数yfft(见式(27))进行拟合。
在频域拟合的基础上进行径向悬浮力模型重构,把yfft补偿至式(24)中可得
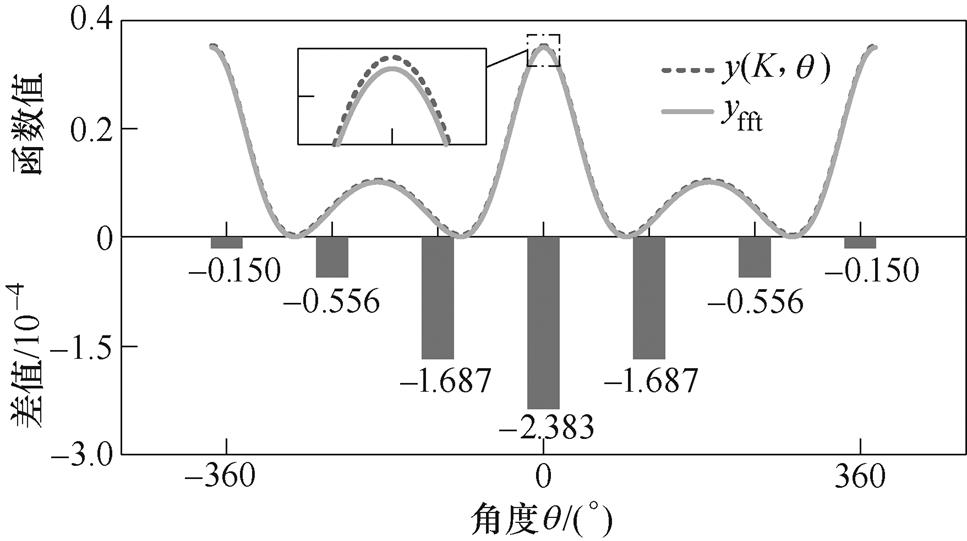
图7 频域拟合示意图
Fig.7 Diagram of frequency domain fitting
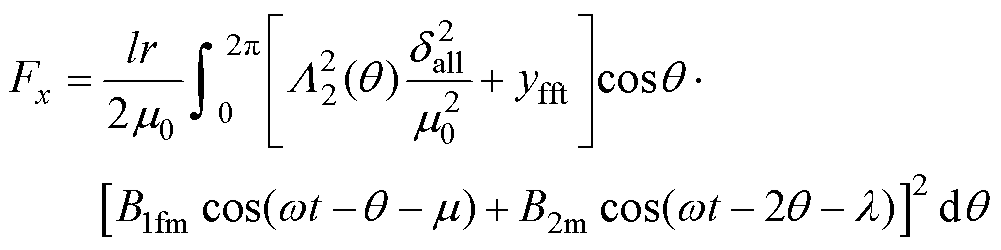 (28)
(28)
将式(28)进行展开,其中仅关注径向悬浮力直流分量,二倍频脉动分量予以忽略可得
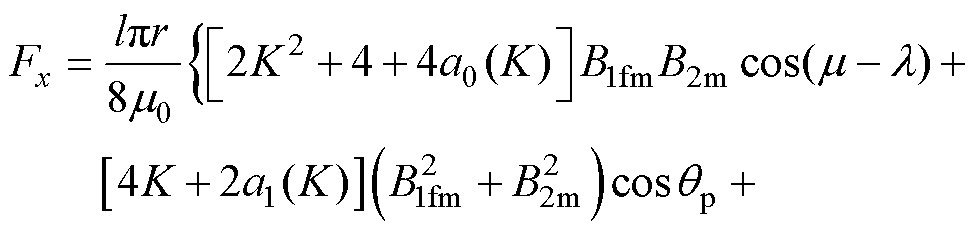
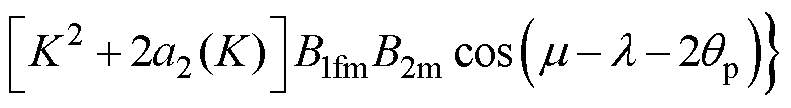 (29)
(29)
同理,y方向径向悬浮力重构模型整理得
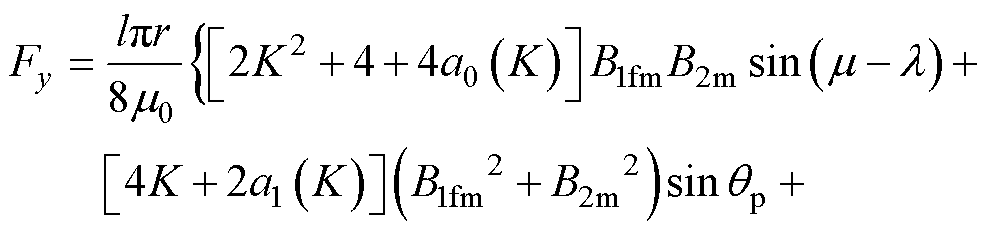
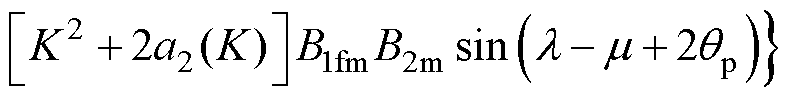 (30)
(30)
下面对拟合函数yfft所包含项数与模型准确度的关系进行探究。联合式(26)与式(28)可知,原磁导函数与拟合函数各谐波项在后续积分计算中相互独立,由和的积分可分立成各项的积分再求和,因此可采用如下一般形式来研究各谐波项对总径向悬浮力的影响,计算公式为
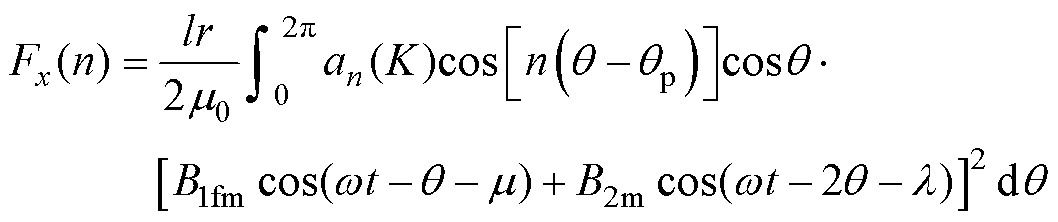 (31)
(31)
将式(31)积分展开并利用三角函数的周期性进行化简整理得
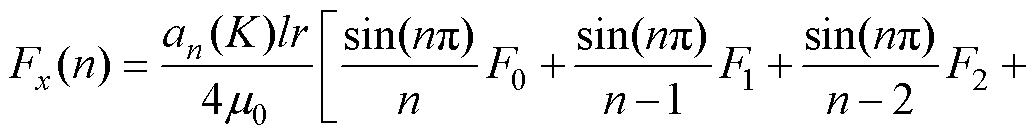
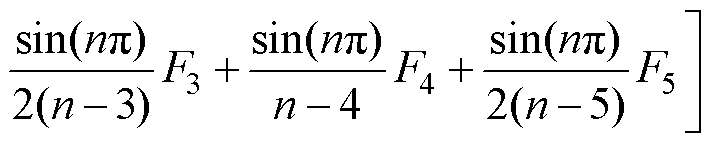 (32)
(32)
式中,F0~F5为关于B1fm、B2m或它们二者的多项式,形式固定而不影响计算。
式(32)为式(31)的等价积分展开式,代入不同n值可对应求得n次谐波项径向悬浮力计算值Fx(n)。分析该式可知:当且仅当自然数n=0、1、2、3、4或5时,式中某一项为“0/0”型可用洛必达法则进行求解,其余项为0。例如,当n=5时可得
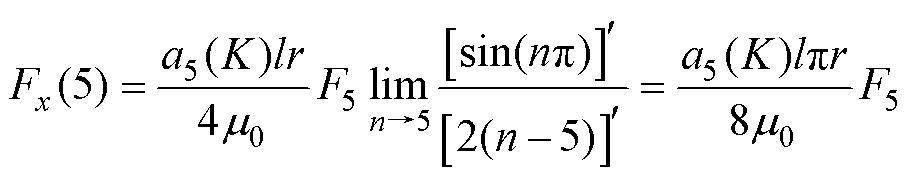 (33)
(33)
当n>5时,Fx(n)中每一项分子为0而分母不为0,故Fx(n)=0。因此,无论yfft中谐波次数大于5的项取多少项,它们在径向悬浮力计算公式中所对应的Fx(n)都为0,即对总径向悬浮力不起作用。分析Fy亦可得相同结论。
因此,取yfft如式(27)所示,在形式简洁的同时涵盖了所有可能形式,从最终结果上而言实现了对差值函数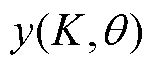 的完美拟合。
的完美拟合。
对重构径向悬浮力模型进行特性分析,以Fx为例,式(29)可以拆写为
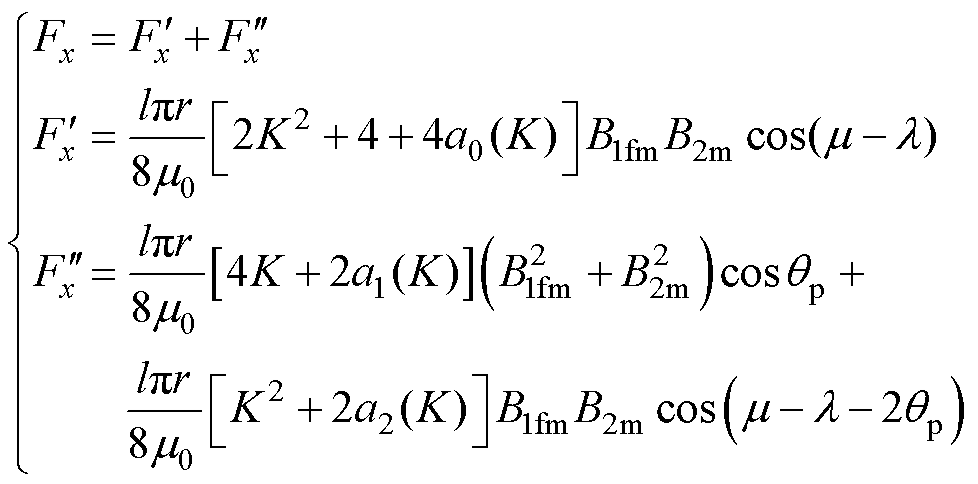 (34)
(34)
式中,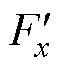 、
、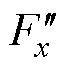 分别为Fx的可控、不可控分量。
分别为Fx的可控、不可控分量。
分析上述模型可得:
(1)x方向径向悬浮力Fx可以分解成可控径向悬浮力分量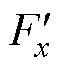 和不可控径向悬浮力分量
和不可控径向悬浮力分量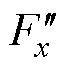 两部分。
两部分。
(2)可控径向悬浮力分量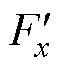 和永磁体与转矩绕组合成气隙磁通密度、悬浮绕组气隙磁通密度以及
和永磁体与转矩绕组合成气隙磁通密度、悬浮绕组气隙磁通密度以及
它们之间夹角的余弦值成正比。虽然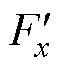 中有与偏心系数K相关部分而呈现一定非线性特性,但以本文样机为例,根据后续4.1节图11的具体数据分析,线性分量仍占绝大部分(约99.2%),从控制而言基
中有与偏心系数K相关部分而呈现一定非线性特性,但以本文样机为例,根据后续4.1节图11的具体数据分析,线性分量仍占绝大部分(约99.2%),从控制而言基
本无影响;且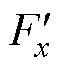 的方向与偏心角度
的方向与偏心角度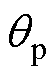 无关,可进行坐标变换。因此,
无关,可进行坐标变换。因此,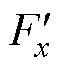 能够以绕组中通入不同幅值相
能够以绕组中通入不同幅值相
位电流的方式实现人为可控性。
(3)不可控径向悬浮力分量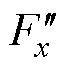 本质为转子偏心所引起的偏心磁拉力,当转子完全处于中心时,该项分量为0。不可控径向悬浮力的大小与转子偏心系数K存在非线性关系,且x、y方向上的偏心磁拉力分量相互耦合,不能实现人为可控性。
本质为转子偏心所引起的偏心磁拉力,当转子完全处于中心时,该项分量为0。不可控径向悬浮力的大小与转子偏心系数K存在非线性关系,且x、y方向上的偏心磁拉力分量相互耦合,不能实现人为可控性。
同理,y方向径向悬浮力Fy也可进行相同分解,模型特性与Fx一致,有
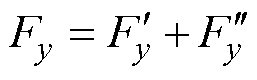 (35)
(35)
式中,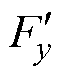 、
、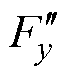 分别为Fy的可控、不可控分量。
分别为Fy的可控、不可控分量。
可控径向悬浮力控制的实现是无轴承电机数字控制系统的关键。将式(34)、式(35)中可控径向悬浮力分量改写为以电流、磁链为自变量的形式为
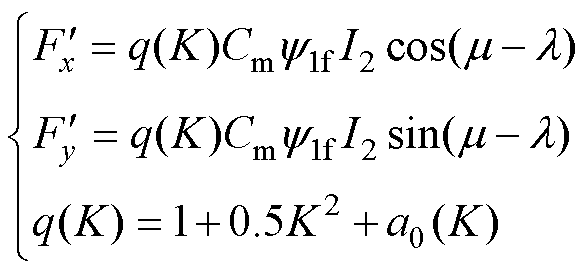 (36)
(36)
其中
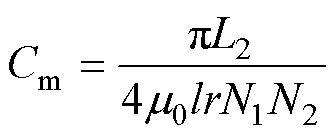
式中,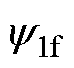 为转矩绕组、永磁体合成磁链;I2为悬浮绕组电流;q(K)为可控径向悬浮力系数项中有关偏心系数K的部分,其值由K唯一确定。q(K)与1的偏差和偏心系数K正相关。
为转矩绕组、永磁体合成磁链;I2为悬浮绕组电流;q(K)为可控径向悬浮力系数项中有关偏心系数K的部分,其值由K唯一确定。q(K)与1的偏差和偏心系数K正相关。
为与电机控制系统中采用同步旋转坐标系的分析习惯相统一,式(36)经坐标变换可得
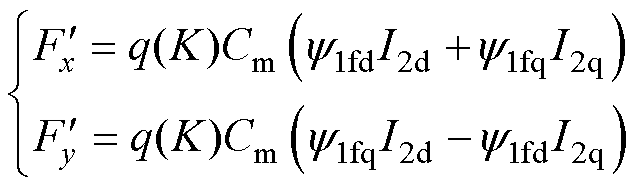 (37)
(37)
式中,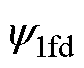 、
、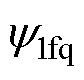 分别为
分别为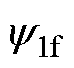 的直轴和交轴分量;I2d、I2q分别为I2的直轴和交轴分量。
的直轴和交轴分量;I2d、I2q分别为I2的直轴和交轴分量。
若转矩系统采用id=0的控制方式,则有
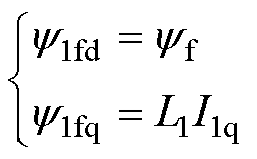 (38)
(38)
式中,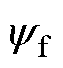 为永磁体磁链;L1为转矩绕组电感;I1q为转矩绕组电流交轴分量。
为永磁体磁链;L1为转矩绕组电感;I1q为转矩绕组电流交轴分量。
将式(38)代入式(37),并写成矩阵形式,最终得可控径向悬浮力控制模型为
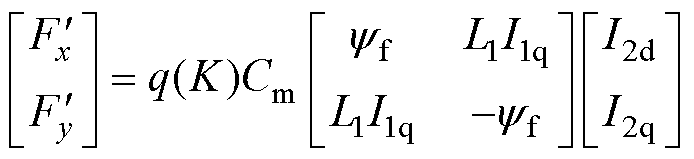 (39)
(39)
综上,本节采用频域拟合方式所建立的重构模型完美消除了第2节所分析的模型误差,与实际磁导函数下的径向悬浮力模型完全等效。
本文运用有限元法对p1=1、p2=2的无轴承永磁薄片电机的径向悬浮力进行仿真分析,并将仿真结果与所建立解析模型的计算值进行对比,从而验证本文所提出的基于频域拟合的径向悬浮力精确建模方法的正确性与有效性。无轴承永磁薄片电机样机参数见表2。
表2 无轴承永磁薄片电机样机参数
Tab.2 The parameters of bearingless permanent magnet motor prototype
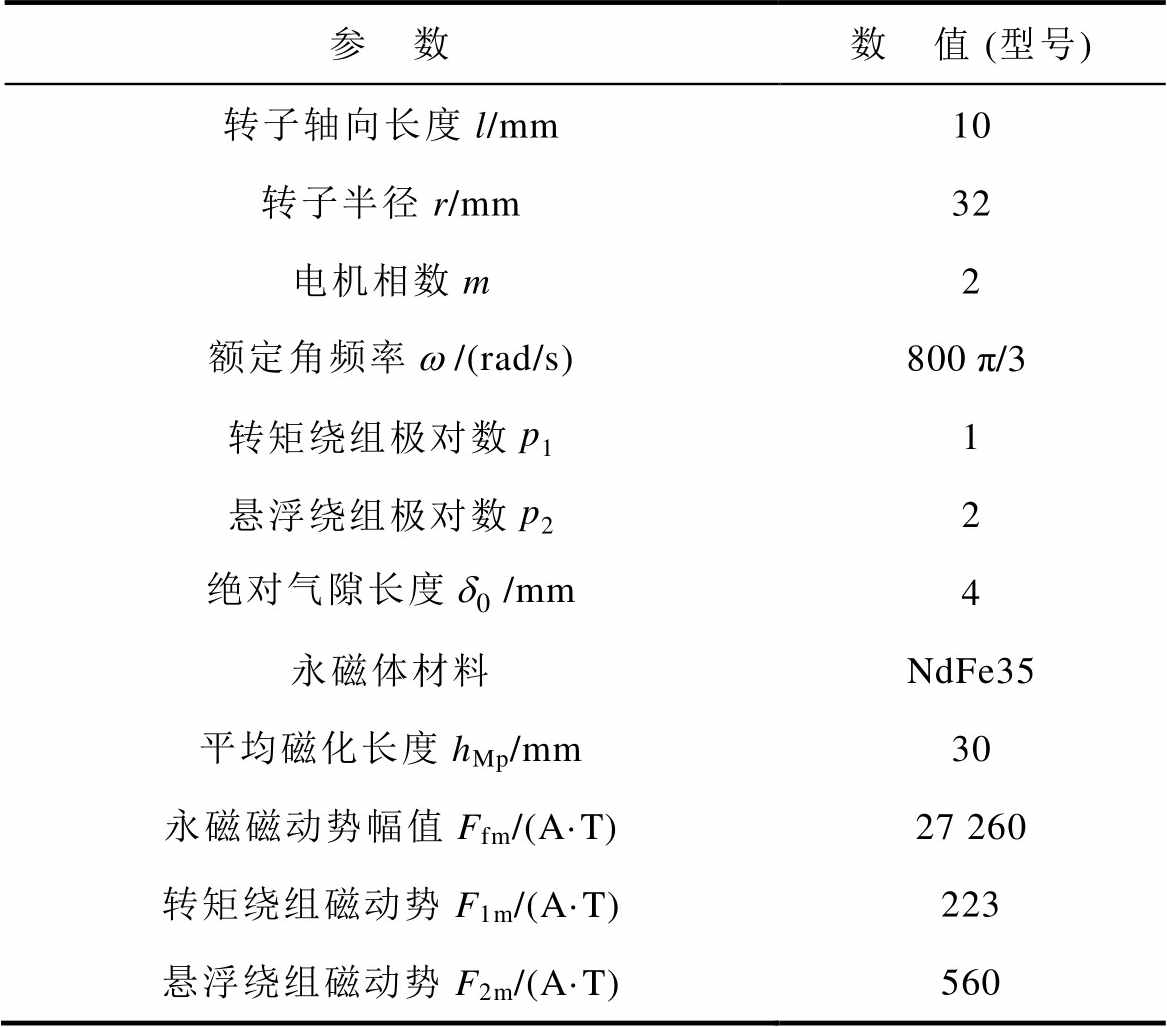
参 数数 值 (型号) 转子轴向长度l/mm10 转子半径r/mm32 电机相数m2 额定角频率/(rad/s)800 转矩绕组极对数p11 悬浮绕组极对数p22 绝对气隙长度/mm4 永磁体材料NdFe35 平均磁化长度hMp/mm30 永磁磁动势幅值Ffm/(A·T)27 260 转矩绕组磁动势F1m/(A·T)223 悬浮绕组磁动势F2m/(A·T)560
根据表2样机参数建立有限元仿真模型如图8所示。
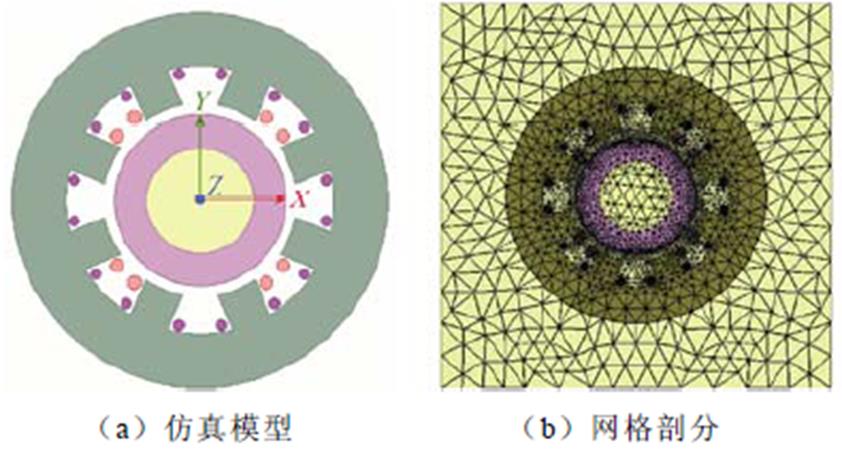
图8 有限元分析模型
Fig.8 Finite element analytical model
设定永磁体转子位于中心,此时径向悬浮力中仅含可控径向悬浮力分量,给定I1=5A、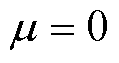 ,可控径向悬浮力x轴分量
,可控径向悬浮力x轴分量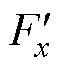 、y轴分量
、y轴分量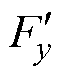 随悬浮绕组电流幅值I2、初相位
随悬浮绕组电流幅值I2、初相位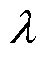 变化而相应变化。图9、图10分别为悬浮力模型计算结果与有限元仿真结果随
变化而相应变化。图9、图10分别为悬浮力模型计算结果与有限元仿真结果随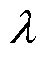 、I2的变化曲线。可以得出,
、I2的变化曲线。可以得出,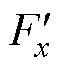 、
、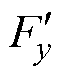 的解析模型计算值和有限元仿真结果基本一致。其中,
的解析模型计算值和有限元仿真结果基本一致。其中,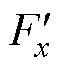 和
和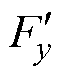 随
随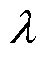 变化呈正余弦分布。在转子不发生偏心情况下,可控径向悬浮力最大值与悬浮绕组电流幅值I2呈线性关系,当I2较大时由于磁饱和,模型计算结果与有限元仿真结果略有偏差。
变化呈正余弦分布。在转子不发生偏心情况下,可控径向悬浮力最大值与悬浮绕组电流幅值I2呈线性关系,当I2较大时由于磁饱和,模型计算结果与有限元仿真结果略有偏差。
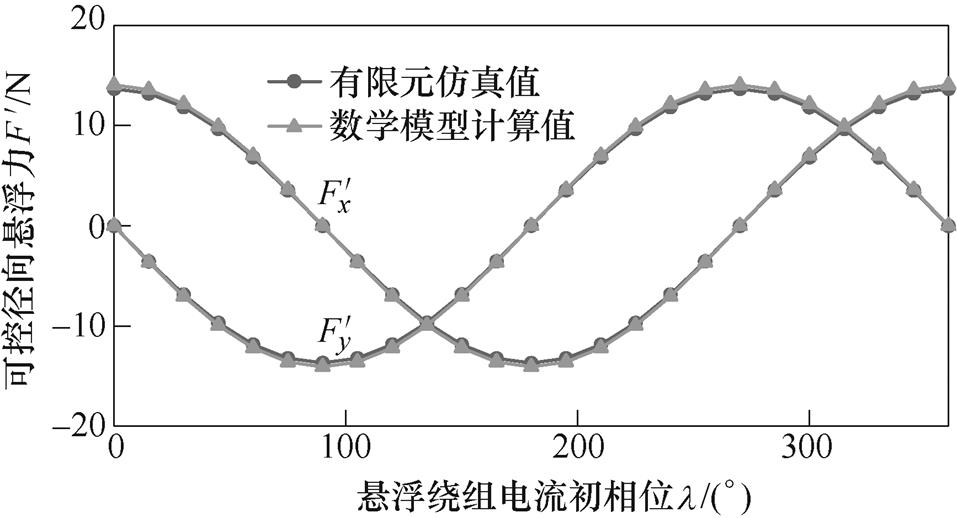
图9 I2=5A时可控径向悬浮力随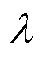 变化曲线
变化曲线
Fig.9 Changing curves of controllable radial suspension force with 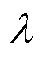 when I2=5A
when I2=5A
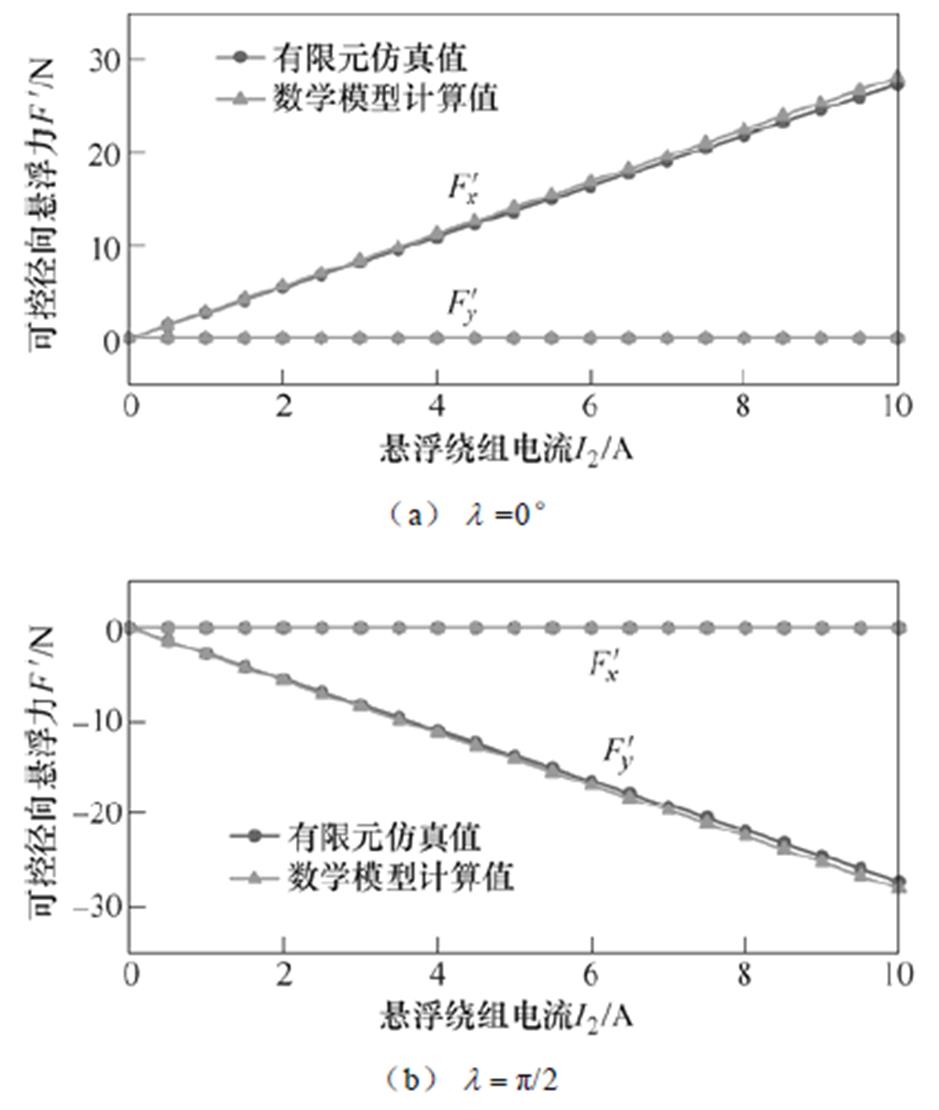
图10 不同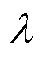 时可控径向悬浮力随I2变化曲线
时可控径向悬浮力随I2变化曲线
Fig.10 Changing curves of controllable radial suspension force with I2under different 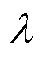
下面对转子偏心时的可控径向悬浮力进行仿真分析,给定转矩绕组电流I1=5A,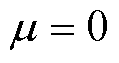 ,悬浮绕组电流I2=5A、
,悬浮绕组电流I2=5A、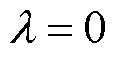 ,永磁转子从中心处沿y轴正方向偏移(
,永磁转子从中心处沿y轴正方向偏移(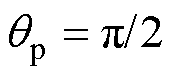 ),此时x轴方向只含可控径向悬浮力(在确定偏心角度下3.4节所定义的不可控径向悬浮力第二项也视为可控径向悬浮力)。在不同转子偏心距离下,将x轴方向可控径向悬浮力
),此时x轴方向只含可控径向悬浮力(在确定偏心角度下3.4节所定义的不可控径向悬浮力第二项也视为可控径向悬浮力)。在不同转子偏心距离下,将x轴方向可控径向悬浮力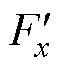 的模型计算值和有限元仿真值整理成曲线如图11所示,上半部分是总值,下半部分是减去固定线性部分所得的非线性值。可以得出,解析模型计算值与有限元仿真值具有相同变化规律,二者曲线大致吻合。其中,有限元仿真值因磁饱和会略小于模型计算值,因仿真时读取一段周期内平均值,个别仿真结果也会有出入。随着y轴方向偏心距离增加,x轴方向可控径向悬浮力非线性部分会从0开始增加,呈非线性趋势,这说明x、y方向径向悬浮力相互耦合。但于可控径向悬浮力总值而言,非线性部分所占比例非常小(不到1%),因此在整个坐标范围内可控径向悬浮力的曲线基本保持原形,所呈现出的非线性很小。
的模型计算值和有限元仿真值整理成曲线如图11所示,上半部分是总值,下半部分是减去固定线性部分所得的非线性值。可以得出,解析模型计算值与有限元仿真值具有相同变化规律,二者曲线大致吻合。其中,有限元仿真值因磁饱和会略小于模型计算值,因仿真时读取一段周期内平均值,个别仿真结果也会有出入。随着y轴方向偏心距离增加,x轴方向可控径向悬浮力非线性部分会从0开始增加,呈非线性趋势,这说明x、y方向径向悬浮力相互耦合。但于可控径向悬浮力总值而言,非线性部分所占比例非常小(不到1%),因此在整个坐标范围内可控径向悬浮力的曲线基本保持原形,所呈现出的非线性很小。
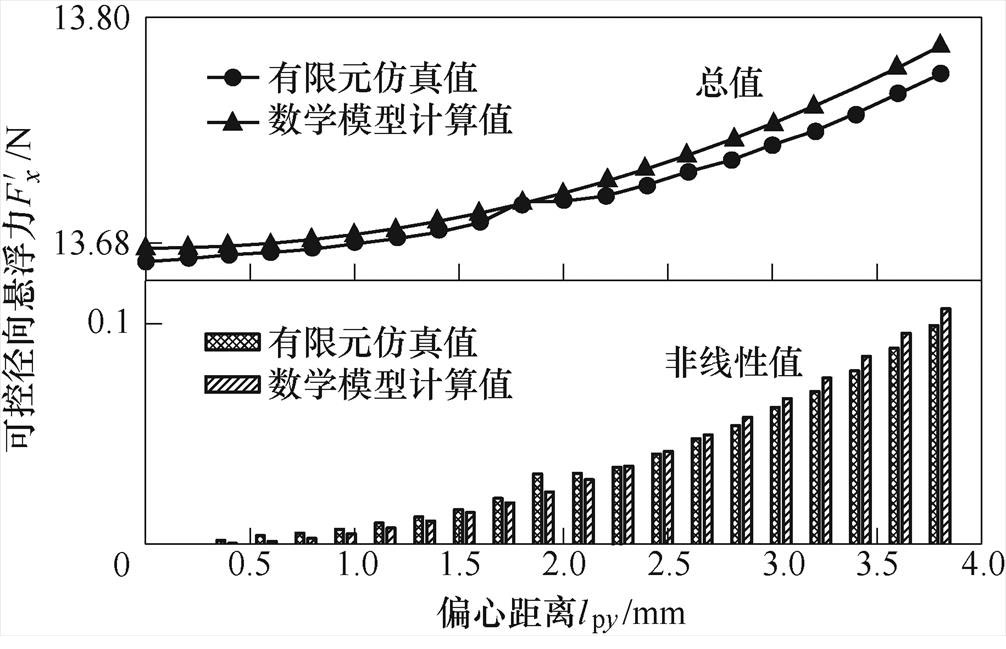
图11 x轴可控径向悬浮力随偏心距离的变化曲线
Fig.11 Changing curves of x-axis controllable radial suspension force with eccentric distance
设定悬浮绕组电流I2=0A、转矩绕组电流I1= 5A,永磁转子从中心处沿x轴正方向偏移,此时径向悬浮力中仅含转子偏心所引起的偏心磁拉力分量。在不同转子偏心距离下,将不可控径向悬浮力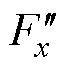 、
、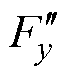 的模型计算值和有限元仿真值整理并绘制成曲线进行比较,如图12所示。由图可以得出,解析模型计算结果与有限元仿真结果偏差很小,二者曲线基本吻合且具有相同变化规律。在lpx较小时,x轴不可控径向悬浮力分量
的模型计算值和有限元仿真值整理并绘制成曲线进行比较,如图12所示。由图可以得出,解析模型计算结果与有限元仿真结果偏差很小,二者曲线基本吻合且具有相同变化规律。在lpx较小时,x轴不可控径向悬浮力分量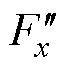 呈线性,但当lpx增大至约2.7mm时,
呈线性,但当lpx增大至约2.7mm时,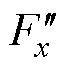 曲线开始略微上扬呈现出非线性趋势,且随着lpx增大曲线非线性程度也逐渐增大;在lpx变化时,y轴不可控径向悬浮力分量
曲线开始略微上扬呈现出非线性趋势,且随着lpx增大曲线非线性程度也逐渐增大;在lpx变化时,y轴不可控径向悬浮力分量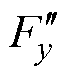 一直保持为0。本文以转子沿x轴正方向偏移为例,当转子从圆心沿其他方向偏移时,也可得到相同分析结果。
一直保持为0。本文以转子沿x轴正方向偏移为例,当转子从圆心沿其他方向偏移时,也可得到相同分析结果。
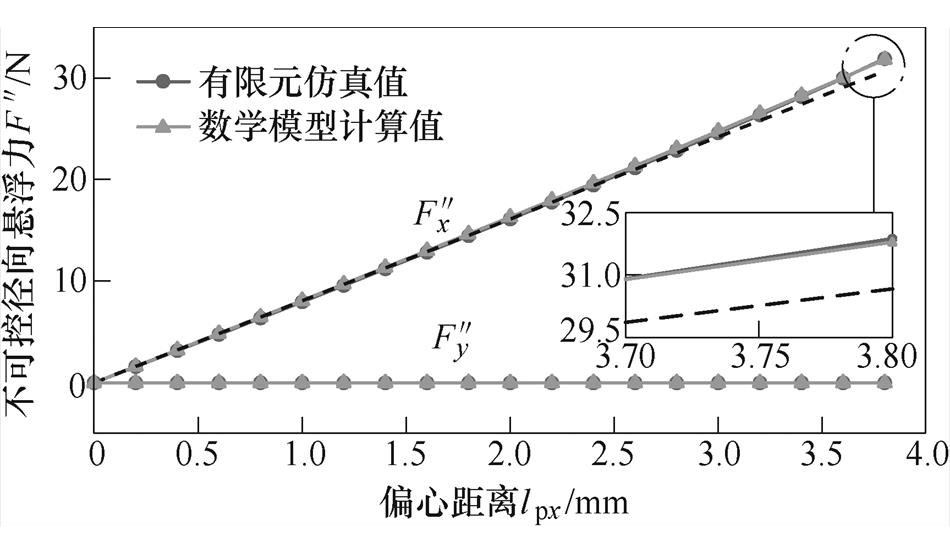
图12 不可控径向悬浮力随偏心距离的变化曲线
Fig.12 Changing curves of uncontrollable radial suspension force with eccentric distance
图12中永磁转子的最大偏心距离不会超过样机绝对气隙长度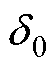 =4mm,
=4mm,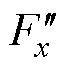 曲线非线性程度并不明显。保持永磁转子大小不变而扩大
曲线非线性程度并不明显。保持永磁转子大小不变而扩大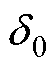 ,绘制出
,绘制出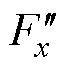 变化曲线如图13所示,同时在图中绘制出仅修正等效气隙长度下一般径向悬浮力的模型计算值曲线。由图13可知,若仅修正等效气隙长度,模型计算值曲线完全呈线性,在偏心距离较小时和有限元仿真结果较好吻合,但随着偏心距离增大二者曲线逐渐偏离;若采用本文方法进行模型重构,在整个偏心距离范围内模型计算值和有限元仿真结果都具有很好吻合度,呈现出一致的非线性特性。图13中的非线性误差本质为转子偏心所引起的实际磁导函数与简化磁导函数的差值在不可控径向悬浮力中的最终体现。根据2.1节分析,磁导函数绝对误差与偏心系数K呈正相关,因此不可控径向悬浮力非线性误差也具有相同变化规律,即转子可偏心范围越大非线性误差数值范围也就越大。
变化曲线如图13所示,同时在图中绘制出仅修正等效气隙长度下一般径向悬浮力的模型计算值曲线。由图13可知,若仅修正等效气隙长度,模型计算值曲线完全呈线性,在偏心距离较小时和有限元仿真结果较好吻合,但随着偏心距离增大二者曲线逐渐偏离;若采用本文方法进行模型重构,在整个偏心距离范围内模型计算值和有限元仿真结果都具有很好吻合度,呈现出一致的非线性特性。图13中的非线性误差本质为转子偏心所引起的实际磁导函数与简化磁导函数的差值在不可控径向悬浮力中的最终体现。根据2.1节分析,磁导函数绝对误差与偏心系数K呈正相关,因此不可控径向悬浮力非线性误差也具有相同变化规律,即转子可偏心范围越大非线性误差数值范围也就越大。
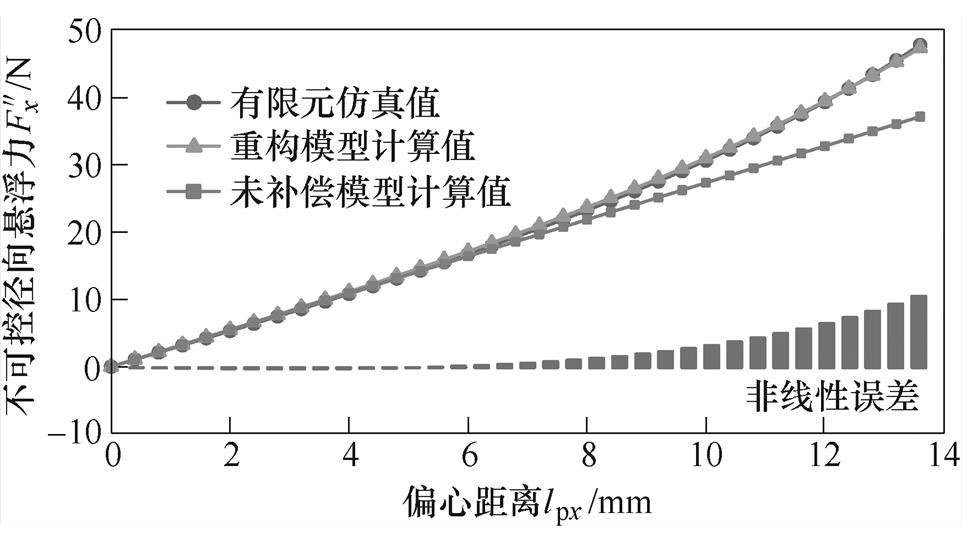
图13 扩大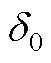 下
下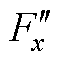 随偏心距离的变化曲线
随偏心距离的变化曲线
Fig.13 Changing curves of 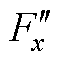 with eccentric distance when extending
with eccentric distance when extending 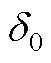
在一般无轴承永磁薄片电机设计时,鉴于较大的径向悬浮力非线性会带来控制难题,绝对气隙长度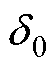 应选取合适值,图13为此提供了很好的设计参考,即转子可偏心范围应限制在图中线性区间内。此外,由于使转子回到圆心所需通入悬浮绕组电流的幅值和转子偏心位移大小呈正相关,在确定
应选取合适值,图13为此提供了很好的设计参考,即转子可偏心范围应限制在图中线性区间内。此外,由于使转子回到圆心所需通入悬浮绕组电流的幅值和转子偏心位移大小呈正相关,在确定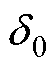 下电机功率限制会进一步压缩转子可偏心范围。以本文样机
下电机功率限制会进一步压缩转子可偏心范围。以本文样机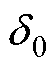 =4mm为例,绘制x轴方向总径向悬浮力Fx关于悬浮绕组电流I2和偏心位移lpx的三维图像如图14所示,相关参数设置为:I1=5A、
=4mm为例,绘制x轴方向总径向悬浮力Fx关于悬浮绕组电流I2和偏心位移lpx的三维图像如图14所示,相关参数设置为:I1=5A、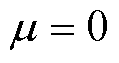 、
、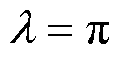 。
。
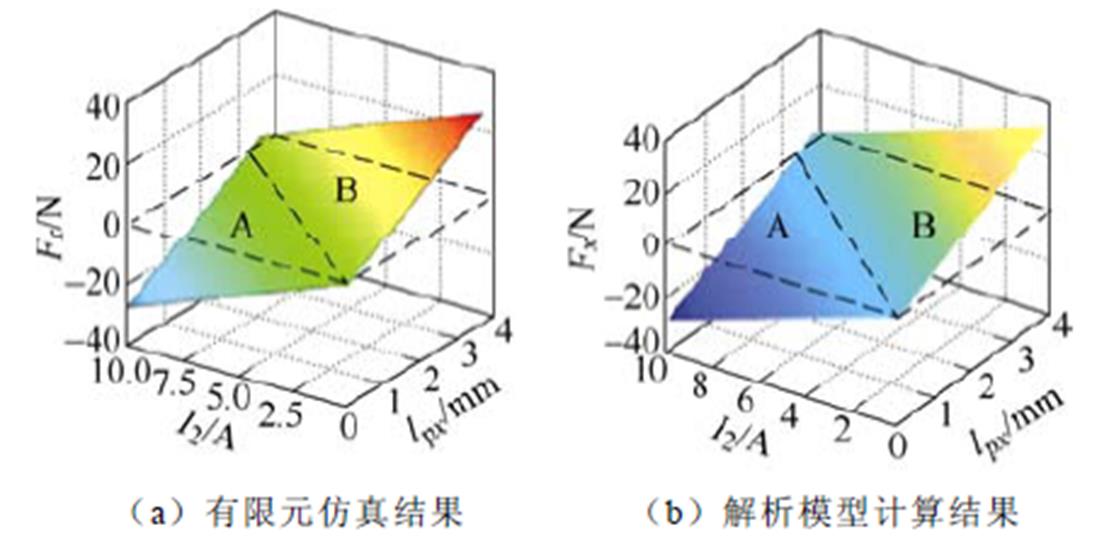
图14 总径向悬浮力Fx三维图像
Fig.14 Three-dimensional diagram of Fx
由图14可知,有限元仿真结果和解析模型计算结果几乎完全一致。图中虚线为Fx三维曲面与Fx=0平面的交线,此时可控径向悬浮力与偏心磁拉力正好相等。在功率限制(I2≤10A)情况下,图中,A区域对应样机的可控区,而在B区域就很难实现转子的稳定径向悬浮。
综上,本节通过可控径向悬浮力、不可控径向悬浮力解析模型计算值与有限元仿真值的比较分析,验证了本文所建立的基于频域拟合径向悬浮力解析模型的正确性与准确性。
针对无轴承永磁薄片电机因转子偏心位移大而引起的径向悬浮力非线性误差问题,本文提出一种基于频域拟合的径向悬浮力精确建模方法,其优势在于:
1)在一般径向悬浮力模型基础上修正了等效气隙长度,补偿了磁导函数近似误差。
2)将径向悬浮力非线性分量转化为偏心系数的函数进行补偿,提高了模型精确度,并运用有限元法进行了验证。
3)虽然对象确定,但建模方法与过程具有普遍性,尤其为转子偏心范围较大的无轴承电机的设计优化和控制手段提供了合理参考和有效依据。
参考文献
[1] Sun Xiaodong, Chen Long, Yang Zebin. Overview of bearingless permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5528-5538.
[2] 黄威, 邓智泉, 李克翔, 等. 一种磁悬浮轴承支承刚性转子现场动平衡方法[J]. 电工技术学报, 2020, 35(22): 4636-4646.
Huang Wei, Deng Zhiquan, Li Kexiang, et al. A filed dynamic balancing method for rigid rotor supported by magnetic bearings[J]. Transactions of China Elec- trotechnical Society, 2020, 35(22): 4636-4646.
[3] 胡烽, 孙宏博, 蒋栋, 等. 基于四相全桥的磁悬浮轴承开关器件开路故障容错控制策略[J]. 电工技术学报, 2022, 37(9): 2295-2305, 2340.
Hu Feng, Sun Hongbo, Jiang Dong, et al. Fault- tolerant strategy of four-phase full-leg for active magnetic bearing in case of open circuit fault of switching device[J]. Transactions of China Electro- technical Society, 2022, 37(9): 2295-2305, 2340.
[4] Bartholet M T, Nussbaumer T, Silber S, et al. Com- parative evaluation of polyphase bearingless slice motors for fluid-handling applications[J]. IEEE Transa- ctions on Industry Applications, 2009, 45(5): 1821- 1830.
[5] Pan Wei, Zhu Huangqiu, Li Hui. Design and opti- mization of bearingless permanent magnetic syn- chronous motors[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 2516908.
[6] 禹春敏, 邓智泉, 梅磊, 等. 基于精确磁路的新型混合型轴向-径向磁悬浮轴承研究[J]. 电工技术学报, 2021, 36(6): 1219-1228.
Yu Chunmin, Deng Zhiquan, Mei Lei, et al. Research of new hybrid axial-radial magnetic bearing based on accurate magnetic circuit[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1219-1228.
[7] 李志, 苏振中, 胡靖华, 等. 磁轴承复合位移传感设计与实验研究[J]. 电工技术学报, 2021, 36(7): 1425-1433.
Li Zhi, Su Zhenzhong, Hu Jinghua, et al. Design and experimental research of magnetic bearing compound displacement sensor[J]. Transactions of China Elec- trotechnical Society, 2021, 36(7): 1425-1433.
[8] 周天豪, 陈磊, 祝长生, 等. 基于自适应变步长最小均方算法的磁悬浮高速电机不平衡补偿[J]. 电工技术学报, 2020, 35(9): 1900-1911.
Zhou Tianhao, Chen Lei, Zhu Changsheng, et al. Unbalance compensation for magnetically levitated high-speed motors based on adaptive variable step size least mean square algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1900-1911.
[9] Zhang Shaoru, Luo Fanglin. Direct control of radial displacement for bearingless permanent-magnet-type synchronous motors[J]. IEEE Transactions on Indu- strial Electronics, 2009, 56(2): 542-552.
[10] 丁强, 邓智泉, 王晓琳. 无轴承交替极永磁电机集中式悬浮绕组结构及其优化设计方法[J]. 电工技术学报, 2015, 30(18): 104-111.
Ding Qiang, Deng Zhiquan, Wang Xiaolin. Structure of concentrated suspension windings and its opti- mization design methods of bearingless consequent- pole permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 104-111.
[11] 仇志坚, 邓智泉, 章跃进. 交替极永磁无轴承电机的直接悬浮力控制[J]. 电工技术学报, 2011, 26(9): 94-99.
Qiu Zhijian, Deng Zhiquan, Zhang Yuejin. Direct levitation force control of a consequent-pole per- manent magnet bearingless motor[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 94-99.
[12] Oshima M, Miyazawa S, Deido T, et al. Characteri- stics of a permanent magnet type bearingless motor[J]. IEEE Transactions on Industry Applications, 1996, 32(2): 363-370.
[13] 孙晓东, 陈龙, 杨泽斌, 等. 考虑偏心及绕组耦合的无轴承永磁同步电机建模[J]. 电工技术学报, 2013, 28(3): 63-70.
Sun Xiaodong, Chen Long, Yang Zebin, et al. Modeling of a bearingless permanent magnet syn- chronous motor considering rotor eccentricity and coupling relationship of windings[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 63-70.
[14] Zhu Huangqiu, Cheng Qiuliang, Wang Chengbo. Modeling of bearingless permanent magnet syn- chronous motor based on mechanical to electrical coordinates transformation[J]. Science in China Series E: Technological Sciences, 2009, 52(12): 3736.
[15] 左文全, 吕艳博, 付向东, 等. 无轴承永磁薄片电机径向悬浮力精确数学建模[J]. 中国电机工程学报, 2012, 32(3): 103-110, 9.
Zuo Wenquan, Lü Yanbo, Fu Xiangdong, et al. Accurate mathematical modeling of radial suspension force on bearingless permanent magnet slice motors[J]. Proceedings of the CSEE, 2012, 32(3): 103-110, 9.
[16] Ooshima M, Yamashita K, Chiba A, et al. An improved control method of buried-type IPM bearingless motors considering magnetic saturation and magnetic pull variation[C]//IEEE International Electric Machines and Drives Conference, 2003, Madison, WI, USA, 2003: 1055-1060.
[17] 李可, 孙晓东, 杨泽斌. 无轴承永磁同步电动机径向力模型[J]. 轴承, 2014(12): 10-13.
Li Ke, Sun Xiaodong, Yang Zebin. Radial force model of bearingless permanent magnet synchronous motors[J]. Bearing, 2014(12): 10-13.
[18] 孙宇新, 钱建林, 朱熀秋, 等. 基于转子偏心坐标系的无轴承永磁薄片电机径向悬浮力模型[J]. 电机与控制学报, 2016, 20(4): 10-16.
Sun Yuxin, Qian Jianlin, Zhu Huangqiu, et al. Radial suspension force model of bearingless permanent magnet slice motor based on coordinate system of rotor eccentricity[J]. Electric Machines and Control, 2016, 20(4): 10-16.
[19] 廖启新. 无轴承薄片电机基础研究[D]. 南京: 南京航空航天大学, 2009.
[20] 邓智泉, 仇志坚, 王晓琳, 等. 无轴承永磁同步电机的转子磁场定向控制研究[J]. 中国电机工程学报, 2005, 25(1): 104-108.
Deng Zhiquan, Qiu Zhijian, Wang Xiaolin, et al. Study on rotor flux orientation control of permanent magnet bearingless synchronous motors[J]. Pro- ceedings of the CSEE, 2005, 25(1): 104-108.
Abstract In bearingless permanent magnet slice motor system, it is a necessary condition for the realization of precise and stable radial suspension control of slice rotor to construct an accurate mathematical model of radial suspension force. However, structural characteristics of large air gap makes the rotor have a large eccentricity space range without bearing support, which brings nonlinear errors of controllable radial suspension force and eccentric magnetic force. To address this issue, this paper proposes a reconstruction method of radial suspension force model based on frequency domain fitting. It improves model accuracy by transforming the nonlinear components into functions of eccentricity coefficient and compensating them.
Firstly, the general radial suspension force model is derived by Maxwell stress tensor method. Factors causing model errors in the process of derivation are summarized as follows: approximation error of permeability function, radial suspension force ellipsis error and difference between equivalent air gap and absolute air gap. The following conclusions can be drawn from the systematic analysis: ① The error of radial suspension force caused by the approximation of permeability function is positively correlated with the eccentricity coefficient. ② Radial suspension force ellipsis has little effect on model accuracy. ③ The modification of equivalent air gap length is a necessary condition for establishing accurate radial suspension force model.
Secondly, the model reconstruction method based on frequency domain fitting is designed in detail. On the basis of correction of eccentricity coefficient and related physical quantity, the difference function is constructed and its frequency domain function is expanded by Fourier transform. The sum of the constant term to the fifth harmonic term in the frequency domain expansion is selected as the fitting function, and compensated to the calculation formula to solve the reconstructed model. By mathematical proof, the analytical model is equivalent to the radial suspension force model under the actual permeability function, which is divided into two parts: controllable radial suspension force and uncontrollable radial suspension force. The nonlinear component of the model is expressed mathematically by the eccentricity coefficient.
Finally, the two-dimensional finite element simulation model is constructed to verify the accuracy of the reconstructed model. The following conclusions can be put forward from the simulation analysis: ① The difference between the analytical model results and the finite element simulation results is small, and the curves of them are consistent with each other and have the same variation rule. ② The nonlinear component of the controllable radial suspension force occupies a small proportion and can be ignored approximately compared with the whole. ③ The nonlinear error of the uncontrollable radial suspension force is positively correlated with the eccentricity coefficient and the range of eccentricity of the rotor must be limited when designing the motor structure.
Keywords:Bearingless permanent magnet slice motors, radial suspension force, Maxwell stress tensor method, frequency domain fitting, finite element simulation
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.220547
国家自然科学基金(52177048)和江苏省自然科学基金(BK20201297)资助项目。
收稿日期 2022-04-11
改稿日期 2022-05-24
E-mail: wangxl@nuaa.edu.cn(通信作者)
石滕瑞 男,1998年生,硕士研究生,研究方向为无轴承永磁同步电机数学模型及控制。
E-mail: storystatham@163.com
(编辑 崔文静)