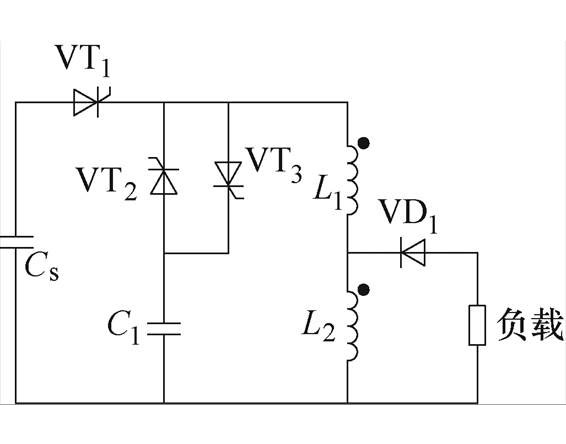
图1 Meat Grinder with SECT电路拓扑
Fig.1 Topology of Meat Grinder with SECT
摘要 由于电感储能型脉冲源单模块的能级受限,无法达到电磁发射的能量要求,需进行多模块协同工作的研究。而电感型脉冲源元件参数众多,工作过程复杂,且多模块运行中存在串扰,给系统设计带来很大的挑战。该文基于Meat Grinder with SECT电路,探究了多模块电感型脉冲源的工作过程,经过磁路和电路的等效处理之后,将多模块系统的运行简化为单模块问题。基于此,建立了详细的多模块脉冲源系统的解算方法,可以利用最底层的几何和电气参数,计算出脉冲源系统的性能指标。使用遗传算法对系统参数进行大规模优化,得到储能密度最高的多模块电感型脉冲源系统的参数,使用8个分立的脉冲源模块,并联、同步为负载放电,可以实现4.58MJ/m3的储能密度和158kA的电流输出。
关键词:电感储能型脉冲源 多模块系统 优化方法 等效电路
电磁发射是一种利用电磁能将弹丸以超高速发射的新型武器系统,由电磁发射器、高功率脉冲电源和测控系统等几部分组成[1-5]。其中,高功率脉冲电源需要为负载提供持续几毫秒的兆安级电流,且体积要尽可能小,以保证武器系统的机动性和灵活性。电感储能型脉冲源(Inductive Pulsed Power Supply, IPPS)凭借高储能密度的优势,成为极具研究价值和应用前景的脉冲电源类型[6-8]。关于电感储能型脉冲电源的研究,可大致分为拓扑设计、模块构建和系统集成三个阶段。
(1)拓扑设计阶段,根据电路结构的不同,电感储能型脉冲电源可以分为两类:一种是XRAM类电路,由W. Koch等在1967年提出[9],利用电感电流的串充并放实现功率倍增。另一类是Meat Grinder类电路,由O. Zucker等在1980年提出[10],利用磁通压缩效应实现电流倍增。经过多次改进,能够显著改善主回路换流能力的Meat Grinder with SECT成为了目前最成熟的IPPS拓扑之一[11],如图1所示,本文也将以该电路为例,进行具体分析。
(2)模块构建阶段,在国内外研究者的努力下,多种类型的电感储能型脉冲源模块已经研制成功并可以稳定输出脉冲电流[12-14],但目前所实现的储能密度距离理论上限10MJ/m3还有很远。为了进一步提高性能,需要引入大规模优化算法来辅助设计。本课题组之前的研究探究了脉冲电容参数的选取与电源性能的关系[15],给出了单个电源模块的优化设计方法[16]。

图1 Meat Grinder with SECT电路拓扑
Fig.1 Topology of Meat Grinder with SECT
(3)系统集成阶段,需考虑实际发射的能级和工作场景需求。受半导体开关性能、材料机械力和加工工艺的限制,单个电感型脉冲源模块的能级和电流输出能力无法做到很大,为了达到电磁发射的能量和电流幅值要求,在实际发射时需要多个脉冲电源模块协同工作。而电感型脉冲源电路工作过程较为复杂,电气及结构参数众多且大多数对模块性能的影响是间接且非线性的,这使得模块的设计非常困难。此外,包含多个模块的脉冲电源系统参数更多,运行过程更加复杂,这给系统设计带来了更大的挑战。
本文以Meat Grinder with SECT电路为例,研究了并联、同步放电的多模块电感储能型脉冲电源的工作原理,提出了一套适用于多模块系统的优化方法,能够在固定能级和输出电流的约束下,给出储能密度最高的电感型脉冲源系统设计方案,得到的最优解性能优异,经验证,可以实现4.58MJ/m3的储能密度和158kA的电流输出。
处于同一系统中的各个模块需要并联、同步放电,为了降低系统复杂度、方便检测检修、充分发挥各元件性能,各模块的构成和运行状态最好是完全对称的。下面首先确定系统中单个模块的电路拓扑和元件构成。
如图1所示,Meat Grinder with SECT电路构成的模块一般由一对紧密耦合的电感L1、L2,一个脉冲电容器C1,3个晶闸管VT1、VT2、VT3,一个二极管VD1和若干机械固定装置构成。图2展示了本课题组研制的脉冲源模块结构示意图。
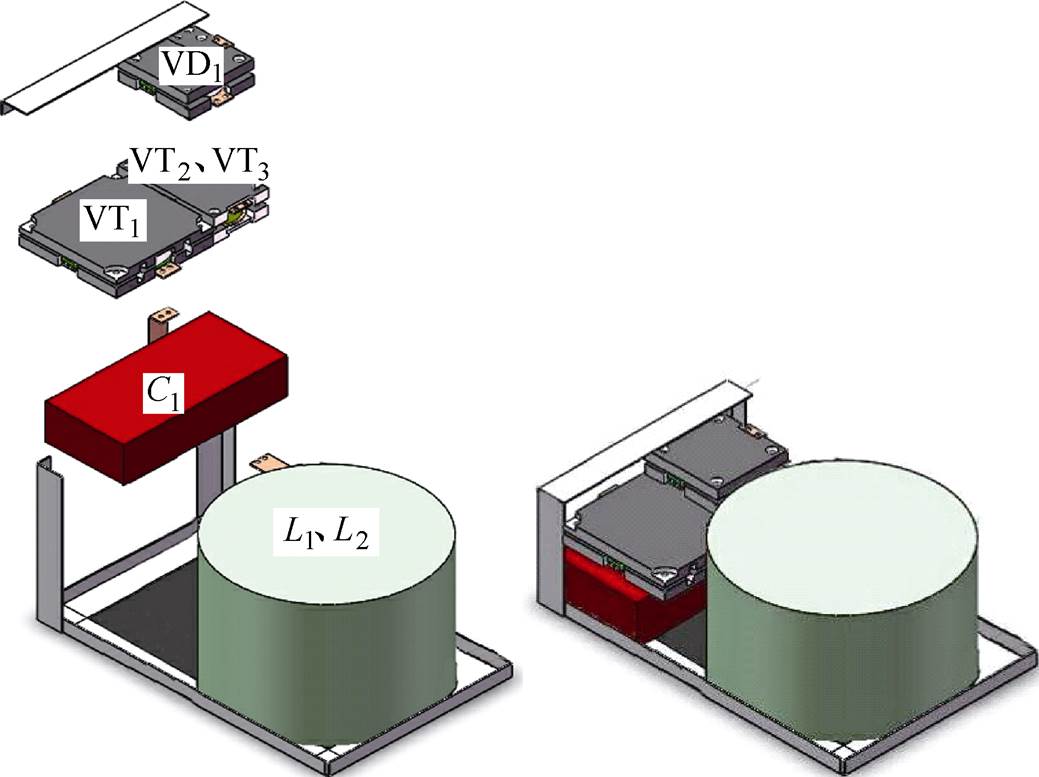
图2 脉冲源模块结构示意图
Fig.2 Structure diagram of pulsed power module
电感是模块中最复杂且最关键的元件,L1和L2在外观上是同一个器件,由一系列同轴的、内外径相等的导体饼构成,内部采用单元化设计。电感器的结构可由以下几个参数完全确定:单元数N、单元内一次侧线饼数m1、二次侧线饼数m2、一次侧线饼匝数n1、二次侧线饼匝数n2、一次侧线饼厚度h1、二次侧线饼厚度h2、线饼内径ri、线饼外径ro。此外,绝缘距离、机械固定件的尺寸等工程常数一般由经验和实际需求给出。
C1选用脉冲电容,其容值C1和最大耐压UCmax均可自由改变,体积由电容器最大能量和储能密度共同确定。
VT1、VT2和VT3都是快速晶闸管,VD1为二极管。半导体开关的最大通流和耐压是限制模块性能的主要因素,而且不同类型的半导体开关的体积和成本差别不很大,因此应尽量使用性能较好的型号。
综上所述,由m1、m2、N、n1、n2、h1、h2、ro、ri、C1、UCmax共11个参数就可以描述并确定各个元件,进而描述整个模块。
对于单模块运行的Meat Grinder with SECT电路,工作原理可以大致描述为:导通VT1,初级电源Cs为电感L1和L2串联充电;随后导通VT2,主开关VT1被带有预充电压的辅助电容C1关断,L1电流因失去通路而快速下降,其自感和互感中的磁场能量快速转移到回路L2-负载-VD1中,使其电流倍增;随后辅助电容C1上的负电压还可以通过VT3继续向负载放电。
如果多个上述电路模块要协同对负载放电,则需要将各个模块的负载端并联,多模块电感型脉冲源系统电路如图3所示。
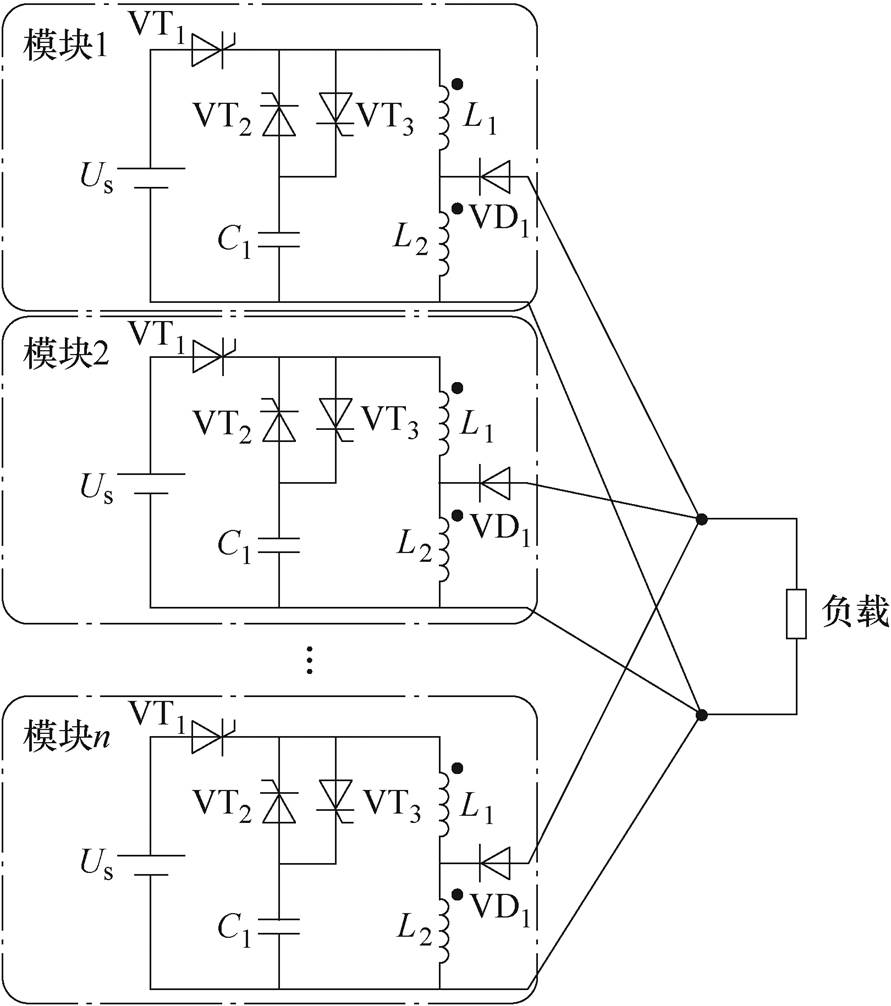
图3 多模块电感型脉冲源系统电路
Fig.3 Circuit diagram of multi-module inductive pulsed power system
在多模块系统运行时,各个模块之间会受到电路和磁路的干扰,造成不对称性出现,提高系统复杂度,下面分别进行探究。
为保证储能密度和脉冲输出效果,储能电感一般采用空芯同轴线饼的结构,这种布线方式使得线圈磁场是空间发散的,对于多模块构成的系统,各电感之间的磁场会相互干扰,由此产生的不均匀互感会损害模块间的对称性,且使波形产生畸变。解决磁路串扰问题的方案有两个:
一是在空间中对称排布各模块,使电感之间的互感完全对称,随后准确量化各模块之间的耦合感值。但由于对称性给模块间空间排布带来很多限制,且空间中任意位置线圈的互感计算较为繁琐,该方法将会使得多模块系统复杂度和设计难度极大提高。
二是通过恰当的空间排布方式,使得模块间磁场干扰降低到可被忽略的程度。经验证,如果将各个模块的电感都放置于同一个水平面,则互感耦合系数一般不会超过2%,可以忽略。在本文的研究中,采取该方法来解决磁路干扰问题。
系统中各个模块相互并联,一同对负载放电。则其他模块的放电电流会明显改变负载状态,进而影响模块内部的工作状态。这种串扰问题可以使用等效电路进行分析。
由于各模块同步运行,且相互对称(电气参数、性能、运行状态一致),因此各输出电流是完全相同的。在n模块系统中,当任意一个模块输出电流为i时,其他各模块输出总电流为(n-1)i,其等效电路如图4所示,右侧电流源即代表其余n-1个模块。所研究模块输出端口电压uload可以表示为
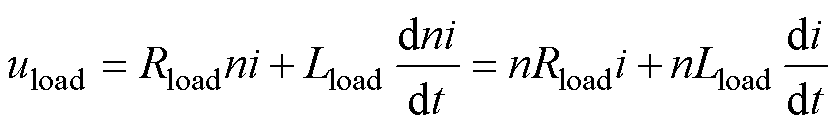 (1)
(1)
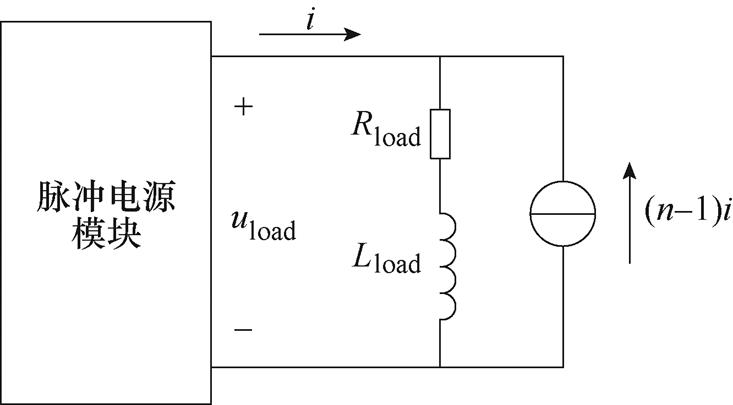
图4 模块间电路串扰等效电路
Fig.4 Equivalent circuit for exploring the interaction between modules
可以看到,输出端电压完全等效于n倍负载产生的效果。因此可以得出结论:对称的n个模块并联、同步对负载放电时,其中任一模块的运行状态与单模块带n倍负载的运行状态完全一致。所以可以用单模块的电路解算方法分析多模块系统的运行状态。
在解决磁路和电路串扰问题后,对于完全对称的多模块系统,只需在上述11个模块相关参数的基础上增加模块数n,共12个参数即可描述和唯一确定该系统。
在经过电路和磁路的等效处理之后,多模块系统的工作过程被大大简化,因此可以基本参照单模块的参数设计方法,使用大规模优化来指导多模块系统的设计。
本文所进行的优化设计的目标为:找到一种总储能600kJ的电感型脉冲源系统的构型及参数,使其储能密度尽可能地大,且可以稳定安全运行,以指导下一步的实际系统搭建。
遗传算法(Genetic Algorithm, GA)是一种基于自然选择和遗传机制的全局优化搜索算法,本文选用该算法进行优化,算法的运行流程如图5所示。算法首先随机生成由多个个体构成的种群,其中每一个体都代表一组参数的取值,即表示多模块电源系统的一种配置。每个个体对应的多模块系统的性能都被分别解算,以得出目标函数值,其解算方法将会在2.2节中说明。算法会参考目标函数值对种群中个体进行选择、杂交和变异操作,以产生新的种群。经过多次迭代后,选取性能最好的个体作为优化结果。算法使用的参数见表1。
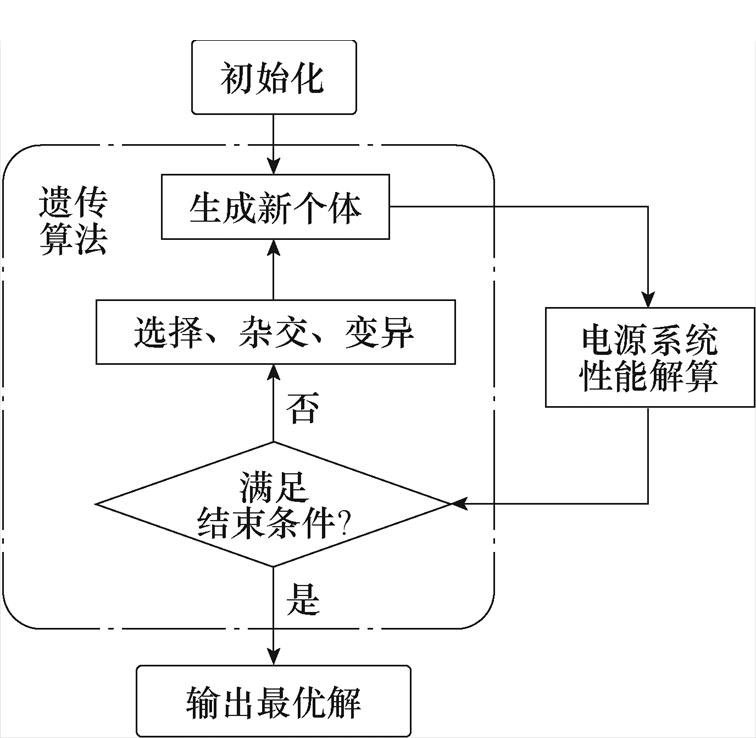
图5 脉冲源系统优化算法流程
Fig.5 Flow chart of pulsed power system optimization
算法选取ro、ri、m1、m2、n、n1、n2、kC1共8个量作为自变量,其取值范围同见表1。前述描述系统的另外四个变量(n、h1、h2、UCmax)可以作为中间变量由推导得到,计算方法也将在2.2节中介绍。
表1 算法参数
Tab.1 Algorithm-related parameters
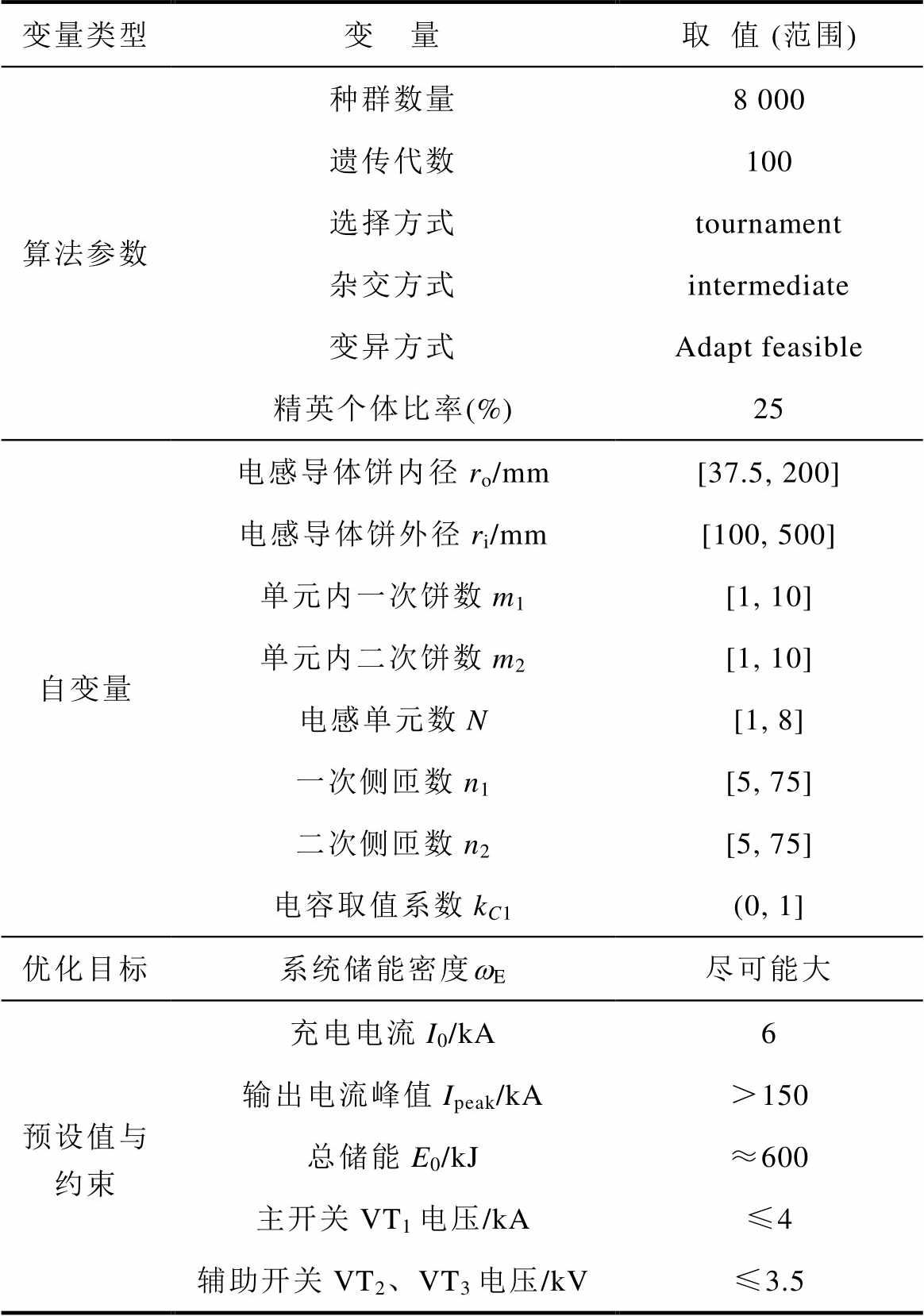
变量类型变 量取值 (范围) 算法参数种群数量8 000 遗传代数100 选择方式tournament 杂交方式intermediate 变异方式Adapt feasible 精英个体比率(%)25 自变量电感导体饼内径ro/mm[37.5, 200] 电感导体饼外径ri/mm[100, 500] 单元内一次饼数m1[1, 10] 单元内二次饼数m2[1, 10] 电感单元数N[1, 8] 一次侧匝数n1[5, 75] 二次侧匝数n2[5, 75] 电容取值系数kC1(0, 1] 优化目标系统储能密度wE尽可能大 预设值与约束充电电流I0/kA6 输出电流峰值Ipeak/kA>150 总储能E0/kJ≈600 主开关VT1电压/kA≤4 辅助开关VT2、VT3电压/kV≤3.5
系统优化选取多模块系统的储能密度为目标函数。储能密度wE的计算公式为
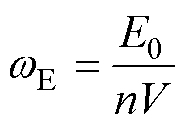 (2)
(2)
其中
 (3)
(3)
式中,E0为多模块系统的总储能;Ltot为单个模块中两串联电感的总电感值;I0为单模块充电电流;V为单个电源模块的体积,模块体积V由各元件体积相加得到,计算过程中充分考虑冗余,以补偿元件间隙、机械固定件等带来的体积增加。
系统优化的几个约束条件被定义如下:根据初级电源的输出性能和主开关的耐受电流,各模块的充电电流I0取为6kA。考虑到电磁发射的应用场景,脉冲源系统在驱动电参数为2mH、2mW 的负载时,输出电流峰值不低于150kA。根据系统规模,确定多模块系统总储能在600kJ左右。在电路运行时,VT1两端电压不能超过4kV,VT2和VT3电压不能超过3.5kV。需要说明的是,上述约束的具体取值取决于实际物理场景,如果所需的优化场景变化,可以改变约束参数的取值,优化流程保持不变。
对于优化进程中的每一个个体,都需要根据8个自变量的取值组合,解算得到相应系统的性能,并计算得到相应的适应值函数。系统性能解算可按照以下几个流程进行。
(1)电感几何参数预处理。根据自变量中导体饼内外径和匝数可以计算得到匝宽取值,随后根据估算得到的导体通流和预设的通流密度计算得到导体饼厚度。将尽可能多的几何参数作为导出量,可以减少自变量数,极大减轻优化算法负担。
(2)电感参数计算。本课题组之前的研究,给出了多个同轴导体饼的电参数求解方法:单个导体饼的自感可由经验公式计算得到;导体饼之间的互感可以参照预计算的结果,由参数扫描和插值的方式快速得到;电感内阻可以由阿基米德螺线公式计算得到。更多详细信息,可参见文献[17-19]。
(3)模块数推算。经过上一步骤,两电感的串联总感值Ltot被计算得到,再根据充电电流I0求得此时单个模块的储能,随后便可根据预设的总储能E0,使用四舍五入计算系统中应包含的模块数n。
(4)电路求解。首先根据C1容值最大值和自变量容值系数kC1相乘得到C1取值;然后根据1.4节的结论,将负载支路的感值和阻值都增大n倍,以便使用单模块电路来等效n模块并联运行的情况。关于电路计算,使用Dommel EMTP梯形法[20],在Matlab中编制单模块电路仿真程序,以便能快速得到电路运行时各元件的电压、电流变化情况。
(5)性能计算。根据上一步中得到的电压电流数据,提取各半导体开关最大承受电压,判断如果超过安全阈值,则直接记录该个体适应值为0,结束计算,否则继续进行性能计算:提取C1电压最大值UCmax并计算C1储能和体积;根据各元件参数计算模块体积V和系统储能密度wE;提取模块输出电流最大值,乘以n以后得到系统总输出电流的峰值Ipeak;最后根据式(4)、式(5)进行适应值计算。
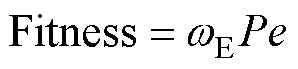 (4)
(4)
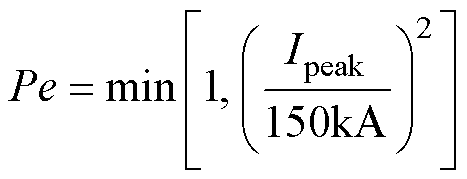 (5)
(5)
式中,Pe为罚函数,可以迫使被优化个体的输出电流的幅值不小于150kA。
在Matlab中搭建并运行优化程序,100代遗传、10万次系统性能解算共花费0.4h。
在随机生成的第一代个体中,满足半导体电压约束要求的有效个体占比80%,个体平均适应值(即储能密度)仅为0.78MJ/m3。经过100代演化,每代个体的平均储能密度和最高储能密度如图6所示。可见,演化后期得到的能量密度显著高于第一代,遗传算法寻优效果较好,相比随机构型(第一代)的性能具有极大提升。最后得到的最优解的参数及性能见表2。
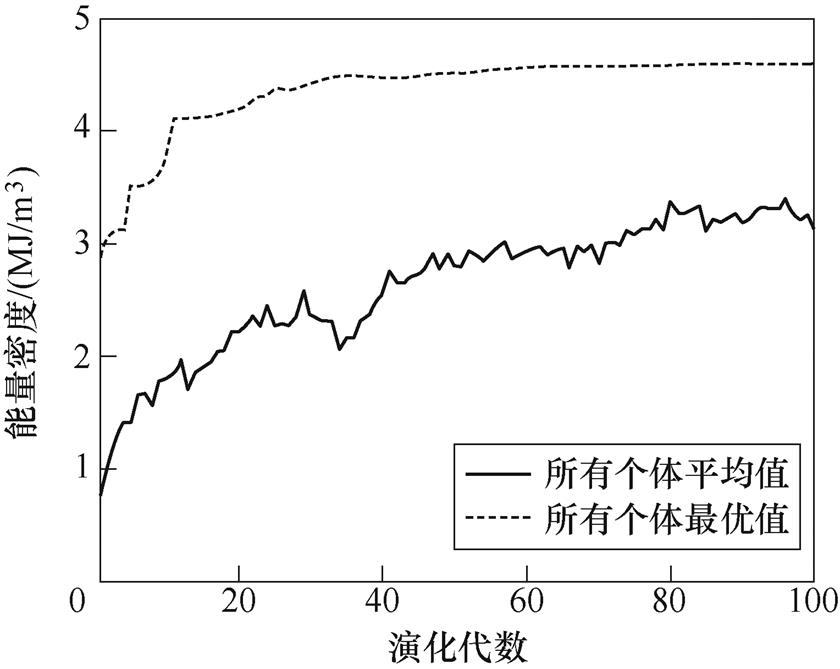
图6 演化过程各代适应值数据
Fig.6 Fitness value of each generation in the evolution process
表2 多模块脉冲源系统优化最优解参数取值
Tab.2 Parameter value of optimal solution for multi-module pulsed power system optimization
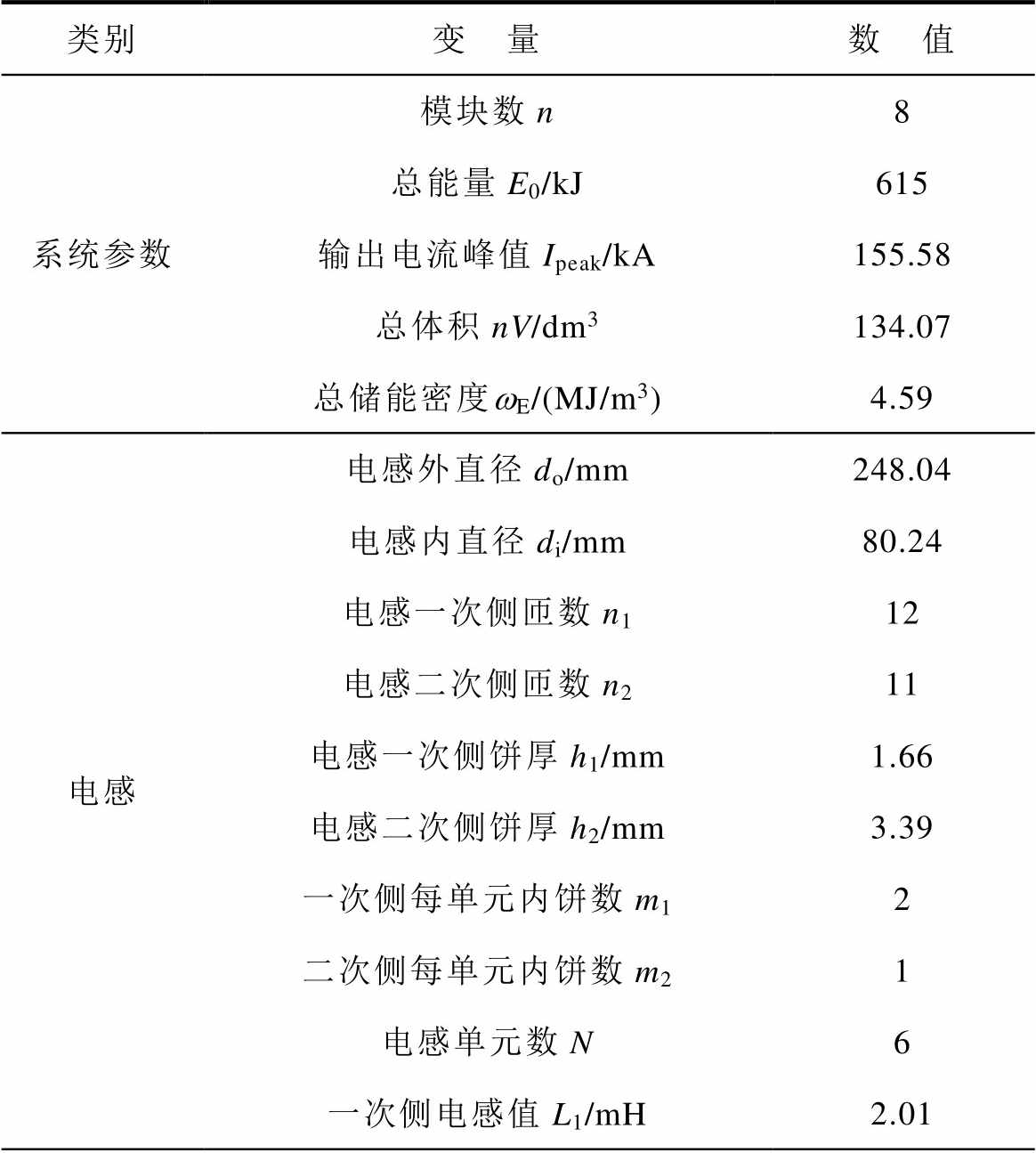
类别变 量数 值 系统参数模块数n8 总能量E0/kJ615 输出电流峰值Ipeak/kA155.58 总体积nV/dm3134.07 总储能密度wE/(MJ/m3)4.59 电感电感外直径do/mm248.04 电感内直径di/mm80.24 电感一次侧匝数n112 电感二次侧匝数n211 电感一次侧饼厚h1/mm1.66 电感二次侧饼厚h2/mm3.39 一次侧每单元内饼数m12 二次侧每单元内饼数m21 电感单元数N6 一次侧电感值L1/mH2.01
(续)
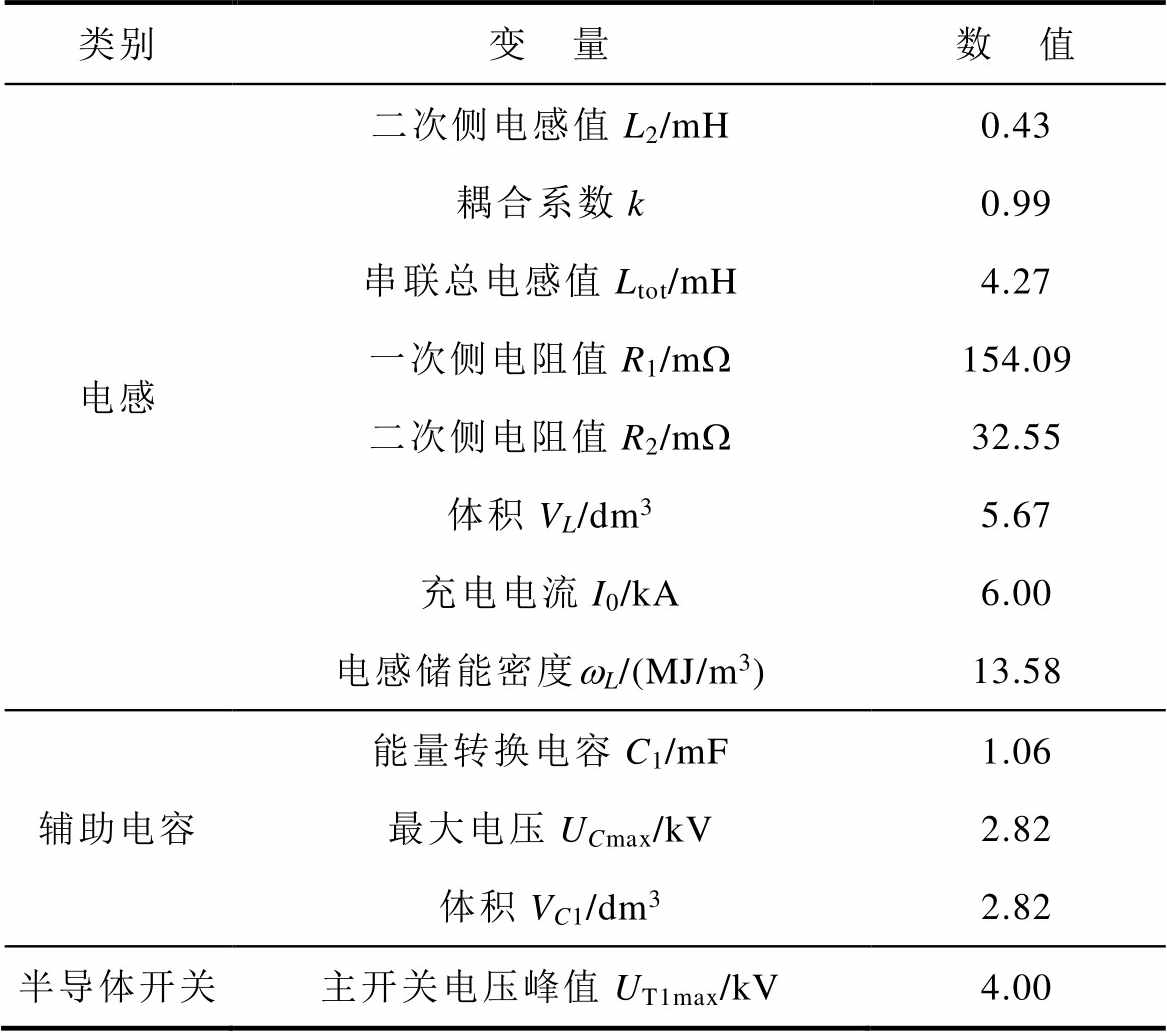
类别变 量数 值 电感二次侧电感值L2/mH0.43 耦合系数k0.99 串联总电感值Ltot/mH4.27 一次侧电阻值R1/mW154.09 二次侧电阻值R2/mW32.55 体积VL/dm35.67 充电电流I0/kA6.00 电感储能密度wL/(MJ/m3)13.58 辅助电容能量转换电容C1/mF1.06 最大电压UCmax/kV2.82 体积VC1/dm32.82 半导体开关主开关电压峰值UT1max/kV4.00
可见,最优解用8个模块实现了156kA的电流输出,其中每个模块的能级约为76.9kJ,最终系统的储能密度高达4.59MJ/m3。
本优化结果与美国先进技术研究所(Institute for Advanced Technology, IAT)、德法联合实验室(French-German research Institute of Saint-Louis, ISL)、本课题组的试验结果对比见表3。可以看到本课题组的试验和优化结果在能量密度方面优势巨大,这也意味着可以用更小体积的脉冲电源为电磁发射器供能。
表3 IPPS系统性能比较
Tab.3 Performance optimization of several IPPS system
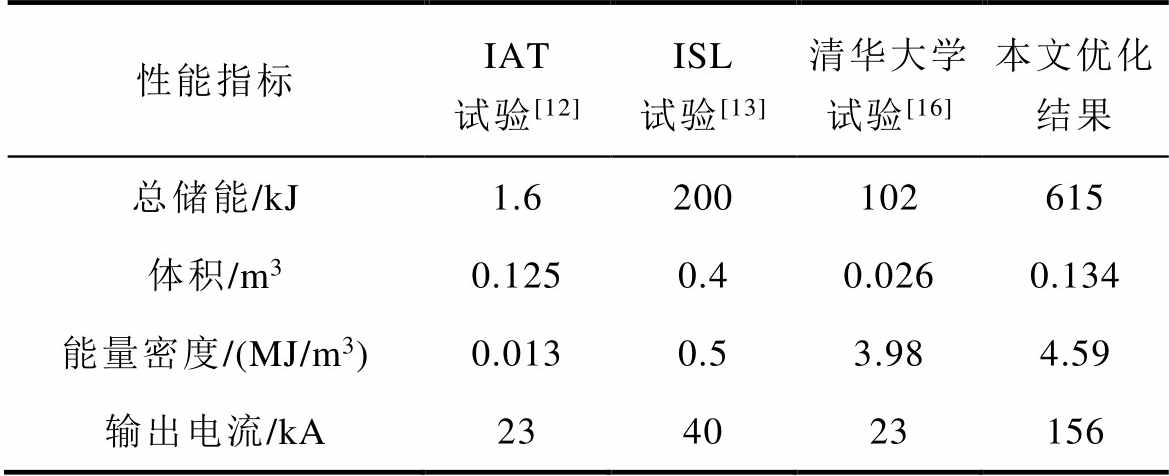
性能指标IAT试验[12]ISL试验[13]清华大学试验[16]本文优化结果 总储能/kJ1.6200102615 体积/m30.1250.40.0260.134 能量密度/(MJ/m3)0.0130.53.984.59 输出电流/kA234023156
使用Simplorer搭建仿真电路进行验证,得到电压电流波形如图7~图9所示,各关键电气参数的性能对比见表4。
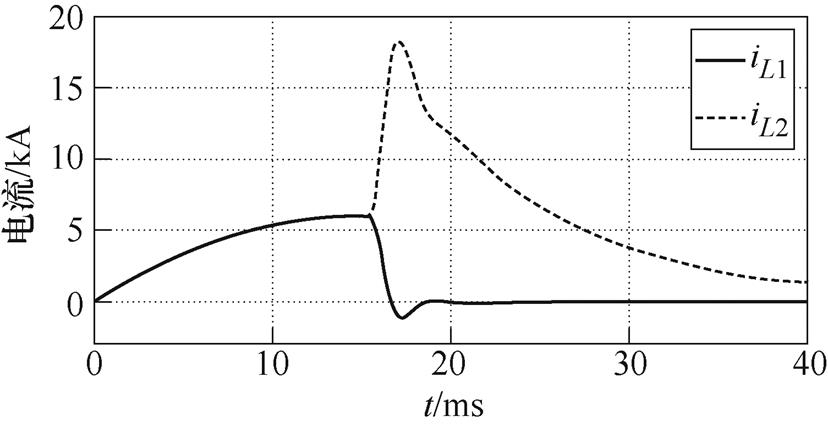
图7 电感线圈电流仿真验证波形
Fig.7 Inductor current waveforms of the verification simulation
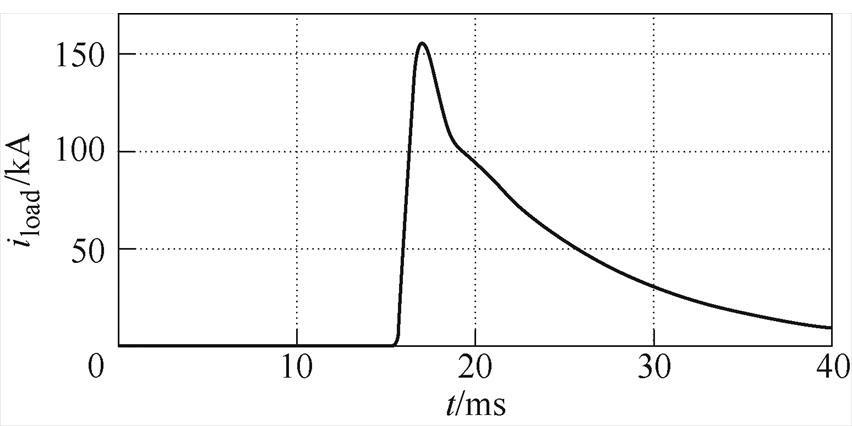
图8 负载电流仿真波形
Fig.8 Load current waveform of the verification simulation
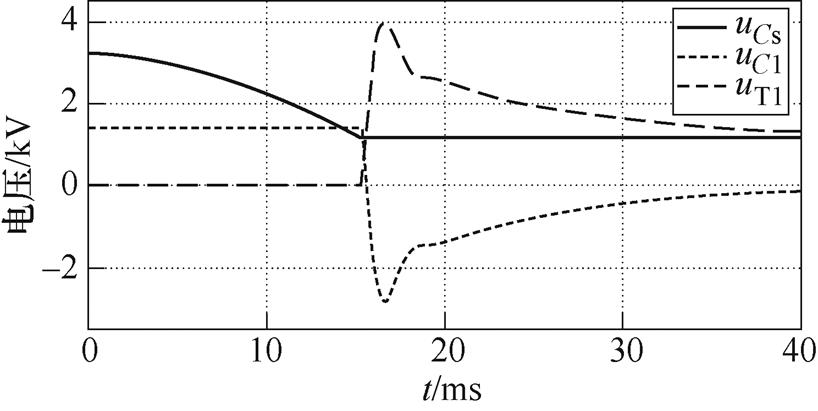
图9 电容及主开关电压仿真验证波形
Fig.9 Voltage waveforms of the verification simulation
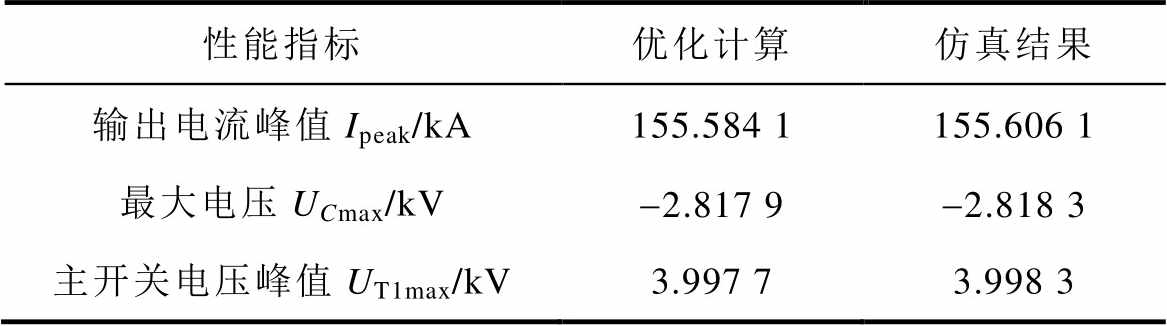
表4 优化计算与仿真验证结果比较
Tab.4 Comparison of optimization calculation and simulation verification results
性能指标优化计算仿真结果 输出电流峰值Ipeak/kA155.584 1155.606 1 最大电压UCmax/kV-2.817 9-2.818 3 主开关电压峰值UT1max/kV3.997 73.998 3
可以看到,电路运行正常,负载端成功实现了脉冲电流输出。优化计算和仿真结果的各项性能参数均吻合得较好,证明了模块解算的准确性和优化方法的有效性。当然,优化结果的有效性还需经过将来硬件试验的检验。
本文探究了多模块电感性脉冲源的工作过程,经过磁路和电路的等效处理之后,将多模块系统的问题简化为单模块运行的问题。此外,本文还建立了详细的多模块脉冲源系统的解算方法,可以利用最底层的几何和电气参数,求解得到各元件的性能,并计算得到脉冲源的输出电流等性能参数。
基于此,本文使用遗传算法对系统参数进行了大规模优化,在充分考虑元件裕度、工程实现等的基础上,得到了储能密度最高的多模块电感型脉冲源系统的参数:使用8个分立的脉冲源模块,并联、同步为负载放电,可以实现4.58MJ/m3的储能密度和158kA的电流输出。
需要说明的是,本文虽然是基于特定拓扑Meat Grinder with SECT,但是对于电感型脉冲电源的其他拓扑,系统分析和优化的方法仍然适用。
参考文献
[1] McNab I R. Developments in pulsed power tech- nology[J]. IEEE Transactions on Magnetics, 2001, 37(1): 375-378.
[2] 阮景煇, 陈立学, 夏胜国, 等. 电磁轨道炮电流分布特性研究综述[J]. 电工技术学报, 2020, 35(21): 4423-4431.
Ruan Jinghui, Chen Lixue, Xia Shengguo, et al. A review of current distribution in electromagnetic railguns[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4423-4431.
[3] 张晓, 鲁军勇, 李湘平, 等. 电磁感应线圈发射子弹系统优化设计[J]. 电工技术学报, 2021, 36(22): 4658-4665.
Zhang Xiao, Lu Junyong, Li Xiangping, et al. System optimization of electromagnetic induction coil launch bullet[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4658-4665.
[4] 李湘平, 鲁军勇, 张晓, 等. 基于NSGA-Ⅱ的过载磁场发生器优化设计[J]. 电工技术学报, 2021, 36(21): 4399-4407.
Li Xiangping, Lu Junyong, Zhang Xiao, et al. Opti- mization of generator of high overload and strong magnetic field based on NSGA-Ⅱ[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4399- 4407.
[5] 徐麟, 张军, 刘佳, 等. 脉冲功率源瞬态反向过电流机理及优化[J]. 电工技术学报, 2020, 35(增刊2): 629-635.
Xu Lin, Zhang Jun, Liu Jia, et al. Mechanism and optimization of transient reverse overcurrent in pulse power system[J]. Transactions of China Electro- technical Society, 2020, 35(S2): 629-635.
[6] Li Jun, Cao Ronggang, Li Shizhong. The deve- lopment of EML technology in China[J]. IEEE Transactions on Plasma Science, 2013, 41(5): 1029- 1033.
[7] 马山刚, 于歆杰, 李臻. 用于电磁发射的电感储能型脉冲电源的研究现状综述[J]. 电工技术学报, 2015, 30(24): 222-228, 236.
Ma Shangang, Yu Xinjie, Li Zhen. A review of the current research situation of inductive pulsed-power supplies for electromagnetic launch[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 222-228, 236.
[8] 王延, 张东东, 付荣耀, 等. 电感储能型大电流毫秒级脉冲源研制[J]. 电工技术学报, 2020, 35(23): 5025-5030.
Wang Yan, Zhang Dongdong, Fu Rongyao, et al. Design of a high current inductive pulsed power supply with millisecond pulse width[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 5025-5030.
[9] Ford R D, Hudson R D, Klug R T. Novel hybrid XRAM current multiplier[J]. IEEE Transactions on Magnetics, 1993, 29(1): 949-953.
[10] Zucker O, Wyatt J, Lindner K. The meat grinder: theoretical and practical limitations[J]. IEEE Transa- ctions on Magnetics, 1984, 20(2): 391-394.
[11] Yu Xinjie, Liu Xukun. Review of the meat grinder circuits for railguns[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1086-1094.
[12] Sitzman A, Surls D, Mallick J. Design, construction, and testing of an inductive pulsed-power supply for a small railgun[J]. IEEE Transactions on Magnetics, 2007, 43(1): 270-274.
[13] Liebfried O, Brommer V. A four-stage XRAM generator as inductive pulsed power supply for a small-caliber railgun[J]. IEEE Transactions on Plasma Science, 2013, 41(10): 2805-2809.
[14] Yu Xinjie, Sun Hao, Liu Xukun, et al. Design, construction, and testing of an 80kJ and 2.4MJ/m3 inductive pulsed power module for electromagnetic launchers[J]. IEEE Transactions on Plasma Science, 2020, 48(1): 285-290.
[15] Liu Xukun, Yu Xinjie, Ban Rui, et al. Parameter analysis of the energy transfer capacitor in the meat grinder with SECT circuit[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1239-1244.
[16] Sun Hao, Yu Xinjie, Li Bei, et al. Parameter optimization and experimental test of 4MJ/m3 IPPS module[J]. IEEE Transactions on Plasma Science, 2021, 49(2): 921-927.
[17] 李臻, 于歆杰. 高储能密度电感的设计[J]. 电工技术学报, 2017, 32(13): 125-129.
Li Zhen, Yu Xinjie. Design of inductors with high energy density[J]. Transactions of China Electro- technical Society, 2017, 32(13): 125-129.
[18] Liu Xukun, Yu Xinjie, Li Zhen. Inductance calcu- lation and energy density optimization of the tightly coupled inductors used in inductive pulsed power supplies[J]. IEEE Transactions on Plasma Science, 2017, 45(6): 1026-1031.
[19] Sun Hao, Yu Xinjie, Li Zhen, et al. Inductance calculation and structural optimization of toroidal circular disk-type inductors in IPPS[J]. IEEE Transa- ctions on Plasma Science, 2021, 49(7): 2247-2255.
[20] Dommel H W. Digital computer solution of electro- magnetic transients in single-and multiphase net- works[J]. IEEE Transactions on Power Apparatus and Systems, 1969, PAS-88(4): 388-399.
Analysis and Optimization of Multi-Module Inductive Pulsed Power Supply System
Abstract High-power pulsed power supply is an important part of the electromagnetic launch system. The pulsed power supply needs to provide the load with a current of mega-ampere magnitude and lasting for several milliseconds, and its volume should be as small as possible to ensure the mobility and concealment of the launch system. According to the form of energy storage, the pulsed power supply can be divided into different types. Among them, the inductive pulsed power supply (IPPS) with high energy density has great research value and application prospects. With the efforts of researchers from various countries, many IPPS modules have been developed and can output pulse current stably. But in practice, due to the limitations of inductor production technology, material characteristics and semiconductor switch performance, it is difficult for a single IPPS module to store too much energy. In order to meet the energy and current requirements of electromagnetic launch, it is necessary to study the cooperative work of a multi-module system. However, the many parameters, complex working processes, and crosstalk in multi-module operation bring significant challenges to the design of multi-module IPPS system.
Firstly, this paper explores the working process of the multi-module IPPS system. In order to improve the efficiency and safety of system operation, it is necessary to avoid the asymmetry of magnetic and electric circuit: For the crosstalk of magnetic circuit, it is found that the mutual inductance between the tiled inductors is very small and can be ignored; For the crosstalk of electric circuit, the method of load parameter multiplication can be used for equivalent analysis. With the equivalence of magnetic and electric circuits, the operation of the multi-module IPPS system can be simplified as a single-module problem that we are relatively familiar with.
Then, the numerical solution model of the multi-module IPPS system is established, which can use the geometric and electrical parameters and directly calculate the performance indicators. The numerical solution model includes the following five sub-blocks: geometric parameter preprocessing, inductance parameter calculation, module number calculation, circuit solution, and performance calculation. Based on this, this paper introduces genetic algorithm (GA) to optimize the system parameters. On the basis of fully considering the component performance margin and engineering implementation, the optimization is operated, and the parameters of the multi-module IPPS system with the highest energy density are obtained: Eight identical IPPS modules power the load parallelly and synchronously, achieving an energy density of 4.58MJ/m3 and a current output of 158kA, and its total energy slightly exceeds 600kJ.
Through simulation analysis, the multi-module IPPS system corresponding to the optimal solution can operate successfully. The performance indicators of the optimization calculation and simulation results are in good agreement, which preliminarily verifies the accuracy of the numerical solution and the effectiveness of the optimization method. The optimization results given in this paper can guide the actual system construction in the next step. In addition, although this paper is based on the analysis of the Meat Grinder with SECT circuit, the proposed numerical solution and optimization methods are still applicable to other topologies and scenarios.
Keywords:Inductive pulsed power supply, multi-module power system, optimization method, equivalent circuit
中图分类号:TM33
DOI: 10.19595/j.cnki.1000-6753.tces.211884
收稿日期 2021-11-18
改稿日期 2021-12-07
E-mail: sunhao3990@163.com
于歆杰 男,1973年生,教授,博士生导师,研究方向为脉冲功率电源、教育数据挖掘、磁电层合材料和无线能量传输等。
E-mail: yuxj@tsinghua.edu.cn(通信作者)
(编辑 崔文静)