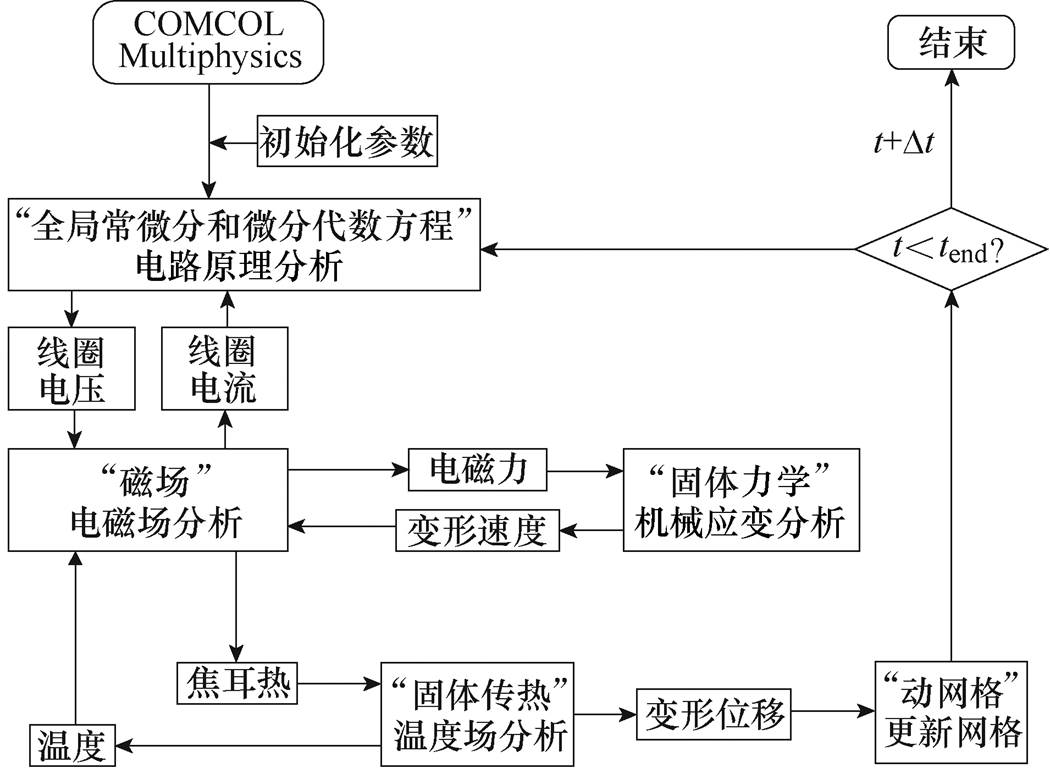
图1 EMF建模流程
Fig.1 EMF modeling flowchart
摘要 在电磁成形的过程中，驱动线圈的发热是影响线圈使用寿命和放电频次的关键因素；集磁器作为一种常用的电磁成形辅助工具，目前被广泛用于改善电磁场的分布，提高工件的成形质量。然而，集磁器的引入也会影响等效电路中的等效电感参数，从而改变线圈中的电流，进而影响线圈的发热。故该文提出使用集磁器作为降低管件电磁胀形中驱动线圈发热的措施；通过理论分析和仿真模拟分析了有/无集磁器的两种方案中线圈的发热和管件的成形效果变化，以及集磁器上的温度变化。结果表明，在内径49.6mm、外径68mm、4×10匝的线圈胀形过程中，通过引入集磁器辅助，在放电电压为10.5kV时，线圈上的焦耳热减少了12.32%，最高温度降低了3.42℃，工件的最大成形深度提升至约为原来的2.76倍；进一步的分析则表明，集磁器的引入降低了等效电路中的电感和电压，使得线圈电流具有更陡的下降沿，衰减速度变快的同时减小了电流峰值，从而让线圈的热量损耗更小。该方法成本较低，容易实现，且对于线圈发热问题具有明显的优化效果，对提高电磁成驱动线圈的使用寿命和放电频次具有重要意义。
关键词：电磁成形 驱动线圈 集磁器 线圈发热 耦合互感
电磁成形（Electromagnetic Forming, EMF）是一种无接触式的高速成形技术[1-3]，其利用脉冲电磁力来对工件进行成形，从20世纪60年代起便有大量的研究成果。相比于传统的准静态成形工艺，EMF在加工中具有更大的优势：提高了金属的成形极限、改善了轻质合金加工中的回弹和起皱问题、同时又保证了金属的表面光洁度[4-5]；EMF因其独特的技术特性被广泛地运用于金属材料加工、焊接等领域内[6-9]。
在EMF的放电过程中，驱动线圈的热负荷是影响线圈机械强度和寿命的重要因素；1956年，Furth 和Waniek等率先提出线圈过热会导致线圈绕组材料的电阻增大，针对线圈的热负荷和机械强度问题提出了“磁矩效应”。根据这一理论，线圈材料中接近熔融温度的部分会出现局部电导率下降的现象，这将导致焦耳热增多，从而使得线圈更多部位出现熔融现象；P. Werdelmann通过实验和数值分析得出结论，在成形过程中仅有一小部分能量被传递到工件中，约有49%的初始能量在放电过程中以焦耳热的形式损失[10]，这也是系统能量传递效率低的主要原因，这种大量的能量损失会使得线圈温度升高，在批量生产过程中热量会随着时间逐渐积累，最终影响线圈的寿命。
在温度特性方面，S. Gies等测量了长期放电下平板线圈的温度变化，对影响温度变化的因素进行了深入探讨[11]；并在2017年提出了一种简单便捷的方法评估在不同放电能量、电流波形和材料导电特性下的线圈焦耳热[12]。S. Golovashchenko等于2006年在仿真中使用空气冷却系统来降低连续放电中的线圈发热，得到了一系列结果，但并没有得到实验结果来证明模型的可靠性[13]。曹全梁等在2015年创新性地在放电电路中引入了一个续流回路，以调节电流波形并消除热量积聚效应，同时不影响成形效率[14]；邱立等提出在线圈绕组间添加加固材料的方法来加强线圈的机械强度和高强度，利用散热线圈进行耦合散热的方式来降低线圈发热，并且在数值上证明了半波电流方法在降低线圈发热问题中的有效性[15]。邱磊和刘良云等探讨了连续放电过程中的平板成形线圈的热负荷和温度特性并进行了优化，以抑制线圈温升。王紫叶等探讨了线圈结构对于发热的影响并做了优化[16]。
在上述研究的基础上，本文提出了一种新的方法来减少驱动线圈中的焦耳热，即在线圈与工件之间引入集磁器；以往对于集磁器的研究与应用侧重于其对成形效果的改善，但是引入集磁器后带来的耦合互感对于原电路中线圈发热的影响却很少涉及。事实上，引入集磁器后，线圈与工件间的耦合关系得到加强，整个系统的等效电感降低，电路的时间常数减小，使得线圈中的电流具有更为陡峭的下降沿而幅值基本不变，因此整个放电过程中焦耳热减少，发热降低。本文通过理论分析，针对内径49.6mm、外径64mm、4×10匝的铜制线圈胀形过程进行了研究，计算了有/无集磁器两种工况下，线圈的电流、焦耳热和最大温度；集磁器的温度变化情况以及工件的感应涡流、磁通变化和工件的成形效果。结果表明，集磁器的引入显著降低了线圈的发热，同时也提升了成形效果，在改变初始放电参数的情况下，集磁器仍然具有较好的降温能力；与现有的方法相比，该方法实施起来更为简便，成本较低。
EMF过程涉及多学科交叉，电磁场、温度场、机械结构场相互耦合作用。本文选取全耦合的方式进行物理场建模，考虑了电流的趋肤效应、工件位移及速度对放电电流与磁场的影响和线圈电阻率对驱动线圈发热的影响，建立电磁场-机械结构场-温度场耦合模型，为研究如何降低线圈的热损耗提供了新思路。
本文使用COMSOL软件，选取“全局常微分和微分代数方程”、“磁场”、“固体力学”、“固体传热”、“动网格”这五个模块进行建模。其中前四个模块分别用于电路原理分析、电磁场分析、机械应变分析和温度场分析，动网格模块运用ALE（拉格朗日-欧拉）方法对变形网格进行更新，实现EMF中的多物理场耦合。模型的求解流程如图1所示，各个物理场的数学模型见后文。
图1 EMF建模流程
Fig.1 EMF modeling flowchart
EMF的成形系统通常包括电容电源、开关、连接电路线、一个驱动线圈和金属工件。当开关关闭时，带有初始储存能量的电容器电流流经线圈，在线圈和工件之间产生强烈的电磁耦合，然后对两个部件产生热和机械效应。本文根据曹全梁等的研 究[14]，选用带有续流回路的EMF放电电路；续流回路可以有效改善电流波动，从而显著减少驱动线圈产生的焦耳热，并在此基础上引入了一个集磁器作为辅助，其系统如图2所示。
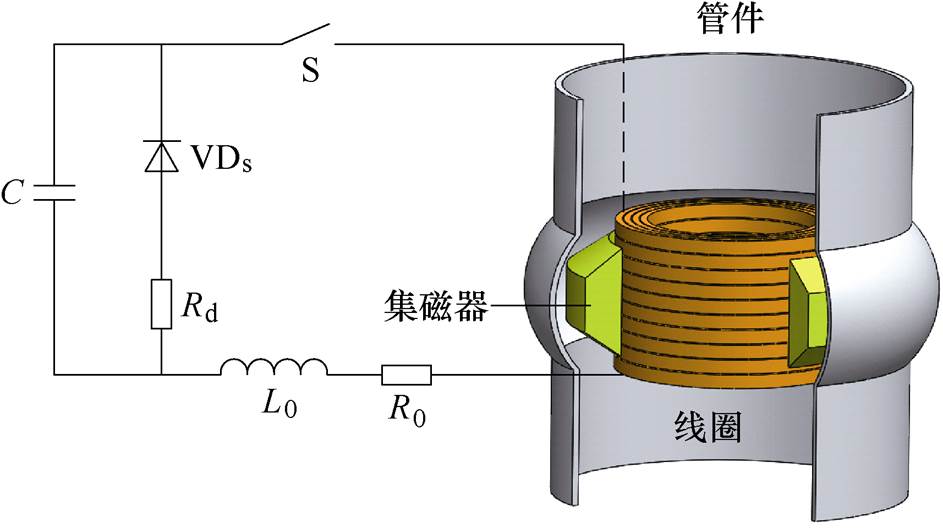
图2 含有集磁器的电磁胀形系统
Fig.2 Electromagnetic bulging system with field shaper
与传统的电动势系统不同，引入集磁器后需要考虑集磁器对于原电路带来的影响，因此其等效电路模型如图3所示，主要包括电容器组C、连接线路的电阻R0和电感L0、续流回路的二极管VDS和续流电阻Rd以及与工件耦合的驱动线圈和集磁器；续流回路与电容电源并联，二极管在电容电源输出正向电压时截断，输出反向电压时导通，即该续流回路只有在输出电压为负值时才可以正常工作。
当引入集磁器后，原电路中工件与成形线圈间的等效耦合电感将发生改变[17-18]，此时板件、集磁器与线圈间的互感之和为Mc-w+Mc-f，集磁器与工件间的耦合等效电感为Mf-w；集磁器起到了类似于“变压器”的作用，故在含有集磁器的电路系统中，其等效电路方程对比文献[11]将有所改变，即
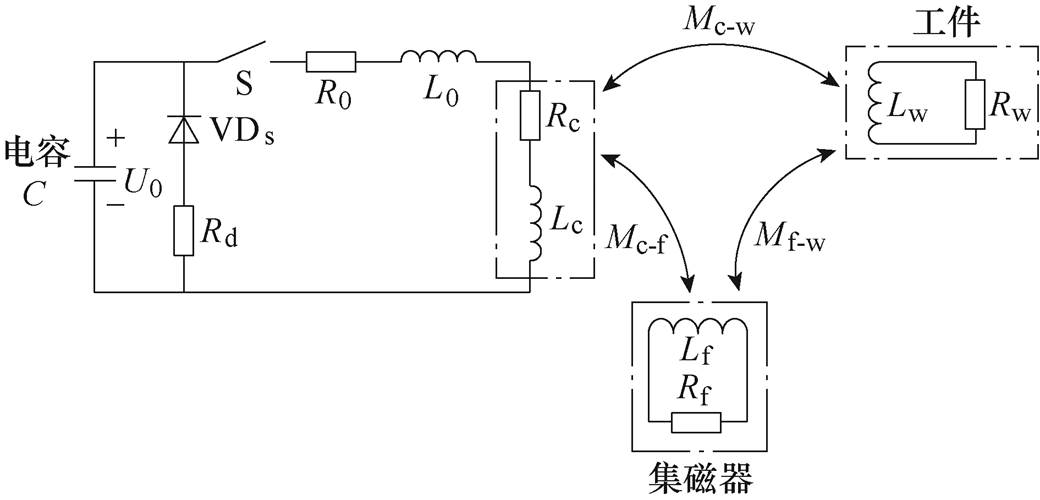
图3 引入集磁器的EMF系统等效电路图
Fig.3 EMF system equivalent circuit diagram for introducing field shaper
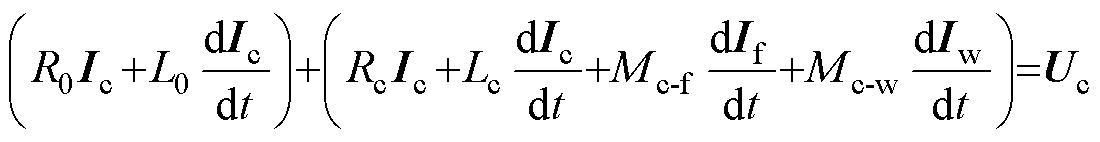（1）
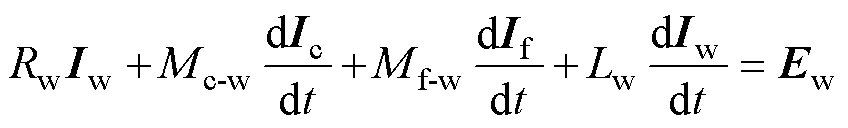（2）
式中，Uc为线圈电压；Ic为线圈中流过的电流；Rc和Lc为驱动线圈的等效电阻和等效电感；Mc-f、Mc-w为线圈与集磁器、工件间的互感系数；Mf-w为集磁器与工件间的互感系数；Rw、Lw分别为工件的等效电阻和电感；Iw为工件中的感应电流；Ew为工件的动生电动势；If为集磁器中的感应电流。
由于EMF过程中电流的频率很大，由此带来的电流趋肤效应和邻近效应不可忽略，因而驱动线圈的电流在横截面上观察是不均匀的，线圈的电流密度计算公式[19]为
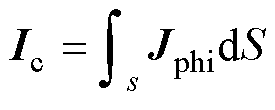（3）
式中，Jphi为线圈电流密度；S为线圈的截面积。
在EMF系统中，集磁器是一种常见的辅助工具，制作集磁器的材料通常为铍青铜、纯铜、铝等高电导率材料。它可以改变电磁场的空间分布，使得磁场的强弱分布在工件成形区域内可控，从而使成形更加灵活多变。本文所使用的胀形用集磁器如图4所示，其剖面如图5所示。
当系统开始放电后，脉冲大电流会使得集磁器的感应区域产生感应涡流，由于趋肤效应，涡流靠近于内表面。感应涡流流经狭缝至工作区域外表面，形成回路。工作区域的外表面面积小于感应区域面积，故此处涡流密度更大，达到了加强工作区域磁场的效果。
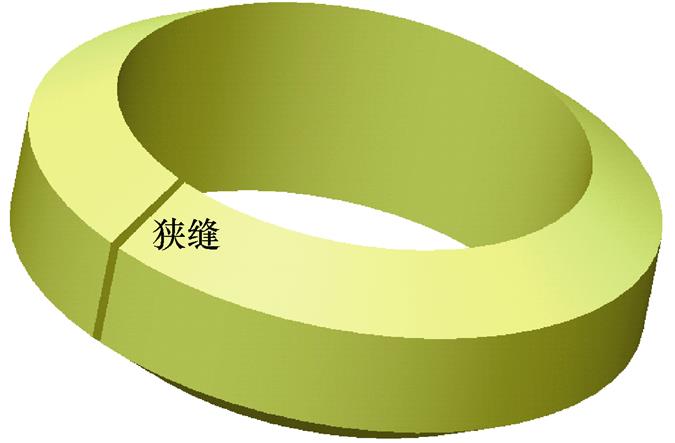
图4 集磁器三维模型
Fig.4 Three dimensional model of field shaper
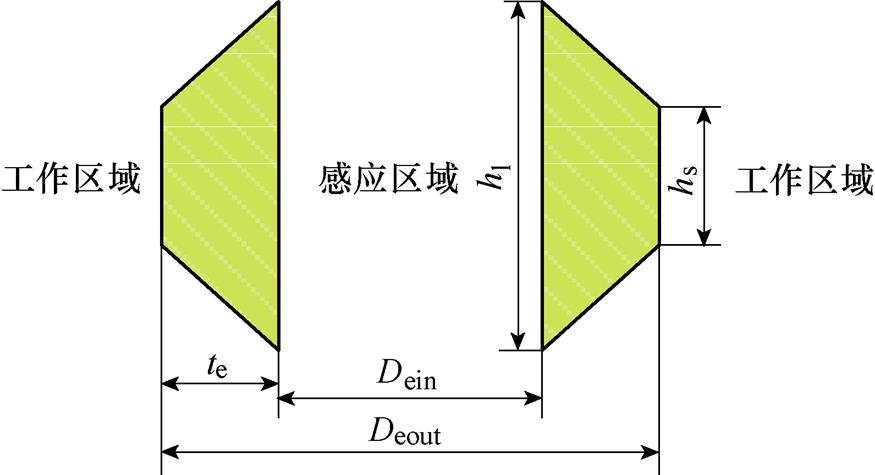
图5 集磁器剖面图
Fig.5 Section drawing of field shaper
成形过程中的热平衡方程为
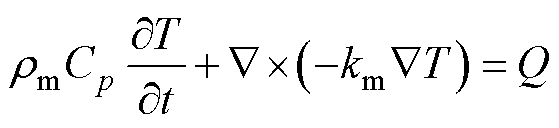（4）
式中，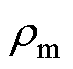
为材料密度；T为温度；Cp为恒压热容；km为热传递系数；Q为热源。根据文献[11]中对铝合金材料热容量与温度变化的研究，在本次模型中所有材料的热性能参数都简单地定义为常数。在模拟中，材料并非处于绝缘环境，考虑到空气在温度变化下引起的自然换流，在仿真中需要将边界设置为“对流热通量”。线圈产生的焦耳热计算公式为
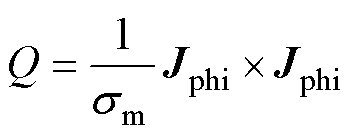（5）
式中，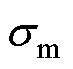
为线圈的电导率；Jphi为线圈的电流密度。集磁器可等效为一个单匝的线圈，其产生的焦耳热也可使用式（5）计算。
在本次的仿真设计中，应该注意到材料的电阻率不是一个定值，它会随着温度的上升发生改变，因此，考虑到温度对电导率的影响，可以根据EMF过程中的焦耳热变化拟合成一个时变函数，即
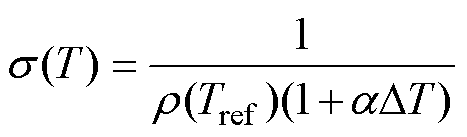（6）
式中，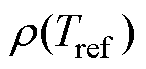
为参考温度20℃时的导体电阻率；
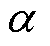为已知的线圈电阻温度系数；
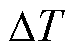为实际温度T与参考温度Tref的差值，T可通过后续的温度场模型中求解。
本文选用型号为AA-6063的铝合金管材进行仿真模拟，根据张骁的研究[20]，其弹性模量为69GPa，泊松比为0.33，初始屈服应力为270MPa，EMF过程有别于准静态成形，考虑到应变率的影响，采用Cowper-Symonds本构模型来构建方程，即
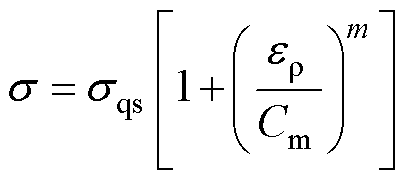（7）
式中，
为高速变形中的流动应力；
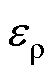为材料的应变率；m为应变率硬化参数；Cm为粘性参数；
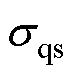为准静态下的流动应力。对于铝合金材料，Cm与m分别取为6 500、0.25。
在仿真时，由于三维模型的建立与计算十分复杂，为了在减小计算量的同时减小计算误差，本文参照了文献[11]中的材料数据并根据实际情况构建了二维轴对称的几何模型，设定了合理的计算域与边界条件，并划分单元大小合适的网格。其中，所用EMF系统仿真的二维几何模型示意图如图6所示；材料属性参数见表1，模型的几何结构与电气参数见表2。本文根据是否引入集磁器辅助成形的情况分别建立了两套模型进行比对，其他参数保持不变，以此来探讨集磁器对线圈温度的影响。
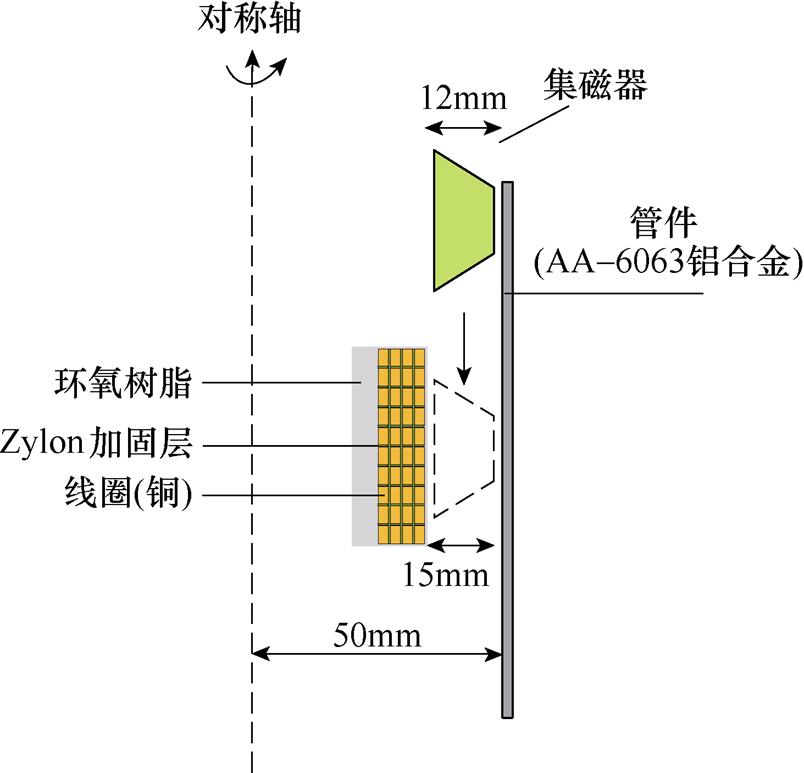
图6 系统二维几何模型
Fig.6 Two dimensional geometric model of the system
为了探讨集磁器对于线圈温度的影响，将变量控制为有/无集磁器辅助成形，在保证其他参数不变的情况下，先讨论两种工况下驱动线圈和集磁器上不同时刻的温度变化情况；其次对集磁器降低线圈发热的原理进行分析，计算了引入集磁器后对原电路带来的互感；然后对比了线圈电流和焦耳热的变化曲线；接着比较了管件上的磁通、涡流和成形质量；最后探究了不同放电电压下集磁器对线圈发热的优化效果。结果表明：当放电电压U0=10.5kV时，引入集磁器后减少了线圈的焦耳热，线圈的最大温升降低了约12.32%；工件的径向位移在使用集磁器后从2.52mm增加到了6.96mm，提高至约2.76倍，成形质量和效率均得到了提高。集磁器对于线圈发热的优化具有普适性，其优化能力随放电电压的升高而略有降低。
表1 材料属性参数
Tab.1 Material property parameter
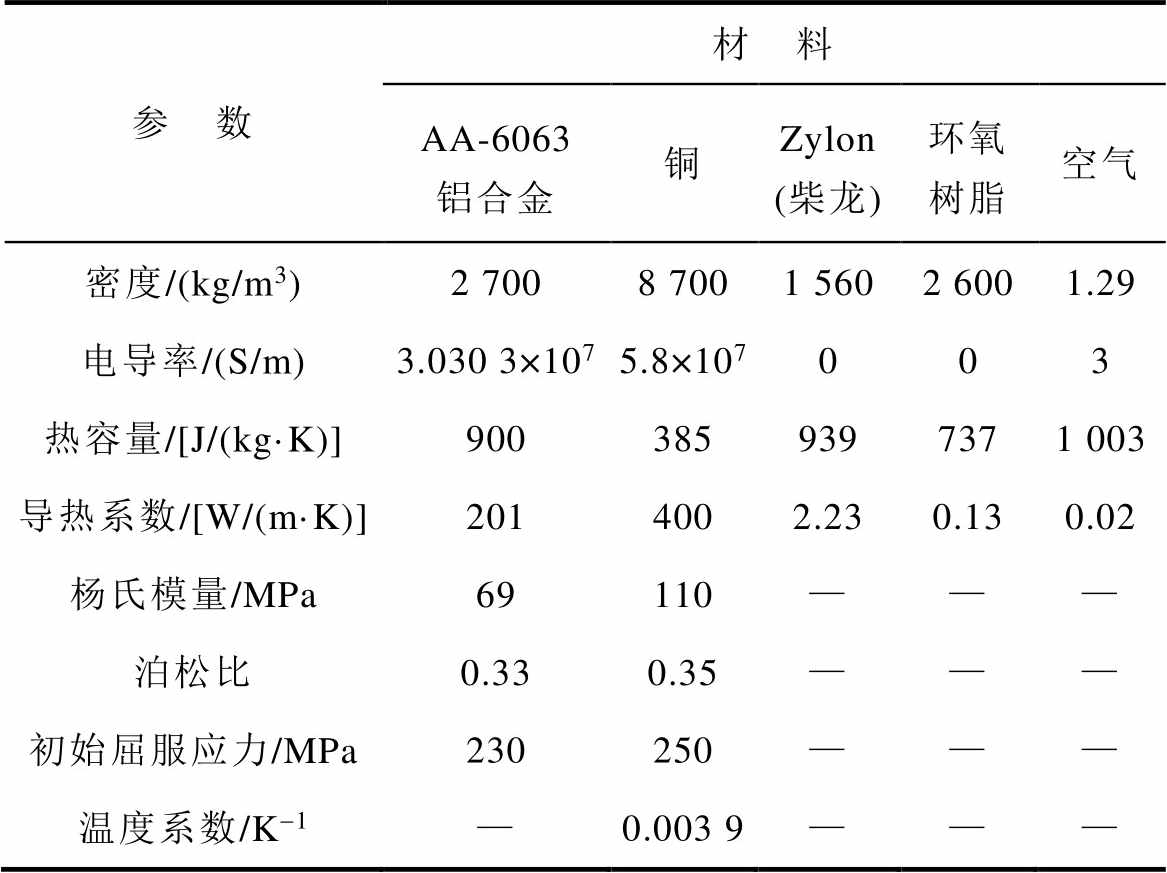
参 数材 料 AA-6063铝合金铜Zylon (柴龙)环氧树脂空气 密度/(kg/m3)2 7008 7001 5602 6001.29 电导率/(S/m)3.030 3×1075.8×107003 热容量/[J/(kg·K)]9003859397371 003 导热系数/[W/(m·K)]2014002.230.130.02 杨氏模量/MPa69110——— 泊松比0.330.35——— 初始屈服应力/MPa230250——— 温度系数/K-1—0.003 9———
表2 EMF系统的几何结构与电气参数
Tab.2 EMF system geometry and electrical parameters
参 数数 值 电源及线路放电电压U0/kV10.5 放电电容C/mF320 线路电感L0/mH7 线路电阻R0/mW15 续流电阻Rd/mW15 线圈线圈高度hc/mm43.6 线圈内径Dcin/mm49.6 线圈外径Dcout/mm68 匝间距dn/mm0.4 线圈总匝数N4×10 管件管件高度hw/mm120 管件厚度Dth/mm2 管件内径Dwin/mm100 管件外径Dwout/mm104 集磁器集磁器内、外高度hl, hs/mm32, 16 集磁器内、外径Dein, Deout/mm72, 96 集磁器厚度te/mm12 初始参考温度T/K293.15(20℃)
3.1.1 线圈温度变化情况
为了更明显地观察驱动线圈上温度随时空的变化情况，依据线圈电流的变化（线圈电流如图7所示）选取了三个时间点：分别是初始时刻（0ms），线圈中电流达到峰值的时刻（0.2ms）以及线圈电流基本衰减至0的时刻（10ms），求取这三个时刻线圈的温度云图，如图8a～图8c所示。可以看出，当线圈电流达到峰值时，线圈上的温度变化很小，而当整个电流的衰减过程结束时，线圈达到了最高温度，这也说明线圈上的热损耗是电流不断积累的结果。
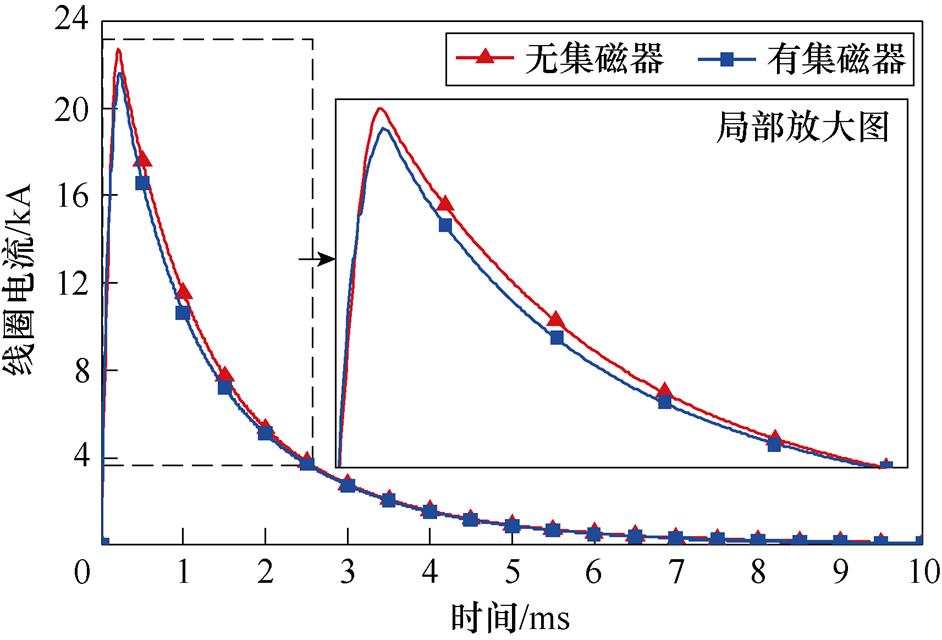
图7 有/无集磁器系统的线圈电流
Fig.7 Coil current of a system with/without a field shaper
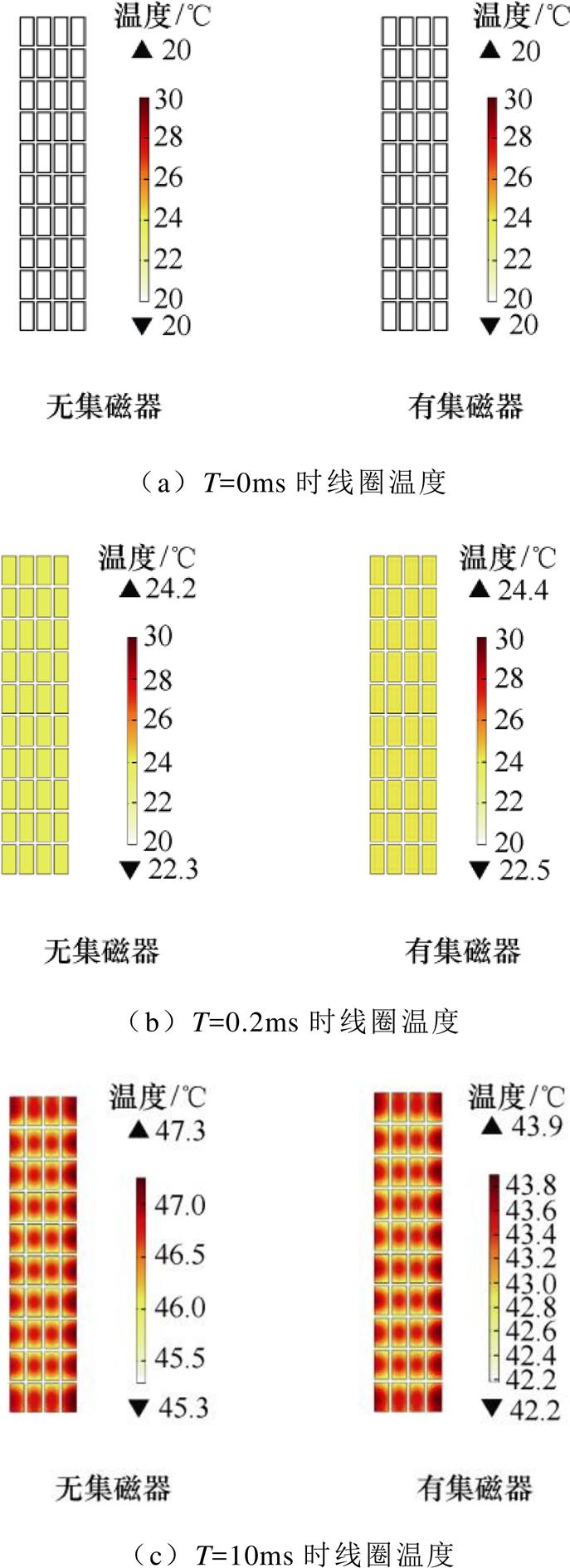
图8 线圈温度变化云图
Fig.8 Cloud diagram of coil temperature change
图9显示了有/无集磁器成形系统中驱动线圈的最大温度变化。可以发现，在20℃的初始温度下，没有使用集磁器时，单次放电后线圈产生的最大温升为27.70℃，引入集磁器后，最大温升降低至24.28℃，约减小了12.35%。
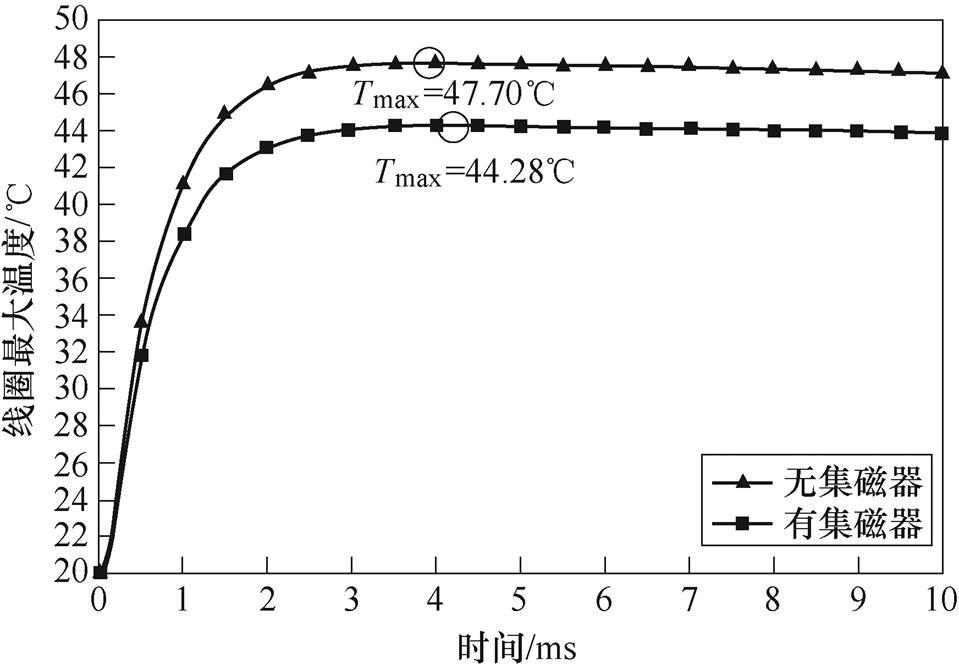
图9 线圈最大温度
Fig.9 Maximum coil temperature
3.1.2 集磁器的温度变化情况
在成形的过程中，集磁器由于感应涡流的作用，也会有一定的温度变化，其感应涡流如图10所示，可以看到，在0.15ms时集磁器中的感应涡流达到最大，在0.2ms时基本衰减至0；为了与线圈的温度变化做比对，选取了0ms、0.15ms、0.2ms和10ms这四个时刻来分析集磁器上的温度，如图11所示。与线圈类似，集磁器上的温度上升也是一个电流累积作用的结果，且由于感应涡流变化比线圈电流更为迅速，在线圈中电流逐步衰减至0时（10ms），集磁器上的温度已由最高时的45℃降低至31.7℃。从图11可以清楚地看到，集磁器温度最高的区域对应其内外表面的工作区，也正是感应涡流由于趋肤效应汇聚的主要区域。
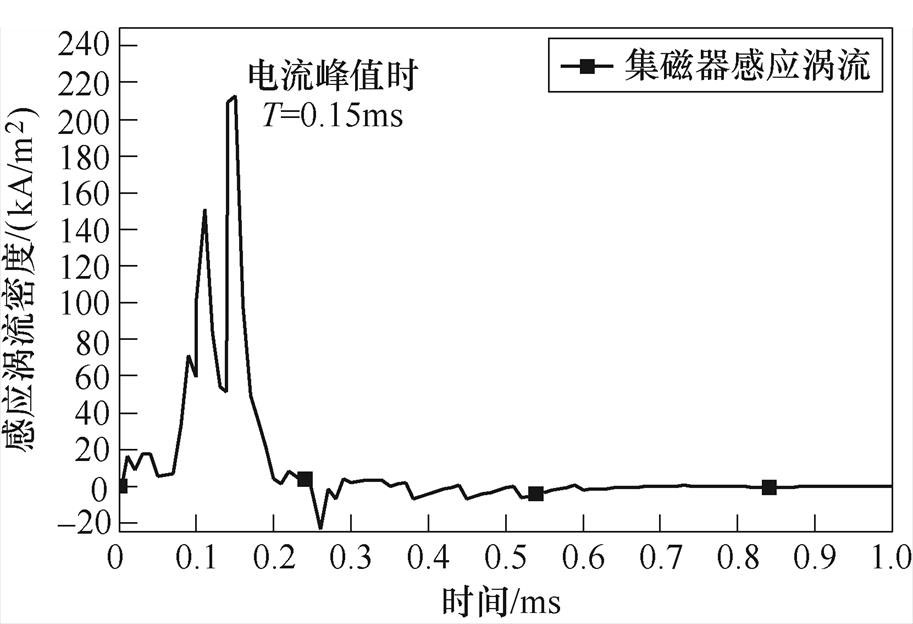
图10 集磁器中的感应涡流
Fig.10 Induction eddy current in the field shaper
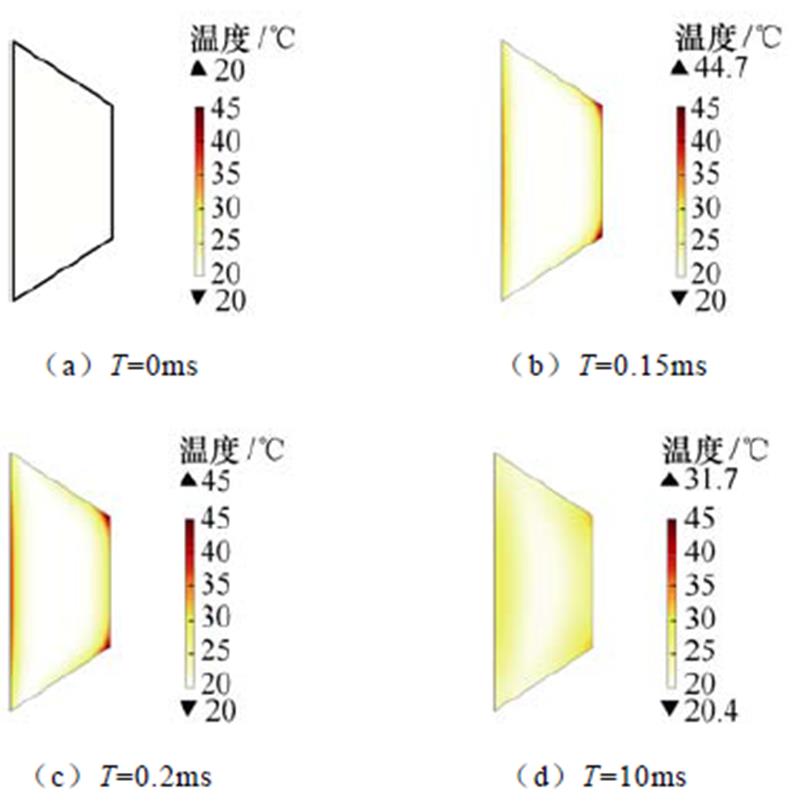
图11 不同时刻集磁器的温度变化
Fig.11 Temperature change of field shaper at different times
3.2.1 集磁器带来的互感变化
在传统的EMF系统中，线圈的发热主要来自线圈电流的损耗，它是一个不断衰减的正弦波，现有的减小线圈发热的做法本质上都是改善线圈电流的波形，例如：文献[21]发现线圈电流中的第一个脉冲波在成形中起到了主导作用，进而提出使用续流回路来吸收多余能量，减少了线圈中的电流振荡。根据式（3）可知，若能优化线圈的电流波形，减少整个脉冲电流所对应的面积，就能达到减少热损耗的目的。
根据第1节对于含有集磁器的等效电路模型的分析，加入集磁器后，为原电路带来了集磁器与线圈间的耦合互感；线圈的磁场作用于集磁器，根据楞次定律，集磁器将产生一个反向的磁链以抵消这种变化，这种变化使得互感反作用于原线圈，将导致原线圈电路中的等效电感L减小，从而使得线圈中的电流能量更小。对于无集磁器和加入集磁器后的模型，分别计算其自感与互感。线圈、工件、集磁器之间的自互感矩阵为
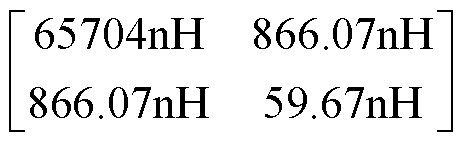
引入集磁器后，多出了线圈与集磁器之间的互感Mc-f =1 617.6nH（其反作用于原电路）和集磁器与工件之间的互感Mf-w=43.41nH，线圈与工件中的互感Mc-w不变，仍为866.07nH。
3.2.2 集磁器对线圈电流的影响
一个EMF系统可以等效看作一个简单的二阶RLC电路，等效电路如图12所示。图12中C为脉冲电源，R为线路中的等效电阻，L为导线、成形线圈的自感Lc与所有互感M之和。经过对电路的分析可知，欠阻尼状态下的电流波形对成形最为有利，本文后面的讨论也都满足这一先决条件，即
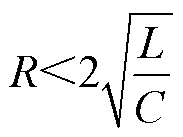（8）
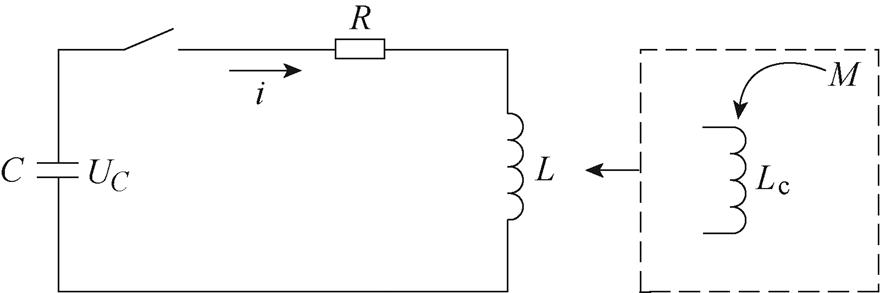
图12 二阶RLC等效电路
Fig.12 Second order RLC equivalent circuit
根据基尔霍夫电压定律，可列得二阶电路方 程为
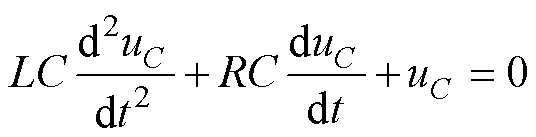（9）
初始条件
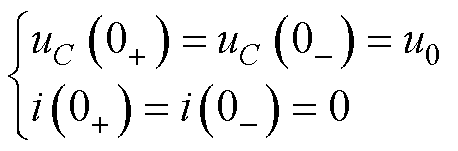（10）
求解该微分方程可得到两个特征根
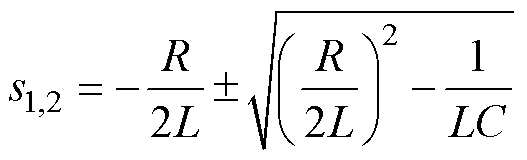（11）
设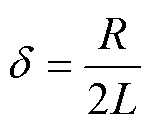
，
，
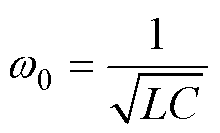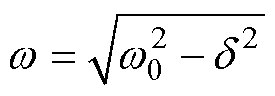；由此，可以得到欠阻尼状态下回路的电流为
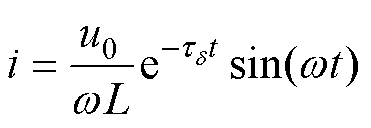（12）
在此对回路电流的最大值和衰减速率进行讨论，通过对RLC电路进行实验得知，电感L的变化对电流幅值的影响十分有限，在本文中，集磁器带来的互感相对于线圈自感是一个较小的值，而且集磁器的引入会带来反向的电压变化，从而使得u0减小，致使线圈电流的幅值减小；耦合互感对电流衰减带来的影响更为显著，电流衰减的时间常数为
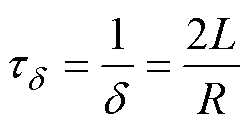（13）
当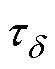
越小时，电流的衰减速度越快，两次成形中的线圈电流如图7所示。由图7不难发现，当引入集磁器后，耦合互感使原电路中的等效电感减少，电路的时间常数减小，线圈中的电流衰减更加迅速；电流的峰值则在集磁器带来的电压作用下减小；引入集磁器后，线圈电流于0.22ms时到达峰值21.59kA，峰值电流减小了1.09kA；故电流对应的积分区域明显减小，总体的热量损耗也相应减小，线圈焦耳热的变化如图13所示。
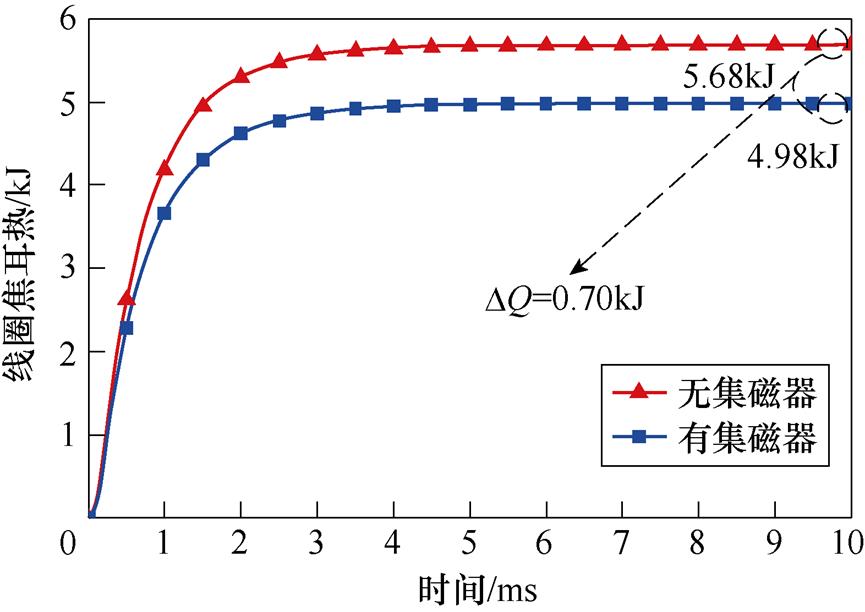
图13 有/无集磁器系统的线圈焦耳热
Fig.13 Joule heat of coil with/without field shaper system
在未引入集磁器的成形系统中，线圈产生的焦耳热为5.68kJ；引入集磁器后，焦耳热减小至4.98kJ，约减小了12.3%，DQ=0.70kJ。
上述分析解释了集磁器降低线圈发热的原理，并对结果进行了比对，证明了其具有良好的降温效果和实施的便捷性；然而，集磁器不仅会对线圈的温度造成影响，同时还会对工件的成形效果产生影响，故本文也对EMF系统加入集磁器后带来的磁场和工件所受电磁力变化进行分析，并且对比最终的变形效果，以总结出可以抑制线圈温升（提高线圈使用率），又可以增加成形的优化方案。
集磁器最主要的作用是对磁场分布进行改变，其施加于线圈与工件之间后，会引起工件中感应涡流的变化，进而改变工件所受到的径向电磁力；在有/无集磁器的两种工况下，工件上的最大磁通密度在0.08ms和0.17ms时达到了最大的6.86T和5.66T，增大了1.2T，管件上的最大磁通密度分布对比如图14所示。两种情况下工件中的感应涡流密度和受到的径向电磁力如图15所示。可以看到，在有/无集磁器的系统中，感应涡流密度分别在0.22ms、0.2ms时达到最大，最大值为92.62kA/m2和89.11kA/m2，增加了3.94%；径向电磁力在0.17ms和0.2ms时达到了最大，分别为194.07kN和183.56kN，增加了5.72%。分析得知，线圈电流的前半段上升沿主导了工件的成形过程（约0.25ms），线圈焦耳热的大量积累发生在下降的后半段。
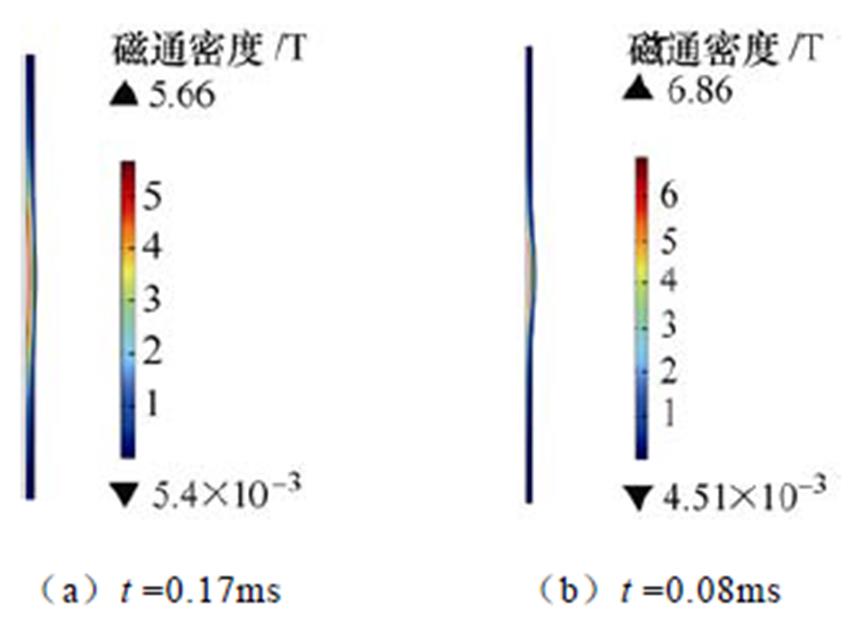
图14 管件上的最大磁通密度分布对比
Fig.14 Comparison of maximum flux density distribution on pipe fittings
图15 感应涡流密度和径向电磁力
Fig.15 Induced eddy current density and radial electromagnetic force
同样的放电初始能量下，引入集磁器后，工件的成形速率与最大成形量均得到了提高，为了更好地体现集磁器带来的影响，选取了工件的内侧中点进行分析，这个点上受到的径向电磁力和位移如图16所示，在集磁器的作用下，工件内侧中点受到的电磁力明显增大；在电磁排斥力的成形过程中最后会有一个吸引力的产生，但这个吸引力十分小，对于工件变形基本无影响[22]；可以看出，两次成形中，电磁力都有一个较小的负值（吸引力），分别为-6.05×107N/m3和-2.2×107N/m3，这与结论吻合。内侧中点的最大径向位移为6.96mm，比无集磁器时增加了4.44mm，整体胀形量提高至约2.76倍；不难看出，工件在0.25ms左右便已基本完成成形，工件整体的成形效果如图17所示。
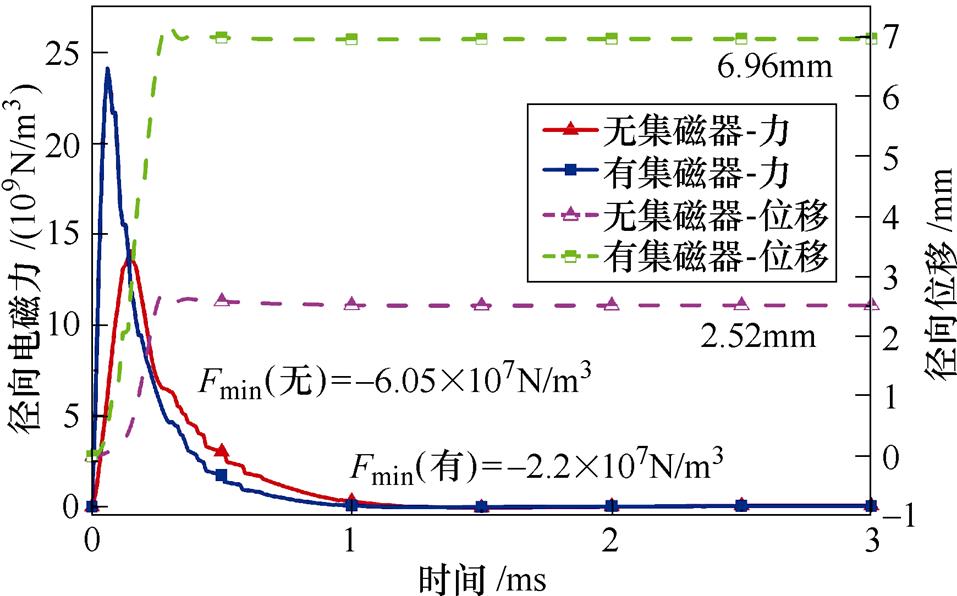
图16 工件内侧中点径向电磁力与位移对比
Fig.16 Comparison of radial electromagnetic force and displacement at midpoint inside the workpiece
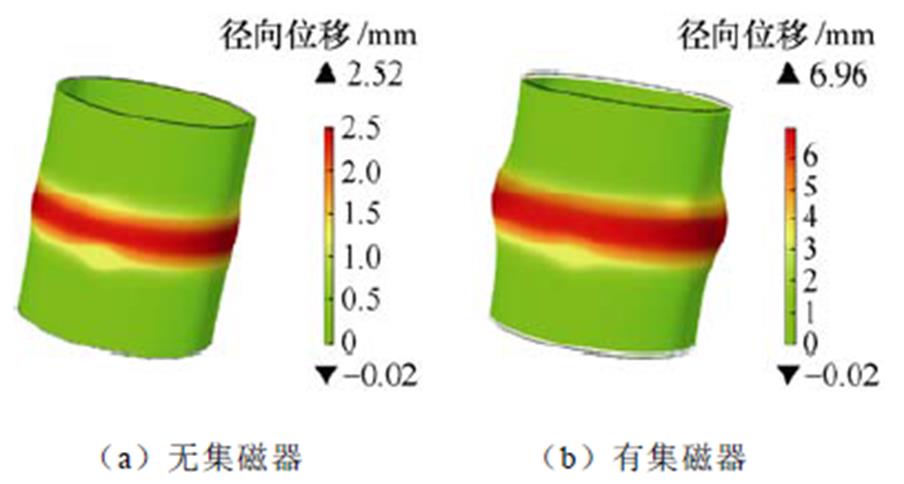
图17 工件成形效果对比
Fig.17 Workpiece forming effect comparison
引入集磁器后，使得磁场集中于管件中点附近（集磁器所在区域），其边缘区域的磁场略有降低，管件的整体径向变形结果如图18所示。不难看出，引入集磁器后并未使管件的可成形范围变小，其主要原因为：电磁成形过程中，管件的主要受力区域高速变形，其余区域的变形往往不是电磁力本身驱动的，而是被高速变形区域“带下去”的，集磁器虽然削弱了部分区域的磁场和电磁力，但反而增大了高速变形区域的电磁力，让这一“带动”效应更明显；同时，引入集磁器后提高了EMF成形过程中的能量效率[15]，整体体现为成形效果更好；在这二者的影响下，管件的可成形区域并未减少。
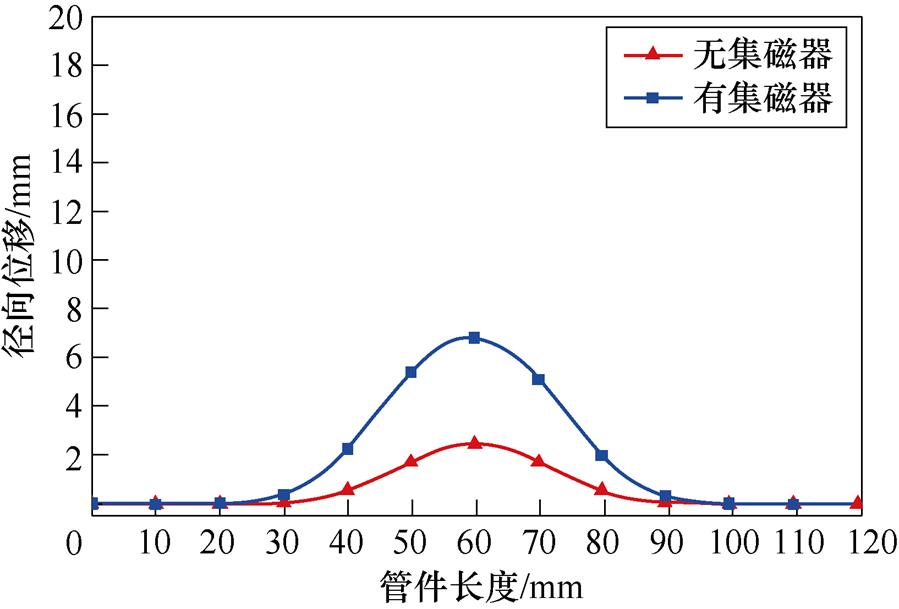
图18 管件整体的径向位移
Fig.18 The radial displacement of the whole workpiece
为了分析不同放电参数下集磁器优化线圈发热的能力，分别仿真了不同初始放电电压下线圈的温度变化情况，其温升降低数据见表3。不难发现，当放电电压从9.5kV增大到12.5kV时，集磁器都能显著降低驱动线圈的温升，但从百分比角度考虑，其能力随着放电电压的提高而略有降低。
表3 不同放电电压下线圈的温升情况
Tab.3 Coil temperature rise at different discharge voltages
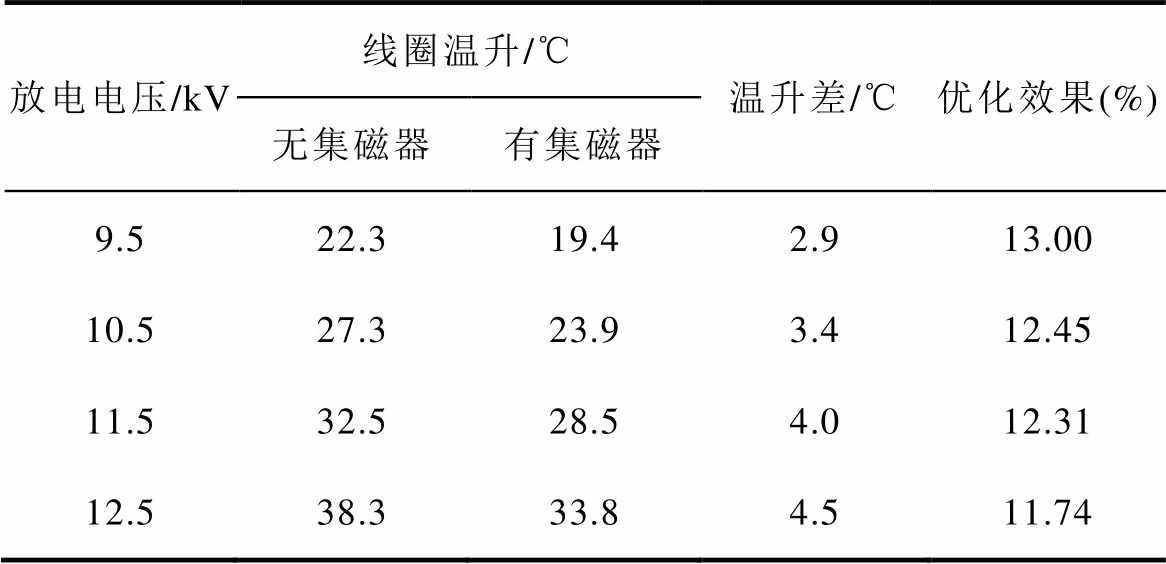
放电电压/kV线圈温升/℃温升差/℃优化效果(%) 无集磁器有集磁器 9.522.319.42.913.00 10.527.323.93.412.45 11.532.528.54.012.31 12.538.333.84.511.74
而当集磁器的制作材料由铜制改为纯铝制时，线圈的最终温度和管件的径向位移分别如图19和20所示；在初始放电电压10.5kV时，线圈温升为23.8℃，管件径向位移为6.26mm，与铜制的集磁器相比，效果有所降低；引起这种变化的主要原因是因为不同材料的电导率不同，会给电磁场分布带来一定影响，但目前工程应用中，综合考虑成本和加工性能，一般集磁器都由铜或者钢等良导体制成，电导率差异不显著，因而其带来的影响不大。同时，集磁器的尺寸与位置也会对效果带来影响，存在一定的优化空间。
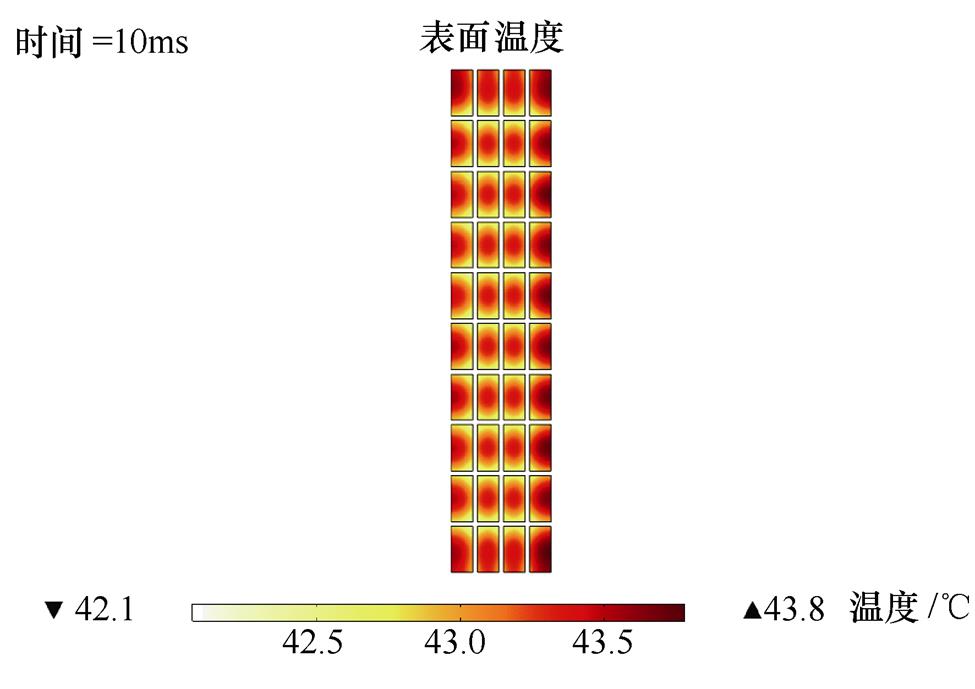
图19 线圈温度变化（铝制集磁器，U0=10.5kV）
Fig.19 Coil temperature change (aluminum field shaper, U0=10.5kV)
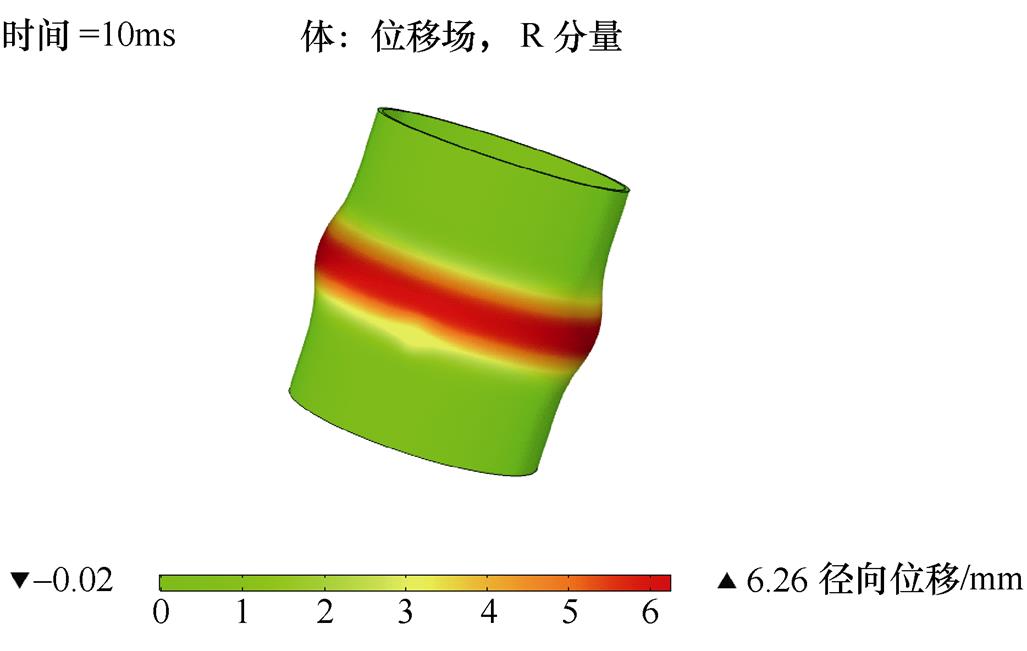
图20 管件径向位移（铝制集磁器，U0=10.5kV）
Fig.20 Radial displacement of workpiece (aluminum field shaper, U0=10.5kV)
通过上述分析可知，作为一种便于实施的优化方法，在EMF系统中使用集磁器可以适当地降低驱动线圈的发热，抑制其温度上升，进而提高线圈的使用寿命；同时，在同样的初始放电能量下，由于集磁器对于磁场分布的改善，可以改变工件所受的电磁力，提高成形质量，增加了能量利用率。
本文提出了一种更为简便的方法可用于优化EMF过程中驱动线圈的发热问题，即在不改变原成形系统时，引入一个辅助成形装置——集磁器；为了验证本文的想法，构建了电磁场-温度场-机械结构场耦合的多物理场模型，通过仿真详细研究了引入集磁器前后对于线圈温度和工件成形的影响。仿真结果如下：
1）线圈的热损耗是线圈电流逐步积累的过程，电流的积分区域正比于线圈产生的焦耳热；引入集磁器后线圈的最大温度上升降低了3.42℃，产生的焦耳热减少了0.7kJ。这是由于引入集磁器后带来了耦合互感和反向电压，影响了原EMF电路的动态过程，在保证欠阻尼的前提下，互感使得原动态电路中的等效电感值减小，进而加快了线圈中电流的衰减速率；反向电压使得等效电压减小，导致电流的峰值减小；二者作用减少了电流的额外损耗；其对减少线圈的发热具有显著的作用。
2）集磁器上产生的感应涡流作用时间十分短暂，使得其在0.2ms时达到了最高温度45℃，但在10ms时（线圈电流衰减至0时刻）降至31.7℃；集磁器相较于线圈，周围的空气流通更加良好，易作降温处理。
3）在相同的初始放电能量下，集磁器由于其对于磁场分布的改善，使得流经工件的磁通密度由5.66T提高到6.86T，同时工件中的感应涡流密度增加了3.94%，工件受到的洛伦兹力提高了5.72%，成形量从2.52mm提升到6.96mm；这也意味着，在相同的变形条件要求下，只需额外引入一个集磁器辅助就可以使用更少的初始放电能量，是一种提高线圈使用寿命和效率的简单而有效的办法。
参考文献
[1] 邱立, 李彦涛, 苏攀, 等. 电磁成形中电磁技术问题研究进展[J]. 电工技术学报, 2019, 34(11): 2247- 2259.
Qiu Li, Li Yantao, Su Pan, et al. Research on electromagnetic problems in electromagnetic forming process[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2247-2259.
[2] 熊奇, 唐红涛, 王沐雪, 等. 2011年以来电磁成形研究进展[J]. 高电压技术, 2019, 45(4): 1171-1181.
Xiong Qi, Tang Hongtao, Wang Muxue, et al. Research progress of electromagnetic forming technique since 2011[J]. High Voltage Engineering, 2019, 45(4): 1171-1181.
[3] Xiong Qi, Zhao Xiang, Zhou Hang, et al. A triple-coil electromagnetic two-step forming method for tube fitting[J]. The International Journal of Advanced Manufacturing Technology, 2021, 116(11/12): 3905- 3915.
[4] 熊奇, 杨猛, 周丽君, 等. 双线圈吸引式板件电磁成形过程中的涡流竞争问题[J]. 电工技术学报, 2021, 36(10): 2007-2017.
Xiong Qi, Yang Meng, Zhou Lijun, et al. Eddy Currents competition in electromagnetic forming process of plates by double-coil attraction[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(10): 2007-2017.
[5] Xiong Qi, Gao Dun, Li Zhe, et al. Electromagnetic attraction bulging of small aluminum alloy tube based on a field shaper[J]. The International Journal of Advanced Manufacturing Technology, 2021, 117(1/2): 511-521.
[6] Dong Pengxin, Li Zhangzhe, Feng Sheng, et al. Fabrication of titanium bipolar plates for proton exchange membrane fuel cells by uniform pressure electromagnetic forming[J]. International Journal of Hydrogen Energy, 2021, 46(78): 38768-38781.
[7] 李成祥, 石鑫, 周言, 等. 针对H型线圈的电磁脉冲焊接仿真及线圈截面结构影响分析[J]. 电工技术学报, 2021, 36(23): 4992-5001.
Li Chengxiang, Shi Xin, Zhou Yan, et al. Electro- magnetic pulse welding simulation for H-type coil and analysis of the influence of coil cross-sectional structure[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4992-5001.
[8] 李成祥, 杜建, 周言, 等. 电磁脉冲板件焊接设备研制及镁/铝合金板焊接实验研究[J]. 电工技术学报, 2021, 36(10): 2018-2027.
Li Chengxiang, Du Jian, Zhou Yan, et al. Develop- ment of electromagnetic pulse welding equipment for plates and experimental research on magnesium/ aluminum alloy welding[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2018-2027.
[9] 张望, 王于東, 李彦涛, 等. 基于双向电磁力加载的管件电磁翻边理论与实验[J]. 电工技术学报, 2021, 36(14): 2904-2911.
Zhang Wang, Wang Yudong, Li Yantao, et al. Theory and experiment of tube electromagnetic flanging based on bidirectional electromagnetic force loading[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2904-2911.
[10] Werdelmann P, Rosendahl J, Peier D. Assessing the effective energy for magnetic forming processes by means of measurements and numerical calculation[C]// 3rd International Conference on High Speed Forming, Dortmund, Germany, 2008: 283-290.
[11] Gies S, Löbbe C, Weddeling C, et al. Thermal loads of working coils in electromagnetic sheet metal for- ming[J]. Journal of Materials Processing Technology, 2014, 214(11): 2553-2565.
[12] Gies S, Tkkaya A. Analytical prediction of Joule heat losses in electromagnetic forming coils[J]. Journal of Materials Processing Technology, 2017, 246: 102-115.
[13] Golovashchenko S, Bessonov N, Davies R. Design and testing of coils for pulsed electromagnetic forming[C]//2nd International Conference on High Speed Forming, Dortmund, Germany, 2006: 141-151.
[14] Cao Quanliang, Han Xiaotao, Lai Zhipeng, et al. Analysis and reduction of coil temperature rise in electromagnetic forming[J]. Journal of Materials Processing Technology, 2015, 225: 185-194.
[15] Qiu Li, Deng Kui, Li Yantao, et al. Analysis of coil temperature rise in electromagnetic forming with coupled cooling method[J]. International Journal of Applied Electromagnetics and Mechanics, 2020, 63(1): 45-58.
[16] 王紫叶, 杨猛, 熊奇. 电磁成形过程中线圈温升及结构优化[J]. 电工技术学报, 2021, 36(18): 3891- 3901.
Wang Ziye, Yang Meng, Xiong Qi. Coil temperature rise and structure optimization in electromagnetic forming[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3891-3901.
[17] 黄浩. 基于集磁器的板材电磁成形校形研究[D]. 宜昌: 三峡大学, 2019.
[18] Xiong Qi, Li Zhe, Tang Jianhua, et al. A flexible and economical method for electromagnetic flanging of tubes with field shapers[J]. The International Journal of Advanced Manufacturing Technology, 2021, 116(3/4): 1169-1177.
[19] 黎镇浩, 曹全梁, 赖智鹏, 等. 电流丝法在电磁成形线圈电流和工件电磁力计算中的应用[J]. 电工技术学报, 2018, 33(18): 4181-4190.
Li Zhenhao, Cao Quanliang, Lai Zhipeng, et al. Application of current filament method on the calculation of current and force in electromagnetic forming[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4181-4190.
[20] 张骁. 脉冲强磁场作用下管件胀拉成形数值模拟与实验研究[D]. 武汉: 华中科技大学, 2017.
[21] Du Limeng, Xia Liangyu, Li Xian, et al. Adjustable current waveform via altering the damping coefficient: a new way to reduce Joule heating in electromagnetic forming coils[J]. Journal of Materials Processing Technology, 2021, 293: 117086.
[22] Xiong Qi, Tang Hongtao, Deng Changzhen, et al. Electromagnetic attraction-based bulge forming in small tubes: fundamentals and simulations[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 1-5.
Abstract As an emerging metal processing and forming technology, electromagnetic forming (EMF) has been widely studied by domestic and foreign experts because of its unique technical advantages. The electromagnetic environment in the process of EMF is very harsh. Existing studies have confirmed that the electromagnetic heat loss of the drive coil is caused by the accumulation of Joule heat, and the electromagnetic heat in the EMF process will affect the structural strength of the drive coil, which in turn reduces the service life and frequency of the coil. The coil performance will be improved by reducing the electromagnetic heat loss of the coil. The integral area of the coil current will be reduced, as the electromagnetic heat loss of the drive coil is due to the accumulation of Joule heat. Based on this, this paper proposes an optimization method for solenoid coil heating.
Firstly, by analyzing the temperature field in the EMF system, it is proposed to use a filed shaper to assist the forming to reduce the coupling mutual inductance of the system, the reduction of time constant results in the decrease of the integral area of the coil current and finally achieving the purpose of reducing the electromagnetic heat generated by the coil. At the same time, the inductance matrix of the solenoid coil, the forming workpiece, and the field shaper is calculated to support this. Through the finite element method, the temperature field is introduced on the basis of the electromagnetic-structural field coupling model, and a fully coupled electromagnetic-structural-temperature field model considering the change of the resistivity of the materials used in each component of the EMF device with temperature is established to verify the feasibility of the forming scheme.
The simulation results show that the electromagnetic expansion of pipe fittings is carried out by using a drive coil with an inner diameter of 49.6mm, an outer diameter of 68mm, and a turn count of 4×10 turns, with the help of introducing a filed shaper when the discharge voltage is 10.5kV, the maximum temperature of the coil is reduced by 12.35%, which is 3.42℃. The Joule heat generated by the coil decreased by 12.3%, a reduction of 0.7kJ. The filed shaper reaches a maximum temperature of 45℃ at 0.2ms, but drops to 31.7℃ at 10ms (when the coil current decays to 0); The magnetic flux density in the workpiece is increased by 21.2% and the induced eddy current density is improved by 3.94%, resulting in a 5.72% enhancement in the Lorentz force on the workpiece. The final forming volume has grown 176%, from 2.52mm to 6.96mm.
The results show that: ① The heat loss of the coil is the result of the gradual accumulation of coil current, and the integral region of the current is proportional to the Joule heat generated by the coil. After the introduction of the field shaper, the coupling mutual inductance in the system is reduced, thereby reducing the equivalent inductance value in the original dynamic circuit and accelerating the attenuation rate of the current in the coil. It alsobrings a reverse voltage, so that the equivalent voltage decreases, resulting in a decrease in the peak value of the current; The combination of the two reduces the additional current losses. ② The induced eddy current in the field shaper has a very short acting time, and compared with the coil, the surrounding air circulation is better, which is easy to do the cooling treatment. ③Under the same deformation conditions, the introduction of magnetizer assistance can reduce the initial discharge energy and reduce the temperature rise of the coil, which is a simple and effective way to improve the service life and efficiency of the coil.
Keywords：Electromagnetic forming, drive coil, field shaper, coil heating, coupling mutual inductance
中图分类号：TM154
DOI: 10.19595/j.cnki.1000-6753.tces.211564
国家自然科学基金（51707104）和武汉强磁场学科交叉资金（WHMFC202121）资助项目。
收稿日期 2021-09-30
改稿日期 2022-02-17
E-mail: pandaqi0218@gmail.com（通信作者）
李青山 男，1998年生，硕士研究生，研究方向为电磁场分析与应用。
E-mail: rillusion4682@gmail.com
（编辑 郭丽军）