图1 变换器拓扑结构
Fig.1 Converter topology
摘要 直流变换器是中压直流（MVDC）汇集系统中的关键部分，起着升压、隔离、电能传输等功能。相比传统的中压交流汇集方案中体积巨大的变压器，中压直流方案中的变换器由于采用中高频控制可大幅减少装置体积。为适应新能源发电端口电压越来越高的发展趋势，该文提出一种无环流零电流软开关（ZCS）三电平复合全桥变换器，其由一个半桥三电平电路和全桥电路共同复用2个开关管而构成，从而所有开关管的电压应力只有输入电压一半，不仅有利于该变换器应用于高输入电压场合，同时还保留所有开关管的软开关特性且消除一次侧环流。为进一步降低所有开关管的峰值电流和辅助开关管的关断电流，又引入了LC串联谐振技术，可大幅降低辅助开关管的关断电流，从而使其开关损耗得到进一步降低。该文对变换器中关键参数进行分析设计，通过PLECS进行仿真，并制作了一台150 V/750 V/1 kW的样机进行了实验验证。
关键词：中压直流汇集 谐振式复合全桥三电平变换器 LC串联谐振 DC-DC变换器
随着传统化石能源的枯竭以及全球环境问题的日益严重，新能源受到了世界各国的广泛关注。利用新能源逐步取代传统化石能源进行发电将成为今后发展的必然趋势。相比于传统的中压交流汇集方案，新能源发电采用中压直流（Medium-Voltage DC, MVDC）汇集具有较多的优势，如去除了笨重的工频变压器、没有交流振荡稳定问题等，是新能源发电汇集重要的发展方向之一[1]。
大功率直流升压变换器是新能源发电中压直流汇集方案中的重要组成部分，目前在大功率场合，IGBT仍然是最主要的功率器件，而大功率工况下实现IGBT的零电流软开关（Zero Current Switching, ZCS）对于降低开关损耗、提高变换效率、实现新能源发电的更高效利用具有重要意义。国内外有关学者对直流升压变换器展开了一系列研究，文献[1-6]提出在变压器二次或一次绕组上并联由两只辅助开关管与一个谐振电容串联的辅助电路，显著地增加了导通损耗。
瑞士苏黎世联邦理工学院J. W. Kolar教授等提出了一种全桥结构与中性点钳位混合型的LC串联谐振变换器，在高压侧采用三电平结构以降低器件电压应力[7-10]。该串联谐振变换器根据谐振频率与开关频率的不同可以工作于多种模式，但工作于电流断续模式时可实现所有开关管的零电流软开关，而此时相当于工作于直流变压器模式，不能调节端口电压。
文献[11-12]提出了一种可实现4个单向导通主开关管ZCS的电流型全桥变换器，单向导通性可保证电流谐振到零后不会反向过零继续增加，以方便主开关管实现ZCS。但由于在主功率回路中增加了4个二极管，所以该变换器效率有所降低。文献[13]提出了一种电流型ZCS全桥变换器，同样需要在一次侧IGBT中串入二极管，增加了导通损耗。
文献[14-18]提出了一种复用桥臂组合型ZCS全桥变换器，基于器件复用原理[19-21]，采用两个全桥变换器的复用方案，减少了器件及相应驱动器的数量，4个开关管可实现零电流的开通与关断，两个辅助开关管实现零电压开通与零电压关断，同时除去了高压侧的滤波电感，消除了高压电感存在的绝缘问题。但该电路同样存在一些不足，如在一次电流续流期间，辅助全桥电路一次电流其实是不向二次侧传递能量的，因此其在一次侧续流无意义，只会在辅助全桥变换器的开关管和变压器的一次侧增加无谓的导通损耗，降低了变换器效率。
文献[22]也提出了一种复用桥臂组合型ZCS全桥变换器，电路相对简单，但在中高压侧需要一个高压滤波电感，给滤波器的设计与制造带来了较大挑战。
综上所述，现有的中压大容量DC-DC变换器应用于MVDC汇集系统时或多或少存在一些问题，如模块组合型双有源桥（Dual-Active-Bridge, DAB）变换器的单个模块容量难以做大，且二次侧采用二极管整流桥时会增大器件的电流应力；模块化多电平变换器（Modular Multilevel Converter, MMC）所需的开关器件数目多、成本高等。
针对上述DC-DC变换器存在的问题，本文提出了一种适用于新能源MVDC汇集的无环流ZCS三电平谐振式复合全桥变换器，借助LC谐振技术，在相同的变换器端口电气参数情况下，该变换器可有效降低电流峰值，并可以实现辅助开关管的关断电流低于其峰值电流，有助于降低关断损耗。
在引言中所述的复用桥臂组合型ZCS全桥变换器，电路复杂度较低，但在中高压侧需要一个高压滤波电感，给滤波器设计与制造带来了较大挑战，因此将该高压滤波电感去除，利用变压器漏感或外接的低压电感来实现能量传输，同时引入阻断电容Cb，实现变压器一次侧无环流，如图1a所示。为了降低输入侧开关器件电压应力，将全桥结构改为三电平结构，形成无环流ZCS三电平复合全桥变换器，有利于开关器件的选型，如图1b所示。此时变换器的电流波形为三角形，在相同的传输功率下其电流峰值偏高，且辅助开关管Q5/Q6的关断电流一定等于其峰值电流，为了降低电流峰值，引入谐振电容Cr，提出无环流ZCS三电平谐振式复合全桥变换器，如图1c所示。
图1中，在变压器一次侧，输入分压电容Cin1和Cin2、续流二极管VDc1和VDc2、飞跨电容Css、主变压器Tr1的一次绕组、电感Lt、谐振电容Cr、开关管Q1～Q4组成半桥三电平结构单元。开关管Q2、Q3、Q5和Q6、阻断电容Cb、辅助变压器Tr2的一次绕组组成辅助全桥结构单元，Q5和Q6分别额外有一个并联电容C5和C6，可见，开关管Q2和Q3为两个单元所复用。在变压器二次侧，Tr1的二次绕组和4个整流二极管VDR1～VDR4组成主整流单元，Tr2的二次绕组和4个整流二极管VDR3～VDR6组成辅助整流单元，类似地，VDR3和VDR4为主辅两个整流单元所复用。两个变压器的二次绕组匝数与一次绕组匝数之比分别为N1和N2。通过合理设计N1和N2，三电平电路将传输90%或者更高的总功率，而剩下的小部分功率则由辅助全桥电路传输。
图1 变换器拓扑结构
Fig.1 Converter topology
图2给出了所提变换器无环流ZCS三电平谐振式复合全桥变换器的典型工作波形，Q1/Q2、Q3/Q4分别以50%的固定占空比同时开通和关断。Q5和Q6则采用PWM斩波控制。由于变换器结构和工作原理的对称性，下面仅分析半个开关周期[t0, t4]内的工作原理，在具体分析前，先作如下假设：Cin1、Cin2和Co都足够大且Cin1=Cin2，因此认为稳态下的输入电压Vin和输出电压Vo恒定，且Cin1和Cin2均分输入电压，即VCin1=VCin2=Vin/2。
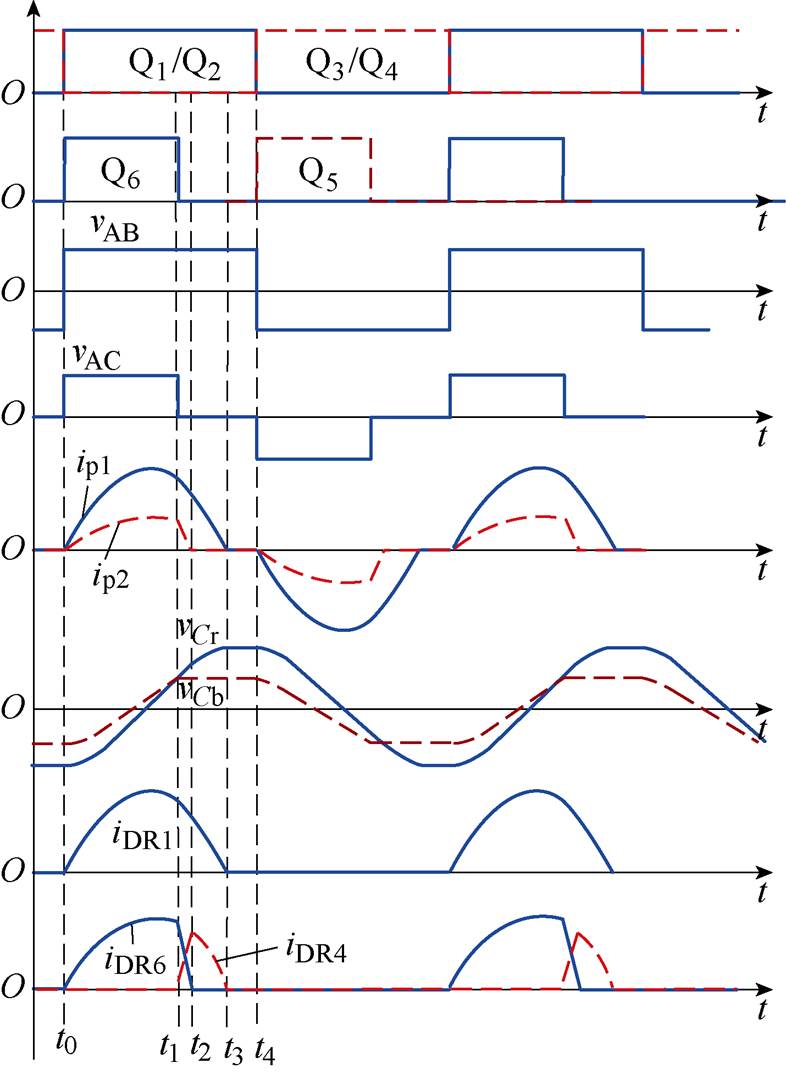
图2 工作主要波形
Fig.2 Main waveforms of work
由图2可知，该变换器在半个中频开关周期内可分为四个模态，各模态相应的电流通路如图3所示。
（1）t0：t0是一个新开关周期的起点，在该时刻，Q3和Q4被关断，而Q1、Q2和Q6则被开通。从所给的电流波形可知，在t0时刻之前所有开关管中都没有电流流过。因此，Q3和Q4是ZCS关断，而Q1、Q2和Q6是ZCS开通。
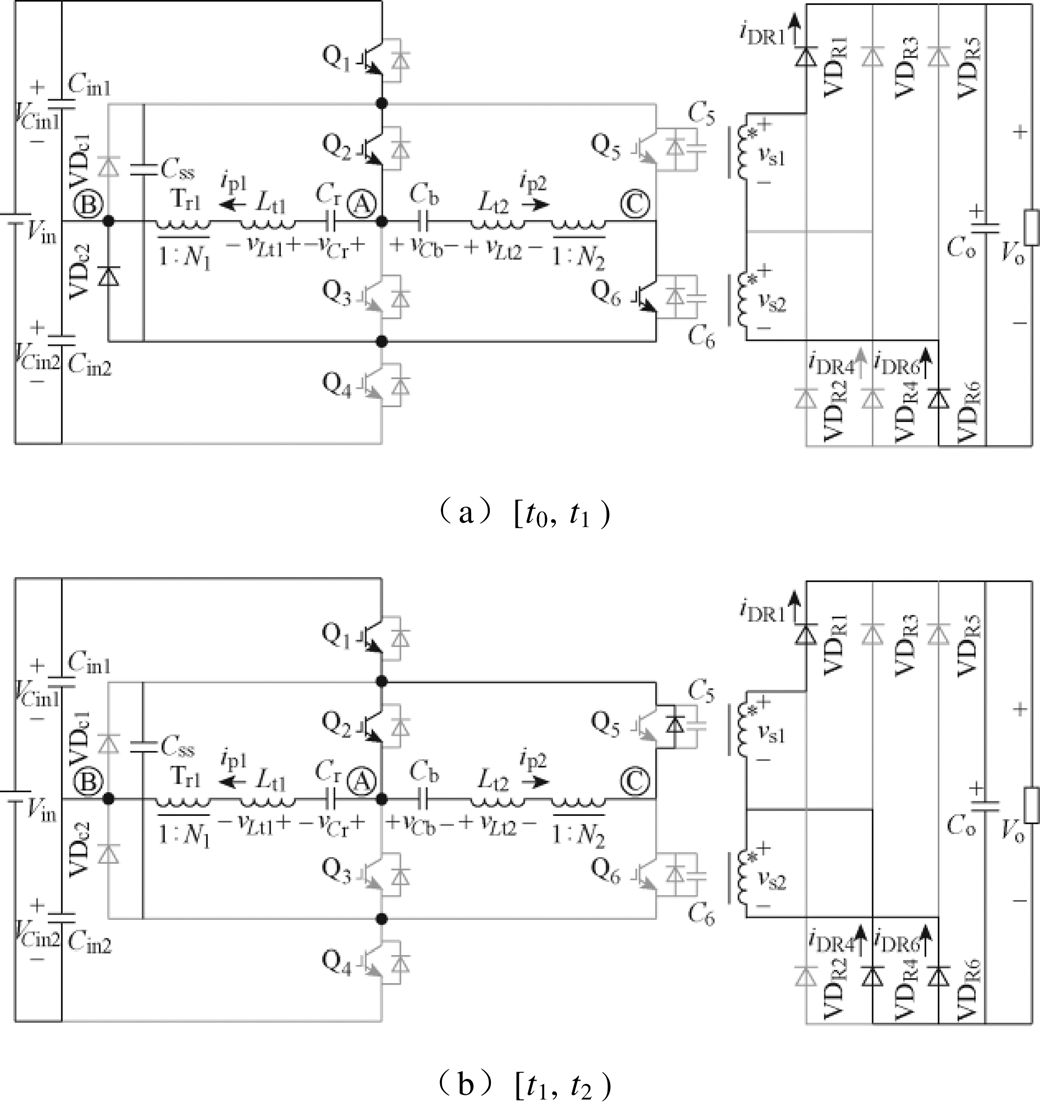
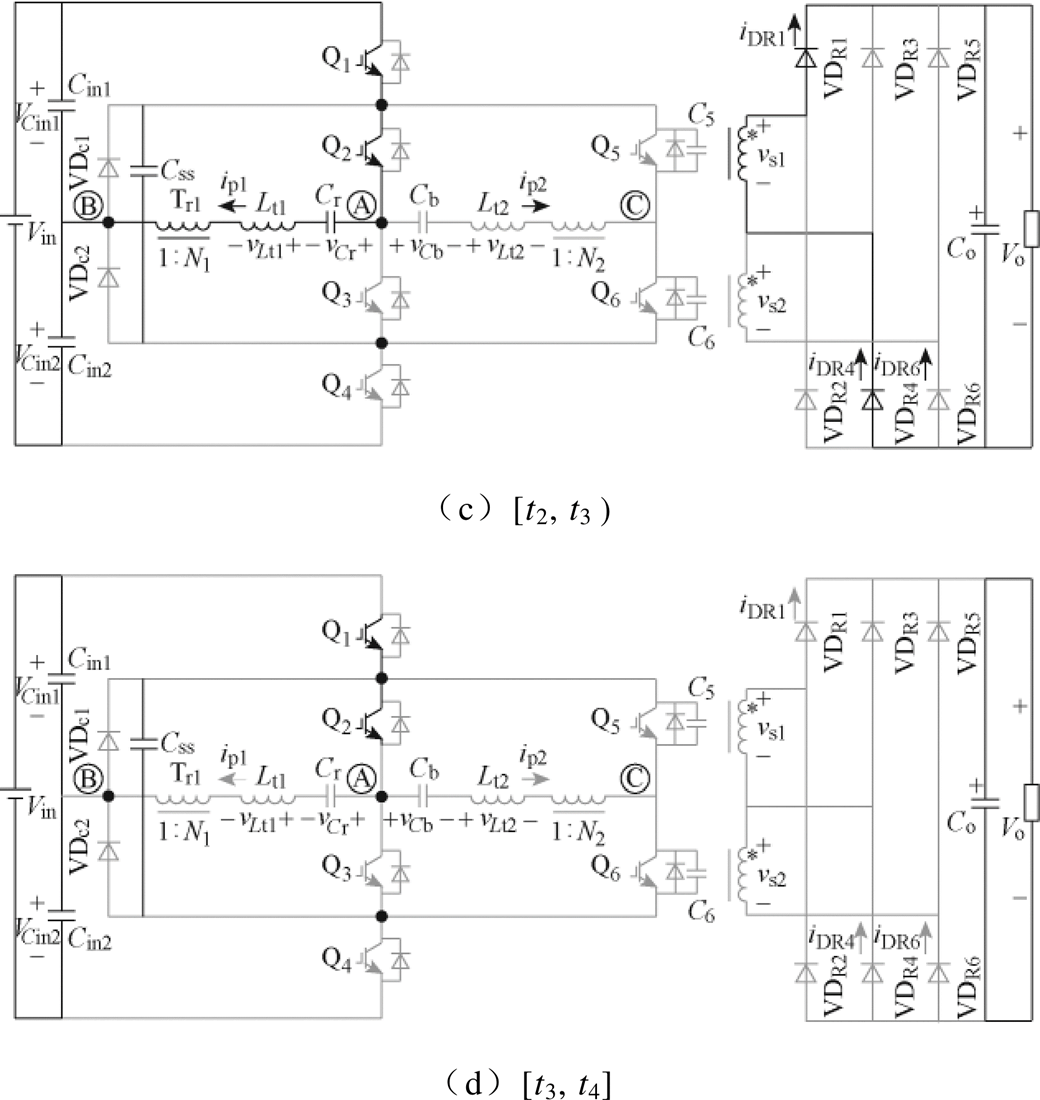
图3 各模态电流通路
Fig.3 Each modal current path
（2）模态1 [t0, t1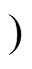
（等效电路见图3a）：可见，vAB=vAC=Vin/2。此时两个变压器的电流都流经Q1和Q2向二次侧供电。二次整流侧两个绕组串联，模态1的等效电路如图4所示。根据电流通路可知本模态中
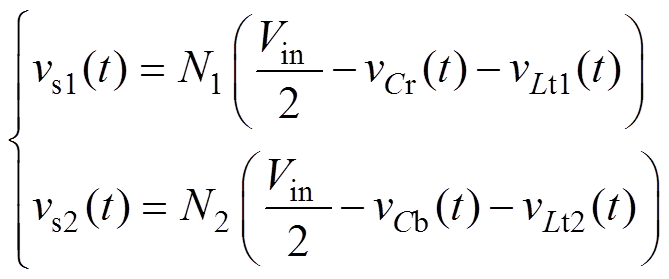（1）
式中，vs1和vs2分别为变压器Tr1和Tr2二次绕组电压；vLt1和vLt2分别为电感Lt1和Lt2两端电压；vCb为阻断电容Cb两端电压；vCr为谐振电容Cr两端电压。
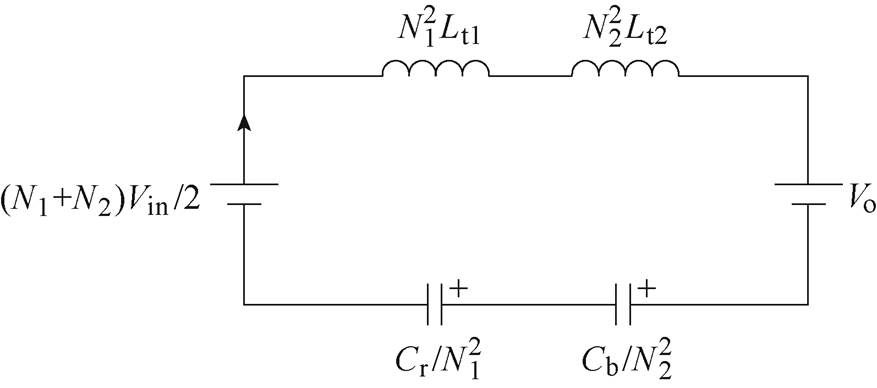
图4 模态1等效电路
Fig.4 Equivalent circuit of mode 1
显然，vLt1和vLt2的表达式分别为
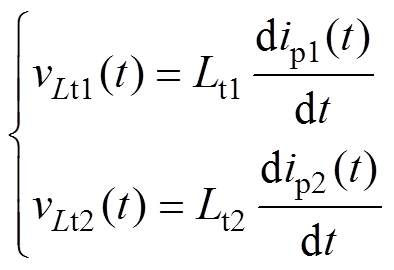（2）
式中，ip1和ip2分别为Tr1和Tr2的一次电流。此外，vCr和ip1、vCb和ip2之间满足
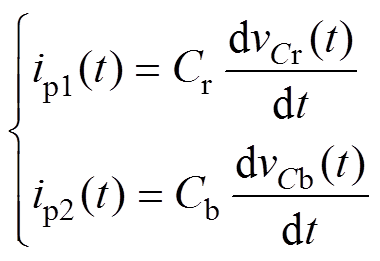（3）
根据本模态中二次电流通路可知，电流和电压的关系应分别满足
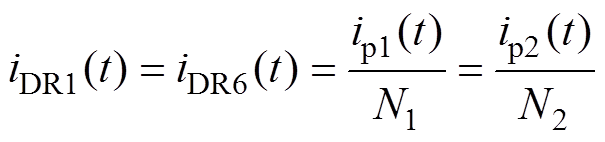（4）
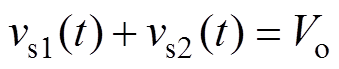（5）
式中，iDR1、iDR6分别为VDR1和VDR6的电流。
将式（1）～式（4）代入式（5）中可得
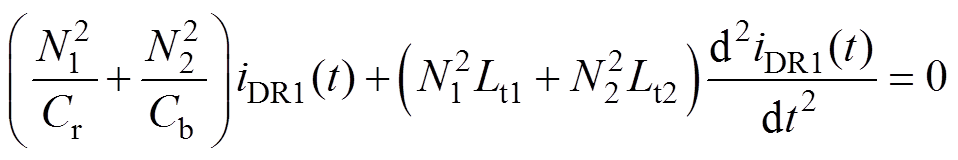（6）
取vCr的初始值为vCr(t0)、vCb的初始值为vCb(t0)，且ip2的初始值为零（当ip1与ip2为正时，其对应的初始值vCr(t0)和vCb(t0)为负），则对式（6）进行简化可得
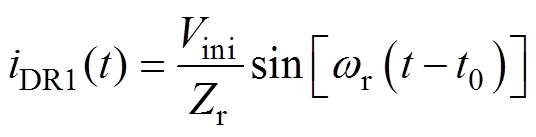（7）
其中
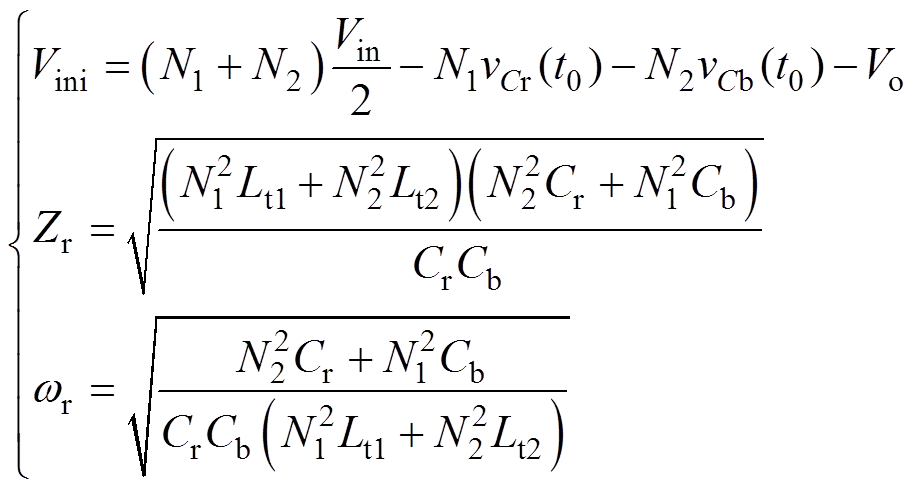（8）
（3）模态2 [t1, t2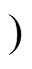（等效电路见图3b）：在t1时刻关断Q6，辅助变压器电流ip2给C5放电，其电压下降，同时ip2给C6充电，其电压上升，因此，两个电容抑制了Q6端电压的上升率，帮助Q6实现了近似零电压关断。当C5放电至零时，ip2则从Q5的反并联二极管流过，因此vAB=Vin/2，vAC=0。同时，二次整流侧进行从VDR6到VDR4的换相，即VDR4的电流iDR4在t1时刻从零开始上升（VDR4自然导通），而iDR6从t1时刻开始下降。可见，本模态中VDR4和VDR6同时导通，意味着Tr2二次绕组电压一直为零。因此，Tr2一次绕组电压也一直为零，本模态中的Cb相当于一个直流阻断源，在其电压的抑制作用下，ip2和iDR6会快速下降，并于t2时刻下降至零，从而完成从VDR6到VDR4的换相，且VDR6实现了ZCS关断。设ip2(t1)=ip2_t1，vCb(t1)=vCb_t1，由于Lt2和Cb谐振，可得Lt2的电流（即ip2）和iDR6的表达式分别为
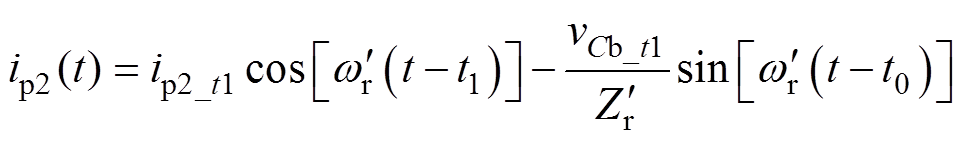（9）
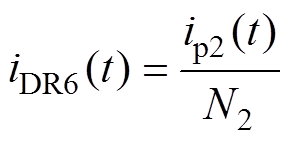（10）
其中
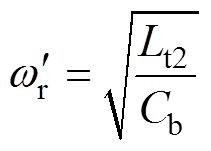
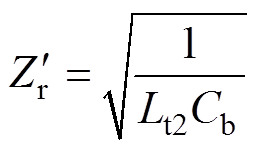
另外，ip1的电流通路不变，设ip1(t1)=ip1_t1，vCr(t1)=vCr_t1，Tr1二次绕组电压被钳位为Vo，将其折算至Tr1一次侧后可得ip1和iDR1分别为
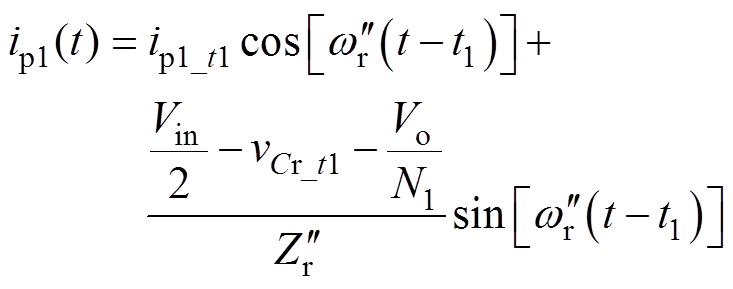（11）
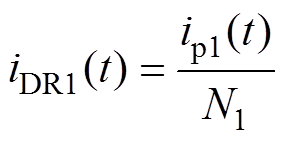（12）
其中
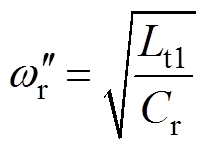
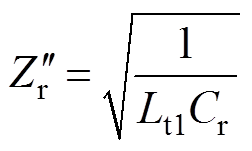
（4）模态3 [t2, t3（等效电路见图3c）：在t2时刻ip2和iDR6下降为零，VDR4和VDR6完成了换相，ip1的电流通路依旧保持与模态1和模态2中的相同，二次整流侧的电流通路则只由VDR4、Tr1二次绕组、VDR1组成。因此，本模态中Tr1二次绕组电压依旧被钳位为Vo，ip1与模态2相同，直接代入模态3所对应的时刻即可。可见，ip1在本模态中也是以谐振形式下降，并且于t3时刻下降为零。另外，vCb在本模态中恒定不变，即满足
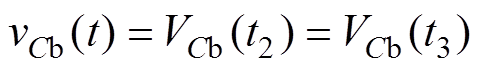（13）
（5）模态4 [t3, t4]（等效电路见图3d）：在t3时刻，ip1、iDR1、iDR4也均已下降为零，VDR1和VDR4实现了ZCS关断。尽管Q1和Q2处于开通状态，但电流ip1、ip2、iDR1、iDR4、iDR6一直为零，所以vCb在本模态中也恒定不变。在t4时刻关断Q1和Q2，由于此时两个开关管的电流都为零，因此实现了零电流关断。经过死区时间后再开通Q3、Q4和Q5，由于其电流上升率受到了限制，因此实现了零电流开通。由于在此之前Q5的端电压已经下降为零，所以Q5实现了零电压零电流软开关（ZVZCS）开通。
综合上面的模态分析，可得Q1～Q6的软开关特性见表1，可见，主开关管都实现了ZCS。
表1 半导体器件的开关特性
Tab.1 Switching characteristics of semiconductor devices
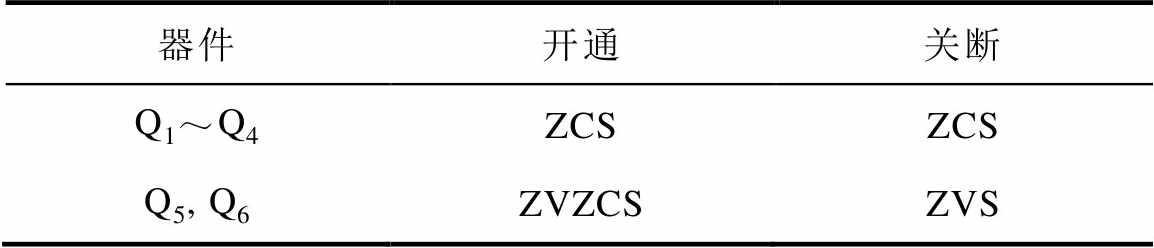
器件开通关断 Q1～Q4ZCSZCS Q5, Q6ZVZCSZVS
该变换器的主要电气参数为主变压器匝比N1、辅助变压器匝比N2、谐振电容Cr、阻断电容Cb、以及电感Lt1和Lt2，为了使变换器正常工作且效率更高，需要对这些参数（尤其是谐振参数）进行优化设计。为了方便分析和仿真对比，本节采用下列变换器参数：输入电压Vin=1.5 kV，输出电压Vo= 15 kV，额定功率PN=1 MW，开关频率fs=2 kHz，开关周期Ts=1/fs=0.5 ms。
主辅两个变压器的二次侧匝数与一次侧匝数之比分别为N1和N2，由于三电平主回路中4个开关管都实现了ZCS，所以希望三电平主回路传输绝大部分功率以提高变换效率，而功率与变压器匝比密切相关，本节将详细阐述变压器匝比的选择。由于下半个开关周期的工作模式与上半个开关周期类似，下面将只分析 [t0, t4] 区间工作情况。
假设变换器为无损耗，[t0, t4] 的总功率Ptot可以表示为
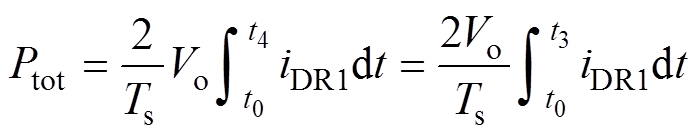（14）
同理，主电路传输的功率Ptr1为
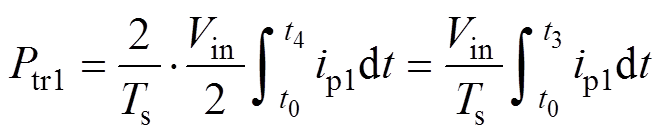（15）
根据时间区间 [t0, t3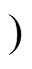 内ip1和iDR1的比例关系，Ptr1也可表示为
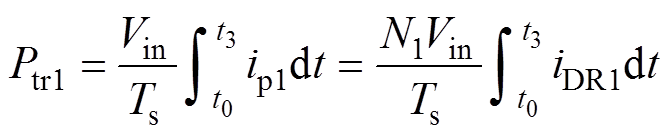（16）
由式（14）和式（16）可得
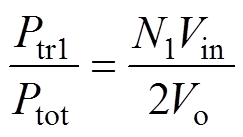（17）
根据能量守恒可知，Tr2传输的功率Ptr2为
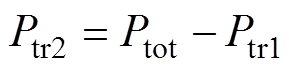（18）
因此可得
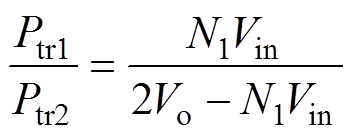（19）
从式（19）可以看出，当Vin与Vo已知时，变压器匝比N1决定了两个变压器的功率。且N1越大，Ptr1占整个功率的比例越大，而Ptr2占整个功率的比例越小，因此，为了让主变压器Ptr1传输绝大部分功率，N1取数应当比较大。不失一般性，当N1取18时，Ptr1占整个功率的90%、而Ptr2仅占整个功率的10%。
假设满载条件下模态4时间区间为零，因此有
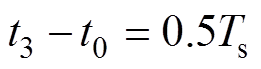（20）
电感Lt1两端的伏秒积平衡应满足
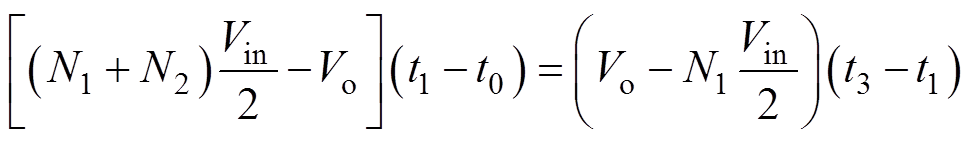（21）
整理式（20）、式（21）可得
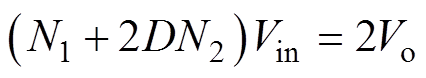（22）
式中，D为Q5和Q6的占空比，即DTs=t1-t0。
显然D＜0.5，因此N2应满足
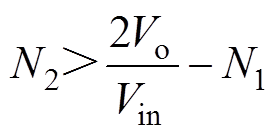（23）
因此，当N1=18时，N2应大于2。此外，由模态1的分析可得
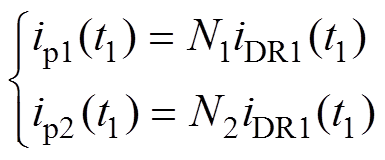（24）
可见，ip2(t1)会随着N2的减小而降低，实际上也就降低了Q5和Q6的峰值电流以及关断电流。因此选择较小的N2可使得ip2(t1)较小，从而减小整体损耗。
Cr、Cb的取值：①会影响vCr(t0)、vCb(t0)绝对值的大小，即谐振电容和阻断电容电压应力的大小，从而影响谐振电容和阻断电容的体积；②可能会影响ip1_max、ip2_max和ip1(t1)、ip2(t1)的大小，即电流应力和Q5和Q6关断电流的大小，后者影响变换器整体的开关损耗；③会影响ip1、ip2下降为零的时间，即模态2、模态3的时间长度，辅助单元的续流时间相对于主单元的续流时间越短、导通损耗越小；④需要保证谐振的周期小于开关周期。为此，下面将详细介绍不同Cr、Cb下|vCr(t0)|、|vCb(t0)|、ip1(t1)、ip2(t1)和t2-t1、t3-t1的变化规律。
由模态1的等效电路可得流过电感的电荷分别为
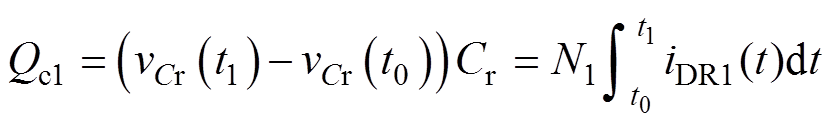（25）
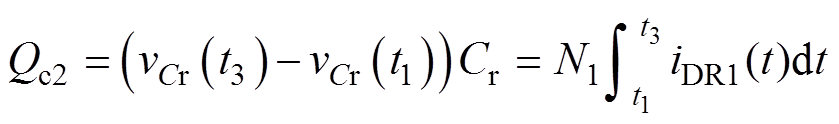（26）
又因为vCr(t3)=-vCr(t0)=VCrmax，则可得主变压器Tr1在上半周期传输的功率为
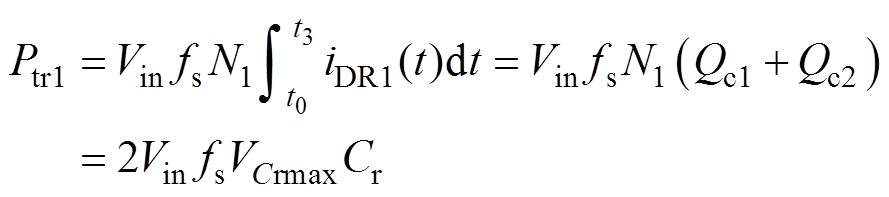（27）
再结合式（17），则Cr可表示为
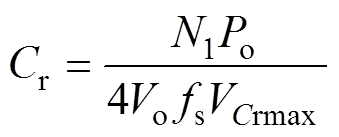（28）
可见，当N1确定时，Cr的值仅与VCrmax有关，且由各个模态的分析可知，在模态4中应满足
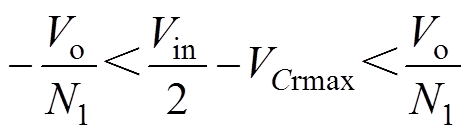（29）
可得
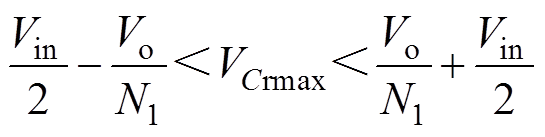（30）
由式（22）可得
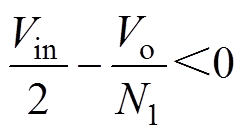（31）
综合式（28）、式（30）和式（31）可知，Cr应满足
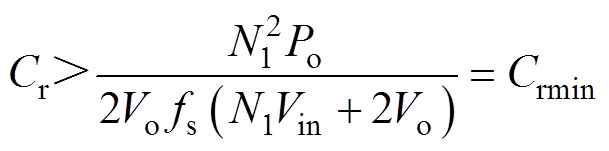（32）
分析可知，主变压器的匝比N1约等于辅助变压器匝比N2的9倍，又因为Cr和Cb的大小相差并不大（由后续仿真和实验的参数选取可知），所以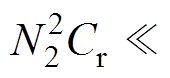
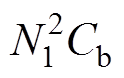，类似地，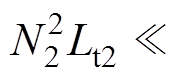
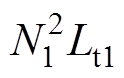，所以模态1中的谐振角频率可简化为
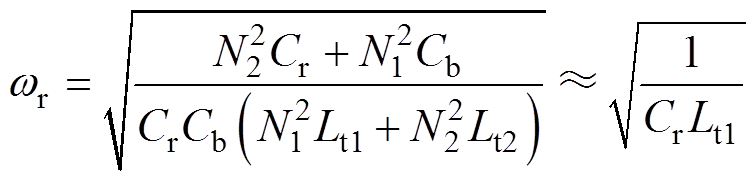（33）
根据模态1的谐振频率大于开关频率可得
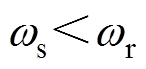（34）
因此可得
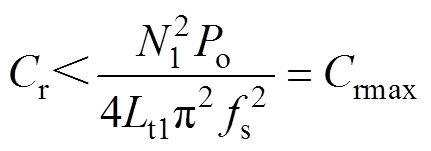（35）
由于模态2时间很短，因此vCb(t)在整个模态2中变化很小，所以可以认为
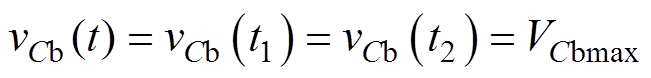（36）
故Lt2两端的电压为恒定值，有
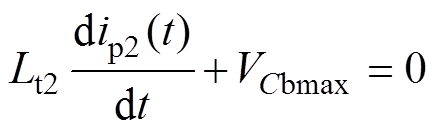（37）
所以ip2(t)被简化为
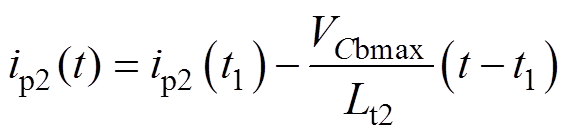（38）
由式（38）可见，在模态2中辅助电路电流ip2下降的速度与VCbmax的大小成正比，与漏感Lt2成反比，又因为VCrmax的大小与电容Cb的大小成反比，因此ip2下降的速度与Cb以及Lt2皆成反比。为了使辅助单元的续流时间尽可能短，进而降低导通损耗，Cb以及Lt2都应选取小容量和感量。
在模态1中流过电容Cb的电荷为
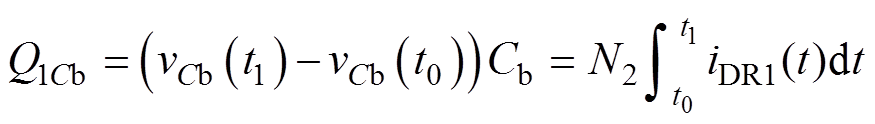（39）
又因为vCb(t1)≈-vCb(t0)=VCbmax，则可得辅助单元在上半周期传输的功率为
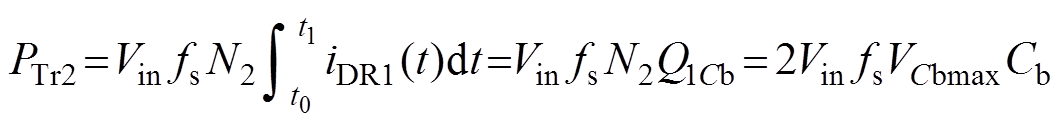（40）
再结合式（17）和式（18），可得
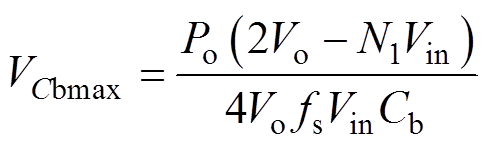（41）
由式（41）可见，VCbmax会随着N1的增大而减小，但会随着Cb的减小而增大，VCbmax即为Cb的电压应力，Cb的电压应力越大，其体积越大、成本越高，因此从选型的角度出发，Cb则应设计选取大电容值。
综上所述，阻断电容Cb的减小有利于降低导通损耗，但会使得其电压峰值增大，因此Cb的选值应折中考虑。
由模态1的等效电路可知，Lt1和Lt2相当于是串联在一起的，由于Ptr2
Ptr1，所需变压器Tr2较小，其漏感Lt2本身就较小，且由前述分析可知，N1
N2，因此
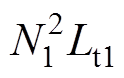，由2.2节的分析可知，为了降低导通损耗，Lt2取值应该较小。因此在参数设计分析时可以将Lt2忽略不计。
为便于分析，定义如下电路参数：
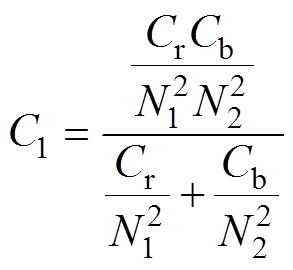
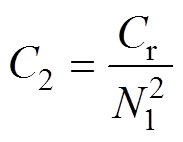
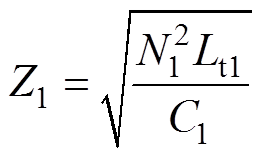
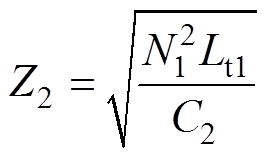
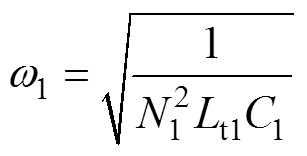
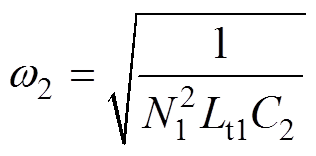
则上半周期各模态的等效电路如图5所示。
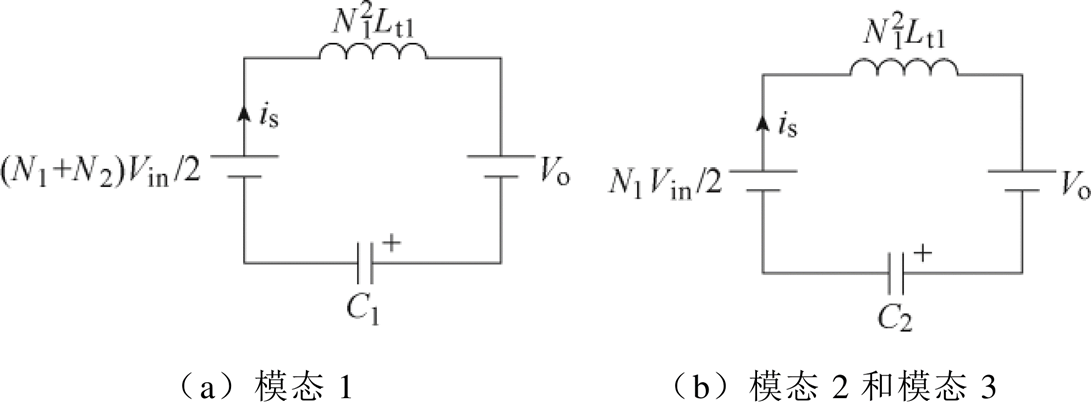
图5 各模态等效电路
Fig.5 Equivalent circuit of each mode
由图5a和基尔霍夫电压定律，可以得到模态1的等效电路的二阶微分方程为
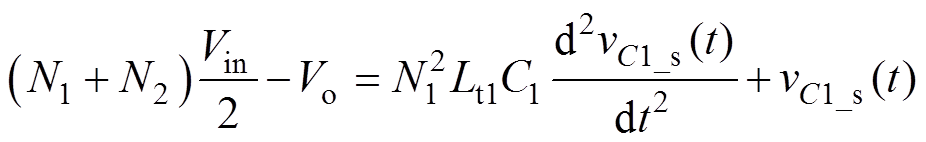（42）
式中，vC1_s为C1的端电压。
同理，模态2和模态3的等效电路可由二阶微分方程表示为
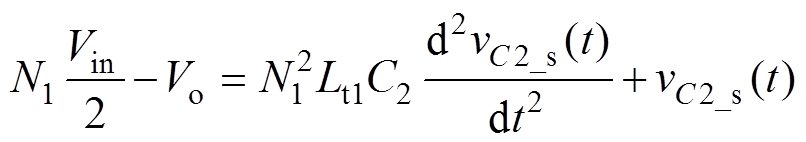（43）
式中，vC2_s为C2的端电压。
对式（42）、式（43）进行降阶计算可得
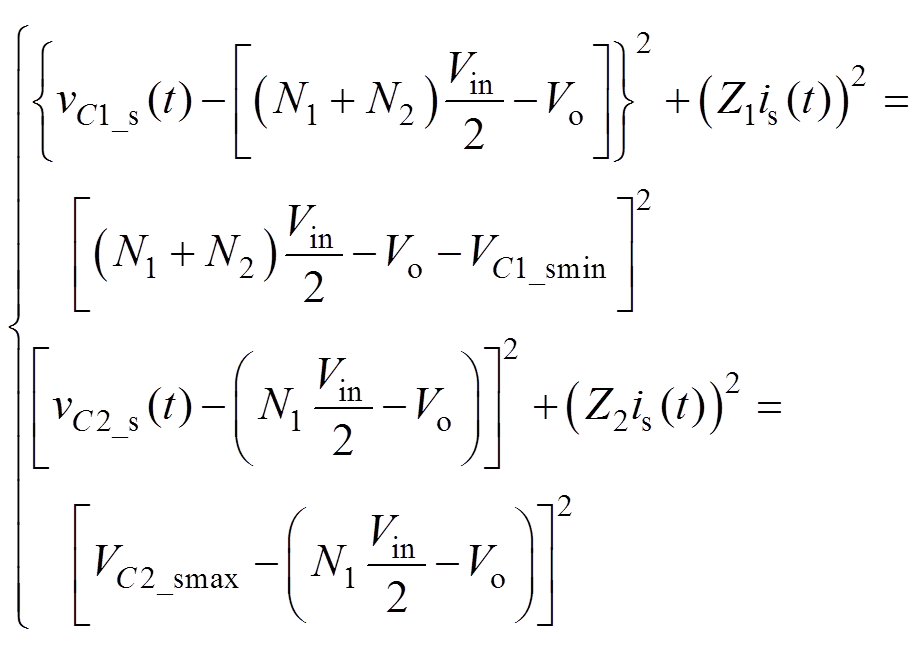（44）
式中，VC1_smin为VC1的最小值，且满足VC1_smin=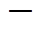 
(VCr_smax+VCb_smax)，VCr_smax、VCb_smax分别为VCr、VCb的最小值；VC2_smax为VC2的最大值，且满足VC2_smax= VCr_smax。
如果将vC1_s(t)看成是平面直角坐标系中的横轴变量，Z1is(t)看成是平面直角坐标系中的纵轴变量，则模态1轨迹是该坐标系上的一段圆弧，因此根据式（44）可绘制出该模态的稳态轨迹。同理将vC2_s(t)和Z2is(t)分别看成是平面直角坐标系中的横轴变量和纵轴变量也可得到模态2、模态3的稳态轨迹，如图6所示。
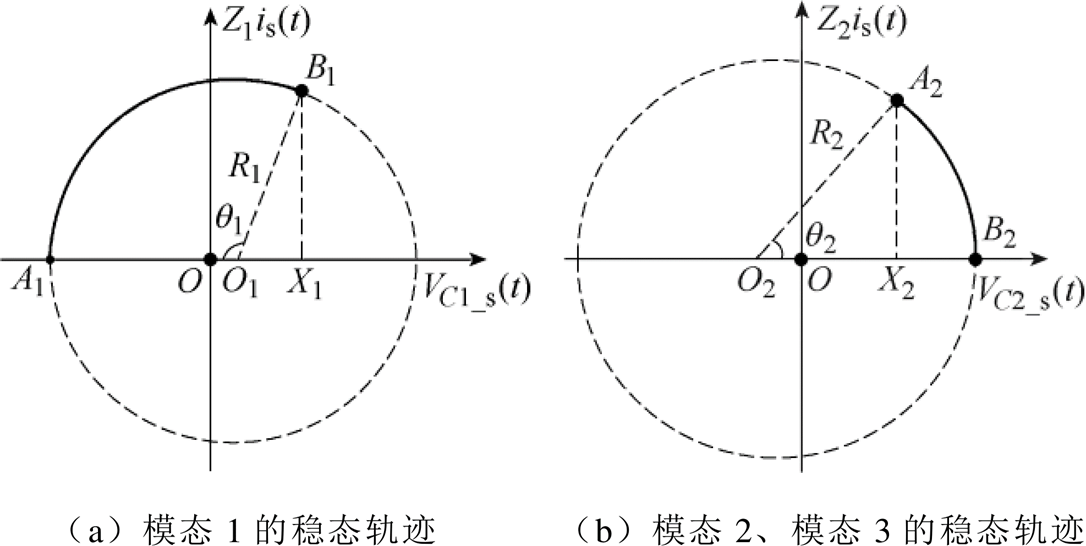
图6 各模态稳态轨迹
Fig.6 Steady state trajectory of each mode
图6中，A1到B1的曲线表示模态1，A2到B2的曲线表示模态2和模态3，节点B2由于模态4中电压、电流都不变，因此只用一个节点B2表示，电压vC2_s不变。故节点A1（VC1_smin, 0）表示开关周期的起点状态，节点B2（VC2_smax, 0）表示上半个周期的结束状态。圆弧A1B1和A2B2的半径可分别表示为
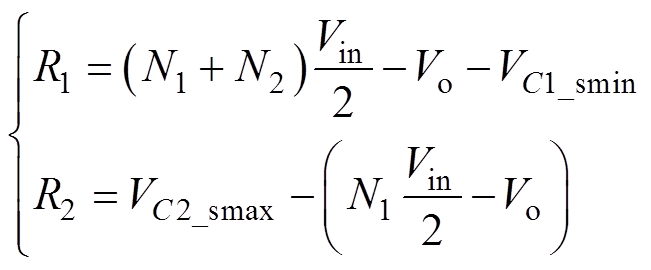（45）
圆心O1和O2的横坐标分别为(N1+N2)Vin/2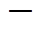Vo、N1Vin/2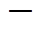Vo，分别记为x(O1)和x(O2)。由上述分析可近似认为vCb(t1)=VCbmax，又vC1_s(t1)=vCr_s(t1)+vCb_s(t1)，vC2_s(t1)=vCr_s(t1)，故可由式（44）得到关于vC2_s(t1)、is(t1)的方程组为
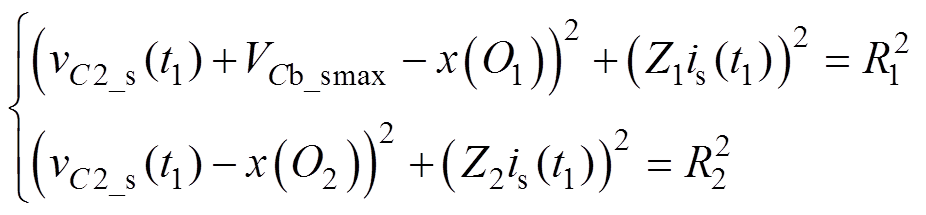（46）
通过解上述方程组，可得
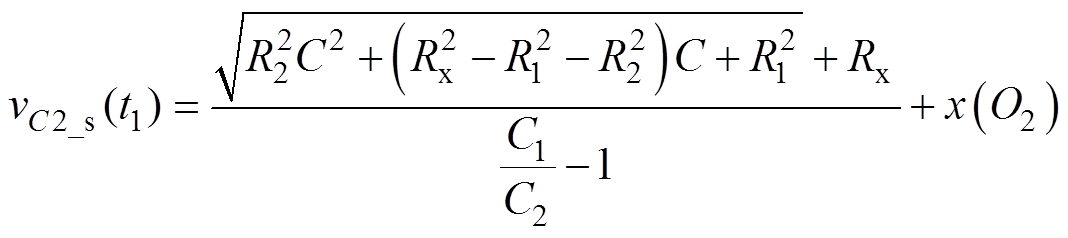（47）
式中，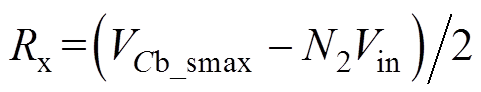
。
因此可得图6中节点A2的横坐标x(A2)=vC2_s(t1)，节点B1的横坐标x(B1)=vC2_s(t1)+VCb_smax。q1和q2分别为模态1和模态2、3的角度，且满足
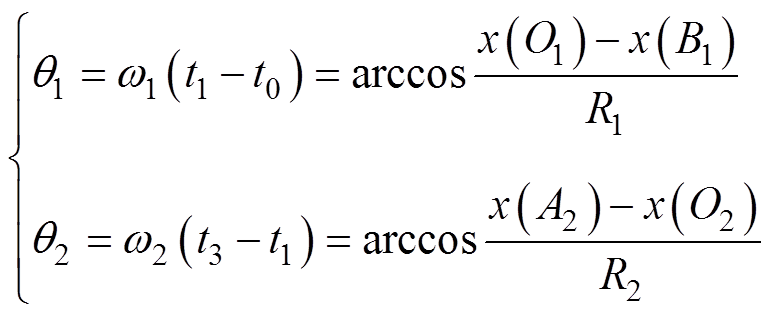（48）
由模态1到模态3的时间之和小于半个开关周期可得
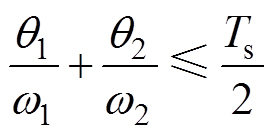（49）
将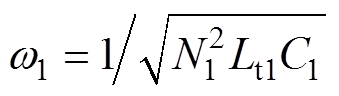
，
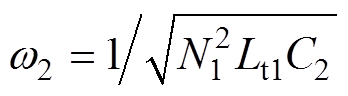代入式（49）可得
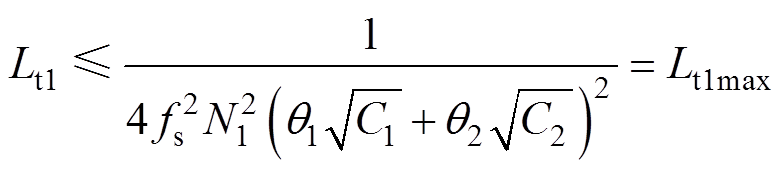（50）
本节按照第2节所给的参数进行仿真，并按Ptr1/ Ptot=90%的功率比例设计变压器匝比N1=18，因此可由式（32）求出Crmin=94.7 mF，取Cr=100 mF，且不失一般性地给定漏感Lt2=1 mH。
为了验证上述分析中N2与Cb的影响，对三种不同工况进行对比分析，见表2，为公平对比，三种工况下主、辅变压器功率相同，即N1相同。Lt1是按照式（50）计算结果给出。
表2 A、B、C三种工况下的主要参数
Tab.2 Main parameters under three working conditions A, B and C
参 数数 值 ABC N1181818 N22.22.52.2 Lt1/mH67.167.864.9 Cr/mF100100100 Lt2/mH111 Cb/mF2525250
图7为不同工况下谐振电容电压vCr、阻断电容电压vCb和变压器Tr1、Tr2一次电流ip1和ip2波形和开关管Q5、Q6驱动电压仿真波形对比，可见，由于A和C工况的N2较小，所以ip2的峰值以及Q5和Q6的关断电流都比工况B的小。此外，通过工况A和C的波形对比可以发现，由于工况A的Cb小，所以其VCbmax大，说明工况A中Cb的电压应力大，这与理论分析相符。
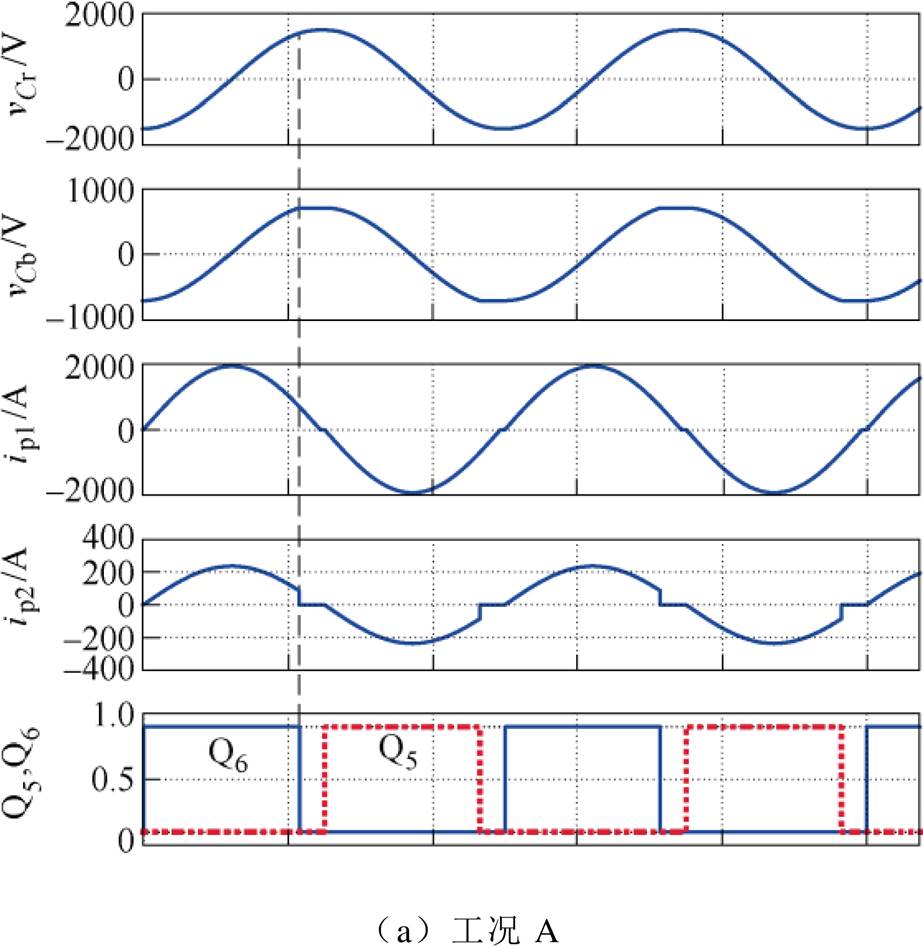
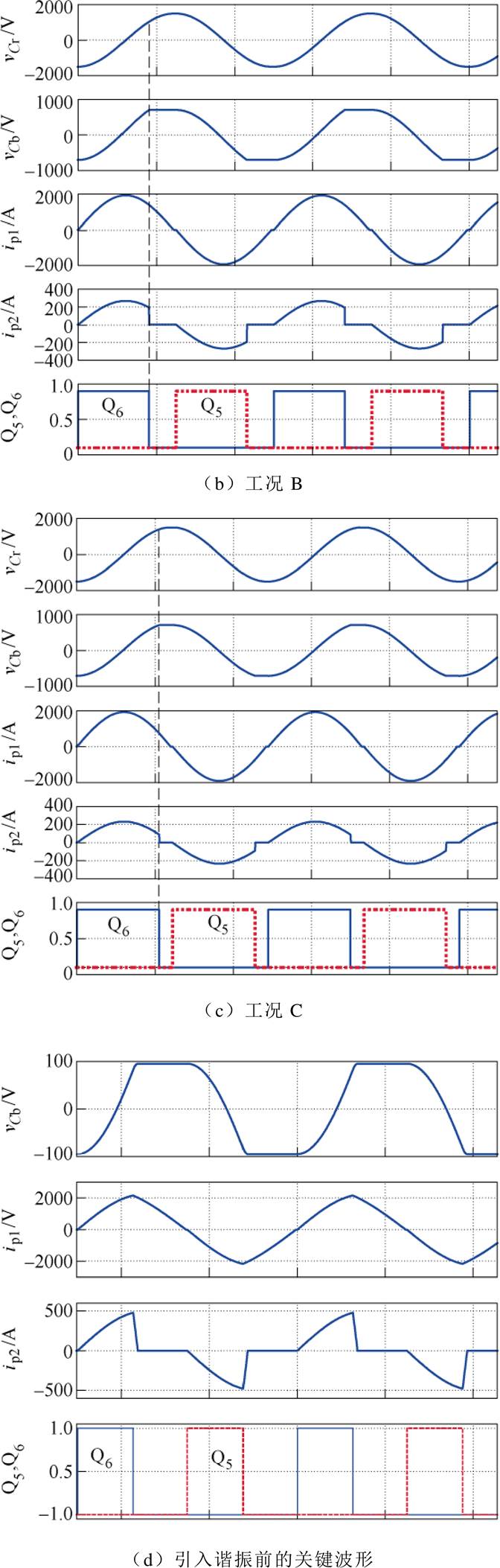
图7 A、B、C三种工况下谐振电容电压vCr、阻断电容电压vCb、变压器Tr1、Tr2一次电流ip1和ip2波形和开关管Q5、Q6驱动电压的仿真波形
Fig.7 Simulation waveforms of resonant capacitor voltage vCr, blocking capacitor voltage vCb, the primary current ip1 and ip2 waveforms of transformer Tr1, Tr2, and switch Q5 and Q6 driving voltages under three working conditions of A, B and C
引入谐振技术前的无环流ZCS三电平复合全桥变换器如图1b所示，其典型工作波形可见参考文献[23]，以工况A参数同样对该电路进行仿真，波形如图7d所示，其ip1的峰值电流和ip2的关断电流分别为2 156 A和479 A，而引入谐振技术的图7a中，ip1的峰值电流和ip2的关断电流分别为1 932 A和191 A。可见，引入本文提出的谐振型电路无论在ip1的峰值电流和ip2的关断电流都有所降低。
为了验证所提中频DC-DC变换器的工作原理和控制方法，本节搭建了一个额定功率为1 kW的150 V/750 V实验样机，该样机的开关频率fs= 10 kHz。设计变压器匝比时将两个变压器的传输功率之比设置为Ptr1/Ptr2=9，根据式（19）和给定的输入/输出电压参数，可得N1=9；进一步地，根据式（23）可得N2＞1，不失一般性，取N2=2；根据式（41），设VCbmax=10 V，可得Cb=3.3 mF，实际中取5 mF；根据式（32）可得Cr＞1.89 mF，根据式（28），设VCrmax=40 V，可得Cr=7.5 mF，从式（33）、式（35）和式（50）可以看出，Cr与Lt1是个耦合的谐振关系，取Cr=8 mF时，根据式（34），当Lt1=30 mH时谐振频率为10.27 kHz，高于开关频率的10 kHz，满足条件；Lt2则为变压器的漏感，实际中取3 mH，飞跨电容Css用于高频纹波滤波，样机中取1 mF。功率开关管Q1～Q6的型号为CRG60T60AK3HD，整流二极管VDR1～VDR6的型号为RHRG30120。样机照片如图8所示。
图8 实验样机照片
Fig.8 Photos of experimental prototype
图9为额定负载下的主要实验波形，可见所有的实验波形都与理论波形（见图2）和仿真波形（见图7）一致。从图9a中可以发现，电流ip2相比于ip1快速下降到0，从图9b～图9d中可以发现，所有整流二极管均在无反向恢复损耗的情况下关闭。
图10给出了开关器件Q1、Q3和Q6的软开关波形。可见，Q1、Q3实现了ZCS开通和关断，辅助开关管Q6实现了ZVS关断，ZVZCS开通。由于模态1中两个变压器电流都经过Q1，而模态2中的iQ1仅为主变压器电流，因此iQ1存在电流跌落现象。
通过引入阻断电容Cb，可以减小一次侧的通态损耗，如果没有阻断电容Cb（此时VDR3和VDR4也不起作用），则主要波形如图11所示，可见电流ip2会与电流ip1同时降为0，因此通态损耗会更大。
图12为样机负载跳变实验结果，实验模拟了样机由额定功率1 kW跳变到半载500 W的情况。图12a给出了变压器一次电流的整个动态响应过程，图12b给出了谐振电容Cr和阻断电容Cb的整个动态响应过程；图12c、图12d和图12e、图12f则分别给出了负载跳变前后变换器一次电流以及谐振电容和阻断电容两端电压的稳态波形。可见，当负载发生跳变时，该变换器动态响应速度较快且进入稳态后较为平稳，实验结果验证了该变换器在应对负载跳变情况下良好的动态性能。
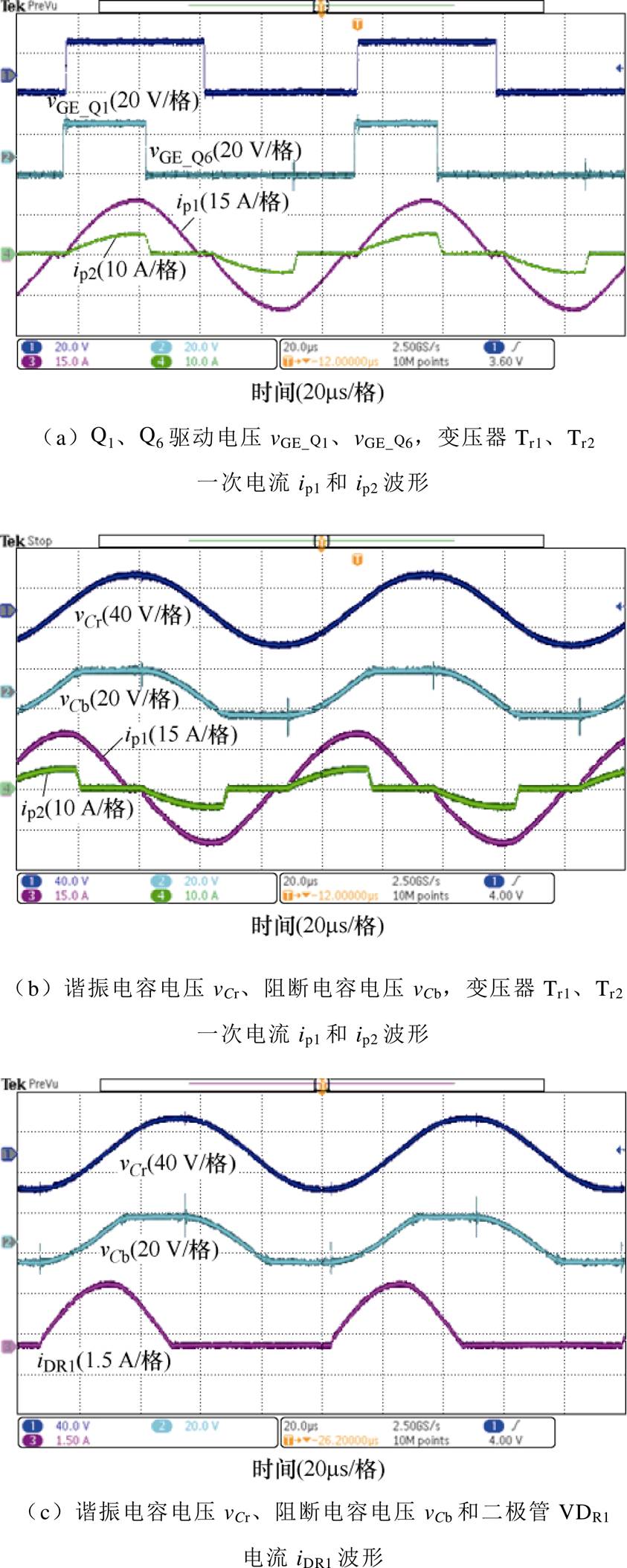
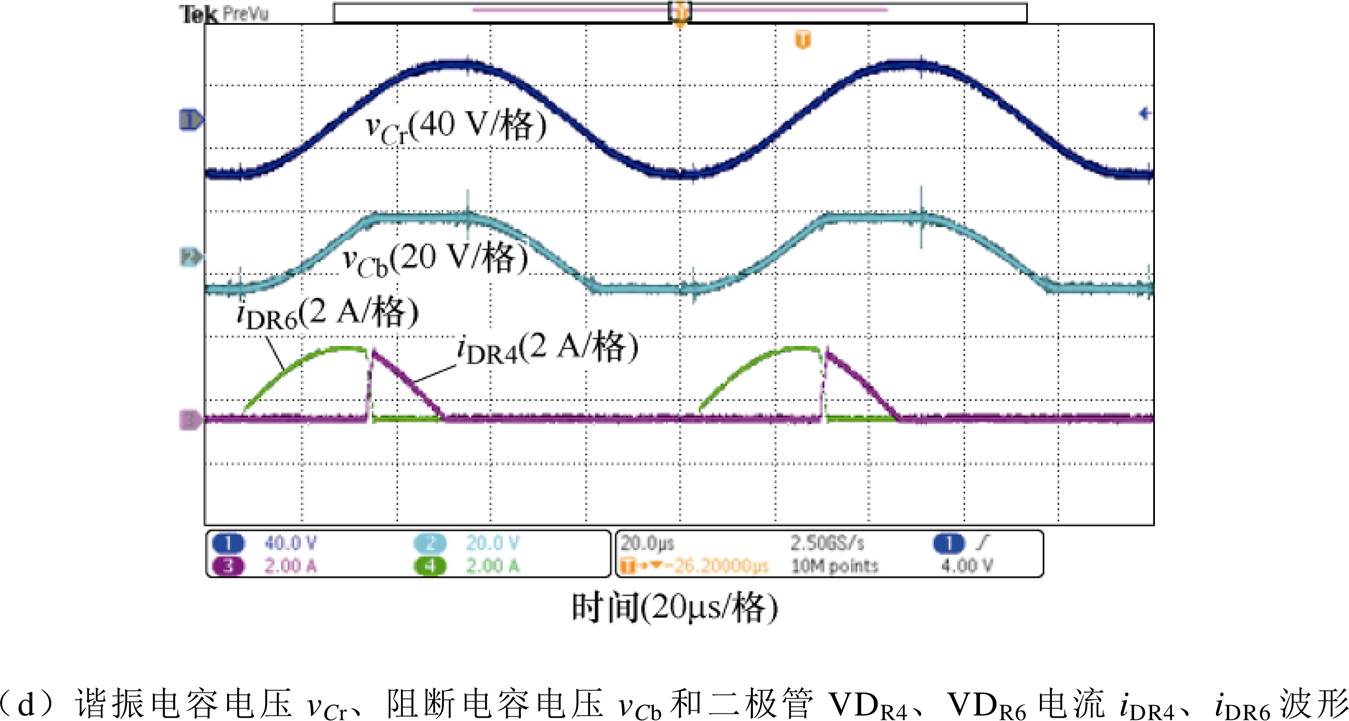
图9 额定负载下的主要工作波形
Fig.9 Main working waveforms under rated load
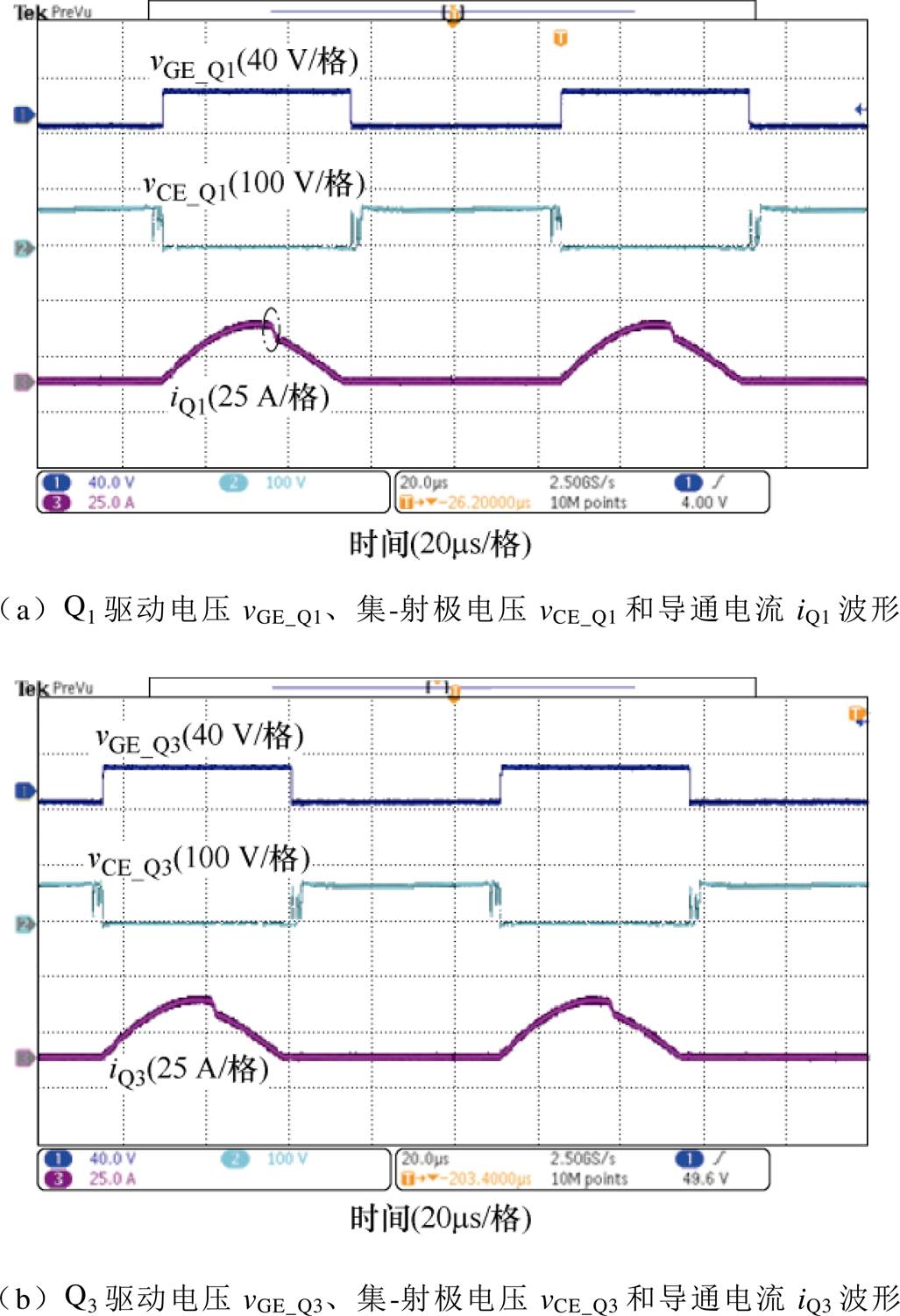
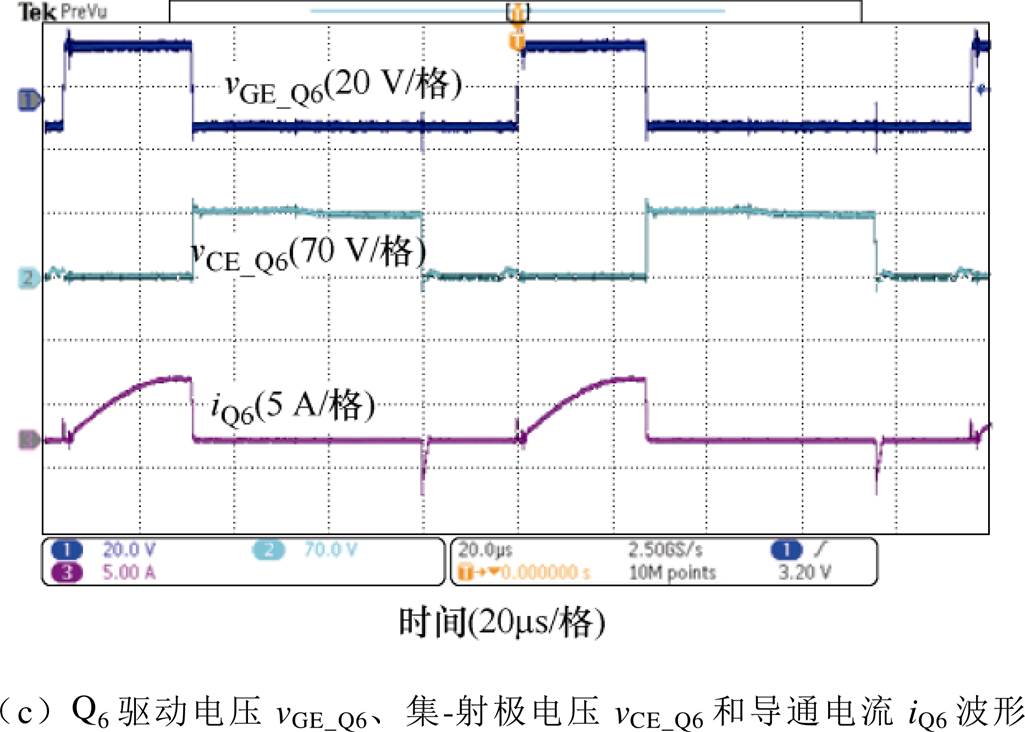
图10 Q1、Q3和Q6的软开关波形
Fig.10 Soft switching waveforms for Q1, Q3 and Q6
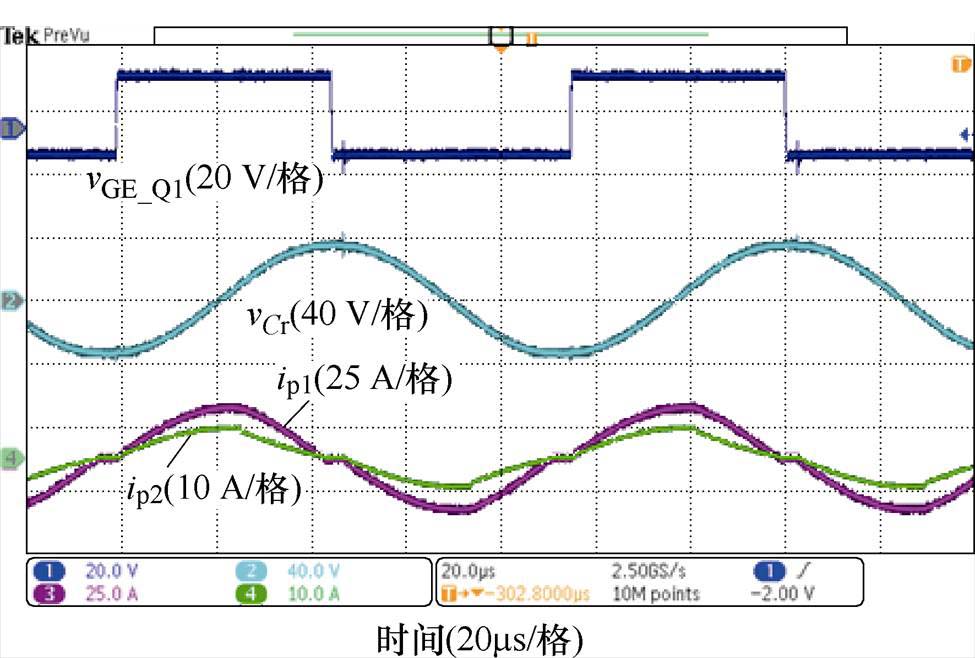
图11 无阻断电容Cb时Q1驱动电压vGE_Q1、谐振电容电压vCr和Tr1、Tr2一次电流ip1和ip2波形
Fig.11 when without blocking capacitor Cb, the waveforms of driving voltage for Q1vGE_Q1, resonant capacitor voltage vCrand Tr1, Tr2 primary side current ip1 and ip2
图13给出了有阻断电容和没有阻断电容两种情况下所测得的效率曲线，由图可见，引入阻断电容的电路效率总是高于没有阻断电容的电路。对比图9a与图11可见，两种工况下的ip1电流基本相同，而没有引入阻断电容前，图11中的ip2波形明显比图9a中的ip2波形多了一段，而这一段电流将在变压器Tr2的一次绕组和一次侧开关管、二极管（ip2正半周时从Q1、Q2、Q6和VDc2中流通，ip2负半周时从Q3、Q4、Q5和VDc1中流通）中形成导通损耗。而引入阻断电容后，这一时段的损耗可以消除，因此可以提高变换效率。
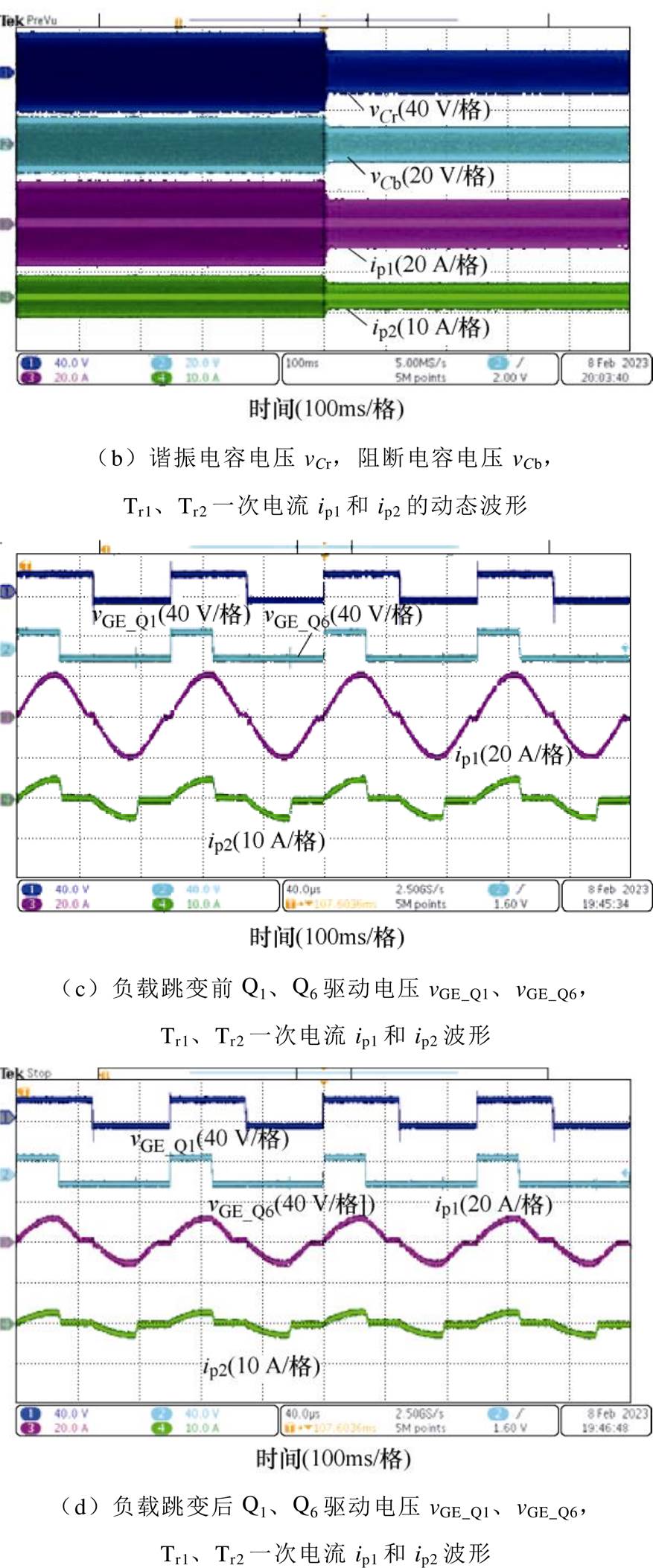
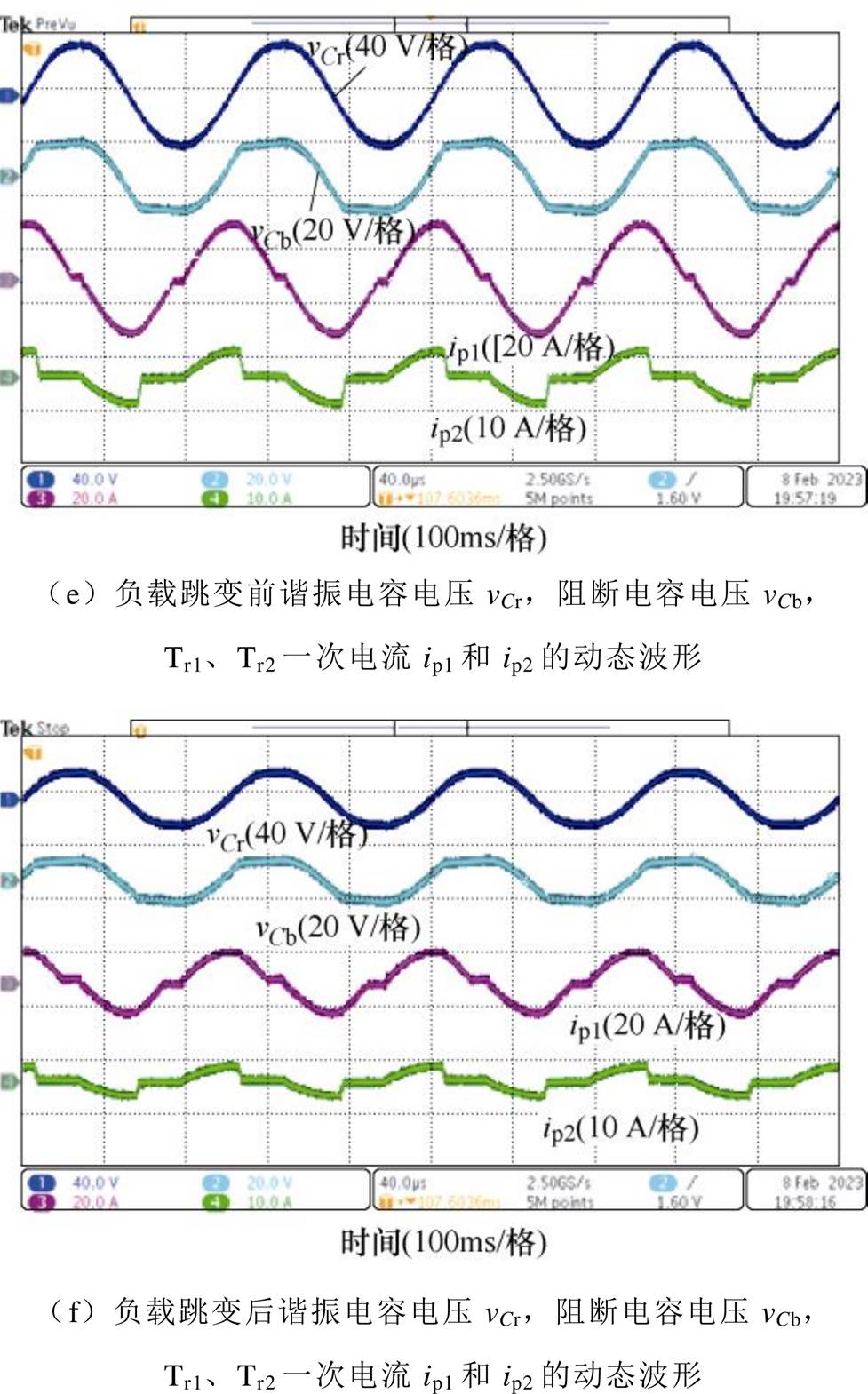
图12 负载跳变动态实验波形
Fig.12 Dynamic experimental waveforms of load jump
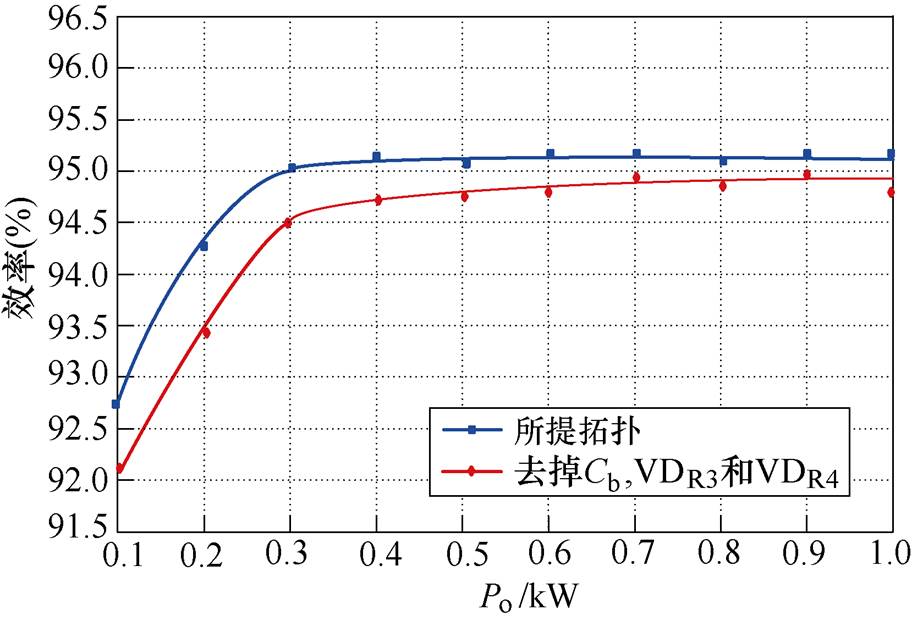
图13 效率对比
Fig.13 Efficiency comparison
本文提出一种无环流三电平复合全桥变换器，在半桥三电平结构单元中引入一个谐振电容，从而形成以LC串联谐振的形式向变压器二次侧传输能量，将三角形电流波形改进为正弦波形，不但降低了所有开关器件的峰值电流，还可减小辅助开关管关断电流。最后，根据得到的谐振电容的取值上、下限，对该变换器进行了仿真和实验，验证了该变换器的正确性。
参考文献
[1] 陈孝莺, 许国, 韩华, 等. 基于脉宽调制的电流断续型谐振变换器[J]. 电工技术学报, 2022, 37(24): 6252-6261.
Chen Xiaoying, Xu Guo, Han Hua, et al. Dis- continuous current mode resonant converter with pulse width modulation control[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6252- 6261.
[2] 吴世伟, 刘文彪, 纪陵, 等. 新能源发电功率预测系统数据流容错研究[J]. 电气技术, 2018, 19(12): 107-111.
Wu Shiwei, Liu Wenbiao, Ji Ling, et al. Research on data flow fault tolerance of new energy power gen- eration forecasting system[J]. Electrical Engineering, 2018, 19(12): 107-111.
[3] 杨晓光, 王德鑫, 贾哲, 等. 负载和输入电压自适应零电压软开关全桥变换器[J]. 电工技术学报, 2022, 37(12): 3061-3072.
Yang Xiaoguang, Wang Dexin, Jia Zhe, et al. A load and input voltage adaptive zero-voltage-switching full-bridge converter[J]. Transactions of China Elec- trotechnical Society, 2022, 37(12): 3061-3072.
[4] Yin Zhijian, Chen Manxin, Li Kerui, et al. A new ZCS PWM full-bridge converter of Buck-type for applications with very high input voltage[C]//IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 2016: 1495- 1500.
[5] Zhang Xin, Chung H S H, Ruan Xinbo, et al. Analysis, optimized design and adaptive control of a ZCS full-bridge converter without voltage over-stress on the switches[C]//2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Expo- sition (APEC), Palm Springs, CA, USA, 2010: 1214- 1221.
[6] Yin Zhijian, Hu Jiefeng, Chung H S H, et al. A ZCS-PWM voltage-driven three-level converter with a secondary-side simple soft-switching snubber[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7542-7552.
[7] Ortiz G, Leibl M G, Huber J E, et al. Design and experimental testing of a resonant DC-DC converter for solid-state transformers[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7534-7542.
[8] Cao Guoen, Guo Zhicheng, Wang Yibo, et al. A DC-DC conversion system for high power HVDC- connected photovoltaic power system[C]//2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 2017: 1-6.
[9] 李福, 邓红雷, 张国驹, 等. 一种中间电容谐振型级联双向DC-DC变换器[J]. 电工技术学报, 2022, 37(20): 5253-5266.
Li Fu, Deng Honglei, Zhang Guoju, et al. A cascaded bidirectional DC-DC converter with intermediate capacitor resonance[J]. Transactions of China Elec- trotechnical Society, 2022, 37(20): 5253-5266.
[10] 王议锋, 韩富强, 杨良, 等. 一种双变压器结构的多谐振型软开关直流变换器[J]. 电工技术学报, 2019, 34(4): 738-746.
Wang Yifeng, Han Fuqiang, Yang Liang, et al. A dual transformer-structured multi-resonant soft-switching DC-DC converter[J]. Transactions of China Electro- technical Society, 2019, 34(4): 738-746.
[11] Suryadevara R, Parsa L. Full-bridge ZCS-converter- based high-gain modular DC-DC converter for PV integration with medium-voltage DC grids[J]. IEEE Transactions on Energy Conversion, 2019, 34(1): 302-312.
[12] 朱选才, 徐德鸿, Hidetoshi Umida, 等. 应用逆阻型IGBT的移相控制电流型全桥零电流开关DC/DC变换器[J]. 中国电机工程学报, 2006, 26(12): 45-49.
Zhu Xuancai, Xu Dehong, Umida H, et al. Current-fed phase shift controlled full bridge ZCS DC/DC converter with reverse block IGBT[J]. Proceedings of the CSEE, 2006, 26(12): 45-49.
[13] Wang Huai, Sun Qian, Chung H S H, et al. A ZCS current-fed full-bridge PWM converter with self- adaptable soft-switching snubber energy[J]. IEEE Transactions on Power Electronics, 2009, 24(8): 1977-1991.
[14] Ning Guangfu, Chen Wu, Shu Liangcai, et al. A hybrid resonant ZVZCS three-level converter for MVDC-connected offshore wind power collection systems[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 6633-6645.
[15] Ning Guangfu, Chen Wu. A hybrid resonant ZCS PWM converter for renewable energy sources connecting to MVDC collection system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 7911-7920.
[16] Shu Liangcai, Chen Wu, Ning Guangfu, et al. A resonant ZVZCS DC-DC converter with two uneven transformers for an MVDC collection system of offshore wind farms[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 7886-7895.
[17] Ning Guangfu, Chen Wu, Shu Liangcai, et al. Hybrid resonant ZVZCS PWM full-bridge converter for large photovoltaic parks connecting to MVDC grids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 1078-1090.
[18] Ning Guangfu, Chen Wu, Shu Liangcai, et al. A hybrid ZVZCS dual-transformer-based full-bridge converter operating in DCM for MVDC grids[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5162-5170.
[19] Chen Yu, Kang Yong, Nie Songsong, et al. The multiple-output DC-DC converter with shared ZCS lagging leg[J]. IEEE Transactions on Power Elec- tronics, 2011, 26(8): 2278-2294.
[20] Chen Yu, Kang Yong. A fully regulated dual-output DC-DC converter with special-connected two trans- formers (SCTTs) cell and complementary pulse width modulation-PFM (CPWM-PFM)[J]. IEEE Transactions on Power Electronics, 2010, 25(5): 1296-1309.
[21] 陈宇. 电力电子变换系统的元件复用理论与方法[D]. 武汉: 华中科技大学, 2011.
[22] Pal A, Basu K. A zero-current-switched PWM full bridge DC-DC converter[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 2019: 6424-6429.
[23] He Xiaokun, Hu Renjie, Chen Wu. A hybrid three- level ZVZCS converter for photovoltaic power con- necting to MVDC collection system[J]. Energies, 2022, 15(15): 5365.
Abstract DC converter is a key part of a medium-voltage DC (MVDC) convergence system. Its role is to convert DC power into load-required voltage or current-controllable DC power, which plays a boost, isolation, power transmission, and other functions. The research on the flow converter has always been a hot spot in domestic and foreign power electronics technology.Compared with the huge transformer in the traditional medium-voltage AC convergence scheme, the converter in the medium-voltage DC scheme can significantly reduce the size of the device due to medium and high-frequency control. With the increasing output port voltage and capacity of photovoltaic and wind power, higher requirements are placed on bridge converters with the ability to adapt to high input voltages.
In order to adapt to the development trend of new energy power generation with higher and higher port voltage, this paper proposes a circulating current-free ZCS (zero-current-switching) three-level composite full-bridge converter. The converter consists of a half-bridge three-level circuit and a full-bridge circuit multiplexed with two switching tubes. The three-level circuit with a resonant capacitor will transmit 90% or more of the total power. In contrast, the auxiliary full-bridge circuit transmits the remaining power so that the voltage stress on all switching tubes is only half of the input voltage. This structure facilitates the converter to high input voltages, preserves the soft-switching characteristics of all switching tubes, and eliminates the primary-side loop current. However, since the current waveform of the converter is triangular, the peak current is high under the same transmission power, and the turnoff current of two multiplexed switch tubes is the maximum, resulting in large shutdown losses. Therefore, LC series resonance technology is introduced in the half-bridge three-level structure unit, forming LC series resonance to transmit energy to the secondary side of the transformer. With the same electrical parameters as the converter ports, the proposed converter can improve the triangular current waveform to a sinusoidal waveform. Accordingly, the peak currents of all the switching devices and the turn-off currents of auxiliary switching tubes can be reduced, which further decreases their switching losses.
Through theoretical analysis, when the input voltage Vinand output voltage Vo are known, the transformer turns ratio N1 determines the power of the two transformers. Moreover, the larger N1 is, the larger the proportion of the whole power transferred by the main circuit Ptr1 is, and the smaller the power transferred by the auxiliary transformer Ptr2 is. Therefore, for the main transformer Ptr1 to transmit the majority of power, N1 should be taken large. Decreasing the blocking capacitor Cb is beneficial for reducing conduction loss but will increase its voltage peak. Therefore, the selection of Cb should be considered in a compromise. According to the requirement that the resonant frequency of the converter is greater than the switching frequency, the upper limit of the resonant capacitor value can be obtained. At the same time, the lower limit of the resonant capacitor value can be determined based on the rated power of the converter. This paper analyzes and designs the key parameters of the converter, conducts simulation verification through Plecs, and produces a 150 V/750 V/1 kW prototype for experimental verification.
keywords：Medium-voltage DC collection, resonant composite full bridge three-level converter, LC series resonance, DC-DC converter
DOI: 10.19595/j.cnki.1000-6753.tces.231067
中图分类号：TM46
收稿日期 2023-07-09
改稿日期 2023-07-27
何晓坤 女，1983年生，博士研究生，研究方向为功率变换器、软开关变换器技术。E-mail: 30869655@qq.com（通信作者）
胡仁杰 男，1963年生，教授，博士生导师，研究方向为电气检测、智能仪器、工业控制网络、电力电子、电工电子实验教学技术等。E-mail: hurenjie@seu.edu.cn
（编辑 陈诚）