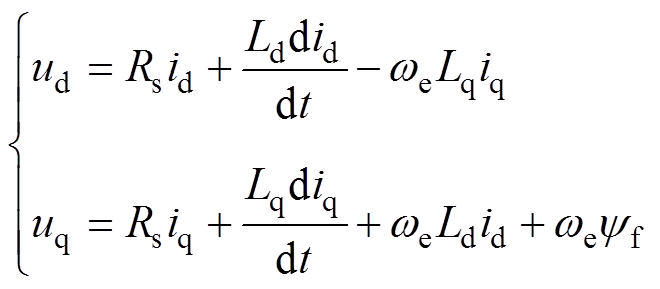（1）
摘要 为实现内嵌式永磁同步电机（IPMSM）高性能运行，该文提出一种最大转矩电流比（MTPA）决策与控制算法，旨在简化控制结构、加快系统动态响应、增强系统鲁棒性。该算法根据dq轴电流直接计算电磁转矩的微分项，并以此作为MTPA状态的决策判据。根据判据值对d轴电流参考值进行补偿，实现对MTPA状态的在线追踪。所提算法无需实际或虚拟信号注入和解算环节，系统动态性能得以提高。d轴电流补偿控制解决了算法收敛速度对负载条件较敏感的问题，提升了控制系统的鲁棒性。理论分析、仿真计算和实验结果验证了该方法的有效性和优越性，与虚拟信号注入法相比，所提出的算法在不同负载下对MTPA状态的收敛时间降低为原来的1/5～1/2。
关键词：内嵌式永磁同步电机 最大转矩电流比 判据计算 直轴电流补偿
内嵌式永磁同步电机（Interior Permanent Magnet Synchronous Motor, IPMSM）具有转矩密度高、恒功率区宽、永磁体涡流损耗低等特点，在诸多领域得到广泛应用[1-2]。由于交直轴磁路不对称，IPMSM的电磁转矩中同时存在永磁转矩和磁阻转矩[3]。为了提高磁阻转矩的利用率，最大转矩电流比（Maximum Torque Per Ampere, MTPA）控制成为IPMSM的首选控制策略。对应于某一负载转矩，MTPA控制通过分配dq轴电流使维持电机运行所需的电枢电流最小，从而减小铜耗，提升效率[4]。
为实现MTPA控制，国内外学者主要提出了解析法、查表法、搜索法和信号注入法四种方法[5]。解析法根据IPMSM的数学模型直接求取MTPA控制的最佳矢量角[6]；查表法根据大量离线测试所得数据查找当前工况最优解，具有较好的工程实用 性[7]；搜索法不依赖电机数学模型和先验数据，可以在线搜索MTPA控制最优解[8]，但在稳定状态下存在周期性振荡现象；信号注入法结合了数学模型求解法与搜索法，是一种较新颖的方法，包括实际信号注入法[9-11]和虚拟信号注入法[12-13]。现有信号注入法均通过注入高频信号并进行信号解调制以获取响应信号中的特定高频分量，从而提取所需控制信号实现MTPA控制。实际信号注入法不受电机参数变化影响，具有较高的控制精度，但会带来额外损耗。虚拟信号注入（Virtual Signal Injection, VSI）法克服了实际信号注入法存在的问题，但电机参数偏导项对算法的控制精度存在影响[14]。这两种信号注入法均采用级联滤波技术实现信号解调制，在一定程度上限制了MTPA状态的动态追踪速度。多虚拟信号注入（Multiple Virtual Signals Injection, MVSI）法通过数学运算方式提取所需控制信号，加快了算法的收敛速度[15]。除正弦信号外，注入实际/虚拟的方波信号亦有助于信号解调制机构的改进设计，缩短系统收敛到MTPA状态的响应时间[16-18]。但现有针对信号注入法的改进措施均增加了算法复杂度，致使处理器运算负担倍增。此外，现有信号注入法在不同工况下的收敛速度不一致，即收敛速度对负载工况较敏感[18-19]，致使MTPA控制增益选取困难，限制了算法的实际应用。针对MTPA控制方法中的计算量大、复杂度高、实用性低等问题，研究改进方法，优化算法控制性能、简化求解过程、降低计算量、提高实用性成为MTPA控制在工程应用中的难点和亟待突破及解决的关键问题。
本文提出一种新颖的MTPA在线控制算法，给出了详细的数学推导、理论分析、仿真和实验验证结果。所提出的算法无需高频信号注入以及复杂的信号解调机构，加快了MTPA控制的决策速度，降低了算法复杂度与计算量。同时，该方法避免了电流分配引起的负载耦合，加快了算法的收敛速度，降低了算法对负载工况的敏感度。最后，仿真和实验验证了新方法在全工况范围内的响应性能。
为了建立正弦波永磁同步电机在dq轴同步旋转坐标系下的线性化数学模型，做如下假设[20-21]：①忽略电机铁心材料饱和；②不计电机铁心中的涡流损耗和磁滞损耗；③电枢电流为对称的三相正弦波电流。
IPMSM的dq轴电压方程可表示为
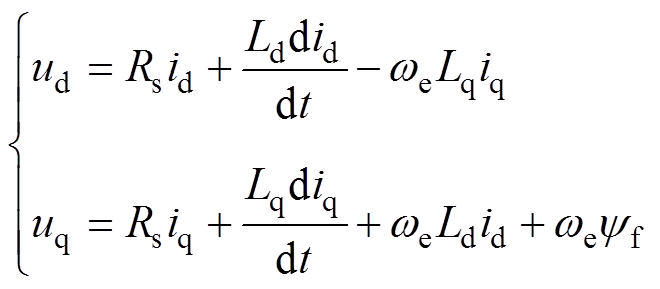（1）
式中，ud, uq、id, iq分别为定子绕组d、q轴电压和电流；Ld、Lq分别为定子绕组d、q轴电感；Rs为定子绕组电阻；yf为永磁磁链；we为转子电角速度。
IPMSM的电磁转矩方程可表示为
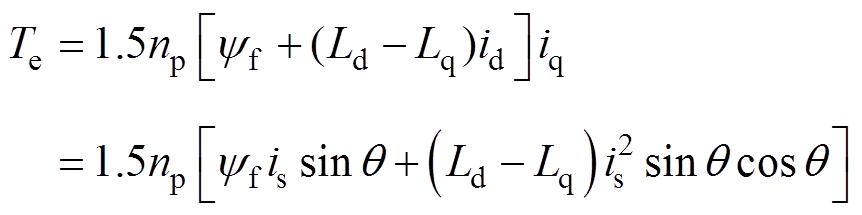（2）
式中，Te为电磁转矩；np为转子极对数；is为定子绕组电流矢量的幅值；q 为电流矢量角，即定子绕组电流矢量与d轴正方向的夹角。
根据式（2），IPMSM的电磁转矩由永磁转矩和磁阻转矩组成。当定子电流幅值一定时，转矩随电流矢量角的变化如图1所示。
当电流矢量角q=qMTPA时，电磁转矩值最大，该状态为MTPA状态。考虑转矩输出及电流约束，MTPA控制问题可以描述为具有约束条件的非线性动态规划问题，写成一般形式为
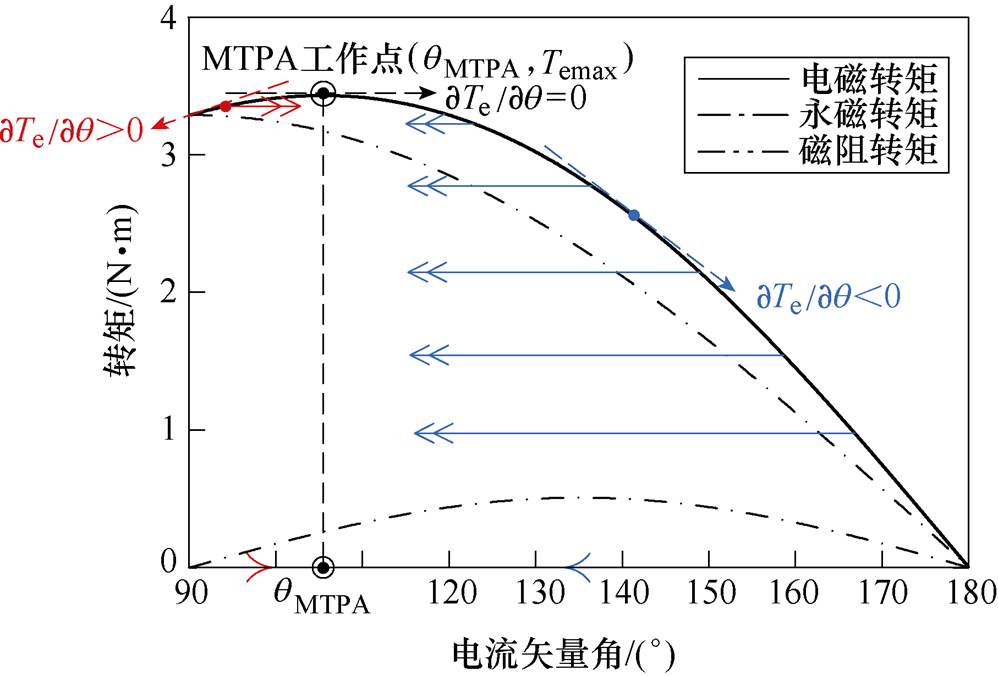
图1 转矩与电流矢量角q 的关系
Fig.1 Torques variation with current vector angle q
（3）
在恒定电枢电流作用下，电磁转矩曲线有且仅有一个极大值点，在该点处，∂Te/∂q 的值为零，对应于MTPA状态。定义∂Te/∂q 为MTPA状态决策判据。为实现对最优电流矢量角qMTPA的跟踪，根据图1所示曲线，可建立如下对应关系：①∂Te/∂q＞0，q 需逐渐增大，即dq/dt＞0；②∂Te/∂q＜0，q 需逐渐减小，即dq/dt＜0；③∂Te/∂q=0，q 收敛到qMTPA。
根据MTPA判据与dq/dt项的收敛关系，当电机处于非MTPA状态时，∂Te/∂q 项的值不为零，需调整电流矢量角q。当∂Te/∂q 项的值为零时，系统达到MTPA状态。为使系统维持稳定的MTPA运行状态，根据前述收敛关系，采用一种误差驱动的闭环控制结构即可实现MTPA控制，如图2所示。由图2可见，MTPA控制过程主要被分为两个部分：
（1）根据设计的状态决策判据提取算法，在线计算MTPA状态决策判据值。
（2）以判据值等于零为控制目标，构建误差驱动的闭环控制结构，在电流矢量角初始值qini的基础上实时调整电流矢量角给定值qref。
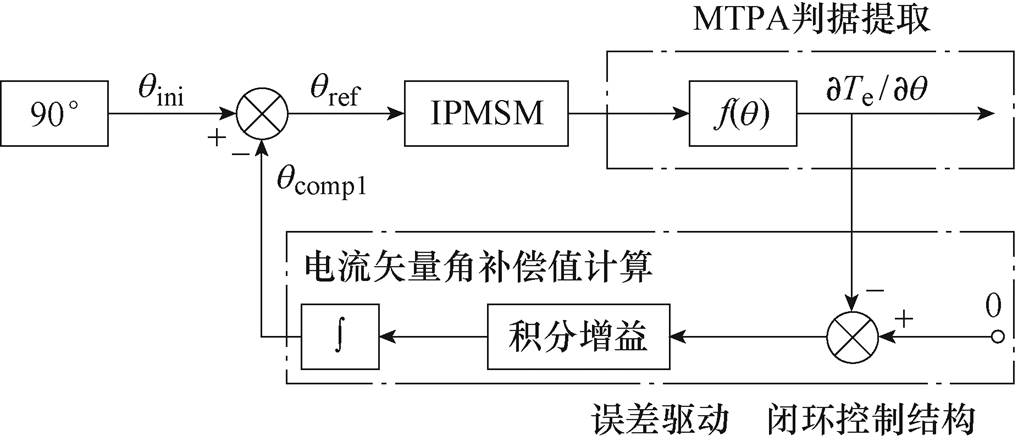
图2 MTPA闭环控制结构
Fig.2 Closed-loop control structure of MTPA
MTPA状态决策判据项提取方法设计如下。根据电流矢量角q 的定义，可得
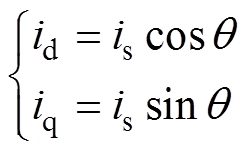（4）
另外，根据式（2）所示电磁转矩表达式，可得
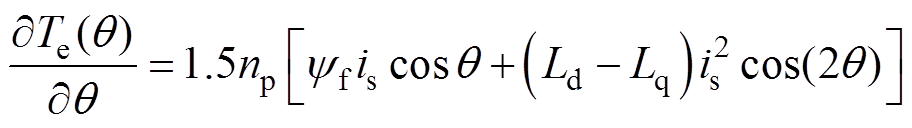（5）
将式（4）代入式（5），重新整理MTPA判据项的表达式，并进行等效变换，可得一种无需信号注入的MTPA状态决策判据计算方法为
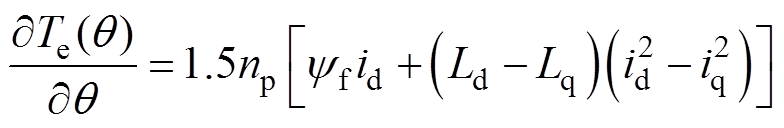（6）
式中，id和iq均为实际电流的采样值。
进一步地，对式（6）所示MTPA判据项提取表达式进行积分可得MTPA判据对时间的误差累加值err为
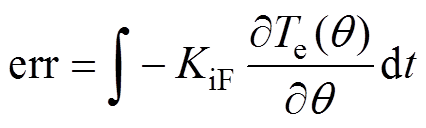（7）
式中，KiF为大于零的积分增益系数，用于调节系统达到稳定状态的收敛速度。KiF值越大，系统趋于稳定所需的时间越短。
当∂Te/∂q =0时，系统达到MTPA状态。由于积分器随着时间对输入值进行数值累积所得到的输出值可以起到稳定的驱动作用，因此，将积分器的输出作为电流矢量角补偿值qcomp1，有
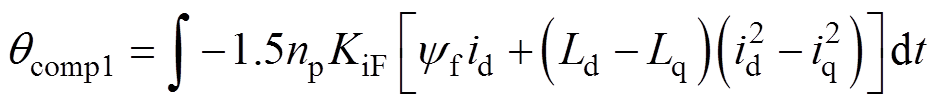（8）
根据图1所示曲线和图2所示闭环控制结构，本文设置qini=90 °，以id=0控制为IPMSM的初始运行状态。同时，将电流矢量角初始值与稳定状态下的电流矢量角补偿值作差，得到新的给定值qref。由此可得一种基于直接判据计算方式在线求取电流矢量角给定值的固定增益（Fixed-Gain current vector Angle Compensation, FGAC）MTPA控制算法，有
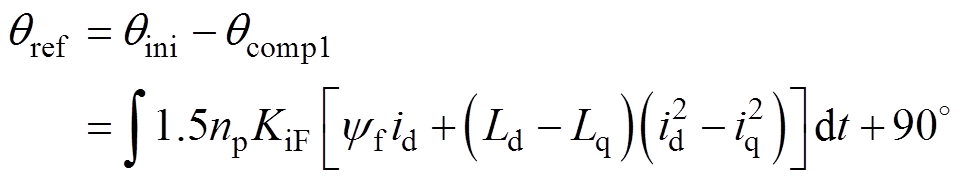（9）
前述FGAC算法建立了电流矢量角随时间变化的收敛关系，以∂Te/∂q=0为控制目标，采用误差驱动的闭环控制结构实现了MTPA控制。但所提取出的MTPA判据与负载电流存在耦合，固定积分增益KiF难以兼顾不同负载工况，致使不同负载工况下的电流矢量角收敛速度不一致：轻载时收敛慢，重载时收敛快。因此，算法适用性受限。
为保证控制算法对不同负载工况具有一致的收敛速度，根据图1可重新建立如下对应关系：①∂Te/∂q＞0，q 需逐渐增大，q-qMTPA＜0；②∂Te/∂q＜0，q 需逐渐减小，q-qMTPA＞0；③∂Te/∂q=0，q 收敛到qMTPA，q=qMTPA。
根据上述收敛关系，以q-qMTPA=0为控制目标，可以得到一种改进型MTPA控制算法。不同于FGAC算法，改进方法将q-qMTPA作为新的MTPA判据项。若电机处于非MTPA状态，q-qMTPA≠0，需调整电流矢量角q；当q-qMTPA=0时，系统达到MTPA状态。此时，算法收敛速度仅与当前电流矢量角和最优电流矢量角间的差值有关，解除了前述判据项∂Te/∂q与负载电流间的耦合。
考虑到q-qMTPA项的值无法直接计算，为获取q-qMTPA项的近似表达式，令f(q)=∂Te/∂q，当|q-qMTPA|＜d 时（d 为充分小的实数），对f(q)在qMTPA处泰勒展开，忽略二阶及以上无穷小项，得
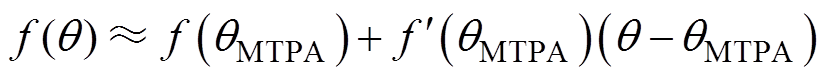（10）
根据式（6）可进一步得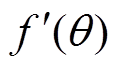
的表达式为
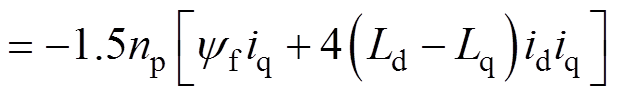（11）
根据MTPA状态定义，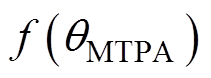
项等于零。考虑到
项难以直接求取，而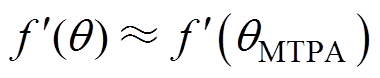
。因此，结合式（6）与式（11），式（10）可近似改写为
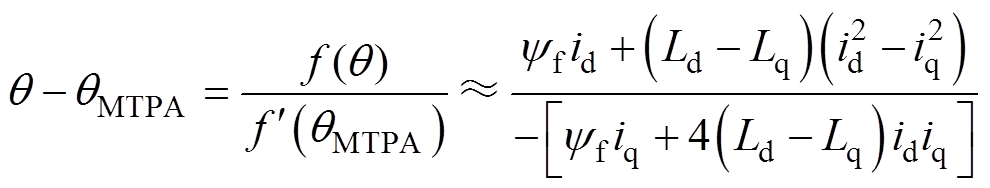（12）
式（12）为线性化后的MTPA状态决策判据，可根据电流采样值直接计算判据值。采用与FGAC算法相同的MTPA闭环控制结构，可以得出改进的MTPA电流矢量角补偿量qcomp2的计算表达式为
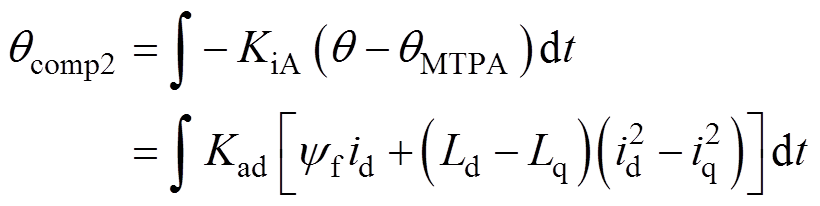（13）
式中，KiA为大于零的积分增益系数；id和iq为时变量，对应的严格表示为id(t)和iq(t)，为简化公式省去时间变量t，简化为id和iq；Kad为Kad(t)的简化表示，且Kad(t)=KiA/[yfiq(t)+4(Ld-Lq)id(t)iq(t)]为自适应增益，其值随dq轴电流变化而变化，因此也是时变量，具备自适应作用。
改进型MTPA控制算法的实现原理及其等效控制结构如图3所示。在图3中，同样以id=0控制作为IPMSM的初始运行状态，叠加电流矢量角补偿量后，可得一种基于直接判据计算方式在线求取qref的自适应增益型（Adaptive-Gain current vector Angle Compensation, AGAC）MTPA控制算法，有
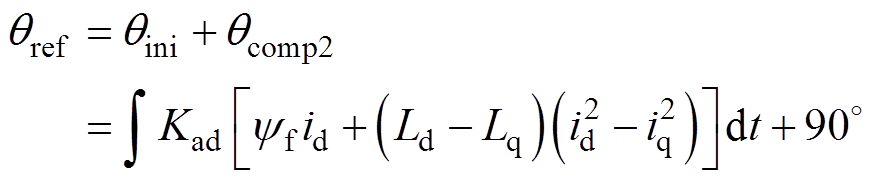（14）
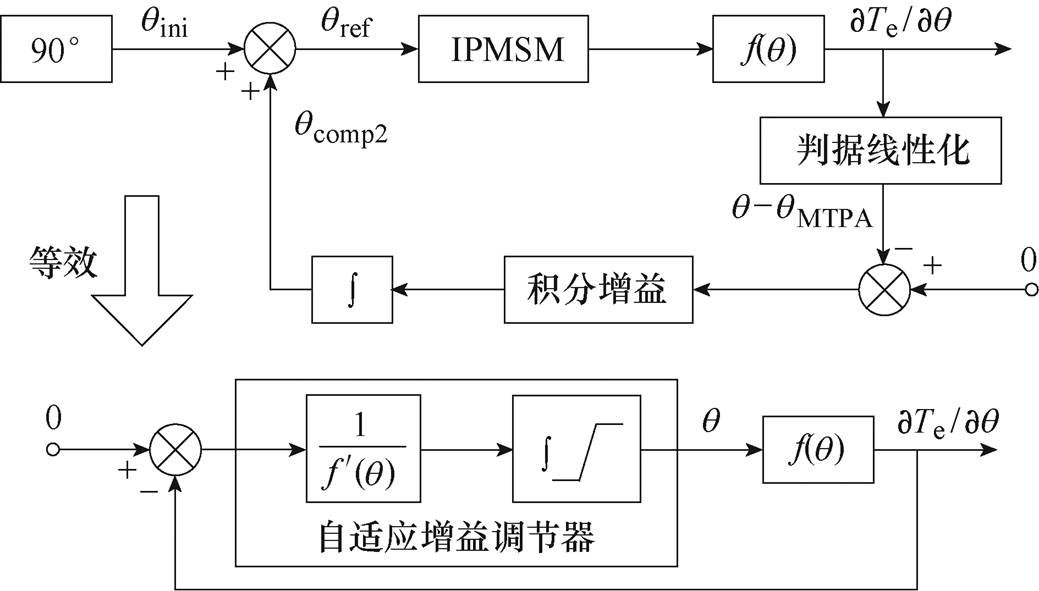
图3 改进的MTPA闭环控制结构
Fig.3 Improved closed-loop control structure of MTPA
AGAC根据负载工况动态调整积分增益，保证算法在不同负载条件下的收敛速度一致，增强系统稳定性及控制算法收敛速度对负载变化的鲁棒性。
假设在电流矢量角q（90 °＜q＜180 °）上叠加扰动信号qh，则对应的电磁转矩Te可表示为
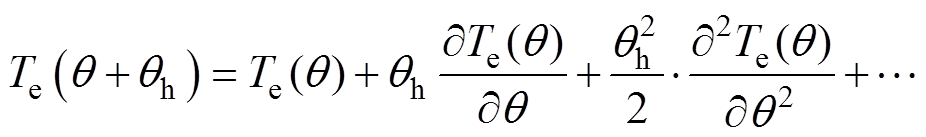
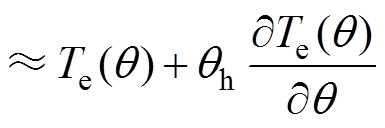（15）
作如下定义：e=Te(q+qh)-Te(q)。选取二次型Lyapunov函数为
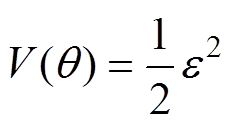（16）
电磁转矩Te及其对电流矢量角q 的一阶、二阶导数的定性描述如图4所示。由于Te(q)为凸函数，根据凸函数性质可得，Te(q)的二阶偏导数小于零。
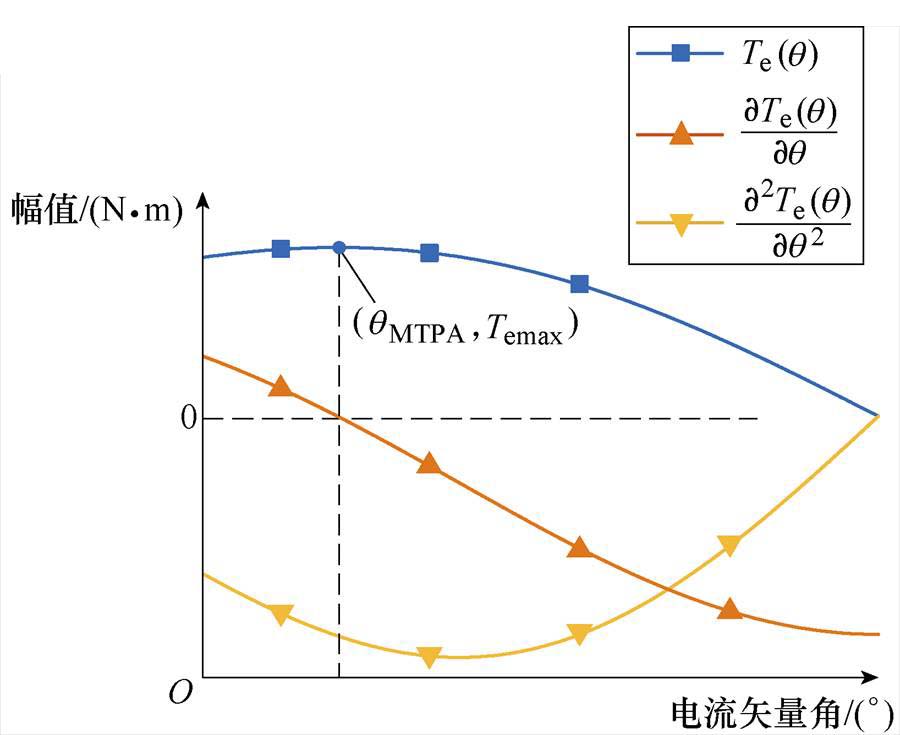
图4 电磁转矩及其一、二阶导数曲线
Fig.4 Curves of Te and its first and second derivative
因此，式（15）可重新写为
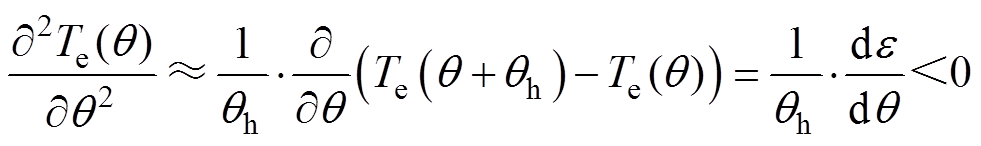（17）
根据式（16）和式（17）可得
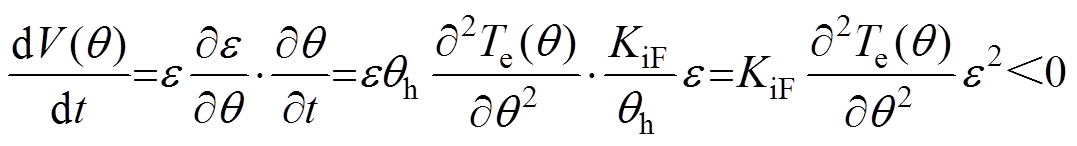（18）
根据图4可得，Te(q)关于q 的二阶偏导数值小于零，故式（14）中的Kad值总大于零，即Kad值与式（9）中的KiF值有相同的正负性。因此，在理想情况下，针对式（9）所示FGAC算法和式（14）所示AGAC算法，根据式（16）～式（18）可得到如下结论：
（1）V(q)是有连续一阶偏导数的正定标量函数。
（2）沿系统任意轨迹，Lyapunov函数V(q)关于时间的导数是负定的。
根据Lyapunov稳定性判别定理，系统在qMTPA处的平衡状态是渐近稳定的，即所提出的MTPA控制算法是稳定的。
将电流给定到实际电流生成环节视为二阶振荡系统，时间常数由PWM控制周期TPWM决定，线性增益由PWM逆变环节的增益KPWM决定。所提算法根据实际电流计算角度偏差，该过程可视为函数运算环节，将其与积分增益合并得到时变的等效积分增益Kad，积分后生成的补偿量叠加到系统给定环节。根据上述描述，得到如图5所示的MTPA控制内部电流环的结构框图。
根据图5建立系统的闭环特征方程为
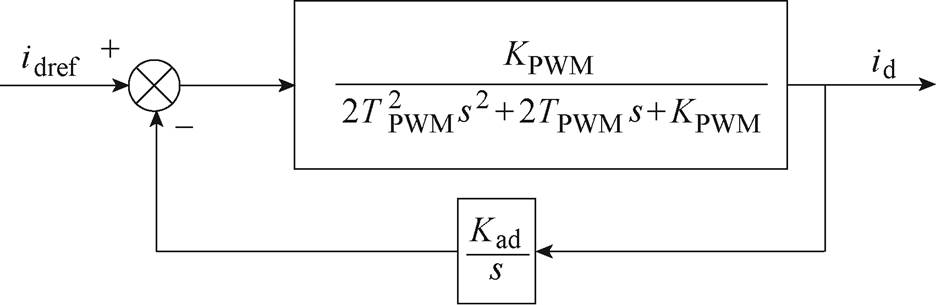
图5 简化后的MTPA控制内部电流环的结构框图
Fig.5 Simplified MTPA current control system block
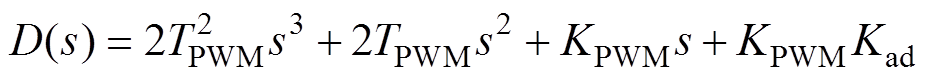（19）
式中，TPWM为PWM周期；KPWM为PWM增益；变量Kad、TPWM和KPWM均大于零。
根据劳斯判据可得系统稳定的充要条件为： Kad＜1/TPWM。在保证系统稳定的条件下，等效积分增益系数Kad取值不能超过PWM的控制频率（电流环控制频率）。为保证系统远离临界稳定状态具有足够的稳定裕度，同时兼顾较快响应速度，Kad初始值不宜过大，建议取PWM控制频率的1/10左右。
采用AGAC的IPMSM控制系统结构如图6所示。
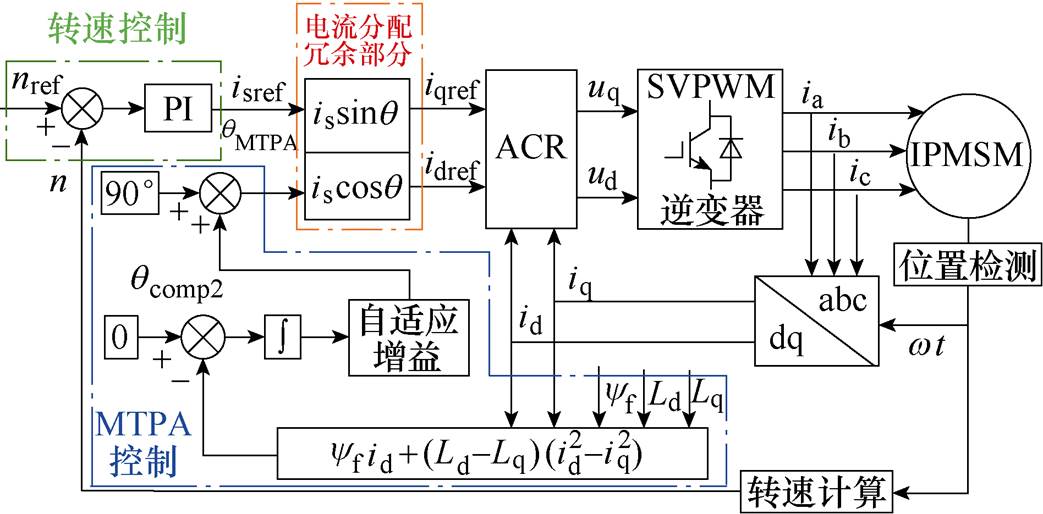
图6 基于AGAC的MTPA控制系统结构
Fig.6 Structure of MTPA control system based on AGAC
结合式（14），采用AGAC算法所得直轴电流给定值的数学响应表达式为
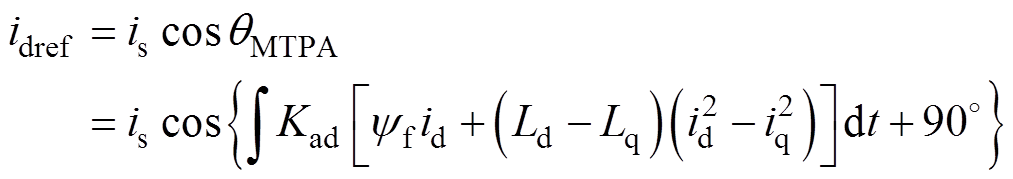（20）
由式（20）可见，虽然控制算法通过引入自适应积分增益控制降低了MTPA控制算法收敛速度对负载工况的敏感度，但在采用AGAC算法的控制系统中，dq轴电流分配仍与负载电流is存在耦合。为降低系统冗余度，简化控制结构，将MTPA控制量补偿点后移至d轴电流给定值处，可以消除电流分配环节，从而降低控制算法对负载工况的敏感度。
假设定子电流幅值不变，在电流矢量角有效范围内，随着q 的增加直轴电流单调减小，两者存在直接映射关系。类比1.1节和1.2节分析方法，可得一种直轴电流补偿型（d-axis Current Compensation, DCC）MTPA控制算法，表达式为
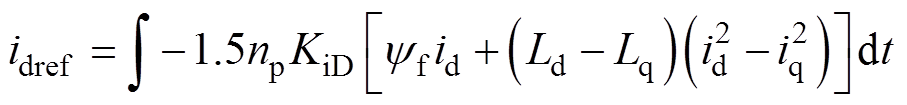（21）
式中，KiD为大于零的积分增益系数。
相比式（20），式（21）所示DCC MTPA控制算法去除了基于三角函数的dq轴电流分配过程，消除了d轴电流给定值响应表达式中的负载电流项，降低了算法对负载工况敏感度，保证了算法的简易性。改进的DCC算法对直轴电流的给定值进行在线修正，使控制系统稳定在MTPA工作状态，采用该算法的控制系统结构如图7所示。
图7 基于DCC的MTPA控制系统
Fig.7 Structure of MTPA control system based on DCC
在Matlab/Simulink中搭建仿真模型，验证所提出的控制算法的有效性，并就仿真结果进行对比分析。本文中所采用的两种永磁同步电机参数见表1，本节采用的电机仿真对象为PMSM-1。
表1 PMSM参数
Tab.1 The parameters of PMSMs
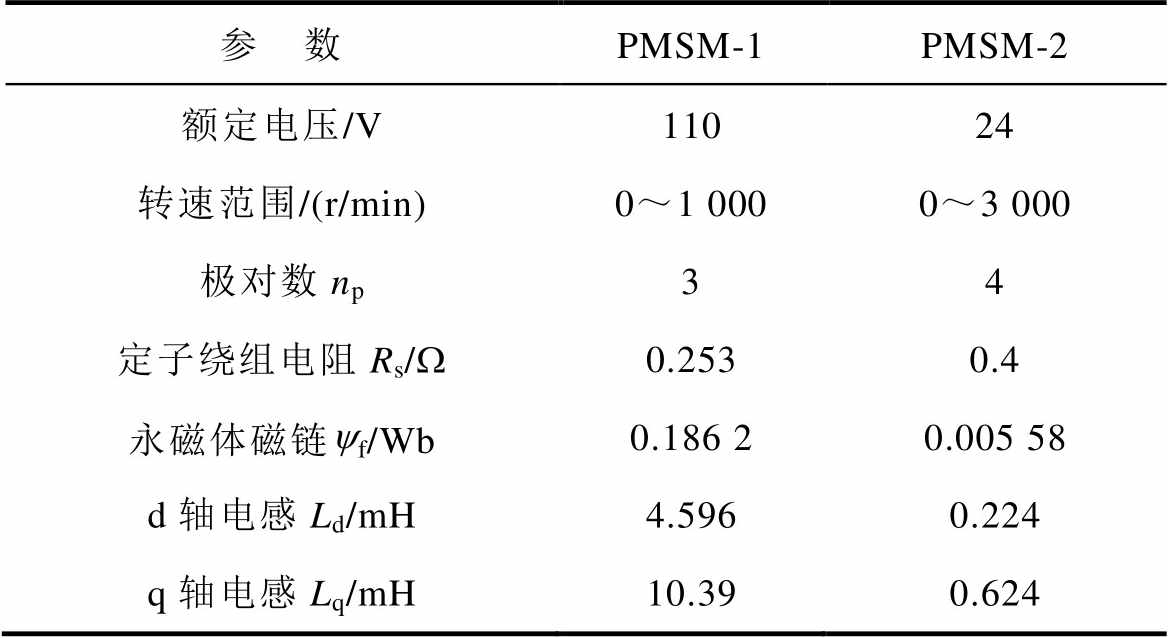
参 数PMSM-1PMSM-2 额定电压/V11024 转速范围/(r/min)0～1 0000～3 000 极对数np34 定子绕组电阻Rs/W0.2530.4 永磁体磁链yf/Wb0.186 20.005 58 d轴电感Ld/mH4.5960.224 q轴电感Lq/mH10.390.624
在不同负载条件下，采用所提三种MTPA控制算法（FGAC、AGAC、DCC）得到的仿真结果如图8所示。图8a中，电机空载起动，第10 s突加1 N·m负载，三种算法对应的dq轴电流收敛到MTPA状态所需时间分别为t1（t1≈6 s）、t2和t3（t2≈t3≈1.8 s）。图8b中，第10 s突加4 N·m负载，三种算法所需的收敛时间分别为t4、t5和t6（t4≈t5≈t6≈2.2 s）。
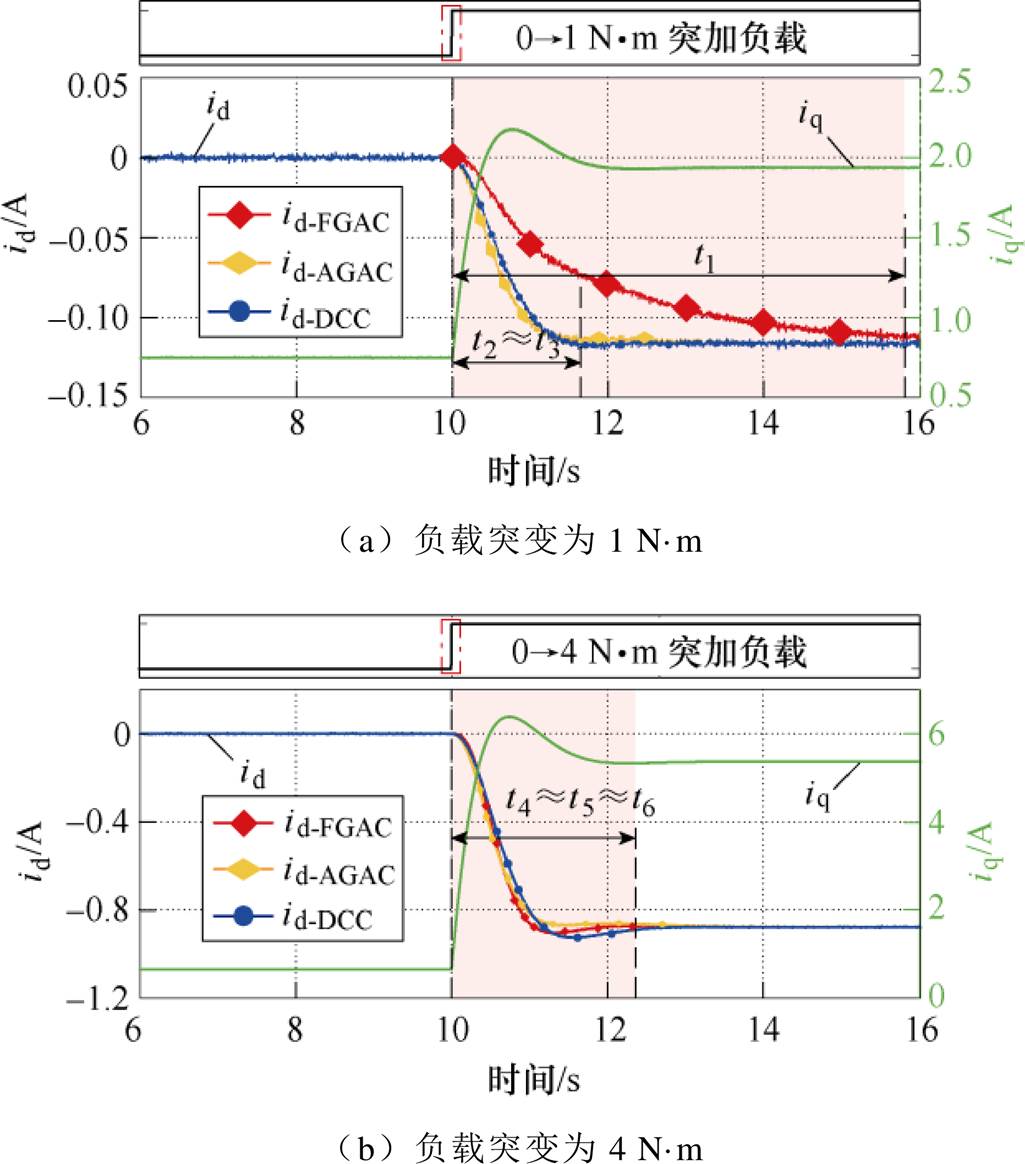
图8 所提出的MTPA算法仿真结果
Fig.8 Simulation results of the proposed MTPA algorithms
由图8可见，FGAC的收敛速度对负载工况较敏感，负载越小，系统收敛到MTPA状态的速度越慢（t1＞t4）。而AGAC和DCC在不同工况下的收敛速度基本一致，即两种算法的收敛速度对负载工况敏感度较低，其原因是引入了自适应增益，以及消除了由dq轴电流分配模块引起的负载耦合。
负载突变情况下，本文所提出的MTPA控制算法与现有VSI算法的动态响应速度对比结果如图9所示。鉴于AGAC与DCC收敛速度基本一致，因此，图中仅给出FGAC、DCC和VSI的对比。由图9可见，在不同负载条件下，本文所提算法对MTPA状态的收敛速度相比VSI算法快4～5倍。并且，在所提出的算法中，DCC在不同负载工况下的收敛速度基本一致，即消除dq轴电流分配模块这一措施有效降低了算法收敛速度与负载的耦合。
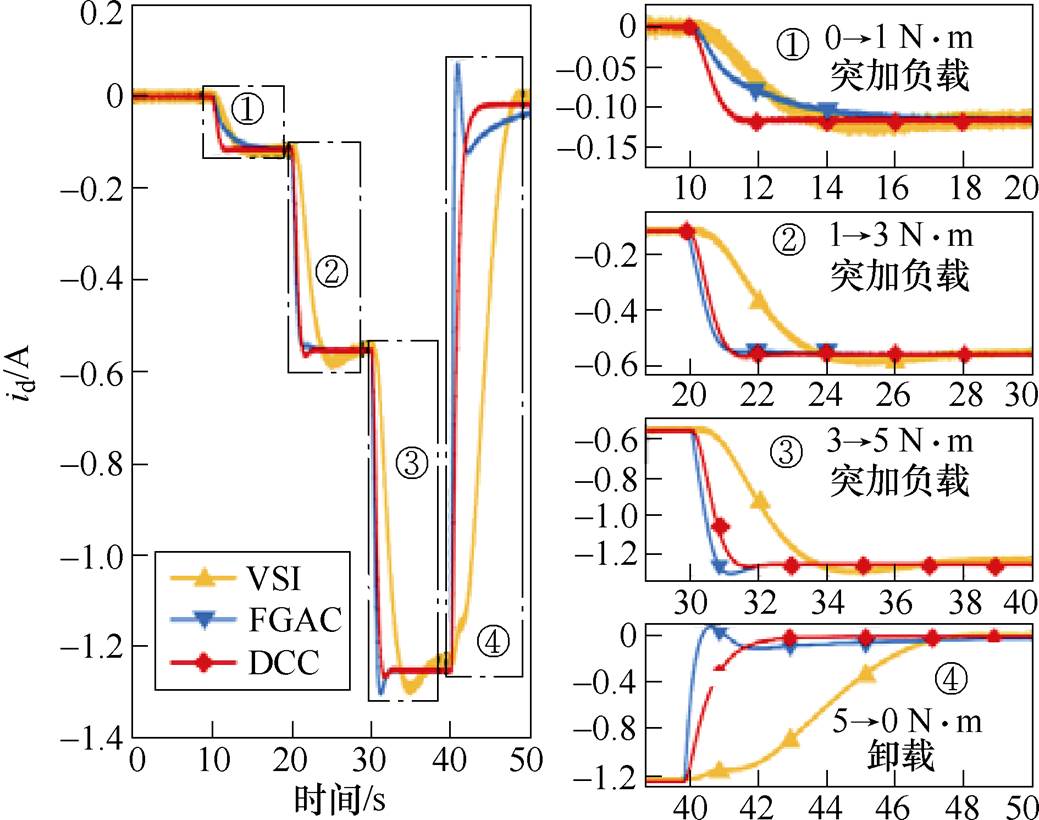
图9 MTPA控制算法动态响应速度对比
Fig.9 Dynamic response comparison of MTPA algorithms
图10进一步仿真对比了MVSI和DCC两种算法的性能。由图10可见，虽然MVSI在收敛速度的快速性方面有一定改善，但其需借助功率方程提取MTPA判据导致算法与转速存在强烈耦合，故MVSI在高转速下的收敛速度快于低转速工况。本文所提出的DCC算法基于转矩方程进行推导，实现了与转速的完全解耦，算法动态收敛速度与转速无关。
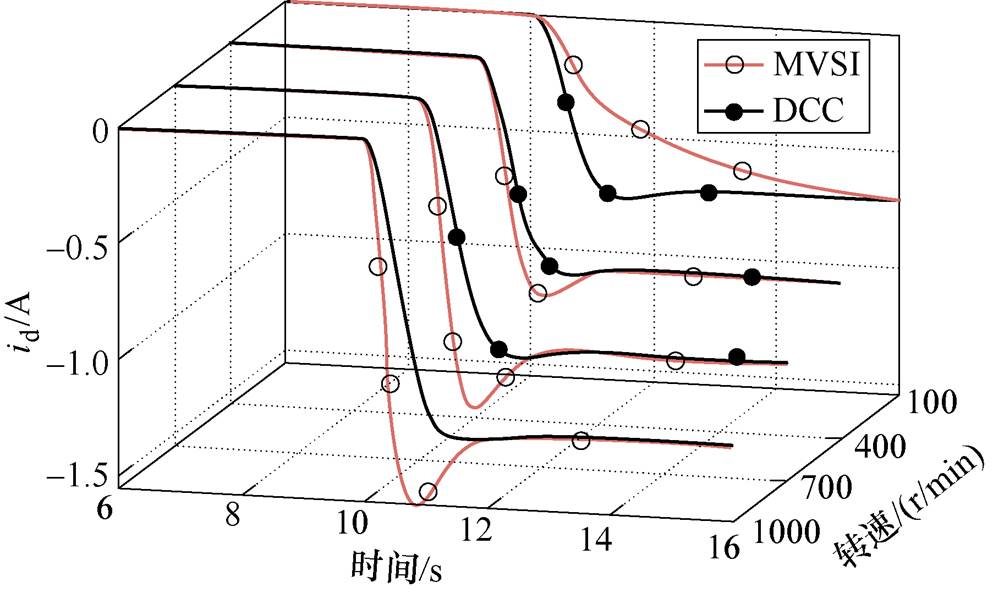
图10 控制算法的动态响应与转速的耦合
Fig.10 Coupling of the dynamic response and the speed
理论分析和仿真计算结果表明，FGAC收敛速度对负载工况较敏感，需结合自适应增益控制进行改进。AGAC和DCC两种方法性能不尽相同。DCC去除了电流分配环节，本质上对负载敏感度较低，采用固定增益即可达到AGAC算法的控制效果。并且，DCC算法中无余弦函数带来的非线性。综上所述，所提d轴电流补偿型MTPA控制方法无需信号注入、取消了信号解调制机构，系统响应速度快、算法运算量小、复杂度低，是一种较为理想的方案。
MTPA状态决策判据与yf、Ld和Lq三个参数有关，分析各参数偏差对控制精度的影响，参数偏差引起的MTPA追踪误差如图11所示。结果表明，yf和Ld偏差对MTPA状态跟踪精度的影响较小，约2 °左右（按±25 %的参数变化计算）。对于IPMSM，磁路饱和导致Lq的变化幅度大于Ld变化幅度[13, 17]，因此Lq偏差对MTPA算法控制精度的影响更为突出，可以结合参数辨识算法实时在线估计Lq，提高MTPA状态的跟踪精度。
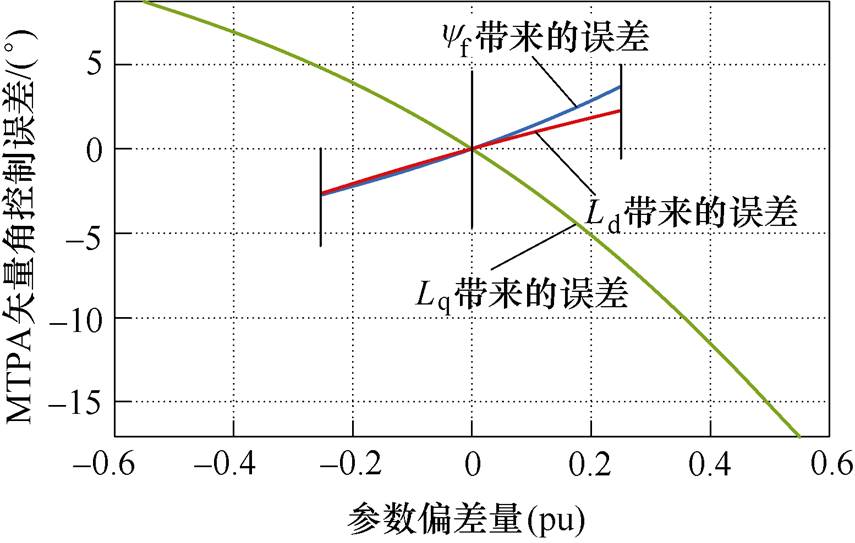
图11 参数偏差引起的MTPA追踪误差
Fig.11 MTPA tracking error caused by parameter deviation
考虑电机稳态方程及本文所建立的MTPA判据形式，可以将yf和Ldid合并考虑，建立依托单变量Rs的yf+Ldid和Lq辨识方法，即
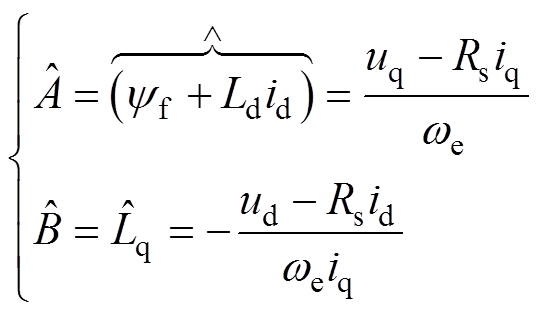（22）
式中，
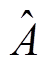和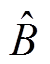
分别为参数yf+Ldid和Lq的估计值。
此时，所提出的MTPA控制算法仅依赖Rs和Ld参数，Ld偏差引起的MTPA状态误差与图11一致，计算DRs引起的MTPA状态误差如图12所示。图11和图12表明，MTPA状态误差与DLd/Ld、以及与DRs/Rs的关系近似呈线性；电机转速越低，DRs引起的MTPA的跟踪误差越大；在全速域范围内，DLd引起的误差相对较大，DRs引起的误差则较小，电阻参数偏差对MTPA控制精度的影响较弱。
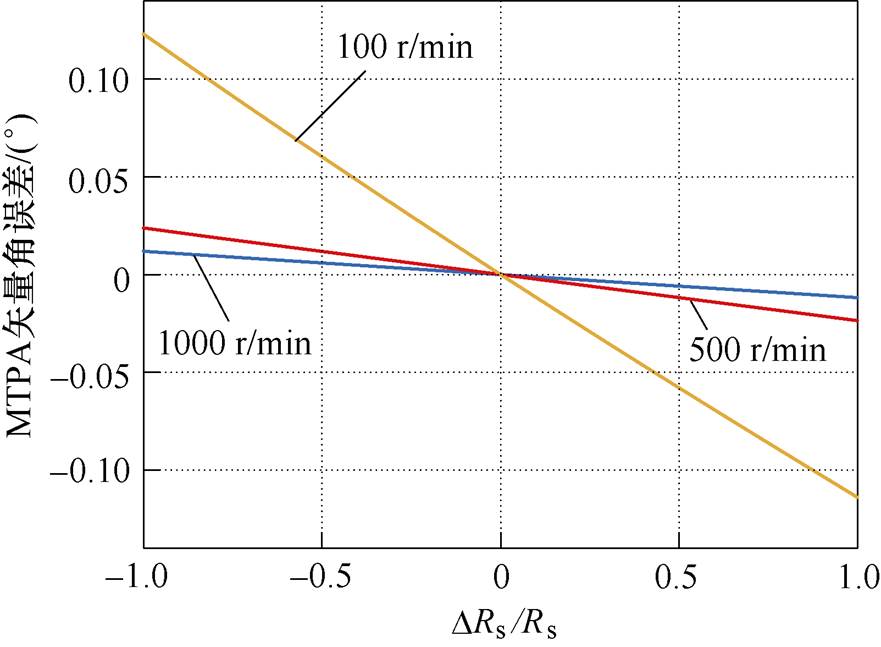
图12 DRs偏差引起的MTPA的跟踪误差
Fig.12 MTPA tracking error caused by DRs
本文在不同实验平台上分别对所提出的算法的控制性能进行实验验证。实验测试平台如图13所示，其中，实验平台1采用的电机为PMSM-1。实验过程中，逆变器开关频率设置为10 kHz，控制系统采样周期设置为100 ms，电流环PWM控制周期设置为100 ms，而MTPA控制算法执行周期与转速环控制周期相同，均设置为1 ms。
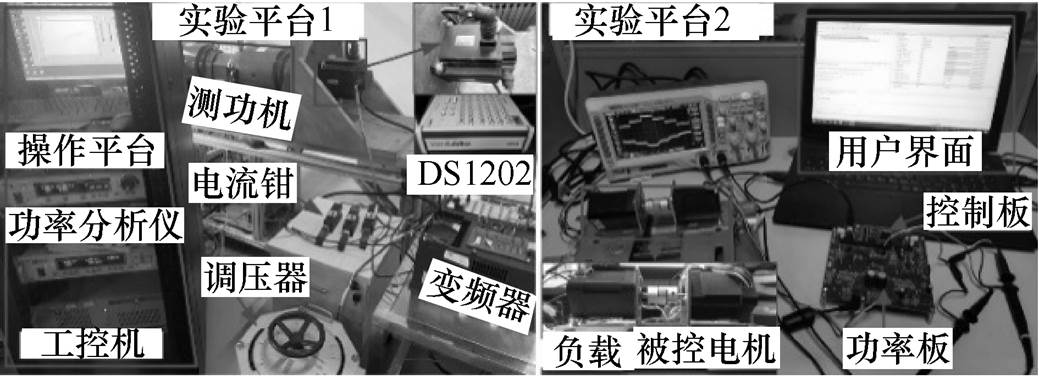
图13 测试平台
Fig.13 Test platform
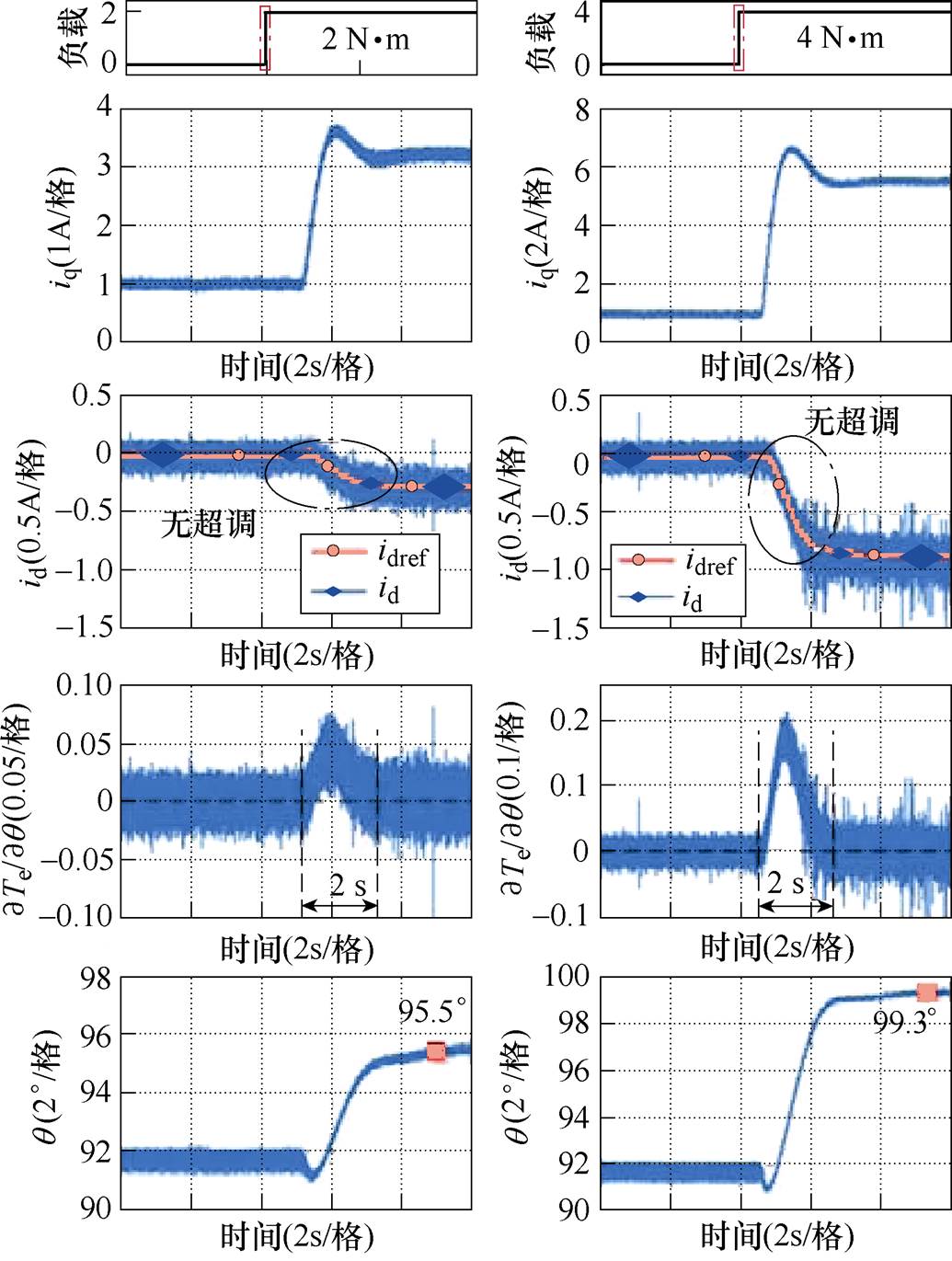
经过3.1节对比分析，DCC算法的综合性能较为优秀。因此，本节实验仅对所提出的DCC算法进行验证。为验证DCC收敛速度对不同负载工况的鲁棒性，图14和图15分别为不同给定转速时，转矩突变工况下的DCC MTPA算法动态响应过程。由图14和图15可见，在2 N·m和4 N·m的不同工况下，DCC算法收敛速度基本相同（约2 s）。在所有控制器参数均不变的情况下，算法收敛速度与转速无关，验证了DCC收敛速度与转速的解耦关系。
在相同的实验平台条件下，本文对VSI和MVSI进行实验验证，给出了详细的实验结果，并与本文所提出的DCC算法进行比较。
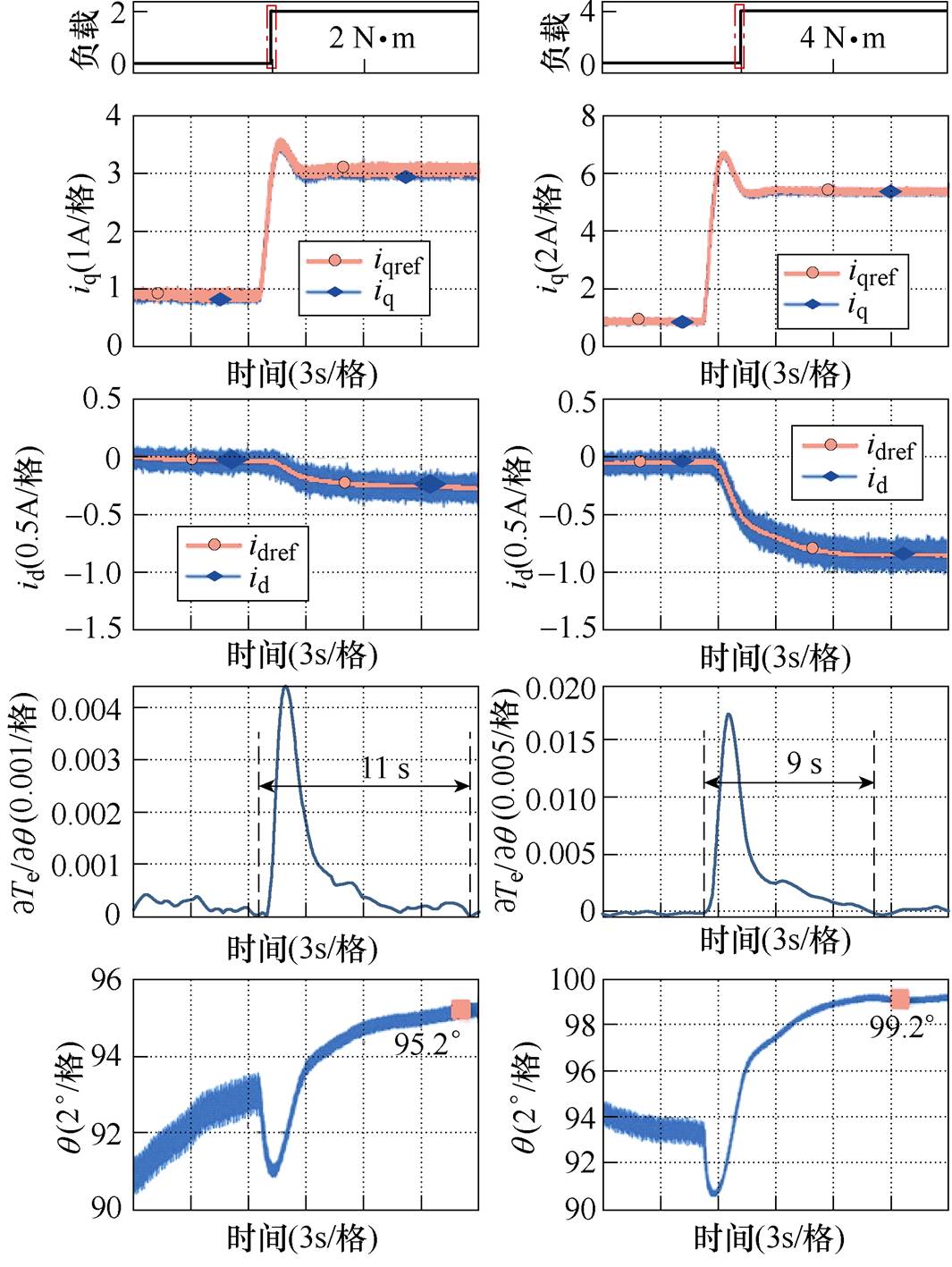
当采用VSI方法时，在400 r/min工况下，负载转矩阶跃变化和连续递增/递减的实验结果分别如图16和图17所示。可见，VSI收敛到MTPA状态所需时间约为10 s，与现有文献所得结果一致。VSI利用级联滤波器结构对注入的正弦信号进行解调制以提取MTPA状态决策判据，该过程限制了MTPA控制环节的带宽。因此，在轻载和重载工况下，VSI的动态收敛速度均慢于DCC算法。
当采用MVSI方法时，在不同转速条件下，负载转矩阶跃变化和连续递增/递减的实验结果分别如图18和图19所示。
（a）0～2 N·m负载突变 （b）0～4 N·m负载突变
图14 在400 r/min工况下所提出的算法的控制性能
Fig.14 Waveforms of the proposed algorithm at 400 r/min
（a）0～2 N·m负载突变 （b）0～4 N·m负载突变
图15 在800 r/min工况下所提出的算法的控制性能
Fig.15 Waveforms of the proposed algorithm at 800 r/min
（a）0～2 N·m负载突变 （b）0～4 N·m负载突变
图16 在400 r/min时VSI方法的实验结果
Fig.16 Experimental results of the VSI at 400 r/min
图17 在400 r/min和负载连续阶跃变化时VSI的波形
Fig.17 Waveforms of VSI under 400 r/min and continuous step change of load
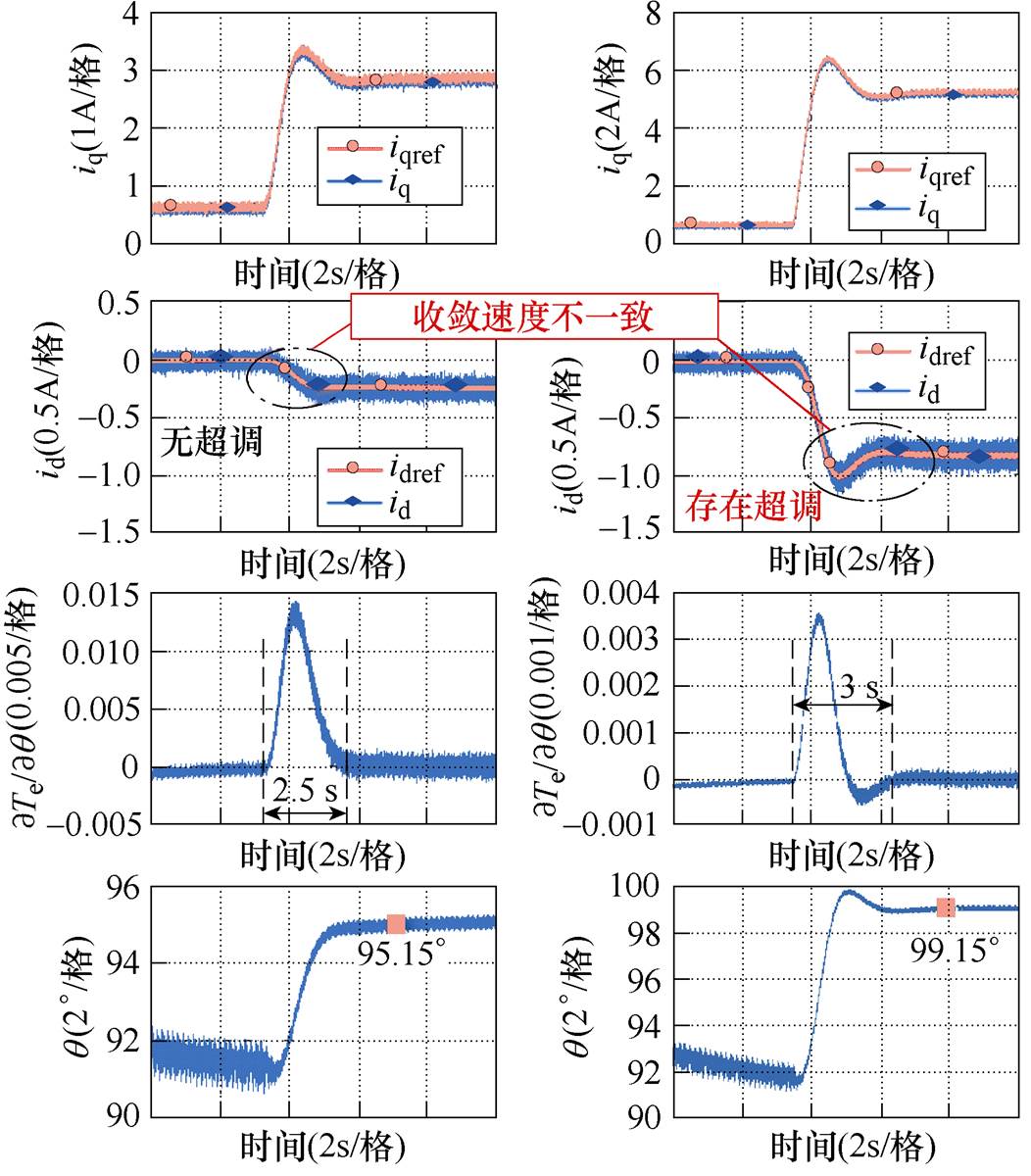
（a）400 r/min突增2 N·m负载 （b）800 r/min突增4 N·m负载
图18 在不同工况下MVSI方法的实验结果
Fig.18 Experimental results of the MVSI
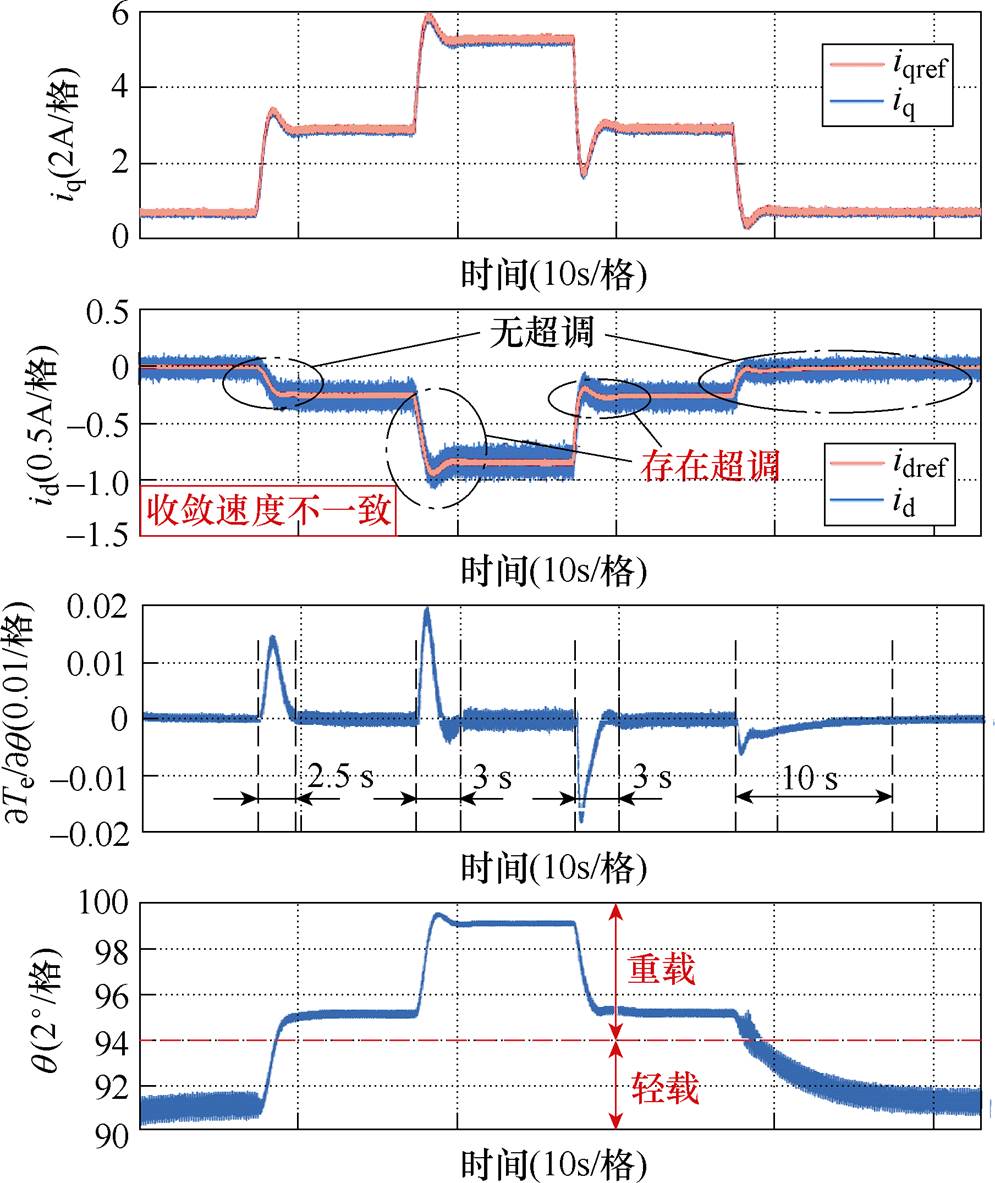
图19 在400 r/min和负载连续阶跃变化时MVSI的波形
Fig.19 Waveforms of MVSI under the condition of 400 r/min and continuous step change of load
图18a中，在400 r/min时，负载转矩从0突变为2 N·m，id约2.5 s后收敛到最优解，且不产生超调。图18b中，在800 r/min时，负载转矩从0突变为4 N·m，id经过约3 s收敛到最优解，但调节过程出现了明显超调。图18和图19表明：MVSI的收敛速度较快，但由于其信号解调制过程依赖功率方程，算法收敛速度与电机实际转速之间存在耦合。并且，MVSI的收敛速度对负载工况较敏感，在转速或负载变化剧烈的场合下，追求轻载工况下的快速动态响应会导致重载时负载突变过程中的d轴电流超调增大，严重时甚至会导致系统运行失去稳定。
表2给出了三种MTPA控制算法所得最优电流矢量角值，以及对应的实际最优矢量角值。表2表明，三种算法在相同工况下的稳态控制误差均在1 °～2 °范围内，具有近似的控制精度。
表2 不同方法所得的电流矢量角对比
Tab.2 Comparison of qMTPA obtained by different methods（单位: °）
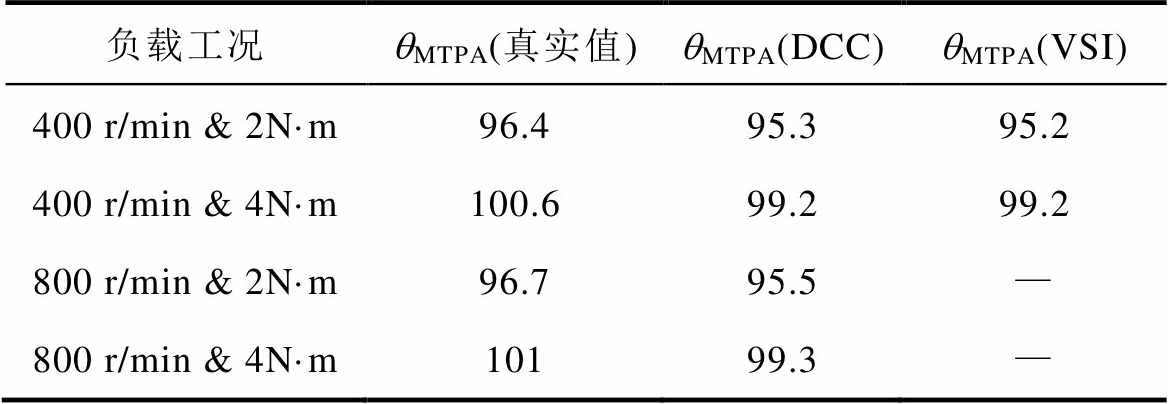
负载工况qMTPA(真实值)qMTPA(DCC)qMTPA(VSI) 400 r/min & 2N·m96.495.395.2 400 r/min & 4N·m100.699.299.2 800 r/min & 2N·m96.795.5— 800 r/min & 4N·m10199.3—
MTPA控制算法的收敛速度上限受制于转速环带宽。实验平台1转速环带宽较小，故MTPA算法收敛速度较慢。针对此问题，以PMSM-2为控制对象，在基于TI F28069M和TI DRV8312的实验平台2上开展转速环带宽不受限情况下的实验验证。
在转矩控制模式下，图20为采用不同积分增益调节DCC算法的动态收敛速度的实验结果。为便于叙述，本文以逆变器开关频率为基准值对积分增益KiD进行归一化处理。由图20可见，随着积分增益增大，算法收敛速度加快。
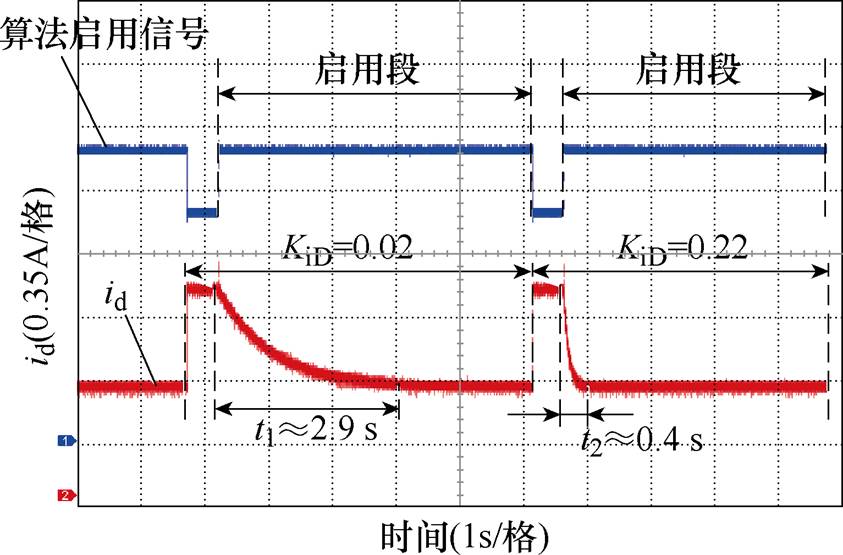
图20 DCC收敛速度调节实验
Fig.20 Adjustment of DCC convergence speed
采用转速、电流双闭环控制策略进行实验，所得结果如图21所示。当KiD=0.05时，id收敛至最优解所需时间约为2.2 s，当KiD=0.5时，id收敛至最优解所需时间则约为1.2 s，算法收敛速度加快。相比图20，当KiD=0.22时，算法收敛时间仅需0.4 s。对比实验结果表明，MTPA收敛速度受转速环带宽制约。即采用双闭环控制时，增大积分增益对MTPA收敛速度的改善效果受转速环带宽限制，达到带宽上限后，若继续增加KiD，算法收敛速度改善有限，且易导致系统失去稳定。考虑KiD取值范围与电流环PWM控制频率的联系，本文设置MTPA控制算法执行频率与转速环相同，并选择KiD初始值为电流环PWM控制频率的1/10，再根据实际系统需要进行微调，进一步优化算法收敛速度。
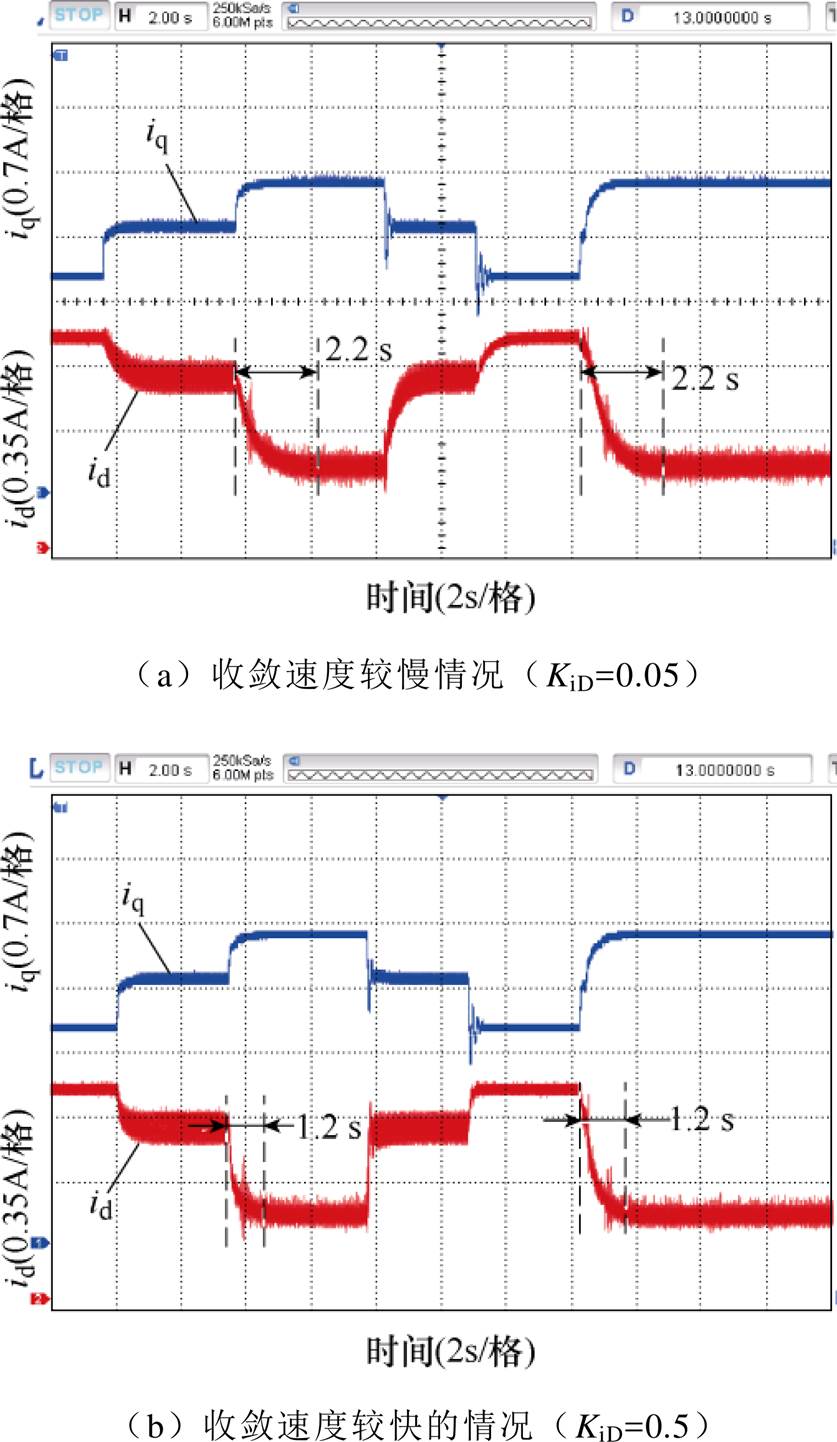
图21 受限于转速环带宽时的DCC算法实验结果
Fig.21 Experimental results of DCC algorithm limited by the bandwidth of speed loop
由于硬件条件限制，不同文献中MTPA控制算法动态过程持续时间各不相同。为客观比较不同算法的动态收敛速度，本文采用归一化方法，将轻载下VSI的收敛时间作为参考值1(pu)，计算不同方法收敛所需时间的归一化值。
表3为不同MTPA算法的动态性能对比结构。相比而言，所提DCC算法收敛速度较快，并且对转速和转矩等工况不敏感，对于工况变化复杂、剧烈的场合有较强的适用性。
表3 不同MTPA方法的性能比较
Tab.3 Comparison of dynamic performance
方法VSI(1)[12]VSI(2)[17]MVSI[15]DCC本文 轻载收敛时间(pu)1110.2 重载收敛时间(pu)10.110.40.2 是否对转速敏感否否是否 是否对负载敏感否是是否 信号注入形式正弦波方波多正弦波—
实验中，为比较不同MTPA算法的复杂度，以DCC和MVSI为例，分别统计执行MTPA算法相关代码所需的时钟周期数、运算时长以及内存占用等性能指标，所得结果见表4。表4表明，所提出的DCC MTPA控制算法计算量最小，运算时长仅需1.24 ms。而MVSI算法在线计算量较大，所需计算时长为8.81 ms。相比MVSI，DCC的时间复杂度（在线计算量）减少了约86 %，空间复杂度（内存占用）减少了约56 %。
表4 算法复杂度对比
Tab.4 Comparison of complexity
性能指标MVSIDCC 时钟周期数量/个793112 运算时间/ms8.811.24 占用内存数量/字节3 2071 419
所提无需信号注入的DCC MTPA控制算法直接在线计算判据值，消除了解调制过程对MTPA算法收敛速度的限制，而补偿点后移至直轴电流给定环节实现了算法收敛速度与负载工况的解耦。在降低算法复杂度的基础上，DCC MTPA控制算法在不同工况下的收敛速度均优于现有大多数方法。
本文提出了一种基于直接判据提取方式的直轴电流补偿型最大转矩电流比控制算法，该方法无需任何形式的信号注入过程，具有以下优点：
1）所提出的算法建立了MTPA状态直接决策判据，缩短了算法的解算收敛时间。以VSI动态收敛过程持续时间为基准值1(pu)，不同工况下，所提算法收敛时间均仅需0.2(pu)，快于现有大多数方法。
2）所提出的算法通过直接计算方式提取MTPA状态决策判据，无需向系统中注入实际/虚拟信号，无需信号解调制过程。相比MVSI，所提算法的时间复杂度减少约86 %，空间复杂度减少约56 %。
3）通过设置自适应积分增益和对MTPA控制系统进行结构优化，降低了算法的动态收敛速度对负载、转速等工况的敏感度，增强了算法适用性。
参考文献
[1] 佟文明, 姚颖聪, 李世奇, 等. 考虑磁桥不均匀饱和的内置式永磁同步电机等效磁网络模型[J]. 电工技术学报, 2022, 37(12): 2961-2970.
Tong Wenming, Yao Yingcong, Li Shiqi, et al. Equivalent magnetic network model for interior permanent magnet machines considering non-uniform saturation of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2961- 2970.
[2] Liu Feng, Wang Xiuhe, Xing Zezhi, et al. Reduction of cogging torque and electromagnetic vibration based on different combination of pole arc coefficient for interior permanent magnet synchronous machine[J].CES Transactions on Electrical Machines and Systems, 2021, 5(4): 291-300.
[3] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet syn- chronous motor based on adaptive Notch filter online decoupling[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 344-354.
[4] 李峰, 夏超英. 考虑磁路饱和的IPMSM电感辨识算法及变参数MTPA控制策略[J]. 电工技术学报, 2017, 32(11): 136-144.
Li Feng, Xia Chaoying. Inductance identification algorithm and variable-parameters MTPA control strategy for IPMSM considering magnetic circuit saturation[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 136-144.
[5] 付兴贺, 陈锐, 董婷, 等. 考虑参数不确定的永磁同步电机MTPA控制综述[J]. 中国电机工程学报, 2022, 42(2): 796-807, 30.
Fu Xinghe, Chen Rui, Dong Ting, et al. Overview of MTPA control of permanent magnet synchronous motor considering parameter uncertainty[J]. Pro- ceedings of the CSEE, 2022, 42(2): 796-807, 30.
[6] Wang Huimin, Li Chongyuan, Zhang Guozheng, et al. Maximum torque per ampere (MTPA) control of IPMSM systems based on controller parameters self-modification[J]. IEEE Transactions on Vehicular Technology, 2020, 69(3): 2613-2620.
[7] Kim Y S, Sul S K. Torque control strategy of an IPMSM considering the flux variation of the per- manent magnet[C]//2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 2007: 1301-1307.
[8] Dianov A, Young-Kwan K, Sang-Joon L, et al. Robust self-tuning MTPA algorithm for IPMSM drives[C]//34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 2009: 1355-1360.
[9] Bolognani S, Petrella R, Prearo A, et al. Automatic tracking of MTPA trajectory in IPM motor drives based on AC current injection[J]. IEEE Transactions on Industry Applications, 2011, 47(1): 105-114.
[10] Liu Guohai, Wang Jian, Zhao Wenxiang, et al. A novel MTPA control strategy for IPMSM drives by space vector signal injection[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9243-9252.
[11] 刘国海, 张嘉皓, 陈前. 基于空间电压矢量注入的频率可变型五相永磁同步电机最大转矩电流比控制[J]. 电工技术学报, 2020, 35(20): 4287-4295.
Liu Guohai, Zhang Jiahao, Chen Qian. Variable frequency maximum-torque-per-ampere control for five-phase permanent-magnet motor based on space voltage vector injection[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4287-4295.
[12] Sun Tianfu, Wang Jiabin, Chen Xiao. Maximum torque per ampere (MTPA) control for interior per- manent magnet synchronous machine drives based on virtual signal injection[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 5036-5045.
[13] 赵文祥, 刘桓, 陶涛, 等. 基于虚拟信号和高频脉振信号注入的无位置传感器内置式永磁同步电机MTPA控制[J]. 电工技术学报, 2021, 36(24): 5092- 5100.
Zhao Wenxiang, Liu Huan, Tao Tao, et al. MTPA control of sensorless IPMSM based on virtual signal and high-frequency pulsating signal injection[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5092-5100.
[14] Sun Tianfu, Wang Jiabin, Koc M. On accuracy of virtual signal injection based MTPA operation of interior permanent magnet synchronous machine drives[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7405-7408.
[15] Chen Bao, Shen Anwen, Luo Xin, et al. Novel MTPA control strategy for IPMSM based on multiple virtual signals injection[J]. IET Electric Power Applications, 2020, 14(3): 457-463.
[16] Zhao Yue. Virtual square-wave current injection based maximum torque per ampere control for interior permanent-magnet synchronous machines[C]//2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 2016: 1-6.
[17] Wang Jun, Huang Xiaoyan, Yu Dong, et al. An accurate virtual signal injection control of MTPA for an IPMSM with fast dynamic response[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7916-7926.
[18] Zhou Xinxiu, Zhou Yongping, Wang Huijun, et al. An improved MTPA control based on amplitude-adjustable square wave injection[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 956-965.
[19] Bedetti N, Calligaro S, Olsen C, et al. Automatic MTPA tracking in IPMSM drives: loop dynamics, design, and auto-tuning[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 4547-4558.
[20] 李祥林, 薛志伟, 阎学雨, 等. 基于电压矢量快速筛选的永磁同步电机三矢量模型预测转矩控制[J]. 电工技术学报, 2022, 37(7): 1666-1678.
Li Xianglin, Xue Zhiwei, Yan Xueyu, et al. Voltage vector rapid screening-based three-vector model predictive torque control for permanent magnet synchronous motor[J]. Transactions of China Electro- technical Society, 2022, 37(7): 1666-1678.
[21] 肖飞, 许观达, 连传强, 等. 永磁同步电机单电流传感器系统的三相电流重构策略[J]. 电工技术学报, 2022, 37(7): 1609-1617.
Xiao Fei, Xu Guanda, Lian Chuanqiang, et al. Three- phase current reconstruction strategy of permanent magnet synchronous machine drives using a single current sensor[J]. Transactions of China Electro- technical Society, 2022, 37(7): 1609-1617.
Abstract Due to the asymmetry of the magnetic circuit of the quadrature axis and direct axis, there are both permanent magnet torque and reluctance torque in the electromagnetic torque of the interior permanent magnet synchronous motor (IPMSM). In order to improve the utilization rate of reluctance torque, the maximum torque per ampere (MTPA) control has become the preferred control strategy of IPMSM. Corresponding to a certain load torque, the MTPA control minimizes the armature current required to maintain the operation of the motor by distributing the d-q axis current, thereby reducing copper consumption and improving efficiency. Some of the existing MTPA control methods have the problems of immense computation, high complexity, and low practicability. An improved MTPA control algorithm to realize the high-performance operation of IPMSM is proposed in this paper, which aims to simplify the control structure, speed up the dynamic response and enhance the robustness of the system.
The proposed algorithm directly calculates the differential term of electromagnetic torque according to d-q axis currents, which is taken as the decision criterion of the MTPA state. According to the convergence relationship between the MTPA criterion and the dq/dt term, when the motor is in a non-MTPA state, the ∂Te/∂qis not zero, and the current vector angle q needs to be adjusted. Then, an error-driven closed-loop control structure is constructed with the criterion value equal to zero as the control target. Finally, the given value of the current vector angle qref is adjusted in real time based on the initial value of the current vector angle qini. The criterion is utilized to compensate for the reference value of the d-axis current to realize the tracking and maintenance of the MTPA state. The proposed method does not need an actual or virtual signal injection and demodulation, and the dynamic performance of the system is improved. The d-axis current compensation control solves the problem that the convergence speed of the conventional algorithm is sensitive to load conditions, and improves the robustness of the control system.
This paper has compared the proposed algorithms, including fixed-gain current vector angle compensation (FGAC), adaptive-gain current vector angle compensation (AGAC), and d-axis current compensation (DCC), with the current virtual signal injection (VSI) and multiple virtual signals injection (MVSI). The 1 N·m load test show that the time required for the d-q axis current corresponding to converge to the MTPA state is about 6 s (FGAC), 1.8 s (AGAC), and 1.8 s (DCC). When the load is changed to 4 N·m, the response time of the three methods is about 2.2 s. The convergence speed of the proposed algorithm for the MTPA state is 4～5 times faster than that of the VSI algorithm. Experiments show that the convergence speed of the DCC algorithm is mostly the same (about 2 s) under different working conditions of 2 N·m and 4 N·m. The dynamic convergence speed of VSI is slower than that of the DCC algorithm under light load and heavy load. Compared with MVSI, DCC’s time complexity (online computation) is reduced by about 85%, and the space complexity (memory footprint) is reduced by about 55%.
The following conclusions can be drawn from simulation and experimental analysis: (1) The proposed algorithm establishes the MTPA state direct decision criterion, which shortens the solution convergence time. Taking the VSI dynamic convergence process duration as the benchmark value 1(pu), the convergence time of the proposed algorithm is only 0.2(pu) under different working conditions, faster than most existing methods. (2) The proposed algorithm extracts the MTPA state decision criterion using direct calculation without injecting real/virtual signals into the system and the signal demodulation process. Both time complexity and space complexity are reduced. (3) By setting the adaptive integral gain and optimizing the structure of the MTPA control system, the sensitivity of the dynamic convergence speed of the algorithm to the load, speed, and other working conditions is reduced, and the applicability of the algorithm is enhanced.
keywords：Interior permanent magnet synchronous motor (IPMSM), maximum torque per ampere (MTPA), criterion calculation, d-axis current compensation
DOI: 10.19595/j.cnki.1000-6753.tces.221091
中图分类号：TM351
江苏省自然科学基金（BK20201275）、国家自然科学基金（51977035）和特种电机与高压电器教育部重点实验室开放课题（KFKT202001）资助项目。
收稿日期 2022-06-10
改稿日期 2022-06-28
付兴贺 男，1978年生，博士，副教授，博士生导师，研究方向为高温特种电机及其控制、伺服系统多源异构扰动抑制。E-mail: fuxinghe@seu.edu.cn（通信作者）
陈 锐 男，1997年生，硕士，研究方向为永磁电机控制。E-mail: 220192697@seu.edu.cn
（编辑 崔文静）