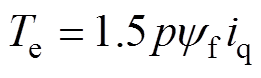 (1)
(1)
摘要 为了提高永磁同步电机位置伺服系统的控制性能,该文提出一种鲁棒性无差拍预测转速控制策略。首先,根据无差拍控制原理对速度环和电流环进行设计。其次,采用增量模型消除了永磁磁链对电流预测的影响。再次,设计扩展状态观测器,对参数不匹配、负载和逆变器非线性造成的扰动进行观测。然后,根据位置伺服系统的特点提出一种补偿策略。最后,通过实验对提出的控制策略进行研究,实验结果表明,该方法能提高系统的稳态控制精度和动态响应速度。
关键词:位置伺服系统 无差拍预测转速控制 扩展状态观测器 补偿策略
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)驱动系统[1-2]由于具有高功率密度、高效率和结构紧凑等特点,被广泛地应用于伺服系统中。磁场定向控制是PMSM驱动广泛应用的控制策略。在位置伺服系统中,为了获得精确的稳态跟踪效果和快速的动态响应,传统PI控制[3]是设计速度环和电流环时常用的方法。伺服电动机要求在各种工况、电机内部参数变化和外部扰动的影响下都能保持理想的工作性能,因此对PI控制器的参数提出了更高的要求。
近些年,预测控制由于具有较好的自适应能力和良好的动态性能,逐渐成为研究热点[4-8]。预测控制主要可以分为两类:模型预测控制(Model Predictive Control, MPC)[9-11]和无差拍预测控 制[12-13]。MPC利用电机离散模型预测未来的工作状态,进而可以根据价值函数确定最优的工作电压矢量。文献[10]提出了一种用于永磁同步电机的模型预测直接转速控制(Model Predictive Direct Speed Control, MPDSC)方法。该方法结构简单,无需脉冲宽度调制(Pulse Width Modulation, PWM),但精确的预测需要较大的计算量,对硬件条件要求较高,限制了其在工业中的应用。无差拍预测控制基于系统离散模型计算每个采样周期的参考电压矢量,通过PWM转换为开关信号,能在较小的计算量下获得相近的动态性能和更好的稳态跟踪效果。因此,无差拍预测电流控制(Deadbeat Predictive Current Control, DPCC)被应用在很多工业领域。但是,目前很少有文献提到速度环和电流环均采用基于离散模型设计的无差拍预测转速控制(Deadbeat Predi- ctive Speed Control, DPSC)方法,因此将无差拍预测控制同时用于永磁同步电机电流环与速度环,改善位置伺服电动机的性能还值得进一步深入研究。
无论是MPDSC还是DPSC都需要精确的控制模型,包括电机的电气参数、机械参数以及负载信息。一方面,电机的电气参数会随着运行工况以及温度的变化而发生变化,机械参数无法通过直接测量获得,而负载转矩则需要通过额外的装置进行测量。另一方面,逆变器非线性会影响预测的精度从而降低系统的性能。可以采用电机在线参数辨识的方法来解决模型预测控制中的模型准确度问题。文献[14]中提出了一种基于模型参考自适应系统(Model Reference Adaptive System, MRAS)的参数估计方法,为了解决欠秩问题,通过将一些参数作为已知的固定值来估计其他参数。但由于电机参数实时变化而无法固定,因此会导致MRAS得到参数辨识结果不准确。文献[15]提出了一种基于磁链注入的参数辨识方法,能够实现对电机电气参数的辨识,但是额外的信号注入会影响系统正常的运行状态。文献[16]提出了一种基于粒子群优化算法的参数辨识方法,可以对电机参数以及逆变器非线性进行全局辨识。但是该方法必须在空载情况下应用,并且这种生物启发式算法需要对大量数据进行迭代寻优,难以应用于实时数字处理器中。
另一种解决模型预测控制中模型准确度问题的方法是采用扰动观测器[17-18]进行补偿。文献[17]基于滑模控制理论设计了一种全局参数扰动和负载观测器,有效地提高了电机系统的鲁棒性。但是滑模观测器的效果依赖相关参数的合理选择,目前尚未有相关文献提出具体的选择标准。文献[18]提出了一种扩展状态观测器(Extended State Observer, ESO),可以对未知扰动进行准确观测。ESO独立于系统的数学模型,因此具有较强的鲁棒性,但该文献仅讨论了其对电流环的性能改进,并没有将其同时用于速度环和电流环预测控制中。文献[19]采用无差拍控制策略来减小系统的动态响应时间,提出一种指数ESO加快观测状态的收敛速度,提升了系统的扰动抑制性能。文献[20]针对电机周期性转矩波动问题,提出了一种模块化ESO,将指定次转矩纹波作为待观测状态,有效减小周期性扰动对系统的影响。文献[21]采用超螺旋滑模策略进行速度控制,提出一种有限时间ESO用于对系统的集中扰动进行观测,从而进行控制器补偿。与传统ESO相比,有限时间ESO通过非线性函数的引入具有更高的观测速度与精度。
本文针对PMSM位置伺服系统提出了一种鲁棒性DPSC策略。相比于之前相关文献,本文提出的控制策略具有如下特点:①基于PMSM离散模型和无差拍控制原理,设计了速度环和电流环,避免了级联式PI控制器的设计,提高了系统的动态性能;②将ESO方法扩展应用至电流环与速度环同时采用预测控制的控制方法中,针对预测电流和预测转速进行实时补偿,提高了系统的鲁棒性,避免了复杂的全局参数辨识过程;③结合位置伺服系统的特点,提出的控制方法采用位置跟随补偿策略,有效地提高了系统位置跟随效果。
本文研究对象为用于位置伺服的表贴式PMSM(Surface PMSM, SPMSM),d轴和q轴电感值相等,因此电磁转矩和定子电压可以表示为
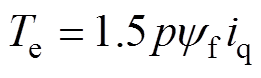 (1)
(1)
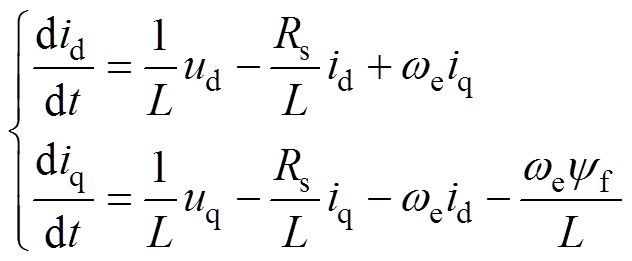 (2)
(2)
式中,Te为电磁转矩;p为极对数;ud和uq分别为d轴和q轴电压;id和iq分别为d轴和q轴电流;Rs和L分别为定子电阻和电感;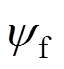 为永磁磁链;
为永磁磁链;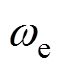 为电角速度。
为电角速度。
令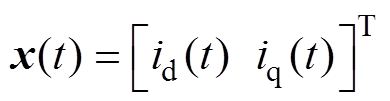 ,
,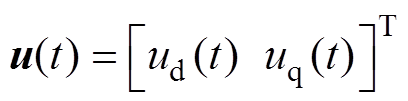 ,式(2)可改写为
,式(2)可改写为
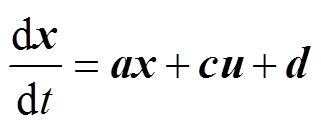 (3)
(3)
其中
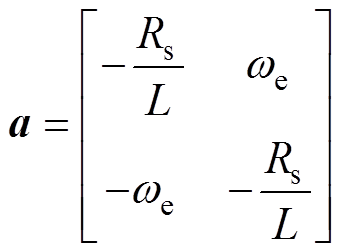
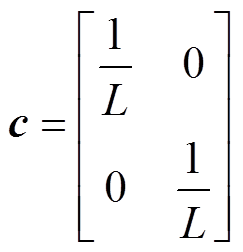
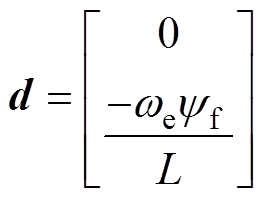
PMSM的机械方程可表示为
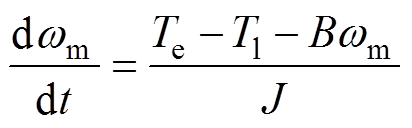 (4)
(4)
式中,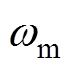 为机械角速度;Tl为负载转矩;B为黏滞摩擦系数;J为转动惯量。
为机械角速度;Tl为负载转矩;B为黏滞摩擦系数;J为转动惯量。
将式(1)代入式(4),机械方程可以改写为
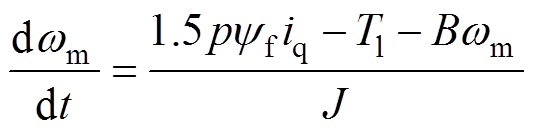 (5)
(5)
通过前向欧拉差分可得n+1时刻预测的电机转速为
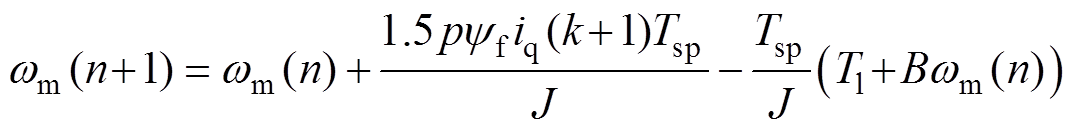 (6)
(6)
式中,Tsp为转速采样周期;iq(k+1)为k+1时刻的q轴电流值。为实现无差拍转速控制(DPSC),将式(6)中wm(n+1)用转速参考值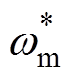 替代,iq(k+1)用q轴电流参考值
替代,iq(k+1)用q轴电流参考值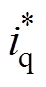 替代,则可得
替代,则可得
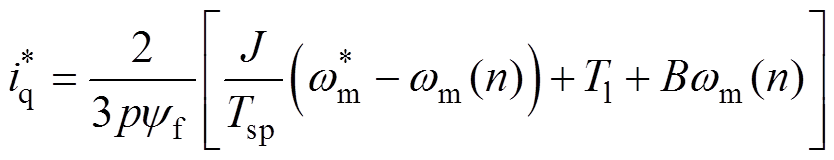 (7)
(7)
为实现电机电流环的无差拍控制,将电机电压方程式(3)进行离散化,根据k时刻电压、电流,可预测获得k+1时刻的电流为
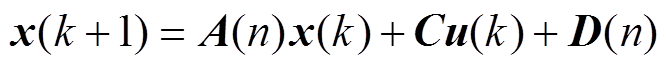 (8)
(8)
其中
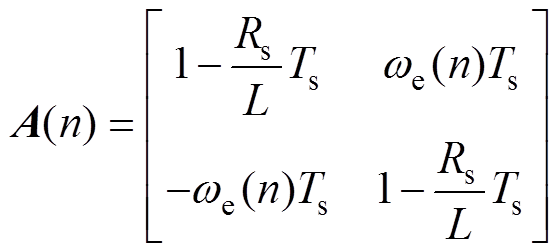
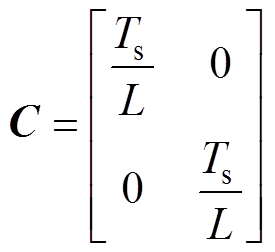
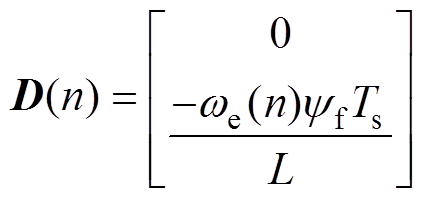
式中,Ts为电流采样周期。根据式(8)可以推导出k+1时刻的电压方程为
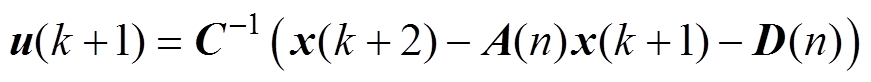 (9)
(9)
式中,x(k+2)用电流参考值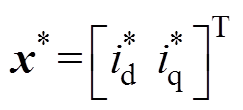 表示,u(k+1)用电压参考值
表示,u(k+1)用电压参考值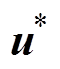 表示,可得k+1时刻的
表示,可得k+1时刻的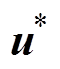 值为
值为
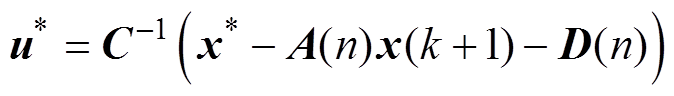 (10)
(10)
由于本文研究对象为SPMSM,因此采用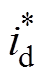 =0的控制方法。图1所示为基于DPSC策略的SPMSM位置伺服系统控制框图。
=0的控制方法。图1所示为基于DPSC策略的SPMSM位置伺服系统控制框图。
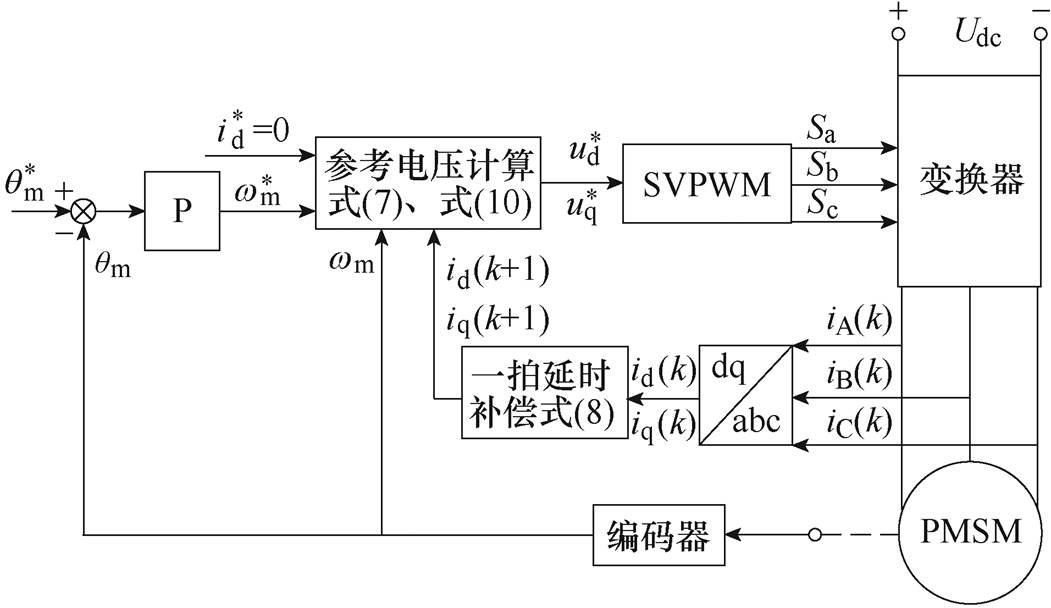
图1 基于DPSC策略的SPMSM位置伺服系统控制框图
Fig.1 Block diagram of SPMSM position servo system based on DPSC strategy
为了提高DPSC的鲁棒性,本文采用增量模型消除电流预测模型中永磁磁链的影响,并且设计了ESO对SPMSM其他参数不匹配、负载扰动以及逆变器非线性造成的扰动进行补偿。
由于电机机械时间常数远大于电气时间常数,可近似认为相邻电流采样周期中电机转速不变,因此k时刻的电压方程中参数矩阵D(n)与A(n)不变。根据式(9)可得k时刻的电压为
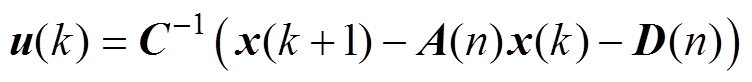 (11)
(11)
将式(9)与式(11)相减,可得增量模型为
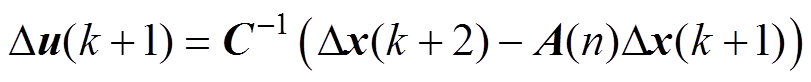 (12)
(12)
其中
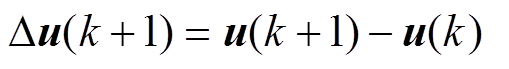
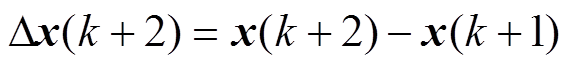
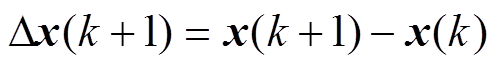
考虑到系统参数不匹配、负载扰动以及逆变器非线性等扰动时,电机定子电压和转速分别为
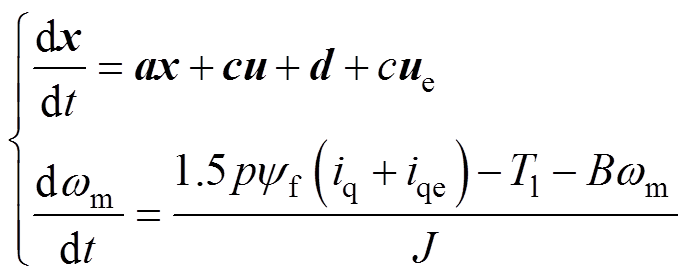 (13)
(13)
其中
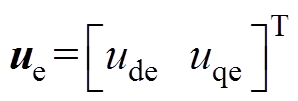
式中,ue和iqe分别为电压误差和电流误差。电压和电流误差可以扩展为ESO中的新状态,通过ESO可以对电压和电流误差进行估算,在此基础上可以针对预测电流和转速进行实时补偿。根据式(13),ESO可设计为
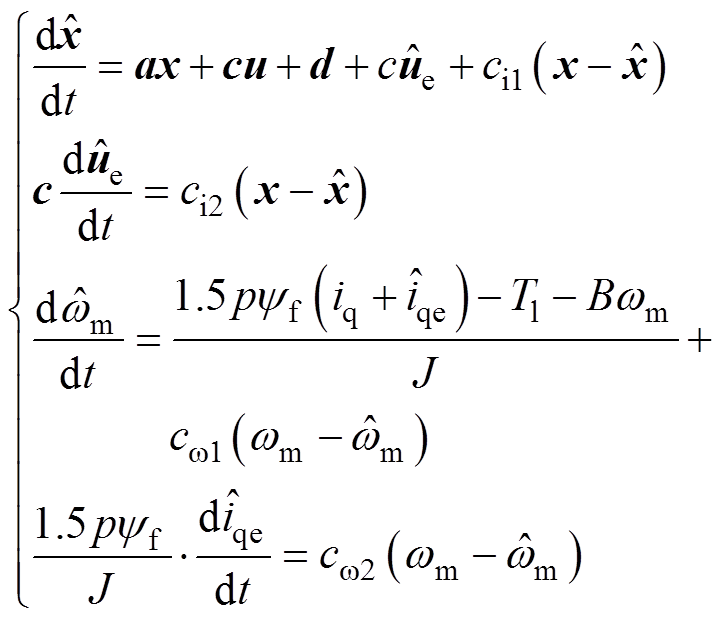 (14)
(14)
式中,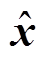 和
和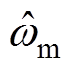 分别为x和
分别为x和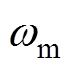 的估计值;
的估计值;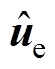 和
和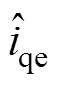 分别为
分别为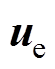 和
和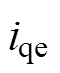 的估计值;ci1、ci2、
的估计值;ci1、ci2、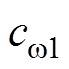 和
和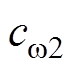 为ESO增益。
为ESO增益。
将式(14)进行离散化,并在电流预测中采用增量模型,可得d、q轴电流和转速预测方程分别为
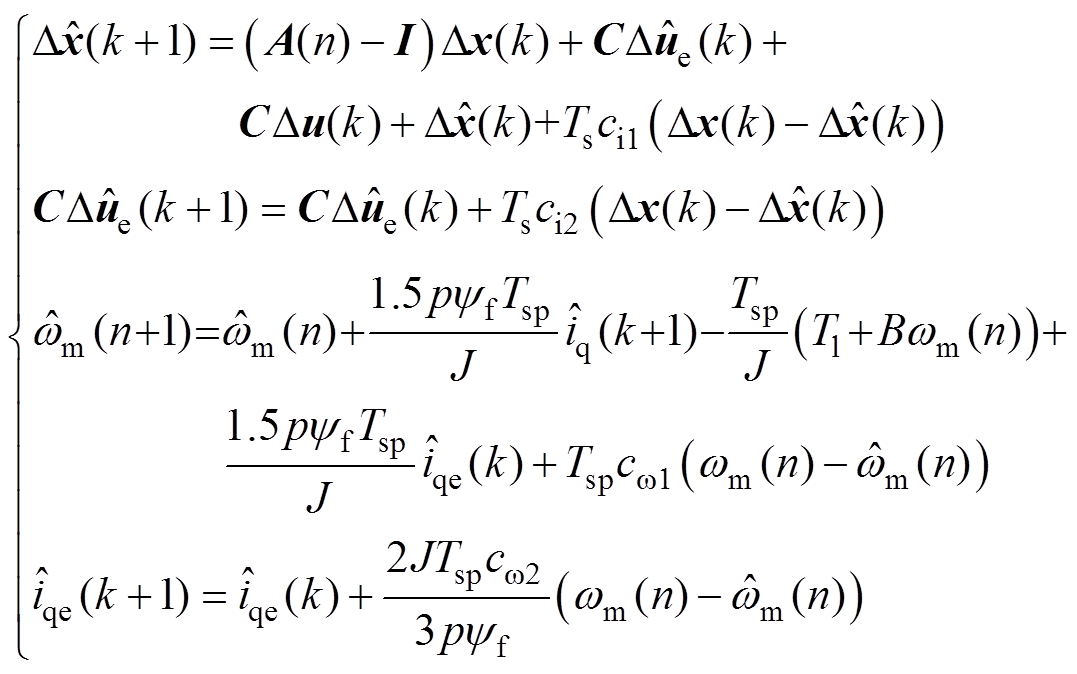 (15)
(15)
式中,I为单位矩阵。
根据上述ESO对电压误差和电流误差进行观测,并对q轴参考电流和参考电压进行实时补偿。为了获得更好的控制性能,分别用电流和转速估计值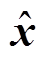 和
和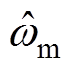 代替式(7)和式(10)中的电流和转速的实测值
代替式(7)和式(10)中的电流和转速的实测值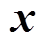 和
和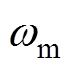 。补偿后的q轴参考电流和d、q轴参考电压分别为
。补偿后的q轴参考电流和d、q轴参考电压分别为
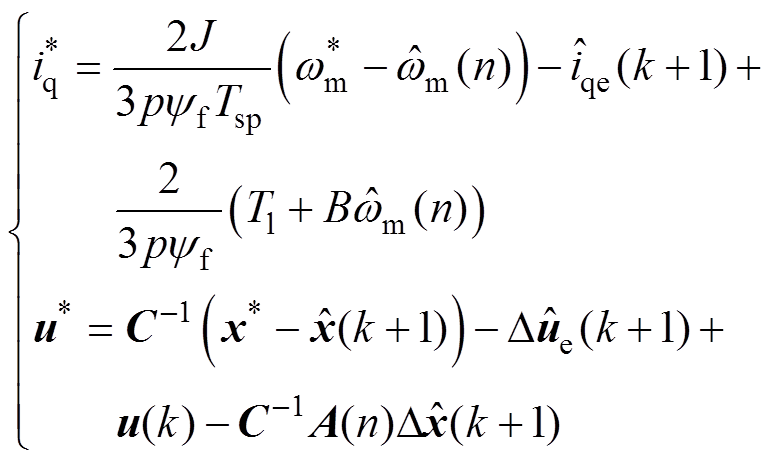 (16)
(16)
由于逆变器和电机受最大导通电流影响,因此需要对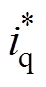 进行限制,设定为
进行限制,设定为
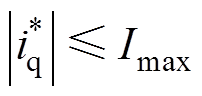 (17)
(17)
考虑到逆变器输出电压的能力,同样需要对参考电压幅值进行限制。当式(16)中参考电压值大于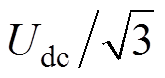 时,对参考电压进行重新计算,有
时,对参考电压进行重新计算,有
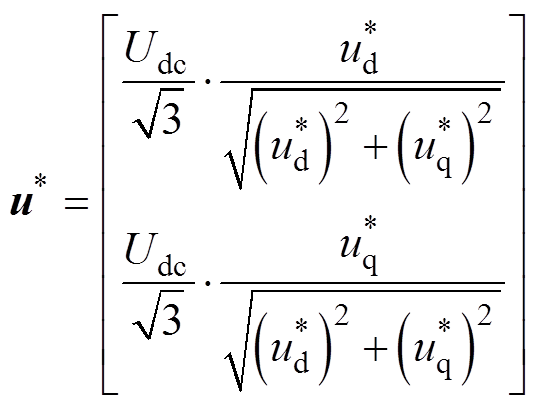 (18)
(18)
由式(16)可知,q轴电流参考值和电压参考值计算依赖ESO得到的转速、电流估计值以及电流、电压误差估计值,所以ESO是整个系统稳定的基础。式(13)可以变为
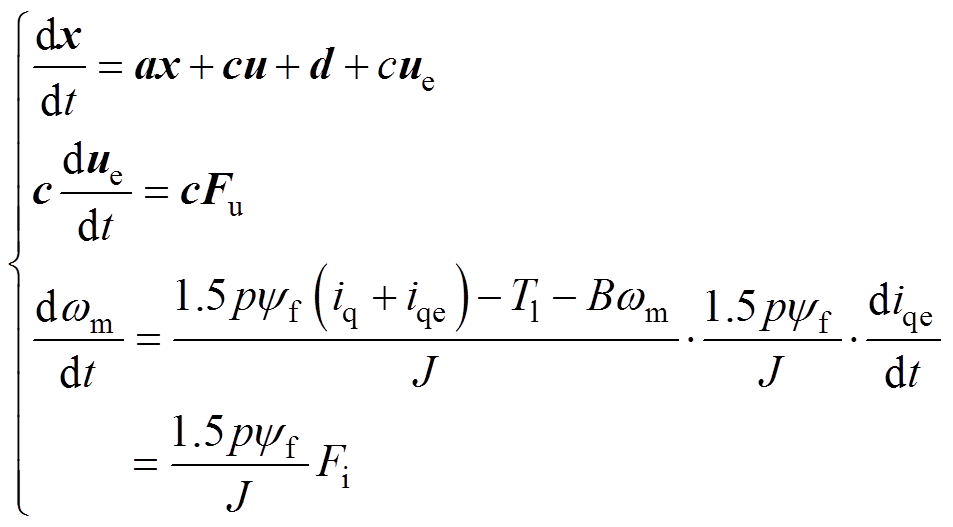 (19)
(19)
式中,Fu和Fi分别为ue和iqe的变化率。
然后,根据式(14)和式(19),可得
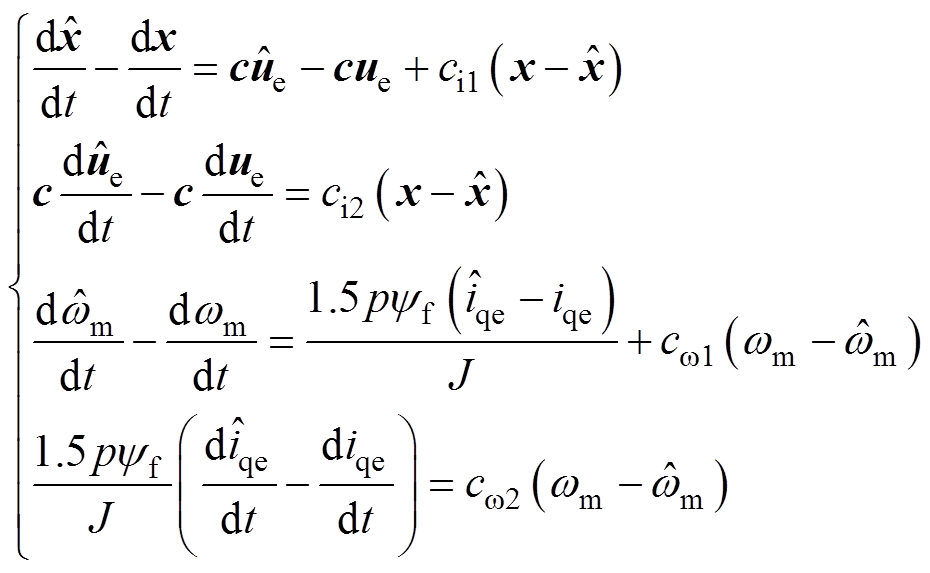 (20)
(20)
采用e1、e2、e3和e4分别代替式(20)中的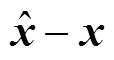 、
、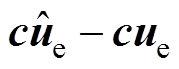 、
、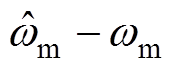 和
和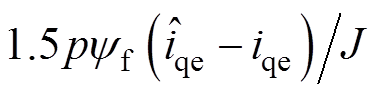 ,式(20)可以重新表示为
,式(20)可以重新表示为
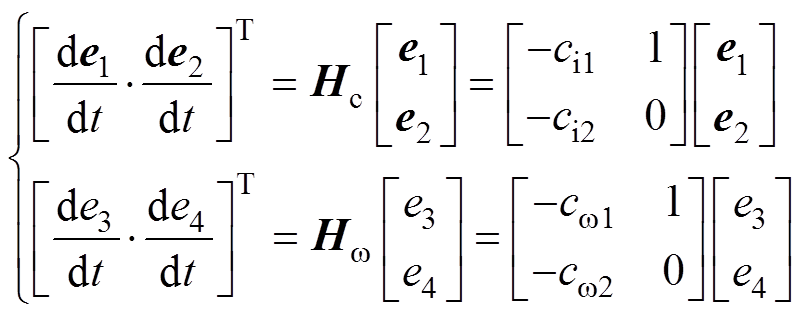 (21)
(21)
ESO稳定性和系数矩阵Hc及Hw 有关,相应特征方程为
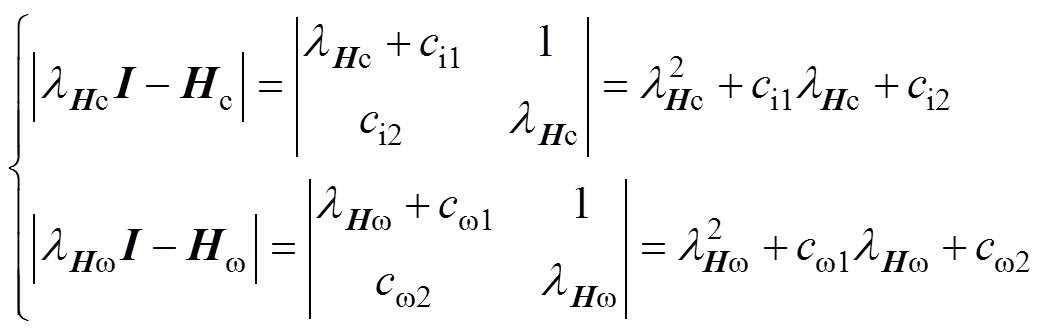 (22)
(22)
式中,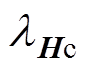 和
和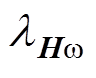 分别为系数矩阵Hc和Hw 的特征值。
分别为系数矩阵Hc和Hw 的特征值。
根据Routh-Hurwitz判据,当式(22)中系数均为非负,即ci1>0、ci2>0、cw1>0、cw2>0时,ESO是稳定的。式(23)以期望观测带宽形式给出了ESO参数整定方法[22],有
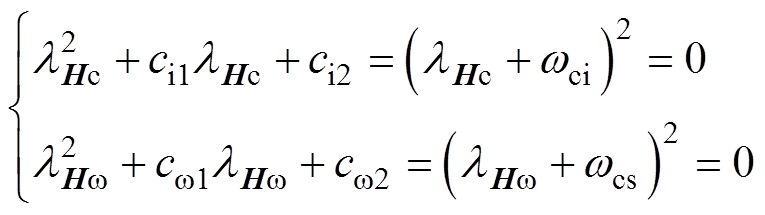 (23)
(23)
式中,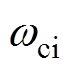 、
、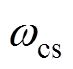 为所期望的ESO电流环、转速环带宽。经过系数对比,ESO增益选择如下:ci1=
为所期望的ESO电流环、转速环带宽。经过系数对比,ESO增益选择如下:ci1=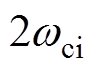 ,ci2=
,ci2=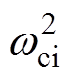 ,cw1=
,cw1=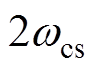 ,cw2=
,cw2=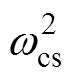 。为了说明所设计的ESO稳定性,对式(20)进行Laplace变换,可得到q轴电流ESO和转速ESO的传递函数分别为
。为了说明所设计的ESO稳定性,对式(20)进行Laplace变换,可得到q轴电流ESO和转速ESO的传递函数分别为
 (24)
(24)
本文选取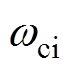 =2 000 rad/s,
=2 000 rad/s,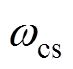 =600 rad/s,获得式(24)中传递函数的伯德图,如图2所示。可见,iq和w 观测器相频裕度均大约为140°。
=600 rad/s,获得式(24)中传递函数的伯德图,如图2所示。可见,iq和w 观测器相频裕度均大约为140°。
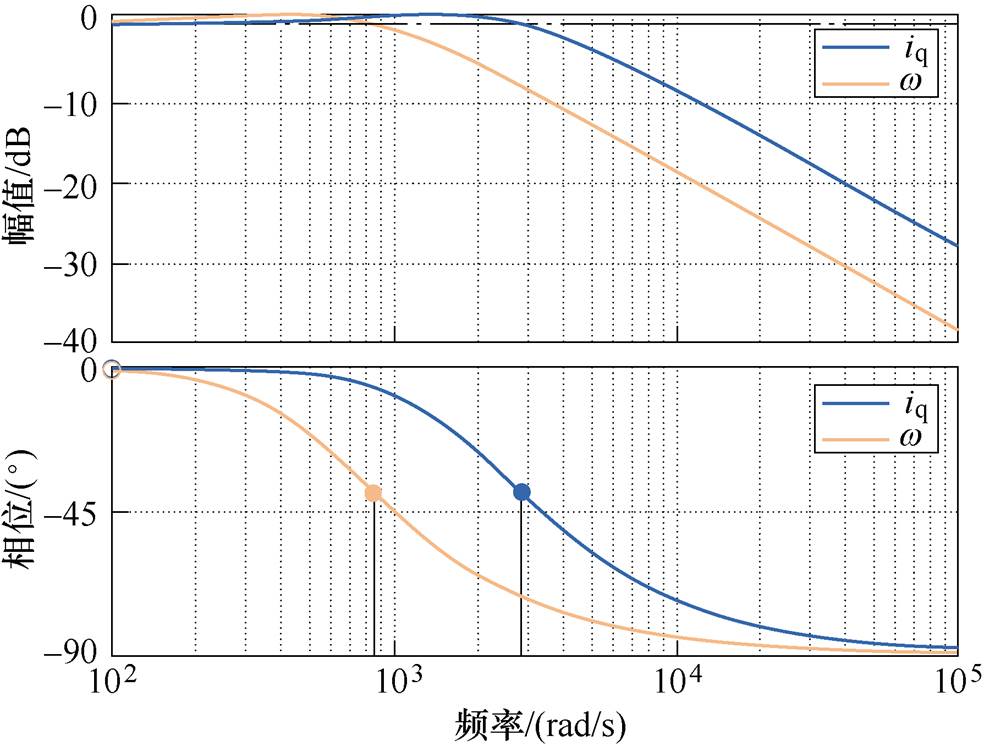
图2 扩张状态观测器伯德图
Fig.2 Bode diagram of ESO
在实际位置即将达到给定位置信号时,若采用观测器获得的实时误差对系统进行补偿,会影响系统的动态性能,增加到达给定位置的整定时间。为此,本文提出一种位置跟随补偿策略。由于位置伺服系统总是在静止和跟随给定位置的工作状态之间不断切换,在系统静止时可以认为电压和电流误差的估计值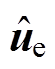 和
和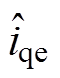 不变,将其记为
不变,将其记为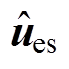 和
和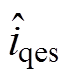 并保存在控制器中。本文提出的补偿策略中不同补偿量之间的切换原则为
并保存在控制器中。本文提出的补偿策略中不同补偿量之间的切换原则为
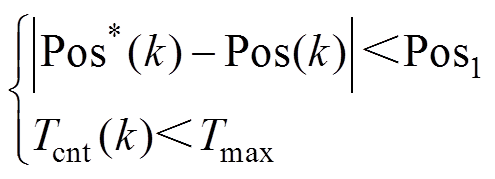 (25)
(25)
式中,Pos*和Pos分别为系统给定位置和实际位置;Pos1为设定的给定位置和实际位置差值绝对值的阈值,本文选取Pos1=80脉冲;Tcnt为计数值;Tmax为最大计数值。
图3为预测误差补偿策略流程。其中,Tcnt初始值设为Tmax,当给定的参考位置发生变化时,将Tcnt设置0。当实际位置即将到达给定位置信号时,即满足式(25)中第一个不等式时,可以认为系统已经接近位置追踪稳定状态。此时,由于式(25)中两个不等式均成立,采用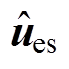 和
和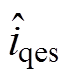 对系统进行补偿,Tcnt开始计数。当Tcnt=Tmax时,继续采用通过ESO实时得到的
对系统进行补偿,Tcnt开始计数。当Tcnt=Tmax时,继续采用通过ESO实时得到的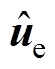 和
和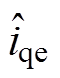 对系统进行补偿。本文中将采用所提出的补偿策略的R-DPSC策略称作PR- DPSC策略。图4为基于PR-DPSC策略的PMSM位置伺服系统控制框图。
对系统进行补偿。本文中将采用所提出的补偿策略的R-DPSC策略称作PR- DPSC策略。图4为基于PR-DPSC策略的PMSM位置伺服系统控制框图。
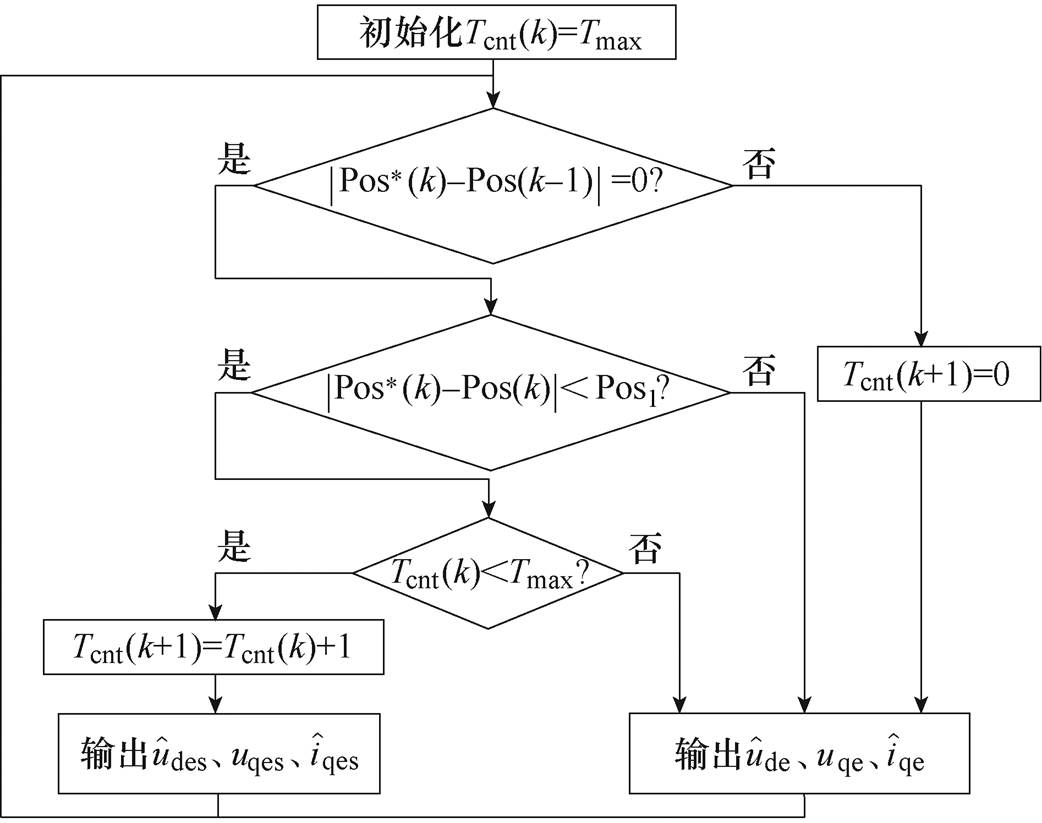
图3 预测误差补偿策略流程
Fig.3 Flow chart of predictive error compensation strategy
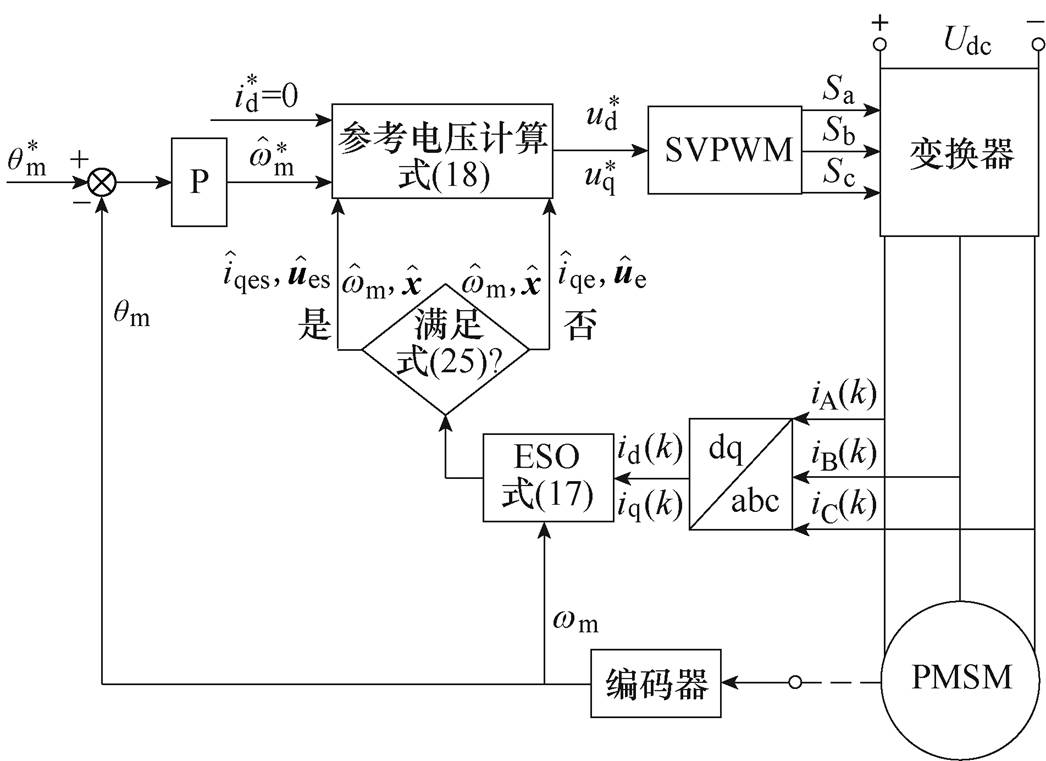
图4 基于PR-DPSC策略的PMSM位置伺服系统控制框图
Fig.4 Block diagram of PMSM position servo system based on PR-DPSC strategy
为了验证本文所提出的控制策略,搭建了两电平三相PMSM实验平台,控制器为TMS320F28346,负载电机工作在恒转矩模式。伺服系统的实验参数见表1,均选取了电机铭牌标定值,负载转矩采用人为给定方式。
图5所示为采用DPSC策略时的实验结果,当控制程序参数以及负载转矩值和实际值一致时,可以看出稳态情况下实际位置与给定位置之间没有误差。当控制程序参数设置为额定值的两倍、负载转矩值设置为0 N·m时,由于程序控制参数以及负载转矩值和实际负载转矩值不一致,稳态情况下实际位置与给定位置之间出现了误差,如图5b所示。
表1 实验参数
Tab.1 Experimental parameters
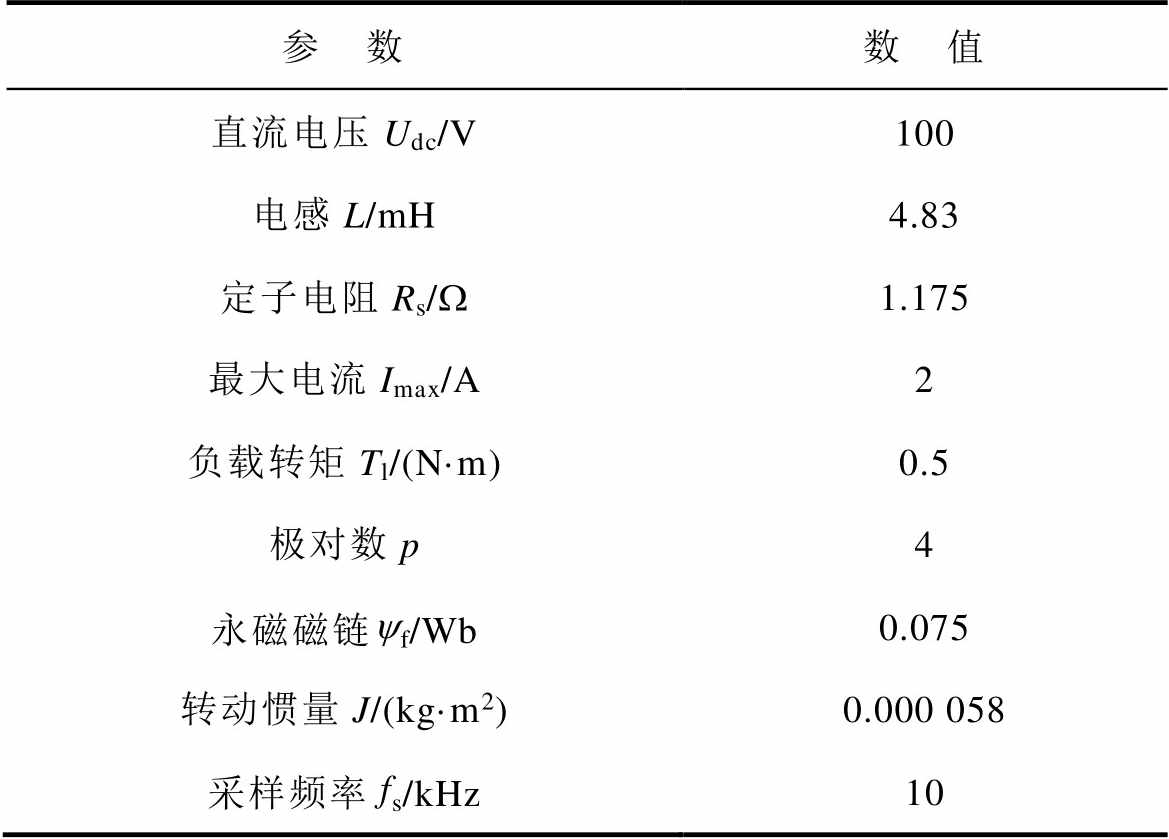
参 数数 值 直流电压Udc/V100 电感L/mH4.83 定子电阻Rs/W1.175 最大电流Imax/A2 负载转矩Tl/(N·m)0.5 极对数p4 永磁磁链yf/Wb0.075 转动惯量J/(kg·m2)0.000 058 采样频率fs/kHz10
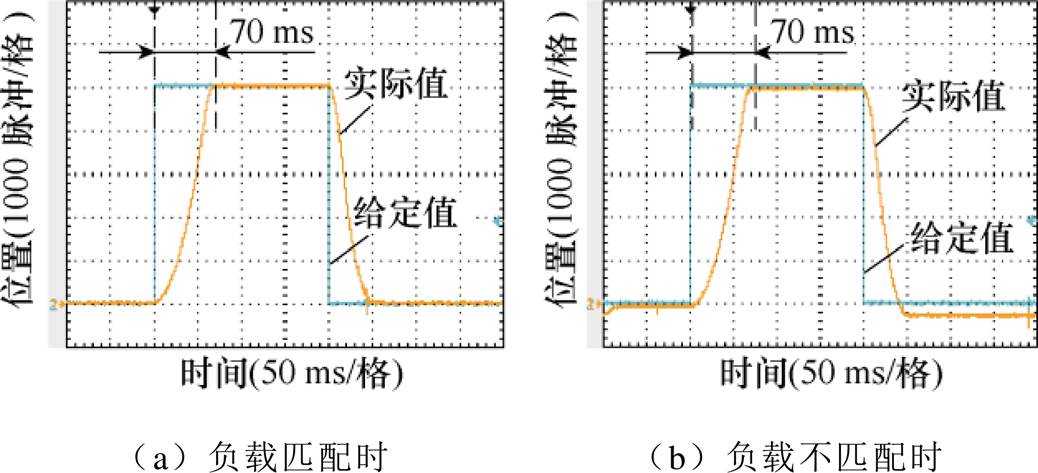
图5 采用DPSC策略时给定阶跃信号的实验波形
Fig.5 Experimental waveforms of step signal using DPSC strategy
图6所示为在参数和负载转矩值设置与实际值不匹配的情况下采用鲁棒-无差拍预测转速控制(Robust-DPSC, R-DPSC)策略时的实验波形。由于ESO的作用,稳态情况下实际位置与给定位置之间的误差得到了消除,并且电流可以控制在最大电流范围之内。由2.3节中的分析可知,因为对误差的估计是一个积分过程,在实际位置接近给定位置时系统会出现振荡,到达给定位置的时间也由图5a中所示的70 ms增加到84 ms。
图7为采用预测误差补偿鲁棒-无差拍预测转速控制(PR-DPSC)策略的实验波形。控制信号电平高低表示采用不同补偿量的切换过程,式(25)中,Tmax的值可以根据位置振荡过程具体时间来选取。
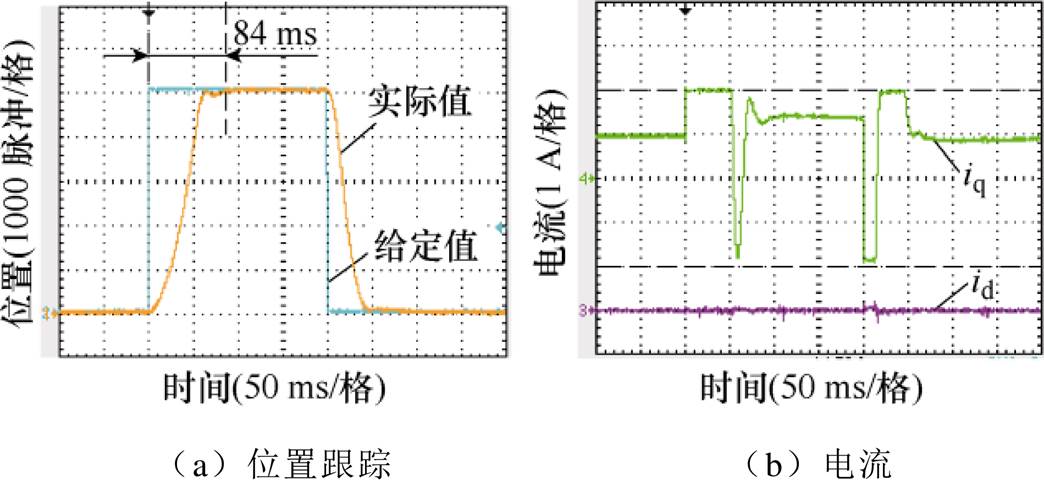
图6 采用R-DPSC策略时给定阶跃信号的实验波形
Fig.6 Experimental waveforms of step signal using R-DPSC strategy
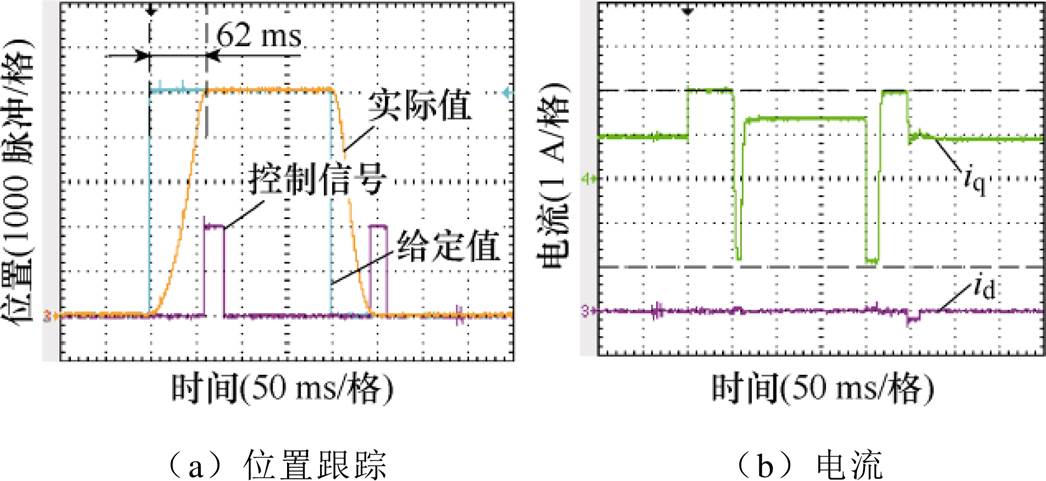
图7 采用PR-DPSC策略时给定阶跃信号的实验波形
Fig.7 Experimental waveforms of step signal using PR-DPSC strategy
同样地,在控制参数以及负载转矩值设置与实际值不匹配的情况下,可以看出采用所提出的补偿策略后,稳态情况下实际位置与给定位置之间没有误差,并且实际位置接近给定位置时振荡现象得到消除,系统到达给定位置的时间也由84 ms减少到了62 ms。
为了进一步评估所提出的PR-DPSC策略控制性能,在相同的实验条件下,分别采用PI控制和DPCC策略进行了相关实验比较。如图8、图9所示,PI控制的速度环和电流环以及DPCC策略的速度环均已调至最优,可以看出采用PI控制和DPCC策略时,系统到达给定位置的时间分别为94 ms和86 ms。通过三种不同控制方法实验结果的比较,可以证明PR-DPSC策略具有更好的控制效果。
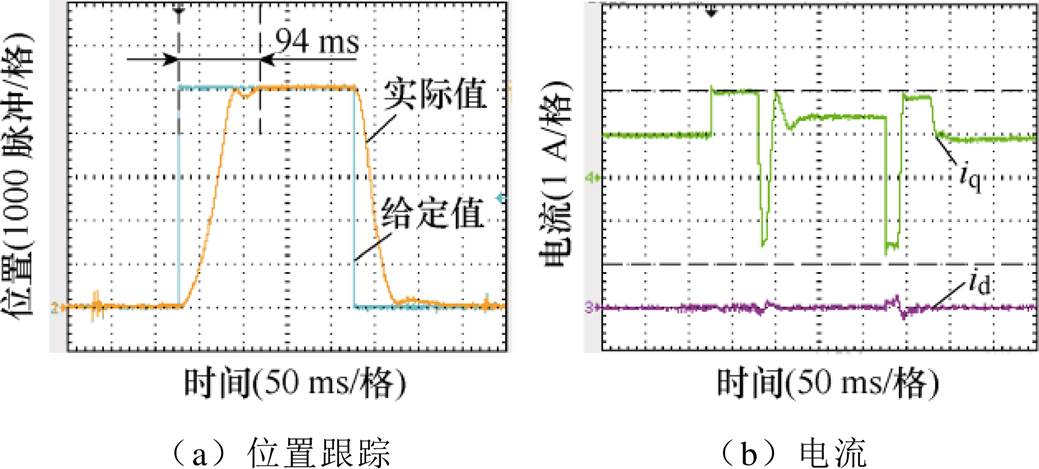
图8 采用PI控制时给定阶跃信号的实验波形
Fig.8 Experimental waveforms of step signal using PI control
图10为采用不同预测控制策略时系统抗扰动性能实验波形对比。由于在负载突变时系统给定位置没有发生变化,此时R-DPSC与PR-DPSC是等价的,因此仅给出了PR-DPSC和DPSC的对比结果。
采用DPCC策略时,系统在负载突变时实际位置偏离给定位置的最大误差为122脉冲,75 ms后实际位置与给定位置间的误差得到消除。采用PR- DPSC时,系统在负载突变情况下实际位置偏离给定位置的最大误差为70脉冲,55 ms后实际位置与给定位置间的误差得到消除。可以看出,相比DPCC策略,所提出的PR-DPSC策略具有更好的抗扰动性能。
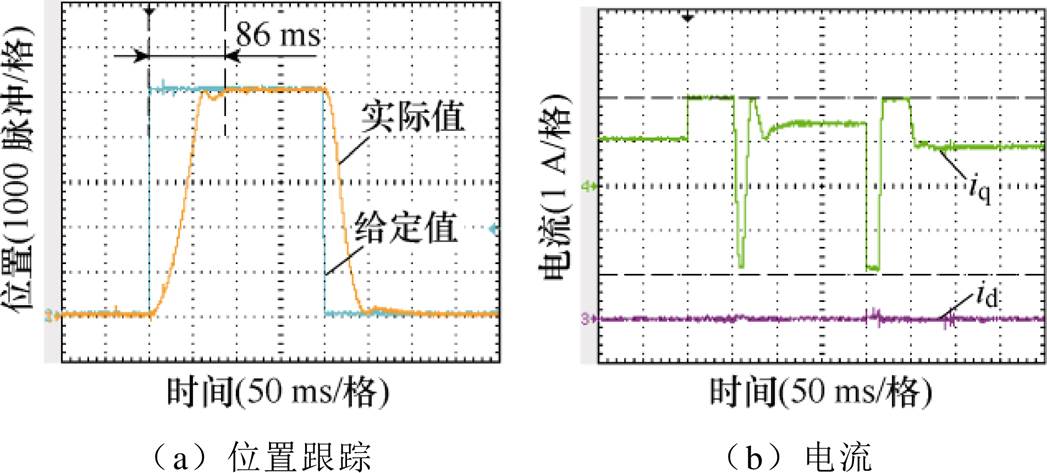
图9 采用DPCC策略时给定阶跃信号的实验波形
Fig.9 Experimental waveforms of step signal using DPCC strategy
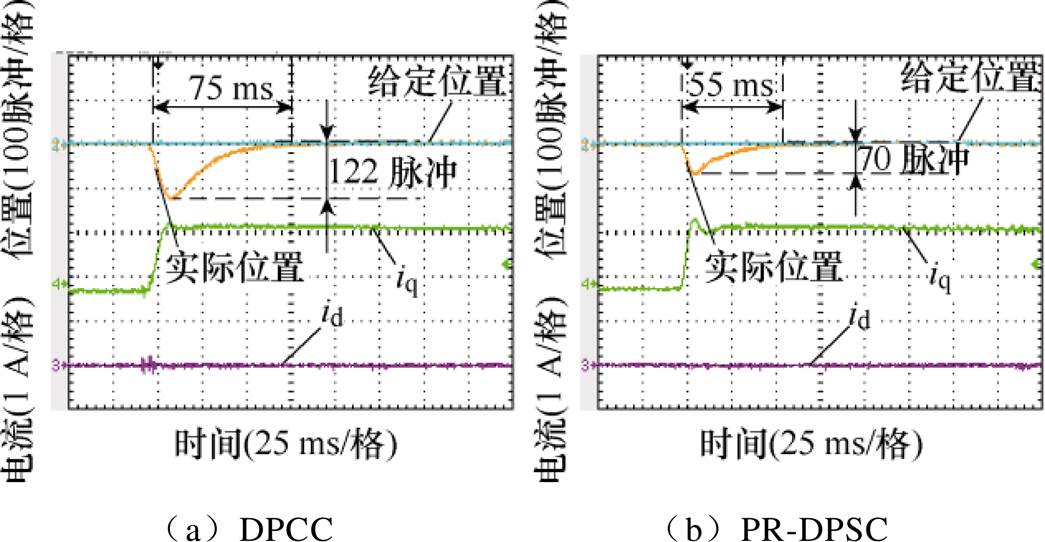
图10 负载突变情况下采用DPCC策略和 PR-DPSC策略时的实验波形
Fig.10 Experimental waveforms of load changing using DPCC strategy and PR-DPSC strategy
本文研究了基于DPSC策略的鲁棒性位置伺服PMSM系统,研究结论如下:
1)提出的DPSC策略提高了系统的动态响应,使得系统能更快到达给定位置。
2)设计的ESO能对参数不匹配、负载和逆变器非线性造成的扰动进行观测,结合提出的补偿策略,消除了系统到达给定位置时的振荡现象,提高了控制精度和动态性能。
通过实验验证了本文提出的基于DPSC鲁棒性位置伺服永磁电机控制器具有较好的位置跟随效果和鲁棒性。
参考文献
[1] 付兴贺, 江政龙, 吕鸿飞, 等. 电励磁同步电机无刷励磁与转矩密度提升技术发展综述[J]. 电工技术学报, 2022, 37(7): 1689-1702.
Fu Xinghe, Jiang Zhenglong, Lü Hongfei, et al. Review of the blushless excitation and torque density improvement in wound field synchronous motors[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1689-1702.
[2] 王一波, 王政, 温从剑, 等. 多通道三电平风力发电系统协同控制策略研究[J]. 中国电机工程学报, 2019, 39(2): 366-375, 634.
Wang Yibo, Wang Zheng, Wen Congjian, et al. Collaborative control strategies for multi-channel three-level wind energy conversion system[J]. Pro- ceedings of the CSEE, 2019, 39(2): 366-375, 634.
[3] Kazmierkowski M P, Malesani L. Current control techniques for three-phase voltage-source PWM con- verters: a survey[J]. IEEE Transactions on Industrial Electronics, 1998, 45(5): 691-703.
[4] 李祥林, 薛志伟, 阎学雨, 等. 基于电压矢量快速筛选的永磁同步电机三矢量模型预测转矩控制[J]. 电工技术学报, 2022, 37(7): 1666-1678.
Li Xianglin, Xue Zhiwei, Yan Xueyu, et al. Voltage vector rapid screening-based three-vector model predictive torque control for permanent magnet syn- chronous motor[J]. Transactions of China Electro- technical Society, 2022, 37(7): 1666-1678.
[5] 郭磊磊, 王朋帅, 李琰琰, 等. 不同代价函数下永磁同步电机模型预测控制参数失配可视化分析[J]. 电工技术学报, 2023, 38(4): 903-914.
Guo Leilei, Wang Pengshuai, Li Yanyan, et al. Visual analysis of parameters mismatch in model predictive control for permanent magnet synchronous motor under different cost functions[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 903-914.
[6] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[7] 李昱, 郭宏, 平朝春, 等. 基于电流源变流器的永磁同步电机驱动系统全状态变量预测转矩控制[J]. 电工技术学报, 2021, 36(1): 15-26.
Li Yu, Guo Hong, Ping Zhaochun, et al. A full-state variable predictive torque control of current source converter fed permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 15-26.
[8] 谷鑫, 鲁金月, 王志强, 等. 基于无差拍电流预测控制的永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2022, 37(24): 6345-6356.
Gu Xin, Lu Jinyue, Wang Zhiqiang, et al. Harmonic current suppression strategy for permanent magnet synchronous motor based on deadbeat current predi- ction control[J]. Transactions of China Electro- technical Society, 2022, 37(24): 6345-6356.
[9] Gu Minrui, Wang Zheng, Yu Kailiang, et al. Inter- leaved model predictive control for three-level neutral- point-clamped dual three-phase PMSM drives with low switching frequencies[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11618-11630.
[10] Kawai H, Zhang Zhenbin, Kennel R, et al. Direct speed control based on finite control set model predictive control with voltage smoother[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 2363-2372.
[11] Gu Minrui, Wang Zheng, Wen Congjian, et al. Collaborative mid-point voltage regulation in low- switching-frequency MPC for three-level NPC inver- ters fed dual three-phase PMSM drives[J]. IEEE Open Journal of Power Electronics, 2021, 2: 673-682.
[12] Yu Kailiang, Wang Zheng, Hua Wei, et al. Robust cascaded deadbeat predictive control for dual three- phase variable-flux PMSM considering intrinsic delay in speed loop[J]. IEEE Transactions on Industrial Electronics, 2022, 69(12): 12107-12118.
[13] Yu Kailiang, Wang Zheng. Improved deadbeat predi- ctive current control of dual three-phase variable-flux PMSM drives with composite disturbance observer[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 8310-8321.
[14] Kim H S, Lee K. Model predictive current control with online parameter estimation for synchronous reluctance machine controlled by high-frequency signal injection position-sensorless[J]. IEEE Access, 2022, 10: 25267-25277.
[15] Wang Kang, Lorenz R D, Baloch N A. Enhanced methodology for injection-based real-time parameter estimation to improve back EMF self-sensing in induction machine deadbeat-direct torque and flux control drives[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6071-6080.
[16] Liu Zhaohua, Wei Hualiang, Li Xiaohua, et al. Global identification of electrical and mechanical parameters in PMSM drive based on dynamic self-learning PSO[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10858-10871.
[17] Zhang Xiaoguang, Cheng Yu, Zhao Zhihao, et al. Robust model predictive direct speed control for SPMSM drives based on full parameter disturbances and load observer[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8361-8373.
[18] Yang Ming, Lang Xiaoyu, Long Jiang, et al. Flux immunity robust predictive current control with incremental model and extended state observer for PMSM drive[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(12): 9267-9279.
[19] Wang Fengxiang, Ke Dongliang, Yu Xinhong, et al. Enhanced predictive model based deadbeat control for PMSM drives using exponential extended state observer[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(3): 2357-2369.
[20] Hu Mingjin, Hua Wei, Wang Zuo, et al. Selective periodic disturbance elimination using extended harmonic state observer for smooth speed control in PMSM drives[J]. IEEE Transactions on Power Electronics, 2022, 37(11): 13288-13298.
[21] Hou Qiankang, Ding Shihong. Finite-time extended state observer-based super-twisting sliding mode controller for PMSM drives with inertia identi- fication[J]. IEEE Transactions on Transportation Electrification, 2022, 8(2): 1918-1929.
[22] Zhang Yongchang, Jin Jialin, Huang Lanlan. Model- free predictive current control of PMSM drives based on extended state observer using ultralocal model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
Abstract For the predictive control strategy of the permanent magnet synchronous motor position servo system, both model predictive direct speed control (MPDSC) and deadbeat predictive speed control (DPSC) depend on an accurate control system model. However, in practical applications, the motor parameters are changing and challenging to measure, which makes the control performance worse. Moreover, the nonlinearity of the inverter will also affect the prediction accuracy and reduce the performance of the control system. Recently, some methods have been proposed to solve the issues of parameter inaccuracy, but most are computationally expensive and hard to implement in practice. This paper proposes a robust deadbeat predictive speed control (R-DPSC) strategy to improve the control performance of the permanent magnet synchronous motor position servo system by incorporating the deadbeat control and the disturbance observer.
Firstly, according to the mathematical model of PMSM in the synchronous coordinate frame and the deadbeat control principle, the current and speed loops are designed for the servo drive. A proportional controller is used to design the position loop. Then, according to the discrete-state model of the motor, the reference voltages are predicted and converted into the switching signals of the inverter by space vector pulse-width modulation (SVPWM). In this paper, the incremental model is adopted to predict the current without the permanent-magnet flux value, and an extended state observer (ESO) is designed with the incremental model to estimate and compensate for the prediction errors caused by inaccurate parameters and load disturbance. The R-DPSC strategy combined with ESO can accurately track the desired position in the case of inaccurate parameters and external disturbance in load. In order to reduce the oscillation caused by the observer when the system approaches the given position reference, a prediction error compensation method is proposed, which uses different compensation quantities according to different working states of the system. The R-DPSC strategy with prediction error compensation method (PR-DPSC) can improve the robustness of the system and maintain the good dynamic performance of the DPSC strategy. Thus, the system can achieve better position-tracking performance.
The experimental results show that when the control parameters and the load torque settings do not match the actual values, the position tracking error is eliminated by the R-DPSC strategy. After adopting the PR-DPSC strategy, the position tracking error can be eliminated, and the oscillation phenomenon disappears when the actual position is close to the given position. Furthermore, the time for the system to reach the given position is reduced. Under the same experimental conditions, comparative experiments were carried out for different control schemes, which proved that the PR-DPSC strategy has faster position tracking speed and better anti-disturbance performance.
The research conclusions are as follows: (1) The proposed DPSC strategy improves the dynamic response of the system, enabling the system to reach a given position faster; (2) The designed ESO can observe the disturbance caused by parameter mismatch, load, and inverter nonlinearity. The proposed compensation strategy eliminates the oscillation phenomenon when the system reaches a given position, and the control accuracy and dynamic performance are improved.
keywords:Position servo system, deadbeat predictive speed control, extended state observer, compensation strategy
DOI: 10.19595/j.cnki.1000-6753.tces.221921
中图分类号:TM383.4
收稿日期 2022-10-09
改稿日期 2023-03-24
王 政 男,1979年生,教授,博士生导师,研究方向为电机驱动及控制、新能源与分布式发电。E-mail: zwang@seu.edu.cn(通信作者)
温从剑 男,1995年生,硕士研究生,研究方向为电机驱动及控制。E-mail: wcj19951026@163.com
(编辑 崔文静)