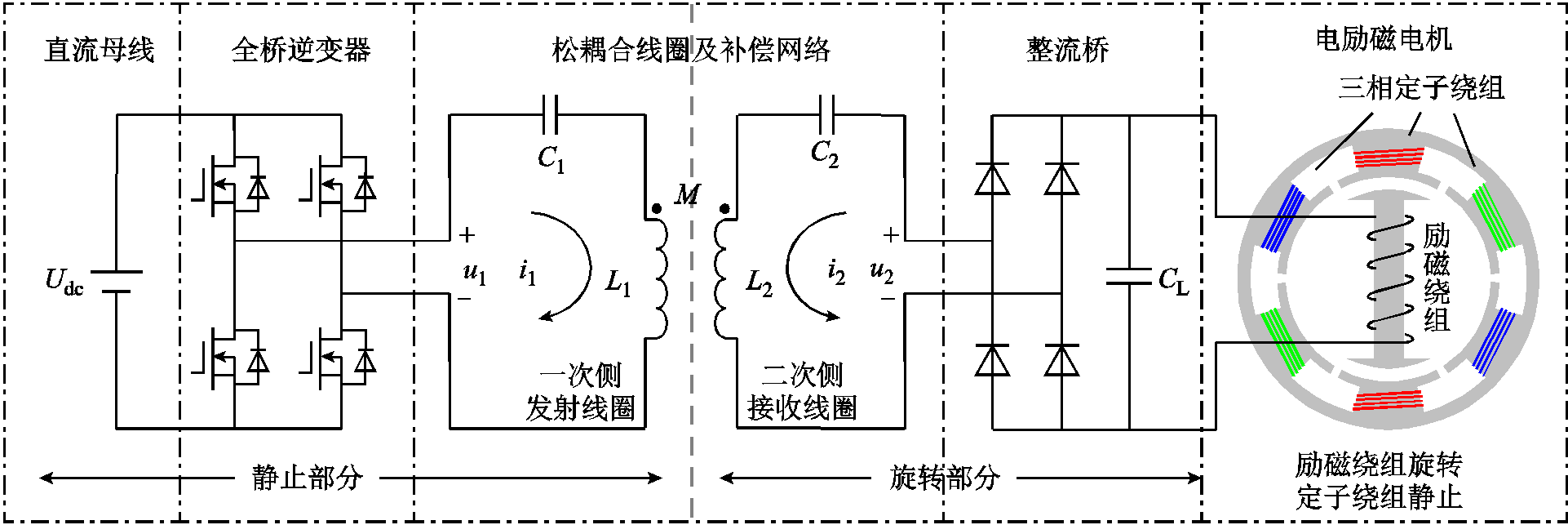
图1 串联-串联补偿型感应耦合式无刷励磁系统结构
Fig.1 Schematic diagram of series–series compensated wireless power transfer system
摘要 电励磁同步电机（EESM）具有稀土永磁材料依赖性低、励磁磁场可控、调速范围广的优点，在新能源汽车驱动领域拥有良好的应用前景。利用电感耦合式无刷励磁技术可以有效降低传统有刷EESM的摩擦损耗和维护成本。但是，无刷励磁技术的引入导致励磁电流无法直接测量，因此提出一种基于降阶动态相量模型的间接式励磁电流估计方法。首先利用电感耦合关系将励磁电流的直接估计转换为间接估计，有效地提高了算法的鲁棒性；然后推导出励磁电流降阶动态相量估计模型，进一步提高间接估计方法的精度；接着考虑电流谐波影响，提出变系数改进方法；最后通过仿真和实验验证了估计方法的有效性。
关键词：电励磁同步电机 电感耦合式无刷励磁技术 电流估计 动态相量模型
电励磁同步电机（Electrically Excited Synch-ronous Machine, EESM）具有稀土永磁材料依赖性低、励磁调节灵活、调速范围广等优点，在新能源汽车电驱动领域展现出特有的技术和成本优势[1]。但传统EESM的电刷集电环结构会引起摩擦损耗、增加维护成本、降低电机工作可靠性[2]。因此，无刷励磁技术已成为EESM应用发展的迫切需求和亟待解决的关键问题[3]。现有无刷励磁方式主要包括励磁机式、谐波励磁及无线电能传输式[4-6]。无线电能传输励磁方式又可以分为电感耦合式和电容耦合式。其中，电感耦合式励磁方法结构简单、传输效率高，具有广阔的应用前景[7]。
对于无刷励磁系统，采用开环方式控制励磁电流难以满足EESM高精度励磁磁场调节和速度控制要求，必须依靠励磁电流反馈构建闭环控制系统才能提高励磁电流的控制精度和抗干扰能力[8-9]。但无刷励磁系统的励磁绕组随转子一起旋转，励磁能量发送回路和接收回路之间无直接电气连接，致使励磁电流反馈的获取面临技术挑战[10]。
无刷励磁方案的差异和特点决定了励磁电流获取方法各有区别。在励磁机方案中，可以根据励磁机模型计算出励磁机转子的电压、电流，再根据整流器模型计算励磁电流估计值[11]。在谐波励磁方案中，可以通过静态实验建立离线表格，根据定子谐波绕组电流估计励磁电流[12]。电容耦合式励磁方案比较特殊，励磁静止侧和旋转侧共用同一电流回路，经过处理和折算便可直接获得励磁电流[13]。在电感耦合式励磁系统中，获取励磁电流的方式包括：无线通信式、模型估计式。无线通信方式需要在二次回路增加采样电路，利用无线通信装置将采样到的励磁电流数据发送至一次回路[14]。该方法原理简单，但是需要额外增加电路装置，且传递的反馈信号易受到电机内磁场的干扰。模型估计方式包括基于电机绕组模型估计和基于线圈耦合电感模型估计。基于电机绕组模型的电流估计方式需要先建立电机绕组与励磁绕组之间的磁链和电压关系，再根据采集到的定子端电压和电流计算出励磁电流[15]；基于线圈耦合电感模型估计则需建立电感等效电路模型，利用一次电压、电流信息计算出励磁电流[16]。模型估计方式获取励磁电流对硬件要求较小，但是估计效果受数学模型精度及参数扰动的影响。
反映励磁系统电路中物理关系的数学模型主要包括稳态模型和瞬态模型[17]。前者计算简单但是精度较低；后者精度高但计算复杂。除此之外，还有精度较高且计算相对简单的全阶和降阶动态相量模型[18]。但目前上述模型多用于无线电能传输系统建模和参数优化，鲜有研究将其应用于无刷电励磁电机的励磁电流估计。
针对模型估计中存在的参数扰动问题，文献[19]提出一种利用母线电流修正励磁电流估计值的方法，在一台最大励磁电流为18 A的样机上进行验证，变负载工况下的估计误差在2%以内。该方法具有一定的估计精度，但是实现过程依赖大量实验结果，普适性低，且需要增加一个电流传感器用于检测母线电流。文献[20]利用一次侧LCL型谐振补偿结构的特点，提出一种适用于变负载工况的电流估计方法，并考虑了一次电流的谐波影响，在一台额定励磁电流为2 A的样机上完成了实验验证，最终的电流估计误差约为5.7%。该方法计算简单，但受限于一次侧特定的补偿形式，需要用到两个电流传感器，且并未考虑负载参数变化对电流估计的影响。
鉴于此，本文针对串联-串联补偿型电感耦合式无刷励磁系统，提出了一种基于系统降阶动态相量模型的间接励磁电流估计方法，具有计算简单、负载适应性强、硬件成本低等特点。本文首先设计了励磁能量传输电路的拓扑结构，建立励磁系统的等效电路模型；然后为避免负载参数扰动的影响，利用电感耦合关系，选取二次侧反射电压作为中间变量，提出一种间接式电流估计方法，建立降阶动态相量估计模型，进一步提高间接估计方法的估计精度；接着考虑二次电流的谐波影响，提出变波形系数改进方法；最后通过仿真和实验验证了上述电流估计方法的有效性。
根据电励磁电机励磁传输功率的要求，建立图1所示的串联-串联感应耦合式无线电能传输系统的电路拓扑。该结构高阶非线性的特性不利于励磁电流的在线估计。但无刷励磁系统正常工作时处于谐振状态，可以采用基波分析法对系统非线性环节进行简化并建立等效电路模型[21]，在一定误差范围内可以降低模型复杂度但又不失电流估计的有效性。
图1 串联-串联补偿型感应耦合式无刷励磁系统结构
Fig.1 Schematic diagram of series–series compensated wireless power transfer system
无刷励磁系统中移相全桥逆变器输出电压
的傅里叶展开式[22]为
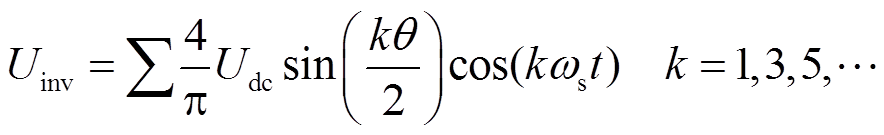（1）
式中，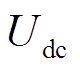
为直流母线电压；
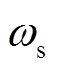为逆变器输出电压频率；
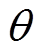为在0°～180°内变化的移相角。根据式（1）可以得到逆变器输出电压的基波有效值
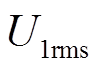为
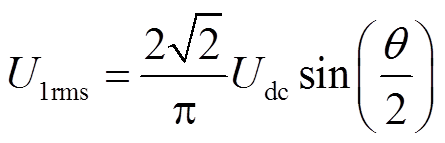（2）
当母线电压保持不变时，根据系统实际的移相角即可计算出逆变器输出电压的基波有效值。在后续分析中利用式（2）将非线性的逆变器环节等效为一个电压源。
励磁系统中作为负载的励磁绕组端电压满足
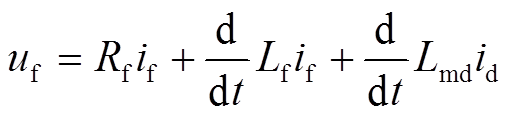（3）
式中，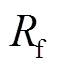
为励磁绕组电阻；
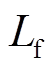为励磁绕组自感；if
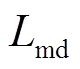为定子d轴与转子之间的等效互感；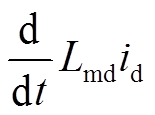
电枢电流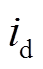
变化及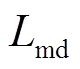变化在励磁绕组上产生的反电动势。根据式（3）可以将负载等效为电阻、电感及反电动势
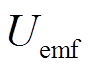的串联模型。
由式（3）可知，根据励磁端电压uf求励磁电流
会受到
参数变化及反电动势的干扰。为了提高励磁电流估计的准确性和鲁棒性，可以将整流桥输出端等效成电流源
。建立整流桥、滤波电容和励磁绕组的等效电路模型如图2所示，以此推导励磁电流和二次电流之间的关系。
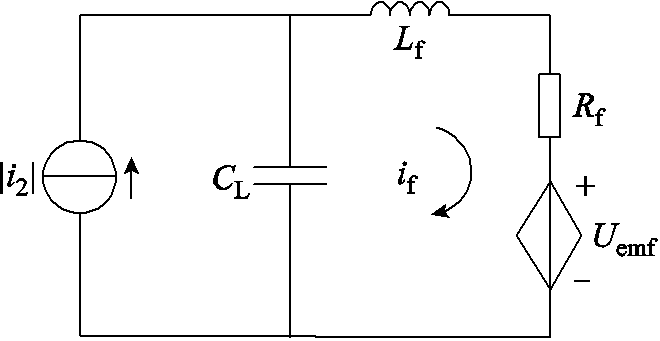
图2 整流桥和负载等效电路模型
Fig.2 Equivalent model of rectifier and load
当滤波电容
足够大时，
近似为直流量。基于串联-串联型感应耦合电能传输系统的二次侧输出特性[23]和基波分析法，二次电流满足
，其中，
为二次电流基波有效值，
为补偿网络谐振频率。
与的平均值满足
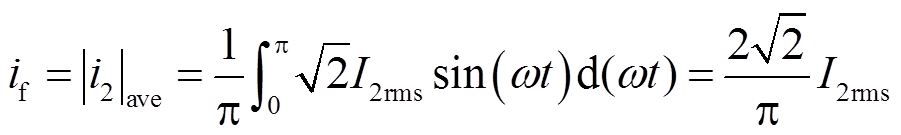（4）
由式（4）可知，励磁电流与二次电流基波有效值
之间为线性关系，因此只要估计出二次电流基波有效值即可间接估计出励磁电流，避免引入负载变化带来的干扰，能有效提高励磁电流估计的鲁棒性。
根据二端口网络理论，相对于二次线圈，整流桥和励磁绕组负载可以直接等效成电阻
，满足
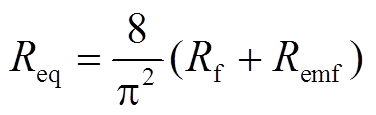（5）
式中，
为一个虚拟电阻，用于表征反电动势
的影响，且
。大小可反映负载及工况变化情况。
综合上述分析，将图1所示的无线励磁能量传输系统电路拓扑简化并等效为图3所示结构。其中
、
分别为一、二次线圈内阻，
、
分别为一、二次线圈自感，
、
分别为一、二次侧谐振补偿电容，
为线圈互感，
表示逆变器输出电压，
、
表示线圈互感产生的耦合电动势。
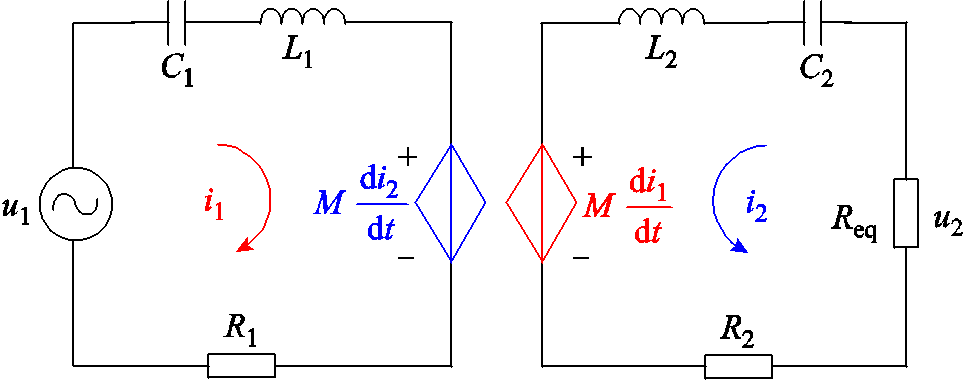
图3 无刷励磁系统等效电路模型
Fig.3 Equivalent model of wireless power transfer systems
考虑到负载工况变化，
参数是时变且未知的，直接利用图3所示的等效电路模型构建励磁电流估计模型的方法鲁棒性较差，需要进行调整。
定义
为二次侧电路反射电压，满足
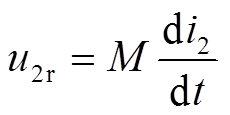（6）
由于发射和接收线圈的相对位置不变，且松耦合线圈互感基本不受饱和影响，故线圈互感
不变且可测。因此，根据可测的逆变器输出电压
和一次电流
估计出
，再根据式（6）计算出二次电流，最后利用式（4）即可计算出励磁电流。上述过程本质上是将励磁电流的直接估计转换为二次侧反射电压和二次电流有效值的间接估计。将图3结构等效至一次侧，构建图4所示的一次侧等效电路模型。
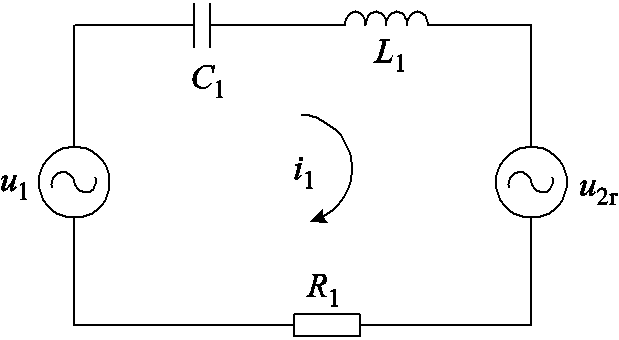
图4 一次侧等效电路模型
Fig.4 Equivalent model of wireless power transfer systems
利用一次侧等效模型开展励磁电流间接估计摆脱了对负载参数的依赖，提高了估计方法的鲁棒性，同时降低了等效电路的储能元件数量和模型阶数。
对于含谐振环节的系统，可以采用动态相量法进行数学建模，计算复杂度低于瞬态模型并且精度高于稳态模型，还可以进行降阶处理简化计算。本节将推导基于降阶动态相量模型的励磁电流估计数学表达式。
记一次侧补偿电容和电感
两端电压分别为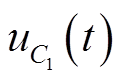
、
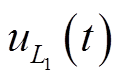，一次电流为
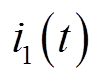，对应的一阶动态相量分别为
、
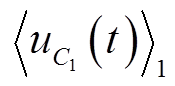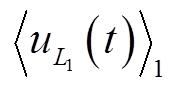和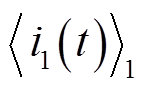
，则由动态相量的微分特性[18]可以写出电感和电容元件特性的动态相量表达式为
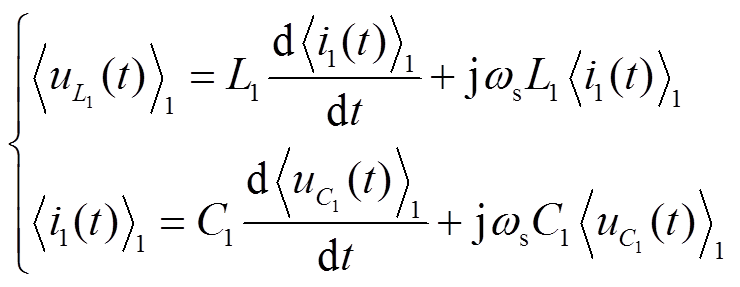（7）
动态相量模型的每个状态量对应两个微分方程，分别为实部方程和虚部方程，因此系统一次侧等效电路模型对应的全阶动态相量模型为4阶。为了方便计算，可以利用谐振网络的特点对全阶动态相量方程进行降阶处理。根据式（7）写出原始的谐振网络动态相量模型在s域下的表达式为
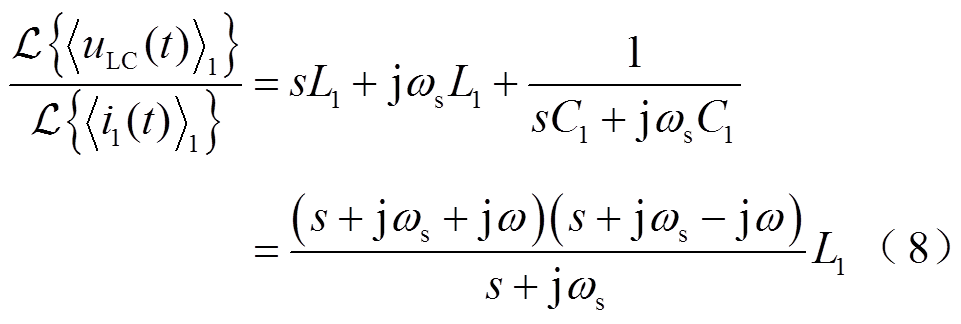
式中，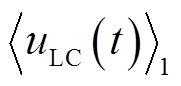
为电感和电容串联后的端电压对应的一阶动态相量。谐振时满足
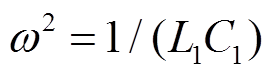，利用谐振关系可以将式（8）简化为仅含参数
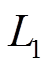的形式。
正常工作时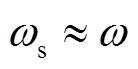
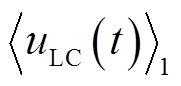，且和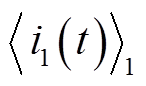
变化的频率远小于
，满足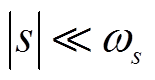
，式（8）可近似为
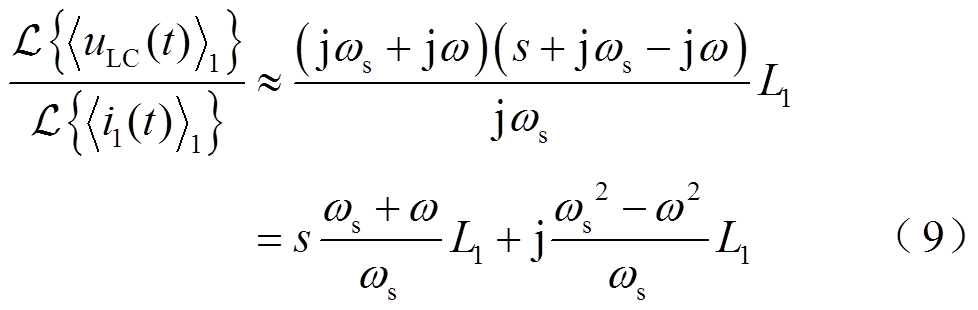
利用式（9）即可将谐振网络的动态相量模型的阶数由二阶降为一阶，如图5所示。
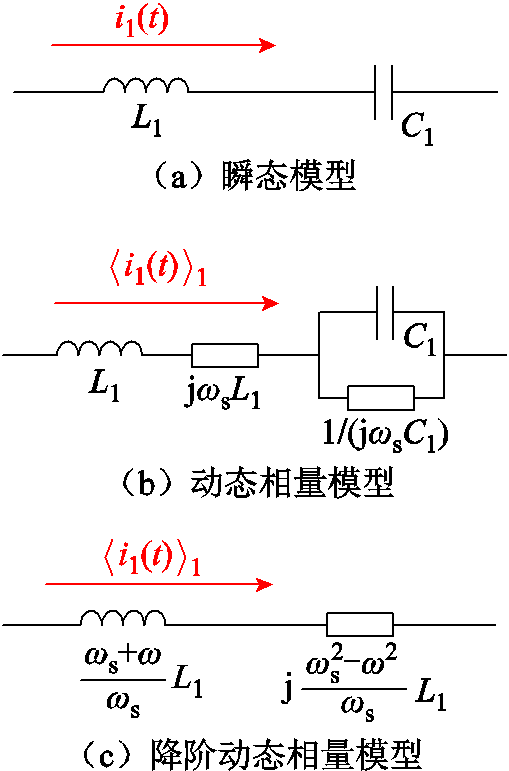
图5 一次侧谐振网络模型示意图
Fig.5 Models of series LC resonator
降阶动态相量模型精度高于稳态模型，计算复杂度远低于瞬态时域模型。就模型本身精度而言，全阶动态相量模型略微高于降阶动态模型，但降阶动态模型方程阶数更低，计算简单，更适用于在线计算[18]。因此本文基于降阶动态相量模型来描述励磁系统一次侧等效电路，并在此基础上推导出励磁电流估计表达式。
针对无刷励磁系统，基于基波假设，一次侧输入电压
和二次侧反射电压
的动态相量分别为
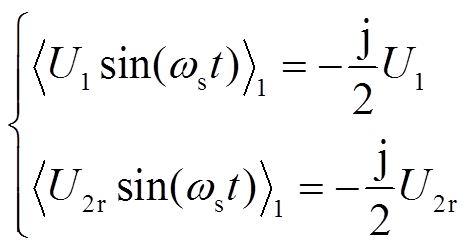（10）
式中，
和
分别为
和的基波幅值。
一次侧等效电路模型对应的微分方程为
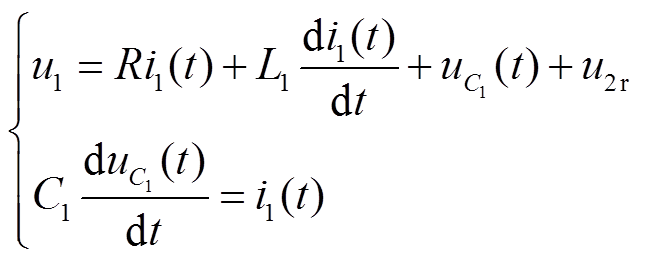（11）
记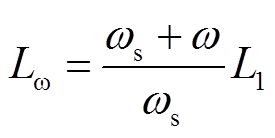
，
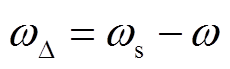，利用降阶动态相量模型将微分方程式（11）改写为
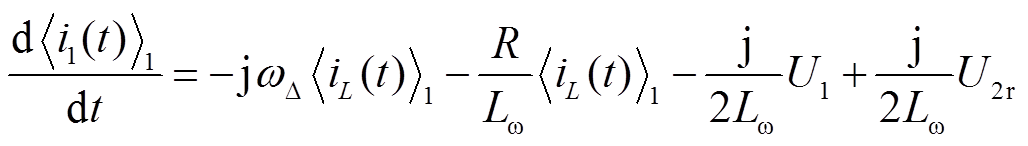（12）
将方程中的实部和虚部进行分离，得
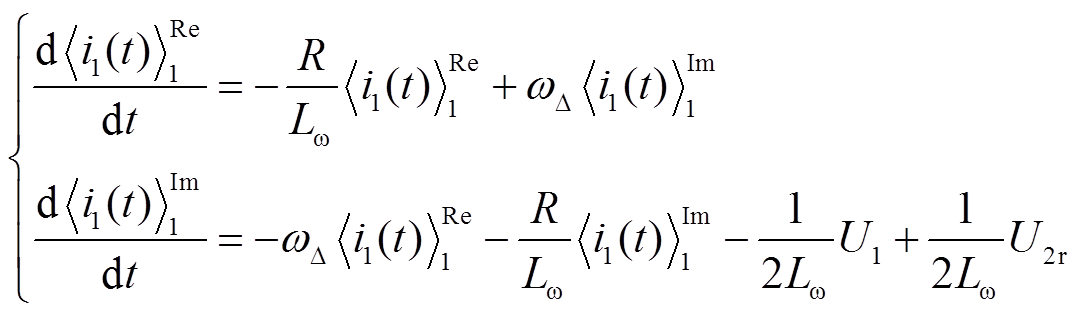（13）
为了将降阶动态相量模型中的中间变量
解算出来，将
视为系统扰动，此时式（13）可以改写成状态空间方程的形式为
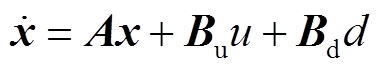（14）
式中
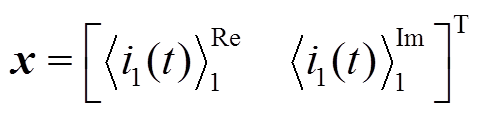
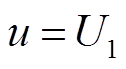
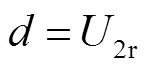
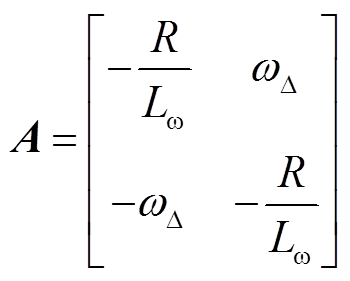
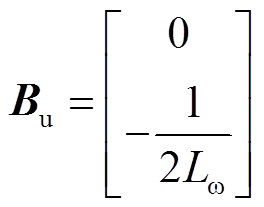
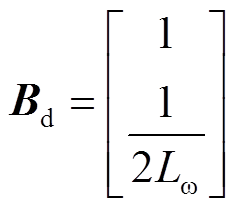
构造扰动观测器对进行估计，表达式为
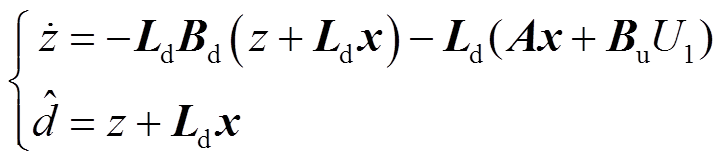（15）
式中，z为辅助变量；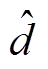
为扰动的估计值；
为观测增益矩阵。定义扰动估计误差ed为
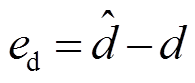（16）
对式（16）两边进行求导并化简可得
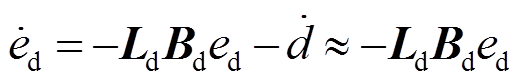（17）
在系统降阶动态相量模型中，扰动项相对于观测器的动态过程是慢变的，故
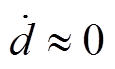。此时只要矩阵
满足Hurwitz稳定即可保证干扰观测器的收敛性。扰动观测器的结构框图如图6所示。
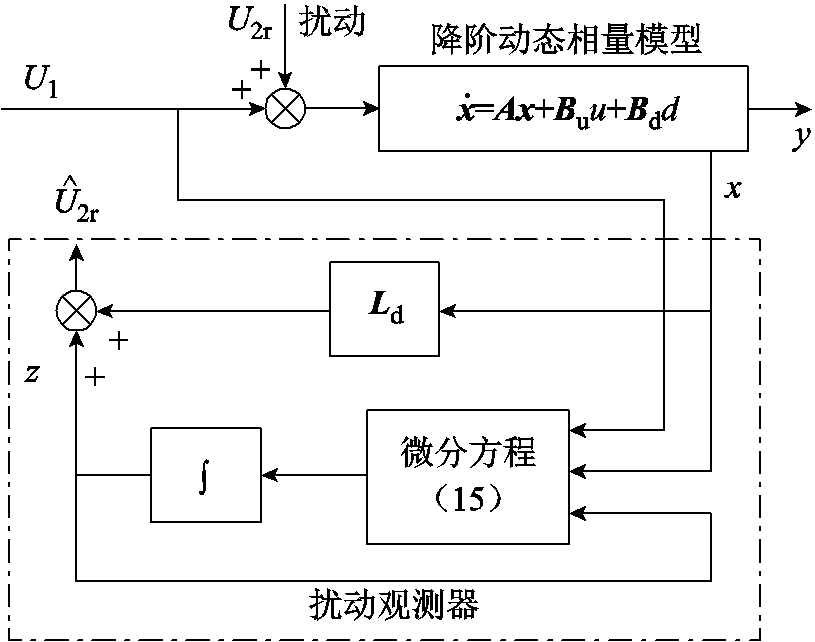
图6 扰动观测器结构框图
Fig.6 Block diagram of the disturbance observer
在动态相量模型中，扰动项二次侧反射电压可以表示为
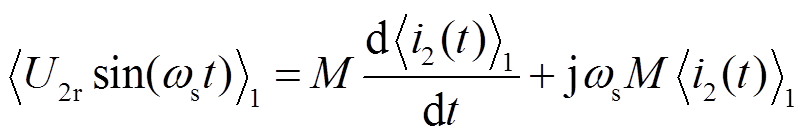（18）
同样在
条件下，做拉氏变换可得
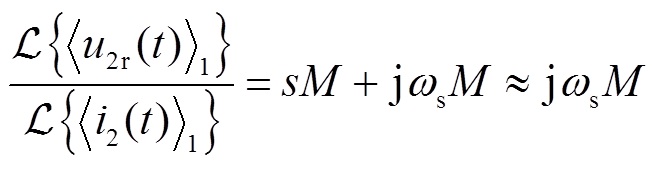（19）
整理可得
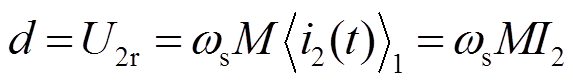（20）
结合扰动观测器输出结果及式（4），可以写出基于降阶动态相量估计模型的励磁电流表达式为
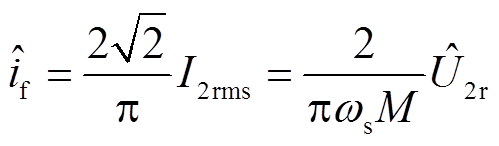（21）
为了更直观地表现基于降阶动态相量间接励磁电流估计方法的效果，给出基于稳态模型的励磁电流估计式用于对比分析。
结合一次侧等效电路模型中各元件的稳态模型和基尔霍夫电压方程，推导出基于稳态模型的励磁电流估计表达式为
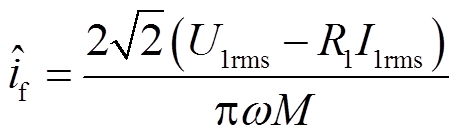（22）
式中，I1rms为一次电流有效值。
当电励磁电机稳定运行时，励磁电流可视为稳定的直流量。因此在分析估计误差时忽略励磁电流的暂态变化过程，以励磁电流稳定值为基准进行估计误差分析。另外需要说明的是，由估计式（21）、式（22）可知，电流估计结果必然会对互感参数
十分敏感。但2.1节强调了本文所研究的无刷励磁系统中互感是不变且已知的，因此在后续误差分析中不再对参数M进行敏感性分析，而是重点关注负载参数敏感性。
在Simulink中搭建无刷励磁系统的模拟电路仿真模型，系统相关参数见表1，观测增益矩阵配置为[0, 0.5]。（注：互感参数设计得相对较大，主要是为了提高传输效率[24]，且经过验证感应耦合线圈的输出功率在所设计的互感参数和工作频率下能够满足最大励磁功率要求。）
表1 无刷励磁系统参数
Tab.1 Parameters of wireless excitation system
参数数值 励磁绕组电阻（常温）Rf0/Ω15 励磁绕组自感Lf/mH400 励磁侧直流母线电压Udc/V48 一、二次线圈电阻R1、R2/Ω0.2 一、二次线圈自感L1、L2/mH100 耦合线圈互感M/mH60 谐振补偿电容C1、C2/nF400 逆变器工作频率f/kHz25 励磁电流额定值ifN/A3.6 额定励磁功率PfN/W200
在给定工况下验证所提电流估计方法的效果：在0～0.1 s内保持移相占空比α为1，0.1 s时降为0.75，0.2 s时α降为0.5，0.3 s时α重新变为1；在0.35 s后加入正弦反电动势
。
当励磁绕组电阻
时，仿真结果如图7所示。图7中
为励磁电流，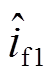
表示稳态模型估计值，
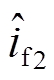表示降阶动态模型估计值，
和
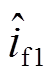分别表示和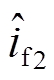的绝对估计误差。
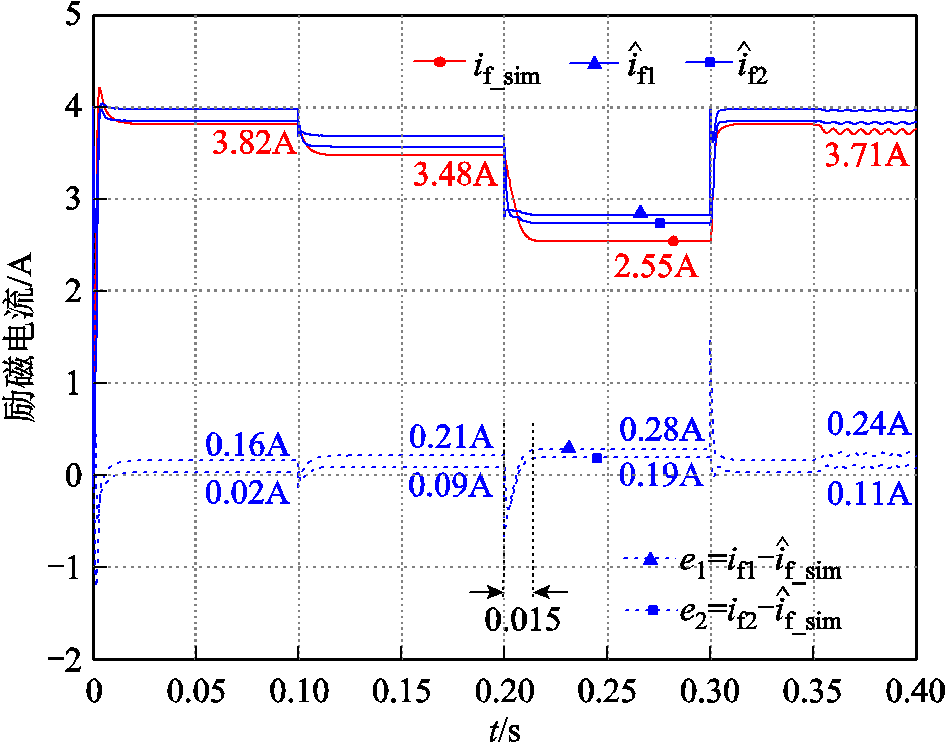
图7 
时两种估计模型结果对比
Fig.7 Comparison results of two estimation models when
仿真结果表明，稳态估计模型和降阶动态相量估计模型的收敛时间相当，输入阶跃变化时的收敛时间基本维持在0.015 s左右，与励磁电流振荡收敛时间相当，几乎不存在估计延时。故所提电流估计方法的响应速度足够用于闭环反馈。且相较于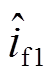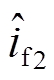，的估计误差总是更小。当
时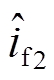，的相对误差仅有0.52%，但当
变小至0.5时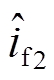，的相对误差增大至7.4%。在0.35 s后加入正弦反电动势干扰后，励磁电流
出现了波动，且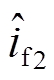相较于无反电动势时误差略微增大，此时的相对误差约为2.96%。
在不同温度下，励磁绕组电阻可由式（23）计算。
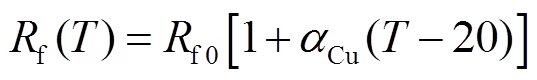（23）
式中，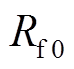
为常温（20℃）下的电阻值；
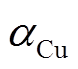为铜的电阻温度系数，一般取0.041℃-1；T为温度。
考虑电励磁电机工作时励磁绕组温度上升，以50℃温升为例，此时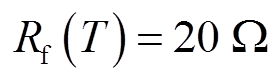
。在仿真中令励磁绕组电阻参数
，仿真结果如图8所示。
对比分析图7和图8可知，当励磁绕组电阻参数增大时，励磁电流会略微下降。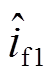在给定工况下最大估计误差从10.9%增加至12.9%，而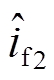的最大估计误差则仅仅从7.4%增加至7.6%。
上述结果表明，本文所提的间接式估计方法是可行的，且相较于稳态估计模型，基于降阶动态相量模型的估计方法具有更高的估计精度和鲁棒性。
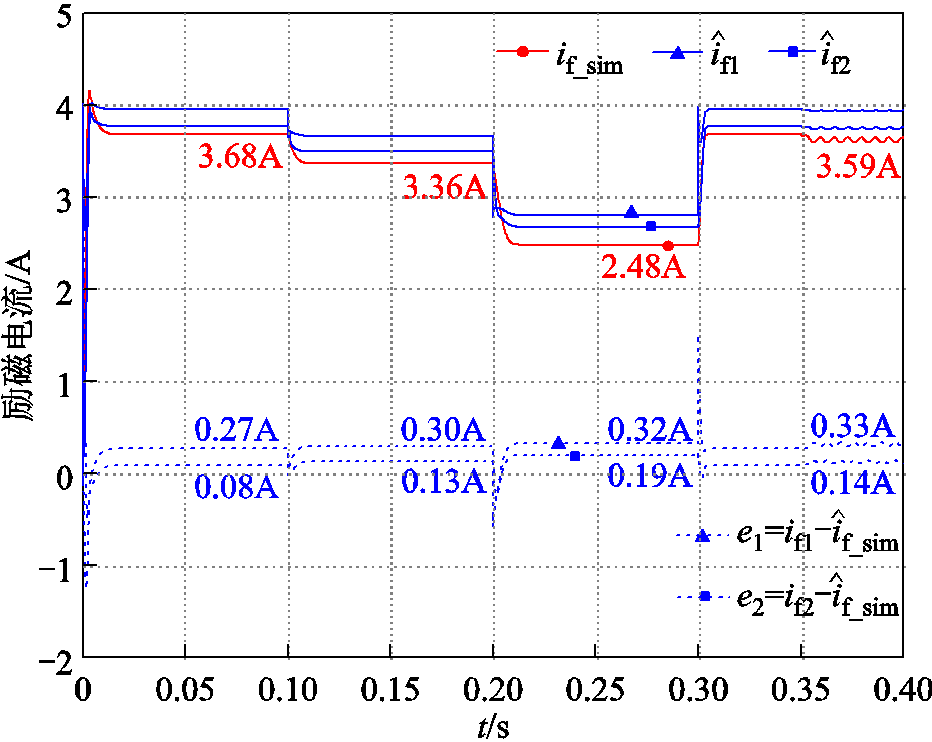
图8 
时两种估计模型结果对比
Fig.8 Comparison results of two estimation models when 
上述仿真结果表明，在
时励磁电流的估计误差明显变大。本文提出的间接式励磁电流估计方法需要先估计出二次侧反射电压和二次电流有效值
，再利用整流桥模型计算励磁电流估计值。在分析误差时可以先检验中间变量的估计误差，校核二次电流估计值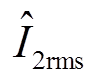
是否准确。
当
和
时，仿真结果分别如图9和图10所示。图中
表示和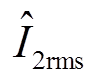之间的绝对估计误差。
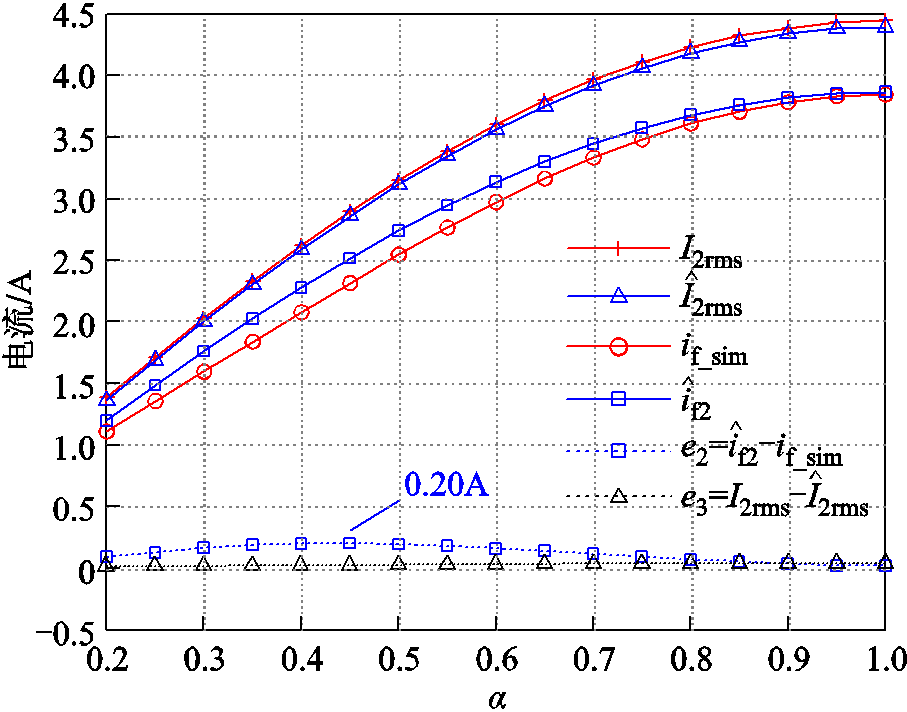
图9 Rf =15 Ω时二次电流有效值及励磁电流估计结果
Fig.9 The estimation results of RMS value of secondary side current and field current when Rf=15 Ω
结果表明，在不同的负载参数下，励磁电流估计误差
均会随着a的减小先增大后减小。且随着变大，整体略微变大。但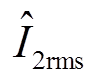的估计误差并不会受a和变化的影响，最大估计误差始终不超过2%。由此可知，所提方法对
的估计具有较高的精度和鲁棒性，间接说明扰动观测器估计出的也是准确的。因此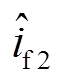
的估计误差受a影响的现象只能是由整流模型，即式（4）的误差造成的。
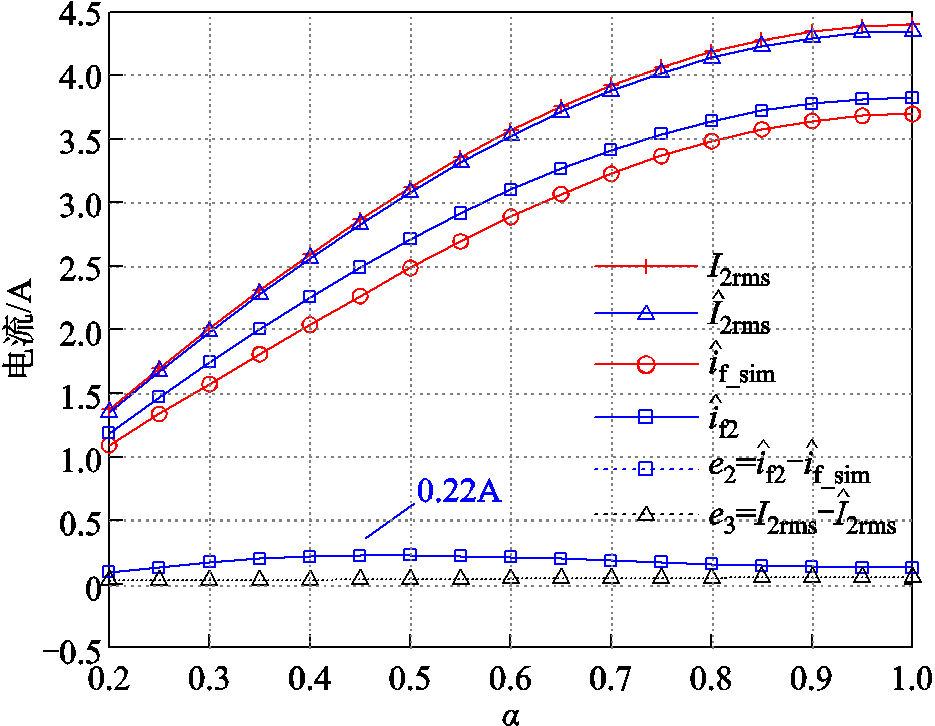
图10 Rf =20 Ω时二次电流有效值及励磁电流估计结果
Fig.10 The estimation results of RMS value of secondary side current and field current with resistance parameter changed when Rf =20 Ω
定义波形系数
为
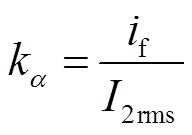（24）
式（4）中基于基波假设的
始终为0.9。但实际上受二次电流谐波影响，波形系数
是一个与
和相关的时变系数。不同工况下仿真计算得到的随和变化曲线如图11所示。
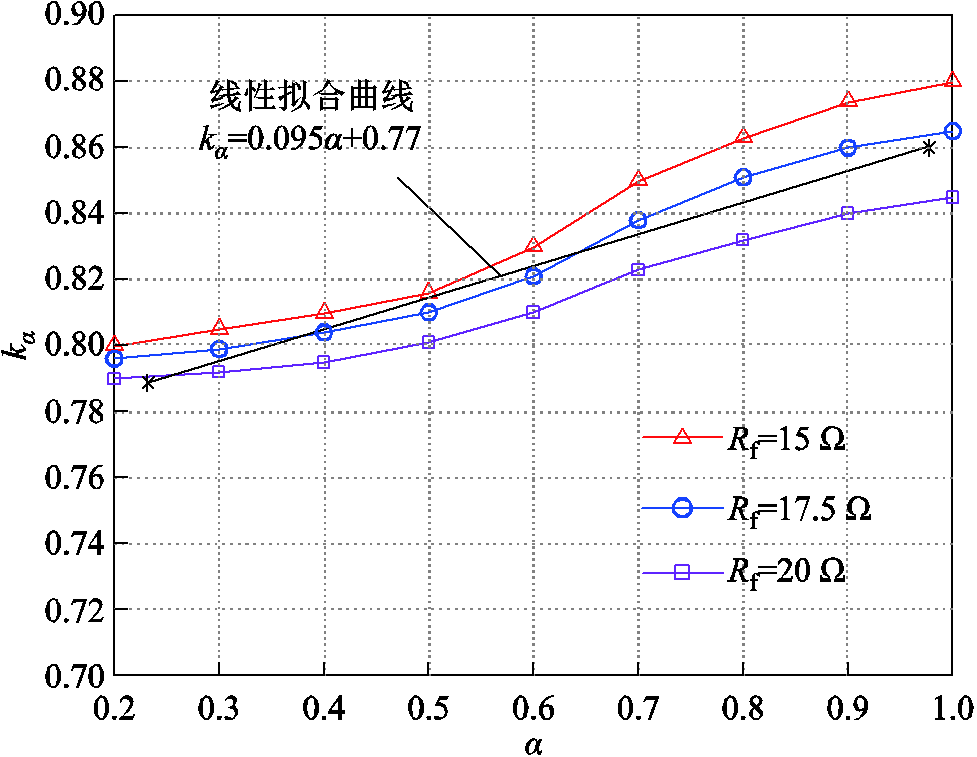
图11 波形系数变化曲线
Fig.11 Curves of waveform coefficient
在电流估计过程中时变电阻未知，无法将拟合成和的函数。但从工程实现的角度可以求出不同下的平均曲线。假设仅与有关，对其进行线性拟合，记为
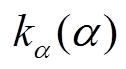，代入式（21）可得修正后的电流估计表达式为
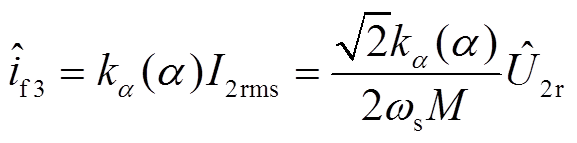（25）
当时，变系数估计方法仿真结果如图12所示，图中
表示
的绝对估计误差。结果表明，变系数估计方法的电流估计误差整体变小，最大估计误差绝对值从原来的0.2 A减小为0.07 A。
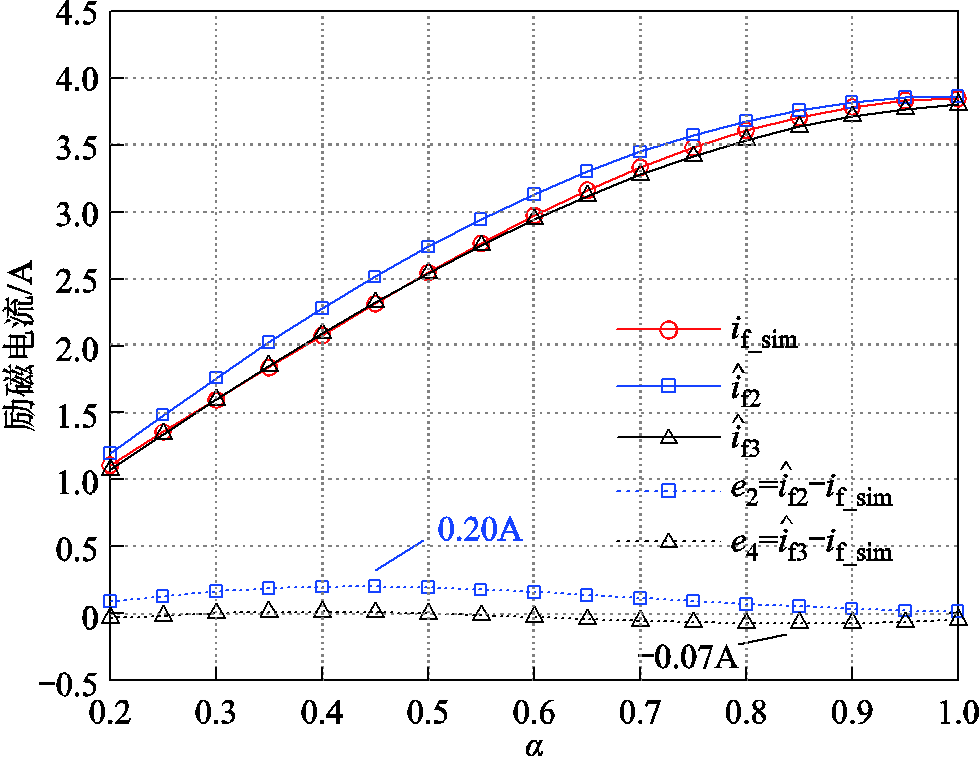
图12 变系数励磁电流估计结果
Fig.12 Results of variable coefficient estimator
和
时的仿真结果分别如图13和图14所示。仿真结果表明，在负载电阻变化及不同占空比下，变系数估计结果均有较高的精度，近似拟合出的能够满足需要。在给定工况下，变波形系数估计结果的最大相对误差仅为3.3%，明显小于定波形系数估计方法的7.6%。
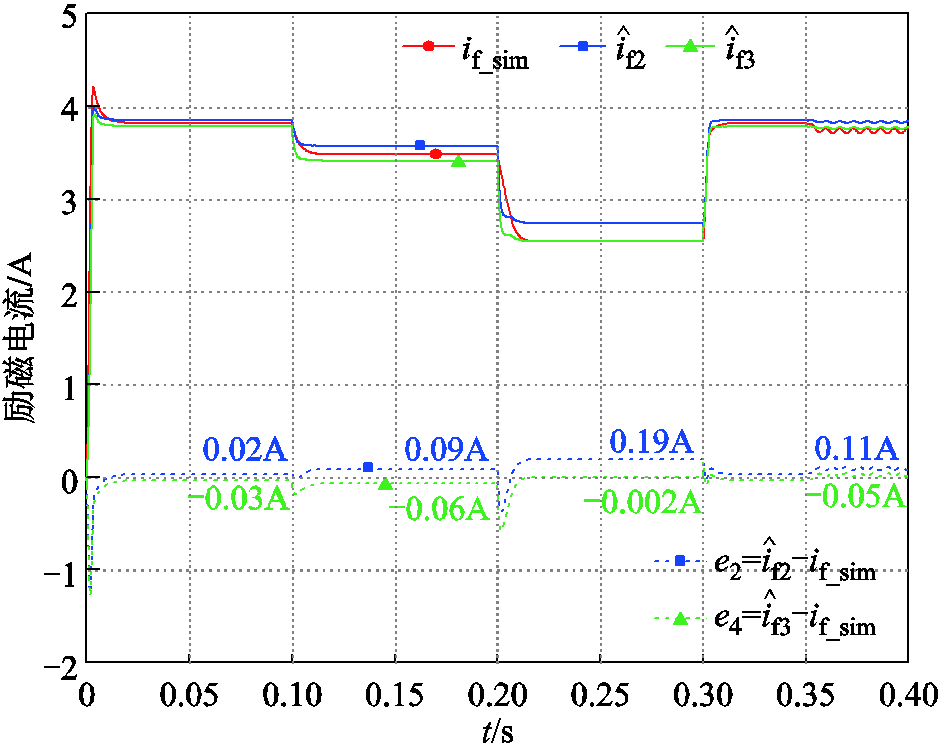
图13 
时变系数励磁电流估计结果
Fig.13 Variable coefficient estimation results when 
事实上的大小不仅与占空比和励磁电阻有关，还与无刷励磁系统参数（包括谐振频率、线圈自感以及线圈互感等）有关。但是对不同的电感耦合式励磁系统都可以应用上述近似拟合的方法获取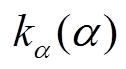，仅需要增加简单的仿真或实验步骤就可以有效地提高估计结果的精度和鲁棒性。
综上所述，基于降阶动态相量模型的估计方法精度显著高于稳态模型估计方法，并且采用考虑谐波影响的变波形系数改进估计方法可以进一步提高电流估计的精度和鲁棒性。
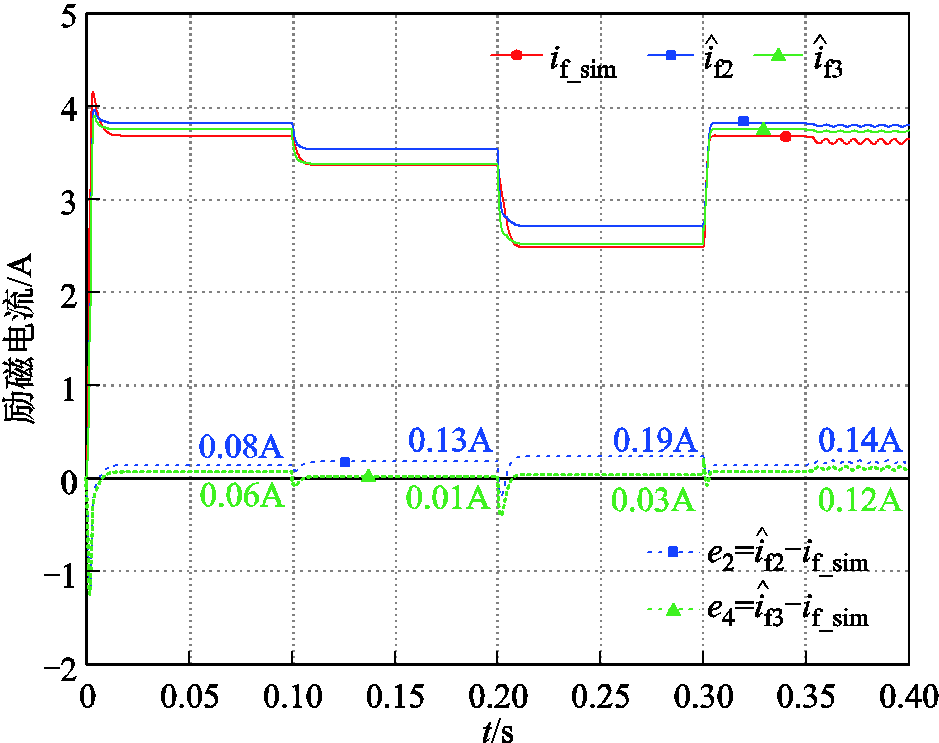
图14 
时变系数励磁电流估计结果
Fig.14 Variable coefficient estimation results when 
本文搭建的实验平台如图15所示。
图15 实验平台
Fig.15 Experimental platform
为了获取励磁电流真实值来验证电流估计效果，对电机转子进行改造，利用电刷集电环将励磁绕组引出，如图16所示。
在励磁绕组引出线两端串联电阻箱用于改变励磁回路总电阻以验证电流估计方法的鲁棒性。记此时励磁回路总电阻为
。当
，
和
时，逆变器输出电压和二次电流
波形分别如图17和图18所示。
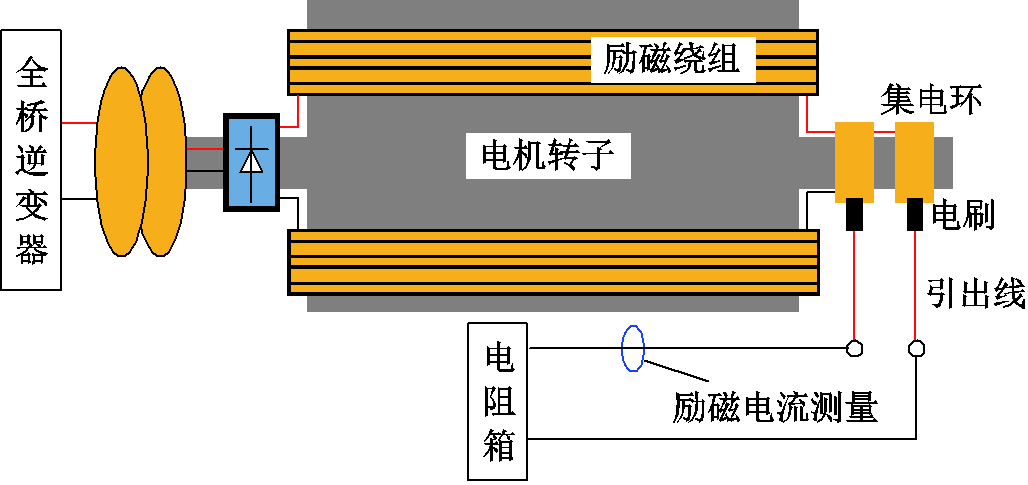
图16 励磁电流测量原理
Fig.16 Field current measurement schematic diagram
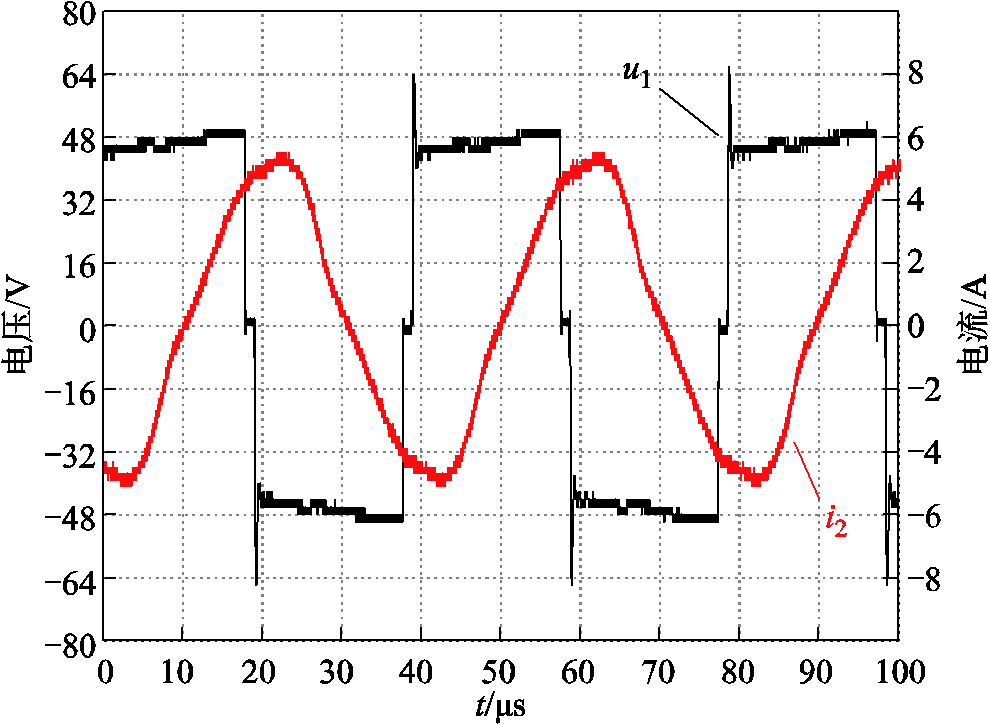
图17 
时的实验波形
Fig.17 Experimental waveforms when
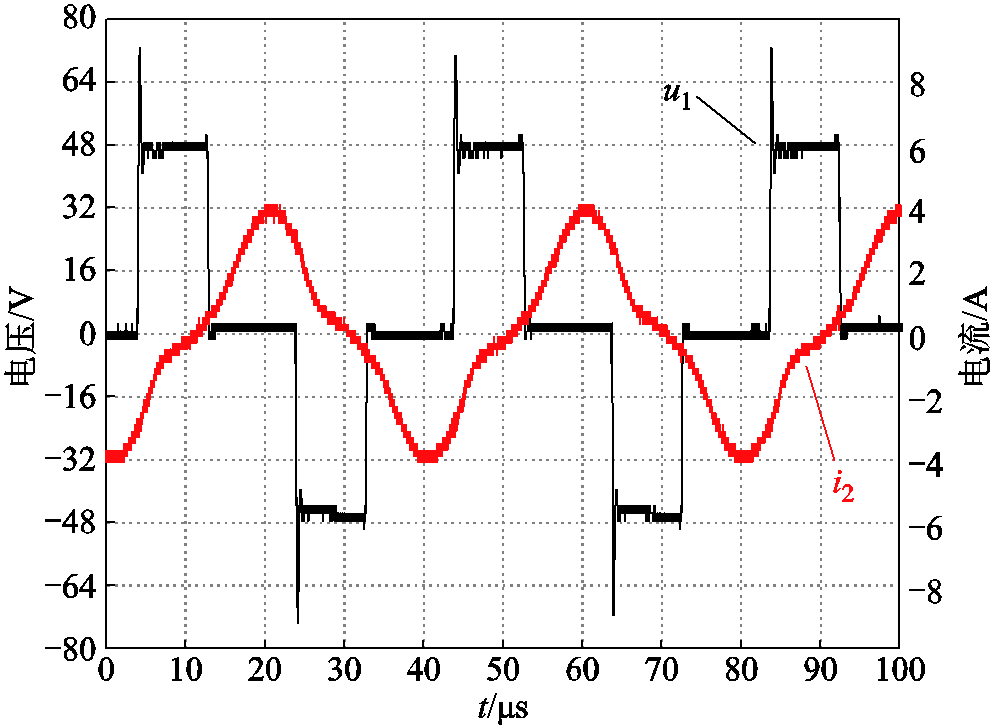
图18 
时的实验波形
Fig.18 Experimental waveforms when 
对二次电流进行快速傅里叶变换分解可得，
时二次电流谐波畸变率（Total Harmonic Distortion, THD）为8.18%，而
时的THD增加至21.52%。实验结果表明，随着的减小，二次电流谐波含量增加，对应波形系数减小，与仿真分析结果一致。
实验中选取与仿真一致的
拟合系数（图11）。当电阻箱电阻为0、
时，电流估计结果如图19所示。图中
为励磁电流实际值，
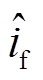为励磁电流估计值。改变电阻箱电阻，令
，此时电流估计结果如图20所示。
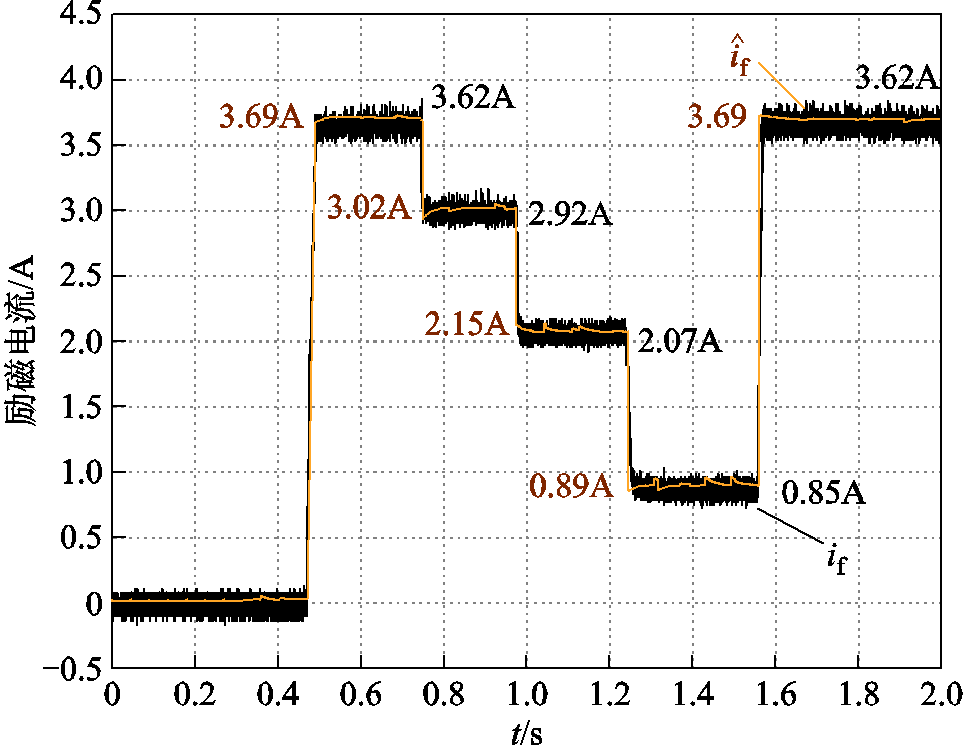
图19 
的励磁电流跟踪曲线
Fig.19 Tracking curve of field current when
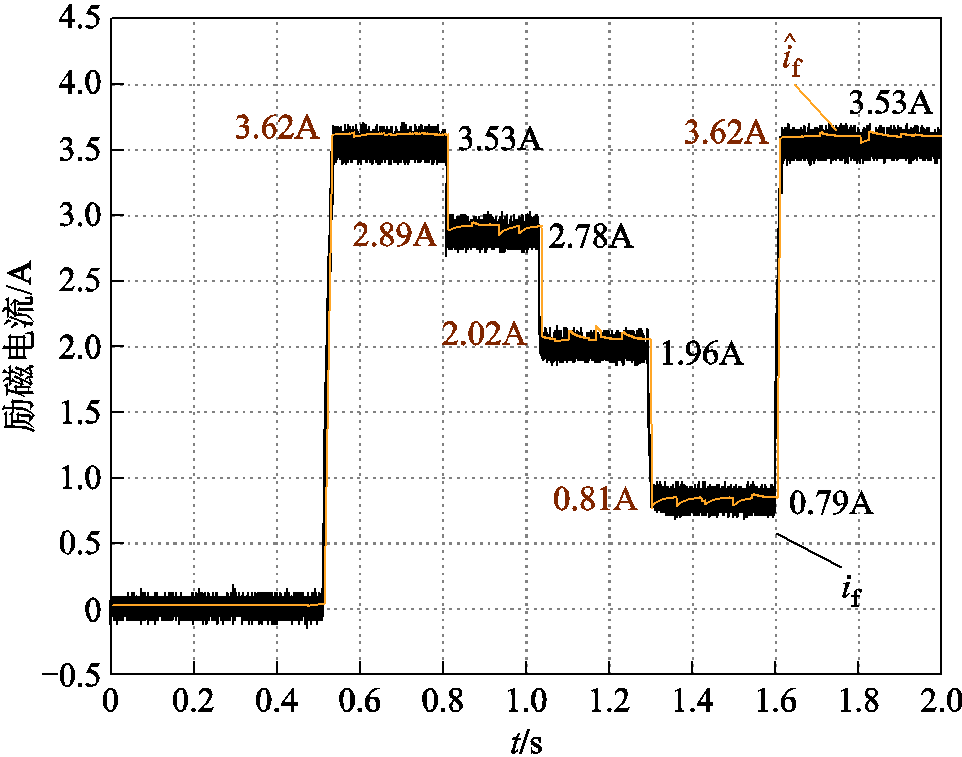
图20 
的励磁电流跟踪曲线
Fig.20 Tracking curve of field current when
为了使励磁电流估计结果更加平稳，增加了软件滤波环节。图19和图20中曲线左侧数值为励磁电流估计值的平均值，右侧数值为励磁电流的平均值。结果表明，所提电流估计方法具有较高的精度和鲁棒性，给定工况下最大相对估计误差约为4.7%。
综上所述，实验结果与仿真结果基本一致，变波形系数改进方法的假设和应用都是合理的，所提的电流估计方法具有较高的精度和鲁棒性。
针对串联-串联补偿型电感耦合式无刷励磁系统，本文提出了一种基于降阶动态相量模型的励磁电流间接估计方法。该方法建立了励磁系统的一次侧等效电路模型，对励磁电流进行间接估计，提高了估计方法的鲁棒性；建立降阶动态相量估计模型并考虑二次电流的谐波影响，提出变系数改进方法，进而获得更高的电流估计精度。
通过仿真和实验分析可以验证：基于降阶动态相量模型的励磁电流间接估计方法具有较高的精度和鲁棒性，且仅需要一个电流传感器，硬件成本较低；采用近似拟合的变波形系数
对估计模型进行修正能有效地减小二次电流谐波带来的估计误差。
本文所提的励磁电流估计方法在串联-串联电感耦合励磁系统中具有较好的效果，但对整流模型中的波形系数的细致分析和准确获取还有待进一步的研究。此外，利用间接估计思想及动态相量模型，可以实现对更多非串联-串联型拓扑的电感耦合式励磁系统高精度、高鲁棒性的电流估计，拓宽所提电流估计方法的应用范围。
参考文献
[1] Fallows D, Nuzzo S, Galea M. Exciterless wound-field medium-power synchronous machines: their history and future[J]. IEEE Industrial Electronics Magazine, 2022, 16(4): 44-51.
[2] 寇佳宝, 高强, 滕咏哮, 等. 负载换流逆变器驱动电励磁同步电机无速度传感器模型预测控制方法[J]. 电工技术学报, 2021, 36(1): 68-76. Kou Jiabao, Gao Qiang, Teng Yongxiao, et al. Speed sensorless model predictive control for load commutated inverter-fed electrically excited synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 68-76.
[3] 付兴贺, 江政龙, 吕鸿飞, 等. 电励磁同步电机无刷励磁与转矩密度提升技术发展综述[J]. 电工技术学报, 2022, 37(7): 1689-1702. Fu Xinghe, Jiang Zhenglong, Lü Hongfei, et al. Review of the blushless excitation and torque density improvement in wound field synchronous motors[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1689-1702.
[3] 卿晓东, 苏玉刚. 电场耦合无线电能传输技术综述[J]. 电工技术学报, 2021, 36(17): 3649-3663. Qing Xiaodong, Su Yugang. An overview of electric-filed coupling wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3649-3663.
[5] Dajaku G, Gerling D. Self-excited synchronous machine with high torque capability at zero speed[C]// 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 2018: 1165-1171.
[6] Di Gioia A, Brown I P, Nie Yue, et al. Design and demonstration of a wound field synchronous machine for electric vehicle traction with brushless capacitive field excitation[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1390-1403.
[7] Maier M, Parspour N. Operation of an electrical excited synchronous machine by contactless energy transfer to the rotor[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3217-3225.
[8] Song Kai, Li Zhenjie, Jiang Jinhai, et al. Constant Current/voltage charging operation for series–series and series–parallel compensated wireless power transfer systems employing primary-side controller[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 8065-8080.
[9] Zaghrini C, Khoury G, Fadel M, et al. Minimum copper losses per torque optimization on electrically excited synchronous motors for electric vehicles applications[C]//2022 IEEE 20th International Power Electronics and Motion Control Conference (PEMC), Brasov, Romania, 2022: 661-666.
[10] Stancu C, Ward T, Rahman K M, et al. Separately excited synchronous motor with rotary transformer for hybrid vehicle application[J]. IEEE Transactions on Industry Applications, 2018, 54(1): 223-232.
[11] Jiao Ningfei, Liu Weiguo, Zhang Zan, et al. Field Current estimation for wound-rotor synchronous starter–generator with asynchronous brushless exciters[J]. IEEE Transactions on Energy Conversion, 2017, 32(4): 1554-1561.
[12] Yao Fei, An Quntao, Sun Lizhi, et al. Optimization design of stator harmonic windings in brushless synchronous machine excited with double-harmonic-windings[C]//2017 International Energy and Sustainability Conference (IESC), Farmingdale, NY, USA, 2017: 1-6.
[13] Hagen S, Dai Jiejian, Brown I P, et al. Low-cost, printed circuit board construction, capacitively coupled excitation system for wound field synchronous machines[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 2019: 5358-5364.
[14] Zhong Wenxing, Ron Hui S Y. Charging time control of wireless power transfer systems without using mutual coupling information and wireless communication system[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 228-235.
[15] Tang Junfei, Jiang Bowen, Boscaglia L, et al. Observations of field current and field winding temperature in electrically excited synchronous machines with brushless excitation[C]//2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 2022: 841-847.
[16] Berweiler B, Ponick B. Current and average temperature calculation for electrically excited synchronous machines in case of contactless energy supply[C]//2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 2020: 1730-1735.
[17] Chen Fengwei, Garnier H, Deng Qijun, et al. Control-oriented modeling of wireless power transfer systems with phase-shift control[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 2119-2134.
[18] Li Hongchang, Fang Jingyang, Tang Yi. Dynamic phasor-based reduced-order models of wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11361-11370.
[19] Tang Junfei, Liu Yujing, Lundberg S. Estimation algorithm for current and temperature of field winding in electrically excited synchronous machines with high-frequency brushless exciters[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3512-3523.
[20] Kang Jinsong, Liu Yusong, Sun Liangrong. A primary-side control method of wireless power transfer for motor electric excitation[C]//2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi'an, China, 2019: 2423-2428.
[21] 郑广策, 赵凯, 王浩宇, 等. 基于LCC-S补偿网络的无线充电系统小信号模型[J]. 电工技术学报, 2022, 37(21): 5369-5376. Zheng Guangce, Zhao Kai, Wang Haoyu, et al. Small-signal model for inductive power transfer systems using LCC-S compensation[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5369-5376.
[22] Kang Jinsong, Liu Yusong, Sun Liangrong, et al. A reduced-order model for wirelessly excited machine based on linear approximation[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12389-12399.
[23] Cao Pengju, Tang Yunyu, Zhu Fan, et al. An IPT system with constant current and constant voltage output features for EV charging[C]//IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 2018: 4775-4780.
[24] 赵进国, 赵晋斌, 张俊伟, 等. 无线电能传输系统中有源阻抗匹配网络断续电流模式最大效率跟踪研究[J]. 电工技术学报, 2022, 37(1): 24-35. Zhao Jinguo, Zhao Jinbin, Zhang Junwei, et al. Maximum efficiency tracking study of active impedance matching network discontinous current mode in wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 24-35.
Abstract Electrically excited synchronous machines (EESM) has the advantages of low dependence on rare earth permanent magnet materials, controllable excitation field and wide speed regulation range, and has a good application prospect in electric vehicles. However, the traditional EESM's brush-slip ring structure caused friction loss, increased maintenance costs, and reduced reliability. Therefore, brushless excitation has become an urgent requirement and a critical issue to be solved for EESM applications. Inductively coupled brushless excitation technology can effectively reduce friction losses and maintenance costs. Currently, mainstream brushless excitation methods include exciter type, harmonic excitation type, and wireless power transfer type. Wireless power transfer excitation can be divided into inductive coupling and capacitive coupling types. Inductive coupling excitation has a simple structure and high transmission efficiency, making it promising for applications.
However, the usage of brushless excitation technology will bring a new challenges. The excitation winding of brushless excitation system rotates with the rotor, and there is no direct electrical connection between the transmitting circuit and the receiving circuit, resulting in the acquisition of excitation current value facing technical challenges. To estimate the field current in similar scenarios has been the scope of some previous studies. The existing current estimation methods can achieve good results in their respective application fields, but there are some limitations and shortcomings, which need to be further developed.
In view of this, an indirect excitation current estimation method based on reduced order dynamic phasor model is proposed for series-series compensation inductively coupled brushless excitation system, which has the characteristics of simple calculation, strong load adaptability and low hardware cost. The topology structure of excitation energy transmission circuit is designed. The equivalent circuit model of excitation system is established. In order to avoid the influence of load parameter disturbance, an indirect current estimation method is proposed by using the inductive coupling relation and the secondary side reflection voltage as the intermediate variable. A reduced order dynamic phasor estimation model is established to further improve the estimation accuracy of the indirect estimation method. Considering the harmonic effect of subside current, an improved method of variable waveform coefficient is proposed. Finally, the validity of the current estimation method is verified by simulation and experiment.
The experimental results show that indirect estimation method has high robustness, the maximum relative estimation error is 4.7% under load variation. Compared with the steady-state estimation model, the reduced order dynamic phasor estimation model can maintain higher estimation accuracy when the load condition changes. Using approximately fitted variable waveform coefficientto modify the estimation model can effectively reduce the estimation error caused by secondary current harmonics.
The proposed excitation current estimation method has a good effect in series-series inductively coupled excitation system. And only one current sensor is required, resulting in low hardware cost. However, the detailed analysis and accurate acquisition of waveform coefficients in the rectification model need further research. In addition, the indirect estimation idea and the dynamic phasor model can be used to estimate the current of more inductively coupled excitation systems with non-series-series topology with high accuracy and high robustness, and broaden the application range of the proposed current estimation method.
keywords：Electrically excited synchronous machines, inductively coupled brushless excitation technology, current estimation algorithm, dynamic phasor model
DOI:10.19595/j.cnki.1000-6753.tces.230946
中图分类号：TM341
国家自然科学基金资助项目（51977035）。
收稿日期 2023-06-23
改稿日期 2023-08-06
付兴贺 男，1978年生，博士，副教授，研究方向为高温特种电机及其控制、伺服系统多源异构扰动抑制。E-mail：fuxinghe@seu.edu.cn （通信作者）
夏宏伟 男，1998年生，硕士研究生，研究方向为电机控制。E-mail：220213084@seu.edu.cn
（编辑 赫蕾）