图1 车辆运行工况
Fig.1 The vehicle operating conditions
摘要 针对无人配送车用低速大转矩电机驱动系统的多工况运行需求，结合前期针对不等Halbach交替极游标轮毂电机的研究，提出一种基于电机整体运行工况的优化框架。该电机采用磁场调制原理与不等Halbach阵列拓扑，具备强聚磁特性以及高输出性能，但存在转矩脉动、成本高、损耗较大等问题。并且传统基于额定点的多目标优化方式，难以在全工况域满足车辆性能需求。因此结合所提出的优化框架，针对电机成本、效率、转矩脉动进行参数寻优，以满足全工况需求。为提升优化速度，利用聚类分析选出代表性工作点，并基于灵敏度分析建立高敏参数响应面模型，结合非支配排序遗传算法（NSGA-Ⅱ）确定全局全工况下的最优解。最后，基于优化后的参数制作样机并进行实验验证，以证明所提出电机和方法的可行性与准确性。
关键词：轮毂电机 磁场调制 聚类分析 多目标优化 遗传算法
随着社会的发展，智能化无人配送车的出现能够帮助人类进行部分劳动，而电机作为其驱动部件，需要满足高转矩密度、低成本、高效率等实际需求[1]。因此，为了满足实际工作需求，诸如开关磁阻、永磁同步等电机拓扑被陆续研究[2-3]，但是转矩密度难以进一步提升。而随着磁场调制原理的完善，磁场谐波能被充分地利用以提升电机的输出性能，因此许多新型拓扑被提出。其中，游标电机因其结构简单、转矩密度高和转矩脉动小等优点而受到广泛关注[4]。
基于场调制原理，游标电机将高速旋转的定子磁场转变为较低速度的转子磁场以实现“自减速”效应。电枢绕组部分可以按照高速电机设计，以解决直驱电机由于极槽数量较多而导致体积增大的问题，从而提高了电机的转矩密度。为进一步降低制造成本，诸如“交替极”“少稀土永磁”等措施被提出[5-6]。并且为平衡制造成本、输出能力与电机性能需求，应该针对结构参数进行优化处理。因此，需要针对前期提出的具有高聚磁能力的交替极不等Halbach游标轮毂电机（Consequent Pole Unequal Halbach Vernier Wheel Motor, CPUHVWM）进行多目标优化分析[7]。
电机优化是一种带有多个不等式约束的非线性优化问题。利用有限元软件对电机进行优化设计已成为一种主要手段，其具有准确度高的特点。但是在优化过程中，由于电机中包含有大量结构参数，导致该方法运算量大、效率较低，并且大多以单目标寻优为主。为了提升电机的优化效率，利用代理模型，建立结构参数与目标函数之间的关系，并结合如遗传算法、粒子群等算法进行大规模参数寻优处理，可对多个目标同时进行寻优。文献[8]采用粒子群优化算法，以高功率因数与低转矩脉动为目标，对结构参数进行寻优，并进行实验，验证了其有效性。为了进一步提升优化效率，文献[9]通过Kriging模型辅助结合多目标粒子群优化算法，以此获得优化目标的Pareto前沿。但是粒子群算法属于随机搜索算法，容易陷入局部最优解。因此，文献[10]采用多种群遗传算法对永磁直线电机进行参数寻优，以寻求高推力密度、低推力波动和低铜耗。为了进一步加快寻优速度，文献[11]采用响应面与差分进化算法相结合的形式，以快速生成Pareto解集。
但是，上述研究大多基于单一额定工况进行多目标优化，未考虑其他工况下，电机性能是否满足需求。因此，文献[12]考虑了三种典型运行工况，以全面提升电机性能为前提，利用响应面法结合优化算法进行分析。而文献[13]基于勒芒赛车的驾驶工况循环，将运行工况分为7个区域，对电机进行优化设计，但是工作点较多，分析过程较为复杂。文献[14]通过对驾驶工况的分析，引入对工况代表点的性能评估，以此对整体性能进行优化分析，但是在后续优化中，存在较多工况点，优化效率仍然不高。因此，如何基于实际工况，对电机进行高效快速的参数寻优，值得深入研究。
本文基于所提出的具有高聚磁能力的CPUHVWM，以降低电机转矩脉动、降低成本与提升效率为优化目标，提出一种考虑全工况域的多目标优化框架，以准确获取电机在全工况域下的最优参数。主要创新点如下：①将不等Halbach阵列与交替极相结合，既减少了永磁体的使用，又增加了聚磁能力；②引入了轮廓系数对k聚类法进行评判以达到最优聚类效果；③优化前，考虑了电流分配方案与永磁体退磁情况，能够保障后续优化的有效性。在上述创新点的基础上，基于灵敏度分析建立高敏参数响应面模型，结合非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm-Ⅱ, NSGA-Ⅱ）对参数进行寻优。最终，在电机电磁性能分析的基础上制作样机并进行实验测试，证实所提出模型和方法的有效性和准确性。
该电机应用于校园无人配送机器人，该类机器人具有较为固定的路况及行驶路径。因此，基于园区内的限速、坡度，对无人配送车辆行驶状态进行了采样，车辆运行工况如图1所示。可见，其车辆运行存在频繁起停工况。
图1 车辆运行工况
Fig.1 The vehicle operating conditions
轮毂电机转速n与配送车辆的车速va以及轮胎外径Dw密切相关，而车辆在行驶过程中其电机的驱动力Tw（即电机输出转矩）和所受到的阻力应保持平衡，可建立一个动态的平衡方程，即
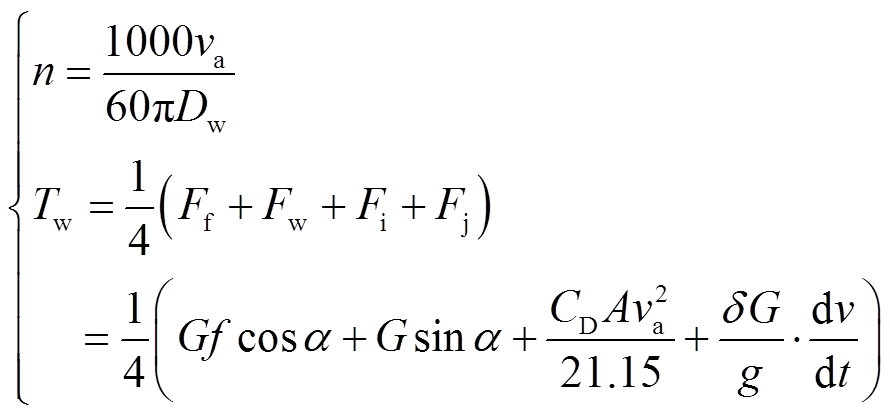（1）
式中，Ff、Fw分别为车辆行驶过程中所受到的滚动阻力和空气阻力；Fi、Fj分别为行驶过程中受到的坡道阻力和加速阻力；G为车辆与货物的总重量；f为滚动阻力系数；CD为空气阻力系数；A为该车辆的迎风面积；δ为旋转质量换算系数；α为路面的坡度角。
根据式（1），可分别对不同时段的转速-转矩模型加以确定，标注出了在该时间段内的全部工作点，如图2所示。
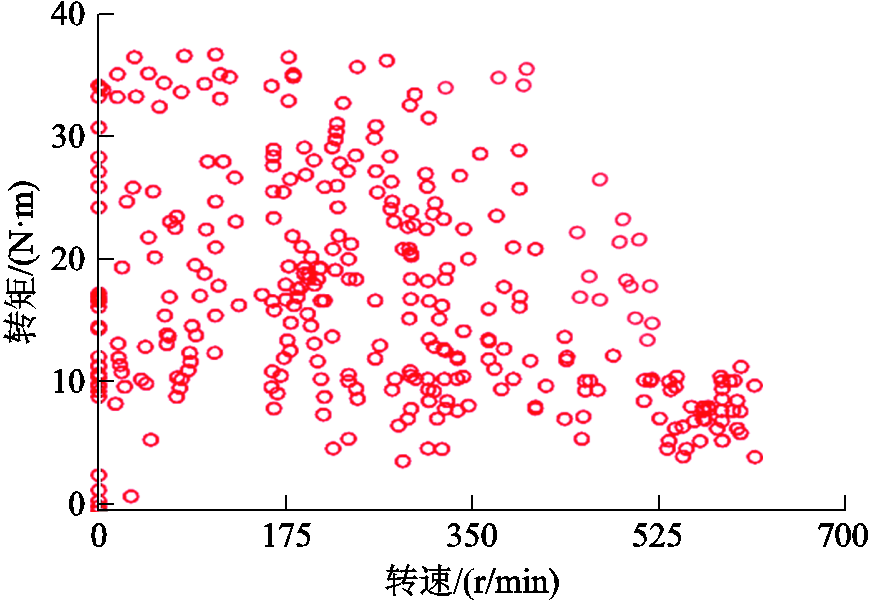
图2 电机运行工作点
Fig. 2 The machine operating condition points
通过观测，可以大致将电机的运行阶段分为：频繁起停、低速爬坡、低速巡航、中速巡航与高速巡航。然而，电机工作点数量较多，需要引入数据挖掘技术对数据点进行聚类分析预处理，从而简化后续优化流程。因此，采用k聚类法[15]对数据点进行处理，并引入轮廓系数s，以评判不同分区的优劣，可以写为
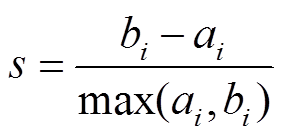（2）
式中，ai为第i个点到与i相同聚类中其他点的平均距离；bi为第i个点到不同聚类中点的最小平均距离。分别对不同簇数的轮廓系数进行分析，如图3所示，其数值越接近1，聚类效果越好。
图3 聚类数量与轮廓系数的关系
Fig.3 The relationship between cluster quantity and contour coefficient
从图3中能够看出，当聚类数量（簇）k=5时，轮廓系数最大，因此将图2的工况点分为5个簇，并且每个数据簇均包含一个质心，工况预处理如图4所示。
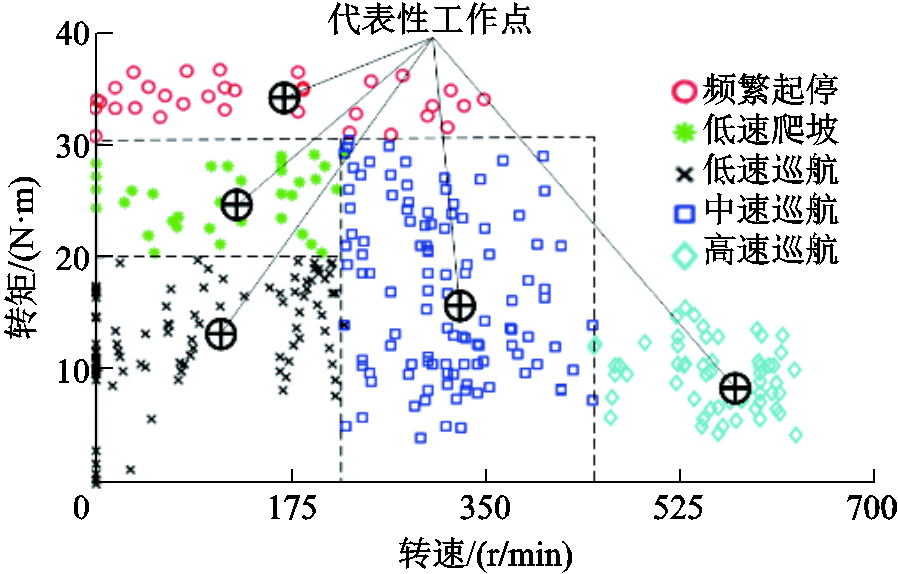
图4 工况预处理
Fig.4 The condition pretreatment
根据持续更新迭代选择出最终的质心，并依据所在工况区域内点数占比引入权重。最终的质心与权重见表1。
表1 代表性工作点
Tab.1 The representative working points
运行阶段转速/(r/min)转矩/(N×m)权重(%) 频繁起停172.835.611.08 低速爬坡136.125.49.91 低速巡航110.212.127.99 中速巡航302.716.932.36 高速巡航592.49.918.66
本文所提出并用于优化设计的CPUHVWM具有27个定子槽、23对永磁体极以及4对电枢绕组极，电机拓扑结构如图5所示。与传统的Halbach电机相比，该电机采用了不等Halbach结构，将永磁体分为三段，两端永磁体宽度小于中间部分，其充磁方向如图5b所示。该结构能够提升聚磁能力，进而提升转矩密度。此外，相较于表贴式结构，交替极结构中每个极对的永磁磁通仅由一个永磁体产生，因此降低了电机成本。并且由于交替极的使用d/q轴磁路不对称，因此提升了电机的凸极性。
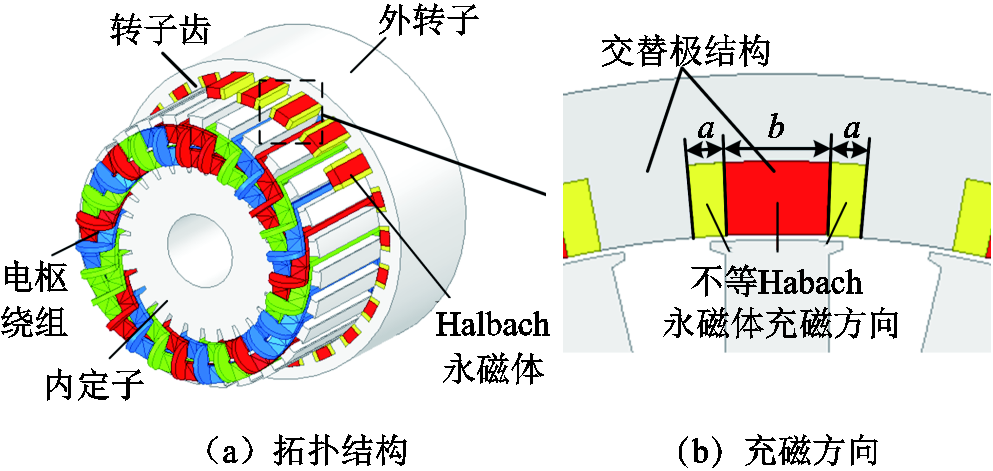
图5 CPUHVWM拓扑结构
Fig.5 The topology of CPUHVWM
图6a～图6c分别展示了径向充磁、常规Halbach与所提出的不等Halbach的转子结构，并在相同初始参数的前提下，对三种结构的气隙磁通密度进行了对比分析，如图6d和图6e所示。从图6e中能够看出，三种结构的气隙磁通密度经过FFT分解出现了诸多有效次工作谐波，其中4次与23次谐波分别为定转子极对数所生成的，其他较小的谐波次数，均为调制谐波。综合来看，所提出的不等Halbach结构，在相同铜耗与永磁体用量的情况下，其波形与幅值均大于其他两种结构，能够说明其性能优势。
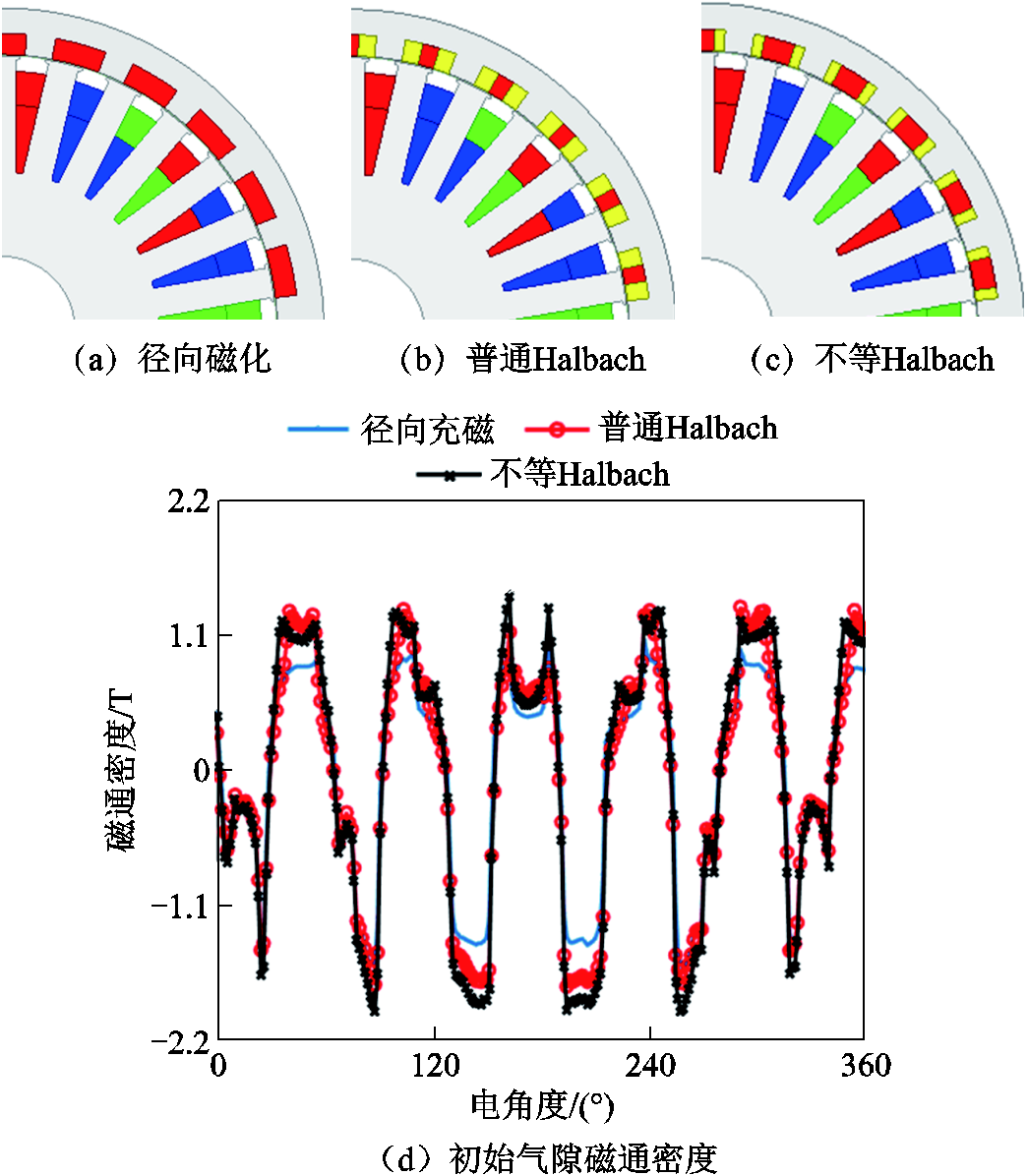
图6 初始结构与气隙磁通对比
Fig.6 Comparative of initial structure and air-gap flux
基于图2中的运行工况，并结合给定冗余设计，设定电机的性能需求见表2，其中也考虑了电机过载及弱磁性能。
表2 电机性能需求
Tab.2 The motor performance requirements
参数数值参数数值 额定功率/kW2.3轴向长度/mm50 额定转速/(r/min)500过载电流/A9 额定转矩/(N×m)45峰值转矩/(N×m)65 额定电流/A6最高转速/(r/min)900 转子外径/mm170效率(%)90
该结构基于磁场调制原理，利用定转子齿代替磁齿轮复合电机中的调磁环进行磁场调制，实现了不同定转子磁极对数之间的空间调制，以产生更多的有效谐波分量，从而提升转矩[16]。
为了满足磁场调制原理，电机的调磁齿Z、转子极对数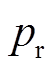
与电枢绕组极对数ps应满足
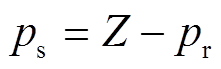（3）
电机的极比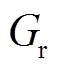
可以表示为
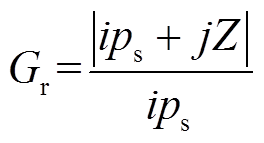（4）
式中，i为正奇数；j为全部整数。在众多数字组合中，当i=1及j=-1时，能够得到最大调制谐波幅值。
基于上述分析，并结合需选择较高的极槽最小公倍数的条件，最终选择了27槽、23对转子极和4对电枢绕组极的极槽组合形式。
根据电机参数需求的设定能够看出，电机的额定及过载参数均设有余量。为了满足各工况下的需求，需要对电机转矩脉动、效率、制造成本进行优化。而在多目标优化之前，需要对电机弱磁工作点、永磁体退磁情况等进行分析，以确保后续优化的有效性[17]。
根据电机实际需求，该电机的运行工况点可以简要分为恒转矩区域、恒功率区域及过载区域，如图7a所示。在恒转矩区域及过载区域中，以最大转矩电流比（Maximum Torque Per Ampere,MTPA）为约束，精准施加电流[18]。而在恒功率区域采用弱磁控制，施加-d轴电流，在电压约束限制下，提升电机转速，需保障永磁体不会发生不可逆退磁。电机稳态下的电压方程可写为
（5）
式中，ud、uq分别为直轴与交轴电压；id、iq分别为直轴与交轴电流；Ld、Lq分别为直轴与交轴电感；Rs为相电阻；ω为电流频率；ypm为永磁磁链。转矩方程可写为
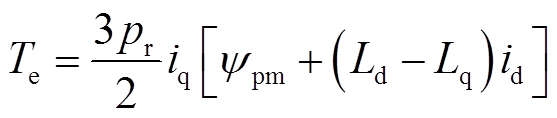（6）
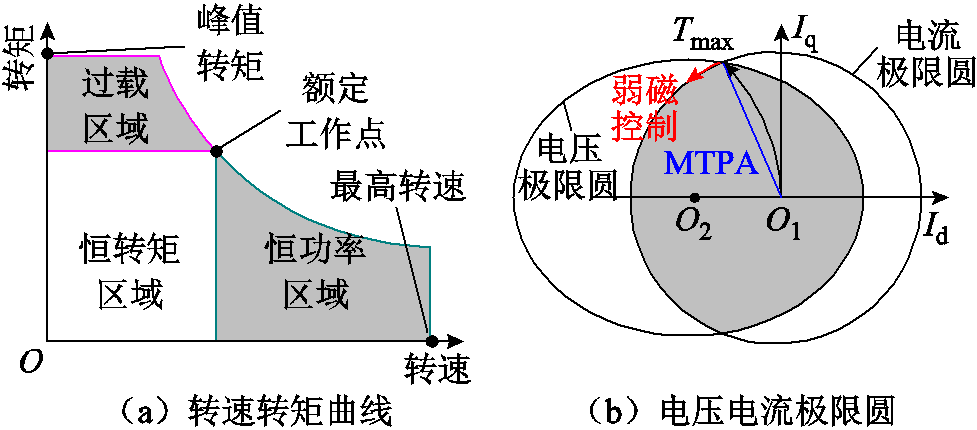
图7 性能原理研究
Fig.7 The research on performance principle
由于采用交替极转子结构，除电磁转矩外，其包含一部分磁阻转矩。在dq轴坐标系下，其电压电流极限圆如图7b所示。且电压与电流的约束条件为
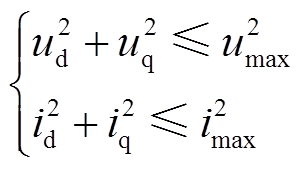（7）
式中，umax和imax分别为所选择逆变器的最大输出电压与电流。
为了获取电流分配方案，并对永磁体状态进行评估，选取了部分关键工况点拟合d、q轴第二象限平面，分析不同d、q轴电流情况下转矩变化情况，以及弱磁状态下，反向励磁电流是否会对永磁体造成不可逆退磁影响，其输出性能结果如图8所示。
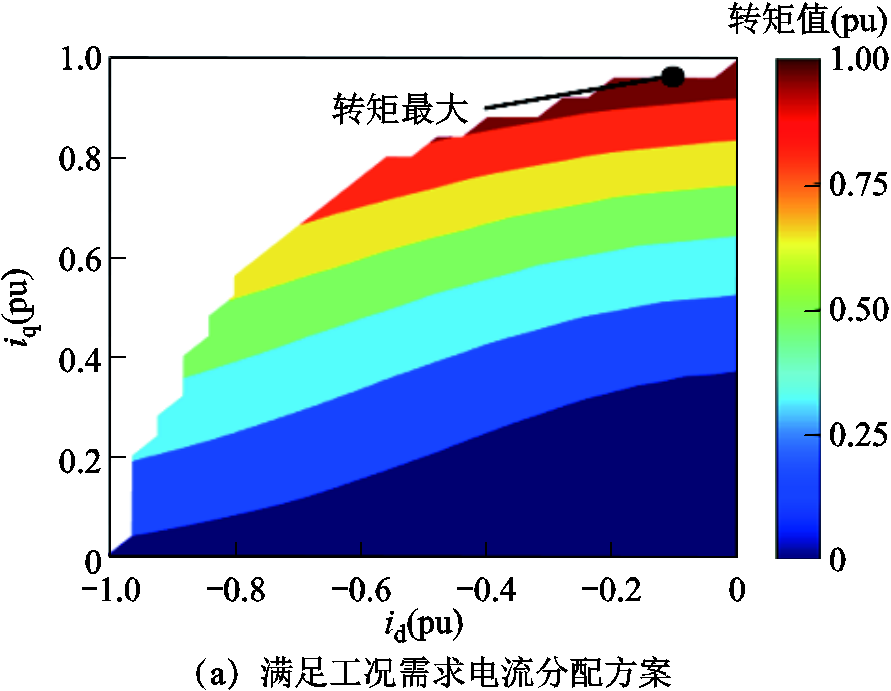
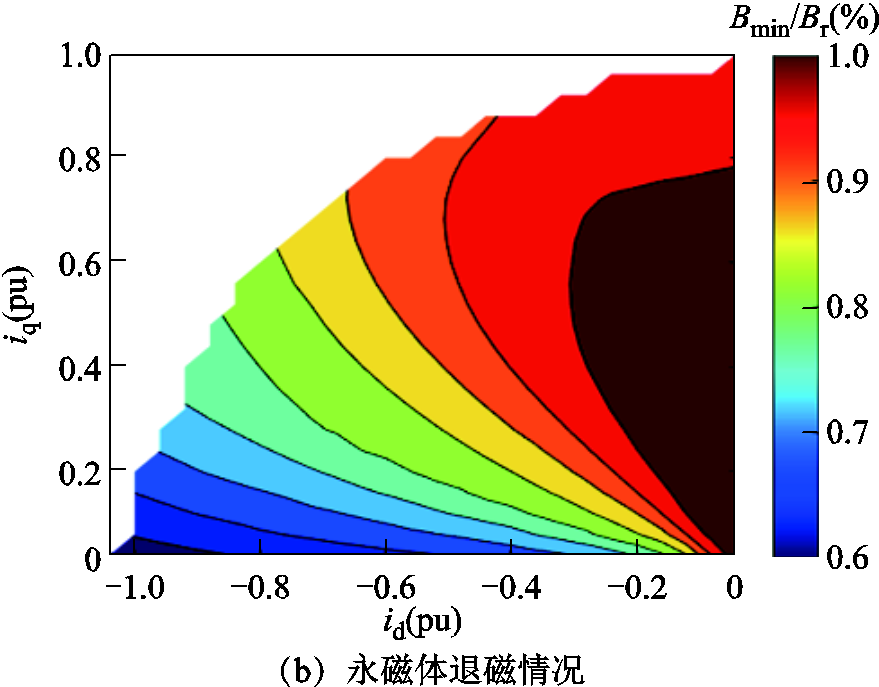
图8 输出性能结果
Fig.8 The output performance analysis
电机最大转矩处用黑点标记，如图8a所示，随着iq的增大，电机的转矩相应增加；随着id的增大，电机的转矩逐渐减少，同时转速相应提高，起到了弱磁作用。图8b展示了在现有的电流分配方案中，通入不同的d、q轴电流下永磁体的退磁率。能够看出，在该电流分配方案中，对永磁体的影响不大，均在可逆的退磁区域。因此，在后续优化中，仅需考虑母线电压对输出性能的限制即可。
在满足转矩和转速需求的前提下，需针对电机转矩脉动、有效材料成本（Active Material Cost, AMC）及效率进行优化，以保障电机整体优势。
1）电机有效材料成本
所提出的电机结构主要由永磁体、硅钢片及铜线组成，其材料成本主要由上述部分构成，以硅钢片材料为基准，其有效材料成本方程可以写为
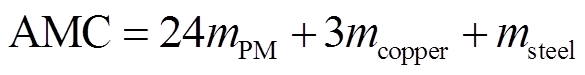（8）
式中，mPM、mcopper、msteel分别为电机永磁体、绕组和硅钢片的有效质量。
2）电机效率
电机效率同样尤为重要，为方便后续计算，针对电机铜耗、铁耗及涡流损耗进行分析，将风摩、机械损耗设为定值放入不同工况，基于表1中给出的工况及权重分配，引出电机加权效率，可以写为
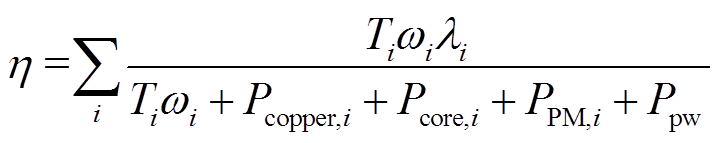（9）
式中，Ti和ωi分别为不同工况点的转矩和转速；λi为电机不同工况所占权重；Pcopper,i、Pcore,i和PPM,i分别为不同工况下的铜耗、铁耗及涡流损耗；Ppw为电机除上述三种以外的损耗，作为定值加入。
完成电机性能分析后，需选择对优化目标影响较大的关键参数，对其进行优化。因此，构建一个综合框架来指导该电机多目标优化，如图9所示。
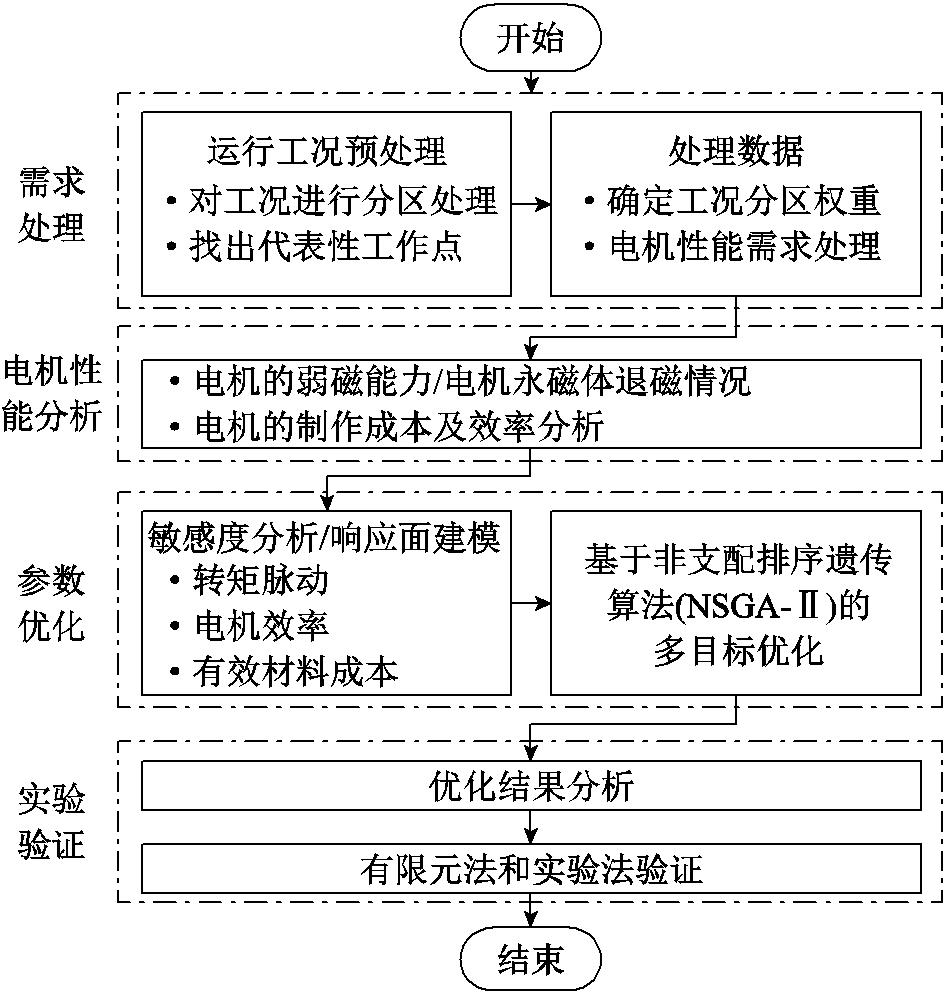
图9 多目标优化框架
Fig.9 The multi-objective optimization framework
为保障优化结果的可靠性，将电机的气隙、转子外径、轴向长度及槽满率设为固定值，并将其代入后续分析中。针对下述参数进行优化扫描，详细的参数模型如图10所示。由于在优化参数时，转矩会发生变化，因此将加权转矩作为优化约束，以满足输出条件。
为确保未来结果的收敛性并保障灵敏度分层的公平性，根据优化目标的重要性分配了权重系数。其中，电机效率和有效材料成本权重系数均为0.4，转矩脉动权重系数为0.2。通过综合灵敏度指数定量分析各设计变量对优化目标的敏感度，其综合灵敏度指标可以写为
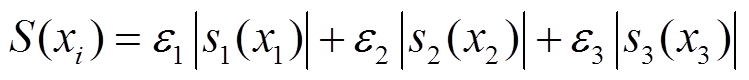（10）
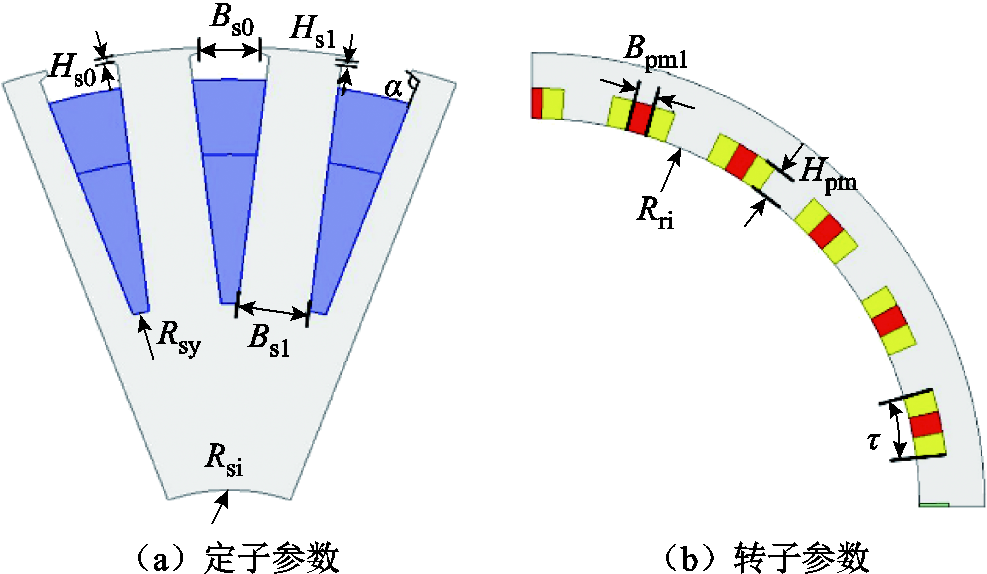
图10 参数模型
Fig.10 The parameters model
式中，si(xi)为第i个变量对目标函数的灵敏度指数；εi为第i个变量的权重系数。
将该结构进行参数化建模，并对图10中共计11个参数定义选值范围，对不同参数在所定义的范围内进行敏感度分析，如图11所示。图11中敏感度的正负仅代表在其他参数不变的情况下，单一参数变化对目标是正相关还是负相关；而敏感度绝对值的大小代表了该参数对优化目标的影响程度。从图11中能够看出，转矩脉动s1与定子槽开口、永磁体弧长等相关度较大；而有效材料成本s2主要与永磁体尺寸、绕组匝数等参数密切相关；电机效率s3与永磁体弧长相关度较大，这是由于交替极处磁通较小，在相同电流下，整体效率下降。根据式（10），得到参数敏感度计算结果见表3。综合判断灵敏度指标，将S≥0.09的参数划入高灵敏区，利用算法进行寻优；其他参数划入低灵敏区，利用单目标扫描进行分析。具体分配方案见表3，其中符号△表示划入低灵敏区。
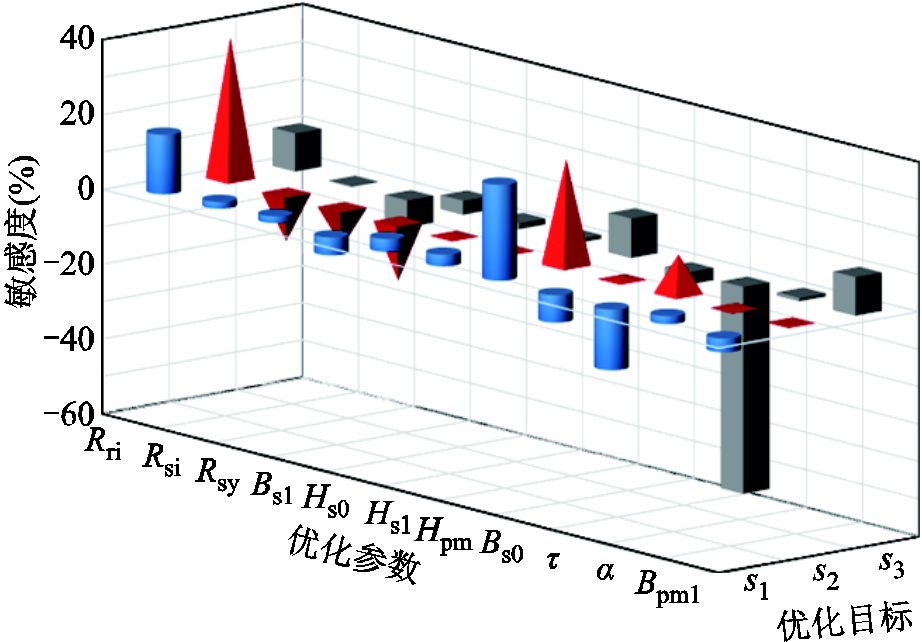
图11 参数敏感度分析
Fig.11 The parameter sensitivity analysis
表3 参数敏感度计算
Tab. 3 The parameter sensitivity calculation
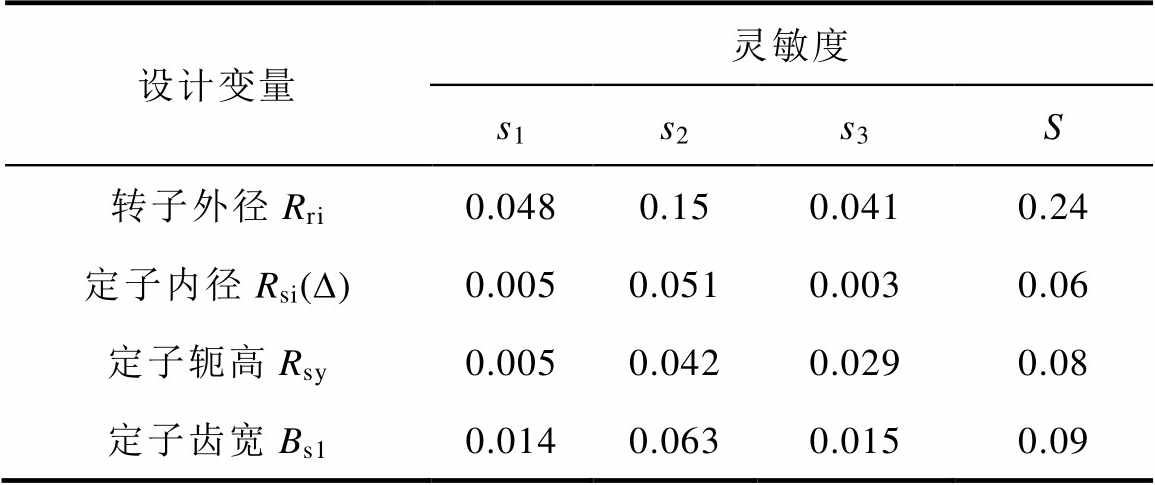
设计变量灵敏度 s1s2s3S 转子外径Rri0.0480.150.0410.24 定子内径Rsi(D)0.0050.0510.0030.06 定子轭高Rsy0.0050.0420.0290.08 定子齿宽Bs10.0140.0630.0150.09
（续）
设计变量灵敏度 s1s2s3S 调制齿高Hs0(D)0.010.0020.0060.02 槽肩高Hs1(D)0.0090.0010.0040.01 永磁体高Hpm0.0770.1130.0420.23 齿间距Bs0(D)0.0220.0030.0130.04 极弧长度τ0.0490.0420.2210.3 槽肩角α(D)0.0060.0010.0040.01 永磁体宽Bpm10.01100.0760.09
为了明确设计变量及优化目标之间的关系，本文采用响应面法的中心组合设计（Central Composite Design,CCD），通过较少的试验点来估计回归模型，并且保证空间内的自变量得到覆盖。通过CCD能够快速拟合响应面模型，以构建出多项式函数。分别选取了4.1节中的高敏参数，通过该方法拟合参数与目标函数之间的关系，目标响应面模型如图12所示。从图12中能够看出，参数变化会对不同目标造成不同影响，为解决目标冲突问题将采用智能算法，进一步进行寻优分析。
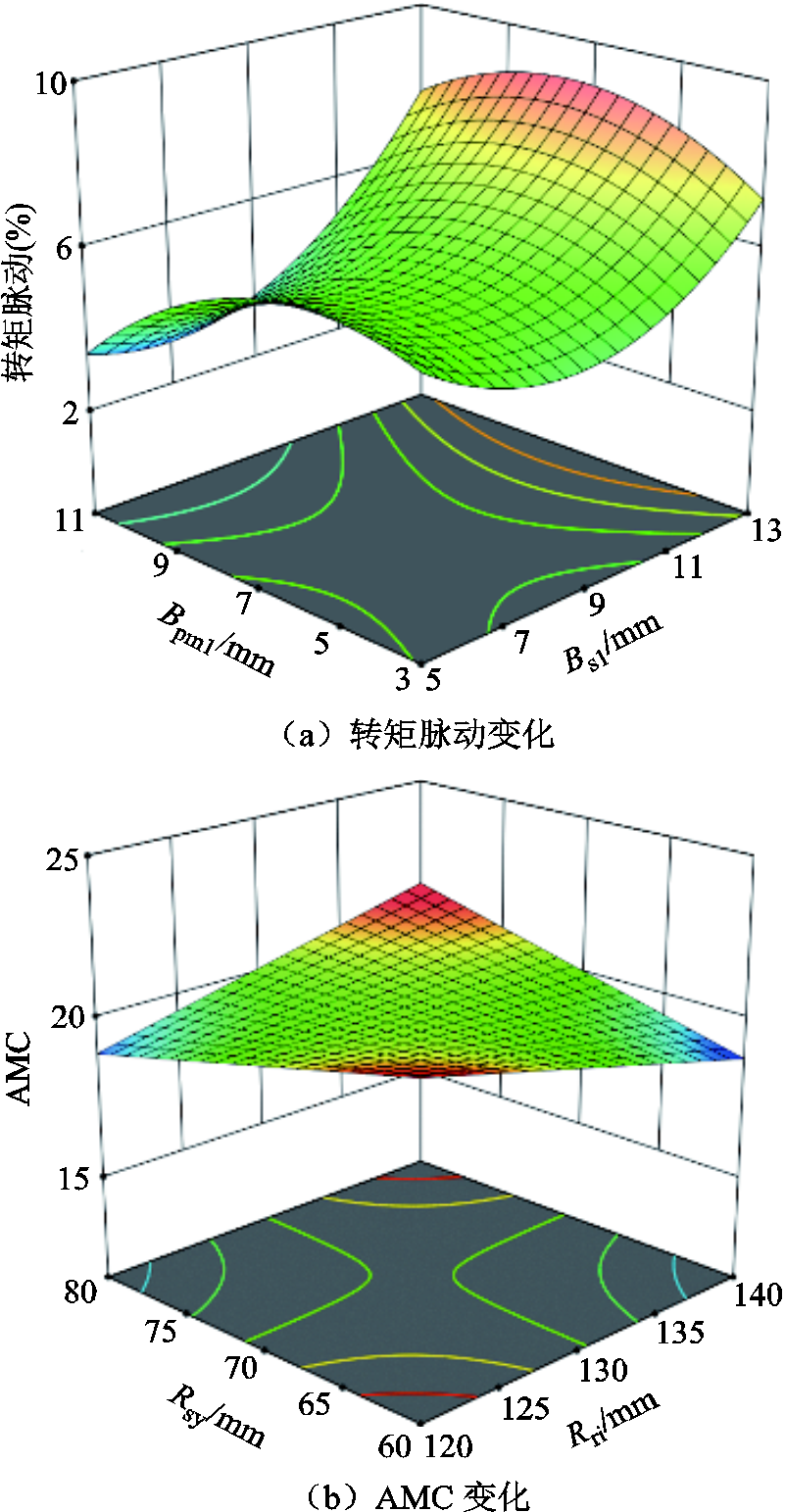
图12 目标响应面模型
Fig.12 The target response surface model
NSGA-Ⅱ算法是基于Pareto优势的典型多目标优化算法之一，该算法采用带有精英策略的快速非支配排序算法，能有效降低计算复杂度，更加高效地找到整个Pareto前沿。因此，利用该算法对三种目标同时进行寻优处理，通过多次迭代生成Pareto前沿，如图13所示。
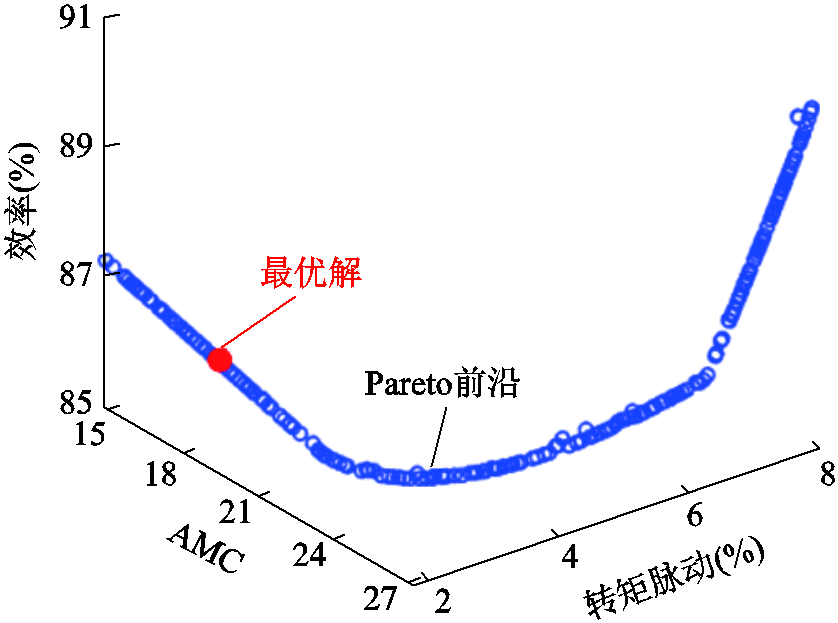
图13 Pareto前沿解集
Fig.13 The Pareto frontier solution set
从图13中的Pareto前沿中能够看出，三种优化目标解集较多且分布较广，仅根据解集无法判断最优值点。因此，根据前文提出的权重系数对每个目标进行权重分配，并定义评价函数为
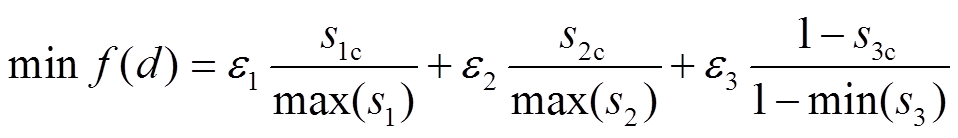（11）
式中，f(d)为Pareto的解集；s1c、s2c、s3c分别为当前状态下不同优化目标值；max(s1)、max(s2)、min(s3)分别为该Pareto解集中对应目标的最大或最小值。最终通过计算选择出最优解，如图13中红色标记所示。
根据上述分析结果，分别列出电机的初始及最优参数，见表4。
表4 参数对比
Tab.4 The representative working points
参数初始参数最优参数 Rri /mm6365.5 Rsy /mm3337.5 Bs1 /mm57.1 Hpm /mm75 τ /(°)7.810 Bpm1 /(°)2.66.5
为验证所提出模型与优化方法的有效性，在同等铜耗与同等永磁体用量的情况下，利用有限元法对优化后的模型进行了对比分析，并对初始与最优参数在额定点和弱磁点的转矩脉动进行比较，如图14所示。从图14中能够看出，所提出的不等Halbach结构具有更优的转矩特性，相较于径向充磁与普通Halbach转子结构，转矩分别提升了13.25%与4.65%。同样也能够看出，基于额定点处，优化后较初始参数的转矩脉动，从4.05%下降至2.53%。基于弱磁点处，优化后的转矩脉动较初始参数从6.54%下降到4.22%。验证了该参数优化后，转矩脉动进一步得到降低。
图14 输出性能对比
Fig.14 The output performance comparison
基于相同转矩对两种参数下电机的效率进行了仿真分析，如图15所示。从图15中能够看出，在不计母线电压情况下，两种参数的电机均能达到需求转速。但是初始参数下的绕组匝数较多，导致电感增大，致使弱磁转速受到母线电压限制，达不到预设区域；而在相同转矩下，最优参数与初始参数相比，其电感较小，弱磁状态下，能够满足直流母线电压限制。从电机效率中看，最优参数额定点效率最大值能够达到90.7%，较初始参数增长7.7%。针对整体效率进行对比，最优参数在全工况域下的电机效率分布同样具有较大优势。
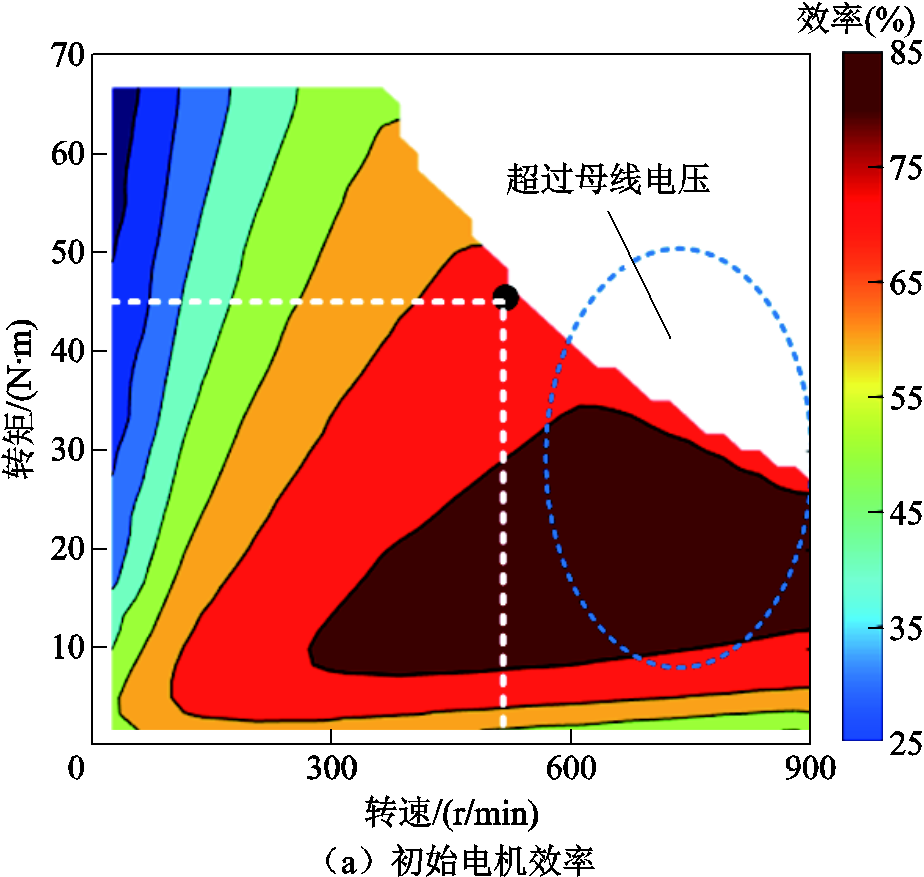
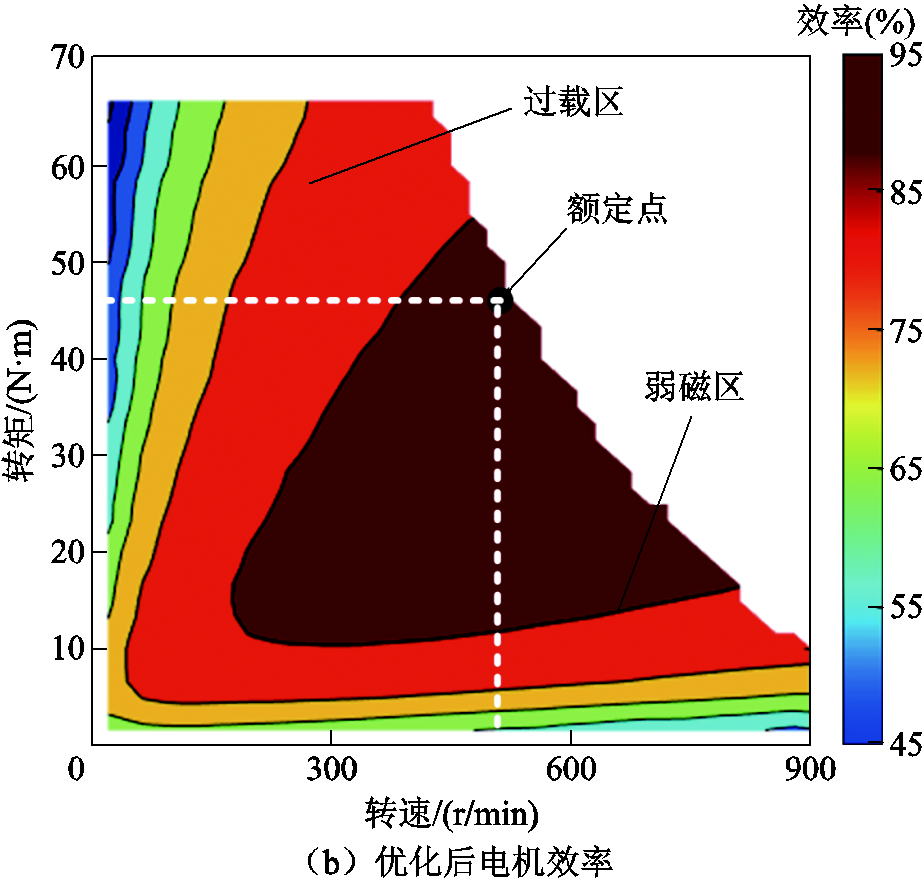
图15 电机效率对比
Fig.15 The motor efficiency comparison
针对电机AMC的对比如图16所示。从图中能够看出，在保障性能的前提下，有效减少永磁体材料，能大幅降低电机制作成本，因此交替极的使用具有较大成本优势。通过对比初始参数与最优参数的AMC能够看出，在保障输出转矩条件下，有效材料成本能够减少16.8%，证明了优化方法的有效性。
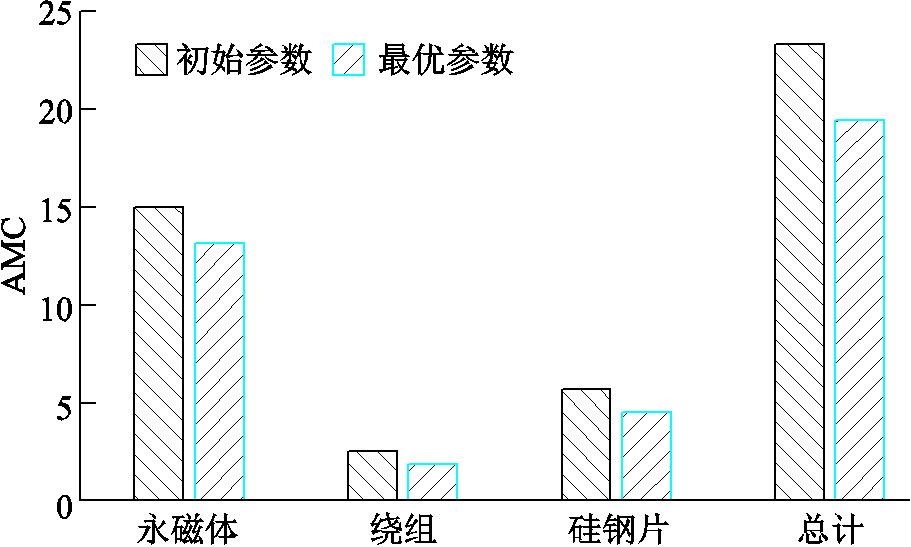
图16 电机材料有效成本
Fig.16 The active material cost of motor
为验证所提出CPUHVWM的合理性及多目标优化框架的有效性，制作了一台27槽24对极的样机，并搭建了实验平台，如图17所示。
图17 样机实验平台
Fig.17 The prototype experiment platform
基于上述实验平台，针对额定转速下的反电动势及谐波组成进行了分析，反电动势波形如图18所示。从图18中能够看出，实验反电动势正弦度良好，较有限元计算结果低7.8%，其总谐波畸变率（Total Harmonic Distortion, THD）升高约2.9%。
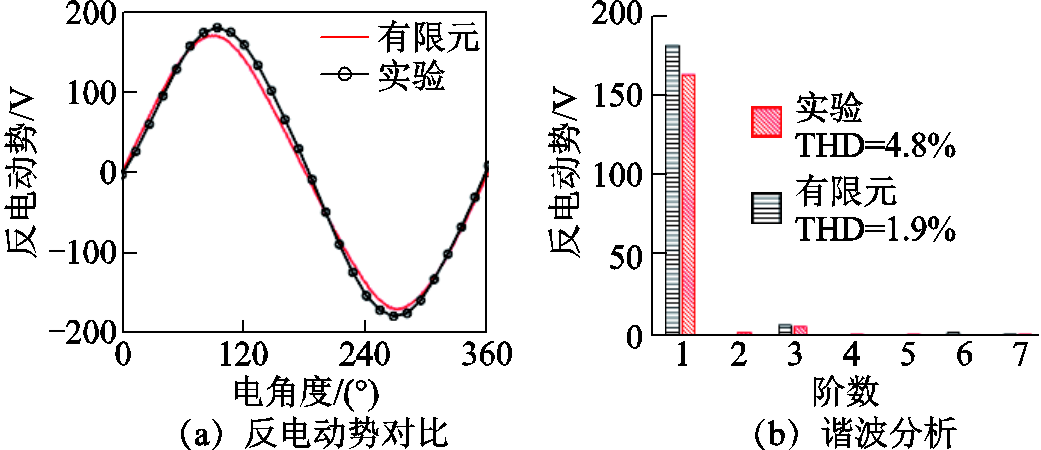
图18 反电动势波形
Fig.18 The back EMF waveforms
此外，对不同电流下的转矩进行了实验验证，转矩分析如图19所示。在额定电流下，实验测得的输出转矩为42.2 N·m，较有限元分析结果低5.5%。该误差主要是由于零件加工或装配造成的，其结果在可接受范围内。在此基础上，利用功率分析仪，对电机不同电流、不同转速下的效率进行了分析，如图20所示。
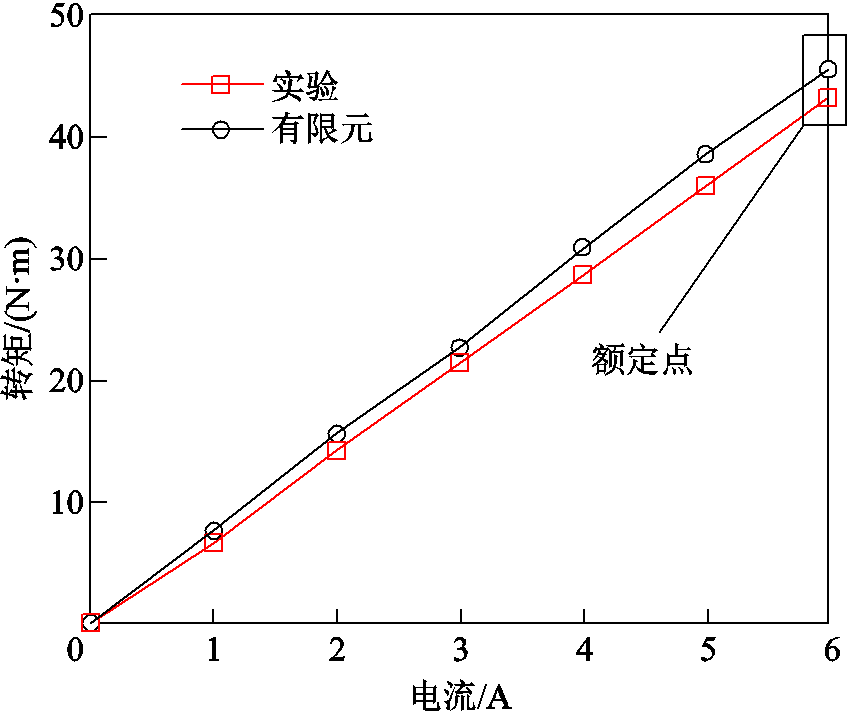
图19 转矩分析
Fig.19 The torque analysis
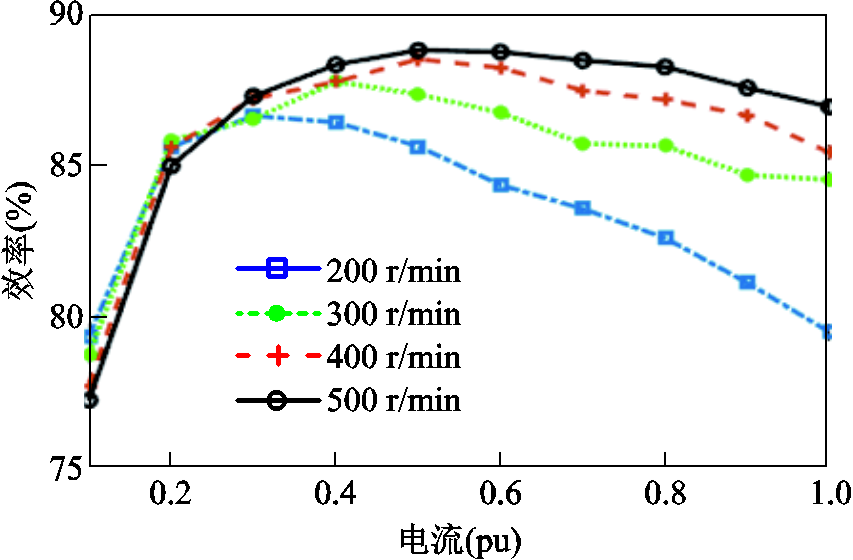
图20 效率分析
Fig.20 The efficiency analysis
从图20中能够看出，在相同电流下，效率随着转速的增加而增加。而在同一转速下，效率随着电流先上升后下降，这主要是由于铜耗加大导致的。在额定电流及额定转速下，该电机效率能达到87.3%，较有限元分析结果降低3.4%，并且代表性工作点与有限元分析结果相差均小于5%，因此验证了所提出优化框架有效性与准确性。
针对无人送货机器人驱动系统，本文基于不等Halbach游标轮毂电机，提出了一种多目标优化框架，以进一步提高该电机性能。该优化方法基于电机的实际工况，通过灵敏度分层，以高敏参数拟合响应面模型，并通过算法进行寻优。主要结论如下：
1）该优化框架能够快速且全面地对电机结构参数进行寻优，同时考虑到最大母线电压及永磁体退磁程度的限制，能够保障求解出最优参数的有效性与合理性。
2）对工况点进行聚类分析，能够快速选出代表性工况点代表全工况域，对复杂工况进行精练简化，可减少后续有限元计算的时间成本，并且提升了电机性能优化的准确性。
3）响应面结合NSGA-Ⅱ算法优化能够快速准确地对参数进行寻优，并保障优化参数在合理范围，避免陷入局部最优解的风险，减少计算成本。
因此，本文采用的不等Halbach游标轮毂电机及其优化框架能够在保障性能需求的同时有效地降低电机材料成本、提升效率，验证了所提出方法的有效性与准确性。
参考文献
[1] 马伟明, 王东, 程思为, 等. 高性能电机系统的共性基础科学问题与技术发展前沿[J]. 中国电机工程学报, 2016, 36(8): 2025-2035. Ma Weiming, Wang Dong, Cheng Siwei, et al. Common basic scientific problems and technological development frontier of high performance motor system[J]. Proceedings of the CSEE, 2016, 36(8): 2025-2035.
[2] Yue Yan, Jia Shaofeng, Liang Deliang. New topologies of high torque density machine based on magnetic field modulation principle[J]. CES Transactions on Electrical Machines and Systems, 2023, 7(1): 1-10.
[3] 丁文, 李可, 付海刚. 一种12/10极模块化定子混合励磁开关磁阻电机分析[J]. 电工技术学报, 2022, 37(8): 1948-1958. Ding Wen, Li Ke, Fu Haigang. Analysis of a 12/10-pole modular-stator hybrid-excited switched reluctance machine[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 1948-1958.
[4] 梁子漪, 曲荣海, 李大伟, 等. 一种交替极切向励磁游标永磁电机的分析与设计[J]. 电工技术学报, 2020, 35(15): 3173-3181. Liang Ziyi, Qu Ronghai, Li Dawei, et al. Analysis of a consequent-pole spoke-array vernier permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3173-3181.
[5] 阳辉, 王逸贤, 郑昊, 等. 新型双层串联混合永磁记忆电机设计优化与特性分析[J]. 中国电机工程学报, 2022, 42(24): 9042-9052. Yang Hui, Wang Yixian, Zheng Hao, et al. Design optimization and characteristics analysis of a novel dual-layer series hybrid permanent magnet memory machine[J]. Proceedings of the CSEE, 2022, 42(24): 9042-9052.
[6] 李亚, 周庆林, 丁石川, 等. 表嵌式交替极永磁电机拓扑演化及气隙磁场调制效应研究[J]. 电工技术学报, 2023, 38(12): 3188-3198. Li Ya, Zhou Qinglin, Ding Shichuan, et al. Investigation of topologies evolution and air-gap field modulation effect on surface-inset consequent-pole PM machines[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3188-3198.
[7] Fan Ying, Gu Lingling, Luo Yong, et al. Investigation of a new flux-modulated permanent magnet brushless motor for EVs[J]. The Scientific World Journal, 2014, 2014: 540797.
[8] 赵玫, 于帅, 邹海林, 等. 聚磁式横向磁通永磁直线电机的多目标优化[J]. 电工技术学报, 2021, 36(17): 3730-3740. Zhao Mei, Yu Shuai, Zou Hailin, et al. Multi-objective optimization of transverse flux permanent magnet linear machine with the concentrated flux mover[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3730-3740.
[9] 李雄松, 崔鹤松, 胡纯福, 等. 平板型永磁直线同步电机推力特性的优化设计[J]. 电工技术学报, 2021, 36(5): 916-923. Li Xiongsong, Cui Hesong, Hu Chunfu, et al. Optimal design of thrust characteristics of flat-type permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 916-923.
[10] Yu Hao, Yu Guodong, Xu Yongxiang, et al. Torque performance improvement for slotted limited-angle torque motors by combined SMA application and GA optimization[J]. IEEE Transactions on Magnetics, 2021, 57(2): 1-5.
[11] Zhao Wenxiang, Ma Anqi, Ji Jinghua, et al. Multiobjective optimization of a double-side linear vernier PM motor using response surface method and differential evolution[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 80-90.
[12] Zheng Shiyue, Zhu Xiaoyong, Xu Lei, et al. Multi-objective optimization design of a multi-permanent-magnet motor considering magnet characteristic variation effects[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3428-3438.
[13] Fatemi A, Ionel D M, Popescu M, et al. Design optimization of a high torque density spoke-type PM motor for a formula E race drive cycle[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4343-4354.
[14] Fatemi A, Demerdash N A O, Nehl T W, et al. Large-scale design optimization of PM machines over a target operating cycle[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 3772-3782.
[15] 吉敬华, 沈人洁, 徐亮, 等. 考虑运行工况的模块化双永磁游标电机多工作点优化设计[J]. 电工技术学报, 2022, 37(22) : 5649-5659. Ji Jinghua, Shen Renjie, Xu Liang, et al. Multi-working point optimization of modular double permanent-magnet vernier motor considering operation condition[J]. Transactions of China Electrotechnical Society, 2022, 37(22) : 5649-5659.
[16] Cheng Ming, Han Peng, Hua Wei. General airgap field modulation theory for electrical machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6063-6074.
[17] Yang Yinye, Rahman M M, Lambert T, et al. Development of an external rotor V-shape permanent magnet machine for E-bike application[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1650-1658.
[18] 樊英, 雷宇通, 张秋实. 新型交替极混合励磁电机宽速域电流高效协调控制[J]. 中国电机工程学报, 2020, 40(24): 7918-7927. Fan Ying, Lei Yutong, Zhang Qiushi. Wide speed area and efficient current coordinated control of new consequent-pole hybrid excitation motor[J]. Proceedings of the CSEE, 2020, 40(24): 7918-7927.
Abstract Aiming at the multiple operating conditions of the low speed and high torque motor drive system for unmanned delivery vehicles, combined with practical goals such as reducing manufacturing costs and increasing magnetic gathering capacity, a consequent pole unequal Halbach vernier wheel motor (CPUHVWM) is adopted to meet the performance requirements. However, there are problems such as torque ripple, high cost, and high loss that require optimization.The optimization methods can be divided into two main types.The first method is based on finite element method (FEM), which has low computational efficiency and focuses on single-objective optimization, making it difficult to find a global optimal solution. The other is algorithm optimization, which mainly establishes the relationship between structural parameters and objective functions and performs optimization processing through algorithms. The large number of operating points makes it challenging for single point based optimization techniques to fully satisfy vehicle performance requirements. This paper introduces an optimization framework that is predicated upon comprehensive operational conditions.The optimization goals center around reducing the motor costs, minimizing torque ripple, and enhancing efficiency, all while accounting for potential permanent magnet demagnetization and limitations in DC bus voltage.
Due to the large number of motor driving operating points, the motor operation stages are divided into frequent start and stop, low speed climbing, low speed cruising, medium speed cruising, and high speed cruising.Utilizing K-means clustering analysis, the centroid of each data cluster is ascertained, and the weight of the region is assigned, thereby ensuring that each operating point is duly considered in the subsequent optimization design.After that, combined with redundancy design, the performance parameters required for the final motor were selected, and the operating principle of the motor and the selection of pole slot ratio were analyzed.
To ensure the effectiveness of subsequent motor parameter optimization, the current distribution scheme within the voltage and current limit circles and the demagnetization of the PMs are analyzed, respectively. It can be seen that in this current distribution scheme, the impact on the PMs is not significant, and it is in the reversible demagnetization region. Therefore, in subsequent optimization, only the limitation of bus voltage on output performance needs to be considered.
The motor parameters are divided into high-sensitivity regions and low-sensitivity regions. Only the high-sensitivity parameters are modeled using regression models, and a polynomial function is constructed. Subsequently, non-dominated sorting genetic algorithm-Ⅱ(NSGA-Ⅱ) is adopted to simultaneously optimize the three objectives, facilitate Pareto-front creation via multiple iterations, and establish evaluation functions grounded on the prescribed weight coefficients in order to attain the optimal solution.After comparison, it is found that after optimization, compared with the initial parameters, the torque ripple at the rated point can be reduced by 37.5%, the efficiency can be increased by 7.7%, and the effective material cost can be reduced by 16.8%.
Finally, a 2 kW prototype is made for performance test. Compared with FEM, the experimental back EMF is 7.8% lower, and its THD is about 2.9% higher. At the rated current, the measured output torque is 42.2 Nm, which is 5.5% lower than FEM, and the efficiency is 87.3%, which is 3.4% lower than FEM.The above errors are mainly caused by the processing or assembly of parts and components, and the errors are within an acceptable range.
The following conclusions can be drawn from the simulation analysis: (1) The structural parameters of the motor can be comprehensively and quickly optimized through the proposed optimization framework. Considering the limitations of maximum bus voltage and demagnetization of PMs, respectively, the effectiveness and rationality of the results are ensured. (2) Cluster analysis of operating points can reduce the time and cost of subsequent finite element calculations. (3) RSM is combined with the NSGA-Ⅱ algorithm optimization to quickly and accurately optimize parameters while decreasing the possibility of entering local optima.
keywords：Wheel motor, magnetic field modulation, cluster analysis, multi-objective optimization, genetic algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.230335
中图分类号：TM351
国家自然科学基金重大项目（51991382）和国家自然科学基金（62173086）资助。
收稿日期 2023-02-08
改稿日期 2023-08-08
樊 英 女，1970年生，教授，博士生导师，研究方向为电动汽车驱动控制、新型永磁电机设计分析与控制、新能源发电。E-mail：vickifan@seu.edu.cn（通信作者）
陈秋蒴 男，1993年生，博士研究生，研究方向为游标电机设计与控制。E-mail：chenqiushuo@seu.edu.cn
（编辑 郭丽军）