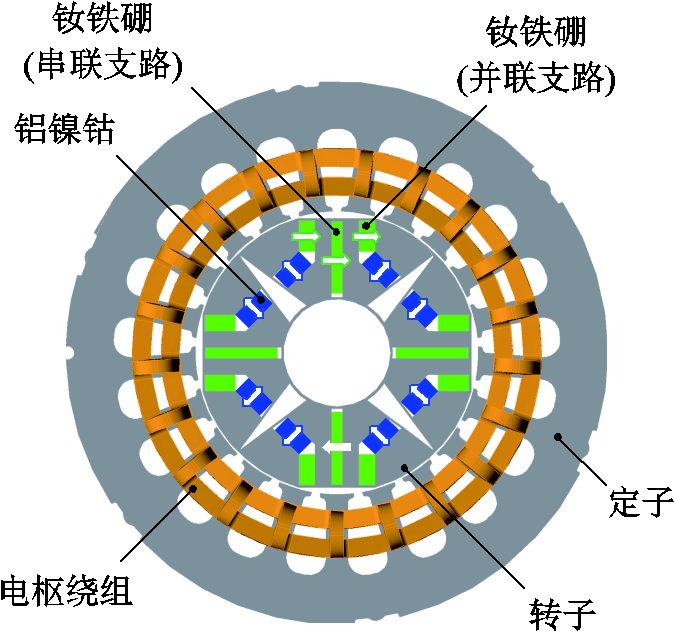
图1 HMC-VFMM拓扑结构
Fig.1 Topology of the HMC-VFMM
摘要 变磁通记忆电机（VFMM）克服了传统永磁同步电机（PMSM）气隙磁场不可调节、调速范围受限等缺点，可根据运行工况需求实时地在线调节气隙磁场，具有全域高效运行的优势。该文针对一台混联磁路型VFMM（HMC-VFMM）磁路复杂及非线性强等问题，研究非线性模型的建立及调磁电流脉冲轨迹的优化。首先，测试磁化曲线、电枢磁链特性与电感特性，建立VFMM的非线性模型，以实现电机特性的精确描述；其次，分析正弦型电流脉冲轨迹与所需电压变化特性，并基于此提出一种非对称电流脉冲轨迹与优化方案，在实现充去磁的同时，降低调磁过程产生的损耗；再次，为实现调磁电流的精确控制，基于上述非线性模型，提出一种基于实测参数的前馈电流控制器；最后，通过实验验证所提电流控制器的有效性以及理论分析的正确性。
关键词：变磁通记忆电机 永磁同步电机 非线性模型 电流脉冲轨迹 前馈电流控制器
永磁同步电机（Permanent Magnet Synchronous Machine, PMSM）因其高效率、高功率密度与高可靠性等优势，已被广泛应用于电动汽车、高端制造与航空航天等重点战略领域[1-3]。然而，传统PMSM一般采用钕铁硼等高矫顽力（High Coercive Force, HCF）永磁体（Permanent Magnet, PM），气隙磁场难以调节，调速范围受限。为拓宽调速范围，最常用的措施是施加d轴弱磁电流抵消部分永磁磁链以降低反电动势，除了带来额外铜耗、降低系统效率外，还可能导致钕铁硼永磁材料的不可逆退磁[4]。
针对上述问题，国内外学者提出了一类全新概念的永磁电机——变磁通记忆电机（Variable Flux Memory Machine,VFMM）[5]，采用铝镍钴与钐钴等低矫顽力（Low Coercive Force, LCF）PM，仅需施加瞬时脉冲电流即可在线调节LCF PM的磁化状态（Magnetization State, MS），实现“变磁通”运行，几乎无励磁损耗。比起传统永磁电机，VFMM可以根据运行工况需求实时地调整气隙磁场，具有全域高效的优势，在电动汽车、轨道交通、家用电器等宽调速应用场合中具有广阔的应用前景[6-7]。
磁通可调无疑是VFMM区别于传统PMSM的最重要特征，LCF PM的MS调节是研究VFMM控制技术时需要考虑的最核心问题[8]。一般地，用于调磁的瞬时电流脉冲通常仅持续数十毫秒且幅值可达绕组电流额定值的3～4倍，这对控制器的动态性能与控制精度提出了极高要求。现有文献提出了诸如无差拍电流控制器[9]、模糊PI控制器[10]、改进前馈PI控制器[11]、自抗扰控制器[12]等高性能电流控制器，以实现调磁电流的高精度控制。与此同时，注入高幅值d轴电流会引起电磁转矩的剧烈波动，大大影响系统稳定性，鉴于此，如何抑制调磁带来的转矩波动是VFMM控制的关键技术难题。针对该问题，文献[13]提出了一种电流型观测器与电压型观测器级联的强鲁棒性定子磁链观测器，在此基础上，根据转矩方程求解出q轴解耦电流给定值，以保证调磁过程中电磁转矩输出恒定[14]。文献[15]提出一种滑模转矩观测器，用于观测负载转矩，将其补偿至转速控制[16]，并基于此设计了一种滑模转速控制器，具有优越的动态性能。
从电机运行状态来看，调磁过程中转矩波动的最终表现形式是其进一步引发的电机转速波动。由于电机存在惯量，影响电机转速波动大小的因素包括转矩波动的幅值与持续时间两方面，鉴于此，也有部分文献以提升调磁速度为目标开展研究工作，即减小调磁电流持续时间。文献[10]基于梯形调磁电流轨迹，提出了一种调磁时间优化方法，该方法根据电机运行状态与目标MS等信息计算出可用的最大电压，进而得到最短调磁时间。文献[17]提出一种非线性调磁电流控制策略，以最大化电压利用率为目标，在线计算调磁电流轨迹，从而缩短调磁时间。上述两种方法均得到了较好的控制效果，在保证调磁准确度的基础上，显著提升了调磁速度。
理论上，除了改善调磁带来的转速波动外，提升调磁速度还有助于减小调磁电流产生的损耗，但尚未有学者针对调磁电流轨迹与损耗之间的联系进行深入研究。除此以外，为实现调磁，VFMM磁路结构通常较为复杂，其电磁参数表现出极强的非线性，传统数学模型难以精准描述电机的非线性变化特性。因此，本文在建立VFMM非线性模型的基础上，以减小调磁过程带来的损耗为目标，深入研究VFMM调磁电流轨迹的优化设计方法。
本文的研究对象为一台混联磁路型VFMM（Hybrid Magnetic Circuit-VFMM，HMC-VFMM）[18]。首先，考虑到VFMM参数（尤其在调磁过程中）具有较强的非线性，本文通过离线测试获得电机电感与磁链的变化特性，基于此建立VFMM的非线性模型，用于精确描述电机特性；其次，研究常规对称正弦型电流脉冲轨迹的优化与所需相电压的变化特性，而后提出一种非对称电流脉冲轨迹的设计和优化方法，在实现充、去磁的基础上，降低调磁过程产生的损耗；然后，为提高调磁电流控制精度，结合所构建的非线性模型设计了一种基于实测参数的前馈电流控制器；最后，通过实验验证所提电流控制器与调磁电流轨迹优化方案的有效性。
本文所研究的HMC-VFMM拓扑结构如图1所示。可以看出，HMC-VFMM转子采用双层混合永磁结构，HCF PM（钕铁硼）分置两层，分别与LCF PM（铝镍钴）构成串联和并联磁路，该类混联结构兼具串联磁路与并联磁路两种结构的优势。一方面，在串联磁路中放置HCF PM能够有效提升LCF PM的抗去磁能力；另一方面，当LCF PM反向磁化时，并联磁路中的HCF PM将通过其形成短路磁场，从而显著拓宽电机的调磁范围。
图1 HMC-VFMM拓扑结构
Fig.1 Topology of the HMC-VFMM
HMC-VFMM的调磁原理可以用图2进行说明，可以看到，通过施加充去磁电流脉冲，永磁体工作点能够在不同的回复线上移动。因此，利用电流脉冲能够有效改变低矫顽力永磁体的磁化状态以及电机整体的永磁磁链，从而实现转速范围和高效率运行区域的扩展。图2还对比了不同磁路类型VFMM的特性。总的来看，并联磁路型VFMM的负载线更接近拐点，更加容易去磁，但永磁工作点的变化范围更宽，因此拥有更宽的调磁范围；相比之下，串联磁路型VFMM负载线远离拐点，因此该类VFMM拥有更好的抗负载去磁能力，但这也导致其充去磁困难，且永磁工作点的变化范围较窄；本文研究的HMC-VFMM能够在抗负载去磁能力和调磁范围之间得到更好的平衡，其负载线在上述两类电机之间，兼具两者优势。图3为通过有限元仿真得到的不同磁化状态下电机的空载磁通密度分布，可以看出该电机具有良好的调磁能力。
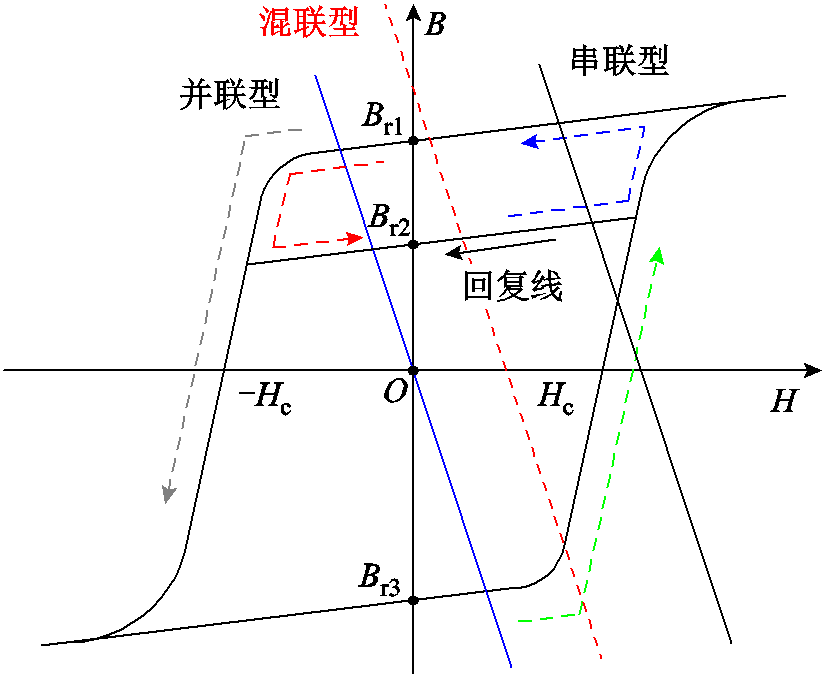
图2 HMC-VFMM调磁原理
Fig.2 Flux regulation principle of the HMC-VFMM
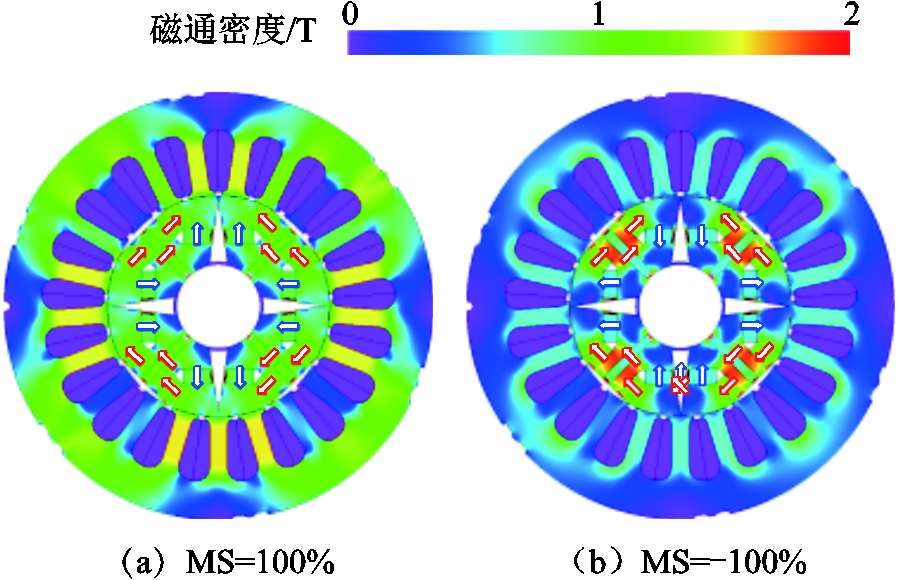
图3 不同磁化状态下空载磁通密度分布
Fig.3 No-load flux density distribution in differentmagnetization states
1.2.1 数学模型
由于具有相同的定转子结构，VFMM与传统PMSM的电路方程和转矩激励原理基本一致。dq坐标系下，VFMM的电压方程与转矩方程分别为
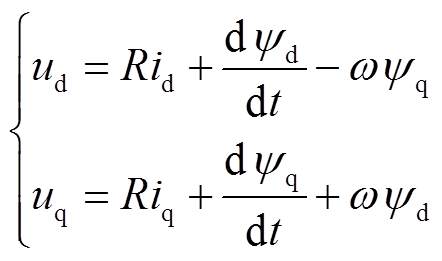（1）
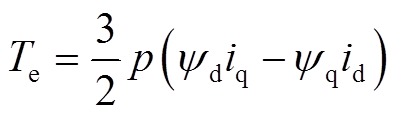（2）
式中，ud和uq分别为d轴和q轴电压；R为定子电阻；id和iq分别为d轴和q轴电流；ω为电角速度；ψd和ψq分别为d轴和q轴磁链；p为极对数。d轴磁链包含了电枢磁链与永磁磁链[19]，即
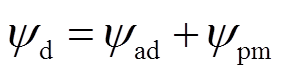（3）
式中，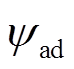
为d轴电枢磁链；
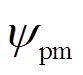为永磁磁链。
1.2.2 磁化曲线
1.2.1节建立了考虑充、去磁特性与磁路饱和的VFMM磁链模型，包含永磁磁链与电枢磁链两部分。本节分析永磁磁链相对于调磁电流幅值的变化曲线，后文称之为磁化曲线。
获取磁化曲线的关键在于测试电机空载调磁特性，包括主充磁曲线和主去磁曲线。主充磁曲线的测试需要先将电机完全去磁，之后逐步增加充磁电流脉冲幅值，通过对拖平台测试电机反电动势幅值进而计算相应的永磁磁链幅值，直至永磁磁链几乎不再变化为止。相应地，主去磁曲线可以通过同样的方式获取。本文所研究的HMC-VFMM样机的磁化曲线如图4所示。理论上，VFMM的永磁磁链能够实现连续无极调节，但为简化充、去磁操作，通常只考虑若干个离散的磁化状态。本文后续的研究工作将重点考虑图4中的MS1（永磁磁链为0.24 Wb）与MS2（永磁磁链为0.14 Wb）两个磁化状态，对应的充、去磁电流幅值分别为30 A与-25 A。
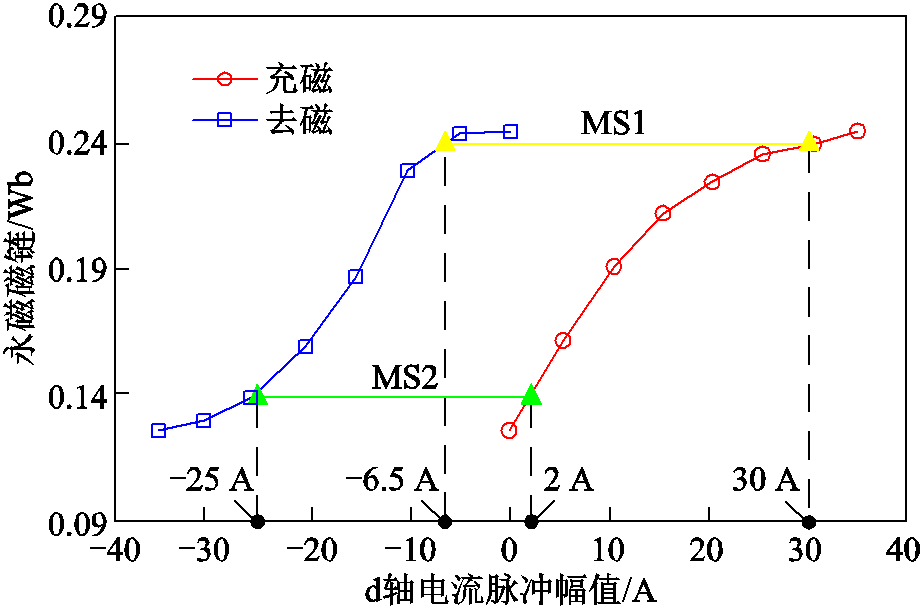
图4 HMC-VFMM样机磁化曲线
Fig.4 Magnetization curves of the HMC-VFMM prototype
1.2.3 电枢磁链与电感变化特性
在得到磁化曲线的基础上，本节进一步分析电枢磁链特性，并在此基础上获得电机电感的变化特性。由于调磁过程中需注入高幅值d轴电流，测试磁链特性时需考虑两方面因素：①注入高幅值定子电流会导致严重的磁路饱和现象；②长时间过电流会造成电机发热甚至损毁。综合对比已有的磁链测试方法，电压脉冲注入法[20]仅会产生一个短时间的电流脉冲，不会造成电机的大量发热，十分适合对VFMM的d轴磁链进行测量。令电机保持静止状态，通过逆变器注入短时的电压脉冲并观测电流响应，然后通过计算得到对应的磁链结果。假设在测试过程中施加幅值为uin的d轴电压脉冲，在施加该电压脉冲时t时刻的d轴磁链可以表示为
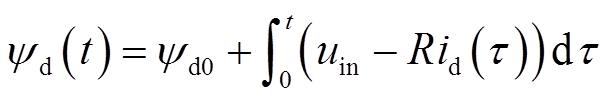（4）
式中，
为初始d轴磁链，数值上与空载状态下的永磁磁链相等。
以由MS2至MS1的充磁过程为例，施加60 V电压脉冲与对应的电流响应结果如图5a所示。初始状态下施加60 V电压并记录其电流响应，当电流上升至30 A时改变电压极性，直至电流下降至0，撤去电压脉冲。根据测试结果，通过式（4）可以计算得到图5b所示的d轴磁链变化曲线。可以看出，由于永磁磁链变化，电流上升与下降过程中的磁链曲线轨迹并不重合。撤去电压脉冲后，d轴磁链由初始状态的0.14 Wb增加至0.24 Wb，实现了充磁操作。相应地，去磁过程中的电压脉冲/电流响应以及相应的磁链曲线如图5c与图5d所示。
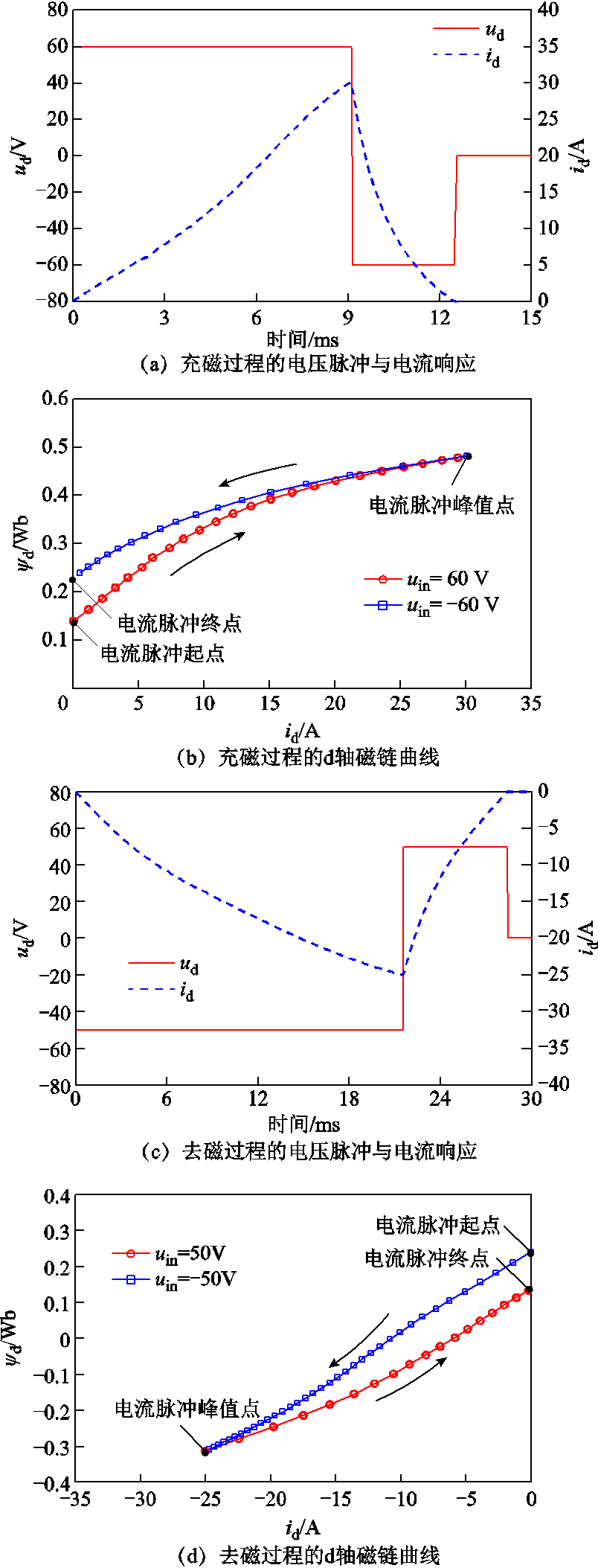
图5 电压脉冲注入法磁链测试结果
Fig.5 Flux test results by voltage pulse injection method
结合图5测试结果与图4所示磁化曲线，可根据式（5）计算出d轴电枢磁链。
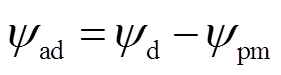（5）
需要注意的是，当调磁电流处于激励过程中，永磁磁链随电流不断上升（或降低），因此，须根据电流幅值与磁化曲线确定式（5）中的永磁磁链项；而在调磁电流处于回复过程中，充磁（或去磁）过程已完成，式（5）中的永磁磁链项为恒定值。最终得到的d轴电枢磁链特性如图6所示。可以发现，对于所研究的HMC-VFMM样机，d轴电枢磁链会受到调磁过程的影响，且充磁过程影响更大，但整体上电流激励与回复过程中的电枢磁链曲线基本重合，本文采用二者的平均数值进行替代，简化磁链模型。
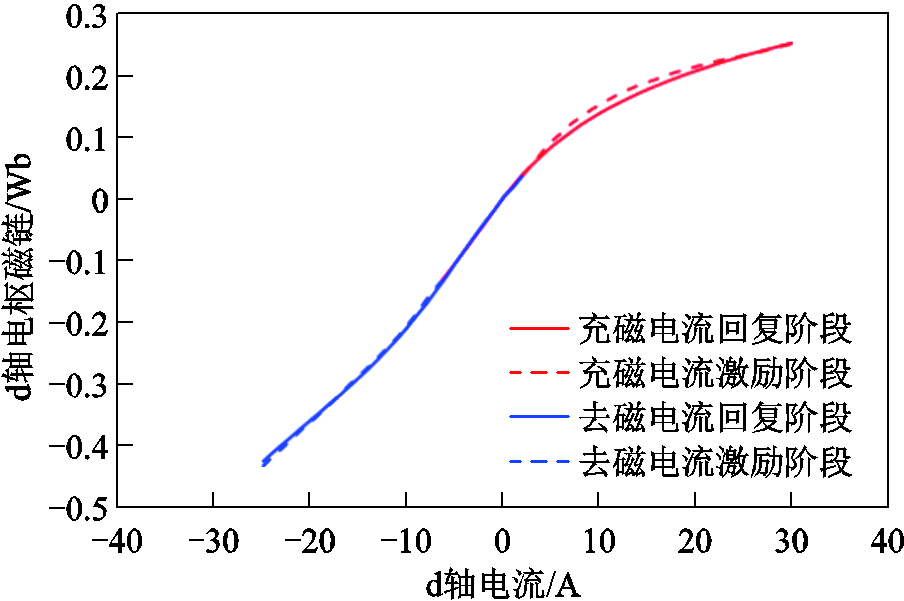
图6 d轴电枢磁链曲线
Fig.6 Curves of d-axis armature flux
同样地，q轴磁链也可以采用电压脉冲注入法进行测量，测试结果如图7所示。可以看出，q轴磁链基本不受磁化状态的影响。基于磁化曲线与dq轴电枢磁链变化特性，可以基于查表法进一步得到所研究HMC-VFMM的磁链模型，如图8所示。
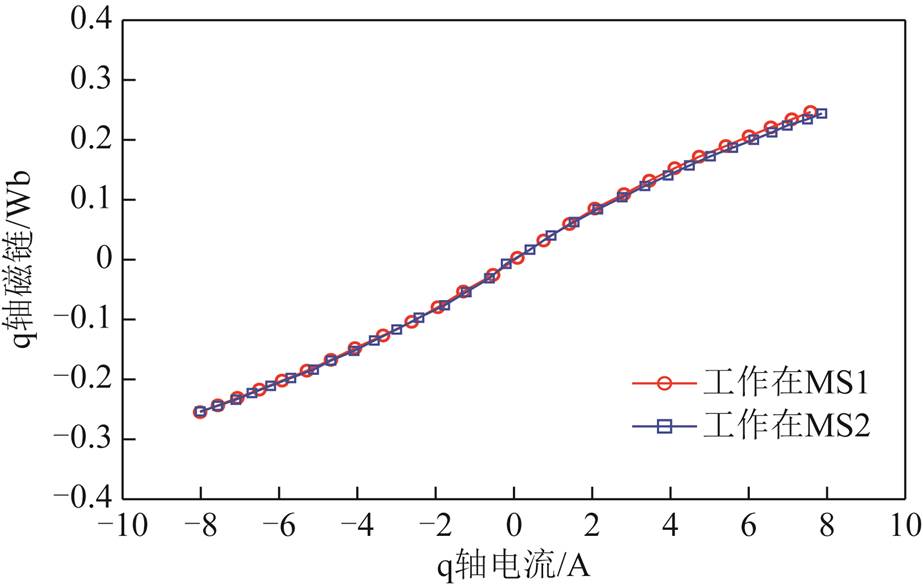
图7 q轴电枢磁链曲线
Fig.7 Curves of q-axis armature flux
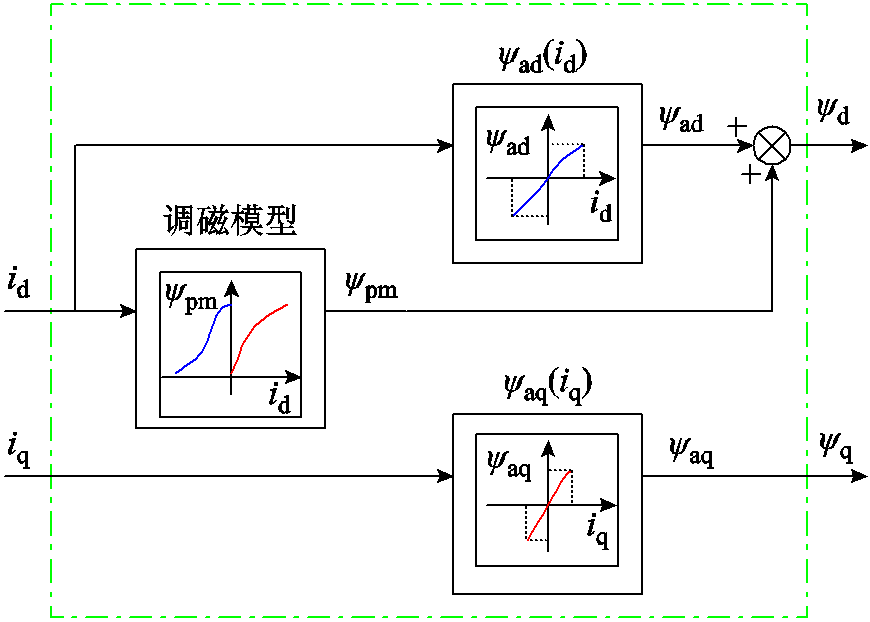
图8 HMC-VFMM磁链模型
Fig.8 Flux model of the HMC-VFMM
电感变化特性可根据电枢磁链特性计算得到，如图9所示，可以看出，dq轴电感随电流的变化范围能够覆盖整个充、去磁过程。
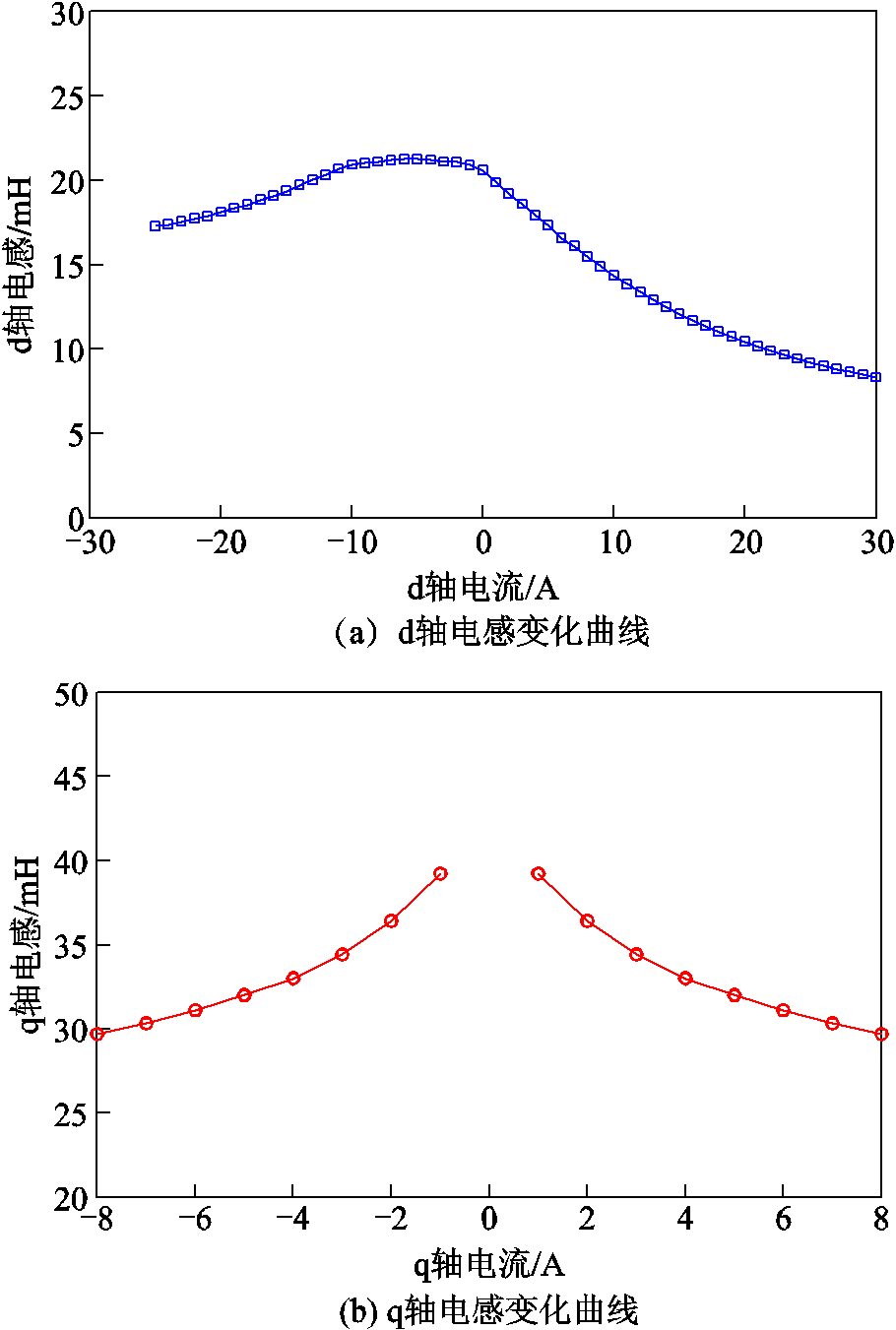
图9 HMC-VFMM电感变化曲线
Fig.9 Curves of dq-axes inductances of the HMC-VFMM
VFMM的核心特征是能够通过施加电流脉冲来改变永磁体磁化状态，而无需持续施加弱磁电流实现扩速。由于脉冲持续时间极短，其产生的损耗相对而言可以忽略不计，因此VFMM系统整体运行效率能够得到提升。但在实际运行过程中，频繁的充去磁操作也会造成累积损耗，降低整体的运行效率，采用降低调磁频率或充去磁过程损耗的方式能够进一步提高系统效率。充去磁过程中的损耗类型包括磁滞损耗、铜耗、永磁体涡流损耗、定转子铁心损耗等，其中，磁滞损耗和铜耗为最主要的损耗。充去磁过程中的磁滞损耗为
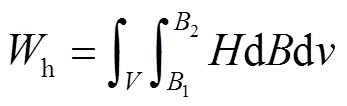（6）
式中，B1和B2分别为充、去磁前后永磁体工作点磁通密度，可以看出磁滞损耗大小与充、去磁前后的磁通密度有关，调磁电流轨迹的变化无法影响磁滞损耗。另外，充去磁过程中的铜耗为
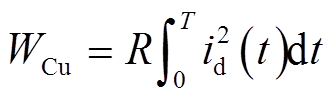（7）
可以看出，铜耗与所施加电流脉冲轨迹的形状及其持续时间有关。总的来说，若当前磁化状态和目标磁化状态确定，充去磁过程中的磁滞损耗基本不变，但可以通过改变电流脉冲形状或缩短持续时间来减少铜耗，从而降低整个充去磁过程的损耗。
最常用的调磁电流轨迹为梯形波与正弦波，本文选择正弦型电流脉冲轨迹进行分析和优化。正弦波形可以通过幅值、周期和相位进行整定，但对于充、去磁电流脉冲，其起始电流和峰值电流由目标磁化状态决定，本文尝试通过设置偏移角，截取部分正弦波作为充、去磁电流脉冲。正弦型电流脉冲轨迹如图10所示，图中脉冲轨迹可以通过调整脉冲持续时间T和偏移角度φ进行调整，调整后的d轴电流脉冲可以描述为关于T和φ的函数，即
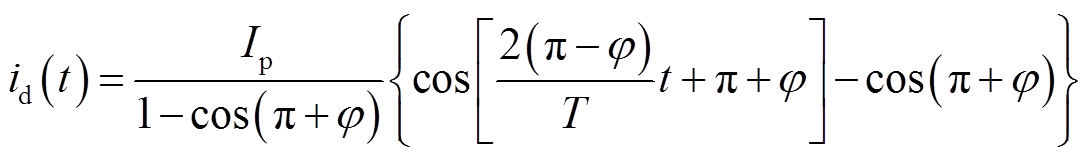（8）
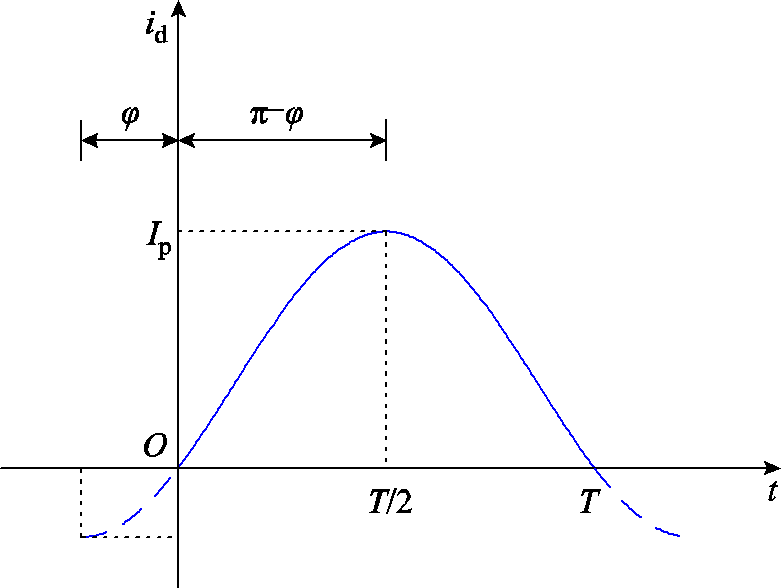
图10 正弦波脉冲轨迹示意图
Fig.10 Schematic of a sine-shaped pulse trajectory
为分析偏移角对充去磁过程的影响，分别在500 r/min与900 r/min转速条件下进行了充磁与去磁操作，电流脉冲持续时间为0.06 s，充去磁电流分别为30 A与-25 A。图11和图12分别为不同偏移角下的充、去磁电流脉冲及对应的相电压幅值曲线。可以看出，改变偏移角能够对电流脉冲波形及调磁所需相电压产生影响。当电流上升接近峰值时，相电压达到峰值，且随着偏移角的增大逐渐降低。相比之下，去磁过程中的相电压峰值变化相对较为明显，而充磁过程的电压几乎无变化。特别地，偏移角为0°时，去磁过程中的相电压峰值将会超出70 V，这意味着相同的电压限制可能无法成功激励出该电流脉冲，导致调磁失败。此外，随着偏移角的增加，充去磁起始点的电流变化率更大，因此所需电压初始值也会随之增加。
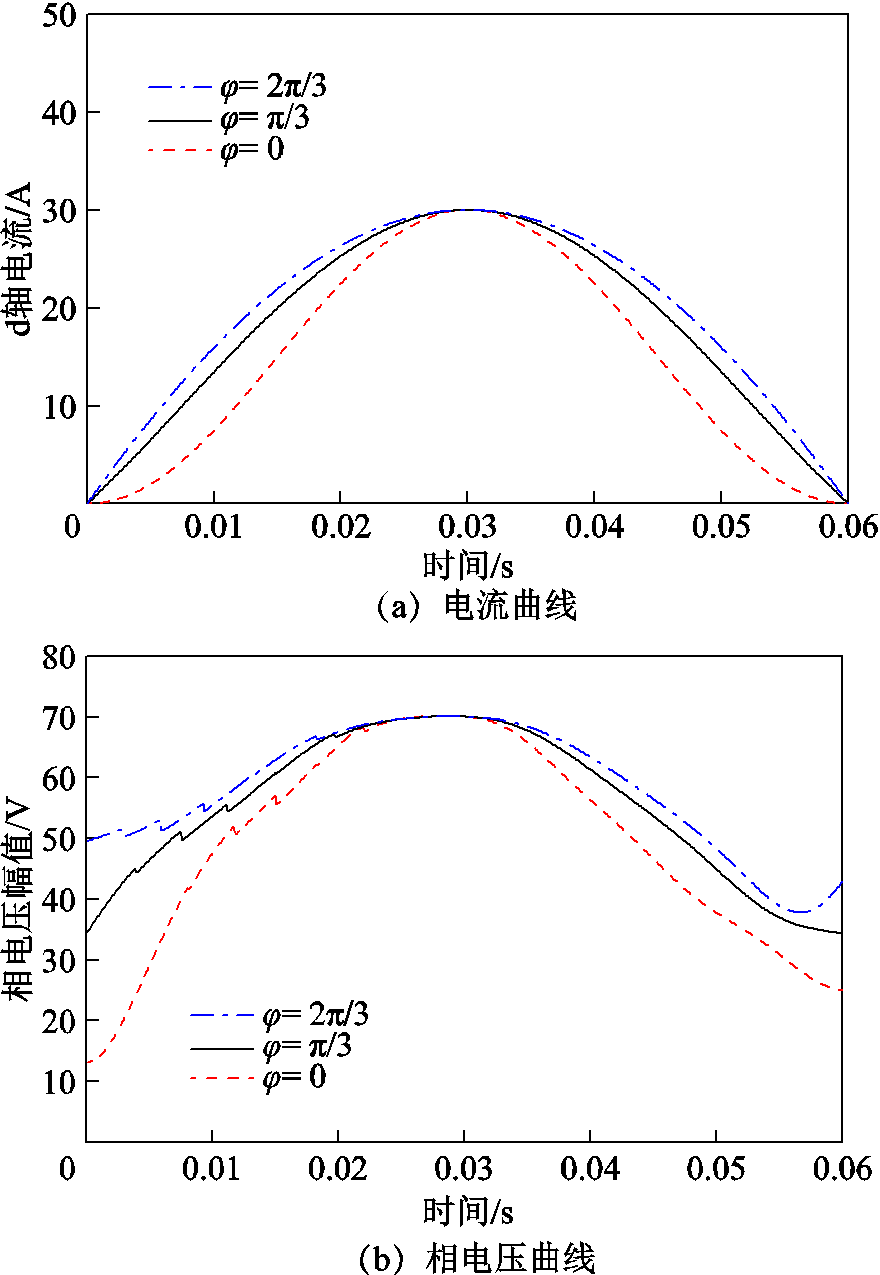
图11 不同偏移角下充磁电流脉冲与相电压曲线
Fig.11 Curves of re-magnetizing current and phasevoltage by setting different skewing angles
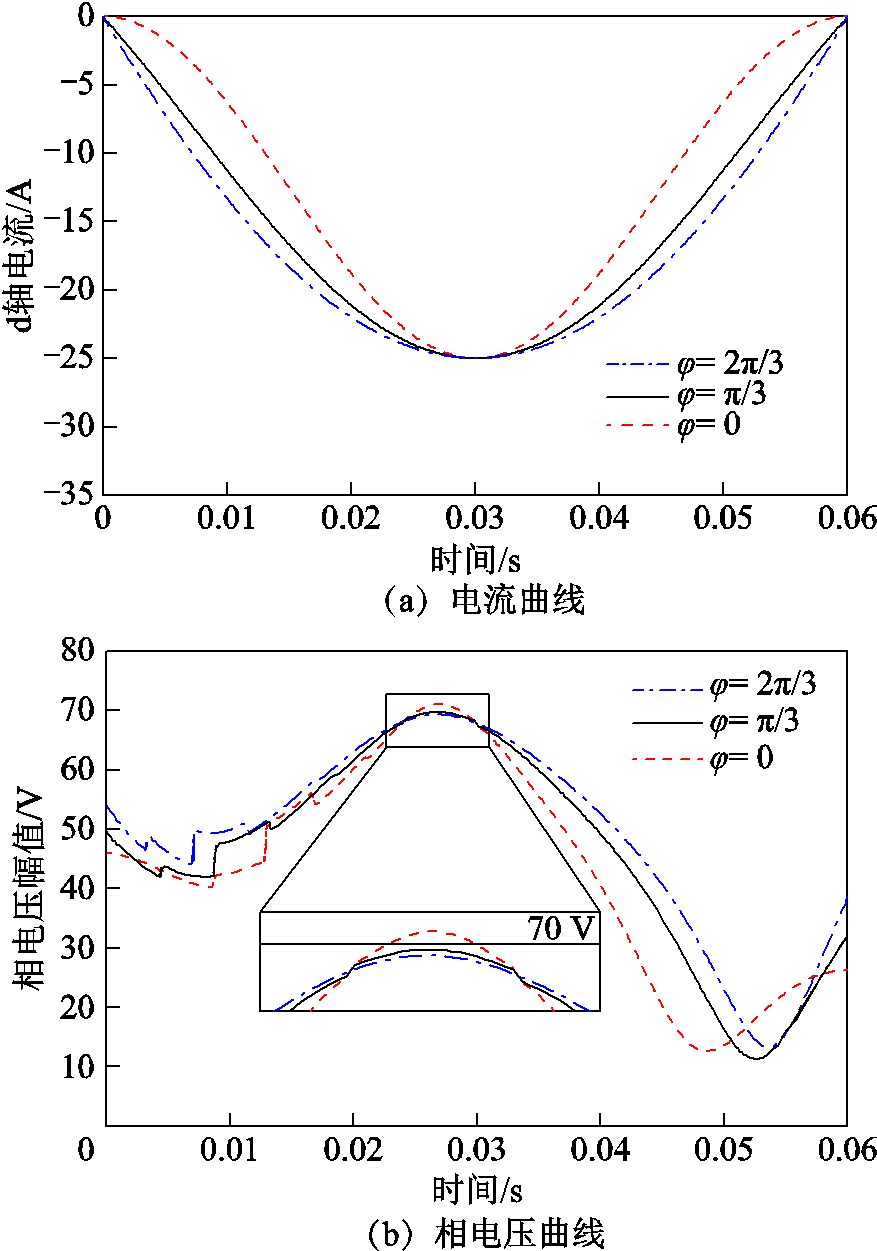
图12 不同偏移角下去磁电流脉冲与相电压曲线
Fig.12 Curves of demagnetizing current and phasevoltage by setting different skewing angles
根据2.2节的分析，调磁所需电压在电流峰值左右达到最大值。本文根据电流到达峰值的时间将其分为两个部分，如图13所示。整个充去磁过程中的最大电压将由峰值前这一阶段决定，而通过调节电流回复阶段的脉冲持续时间和偏移角则可以改变充去磁过程产生的损耗。d轴电流脉冲可以写成
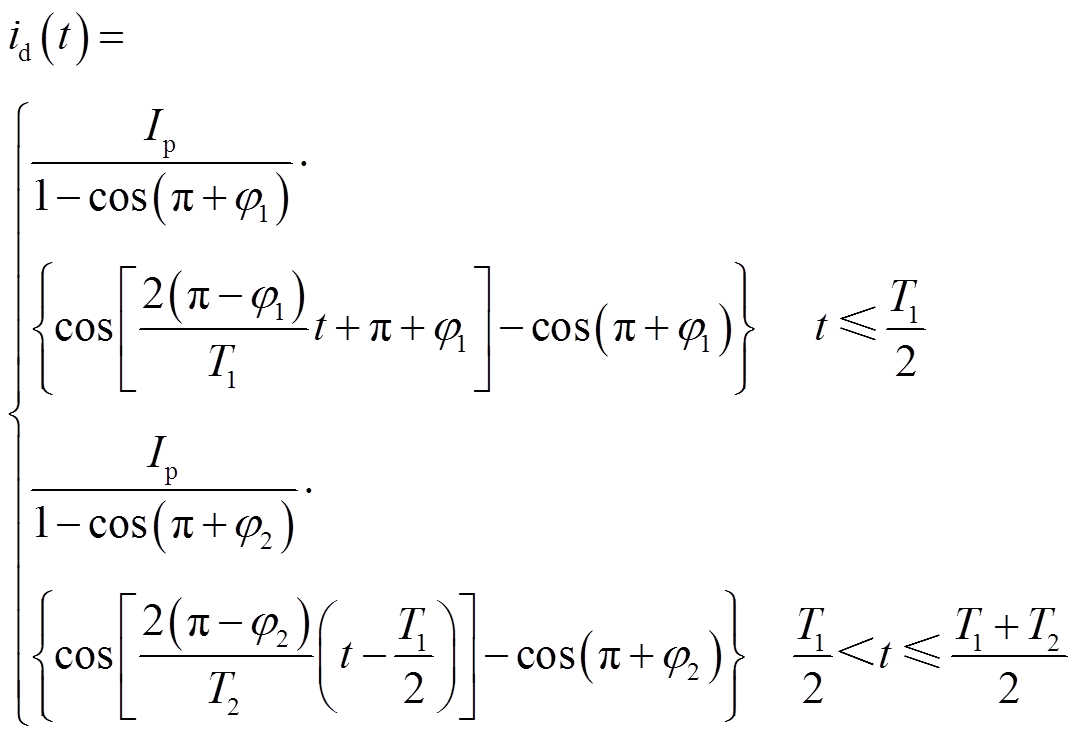（9）
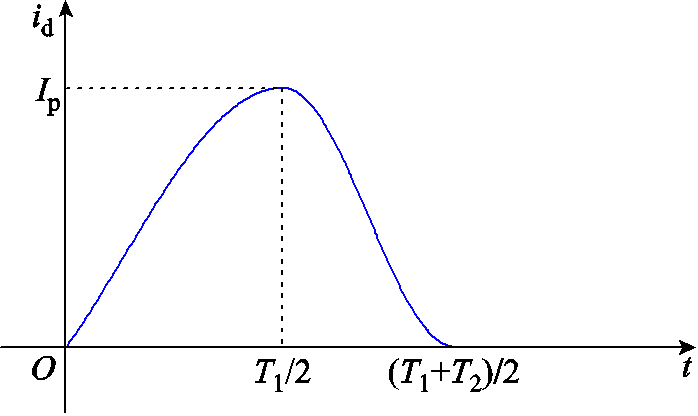
图13 非对称脉冲轨迹示意图
Fig.13 Schematic of an asymmetrical pulse trajectory
根据图11和图12，可以发现在偏移角为0°时，电流回复阶段所需的电压较低，这里直接令偏移角φ2 = 0，于是式（9）可以改写为
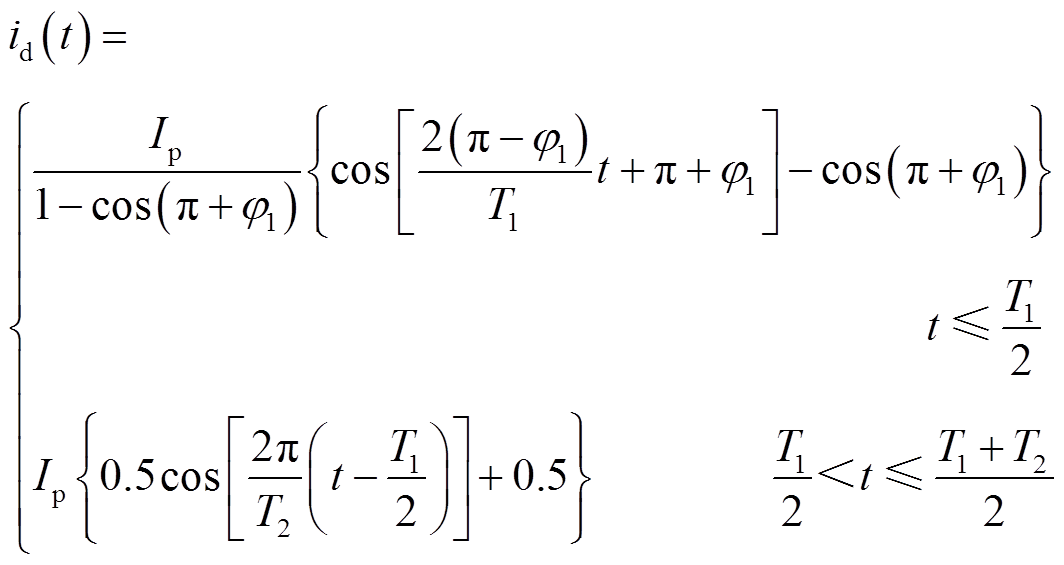（10）
为分析电流回复阶段持续时间（即T2）对充去磁过程的影响，分别在500 r/min与900 r/min转速条件下进行了充磁与去磁操作，电流上升阶段持续时间为0.03 s（即T1 = 0.06 s），偏移角φ1 = 2π/3，充、去磁电流分别为30 A与-25 A。图14和图15分别为不同电流回复阶段持续时间充、去磁电流脉冲及对应的相电压幅值曲线。可以看出，当T2为0.06 s和0.02 s时，充去磁过程中的相电压幅值最大值与对称正弦波形相同。因此，该方式配置的电流脉冲理论上能在相同的母线电压限制下产生，且通过非对称设计能够改变电流脉冲轨迹从而改变充去磁过程中的损耗。然而，进一步减小T2也会产生更大的电压需求，当T2 = 0.018 s时，相电压峰值出现在电流回复阶段，超出70 V，可能会由于直流母线电压的限制无法施加预期的电流脉冲。总的来说，适当地减小电流回复阶段持续时间能够在不影响调磁所需电压峰值的前提下，降低调磁电流包络面积，进而减小损耗。
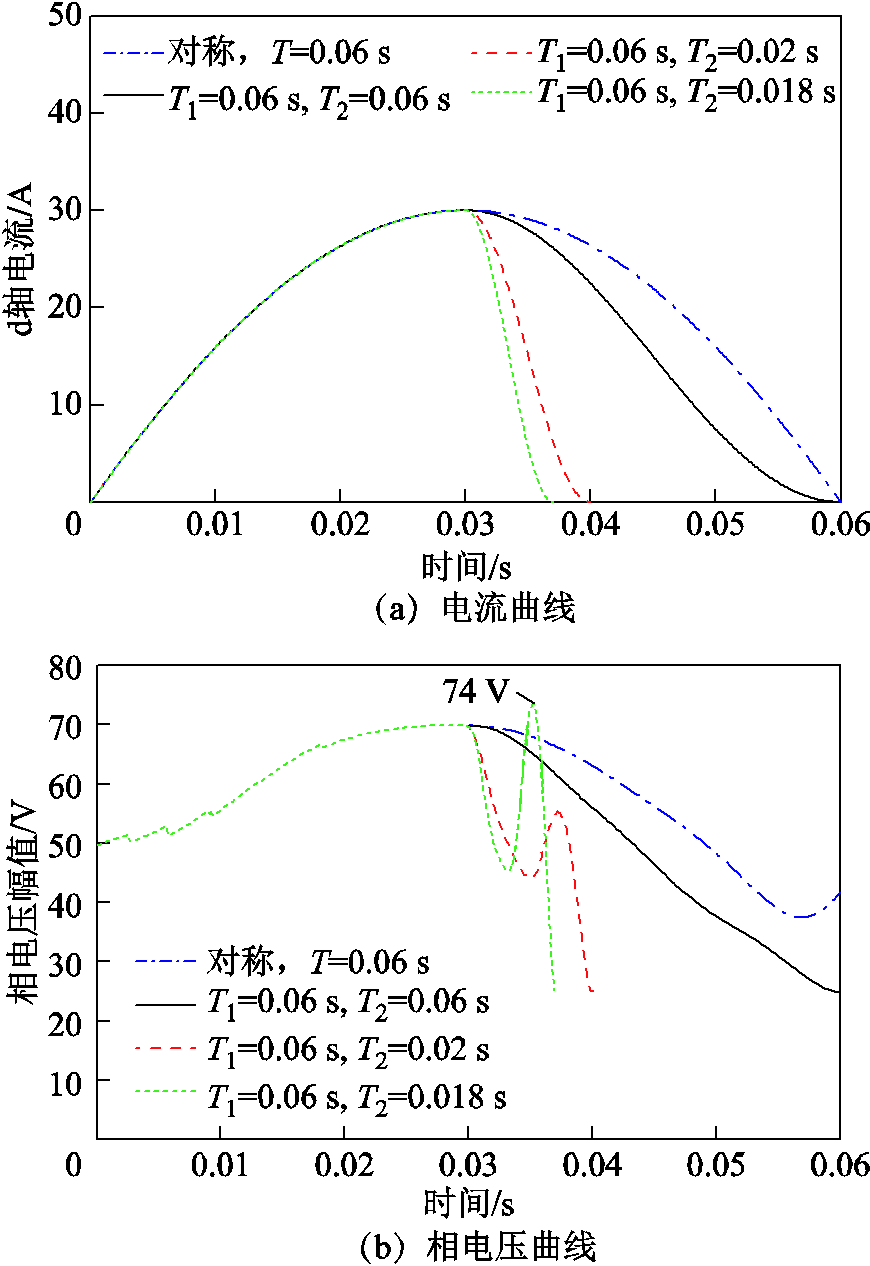
图14 非对称充磁电流脉冲与相电压曲线
Fig.14 Curves of asymmetrical re-magnetizing currentand phase voltage
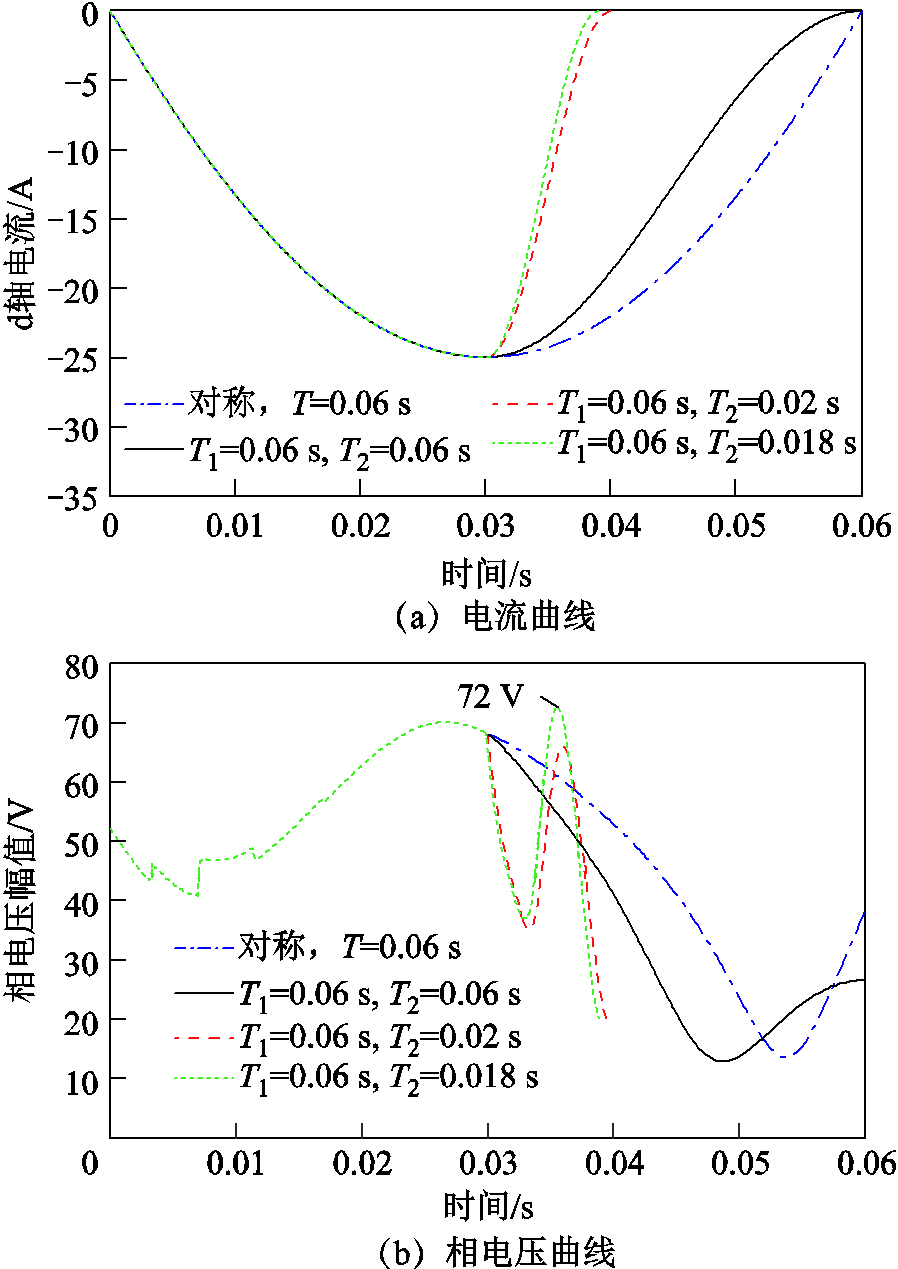
图15 非对称去磁电流脉冲与相电压曲线
Fig.15 Curves of asymmetrical demagnetizing currentand phase voltage
VFMM特有的调磁控制极大地增加了控制器的设计难度。在第1节所构建HMC-VFMM非线性数学模型的基础上，参考传统前馈电流控制器，本文提出一种基于实测参数的前馈电流控制器。VFMM系统的整体控制结构采用相对成熟的磁场定向控制，如图16a所示，所提基于实测参数的前馈电流控制器如图16b所示。图16中，ωm_ref和ωm分别为转速参考值与实际值，id_ref和iq_ref分别为d、q轴电流给定值，ud_ref和uq_ref为电流控制器输出量，Ld和Lq分别为d轴与q轴电感，ud_PI和uq_PI分别为d、q轴PI控制器输出。根据图16b，d、q轴电压给定值可以表示为
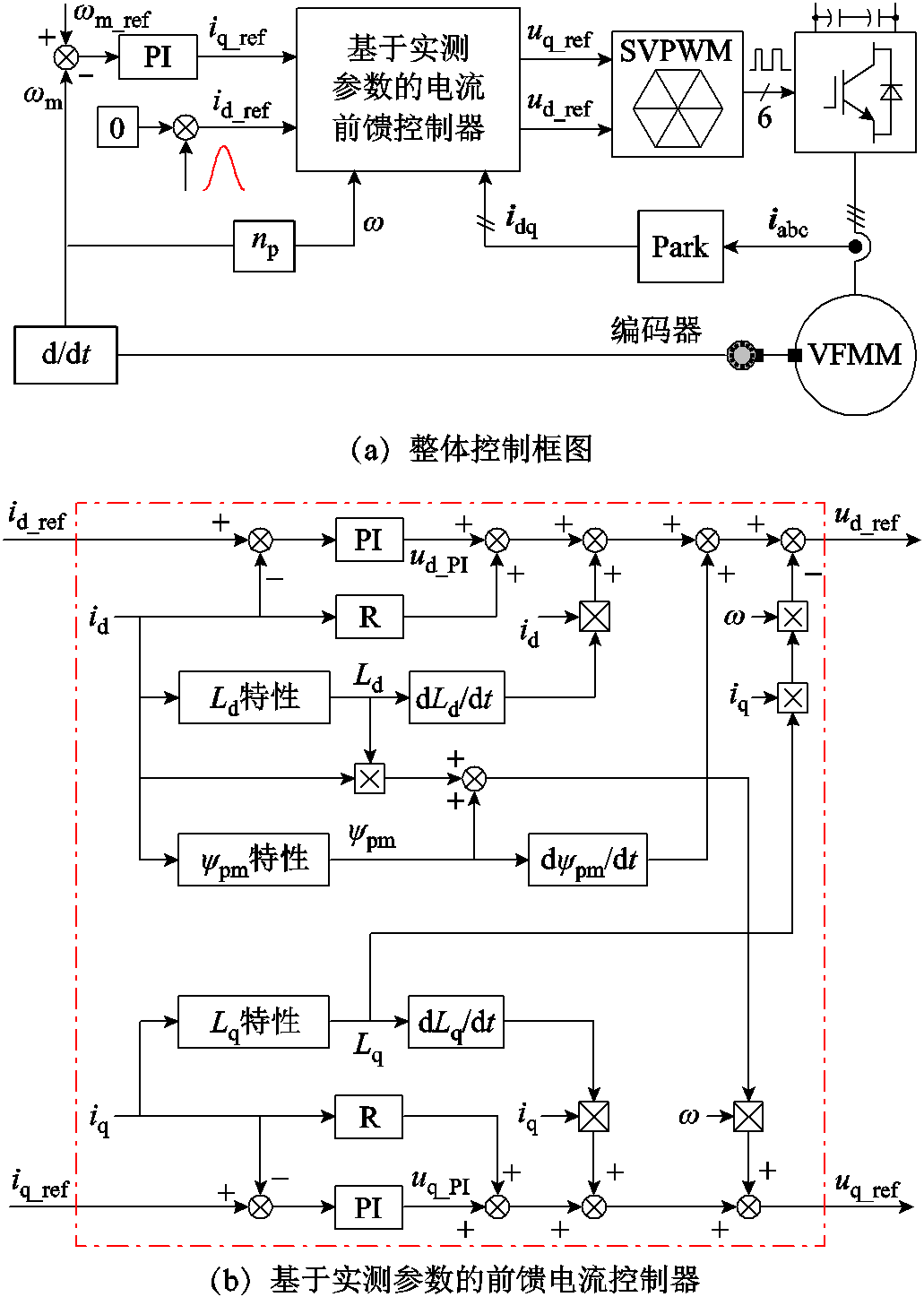
图16 VFMM系统控制框图
Fig.16 Control diagram of the VFMM drive system
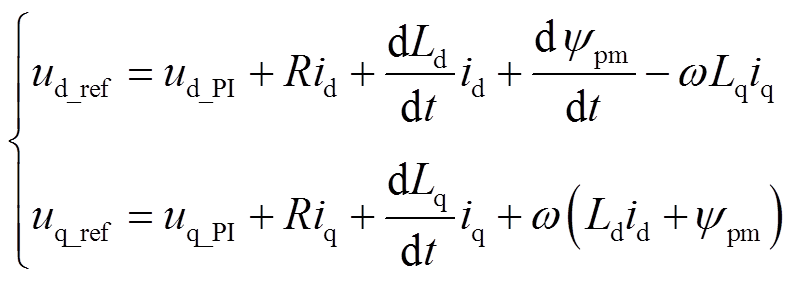（11）
本文将式（11）等号右侧含参部分定义为d、q轴电压的前馈补偿量，即有
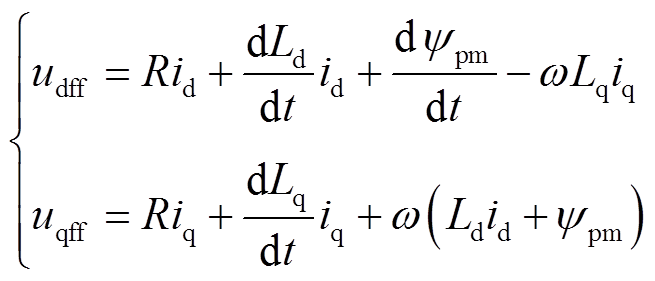（12）
式中，udff与uqff分别为d、q轴电压补偿量。
为了验证前述理论分析的正确性，基于所研究的HMC-VFMM样机搭建了实验测试平台，如图17所示，电机的主要参数见表1，永磁磁链与dq轴电感参数已在图4与图9中给出。被测样机安装于对拖台架，伺服电动机由上位机控制，用于拖动被测样机或提供负载。转矩传感器选用Burster的8661系列高精度转矩传感器，能够实现转矩/转速的高精度测量。控制器方面，主控芯片选用STM32F407单片机，开关器件选用型号为FDA59N30的MOSFET，额定电压与额定电流分别为300 V与59 A，能够满足实验需求。需要指出的是，为利用图4与图9所示实测数据，实验中采用“查表+插值”的方法对相关参数进行在线更新。
图17 实验测试平台
Fig.17 Experimental test rig
表1 所研究的HMC-VFMM样机的主要参数
Tab.1 Main parameters of the proposed tested HMC-VFMM
参数数值 额定功率PR/ W500 额定转速nR/(r/min)800 极对数p2 直流母线电压Udc/ V100 额定电流IR/ A7.5 相电阻R/Ω1.2
为验证所提前馈电流控制器的有效性，实验对比了有无参数前馈环节的电流控制效果。电流脉冲轨迹采用正弦型，持续时间设置为50 ms，充、去磁电流幅值分别为30 A与-25 A，电机转速设置为500 r/min且无负载，实验结果如图18与图19所示。
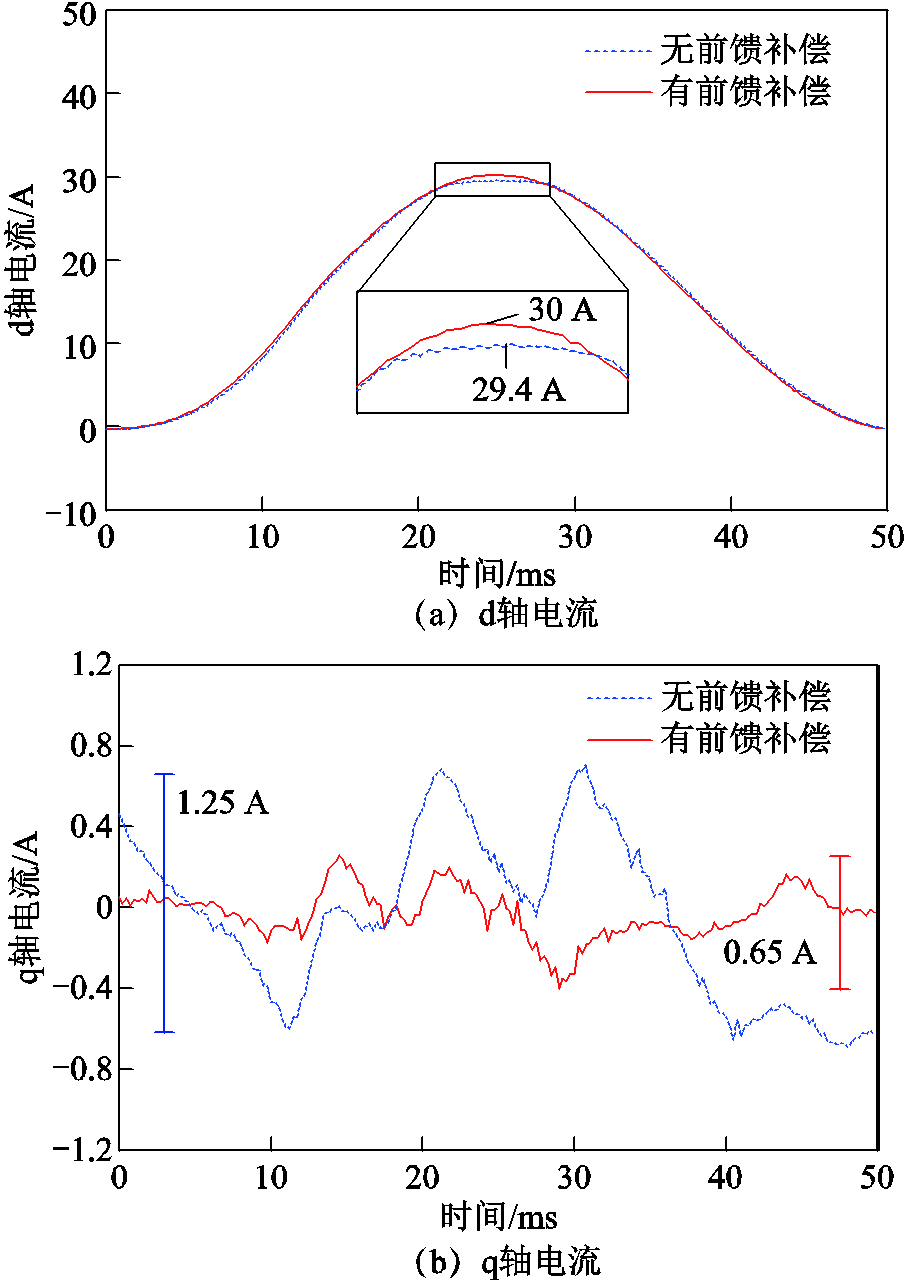
图18 充磁实验结果
Fig.18 Experimental results of re-magnetization
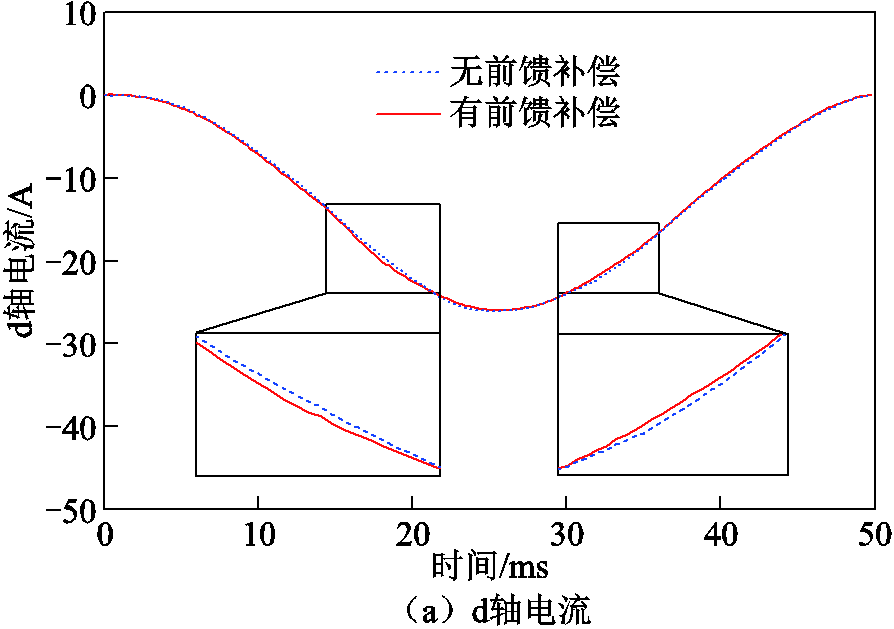
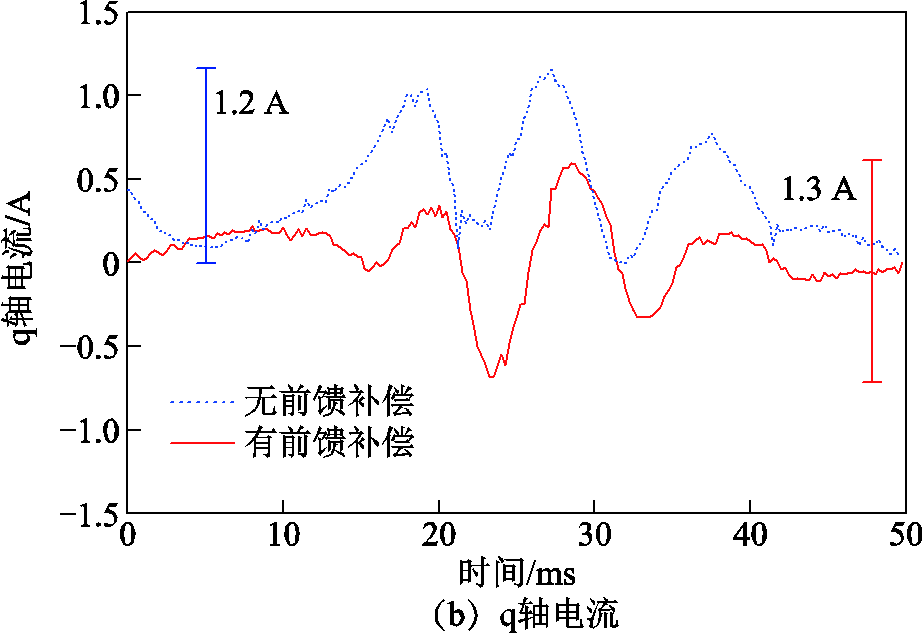
图19 去磁实验结果
Fig.19 Experimental results of de-magnetization
由图18和图19可以看出，充磁过程中，不采用参数前馈时，d轴电流脉冲峰值约为29.4 A，稍低于所需30 A峰值，且q轴电流波动较大，波动幅值约1.25 A；而采用参数前馈时，d轴电流能够较好地跟踪给定轨迹，同时q轴电流波动范围较小，波动幅值仅约0.65 A。去磁过程中，两种方法均能够控制d轴电流达到所需的-25 A峰值，电流轨迹仅存在细微差异，q轴电流波动幅值相当，分别为1.3 A与1.2 A。但未加入参数前馈环节时，q轴电流呈现明显正偏置，而加入参数前馈环节后q轴电流能够在给定值附近波动，控制效果得到了有效提升。上述实验结果验证了所提基于实测参数的前馈电流控制器能够有效改善充、去磁过程中的电流控制效果。
在高性能电流控制器的基础上，进一步通过实验对比了不同充、去磁电流脉冲轨迹给定下d轴电流的控制效果与相电压幅值大小。充、去磁电流幅值分别为30 A与-25 A，电机转速设置为500 r/min且无负载。图20与图21给出了正弦波脉冲轨迹（T = 50 ms）和三种非对称脉冲轨迹（T1 = 50 ms，T2 = 20, 30, 40 ms）给定下的充、去磁实验结果。可以看出，在四种脉冲轨迹给定下，d轴电流均能达到所需要的峰值。由于电流上升阶段轨迹一致，在此过程中，d轴电流和相电压幅值曲线均保持一致，几种非对称电流脉冲均能实现去磁操作。同时，充、去磁过程所需要的相电压峰值均出现于电流上升阶段。
对于电流回复阶段，比较图20与图21可以发现，在充磁工况下，相电压峰值并没有由于持续时间的缩短而明显增大，回复阶段持续时间T2越短，对应的相电压幅值下降速度越快；去磁工况下，缩短T2则会显著提高所需相电压，T2越小，相电压曲线的波峰出现越早，在T2 = 20 ms时，电流回复阶段所需最大相电压达到55 V左右，略高于对称轨迹下回复阶段所需最大相电压。可以预见，进一步缩短T2可能使得去磁所需相电压峰值出现在电流回复阶段，提高调磁所需电压幅值。因此，调磁电流时间的选取须考虑电压裕度，在不提高所需电压需求的前提下，缩短整个调磁过程，降低其带来的损耗。
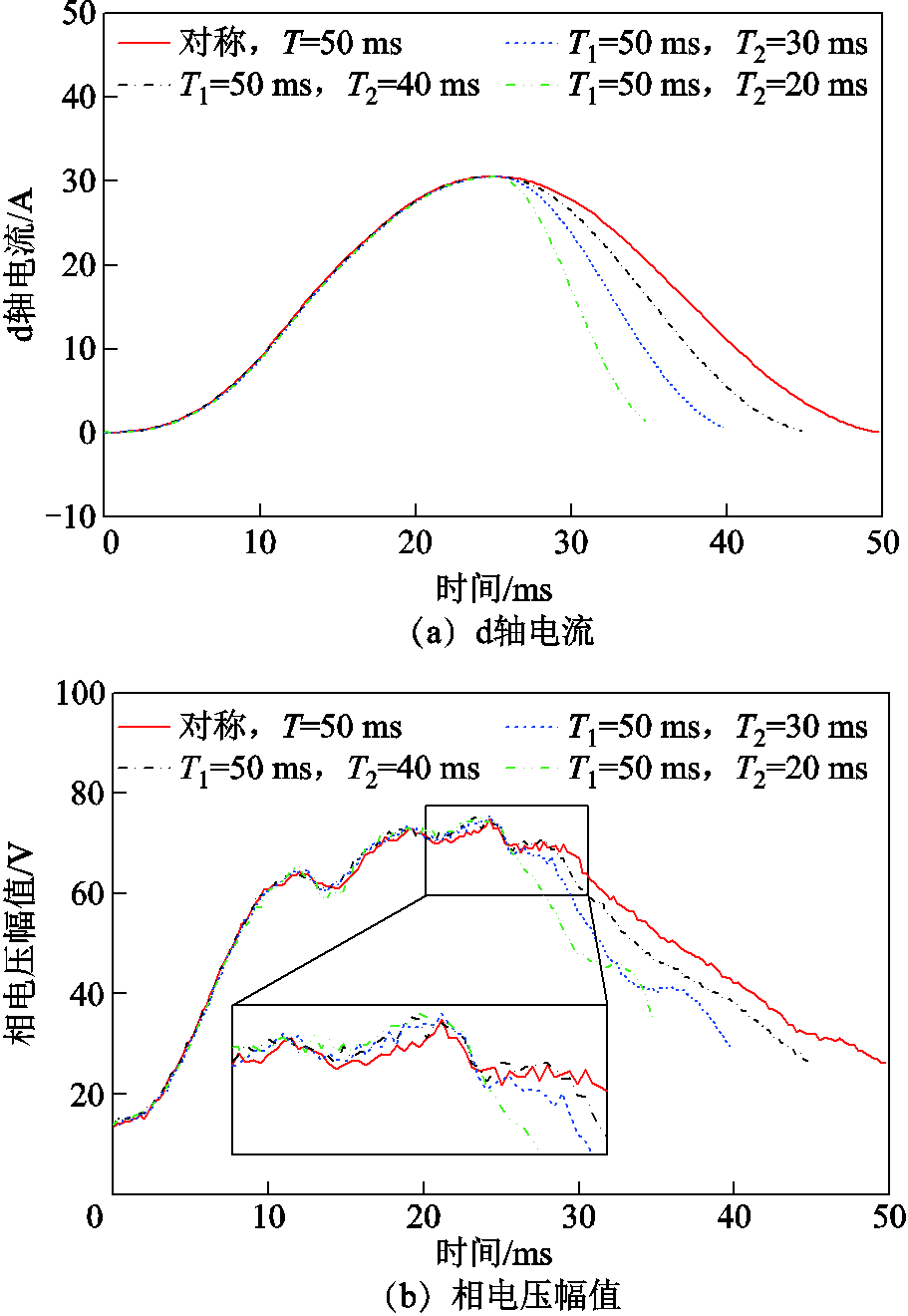
图20 不同电流脉冲轨迹下充磁实验结果
Fig.20 Experimental results in re-magnetizationoperations of different current pulse trajectories
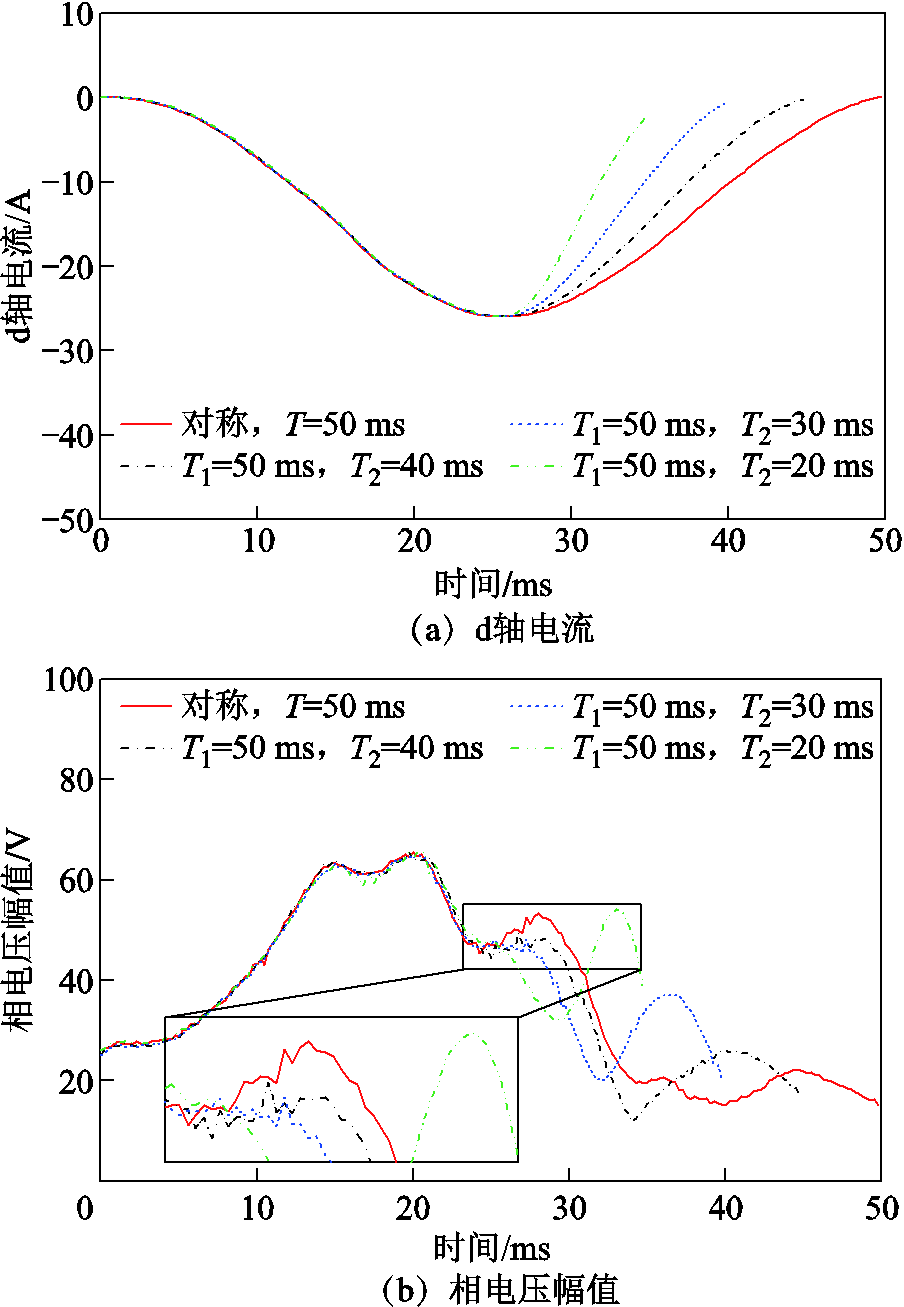
图21 不同电流脉冲轨迹下去磁实验结果
Fig.21 Experimental results in demagnetizationoperations of different current pulse trajectories
最后，测量并对比了不同充、去磁电流脉冲带来的损耗情况。为检测调磁过程中的损耗，采用图22所示测量电路，在测量开始前，首先需要锁定转子使其位于零位置，通过逆变器产生电流脉冲对电机进行调磁。调磁过程中，采集充、去磁过程中逆变器输出电压与电流，然后计算损耗，计算式为
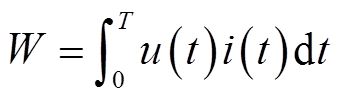（13）
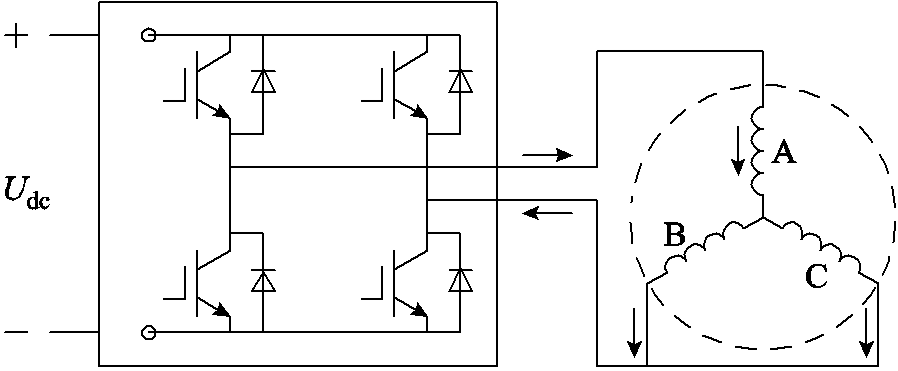
图22 调磁损耗测量电路
Fig.22 Circuit for measuring the loss duringre-/de-magnetization processes
实验采集了4.3节中测试的几种调磁电流轨迹对应的损耗，总结见表2，表中“损耗降低”描述了几种非对称脉冲总损耗相对于对称脉冲总损耗下降的百分比。可以看出，调磁过程中产生的损耗主要为铜耗。对于对称脉冲轨迹，充磁与去磁两种工况下产生的总损耗分别为33.58 J与27.88 J，其中铜耗分别占82.13%与70.16%。对于非对称脉冲轨迹，在保持第一部分脉冲相同的情况下，通过缩短第二部分的持续时间能够降低充去磁过程中的损耗。与对称脉冲轨迹相比，三种非对称脉冲轨迹充磁工况下的损耗分别降低约22.57%、11.97%与1.46%，去磁工况下的损耗分别降低约27.69%、18.62%与9.43%。
表2 不同电流脉冲产生的损耗
Tab.2 Losses generated by different current pulse trajectories
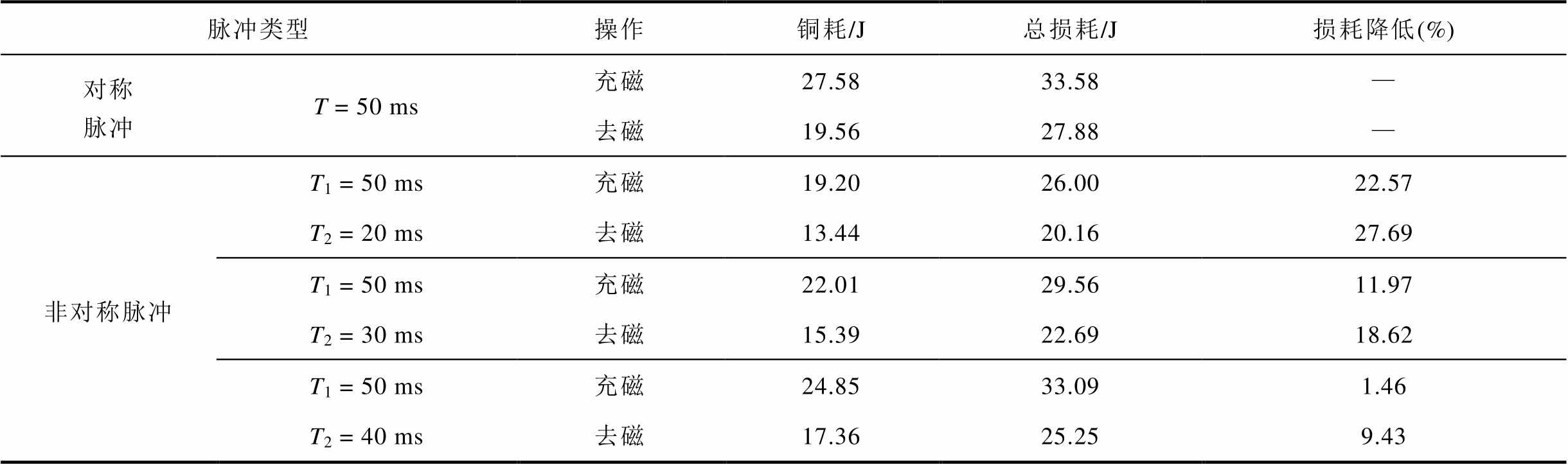
脉冲类型操作铜耗/J总损耗/J损耗降低(%) 对称脉冲T = 50 ms充磁27.5833.58— 去磁19.5627.88— 非对称脉冲T1 = 50 msT2 = 20 ms充磁19.2026.0022.57 去磁13.4420.1627.69 T1 = 50 msT2 = 30 ms充磁22.0129.5611.97 去磁15.3922.6918.62 T1 = 50 msT2 = 40 ms充磁24.8533.091.46 去磁17.3625.259.43
本文针对一台HMC-VFMM，研究了非线性模型的建立与调磁电流脉冲轨迹的优化，提出了基于非线性模型的前馈电流控制器，给出了详细的理论分析与实验验证。主要结论如下：
1）本文基于非线性模型设计的前馈电流控制器能够获得更加优越的电流控制效果，提高调磁电流控制精度。
2）对于常规对称正弦型电流脉冲轨迹，调磁所需相电压峰值出现于电流上升阶段且随着偏移角的增大逐渐降低。
3）对于本文所提非对称电流脉冲轨迹，通过优化电流回复阶段的持续时间，能够在顺利实现调磁的基础上，有效降低调磁过程产生的损耗。
4）比起充磁工况，电流轨迹的优化对去磁工况的影响更为显著，可能会导致所需相电压峰值出现在电流回复阶段，进而带来调磁失败等问题，因此，调磁电流时间的选取须考虑电压裕度。
参考文献
[1] 黄海林, 李大伟, 曲荣海, 等. 磁齿轮复合永磁电机拓扑及应用综述[J]. 电工技术学报, 2022, 37(6): 1381-1397. Huang Hailin, Li Dawei, Qu Ronghai, et al. A review of magnetic geared machines: topologies and applications[J]. Transactions of China Electrotechnical Society, 2022, 37(6) : 1381-1397.
[2] 梁子漪, 曲荣海, 陈智, 等. 双机电端口电机系统综述与发展展望[J]. 电工技术学报, 2022, 37(19): 4923-4937. Liang Ziyi, Qu Ronghai, Chen Zhi, et al. Overview of dual-electrical-port dual-mechanical-port machine system and their development[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4923-4937.
[3] 孙玉华, 赵文祥, 吉敬华, 等. 高转矩性能多相组永磁电机及其关键技术综述[J]. 电工技术学报, 2023, 38(6): 1403-1420. Sun Yuhua, Zhao Wenxiang, Ji Jinghua, et al. Overview of multi-star multi-phase permanent magnet machines with high torque performance and its key technologies[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1403-1420.
[4] 沈月芬, 刘旭. 考虑互感的多齿开关磁链永磁记忆电机的精确磁路模型[J]. 电工技术学报, 2022, 37(10) : 2435-2445. Shen Yuefen, Liu Xu. Accurate magnetic circuit model of multi-tooth switched flux permanent magnet memory machine considering the mutual inductance[J]. Transactions of China Electrotechnical Society, 2022, 37(10) : 2435-2445.
[5] Ostovic V. Memory motors[J]. IEEE Industry Applications Magazine, 2003, 9(1): 52-61.
[6] 胡俊杰, 赖信辉, 郭伟, 等. 考虑电动汽车灵活性与风电消纳的区域电网多时间尺度调度[J]. 电力系统自动化, 2022, 46(16) : 52-60. Hu Junjie, Lai Xinhui, Guo Wei, et al. Multi-time-scale scheduling for regional power grid considering flexibility of electric vehicle and wind power accommodation[J]. Automation of Electric Power Systems, 2022, 46(16) : 52-60.
[7] 王晓姬, 王道涵, 王柄东, 等. 电动汽车驱动/充电一体化系统及其控制策略综述[J]. 电工技术学报, 2023: 1-18. http://doi.org/10.19595/j.cnki.1000-6753. tces.230583. Wang Xiaoji, Wang Daohan, Wang Bingdong, et al. A review of drive-charging integrated systems and control strategies for electric vehicles[J]. Transactions of China Electrotechnical Society, 2023: 1-18. http:// doi.org/10.19595/j.cnki.1000-6753. tces.230583.
[8] Yu Chuang, Chau K T. Design, analysis, and control of DC-excited memory motors[J]. IEEE Transactions on Energy Conversion, 2011, 26(2): 479-489.
[9] Yu Kailiang, Wang Zheng. Improved deadbeat predictive current control of dual three-phase variable-flux PMSM drives with composite disturbance observer[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 8310-8321.
[10] Zhong Yuxiang, Lin Heyun, Wang Jiyao, et al. Variable time magnetization current trajectory control method for variable flux memory machines[J]. IEEE Transactions on Transportation Electrification, 2022, 8(3): 3100-3110.
[11] Chen Junhua, Li Jian, Qu Ronghai. Analysis, modeling, and current trajectory control of magnetization state manipulation in variable-flux permanent magnet machines[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 5133-5143.
[12] Chen Zhiyong, Lin Heyun, Zhong Yuxiang, et al. A novel current control strategy for magnetization state manipulation of variable flux memory machine based on linear active disturbance rejection[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1962-1971.
[13] Yu C Y, Fukushige T, Limsuwan N, et al. Variable-flux machine torque estimation and pulsating torque mitigation during magnetization state manipulation[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3414-3422.
[14] Yuuki K, Sakai K, Mochikawa H. Variable-flux motor drive system: US8179068[P]. 2012-05-15.
[15] 仲宇翔, 林鹤云, 王激尧, 等. 基于滑模控制的记忆电机调磁转速波动抑制[J]. 中国电机工程学报, 2023, 43(7): 2512-2520. Zhong Yuxiang, Lin Heyun, Wang Jiyao, et al. Speed variation suppression for memory machine during magnetization state manipulation based on sliding mode control[J]. Proceedings of the CSEE, 2023, 43(7): 2512-2520.
[16] Zhong Yuxiang, Lin Heyun, Wang Jiyao, et al. Speed fluctuation mitigation control for variable flux memory machine during magnetization state manipulations[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 222-232.
[17] Chen Junhua, Fang Haiyang, Qu Ronghai. Online magnetization trajectory prediction and current control for a variable-flux permanent magnet machine[J]. IEEE Access, 2020, 8: 41325-41334.
[18] Yang Hui, Lyu Shukang, Lin Heyun, et al. A novel hybrid-magnetic-circuit variable flux memory machine[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5258-5268.
[19] Chen Junhua, Li Jian, Qu Ronghai, et al. Magnet-frozen-permeability FEA and DC-biased measurement for machine inductance: application on a variable-flux PM machine[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4599-4607.
[20] 王锐, 刘卫国, 孙承浩. 基于电压脉冲注入和傅里叶拟合的转子绕线式同步起动/发电机初始位置检测方法[J]. 中国电机工程学报, 2022, 42(5): 1981-1991. Wang Rui, Liu Weiguo, Sun Chenghao. Initial rotor position estimation method for a wound-rotor synchronous starter/generator based on voltage pulse injection and Fourier fitting[J]. Proceedings of the CSEE, 2022, 42(5): 1981-1991.
Abstract The development of variable flux memory machine (VFMM) is to tackle the issues of unchangeable air-gap flux and hence limited speed range, which are the main drawbacks of the traditional permanent magnet synchronous machine (PMSM). According to the operating condition, the air-gap flux of VFMM can be adjusted online by injecting a pulse-shaped d-axis current, so that the efficiency under different working points can be enhanced. The existing works in relation to the VFMM drives are rare. Most of them focus on improving the dynamic response of current controller and suppressing the torque fluctuation due to the injection of d-axis current pulse. No scholars have studied the relationship between the re-/de-magnetization current pulse trajectories and the resulted losses. To fulfill the gap, this paper gives a research on the key technical issue.
This work is based on a hybrid magnetic circuit VFMM (HMC-VFMM). Firstly, in order for an accurate description on the HMC-VFMM with complex electromagnetic properties, the magnetizing curve, the armature flux characteristic and the inductance characteristic are tested, on which basis, the nonlinear mathematical model is established. Secondly, the sine-shaped current pulse trajectories and the required voltages are analyzed. Then, an asymmetrical current pulse trajectory and its improved method are proposed in order to realize re-/de-magnetization and reduce the associated losses simultaneously. The corresponding voltage curves are analyzed in terms of the maximum amplitude. Thirdly, based on the established nonlinear mathematical model, a feedforward current controller considering the measured parameters is proposed. The proposed current controller is integrated into the mature flux-oriented control.
Finally, an experimental test rig based on the prototype of HMC-VFMM is constructed to verify the effectiveness of the foregoing theoretical analyses. The proposed feedforward current controller is tested at first. The control methods with and without the proposed feedforward current controller are compared. The results show that the dq-axis currents regulated by the method with the proposed controller perform better in terms of tracking errors. With the high-performed controller, the control performances of d-axis current with different trajectories and the corresponding voltage values are compared. For re- and de-magnetization operations, the magnitudes of the d-axis current pulse trajectories are set to +30 A and −25 A, respectively. Four trajectories including a sine-shaped current pulse trajectory and three asymmetrical current pulse trajectories with different durations are tested. The results show that the tested three asymmetrical current pulse trajectories can shorten the total time of magnetization processes and don’t enhance the voltage requirement. Then, the losses resulted from the magnetization operations with the four trajectories are measured and compared. The obtained data indicates that using the sine-shaped current pulse trajectory, the losses during re-and de-magnetization processes are 33.58 J and 27.88 J, respectively, and the copper losses account for 82.13% and 70.16%, respectively. With the three asymmetrical current pulse trajectories, the losses can be reduced by 22.57%, 11.97% and 1.46% for the re- magnetization operation and are 27.69%, 18.62% and 9.43% for the de- magnetization operation.
The following conclusions can be drawn according to the experimental results. (1) The proposed feedforward current controller considering measured parameters can improve the current control accuracy. (2) For the conventional sine-shaped current pulse trajectories, the peak value of voltage required for re- or de-magnetization operation appears at the rising stage and decreases gradually with the increase of the designed offset angle. (3) For the proposed asymmetric current pulse trajectories, by improving the duration of the recovery stage, the loss generated in the re-/de-magnetization processes can be effectively reduced without sacrificing the realization of re-/de-magnetization. (4)The improvement of current trajectory has a more significant impact on the demagnetization operation over the re-magnetization operation. This can lead to the peak value of the required phase voltage appearing in the recovery stage, thus causing the failure of demagnetization operation. Therefore, the selection of the duration of current pulse trajectory must consider the voltage allowance.
keywords：Variable flux memory machine, permanent magnet synchronous machine, nonlinear mathematical model, current pulse trajectory, feedforward current controller
DOI:10.19595/j.cnki.1000-6753.tces.230965
中图分类号：TM341
国家自然科学基金（52037002, 52077033）、江苏省重点研发计划项目（BE2021052）、江西省“千人计划”项目（jsxq2020102088）、科技部高端外国专家引进计划（G2022141003L）、GF装备预研科技基金和电磁能技术全国重点实验室资助课题（6142217210201）资助。
收稿日期 2023-06-20
改稿日期 2023-07-26
阳 辉 男，1988年生，副教授，博士生导师，研究方向为电动汽车永磁电机系统、机器人伺服系统等。E-mail：huiyang@seu.edu.cn（通信作者）
刘 兴 男，1995年生，博士研究生，研究方向为永磁同步电机控制技术。E-mail：lyousying1996@163.com
（编辑 郭丽军）