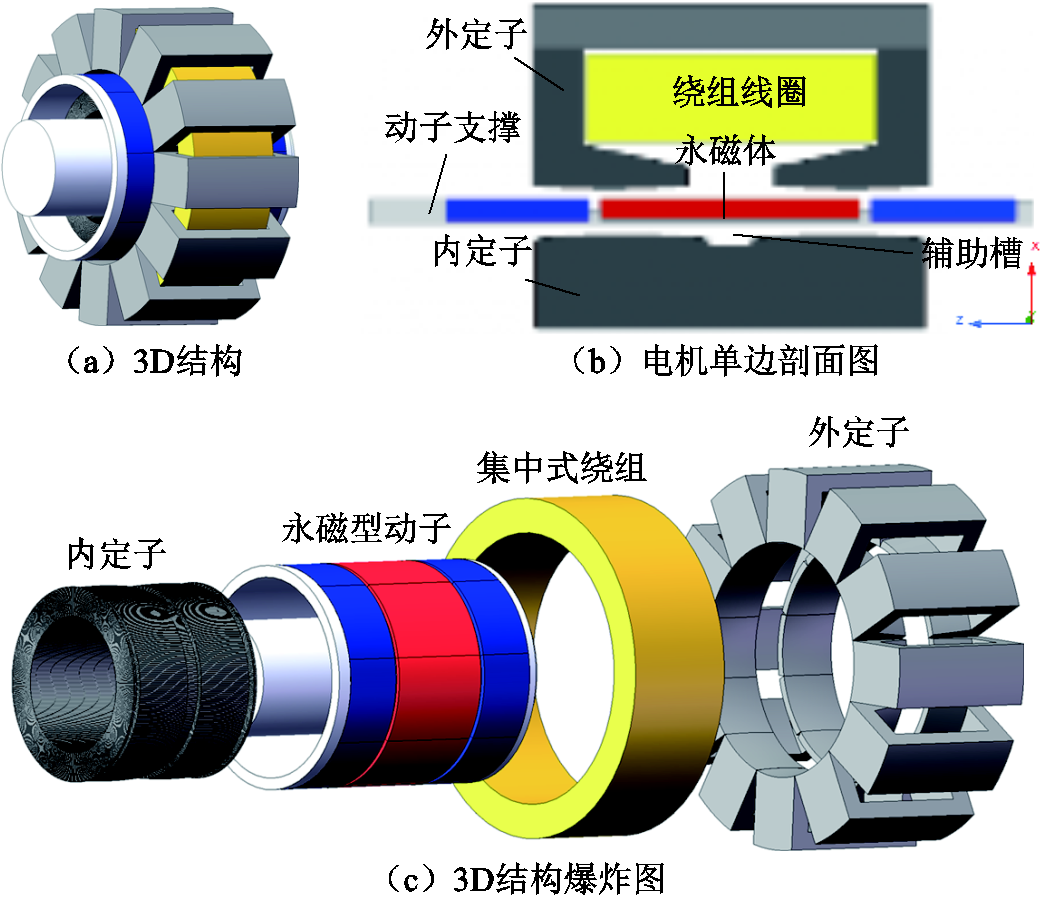
图1 新型单相永磁直线振荡电机结构
Fig.1 Structure of novel single-phase permanent magnet linear oscillation actuator
摘要 圆筒型双定子永磁直线振荡电机因其结构简单、功率密度高而广泛应用于压缩机领域。然而,电机的定子通常采用传统的硅钢片周向叠压方式,导致其叠压系数低、磁路易饱和。因此,该文提出一种新的混合叠压方法。首先,介绍了双定子永磁直线振荡电机的基本拓扑结构和工作原理,给出磁路特有的分布方式;然后,对采用电工纯铁和硅钢片混合叠压方式进行分析,推导了硅钢片数量与电工纯铁之间的占比关系,并对不同硅钢片数量对电机反电动势、电磁推力和损耗的影响进行分析;最后,通过三维有限元分析对采用传统叠压方式和混合叠压方式的双定子永磁直线振荡电机的电磁特性进行了比较和分析。实验结果验证了混合叠压方式在提高电磁推力和简化制作工艺方面的优势。
关键词:永磁直线振荡电机 混合叠压 圆筒型 有限元法 电磁性能
直线压缩机采用直线振荡电机直接驱动的方式能够显著地调高制冷系统的效率,同时减小整体的体积。相比于传统的三相直线振荡电机,单相永磁直线振荡电机具有机械结构简单、制造成本低、反应速度快和没有运动转换装置等优点,被广泛地运用在短行程高频率的场所[1-2]。通常,单相永磁直线振荡电机多采用圆筒型结构,这种结构可以有效地减少端部绕组,同时获得更高的气隙磁通密度和效率。但是,由于电机的主磁路与动子的移动方向在同一平面,因此需要对硅钢片进行周向排布以减小磁阻。周向叠压的硅钢片[3-4]不仅增加了装配难度,而且降低了定子的叠压系数,从而影响了电机的性能。因此众多学者采用了不同的叠压方式[5-12]来解决这一问题。
相较于电工纯铁,软磁复合材料[5-7]涡流损耗更低,导磁性能更好,能够实现电机定子的整体加工。文献[5]对一台采用准哈尔巴赫动磁式直线振荡电机进行了研究,其定子采用软磁复合材料进行加工,样机实验验证了该方法的可行性。尽管这种方式能够简化电机的装配方式,但是相较于硅钢片材料,其导磁性能不高,而产生的损耗较高,同时较高的材料价格制约了应用的领域[8]。文献[9]提出了一种新型的横向磁通双定子动磁式直线振荡电机,该电机的动子和定子铁心由硅钢片沿轴向叠压而成,这种方式有效地降低了装配难度。基于这种装配方式,文献[10]提出了一种动铁式横向磁通直线振荡电机,其将永磁体嵌入到定子内部,有效地提高了单位永磁体的出力,降低了永磁体的使用量。而针对硅钢片周向叠压方式的特点,文献[11]介绍了一种新的装配方式,该方式将外定子齿和轭部分别进行叠压,其叠压系数由最初的0.62提高到了0.75。在文献[11]的基础上,文献[12]采用三层混合叠片方式,根据磁路中不同的分布,将轴向叠压与周向叠压相结合,通过多种模块拼装方式使得外圈叠压系数增大了65%,定子整体的体积系数增大了35%。尽管这种多层叠压方式能够起到一定增大叠压系数的能力,但是往往会导致装配工艺过于复杂,从而影响电机的加工效率。文献[13]针对横向磁通永磁电机提出了一种硅钢片和软磁复合材料的混合铁心,并通过3D有限元法计算了电机的基本电磁参数。文献[14]采用混合铁心方式设计了一台磁通切换永磁圆筒电机,并根据不同的运行频率,给出了硅钢片和软磁复合材料的不同用量。
对于电机磁场的计算,目前使用最为广泛的是解析法[15]和数值计算法。电磁场解析法基于电磁场基本理论,针对电机各部分建立偏微分方程,并结合边界条件和介质的本构关系进行求解。电磁场数值计算是在电磁场解析法的基础上,通过把连续的数学模型离散化处理,结合计算机程序进行数值求解。在数值计算方法中有限元法适应性强,可以较好地处理复杂的电磁结构和非线性问题,应用最为广泛[16-19]。文献[16]采用有限元法对一台U型永磁开关磁链直线电机的特性进行了分析。并与隐机式电机进行了对比,结果表明气隙磁通密度增大了38.2%,电磁推力提高了20.54%。文献[17]结合实际应用环境,采用二维有限元分析对次级分段型直线磁通切换永磁电机进行了分析,验证了电机设计的合理性。文献[18]对一台圆筒型永磁同步直线电机进行了精确建模,并采用有限元和样机测试的方式验证了模型的正确性。同时,对于圆筒型横向磁通切换直线电机的研究,文献[19]采用等效磁路的方式建立了电机的数学模型,并通过二维和三维有限元仿真计算了电机磁场分布,同时与传统的圆筒型初级永磁直线电机进行了对比。
本文针对传统的圆筒型双定子永磁直线振荡电机定子装配形式进行了分析,提出了一种混合型的叠压方式。首先介绍了直线振荡电机的基本结构和运行原理,然后根据电机磁路特点分析了内外定子采用混合叠压方式的情况和装配方式。由于是将电工纯铁和硅钢片混合使用,因此推导了两种材料在不同结构下的占比情况。通过3D有限元法分析了不同硅钢片数量对电机性能的影响。最后利用有限元法和样机实验验证了该方法的有效性,实验结果表明,混合叠压方式不仅能够显著提高电磁推力,还可以较大程度地降低装配难度,避免装配误差。
图1为本文研究的新型C型铁心双定子永磁直线振荡电机。其中图1a为电机的三维结构图,图1b为电机单边剖面图,图1c为电机的三维结构爆炸图。如图中所示,新型直线振荡电机采用双定子和单个动子结构。外定子采用C型铁心,集中式绕组放置于外定子内部。内定子上设置有辅助槽用于抑制定位力,同时电机的定子采用弧形齿结构,能够平滑气隙磁阻。由于电机特殊的磁路,定子由周向叠压的硅钢片组成,从而导致内紧外松的特点。动子支撑采用非导磁金属材料加工而成,其表面放置有三块永磁体环,相邻两块永磁体的充磁方向相反。

图1 新型单相永磁直线振荡电机结构
Fig.1 Structure of novel single-phase permanent magnet linear oscillation actuator
新型C型铁心双定子永磁直线振荡电机采用双定子和三块永磁体组成的动子结构。电机的主磁路平面与动子移动方向共面,因此需要采用硅钢片周向叠压的方式来构成定子,以减小电机的涡流损耗和主磁路磁阻。图2给出了电机在不同位置的磁通路线。当动子在初始位置时,永磁体产生的磁通在外定子齿上产生回路,此时磁通不经过定子轭部,磁通以漏磁的形式存在,如图2a所示。当动子运动到最大位置时,永磁体产生的磁通经过左边外气隙、左边外定子齿、外定子轭部、右边外定子、右边外气隙最后回到永磁体,从而形成完整的磁通回路,如图2b所示。
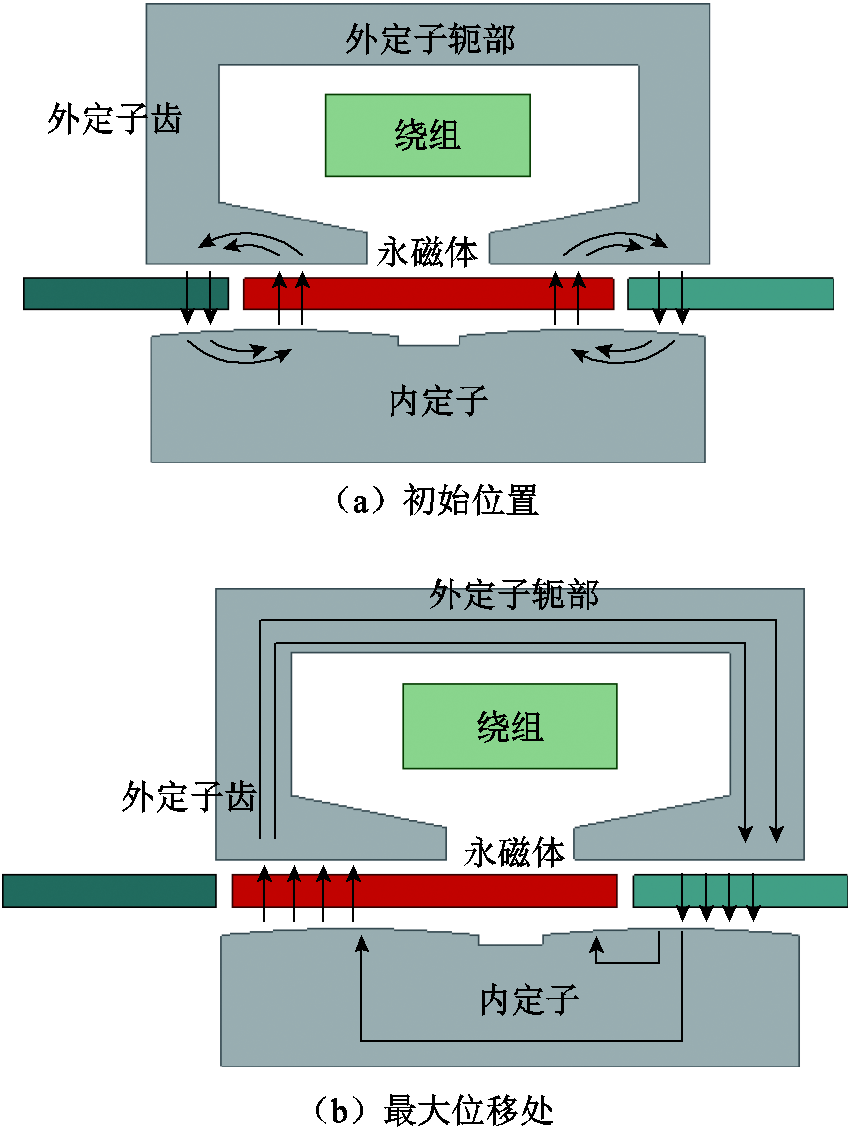
图2 电机在不同位置的磁通路线
Fig.2 Magnetic flux path of motor at different positions
在空载状态下,当动子匀速运行时,集中绕组所匝链的磁通逐渐增大或减小,因此在有效行程内反电动势近似为恒定值。当动子的运动速度为正弦时,所感应出的反电动势也为正弦形式。直线振荡电机在作为压缩机使用时,电枢绕组通常施加单相的正弦交流电,所产生的磁场与永磁体所产生的磁场相互作用,从而使得电机动子在轴向上周期性往复运动,其频率与电流的频率相同,从而实现对外功率的最高效输出。
通过前文对双定子永磁直线振荡电机的基本结构和运行原理的介绍可知,电机的磁路处于轴向空间内,而电机采用圆筒型结构,因此无法像平板型电机那样高效地利用硅钢片。目前对于圆筒型直线振荡电机定子的装配常采用软磁复合材料和硅钢片周向叠压的方式。软磁复合材料的磁场饱和点较低、材料成本较高,不适用于小功率直线振荡电机的场景。而硅钢片的叠压系数和装配难度尚未解决,因此本文提出了一种新的混合叠片方式。
通过对圆筒型双定子永磁直线振荡电机现有的硅钢片叠压方式的分析,了解了每种叠压方式的优势和局限性,因此本文为了降低工艺装配难度,提出了一种采用整块导磁材料内嵌硅钢片的混合叠片形式。混合叠压方案是结合整块钢板和硅钢片各自的优势,从而在提高电机定子的叠压系数的同时,避免涡流损耗大幅度增加。
图3所示为本文所提出的一种混合叠压方案。图3a中内定子采用整块电工纯铁压铸成圆筒型结构,在圆筒型电工纯铁的外表面沿周向加工一定数量的槽,槽的宽度与硅钢片的厚度相同,深度与电机设计的内定子高度相同。将硅钢片嵌入相应的槽中,采用端部焊接的形式进行固定,最后将圆筒钢板内圆处连接部分撤掉,从而构成一个完整的内定子。为了降低电机的涡流损耗,防止硅钢片与软磁材料之间有电导通,因此需要在硅钢片的表面进行电绝缘处理。外定子采用齿部和轭部分别装配的形式。其中齿部采用混合叠片方案,在开槽时应在定子齿的顶端留有一部分余量,从而保持外定子齿结构的完整性以便装配硅钢片,如图3b所示。由于外定子轭部内、外半径之比较大,因此仅采用硅钢片周向叠压的方式。硅钢片组成的轭部与定子齿上都设置有相应的定位槽,将固定圆环放置槽中便可起到固定外定子的作用。
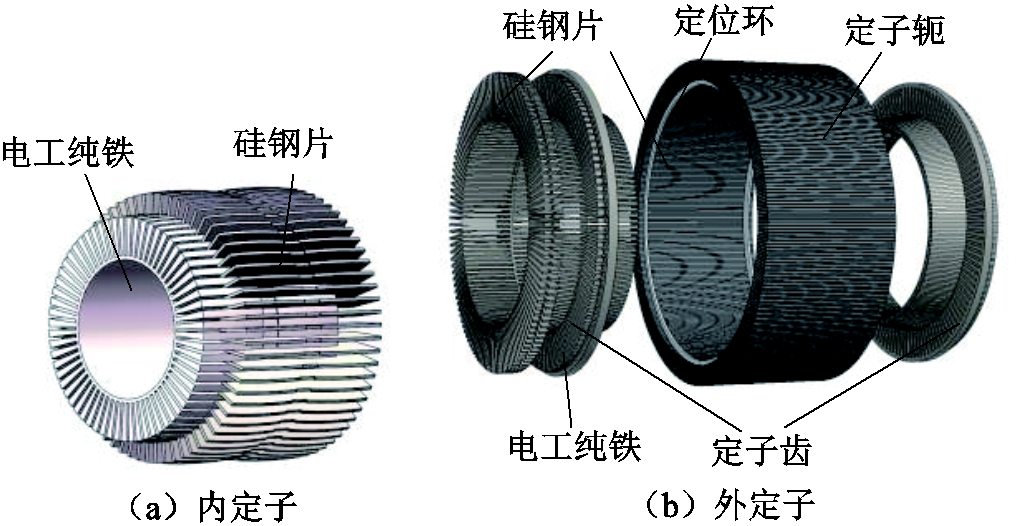
图3 定子混合叠压方案
Fig.3 Hybrid lamination method of the stator
由混合叠片加工而成的定子铁心包括硅钢片和电工纯铁,两种材料在定子中所占比例的大小会对电机整体性能产生较大的影响,因此需要通过计算两种材料所占比例的参数,为后续电磁性能的设计做铺垫。
内定子叠片开槽示意图如图4所示。在电工纯铁上加工出相应的内嵌槽,其形状如图4中(红色)方框所示。如图所示,以圆心O点作为坐标轴的原点,线段OA与内定子内半径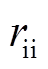 相等,OD与内定子外半径
相等,OD与内定子外半径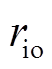 相等。AB=CD表示槽的宽度,由于需要嵌入硅钢片,因此其值应为硅钢片厚度
相等。AB=CD表示槽的宽度,由于需要嵌入硅钢片,因此其值应为硅钢片厚度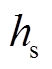 的Ns倍,即
的Ns倍,即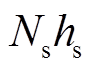 ,Ns为整数。AD为矩形槽的深度,由于内定子为环形,实际切割深度
,Ns为整数。AD为矩形槽的深度,由于内定子为环形,实际切割深度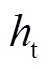 应大于AD的长度。
应大于AD的长度。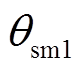 为扇形电工纯铁剩余齿最窄处的角度,
为扇形电工纯铁剩余齿最窄处的角度,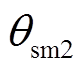 为扇形电工纯铁剩余齿最宽处的角度。角度
为扇形电工纯铁剩余齿最宽处的角度。角度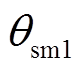 、
、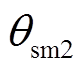 的大小与槽宽度和数量有关。
的大小与槽宽度和数量有关。
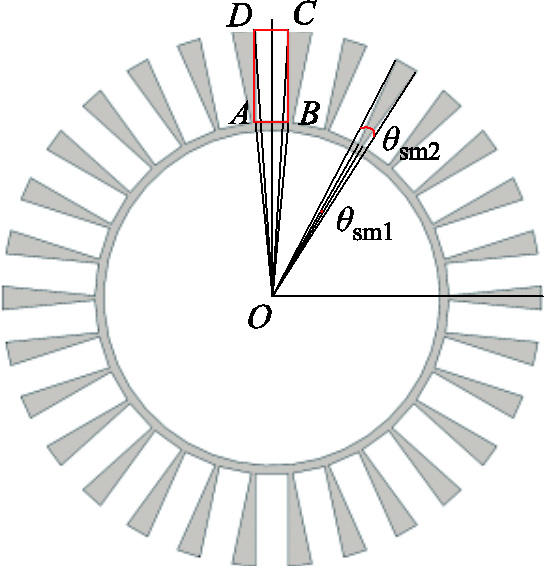
图4 内定子叠片开槽示意图
Fig.4 Slot diagram of the inner stator lamination
根据勾股定理可知,槽底部所占的角度为
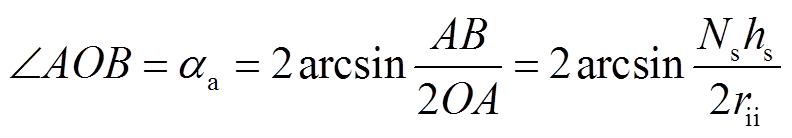 (1)
(1)
槽顶部所占的角度为
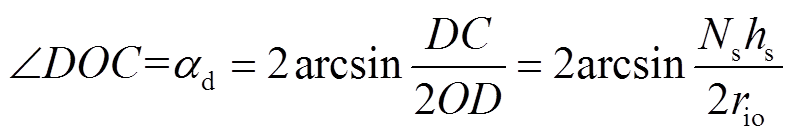 (2)
(2)
槽深度为
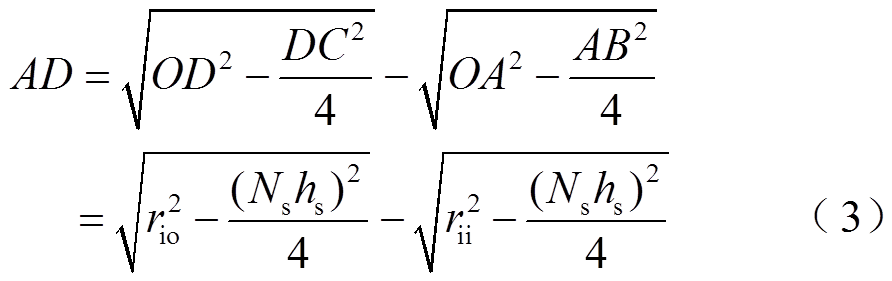
实际切割深度为
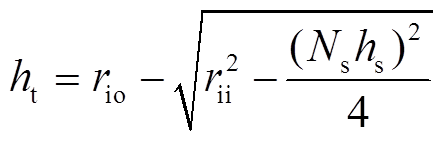 (4)
(4)
单个槽的面积为
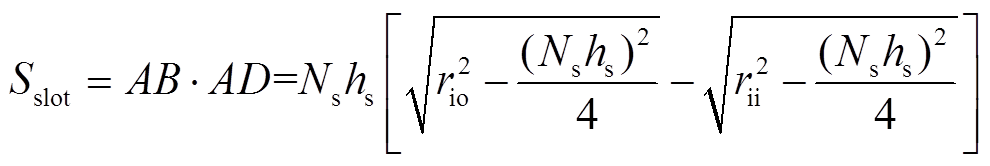 (5)
(5)
扇形电工纯铁的下端和上端弧形角度分别为
![]() (6)
(6)
式中,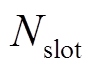 为开槽的数量。
为开槽的数量。
扇形电工纯铁的下端和上端弧形宽度分别为
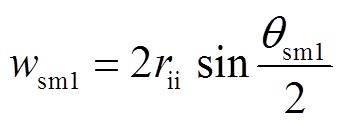 (8)
(8)
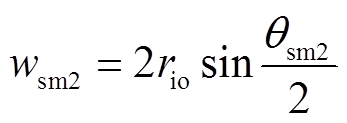 (9)
(9)
单个扇形电工纯铁的面积为
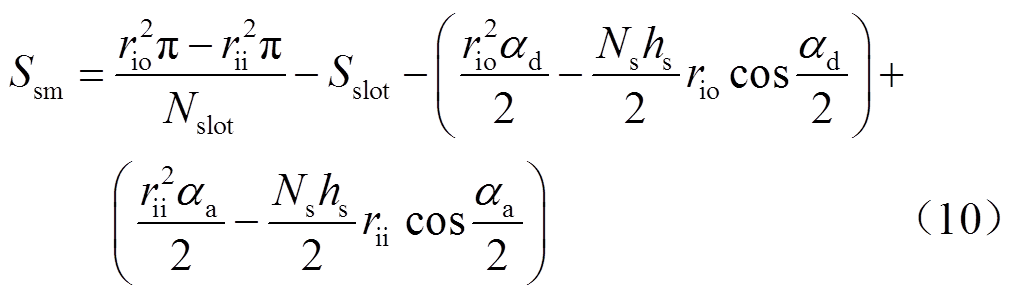
整理得
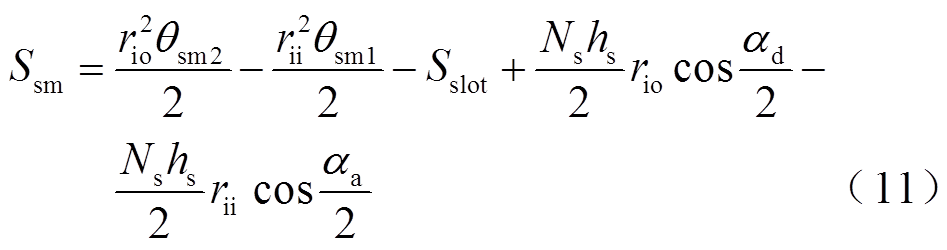
根据叠片叠压的方式,为保持叠片之间互相不重叠,扇形电工纯铁的下端弧形角度约束为
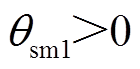 (12)
(12)
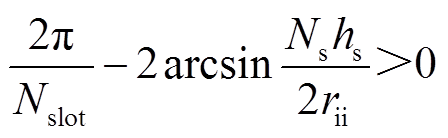 (13)
(13)
因此电工纯铁开槽数量存在上限为
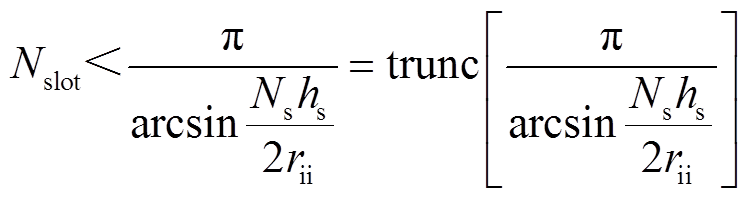 (14)
(14)
式中,trunc[·]为取整函数。
为了保证开槽过程中铁心部分的结构强度,依据经验,设置电工纯铁下端最窄处宽度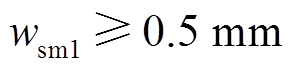 。采用0.5 mm厚度的硅钢片,通过公式计算,获得内定子电工纯铁上开槽数量与硅钢片装叠总数量的关系见表1。
。采用0.5 mm厚度的硅钢片,通过公式计算,获得内定子电工纯铁上开槽数量与硅钢片装叠总数量的关系见表1。
表1 内定子开槽工艺参数
Tab.1 Inner stator slotting process parameters

单槽硅钢片数槽数硅钢片总数下端宽度/mm上端宽度/mm电工纯铁总面积/mm2 11251250.511.161 352.05 2831660.511.51 085.49 3621860.531.84955.39 4502000.512.15864.23 5412050.562.56831.53 6352100.592.92798.78 7312170.553.19752.96 8272160.653.68759.13 9252250.523.79700.18 10222200.74.42732.29
硅钢片中的损耗通常是由相应的损耗系数计算获得。在传统的旋转永磁电机中,根据Bertotti等的研究,铁心损耗由磁滞损耗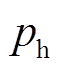 、涡流损耗
、涡流损耗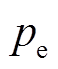 、附件损耗
、附件损耗![]() 三部分组成。硅钢片单位质量下铁心损耗为
三部分组成。硅钢片单位质量下铁心损耗为
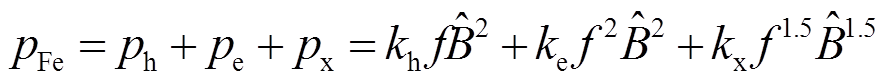 (15)
(15)
式中,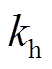 为磁滞损耗系数;
为磁滞损耗系数;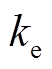 为涡流损耗系数;
为涡流损耗系数;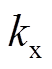 为附加损耗系数;
为附加损耗系数;![]() 为磁通密度幅值;
为磁通密度幅值;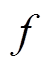 为磁通密度波形变化频率。由于直线振荡电机磁路中不同位置的磁通密度变化幅值不同,因此需要将电机中的硅钢片划分为不同区域从而计算出相应的磁通密度和体积。电机总的铁心损耗为
为磁通密度波形变化频率。由于直线振荡电机磁路中不同位置的磁通密度变化幅值不同,因此需要将电机中的硅钢片划分为不同区域从而计算出相应的磁通密度和体积。电机总的铁心损耗为
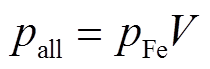 (16)
(16)
式中,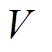 为铁心的体积。
为铁心的体积。
硅钢片中的涡流损耗通常是由式(15)中的涡流损耗系数计算获得,因此无需通过涡流幅值计算涡流损耗。而其他导磁材料中需要根据磁场变化所产生的涡流来计算涡流损耗,根据电磁场原理,磁路中的电流密度计算过程如下。
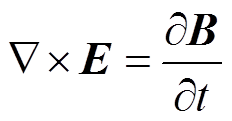 (17)
(17)
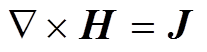 (18)
(18)
电流密度J可通过电场强度E和电导率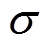 的乘积获得。
的乘积获得。
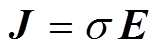 (19)
(19)
由功率的计算公式可以获得一定体积中电磁的损耗功率。
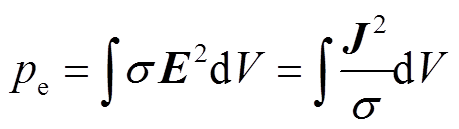 (20)
(20)
由于非硅钢片材料中相应的铁心损耗系数未知,因此在计算过程中可以忽略,仅考虑由涡流引起的损耗。
上文对混合叠片方式可以采用的不同形式进行了研究,给出了内外定子开槽数量与硅钢片数量的关系。同时,根据分析可知,不同的叠片方案会对电机的性能产生较大的影响,因此下面将对内定子采用不同的叠片方式对电磁特性的影响进行分析,主要对磁路中磁场密度、电磁出力特性、铁心损耗性能进行比较。
采用3D有限元仿真模型对采用不同混合叠片的直线振荡电机进行仿真分析。根据机械加工经验,将扇形电工纯铁最窄处宽度定为大于等于0.5 mm,分别选取每槽放置硅钢片数量为1~10时的模型进行对比。为了保持对比结果的一致性,所有模型的外定子硅钢片采用统一的单个硅钢片开槽方式,开槽数量为250个,其结构如图3b中的外定子部分。硅钢片采用的牌号为50WW470,电工纯铁为steel010。图5给出了通过SolidWorks绘制的不同内定子结构的示意图,由于结构众多,此处仅给出四种方案。图5中深色部分为硅钢片,浅色部分为扇形电工纯铁。
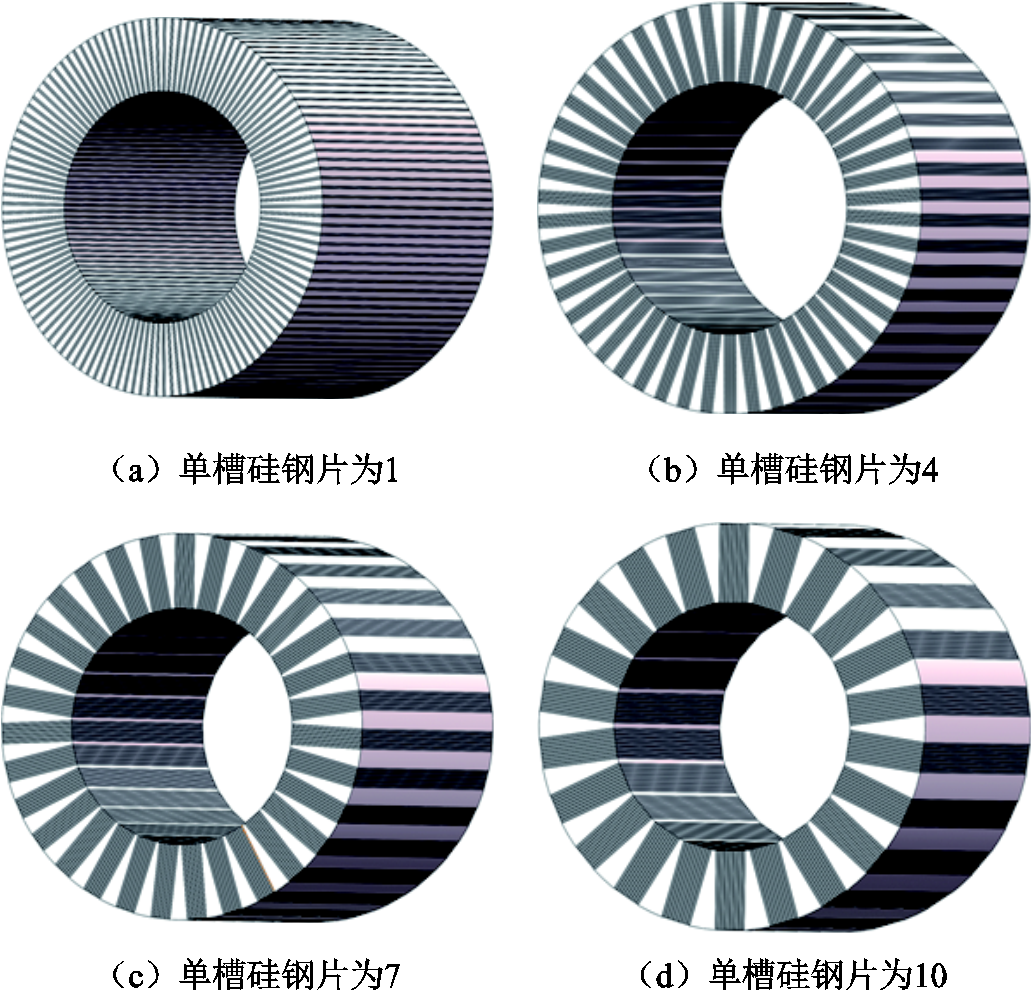
图5 采用不同混合叠片方案内定子
Fig.5 Different hybrid laminations of internal stators
采用Maxwell软件中的3D模块对直线振荡电机进行仿真分析。为了降低模型计算时间,对模型进行切割处理,选取模型的1/12部分,由于圆筒型电机关于轴线对称,因此切割处理不会影响计算结果。分别对采用不同内定子结构的直线振荡电机进行有限元仿真分析,从而获得电机在空载和负载状态下的电磁性能参数。
对比不同直线振荡电机电磁推力随着动子的位移的变化情况,设置动子以匀速1 m/s的方式从左边最大位移处移动到右端,行程为20 mm。电枢绕组中通入电流为0,仿真获得不同内定子的反电动势系数对比图。图6所示为每槽硅钢片数量对反电动势系数的影响情况。由图可知,当每槽硅钢片数量为1时,反电动势系数为22.018 V,而随着每槽硅钢片数量的增加反电动势系数逐渐降低,这主要是由于随着单槽硅钢片数量的增加,每槽中硅钢片与气隙接触的面为平面,实际气隙长度大于弧形面,因此相应的气隙磁通密度有所下降。
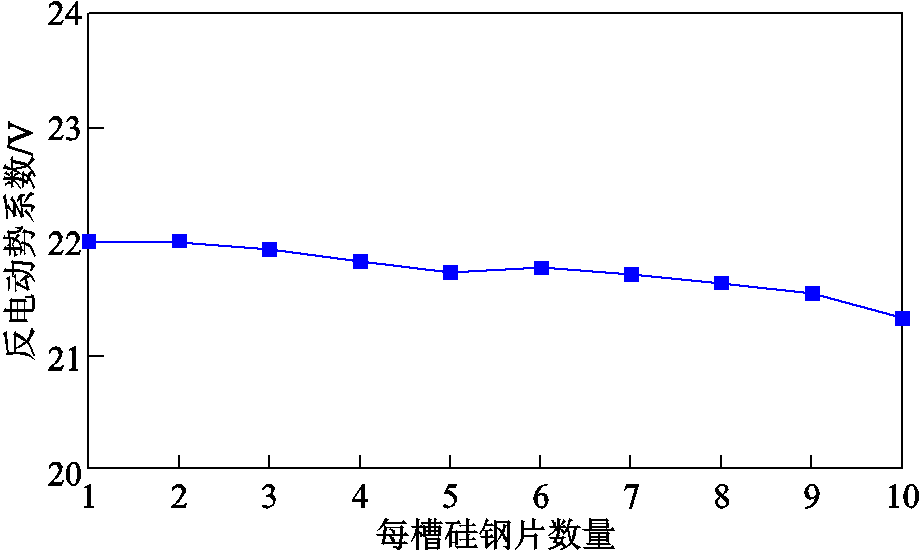
图6 每槽硅钢片数量对反电动势系数的影响
Fig.6 Influence of the number of silicon steel sheets per slot on the back-EMF coefficient
电枢绕组通入幅值为20 A的交流电,使得动子以正弦速度作往复运动。对比分析不同硅钢片数量下电磁推力波形的幅值和谐波畸变率(Total Harmonic Distortion, THD),电磁推力随每槽硅钢片数量的变化曲线如图7所示。由图7中可知,相较于采用单个硅钢片开槽方式的内定子,随着每槽硅钢片数量的增加,电磁推力先增大后逐渐减小,当每槽硅钢片数量为2时,电磁推力最大为456.5 N。电磁推力与上文获得反电动势系数波形的变化规律相同。而电磁推力波形的THD变化不明显,所有状态都围绕着4%波动,因此考虑到仿真剖分精度不高的问题,可以认为每槽硅钢片数量对于电磁推力波形的THD影响不大,可以忽略。
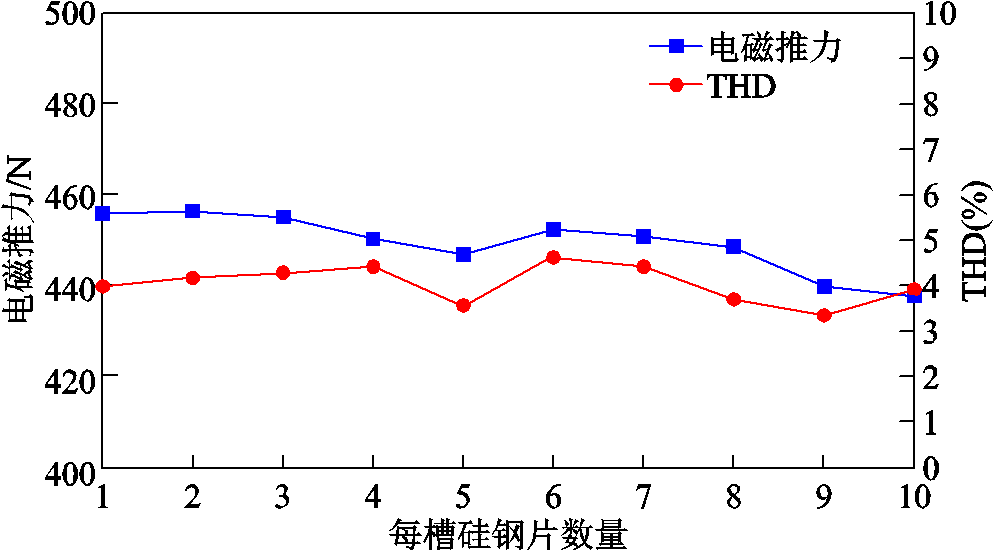
图7 电磁推力随每槽硅钢片数量的变化曲线
Fig.7 The curve of electromagnetic thrust with the number of silicon steel sheets per slot
图8为内定子损耗随每槽硅钢片数量变化的曲线。为了更加直观地展现内定子开槽情况对损耗的影响情况,在3D模型仿真计算时只计算内定子硅钢片中的铁心损耗和电工纯铁的涡流损耗,由于其他尺寸参数和使用材料都相同,因此可以在对比分析中忽略。如图8所示,由于磁场在内定子铁心中的变化不大,因此所产生的总损耗也相对较小。随着每槽硅钢片数量的增加,总的硅钢片使用量也增加,但是铁心损耗的变化情况并非单调增加,而是先增大后减小。当每槽硅钢片数为9时,铁心损耗达到最大值,这主要是由于每槽硅钢片为10时,硅钢片的总用量有所减小,同时硅钢片与永磁体之间的气隙长度也在增大,导致铁心中的磁通密度略有减小,从而导致铁心损耗降低。而电工纯铁中的涡流损耗随着每槽硅钢片数量的增加而逐渐增大。尽管电工纯铁的用量逐渐减小,但是由于每个电工纯铁的体积在逐渐增大,因此单位体积所产生的涡流损耗明显增大。如图8所示,当每槽硅钢片的数量分别为3、6、8、10时,其扇形电工纯铁下端宽度相较于其他状态时明显较大,因此所产生的涡流损耗明显增加。
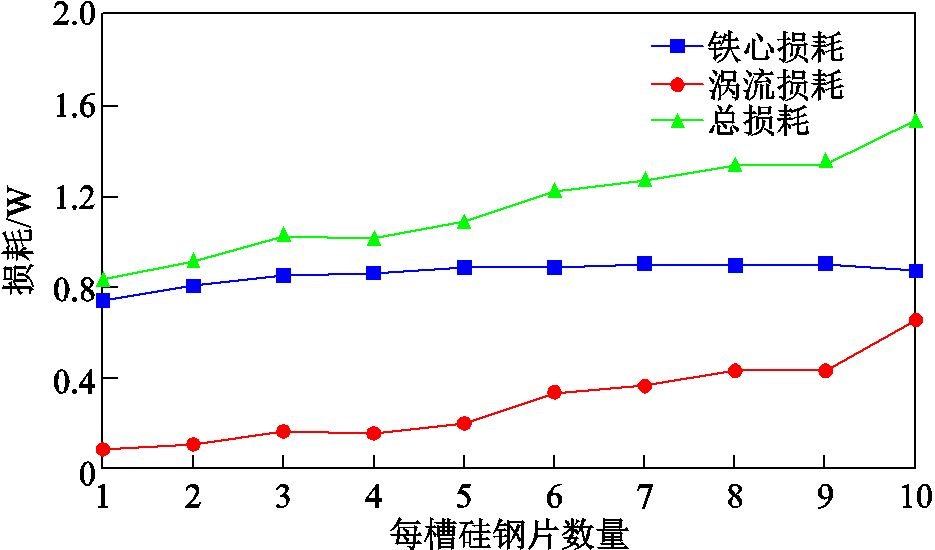
图8 损耗随每槽硅钢片数量的变化曲线
Fig.8 Loss waveforms with the number of silicon steel sheets per slot
通过对比可知,通过增大每个槽的宽度来减小电工纯铁的使用量并没有提高电机的性能,损耗和电磁推力都有所下降,因此在样机加工过程中选择单槽硅钢片数量为1的方案。
采用一台300 W直线振荡电机的结构模型,对对比分析两种叠压方式对电机性能的影响,电机的结构参数见表2。利用3D有限元仿真对模型进行仿真分析从而获得相应的电磁特性。
表2 300 W直线振荡电机结构参数
Tab.2 Structure parameters of 300 W linear oscillation actuator(单位:mm)

参数数值 定子长度55 内定子高度13 永磁体厚度3 中间永磁体宽度36 端部永磁体宽度20 永磁体间隔1.5 气隙1.5 槽口宽度12 外定子内半径39.5 外定子高度25.5 外定子轭部厚度6 外定子齿宽6
图9所示为两种叠压方式下电机开路磁场分布。其中图9a和图9b为空载状态下的磁场分布,图9c和图9d为负载电流为20A下的磁场分布。如图9所示,仅采用硅钢片叠压而成的内定子在空载状态时的磁通密度就远大于混合叠压的,这主要是由于硅钢片的叠压系数较小,磁通集中在硅钢片上导致磁通密度较大。而当电机运行在负载状态时,内定子硅钢片便处于磁饱和状态,如图9c所示,而混合叠压的内定子磁通密度仅为1.6 T左右。

图9 开路磁场分布
Fig.9 Open-circuit flux distribution
电机动子以匀速状态运行,从而获得空载状态下磁链的对比模型,如图10所示。采用硅钢片周向叠压的电机的磁链与混合叠压电机的磁链基本相同,主要是空载状态下两种电机磁路都未达到饱和,其总磁通相差不大。
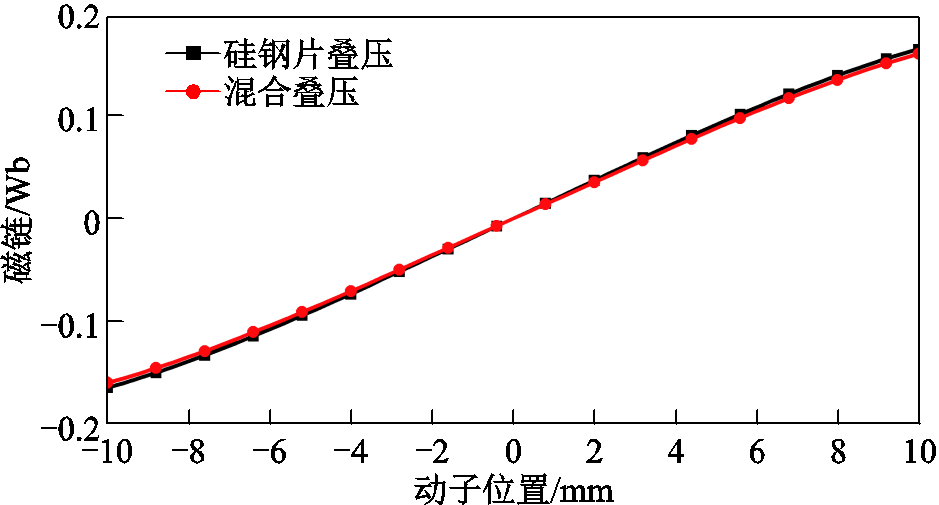
图10 绕组空载磁链
Fig.10 Flux linkage of open-circuit
图11所示为电机在不同叠压方式下电磁推力的对比图,此时,对电枢绕组施加20 A直流电。如图所示,当动子位于-10~0 mm之间时,两种电机所产生的电磁推力基本相同,这主要是由于此时永磁体所产生的磁路方向与电枢绕组所产生的磁路方向相反,因此不会导致磁路出现磁饱和。而当动子由位置0 mm运行到最大位置10 mm处时,两个磁场方向相同且叠加在一起,从而导致内定子中存在磁饱和现象,而混合叠压的内定子磁饱和程度明显小于仅有硅钢片叠压的内定子,因此其电磁推力在最大位移处时幅值为221 N,相较于前者提高了26%。
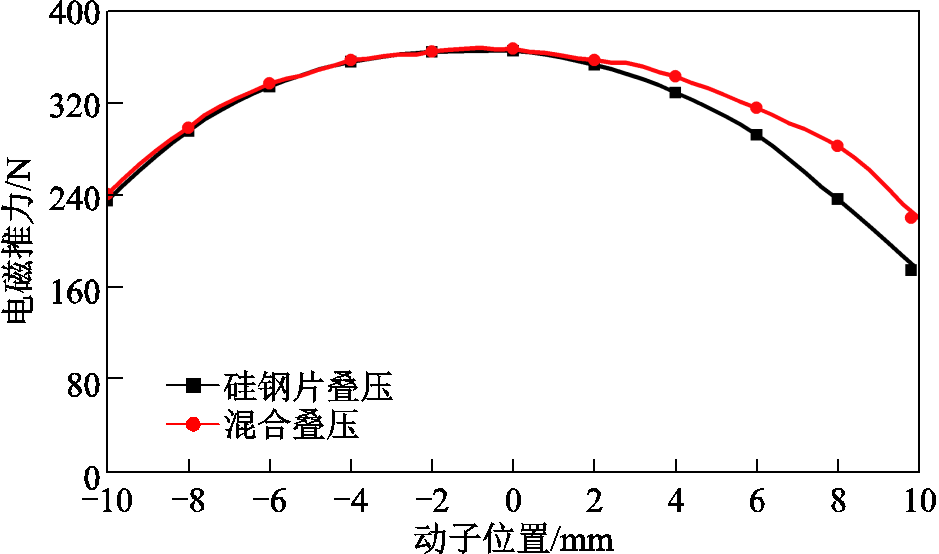
图11 电磁推力对比
Fig.11 Comparison of the excitation force
图12对比分析了两种模型所获得的损耗波形。此时电机运行在正弦速度下,运行频率为40 Hz,电枢电流为20 A,损耗包含磁滞损耗和涡流损耗。如图12所示,在相同负载电流下,混合叠压电机的平均总损耗为13.8 W,大于采用传统硅钢片叠压的电机平均损耗11.38 W,这主要是由于混合叠压的内定子中采用电工纯铁,导致总的涡流损耗增加。同时根据电机各部位的磁通密度通过式(15)和式(20)计算出混合叠压的损耗结果,如图中点线波形。从图12中可以看出,解析计算结果明显大于有限元仿真分析的结果,这是由于有限元仿真能够通过剖分精确计算每个部位的磁通密度分布,从而获得更加准确的结果;而解析计算中选取的计算部位数量有限,无法精确到每个位置的磁通密度。
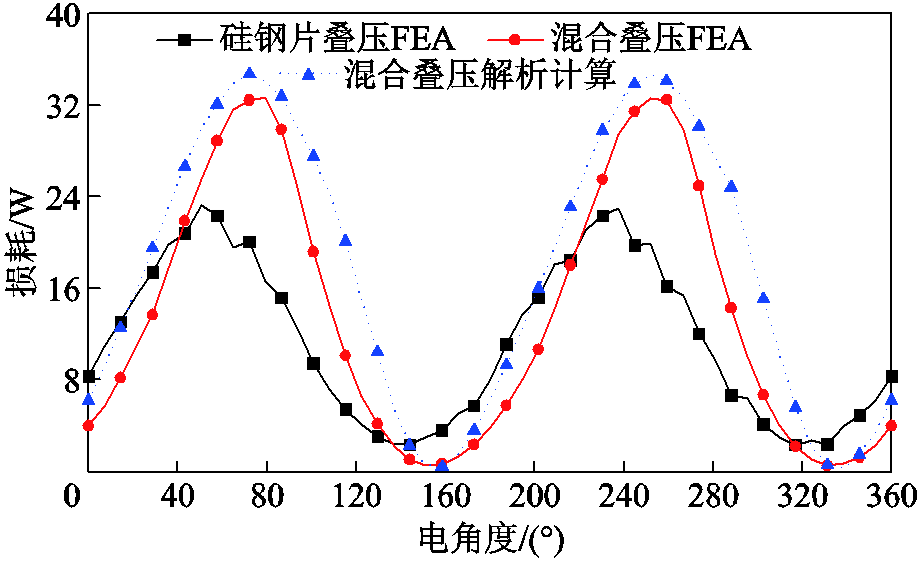
图12 铁心损耗对比
Fig.12 Comparison of the core loss
图13所示为混合叠压电机损耗随频率变化波形。电枢电流保持为20 A,运行频率在20~60 Hz的范围内变化。如图13所示,随着频率的增加,铁心损耗和涡流损耗都逐渐增大,而涡流损耗的增长幅度明显大于铁心损耗。因此在加工混合叠压电机的电工纯铁部件时,可根据实际装配条件,对电工纯铁进行分块化处理以减少涡流损耗。
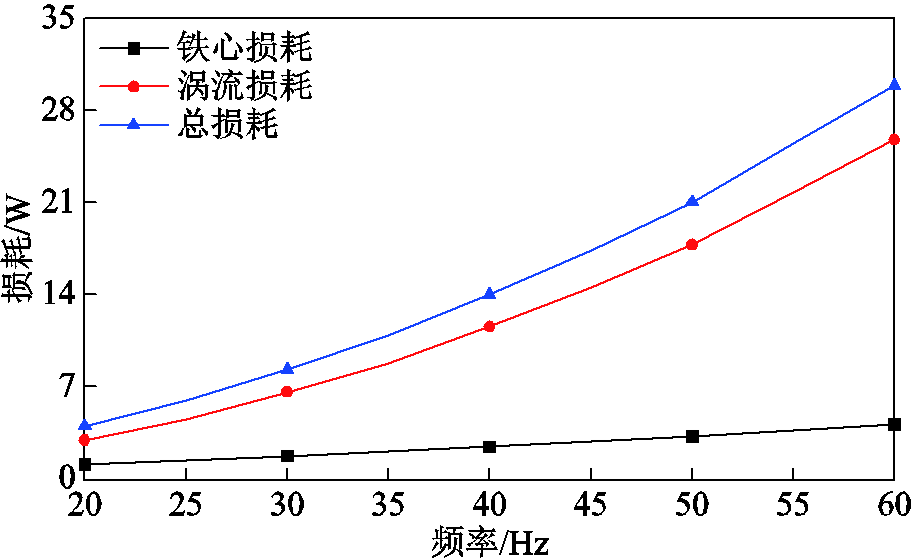
图13 混合叠压电机损耗随频率变化波形
Fig.13 Waveforms of loss variation with frequency in hybrid laminated motor
为了验证所提出的混合叠压方式对永磁直线振荡电机的影响,对电机进行了样机制造,如图14所示。图14中分别给出了电机的外定子、内定子、动子和电机整机装配结构。从图14可以看出,样机的外定子采用分段齿和轭的形式,这种方法有助于放置集中绕组。同时,两个钢板弹簧固定在电机壳体上,以支撑动子的移动。这种安装方法无需端盖和轴承,从而有效降低了电机的质量。

图14 实验样机
Fig.14 Developed test prototype
图15显示了电机原型测试平台。测试平台主要包括示波器、新型电机样机、旋转电机、磁力丝杠和推力传感器。磁力丝杠和旋转电机的组合可以实现直线运动。因此,可以通过调整旋转电机来测试实验样机的电磁性能。

图15 电机原型测试平台
Fig.15 Test platform of the proposed novel single-phase permanent magnet linear oscillation actuator
通过测试平台检测样机的电磁推力随动子位移的变化。采用抱闸将旋转电机固定在不同位置,然后对直线电机通入直流电流获得电磁推力。电磁推力随位移变化的对比波形如图16所示。由图16可以看出,实验得到的电磁推力与三维有限元模拟结果吻合得较好。由于装配过程中无法避免工艺误差的存在,样机的实际电磁推力比三维仿真的电磁推力小7%左右。但是与传统硅钢片的电磁推力仿真结果相比,在位置为10 mm处的饱和程度明显降低。
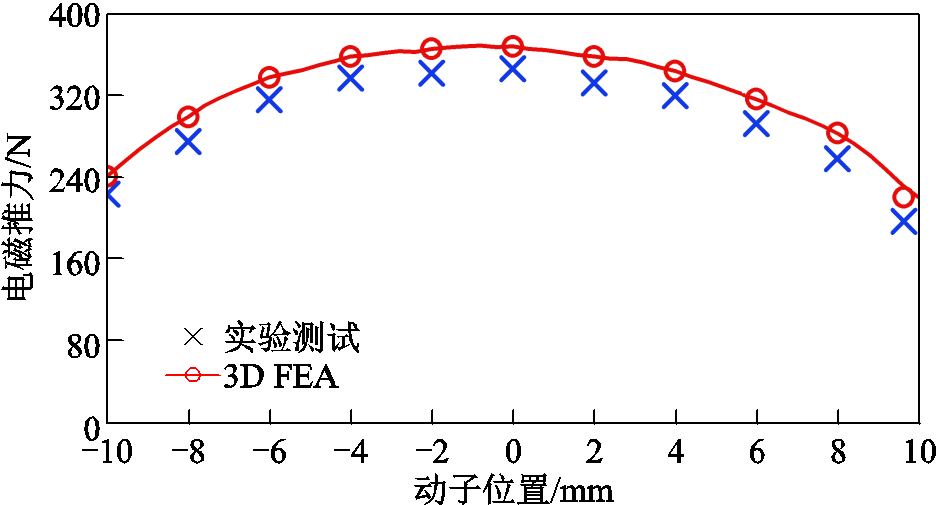
图16 实验与三维仿真定位力结果对比
Fig.16 Tested and 3-D simulated results of detent force
为了验证所提出直线振荡电机的电磁性能,图17显示了电机的三维模拟和测试反电动势随位移变化的波形。采用对拖测试平台实现反电动势测试,主要通过旋转电机和磁力丝杠带动直线振荡电机动子以频率为10 Hz进行正弦运动,有效行程为 ±8 mm。从图17中可以看出,测试的反电动势波形在动子减速阶段与仿真数据存在一定的误差,这主要与整个测试系统的测试精度有一定的关系,但总体趋势保持一致。同时由于测试电机采用的旋转电机,在做往复运动时存在一定的换向波动,因此导致实测反电动势中存在一定的波动。实验测试数据整体小于3D仿真结果,这还与电机装配过程中出现的装配误差有关,在理论计算时没有考虑绕组的出线孔,同时硅钢片齿与轭部之间存在装配气隙,这都会引起电机内部磁阻的增大,从而导致实际测试反电动势小于仿真结果。
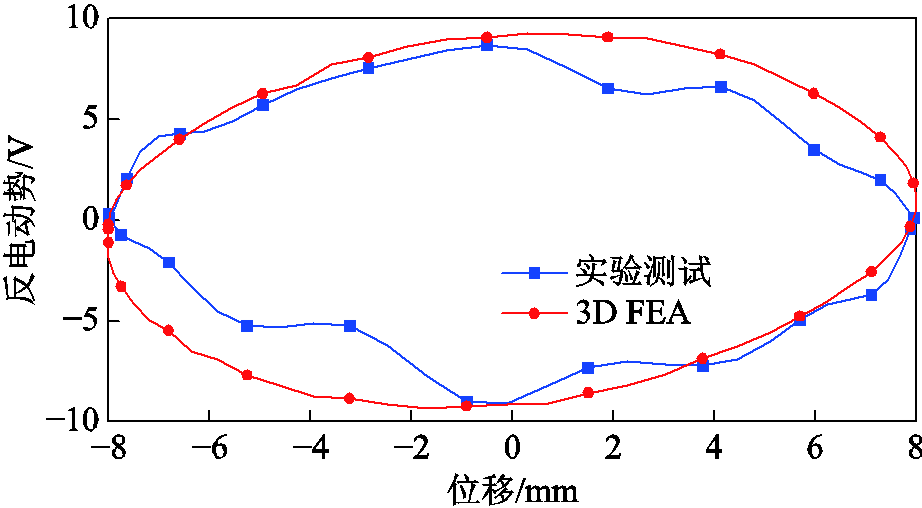
图17 实验与三维仿真空载反电动势对比
Fig.17 Tested and 3-D simulated results of back-EMF waveforms at no-load
图18所示为直线振荡电机在负载状态下的位移电流比和效率与频率的关系。此时保持输入电压不变,频率由40 Hz变化到65 Hz。如图18所示,随着频率的变化,电机的位移电流比先增大后减小,当其达到最大值时,频率等于52 Hz,即为机械谐振频率,而电机的效率也在此时达到最大值为84.5%。当频率由52 Hz增大到65 Hz时,效率从最大值下降到52%,下降幅度高达38.5%。同时根据图18可知,频率在48~52 Hz之间时,效率的变化幅度较小仅为4.8%,因此在直线振荡电机运行过程中可将频率控制在低于谐振频率的一定范围内,从而减小电机的控制难度。

图18 负载时位移电流比、效率与频率关系
Fig.18 Curves of displacement current ratio and efficiency with frequency under load
本文针对圆筒型双定子永磁直线振荡电机提出了一种新的混合叠压方式,对电机的定子采用电工纯铁和硅钢片混合装配的形式,推导了两种材料在内定子所占比例,并给出了电机损耗的计算公式,同时讨论了电工纯铁中硅钢片的数量对电机整体性能的影响,对比分析了电工纯铁的大小对涡流损耗的影响。另外采用3D有限元法对比分析了传统叠压方式和本文所提出的混合叠压方式对电机的影响。通过仿真和实验结果表明,本文所提出的混合叠压方式能够有效地降低直线振荡电机负载时的磁路饱和情况。同时,相较于仅有硅钢片叠压的直线振荡电机,采用混合叠压方式的电机能够将最大位置处的电磁推力提高26%。
参考文献
[1] Chen X, Zhu Z Q, Howe D. Modeling and analysis of a tubular oscillating permanent-magnet actuator[J]. IEEE Transactions on Industry Applications, 2009, 45(6): 1961-1970.
[2] 柴嘉伟, 贵献国. 音圈电机结构优化及应用综述[J].电工技术学报, 2021, 36(6): 1113-1125. Chai Jiawei, Gui Xianguo. Overview of structure optimization and application of voice coil motor[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1113-1125.
[3] Kim W H, Kim C W, Shin H S, et al. Optimal design of short-stroke linear oscillating actuator for minimization of side force using response surface methodology[J]. IEEE Transactions on Magnetics, 2022, 58(2): 1-5.
[4] 徐伟, 李想, 廖凯举, 等. 直线振荡电机拓扑结构及应用综述[J]. 电工技术学报, 2022, 37(21): 5377-5401. Xu Wei, Li Xiang, Liao Kaiju, et al. Overview of linear oscillatory machines: topology and application[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5377-5401.
[5] Wang J, Howe D, Lin Z. Analysis of a short-stroke, single-phase, quasi-Halbach magnetised tubular permanent magnet motor for linear compressor applications[J]. IET Electric Power Applications, 2008, 2(3): 193-200.
[6] 徐衍亮, 崔波, 张文晶, 等. 软磁复合材料-Si钢组合铁心盘式横向磁通永磁无刷电机[J]. 电工技术学报, 2020, 35(5): 983-990. Xu Yanliang, Cui Bo, Zhang Wenjing, et al. Disk transverse flux permanent magnet brushless motor based on soft magnetic composite-Si steel core[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 983-990.
[7] Wang Jiabin, Howe D, Lin Zhengyu. Design optimization of short-stroke single-phase tubular permanent-magnet motor for refrigeration applications[J]. IEEE Transactions on Industrial Electronics, 2010, 57(1): 327-334.
[8] 赵国新, 孔德财, 高晓林. 软磁复合材料与硅钢片材料的永磁电机性能差异研究[J]. 电工技术学报, 2018, 33(增刊1): 75-81. Zhao Guoxin, Kong Decai, Gao Xiaolin. Performance difference study on permanent magnet synchronous motor based on soft magnetic composite material and silicon steel sheet[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 75-81.
[9] 夏永明, 卢琴芬, 叶云岳, 等. 新型双定子横向磁通直线振荡电机[J]. 中国电机工程学报, 2007, 27(27): 104-107. Xia Yongming, Lu Qinfen, Ye Yunyue, et al. Novel flux reversal linear oscillatory motor with two divided stators[J]. Proceedings of the CSEE, 2007, 27(27): 104-107.
[10] 李想, 徐伟, 叶才勇. 新型定子永磁型动铁心式横向磁通直线振荡电机[J]. 中国电机工程学报, 2017, 37(21): 6209-6217. Li Xiang, Xu Wei, Ye Caiyong. Novel stator-magnet moving-iron transversal-flux linear oscillatory machine[J]. Proceedings of the CSEE, 2017, 37(21): 6209-6217.
[11] Kim K H, Park H I, Jeong S S, et al. Comparison of characteristics of permanent-magnet linear oscillating actuator according to laminated method of stator core[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1-4.
[12] 施振川. 圆筒型直线振荡电机关键问题研究[D]. 南京: 东南大学, 2018.
[13] 卢琴芬, 谢舸, 金勇等. 混合铁心横向磁通永磁电机的设计与分析[J] .中国电机工程学报, 2011, 31(9): 66-70. Lu Qinfen, Xie Ge, Jin Yong, et al. Design and analysis of a transverse-flux permanent magnet motor with hybrid iron-core[J]. Proceedings of the CSEE, 2011, 31(9): 66-70.
[14] Wang S P, Liu C C, Wang Y H, et al. Electromagnetic performance analysis of flux-switching permanent magnet tubular machine with hybrid cores[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(1): 43-52.
[15] 张春雷, 张辉, 叶佩青. 高霍尔位置检测精度的圆筒型永磁同步直线电机设计[J]. 电工技术学报, 2022, 37(10): 2481-2490. Zhang Chunlei, Zhang Hui, Ye Peiqing. Design of tubular permanent magnet synchronous linear motor by reliability-based robust design optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2481-2490.
[16] 许孝卓, 封海潮, 艾立旺等. U型永磁凸极直线电机结构及电磁特性[J]. 电工技术学报, 2021, 36(6): 1179-1189. Xu Xiaozhuo, Feng Haichao, Ai Liwang, et al. Structure and electromagnetic characteristics of U-shaped permanent magnet salient pole linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1179-1189.
[17] 曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020, 35(5): 1001-1012. Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001-1012.
[18] 张春雷, 张辉, 叶佩青, 等. 两相无槽圆筒型永磁同步直线电机电感计算与分析[J]. 电工技术学报, 2021, 36(6): 1159-1168. Zhang Chunlei, Zhang Hui, Ye Peiqing, et al. Inductance analysis of two-phase slotless tubular permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1159-1168.
[19] 付东山, 贾泽宇, 吴富强, 等. 新型斜气隙圆筒型横向磁通切换直线电机及其建模分析[J]. 中国电机工程学报, 2022, 42(15): 5706-5718. Fu Dongshan, Jia Zeyu, Wu Fuqiang, et al. Novel oblique air-gap tubular transverse flux switching permanent magnet linear motors and its modeling analysis[J]. Proceedings of the CSEE, 2022, 42(15): 5706-5718.
Abstract Tubular permanent magnet linear oscillating actuators (TPMLOA) have widely used in the application field of short-stroke and high frequency linear reciprocating, because of simple mechanical structure, without the rotary-to-linear conversion, low maintenance costs and fast dynamic response. However, the tubular structure and the special distribution of magnetic circuit pose significant challenges to the assembly of silicon steel sheets. The traditional assembly method is to laminate the silicon steel sheets in a circumferential direction, which leads to a low stacking coefficient of the silicon steel sheet of stator and can easily cause magnetic circuit saturation. At present, scholars have proposed some ways to increase the stacking coefficient and improve the performance of the TPMLOA, but these methods also increase the assembly difficulty and processing cost. Therefore, this paper proposes a hybrid lamination method to solve the above problems. The combination of silicon steel sheets and electrical iron materials can effectively reduce the assembly difficulty and increase stacking coefficient.
Firstly, the basic structure of a C-core double stator TPMLOA with three permanent magnets is introduced, and the magnetic circuit distribution and the operating principle of the motor at different positions is given. Secondly, the implementation method and related parameter determination of the hybrid lamination scheme proposed in this article is explained and derived, and the upper limit of the number of slots for electrical iron is determined. Thirdly, the influence of different quantities of silicon steel sheets in each slot on the electromagnetic performance of TPMLOA is compared and analyzed, and the optimal number of slots for electrical iron materials is determined. Finally, through three-dimensional finite element analysis (3D-FEA) and prototype experiments, the advantages of using a hybrid lamination TPMLOA in reducing magnetic circuit saturation and improving electromagnetic thrust capacity are verified.
By analyzing the impact of different numbers of silicon steel sheets in each slot on the performance of the TPMLOA, it can be concluded that as the number of silicon steel sheets in each slot increases, the amplitude of the back electromotive force (EMF) and electromagnetic thrust of the TPMLOA gradually decreases, while the iron core loss and eddy current loss also increase. Therefore, when the number of silicon steel sheets in each slot is 1, it is more conducive to improving the performance of the motor. The 3D-FEA results show that when the armature current is 20 A, compared to the traditional TPMLOA in a magnetic circuit saturation state, the magnetic field density of the stator in the hybrid lamination TPMLOA is only about 1.6T. Although the electromagnetic thrust of the two lamination methods is the same at the center position, the electromagnetic thrust of the hybrid lamination TPMLOA at the maximum position of 10 mm is 221 N, which is 26% higher than that of traditional TPMLOA. However, the effect of hybrid lamination method on the eddy current loss of the motor cannot be ignored. When the operating frequency is 40 Hz and the armature current is 20 A, the total core loss of the hybrid lamination TPMLOA is 13.8 W, which is greater than the 11.38 W of traditional TPMLOA. The comparison between prototype experiments and the simulation analysis shows that the electromagnetic thrust of the actual prototype is 7% smaller than that of the 3D-FEA, and the amplitude of the actual test back EMF is also smaller than the simulation results. Finally, load test is conducted on the prototype, and the resonance frequency of the surface linear oscillation motor is 52 Hz, and the efficiency of the TPMLOA reaches a maximum of 84.5%.
Through comparative analysis, the following conclusions can be drawn: (1) Compared with traditional lamination method, the hybrid lamination method proposed in this paper can effectively improve the saturation of the magnetic circuit and increase the electromagnetic thrust at the maximum position. (2) The hybrid lamination method causes an increase in eddy current loss, which reduces efficiency of the TPMLOA. Therefore, a block-based approach should be adopted to reduce eddy current loss. (3) TPMLOA has the highest efficiency at resonance frequency.
keywords:Permanent magnet linear oscillation actuator, hybrid lamination, tubular structure, finite element analysis, electromagnetic performance
DOI:10.19595/j.cnki.1000-6753.tces.230979
中图分类号:TM359.4
国家自然科学基金资助项目(51777029)。
收稿日期 2023-06-25
改稿日期 2023-07-23
张洪彬 男,1990年生,博士,研究方向为直线振荡电机设计及其控制。E-mail:hongbinzhang2014@163.com
徐志科 男,1978年生,副教授,硕士生导师,研究方向为新型超声波电机的运行理论及控制。E-mail:xuzhike@seu.edu.cn(通信作者)
(编辑 郭丽军)