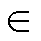(IDn0, IDn)，则在不同剩余电流激励下，漏电保护器均处于正常工作状态。摘要 漏电保护器在实际服役过程中可能会发生故障，但诱发其故障暴露的激励条件不具备时，其故障并不能显现出来。针对这一问题，提出一种计及隐藏故障的漏电保护器运行状态划分方法，建立基于马尔可夫过程的运行状态转移模型，实现漏电保护器的实际服役状态准确描述；设计基于蒙特卡洛法的漏电保护器可靠性仿真模型，以漏电故障频次、漏电流大小、保护器可靠性水平和运行时间为主要变量，对无检查和有检查下漏电保护器的状态概率进行仿真分析，确定了保证供电系统可靠性和安全性条件下的最低定期检查频次。该方法适用于不同可靠性水平的漏电保护器的分析与评估，对其定期检查策略的制定具有指导意义。
关键词：漏电保护可靠性 激励响应法 马尔可夫过程 定期检查 服役可靠性
漏电保护器（Residual Current Device, RCD）是非常重要的保护类电器，广泛应用于低压配电系统中，可防止电气线路和设备接地故障造成的漏电事故[1-4]。在服役过程中，漏电保护器可能会发生拒动或误动，丧失漏电保护功能，存在引发人身触电或漏电火灾的安全隐患。因此，进行漏电保护器可靠性研究具有重要的意义。
在漏电保护器可靠性研究方面，一般采用成功率来考核漏电保护可靠性[2-4]，该方法能有效检验漏电保护器是否存在故障，但在保护成功率验证方法上还有缺陷，同一时刻保护功能测量次数的多少几乎不影响漏电保护器是否可靠动作，无法准确反映漏电保护可靠性实际变化情况，因此需要对漏电保护器的实际服役状态进行研究。在服役过程中，漏电保护器存在多个运行状态，其自身发生故障后，只有诱发故障暴露的激励条件出现时，其故障状态才会显现，因此可以将漏电保护器的故障状态分为故障隐藏状态和故障显现状态。一般情况下，诱发漏电保护器故障暴露的激励条件主要是供电线路或用电设备产生的剩余电流，该特点符合激励响应的基本特征。许多学者通过激励响应模型进行可靠性预测和评估研究[5-10]，文献[8]研究了随机振动激励下电路板的响应情况，随机激励振动造成电路板疲劳破坏，存在疲劳极限，结合应力强度干涉模型得到电路板的疲劳寿命可靠性；文献[9]考虑非随机过程地震激励下埋地管道遭受应力情况，得到其动力响应，结合非概率可靠性理论得到小样本的实际工程情况下的抗震可靠性。
马尔可夫过程一般可以用来描述设备或系统不同运行状态的转移[11-25]，其在考虑状态转移随机性的同时，也考虑了各个状态出现的时序关联性，更贴近于实际运行情况。文献[13]运用马尔可夫理论分析了储能装置所处状态以及状态间相关转换过程，建立了可靠性模型，对比传统串联可靠性系统的可用度等指标，证明了该可靠性模型更符合实际工作场景；文献[14]针对综合能源系统，应用马尔可夫过程建立了状态转移模型，采用蒙特卡洛法分析该系统不同运行状态的转移情况，并结合能量指标，为能量转化设备在系统中的规划和运行提供参考；文献[15]将大型电力系统作为研究对象，通过蒙特卡洛模拟法反复抽样，得到与系统状态概率分布相同的马尔可夫链，模拟了电力系统实际运行情况。马尔可夫过程广泛应用于系统的可靠性建模和分析，对研究设备在不同运行环境的可靠性指标起到显著作用[11-23]。
本文根据漏电保护器在实际服役过程中的运行状态对其可靠性进行研究，解决保护类电器的可靠性评估问题，并反映隐藏故障对其服役状态的影响。
漏电保护器属于保护类电器，正常运行时长期保持不动作，供电线路或用电设备发生故障漏电时对其进行保护。
在实际服役过程中，漏电保护器有两种故障模式，即：供电线路或用电设备发生故障漏电时，漏电保护器不能迅速可靠动作，无法切断故障线路，漏电保护器拒动作，此时，若供电线路或用电设备产生的剩余电流小于漏电动作值时，则漏电保护器一直处于闭合状态，无法判断漏电保护器是否存在拒动故障，只有当供电线路或用电设备产生的剩余电流达到或超过漏电保护器动作值时，漏电保护器应当动作而没有动作，呈现出拒动故障状态；供电线路或用电设备没有故障漏电时，漏电保护器断开正常运行的线路，漏电保护器误动作，若供电线路或用电设备产生的剩余电流大于漏电动作值，则漏电保护器断开供电线路，也无法判断漏电保护器是否存在误动故障，只有当供电线路或用电设备产生的剩余电流小于漏电动作值时，漏电保护器不应当动作而动作，呈现出误动故障状态。
因此，漏电保护器处于不同状态时，在剩余电流激励下产生不同的响应，通过其响应可以判断出漏电保护器的状态，并对其可靠性进行评估。
漏电保护器的实际服役状态受其保护特性的影响，可以根据表征保护特性的所有参数来分析其可靠性，也可以将其中之一作为代表来分析其可靠性。漏电保护特性主要包括漏电动作值和漏电动作时间，当漏电保护特性符合要求时，无论供电线路或用电设备是否存在故障漏电，漏电保护器均处于正常工作状态。漏电保护器自身发生故障后，其漏电保护特性不符合要求，若没有诱发故障显现的条件出现，虽然漏电保护功能丧失，但仍可以保持线路正常供电或用电设备的正常工作，漏电保护器处于故障隐藏状态。若某一时刻漏电保护器故障显现的激励条件出现，其故障就会立刻显现，此时漏电保护器进入故障显现状态。
实际服役过程中漏电保护器对应为五种工作状态，即：正常工作状态、拒动故障隐藏状态、误动故障隐藏状态、拒动故障显现状态、误动故障显现状态。若将漏电动作值IDd作为漏电保护特性的判断依据，并对比IDd与额定剩余不动作电流IDn0和额定剩余动作电流IDn的大小，则根据供电线路或用电设备的剩余电流ID 进行漏电保护器运行状态描述，其状态如下：
状态1（正常工作状态）：漏电保护器自身没有故障，即IDd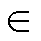(IDn0, IDn)，则在不同剩余电流激励下，漏电保护器均处于正常工作状态。
状态2（拒动故障隐藏状态）：漏电保护器发生拒动故障，即IDd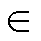(IDn, ∞)、ID
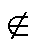(IDn, IDd)，则漏电保护器处于拒动故障隐藏状态。此时虽能保持供电线路或用电设备的正常用电，但存在重大安全隐患。
状态3（误动故障隐藏状态）：漏电保护器发生误动故障，即IDd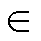[0, IDn0
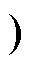、ID(ID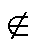d, IDn0]，则漏电保护器处于误动故障隐藏状态。此时虽能保持供电线路或用电设备的正常用电，但随时会中断供电线路或用电设备的正常用电。
状态4（拒动故障显现状态）：漏电保护器发生拒动故障，即IDd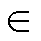(IDn,∞)、ID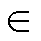(IDn, IDd)，则漏电保护器处于拒动故障显现状态。此时无法对供电线路或用电设备的故障漏电进行有效保护，可能引起人身伤亡或漏电火灾事故的发生。
状态5（误动故障显现状态）：漏电保护器发生误动故障，即IDd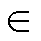[0, IDn0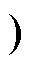、ID(ID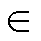d, IDn0]，则漏电保护器处于误动故障显现状态。此时无法保障供电线路或用电设备的正常运行，可能造成不必要的经济损失。
若考虑漏电动作时间的影响，只需要依据其是否满足漏电保护特性，仍可以将漏电保护器的运行状态划分为以上五种状态。虽然以下分析中仅以漏电动作值为例进行分析，但很容易将其方法拓展到同时考虑漏电动作值和动作时间影响下的状态分析。
马尔可夫过程是一种基于概率统计的随机过程，可以描述设备或系统在开始运行后各状态之间的转移过程，该过程具有无记忆性，假设设备或系统在运行过程中所处状态{X(t), t≥0}对于任意时间t1＜t2＜…＜tn，离散状态空间为E{x1, x2,…, xn}，在tn+1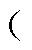
tn＜tn+1
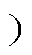时刻，其状态X(tn+1)仅与X(tn)=xn有关，与X(t1)=x1,…, X(tn-1)=xn-1无关，即设备或系统的下一个状态只与当前状态有关，与之前状态无关。对比漏电保护器的五种状态之间关系，状态4和状态5对应的当前时刻状态必然是状态2和状态3，而与状态1（之前状态）无关，即下一时刻状态仅与当前状态有关，满足马尔可夫性，可以用马尔可夫过程描述漏电保护器状态转移情况。
为了更加清晰地利用马尔可夫过程描述漏电保护器的状态转移情况，进行如下假设：
（1）指数分布适用于描述偶然发生的故障，其可靠性特征量可用简单而精确的公式计算，使用方便，因此假设漏电保护器的误动故障和拒动故障偶然发生且相互独立，服从指数分布，拒动故障或误动故障均会使漏电保护器失去漏电保护功能，二者构成串联关系。
（2）泊松分布常用于分析单位时间内随机事件发生的次数，可以用来描述故障漏电发生频次，满足随机性和不确定性。因此，用参数为ll的指数分布描述线路中故障漏电的发生时间序列，则故障漏电发生次数服从参数为ll的泊松分布，即故障漏电频次为ll。
（3）正态分布常用于分析生产过程或环境影响带来的质量差异，因此供电线路或用电设备正常运行时的剩余电流ID 和故障漏电时产生的剩余电流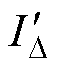
的大小用正态分布描述，即ID～N(mD, 
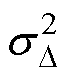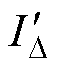)和～N(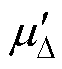
, 
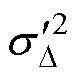)，剩余电流均值和方差反映了漏电严重程度。
（4）当漏电保护器发生故障后，存在满足故障显现条件的正常漏电电流或故障漏电电流，其故障将暴露，因此激励条件和漏电保护器故障情况满足并联关系。
（5）漏电保护器在初始投入使用时处于正常状态，同时其保持原有状态和转移到下一状态的概率和为1。
不考虑激励作用时，影响漏电保护器运行状态的因素只有保护器可靠性水平，此时，可靠性框图如图1所示。
不考虑激励作用时漏电保护器状态转移如图2所示。
图1 不考虑激励时漏电保护器的可靠性框图
Fig.1 Reliability block diagram of RCD without excitation conditions
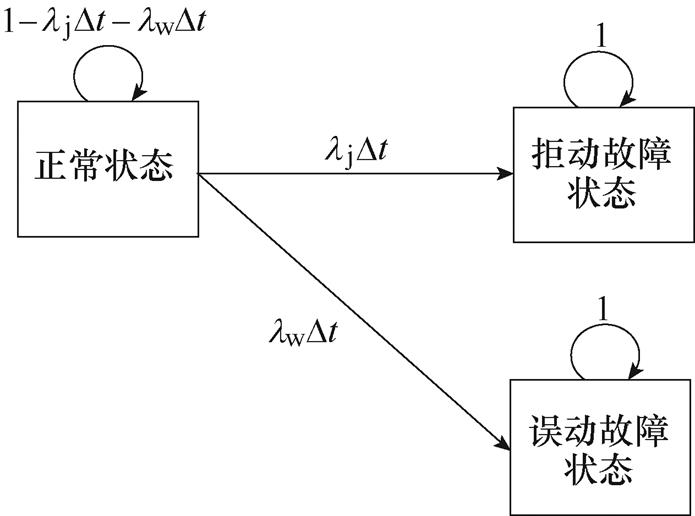
图2 不考虑激励作用时漏电保护器状态转移
Fig.2 State transition diagram of RCD without excitation conditions
图2中，正常工作状态为状态1，拒动故障状态包括状态2（拒动故障隐藏状态）和状态4（拒动故障显现状态），误动故障状态包括状态3（误动故障隐藏状态）和状态5（误动故障显现状态），每条线段表征两个状态之间的转移。由于拒动率lj或误动率lw是单位时间内漏电保护器拒动或误动发生的概率，即在单位时间内由正常状态转移到拒动故障状态或误动故障状态的概率，则转移概率ljDt、lwDt为Dt时间内漏电保护器由正常工作状态转移到拒动或误动故障状态的概率。
漏电保护器可靠性水平影响了正常工作状态和故障状态的概率（包括故障隐藏状态和显现状态的概率），由于假设漏电保护器故障服从指数分布，此时正常工作状态概率p1(t)和故障状态概率p2～5(t)满足
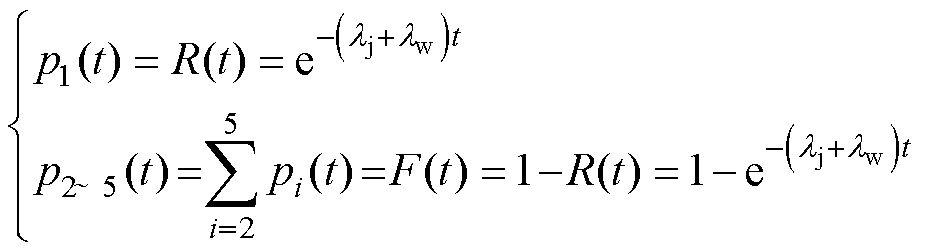
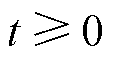（1）
式中，F(t)为累积失效概率；pi(t)（i=2～5）分别对应状态2～状态5的概率。
漏电保护器可靠性水平越高，拒动率和误动率越小，处于正常工作状态的概率越高，处于故障状态的概率越低。
在实际服役过程中，漏电保护器运行状态受到供电线路或用电设备产生的剩余电流（激励）影响，其可靠性框图如图3所示。
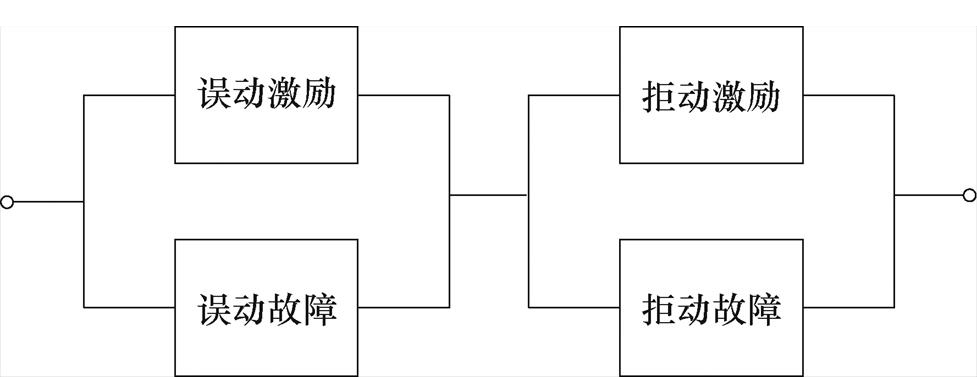
图3 激励作用下漏电保护器的可靠性框图
Fig.3 Reliability block diagram of RCD under excitation conditions
结合图3，利用马尔可夫过程来描述漏电保护器状态1～状态5对应的状态转移过程，如图4所示。
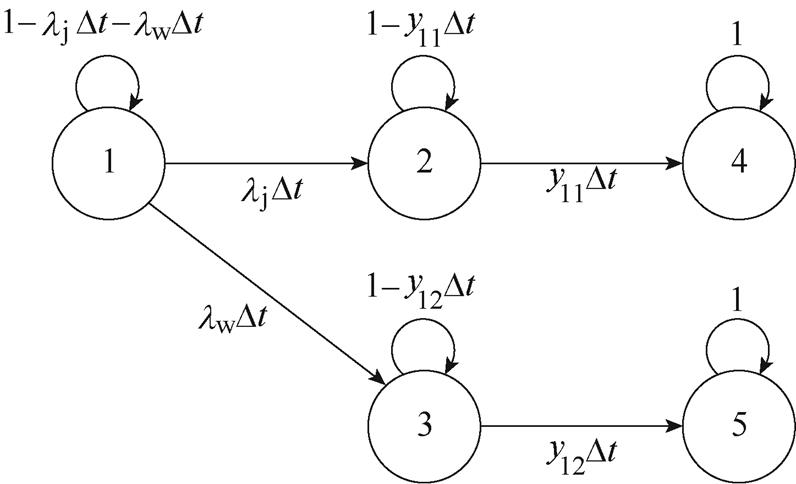
图4 基于马尔可夫过程的漏电保护器状态转移
Fig.4 State transition diagram of RCD based on Markov process
图4中，转移概率yl1Dt是Dt时间内漏电保护器由拒动故障隐藏状态转移到显现状态的概率，转移概率yl2Dt是Dt时间内使漏电保护器由误动故障隐藏状态转移到显现状态的概率，转移率yl1和yl2取决于满足漏电保护器故障隐藏状态转移到显现状态的条件，即供电线路或用电设备中漏电发生率。拒动激励是故障漏电，所以拒动转移概率应是故障漏电发生率与故障漏电剩余电流ID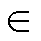(IDn, IDd)的概率的积，而误动激励是正常漏电，正常漏电是一直存在的，其发生概率为1，所以误动转移概率就是正常漏电剩余电流ID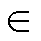(IDd, IDn0)的概率。因此，转移率yl1和yl2计算方法[26]分别为
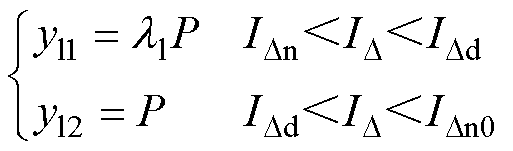（2）
漏电保护器状态转移概率满足
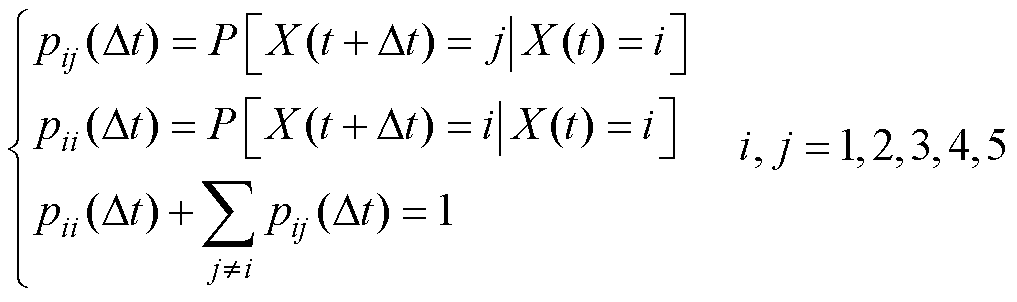（3）
式中，pii(Dt)为漏电保护器状态转移概率，t时刻漏电保护器处于状态i条件下，在t+Dt时刻保持状态i的概率；pij(Dt)为t时刻漏电保护器处于状态i条件下，在t+Dt时刻状态转移到状态j的概率。
根据式（3），将转移概率写成矩阵形式，记为
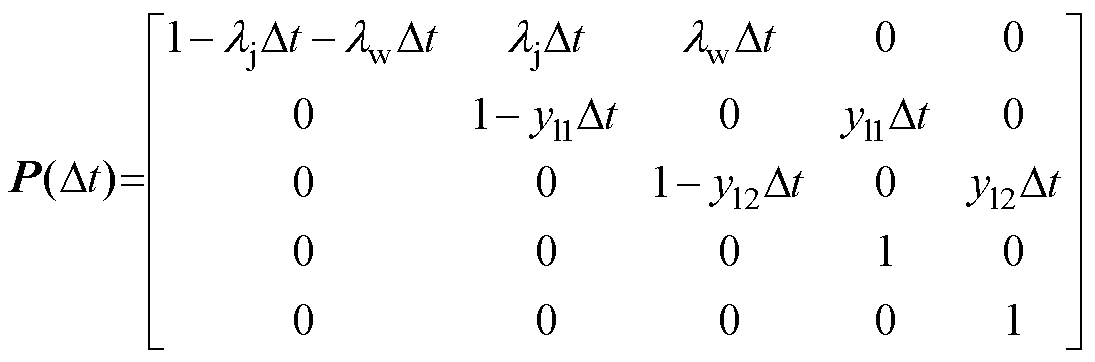（4）
对有限状态空间的马尔可夫过程，转移密度qij和qii定义[21]为
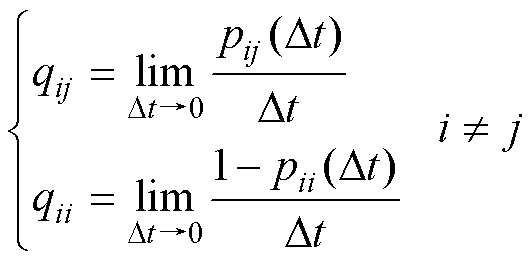（5）
即构成的转移密度矩阵M为
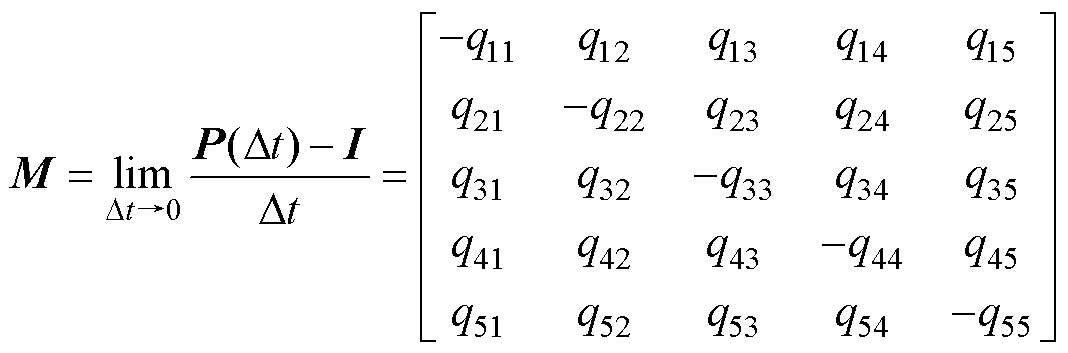
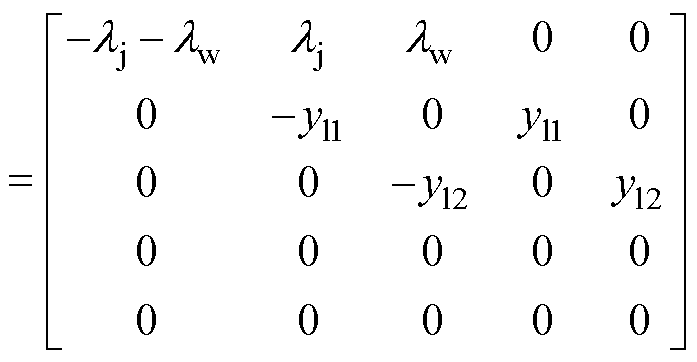（6）
式中，I为单位矩阵。
根据全概率公式，t+Dt时刻处于任意状态j的状态概率[13]为
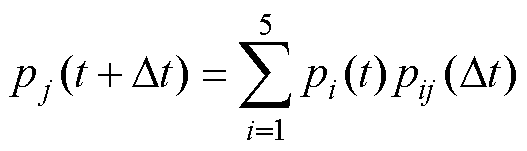（7）
矩阵形式为
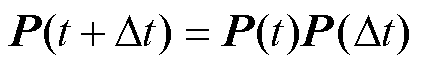（8）
式中，t时刻处于状态i的概率pi(t)=P(X(t)=i), i=1～5，状态概率P(t+Dt)=
p1(t+Dt) p2(t+Dt) p3(t+Dt) p4(t+Dt) p5(t+Dt)
，P(t)=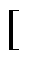p1(t) p2(t) p3(t) p4(t) p5(t)。
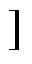由微分定义，令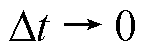
得
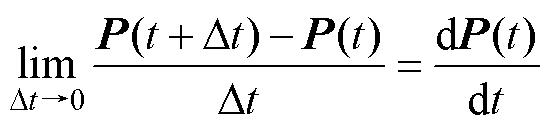（9）
将式（8）、式（9）联立求解，且初始时刻各个状态的概率为P(0)=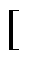1 0 0 0 0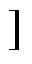，则P(t)满足
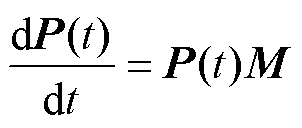（10）
展开后得到
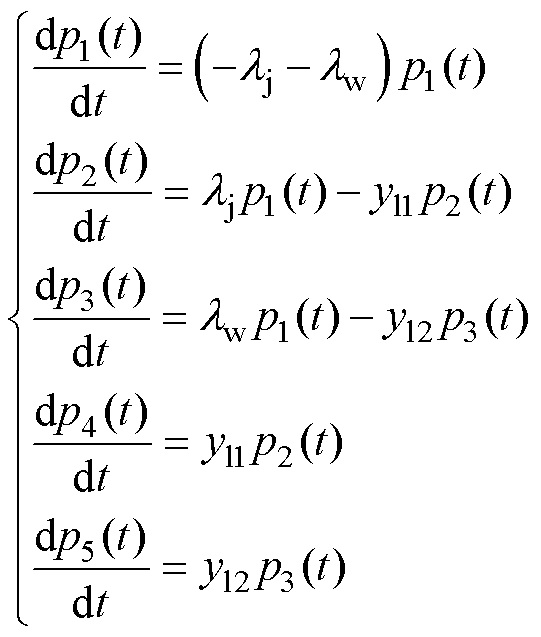（11）
通过式（11）可以得到漏电保护器服役过程中运行状态的状态概率。
结合图4及上述分析可知，漏电保护器故障是否显现，受故障严重程度和运行环境的影响。其故障严重程度可以采用保护器可靠性水平和动作值大小进行描述；同时对漏电保护器服役环境进行划分，不同场所下正常漏电和故障漏电不同，可以将其划分为三种环境条件。
（1）良好运行环境。如一般住宅或办公等场所，当漏电保护器服役于该环境下时，供电线路或用电设备正常运行时的剩余电流较小，漏电保护器应长期保持不动作，确保正常供电，且故障漏电发生频次低，剩余电流幅值不大。运行条件可以假设为：正常漏电电流ID1～N(mD1,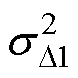 
)满足mD1+2sD1≤0.25IDn0和mD1-3sD1≥0，即正常漏电电流ID1～N(0.15IDn0, (0.05IDn0)2)，故障漏电电流发生频次ll为0.1或0.5次/年，分别表示10年或两年出现一次漏电故障，故障剩余电流分布满足
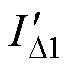～N(IDn, (0.1IDn)2)。
此时，若漏电保护器发生拒动故障，其动作值IDd大于额定动作值IDn，由于供电线路或用电设备正常运行时的剩余电流不满足拒动故障显现条件（ID∈(IDn, IDd)），拒动故障一般会处于隐藏状态；若漏电保护器发生误动故障，其动作值IDd小于额定不动作值IDn0，供电线路或用电设备正常运行时的剩余电流容易满足ID∈(IDd, IDn0]，误动故障显现出来。因此，在实际用电过程中人们感受到的误动故障会多于拒动故障。
（2）一般运行环境。如商业、一般实验或轻工业生产等场所，当漏电保护器服役于该环境，供电线路或用电设备正常运行时的剩余电流高于良好环境下的值，但漏电保护器也长期保持不动作，能保证正常供电。在该环境下故障漏电发生频次高于良好环境下的值，且剩余电流幅值也较大，其数值分散性增大。运行条件可以假设为：正常漏电电流ID2～N(mD2,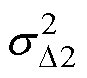 
)满足mD2+2sD2≤0.5IDn0和mD2-3sD2≥0，即正常漏电电流ID2～N(0.3IDn0, (0.1IDn0)2)；故障漏电发生频次ll为0.5或2次/年，分别表示两年或半年出现一次漏电故障，故障剩余电流
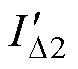～N(1.5IDn, (0.2IDn)2)。
一般运行环境下，若漏电保护器发生拒动故障，其动作值IDd大于额定动作值IDn，当供电线路或用电设备产生的漏电电流满足拒动故障显现条件（ID(IDn, IDd)）时，拒动故障显现，且在相同拒动率下，拒动作显现频率高于良好运行环境；若漏电保护器发生误动故障，其动作值IDd小于额定不动作值IDn0，供电线路或用电设备正常运行时的剩余电流较大，误动作显现频率高于良好运行环境。因此，该运行环境下，漏电保护器显现出的故障既有误动故障又有拒动故障。
（3）恶劣运行环境，如户外、农网及重工业生产等场所，当漏电保护器服役于该环境，供电线路或用电设备正常运行时的剩余电流高于一般环境下的值，甚至可能接近漏电保护器的剩余电流动作值。在该环境下故障漏电发生频次明显增大，且剩余电流幅值也增大。运行条件可以假设为：正常漏电电流ID3～N(mD3,
)满足mD3+2sD3≤IDn0和mD3-3sD3≥0，即正常漏电电流ID3～N(0.6IDn0, (0.2IDn0)2)；故障漏电发生频次ll为2或5次/年，分别表示半年或两个半月出现一次漏电故障，故障剩余电流满足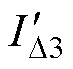
～N(5IDn, (0.3IDn)2)。
在恶劣运行环境下，若漏电保护器发生拒动故障，其动作值IDd大于额定动作值IDn，由于该环境下故障漏电发生频次增加，拒动故障更容易显现出来；若漏电保护器发生误动故障，供电线路或用电设备正常运行时的剩余电流较大，误动作显现频率明显增加。因此，拒动作和误动作显现频率高于一般环境和良好运行环境。
根据漏电保护器运行规范，需要通过定期按其试验按钮来检查漏电保护功能是否正常。定期检查是在漏电保护器可靠性水平不改变的前提下，通过及时更换处于故障隐藏状态的保护器，使其恢复到初始工作状态，在保证供电系统安全性的前提下，提升供电线路或用电设备的供电可靠性。因此，通过定期检查漏电保护器的漏电保护功能，可以尽早发现其故障隐藏状态，消除隐藏故障带来的隐患，通过减少拒动故障隐藏状态出现次数提高供电安全性，或者减少误动故障隐藏状态出现次数提高连续供电能力，并减少故障显现状态出现次数，从而提升供电线路或用电设备的供电可靠性和安全性。基于定期检查的漏电保护器状态转移模型如图5所示。
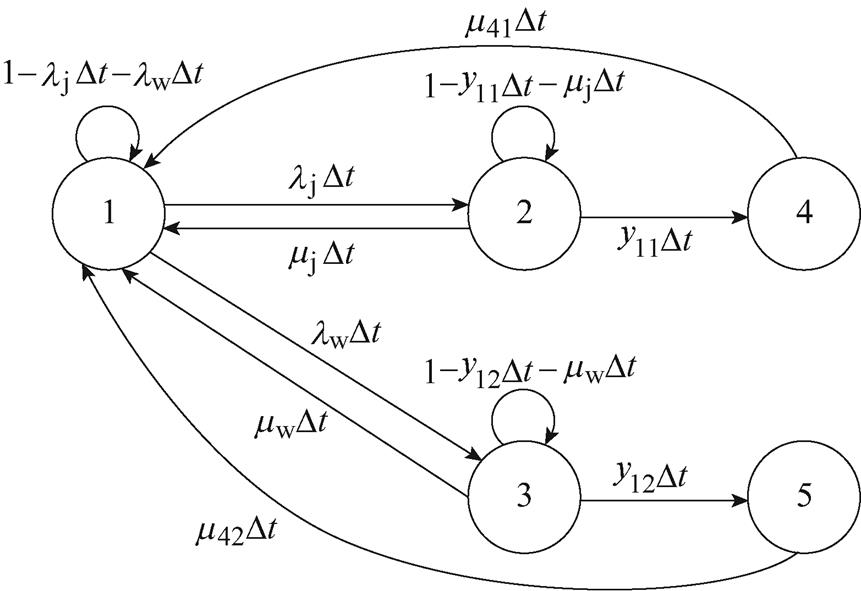
图5 基于定期检查的漏电保护器状态转移
Fig.5 State transition diagram of RCD based on periodic inspection
图5中，转移率mj、mw为定期检查率，转移概率mjDt、mwDt为Dt时间内漏电保护器由拒动或误动故障隐藏状态转移到正常工作状态的概率；m41、m42为更换率，转移概率m41Dt、m42Dt为Dt时间内更换漏电保护器（维修）使其从故障显现状态转移到正常工作状态的概率。
对应的转移密度矩阵M为
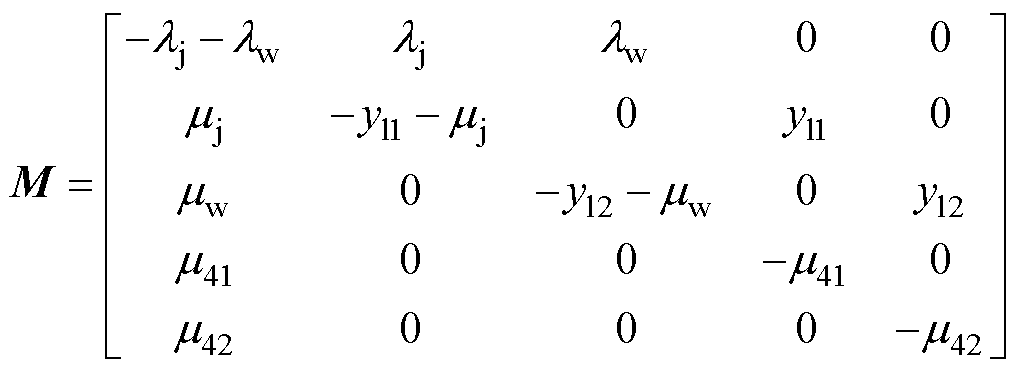（12）
结合式（10），得到此时的瞬时状态概率为
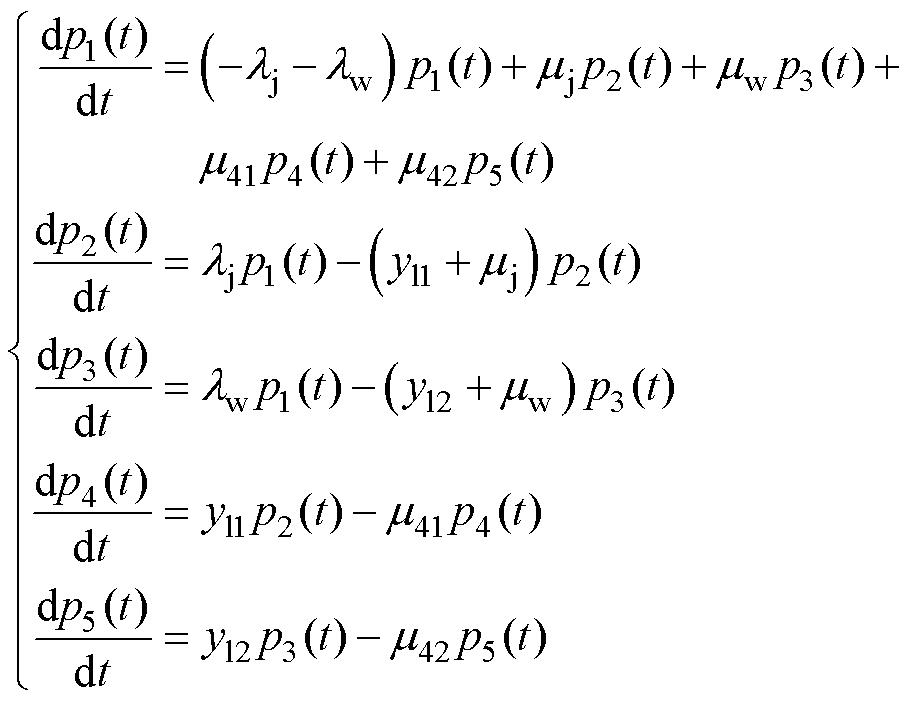（13）
在第一次检查前，漏电保护器状态概率分布与无定期检查时相同。通过定期检查发现故障隐藏状态后，立即更换漏电保护器，使其状态返回到正常工作状态（状态1），从第二个检查周期开始，各个状态的概率改变，使得漏电保护器处于正常工作状态（状态1）的概率增加，故障状态（状态2～状态5）的概率降低，降低出现故障显现状态时进行漏电保护器更换的次数，减少有害影响，有效保障供电线路和用电设备的正常运行。
由于故障漏电发生次数比较少，较低的定期检查频次可以及时发现处于拒动故障隐藏状态的保护器，但供电线路或用电设备长期存在正常漏电，误动故障显现状态概率仍然较高，需要大幅度提高检查频次，才能及时发现误动故障隐藏状态。因此，定期检查频次如何选取至关重要，检查频次低可能会造成不能及时发现处于故障隐藏状态的漏电保护器，而检查频次过高可能会由于过度检查而造成检查费用过高。定期检查频次较高时，无法通过人工检查实现，需要带有自检功能的漏电保护器自动完成检查，否则人工成本和费用太高，实际中无法实现。在满足电力系统供电可靠性水平条件下，进行定期检查频次对运行状态影响分析，可以为确定漏电保护器检查频次提供参考。
利用蒙特卡洛法[27]模拟漏电保护器运行场景，包括拒动率、误动率、正常漏电电流、故障漏电发生频次、定期检查频次等参数，验证漏电保护器实际运行状态和服役状态概率的影响，可靠性模拟仿真分析流程如图6所示。
为便于模拟仿真，漏电保护器特征及其运行条件处理方法如下：
（1）样本数量越多，越能接近实际，本文选取漏电保护器样本数量n=1 000。考虑漏电保护器服役10年的可靠性，因此仿真年限选取为10年，若要求漏电保护器服役10年时可靠度在0.9或0.95以上，且满足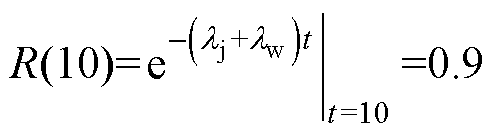
或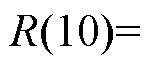
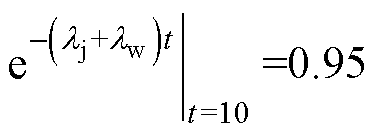。为了简化分析过程，认为漏电保护器拒动率和误动率相同，则拒动率和误动率满足lj=lw≤0.005 26（1次/年）或lj=lw≤0.002 56（1次/年）。
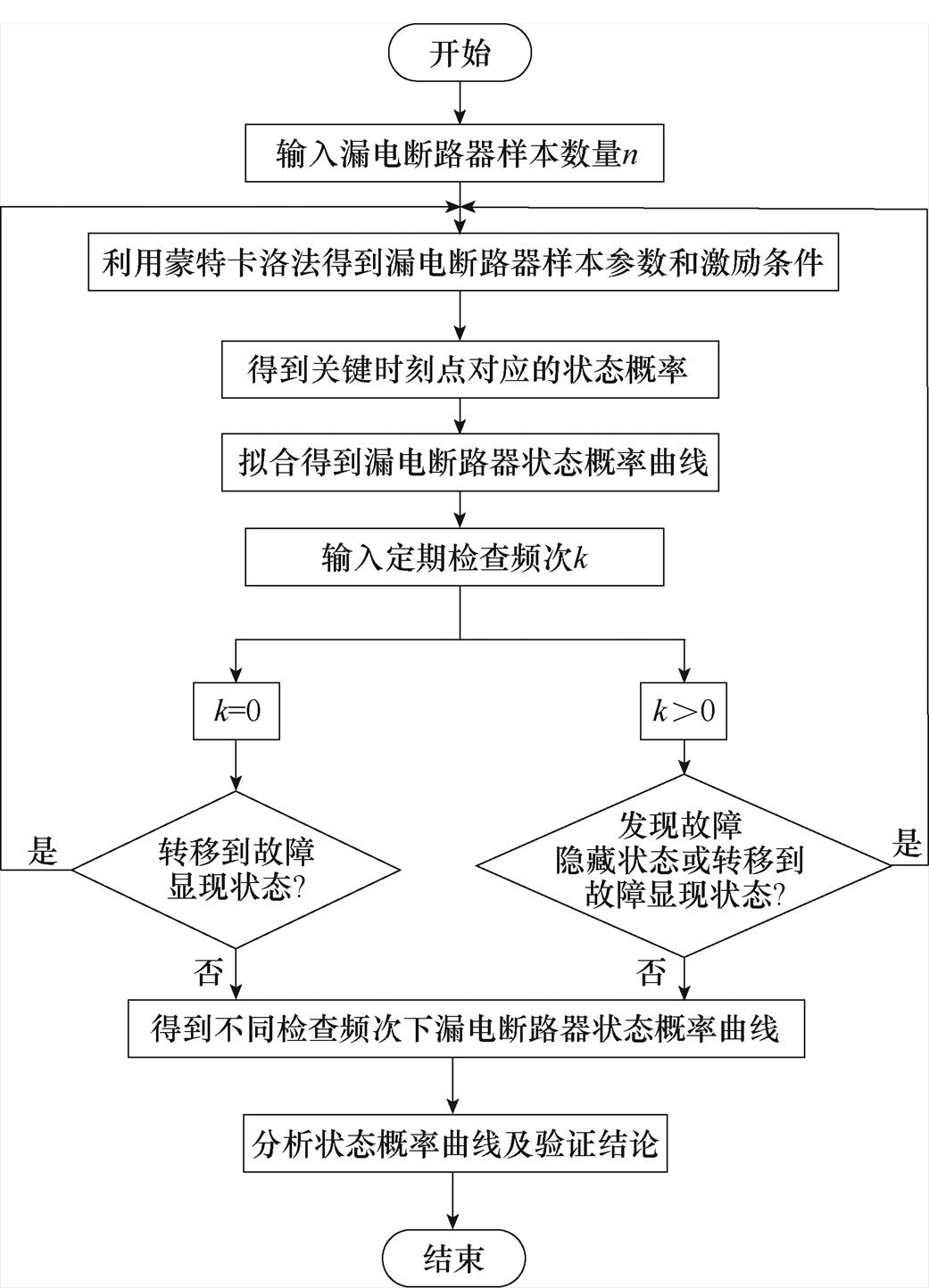
图6 漏电保护器服役可靠性仿真过程
Fig.6 Service reliability simulation process of RCD
（2）漏电保护器动作值的标幺化。额定剩余动作电流值IDn的标幺值为1(pu)，额定剩余不动作电流IDn0的标幺值为0.5(pu)。
（3）漏电保护器样本数据的产生。按照一定分布规律产生样本数据，包括故障类型（拒动、误动）、故障时间。漏电保护器故障程度不同，其故障后的动作值也会不同，并对服役状态产生影响。因此，将误动故障分为五种不同程度的故障，其动作值IDd分别为0、0.1IDn、0.2IDn、0.3IDn和0.4IDn。将拒动故障分为六种不同程度的故障，其动作值IDd分别为1.1IDn、1.5IDn、2.5IDn、5IDn、6IDn和10IDn。通过上述参数反映不同可靠性水平的漏电保护器服役情况。
（4）激励条件的产生。用于模拟供电线路和用电设备（被保护对象）的漏电数据，包括正常剩余电流、漏电故障频次及发生时间、故障剩余电流，其值大小反映不同激励强度，代表不同故障严酷程度。
（5）定期检查影响分析。无定期检查（k=0）时，只有故障显现才能发现其故障。有定期检查（k＞0）时，可以通过定期检查，发现其故障隐藏状态。在漏电保护器自身可靠性无法满足供电线路或用电设备的供电可靠性要求下，通过定期检查可以提高供电可靠性。
（6）漏电保护器运行状态可靠性的计算。统计某一时刻漏电保护器的工作状态，可以得到该时刻不同状态的概率值为
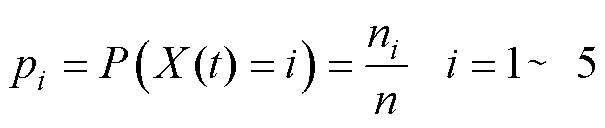（14）
式中，ni（i=1～5）指t时刻n个漏电保护器中处于状态i的数量。最后对各时刻点进行拟合，得到漏电保护器的状态概率曲线，分析并验证漏电保护器可靠性水平、激励条件及检查策略对漏电保护器服役可靠性的影响。
漏电保护器实际服役过程中，供电线路或设备运行环境不同，正常漏电电流大小和故障漏电严酷程度不同。结合2.1节中设定的数值，将三种运行环境下的正常漏电电流分布和故障漏电对应的剩余电流值进行标幺化，见表1。
表1 不同运行环境下漏电参数设定
Tab.1 Setting of leakage parameters under different operating environments
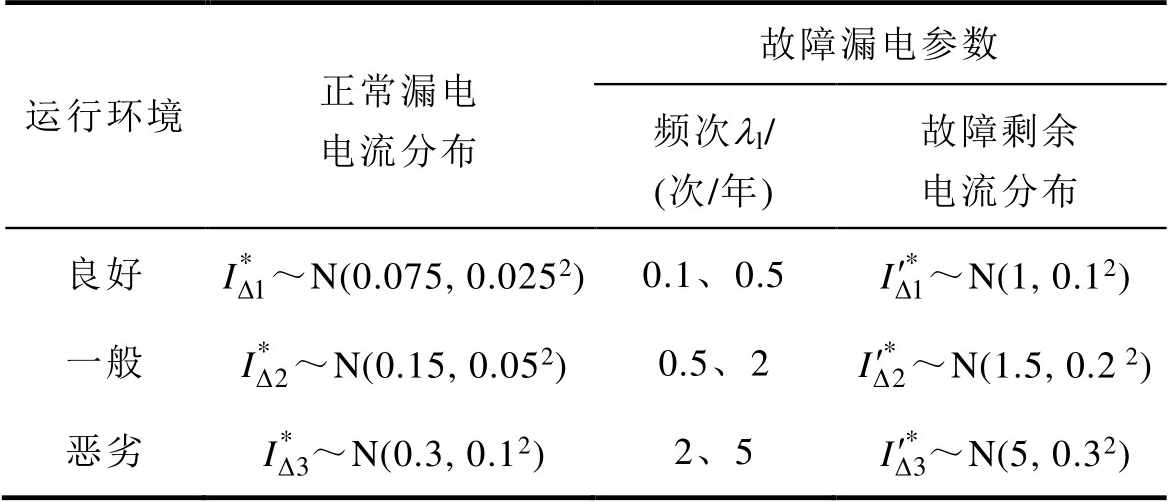
运行环境正常漏电电流分布故障漏电参数 频次ll/ (次/年)故障剩余电流分布 良好～N(0.075, 0.0252)0.1、0.5～N(1, 0.12) 一般～N(0.15, 0.052)0.5、2～N(1.5, 0.2 2) 恶劣～N(0.3, 0.12)2、5～N(5, 0.32)
为了研究漏电保护器可靠性水平对其运行状态的影响，保证同一运行环境下，对服役10年时可靠度为0.9（R(10)=0.9）和0.95（R(10)=0.95）的漏电保护器分别进行模拟分析，状态概率曲线如图7所示。可以看出，正常工作状态和故障状态的概率曲线符合指数分布，即与漏电保护器可靠度函数式（1）近似相同。漏电保护器服役时间越长，发生故障的概率越高，且漏电保护器可靠性水平越高，正常工作状态概率越高，而故障状态概率越低。在拒动率和误动率相等情况下，两种故障模式发生的概率相同。
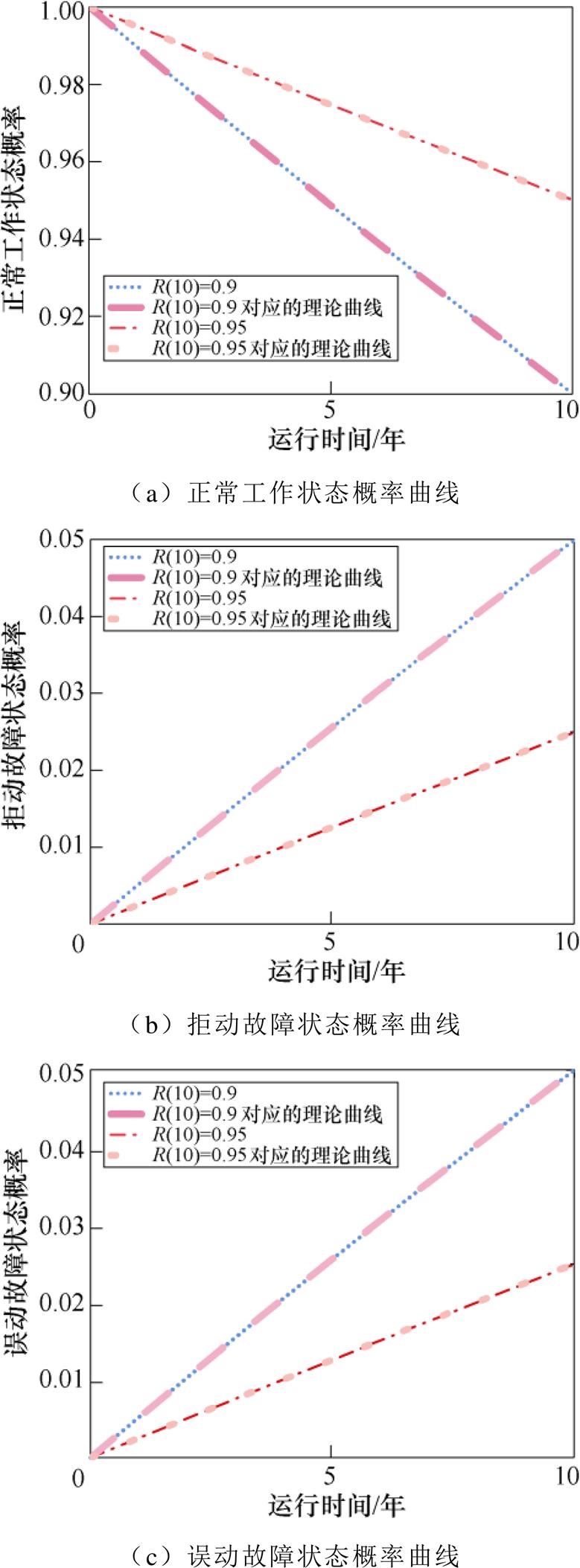
图7 漏电保护器的服役状态概率
Fig.7 Service state probability diagram of RCD
为了验证激励条件和漏电保护器故障程度对漏电保护器服役状态的影响，以R(10)=0.9为例进行漏电保护器运行状态的模拟仿真。三种不同运行环境下漏电保护器故障隐藏和显现状态概率（状态2～状态5）曲线如图8～图10所示。可以看出，不同运行环境和不同故障程度（动作值不同）条件下故障隐藏和显现状态概率存在较大差别。在同一运行环境下，漏电保护器故障程度越严重，其动作值偏离正常范围（0.5IDn～IDn）越大，故障显现状态概率越大，即验证了误动故障发生后其动作值越小，误动显现概率越高，拒动故障发生后其动作值越大，拒动显现概率越高。
图8和图9分别为三种运行环境下拒动故障隐藏和显现状态概率曲线。图中，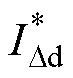
为漏电电流标幺值。可以发现，拒动故障隐藏状态和显现状态的概率受故障漏电发生频次和故障程度的影响，故障漏电频次越大，拒动故障显现状态概率越高，但由于供电线路或用电设备产生的故障漏电发生频次很低，所以部分拒动故障仍会处于隐藏状态。在良好运行环境下，漏电保护器拒动后动作值为1.5IDn～10IDn时状态概率曲线重合，这是由于良好运行环境时故障漏电电流范围在（0.7IDn, 1.3IDn）（正态分布3s 原则），动作值大于1.3IDn后，线路或用电设备只要发生故障漏电，均满足拒动故障显现条件，显现概率相同，如图8a和图9a所示。但由于故障漏电频次很小，很少发生，所以拒动故障显现概率很低。
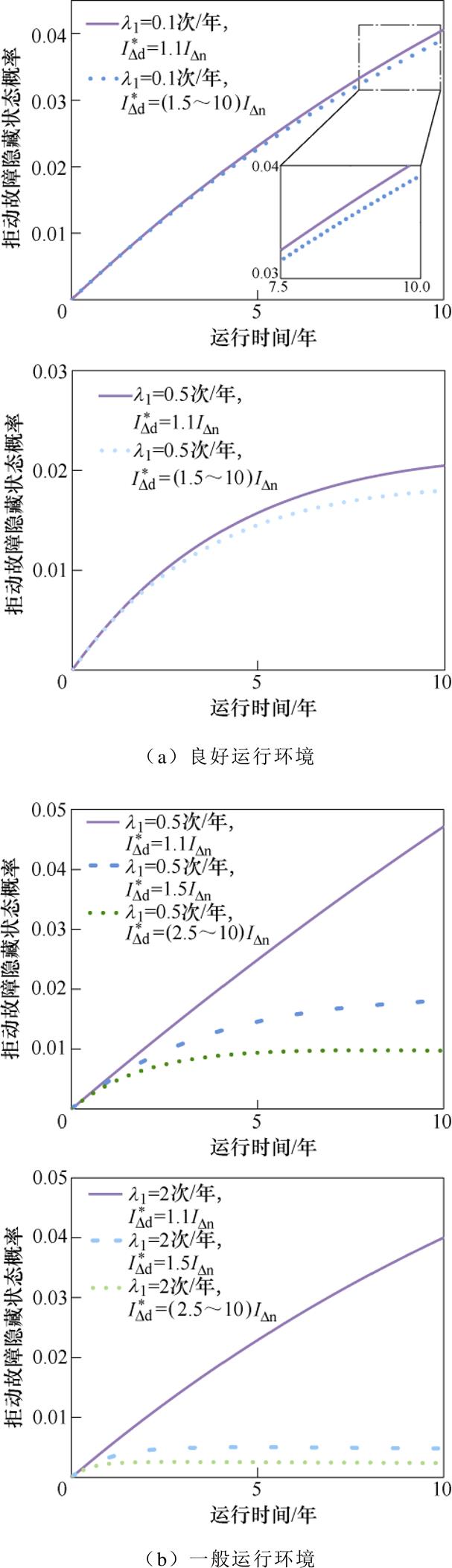
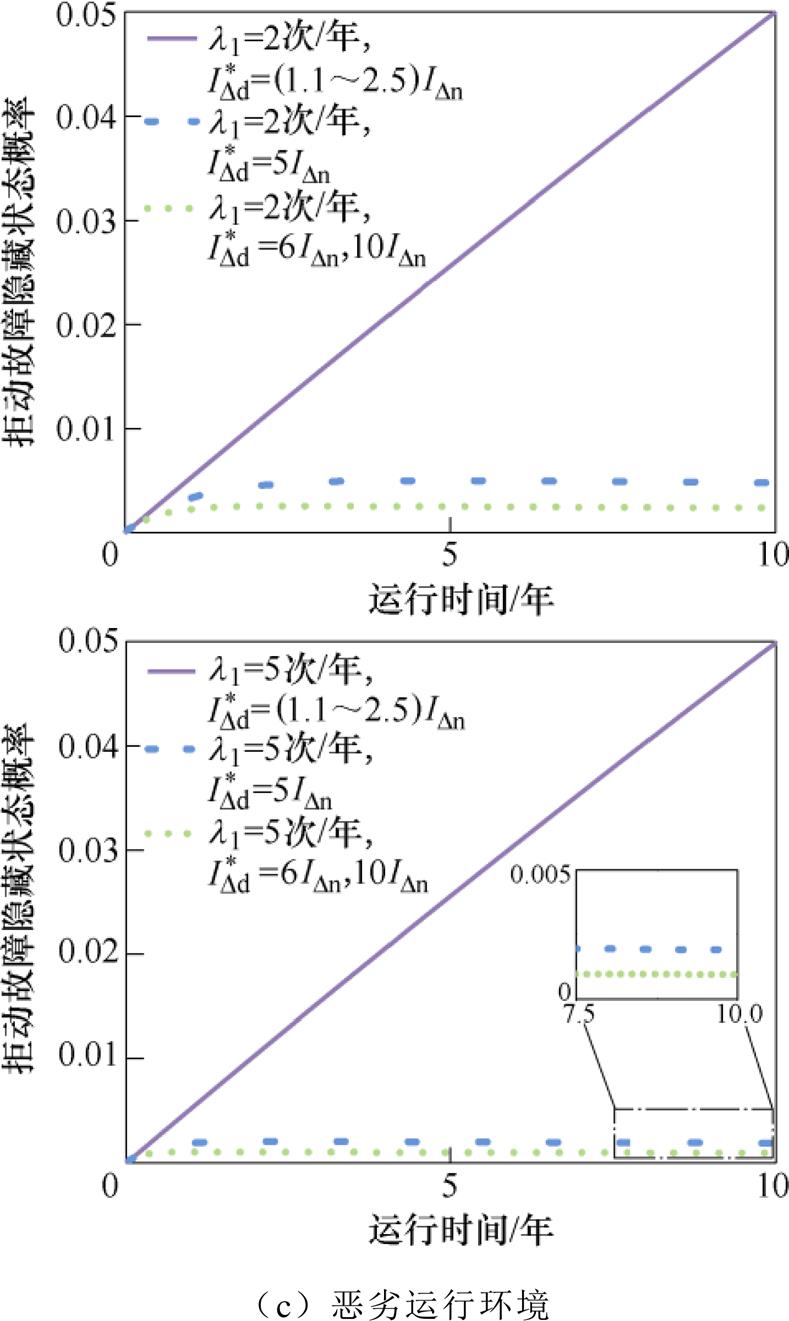
图8 不同故障漏电频次下拒动故障隐藏状态概率
Fig.8 Probability diagram of the hidden reject-operation state under different fault leakage frequencies
在一般运行环境下，动作值为2.5IDn～10IDn时曲线重合，如图8b和图9b所示。这是由于一般运行环境时故障漏电电流范围基本处于（0.9IDn, 2.1IDn），动作值小于2.1IDn时，拒动后动作值增大，拒动故障显现概率随之增大，但动作值大于2.1IDn后，线路或用电设备只要发生故障漏电，均满足拒动故障显现条件，故障漏电频次较低，所以该运行环境下拒动故障显现概率较低，不会完全显现。
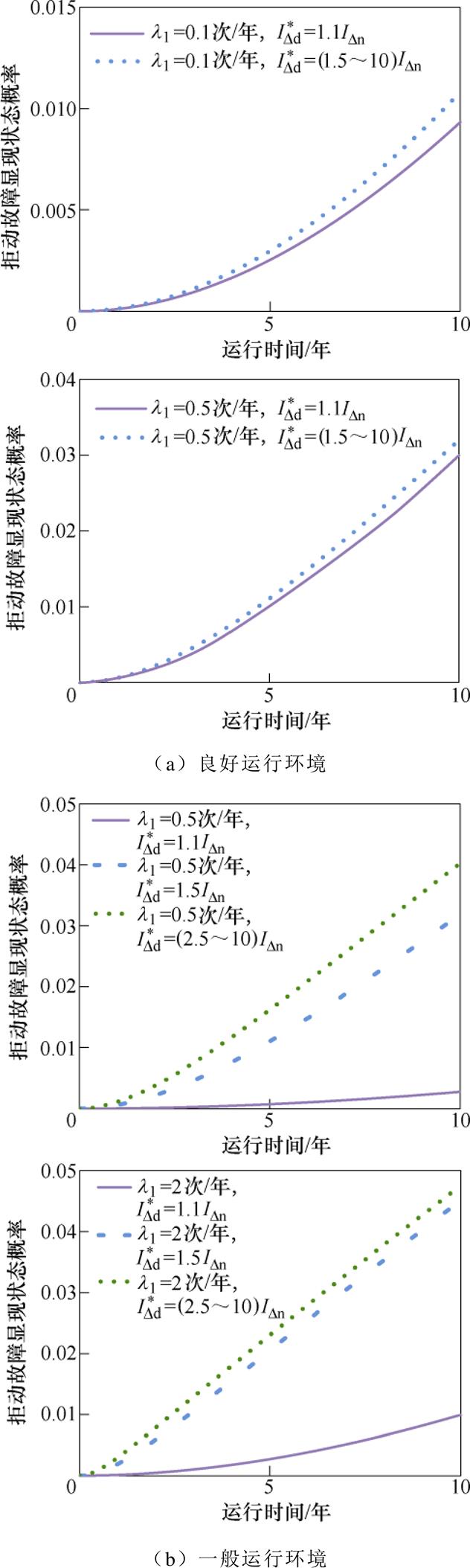
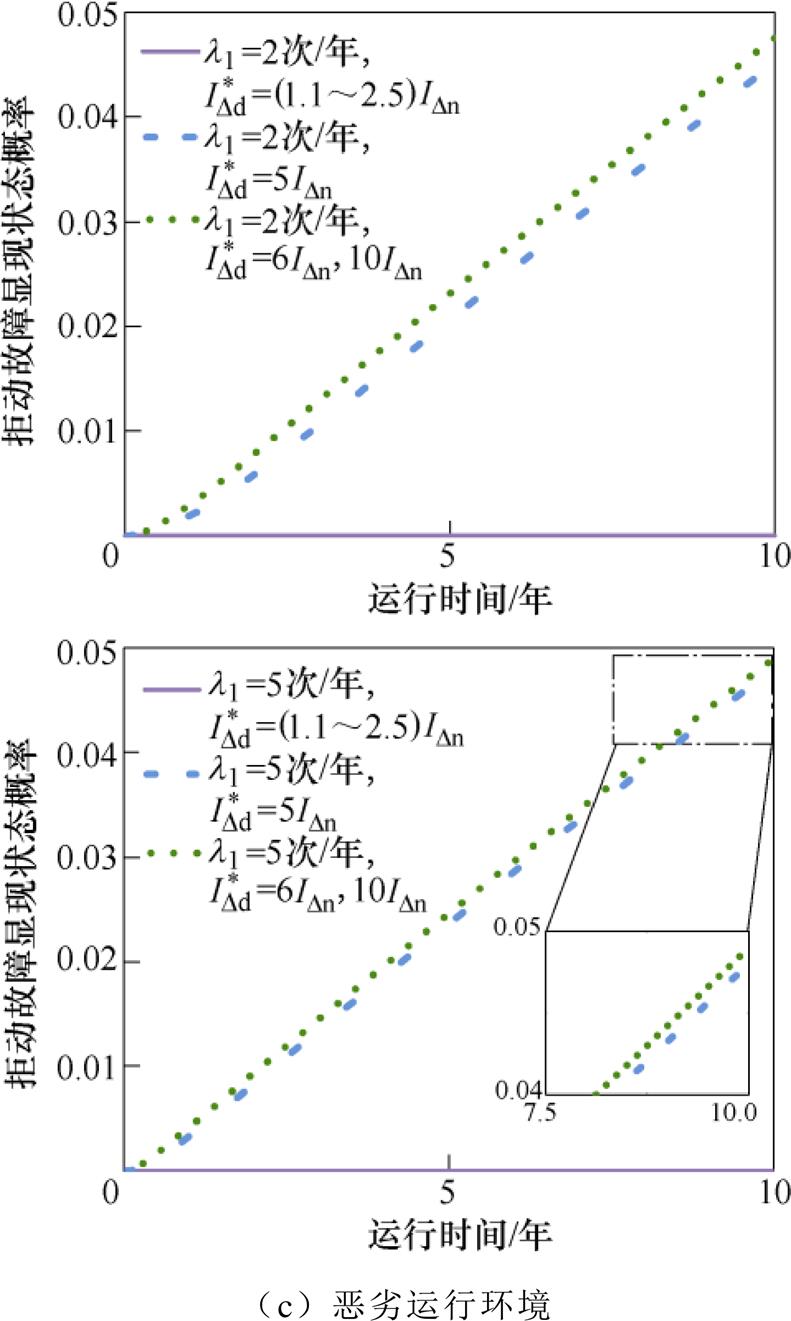
图9 不同故障漏电频次下拒动故障显现状态概率
Fig.9 Probability diagram of the appearing reject- operation state under different fault leakage frequencies
在恶劣运行环境下，动作值为1.1IDn～2.5IDn，以及动作值对应为6IDn、10IDn，状态曲线分别重合，如图8c和图9c所示。这是由于恶劣运行环境下故障漏电电流范围基本处于（4.1IDn, 5.9IDn），动作值小于4.1IDn，发生故障漏电后漏电保护器可以正确动作，拒动故障均处于隐藏状态；而当动作值大于5.9IDn时，发生故障漏电，均满足拒动故障显现条件，此时故障漏电频次较高，所以该运行环境下拒动故障显现概率较高。
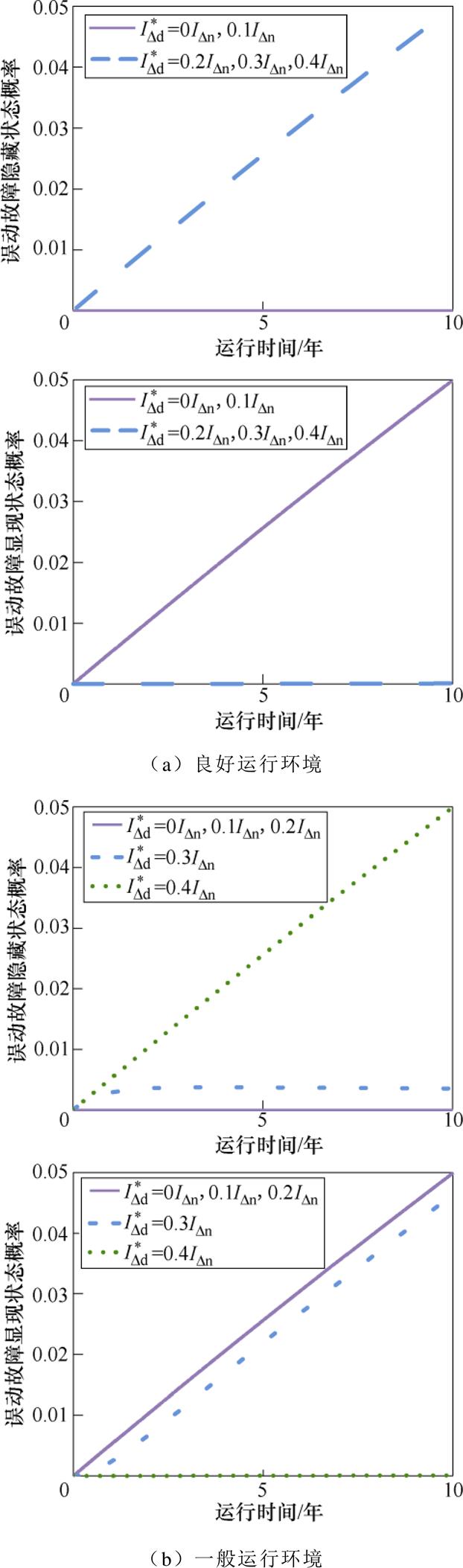
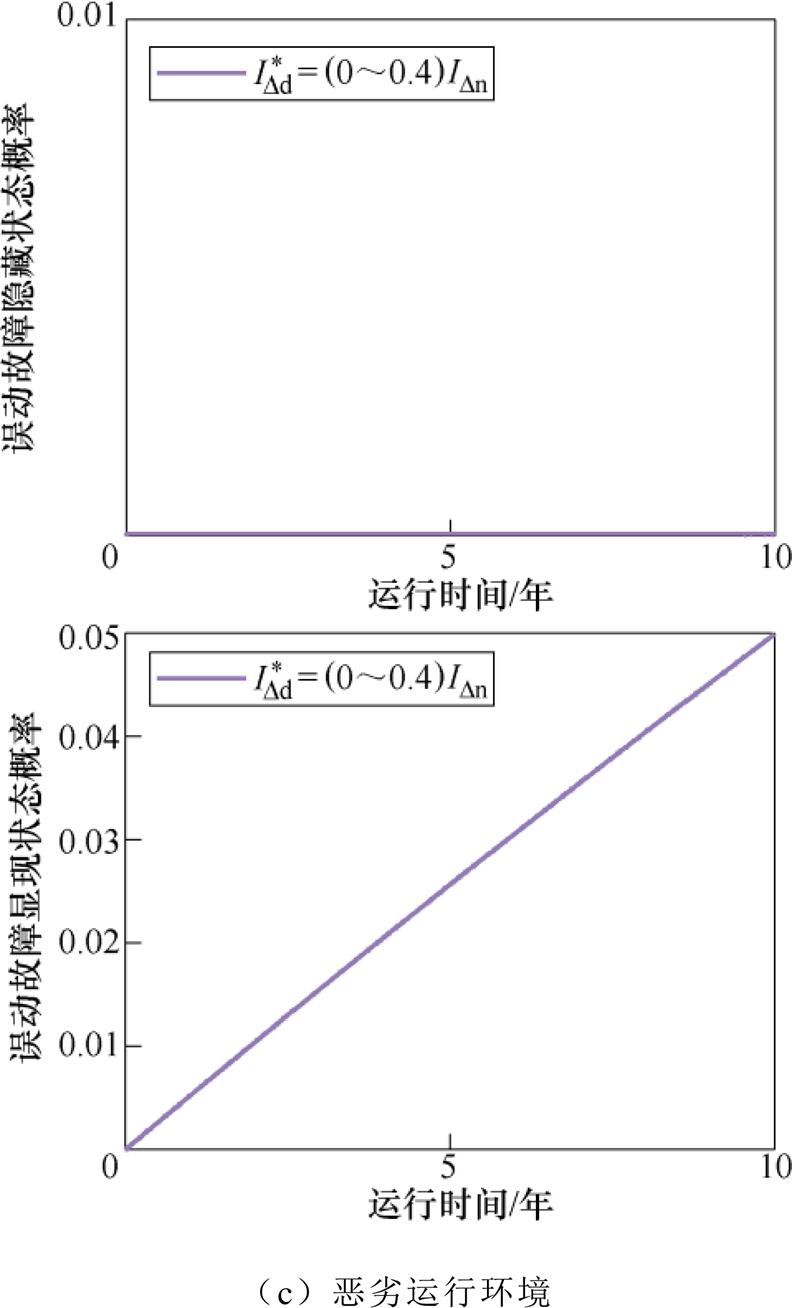
图10 误动故障隐藏和显现状态概率
Fig.10 Probability diagram of hidden state and appearing state states of the wrong-operation
图10为三种运行环境下误动故障隐藏和显现状态概率曲线，由于线路或用电设备一直存在正常漏电，所以误动故障显现概率就是正常漏电ID∈ (IDd, IDn0]的概率，一旦发生误动故障，几乎都会立即显现出来。
在良好运行环境下，漏电保护器误动后其动作值为0和0.1IDn时误动故障均处于显现状态，而动作值为0.2IDn、0.3IDn和0.4IDn时均处于隐藏状态，这是由于此时正常漏电电流范围在（0, 0.15IDn），动作值小于0.15IDn时，误动故障显现条件才会满足，大于0.15IDn后不满足误动故障显现条件，如图10a所示。
在一般运行环境下，漏电保护器误动后动作值为0、0.1IDn和0.2IDn时误动故障均处于显现状态，0.3IDn显现状态概率远高于隐藏状态概率，而动作值为0.4IDn时均处于隐藏状态，这是由于一般运行环境下正常漏电电流范围在（0, 0.3IDn），动作值小于0.3IDn时曲线重合，误动故障都会显现，而大于0.3IDn时均处于隐藏，如图10b所示。
在恶劣运行环境下，漏电保护器误动后动作值为0、0.1IDn、0.2IDn、0.3IDn和0.4IDn时误动故障均处于显现状态，这是因为恶劣运行环境下正常漏电电流范围在（0, 0.6IDn），动作值小于0.5IDn时，满足误动故障显现条件，所以此时对应曲线均重合，均处于误动故障显现状态，如图10c所示。考虑到漏电保护器误动后动作值在（0, 0.5IDn）分布的随机性，在恶劣运行环境下，误动故障更容易显现，而在良好环境下，误动故障可能处于隐藏状态。
结合图8～图10，由于拒动故障后动作值随机分布范围是（IDn, ∞），漏电保护器处于良好运行环境时，存在拒动故障后动作值在（0.7IDn, 1.3IDn）概率小于误动故障后动作值在（0, 0.15IDn）的概率。由于正常漏电一直存在，其发生频次远远高于故障漏电频次。因此，良好运行环境下误动故障显现概率高于拒动故障；一般运行环境下故障漏电频次增加，且其电流分布范围增大，拒动故障显现概率增加；恶劣环境下故障漏电严重程度进一步增大，拒动故障显现概率进一步增大，造成该环境下拒动和误动故障均容易显现，漏电保护器故障后影响较大。
通过仿真分析可以发现，基于马尔可夫过程的漏电保护器可靠性模型可以真实模拟出实际服役过程中保护器可靠性变化情况，能够解释漏电保护器的误动更容易出现的原因。
若漏电保护器服役10年的可靠性保持在0.9或0.95以上，则供电线路和用电设备的供电可靠性也仅为0.9或0.95，但是一般要求电力系统的可靠性在0.999及以上，因此需要通过漏电保护器的定期检查来保障供电可靠性和安全性。
在良好运行环境中，R(10)=0.9的漏电保护器在故障漏电频次为0.1次/年情况下，选取误动故障后的动作值为0.1IDn、拒动故障动作值1.5IDn，得到不同定期检查频次时正常工作状态和故障隐藏状态的概率曲线如图11所示。
随着定期检查频次的增加，故障隐藏状态概率明显降低，正常工作状态概率增加。k=1时漏电保护器处于正常工作状态概率保持在0.994及以上，k=6时正常工作状态概率保持在0.997及以上，并且10年内1 000台样本漏电保护器在定期检查频次k=0、1、6时故障显现后更换次数分别为49、49、37，且均为因误动故障显现后进行的更换。这是因为供电线路和用电设备正常运行时就存在正常漏电，一旦发生误动作故障，很快就会显现出来。而供电线路和用电设备故障漏电发生频次相对较低，即使发生拒动故障，由于激励条件没有出现，拒动故障也显现不出来。通过定期检查，可以发现处于隐藏状态的故障，大幅度降低拒动故障显现状态概率，保证了线路或用电设备运行的安全性；同时部分误动故障隐藏状态也会被发现，提高了线路或用电设备运行的连续供电可靠性，但误动故障显现状态概率仍然较高，需要更高的检查频次。
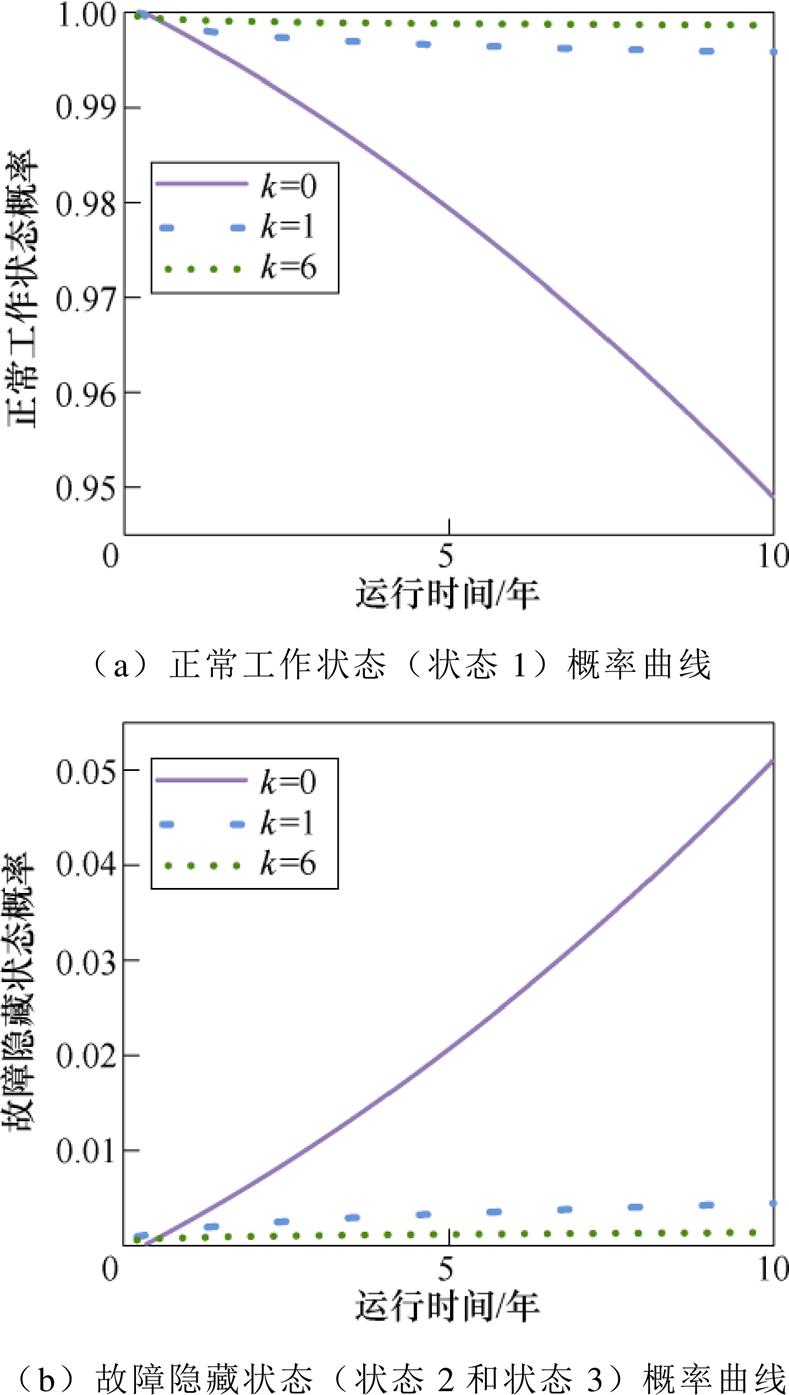
图11 不同检查频次下漏电保护器的状态概率
Fig.11 State probability diagram of RCD under different inspection frequencies
在一定的漏电保护器可靠性水平和运行环境下，保障电力系统供电可靠性水平在0.999以上，即漏电保护器故障不显现的概率在0.999以上。保持误动故障后的动作值为0.1IDn、拒动故障动作值1.5IDn不变，进行三种运行环境下的最低定期检查频次仿真，其结果见表2。
从表2可以看到，在保障相同供电可靠性下，漏电保护器可靠性水平越高所需定期检查频次越少，漏电保护器运行环境改善也可以降低故障显现概率，从而提高供电线路或用电设备的供电可靠性和安全性；通过定期检查可以显著减少因故障显现需要更换漏电保护器的次数，也就避免了因漏电保护器故障引起的供电损失。同时，还可以看到，漏电保护器可靠性水平不是很高情况下，要提高供电可靠性和安全性，需要的定期检查频次很高，在漏电保护器可靠性为0.90时，工作在恶劣环境下时，定期检查周期为5.82 h/次，相当于一天要检查将近4次，而在漏电保护器可靠性为0.95时，恶劣运行环境下，定期检查周期为16.49 h/次，相当于一天要检查1次以上。因此，要大幅提高系统的供电可靠性和安全性，检查频次就必须很高。一般情况下，很难通过人工来完成频次很高的检查，但可以通过漏电保护器的自检功能实现很高的检查频次，即可以通过自检大幅提高供电系统的可靠性和安全性。
表2 最低定期检查频次
Tab.2 Minimum periodic inspection frequency
漏电保护器可靠性水平定期检查频次k/(次/年) 良好一般恶劣 R(10)=0.96921 1671 505 R(10)=0.95201238531
漏电保护器主要用于供电线路或用电设备的漏电故障保护，在实际服役过程中漏电保护器可能会发生拒动或误动故障，丧失漏电保护功能，存在引发人身触电或漏电火灾的安全隐患。本文通过漏电保护器可靠性研究，提出了一种存在误动故障和拒动故障的保护类电器可靠性分析方法，能够解释实际服役中漏电保护器误动故障多于拒动故障的现象，并分析了漏电保护器质量水平、服役环境的恶劣程度以及定期检查等对其可靠性的影响，为提升其服役系统的可靠性和安全性具有重要指导意义。主要结论如下：
1）通过漏电保护器实际服役情况分析，发现其有五种典型运行状态，即正常工作状态、拒动故障隐藏状态、误动故障隐藏状态、拒动故障显现状态和误动故障显现状态。漏电保护器发生拒动和误动故障后，在没有诱发其故障显现条件时，漏电保护器自身故障不能立即显现出来，而是处于故障隐藏状态。
2）建立了基于马尔可夫过程的漏电保护器服役状态转移模型，分析了供电线路或用电设备产生的漏电（激励）和保护器可靠性水平对漏电保护器运行状态的影响，阐明了不同运行环境下漏电保护器拒动故障或误动故障出现次数不同的原因。
3）漏电保护器处于故障隐藏状态时存在隐患，需要通过定期检查来消除漏电保护器的故障隐藏状态，并分析了不同检查频次对漏电保护器故障隐藏状态和服役可靠性的影响，得到了满足一定系统供电可靠性和安全性的漏电保护器最低检查频次，可为带自检功能的漏电保护器自检周期的选取提供参考。
4）通过蒙特卡洛法模拟产生了不同质量水平下漏电保护器的可靠性参数和不同运行环境下的激励参数，进行了漏电保护器服役可靠性仿真分析，证明了采用激励响应法和马尔可夫过程建立漏电保护器服役可靠性模型能更好地揭示漏电保护器实际服役状态。
参考文献
[1] 高洁馨. 常村煤矿地面供电系统中漏电断路器的应用分析[J]. 机电工程技术, 2019, 48(1): 122-124.
Gao Jiexin. Application analysis of leakage circuit breaker in ground power supply system of Changcun coal mine[J]. Mechanical & Electrical Engineering Technology, 2019, 48(1): 122-124.
[2] 边鑫磊. 温湿度对电子式漏电断路器性能影响的研究[D]. 天津: 河北工业大学, 2017.
[3] 李奎, 李常宇, 牛峰, 等. 电磁式漏电断路器的空间磁场抗扰分析及屏蔽结构设计[J]. 电工技术学报, 2022, 37(9): 2161-2169.
Li Kui, Li Changyu, Niu Feng, et al. Anti-magnetic field interference analysis and shielding structure design of electromagnetic residual current circuit breaker[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2161-2169.
[4] 刘帼巾, 李想, 王泽, 等. 基于Wiener过程电子式漏电断路器的剩余寿命预测[J]. 电工技术学报, 2022, 37(2): 528-536.
Liu Guojin, Li Xiang, Wang Ze, et al. Remaining life prediction of electronic residual current circuit breaker based on Wiener process[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 528-536.
[5] 魏永祥, 陈建军, 马洪波, 等. 随机参数弹性连杆在平稳随机激励下的动力可靠性分析[J]. 机械工程学报, 2012, 48(2): 36-43.
Wei Yongxiang, Chen Jianjun, Ma Hongbo, et al. Dynamic reliability analysis of elastic linkage mech- anism with stochastic parameters under stationary random excitation[J]. Journal of Mechanical Engin- eering, 2012, 48(2): 36-43.
[6] Song J, Der Kiureghian A. Joint first-passage pro- bability and reliability of systems under stochastic excitation[J]. Journal of Engineering Mechanics, 2006, 132(1): 65-77.
[7] 彭文昊, 陆俊, 冯勇军, 等. 计及用户参与不确定性的需求响应策略优化方法[J]. 电网技术, 2018, 42(5): 1588-1594.
Peng Wenhao, Lu Jun, Feng Yongjun, et al. Optimization method of demand response strategy considering user participation uncertainty[J]. Power System Technology, 2018, 42(5): 1588-1594.
[8] 金有刚, 姚军. 随机振动环境下电路板的疲劳寿命与可靠性研究[J]. 强度与环境, 2007, 34(3): 58-62.
Jin Yougang, Yao Jun. The method research on fatigue life analysis and reliability of the typical circuit board in random-vibration environment[J]. Structure & Environment Engineering, 2007, 34(3): 58-62.
[9] 张鹏, 王艺环, 秦国晋. 非随机过程的地震激励下埋地压力管道的非概率可靠性分析[J]. 中国安全生产科学技术, 2018, 14(6): 134-141.
Zhang Peng, Wang Yihuan, Qin Guojin. Non- probabilistic reliability analysis of buried pressure pipeline under non-random process earthquake excitation[J]. Journal of Safety Science and Tech- nology, 2018, 14(6): 134-141.
[10] Zhang Hailong, Zhang Tinghui, Shen Shuyu, et al. Reliability analysis of a novel magneto-rheological regenerative suspension system under road excita- tion[C]//2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 2018: 1033-1038.
[11] 杨墨缘, 欧阳森, 张真, 等. 考虑不同运行状态的多端口直流断路器可靠性模型[J]. 电网技术, 2021, 45(10): 4037-4046.
Yang Moyuan, Ouyang Sen, Zhang Zhen, et al. Reliability model of multi-port DC circuit breaker considering different operating states[J]. Power System Technology, 2021, 45(10): 4037-4046.
[12] Prodanov P I, Dankov D D. Applying Markov analysis for reliability modeling of energy storage devices[C]//2020 XI National Conference with International Participation (ELECTRONICA), Sofia, Bulgaria, 2021: 1-4.
[13] 于明丽, 崔利荣. 两阶段有向网络马尔可夫系统维修模型与分析[J]. 北京理工大学学报, 2011, 31(6): 753-756.
Yu Mingli, Cui Lirong. Modeling and analysis of two- stage directed network Markov repairable system[J]. Transactions of Beijing Institute of Technology, 2011, 31(6): 753-756.
[14] 倪伟, 吕林, 向月, 等. 基于马尔可夫过程蒙特卡洛法的综合能源系统可靠性评估[J]. 电网技术, 2020, 44(1): 150-158.
Ni Wei, Lü Lin, Xiang Yue, et al. Reliability evaluation of comprehensive energy system based on Markov process Monte Carlo method[J]. Power System Technology, 2020, 44(1): 150-158.
[15] 石文辉, 别朝红, 王锡凡. 大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J]. 中国电机工程学报, 2008, 28(4): 9-15.
Shi Wenhui, Bie Zhaohong, Wang Xifan. Appli- cations of Markov chain Monte Carlo in large-scale system reliability evaluation[J]. Proceedings of the CSEE, 2008, 28(4): 9-15.
[16] 赵志欣, 唐慧, 刘仁云. 基于马尔可夫过程的风电系统可靠性分析[J]. 吉林大学学报(工学版), 2021, 51(2): 697-703.
Zhao Zhixin, Tang Hui, Liu Renyun. Reliability analysis of wind power system based on Markov process[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(2): 697-703.
[17] 边晓燕, 史越奇, 裴传逊, 等. 计及经济性和可靠性因素的区域综合能源系统双层协同优化配置[J]. 电工技术学报, 2021, 36(21): 4529-4543.
Bian Xiaoyan, Shi Yueqi, Pei Chuanxun, et al. Bi- level collaborative configuration optimization of integrated community energy system considering economy and reliability[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4529-4543.
[18] 赵书涛, 王波, 华回春, 等. 基于马尔科夫模型的直流断路器可靠性评估方法[J]. 电工技术学报, 2019, 34(增刊1): 126-132.
Zhao Shutao, Wang Bo, Hua Huichun, et al. Reliability evaluation method of DC circuit breaker based on Markov model[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 126-132.
[19] Khalilnejad A, Pour M M, Zarafshan E, et al. Long term reliability analysis of components of photo- voltaic system based on Markov process[C]// SoutheastCon, Norfolk, VA, USA, 2016: 1-5.
[20] Tan Yifang, Feng Ding. Reliability evaluation for unmanned aerial vehicle components based on Markov degradation process[C]//IEEE Advanced Infor- mation Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi'an, China, 2017: 1804-1807.
[21] 刘帼巾, 王泽, 李想, 等. 基于改进Bootstrap- Bayes的电子式剩余电流动作断路器可靠性评估[J]. 电工技术学报, 2022, 37(16): 4250-4258.
Liu Guojin, Wang Ze, Li Xiang, et al. Reliability evaluation of electronic residual current operated circuit breaker based on improved Bootstrap-Bayes[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4250-4258.
[22] 李谦. 计及极端天气与风电接入的系统运行风险评估[D]. 济南: 山东大学, 2015.
[23] Ghaderi A, Haghifam M R, Mostafa Abedi S. Application of Monte Carlo simulation in Markov process for reliability analysis[C]//IEEE 11th Inter- national Conference on Probabilistic Methods Applied to Power Systems, Singapore, 2010: 293-298.
[24] 潘仲立. 可靠性分析的理论基础[M]. 北京: 水利电力出版社, 1988.
[25] Ugurlu O F, Kumral M. Reliability-based perfor- mance analysis of mining drilling operations through Markov chain Monte Carlo and mean reverting process simulations[J]. Simulation, 2020, 96(7): 593- 604.
[26] 郭一帆, 唐家银. 伴有衰减型随机冲击的竞争失效可靠性综合评估模型[J]. 湖北大学学报(自然科学版), 2021, 43(1): 6-15.
Guo Yifan, Tang Jiayin. Comprehensive evaluation model of competitive failure reliability with atten- uated random shock[J]. Journal of Hubei University (Natural Science Edition), 2021, 43(1): 6-15.
[27] 赵营鸽, 李颖, 王灵月, 等. 基于均值点展开的单变元降维法在EIT不确定性量化研究中的应用[J]. 电工技术学报, 2021, 36(18): 3776-3786.
Zhao Yingge, Li Ying, Wang Lingyue, et al. The application of univariate dimension reduction method based on mean point expansion in the research of electrical impedance tomography uncertainty quanti- fication[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3776-3786.
Abstract The residual current Device (RCD) is mainly used to protect power supply lines or electrical equipment leakage faults. During the service of the RCD, it may occur to the reject-operation or the wrong-operation. If the RCD loses its leakage protection function, the lines or equipment have safety hazards, such as personal electric shock or leakage fire. Therefore, it is necessary to study the reliability of RCD.
If the RCD fails, its fault state is exposed only when the corresponding excitation condition occurs. The higher the reliability level of RCD, the lower the reject-operation rate and wrong-operation rate. The higher the probability of a normal service state, the lower the probability of a fault state. The reliability block diagram is shown in Fig.A1.
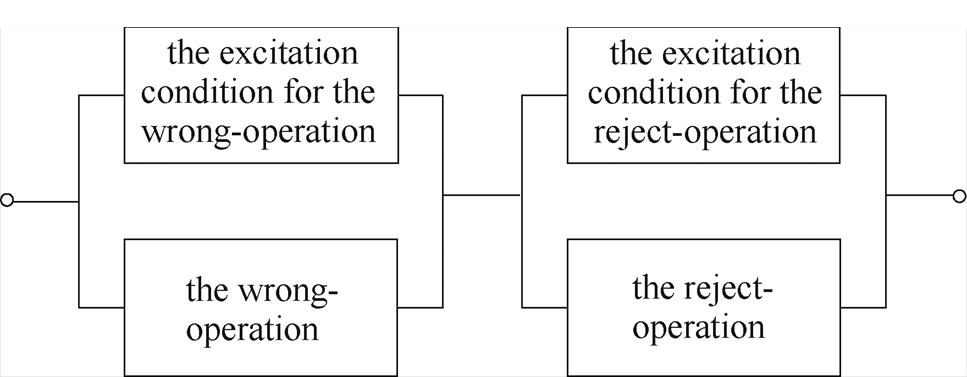
Fig.A1 Reliability block diagram of RCD under fault conditions
The fault state of RCD is divided into two categories: the hidden failure state and the appearing fault state. Therefore, there are five service conditions of RCD: normal service state (State 1), the hidden reject-operation state (State 2), the hidden wrong-operation state (State 3), the appearing reject-operation state (State 4), and the appearing wrong-operation state (State 5). The current moment states corresponding to State 4 and State 5 are necessarily State 2 and State 3, not State 1 (previous state). The state at the next moment only relates to the current state, which satisfies the Markov property. Markov process can be used to describe the state transfer of RCD. There are safety hazards when RCD is in the hidden failure state, and it is necessary to eliminate the hidden fault state of RCD by periodic inspection. The state transition diagram of RCD based on periodic inspection is shown in Fig.A2.
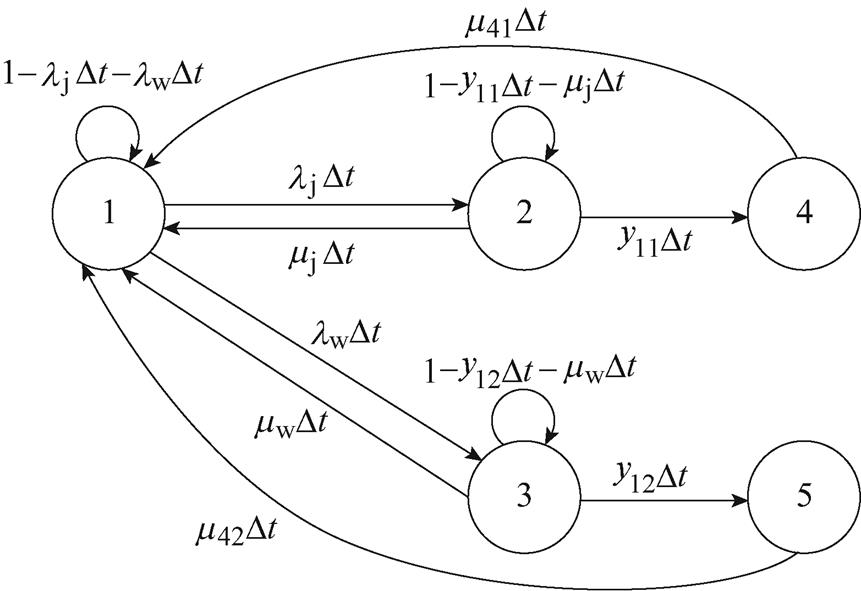
Fig.A2 State transition diagram of RCD based on periodic inspection
In general, if the frequency of fault leakage of power supply lines or electrical equipment is low, the RCD in the hidden reject-operation state can be found at a lower periodic inspection frequency. However, the normal leakage of power supply lines or electrical equipment exists permanently, so the probability of the wrong- operation appearance state is still high. If the RCD reliability level is low, self-inspection can be used to achieve a high frequency of periodic inspections, thereby significantly improving the reliability and safety of the power supply system.
In different service environments, the frequency of fault leakage and the residual current are different for power supply lines or electrical equipment. So the service environment can be divided into three grades: good, general, and bad. The Poisson distribution describes the frequency of fault leakage, and the Normal distribution describes the amplitude of normal residual current and fault leakage current. Under the same power supply reliability conditions, the higher the reliability level of RCD is, the fewer periodic inspections are required. In addition, a periodic inspection can significantly reduce the frequency of replacing the leakage protector due to apparent failure and can avoid power loss caused by RCD failure.
The simulation experiment takes leakage fault frequency, the magnitude of the leakage current, the reliability level of the RCD, and running time as the variables. The probabilities for each running status with and without the inspected RCD are analyzed. The minimum periodic inspection frequency is obtained to ensure the reliability and safety of the power supply system. The simulation results not only explain that the wrong operation is more than the reject-operation of RCD in actual service, but also prove that the service reliability analysis model of RCD based on the Markov process can describe the actual operation of RCD.
keywords：Residual current protection reliability, excitation response method, Markov process, periodic inspection, service reliability
DOI: 10.19595/j.cnki.1000-6753.tces.221171
中图分类号：TM56
国家自然科学基金（51937004, 51777056）和河北省自然科学重点基金（E2019202124）资助项目。
收稿日期 2022-06-20
改稿日期 2022-10-19
李 奎 男，1965年生，教授，博士生导师，研究方向为电器可靠性与试验技术、电器智能化理论与技术。E-mail: likui@hebut.edu.cn（通信作者）
郝运佥 女，1996年生，硕士，研究方向为电器可靠性。E-mail: 906332947@qq.com
（编辑 崔文静）