图1 EMFA示意图
Fig.1 Schematic diagram of EMFA
摘要 为减少接触器的触头弹跳，针对恒定气隙接触器提出一种位置预测方法，使用等效磁路法与参数辨识从永磁体磁链中提取位置信息，随后依据位置信息实施控制。建立磁力机构等效磁路模型，推导出动态磁链、位移与电流的映射关系，实验验证了映射关系的合理性。通过实验获得位移、电压与电流，根据实验数据计算磁链，采用多元回归的方法获取位移的映射的参数，完成了接触器位置预测。通过有限元模型的参数扫描功能，建立驱动力、磁链的两个曲面，通过插值的方法完成接触器的建模，从而进行位置预测以及无位置控制的仿真。使用磁力机构驱动的接触器进行实验，实验结果表明，新型无位置传感器控制方法适用于恒定气隙接触器，验证了位置预测的准确性与控制方法的有效性。
关键词：恒定气隙接触器 控制 触头弹跳 磁力机构（EMFA） 动态特性
接触器是一种用于接通与分断电路的电器，广泛应用于电源切换、电机控制、轨道交通及新能源发电等场景之中[1-6]。操动机构作为执行部件是接触器的重要组成部分，它将电能转化为机械能，驱动接触器触头运动实现合/分闸。磁力机构（Electro- magnetic Force driving Actuator, EMFA）作为一种新型操动机构，逐步应用于多种电压等级的开关设备之中[7-11]。
接触器合闸过程中的触头弹跳碰撞将产生电弧，高频率长时间的弹跳过程将显著缩短接触器的电寿命[12-18]。因此，在合闸过程中通过对操动机构合理调速，实现操作运动的柔性化，改善操动机构的动态特性，减小弹跳的发生，对提升接触器的寿命及可靠性至关重要。
对接触器的调速方法已展开深入研究[19-21]，其中无位置传感器控制具有一定的经济优势，因此得到了研究学者的广泛关注。无位置触感器可分为位置预测与动态控制两部分，位置预测主要通过输入电压、电流等电信号完成，而动态控制通过预测位移执行控制策略，因此位置预测是动态控制的输入条件，而动态控制是验证控制效果的方法。永磁接触器的无位置传感器控制已取得显著成果[22-26]，由于在合闸的过程中气隙逐渐减小，主磁路的磁阻也随之降低，线圈动态电感将逐渐增加。因此，通过线圈电压与电流计算动态电感反推气隙变化量即可获得动态位置。然而，这种位置预测方式不适用于运动气隙不发生变化的磁力机构，磁力机构是一种动线圈结构，运动过程中气隙保持恒定，无法从气隙中提取位置信息，因此需要一种新型的位置预测方法，随后依据位置信息实现动态控制，从而有效地抑制触头弹跳。
本文提出了一种新型位置预测方法，从永磁体磁链中提取接触器的位置信息，在位置预测的基础上实现了恒定气隙接触器的动态控制。首先，基于EMFA拓扑结构建立等效磁路模型，推导出永磁体磁链、线圈磁链、位置以及电流的公式，通过实验完成了公式参数的辨识，并验证了预测位置的准确性。随后，基于预测位置完成了恒定气隙接触器的动态控制，在仿真的基础上完成了相关实验，验证了通过动态控制来抑制触头弹跳的有效性。
本文研究的恒定气隙接触器由EMFA驱动，其二维原理如图1所示。主要结构包括：顶盖、轭铁、静铁心、永磁体、动铁心以及线圈。其中，线圈与动铁心为机构的动作部件。由电容储能，电容与线圈组成二阶放电电路。线圈中电子在磁场中产生洛伦兹力，推动EMFA运动。由于EMFA为动线圈结构，因此在运动过程中，磁路的气隙不发生变化，故EMFA可称为恒定气隙操动机构[9]。由于磁力机构包含了四块永磁体，因此相对于永磁接触器，磁力机构的成本略高。然而，凭借着较小的体积以及较短的励磁时间，磁力机构接触器在互联网数据中心的配电模块中得到了应用。在图1中，Rm1、Rm2为顶盖气隙磁阻；Rm3、Rm4、Rm7、Rm8为动铁心磁阻；Rm5、Rm6为线圈气隙磁阻；Rm9、Rm10为轭铁气隙磁阻；Rm11、Rm12为静铁心；Rm13～Rm16为轭铁磁阻；IN1～IN4为永磁体磁动势。
图1 EMFA示意图
Fig.1 Schematic diagram of EMFA
接触器机构EMFA的尺寸小于30 mm×30 mm× 30 mm。电路采用电容器放电。接触器的铁磁材料为DT4E，永磁材料为N35，永磁体的剩磁为1.1 T，接触材料为AgSnO2。线圈匝数为180，线圈电阻为2.73 W。行程为2.5 mm，开距为2 mm，超行程为0.5 mm。
为抑制触头弹跳，本文采用无位置传感器控制方案，无位置传感器控制主要包括位置预测与动态控制两个方面，位置预测为动态控制提供位置信息，动态控制采用分段脉冲宽度调制（Pulse Width Modulation, PWM）控制方法，用于验证方案对触头弹跳的抑制效果。
首先，基于EMFA拓扑结构建立磁路模型，推导出不含参数的磁链、电流以及位移公式。随后，通过实验完成参数的辨识，即可获得完整的位置预测公式。
EMFA的磁场激励源由永磁体与线圈两部分组成，其中四块永磁体横向排布，为线圈提供磁场。以静铁心为对称轴，左侧两块永磁体与右侧两块永磁体充磁方向相反，同侧永磁体充磁方向相同。
由于EMFA截面磁路相同，建立EMFA等效磁路模型，各个部分的磁阻分布如图2所示。由于动态过程中经过动铁心Rm3、Rm4、Rm7、Rm8的磁通不影响线圈磁链的大小，因此将其折算至漏磁之中。
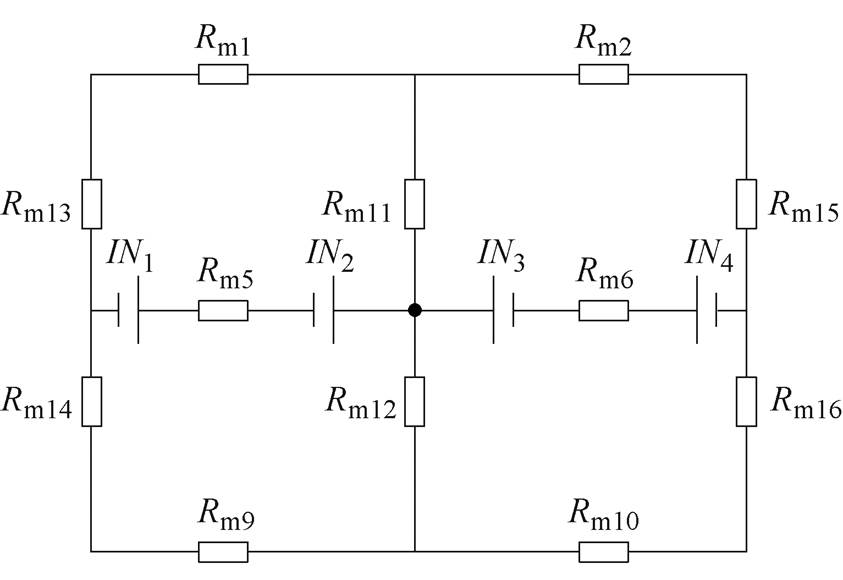
图2 EMFA永磁体磁路
Fig.2 EMFA permanent magnet magnetic circuit diagram
动态特性方面，通电线圈在永磁体提供的恒定磁场中受到安培力的作用，而EMFA运动过程中气隙不变。总磁链y 与运动位置x和励磁电流i有关。下文将总磁链分解为永磁体产生的磁链以及线圈产生的磁链两部分分析计算。
永磁体磁路与线圈励磁磁路如图3所示，左图实线为永磁体产生的磁通方向，由4个独立的主磁路组成。右图虚线为线圈励磁产生的磁通方向，主要路径由电工纯铁组成。可见，在EMFA动作的过程中，线圈磁路的气隙不发生变化，这与气隙变化的操动机构具有较大差异。
图3 永磁体磁路与线圈励磁磁路
Fig.3 Permanent magnet circuit and coil flux
永磁体磁通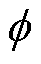
是瞬态计算的重要参数，由图3可知，EMFA永磁体磁路由四条支路组成，将四条磁路拆分计算，以左下方支路为例，磁路由激励源IN1、IN2，以及磁阻Rm5、Rm12、Rm9、Rm14组成。而Rm5的计算公式为
（1）
式中，Rma为永磁体之间气隙磁阻；Rmy1、Rmy2为永磁体磁阻。由磁路定则可知
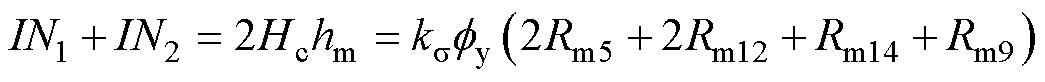（2）
式中，kσ为漏磁系数；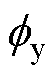
为图3永磁体产生四条磁路中其中一条的总磁通；Hc为永磁体矫顽力；hm为永磁体厚度。
关于永磁体磁链，即由永磁体产生穿过线圈的磁链。将永磁体视为分布参数，如图3中永磁体磁路所示，静铁心中上半部分磁通方向向上，下半部分向下。由于线圈交链部分包含两个方向的磁通，因此永磁体产生的磁链有一部分相互抵消。以分闸位置为例，永磁体产生的磁链数值上等于线圈上方永磁体的磁通乘以匝数，即图3的虚线部分。随着线圈运动位置的不同，永磁体产生的磁链也不相同。此处认为单位高度永磁体产生的磁通相同，永磁体产生的磁链满足
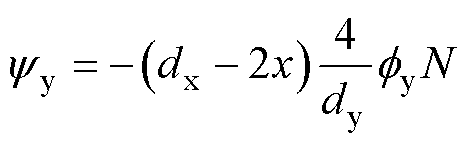（3）
式中，yy为永磁体磁链；dx为接触器行程；x为线圈运动位置；dy为永磁体高度；N为线圈匝数。当x=0时yy为接触器的初始磁链。由式（3）可知，永磁体磁链与EMFA的位移呈线性关系，因此计算得到永磁体磁链后即可获得EMFA运动位置。
为验证式（3）的有效性，本文使用“推动法”验证了永磁体磁链与EMFA位移的映射关系。使用推拉力计推动EMFA运动，线圈保持开路，线圈的磁链中只包含永磁体磁链，而不包含线圈励磁磁链，因此磁链计算为
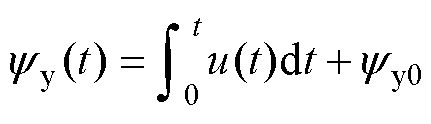（4）
式中，u(t)为线圈切割永磁体磁力线产生的电压，即此时测量的线圈电压；t为时间；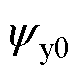
为初始位置的永磁体磁链。实验获得的位移以及磁链将成为“推动法”拟合的输入。
测量线圈电压以及EMFA位移，积分得到永磁体磁链，使用最小二乘法将磁链与位移进行线性拟合。映射的基本形式见式（3），其中输入为磁链与位移，输出磁链对位移的映射参数。随后将磁链代入具体参数的式（3）中计算得到拟合结果。“推动法”中位移测量值与拟合结果如图4所示。
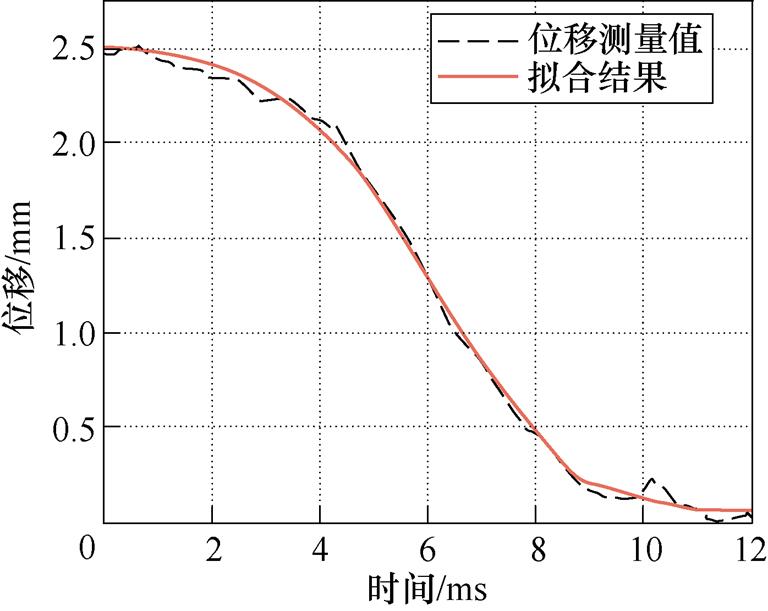
图4 “推动法”中位移测量值与拟合结果
Fig.4 Displacement measurements and fitting results in the “push method”
其物理意义在于，EMFA的动作线圈切割永磁体产生的磁力线，将在线圈处产生电动势，其中动态电压与线圈运动速度成正比。由于计算磁链需完成电压的积分，同时相当于速度积分计算位移，因此永磁体磁链中含有EMFA的运动位置信息。综上所述，永磁体磁链与位移存在线性映射关系，这与式（3）是相吻合的。
除永磁体磁链外，磁链中还有线圈磁链，而线圈磁链满足
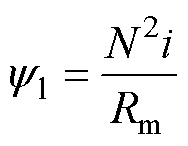（5）
其中
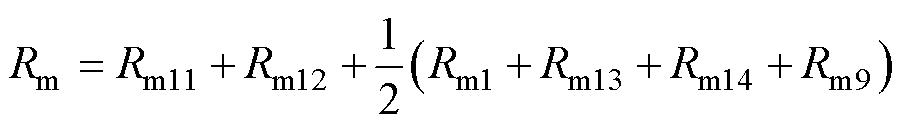（6）
式中，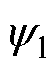
为线圈磁链；i为线圈电流；Rm为线圈磁路的磁阻。铁磁材料的局部磁饱和现象在磁路气隙较小的情况下较为严重，而EMFA的永磁体磁路与线圈磁路中存在恒定气隙。如式（2）中气隙磁阻Rm5为磁阻的主要组成部分，式（6）中气隙磁阻Rm1与Rm9为磁阻的主要组成部分，因此区域磁饱和现象对磁路计算的影响较小。
为验证铁磁材料的非线性特性，需对式（5）中的N2/Rm进行分析。理论上，由于铁磁材料的非线性特性，磁阻Rm随电流的变化而变化。在“固定法”的实验条件下，把式（7）计算出的磁链除以电流i即可获得N2/Rm。实验获得的N2/Rm在不同电流条件下几乎不发生变化，这是由于在实验电流之内，气隙磁阻Rm1与Rm9远远大于铁磁磁阻Rm11、Rm12、Rm13与Rm14，而N2/Rm可视为常数。
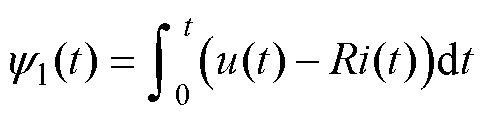（7）
式中，R为线圈电阻。
为排除永磁体磁链变化对计算结果的影响。使用工装夹具将EMFA动作部分固定，使用电容为线圈通电，即“固定法”。测量线圈的电流与电压，通过式（7）计算得到线圈磁链，由于EMFA线圈固定，因此永磁体产生的磁链不发生变化，此时测得的磁链可认为是线圈励磁产生的磁链。其中实验获得的电流以及磁链将成为“固定法”拟合的输入。
于是使用最小二乘法将励磁磁链与电流进行线性拟合。其中映射的基本形式见式（5），输入磁链与电流，输出磁链对电流的映射参数。随后，将磁链代入获得具体参数的式（5）中计算得到拟合结果。“固定法”中电流测量值与拟合结果如图5所示，拟合结果较好。用实验的方法验证了建模的合理性。
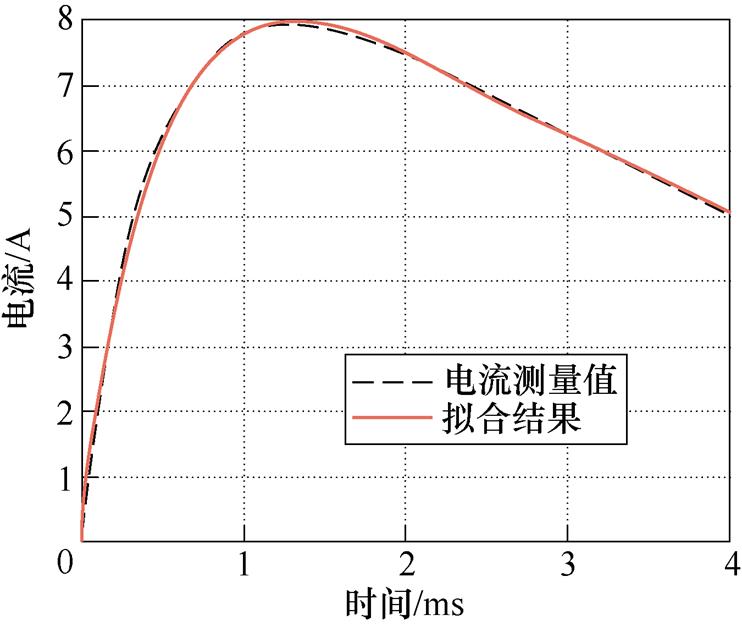
图5 “固定法”中电流测量值与拟合结果
Fig.5 Current measurement value and fitting results in “fixed method”
结合式（2）、式（3）与式（5），EMFA的动态位移可表示为
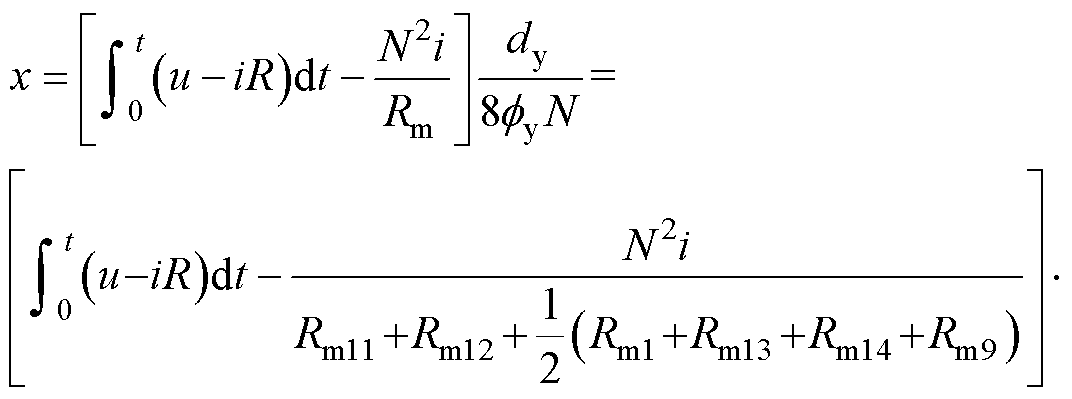
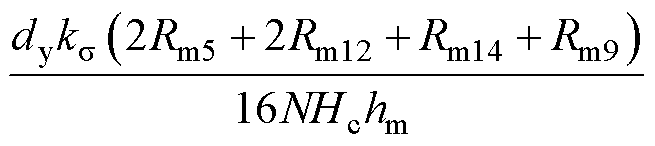（8）
式中，u为线圈两端电压。式（8）中，dx分量作为积分的初值被消去了，可凭借其完成EMFA在瞬态过程中的位置预测。通过磁路模型完成接触器数学模型搭建后需确定公式的具体参数，使用参数辨识的方法确定函数的具体系数，最终用于控制器的设计之中。
关于位移预测方法的适用范围，由于电磁设备往往具有不同的拓扑结构，其磁路方程也不尽相同，因此本文所述的磁路方程仅适用于磁力机构。而等效磁路法与参数辨识相配合的建模方法同样适用于其余恒定气隙接触器。位置预测的具体流程如下：
（1）基于特定的电磁操动机构拓扑结构，建立等效磁路模型，推导磁链、电流及位移的公式，其中公式中的具体参数不需要计算。
（2）进行操动机构动作实验，测量线圈的电压、电流以及操动机构的位移，并根据电压电流计算动态磁链。
（3）将步骤（2）实验数据代入步骤（1）的公式之中，完成参数辨识，即可获得完整的位置预测公式。
（4）基于完整的位置预测公式，即可根据线圈的电压及电流预测操动机构的动态位置。
恒定气隙接触器的磁路模型是为了推导磁链、电流与位移的基本映射关系，映射关系中位移为输出，磁链与电流为输入。在根据磁路模型确定模型的基本形式之后，需完成对模型参数的辨识。完成参数的辨识后，即可将完整的映射关系应用于位置预测之中。
多元线性回归的基本模型为
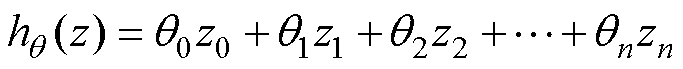（9）
代价函数为
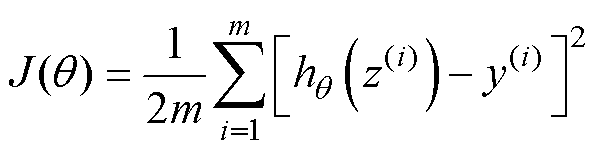（10）
通过代价函数获得模型的参数，求解获得模型的参数q 的值。
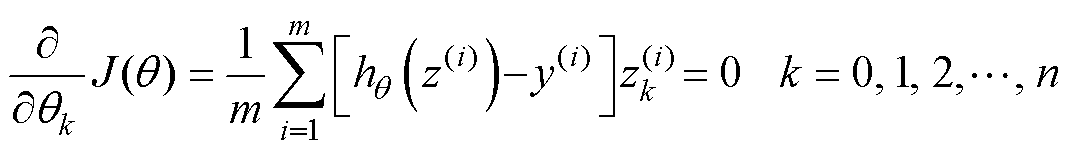（11）
式中，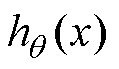
为拟合函数；z为自变量；
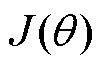为代价函数；y为因变量；m为样本数；n为自变量数。
等效磁路模型建立了式（8）的基本形式，其中q 为式（8）的相关参数，在获得完整的预测模型后即可进行位置预测。位移的计算与实验结果如图6所示，图中，实线为预测位移而虚线为EMFA的位移测量值。实验证明不同驱动电压下实验的测量值与计算值相差较小，满足无位置传感器控制的需要。
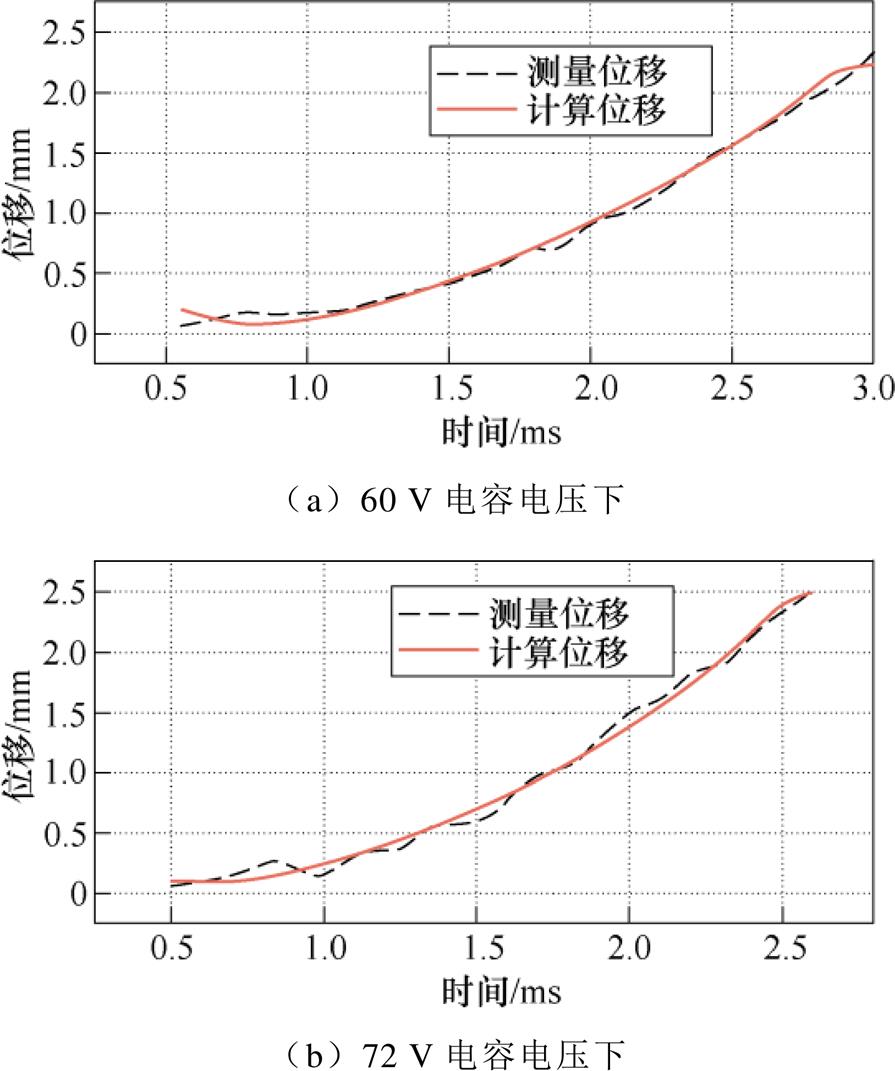
图6 位移的计算与实验结果
Fig.6 Calculation of displacement and experimental results
将第2节中的预测位置作为输入，即可对EMFA进行动态控制。在开展实验之前，需对控制策略的有效性进行定量分析，并对占空比组合进行合理的配置。通过Ansoft建立磁链、电流、位移以及电磁力、电流、位移的双曲面，使用龙格库塔法求解达朗贝尔运动方程计算EMFA动态特性。在静态数值插值法的基础上，引入了参数辨识模块，在动态特性仿真的同时实现位移映射关系的参数辨识。
由于磁力机构运动过程中工作气隙不发生变化，经典的动态电感法不能直接应用在磁力机构的位置预测中。因此，本文首先建立磁路模型确定不含参数的位移映射关系，发现磁力机构的位置仅与总磁链中永磁体产生的部分相关，再通过参数辨识完善模型，最终实现位置预测。本质上不同于动态电感法直接寻找总磁链中的位移信息，磁力机构需要在总磁链中提取有效部分再完成位移的折算。
在磁路法与参数辨识建立位置预测模型的基础上，对比仿真计算位移与预测位移，验证位移预测的准确性。在控制策略的基础上根据预测位移完成接触器的动态斩波控制，根据仿真完成了占空比对动态特性的影响分析，仿真可为相关实验提供指导。
接触器的控制电路如图7所示，直流电源为电容C充电，由驱动电容C为线圈放电。放电过程中使用DSP产生PWM信号，由IGBT斩波对EMFA进行动态控制。电路中，L、R分别为EMFA线圈的电感与电阻。其中电力电子开关型号为G160N60，驱动光耦为A316J，DSP型号为TMS320F28335，PWM频率为20 kHz。
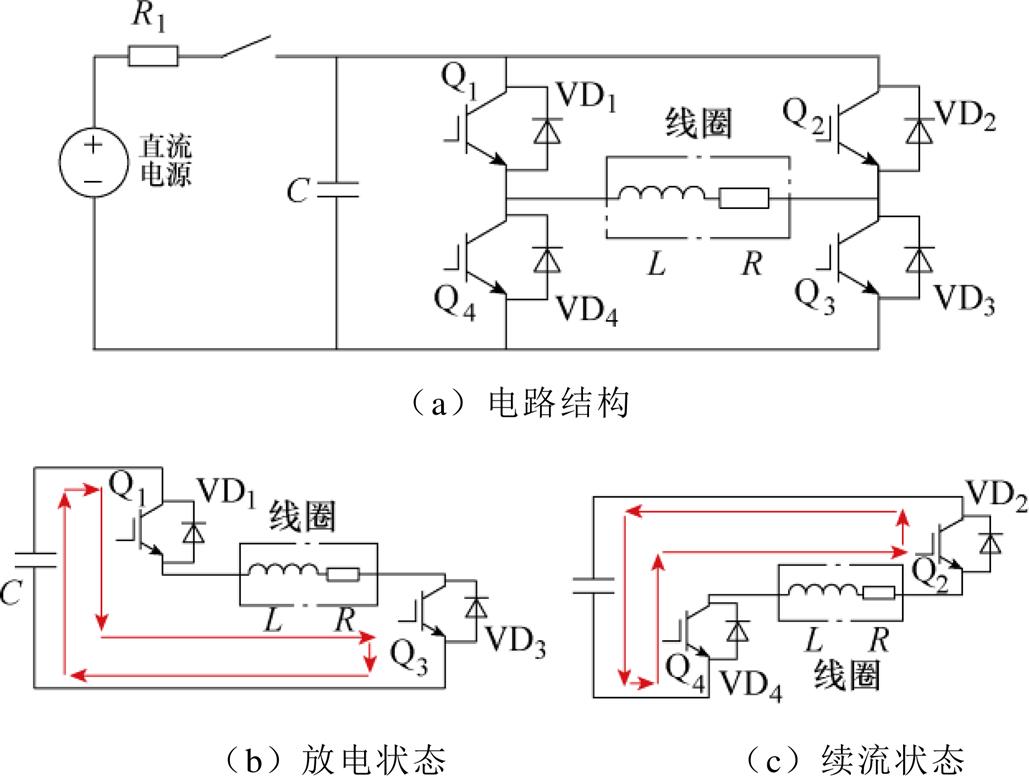
图7 控制电路
Fig.7 Control circuit
斩波的过程分为放电与续流两个阶段，其中放电方程为
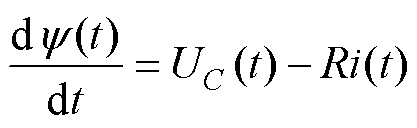（12）
而续流方程为
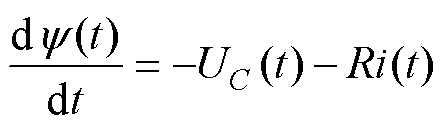（13）
式中，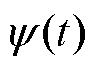
为线圈磁链；UC为电容电压；i(t)为电流。当电容向线圈放电时UC取正；当线圈向电容续流时UC取负。式（12）、式（13）中忽略了二极管及电力电子器件的导通压降。
如图7所述，在斩波的过程中，由于电路拓扑发生变化，电路状态方程亦发生变化。此时计算磁链需采集电压及电流，由于线圈电压在放电与续流过程中极性相反，而DSP仅能输入0～3 V正极性信号，因此不能将电压信号直接输入DSP之中。因此本文采集了电容电压信号，在分压后输入DSP中完成磁链计算。在计算的过程中将斩波周期与采样周期的比值称为T，Tc为采样周期，斩波周期共o个，占空比为D，电容电压为UC，线圈电流为i，电阻为R，
为磁链。则磁链计算为
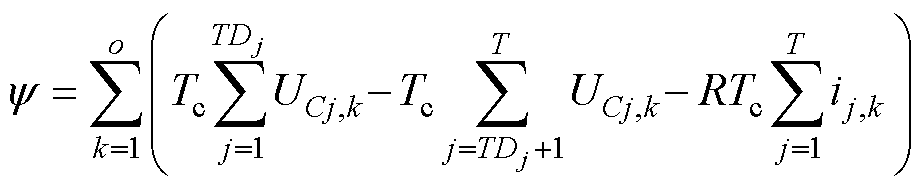（14）
为完成恒气隙接触器动态控制的建模仿真，需建立EMFA的动态仿真模型。使用有限元软件Ansoft的参数扫描功能计算获得电磁力、磁链、位移与电流的曲面如图8所示。此外，如图8a所示，磁链、电流与位移的曲面近似一个平面，因此2.3节中使用多元线性回归计算相关映射关系是合理的。
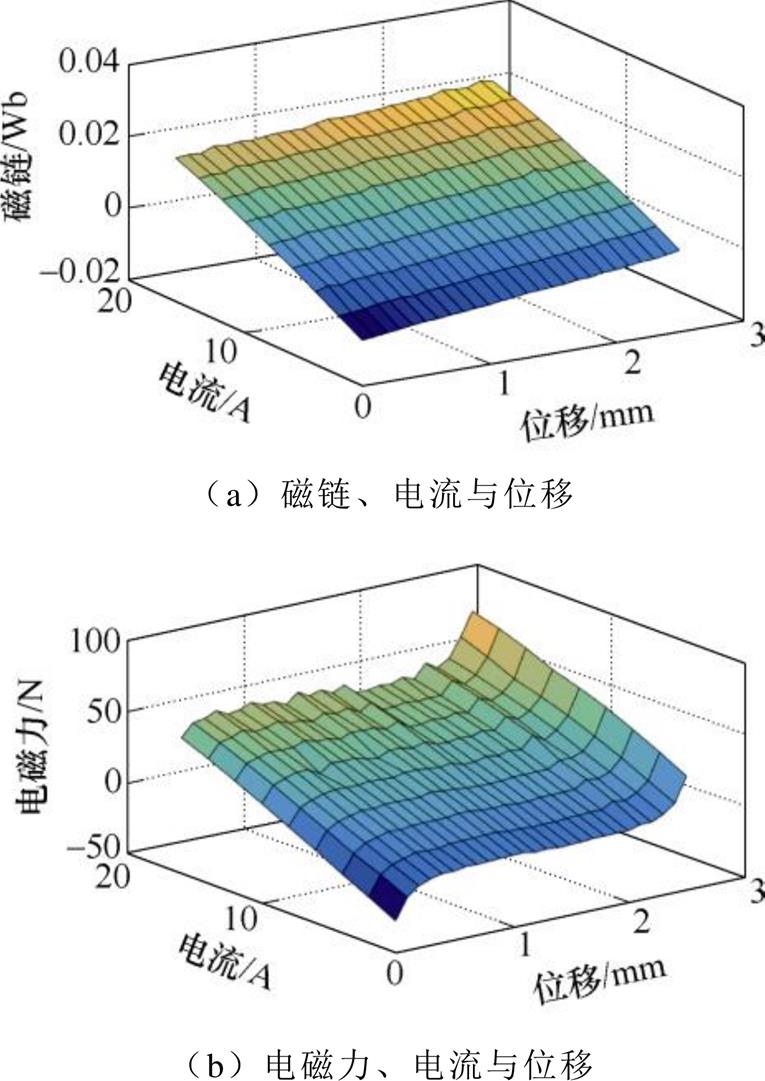
图8 电磁力、磁链、电流与位移的曲面
Fig.8 Surfaces of force, flux, current and displacement
图8a用于插值计算线圈电流，图8b用于计算EMFA电磁力，本质上两个曲面完成了电流与位移到磁链与电磁力的映射。使用式（15）求解机械运动方程即可获得EMFA的电气特性及机械特性。
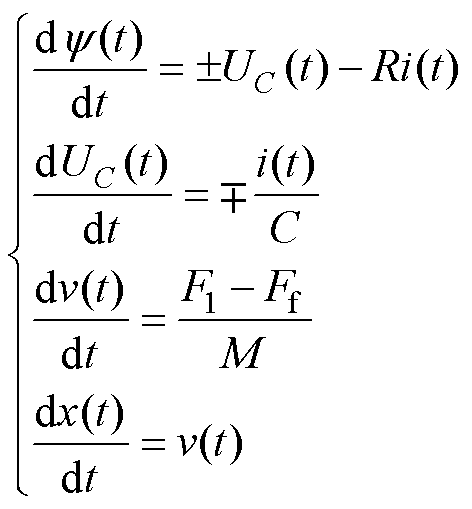（15）
式中，F1为安培力；Ff为运动反力；x为位移；v(t)为运动速度；M为质量。式（15）中当电路处于放电状态时，UC取正而i(t)取负；电路处于续流状态时，UC取负而i(t)取正。
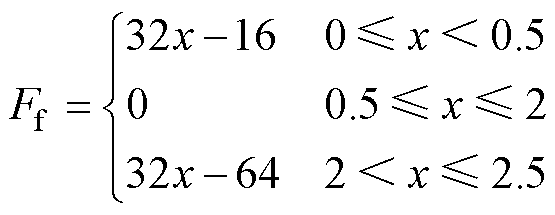（16）
由于测试用接触器为切换型接触器，因此在两个保持位置触头反力方向相反。
在求解微分方程式时使用四阶龙格库塔法进行计算，有
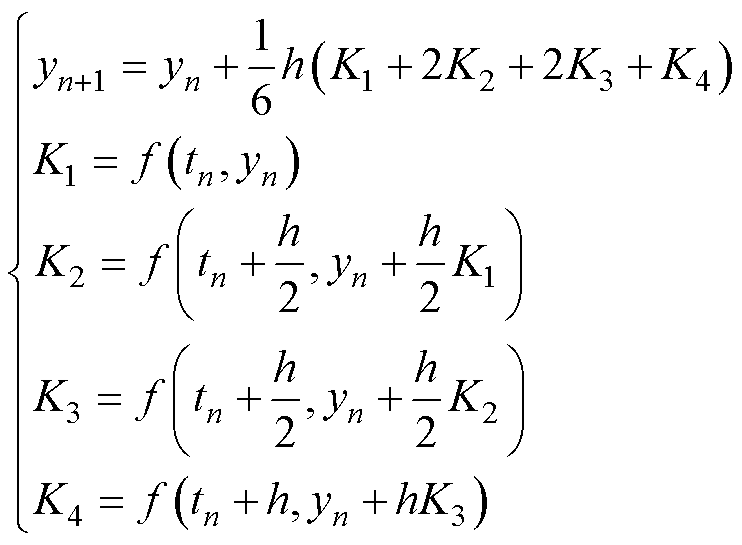（17）
式中，yn+1为下一时间步的值；yn为当前时间步值；h为步长；K1～K4为斜率；f为状态方程；tn为当前时间。
为验证无位置传感器控制的有效性，在EMFA位置预测的基础上，制定了分段PWM控制策略。分段PWM是永磁接触器的一种经典控制方法[26]，在接触器运动至不同的位置时施加不同占空比的PWM，通过桥式电路完成电流斩波，合理地控制线圈电流，从而完成速度调控，抑制触头弹跳。
恒定气隙接触器控制策略如图9所示，虚线为无控制情况下的速度曲线，在电磁力的不断作用下，EMFA的运动速度不断提升，在合闸时刻将引起触头的弹跳，弹跳时间过长将加大触头烧蚀，不利于接触器寿命的延长。因此，在起始阶段，使用较高的占空比有利于接触器快速动作，随着位移的不断增加逐步降低PWM占空比，有利于降低接触器末速度，从而降低触头弹跳。
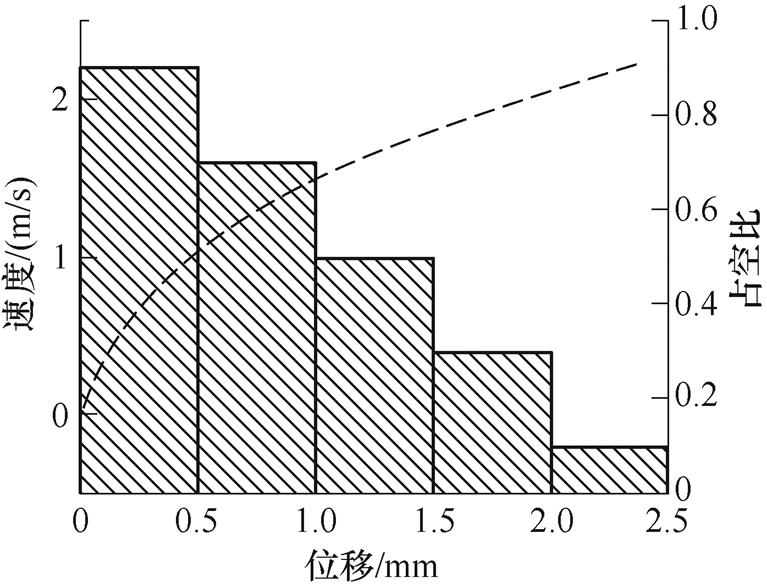
图9 恒定气隙接触器控制策略
Fig.9 Constant air gap contactor control strategy
仿真原理如图10所示，主要包括：PWM模块、u模块、psi模块、预测模块、双曲面模块、辨识模块以及位移模块。其中，PWM模块根据预测位移执行图9的控制策略；u模块与psi模块根据PWM判断电路状态，从而执行式（15）的计算；预测模块在获得辨识模块参数的基础上根据式（8）完成位置预测；双曲面模块存储了图8曲面用于插值计 算[24]；辨识模块完成了式（8）参数的辨识；位移模块输入电磁力用于计算EMFA动态位移。通过此模型能够完成EMFA的动态位置的预测以及无位置传感器控制仿真。
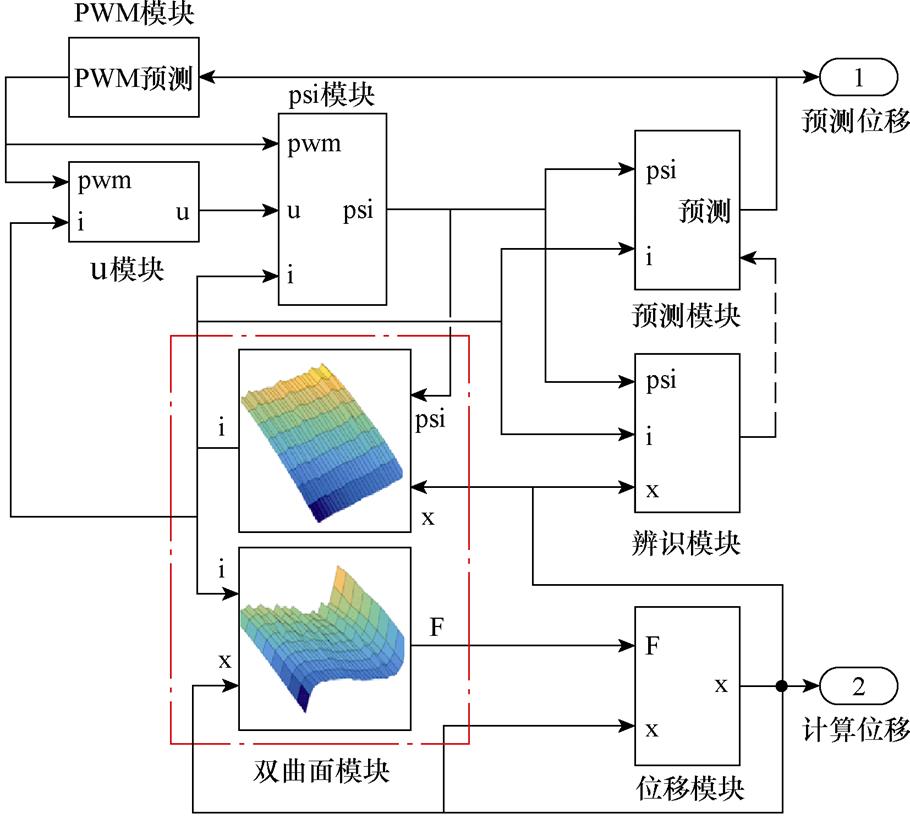
图10 仿真原理
Fig.10 Simulation schematic
通过上述数学模型进行建模，完成EMFA电磁模型及电路模型的搭建。根据双曲面配合式（15）计算EMFA动态电磁力，减去反力并经过两次积分模块可获得位移，如图11的虚线所示。仿真中包括了参数辨识模块，输入无控制条件下的磁链、电流及位移辨识式（8）的参数。在使用上述参数的式（8）的基础上，完成控制条件下的位移预测，如图11实线所示，输入磁链以及电流，即可输出对应的预测位移。如图11所示，基于式（15）的计算位移与基于式（8）的预测位移具有较强的一致性，验证了仿真的有效性以及位移预测的准确性。
逐步降低PWM占空比在降低接触器末速度的同时，不可避免地延长了接触器的闭合时间。因此，对不同PWM占空比组合下的动态特性进行了分析。末速度直接影响弹跳时间，表1使用末速度对触头的弹跳情况进行表征。
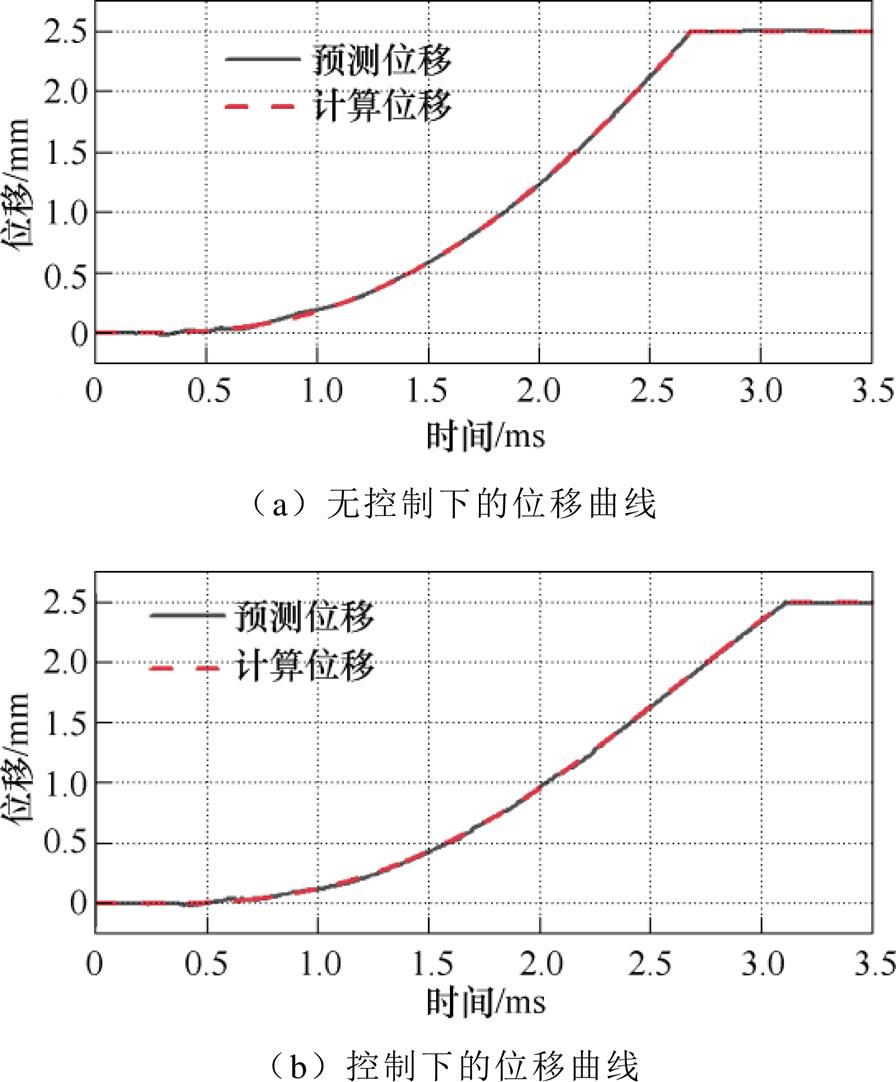
图11 仿真结果
Fig.11 Simulation result
表1 PWM占空比对动态特性的影响
Tab.1 PWM duty cycle on dynamic characteristics
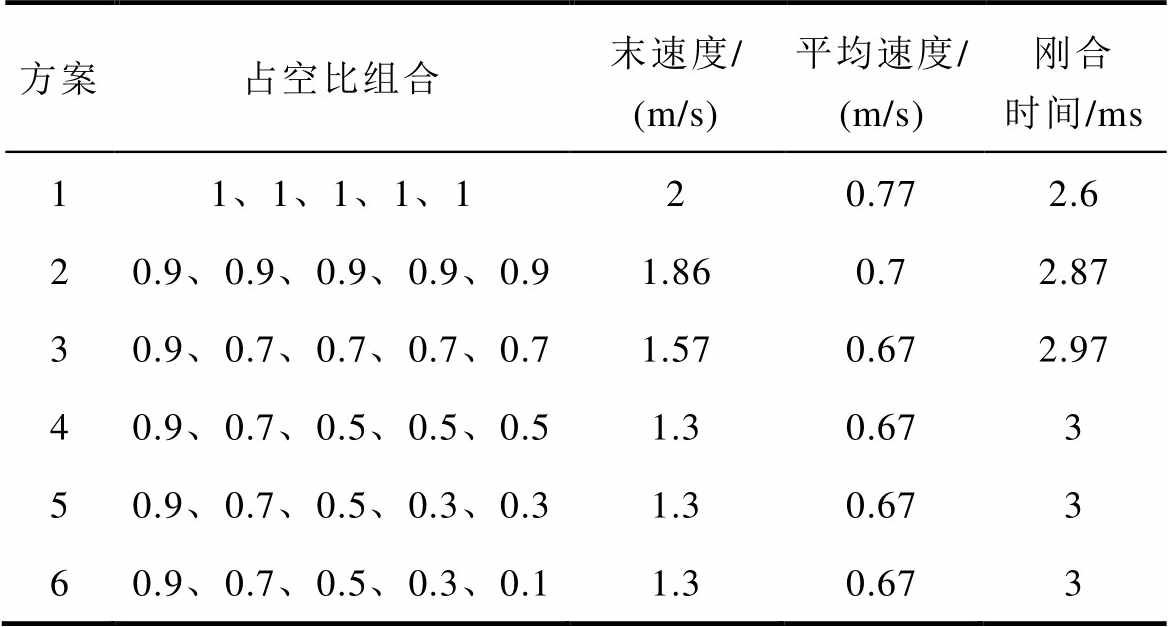
方案占空比组合末速度/ (m/s)平均速度/ (m/s)刚合时间/ms 11、1、1、1、120.772.6 20.9、0.9、0.9、0.9、0.91.860.72.87 30.9、0.7、0.7、0.7、0.71.570.672.97 40.9、0.7、0.5、0.5、0.51.30.673 50.9、0.7、0.5、0.3、0.31.30.673 60.9、0.7、0.5、0.3、0.11.30.673
由表1所示，对比方案1、2与3，随着占空比组合的不断下降，刚合时间延长而末速度下降。对比方案1与6，控制情况下末速度下降了35%，而平均速度仅下降了13%，相对于平均速度末速度的下降幅度更大。
在仿真的基础上，依据预测位移展开动态控制实验，通过触头弹跳时间验证弹跳抑制效果。搭建实验测试平台如图12所示。平台主要包括：电源模块、斩波模块、DSP模块、接触器与传感器、分压器。
为验证控制对接触器弹跳抑制的效果，同时验证占空比配置对动态特性的影响，本节完成了不同占空比的动态特性实验。
图12 实验平台
Fig.12 Experiment platform
方案2～5的测试波形如图13所示，其中包含了触头弹跳波形以及电流波形。由于位移曲线相似，因此将差异最大的波形在图14中进行了描述。由电流曲线可以看出，逐渐减低占空比将减少线圈电流，在占空比低于50%的情况下，电流快速降低至0并小范围波动，而占空比大于70%的情况下，电流波形保持稳定下降的趋势。而从负载电压处可看到触点的弹跳波形，随着占空比组合的不断降低，合闸时间逐渐延长而弹跳时间逐渐减小。在占空比不断变化的情况下，合闸时间的变化范围较小，而弹跳时间变化较大。详细的实验数据见表2，其中表2的实验结果与仿真结果相吻合，验证了仿真的准 确性。
对比方案1与方案6，即无控制与有控制的实验波形。如图14所示，分别为触头弹跳、线圈电流、位移波形。恒定气隙接触器的弹跳时间为1.2 ms。这是由于末速度较快，触头碰撞能量较大，使得弹跳时间较长，不利于接触器寿命的延长。
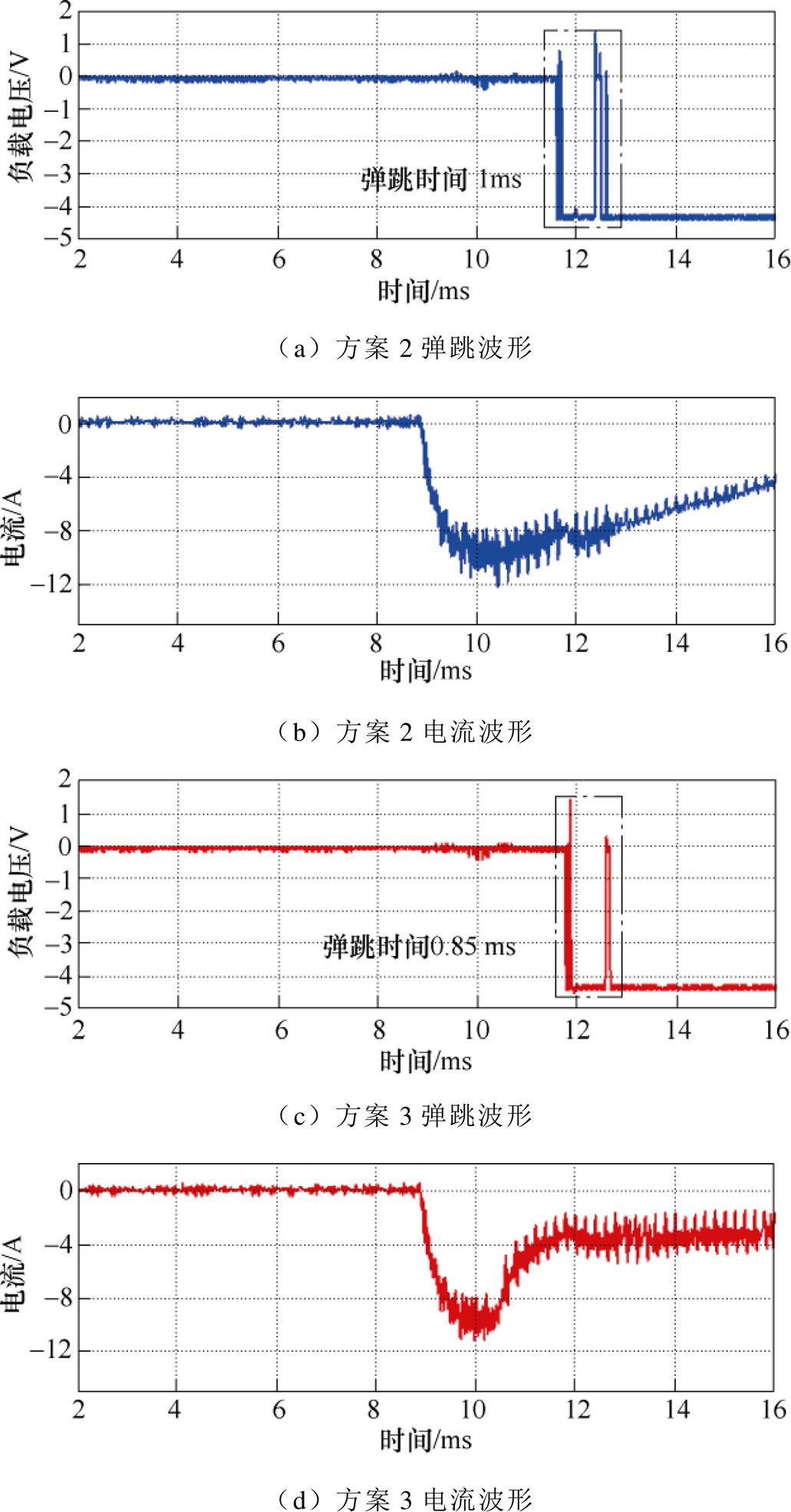
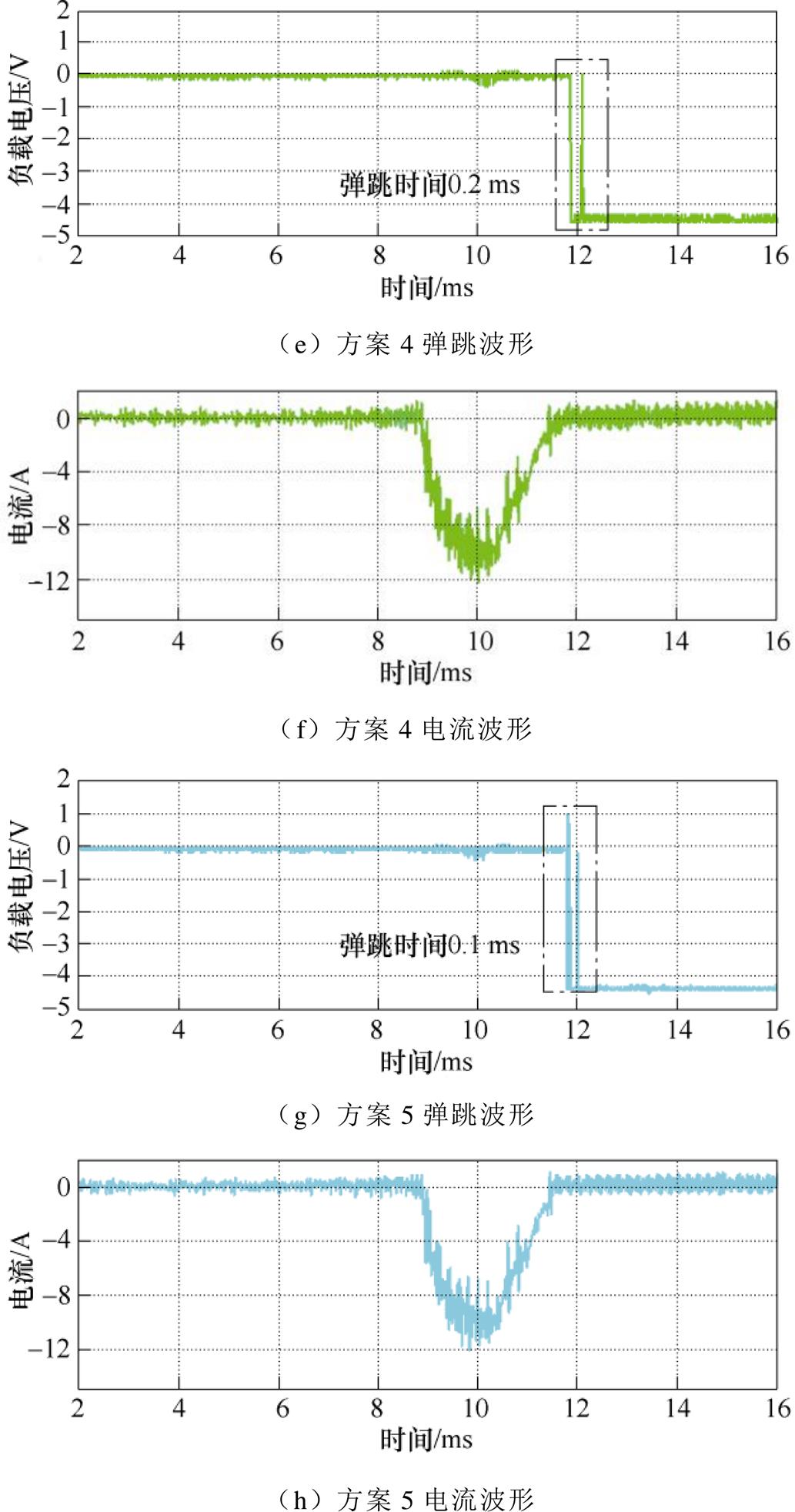
图13 方案2～5的测试波形
Fig.13 Test waveforms for schemes 2～5
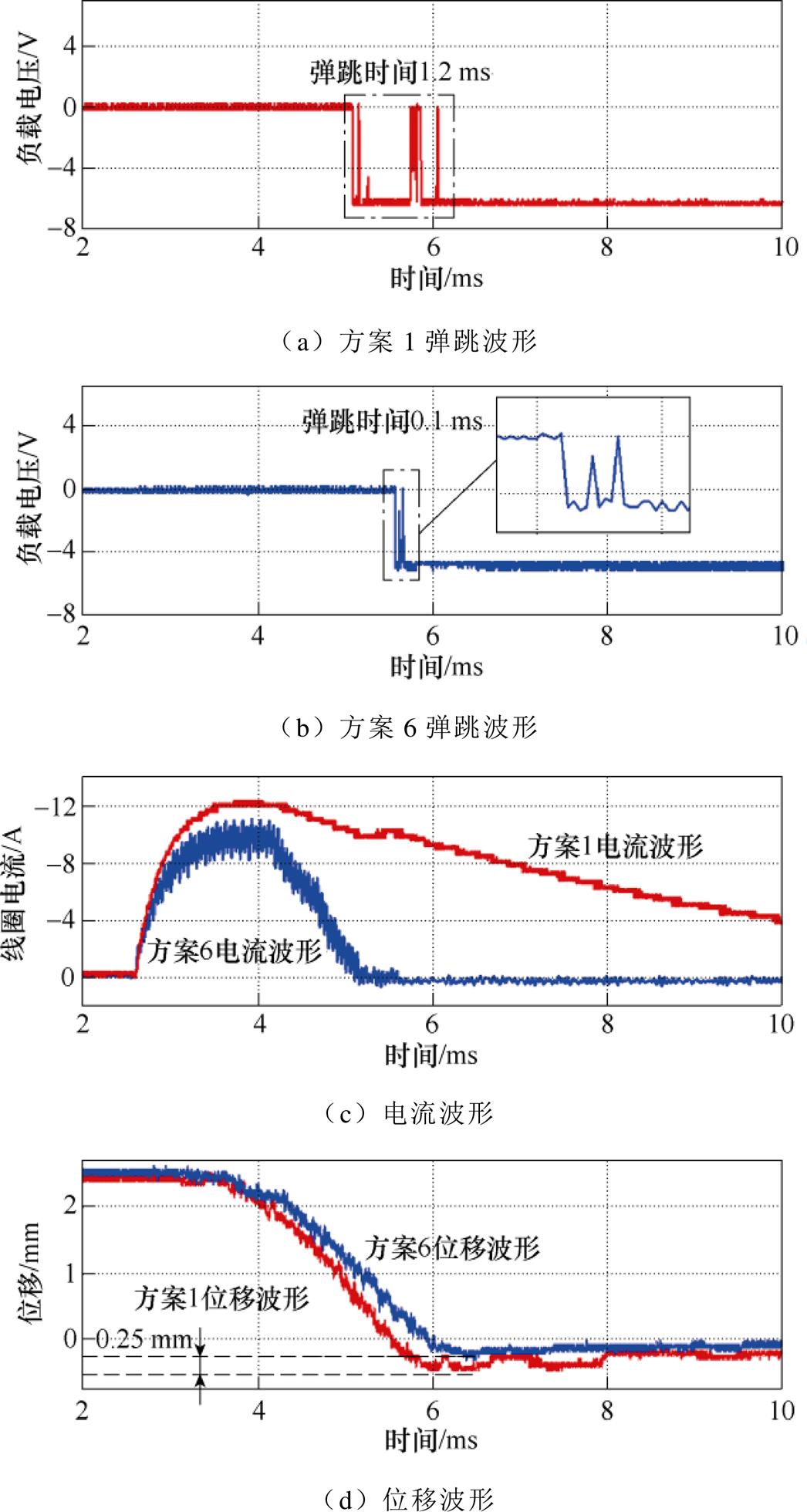
图14 方案1与6的测试波形
Fig.14 Test waveforms for scenarios 1 and 6
表2 实验结果
Tab.2 Experiment results
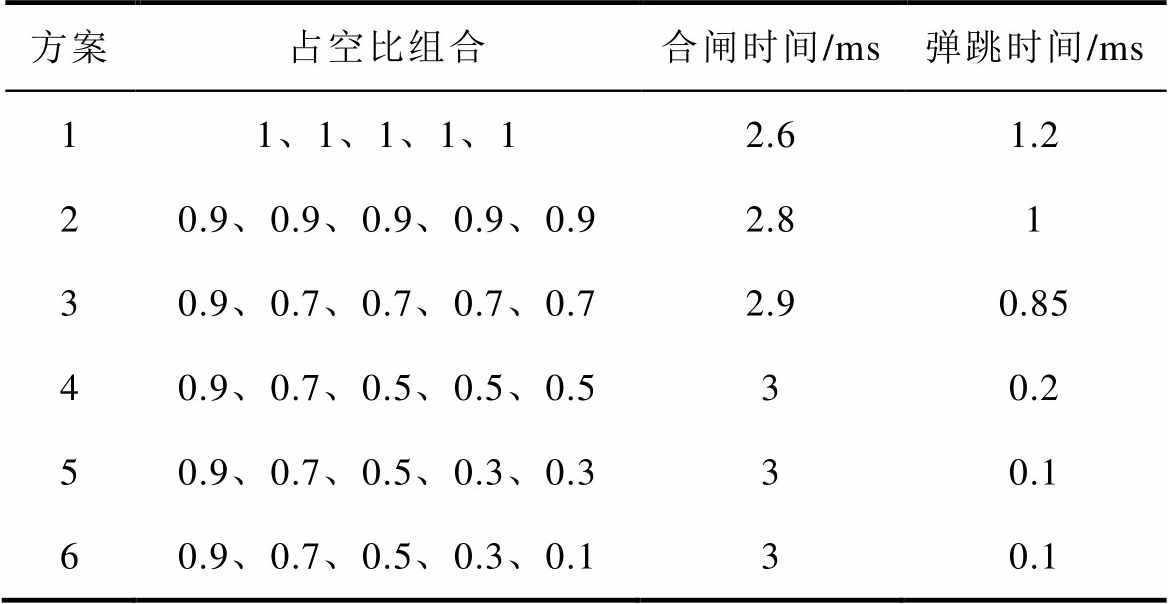
方案占空比组合合闸时间/ms弹跳时间/ms 11、1、1、1、12.61.2 20.9、0.9、0.9、0.9、0.92.81 30.9、0.7、0.7、0.7、0.72.90.85 40.9、0.7、0.5、0.5、0.530.2 50.9、0.7、0.5、0.3、0.330.1 60.9、0.7、0.5、0.3、0.130.1
方案6的测试波形如图14蓝线所示，其中占空比组合以0.9、0.7、0.5、0.3、0.1为例进行测试。在EMFA运动至不同的位置时施加不同的占空比，以达到控制EMFA末速度降低弹跳时间的目的。方案6接触器的弹跳时间为0.1 ms，对比方案1的弹跳波形，弹跳时间减小了92%，减少了最大回弹距离约0.25 mm。其中，方案6电流波形的高频分量是IGBT斩波造成的。
实验证明分段PWM控制能够减少弹跳时间，验证了动态控制方法的有效性。
针对恒定气隙接触器提出一种位置预测方法，使用等效磁路法与参数辨识从永磁体磁链中提取位置信息，随后依据位置信息实施控制。通过实验的方法验证了位置预测的准确性与控制的有效性。在此基础上，得到以下结论：
1）通过等效磁路模型，建立了恒定气隙接触器位移、磁链与电流的基本映射模型，并通过实验验证了模型的有效性。
2）使用多元回归的方法完成了位移、磁链与电流映射关系的参数辨识，在完成映射关系的基础上进行实验，并通过实验验证了其准确性。
3）通过有限元软件计算磁链、电磁力、电流与位移的双曲面，通过双曲面插值模拟EMFA动态特性，建立了位置预测及动态控制模型，动态控制能够有效降低末速度。
4）在仿真的基础上完成了动态控制实验，对比了有无控制条件下的动态特性，实验证明该控制方法适用于恒定气隙接触器，分段控制条件下能够减少92%的弹跳时间。
参考文献
[1] 游颖敏, 王景芹, 舒亮, 等. 基于音频特征的交流接触器电寿命预测方法[J]. 电工技术学报, 2021, 36(9): 1986-1998.
You Yingmin, Wang Jingqin, Shu Liang, et al. The method of electrical life prediction considering the audio characteristics of AC contactor[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1986- 1998.
[2] 李奎, 张国盼, 郑淑梅, 等. 基于实时服役参数的交流接触器电寿命最大化控制策略[J]. 电工技术学报, 2021, 36(9): 1976-1985.
Li Kui, Zhang Guopan, Zheng Shumei, et al. A control strategy for maximizing the electrical life of AC contactors based on real-time operating para- meters[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1976-1985.
[3] 贾博文, 武建文, 夏尚文, 等. 直流自然换流式接触器设计与均压开断研究[J]. 电工技术学报, 2021, 36(20): 4371-4378.
Jia Bowen, Wu Jianwen, Xia Shangwen, et al. Design and uniform voltage breaking research of a DC natural current commutation contactor[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4371-4378.
[4] 刘帼巾, 李想, 王泽, 等. 基于Wiener过程电子式漏电断路器的剩余寿命预测[J]. 电工技术学报, 2022, 37(2): 528-536.
Liu Guojin, Li Xiang, Wang Ze, et al. Remaining life prediction of electronic residual current circuit breaker based on Wiener process[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 528-536.
[5] 唐昭晖, 许志红. 基于响应面法的交流接触器弹簧系统优化设计方法[J]. 电工技术学报, 2022, 37(2): 515-527.
Tang Zhaohui, Xu Zhihong. Optimal design method for AC contactor spring system based on response surface method[J]. Transactions of China Electro- technical Society, 2022, 37(2): 515-527.
[6] 汤龙飞, 庄剑雄, 孙怀懿, 等. 电磁开关高频吸持噪声抑制策略[J]. 电工技术学报, 2022, 37(10): 2631-2643.
Tang Longfei, Zhuang Jianxiong, Sun Huaiyi, et al. Suppression strategies of electromagnetic switch high-frequency holding noise[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2631- 2643.
[7] 董恩源, 刘罡, 邹启涛, 等. 长行程断路器操动用新型磁力机构[J]. 高电压技术, 2010, 36(3): 816- 820.
Dong Enyuan, Liu Gang, Zou Qitao, et al. New type magnetic force actuator (MFA) for long stroke circuit breaker[J]. High Voltage Engineering, 2010, 36(3): 816-820.
[8] 田宇, 许家源, 王永兴, 等. 配126kV单断口选相真空断路器长行程磁力机构设计及性能试验[J]. 电网技术, 2020, 44(11): 4445-4453.
Tian Yu, Xu Jiayuan, Wang Yongxing, et al. Design and performance test of electro-magnetic force actuator for 126kV single break vacuum circuit breaker with controlled switching[J]. Power System Technology, 2020, 44(11): 4445-4453.
[9] Ro J S, Bak H J, Jung H K. Characteristic analysis and design of a novel Lorentz force driving actuator for a molded case circuit breaker[J]. IET Electric Power Applications, 2015, 9(1): 1-9.
[10] Wang Gongrun, Wang Yongxing, Zhang Lifan, et al. A novel model of electromechanical contactors for predicting dynamic characteristics[J]. Energies, 2021, 14(22): 7466.
[11] 茹晶晶, 方春恩, 瞿绪龙, 等. 新型磁力操动机构EMFA的动态特性仿真研究[J]. 高压电器, 2011, 47(11): 6-10.
Ru Jingjing, Fang Chun'en, Zhai Xulong, et al. Dynamic characteristic simulation of a new type of electromagnetic force driving actuator EMFA[J]. High Voltage Apparatus, 2011, 47(11): 6-10.
[12] 李奎, 李晓倍, 郑淑梅, 等. 基于BP神经网络的交流接触器剩余电寿命预测[J]. 电工技术学报, 2017, 32(15): 120-127.
Li Kui, Li Xiaobei, Zheng Shumei, et al. Residual electrical life prediction for AC contactor based on BP neural network[J]. Transactions of China Electro- technical Society, 2017, 32(15): 120-127.
[13] 李奎, 段宇, 黄少坡, 等. 基于Wiener过程的交流接触器剩余电寿命预测[J]. 中国电机工程学报, 2018, 38(13): 3978-3986, 4039.
Li Kui, Duan Yu, Huang Shaopo, et al. Residual electrical life prediction of AC contactor based on the Wiener process[J]. Proceedings of the CSEE, 2018, 38(13): 3978-3986, 4039.
[14] 张长坤, 许志红. 基于磁链变量的宽电压智能交流接触器触头弹跳抑制策略[J]. 电工技术学报, 2018, 33(21): 4998-5006.
Zhang Changkun, Xu Zhihong. Contact bounce suppression based on flux linkage of wide voltage range intelligent AC contactor[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4998- 5006.
[15] 张长坤, 许志红. 基于磁链反馈的智能交流接触器串级控制策略[J]. 中国电机工程学报, 2020, 40(4): 1329-1338, 1424.
Zhang Changkun, Xu Zhihong. A cascade control strategy for intelligent AC contactors based on flux linkage feedback[J]. Proceedings of the CSEE, 2020, 40(4): 1329-1338, 1424.
[16] 翟国富, 薄凯, 周学, 等. 直流大功率继电器电弧研究综述[J]. 电工技术学报, 2017, 32(22): 251-263.
Zhai Guofu, Bo Kai, Zhou Xue, et al. Investigation on breaking arc in DC high-power relays: a review[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 251-263.
[17] 翟国富, 许峰, 刘茂恺. 基于超程时间减小速率建模的电磁继电器可靠性寿命分析方法的研究[J]. 电子器件, 2002, 25(3): 301-304.
Zhai Guofu, Xu Feng, Liu Maokai. The research of a method for life analysis on reliability of elec- tromagnetic relays based on the model of rate of decrease of super-path time[J]. Journal of Electron Devices, 2002, 25(3): 301-304.
[18] 纽春萍, 陈德桂, 李兴文, 等. 交流接触器触头弹跳的仿真及影响因素[J]. 电工技术学报, 2007, 22(10): 85-90, 108.
Niu Chunping, Chen Degui, Li Xingwen, et al. Simulation of contact bounce of AC contactor and study of its influence factors[J]. Transactions of China Electrotechnical Society, 2007, 22(10): 85-90, 108.
[19] Dong Enyuan, Qin Taotao, Wang Yongxing, et al. Experimental research on speed control of vacuum breaker[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2594-2601.
[20] 刘颖异, 陈德桂, 袁海文, 等. 带电流反馈的永磁接触器动态特性仿真与分析[J]. 中国电机工程学报, 2010, 30(15): 118-124.
Liu Yingyi, Chen Degui, Yuan Haiwen, et al. Simu- lation and analysis on dynamic characteristics of permanent magnetic contactor with current feed- back[J]. Proceedings of the CSEE, 2010, 30(15): 118-124.
[21] 吴自然, 舒亮, 许成文, 等. 一种新型永磁交流接触器及其控制电路[J]. 中国电机工程学报, 2016, 36(13): 3667-3673, 3387.
Wu Ziran, Shu Liang, Xu Chengwen, et al. A new permanent magnet AC contactor and its control circuit[J]. Proceedings of the CSEE, 2016, 36(13): 3667-3673, 3387.
[22] Wang Xianbing, Lin Heyun, Ho S L, et al. Analysis of dynamic characteristics of permanent magnet con- tactor with sensorless displacement profile control[J]. IEEE Transactions on Magnetics, 2010, 46(6): 1633- 1636.
[23] Fang Shuhua, Liu Qingdong, Lin Heyun, et al. A novel flux-weakening control strategy for permanent- magnet actuator of vacuum circuit breaker[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2275-2283.
[24] Wang Xianbing, Lin Heyun, Fang Shuhua, et al. Dynamic performance analysis of permanent magnet contactor with a flux-weakening control strategy[J]. Journal of Applied Physics, 2011, 109(7): 07E707.
[25] 汪先兵, 林鹤云, 房淑华, 等. 无位置传感器的智能永磁接触器弱磁控制及合闸动态特性分析[J]. 中国电机工程学报, 2011, 31(18): 93-99.
Wang Xianbing, Lin Heyun, Fang Shuhua, et al. Analysis of flux-weakening control and dynamic characteristic for making process of sensorless intelligent permanent magnet contactor[J]. Pro- ceedings of the CSEE, 2011, 31(18): 93-99.
[26] 汪先兵, 林鹤云, 房淑华, 等. 永磁接触器位移分段PWM控制及吸合过程动态特性分析[J]. 中国电机工程学报, 2010, 30(3): 113-118.
Wang Xianbing, Lin Heyun, Fang Shuhua, et al. Segmented PWM control of permanent magnet contactor displacement and dynamic characteristics analysis of pull-in process[J]. Proceedings of the CSEE, 2010, 30(3): 113-118.
Abstract A contactor is an electrical appliance that connects and disconnects circuits, widely used in power switching, motor control, rail transit, and new energy power generation. During the closing process, the contact bounce collision will produce arcs, and the high-frequency long-time bounce process will significantly shorten the electrical life of the contactor. It is feasible to use sensorless control to suppress contact bounce. The sensorless control technology of the constant air gap contactor is studied. Position sensorless control includes position prediction and dynamic control. The equivalent magnetic circuit method and parameter identification are used to realize position prediction. Based on position prediction, the simulation and experimental research of dynamic control are carried out.
A position sensorless control method is proposed for the constant air gap contactors to reduce the contact bounce of the contactor. The position information is extracted from the permanent magnet flux linkage through the equivalent magnetic circuit method and parameter identification. Then the actuator is controlled according to the location information. The equivalent magnetic circuit model of the electromagnetic force driving actuator (EMFA) is established. The mapping relationship between dynamic flux linkage, displacement, and current is then deduced. The rationality of the mapping relationship is verified by the “fixed method” and “prediction method”. The displacement, voltage, and current are obtained through experiments, the flux linkage is calculated according to the experimental data, and the parameters of the displacement mapping are obtained by the multiple regression method. Afterward, the position prediction of the contactor is completed. The predicted displacement is compared with the measured displacement, verifying the accuracy of position prediction.
Two surfaces of the driving force and flux linkage are established through the parameter scanning function of the finite element model. The modeling of the contactor is completed by interpolation, position prediction, and simulation without carrying out position control. Based on the simulation model, the calculated displacement is compared with the predicted displacement, and the accuracy of displacement prediction is verified. Based on the subsection PWM control strategy, the influence of duty cycle combinations on the dynamic characteristics of the contactor is analyzed. The simulation results show that the terminal speed of the contactor is reduced with the gradual reduction of the duty cycle combination.
The experimental platform is built, including power module, chopper module, DSP module, contactor, sensor, and voltage divider module. In the experiment, the coil current, contact bounce, and contactor displacement under different duty cycle combinations are collected. The influence of the duty cycle combination on closing time and bouncing time is analyzed. With the decrease in duty cycle combination, the bouncing time decreases while the closing time increases gradually. The experimental results show that the new position sensorless control method is suitable for constant air gap contactors. The accuracy of the position prediction and the effectiveness of the control method are verified.
Based on simulation and experiment, the following conclusions are drawn:(1) The equivalent magnetic circuit method and parameter identification can be used to predict the position of the constant air gap contactor. (2) The EMFA simulation model is established by the difference method, and the dynamic control can effectively reduce the terminal speed. (3) The experiment proves that the control method is suitable for the constant air gap contactor, and the bounce time can be reduced by 90% under subsection control.
keywords：Constant air gap contactor, control, contact bounce, electromagnetic force driving actuator (EMFA), dynamic characteristics
DOI: 10.19595/j.cnki.1000-6753.tces.221438
中图分类号：TM572
省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学）开放课题基金资助项目（EERI_KF2020009）。
收稿日期 2022-07-26
改稿日期 2022-08-19
王公润 男，1996年生，博士研究生，研究方向为快速机械开关、电磁设备建模。E-mail: 875199959@qq.com
王永兴 男，1973年生，副教授，硕士生导师，研究方向为智能电器、高压电器的可靠性理论。E-mail: yxwang@dlut.edu.cn（通信作者）
（编辑 崔文静）