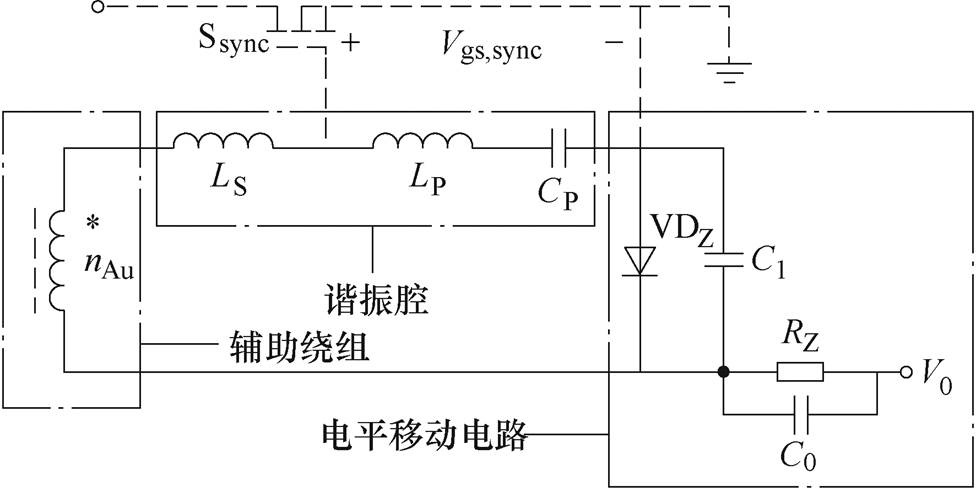
图1 自驱动同步整流技术电路
Fig.1 Self-driven synchronous rectification technology circuit diagram
摘要 该文设计一种具有准零相位差同步驱动信号的10 MHz DC-DC功率变换器,通过设计逆变器输出电压与整流器输入电压近似同相位,整流器和逆变器可以采用同一驱动信号,简化了同步整流开关管的控制难度,实现了10 MHz下可靠、简洁的同步整流控制。同时,为满足主拓扑要求,构建具有二次侧准无漏感特性的嵌套环形3D变压器,大大减少了传统变压器二次侧漏感对于同步整流控制的影响,并提出由多个印制电路板(PCB)结合来制作嵌套环形3D变压器的方法。最终,设计了一台48 V输入、12 V/28 W输出的实验样机,实验结果验证了所提出的控制方法和数值设计方法的可行性。
关键词:高频DC-DC变换器 同步整流 PCB变压器 准无漏感
随着电力电子技术的不断发展,对电力电子系统的效率和体积的要求越来越高[1-7]。较高的工作频率可以减少无源元件在每个周期内所需转换的能量,使电感、电容和变压器的体积和数值较小[8]。因此,提高开关频率是降低电力电子变换器体积的最有效途径。随着无源元件的数值减小,寄生元件的数值与所需谐振元件的数值变得相近。因此,提高系统的工作频率不仅可以减小系统的体积,还可以利用系统的寄生元件作为谐振元件,减小元件数目[9-14]。例如,当频率提高到几MHz至几十MHz后,谐振电感的感值将下降到与各类空心变压器的漏感相近似,可以将空心变压器的漏感作为谐振元件,但其影响也日益凸显。
在高频DC-DC变换器中,整流器通常采用具有极快开关速度的肖特基二极管。然而,肖特基二极管的正向压降仍然很高。为了提升高频DC-DC变换器的效率,越来越多的高频开关电源采用同步整流技术[14-17]。但是,在几十MHz的频率下,同步整流驱动技术有较大挑战:由于谐振电路中存在无源元件、寄生电感和变压器漏感,造成整流器输入电压与逆变器输出电压存在一定相位差。如果不能精确计算或测定相位差,错误的时钟信号将会导致同步整流开关管误动作,开关管的体二极管导通并增加反向导通损耗[18]。另外,在如此高的频率下,目前没有同步整流模拟控制芯片可以可靠运行。
图1为在低压/低功率的高频DC-DC功率变换器中,采用的同步整流器的自驱动导通方法。然而,自驱动导通方法需要额外的谐振电路,很难精确地驱动同步整流开关,特别是开关频率在几十MHz的情况下[19-20]。因此,如何在几十MHz频率下使同步整流更准确、高效,具有十分重要的意义。

图1 自驱动同步整流技术电路
Fig.1 Self-driven synchronous rectification technology circuit diagram
在高频情况下,为了解决上述问题,整流侧和逆变侧的同步驱动信号必须具有零相位差特性。为了实现这一性能,本文采用了具有单侧准无漏感特性的嵌套环形3D变压器。基于嵌套环形变压器的准无漏感特性,可以大大减少整流器输入电压与逆变器输出电压之间的相位差。此时整流器和逆变器可以使用相同的驱动信号,解决了几十MHz下同步整流技术的难题。
首先,本文对实现同步驱动的根本元件——嵌套环形3D变压器进行了理论分析。并且进一步提出了应用该变压器实现同步整流的10 MHz变换器的方案。其次,对嵌套环形3D变压器进行了设计、仿真及实验验证。基于上述分析,对所提拓扑搭建了样机,进行实验验证。最后,对全文进行了总结。
嵌套环形3D变压器示意图如图2所示,嵌套环形3D变压器由内、外两个绕组组成。其中,外部、内部绕组分别为变压器一次侧、二次侧,外部绕组环绕包围内部绕组。绕组电流及磁场分布示意图如图3所示,绕组中总电流可分为径向电流iN2和周向电流i1-t,分别产生径向磁场HN2和周向磁场H1-t。其中,内、外部绕组会耦合共同的HN2磁场,并且,内部绕组沿圆周方向所产生的磁通全部被外部绕组横截面所封闭,即内部绕组产生的磁通全部充当内、外绕组的共有磁通。因此,内部绕组的漏磁可看作零。嵌套环形变压器的等效原理如图4所示,嵌套环形3D变压器可用图4所示电路等效(外部绕组为变压器一次侧,内部绕组为变压器二次侧),可大大减小其二次侧漏感。
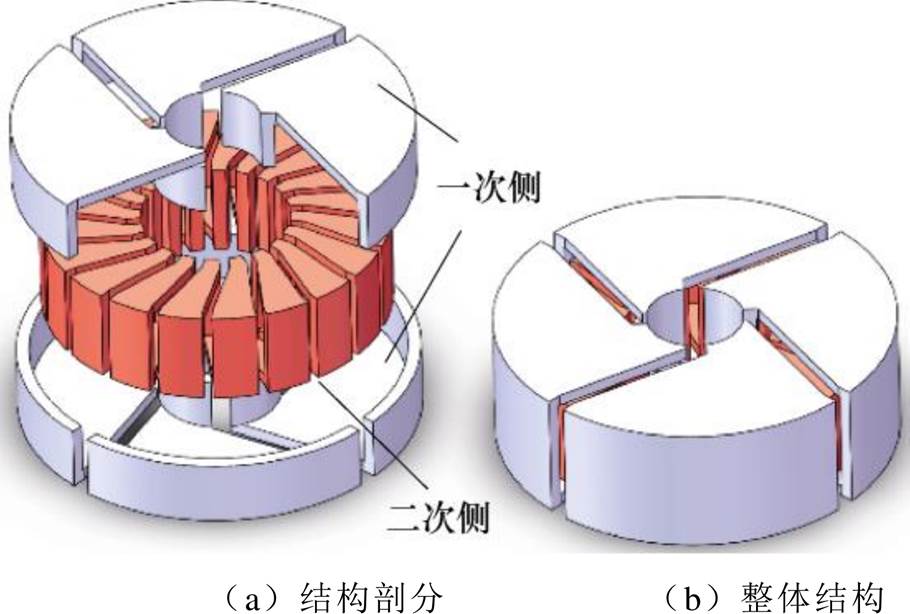
图2 嵌套环形变压器示意图
Fig.2 The schematic diagram of nested toroidal transformer
图4中,LS1、LS2分别为变压器一、二次侧漏感,Lm为励磁电感,n为变压器电压比。变压器横截面示意图如图5所示。为了计算等效电路中的上述参数,必须先计算图5中所示的由外、内部绕组(一次、二次侧)共有的磁通路径引起的磁阻Rm和由在外绕组内部并在内绕组外部的磁通路径引起的磁阻R11。图中,ri,prim、ri,sec分别为变压器一、二次侧的内径,ro,prim、ro,sec分别为变压器一、二次侧的外径,hprim、hsec分别为变压器一、二次侧的高度。
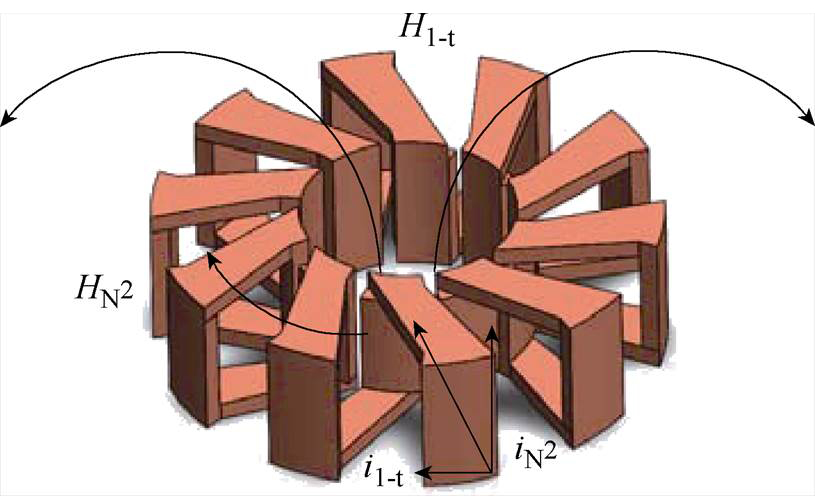
图3 绕组电流及磁场分布示意图
Fig.3 Schematic diagram of winding current and magnetic field distribution
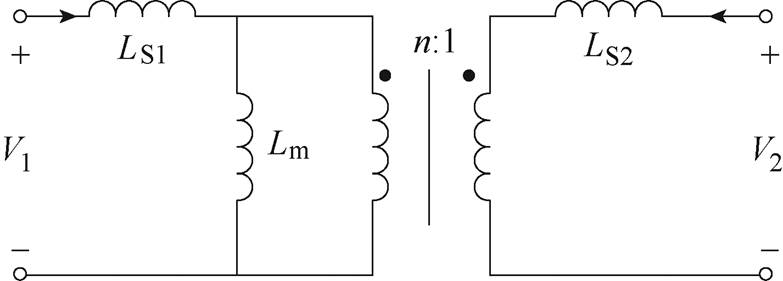
图4 嵌套环形变压器的等效原理
Fig.4 Equivalent schematic of nested toroidal transformer
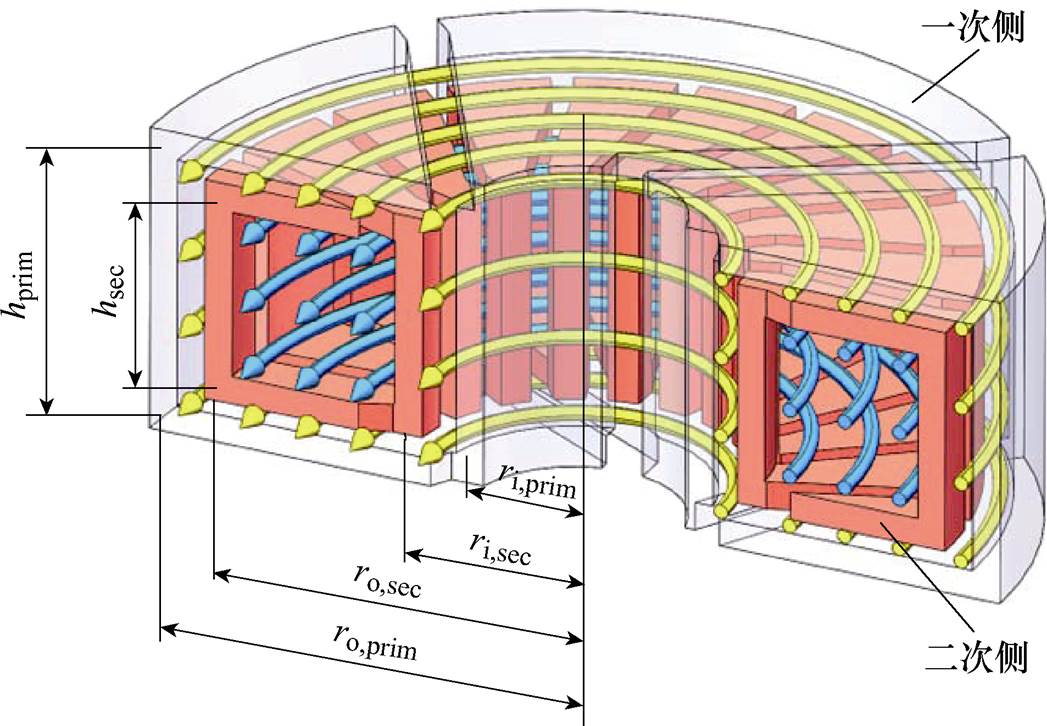
图5 变压器横截面示意图
Fig.5 The cross section diagram of the nested toroidal transformer
首先,利用安培定律式(1),可得到绕组内磁场强度的表达式H=Ni/(2pr),其中,N为绕组的匝数,i为电流,r为距绕组的距离。其次,利用内环内部的磁场强度和内外环之间区域的磁场强度的积分可分别计算出内、外部(一次、二次侧)绕组共有的磁通Fm和在外绕组内部并在内绕组外部的磁通F11。最后,可以通过式(2)和式(3)来计算相应的磁阻Rm和R11。
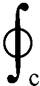
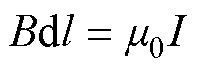 (1)
(1)
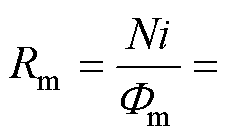
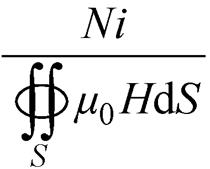
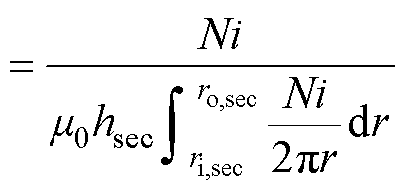
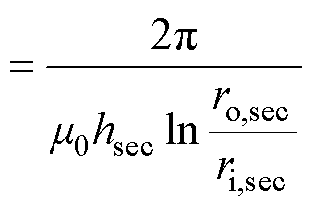 (2)
(2)
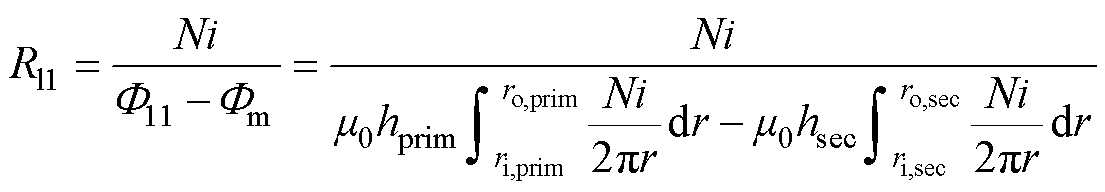
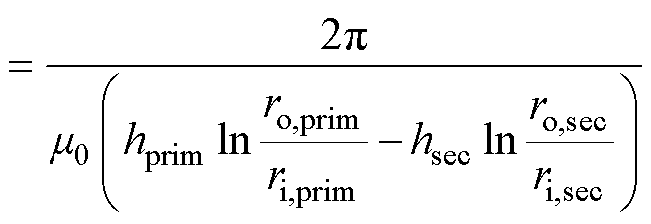 (3)
(3)
式中,B为dl处的磁感应强度;l为空间内垂直于电流方向的任一平面的闭合回路;m0为真空磁导率,m0=4p×10-7 H/m;I为闭合回路内的总电流;Fm为一次、二次绕组共有的磁通;H为在dS处的磁场强度。
得到各部分磁阻值后,可得到式(4)所示的电感矩阵。
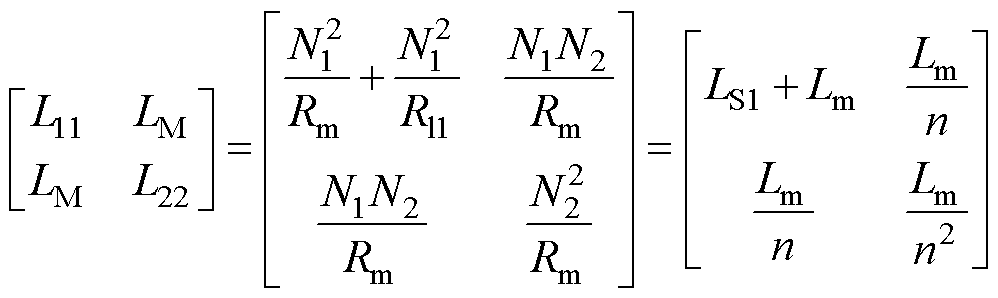 (4)
(4)
式中,N1、N2为变压器一、二次侧匝数;L11、L22、LM为变压器一次、二次侧的自感和互感。
电感矩阵提供了不同变压器模型之间的转换公式,但式(4)忽略了周向电流i1-t产生的电感。为了进一步提高电感矩阵的精度,L11和L22应分别增加由图3中的电流i1-t引起的外环和内环绕组的单匝电感L1-t-1和L1-t-2。其近似计算公式[21]为
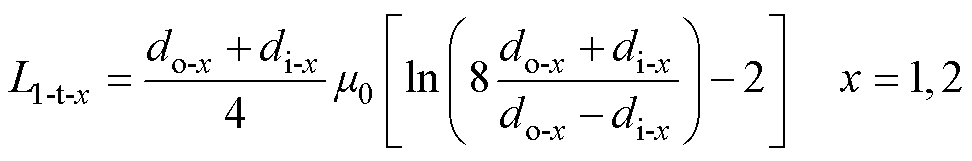 (5)
(5)
式中,do-x和di-x分别为内、外绕组的外直径和内直径。因此,电感矩阵可以进一步修正为
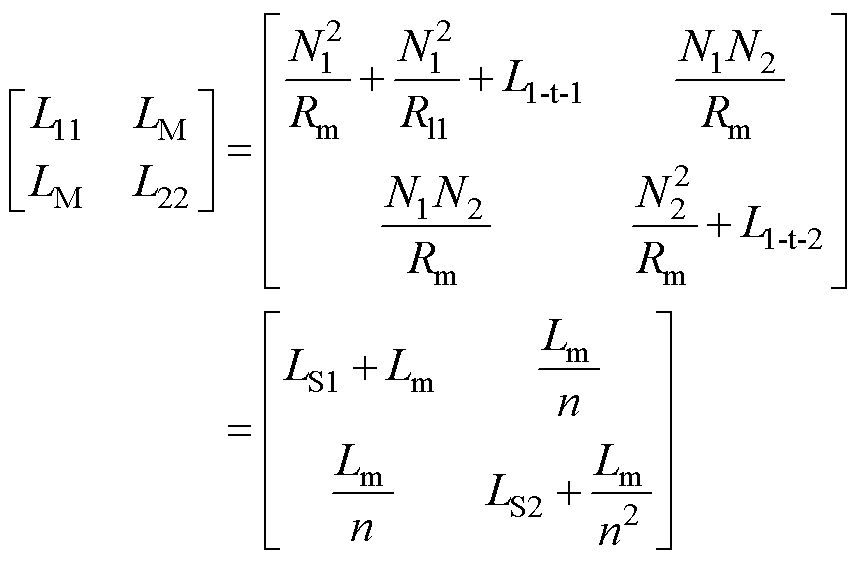 (6)
(6)
通过式(6)可知,可以调节变压器一、二次侧匝数N1、N2来改变变压器的电压比n。根据具体的应用场景,通过设计电压比,可以实现升压或降压变压器的功能。针对嵌套环形3D变压器二次侧准无漏感的特性,在高频情形下可以应用到如下的同步整流场景中。
图6所示为在10MHz开关频率下,应用嵌套环形3D变压器准无漏感特性的零相位差同步驱动型拓扑。它由Class DE逆变器、LC串联支路、变压器和全桥同步整流器组成。其中,Cin、Cout为输入电容和输出电容,Vin、VO为输入电压和输出电压,VA、VB为逆变器输出电压和整流器输入电压,VP、VS为变压器一次侧输入电压和二次侧输出电压,变压器用于吸收谐振电感Lr,提供电气隔离并提高电压降比。此外,功率在由输入侧传输到输出侧的过程中经过由谐振电感Lr、谐振电容Cr构成的串联谐振网络,因此流过谐振腔的电流可近似为正弦波。在应用基波分析法后,谐振腔的交流等效电路如图7所示[21]。
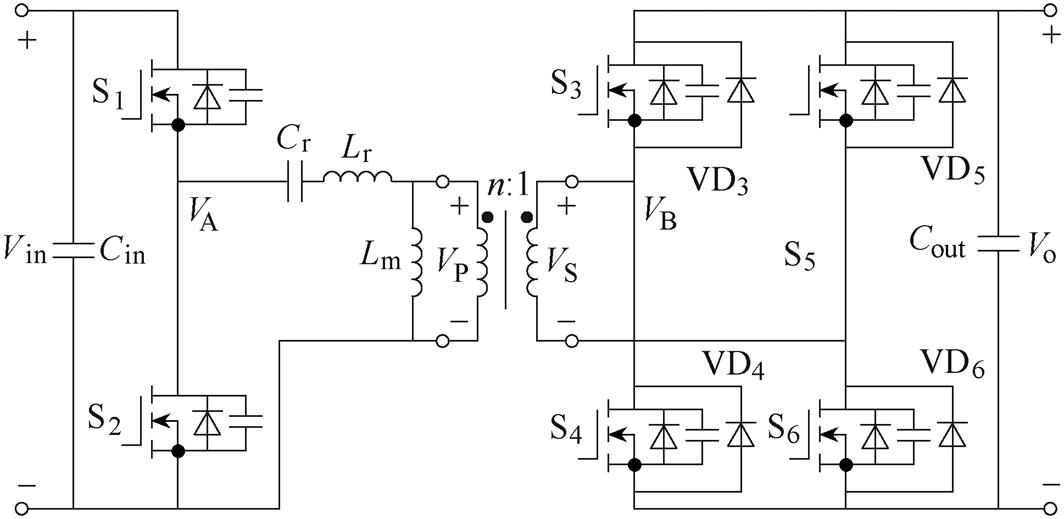
图6 基于Class DE逆变器、LC串联支路和全桥同步整流的高频变换器
Fig.6 Proposed high frequency converter based on Class DE inverter, LC branch and full-bridge synchronous rectifier
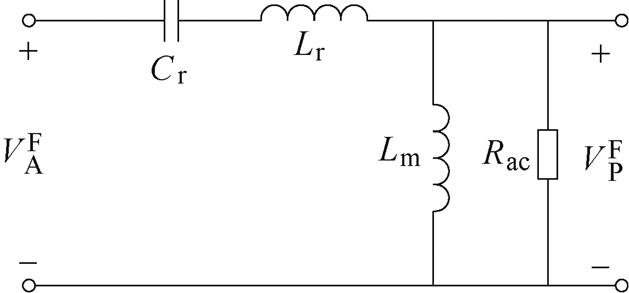
图7 基于基波分析法的谐振腔交流等效电路
Fig.7 AC equivalent circuit of the resonant tank based on FHA
图7中,Rac为负载经过整流器和变压器的等效电阻,表示为
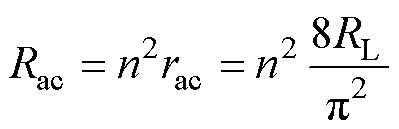 (7)
(7)
式中,rac为整流桥等效电阻;RL为负载电阻。
谐振腔增益M可表示为
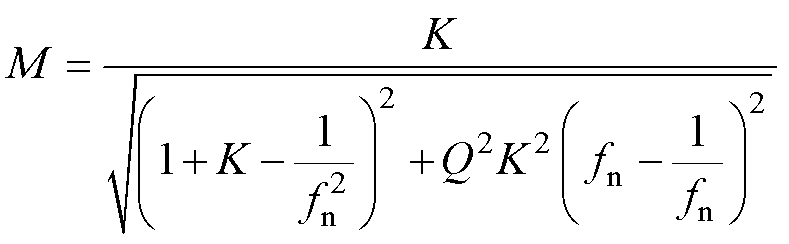 (8)
(8)
式中,K为电感系数,K=Lm/Lr;fn为归一化频率,fn= fs/fr,fs为开关频率,fr为谐振频率,fr=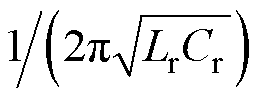 ;品质因数Q=2pfrLr/Rac。
;品质因数Q=2pfrLr/Rac。
对于传统的空心变压器来说,由于其耦合系数一般较低,会在变压器一、二次侧均引入较大的漏感,在高频情况下此漏感与电路中谐振元件数值相近,可被用作谐振元件。在上述谐振腔中,一次侧漏感LS1可作为谐振电感Lr与谐振电容Cr在频率fr处谐振。而二次侧漏感LS2则会串联在变压器输出端与整流桥之间,如图8所示。
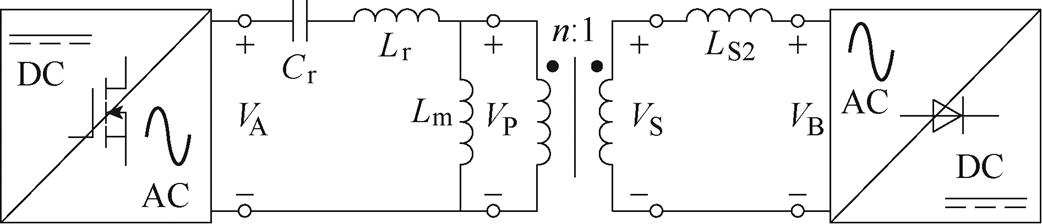
图8 将变压器等效后所提拓扑的简化等效电路
Fig.8 The simplified equivalent circuit diagram of the proposed topology after equivalent transformers
当变换器正常工作时,可设定Lr与Cr的谐振频率fr与开关频率fs相同。此时,对于基波来说,由于Lr与Cr串联谐振,所以逆变器输出电压VA、一次侧输入电压VP和二次侧输出电压VS相位差可以看作零。但是由于变压器二次侧漏感LS2的存在,VB与VA之间的相位差可表示为
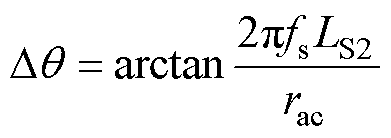 (9)
(9)
此时对整流桥进行同步整流,需要对逆变器和整流器的驱动信号相位差进行精确的控制。但随着系统工作频率的增加,每个周期的时间越来越短,这使得驱动信号的控制越来越困难。理论上,此相位差可以通过使Cr不与Lr在开关频率下谐振来补偿。为了简化分析,将图7中谐振腔转化为如图9所示的谐振腔电路。变换器等效谐振腔电路如图9所示。
对图9所示谐振腔两端电压VA和VB进行分析,此时补偿电容Cr的值表示为
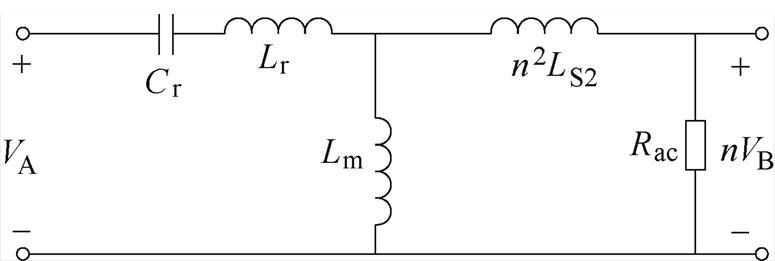
图9 变换器等效谐振腔电路
Fig.9 The circuit diagram of equivalent resonant cavity in the converter
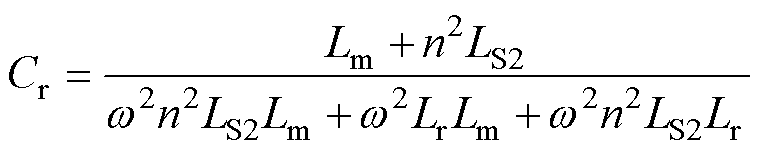 (10)
(10)
由式(10)可知,在变压器的一、二次侧均含有漏感的设计条件下,补偿电容Cr的值将受许多参数的影响,如Lm、n、LS2、Lr。这些参数的小偏差将可能造成补偿电容Cr值的大误差,导致一次侧和二次侧相位差增大。所以,变压器二次侧漏感的存在使得驱动信号的控制更加严格,特别是在几十MHz的情况下。
为了减少变压器二次侧漏感LS2,可利用内环准无漏感的嵌套环形3D变压器来代替一、二次侧均有较大漏感的传统空心变压器。此时VB与VA之间的相位差可近似看作是零,当负载变化时相位差也将保持为0,不需要重新进行校准,整流器与逆变器可以使用同一个驱动信号,进而简化对同步整流驱动信号的控制,使同步整流的易控性和可靠性得到提高。
在这种情况下,对于选定的输入电压Vin、VA、VP、VS和VB波形如图10所示,整流桥输入电压VB可看作占空比0.5,幅值±Vin/(2n)的方波电压,整流后输出电压为Vin/(2n)。变压器电压比应为
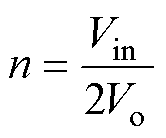 (11)
(11)
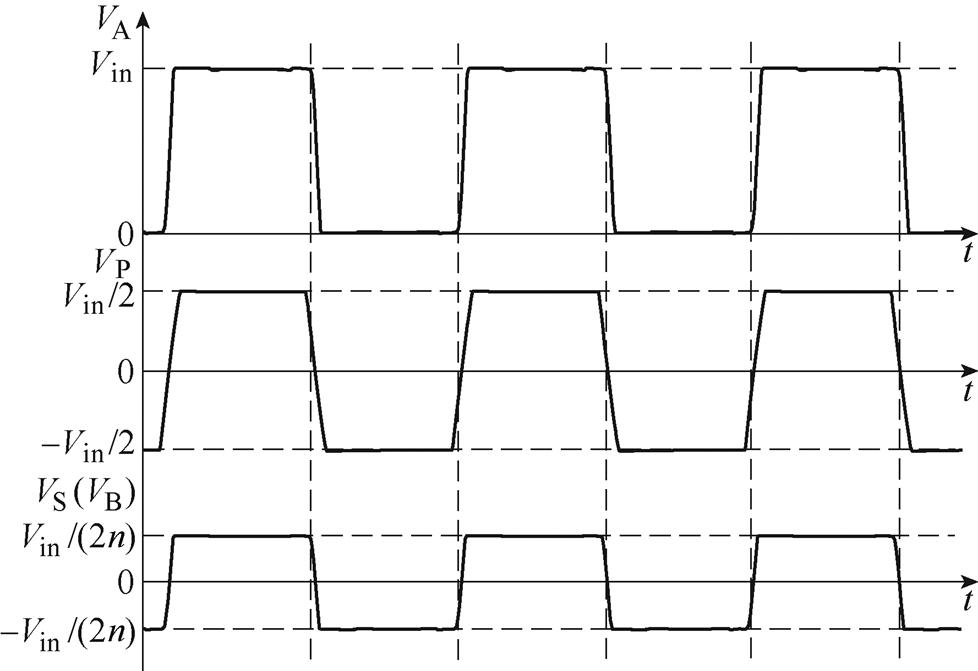
图10 变压器二次侧无漏感时VA、VP、VS和VB波形
Fig.10 Waveforms diagram of VA、VP、VS and VB without leakage inductance on the secondary side of transformer
由于各类空心变压器的耦合系数一般较低,为了便于设计空心变压器,变压器的电感系数K可以取0.7左右。当变压器设计好后,谐振电容Cr就可以根据设计好的变压器一次侧漏感Lr表示为
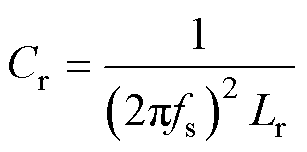 (12)
(12)
针对零相位差同步驱动型拓扑,本文设计了嵌套环形变压器结构,变压器内、外环的详细设计参数见表1。
表1 变压器内环和外环结构参数
Tab.1 Parameters of inner and outer windings of transformer

参 数一次侧 (外环)二次侧 (内环) 外直径/mm4237 内直径/mm1217 高度/mm1411 厚度/mm0.030.03 匝间距/mm22 匝数126 铜厚/mm0.035—
根据表1中的数据及式(2)、式(3)、式(5)、式(6)可计算出嵌套环形3D变压器电感矩阵的理论计算值,计算过程如下:
首先,根据表1的变压器设计参数,代入式(2)和式(3)计算可得,磁阻Rm和R11分别为5.84× 108 H-1,5.57×108 H-1。
其次,将表1中的参数代入式(5)中,分别计算内环和外环的单匝电感。计算结果为
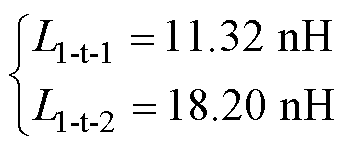 (13)
(13)
利用磁阻值、N1、N2、L1-t-1和L1-t-2,通过式(6)得到电感矩阵为
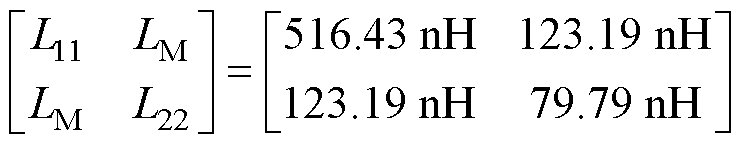 (14)
(14)
在嵌套环形3D变压器的制造方面,采用焊接多个PCB的方法制作嵌套环形3D空心变压器的内部与外部绕组。
图11为内部与外部绕组示意图,对于匝数为N的绕组而言,PCB线路可分为顶部线路(N股线)、底部线路(N股线)以及内、外侧垂直连接线(内、外各N股),因此,在具体制作变压器绕组时,可根据不同的线路画出不同的PCB,并利用PCB半孔工艺和PCB边缘的焊盘将位置相邻应焊接到一起的PCB连接为一个整体,从而完成整个嵌套环形空心变压器的制作。
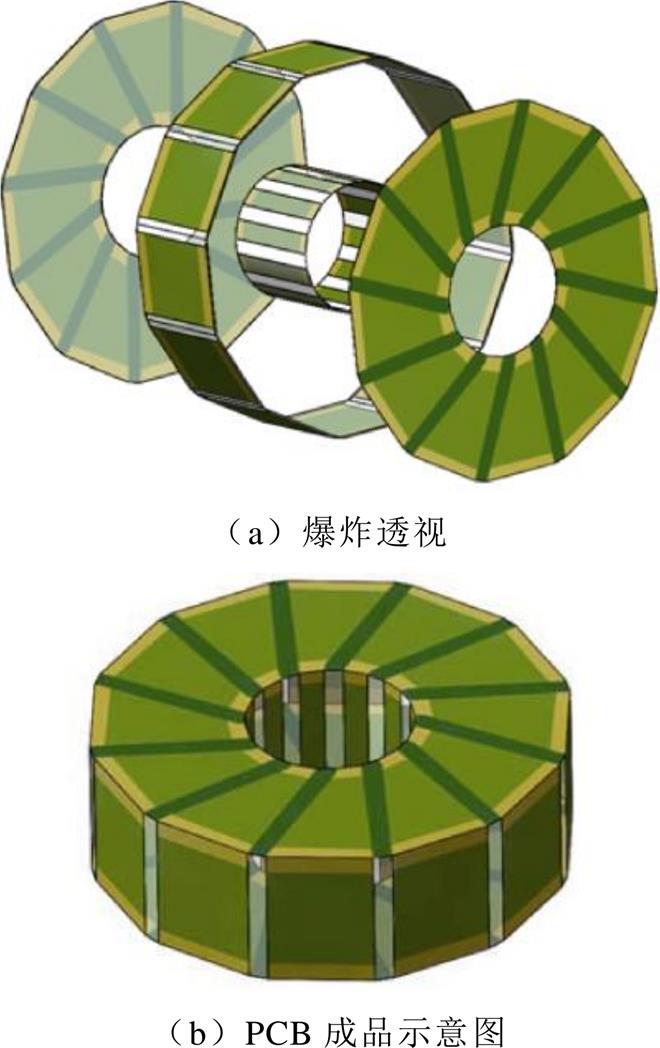
图11 PCB制作内、外部绕组示意图
Fig.11 Schematic diagram of inner and outer winding coils in PCB fabrication
如图11a所示,在利用PCB制作绕组时,根据不同线路是否在一个水平面可将绕组分为1块顶部线路板、1块底部线路板和2N块侧面垂直连接线路板,完整绕组的示意图如图11b所示。
图12a展示了采用多PCB结合的方法制作整个嵌套环形3D变压器的内、外绕组的结构剖分。为详细展示嵌套环形空心变压器的结构,其中内部绕组为焊接后状态,外部绕组为焊接前状态(爆炸图视角)。图12b展示了采用PCB结合制作嵌套环形3D变压器的整体结构,图中内、外绕组均为焊接后状态。
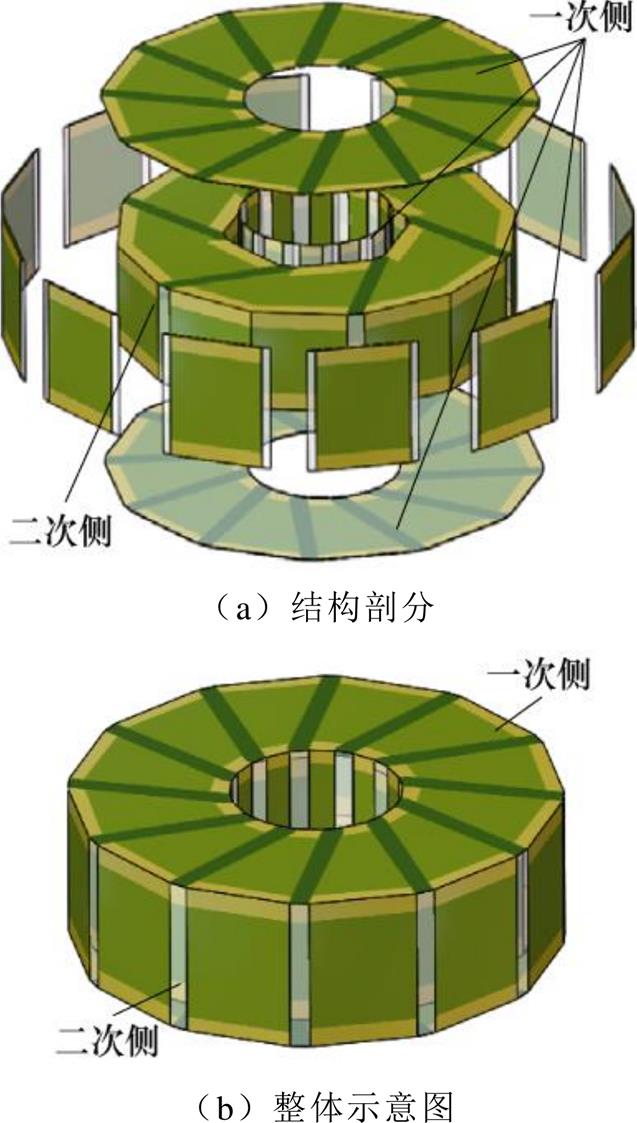
图12 PCB制作变压器示意图
Fig.12 Schematic diagram of PCB manufacturing transformer
为了能通过实验仪器测量得到图4中变压器的参数LS1、LS2、Lm和n,可分别测定L1,open、L2,open、L1,short和L2,short。其中,L1,open为二次侧开路时在一次侧测得的电感,L2,open为一次侧开路时在二次侧测得的电感,L1,short为二次侧短路时在一次侧测得的电感,L2,short为一次侧短路时在二次侧测得的电感。
对于图13所示变压器模型及其等效电路,L1,open、L2,open和L2,short可分别由式(15)和式(16)计算,联立二者可得式(17)。式(17)给出了测量值和变压器参数的数值关系,式(6)也可由式(17)导出。
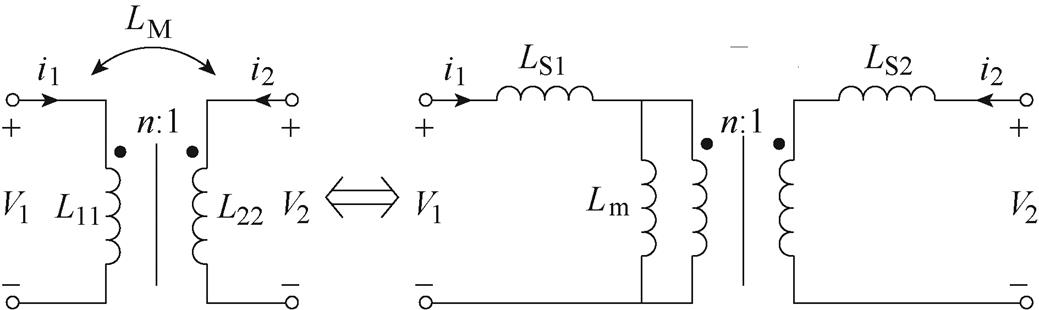
图13 变压器的等效电路
Fig.13 The equivalent circuit diagram of transformer
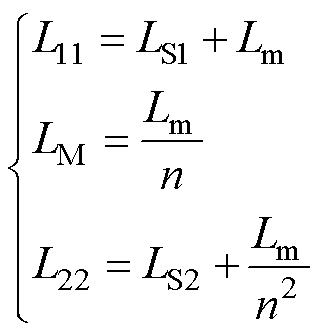 (15)
(15)
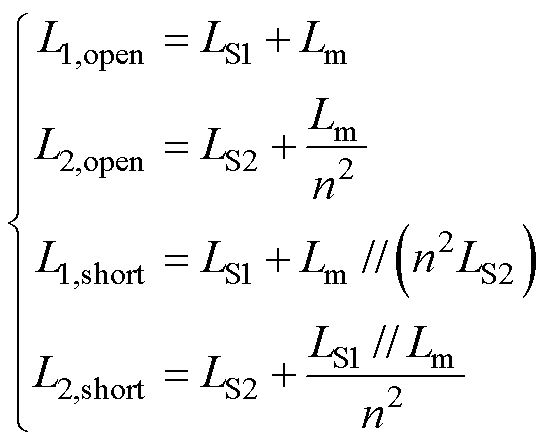 (16)
(16)
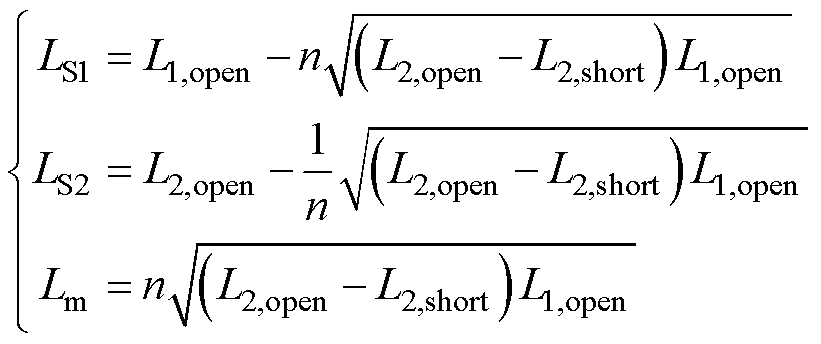 (17)
(17)
表2比较了电感矩阵和变压器参数的计算值、Maxwell仿真值和实验测试值。结果表明,理论计算、仿真和实验结果吻合度良好。
表2 电感矩阵和变压器参数的计算值、Maxwell仿真值和实验测试值比较
Tab.2 Comparison of inductance matrix values and transformer parameters between calculation, Maxwell simulation and experiment (单位: nH)
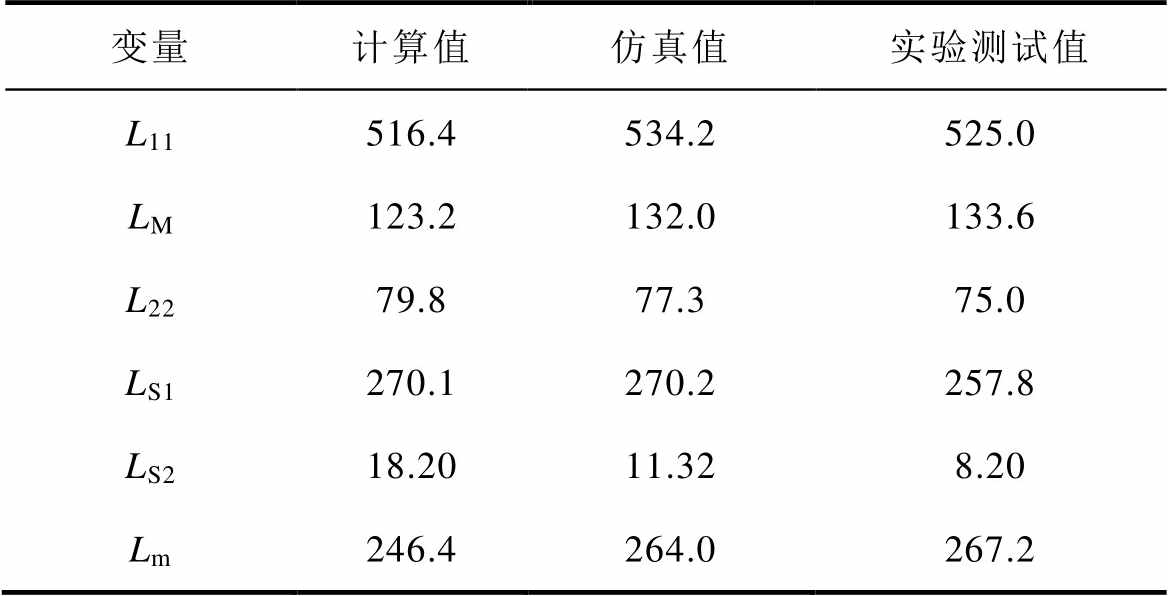
变量计算值仿真值实验测试值 L11516.4534.2525.0 LM123.2132.0133.6 L2279.877.375.0 LS1270.1270.2257.8 LS218.2011.328.20 Lm246.4264.0267.2
本文基于所提出的拓扑结构和设计方法,搭建了一台开关频率10 MHz、48 V/12 V、28 W的样机,对上述设计方法进行验证。图14为所设计变换器的样机实物,样机体积大小为4.2 cm×4.0 cm×2.4 cm。多个PCB结合的实验样机整体包括以焊接多个PCB制作内部与外部绕组的方法制作的嵌套环形3D变压器部分。图15所示为Class DE逆变部分,图16所示为全桥同步整流器部分,该样机使用的实验元件参数见表3。
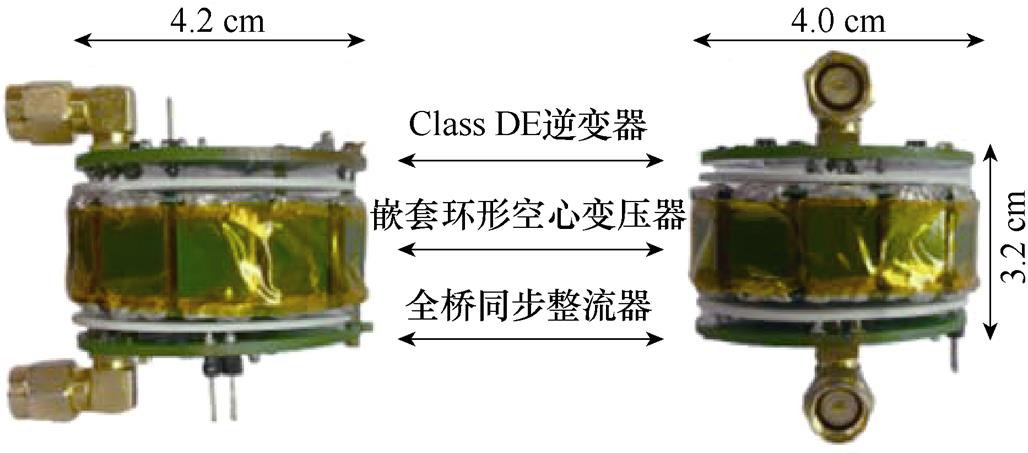
图14 所提拓扑的样机实物
Fig.14 The photographs of proposed converter
图17展示了Class DE逆变器中开关管的漏源极电压VDS和驱动电压VGS实验波形,从图中可知,在开关管的驱动电压VGS开始上升前,开关管的漏源极电压VDS已经下降到零,使得开关管S1和S2实现软开关,降低了开关损耗。
图18展示了逆变器输出电压VA(开关管S1的漏源极电压VDS)与整流器输入电压VB的实验波形。从图中可知,VA与VB保持良好的同相性,这为逆变器和全桥同步整流器使用相同的时钟信号驱动开关实现简单可靠的同步整流提供了保障。

图15 多PCB结合Class DE逆变器样机
Fig.15 Multi-PCB combined with Class DE inverter prototype diagram
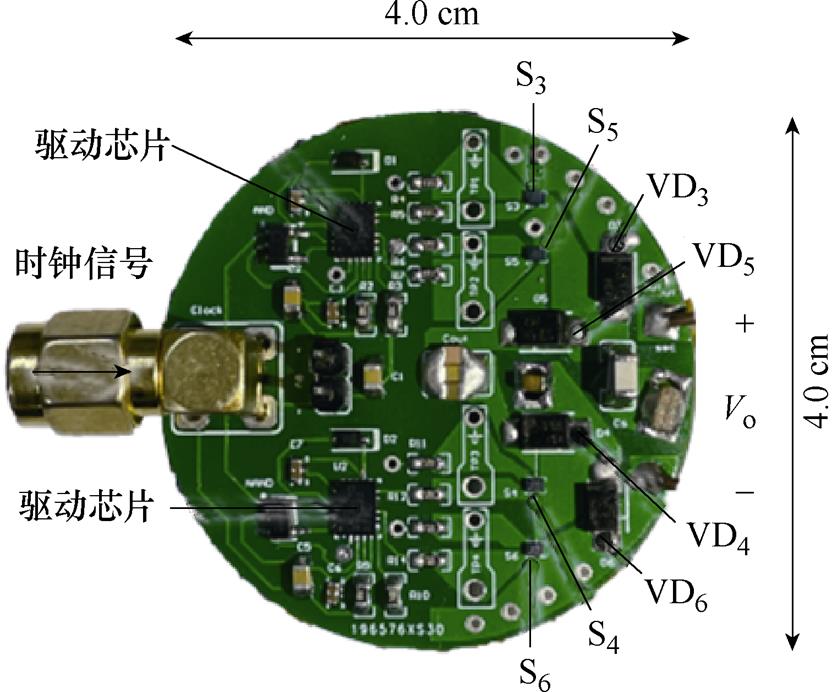
图16 多PCB结合全桥同步整流器样机
Fig.16 Multi-PCB combined with full-bridge rectifier prototype diagram
表3 实验元件参数
Tab.3 Experimental parameters of the prototype
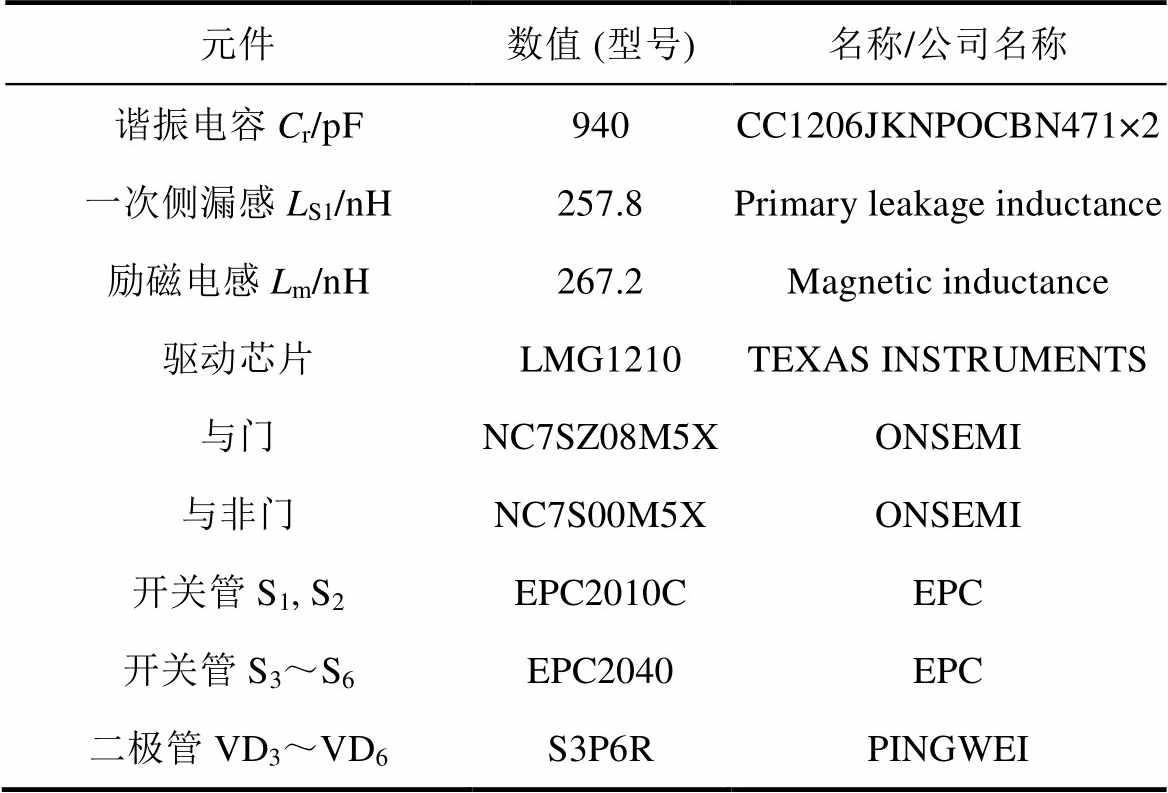
元件数值 (型号)名称/公司名称 谐振电容Cr/pF940CC1206JKNPOCBN471×2 一次侧漏感LS1/nH257.8Primary leakage inductance 励磁电感Lm/nH267.2Magnetic inductance 驱动芯片LMG1210TEXAS INSTRUMENTS 与门NC7SZ08M5XONSEMI 与非门NC7S00M5XONSEMI 开关管S1, S2EPC2010CEPC 开关管S3~S6EPC2040EPC 二极管VD3~VD6S3P6RPINGWEI
图19展示了整流器中开关管的漏源极电压VDS与驱动电压VGS实验波形。从图中可知,二极管的正向压降在开关管导通期间显著降低,可有效减小整流损耗,实现了高频同步整流,验证了零相位差同步驱动控制策略在高频情形下的有效性。
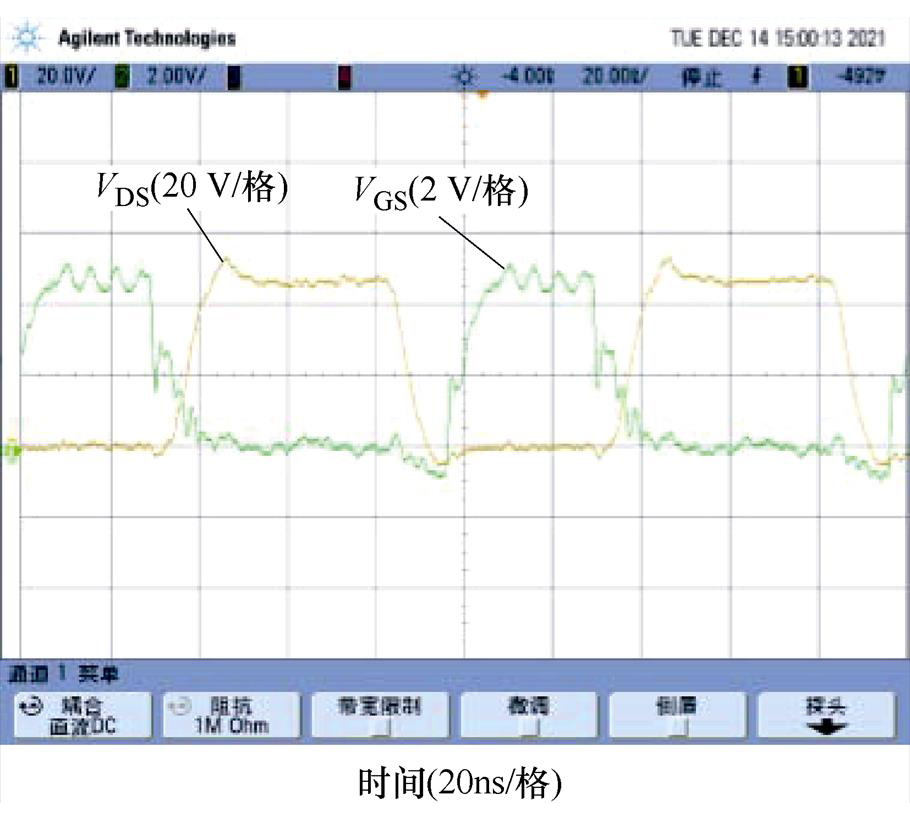
图17 Class DE逆变器开关管软开关实验波形
Fig.17 Soft switching experimental waveforms of switches in Class DE inverter
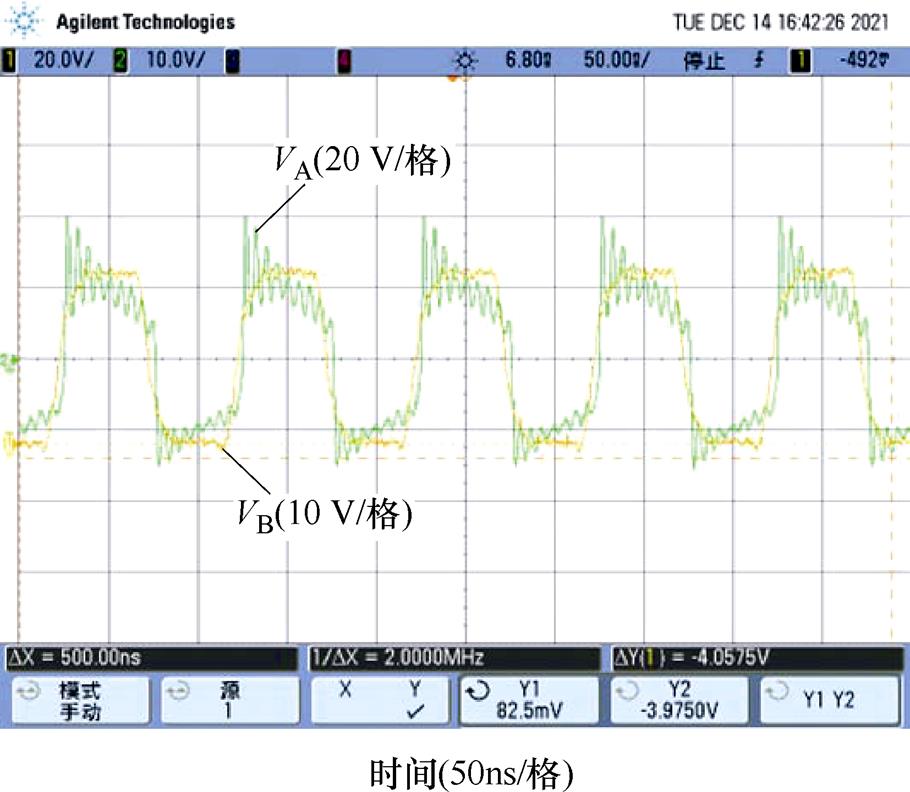
图18 额定条件下逆变器输出电压和整流器输入电压波形
Fig.18 The waveforms of inverter output voltage and rectifier input voltage when the converter works under rated condition
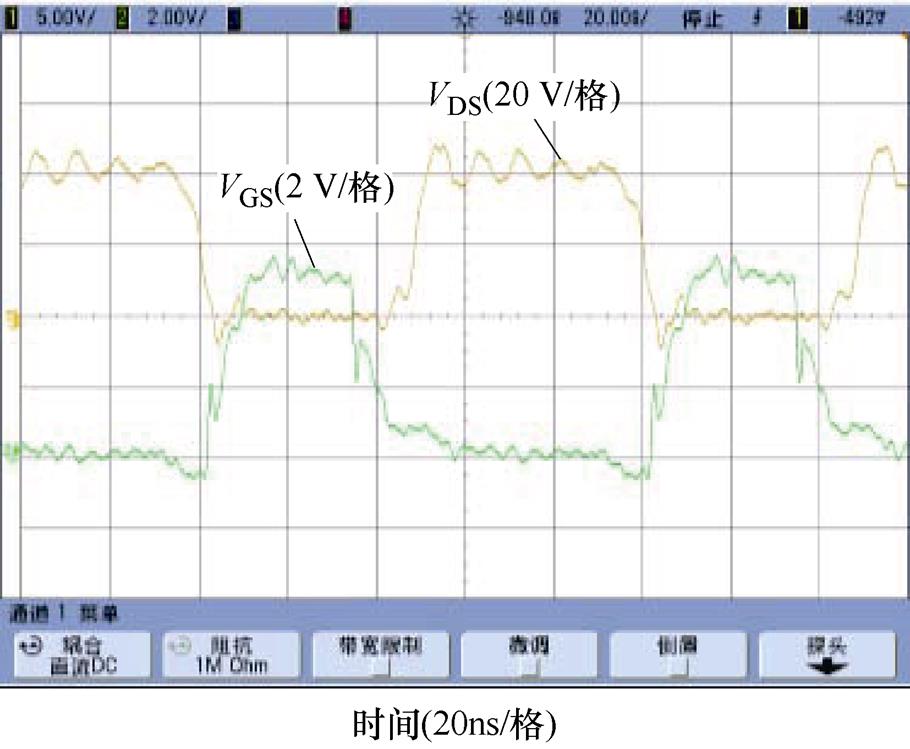
图19 开关管及肖特基二极管的电压波形和驱动信号波形
Fig.19 The voltage waveforms and driving signal waveform of the switch and Schottky diode
图20展示了样机当负载从5 W 切换到40 W 直流输出电压波形。由实验波形可知,系统工作稳定时,输出电压恒定为12 V。随着负载切换至40 W,系统输出电压略微上升,响应速度较快。开关机时,输出电压无过冲,且响应速度较快。
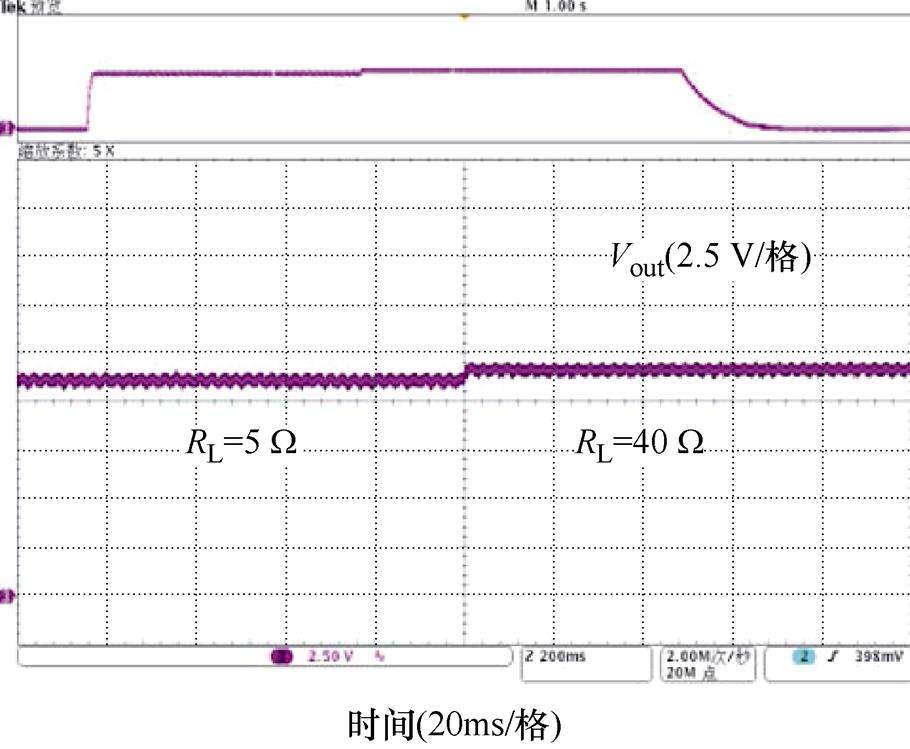
图20 负载变化下输出电压实验波形
Fig.20 Experimental waveforms of output voltage under the load change
图21展示了根据实验数据所得的多PCB结合实验样机效率曲线。运用准零相位差同步驱动控制策略进行高频同步整流后,多PCB结合实验样机的系统效率在满载和轻载情形下分别较之普通全桥整流提升了1.7%~14.2%不等,验证了所提控制策略的有效性。
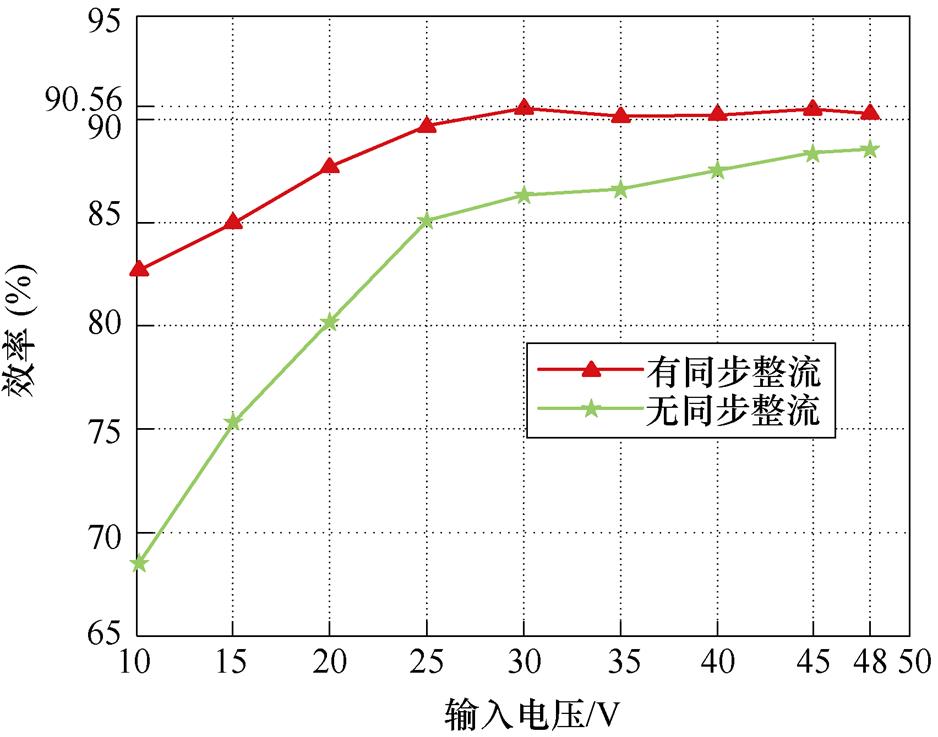
图21 实验样机效率曲线
Fig.21 Experimental prototype efficiency curves
本文设计了一款48 V转12 V,输出功率21 W,开关频率10 MHz的DC-DC变换器,并且采用多PCB结合方式制作的嵌套环形3D变压器。利用嵌套环形3D变压器二次侧准无漏感的特点,将变换器输出电压与整流器输入电压的相位差近似调节为零,使整流器和逆变器可用同一驱动信号驱动开关,解决了高频下同步整流的驱动问题,简化了同步整流的控制,系统峰值效率为92.56%,提高了系统性能。
参考文献
[1] Sun Bainan, Zhang Zhe, Andersen M A E. A com- parison review of the resonant gate driver in the silicon MOSFET and the GaN transistor appli- cation[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7776-7786.
[2] Huang Nantian, Wang Da, Lin Lin, et al. Power quality disturbances classification using rotation forest and multi-resolution fast S-transform with data compression in time domain[J]. IET Generation, Trans- mission & Distribution, 2019, 13(22): 5091-5101.
[3] Park S, Rivas-Davila J. Duty cycle and frequency modulations in Class-e DC-DC converters for a wide range of input and output voltages[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(12): 10524- 10538.
[4] Park H P, Jung J H. Power stage and feedback loop design for LLC resonant converter in high-switching- frequency operation[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7770-7782.
[5] Alonso J M, Martínez G, Perdigão M, et al. A systematic approach to modeling complex magnetic devices using SPICE: application to variable indu- ctors[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7735-7746.
[6] Sun Bainan, Zhang Zhe, Andersen M A E. Research of low inductance loop design in GaN HEMT application[C]//44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 2018: 1466-1470.
[7] Perreault D J, Hu Jingying, Rivas J M, et al. Opportunities and challenges in very high frequency power conversion[C]//Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Expo- sition, Washington, DC, USA, 2009: 1-14.
[8] 徐殿国, 管乐诗, 王懿杰, 等. 超高频功率变换器研究综述[J]. 电工技术学报, 2016, 31(19): 26-36.
Xu Dianguo, Guan Yueshi, Wang Yijie, et al. Review on very high frequency power converters[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(19): 26-36.
[9] Knott A, Andersen T M, Kamby P, et al. Evolution of very high frequency power supplies[J]. IEEE Journal of Emerging and Selected Topics in Power Elec- tronics, 2014, 2(3): 386-394.
[10] Liu Ming, Fu Minfan, Ma Chengbin. Parameter design for a 6.78-MHz wireless power transfer system based on analytical derivation of Class E current- driven rectifier[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4280-4291.
[11] 管乐诗, 施震宇, 王懿杰, 等. 基于 Class E谐振电路的隔离型高频DC-DC变换器[J]. 电工技术学报, 2020, 35(22): 4750-4760.
Guan Yueshi, Shi Zhenyu, Wang Yijie, et al. An isolated high frequency DC-DC converter based on Class E resonant circuit[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4750-4760.
[12] 伍梁, 孙晓玮, 赵钧, 等. 基于大信号模型的多模块LCC级联变换器输出电压不均衡分析法[J]. 电工技术学报, 2020, 35(24): 5142-5151.
Wu Liang, Sun Xiaowei, Zhao Jun, et al. Analysis of output voltage imbalance for cascaded multi-module LCC converters based on large-signal model[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5142-5151.
[13] 高璐, 徐策, 董光冬, 等. 基于电磁仿真软件的平面变压器共模电磁干扰建模方法及其应用[J]. 电工技术学报, 2020, 35(24): 5057-5063.
Gao Lu, Xu Ce, Dong Guangdong, et al. Common mode electro-magnetic interference modeling method of planar transformers based on CST software and its application[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5057-5063.
[14] Zhang Junming, Liao Jiawen, Wang Jianfeng, et al. A current-driving synchronous rectifier for an LLC resonant converter with voltage-doubler rectifier structure[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1894-1904.
[15] Fu Dianbo, Liu Ya, Lee F C, et al. A novel driving scheme for synchronous rectifiers in LLC resonant converters[J]. IEEE Transactions on Power Elec- tronics, 2009, 24(5): 1321-1329.
[16] 张少腾, 赵晋斌, 吴月宝, 等. 基于自互感调节的无线电能传输用E类逆变器软开关技术研究[J]. 电工技术学报, 2021, 36(21): 4558-4566.
Zhang Shaoteng, Zhao Jinbin, Wu Yuebao, et al. Research on soft switching technology of Class E inverter based on self mutual-inductance regulation in wireless power transfer[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4558-4566.
[17] Wang Fan, McDonald B A, Langham J, et al. A novel adaptive synchronous rectification method for digitally controlled LLC converters[C]//2016 IEEE Applied Power Electronics Conference and Expo- sition, Long Beach, CA, USA, 2016: 334-338.
[18] Xu Shengyou, Qian Qinsong, Tao Tao, et al. Syn- chronous rectification using resonant capacitor voltage for secondary side resonant active clamp flyback converter[C]//2020 IEEE Applied Power Electronics Conference and Exposition, New Orleans, LA, USA, 2020: 2926-2931.
[19] Tong Zikang, Braun W D, Rivas-Davila J M. Design and fabrication of three-dimensional printed air-core transformers for high-frequency power applications[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8472-8489.
[20] Hurley W G, Duffy M C, Zhang Jun, et al. A unified approach to the calculation of self-and mutual- inductance for coaxial coils in air[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(11): 6155- 6162.
[21] Ramo S, Whinnery J R, Van Duzer T. Fields and waves in communication electronics[M]. Hoboken: John Wiley & Sons, 1994.
[22] 刘晓东, 董保成, 吴慧辉, 等. 基于并联变压器切换的LLC谐振变换器宽范围效率优化控制策略[J].电工技术学报, 2020, 35(14): 3018-3029.
Liu Xiaodong, Dong Baocheng, Wu Huihui, et al. Wide range efficiency optimization control strategy for LLC resonant converter based on parallel trans- former switching[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3018-3029.
Abstract High-frequency power DC-DC converters are widely used in consumer electronics for their smaller size and higher power density. Under high-frequency conditions, the rectifiers use Schottky diodes with extremely fast switching speed. However, the forward voltage drop of Schottky diodes is still high, which limits efficiency. Due to the small switching period, the synchronous rectification control methods are no longer suitable for high-frequency conditions. Therefore, the method to realize synchronous rectification accurately and efficiently at tens of megahertz helps to improve the efficiency of high-frequency power converters.
The key to realizing synchronous rectification is the accuracy of a given driving signal. Due to the high-frequency conditions, the traditional synchronous rectification control method can easily generate the error driving signal, which will cause a straight through in the arm in severe cases. To avoid the error of the driving signal, the method of providing the same driving signal for the switches on the primary and secondary sides is adopted. Therefore, there is no inductive component on the non-resonant branch side of the transformer, so the output voltage of the inverter and the input voltage of the rectifier maintain the characteristic of zero phase difference. Meanwhile, the resonant branch is constructed in another side of the transformer, which consists of the leakage inductance and resonant capacitance. In addition, it is necessary to carry out precise parameter design to ensure that the switch works under soft-switching conditions.
The difficulty in realizing the abovementioned zero-phase-difference synchronous driving is constructing an air-core transformer with single-side leakage inductance. The nested toroidal air-core transformer without leakage inductance in the inner winding is designed by the outer winding completely wrapping the inner winding. The magnetic flux generated by the inner winding acts as the common magnetic flux of the inner and outer windings. That is, there is almost no leakage inductance on the secondary side. Further, this paper analyzes the modeling and design method of the nested toroidal air-core transformer. By synthesizing the relationship between the reluctance, the magnetic flux, and the transformer inductance matrix, the numerical relationship between the physical structure parameters of the nested toroidal air-core transformer and the transformer parameters is derived from the precise design of the air-core transformer. Moreover, the calculation and Maxwell simulation of the nested toroidal air-core transformer verify the feasibility of the modeling method of the nested toroidal air-core transformer.
Based on the nested toroidal air-core transformer manufactured with the combination of multiple PCBs, an experimental prototype with 48 V input and 12 V/28 W output is built. The experimental results verify the effectiveness of the design method of the nested toroidal air-core transformer and the improved frequency synchronous rectification control method.
The nested toroidal 3D transformer can optimize to achieve single-side leakage inductance characteristics, further decreasing the small leakage inductance. Additionally, the inductance of the power loop needs to be optimized to reduce the switch voltage oscillation. The parasitic parameters of the circuits affecting synchronous rectification must be considered.
keywords:High frequency DC-DC converter, synchronous rectification, PCB transformer, quasi-no leakage inductance
DOI: 10.19595/j.cnki.1000-6753.tces.221316
中图分类号:TM46
国家自然科学基金资助项目(52007041)。
收稿日期 2022-07-06
改稿日期 2022-08-10
管乐诗 男,1990年生,副教授、博士生导师,研究方向为高频、超高频功率变换技术。E-mail: hitguanyueshi@163.com(通信作者)
程 怡 男,1999年生,硕士研究生,研究方向为高频功率变换技术。E-mail: 2073424024@qq.com
(编辑 陈 诚)