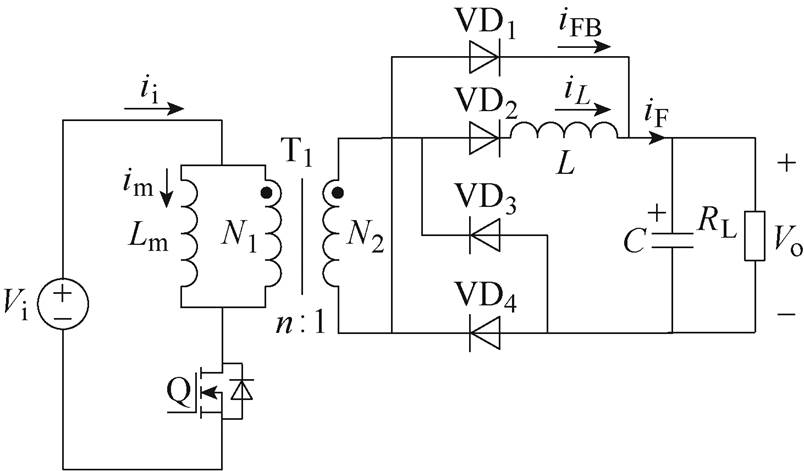
图1 正-反激变换拓扑
Fig.1 Forward-flyback topology
摘要 通过分析正-反激变换拓扑工作于不同模式时的功率传输特性及其与负载电阻的关系,发现工作于励磁电流断续导电模式(MDCM)时的正激功率和反激功率均随负载电阻的减小而增大,工作于励磁电流连续导电模式(MCCM)时的正激功率维持不变,而反激功率随负载电阻的减小单调增加。对于给定输出功率,推导得出了开关管电流应力与正激功率和反激功率之间的解析关系式,探讨了功率分配对正-反激变换拓扑效率的影响,并指出减小正激功率有利于降低开关管电流应力,而减小反激功率有利于提高正-反激变换拓扑效率。综合考虑功率传输特性对正-反激变换拓扑电气性能的影响,提出一种在给定负载变化范围内,确保输出功率最大时使得正激功率与反激功率相等的磁性元件参数设计方法,实验结果验证了理论分析的正确性和设计方法的可行性。
关键词:正-反激变换拓扑 功率传输分配 正激功率 反激功率 设计
正激变换拓扑因其结构简单、不存在开关直通的高可靠性等优势成为应用最广的拓扑之一,特别是在中小功率开关电源中占据了主导地位[1-3]。但由于基本正激变换拓扑的单向磁化可能导致变压器磁心饱和,因此必须采取磁复位措施。针对这一问题,目前已提出了多种解决方案[4-6],但是各种方案在实现磁复位的同时,总会影响到正-反激变换拓扑某些方面的电气性能:RCD(R—电阻、C—电容、D—二极管)复位会将励磁能量全部消耗于电阻[7],只能应用于小功率场合;一次侧附加绕组复位[8]可将励磁能量反馈回输入电源,但增加了变压器绕制的复杂性。一次侧LCD(L—电感、C—电容、D—二极管)复位[9]可实现无损复位,但会增加开关管及钳位二极管电流应力,使得通态损耗增加;双管正激变换器[10]虽然降低了开关管电压应力,但增加了电路复杂性,且由于最大占空比不能超过0.5,因此其在宽输入电压场合中的应用受到了限制;一次侧有源钳位技术[11-12]理论上可实现开关管的零电压软开关(Zero Voltage Switching, ZVS)及磁心双向磁化,但若需确保ZVS性能良好,还必须另外添加辅助电路[13]。
可见,一次侧磁复位方式不能将励磁能量传输至负载,因此不利于提升变换器的能量利用率。而采用二次侧复位的正激变换拓扑既可在正激期间(开关管导通期间)将电源能量传输到输出部分,还可在反激期间(开关管关断期间)将励磁能量传输至负载,因此称为正-反激变换拓扑,显然,正-反激变换拓扑可有效提高能量传输效率。目前已经提出了多种正-反激组合变换拓扑,文献[14]提出的双管二次侧双绕组正-反激组合变换拓扑,可将励磁能量传输至负载的同时减小开关管电压应力,但双管结构需要额外增加开关管及其驱动电路,导致系统成本增加。为此,文献[15]提出了一种单管二次侧双绕组复位结构,但是双绕组结构会导致变压器设计和绕制工艺复杂。为了进一步简化结构,文献[16]研究了二次侧附加LCD的正激变换拓扑,但附加电感与正激电感的工作模式和功率传输相互制约,导致参数设计复杂,且会影响大功率传输。
单管、单变压器、单二次绕组的四二极管正-反激变换拓扑可避免上述问题[17],且还可应用于功率因数校正[18-19],因此,具有重要研究价值。但是,该拓扑的工作模式要比正激变换拓扑和反激变换拓扑复杂得多[20-23],文献[24]对其不同工作模式时的能量传输过程进行了分析,并推导得出了工作于各模式时的临界电感和输出纹波电压解析式。然而,目前还少见关于该正-反激变换拓扑功率传输特性及其相应磁性元件参数设计方法的研究报道,其磁性元件包括变压器及正激电感。
为此,本文将对四二极管正-反激变换拓扑的功率传输特性展开深入研究,并通过综合考虑正激部分与反激部分传输功率比例对正-反激变换拓扑电气性能的影响,得出磁性元件参数的设计方法。对于正-反激变换拓扑的研制及推广应用具有重要理论指导意义。
本文研究的单管、单变压器、二次侧单绕组结构的正-反激变换拓扑如图1所示。图1中,Vi和Vo分别为输入电压和输出电压;ii为输入电流,im为励磁电感电流;Q为一次侧开关管;T1为匝比等于n的变压器;VD1、VD2和VD4为二次侧整流二极管;VD3为续流二极管;C为输出滤波电容;RL为负载电阻。

图1 正-反激变换拓扑
Fig.1 Forward-flyback topology
正-反激变换拓扑的工作原理:在开关导通期间,直流输入电源加在变压器一次绕组两端,励磁电感电流im线性增加,同时通过变压器耦合将输入电能传递到二次侧,此时二次绕组两端电压为上正下负,大小为Vi/n,整流二极管VD2和VD4正向导通,流过正激电感的电流iL线性增加。在此期间,输入电能一部分转化为磁能储存在励磁电感Lm和正激电感L中,另一部分能量通过正激电感L传递到输出负载。在开关关断期间,正激电感L中储存的能量通过二极管VD2和VD3构成回路向负载提供能量,正激电感电流iL线性减小,同时变压器二次电压为上负下正,二极管VD1正向导通,储存在励磁电感Lm中的能量通过二极管VD1和VD3构成回路向负载释放能量,反激回路电流iFB线性减小。
当正-反激变换拓扑工作于稳定状态时,电路中的正激电感L与变压器励磁电感Lm均需满足伏秒平衡,但是根据正-反激变换拓扑工作原理可知,若正激电感电流处于连续状态,励磁电感将无法满足伏秒平衡,即励磁电流im的上升量总是大于其下降量,因而正激电感只能工作于断续导通模式(Dis- continous Conduction Mode, DCM)。为此,依据励磁电感电流在开关关断期间是否下降为零,将正-反激组合变换拓扑划分为两种工作模式:若励磁电感电流在开关关断期间未下降到零,正-反激变换拓扑工作在励磁电流连续导通模式(Magnetizing current Continuous Conduction Mode, MCCM);若励磁电感电流在开关关断期间已下降到零,正-反激变换拓扑工作于励磁电流断续导通模式(Mag- netizing current Discontinuous Conduction Mode, MDCM)。
四二极管正-反激变换拓扑的输出功率由正激回路和反激回路同时提供,而由于正激电感只能工作于DCM,因此正-反激变换拓扑的功率传输特性受到励磁电感工作模式的影响。为探究励磁电感对正-反激变换拓扑功率传输特性的影响,从而为正-反激变换拓扑的设计提供理论指导,因此有必要分析励磁电感工作于不同模式时的功率传输特性。
当正-反激变换拓扑工作于MCCM时,根据励磁电感的伏秒平衡可得输出电压为
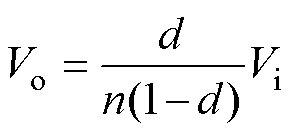 (1)
(1)
因此,MCCM下占空比d可表示为
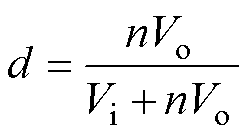 (2)
(2)
同时,由于正激电感只能工作于断续状态,因而正激电感的峰值电流可表示为
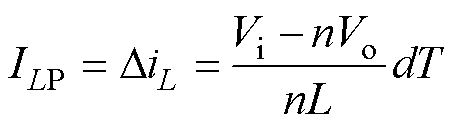 (3)
(3)
式中,T为开关周期。设正、反激变换拓扑的工作频率为f,结合式(2)、式(3)可得变换拓扑工作于MCCM时,其正激电感峰值电流为
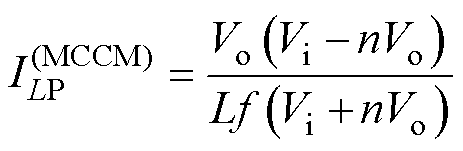 (4)
(4)
设开关管导通期间储存在正激电感L中的能量和传递给负载的能量分别为E1和E2,则
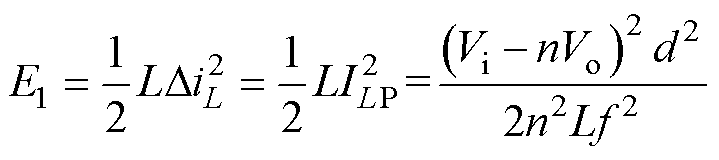 (5)
(5)
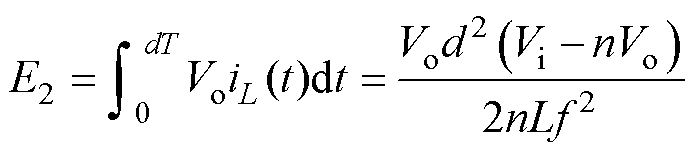 (6)
(6)
因此,一个开关周期内正激部分传递的能量EFW表示为
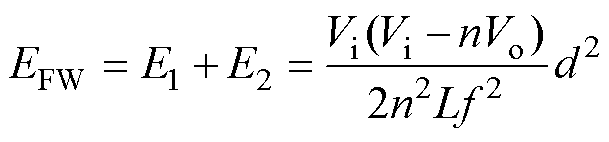 (7)
(7)
此时,将式(2)代入式(7)可得
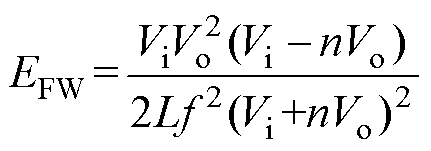 (8)
(8)
所以,当正-反激变换拓扑工作于MCCM时,一个开关周期内正激部分提供给负载的功率——正激功率PFW表示为
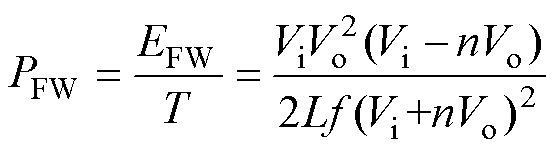 (9)
(9)
由功率守恒可知,一个开关周期内反激部分提供给负载的功率——反激功率PFB表示为
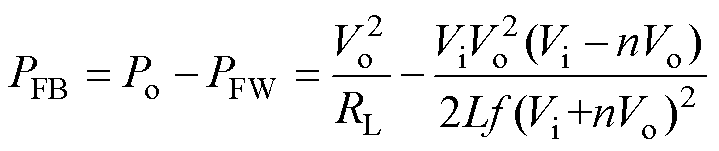 (10)
(10)
由式(9)可见,当正-反激变换拓扑工作于MCCM时,正激功率PFW与负载电阻RL无关,但会随正激电感的减小而增大。同时由式(4)可见,正激电感峰值电流与负载无关。因此,MCCM时正激功率不随负载电阻变化,而其余的功率由反激回路进行传输。
当正-反激变换拓扑工作于MDCM时,设在开关管导通期间,变压器励磁电感Lm和正激电感L中所储存的能量以及由输入电源传递给输出负载的能量分别为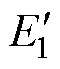 、
、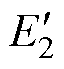 和
和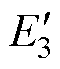 ,则可分别表示为
,则可分别表示为
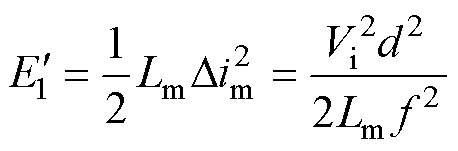 (11)
(11)
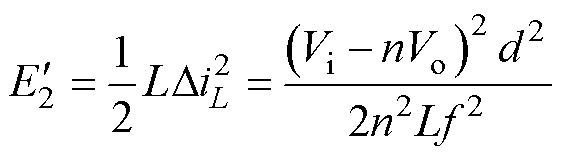 (12)
(12)
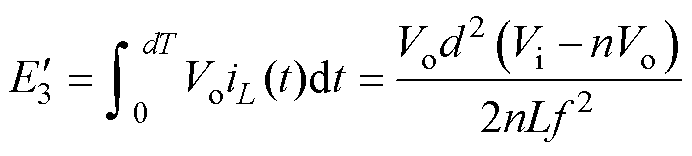 (13)
(13)
式中,Dim为励磁电感电流变化量。
因此,当正-反激变换拓扑工作于MDCM时,一个开关周期内传输到输出端的能量E为
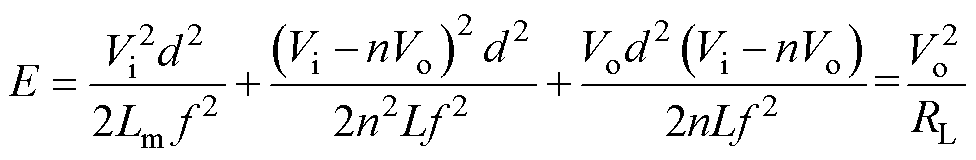 (14)
(14)
由式(14)可得工作于MDCM时的占空比为
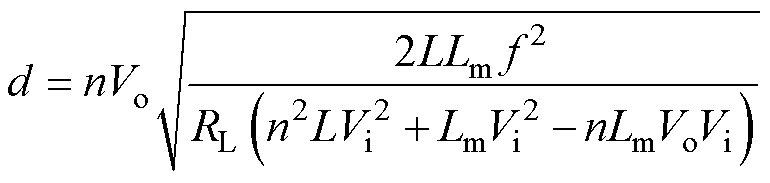 (15)
(15)
正激部分传输的能量包含两部分:正激电感中存储的能量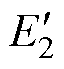 和在开关导通期间传递到负载的能量
和在开关导通期间传递到负载的能量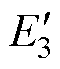 。因此可得正激功率PFW为
。因此可得正激功率PFW为
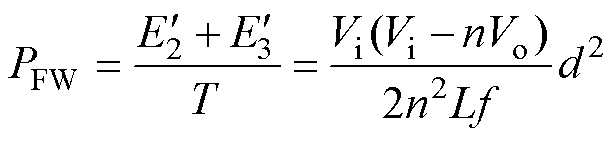 (16)
(16)
反激功率PFB等于开关管导通期间在励磁电感中储存的能量与开关周期T的比值,即有
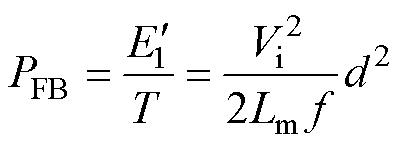 (17)
(17)
将式(15)代入式(16)可得正-反激变换拓扑工作于MDCM时的正激功率为
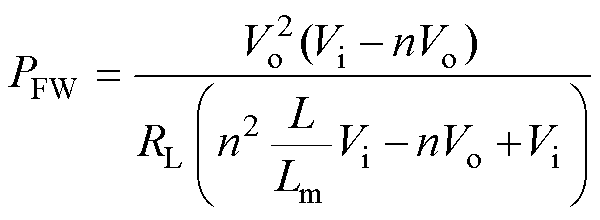 (18)
(18)
由式(18)可以看出,正激功率随励磁电感Lm的减小而减小,随正激电感L的减小而增加。
将式(15)代入式(17),可得正-反激变换拓扑工作于MDCM时的反激功率为
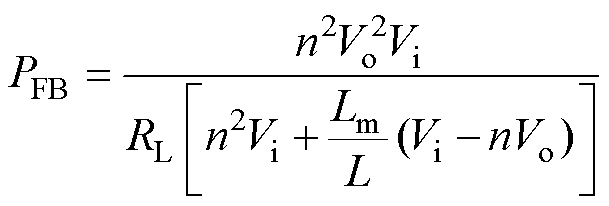 (19)
(19)
由式(19)可以看出,对于正-反激变换拓扑,反激功率将随正激电感L的增大而增大,随励磁电感Lm的增大而减小。
对于正-反激变换拓扑而言,最大功率传输时正激功率和反激功率的比例对其工作性能的影响尤为重要,因此需分析正-反激变换拓扑工作模式及电路中的磁性元件参数对正-反激变换拓扑功率传输特性的影响,从而为该拓扑的设计提供理论指导。
当励磁电感工作于MCCM时,流过励磁电感的最小电流IMV可表示为
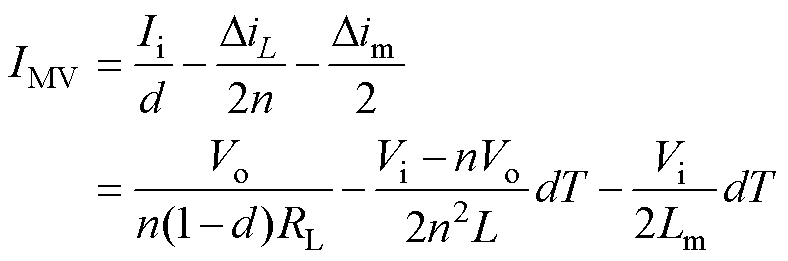 (20)
(20)
结合式(2),并令IMV=0可得励磁电感工作于MCCM与MDCM的临界负载电阻RLC为
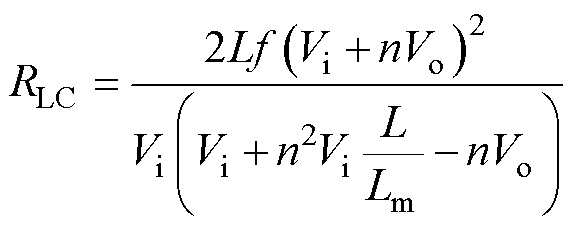 (21)
(21)
当RL>RLC时,正-反激变换拓扑工作于MDCM;当RL<RLC时,正-反激变换拓扑工作于MCCM。
为分析正-反激变换拓扑工作于MCCM与MDCM时正、反激功率的传输特性,在给定Vo、Vi、L、n的情况下,依据式(9)、式(10)、式(18)、式(19)、式(21)可得不同工作模式下正激功率与反激功率随负载电阻的变化曲线如图2所示。
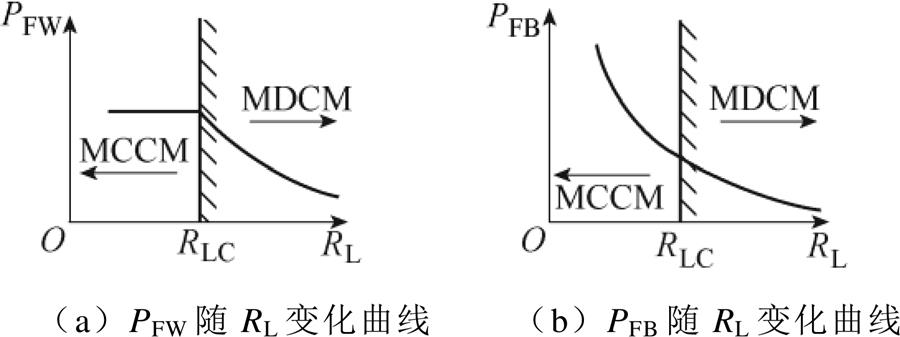
图2 MCCM及MDCM下正激功率与反激功率随负载电阻的变化曲线
Fig.2 Variation curves of forward power and flyback power versus load resistance under MCCM and MDCM
由图2可见,反激功率PFB在MCCM与MDCM时均随负载电阻的减小而增加,而正激功率PFW在MDCM时随负载电阻的减小而增大,当负载电阻减小至RLC,即进入MCCM时,PFW达到最大值,且不再随负载电阻的减小而发生变化。
为进一步分析正-反激变换拓扑工作模式对功率分配特性的影响,结合式(9)、式(10)和式(18)、式(19)可得整个负载范围内正激和反激部分的传输功率比为
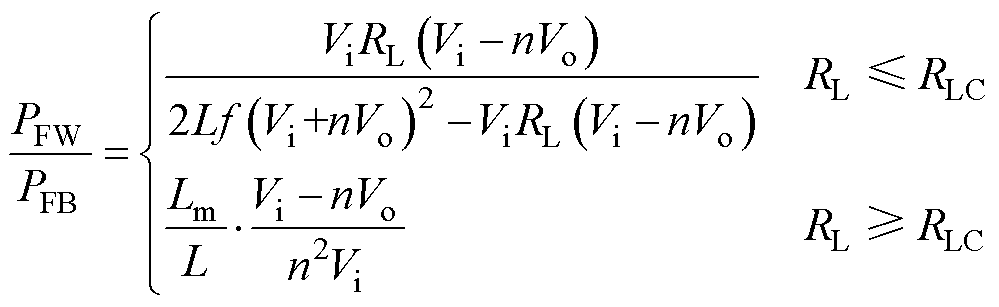 (22)
(22)
依据式(22)可得整个负载范围内正激功率与反激功率之比与负载电阻的关系示意图,如图3所示。
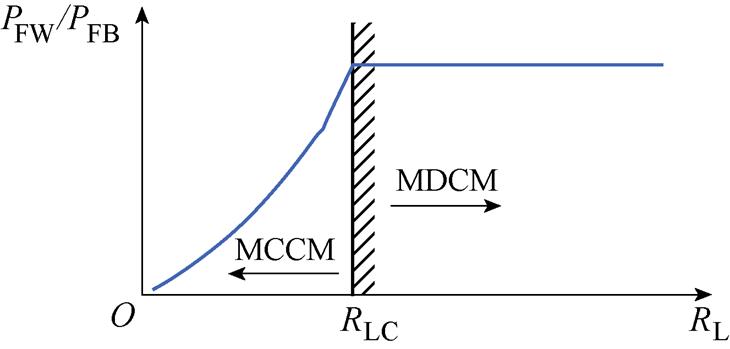
图3 功率传输比与负载电阻的关系
Fig.3 The relationship between the transmission power ratio and the load resistance
从图3可以看出,当正-反激变换拓扑工作于MCCM时,正激功率与反激功率之比随负载电阻RL的增加而增加,而当正-反激变换拓扑工作于MDCM时,正激功率与反激功率之比达到整个负载范围内的最大值且不随负载电阻发生变化。
综上所述,当正-反激变换拓扑工作于MDCM时,PFW、PFB均随负载电阻的减小而增加,且二者之比与负载电阻无关。当负载电阻减小到使得正-反激变换拓扑进入MCCM时,正激功率达到给定负载范围内的最大值,随着负载电阻的进一步减小,正激功率不再变化,而反激功率继续增加。
依据式(9)、式(10)可得MCCM时对应正激功率与反激功率相等的临界负载电阻RLE为
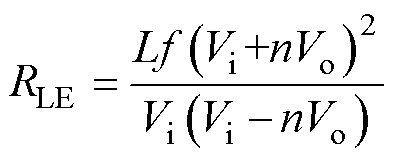 (23)
(23)
由式(21)、式(23)可得RLC与RLE相等时(在图4中,将此时对应的负载电阻用RCE表示)对应的临界励磁电感Lmc为
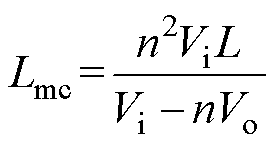 (24)
(24)
令励磁电感Lm=Lmc,并将式(24)代入式(18)和式(19)可得
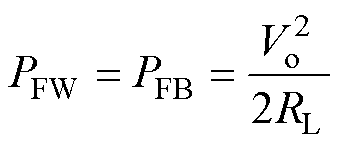 (25)
(25)
根据上述定义的临界励磁电感Lmc以及对应RLC与RLE相等的负载电阻用RCE,为分析励磁电感Lm对正-反激变换拓扑功率传输分配的影响,在给定Vo、Vi、L、n的情况下,结合图2及式(23)~式(25)可得不同励磁电感下PFW与PFB随负载电阻变化的示意关系如图4所示。
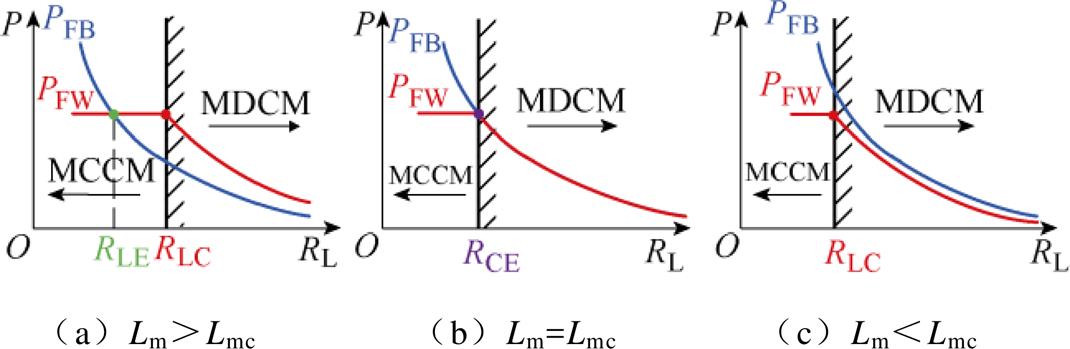
图4 不同励磁电感下正激功率及反激功率随负载电阻的变化曲线
Fig.4 Variation curves of forward power and flyback power versus load resistance under different excitation inductance
由图4a可以看出,当Lm>Lmc时,若负载电阻RL<RLE,则PFW<PFB;若RL>RLE,则PFW>PFB。而由图4b可知,当Lm=Lmc时,若RL>RCE,即正-反激变换拓扑工作于MDCM时,PFW=PFB;若RL<RCE,即正-反激变换拓扑工作于MCCM时,PFW<PFB。在此基础上,若进一步减小励磁电感Lm使其满足Lm<Lmc,则由图4c可见,此时在整个负载范围内PFW<PFB。
正、反激功率传输分配还受到励磁电感与正激电感比值的影响。由式(22)可知,当RL>RLC,即正-反激变换拓扑工作于MDCM时,随着电感Lm和L比值的增大,PFW与PFB的比值会随之增大。因此,对于给定的输出功率,减小变压器励磁电感Lm或增大正激电感L,都将使反激功率增加,而正激功率减小。
不仅两电感取值对正-反激变换拓扑的传输功率比例有影响,变压器匝比对功率传输功率比例也有影响。在输入电压动态范围内,根据式(22)可得出变压器匝比n不同时,传输功率比与输入电压的关系曲线,如图5所示。其中,ViC1、ViC2及ViC3为变压器匝比n不同时,使得对应正-反激变换拓扑工作于MCCM与MDCM临界模式的临界输入电压。由图5可以看出,正激功率与反激功率的传输比例会随变压器匝比n的增加而减小。
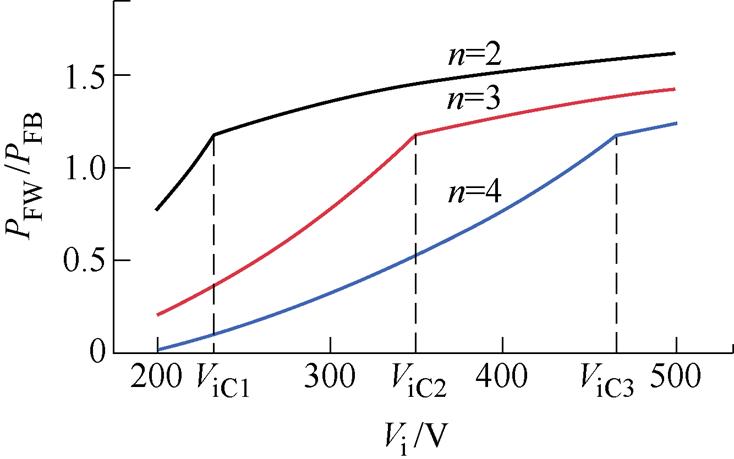
图5 传输功率比与变压器匝比n的关系
Fig.5 The relationship between the transmission power ratio and the transformer turns ratio n
由上述分析可知,若Lm>Lmc,正-反激变换拓扑工作于MDCM时,PFW>PFB;工作于MCCM时,若RL>RLE,则PFW>PFB,若RL<RLE,则PFW<PFB。若Lm=Lmc,工作于MDCM时,PFW=PFB,而工作于MCCM时,PFW<PFB。若Lm<Lmc,则在整个负载范围内PFW<PFB。且对于给定的输出功率,随着变压器励磁电感Lm的增加,PFW增加,PFB减小;随着正激电感L或匝比n的增加,PFB增加,PFW减小。
正-反激变换拓扑的功率传输分配还会对开关管的电流应力产生影响,下面就功率传输分配对电流应力的影响进行分析。
结合式(3)、式(7)可得正激功率与正激电感峰值电流的关系式为
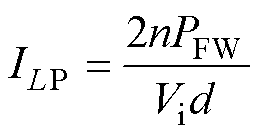 (26)
(26)
同时,无论励磁电感工作于MCCM还是MDCM都可将一个开关周期内的反激能量EFB用励磁电感峰值电流ILmp表示为
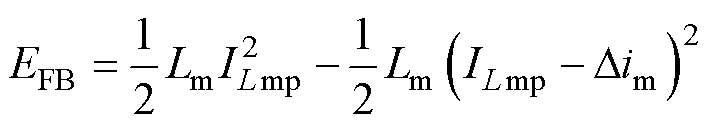 (27)
(27)
且有
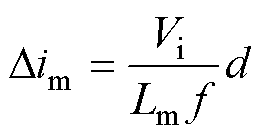 (28)
(28)
则将式(28)代入式(27)可得EFB为
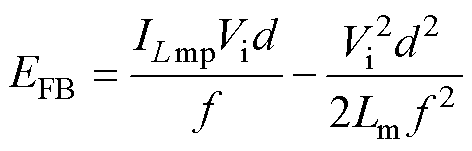 (29)
(29)
依据式(29)可得ILmp与反激功率的关系式为
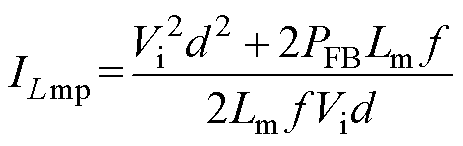 (30)
(30)
结合式(26)、式(30),并考虑到Po=PFW+PFB,可得开关管电流应力IS,max为
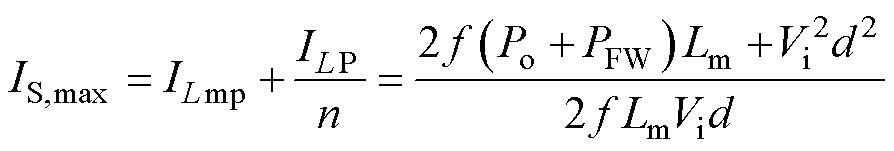 (31)
(31)
由式(31)可以看出,当Po一定时,PFW越小,开关管电流应力越小,因此,减小正激功率有利于降低开关管电流应力。
结合图4c分析可知,当励磁电感Lm<Lmc时,正激功率在整个负载范围内均小于反激功率,有利于降低开关管的电流应力。但是,反激功率太大,需要增加变压器气隙来减小励磁电感,这又会增大漏感和变压器损耗[25]。因此,为提升正-反激变换拓扑效率,并不致使开关管电流应力太大,建议Lm= Lmc。若励磁电感Lm=Lmc,当RL<RCE,即正-反激变换拓扑工作于MCCM时,正激功率小于反激功率;而当RL>RCE,即正-反激变换拓扑工作于MDCM时,正激功率等于反激功率。因此,在给定输出功率下且Lm=Lmc时,正-反激变换拓扑在MCCM下的正激功率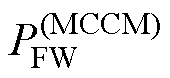 较其工作于MDCM下的正激功率
较其工作于MDCM下的正激功率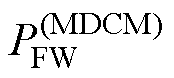 更小,即
更小,即
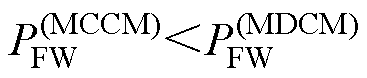 (32)
(32)
将Lm=Lmc时正-反激变换拓扑工作于MCCM及MDCM时的开关管电流应力分别表示为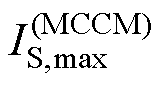 及
及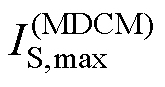 ,则结合式(31)、式(32)可得
,则结合式(31)、式(32)可得
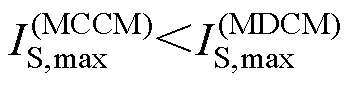 (33)
(33)
上述分析可见,当Lm=Lmc时,有利于提高正-反激变换拓扑效率,且此时正-反激变换拓扑工作于MCCM的开关管电流应力更小。
由上述分析可知,正激电感和变压器共同影响着正-反激变换拓扑的传输功率和开关管电流应力,因此,必须对其进行合理设计。
对正激电感及变压器的设计主要考虑其取值对开关管电流应力及正-反激变换拓扑效率的影响。结合第4节分析可知,将对应RCE的临界励磁电感Lmc作为变压器励磁电感Lm的设计值可提升正-反激变换拓扑效率,并不致使开关管电流应力太大,则由式(24)可得变压器励磁电感设计值Lm为
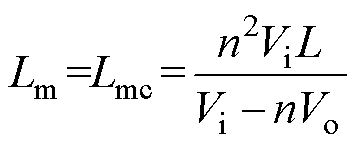 (34)
(34)
当Lm=Lmc时,由式(33)可知,工作于MCCM时开关管电流应力更小。但由图4b可得,MCCM时的反激功率会大于正激功率,使得损耗相对较大,而工作于MDCM时,正激功率与反激功率相等,有利于提升正-反激变换拓扑效率。因此,为提升正-反激变换拓扑效率,并不致使开关管电流应力过大,令正-反激变换拓扑在最大输出功率时工作于MCCM与MDCM的临界模式,即可确保在给定负载范围内正激功率始终与反激功率相等。假设正-反激变换拓扑输入电压及输出负载范围分别为[Vi,min, Vi,max],[RL,min, RL,max],则令RL,min=RLC,由式(21)可得临界模式下正激电感L为
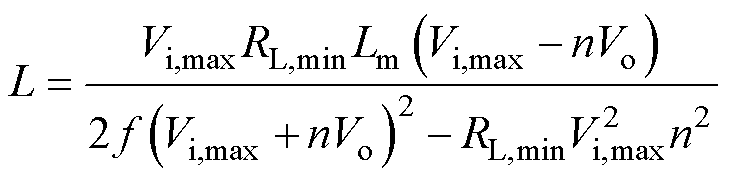 (35)
(35)
由式(34)、式(35)可得输出功率最大时,工作于MCCM与MDCM的临界时正激电感设计值表示为
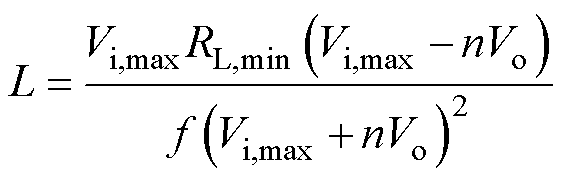 (36)
(36)
将式(36)代入式(34)可得励磁电感设计值Lm为
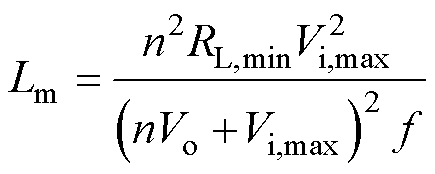 (37)
(37)
由式(37)可以看出,在给定动态范围内,励磁电感设计值会随正-反激变换拓扑工作频率的增加而减小,并且其值还与变压器匝比有关。而对于变压器匝比的设计,仍需综合考虑多种因素。
对于正-反激变换拓扑,为确保MCCM下输入电压为最小值Vi,min,同时占空比达到最大值dmax时,输出电压能够满足给定指标要求,则依据式(1)可得在给定动态范围内,变压器匝比n需满足
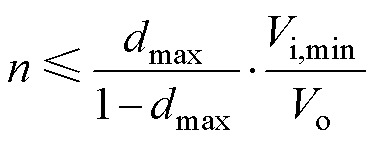 (38)
(38)
此外,结合式(22)可知,正激功率和反激功率的传输比会随匝比n的减小而增加,因此对于给定的输出功率,减小匝比n可增大正激功率。结合第4节分析可知,正激功率越大,正-反激变换拓扑效率越高,因此减小变压器匝比有利于提高正-反激变换拓扑效率。但考虑到正激功率越大,开关管电流应力越大,因此,为了不致使开关管电流应力过大,匝比n也不可太小。
综上所述,为提高正-反激变换拓扑的整体性能,在满足式(38)的前提下,需综合考虑各因素来选取变压器的匝比。
为了验证理论分析的正确性和所提出设计方法的可行性,设计并制作实验样机,其中,样机的主要参数见表1。
表1 样机的主要参数
Tab.1 prototype parameters
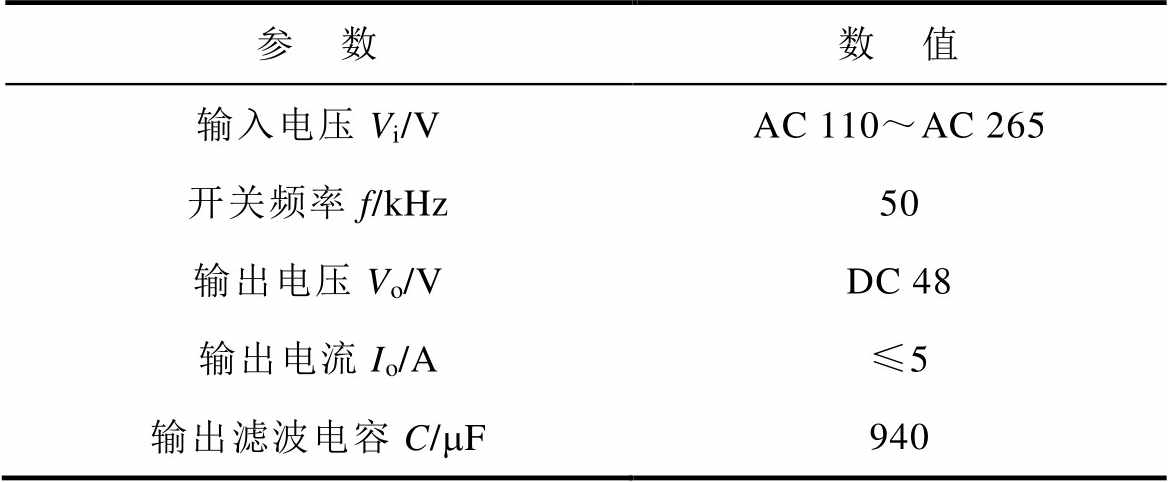
参 数数 值 输入电压Vi/VAC 110~AC 265 开关频率f/kHz50 输出电压Vo/VDC 48 输出电流Io/A≤5 输出滤波电容C/mF940
将样机参数代入式(36)和式(37)可得,正激电感的临界电感为90 mH,励磁电感为486 mH。样机选取UC3845为控制芯片,并令最大占空比dmax=0.45,则依据式(38)可得变压器匝比n≤2.3。综合考虑n对电流应力及能量传输效率的影响,本实验取n=2。基于所研制实验样机,搭建实验系统如图6所示。

图6 实验系统
Fig.6 Experimental prototype
为验证正-反激变换拓扑工作在MDCM与MCCM时正、反激功率传输分配与负载的关系,本实验取L=100 mH,使其在负载电流较小时工作于MDCM,较大时进入MCCM。在输入电压为AC 220 V时,分别测得输出负载1、3和5 A时的各电感电流实验波形如图7所示。由图7可见,当正-反激变换拓扑工作于MDCM时,随着负载电流的增加,正激电感电流iL随之增加。然而,当正-反激变换拓扑进入MCCM后,iL不再随负载变化,而反激回路电流iF随负载电流的增大而增大,此时正激功率达到最大值且不再变化,增加的功率将由反激功率进行补足。此外,随着负载电流的增大,正激电感始终处于DCM,验证了理论分析的正确性。
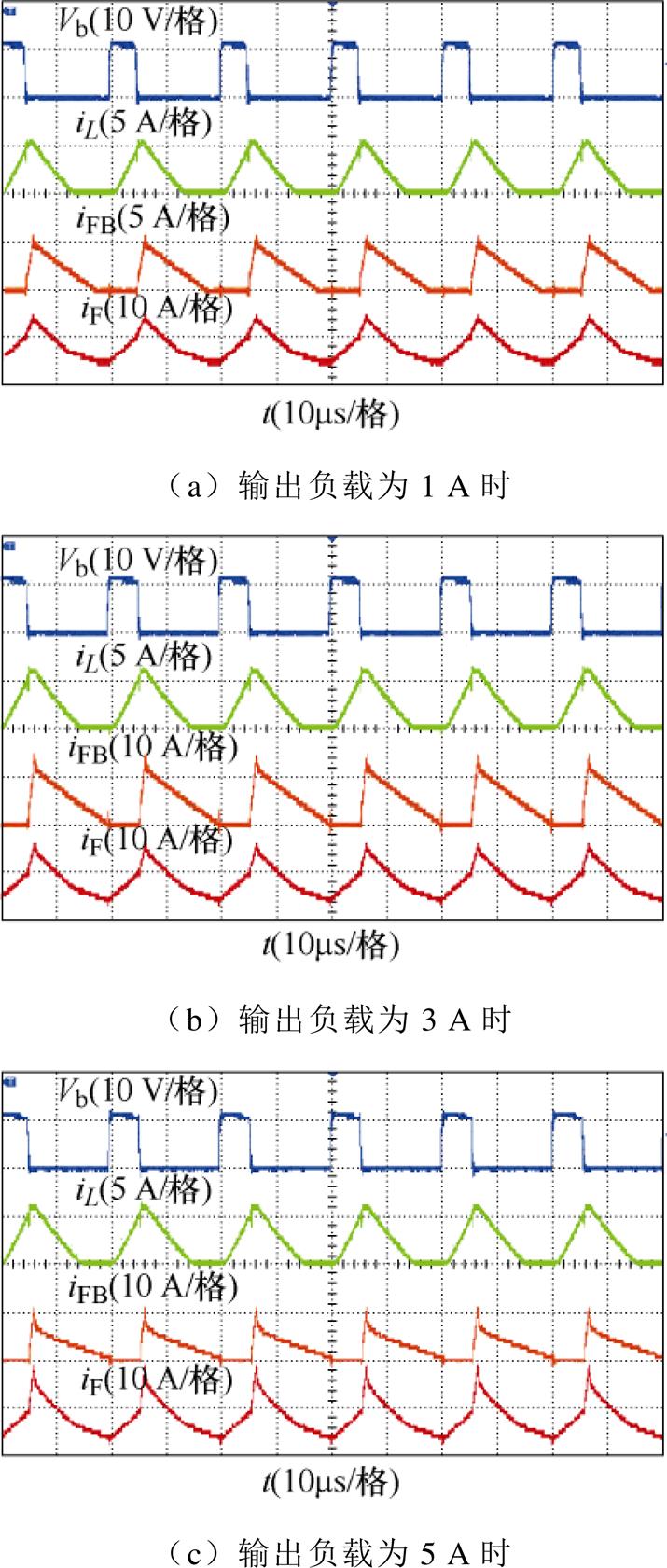
图7 不同负载下的电感电流实验波形
Fig.7 Experimental waveforms of inductor current under different loads
为验证正激功率与开关管电流应力之间的关系,分别测试正激电感L为90、80和70 mH下的开关管电流波形如图8所示。
由图8可见,随着正激电感的减小,开关管的电流应力IS,max逐渐增加。根据3.2节及第4节分析,减小正激电感会增大正激功率,同时变压器二次侧折合到一次侧的电流增大,导致正激期间开关管的电流应力变大。实验验证了理论分析的正确性。
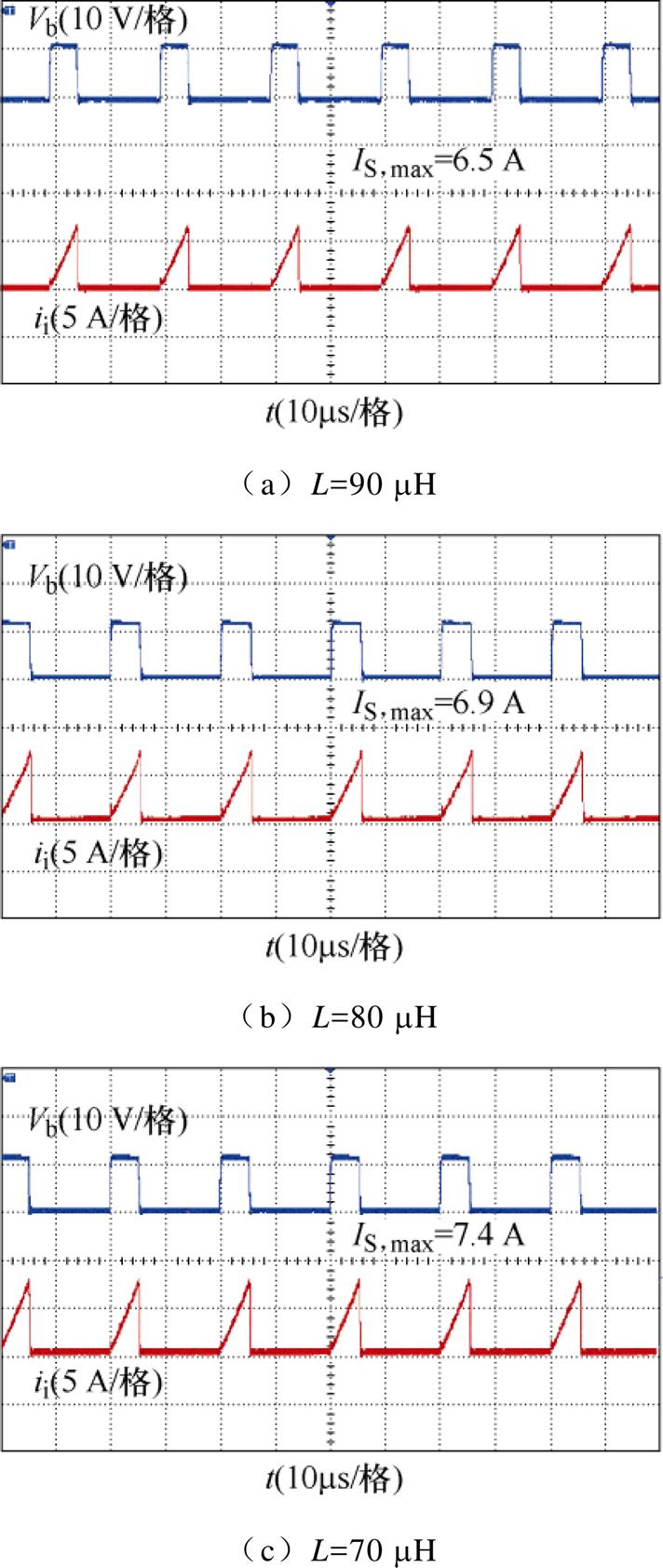
图8 不同正激电感值下的开关管电流实验波形
Fig.8 Current experimental waveforms through the switch under different forward inductance
为验证传输功率的分配比例对正-反激变换拓扑效率的影响,分别测试了变压器匝比为2时不同电感比值下样机的效率,以及励磁电感Lm=486 mH、正激电感L=90 mH时不同变压器匝比下样机的效率,测试的效率曲线如图9所示。
图9a为不同电感比值时的效率曲线,图9b为不同匝比下的效率曲线。当变压器励磁电感Lm与正激电感L的比值(Lm/L=7)较大时,由于正激功率大于反激功率,功率得到了更有效地传输,因此其变换效率高于电感比值(Lm/L=4)较小时的变换效率;当变压器匝比(n=2)较小时,由于正激功率增大,有益于功率有效传输,因此正-反激变换拓扑的效率高于匝比(n=4)较大时的效率。
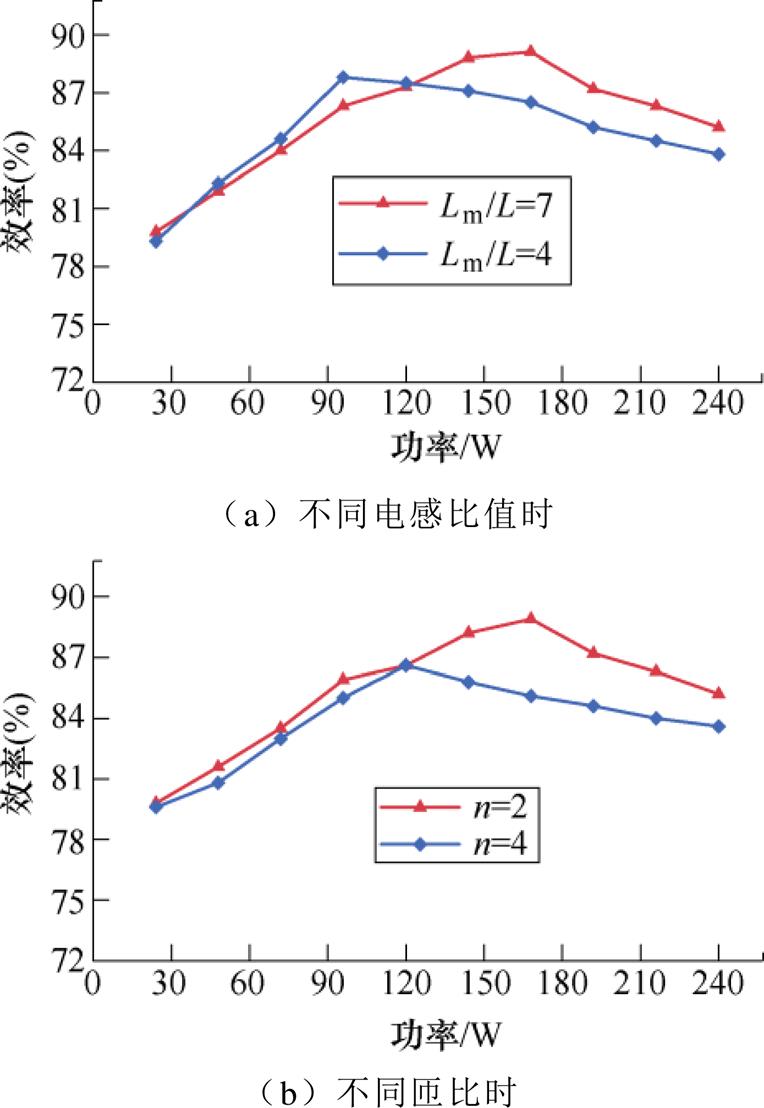
图9 给定负载范围内的效率曲线
Fig.9 Efficiency curves within the given load range
通过分析二次侧四二极管正-反激变换拓扑的功率传输特性及正、反激功率分配对开关管电流应力、正-反激变换拓扑效率的影响,综合得出了正激电感和变压器的设计方法,并研制样机进行了实验研究,验证了理论分析的正确性及设计方法的可行性。通过本文的研究,得出的主要结论如下:
1)MDCM及MCCM时的反激功率均随负载电阻的减小单调增加;而随着负载电阻的减小,正激功率在MDCM时单调增加,临界时达到最大值,在MCCM时不再变化。
2)对于给定的输出功率,随着励磁电感Lm的增加,PFW增加,PFB减小,且当Lm与对应PFW=PFB的临界励磁电感Lmc相等时,MDCM时的PFW=PFB;而随着匝比n的增加,PFB增加,PFW减小。
3)对于给定的输出功率,开关管电流应力随着正激功率的减小而减小,因此,减小正激功率有利于降低开关管电流应力。但是,减小正激功率又不利于提高正-反激变换拓扑效率。
4)综合考虑正、反激传输功率分配对正-反激变换拓扑电气性能的影响,提出了一种在给定负载范围内,确保最大输出功率时使得正激功率与反激功率相等的元件参数设计方法。
本文基于功率传输特性分析,所提出的正-反激变换拓扑元件参数设计方法,有助于高性能正-反激变换拓扑的研制,并促进其推广应用。
参考文献
[1] Severns R. The history of the forward converter[J]. Switching Power Magazine, 2000: 20-22.
[2] Xu Congwen, Ma Qishuang, Xu Ping, et al. Closed-loop gate drive for single-ended forward converter to reduce conducted EMI[J]. IEEE Access, 2020, 8: 123746-123755.
[3] Lin Jingyuan, Liu P J, Yang Chengyan. A dual- transformer active-clamp forward converter with nonlinear conversion ratio[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4353-4361.
[4] 李学峰, 吴德军, 王仕韬. 一种变模态恒定磁芯复位电压双管正激变换器[J]. 电源学报, 2018, 16(1): 19-23.
Li Xuefeng, Wu Dejun, Wang Shitao. Flexible mode double-switch forward converter with variable mode constant magnetic-reset voltage[J]. Journal of Power Supply, 2018, 16(1): 19-23.
[5] 李洪珠, 刘歆俣, 李洪璠, 等. 正激变换器磁集成分析与设计准则[J]. 中国电机工程学报, 2019, 39(12): 3667-3676.
Li Hongzhu, Liu Xinyu, Li Hongfan, et al. Analysis and design criteria of integrated magnetic in forward converters[J]. Proceedings of the CSEE, 2019, 39(12): 3667-3676.
[6] 吴琨, 钱挺, 王浩. 一种开关频率固定的输出可调型有源钳位正激双向谐振变换器[J]. 电工技术学报, 2018, 33(20): 4771-4779.
Wu Kun, Qian Ting, Wang Hao. An novel fixed switching frequency active-clamp forward dual resonant converter with requlation capability of output voltage[J]. Transactions of China Electro- technical Society, 2018, 33(20): 4771-4779.
[7] 吴红飞, 刘薇, 邢岩. 一族宽输入电压范围正激变换器拓扑[J]. 中国电机工程学报, 2012, 32(36): 29-35, 17.
Wu Hongfei, Liu Wei, Xing Yan. A family of forward converter topologies for wide input voltage range[J]. Proceedings of the CSEE, 2012, 32(36): 29-35, 17.
[8] 陈道炼, 范玉萍, 严仰光. 正激变换器的磁复位技术研究[J]. 电力电子技术, 1998, 32(1): 72-74, 91.
Chen Daolian, Fan Yuping, Yan Yangguang. Research on magnetic reset technology of forward converter[J]. Power Electronics Technology, 1998, 32(1): 72-74, 91.
[9] 王国礼, 金新民. 采用LCD箝位电路的正激DC- DC变换器[J]. 电工技术杂志, 2000, 19(12): 24-26.
Wang Guoli, Jin Xinmin. A forward DC-DC converter with LCD clamp circuit[J]. Electrotechnical Appli- cation, 2000, 19(12): 24-26.
[10] Meng Tao, Ben Hongqi, Song Yilin, et al. Analysis and design of an input-series two-transistor forward converter for high-input voltage multiple-output applications[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 270-279.
[11] Youn H S, Baek J I, Kim J K. Interleaved active clamp forward converter with extended operating duty ratio by adopting additional series-connected secondary windings for wide input and high current output applications[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4423-4433.
[12] Jeong Y, Park J D, Moon G W. An interleaved active- clamp forward converter modified for reduced primary conduction loss without additional com- ponents[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 121-130.
[13] Lin Jingyuan, Lee S Y, Ting C Y, et al. Active-clamp forward converter with lossless-snubber on secondary- side[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7650-7661.
[14] Murthy-Bellur D, Kazimierczuk M K. Two-switch flyback-forward PWM DC-DC converter with reduced switch voltage stress[C]//Proceedings of 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 2010: 3705-3708.
[15] 刘树林, 王航杰, 胡传义, 等. 附加LC的正反激组合变换器辅助电感最佳工作模态及LC参数优化设计[J]. 电工技术学报, 2022, 37(2): 389-396.
Liu Shulin, Wang Hangjie, Hu Chuanyi, et al. Analysis of the optimal operating mode of auxiliary inductance and LC parameter optimization design of forward and flyback combined converter with additional LC[J]. Transactions of China Electro- technical Society, 2022, 37(2): 389-396.
[16] 刘树林, 张海亮, 王航杰, 等. 抑制输出能量倒灌的二次侧自复位正激变换器的能量传输过程分析[J]. 电工技术学报, 2020, 35(增刊2): 477-483.
Liu Shulin, Zhang Hailiang, Wang Hangjie, et al. Analysis of the energy transmission process of the secondary-side self-resetting forward converter with suppressing output energy backflow[J]. Transactions of the China Electrotechnical Society, 2020, 35(S2): 477-483.
[17] Cao Jian, Liu Shulin, Yan Liqian, et al. Research on power transmission characteristic of forward-flyback converter[C]//2018 13th IEEE Conference on Indu- strial Electronics and Applications (ICIEA), Wuhan, China, 2018: 1342-1346.
[18] Tacca H E. Power factor correction using merged flyback-forward converters[J]. IEEE Transactions on Power Electronics, 2000, 15(4): 585-594.
[19] Dong Hanjing, Xie Xiaogao, Jiang Lei, et al. An electrolytic capacitor-less high power factor LED driver based on a “one-and-a-half stage” forward- flyback topology[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1572-1584.
[20] 孟涛, 安彦桦, 贲洪奇. 输入串联型变换器集成变压器的分布电容影响机制与绕组布局方法[J]. 电工技术学报, 2021, 36(24): 5272-5282.
Meng Tao, An Yanhua, Ben Hongqi. Stray capa- citances influences and windings layout of the integrated-transformer in the input-series converter[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5272-5282.
[21] 王迎迎, 程红. 应用于功率变换器的多绕组高频变压器模型[J]. 电工技术学报, 2021, 36(19): 4140-4147.
Wang Yingying, Cheng Hong. Dual multi-winding high-frequency transformer equivalent circuit for power converter applications[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4140-4147.
[22] 郭向伟, 耿佳豪, 刘震, 等. 基于反激变换器的双目标直接均衡方法[J]. 电工技术学报, 2021, 36(6): 1269-1278.
Guo Xiangwei, Geng Jiahao, Liu Zhen, et al. The dual-objective direct balancing method based on flyback converter[J]. Transactions of China Electro- technical Society, 2021, 36(6): 1269-1278.
[23] 李科峰, 肖飞, 刘计龙, 等. 多电平有源中点钳位逆变器串联IGBT均压方法[J]. 电力系统自动化, 2022, 46(2): 163-170.
Li Kefeng, Xiao Fei, Liu Jilong, et al. Voltage balancing method of series-connected IGBTs for multi-level active neutral point clamped inverter[J]. Automation of Electric Power Systems, 2022, 46(2): 163-170.
[24] 刘树林, 曹剑, 胡传义, 等. 正-反激组合变换器的能量传输模式及输出纹波电压分析[J]. 电工技术学报, 2019, 34(8): 1647-1656.
Liu Shulin, Cao Jian, Hu Chuanyi, et al. Energy transmission modes and output ripple voltage of forward-flyback converter[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1647-1656.
[25] 尹浩, 苏建徽, 赖纪东, 等. 中频圆导线变压器漏感的精确解析计算[J]. 电工技术学报, 2021, 36(15): 3211-3220.
Yin Hao, Su Jianhui, Lai Jidong, et al. Accurate analytical calculation of leakage inductance of round conductor transformer under the medium frequency[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3211-3220.
Abstract The unidirectional magnetization of the basic forward conversion topology will lead to the transformer’s saturation, and various magnetic reset measures have been proposed. Among them, the primary side magnetic reset only consumes the excitation energy on the resistance or feedback to the input side, so the excitation energy can not be fully utilized. Therefore, it is not beneficial to improve energy transmission efficiency of the converter. The secondary-side reset forward-flyback conversion topology composed of four diodes on the secondary side can forward energy and excitation energy to the load, thus improving the energy efficiency. However, the excitation inductor and the forward inductor affect the power transmission and distribution characteristics and the switch current stress of the conversion topology. Therefore, this paper studies the relationship between power transmission characteristics, switch current stress and the magnetic components parameters. The design method of magnetic components parameters is proposed by comprehensively considering the influence of forward and flyback transmission power ratio on the electrical performance of the conversion topology.
For the forward-flyback converter, the forward inductor can only work in DCM. Compared with the minimum excitation inductor current in one cycle with zero, its working mode can be divided into Magnetizing current continuous conduction mode (MCCM) and Magnetizing current Discontinuous Conduction Mode (MDCM). Its power transmission characteristics and its relationship with a load resistance RL under different modes show that both the forward power PFW and flyback power PFB increase with the decrease of the RL when the conversion topology works in the MDCM. When the RL is reduced to make the conversion topology enter the MCCM, the PFW increases to the maximum value and no longer increases with the decrease of the RL, while the PFB still increases with the decrease of the RL.
The critical excitation inductance Lmc corresponding to PFW=PFB is defined by analyzing the influence of excitation inductance on the power transmission and distribution characteristics of the conversion topology. For the given output power, the PFW increases, and the PFB decreases with the increase of excitation inductance. When the excitation inductor equals Lmc, and the conversion topology works in MDCM, the PFW equals PFB. The PFB increases, and the PFW decreases with the increase of the transformer turn ratio.
Regarding the influence of power transmission distribution on the switch current stress, for the given output power, the switch current stress decreases with the decrease of PFW. Therefore, reducing the PFW can reduce the switch current stress. However, reducing the PFW will increase the PFB, while increasing the PFB requires increasing the transformer air gap to reduce the magnetizing inductance, which will increase the transformer loss. Therefore, reducing the PFW is not beneficial to improving the efficiency of the conversion topology.
Regarding the influence of the distribution of PFW and PFB on the electrical performance of the conversion topology, reducing the PFW is beneficial to reducing the current stress of the switch, and reducing the PFB can improve the efficiency of the conversion topology. Therefore, to improve the efficiency of the conversion topology and not cause the current stress of the switch to be too high, a component parameter design method is proposed to guarantee that PFW=PFB when the output power reaches the maximum within the given load range.
Experimental results verify the correctness of the theoretical analysis and the feasibility of the proposed design method. The proposed design method for component parameters can develop a high-performance forward-flyback conversion topology and promote its popularization and application.
keywords:Forward-flyback conversion topology, power transmission distribution, forward power, flyback power, design
DOI: 10.19595/j.cnki.1000-6753.tces.221472
中图分类号:TM46
国家自然科学基金资助项目(51777167, 51604217)。
收稿日期 2022-07-30
改稿日期 2022-09-09
刘树林 男,1964年生,博士,教授,博士生导师,研究方向为开关变换器的分析与设计及本质安全电路等。E-mail: lsigma@163.com(通信作者)
沈一君 女,1998年生,硕士研究生,研究方向为开关变换器的分析与设计及本质安全电路。E-mail: 20206029003@stu.xust.edu.cn
(编辑 陈 诚)