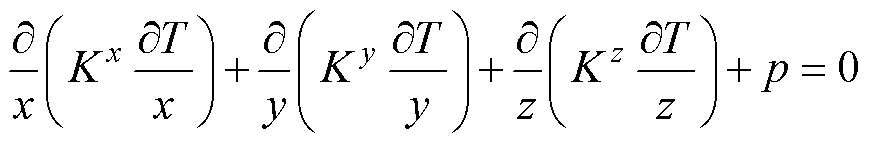 (1)
(1)
摘要 三维温升计算是大功率高频变压器(HFT)建模中的难点问题,准确、快速的热模型对于HFT的优化设计和稳定运行有着重要意义。目前,普遍采用降维方式建立集总参数热网络模型,其计算精度易受结构参数影响,在宽参数范围寻优中难以实现准确的热点预测。该文基于有限差分方法(FDM)构建了HFT三维热模型,并对离散化误差及其控制方法进行分析。借助有限元仿真对三维热模型的参数适应性进行详细校验,包括结构尺寸、损耗密度及散热条件,校验结果表明,该模型在宽参数范围内的最大误差小于10%。以10 kHz、150 kW变压器为例进行优化设计,单次三维温升计算平均耗时2.8 ms,最优设计边界上的最高温升计算误差低于5.5%。根据优化设计结果加工150 kW变压器原型样机并进行额定功率测试,最高温升计算误差为3%。
关键词:高频变压器 三维热模型 有限差分 优化设计
在智能电网快速发展背景下,电力电子变压器(Power Electronic Transformer, PET)成为构建新一代交直流配电网的关键设备[1-3],其中高频变压器(High-Frequency Transformer, HFT)是实现电气隔离、电压转换的核心部件。
提高工作频率是降低HFT体积、质量及成本的有效手段,但随着工作频率提高,磁心和绕组的损耗密度增加,同时变压器的散热面积却相对减小[4]。以环氧树脂、硅胶为代表的固体灌封材料,因其优异的绝缘性能及高安全性、易维护等特点,得到了广泛应用[5],但高介电强度的固体绝缘材料导热性能普遍较差,难以将变压器内部的热量导出,容易导致局部过热。运行温度是考核HFT性能的重要指标,过高的运行温度将导致绝缘材料老化,因此准确的热模型和温升计算方法对于HFT的设计和寿命预测有着重要意义[6]。
目前,磁性器件优化设计中普遍采用的温升计算方法为有限元方法(Finite Element Method, FEM)和热网络法(Thermal Network Method, TNM)。
基于精细化的结构建模和网格单元划分,FEM的计算精度得到广泛认可,能够实现准确的三维温度分布预测。另一方面,FEM对计算资源消耗巨大,单次计算耗时长,难以用于优化设计中的寻优过程,通常只用于对比分析和校验优化结果[7-8]。文献[9]采用FEM精确模拟了一台2 500 kV·A干式变压器的对流换热过程,并实现变压器结构件温升计算和绕组热点预测,温升试验结果表明,FEM预测值与试验值误差小于±6%。
TNM是一种基于热阻参数的温升计算方法,与FEM相比具有模型相对简单、易于参数化和快速求解的优点,是目前磁性器件优化设计中的主要温升计算方法。
为了增大散热面积降低温升,传统工频干式变压器一般采用圆筒式绕组,一次、二次绕组间留有散热气道。由于圆筒式绕组和散热风道为圆周对称结构,故可忽略绕组在圆周切线方向上的热量流动和温度梯度,文献[10-12]中建立了圆筒绕组的径向和轴向TNM热模型,TNM温升计算结果与FEM及试验结果相比具有较高精度。
平面磁性器件近年来被广泛应用于中小功率变换器中,除了具有高度低、易于自动化制造的优点,其内部热量主要在垂直方向上传递,热传递路径较短,具有较好的散热性能,因此能够实现更高的功率密度。文献[13]建立了平面电感在磁心窗口平面内的二维TNM模型,该平面电感被铝外壳包裹并安装水冷底板,电感热量通过绕组、磁心及铝外壳传导至底部水冷板。文献[8]同样基于磁心窗口平面建立平面变压器的TNM模型,另外考虑了磁心窗口外绕组的散热量,形成三维TNM模型。
对于高压大功率HFT,为了缩短绝缘间距实现高耐压并提高功率密度,通常采用整体灌封结构[6]。与传统干式变压器和平面磁性器件不同,整体灌封HFT中没有主导的热传导方向和散热面,难以通过降维方式简化HFT的热模型。对于大功率HFT的温升计算和优化设计,目前文献普遍以磁心窗口平面为建模对象,假设窗口平面垂直方向上无温度梯度,忽略了磁心端部及绕组端部的散热量以及对三维温升分布的影响[14-17]。
HFT热模型的另一个难点是,绕组和磁心均为体热源,其内部温度分布呈非线性,难以通过集总参数模型准确估计内部温升。若采用传统TNM,将分布的损耗集中于建模对象中心,将导致温升过高估计[18]。
为了实现HFT温升的准确计算,并满足HFT优化设计所需的快速性和宽范围参数适应性,本文提出基于有限差分方法(Finite Difference Method, FDM)的HFT三维温升计算方法。首先建立了三维热传导差分方程,并对其离散化误差进行分析。以心式变压器为例,考虑磁心和绕组的各向异性导热特征,给出差分单元划分方法。借助有限元仿真工具对三维热模型的参数适应性进行了详细校验,并与传统热网络方法进行计算精度对比。最后基于三维温升计算方法进行150 kW变压器的优化设计,并根据最优设计结果实际加工样机,进行额定工况下的温升测试。
对于具有内热源的三维实体,达到热平衡后其内部温度分布满足傅里叶方程,在直角坐标系中有
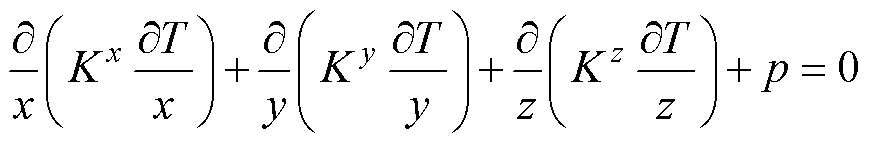 (1)
(1)
式中,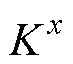 、
、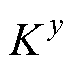 、
、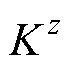 分别为x、y、z坐标方向上的热导率;p为位置(x, y, z)处的单位体积热功率;T为位置(x, y, z)处的温度。
分别为x、y、z坐标方向上的热导率;p为位置(x, y, z)处的单位体积热功率;T为位置(x, y, z)处的温度。
有限差分方法的基础为离散化,三维空间中的离散化过程如图1所示,使用标号i、j、k表示各个节点在三维坐标方向上的位置,节点与周围节点连接线的中垂面构成的封闭空间为该节点的代表区域,节点(i, j, k)所代表单元在坐标方向上的尺寸分别为Wi、Lj、Hk。

图1 三维有限差分单元
Fig.1 Three-dimensional finite difference element
一般采用替代微分算子的方式将微分方程直接离散化为差分方程,变压器内部磁心、绕组、绝缘层等各部分尺寸、热导率、热密度均不相同,故各部分材料交界面处难以直接离散化。傅里叶方程的本质为流入任意微元的热量与其自身产生热量之和为零,故可先求得相邻单元界面处的热流量表达式,再根据热平衡建立任意节点的差分方程。
差分单元间的典型热传递过程如图2所示,包括计算域内部单元i、边界单元i-1及计算域外部虚拟单元0,三者的尺寸、热导率、热密度均不相同,对应的节点温度分别为Ti、Ti-1、T0,其中虚拟单元0用于实现边界上的对流及辐射换热过程,T0为外部环境温度。
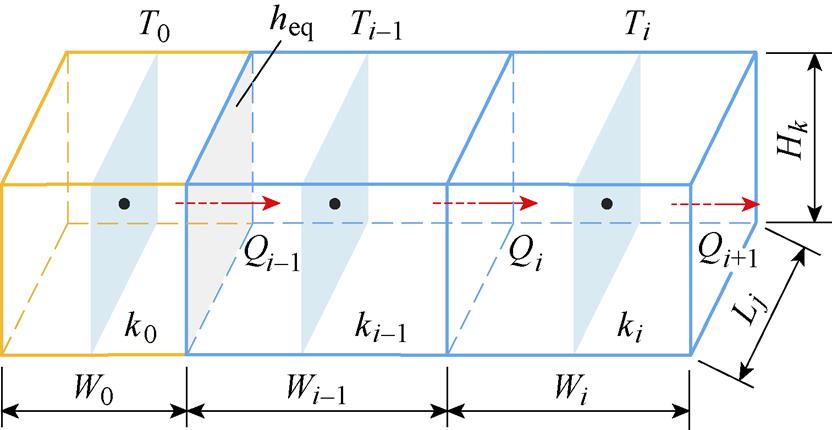
图2 相邻单元间的热传递过程
Fig.2 Heat transfer process between adjacent elements
根据热阻定义,单元i-1至单元i的热流量Qi可表示为
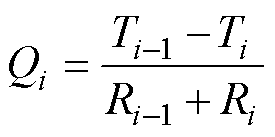 (2)
(2)
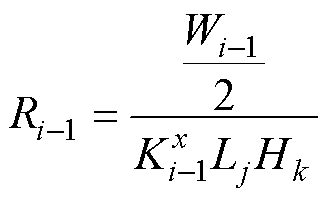 (3)
(3)
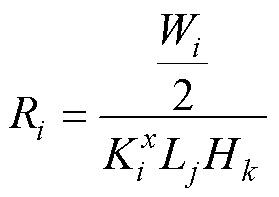 (4)
(4)
式中,Ri-1和Ri分别为单元i-1中心、单元i中心至交界面的连接热阻;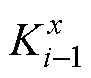 和
和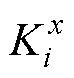 分别为单元i-1、单元i在x轴方向上的热导率,故
分别为单元i-1、单元i在x轴方向上的热导率,故
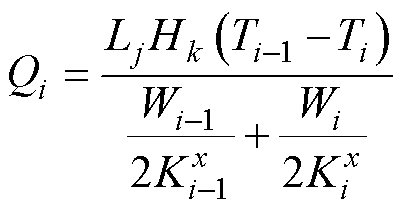 (5)
(5)
同样地,外部虚拟单元0至边界单元i-1的热流量Qi-1可表示为
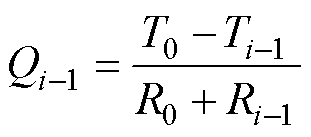 (6)
(6)
外部单元至交界面的连接热阻R0为
 (7)
(7)
式中,heq为表面等效传热系数,包括对流和辐射两种传热形式的综合影响。
为了使连接热阻R0与式(3)和式(4)的形式一致,便于差分方程构建,定义表面虚拟热导率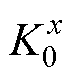 为
为
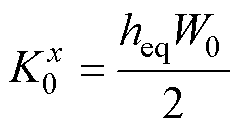 (8)
(8)
故外部单元至边界单元的热流量可表示为
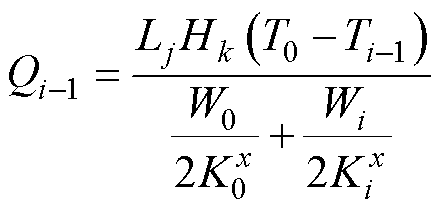 (9)
(9)
对于任意节点(i, j, k),将该单元所有交界面的热流量表达式代入式(10),即可建立该节点的差分方程。对于内部节点,差分方程如式(11)所示,差分方程式(11)中具体系数表达式在附录中列出。
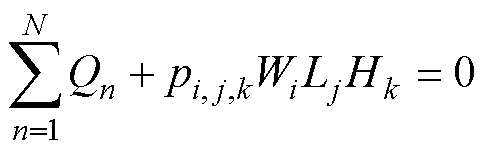 (10)
(10)
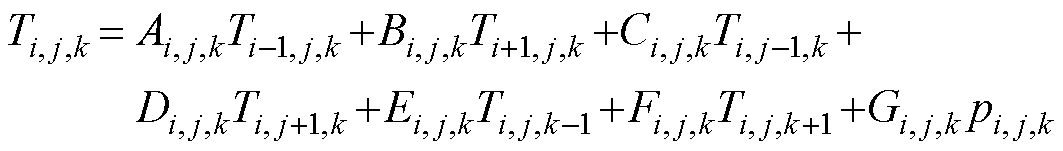 (11)
(11)
式中,N为该节点周围相邻节点的数量;Qn为节点(i, j, k)至相邻节点的热流量; 为节点(i, j, k)所在单元的热功率密度;
为节点(i, j, k)所在单元的热功率密度;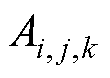 ~
~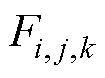 为节点(i, j, k)至周围节点的连接系数;
为节点(i, j, k)至周围节点的连接系数;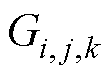 为该节点热功率系数,若该节点无热源,则
为该节点热功率系数,若该节点无热源,则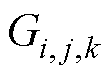 =0。
=0。
求得计算区域内所有节点的连接系数和热功率系数,建立差分方程组,由于节点数量较多,本文采用逐次超松弛迭代方法求解该差分方程组[19]。
采用有限差分方法求解三维热传导问题时,在单元内温度呈线性分布的假设条件下求得相邻单元间的热流量以及温度差分方程。然而,热源功率将使单元内温度分布呈现非线性,从而影响有限差分方法求解精度。以下在一维条件下分析内热源功率对单元内温度分布的影响。
令图2中的单元i内部沿x轴方向的温度分布函数为ti(x),单元内部热功率密度为pi,根据式(1)的一维形式可得
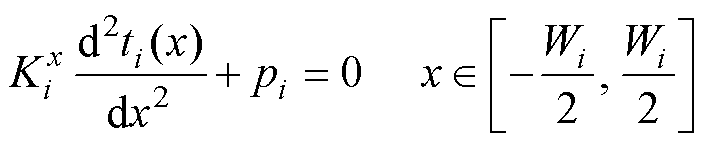 (12)
(12)
式(12)的通解为
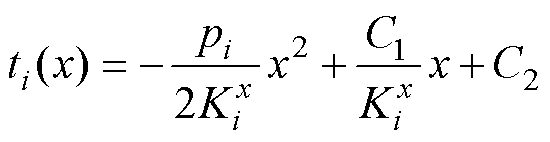 (13)
(13)
式中,C1和C2为待定系数。
令单元i中心温度ti(0)=Ti,x=Wi/2位置处的热流量为Qi+1可由温度分布函数ti(x)的导数表示。
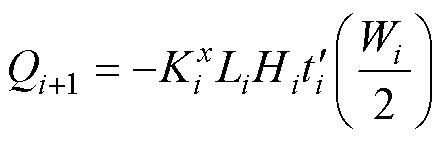 (14)
(14)
联立方程求解式(13)中待定参数,可得
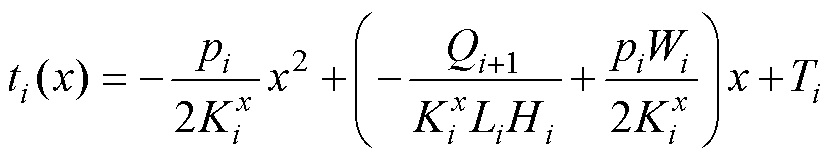 (15)
(15)
根据ti(x),差分单元两端的温差DTi可表示为
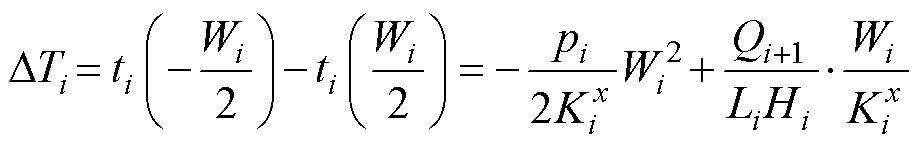 (16)
(16)
若假设单元i内温度呈线性分布,根据热阻定义,则单元i两端的温差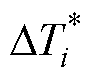 为
为
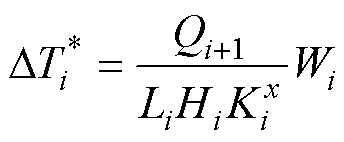 (17)
(17)
对比式(16)和式(17),当假设温度线性分布时,单元i内温度梯度估计误差为
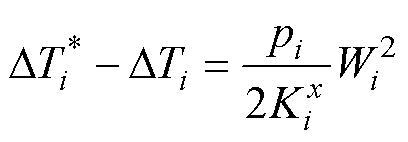 (18)
(18)
对于体热源,如变压器中的磁心部分,假设体热源内热密度为p,当内部热量只沿单方向传递时,线性假设下的温升累计误差达到最大,可表示为
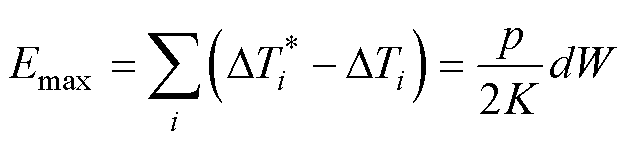 (19)
(19)
式中,K、d分别为热量传导方向的热导率和单元尺寸;W为热源整体在该方向上的总长度。
根据式(19),差分单元尺寸是影响结果精度的重要因素。在具体问题中,为了将线性假设导致的误差控制在一定范围内,需要根据热源功率和材料热导率调整差分单元尺寸。
变压器等磁性器件内的热源为体热源,根据傅里叶方程,需要确定热量体密度才能确定温度分布。对于磁心损耗,由于方波电压激励下广义Steinmetz改进式(Improved Generalized Steinmetz Equation, IGSE)的计算精度最高,因此一般选择IGSE计算磁心损耗[20]。采用IGSE的磁心损耗体积密度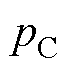 (W/m3)[21]为
(W/m3)[21]为
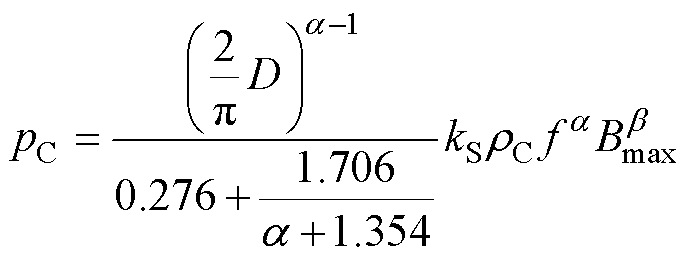 (20)
(20)
式中,D为方波电压占空比;Bmax为峰值磁通密度;f为工作频率;kS、a、b 分别为正弦激励下的Steinmetz比例、频率和磁通幅值系数;rC为磁心材料密度。
为了降低高频损耗,高频变压器一般采用利兹线绕组,绕组截面如图3a所示,包含m层线圈,每层NW匝,绕组截面整体宽度和高度分别为wW、hW。利兹线绕组结构复杂且内部导线分布具有随机性,难以采用实际模型进行变压器热仿真或温升计算,等效替代方法是采用绕组等效均一化模型[22-24]:将绕组中铜导体、绝缘漆及环氧树脂填充物的组合视为单一均质材料,将不同材料的热导率合成为单一有效热导率,同时将损耗均匀分配在整个绕组区域。
考虑高频效应的绕组总损耗Ploss,W[14]为
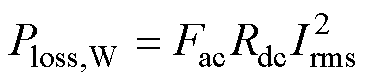 (21)
(21)
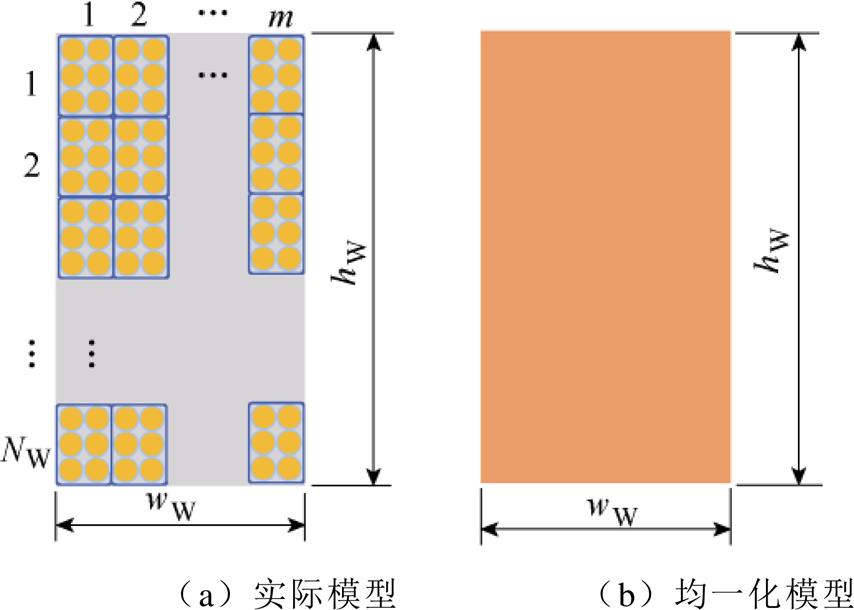
图3 利兹线绕组截面
Fig.3 Cross section of Litz wire winding
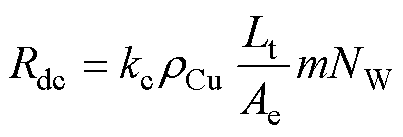 (22)
(22)
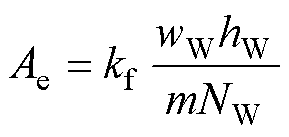 (23)
(23)
式中,Rdc为绕组直流电阻;Irms为绕组电流有效值;Fac为工作频率下的交流电阻系数;rCu为铜导体电阻率;Lt为绕组平均匝长;Ae为单匝利兹线有效截面积;kf为绕组填充率;kc为补偿系数,用于校正单股线束换位、缠绕导致的长度增加以及单股线断线导致的阻值增大;kf和kc为系数,主要受单股线直径和绞合方式影响,是利兹线型号有关的常数。
绕组总体积VW=wWhWLt,故绕组的单位体积损耗可表示为
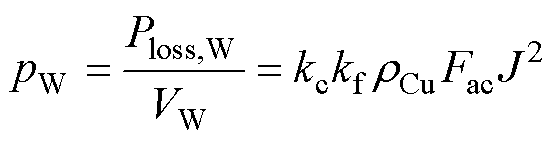 (24)
(24)
式中,J为绕组中铜导体电流密度。根据式(24),若采用同型号利兹线,根据交流电阻系数Fac和电流密度J即可确定单位体积损耗pW,其中工作频率下的Fac可采用辅助绕组方法测量得到[25]。
变压器中热源包括磁心和绕组两部分,根据式(19),热源的损耗密度、材料热导率和差分单元网格尺寸共同影响了单元内部温度梯度估算误差。为了降低损耗、提高变压器效率和功率密度,本文中磁心材料采用纳米晶,绕组采用矩形利兹线,两者的热导率参数见表1,其中绕组的热导率是经环氧树脂浇注固化后的测量数据。纳米晶磁心为多层带材缠绕结构,利兹线为多股线绞合结构,故两者都存在显著的导热各向异性特征,特别是利兹线绕组,其线材横截平面内的热导率远低于其轴向热导率。
低热导率将导致较大的温度梯度估计误差,结合表1中的热导率参数,需要控制利兹线绕组横截平面内以及纳米晶磁心在垂直于带材方向上的单元尺寸。根据式(19),为保证温升估计误差小于最大误差Emax,热源部分差分单元尺寸应小于上限值dmax。
表1 高频变压器中主要材料的热导率参数
Tab.1 Thermal conductivity parameters of main materials in HFT

材料方向热导率/[W/(m·K)] 纳米晶磁心垂直于带材平面1.1 纳米晶磁心平行于带材平面8.5 利兹线绕组线材轴向160 利兹线绕组线材截面1.2 环氧树脂—1.0
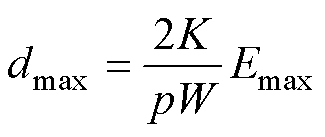 (25)
(25)
式中,K和W分别为对应方向上的热导率和总长度;p为损耗体积密度。考虑到工程实践中变压器内部最高温升一般设计为50~100 K,在保证计算精度前提下为了尽量减少单元数量,在本文中将Emax设为5 K。
心式变压器在三维坐标方向均具有几何对称性,为了减少热模型计算单元数量,以1/8结构模型为计算对象,如图4所示。1/8心式变压器的差分单元划分如图5所示,为了便于构建和求解差分方程,将磁心、一次绕组、二次绕组及绝缘层中的六面体差分单元对齐设置。根据纳米晶磁心和利兹线绕组的热导率特征,按照式(25)限制一次绕组宽度wW1、二次绕组宽度wW2、绕组高度hW以及磁心柱厚度tC方向上的最大尺寸。
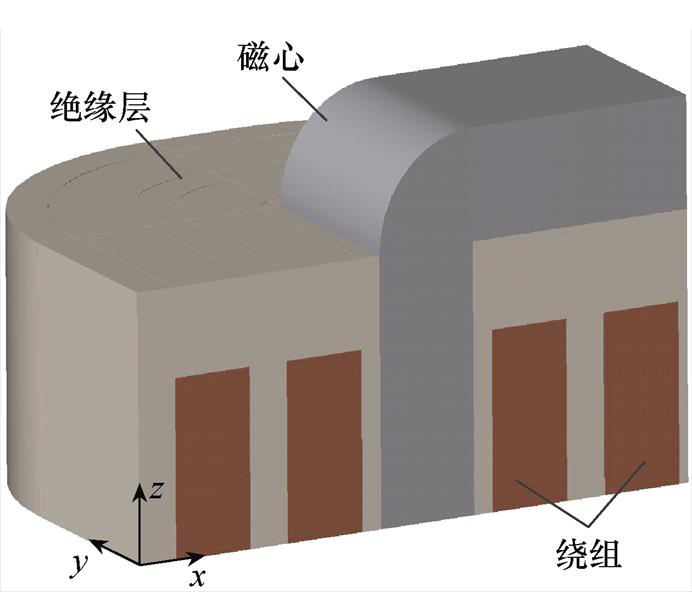
图4 1/8心式变压器结构模型
Fig.4 Structure model of one-eighth core type transformer
2.3.1 变压器温升仿真模型
为了验证有限差分温升模型的计算精度,基于Ansys Workbench软件工具按照图4建立了1/8心式变压器的参数化三维FEM热仿真模型。在热仿真模型中,根据材料热导率特征将磁心和绕组分为多个部分,分别设置各个方向的热导率参数。为了减少网格数量,仿真模型中采用六面体结构化网格。
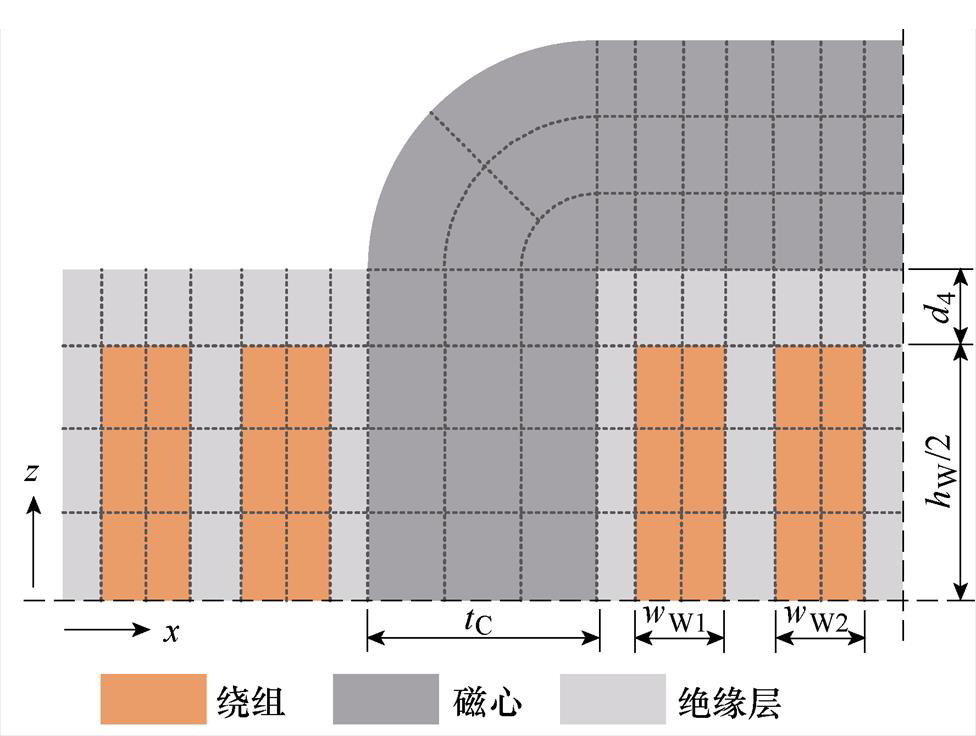
(a)xz平面
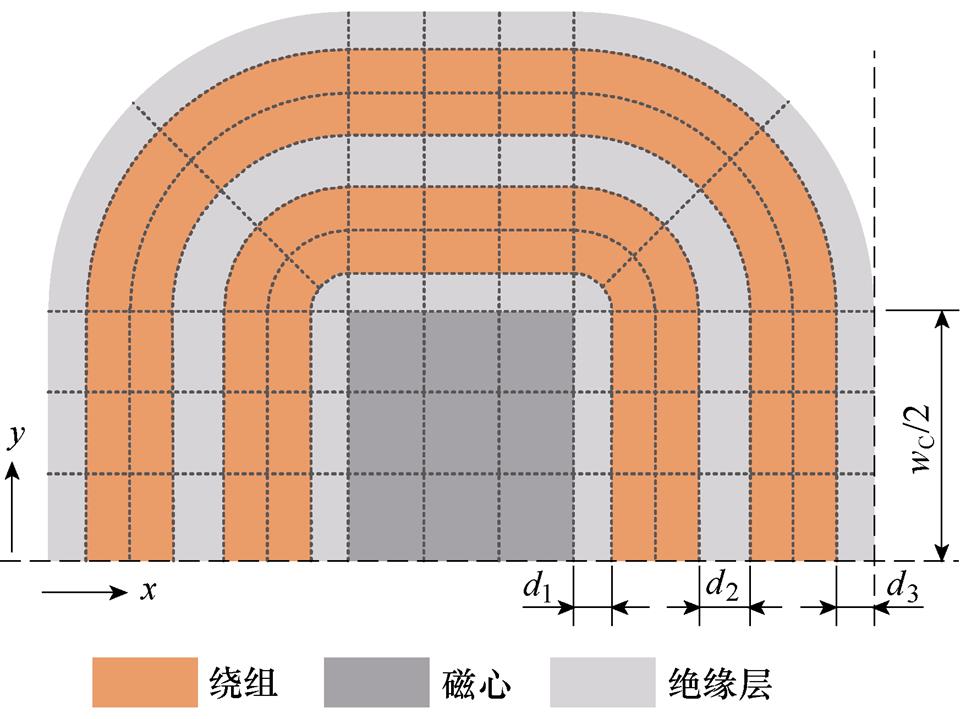
(b)xy平面
图5 心式变压器有限差分单元划分方法
Fig.5 The partition of finite difference element in core type transformer
图6给出了绕组的仿真模型和仿真结果,图6a中绕组被划分为五个部分,并标出了各部分的高热导率方向。图6b所示仿真结果中利兹线绕制方向上的温度梯度很小,温度梯度方向与高热导率方向垂直,符合利兹线绕组的各向异性导热特征。
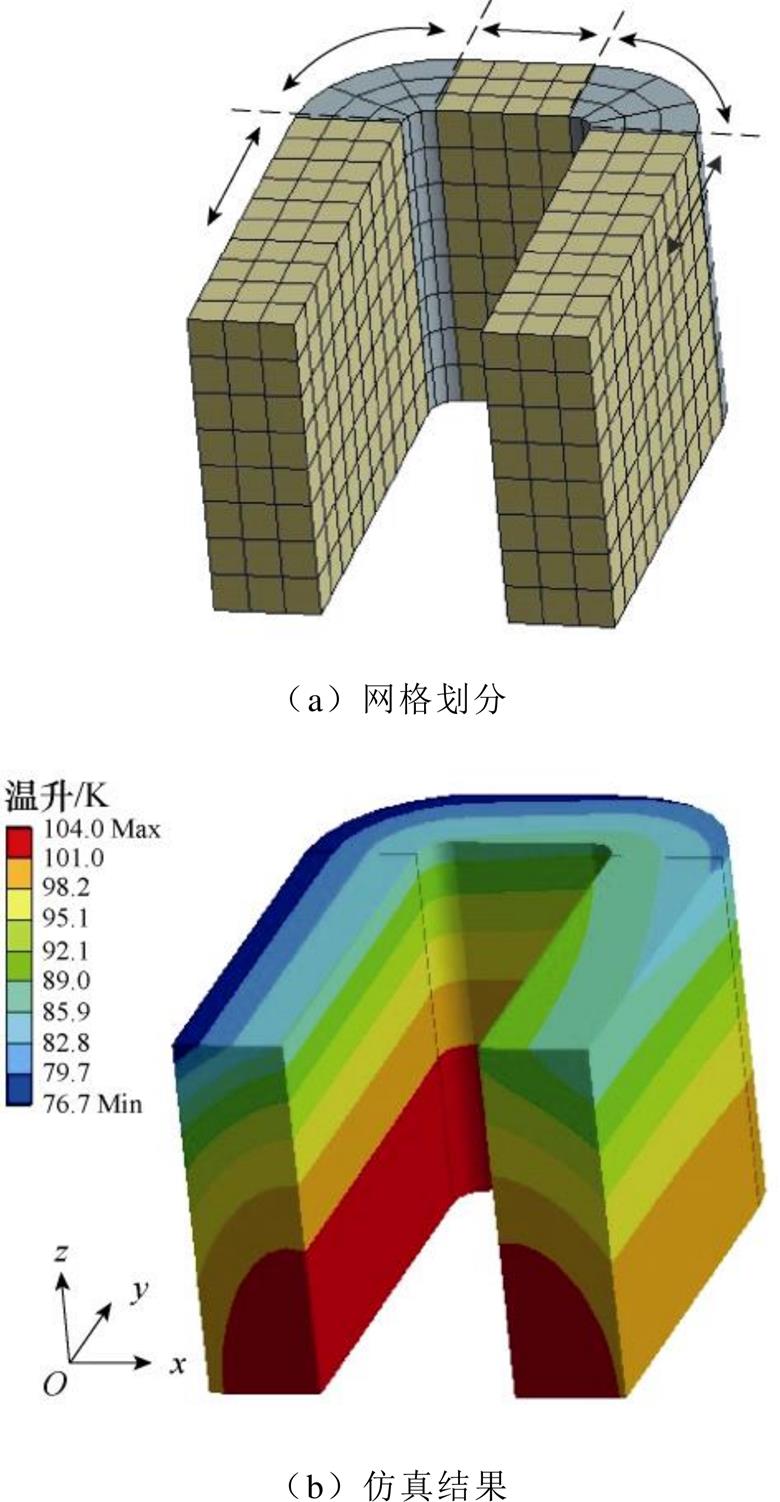
图6 绕组FEM温升仿真
Fig.6 FEM temperature rise simulation of winding
2.3.2 FDM计算误差分析
与确定变压器的温升计算相比,在变压器优化设计中,需要保证在变压器设计参数变化情况下均能准确预测温升信息,与温升相关的具体参数包括:①磁心和绕组的结构尺寸;②磁心和绕组的损耗密度或总损耗;③表面等效传热系数。
以心式高频变压器为例,表2给出了用于温升计算模型校验的变压器参数。对于结构参数,定义rW为绕组高度hW与宽度wW的比值,rC为磁心宽度wC与厚度tC的比值。将绕组宽度wW、磁心厚度tC以及绝缘距离设为固定值,通过调整rW和rC实现变压器整体三维尺寸比例变化。按照工程设计经验,磁心和绕组的损耗密度范围设为2×104~8×104 W/m3。干式变压器通常采用自然风冷或强制风冷方式散热,部分应用通过在变压器表面加装肋片式散热器进一步降低温升[14, 16],同样可使用表面等效传热系数heq等价表示散热器的散热效果[26]。考虑以上三种风冷散热形式,heq的范围设为10~800 W/(K·m2)。
表2 心式变压器参数
Tab.2 The parameters of core type transformer

参 数数 值 绕组宽度wW1、wW2/mm20 磁心厚度tC/mm25 磁心至绕组的绝缘距离d1/mm5 绕组间的绝缘距离d2/mm10 绕组至磁心轭部的绝缘距离d3/mm10 绕组至变压器表面的绝缘距离d4/mm20 归一化绕组高度rW2~16 归一化磁心宽度rC2~16 绕组损耗密度pW/(W/m3)2×104~8×104 磁心损耗密度pC/(W/m3)2×104~8×104 表面等效传热系数heq/[W/(K·m2)]10~800
磁心和绕组的最高温升DTC_max、DTW_max是变压器优化设计中的主要关注指标。基于FDM,首先将损耗密度pW、pC和表面等效传热系数heq设为恒定值,图7a中给出rW和rC变化时DTC_max和DTW_max相对于仿真结果的计算误差。当rW和rC在2~16范围内变化时,DTC_max和DTW_max的最大误差为6.6%。
为了对比FDM和TNM的温升计算精度,参考文献[14-17]建立如图8所示的心式变压器6节点热网络温升计算模型。
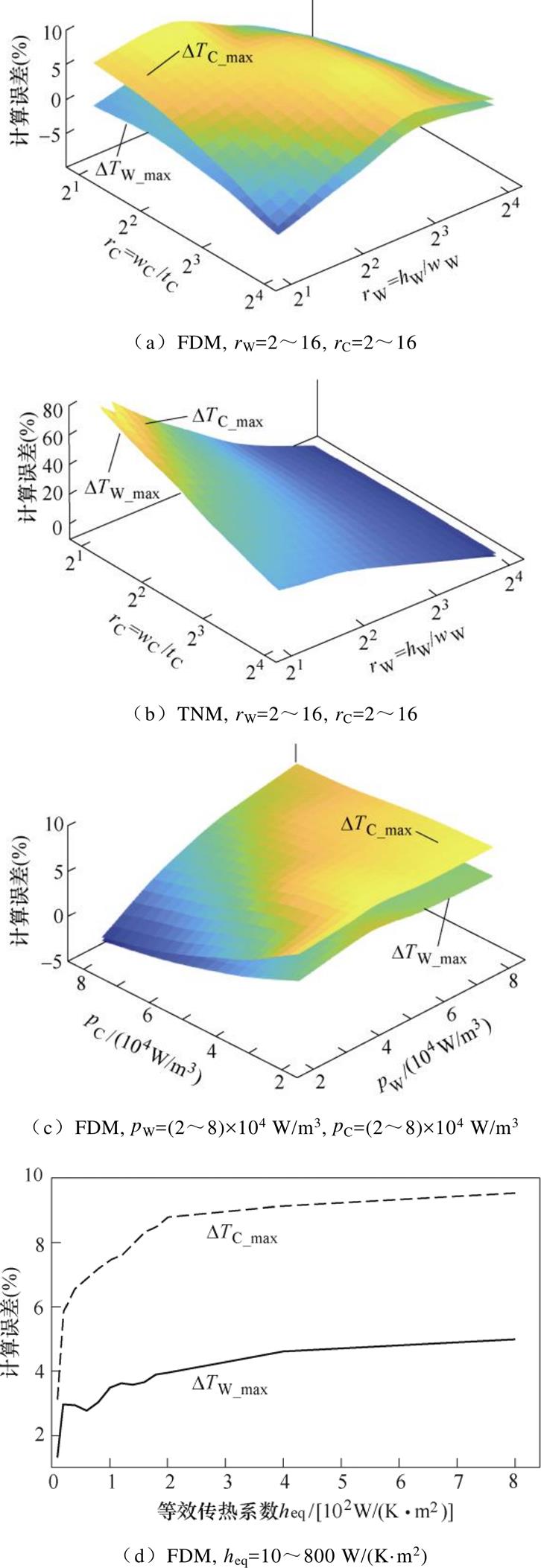
图7 参数变化时的温升计算误差
Fig.7 The calculation error of temperature rise in the case of parameter variation
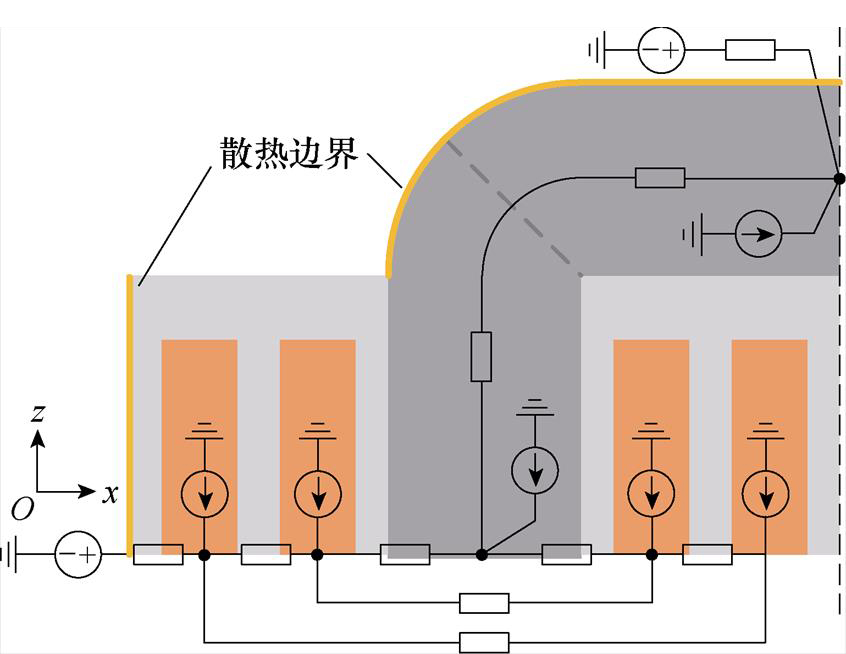
图8 心式变压器六节点热网络模型
Fig.8 Thermal network model of core type transformer with six nodes
在相同参数条件下,考虑rW和rC变化时TNM的温升计算误差如图7b所示。图7b中当绕组高度hW和磁心宽度wC取最小值时TNM的误差最大,温升计算误差为80%。随着hW和wC的增大,TNM的温升计算误差显著减小至约10%。TNM温升计算结果偏高的主要原因是:①仅将绕组侧面和磁心轭部顶面作为换热边界,忽略了磁心窗口端部及绕组端部的散热量,绕组高度和磁心宽度越小则该假设引起的误差越大;②将三维分布损耗集中为面热源将导致温升计算值偏高[18]。
变压器中绕组和磁心的温升不仅受自身损耗的影响,两者之间还存在耦合作用,故需要评估绕组和磁心损耗密度独立变化时的温升计算误差。基于FDM,变压器结构尺寸和表面等效传热系数heq设为定值,绕组损耗密度pW和磁心损耗密度pC变化时DTC_max和DTW_max的计算误差如图7c所示。以FEM仿真结果为参考,损耗密度对FDM的计算误差的影响较小,当pW和pC在2×104~8×104 W/m3范围内独立变化时,DTC_max和DTW_max的最大误差为7.5%。
除绕组、磁心尺寸及损耗密度外,变压器散热条件即表面等效传热系数是影响变压器温升的关键参数。基于FDM,变压器表面等效传热系数heq变化时DTC_max和DTW_max的计算误差如图7d所示。变压器温升模型可分解为内部至表面、表面至外部空气两部分。当传热系数heq增大时,变压器表面至周围环境的热阻和温升大幅降低,而变压器内部热阻不变,故变压器内部至表面的热阻和温升计算误差被放大,整体温升计算误差最终趋于内部至表面的温升计算误差。以有限元仿真结果为参考,当heq在10~800 W/(K·m2)范围内变化时,DTC_max和DTW_max的最大误差为9.5%。
采用归一化绕组模型进行变压器设计,变压器结构自由设计参数包括一次绕组厚度wW1、二次绕组厚度wW2、绕组高度hW、磁心厚度tC及宽度wC,另外还包括一次绕组匝数N1。变压器中绝缘距离由工作电压等级确定,本文按照10 kV工作电压要求设置图5中绝缘层厚度d1、d2、d3、d4,具体数值见表2。
对于具体的变压器绕组电压、电流参数,难以直接确定结构尺寸的优化范围,而绕组电流密度和磁心工作磁通密度容易根据材料类型和工程经验确定。对于绕组结构参数,绕组厚度受到绕组层数和单匝线圈尺寸的限制,而绕组高度hW不受限。以一次绕组为例,使用其电流密度J1作为优化变量,由wW1和J1计算得到绕组高度hW为
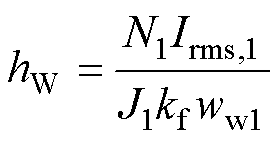 (26)
(26)
式中,Irms,1为一次绕组电流有效值。令一次绕组和二次绕组高度相同,则二次绕组宽度wW2=wW1J1/J2,其中,J2为二次绕组的电流密度。
对于磁心结构参数,受到趋肤深度的限制,磁心厚度tC一般只能在固定尺寸范围内选择,而磁心宽度wC可通过多个磁心单元叠加灵活调整。本文中使用峰值磁通密度Bmax作为优化变量,由磁心厚度tC和磁通密度Bmax计算得到磁心宽度wC为
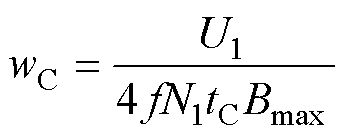 (27)
(27)
式中,U1为一次电压幅值。
基于自由参数扫描方法的高频变压器优化设计流程如图9所示,首先确定变压器电气参数、优化指标、约束条件、运行条件以及磁心、绕组、绝缘材料属性,根据上述条件并结合工程设计经验确定优化变量范围及绝缘间距,对6个优化变量N1、wW1、J1、J2、tC、Bmax组合得到的所有设计方案进行基本电磁关系、磁心及绕组损耗密度等参数计算,再采用FDM计算变压器中最高温升,最终输出所有符合温升要求的设计结果。
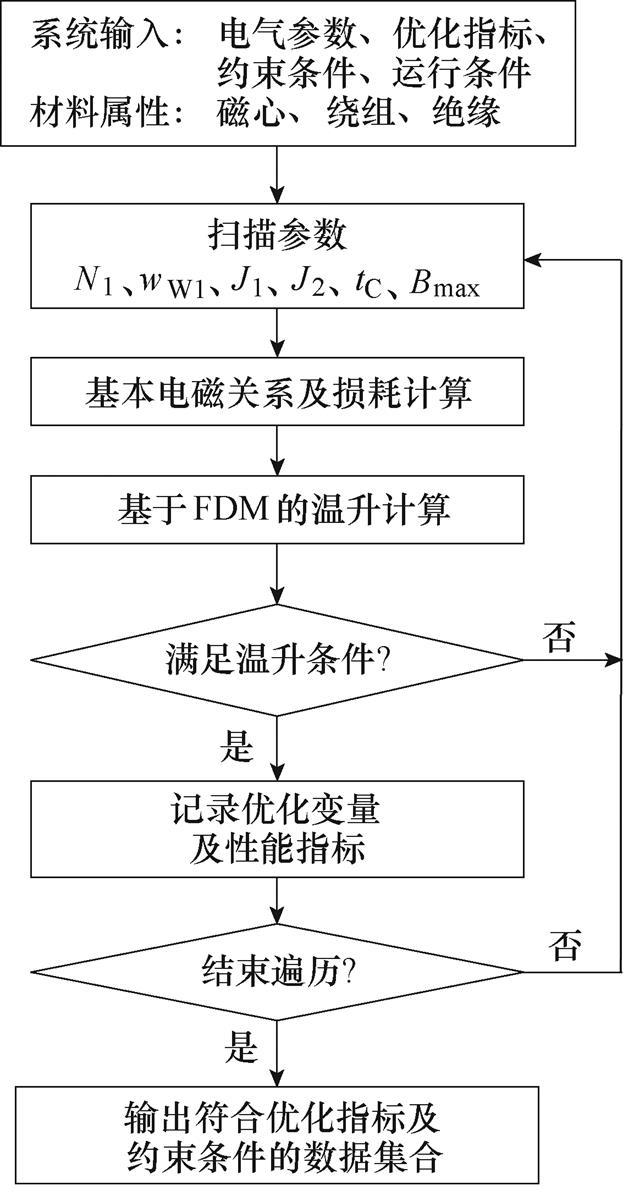
图9 高频变压器优化设计流程
Fig.9 Optimization design procedure of HFT
采用图9所示优化流程进行心式变压器优化设计,变压器额定参数见表3。绕组材料采用矩形利兹线,磁心材料使用纳米晶,绝缘材料为环氧树脂,材料热导率参数见表1。考虑强迫风冷方式,风速约为1~2 m/s,实测该风速下等效传热系数为20 W/(K·m2)。变压器最高运行环境温度为50℃,变压器中磁心、绕组、绝缘材料最高使用温度为150℃,故变压器内部最高允许温升为100 K。
表3 高频变压器样机额定参数
Tab.3 Rated parameter of HFT prototype

参 数数 值 一次绕组额定电压/V1 000 一次绕组额定电流/A170 额定功率/kW150 工作频率/kHz10
为了缩短优化程序运行时间,将所有变量组合平均分配给4个线程,设计点总数量为50万。基于Intel i5-7500处理器,优化程序运行总时间为371 s,单个设计点的温升计算平均耗时为2.8 ms,表明基于FDM的三维温升计算方法满足变压器优化设计所需的计算速度要求。作为对比,2.3.1节中有限元软件单次运行时间约为20 s。
在100 K温升范围内的150 kW心式变压器的效率-功率密度优化设计结果如图10所示,每个点表示一个优化设计变量组合,点的颜色表示变压器内部的最高温升。
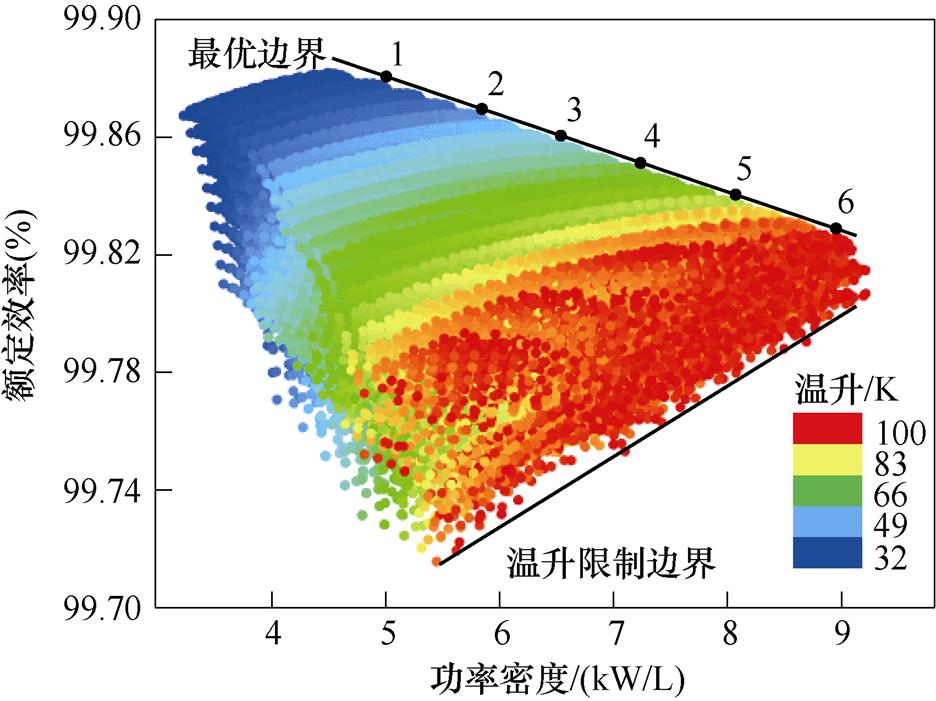
图10 150 kW心式变压器效率-功率密度优化设计结果
Fig.10 Results of efficiency-power density optimization design of 150 kW core type transformer
在效率-功率密度坐标系中,优化结果区域上边沿为最优设计边界,右下边沿为温升限制边界。在最优边界上随着功率密度的增加,变压器效率逐渐降低,温升逐渐升高,满足100 K温升要求的最大功率密度约为9 kW/L,此时变压器效率约为99.82%。
为了校验变压器结构尺寸以及损耗密度自由变化情况下FDM的温升计算精度,在图10的最优边界上随功率密度增大依次选取6个设计点。从优化数据中提取6个设计点的结构尺寸和损耗密度数据并导入有限元仿真软件,磁心最高温升的有限元仿真结果、FDM计算结果以及相对误差如图11所示。FDM计算结果略高于有限元仿真结果,6个设计点中磁心最高温升的最大误差为5.5%。
为了提高功率密度,选择图10中的设计点6作为最优设计点,根据该设计点的结构尺寸参数进行样机加工,150 kW变压器以及DC-DC变换器样机如图12a所示。根据仿真结果,变压器温升最高点是磁心柱中部且靠近内侧绕组的位置,故在样机中对应位置布置热电偶测温探头,固化在绝缘层内。变压器样机长0.3 m、宽0.3 m、高0.2 m,功率密度8.3 kW/L,由于实际变压器样机包含绕组出线部分,故样机功率密度略低于设计值9 kW/L。150 kW变压器样机的测试电路如图12b所示,其中一次侧电路采用3.3 kV SiC功率器件,二次侧电路采用1.2 kV SiC器件,该电路可实现2 kV至750 V的双向直流功率传输。

图11 最优边界上的温升计算误差
Fig.11 Temperature rise calculation error on the optimum boundary
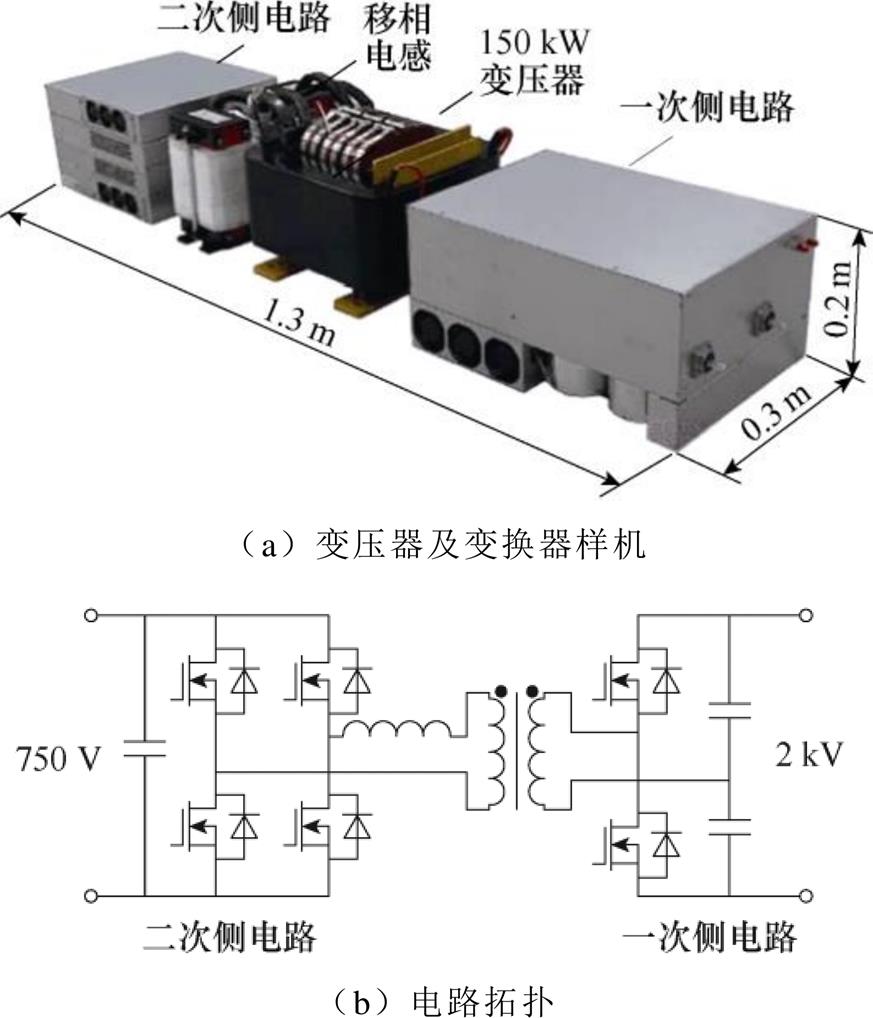
图12 150 kW DC-DC变换器
Fig.12 150 kW DC-DC converter
在10 kHz频率下,变压器样机额定功率运行时一次电压u1和电流i1的波形如图13a所示,绕组电压幅值为1 000 V,绕组电流有效值为166 A。环境温度为20℃时,变压器样机在额定工况运行并达到热平衡,磁心轭部红外热成像如图13b所示。该变压器样机的磁心由3个磁心单元组成,磁心单元间留有空隙便于红外测量磁心轭部内部温度及布置热电偶探头。磁心轭部空隙内最高温升为93 K,由热电偶测得的变压器内部最高温升为103 K。150 kW变压器样机额定工况下温升测试结果与设计温升目标100 K接近,表明基于FDM的变压器三维温升计算及优化方法可用于实际工程且具有较高精度。
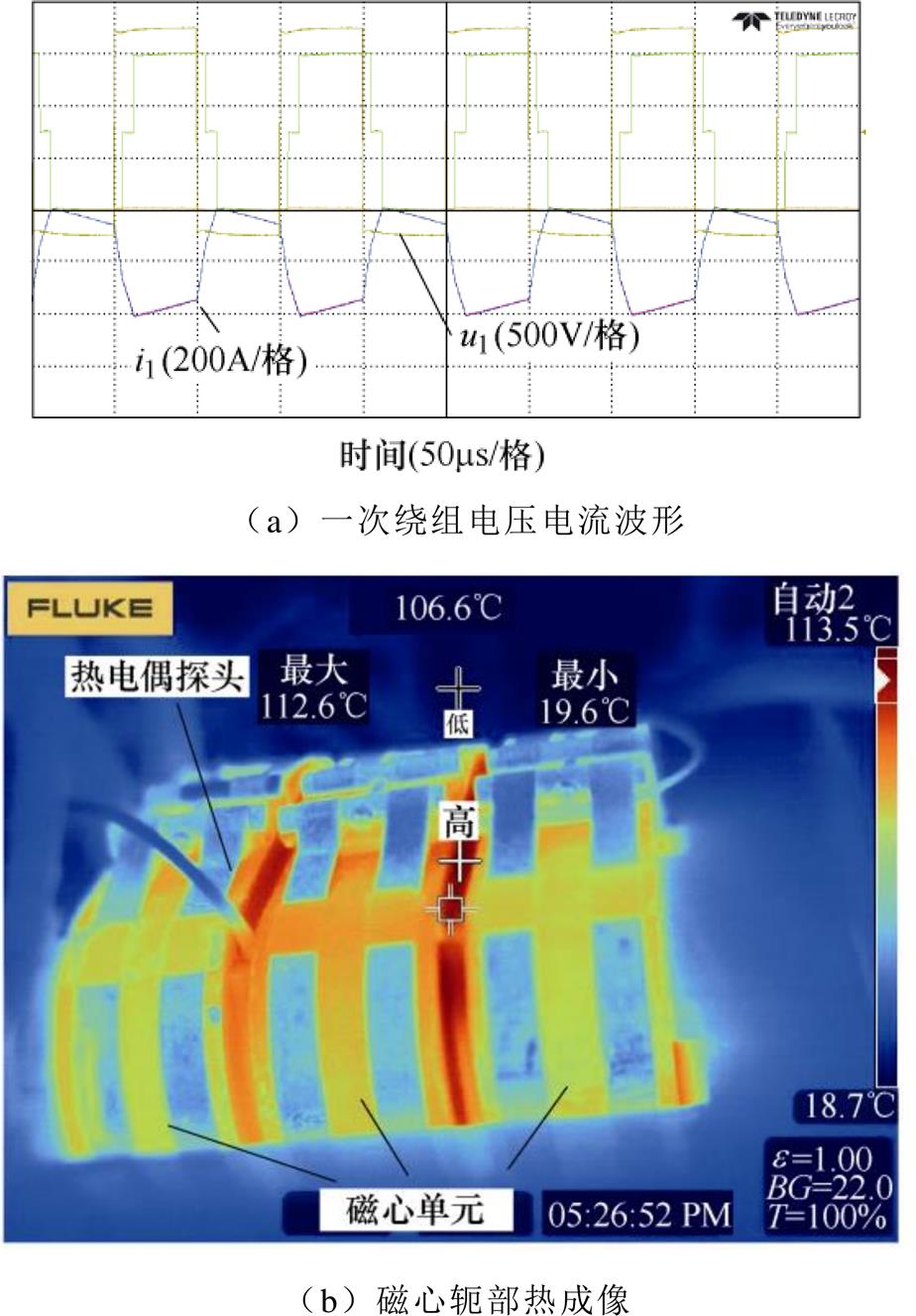
图13 150 kW变压器样机额定功率运行情况
Fig.13 Rated power operation of 150 kW transformer prototype
本文基于FDM建立了固体灌封HFT三维热模型,解决了传统方法参数适应性差的问题,实现了变压器内部热点的快速、准确预测,主要结论如下:
1)TNM对变压器的三维热模型进行了降维简化,忽略了磁心窗口端部及绕组端部的热传导路径,变压器三维尺寸对其温升计算精度有较大影响,难以适用于固体灌封变压器的优化设计。
2)对于FDM,其温升计算误差主要受建模对象的热功率密度、热导率、尺寸以及差分单元尺寸影响。对于固体灌封HFT,磁心和绕组的高损耗密度、低热导率特征增大了温升分布的非线性,需根据具体参数调整差分单元尺寸以满足精度要求。
3)相对于FEM和TNM,基于FDM的三维温升计算方法实现了计算精度和计算速度之间的平衡,为HFT的优化设计提供了模型基础。
附录 差分方程系数
 (A1)
(A1)
 (A2)
(A2)
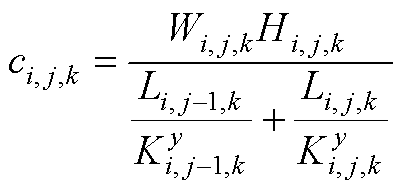 (A3)
(A3)
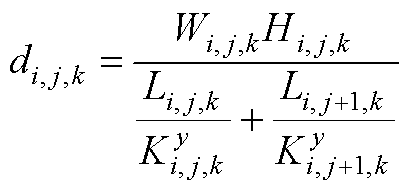 (A4)
(A4)
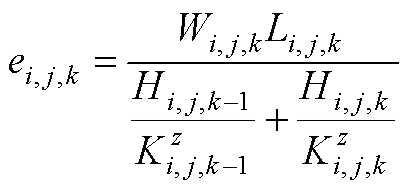 (A5)
(A5)
 (A6)
(A6)
 (A7)
(A7)
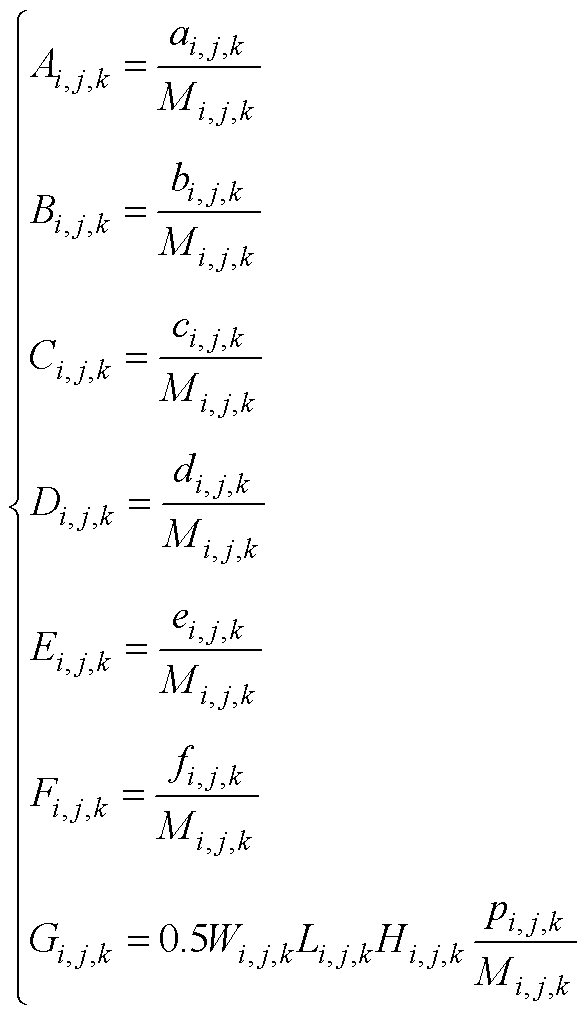 (A8)
(A8)
参考文献
[1] 赵晓君, 张纯江, 柴秀慧, 等. 串并联架构区域电能路由器柔性运行与功率流控制策略[J]. 电工技术学报, 2021, 36(7): 1480-1491.
Zhao Xiaojun, Zhang Chunjiang, Chai Xiuhui, et al. Flexible operation and power flow control strategies for series-parallel architecture region electric power router[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1480-1491.
[2] 高范强, 李子欣, 李耀华, 等. 面向交直流混合配电应用的10kV-3MV·A四端口电力电子变压器[J]. 电工技术学报, 2021, 36(16): 3331-3341.
Gao Fanqiang, Li Zixin, Li Yaohua, et al. 10kV- 3MV·A four-port power electronic transformer for AC-DC hybrid power distribution applications[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3331-3341.
[3] 周兵凯, 杨晓峰, 张智, 等. 能量路由器中双有源桥直流变换器多目标优化控制策略[J]. 电工技术学报, 2020, 35(14): 3030-3040.
Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Multi-objective optimization control strategy of dual- active-bridge DC-DC converter in electric energy router application[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3030-3040.
[4] Leibl M, Ortiz G, Kolar J W. Design and experimental analysis of a medium-frequency transformer for solid- state transformer applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 110-123.
[5] 孙凯, 卢世蕾, 易哲嫄, 等. 面向电力电子变压器应用的大容量高频变压器技术综述[J]. 中国电机工程学报, 2021, 41(24): 8531-8546.
Sun Kai, Lu Shilei, Yi Zheyuan, et al. A review of high-power high-frequency transformer technology for power electronic transformer applications[J]. Pro- ceedings of the CSEE, 2021, 41(24): 8531-8546.
[6] 靳艳娇, 乔光尧, 邓占锋, 等. 全环氧固封高频变压器散热优化设计研究[J]. 电网技术, 2022, 46(7): 2531-2537.
Jin Yanjiao, Qiao Guangyao, Deng Zhanfeng, et al. Heat dissipation optimization design of epoxy resin sealing high frequency transformer[J]. Power System Technology, 2022, 46(7): 2531-2537.
[7] Scoltock J, Wang Yiren, Calderon-Lopez G, et al. Rapid thermal analysis of nanocrystalline inductors for converter optimization[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2276-2284.
[8] Shafaei R, Ordonez M, Ali Saket M. Three- dimensional frequency-dependent thermal model for planar transformers in LLC resonant converters[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4641-4655.
[9] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491.
Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal- fluid model[J]. Transactions of China Electrotech- nical Society, 2020, 35(21): 4483-4491.
[10] 唐钊, 刘轩东, 陈铭. 考虑流体动力学的干式变压器热网络模型仿真分析[J]. 电工技术学报, 2022, 37(18): 4777-4787.
Tang Zhao, Liu Xuandong, Chen Ming. Simulation analysis of thermal network model of dry-type transformer considering fluid dynamics[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(18): 4777-4787.
[11] Yuan Shuai, Zhou Lijun, Gou Xiaofeng, et al. Modeling method for thermal field of turbulent cooling dry-type on-board traction transformer in EMUs[J]. IEEE Transactions on Transportation Elec- trification, 2022, 8(1): 298-311.
[12] Chen Yifan, Yang Qingxin, Zhang Changgeng, et al. Thermal network model of high-power dry-type trans- former coupled with electromagnetic loss[J]. IEEE Transactions on Magnetics, 2022, 58(11): 1-5.
[13] Gao Yucheng, Sankaranarayanan V, Dede E M, et al. Modeling and design of high-power, high-current- ripple planar inductors[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5816-5832.
[14] 陈彬, 梁旭, 唐波, 等. 大功率中频三相变压器优化设计方法[J]. 中国电机工程学报, 2021, 41(8): 2877-2890.
Chen Bin, Liang Xu, Tang Bo, et al. Optimization method of high-power medium-frequency three-phase transformer[J]. Proceedings of the CSEE, 2021, 41(8): 2877-2890.
[15] Booth K, Subramanyan H, Liu Jun, et al. Parallel frameworks for robust optimization of medium- frequency transformers[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 5097-5112.
[16] Mogorovic M, Dujic D. 100 kW, 10 kHz medium- frequency transformer design optimization and experimental verification[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1696-1708.
[17] Bahmani M A, Thiringer T, Kharezy M. Optimization and experimental validation of medium-frequency high power transformers in solid-state transformer applications[C]//2016 IEEE Applied Power Electro- nics Conference and Exposition (APEC), Long Beach, CA, USA, 2016: 3043-3050.
[18] Wrobel R, Mellor P H. A general cuboidal element for three-dimensional thermal modelling[J]. IEEE Transa- ctions on Magnetics, 2010, 46(8): 3197-3200.
[19] 孙志忠, 袁慰平, 闻震初. 数值分析[M]. 3版. 南京: 东南大学出版社, 2011.
[20] 王佳宁, 邹强, 胡嘉汶, 等. 一种中压绝缘大功率中频变压器的优化设计方法[J]. 电工技术学报, 2022, 37(12): 3048-3060.
Wang Jianing, Zou Qiang, Hu Jiawen, et al. An optimal design method for medium-voltage insulated high-power medium-frequency transformer[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(12): 3048-3060.
[21] Lu Rui, Yu Jianxiong, Feng Dingyi, et al. Modeling and design of a medium frequency transformer with high isolation and high power-density[C]//2021 IEEE Applied Power Electronics Conference and Expo- sition (APEC), Phoenix, AZ, USA, 2021: 1694- 1700.
[22] Jaritz M, Hillers A, Biela J. General analytical model for the thermal resistance of windings made of solid or Litz wire[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(1): 668-684.
[23] Liu Xiaomei, Gerada D, Xu Zeyuan, et al. Effective thermal conductivity calculation and measurement of Litz wire based on the porous metal materials structure[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(4): 2667-2677.
[24] Salinas López G, Expósito A D, Muñoz-Antón J, et al. Fast and accurate thermal modeling of magnetic components by FEA-based homogenization[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1830-1844.
[25] 汪涛, 骆仁松, 文继峰, 等. 基于辅助绕组的高频变压器绕组损耗测量方法[J]. 电工技术学报, 2022, 37(10): 2622-2630, 2655.
Wang Tao, Luo Rensong, Wen Jifeng, et al. A measurement method of winding loss for high- frequency transformer based on auxiliary winding[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2622-2630, 2655.
[26] Wu H H, Hsiao Y Y, Huang H S, et al. A practical plate-fin heat sink model[J]. Applied Thermal Engineering, 2011, 31(5): 984-992.
Abstract Temperature rise calculation is a complex problem in modeling high-power high-frequency transformers (HFT). An accurate and fast thermal model is significant for the optimal design and stable operation of HFT. At present, lumped parameter thermal network model is usually built through dimensionality reduction, and its calculation precision is easily affected by structural parameters. It is difficult to achieve accurate hot spot prediction in optimizing a wide parameter range.
A three-dimensional thermal model of HFT considering anisotropic thermal conductivity is constructed based on the finite difference method (FDM). The discretization error of the three-dimensional thermal model is quantitatively analyzed, which is mainly affected by the loss density, thermal conductivity, and size of the finite difference element. In order to minimize the number of finite differential elements while ensuring the calculation accuracy of the thermal model, three-dimensional sizes of the differential element are adjusted actively according to the discretization error expression. For HTF with nanocrystalline core and litz wire winding, the element sizes in the direction along the width, height of winding and the thickness of core are the key parameters affecting the accuracy of temperature rise calculation.
The parameter adaptability of the proposed thermal model is verified in detail with finite element simulation, including structural parameters, loss density, and heat dissipation conditions. The results show that the maximum error of the model is less than 10% in a wide range of parameters. However, the error of the traditional lumped parameter thermal network model is significantly affected by the structural parameters, and the error varies in the range of 10%~80% within the same parameter variation range.
Based on the proposed thermal model, the efficiency-power density optimal design of a 10 kHz 150 kW transformer was carried out with the parameter scanning method. The upper limit of temperature rise was set to 100 K, and the differential element sizes were adjusted according to the error of less than 5 K. The optimization design program calculated 500 000 design points within 371 s with parallel computing, and the average time of three-dimensional thermal model calculation for a single design point was 2.8 ms. The temperature rise calculation results of the design points on the optimal design boundary were verified, and the error was less than 5.5%. Compared with finite element simulation and the lumped parameter thermal network model, the proposed three-dimensional thermal model based on FDM balances calculation accuracy and calculation speed.
On the optimal design boundary, with the increase of power density, the transformer efficiency gradually decreases, and the temperature rise gradually increases. The maximum power density to meet the 100 K temperature rise requirement was about 9 kW/L, and the transformer efficiency was about 99.82%. A 150 kW transformer prototype was processed according to the optimized design point with maximum power density, and the maximum temperature rise was 103 K under rated working conditions.
keywords:High-frequency transformer, three-dimensional thermal model, finite difference, optimization design
DOI: 10.19595/j.cnki.1000-6753.tces.221305
中图分类号:TM433
南瑞集团有限公司科技资助项目(JS2101854)。
收稿日期 2022-07-04
改稿日期 2022-07-29
骆仁松 男,1992年生,硕士,研究方向为大功率电力电子变换器的设计与优化。E-mail: luors@nrec.com
汪 涛 男,1981年生,硕士,研究方向为柔性直流输电及柔性交流输电。E-mail: wangtao@nrec.com
(编辑 崔文静)