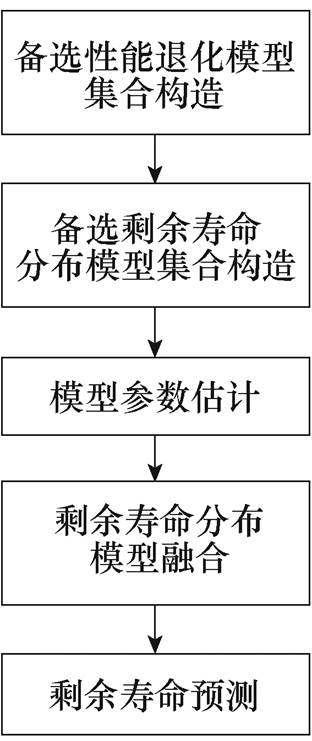
图1 基于模型融合的电子元器件个体剩余寿命建模与预测方法流程
Fig.1 Flow chart of residual life modeling and prediction method for electronic components based on model fusion
摘要 电子元器件通常为整个系统中较易发生故障的薄弱环节,并且往往承担着较为关键的任务,一旦未及时更换引发故障,可能会导致整个系统的失效。因此,对系统中电子元器件的剩余寿命进行精准预测至关重要。由于失效机理复杂、先验信息不充分、监测数据不足等原因,电子元器件的退化模型存在不确定性问题,会对剩余寿命的预测结果产生较大的影响。针对模型不确定性问题,现有研究未考虑模型的预测能力,且需要大量的先验信息或退化数据。为解决上述问题,该文提出一种基于模型融合的电子元器件剩余寿命预测方法。具体而言,提出一种综合考虑了模型的拟合能力、复杂度与预测精度的新模型优劣性指标,并依据新指标构造了各备选模型为真实模型的概率,进而利用全概率公式对所有备选模型进行融合,最后通过融合模型求解出电子元器件个体的剩余寿命。经实际案例分析,验证了该文所提出方法的有效性和精确性。
关键词:电子元器件 个体剩余寿命预测 模型不确定性 模型优劣性指标 模型融合
随着电力电子技术的高速发展,电子元器件在电力、通信、航天、激光等诸多领域得到广泛应用,因其往往需要承受高电应力及高开关频率的作用,使得电子元器件成为整个系统中较易发生故障的薄弱环节[1]。一旦未及时更换而引发故障,可能会导致整个系统失效,造成严重的损失。因此,对电子元器件剩余寿命的准确预测至关重要,在其发生故障之前将其更换,从而确保整个系统的稳定运行[2-3]。
对剩余寿命进行准确预测的重要前提是建立合适的性能退化模型,用于描述电子元器件个体的性能指标随时间的变化规律,这需要对退化模型的不确定性问题进行分析[4]。导致模型不确定性问题的原因主要有以下几个方面:
(1)对于新型或复杂的电子元器件,因其失效机理复杂,导致失效物理过程无法确定,使得其性能退化规律难以掌握[5]。
(2)对于一些已经得到广泛研究的电子元器件,不同的学者可能有不同的认识。以电解电容器为例,文献[6]指出电解电容器的容值是时间的线性函数;文献[7]则认为电解电容器的容值退化过程服从时间的指数函数。
(3)由于一些电子元器件的退化过程存在很强的随机性,当退化数据不充足时,难以确定合适的性能退化模型[8]。
(4)针对性能退化规律呈现非线性特征的电子元器件,如果只重视其明显退化后的数据,而忽视产品未明显退化时期的状态演变过程,甚至不记录这个时期产品的退化数据,可能造成难以准确刻画产品从初始状态到明显退化状态之间的过渡过程,使得与当前数据拟合程度较好的模型不一定具有良好的预测能力[9]。
针对模型的不确定性问题,现有文献中有如下四种方法:基于模型优劣性指标的选择法、贝叶斯估计法、贝叶斯模型平均(Bayesian Model Averaging, BMA)法、基于小波密度估计(Wavelet Density Estimation, WDE)的方法。其中,基于模型优劣性指标的选择法是利用可以考虑到模型拟合能力以及复杂度等方面的模型优劣性指标,对备选模型进行选择。如,Yan Bingxin[10]等针对某型电连接器接触电阻的退化数据,利用模型优劣性指标中的赤池信息准则(Akaike Information Criterion, AIC),对维纳过程模型与考虑了退化机理等效性的改进维纳过程模型进行了比较,得出了后者优于前者的结论。贝叶斯估计法是依据贝叶斯公式融合先验信息和现场数据,对模型参数的后验分布进行更新,从而得到校正后的模型[11]。如,王浩伟等[12]针对某型导弹电连接器接触电阻的退化数据,利用贝叶斯估计法求得了伽马过程中模型参数的后验均值,从而建立了融合先验数据与现场测量数据的性能退化模型。BMA法是在贝叶斯框架下,构造每个备选模型相应的权重,从而实现模型融合[13]。如,Liu Le等[14]针对电连接器应力松弛的退化数据,利用BMA法对维纳过程、伽马过程及逆高斯过程依权重进行融合,得到与数据匹配程度较高的性能退化模型,进而依据该模型进行加速退化试验设计。WDE法既可对备选模型进行选择,也可在退化数据与备选模型的匹配程度均不高时对备选模型进行校正。如,Lin Yanhui等[9]针对某型列车车轮直径的退化数据,利用基于WDE的集成退化建模框架,将备选模型按与退化数据的匹配程度进行选择或融合,从而得到最优模型。
在上述现有方法中,有如下几个问题:
(1)基于模型优劣性指标的选择法仅考虑了模型的复杂度以及对当前数据的拟合程度等方面,并未考虑模型的预测能力,不能保证剩余寿命的预测精度,且只是挑选出单个模型,可能将真正好的模型舍弃掉了。
(2)贝叶斯法依赖产品的先验信息,而在现实中,尤其是对于新型电子元器件,先验信息通常难以获取。
(3)基于小波密度估计的方法引入了大量的未知参数,因此当数据量较少时,可能存在参数估计精度较差的问题。
针对上述问题,本文提出了一种新的解决方法,即基于模型融合的电子元器件个体剩余寿命建模与预测方法,该方法针对退化过程可以用单一特征量表征的电子元器件,其过程如下:
(1)建立备选性能退化模型集合。
(2)由备选性能退化模型集合推导出备选剩余寿命分布模型集合。
(3)基于实际数据估计模型参数。
(4)提出综合考虑模型拟合能力、复杂度与预测精度的新模型优劣性指标,并基于所提出的指标对所有备选剩余寿命分布模型进行融合。
(5)利用融合后的模型求解产品的剩余寿命。
本文所提出的模型优劣性指标考虑了模型的预测能力,且针对备选模型采用模型融合的策略,在一定程度上降低了放弃最佳模型的风险;本文所提出的预测方法,不依赖先验信息,同时不会引入过多的未知参数,在现实中具有较高的可操作性和适用性。
本文所提出的基于模型融合的电子元器件个体剩余寿命建模与预测方法,针对退化过程可以用单一特征量表征的电子元器件,其整体思路如下:
(1)针对各类电子元器件典型和常见的性能退化规律,构建备选性能退化模型集合。
(2)根据故障判据,由备选性能退化模型集合推导得到备选剩余寿命分布模型集合。
(3)利用极大似然估计法对备选模型中的未知参数进行求解。
(4)依据本文所提出的综合考虑模型拟合能力、复杂度与预测精度的新模型优劣性指标,构造各备选模型为真实模型的概率,并根据所构造的概率利用全概率公式对备选模型进行融合,得到剩余寿命分布的融合模型。
(5)由剩余寿命分布的融合模型与剩余寿命点估计的数学关系,对剩余寿命的预测值进行求解。
基于模型融合的电子元器件个体剩余寿命建模与预测方法流程如图1所示。
性能退化模型由退化趋势模型与随机效应模型两部分组成。退化趋势表征了退化量(即性能参数值)在平均意义下的变化趋势;随机效应表征了退化量在退化趋势附近的分布情况,体现了由于环境的波动性、产品退化的动态性等不确定性因素造成的随机影响[15]。
1.2.1 退化趋势模型
为不失一般性,首先对一些常用电子元器件的机理或经验模型进行梳理。文献[6]指出电解电容器的容值退化趋势为直线型,电解电容器的等效串联电阻的阻值退化趋势为指数型;文献[7]则认为电解电容器的容值退化趋势为指数型;文献[16]指出薄膜电阻的阻值退化趋势为幂律型;文献[17]指出功率MOSFET的阈值电压退化趋势为幂律型。上述电子元器件的退化趋势有直线型、幂律型及指数型。

图1 基于模型融合的电子元器件个体剩余寿命建模与预测方法流程
Fig.1 Flow chart of residual life modeling and prediction method for electronic components based on model fusion
此外,对现有研究中常用的电子元器件退化趋势模型进行总结。G. A. Whitmore等[18]将备选退化趋势模型设为幂律型与复合指数型;Liu Le等[19]将备选退化趋势模型设为幂律型;文献[20]指出退化趋势模型一般有直线型、幂律型、指数型、对数型及复合指数型。
因此,通过合并常用电子元器件的机理或经验模型及现有研究中常用的退化趋势模型,本文考虑直线型、幂律型、指数型、对数型和复合指数型五种退化趋势模型,表达式如下:
(1)直线型: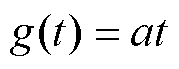 。
。
(2)幂律型: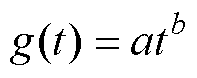 。
。
(3)指数型: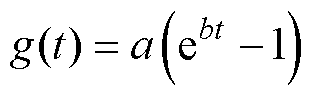 。
。
(4)对数型: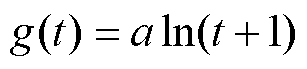 。
。
(5)复合指数型: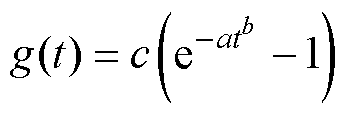 。
。
式中,t为时间;a、b、c为模型参数;g(t)为退化趋势,且g(t)为单调递增函数。
1.2.2 随机效应模型
考虑两种随机效应的刻画方法,一种是混合效应模型[21],这是当前性能退化研究中应用最为广泛的建模方法之一;另一种是随机过程模型[22],这是较为先进的一种建模方法。常用的随机过程模型有维纳过程、伽马过程和逆高斯过程,由于后两种模型针对严格单调的退化过程,更适用于机械产品,因此这里只采用维纳过程刻画电子元器件性能退化过程中的随机效应。
1)混合效应模型为
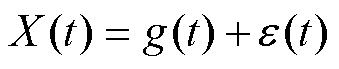 (1)
(1)
式中,X(t)为退化量,且X(0)=0;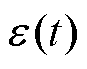 为随机效 应,且在任意时刻独立同分布于期望为零、方差为
为随机效 应,且在任意时刻独立同分布于期望为零、方差为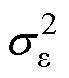 的正态分布,即
的正态分布,即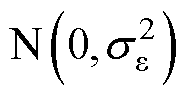 。
。
2)维纳过程模型[23-24]为
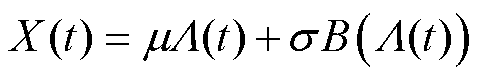 (2)
(2)
式中,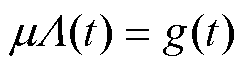 为退化趋势;
为退化趋势;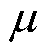 为漂移系数,表征退化速率;
为漂移系数,表征退化速率; 为扩散系数;
为扩散系数;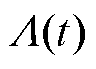 为时间函数;
为时间函数;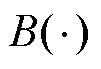 为标准布朗运动。
为标准布朗运动。
维纳过程具有如下三种性质:
(1)X(t)在t=0处连续,且有X(0)=0。
(2)对任意的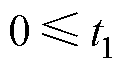 ,
, 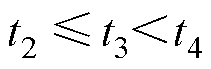 ,增量
,增量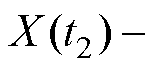
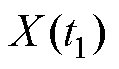 与
与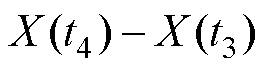 相互独立。
相互独立。
(3)独立增量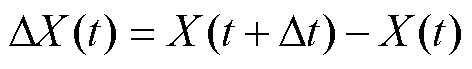 服从正态分布
服从正态分布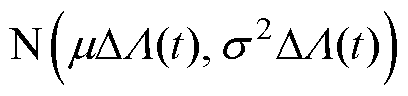 ,其中
,其中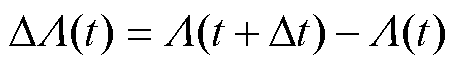 。
。
综上所述,考虑五种退化趋势模型和两种随机效应模型,所建立的备选性能退化模型集合共有十种性能退化模型。
具体而言,将式(1)中的g(t)替换为1.2.1节中的五种退化趋势模型,进而得到如下五种性能退化模型:
(1)基于直线型退化趋势的混合效应模型为
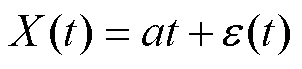 (3)
(3)
(2)基于幂律型退化趋势的混合效应模型为
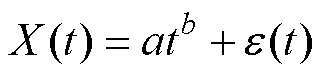 (4)
(4)
(3)基于指数型退化趋势的混合效应模型为
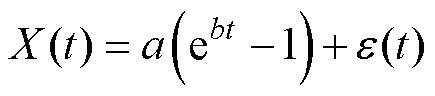 (5)
(5)
(4)基于对数型退化趋势的混合效应模型为
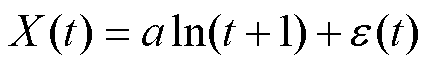 (6)
(6)
(5)基于复合指数型退化趋势的混合效应模型为
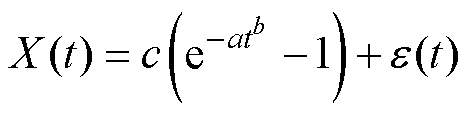 (7)
(7)
将式(2)中的 替换为1.2.1节中的五种退化趋势模型,其中对于直线型、幂律型、指数型、对数型和复合指数型退化趋势模型,分别有
替换为1.2.1节中的五种退化趋势模型,其中对于直线型、幂律型、指数型、对数型和复合指数型退化趋势模型,分别有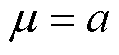 且
且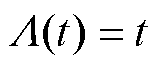 、
、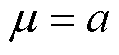 且
且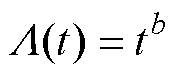 、
、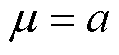 且
且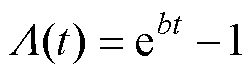 、
、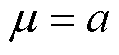 且
且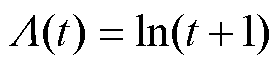 和
和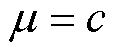 且
且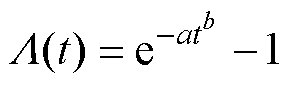 ,进而可得如下五种性能退化模型:
,进而可得如下五种性能退化模型:
(1)基于直线型退化趋势的维纳过程模型为
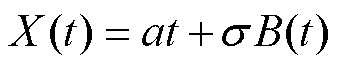 (8)
(8)
(2)基于幂律型退化趋势的维纳过程模型为
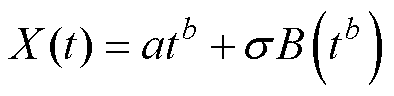 (9)
(9)
(3)基于指数型退化趋势的维纳过程模型为
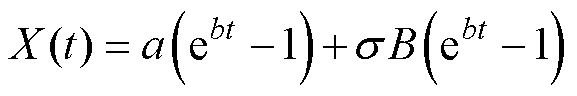 (10)
(10)
(4)基于对数型退化趋势的维纳过程模型为
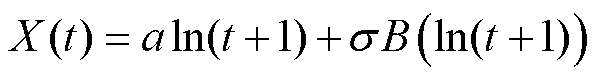 (11)
(11)
(5)基于复合指数型退化趋势的维纳过程模型为
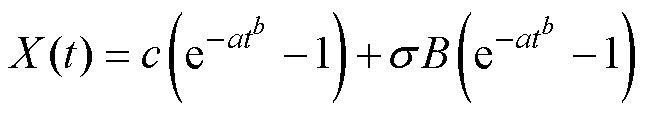 (12)
(12)
(1)对于混合效应模型,记当前时刻为tk,剩余寿命为t,失效阈值为D。当产品退化量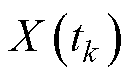 <D时,令
<D时,令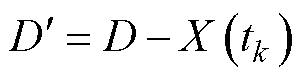 ,则产品剩余寿命的累积分布函数(Cumulative Distribution Function, CDF)为
,则产品剩余寿命的累积分布函数(Cumulative Distribution Function, CDF)为
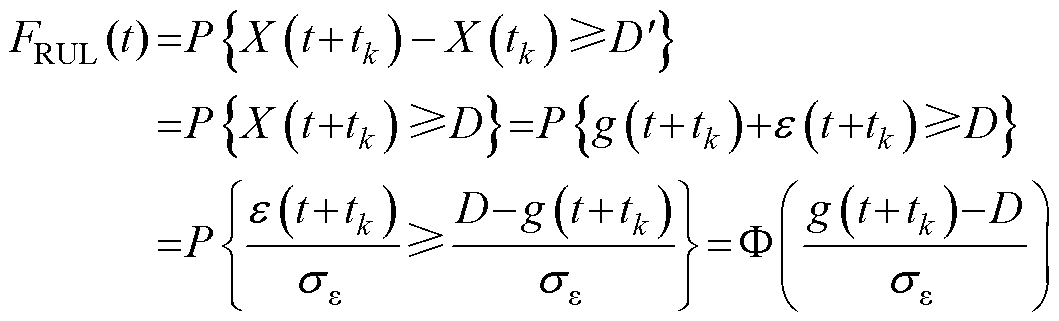 (13)
(13)
式中,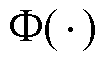 为标准正态分布的CDF。
为标准正态分布的CDF。
(2)对于维纳过程模型,文献[18]指出时间函数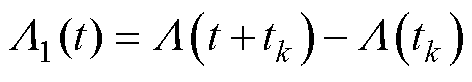 服从逆高斯分布,则产品剩余寿命的CDF为
服从逆高斯分布,则产品剩余寿命的CDF为
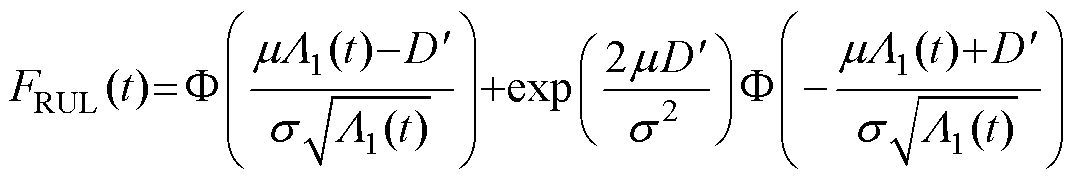 (14)
(14)
综上所述,考虑五种趋势性刻画方法和两种随机性刻画方法,共有十种性能退化模型,相应形成包含十个模型的备选剩余寿命分布模型集合。与1.2.2节相同,将式(13)中的g(t)及式(14)中的 均替换为1.2.1节中的五种退化趋势模型,进而得到十种备选剩余寿命分布模型的表达式。记十种剩余寿命分布模型依次为Mz(z=1, 2,…, 10),其中Mz(z=1, 2, 3, 4, 5)依次为基于直线型、幂律型、指数型、对数型、复合指数型退化趋势的混合效应模型下的剩余寿命分布模型,Mz(z=6, 7, 8, 9, 10)依次为基于直线型、幂律型、指数型、对数型、复合指数型退化趋势的维纳过程模型下的剩余寿命分布模型。
均替换为1.2.1节中的五种退化趋势模型,进而得到十种备选剩余寿命分布模型的表达式。记十种剩余寿命分布模型依次为Mz(z=1, 2,…, 10),其中Mz(z=1, 2, 3, 4, 5)依次为基于直线型、幂律型、指数型、对数型、复合指数型退化趋势的混合效应模型下的剩余寿命分布模型,Mz(z=6, 7, 8, 9, 10)依次为基于直线型、幂律型、指数型、对数型、复合指数型退化趋势的维纳过程模型下的剩余寿命分布模型。
对每种模型,采用极大似然估计方法估计模型中的参数。
(1)对于随机效应模型为混合效应模型的备选模型Mz(z=1, 2, 3, 4, 5),设xi为ti时刻某电子元器件的退化量测量值(i=1, 2,…, n),n为截止至当前时刻的总测量次数。由式(1)可知,X(t)服从正态分布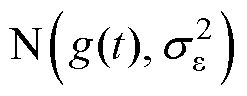 ,从而可构造似然函数如式(15)所示,并估计出未知参数
,从而可构造似然函数如式(15)所示,并估计出未知参数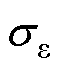 和
和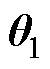 。
。
 (15)
(15)
式中,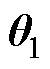 为g(t)中的未知参数向量。
为g(t)中的未知参数向量。
(2)对于随机效应模型为维纳过程模型的备选模型Mz(z=6, 7, 8, 9, 10),记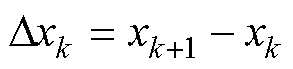 ,
,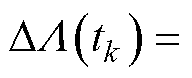
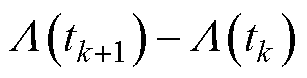 ,其中k=1, 2,…, n-1。根据维纳过程的独立增量
,其中k=1, 2,…, n-1。根据维纳过程的独立增量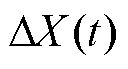 服从正态分布
服从正态分布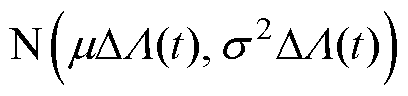 的性质,可构造似然函数如下,并估计出未知参数
的性质,可构造似然函数如下,并估计出未知参数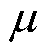 、
、 、
、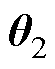 。
。
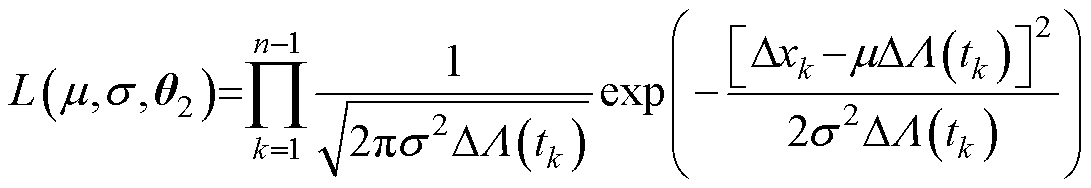 (16)
(16)
式中,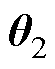 为
为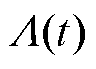 中的未知参数向量。
中的未知参数向量。
为了求解模型中未知参数的极大似然估计值,需要对式(15)和式(16)中的待估参数求偏导数,进而得到使似然函数取得最大值的待估参数值,即模型中未知参数的极大似然估计值。由于式(15)和式(16)相对复杂,通过求解偏导数的方法得出模型中未知参数的解析解较为困难,因此以最大化似然函数为优化目标,以模型中未知参数为决策变量,构造一个优化问题。内点算法[25]是解决最值最优化问题的一种常用且高效的方法,采用该算法求解所构造的优化问题,从而解决模型中未知参数的极大似然估计值求解问题。
本节将构造一个新的模型优劣性指标,并利用该指标形成各备选剩余寿命分布模型是真实模型的概率,进而通过全概率公式对备选模型进行融合,得到剩余寿命分布的融合模型。
1.5.1 新模型优劣性指标
本文所提出的新模型优劣性指标综合考虑了模型的复杂度、拟合能力及预测精度。上述三点分别由模型中的未知参数个数、对数似然函数值及剩余寿命预测值的平均相对误差来表征。有关于剩余寿命预测值平均相对误差的具体解释如下:
记Mz为第z个备选剩余寿命分布模型(z=1, 2,…, m),m为备选模型总个数,性能退化数据为(ti, xi)(i=1, 2,…, n),xi为ti时刻的性能退化量。将tk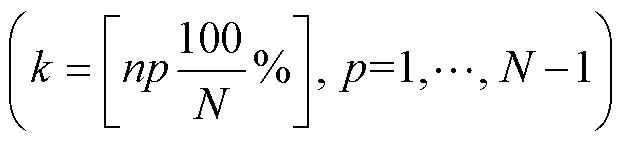 定义为伪当前时刻,其中N为大于1的整数,[∙]代表向下取整。将dpr(r=1, 2,…, sp)定义为伪当前时刻为tk时所对应的伪失效阈值,其中sp为伪当前时刻为tk时,伪失效阈值的数量。dpr的计算公式为
定义为伪当前时刻,其中N为大于1的整数,[∙]代表向下取整。将dpr(r=1, 2,…, sp)定义为伪当前时刻为tk时所对应的伪失效阈值,其中sp为伪当前时刻为tk时,伪失效阈值的数量。dpr的计算公式为
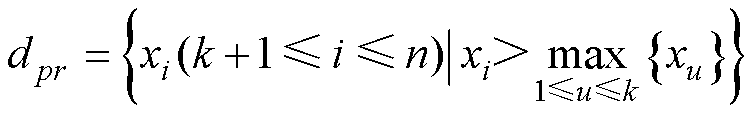 (17)
(17)
即,当伪当前时刻为tk时,在所有位于tk之后的退化数据(ti, xi)(i=k+1, 2,…, n)中,满足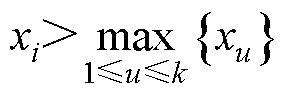 的性能退化量xi均为该伪当前时刻tk所对应的伪失效阈值dpr,此外,tpr为dpr所对应的时刻。在伪当前时刻tk以及其所对应的伪失效阈值dpr下,利用性能退化数据(ti, xi)(i=1, 2,…, k)进行剩余寿命预测。记剩余寿命的预测值为
的性能退化量xi均为该伪当前时刻tk所对应的伪失效阈值dpr,此外,tpr为dpr所对应的时刻。在伪当前时刻tk以及其所对应的伪失效阈值dpr下,利用性能退化数据(ti, xi)(i=1, 2,…, k)进行剩余寿命预测。记剩余寿命的预测值为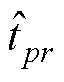 ,剩余寿命的真实值为Tpr=tpr-tk。求解伪当前时刻tk时的剩余寿命预测值的相对误差epr,其中p=1, 2,…, N-1;r=1, 2,…, sp,N为大于1的整数。则模型Mz下平均相对误差Ez的计算公式为
,剩余寿命的真实值为Tpr=tpr-tk。求解伪当前时刻tk时的剩余寿命预测值的相对误差epr,其中p=1, 2,…, N-1;r=1, 2,…, sp,N为大于1的整数。则模型Mz下平均相对误差Ez的计算公式为
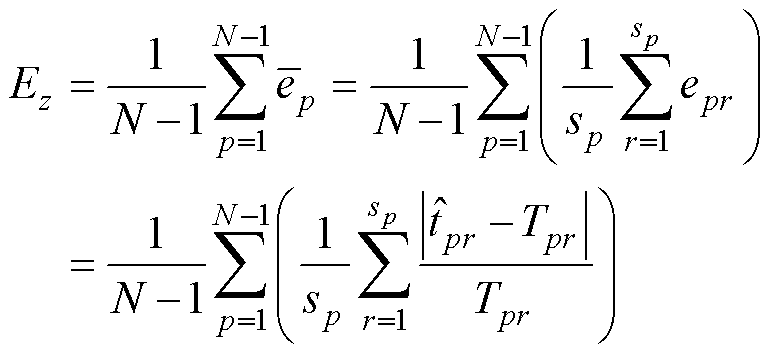 (18)
(18)
在计算每个伪当前时刻tk所对应的平均相对误差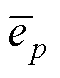 时,可能存在以下三种特殊情况:
时,可能存在以下三种特殊情况:
(1)如果伪当前时刻tk前数据的退化趋势单调性与整体数据相悖,这会导致利用tk之前数据得到的退化趋势模型无法达到失效阈值,从而得出剩余寿命为无穷大的结果,与客观实际不符。
(2)如果伪当前时刻tk前的数据量过少,依据其建立的退化模型和剩余寿命模型无法客观地描述产品的退化规律和失效行为,使得求解出的误差值不具有参考性。例如,当伪当前时刻tk前仅有一个数据点时,只能利用两个数据点进行退化建模,此时无法对复杂的非线性退化过程进行准确刻画。
(3)如果伪当前时刻tk所对应的伪失效阈值数sp=0,则由式(13)和式(14)可知,此时无法获得剩余寿命分布模型,从而无法对剩余寿命预测值以及预测误差进行求解。
上述三种情况中,在前两种情况下无法获得符合客观实际的误差值,在第三种情况下无法对误差值进行求解。为解决这个问题,本文采用了不确定理论中的最大不确定性原理[26]。该原理表明,对于某事件,如果根据现有信息无法确定其测度,则取中间值,使得不确定性达到最大。基于此原理,记第z个模型的第q个伪当前时刻所对应的平均相对误差为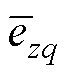 (z=1, 2,…, m; q=1, 2,…, hz),其中hz为第z个模型下未发生上述三种情况的伪当前时刻数。在上述三种情况发生时,令
(z=1, 2,…, m; q=1, 2,…, hz),其中hz为第z个模型下未发生上述三种情况的伪当前时刻数。在上述三种情况发生时,令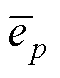 为
为
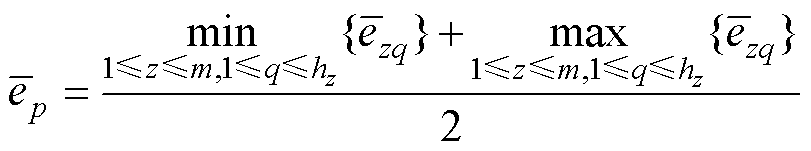 (19)
(19)
式(19)表明,对于某个模型,如果在某个伪当前时刻下无法获得正常的平均相对误差,则令平均相对误差等于所有模型下所有不存在上述三种情况的伪当前时刻所对应的平均相对误差的中间值,使其不确定性最大。进而,所提出的新模型优劣性指标的构造方法如下。
令
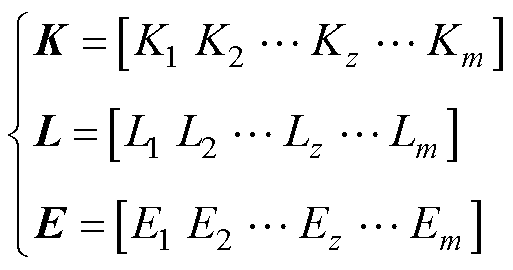 (20)
(20)
式中,Kz为第z个模型中的未知参数个数的相反数;Lz为第z个模型的对数似然函数值;Ez为第z个模型的剩余寿命预测值平均相对误差的相反数。
对于综合性指标的构造,现有研究通常采用加权和的方式,将综合性的指标表示为各方面指标的线性函数,并将不同方面指标相应的权重直观理解为该指标的重要性[14, 27]。此外,考虑到指标Kz、Lz、Ez的取值范围不同,因此若新指标等于三者直接加权和,会使其数值受取值范围较广的指标的影响较大。又因为各指标单位化后的变化范围相同,所以令新指标等于各指标单位化后的加权和,可以解决上述问题。
将Kz、Lz、Ez单位化,有
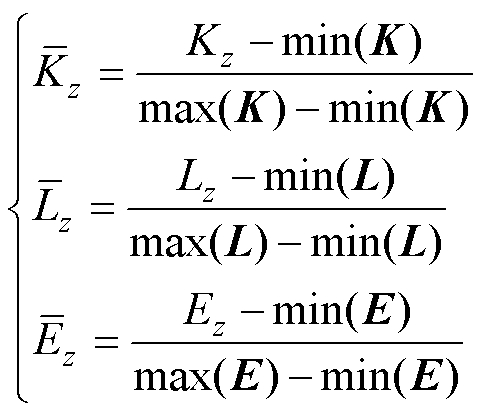 (21)
(21)
进而,对于第z个模型,其新指标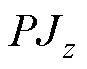 为
为
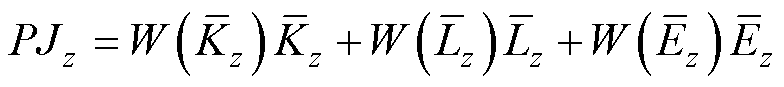 (22)
(22)
式中,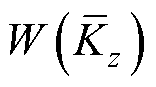 、
、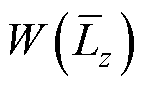 和
和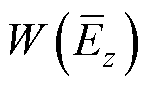 分别为模型复杂度、拟合能力和预测精度三个方面的权重,表征了模型复杂度、拟合能力和预测精度的重要性。权重的取值[28]一般满足
分别为模型复杂度、拟合能力和预测精度三个方面的权重,表征了模型复杂度、拟合能力和预测精度的重要性。权重的取值[28]一般满足
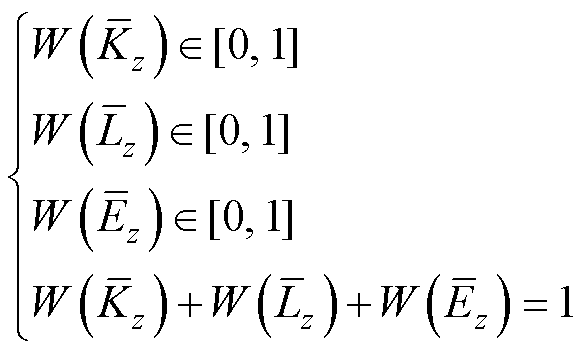 (23)
(23)
对于权重的设置,可根据专家经验信息或先验信息进行判断。针对专家经验信息和先验信息缺乏的情形,本文依据最大熵原理[29]解决权重的设置问题。最大熵原理指出,在进行一项决策时,如果缺乏明确的信息,应在约束条件下采取不具有倾向性的策略,这样可以使得信息熵达到最大,即使得各方面信息的信息量总和最大化。因此,针对专家经验信息和先验信息缺乏的情形,依据最大熵原理,在约束条件式(23)下,令
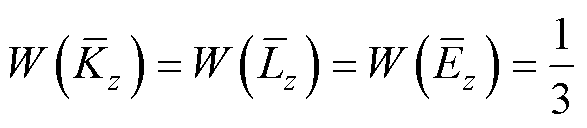 (24)
(24)
式(24)表明,模型的复杂度、拟合能力和预测精度有相同的重要性,即在对模型进行综合性评价时,对每个方面都不具有倾向性。
由于Kz、Lz、Ez的取值越大,其所对应模型Mz的复杂度、拟合能力及预测精度就越优,且根据式(22)和式(24),所构造的新指标PJz是Kz、Lz、Ez单位化后的加权和,因此PJz的值越大,其所对应的模型Mz关于复杂度、拟合能力及预测精度的综合性能就越好。
1.5.2 模型融合
构造模型Mz为真实模型的概率为
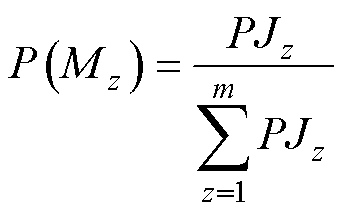 (25)
(25)
记模型Mz下剩余寿命的CDF为Fz(t),基于全概率公式融合各备选模型下剩余寿命的CDF,得到融合模型下剩余寿命的CDF为
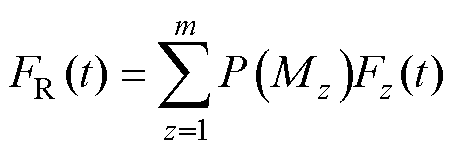 (26)
(26)
采用剩余寿命的期望作为剩余寿命的点估计,有
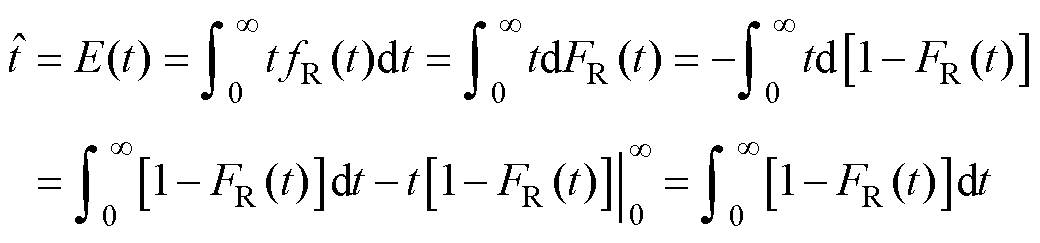 (27)
(27)
式中,fR(t)为剩余寿命的概率密度函数。由于被积函数相对复杂,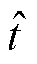 通常没有解析表达式,因此使用数值积分的方法对
通常没有解析表达式,因此使用数值积分的方法对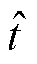 进行求解。由于自适应辛普森算法[30]是一种高效且精度较高的数值积分方法,所以采用该方法对
进行求解。由于自适应辛普森算法[30]是一种高效且精度较高的数值积分方法,所以采用该方法对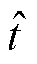 进行数值积分,进而求得电子元器件的剩余寿命预测值。
进行数值积分,进而求得电子元器件的剩余寿命预测值。
本节通过3个实际案例验证所提出方法的有效性和准确性。基于3个电子元器件的实际退化数据,应用不同的剩余寿命预测方法,并对各预测方法的预测效果进行对比分析。记3个电子元器件分别为产品1、2、3,其中产品1的退化数据为某型号锂离子电池的容量[31],产品2的退化数据为某型号GaAs激光器的工作电流测量值相对于初始值的增量百分比[32],产品3的退化数据为某型号精密电阻的电阻测量值相对于初始值的增量百分比[33]。
由于在实际的剩余寿命预测过程中,往往很难获取电子元器件的先验信息和大量退化数据,所以通常无法应用贝叶斯法和小波密度估计法,故本案例将使用模型优劣性指标作为剩余寿命建模与预测的依据,采用的指标分别为似然函数值、AIC与本文所提出的新指标。似然函数值用于表征模型的拟合能力,似然函数值越大则说明模型与现有数据的拟合程度越高,即模型越优[10]。AIC由模型中未知参数的数量及似然函数值两部分组成,综合考虑模型的复杂度和拟合能力[34],其计算公式为
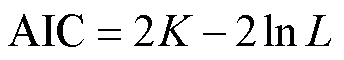 (28)
(28)
式中,K为模型中未知参数的数量;L为似然函数值。AIC值越小说明模型越优。
具体的建模与预测方法如下:
(1)方法1:似然函数值选择法。该方法通过模型的似然函数值表征各模型的拟合能力,由于似然函数值越大模型的拟合能力越强,因此以似然函数值最大的备选模型为最优模型,并根据该模型进行剩余寿命预测。
(2)方法2:AIC选择法。这是当前应用非常广泛的一种方法[10, 34-35],该方法根据各备选模型的AIC值大小进行选择,由于AIC值越小模型越好,因此以AIC值最小的备选模型为最优模型,并根据该模型进行剩余寿命预测。
(3)方法3:新指标选择法。该方法根据各备选模型的新指标值大小进行选择。在计算各模型的新指标时,本文考虑专家和先验信息缺乏的情形,所以按照式(24)给定的权重对新指标进行计算。由于新指标值越大模型越好,因此以新指标值最大的备选模型为最优模型,并根据该模型进行剩余寿命预测。
(4)方法4:新指标融合法。该方法即本文所提出的建模与预测方法。在计算新指标时,权重的取值同方法3。
对各电子元器件的退化数据做标准化处理,记原退化数据为(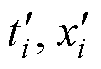 )(i=1, 2,…, n),若原数据的平均退化趋势为递增,则标准化后的退化数据为(
)(i=1, 2,…, n),若原数据的平均退化趋势为递增,则标准化后的退化数据为(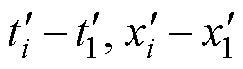 );若原数据的平均退化趋势为递减,则标准化后的退化数据为(
);若原数据的平均退化趋势为递减,则标准化后的退化数据为(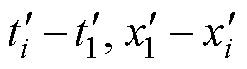 );将标准化后的数据记作(
);将标准化后的数据记作(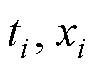 )。
)。
电子元器件的失效阈值取决于产品的实际使用要求,在现有的剩余寿命预测研究中,为了比较分析不同预测方法的预测效果,通常假设失效阈值为一个给定的固定值[6]。因此,本案例将各产品标准化后退化数据(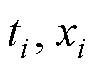 )(i=1, 2,…, n)的最大值xj作为失效阈值,进而xj所对应的时刻tj为产品的真实寿命,分别以不同的当前时刻tk进行剩余寿命预测,并以Tk=tj-tk为真实剩余寿命,对预测结果的绝对误差进行求解。
)(i=1, 2,…, n)的最大值xj作为失效阈值,进而xj所对应的时刻tj为产品的真实寿命,分别以不同的当前时刻tk进行剩余寿命预测,并以Tk=tj-tk为真实剩余寿命,对预测结果的绝对误差进行求解。
下面将对3个电子元器件的剩余寿命预测值进行计算,并对各方法的预测效果进行比较。为了度量预测效果,采用了两种指标,分别为绝对误差和相对优势指数[36]。记由方法1~4得到的剩余寿命预测结果的绝对误差分别为AEi(i=1, 2, 3, 4),则第i种方法的相对优势指数RSi的计算公式为
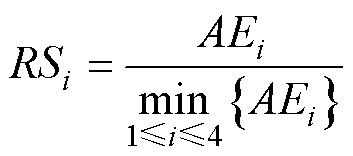 (29)
(29)
由式(29)可以看出,某种方法的相对优势指数越大,说明其绝对误差越大,则该方法的相对优势越小,也即绝对误差最小的方法相对于该方法的优势越明显。当RSi=1时,表明指数RSi所对应的方法为绝对误差最小的方法。
产品1的原始退化数据为某型号锂离子电池的容量x随循环次数增加的变化情况,测量间隔为1次。其标准化后的退化数据如图2所示。
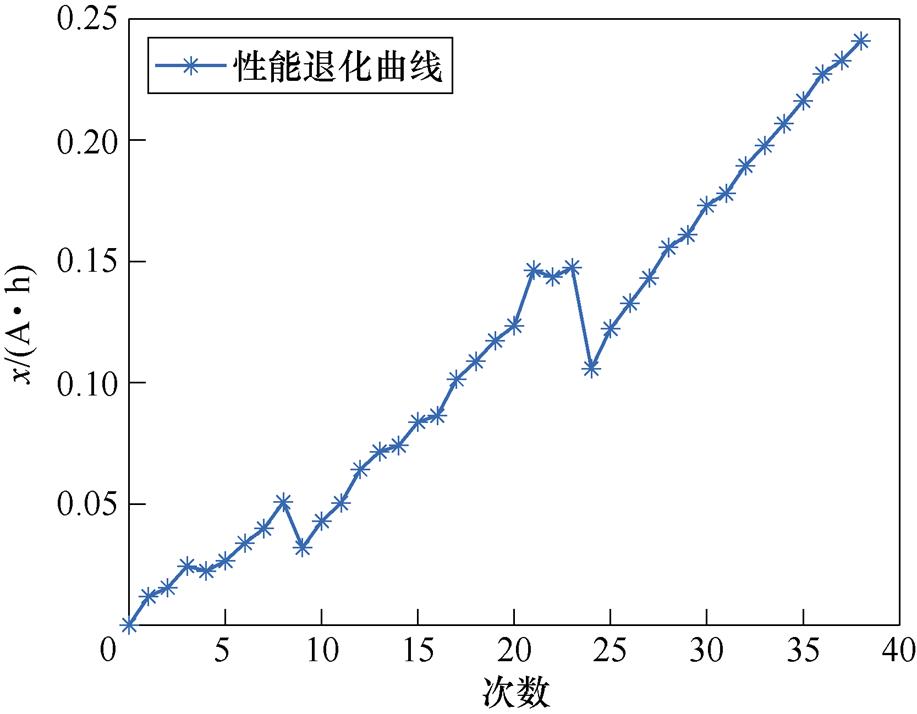
图2 产品1的性能退化曲线
Fig.2 Performance degradation curve of product 1
在产品1的退化数据下,利用四种方法所得到的最优模型见表1,其中Mz(z=1, 2,…, 10)所指代的模型与1.3节中相同。方法1、2、3为选择法,而方法4为融合法,方法4不是从备选模型集合中多选一,而是利用各备选模型为真实模型的概率将备选模型进行融合。因此,表1展示了由方法1、2、3所选择出的最优模型,以及由方法4所得出的模型Mz(z=1, 2,…, 10)为真实模型的概率向量[P(M1) P(M2) …P(M10)]。
利用新指标融合法对产品1的退化数据进行剩余寿命预测,其结果如图3所示。
由于该产品的退化数据非单调,且规律性相对较差,因此如图3所示,对于新指标融合法,当前时刻较小时,退化数据相对较少,导致其对产品退化规律的刻画效果相对较差,使得预测结果相较于真实值有较大偏移。随着当前时刻的增加,退化数据随之增多,预测值相较于真实值的偏移也有所降低。
表1 产品1下不同方法所得到的最优模型
Tab.1 Optimal models under different methods for product 1

tk似然函数值选择法AIC选择法新指标选择法新指标融合法 5M2M2M4[0.094 0.124 0.114 0.126 0.082 0.065 0.117 0.063 0.107 0.104] 9M8M8M8[0.092 0.112 0.104 0.077 0.103 0.106 0.105 0.118 0.106 0.073] 13M1M3M6[0.060 0.084 0.111 0.103 0.113 0.116 0.102 0.093 0.105 0.109] 17M7M7M10[0.069 0.099 0.104 0.072 0.107 0.118 0.115 0.073 0.118 0.121] 21M5M5M7[0.090 0.058 0.099 0.120 0.101 0.092 0.136 0.055 0.133 0.112] 25M1M4M4[0.109 0.094 0.113 0.139 0.115 0.092 0.121 0.055 0.064 0.093] 29M10M10M10[0.142 0.105 0.091 0.075 0.062 0.085 0.066 0.124 0.086 0.161] 33M3M3M1[0.123 0.117 0.079 0.102 0.067 0.115 0.068 0.097 0.121 0.106] 37M6M6M7[0.113 0.068 0.079 0.099 0.082 0.114 0.129 0.125 0.081 0.104]
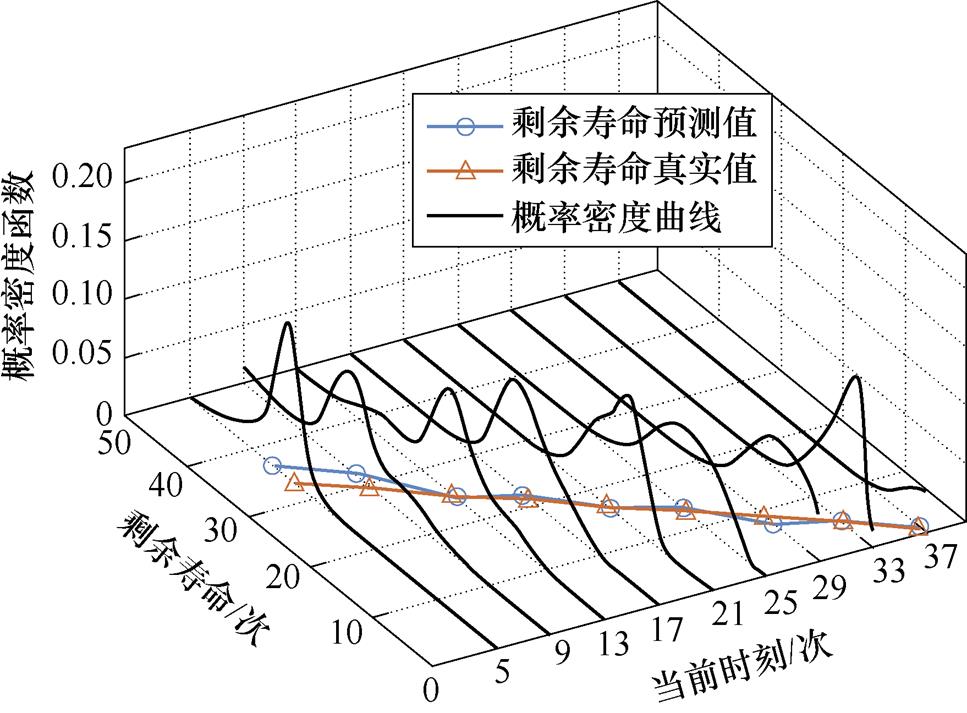
图3 产品1的剩余寿命真实值、基于新指标融合法的剩余寿命预测值及其概率密度曲线
Fig.3 True residual life value, predicted residual life value and probability density curves based on the new index fusion method for product 1
利用似然函数值选择法、AIC选择法、新指标选择法及新指标融合法,对产品1的退化数据进行剩余寿命预测,其结果如图4所示。绝对误差如图5和表2所示,相对优势指数见表3。表2中的“均值”行表示所对应的方法在各当前时刻下绝对误差的平均值,表3中的“平均绝对误差下的相对优势指数”行是依据各方法下绝对误差的平均值计算得到的相对优势指数。
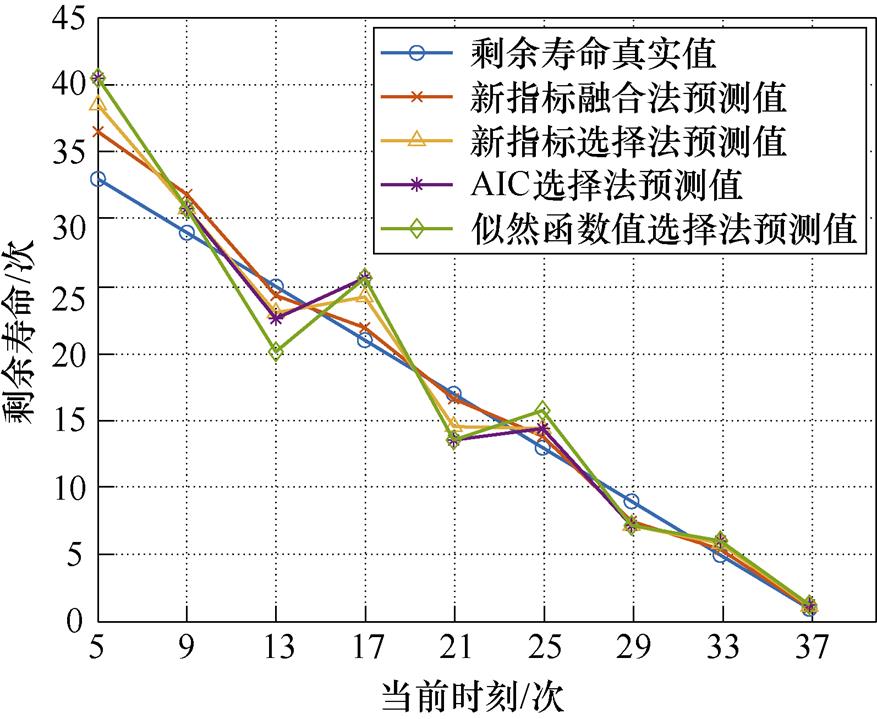
图4 产品1下不同方法的剩余寿命预测值
Fig.4 Predicted residual life values under different methods for product 1
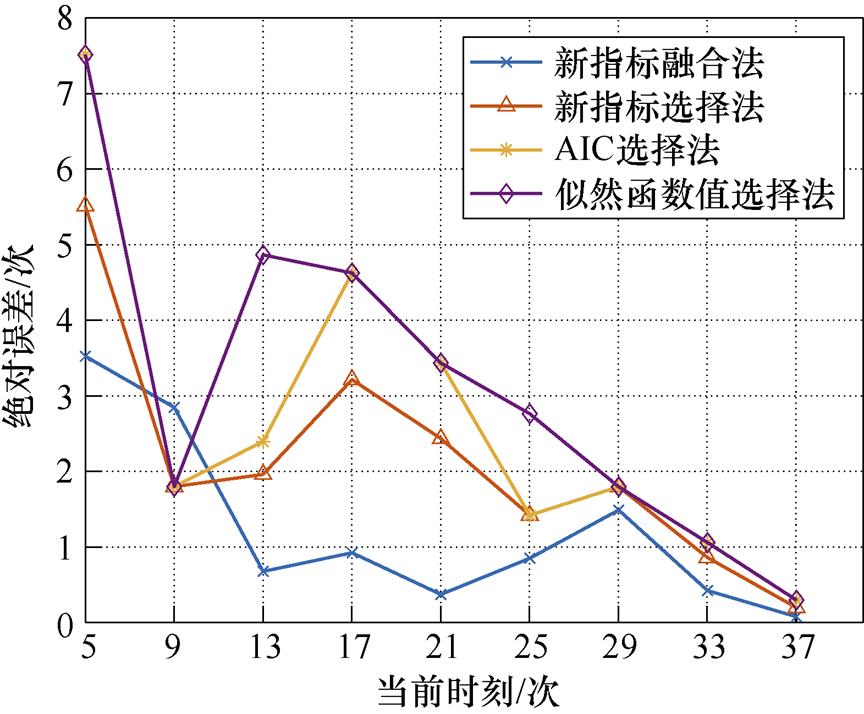
图5 产品1下不同预测方法的绝对误差
Fig.5 Absolute errors under different prediction methods for product 1
表2 产品1下不同方法的绝对误差(次)
Tab.2 Absolute errors (times) under different methods for product 1
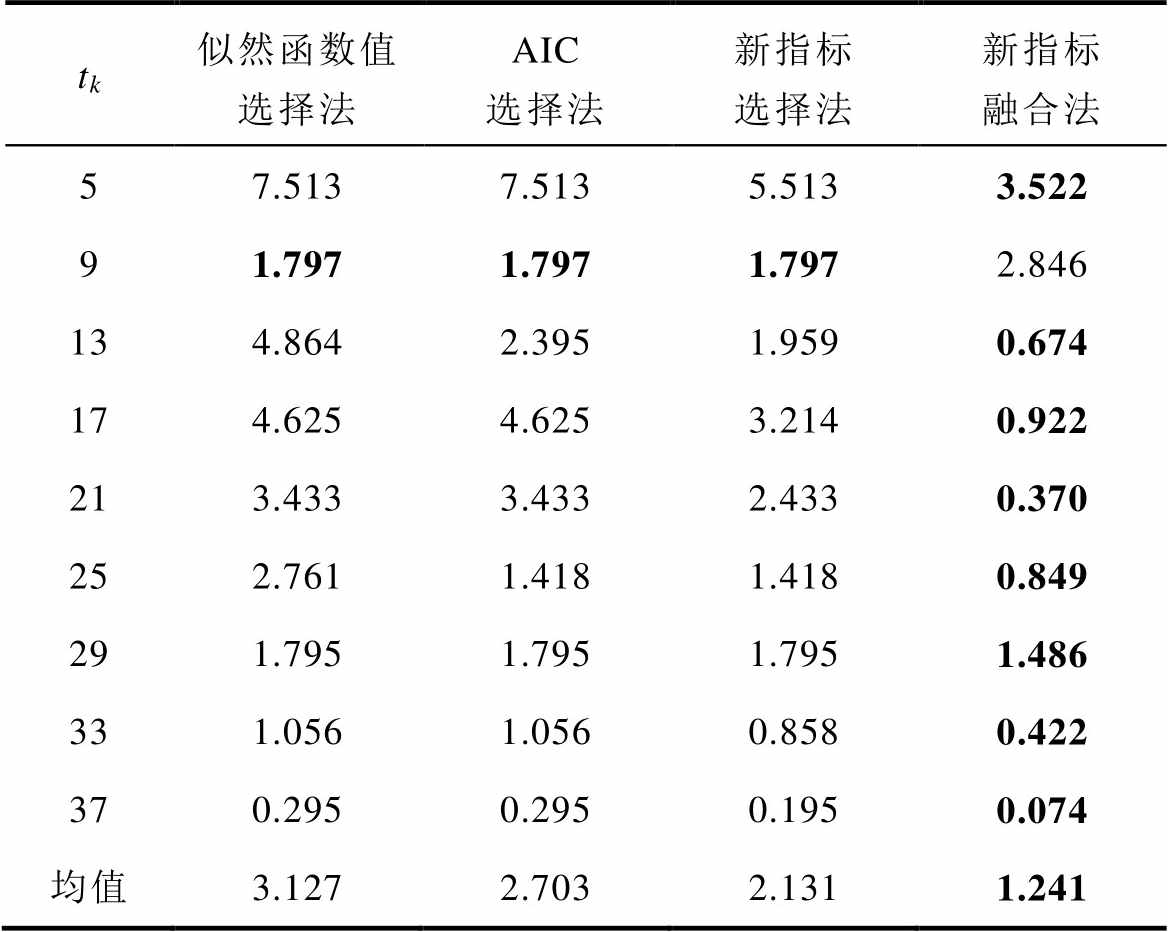
tk似然函数值选择法AIC选择法新指标选择法新指标融合法 57.5137.5135.5133.522 91.7971.7971.7972.846 134.8642.3951.9590.674 174.6254.6253.2140.922 213.4333.4332.4330.370 252.7611.4181.4180.849 291.7951.7951.7951.486 331.0561.0560.8580.422 370.2950.2950.1950.074 均值3.1272.7032.1311.241
表3 产品1下不同方法的相对优势指数
Tab.3 The index of relative superiority under different methods for product 1
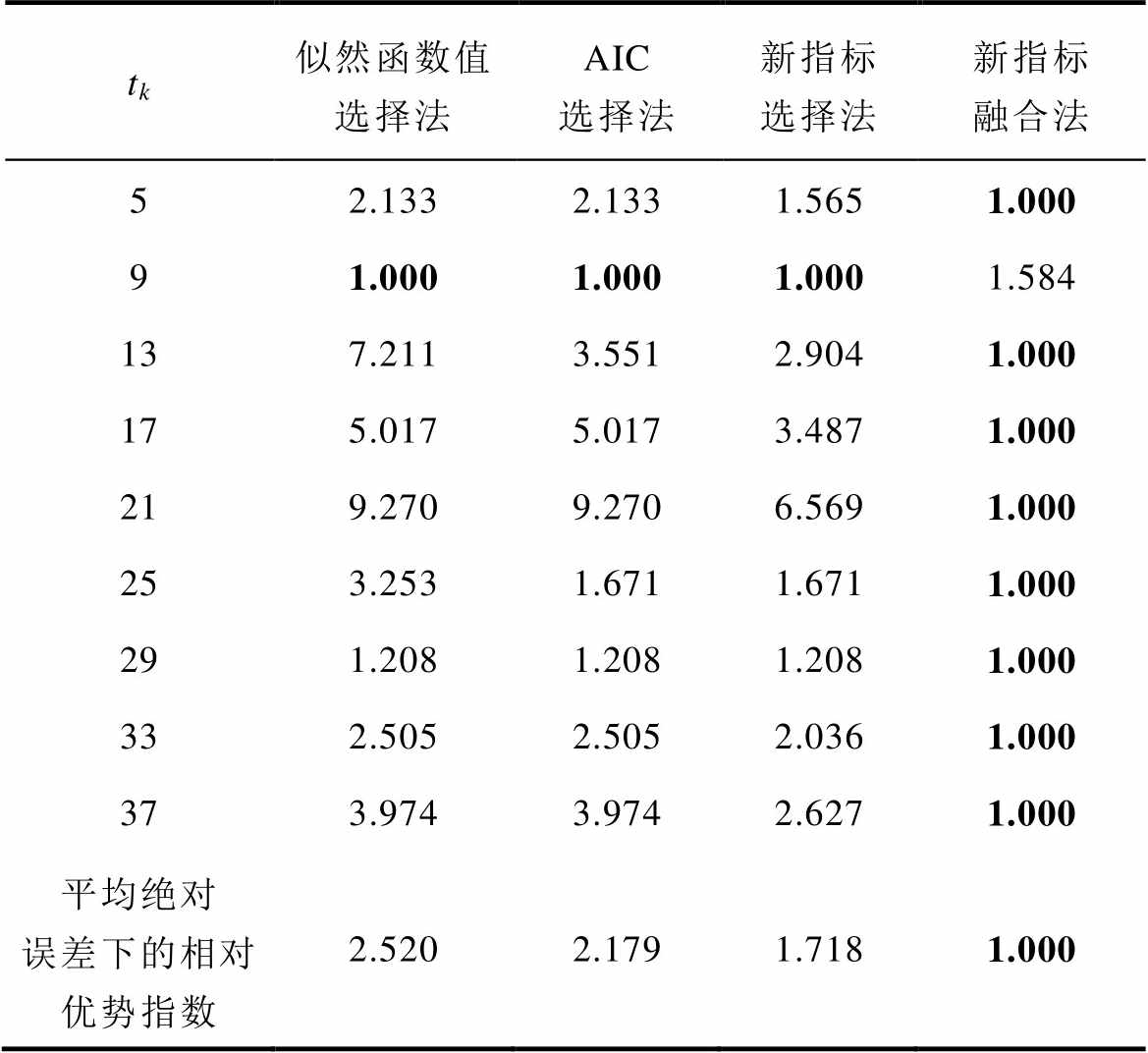
tk似然函数值选择法AIC选择法新指标选择法新指标融合法 52.1332.1331.5651.000 91.0001.0001.0001.584 137.2113.5512.9041.000 175.0175.0173.4871.000 219.2709.2706.5691.000 253.2531.6711.6711.000 291.2081.2081.2081.000 332.5052.5052.0361.000 373.9743.9742.6271.000 平均绝对误差下的相对优势指数2.5202.1791.7181.000
由表2、表3可以看出,对于产品1,新指标融合法相较于其他三种方法的预测效果最好。由平均绝对误差下的相对优势指数可知,似然函数值选择法、AIC选择法、新指标选择法的平均绝对误差约为新指标融合法的2.5倍、2.2倍和1.7倍,新指标融合法的平均绝对误差相较于上述三种方法下降了约60 %、54 %和42 %。当前时刻tk为5、13、17、21、33、37时,新指标选择法的预测效果优于AIC选择法及似然函数值选择法;当前时刻tk为9、25、29时,新指标选择法的预测效果与AIC选择法相同。除tk=9外,新指标融合法的预测效果均为最优。对于平均预测效果,按新指标融合法、新指标选择法、AIC选择法、似然函数值选择法的顺序依次递减。
新指标相较于AIC和似然函数而言,对备选模型的预测精度有所考量,降低了放弃预测效果较好模型的风险。因此,利用新指标所选择出的模型的平均预测效果,要优于利用AIC或似然函数进行选择。在新指标下,融合法的预测效果优于选择法,这是因为选择法的本质是从各备选模型中选择出一个作为最终模型,并用其进行剩余寿命预测,必然存在抛弃预测效果较好模型的风险,而融合法可以将所有备选模型进行融合,这不仅不会抛弃任何模型,还可以在一定程度上抑制单一模型的缺点,同时融合模型还具有不同备选模型的特征。因此,单一模型对退化过程的刻画能力相对于融合模型较弱,使得在新指标下,融合法的预测效果优于选择法。由上述分析可知,新指标融合法同时应用了考虑预测精度的新指标及对所有备选模型进行融合的融合策略,因此,新指标融合法相较于其他三种方法具有更好的预测效果。
产品2为某型号GaAs激光器,是激光切割机中常用的一种电子器件,其所发出的激光经光路系统聚焦成高功率密度的激光束,从而起到切割工件的作用。产品2的原始退化数据为该产品在80 ℃下的工作电流相对于初始值的增量百分比,测量间隔为250 h。其标准化后的退化数据如图6所示。
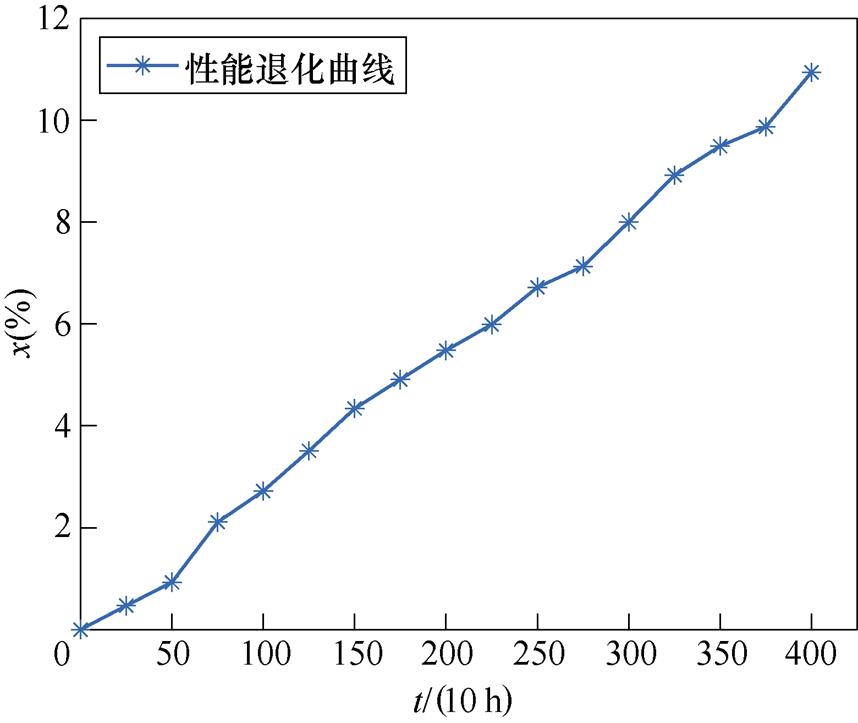
图6 产品2的性能退化曲线
Fig.6 Performance degradation curve of product 2
在产品2的退化数据下,利用似然函数值选择法、AIC选择法、新指标选择法以及新指标融合法所得到的最优模型见表4。
利用新指标融合法对产品2的退化数据进行剩余寿命预测,其结果如图7所示。
不同于产品1,产品2的退化数据具有较强的线性规律,使得利用较少的数据就可对该产品的退化过程进行较准确的刻画。如图7所示,针对于新指标融合法,即使在当前时刻较小时,剩余寿命的预测结果也没有相对于真实值有较大偏移。
利用似然函数值选择法、AIC选择法、新指标选择法及新指标融合法,对产品2的退化数据进行剩余寿命预测,其结果如图8所示。绝对误差如图9和表5所示,相对优势指数见表6。
由表5、表6可以看出,对于产品2,新指标融合法相较于其他三种方法的预测效果最好。由平均绝对误差下的相对优势指数可知,似然函数值选择法、AIC选择法、新指标选择法的平均绝对误差约为新指标融合法的2.2倍、2.1倍和1.8倍,新指标融合法的平均绝对误差相较于上述三种方法下降了约54 %、52 %和45 %。当前时刻tk为175、225、375时,新指标选择法的预测效果优于AIC选择法以及似然函数值选择法;当前时刻tk为75、125、275、325时,新指标选择法的预测效果与AIC选择法相同。对于任意当前时刻,新指标融合法的预测效果均为最优。对于平均预测效果,按新指标融合法、新指标选择法、AIC选择法、似然函数值选择法的顺序依次递减。因此,在产品2的退化数据下仍有新指标融合法相较于其他三种方法具有最好预测效果的结论。
表4 产品2下不同方法所得到的最优模型
Tab.4 Optimal models under different methods for product 2

tk似然函数值选择法AIC选择法新指标选择法新指标融合法 75M1M1M1[0.125 0.108 0.082 0.100 0.107 0.098 0.095 0.062 0.105 0.114] 125M6M6M6[0.093 0.110 0.111 0.099 0.110 0.113 0.101 0.075 0.082 0.103] 175M7M3M2[0.075 0.135 0.118 0.110 0.060 0.088 0.095 0.128 0.096 0.090] 225M4M4M8[0.111 0.056 0.078 0.103 0.117 0.126 0.116 0.128 0.068 0.092] 275M1M1M1[0.130 0.089 0.093 0.079 0.101 0.086 0.102 0.098 0.105 0.112] 325M5M5M5[0.079 0.112 0.101 0.068 0.124 0.092 0.103 0.091 0.113 0.113] 375M2M2M6[0.040 0.108 0.093 0.114 0.079 0.129 0.108 0.106 0.089 0.128]
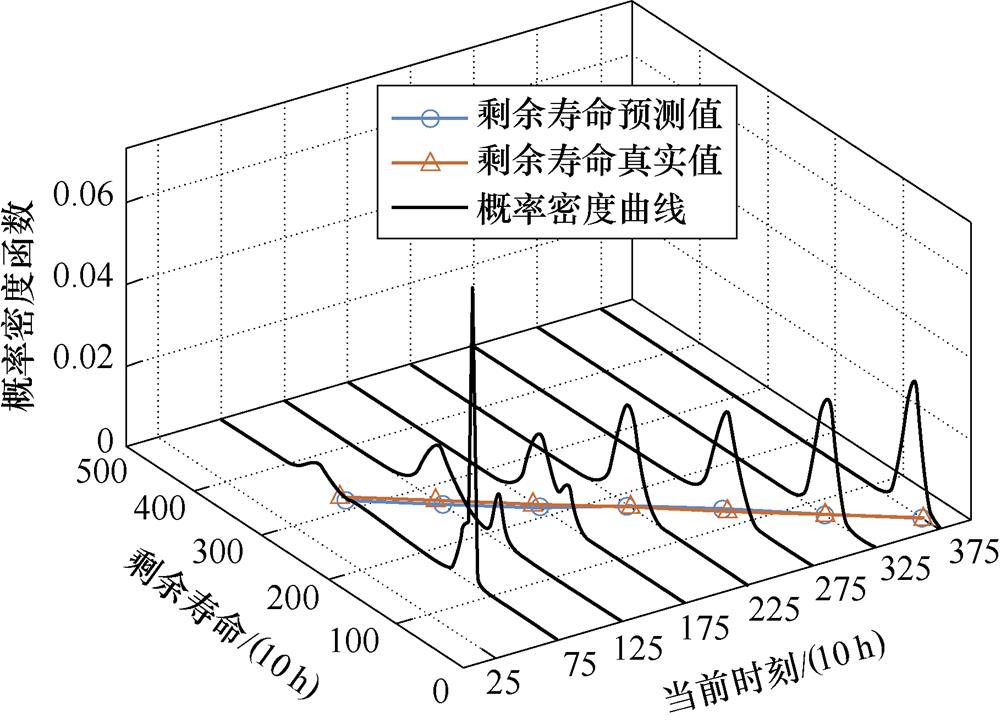
图7 产品2的剩余寿命真实值、基于新指标融合法的剩余寿命预测值及其概率密度曲线
Fig.7 True residual life value, predicted residual life value and probability density curves based on the new index fusion method for product 2
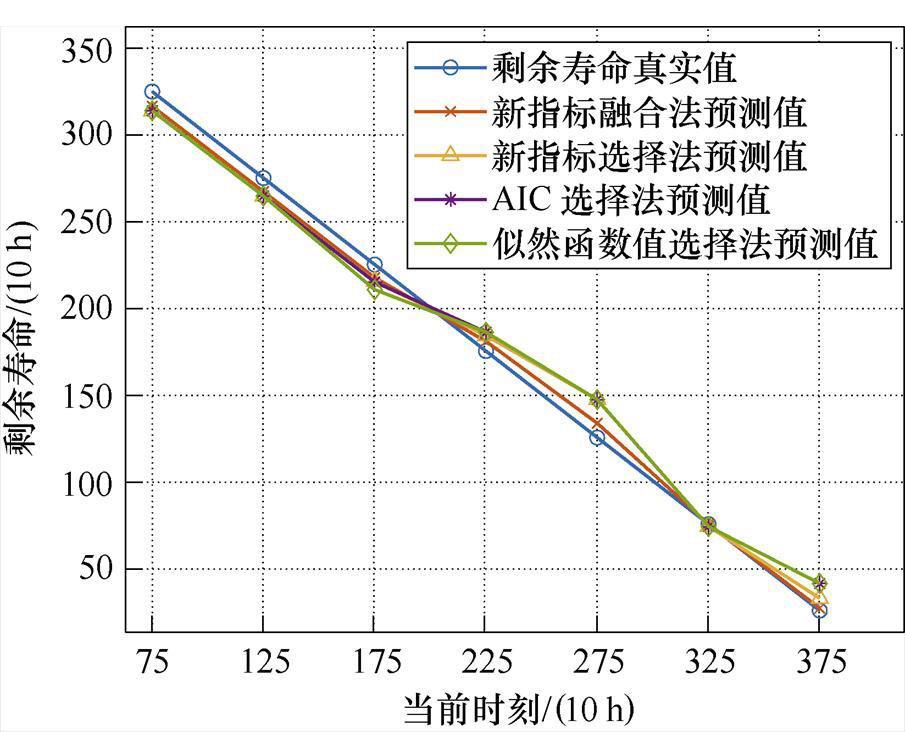
图8 产品2下不同方法的剩余寿命预测值
Fig.8 Predicted residual life values under different methods for product 2
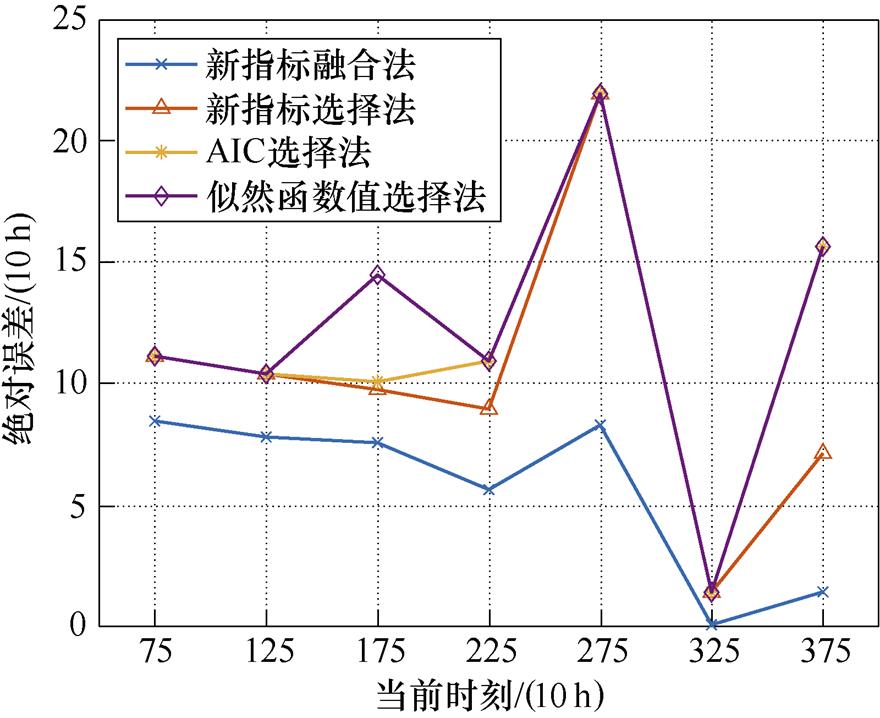
图9 产品2下不同预测方法的绝对误差
Fig.9 Absolute errors under different prediction methods for product 2
表5 产品2下不同方法的绝对误差(10 h)
Tab.5 Absolute errors (10 h) under different methods for product 2
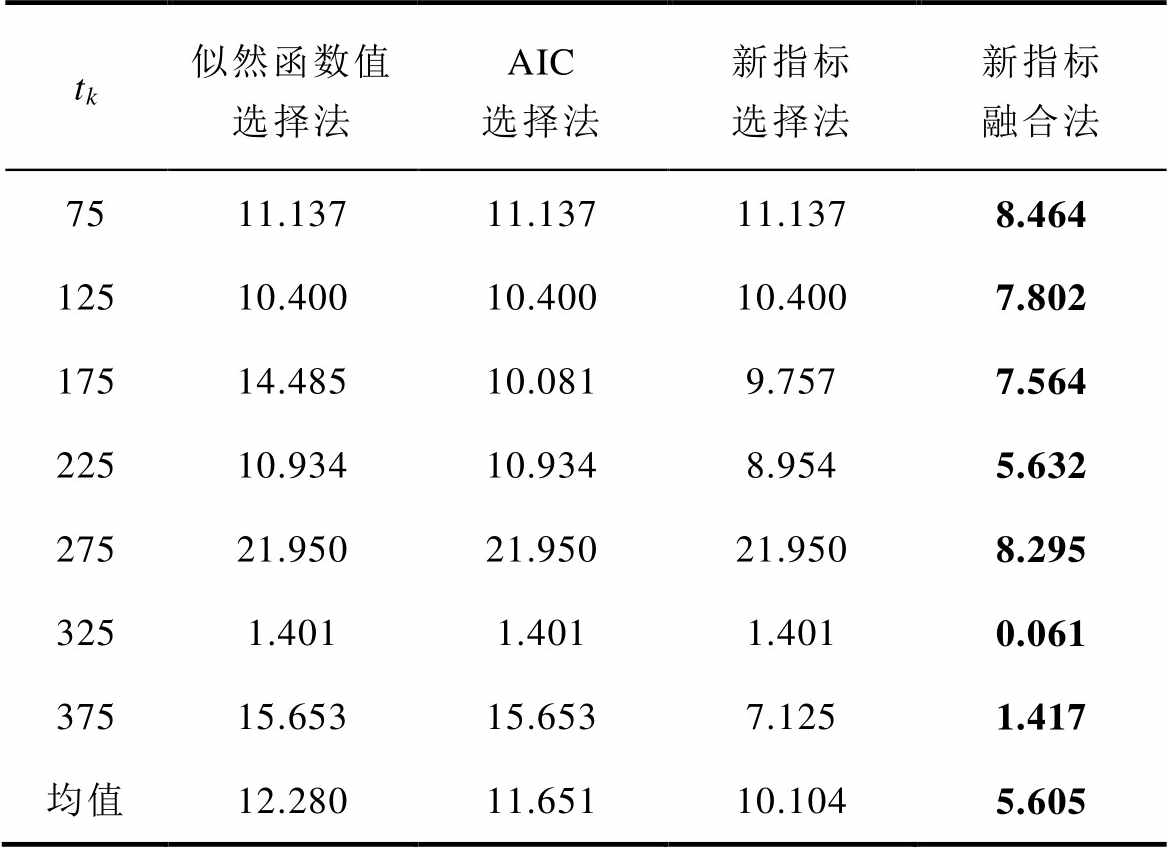
tk似然函数值选择法AIC选择法新指标选择法新指标融合法 7511.13711.13711.1378.464 12510.40010.40010.4007.802 17514.48510.0819.7577.564 22510.93410.9348.9545.632 27521.95021.95021.9508.295 3251.4011.4011.4010.061 37515.65315.6537.1251.417 均值12.28011.65110.1045.605
表6 产品2下不同方法的相对优势指数
Tab.6 The index of relative superiority under different methods for product 2
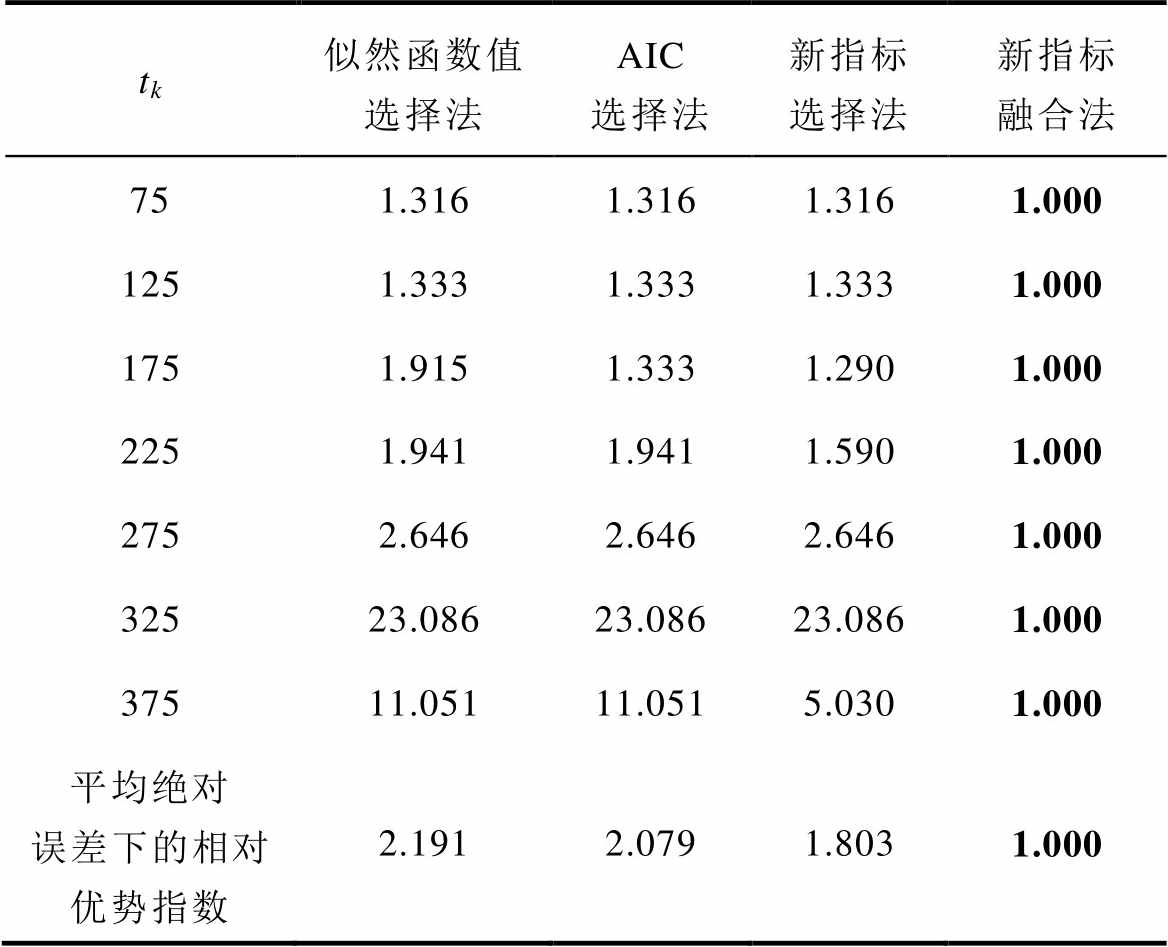
tk似然函数值选择法AIC选择法新指标选择法新指标融合法 751.3161.3161.3161.000 1251.3331.3331.3331.000 1751.9151.3331.2901.000 2251.9411.9411.5901.000 2752.6462.6462.6461.000 32523.08623.08623.0861.000 37511.05111.0515.0301.000 平均绝对误差下的相对优势指数2.1912.0791.8031.000
产品3的原始退化数据为某型号精密电阻在60 ℃下的电阻测量值相对于初始值的增量百分比,测量间隔为120 h。其标准化后的退化数据如图10所示。
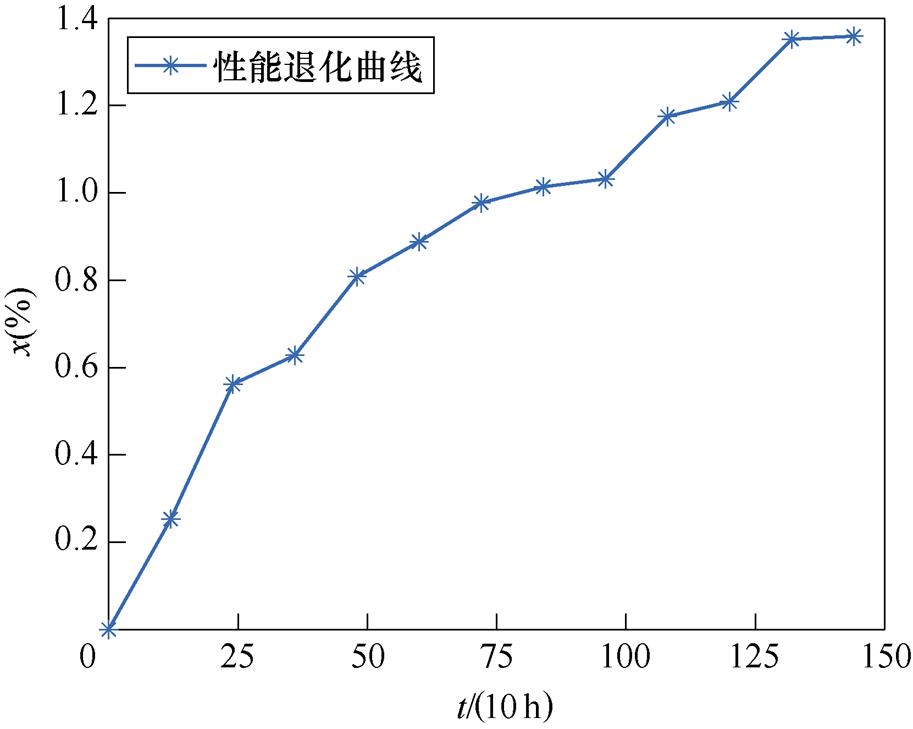
图10 产品3的性能退化曲线
Fig.10 Performance degradation curve of product 3
在产品3的退化数据下,利用似然函数值选择法、AIC选择法、新指标选择法以及新指标融合法所得到的最优模型见表7。
利用新指标融合法对产品3的退化数据进行剩余寿命预测,其结果如图11所示。
利用似然函数值选择法、AIC选择法、新指标选择法以及新指标融合法,对产品3的退化数据进行剩余寿命预测,其结果如图12所示。绝对误差如图13和表8所示,相对优势指数见表9。
通过对比产品3与产品1、2的退化数据可以发现,产品3不像产品2一样具有较强的线性规律,也不像产品1一样虽然数据规律性不强,但数据量相对较大。产品3的退化趋势具有明显的非线性特征,且数据量相对较小。因此,如图12所示,在利用似然函数值选择法、AIC选择法和新指标选择法对产品3进行剩余寿命预测时,预测值相对于真实值均出现了较大的偏移,且偏移量在当前时刻较小时尤为明显,但随着当前时刻的增加,偏移量逐步降低。如图12所示,虽然新指标融合法的预测值也具有上述特征,但相较于其他方法,新指标融合法在各个当前时刻的偏移量明显较小。
表7 产品3下不同方法所得到的最优模型
Tab.7 Optimal models under different methods for product 3

tk似然函数值选择法AIC选择法新指标选择法新指标融合法 36M6M6M9[0.106 0.115 0.078 0.076 0.077 0.053 0.125 0.121 0.127 0.119] 60M3M3M6[0.088 0.105 0.093 0.084 0.121 0.144 0.091 0.087 0.098 0.086] 84M1M1M1[0.132 0.103 0.085 0.071 0.104 0.096 0.073 0.084 0.124 0.123] 108M4M9M9[0.089 0.107 0.083 0.125 0.072 0.080 0.085 0.127 0.130 0.095] 132M7M7M10[0.108 0.094 0.108 0.103 0.081 0.073 0.094 0.105 0.112 0.118]
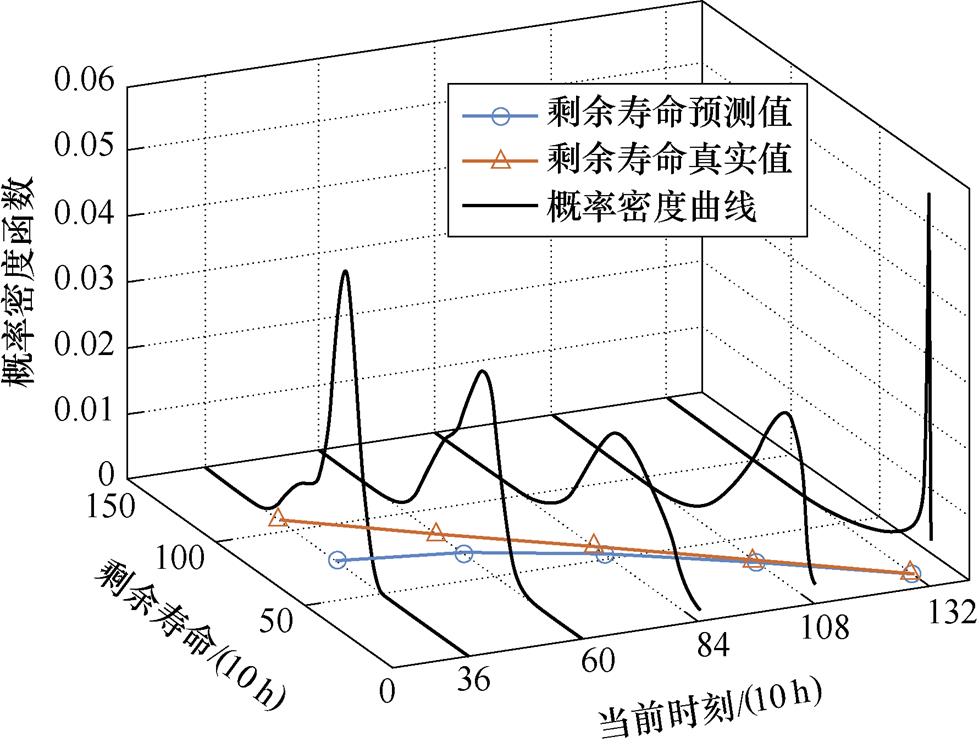
图11 产品3的剩余寿命真实值、基于新指标融合法的剩余寿命预测值以及概率密度曲线
Fig.11 True residual life value, predicted residual life value and probability density curve based on the new index fusion method for product 3
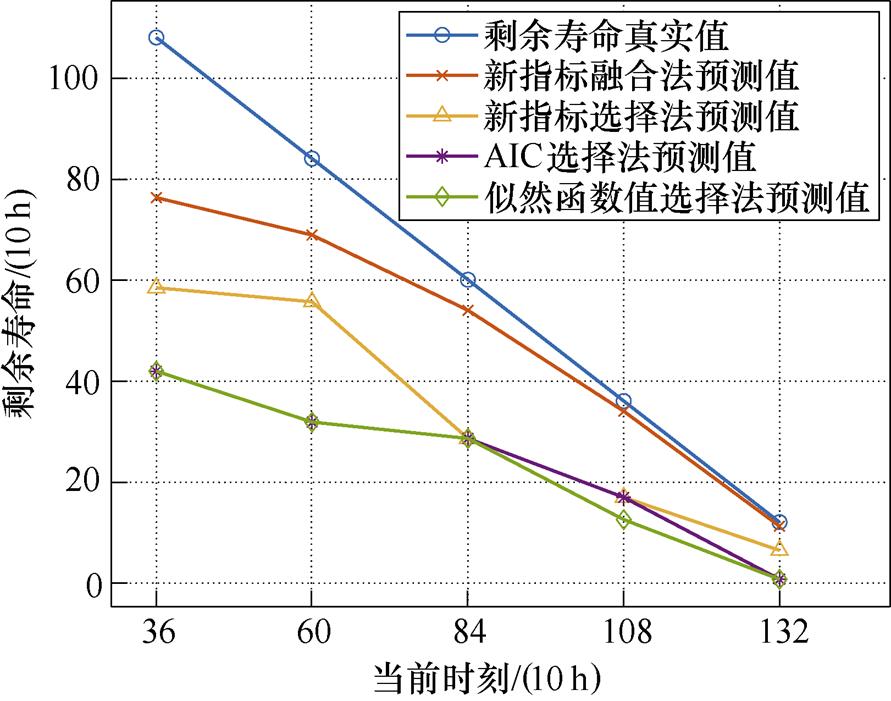
图12 产品3下不同方法的剩余寿命预测值
Fig.12 Predicted residual life values under different methods for product 3
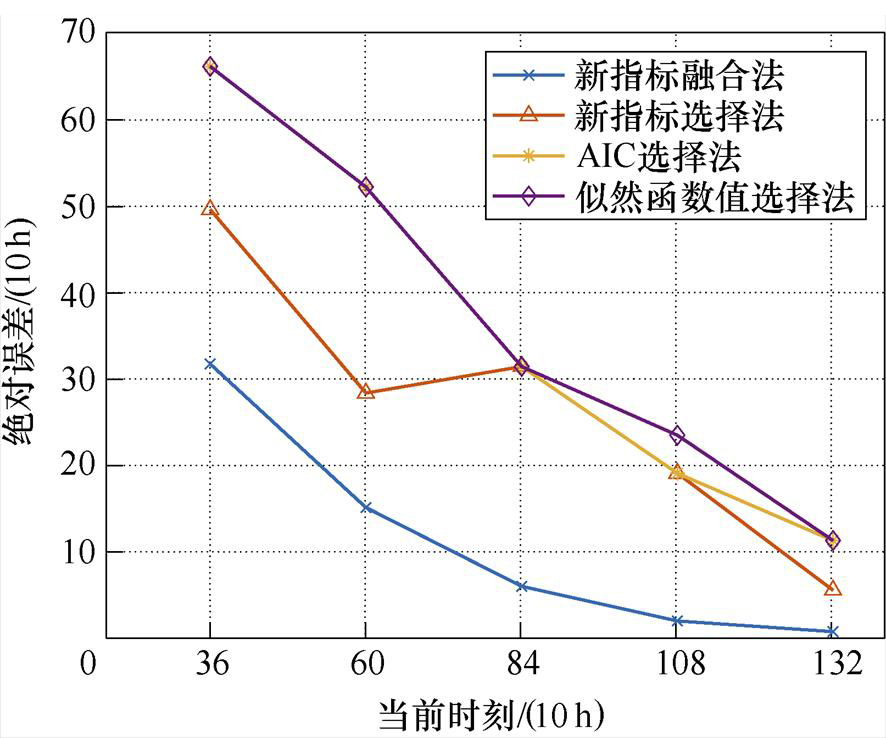
图13 产品3下不同预测方法的绝对误差
Fig.13 Absolute errors under different prediction methods for product 3
表8 产品3下不同方法的绝对误差(10 h)
Tab.8 Absolute errors (10 h) under different methods for product 3
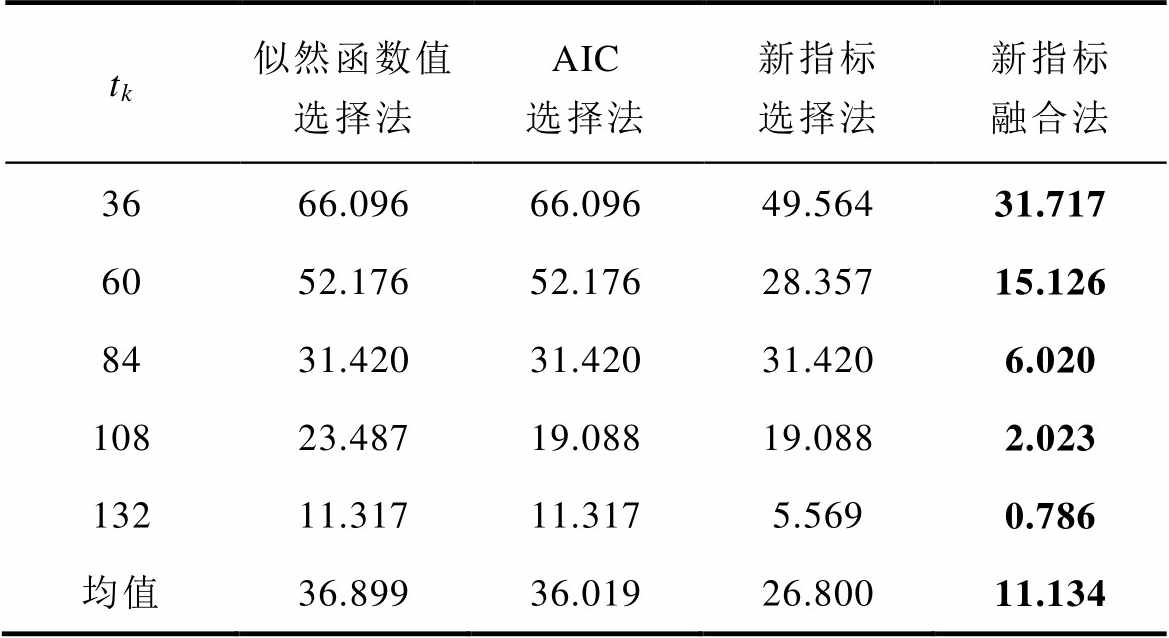
tk似然函数值选择法AIC选择法新指标选择法新指标融合法 3666.09666.09649.56431.717 6052.17652.17628.35715.126 8431.42031.42031.4206.020 10823.48719.08819.0882.023 13211.31711.3175.5690.786 均值36.89936.01926.80011.134
表9 产品3下不同方法的相对优势指数
Tab.9 The index of relative superiority under different methods for product 3

tk似然函数值选择法AIC选择法新指标选择法新指标融合法 362.0842.0841.5631.000 603.4493.4491.8751.000 845.2195.2195.2191.000 10811.6139.4389.4381.000 13214.40014.4007.0861.000 平均绝对误差下的相对优势指数3.3143.2352.4071.000
由表8、表9可以看出,对于产品3,新指标融合法相较于其他三种方法的预测效果最好。由平均绝对误差下的相对优势指数可知,似然函数值选择法、AIC选择法、新指标选择法的平均绝对误差约为新指标融合法的3.3倍、3.2倍和2.4倍,新指标融合法的平均绝对误差相较于上述三种方法下降了约70 %、69 %和58 %。当前时刻tk为36、60、132时,新指标选择法的预测效果优于AIC选择法及似然函数值选择法;当前时刻tk为84、108时,新指标选择法的预测效果与AIC选择法相同。对于任意当前时刻,新指标融合法的预测效果均为最优。对于平均预测效果,按新指标融合法、新指标选择法、AIC选择法、似然函数值选择法的顺序依次递减。
通过产品3的预测结果可以发现,即使退化数据的规律性较差、数据量较小,新指标融合法仍然可以得到较好的预测效果,因此该方法具有较为广泛的适用性。
本文针对退化过程可以用单一特征量表征的电子元器件性能退化模型的不确定性问题,提出了一种新的模型优劣性指标,并依据该指标对备选模型进行融合,得到了电子元器件个体的剩余寿命融合模型,进而通过该融合模型实现了剩余寿命预测,最终形成了一种基于模型融合的电子元器件个体剩余寿命预测方法。主要结论如下:
1)本文所提出的新模型优劣性指标不同于传统指标,新指标综合考虑了备选模型的拟合程度、复杂度和预测精度,因此新指标可以对备选模型进行较为全面的度量。
2)对所有备选模型进行融合的融合策略,不仅降低了放弃预测效果较好的模型的风险,其所建立的模型还同时具有多种模型的特征,可以在一定程度上抑制单一模型的缺点。
3)本文所提出的新指标融合法,不依赖大量的先验信息或退化数据,且具有较高的预测精度及较为广泛的适用性。
本文针对电子元器件共选取了十种备选模型,未来可以将更多的电子元器件退化趋势模型和随机效应模型纳入备选模型集合中,使得新指标融合法所建立的融合模型对于电子元器件更具一般性和广泛适用性。还可以通过对备选模型集合进行调整,使得本文所提出的新指标融合法可以对其他类型的产品进行性能退化建模和剩余寿命预测。
参考文献
[1] 周荔丹, 闫朝鑫, 姚钢, 等. 空间辐射环境对航天器分布式电力系统关键部件的影响及应对策略[J]. 电工技术学报, 2022, 37(6): 1365-1380.
Zhou Lidan, Yan Chaoxin, Yao Gang, et al. Influence of space radiation environment on critical components of spacecraft distributed power system and counter- measures[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1365-1380.
[2] 韩乔妮, 姜帆, 程泽. 变温度下IHF-IGPR框架的锂离子电池健康状态预测方法[J]. 电工技术学报, 2021, 36(17): 3705-3720.
Han Qiaoni, Jiang Fan, Cheng Ze. State of health estimation for lithium-ion batteries based on the framework of IHF-IGPR under variable tempe- rature[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3705-3720.
[3] 李辉, 刘人宽, 王晓, 等. 压接型IGBT器件封装退化监测方法综述[J]. 电工技术学报, 2021, 36(12): 2505-2521.
Li Hui, Liu Renkuan, Wang Xiao, et al. Review on package degradation monitoring methods of press- pack IGBT modules[J]. Transactions of China Elec- trotechnical Society, 2021, 36(12): 2505-2521.
[4] 郭劲言. 模型不确定的电主轴加速退化试验多目标优化设计方法[D]. 长春: 吉林大学, 2021.
[5] Jiao Jian, De Xinlin, Chen Zhiwei, et al. Integrated circuit failure analysis and reliability prediction based on physics of failure[J]. Engineering Failure Analysis, 2019, 104: 714-726.
[6] Zhou Yuege, Ye Xuerong, Zhai Guofu. Degradation model and maintenance strategy of the electrolytic capacitors for electronics applications[C]//2011 Pro- gnostics and System Health Managment Confernece, Shenzhen, China, 2011: 1-6.
[7] Celaya J R, Kulkarni C, Saha S, et al. Accelerated aging in electrolytic capacitors for prognostics[C]// 2012 Proceedings Annual Reliability and Maintaina- bility Symposium, Reno, NV, USA, 2012: 1-6.
[8] 孟晓凯, 王志强, 李国锋. 基于硬度保留率的船用电缆剩余寿命快速评估[J]. 电工技术学报, 2016, 31(15): 197-203.
Meng Xiaokai, Wang Zhiqiang, Li Guofeng. Rapid assessment of marine cable remaining life based on retention rate of hardness[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 197-203.
[9] Lin Yanhui, Ding Zeqi. An integrated degradation modeling framework considering model uncertainty and calibration[J]. Mechanical Systems and Signal Processing, 2022, 166: 108389.
[10] Yan Bingxin, Ma Xiaobing, Wang Han. Analysis of an improved Wiener deterioration model considering mechanism equivalence[J]. Journal of Physics: Con- ference Series, 2018, 1053: 012115.
[11] Wang Lizhi, Pan Rong, Li Xiaoyang, et al. A Bayesian reliability evaluation method with integrated accelerated degradation testing and field infor- mation[J]. Reliability Engineering & System Safety, 2013, 112: 38-47.
[12] 王浩伟, 徐廷学, 刘勇. 基于随机参数Gamma过程的剩余寿命预测方法[J]. 浙江大学学报(工学版), 2015, 49(4): 699-704, 762.
Wang Haowei, Xu Tingxue, Liu Yong. Remaining useful life prediction method based on Gamma processes with random parameters[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(4): 699-704, 762.
[13] Yu Yong, Hu Changhua, Si Xiaosheng, et al. Modified Bayesian D-optimality for accelerated degradation test design with model uncertainty[J]. IEEE Access, 2019, 7: 42181-42189.
[14] Liu Le, Li Xiaoyang, Jiang Tongmin, et al. Optimal design for accelerated degradation tests with stochastic model uncertainty[M]. Risk, Reliability and Safety: Innovating Theory and Practice. Taylor & Francis Group, 6000 Broken Sound Parkway NW, Suite 300, Boca Raton, FL 33487-2742: CRC Press, 2016: 10-15.
[15] Kang Rui, Gong Wenjun, Chen Yunxia. Model-driven degradation modeling approaches: investigation and review[J]. Chinese Journal of Aeronautics, 2020, 33(4): 1137-1153.
[16] Schössler T, Schön F, Lemier C, et al. Reliability improvements of thin film platinum resistors on wafer-level and micro-hotplates at stress temperatures in the range of 140-290℃[J]. Microelectronics Reliability, 2020, 104: 113557.
[17] 张月, 卓青青, 刘红侠, 等. 功率MOSFET的负偏置温度不稳定性效应中的平衡现象[J]. 物理学报, 2013, 62(16): 167305.
Zhang Yue, Zhuo Qingqing, Liu Hongxia, et al. Flat-roof of dynamic equilibrium phenomenon in static negative biase temperature instability effect on power metal-oxide-semiconductor field-effect transi- stor[J]. Acta Physica Sinica, 2013, 62(16): 167305.
[18] Whitmore G A, Schenkelberg F. Modelling acceler- ated degradation data using Wiener diffusion with a time scale transformation[J]. Lifetime Data Analysis, 1997, 3(1): 27-45.
[19] Liu Le, Li Xiaoyang, Zio E, et al. Model uncertainty in accelerated degradation testing analysis[J]. IEEE Transactions on Reliability, 2017, 66(3): 603-615.
[20] 潘广泽, 张铮, 罗琴, 等. 基于性能退化的电力电子器件寿命评估[J]. 中国电力, 2020, 53(10): 156- 162.
Pan Guangze, Zhang Zheng, Luo Qin, et al. Per- formance degradation based lifetime evaluation of power electronic devices[J]. Electric Power, 2020, 53(10): 156-162.
[21] Zhou Rensheng, Serban N, Gebraeel N. Degradation- based residual life prediction under different envi- ronments [J]. Annals of Applied Statistics, 2014, 8(3): 1671-1689.
[22] Ye Zhisheng, Xie Min. Stochastic modelling and analysis of degradation for highly reliable products[J]. Applied Stochastic Models in Business and Industry, 2015, 31: 16-32.
[23] 李奎, 高志成, 武一, 等. 基于统计回归和非线性Wiener过程的交流接触器剩余寿命预测[J]. 电工技术学报, 2019, 34(19): 4058-4070.
Li Kui, Gao Zhicheng, Wu Yi, et al. Remaining lifetime prediction of AC contactor based on statistical regression and nonlinear Wiener process[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4058-4070.
[24] 刘帼巾, 李想, 王泽, 等. 基于Wiener过程电子式漏电断路器的剩余寿命预测[J]. 电工技术学报, 2022, 37(2): 528-536.
Liu Guojin, Li Xiang, Wang Ze, et al. Remaining life prediction of electronic residual current circuit breaker based on Wiener process[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 528-536.
[25] Byrd R H, Gilbert J C, Nocedal J. A trust region method based on interior point techniques for nonlinear programming[J]. Mathematical Program- ming, 2000, 89(1): 149-185.
[26] Liu Baoding. Uncertainty theory[M]. Berlin: Springer, 2010.
[27] 何志鹏, 赵虎. 微型断路器电寿命评估[J]. 电工技术学报, 2022, 37(4): 1031-1040.
He Zhipeng, Zhao Hu. Electrical lifespan evaluation of miniature circuit breakers[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 1031- 1040.
[28] Coello C A. A comprehensive survey of evolutionary- based multiobjective optimization techniques[J]. Knowledge and Information Systems, 1999, 1(3): 269-308.
[29] 夏冬, 吴俊勇, 贺电, 等. 一种新型的风电功率预测综合模型[J]. 电工技术学报, 2011, 26(增刊1): 262-266.
Xia Dong, Wu Junyong, He Dian, et al. A novel combined model for wind power forecasting based on maximum entropy principle[J]. Transactions of China Electrotechnical Society, 2011, 26(S1): 262-266.
[30] Campagnolo L Q, Celes W, de Figueiredo L H. Accurate volume rendering based on adaptive nume- rical integration[C]//2015 28th SIBGRAPI Confer- ence on Graphics, Patterns and Images, Salvador, Brazil, 2015: 17-24.
[31] Cadini F, Sbarufatti C, Cancelliere F, et al. State- of-life prognosis and diagnosis of lithium-ion batteries by data-driven particle filters[J]. Applied Energy, 2019, 235: 661-672.
[32] Nelson W, Meeker W Q, Escobar L A. Statistical methods for reliability data[J]. Technometrics, 1998, 40(3): 255.
[33] 王浩伟. 加速退化数据建模与统计分析方法及工程应用[M]. 北京: 科学出版社, 2019.
[34] Park C, Padgett W J. New cumulative damage models for failure using stochastic processes as initial damage[J]. IEEE Transactions on Reliability, 2005, 54(3): 530-540.
[35] Park C, Padgett W J. Stochastic degradation models with several accelerating variables[J]. IEEE Transa- ctions on Reliability, 2006, 55(2): 379-390.
[36] Li Xiaoyang, Chen Dayu, Wu Jipeng, et al. 3- Dimensional general ADT modeling and analysis: considering epistemic uncertainties in unit, time and stress dimension[J]. Reliability Engineering & System Safety, 2022, 225: 108577.
Abstract Electronic components are usually the weak parts of a system and are generally required to fulfill critical tasks. If a seriously degraded electronic component is not replaced in time, its failure may result in the failure of the whole system. Therefore, it is significant to accurately predict the residual life of electronic components in the system. Due to factors such as complex failure mechanisms, little prior information, and insufficient monitoring data, the degradation model of an electronic component is usually uncertain, which may cause an inaccurate prediction of the residual life. However, the existing studies did not consider the predictive ability of a model and required much prior information or degradation data. Therefore, a residual life prediction method for an individual electronic component based on model fusion is proposed in this paper. Alternative models are fused based on a novel model evaluation index that incorporates the fitting ability, complexity, and prediction accuracy of a model. Then the residual life of an electronic component is predicted based on the fused model.
The proposed residual life prediction method is focused on the case that a single performance parameter can characterize the performance of an electronic component. Firstly, the alternative degradation model is established for typical and common degradation patterns of electronic components. Secondly, the alternative residual life distribution model is derived based on the alternative degradation model. Thirdly, the maximum likelihood estimation method is adopted to estimate the unknown parameters in the alternative model using the available degradation data collected up to the current time. Fourthly, the probability that an alternative model is the true one is constructed according to the proposed novel model evaluation index. Then the alternative residual life distribution models are fused via the law of total probability to obtain the fused model of the residual life distribution. Fifthly, the expected residual life is taken as the point estimate of the residual life and calculated based on the fused residual life distribution model.
Three real cases are carried out to verify the proposed residual life prediction method. Through comparison analysis, it is shown that the proposed method is superior to the methods that predict the residual life based on the best model selected according to a traditional model evaluation index, such as the Akaike information criterion (AIC) and the value of the likelihood function, or the proposed index. Moreover, it is verified that the proposed method can ensure good prediction accuracy, even if the regularity of the degradation data is poor and the amount of the data is small.
Some specific conclusions are summarized as follows. (1) The proposed novel model evaluation index is comprehensive since it simultaneously considers the fitting ability, complexity, and prediction accuracy of a model. (2) The strategy of model fusion can reduce the risk of abandoning a model with better prediction results and make a fused model have the characteristics of all the alternative models. The drawbacks of using a single model can be overcome to a certain extent. (3) The proposed residual life prediction method for electronic components is independent of much prior information or degradation data and has a high prediction accuracy and powerful practicability.
keywords:Electronic component, individual residual life prediction, model uncertainty, model evaluation index, model fusion
DOI: 10.19595/j.cnki.1000-6753.tces.221359
中图分类号:TB114.3; TM07
国家自然科学基金(72101081, 51937004)和中央引导地方科技发展资金(226Z2102G)资助项目。
收稿日期 2022-07-16
改稿日期 2022-07-29
赵昌东 男,1997年生,硕士研究生,研究方向为电器可靠性等。E-mail: 1159732872@qq.com
项石虎 男,1992年生,博士,研究方向为电器可靠性等。E-mail: 2020070@hebut.edu.cn(通信作者)
(编辑 崔文静)