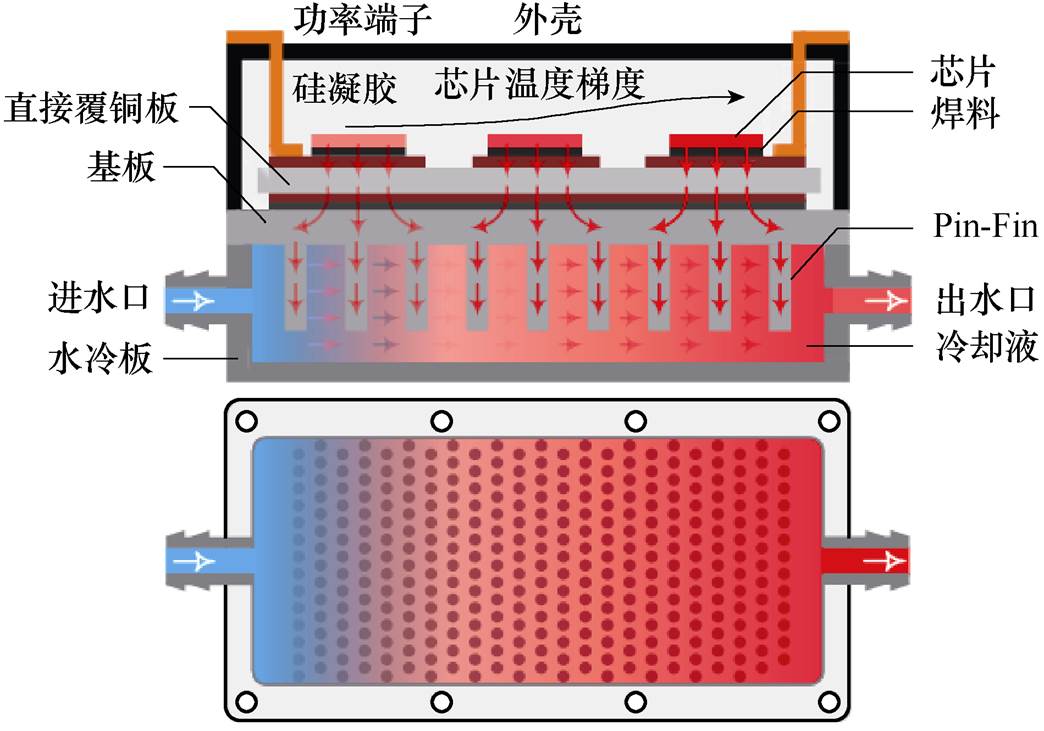
图1 传统Pin-Fin散热器存在的问题
Fig.1 Obstacles of traditional Pin-Fin heatsink
摘要 集成Pin-Fin散热器可以降低功率模块的结-流热阻，是车用电机控制器热管理的发展趋势。然而，传统参数设计方法无法定量表征Pin-Fin的形貌结构，设计自由度低、设计效果欠佳，难以实现Pin-Fin的热-流协同设计。基于变密度拓扑优化方法，该文提出一种Pin-Fin形貌结构的设计方法，建立Pin-Fin设计的变密度拓扑优化模型，分析模型参数对优化结果和收敛性的影响规律，形成以结-流热阻和冷却液压降为目标的协同优化方法，探索Pin-Fin结构的热-流耦合规律和强化换热方法，得到最优的Pin-Fin散热器形貌结构，搭建变流器实验平台和车用电机控制器样机，对标商业化圆形Pin-Fin结构，以及三角形、菱形和水滴形等其他形貌结构，计及母线电压、负荷电流和冷却液流量的影响，实验结果验证了所提模型方法的可行性和有效性。实验结果表明：基于拓扑优化方法设计的Pin-Fin结构，与传统结构相比可以降低12 %的结-流热阻，消除了多芯片结温差异的80 %，为车用功率模块和电机控制器研究提供新的思路。
关键词：车用功率模块 集成Pin-Fin散热器 拓扑优化方法 热-流协同优化设计
面向“双碳目标”国家战略和“创新、绿色”发展理念，电动汽车将逐渐取代燃油车，成为电气化交通的重要发展趋势。电机控制器是电动汽车能量传输的纽带，是电动汽车的“心脏”[1]。高压大容量、高功率密度、高可靠、低成本，是车用电机控制器的追求目标[2]。得益于SiC等宽禁带器件的快速发展，车用电机控制器越来越小型化、轻量化、集成化，芯片单位面积的热通量显著提高，给电机控制器的热管理带来严峻挑战[3]。相对于传统水冷板结构，集成Pin-Fin散热器物理结构简单、扰流效果好、换热面积大，可以降低40 %的结-流热阻[4]，在车用功率模块中得到了广泛应用。现有车用Si IGBT芯片的热通量通常为0.1～0.15 kW/cm2，预计5年内将提升到0.5 kW/cm2，SiC芯片的热通量甚至将超过1 kW/cm2。然而，车用电机控制器缺乏高热通量管理方法，难以匹配车用功率芯片的快速发展，已经成为制约其功率密度提升的瓶颈。如何优化设计集成Pin-Fin散热器，适应车用功率芯片的高热通量需求，有待进一步的深入研究。
针对Pin-Fin散热器优化设计的研究，主要集中在排列布局和形貌结构两个方面。在排列布局方面，受端壁效应影响[5]，Pin-Fin的尾端会出现回流现象，增加动能损耗，不利于能量传递[6]。适当减小Pin-Fin间距，可以削弱端壁效应，增加传热效率[7]。但是，过于密集的Pin-Fin排布，会增加流道间的阻力，不利于热交换。基于排列组合[8]、响应面法[9]等数值计算方法，以Pin-Fin阵列排布为优化变量，以散热器热阻和流体动能损耗为目标，能够构建Pin-Fin优化设计模型，优化Pin-Fin的排列布局参数。此外，传统Pin-Fin结构大多均匀排布，沿着水冷流道来看，由于上游Pin-Fin阻碍，下游冷却液存在温度的大幅增加和动能损失，降低冷却液的利用效率和换热效果，将导致芯片之间的温度梯度较大[10]。在形貌结构方面，Pin-Fin的形貌结构会直接影响共轭传热效率和流体动能损耗。在车用电机控制器的热管理中，冷却液直接与Pin-Fin接触，带走功率芯片的功率损耗。因此，选择合适的Pin-Fin形貌结构，至关重要。常见的形貌结构有圆形、锥形、三角形[11]、椭圆形、流线形、矩形、五边形和六边形等[12]。其中圆形和锥形的Pin-Fin结构，换热面积大，具有较高的表面传热系数[13]；流线形和菱形结构可以降低系统的热阻和压降。针对Pin-Fin形貌结构的设计，大都采用经验-试凑方法，根据常见几何结构，通过经验枚举和排列组合的方式，对初始结构的各项参数进行仿真和实验分析，耗时长、成本高、自由度低，且难以获得最优的Pin-Fin形貌结构。除此之外，在Pin-Fin附近增添更小的圆形、半圆形和矩形等结构[14]，改变流线轨迹，可以在边界之间产生剪切层，增强流体的扰动性以起到强化换热的效果[15]。但是，强化换热的提升会大幅增加进-出水口的压降，增加水泵的功率和成本。
传统的Pin-Fin形貌结构优化方法仅有响应面法[16]和粒子群算法[17]等数值优化方法，根据常见几何结构（如圆形、三角形等），通过经验枚举和排列组合的方式，对初始结构的各项参数进行仿真和实验分析，无法涵盖目前已知的所有形貌结构，并定量表征形貌结构问题，设计周期长、成本高、自由度低，难以获得最优的Pin-Fin形貌结构。综上所述，目前关于传统的数值优化方法，均无法定量表征Pin-Fin形貌结构，难以实现热-流协同设计，设计结果温度梯度高、设计自由度低、设计效果欠佳，急需突破Pin-Fin流-固耦合系统的交互机制，实现Pin-Fin结构的定量表征和协同优化，提升功率模块和电机控制器的热-流性能。
与传统参数优化方法相比，拓扑优化方法可根据设计目标实现散热结构的定量表征与协同优化，设计自由度极高，优化效果好。针对车用功率模块的高热通量管理问题，本文基于拓扑优化方法，结合变密度插值模型、有限元方法和梯度下降算法，提出了Pin-Fin形貌结构的表征模型和设计方法，弥补了传统设计方法缺乏模型指导、设计自由度低、缺少热-流协同等问题。结合变密度插值、投影过滤和灵敏度分析等方法，构建了Pin-Fin形貌结构的表征模型，分析了模型参数对优化结果的影响规律，采用连续梯度法提升了优化结果的准确性，以芯片结-流热阻和冷却液压降最小为协同优化目标，建立了Pin-Fin的热-流协同优化设计方法，结合车用功率模块损耗模型，构建了Pin-Fin散热器的热-流协同设计方法，对标商业化车用功率模块以及三角形、菱形和水滴形等其他形貌结构，基于车用电机控制器的原型样机及实验平台，通过固定工况和实际工况的大量实验结果，验证了所提模型方法在降低结-流热阻、均衡芯片结温等方面的有效性，为高热通量车用功率模块的设计，以及高可靠车用电机控制器的研发，提供新的理论模型和技术方法。
基于图1所示的车用电机控制器，芯片产生的功率损耗通过热传导的方式传导至集成Pin-Fin，Pin-Fin直接浸没在冷却液中，通过热对流的方式将将芯片产生的大量热量带走。在传统Pin-Fin结构中，翅片均匀交错排列，以增强流体扰动性，提高换热效率。然而，由于上游翅片的阻碍，冷却液动能在冲击翅片过程中不断降低，同时冷却液在流动过程中被不断加热，导致传热效率不断降低，芯片温度梯度较大，温度最高的芯片和温度最低的芯片间存在5～15 ℃的差异[18]。为了降低芯片结温，并消除芯片结温差异，基于拓扑优化方法，本文提出Pin-Fin的热-流协同设计方法，提升功率模块和电机控制器的综合性能。
图1 传统Pin-Fin散热器存在的问题
Fig.1 Obstacles of traditional Pin-Fin heatsink
对于不可压缩的流体，可以采用连续性方程及其运动方程来描述，即Navier-Stokes方程[19]。
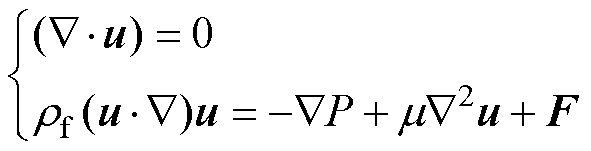（1）
式中，rf、u、P和m 分别为流体的密度、速度矢量、压力和动力粘度；F为无量纲的体积力，表征多孔介质流的流体阻力。
根据达西定律，体积力与速度u成正比，得
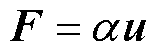（2）
式中，a 为多孔介质反射率。对于流体域，流体可以自由流动而不受体积力的限制，a =0；对于固体域，流体在固体域中受到无穷大的阻力，不能自由流动，a 为无穷大，设计域内的拓扑优化示意图如图2所示。
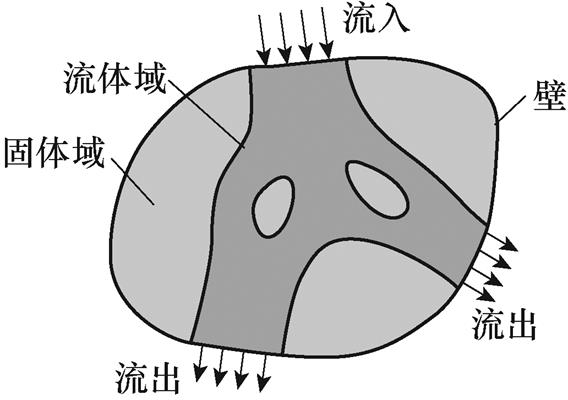
图2 设计域内的拓扑优化示意图
Fig.2 Topology optimization diagram in design domain
为了表征固体域和流体域所对应的密度与体积力之间的关系，可以采用材料属性的合理近似模型（Rational Approximation of Material Properties, RAMP）插值函数对a 进行插值[19]，即
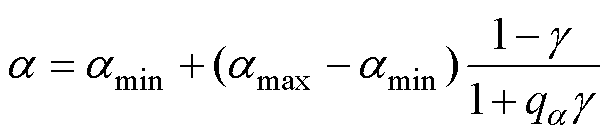（3）
式中，amin=0代表流体域的极低反射率；amax=106代表固体域的最大渗透反射率；qa为插值函数的惩罚因子；g 为拓扑优化过程中的各离散网格内的设计变量。根据式（2）、式（3），式（1）可以转换为
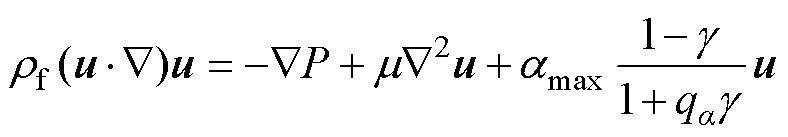（4）
在传热过程中，存在流体域与固体域的耦合，引入与材料密度相关的比定压热容和热导率，流-固传热的能量方程可以表示为
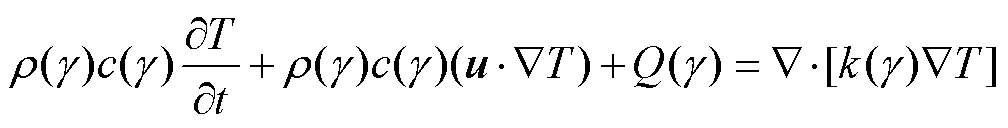（5）
式中，T为设计域的温度；r(g)、c(g)和k(g)为经过密度插值后的材料密度、比定压热容和热导率；Q(g)为外部热源的发热功率。对于稳态传热，有
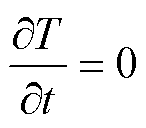（6）
根据式（6），热传导和热对流过程与流速、比热容、热导率直接相关。在流体流动过程中，能量方程描述了设计域内固体与流体之间的热对流和热传导过程。对比定压热容c(g)、热导率k(g)和外部热源Q(g)采用RAMP插值，有
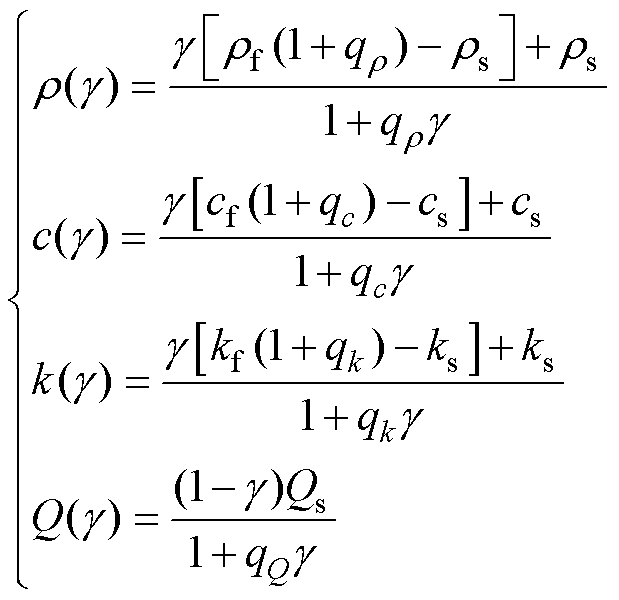（7）
式中，rs为固定的密度；cf和cs为流体域和固体域的比定压热容；kf和ks为流体域和固体域的热导率；Qs为固体域发热功率，经过密度插值后表示仅仅在固体区域内产生热量；qr、qc、qk和qQ分别为密度比定压热容、热导率和功率插值的惩罚因子。通过设置惩罚因子，对中间密度值进行惩罚，使原来[0, 1]区间变化的设计变量进行离散化，最终得到近似0和1的优化结果[20]。
对于车用功率模块的集成Pin-Fin散热器，固体材料为金属，流体材料为50 %水和50 %乙二醇混合溶液，各种材料的物理属性，见表1。惩罚因子的大小会影响模型收敛性和准确度，不同惩罚因子下密度和比热容插值函数如图3所示。因此，可以通过优化各离散区域的设计变量g，改变Pin-Fin的材料属性和拓扑结果，优化Pin-Fin散热器的热-流性能。
表1 Pin-Fin散热器的材料属性
Tab.1 Material properties of Pin-Fin heatsink
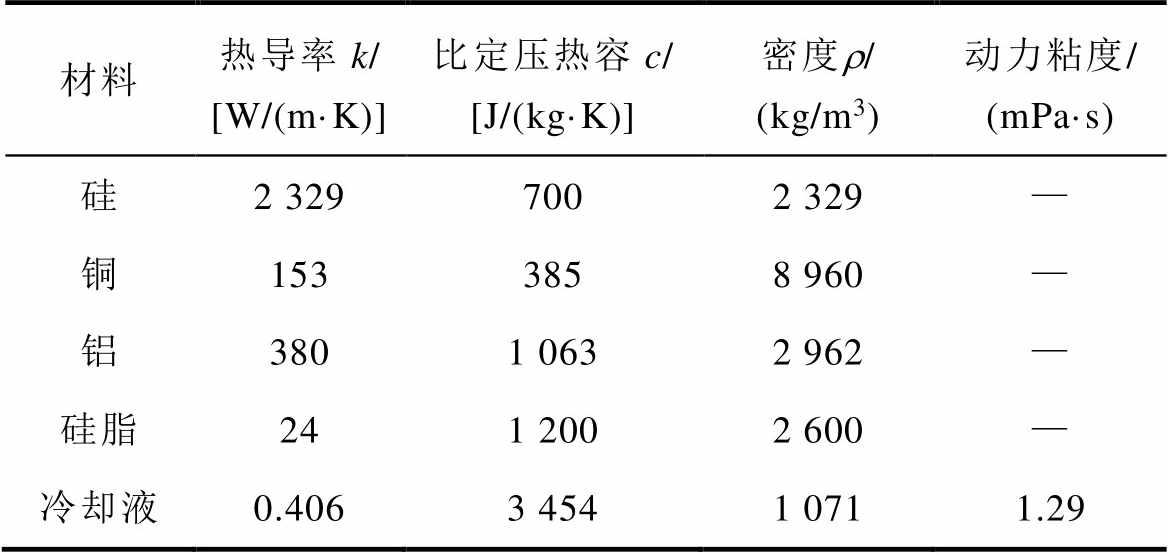
材料热导率k/ [W/(m·K)]比定压热容c/ [J/(kg·K)]密度r/ (kg/m3)动力粘度/ (mPa·s) 硅2 3297002 329— 铜1533858 960— 铝3801 0632 962— 硅脂241 2002 600— 冷却液0.4063 4541 0711.29
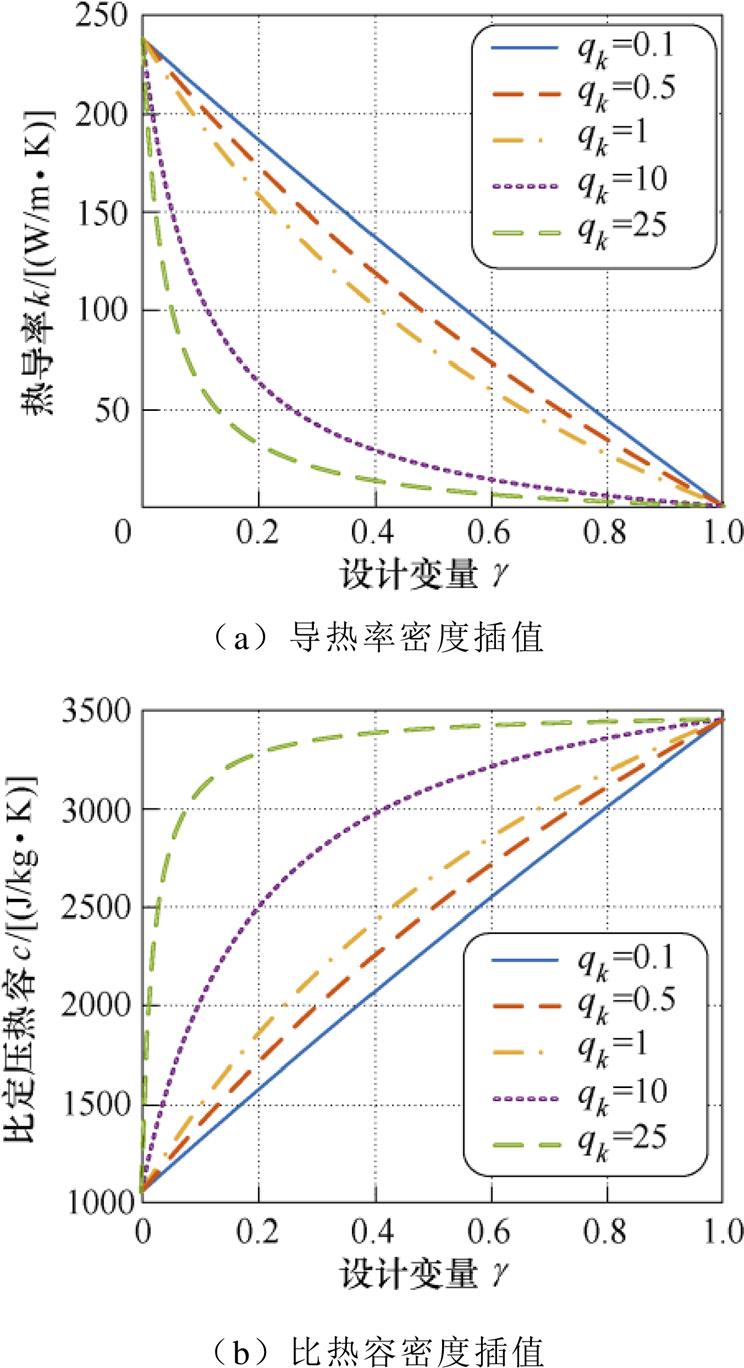
图3 不同惩罚因子下导热率和比热容插值函数
Fig.3 The interpolation functions of thermal conductivity and specific heat capacity under different penalty factors
密度过滤可以避免对网格的依赖性，提升算法的收敛性和鲁棒性，双曲正切投影可以解决因密度过滤产生的灰度问题，得到清晰的拓扑形态。这里采用基于霍尔姆兹偏微分方程进行密度过滤方法[21]，即
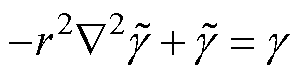（8）
式中，r为过滤半径；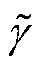
为过滤后的设计变量。通常，过滤半径选为设计域内最大网格尺寸的1.5倍。
密度过滤和投影对拓扑形态的影响如图4所示。上述密度过滤虽然可以提高求解时数值的稳定性，但同时也会产生大量灰度单元，如图4b所示。为了解决因密度过滤产生的灰度问题，采用双曲正切投影的方法[22]，以得到清晰的拓扑形态，即
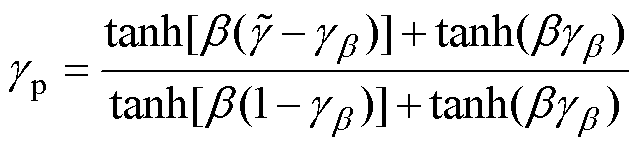（9）
式中，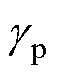
为投影后的设计变量；
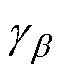为投影点；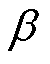
为斜率。通常，为了确保优化问题为凸规划问题，同时使流-固边界更加清晰稳定，取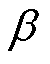=8[23]。
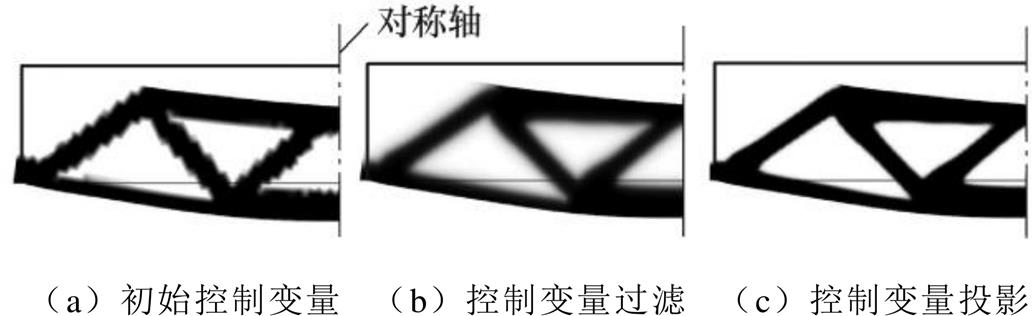
图4 密度过滤和投影对拓扑形态的影响
Fig.4 Topological morphology affected by filter and projection tools
结-流热阻Rthjf和冷却液压降ΔPf是衡量Pin- Fin散热器性能的关键指标，可以采用在单位发热功率下散热器温度的变化G 表征Rthjf，采用流体动能损耗F 表征ΔPf [19]，即
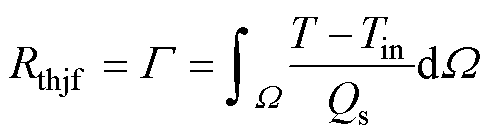（10）
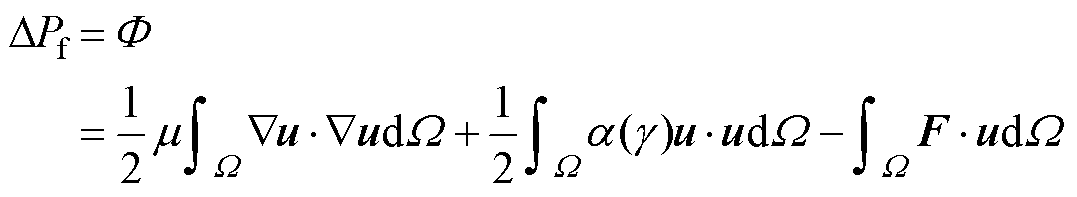（11）
式中，T和Tin为设计域W 的实际温度和初始温度。
由于两个目标函数的量纲和梯度不同，容易造成单个目标函数变化过大，导致求解过程不稳定，影响优化模型收敛性。将优化目标通过F0和G0进行无量纲化处理，构建归一化的目标函数。此外，采用对数函数进行多目标优化设计，提升数值计算的收敛性和稳定性，建立优化设计的目标函数为
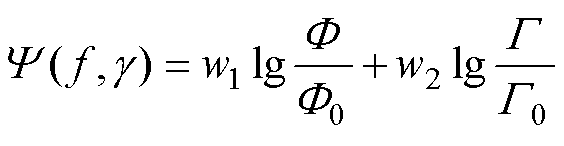（12）
式中，f为控制方程；w1和w2为加权因子，改变w1和w2的大小，可以在热阻与压降之间寻求折中。优化设计的约束条件为
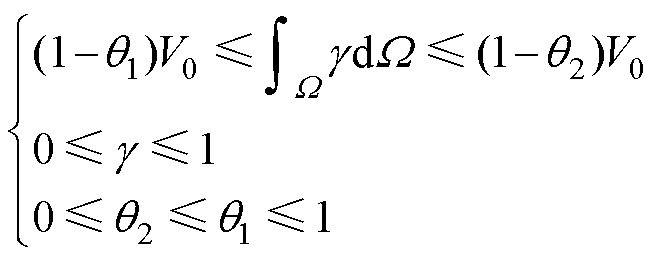（13）
式中，W 为设计域；V0为设计域总体积；流体域的体积为W 内设计变量g 的积分（流体域g=1、固体域g=0）；固体域的体积为设计域总体积减流体域体积；q1和q2为体积约束因子，表示固体域体积与设计域体积占比的上限和下限；g、q1和q2的范围均在0～1之间。因此可以通过设置体积约束因子在一定约束条件下，合理分配固体材料，实现最优形貌结构设计。控制方程的弱形式可以表示[24]为
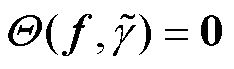（14）
式中，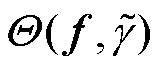
为控制方程中状态变量的残差向量。
伴随灵敏度方法具有的内存消耗低、求解效率高、计算速度快的优点。在迭代过程中求解设计域内大量单元密度g 的灵敏度，通过全局收敛的移动渐近线（Globally Convergent version of Method of Moving Asymptotes, GCMMA）算法寻优，不断更新设计变量g 的值，以找到满足约束条件下，目标函数的最大值或最小值。因此，在不断迭代过程中构建伴随灵敏度方程为
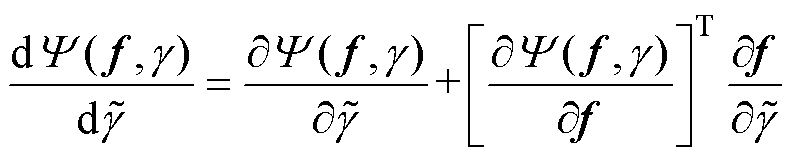（15）
由于无法直接求解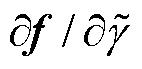
，因此通过构建控制方程的弱形式进行间接求解。根据式（15），有
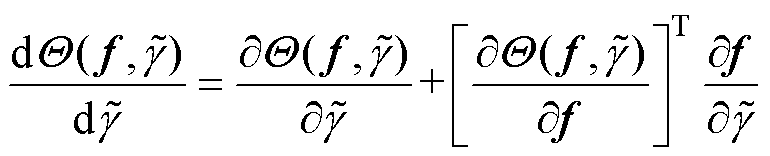（16）
因此，有
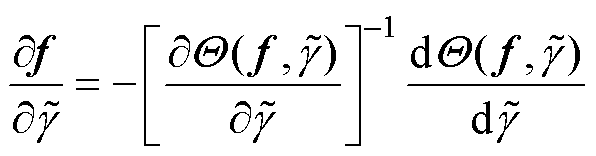（17）
定义伴随变量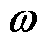
，有
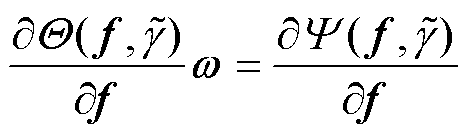（18）
因此，式（18）可以表示为
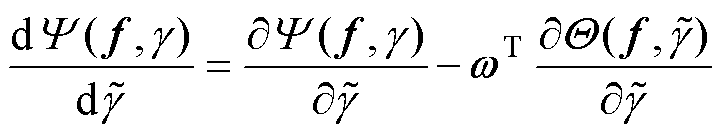（19）
需要指出的是，残差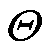
对设计变量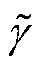的偏导数，可以通过求解状态变量T的弱形式得到。
本文采用COMSOL进行多物理的求解和拓扑优化的仿真设计。通过Navier-Stokes方程求解速度和压力场，通过能量守恒方程求解速度场和温度场。为了得到更准确的求解结果，通过“非等温流动”模块进行上述两个方程全耦合求解，由此便可得到温度、速度和压力等状态变量。
拓扑优化方法的设计流程如图5所示，在初始化设计变量和一系列边界条件后，通过有限元软件进行多物理场的求解得到一系列状态变量。在得到初始解后，判断求解目标函数并判断是否满足迭代收敛条件。如果不满足收敛条件，则在每个网格单元内求解伴随灵敏度，并进行密度过滤和投影，采用逐次逼近的移动渐近寻优算法更新设计变量，重新分配每个网格单元内的设计变量，进行下一轮计算，直至满足收敛条件，求得最优设计变量。
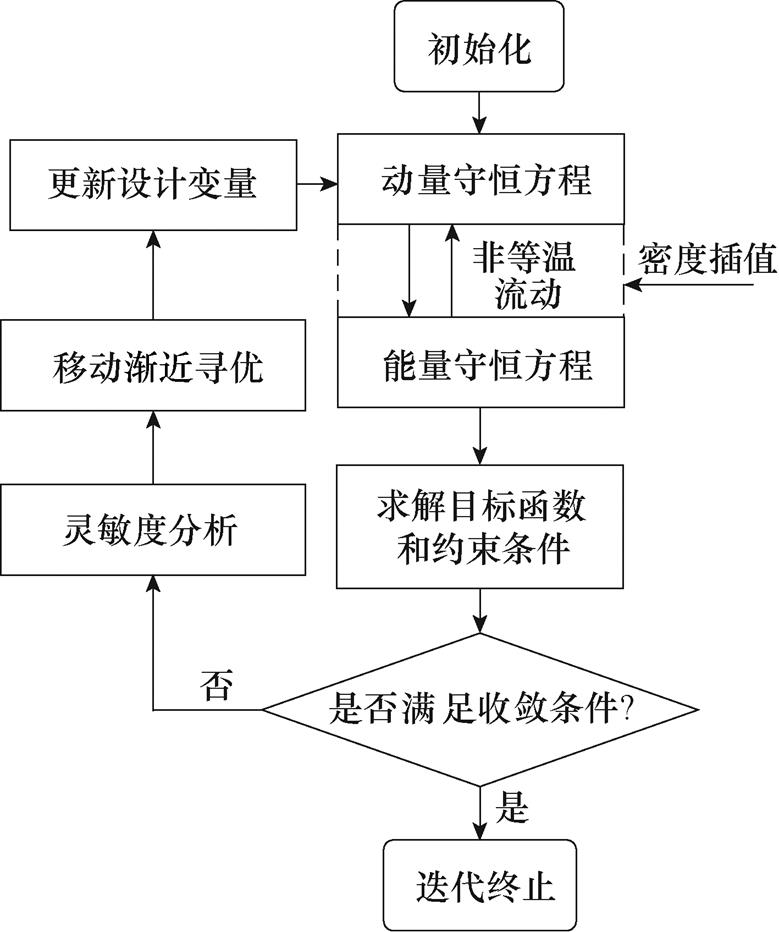
图5 车用功率模块Pin-Fin拓扑优化设计的流程
Fig.5 Flow-chart of Pin-Fin topology optimization for automotive power module
以英飞凌公司HybridPack封装的车用功率模块FS400R07A3E3为例，建立车用电机控制器的电-热模型，实现Pin-Fin散热器的拓扑优化设计。
车用功率模块的典型结构如图6所示，传统圆形Pin-Fin的主要特征参数包括：半径R、纵向距离D1和横向间距D2。为了设计Pin-Fin的形貌结构，首先需要确定设计域的大小，在不改变散热器体积的情况下，采用拓扑优化方法，合理分配材料，寻找最优的Pin-Fin拓扑结构。在不改变D1和D2的情况下，开展R的单因素实验。入水口流速设置为1 m/s，IGBT和二极管分别设置390 W和170 W的功率损耗。
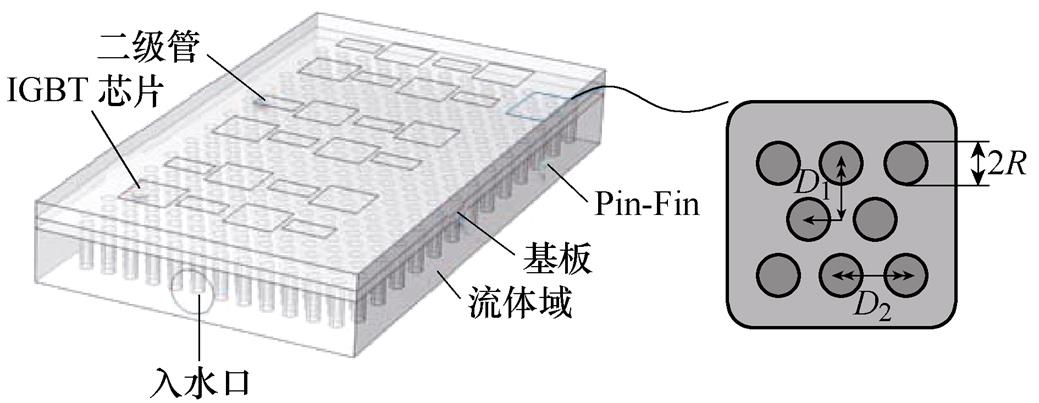
图6 车用功率模块的传统Pin-Fin散热器结构
Fig.6 Configuration of traditional Pin-Fin heat-sink in automotive power module
不同Pin-Fin直径对芯片结温ΔTj和冷却液压降ΔPf的影响，Pin-Fin半径R的单因素仿真结果如图7所示。增加Pin-Fin半径，可以降低散热器热阻，降低芯片温升，同时压降线性上升。但是，当半径增大到一定程度后，密集的Pin-Fin减少了冷却液的流动性，以及Pin-Fin与冷却液的换热空间，散热器热阻反而会增加。为了取得最优的拓扑结构，避免局部最优解的出现，选择设计域Rmax=1.5 mm，确保足够的设计自由度。为了不改变Pin-Fin的排列布局，规定R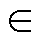
(0, Rmax
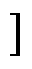范围内，g 的初始值为0。
惩罚因子决定了插值函数的凹凸性和模型的收敛性与准确性。三维拓扑优化计算得出的结果太过复杂，在实际加工中难以加工制作[25]；而Pin-Fin的形貌结构可以简化为由二维模型（如圆形，三角形等）拉伸得到，因此本文建立如图8所示二维简化模型，探究拓扑优化参数对优化结果的影响。设计域和横纵间距保持不变，最大设计域为Rmax，入口流速为0.5 m/s，并将热源均匀分布在设计域内。
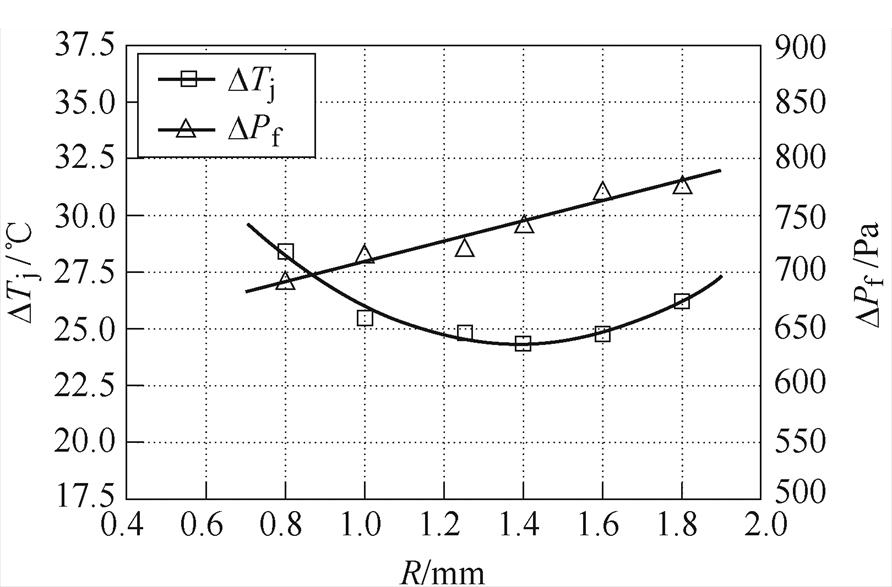
图7 Pin-Fin半径R的单因素仿真结果
Fig.7 Single factor influence of Pin-Fin radius R based on simulation results
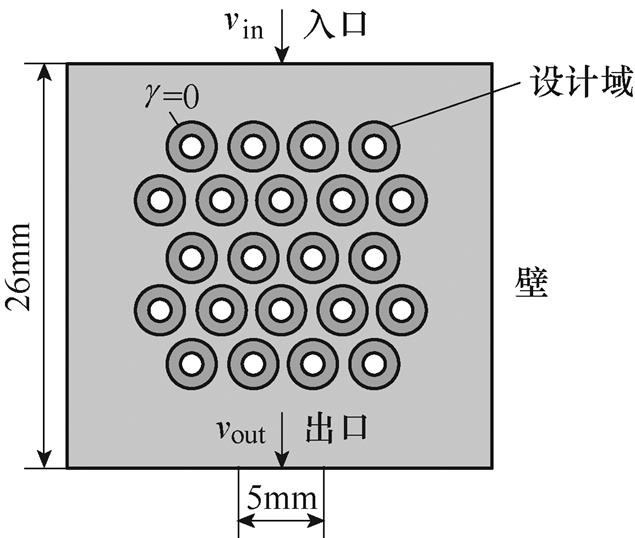
图8 拓扑优化的简化模型
Fig.8 Topology optimization using simplified model
下面详细分析惩罚因子对优化结果的影响。较大的惩罚因子会提高函数的凹凸性，增强函数的收敛性；较小的惩罚因子可以减小梯度，但是会模糊固体域和流体域界限，减小优化结果的准确性[20]。惩罚因子对拓扑优化结果的影响如图9所示。当惩罚因子都为0.1时，模型并不收敛。逐渐增大惩罚因子，模型收敛性提高，但是流-固边界相对模糊，影响模型的准确性。当惩罚因子增大至50时，模型收敛，边界清晰。
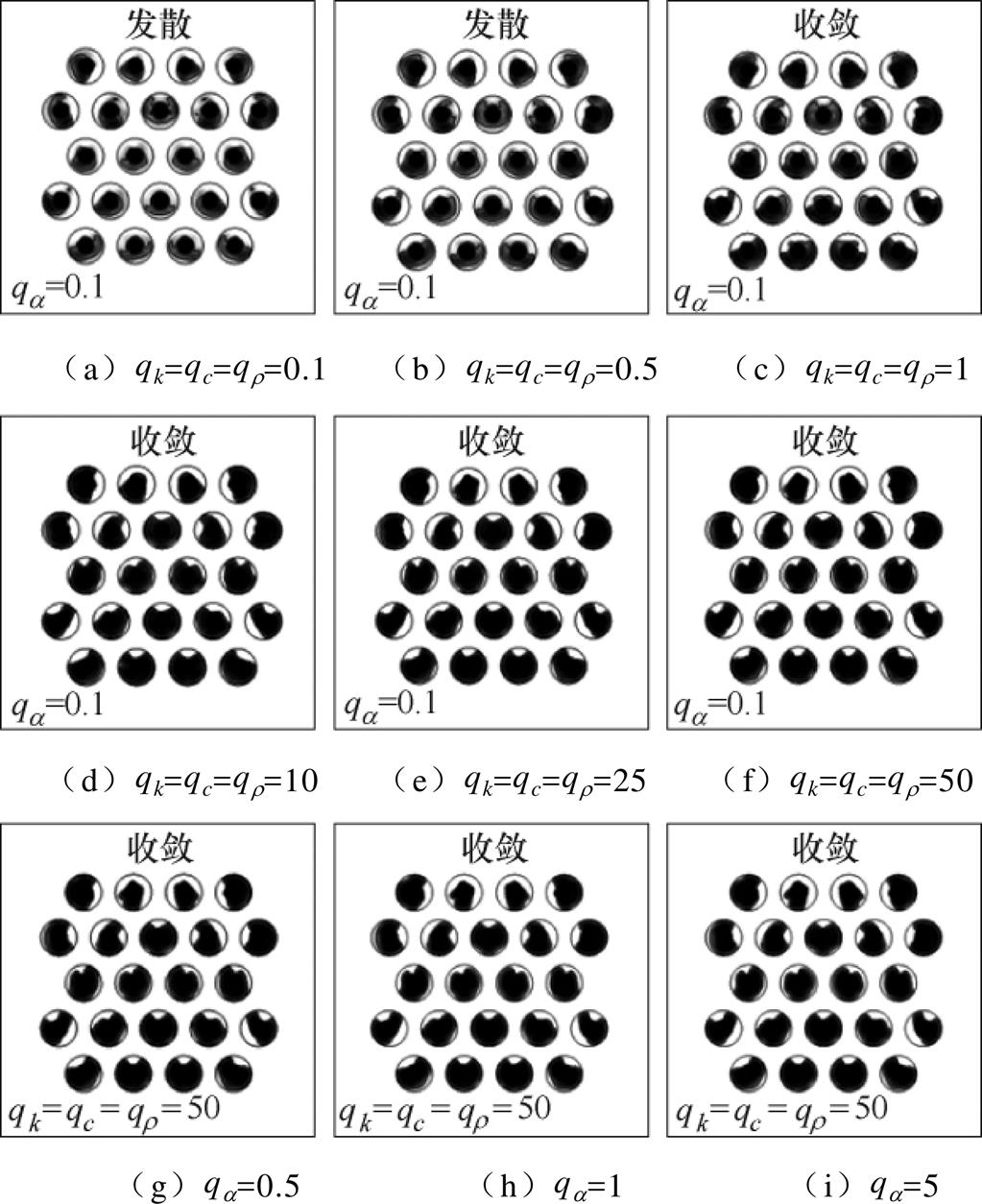
图9 惩罚因子对拓扑优化结果的影响
Fig.9 Topology optimization results affected by penalty factor
为了得到清晰的流-固边界，并避免产生局部最优解，采用连续变化迭代法，在迭代过程中逐渐增加惩罚因子。在迭代过程中分三步进行计算：①惩罚因子取值为qa=qk=qc=qr=0.1；②惩罚因子增大为qa=0.1、qk=qc=qr=10；③将惩罚因子设置为qa=0.5、qk=qc=qr=50。在保证模型的准确性的同时，减小了相对误差来提高模型的收敛性，连续变化迭代法迭代误差及收敛结果如图10所示。
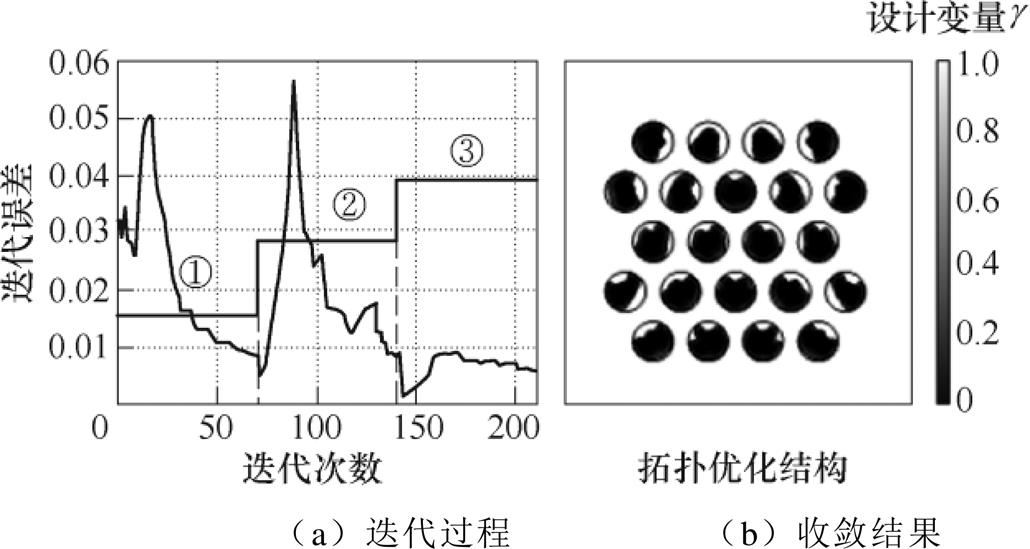
图10 连续变化迭代法迭代误差及收敛结果
Fig.10 Continuous variation iterative method iterative error and final result
下面详细分析材料约束因子q1和q2对求解结果的影响。分别取q2=0.4, 0.5, 0.6，q1=0.45, 0.55, 0.65时，拓扑优化结果，体积约束因子对拓扑优化结果的影响如图11所示。不断增大q1与q2值，固体域的体积始终收敛于约束因子的下限q2，验证了材料体积约束的可行性。选择q2=0.4和q1=0.45，以保证固体体积在相同情况下，自由分配材料，实现协同优化设计。
对于式（11）的加权因子w1和w2，当w1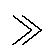
w2时，以散热器动能损耗最小为优化目标，当w2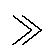w1时，以散热器结-流热阻最小为优化目标。分别设置加权因子为1、5和50，分析不同加权因子对拓扑优化结果的影响，结果如图12所示，图12中，DTj为平均温升，Pf为入口-出口的压降。当增大w1时，DPf在不断增大，但是也会增加DPf。需要注意的是，在不断提高加权因子w1的同时，输出材料体积因子也在不断增加，表明为了进一步降低动能损耗，固体域也在相应减少，与实际情况相符，证明多目标优化和材料约束条件的合理性。
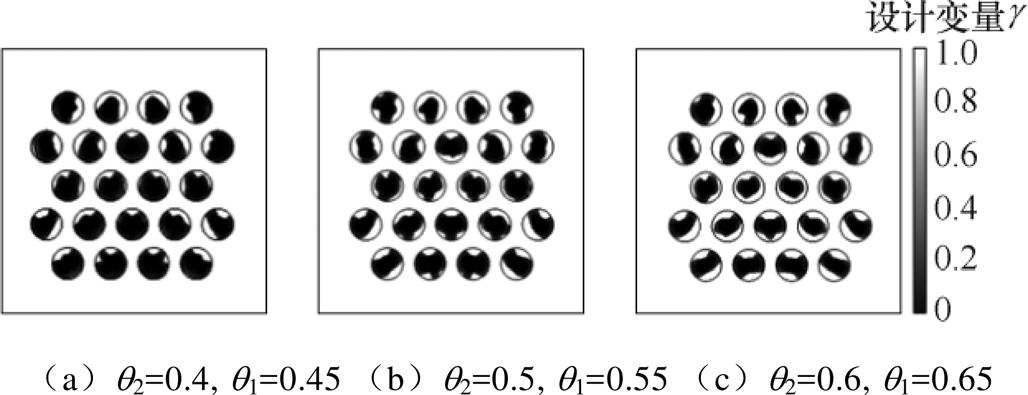
图11 体积约束因子对拓扑优化结果的影响
Fig.11 Topology optimization results affected by material volume factor
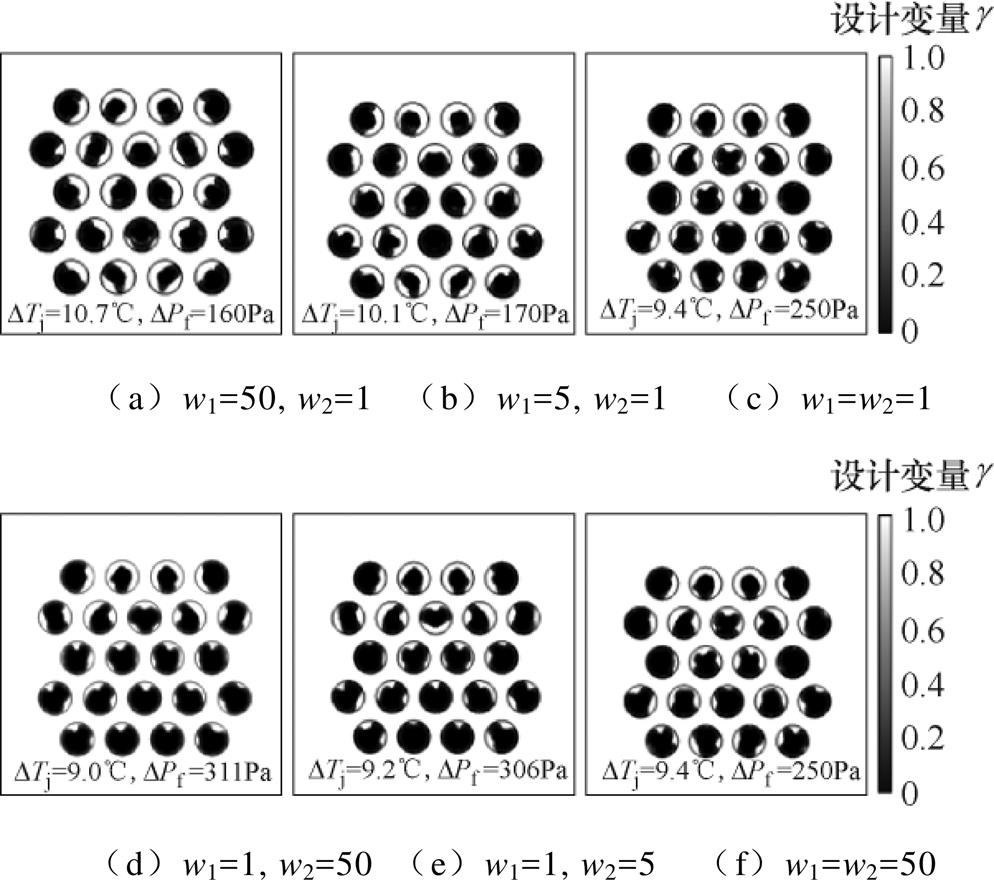
图12 多目标加权因子对拓扑优化结果的影响
Fig.12 Topology optimization results affected by multi-objective weights
考虑Pin-Fin对均温热源的耗散能力，当加权因子分别设置为w1=1和w2=50时，与商业化Pin-Fin相比，均匀热源下Pin-Fin优化前后的温度场、速度场和流体场分布如图13所示。
根据图13a，Pin-Fin优化前后，平均温度降低了1.8 ℃，优化前DTjmax为13.7 ℃，而优化后的DTjmax为11.8 ℃，证明了优化结果的有效性。根据图13b和图13c，传统圆柱Pin-Fin结构的尾部流速很低，尾迹区存在明显的回流现象，尾迹区的温度梯度变化非常小，不利于对流换热，降低了冷却液的利用效率。拓扑优化Pin-Fin结构改变了材料的空间分布，重构了流体的流速场，尾迹区得到拉伸，并且朝着强化换热的方向延展。由于上游Pin-Fin结构的改变，在流体场内产生了二次回流，加强了对流换热效果，形成了类似纵向涡流发生器的效果。
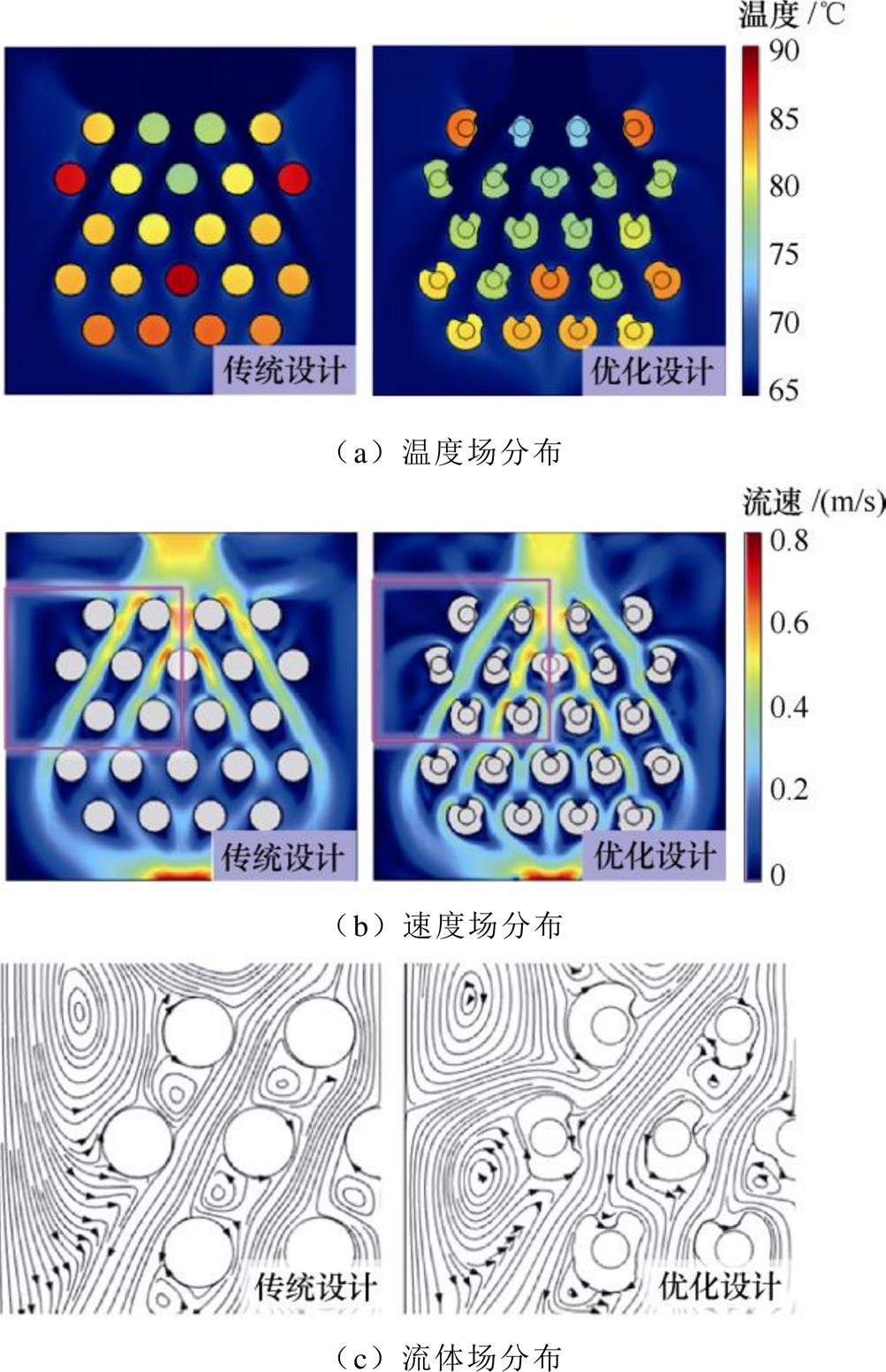
图13 均匀热源下Pin-Fin优化前后的多物理场分布
Fig.13 Multi-physics distribution before and after Pin-Fin optimization considering uniformed power dissipation
在车用功率逆变器中，功率芯片一般为不对称布局，不均匀热源设置对拓扑优化结果的影响如图14所示。为了实现Pin-Fin散热器的全局优化设计，需要考虑不均匀热源的影响。通常，芯片下方的热耗散功率高于其他区域，典型不均匀热源分布如图14a所示，拓扑优化结果如图14b所示。
相对于商业化Pin-Fin结构，不均匀热源下Pin-Fin优化前后温度场、速度场和流体场的分布如图15所示。拓扑优化方法可以根据不均匀热源分布，合理分配材料，实现整体热阻最小的目标。采用传统Pin-Fin和拓扑优化Pin-Fin，最高温度分别为90 ℃和85.6 ℃，降低4.4 ℃。拓扑优化Pin-Fin在入水口处减少材料分布，增加热耗散功率较高区域的流量，大幅度降低最高结温处的温度，验证了不均匀热源条件下，拓扑优化设计的有效性。
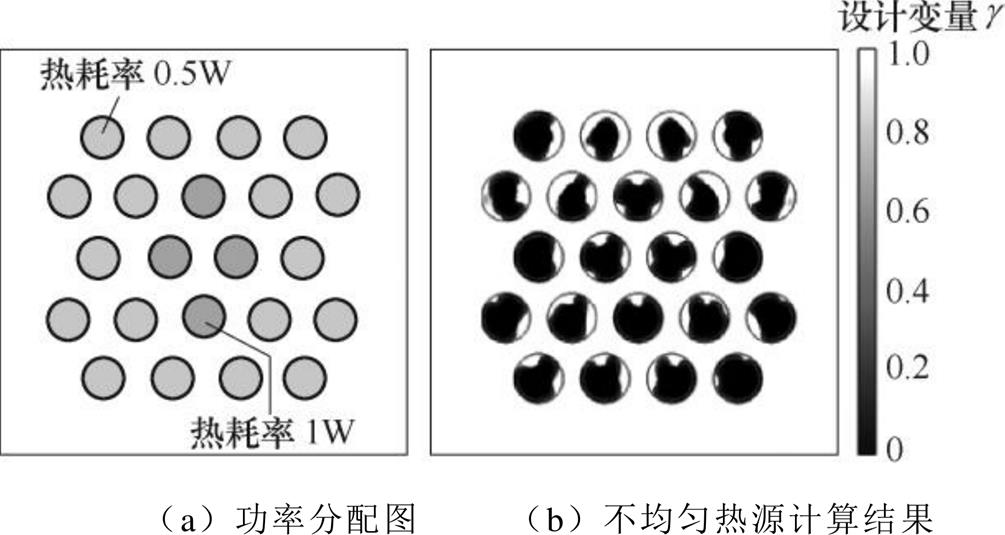
图14 不均匀热源设置对拓扑优化结果的影响
Fig.14 Influence of uneven heat source settings on topology optimization results
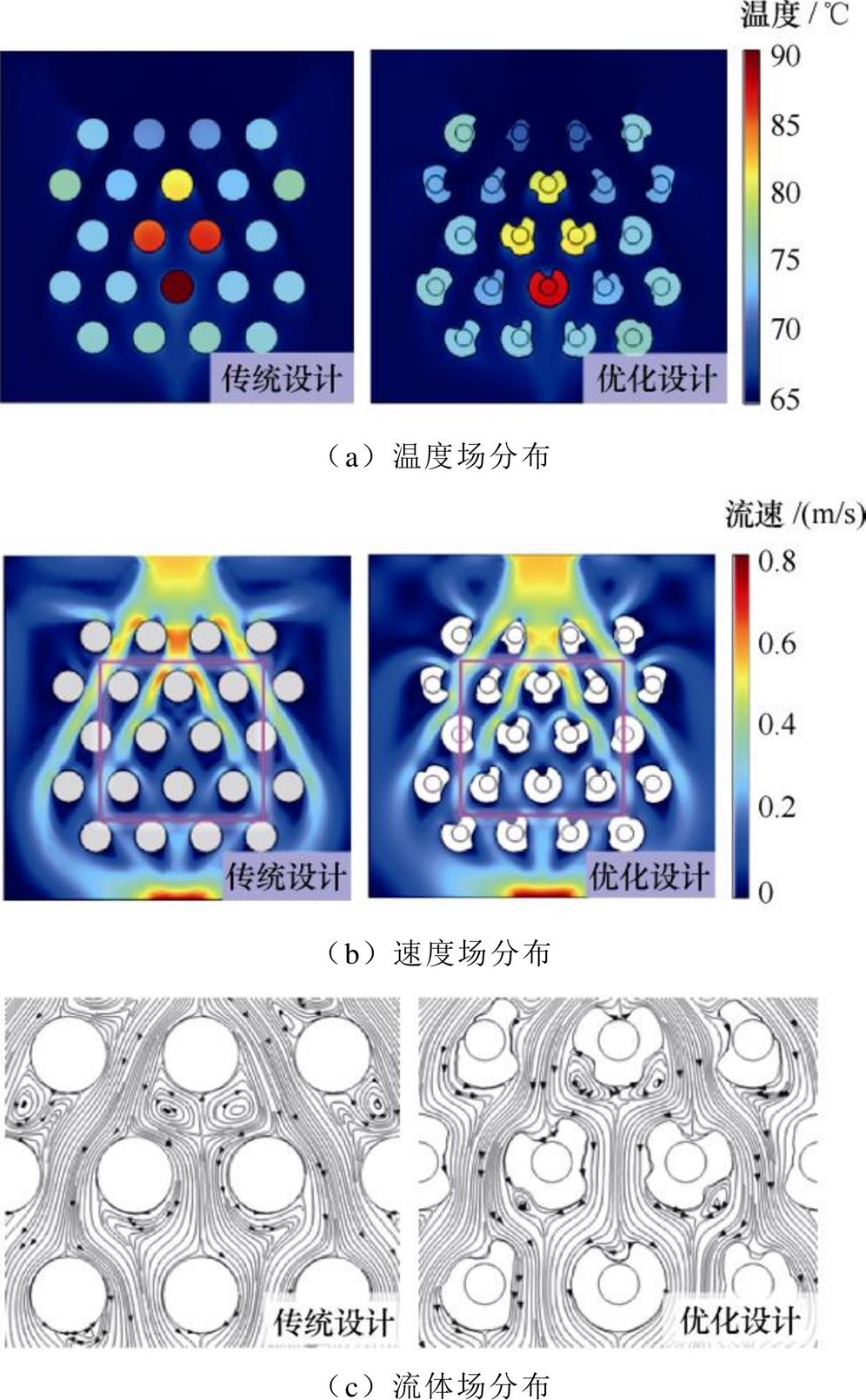
图15 不均匀热源下Pin-Fin优化前后的多物理场分布
Fig.15 Multi-physics distribution before and after Pin-Fin optimization considering unbalanced power dissipation
对于车用电机控制器，芯片结温的升高主要由IGBT和二极管的导通损耗和开关损耗组成。为实现散热器协同优化设计，需要建立功率模块的损耗模型[26]。
对于SVPWM，IGBT的导通损耗为
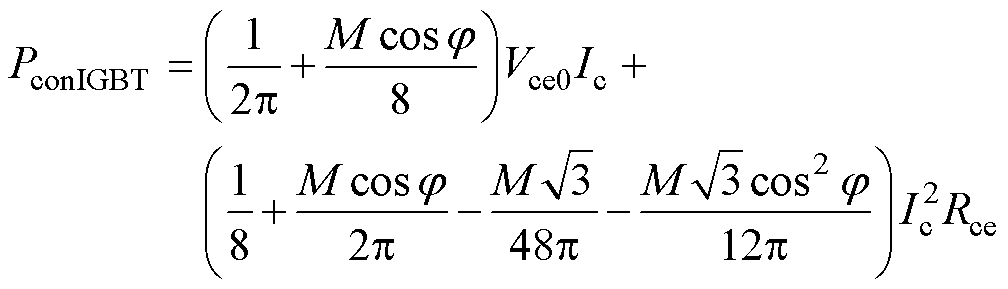（20）
式中，Vce0和Ic为IGBT的饱和压降和集电极电流；Rce为IGBT的导通电阻；M为调制比。IGBT的开关损耗为
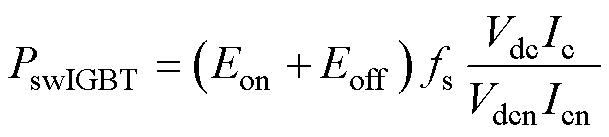（21）
式中，Eon和Eoff为IGBT的开通损耗和关断损耗；fs为开关频率；Vdc为直流母线电压；Vdcn和Icn分别为数据手册中开关断损耗测试所用的直流母线电压和集电极电流。对于SVPWM，二极管的导通损耗为
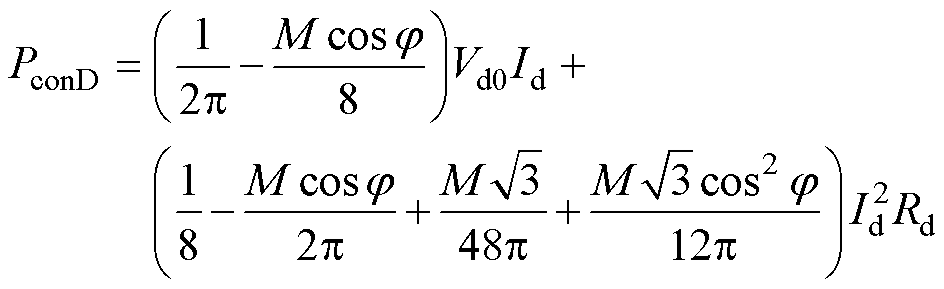（22）
式中，Vd0和Rd分别为二极管的门槛电压和导通电阻；Id为二极管的负荷电流。二极管的开关损耗主要为反向恢复损耗，可以表示为
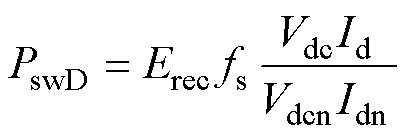（23）
式中，Erec为二极管的反向恢复损耗。
因此，以车用功率模块FS400R07A3E3为例，根据其数据手册，有：Vce0=0.75 V、Rce=2.3 mW、Vd0=0.82 V、Rd=1.7 mW、Eon=6.8 mJ、Eoff =12 mJ、Erec=6.9 mJ、Vdcn=300 V、Icn=Idn=400 A，当Vdc=50 V、Ic=Id=90 A、fs=10 kHz时，可以计算得到，IGBT的损耗为390 W，二极管的损耗为170 W。
功率模块的功率损耗分布如图16所示。由于热传递过程存在扩散角的影响，异质材料计算过于复杂，于是采用构建有限元模型求解，模型如图16a所示。设置IGBT和二极管的材料为硅，基板材料设置为铜，冷却液温度65 ℃，进行有限元求解。
从图16b Pin-Fin热通量分布可以看出，在芯片下方的热通量较高，在二维模型中需要分配更高的功率且由于芯片之间的热耦合同样也需要分配较高功率。将不均匀热通量分配给相应的二维模型（边界条件与三维模型相同）中便可得到拓扑优化结果。由于优化结构过于复杂，采用有限元软件对优化结构与传统结构进行仿真对比，如图17所示。其中冷却液流量为2.7 L/min，热源设置与模块功率损耗相同。拓扑优化结构如图17b所示，整个Pin-Fin排列布局呈现疏-密-疏的分布，在入口处和出口处流速较高且发热功率较低，因此Pin-Fin较为稀疏，以便增加中部区域发热最严重区域的流量，降低系统的整体热阻。
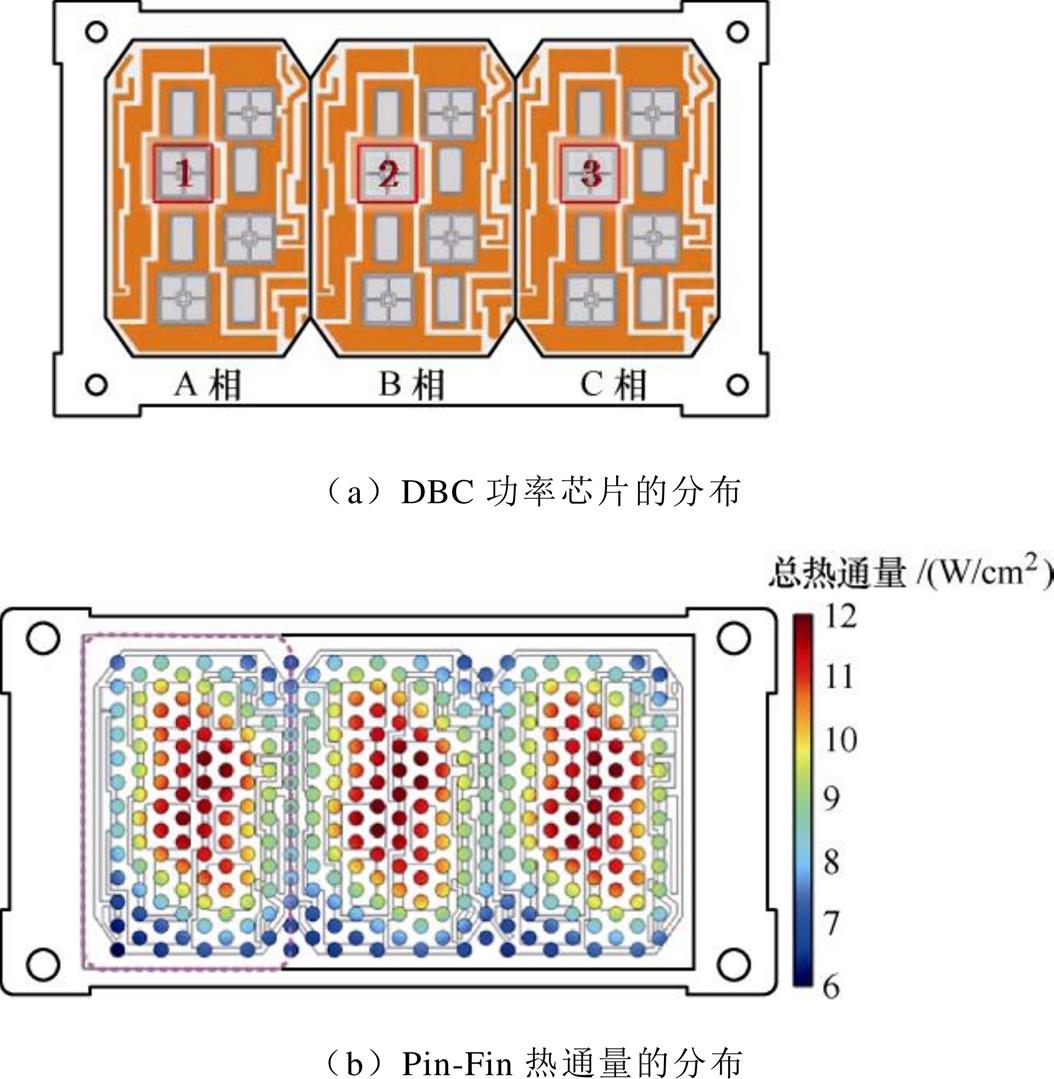
图16 功率模块的功率损耗分布
Fig.16 Power dissipation distribution in power module
优化前后有限元仿真结果如图17a、图17b所示，芯片的最大结温分别为90.4 ℃和86.3 ℃，可以明显看到优化结构的芯片结温小于传统设计。在传统设计中，芯片结温差异为5.5 ℃，优化设计芯片结温差异为1.2 ℃，改善了多芯片并联温度分布的一致性。芯片结温分布情况如图17c所示，优化Pin-Fin不仅可以降低芯片结温，也可降低芯片结温差异，提高冷却液利用效率。
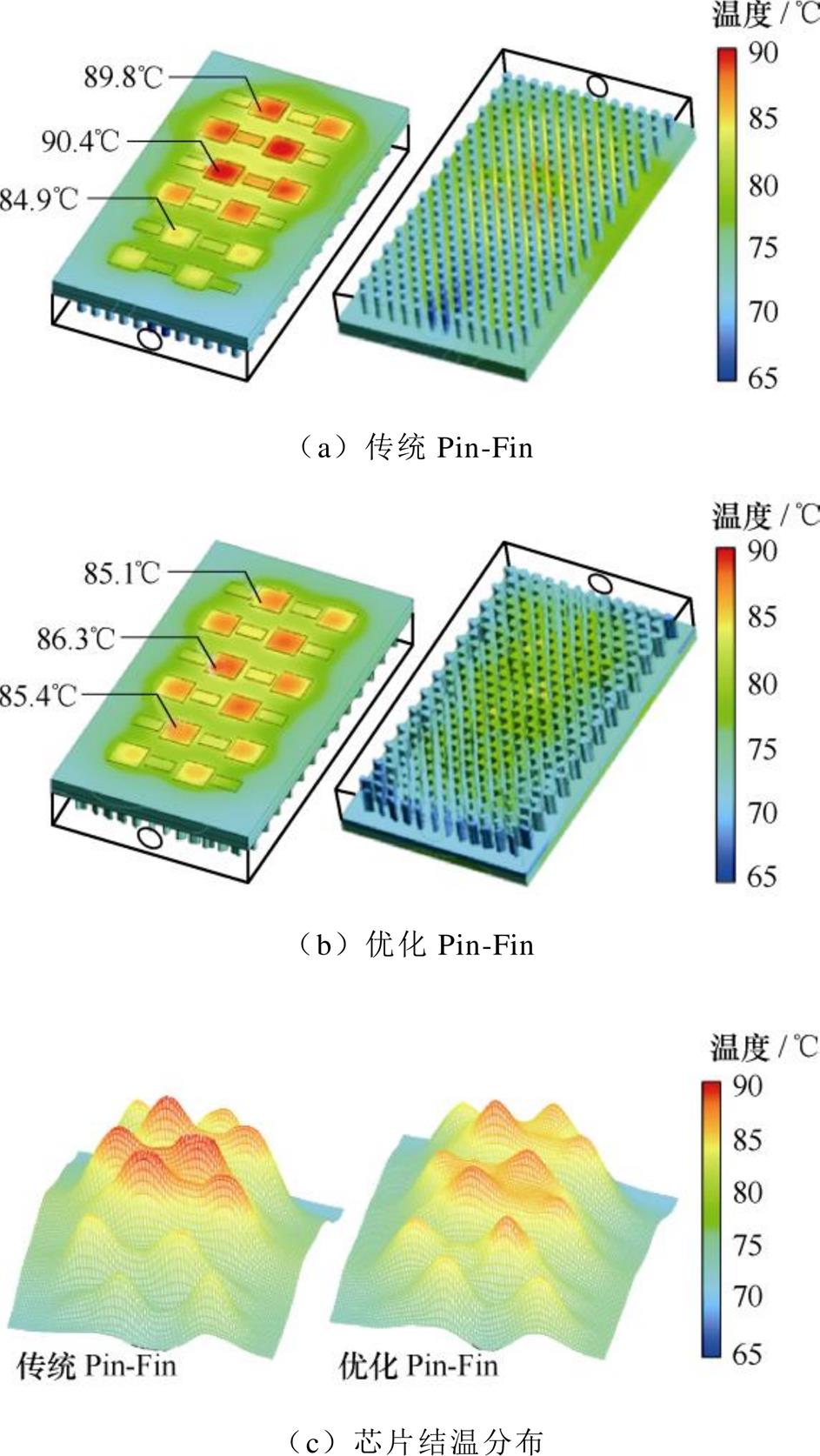
图17 传统Pin-Fin与优化Pin-Fin有限元仿真结果对比
Fig.17 Comparison of finite element simulation results between traditional Pin-Fin and optimized Pin-Fin
为了评估Pin-Fin的性能，搭建了车用电机控制器模拟平台，如图18所示。被测功率模块FS400R07A3E3用作电机控制器，对拖功率模块用于模拟电机。根据电动汽车的实际工况，给定电机控制器的转速和转矩。功率在两个逆变器之间循环流动，直流电源仅需提供很小的损耗功率，即可实现较大功率的模拟加载。采用红外热成像仪监测功率芯片的结温，采用电磁流量计测量循环液的流量，在水冷槽的进-出水口放置压力计，测量Pin-Fin的冷却液压降。
为了验证基于拓扑优化方法设计的Pin-Fin散热器设计，针对英飞凌公司FS400R07A3E3功率模块，通过金属3D打印技术，采用铝合金材料研制了如图19所示的电机控制器样机。
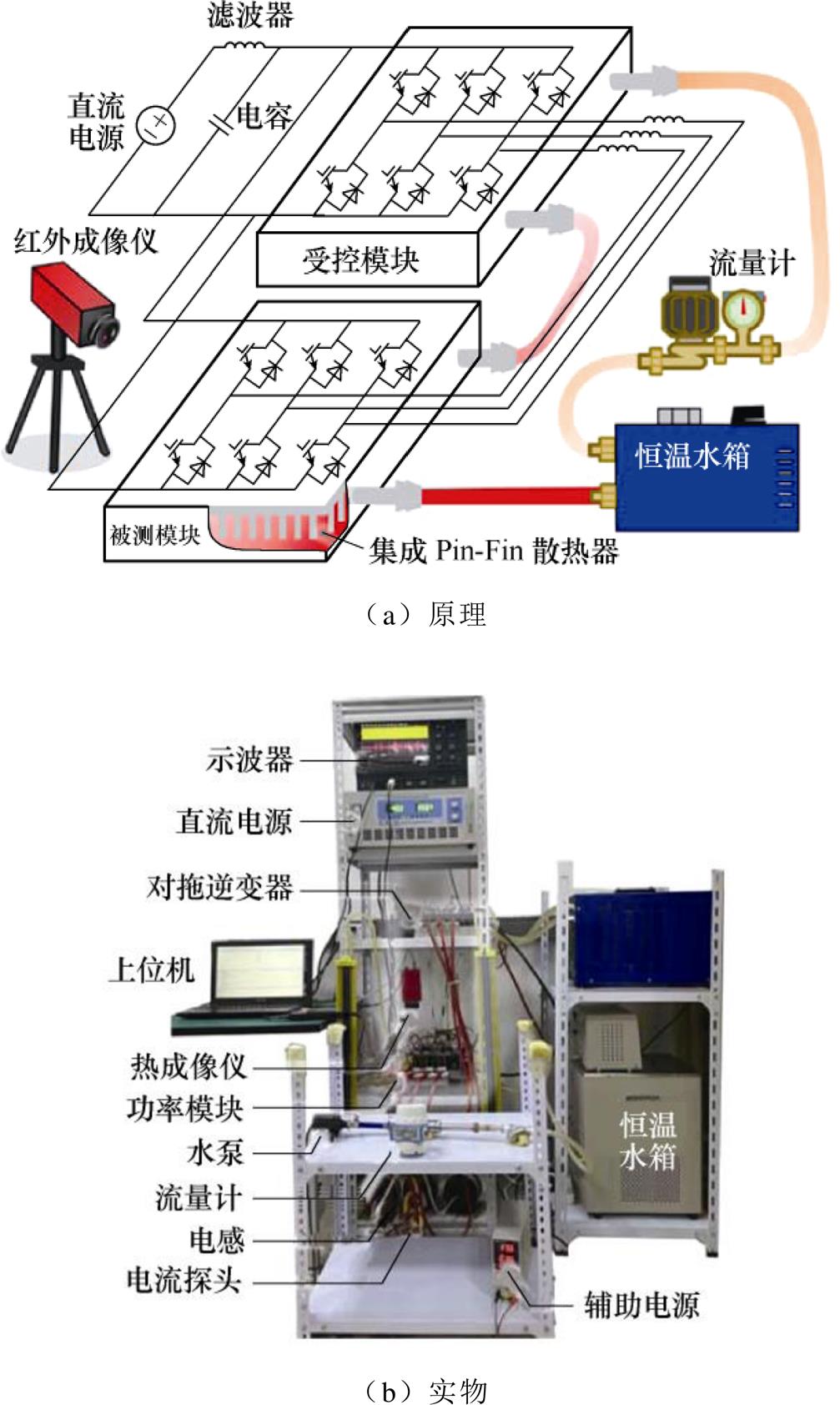
图18 面对面变流器三相对拖实验原理
Fig.18 Schematic diagram of front-to-front converter
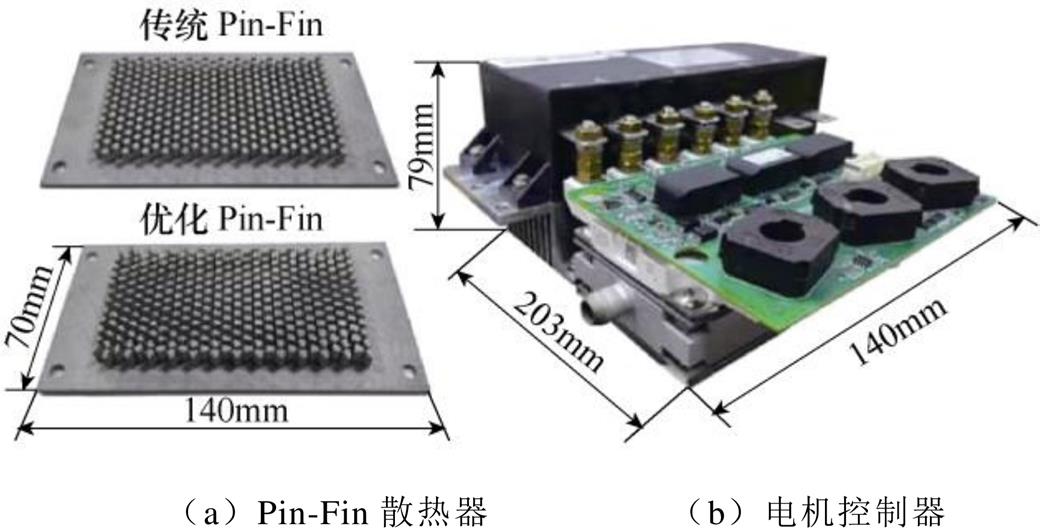
图19 Pin-Fin散热器和电机控制器样机
Fig.19 Prototypes of Pin-Fin heatsink and power control unit
在母线电压350 V、负荷电流90 A、冷却液流量2.7 L/min条件下，电压电流波形及功率模块的稳态温度分布，如图20所示。在相同条件设置下，以A、B、C三相的IGBT芯片为例，不同Pin-Fin散热器功率模块的瞬态结温分布如图21所示。可见，对于传统Pin-Fin，芯片之间存在明显的温度梯度，B相芯片居于模块中心，由于热耦合，结温最高；A相芯片靠近入水口，环境温度最低，结温最低，芯片结温差异接近5 ℃，如图21a所示；相反，采用优化Pin-Fin，芯片之间的温度梯度小于1 ℃，如图22b所示，芯片之间的结温差异降低80 %。此外，相对于传统Pin-Fin，优化Pin-Fin能降低芯片结温5 ℃。因此，优化Pin-Fin设计可以降低芯片结温差异和结温幅值，提高冷却液的利用效率和功率模块的预期寿命。改变负荷电流大小，不同负荷电流下功率模块的结温实验结果，如图22所示。可见，随着负荷电流增加，电机控制器的损耗功率增加，芯片结温也在不断升高。与传统Pin-Fin相比，采用优化后的Pin-Fin，芯片结温最高下降6 ℃。
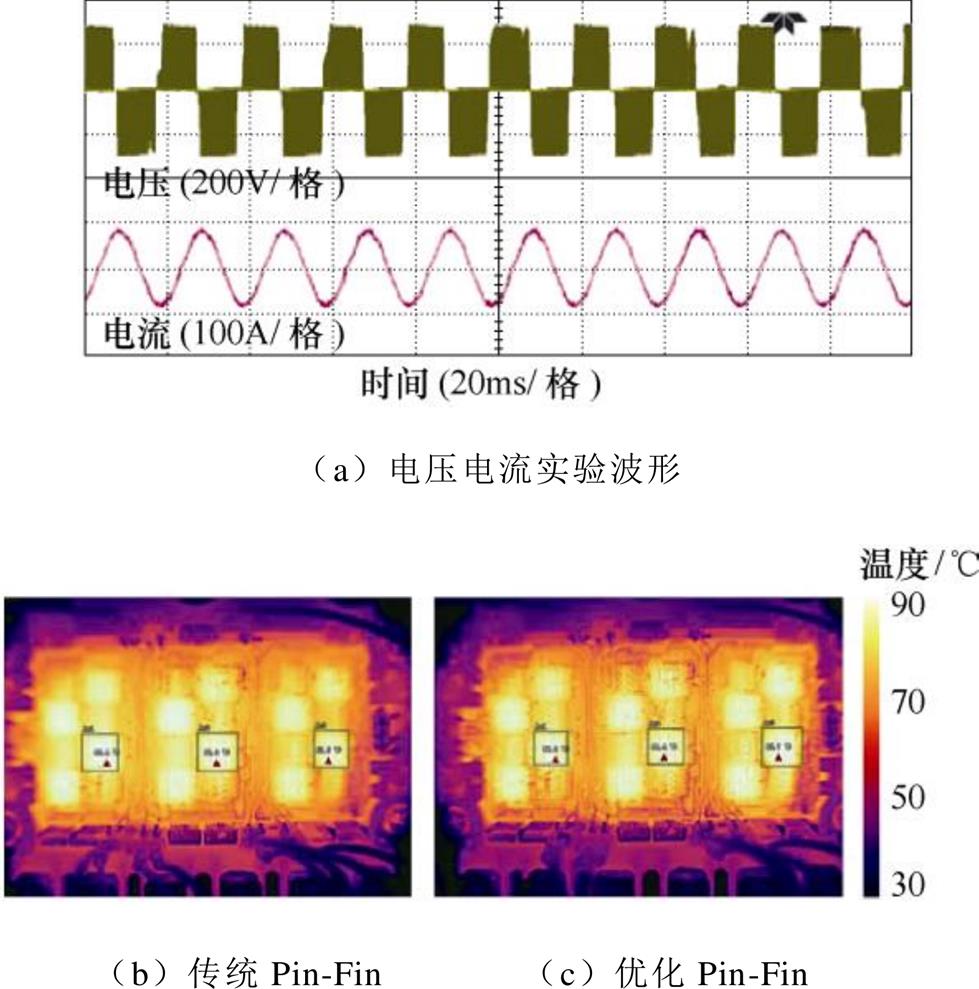
图20 不同直流母线电压下功率模块的结温实验结果
Fig.20 Experimental results of junction temperature of power module under different DC-link voltages
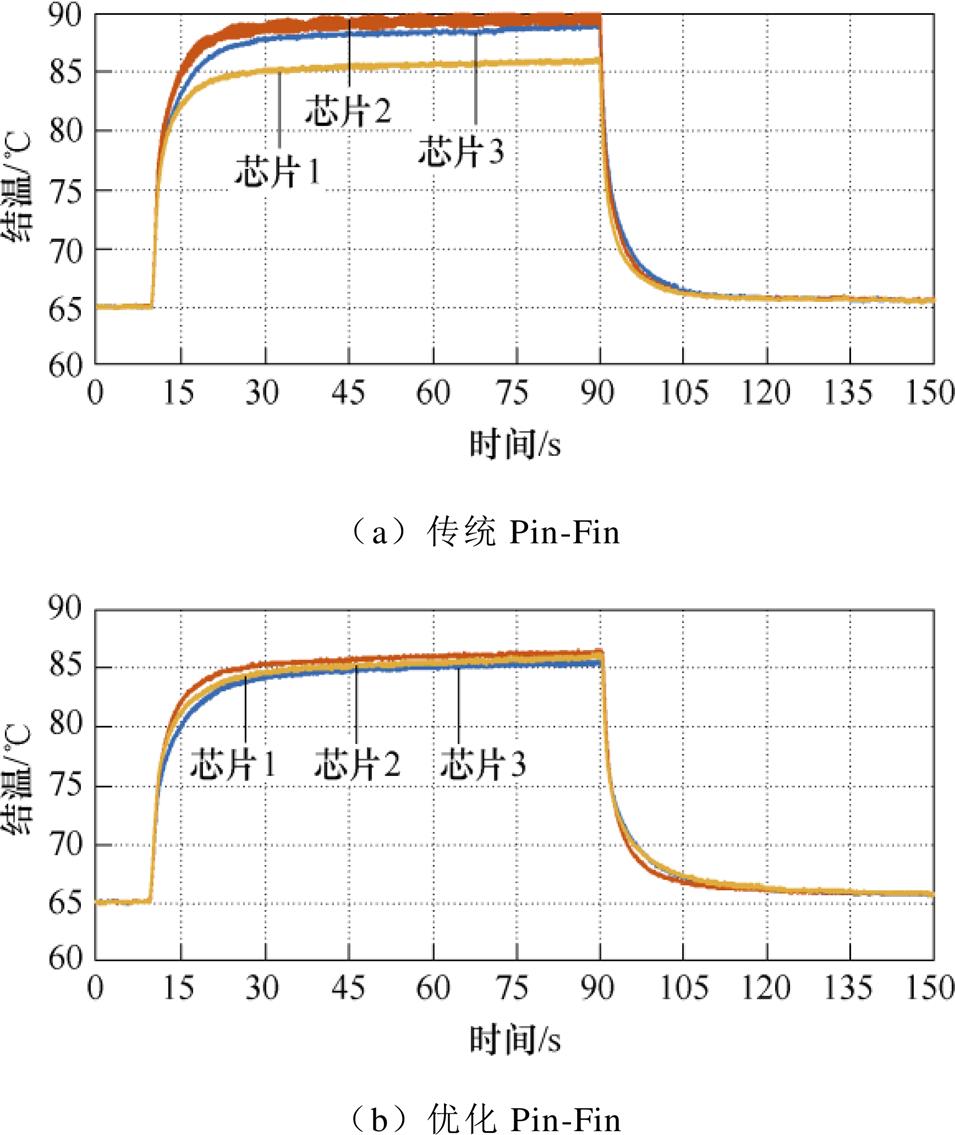
图21 不同Pin-Fin散热器功率模块的瞬态结温分布
Fig.21 Experimental results of junction temperature of power module using different Pin-Fins
维持负荷电流135 A、流量2.7 L/min，改变母线电压，功率模块温度最高的芯片2的结温分布，如图23所示。可见，随着母线电压的提高，模块损耗的提高，芯片结温也不断升高。采用优化的Pin-Fin散热器，可以大幅度降低芯片的结温，提升模块的寿命。
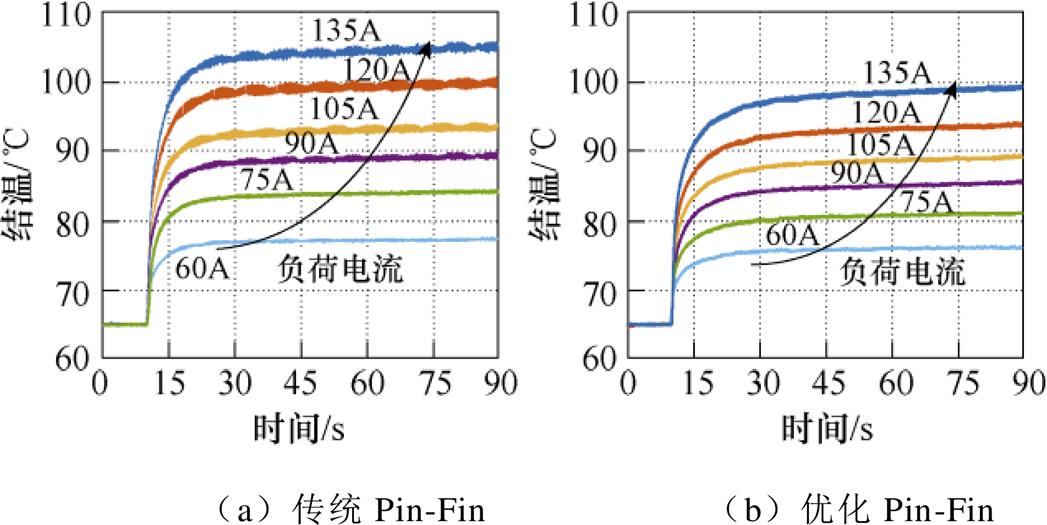
图22 不同负荷电流下功率模块的结温实验结果
Fig.22 Experimental results of junction temperature of power module under different load currents
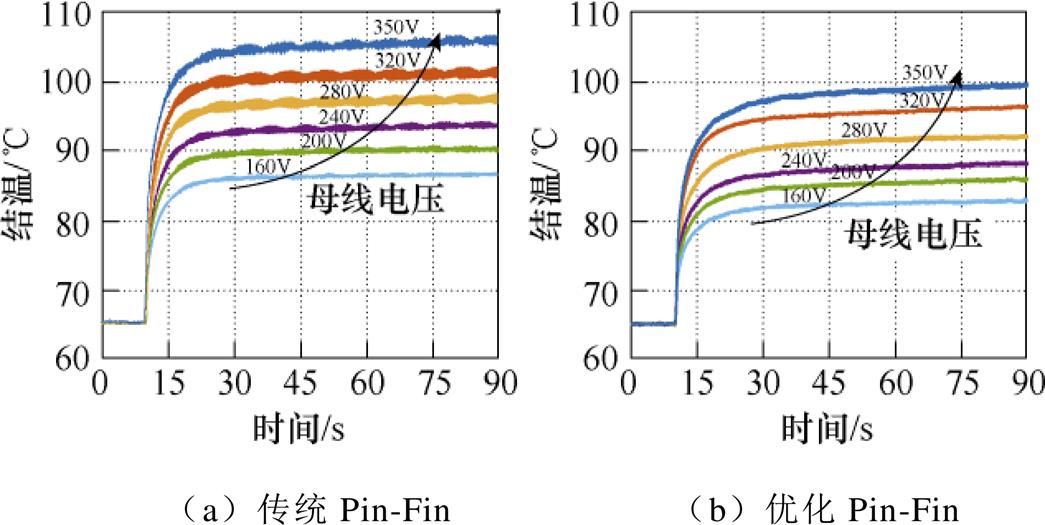
图23 不同母线电压下功率模块的结温实验结果
Fig.23 Experimental results of junction temperature of power module under different DC-link voltages
综上所述，当流量为2.7 L/min时，母线电压和负荷电流与芯片温升DTj之间，呈线性关系，置信度均在95 %以上，不同负荷电流和母线电压与芯片温升的关系如图24所示，可以描述为
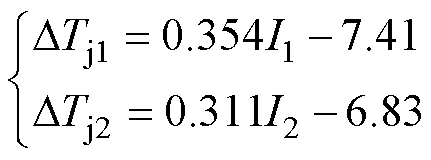（24）
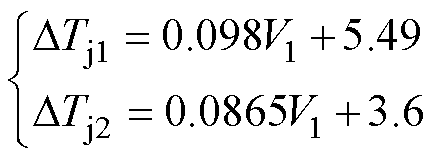（25）
式中，DTj1、I1和V1为传统Pin-Fin结构的芯片温升、负荷电流和母线电压；DTj2、I2和V2为优化Pin-Fin结构的芯片温升、负荷电流和母线电压。
维持直流母线电压350 V、负荷电流峰值90 A，改变冷却液流量，芯片2的结温，流量对散热器热阻和结温的影响如图25所示。可见，流量越大，结温越低，换热效率越高。与传统Pin-Fin相比，优化Pin-Fin显著降低了芯片结温。
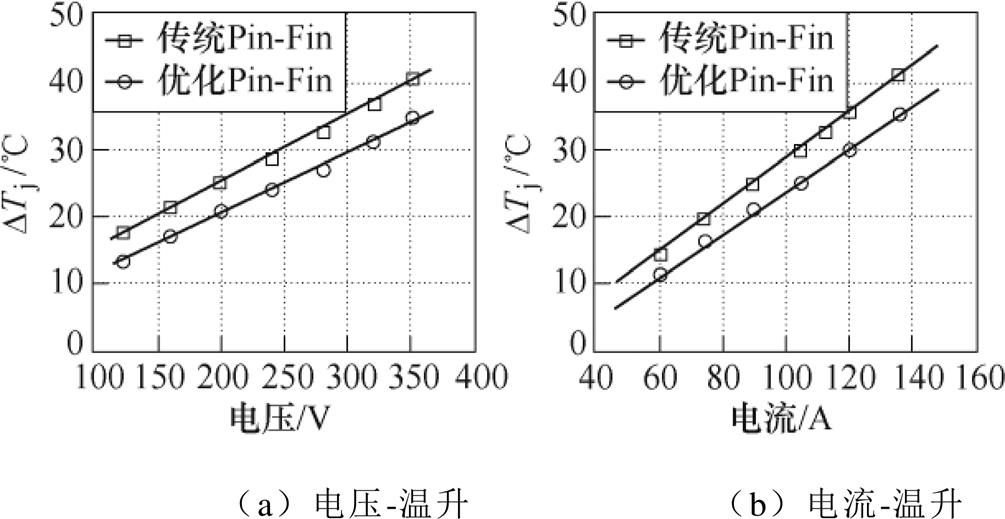
图24 不同负荷电流和母线电压与芯片温升的关系
Fig.24 Relationship between junction temperature rise and load current or DC-link voltage
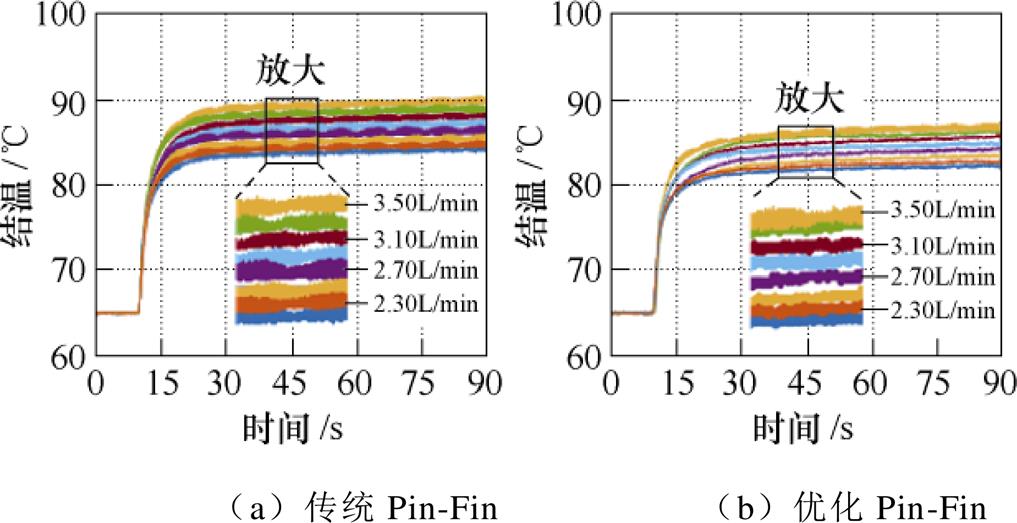
图25 流量对散热器热阻和结温的影响
Fig.25 Thermal resistance and presure drop of heat-sinks affected by flow rate
此外，得到冷却液流量对芯片结-流热阻和Pin- Fin压降的影响，如图26所示。随着流量增加，芯片结-流热阻降低，Pin-Fin压降增加，有
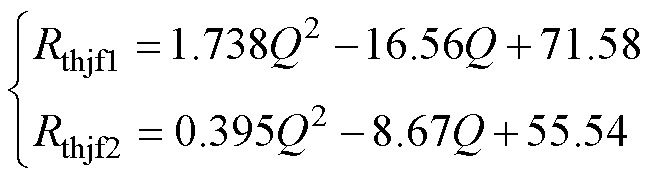（26）
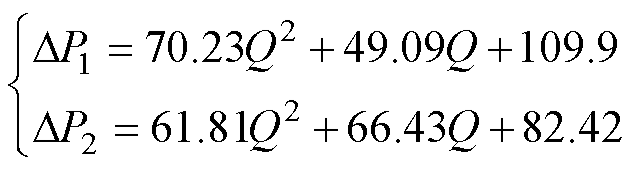（27）
式中，Q为冷却液流量；Rthjf1和Rthjf2分别为传统和优化Pin-Fin的结-流热阻；ΔP1和ΔP2分别为传统和优化Pin-Fin的冷却液压降。当Q=3 L/min时，对于传统Pin-Fin，Rthjf1=37.54 K/kW，ΔP1=889.24 Pa；对于优化Pin-Fin，Rthjf2=33.05 K/kW，ΔP2=838 Pa。相对于传统Pin-Fin，优化Pin-Fin的热阻降低12 %，压降减小约50 Pa，意味着在同等泵送功率下，优化Pin-Fin可以获得更好的散热效果。
综上所述，拓扑优化后的Pin-Fin散热器，可以有效降低结-流热阻，减小芯片之间的温度梯度，提高冷却液的利用效率，验证了优化方法的可行性和有效性。
为进一步验证所提设计方法的有效性，本文通过金属3D打印的方法，制备了菱形、三角形和水滴形[27]结构的Pin-Fin散热器如图27所示，各项参数均参见图27，排列布局与传统Pin-Fin完全相同。
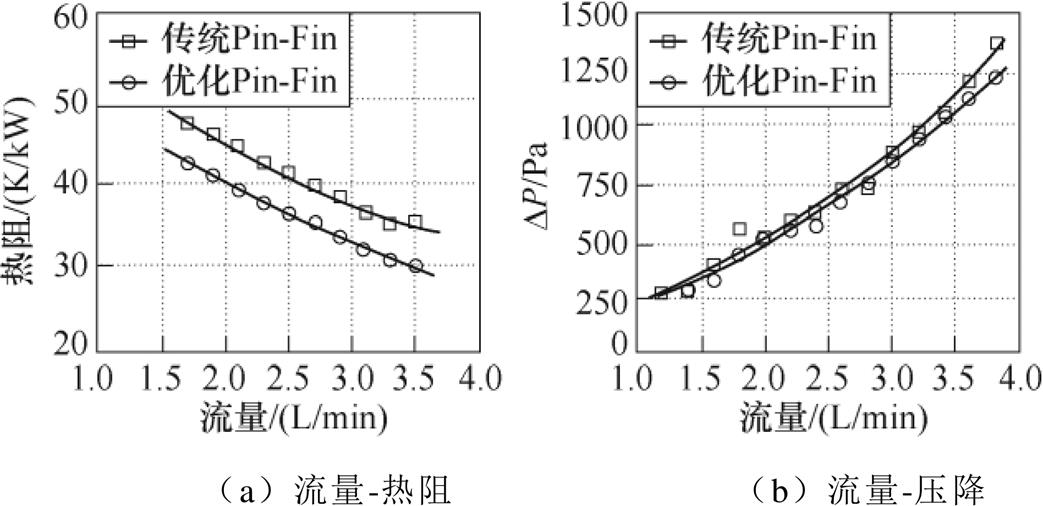
图26 流量对散热器热阻和压降的影响
Fig.26 Thermal resistance and presure drop of heat-sinks affected by flow rate
图27 菱形-三角形-水滴形Pin-Fin散热器
Fig.27 Prototypes of diamond-triangle-teardrop shape Pin-Fin heatsink
计及不同母线电压、负荷电流的情况下，得到了如图28所示的不同母线电压和负荷电流下功率模块的结温实验结果。在2.7 L/min的流量条件下，控制负荷电流为135 A，随着母线电压和负荷电流的不断增加，电机控制器的损耗功率在不断增加，芯片结温也在不断升高，不同形貌结构的散热器一致性明显。
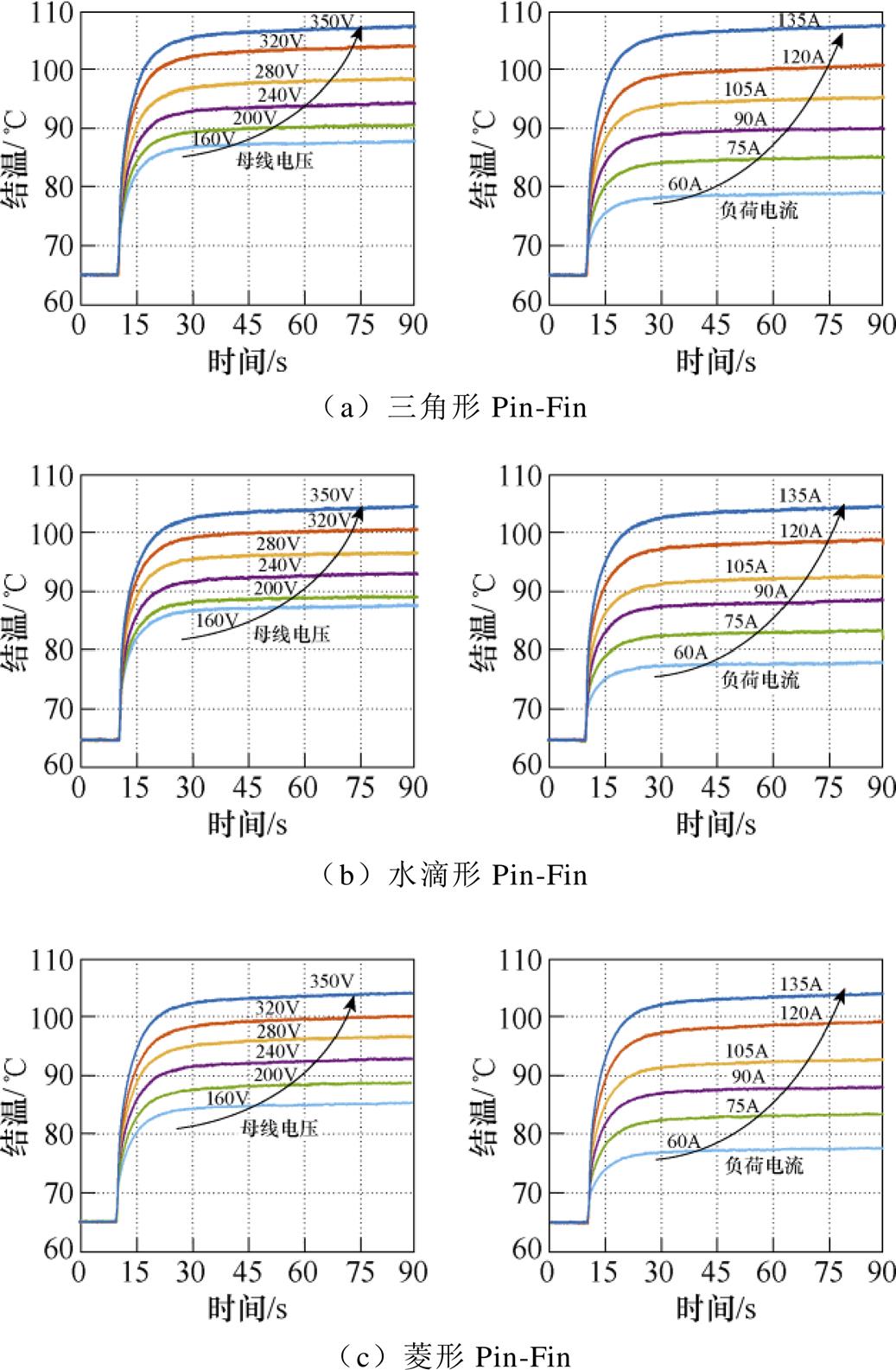
图28 不同母线电压和负荷电流下功率模块的结温实验结果
Fig.28 Experimental results of junction temperature of power module under DC-link voltages different load currents
得到的电压-电流与芯片结温的关系如图29所示。图中，水滴形结构与传统圆形结构的电压-结温特性基本相同，图中两种结构线也基本重合；而优化后的三角形结构反而会增加芯片结温，不利于电机控制器的可靠运行；菱形结构则优于传统圆形Pin-Fin结构。在母线电压350 V和负荷电流135 A的情况下，传统Pin-Fin的芯片结温为40.5 ℃；而菱形结构则为39.2 ℃，结温降低约1.3 ℃。即使是最优的菱形结构，结温降低方面仍然低于本文所提出的优化结构，验证了设计方法的有效性。
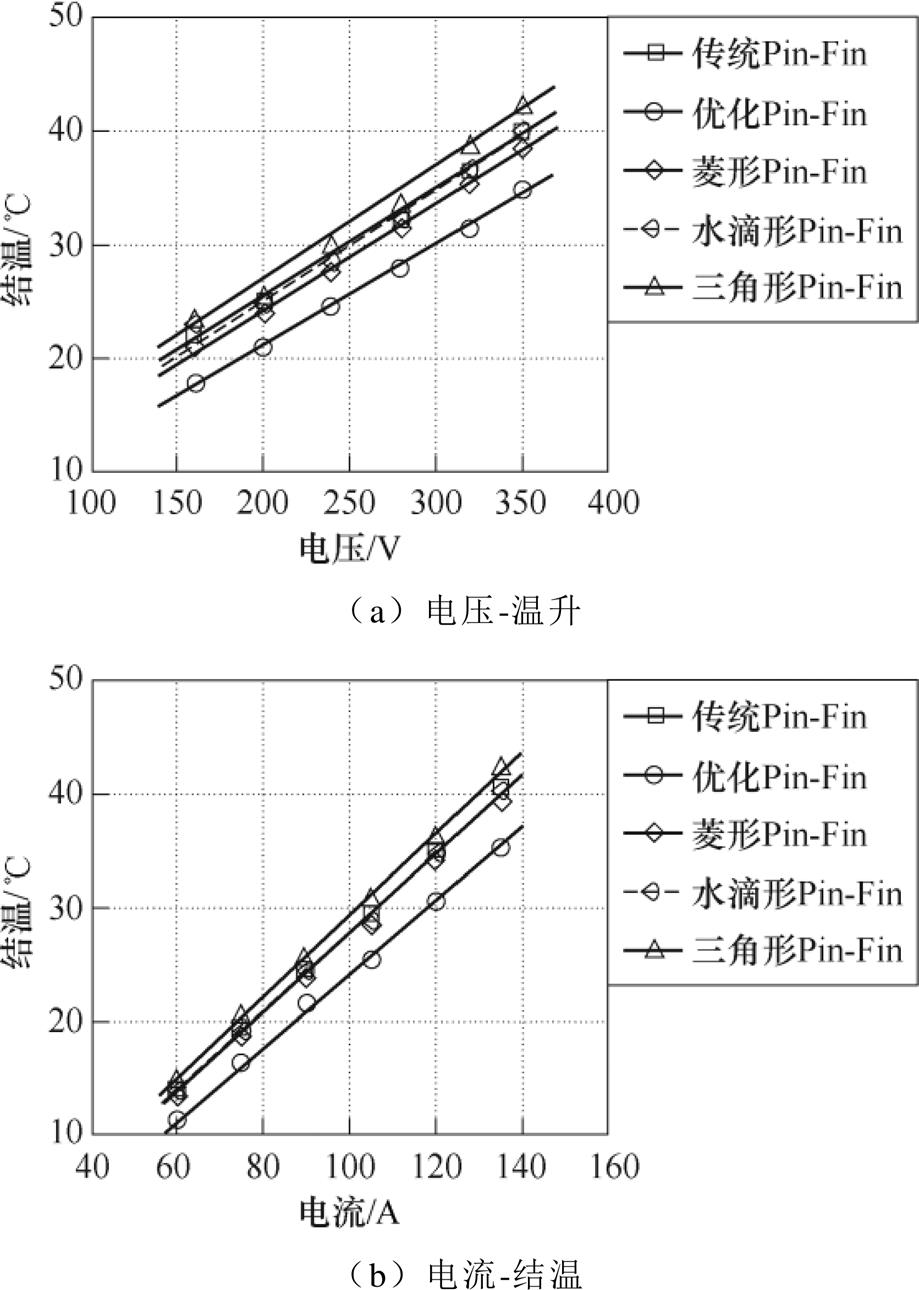
图29 不同负荷电流和母线电压与芯片结温的关系
Fig.29 Relationship between junction temperature rise and load current or DC-link voltage
相较于传统结构，菱形结构可有效增加换热面积，降低功率模块的热阻。于是采用效果较优的菱形结构与优化前后的Pin-Fin结构进行实际运行工况下的结温波动实验，电机控制器在30 min内的电-热特性，如图30所示。由于实际工况的波动性，负荷电流幅值持续波动。此外，采用优化后的Pin-Fin，芯片结温降低7～8 ℃，菱形结构结温降低约1～2 ℃，优化效果并不明显。
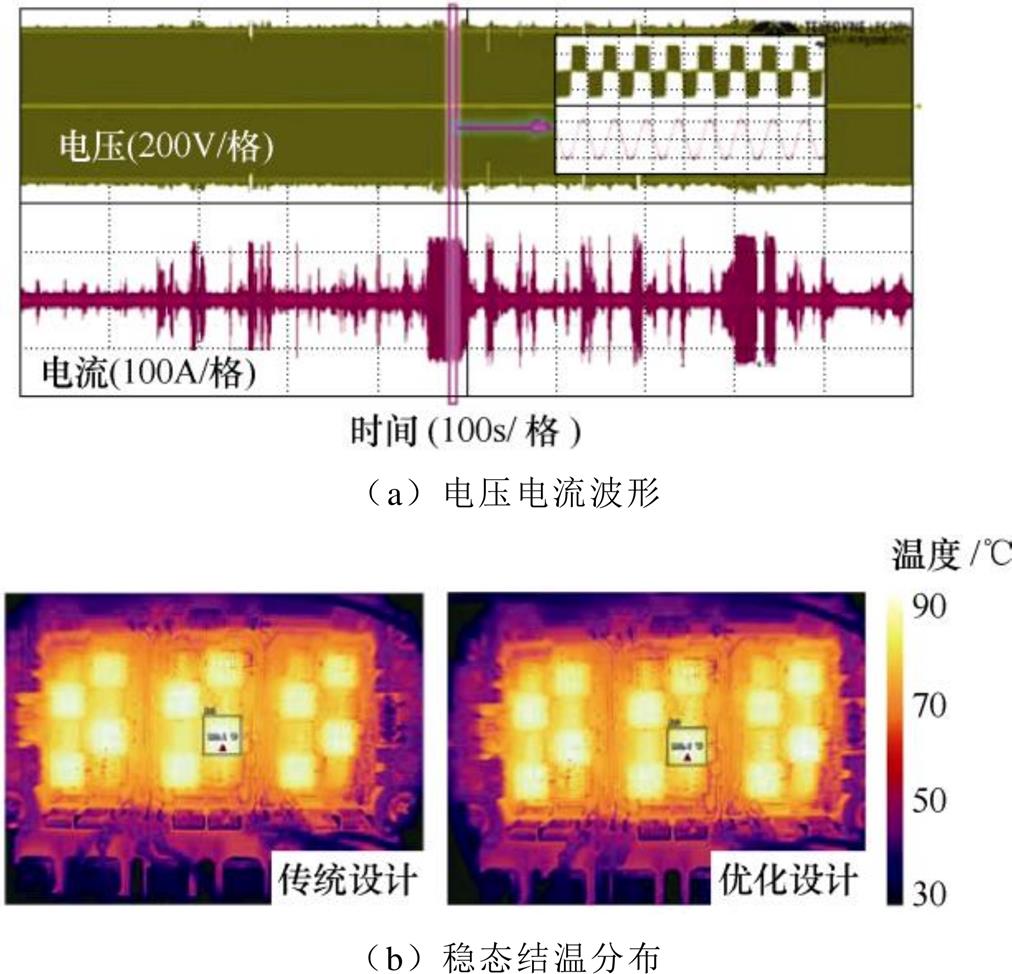
图30 实际工况下电压电流波形和芯片结温分布
Fig.30 Voltage and current waveforms and junction temperature distribution under real mission profile
优化Pin-Fin前后，实际工况下不同Pin-Fin的对比实验结果如图31所示。可见，采用优化Pin-Fin散热器，芯片结温显著降低。采用传统Pin-Fin，芯片最高结温和平均温升分别为110 ℃和74.8 ℃，采用优化Pin-Fin后，芯片最高结温和平均温升降至102.8 ℃和73.3 ℃。采用优化Pin-Fin，芯片最高结温降低7.2 ℃，可以有效提升车用电机控制器的寿命。相较于优化Pin-Fin，菱形Pin-Fin的优化效果并不明显，最高结温降低大约为1.7℃。综上所述，本文提出的优化设计方案可明显降低芯片结温波动，提升车用电机控制器的可靠性。
图31 实际工况下不同Pin-Fin的对比实验结果
Fig.31 Experimental results of compared Pin-Fins under real mission profile
集成Pin-Fin散热器能够降低车用功率模块的结-流热阻，提高车用电机控制器的可靠性。Pin-Fin散热器的设计面临电-热-流多物理场耦合的挑战，传统参数设计方法难以定量表征形貌结构，亟需有效的基础理论模型和定量设计方法。针对Pin-Fin形貌结构的设计难题，本文基于拓扑优化方法，将形貌结构设计问题，转换为低维度多目标优化模型，以结-流热阻和冷却液压降为优化目标，提出了Pin-Fin形貌结构的设计方法，对标商业化车用功率模块，基于大量的实验结果和仿真设计，验证了模型和方法的有效性，可以得到以下结论：
1）惩罚因子是影响拓扑优化的主要因素。增大惩罚因子会加强收敛性，但是会陷入局部最优解；减小惩罚因子能避免局部最优解，但是会模糊流-固边界。采用连续变换法，可以提高模型收敛性，并避免陷入局部最优解。此外，构建多目标优化模型，可以根据设计目标，加快设计速度，降低研发周期和成本，实现Pin-Fin形貌结构的定制化设计。
2）基于拓扑优化的Pin-Fin结构，可以提高冷却液的利用效率，降低芯片结温，以及芯片之间的温度梯度，实现热-流协同设计。通过拓扑优化方法，综合考虑入水口与出水口的影响，分配不均匀功率，得到了全新的Pin-Fin形貌结构。基于大量的实验证明了所提出的设计方法的有效性。实验结果表明，采用拓扑优化设计的Pin-Fin散热器，各芯片之间的温度梯度小于1 ℃。
3）与传统结构相比，优化后的Pin-Fin结构可以降低功率模块12 %的结-流热阻，在实际工况中可以降低15.3 %的平均温升，降低7.2 ℃的最大温升。详细对比了其他形貌结构以及参数设计方法，实验结果均验证了本文提出的拓扑优化方法在提升功率模块热管理性能、降低模块热阻以及车用电机控制器可靠性方面的应用前景。
参考文献
[1] Bhunia A, Chen C L. Jet impingement cooling of an inverter module in the harsh environment of a hybrid vehicle[C]//ASME Summer Heat Transfer Conference, San Francisco, USA, 2009: 561-567.
[2] 曾正, 欧开鸿, 吴义伯, 等. 车用双面散热功率模块的热-力协同设计[J]. 电工技术学报, 2020, 35(14): 3050-3064.
Zeng Zheng, Ou Kaihong, Wu Yibo, et al. Thermo- mechanical co-design of double sided cooling power module for electric vehicle application[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(14): 3050-3064.
[3] Narumanchi S. Thermal management and reliability of power electronics and electric machines[C]//IEEE 3D-PEIM, Raleigh, USA, 2016: 1-13.
[4] 付和平, 陈杰, 邱瑞昌, 等. 电力电子变流装置散热器状态智能预测方法[J]. 电工技术学报, 2021, 36(20): 4350-4358.
Fu Heping, Chen Jie, Qiu Ruichang, et al. Intelligent prediction method for thermal dissipation state of heatsink in power electronic converter[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(20): 4350-4358.
[5] Chang S W, Yang T L, Huang C C, et al. Endwall heat transfer and pressure drop in rectangular channels with attached and detached circular Pin-Fin array[J]. International Journal of Heat and Mass Transfer, 2008, 51(21-22): 5247-5259.
[6] Chai Lei, Xia Guodong, Wang Huasheng. Numerical study of laminar flow and heat transfer in micro- channel heat sink with offset ribs on sidewalls[J]. Applied Thermal Engineering, 2016, 92: 32-41.
[7] Ostanek J K, Thole K A. Effect of streamwise spacing on periodic and random unsteadiness in a bundle of short cylinders confined in a channel[J]. Experiments in Fluids, 2012, 53(6): 1779-1796.
[8] Culham J R, Muzychka Y S. Optimization of Pin-Fin heat sinks using entropy generation minimization[J]. IEEE Transactions on Components and Packaging Technologies, 2001, 24(2): 159-165.
[9] Chiang K T, Chou C C, Liu N M. Application of response surface methodology in describing the thermal performances of a Pin-Fin heat sink[J]. International Journal of Thermal Sciences, 2009, 48(6): 1196-1205.
[10] Lee T Y. Design optimization of an integrated liquid- cooled IGBT power module using CFD technique[J]. IEEE Transactions on Components and Packaging Technologies, 2000, 23(1): 55-60.
[11] Menrath T, Rosskopf A, Simon F B, et al. Shape optimization of a pin fin heat sink[C]//IEEE SEMI- THERM, San Jose, USA, 2020: 10-16.
[12] Gupta D, Saha P, Roy S. Numerical investigation on heat transfer enhancement with perforated Square micro-Pin Fin heat sink for electronic cooling application[C]//IEEE EPTC, Singapore, 2019: 241- 246.
[13] Kosar A, Peles Y. Micro scale pin fin heat sinks: parametric performance evaluation study[J]. IEEE Transactions on Components and Packaging Tech- nologies, 2007, 30(4): 855-865.
[14] Xie Gongnan, Song Yidan, Asadi M, et al. Opti- mization of Pin-Fins for a heat exchanger by entropy generation minimization and constructal law[J]. Journal of Heat Transfer, 2015, 137(6): 061901.
[15] Chang S, Wu P, Cai Weiling, et al. Experimental heat transfer and flow simulations of rectangular channel with twisted-tape Pin-Fin array[J]. International Journal of Heat and Mass Transfer, 2021, 166: 120809.
[16] 袁发庭, 吕凯, 刘健犇, 等. 基于电磁-热-结构多物理场耦合的铁心电抗器线圈结构优化方法[J]. 电工技术学报, 2022, 37(24): 6431-6441.
Yuan Fating, Lü Kai, Liu Jianben, et al. Coil structures optimization method of iron core reactor based on electromagnetic-thermal-structure multi- physical field coupling[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6431-6441.
[17] 王玲, 李俐, 朱翔鸥, 等. 基于粒子群算法的强迫风冷散热器多目标优化[J]. 电气技术, 2022, 23(2): 20-25.
Wang Ling, Li Li, Zhu Xian’gou, et al. Multi- objective optimization of forced air-cooled heatsink based on particle swarm optimization algorithm[J]. Electrical Engineering, 2022, 23(2): 20-25.
[18] 丁雪妮, 陈民铀, 赖伟, 等. 多芯片并联IGBT模块老化特征参量甄选研究[J]. 电工技术学报, 2022, 37(13): 3304-3316, 3340.
Ding Xueni, Chen Minyou, Lai Wei, et al. Selection of aging characteristic parameter for multi-chips parallel IGBT module[J]. Transactions of China Elec- trotechnical Society, 2022, 37(13): 3304-3316, 3340.
[19] Borrvall T, Petersson J. Topology optimization of fluids in Stokes flow[J]. International Journal for Numerical Methods in Fluids, 2003, 41(1): 77-107.
[20] Koga A A, Lopes E C C, Villa Nova H F, et al. Development of heat sink device by using topology optimization[J]. International Journal of Heat and Mass Transfer, 2013, 64: 759-772.
[21] Sigmund O, Petersson J. Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima[J]. Structural Optimization, 1998, 16(1): 68-75.
[22] Wang Fengwen, Lazarov B S, Sigmund O. On pro- jection methods, convergence and robust formulations in topology optimization[J]. Structural and multi- disciplinary optimization, 2011, 43(6): 767-784.
[23] Comsol. Topology optimization of an MBB beam[EB/OL]. www.comsol.com/model/topology-optimization-of-an- mbb-beam-7428, 2022-2-1.
[24] Zhang Bin, Zhu Jihong, Xiang Gaoxiang, et al. Design of nanofluid-cooled heat sink using topology optimization[J]. Chinese Journal of Aeronautics, 2021, 34(2): 301-317.
[25] Sun Sicheng, Liebersbach P, Qian Xiaoping. 3D topology optimization of heat sinks for liquid cooling[J]. Applied Thermal Engineering, 2020, 178: 115540.
[26] 罗旭, 王学梅, 吴海平. 基于多目标优化的电动汽车变流器IGBT及开关频率的选择[J]. 电工技术学报, 2020, 35(10): 2181-2193.
Luo Xu, Wang Xuemei, Wu Haiping. Selections of IGBTs and switching frequency of the electric vehicle converter based on multi-objective optimization[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2181-2193.
[27] Kosar A, Peles Y. TCPT-2006-096. R2: Micro scale pin fin heat sinks—parametric performance evalu- ation study[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2007, 30(4): 855-865.
Abstract The integrated Pin-Fin heatsink can effectively reduce the junction-fluid thermal resistance of the automotive power module, which is a state-of-the-art and promising solution for the thermal management of the power control unit. It has shown that topological characterization plays a crucial role in the overall performance of the Pin-Fin heatsink. According to the basic geometric structures, such as circles, squares, and ellipses, the parameters of initial structures are simulated and experimentally analyzed using empirical enumeration or arrangement and combination. However, there are only numerical solution methods to optimize the Pin-Fin structure, which are time-consuming, high cost, and have a low degree of freedom. Limited by the existing geometry aspects, there needs to be a method capable enough to contain all geometrical aspects of the Pin-Fin structure to make the thermal-fluid co-optimal design.
Inspired by these research gaps, based on the topology optimization method and gradient descent algorithm, the varied-density-oriented mathematical model is proposed to characterize the Pin-Fin heatsink. Firstly, the detailed fluid field and thermal field control functions are analyzed, focusing on the PCU model. Then, penalty factors are applied in the material interpolation to characterize the relationship between the fluid and solid domains. The junction resistance and pressure drop are key indicators in the topology optimization formulation. Adjusting the weight factors achieves topology optimization results under specific design requirements. Besides the even power dissipation, the principle of unbalanced power dissipation on optimization results is analyzed. The topology optimization method can reasonably distribute materials under the unbalanced heat source and achieve the goal of minimizing the thermal-fluid co-optimal design.
The front-to-front converter is constructed to evaluate the performance of the optimized Pin-Fin structure. Comprehensive experiments are presented to ensure the feasibility and validity of proposed models and methodologies compared with the commercial circle, diamond, triangle, and teardrop structures. It is found that with the help of the topology optimization, the designed Pin-Fin heatsink reduces the junction-fluid thermal resistance by 12 % and eliminates the mismatched junction difference by 80 % compared with the traditional circular design. The diamond, triangle, and teardrop shape Pin-Fin heatsink prototypes are also analyzed under the same load current and busbar voltage. Even for the optimal diamond-shape Pin-Fin, the junction temperature is still higher than that of the structure proposed in this paper, which verifies the effectiveness of the design method.
The following conclusions can be drawn from the simulation and experiment analysis. Penalty factors affect the convergence of topology optimization. Building the multi-objective optimization model can accelerate the design speed and reduce the research and development cost. The topology optimization method has a high degree of design freedom to achieve the co-optimized design. The optimized structure can reduce chip temperature differences by 80 %, and the temperature gradient between each chip is less than 1 ℃. The thermal resistance can be reduced by 12 %, and the maximum temperature rise can be reduced by 6 ℃ under different load conditions. Experimental results verify that the optimized Pin-Fin structure can effectively improve the thermal performance and the reliability of the automotive power module.
keywords：Automotive power module; integrated Pin-Fin heatsink, topology optimization method, thermal-fluid co-optimal design
DOI: 10.19595/j.cnki.1000-6753.tces.221088
中图分类号：TM464
国家自然科学基金项目（52177169）、重庆市基础研究与前沿探求项目（cstc2021zdyjA0035）和重庆市研究生科研创新项目（CYS22023）资助。
收稿日期 2022-06-10
改稿日期 2022-08-01
李恺颜 男，1998年生，硕士研究生，研究方向为新型电力电子器件封装集成与应用。E-mail: 535306488@qq.com
曾 正 男，1986年生，博士，教授，研究方向为新型电力电子器件封装集成与应用。E-mail: zengerzheng@126.com（通信作者）
（编辑 陈 诚）