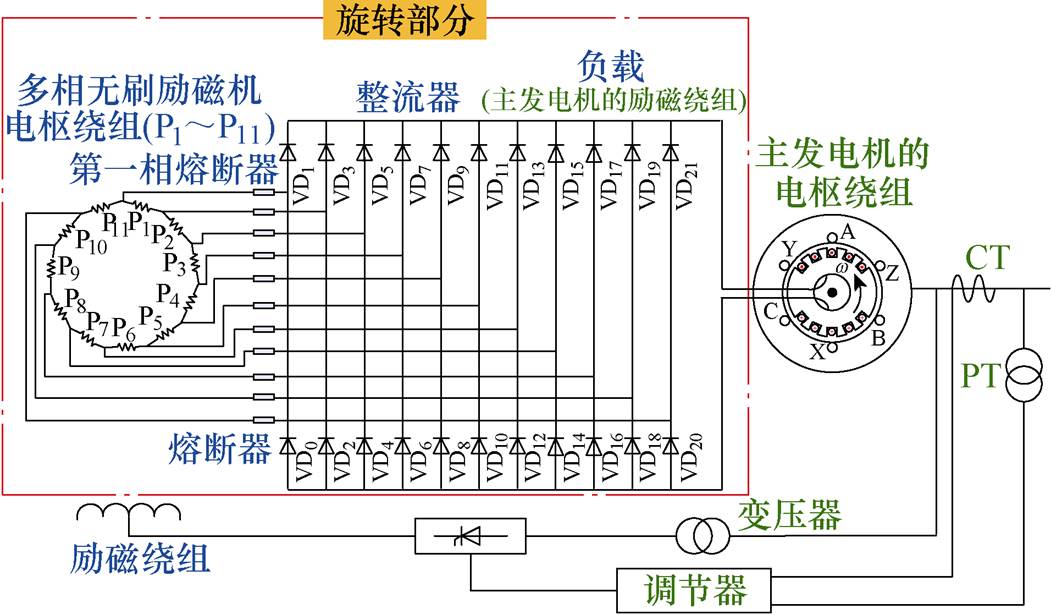
图1 11相环形无刷励磁系统示意图
Fig.1 11-phase annular brushless exciter
摘要 对于核电站频繁发生的多相旋转整流器开路故障，实际现场不仅需要可靠诊断，还需要对故障模式进行准确区分。利用故障在励磁机定子励磁电流中反映的特征来诊断无法被直接测量到的旋转整流器故障是一种有效的途径，但是以往研究均仅关注故障励磁电流的频域特征，能识别故障的发生而无法进一步对故障模式进行分类。为此，该文对旋转整流器一管开路、一相开路以及不同位置的两相开路故障后励磁电流时域、频域及频谱分布特征进行研究。首先，对某11相环形无刷励磁系统的运行特性进行理论分析，基于二极管导通顺序及故障二极管在电机运行周期中所处的位置，对故障励磁电流时域特征进行分析；其次，基于故障对励磁电流的影响机理，对励磁电流故障分量进行解析，得到了旋转二极管不同模式故障下的频域及频谱分布特征，并通过某11相动模样机实验验证了理论分析的正确性；最后，结合励磁电流时域、频域以及频谱分布三者特征，提出了二极管不同模式故障的诊断方法。样机实验表明，该文提出的诊断方法能实现所有故障模式的区分，可为一般多相环形无刷励磁系统旋转整流系统故障的保护提供依据。
关键词：多相环形无刷励磁机 整流器故障 励磁电流 时域 频域 频谱分布
核能因其清洁高效性，近年来得到了大力发 展[1]，核电单机发电及励磁容量也不断增大，无刷励磁机由于没有碳刷及滑环对励磁容量的限制而成为主要励磁方式[2]，尤其是近年来出现的一种多相环形结构的无刷励磁机，由于其容错性强和励磁功率高[3]而被广泛用于超大容量核电站。
某核电11相环形无刷励磁系统的结构如图1所示，其励磁绕组位于定子侧，电枢绕组位于转子侧，多相整流器与转子一起高速旋转，负载为主发电机的励磁绕组。为了防止二极管过电流烧毁，励磁机每一相电枢绕组与整流器之间均设有熔断器。
图1 11相环形无刷励磁系统示意图
Fig.1 11-phase annular brushless exciter
旋转整流器是为发电机提供高品质直流电的关键，但因为二极管长期处于高温且高速旋转状态，实际运行中由于二极管损坏导致的整流器故障时有发生。实际二极管可能发生短路故障和开路故障，但是实际现场对二极管配置了过电流熔断器，二极管短路时产生的大电流将致使熔断器短时过电流高温熔断，进而最终导致一相开路故障，因此实际只需要考虑开路故障即可。除了一管开路故障之外，根据熔断器故障数量的不同，故障模式还可分为一相开路、不同位置的两相开路等。对于多相整流器而言，一管开路及一相开路故障初期励磁机仍能给主发电机提供正常工作电流，但长时间带故障运行容易导致更多的熔断器断开而造成故障扩大，影响发电系统的安全运行[4]。
因此，即使是一管开路故障，也非常有必要进行及时的诊断。然而，正常运行时整流系统处于高速旋转状态，二极管及电枢电流无法直接测量，所以常规静止励磁系统的故障检测方式不再适用。为此，国内外专家学者对旋转整流器故障诊断方法进行了大量研究，部分学者利用励磁绕组回路的磁链关系重构电枢电流的方式进行故障诊断[5-8]。例如，文献[5]通过重构电枢电流对双励磁绕组异步发电机旋转整流器正常运行及故障特征进行了分析，利用主励磁机电枢电流轨迹几何特征对旋转整流器进行诊断，但该重构电枢电流的方法并不适用于单励磁绕组同步发电机，尤其是多相结构的无刷励磁机；此外，有学者采用发电机端电气量进行故障诊断，在文献[9]中，主发电机三相定子电压被用于旋转整流器一管开路故障和两管开路故障诊断，文献[10]同样表明，主发电机定子电压的6次谐波也可用于故障诊断。然而，基于主发电机端电气量的诊断方法对故障的分类能力仍然局限于电阻和非线性负载的情况。基于探测线圈的故障诊断方法也有较多研究[11-12]，文献[11]采用两个空间相对位置分布的探测线圈感应电动势差值来检测某48相旋转整流器中二极管一管和两管开路故障，与文献[13-15]一致，该48相实际为多组三相整流器并联而成，与环形结构励磁机在运行机理及分析方法上有较大不同[16-17]，且探测线圈法需要对目前现场运行的励磁机进行改造而实用性较差。
依据故障在励磁机定子侧励磁绕组中反映的特征来实现监测是一种有效且通用的途径。文献[18]和文献[19-20]分别对多相环形无刷励磁机的定子和转子绕组短路故障后的定子励磁电流特征进行了分析。文献[21-23]分析了故障后电枢电流及电枢反映磁动势的变化，基于定、转子电磁相互作用关系对定子励磁侧故障谐波电流特征进行分析，提出利用定子励磁电流谐波对旋转二极管一管开路故障进行诊断。与文献[21-23]类似，文献[24]对某39相环形无刷励磁系统旋转二极管一管开路故障进行了分析，但均未对旋转整流器更易发生的相开路故障进行研究，并且均只关注故障后电气量的频域特征，没有对频谱分布规律及励磁电流的故障时域特征进行研究。
利用励磁机定子励磁电流的频域特征来识别故障的发生是一个有效的方法，但是多相旋转整流器的故障模式众多，难以可靠区分。不同故障模式对励磁系统的影响并不相同，为了减小故障停机造成的经济损失，实际现场对不同的二极管故障模式有着不同的处理规程：一管和一相开路故障仅报警，两相开路故障需要停机。因此，不仅要求能够识别故障的发生，还需要区分二极管的故障类型。而要区分多相旋转整流器故障类型并不容易，尤其是现有研究中仅利用频域中总谐波有效值的诊断方法，因为研究发现，部分两相开路故障的总谐波有效值是接近甚至小于一相开路故障下的总谐波有效值的。其次，现有分析方法中励磁电流的频域特征均为通过分析电枢绕组中故障谐波电流及定转子电流感应过程得到的，丢失了故障位置信息而不能得到各特征谐波电流的相对大小。
实际上不仅频域特征，不同故障在励磁电流时域特征和频谱分布特征上也有不同的体现，可作为不同故障模式诊断的依据。本文深入研究了故障二极管对励磁绕组时域波形的影响机理，分析了不同类型故障下励磁电流时域波形的独有特征，并基于该影响对故障励磁电流进行了解析，不仅揭示了故障励磁电流的频域特征，还分析得到了故障谐波电流的分布规律，最终提出了基于励磁机定子电流时域、频域及频谱分布特征三者结合的故障诊断方法，可为一般多相无刷励磁机旋转整流器的故障诊断和模式分类提供依据。
实际11相励磁机电枢绕组接线如附录所示，励磁机正常运行时，线电压最大的电枢绕组两端二极管导通。根据已有研究[25]，三相串联电枢绕组感应电动势最大，22个二极管将随着合成最大电动势的相序变化而轮流导通，二极管导通顺序如图2所示，按照VD9、VD2、VD19等顺序依次导通。
励磁机一个电周期中，二极管将换相22次，理想状态下电枢电流值将对应变化22次，即第1相电枢绕组的电流波形如图3中曲线1所示，具体分析见文献[25]。图中，i1为第一相电枢电流，i11为第11相电枢电流，Ild为负载电流有效值，电枢电流由宽度为p/11，高度为3Ild/11或8Ild/11的22个矩形波组成。由于电枢回路电感的作用，电枢电流的实际波形如曲线2所示，I为等效电枢电流有效值。相邻第11相电枢电流滞后第一相电枢电流4p/11电角度，如曲线3所示。
图2 二极管导通顺序
Fig.2 Diode conduction sequence
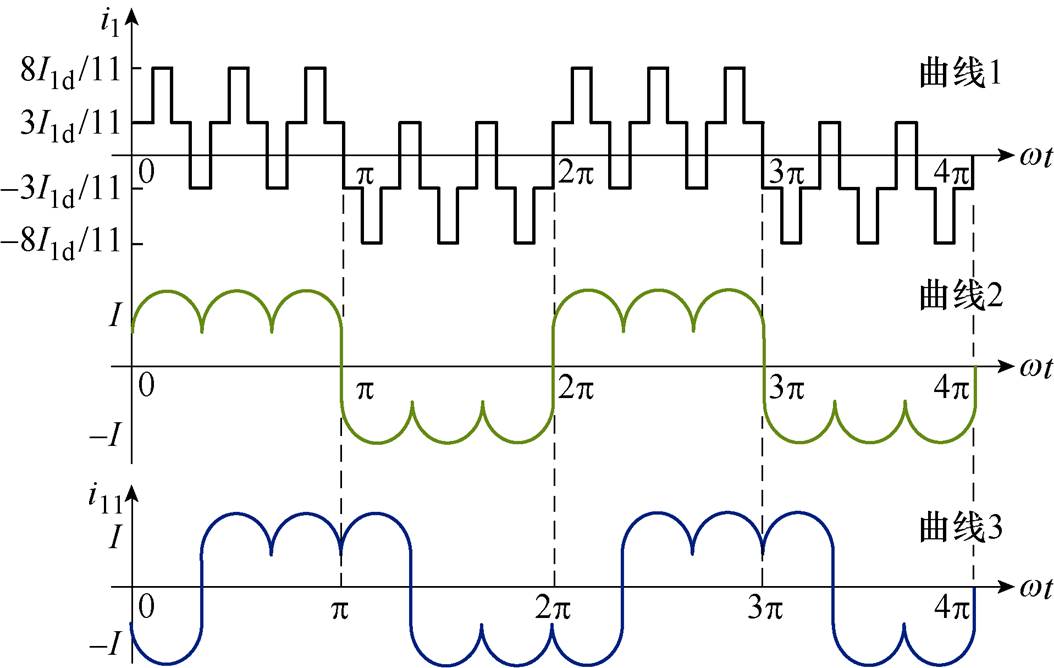
图3 正常运行时的电枢电流波形
Fig.3 Armature current waveforms during normal operation
为便于理论分析，假设电枢绕组的电感足够大，则电枢电流波形纹波消失，变成宽度为p，高度为I的矩形波，如图4所示。
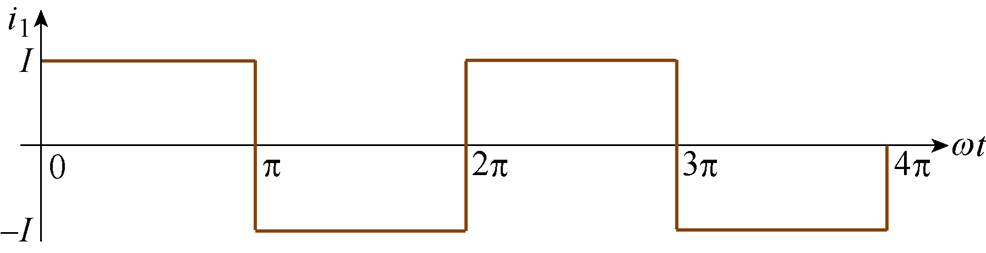
图4 第一相等效电枢电流波形
Fig.4 Equivalent armature current waveform of the 1st phase
电枢电流满足奇谐函数性质仅含有奇数次谐波电流。因此，第k相电枢绕组的m 次谐波电流表达式为
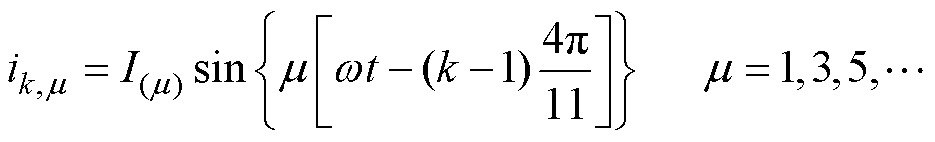（1）
式中，m 为谐波电流次数；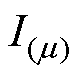
为m 此谐波电流有效值；
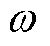为旋转角速度；t为时间。
各相电枢电流均会产生各次空间谐波磁动势。其中，分数次谐波磁场在所有磁极上的感应电动势合成为零，而偶数次谐波磁场在一个磁极内的感应电动势为零。因此，本文的理论分析均只考虑电枢电流产生的奇数次谐波磁动势对励磁绕组的感应作用。则第k相电枢绕组的m 次谐波电流产生的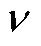
次空间谐波磁动势为
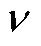=1, 3, 5,… （2）
式中，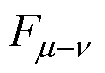
为谐波磁动势幅值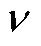；为电枢磁动势谐波次数；
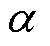为沿电机转子圆周方向的电角度。
各相电枢绕组产生的磁动势均为脉振磁动势，分解为正、反转磁动势并分别合成后可以表示为
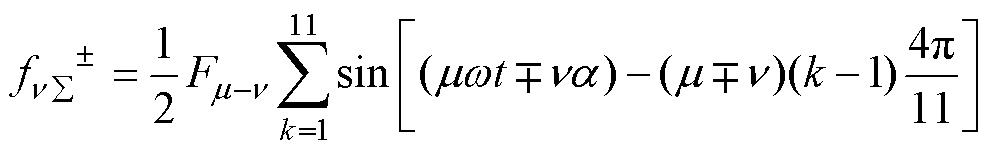（3）
对式（3）进行分析可知，当且仅当v±m=11n（n=0, 2, 4,…）时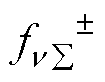
才不为0，即电枢反应磁动势中只存在11n±m 次分量。11n±m 次正转谐波磁动势转速为m/(11n±m) 倍同步转速，相对定子为1-m/(11n±m)倍同步转速，将在定子励磁绕组中感应出11n倍基频的电动势。因此，11相环形无刷励磁机正常运行时，励磁电流除直流分量外主要含有22及其倍数次谐波分量。
不考虑励磁绕组电感及二极管换相过程时，可将励磁电流绘制成如图5所示的22脉波。实际上，这也是由于二极管每隔p/11电角度换相，电枢电流一个电周期经二极管22次换相调制后在励磁绕组上感应出来的结果。每一次二极管换相，即有一相电枢绕组电流反向，也对应着励磁电流中一个极小值点。每一个二极管持续导通时间为2p/11，导通结束时换相至下一个二极管继续导通。由于此时没有故障，二极管均正常运行，不会导致励磁电流发生畸变。
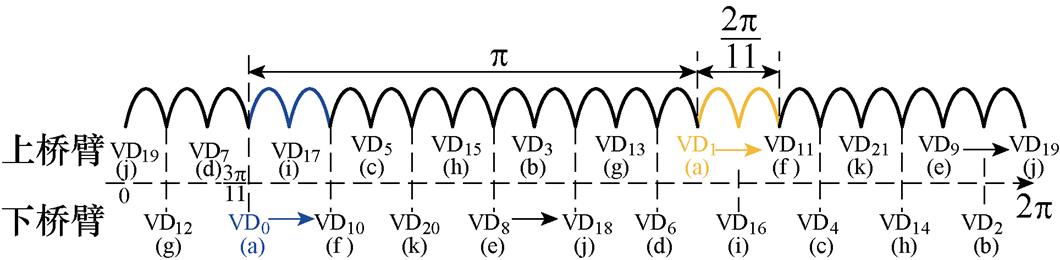
图5 励磁机正常运行时励磁电流波形
Fig.5 Excitation current waveform during normal operation
二极管故障将导致整流器工作状态的缺失，在故障二极管没有参与运行的时刻，励磁机励磁电流以及各电枢电流将与正常运行时刻一致，而当励磁机运行到故障二极管原本应该导通的时刻时，电枢电流将发生不同于正常运行时的畸变，励磁电流时域波形对应位置将出现一定时长的畸变。由于本文只关注励磁电流畸变个数及位置，因此忽略励磁绕组电感作用和二极管换相过程时，同一周期中励磁电流时域波形上畸变将只与二极管发生故障的数量与相对位置有关。
不失一般性，假设VD0管发生开路故障，故障后各相电枢绕组电压（感应电动势）不变。此时故障只会影响与VD0二极管相关的运行状态，其余时刻电枢电流将与正常运行时一致。VD0二极管参与的两个运行状态如图6所示，由图可知，在第一个运行状态中，故障将主要改变第1、2、3相电枢电流，并且电枢电流的改变发生在同一时刻；同理在第二个运行状态中，故障将主要影响第9、10、11相电枢电流。
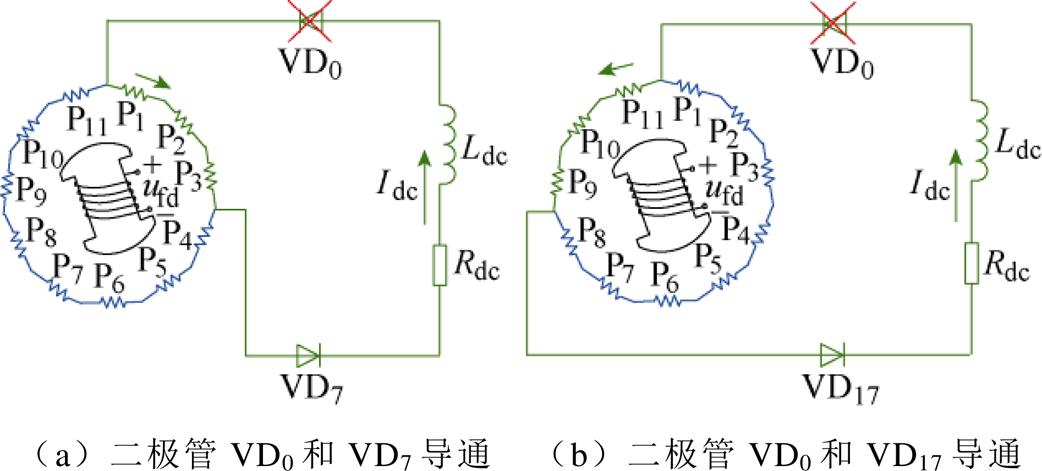
图6 故障二极管运行拓扑
Fig.6 Operation topology after diode fault
由于两个状态中三相电枢电流变化是分别相同的，因此分别以故障后第1和第11相电枢电流变化为例对两个状态进行分析。图7a为故障后第1相电枢绕组理想状态下的电流波形，由于故障二极管无法通过工作电流，上一个二极管，即VD12无法换相至VD0，因此与故障二极管相关的导通状态缺失，但是由于上一个工作状态二极管VD12的续流作用，故障时刻第1、11相电枢电流不为零，而是维持上一状态电流p/11时间后，直接向下一个二极管VD10完成换相，因此故障二极管仅在其工作状态对应时刻影响电枢电流，而其他二极管导通时刻电枢电流保持不变。故障电枢电流的变化量如图7中的虚线填充部分所示。考虑实际电枢绕组电感作用，可以将第1相故障电枢电流等效为如图7a中的曲线2所示。同理分析可知，故障后第11相电枢电流如图7b所示。
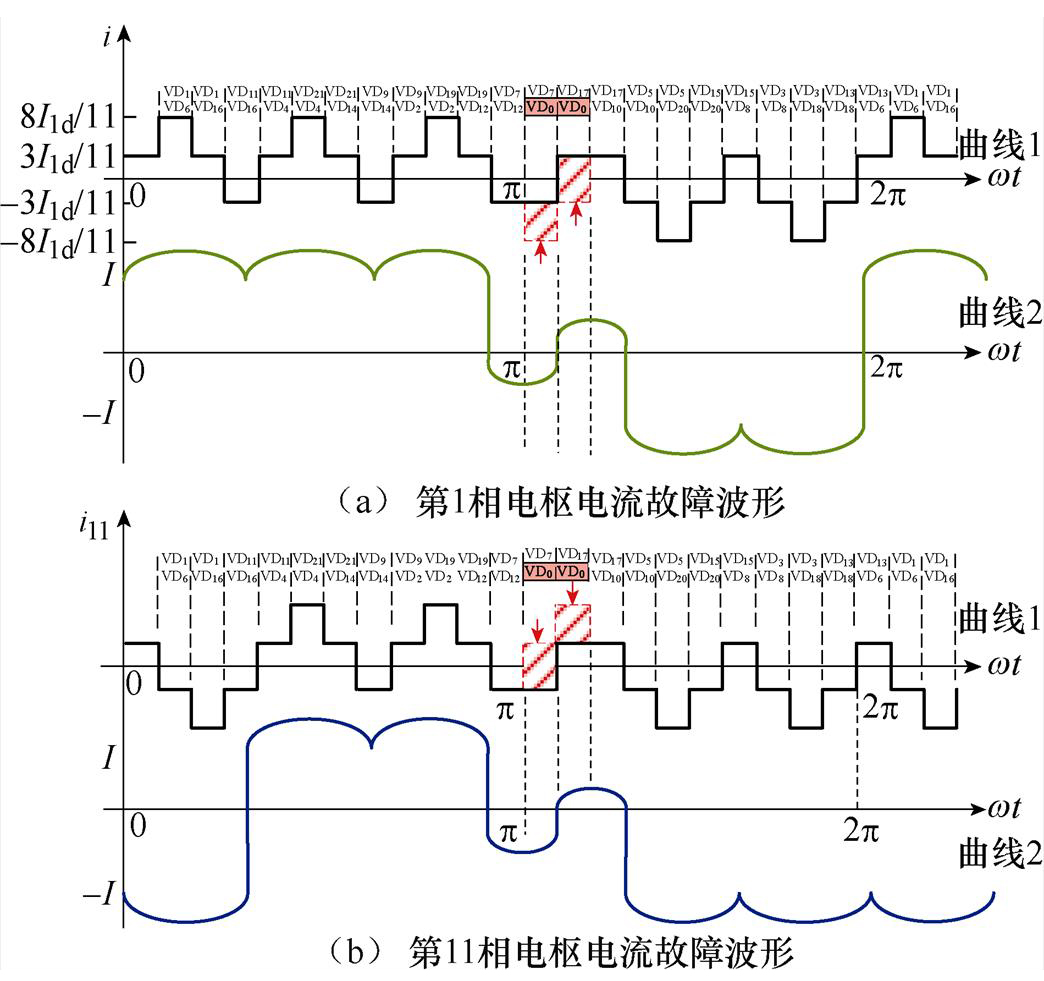
图7 故障对第1、11相电枢电流的影响
Fig.7 Effect of fault on armature current of phase 1 and 11
将VD0开路故障后第1、11相电枢电流看成正常运行时电枢电流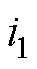
、
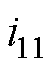与故障分量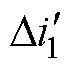
、
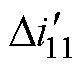的叠加，则可得故障分量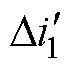、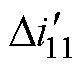的波形如图8所示。
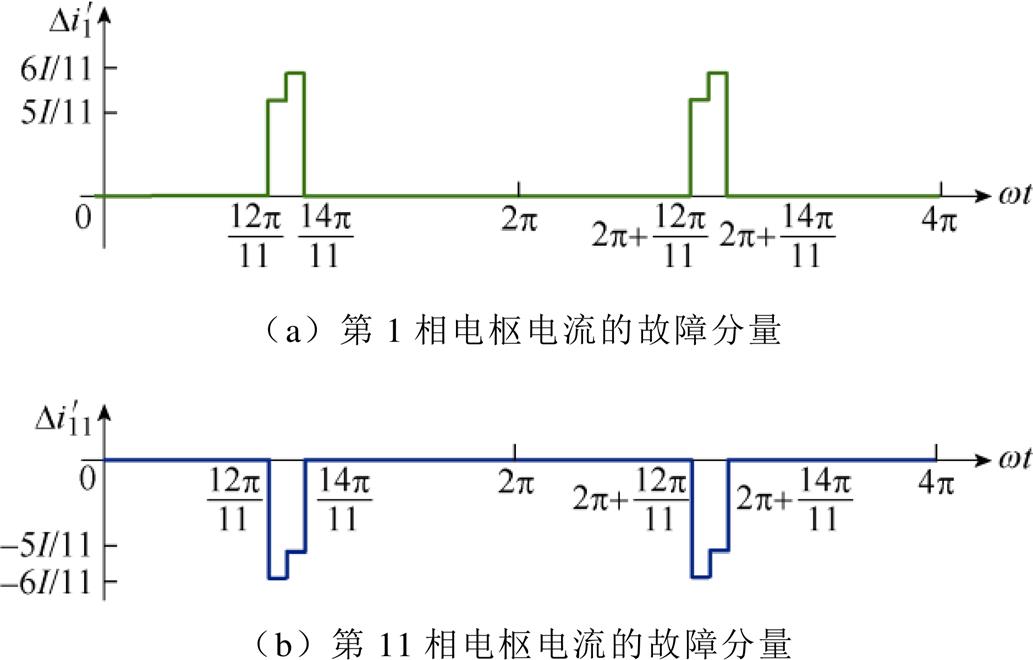
图8 一管开路时电枢电流的故障分量
Fig.8 Fault component under one-tube open-circuit
分析励磁绕组故障电流特性时，仅需要考虑电枢电流故障分量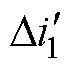、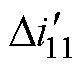对励磁电流的影响即可。以第1相电枢绕组为例，在故障时刻（12p/11, 14p/11）期间，对第1相电枢绕组中通以故障分量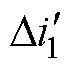，故障初始时刻电枢绕组与磁极的相对位置如图9所示。此时，故障后第1相电枢电流下降沿出现畸变，则S磁极下对应的电枢空间气隙故障磁动势方向向下，并且随着转子的运动，S极方向为下的总磁通将逐渐减小，根据楞次定律，将在励磁绕组中感应出对应的故障电动势。
励磁绕组电动势正方向与磁链方向满足右手定则，则故障时刻期间，第1相电枢绕组故障电流在励磁绕组上的感应电动势为
图9 第1相电枢绕组故障分量对励磁电流的影响
Fig.9 Influence of the 1st phase armature winding fault component on excitation current
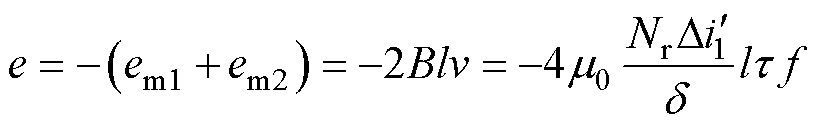（4）
式中，em1为线圈第一个有效边的感应电动势；em2为线圈第二个有效边的感应电动势；B为气隙磁场强度；v为转子旋转线速度；l为励磁线圈的有效长度；Nr为电枢绕组匝数；m0为真空磁导率；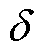
为气隙长度；f为励磁机基波频率；
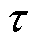为定子内表面用长度表示的每极所占的空间距离。
由于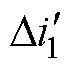方向为正，由式（4）可知，其在励磁绕组上感应出方向为负的电动势，同理可知，在故障时刻（12p/11, 14p/11）期间，对第11相电枢电流通以电流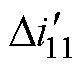时，由于第11相电枢绕组位于N极下，励磁绕组上的感应电动势为
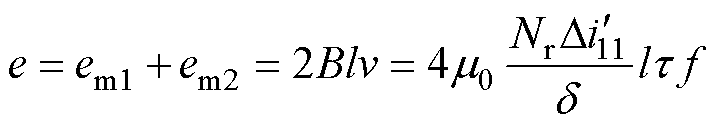（5）
由于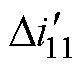方向为负，由式（5）可知，其在励磁绕组上将同样感应出方向为负的电动势。
因此，可知在二极管故障对应的时刻内，励磁绕组上除了固有的直流分量外，将出现由故障电枢电流感应出的方向为负的电动势，对应产生方向为负的故障电流。二极管一管开路故障时励磁电流波形示意图如图10所示。当考虑励磁绕组电感作用时，励磁电流波形将出现由故障造成的下降坑，如图10b所示，VD0管开路故障后，励磁电流对应点a～f段波形将发生畸变，畸变持续时间与VD0二极管导通时长2p/11相等。用2p 表示定子励磁电流的周期，用nd表示定子励磁电流一个周期内的畸变个数，td为畸变持续时间，则可以得到发生一管开路故障时，定子励磁电流的时域特征为：nd=1，td=2p/11。其他二极管导通时刻，励磁电流波形与正常运行时一致。
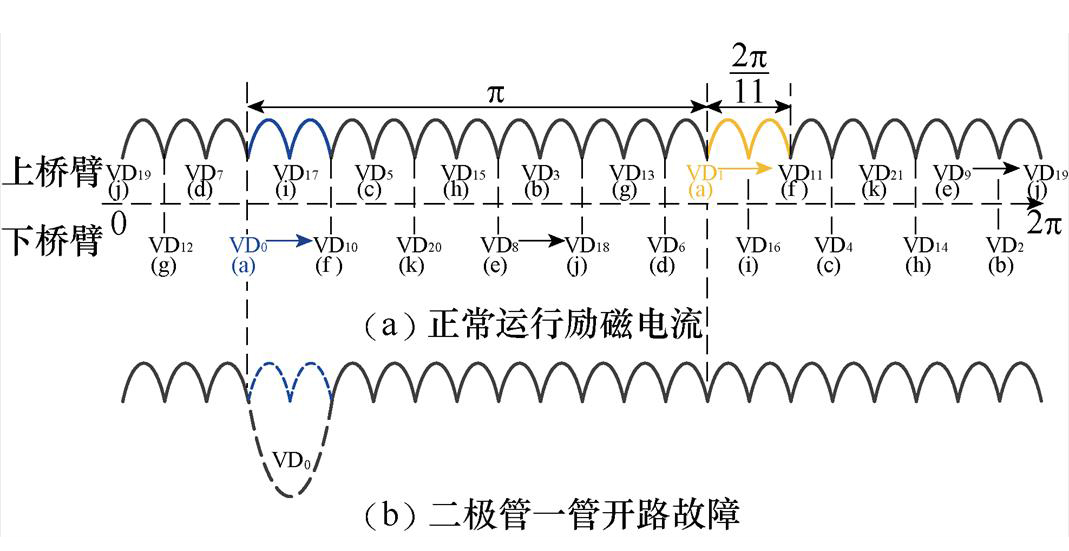
图10 二极管一管开路故障时励磁电流波形示意图
Fig.10 Schematic diagram of excitation current waveforms in the case of one-tube open-circuit fault
由于所有二极管均按照顺序依次导通，因此，励磁电流中的畸变坑仅与故障二极管数量及位置相关，其他时刻励磁电流波形与正常运行时一致。一相及第1、5相二极管故障励磁电流波形示意图如图11所示。以第1相开路故障为例，对应第1相熔断器熔断，可以等效为上桥臂二极管VD1和下桥臂二极管VD0同时发生开路故障，励磁电流波形中将出现两个持续时间均为2p/11且间隔p 电角度的畸变，定义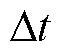
为畸变坑的间隔时间，则二极管一相开路故障时定子励磁电流的时域特征为nd=2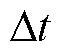，=p，td=2p/11，如图11b所示。
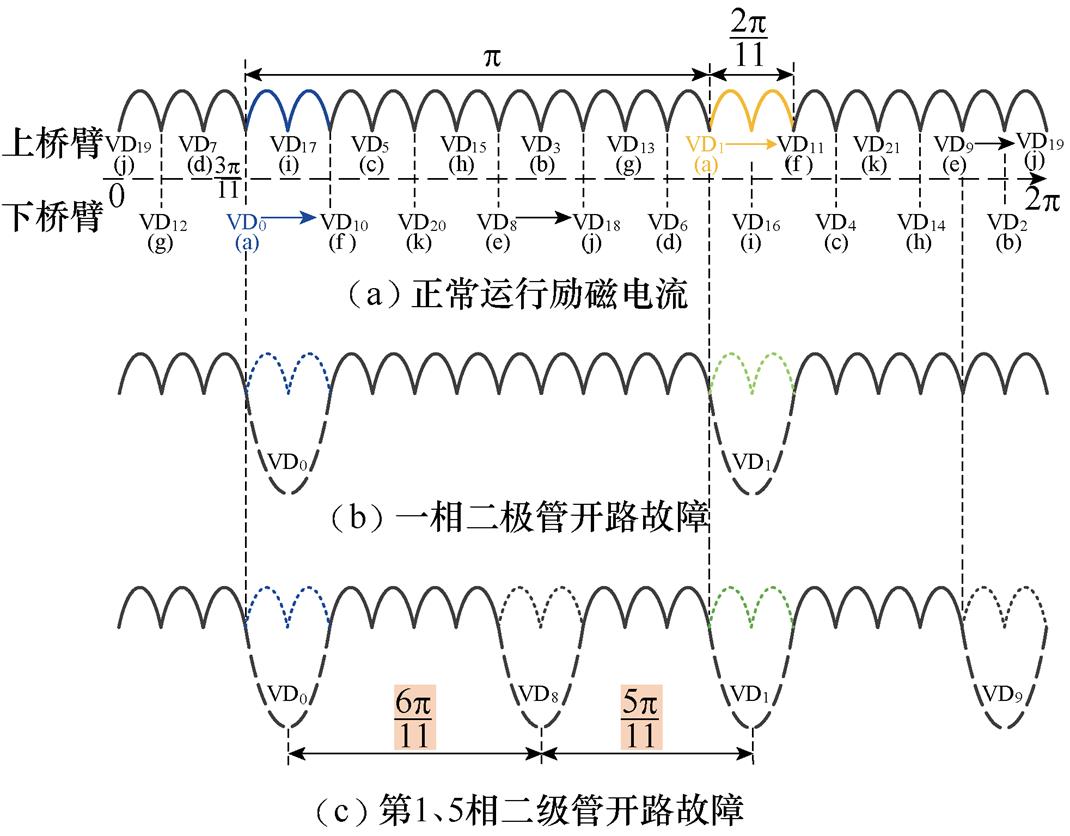
图11 一相及第1、5相二极管故障励磁电流波形示意图
Fig.11 Influence of one-phase open-circuit fault and the 1st phase and 5th phase open-circuit fault on excitation current
可以发现，不同数量和位置的二极管发生故障，对励磁电流的影响均可等效为所有故障二极管单独故障时对励磁电流影响的叠加。例如，当第1、5相（物理上相隔4相）二极管发生开路故障时，如图11c所示，励磁电流波形中将出现分别由第1相（VD0、VD1）和第5相（VD8、VD9）二极管故障造成的4个畸变，每个畸变持续时间均为2p/11，相邻两个畸变间隔分别为5p/11和6p/11。可知，励磁电流的时域特征为nd=4，
=5p/11，td=2p/11。
但是，并非所有两相二极管开路故障励磁电流波形都会出现4个畸变坑，当两个故障二极管工作时刻相邻时，两个持续时间为2p/11的畸变合成为一个畸变坑。第1、4相及第1、6相故障对励磁电流影响如图12所示，第1、4相（物理上相隔3相）与第1、6相（物理上相隔5相）二极管故障，励磁电流中将只出现两个间隔p 时间电角度的畸变。可以得到发生第1、4相与第1、6相二极管故障时，定子励磁电流的时域特征为nd=2，=p，td分别为3p/11和4p/11。
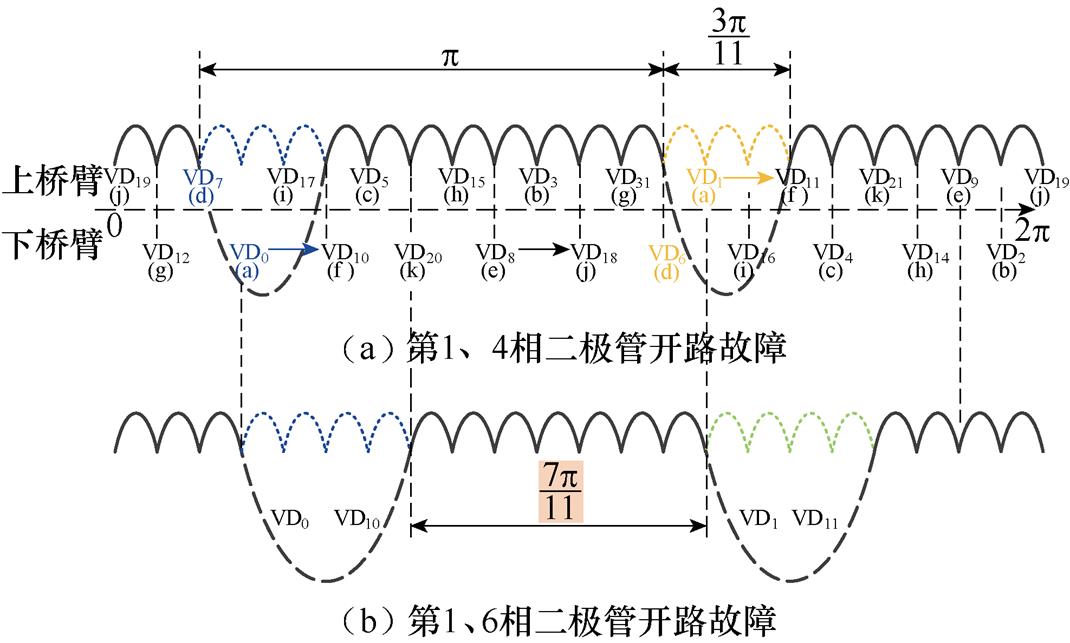
图12 第1、4相及第1、6相故障对励磁电流影响
Fig.12 Influence of the 1st phase and 4th phase fault and the 1st phase and 6th phase fault on excitation current
由理论分析可知，二极管开路造成励磁电流波形出现畸变坑，并且该畸变坑的数量和位置仅与故障二极管的数量及位置相关。因此实际上，对励磁电流波形变化量进行分析即可得到故障后励磁电流的频域特征。同时由式（4）、式（5）可知，故障感应电动势的大小正比于电枢电流的故障分量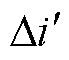
，因此当不考虑励磁绕组电感时，励磁电流的畸变坑可以等效为与故障分量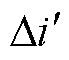相同的矩形波，矩形波的有效值仅与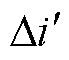相关，忽略电枢电流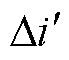中幅值的微小差异，则可以得到一管开路故障下励磁电流的等效矩形波如图13所示。
对一管开路后的励磁电流故障分量进行傅里叶谐波分解，结果为
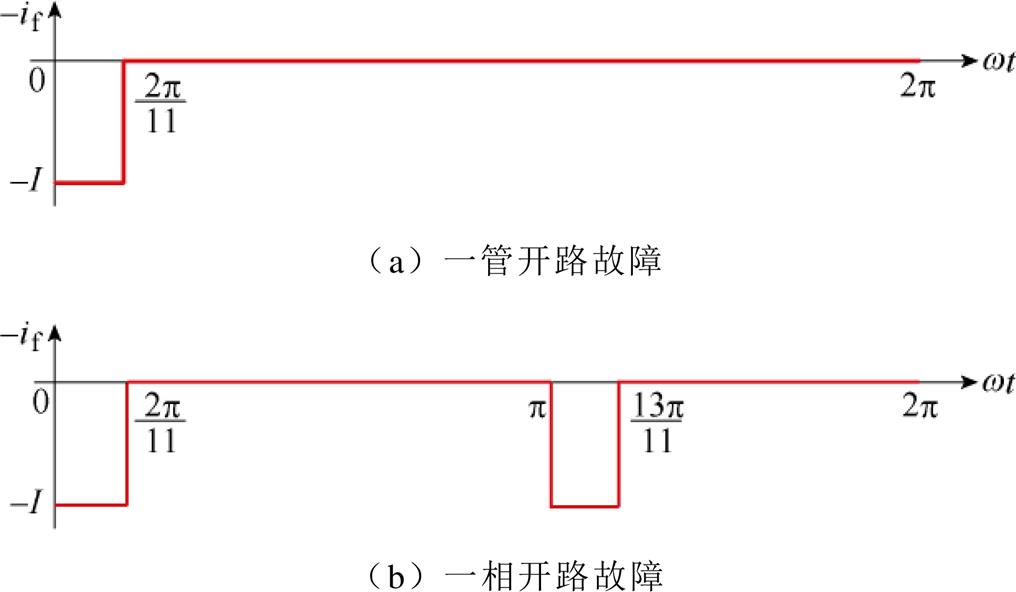
图13 一管及一相开路故障励磁电流等效波形
Fig.13 Equivalent waveform of excitation current under open circuit fault of one-tube and one-phase
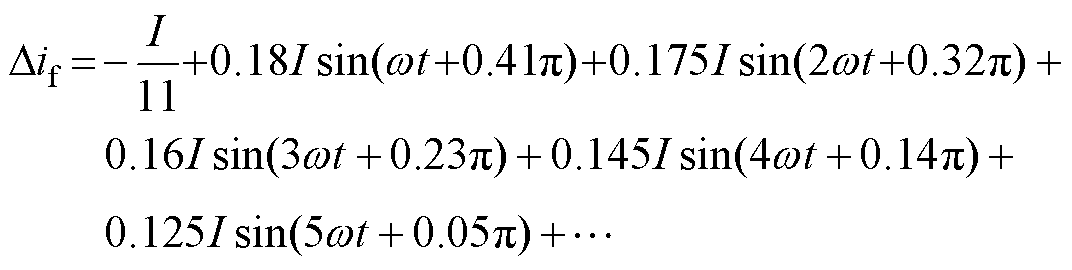
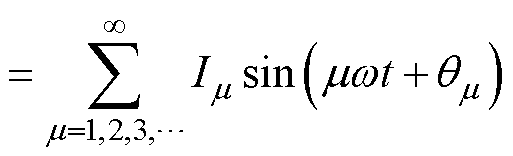（6）
同理，一相开路故障后的励磁电流故障分量进行傅里叶分解，结果为
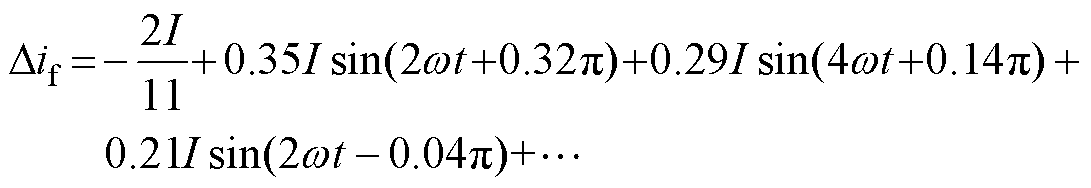
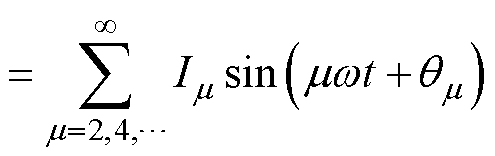（7）
由分解结果可知，一管开路故障后励磁电流中将含有各次谐波电流，而一相开路故障之后，励磁电流中仅含有偶数次谐波电流，实际上这是由于一相开路之后励磁电流的故障分量为偶谐函数的原因。同理可知，两相开路故障时励磁电流中的傅里叶分解结果中也均仅含有偶数次谐波电流分量。
理论分析结果中，一管开路故障时励磁电流中将出现各整数次谐波电流，而一相与两相开路故障时，励磁电流中将仅出现偶数次谐波电流。实际上，除了谐波次数，故障分量的傅里叶分解中各次谐波有效值的分布特征也存在差异。由式（6）和式（7）可以看出，一管及一相开路故障时各次谐波电流有效值随着次数增大而依次递减，故障励磁电流中主要含有2次谐波电流。但是，两相开路故障时励磁电流中将出现2个或者4个畸变坑，因此不同位置的两相开路故障时，谐波电流有效值的分布将随着间隔位置不同而不同。
对于图12所示的第1、4及第1、6两相开路故障，由于故障二极管运行状态相邻，其故障励磁电流的等效波形如图14所示，结合对第1相的分析可知，其故障谐波电流的分布特征同样将随着谐波次数增大而依次递减，故障励磁电流中将主要含有2次谐波电流。但是第1、4相开路时故障分量脉冲宽度更窄，傅里叶分解后较第1、6相开路故障将含有更多的高频分量。
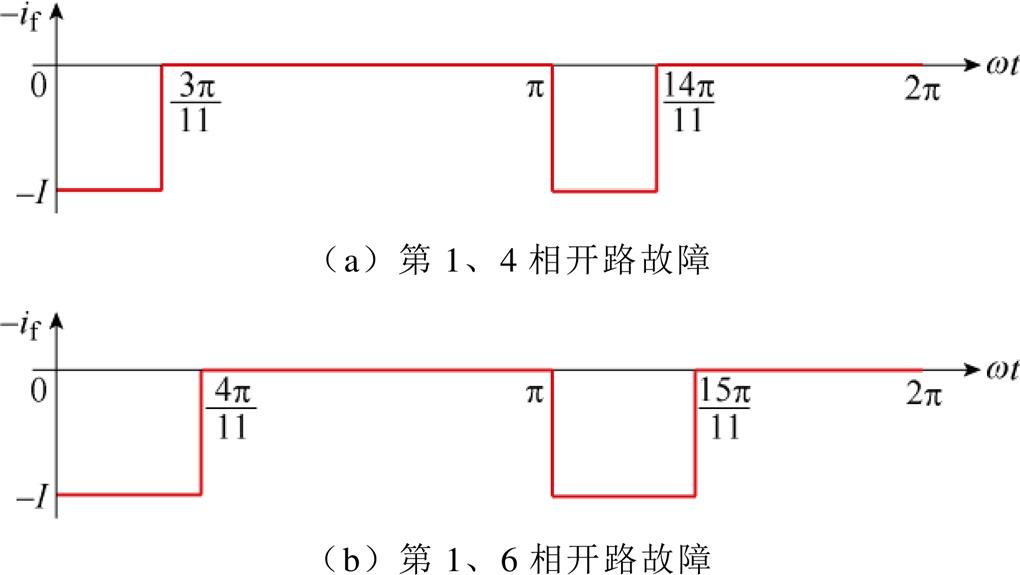
图14 第1、4和第1、6相开路故障励磁电流等效波形
Fig.14 Equivalent waveforms of excitation current under the 1st、4th and the 1st、6th phase faults
但是对于第1、2和第1、3以及第1、5两相开路故障，由于故障二极管运行状态并不相邻，励磁电流波形中将含有4个畸变坑，故障励磁电流中谐波电流的分布特征将与以上故障并不相同，故障分量等效波形如图15所示。
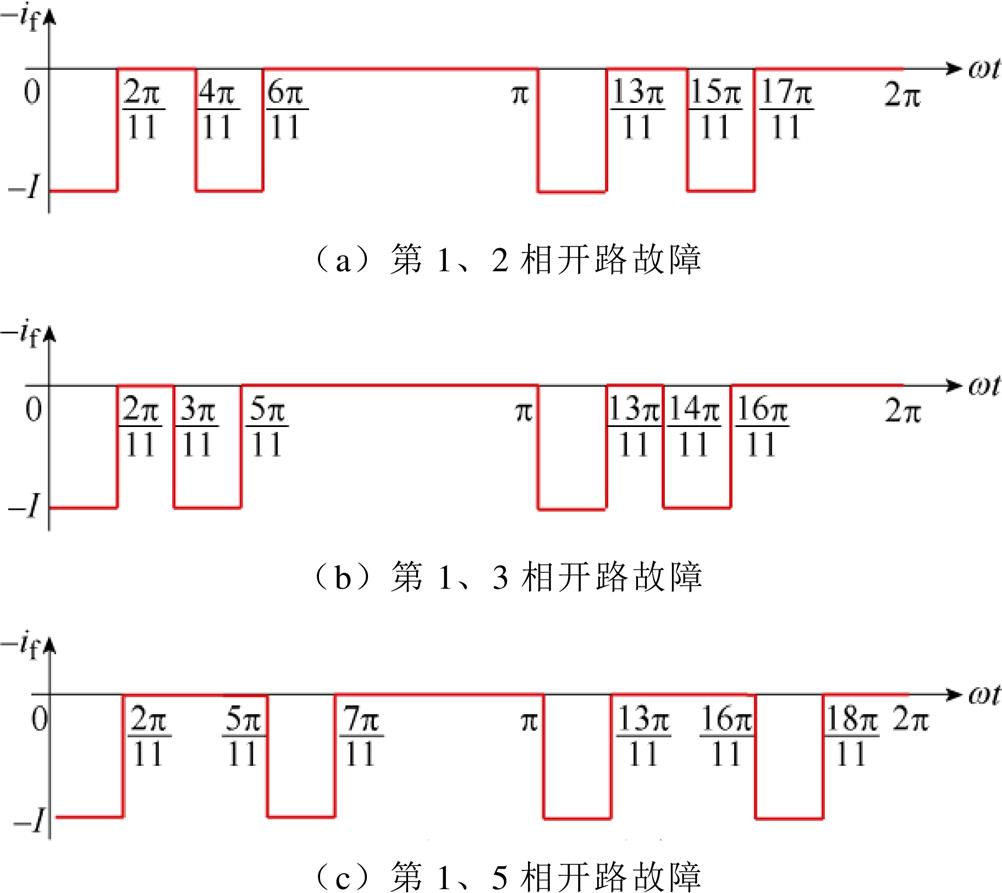
图15 不同位置两相开路故障励磁电流等效波形
Fig.15 Equivalent waveforms of excitation current under two-phase open circuit fault at different positions
可知，随着故障相对位置的不同，故障分量中谐波电流的分布特征也将不一致，但是均将满足偶谐函数条件，傅里叶分解结果中均仅含有偶数次谐波电流，可写为
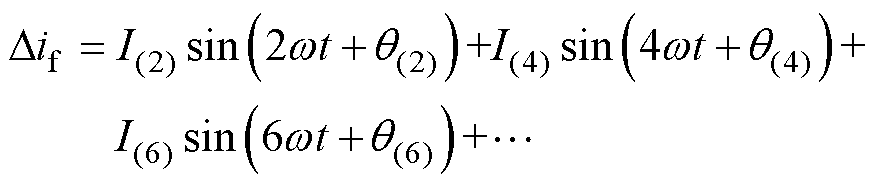（8）
对于图15所示三种故障，励磁电流谐波有效值分布特征如下（计算过程从略）：
第1、2相开路故障：I(2)=0.286I，I(4)=0.379I，I(6)=0.403I。
第1、3相开路故障：I(2)=0.451I，I(4)=0.082I，I(6)=0.353I。
第1、5相开路故障：I(2)=0.098I，I(4)=0.556I，I(6)=0.175I。
可以看到，第1、2相开路故障后励磁电流中谐波电流的分布特征为I(6)＞I(4)＞I(2)，故障励磁电流中主要含有6次谐波电流；而对于第1、3相开路故障谐波电流的分布特征为I(2)＞I(6)＞I(4)，即故障励磁电流中主要含有2次及6次谐波电流；同理，第1、5相开路故障谐波电流的分布特征为I(4)＞I(6)＞I(2)，即故障励磁电流中主要含有4次谐波电流。
为验证上述理论分析的正确性，本文在一台与实际励磁机结构相同的11相环形励磁机动模样机上进行了实验，样机的基本参数见表1。
表1 11相环形励磁机动模样机的基本参数
Tab.1 Basic parameters of 11-phase exciter prototype
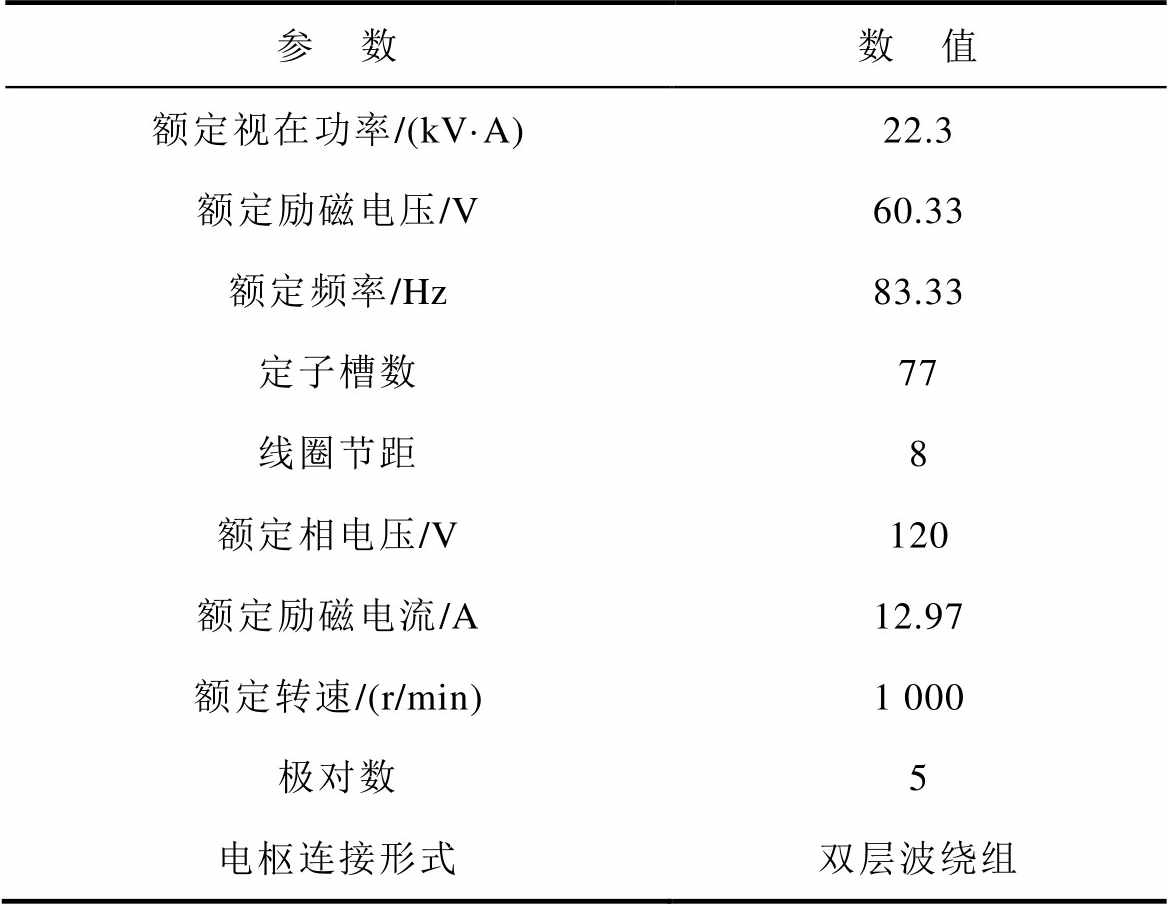
参 数数 值 额定视在功率/(kV·A)22.3 额定励磁电压/V60.33 额定频率/Hz83.33 定子槽数77 线圈节距8 额定相电压/V120 额定励磁电流/A12.97 额定转速/(r/min)1 000 极对数5 电枢连接形式双层波绕组
实验装置如图16所示。11相环形无刷励磁机由直流电动机拖动，直流电动机转速为960 r/min，此时电枢绕组感应电动势的基波频率为80 Hz，周期为12.5 ms。电枢绕组经过11相整流桥连接至阻感负载，断开相应位置的二极管断路器分别进行一管、一相和不同位置两相开路实验。
图16 实验装置
Fig.16 The actual experiment device
为保证实验安全，在实验中给励磁机励磁绕组施加15 V直流电压（约为额定励磁电压的25 %），励磁电流约为3.5 A，负载为Rdc=12.5 W, L=0.1 H。励磁机正常运行时及二极管一管开路故障后的二极管及电枢电流波形如图17所示。由图17可知，正常运行时二极管的换相顺序及电枢电流波形与理论分析结果完全一致，发生一管开路故障后，第1、11相电枢电流的变化也与图7完全一致，验证了理论分析的正确性。
对正常运行及故障后一个周期（12.5 ms）的励磁电流进行滤波，结果如图18所示。由图18可知，励磁电流一管开路故障后励磁电流中将出现一个畸变坑，一相开路故障后励磁电流波形中将出现两个畸变坑，不同位置二极管开路故障后励磁电流的波形均与理论分析结果一致。此外，还关注了两次畸变间隔的时间。从图18中可以看出，发生一相开路故障时，励磁电流中两次畸变时间为半个周期，即6.25 ms，第1、4相（物理上间隔3相）和第1、6相（物理上间隔5相）二极管开路故障时也是如此；当发生第1、5相（物理上相隔4相）开路故障时，两次畸变间隔时间分别为2.90 ms和3.35 ms，实验结果与理论分析结果基本一致，同理发生第1、2相（物理上相隔1相）和第1、3相（物理上相隔2相）开路故障时也是如此。虽然，实际实验时受到电机转速及绕组电感的作用，大小无法与理论分析结果保持完全一致，但是误差在允许范围内，同时不同间隔二极管故障下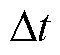的相对大小也验证了理论分析结果。
图17 励磁机正常运行及一管开路时二极管及电枢电流
Fig.17 Diode and armature current under normal operation of exciter and one-tube open circuit
为了验证故障频域及分布特征的理论分析结果，对正常运行及故障之后的一个周期励磁电流数据进行傅里叶分解，选择基波频率为80 Hz，一管及一相开路故障后励磁电流中所有7次之内的谐波结果见表2。
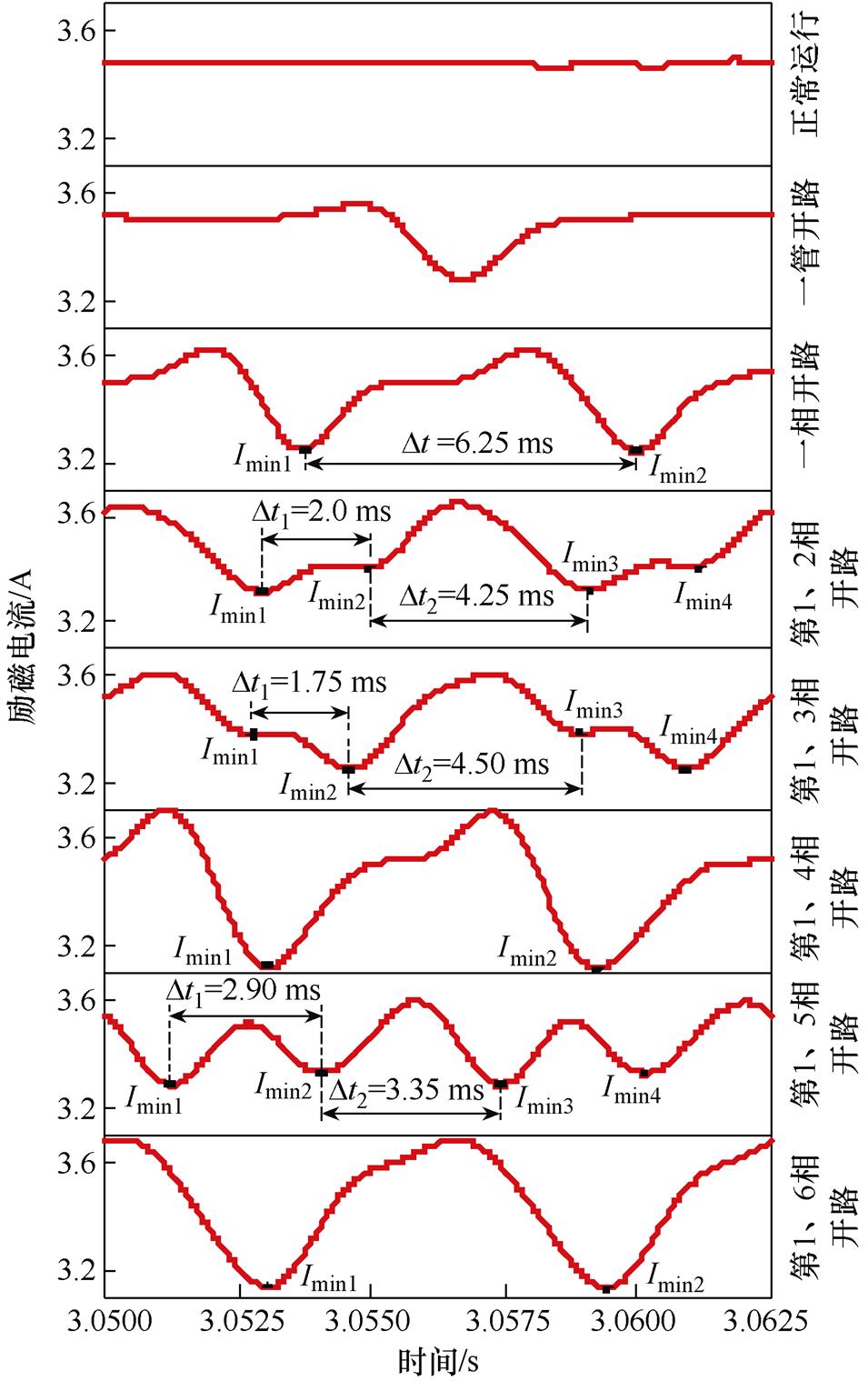
图18 故障实验励磁电流（滤波后）
Fig.18 Experimental waveforms of the excitation current (after filtering)
表2 旋转整流器故障下励磁电流谐波结果
Tab.2 Harmonics of excitation current under rectifier fault （单位: A）
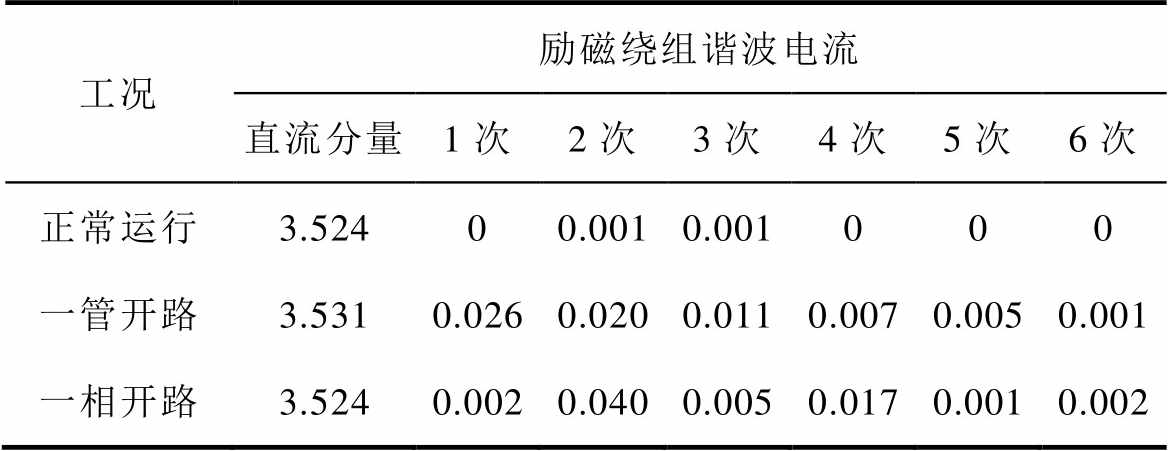
工况励磁绕组谐波电流 直流分量1次2次3次4次5次6次 正常运行3.52400.0010.001000 一管开路3.5310.0260.0200.0110.0070.0050.001 一相开路3.5240.0020.0400.0050.0170.0010.002
由表2可知，励磁机正常运行时，励磁电流中基本不含有任何数次的谐波电流；一管开路故障后，励磁电流中出现整数次谐波电流，一相开路故障后，励磁电流中仅出现偶数次谐波电流。此外，两者特征谐波分布规律均为依次递减，与理论分析完全一致。
同理，不同位置两相开路故障后，励磁电流中同样将仅含有偶数次谐波电流。图19为两相开路故障后励磁电流的傅里叶分解结果，从图可知，故障后偶数次谐波电流增大，并且第1、3相开路故障后，故障励磁电流主要以2次与6次谐波电流为主，第1、5相开路故障后，励磁电流4次谐波电流为最大，第1、4相和第1、6相开路故障后，励磁电流中主要为2次及4次谐波电流，但是第1、4相开路故障时励磁电流中4次与6次谐波电流有效值均高于第1、6相开路故障，尤其是6次谐波电流。虽然实际受到励磁绕组电感的低通滤波影响，故障励磁电流中的6次谐波电流有所削弱，但是故障后励磁电流中的主要特征分量与理论分析结果完全一致。
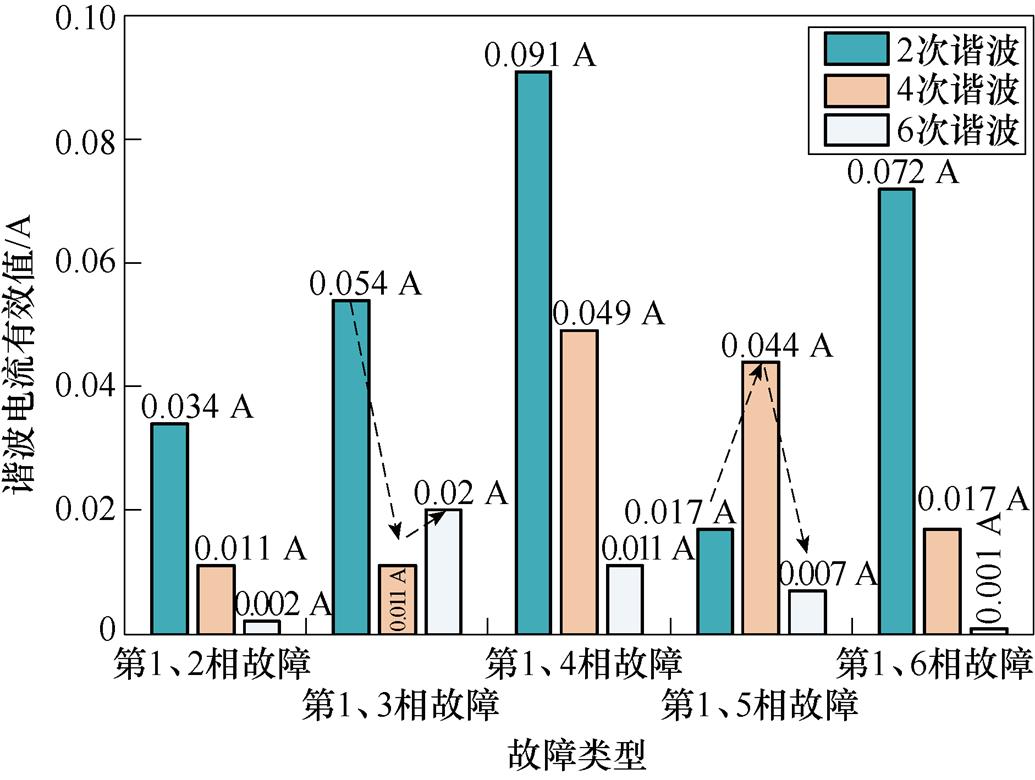
图19 两相开路故障谐波及分布规律
Fig.19 Harmonic and frequency spectrum distribution under two-phase open-circuit fault
但是不同于理论分析，第1、2相发生开路故障后，励磁电流中的特征谐波电流的分布规律为逐渐递减的，这是因为，特征谐波电流不仅受到励磁绕组的电感作用影响，还将受到电枢绕组电感作用的影响。尤其是第1、2相二极管开路故障，因为第1、2相电枢绕组空间相差4p/11电角度，同一相电枢电流内由两相二极管造成的故障分量也将间隔4p/11电角度（第1、3相二极管开路时为8p/11电角度），受到电枢电感影响，这两相二极管单独造成的电枢电流故障分量将出现暂态过程甚至将合并为一个。并且电枢绕组电感在负载电流较大时对结果影响较大，因为负载电流越大，意味着负载电阻更小，电枢绕组与负载回路中的时间常数更大，故障电流的暂态过程相应更长。为此，本文还进行了轻载工况下（Rdc=25 W, L=0.1 H）的第1、2相开路故障实验，对故障励磁电流进行傅里叶分解，结果见表3。可以发现，轻载工况下，第1、2相开路故障后励磁电流的谐波同样含有较大的偶数次谐波电流，并且分布规律为逐渐递增，故障后励磁电流中主要含有6次谐波电流，与理论分析一致。
表3 轻载工况下第1、2相开路故障谐波结果
Tab.3 Harmonics result in the case of the 1st and 2nd phases open-circuit fault under light load condition （单位: A）
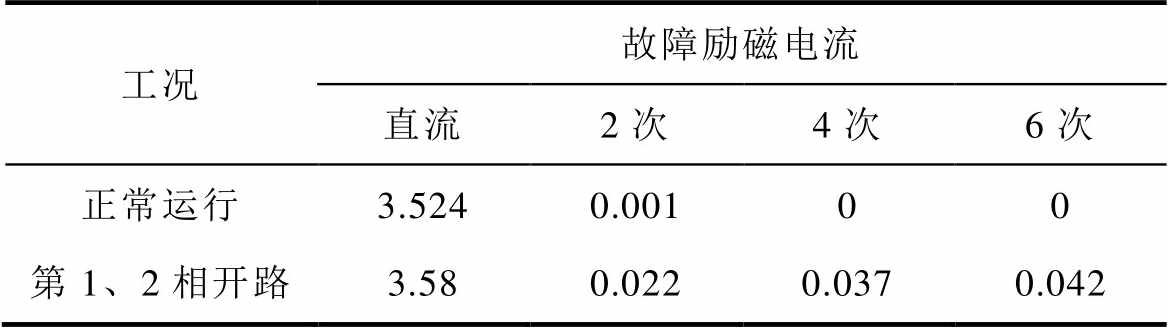
工况故障励磁电流 直流2次4次6次 正常运行3.5240.00100 第1、2相开路3.580.0220.0370.042
由于励磁机实际负载为主发电机励磁绕组，可看成一个大电感，因此本文在故障诊断时考虑与样机实验负载相一致下的谐波电流分布特征。
通过前文理论及实验分析，得到了旋转整流器不同故障模式下定子励磁电流的时域和频域特征，总结见表4。表中，dc为直流分量，为使结果更直观，频谱分布中考虑含量最大的两个频谱分量。
表4 旋转二极管不同故障模式下励磁电流的特征总结
Tab.4 Characteristics of exciter stator excitation current under different faults of rotating rectifier
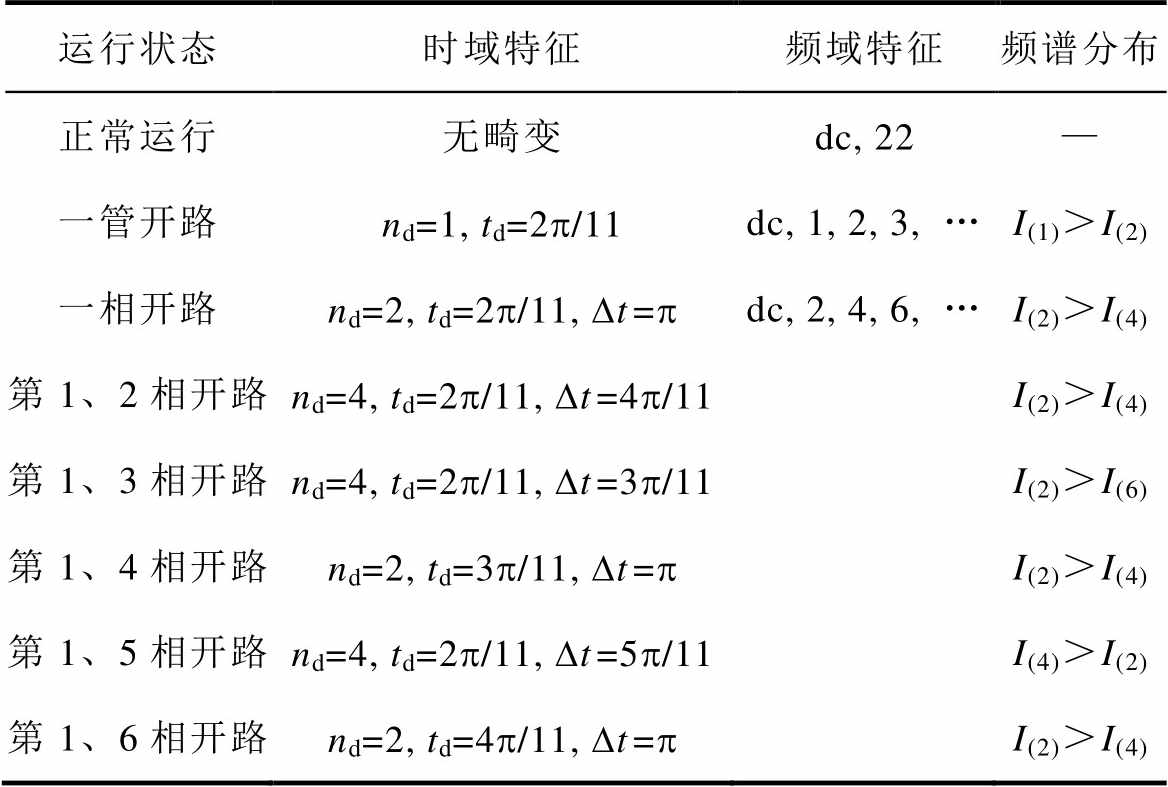
运行状态时域特征频域特征频谱分布 正常运行无畸变dc, 22— 一管开路nd=1, td=2p/11dc, 1, 2, 3, …I(1)＞I(2) 一相开路nd=2, td=2p/11, Dt=pdc, 2, 4, 6, …I(2)＞I(4) 第1、2相开路nd=4, td=2p/11, Dt=4p/11I(2)＞I(4) 第1、3相开路nd=4, td=2p/11, Dt=3p/11I(2)＞I(6) 第1、4相开路nd=2, td=3p/11, Dt=pI(2)＞I(4) 第1、5相开路nd=4, td=2p/11, Dt=5p/11I(4)＞I(2) 第1、6相开路nd=2, td=4p/11, Dt=pI(2)＞I(4)
由故障特征可知，不同旋转整流器故障模式由于二极管故障数量及位置的不同，励磁电流时域波形在畸变坑数量、畸变坑的间隔以及持续时间上区分明显，可用于区分旋转整流器故障模式。但是值得注意的是，仅依赖励磁电流时域特征并不能可靠识别出故障的发生，仅能用于在可靠确定旋转整流器故障发生后的模式区分。与时域特征同理，不同故障下频谱分布特征也将不同，由表4可知，两者互相辅助可对故障模式进行一一区分，但同样无法可靠识别出故障的发生。与此相反，仅依赖频域特征对于一相开路故障和两相开路故障区分度不足，如表2和图19中，第1、2相二极管开路故障后励磁电流总有效值小于一相开路故障下的，但依据故障前后总谐波含量的变化能可靠识别故障的发生，同时利用奇数次谐波含量与偶数谐波电流含量的比值也能识别出一管开路故障。
综上所述，本文提出一种基于励磁机定子励磁电流时域、频域以及频谱分布特征的旋转二极管开路故障保护原理，诊断步骤如下：
（1）采集滤波。采集励磁机的定子励磁电流并进行滤波。
（2）故障特征量计算。首先计算步骤（1）采集并经过滤波的励磁电流时域波形的极小值nd，并对结果进行取整；其次对励磁电流进行快速傅里叶变换（Fast Fourier Transform, FFT）分析，计算奇数次谐波有效值I1、偶数次谐波有效值I2及总谐波有效值I3；直流量记为I0，2次、4次和6次谐波电流分别记为I(2)、I(4)和I(6)，有
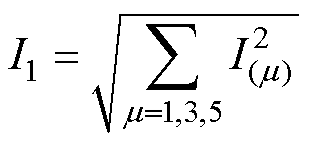
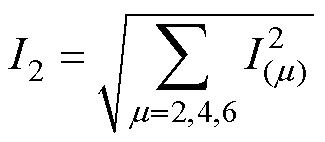
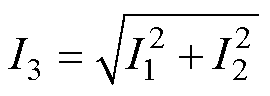
（3）进行故障判断。
总体故障诊断流程如图20所示。本文提出的方法结合励磁电流时域、频域以及频谱分布三者特征，不仅能有效提高诊断的可靠性，还能大大提高对不同故障模式的区分度，从而实现利用单一电气量实现对旋转整流器不同故障模式的可靠诊断及准确区分。
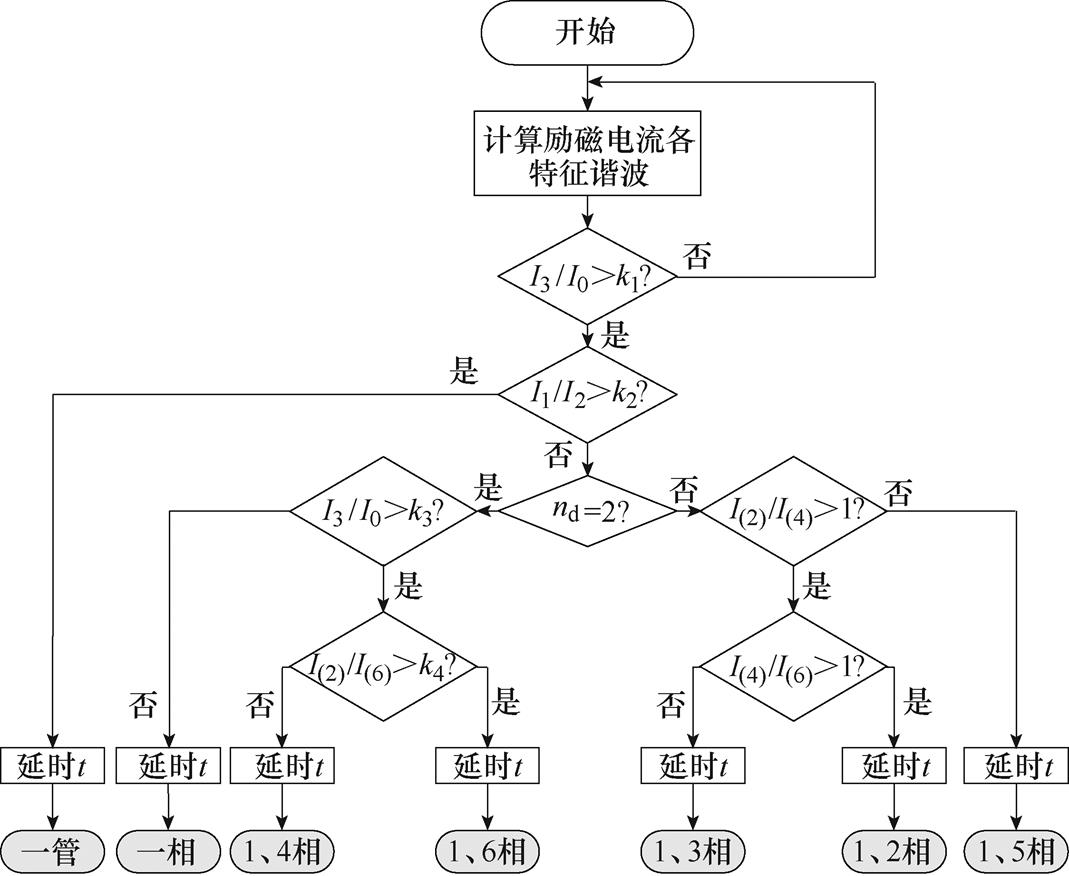
图20 故障诊断流程
Fig.20 Fault diagnosis process
为了验证保护方法的正确性，本文根据图20编制了相应的诊断程序，并在样机上进行了一管、一相等不同开路故障模式的实验，保护门槛定值根据理论分析或者实验结果确定，考虑一定的可靠系数，实际应用时可以根据与真机匹配的仿真结果确定。实验时对励磁电流进行傅里叶分解，通过选取1～6次谐波电流叠加合成原励磁电流的方式进行滤波，为保证准确度，计算nd值时通常选取10个周期以上的数据。图21为一相开路及两相开路故障实验励磁电流的nd计算值，可以看出，故障期间一相开路故障nd值稳定在2左右，而第1、2相和第1、3相以及第1、5相开路故障励磁电流nd值稳定在4左右，与理论分析结果一致，实验过程中保护方法可靠识别励磁电流的时域特征。
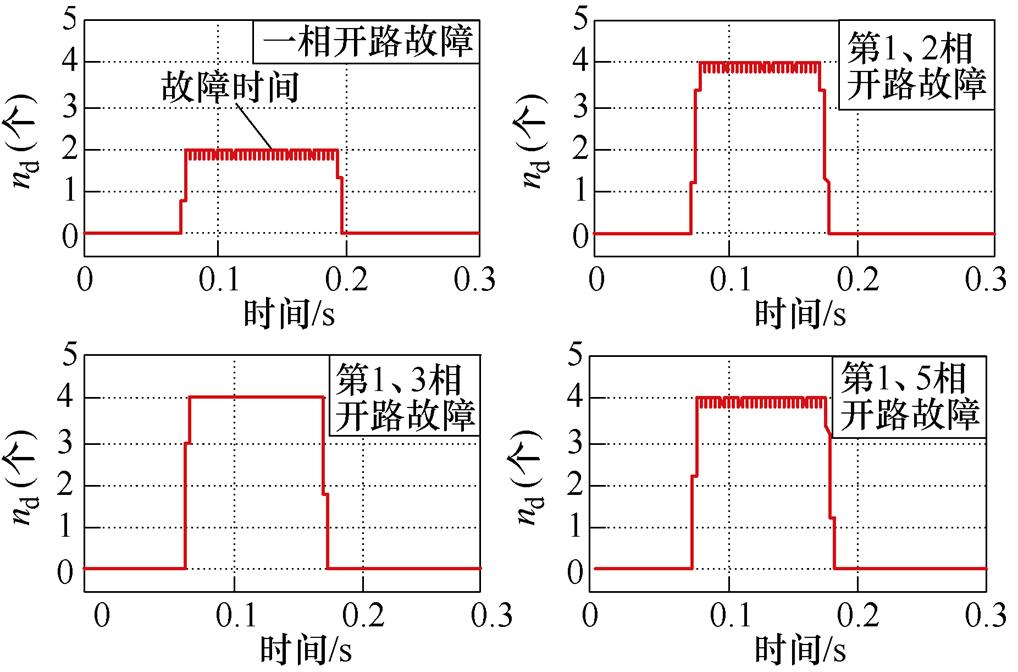
图21 整流器开路故障下的nd值
Fig.21 The nd value under rectifier open-circuit fault
5.4.1 一管开路故障的识别
与一相开路故障和两相开路故障不同，一管开路故障下励磁电流同时含有奇数次和偶数次谐波电流。图22为实验过程中奇偶次谐波电流有效值的比值变化，可以看到，一管开路故障时I1/I2显著大于门槛定值，保护方法可靠识别一管开路故障。
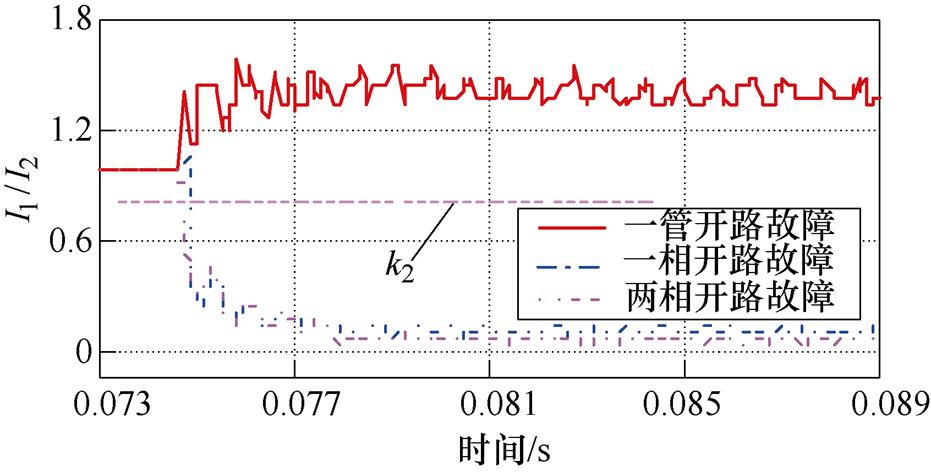
图22 一管开路故障的诊断
Fig.22 Diagnosis of one-tube open circuit fault
5.4.2 一相开路故障的识别
根据图21可知，一相开路故障、第1～4相开路以及第1～6相开路故障励磁电流nd值都为2，但是总谐波有效值不同。图23为一相故障及两种两相开路故障前后的实验励磁电流总谐波有效值与直流分量比值的变化，可看出一相开路故障时总谐波有效值比值明显小于第1～4和第1～6相开路故障，且小于门槛定值，诊断方法可靠区分一相开路故障。
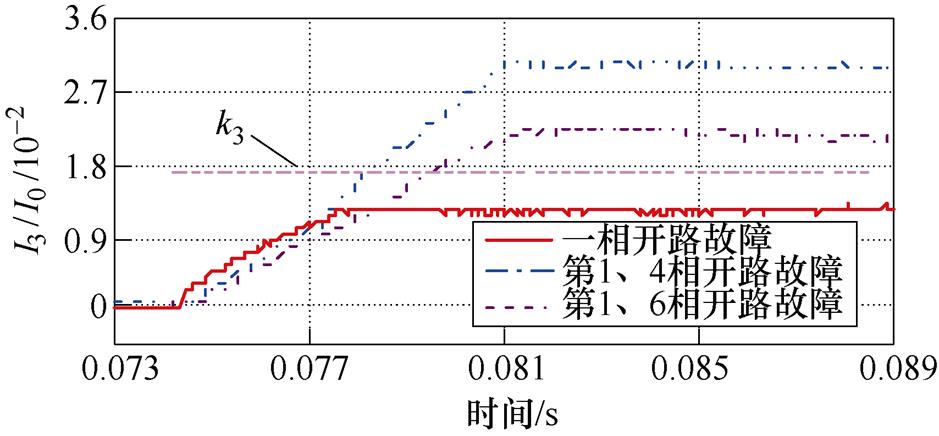
图23 一相开路故障的诊断
Fig.23 Diagnosis of one-phase open circuit fault
5.4.3 两相开路故障的识别及区分
对于总谐波有效值大于一相开路故障的第1、4相开路和第1、6相开路故障，根据图20可知，保护利用I(2)/I(6)进行区分。从图24可知，第1、6相开路故障后I(2)/I(6)比值显著大于第1、4相开路故障，超过门槛定值，保护可靠区分两种故障模式。
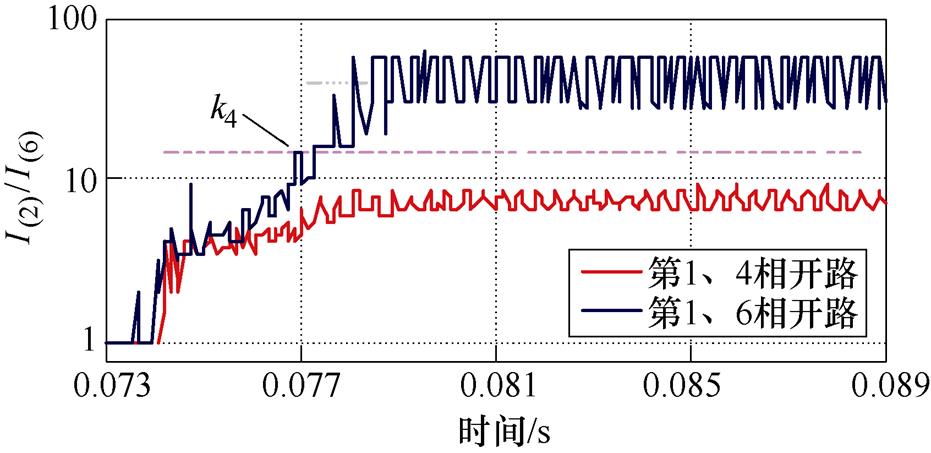
图24 第1、4相和第1、6相开路故障的诊断
Fig.24 Diagnosis of the 1st、4th and the 1st、6th fault
而对于故障励磁电流nd值都为4的第1、2相和第1、3相以及第1、5相开路故障，保护方法利用谐波有效值的分布特征进行诊断并区分。图25为三种两相开路模式故障前后I(2)/I(4)、I(4)/I(6)的比值变化。比值判据门槛定值为1，从图25a可以看出，第1、5相开路故障时，I(2)/I(4)比值显著低于门槛定值，保护可靠识别。同理，从图25b可以看出，第1、2相和第1、3相开路故障时，I(4)/I(6)比值有显著差异，第1、3相开路故障下，I(4)/I(6)比值远低于门槛定值1。在实验过程中保护可靠识别并区分以上三种两相开路故障。
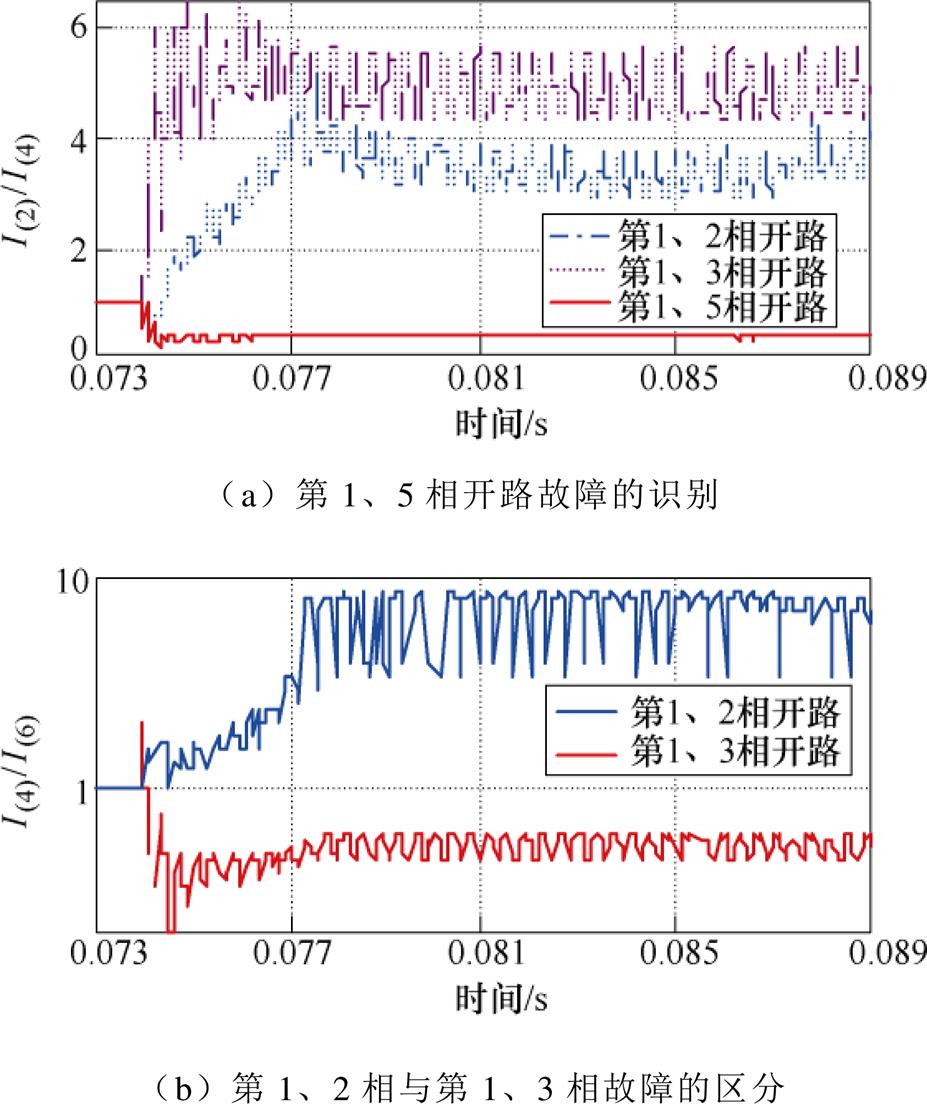
图25 两相开路故障的诊断
Fig.25 Diagnosis of two-phase open circuit fault
本文从多相环形无刷励磁机正常运行机理出发对二极管故障后励磁电流时频特征进行了深入研究，全面分析了一管、一相及不同位置二极管两相开路故障后对励磁电流时域波形的影响机理，深入揭示了故障后励磁电流频域及频谱分布特征，理论分析与样机实验结果完全一致，结论如下：
1）一管开路故障后一周期励磁电流波形含有一个畸变坑，对应频域特征为各整数次谐波电流，有效值分布特征为依次递减。
2）一相开路故障后一周期励磁电流波形中含有两个畸变，对应频域特征为偶数次谐波电流，有效值分布特征为依次递减。
3）两相开路故障后一周期励磁电流中含有2个或者4个畸变坑，频域为偶数次谐波电流，在分布特征上第1、3相开路故障主要为2、6次谐波电流，第1、5相开路故障主要为4次谐波电流。
基于以上故障特征，本文提出了基于励磁机定子励磁电流频域、时域以及频谱分布特征三者结合的诊断方法，动模样机实验表明本文提出的保护方法能可靠识别所有不同模式二极管开路故障。本文提出的保护方法简单可靠，可应用于一般多相环形无刷励磁机的旋转整流器故障保护。
附 录
11相环形无刷励磁机电枢绕组连接：
第1相：1-16-31-46-61-76-14
第2相：29-44-59-74-12-27-42
第3相：57-72-10-25-40-55-70
第4相：8-23-38-53-68-6-21
第5相：36-51-66-4-19-34-49
第6相：64-2-17-32-47-62-77
第7相：15-30-45-60-75-13-28
第8相：43-58-73-11-59-41-56
第9相：71-9-24-39-54-69-7
第10相：22-37-52-67-5-20-35
第11相：50-65-3-18-33-48-63
参考文献
[1] 赵冬梅, 王浩翔, 陶然. 计及风电-负荷不确定性的风-火-核-碳捕集多源协调优化调度[J]. 电工技术学报, 2022, 37(3): 707-718.
Zhao Dongmei, Wang Haoxiang, Tao Ran. A multi- source coordinated optimal scheduling model con- sidering wind-load uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 707-718.
[2] 付兴贺, 江政龙, 吕鸿飞, 等. 电励磁同步电机无刷励磁与转矩密度提升技术发展综述[J]. 电工技术学报, 2022, 37(7): 1689-1702.
Fu Xinghe, Jiang Zhenglong, Lü Hongfei, et al. Review of the blushless excitation and torque density improvement in wound field synchronous motors[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1689-1702.
[3] 孙嘉伟, 郑泽东, 李驰, 等. 对称型多相电机断相容错运行下的电流谐波分析与补偿[J]. 电工技术学报, 2022, 37(21): 5424-5434.
Sun Jiawei, Zheng Zedong, Li Chi, et al. Analysis and compensation of current harmonics in symmetrical multiphase machines in fault-tolerant operation against open-phase faults[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5424-5434.
[4] Zouaghi T, Poloujadoff M. Modeling of polyphase brushless exciter behavior for failing diode oper- ation[J]. IEEE Transactions on Energy Conversion, 1998, 13(3): 214-220.
[5] Jiao Ningfei, Han Xu, Wei Zhihuang, et al. Online fault diagnosis for rotating rectifier in wound-rotor synchronous starter-generator based on geometric features of current trajectory[J]. IEEE Transactions on Industrial Electronics, 2021, 68(4): 2952-2963.
[6] Pang Ji, Liu Weiguo, Wei Zhihuang, et al. Online diode fault detection in rotating rectifier of the brushless synchronous starter generator[J]. IEEE Transactions on Industrial Informatics, 2020, 16(11): 6943-6951.
[7] Zhang Zan, Liu Weiguo, Peng Jichang, et al. Identification of TBMES rotating diode failure[J]. IET Electric Power Applications, 2017, 11(2): 260- 271.
[8] Wei Zhihuang, Liu Weiguo, Pang Ji, et al. Fault diagnosis of rotating rectifier based on waveform distortion and polarity of current[J]. IEEE Transa- ctions on Industry Applications, 2019, 55(3): 2356- 2367.
[9] Rahnama M, Vahedi A, Alikhani A M, et al. Diode open-circuit fault detection in rectifier bridge of the brushless synchronous generator[C]//2018 XIII Inter- national Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 2018: 1821-1826.
[10] Salah M, Bacha K, Chaari A, et al. Brushless three- phase synchronous generator under rotating diode failure conditions[J]. IEEE Transactions on Energy Conversion, 2014, 29(3): 594-601.
[11] Wu Yucai, Cai Bochong, Ma Qianqian. Research on an online diagnosis for rotating diode faults in three-phase brushless exciter with two coils[J]. IET Electric Power Applications, 2019, 13(1): 101-109.
[12] 孙宇光, 杜威, 桂林, 等. 用于多相无刷励磁机开路与短路故障检测的磁极探测线圈设计[J]. 电工技术学报, 2022, 37(14): 3542-3554.
Sun Yuguang, Du Wei, Gui Lin, et al. Design of pole detection coils for open-circuit and short-circuit faults in multiphase brushless exciter[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3542- 3554.
[13] 吴新振, 张伟玲, 董海涛, 等. 十二相整流发电机二极管开路的故障运行分析[J]. 电工技术学报, 2017, 32(3): 157-163.
Wu Xinzhen, Zhang Weiling, Dong Haitao, et al. Analysis of diode-open fault operation for 12-phase rectifier generators[J]. Transactions of China Electro- technical Society, 2017, 32(3): 157-163.
[14] 孙宇光, 黄子果, 陈丽, 等. 十二相整流同步发电机定子匝间短路故障计算[J]. 电工技术学报, 2014, 29(3): 57-64.
Sun Yuguang, Huang Ziguo, Chen Li, et al. Calcu- lation of stator winding inter-turn short circuit in 12-phase synchronous generators with rectifier load system[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 57-64.
[15] 张艳辉, 郑晓钦, 吴新振, 等. 基于有限元场路耦合的十二相整流发电机系统定子匝间短路分析[J]. 电工技术学报, 2019, 34(9): 1842-1849.
Zhang Yanhui, Zheng Xiaoqin, Wu Xinzhen, et al. Analysis of stator winding inter-turn short circuit on a 12-phase rectifier generator system based on finite element field-circuit coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1842- 1849.
[16] 郝亮亮, 张扬, 屈天龙, 等. 多相多边形无刷励磁机及旋转整流系统的运行状态分析[J]. 电力自动化设备, 2020, 40(4): 159-165.
Hao Liangliang, Zhang Yang, Qu Tianlong, et al. Operating state analysis of multi-phase angular brushless exciter and rotating rectifier system[J]. Electric Power Automation Equipment, 2020, 40(4): 159-165.
[17] 郝亮亮, 胡启昊, 张扬, 等. 多相环形无刷励磁系统的运行特性分析[J]. 电机与控制学报, 2021, 25(7): 30-39.
Hao Liangliang, Hu Qihao, Zhang Yang, et al. Analysis of operation characteristics of multiphase annular brushless excitation system[J]. Electric Machines and Control, 2021, 25(7): 30-39.
[18] Hao Liangliang, Chang Jiang, Hu Liang, et al. Analysis of the interturn short circuits of stator field windings in multiphase angular brushless exciter at nuclear power plant[J]. IEEE Transactions on Energy Conversion, 2019, 34(4): 2126-2136.
[19] Hao Liangliang, Chen Jianlin, Li Jiahui, et al. Diagnosis of rotor winding short-circuit fault in multi-phase annular brushless exciter through stator field current harmonics[J]. IEEE Transactions on Energy Conversion, 2021, 36(3): 1808-1817.
[20] 郝亮亮, 李佳慧, 段贤稳, 等. 核电多相环形无刷励磁机转子绕组短路故障特征分析[J]. 电工技术学报, 2020, 35(6): 1251-1261.
Hao Liangliang, Li Jiahui, Duan Xianwen, et al. Analysis of short circuit fault characteristics of rotor winding of nuclear power multiphase ring brushless exciter[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1251-1261.
[21] 郝亮亮, 王善铭, 邱阿瑞, 等. 多相无刷励磁系统励磁机定子电流谐波特性[J]. 清华大学学报(自然科学版), 2011, 51(1): 58-62.
Hao Liangliang, Wang Shanming, Qiu Arui, et al. Harmonic characteristics of exciter stator current in multiphase brushless excitation system[J]. Journal of Tsinghua University (Science and Technology), 2011, 51(1): 58-62.
[22] 郝亮亮, 王善铭, 邱阿瑞, 等. 多相无刷励磁系统旋转整流器故障的仿真与识别[J]. 电工技术学报, 2012, 27(4): 138-144.
Hao Liangliang, Wang Shanming, Qiu Arui, et al. Simulation and identification of rotating rectifier fault in multiphase brushless excitation system[J]. Transa- ctions of China Electrotechnical Society, 2012, 27(4): 138-144.
[23] 郝亮亮, 李佳慧, 李洪学, 等. 核电多相角形无刷励磁系统旋转二极管开路故障特征分析[J]. 电力系统自动化, 2019, 43(11): 112-120.
Hao Liangliang, Li Jiahui, Li Hongxue, et al. Characteristic analysis of open-circuit fault of rotating diode in nuclear multi-phase angular brush- less excitation system[J]. Automation of Electric Power Systems, 2019, 43(11): 112-120.
[24] 蔡波冲, 武玉才, 赵艳军. 基于定子电流谐波法的无刷励磁机旋转二极管开路故障检测[J]. 大电机技术, 2018(4): 61-65.
Cai Bochong, Wu Yucai, Zhao Yanjun. The detection of open-circuit fault of rotary diode in brushless exciter using stator current harmonic method[J]. Large Electric Machine and Hydraulic Turbine, 2018(4): 61-65.
[25] Chen Jianlin, Hao Liangliang, Wang Xiaoming, et al. Analysis of armature winding open-phase fault in multi-phase annular brushless exciter at nuclear power plant[J]. IET Electric Power Applications, 2021, 15(3): 271-283.
Abstract The excitation system with a multi-phase annular brushless exciter (MPABE) is widely used in large-capacity nuclear power plants. However, the rectifier open-circuit fault caused by diodes or fuses damage often occurs in field operation. The fault types can be classified as one-tube open-circuit fault, one-phase open-circuit fault, and two-phase open-circuit fault. The actual site needs to reliably diagnose the open-circuit fault occurrence of multi-phase rotating rectifiers and accurately distinguish the fault modes. Since the field winding of the exciter is located at the stator and the rectifier rotates with the rotor at high speed, the rectifier fault cannot be monitored directly. Therefore, it is an effective way to diagnose the rotating rectifier fault using the excitation current characteristics. Hence, this paper analyzes the rectifier fault mechanism and proposes a new rectifier open-circuit fault diagnosis method based on the time-frequency characteristics of the fault excitation current.
Firstly, the operation mechanism of an 11-phase annular brushless excitation system is analyzed theoretically. Based on the diode conduction sequence and the position of the fault diode in the motor operation period, the time-domain waveform of the fault excitation current is analyzed. Secondly, based on the influence mechanism of the fault diode on excitation current, the fault component of excitation current is analyzed, and the frequency-domain characteristics and spectrum distribution of one-tube open-circuit, one-phase open-circuit and two-phase open-circuit of the rotating diode are obtained. The experiments were carried out on a particular 11-phase exciter prototype. The theoretical analysis is consistent with the prototype experimental results. Finally, based on the combination of time-domain, frequency-domain, and spectrum distribution characteristics of exciter stator excitation current, a new fault diagnosis method of rotating rectifier open-circuit fault in MPABE is proposed for the rectifier one-tube open-circuit fault, one-phase open-circuit fault and two-phase open-circuit fault. The prototype experiment shows that this method can reliably identify all diode open-circuit faults of different modes.
Frequency-domain characteristics indicate the occurrence of a fault. The frequency-domain characteristics of excitation current after rectifier one-phase open-circuit fault and two-phase open-circuit fault are the same, and the harmonic quantity of two-phase fault is not always greater than that of one-phase fault. However, there is a more significant difference between two-phase fault and one-phase fault in time-domain characteristics and spectrum distribution characteristics of excitation current. Therefore, this paper combines the time-domain characteristics with the frequency-domain characteristics to diagnose different faults of the rectifier. The frequency-domain characteristics activate the protection and identify the rectifier’s one-tube open-circuit fault and one-phase open-circuit fault. Then the time-domain and spectrum distribution characteristics are used to distinguish the rectifier’s two-phase open-circuit faults at different locations.
The following conclusions can be drawn from the theoretical analysis and experimental results: (1) After a one-tube open-circuit fault, one period excitation current waveform contains a distortion, the corresponding frequency-domain characteristics are all integer-order harmonic currents, and the distribution characteristics of RMS are decreasing in sequence. (2) After a one-phase open-circuit fault, there are two distortions in the excitation current waveform of one period, the corresponding frequency-domain characteristics are even-order harmonic currents, and the distribution characteristic of RMS decreases in sequence. (3) After a two-phase open-circuit fault, one period of excitation current contains two or four distortions. The frequency domain is even-order harmonic currents. Regarding distribution characteristics, the 1st and 3rd phase open-circuit faults are mainly 2nd and 6th harmonic current, and the 1st and 5th phase open-circuit faults are mainly 4th harmonic current. (4) The proposed diagnosis method can reliably distinguish diode open-circuit faults of all modes.
keywords：Multi-phase annular brushless exciter, rectifier fault, excitation current, time-domain, frequency-domain, spectral distribution
DOI: 10.19595/j.cnki.1000-6753.tces.221408
中图分类号：TM341
中央高校基本科研业务费专项资金项目（2021YJS153, 2020JBM070）和中广核集团公司科技项目（3100077013）资助。
收稿日期 2022-07-22
改稿日期 2022-11-02
郝亮亮 男，1985年生，副教授，博士生导师，研究方向为电力系统主设备故障分析及保护、直流输电控制与保护、励磁控制。E-mail: llhao@bjtu.edu.cn（通信作者）
陈建林 男，1994年生，博士研究生，研究方向为多相无刷励磁系统故障监测及其保护。E-mail: 20117018@bjtu.edu.cn
（编辑 崔文静）