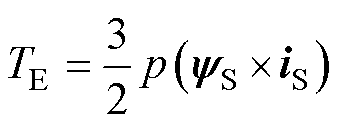（1）
摘要 内置式永磁同步电机的电磁转矩主要包括永磁转矩和磁阻转矩两种成分，转矩成分的准确分离和分析有助于进一步优化设计电机拓扑结构，提高电机的功率密度，而电磁转矩成分精确分析的关键在于交直轴电感的准确计算。该文针对内置式永磁同步电机的交直轴电感求解与转矩成分分析的实际问题，以一台8极11 kW的内置式永磁同步电机为例，对其进行建模仿真计算；通过对采用静磁场求解电感与瞬态场求解电感两类求解电感的方法进行对比分析，在此基础上提出了一种改进的静磁场快速求解交直轴电感的方法，并实现了对电机转矩组成的高精度分离提取和在电磁设计阶段对电磁转矩成分的预测。改进的静磁场求解电感的方法既能精确考虑交叉耦合效应，又能考虑不同负载下饱和效应的影响。此外，相较于瞬态场求解电感的方法，该方法有效减少了仿真步数从而缩短了仿真时长。最后，构建实验测试平台对目标样机进行了转矩测试，并与预测模型结果进行比较，实验结果验证了所提方法的准确性和有效性。
关键词：永磁同步电机 电感计算 转矩分析 有限元分析
永磁同步电机凭借其体积小、功率密度高和控制简单等诸多优点，被广泛应用于电动汽车、伺服驱动、家用电器、高端数控机床和高速主轴等领域[1-5]。
永磁同步电机相较于其他电机，由于采用永磁体进行励磁，其电机结构相对简单，方便解析计算或控制。但无论是对永磁同步电机进行高精度解析建模从而实现优化设计，亦或是对其进行精确驱动控制，都需要准确地求解永磁同步电机的交直轴（d、q轴）电感[6-8]。
目前主要求解d、q轴电感的方法分为解析计算法、有限元数值计算法及实验测量法[9-12]。其中实验测量法是通过搭建实验平台对样机实体进行测试得到交直轴电感。如文献[12]中，作者提出了一种同时注入高频旋转电压和脉动电压的新技术，基于此技术对内置式永磁同步电机d、q轴电感进行估算。通过与只使用旋转电压注入或者脉动电压注入来测试电感相比，新方法不需要位置传感器，也在一定程度上避免了数字滤波器和电压合成引起的延迟效应。但是实验测量电感的方法，需要昂贵的测试设备，以及搭建复杂的实验平台。此外，实验测量法需要具体的样机实体进行测试，因此无法在电机前期优化设计阶段进行应用，其适用范围具有一定的局限性。
解析计算法是通过搭建电机的等效磁路模型，利用电机模型实现d、q轴电感的快速计算。使用解析计算法求解电感有助于在设计过程中，对电机的拓扑结构进行设计优化[13-15]。文献[15]以一台8极100 kW的电机为例，对电机模型中的d、q轴电流进行插值计算，利用插值计算结果解析重建磁链，最后对磁链结果处理后进一步得到电感和转矩的解析表达式。此方法相较于搭建实验平台测试电感的方法更为简便，但其求解精度相对较差。而且内置式永磁同步电机的磁路相对复杂，较难建立精确的磁网格模型，因此解析法的应用范围具有一定的局限性。而在电机的解析模型或精准控制模型的搭建上，必须考虑在实际运行中，电机部分参数非线性变化对其准确性和可靠性的影响[16]。
通过有限元数值计算法求解电感，一定程度上避免了解析法计算结果不精确的缺点，同时规避了实验测试法无法应用于电机电磁设计初期的问题。文献[17]通过有限元工具对双三相电机的电感进行了研究，利用磁路中的磁导，对非线性饱和电感进行了公式化处理，最后利用公式求解出电感。但文献[17]的研究仅考虑磁路饱和效应的影响，并未考虑d、q轴电流交叉耦合的影响。文献[18]以一台4极30 kW的驱动用内置式永磁同步电机为例，采用静磁场求解电机的d、q轴电感。文献[18]具体通过冻结磁导率法对电感进行求解，此方法有助于进一步考虑磁路饱和效应的影响，提高了求解精度。但文献[18]仍然忽略了交叉耦合效应的影响，且求解的仿真模型数量较少，其计算结果的精确性存在不足。文献[19]采用瞬态场进行电感求解，以一台22 kW的自起动永磁同步电机为例，通过冻结磁导率法得到当前磁路饱和条件下的非线性磁场分布，避免了电机磁场非线性导致的求解困难，再通过磁储能法与磁链电流公式进一步成功求解出考虑电流交叉耦合影响下d、q轴电感。但瞬态场求解器本身的处理时间相对较长，且求解电感需对大量不同工作电流下的电机模型进行计算和处理，所以该方法仍然存在求解过程复杂和求解器计算量较大的问题。
由于上述现有求解d、q轴电感的方法，存在精度较差、结果不够准确、求解过程复杂和耗时长以及应用范围具有一定局限性等问题。本文针对内置式永磁同步电机d、q轴电感准确求解的问题，在综合比较了静磁场求解电感和瞬态场求解电感的优缺点后，在两类有限元求解电感方法的思路基础上提出了一种改进的静磁场求解电感的方法：通过对电机机械角与电流超前角进行换算后，变换定转子的机械相对位置；再用有限元计算得到不同d、q轴电流组合下的三相磁链，对三相磁链进行Park变换得到d、q轴磁链；最后通过与采用冻结磁导率法求解得到的永磁体磁链进行联立求解，得到了考虑d、q轴电流交叉耦合及磁路饱和等影响的d、q轴电感。此外本文依据上述方法计算得到的d、q轴电感，进一步构建转矩预测模型，实现了对电机电磁转矩的预测及转矩成分的高精度分离提取。最后，通过样机实验结果与预测模型的数据进行分析对比，验证了电感求解与分析模型的准确性。
以一般常见的三相永磁同步电机为例，正常电机的输入与输出均为三相变量，所以电机的磁场模型是一个三相的空间-时间状态模型。但是为便于分析和观测，对电机的磁场模型进行处理，将其转变为基于同步转子位置定义的交直轴模型。交直轴模型更方便同步电机进行矢量控制，且交直轴模型也有助于电机中的磁场饱和、空间谐波影响、铁损耗等具体问题的分析。
交直轴模型在具体的数学建模中，根据所选变量的差别，可以细分为电流模型与磁链模型[20]。而对于电机的电磁转矩TE，两种数学模型中的转矩公式均可以表示为
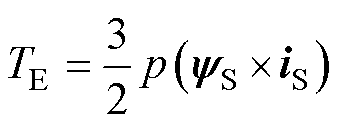（1）
式中，p为电机的极对数；yS=[yd yq]T，yd、yq分别为电机在d、q轴上的磁链，yS代表着dq轴磁链的合成磁链；iS=[id iq]T，id、iq分别为电机在d、q轴上的电流。
两种模型的差异在于，电流模型将合成磁链yS进一步表达为随iS变化，即
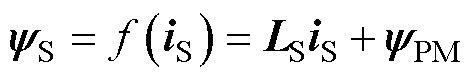（2）
式中，yPM为转子永磁体产生的永磁体磁链；LS为由直轴（d轴）分量电感Ld和交轴（q轴）分量电感Lq组成的对角矩阵，可以表示为
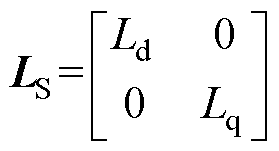（3）
基于式（3）得出电机分别在的d轴和q轴上的磁链方程为
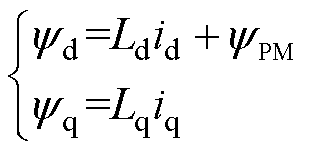（4）
电机中具体各相量之间的关系可以从图1所示的相量图中直观的表示。
在图1中，定义x轴与电机UVW三相中的U相对齐；y0为电流iS产生的磁链；g 为电流超前角，图中显示为iS与d轴的夹角；c 为电机d轴与U相x轴之间相差的角度。由图1可以看出电机的空间状态模型由两套坐标系组成，分别是固定在定子上的xy坐标轴和固定在转子的dq轴坐标系。
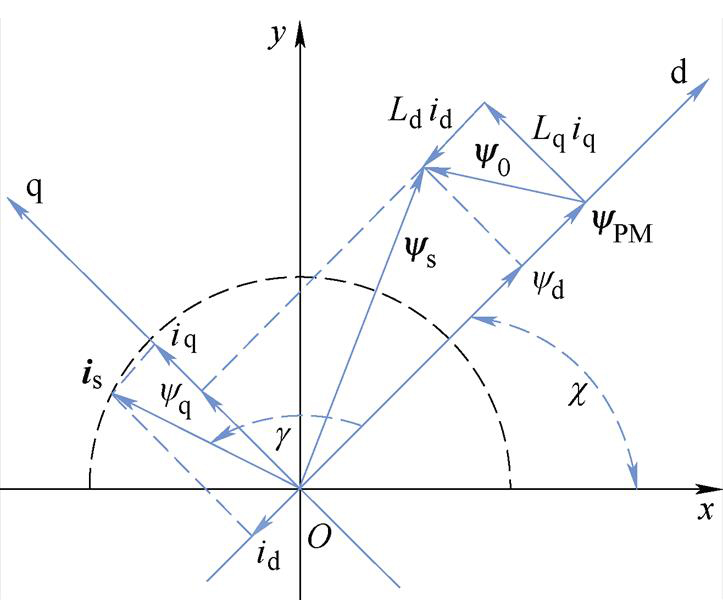
图1 永磁同步电机空间相量
Fig.1 Space phasor diagram of permanent magnet synchronous machine
在磁链模型中其各式的表达则与电流模型刚好相反，将电机电流iS表达为随电机磁链yS变化[21]，即
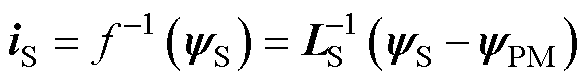（5）
式中，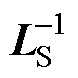
为电感矩阵的LS逆矩阵。
采用式（1）能够快速计算出电机电磁转矩的平均值，然而针对内置式永磁同步电机或者磁阻电机的转矩成分精确分离的问题，需要由式（1）～式（4）对电磁转矩的组成成分磁阻转矩和永磁转矩进行分离提取。即
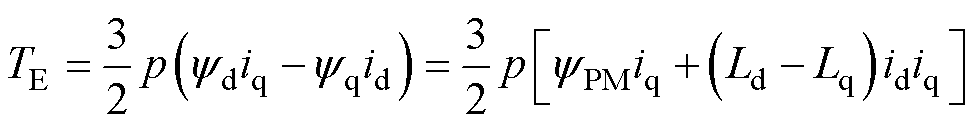（6）
从上述电流模型或者磁链模型中均能发现，若要准确地分析电机的各项转矩成分，需预先通过有限元建模计算求解电机的d、q轴电感。而实际的计算过程中，在负载情况下内置式永磁同步电机通常存在较强的磁路饱和效应与交叉耦合效应，具体表现为电机的d、q轴电感与永磁体磁链会随d、q轴电流组合的改变而变化。所以，若追求模型的准确性与实用性，需要进一步精确求解考虑磁路饱和与交叉耦合效应下，不同d、q轴电流组合下的d、q轴电感与永磁体磁链。因此，d、q轴电感是与d、q轴电流成非线性相关的函数，具体为
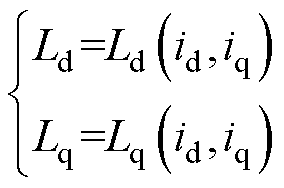（7）
值得注意的是，国内外学者对交叉耦合的定义也有所不同，本文研究的交叉耦合特指Zhu Ziqiang所定义的交轴电流与直轴电流的相互影响[12]。在进一步考虑了磁路饱和效应与交叉耦合效应的电磁转矩公式具体表示为
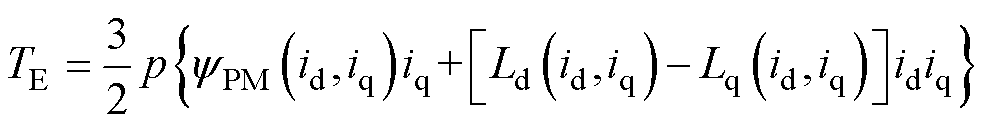（8）
结合式（4），可以得出电感在非线性函数中的求解公式为
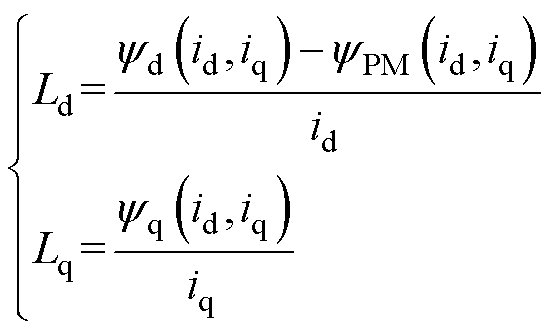（9）
由式（9）可知，准确求解d、q轴电感需先求解出电机的d、q轴磁链。有限元计算求解电感的方法，根据求解器的不同，大致分为通过静磁场和瞬态场求解电感的两类方法。本文通过对上述两类方法进行梳理总结，提出了一种改进的静磁场求解电感的方法。
本文具体以一台8极11 kW的内置式永磁同步电机为样机，电机的具体参数见表1。
表1 永磁同步电机样机参数
Tab.1 The parameters of permanent magnet synchronous machine
参 数数 值 定子外径Dse/mm222 定子内径Ds/mm158 转子内径Dr/mm48 铁心长度l/mm110 气隙长度d/mm0.6 定子槽数Qs36 每相串联匝数N120 永磁体剩余磁感应强度Br/T1.2 永磁体相对磁导率mr1.05 永磁体厚度h/mm5 额定功率P/kW11 并联支路数a1 永磁体极对数p4 额定转速n1/(r/min)1 500
一般认为，有限元静磁场是一个相对静止的求解器，只考虑电机在某一个位置下，电机定转子之间的电磁耦合关系。在静磁场中电机的三相电流不再是随时间变化的正弦函数，而是某一时刻符合基尔霍夫定律的定值，具体公式[22]为
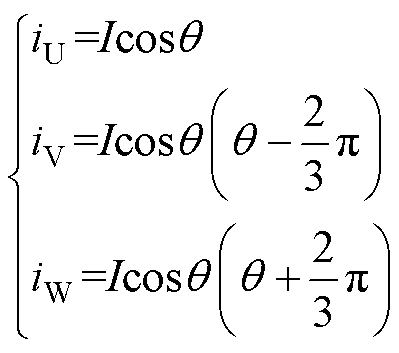（10）
式中，I为通入U相电流的幅值；iU、iV、iW为定子U、V、W三相的相电流瞬时值；q 为此时刻与电机转子机械位置相对应的电角度。
永磁同步电机定转子位置调整示意图如图2所示，采用静磁场直接求解电感的方法，是预先通过调节定转子之间的相对位置，实现电机转子的d、q轴坐标系与定子U相的xy坐标系相重合的目的（电机的d轴对准U相）。此时，式（10）中的q 角为0，通过注入的三相电流为I、-0.5I、-0.5I，等价为只在d轴注入电流，根据磁链结果可以直接计算d轴电感，同样的原理也可以求解出q轴的电感，其直接计算电感的公式为
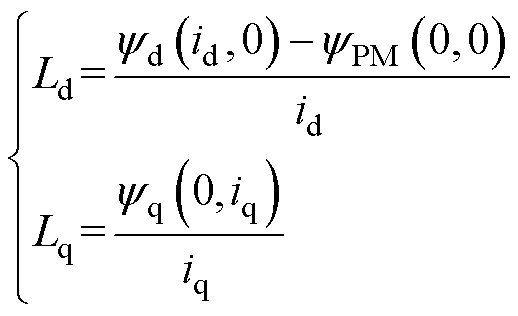（11）
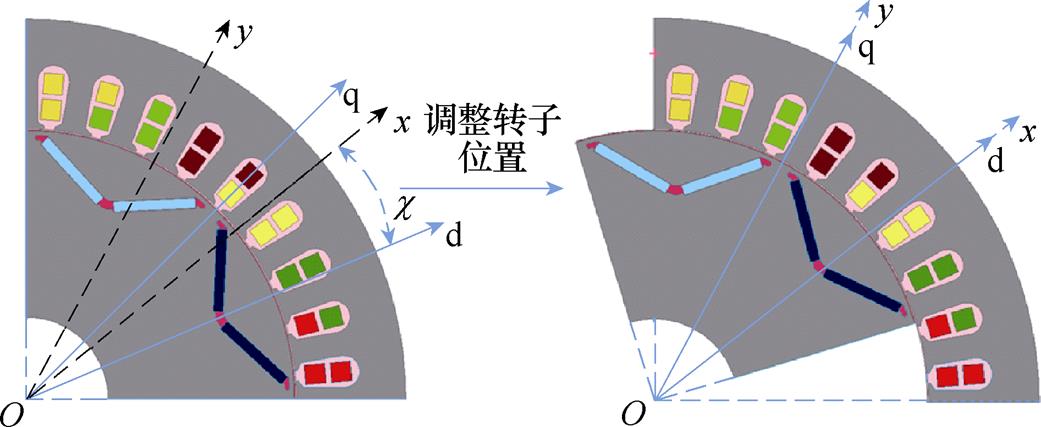
图2 永磁同步电机定转子位置调整示意图
Fig.2 Schematic diagram of position adjustment of stator and rotor of permanent magnet synchronous machine
采用上述方法能够快速求出d、q轴电感，但其计算精度不高，且无法考虑永磁体的工作点在通入不同电流时所产生的变化。此外，该方法也无法顾及磁路饱和与交叉耦合效应对电感的影响，因此上述方法不适用于高精度定量分离内置永磁同步电机的电磁转矩成分。
不同电流下的电机相对磁导率云图如图3所示。分别比较模型在不同电流下的定转子相对磁导率mr的云图，不同电流下定转子mr有较大差异，引起电机磁路中的磁阻发生较大变化，从而导致永磁体磁链幅值的差异，以及电机磁路中饱和程度的变化。所以，为了保证d轴电感计算的准确性，可以采用冻结磁导率法对永磁体磁链进行精确计算，对通入d轴电流时的定转子相对磁导率进行冻结，代入重新构建的电机模型中，计算电流iS为0时刻的永磁体磁链，因此d轴电感计算公式可以进一步修正为
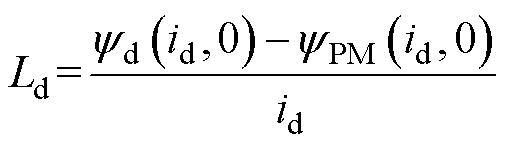（12）
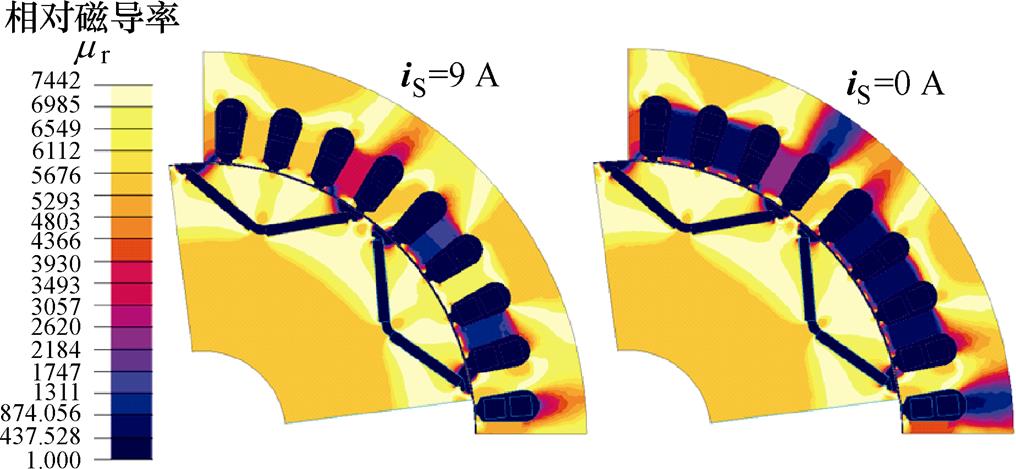
图3 不同电流下的电机相对磁导率云图
Fig.3 Relative permeability cloud of machine at different currents
静磁场求解电感及永磁体磁链如图4所示。由图4a可知，在静磁场求解电感的过程中，采用冻结磁导率法和未采用冻结磁导率法的d轴电感计算结果差异较大。由于未采用冻结磁导率法求解电感时选取的永磁体磁链为定值，均是d轴电流id和q轴电流iq为0时的永磁体磁链，即yPM(0, 0)=0.472 Wb。而采用冻结磁导率法求解永磁体磁链能够有效考虑d轴电流id对永磁体磁链的影响，即yPM(id, 0)。从图4b采用冻结磁导率法求解的永磁体磁链曲线中可以发现，随着去磁电流的增加（由0至-30 A），永磁体工作点将发生偏移，导致永磁体磁链也逐渐增大，结合式（12）所求解的d轴电感，随去磁电流的增加而减小。图4c为采用静磁场求解的q轴电感，q轴电感随q轴电流的增加而减少，原因为q轴磁路随q轴电流增加逐渐趋于饱和。
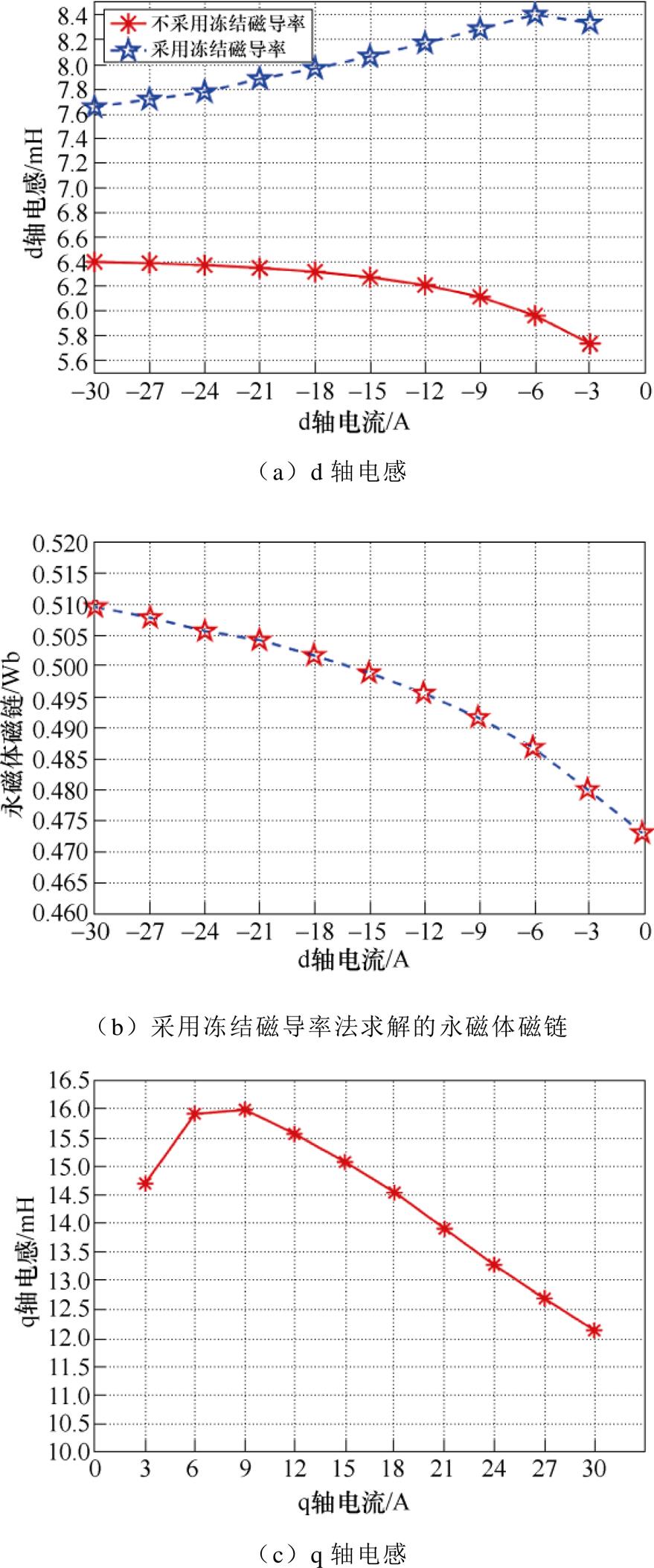
图4 静磁场求解电感及永磁体磁链结果
Fig.4 Calculation of inductances and permanent magnet flux by stacic magnetic field
采用上述静磁场求解电感的方法，可以较快且简便地求解出d、q轴电感，但其求解精度不高，且并未考虑d、q轴电流交叉耦合效应对电感的影响。采用瞬态场的电感计算，在一定程度上可以解决此问题，能计算不同d、q轴电流组合下的d、q轴电感，且同时考虑了磁路饱和效应与交叉耦合效应的影响。
采用瞬态场的电感计算方法需采用d、q轴电流来进一步表述所耦合的场路模型中的三相电流源表达式，可以表述为
（13）
为了能在d、q轴施加特定的定子电流，与静磁场求解电感类似，采用瞬态场的电感计算方法同样需要将转子d轴与定子的U相对齐。从式（13）中可以看出，输入不同的d、q轴电流组合，将对应产生不同的电流超前角g。通过计算电机模型在不同d、q轴电流组合下的三相磁链，再对三相磁链进行Park变换得到d、q轴磁链[23]为
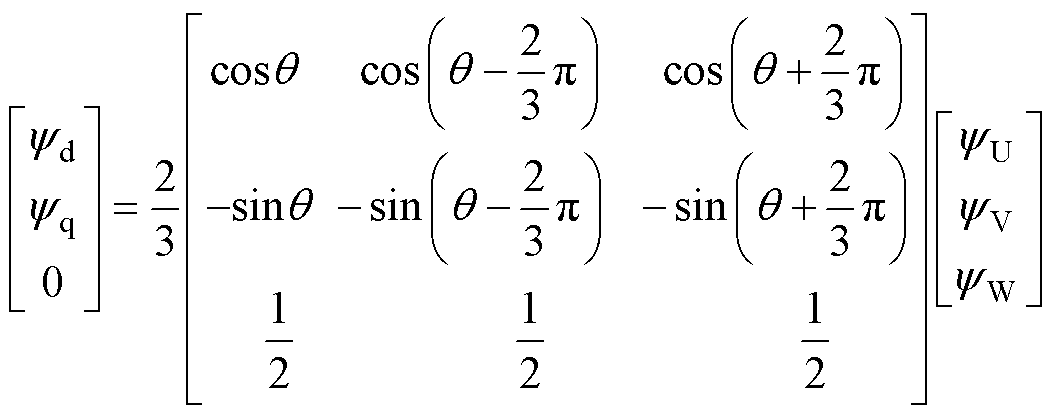（14）
式中，yU、yV、yW分别为电机U、V、W三相的磁链。
在瞬态场的电感计算过程中，是通过调节电流模型中的输入量，达到控制输入电流超前角g 的效果，得到不同g 下的磁链结果，对磁链结果进行Park变换处理，最后再通过式（9）所示的考虑饱和效应和交叉耦合效应的磁链电流公式，计算出不同d、q轴电流组合下的d、q轴电感。通过上述瞬态场求解电感的方法可以有效地考虑饱和效应及交叉耦合效应对电机d、q轴电感的影响，得到较为精确的d、q轴电感数值三维图，如图5所示。
对上述不同求解电感的方法，进行优缺点比较见表2。尽管瞬态场的计算方法能够较好地考虑电机磁路饱和效应和d、q轴电流相互耦合效应等问题，满足对d、q轴电感的求解需求。然而，通过瞬态场对电机电磁性能的求解需要进行若干个电周期的仿真计算，且为了保证计算精度，每个电周期内通常需要求解50～200步，因此其求解时间相对较长，在实际的使用中存在一定的局限性。
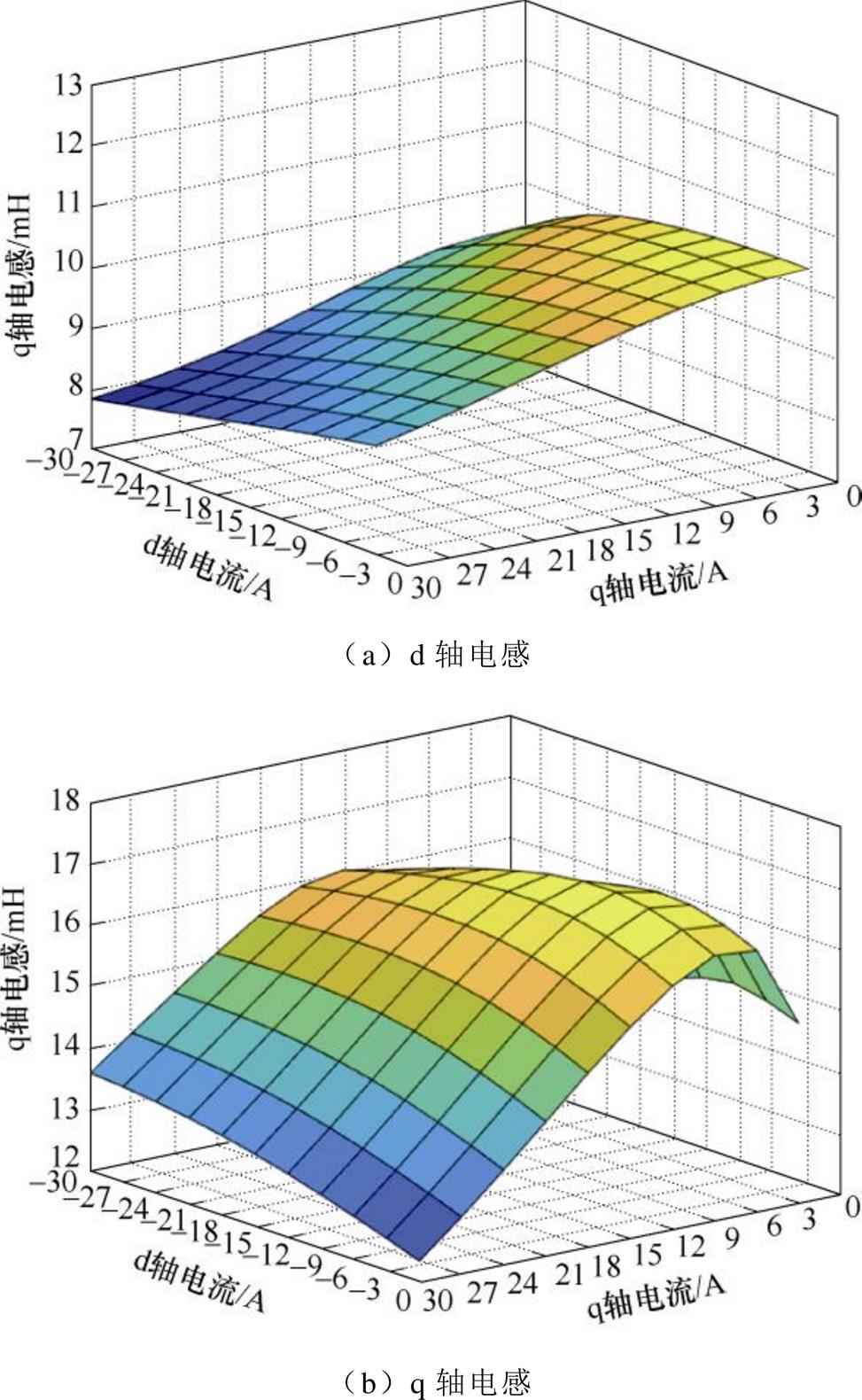
图5 瞬态场求解电感数值三维图
Fig.5 Calculating inductance of transient field
表2 电感计算方法优缺点比较
Tab.2 Comparison of advantages and disadvantages of inductance calculation methods
电感计算方法优 点缺 点 静磁场电感计算计算迅速，求解简便计算结果不准确，且不能考虑交叉饱和影响 瞬态场电感计算考虑交叉饱和影响，结果相对准确求解时间过长
采用静磁场求解电感的方法，具备的优点是计算快捷，该特性受益于求解器自身收敛迅速以及仿真步长的缩减。因此本文利用此特点，提出一种能避免瞬态场求解电感计算时间长，且能考虑d、q轴电流交叉耦合影响的静磁场电感计算方法。
在原有的瞬态场计算不同d、q轴电流组合的电感求解过程中，一般是通过对式（13）中的id和iq的幅值进行调整，实现电流空间相位的改变，从而获得不同电流超前角下的三相磁链和d、q轴电感。针对该计算原理，改进后考虑交叉耦合的静磁场求解电感流程如图6所示。对上述计算逻辑进行重构，并采用静磁场下冻结磁导率方法快速计算不同d、q轴电流组合下的永磁体磁链，从而确保进一步考虑交叉耦合效应和饱和效应的d、q轴电感的精确计算。此外，上述静磁场求解方法依据磁链模型理论上只需要1步仿真即可获得平均电磁转矩，从而显著缩短了有限元仿真步数，缩短仿真耗时。
如图6所示，具体的流程为先根据电机的额定工作点以及目标精度确定求解d、q轴电流组合的范围。然后根据d、q轴电流组合计算得到相应的电流超前角g，再依据式（15）所示的换算公式进行转子机械角s 与相应电流超前角g 的换算；调整电机模型的机械角s 后，进行静磁场计算；提取不同d、q轴电流组合下计算结果的三相磁链，并同时采用冻结磁导率法得到该d、q轴电流组合下的定转子相对磁导率mr(id, iq)；对三相磁链进行Park变换得到d、q轴磁链，并将定转子相对磁导率mr(id, iq)重新代入电机模型求解永磁体磁链yPM(id, iq)。最后，通过式（9）的磁链电流公式求解得到考虑了磁路饱和效应与交叉耦合效应的d、q轴电感。
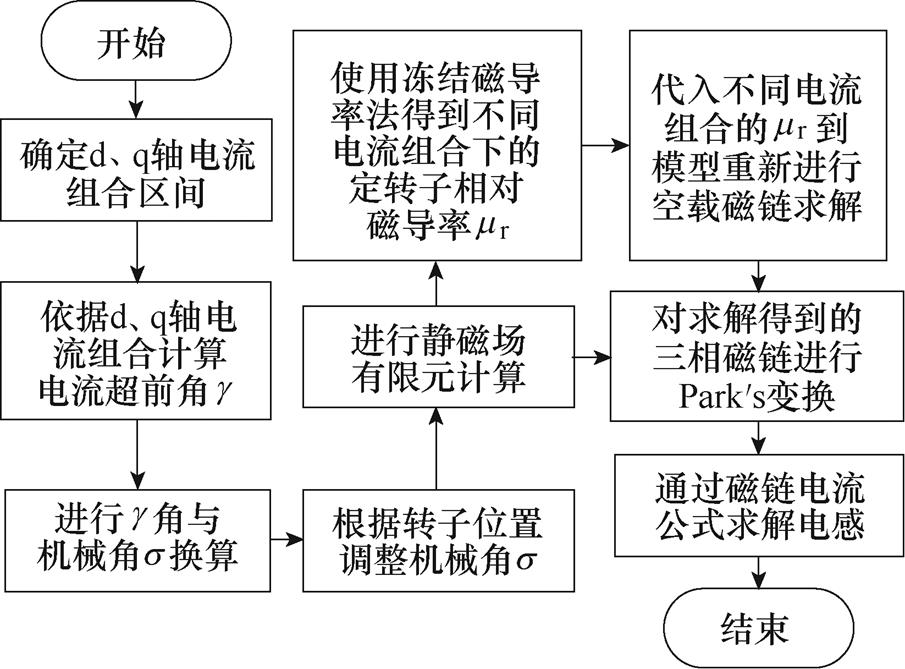
图6 改进后考虑交叉耦合的静磁场求解电感流程
Fig.6 Flow chart of the improved solution of static magnetic field inductance considering cross coupling effects
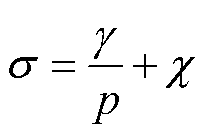（15）
对瞬态场求解电感和改进的静磁场求解电感的两种方法中计算得到的永磁体磁链绘制三维图如图7所示。对比两种不同方法求取的永磁体磁链幅值可以发现，两者较为接近，且由于d轴通入的是去磁电流，随着d轴电流的增加，求解的永磁体的磁链反而减小，而随着q轴电流的增加，由于交叉耦合的影响，永磁体磁链在一定程度上增加。但是由于改进的静磁场计算方法的步数相较于瞬态场计算方法，有较为显著的缩减，且瞬态场计算方法所得到的磁链值为多个仿真周期内的平均值，所以两者对比发现，其计算结果仍然存在一定差异，但并不显著。
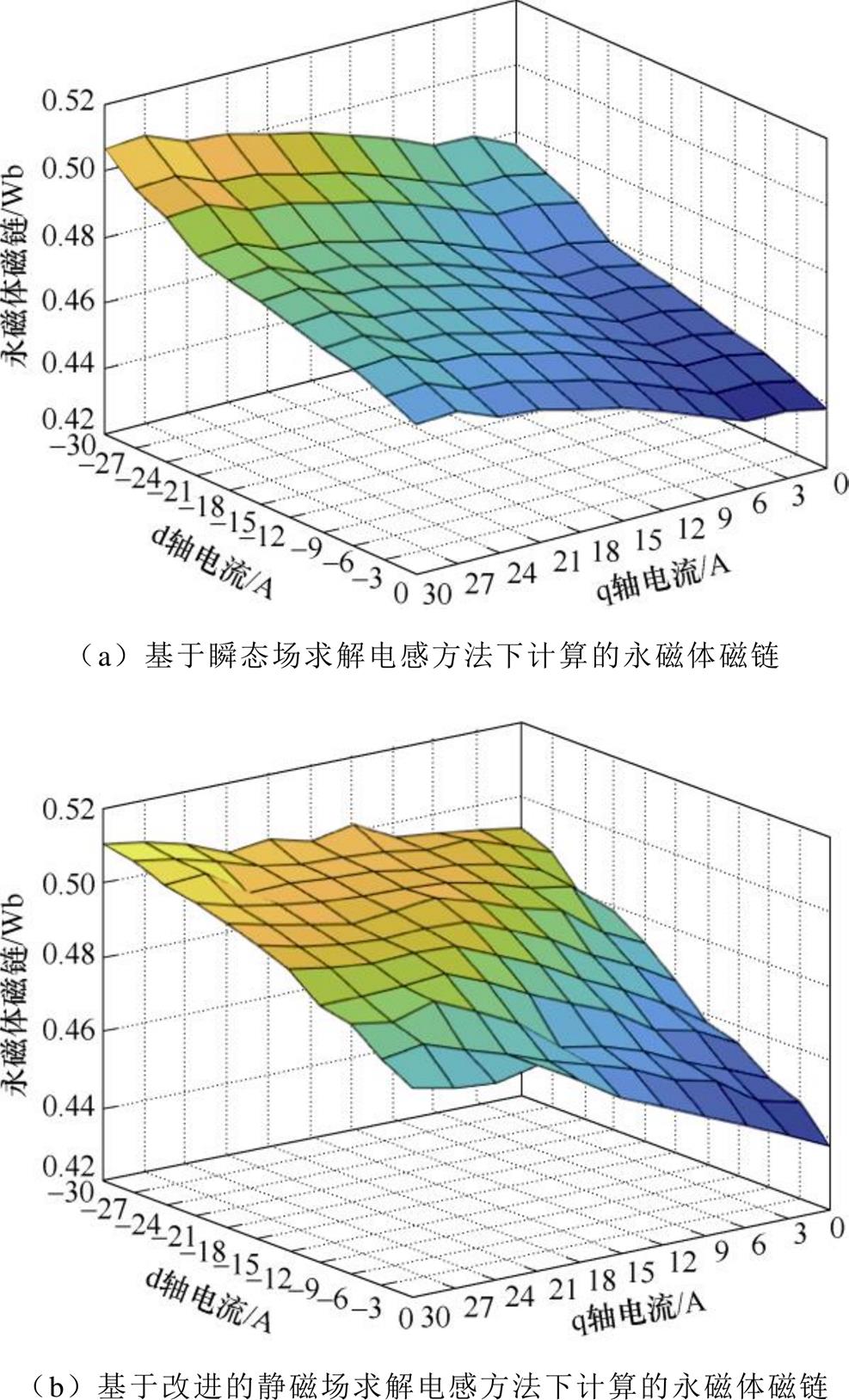
图7 永磁体磁链数值三维图
Fig.7 Three dimensional numerical diagram of permanent magnet flux linkage
同样对此方法下d、q轴电感进行三维图绘制如图8所示。将其与瞬态场电感计算结果相比较，两者计算得到的q轴电感大致相同。而计算得到的d轴电感在id较小而iq较大的电流组合时存在一定的误差，在整个计算范围内还较为相似，而且结合图7可以发现，d轴电感的求解误差主要来自永磁体磁链求解的差异上，可能由于d轴电流较小而q轴电流较大时，q轴电流对d轴电流的互感影响较大，导致永磁体磁链求解的差异性。（但通过后文在转矩预测模型中的验证，表明基于两种有限元求解电感方法得到的预测转矩误差较小，说明永磁体磁链求解的误差在可接受范围内。）通过对比图5瞬态场电感计算结果和图8改进的静磁场电感计算结果可以发现，两者的计算结果较为接近，但是在计算的仿真步数和求解时间上，改进的静磁场求解电感的方法有较大的优势。
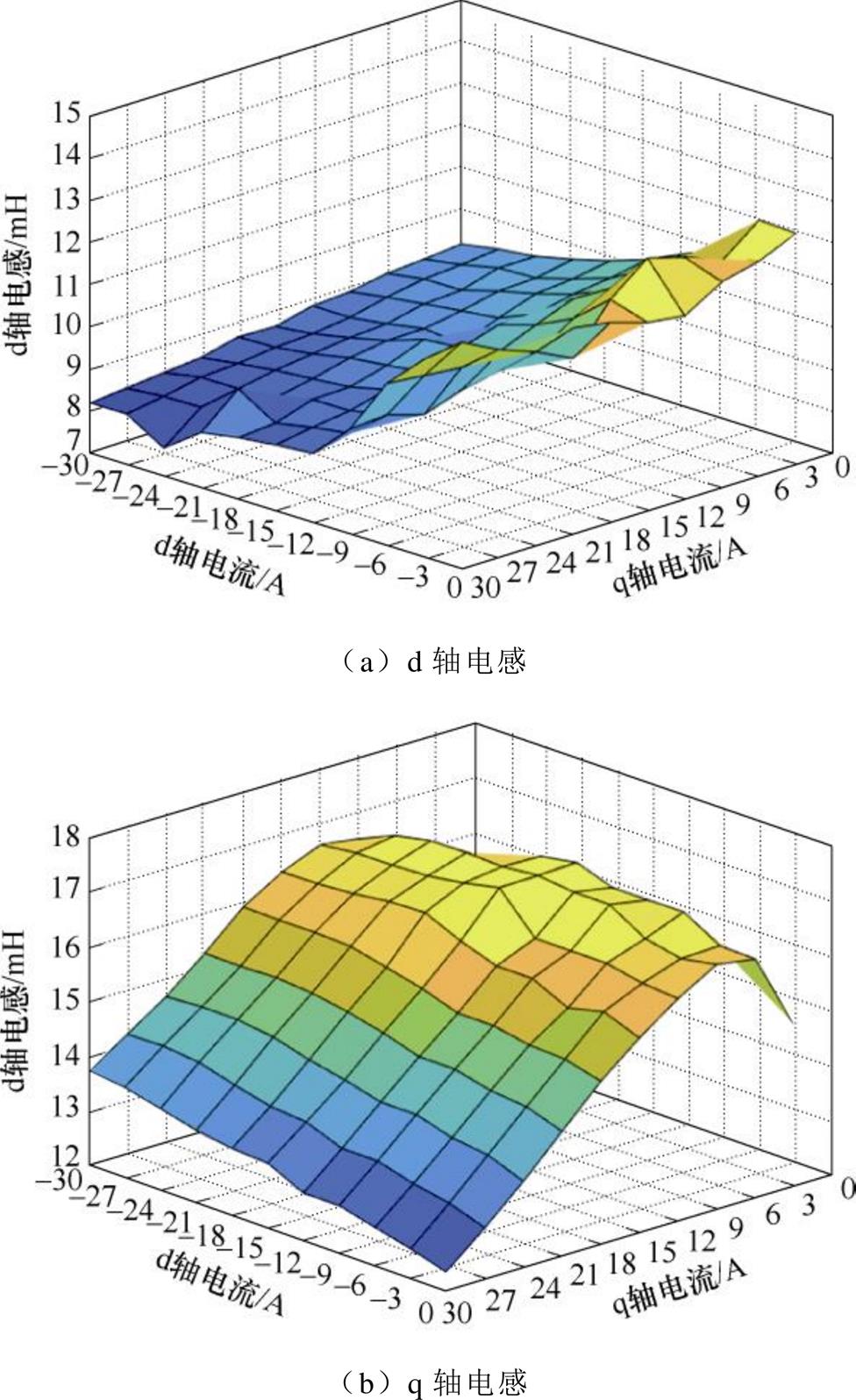
图8 改进的静磁场求解电感数值三维图
Fig.8 3-D inductance diagram based on the improved static magnetic field calculation method
表3对比了在相同d、q轴电流组合下采用瞬态场和改进静磁场法计算d、q轴电感所需要的仿真步数与时间。其中所有仿真计算都是在采用AMD Ryzen 9 3900X CPU和64 GB RAM的计算机上进行。从表3可以发现，原瞬态场求解电感的方法，其仿真步数为6 171步（d轴电流与q轴电流分别仿真11步，每个模型在时间维度上仿真51步，总步数为11×11×51=6 171步）仿真时间为16 h24 min。而改进的静磁场求解电感的方法，其仿真步数为242步（每个模型在空间维度上仅仿真1步，采用冻结磁导率法后，对模型重新仿真1步，总步数为11×11×2=242步），仿真时间为38 min，缩减为瞬态场计算方法仿真时间的3.86 %左右。
表3 不同有限元电感计算方法的仿真步数与时间对比
Tab.3 Comparison of simulation steps and time of different finite element inductor calculation methods
电感计算方法仿真步数仿真时间 改进的静磁场电感计算24238 min 瞬态场电感计算6 17116 h24 min
通过上述方法可以求解出相对准确的d、q轴电感，再通过式（8）的转矩方程，可以对电机模型进行转矩组成分析以及转矩预测。通过式（8）与不同dq轴电流组合下求解的电感，可以得到如图9所示以dq轴电流组合为变量的等转矩线。通过读取图9的等转矩线，可以快速估算出不同dq轴电流组合所对应的电磁转矩，实现对电机的转矩预测。而且可以通过缩减电感计算中电流组合的间隔，进一步提高转矩预测的精度，更精准地分析、设计电机。
图9 基于有限元求解电感方法的转矩预测
Fig.9 Torque prediction based on solving inductance
对比图9中两种不同计算方法所预测的电磁转矩可以得到如图10所示的不同电流组合下的绝对误差柱状图。从图中可以看出，基于改进的静磁场求解电感预测的电磁转矩具有较高精度与基于瞬态场求解方法的预测转矩两者之间的绝对误差整体较小，绝对误差均在4 N·m以内，两种预测结果有相同的参考价值。
图10 电磁预测转矩绝对误差
Fig.10 Absolute error of electromagnetic torque
在永磁同步电机，特别是内置式永磁同步电机的设计中，磁阻转矩和电磁转矩均是电磁转矩的重要组成部分，电机的输出转矩受到磁阻转矩和永磁转矩两种成分的影响，所以分析电机的转矩性能需要对两种成分进行准确分离。
根据式（7）变化可得电机的转矩组成为
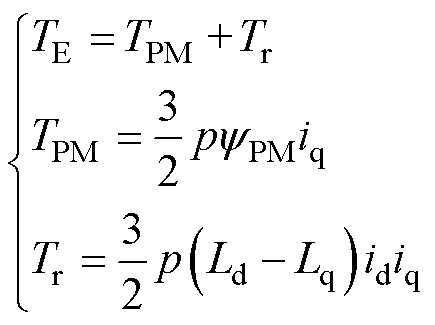（16）
式中，TPM为电机的永磁转矩；Tr为电机的磁阻转矩。如式（16）所示，准确计算了电机的dq轴电感就能对电机的转矩成分进行分离。图11所示为以样机的额定电流下的工况为例，对电机在电流超前角g从0 °到180 °下输出的电磁转矩进行转矩组成分离。图11采用改进的静磁场求解电感的方法对电机d、q轴电感进行快速预测，并结合式（16）定量计算了电磁转矩的平均值以及其各组成成分。从图11中可以看出，该样机电磁转矩输出成分中主要以永磁转矩为主，在额定工况下，采用最大转矩电流比控制逻辑得到的最大电磁转矩，其中，磁阻转矩的数值为2.55 N·m，占比约3.72 %，永磁转矩的数值为66.07 N·m，占比约97.20 %。
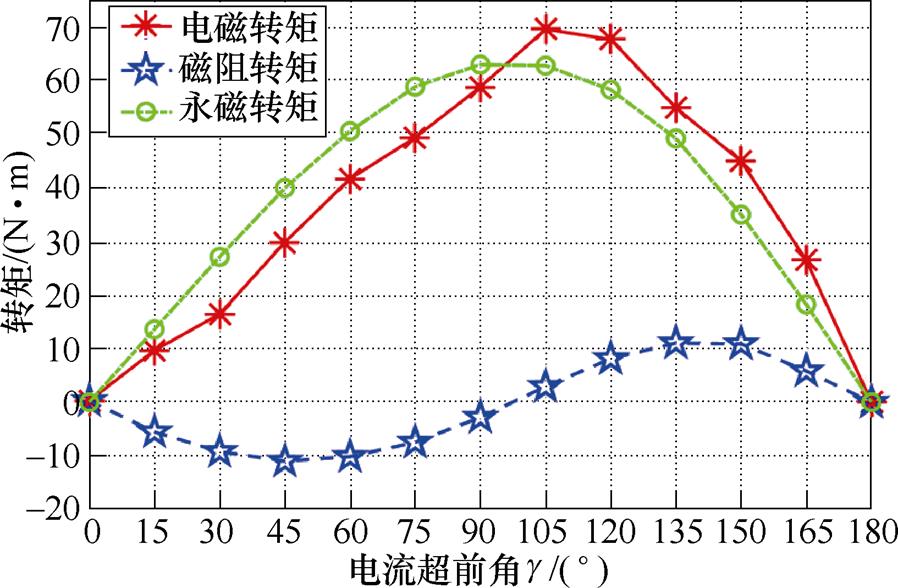
图11 不同电流超前角下的电磁转矩组成成分分离
Fig.11 Separation of components of electromagnetic torque for different current lead angles
搭建实验平台如图12所示，对目标样机进行测试，实验中对目标样机选取了七个不同电流下的工作点，进行转矩测试。由于目标样机设计为恒转速电机，其七个不同工作点电流分别选择为额定电流的0.2、0.4、0.6、0.8、1.2倍以及额定电流。
图12 样机实验测试平台
Fig.12 Test platform for prototype testing
实验通过控制器对电机进行最大转矩电流比控制，对其实测转矩与通过瞬态场或静磁场直接求解的电磁转矩，以及基于改进的静磁场求解电感的方法的预测转矩之间进行对比。具体数据对比见表4。由表4可以发现，测试电流为0.2倍额定电流时，由于相对额定电流，该测试电流过小，导致误差较大。除此之外，在其他不同测试电流下，瞬态场直接求解的电磁转矩和基于改进的静磁场求解电感的方法的预测转矩与实测数据更为接近。瞬态场直接计算得到的电磁转矩是对求解区间内的输出转矩取平均值，所以一定程度上抵消了转矩脉动的影响，使其与实测转矩更为接近。基于改进的静磁场求解电感的方法的预测转矩，由于是电感电流得到的磁阻转矩与永磁体磁链电流得到的永磁转矩相加所得，避开了电机齿槽效应所导致的影响，得到相对准确的转矩结果。
表4 实测数据与求解器仿真数据对比
Tab.4 Comparison between measured data and simulated data of solver
电流/A转矩/(N·m) 实测瞬态场直接求解静磁场直接求解基于改进的静磁场求解电感方法的预测结果 0.490.81.752.251.74 4.0314.3914.6415.8314.61 7.4727.8227.6729.4727.56 11.0442.2341.3544.3841.18 14.7356.4755.3559.2955.07 18.4069.8868.9473.4668.62 22.3983.9585.0487.9684.77
采用上述基于改进的静磁场求解电感方法的转矩预测模型对各个工作点下的转矩成分进行分离比较，具体数值如图13所示。通过图13可以发现，内置式永磁同步电机的输出转矩主要由永磁转矩组成，磁阻转矩的占比相对较小。而且通过对分离出的各转矩成分，与图11中的各转矩成分进行对比分析，可以发现在额定工况下，即便保持电机转子拓扑结构不变，样机的磁阻转矩最大能达到11 N·m左右，而在实际最大输出转矩点的磁阻转矩是2.55 N·m左右。上述对比说明这台样机的磁障设计还有较大的优化空间。可以在原基础上通过优化转子拓扑结构来进一步提高目标电机的转矩密度。
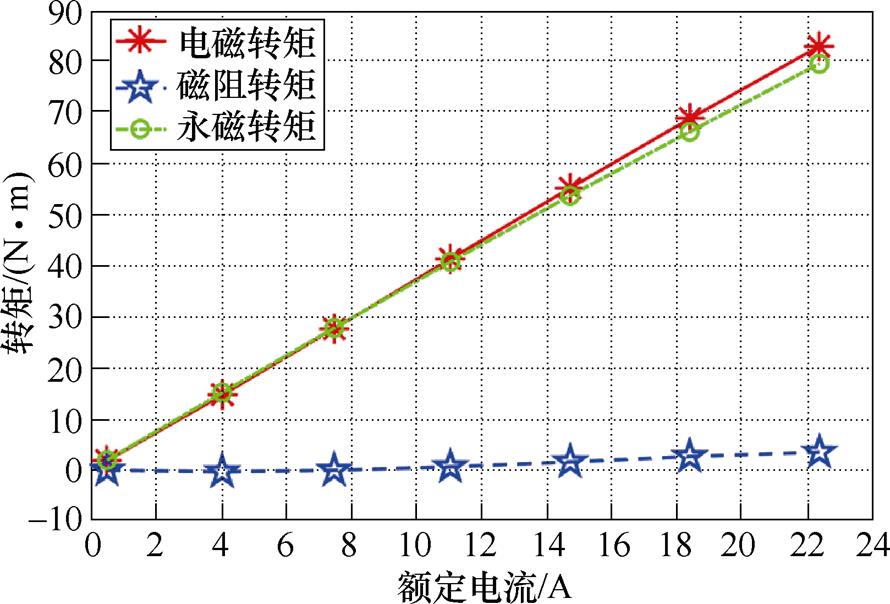
图13 多工作点下静磁场转矩分离
Fig.13 Static magnetic field torque separation at multiple operating points
本文通过对多种传统的有限元求解交、直轴电感的方法进行梳理总结，并在此基础上提出了一种改进的有限元电感计算方法。改进的方法是基于静磁场求解器的电感计算，相较于传统的静磁场计算，它能够有效考虑d、q轴的交叉耦合效应和磁路饱和效应对d、q轴电感的影响，提高了电感计算的准确性。而其相较于传统的瞬态场电感计算，在保证相同计算范围的情况下，由于求解器与仿真步数的不同，改进的静磁场求解电感的方法在仿真计算时间上缩减主原瞬态场方法仿真时长的3.86 %，而两种方法求解的交、直轴电感的相对误差在6 %以内。
本文同时对计算得到的d、q轴电感进行了转矩预测和转矩分离的后处理应用。通过将瞬态场方法和改进的静磁场方法两种不同方法求解的电感进行电磁转矩预测。其转矩预测结果的相对误差在较大范围内都维持在2 %左右，在d、q轴电流较大的情况下，相对误差变高，但也未超过5 %。在后续的实验中，通过对比实测转矩与预测转矩，发现两者的相对误差均在3 %以内，证明了预测结果的准确性，也说明了上述交、直轴电感求解方法与转矩模型有助于电机的设计分析。
参考文献
[1] EL-Refaie A M. Fractional-slot concentrated- windings synchronous permanent magnet machines: opportunities and challenges[J]. IEEE Transactions on Industrial Electronics, 2010, 57(1): 107-121.
[2] 倪有源, 王磊, 王群京. 凸形不等厚磁极永磁电机建模与分析[J]. 电工技术学报, 2020, 35(11): 2406- 2414.
Ni Youyuan, Wang Lei, Wang Qunjing. Modeling and analysis of permanent magnet motor with convex unequal thickness poles[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2406-2414.
[3] Lai Chunyan, Feng Guodong, Mukherjee K, et al. Investigations of the influence of PMSM parameter variations in optimal stator current design for torque ripple minimization[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1052-1062.
[4] 刘凯, 张炳义, 冯桂宏. 基于非对称绕组函数法永磁同步电机偏心电感参数的研究[J]. 电工技术学报, 2020, 35(增刊2): 387-394, 431.
Liu Kai, Zhang Bingyi, Feng Guihong. Research on eccentric inductance parameters of permanent magnet synchronous motor based on asymmetric winding function method[J]. Transactions of China Elec- trotechnical Society, 2020, 35(S2): 387-394, 431.
[5] 郭凯凯, 郭有光. 磁通反向直线旋转永磁电机三维非线性等效磁路模型分析[J]. 电工技术学报, 2020, 35(20): 4278-4286.
Guo Kaikai, Guo Youguang. Analysis of three- dimensional nonlinear equivalent magnetic circuit model of permanent magnet motor with reverse flux linear rotation[J]. Transactions of China Electro- technical Society, 2020, 35(20): 4278-4286.
[6] 李文真, 刘景林. 考虑磁路饱和及交叉耦合效应的内置式永磁同步电机无传感器优化方法[J]. 电工技术学报, 2020, 35(21): 4465-4474.
Li Wenzhen, Liu Jinglin. Sensorless optimization method of built-in permanent magnet synchronous motor considering magnetic circuit saturation and cross-coupling effect[J]. Transactions of China Elec- trotechnical Society, 2020, 35(21): 4465-4474.
[7] 陈卓易, 屈稳太. 基于PID型代价函数的永磁同步电机模型预测电流控制[J]. 电工技术学报, 2021, 36(14): 2971-2978.
Chen Zhuoyi, Qu Wentai. Model predictive current control for permanent magnet synchronous motors based on PID-type cost function[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2971- 2978.
[8] Zhong Yuxiang, Lin Heyun, Chen Zhiyong, et al. Online-parameter-estimation-based control strategy combining MTPA and flux-weakening for variable flux memory machines[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4080-4090.
[9] 刘金海, 陈为, 胡金高. 永磁同步电机dq电感参数新实验获取法[J]. 电工技术学报, 2014, 29(7): 97-103.
Liu Jinhai, Chen Wei, Hu Jingao. Novel experimental methods of acquiring dq inductance of permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 97-103.
[10] Sarikhani A, Nejadpak A, Mohammed O A. Coupled field-circuit estimation of operational inductance in PM synchronous machines by a real-time physics- based inductance observer[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2283-2286.
[11] Lai Chunyan, Feng Guodong, Mukherjee K, et al. Torque ripple minimization for interior PMSM with consideration of magnetic saturation incorporating on-line parameter identification[C]//2016 IEEE Con- ference on Electromagnetic Field Computation (CEFC), Miami, FL, USA, 2017: 1.
[12] Shuang Bo, Zhu Ziqiang. A novel method for estimating the high frequency incremental DQ-axis and cross-coupling inductances in interior permanent magnet synchronous machines[J]. IEEE Transactions on Industry Applications, 2021, 57(5): 4913-4923.
[13] Shin K H, Park H I, Lee S H, et al. Armature reaction field and inductance calculations for a permanent magnet linear synchronous machine based on subdomain model[C]//2016 IEEE Conference on Electromagnetic Field Computation (CEFC), Miami, FL, USA, 2017: 1.
[14] Lee K D, Lee Ju, Lee H W. Inductance calculation of flux concentrating permanent magnet motor through nonlinear magnetic equivalent circuit[J]. IEEE Transactions on Magnetics, 2015, 51(11): 1-4.
[15] Jeong I, Nam K. Analytic expressions of torque and inductances via polynomial approximations of flux linkages[J]. IEEE Transactions on Magnetics, 2015, 51(7): 1-9.
[16] Silvester P, Chari M V K. Finite element solution of saturable magnetic field problems[J]. IEEE Transa- ctions on Power Apparatus and Systems, 1970, PAS-89(7): 1642-1651.
[17] 郑萍, 王勃, 吴帆, 等. 电动汽车用双三相永磁同步电机饱和电感特性分析及计算方法[J]. 电工技术学报, 2013, 28(7): 19-25.
Zheng Ping, Wang Bo, Wu Fan, et al. Analysis and calculation method of saturated inductance of a dual-three phase permanent-magnet synchronous machine for electric vehicles[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 19-25.
[18] 符荣, 窦满峰. 电动汽车驱动用内置式永磁同步电机直交轴电感参数计算与实验研究[J]. 电工技术学报, 2014, 29(11): 30-37.
Fu Rong, Dou Manfeng. D-axis and Q-axis inductance calculation and experimental research on interior permanent magnet synchronous motors for EV[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 30-37.
[19] 李和明, 张健, 罗应立, 等. 考虑交叉饱和影响的永磁同步电机稳态参数有限元分析[J]. 中国电机工程学报, 2012, 32(12): 104-110.
Li Heming, Zhang Jian, Luo Yingli, et al. Finite element analysis of PMSM steady state parameters considering cross-saturation effect[J]. Proceedings of the CSEE, 2012, 32(12): 104-110.
[20] 王艾萌. 内置式永磁同步电动机的优化设计及弱磁控制研究[D]. 北京: 华北电力大学, 2010.
[21] Drobnič K, Gašparin L, Fišer R. Fast and accurate model of interior permanent-magnet machine for dynamic characterization[J]. Energies, 2019, 12(5): 783.
[22] 刘健. 电路分析[M]. 北京: 电子工业出版社, 2005.
[23] 袁雷, 胡冰新, 魏克银. 现代永磁同步电机控制原理及MATLAB仿真[M]. 北京: 北京航空航天大学出版社, 2016.
Abstract The electromagnetic torque of an IPMSM (Interior permanent magnet synchronous machine) mainly consists of two components: permanent magnet torque and reluctance torque. The accurate separation and analysis of the torque components can optimize the topology and improve the power density of the machine. The key to accurate analysis of the components of the electromagnetic torque is the accurate calculation of the d-q-axis inductance. This paper uses an IPMSM with 8 poles and 11 kW as an example to solve the d-q-axis inductance and analyze the torque components. By comparing and analyzing two kinds of inductance solving methods, static magnetic field solving inductance and transient field solving inductance, an improved method for fast solving the inductance by the static magnetic field is presented, which achieves high-precision separation and extraction of machine torque components and prediction of electromagnetic torque components in the stage of electromagnetic design.
The improved method determines the current lead angle according to different d-q-axis current combinations, converts the mechanical angle of the machine to the current lead angle, and transforms the relative mechanical position of the stator and rotor to control the machine operation under different current amplitudes or current lead angles. Then, the three-phase flux linkage under different d-q-axis current combinations is obtained by finite element calculation, and the d-q-axis flux linkage is obtained by Park's transformation of the three-phase flux linkage. Finally, the d-q-axis inductance is obtained by solving the d-q-axis flux linkage, and the permanent magnet flux linkage is obtained using the frozen permeability method. The improved method can consider both the cross-coupling and saturation effects under different loads. In addition, the d-q-axis inductance calculated by the above method is combined with the electromagnetic torque equation considering the effect of magnetic saturation and cross-coupling.
The d-q-axis inductances of the target prototype are solved by the transient field method and the improved static magnetic field method, respectively. The relative errors of the d-q-axis inductances solved by the two methods are within 6 %. Compared with the transient field method, the improved static magnetic field method reduces the simulation steps by 96.08 % and the calculation time by 96.14 %. It shows that the improved method can effectively reduce the number of simulation steps and shorten the simulation time. Finally, an experimental test platform is built to test the torque of the target prototype under different operating point currents. The relative errors between the measured torque and the predicted torque are within 3 %. Taking the working condition of the prototype under the rated current as an example, the electromagnetic torque of the machine output at different current lead angles of 0 °to 180 °is separated. At the same time, the composition of the maximum electromagnetic torque obtained by the maximum torque current ratio control logic is analyzed. In the composition, the value of the reluctance torque is 2.55 N·m, accounting for about 3.72 %; and the value of the permanent magnet torque is 66.07 N·m, accounting for about 97.20 %. Moreover, the maximum reluctance torque of the prototype can reach about 11 N·m, while the actual reluctance torque at the maximum electromagnetic torque point is 2.55 N·m, which shows that the magnetic barrier design of this prototype still has a large space for optimization. The torque density of the target machine can be further improved by optimizing the rotor structure combined with the fast torque analysis and the prediction model in this paper. The experimental results verify the accuracy and validity of the new method.
keywords：Permanent magnet synchronous machines, inductance calculation, torque analysis, finite element analysis
DOI: 10.19595/j.cnki.1000-6753.tces.221385
中图分类号：TM351
国家自然科学基金项目（51977055），中央高校基本科研业务费专项资金项目（JZ2022HGTA0322）和安徽省科技重大专项项目（201903a05020042）资助。
收稿日期 2022-07-19
改稿日期 2022-08-03
李仕豪 男，1995年生，博士研究生，研究方向为永磁电机的设计及优化。E-mail: lishihao@mail.hfut.edu.cn
鲍晓华 男，1972年生，博士，教授，博士生导师，研究方向为电机的设计理论和技术等。E-mail: baoxh@hfut.edu.cn（通信作者）
（编辑 郭丽军）