Tab.1 Prototype parameters
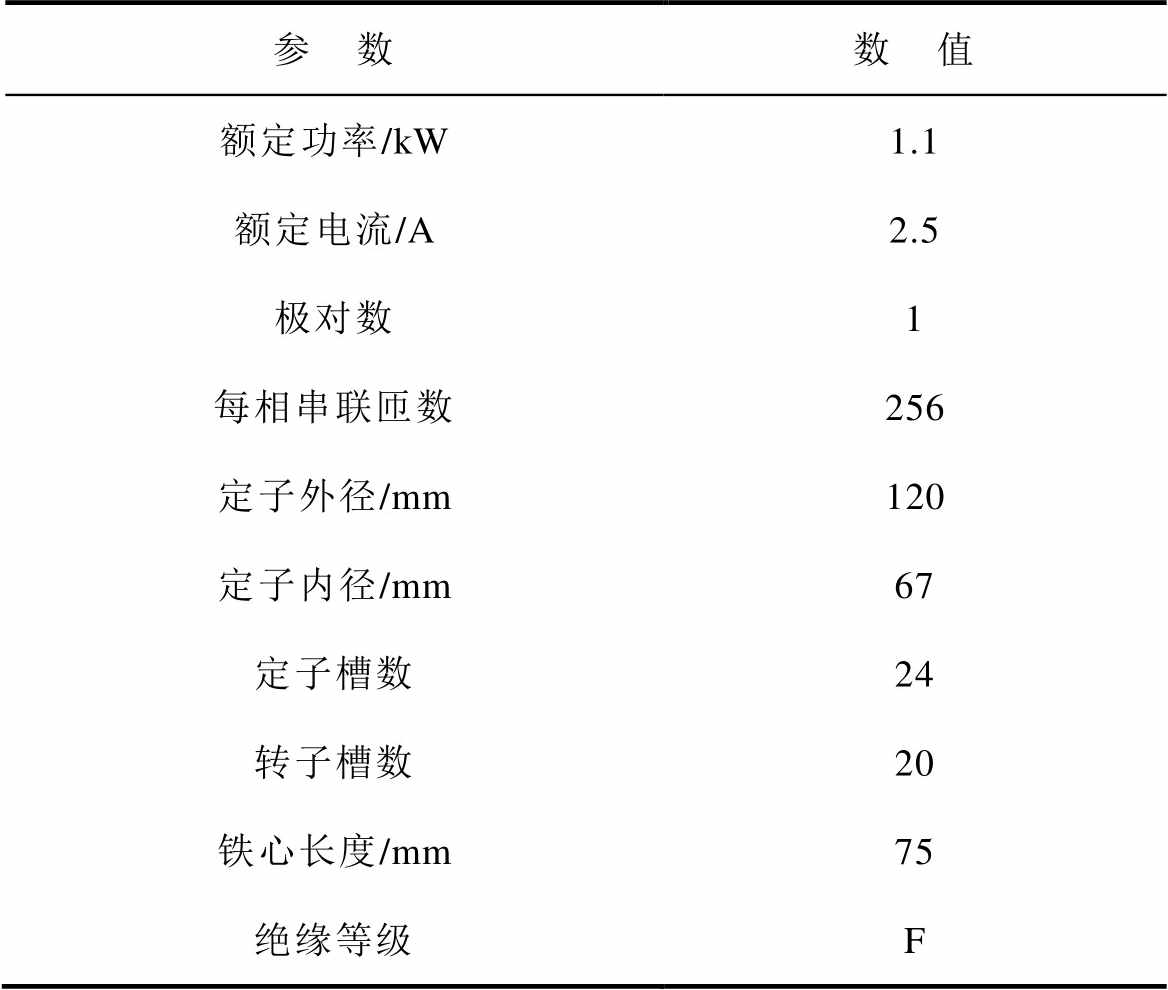
参 数数 值 额定功率/kW1.1 额定电流/A2.5 极对数1 每相串联匝数256 定子外径/mm120 定子内径/mm67 定子槽数24 转子槽数20 铁心长度/mm75 绝缘等级F
摘要 感应电机匝间短路故障的温升特性是故障的明显特征之一，针对该问题研究不同工况下匝间短路故障对电机温度场的影响，旨在从电机温度场分布与温升特性角度给出电机故障预警与诊断的方法。以一台笼型感应电机为例，经过合理等效建立电机三维瞬态温度场仿真模型，分别对空、轻、满载三种工况下的正常与故障电机进行温度场仿真计算。通过与各情况下的电机温升实验数据对比，验证了仿真结果的准确性。综合分析电机温升实验与温度场仿真结果，揭示了电机故障前后传热特性差异，并通过对比电机温升的时间特性与空间分布特性的变化情况，得到了与匝间短路故障相关的温度分布特征。针对故障后电机绕组温度的差异特性提出了相应的温度监测与诊断方法，为电机实际运行监测提供参考。
关键词：感应电机 匝间短路故障 多工况 温度场 温升特性
感应电机具有成本低、易于维护的优点，是工业传动领域最常见的交流电机类型，一旦电机由于故障造成系统停机将引起较大的经济损失。据统计，匝间短路故障约占电机总故障的26 %～36 %[1]，故障发生后会引起电机磁场、温度、振动噪声等多场量的变化，其中由于故障引发的过热问题会加速绕组绝缘恶化进而使故障扩散或程度加深[2]。
许多专家学者针对电机匝间短路故障问题进行研究，提出了多种基于电机电气量与多场量的监测和故障诊断方法。例如，电机电流信号分析[3]、气隙磁场[4-5]与漏磁场探测[6]、基于电机振动信号[7-8]的诊断方法等，均取得了较好的结果。电机的温度特征除了可以作为性能指标用于电机的设计过程[9-10]，其也是匝间短路故障的明显特征，通过相应热特征的研究可以实现故障的监测与诊断以及对故障发展和电机寿命的预测。目前，对于故障引发电机热特征与温度场分布变化的研究主要集中于两方面：一方面是利用传感器等探测手段对故障电机温升进行测量[11-16]；另一方面是利用集总参数热网络或有限元模型对故障电机进行建模与仿真研究[17-22]。
对于电机故障前后温度变化较为直接的探测方法是在电机定子槽内或电机某部件上埋置热敏电阻温度传感器[11]，该方法可以直接得到探测点的温升情况，但是受限于传感器布置数量仅能对部分关键测温点进行温度监测。文献[12-13]提出了一种更为灵敏的利用光纤光栅温度传感器进行温度测量的方法。通过监测电机绕组温度可以有效识别电机的热点信息并实现故障的有效诊断，但是该方法的实现依赖传感器位置的准确布置且成本较高。热成像技术也在探测匝间短路故障引起的电机温度变化方面有所应用，文献[14]将红外热电堆传感器阵列安装在机壳内表面，实现了对电机端部绕组的温度监测和故障诊断与定位。文献[15-16]利用红外成像仪对故障后电机的红外图像进行分析，探测结果虽然可以表征匝间短路故障的现象，但是由于红外图像展示的是电机机壳的红外特征，不能表征电机内部的热特性，且机壳的升温速度远低于内部部件，因此该方法只适用于温度监测。
受限于传感器的数量与布置位置，温度测量只能针对某些测温点或者测温区域，还需要借助温度场仿真手段研究电机故障前后的温度分布。文献[17]针对感应电机的故障温度场问题，考虑不同接触电阻条件，利用集总参数模型和有限元模型对匝间短路故障的二维温度场进行仿真研究。文献[18]同样以二维有限元仿真得到了不同极槽配合下容错永磁同步电机匝间短路故障的槽内导体温度分布。二维温度场仿真虽然可以得到一些故障温度分布规律，但是由于其无法考虑电机轴向的散热条件差异，因此结果和工程实际情况差别较大。文献[19-20]针对两种新型永磁电机的匝间短路问题，利用三维集总参数模型和有限元仿真模型分别进行了稳态和瞬态故障温度场研究，并利用实验验证了所用方法的准确性。对于本文所研究的封闭型自扇冷式电机，文献[21-22]利用1/2等效三维有限元模型仿真了感应电机匝间短路的稳态温度场，得到了不同短路电流下电机各部件稳态温度分布。但是在建模过程中没有根据该类型电机的结构特点考虑接线盒处的不良散热条件，且稳态温度分布无法反映出故障造成的温度瞬态特性。
综上所述，目前针对匝间短路故障引发电机热特性变化的问题，从温度探测、故障识别、建模与仿真等角度的研究取得了良好的效果，但是多种研究手段仍存在缺点与不足。如槽内布置传感器受限于测温点数量与布置准确性，红外探测又会受到内部空间限制或者外部机壳表面温度与故障特征不敏感的影响。并且，对于封闭自扇冷式电机在不同负载条件下的匝间短路瞬态温度分布与故障温升特性仍缺乏相关研究。
本文充分考虑电机实际冷却结构特点，采用电机内部埋置热敏电阻进行多测温点温度测量与三维全域瞬态温度场仿真相结合的方法，对空载、轻载、满载三种工况下匝间短路故障对电机温升特性的影响进行研究。通过分析故障前后电机温度变化的时空特性与绕组温度差异，总结出故障相关热特征，为电机匝间短路故障监测与诊断提供依据。
本文以一台YE2-80M2-2笼型感应电机作为研究对象，样机参数见表1。电机发生匝间短路故障时，电机绕组拓扑结构由原来三相对称结构变为故障相绕组和短路环部分以及两个非故障相绕组的非对称结构。以A相绕组发生匝间短路故障为例，故障电机的等效电路如图1所示。根据样机参数与故障情况建立了二维电磁有限元仿真模型如图2所示，图中标注了电机各相绕组分布与故障相绕组接线。在建模过程中对电机铁心的轭部、齿中、齿顶位置分块建模，规定故障发生处绕组为故障槽绕组，A相其他槽绕组为故障相非故障槽绕组，B、C相绕组为非故障相绕组。
表1 样机参数
Tab.1 Prototype parameters
参 数数 值 额定功率/kW1.1 额定电流/A2.5 极对数1 每相串联匝数256 定子外径/mm120 定子内径/mm67 定子槽数24 转子槽数20 铁心长度/mm75 绝缘等级F
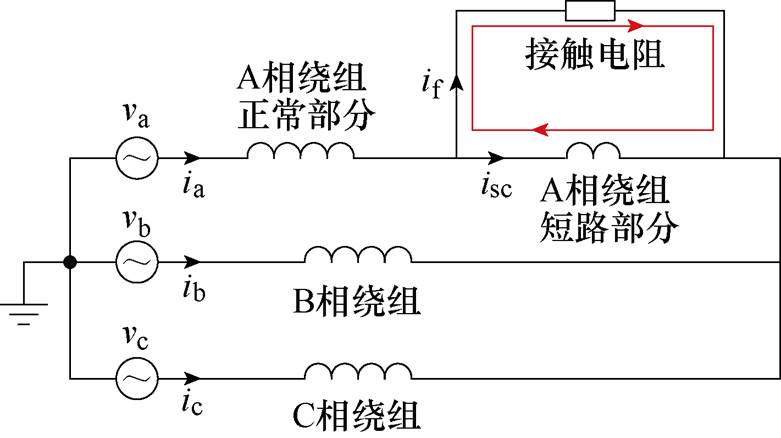
图1 匝间短路故障的绕组等效电路
Fig.1 Winding equivalent circuit of inter-turn fault
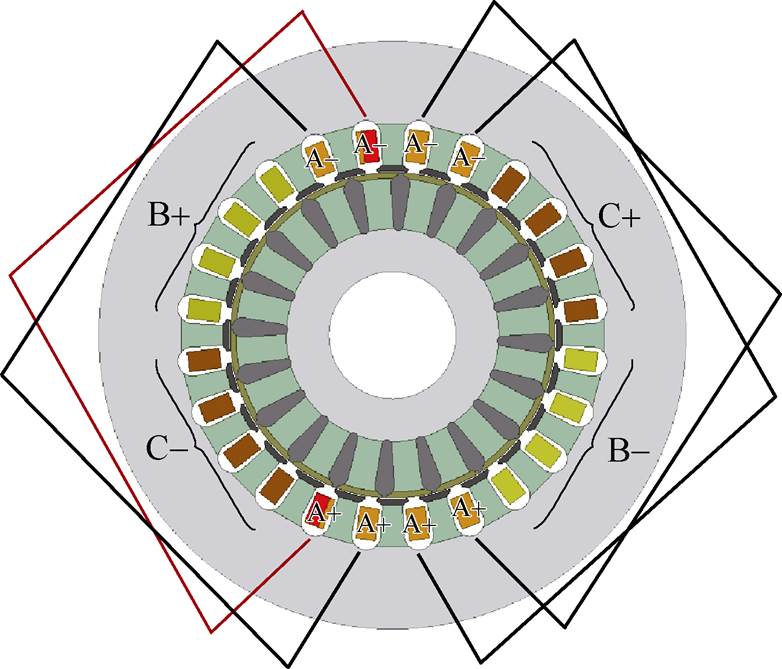
图2 电磁有限元仿真模型
Fig.2 Finite element simulation model of the electromagnetic field
为了对电机匝间短路故障的温升特性进行研究，分别对正常和故障电机进行空载、轻载（40 %额定负载）和满载温升实验。空载温升实验平台如图3所示，样机的定子绕组经过重新绕制并引出若干抽头连接在电机外部的绝缘板上，通过将抽头之间短接即可实现电机匝间短路故障的模拟。电机故障程度设置为A相5、15、25、35、45匝短路（与电机绕组每相串联匝数之比可得故障度为1.95 %～17.58 %）。绕组下线过程中在电机内轴向中部的不同位置放置了多个K型测温线，测温位置示意图如图4所示，通过搭配电子测温仪即可实现对电机内部多个测温点的实时温度监控。空载实验中，利用调压器保证输入电压稳定，通过电能质量分析仪对电机的相电压和电流进行测量，在轻载和满载实验中，负载由磁粉制动器搭配直流电源提供。本文在实验中针对匝间短路故障引发的温升特性在不同负载条件下的特征进行研究，仅考虑工况变动与单一故障程度情况，进行三种负载条件下正常与故障45匝电机的温升实验，且为了保障样机和实验设备的安全，两短路匝间经过一个接触电阻连接用以限制过大的短路电流。
图3 空载温升实验平台
Fig.3 Experimental platform of temperature rise under no-load condition
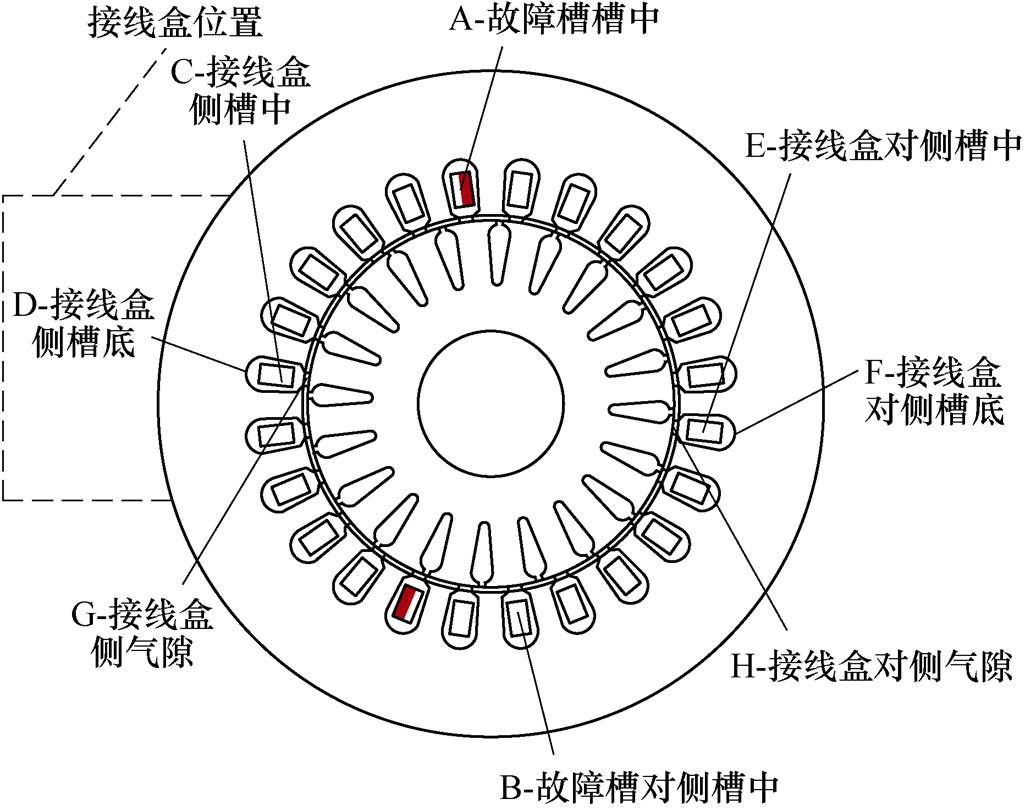
图4 电机测温点埋置位置示意图
Fig.4 Embedded positions of the motor temperature measurement point
2.1.1 模型等效
1）槽内等效
为了简化定子槽内复杂的热交换过程，参照文献[23]对定子槽内模型的等效方法，对故障槽绕组进行区分建模。图5所示为本文采用的故障工况下定子槽内等效模型。等效绝缘导热系数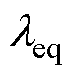
为
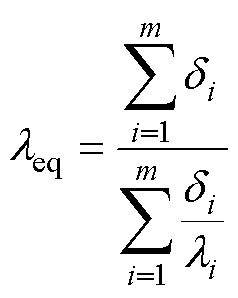（1）
式中，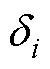
为各绝缘材料等效厚度；
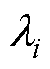为各绝缘材料导热系数。
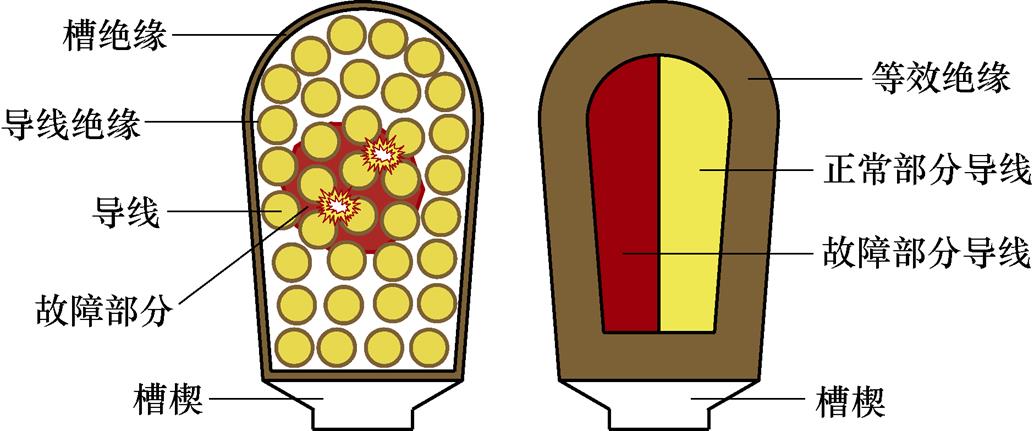
图5 定子槽内等效模型
Fig.5 Equivalent model of the components in stator slot
2）气隙等效
气隙是电机定转子间热交换的媒介，但由于转子转动带动气隙空气的流动会造成气隙处空气流速的非线性变化。本文为了简化这种复杂的换热过程，将气隙传热等效为实体热传导的方式。首先计算气隙流体的临界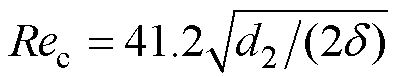雷诺数
与雷诺数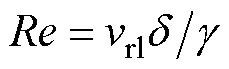
，其中，d2为转子外径，
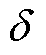为气隙长度，vrl为转子外圆线速度，
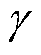为空气运动粘度。若Re＜Rec，则气隙中空气为层流，其导热系数即为空气导热系数；若Re＞Rec，则气隙中空气为湍流，气隙等效导热系数
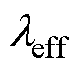[24]为
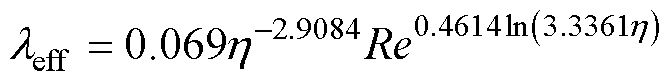（2）
式中，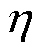
为转子外径与定子内径之比。
2.1.2 温度场仿真模型与边界条件
三维瞬态温度场计算基本方程和边界条件分别为
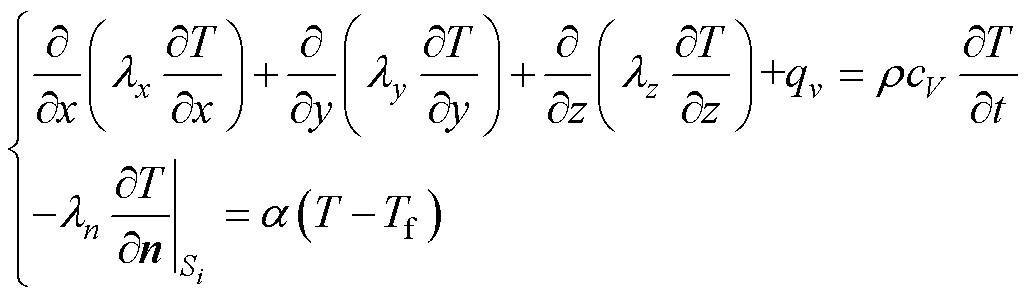（3）
式中，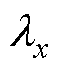
、
、
、
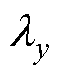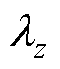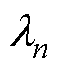为x、y、z、n方向的热导率；T为物体上的温度；
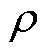为物质的密度；cV为物体比定容热容；qv为内部热流密度；Si为各散热面边界；n为各边界面法向量；
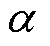为n方向上的表面传热系数；Tf为介质温度。
在建立模型过程中做出如下假设：①槽内导体与绝缘的等效模型中认为绕组与绝缘、绝缘与铁心间紧密贴合；②不考虑转子导条与铁心间的接触热阻；③电机换热主要集中于电机轴向有效部分，忽略定子绕组端部的影响。电机的三维温度场仿真模型与散热边界如图6所示，在图中标出了各散热面位置（见图中S1～S7，各散热面表面传热系数计算方法列于附录）。由于所研究样机属于封闭型自扇冷式电机，机壳轴向散热条件差异较大。将电机外壳分为六个部分，依次利用风速仪在室温环境下测量正常运行电机机壳各段位置处的空气流速，进而换算为各段的散热系数，计算方法见附录式（A1），并认为每段机壳在周向方向的散热系数一致。
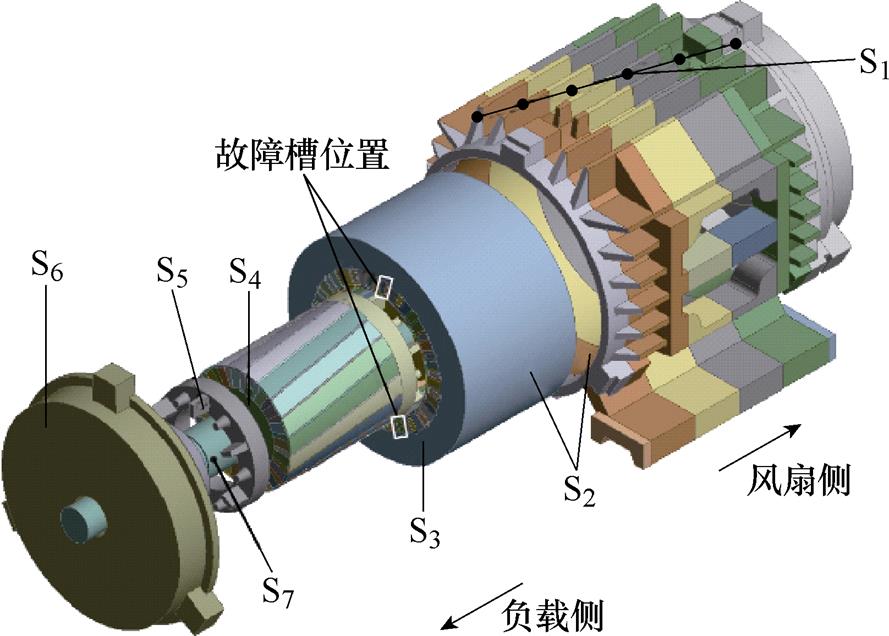
图6 三维温度场仿真模型与散热边界
Fig.6 Three-dimensional thermal field simulation model and heat dissipation boundaries
电机运行过程中各部分产生的损耗是导致电机温升的热源。感应电机的总损耗由绕组铜耗、铁心损耗、转子铝耗、机械和杂散损耗组成[25]。
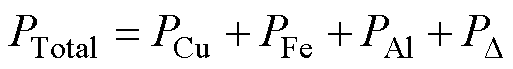（4）
式中，PTotal为电机总损耗；PCu为定子绕组铜耗；PFe为铁心损耗；PAl为转子铝耗；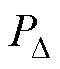
为机械与杂散损耗。PCu可由各工况下的实测数值计算，PFe和PAl由有限元计算所得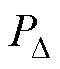，由经验公式计算，各部分损耗的具体计算方法可参见文献[25]。正常的三相绕组电机，其各相电阻与电流均相等，铜耗可按
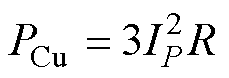计算，其中，IP为相电流有效值，R为相电阻。当发生匝间短路故障时，电机的等效电路拓扑结构发生改变，如图1所示，除三相电流外，在电机内部的短路环位置还会出现一个短路环流。此时，原本相等的三相电流变得各不相同，且故障相绕组被分为正常与短路两部分。故障时电机的铜损为
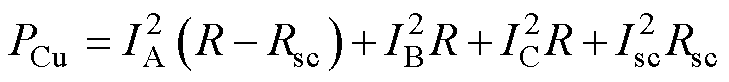（5）
式中，IA、IB、IC各相电流有效值；Isc为短路电流有效值；Rsc为短路匝电阻。
表2列出了电机故障前后三种负载条件下的各部分损耗值。由于感应电机转子铁耗数值较小以及PD计作常数，本文对这两部分损耗不做讨论。表2中数据表明，定子齿部与轭部铁耗在故障前后变化很小，这说明短路线圈产生的脉振磁场仅对故障槽两侧齿部铁耗有较大影响而对铁心整体铁耗影响较小，并且从铁耗数值在总损耗的占比而言，定子铁耗是本文研究样机的非主要热源。转子铝耗随着工况变化即转子转差增大而增大，且故障后有明显增长，在满载工况下该部分损耗占比较高，会导致转子的温升增大。铜耗是电机的主要热源，匝间短路故障发生后，定子各相电流发生较大变化且由于短路环电流存在会引起定子铜耗的剧烈增加。作者之前的研究中针对匝间短路故障前后电机电流的变化规律进行了详细的分析[26]，可为匝间短路故障电机的铜耗评估提供参考，本文不再赘述。
表2 正常与故障电机损耗对比
Tab.2 Comparison of losses on normal and faulty conditions （单位: W）
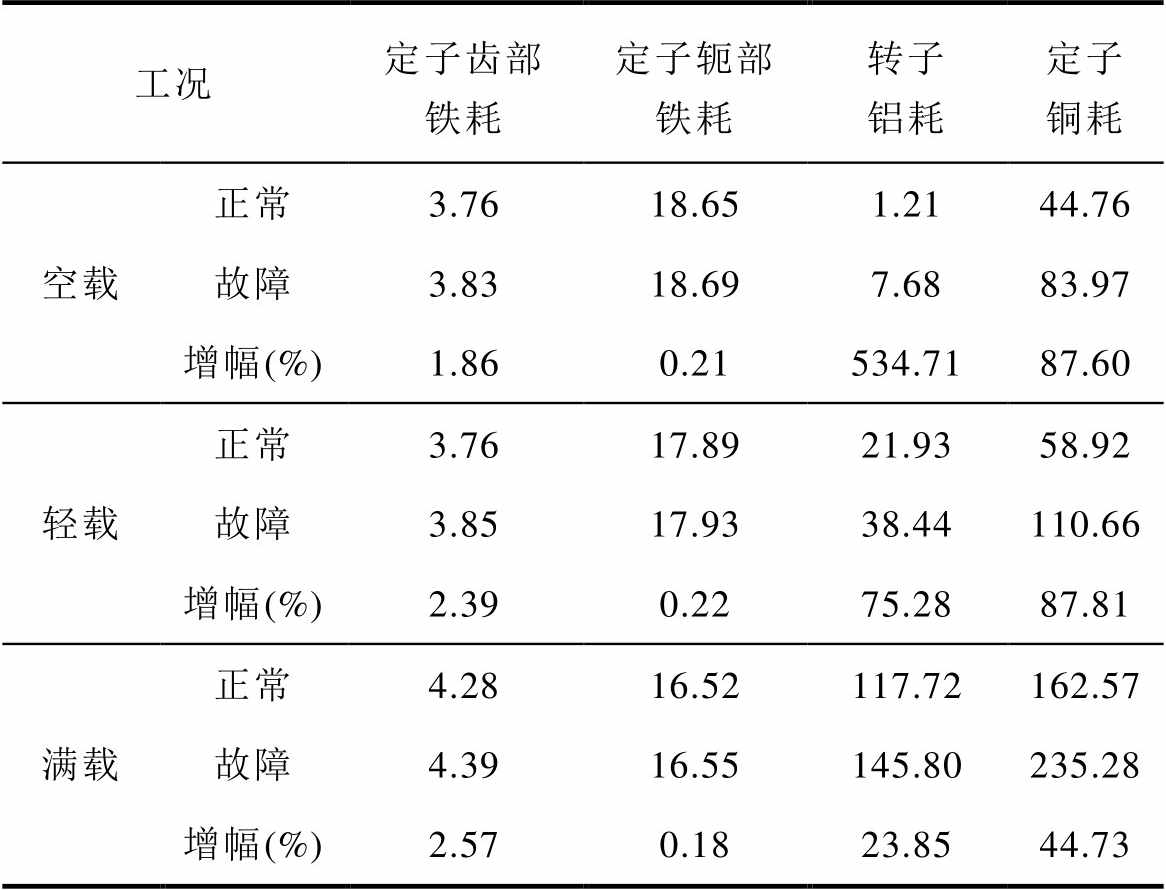
工况定子齿部铁耗定子轭部铁耗转子铝耗定子铜耗 空载正常3.7618.651.2144.76 故障3.8318.697.6883.97 增幅(%)1.860.21534.7187.60 轻载正常3.7617.8921.9358.92 故障3.8517.9338.44110.66 增幅(%)2.390.2275.2887.81 满载正常4.2816.52117.72162.57 故障4.3916.55145.80235.28 增幅(%)2.570.1823.8544.73
空载、轻载、满载条件下的正常与故障电机温升实验的环境初始温度列于表3（各测温点初始温度以测量值为准）。将表中数值作为各工况下仿真的初始温度条件，结合2.1节的温度场模型各边界条件，并将电磁计算得到的损耗作为热源加载至电机各区域，即可计算得到各工况下电机三维瞬态温度场分布。
表3 电机温升实验环境初始温度
Tab.3 Initial environment temperature of motor temperature rise experiment （单位: ℃）
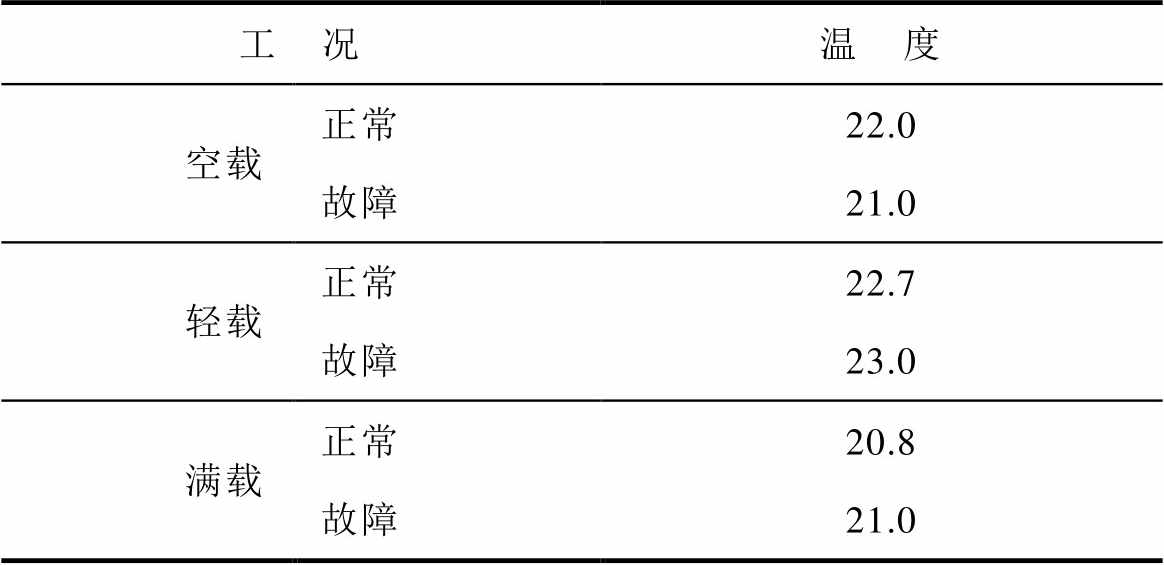
工 况温 度 空载正常22.0 故障21.0 轻载正常22.7 故障23.0 满载正常20.8 故障21.0
匝间短路故障会引发绕组温度的剧烈变化，图7为三种工况下故障前后稳态时电机定子绕组的温度分布（认为电机运行至90 min时到达热稳态）。从图7中可以看出，绕组轴向温差小，周向温差大，正常时由于接线盒位置的不良散热条件，绕组最高温度出现在接线盒一侧。但是绕组整体温度差异不大，三种工况的绕组温差分别仅有1.4 ℃、1.9 ℃和4.4 ℃。故障打破了电机正常时的温度分布规律，最高温度出现在故障槽绕组，绕组整体温差增加至39.2 ℃、37.1 ℃、38.3 ℃，且各相绕组平均温度也差异较大。
故障对定子铁心温度的影响规律与绕组相似，且在三种工况下表现一致，满载工况下正常和故障电机定子铁心的稳态温度分布情况如图8所示。由于电机机壳各处的散热条件差异，造成了铁心温度沿轴向和周向的不均匀分布。正常时，铁心温度轴向负载侧高于风扇侧，周向接线盒侧温度高于其他位置，且由于接线盒处的不良散热条件与气隙较低的导热系数，铁心最高温度出现在接线盒位置齿顶处。故障后，电机铁心温度整体升高，温差较正常时略有提升，且由于故障槽绕组温度的剧烈提升，铁心最高温度点出现在故障槽齿顶位置。
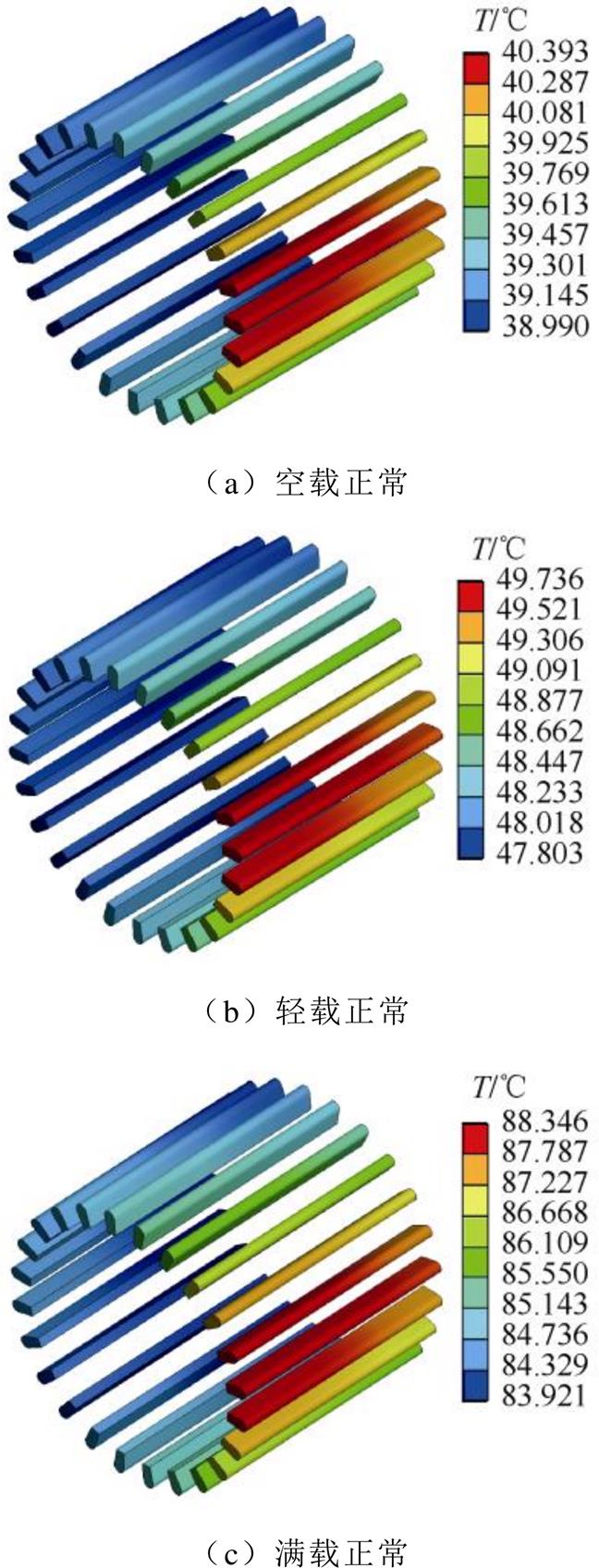
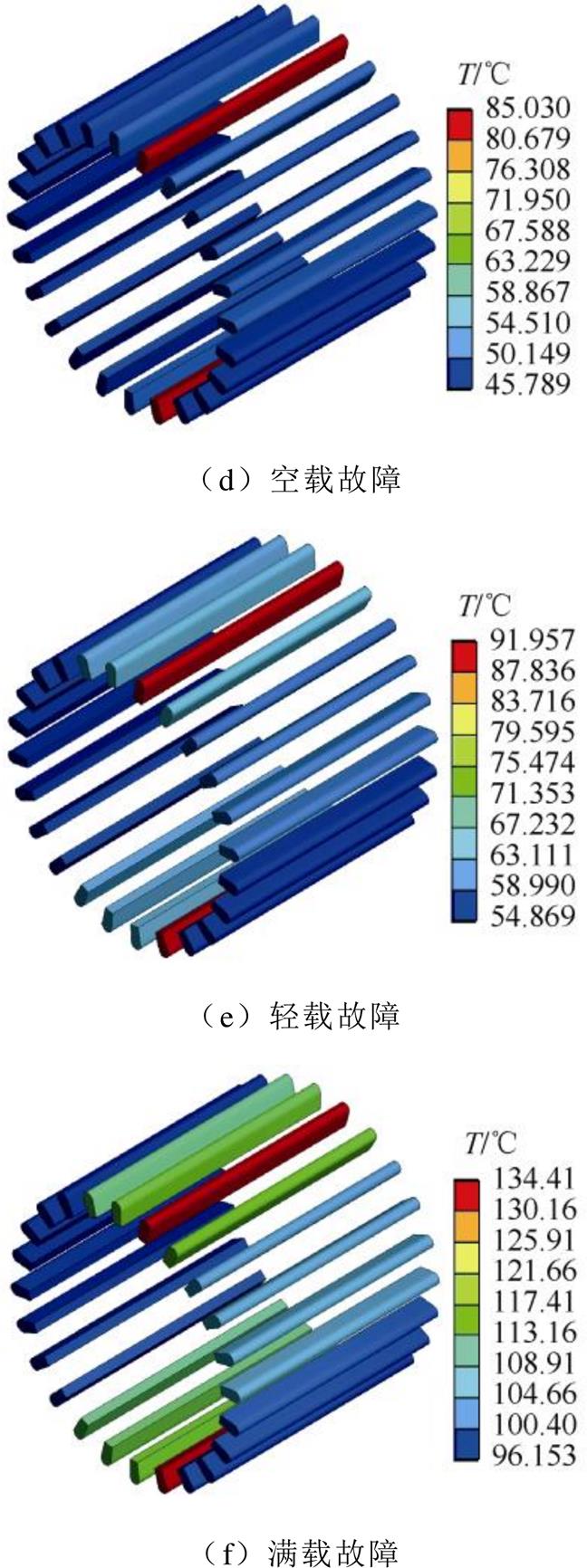
图7 三种工况下正常与故障电机绕组温度分布
Fig.7 Temperature distribution of windings in normal and faulty motor under three load conditions
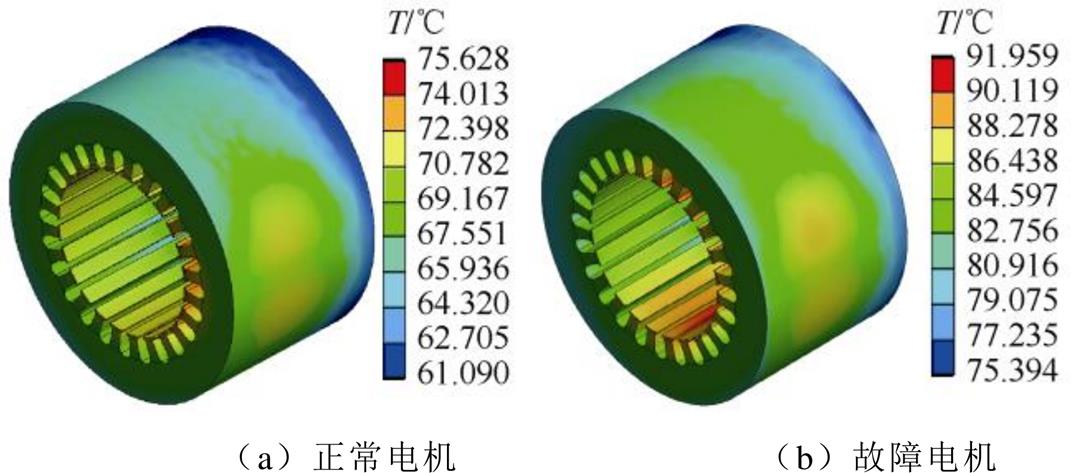
图8 满载工况定子铁心温度分布
Fig.8 Temperature distributions of stator core under rated load condition
在空载与轻载工况下正常与故障电机的转子温度均较低，图9为满载工况下电机故障前后的转子稳态温度分布。转子整体轴向温差较小，径向温差较大，负载侧温度高于风扇侧，最高温度在转子中部靠近负载侧的导条位置。故障后转子温度明显升高，增长幅度为17.5 %，这会导致转子关键位置热应力增大，进而增加了转子故障的风险。
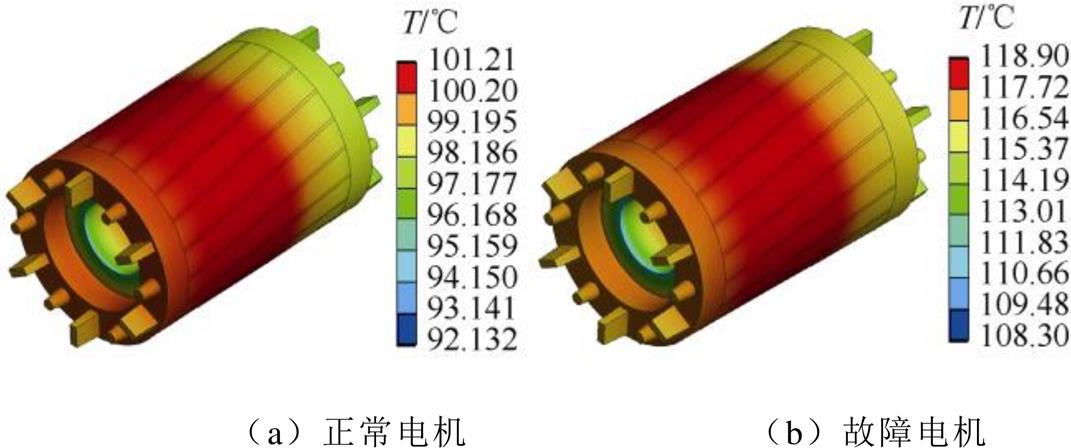
图9 满载工况转子温度分布
Fig.9 Temperature distributions of rotor under rated load condition
通过对电机内部测温点在不同工况下的温升进行测量，并将测量数据与三维仿真模型中相应位置的温度数据对比，即可验证温度场仿真结果的准确性。图10所示为空载工况下正常与故障电机两测温点A和D的仿真与实测温度曲线，实验中由于电机运行前期升温较快，数据记录间隔较小。从仿真曲线与实测数据的对比可以看出，二者趋势一致，电机温升稳定时的温度相近，说明建模与仿真的准确性较高，仿真结果可以反映出电机的实际温度。
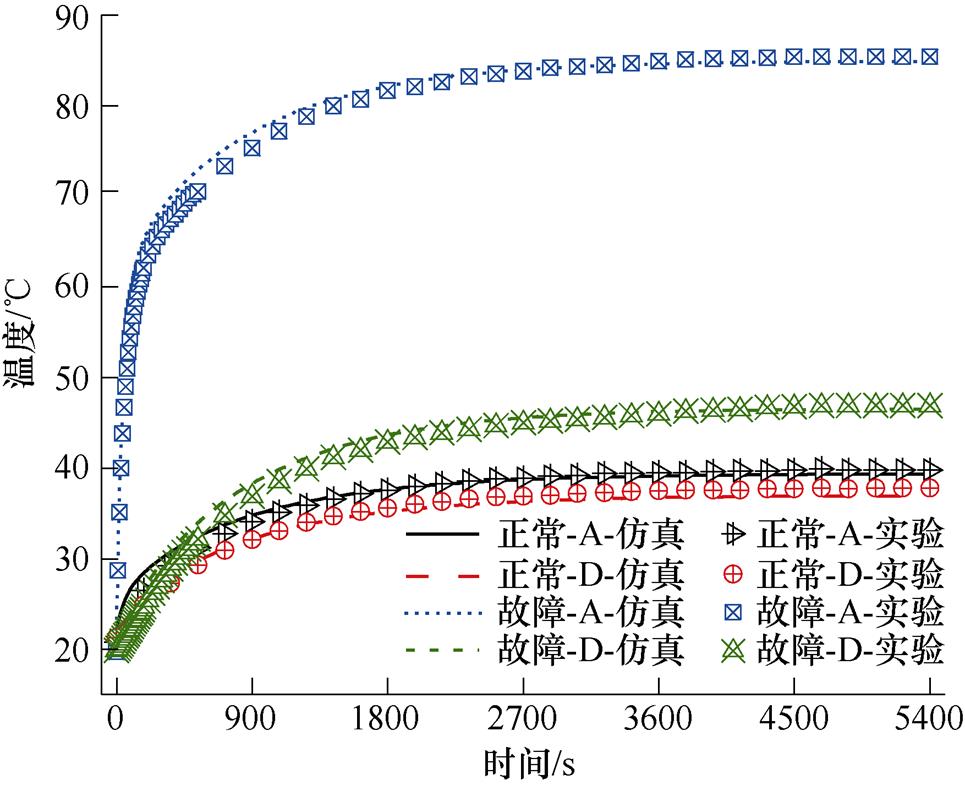
图10 空载工况下正常与故障电机温升曲线
Fig.10 Temperature rise variations of normal and faulty motor under no-load condition
需要说明的是，满载故障实验时故障槽的实测温升在电机运行45 min时达到了112.8 K，超过了F级绝缘最大温升限度，为了保证设备的安全随即停止了实验。后文如无特别说明，各工况下正常电机与空、轻载故障电机稳态温度均指90 min时刻，满载故障稳态温度指45 min时刻。
表4列出了三种工况下正常与故障电机的稳态温度与温升数据，受限于篇幅只列出4个关键测温点（A—故障槽绕组、C—非故障相绕组、F—槽底定子铁心和H—气隙）的相关数据。由于这4个测温点位于电机内部的不同部位，可以认为表中数据能反映出电机整体温度分布。综合分析图10与表4中仿真和实测数据的差异可以看出，各工况下仿真值略低于实测值，这是由于在槽部等效绝缘模型的建立过程中虽然考虑了槽绝缘和导线绝缘的实际厚度以及无浸渍漆等因素，等效绝缘的导热系数计算值仍比实际情况大而造成的。从表4中的测温点温升数据对比可以看出，各工况正常与故障情况下的仿真数据与实测数据接近，进一步说明温度场模型的合理性以及仿真结果的准确性。
匝间短路故障会造成电机各部分的热生成率与故障前发生较大变化，进而引发故障前后温度场的时空分布特性差异，具体体现为电机同一部件温度的时间变化特性与电机整体温度的空间分布特性。通过对实测与仿真结果的分析可以得到故障的相关热特征，并为电机监测与故障诊断提供依据。为了和实验结果保持一致，本节分析内容中满载故障稳态温度取为45 min时刻，其余工况取为90 min时刻。
表4 三种工况下电机关键测温点故障前后温升值对比
Tab.4 Comparison of temperature rise of key temperature measurement points before and after fault under three load conditions
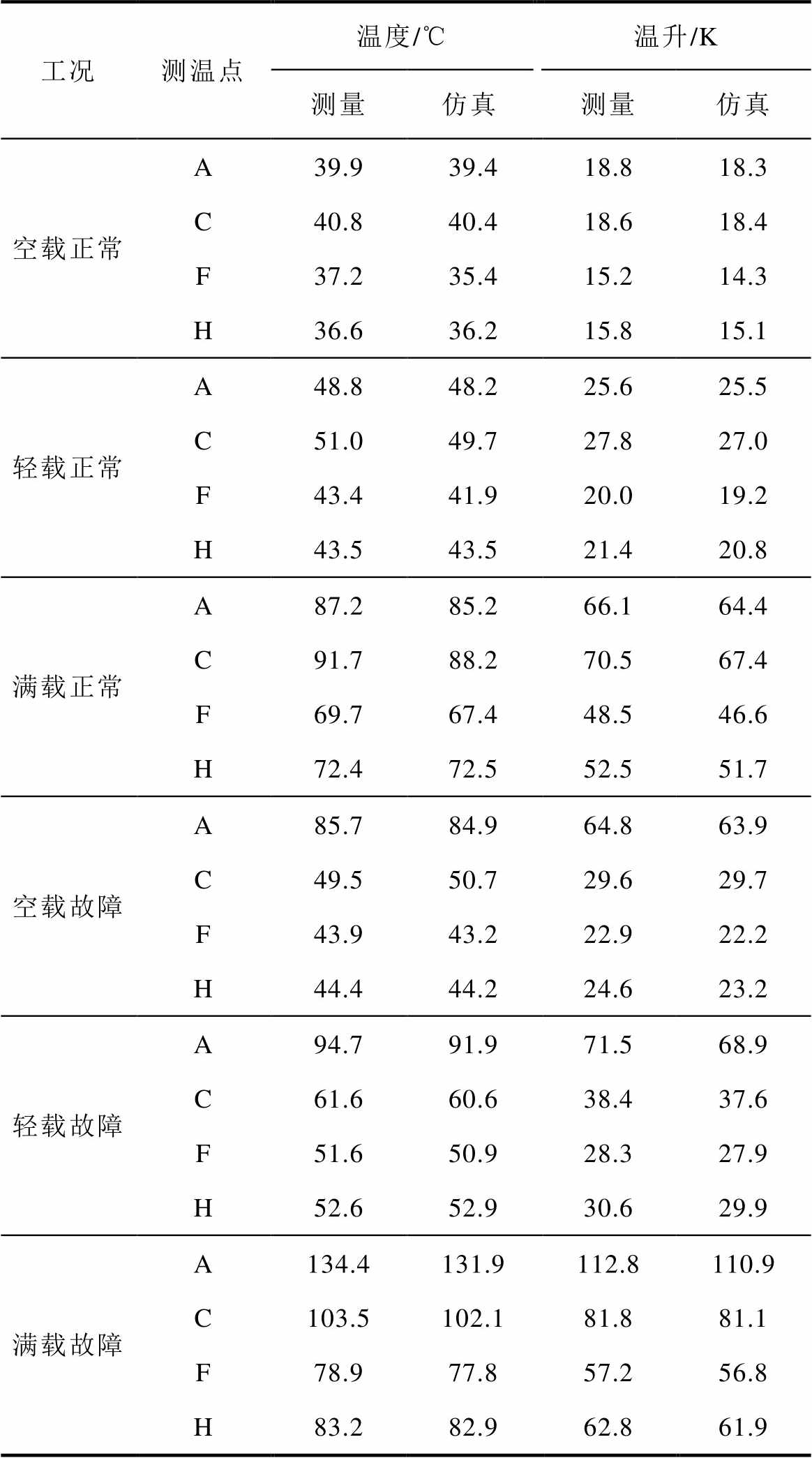
工况测温点温度/℃温升/K 测量仿真测量仿真 空载正常A39.939.418.818.3 C40.840.418.618.4 F37.235.415.214.3 H36.636.215.815.1 轻载正常A48.848.225.625.5 C51.049.727.827.0 F43.441.920.019.2 H43.543.521.420.8 满载正常A87.285.266.164.4 C91.788.270.567.4 F69.767.448.546.6 H72.472.552.551.7 空载故障A85.784.964.863.9 C49.550.729.629.7 F43.943.222.922.2 H44.444.224.623.2 轻载故障A94.791.971.568.9 C61.660.638.437.6 F51.650.928.327.9 H52.652.930.629.9 满载故障A134.4131.9112.8110.9 C103.5102.181.881.1 F78.977.857.256.8 H83.282.962.861.9
图10结果表明，故障后电机在运行前期升温明显，为了研究故障对电机温升特性的影响，将A、C、F、H 4个测温点空载运行前9 min的测量数据绘于图11。故障发生后，在前9 min的时间内各测温点温升值均大于正常电机温升（C、F、H三测温点温升量分别增大36 %、38 %、49 %），故障槽的温升值（测温点A）甚至达到了正常电机的4.88倍。若以正常电机前9 min的温升量作为标准，电机不同位置的温升时间特性差异较大，故障后各测温点达到此温升量的时间（图11中标记为t1）分别缩短了97.6 %、38.9 %、34.3 %和37.0 %。上述电机温升特性规律同样适用于轻载和满载工况，图12所示为两工况下测温点A的实测温升曲线，在两工况下故障后A点温升值分别达到正常电机的3.63倍和2.18倍，且相应温升时间分别缩短95.4 %和88.9 %。图11和图12的结果表明，匝间短路故障会缩短故障相关部件的温升时间，且故障温度特征以故障槽绕组温度变化最为显著。
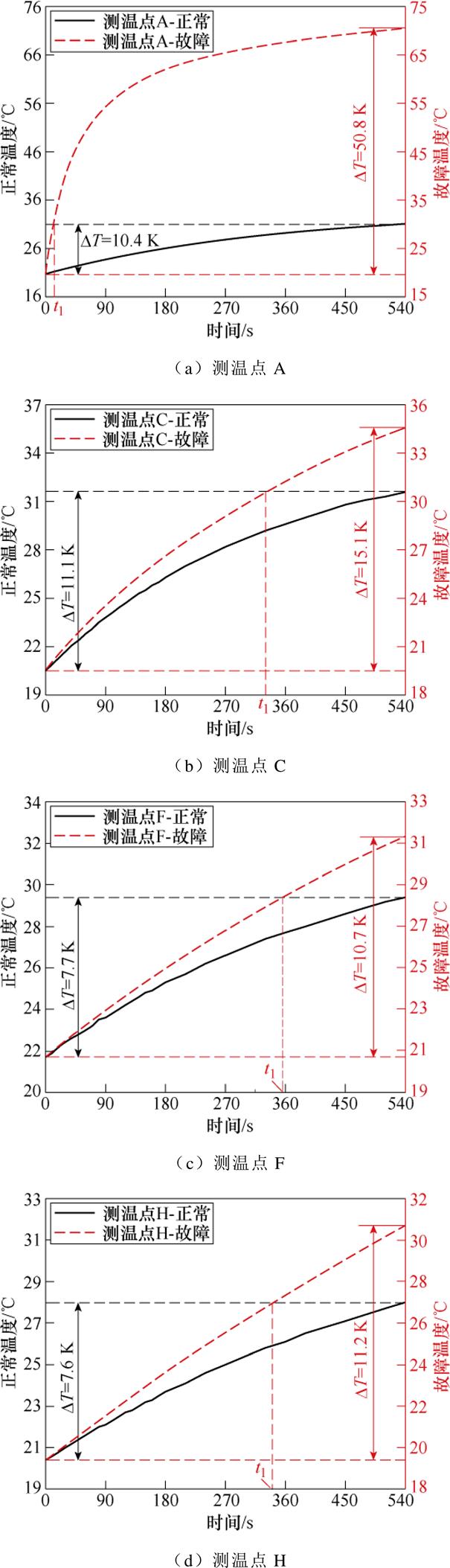
图11 空载工况运行前9 min实测温升曲线
Fig.11 Measured temperature rise curves under no-load condition in first nine minutes
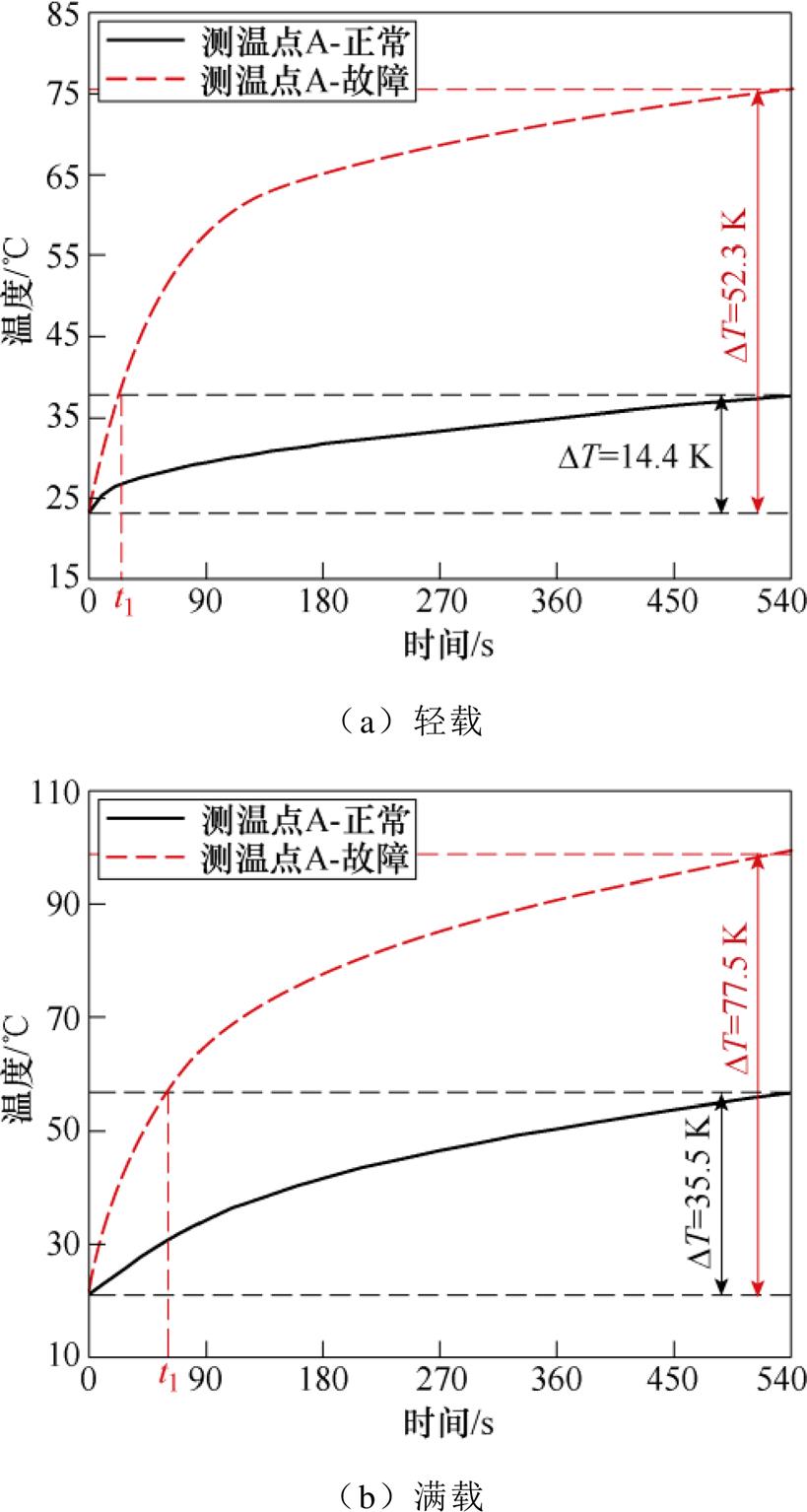
图12 轻载与满载工况运行前9 min A点实测温升曲线
Fig.12 Measured temperature rise curves of point A under light load and rated load conditions in first nine minutes
由于电机周向散热条件以及电机故障后各部件产生热量的差异，造成了电机故障前后不均匀的空间温度分布。为了研究故障温度场变化的空间特征，分别对电机两条路径下的温度分布进行分析，温度测量路径如图13所示，图中，L1和L2分别为电机轴向中部故障槽位置和接线盒位置的径向路径。
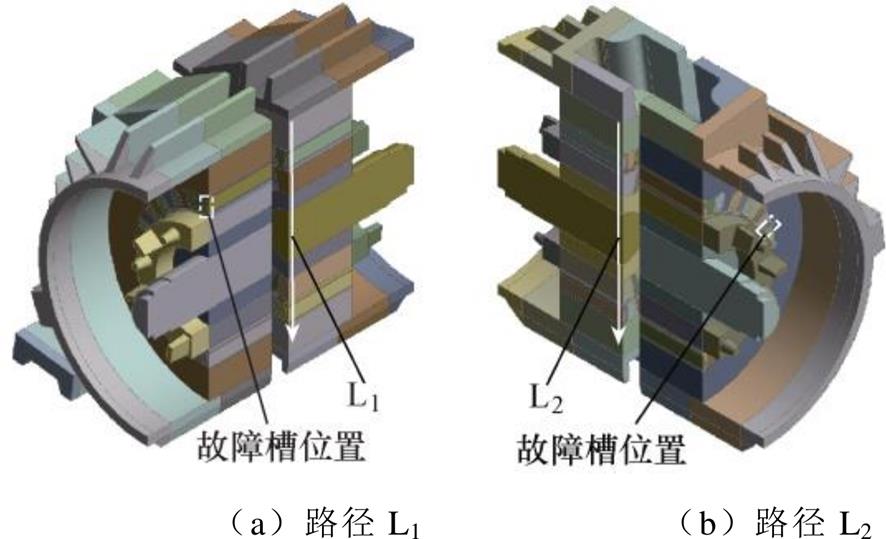
图13 温度测量路径
Fig.13 Temperature measurement paths of motor
图14、图15分别为三种工况下正常与故障电机沿两条路径的稳态温度分布。从图中可以看出，轻载与满载工况下电机正常运行时最高温度位于转子，且由于转子与转轴材料的良好导热性，其温度分布较为均匀，而空载下电机转子温度较低，最高温度位于定子绕组位置。由于L1路径两侧的散热条件一致，三种工况下正常电机温度分布近乎对称，而L2路径接线盒一侧的散热条件较差造成了接线盒侧的铁心和绕组温度均高于另一侧。当故障发生后，电机各部件温度提升明显，从图14b可以看出，原有对称的温度分布被打破，最高温度出现在故障槽绕组且电机沿L1路径温度差异很大。故障后路径L2的温度较正常电机有所升高，但分布规律与正常电机相同。
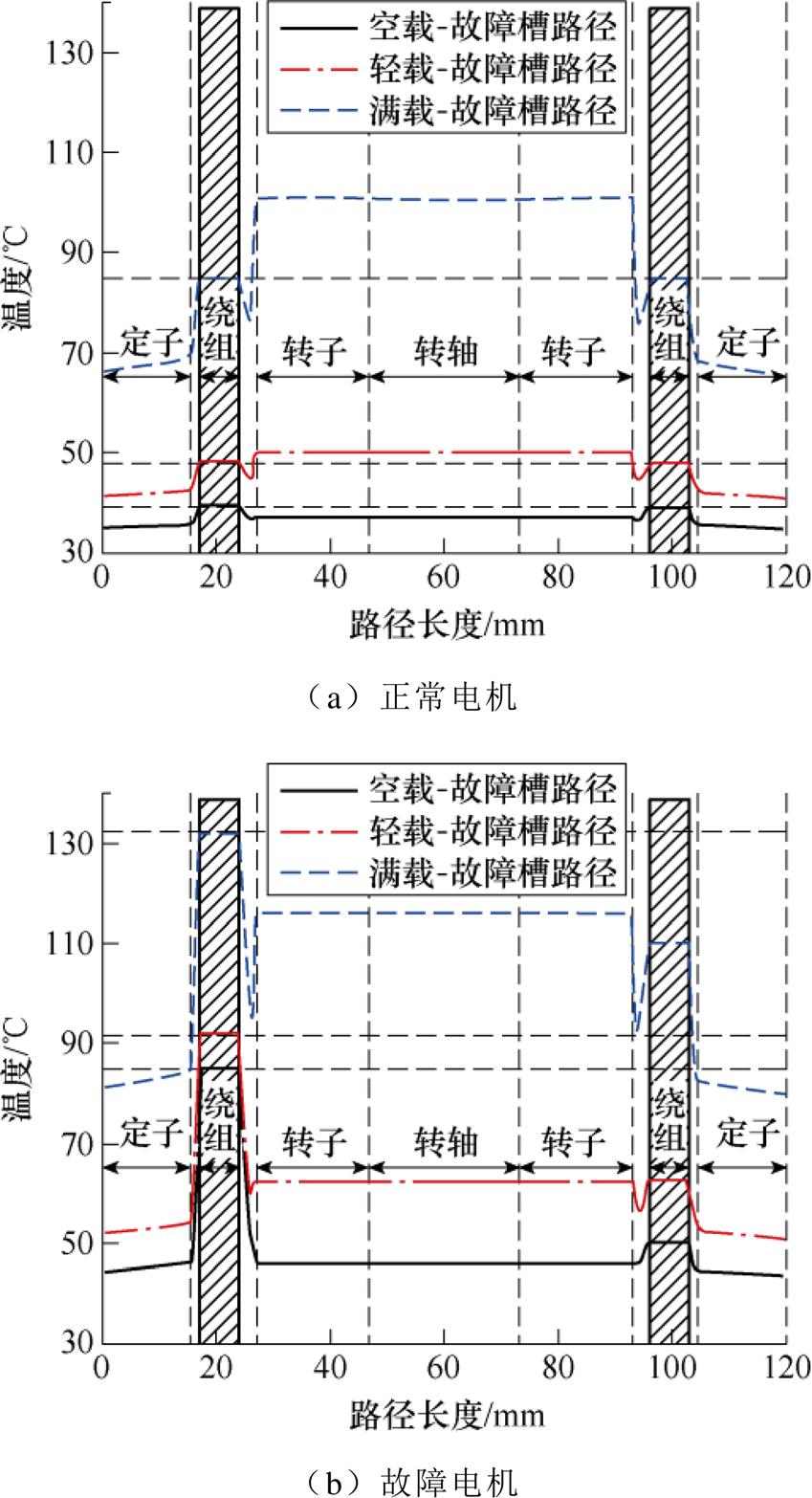
图14 三种工况下L1路径稳态温度分布
Fig.14 Steady-state temperature distributions of L1 under three load conditions
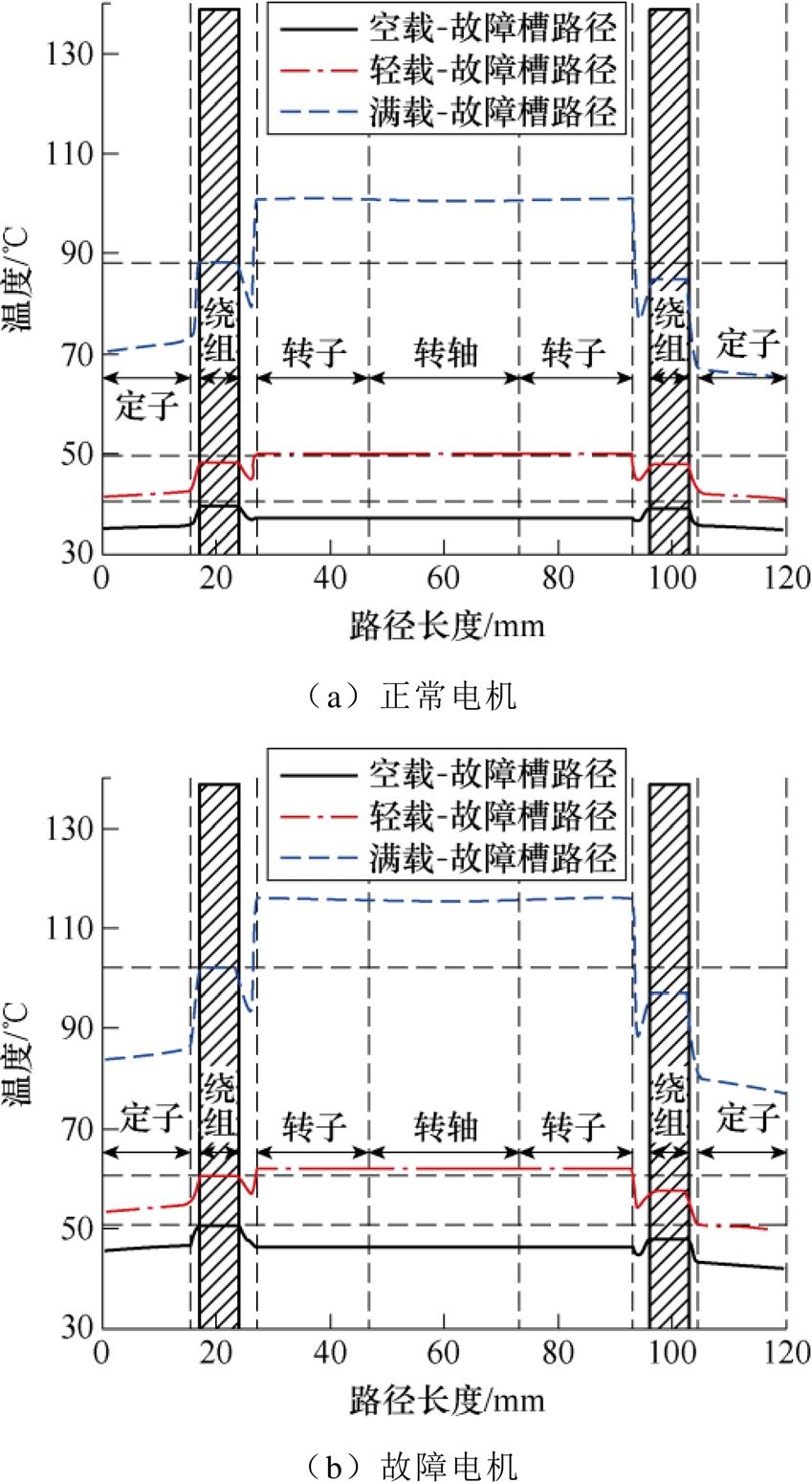
图15 三种工况下L2路径稳态温度分布
Fig.15 Steady-state temperature distributions of L2 under three load conditions
故障引发的电机各部件温度变化中绕组温度差异特征表现得最为显著，图16为三种工况下正常与故障电机各相绕组稳态平均温度的变化情况。电机正常运行时，由于电机周向散热条件差别会造成各相绕组平均温度存在轻微差异（图7a～图7c中数据，空载最大温差为1.4 ℃、轻载最大温差为1.9 ℃、满载最大温差为4.4℃），但是总体温差很小，可以认为各相绕组平均温度值是一致的。以电机达到稳态温度时的温升量计算，三种工况下故障后故障槽绕组温升比正常情况分别增大了249.2 %、170.2 %、72.2 %。而各相绕组平均温度也从正常时的几乎一致，变为温度相差37.7 ℃、35.3 ℃和35.6 ℃。从故障前后温度对比数据可以看出，故障发生后各相绕组的平均温度与正常状态相比体现出两个明显的特征，即故障槽绕组温升量大和各相绕组间温差增大。
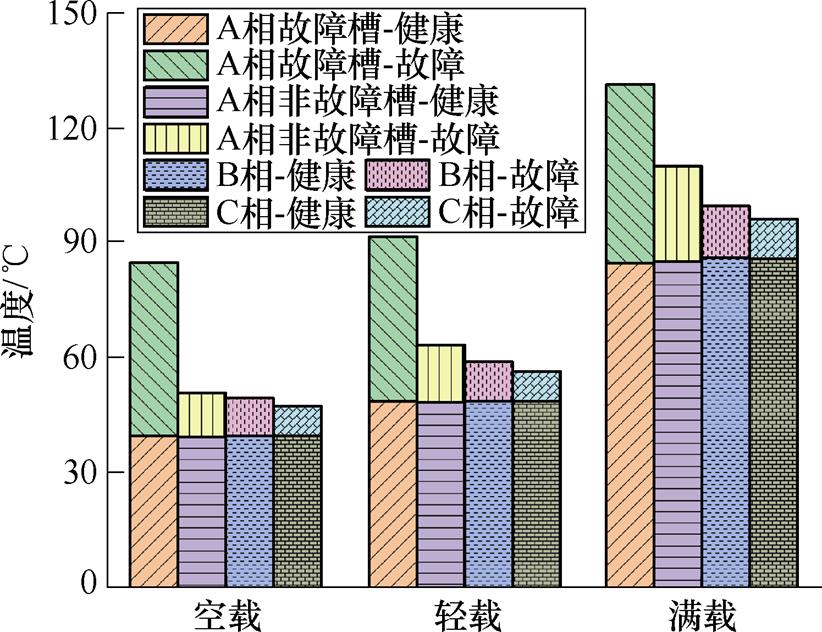
图16 三种工况下各相绕组稳态温度差异
Fig.16 Steady-state temperature difference of each phase winding under three load conditions
故障前后绕组的温差特征在电机的整个升温过程中同样显著。图17为空载情况下正常与故障电机运行3个时刻下的各相绕组平均温升值曲线（轻载和满载工况下该规律与空载相同）。正常时，电机在各时刻下温度分布均匀，分布规律与图16所示的稳态状态一致。故障后电机在各时刻下绕组温度分布同样表现为故障槽绕组温升高和各相绕组间温差大的特点。通过综合分析图16与图17的结果可以说明，从电机运行初期至稳态的全过程均可利用此特征进行故障监测与诊断。
电机绕组温度的差异性变化是最明显的故障特征，利用4.1和4.2小节所述故障前后绕组温度的变化规律并通过计算绕组温度监测数据的方差值D即可判定故障是否发生。图18所示为绕组温度监测传感器位置排布示意图，图中标注了各相绕组分布与各槽编号，监测中采用Pt100温度传感器测量槽内绕组的温度。考虑到匝间短路故障发生位置的不确定性，本文比较了三种监测方案在不同工况下的研究结果。其中：方案1监测全部24槽绕组的温度；方案2采取每相绕组取一个槽的方式进行监测，且在故障相取到了故障槽绕组（B2-A6-C11）；方案3同样采取每相绕组取一个槽的方式进行监测，但在故障相未取到故障槽绕组（B14-A18-C23）。
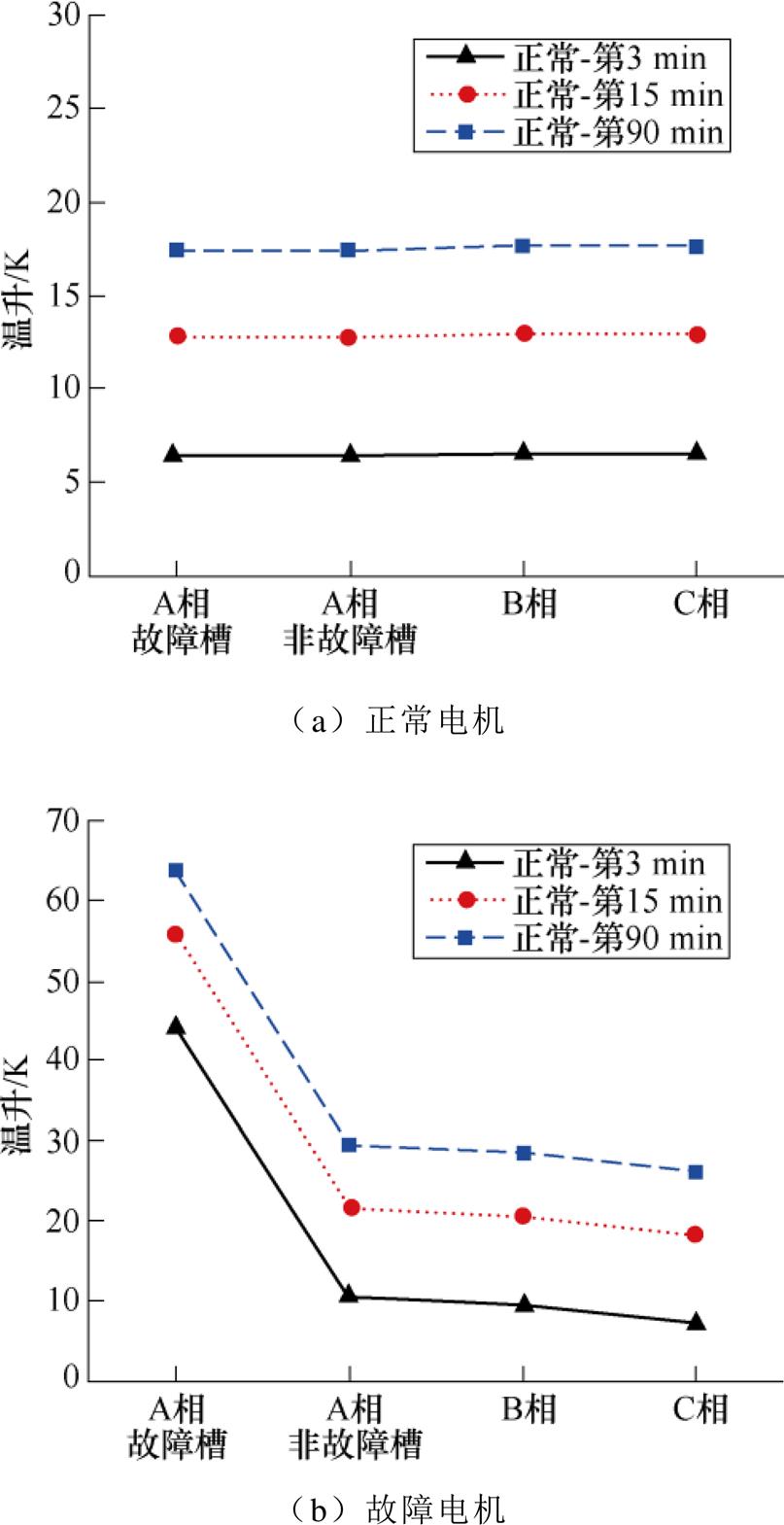
图17 不同时刻下空载工况各相绕组温度差异
Fig.17 Temperature difference of each phase winding under no-load condition at different moment
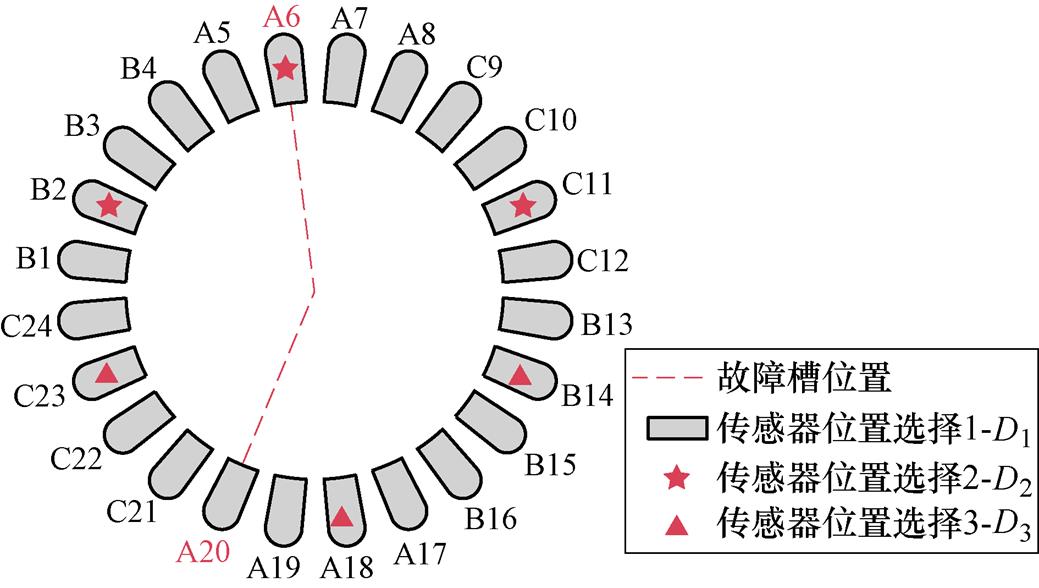
图18 绕组温度传感器位置排布方案
Fig.18 Position arrangement scheme of winding temperature sensors
将三种方案在不同时刻下绕组温度监测数据的方差值列于表5。电机正常运行时，三种方案计算得到的绕组温度方差值均很小，说明正常电机的绕组温度分布均匀。故障发生后，电机绕组温度分布的离散程度明显提高，造成计算得到的D值相较于正常值有明显差异，且这种巨大的差异伴随着电机运行的不同时刻，说明绕组温度方差值可以作为特征量用来进行故障诊断。
故障后不同负载工况下的D值均表现为D2最大、D1次之、D3最小。D2采样样本小且取到了故障槽绕组，计算值具有一定的特殊性；D1样本量大，整体性高，但是工程实际中不可能对所有槽绕组进行温度监控；D3虽然在三个方案中故障计算值最小，但是其故障值相较于正常值依然存在数量级差异，可以作为有效的诊断特征量。并且，方案3在传感器布置上具有任意性，即只需在每相绕组中各取任意一个槽绕组进行监控即可，这降低了传感器监测位置的选取难度，增强了工程实用性。
表5 三种工况下故障前后电机绕组温度方差统计值对比
Tab.5 Variance value comparisons of winding temperature before and after fault under three load conditions
时刻工况空载轻载满载 D1D2D3D1D2D3D1D2D3 3 min正常0.0030.0050.0020.0040.0070.0030.0080.0140.007 故障97.455291.3361.50084.510253.3566.83999.112254.45638.536 15 min正常0.0600.0860.0560.0940.1320.0890.3850.5350.367 故障101.292302.2901.87787.819262.9646.240102.500263.41337.819 90 min正常0.1670.2310.1580.3210.4370.3081.6571.4401.605 故障101.576301.5961.59588.015262.3795.402102.353263.30534.470
综上所述，本文提出的利用绕组温度方差值的诊断方法对于不同负载条件运行的单一故障电机是十分有效的。并且由于匝间短路故障最主要的热特征是绕组的温度变化，因此采用电机每相绕组任取一个槽绕组的温度监测方式与利用绕组温度方差值的诊断方法对于不同功率的电机也具有适用性。在未来的研究工作中还将结合电机在多种负载条件下不同故障程度时表现出的温度变化特征，总结出相应的故障判定阈值，建立更加完善的故障预警与监测体系。
本文针对感应电机定子匝间短路故障问题，从电机温升特性变化的角度，研究了不同负载条件下故障对电机温升特性的影响以及故障相关的热特征，得到如下结论：
1）通过电机内部多测温点温升测量与三维全域温度场仿真相结合的研究方法，得到了故障后电机各关键位置的温升情况与电机全域的温度分布特征，以及故障对电机不同工况下的温度场分布规律的影响。
2）匝间短路故障会造成电机瞬态和稳态温度的差异性分布，即故障引发电机各部件温升速率不同引起的温升时间变化特性差异与各部件温升量不同导致的电机整体温度空间分布特性差异。故障发生后，绕组是温度变化最剧烈的部分，上述特征在绕组温度差异性方面体现得最为显著。
3）电机绕组故障温度特征在不同工况下的变化趋势近似相同，故障槽绕组表现出剧烈变化的温升瞬态特性，即故障槽绕组温升速率的加快以及温升量的增大。此外，绕组间温度分布也从正常时各相绕组平均温度几乎一致变为故障后温度相差巨大，且该特征伴随从电机运行初期到稳态的全过程。
4）电机温升特性在匝间短路故障后发生明显变化，利用本文提出的绕组温度监测与方差分析方法可以从电机温度场变化角度对电机进行有效诊断。后续工作也将针对电机不同故障程度时的温度差异特征进行研究，为电机实际运行监测与故障预警提供参考。
附 录
将电机等效模型中各散热面的表面传热系数计算方法[27-28]列写如下。
1. 机壳表面（S1）传热系数
根据机壳表面实测风速不同将机壳分为六部分，各段换热系数可按式（A1）计算。由于接线盒部分相对封闭，所以该处按照自然对流散热处理。
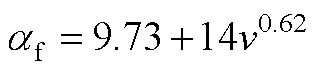（A1）
式中，af为机壳表面传热系数；v为机壳表面风速。
2. 铁心与机壳接触面（S2）热阻与传热系数
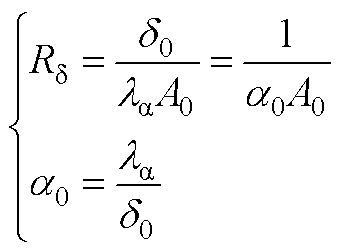（A2）
式中，Rd为等效导热热阻，且假定等效传热热阻与之相等；d0为机壳和定子铁心间的气隙长度；la为空气的导热系数；A0为定子铁心和机壳间的导热面积。
3. 定子铁心端面（S3）传热系数
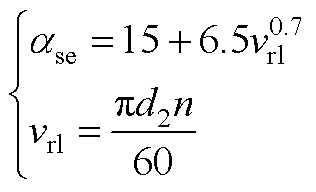（A3）
式中，ase为定子铁心端面传热系数；vrl为转子表面线速度；n为转子转速。
4. 转子铁心端面（S4）传热系数
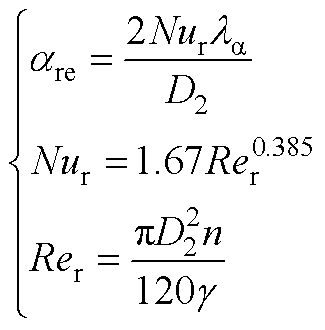（A4）
式中，are为转子铁心端面传热系数；Nur为努塞尔系数；Rer为转子端面空气的雷诺数。
5. 转子端环表面（S5）传热系数
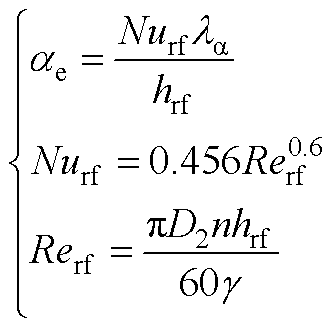（A5）
式中，ae为转子端环表面传热系数；Nurf为转子端环处努塞尔系数；Rerf为转子端环表面空气的雷诺数；hrf为转子风叶高度。
6. 端盖外表面（S6）传热系数
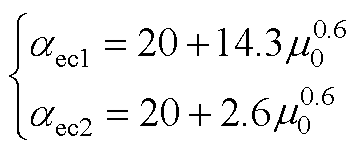（A6）
式中，aec1为风扇侧端盖外表面传热系数；aec2为负载侧端盖外表面传热系数；m0为外风扇外径处圆周速度一半。
7. 转轴表面（S7）传热系数
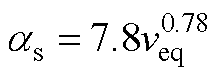（A7）
式中，as为转轴表面传热系数；veq为相应圆周速度的75 %。
参考文献
[1] Singh G K, SASA Kazzas. Induction machine drive condition monitoring and diagnostic research-a survey[J]. Electric Power Systems Research, 2003, 64(2): 145-158.
[2] Ojaghi M, Sabouri M, Faiz J. Diagnosis methods for stator winding faults in three-phase squirrel-cage induction motors[J]. International Transactions on Electrical Energy Systems, 2014, 24(6): 891-912.
[3] 张业成, 刘国海, 陈前. 基于电流波动特征的永磁同步电机匝间短路与局部退磁故障分类诊断研究[J]. 电工技术学报, 2022, 37(7): 1634-1643, 1653.
Zhang Yecheng, Liu Guohai, Chen Qian. Discri- mination of interturn short-circuit and local demag- netization in permanent magnet synchronous motor based on current fluctuation characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1634-1643, 1653.
[4] Mirzaeva G, Saad K I. Advanced diagnosis of stator turn-to-turn faults and static eccentricity in induction motors based on internal flux measurement[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3961-3970.
[5] Praveen K N, Isha T B. FEM based electromagnetic signature analysis of winding inter-turn short-circuit fault in inverter fed induction motor[J]. CES Transa- ctions on Electrical Machines and Systems, 2019, 3(3): 309-315.
[6] Filho P C M L, Santos D C, Batista F B, et al. Axial stray flux sensor proposal for three-phase induction motor fault monitoring by means of orbital analysis[J]. IEEE Sensors Journal, 2020, 20(20): 12317-12325.
[7] 何玉灵, 张文, 张钰阳, 等. 发电机定子匝间短路对绕组电磁力的影响[J]. 电工技术学报, 2020, 35(13): 2879-2888.
He Yuling, Zhang Wen, Zhang Yuyang, et al. Effect of stator inter-turn short circuit on winding elec- tromagnetic forces in generators[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2879- 2888.
[8] 王栋悦, 谷怀广, 魏书荣, 等. 基于机电信号融合的DFIG定子绕组匝间短路故障诊断[J]. 电力系统自动化, 2020, 44(9): 171-178.
Wang Dongyue, Gu Huaiguang, Wei Shurong, et al. Diagnosis of inter-turn short-circuit fault in stator windings of DFIG based on mechanical and electrical signal fusion[J]. Automation of Electric Power Systems, 2020, 44(9): 171-178.
[9] 吴柏禧, 万珍平, 张昆, 等. 考虑温度场和流场的永磁同步电机折返型冷却水道设计[J]. 电工技术学报, 2019, 34(11): 2306-2314.
Wu Boxi, Wan Zhenping, Zhang Kun, et al. Design of reentrant cooling channel in permanent magnet synchronous motor considering temperature field and flow field[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2306-2314.
[10] 秦雪飞, 沈建新, Nilssen R, 等. 高速永磁同步电机在多物理场和变流器约束下的设计[J]. 电工技术学报, 2022, 37(7): 1618-1633.
Qin Xuefei, Shen Jianxin, Nilssen R, et al. Design of high-speed PMSM considering multi-physics fields and power converter constraints[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1618- 1633.
[11] 谢颖, 胡圣明, 陈鹏, 等. 永磁同步电机匝间短路故障温度场分析[J]. 电工技术学报, 2022, 37(2): 322-331.
Xie Ying, Hu Shengming, Chen Peng, et al. Thermal field analysis on inter-turn short circuit fault of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(2): 322-331.
[12] Mohammed A, Melecio J I, Djurović S. Stator winding fault thermal signature monitoring and analysis by in situ FBG sensors[J]. IEEE Transactions on Industrial Electronics, 2018, 66(10): 8082-8092.
[13] Mohammed A, Djurović S. FBG thermal sensing ring scheme for stator winding condition monitoring in PMSMs[J]. IEEE Transactions on Transportation Electrification, 2019, 5(4): 1370-1382.
[14] Kumar P S, Xie Lihua, Halick M S M, et al. Stator end-winding thermal and magnetic sensor arrays for online stator inter-turn fault detection[J]. IEEE Sensors Journal, 2021, 21(4): 5312-5321.
[15] Singh G, Kumar T C A, Naikan V N A. Induction motor inter turn fault detection using infrared thermo- graphic analysis[J]. Infrared Physics and Technology, 2016, 77: 277-282.
[16] Glowacz A, Glowacz Z. Diagnosis of the three-phase induction motor using thermal imaging[J]. Infrared Physics & Technology, 2017, 81: 7-16.
[17] Bento F, Adouni A, Muxiri A C P, et al. On the risk of failure to prevent induction motors permanent damage, due to the short available time-to-diagnosis of inter- turn short-circuit faults[J]. IET Electric Power Appli- cations, 2021, 15(1): 51-62.
[18] Dusek J, Arumugam P, Brunson C, et al. Impact of slot/pole combination on inter-turn short-circuit current in fault-tolerant permanent magnet machines[J]. IEEE Transactions on Magnetics, 2016, 52(4): 1-9.
[19] Li G J, Ojeda J, Hoang E, et al. Thermal- electromagnetic analysis of a fault-tolerant dual-star flux-switching permanent magnet motor for critical applications[J]. IET Electric Power Applications, 2011, 5(6): 503-513.
[20] Shi Yanwen, Wang Jiabin, Wang Bo. Transient 3-D lumped parameter and 3-D FE thermal models of a PMASynRM under fault conditions with asymmetric temperature distribution[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 4623-4633.
[21] 刘慧开, 杨立, 孙丰瑞. 异步电动机定子绕组槽内匝间短路早期故障的表面温升[J]. 电工技术学报, 2007, 22(3): 49-54.
Liu Huikai, Yang Li, Sun Fengrui. Study of surface temperature rise of induction motor with stator winding inter-turn short circuit fault in slot[J]. Transactions of China Electrotechnical Society, 2007, 22(3): 49-54.
[22] 王艳武, 杨立, 孙丰瑞. 异步电动机定子绕组匝间短路三维温度场计算与分析[J]. 中国电机工程学报, 2009, 29(24): 84-90.
Wang Yanwu, Yang Li, Sun Fengrui. Simulation and analysis of 3D temperature field for stator winding short-circuit in asynchronous motor[J]. Proceedings of the CSEE, 2009, 29(24): 84-90.
[23] Boglietti A, Carpaneto E, Cossale M, et al. Stator winding thermal conductivity evaluation: an industrial pro- duction assessment[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 3893-3900.
[24] Ball K S, Farouk B, Dixit V C. An experimental study of heat transfer in a vertical annulus with a rotating inner cylinder[J]. International Journal of Heat and Mass Transfer, 1989, 32(8): 1517-1527.
[25] 谢颖, 郭金鹏, 单雪婷, 等. 油田抽油机用感应电动机三维瞬态温度场计算分析[J]. 电机与控制学报, 2019, 23(10): 59-67.
Xie Ying, Guo Jinpeng, Shan Xueting, et al. Three- dimensional transient temperature field calculation and analysis of induction motor for oilfield pumping unit[J]. Electric Machines and Control, 2019, 23(10): 59-67.
[26] Chen Peng, Xie Ying, Hu Shengming. Electromagnetic performance and diagnosis of induction motors with stator interturn fault[J]. IEEE Transactions on Industry Applications, 2020, 57(2): 1354-1364.
[27] 黄国治, 傅丰礼. 中小旋转电机设计手册[M]. 北京: 中国电力出版社, 2007.
[28] 魏永田, 孟大伟, 温嘉斌. 电机内热交换[M]. 北京: 机械工业出版社, 1988.
Abstract The induction motor is the most common AC motor type in industrial applications. Due to its complex working conditions, various stator, rotor, or bearing faults will occur. According to statistics, the inter-turn fault (ITF) accounts for about 26%～36% of the total motor fault. After the fault occurs, it will cause changes in the magnetic field, thermal field, vibration, and motor noise. Besides, the overheating problem caused by the fault will accelerate the deterioration of winding insulation and deepen the fault degree. Recently, the research focused on the thermal characteristics caused by ITF, which has achieved good results in temperature detection, fault identification, modeling, and simulation. However, there are still areas for improvement in many research methods. Therefore, the transient thermal field simulation and temperature rise (TR) experiment are adopted to analyze the temporal-spatial characteristics of motor thermal field distribution and the differences in winding temperature before and after the fault. In addition, the thermal characteristics related to the fault can be summarized.
Firstly, the 3D transient simulation model of the motor is established after reasonable equivalence. The motor loss values under no-load, light load, and rated load conditions before and after the fault are used as the heat source, and the whole domain thermal field distribution of the normal and faulty motor under different conditions is obtained by simulation. Secondly, the thermistors are embedded at several key temperature measuring points inside the prototype to carry out the TR experiment of the motor under various working conditions. Also, the results of TR experiments verify the simulation accuracy. Finally, according to the simulation and measured temperature results, three TR characteristics caused by ITF are summarized, and a fault diagnosis method based on the winding temperature difference is proposed.
The simulation and experimental results show that ITF will cause three characteristics of the motor TR: time, space, and winding temperature difference. As the heat generation rate of each part of the faulty motor changes greatly, the TR time of the four critica positions of the motor after the fault is shortened by 97.6%, 38.9%, 34.3%, and 37.0%, respectively, compared with the normal time, and the TR of each part will rise significantly, especially in the faulty slot. In addition, the spatial temperature distribution after the fault is uneven due to the differences in the circumferential heat dissipation conditions of the motor and the heat generation of each component after the fault. The temperature difference characteristics of winding are the most obvious in the temperature variation of each motor component caused by faults. By analyzing the temperature data of winding at different times, a fault diagnosis method using the variance value of winding temperature is proposed. The results show that the data with the variance value as the characteristic quantity after the fault is more than 20 times larger than the normal one, which indicates that the method can diagnose faults under different load conditions.
The following conclusions can be drawn from the comprehensive analysis of the research results: (1) ITF will cause the differential distribution of the transient and steady thermal field of the motor, and the above characteristics are most obvious in the winding temperature difference. (2) The variation trend of temperature characteristics of motor winding under different working conditions is approximately the same. The faulty slot winding shows the transient characteristics of TR with drastic changes. In addition, the temperature distribution among windings also changes from almost the same at the normal time to a considerable difference after the fault. (3) The TR characteristics of the motor change obviously after ITF. The winding temperature monitoring and variance analysis method proposed in this paper can effectively diagnose the fault from the perspective of the thermal field.
keywords：Induction motor, inter-turn fault, multiple load conditions, thermal field, temperature rise characteristics
DOI: 10.19595/j.cnki.1000-6753.tces.221136
中图分类号：TM343
国家自然科学基金项目（51977052）、国家自然科学基金区域创新发展联合基金重点支持项目（U21A20145）和黑龙江省自然科学基金重点项目（ZD2022E006）资助。
收稿日期 2022-06-16
改稿日期 2022-07-13
陈 鹏 男，1993年生，博士研究生，研究方向为电机多物理场计算与感应电机故障诊断。E-mail: chenp_7@163.com
谢 颖 女，1974年生，教授，博士生导师，研究方向为电机内综合物理场计算、新能源汽车用电机设计及多目标优化。E-mail: xieying_1975@163.com（通信作者）
（编辑 崔文静）