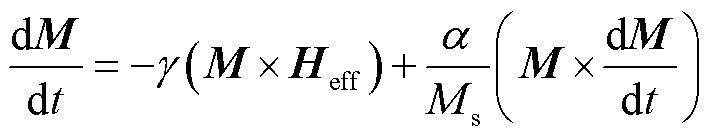（1）
摘要 为明确纳米晶合金高频磁损耗与其微观结构的关系，基于随机各向异性理论，建立了介观尺度下纳米晶合金的三维模型。以晶体相体积分数V和晶粒尺寸d为研究参数，从介观层面探究了微观结构的变化对高频磁损耗pv的影响，并得出材料pv与V和d的函数关系式。结果表明：材料pv会随着V和d的增加而增加，且d对于材料pv的影响更为显著。当外部磁场频率保持10 kHz不变、V从60%增大为80%时，材料pv增长率为27.11%；相应地，d从6 nm增大到15 nm时，材料pv增长率为51.83%。从三者之间的函数关系式也可看出，晶粒尺寸d和体积分数V都与高频磁损耗pv正相关，但两者的指数系数却不相同，d的指数系数大于V的指数系数，因此，d的变化对于材料pv的影响更为显著。
关键词：纳米晶合金 晶粒尺寸 体积分数 高频磁损耗
随着我国远距离直流输电和储能系统并网技术的不断发展，通过大功率电力电子器件及其控制技术以实现直流电压变换的高频变压器（High Frequency Transformer, HFT）逐渐获得应用，并得到了广泛的关注[1-6]。与工频变压器相比，高频变压器具有体积小、功率密度高、负荷侧电压输出恒定等优势，但随着工作频率逐渐提高至kHz，高频复杂磁场下的铁心损耗将大幅增加，对高频变压器用铁心材料的性能提出了更高的要求。纳米晶合金（FINEMET、NANOPERM、HITPERM系列合金）是一种双相复合铁磁材料，其微观结构表现为球状纳米晶粒弥散分布于非晶基体上，不仅具有高饱和磁感应强度、高有效磁导率、低损耗和低矫顽力等优异的综合软磁性能，而且成本较低、制备工艺简单、耐热性能高，已逐渐成为应用广泛的中高频铁磁材料[7-10]。
近年来，国内外学者针对纳米晶合金材料的磁损耗及磁性能表征等开展了一系列研究工作，并取得了重要进展。高频激励条件下对于磁损耗的计算方法主要分为工程经验公式法和损耗分离法。文献[11]采用相似元素协同取代的方法，用P元素替换Fe84Nb7B9合金中的B元素，发现元素替换后降低了合金的晶粒尺寸，提高了α-Fe相的尺寸均匀性和体积分数，使饱和磁感应强度从1.50 T提高到1.57 T。文献[12]研究了一步和两步退火工艺分别对淬火后的Fe73.5Cu1Nb3Si13.5B9的磁性能（磁损耗和动态矫顽力）、结晶动力学和显微组织的影响，结果表明，两步退火工艺能有效地改善合金的磁性能，优化微观组织。文献[13]采用熔体纺丝法制备了Fe79Si9B4.5P1.5CuNbx合金，发现Nb能使合金的晶粒尺寸减小，x=2时合金的单位磁损耗为5.84 W/kg，比x=1时的单位磁损耗降低了19%。然而，上述研究主要从材料制备工艺的宏观实验出发，通过对制备工艺的改进来完善纳米晶合金的磁性能，难以表征外部工况改变对磁损耗（因材料内部磁矩旋转运动引起的）的影响机理。为此，伍珈乐对纳米晶合金进行了微磁学仿真，发现磁化时畴壁的位移明显滞后于磁矩偏转，可以看作是磁矩偏转的结果[14]。韩智云等通过界定“动态饱和”和“静态饱和”，探究了外部交变磁场幅值或频率分别变化时对纳米晶合金磁化过程的影响[15]。
然而，上述文献仅研究了外部工况改变时纳米晶合金磁化过程中的磁矩旋转和畴壁位移，难以表征高频激励下材料内部晶粒尺寸、晶体相体积分数对高频磁损耗的影响机理，缺乏纳米晶合金运用于高频变压器铁心的理论支持。一方面，纳米晶合金制备时退火温度的不同，将导致合金的晶粒尺寸及晶体相体积分数出现差异，造成晶体相内部磁畴微应力、晶体相与非晶相之间的界面微应力及磁化时内部的涡流回路发生变化，最终影响合金的磁损耗；另一方面，相较于工频变压器，高频变压器运行工况复杂，工作频率高，频率的提高会加快合金内部磁矩的偏转以及磁畴壁的位移，增加纳米晶合金的高频磁损耗。因此，有必要研究高频激励下纳米晶合金晶体相体积分数V和晶粒尺寸d对于材料高频磁损耗的影响。
本文首先基于环形样件法构建交流测试系统，测量V=60%、d=10 nm的纳米晶合金在磁感应强度B= 0.7 T、频率f=10 kHz的交变磁场激励下的磁损耗；然后，建立相应介观尺度下纳米晶合金的三维模型，通过施加相同的交变磁场，得到模型的磁损耗，并将上述的两个损耗值进行对比，验证模型的正确性；最后，通过分别改变模型的晶体相体积分数和晶粒尺寸，探究了V为60%、70%和80%，d为6 nm、10 nm和15nm的纳米晶合金的高频磁损耗，并对结果进行分析。本文可为高频变压器新型铁心材料的设计与应用奠定理论基础并提供关键技术。
微磁学模拟源自LLG（Landau-Lifshitz-Gilbert）方程，能够精确地模拟宏观模型较难以计算的多种参数，包括材料磁化时内部因畴壁位移而产生的钉扎效应、动态磁化过程中的弛豫机制等多种微观动态磁化过程，可通过图形界面直接观测材料磁化的内部物理过程，这对于研究材料的高频磁化过程至关重要[16-20]。同时，利用LLG方程可以数值求解磁化的动态运动，其计算式为
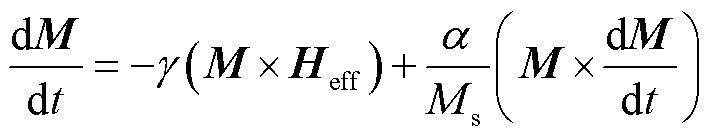（1）
式中，M为磁化强度矢量；Heff为有效场；Ms为饱和磁化强度；α为无量纲吉尔伯特阻尼常数，为计算方便，本文选取α=0.5；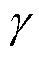
为吉尔伯特回旋磁比，
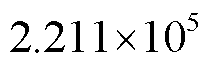。有效场由交换场、静磁场、磁晶各向异性场和塞曼场组成[21]。
选取样品材料为具有极高磁导率、高饱和磁感应强度和低矫顽力的FINEMET纳米晶合金，其化学式为Fe37.5Cu1Nb3Si13.5B9。通过ZEISS-40MAT光学显微镜[22]可以观察到合金的微观结构为大小不一的球状纳米晶相随机地分布在非晶基体上，如图1所示。并且，当材料内部球状纳米晶相的体积分数为60%～70%时，纳米晶合金具有最佳的软磁性能。
图1 纳米晶合金的微观结构
Fig.1 Microstructure of nanocrystalline alloy
基于G. Herzer的随机各向异性理论[23]，通过微磁学模拟软件，构建纳米晶合金的三维微磁学模型。模型建立时，晶胞的结构分为立方体晶胞和球状晶胞两种，如图2所示。图中最内部的球体为晶粒的晶体相，其余部分为非晶相。
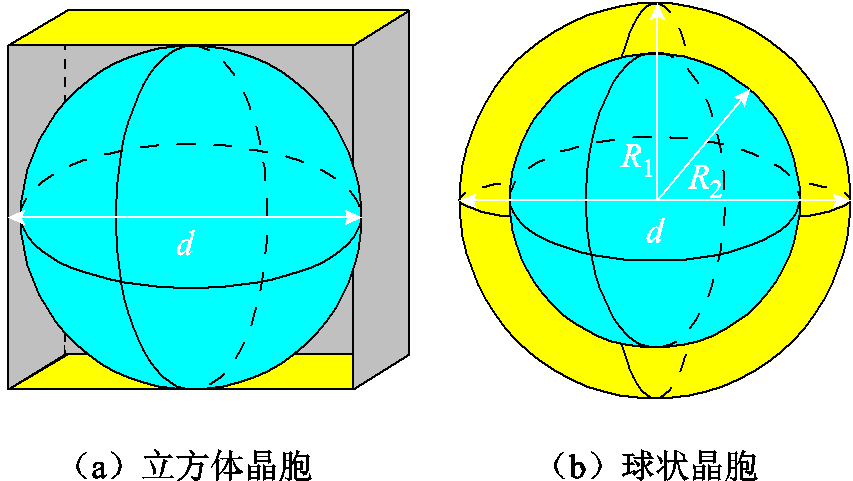
图2 纳米晶粒示意图
Fig.2 Schematic diagram of nanocrystals
相比于立方体晶胞，球状晶胞具有如下优势：一方面，若假定纳米晶胞为正方体结构，即球状纳米晶相内切于正方体非晶相之中，此时，纳米晶相占整个晶胞的体积分数最大值仅为52.35%，与实际情况60%～70%[22]不符。而球状晶胞可通过调整纳米晶粒半径R1和晶体相半径R2的大小来改变纳米晶相的体积分数值，并且方便之后研究体积分数变化对于材料磁损耗的影响。另一方面，立方体晶胞特有的边缘棱角会产生高度不均匀的杂散场，由杂散场产生的退磁效应会造成相邻晶胞之间交换耦合作用的减弱[24]，最终导致立方体晶胞的相应磁能积小于球状晶胞的磁能积。
综上所述，相比于立方体晶胞，球状纳米晶胞能够达到纳米晶合金体积分数为60%～70%的目标，并可通过调整半径R1和R2的大小改变纳米晶相的体积分数，方便之后研究体积分数变化对材料磁损耗的影响。同时，球状纳米晶胞具有最大的磁能积，保证了相邻晶胞之间的强交换耦合，能够最大程度地发挥交换耦合效应。
晶粒晶体相与非晶相之间的交换耦合对纳米晶合金材料的铁磁特性有着重要影响，它们之间的交换作用系数Acry-Amor可表示为
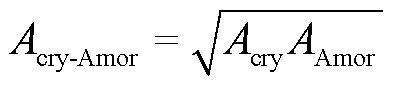（2）
式中，Acry和AAmor分别为晶体相和非晶相的交换作用常数。
当纳米晶粒为球状结构时，相邻的球状晶粒之间会存在空隙，称为“空白区域”，如图3所示。模型建立时各个区域的重要磁特性参数见表1。为了忽略空白区域对模型的影响，空白区域的磁特性参数均设置为0。
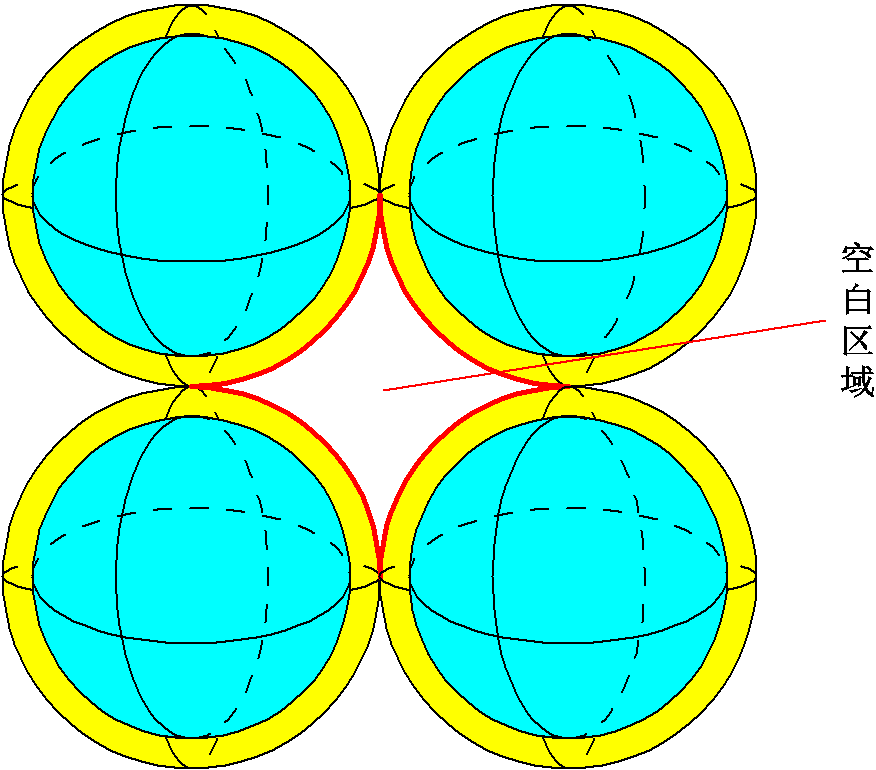
图3 相邻球状纳米晶粒
Fig.3 Adjacent spherical nanocrystals
表1 纳米晶合金材料的重要磁性参数
Tab.1 Important magnetic parameters of nanocrystalline alloy materials
磁性参数晶体相非晶相空白区域 交换作用常数A/(J/m)1×10-116×10-120 磁晶各相异性常数K1/(J/m3)8×10200 饱和磁化强度Ms/T1.311.160
同时，为了简化分析，对模型作出以下几点假设：
1）非晶相的内部由于不存在晶体结构，因此可以理想地认为其磁晶各项异性常数为零。
2）纳米晶粒均匀地分布在非晶相基体中，发生在纳米晶粒与晶粒之间的铁磁交换作用是通过非晶相耦合来实现的。
3）为了使磁性体系的能量最小，纳米晶粒在模型中平行排列。
纳米晶合金的三维介观微磁学模型如图4所示，直径为10 nm的球状纳米晶粒水平排列，模型整体的大小为3 000 nm×1 500 nm×40 nm。
图4 纳米晶合金模型示意图
Fig.4 Schematic diagram of nanocrystalline alloy model
为验证模型的正确性，本文基于环形样件法搭建了磁性能测试系统，测量纳米晶合金的高频磁损耗，测试系统装置如图5所示。
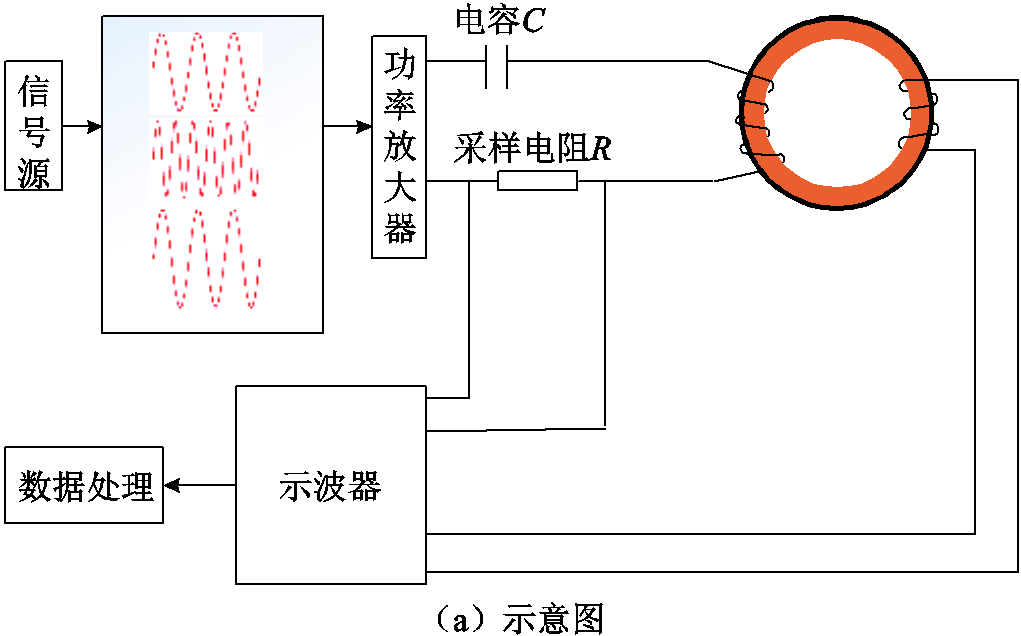
图5 测试系统装置
Fig.5 Test system installation diagram
如图5所示，测试系统主要由激励模块、测试模块和数据处理模块组成。激励模块由信号源和功率放大器构成，信号源用于产生不同频率和不同幅值的正弦交变磁场，经功率放大器放大后施加于测试样品的一次侧。测试模块由测试样品和隔直电容串联组成，隔直电容可以消除直流偏磁对纳米晶合金磁损耗的影响。示波器则用于采样圆环试样一次侧励磁电流及二次侧感应电压，并传输给计算机进行处理，其中，一次侧励磁电流通过测量采样电阻上的电压获取。
本文重点研究纳米晶合金微观结构对高频磁损耗的影响。测试时交变磁场的频率选定在纳米晶常用的应用频率10 kHz左右。
测试样品选用圆环试样，其实物及结构参数如图6所示。样品尺寸为：内圆直径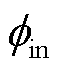
=32 mm，外圆直径
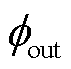=50 mm、厚度h=20 mm。其微观参数为：体积分数V=60%，晶粒尺寸d=10 nm。相应纳米晶合金微磁学模型中球状纳米晶粒如图7所示。
图6 磁性测试用圆环试样
Fig.6 Ring for magnetic testing
图7 球状纳米晶粒（V=60%, d=10 nm）
Fig.7 Spherical nanocrystals (V=60%, d=10 nm)
在交变磁场作用下，铁磁材料被周期性反复磁化的过程称为动态磁化。铁磁材料磁化一周的单位体积磁损耗在数值上等于动态磁滞回线所包围的面积[25]。通过图5中搭建好的测试系统，对圆环纳米晶合金施加幅值为0.7 T，频率为1～10 kHz的正弦交变磁场，得到其动态磁滞回线，进而获得不同频率下的磁损耗。圆环试样在不同频率交变磁场激励下的动态磁滞回线如图8所示。
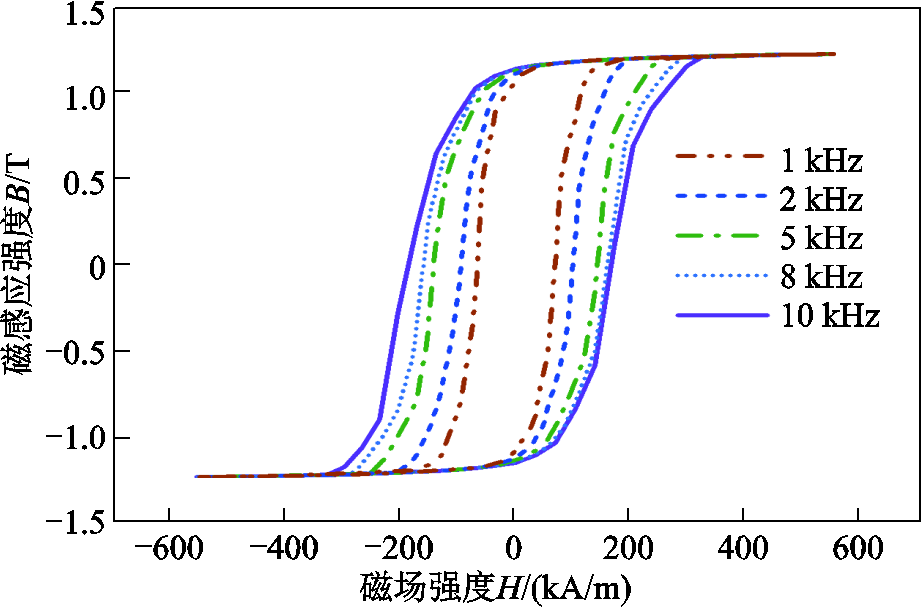
图8 圆环试样不同频率下的动态磁滞回线
Fig.8 Dynamic hysteresis loops of ring samples at different frequencies
从图8中可以发现，动态磁滞回线与静态磁滞回线形状类似，但动态磁滞回线所包围的面积远比静态回线的大，并且其形状与大小也随交变磁场的改变而变化。这是因为材料在动态磁化的过程中，磁损耗除了磁滞损耗之外，还包含涡流损耗与剩余损耗。
为验证模型的正确性，对建立的微磁学模型施加幅值为0.7 T，频率为1～10 kHz的正弦交变磁场，得到模型的动态磁滞回线，并通过计算其包围的面积得到纳米晶合金的磁损耗。图9给出了10 kHz激励下模型的动态磁滞回线。
对图9中动态磁滞回线所包围的面积（即图中阴影部分）进行计算，得到模型在10 kHz激励下的损耗值为141.98 kW/m3。表2列举了不同频率激励下实验测得的磁损耗与仿真得到的损耗值，并对两者进行了对比。
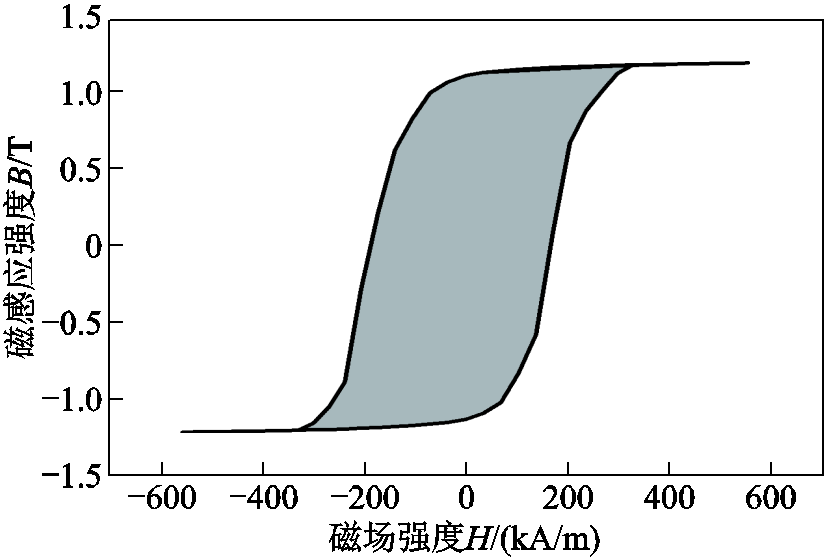
图9 10 kHz激励下模型的动态磁滞回线
Fig.9 Dynamic hysteresis loop of the model under 10 kHz excitation
表2 纳米晶合金磁损耗实验数据与仿真数据对比
Tab.2 Comparison of experimental data and simulation data on magnetic loss of nanocrystalline alloy
数据来源高频磁损耗pv 1 kHz2 kHz5 kHz8 kHz10 kHz 实验数据/(kW/m3)7.1115.2751.11100.63140.01 仿真数据/(kW/m3)7.6416.3553.24102.36141.98 误差(%)7.457.074.171.721.41
从表2可以看出，通过模型仿真得到的磁损耗与实验测得的磁损耗相差不大，交变磁场频率为10 kHz时，误差最小为1.41%。并且，随着频率的减小误差逐渐增加，交变磁场频率为1 kHz时，误差最大为7.45%，但仍小于10%，验证了模型的预测精度。
目前对于纳米晶合金微观结构的研究表明，要实现纳米晶合金晶体相体积分数V和晶粒尺寸d的变化，主要是通过改变制备过程中各合金元素的配比及退火温度等工艺。本文基于微磁学仿真软件oommf，构建了纳米晶合金的微磁学模型，并通过改变模型的微观参数，实现微观结构对材料高频磁损耗的研究。
由图2可知，纳米晶粒由晶体相和非晶相两部分组成，并且晶体相分布于非晶相内。因此，晶粒尺寸包含外部的非晶相部分，纳米晶粒微观结构示意图如图10所示。
晶体相体积分数V计算式为
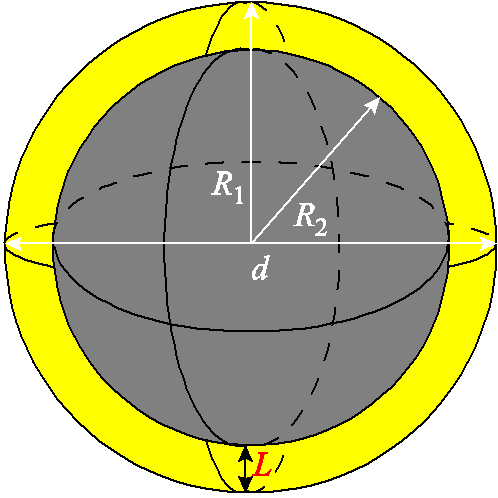
图10 纳米晶粒微观结构示意图
Fig.10 Schematic diagram of microstructure of nanocrystals
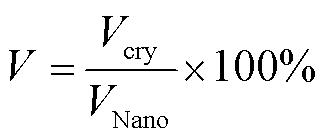（3）
式中，Vcry为晶体相的体积；VNano为纳米晶粒的体积。
当d确定之后，首先通过球形体积公式即可计算出纳米晶粒的体积VNano；然后，根据式（3）计算出晶体相的体积Vcry；接着，通过晶体相的体积计算出晶体相的半径R2；最后，通过纳米晶粒半径R1和晶体相的半径R2即可计算出非晶相与晶体相之间的间隙长度L。微观结构参数计算过程如图11所示。
图11 微观结构参数计算过程
Fig.11 Calculation process of microstructure parameters
为探究d对纳米晶合金高频磁损耗的影响，保持V=60%不变，d分别设置为6、10、15 nm，按照图11的计算过程计算出相应条件下的晶粒微观结构。不同尺寸的单个纳米晶粒示意图如图12所示。
接着，施加磁感应强度为0.7 T，频率为1～10 kHz的交变磁场。仿真过程中，通过软件的mmData Table（数据储存功能）对数据进行储存，并利用Python脚本对数据进行筛选，得到材料的磁感应强度B和磁场强度H；然后通过绘图软件绘制纳米晶合金在不同交变磁场激励下的动态磁滞回线；最后对动态磁滞回线进行积分计算得到其包围的面积，即纳米晶合金的磁损耗。图13展示了不同晶粒尺寸d的纳米晶合金在10 kHz激励下的动态磁滞回线。
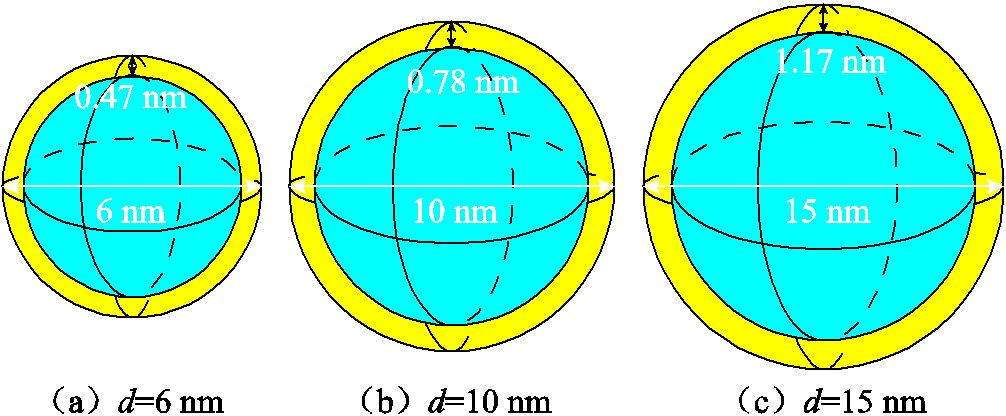
图12 不同尺寸的单个纳米晶粒示意图
Fig.12 Nanocrystals of different sizes
图13 不同晶粒尺寸d的纳米晶合金在10 kHz激励下的动态磁滞回线
Fig.13 Dynamic hysteresis loops of nanocrystalline alloy with different grain size d under 10 kHz excitation
从图13中可以发现，随着d的增加，纳米晶合金动态磁滞回线所包围的面积逐渐增大，意味着材料的高频磁损耗逐渐增大。表3列出了d为6、10、15 nm的纳米晶合金在1～10 kHz激励下的高频磁损耗，并根据表中的数据绘制了纳米晶合金高频磁损耗随d变化的曲线，如图14所示。
表3 不同晶粒尺寸d纳米晶合金的高频磁损耗
Tab.3 High frequency loss of nanocrystalline alloy with different grain sizes d
晶粒尺寸d/nm高频磁损耗pv/(kW/m3)1 kHz2 kHz5 kHz8 kHz10 kHz66.9113.8842.5981.89113.58107.6416.3553.24102.36141.98159.3621.8265.88120.83172.45
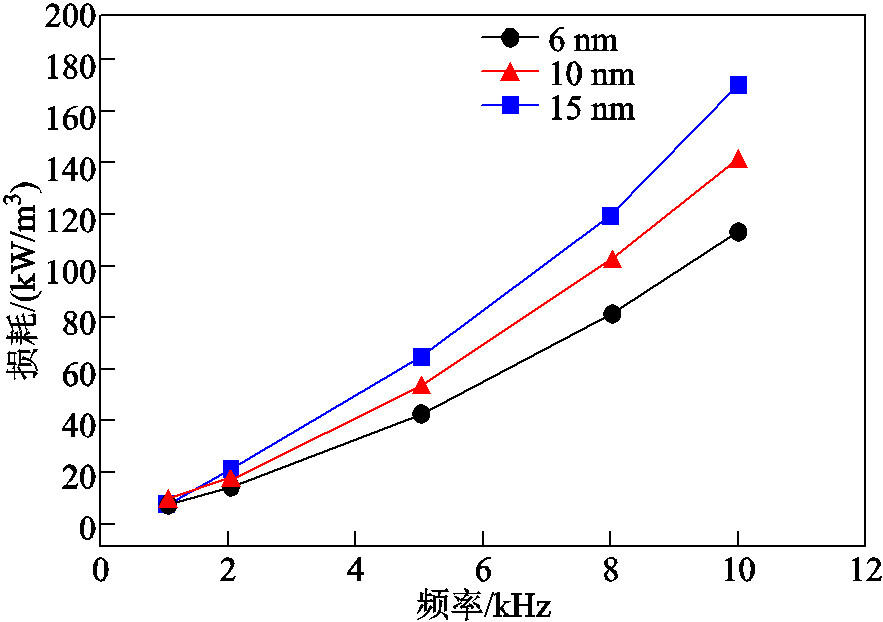
图14 纳米晶合金高频磁损耗与不同晶粒尺寸d的关系
Fig.14 Variation curves of high frequency loss of nanocrystalline alloy with different grain size d
从图14中可以发现，随着d的增大，纳米晶合金高频磁损耗逐渐增加，并且随着频率f的提升，高频磁损耗增加程度更为显著。当外部磁场频率保持1 kHz不变、d从6 nm增大为15 nm时，材料的高频磁损耗从6.91 kW/m3增加到9.36 kW/m3，增长率为35.46%；当外部磁场频率保持10 kHz不变，d从6 nm增大为15 nm时，材料的高频磁损耗从113.58kW/m3增加到172.45kW/m3，增长率为51.83%。
上述现象可由损耗分离法进行解释，铁磁材料的磁损耗包括静态损耗和动态损耗。其中，静态损耗也被描述为磁滞损耗，是铁磁材料在磁化过程中内部磁畴旋转摩擦而产生的内能损耗；动态损耗则分为涡流损耗和剩余损耗。与涡流损耗和磁滞损耗相比，剩余损耗很小，一般可以忽略[26]。损耗分离法计算铁磁材料的表达式为
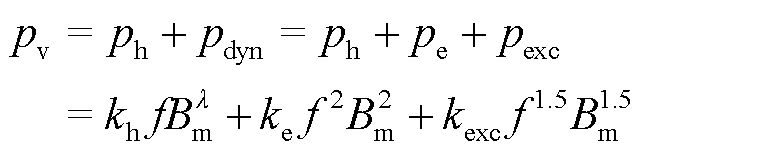(4)
式中，pv为铁磁材料的磁损耗；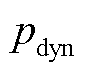
为铁磁材料的动态磁损耗；ph为铁磁材料的磁滞损耗；pe为铁磁材料的涡流损耗；pexc为铁磁材料的剩余损耗；
为斯坦梅茨系数；kh、ke、kexc分别为磁滞损耗系数、涡流损耗系数和剩余损耗系数；Bm为磁感应强度最大值。
由式（4）可知，磁滞损耗的频率指数系数要低于涡流损耗的频率指数系数，因此随着频率的提升（达到kHz级时），涡流损耗值将远大于磁滞损耗，此时磁滞损耗可忽略不计。因此，本文的高频磁损耗主要由涡流损耗组成。由于铁磁材料的晶粒为球形结构，材料内部单位体积中的涡流损耗可由式（5）计算。对于正弦变化的交变磁场，式（5）又可简化为式（6）[27-28]。
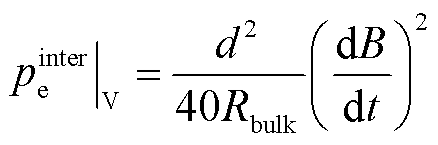（5）
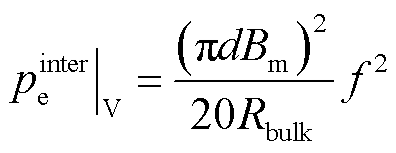（6）
式中，Rbulk为材料的电阻率。
纳米晶合金材料中晶粒晶体相的体积可以表示为
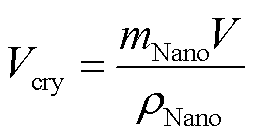（7）
式中，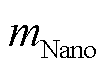
为材料的质量；
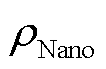为铁磁材料的密度。
材料总的涡流损耗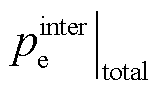
可以通过式（6）和式（7）的乘积表示，即
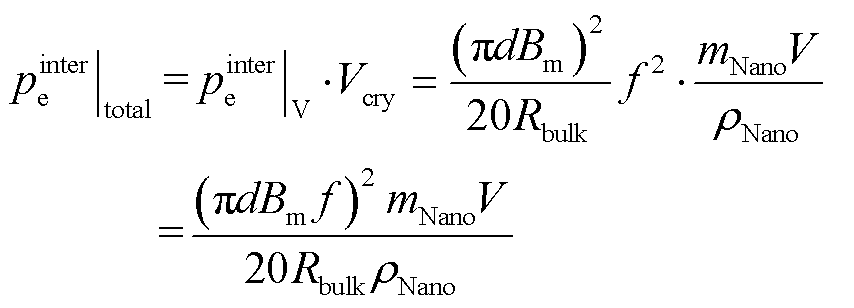(8)
从式（8）可以看出，材料的涡流损耗与晶粒尺寸呈正相关，因此，当d增大时，材料的高频磁损耗会随之增加。
为探究体积分数对纳米晶合金高频磁损耗的影响，保持d=10 nm不变，V分别设置为60%、70%、80%，按照图11的计算过程计算出相应条件下的晶粒微观结构。不同体积分数的单个纳米晶粒示意图如图15所示。
图15 不同体积分数的单个纳米晶粒示意图
Fig.15 Nanocrystals of different volume fractions
按照不同晶粒尺寸对损耗影响的数据处理步骤，得到不同体积分数的纳米晶合金在幅值为0.7 T、频率为1～10 kHz的交变磁场激励下的磁感应强度B及磁场强度H，绘制了不同体积分数的纳米晶合金在不同频率激励下的动态磁滞回线。其中，不同体积分数的纳米晶合金在10 kHz激励下的动态磁滞回线如图16所示。
图16 不同体积分数V的纳米晶合金在10 kHz激励下的动态磁滞回线
Fig.16 Dynamic hysteresis loops of nanocrystalline alloy with different volume fraction V under 10 kHz excitation
从图16中可以发现，随着V的增加，纳米晶合金动态磁滞回线所包围的面积逐渐增大，意味着材料的高频磁损耗逐渐增大。同时，相较于晶粒尺寸的变化，体积分数改变时，对于纳米晶合金动态磁滞回线的变化并不明显。表4列出了V为60%、70%、80%的纳米晶合金在1～10 kHz激励下的高频磁损耗，并根据表中的数据绘制了纳米晶合金高频磁损耗随V变化的曲线，如图17所示。
表4 不同体积分数V纳米晶合金的高频磁损耗
Tab.4 High frequency loss of nanocrystalline alloy with different volume fraction V
体积分数V(%)高频磁损耗pv/(kW/m3) 1 kHz2 kHz5 kHz8 kHz10 kHz 607.6416.3553.24102.36141.98 709.5119.0958.56112.60156.18 8010.2523.6867.55128.95180.47
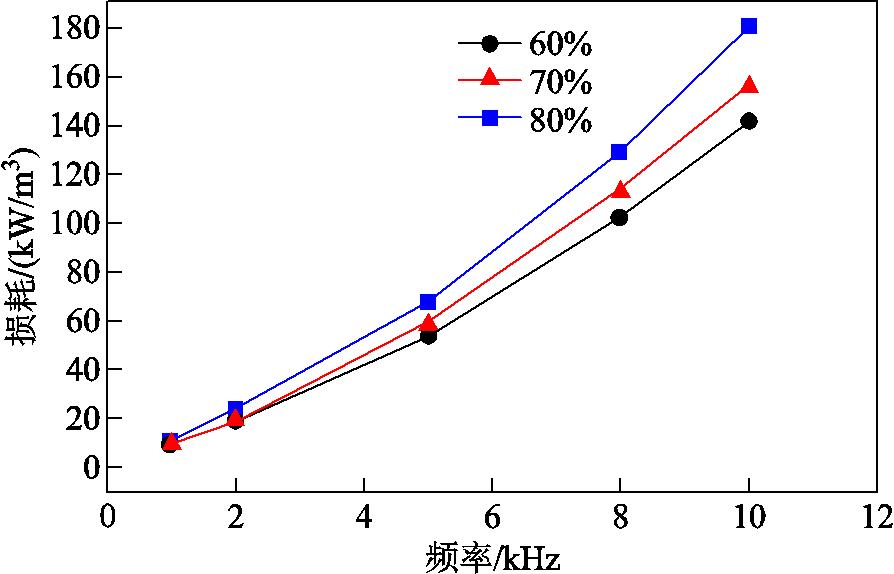
图17 纳米晶合金高频磁损耗与体积分数V的变化曲线
Fig.17 The variation curves of high frequency loss and different volume fraction V of nanocrystalline alloy
从图17中可以发现，随着V的增大，纳米晶合金高频磁损耗逐渐增加，并且，随着f的提升高频磁损耗增加程度更为显著。当外部磁场频率f保持1 kHz不变、V从60%增大为80%时，材料的高频磁损耗从7.64 kW/m3增加到10.25 kW/m3，增长率为34.16%；当外部磁场频率f保持10 kHz不变、V从60%增大为80%时，材料的高频磁损耗从141.98 kW/m3增加到180.47 kW/m3，增长率为27.11%。
出现上述现象的原因有以下两点：
1）由材料涡流损耗的计算式（8）可知，涡流损耗值与V呈正相关。因此，高频磁损耗随着V的增加而增大。
2）由材料涡流损耗的计算式（8）可知，涡流损耗值与材料的电阻率成反比，而纳米晶合金的电阻率会随着V的增加而减小。因此，高频磁损耗随着V的增加而增大。
同时，通过与晶粒尺寸变化的数据进行比较可以发现：相较于d的变化对于纳米晶合金高频磁损耗的影响，V的变化对于材料高频磁损耗的影响不是很显著。当外部磁场f保持1 kHz不变，V从60%增大为80%时，材料高频磁损耗的增长率为34.16%；相应地，d从6 nm增大到15 nm时，材料的高频磁损耗增长率为35.45%。当外部磁场f保持10 kHz不变，V从60%增大为80%时，材料的高频磁损耗增长率为27.11%；相应地，d从6 nm增大到15 nm时，材料的高频磁损耗增长率为51.83%。
晶粒尺寸变化对于纳米晶合金高频磁损耗影响更为显著的原因同样可以由涡流损耗计算式（8）解释。d和V虽然都与涡流损耗呈正相关，但两者的指数系数不同，晶粒尺寸的指数系数为2，体积分数的指数系数为1。因此，d的变化对于纳米晶合金高频磁损耗影响更为显著。
为探究微观结构变化对纳米晶合金高频磁损耗的影响，本文首先基于环形样件法，构建了高频磁损耗测试系统，测量了体积分数V=60%、晶粒尺寸d=10 nm的纳米晶合金高频磁损耗；然后，建立了相应介观尺度下纳米晶合金的三维模型，通过施加相同的交变磁场，得到了模型的磁损耗，并将上述的两个损耗值进行对比，验证了模型的正确性；最后，利用控制变量法，分别改变模型的V和d，探究了晶体V和d变化时对纳米晶合金的高频磁损耗的影响，得到以下结论：
1）对于晶粒尺寸而言，当纳米晶合金的d逐渐增大时，材料的高频磁损耗也随之增加。由损耗分离法可知，材料的高频磁损耗主要由涡流损耗组成。而材料的涡流损耗与d呈正相关，因此，当d增大时，材料的高频磁损耗会随之增加。
2）对于体积分数而言，当纳米晶合金的V逐渐增大时，材料的高频磁损耗也随之增加。出现上述现象的原因与晶粒尺寸相似。材料的涡流损耗与V呈正相关，因此，当V增大时，材料的高频磁损耗会随之增加。同时，材料的电阻率也会随着V的增大而减小，而涡流损耗与材料的电阻率成反比，因此，纳米晶合金的涡流损耗会随着V的增大而增加。
3）d和V都与纳米晶合金的高频磁损耗正相关。其中，d对于材料高频磁损耗的影响更为显著。当外部磁场频率保持10 kHz不变、V从60%增大为80%时，材料的高频磁损耗增长率为27.11%；相应地，d从6 nm增大到15 nm时，材料的高频磁损耗增长率为51.83%。这是因为由涡流损耗的计算式可知，d和V都与涡流损耗呈正相关。但两者的指数系数不同，d的指数系数为2，V的指数系数为1。因此，d的变化对于纳米晶合金高频磁损耗影响更为显著。
参考文献
[1] 赵志刚, 徐曼, 胡鑫剑. 基于改进损耗分离模型的铁磁材料损耗特性研究[J]. 电工技术学报, 2021, 36(13): 2782-2790. Zhao Zhigang, Xu Man, Hu Xinjian. Research on magnetic losses characteristics of ferromagnetic materials based on improvement loss separation model[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2782-2790.
[2] 孙鹤, 李永建, 刘欢, 等. 非正弦激励下纳米晶铁心损耗的计算方法与实验验证[J]. 电工技术学报, 2022, 37(4): 827-836. Sun He, Li Yongjian, Liu Huan, et al. The calculation method of nanocrystalline core loss under non-sinusoidal excitation and experimental verification[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 827-836.
[3] 袁发庭, 吕凯, 刘健犇, 等. 基于电磁-热-结构多物理场耦合的铁心电抗器线圈结构优化方法[J]. 电工技术学报, 2022, 37(24): 6431-6441. Yuan Fating, Lü Kai, Liu Jianben, et al. Coil structures optimization method of iron core reactor based on electromagnetic-thermal-structure multi-physical field coupling[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6431-6441.
[4] 孙鹤, 李永建, 刘欢, 等. 非正弦激励下纳米晶铁心损耗的计算方法与实验验证[J]. 电工技术学报, 2022, 37(4): 827-836. Sun He, Li Yongjian, Liu Huan, et al. The calculation method of nanocrystalline core loss under non-sinusoidal excitation and experimental verification[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 827-836.
[5] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883. Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of loss and magnetostrictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
[6] 赵志刚, 徐曼, 胡鑫剑. 基于改进损耗分离模型的铁磁材料损耗特性研究[J]. 电工技术学报, 2021, 36(13): 2782-2790. Zhao Zhigang, Xu Man, Hu Xinjian. Research on magnetic losses characteristics of ferromagnetic materials based on improvement loss separation model[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2782-2790.
[7] 王哲, 谢基表, 张忠福, 等. 铁基非晶、纳米晶软磁合金研究概况[J]. 山东冶金, 2019, 41(3): 42-46. Wang Zhe, Xie Jibiao, Zhang Zhongfu, et al. Research status of Fe based amorphous and nanocrystalline soft magnetic alloys[J]. Shandong Metallurgy, 2019, 41(3): 42-46.
[8] 杨庆新, 李永建. 先进电工磁性材料特性与应用发展研究综述[J]. 电工技术学报, 2016, 31(20): 1-29. Yang Qingxin, Li Yongjian. Characteristics and developments of advanced magnetic materials in electrical engineering: a review[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 1-29.
[9] Füzer J, Dobák S, Kollár P. Magnetization dynamics of FeCuNbSiB soft magnetic ribbons and derived powder cores[J]. Journal of Alloys and Compounds, 2015, 628: 335-342.
[10] Kenzelmann S, Rufer A, Dujic D, et al. Isolated DC/DC structure based on modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 89-98.
[11] Li T, Li Yanhui, Wu Licheng, et al. Improvement of soft magnetic properties of a Fe84Nb7B9 nanocrystalline alloy by synergistic substitution of P and Hf[J]. Journal of Alloys and Compounds, 2022, 918: 165735.
[12] Zhou Jian, Meng Li, Yang Fuyao, et al. Effect of heat treatment on dynamic magnetic properties and microstructures of Fe73.5Cu1Nb3Si13.5B9nanocrystalline alloy[J]. Journal of Materials Science: Materials in Electronics, 2017, 28(9): 6829-6836.
[13] Zhang Zongyang, Liu Xiansong, Feng Shuangjiu, et al. The glass formation ability and soft magnetic properties of the Fe79Si9B4.5P1.5CuNbx nanocrystalline alloys[J]. Journal of Magnetism and Magnetic Materials, 2020, 497: 165990.
[14] 伍珈乐. 纳米晶合金介观高频饱和机理的微磁学分析[D]. 济南: 山东大学, 2018.
[15] 韩智云, 邹亮, 伍珈乐, 等. 外部和内部因素对纳米晶合金kHz级饱和磁化过程影响的微磁学分析[J]. 电工技术学报, 2019, 34(8): 1589-1598. Han Zhiyun, Zou Liang, Wu Jiale, et al. Micromagnetic analysis of external and internal impact factors on kHz level saturation magnetization for nanocrystalline alloy[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1589-1598.
[16] 张长庚. 电工软磁材料三维磁特性测量及耦合磁滞和各向异性的电磁有限元模拟[D]. 天津: 河北工业大学, 2016.
[17] Zhi Q Z, Dong B S, Chen W Z, et al. Elevated temperature initial permeability study of Fe73.5Cu1Nb3Si13.5B9 alloy[J]. Materials Science and Engineering: A, 2007, 448(1/2): 249-252.
[18] Bottauscio O, Manzin A. Comparison of multiscale models for eddy current computation in granular magnetic materials[J]. Journal of Computational Physics, 2013, 253: 1-17.
[19] Fan Xingdu, Zhang Tao, Jiang Mmufeng, et al. Synthesis of novel FeSiBPCCu alloys with high amorphous forming abilityand good soft magnetic propertie[J]. Journal of Non-Crystalline Solids, 2019, 503-504: 36-43.
[20] Matsumori H, Shimizu T, Wang Xiongfei, et al. A practical core loss model for filter inductors of power electronic converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(1): 29-39.
[21] Zhang Zhidong. Magnetic structures, magnetic domains and topological magnetic textures of magnetic materials[J]. Acta Physica Sinica, 2015, 64(6): 067503.
[22] 马海健, 魏文庆, 鲍文科, 等. 铁基纳米晶软磁合金研究进展及应用展望[J]. 稀有金属材料与工程, 2020, 49(8): 2904-2912. Ma Haijian, Wei Wenqing, Bao Wenke, et al. Research progress and application prospect of Fe-based nanocrystalline soft magnetic alloys[J]. Rare Metal Materials and Engineering, 2020, 49(8): 2904-2912.
[23] Herzer G. Modern soft magnets: amorphous and nanocrystalline materials[J]. Acta Materialia, 2013, 61(3): 718-734.
[24] 贺佳. Nd2Fe14B/α''-Fe16N2核/壳结构纳米复合材料的微磁学模拟[D]. 临汾: 山西师范大学, 2021.
[25] 吴琛, 严密. 金属软磁复合材料研究进展[J]. 中国材料进展, 2018, 37(8): 582-589. Wu Chen, Yan Mi. Research progress on soft magnetic composites[J]. Materials China, 2018, 37(8): 582-589.
[26] 赵青. 非晶纳米晶磁材料在复杂激磁条件下的损耗特性研究[D]. 天津: 河北工业大学, 2017.
[27] Taghvaei A H, Shokrollahi H, Janghorban K, et al. Eddy current and total power loss separation in the iron-phosphate-polyepoxy soft magnetic composites[J]. Materials & Design, 2009, 30(10): 3989-3995.
[28] Hossein Taghvaei A, Ebrahimi A, Gheisari K, et al. Analysis of the magnetic losses in iron-based soft magnetic composites with MgO insulation produced by sol-gel method[J]. Journal of Magnetism and Magnetic Materials, 2010, 322(23): 3748-3754.
Abstract With the continuous development of long distance DC power transmission and energy storage system in China, High Frequency Transformer which can realize DC voltage transformation through high power electronic devices and their control technology has been gradually applied.However, as the working frequency gradually increases to kilohertz, the core loss will increase greatly under the complex magnetic field at high frequency, and higher requirements are put forward for the performance of the core materials used in High Frequency Transformer.Nanocrystalline alloy is a kind of composite bipolar ferromagnetic material, not only has high saturation magnetic induction intensity, high effective magnetic permeability, low loss and low coercivity excellent soft magnetic properties, and low cost, simple preparation, high heat resistance, has widely used in high frequency ferromagnetic material.
In order to clarify the relationship between high-frequency magnetic loss and internal microstructure of nanocrystalline alloy, a three-dimensional model of nanocrystalline alloy at mesoscopic scale was established based on G. Herzer's random anisotropy theory. Then, based on the ring sample method, an AC test system was constructed to measure the magnetic loss of nanocrystalline alloy with the volume fraction V=60% and the grain size d=10nm under alternating magnetic field excitation with amplitude H=0.7 T and frequencyf =10 kHz. Next, to obtain magnetic loss of the model, a sinusoidal alternating magnetic field withthe same amplitude and frequency was applied to the model. And the above two loss values are compared to verify the correctness of the model. Finally taking crystal phase volume fraction V and grain size d as research parameters, the influence of microstructure change on high frequency magnetic loss was investigated from the mesoscopic level, and the functional relationship between high frequency magnetic loss and volume fraction V and grain size d was obtained.
The results show that the high frequency magnetic loss increases with the increase of volume fraction V and grain size d.This is because the high frequency loss of the material is mainly composed of eddy current loss. And the eddy current loss of the material is positively correlated with volume fraction V and grain size d, so when V and d increases, the high frequency loss of the material will increase.Meanwhile, the resistivity of the material will also increase with the increase of V and d, and the eddy current loss is inversely proportional to the resistivity of the material. Therefore, the eddy current loss of the nanocrystalline alloy will increase with the increase of V and d. Among them, grain size d has a more significant effect on high frequency loss of materials. When the external magnetic field frequency f remains constant (10 kHz) and the volume fraction V increases from 60% to 80%, the increase rate of high frequency magnetic loss is 27.11%. Accordingly, when the grain size d increases from 6 nm to 15 nm, the increase rate of high frequency loss is 51.83%. As can be seen from the functional relations among the three, both grain size d and volume fraction V are positively correlated with eddy current loss, but their coefficients are different. The coefficient of grain size d is larger than that of volume fraction V. Therefore, the change of grain size d has a more significant impact on the high frequency loss of materials.
keywords: Nanocrystalline alloy, grain size, volume fraction, high-frequency magnetic loss
DOI:10.19595/j.cnki.1000-6753.tces.221704
中图分类号：TM274
国家自然科学基金项目（51977122, 51307102）和省部共建电工装备可靠性与智能化国家重点实验室立项（EERI_KF2021011）资助。
收稿日期 2022-09-06
改稿日期 2022-10-10
代岭均 女，1999年生，硕士研究生，研究方向为高电压与绝缘技术。E-mail：202114542@mail.sdu.edu.cn
邹 亮 男，1983年生，博士，副教授，研究方向为高电压与绝缘技术、应用电磁学等。E-mail：zouliang@sdu.edu.cn（通信作者）
（编辑 李 冰）