图1 WPT系统电路
Fig.1 Circuit topology of the WPT system
摘要 针对电动汽车进行静态无线充电时，发收机构相对偏移偏转会导致耦合系数和传输能效性急剧下降的问题，该文提出一种基于双极性耦合磁场调控的高抗偏移偏转无线电能传输（WPT）系统，该系统发射机构采用双层正交DD（DQDD）线圈，接收机构采用交叠式DD（OLDD）线圈。首先，给出空间位置和导磁机构特征参数与耦合系数之间的作用规律，并分析了发射机构激发磁场的分布特性；其次，构建基于双路逆变器-单路整流器的LCC-S补偿网络拓扑，并推导具有发射激励电流恒定特性以及系统输出电压不受负载影响的谐振参数配置条件；然后，给出一种将最大耦合系数作为期望目标的磁场调控策略；最后，通过实验样机验证了所构建耦合机构的抗偏移偏转性能。实验结果表明：在水平面±70 %的偏移范围内，输出功率维持在1.8 kW左右，系统效率不低于88 %。
关键词：无线电能传输 电动汽车 偏移偏转 磁场调控
采用无线电能传输（Wireless Power Transfer, WPT）方式的电动汽车充电系统无需线缆连接充电设备和车体，不存在接触损耗、积尘和机械磨损等问题，充电模式更加便捷、安全、灵活，可适应恶劣环境，故电动汽车无线充电系统受到了国内外专家学者的高度关注[1-3]。电动汽车静态无线充电过程中，发射机构与接收机构不可避免地出现偏移偏转的错位情况，这种错位会导致发收机构耦合系数和充电能效性的急剧下降[4-5]。因此，提高耦合机构的抗偏移偏转性能，同时保证接收机构拾取功率的稳定性是电动汽车静态WPT系统待解决的关键问题[6-7]。
现有文献为了提高静态WPT系统的抗偏移能力，主要采用了两种方式：调整耦合线圈绕制形式、采用复合型补偿拓扑。
在耦合线圈绕制方面，螺旋管（Solenoid Pad, SP）线圈和圆形（Circular Pad, CP）线圈的激励磁场均具有单极分布特征，两者分别使用激励磁场的水平分量和垂直分量进行能量耦合。相比于CP线圈，SP线圈具有更高的耦合磁通密度和更大的耦合系数[8-9]。然而，基于SP线圈发、收机构的耦合磁场呈双侧分布，存在较大的漏磁通，因此增加了屏蔽铝板中的涡流损耗；相比于单极性线圈，双D（Double-D, DD）线圈产生的磁场具有两个相反的极性，使得DD线圈在宽范围气隙内保持较大的耦合系数[10]。但在偏移过程中两个反极性磁场将导致耦合系数为零的功率拾取盲点；为克服DD线圈横向偏移过程中存在拾取盲点的不足，DDQ（Double- D Quadrature）线圈在DD线圈的中心位置上绕制正交解耦Q线圈。基于DDQ线圈的耦合机构在横向偏移时，随着DD线圈的耦合磁通的逐渐减小，而Q线圈的耦合磁通则逐渐增大，实现了总耦合磁通维持基本不变[11-12]；交叠式DD（Overlapping DD, OLDD）线圈综合了DD线圈和DDQ线圈的特点。通过调节OLDD线圈中两个D形线圈的交叠面积，两个D形线圈可实现相互解耦。与DDQ线圈类似，在偏移时也可进行独立补偿和控制。此外，在相同耦合面积下，OLDD线圈用铜量小于DDQ线圈[13]；由于DD、DDQ和OLDD线圈在横向偏移时的磁通变化特征具有方向性，而三极性（Triple Polar, TP）线圈可以形成多个方向上的极化磁场[14]。然而，TP线圈中三个扇形线圈的解耦需要调整三者的重叠面积。此外，其极化磁场需要三路激励电流幅值和相位的独立控制，由此增加了控制电路的复杂度。除了上述线圈形式以外，文献[15-16]通过增加发射机构的线圈数量，利用不同位置的多个线圈来获得分布均匀的磁场，从而增大耦合面积并保证接收机构不同偏移位置拾取功率的稳定性，提升系统抗偏移性能。但这种方式所绕制的耦合机构耗铜量大，导致损耗增大，降低了系统的效率。
在复合型补偿拓扑方面，文献[17]提出了SP-S复合型补偿拓扑，实现了发射端激励电流在偏移过程中近似恒定，克服了四种基本补偿拓扑（SS、SP、PS、PP）的传输特性受耦合机构偏移影响较大的问题；文献[18-19]提出了具有高抗偏移特性的双侧LCC补偿拓扑，降低了系统参数的设计难度，减小了线圈自感对系统阻抗的影响，实现了发射端线圈电流不受耦合系数变化的影响；为减小接收端的体积和减轻重量，文献[20-21]采用结构相对更简单的LCC-S拓扑，在具有双侧LCC拓扑相同优点的情况下，同时减少了双侧LCC拓扑的谐振元件。
综合现有两种抗偏移提升方式的特点并针对其存在的局限性，本文提出了一种基于双极性耦合磁场调控的高抗偏移偏转WPT系统。该系统发射机构采用双层正交DD（Double-layer Quadrature DD, DQDD）线圈，接收机构采用OLDD线圈。DQDD线圈由双层正交排列的两对解耦DD线圈组成，其激发的磁场分布通过两组DD线圈激励电流的幅值及相位来进行调控；接收机构OLDD线圈借助切换开关可变换为单极性CP线圈，从而改变接收机构可拾取的磁场极性。构建了基于双路逆变器-单路整流器的LCC-S补偿网络拓扑，推导了发射机构激励电流恒定且系统输出电压与负载无关的网络参数配置条件；提出了一种将最大耦合系数作为期望目标的磁场调控策略，通过调控发射DQDD线圈的激励电流相位差以及接收OLDD线圈的拾取极性，实现了偏移偏转情况下WPT系统的高能效传输。最后搭建了传输间距为130 mm的1.8 kW实验样机，在±270 mm水平面及±45 °的偏移偏转范围内，验证了所提磁耦合机构的传输能效性。
本文参照国际电工委员会设定的电动汽车无线充电系统标准IEC TS 61980所定义的空间直角坐标系。其原点O定义为发、收机构正对时，发射机构的中心位置；X轴为车辆行驶方向，即纵向；Y轴为正交于车辆行驶的方向，即横向。
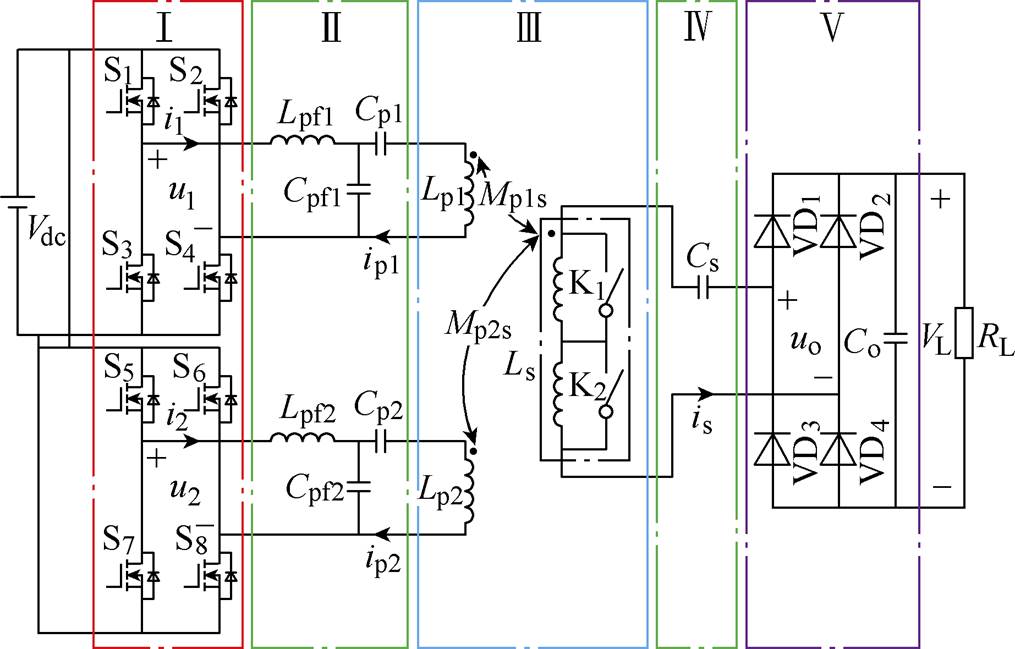
图1为基于双极性耦合磁场调控的高抗偏移偏转WPT系统电路，图中Ⅰ～Ⅴ分别为逆变器、发射侧补偿拓扑、DQDD-OLDD磁耦合机构、接收侧补偿拓扑、以及整流器。本系统采用两路逆变器独立激励DQDD发射机构的两组DD线圈。图中u1、u2为逆变器输出电压，i1、i2为逆变器输出电流，ip1、ip2、is分别为发射机构两组DD线圈和接收线圈的电流，Lp1、Lp2、Ls分别为两组DD线圈和接收线圈的自感，Lpfi、Cpi、Cpfi（i=1, 2）构成了两组DD线圈的LCC补偿网络，Cs为接收线圈的串联补偿电容，Mp1s、Mp2s分别为两组DD线圈与接收线圈间的互感。
图1 WPT系统电路
Fig.1 Circuit topology of the WPT system
图2a为基于双极性耦合磁场调控所采用的磁耦合机构，发射机构由双层正交DD线圈和磁心组成，接收机构由OLDD线圈和磁心组成。图2b给出了磁耦合机构的堆叠次序，DQDD线圈由叠放于磁心上的两组DD线圈组成，且同组两个D形线圈的间距为WWD，OLDD线圈由两组CP线圈交叠组成，其交叠形成的窗口宽度同样为WWD。
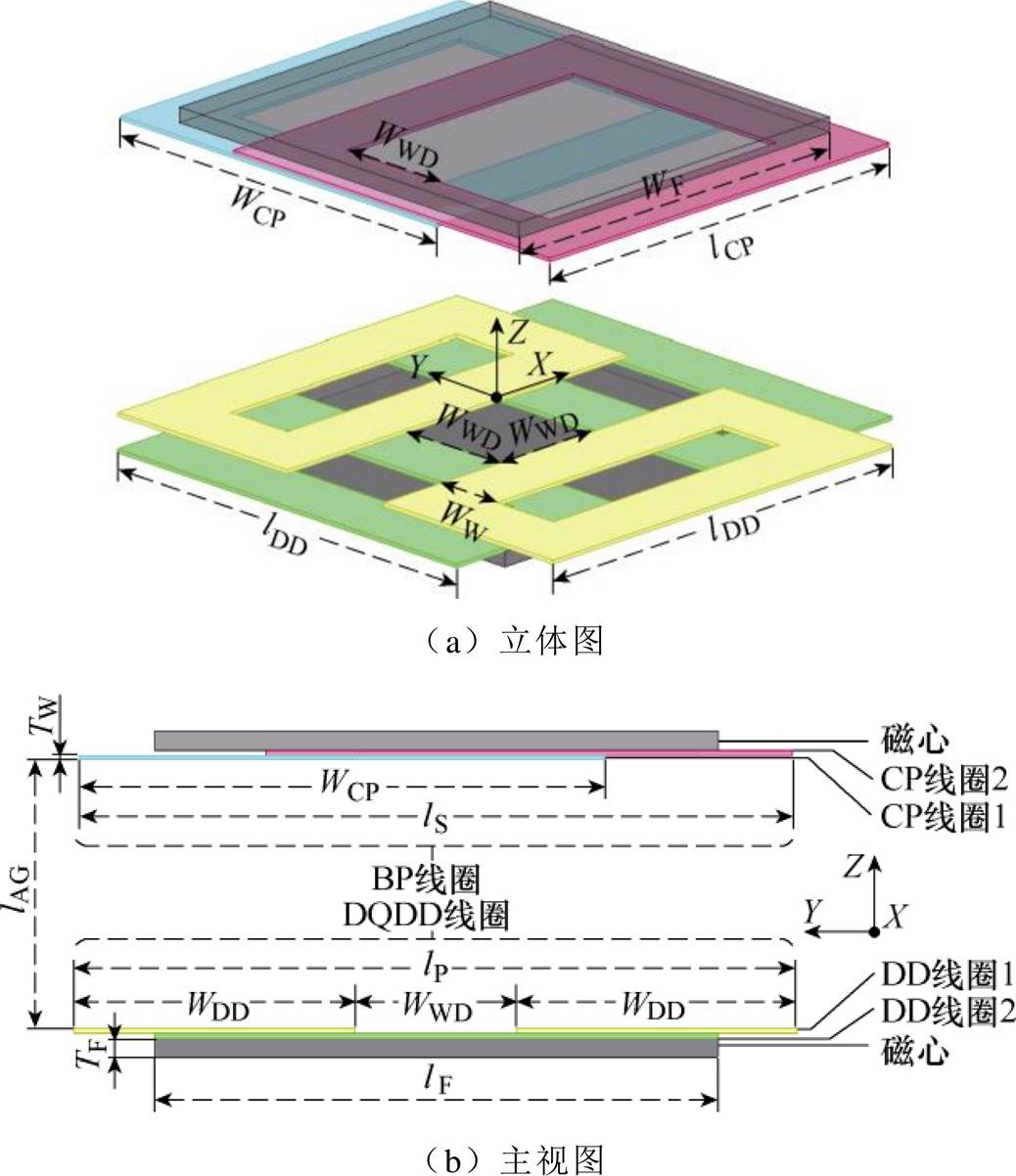
图2 磁耦合机构
Fig.2 Magnetic coupling structure
1.2.1 基于DQDD线圈的发射机构
图3a给出了DQDD线圈绕制方案。DD线圈1激发沿Y轴方向的磁通量，记为FDD1；DD线圈2激发沿X轴方向的磁通量，记为FDD2。两组DD线圈空间正交摆放位置使得磁通量FDD1和FDD2在空间上处于正交位置，同组DD线圈与非同组DD线圈的净磁通量接近于0，因此，上、下两组DD线圈相互解耦。相互解耦的线圈结构意味着线圈中的激励电流可独立控制而不受彼此的影响，降低了电路分析的难度。
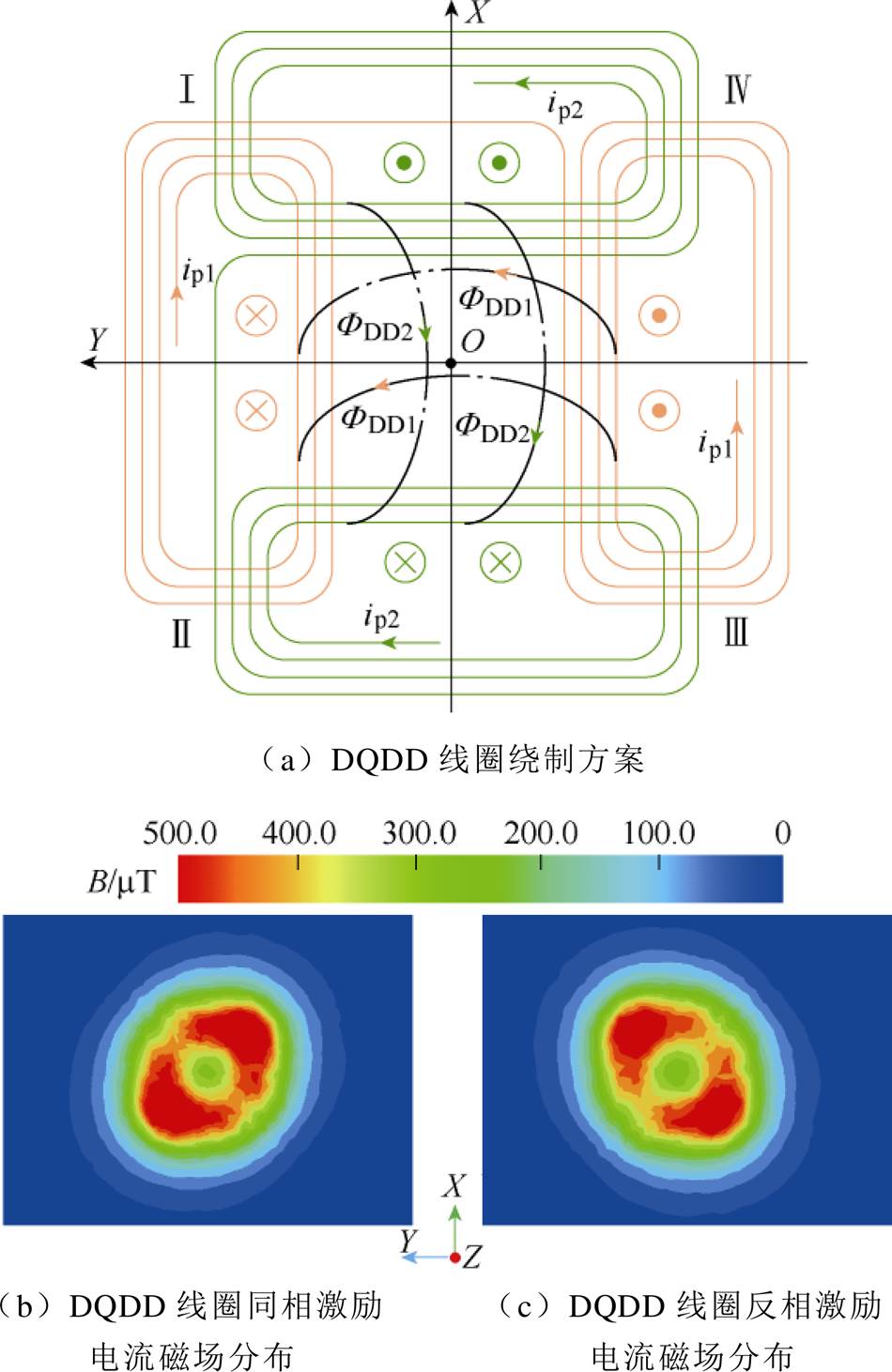
图3 DQDD线圈绕制方案及激发磁场
Fig.3 Winding scheme of DQDD coil and excitation magnetic field
设DD线圈1和DD线圈2的激励电流幅值相同，相位相差b，其表达式为
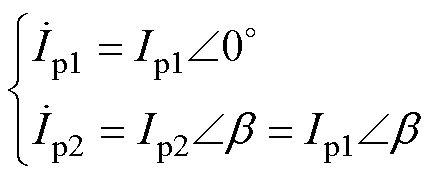（1）
结合两组DD线圈的正交位置关系，两个DD线圈激励电流产生的磁动势fDD1、fDD2可表示为
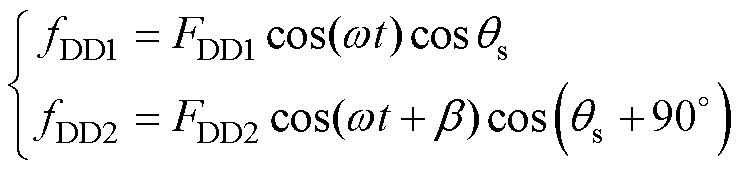（2）
式中，qs为参考空间角；w 为系统角频率。FDD1= FDD2，这是由于两组DD线圈具有相同的结构。
由式（2）可得出，在XOY面内任意点的合成磁动势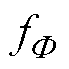
为
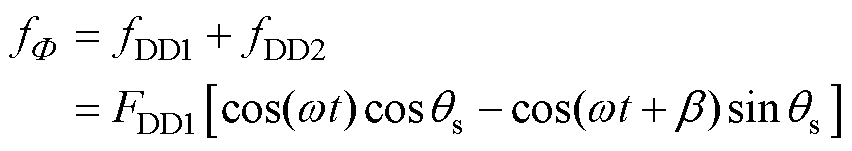（3）
式（3）意味着合成磁动势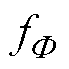与激励电流的相位差b 有关。
当b 分别为0 °、180 °和90 °时，合成磁动势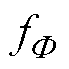为
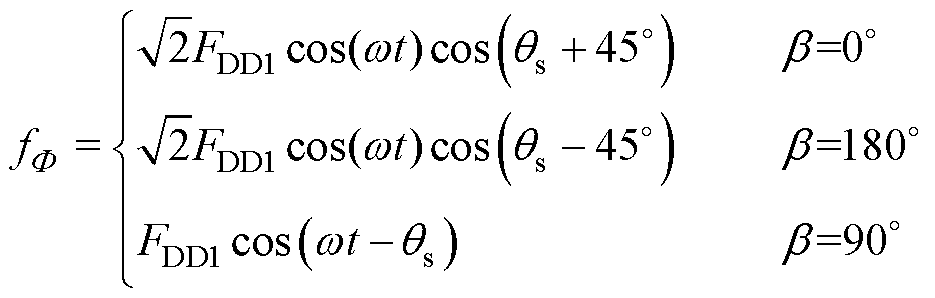（4）
式（4）说明了当激励电流ip1和ip2的相位差为0 °或180 °时，磁感应强度是单个DD线圈激发的磁感应强度的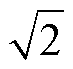
倍；而当两路激励电流相差90 °时，磁感应强度则相同。而且，当b=0 °即DQDD同相激励，DQDD线圈的两极磁场主要分布在负45 °对角，如图3b所示；对于b=180 °即DQDD反相激励，两极磁场则主要集中在正45 °对角如图3c所示。至于b=90 °，两极磁场呈等幅值周期性旋转分布，如图4所示。图中，T表示时刻，Ts表示周期。
1.2.2 基于OLDD线圈的接收机构
图5给出了接收机构OLDD线圈绕制方案和结构变换方法。其中开关K1、K2用以接收机构的结构变换。当接收机构需要OLDD线圈时，K1和K2的COMi（i=1, 2）端点均与NOi端点闭合，如图5a所示。此时，接收机构可拾取发射线圈激发的双极性磁场。在双极性磁场中，穿过OLDD线圈两个耦合区域内的磁场方向一致，而解耦区域内的磁场相反。OLDD线圈所采用的反向串联绕制方式使得解耦区的感应电动势为零，而两个耦合区的感应电动势顺向串联。当拾取机构需要CP线圈时，K1和K2的其中一个COMi端点与对应NCi端点闭合，如图5b、图5c所示。若K2端点与NC2闭合，则左侧线圈接入，此时接收机构在双极性磁场中拾取垂直向内的磁场；反之，则右侧线圈接入，此时拾取的磁场方向垂直向外。
图4 相位差b=90 °时合成磁场分布
Fig.4 Composite magnetic field distribution with phase difference b=90 °
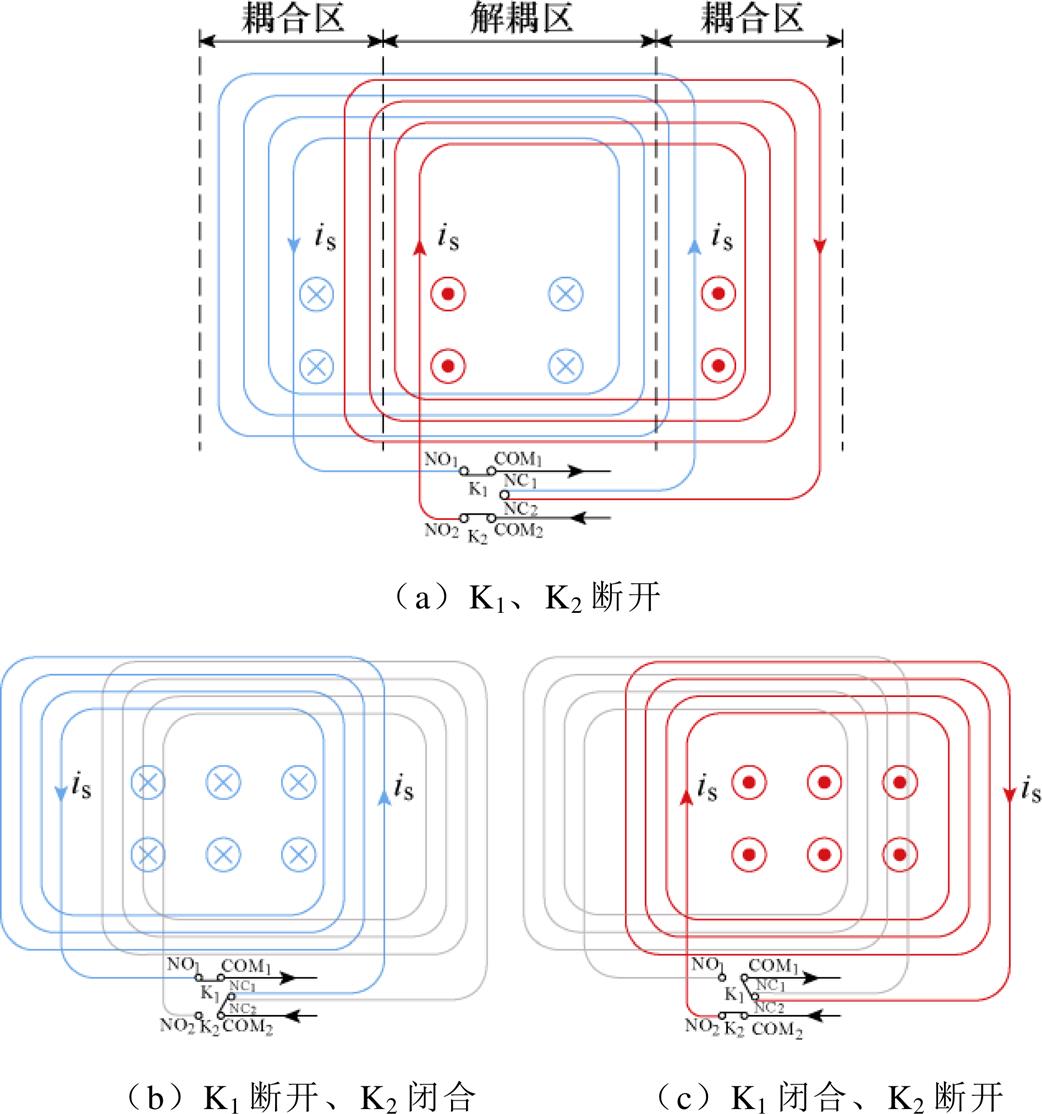
图5 OLDD线圈绕制方案
Fig.5 Winding scheme of OLDD coil
综合DQDD发射机构四种激励方式以及OLDD接收机构两种拾取方式，双极性耦合机构可分为如图6所示八种工作模式：即①DD1-OLDD、②DD1- CP、③同相DQDD-OLDD、④同相DQDD-CP、⑤DD2-OLDD、⑥DD2-CP、⑦反相DQDD-OLDD、⑧反相DQDD-CP。
1.2.3 基于双极性耦合机构的等效耦合系数
耦合系数是评判WPT系统耦合机构抗偏移偏转性能的关键参数之一。在多组发射线圈的激励电流和激发磁场彼此解耦的条件下，原、副边多个线圈的耦合作用可通过等效自感和互感描述[14]，对于本文由两组发射线圈和一组接收线圈组成的双能道耦合机构，在发射端实现解耦控制的条件下，则可等效为单能道耦合机构，引入等效耦合系数keff表示其耦合程度，即
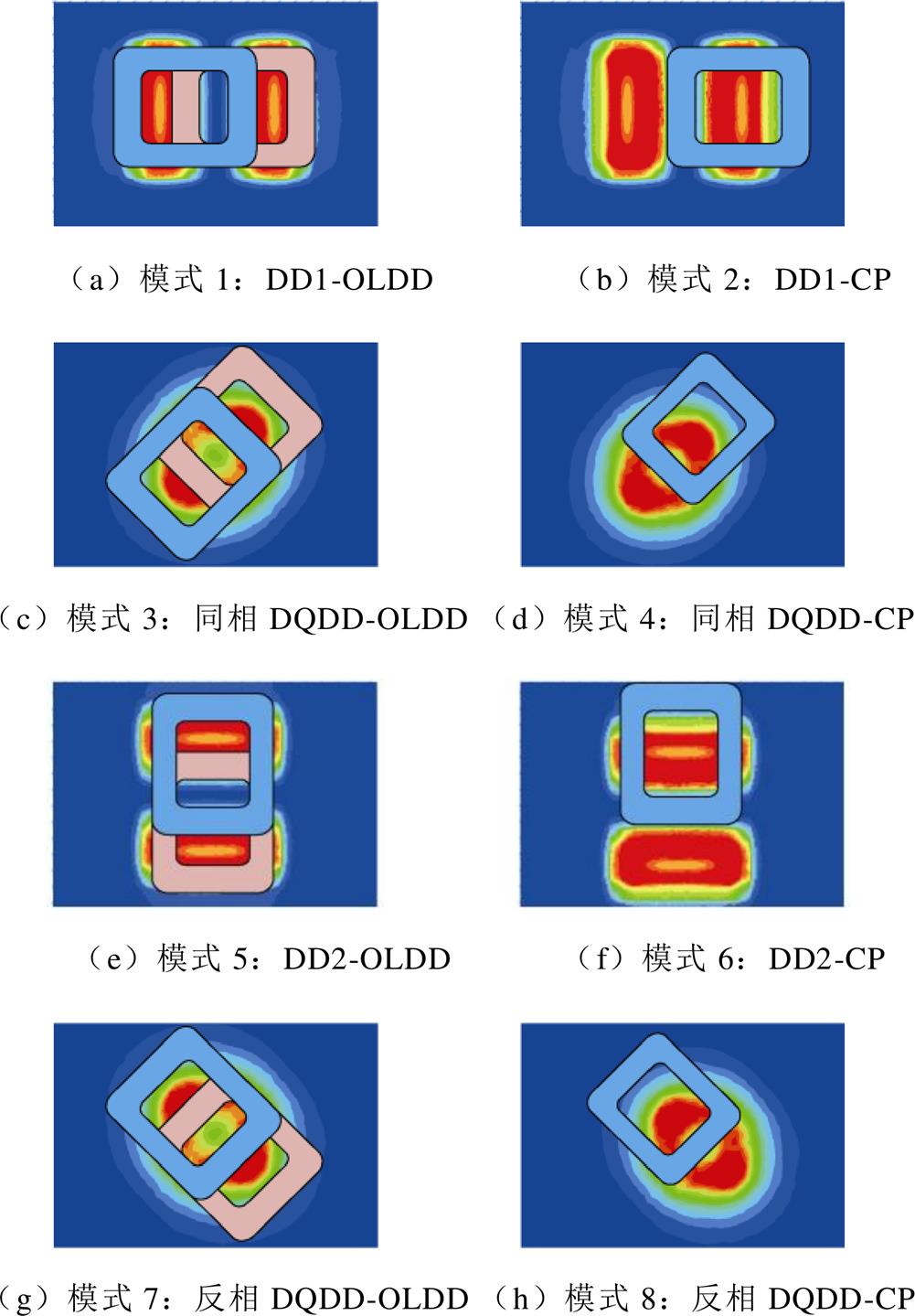
图6 双极性耦合机构工作模式
Fig.6 Working mode of bipolar coupling structure
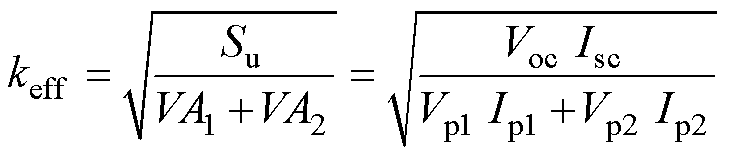（5）
式中，Su为接收线圈拾取的容量；VAi为发射线圈传输的容量；Voc和Isc分别为接收线圈的开路电压和短路电流，Vpi和Ipi依次为发射线圈的端电压和激励电流，其中Su和VAi可具体表示为
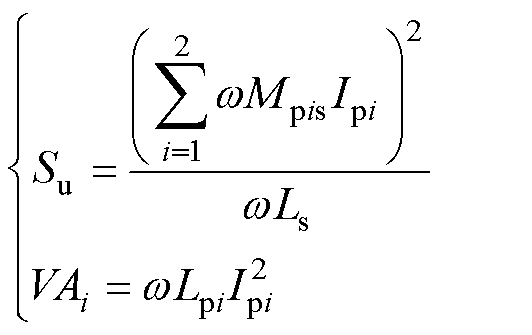（6）
将式（6）代入式（5），keff可简化为
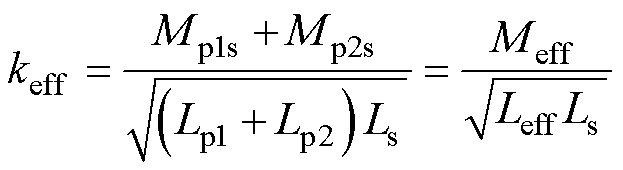（7）
式中，Meff和Leff分别为系统的等效互感和等效自感，当系统仅激励DD线圈1或DD线圈2，此时Meff =Mpis，Leff =Lpi（i=1, 2）。本节所推导的等效耦合系数keff将用于后续的双极性耦合机构参数配置及耦合机构性能对比。
图7为图1的等效互感模型，据此列写KVL方程为
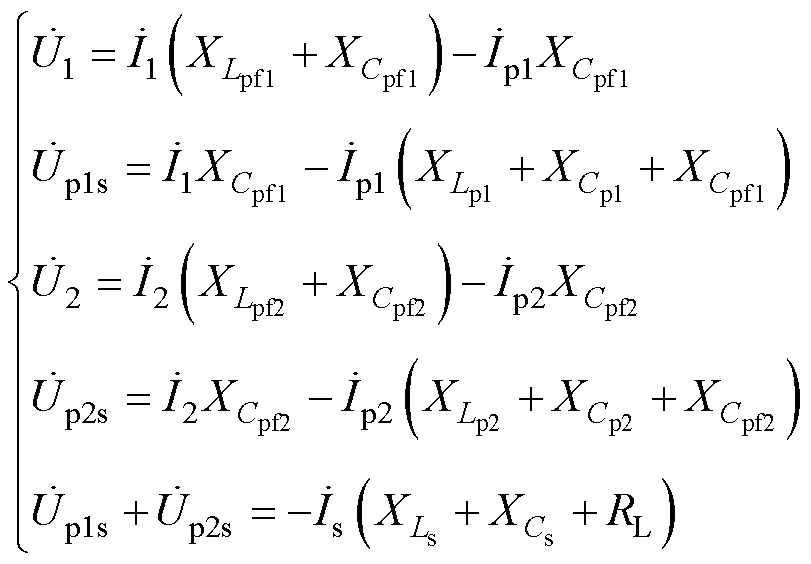（8）
式中，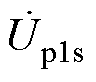
、
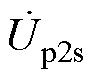为两组互感Mp1s、Mp2s产生的感应电压；XL、XC分别为补偿网络及线圈的电抗，其具体表示为
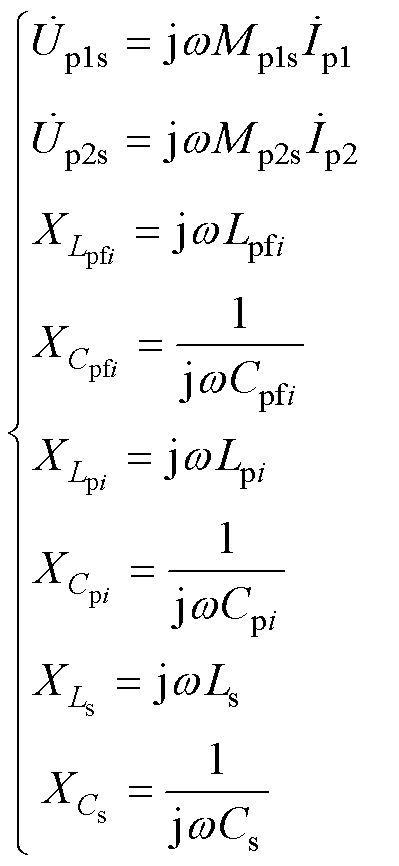（9）
式（10）给出了LCC-S补偿电路参数配置方法。
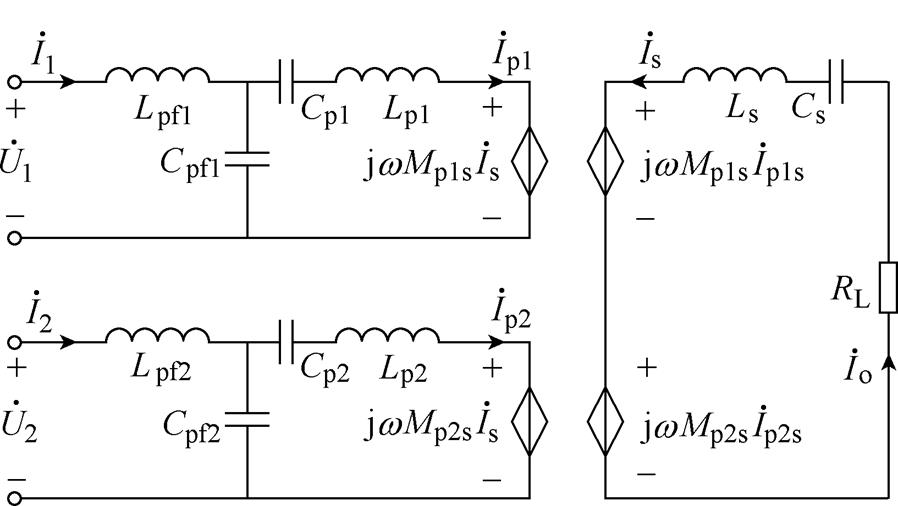
图7 LCC-S补偿拓扑
Fig.7 LCC-S compensation topology
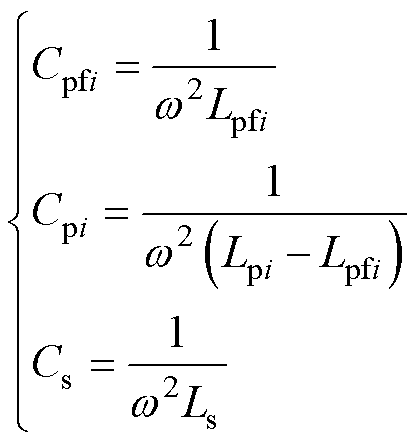（10）
由式（8）～式（10），可求得各回路电流为
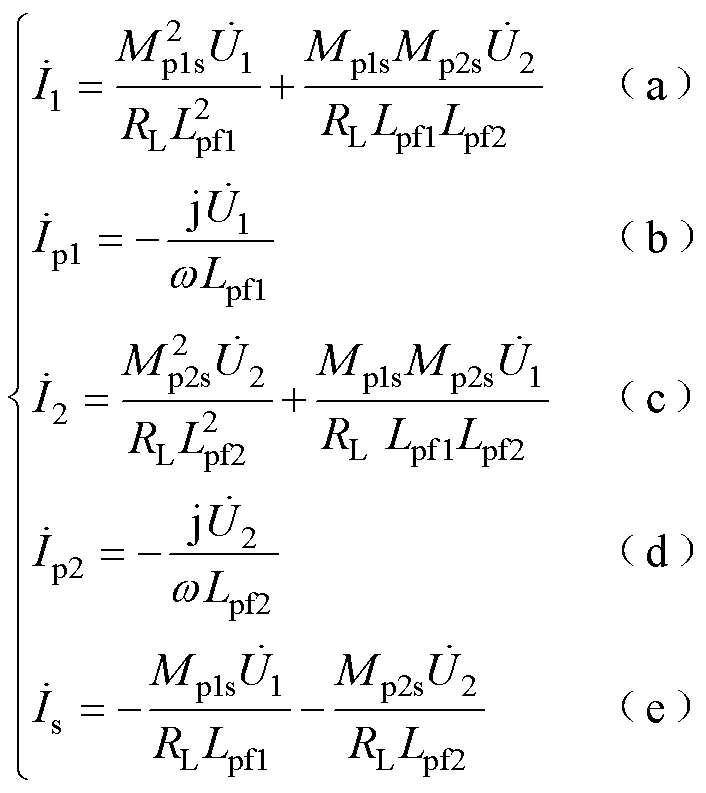（11）
由式（11）可知，当发射端补偿网络采用LCC拓扑，在工作频率保持不变时，发射机构中两组DD线圈的激励电流ipi的幅值仅取决于逆变器输出电压的幅值和电感Lpfi，与负载及互感无关。此特性实现了两组DD线圈的激励电流的独立控制，且当逆变器输出电压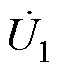
、
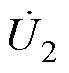的幅值相等且补偿电感Lpf1、Lpf2的电感值相等时，激励电流ip1、ip2的幅值相等。
由于耦合系数受窗口宽度WWD及磁心尺寸TF、lF的影响，面向发射机构与接收机构完全对准的位置情况，参照国家以及相关组织发布的电动汽车WPT系统设计标准，给出了磁耦合机构部分尺寸，并对窗口宽度WWD及磁心尺寸lF、TF进行了优化。
根据标准IEC TS 61980，选定发射机构与接收机构的间距lAG=130 mm；D形线圈lDD=300 mm，WDD=150 mm，TW=2.5 mm，匝数N=20，WW=50 mm；CP线圈lCP=300 mm，WCP=200+WWD。因此DQDD线圈lp=300+WWD；OLDD线圈ls=300+WWD，Ws= lCP=300 mm。表1第一、二列给出了磁耦合机构待优化的尺寸参数、优化范围。其中，窗口宽度WWD和磁心长度lF决定了磁场的覆盖区域，其优化范围以lp为归一化基准；磁心厚度TF决定了磁场的强度，其优化范围以lAG为归一化基准。
表1 待优化的尺寸参数、优化范围及优化值
Tab.1 Size parameters to be optimized、optimized range and value
参数优化范围(%)优化值 窗口宽度WWD0～5023[(WWD/lp)×100%] 磁心长度lF15.4～102.676.9[(lF/lp)×100%] 磁心厚度TF2.3～23.19.2[(TF/lAG)×100%]
图8给出了窗口宽度WWD对线圈自感、互感和耦合系数的影响规律，此时磁心长度lF归一化数值选取为76.9 %，磁心厚度TF为9.2 %。由图8可知，随着WWD的增大，自感曲线先下降而后趋于平缓；互感和耦合系数曲线先上升而后略微下降。为实现高传输效率以及低线圈端电压的目的，选取WWD的优化值为23 %，此时耦合系数最大且线圈自感较小。
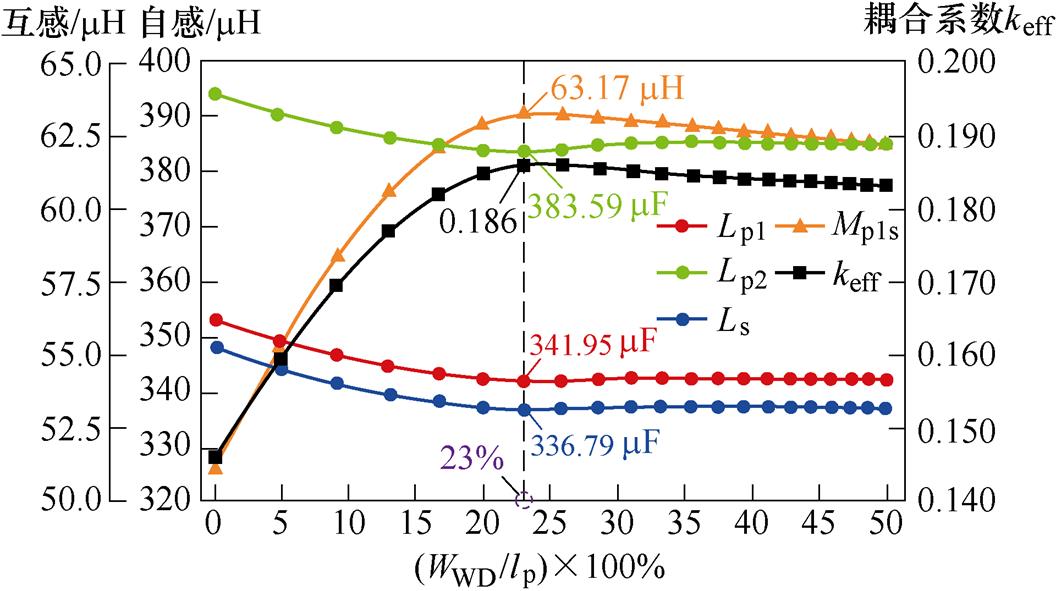
图8 窗口宽度对自感、互感和耦合系数的影响规律
Fig.8 Influence of window width on self-inductance, mutual inductance and coupling coefficient
图9a、图9b分别为磁心长度lF、磁心厚度TF对耦合系数的影响规律。在对磁心尺寸进行优化时，窗口宽度WWD归一化数值设定为23 %。由图9a可知，随着lF的增大耦合系数曲线先急剧上升而后小幅度下降，当磁心长度lF归一化后的数值为76.9 %，耦合系数达到最大为0.186，其原因是(lF/lp)×100 %＞76.9 %会减小发射线圈自耦合区磁阻导致耦合系数降低，而小于76.9 %会增大发射线圈与接收线圈的互耦合区磁阻导致耦合系数降低。根据此影响规律，可确定接收机构的磁心长度lF=300 mm，以及磁心宽度WF=230 mm。由图9b可知，随着TF的增大耦合系数曲线先快速上升而后趋于平缓，当磁心厚度TF归一化后的数值为9.2 %，耦合系数达到最大为0.189，综合考虑磁心的质量和体积以及现有磁心尺寸，最终选定铁氧体厚度TF=10 mm。
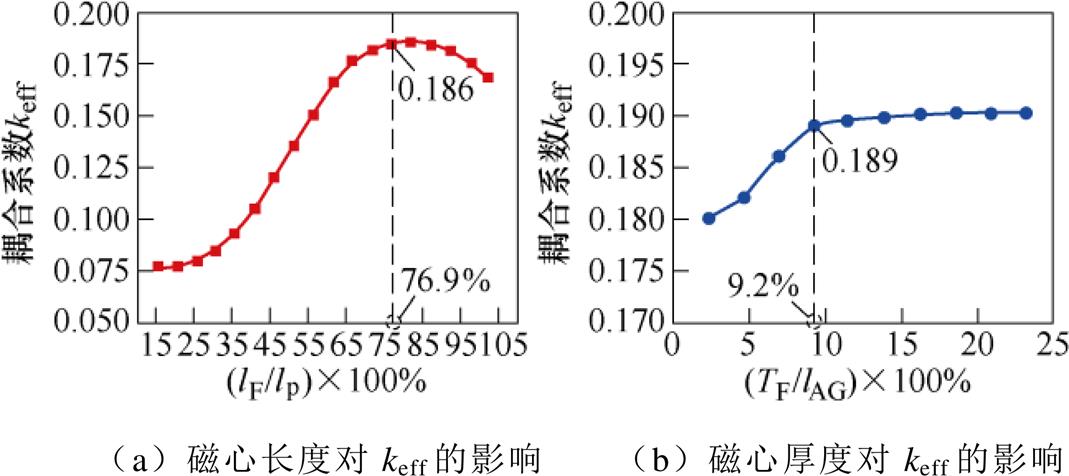
图9 磁心尺寸对耦合系数的影响规律
Fig.9 Influence of core size on coupling coefficient
综合窗口宽度和磁心尺寸的优化结果，对于本文选定的传输间距lAG=130 mm，D形线圈宽度WDD= 150 mm，可得DQDD耦合机构的整体尺寸参数，见表2，表2中参数将作为实验样机设计依据。需要指出的是，优化所得的窗口宽度和磁心尺寸的归一化结果同样适用于其他尺寸参数的DQDD- OLDD耦合机构。
表2 磁耦合机构尺寸参数
Tab.2 Parameters of magnetic coupling structure （单位: mm）
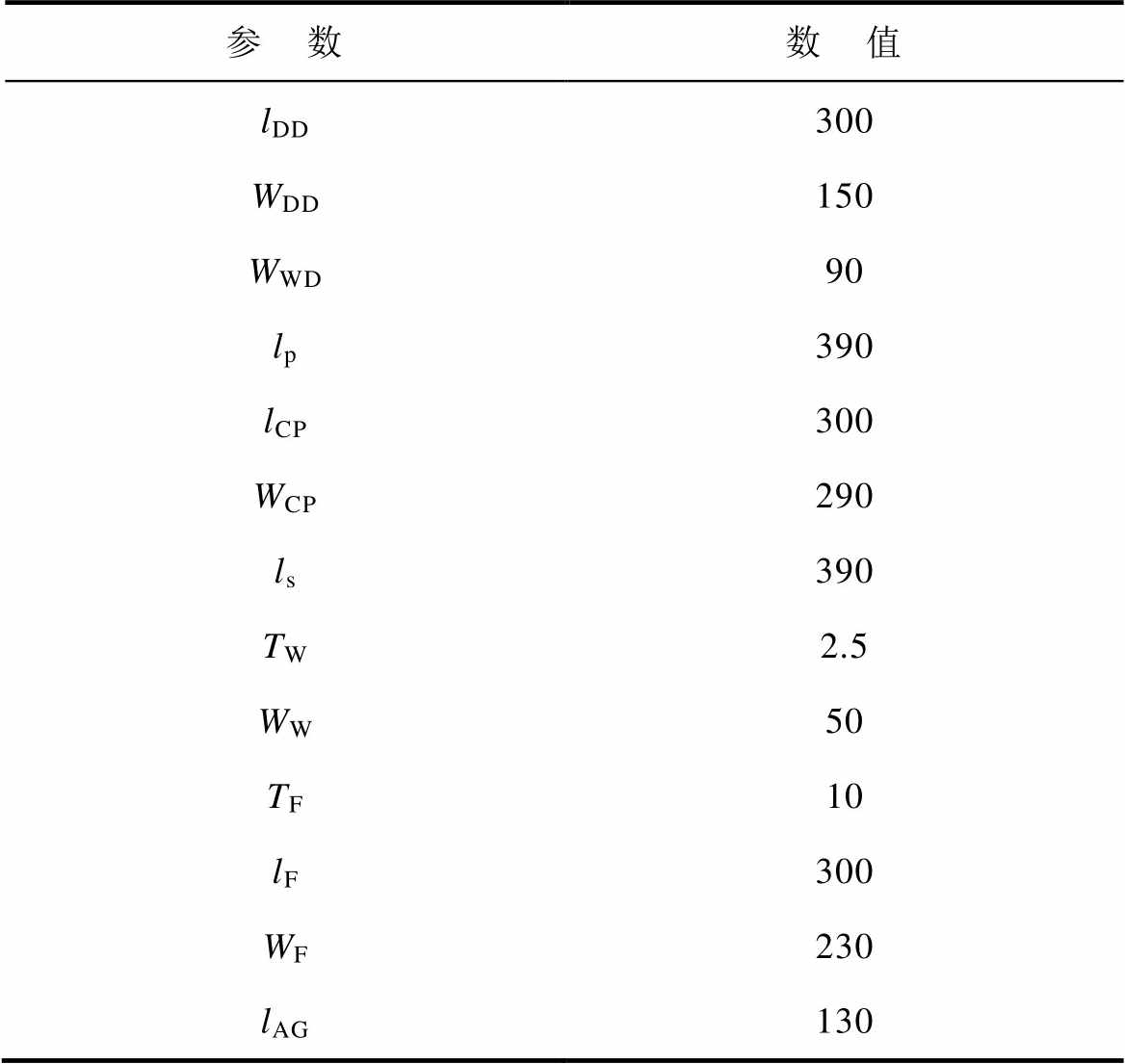
参 数数 值 lDD300 WDD150 WWD90 lp390 lCP300 WCP290 ls390 TW2.5 WW50 TF10 lF300 WF230 lAG130
基于双极性耦合机构的八种工作模式提出了图10所示的变结构及磁场调控策略。其中，图10a给出了发射机构激励方式与绕Z轴偏转角度q 的关系，根据绕Z轴的偏转程度划分为八个区域，依次为：当q∈(-15, 15 °)∪(165, 195 °)发射机构选用DD线圈1激励方式，当q∈(15, 75 °)∪(195, 255 °)发射机构选用DQDD线圈同相激励方式，当q∈ (75, 105 °)∪(255, 285 °)发射机构选用DD线圈2激励方式以及当q∈(105, 165 °)∪(285, 345 °]发射机构选用DQDD线圈反相激励方式。
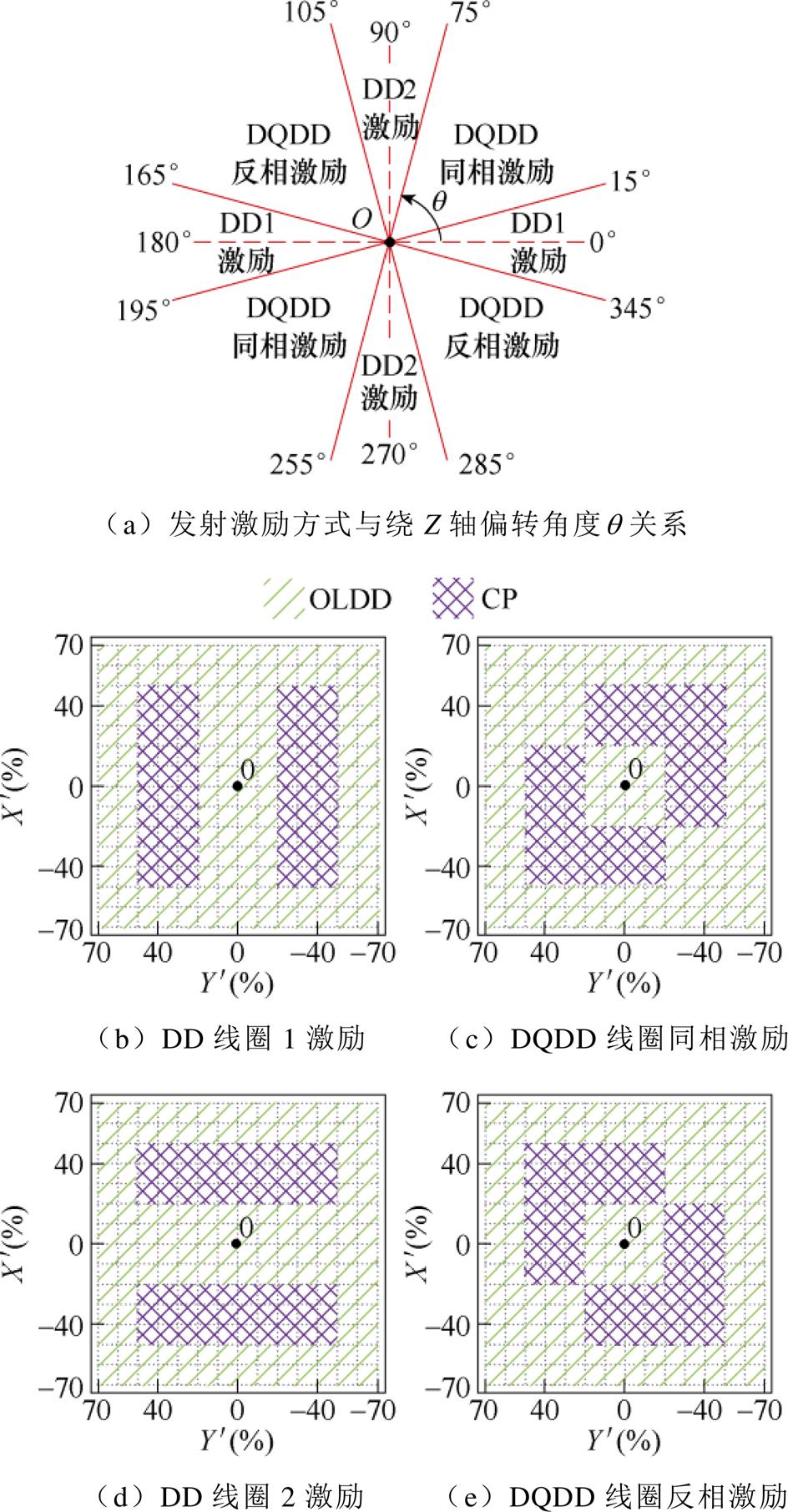
图10 变结构及磁场调控策略
Fig.10 Strategy of variable structure and magnetic-field control
图10b～图10e给出了不同激励方式下接收拾取结构与偏移位置的关系。图中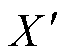
表示归一化的偏移距离，即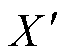=DX/lP×100 %，同理
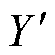=DY/lP×100 %。虚线交点表示接收机构中心点位置，每两个点之间的横向和纵向距离均为10 %，即每个点之间的横、纵向偏移距离为39 mm。本文所划定的纵向和横向的偏移范围均选取为±70 %，分别是标准IEC TS 61980中MF-WPT2/Z3等级系统设定范围的3.3倍和2.8倍。
在以发射机构为中心划定的±70 %偏移范围内，据此选取接收机构角度偏转q=0 °、q=45 °两种情况并分析变结构及磁场调控后的等效耦合系数变化规律，如图11所示。
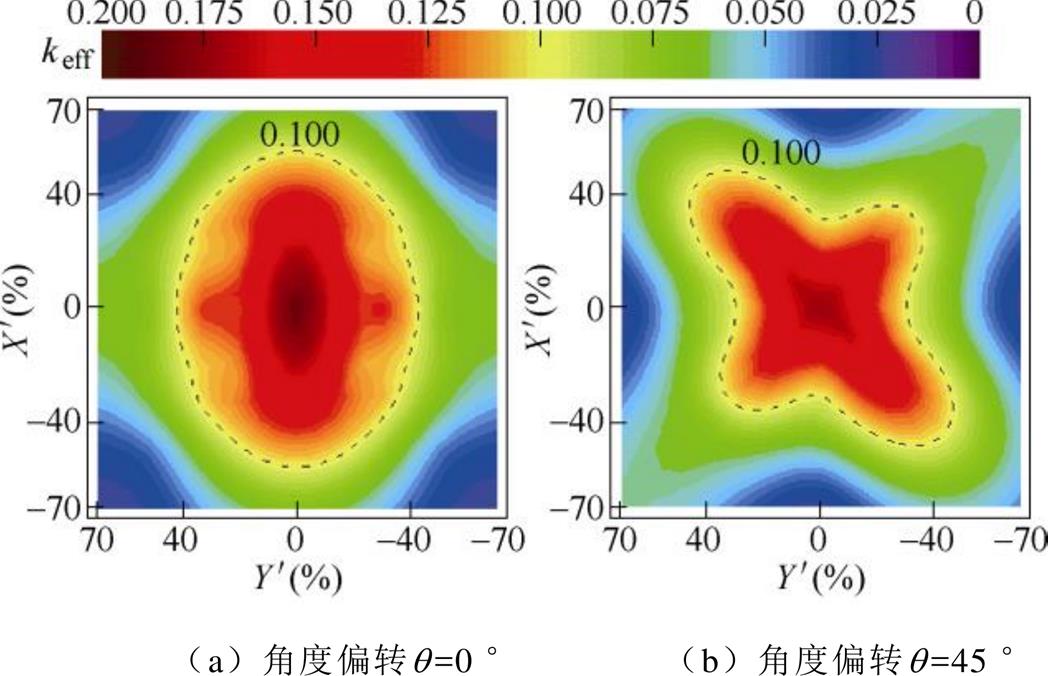
图11 变结构及磁场调控后等效耦合系数变化规律
Fig.11 Variation of coupling coefficient with variable structure and magnetic-field control
图11a给出了接收机构角度偏转q=0 °时keff的变化规律。由图11a可知，等效耦合系数不低于0.1的区域在划定的偏移范围内占比为0.36，相比于传统的DD-DD磁耦合机构，在特定位置将接收机构拾取结构由OLDD线圈变换为CP线圈消除了拾取盲点，使得keff在Y方向上的变化率更平缓，提高了Y方向上抗偏移能力。据图11b给出的角度偏转q=45 °时keff变化规律不难看出，在接收机构存在较大角度偏转时，虽然原点处keff数值有所下降，但keff≥0.1的区域仍然较大，占划定的偏移范围的比值为0.28。通过对图11分析可得，所提磁耦合机构引入变结构及磁场调控后，具有较高的抗水平偏移能力和抗角度偏转能力。
结合所提调控策略，给出了双极性耦合磁场调控流程，如图12所示。首先依次激励发射机构DQDD中的两组DD线圈，此时接收拾取结构为OLDD线圈，分别测取两组DD线圈被激励时接收端负载电压VL1、VL2。然后判断负载电压VL1、VL2的比值是否属于（e1, e2），若满足此条件，则发射机构采用DD线圈激励。再判断VL1、VL2的大小，若VL1＞VL2，则由DD线圈1激励。再后，测量接收拾取结构为OLDD、CP线圈时对应的负载电压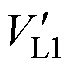
、
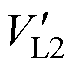，并判断二者大小。若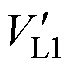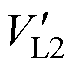＞，则系统工作在模式1；反之，则系统工作在模式2。若VL1＜VL2，由DD线圈2激励，其调控流程同理。
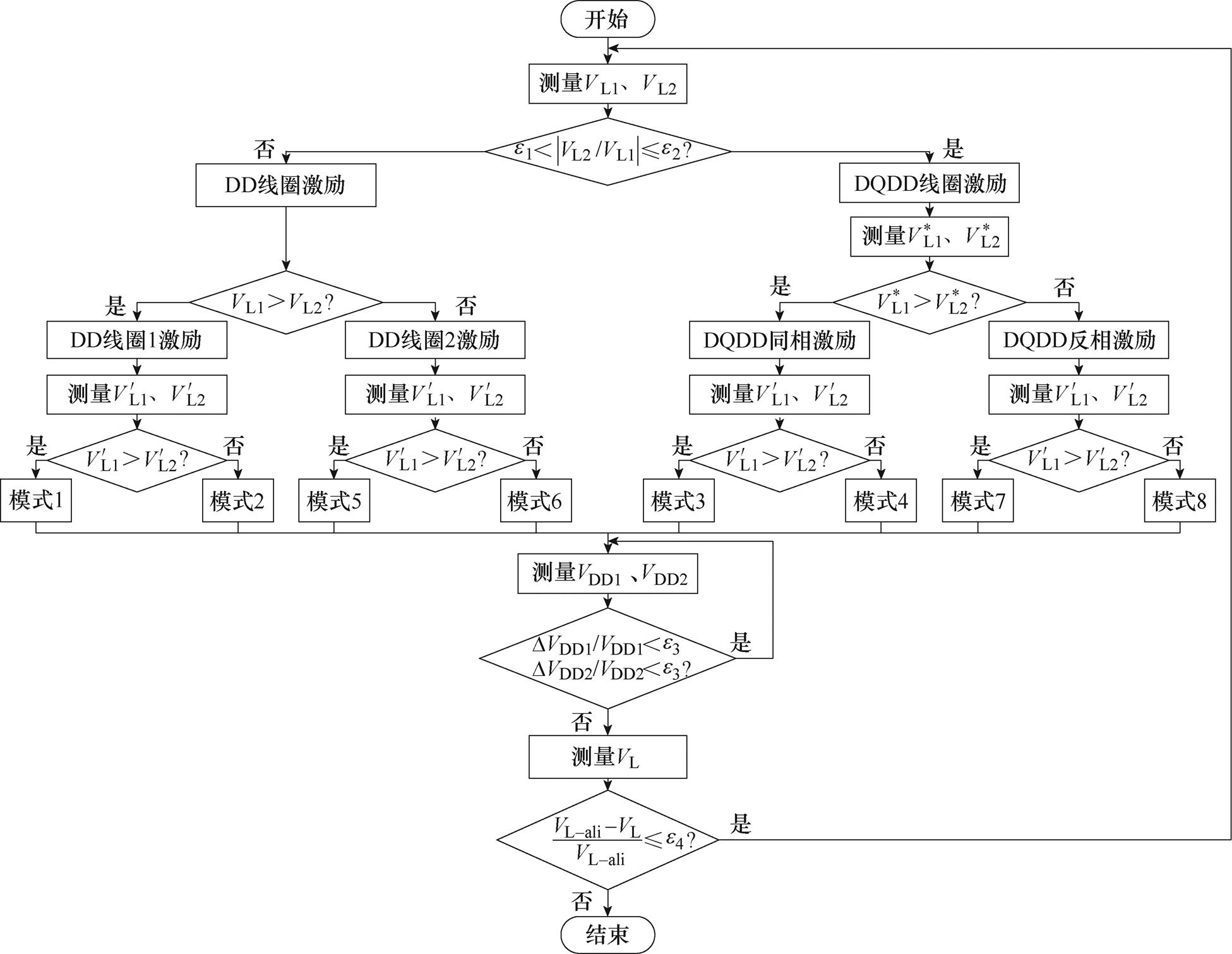
图12 调控流程
Fig.12 Flow chart of control
若负载电压VL1、VL2的比值不属于区间（e1, e2），则发射机构的激励方式为DQDD线圈激励，此时依次测量DQDD同相激励和反相激励时的负载电压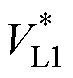
、
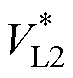，并判断其大小，若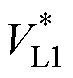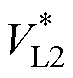＞，则由DQDD同相激励。再测量变换拾取结构后的负载电压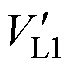、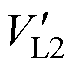，并判断二者大小，最终确定系统处于工作模式3或工作模式4。若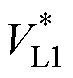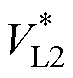＜，由DQDD反相激励，其调控流程同理。
为了应对收发线圈相对位置随机移变所导致的激励模式与拾取结构失配的问题，同时避免调控程序被频繁地执行，调控策略采用了基于收发线圈相对位置的模式匹配监控方法。在功率传输阶段，实时检测发射端两组DD线圈的端电压VDD1、VDD2，从而监测线圈端电压的变化率DVDDi/VDDi（i=1, 2）是否超过设定阈值e3。当两组DD线圈的端电压变化率都低于e3，即说明接收端未移出初始匹配区域。
若移出初始匹配区域，测量该位置下的负载电压VL，检测此时负载电压VL与对准位置下负载电压VL-ali的衰减率，若衰减率小于设定阈值e4，即说明接收端未移出所划定的偏移范围。此时控制器重启磁场调控程序，重新匹配发射线圈的激励模式与接收线圈拾取结构；反之，则说明接收端移出所划定的偏移范围，不再激励发射线圈以保证系统运行的安全性。
本文所提双极性耦合机构具有中心对称性，由于q=0 °与q=90 °的变结构及磁场调控类似，q=15 °与q=-15 °，q=45 °与q=-45 °的变结构及磁场调控类似，故后续主要讨论角度无偏转和角度偏转15 °和45 °这两种情况。
定义衡量耦合机构抗偏移能力的指标为耦合系数衰减率（Coupling Coefficient Attenuation Ratio, CCAR）[22]为
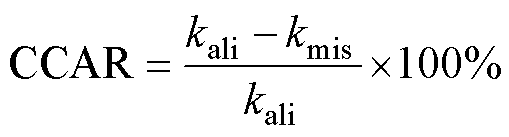（12）
式中，kali和kmis分别为对准时和偏移后的等效耦合系数。在相同偏移偏转情况下，CCAR的数值越小表示偏移的容忍度越高。本文选择CP线圈和DD线圈作为比较的磁耦合机构，分析过程中耦合机构所采用的匝数、线圈和导磁机构尺寸以及传输间距均相同。相比于WPT系统常用的CP和DD耦合机构，基于变结构及磁场调控的双极性耦合机构兼备更强的抗水平偏移能力和抗角度偏转能力。图13为不同磁耦合机构在不同角度偏转情况下CCAR的变化规律。
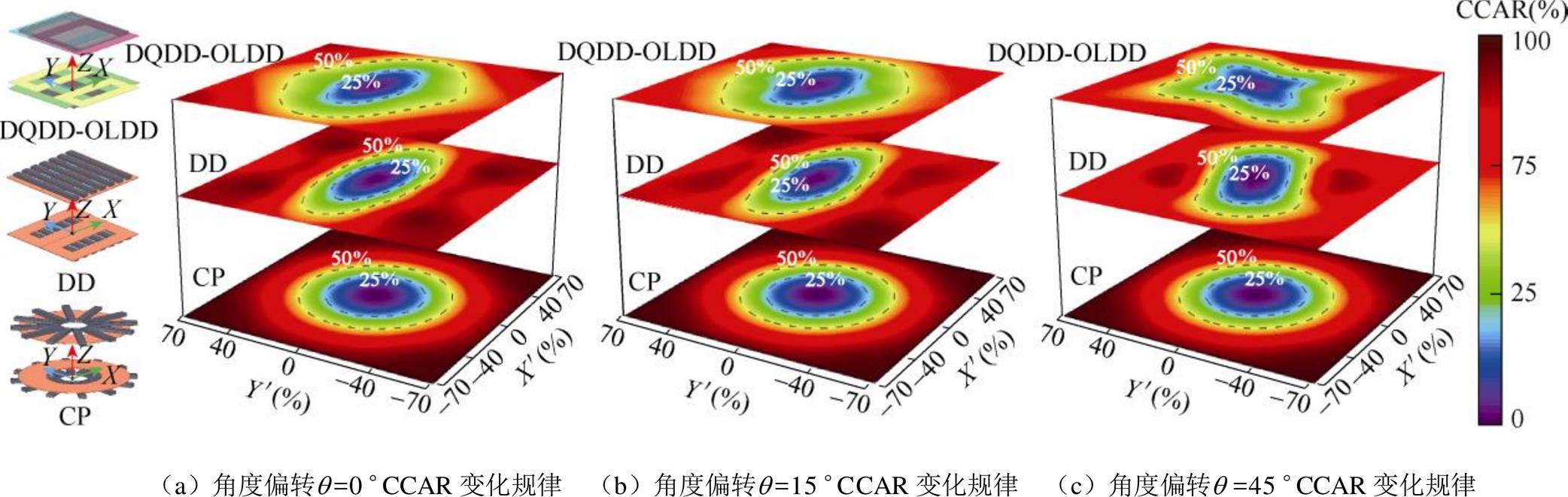
图13 不同磁耦合机构的CCAR变化规律
Fig.13 Variation of CCAR of different coupling structures
图13a给出了角度偏转q=0 °情况下三种耦合机构的CCAR变化规律。相比于CP线圈，所提磁耦合机构的CCAR不高于25 %和50 %的对应区域面积依次是CP线圈的0.9倍和1.43倍。偏移距离为20 %时，所提磁耦合机构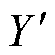方向上CCAR增大速度略快于CP线圈，但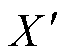方向上CCAR增大速度明显慢于CP线圈。其次，所提磁耦合机构偏移50 %的CCAR才增大到50 %，而CP线圈偏移40 %的CCAR就已增大到50 %，这表明所提磁耦合机构比CP线圈具有更高的抗偏移能力且偏移程度越大其性能越突出；与DD线圈相比，所提磁耦合机构的CCAR不高于25 %对应区域面积与DD线圈相等，CCAR不高于50 %对应区域面积是DD线圈的1.5倍，且DD线圈在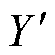方向偏移40 %处的CCAR约为100 %，这表明所提磁耦合机构比DD线圈具有全方位和更宽范围的抗偏移性能。图13b为角度偏转q=15 °情况下三种耦合机构的CCAR变化规律。可见，在偏转15 °情况下，CP线圈、DD线圈以及本文所提耦合机构的CCAR不高于25 %的区域基本相等；而CCAR不高于50 %的区域占比则依次为26.5 %，21.9 %以及42.3 %。由此表明：存在较小角度偏转时，相比于CP线圈和DD线圈，所提磁耦合机构具有更宽范围的抗偏移偏转性能。图13c给出了角度偏转q=45 °情况下三种耦合机构的CCAR变化规律。与CP、DD线圈相比，所提磁耦合机构CCAR低于25 %的对应区域面积与CP、DD线圈面积基本相等；而CCAR不高于50 %的对应区域面积分别是CP、DD线圈的1.55倍和1.49倍，这表明在较大偏转情况下所提磁耦合机构相比于CP、DD线圈具有更强的抗偏移偏转性能且偏移距离越大其性能更优越。
综合上述的对比分析后可知，本文所提磁耦合机构在水平面内位置、角度抗偏移性能都优于CP和DD磁耦合机构，且偏移程度越大其性能越突出。
根据表2给出的磁耦合机构尺寸参数，结合LCC-S补偿电路的参数配置方法搭建如图14所示的实验样机，验证所提的磁耦合机构加入变结构及磁场调控后的抗偏移性能和传输特性。
图14给出了①直流电源、②逆变电路、③补偿电路、④磁耦合机构、⑤开关投切电路、⑥整流电路、⑦电子负载、⑧示波器、⑨线圈绕组、+磁心、,铝板及-绝缘纸。其中，开关投切电路采用了实验室现成的继电器模块，其型号为松下公司生产的HE1AN-W-DC12V-Y6，工频情况下其触点间耐受电压和额定通流分别为2 000 V和90 A；发射机构和接收机构的线圈绕组由直径0.2 mm×300股的利兹线绕制；磁心材料为PC44锰锌铁氧体；铝板采用厚度3 mm的6061铝材，其作用是屏蔽泄漏的磁场；绝缘纸用于防止上、下两层线圈短路。
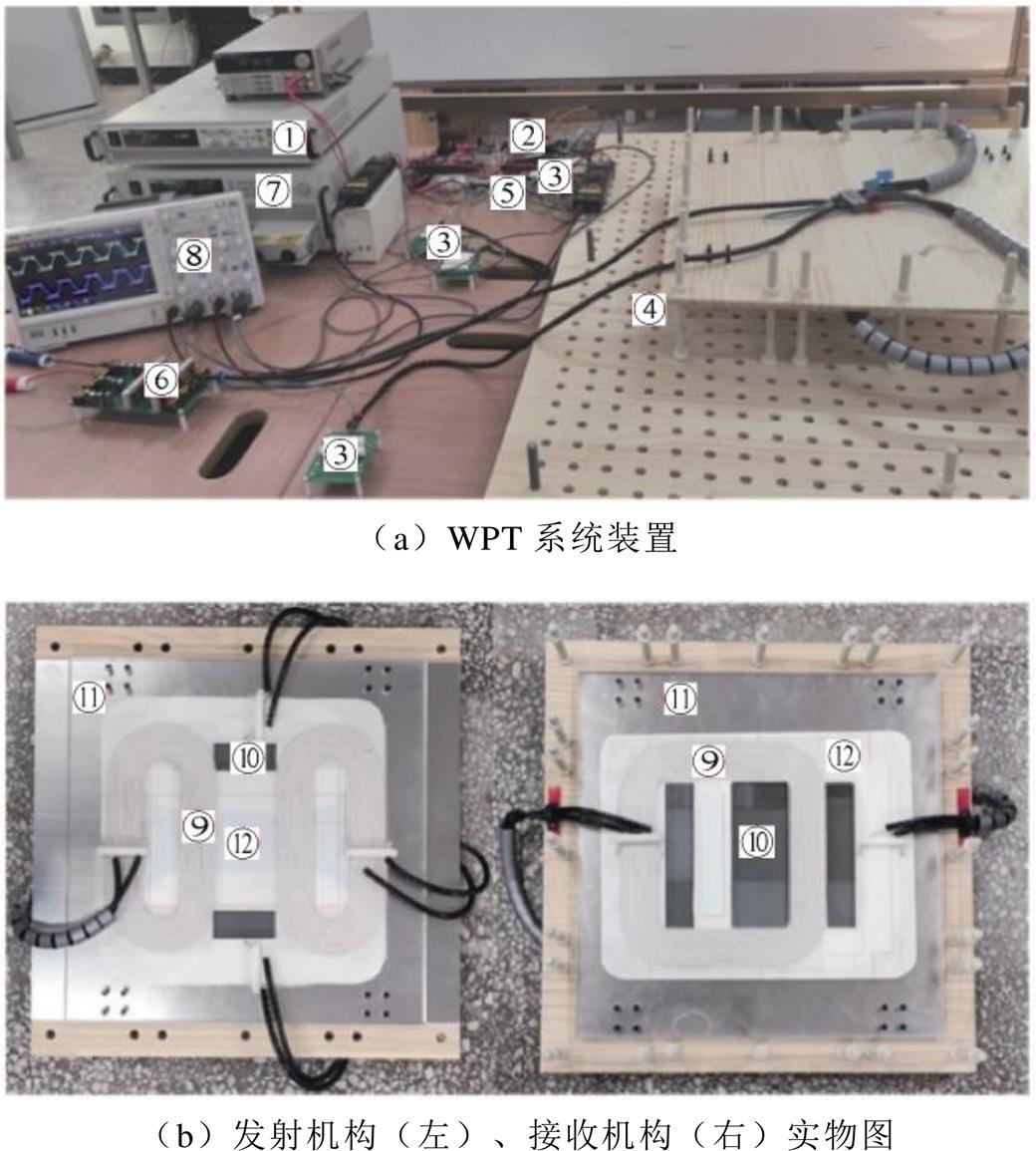
图14 实验样机
Fig.14 Experimental prototype
表3列出了系统的主要参数值和元器件型号。需要指出的是，发射机构中所绕制的单个DD线圈的内阻为0.26 W，且两层DD线圈间的互感为0.3 mH，相比于其自感可忽略，即可认为两层DD线圈间实现了解耦。另外，发、收机构之间的信号通信由蓝牙模块实现。负载电压VL经电阻分压后，再由MCU内置ADC模块采样后传送给发射端；发射端根据负载电压信息确定接收机构激励方式，调控发射磁场并向接收端开关发出控制信号。为了验证本文所提耦合机构XOY面内位置、角度的抗偏移性能，以气隙高度130 mm的位置为参考基准，10 %（39 mm）作为步进长度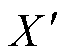，=±70 %、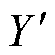=±70 %（X=±273 mm、Y=±273 mm）作为边界，给出了不同位置偏移及角度偏转下双能道的耦合系数测量值和误差，如图15所示。
表3 样机主要参数值及元件型号
Tab.3 Parameters and component type of the prototype
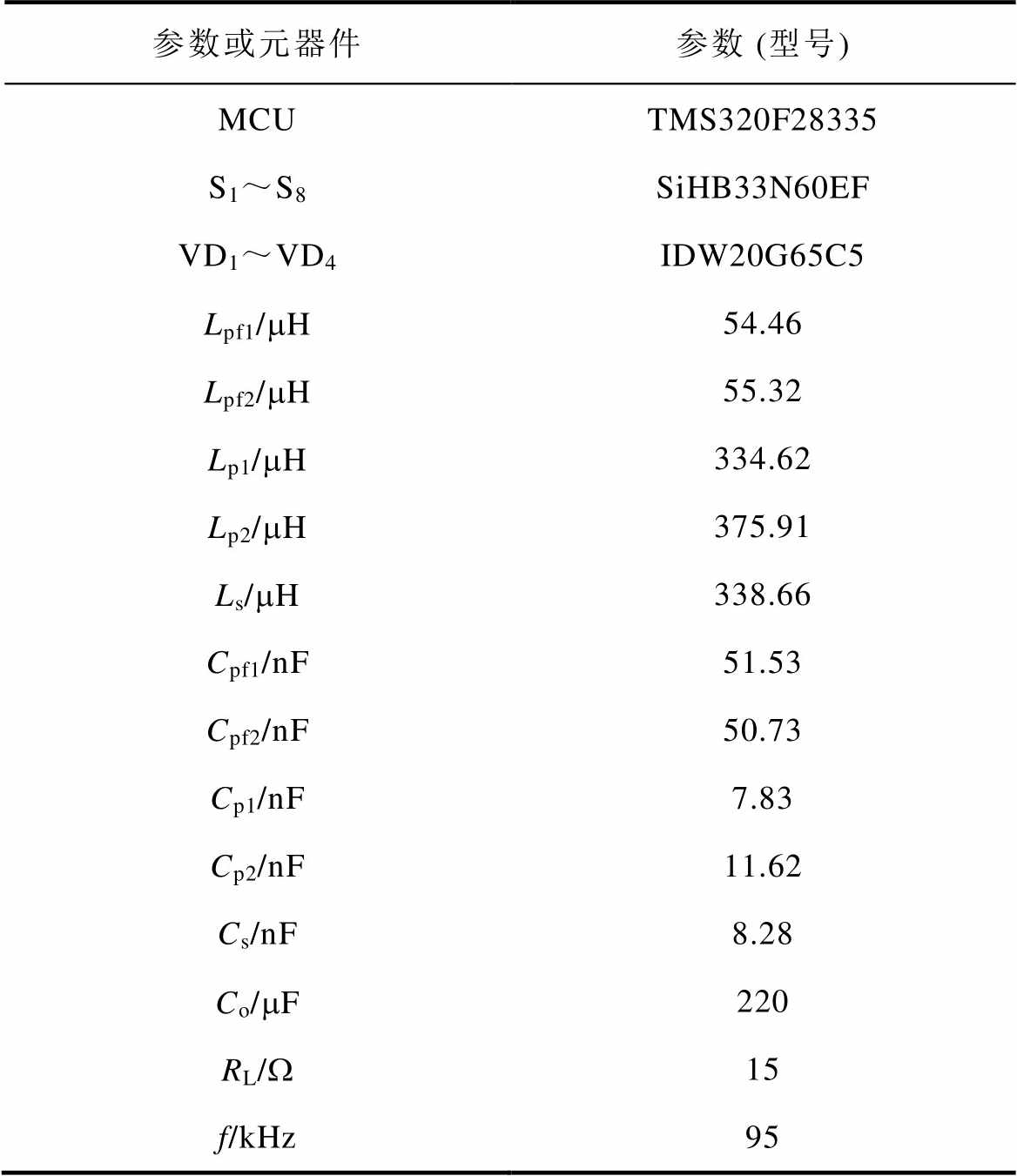
参数或元器件参数 (型号) MCUTMS320F28335 S1～S8SiHB33N60EF VD1～VD4IDW20G65C5 Lpf1/mH54.46 Lpf2/mH55.32 Lp1/mH334.62 Lp2/mH375.91 Ls/mH338.66 Cpf1/nF51.53 Cpf2/nF50.73 Cp1/nF7.83 Cp2/nF11.62 Cs/nF8.28 Co/mF220 RL/W15 f/kHz95
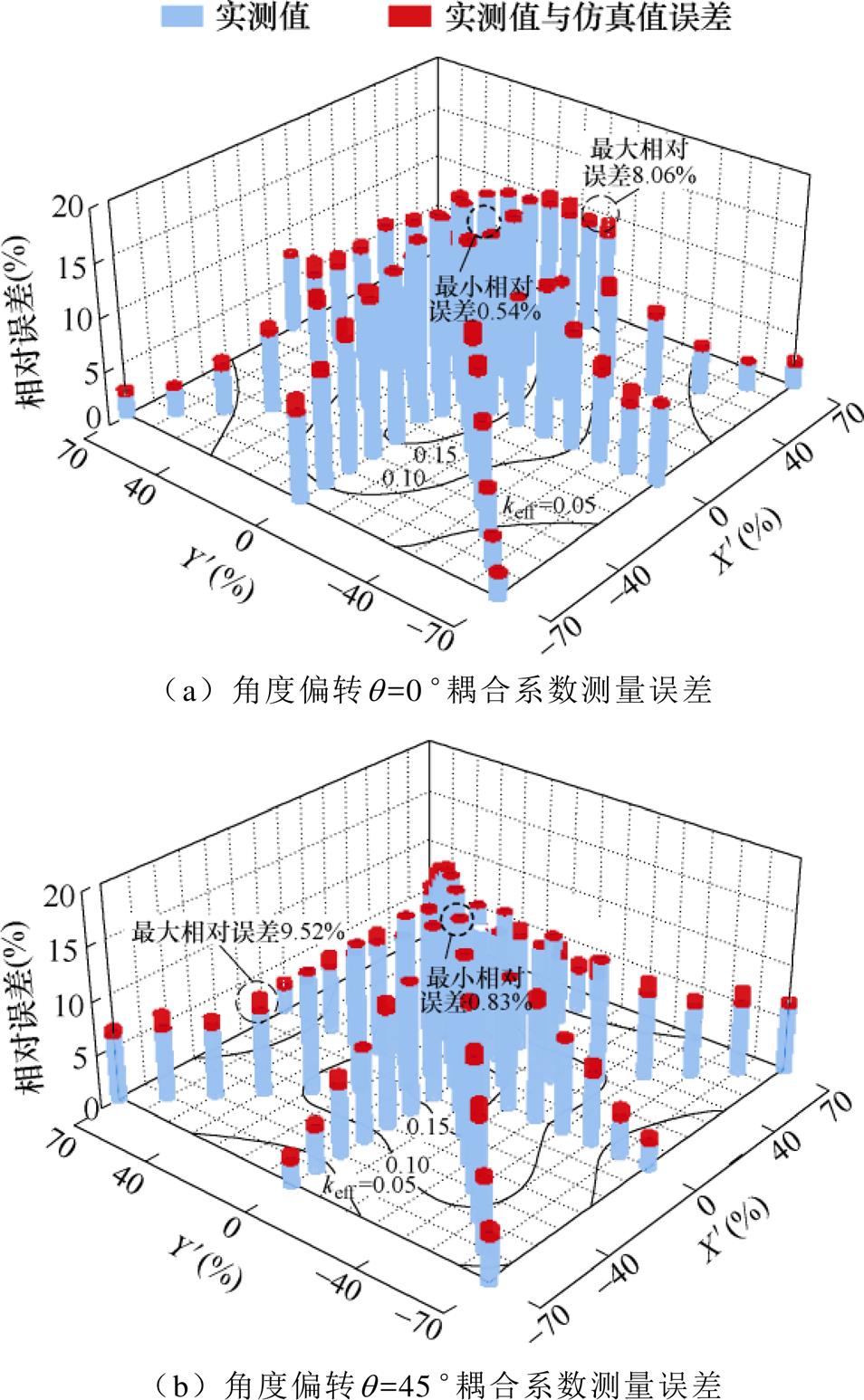
图15 等效耦合系数测量误差
Fig.15 Measurement of effective coupling coefficient
图15a中正对准位置下keff=0.183，整个偏移范围内实验测量值与仿真等效耦合系数的最大相对误差为8.06 %，最小相对误差为0.54 %，平均相对误差为3.49 %。图15b中正对准位置下keff =0.179，整个偏移范围内实验测量值与仿真等效耦合系数的最大相对误差为9.52 %，最小相对误差为0.83 %，平均相对误差为3.7 %。总体上来看，测量结果与仿真的误差较小，等效耦合系数及其CCAR变化规律的仿真分析结果基本一致，因此验证了本文所提磁耦合机构在XOY面内位置、角度的抗偏移性能。
表4给出了功率传输前低功率激励Vdc=10 V时，位置1角度偏转0 °正对准、位置2角度偏转0 °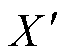偏移40 %、位置3无角度偏转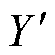偏移40 %、位置4角度偏转45 °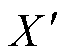偏移40 %且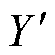偏移40%以及位置5角度偏转45 °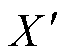偏移40 %且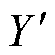偏移-40 %五种位置不同模式下的负载电压VL。此外，图12调控流程中e1、e2分别为正对准位置下角度偏转15 °、75 °时所对应的VL2、VL1的电压比值，其具体数值分别为0.28和3.15；e3设定为1，即线圈端电压变化两倍则认为接收机构移出初始匹配区域；e4设定为0.75。这是因为由图13可知，接收机构偏移距离为70 %时，CCAR为75 %，再结合式（11e）中负载电流与互感的正比例关系，即可设定e4。
表4 五种位置不同模式下负载电压
Tab.4 Load voltage of different modes under five positions
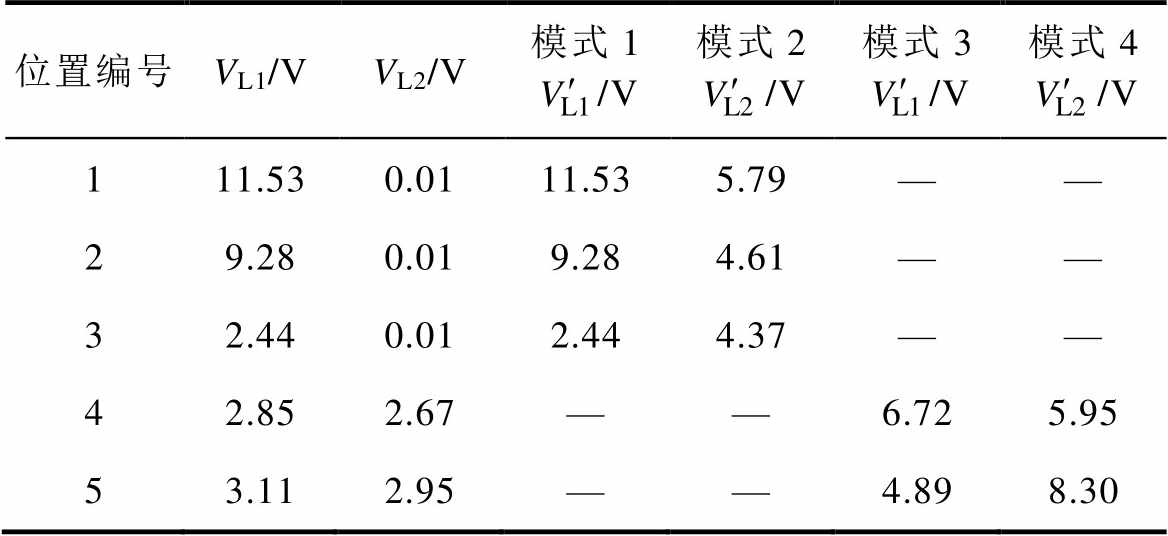
位置编号VL1/VVL2/V模式1/V模式2/V模式3/V模式4/V 111.530.0111.535.79—— 29.280.019.284.61—— 32.440.012.444.37—— 42.852.67——6.725.95 53.112.95——4.898.30
由表4可知，处于1号、2号、3号位置，VL2/VL1为0，不属于（0.28, 3.15）区间内，不满足此条件，此时发射机构由DD线圈1激励。处于4号、5号位置时，VL2/VL1分别为0.92、0.94，均包含于（0.28, 3.15）区间内，满足判断条件，此时发射机构由DQDD线圈激励。处于1号、2号、4号位置，变换接收拾取结构后的负载电压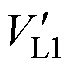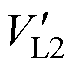＞，此时接收拾取结构选用OLDD线圈。处于3号、5号位置，变换接收拾取结构后的负载电压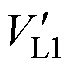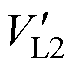＜，此时接收拾取结构选用CP线圈。综上所述，1号位置系统工作在模式1，即DD1-OLDD；2号位置系统同样工作在模式1，即DD1-OLDD；3号位置系统工作在模式2，即DD1-CP；4号位置系统工作在模式3，即同相DQDD-OLDD；5号位置系统工作在模式4，即同相DQDD-CP。
此外，为了验证双路逆变器-单路整流器的LCC-S补偿网络的系统传输特性，测取了上述五种位置下实验样机功率变换电路和补偿电路的电压电流波形，如图16所示。
图16 五种位置下实验样机波形图
Fig.16 Waveform diagram of experimental prototype under five positions
表5 五种位置下实验样机的功率及效率
Tab.5 Power and efficiency of experimental prototype under five positions
位置工作模式输入功率/W输出功率/W效率(%) q=0 °正对准模式1：DD1-OLDD2 027.61 831.690.3 q=0 °偏移40 %模式1：DD1-OLDD2 079.61 834.388.2 q=0 °偏移40 %模式2：DD1-CP2 048.81 821.288.9 q=45 °偏移40 %且偏移40 %模式3：同相DQDD-OLDD2 068.81 833.288.6 q=45 °偏移40 %且偏移-40 %模式4：同相DQDD-CP2 002.81 776.488.7
图16a给出了五种位置下系统在单路逆变工作以及两路逆变工作时输出的电压和电流波形。在不同位置下逆变输出电压与电流的相位差处于5 °～10 °的范围，说明系统输入阻抗呈弱感性，保证了开关器件均工作在ZVS模式。图16b给出了五种位置下发射机构线圈的电流波形，其相位与逆变电压相位差值始终保持为90 °，由图16b第4图、第5图可知，当两路逆变工作时，发射机构线圈的激励电流ip1与ip2的幅值相等，满足DQDD线圈磁场激励电流的需求。此外，i1、i2的实测有效值与对应仿真值的误差百分比在2 %～8 %内；ip1、ip2的实测有效值与对应仿真值的误差百分比在3 %～7 %范围内，验证了所推导LCC补偿拓扑传输特性的准确性。图16c给出了五种位置下整流前的电压电流波形，据此计算了五种位置下实验样机输出功率与效率，见表5，五种位置下实验样机的输出功率在1.8 kW左右，系统效率均不小于88 %。需要指出的是，在此功率等级下，继电器端电压始终不高于1 300 V且电流保持在11 A左右。对于更高功率等级的应用场合，接收线圈的结构变换可采用SiC MOSFET构成的电力电子开关。适用于中大功率应用场合的DQDD-OLDD耦合机构将会在本文后续的研究中展开。
本文提出了基于双极性耦合磁场调控的高抗偏移偏转WPT系统，分析了DQDD发射机构激励磁场的分布特性和可变结构OLDD线圈的拾取特性，给出了磁耦合机构特征参数与耦合系数之间的作用规律，提出了变换拾取结构及调控发射磁场的控制策略，实验验证了系统的可行性和有效性。所搭建的磁耦合机构，相比于目前常用的磁耦合机构，具有更强的抗偏移偏转性能。该系统的抗偏移性能及系统效率均高于现行标准的设定值，在电动汽车静态无线充电场合具有良好的应用前景。
参考文献
[1] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[2] 贾金亮, 闫晓强. 磁耦合谐振式无线电能传输特性研究动态[J]. 电工技术学报, 2020, 35(20): 4217- 4231.
Jia Jinliang, Yan Xiaoqiang. Research tends of magnetic coupling resonant wireless power transfer characteristics[J]. Transactions of China Electro- technical Society, 2020, 35(20): 4217-4231.
[3] 吴理豪, 张波. 电动汽车静态无线充电技术研究综述(上篇)[J]. 电工技术学报, 2020, 35(6): 1153-1165.
Wu Lihao, Zhang Bo. Overview of static wireless charging technology for electric vehicles: part Ⅰ[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1153-1165.
[4] 谢文燕, 陈为. 全方向无线电能传输技术研究进展[J]. 电力系统自动化, 2020, 44(4): 202-215.
Xie Wenyan, Chen Wei. Research progress of omni- directional wireless power transfer technology[J]. Automation of Electric Power Systems, 2020, 44(4): 202-215.
[5] 郁继栋, 曲小慧, 王国雨, 等. 基于极简三电容补偿的单级式无线电池充电器[J]. 电力系统自动化, 2021, 45(14): 165-172.
Yu Jidong, Qu Xiaohui, Wang Guoyu, et al. Single- stage inductive power transferred battery charger based on minimal three-capacitor compensation[J]. Automation of Electric Power Systems, 2021, 45(14): 165-172.
[6] 吴理豪, 张波. 电动汽车静态无线充电技术研究综述(上篇)[J]. 电工技术学报, 2020, 35(6): 1153-1165.
Wu Lihao, Zhang Bo. Overview of static wireless charging technology for electric vehicles: part Ⅰ[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1153-1165.
[7] 孔令超, 李厚基, 潘搏, 等. 无线电能传输中的QDS线圈偏移特性研究[J]. 电工技术学报, 2022, 37(13): 3361-3371.
Kong Lingchao, Li Houji, Pan Bo, et al. Research on quadruple D square coil with high misalignment tolerance for wireless power transfer[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3361-3371.
[8] Budhia M, Covic G, Boys J. A new IPT magnetic coupler for electric vehicle charging systems[C]// IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 2010: 2487-2492.
[9] Boys J T, Covic G A. The inductive power transfer story at the university of Auckland[J]. IEEE Circuits and Systems Magazine, 2015, 15(2): 6-27.
[10] Budhia M, Boys J T, Covic G A, et al. Development of a single-sided flux magnetic coupler for electric vehicle IPT charging systems[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 318-328.
[11] Huang Zhicong, Wong S C, Tse C K. Design of a single-stage inductive-power-transfer converter for efficient EV battery charging[J]. IEEE Transactions on Vehicular Technology, 2017, 66(7): 5808-5821.
[12] 任洁, 周坤卓, 李宏超, 等. 基于DDQ线圈的双耦合LCL拓扑IPT系统及其抗偏移方法研究[J]. 中国电机工程学报, 2019, 39(9): 2778-2787.
Ren Jie, Zhou Kunzhuo, Li Hongchao, et al. Study of dual coupled LCL topology IPT system based on DDQ coils and its anti-misalignment method[J]. Pro- ceedings of the CSEE, 2019, 39(9): 2778-2787.
[13] Zaheer A, Covic G A, Kacprzak D. A bipolar pad in a 10-kHz 300-W distributed IPT system for AGV applications[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3288-3301.
[14] Kim S, Covic G A, Boys J T. Tripolar pad for inductive power transfer systems for EV charging[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5045-5057.
[15] Hui S Y R, Ho W W C. A new generation of universal contactless battery charging platform for portable consumer electronic equipment[J]. IEEE Transactions on Power Electronics, 2005, 20(3): 620-627.
[16] Zhong W X, Liu Xun, Hui S Y R. A novel single- layer winding array and receiver coil structure for contactless battery charging systems with free- positioning and localized charging features[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4136-4144.
[17] Hou Jia, Chen Qianhong, Wong S C, et al. Analysis and control of series/series-parallel compensated resonant converter for contactless power transfer[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(1): 124-136.
[18] Li Siqi, Li Weihan, Deng Junjun, et al. A double- sided LCC compensation network and its tuning method for wireless power transfer[J]. IEEE Transa- ctions on Vehicular Technology, 2015, 64(6): 2261- 2273.
[19] 王佩月, 左志平, 孙跃, 等. 基于双侧LCC的全双工无线电能传输能量信号并行传输系统[J]. 电工技术学报, 2021, 36(23): 4981-4991.
Wang Peiyue, Zuo Zhiping, Sun Yue, et al. Full- duplex simultaneous wireless power and data transfer system based on double-sided LCC topology[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4981-4991.
[20] Wang Yijie, Wang Haoyu, Liang Tian, et al. Analysis and design of an LCC/S compensated resonant converter for inductively coupled power transfer[C]// 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 2017: 1-5.
[21] Yang Junfeng, Zhang Xiaodong, Zhang Kaijian, et al. Design of LCC-S compensation topology and optimi- zation of misalignment tolerance for inductive power transfer[J]. IEEE Access, 2020, 8: 191309-191318.
[22] 王懿杰, 陆凯兴, 姚友素, 等. 具有强抗偏移性能的电动汽车用无线电能传输系统[J]. 中国电机工程学报, 2019, 39(13): 3907-3917.
Wang Yijie, Lu Kaixing, Yao Yousu, et al. An electric vehicle (EV)-oriented wireless power transfer system featuring high misalignment tolerance[J]. Proceedings of the CSEE, 2019, 39(13): 3907-3917.
Abstract During the static wireless charging of electric vehicles, misalignment between the transmitting and the receiving structures is inevitable. Such misalignment may cause a rapid decrease in the coupling coefficient and transfer efficiency of the magnetic coupling structure. Therefore, a critical issue for the static wireless power transfer (WPT) system of the electric vehicle is to improve the coupling structure's misalignment tolerance with high stability of the pickup power of the receiving structure. A WPT system with high misalignment tolerance based on bipolar coupling magnetic-field control is proposed. A double-layer quadrature DD (DQDD) coil is used for the transmitting structure, and an overlapping DD (OLDD) coil is adopted for the receiving structure. The DQDD coil comprises two sets of DD coils decoupling each other in a double-layer quadrature layout. The quadrature layout enables the magnetic fluxes induced from two sets of DD coils to be in an orthogonal position in space. Meanwhile, the dominant magnetic flux between two sets of DD coils is close to zero.The OLDD coil of the receiving structure can be changed into the CP coil by controlling two switches, so that the magnetic field picked up by the OLDD can change from bipolarity to unipolarity.
Firstly, an LCC-S circuit based on a dual inverter-single rectifier is constructed. To achieve decoupling for control, the two sets of DD coils in the transmitting structure are excited by the two channels of inverters separately to adjust the output voltage amplitude and phase of the two channels of inverters, respectively. The parameter configuration for the constant excitation current of the transmitting coil and output voltage are deduced. Secondly, the interaction between the characteristic parameters of the coupling structure and coupling coefficient is given when the transmitting structure and the receiving structure are entirely aligned. Accordingly, the size of the DQDD-OLDD coupling structure is optimized. Then, a magnetic-field control strategy is given to achieve the desired maximum coupling coefficient. By controlling the phase difference between the excitation current of the transmitting DQDD coil and the pickup polarity of the receiving OLDD coil, the high transfer efficiency of the WPT system is maintained when misalignment occurs. Combined with the magnetic-field control strategy, a pattern-matching monitoring method based on the position of the receiving structure is proposed. Thus, the excitation mode and the picking structure can match regardless of the random movement of the receiving structure, avoiding the frequent execution of the control program. Finally, an indicator, coupling coefficient attenuation ratio (CCAR), is defined to measure the anti-misalignment performance of the coupling structure. The proposed coupling structure has higher misalignment tolerance than the conventional circle pad and DD coupling structure.
An experimental prototype was built, and the equivalent coupling coefficient was measured. The anti-misalignment performance of the DQDD-OLDD coupling structure in the XOY plane has been verified. In addition, the power converter circuit and the compensation circuit of the prototype at five positions were- measured, which verifies the system transfer characteristics of the dual inverter-single rectifier. The experimental results indicate that the output power is maintained at 1.8 kW in the 270 mm horizontal misalignment range, and the system efficiency is maintained above 88 %.
keywords：Wireless power transfer, electric vehicle, misalignment, magnetic-field control
DOI: 10.19595/j.cnki.1000-6753.tces.221182
中图分类号：TM724
收稿日期 2022-06-21
改稿日期 2022-07-09
谢诗云 男，1987年生，博士，讲师，研究方向为电力电子与电能变换、无线电能传输。E-mail: xieshiyun1987@cqut.edu.cn
李 恋 男，1998年生，硕士研究生，研究方向为无线电能传输。E-mail: 935357999@qq.com（通信作者）
（编辑 郭丽军）