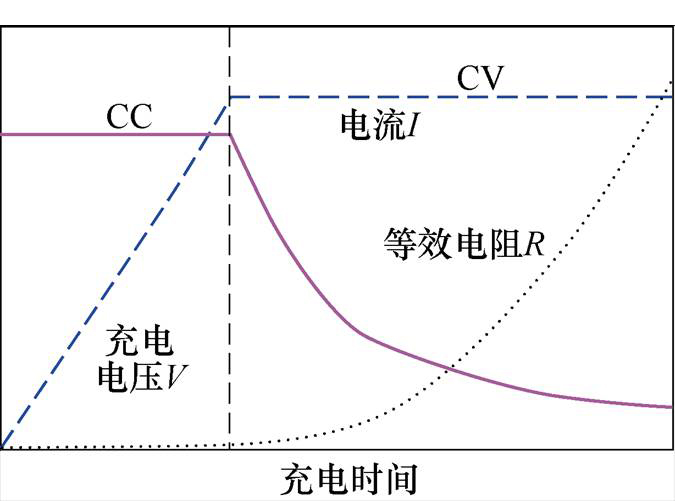
图1 典型蓄电池充电曲线
Fig.1 Typical battery charging curves
摘要 为了解决蓄电池充电过程中的恒流过充或恒压欠充问题，该文提出一种LCC-LCC/S自切换恒流-恒压复合型无线电能传输系统。通过副边电力开关切换，该系统不仅可实现恒流-恒压输出，且能有效应对蓄电池充电过程中的各种异常工况；另外，在充电完成负载移除时，该系统能自动进入低功耗待机状态。首先，给出LCC-LCC/S自切换复合拓扑，分析恒压-恒流及零相角（ZPA）特性；其次，分析恒流-恒压切换点并验证其最优性；然后，通过分析充电过程中出现的副边缺失、负载短路、负载断路等异常工况，系统能通过开关切换有效应对以上异常工作情况，并且充电完成负载移除后系统能自动进入低功耗待机状态；接着，通过与目前研究较多的S-SP拓扑的系统特性进行对比，突出了LCC-LCC/S拓扑的优势；最后，搭建仿真和实验平台，实现最大电流为5.03 A、最大电压为48.92 V的高效率输出，验证了所提理论的正确性。
关键词：无线电能传输 自切换 恒流-恒压 复合拓扑
无线电能传输（Wireless Power Transfer, WPT）的概念是由尼古拉·特斯拉在近100年前提出的[1]，WPT技术目前正成为一种为现代设备充电的研究热点，其广泛应用在诸如心脏起搏器、电动汽车、太阳能卫星、自主水下航行器、无人驾驶飞行器等先进设备[2-7]。这种安全、便捷的充电技术正成为未来电子装置的主流充电方式[8-9]。
WPT技术应用在电动自行车蓄电池的充电上，存在电能传输效率低、电池充放电次数少和充电安全等问题。基于这些问题，需要对蓄电池的充电模式做出深刻的分析。蓄电池的传统充电方式采用恒流输出（Constant Current Output, CCO）和恒压输出（Constant Voltage Output, CVO）[10-11]两阶段充电方式。当电池充电时，CCO模式用于向电池施加恒定的直流电流，直到充电电压达到最大额定电压，然后控制器切换到CVO模式， CVO模式下充电电流会逐渐降低，然后一直到充电完成，这种两阶段充电方式能减少充电时间，延长电池使用寿命。典型蓄电池充电曲线如图1所示。
图1 典型蓄电池充电曲线
Fig.1 Typical battery charging curves
目前，有以下几种方式可以实现无线电能传输系统的恒流-恒压输出：第一种是通过控制系统工作频率来实现[12-15]；第二种是通过控制占空比来实 现[16]；第三种是通过在副边加入一个直流斩波器来实现[17-20]，以上几种控制方式虽然控制精度较高，但存在闭环控制系统复杂的问题；第四种是通过在原边或副边加入交流开关用于切换拓扑来实现。文献[21]采用变结构LC-CLCL拓扑来实现恒流-恒压输出，但开关切换时输出的电流和电压波动较大，会对电池造成冲击，减少电池使用寿命。文献[22]提出了S/P-S/SP混合补偿拓扑电路，虽然电路结构较为简单，但未分析交流开关耐压能力的问题，并且开关切换瞬间输出电压有20 V左右的尖峰，对电池冲击较大。文献[23]提出了一种基于F-F/T变结构谐振网络的恒压-恒流型电场耦合电能传输系统，虽然无需任何检测与通信电路，但是整个系统阶数较高、结构较为复杂；另外，该系统较难实现三个交流开关的同开同闭，且开关切换时会产生过高的电压/电流尖峰。文献[24]提出在原边加入两个交流开关的方法将串联-串联（Series-Series, SS）型拓扑和并联-串联（Parallel-Series, PS）型拓扑混合起来实现恒流-恒压输出，该系统虽然结构简单，但并未考虑到异常工作情况下系统如何做出反应来保护系统。
鉴于以上文献的不足，本文提出一种LCC- LCC/S自切换恒流-恒压复合型拓扑，该复合型拓扑只需在副边加入两个交流开关和一个补偿电容。通过两个交流开关的同开同闭，不仅能实现分段恒流-恒压输出，而且异常工作情况下进行开关切换也能有效保护系统，充电完成负载移除时能自动进入低功耗待机状态且原副边之间无需通信。所提出的复合型无线电能系统在恒流模式和恒压模式下均能实现零相角（Zero Phase Angle, ZPA），开关切换时输出电压和电流波动极小，并且在仿真与实验中验证了本文所提出的系统性能优于目前应用较多的SS/PS混合拓扑。
本文所提出的LCC-LCC/S自切换恒流-恒压复合型拓扑结构如图2所示。图中，Vin为输入直流电压；Q1～Q4为组成全桥逆变电路的MOSFET管；L1、C1和L2、C2分别构成原、副边谐振网络；LP和LS分别为发射线圈和接收线圈上的自感；CP和CS1、CS2分别为发射线圈和接收线圈上的补偿电容；VD1～VD4为组成不可控整流电路的快恢复二极管；S1和S2均为两个反向串联的IGBT组成的交流开关，其内部结构如图3所示；Co为滤波电容；Ro为蓄电池等效电阻。
开关S1、S2导通或关断时，将控制CS2和C2的切入或切出。当S1和S2导通时，CS2被短路，C2接入电路，系统进入LCC-LCC拓扑的恒流充电模式；当S1和S2关断时，CS2接入电路，C2被切出，系统进入LCC-S拓扑的恒压充电模式。开关状态与输出模式的关系见表1。
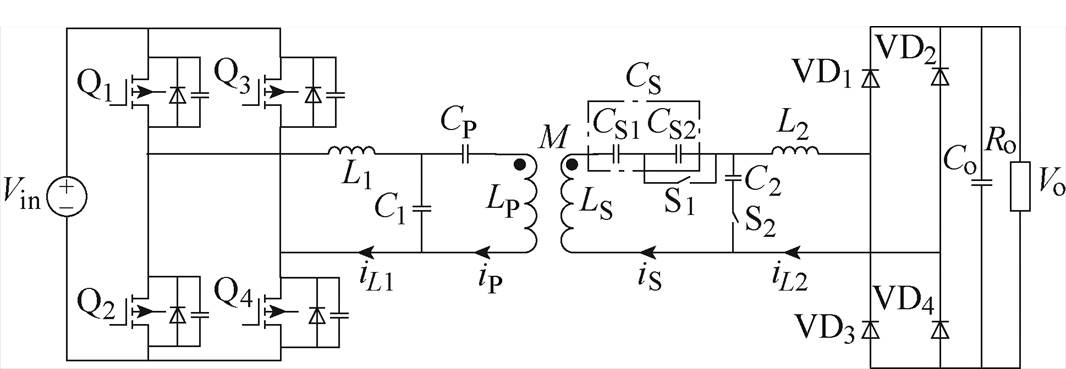
图2 LCC-LCC/S自切换恒流-恒压复合型拓扑结构
Fig.2 LCC-LCC/S self-switching constant current and constant voltage composite topology
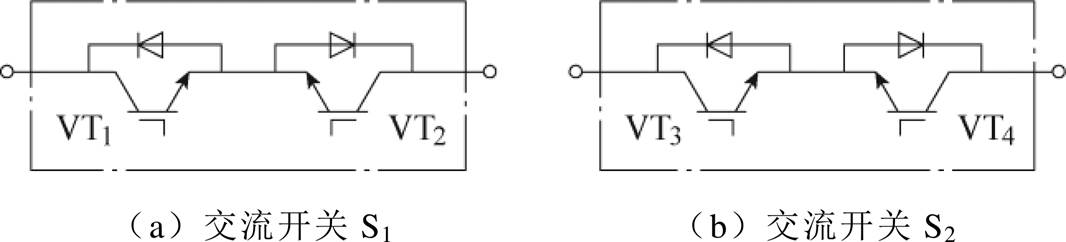
图3 2个IGBT反向串联的交流开关
Fig.3 AC switch with 2 IGBTs connected in reverse series
表1 开关状态与输出模式关系
Tab.1 The relationship between switching state and output mode
工作模式补偿网络开关状态 恒流LCC-LCCS1、S2导通 恒压LCC-SS1、S2关断
当开关S1和S2导通时，系统处于恒流模式，拓扑结构如图4所示。图4中，Uin为输入交流电压；L1、C1和L2、C2分别构成原、副边谐振网络；LP和LS分别为发射线圈和接收线圈上的自感；RP和RS分别为发射线圈和接收线圈的寄生内阻；R1和R2分别为原、副边补偿电感的寄生内阻；CP和CS1分别为发射线圈和接收线圈上的补偿电容；R为蓄电池等效电阻。
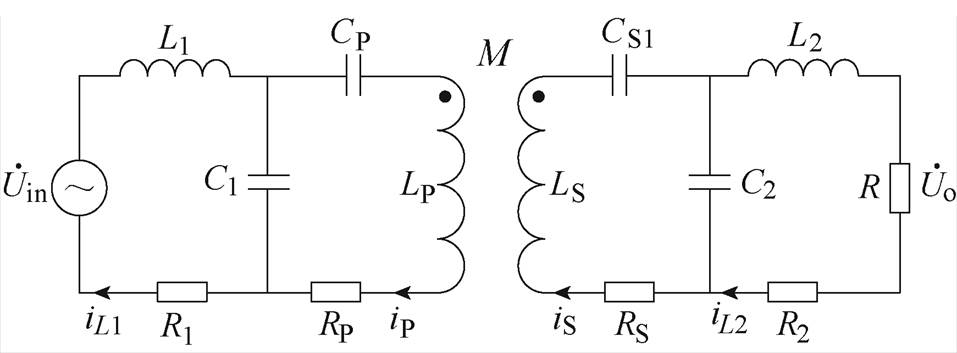
图4 LCC-LCC恒流模式拓扑结构
Fig.4 The LCC-LCC topology of CC mode
w 为输入电源的频率，wP为原边回路谐振频率，wS为副边回路谐振频率。当系统处于谐振状态下，L1、C1、L2、C2、LP、LS、CS1、CP满足
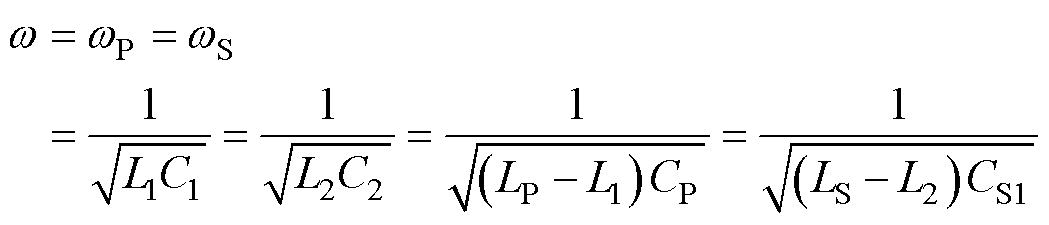（1）
在谐振频率下，副边回路阻抗为
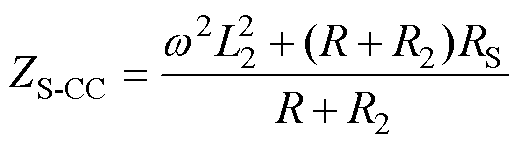（2）
副边折射到原边的引入阻抗为
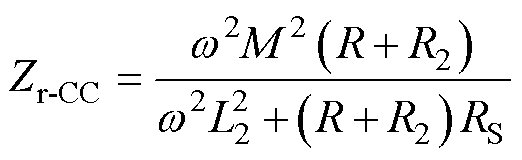（3）
则原边的输入阻抗为
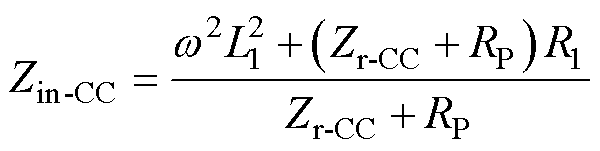（4）
因此在谐振频率下，LCC-LCC拓扑的原边输入阻抗为纯阻性，具有功率因数为1的特性。
LCC-LCC拓扑的输入功率为
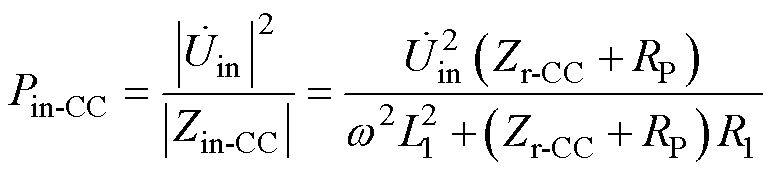（5）
将原副边补偿电感的寄生内阻R1、R2忽略不计，k为发射线圈与接收线圈之间的耦合系数，则LCC-LCC拓扑的输出功率可表示为
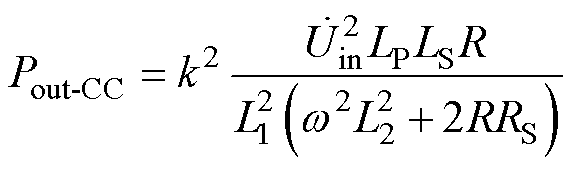（6）
传输效率可表示为
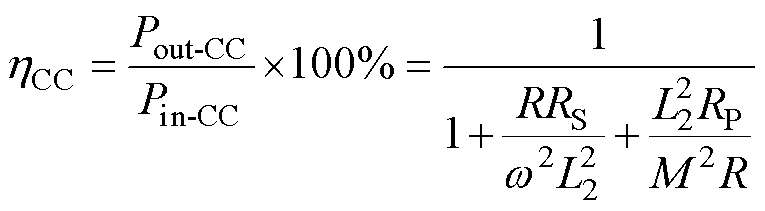（7）
忽略接收线圈的寄生内阻RS，则LCC-LCC拓扑的输出电流可表示为
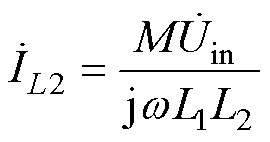（8）
由式（8）可知，LCC-LCC拓扑电路在完全谐振的状态下，可实现与负载无关的恒流特性，且输入阻抗Zin没有虚部，具有ZPA特性。
当开关S1和S2关断时，系统处于恒压模式，拓扑结构如图5所示。
当系统处于谐振状态下，L1、C1、LP、LS、CS、CP满足
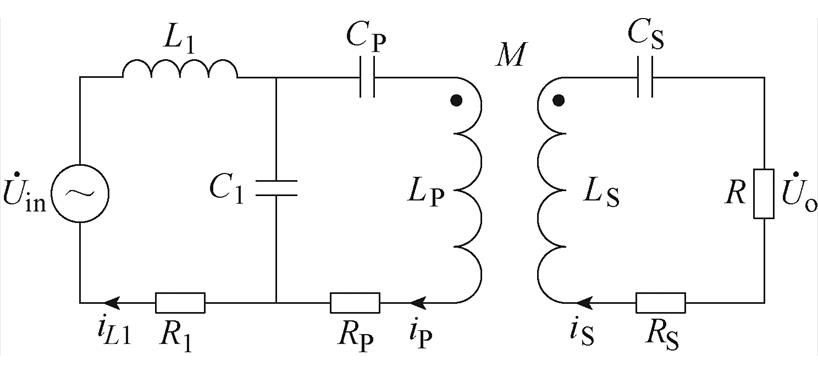
图5 LCC-S恒压模式系统
Fig.5 The LCC-S topology of CV mode
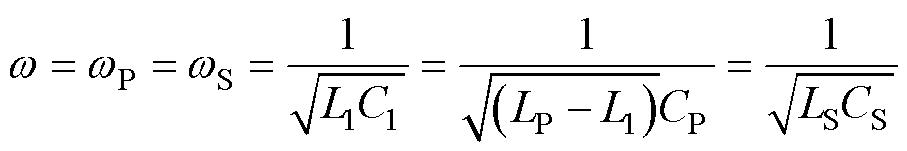（9）
在谐振频率下，副边折射到原边的引入阻抗为
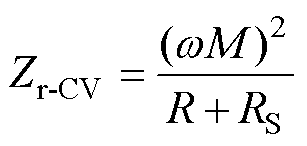（10）
则原边输入阻抗为
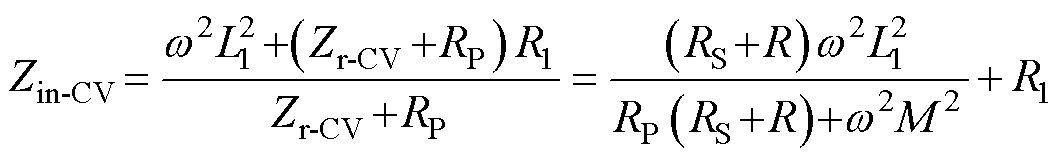（11）
因此在谐振频率下，LCC-S拓扑的原边输入阻抗为纯阻性，具有功率因数为1的特性。
LCC-S拓扑的输入功率为
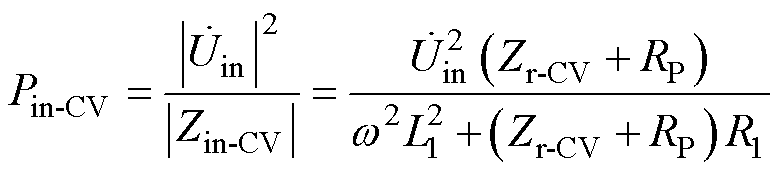（12）
将原边补偿电感的寄生内阻R1忽略不计，则LCC-S拓扑的输出功率可表示为
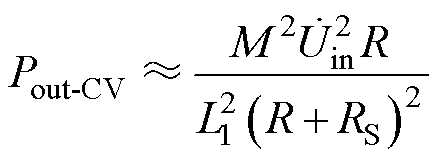（13）
传输效率为
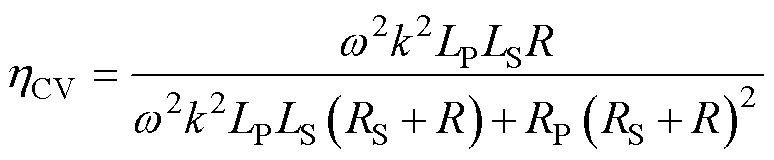（14）
忽略接收线圈的寄生电阻RS，则LCC-S拓扑的输出电压可表示为
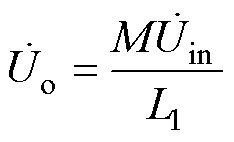（15）
由式（15）可知，LCC-S拓扑在完全谐振的状态下，可实现与负载无关的恒压特性，且输入阻抗Zin-CV没有虚部，具有ZPA特性。
因此，通过对原副边参数以及输出功率的合理设计，便可将LCC-LCC拓扑与LCC-S拓扑复合，实现两阶段的恒流-恒压充电。
为了使开关切换前后输出功率没有太大的波动，令LCC-LCC的输出功率Pout1和LCC-S的输出功率Pout2相等，则
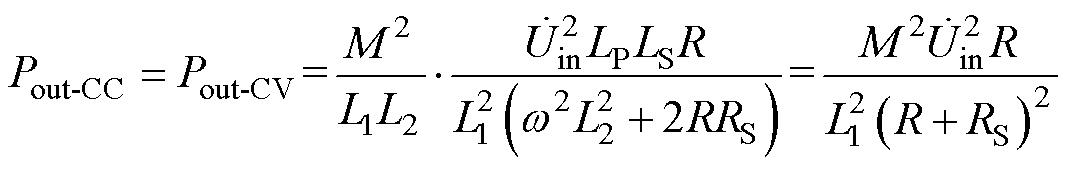（16）
以负载电阻R为变量，式（16）中的其他参数为常量，便可求出两拓扑输出功率相等时对应的负载等效电阻R=8.1 W。
当负载等效电阻为8.1 W 时，LCC-LCC拓扑的输出电流和电压分别为
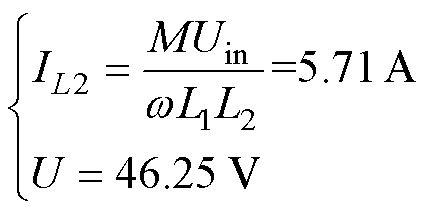（17）
LCC-S拓扑的输出电流和电压分别为
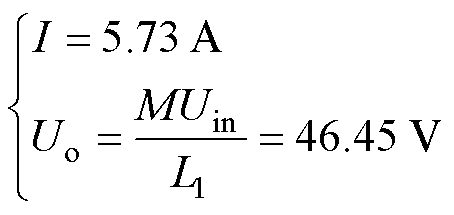（18）
由式（18）可看出，两种拓扑的输出电流差值仅为0.02 A、输出电压差值仅为0.2 V，因此将8.1 W 作为恒流-恒压切换点时，切换前后的电压电流落差极小，可有效减小开关切换时负载上电压电流的波动。式（16）左右两边M2相互抵消，因此理论上最优切换点与互感无关。
通过对LCC-LCC拓扑和LCC-S拓扑建模，获得了各自的效率和输出功率，如式（6）、式（7）、式（13）、式（14）所示，可得LCC-LCC和LCC-S拓扑输出功率和效率随R变化曲线如图6与图7 所示。
从图6中可以看出，LCC-LCC拓扑的输出功率曲线与LCC-S拓扑的输出功率曲线交点对应的阻值为8.1 W，与式（16）计算的结果一致。
从图7中可以看出，在负载阻值为8.1 W 时，两拓扑效率的差值很小，说明在开关切换前后输入功率没有太大的波动，且整个充电过程中系统始终处于高效率的状态。
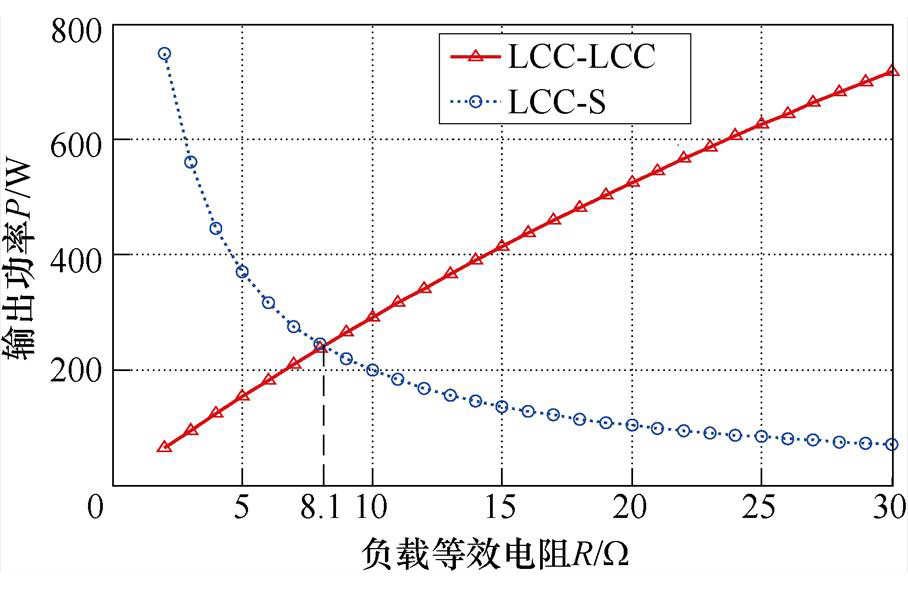
图6 LCC-LCC和LCC-S拓扑的输出功率随R变化曲线
Fig.6 The curves of the output power vs R for LCC-LCC topology and LCC-S topology respectively
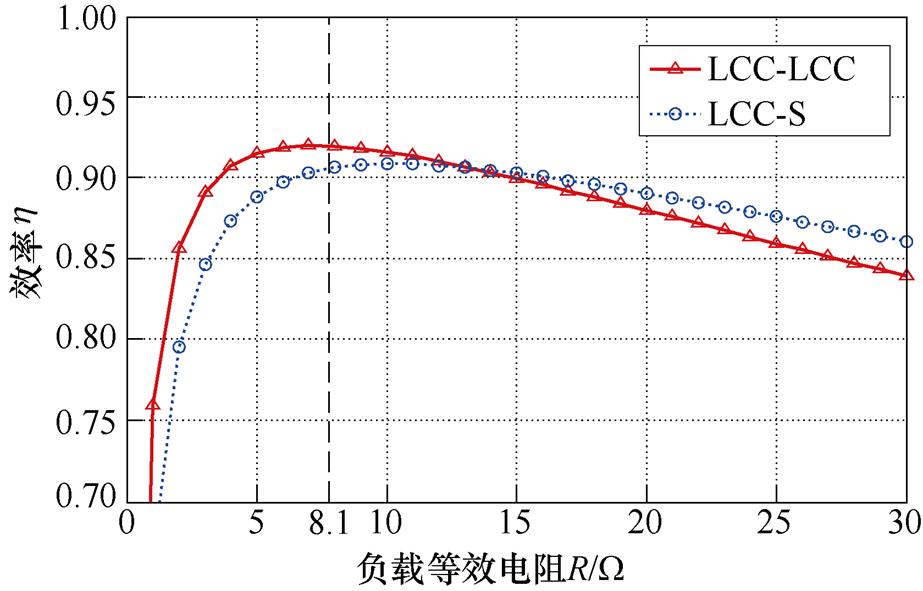
图7 LCC-LCC和LCC-S拓扑的效率随R变化曲线
Fig.7 The curves of efficiency vs R for LCC-LCC topology and LCC-S topology respectively
R是包含副边整流桥以及后端电路的等效电阻，故可得出整流桥后负载转折电阻Ro为
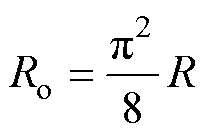（19）
当负载等效电阻为8.1 W 时，整流桥后负载转折电阻为10 W。
为验证负载转折电阻为10 W 时为开关切换点的最优性，选择了8 W 和12 W 两个阻值作为样本进行观察。图8为不同负载转折电阻切换前后的电流与电压的波形，由图8可知，在负载转折电阻为8 W 和12 W 时进行切换，电流电压落差较大，在负载转折电阻为10 W 时进行切换，电流电压落差最小，验证了理论分析的正确性。
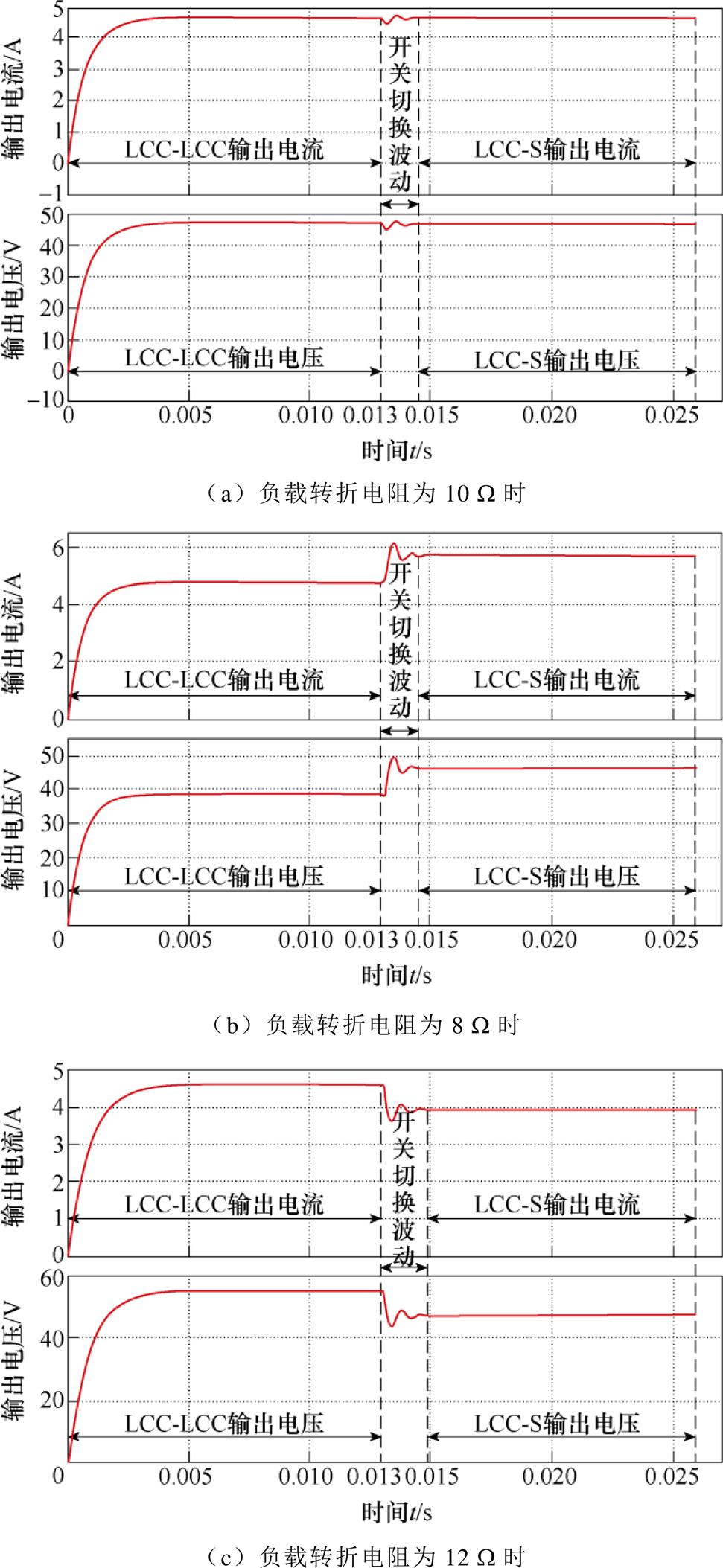
图8 不同负载转折电阻切换前后的电流与电压波形
Fig.8 Waveforms of the current and voltage for the duration of the different resistors switching
图9为充电完成负载移除前后逆变器输出电流仿真波形，在恒压模式为负载充电时，当充电完成负载移除后，引入阻抗为
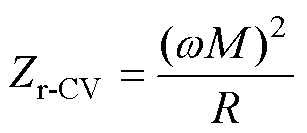（20）
由于副边负载移除，R趋于无穷大，Zr-CV趋于无穷小，原边反射阻抗为零，则原边总阻抗为
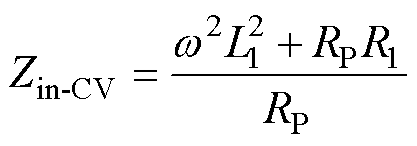（21）
因为发射线圈寄生电阻非常小，所以原边总阻抗Zin-CV较大，逆变器输出电流下降到一个较小值，即无需任何控制便可使系统自动进入低功耗待机状态，系统具有负载自适应性。
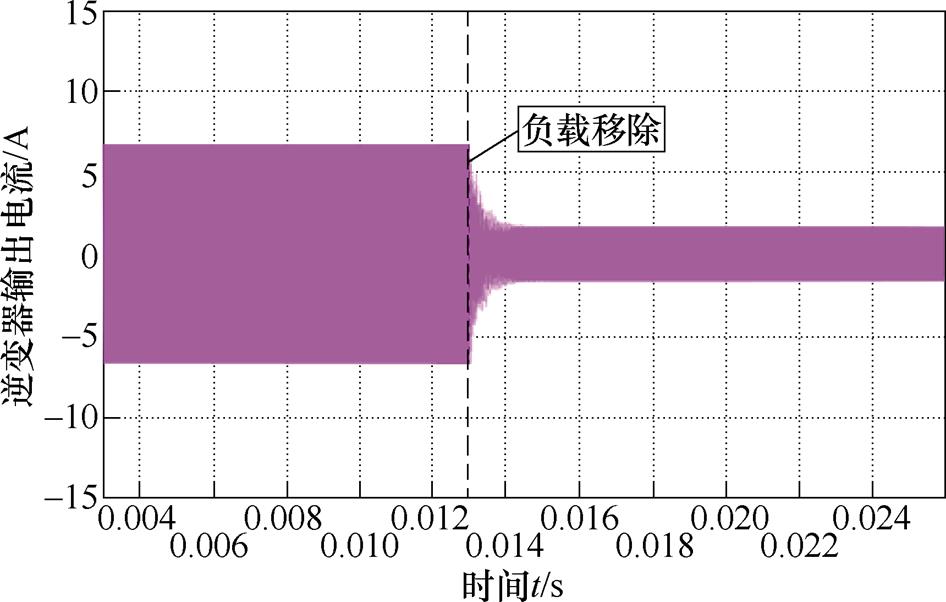
图9 充电完成负载移除前后逆变器输出电流仿真波形
Fig.9 Output current simulation waveforms of the inverter for the duration of charging completion and load removal
在实际充电过程中，难免会出现副边缺失、负载开路、负载短路等异常工作情况，因此，有必要对异常工作情况进行分析，使系统能对异常工作情况及时做出处理，以免损坏电路中的器件。
首先对副边缺失的情况进行分析，当副边缺失时，无论是LCC-LCC还是LCC-S，都只剩下原边拓扑电路，LCC-LCC和LCC-S副边缺失时的等效电路如图10所示。
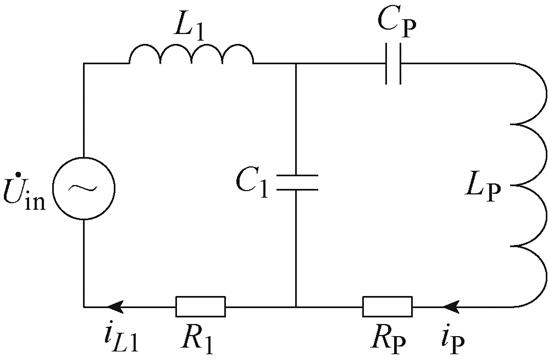
图10 LCC-LCC和LCC-S副边缺失时的等效电路
Fig.10 Equivalent circuit diagrams for LCC-LCC and LCC-S with secondary side missing
副边缺失时，副边的等效阻抗视为无穷大，根据式（3）和式（10），引入原边的阻抗为零，则
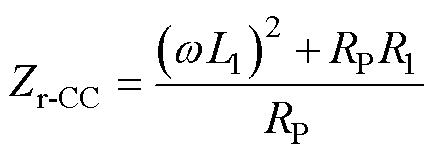（22）
寄生电阻RP较小，可忽略不计，输入阻抗可视为无穷大，则输入电流和发射线圈电流分别为
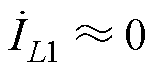（23）
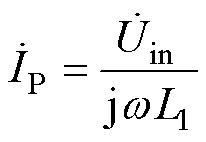（24）
副边缺失时流过原副边器件的电流波形如图11所示。在0.013 s发生副边缺失时，逆变器输出电流含有大量谐波分量，逆变器输出的高次谐波在L1和C1中反复传递且发射线圈LP中的电流基本保持不变，发射线圈的电流仅在LP、CP、C1中流动，并且具有一定的流动损耗，因此无论是LCC-LCC还是LCC-S拓扑发生副边缺失，原边电路中的器件均不会出现过电流现象，且无需任何检测装置便能自动应对充电过程中副边缺失的情况。
图11 副边缺失时流过原副边器件的电流波形
Fig.11 The waveforms of IP, IS, IL1 and IC1 for the duration of the secondary side missing
在恒压-恒流两种充电模式中都有可能会出现负载开路的情况如图12所示。因此负载开路时的拓扑分为图12a、图12b两种情况。
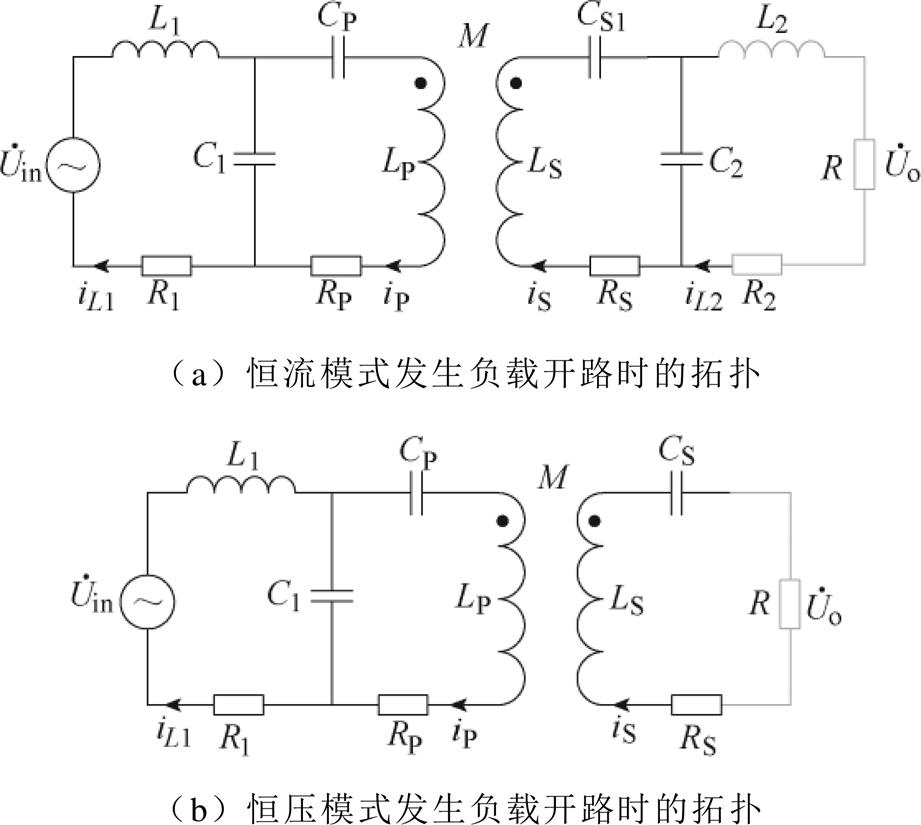
图12 复合拓扑发生负载开路时的两种等效拓扑
Fig.12 Two equivalent topologies in case of load open circuit
由图12a可以看出，当恒流模式发生负载开路时，引入阻抗为
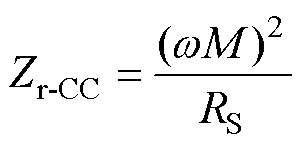（25）
RS极小，则Zr-CC极大，此时的原边输入阻抗为
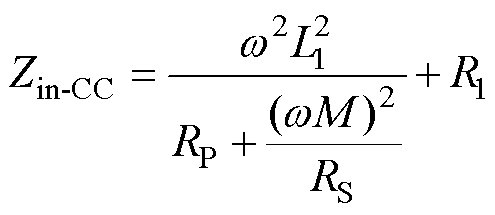（26）
原边输入电流为
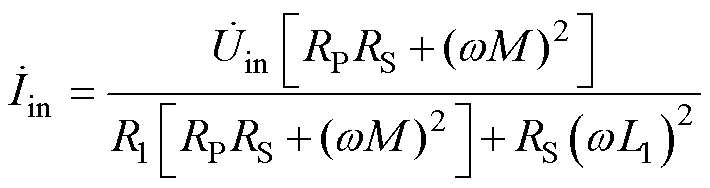（27）
由于R1、RS极小，则输入电流Iin极大，在电路中表现为输入电流迅速增加，如图13中的电流IL1的波形所示。
图13 恒流模式下负载开路时的原副边电流波形
Fig.13 The waveforms of IP, IS, IL1 and IC1 in CC mode for the duration of the load open circuit
发射线圈中的电流为
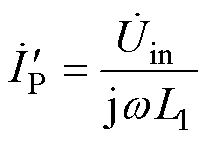（28）
则发射线圈中的电流基本保持不变，不会出现迅速增加的情况，如图13中的电流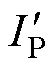
的波形所示。
流过电容C1的电流为
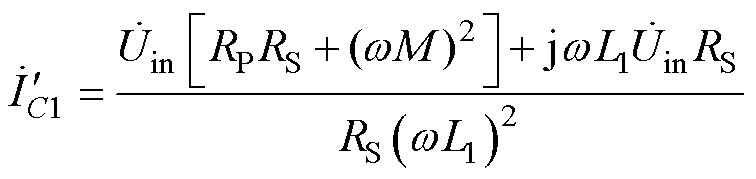（29）
由于RS极小，则C1中的电流也会出现激增现象，如图13中电流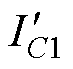
的波形所示。
接收线圈中的电流为
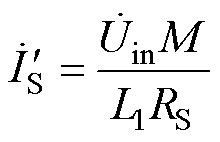（30）
同理接收线圈中也会出现电流激增现象，如图13中的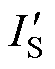
所示。
恒压模式下发生负载开路时的等效电路与其副边缺失时的等效电路相同，在此不做赘述。
当发生负载短路或副边的不可控整流电路中的快恢复二极管被击穿等异常工作情况时，可根据恒流-恒压两种工作模式分为复合拓扑发生负载短路时的两种等效电路，如图14所示。
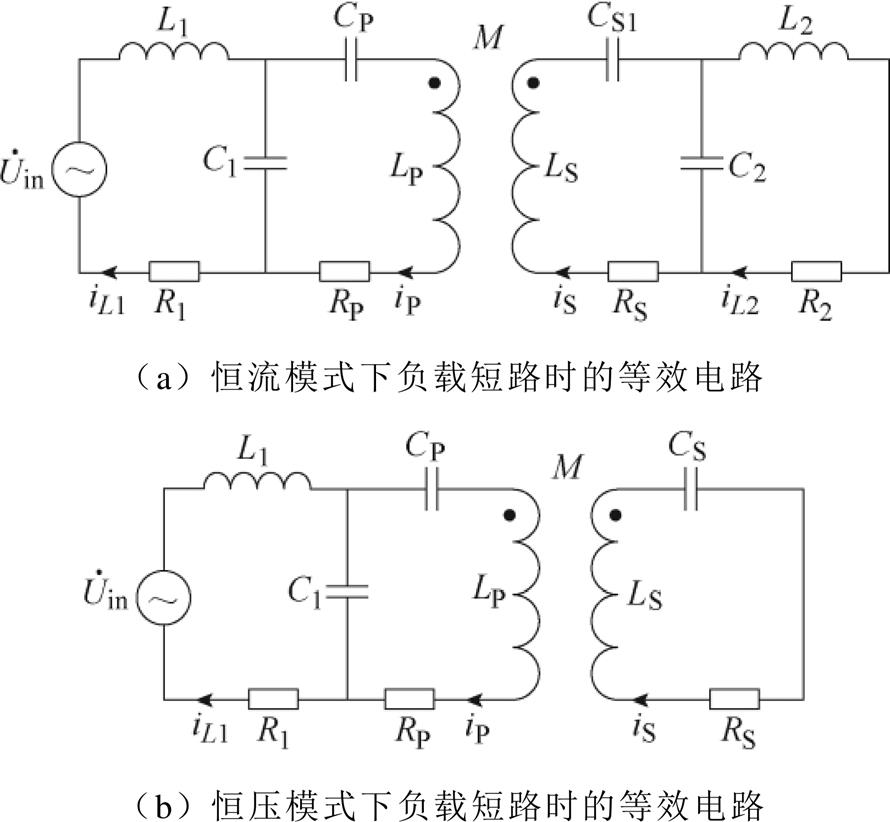
图14 复合拓扑发生负载短路时的两种等效电路
Fig.14 Two equivalent topologies with load short circuit
正常工作时恒流模式下的接收线圈中电流为
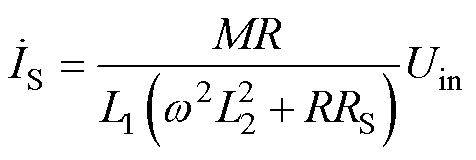（31）
由式（31）可知，当恒流模式下发生负载短路时，R=0，则IS=0，即接收线圈中的电流为零，与副边缺失时的工作情况基本一致，在此不做赘述。
正常工作时恒压模式下的系统输入电流为
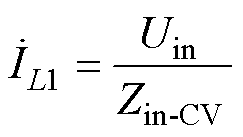（32）
根据基尔霍夫定律，发射线圈中的电流为
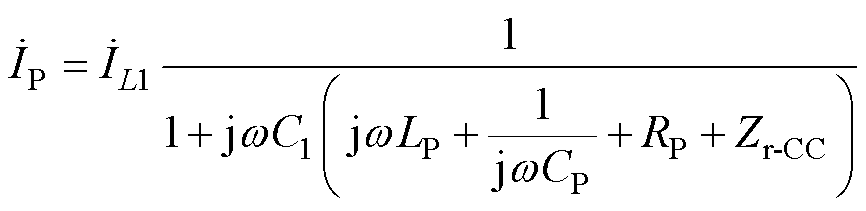（33）
则副边接收线圈中的电流为
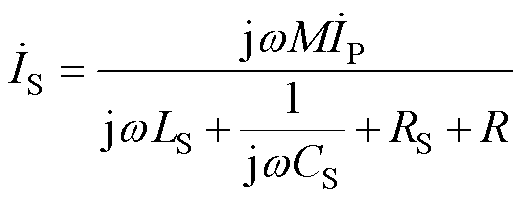（34）
则可将输入电流简化为
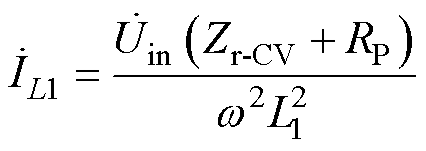（35）
接收线圈电流可简化为
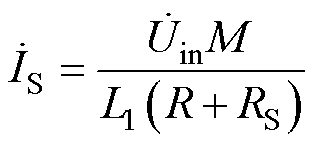（36）
从式（35）和式（36）中可以看出，当恒压模式下发生负载短路，即R=0时，输入电流IL1和接收线圈电流IS均会迅速增加，同理IC1也会出现激增现象，仿真波形如图15所示。
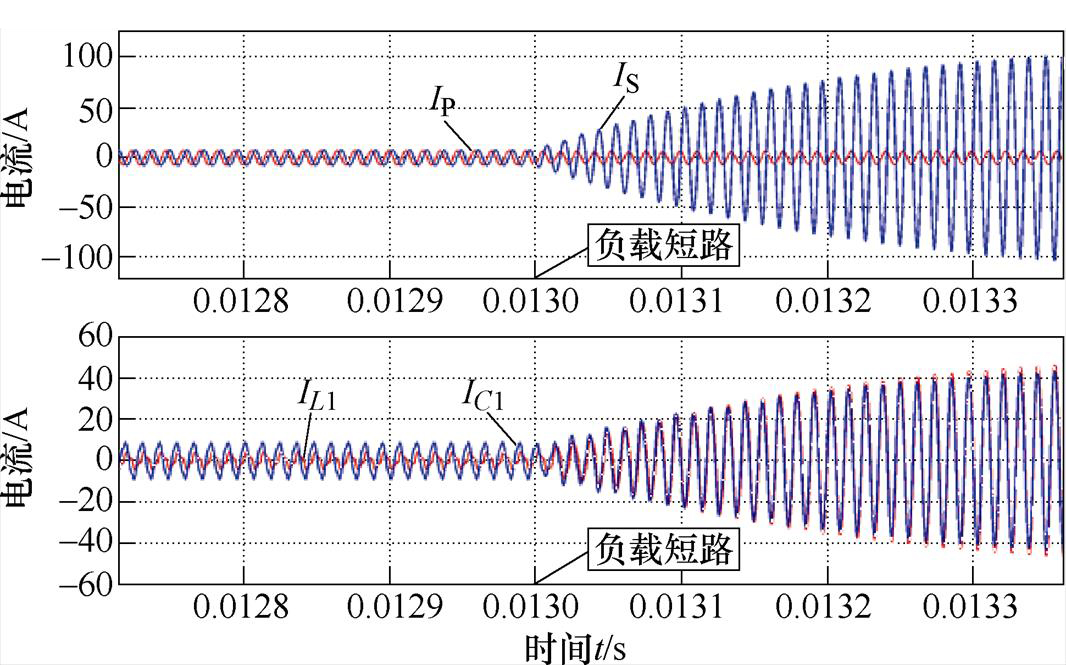
图15 恒压模式下负载短路时的原副边电流仿真波形
Fig.15 The waveforms of IP, IS, IL1 and IC1 in CV mode for the duration of the load short circuit
当电路中出现电流激增现象时，会使全桥逆变器的开关管过热并击穿补偿电容。
在应对各种异常工作情况时LCC-LCC和LCC- S拓扑的稳定性分析见表2。从表2中可以看出，这两种拓扑都可以有效应对副边丢失的情况，但LCC-LCC拓扑不能应对负载开路的情况，LCC-S拓扑不能应对负载短路的情况。因此，当恒流模式下发生负载开路时，通过副边开关切换到LCC-S拓扑；当恒压模式下发生负载短路时，通过副边开关切换到LCC-LCC拓扑，从而实现在异常工作情况下有效的保护系统。
表2 两拓扑的稳定性分析
Tab.2 Stability analysis of the two topologies
工作模式LCC-LCCLCC-S 副边缺失保护系统保护系统 负载开路损坏系统保护系统 负载短路保护系统损坏系统 充电完成负载移除—低功耗待机
为了降低S2切换期间的瞬态电压，必须在IC2为零时切换开关，IC2为零时IL2和ILs大小相等，相位相同，这样就不会对开关断开之后电路中的电流平衡造成影响。
S1由VT1、VT2两个IGBT反向串联组成，如图3a所示，S2由VT3、VT4两个IGBT反向串联组成，如图3b所示。通过检测电流IC2流向，在IC2流进开关S2时，即电流流经VT3（非VT3中体二极管）和VT4中反并联的体二极管，关断VT4。而电流IC2流出开关S2时，由于VT4已经关断，此时IC2为零。此时，关断VT1、VT2、VT3即可实现系统输出模式的平滑切换，如图16所示。因此，S2切换期间的瞬态电压大大降低，如图17所示，开关瞬间有向下200多伏的电压，经过短暂调整，S2两端电压逐渐变为电路中的谐振电压，因此开关瞬间没有较大的电压冲击。
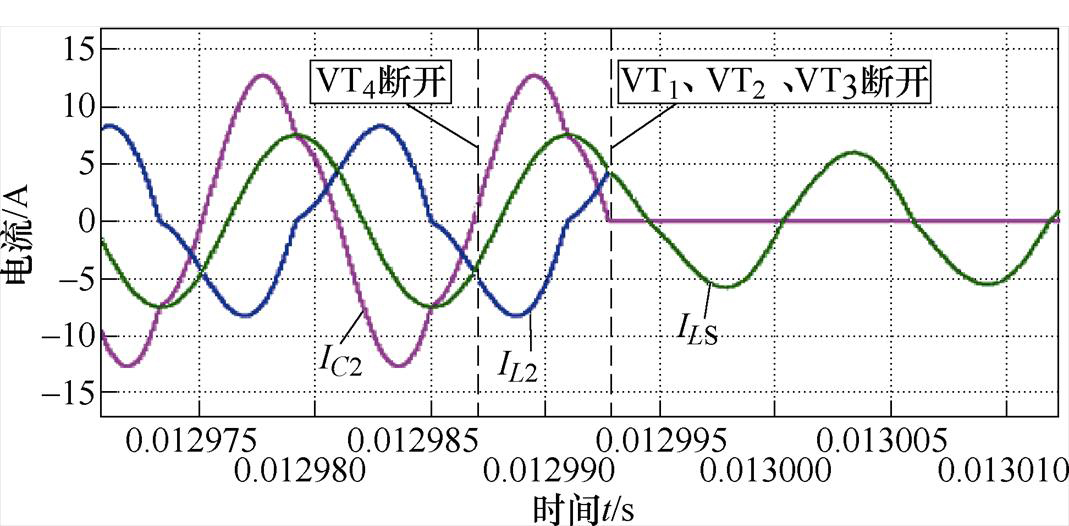
图16 开关顺序切换时副边电流
Fig.16 The current of IC2, ILS and IL2 for the duration of the switches switching in sequence
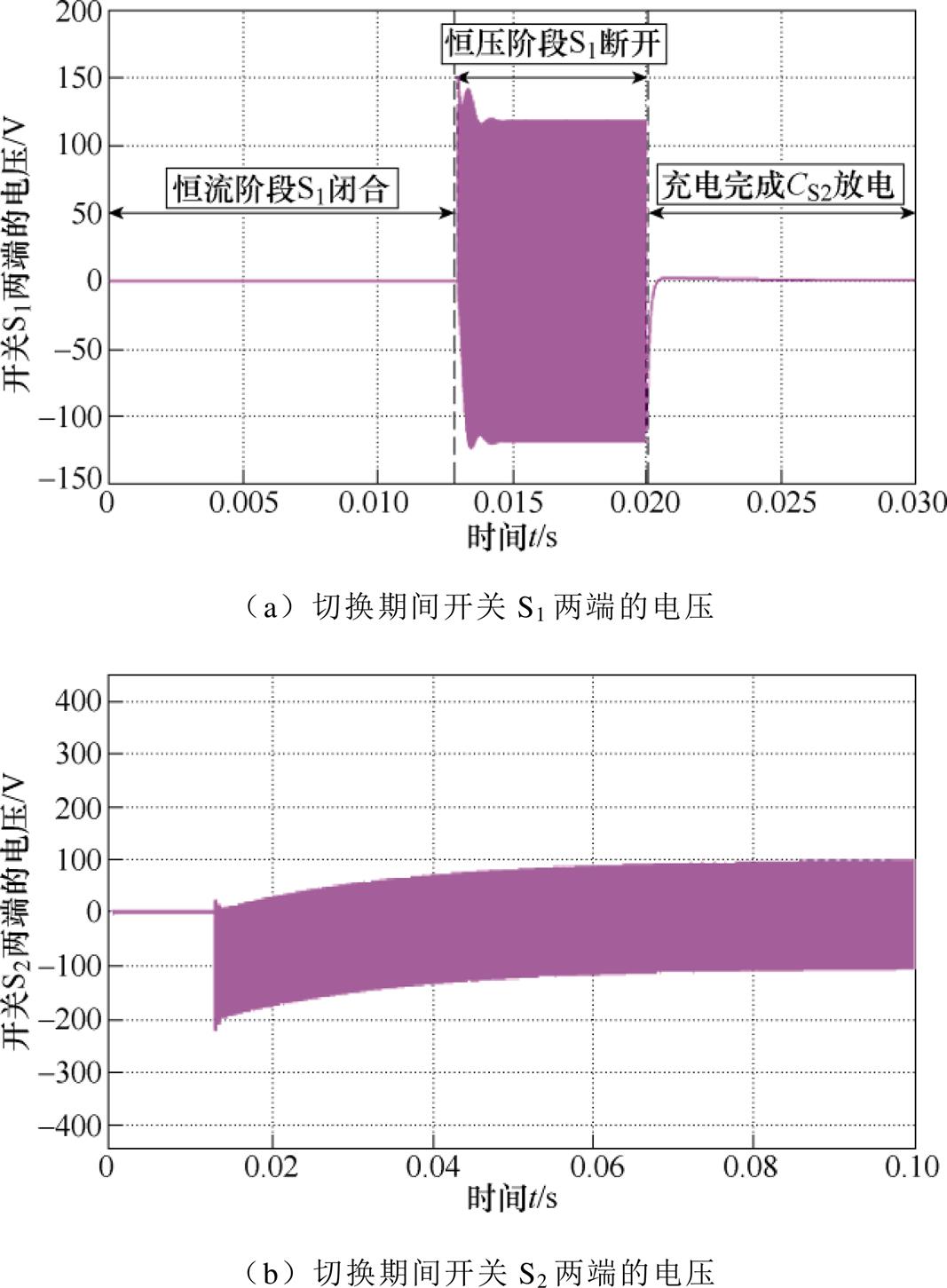
图17 开关瞬态电压
Fig.17 Voltage of S1 and S2
开关S1关断时，其两端电压波形如图17a所示，S1与谐振电容CS2并联，电容两端电压不会突变，因此开关S1两端的电压也不会突变。
根据此开关时序控制方案设计了开关切换流程如图18所示。
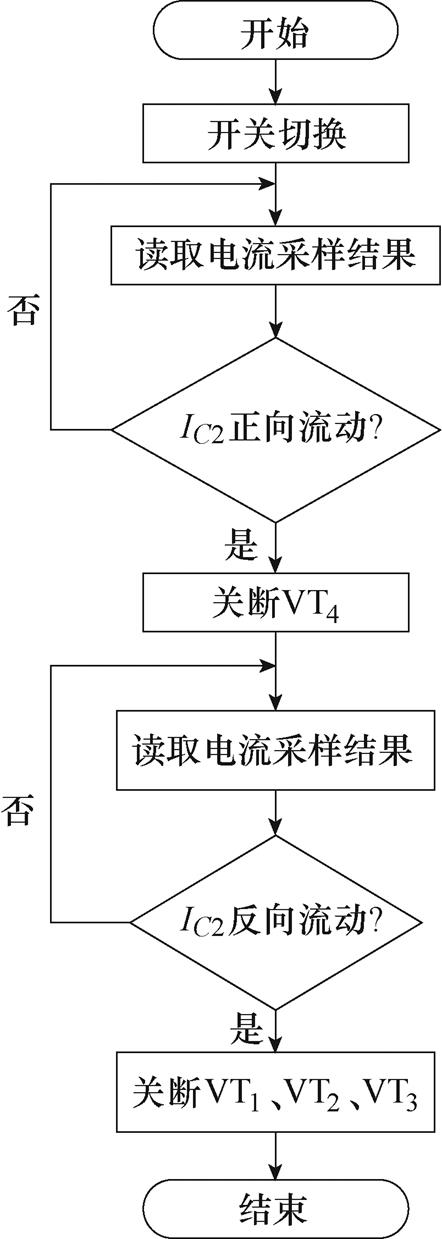
图18 开关控制流程
Fig.18 Block diagram of the switch control program
本文设计的开关S1和S2只用于恒流-恒压、异常工作情况和待机状态下的一次切换，因此S1、S2导通损耗可忽略不计。
LCC-LCC/S自切换系统结构电路如图19所示，全桥逆变器将输入的直流电逆变成交流电供给发射线圈LP，发射线圈LP通过磁场耦合将能量传递到副边接收线圈LS，再经副边不可控整流装置将交流电转变为直流电给负载供电，电压采样电路将采集到的电压信号发送给控制芯片，当检测到负载电压达到46.91 V时，控制芯片向驱动电路发送信号将开关断开，系统进入恒压充电模式，一直到充电结束。
在整个充电过程中，若检测到接收线圈中的电流IS发生异常，则控制芯片可向驱动电路发送信号将开关导通或断开，从而实现异常工作情况下停机有效保护电路，系统程序控制框图如图20所示。
对于本文两阶段恒流-恒压充电来讲，充电过程先是恒流充电，电压逐渐升高。在本文选用的负载情况下，负载等效电阻为8.1 W 时，电压升高至46.91 V，立即切换开关。在其他负载情况下，负载等效电阻为8.1 W 时，升高的电压值是有差别的。因此，不同负载情况下，只需将程序中的切换电压46.91 V修改成相应的负载电压，就能实现不同电池负载的最优切换。
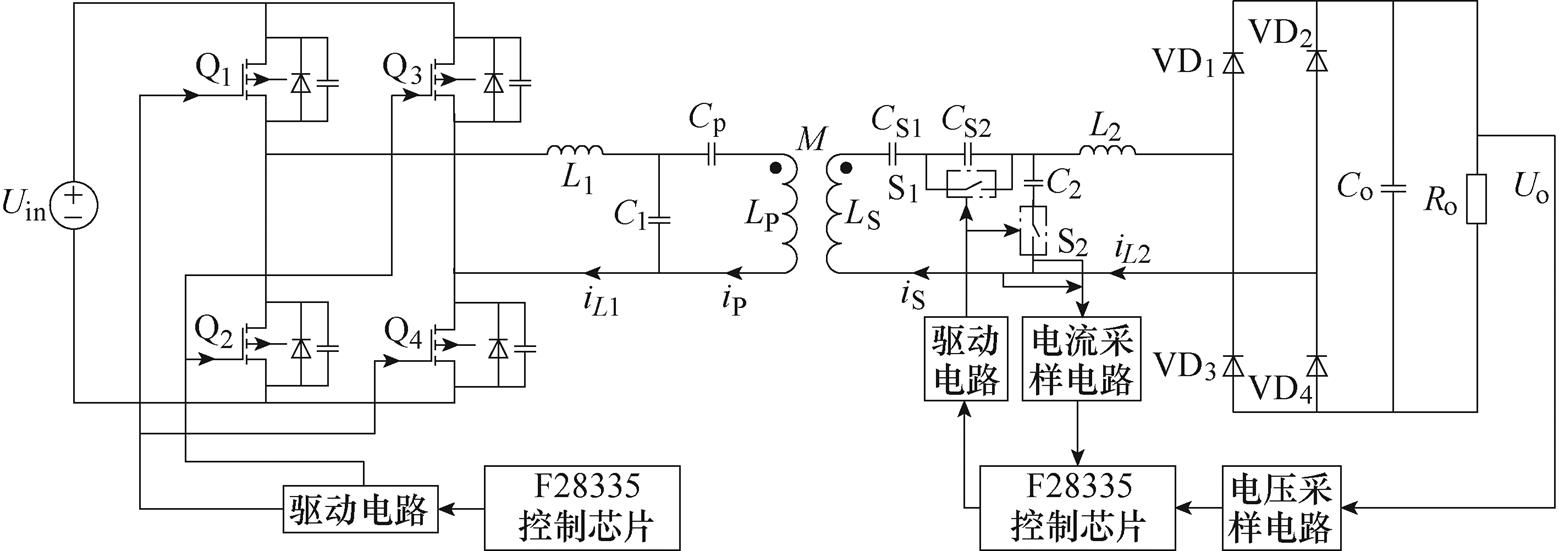
图19 LCC-LCC/S自切换系统结构
Fig.19 LCC-LCC/S self-switching system
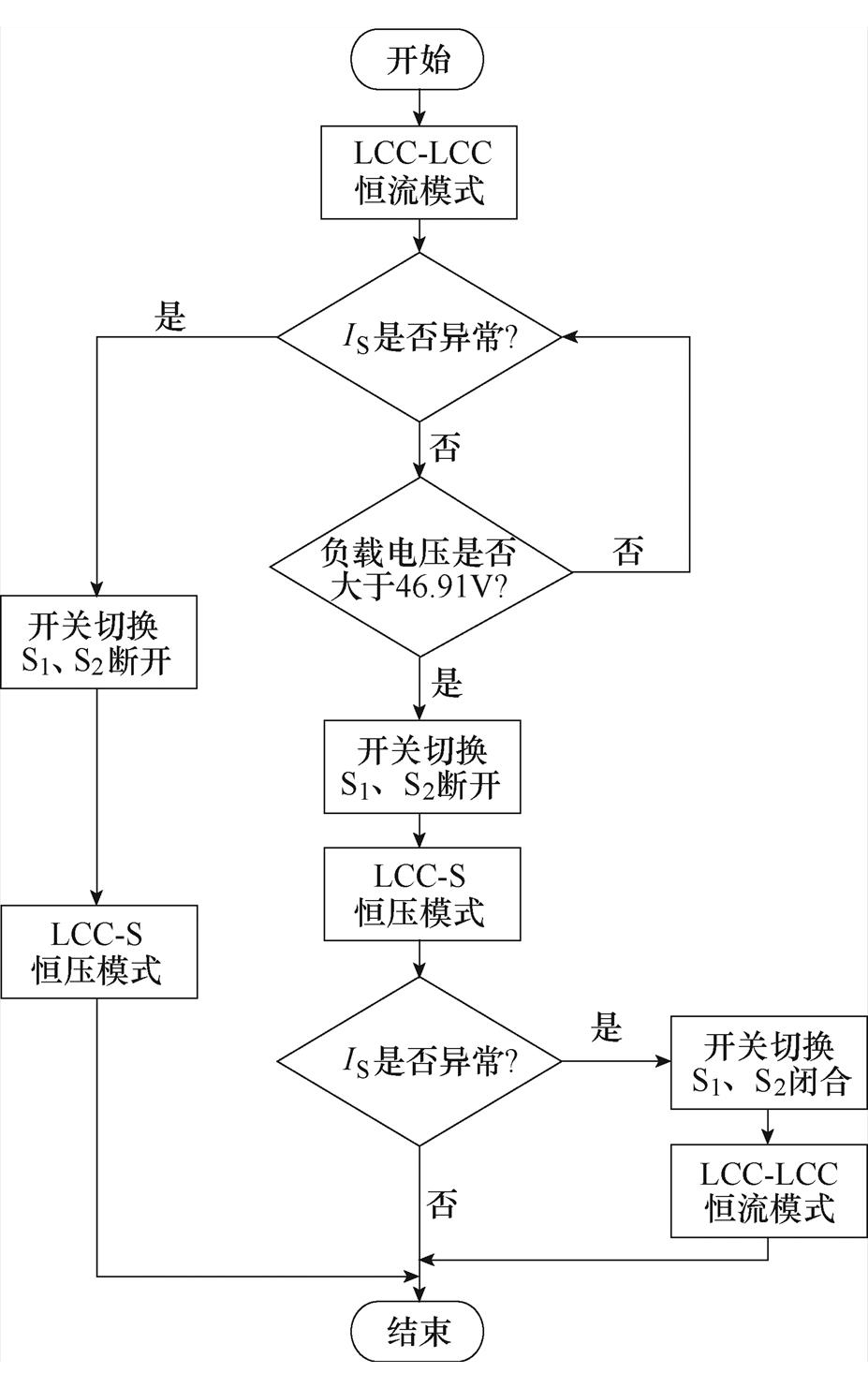
图20 LCC-LCC/S自切换系统程序控制框图
Fig.20 Block diagram of the program control of the LCC-LCC/S self-switching system
在整个正常充电过程中，负载上的电压电流变化曲线如图21所示。
从图21中可以看出，在恒流充电阶段最大电流为5.03 A，最小电流为4.69 A，在恒压阶段的最大电压为48.92 V，最小电压为46.91 V，故可认为恒流阶段的输出电流和恒压阶段的输出电压基本保持恒定，且在恒流-恒压切换点即负载电阻为10 W 时的输出电流与电压基本不存在落差。
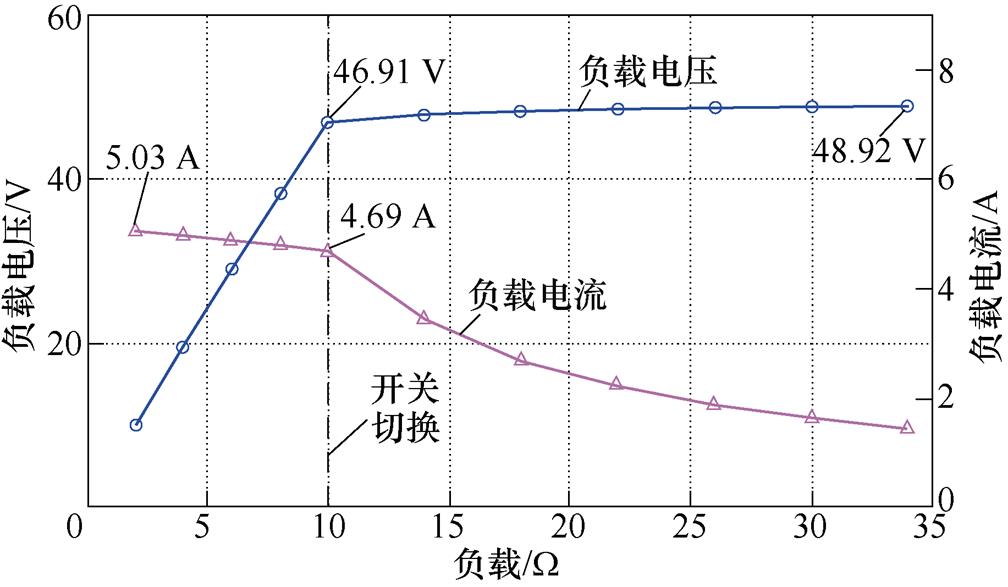
图21 全范围充电的输出电压与电流变化曲线
Fig.21 The output voltage and current curves for full-range charging process
开关切换前后逆变器输出电压和电流的波形如图22所示。
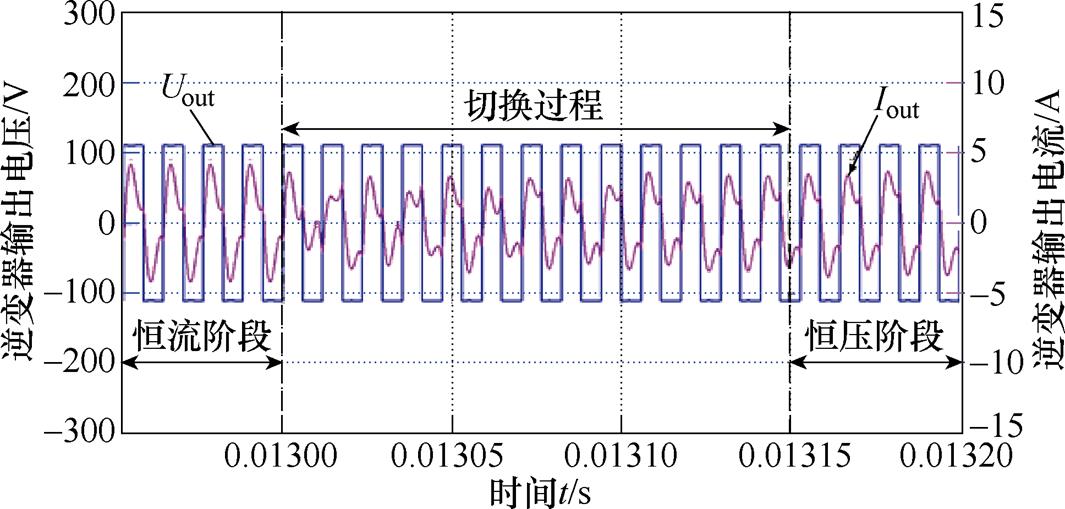
图22 开关切换前后逆变器输出电压与电流仿真波形
Fig.22 The simulation waveforms of inverter output voltage and current during charging mode switching
从图22中可以看出，开关切换前中后逆变器输出电压与电流基本保持同相位且切换过程中逆变器输出的电压与电流没有太大的波动，具有良好的ZPA特性。
复合拓扑的输出功率与效率曲线如图23所示，图23a中的仿真曲线与理论计算的输出功率曲线高度吻合，整个充电过程的输出功率先增大、后减小，最高输出功率为242.2 W，且恒流-恒压切换点处输出功率波动较小。
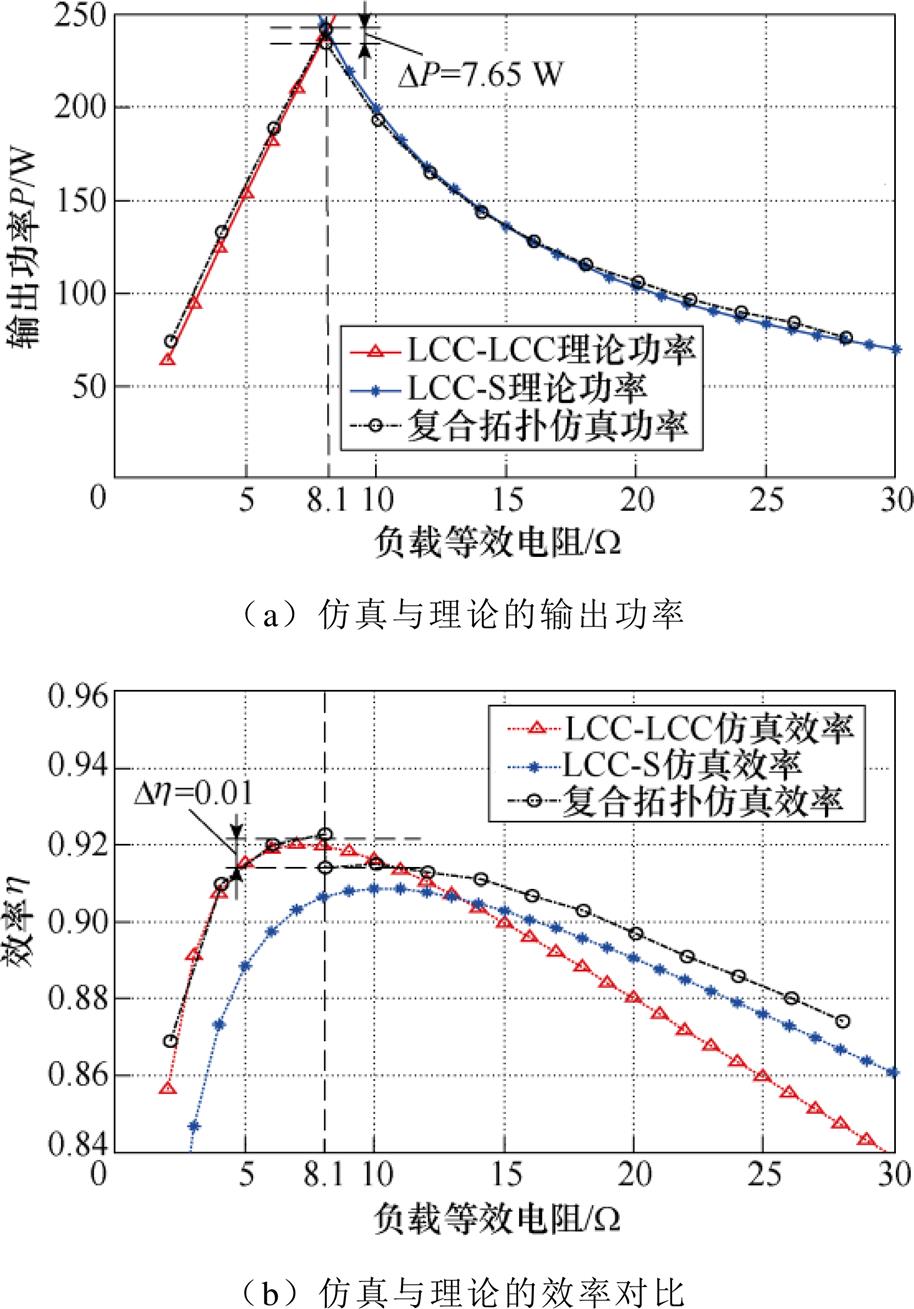
图23 复合拓扑的输出功率与效率
Fig.23 Output power and efficiency of composite topology
从图23b中可以看出，整个充电过程中复合拓扑的理论计算效率与仿真效率基本吻合且复合拓扑始终保持着86 %～92 %的充电效率，充分利用了这两种拓扑充电效率高的区段，避开了这两种拓扑充电效率低的区段。
本文设计的LCC-LCC/S复合拓扑相对于目前设计较多的S-S/P拓扑有很多优势，如图24a所示，在恒流充电阶段LCC-LCC拓扑的充电效率始终高于SS拓扑。
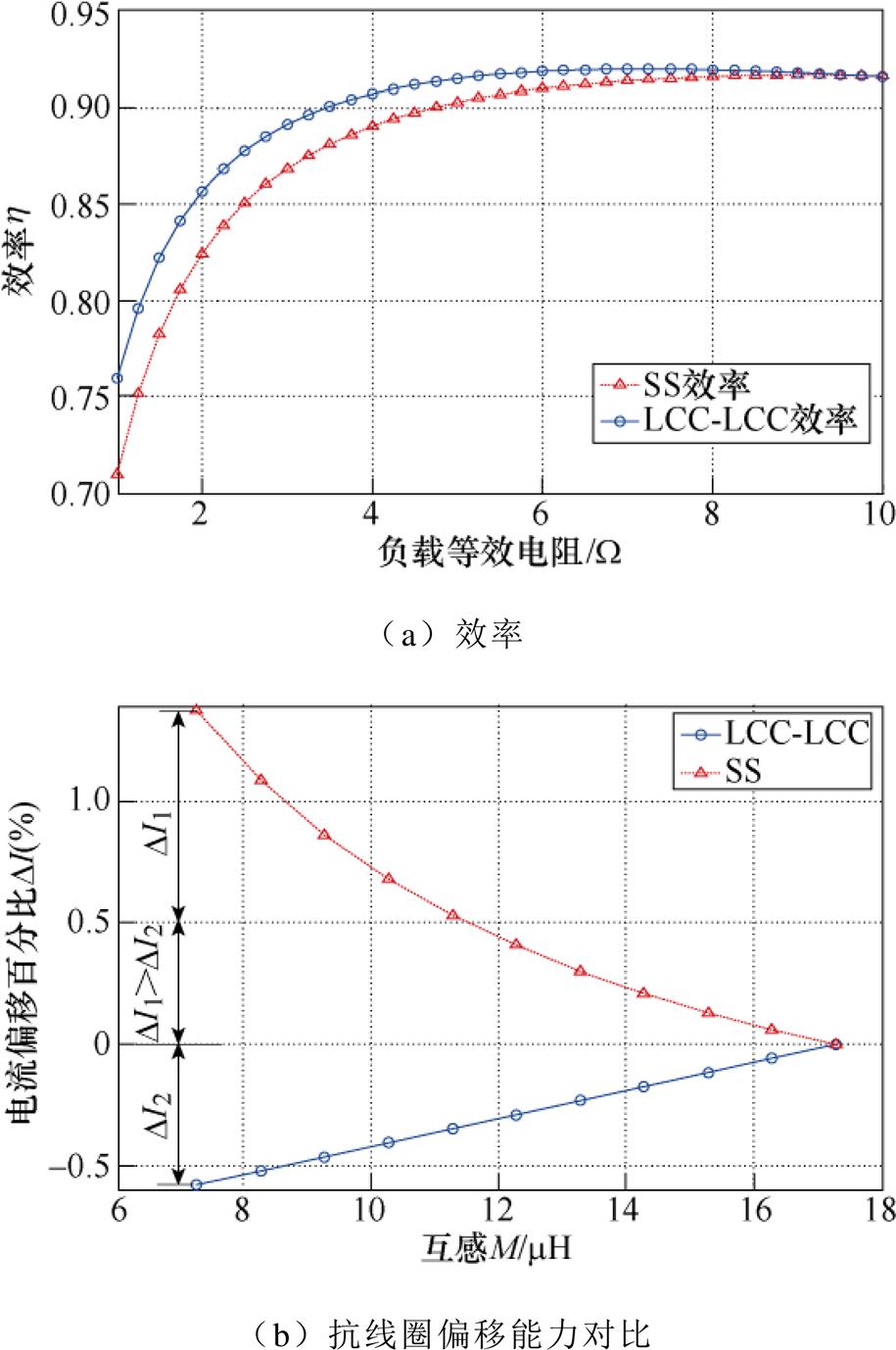
图24 LCC-LCC拓扑与SS拓扑特性的对比
Fig.24 Comparison between the characteristics of LCC-LCC topology and SS topology
另外，LCC-LCC拓扑的抗线圈偏移能力也优于SS拓扑，在图24b中，定义电流偏移百分比DI为
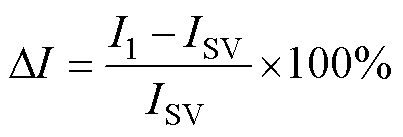（37）
式中，ISV为发射线圈与接收线圈对齐时，M= 17.28 mH的输出电流；I1为发射线圈与接收线圈发生偏移，即M减小时的输出电流。
从图4中可以看出，当线圈发生偏移即发射线圈与接收线圈互感减小时，LCC-LCC与零轴之间的落差小于SS与零轴之间的落差，因此，LCC-LCC拓扑输出电流的抗线圈偏移能力优于SS拓扑。
除了恒流阶段LCC-LCC拓扑有很大的优势之外，在恒压阶段LCC-S拓扑相对于PS拓扑也有较大的优势。LCC-S拓扑与PS拓扑特性的对比如图25所示。图25a中，恒压充电阶段LCC-S拓扑的效率始终大于PS拓扑的效率。在图25b中，定义电压偏移百分比DU为
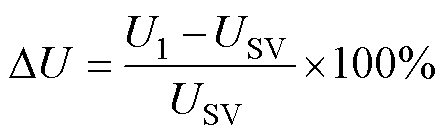（38）
式中，USV为发射线圈与接收线圈对齐时，M= 17.28 mH的输出电压；U1为发射线圈与接收线圈发生偏移，即M改变时的输出电压。
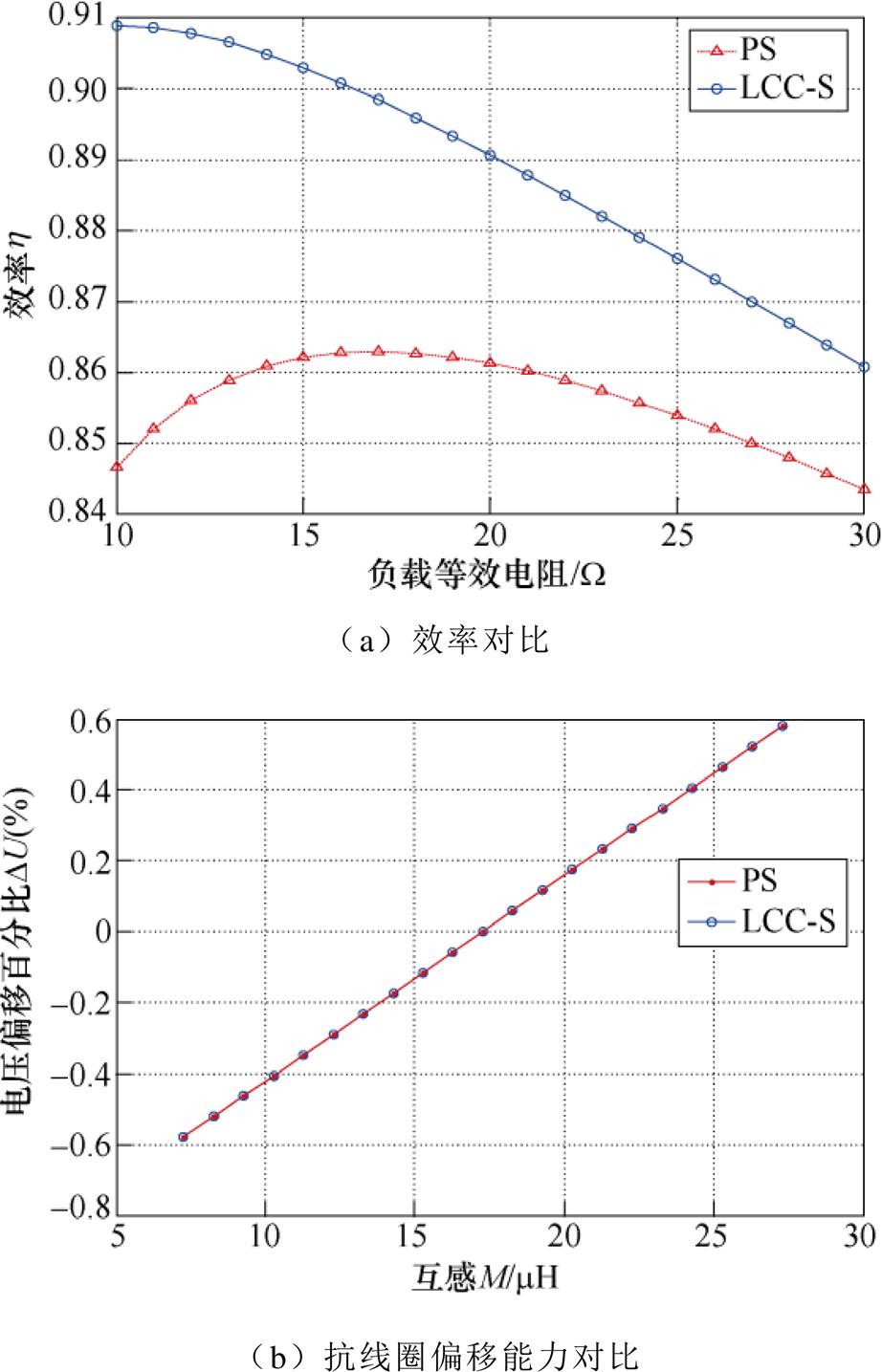
图25 LCC-S拓扑与PS拓扑的特性对比
Fig.25 Efficiency comparison between LCC-S topology and PS topology
则从图25b中可以看出，两条曲线完全重合，LCC-S拓扑与PS拓扑的抗线圈偏移能力相同。
在发射线圈与接收线圈之间互感发生变化的过程中，会导致系统中的工作频率发生短暂的波动；且在实际应用过程中，系统的工作频率很有可能受到环境温度等影响使电气参数发生变化致工作频率发生变化，因此有必要对系统的抗频率偏移特性进行分析。
在抗频率偏移这一方面，LCC-LCC拓扑也要优于SS拓扑，LCC-LCC拓扑与SS拓扑的抗频率偏移能力对比如图26所示。图26中，定义效率偏移百分比Dh 为
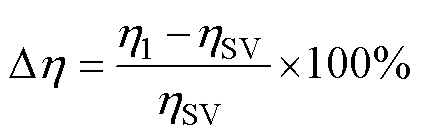（39）
式中，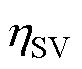
为工作频率为85 kHz时系统的效率；
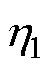为工作频率偏移85 kHz时系统的效率。
则从图26a和图26b对比可以看出，当工作频率发生偏移、负载较小时，LCC-LCC和SS拓扑抗频率偏移能力基本一致，但随着负载电阻的增加，LCC-LCC的曲线比SS拓扑的曲线更贴近零轴且更平稳，意味着LCC-LCC拓扑有着更好的抗频率偏移能力。
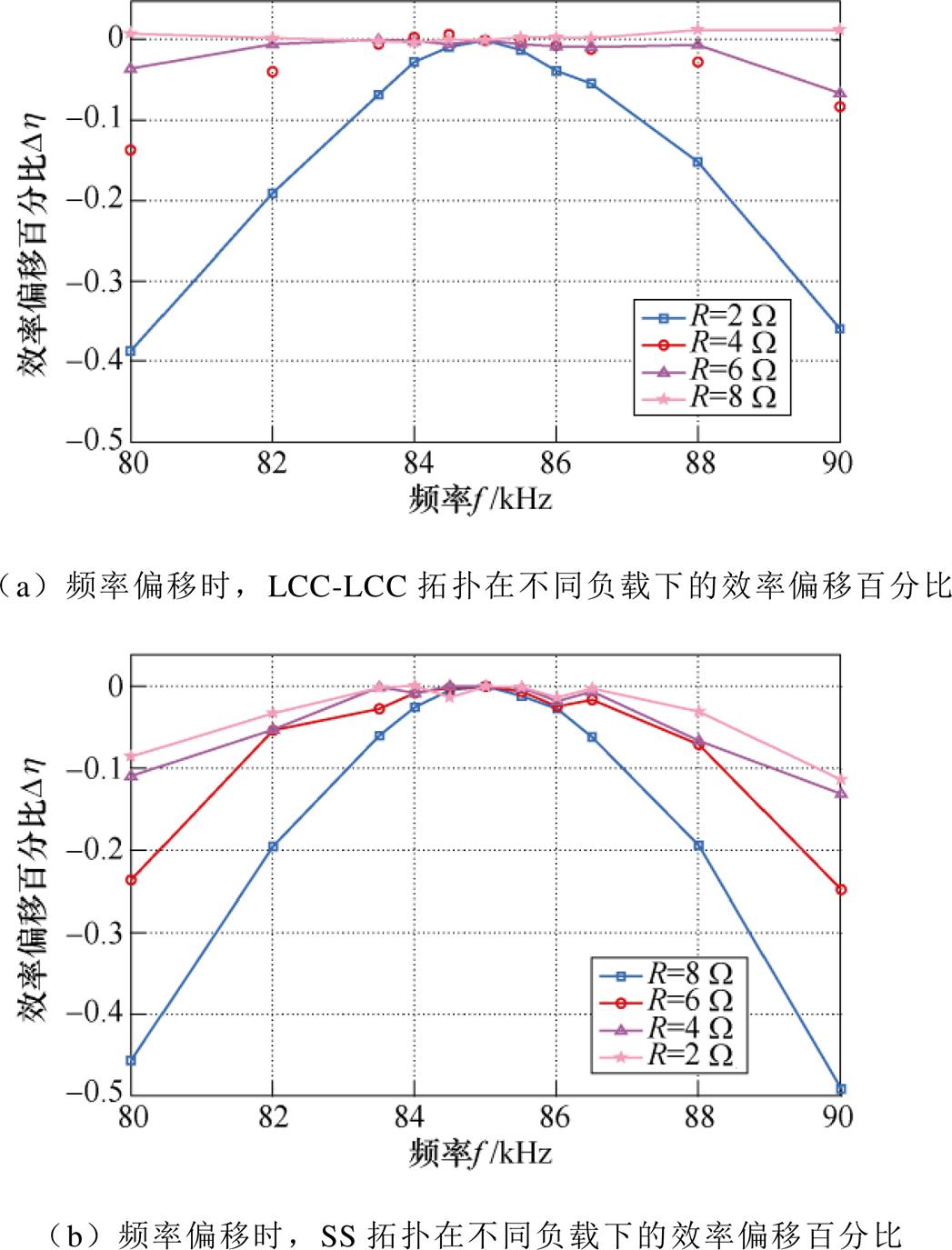
图26 LCC-LCC拓扑与SS拓扑的抗频率偏移能力对比
Fig.26 Comparison between anti-frequency offset of LCC-LCC topology and SS topology
实验平台如图27所示，实验参数见表3。
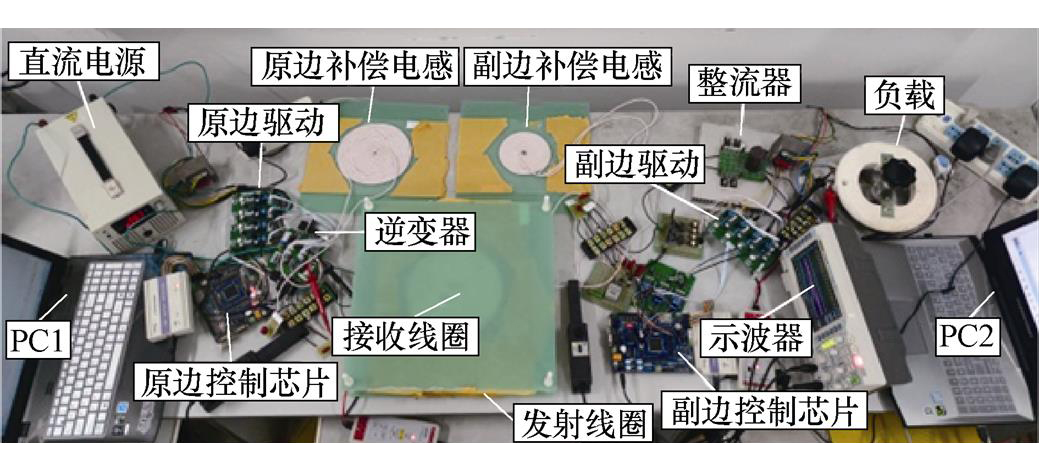
图27 实验平台
Fig.27 Experimental platform
表3 实验参数
Tab.3 Experimental parameters
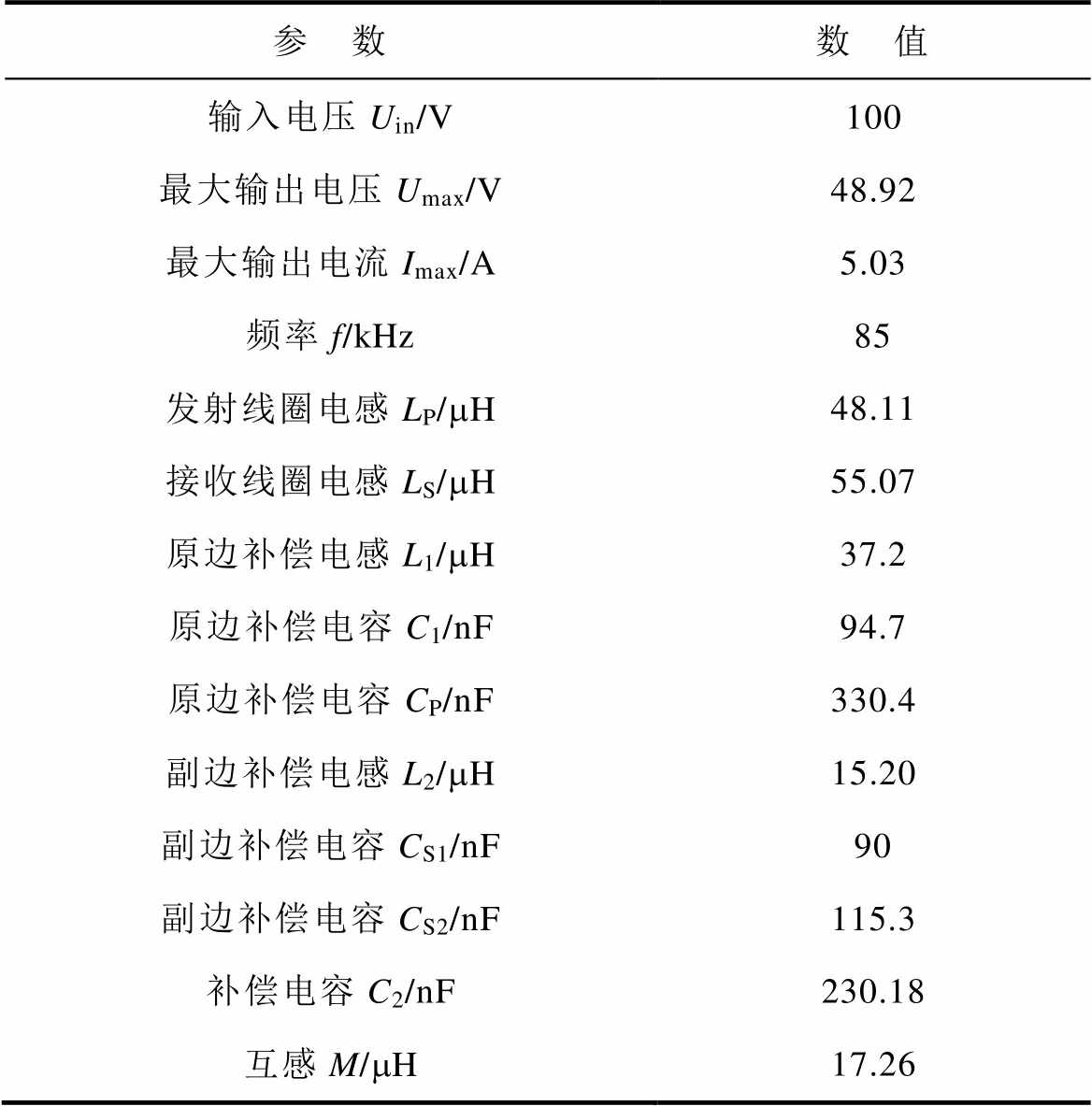
参 数数 值 输入电压Uin/V100 最大输出电压Umax/V48.92 最大输出电流Imax/A5.03 频率f/kHz85 发射线圈电感LP/mH48.11 接收线圈电感LS/mH55.07 原边补偿电感L1/mH37.2 原边补偿电容C1/nF94.7 原边补偿电容CP/nF330.4 副边补偿电感L2/mH15.20 副边补偿电容CS1/nF90 副边补偿电容CS2/nF115.3 补偿电容C2/nF230.18 互感M/mH17.26
图28为恒流模式下不同负载大小时系统输出电流，从图28中可以看出，即使负载大小发生变化，输出电流也基本保持不变，故可认为其恒流模式下的输出电流与负载无关。
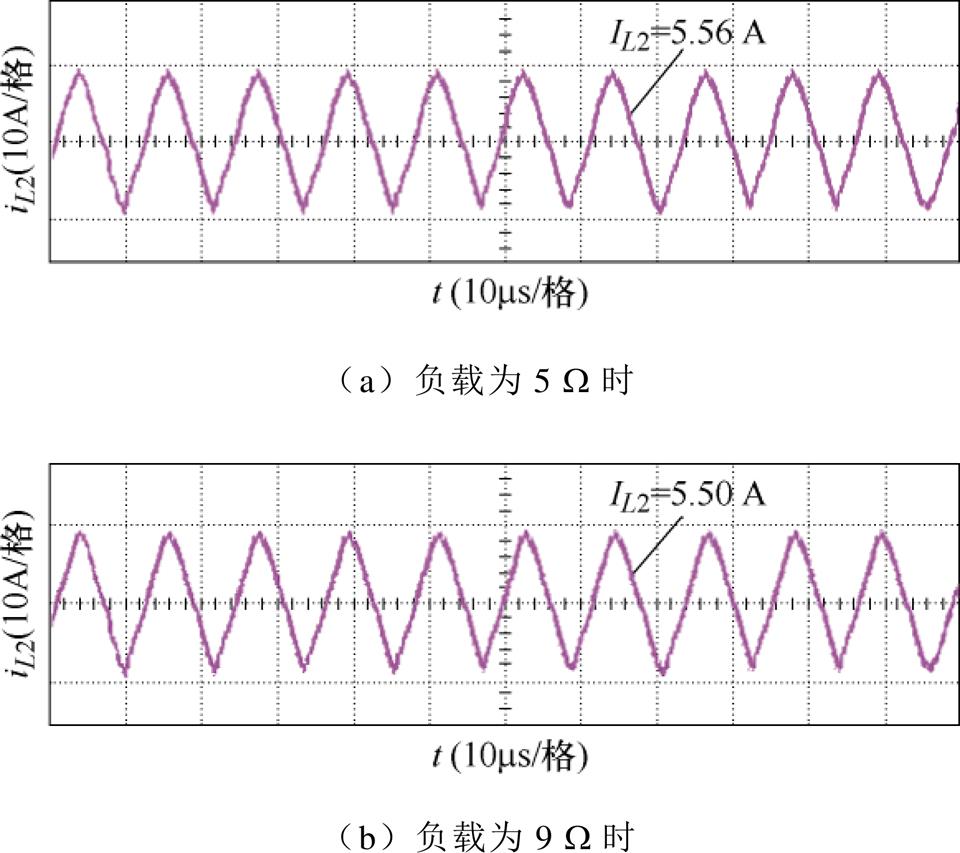
图28 恒流模式下不同负载大小时的输出电流
Fig.28 Output current at different loads in CC mode
图29为恒压模式下不同负载大小时系统输出电压，图29中可以看出，即使负载大小发生变化，输出电压也基本保持不变，故可认为其恒压模式下的输出电压与负载大小无关。
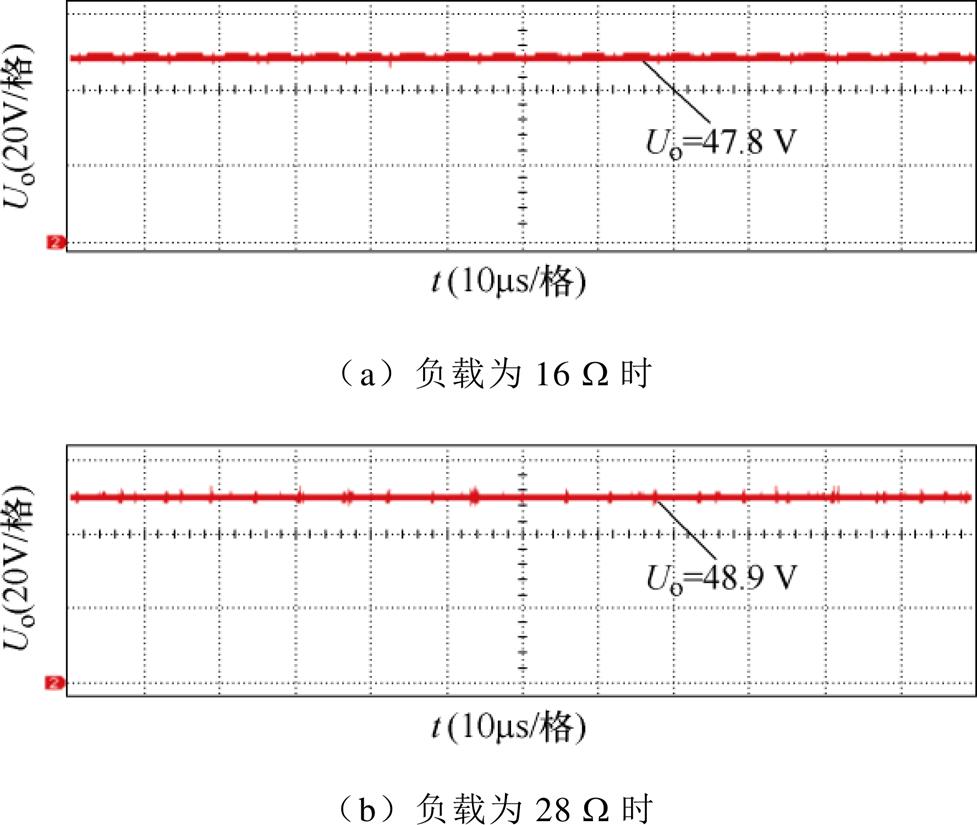
图29 恒压模式下不同负载大小时的输出电压
Fig.29 Output voltage at different loads in CV mode
为了验证开关切换时系统的稳定性，让系统先处于LCC-LCC恒流模式，当转折电阻为10 W 时，开关S1、S2断开，进入LCC-S恒压模式，开关切换时的输出电压与电流暂态响应实验波形如图30所示。从图30中可以看出，开关切换前后系统的输出电流仅变化了0.02 A，输出电压仅变化了0.2 V，切换过程中的落差极小，不会对蓄电池造成损坏。
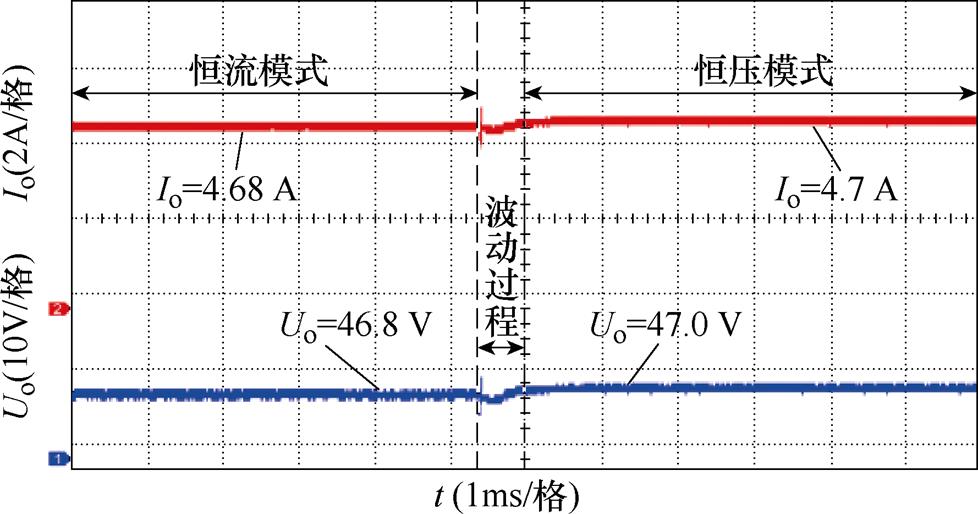
图30 开关切换时的输出电压与电流暂态响应实验波形
Fig.30 Experimental waveforms of output voltage and currenttransient response during charging mode switching
图31给出了恒流和恒压模式下逆变器输出的电压与电流波形。一般情况下，为了避免无功能量的产生，恒流和恒压模式的逆变器输出电压与电流基本同相位，实现ZPA特性。但为了实现软开关特性，本文使输入阻抗为弱感性，输出电流略滞后于输出电压。
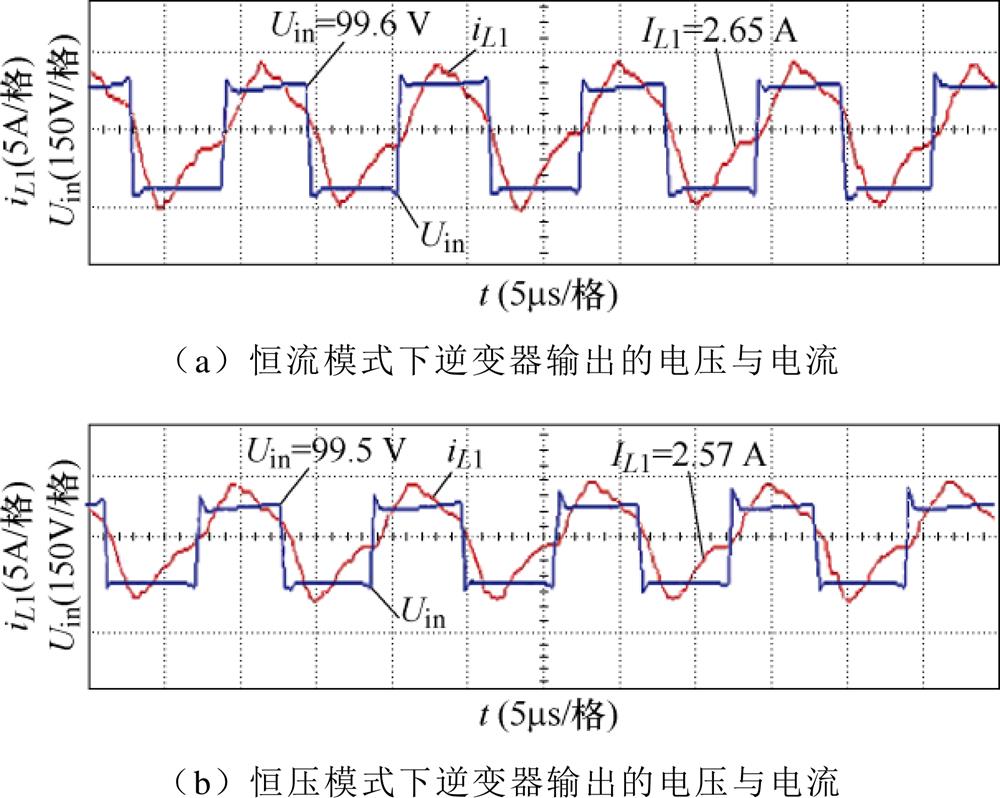
图31 逆变器输出电压与电流实验波形
Fig.31 Experimental waveforms of inverter output voltage and current
复合拓扑实验与仿真效率对比如图32所示，从图中可以看出，仿真与实验测试的效率结果基本一致。
图33为负载切除时逆变器输出电流的暂态响应实验波形，从图33中可以看出，当充电完成负载移除后，输出电流迅速下降到一个较小值，即无需任何检测和控制电路，便能使系统自动进入低功耗待机状态，具有良好的负载自适应性，与图9中的仿真结果一致。
图34为恒流-恒压模式下副边缺失时的原副边器件中的电流波形，从图34中可以看出，当发生副边缺失时，发射线圈电流基本保持不变，逆变器输出的高次谐波在L1和C1中反复传递，与理论分析和仿真结果一致。
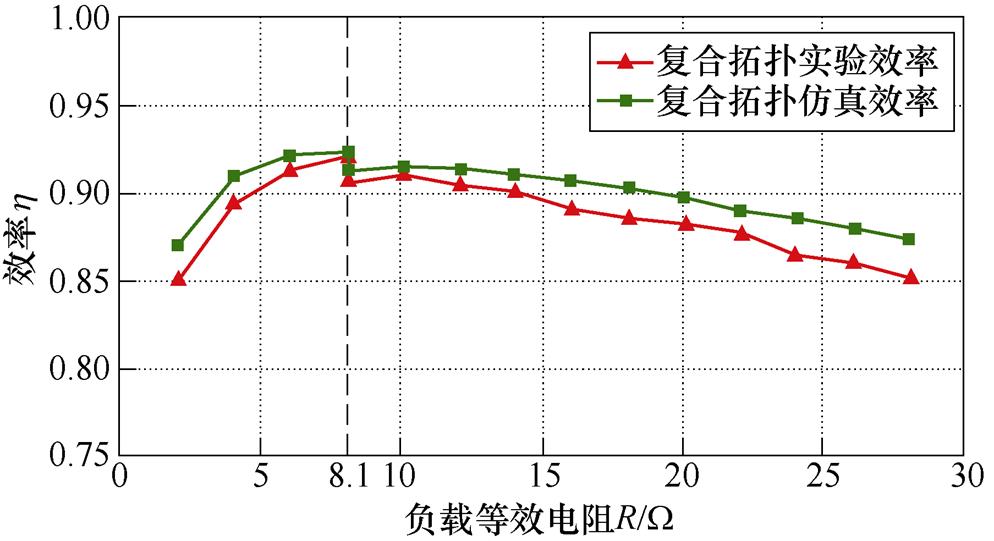
图32 复合拓扑实验与仿真效率对比
Fig.32 Comparison between experimental efficiency and simulated efficiency
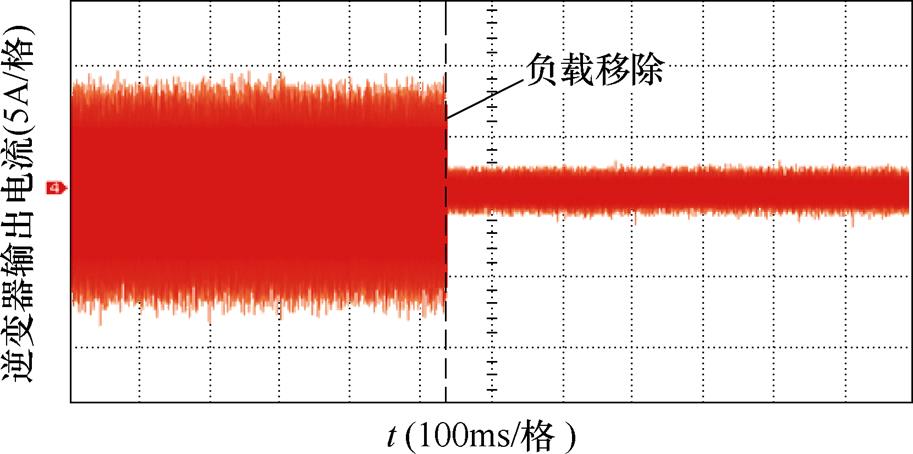
图33 负载切除时逆变器输出电流暂态响应实验波形
Fig.33 Experimental waveform of inverter output current transient response during the load removal
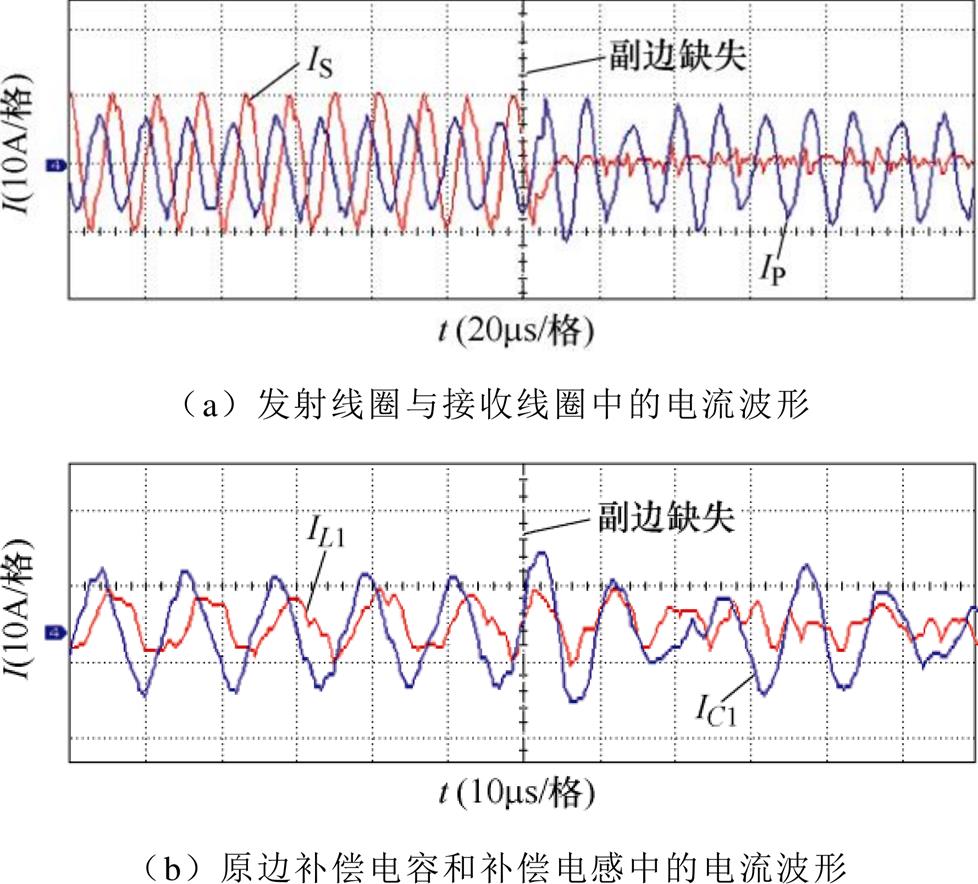
图34 副边缺失时的原副边器件实验电流波形
Fig.34 Experimental current waveform for the duration of the secondary side missing
本文提出了一种基于LCC-LCC/S复合拓扑的电路模型，通过在副边加交流开关和附加电容的方法，实现由恒流切换恒压的两阶段充电，有效地解决了恒流过冲和恒压欠冲的问题，并验证了所提出的系统性能优于目前应用较多的S/SP复合拓扑。另外所提出的系统能有效应对充电过程中出现的副边缺失、负载短路、负载开路等异常工作情况，并在充电完成负载移除时，无需任何检测或控制装置系统便能自动进入低功耗待机状态，开关切换前后电流落差仅为0.02 A，电压落差仅为0.2 V，最大输出电压48.92 V，最大输出电流5.03 A，最大输出功率为242.26 W，效率处在86 %～92 %之间，本文所提出的系统具有安全性、可靠性和高效性，可广泛应用于蓄电池充电，为WPT技术在电动车上的应用夯实了基础。
参考文献
[1] Nikola T. System of transmission of electrical energy: US0645576[P]. 1900-03-20.
[2] Li Zhenjie, Zhu Chunbo, Jiang Jinhai, et al. A 3kW wireless power transfer system for sightseeing car supercapacitor charge[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3301-3316.
[3] 赵军, 赵毅航, 武志军, 等. 电动汽车无线充电系统对心脏起搏器的电磁兼容与热效应影响[J]. 电工技术学报, 2022, 37(增刊1): 1-10.
Zhao Jun, Zhao Yihang, Wu Zhijun, et al. The influence of electric vehicle wireless charging system on electromagnetic compatibility and thermal effect of cardiac pacemaker[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 1-10.
[4] 吴丽君, 李冠西, 张朱浩伯, 等. 一种具有恒流恒压输出自切换特性的电动汽车无线电能传输系统拓扑[J]. 电工技术学报, 2020, 35(18): 3781-3790.
Wu Lijun, Li Guanxi, Zhang Zhuhaobo, et al. A wireless power transfer system topology with automatic switching characteristics of constant current and constant voltage output for electric vehicle charging[J]. Transactions of China Elect- rotechnical Society, 2020, 35(18): 3781-3790.
[5] 程志远, 陈坤, 李东东, 等. 旋转式无线充电系统偏移特性研究[J]. 电工技术学报, 2021, 36(22): 4648-4657.
Cheng Zhiyuan, Chen Kun, Li Dongdong, et al. Research on offset characteristics of rotary wireless charging system[J]. Transactions of China Electro- technical Society, 2021, 36(22): 4648-4657.
[6] Obayashi S, Kanekiyo Y, Nishizawa K, et al. 85-kHz band 450-W inductive power transfer for unmanned aerial vehicle wireless charging port[C]//Proceedings of IEEE Wireless Power Transfer Conference (WPTC), London, UK, 2020: 80-84.
[7] Yang Lei, Zhang Yuanqi, Li Xiaojie, et al. Analysis and design of four-plate capacitive wireless power transfer system for undersea applications[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 202-211.
[8] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[9] Han Wei, Chau K T, Jiang Chaoqiang, et al. Design and analysis of quasi-omnidirectional dynamic wireless power transfer for fly-and-charge[J]. IEEE Transactions on Magnetics, 2019, 55(7): 1-9.
[10] 姚若玉, 曲小慧, 郁继栋, 等. 自适应电池充电曲线的三线圈电池无线充电器[J]. 电力系统自动化, 2022, 46(7): 170-177.
Yao Ruoyu, Qu Xiaohui, Yu Jidong, et al. Three-coil wireless battery charger with self-adaptation to battery charging curve[J]. Automation of Electric Power Systems, 2022, 46(7): 170-177.
[11] 郁继栋, 曲小慧, 王国雨, 等. 基于极简三电容补偿的单级式无线电池充电器[J]. 电力系统自动化, 2021, 45(14): 165-172.
Yu Jidong, Qu Xiaohui, Wang Guoyu, et al. Single-stage inductive power transferred battery charger based on minimal three-capacitor com- pensation[J]. Automation of Electric Power Systems, 2021, 45(14): 165-172.
[12] 王春芳, 岳睿, 李厚基, 等. 基于单管电路的恒流恒压无线充电系统研究[J]. 电工技术学报, 2021, 36(22): 4637-4647, 4657.
Wang Chunfang, Yue Rui, Li Houji, et al. Research on constant-current and constant-voltage wireless charging system based on single-switch circuit[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4637-4647, 4657.
[13] Kim M, Byeon J, Lee B K, et al. Performance analysis of magnetic power pads for inductive power transfer systems with ferrite structure variation[C]//Pro- ceedings of Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, 2017: 1-6.
[14] Wang Meng, Feng Jing, Shi Yanyan, et al. Demag- netization weakening and magnetic field con- centration with ferrite core characterization for efficient wireless power transfer[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(3): 1842- 1851.
[15] Wang C S, Stielau O H, Covic G A. Design considerations for a contactless electric vehicle battery charger[J]. IEEE Transactions on Industrial Electronics, 2005, 52(5): 1308-1314.
[16] Wu H H, Gilchrist A, Sealy K D, et al. A high efficiency 5kW inductive charger for EVs using dual side control[J]. IEEE Transactions on Industrial Informatics, 2012, 8(3): 585-595.
[17] Huang Mo, Lu Yan, Martins R P. A reconfigurable bidirectional wireless power transceiver for battery- to-battery wireless charging[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7745-7753.
[18] Buja G, Bertoluzzo M, Mude K N. Design and experimentation of WPT charger for electric city car[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7436-7447.
[19] Li Hongchang, Li Jie, Wang Kangping, et al. A maximum efficiency point tracking control scheme for wireless power transfer systems using magnetic resonant coupling[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3998-4008.
[20] Boys J T, Covic G A, Xu Yongxiang. DC analysis technique for inductive power transfer pick-ups[J]. IEEE Power Electronics Letters, 2003, 1(2): 51-53.
[21] 廖志娟, 周磊, 吴镇, 等. 变结构LC-CLCL拓扑恒压恒流型电场耦合电能传输系统[J]. 中国电机工程学报, 2021, 41(17): 6039-6050.
Liao Zhijuan, Zhou Lei, Wu Zhen, et al. An electric-field coupled power transfer system with constant voltage and constant current output based on changeable LC-CLCL resonant circuit[J]. Pro- ceedings of the CSEE, 2021, 41(17): 6039-6050.
[22] 张辉, 王换民, 李宁, 等. 电动汽车无线充电混合补偿拓扑电路分析[J]. 电力系统自动化, 2016, 40(16): 71-75.
Zhang Hui, Wang Huanmin, Li Ning, et al. Analysis on hybrid compensation topology circuit for wireless charging of electric vehicles[J]. Automation of Electric Power Systems, 2016, 40(16): 71-75.
[23] 苏玉刚, 谢诗云, 王智慧, 等. 基于F-F/T变结构谐振网络的恒压-恒流型电场耦合电能传输系统[J]. 电工技术学报, 2019, 34(6): 1127-1136.
Su Yugang, Xie Shiyun, Wang Zhihui, et al. An electric-field coupled power transfer system with constant voltage and constant current output based on F-F/T changeable resonant circuit[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1127- 1136.
[24] 孙跃, 张欢, 陶维, 等. 基于变结构模式的宽负载恒压感应耦合电能传输系统[J]. 电力系统自动化, 2016, 40(5): 109-114, 126.
Sun Yue, Zhang Huan, Tao Wei, et al. Constant- voltage inductively coupled power transfer system with wide load range based on variable structure mode[J]. Automation of Electric Power Systems, 2016, 40(5): 109-114, 126.
Abstract The two-stage charging mode can solve CC overcharge and CV undercharge during battery charging. There are several ways to achieve CC/CV charging for WPT systems, such as working frequency adjustment, duty cycle adjustment, and adding a DC-DC chopper at the secondary side. Such methods can achieve CC/CV charging with high accuracy, but their control schemes need to be simplified. Moreover, the output current and voltage fluctuate greatly during the charging mode switching. The spike will impact the battery on the battery life. Therefore, this paper proposes a LCC-LCC/S self-switching CC and CV composite topology, only requiring two AC switches and a compensation capacitor on the secondary side. By simultaneously opening and closing the two AC switches, the proposed WPT system can achieve the segmented CC/CV charging and improve system safety under abnormal working conditions. Moreover, ZPA in both CC and CV charging modes can be realized, and the output voltage and current fluctuate very small during switching. At last, the performance evaluation is also given by comparing the LCC-LCC/S topology with SS/PS hybrid topology.
Firstly, the self-switching LCC-LCC/S-based composite topology is presented. The characteristics of CC/CV, ZPA, and the load optimal switching point are also analyzed. Secondly, several abnormal working conditions are analyzed, including the secondary side missing, load short-circuit, and load open-circuit. The corresponding solutions are presented. Thirdly, by comparing the system characteristics of the currently popular S/SP topology, the advantages of the LCC-LCC/S topology are highlighted. Finally, an experimental platform is built. The experimental results indicate that a highly efficient, reliable and safe WPT system is manufactured. The transmission efficiency is 86 %～92 % during the charging process, the maximum current is 5.03 A, and the maximum voltage is 48.92 V.
The simulated and experimental results show that the LCC-LCC and the LCC-S topology can achieve load-independent CC and CV output with ZPA characteristics, respectively. The output current changes only below 0.02 A, and the output voltage changes below 0.2 V during the charging mode switching. Therefore, they will not damage the battery. In order to improve charging safety and avoid WPT system damage under abnormal operating conditions, the proposed WPT system can achieve the two charging modes freely, switching the LCC-LCC topology to the LCC-S topology in the load open-circuit and the LCC-S topology to the LCC- LCC topology in the load short circuit. Moreover, the voltage peak across the switches can be effectively reduced by controlling the switching sequence for the duration of the charging mode switching. The proposed system has higher efficiency and better anti-misalignment capability than the S/PS composite system. The experimental WPT system can produce a maximum output voltage of 48.92 V, a maximum output current of 5.03 A, a maximum output power of 242.26 W, and an efficiency of 86 % to 92 %.
The following conclusions can be drawn from the simulation and the experiments: (1) The proposed LCC-LCC/S composite topology can realize a two-stage CC/CV charging output and effectively solve CC overcharge and CV undercharge problems. (2) The proposed system can effectively deal with abnormal working conditions such as secondary side missing, load short circuit, and load open circuit. In addition, the WPT system can automatically run a low-power standby state without any control after the charging completion and the load removal. (3) The voltage spike across the switches is effectively reduced through the optimal control of the switching timing. (4) The performance of the LCC-LCC/S topology on the anti-misalignment capability is better than that of the current popular S/PS composite topology.
keywords：Wireless power transfer, self-switching, constant current (CC) and constant voltage (CV), composite topology
DOI: 10.19595/j.cnki.1000-6753.tces.221236
中图分类号：TM724
国家自然科学基金面上项目（5157702）和安徽省自然科学基金面上项目（1508085）资助。
收稿日期 2022-06-28
改稿日期 2022-08-06
杨云虎 男，1973年生，博士，副教授，硕士生导师，研究方向为无线电能传输、电力电子与电力传动、控制理论与应用。E-mail: roye_yang@126.com（通信作者）
贾维娜 女，1998年生，硕士研究生，研究方向为无线电能传输。E-mail: 2219353078@qq.com
（编辑 陈 诚）