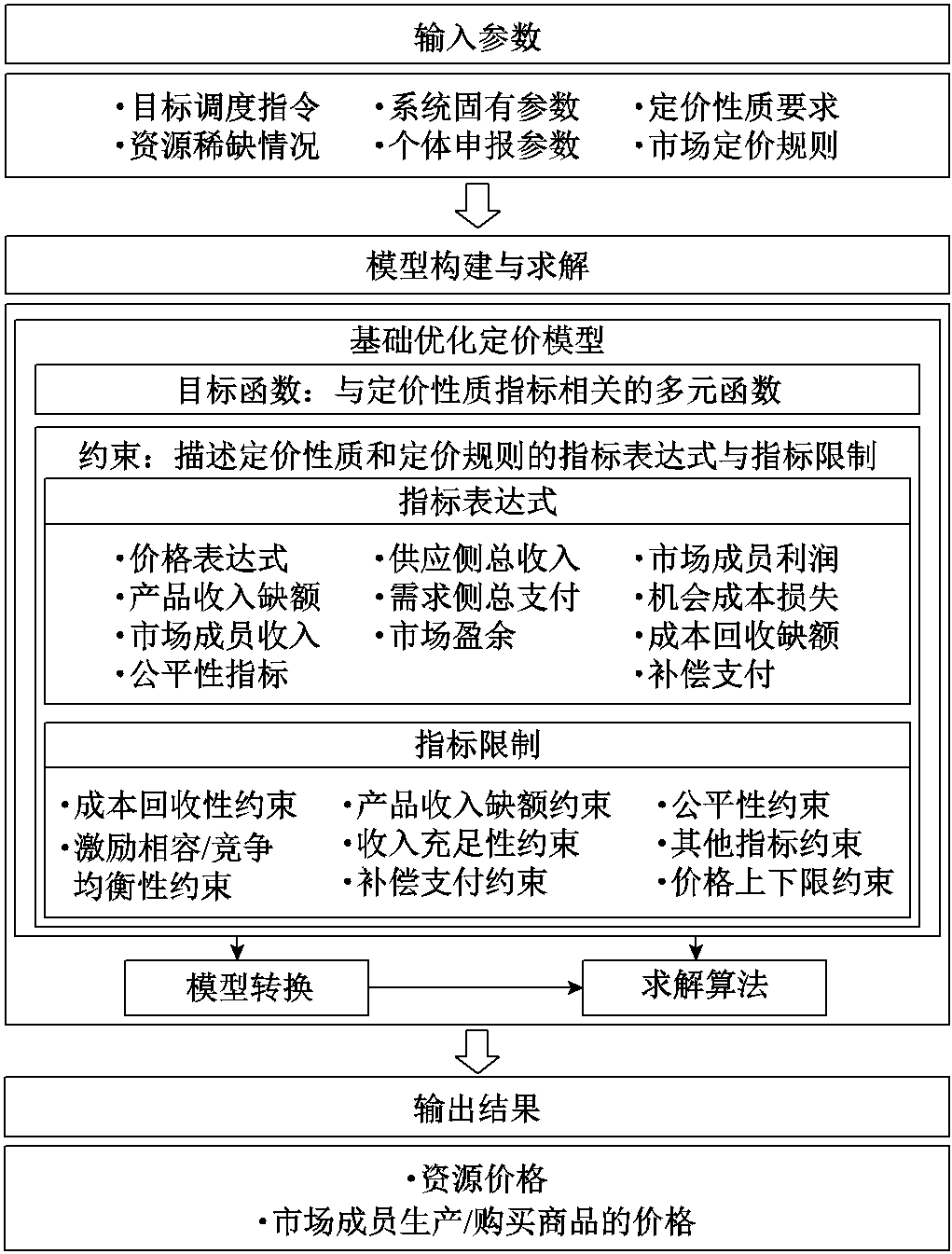
图1 通用性优化定价框架
Fig.1 The basic framework of price optimization
摘要 在电力市场中,电价通常由市场出清或优化调度等原问题的对偶解构成,具有良好的经济学意义。然而,当原问题面临退化、约束越限等问题时,基于原问题对偶解的定价方法难以保证理想的定价性质。为此,该文提出一种计及定价性质要求的通用性优化定价框架与几种不同形式的优化定价模型,以满足市场运营机构对定价性质的调控需求。首先,从优化视角剖析定价问题,总结提炼了一种通用性优化定价框架,构建通用形式的基础优化定价模型;其次,分析基础优化定价模型的典型目标函数与约束设置,基于最优化理论与对偶理论,分别构建与双层规划定价模型等价的线性规划定价模型,解析其与现有定价方法的区别与联系;再次,以特定市场出清模型及定价问题场景为例,说明所提方法的实用性;最后,基于IEEE 30节点系统和Polish 2 383节点系统进行仿真分析,结果表明所提方法可灵活优化定价性质,满足市场定价的多重需求。
关键词:电力市场 定价机制 双层规划 线性规划 对偶理论
价格是市场中协调供需双方行为,引导资源优化配置的重要工具[1-5]。合理的定价机制是我国电力市场稳定运行的核心与基础[6]。一般而言,定价机制设计时期望满足的理想性质包括:市场成员成本回收性、激励相容性(即价格与配置构成市场竞争均衡)、市场运营机构收入充足性、公平性等[7-8]。
在电力市场中,若称市场出清问题为原问题,市场出清价格通常由原问题的对偶解(或称对偶乘子、影子价格等)表述。例如,节点边际电价(Locational Marginal Price, LMP)由经济调度(Economic Dispatch, ED)问题的对偶解构成,被定义为满足节点新增单位负荷需求的系统边际成本增量[9]。对于线性规划问题而言,其对偶解可反映原问题各约束对应资源的稀缺性,具有良好的经济学意义。因此,以LMP为代表的边际定价方法在国内外电力现货市场得到了广泛的应用,且以配电网节点边际电价(Distribution Locational Marginal Price, DLMP)的形式扩展到配电侧电力市场[10-11]。
然而,在某些情况下,直接求解原问题(调度或市场出清问题)对偶解得到的电价可能无法满足实际市场需求,例如:①原问题退化,对偶问题多解,非唯一性节点电价可能导致歧视性社会福利分配等问题[12];②原问题约束达界或越限(约束松弛变量在目标函数中具有较大的惩罚系数),对偶解数值极高,节点电价出现异常尖峰,市场风险较高,市场成员难以接受[13];③原问题并未充分计及市场成员的实际可行域(如非凸成本特性[14]、时段耦合特性[15]等),由对偶解构成的节点电价难以引导市场成员跟随目标调度指令。当前,针对上述问题的相关研究可综述如下。
首先,针对原问题退化导致的价格多解问题,在工业界,市场运营主体拟在调度问题的约束或目标函数中添加扰动项来缓解对偶多解问题[16-17]。在学术界,文献[18]基于单时段市场出清问题的对偶问题与强对偶条件构造优化定价问题,以市场各类盈余的加权组合为目标引导价格的优化;文献[19]基于单时段市场出清问题的最优性条件构造优化定价问题,以最小化阻塞盈余为目标优化价格;文献[20]在文献[19]的基础上,进一步结合基于满意度的定价方法解决不同阻塞场景下的价格多解问题。文献[18-20]本质上是基于市场出清原问题的最优性条件严格约束对偶变量(价格)的优化空间。
其次,针对原问题约束越限(或达界)导致的价格尖峰问题,在工业界,PJM曾根据约束违反程度修改线路容量约束的限值,基于修改后的原问题的对偶解获得价格[21]。广东电力市场修改松弛变量在原问题目标函数中的惩罚因子,并添加约束限制机组调度变量的取值,基于修改后的原问题的对偶解获得价格。在学术界,文献[22]以最小化机会成本损失为目标,考虑价格限制,构建了双层规划优化定价模型。文献[23]解析了对偶乘子与价格的关系,在优化定价模型中嵌入一般化的价格表达式以进一步挖掘价格的优化空间。然而,文献[22-23]均采用极点遍历法处理下层优化问题,将双层规划模型转换为线性规划模型,所得模型约束数量将随时段数的增加呈指数式增长,难以适用于多时段市场出清。
再次,针对原问题未考虑市场成员的非凸特性导致的价格激励问题,文献[24]提出整数规划定价方法(Integer Programming Pricing, IP Pricing),添加个体约束将机组启停变量固定为最优解,并以约束的对偶乘子对启停定价,弥补其机会成本损失。文献[25]提出凸包定价方法(Convex Hull Pricing, ConvHP),定价问题有原问题和拉格朗日对偶问题两种表达形式,价格由对偶乘子构成[26-27]。文献[28]提出一种统一非凸定价模型,在一定目标函数设置下等价于凸包定价。
最后,针对原问题未考虑市场成员的时段耦合特性导致的价格激励问题,文献[15]提出在节点电价中引入爬坡约束的对偶乘子作为新增价格分量,以实现单时段的局部均衡和全时段的总体均衡。文献[29]基于目标调度指令构建考虑多周期激励性质的定价辅助模型,价格由系统约束的对偶乘子构成。
综上所述,解决市场定价问题的思路主要分为两类:①从原问题角度出发,修改调度或市场出清模型的约束或目标函数得到定价辅助模型,价格由定价辅助模型的对偶解构成;②从对偶角度出发,根据市场对定价性质的需求构建优化定价模型,价格是优化定价模型的决策变量。与前者相比,后者的主要优势在于:可根据市场需求直接调控价格的优化空间与优化目标,保证重要的定价性质。然而,现有研究在构造优化定价模型时,或依赖市场出清原问题的对偶问题与最优性条件,未能明确解析具体的定价性质,导致模型的可扩展性受限,难以适应于不同问题场景和多重市场需求;或未能充分利用原问题的参数、目标调度指令以及定价性质的内在特征,导致模型结构复杂,增加了计算负担。
本文的主要贡献在于:
1)提出了基于优化视角的定价问题剖析方法。归纳总结了由“输入参数-模型构建与求解-输出结果”构成的通用性优化定价框架,建立了以目标调度指令为参数,以价格为决策变量,以满足多种定价性质、定价规则为目标或约束的双层规划基础优化定价模型,解析表征了成本回收性、激励相容性、收入充足性、公平性等定价要求。
2)给出了典型优化定价模型及其转换方法。根据优化定价模型目标与约束的设置,构造了四种典型的基础优化定价模型,基于最优化理论与对偶理论,提出了原问题形式与对偶问题形式两种模型转换方法,可将双层规划基础优化定价模型转换为线性规划模型,探讨了所提定价方法与现有定价方法的区别与联系。
3)针对电力市场多时段经济调度下的价格尖峰问题,说明了所提定价方法的合理性。根据问题性质选取合适的基础定价模型与模型转换方法,建立了考虑多重定价性质约束的线性规划定价优化模型。算例分析表明,所提优化定价方法可实现不同定价性质的灵活权衡,通过合理调控价格优化空间,所提方法在计算时间上与节点边际定价方法相当,适应于实际市场需求。
本小节基于优化视角分析定价问题,总结归纳出一种通用性优化定价框架,然后,基于定价性质的内涵分析,构建通用基础优化定价模型。
从优化视角来看,定价问题是以目标调度指令为参数,以价格为决策变量,以满足定价性质(如引导市场成员优化配置资源)和市场定价规则为目标或约束的优化问题。本文所提通用性优化定价框架由输入参数、模型构建与求解、输出结果三部分构成,如图1所示。构造定价问题的关键在于:充分利用目标调度指令、资源稀缺情况、系统固有参数、市场成员申报的个体参数等已知信息,准确解析市场所需定价性质与定价规则,合理构造价格表达式,有效计及市场成员在价格信号下的响应行为等。

图1 通用性优化定价框架
Fig.1 The basic framework of price optimization
首先,输入参数是模型构建的前提条件,主要包括:①目标调度指令:市场运营主体期望市场成员遵循的调度指令,即价格信号的指引方向,如机组组合或经济调度问题的最优解(包括机组出力、负荷需求等);②资源稀缺情况:调度问题中系统约束或个体约束的达界情况(其中,系统约束是功率平衡约束、线路传输容量约束等耦合多个市场成员的约束;个体约束是机组出力上下限、爬坡约束等只与单个市场成员相关的约束),达界约束对应的资源即为稀缺资源,该信息可用于设置资源价格的优化空间;③系统固有参数:调度模型中系统约束的系数和限制(如功率转移分布因子、线路传输容量限制等),可用于构造价格表达式,即市场成员价格与系统资源价格之间的耦合关系,利用②和③的信息本质上是利用原问题的对偶信息,以保证价格在经济学意义上的可解释性;④个体申报参数:市场成员向运营主体申报的成本函数与个体约束,基于此,在优化定价模型中构成其预期自调度可行域,刻画市场成员对价格信号的响应行为;⑤定价性质要求:市场运营机构对于定价机制满足特定经济性质(如成本回收性、激励相容性、收入充足性、公平性等)的要求或权衡不同性质时的偏好,基于此,设置优化定价模型的目标和约束;⑥市场定价规则:市场运营机构为避免过大的市场风险、考虑相关政策要求所采取的干预措施(如价格上下限、市场成员收入限制等),基于此,在优化定价模型中添加约束。
其次,模型的构建与求解是定价框架的核心内容,主要包含基础优化定价模型构建、模型转换与模型求解。其中,基础优化定价模型是指根据市场需求与定价性质内涵直接构造的定价模型,该模型的目标函数与约束表达式直接体现其物理含义,模型结构可能较为复杂,如双层规划模型。模型转换是指基于模型的结构特性与最优化理论等,将模型转换为易于求解的形式,如将双层规划模型转换为单层线性规划模型。模型求解则分为两种情况:①直接求解基础模型,通常需基于模型结构特征来设计求解算法;②求解转换后的模型,由于转换后的模型为线性规划模型,故可直接采用现有成熟的求解算法。本文主要研究基础模型的构建与模型转换方法,所得模型采用现有线性规划算法求解。
最后,输出结果是满足市场需求的稀缺资源价格和市场成员生产/购买商品的价格。
在上述定价框架下,本小节基于定价性质的物理内涵分析,构造定价性质量化指标的表达式和限制,可得基础优化定价模型的通用形式如下。
1)目标函数
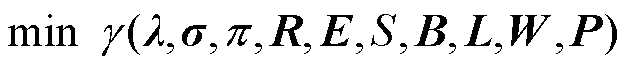 (1)
(1)
式中, 为市场成员生产/购买商品的价格向量;
为市场成员生产/购买商品的价格向量;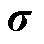 为系统或个体资源的价格向量;
为系统或个体资源的价格向量;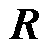 为市场成员的收入向量;
为市场成员的收入向量; 为产品收入缺额(Product Revenue Shortfall, PRS)[30];E为公平性指标;
为产品收入缺额(Product Revenue Shortfall, PRS)[30];E为公平性指标;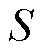 为市场运营机构的市场盈余;
为市场运营机构的市场盈余;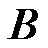 为市场成员的利润向量;
为市场成员的利润向量;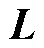 为市场成员的机会成本损失向量;
为市场成员的机会成本损失向量;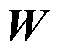 为市场成员的成本回收缺额向量;
为市场成员的成本回收缺额向量;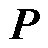 为除收入
为除收入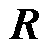 外的补偿支付向量。目标函数通常是市场对于定价性质要求的集中体现,对于定价问题而言,在某些情况下,不同定价要求之间存在冲突,并不存在同时严格满足所有理想定价性质的价格,此时需松弛部分定价性质约束,并构造描述相关定价性质的指标,将目标函数设置为与单个或多个定价性质指标变量相关的函数
外的补偿支付向量。目标函数通常是市场对于定价性质要求的集中体现,对于定价问题而言,在某些情况下,不同定价要求之间存在冲突,并不存在同时严格满足所有理想定价性质的价格,此时需松弛部分定价性质约束,并构造描述相关定价性质的指标,将目标函数设置为与单个或多个定价性质指标变量相关的函数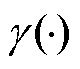 ,以实现定价性质的灵活权衡。常见的目标设置有:最小化机会成本损失、最小化市场盈余、最小化需求侧总支付,以及考虑权重的多目标组合等。
,以实现定价性质的灵活权衡。常见的目标设置有:最小化机会成本损失、最小化市场盈余、最小化需求侧总支付,以及考虑权重的多目标组合等。
2)指标表达式
价格表达式描述了商品价格信号的来源,构建了不同市场成员所得价格信号之间的耦合关系,决定了价格的优化维度,其一般形式为
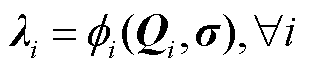 (2)
(2)
式中, 为市场成员的索引;
为市场成员的索引; 为价格函数。
为价格函数。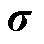 包括:①真实的系统资源(如功率平衡资源、线路容量资源等)价格
包括:①真实的系统资源(如功率平衡资源、线路容量资源等)价格 ,对应于调度模型中的系统约束,根据资源的稀缺情况(约束达界情况),系统资源价格
,对应于调度模型中的系统约束,根据资源的稀缺情况(约束达界情况),系统资源价格 可进一步分为稀缺系统资源价格
可进一步分为稀缺系统资源价格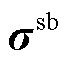 和非稀缺系统资源价格
和非稀缺系统资源价格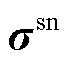 ;②真实的个体资源(如机组容量资源、机组爬坡资源等)价格
;②真实的个体资源(如机组容量资源、机组爬坡资源等)价格 ,对应于调度模型中的个体约束;③虚拟的资源价格
,对应于调度模型中的个体约束;③虚拟的资源价格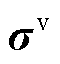 ,在调度模型中并无对应约束,属于人为添加的分量。矩阵
,在调度模型中并无对应约束,属于人为添加的分量。矩阵 描述了市场成员i生产的商品对资源的占用情况,由不同资源相关约束中商品生产/调度决策变量的系数构成,如线路容量约束中描述电能商品对线路容量资源占用情况的功率转移分布因子等。
描述了市场成员i生产的商品对资源的占用情况,由不同资源相关约束中商品生产/调度决策变量的系数构成,如线路容量约束中描述电能商品对线路容量资源占用情况的功率转移分布因子等。
产品收入缺额通常表示由于非稀缺线路容量资源具有大于零的资源价格且构成电价的分量,导致金融输电权类商品的收入不足,在此进一步扩展为所有非稀缺资源参与定价导致的商品收入缺额,其一般形式为
 (3)
(3)
式中,矩阵Z描述了目标调度指令下参与定价的资源的稀缺情况;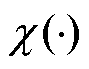 为产品收入缺额函数。以资源w为例,其对应约束为
为产品收入缺额函数。以资源w为例,其对应约束为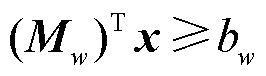 ,其中,向量
,其中,向量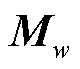 表示各市场成员生产商品对资源w的占用情况;
表示各市场成员生产商品对资源w的占用情况;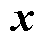 为商品生产/调度决策变量;以
为商品生产/调度决策变量;以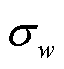 表示资源w的价格。在目标调度指令
表示资源w的价格。在目标调度指令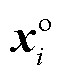 下,资源w的稀缺情况可表示为
下,资源w的稀缺情况可表示为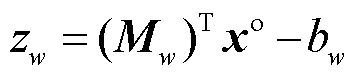 ,通常
,通常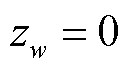 表示资源稀缺,而
表示资源稀缺,而 表示资源并不稀缺,对应产品收入缺额为
表示资源并不稀缺,对应产品收入缺额为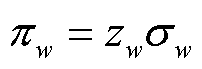 ,即当所有非稀缺资源价格为0,只有稀缺资源价格大于0时,有
,即当所有非稀缺资源价格为0,只有稀缺资源价格大于0时,有 。
。
价格信号下,市场成员遵从市场调度指令时的收入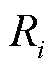 和市场成员自调度的收入
和市场成员自调度的收入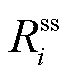 分别为
分别为
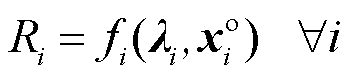 (4)
(4)
 (5)
(5)
式中,向量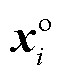 为目标调度指令,即市场运营主体期望市场成员i生产的商品量(商品需求量是负的供应量);
为目标调度指令,即市场运营主体期望市场成员i生产的商品量(商品需求量是负的供应量); 为市场成员i的收入函数。
为市场成员i的收入函数。
价格函数 与收入函数
与收入函数 将共同决定定价的公平性。公平性通常体现为同质商品同价,即不同市场成员生产/购买同质电能商品的单价相同。在电力市场中,为保证市场公平性,价格表达式通常以稀缺系统资源价格
将共同决定定价的公平性。公平性通常体现为同质商品同价,即不同市场成员生产/购买同质电能商品的单价相同。在电力市场中,为保证市场公平性,价格表达式通常以稀缺系统资源价格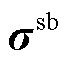 相耦合,按照一定规则将不同市场成员生产/购买商品的价格相互关联,如
相耦合,按照一定规则将不同市场成员生产/购买商品的价格相互关联,如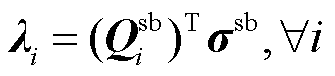 ;常见的收入表达式为
;常见的收入表达式为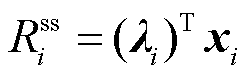 ,即市场成员生产某种商品的收入与对应的商品量成正比(负的收入即为支出)。从而,价格与收入表达式的物理意义解析如下:在市场出清时,市场成员生产/购买商品(如电能、辅助服务等)除需满足自身运行约束外,还需满足系统约束(如商品供需平衡约束、线路容量约束)等;在优化定价问题中,上述系统约束的限制性作用以一种非约束形式体现,即通过系统稀缺资源的价值
,即市场成员生产某种商品的收入与对应的商品量成正比(负的收入即为支出)。从而,价格与收入表达式的物理意义解析如下:在市场出清时,市场成员生产/购买商品(如电能、辅助服务等)除需满足自身运行约束外,还需满足系统约束(如商品供需平衡约束、线路容量约束)等;在优化定价问题中,上述系统约束的限制性作用以一种非约束形式体现,即通过系统稀缺资源的价值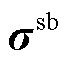 ,根据生产/购买商品对系统资源的贡献/占用情况
,根据生产/购买商品对系统资源的贡献/占用情况 ,以价格信号
,以价格信号 的形式传递给市场成员,影响市场成员的收入
的形式传递给市场成员,影响市场成员的收入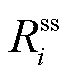 ,从而引导市场成员自发地以最优化资源配置的方式生产/购买商品。
,从而引导市场成员自发地以最优化资源配置的方式生产/购买商品。
由于不同市场对于同质商品或公平性的具体定义及要求存在差异,在实际应用时,需先根据市场要求确定满足公平性原则的价格表达式和收入表达式,如前述价格表达式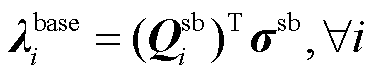 ,收入表达式
,收入表达式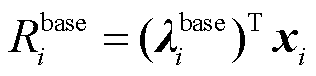 ;而后确定在其基础上的额外分量,即对应等式约束的松弛量,如
;而后确定在其基础上的额外分量,即对应等式约束的松弛量,如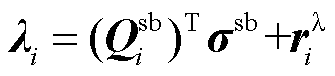 中的
中的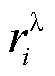 ,
,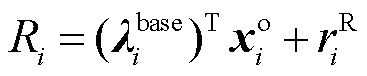 中的
中的 。上述松弛量与补偿支付
。上述松弛量与补偿支付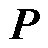 共同构成表征公平性或非歧视性的指标,
共同构成表征公平性或非歧视性的指标,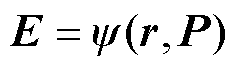 。
。
综合需求侧市场成员遵从调度指令时的支出和供应侧市场成员遵从调度指令时的收入,可得市场盈余为
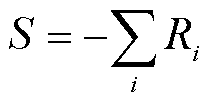 (6)
(6)
考虑市场成员生产商品的成本/报价函数 ,则其遵从调度指令时的利润
,则其遵从调度指令时的利润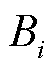 为
为
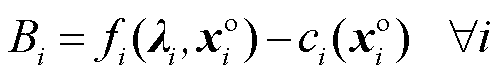 (7)
(7)
价格信号下,市场成员的机会成本损失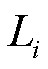 为
为
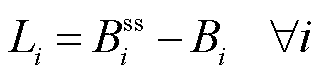 (8)
(8)
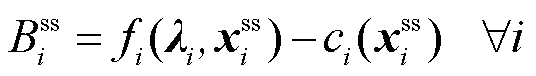 (9)
(9)
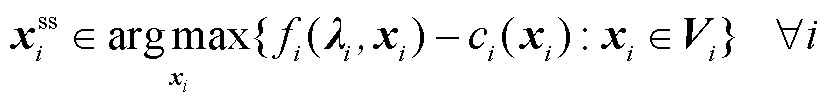 (10)
(10)
式中,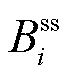 为市场成员在给定价格信号和可行域
为市场成员在给定价格信号和可行域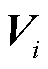 下进行自调度的最大利润;
下进行自调度的最大利润;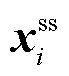 为对应的最优自调度决策;
为对应的最优自调度决策;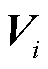 为运营主体在优化价格时所考虑的市场成员预期自调度可行域,由市场成员的个体约束构成,即所得价格信号满足市场成员在可行域
为运营主体在优化价格时所考虑的市场成员预期自调度可行域,由市场成员的个体约束构成,即所得价格信号满足市场成员在可行域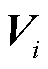 内自调度的激励需求。设置
内自调度的激励需求。设置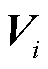 时除需参考市场成员申报的真实可行域
时除需参考市场成员申报的真实可行域 外,还需综合考虑运营主体所期望满足的激励信号及计算负担等因素。当
外,还需综合考虑运营主体所期望满足的激励信号及计算负担等因素。当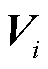 与
与 呈不同关系时,最终价格的实际激励作用也不同。
呈不同关系时,最终价格的实际激励作用也不同。
定理1:当优化定价模型中的预期可行域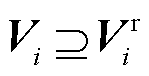 时,所得价格信号可以满足市场成员在其真实可行域
时,所得价格信号可以满足市场成员在其真实可行域 内自调度的激励需求。
内自调度的激励需求。
证明:假设在优化定价模型中,市场成员的激励需求为机会成本损失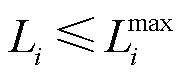 ,优化所得价格信号为
,优化所得价格信号为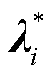 。
。
在价格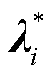 下,以利润最大化为目标进行自调度优化,当可行域为
下,以利润最大化为目标进行自调度优化,当可行域为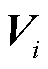 时,得到市场成员i的预期最大自调度利润为
时,得到市场成员i的预期最大自调度利润为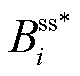 ;当可行域为
;当可行域为 时,得到市场成员i的实际最大自调度利润为
时,得到市场成员i的实际最大自调度利润为 。由于可行域
。由于可行域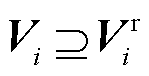 ,基于最优化理论,有
,基于最优化理论,有 ,故有
,故有 。因此,在所得价格信号
。因此,在所得价格信号 下,市场成员的实际机会成本损失
下,市场成员的实际机会成本损失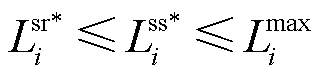 ,仍然满足激励需求,证毕。
,仍然满足激励需求,证毕。
价格信号下,市场成员的成本回收缺额为
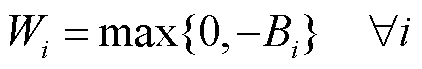 (11)
(11)
3)指标限制
指标限制是指根据市场运营机构的实际需求有选择性地添加关于定价性质和定价规则指标变量的约束。
价格信号下,为保证市场成员参与市场的积极性,需满足成本回收性,即市场成员利润非负。
 (12)
(12)
价格信号下,为保证市场成员自愿遵从目标调度指令,价格与调度指令需构成竞争均衡,即各市场成员的机会成本损失为零。
 (13)
(13)
需要注意的是,当市场成员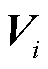 包含
包含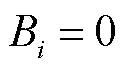 的调度决策时,有
的调度决策时,有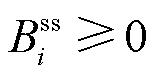 ,此时满足约束(13)即可满足约束(12)。
,此时满足约束(13)即可满足约束(12)。
为保证价格信号的经济学意义,避免产品收入缺额,使非稀缺资源的价格为零,可设置
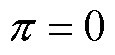 (14)
(14)
价格信号下,考虑到市场运营主体的收入充足性要求,即对于非盈利性运营主体而言,从需求侧的总收入需覆盖其对供应侧的总支出,市场盈余非负,即
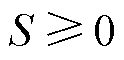 (15)
(15)
考虑到补偿支付的引入是为了弥补价格信号下市场成员的机会成本损失和成本回收缺额,且不能破坏市场运营机构的收入充足性,故需满足
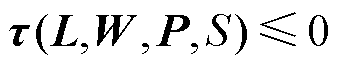 (16)
(16)
此外,还有市场公平性等其他指标要求,对市场公平性等其他指标的限制可统一表达为
 (17)
(17)
最后,为避免过高的价格尖峰或过低的价格低谷引起过大的市场风险,可设置商品价格上、下限约束为
 (18)
(18)
综上所述,式(1)~式(18)构成了通用形式的基础优化定价模型。该模型充分展示了电力市场通过价格信号引导市场成员分散优化决策(自调度)以实现系统整体优化(遵从系统最优调度决策)的本质。本文所提通用性优化定价框架与基础优化定价模型不仅适用于电力现货市场,也适用于配电网、微电网等其他层级的集中式市场。
首先,本节考虑基础优化定价模型目标函数与约束的不同设置,分别构造四种典型的优化定价模型;然后,基于最优化理论与对偶理论提出两种形式的模型转换方法,构建与双层规划基础定价模型等价(价格最优解相同)的线性规划模型,并解析所提优化定价方法与现有定价方法的区别与联系。
1)基础优化定价模型OP1为
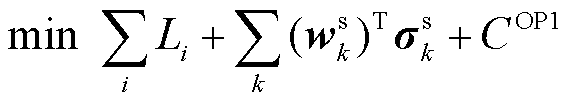 (19)
(19)
 (20)
(20)
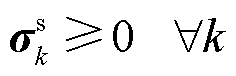 (21)
(21)
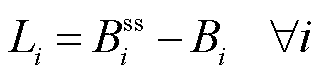 (22)
(22)
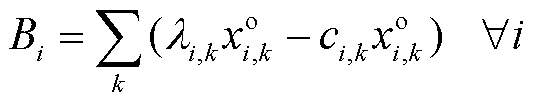 (23)
(23)
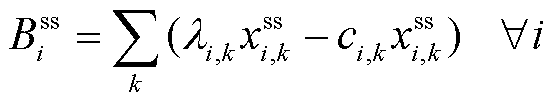 (24)
(24)
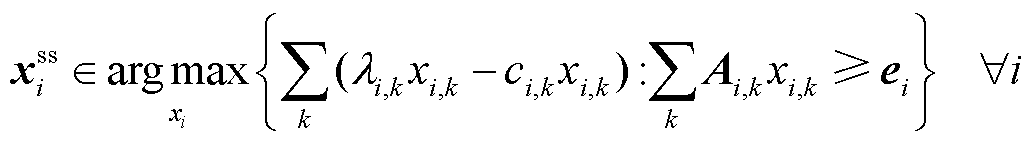 (25)
(25)
式中,k为市场交易商品的索引;K为市场交易商品的集合,集合元素由市场出清时段数(单时段/24时段等)和商品类型(电能商品、启停商品、辅助服务商品等)共同决定,可涵盖各个时段的各类商品;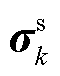 为与商品k相关的系统资源价格变量;
为与商品k相关的系统资源价格变量;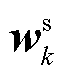 为其系数向量;
为其系数向量;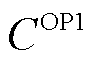 为常数,包含市场成员利润等定价性质指标的常数部分(如当目标函数包含市场成员利润时,
为常数,包含市场成员利润等定价性质指标的常数部分(如当目标函数包含市场成员利润时,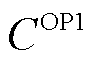 包含市场成员在目标调度指令下的调度成本),不影响模型的最优解,故
包含市场成员在目标调度指令下的调度成本),不影响模型的最优解,故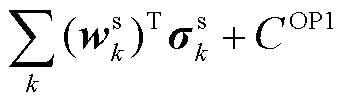 可表征除机会成本损失外,
可表征除机会成本损失外,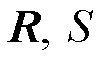 等任意性质指标的线性组合;向量
等任意性质指标的线性组合;向量 表示市场成员i供应单位商品k时对相关系统资源的占用情况;
表示市场成员i供应单位商品k时对相关系统资源的占用情况;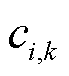 为市场成员i对商品k的报价;向量
为市场成员i对商品k的报价;向量 、
、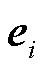 分别为构成预期自调度可行域
分别为构成预期自调度可行域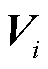 的个体约束的系数和限值,其中,
的个体约束的系数和限值,其中, 表示市场成员i供应单位商品k时对个体资源的占用情况,
表示市场成员i供应单位商品k时对个体资源的占用情况,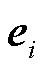 为个体资源限值(如机组出力上限/下限、相邻时段爬坡限值等)。在OP1中,目标函数为机会成本损失与其他性质的线性组合;价格表达式(20)、市场成员利润式(23)等均为线性约束;市场成员预期可行域
为个体资源限值(如机组出力上限/下限、相邻时段爬坡限值等)。在OP1中,目标函数为机会成本损失与其他性质的线性组合;价格表达式(20)、市场成员利润式(23)等均为线性约束;市场成员预期可行域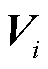 为凸多面体;无个体资源参与定价;不考虑价格限制、收入限制等额外价格约束。
为凸多面体;无个体资源参与定价;不考虑价格限制、收入限制等额外价格约束。
此时,原问题形式的定价辅助模型(记为PP1)可写为
 (26)
(26)
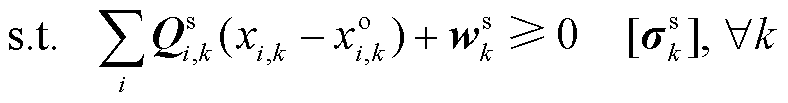 (27)
(27)
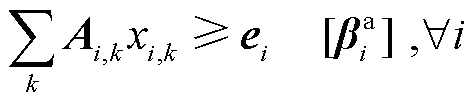 (28)
(28)
式中,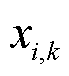 为市场成员i供应商品k的调度决策变量,该问题以社会福利最大化或者系统成本最小化为目标;式(27)是参与定价的系统约束;式(28)是不参与定价的个体约束;
为市场成员i供应商品k的调度决策变量,该问题以社会福利最大化或者系统成本最小化为目标;式(27)是参与定价的系统约束;式(28)是不参与定价的个体约束;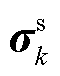 、
、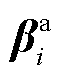 为对应约束的对偶乘子,价格表达式为式(20)。
为对应约束的对偶乘子,价格表达式为式(20)。
定理2:基于双层规划定价模型OP1的定价方法等价于基于调度/定价辅助模型PP1对偶解的定价方法,两者所得价格信号具有相同的性质。
证明:将式(20)~式(25)代入式(19)中整理可得

式(29)与OP1等价。去掉目标函数中的常数项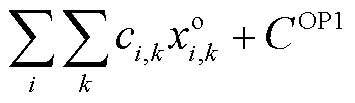 后进一步变换可得
后进一步变换可得
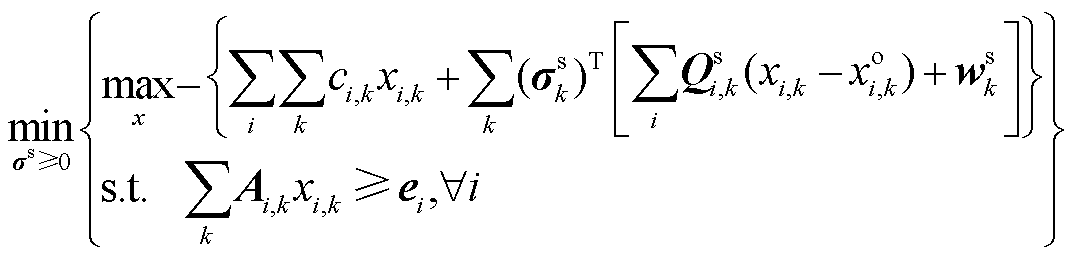 (30)
(30)
由于目标函数的常数项不影响优化问题最优解,故式(30)与OP1等价。此外,式(30)是PP1的拉格朗日对偶问题,且PP1为线性规划问题,故式(30)与PP1等价,即OP1与PP1所得价格信号相同,证毕。
特别地,当OP1的目标函数为
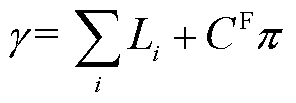 (31)
(31)
式中, 为调度指令下非稀缺系统资源价格大于0导致的产品收入缺额,
为调度指令下非稀缺系统资源价格大于0导致的产品收入缺额,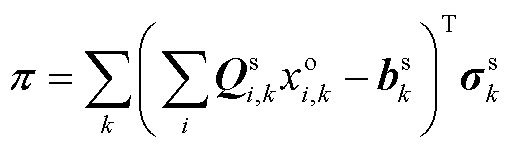 ;
; 为非负常数,表征产品收入缺额对应定价目标的权重系数;向量
为非负常数,表征产品收入缺额对应定价目标的权重系数;向量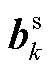 表示与商品k相关的系统资源限值;向量
表示与商品k相关的系统资源限值;向量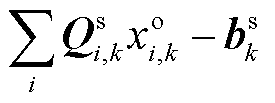 描述了目标调度指令下资源的稀缺情况,其元素为0表示资源限制约束达界,对应资源稀缺。此时,仍可按照上述推导得到等价的原问题形式。对应等价的原问题形式中系统约束(27)将变为
描述了目标调度指令下资源的稀缺情况,其元素为0表示资源限制约束达界,对应资源稀缺。此时,仍可按照上述推导得到等价的原问题形式。对应等价的原问题形式中系统约束(27)将变为
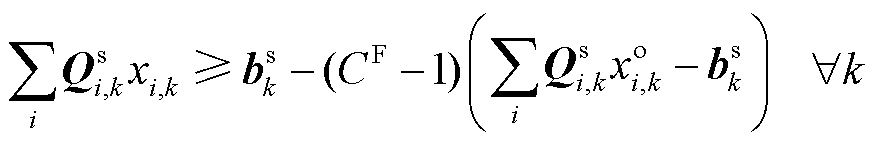 (32)
(32)
文献[26-29]所讨论模型均属于上述OP1类模型,其中,文献[26-28]中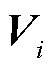 是机组非凸可行域的凸包,目标函数为式(31),且文献[26-27]中
是机组非凸可行域的凸包,目标函数为式(31),且文献[26-27]中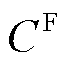 =1;文献[29]中
=1;文献[29]中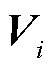 是启停变量固定后的机组可行域。基于经济调度问题(线性规划问题)对偶解得到的LMP也可基于一种特殊的OP1模型得到,其中,
是启停变量固定后的机组可行域。基于经济调度问题(线性规划问题)对偶解得到的LMP也可基于一种特殊的OP1模型得到,其中,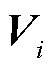 是启停变量固定后的机组可行域,
是启停变量固定后的机组可行域,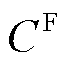 =1,若
=1,若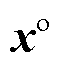 是ED的最优调度解,基于强对偶性定理可知,在不计非凸特性的情况下,LMP可保证机会成本损失与产品收入缺额为0。因此,针对不同市场问题,可根据实际市场需求调整优化定价问题的目标与机组预期可行域等,然后基于对偶理论将其转换为等价的原问题形式的定价辅助模型,基于原问题对偶解获得所需价格。
是ED的最优调度解,基于强对偶性定理可知,在不计非凸特性的情况下,LMP可保证机会成本损失与产品收入缺额为0。因此,针对不同市场问题,可根据实际市场需求调整优化定价问题的目标与机组预期可行域等,然后基于对偶理论将其转换为等价的原问题形式的定价辅助模型,基于原问题对偶解获得所需价格。
2)基础优化定价模型OP2为
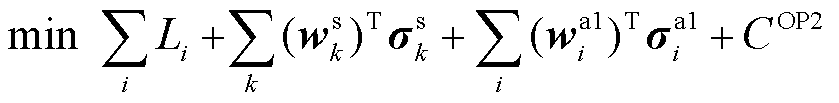 (33)
(33)
 (34)
(34)
 (35)
(35)
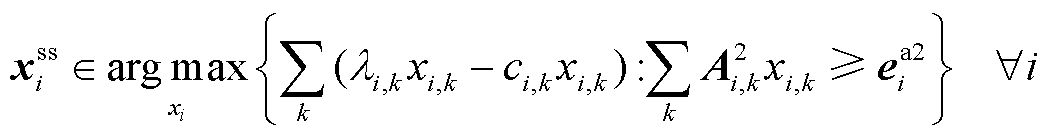 (36)
(36)
约束式(22),式(23),式(24)
式中,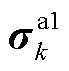 为与商品k相关且参与定价的个体资源价格变量;
为与商品k相关且参与定价的个体资源价格变量;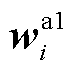 为其目标函数系数向量;
为其目标函数系数向量;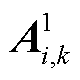 为市场成员i供应单位商品k时对参与定价的相关个体资源的占用情况,可由相关个体约束中
为市场成员i供应单位商品k时对参与定价的相关个体资源的占用情况,可由相关个体约束中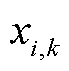 的系数构成;
的系数构成; 为任意常数,与
为任意常数,与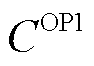 同理,不影响模型最优解;
同理,不影响模型最优解;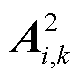 、
、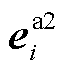 分别为构成
分别为构成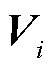 的个体约束的系数与限值;
的个体约束的系数与限值;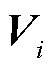 由不参与定价的个体约束构成。在OP2中,目标函数为机会成本损失与其他性质的线性组合;相比于OP1,OP2中部分个体资源也参与定价,价格表达式(34)由系统资源和部分个体资源的价格分量共同构成。个体资源参与定价容易导致歧视性,需根据实际市场要求而定。
由不参与定价的个体约束构成。在OP2中,目标函数为机会成本损失与其他性质的线性组合;相比于OP1,OP2中部分个体资源也参与定价,价格表达式(34)由系统资源和部分个体资源的价格分量共同构成。个体资源参与定价容易导致歧视性,需根据实际市场要求而定。
从而,同理于OP1,与OP2等价的原问题(定价辅助/调度问题)形式(记为PP2)可写为
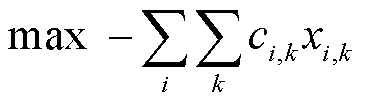 (37)
(37)
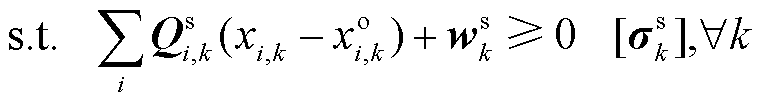 (38)
(38)
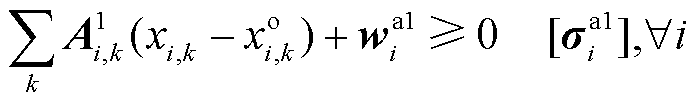 (39)
(39)
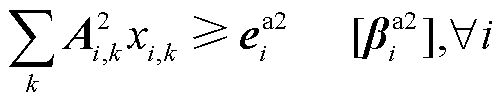 (40)
(40)
综上所述,对于OP1和OP2两种典型的优化定价模型而言,基于优化定价模型最优解所得价格与基于某原问题(调度/定价辅助问题)对偶解所得价格相同,体现了两种定价思路的关联性,即后者本质上是面向特定目标且满足某些定价性质约束的优化定价问题。优化定价问题可视为将原问题中对应对偶乘子参与定价的约束转换为价格信号,并将其作为市场成员自调度问题的目标函数系数,而对应对偶乘子不参与定价的个体约束则构成了市场成员的预期自调度可行域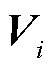 ,然后优化价格信号(对偶乘子)以引导市场成员在预期自调度可行域内自愿满足参与定价的约束或遵从系统调度指令。从优化定价的角度来看,LMP是将系统约束转换为价格信号,其
,然后优化价格信号(对偶乘子)以引导市场成员在预期自调度可行域内自愿满足参与定价的约束或遵从系统调度指令。从优化定价的角度来看,LMP是将系统约束转换为价格信号,其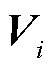 是启停变量固定后的机组可行域;ConvHP是将系统约束转换为价格信号,其
是启停变量固定后的机组可行域;ConvHP是将系统约束转换为价格信号,其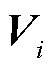 是机组最紧的凸松弛域;IP Pricing是将系统约束和固定启停的个体约束转换为价格信号,其
是机组最紧的凸松弛域;IP Pricing是将系统约束和固定启停的个体约束转换为价格信号,其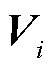 是启停变量松弛后的机组可行域;文献[15]所提TLMP是将系统约束和个体爬坡约束转换为价格信号,其
是启停变量松弛后的机组可行域;文献[15]所提TLMP是将系统约束和个体爬坡约束转换为价格信号,其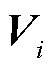 是启停变量固定且去掉爬坡约束后的机组可行域。
是启停变量固定且去掉爬坡约束后的机组可行域。
总体而言,上述原问题形式的模型转换方法是在基础优化定价模型中价格表达式为线性约束,且没有价格上下限等额外价格约束的条件下成立的。当不满足上述条件时,该转换方法将不再适用。为此,本文针对考虑额外价格约束的优化定价模型进一步提出了对偶问题形式的模型转换方法。
1)基础优化定价模型OP3为
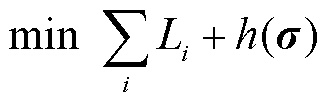 (41)
(41)
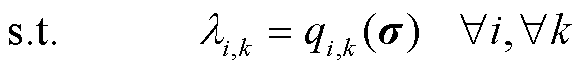 (42)
(42)
约束式(6),式(12),式(15),式(17),式(18),式(22)~式(25)
式中,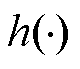 为除机会成本损失
为除机会成本损失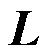 之外,其他性质指标的组合函数(性质指标
之外,其他性质指标的组合函数(性质指标 等均可解析表征为资源价格的函数);
等均可解析表征为资源价格的函数);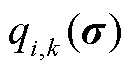 为商品价格
为商品价格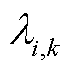 与资源价格
与资源价格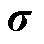 的函数关系。相比于OP1与OP2,OP3中目标函数
的函数关系。相比于OP1与OP2,OP3中目标函数 与价格函数
与价格函数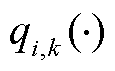 并不局限于线性函数,可扩展为分段线性函数等更一般化的函数形式,下述模型转换方法仍适用。此外,OP3可考虑成本回收性式(12)、价格上下限式(18)等额外价格约束。
并不局限于线性函数,可扩展为分段线性函数等更一般化的函数形式,下述模型转换方法仍适用。此外,OP3可考虑成本回收性式(12)、价格上下限式(18)等额外价格约束。
对偶形式的定价模型(记为DP1)可写为
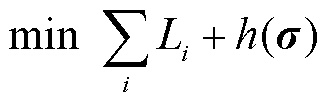 (43)
(43)
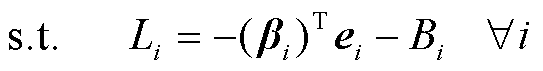 (44)
(44)
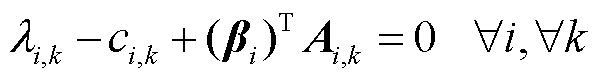 (45)
(45)
 (46)
(46)
约束式(6),式(12),式(15),式(17),式(23),式(18),式(42)
定理3:单层优化问题DP1中变量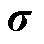 、
、 的最优解即为双层规划问题OP3中变量
的最优解即为双层规划问题OP3中变量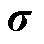 、
、 的最优解。
的最优解。
证明见附录。
将式(25)中的自调度优化问题记为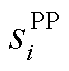 ,其对偶问题记为
,其对偶问题记为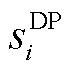 。以DP1代替OP3本质上是以市场成员自调度对偶问题
。以DP1代替OP3本质上是以市场成员自调度对偶问题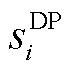 的可行解目标函数值(即
的可行解目标函数值(即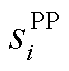 目标函数值的上界)替代原问题
目标函数值的上界)替代原问题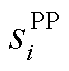 的最优解目标函数值,表征市场成员在价格信号下的响应行为。其中,
的最优解目标函数值,表征市场成员在价格信号下的响应行为。其中,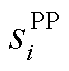 的可行解、最优解的目标函数值可表达为价格响应函数
的可行解、最优解的目标函数值可表达为价格响应函数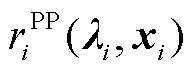 、
、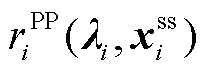 ;
;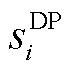 的可行解、最优解的目标函数值可表示为
的可行解、最优解的目标函数值可表示为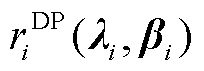 、
、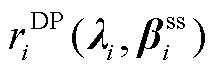 。由弱对偶定理可知,在任意价格信号下,
。由弱对偶定理可知,在任意价格信号下,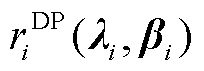 是
是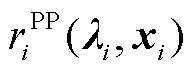 的上界,在定价优化目标(41)下,以
的上界,在定价优化目标(41)下,以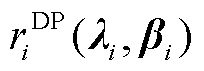 替代
替代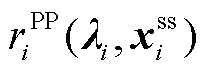 ,价格响应问题可转换为
,价格响应问题可转换为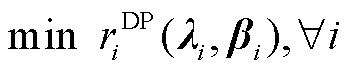 ;由强对偶定理可知,
;由强对偶定理可知, ,从而实现了模型的等价转换。文献[22-23]所提模型属于OP3类模型,可采用本文所提方法将其转换为线性规划模型。
,从而实现了模型的等价转换。文献[22-23]所提模型属于OP3类模型,可采用本文所提方法将其转换为线性规划模型。
2)基础优化定价模型OP4为
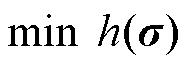 (47)
(47)
 (48)
(48)
约束式(6),式(12),式(15),式(17),式(42),式(18),式(22)~式(25)
相比于定价模型OP3,模型OP4并未在目标函数中考虑机会成本损失的相关项,而是以约束的形式限制机会成本损失。
对偶形式的定价模型(记为DP3)可写为
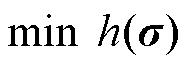 (49)
(49)
约束式(6),式(12),式(15),式(17),式(18),式(23),式(42),式(44)~式(46),式(48)
定理4:单层优化问题DP3中变量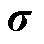 、
、 的最优解即为双层规划问题OP4中变量
的最优解即为双层规划问题OP4中变量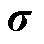 、
、 的最优解。
的最优解。
证明见附录。
对于OP4而言,若同时考虑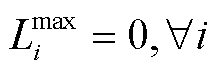 ,式(20),
,式(20),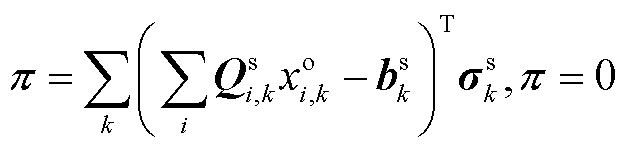 等约束,且无其他价格限制约束,转换后的DP3可涵盖文献[18-19]所提模型。
等约束,且无其他价格限制约束,转换后的DP3可涵盖文献[18-19]所提模型。
综上所述,当针对实际市场定价问题构造的优化定价模型属于上述四种典型模型中的任意一种时,可采用上述模型转换方法将双层规划定价模型转换为单层优化定价模型,若目标函数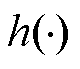 与价格表达式
与价格表达式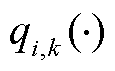 均为线性函数,则可将其转换为线性规划模型进行求解。
均为线性函数,则可将其转换为线性规划模型进行求解。
本小节以多时段经济调度为市场出清原问题,不计机组启停等非凸特性,针对线路越限(或阻塞)导致的价格尖峰问题,构建优化定价模型。
首先,多时段经济调度模型为
 (50)
(50)
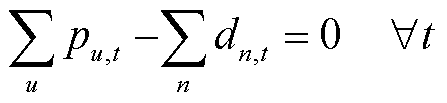 (51)
(51)
 (52)
(52)
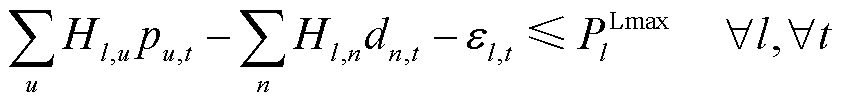 (53)
(53)
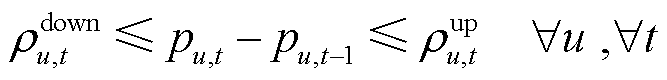 (54)
(54)
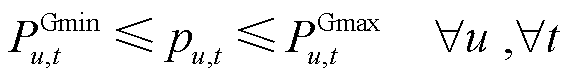 (55)
(55)
 (56)
(56)
式中,n、u、l、t分别为负荷、机组、线路、时段的索引;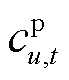 为机组报价;
为机组报价;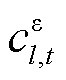 为松弛变量的惩罚因子;
为松弛变量的惩罚因子;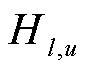 和
和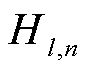 为功率转移分布因子,分别描述了机组u和负荷n的注入/流出功率与线路l的有功潮流之间的灵敏度关系;
为功率转移分布因子,分别描述了机组u和负荷n的注入/流出功率与线路l的有功潮流之间的灵敏度关系;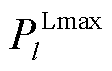 和
和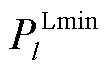 为线路l的功率传输限值;
为线路l的功率传输限值;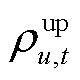 和
和 分别为机组各时段向上、向下爬坡功率限值;
分别为机组各时段向上、向下爬坡功率限值;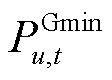 和
和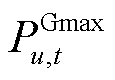 分别为机组各时段出力的下限和上限;
分别为机组各时段出力的下限和上限; 为负荷n在时段t的需求,需求侧报量不报价;
为负荷n在时段t的需求,需求侧报量不报价;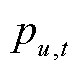 为机组u在时段t的出力;
为机组u在时段t的出力; 为线路l在时段t的潮流约束松弛量。模型优化目标(50)为最小化系统运行成本与线路潮流越限成本之和;式(51)是各时段系统功率平衡约束;式(52)和式(53)是线路容量约束;式(54)是机组爬坡约束;式(55)是机组出力上下限约束;其中,式(51)~式(53)属于系统约束,以
为线路l在时段t的潮流约束松弛量。模型优化目标(50)为最小化系统运行成本与线路潮流越限成本之和;式(51)是各时段系统功率平衡约束;式(52)和式(53)是线路容量约束;式(54)是机组爬坡约束;式(55)是机组出力上下限约束;其中,式(51)~式(53)属于系统约束,以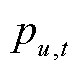 为例,表征其对系统资源占用情况的系数向量
为例,表征其对系统资源占用情况的系数向量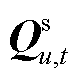 由约束式(51)~式(53)中
由约束式(51)~式(53)中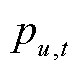 的系数构成,即
的系数构成,即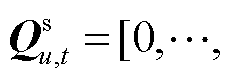
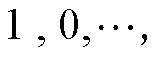
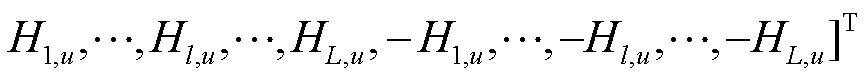 ;式(54)、式(55)属于个体约束。以上标“o”表示上述模型的最优解,即目标调度指令。
;式(54)、式(55)属于个体约束。以上标“o”表示上述模型的最优解,即目标调度指令。
针对价格尖峰问题,需考虑额外价格约束,故可采用OP3或OP4类优化定价模型,并采用对应模型转换方法,其对偶形式的线性规划定价模型为
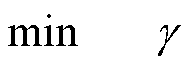 (57)
(57)
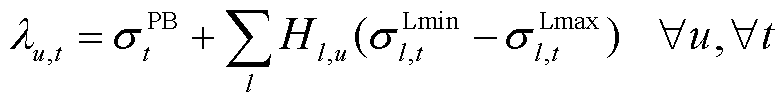 (58)
(58)
 (59)
(59)
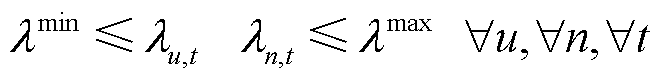 (60)
(60)
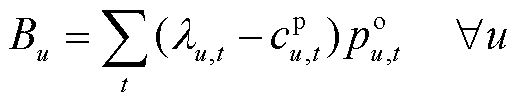 (61)
(61)
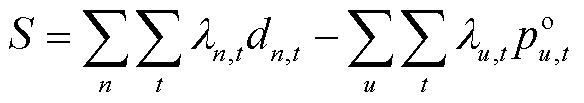 (62)
(62)
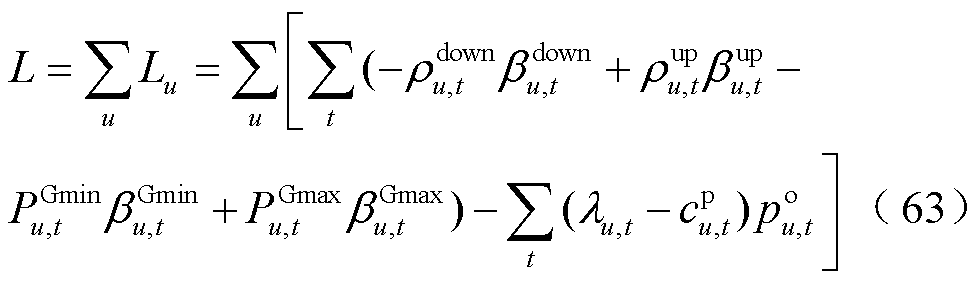
 (64)
(64)
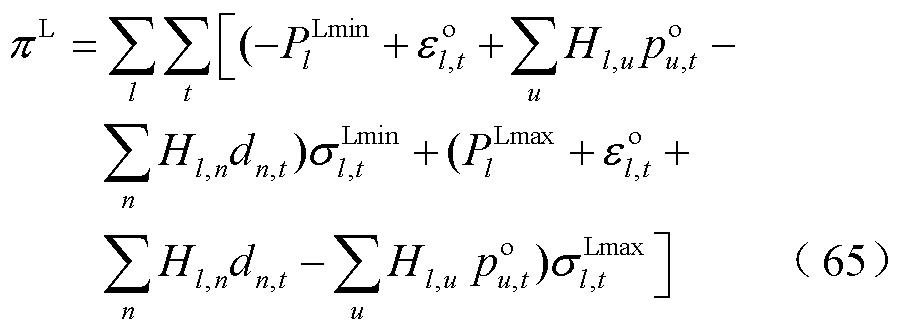
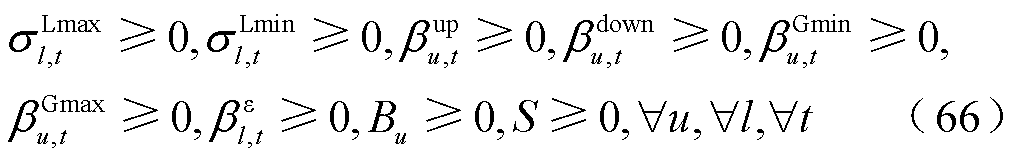
式中,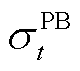 ,
,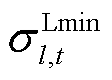 ,
,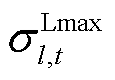 ,
,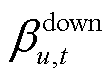 ,
, ,
, ,
, ,
,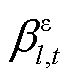 分别为约束式(51)~式(56)所对应的系统或个体资源的价格;
分别为约束式(51)~式(56)所对应的系统或个体资源的价格; 和
和 分别为各市场成员生产/购买电能商品的价格;
分别为各市场成员生产/购买电能商品的价格; 为机组u的机会成本损失;
为机组u的机会成本损失; 为总机会成本损失;
为总机会成本损失;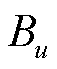 为机组u的利润;
为机组u的利润;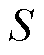 额市场盈余;
额市场盈余;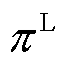 为非稀缺线路容量资源参与定价导致的产品收入缺额。式(58)、式(59)为机组和负荷的电价表达式,由系统资源价格构成,对应于DP1或DP3中的式(42);式(60)为价格上下限约束,对应于式(18);式(61)为机组利润表达式,对应式(23);式(62)为市场盈余表达式,对应于式(6);式(63)为机会成本损失表达式,对应于DP1或DP3中的式(44);式(64)为机组自调度问题对偶问题的约束,对应于DP1或DP3中的式(45);式(65)为产品收入缺额的表达式,对应于
为非稀缺线路容量资源参与定价导致的产品收入缺额。式(58)、式(59)为机组和负荷的电价表达式,由系统资源价格构成,对应于DP1或DP3中的式(42);式(60)为价格上下限约束,对应于式(18);式(61)为机组利润表达式,对应式(23);式(62)为市场盈余表达式,对应于式(6);式(63)为机会成本损失表达式,对应于DP1或DP3中的式(44);式(64)为机组自调度问题对偶问题的约束,对应于DP1或DP3中的式(45);式(65)为产品收入缺额的表达式,对应于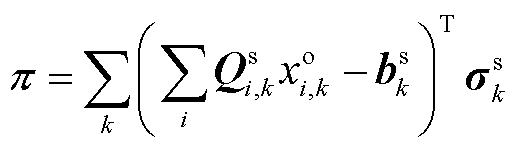 ;式(66)包含成本回收性、收入充足性、资源价格限制等约束,对应于式(12)、式(15)、式(17)、式(46)。在所提模型中,机会成本损失是描述竞争均衡性的定价性质指标,并未考虑针对机会成本损失引入补偿支付(通常称为上抬费用)。
;式(66)包含成本回收性、收入充足性、资源价格限制等约束,对应于式(12)、式(15)、式(17)、式(46)。在所提模型中,机会成本损失是描述竞争均衡性的定价性质指标,并未考虑针对机会成本损失引入补偿支付(通常称为上抬费用)。
对于价格尖峰问题,采用优化定价方法的优势在于,可通过目标和约束的设置来合理引导和保证价格在不同性质上的表现,如减小价格限值对其激励作用的影响、减小用户总支付、解决潜在的价格多解问题等。相比于文献[22-23],本文采用所提模型转换方法构建了线性规划定价模型,模型约束随时段数增加呈线性增长,而非指数式增长,可适用于多时段调度。同时,模型解析表达了市场成员利润、机会成本损失、市场盈余、产品收入缺额等定价性质相关指标,可兼顾多种定价性质。
本小节将基于IEEE 30节点系统和Polish 2 383节点系统进行24时段市场出清(仿真参数见文献[31]),考虑价格尖峰问题场景,验证和解析所提定价方法的特性。
算例将对比分析以下八种定价方法(其中M3~M8是在第3节所提优化定价模型基础上进行不同目标与约束的设置):①M1:节点边际定价,价格由经济调度问题系统约束的对偶乘子构成,价格表达式为式(58)和式(59);该方法本质上属于OP1类模型,可等价为在所提优化定价模型中,将目标函数设置为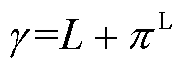 ,将越限线路容量资源价格设置为惩罚因子的值,且不考虑价格上下限、成本回收性等约束。②M2:广东方法,在原经济调度问题基础上,修改惩罚因子与机组出力限制,从而获得定价辅助问题,价格由定价辅助问题系统约束的对偶乘子构成。若同样等价为某种优化定价模型,其与M1的主要区别在于两者的预期自调度可行域与越限线路容量资源价格不同。③M3:将优化目标设置为最小化市场盈余,即
,将越限线路容量资源价格设置为惩罚因子的值,且不考虑价格上下限、成本回收性等约束。②M2:广东方法,在原经济调度问题基础上,修改惩罚因子与机组出力限制,从而获得定价辅助问题,价格由定价辅助问题系统约束的对偶乘子构成。若同样等价为某种优化定价模型,其与M1的主要区别在于两者的预期自调度可行域与越限线路容量资源价格不同。③M3:将优化目标设置为最小化市场盈余,即 ,添加约束
,添加约束 ,不考虑价格上、下限。④M4:将优化目标设置为最大化市场盈余,即
,不考虑价格上、下限。④M4:将优化目标设置为最大化市场盈余,即 ,添加约束
,添加约束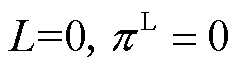 ,考虑市场盈余上限,不考虑价格上、下限。⑤M5:将优化目标设置为最小化机会成本损失,即
,考虑市场盈余上限,不考虑价格上、下限。⑤M5:将优化目标设置为最小化机会成本损失,即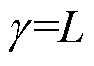 ,添加约束
,添加约束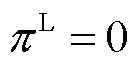 ,考虑价格上、下限。⑥M6:将优化目标设置为最小化机会成本损失与产品收入缺额之和,即
,考虑价格上、下限。⑥M6:将优化目标设置为最小化机会成本损失与产品收入缺额之和,即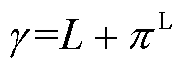 ,考虑价格上、下限。⑦M7:将优化目标设置为多种定价性质的线性组合,目标函数包括机会成本损失、产品收入缺额与需求侧总支出,即
,考虑价格上、下限。⑦M7:将优化目标设置为多种定价性质的线性组合,目标函数包括机会成本损失、产品收入缺额与需求侧总支出,即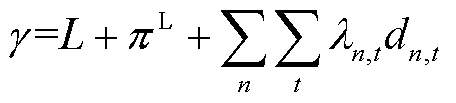 ,不考虑价格上、下限。⑧M8:将优化目标设置为多种定价性质的线性组合,目标函数包括机会成本损失、产品收入缺额与市场盈余,即
,不考虑价格上、下限。⑧M8:将优化目标设置为多种定价性质的线性组合,目标函数包括机会成本损失、产品收入缺额与市场盈余,即 ,不考虑价格上、下限。
,不考虑价格上、下限。
在IEEE 30节点系统中,M1、M2的惩罚因子分别设为106 $/(MW·h)、100 $/(MW·h);M4的市场盈余上限设为106 $;M5、M6的价格限值设为[-100,100] $/(MW·h),机组仿真参数见表1。
表1 IEEE 30节点系统的机组参数
Tab.1 Generator parameters of IEEE 30-bus system

机组G1G2G3G4G5G6 燃料成本/[$/(MW·h)]21.7513.2533 出力上限/MW808060504040 出力下限/MW2020151088 爬坡速率/(MW/h)242418151212
首先,当在目标调度指令下,系统有线路发生阻塞但无线路潮流越限,不同定价方法下的市场定价结果见表2。
如表2所示,由于目标调度指令是经济调度问题的最优调度解,基于经济调度问题对偶解的M1满足机会成本损失与产品收入缺额为零的性质。此外,M2~M6所得价格均满足上述性质,其中,M2与M1的原问题/定价辅助问题因线路松弛变量不起作用而等价,故两者电价相同;基于对偶定理可知,相比于M6,M1中存在对越限线路容量资源的价格限制(越限线路容量资源价格等于罚因子的值),故当无线路越限且价格上下限与成本回收性约束不起作用时,M1与M6等价,但由于存在价格多解问题,故两者定价结果不同;在此算例中,M1、M6所得结果恰好对应于满足机会成本损失与产品收入缺额为零性质的价格集合中市场盈余最小(M3)和最大(M4)的情况;M5所得结果恰好与M1相同。M7引入了非稀缺资源(非阻塞线路容量资源)参与定价,按照相应的定价目标在增加产品收入缺额的同时有效降低了需求侧总支付;M8则为了降低市场盈余,未引入线路容量资源参与定价。
表2 IEEE 30节点系统无约束越限时市场定价结果
Tab.2 Market pricing results of IEEE 30-bus system with no constraint violation

方法最高电价/ [$/(MW·h)]最低电价/ [$/(MW·h)]机会成本损失/$市场盈余/$产品收入缺额/$需求侧总支付 /$ M19.5140.250872.0014 510 M29.5140.250872.0014 510 M39.5140.250872.0014 510 M49.5140.2501 198014 600 M59.5140.250872.0014 510 M69.5140.2501 198014 600 M742.128-100129.30370.58 454 M850.2523.8580013 540
其次,当目标调度指令下,系统有线路发生阻塞且有线路发生潮流越限。在不同定价方法下,时段12(线路10发生潮流越限)各节点电价如图2所示。
图2 不同定价方法下时段12各节点的电价曲线
Fig.2 The electricity prices of nodes in time 12 under different pricing methods
如图2所示,在M1中,各节点价格整体较高,电价尖峰值高达864 600$/(MW·h);在M2~M6中,电价尖峰值大幅削减,电价曲线趋势与M1相似,这是因为在M1~M6方法下,时段12参与定价的线路容量稀缺资源(或形成电价中最大阻塞分量的容量稀缺资源)相同,但资源的具体价值不同;而在M7、M8中,时段12线路容量资源不参与定价,故不同节点之间无价差。
电价尖峰本质上源于电力商品对价格极高的线路容量资源的占用,在不同定价方法下,时段12的潮流越限线路的容量资源价值(对偶乘子)见表3。
表3 IEEE 30节点系统潮流越限线路的容量资源定价结果
Tab.3 Pricing results for capacity resource of line with power flow violating limits in IEEE 30-bus system (单位:$/MW)

方法M1M2M3M4M5M5*M6M6*M7M8 价格10610013526 699113.4100.3113.4100.300
如表3所示,在方法M1、M2下,由于原对偶问题最优性条件的严格限制,越限线路容量资源价格等于惩罚因子的值;在所提优化定价方法M3~M8下,该限制被打破,资源价格将根据定价模型中目标函数与约束的设置有方向地优化,与M1相比,资源价格大幅降低,从而有效缓解了异常电价尖峰。
不同定价方法下,各市场成员的机会成本损失与利润分别见表4、表5。
表4 机组的机会成本损失
Tab.4 Lost opportunity costs of generators (单位:$)
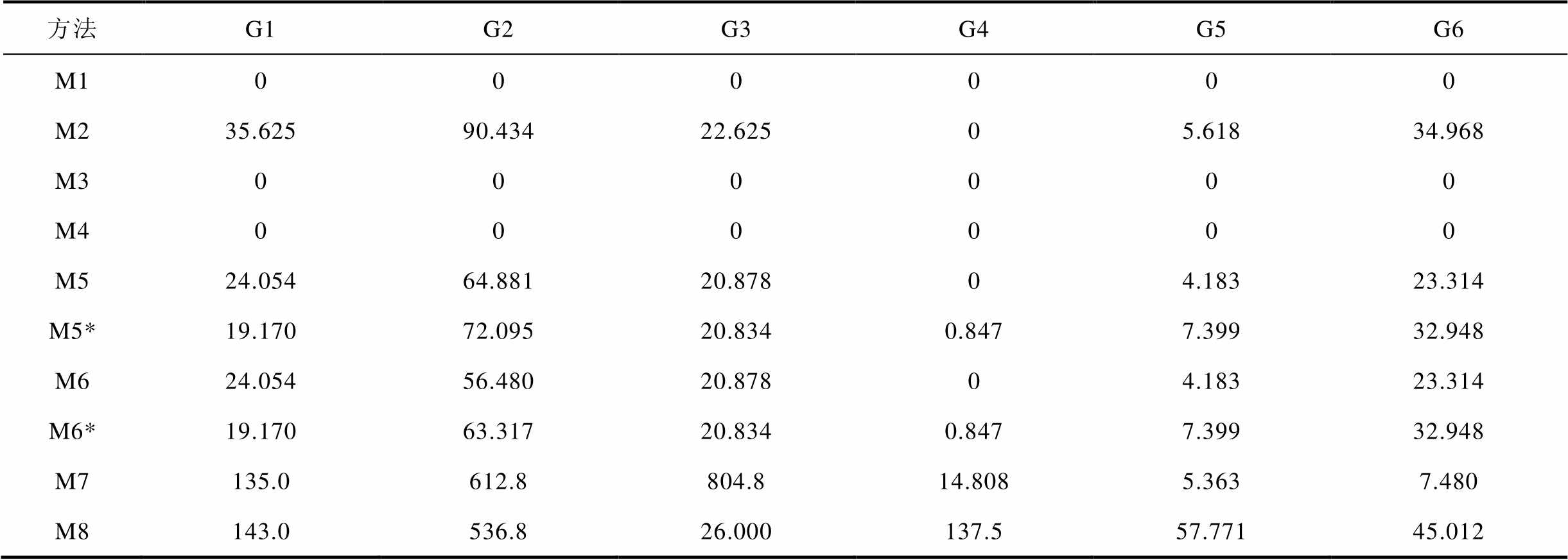
方法G1G2G3G4G5G6 M1000000 M235.62590.43422.62505.61834.968 M3000000 M4000000 M524.05464.88120.87804.18323.314 M5*19.17072.09520.8340.8477.39932.948 M624.05456.48020.87804.18323.314 M6*19.17063.31720.8340.8477.39932.948 M7135.0612.8804.814.8085.3637.480 M8143.0536.826.000137.557.77145.012
如表4所示,M1、M3、M4可以保证所有市场成员无机会成本损失;M2由于修改了原模型约束(本质上缩减了预期自调度可行域),导致市场成员存在不明机会成本损失;M5~M8则为了兼顾价格大小、产品收入缺额、市场盈余、需求侧总支付等方面的性质,导致市场成员存在机会成本损失。
表5 机组的利润
Tab.5 Profits of generators (单位:$)
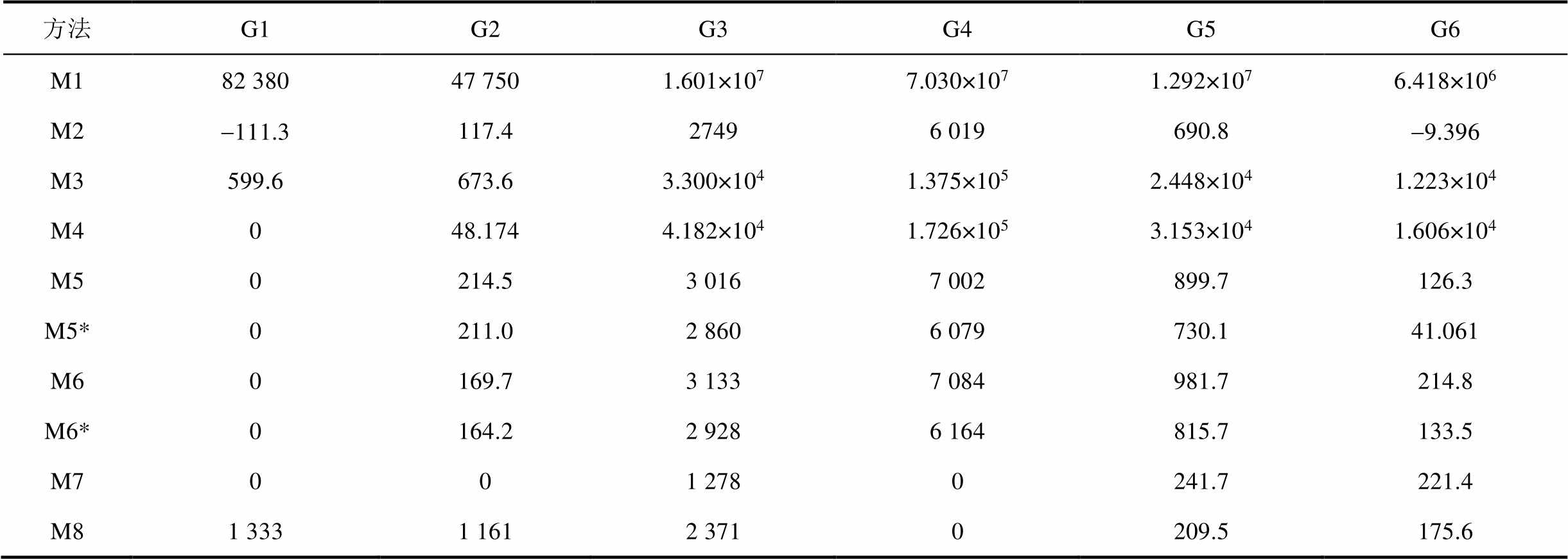
方法G1G2G3G4G5G6 M182 38047 7501.601×1077.030×1071.292×1076.418×106 M2-111.3117.427496 019690.8-9.396 M3599.6673.63.300×1041.375×1052.448×1041.223×104 M4048.1744.182×1041.726×1053.153×1041.606×104 M50214.53 0167 002899.7126.3 M5*0211.02 8606 079730.141.061 M60169.73 1337 084981.7214.8 M6*0164.22 9286 164815.7133.5 M7001 2780241.7221.4 M81 3331 1612 3710209.5175.6
如表5所示,在M1下,所有市场成员均能回收其运行成本;在M2下,机组G1、G6收入不足;在所提优化定价方法M3~M8下,以约束形式保证了成本回收性,其中M7最小化了用户侧支付,机组总利润最小。
不同方法下,市场整体定价结果见表6。
表6 IEEE 30节点系统有约束越限时市场定价结果
Tab.6 Market pricing results in IEEE 30-bus system with constraint violation
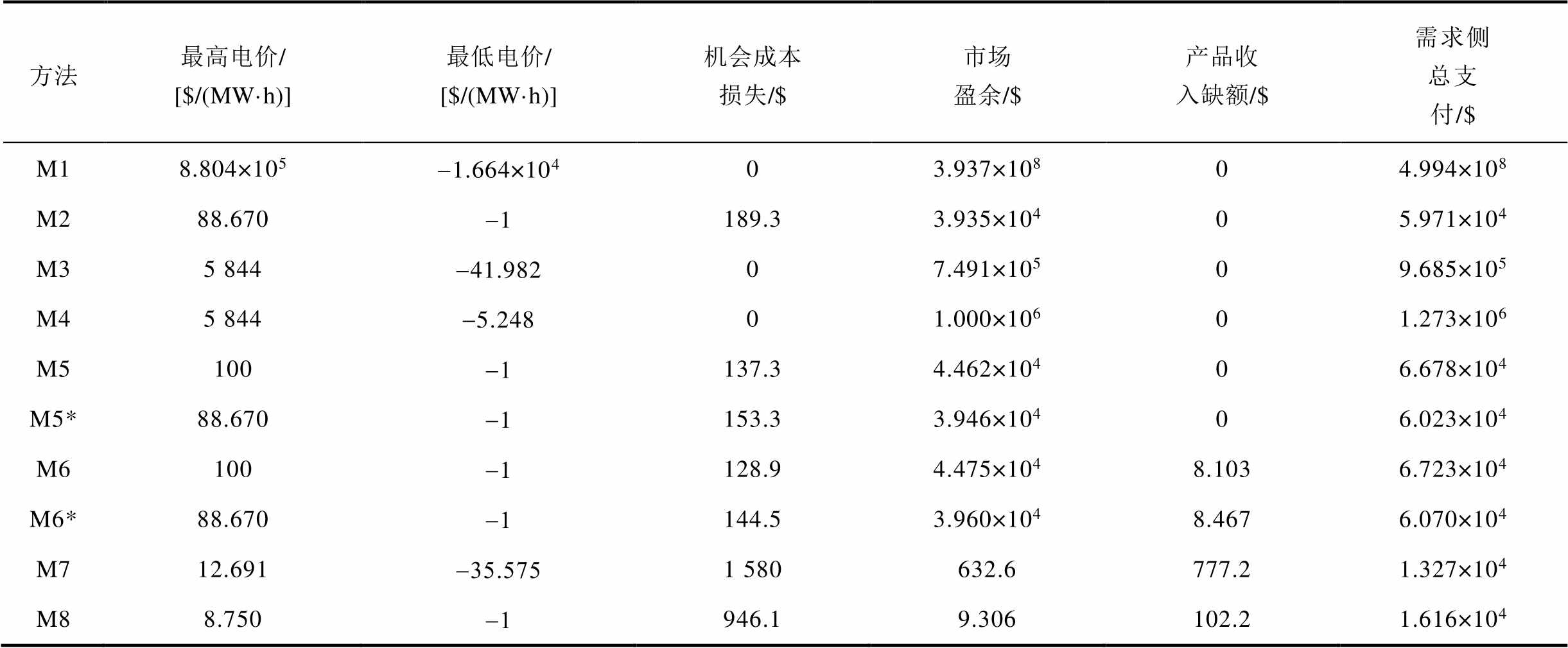
方法最高电价/ [$/(MW·h)]最低电价/ [$/(MW·h)]机会成本损失/$市场盈余/$产品收入缺额/$需求侧总支付/$ M18.804×105-1.664×10403.937×10804.994×108 M288.670-1189.33.935×10405.971×104 M35 844-41.98207.491×10509.685×105 M45 844-5.24801.000×10601.273×106 M5100-1137.34.462×10406.678×104 M5*88.670-1153.33.946×10406.023×104 M6100-1128.94.475×1048.1036.723×104 M6*88.670-1144.53.960×1048.4676.070×104 M712.691-35.5751 580632.6777.21.327×104 M88.750-1946.19.306102.21.616×104
如表6所示,M1、M3、M4均可使机会成本损失与产品收入缺额为零,即满足激励相容性,且只有稀缺资源参与定价,保证了价格信号的经济学意义;相比于M1,M3与M4缓解了电价尖峰;M4以最大化市场盈余为目标,在此算例中,其市场盈余优化结果为设定的上限值;M5、M6在满足价格上、下限的前提下,尽可能减少机会成本损失(与产品收入缺额);为便于对比分析,将M5、M6的价格上限、下限设置为M2的最高电价、最低电价,分析可知,在相同价格峰值下,M5、M6相比于M2进一步降低了机会成本损失,而由于M6引入少量非稀缺资源参与定价,故其机会成本损失相对较小;M7、M8均引入非稀缺资源参与定价,根据各自目标,大幅降低了需求侧总支付与市场盈余。
在M5和M6中,若调整价格上限,对机会成本损失的影响如图3所示。

图3 不同定价方法下价格上限对机会成本损失的影响
Fig.3 The impact of price caps on lost opportunity cost under different pricing methods
如图3所示,随着价格上限的提高,M5和M6的价格优化空间增大,故机会成本损失不断减小。当价格上限大于1 172 $/(MW·h)时,M6不再引入非稀缺资源参与定价,M5和M6所得价格一致;当价格上限大于5 844 $/(MW·h)时,M5和M6所得价格可保证市场成员无机会成本损失。
在M6~M8中,若调整机会成本损失在目标函数中的权重系数,对机会成本损失、产品收入缺额、需求侧总支付、市场盈余等的影响如图4所示。
如图4所示,在方法M6~M8下,随着机会成本损失在目标函数中的权重系数逐渐增加,价格优化越发倾向于减小机会成本损失,机会成本损失逐渐减小直至不变。对M6而言,其目标函数包含机会成本损失与产品收入缺额,当机会成本损失权重系数较高时,其将机会成本损失视为首要关注的性质,在同样的机会成本损失下,可保证较小的产品收入缺额;对于M7而言,其目标函数进一步包含需求侧总支付,当机会成本损失权重系数较高时,其将机会成本损失视为首要关注的性质,在同样的机会成本损失下,可保证较小的产品收入缺额与需求侧总支付;对于M8而言,其在目标函数进一步包含市场盈余,当机会成本损失权重系数较高时,将机会成本损失视为首要关注的性质,在同样的机会成本损失下,可保证较小的产品收入缺额与市场盈余。总体而言,可根据市场运营主体及市场成员对不同性质的重视程度,灵活设置其在目标函数中的权重系数。

图4 不同定价方法下机会成本损失的目标权重对各性质指标的影响
Fig.4 The impact of weight of lost opportunity cost in objective on various property under different pricing methods
在Polish 2 383节点系统中,M1、M2的约束越限惩罚因子分别为107$/(MW·h)、103$/(MW·h);M4的市场盈余上限为5×107$;M5、M6的价格限值为[-103, 103]$/(MW·h)。当系统发生约束越限时,在不同定价方法下,市场整体的定价结果见表7。
表7 Polish 2 383节点系统的定价结果
Tab.7 Pricing results in Polish 2 383-bus system
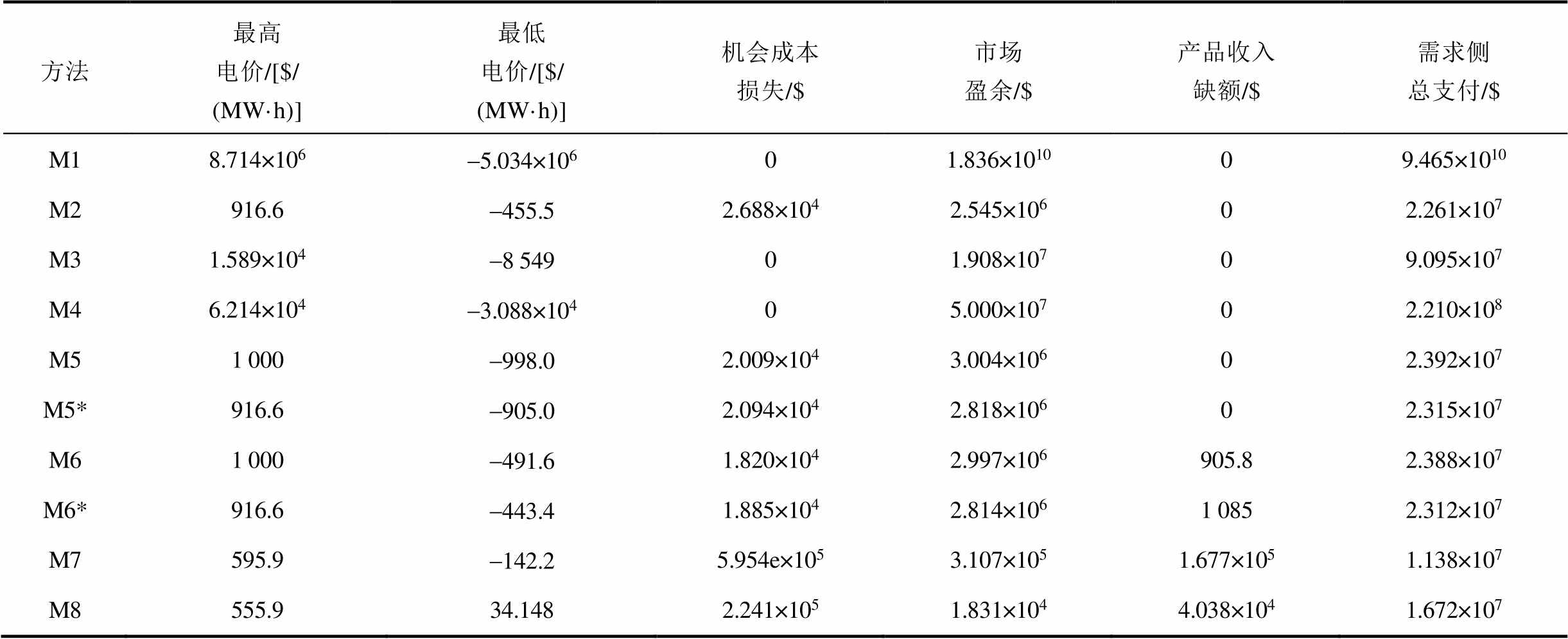
方法最高电价/[$/ (MW·h)]最低电价/[$/ (MW·h)]机会成本损失/$市场盈余/$产品收入缺额/$需求侧总支付/$ M18.714×106-5.034×10601.836×101009.465×1010 M2916.6-455.52.688×1042.545×10602.261×107 M31.589×104-8 54901.908×10709.095×107 M46.214×104-3.088×10405.000×10702.210×108 M51 000-998.02.009×1043.004×10602.392×107 M5*916.6-905.02.094×1042.818×10602.315×107 M61 000-491.61.820×1042.997×106905.82.388×107 M6*916.6-443.41.885×1042.814×1061 0852.312×107 M7595.9-142.25.954e×1053.107×1051.677×1051.138×107 M8555.934.1482.241×1051.831×1044.038×1041.672×107
如表7所示,在2 383节点系统中,不同定价方法呈现出的定价结果特点与30节点系统类似,故不再进一步详述。此外,为进一步验证所提方法的实用性,本文在2 383节点系统测试了15个具有不同负荷曲线的案例,均进行24时段的市场出清。不同定价方法的平均计算时间见表8。
表8 Polish 2 383节点系统的价格求解时间
Tab.8 Price calculation time in Polish 2 383-bus system 单位:s)

方法M1M2M3M4M5M5*M6M6*M7M8 时间4.654.873.673.522.602.6517.1817.419.929.69
上述方法均满足日前市场出清的时间要求。总体而言,优化定价方法M3~M5与边际定价方法M1、M2的计算时间相当;而M6~M8则引入了部分非稀缺资源参与定价,扩大了定价模型的优化维度,故计算时间相对较长,针对非稀缺资源的价格限制,建议根据市场需求进行合理控制。
综上所述,本文所提优化定价方法可通过合理设置模型目标函数与约束来适应市场对定价性质的多重需求。在方法的选择上,若要保证激励相容且不引入非稀缺资源参与定价,可采用M3或M4,此时,价格尖峰与价格多解现象会根据对应目标设置有所缓解;若要在价格限值下尽可能减小机会成本损失,且不引入非稀缺资源参与定价,则可采用M5;若要在价格限值下尽可能减小机会成本损失和产品收入缺额,可采用M6;若要进一步综合考虑市场盈余与需求侧收入,可采用M7或M8。
本文总结提炼了一种通用性优化定价框架,构建了典型的优化定价模型,研究表明,基于最优化理论与对偶理论,可将不同目标及约束设置下的双层规划优化定价模型转换为原问题或对偶问题形式的线性规划模型,从而支撑优化定价模型的实际应用。所提基础优化定价模型与模型转换方法说明了现有多种定价方法之间的区别与联系,不同定价方法本质上是考虑不同定价性质相关目标与约束设置的优化定价模型。此外,针对价格尖峰问题的应用案例表明,所提定价模型可解析表达多种定价性质和定价规则的相关指标,便于市场运营机构根据需求直接调控价格的优化目标与优化空间,实现了价格在不同定价性质之间的灵活权衡,同时,模型求解效率与传统节点边际定价方法相当,满足实际应用要求。总体而言,本文所提优化定价模型及模型转换方法具有实用性与可扩展性,其在考虑非凸性、不确定性等复杂市场问题场景下的应用值得进一步研究。
附 录
定理3:单层优化问题DP1中变量 、
、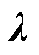 的最优解即为双层规划问题OP3中变量
的最优解即为双层规划问题OP3中变量 、
、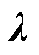 的最优解。
的最优解。
证明:以市场成员i为例,式(25)中的自调度优化问题记为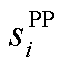 ,有
,有
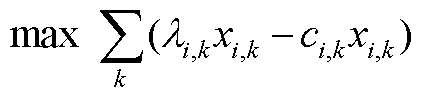 (A1)
(A1)
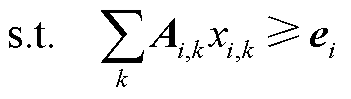 (A2)
(A2)
其对偶问题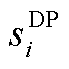 为
为
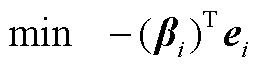 (A3)
(A3)
 (A4)
(A4)
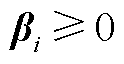 (A5)
(A5)
式中,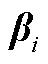 为自调度约束的对偶乘子。
为自调度约束的对偶乘子。
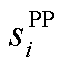 的KKT(Karush-Kuhn-Tucker)条件为
的KKT(Karush-Kuhn-Tucker)条件为
式(A4),式(A5)
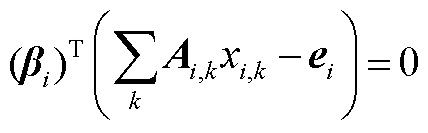 (A6)
(A6)
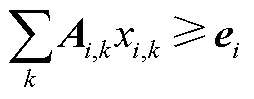 (A7)
(A7)
基于线性规划对偶理论,有强对偶条件,即
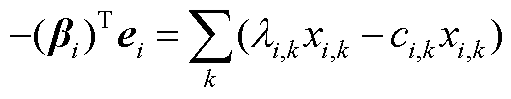 (A8)
(A8)
推导可知,式(A4)、式(A5)、式(A7)、式(A8)与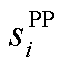 的KKT条件(A4)~式(A7)等价,又令
的KKT条件(A4)~式(A7)等价,又令
 (A9)
(A9)
因此,对于OP3而言,其约束式(22)、式(24)、式(25)可由约束式(A4)、式(A5)、式(A7)~式(A9), 等价替换,将约束替换后的优化问题记为DP0,其与OP3等价,其中式(A8)为非线性约束。由于在优化定价问题中,通常只关注市场成员在给定价格信号下自调度的最优目标函数值,而并不关注自调度最优解,故考虑去掉优化问题DP0中的约束式(A7)、式(A8),
等价替换,将约束替换后的优化问题记为DP0,其与OP3等价,其中式(A8)为非线性约束。由于在优化定价问题中,通常只关注市场成员在给定价格信号下自调度的最优目标函数值,而并不关注自调度最优解,故考虑去掉优化问题DP0中的约束式(A7)、式(A8), ,所得优化问题即为DP1。DP1与OP3之间的关系解析如下。
,所得优化问题即为DP1。DP1与OP3之间的关系解析如下。
令DP1中资源价格和商品价格的最优解为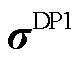 、
、 ;将DP1中资源价格和商品价格变量替换为最优解,去掉与剩余变量无关的约束和目标函数的常数项,整理可得
;将DP1中资源价格和商品价格变量替换为最优解,去掉与剩余变量无关的约束和目标函数的常数项,整理可得
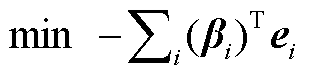 (A10)
(A10)
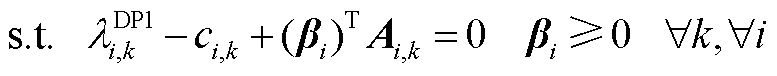 (A11)
(A11)
由于约束式(A11)在不同市场成员间独立,上述问题可拆分为若干个独立的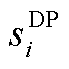 ,故存在
,故存在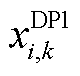 与问题DP1的最优解
与问题DP1的最优解 满足最优性条件,即满足约束
满足最优性条件,即满足约束
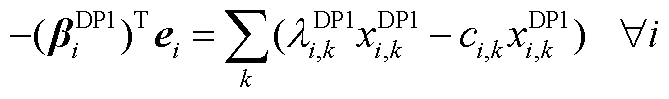 (A12)
(A12)
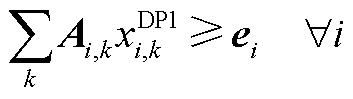 (A13)
(A13)
因此,DP1的最优解满足DP0的约束式(A7),式(A8), ,是DP0的可行解,又DP1的可行域包含DP0的可行域,DP1与OP3等价,故DP1中
,是DP0的可行解,又DP1的可行域包含DP0的可行域,DP1与OP3等价,故DP1中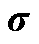 、
、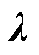 的最优解即为DP0和OP3中对应变量的最优解,证毕。
的最优解即为DP0和OP3中对应变量的最优解,证毕。
定理4:单层优化问题DP3中变量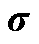 、
、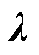 的最优解即为双层规划问题OP4中变量
的最优解即为双层规划问题OP4中变量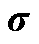 、
、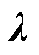 的最优解。
的最优解。
证明:与OP3同理可知,OP4的约束式(22)、式(24)、式(25)可由约束式(A4)、式(A5)、式(A7)~式(A9), 等价替换,所得等价优化问题记为DP2;在DP2的基础上去掉约束式(A7)、式(A8),
等价替换,所得等价优化问题记为DP2;在DP2的基础上去掉约束式(A7)、式(A8), ,所得优化问题记为DP3。DP3与OP4之间的关系解析如下。
,所得优化问题记为DP3。DP3与OP4之间的关系解析如下。
已知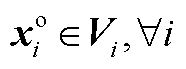 ,基于机会成本损失的定义可知,
,基于机会成本损失的定义可知,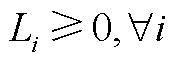 ,故设置
,故设置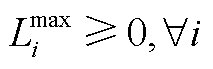 。设DP3中资源价格和商品价格的最优解为
。设DP3中资源价格和商品价格的最优解为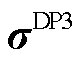 、
、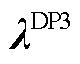 ,
,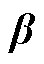 的最优解为
的最优解为 ,对应机会成本损失为
,对应机会成本损失为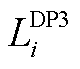 ;将
;将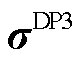 、
、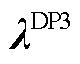 代入OP4中,所得机会成本损失记为
代入OP4中,所得机会成本损失记为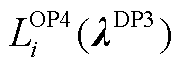 ;令
;令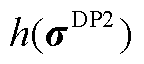 、
、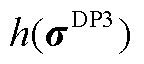 、
、 分别表示DP2、DP3、OP4的最优目标函数。
分别表示DP2、DP3、OP4的最优目标函数。
对于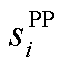 与
与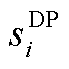 ,基于弱对偶定理可知,对偶问题与原问题的目标函数将满足
,基于弱对偶定理可知,对偶问题与原问题的目标函数将满足
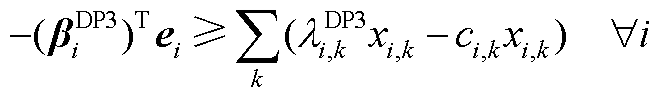 (A14)
(A14)
由式(22)~式(24)、式(A9)可知,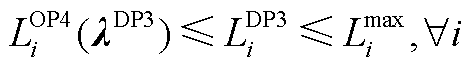 ,即
,即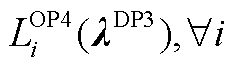 满足约束
满足约束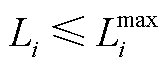 ,故
,故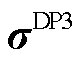 、
、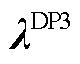 是OP4的可行解,则有
是OP4的可行解,则有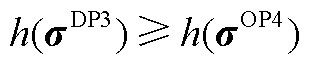 。由于DP3的可行域包含DP2的可行域,有
。由于DP3的可行域包含DP2的可行域,有 ,又DP2与OP4等价,有
,又DP2与OP4等价,有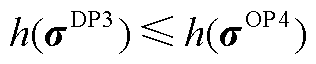 ,即
,即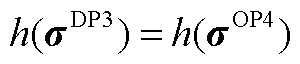 ,故
,故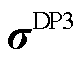 和
和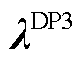 是OP4的最优解,证毕。
是OP4的最优解,证毕。
特别地,当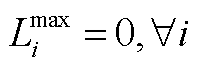 ,由式(A9),
,由式(A9),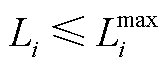 可得
可得
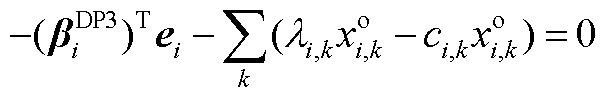 (A15)
(A15)
又因为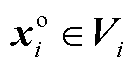 ,故
,故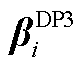 、
、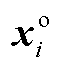 满足条件式(A4)~式(A7),即
满足条件式(A4)~式(A7),即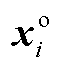 与
与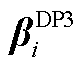 满足
满足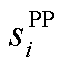 的KKT条件,
的KKT条件,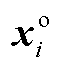 与
与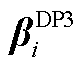 是价格信号
是价格信号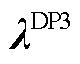 下
下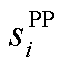 和
和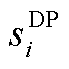 的最优解,此时市场成员遵从调度指令的机会成本损失为0。
的最优解,此时市场成员遵从调度指令的机会成本损失为0。
参考文献
[1] 张显, 史连军. 中国电力市场未来研究方向及关键技术[J]. 电力系统自动化, 2020, 44(16): 1-11.
Zhang Xian, Shi Lianjun. Future research areas and key technologies of electricity market in China[J]. Automation of Electric Power Systems, 2020, 44(16): 1-11.
[2] 张迪, 苗世洪, 周宁, 等. 分布式发电市场化环境下各交易主体响应行为模型[J]. 电工技术学报, 2020, 35(15): 3327-3340.
Zhang Di, Miao Shihong, Zhou Ning, et al. Research on response behavior model of trading entities considering the marketization environment of distributed generation[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3327-3340.
[3] 许刚, 张丙旭, 张广超. 电动汽车集群并网的分布式鲁棒优化调度模型[J]. 电工技术学报, 2021, 36(3): 565-578.
Xu Gang, Zhang Bingxu, Zhang Guangchao. Distributed and robust optimal scheduling model for large-scale electric vehicles connected to grid[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 565-578.
[4] 张衡, 张沈习, 程浩忠, 等. Stackelberg博弈在电力市场中的应用研究综述[J]. 电工技术学报, 2022, 37(13): 3250-3262.
Zhang Heng, Zhang Shenxi, Cheng Haozhong, et al. A state-of-the-art review on Stackelberg game and its applications in power market[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3250-3262.
[5] 涂青宇, 苗世洪, 张迪, 等. 分布式发电市场化环境下基于价格型需求响应的农村光伏交易模式研究[J]. 电工技术学报, 2020, 35(22): 4784-4797.
Tu Qingyu, Miao Shihong, Zhang Di, et al. Research on rural photovoltaic trading pattern based on price-based demand response under marketization environment of distributed generation[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4784-4797.
[6] 唐成鹏, 张粒子, 刘方, 等. 基于多智能体强化学习的电力现货市场定价机制研究(一):不同定价机制下发电商报价双层优化模型[J]. 中国电机工程学报, 2021, 41(2): 536-553.
Tang Chengpeng, Zhang Lizi, Liu Fang, et al. Research on pricing mechanism of electricity spot market based on multi-agent reinforcement learning(part I): Bi-level optimization model for generators under different pricing mechanisms[J]. Proceedings of the CSEE, 2021, 41(2): 536-553.
[7] 安麒, 王剑晓, 武昭原, 等. 高比例可再生能源渗透下的电力市场价值分配机制设计[J]. 电力系统自动化, 2022, 46(7): 13-22.
An Qi, Wang Jianxiao, Wu Zhaoyuan, et al. Benefit allocation mechanism design of electricity markets with penetration of high proportion of renewable energy[J]. Automation of Electric Power Systems, 2022, 46(7): 13-22.
[8] Azizan N, Su Yu, Dvijotham K, et al. Optimal pricing in markets with nonconvex costs[J]. Operations Research, 2020, , 68(2): 480-496.
[9] 史新红, 郑亚先, 薛必克, 等. 机组运行约束对机组节点边际电价的影响分析[J]. 电网技术, 2019, 43(8): 2658-2665.
Shi Xinhong, Zheng Yaxian, Xue Bike, et al. Effect analysis of unit operation constraints on locational marginal price of unit nodes[J]. Power System Technology, 2019, 43(8): 2658-2665.
[10] 边晓燕, 张璐瑶, 周波, 等. 基于知识图谱的国内外电力市场研究综述[J]. 电工技术学报, 2022, 37(11): 2777-2788.
Bian Xiaoyan, Zhang Luyao, Zhou Bo, et al. Review on domestic and international electricity market research based on knowledge graph[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2777-2788.
[11] 郑重, 苗世洪, 李超, 等. 面向微型能源互联网接入的交直流配电网协同优化调度策略[J]. 电工技术学报, 2022, 37(1): 192-207.
Zheng Zhong, Miao Shihong, Li Chao, et al. Coordinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy Internet[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 192-207.
[12] Hogan W W. Multiple market-clearing prices, electricity market design and price manipulation[J]. The Electricity Journal, 2012, 25(4): 18-32.
[13] Applying transmission constraint penalty factors in the market clearing engine, PJM manual 11: Energy & Ancillary Services Market Operations[EB/OL]. Valley Forge, PA: PJM, 2022. https://www.pjm.com/-/media/documents/manuals/m11.ashx.
[14] 王宣元, 高峰, 康重庆, 等. 扩展的节点电价算法研究[J]. 电网技术, 2019, 43(10): 3587-3596.
Wang Xuanyuan, Gao Feng, Kang Chongqing, et al. Analysis of extended locational marginal price[J]. Power System Technology, 2019, 43(10): 3587-3596.
[15] Guo Ye, Chen Cong, Tong Lang. Pricing multi-interval dispatch under uncertainty part I: dispatch-following incentives[J]. IEEE Transactions on Power Systems, 2021, 36(5): 3865-3877.
[16] Hobbs B F. Finding unique prices under degeneracy[EB/OL]. Folsom, CA: CAISO MSC, 2014. http://www.caiso.com/Documents/PricingEnhancementDiscussion-MSC_Presentation-Hobbs.pdf.
[17] CAISO. Tariff amendment to implement pricing enhancements[EB/OL]. Folsom, CA: CAISO, 2016. http://www.caiso.com/Documents/Jun6_2016TariffAmendment-PricingEnhancements_ER16-1886.pdf.
[18] Alguacil N, Arroyo J M, García-Bertrand R. Optimization-based approach for price multiplicity in network-constrained electricity markets[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4264-4273.
[19] Zhang Liang, Feng Donghan, Lei Jinyong, et al. Congestion surplus minimization pricing solutions when Lagrange multipliers are not unique[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2023-2032.
[20] 刘畅, 冯冬涵, 方陈. 实时市场中电价多解情况下的一种定价新方法[J]. 中国电机工程学报, 2020, 40(2): 390-400.
Liu Chang, Feng Donghan, Fang Chen. A new pricing method for price multiplicity in real-time market[J]. Proceedings of the CSEE, 2020, 40(2): 390-400.
[21] Transmission constraint control logic and penalty factors[EB/OL]. Valley Forge, PA: PJM, 2018. https: //www.pjm.com/-/media/committees-groups/committees/ mic/20180510-special/20180510-item-03-transmission-constraint-penalty-factor-education.ashx.
[22] Fang Xinxin, Yang Zhifang, Yu Juan, et al. Electricity pricing under constraint violations[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2794-2803.
[23] 王怡, 杨知方, 余娟, 等. 节点电价与对偶乘子的内在关联分析与扩展[J]. 电力系统自动化, 2021, 45(6): 82-91.
Wang Yi, Yang Zhifang, Yu Juan, et al. Analysis and extension of internal relationship between locational marginal price and dual multiplier[J]. Automation of Electric Power Systems, 2021, 45(6): 82-91.
[24] Richard P, O'Neill, Sotkiewicz P M, et al. Efficient market-clearing prices in markets with nonconvexities[J]. European Journal of Operational Research, 2005, 164(1): 269-285.
[25] Gribik P, Hogan W, Pope S L. Market-clearing electricity prices and energy uplift [Z/OL]. 2007, https://hepg.hks.harvard.edu/publications/market-clearing-electricity-prices-and-energy-uplift.
[26] Andrianesis P, Bertsimas D, Caramanis M, et al. Computation of convex hull prices in electricity markets with non-convexities using Dantzig-Wolfe decomposition[C]//2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 2022: 1.
[27] Stevens N, Papavasiliou A. Application of the level method for computing locational convex hull prices[J]. IEEE Transactions on Power Systems, 2022, 37(5): 3958-3968.
[28] Yang Zhifang, Zheng Tongxin, Yu Juan, et al. A unified approach to pricing under nonconvexity[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3417-3427.
[29] Yang Zhifang, Wang Yi, Yu Juan, et al. On the minimization of uplift payments for multi-period dispatch[J]. IEEE Transactions on Power Systems, 2020, 35(3): 2479-2482.
[30] Schiro D A, Zheng Tongxin, Zhao Feng, et al. Convex hull pricing in electricity markets: formulation, analysis, and implementation challenges[J]. IEEE Transactions on Power Systems, 2016, 31(5): 4068-4075.
[31] Wang Y. 市场仿真参数. Figshare. Dataset[Z/OL]. https://doi.org/10.6084/m9.figshare.20326125.v1.
Abstract In the electricity market, electricity prices usually consist of dual solutions to the primal problem such as market clearing or dispatch problem, which has nice economic significance. However, when the primal problem is faced with problems such as degeneracy and constraint violation, the pricing method based on the dual solutions cannot guarantee the ideal pricing properties. Recently, some methods were presented to solve these pricing problems, but they can hardly balance the diverse market requirements for pricing properties. Therefore, this paper proposes a general optimization pricing framework considering the pricing property requirements, and several different forms of optimization pricing models, to satisfy the regulatory requirements on the pricing properties of the market operator.
First, from an optimization perspective, a general optimization pricing framework is developed, and the universal-form basic optimization pricing model which can analytically characterize cost recovery, incentive compatibility, revenue adequacy, fairness, and other pricing requirements is analyzed in detail. Secondly, typical objective function and constraint settings of the basic optimization pricing model are analyzed, based on the optimization theory and duality theory, linear programming models equivalent to the bi-level programming models are constructed, and the differences and connections between the proposed pricing methods and the existing pricing methods are interpreted. Third, taking a multi-period economic dispatch model and price spiking problem in the electricity market as an example, the practicality of the proposed method is illustrated. A suitable basic pricing optimization model and a model transformation method are selected, and a linear programming pricing optimization model considering multiple pricing property constraints is established. Finally, the proposed optimal pricing method can achieve flexible trade-offs between different properties. By reasonably regulating the prices’ optimization space, the proposed method is comparable to the locational marginal pricing (LMP) method in terms of calculation time.
The numerical simulation is developed in IEEE 30 bus system and Polish 2 383 bus system. We compared pricing methods M1~M8, where M1 and M2 are respectively corresponding to the LMP based on the original dispatch model and modified dispatch model, and M3~M8 are based on the proposed pricing model with different objectives and constraint settings. The results show that M1, M3, and M4 can ensure zero lost opportunity cost (LOC) for all market participants; M2 leads to an unambiguous LOCs for market participants because the real dispatch space is not considered; M5~M8 lead to LOCs for market participants as it attempts to balance the properties of the price cap, product revenue shortfall, market surplus, and total consumer payments.
The following conclusions can be drawn from the simulation analysis: the optimal pricing method proposed in this paper can be adapted to market requirements by reasonably setting the model objective function and constraints. In terms of method selection, M3 or M4 can be used to ensure incentive compatibility and not to introduce non-scarce resources into the pricing, where price spikes and multiple solutions of price are mitigated according to the corresponding objective settings; M5 can be used to minimize LOC under the price limit and not to introduce non-scarce resources into the pricing; M6 can be used to minimize LOC and revenue shortfall under the price limit; M7 or M8 is used to further integrate the market surplus and total consumer payment.
keywords: Electricity market, pricing mechanism, bi-level programming, linear programming, duality theory
中图分类号:TM9
DOI:10.19595/j.cnki.1000-6753.tces.221083
国家自然科学基金资助项目(52177072)。
收稿日期 2022-06-10
改稿日期 2022-12-07
王 怡 女,1998年生,博士研究生,研究方向为电力市场、电力系统规划等。E-mail:20153529@cqu.edu.cn
杨知方 男,1992年生,博士,教授,博士生导师,研究方向为电力系统优化、电力市场等。E-mail:zfyang@cqu.edu.cn(通信作者)
(编辑 赫蕾)